2018届苏教版复数单元测试18
必修第二册第二单元《复数》测试题(含答案解析)

一、选择题1.设()()2225322z t t t t i =+-+++,其中t ∈R ,则以下结论正确的是( ) A .z 对应的点在第一象限B .z 一定不为纯虚数C .z 对应的点在实轴的下方D .z 一定为实数 2.若a b 、为非零实数,则以下四个命题都成立:①10a a+≠;②()2222a b a ab b +=++;③若a b ,=则a b =±;④若2a ab =,则a b ,=则对于任意非零复数a b 、,上述命题中仍为真命题的个数为( )个. A .1 B .2 C .3 D .43.213(1)i i +=+( ) A .3122i - B .3122i + C .3122i -- D .3122i -+ 4.下列各式的运算结果为纯虚数的是A .(1+i)2B .i 2(1-i)C .i(1+i)2D .i(1+i) 5.“复数3i ia z -=在复平面内对应的点在第三象限”是“0a ≥”的 A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件 6.设i 是虚数单位,则2320192342020i i i i +++⋅⋅⋅+的值为( ) A .10101010i -- B .10111010i -- C .10111012i -- D .10111010i - 7.已知复数z 满足()()()1212i z i i -=++,则z 的共轭复数为( )A .1i --B .1i +C .55i +D .55i - 8.复数51i i-的虚部是( ) A .12 B .2i C .12- D .2i - 9.已知复数z 满足()2z i i i -=+,则z =( )A B C D 10.若11i ai ++是纯虚数(其中i 为虚数单位),则实数a 等于( ) A .1B .1-C .2D .2- 11.已知复数z 满足|z |=1,则|z +1-2i |的最小值为( )A 1BC .3D .212.设i 为虚数单位,a R ∈,“复数2202021a i z i =--不是纯虚数“是“1a ≠”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件第II 卷(非选择题)请点击修改第II 卷的文字说明参考答案二、填空题13.设复数z 满足341z i --=,则z 的最大值是_______.14.设复数z 满足1z =,且使得关于x 的方程2230zx zx ++=有实根,则这样的复数z 的和为______.15.化简:2020201921i z i i ⎛⎫=+= ⎪ ⎪+⎝⎭________.16.在复平面内,复数(3)2a a z i =-+表示的点在直线y x =上,则z =_______. 17.在实数集R 中,我们定义的大小关系“>”为全体实数排了一个“序”.类似地,我们在复数集C 上也可以定义一个称为“序”的关系,记为“>”.定义如下:对于任意两个复数:()111222121212z a bi z a b i a a b b R z z =+=+∈,,,,,>当且仅当“12a a >”或“12a a =”且“12b b >”.按上述定义的关系“>”,给出以下四个命题:①若12z z >,则12z z >;②若1223z z z z >,>,则13z z >;③若12z z >,则对于任意12z C z z z z ∈++,>;④对于复数0z >,若12z z >,则12zz zz >.其中所有真命题的序号为______________.18.设b R ∈,i 是虚数单位,已知集合{}|2A z z i =-≤,{}11|1,B z z z bi z A ==++∈,若A B ⋂≠∅,则b 的取值范围是________. 19.已知复数z =a +3i 在复平面内对应的点位于第二象限,且|z|=2,则复数z 等于________.20.如果复数z 的模不大于1,而z 的虚部的绝对值不小于,则复平面内复数z 的对应点组成图形的面积是___.三、解答题21.已知m R ∈,复数2(1i)(5i 3)(46i)z m m =+-+-+,当m 为何值时,(1)z 为实数?(2)z 为虚数?(3)z 为纯虚数?(4)z 在复平面内对应的点在第四象限?22.已知1z i =+,i 为虚数单位.(1)若234z z ω=+-,求ω;(2)若2211z az b i z z ++=--+,求实数a ,b 的值.23.已知复数z 满足|z |=z 的实部、虚部均为整数,且z 在复平面内对应的点位于第四象限.(1)求复数z ;(2)若()22m m n i z --=,求实数m ,n 的值.24.已知复数z 满足z =,2z 的虚部为2,(1)求复数z ;(2)设22,,z z z z -在复平面上对应点分别为,,A B C ,求ABC ∆的面积. 25.已知复数z 使得2z i R +∈,2z R i∈-,其中i 是虚数单位. (1)求复数z 的共轭复数z ; (2)若复数()2z mi +在复平面上对应的点在第四象限,求实数m 的取值范围. 26.i 是虚数单位,且2(1)2(5)3i i a bi i-+++=+(,a b ∈R ). (1)求,a b 的值;(2)设复数1()z yi y R =-+∈,且满足复数()a bi z +⋅在复平面上对应的点在第一、三象限的角平分线上,求||z .【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据()2222110t t t ++=++>,2253t t +-可正可负也可为0,即可判定.【详解】()2222110t t t ++=++>,z ∴不可能为实数,所以D 错误; z ∴对应的点在实轴的上方,又z 与z 对应的点关于实轴对称,z 对应的点在实轴的下方,所以C 正确;213,25302t t t -<<+-<,z 对应的点在第二象限,所以A 错误; 21,25302t t t =+-=,z 可能为纯虚数,所以B 错误; ∴C 项正确.故选:C【点睛】此题考查复数概念的辨析,关键在于准确求出实部和虚部的取值范围.2.B解析:B【解析】【分析】根据复数的概念和性质,利用复数的代数形式的运算法则,即可得出正确选项.【详解】解:对于①,当a i =时,10a a+=,即①不成立, 对于②,根据复数代数形式的运算法则,满足乘法公式,即②在正确,对于③,在复数C 中,1i =,则1,a b i ==时,a b ≠±,即③错误,对于④,根据复数代数形式的运算法则可得,若2a ab =,则a b ,=即④正确, 综上可得上述命题中仍为真命题的序号为②④,故选B.【点睛】本题考查了复数的概念和性质及复数的代数形式的运算法则,属基础题.3.A解析:A【分析】首先计算2(1)i +,之后应用复数的除法运算法则,求得结果.【详解】 ()21313312221ii i i i ++==-+, 故选A.【点睛】该题考查的是有关复数的运算,属于简单题目.4.A【分析】利用复数的四则运算,再由纯虚数的定义,即可求解.【详解】由题意,对于A 中,复数2(1)2i i +=为纯虚数,所以正确;对于B 中,复数2(1)1i i i ⋅-=-+不是纯虚数,所以不正确;对于C 中,复数2(1)2i i ⋅+=-不是纯虚数,所以不正确;对于D 中,复数(1)1i i i ⋅+=-+不是纯虚数,所以不正确,故选A.【点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其四则运算技巧和常规思路. 其次要熟悉复数相关基本概念是解答此类问题的关键,着重考查了推理与计算能力,属于基础题. 5.A解析:A【详解】 因为33ai z a i i-==--,所以由题设可得00a a -<⇒>,因此0a >是0a ≥的充分不必要条件,故应选答案A . 6.B解析:B【分析】利用错位相减法、等比数列的求和公式及复数的周期性进行计算可得答案.【详解】解:设2320192342020S i i i i =+++⋅⋅⋅+,可得:24201920320023420192020iS i i i i i =++++⋅⋅⋅++,则24201923020(1)22020i S i i i i ii -=++++⋅⋅⋅+-, 2019242019202023020(1)(1)202020201i i i S i i i i i i i i i i--=+++++⋅⋅⋅+-+-=-, 可得:2(1)(1)(1)20202020202112i i i i i S i i i i ++-=+-=+-=-+-, 可得:2021(2021)(1)1011101012i i i S i i -+-++===---, 故选:B.【点睛】本题主要考查等比数列的求和公式,错位相减法、及复数的乘除法运算,属于中档题. 7.A解析:A化简得到1z i =-+,再计算共轭复数得到答案.【详解】()()()1212i z i i -=++,故()()()()()()()()()121212131211212125i i i i i i i z i i i i +++++++====-+--+,故1z i =--. 故选:A .【点睛】本题考查了复数的化简,共轭复数,意在考查学生的计算能力.8.A解析:A【解析】【分析】由题意首先化简所给的复数,然后确定其虚部即可.【详解】 由复数的运算法则可知:51i i -()()()1111122i i i i i +==-+-+, 则复数51i i-的虚部是12. 本题选择A 选项.【点睛】本题主要考查复数的运算法则,虚部的定义等知识,意在考查学生的转化能力和计算求解能力.9.A解析:A【分析】首先求得复数z ,然后求解其共轭复数并确定模即可.【详解】 由题意可得:2211i z i i i i i +=+=-++=-,则1,z i z =+=故选A .【点睛】本题主要考查复数的运算法则,复数的模的计算等知识,意在考查学生的转化能力和计算求解能力. 10.B解析:B设11i bi ai+=+,化简后利用复数相等列方程求解即可. 【详解】 设()1,,1i bi a b R ai+=∈+, 所以()11i bi ai ab bi +=⋅+=-+,所以11ab b -=⎧⎨=⎩, 解得11a b =-⎧⎨=⎩, 故选:B .【点睛】本题主要考查复数的乘法运算,考查复数相等的性质,属于基础题.11.A解析:A【分析】 根据1z =分析出z 在复平面内的轨迹方程,再根据12z i +-的几何意义以及圆外一点到圆上点的距离最小值求法求解出结果.【详解】因为|||i |1z x y =+==,所以221x y +=,即z 在复平面内表示圆O :221x y +=上的点;又|12i ||(1)(2)i |z x y +-=++-,所以|12i |z +-表示圆O 上的动点到定点(12)A -,的距离,所以min |12i |z +-为||1OA r -=,故选:A .【点睛】 关键点点睛:解答本题的关键是理解1z =对应的轨迹方程以及掌握12z i +-的几何意义,将复数模的最值问题转化为点到点的距离最值问题. 12.A解析:A【分析】先化简z ,求出a ,再判断即可.【详解】()()2202022211112121211222a i a a i a z i i i i i +=-=-=-=-----+,z 不是纯虚数,则21022a -≠,所以21≠a ,即1a ≠±, 所以1a ≠±是1a ≠的充分而不必要条件.故选:A .【点睛】本题主要考查根据复数的类型求参数,考查充分条件和必要条件的判断,考查逻辑思维能力和计算能力,属于常考题.二、填空题13.6【解析】分析:先找到复数z 对应的点的轨迹再求的最大值详解:设复数则所以复数对应的点的轨迹为(34)为圆心半径为1的圆所以的最大值是故答案为6点睛:(1)本题主要考查复数中的轨迹问题意在考查学生对这 解析:6【解析】分析:先找到复数z 对应的点的轨迹,再求z 的最大值.详解:设复数(,)z x yi x y R =+∈,则22341,(3)(4)1x yi i x y +--=∴-+-=, 所以复数对应的点的轨迹为(3,4)为圆心半径为1的圆,所以z 1516=+=.故答案为6点睛:(1)本题主要考查复数中的轨迹问题,意在考查学生对这些基础知识的掌握水平和数形结合的思想方法.(2)z a bi r ++=表示以点(a,b)为圆心r 为半径的圆,不要死记硬背,直接化成直角坐标,就一目了然. 14.【分析】首先设(且)代入方程化简为再分和两种情况求验证是否成立【详解】设(且)则原方程变为所以①且②;(1)若则解得当时①无实数解舍去;从而此时或3故满足条件;(2)若由②知或显然不满足故代入①得所 解析:74- 【分析】首先设z a bi =+ (a ,b ∈R 且221a b +=),代入方程,化简为()()222320ax ax bx bx i +++-=,再分0b =和0b ≠两种情况求,a x 验证是否成立.【详解】设z a bi =+,(a ,b ∈R 且221a b +=) 则原方程2230zx zx ++=变为()()222320ax ax bx bx i +++-=.所以2230ax ax ++=,①且220bx bx -=,②;(1)若0b =,则21a =解得1a =±,当1a =时①无实数解,舍去;从而1a =-,2230x x --=此时1x =-或3,故1z =-满足条件;(2)若0b ≠,由②知,0x =或2x =,显然0x =不满足,故2x =,代入①得38a =-,8b =±,所以838z =-±.综上满足条件的所以复数的和为3371884⎛⎫⎛⎫-+-++--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 故答案为:74-【点睛】思路点睛:本题考查复系数二次方程有实数根问题,关键是设复数z a bi =+后代入方程,再进行整理转化复数的代数形式,注意实部和虚部为0,建立方程求复数z . 15.【分析】利用的幂的性质化简即可得答案【详解】所以原式故答案为:【点睛】本题考查复数的计算合理利用常见结论可使计算简便如等等解析:1i --【分析】利用i 的幂的性质化简即可得答案.【详解】2019201633i i i i i =⋅==-,()1010202010102101010082222i 2i i i i 11i 2i 1i ⎡⎤⎛⎫-⎛⎫====⋅==-⎢⎥ ⎪ ⎪ ⎪+⎝⎭+⎢⎥⎝⎭⎣⎦,所以原式=1i --.故答案为:1i --.【点睛】 本题考查复数的计算.合理利用常见结论可使计算简便,如4i 1n =,41i i n +=,42i 1n +=-,43i i n +=-,()21i 2i +=,()21i 2i -=-,1i i=-等等. 16.【分析】根据复数几何意义列方程解方程得再根据共轭复数概念得结果【详解】解:由题意可得解得∴∴故答案为:【点睛】本题考查复数几何意义以及共轭复数概念考查基本分析求解能力属基础题解析:66i -【分析】根据复数几何意义列方程,解方程得9a =,再根据共轭复数概念得结果.【详解】解:由题意可得3a =-,解得9a =,∴66z i =+,∴66z i =-.故答案为:66i -【点睛】本题考查复数几何意义以及共轭复数概念,考查基本分析求解能力,属基础题. 17.②③【分析】根据新定义序的关系对四个命题逐一分析由此判断出真命题的序号【详解】对于①由于所以或且当满足但所以①错误对于②根据序的关系的定义可知复数的序有传递性所以②正确对于③设由所以或且可得或且即成解析:②③【分析】根据新定义“序”的关系,对四个命题逐一分析,由此判断出真命题的序号.【详解】对于①,由于12z z >,所以“12a a >”或“12a a =且12b b >”. 当121,2a a =-=-,满足12a a >但12z z <,所以①错误.对于②,根据“序”的关系的定义可知,复数的“序”有传递性,所以②正确.对于③,设z c di =+,由12z z >,所以“12a a >”或“12a a =且12b b >”,可得“12a c a c +>+”或“12a c a c +=+且12b d b d +>+”,即12z z z z +>+成立,所以③正确.对于④,当123,2,2z i z i z i ===时,126,4zz zz =-=-,12zz zz <,故④错误. 故答案为:②③【点睛】本小题主要考查新定义复数“序”的关系的理解和运用,考查分析、思考与解决问题的能力,属于基础题.18.【解析】【分析】根据复数的代数表示法及其几何意义可知集合A 表示的点的轨迹是以(01)为圆心半径为2的圆及内部;集合B 表示圆的圆心移动到了(11+b );两圆面有交点即可求解b 的取值范围【详解】由题意集解析:b ≤≤【解析】【分析】根据复数的代数表示法及其几何意义可知集合A 表示的点的轨迹是以(0,1)为圆心,半径为2的圆及内部;集合B 表示圆的圆心移动到了(1,1+b );两圆面有交点即可求解b 的取值范围.【详解】由题意,集合A 表示的点的轨迹是以(0,1)为圆心,半径为2的圆及内部; 集合B 表示点的轨迹为以(1,1+b )为圆心,半径为2的圆及内部∵A∩B≠∅,说明,两圆面有交点;∴4≤.可得:b ≤≤,故答案:b ≤≤,【点睛】本题考查复数几何意义,圆与圆的位置关系,体现了数学转化思想方法,明确A.B 集合的意义是关键,是中档题19.【分析】由题意可得a <0由|z|=2可得a 的方程解出即得【详解】∵z=a+i 在复平面内对应的点位于第二象限∴a <0由|z|=2得=2解得a=﹣1或1(舍去)∴z=﹣1+i 故答案为﹣1+i 【点睛】该题解析:【分析】由题意可得a <0,由|z|=2,可得a 的方程,解出即得.【详解】∵i 在复平面内对应的点位于第二象限,∴a <0,由|z|=2,解得a=﹣1或1(舍去),∴z=﹣.故答案为﹣【点睛】该题考查复数的模、复数代数形式的表示及其几何意义,属基础题.20.【解析】分析:先根据复数的模以及复数的虚部列不等式再根据扇形面积减去三角形面积得弓形面积详解:设则如图因此复平面内复数z 的对应点组成图形为两个弓形其面积为扇形面积减去三角形面积是点睛:本题重点考查复解析:2-32π 【解析】分析:先根据复数的模以及复数的虚部列不等式,再根据扇形面积减去三角形面积得弓形面积.详解:设(,)z x yi x y R =+∈11,2y ≤≥ ,如图,2.3AOB π∠=因此复平面内复数z 的对应点组成图形为两个弓形,其面积为扇形面积减去三角形面积是21212232(111sin )232332πππ⨯⋅-⨯⨯⨯=- 点睛:本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()()(),(,,.)++=-++∈a bi c di ac bd ad bc i a b c d R . 其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b 22a b +(,)a b 、共轭为.-a bi三、解答题21.(1)6m =或1m =-(2)6m ≠且1m ≠-(3)4m =(4)46m <<【分析】由题意得解得22(34)(56)z m m m m i =--+--,(1)由2560m m --=,求出m 即可;(2)2560m m --≠,即可得出m ; (3)由22340560m m m m ⎧--=⎨--≠⎩,解得m 范围; (4)根据象限特征,由22340560m m m m ⎧-->⎨--<⎩,解得m 范围. 【详解】解:()()()21i 5i 346i z m m =+-+-+=()()223456i m m m m --+--, (1)由2560m m --=得6m =或1m =-,即当6m =或1m =-时,z 为实数;(2)由2560m m --≠得6m ≠且1m ≠-,即当6m ≠且1m ≠-时,z 为虚数;(3)由22340{560m m m m --=--≠,,得4m =, 即当4m =时,z 为纯虚数;(4)由22340{560m m m m -->--<,,解得46m <<, 即当46m <<时,z 在复平面内对应的点在第四象限.【点睛】本题考查复数的有关概念及其运算法则、方程与不等式的解法,考查推理能力与计算能力.22.(1)ω;(2)12a b =-⎧⎨=⎩【分析】(1)求出1z i =+的共轭复数,代入234z z ω=+-化简,再求ω; (2)根据2211z az b i z z ++=--+,得到()()21a b a i i +++=+,列方程组即可求解. 【详解】(1)已知1z i =+,1z i ∴=-,()()213141i i i ω=++--=--∴,ω∴=(2)()()22211a b a z az b i z z i i+++++==--+, ()()21a b a i i ∴+++=+,121a b a +=⎧∴⎨+=⎩,解得12a b =-⎧⎨=⎩. 【点睛】此题考查复数的基本运算,涉及共轭复数,复数的模长,根据两个复数相等列方程组求解. 23.(1) 12z i =-或2i z =-.(2) 3m =±,5n =.【分析】(1)利用已知条件,设出复数z ,通过225(,)a b a b +=∈Z 及所对点所在位置求出即可复数z ;(2)利用(1),结合复数的乘法运算求解m ,n 的值【详解】(1)设(,)z a bi a b =+∈Z ,则225(,)a b a b +=∈Z ,因为z 在复平面内对应的点位于第四象限,所以0a >,0b <,所以12a b =⎧⎨=-⎩或21a b =⎧⎨=-⎩, 所以12z i =-或2i z =-.(2)由(1)知12z i =-或2i z =-,当12z i =-时,234z i =--;当2i z =-时234z i =-.因为()22m m n i z --=,所以234m m n =±⎧⎨-=⎩,解得3m =±,5n =. 【点睛】本题考查复数的模长公式,考查复数的乘法运算,考查计算能力,是基础题24.(1)1i +或1i --;(2)1【分析】(1)设z =a +bi (a ,b ∈R ),由已知列关于a ,b 的方程组,求解可得复数z ; (2)分类求得A 、B 、C 的坐标,再由三角形面积公式求解.【详解】解:(1)设z =a +bi (a ,b ∈R ),由已知可得:22ab ==⎪⎩2221a b ab ⎧+=⎨=⎩, 解得11a b =⎧⎨=⎩或11a b =-⎧⎨=-⎩. ∴z =1+i 或z =﹣1﹣i ;(2)当z =1+i 时,z 2=2i ,z ﹣z 2=1﹣i ,∴A (1,1),B (0,2),C (1,﹣1),故△ABC 的面积S 12=⨯2×1=1; 当z =﹣1﹣i 时,z 2=2i ,z ﹣z 2=﹣1﹣3i ,∴A (﹣1,﹣1),B (0,2),C (﹣1,﹣3),故△ABC 的面积S 12=⨯2×1=1. ∴△ABC 的面积为1.【点睛】 本题考查复数的乘方和加减运算,考查复数相等的条件和复数的几何意义,以及三角形的面积的求法,考查运算能力,属于中档题.25.(1)42i +;(2)()2,2-.【分析】(1)根据2z i R +∈、2z R i∈-,结合复数的加法、除法运算即可求出z ,进而由共轭复数的概念求得z ;(2) 复数()2z mi +在复平面上对应的点在第四象限,即对应复数的实部、虚部都小于0,解不等式即可求得m 的范围【详解】(1)设(),z x yi x y R =+∈,则()22z i x y i +=++∵2z i R +∈∴2y =- 又22242255z x i x x i R i i -+-==+∈--, ∴4x = 综上,有42z i =- ∴42z i =+(2)∵m 为实数,且()()()()2224212482z mi m i m m m i +=+-=+-+-⎡⎤⎣⎦ ∴由题意得()21240820m m m ⎧+->⎪⎨-<⎪⎩,解得22m -<< 故,实数m 的取值范围是()2,2-【点睛】本题考查了复数,利用复数的四则运算及共轭复数的概念求复数,另外依据复数所处的象限求参数范围26.(1)3,1a b ==-(2【解析】分析:(1)由复数的四则运算可化简复数,再由复数相等可知实部与虚部都要相等,可求得,a b .(2)由复数的乘法运算可化简复数式为标准式,再由复数在第一、三象限的角平分线上可知复数实部等于虚部,求得参数y,再由复数模公式求得复数模.详解:(1)∵()()21253i i a bi i -+++=+ 1033i i==-+ , 又∵,a b R ∈ ∴3,1a b ==-(2)()()()31a bi z i yi +⋅=--+()()331y y i =-+++由题意可知:331y y -+=+,解得2y =-∴z ==点睛:本题主要考查复数四则运算与乘方综合运算和复数相等,及复数与坐标对应关系,及复数的模.。
2018苏教版小学数学二年级上册第二单元测试卷.doc
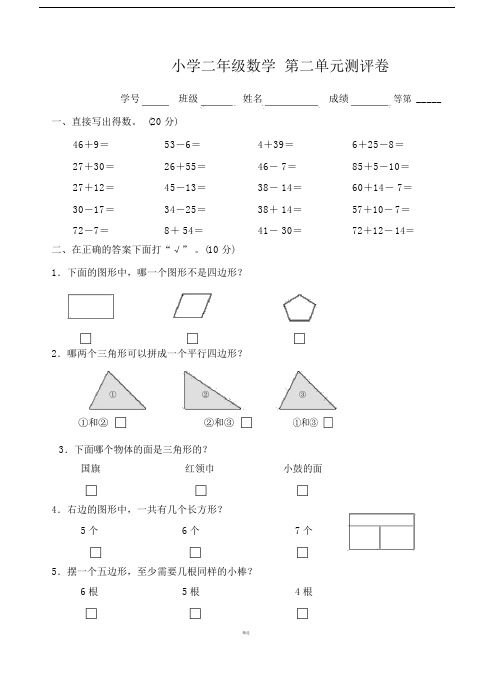
小学二年级数学第二单元测评卷学号班级姓名成绩等第_____ 一、直接写出得数。
(20 分)46+9=53-6=4+39=6+25-8=27+30=26+55=46- 7=85+5-10=27+12=45-13=38- 14=60+14- 7=30-17=34-25=38+ 14=57+10-7=72-7=8+ 54=41- 30=72+12-14=二、在正确的答案下面打“√”。
(10 分)1.下面的图形中,哪一个图形不是四边形?□□□2.哪两个三角形可以拼成一个平行四边形?①②③①和② □②和③ □①和③ □3.下面哪个物体的面是三角形的?国旗红领巾小鼓的面□□□4.右边的图形中,一共有几个长方形?5个6个7个□□□5.摆一个五边形,至少需要几根同样的小棒?6根5根4根□□□三、写出下面各图形的名称。
(10 分)() () () () ()四、把一张长方形纸的一个角剪去,剩下的是什么图形?先画一画,再填一填。
(9分 )剩下的是 ()形剩下的是()形剩下的是()形五、按要求分一分,画一画。
(17 分,7+6+4)1.先写出下面图形的名称,再把下面的图形都分成三角形,最少能分成几个?想一想:八边形最少可以分成 () ( ) ( ) ( ) 个三角形。
( )个( )个( )个2.给下面的四边形增加一条线段,使它们各分成两个不同的多边形。
分成一个三角形分成一个三角形分成两个四边形和一个四边形和一个平行四边形3.在下面的图中描出一个平行四边形和一个六边形。
六、想想填填。
(20分)1.搭两个六边形要用几根小棒呢?(2分 )()根()根2.数一数,填一填。
(6分 )四边形五边形六边形3.七巧板: (12 分)(1)一副七巧板中共有 ( )个三角形, ( )个四边形。
(2)( )号和 ( ) 号可以拼成正方形。
②(3)( )号和 ( ) 号可以拼成平行四边形。
(4)( )号、 ( )号和( )号也可以拼成平行四边形。
复数的单元测试

数系的扩充和复数的概念单元测试姓名 座号 班级一、 选择题1. 下列说法正确的个数是( )①实数是复数; ②虚数是复数; ③实数集和虚数集的交集不是空集; ④实数集和虚数集的并集等于复数集; ⑤虚轴上的点表示的数都是虚数; ⑥实轴上的点表示的数都是实数;A 、3B 、4C 、5D 、62. 复数z满足方程1=+-z z z ,则z对应的点的轨迹是 ( )A 、直线B 、圆C 、两点D 、以上都不对3. 对于复数bi a +,下列结论正确的是( )A 、⇔=0a bi a +为纯虚数;B 、⇔=0b bi a +为实数;C 、i b a )1(-+=3+2i ⇔3=a ,3-=bD 、-1的平方等于i4. 下列说法正确的是( )A 、如果两个复数的实部的差和虚部的差都于0,那么这两个复数相等;B 、在复平面内复数bi a +对应的点为),(a bC 、如果复数yi x +是实数,则0=x ,0=y ;D 、复数i +3大于i +25. 2i i +在复平面内表示的点在( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限6. 设全集I={复数},R={实数},M={纯虚数},则( )A 、I R M =B 、I R MC I = C 、R R M C I =D 、Φ=R C M I7. 以23-i 的虚部为实部,以i i 232+的实部为虚部的复数是( )A 、i 33-B 、i +3C 、i 22+-D 、i 22+8. 若(m 2-3m-4)+(m 2-5m-6)i 是纯虚数,则实数m 的值为 ( )A 、-1B 、4C 、-1或4D 、不存在9. 在复平面内,与复数z=-1-i 的共轭复数对应的点位于 ( )A 、第一象限B 、第二角限C 、第三象限D 、第四象限10. i 21i 2)i 1()i 31(63++-+++-的值是( ) i D i C B A 201、 、、 、 11. 若i 23+是关于x 的方程)R q ,p (0q px x 22∈=++的一个根,则q 的值为( )A 、26B 、13C 、 6 D、512. 221(1)(4),.z m m m m i m R =++++-∈23 2.z i =-则1m =是12z z =的( )条件A 、充分不必要B 、 必要不充分C 、 充要D 、既不充分又不必要二、填空题13. 若x 是实数,y 是纯虚数且满足y i x =+-212,则=x ,=y 。
八年级生物苏教版上册 2017-2018学年 第6单元第18章动物的行为 单元测试题(解析版)

第6单元第17章动物的行为单元测试题一、选择题1.下列属于动物先天性行为的是()A.猴子骑车【答案】C【解析】B.谈虎色变C.蜘蛛结网D.老马识途【分析】(1)先天性行为是动物生来就有的,由动物体内的遗传物质决定的行为,是动物的一种本能,不会丧失.(2)后天学习行为是动物出生后,在动物的成长过程中,通过生活经验和学习逐渐建立起来的新的行为.【详解】A C D、猴子骑车、老马识途、谈虎色变,都是通过生活经验和学习逐渐建立起来的学习行为.不符合题意。
B、蜘蛛结网是生来就有的,由遗传物质决定的先天性行为.因此属于先天性行为的是蜘蛛结网.B符合题意。
【点睛】考查对先天性行为和学习行为的区分。
2.下列成语所描述的动物行为中,属于学习行为的是A.蜻蜓点水C.鹦鹉学舌【答案】D 【解析】B.螳螂捕蝉D.作茧自缚【分析】(1)先天性行为是动物生来就有的,由动物体内的遗传物质决定的行为,是动物的一种本能,不会丧失。
(2)后天学习行为是动物出生后,在动物的成长过程中,通过生活经验和学习逐渐建立起来的新的行为。
【详解】蜻蜓点水、螳螂捕蝉、蜘蛛结网,都是生来就有的,由遗传物质决定的先天性行为,A、B、D不符合题意;鹦鹉学舌,是动物出生后,通过生活经验和学习建立起来的后天学习行为,C符合题意。
【点睛】解答此类题目的关键是理解掌握先天性行为和学习行为的特点。
3.公鸡在清晨一定时刻鸣叫,此行为属于()A.社群行为【答案】B【解析】B.节律行为C.防御行为D.攻击行为节律行为是指生物随着地球、太阳、月亮的周期性变化,逐渐形成的周期性、有节律的行为。
如昼夜节律、月运节律、季节节律等。
公鸡在清晨一定的时刻鸣叫属于昼夜节律行为。
4.下列动物中,“学习能力”最强的是()A.蚂蚁B.黑猩猩C.乌鸦D.蜘蛛【答案】B【解析】动物越高等,形态结构越复杂,学习行为越复杂。
在A蚂蚁、B黑猩猩、C乌鸦、D蜘蛛四种生物中,黑猩猩最高等,其学习能力最强。
2018苏教版小学数学五年级上册第2单元测试卷

CABD(第10题图1) (第11题图2) (第12题图3)小学五年级数学 第二单元测评卷学号 班级 姓名 成绩 等第_____一、填空:(每空1分,共27分) 1.在下面括号内填上适当的单位名称。
(1)我国领土面积大约是960万( )。
(2)一本数学书的封面大约是380( )。
(3)一所学校运动场的占地面积约是2( )。
(4)小华身高140( )。
2.60000平方米=( )公顷 78公顷=( )平方米120平方千米=( )公顷 90000平方分米=( )平方米=( )公顷 1平方千米=( )公顷=( )平方米 40000平方米=( )公顷3.一个三角形和一个平行四边形等底等高。
如果平行四边形的面积是20平方厘米,那三角形的面积是( )平方厘米;如果三角形的面积是20平方厘米,那平行四边形的面积是( )平方厘米。
4.两个完全相同的梯形拼成一个平行四边形,这个平行四边形的底长16厘米,高5厘米。
每个梯形的面积是( )平方厘米。
5.一块平行四边形的水稻田,底边长150米,高是50米。
今年共收水稻15000千克,平均每平方米收水稻( )千克。
6.一块三角形土地底是10米,高15米,面积是( )平方米。
7.一个正方形地的周长是800米,每公顷收稻谷7500千克,则这块地收稻谷( )吨。
8.在一个长9厘米、宽4厘米的长方形内画一个最大的三角形,这个三角形的面积是( )平方厘米。
9.一个梯形的上底与下底的和是40厘米,高是12厘米,这个梯形的面积是( )平方厘米。
10.如图1,在三角形AB C 中,BD 的长度相当于CD 长度的2倍,那么三角形ABD 的面积是三角形ACD 面积的( )倍。
11.如图2,每个方格的边长为1厘米,这只小鱼的面积是( )平方厘米。
12.将木条钉成的长方形拉成一个平行四边形(如图3),原来长方形的面积是( )平方厘米,现在平行四边形的面积是( )平方厘米,周长是( )厘米。
2018届苏教版 无菌操作技术实践 单元测试 (1)

无菌操作技术实践单元测试学校:___________姓名:___________班级:___________考号:___________一、选择题1.花药培养技术与植物组织培养技术的不同之处在于()A.培养基配制方法 B.选材C.接种操作 D.无菌技术【答案】B【解析】试题分析:菊花的组织培养与月季的花药培养都需要制备MS固体培养基,A错误;植物组织培养取材来源植物的体细胞,最后培育得植株是正常的和母本一样的植株,花药离体培养取材来自于植物的花粉,得到的单倍体植株,B正确;菊花的组织培养与月季的花药培养的接种要在无菌条件下进行,所以接种室要消毒;外植体可预先用体积分数为70%的酒精浸泡,取出用无菌水冲洗后,再用0.1%的氯化汞溶液消毒,并用无菌水冲洗干净;接种操作要在酒精灯火焰旁进行,C错误;菊花的组织培养与月季的花药培养都需要无菌操作,D错误。
考点:植物培养的条件及过程【名师点睛】植物组织培养技术与花药培养技术的比较:植物组织培养技术与花药培养技术的相同之处是:培养基的配制、接种要在无菌条件下进行,所以接种室要消毒;外植体可预先用体积分数为70%的酒精浸泡,取出用无菌水冲洗后,再用0.1%的氯化汞溶液消毒,并用无菌水冲洗干净;接种操作要在酒精灯火焰旁进行;接种完毕应立即盖好瓶盖。
但是植物组织培养取材来源植物的体细胞,最后培育得植株是正常的和母本一样的植株,属于无性生殖。
花药离体培养取材来自于植物的花粉,得到的单倍体植株,属于一种特殊的有性生殖方式。
因此,花药离体培养的培育要比植物组织培养复杂一些。
2.在对外植体消毒时以下说法正确的是()A.菊花茎段用流水冲洗后可加少许洗衣粉用软刷子轻轻刷洗,刷洗后在流水下冲洗20minB.用95%的酒精冲刷C.放入0.1%的氯化汞中10minD.用蒸馏水清洗若干次【答案】A【解析】菊花茎段用流水冲洗后可加少许洗衣粉用软刷子轻轻刷洗,刷洗后在流水下冲洗20min,A正确;95%或无水酒精会使菌体表面蛋白质快速脱水凝固,形成一层干燥膜,不能由于外植体的消毒,B错误;用2%次氯酸钠浸泡10~15min或用0.1%升汞浸5~10min,C错误;最后用无菌水冲洗3~5次,D错误。
第七章 复数(单元测试)试卷及答案

第七章复数单元测试一、单选题(共8小题)1.已知a∈R,若复数z=a2+2a+ai是纯虚数,则a=()A.0B.2C.−1D.−22.已知复数z=1+3i,i为虚数单位,则|z|=()1−iA.√2B.√5C.√10D.2√53.若复数z=(1+ai)⋅(1−i)的模等于2,其中i为虚数单位,则实数a的值为()A.−1B.0C.1D.±14.设复数z=i,则复数z的共轭复数z̅在复平面内对应的点位于()1+iA.第一象限B.第二象限C.第三象限D.第四象限5.已知z=1+i,则z(z+1)=()A.3+i B.3−i C.1+i D.1−i6.已知复数z=(3−4i)(2−i),则z的虚部为()A.2B.11C.−11D.−11i7.若z=2−i,则z2−4z=()A.-5B.-3C.3D.58.在复平面内,复数z1,z2所对应的点关于虚轴对称,若z1=1+2i,则复数z2=()A.−1−2i B.−1+2iC.1−2i D.2+i二、多选题(共4小题)9.已知复数z=1+i(其中i为虚数单位),则以下说法正确的有()A.复数z的虚部为i B.|z|=√2C.复数z的共轭复数z=1−i D.复数z在复平面内对应的点在第一象限10.下列命题中,真命题为()A.复数z=a+bi为纯虚数的充要条件是a=0B.复数z=1−3i的共轭复数为z=1+3iC.复数z=1−3i的虚部为−3D.复数√2z=1+i,则z2=i=i,则下列结论正确的是()11.已知复数z满足z+1zA .复数z 的共轭复数为−12+12iB .z 的虚部为12C .在复平面内z 对应的点在第二象限D .|z |=√2212.下列命题中正确的是( )A .已知平面向量a ⃑满足|a ⃑|=1,则a ⃑⋅a ⃑=1B .已知复数z 满足|z |=1,则z ⋅z =1C .已知平面向量a ⃑,b ⃑⃑满足|a ⃑+b ⃑⃑|=|a ⃑−b ⃑⃑|,则a ⃑⋅b ⃑⃑=0D .已知复数z 1,z 2满足|z 1+z 2|=|z 1−z 2|,则z 1⋅z 2=0三、填空题(共4小题)13.已知复数z 满足z ⋅(1−2i )=|3+4i |,则z =___________. 14.已知i 为虚数单位,则i 2020+i 2021=___________.15.复数4+3i 与-2-5i 分别表示向量OA ⃑⃑⃑⃑⃑ 与OB ⃑⃑⃑⃑⃑ ,则向量AB ⃑⃑⃑⃑⃑ 表示的复数是________. 16.已知1+2i 是方程x 2-mx +2n =0(m ,n ∈R )的一个根,则m +n =____.四、解答题(共5小题) 17.计算:(1)(1−4i )(1+i )+2+4i3+4i;(2)(1+i )51−i+(1−i )51+i;(3)(1+2i)2+3(1−i)2+i.18. 已知复数z =m 2−2m −15+(m 2−9)i ,其中m ∈R ,i 为虚数单位. (1)若z 为实数,求m 的值; (2)若z 为纯虚数,求z1+i 的虚部.19.已知复数z =(m 2−2m −3)+(m 2+m −2)i ,(m ∈R). (1)若z >0,求m 的值; (2)若z 是纯虚数,求z ⋅z̅的值.⃑⃑⃑⃑⃑ 对应的复数为1+2i,20.已知复平面内平行四边形ABCD,A点对应的复数为2+i,向量BA⃑⃑⃑⃑⃑ 对应的复数为3−i,求:向量BC(1)点D对应的复数;(2)平行四边形ABCD的面积.−isinθ,其中i为虚数单位,θ∈R.求|z1⋅z2|的21.已知复数z1=3cosθ+isinθ,z2=√24值域.22.已知复数z=3x−(x2−x)i(x∈R)的实部与虚部的差为f(x).(1)若f(x)=8,且x>0,求复数iz的虚部;(2)当f(x)取得最小值时,求复数z的实部.1+2i第七章 复数单元测试一、单选题(共8小题)1.已知a ∈R ,若复数z =a 2+2a +ai 是纯虚数,则a =( ) A .0 B .2 C .−1 D .−2【答案】D【分析】结合复数的概念得到{a 2+2a =0a ≠0,解之即可求出结果.【详解】∵z =a 2+2a +ai 是纯虚数,∴{a 2+2a =0,a ≠0,解得a =−2. 故选:D.2.已知复数z =1+3i 1−i,i 为虚数单位,则|z |=( ) A .√2 B .√5C .√10D .2√5【答案】B【分析】利用复数除法运算进行化简,再求得|z |. 【详解】z =(1+3i )(1+i )(1−i )(1+i )=−2+4i 2=−1+2i ,∴|z |=√(−1)2+22=√5. 故选:B3.若复数z =(1+ai)⋅(1−i)的模等于2,其中i 为虚数单位,则实数a 的值为( ) A .−1 B .0 C .1 D .±1【答案】D【分析】先根据复数的乘法法则得z =(1+a)+(a −1)i ,再根据模的公式列方程求解即可. 【详解】∵z =(1+ai)⋅(1−i)=1−i +ai −ai 2=(1+a)+(a −1)i 则|z|=√(1+a)2+(a −1)2=√2a 2+2=2,解得:a =±1. 故选:D. 4.设复数z =i1+i ,则复数z 的共轭复数z̅在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】D【分析】先求出z ,再求出z ̅,直接得复数z ̅在复平面内对应的点. 【详解】z =i 1+i=i (1-i )(1+i )(1-i )=12+12i ,则z =12−12i ,∴z ̅在复平面内对应的点为(12,−12),位于第四象限;故选:D.5.已知z =1+i ,则z (z +1)=( ) A .3+i B .3−iC .1+iD .1−i【答案】B【分析】根据复数的四则运算法则计算即可.【详解】z ̅(z +1)=(1−i)(1+i +1)=(1−i)(2+i)=3−i ,故选:B. 6.已知复数z =(3−4i)(2−i),则z 的虚部为( )A.2B.11C.−11D.−11i【答案】C【分析】利用复数乘法求出z,即可确定其虚部.【详解】∵z=(3−4i)(2−i)=2−11i,∴z的虚部−11,故选:C7.若z=2−i,则z2−4z=()A.-5B.-3C.3D.5【答案】A【分析】依据复数的运算法则直接求解即可;【详解】z2−4z=z(z−4)=(2−i)⋅(−2−i)=i2−4=−5,故选:A8.在复平面内,复数z1,z2所对应的点关于虚轴对称,若z1=1+2i,则复数z2=()A.−1−2i B.−1+2iC.1−2i D.2+i【答案】B【分析】根据对应的点的特征直接求出即可.【详解】∵z1=1+2i对应的点为(1,2),z1,z2所对应的点关于虚轴对称,∴z2对应的点为(−1,2),∴z2=−1+2i. 故选:B.二、多选题(共4小题)9.已知复数z=1+i(其中i为虚数单位),则以下说法正确的有()A.复数z的虚部为i B.|z|=√2C.复数z的共轭复数z=1−i D.复数z在复平面内对应的点在第一象限【答案】BCD【分析】根据复数的概念判定A错,根据复数模的计算公式判断B正确,根据共轭复数的概念判断C正确,根据复数的几何意义判断D正确.【详解】∵复数z=1+i,∴其虚部为1,即A错误;|z|=√12+12=√2,故B正确;复数z的共轭复数z=1−i,故C正确;复数z在复平面内对应的点为(1,1),显然位于第一象限,故D正确.故选:BCD.【点睛】本题主要考查复数的概念,复数的模,复数的几何意义,以及共轭复数的概念,属于基础题型.11.下列命题中,真命题为()A.复数z=a+bi为纯虚数的充要条件是a=0B.复数z=1−3i的共轭复数为z=1+3iC.复数z=1−3i的虚部为−3D .复数√2z =1+i ,则z 2=i 【答案】BCD【分析】对A,根据纯虚数的定义,可知a =0,b ≠0,故A 错.根据共轭复数,虚部的定义,可判断B,C.运用复数的四则运算,可判断D. 【详解】复数z =a +bi 为纯虚数的充要条件是a =0,b ≠0,故A 错. 复数z =1−3i 的共轭复数为z =1+3i ,复数z =1−3i 的虚部为−3,故B,C 对. 复数√2z =1+i ,则z =√2,z 2=(√2)2=2i 2=i ,故D 对.故选:BCD 11.已知复数z 满足z+1z=i ,则下列结论正确的是( )A .复数z 的共轭复数为−12+12i B .z 的虚部为12 C .在复平面内z 对应的点在第二象限 D .|z |=√22【答案】AD【分析】先由已知求出复数z ,然后再逐个分析判断即可 【详解】由z+1z=i ,得z +1=zi ,∴z =−11−i =−(1+i)(1−i)(1+i)=−12−12i , ∴复数z 的共轭复数为−12+12i ,复数z 的虚部为−12,复数z 在复平面内对应的点在第三象限,|z |=√(−12)2+(−12)2=√22,∴AD 正确,BC 错误,故选:AD 12.下列命题中正确的是( )A .已知平面向量a ⃑满足|a ⃑|=1,则a ⃑⋅a ⃑=1B .已知复数z 满足|z |=1,则z ⋅z =1C .已知平面向量a ⃑,b ⃑⃑满足|a ⃑+b ⃑⃑|=|a ⃑−b ⃑⃑|,则a ⃑⋅b ⃑⃑=0D .已知复数z 1,z 2满足|z 1+z 2|=|z 1−z 2|,则z 1⋅z 2=0 【答案】ABC【分析】结合选项逐个验证,向量的模长运算一般利用平方处理,复数问题一般借助复数的运算来进行.【详解】∵a ⃑⃑⋅a ⃑⃑=|a ⃑⃑|2=1,∴A 正确;设z =a +bi ,则z =a −bi ,∵|z |=1,∴a 2+b 2=1, ∴z ⋅z =(a +bi )(a −bi )=a 2+b 2=1,∴B 正确;∵|a ⃑⃑+b ⃑⃑|=|a ⃑⃑−b ⃑⃑|,∴a ⃑⃑2+2a ⃑⃑⋅b ⃑⃑+b ⃑⃑2=a ⃑⃑2−2a ⃑⃑⋅b ⃑⃑+b ⃑⃑2,即a ⃑⃑⋅b ⃑⃑=0,∴C 正确; ∵|1+i |=|1−i |,然而1⋅i =i ≠0,∴D 不正确. 故选:ABC.三、填空题(共4小题)13.已知复数z 满足z ⋅(1−2i )=|3+4i |,则z =___________. 【答案】1+2i【分析】根据复数的四则运算进行整理化简即可. 【详解】解:∵z ⋅(1−2i )=|3+4i |=5 ∴z =51−2i=5(1+2i )(1−2i )⋅(1+2i )=1+2i ,故答案为:1+2i.14.已知i 为虚数单位,则i 2020+i 2021=___________. 【答案】1+i【分析】根据i n 的周期性求得正确结论. 【详解】i 2020+i 2021=i 4×505+i 4×505+1=1+i . 故答案为:1+i15.复数4+3i 与-2-5i 分别表示向量OA ⃑⃑⃑⃑⃑ 与OB ⃑⃑⃑⃑⃑ ,则向量AB ⃑⃑⃑⃑⃑ 表示的复数是________. 【答案】-6-8i【分析】由复数的几何意义得出向量OA ⃑⃑⃑⃑⃑ 与OB ⃑⃑⃑⃑⃑ 的坐标,再由向量的运算得出AB ⃑⃑⃑⃑⃑ 的坐标,进而得出其复数.【详解】∵复数4+3i 与-2-5i 分别表示向量OA⃑⃑⃑⃑⃑ 与OB ⃑⃑⃑⃑⃑ ,∴OA ⃑⃑⃑⃑⃑ =(4,3),OB ⃑⃑⃑⃑⃑ =(−2,−5) 又AB ⃑⃑⃑⃑⃑ =OB ⃑⃑⃑⃑⃑ −OA ⃑⃑⃑⃑⃑ =(−2,−5)−(4,3)=(−6,−8),∴向量AB ⃑⃑⃑⃑⃑ 表示的复数是-6-8i . 故答案为:-6-8i16.已知1+2i 是方程x 2-mx +2n =0(m ,n ∈R )的一个根,则m +n =____. 【答案】92【分析】将x =1+2i 代入方程,根据复数的乘法运算法则,得到(−3−m +2n )+(4−2m )i =0,再由复数相等的充要条件得到方程组,解得即可;【详解】解:将x =1+2i 代入方程x2-mx +2n =0,有(1+2i)2-m(1+2i)+2n =0,即1+4i −4−m −2mi +2n =0,即(−3−m +2n )+(4−2m )i =0, 由复数相等的充要条件,得{−3−m +2n =04−2m =0解得{n =52m =2 ,故m +n =2+52=92. 故答案为:92 四、解答题(共5小题) 17.计算:(1)(1−4i )(1+i )+2+4i3+4i;(2)(1+i )51−i+(1−i )51+i;(3)(1+2i)2+3(1−i)2+i.【答案】(1)1−i ;(2)0;(3)15+25i 【分析】根据复数四则运算法则计算即可. 【详解】(1)原式=5−3i+2+4i 3+4i=7+i3+4i =(7+i )(3−4i )(3+4i )(3−4i )=25−25i 25=1−i .(2)原式=(1+i )6+(1−i )6(1−i )(1+i )=[(1+i )2]3+[(1−i )2]32=(2i )3+(−2i )32=−8i+8i2=0.(3)(1+2i)2+3(1−i)2+i=−3+4i+3−3i2+i=i 2+i=i(2−i)5=15+25i18. 已知复数z =m 2−2m −15+(m 2−9)i ,其中m ∈R ,i 为虚数单位. (1)若z 为实数,求m 的值; (2)若z 为纯虚数,求z1+i 的虚部. 【答案】(1)m =±3;(2)8【分析】(1)由题意得m 2−9=0,求解即可;(2)先由题意求得z =16i ,再根据复数的除法法则化简复数z 1+i,由此可求得答案.(1)解:若z 为实数,则m 2−9=0,解得m =±3. (2)解:由题意得{m 2−2m −15=0,m 2−9≠0,解得m =5,∴z =16i ,故z 1+i=16i 1+i=16i (1−i )(1+i )(1−i )=8+8i ,∴z1+i的虚部为8.19.已知复数z =(m 2−2m −3)+(m 2+m −2)i ,(m ∈R). (1)若z >0,求m 的值; (2)若z 是纯虚数,求z ⋅z̅的值. 【答案】(1)m =−2;(2)4或100【分析】(1)根据复数z >0,可知z 为实数,列出方程,解得答案;(2)根据z 是纯虚数,列出相应的方程或不等式,再结合共轭复数的概念以及复数的乘法运算,求得答案. 【详解】(1)∵z >0,∴z ∈R ,∴m 2+m −2=0,∴m =−2或m =1. ①当m =−2时,z =5>0,符合题意; ②当m =1时,z =−4<0,舍去. 综上可知:m =−2.(2)∵z 是纯虚数,∴{m 2−2m −3=0m 2+m −2≠0,∴m =−1或m =3,∴z =−2i ,或z =10i ,∴z ⋅z ̅=−2i ×2i =4或z ⋅z ̅=10i ×(−10i)=100, ∴z ⋅z ̅=4或100.20.已知复平面内平行四边形ABCD ,A 点对应的复数为2+i ,向量BA ⃑⃑⃑⃑⃑ 对应的复数为1+2i ,向量BC⃑⃑⃑⃑⃑ 对应的复数为3−i ,求: (1)点D 对应的复数; (2)平行四边形ABCD 的面积. 【答案】(1)5;(2)7【分析】(1)根据复数与向量间的关系运算得BD ⃑⃑⃑⃑⃑ =(4,1),OB ⃑⃑⃑⃑⃑ =(1,−1),则OD ⃑⃑⃑⃑⃑ =OB ⃑⃑⃑⃑⃑ +BD ⃑⃑⃑⃑⃑ =(5,0),从而得到其对应的复数; (2)cosB =BA⃑⃑⃑⃑⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ |BA⃑⃑⃑⃑⃑⃑ ||BC ⃑⃑⃑⃑⃑ |=5√2,则sinB =5√2,利用平行四边形面积公式即可得到答案.【详解】(1)∵向量BA ⃑⃑⃑⃑⃑ 对应的复数为1+2i ,∴向量BA ⃑⃑⃑⃑⃑ =(1,2), BC⃑⃑⃑⃑⃑ 对应的复数为3−i ,∴向量BC ⃑⃑⃑⃑⃑ =(3,−1), BD ⃑⃑⃑⃑⃑ =BA ⃑⃑⃑⃑⃑ +BC ⃑⃑⃑⃑⃑ =(1,2)+(3,−1)=(4,1), OB⃑⃑⃑⃑⃑ =OA ⃑⃑⃑⃑⃑ −BA ⃑⃑⃑⃑⃑ =(2,1)−(1,2)=(1,−1), ∴OD ⃑⃑⃑⃑⃑ =OB ⃑⃑⃑⃑⃑ +BD ⃑⃑⃑⃑⃑ =(1,−1)+(4,1)=(5,0), ∴点D 对应的复数为5 .(2)∵BA ⃑⃑⃑⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ =|BA ⃑⃑⃑⃑⃑ ||BC ⃑⃑⃑⃑⃑ |cosB ,∴cosB =BA⃑⃑⃑⃑⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ |BA⃑⃑⃑⃑⃑⃑ ||BC ⃑⃑⃑⃑⃑ |=√5×√10=5√2, ∵B ∈[0,π],∴sinB =5√2,∴S =|BA⃑⃑⃑⃑⃑ ||BC ⃑⃑⃑⃑⃑ |sinB =√5×√10×5√2=7.故平行四边形ABCD 面积为7.21.已知复数z 1=3cosθ+isinθ,z 2=√24−isinθ,其中i 为虚数单位,θ∈R .求|z 1⋅z 2|的值域. 【答案】[3√24,5√24] 【分析】由复数模的定义,结合三角函数值域的求法即可求解.【详解】|z 1⋅z 2|=|(3cosθ+isinθ)⋅(√24−isinθ)|=|(3cosθ+isinθ)||(√24−isinθ)| =√(1+8cos 2θ)(18+sin 2θ)=√18+sin 2θ+cos 2θ+8sin 2θcos 2θ=√98+2sin 22θ. ∵sin 22θ∈[0,1],∴ √98+2sin 22θ∈[3√24,5√24],即|z 1⋅z 2|∈[3√24,5√24]. 22.已知复数z =3x −(x 2−x )i(x ∈R)的实部与虚部的差为f(x). (1)若f(x)=8,且x >0,求复数iz 的虚部; (2)当f(x)取得最小值时,求复数z 1+2i的实部.【答案】(1)6;(2)−75【分析】(1)由复数的实部、虚部的运算,可得f(x)=x 2+2x ,再结合题意可得x =2,再确定iz 在复平面内对应的点的坐标即可;(2)先求出函数取最小值时x 对应的值,再结合复数的除法运算即可得解.【详解】(1)由题意可得f(x)=3x +(x 2−x )=x 2+2x , ∵f(x)=8,∴x 2+2x =8, 又x >0,∴x =2,即z =6−2i , 则iz =i(6−2i)=2+6i , ∴复数iz 的虚部为6.(2)∵f(x)=x 2+2x =(x +1)2−1,∴当x =−1时,f(x)取得最小值, 此时,z =−3−2i ,则z 1+2i=−3+2i 1+2i=−(3+2i)(1−2i)5=−75+45i ,∴z1+2i 的实部为−75.。
高一数学(必修二)第五章 复数 单元测试卷及答案

高一数学(必修二)第五章 复数 单元测试卷及答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z 满足i 3i z z -=+,则复数z 的实部为( )A.1B.3C.-1D.-32.在复平面内,复数11i 5z =,24i 25z =-,12z z z =+,则复数z 对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.已知复数z 满足4i 63i z +=+,则z 在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限4.当12m <<时,复数()()2i 4i m +-+在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限5.已知复数z 满足()()()293i z a a a =-++∈R ,若z 为纯虚数,则a =( )A.-3B.3±C.3D.06.若,a b ∈R ,i 是虚数单位,i 20212i a b +=-,则2i a b +等于( )A.20212i +B.20214i +C.22021i +D.42021i -7.已知纯虚数,其中i 为虚数单位,则实数m 的值为( )A.1B.3C.1或3D.08.已知复数z 满足,则z =( )A.3i --B.3i -+C.D.二、多选题(本题共4小题,每小题5分,共20分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得5分,有选错的得0分,部分选对的得2分。
)9.若复数z 满足(1i)3i z +=+(其中i 是虚数单位),复数z 的共轭复数为z ,则( ) A.||5z =B.复数z 的实部是2C.复数z 的虚部是1D.复数在复平面内对应的点位于第一象限10.设m ∈R ,复数,则z 在复平面内对应的点可能在( ) ()()21i 4i 3z m m =+-++(3i)10z -=3i -3i +z 2352(1)i z m m m =-++-A.第一象限B.第二象限C.第三象限D.第四象限11.对于复数(,)z a bi a b R =+∈,下列结论错误的是( )A.若,则a bi +为纯虚数B.若32a bi i -=+,则 3,2a b ==C.若0b =,则a bi +为实数D.纯虚数z 的共轭复数是z - 12.复数z 满足23i 3i 232iz -⋅-=+,则下列说法正确的是( ) A.z 的实部为3 B.z 的虚部为2 C.32i z =-+ D.13z =三、填空题:本题共4小题,每小题5分,共20分.13.已知1z 、2z ∈C ,且12i z =+,234i z =-(其中i 为虚数单位),则12z z -=______.14.已知1z 、2z ∈C ,且12i z =+,234i z =-(其中i 为虚数单位),则12z z -=____________.15.复数1i -的虚部的平方是_________________. 16.已知3i 1ia ++(i 为虚数单位,∈R )为纯虚数,则a =____________. 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. (10分)已知复数(3)(3)i z m m m =-+-,其中i 为虚数单位.若z 满足下列条件,求实数m 的值:(1)z 为实数;(2)z 为纯虚数;(3)z 在复平面内对应的点在直线y x =上.18. (12分)已知复数13i 22z =-+,i 为虚数单位. (1)求3z 的值;(2)类比数列的有关知识,求220191z z z ++++的值. 19. (12分)已知复数()()2223232i z m m m m =--+-+.当实数m 取什么值时,复数z 是:(1)实数;(2)纯虚数;20. (12分)复数名12334i,0,(26)i z z z c c =+==+-在复平面内对应的点分别为A ,B ,C ,若BAC∠是钝角,求实数c 的取值范围.21. (12分)已知(){}221,2,3156i ,{1,3},{3}A a a a a B A B =--+--=-⋂=,求实数a 的值.22. (12分)设实部为正数的复数z ,满足||10z =,且复数(12i)z +在复平面内对应的点在第0a =一、三象限的角平分线上.(1)求复数z ;(2)若i ()1im z m -+∈+R 为纯虚数,求实数m 的值.参考答案及解析1.答案:A解析:解法一 设复数i z x y =+,x ,y ∈R ,因为i 3i z z -=+,所以i (i)i 3i x y x y +-+=+,即()i 3i x y y x ++-=+,根据复数相等的充要条件,可得3,1,x y y x +=⎧⎨-=⎩解得1,2,x y =⎧⎨=⎩故复数z 的实部为1,选A.解法二 因为i 3i z z -=+,所以3i (3i)(1i)12i 1i (1i)(1i)z +++===+--+,复数z 的实部为1,故选A. 2.答案:B 解析:因为1214i i 22i 55z z z =+=+-=-+,所以实部小于0,虚部大于0,故复数z 对应的点位于第二象限,故选:B.3.答案:D解析:依题意得,6i z =-,对应复平面的点是(6,1)-,在第四象限. 故选:D.4.答案:B解析:()()2i 4i (24)(1)i z m m m +--+-=+=,若12m <<,则240m -<,10m ->,所以复数z 在复平面内对应的点位于第二象限.故选:B.解析:因为()()()293i z a a a =-++∈R 为纯虚数,所以290a -=且30a +≠,所以3a =. 故选:C.6.答案:D解析:因为i 20212i a b +=-,所以2a =,2021b -=,即2a =,2021b =-,所以2i 42021i a b +=-.故选:D.7.答案:B解析:因为()()21i 4i 3z m m =+-++为纯虚数,故()224i 3m m m z m -++-=,则224300m m m m ⎧-+=⎨-≠⎩,解得3m =. 故选:B.8.答案:D 解析:1010(3i)3i 3i (3i)(3i)z +===+--+. 故选:D.9.答案:ABD解析:(1i)3i z +=+,3i (3i)(1i)42i 2i 1i (1i)(1i)2z ++--∴====-++-,||5z ∴=A 正确;复数z 的实部是2,故选项B 正确;复数z 的虚部是-1,故选项C 错误;复数2i z =+在复平面内对应的点为(2,1),位于第一象限,故选项D 正确.故选ABD.10.答案:ABD解析:由题意得,复数z 在复平面内对应的点为()2352,1m m m -+-. 当10m ->,即1m <时,二次函数2352(32)(1)y m m m m =-+=--的取值有正有负,故z 在复平面内对应的点可以在第一、二象限.当10m -<,即1m >时,二次函数2352(32)(1)0y m m m m =-+=-->,故z 在复平面内对应的点可以在第四象限.故z 在复平面内对应的点一定不在第三象限.故选ABD.解析:解:因为(,)z a bi a b R =+∈当0a =且0b ≠时复数为纯虚数,此时z bi z =-=-,故A 错误,D 正确; 当0b =时,复数为实数,故C 正确;对于B :32a bi i -=+,则32a b =⎧⎨-=⎩即32a b =⎧⎨=-⎩,故B 错误; 故错误的有AB ;故选:AB.12.答案:BD 解析:由23i 3i 232iz -⋅-=+得,(23i)(32i)13i 13i (23i)i(23i)32i 23i 23i (23i)(23i)z ++⋅+====+=-+---+ 所以z 的实部为-3,虚部为2,,13z =,故选BD.13.答案:15i -+解析:122i 34i 15i z z -=+-+=-+.故答案为:15i -+.14.答案:15i -+解析:122i 34i 15i z z -=+-+=-+.故答案为:15i -+.15.答案:1解析:复数1i -的虚部为-1,则其平方为1. 故答案为:1.16.答案:-3 解析:()()()()()()3i 1i 33i 33i 3i 1i 1i 1i 222a a a a a a +⋅-++--++===+++⋅- 因为复数为纯虚数,所以302a +=,3a =-. 故答案为:-3.17.答案:(1)(2)0m =(3)1m =或3m = 32i z =--3m =解析:(1)z 为实数,30m ∴-=,解得:3m =;(2)z 为纯虚数,(3)0030m m m m -=⎧⇒=⎨-≠⎩;(3)z 在复平面内对应的点在直线y x =上, ∴()331m m m m -=-⇒=或3m =.18、(1)答案:31z = 解析:复数13i 22z =-+(i 为虚数单位), 222113313()2()i (i)i 222222z ∴=-+⨯-⨯+=--, 322131313i)(i)i 12222(44z z z ∴=---+==-=⋅, (2)答案:1解析:202022013673911()111z z z z z z z z++++--⋅==-- 111z z-==- 19.答案:(1) 即1m =或2m =时,复数z 为实数(2) 12m =-复数z 为纯虚数解析:(1)当2320m m -+=时,即1m =或2m =时,复数z 为实数;(2)若z 为纯虚数,则222320320m m m m ⎧--=⎨-+≠⎩,解得1 2212m m m m ⎧=-=⎪⎨⎪≠≠⎩或且, 12m ∴=-,即12m =-时,复数z 为纯虚数; 20.答案:49911c c c ⎧⎫>≠⎨⎬⎩⎭∣,且 解析:在复平面内三点坐标为(3,4),(0,0),(,26)A B C c c -, 由BAC ∠为钝角得cos 0BAC ∠<,且A ,B ,C 不共线.(3,4),(3,210),0AB AC c c AB AC =--=--⋅<,且不共线,得c 的取值范围是49911c c c ⎧⎫>≠⎨⎬⎩⎭∣,且. 21.答案:1a =-解析:由题意知,()223156i 3()a a a a a --+--=∈R ,所以22313,560,a a a a ⎧--=⎨--=⎩即 所以1a =-.22.答案:(1)(2)5m =-解析:(1)设,a ,b ∈R ,0a >, 由题意知,2210a b +=.①(12i)(12i)(i)2(2)i z a b a b a b +=++=-++, 得22a b a b -=+.②①②联立,解得3a =,1b =-, 得3i z =-.(2), 所以1302m -+=且, 解得5m =-. 4 1,6 1,a a a a ==-⎧⎨==-⎩或或3i z =-i z a b =+i (i)(1i)113i 31i 1i 222m m m m z ----+⎛⎫+=++=++- ⎪+⎝⎭1102m +-≠。
复数单元测试题+答案

一、复数选择题1.复数11z i=-,则z 的共轭复数为( ) A .1i - B .1i + C .1122i + D .1122i - 2.设复数(,)z a bi a R b R =+∈∈,它在复平面内对应的点位于虚轴的正半轴上,且有1z =,则a b +=( )A .-1B .0C .1D .2 3.若复数1z i i ⋅=-+,则复数z 的虚部为( ) A .-1B .1C .-iD .i 4.在复平面内复数Z=i (1﹣2i )对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限 5.已知复数21i z i =-,则复数z 在复平面内对应点所在象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限6.已知i 为虚数单位,复数12i 1i z +=-,则复数z 在复平面上的对应点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限7.若复数1z i =-,则1z z=-( )A B .2 C .D .4 8.若复数1211i z i +=--,则z 在复平面内的对应点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限 9.满足313i z i ⋅=-的复数z 的共扼复数是( )A .3i -B .3i --C .3i +D .3i -+ 10.已知复数202111i z i-=+,则z 的虚部是( ) A .1- B .i - C .1 D .i11.设复数z 满足方程4z z z z ⋅+⋅=,其中z 为复数z 的共轭复数,若z 的实部为,则z 为( )A .1BC .2D .412.( )A .i -B .iC .iD .i -13.已知()312++=+a i i bi (,a b ∈R ,i 为虚数单位),则实数+a b 的值为( ) A .3 B .5 C .6 D .814.已知i 为虚数单位,则43i i =-( ) A .2655i + B .2655i - C .2655i -+ D .2655i -- 15.复数12z i =-(其中i 为虚数单位),则3z i +=( )A .5BC .2D 二、多选题16.已知复数202011i z i+=-(i 为虚数单位),则下列说法错误的是( )A .z 的实部为2B .z 的虚部为1C .z i =D .||z =17.已知复数z 满足220z z +=,则z 可能为( ).A .0B .2-C .2iD .2i+1-18.已知复数(),z x yi x y R =+∈,则( )A .20zB .z 的虚部是yiC .若12z i =+,则1x =,2y =D .z =19.已知复数012z i =+(i 为虚数单位)在复平面内对应的点为0P ,复数z 满足|1|||z z i -=-,下列结论正确的是( )A .0P 点的坐标为(1,2)B .复数0z 的共轭复数对应的点与点0P 关于虚轴对称C .复数z 对应的点Z 在一条直线上D .0P 与z 对应的点Z 间的距离的最小值为20.已知复数z 满足2724z i =--,在复平面内,复数z 对应的点可能在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限21.已知复数1cos 2sin 222z i ππθθθ⎛⎫=++-<< ⎪⎝⎭(其中i 为虚数单位),则( ) A .复数z 在复平面上对应的点可能落在第二象限B .z 可能为实数C .2cos z θ=D .1z 的实部为12- 22.下列说法正确的是( )A .若2z =,则4z z ⋅=B .若复数1z ,2z 满足1212z z z z +=-,则120z z =C .若复数z 的平方是纯虚数,则复数z 的实部和虛部相等D .“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件 23.已知复数1z i =+(其中i 为虚数单位),则以下说法正确的有( )A .复数z 的虚部为iB .z =C .复数z 的共轭复数1z i =-D .复数z 在复平面内对应的点在第一象限24.已知复数12ω=-(i 是虚数单位),ω是ω的共轭复数,则下列的结论正确的是( )A .2ωω=B .31ω=-C .210ωω++=D .ωω>25.已知1z ,2z 为复数,下列命题不正确的是( )A .若12z z =,则12=z zB .若12=z z ,则12z z =C .若12z z >则12z z >D .若12z z >,则12z z >26.任何一个复数z a bi =+(其中a 、b R ∈,i 为虚数单位)都可以表示成:()cos sin z r i θθ=+的形式,通常称之为复数z 的三角形式.法国数学家棣莫弗发现:()()()n cos sin co i s s nn n z i n r i r n n N θθθθ+==+⎡⎤⎣∈⎦+,我们称这个结论为棣莫弗定理.根据以上信息,下列说法正确的是( )A .22z z =B .当1r =,3πθ=时,31z =C .当1r =,3πθ=时,122z =-D .当1r =,4πθ=时,若n 为偶数,则复数n z 为纯虚数27.已知复数z a =+在复平面内对应的点位于第二象限,且2z = 则下列结论正确的是( ).A .38z =B .zC .z 的共轭复数为1D .24z = 28.若复数21iz =+,其中i 为虚数单位,则下列结论正确的是( )A .z 的虚部为1-B .||z =C .2z 为纯虚数D .z 的共轭复数为1i -- 29.已知复数z 满足23z z iz ai ⋅+=+,a R ∈,则实数a 的值可能是( ) A .1 B .4- C .0 D .530.已知复数i z a b =+(a ,b ∈R ,i 为虚数单位),且1a b +=,下列命题正确的是( )A .z 不可能为纯虚数B .若z 的共轭复数为z ,且z z =,则z 是实数C .若||z z =,则z 是实数D .||z 可以等于12【参考答案】***试卷处理标记,请不要删除一、复数选择题1.D【分析】先由复数的除法化简该复数,再由共轭复数的概念,即可得出结果.【详解】因为,所以其共轭复数为.故选:D.解析:D【分析】先由复数的除法化简该复数,再由共轭复数的概念,即可得出结果.【详解】 因为()()11111111222i i z i i i i ++====+--+, 所以其共轭复数为1122i -. 故选:D.2.C【分析】根据复数的几何意义得.【详解】∵它在复平面内对应的点位于虚轴的正半轴上,∴,又,∴,∴.故选:C .解析:C【分析】根据复数的几何意义得,a b .【详解】∵z 它在复平面内对应的点位于虚轴的正半轴上,∴0a =,又1z =,∴1b =,∴1a b +=.故选:C .3.B【分析】,然后算出即可.【详解】由题意,则复数的虚部为1故选:B解析:B【分析】1i z i-+=,然后算出即可. 【详解】 由题意()11111i i i i z i i i i -+-+--====+⋅-,则复数z 的虚部为1 故选:B 4.A【解析】试题分析:根据复数乘法的运算法则,我们可以将复数Z 化为a=bi (a ,b ∈R )的形式,分析实部和虚部的符号,即可得到答案.解:∵复数Z=i (1﹣2i )=2+i∵复数Z 的实部2>0,虚解析:A【解析】试题分析:根据复数乘法的运算法则,我们可以将复数Z 化为a=bi (a ,b ∈R )的形式,分析实部和虚部的符号,即可得到答案.解:∵复数Z=i (1﹣2i )=2+i∵复数Z 的实部2>0,虚部1>0∴复数Z 在复平面内对应的点位于第一象限故选A点评:本题考查的知识是复数的代数表示法及其几何意义,其中根据复数乘法的运算法则,将复数Z 化为a=bi (a ,b ∈R )的形式,是解答本题的关键.5.B【分析】对复数进行化简,再得到在复平面内对应点所在的象限.【详解】,在复平面内对应点为,在第二象限.解析:B【分析】对复数z 进行化简,再得到z 在复平面内对应点所在的象限.【详解】21i z i =-()()()2111i i i i +=+-()1+1+i i i ==-,z 在复平面内对应点为()1,1-,在第二象限. 故选:B.6.C【分析】利用复数的除法法则化简,再求的共轭复数,即可得出结果.【详解】因为,所以,所以复数在复平面上的对应点位于第三象限,故选:C.解析:C【分析】利用复数的除法法则化简z ,再求z 的共轭复数,即可得出结果.【详解】 因为212(12)(1)11i i i z i i +++==-- 1322i =-+, 所以1322z i =--, 所以复数z 在复平面上的对应点13(,)22--位于第三象限,故选:C. 7.A【分析】将代入,利用复数的除法运算化简,再利用复数的求模公式求解.【详解】由,得,则,故选:A.解析:A将1z i =-代入1z z-,利用复数的除法运算化简,再利用复数的求模公式求解. 【详解】 由1z i =-,得2111z i i i i z i i---===---,则11z i z=--==-,故选:A. 8.B【分析】利用复数的运算法则和复数的几何意义求解即可【详解】,所以,在复平面内的对应点为,则对应点位于第二象限故选:B解析:B【分析】 利用复数的运算法则和复数的几何意义求解即可 【详解】()()12i 1i 12i 33i 33i 111i 2222z +++-+=-=-==-+-, 所以,z 在复平面内的对应点为33,22⎛⎫-⎪⎝⎭,则对应点位于第二象限 故选:B9.A【分析】根据,利用复数的除法运算化简复数,再利用共扼复数的概念求解.【详解】因为,所以,复数的共扼复数是,故选:A解析:A【分析】根据313i z i ⋅=-,利用复数的除法运算化简复数,再利用共扼复数的概念求解.【详解】因为313i z i ⋅=-, 所以()13133i z i i i i-==-=+-, 复数z 的共扼复数是3z i =-,故选:A10.C【分析】求出,即可得出,求出虚部.【详解】,,其虚部是1.故选:C.解析:C【分析】求出z ,即可得出z ,求出虚部.【详解】()()()220211i 1i i 1i 1i 1i z --===-++-,i z ∴=,其虚部是1. 故选:C. 11.B【分析】由题意,设复数,根据共轭复数的概念,以及题中条件,即可得出结果.【详解】因为的实部为,所以可设复数,则其共轭复数为,又,所以由,可得,即,因此.故选:B.解析:B【分析】由题意,设复数(),z yi x R y R =∈∈,根据共轭复数的概念,以及题中条件,即可得出结果.【详解】因为z ,所以可设复数(),z yi x R y R =∈∈,则其共轭复数为z yi =,又z z =,所以由4z z z z ⋅+⋅=,可得()4z z z ⋅+=,即4z ⋅=,因此z =故选:B.12.B【分析】首先,再利用复数的除法运算,计算结果. 【详解】复数.故选:B解析:B【分析】首先3i i=-,再利用复数的除法运算,计算结果.【详解】133i ii+====.故选:B13.D【分析】利用复数的乘法运算及复数相等求得a,b值即可求解【详解】,故则故选:D解析:D【分析】利用复数的乘法运算及复数相等求得a,b值即可求解【详解】()312++=+a i i bi,故332a i bi-+=+则32,38a b a b-==∴+=故选:D14.C【分析】对的分子分母同乘以,再化简整理即可求解.【详解】,故选:C解析:C【分析】对43ii-的分子分母同乘以3i+,再化简整理即可求解.【详解】()()()434412263331055i i i i i i i i +-+===-+--+, 故选:C15.B【分析】首先求出,再根据复数的模的公式计算可得;【详解】解:因为,所以所以.故选:B.解析:B【分析】首先求出3z i +,再根据复数的模的公式计算可得;【详解】解:因为12z i =-,所以31231z i i i i +=-+=+所以3z i +==故选:B . 二、多选题16.AC【分析】根据复数的运算及复数的概念即可求解.【详解】因为复数,所以z 的虚部为1,,故AC 错误,BD 正确.故选:AC解析:AC【分析】根据复数的运算及复数的概念即可求解.【详解】 因为复数2020450511()22(1)11112i i i z i i i i +++=====+---,所以z 的虚部为1,||z =故AC 错误,BD 正确.故选:AC17.AC【分析】令,代入原式,解出的值,结合选项得出答案.【详解】令,代入,得,解得,或,或,所以,或,或.故选:AC【点睛】本题考查复数的运算,考查学生计算能力,属于基础题.解析:AC【分析】令()i ,z a b a b R =+∈,代入原式,解出,a b 的值,结合选项得出答案.【详解】令()i ,z a b a b R =+∈,代入220z z +=,得222i 0a b ab -+=,解得00a b =⎧⎨=⎩,或02a b =⎧⎨=⎩,或02a b =⎧⎨=-⎩, 所以0z =,或2i z =,或2i z =-.故选:AC【点睛】本题考查复数的运算,考查学生计算能力,属于基础题.18.CD【分析】取特殊值可判断A 选项的正误;由复数的概念可判断B 、C 选项的正误;由复数模的概念可判断D 选项的正误.【详解】对于A 选项,取,则,A 选项错误;对于B 选项,复数的虚部为,B 选项错误;解析:CD【分析】取特殊值可判断A 选项的正误;由复数的概念可判断B 、C 选项的正误;由复数模的概念可判断D 选项的正误.【详解】对于A 选项,取z i ,则210z =-<,A 选项错误;对于B 选项,复数z 的虚部为y ,B 选项错误;对于C 选项,若12z i =+,则1x =,2y =,C 选项正确;对于D 选项,z =D 选项正确.故选:CD.【点睛】本题考查复数相关命题真假的判断,涉及复数的计算、复数的概念以及复数的模,属于基础题. 19.ACD【分析】根据复数对应的坐标,判断A 选项的正确性.根据互为共轭复数的两个复数坐标的对称关系,判断B 选项的正确性.设出,利用,结合复数模的运算进行化简,由此判断出点的轨迹,由此判读C 选项的正确解析:ACD【分析】根据复数对应的坐标,判断A 选项的正确性.根据互为共轭复数的两个复数坐标的对称关系,判断B 选项的正确性.设出z ,利用|1|||z z i -=-,结合复数模的运算进行化简,由此判断出Z 点的轨迹,由此判读C 选项的正确性.结合C 选项的分析,由点到直线的距离公式判断D 选项的正确性.【详解】复数012z i =+在复平面内对应的点为0(1,2)P ,A 正确;复数0z 的共轭复数对应的点与点0P 关于实轴对称,B 错误;设(,)z x yi x y R =+∈,代入|1|||z z i -=-,得|(1)(1)i|x yi x y -+=+-,即=y x =;即Z 点在直线y x =上,C 正确; 易知点0P 到直线y x =的垂线段的长度即为0P 、Z 之间距离的最小值,结合点到直线的距=,故D 正确. 故选:ACD【点睛】本小题主要考查复数对应的坐标,考查共轭复数,考查复数模的运算,属于基础题. 20.BD【分析】先设复数,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出,即可确定对应的点所在的象限.【详解】设复数,则,所以,则,解得或,因此或,所以对应的点为或,因此复解析:BD【分析】先设复数(),z a bi a b R =+∈,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出z ,即可确定对应的点所在的象限.【详解】设复数(),z a bi a b R =+∈,则2222724z a abi b i =+-=--,所以2222724z a abi b i =+-=--,则227224a b ab ⎧-=-⎨=-⎩,解得34a b =⎧⎨=-⎩或34a b =-⎧⎨=⎩, 因此34z i =-或34z i =-+,所以对应的点为()3,4-或()3,4-,因此复数z 对应的点可能在第二或第四象限.故选:BD.【点睛】本题主要考查判定复数对应的点所在的象限,熟记复数的运算法则,以及复数相等的条件即可,属于基础题型.21.BC【分析】由可得,得,可判断A 选项,当虚部,时,可判断B 选项,由复数的模计算和余弦的二倍角公式可判断C 选项,由复数的运算得,的实部是,可判断D 选项.【详解】因为,所以,所以,所以,所以A 选解析:BC【分析】 由22ππθ-<<可得2πθπ-<<,得01cos22θ<+≤,可判断A 选项,当虚部sin 20θ=,,22ππθ⎛⎫∈- ⎪⎝⎭时,可判断B 选项,由复数的模计算和余弦的二倍角公式可判断C 选项,由复数的运算得11cos 2sin 212cos 2i z θθθ+-=+,1z 的实部是1cos 2122cos 22θθ+=+,可判断D 选项.【详解】因为22ππθ-<<,所以2πθπ-<<,所以1cos21θ-<≤,所以01cos22θ<+≤,所以A 选项错误;当sin 20θ=,,22ππθ⎛⎫∈- ⎪⎝⎭时,复数z 是实数,故B 选项正确;2cos z θ===,故C 选项正确:()()111cos 2sin 21cos 2sin 21cos 2sin 21cos 2sin 21cos 2sin 212cos 2i i z i i i θθθθθθθθθθθ+-+-===+++++-+,1z 的实部是1cos 2122cos 22θθ+=+,故D 不正确. 故选:BC【点睛】本题主要考查复数的概念,复数模的计算,复数的运算,以及三角恒等变换的应用,属于中档题.22.AD【分析】由求得判断A ;设出,,证明在满足时,不一定有判断B ;举例说明C 错误;由充分必要条件的判定说明D 正确.【详解】若,则,故A 正确;设,由,可得则,而不一定为0,故B 错误; 当时解析:AD【分析】由z 求得z z ⋅判断A ;设出1z ,2z ,证明在满足1212z z z z +=-时,不一定有120z z =判断B ;举例说明C 错误;由充分必要条件的判定说明D 正确.【详解】 若2z =,则24z z z ⋅==,故A 正确;设()11111,z a bi a b R =+∈,()22222,z a b i a b R =+∈由1212z z z z +=-,可得()()()()222222121212121212z z a a b b z z a a b b +=+++=-=-+-则12120a a b b +=,而()()121122121212121212122z z a bi a b i a a bb a b i b a i a a a b i b a i =++=-++=++不一定为0,故B 错误;当1z i =-时22z i =-为纯虚数,其实部和虚部不相等,故C 错误;若复数()()()211z a a i a R =-+-∈是虚数,则210a -≠,即1a ≠± 所以“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件,故D 正确; 故选:AD【点睛】本题考查的是复数的相关知识,考查了学生对基础知识的掌握情况,属于中档题.23.BCD【分析】根据复数的概念判定A 错,根据复数模的计算公式判断B 正确,根据共轭复数的概念判断C 正确,根据复数的几何意义判断D 正确.【详解】因为复数,所以其虚部为,即A 错误;,故B 正确;解析:BCD【分析】根据复数的概念判定A 错,根据复数模的计算公式判断B 正确,根据共轭复数的概念判断C 正确,根据复数的几何意义判断D 正确.【详解】因为复数1z i =+,所以其虚部为1,即A 错误;z ==B 正确;复数z 的共轭复数1z i =-,故C 正确;复数z 在复平面内对应的点为()1,1,显然位于第一象限,故D 正确.故选:BCD.【点睛】本题主要考查复数的概念,复数的模,复数的几何意义,以及共轭复数的概念,属于基础题型.24.AC【分析】根据复数的运算进行化简判断即可.【详解】解:∵所以,∴,故A 正确,,故B 错误,,故C 正确,虚数不能比较大小,故D 错误,故选:AC.【点睛】本题主要考查复数的有关概念解析:AC【分析】根据复数的运算进行化简判断即可.【详解】解:∵12ω=-所以12ω=--,∴2131442ωω=--=--=,故A 正确,3211131222244ωωω⎛⎫⎛⎫⎛⎫==---+=--= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,故B 错误,2111102222ωω++=---++=,故C 正确, 虚数不能比较大小,故D 错误,故选:AC .【点睛】本题主要考查复数的有关概念和运算,结合复数的运算法则进行判断是解决本题的关键.属于中档题.25.BCD【分析】根据两个复数之间不能比较大小,得到C 、D 两项是错误的,根据复数的定义和复数模的概念,可以断定A 项正确,B 项错误,从而得到答案.【详解】因为两个复数之间只有等与不等,不能比较大小解析:BCD【分析】根据两个复数之间不能比较大小,得到C 、D 两项是错误的,根据复数的定义和复数模的概念,可以断定A 项正确,B 项错误,从而得到答案.【详解】因为两个复数之间只有等与不等,不能比较大小,所以C 、D 两项都不正确; 当两个复数的模相等时,复数不一定相等, 比如11i i -=+,但是11i i -≠+,所以B 项是错误的;因为当两个复数相等时,模一定相等,所以A 项正确;故选:BCD.【点睛】该题考查的是有关复数的问题,涉及到的知识点有两个复数之间的关系,复数模的概念,属于基础题目.26.AC【分析】利用复数的三角形式与模长公式可判断A 选项的正误;利用复数的棣莫弗定理可判断B 选项的正误;计算出复数,可判断C 选项的正误;计算出,可判断D 选项的正误.【详解】对于A 选项,,则,可得解析:AC【分析】利用复数的三角形式与模长公式可判断A 选项的正误;利用复数的棣莫弗定理可判断B 选项的正误;计算出复数z ,可判断C 选项的正误;计算出4z ,可判断D 选项的正误.【详解】对于A 选项,()cos sin z r i θθ=+,则()22cos2sin 2z r i θθ=+,可得()222cos 2sin 2z r i r θθ=+=,()222cos sin z r i r θθ=+=,A 选项正确; 对于B 选项,当1r =,3πθ=时,()33cos sin cos3sin3cos sin 1z i i i θθθθππ=+=+=+=-,B 选项错误;对于C 选项,当1r =,3πθ=时,1cos sin 3322z i ππ=+=+,则12z =,C 选项正确;对于D 选项,()cos sin cos sin cos sin 44n n n n z i n i n i ππθθθθ=+=+=+, 取4n =,则n 为偶数,则4cos sin 1z i ππ=+=-不是纯虚数,D 选项错误.故选:AC.【点睛】本题考查复数的乘方运算,考查了复数的模长、共轭复数的运算,考查计算能力,属于中等题.27.AB【分析】利用复数的模长运算及在复平面内对应的点位于第二象限求出 ,再验算每个选项得解.【详解】解:,且,复数在复平面内对应的点位于第二象限选项A:选项B: 的虚部是选项C:解析:AB【分析】利用复数2z =的模长运算及z a =+在复平面内对应的点位于第二象限求出a ,再验算每个选项得解.【详解】解:z a =+,且2z =224a +∴=,=1a ±复数z a =+在复平面内对应的点位于第二象限1a ∴=-选项A : 3323(1)(1)+3(1)+3())8-+=---+=选项B : 1z =-选项C : 1z =-的共轭复数为1z =--选项D : 222(1)(1)+2()2-+=--=--故选:AB .【点睛】本题考查复数的四则运算及共轭复数,考查运算求解能力.求解与复数概念相关问题的技巧:复数的分类、复数的相等、复数的模及共轭复数的概念都与复数的实部、虚部有关,所以解答与复数相关概念有关的问题时,需把所给复数化为代数形式,即()a bi a b R ∈+,的形式,再根据题意求解.28.ABC【分析】首先利用复数代数形式的乘除运算化简后得:,然后分别按照四个选项的要求逐一求解判断即可.【详解】因为,对于A :的虚部为,正确;对于B :模长,正确;对于C :因为,故为纯虚数,解析:ABC【分析】首先利用复数代数形式的乘除运算化简z 后得:1z i =-,然后分别按照四个选项的要求逐一求解判断即可.【详解】 因为()()()2122211i 1i 12i i z i i --====-++-, 对于A :z 的虚部为1-,正确;对于B :模长z =对于C :因为22(1)2z i i =-=-,故2z 为纯虚数,正确;对于D :z 的共轭复数为1i +,错误.故选:ABC .【点睛】本题考查复数代数形式的乘除运算,考查复数的有关概念,考查逻辑思维能力和运算能力,侧重考查对基础知识的理解和掌握,属于常考题.29.ABC【分析】设,从而有,利用消元法得到关于的一元二次方程,利用判别式大于等于0,从而求得a 的范围,即可得答案.【详解】设,∴,∴,∴,解得:,∴实数的值可能是.故选:ABC.【点解析:ABC【分析】设z x yi =+,从而有222()3x y i x yi ai ++-=+,利用消元法得到关于y 的一元二次方程,利用判别式大于等于0,从而求得a 的范围,即可得答案.【详解】设z x yi =+,∴222()3x y i x yi ai ++-=+, ∴222223,23042,x y y a y y x a ⎧++=⇒++-=⎨=⎩, ∴244(3)04a ∆=--≥,解得:44a -≤≤, ∴实数a 的值可能是1,4,0-.故选:ABC.【点睛】本题考查复数的四则运算、模的运算,考查函数与方程思想,考查逻辑推理能力和运算求解能力.30.BC【分析】根据纯虚数、共轭复数、复数的模、复数为实数等知识,选出正确选项.【详解】当时,,此时为纯虚数,A 错误;若z 的共轭复数为,且,则,因此,B 正确;由是实数,且知,z 是实数,C 正确;由解析:BC【分析】根据纯虚数、共轭复数、复数的模、复数为实数等知识,选出正确选项.【详解】当0a =时,1b =,此时z i 为纯虚数,A 错误;若z 的共轭复数为z ,且z z =,则a bi a bi +=-,因此0b =,B 正确;由||z 是实数,且||z z =知,z 是实数,C 正确;由1||2z =得2214a b +=,又1a b +=,因此28830a a -+=,64483320∆=-⨯⨯=-<,无解,即||z 不可以等于12,D 错误. 故选:BC【点睛】本小题主要考查复数的有关知识,属于基础题.。
2018届苏教版(文科数学) 大题规范练4 “17题~19题+二选一”46分练 (1) 单元测试

大题规范练(四) “17题~19题+二选一”46分练(时间:45分钟 分值:46分)解答题(本大题共4小题,共46分,第22~23题为选考题.解答应写出文字说明、证明过程或演算步骤)17.已知数列{a n }中,a 1=511,4a n =a n -1-3(n ≥2).(1)求证:数列{a n +1}为等比数列,并求数列{a n }的通项公式; (2)令b n =|log 2(a n +1)|,求数列{b n }的前n 项和S n .【导学号:07804235】[解] (1)证明:由已知得,a n =14a n -1-34(n ≥2), ∴a n +1=14(a n -1+1),又a 1+1=512,∴数列{a n +1}是以512为首项,14为公比的等比数列. ∴a n +1=512×⎝ ⎛⎭⎪⎫14n -1=211-2n,a n =211-2n-1.(2)b n =|log 2(a n +1)|=|11-2n |,设数列{11-2n }的前n 项和为T n ,则T n =10n -n 2, 当n ≤5时,S n =T n =10n -n 2; 当n ≥6时,S n =2S 5-T n =n 2-10n +50.所以S n =⎩⎨⎧10n -n 2,n ≤5n 2-10n +50,n ≥6.18.如图7所示,四棱锥P -ABCD 的底面ABCD 为矩形,AB =22,BC =2,点P 在底面上的射影在AC 上,E 是AB 的中点.图7(1)证明:DE ⊥平面P AC ;(2)若P A =PC ,且P A 与平面PBD 所成的角的正弦值为63,求二面角D -P A -B 的余弦值.[解] (1)证明:在矩形ABCD 中,AB ∶BC =2∶1,且E 是AB 的中点, ∴tan ∠ADE =tan ∠CAB =12,∴∠ADE =∠CAB . ∵∠CAB +∠DAC =90°,∴∠ADE +∠DAC =90°,即AC ⊥DE .由点P 在底面ABCD 上的射影在AC 上,可知平面P AC ⊥平面ABCD ,且交线为AC ,∴DE ⊥平面P AC . (2)记AC 与BD 的交点为O ,∵P A =PC ,且O 是AC 的中点,∴PO ⊥AC . ∵平面P AC ⊥平面ABCD ,∴PO ⊥平面ABCD .取BC 的中点F ,连接OE ,OF ,∵底面ABCD 为矩形, ∴OE ⊥OF .以O 为坐标原点,分别以OE ,OF ,OP 所在直线为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系,则A (1,-2,0),B (1,2,0),D (-1,-2,0). 设P (0,0,a ), 则AP→=(-1,2,a ). 设平面PBD 的法向量为c =(x 1,y 1,z 1), 又DB→=(2,22,0),OP →=(0,0,a ), 则有⎩⎪⎨⎪⎧c ·DB →=0,c ·OP →=0⇒⎩⎨⎧2x 1+22y 1=0,az 1=0, 令x 1=2,得y 1=-1,∴平面PBD 的一个法向量为c =(2,-1,0).由|c ·AP →||c ||AP→|=63,得a =1.设平面P AD 的法向量为m =(x 2,y 2,z 2),又AD →=(-2,0,0),AP →=(-1,2,1),则有⎩⎪⎨⎪⎧m ·AD →=0,m ·AP →=0⇒⎩⎨⎧-2x 2=0,-x 2+2y 2+z 2=0,令y 2=1,得z 2=-2,∴m =(0,1,-2). 设平面P AB 的法向量为n =(x 3,y 3,z 3), 又AB→=(0,22,0),AP →=(-1,2,1),则有⎩⎪⎨⎪⎧n ·AB →=0,n ·AP →=0⇒⎩⎨⎧22y 3=0,-x 3+2y 3+z 3=0,令x 3=1,得z 3=1,∴n =(1,0,1). ∴cos 〈m ,n 〉=m·n|m ||n |=-23×2=-33,∴二面角D -P A -B 的余弦值为-33.19.近年 我国电子商务行业迎 发展的新机遇.2016年“618”期间,某购物平台的销售业绩高达516亿元人民币,与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.(1)请完成关于商品和服务评价的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全为好评的次数为随机变量X .①求对商品和服务全为好评的次数X 的分布列; ②求X 的数学期望和方差. 附:临界值表K 2的观测值k =(a +b )(c +d )(a +c )(b +d )(其中n =a +b +c +d ).关于商品和服务评价的2×2列联表:[解] (1)k =200150×50×120×80≈11.111>10.828,故能在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关.(2)①每次购物时,对商品和服务全为好评的概率为25,且X 取值可以是0,1,2,3.其中P (X =0)=⎝ ⎛⎭⎪⎫353=27125;P (X =1)=C 13⎝ ⎛⎭⎪⎫25⎝ ⎛⎭⎪⎫352=54125;P (X =2)=C 23⎝ ⎛⎭⎪⎫252⎝ ⎛⎭⎪⎫35=36125;P (X =3)=C 33⎝ ⎛⎭⎪⎫253⎝ ⎛⎭⎪⎫350=8125. 所以X 的分布列为②由于X ~B ⎝ ⎛⎭⎪⎫3,25,则E (X )=3×25=65,D (X )=3×25×⎝ ⎛⎭⎪⎫1-25=1825.(请在第22~23题中选一题作答,如果多做,则按照所做第一题计分) 22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,圆C 的参数方程为⎩⎨⎧x =-5+2cos ty =3+2sin t (t 为参数),在以原点O 为极点,x 轴的非负半轴为极轴建立的极坐标系中,直线l 的极坐标方程为ρcos ⎝ ⎛⎭⎪⎫θ+π4=- 2.(1)求圆C 的普通方程和直线l 的直角坐标方程;(2)设直线l 与x 轴,y 轴分别交于A ,B 两点,点P 是圆C 上任意一点,求A ,B 两点的极坐标和△P AB 面积的最小值.【导学号:07804236】[解] (1)由⎩⎨⎧x =-5+2cos ty =3+2sin t ,消去参数t ,得(x +5)2+(y -3)2=2,所以圆C 的普通方程为(x +5)2+(y -3)2=2. 由ρcos ⎝ ⎛⎭⎪⎫θ+π4=-2,得ρcos θ-ρsin θ=-2,所以直线l 的直角坐标方程为x -y +2=0.(2)直线l 与x 轴,y 轴的交点分别为A (-2,0),B (0,2),化为极坐标为A (2,π),B ⎝ ⎛⎭⎪⎫2,π2, 设点P 的坐标为(-5+2cos t,3+2sin t ),则点P 到直线l 的距离为 d =|-5+2cos t -3-2sin t +2|2=⎪⎪⎪⎪⎪⎪-6+2cos ⎝ ⎛⎭⎪⎫t +π42.所以d min =42=22,又|AB |=2 2. 所以△P AB 面积的最小值是S =12×22×22=4. 23.选修4-5:不等式选讲已知函数f (x )=|x -2|.(1)解不等式:f (x )+f (x +1)≤2;(2)若a <0,求证:f (ax )-af (x )≥f (2a ).[解] (1)由题意,得f (x )+f (x +1)=|x -1|+|x -2|. 因此只要解不等式|x -1|+|x -2|≤2.当x ≤1时,原不等式等价于-2x +3≤2,即12≤x ≤1; 当1<x ≤2时,原不等式等价于1≤2,即1<x ≤2; 当x >2时,原不等式等价于2x -3≤2,即2<x ≤52.综上,原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12≤x ≤52. (2)证明:由题意得f (ax )-af (x )=|ax -2|-a |x -2|=|ax -2|+|2a -ax |≥|ax -2+2a -ax |=|2a -2|=f (2a ), 所以f (ax )-af (x )≥f (2a )成立.。
第七章 复数 单元测试卷(解析版)

第七章 复数单元测试卷一、单选题1.(辽宁省葫芦岛市2021-2022学年高三上学期期末数学试题)已知i 为虚数单位,则复数()i 12i z =-的虚部是( ) A .i B .1 C .2 D .2i【答案】B 【分析】化简复数2i z =+即得解. 【详解】解:由题得()i i 122i z =-=+, 所以复数的虚部为1. 故选:B2.(山东省德州市2021-2022学年高三上学期期末数学试题)已知复数z 满足()121i iz +=-,其中i 为虛数单位,则复数z 在复平面内所对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】A 【分析】根据复数的模长公式以及四则运算得出55z =,最后确定复数z 在复平面内所对应的点的象限. 【详解】 221i 22|2i |2(1)5i i +=+=-=+-=,55(1i)55z +=== 则复数z 在复平面内所对应的点坐标为55⎝⎭,在第一象限.故选:A3.(山东省淄博市2021-2022学年高三上学期期末数学试题)已知复数z 是纯虚数,11i z+-是实数,则z =( )A .-iB .iC .-2iD .2i【答案】B 【分析】由题意设i()z b b R =∈,代入11iz+-中化简,使其虚部为零,可求出b 的值,从而可求出复数z ,进而可求得其共轭复数 【详解】由题意设i()z b b R =∈, 则11i (1i)(1i)(1)(1)i1i 1i (1i)(1i)2z b b b b ++++-++===---+, 因为11iz+-是实数,所以10b +=,得1b =-, 所以i z =-, 所以i z =, 故选:B4.(2022·广东茂名·一模)已知,a b 为实数,且2ii 1ib a +=++(i 为虚数单位),则i a b +=( ) A .34i + B .12i + C .32i -- D .32i +【答案】A 【分析】利用复数的乘除运算化简,再利用复数相等求得,a b ,进而得解. 【详解】()()2i 1i 2i 22i i 22i 1i 2222b b b b b b +-+-+++-===++ 由题意知222=12b a b +⎧=⎪⎪⎨-⎪⎪⎩,解得34a b =⎧⎨=⎩,所以i 34i a b +=+故选:A5.(2022·江苏无锡·高三期末)已知3i1ia ++(i 为虚数单位,a ∈R )为纯虚数,则=a ( ) A .1- B .1C .3-D .3【答案】C 【分析】先利用复数除法法则进行化简,结合纯虚数条件列出方程,求出a 的值. 【详解】3i (3i)(1i)i 3i+31i 22a a a a ++--+==+3(3)i2a a ++-=为纯虚数, 30a ∴+=,3a ∴=-,故选:C.6.(2022·内蒙古包头·高二期末(文))对于非零实数a ,b ,以下四个式子均恒成立,对于非零复数a ,b ,下列式子仍然恒成立的是( ) A .||||||ab a b = B .10a a+≠ C .()20a b +≥D .22a a =【答案】A 【分析】对于选项A :结合复数的乘法和模长公式即可判断;选项B :计算1a a+,然后根据复数运算结果举出反例即可;选项CD :复数的平方可能为虚部不为0的复数,而虚部不为0的复数与实数既不能比较大小也不相等. 【详解】不妨令11i a x y =+,22i b x y =+,选项A :112212121221(i)(i)()i ab x y x y x x y y x y x y =++=-++,从而222222121212211122||()()||||ab x x y y x y x y x y x y a b =-++++,故A 正确; 选项B :111111222211111111i ()i i x y a x y x y a x y x y x y +=++=++-+++, 当10x =,11y =时,10a a+=,故B 错误; 因为复数的平方可能还是虚部不为0的复数,而虚部不为0的复数不能与实数比较大小且不等于实数,故CD 错误. 故选:A7.(2022·湖北·武钢三中高三阶段练习)已知202120221i i 1i z +⎛⎫=+ ⎪-⎝⎭,则在复平面内,复数z 所对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】B 【分析】先利用复数的除法和乘方化简复数z ,再利用复数的几何意义求解. 【详解】21i 12i i i 1i 2+++==-,且i 的乘方运算是以4为周期的运算 所以202120222021202221i i 1i 1i i i i i z +⎛⎫=+++ ===-⎝-⎪+⎭,所以复数z 所对应的点()1,1-,在第二象限. 故选:B8.(2022·全国·高一)复数()()cos2isin3cos isin θθθθ+⋅+的模为1,其中i 为虚数单位,[]0,2πθ∈,则这样的θ一共有( )个. A .9 B .10 C .11 D .无数【答案】C 【分析】先根据复数()()cos2isin3cos isin θθθθ+⋅+的模为1及复数模的运算公式,求得22cos 2sin 31θθ+=即22cos 2cos 3θθ=,接下来分cos2cos3θθ=与cos2cos3θθ=-两种情况进行求解,结合[]0,2πθ∈,求出θ的个数. 【详解】()()cos2isin3cos isin =cos2isin3cos isin 1θθθθθθθθ+⋅++⋅+=,其中cos isin 1θθ+=,所以cos2isin31θθ+=,即22cos 2sin 31θθ+=,222cos 21sin 3cos 3θθθ=-=,当cos2cos3θθ=时,①1232πk θθ=+,1k Z ∈,所以12πk θ=-,1k Z ∈,因为[]0,2πθ∈,所以0θ=或2π;②2232πk θθ=-+,2k Z ∈,所以22π5k θ=,2k Z ∈,因为[]0,2πθ∈,所以0θ=,2π5,4π5,6π5,8π5或2π;当cos2cos3θθ=-时,①()32321πk θθ=++,3k Z ∈,即()321πk θ=-+,3k Z ∈,因为[]0,2πθ∈,所以πθ=,②()42321πk θθ=-++,4k Z ∈,即()421π5k θ+=,4k Z ∈,因为[]0,2πθ∈,所以π5θ=,3π5,π,7π5,9π5,综上:π5mθ=,0,1,10m =,一共有11个. 故选:C二、多选题9.(2022·广东东莞·高三期末)已知复数123,,z z z ,1z 是1z 的共轭复数,则下列结论正确的是( ) A .若120z z +=,则12=z zB .若21z z =,则12=z zC .若312z z z =,则312z z z =D .若1211z z +=+,则12=z z【答案】ABC 【分析】若i z a b =+ ,则i z a b =-,22z z a b ==+,利用复数代数运算,可以判断AB ;利用复数的三角运算,可以判断C ;利用数形结合,可以判断D. 【详解】 对于A :若120z z += ,则12z z =-,故122z z z =-=, 所以A 正确; 对于B :若21z z =,则12=z z , 所以B 正确; 对于C :设11(cos i sin )z r αα=+ ,22(cos i sin )z r ββ=+则()()31212cos()i sin z z z r r αβαβ==+++ ,故312z z z = , 所以C 正确; 对于D :如下图所示,若11OA z =+ ,21OB z =+,则1OC z =,2OD z =,故12z z ≠ , 所以D 错误.故选:ABC10.(2022·江西·高三阶段练习(理))已知复数z 满足()12i 5z -=(其中i 为虚数单位),则下列选项正确的是( ) A .5z =B .复数z 的共轭复数为12i z =+C .复数z 在复平面表示的点位于第一象限D .复数z 的虚部为2 【答案】CD 【分析】利用复数代数形式的乘除运算求出复数z ,然后逐一核对四个选项即可得出答案. 【详解】解:因为()12i 5z -=,所以()()()512i 512i 12i 12i 12i z +===+--+, 所以145z +A 错误; 复数z 的共轭复数为12i z =-,故B 错误;复数z 在复平面表示的点的坐标为()1,2,位于第一象限,故C 正确; 复数z 的虚部为2,故D 正确. 故选:CD.11.(2021·福建福州·高三期中)复数132z =-,其中i 为虚数单位,则下列结论正确的有( )A .1z z ⋅=B .210z z ++=C .21z z= D .2021132z = 【答案】ABC 【分析】根据共轭复数的概念,复数的运算法则,逐一求解验证即可. 【详解】解:因为132z =-,所以132z =-,对于A : 2131313i 12244z z ⎛⎫⎛⎫⋅=-+-=-= ⎪⎪ ⎪⎪⎝⎭⎝⎭,故A 正确; 对于B :22201131313133i 222414z z ⎛⎫⎛⎫--=+= ⎪ ⎪ ⎭⎛⎫++⎪ ⎪⎝⎝+=++⎝⎭⎭ ⎪ ⎪,故B 正确; 对于C :2131132213213i i44z -===---+,2221313313i 2442z ⎛⎫-=+=- ⎪ ⎪⎝=⎭, 所以21z z=,即选项C 正确;对于D :132z =-+,2132z -=,2231313131222z ⎛⎫⎛⎫⎫⎛⎫-⋅-+=--= ⎪ ⎪⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭=⎭⎝,4z z =,所以20212132z z -==,故D 错误.故选:ABC .12.(2021·重庆·万州纯阳中学校高二阶段练习)欧拉公式i cos isin x e x x =+是由瑞士著名数学家欧拉创立,该公式将指数函数的定义域扩大到复数,建立了三角函数与指数函数的关联,在复变函数论里面占有非常重要的地位,被誉为数学中的天骄,依据欧拉公式,下列选项正确的是( ) A .复数2i e 对应的点位于第二象限 B .i 2e π为纯虚数C i 3ix +12D .i 6e π的共轭复数为132-【答案】ABC【分析】利用欧拉公式把选项A ,B ,D 化成复数的代数形式即可计算判断;利用欧拉公式把选项C 的分子化成复数的代数形式,再进行除法运算判断即得. 【详解】对于A ,2i cos 2isin 2e =+,因22ππ<<,即cos20,sin20<>,复数2i e 对应的点位于第二象限,A 正确;对于B ,i2cos isini 22e πππ=+=,i 2e π为纯虚数,B 正确;对于C i (cos isin )(3i)3cos sin 3sin cos 3i 3i(3i)(3i)x x x x x x x+-+-+++-,于是得i 223cos sin 3sin cos 1()()4423ix x x x x +-++,C 正确; 对于D ,6i31cos isini 662e πππ=+=31i 2,D 不正确. 故选:ABC三、填空题13.(2021·天津市第四中学高三阶段练习)已知方程()20R x x m m ++=∈有两个虚根α,β,若3αβ-=,则m 的值是___________. 【答案】52【分析】由已知结合实系数一元二次方程两个虚根互为共轭复数,设出α的代数形式,代入计算作答. 【详解】因α,β是方程()20R x x m m ++=∈有两个虚根,设i(,R)a b a b α=+∈,则i a b β=-,由3αβ-=得:|i (i)||2|3a b a b b +--==,解得3||2b =, 又2(i)(i)0a b a b m ++++=,即22()(2)i 0a b a m ab b -++++=,因R m ∈,于是得:22020a b a m ab b ⎧-++=⎨+=⎩,解得12a =-,52m =,所以m 的值是52.故答案为:5214.(2021·上海长宁·一模)在复平面xoy 内,复数12z ,z 所对应的点分别为12Z Z 、,对于下列四个式子:(1)2211 z z =;(2)1212z z z z ⋅=⋅;(3)2211OZ OZ =;(4)1212OZ OZ OZ OZ ⋅=⋅,其中恒成立的是____________(写出所有恒成立式子的序号) 【答案】(2)(3) 【分析】结合复数运算对四个式子进行分析,由此确定正确答案. 【详解】221111i,2i,2z z z =+==,所以(1)错误.()()121,1,1,1Z Z -,12120,2OZ OZ OZ OZ ⋅=⋅=,所以(4)错误.设()()1212i,i,,,,z a b z c d Z a b Z c d =+=+,()()()2212i z z ac bd ad bc ac bd ad bc ⋅=-++=-++22222222a c b d a d b c =+++22222222222212z z a b c d a c b d a d b c ⋅+++++2)正确.222211OZ OZ a b ==+,所以(3)正确. 故答案为:(2)(3)15.(2021·浙江·模拟预测)已知平面直角坐标系xOy 中向量的旋转和复数有关,对于任意向量x →=(a ,b ),对应复数z =a +ib ,向量x 逆时针旋转一个角度θ,得到复数'(i )(cos isin )cos sin i(sin cos )z a b a b a b θθθθθθ=++=-++,于是对应向量'(cos sin ,sin cos )x a b a b θθθθ→=-+.这就是向量的旋转公式.根据此公式,已知正三角形ABC 的两个顶点坐标是A (1,2),B (3,4),则C 的坐标是___________.(任写一个即可) 【答案】(23,33)-(答案不唯一) 【分析】首先设出C 的坐标,然后分别写出AB →,AC →,利用向量的旋转公式即可求解. 【详解】不妨设C 的坐标为00(,)x y ,且AC →是AB →逆时针旋转60得到, 因为A (1,2),B (3,4),所以(2,2)AB →=,00(1,2)AC x y →=--, 从而AB →对应的复数为22i z =+,AC →对应的复数为'(22i)(cos 60isin 60)13(13)i z =++=-,所以00(1,2)(13,13)AC x y →=--=+,解得023x =033y = 故C 的坐标是(23,33). 故答案为:(23,33).16.(2021·福建·厦门市湖滨中学高三期中)若复数z 满足32i 1z -+=,则62i z --的最小值为__________. 【答案】4 【分析】根据复数模的几何意义得出复数z 对应的点Z 的轨迹是以()3,2C -为圆心,半径为1的圆,然后再根据62i z --的几何意义求最小值即可.【详解】因为复数z 满足32i 1z -+=,则复数z 对应的点Z 的轨迹是以()3,2C -为圆心,半径为1的圆, 又62i z --表示复数z 对应的点Z 与点()6,2P 之间的距离, 所以62i z --的最小值为()()22163221514PC -=-++=-=.故答案为:4.四、解答题17.(2021·贵州遵义·高三阶段练习)已知复数i()z b b =∈R ,31iz +-是实数. (1)求复数z ;(2)若复数2()8m z m --在复平面内所表示的点在第二象限,求实数m 的取值范围. 【答案】 (1)3i z =-(2)(0,9)【分析】 (1)先将i z b =代入31iz +-化简,再由其虚部为零可求出b 的值,从而可求出复数z , (2)先对2()8m z m --化简,再由题意可得2890,60,m m m ⎧--<⎨>⎩从而可求得结果 (1) 因为i z b =,所以33i (3i)(1i)3(3)i 1i 1i 22z b b b b ++++-++===--, 因为31iz +-是实数,所以30b +=,解得3b =-. 故3i z =-.(2)因为3i z =-,所以()222()8(3i)8896i m z m m m m m m --=+-=--+.因为复数2()8m z m --所表示的点在第二象限,所以2890,60,m m m ⎧--<⎨>⎩解得09m <<,即实数m 的取值范围是(0,9).18.(2021·全国·高一课时练习)求复数1i +,1i --2,2i -的辐角主值.【答案】π4,5π4,0,3π2 【分析】计算12r =11cos 2sin 2θθ⎧=⎪⎪⎨⎪⎪⎩结合102πθ≤<,得到辐角主值,同理可得其他答案. 【详解】设这4个复数的模分别为1r ,2r ,3r ,4r ,辐角主值分别为1θ,2θ,3θ,4θ.因为221112r =+11cos 2sin 2θθ⎧=⎪⎪⎨⎪⎪⎩,又102πθ≤<,故1π4θ=. 同理,可以求得:5π5π1i 2cos isin 44⎫--=+⎪⎭, )22cos0isin 0+,3π3π2i 2cos isin 22⎫-=+⎪⎭, 故4个复数的辐角主值分别为π4,5π4,0,3π2. 19.(2021·西藏·拉萨那曲高级中学高二期中(理))已知复数11i z =+,23i z =-.(1)求21z z ; (2)若4i()z a a R =+∈满足2z z +为纯虚数,求||z .【答案】(1)12i -(2)5【分析】(1)根据复数代数形式的运算法则即可求出;(2)根据纯虚数的概念即可求出参数a ,再根据复数模的计算公式即可求出.(1)213i (3i)(1i)33i i 112i 1i (1i)(1i)2z z ------====-++-. (2)因为2(3)3i z z a +=++为纯虚数,∴30a +=,∴3a =-.即34i z =-+,22||(3)45z =-+=.20.(2021·全国·高一课时练习)在复数范围内分解因式:(1)28x +;(2)223x x -+;(3)2321x x -+.【答案】(1)28(22i)(22i)x x x +=+-(2)223(12i)(12i)x x x x -+=--- (3)212123213((x x x x -+-+=) 【分析】利用完全平方公式平方差公式将所给的表达式分解因式. (1)2228=8i (2i)(2i)x x x x +-=+- (2)()22223=12i (12i)(12i)x x x x x -+--=-- (3)∵ 22222112321=3)3[()i ]3339x x x x x -+-+=--( ∴ 212123213[()33x x x x -+=-- ∴ 212123213((x x x x -+-+=) 21.(2021·湖北·高一期末)已知12i +是关于x 的方程20(,)x px q p q R ++=∈的一个根,其中i 为虚数单位. (1)求,p q 的值;(2)记复数i z p q =+,求复数1iz +的模. 【答案】(1)2,5p q =-=(258【分析】(1)由题知()()212i 12i 0p q ++++=,即()()342i 0p q p +-++=,再根据复数相等求解即可; (2)由(1)得25i z =-+,故37i 1i 2z +=+,再求模即可. (1)解:知12i +是关于x 的方程20(,)x px q p q R ++=∈的一个根, 所以()()212i 12i 0p q ++++=,即()()342i 0p q p +-++=, 所以30420p q p +-=⎧⎨+=⎩,解得2,5p q =-=. 所以2,5p q =-=(2)解:由(1)得复数25i z =-+, 所以()()()()25i 1i 25i 37i 1i 1i 1i 1i 2z -+--++===+++- 所以复数1i z +9495844+= 22.(2021·全国·高一课时练习)已知复数()31i 1i z =-. (1)求1arg z 及1z ;(2)当复数z 满足1z =,求1z z -的最大值.【答案】(1)17arg 4z π=,122z = (2)221【分析】(1)化简复数为代数形式后,再化为三角形式,即可求解. (2)z 设为三角形式,和复数1z 的代数形式,共同代入1z z -,化简后可求最大值. (1)解:()31i 1i 22i z =-=-,将1z 化为三角形式,得1772cos isin 44z ππ⎫⎪=⎭+, ∴17arg 4z π=,122z = (2) 解:由于复数z 满足1z =,设cos isin z αα=+,则()()1cos 2sin 2i z z αα-=-++, ()()2221cos 2sin 2924z z πααα⎛⎫-=-++=+- ⎪⎝⎭,当sin 14πα⎛⎫-= ⎪⎝⎭时,21z z -取得最大值942+ 所以1z z -的最大值为221.。
苏教版小学数学五年级上册第一单元《负数的初步认识》单元测试卷(含答案)

第一单元负数的初步认识学校:___________姓名:___________班级:___________考号:___________一、选择题(18分)1.一种饮料外包装上标有“净含量”5005mL ,有4瓶这样的饮料,实际净含量如下,不符合标准的是( )。
A .496mLB .502mLC .495mLD .508mL2.根据5-3=2,4-3=1,3-3=0,可以分析2-3=( )。
A .1B .0C .-1D .-53.下面三个数中,最接近0的是( )。
A .﹣1B .23.5C .32.54.2020年12月30日,滨海县遭遇极寒天气,早上6时,李叔叔测得室外温度为﹣13℃,下午2时温度比早上6时上升了9℃,下午2时的温度是( )。
A .9℃B .5℃C .﹣4℃D .4℃5.磊磊从家先向北走50米,记作﹣50米,然后调头再向南走35米,现在磊磊的位置相对于磊磊家应记作( )米。
A .﹢35B .﹢15C .﹣156.银行存折上“﹢500”元表示客户存入现金500元。
若客户从银行取出350元,存折上应记作( )元。
A .B .C .D .7.下面说法中,正确的有( )个。
①2021年的第一季度共有90天。
②0既不是正数,也不是负数。
③三角形的内角和是180°。
④长度分别为4厘米、5厘米、9厘米的三根小棒能围成一个三角形。
A .1B .2C .3D .48.在下面3个数中,最接近0的是( )。
A .-2B .1C .0.99.在0、9、﹢17、21、﹣0.38、5.9中正数有( )个。
A .3B .4C .510.在下面这些数中,最小的数是( )。
A .12B .﹣12C .0.0012D .0二、填空题(22分)150﹢150﹣350﹢350﹣11.在方框里填上合适的数。
在所填的数中,( )最大。
12.北岳恒山是我省著名的旅游景区,4月27日这天的最高温度是零上7℃,记作( )℃,夜间的最低温度为零下1℃,记作()℃。
复数选择题专项训练单元测试附解析

复数选择题专项训练单元测试附解析一、复数选择题1.若()211z i =-,21z i =+,则12z z 等于( )A .1i +B .1i -+C .1i -D .1i -- 答案:D【分析】由复数的运算法则计算即可.【详解】解:,.故选:D.解析:D【分析】由复数的运算法则计算即可.【详解】解:()2211122z i i i i =-=-+=-,()()212222(1)2222111112z i i i i i i i z i ii i --⨯--+--∴=====--++--.故选:D.2.已知复数()123z i i +=- (其中i 是虚数单位),则z 在复平面内对应点在( )A .第一象限B .第二象限C .第三象限D .第四象限 答案:D【分析】先由复数的运算化简复数z ,再运用复数的几何表示可得选项.【详解】由已知得,所以复数z 在复平面上所对应的点为,在第四象限,故选:D.解析:D【分析】先由复数的运算化简复数z ,再运用复数的几何表示可得选项.【详解】 由已知得()()()()312317171+21+212555i i i iz i i i i ----====--,所以复数z 在复平面上所对应的点为17,55⎛⎫-⎪⎝⎭,在第四象限, 故选:D. 3.已知a 为正实数,复数1ai +(i 为虚数单位)的模为2,则a 的值为( )A B .1 C .2 D .3答案:A【分析】利用复数的模长公式结合可求得的值.【详解】,由已知条件可得,解得.故选:A.解析:A【分析】利用复数的模长公式结合0a >可求得a 的值.【详解】0a >,由已知条件可得12ai +==,解得a =故选:A.4.若复数()()24z i i =--,则z =( )A .76i --B .76-+iC .76i -D .76i + 答案:D【分析】由复数乘法运算求得,根据共轭复数定义可求得结果.【详解】,.故选:.解析:D【分析】由复数乘法运算求得z ,根据共轭复数定义可求得结果.【详解】()()2248676z i i i i i =--=-+=-,76z i ∴=+.故选:D .5.已知复数z 满足()311z i i +=-,则复数z 对应的点在( )上A .直线12y x =-B .直线12y x =C .直线12x =-D .直线12y 答案:C【分析】利用复数的乘法和除法运算求得复数z 的标准形式,得到对应点的坐标,然后验证即可.【详解】解:因为,所以复数对应的点是,所以在直线上.故选:C.【点睛】本题考查复数的乘方和除法运解析:C【分析】利用复数的乘法和除法运算求得复数z 的标准形式,得到对应点的坐标,然后验证即可.【详解】 解:因为33111(1)1(1)2(1)2i i z i i z i i --+=-⇔===-+-,所以复数z 对应的点是1,02⎛⎫- ⎪⎝⎭,所以在直线12x =-上. 故选:C.【点睛】本题考查复数的乘方和除法运算,复数的坐标表示,属基础题.注意:()()()()()3211i 12121i i i i i +=++=-+=-. 6.若复数1z i =-,则1z z =-( )A B .2C .D .4 答案:A【分析】将代入,利用复数的除法运算化简,再利用复数的求模公式求解.【详解】由,得,则,故选:A.解析:A【分析】将1z i =-代入1z z-,利用复数的除法运算化简,再利用复数的求模公式求解. 【详解】由1z i =-,得2111z i i i i z i i---===---,则11z i z =--=- 故选:A.7.若复数z 满足421i z i +=+,则z =( ) A .13i + B .13i - C .3i + D .3i - 答案:C【分析】首先根据复数的四则运算求出,然后根据共轭复数的概念求出.【详解】,故.故选:C. 解析:C【分析】首先根据复数的四则运算求出z ,然后根据共轭复数的概念求出z .【详解】()()()()421426231112i i i i z i i i i +-+-====-++-,故3z i =+. 故选:C. 8.若复数z 满足()322i z i i-+=+,则复数z 的虚部为( ) A .35 B .35i - C .35 D .35i 答案:A【分析】由复数的除法法则和乘法法则计算出,再由复数的定义得结论.【详解】由题意,得,其虚部为,故选:A.解析:A【分析】由复数的除法法则和乘法法则计算出z ,再由复数的定义得结论.【详解】由题意,得()()()()()23343313343434552i i ii z i i i i i ----====-++-+, 其虚部为35, 故选:A. 9.复数z 的共轭复数记为z ,则下列运算:①z z +;②z z -;③z z ⋅④z z ,其结果一定是实数的是( )A .①②B .②④C .②③D .①③ 答案:D【分析】设,则,利用复数的运算判断.【详解】设,则,故,,,.故选:D.解析:D【分析】设(),z a bi a b R =+∈,则z a bi =-,利用复数的运算判断.【详解】设(),z a bi a b R =+∈,则z a bi =-,故2z z a R +=∈,2z z bi -=,22222z a bi a b abi z a bi a b+-+==-+,22z z a b ⋅=+∈R . 故选:D.10.复数112z i =+,21z i =+(i 为虚数单位),则12z z ⋅虚部等于( ). A .1- B .3 C .3i D .i -答案:B【分析】化简,利用定义可得的虚部.【详解】则的虚部等于故选:B解析:B【分析】化简12z z ⋅,利用定义可得12z z ⋅的虚部.【详解】()()1212113z z i i i ⋅=+⋅+=-+则12z z ⋅的虚部等于3故选:B11.在复平面内,复数z 对应的点的坐标是(1,1),则z i =( ) A .1i -B .1i --C .1i -+D .1i + 答案:A【分析】根据复数对应的点的坐标是,得到,再利用复数的除法求解.【详解】因为在复平面内,复数对应的点的坐标是,所以,所以,故选:A解析:A【分析】根据复数z 对应的点的坐标是(1,1),得到1z i =+,再利用复数的除法求解.【详解】因为在复平面内,复数z 对应的点的坐标是(1,1),所以1z i =+, 所以11i i i z i+==-, 故选:A12.设复数202011i z i+=-(其中i 为虚数单位),则z 在复平面内对应的点所在象限为( )A .第四象限B .第三象限C .第二象限D .第一象限 答案:A【分析】根据复数的运算,先将化简,求出,再由复数的几何意义,即可得出结果.【详解】因为,所以,其在复平面内对应的点为,位于第四象限.故选:A.解析:A【分析】根据复数的运算,先将z 化简,求出z ,再由复数的几何意义,即可得出结果.【详解】 因为()()()()4202050550512111121111111i i i z i i i i i i i ++++======+-----+, 所以1z i =-,其在复平面内对应的点为()1,1-,位于第四象限.故选:A.13.已知复数21i z i =-,则复数z 在复平面内对应点所在象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 答案:B【分析】对复数进行化简,再得到在复平面内对应点所在的象限.【详解】,在复平面内对应点为,在第二象限.故选:B.解析:B【分析】对复数z 进行化简,再得到z 在复平面内对应点所在的象限.【详解】21i z i =-()()()2111i i i i +=+-()1+1+i i i ==-,z 在复平面内对应点为()1,1-,在第二象限. 故选:B.14.已知复数z 满足22z z =,则复数z 在复平面内对应的点(),x y ( ) A .恒在实轴上B .恒在虚轴上C .恒在直线y x =上D .恒在直线y x=-上 答案:A【分析】先由题意得到,然后分别计算和,再根据得到关于,的方程组并求解,从而可得结果.【详解】由复数在复平面内对应的点为得,则,,根据得,得,.所以复数在复平面内对应的点恒在实轴上,故解析:A【分析】先由题意得到z x yi =+,然后分别计算2z 和2z ,再根据22z z =得到关于x ,y 的方程组并求解,从而可得结果.【详解】由复数z 在复平面内对应的点为(),x y 得z x yi =+,则2222z x y xyi =-+,222z x y =+, 根据22z z =得222220x y x y xy ⎧-=+⎨=⎩,得0y =,x ∈R . 所以复数z 在复平面内对应的点(),x y 恒在实轴上,故选:A .15.复数z 满足22z z i +=,则z 在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 答案:B【分析】先设复数,根据复数模的计算公式,以及复数相等,求出,得出复数,再由复数的几何意义,即可得出结果.【详解】设复数,由得,所以,解得,因为时,不能满足,舍去;故,所以,其对应的解析:B【分析】先设复数(),z x yi x R y R =+∈∈,根据复数模的计算公式,以及复数相等,求出,x y ,得出复数,再由复数的几何意义,即可得出结果.【详解】设复数(),z x yi x R y R =+∈∈,由22z z i +=得222x yi i ++=,所以2022x y ⎧⎪+=⎨=⎪⎩,解得31x y ⎧=±⎪⎨⎪=⎩,因为1x y ⎧=⎪⎨⎪=⎩时,不能满足20x +=,舍去;故1x y ⎧=⎪⎨⎪=⎩z i =+,其对应的点⎛⎫ ⎪ ⎪⎝⎭位于第二象限, 故选:B.二、复数多选题16.i 是虚数单位,下列说法中正确的有( )A .若复数z 满足0z z ⋅=,则0z =B .若复数1z ,2z 满足1212z z z z +=-,则120z z =C .若复数()z a ai a R =+∈,则z 可能是纯虚数D .若复数z 满足234z i =+,则z 对应的点在第一象限或第三象限答案:AD【分析】A 选项,设出复数,根据共轭复数的相关计算,即可求出结果;B 选项,举出反例,根据复数模的计算公式,即可判断出结果;C 选项,根据纯虚数的定义,可判断出结果;D 选项,设出复数,根据题解析:AD【分析】A 选项,设出复数,根据共轭复数的相关计算,即可求出结果;B 选项,举出反例,根据复数模的计算公式,即可判断出结果;C 选项,根据纯虚数的定义,可判断出结果;D 选项,设出复数,根据题中条件,求出复数,由几何意义,即可判断出结果.【详解】A 选项,设(),z a bi a b R =+∈,则其共轭复数为(),z a bi a b R =-∈, 则220z z a b ⋅=+=,所以0a b ,即0z =;A 正确;B 选项,若11z =,2z i =,满足1212z z z z +=-,但12z z i =不为0;B 错;C 选项,若复数()z a ai a R =+∈表示纯虚数,需要实部为0,即0a =,但此时复数0z =表示实数,故C 错;D 选项,设(),z a bi a b R =+∈,则()2222234z a bi a abi b i =+=+-=+,所以22324a b ab ⎧-=⎨=⎩,解得21a b =⎧⎨=⎩或21a b =-⎧⎨=-⎩,则2z i =+或2z i =--, 所以其对应的点分别为()2,1或()2,1--,所以对应点的在第一象限或第三象限;D 正确. 故选:AD.17.已知复数Z 在复平面上对应的向量(1,2),OZ =-则( )A .z =-1+2iB .|z |=5C .12z i =+D .5z z ⋅= 答案:AD【分析】因为复数Z 在复平面上对应的向量,得到复数,再逐项判断.【详解】因为复数Z 在复平面上对应的向量,所以,,|z|=,,故选:AD解析:AD【分析】因为复数Z 在复平面上对应的向量(1,2)OZ =-,得到复数12z i =-+,再逐项判断.【详解】因为复数Z 在复平面上对应的向量(1,2)OZ =-,所以12z i =-+,12z i =--,|z 5z z ⋅=,故选:AD18.已知复数z 满足220z z +=,则z 可能为( ).A .0B .2-C .2iD .2i+1- 答案:AC【分析】令,代入原式,解出的值,结合选项得出答案.【详解】令,代入,得,解得,或,或,所以,或,或.故选:AC【点睛】本题考查复数的运算,考查学生计算能力,属于基础题.解析:AC【分析】令()i ,z a b a b R =+∈,代入原式,解出,a b 的值,结合选项得出答案.【详解】令()i ,z a b a b R =+∈,代入220z z +=,得222i 0a b ab -+=,解得00a b =⎧⎨=⎩,或02a b =⎧⎨=⎩,或02a b =⎧⎨=-⎩, 所以0z =,或2i z =,或2i z =-.故选:AC【点睛】本题考查复数的运算,考查学生计算能力,属于基础题.19.下面是关于复数21i z =-+的四个命题,其中真命题是( )A .||z =B .22z i =C .z 的共轭复数为1i -+D .z 的虚部为1- 答案:ABCD【分析】先根据复数的除法运算计算出,再依次判断各选项.【详解】,,故A 正确;,故B 正确;的共轭复数为,故C 正确;的虚部为,故D 正确; 故选:ABCD.【点睛】本题考查复数的除法解析:ABCD【分析】先根据复数的除法运算计算出z ,再依次判断各选项.【详解】()()()2121111i z i i i i --===---+-+--,z ∴==,故A 正确;()2212z i i =--=,故B 正确;z 的共轭复数为1i -+,故C 正确;z 的虚部为1-,故D 正确;故选:ABCD.【点睛】本题考查复数的除法运算,以及对复数概念的理解,属于基础题.20.已知复数z 满足2724z i =--,在复平面内,复数z 对应的点可能在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限答案:BD【分析】先设复数,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出,即可确定对应的点所在的象限.【详解】设复数,则,所以,则,解得或,因此或,所以对应的点为或,因此复解析:BD【分析】先设复数(),z a bi a b R =+∈,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出z ,即可确定对应的点所在的象限.【详解】设复数(),z a bi a b R =+∈,则2222724z a abi b i =+-=--,所以2222724z a abi b i =+-=--,则227224a b ab ⎧-=-⎨=-⎩,解得34a b =⎧⎨=-⎩或34a b =-⎧⎨=⎩, 因此34z i =-或34z i =-+,所以对应的点为()3,4-或()3,4-,因此复数z 对应的点可能在第二或第四象限.故选:BD.【点睛】本题主要考查判定复数对应的点所在的象限,熟记复数的运算法则,以及复数相等的条件即可,属于基础题型.21.下列说法正确的是( )A .若2z =,则4z z ⋅=B .若复数1z ,2z 满足1212z z z z +=-,则120z z =C .若复数z 的平方是纯虚数,则复数z 的实部和虛部相等D .“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件 答案:AD【分析】由求得判断A ;设出,,证明在满足时,不一定有判断B ;举例说明C 错误;由充分必要条件的判定说明D 正确.【详解】若,则,故A 正确;设,由,可得则,而不一定为0,故B 错误;当时解析:AD【分析】 由z 求得z z ⋅判断A ;设出1z ,2z ,证明在满足1212z z z z +=-时,不一定有120z z =判断B ;举例说明C 错误;由充分必要条件的判定说明D 正确.【详解】 若2z =,则24z z z ⋅==,故A 正确;设()11111,z a bi a b R =+∈,()22222,z a b i a b R =+∈ 由1212z z z z +=-,可得()()()()222222121212121212z z a a b b z z a a b b +=+++=-=-+-则12120a a b b +=,而()()121122121212121212122z z a bi a b i a a bb a b i b a i a a a b i b a i =++=-++=++不一定为0,故B 错误;当1z i =-时22z i =-为纯虚数,其实部和虚部不相等,故C 错误;若复数()()()211z a a i a R =-+-∈是虚数,则210a -≠,即1a ≠± 所以“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件,故D 正确; 故选:AD【点睛】本题考查的是复数的相关知识,考查了学生对基础知识的掌握情况,属于中档题.22.若复数z 满足()1z i i +=,则( ) A .1z i =-+B .z 的实部为1C .1z i =+D .22z i =答案:BC【分析】先利用复数的运算求出复数z ,然后逐个分析判断即可【详解】解:由,得,所以z 的实部为1,,,故选:BC【点睛】此题考查复数的运算,考查复数的模,考查复数的有关概念,考查共轭 解析:BC【分析】先利用复数的运算求出复数z ,然后逐个分析判断即可【详解】解:由()1z i i +=,得2(1)2(1)1(1)(1)2i i z i i i --====-+-, 所以z 的实部为1,1z i =+,22z i =-,故选:BC【点睛】此题考查复数的运算,考查复数的模,考查复数的有关概念,考查共轭复数,属于基础题23.下列关于复数的说法,其中正确的是( )A .复数(),z a bi a b R =+∈是实数的充要条件是0b =B .复数(),z a bi a b R =+∈是纯虚数的充要条件是0b ≠C .若1z ,2z 互为共轭复数,则12z z 是实数D .若1z ,2z 互为共轭复数,则在复平面内它们所对应的点关于y 轴对称答案:AC【分析】根据复数的有关概念和充分条件和必要条件的定义进行判断即可.【详解】解:对于:复数是实数的充要条件是,显然成立,故正确;对于:若复数是纯虚数则且,故错误;对于:若,互为共轭复数解析:AC【分析】根据复数的有关概念和充分条件和必要条件的定义进行判断即可.【详解】解:对于A :复数(),z a bi a b R =+∈是实数的充要条件是0b =,显然成立,故A 正确;对于B :若复数(),z a bi a b R =+∈是纯虚数则0a =且0b ≠,故B 错误; 对于C :若1z ,2z 互为共轭复数,设()1,z a bi a b R =+∈,则()2,z a bi a b R =-∈,所以()()2122222z a bi a bi a b b z i a =+-=-=+是实数,故C 正确; 对于D :若1z ,2z 互为共轭复数,设()1,z a bi a b R =+∈,则()2,z a bi a b R =-∈,所对应的坐标分别为(),a b ,(),a b -,这两点关于x 轴对称,故D 错误;故选:AC【点睛】本题主要考查复数的有关概念的判断,利用充分条件和必要条件的定义是解决本题的关键,属于基础题.24.下列结论正确的是( )A .已知相关变量(),x y 满足回归方程ˆ9.49.1yx =+,则该方程相应于点(2,29)的残差为1.1B .在两个变量y 与x 的回归模型中,用相关指数2R 刻画回归的效果,2R 的值越大,模型的拟合效果越好C .若复数1z i =+,则2z =D .若命题p :0x R ∃∈,20010x x -+<,则p ⌝:x R ∀∈,210x x -+≥答案:ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当时,,则该方程相应于点(2,29)的残差为,则A 正确;在两个变量解析:ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当2x =时,ˆ9.429.127.9y=⨯+=,则该方程相应于点(2,29)的残差为2927.9 1.1-=,则A 正确;在两个变量y 与x 的回归模型中,2R 的值越大,模型的拟合效果越好,则B 正确;1z i =-,z =C 错误;由否定的定义可知,D 正确;故选:ABD【点睛】本题主要考查了残差的计算,求复数的模,特称命题的否定,属于中档题.25.已知复数()(()()211z m m m i m R =-+-∈,则下列说法正确的是( )A .若0m =,则共轭复数1z = B .若复数2z =,则m =C .若复数z 为纯虚数,则1m =±D .若0m =,则2420z z ++= 答案:BD【分析】根据每个选项里的条件,求出相应的结果,即可判断选项的正误.【详解】对于A ,时,,则,故A 错误;对于B ,若复数,则满足,解得,故B 正确;对于C ,若复数z 为纯虚数,则满足,解得,解析:BD【分析】根据每个选项里的条件,求出相应的结果,即可判断选项的正误.【详解】对于A ,0m =时,1z =-+,则1z =-,故A 错误;对于B ,若复数2z =,则满足(()21210m m m ⎧-=⎪⎨-=⎪⎩,解得m =B 正确; 对于C ,若复数z为纯虚数,则满足(()21010m m m ⎧-=⎪⎨-≠⎪⎩,解得1m =-,故C 错误; 对于D ,若0m =,则1z =-,()()221420412z z ++=+--+=,故D 正确.故选:BD.【点睛】 本题主要考查对复数相关概念的理解,注意不同情形下的取值要求,是一道基础题.26.以下为真命题的是( )A .纯虚数z 的共轭复数等于z -B .若120z z +=,则12z z =C .若12z z +∈R ,则1z 与2z 互为共轭复数D .若120z z -=,则1z 与2z 互为共轭复数 答案:AD【分析】根据纯虚数的概念即可判断A 选项;根据实数、复数的运算、以及共轭复数的定义即可判断BCD 选项.【详解】解:对于A ,若为纯虚数,可设,则,即纯虚数的共轭复数等于,故A 正确;对于B解析:AD【分析】根据纯虚数的概念即可判断A 选项;根据实数、复数的运算、以及共轭复数的定义即可判断BCD 选项.【详解】解:对于A ,若z 为纯虚数,可设()0z bi b =≠,则z bi z =-=-,即纯虚数z 的共轭复数等于z -,故A 正确;对于B ,由120z z +=,得出12z z =-,可设11z i =+,则21z i =--, 则21z i =-+,此时12z z ≠,故B 错误;对于C ,设12,z a bi z c di =+=+,则()()12a c b d i R z z =++++∈,则0b d +=, 但,a c 不一定相等,所以1z 与2z 不一定互为共轭复数,故C 错误;对于D ,120z z -=,则12z z =,则1z 与2z 互为共轭复数,故D 正确. 故选:AD.【点睛】本题考查与复数有关的命题的真假性,考查复数的基本概念和运算,涉及实数、纯虚数和共轭复数的定义,属于基础题.27.复数21i z i +=-,i 是虚数单位,则下列结论正确的是( )A .|z |=B .z 的共轭复数为3122i +C .z 的实部与虚部之和为2D .z 在复平面内的对应点位于第一象限 答案:CD【分析】根据复数的四则运算,整理复数,再逐一分析选项,即得.【详解】由题得,复数,可得,则A 不正确;的共轭复数为,则B 不正确;的实部与虚部之和为,则C 正确;在复平面内的对应点为,位于第一解析:CD【分析】根据复数的四则运算,整理复数z ,再逐一分析选项,即得.【详解】 由题得,复数22(2)(1)13131(1)(1)122i i i i z i i i i i ++++====+--+-,可得||z ==,则A 不正确;z 的共轭复数为1322i -,则B 不正确;z 的实部与虚部之和为13222+=,则C 正确;z 在复平面内的对应点为13(,)22,位于第一象限,则D 正确.综上,正确结论是CD.故选:CD【点睛】本题考查复数的定义,共轭复数以及复数的模,考查知识点全面.28.复数z 满足233232i z i i+⋅+=-,则下列说法正确的是( )A .z 的实部为3-B .z 的虚部为2C .32z i =-D .||z =答案:AD【分析】由已知可求出,进而可求出实部、虚部、共轭复数、复数的模,进而可选出正确答案.【详解】解:由知,,即,所以的实部为,A 正确;的虚部为-2,B 错误;,C 错误;,D 正确;故选:A解析:AD【分析】由已知可求出32z i =--,进而可求出实部、虚部、共轭复数、复数的模,进而可选出正确答案.【详解】 解:由233232i z i i +⋅+=-知,232332i z i i +⋅=--,即()()()2233232232313i i i z i i ---=-=+ 39263213i i --==--,所以z 的实部为3-,A 正确;z 的虚部为-2,B 错误;32z i =-+,C 错误;||z ==D 正确; 故选:AD.【点睛】 本题考查了复数的除法运算,考查了复数的概念,考查了共轭复数的求解,考查了复数模的求解,属于基础题.29.已知i 为虚数单位,则下列选项中正确的是( )A .复数34z i =+的模5z =B .若复数34z i =+,则z (即复数z 的共轭复数)在复平面内对应的点在第四象限C .若复数()()2234224m m m m +-+--i 是纯虚数,则1m =或4m =-D .对任意的复数z ,都有20z答案:AB【分析】求解复数的模判断;由共轭复数的概念判断;由实部为0且虚部不为0求得值判断;举例说明错误.【详解】解:对于,复数的模,故正确;对于,若复数,则,在复平面内对应的点的坐标为,在第四解析:AB【分析】求解复数的模判断A ;由共轭复数的概念判断B ;由实部为0且虚部不为0求得m 值判断C ;举例说明D 错误.【详解】解:对于A ,复数34z i =+的模||5z ==,故A 正确;对于B ,若复数34z i =+,则34z i =-,在复平面内对应的点的坐标为(3,4)-,在第四象限,故B 正确;对于C ,若复数22(34)(224)m m m m i +-+--是纯虚数,则223402240m m m m ⎧+-=⎨--≠⎩,解得1m =,故C 错误; 对于D ,当z i 时,210z =-<,故D 错误.故选:AB .【点睛】本题考查复数代数形式的乘除运算,考查复数的基本概念,考查复数模的求法,属于基础题.30.下列命题中,正确的是( )A .复数的模总是非负数B .复数集与复平面内以原点为起点的所有向量组成的集合一一对应C .如果复数z 对应的点在第一象限,则与该复数对应的向量的终点也一定在第一象限D .相等的向量对应着相等的复数 答案:ABD【分析】根据复数的几何意义逐项判断后可得正确的选项.【详解】设复数,对于A ,,故A 正确.对于B ,复数对应的向量为,且对于平面内以原点为起点的任一向量,其对应的复数为,故复数集与解析:ABD【分析】根据复数的几何意义逐项判断后可得正确的选项.【详解】设复数(),z a bi a b R =+∈,对于A ,0z =≥,故A 正确.对于B ,复数z 对应的向量为(),OZ a b =,且对于平面内以原点为起点的任一向量(),m n α=,其对应的复数为m ni +, 故复数集与复平面内以原点为起点的所有向量组成的集合一一对应,故B 正确. 对于B ,复数z 对应的向量为(),OZ a b =,且对于平面内的任一向量(),m n α=,其对应的复数为m ni +,故复数集中的元素与复平面内以原点为起点的所有向量组成的集合中的元素是一一对应,故B 正确.对于C ,如果复数z 对应的点在第一象限,则与该复数对应的向量的终点不一定在第一象限,故C 错.对于D ,相等的向量的坐标一定是相同的,故它们对应的复数也相等,故D 正确. 故选:ABD .【点睛】本题考查复数的几何意义,注意复数(),z a bi a b R =+∈对应的向量的坐标为(),a b ,它与终点与起点的坐标的差有关,本题属于基础题.。
2018届苏教版 发酵技术 实践 单元测试

发酵技术实践单元测试学校:___________姓名:___________班级:___________考号:___________一、选择题1.如下图所示,在一普通的锥形瓶中,加入含有酵母菌的葡萄糖溶液,则下列有关坐标中表述正确的是A. ①②③B. ①③④C. ②③④D. ①②④【答案】B【解析】刚开始在锥形瓶内氧气比较多,无氧呼吸比较弱,随着氧气的消耗,有氧呼吸减弱,无氧呼吸加强,所以酒精的量逐渐增加,当葡萄糖被消耗尽以后,酒精的产量不再增加,A正确;当锥形瓶中没有糖源的时候,酵母菌就不能再繁殖,数量不再增加,B错误;葡萄糖的浓度随着酵母菌的呼吸作用的消耗,浓度不断下降,C正确;酵母菌的呼吸作用不断的产生二氧化碳,导致pH值不断下降,D正确。
2.某学习小组以樱桃番茄为材料进行果酒、果醋发酵实验。
下列相关叙述正确的是( )A. 酵母菌是嗜温菌,所以果酒发酵所需的最适温度较高B. 先供氧进行果醋发酵,然后隔绝空气进行果酒发酵C. 与人工接种的发酵相比,自然发酵获得的产品品质更好D. 适当加大接种量可以提高发酵速率、抑制杂菌生长繁殖【答案】D【解析】醋酸菌是嗜热菌,果醋发酵所需的最适温度较高,A错误;进行果酒、果醋发酵实验,要先进行隔绝空气果酒发酵,再供氧进行果醋发酵,B错误;人工接种菌种品质更好,且不容易存在杂菌污染,C错误;适当加大接种量,让菌体快速形成优势菌群,可以抑制杂菌生长,提高发酵速率,D正确。
【考点定位】酒酵母制酒及乙酸菌由酒制醋。
3.下列是有关腐乳制作的几个问题,其中正确的是()①腐乳的制作主要是利用了微生物发酵的原理,起主要作用的微生物是青霉、曲霉和毛霉②含水量为70%左右的豆腐适于做腐乳。
用含水量过高的豆腐制腐乳,不易成形,且不利于毛霉的生长③豆腐上生长的白毛是毛霉的白色菌丝,严格地说是直立菌丝,豆腐中还有匍匐菌丝④决定腐乳特殊风味的是卤汤⑤腐乳的营养丰富,是因为大分子物质经过发酵作用分解成小而且易于消化的物质⑥卤汤中含酒量应该控制在21%左右,酒精含量过高,腐乳成熟的时间会延长;含量过低,不足以抑制微生物的生长A. ①②③④B. ②③④⑤C. ③④⑤⑥D. ①④⑤⑥【答案】B【解析】试题分析:腐乳制作的前期发酵中有许多微生物参与,但起主要作用的是毛霉。
三年级英语第一单元测试

三年级英语第一单元测试一、单词部分。
1. 文具类单词。
- ruler(尺子):这是一个可数名词,复数形式是rulers。
例如:I have a ruler.(我有一把尺子。
)- pencil(铅笔):复数形式是pencils。
可以说This is my pencil.(这是我的铅笔。
)- eraser(橡皮):复数是erasers。
如:My eraser is pink.(我的橡皮是粉色的。
)- crayon(蜡笔):复数crayons。
例如:I like my crayons.(我喜欢我的蜡笔。
)- pen(钢笔):复数pens。
例如:Show me your pen.(给我看看你的钢笔。
)- pencil - box(铅笔盒):复数pencil - boxes。
例如:My pencil - box is big.(我的铅笔盒很大。
)2. 打招呼用语相关单词。
- book(书):复数books。
可以说I have a new book.(我有一本新书。
)- hello(你好):用于打招呼,比较随意,例如:Hello, Tom.(你好,汤姆。
)- hi(嗨):和hello用法相似,也是打招呼用语,如:Hi, Lily.(嗨,莉莉。
)二、句型部分。
1. 自我介绍及打招呼句型。
- Hello, I'm...(你好,我是……):这是一个简单的自我介绍句型。
例如:Hello, I'm Mike.(你好,我是迈克。
)- Hi, I'm...(嗨,我是……):与上面句型类似。
如:Hi, I'm Sarah.(嗨,我是萨拉。
)- Goodbye!(再见):用于告别,例如:Goodbye, Miss White.(再见,怀特小姐。
)- Bye!(拜拜):和Goodbye用法相同。
如:Bye, John.(拜拜,约翰。
)2. 询问物品句型。
- What's this?(这是什么?):回答可以是It's a...(它是一个……)。
第9章复数原卷版2

第9章 复数【过关测试】一、填空题(本大题共有12题,满分54分,第16题每题4分,第712题每题5分)考生应在答题纸的相应位置直接填写结果.1.(2021·全国高一课时练习)若x 是实数,y 是纯虚数,且(2x -1)+2i =y ,则x ,y 的值为____________.2.(2021·天津南开区·高三一模)i 是虚数单位,复数212i i-+的共轭复数为______. 3.(2021·天津红桥区·高三一模)i 是虚数单位,则复数312i i -=+___________. 4.(2021·陕西西安市·高三月考(理))若a ∈R ,i 为虚数单位,24a i+=,则a =______________________.5.(2021·全国高一课时练习)若复数z 对应的点在直线y =2x 上,且|z |z =____________6.(2021·全国高一课时练习)若复数z 满足34z z i =--,则z =_______.7.(2021·全国高一课时练习)设z 1=x +2i ,z 2=3-yi (x ,y ∈R ),且z 1+z 2=5-6i ,则z 1-z 2=__________8.(2021·全国高三月考(理))1i 12i-+(其中i 是虚数单位)的共轭复数为___________. 9.(2021·全国高二单元测试)复平面内的点A 、B 、C ,A 点对应的复数为2i +,BA 对应的复数为12i +,BC 对应的复数为3i -,则点C 对应的复数为_________.10.(2021·全国高一课时练习)若复数n 满足i i 43iz +=+,则z =_______11.(2021·全国高一课时练习)已知z 1,z 2∈C,|z 1+z 2,|z 1|=2,|z 2|=2,则|z 1z 2|为________. 12.(2020·上海市进才中学高二月考)若(1)(1)z i i +=-,则z =_______. 二、选择题(本大题共有4题,满分20分,每题5分)每题有且只有一个正确选项,考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.13.(2021·江苏高一单元测试)已知复数1z i =+(i 为虚数单位),若+=a bi z ,则2020+=a b ( )A .1-B .0C .1D .214.(2021·江苏盐城市·高三二模)设复数12,z z 在复平面内的对应点关于实轴对称,134,z i +=则12z z =( )A .25B .25-C .724i -D .724i --15.(2021·全国高三月考(理))已知复数z 满足21z -=,则z 的最大值为( )A .1B .2C .3D .416.(2020·上海市进才中学高二月考)在复数范围内(i 为虚数单位),下列命题正确是( )A .2i i >B .若0(,)a bi a bC +=∈,则0a b ; C .若1z R z+∈,则||1z = D .若z z =,则z R ∈ 三、解答题(本大题共有5题,满分76分)解答下列各题必须在答题纸的相应位置写出必要的步骤.17.(2020·上海市进才中学高二月考)已知z C ∈且2||212z z z i -+=+,求z 的值.18.(2021·江苏高一单元测试)如图,已知复平面内平行四边形ABCD 中,点A 对应的复数为1-,AB 对应的复数为2+2i ,BC 对应的复数为44i .(1)求D 点对应的复数;(2)求平行四边形ABCD 的面积.19.(2021·天津市蓟州区擂鼓台中学高一月考)已知复数122,23z i z i =+=-.(1)计算12z z ⋅;(2)求21z z ;(3)若5z =,且复数z 的实部为复数12z z -的虚部,求复数z .20.(2021·全国高一课时练习)实数m 分别为何值时,复数z 2233m m m +-=++(m 2﹣3m ﹣18)i 是(1)实数;(2)虚数;(3)纯虚数.21.(2020·全国高三专题练习)已知复数1212,34z i z i =-=+,i 为虚数单位.(1)若复数12z az +在复平面上对应的点在第四象限,求实数a 的取值范围;(2)若12z z z =,求z 的共轭复数z .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题(共20小题,每小题5.0分,共100分)
1.等于______________.
2.计算:1+i+i2+i3+…+i100(i为虚数单位)的结果是 __________.
3.已知是虚数单位,则=________
4.已知复数z=k2-3k+(k2-5k+6)i(k∈Z),且z<0,则k=________.
5.设i为虚数单位,若,则实数满足
6.复平面内点A、B、C对应的复数分别为i、1、4+2i,由A→B→C→D按逆时针顺序作平行四边形ABCD,则||等于_______
7.满足条件|z|=1及=的复数z的集合是
8.是虚数单位,i2013=
9.以3i-的虚部为实部,以3i2+i的实部为虚部的复数是
10.已知i是虚数单位,则i+i2+i3+…+i2011=_______(注:指数从1到2011共2011项连加)
11.若,是虚数单位,且b+(﹣2)i=1+i,则a+b的值为
12.已知z1=m2-3m+m2i,z2=4+(5m+6)i,其中m为实数,若z1-z2=0,则m的值为
13.已知复数,复数满足,则复数.
14.已知复数z1=i,z2=1-3,则复数z=z1-z2在复平面内对应的点Z位于复平面内的第象限
15.若复数z满足z=i(2-z)(i是虚数单位),则z=________.
16.已知复数z满足(3+4i)z=25,则z=
17.i+i2+i3+…+i2011的值是________
18.表示为a+bi(a,b∈R),则a+b=________.
19.对于复数a+bi(a,b∈R),下列结论正确的有个
A.a=0⇔a+bi为纯虚数
B.b=0⇔a+bi为实数
C.a+(b-1)i=3+2i⇔a=3,b=-3
D.-1的平方等于i
20.计算:=______.
二、解答题(共5小题,每小题12.0分,共60分)
21.已知z1=cosα+isinα,z2=cosβ-isinβ且z1-z2=+,求cos(α+β)的值.
22.已知a∈R,问复数z=(a2-2a+4)-(a2-2a+2)i所对应的点在第几象限?复数z对应点的轨迹是什么?
23.已知复数z1=2+3i,z2=a-2+i,若|z1-z2||z1|,求实数a的取值范围.
24.计算:
25.计算:
(1)+2000+;
(2)1+i n+i2n+…+i2000n(n∈N).
答案解析
1.【答案】﹣i
【解析】i2011=i4×502+3=i3=﹣i,
2.【答案】1
【解析】由等比数列的求和公式可得:
1+i+i2+i3+ (i100)
而i101=(i4)25•i=i,
故1
3.【答案】﹣2i
【解析】=﹣i﹣i=﹣2i,
4.【答案】2
【解析】∵z<0,k∈Z,∴∴k=2.
5.【答案】,
【解析】由可得,x+1+(1﹣x)i=y,∴,∴
6.【答案】
【解析】∵=+=====
=2+3i.
∴=.
7.【答案】
【解析】设z=x+yi(x、y∈R),依题意得
,解得
∴z=.
8.【答案】i
【解析】2013=i2012•i=(i2)1006•i=(﹣1)1006•i=i.
9.【答案】3-3i.
【解析】∵3i-的虚部为3,3i2+i的实部为-3,∴所求复数为3-3i.
10.【答案】﹣1
【解析】∵i+i2+i3+i4=i﹣1﹣i+1=0
∴复数z=i+i2+i3+i4+…+i2011=i+i2+i3=﹣1
11.【答案】
【解析】∵b+(a﹣2)i=1+i,
∴,∴a=3,b=1.
∴.
12.【答案】-1
【解析】z1-z2=(m2-3m+m2i)-[4+(5m+6)i]
=(m2-3m-4)+(m2-5m-6)i=0
∴解得m=-1,
13.【答案】
【解析】,=
14.【答案】一
【解析】∵z1=3+2,z2=1-3,
∴z=z1-z2=3+2-(1-3i)=(3-1)+(2+3)i=2+5i.
∴点Z位于复平面内的第一象限.
15.【答案】1+
【解析】本题主要考查复数的运算.
∵z=i(2-z),∴z==1+i.
16.【答案】3﹣4i
【解析】∵复数z满足(3+4i)z=25,则z====3﹣4i,
17.【答案】﹣1
【解析】i+i2+i3+…+i2011=502×(i+i2+i3+i4)+i+i2+i3=502×0+i﹣1﹣i=﹣1.
18.【答案】1
【解析】本小题考查复数的除法运算.
∵==i,∴a=0,b=1.
因此a+b=1.
19.【答案】1
【解析】a=0且b≠0时,a+bi为纯虚数,A错误,B正确.a+(b-1)i=3+2i⇒a=3,b=3,C 错误.(-1)2=1,D错误.
20.【答案】16i
【解析】原式=
=(2-5+3)+(7+13-4)i=16i.
21.【答案】
【解析】∵z1=cosα+isinα,z2=cosβ-isinβ
∴z1-z2=(cosα-cosβ)+i(sinα+sinβ)=+i
∴
①2+②2得2-2cos(α+β)=1
即cos(α+β)=.
22.【答案】y=-x+2 (x3)
【解析】由a2-2a+4=(a-1)2+3≥3,-(a2-2a+2)=-(a-1)2-1≤-1得z的实部为正数,虚部为负数.
∴复数z的对应点在第四象限.
设z=x+yi(x、y∈R),则
消去a2-2a得y=-x+2 (x3),
∴复数z对应点的轨迹是一条射线,其方程为y=-x+2 (x3).
23.【答案】的取值范围为(1,7)
【解析】z1-z2=2+3-[(a-2)+i]=[2-(a-2)]+(3-1)=(4-a)+2i 由|z1-z2|<|z1|得
∴
,∴(4-)2,∴1<<7
∴的取值范围为(1,7).
24.【答案】
【解析】解法1:
解法2:
25.【答案】(1)+i(2) 1
【解析】(1)原式=+(-i)100+
=i+1++i=+i.
(2)当n=4k(k∈N)时,原式=1+1+…+1=2001.当n≠4k(k∈N)时,
原式====1.。
