材料力学7—应力状态分析
材料力学第7章应力状态

y
2
2 xy
m m
ax in
m
ax
2
m
in
极值切应力等于极值正应力差的一半。
§7.2 平面应力状态分析的解析法
三、极值切应力和主平面夹角
注意到 则 所以
tan
2 0
2 xy x
y
tan
21
x 2 xy
y
tan
20
1
tan 21
§7.2 平面应力状态分析的解析法
7.2.3 极值切应力及其作用面 一、极值切应力方位角
d 0 d
( x y ) cos 2 2 xy sin 2 0
得
tan
21
x 2 xy
y
二、最大、最小切应力
m m
ax
in
x
2
x
y
2
sin 2
xy cos 2
§7.2 平面应力状态分析的解析法
7.2.2 主应力 主方向 一、主应力
正应力是求极值
d d
x
y
2
(2sin 2 ) xy(2cos2 ) 0
得极值条件为
x
2
y
sin
2
xy
cos
2
0
(1) 极值正应力所在的斜面,恰好是切应力等于零的
平面,即主平面。
(2) 极值正应力就是主应力。
§7.2 平面应力状态分析的解析法
材料力学第七章应力状态和强度理论

x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y
x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2
x
y
2
4 2 xy
x
yx xy x
y
R c
x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2
40
x y
2 0.431MPa
sin( 80 ) xy cos(80 )
C
C
C
例题3:已知梁上的M、Q,试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q = 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa
材料力学 第07章 应力状态分析与强度理论

sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时,导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= -txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心,CD(CD') 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx- sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力
材料力学应力状态分析

材料力学应力状态分析材料力学是研究物质内部力学性质和行为的学科,其中应力状态分析是材料力学中的重要内容之一。
应力状态分析是指对材料内部受力情况进行分析和研究,以揭示材料在外力作用下的应力分布规律和应力状态特征,为工程设计和材料选用提供依据。
本文将从应力状态的基本概念、分类和分析方法等方面展开讨论。
首先,我们来介绍一下应力状态的基本概念。
应力是指单位面积上的力,是描述物体内部受力情况的物理量。
在材料力学中,通常将应力分为正应力和剪应力两种基本类型。
正应力是指垂直于截面的应力,而剪应力是指平行于截面的应力。
在实际工程中,材料往往同时受到多种应力的作用,因此需要对应力状态进行综合分析。
其次,我们将对应力状态进行分类。
根据应力的作用方向和大小,可以将应力状态分为拉应力状态、压应力状态和剪应力状态三种基本类型。
拉应力状态是指材料内部受到拉力作用的状态,压应力状态是指材料内部受到压力作用的状态,而剪应力状态是指材料内部受到剪切力作用的状态。
这三种应力状态在工程实践中都具有重要的意义,需要我们进行深入的分析和研究。
接下来,我们将介绍应力状态分析的方法。
应力状态分析的方法有很多种,常用的有应力分析法、应变分析法和能量方法等。
应力分析法是通过应力分布的计算和分析来揭示应力状态的特征,应变分析法则是通过应变分布的计算和分析来揭示应力状态的特征,而能量方法则是通过能量原理和平衡条件来揭示应力状态的特征。
这些方法各有特点,可以根据具体情况选择合适的方法进行分析。
最后,我们需要注意的是,在进行应力状态分析时,需要考虑材料的本构关系、边界条件和载荷情况等因素,以确保分析结果的准确性和可靠性。
同时,还需要注意应力状态分析的结果对工程实践的指导意义,以便更好地指导工程设计和材料选用。
总之,材料力学应力状态分析是一个复杂而重要的课题,需要我们进行深入的研究和分析。
只有深入理解应力状态的特征和规律,才能更好地指导工程实践,为实际工程问题的解决提供科学依据。
材料力学-应力状态分析
+
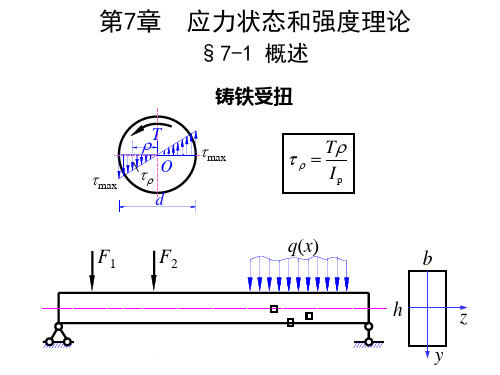
σ x σ y
2
cos 2α τ x sin 2α
sin 2α + τ x cos 2α
注意: 的正负号, 注意:1)σx 、σy 、τx 和 α的正负号, 2) 公式中的切应力是τx ,而非τy, 而非 的正负号。 3) 计算出的σα和τα 的正负号。
τα τ α>0
τα τ α<0
图示圆轴中, 已知圆轴直径d=100mm, 轴向拉 例 : 图示圆轴中 , 已知圆轴直径 , 力 F=500kN,外力矩Me=7kNm。求 C点α = 30°截 , 外力矩 。 点 ° 面上的应力。 面上的应力。 y
σy
τ
D
x
τx τy
σx
o A2
C
A1
σ
D
y
σ1 =
σ x +σ y
2
σ x +σ y + 2
2 +τ x
2
2
σ2 =
σ x +σ y
2
σ x +σ y 2 +τ x 2
σy
τ
D
x
τx τy
σx
o A2
2α0
C
A1
σ
D
y
2τ x 2α 0 = arctan σ x σ y
σ x σ y R= 2
+τ x2
2
σ x +σ y σ α 2
σy
σ x σ y 2 2 + τα = +τ x 2 τ
2 2
D
x
τx τy
σx
o
C D
y
σ
50MPa
材料力学第07章应力状态与应变状态分析

以上由单元体公式
应力圆(原变换)
下面寻求: 由应力圆
单元体公式(逆变换)
只有这样,应力圆才能与公式等价
换句话,单元体与应力圆是否有一一对应关系?
为什么说有这种对应关系?
DE R sin[180o ( 2 20 )] R sin( 2 20 )
( R cos 20 ) sin 2 ( R cos 20 )cos 2
2
cos2
xy
sin 2
同理:
x
y
2
sin 2
xy
cos2
n
Ox
图2
二、极值应力
令:d
d
0
x
y
sin202 xycos200
由此得两个驻点:
01、(
01
2
)和两个极值:
tg20
2 xy x
y
y
mm
ax in
x
y ±(x
2
y
2
)2
2 xy
0 0极值正应力就是主应力 !
y
O
x
七、主单元体、主平面、主应力:
y
y
主单元体(Principal bidy):
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane):
剪应力为零的截面。 x
主应力(Principal Stress ):
主平面上的正应力。
1
主应力排列规定:按代数值大小,
1 2 3
三向应力状态( Three—Dimensional State of Stress): 三个主应力都不为零的应力状态。
A
材料力学 第七章 应力状态和强度理论

y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定: 1 2 3 (按代数值)
§7-3 空间应力状态
与任一截面相对应 的点,或位于应力 圆上,或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正,顺时针转为负。
tg 2a 0
2 x x
y
在主值区间,2a0有两个解,与此对应的a0也有两个解,其中落
在剪应力箭头所指象限内的解为真解,另一解舍掉。
三、应力圆
由解析法知,任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1)轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2)纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律-叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量,应用公式解题时,首先应写清已 知条件。
材料力学-7-应力状态分析

7.1 应力状态的基本概念
y
例题2 1
l
4
z
S
2 3
x
S平面
FP
a
求:取S截面上的一些点的微元,并确定其各个面上 的应力。(忽略剪力影响)
这表明:拉杆的斜截面上存在切应力。
7.1 应力状态的基本概念
受扭之前,圆轴表面为正圆。
Mx Mx
受扭后,变为一斜置椭圆,长轴方向伸长,短轴 方向缩短。这是为什么?
这表明,轴扭转时,其斜截面上存在着正 应力。
7.1 应力状态的基本概念 根据微元的局部平衡
x
n
x'y'
x'
x
x
2 x- y
2
+
cos2q- xy sin 2q
sin 2q xy cos2q
7.2 平面应力状态任意方向面上的应力 ——解析法 例题 3
分析轴向拉伸杆件的最大切应力的作用面, 说明低碳钢拉伸时发生屈服的主要原因。
铸铁拉伸实验
低碳钢拉伸实验
韧性材料拉伸时为什么会出现滑移线?
7.2 平面应力状态任意方向面上的应力 ——解析法
F 0
q dA x dAcosq sinq
xy dAcosq cosq yx dAsinq sinq y dAsinq sinq 0
ζx
q
q
xy
x
q
q
dA
材料力学第七章

若应力状态由主应力表示,并且在max 0 和 min 0 的情况下,则式(7-7) 成为
max min
max
min
2
1 3
2
进一步讨论,由式(7-4)和式(7-6)可知
tan
21
1 tan 20
上式表明1 与 0 之间有如下关系:
1
0
4
可见,切应力取得极值的平面与主平面之间的夹角为 45 。
若三个主应力中,只有一个主应力不等于零,这样的应力状态称为 单向应力状态。若三个主应力中有两个不等于零,称为二向应力状态或 平面应力状态。若三个主应力皆不为零,称为三向应力状态或空间应力 状态。
第二节 平面应力状态分析——解析法
一、斜截面上的应力
图 7-1 所示为平面应力状态的最一般情况。已知 x , y , xy 和 yx 。现 在研究图中虚线所示任一斜截面上的应力,设截面上外法向 n 与 x 轴的夹角 为 。
令 d /d 0 ,由式(7-1)可得
x
2
y
sin
2
xy
cos 2
0
解得
(7-3)
tan 20
2 xy x y
通过运算,可以得到斜截面上正应力的极值为
(7-4)
max min
x
y 2
x
2
y
2
2 xy
(7-5)
由式(7-4)可知, 取得极值的角0 有两个,二者相差 90 ,即最大正应 力 max 和最小正应力 min ,二者分别作用在两个相互垂直的截面上。当 0 , 取得极值时,该斜截面上的切应力 0 ,即正应力就是主应力。
(a)
(b) 图7-6
例 7-4 悬臂梁受力如图 7-7(a)所示。试求截面 n n 上 A 点处的主应力 大小和方向,并按主平面画出单元体。
材料力学第七章知识点总结

规律,确定出最大应力,从而全面考虑构件破坏的原因,建 立适当的强度条件。
材料力学
3、一点的应力状态的描述
研究一点的应力状态,可对一个 包围该点的微小正六面体——单 元体进行分析
在单元体各面上标上应力 各边边长 dx , dy , dz
——应力单元体
三、几个对应关系
点面对应——应力圆上某一点的坐标值对应着单元体某一截面
上的正应力和切应力;
y
σy
n
τ
H (σα ,τα )
τ yxHτ xy来自αxσx
(σy ,Dτyx)
2α A (σx ,τxy)
c
σ
σx +σ y
2
转向对应——半径旋转方向与截面法线的旋转方向一致; 二倍角对应——半径转过的角度是截面法线旋转角度的两倍。
α =α0
=
−2⎢⎡σ x
⎣
−σ y
2
sin 2α0
+τ xy
cos
2α
0
⎤ ⎥
⎦
=0
=
−2τ α 0
τα0 = 0
tg
2α 0
=
− 2τ xy σx −σ y
可以确定出两个相互垂直的平面——主平面,分别为
最大正应力和最小正应力所在平面。
主平面的方位
(α0 ; α0′ = α0 ± 900 )
主应力的大小
材料力学
四、在应力圆上标出极值应力
τ
τ max
x
R
O σ min
2α12α0A(σx ,τxy)
c
σ
σ
max
(σy ,τyx) D
材料力学课件第7章 应力状态分析
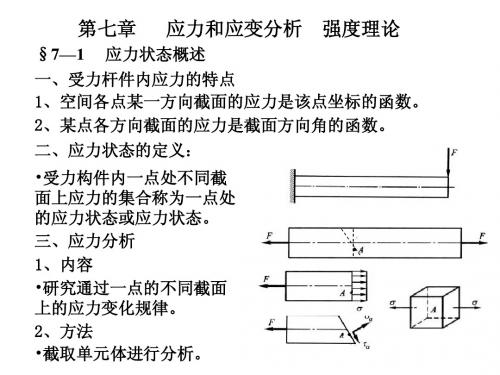
2
(2)主应力值计算 ) 方法一: 方法一: σ x +σ y σ x −σ y + cos 2α 0 − τ xy sin 2α 0 σ α =
2 2 0 σ x +σ y σ x −σ y π π σ = + cos 2 α 0 + − τ xy sin 2 α 0 + α0 + π 2 2 2 2 2
2τ xy
σ x −σ y
2τ xy 1 可取: 可取: α 0 = arctan − σ −σ 2 x y
1 2τ xy , arctan − σ −σ x y 2
π + 2来自3、主应力: 、主应力: (1)性质: )性质: ①主应力为各截面上正应力的极值。 主应力为各截面上正应力的极值。
∗ FS Sz τ= bIz
五、主平面、主应力 主平面、 1、主平面 、 •τ= 0的截面 的截面; 的截面 •过一点有三个相 过一点有三个相 互垂直的主平面. 互垂直的主平面 2、主应力 、 •主平面上的正应力 主平面上的正应力; 主平面上的正应力 •表示符号 1 、σ2、σ3( σ1 ≥σ2≥σ3 ) 。 表示符号σ 表示符号 应力状态分类: 六、应力状态分类: 1、单向应力状态: 只有一个主应力不为零。 、单向应力状态: 只有一个主应力不为零。 •可用平面图形表示应力状态。 可用平面图形表示应力状态。 可用平面图形表示应力状态 2、二向(平面)应力状态:两个主应力不为零。 、二向(平面)应力状态:两个主应力不为零。 •可用平面图形表示应力状态。 可用平面图形表示应力状态。 可用平面图形表示应力状态 3、三向应力状态 :三个主应力都不为零。 三个主应力都不为零。 、 4、简单应力状态:单向应力状态。 、简单应力状态:单向应力状态。 5、复杂应力状态:二向和三向应力状态。 、复杂应力状态:二向和三向应力状态。
材料力学 第七章 应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2
cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2
x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
(1)求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下(只就主应力状态说明) 有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为:
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2
07应力应变分析--材料力学(刘鸿文)

x
切应力以企图使微体沿顺时 针方向旋转者为正; 倾角a :自轴x开始逆时针
y
转向为正,反之为负。
2013-8-7
19
n
x
a
xy yx
Fn 0
Ft 0
a y
a
t
a
dA
dAsina
adA +(xy dA cosa)sina-(x dAcosa)cosa+ (yxdA sina)cos a-(ydA sina)sina=0
a 1.33MPa
max 42.4MPa
a 0 31.72
min 2.4MPa
a 0 90 121.7224
max 42.4MPa
a 0 31.72
得到:
min 2.4MPa
a 0 90 121.72
1
x
a0
3
1 42.4MPa
y
y
yx
yx
xy
x
x
y
2013-8-7
xy
x
纯剪应力状态 ( Shearing State of Stresses )
9
三向应力状态:三个主应力都不为零; 也称空间应力状态( Three-Dimensional State of Stresses )
yz zy
y yx
n
1 3
③主应力大小:
yx
x
a xy
n
x
max
min
1 1 2 ( x y ) ( x y ) 2 4 xy 2 2
y
④由max、、min作用方位(与两个a0如何对应) ⑥
材料力学第七章

x y
2
cos 2 x sin 2
x y
2
sin 2 x cos 2
补充例 题1
T
图示圆轴中,已知:圆轴直径d=100mm, 轴向拉 力F=500kN,外力矩Me=7kN· m。 求C点 =30°截面上的应力。
y T
y
F x
F
C
x
第7章
应力状态和强度理论
§7-1 概 述
低 碳 钢 拉 伸 试 验
铸 铁 拉 伸 试 验
低 碳 钢 扭 转 试 验
铸 铁 扭 转 试 验
1、一点处的应力状态
构件内一点处各截面方向上的应力的情况,称 为该点的应力状态。可由围绕该点的一个单元体面 上的应力表示。
目的:通过应力状态分析求出该点处的 max 、 max 及 其作用面,从而更好地进行强度分析。
30
在二向应力状态下,任意两个垂直面上,其σ的和为一常数。
分析轴向拉伸杆件的最大切应力的作用面,说 补充例 明低碳钢拉伸时发生屈服的主要原因。 题3
低碳钢拉伸时,其上任意一点都是单向应力状态。
x
x y
2
x y
2
cos 2 x sin 2
x
单元体如何取? 在研究点的周围,取一个由三对互相垂直的平 面构成的六面体,该六面体的边长分别为无穷小量 dx、dy和dz,如下图所示。
y
dz dx dy x
z
单元体每个面上应力均布;每对相互平行面上的 性质相同的应力大小相等;可用截面法求任一截面上 的应力。
根据单元体的局部平衡:
y
n
y
材料力学第七章应力状态分析

sin 2α + τ xy cos 2α
(**)
(*) 2 + (**) 2
(σ α −
σ x +σ y
2
) + (τ α ) = (
2 2
σ x −σ y
2
2 ) 2 + τ xy
(7 - 6)
In a given problem, σx, σy, τxy are the three constants, σα,, τα are the variables. This equation is an expression for a circle of radius
σ x −α y
2
cos 2α − τ xy sin 2α
(7-1)
τα =
sin 2α + τ xy cos 2α
3. Principle Stresses in Two-dimensional Problems To find the plane for a maximum or a minimum normal stress, let σ x −α y dσ α = −2[ sin 2α + τ xy cos 2α ] = 0 = −2τ α 2 dα 2τ xy tg 2α1 = − σ x −σ y
σ'=
σ x +σ y
(7 - 5)
∴τ max = ±
min
σ1 − σ 2
2
Example 7-1 For the state of stress shown in the figure, (a) find the stresses acting on the inclined plane with θ=-22.5°; (b) find the principle stresses and shown their sense on a properly oriented element; and (c) find the maximum shear stresses with the associated normal stresses and show the results on a properly oriented element. Solution: For original state of stress σx=3 Mpa σy=1 MPa τxy= -2 Mpa (a) From Eq.(7-1)
材料力学——应力分析

,则α1
405(τx0) 405(τx0)
7-2 二向应力状态分析--解析法
例题1:一点处的平面应力状态如图所示。
已知 x 60MP,a txy 30MPa, y 40MP,a 30。
试求(1) 斜面上的应力; (2)主应力、主平面; (3)绘出主应力单元体。
y t xy
x
目录
7-2 二向应力状态分析--解析法
t
ty(xdsAin)co sy(dsAin)sin0
y
Ft 0
td Atx(ydc Ao )sco sx(dc Ao )ssin ty(xdsAin)siny(dsAin)co s0
目录
7-2 二向应力状态分析--解析法
{ 利用三角函数公式
co2 s 1(1co2s)
2
sin 21(1co2s)
d d (x y)si2 n2 txc y o 2 s
设α=α0 时,上式值为零,即
t (xy )s2 i0 n 2xc y 2 o 0 s 0
2 (x σ 2 σ y) si0n τ x 2 c yα o0s 2 2α α 0 τ 0
即α=α0 时,切应力为零 目录
2
2 s ic n o s si2 n
并注意到 t yx t xy 化简得
t 1
1
2 (xy) 2 (xy)c2 o s xs y 2 in
t1 2(xy)si2 ntxy co 2s
目录
7-2 二向应力状态分析--解析法
3. 正应力极值和方向
确定正应力极值
t 1 2 (xy ) 1 2 (xy )c2 o s xs y 2 in
(2)主平面的位置
tg2α0
2τ xy σx σy
材料力学-07-应力分析和强度理论

§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法: 解析法
1.斜截面上的应力 1.斜截面上的应力
y
σx
a
τ yx
τ xy
σx α
τa
n
τ xy
σa
dA
x
σy
n
τ yx
σy
t
t
∑F = 0
∑F =0
13
§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法: 解析法
tan 2α0 = − 2τ xy
σ x −σ y
由上式可以确定出两个相互垂直的平面, 由上式可以确定出两个相互垂直的平面,分别 为最大正应力和最小正应力所在平面。 为最大正应力和最小正应力所在平面。 所以,最大和最小正应力分别为: 所以,最大和最小正应力分别为:
σmax = σ x +σ y
2 1 + 2 − 1 2
单元体
单元体——构件内的点的代表物, 单元体——构件内的点的代表物,是包围被研究点的 ——构件内的点的代表物 无限小的几何体。 常用的是正六面体。 无限小的几何体。 常用的是正六面体。 单元体的性质—— 平行面上,应力均布; 单元体的性质——1) 平行面上,应力均布; —— 2) 平行面上,应力相等。 平行面上,应力相等。
2 2
σy
τ xy
α
60 − 40 60 + 40 = + cos(−60o ) + 30 sin(−60o ) 2 2
σx
= 9.02 MPa
τα =
σ x −σ y
2 60 + 40 = sin(−60o ) − 30 cos(−60o ) 2
材料力学第七章应力应变分析

x
y
2
x
2
y
cos 2
xy sin 2
x
y
2
sin 2
xy cos 2
1、最大正应力的方位
令
d d
2[
x
y sin 2
2
xy cos 2 ] 0
tg 2 0
2 xy x
y
0 0
90
0 和 0+90°确定两个互相垂直的平面,一个是最大正应 力所在的平面,另一个是最小正应力所在的平面.
的方位.
m
m a
A
l
解: 把从A点处截取的单元体放大如图
x 70, y 0, xy 50
A
tan 20
2 xy x y
2 50 1.429
1
3
(70) 0
0
A
x
0
27.5 62.5
3
1
因为 x < y ,所以 0= 27.5° 与 min 对应
max min
x
2
y
(
x
2
y )2
三、应力状态的分类
1、空间应力状态
三个主应力1 、2 、3 均不等于零
2、平面应力状态
三个主应力1 、2 、3 中有两个不等于零
3、单向应力状态
三个主应力 1 、2 、3 中只有一个不等于零
2 3
2
1
1
1
1
1
3 2
2
1
例题 1 画出如图所示梁S截面的应力状态单元体.
F
5
S平面
4
3
l/2
2
l/2 1
任意一对平行平面上的应力相等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p =n σ
T T
p
τa
y σx α
n
切应力分量
τxy τyx σy
∆A
τα = p t = n σt
T
T
σ x τ xy − sinα τ α = (cosα sinα ) ⋅ ⋅ τ yx σ y cosα 1 τ α = − (σ x − σ y ) sin2α + τ xy cos2α 2
垂直于截面的应力称为 “ 正应力” 正应力”
(Normal Stress); Stress);
位于截面内的应力称为 “ 切应力” 切应力”
(Shearing
Stress).
应力状态概念
P1 ∆FQy ∆A y
若干概念和定义
应力的矢量表示
∆FR
∆FN x
σ x = σ ,τ = [τ xy τ xz ]
应力状态的概念及其描述
应力的三个重要概念 应力的点的概念; 应力的点的概念; 应力的面的概念; 应力的面的概念; 应力状态的概念. 应力状态的概念.
应力状态的概念及其描述
FQ FN x
M z
横截面上正应力分析和切应力分析 的结果表明: 的结果表明:同一面上不同点的应力 各不相同, 各不相同,此即应力的点的概念。
( px py ) = (nx
T
σx τxy τyx
∆A α px ∆A ∆A ny∆A ny∆A
σy
x
σ x τ xy ny ) τ yx σ y
T
p =n σ
px = nxσx + nyτ yx py = nxτ xy + nyσ y
正应力分量由公式可得:
p n
2
cos2 −τxy sin 2 θ θ
sin 2 +τxy cos2 θ θ
σx′= 0
τx′y′= 0
0=
σx −100 σx+ 100
2 + 2
cos(2×30°) -τxysin 2×30°) (
0=
0+100 sin 2×30°) +τxycos(2×30°) ( 2
The First Kind of Exercise: The Analysis of the Stress-State
y
σx
θ θ
τ x'y'
x´
τ xy
σx'
τ yx
dA dA
σy
平面应力状态分析
平衡原理的应用
∑F
x xy
y′
=0
−τx´y ´ dA +σ (dA cos θ ) sin θ +τ (dA cos θ ) cos θ −τ (dA sin θ ) sin θ −σ (dA sin θ ) cos θ = 0
应力状态的概念及其描述
τ x'y'
σx'
τ x'y'
τ xy
τ yx
σx'
σx
微元平衡分析结果表明:即使同一 微元平衡分析结果表明: 点不同方向面上的应力也是各不相同 的,此即应力的面的概念。
应力状态的概念及其描述
应 力
指明
1.哪一个面上? 哪一点? 2.哪一点? 哪个方向面?
过一点不同方向面上应力的集合,称 过一点不同方向面上应力的集合, 之为这一点的 应力状态(State of Point)。 the Stresses of a Given Point)。
Problem 3
0=
σx −100 σx+ 100
2 + 2
cos(2×30°) -τxysin 2×30°) (
0+100 0= sin( 2×30°) +τxycos(2×30°) 2
σx = −33.3M Pa
τxy = − yx = −57.7M τ Pa
2、坐标变换,平面应力分析 应力分析
1
示例二 z
4 2 3 S平面
x
应力状态的概念及其描述
y
示例二
FQy
1
1
τ1 =
Mz σx1 = W z
z
4
Mx Wp
4 2 3
Mz
Mx τ3 = Wp
x
Mx
Mx τ3 = W p
3
Mz σx = − W z
3
平面应力状态分析
正负号规则
正 负 号 规 则
σx
正 应 力
σx
σx
拉为正
σx
压为负
平面应力状态分析
τ x'y'
σx'
σx
σx
拉 中 有 切
应力状态的概念及其描述
y'
根据微元的局部平衡
τ yx
x'
τ xy τ xy
τ x'y'
τ yx
σx'
切 中 有 拉
应力状态的概念及其描述
重要结论
不仅横截面上存在应力, 不仅横截面上存在应力 , 斜截 面上也存在应力; 面上也存在应力 ; 不仅要研究横 截面上的应力, 截面上的应力 , 而且也要研究斜 截面上的应力。 截面上的应力。
Problem 3
y´
y x´
30°
Solution:Us the coordinate : conversion equation:
σx′ =
x
σx +σy σx −σy
2 +
2 Because the section AC is free surface, we have
τx′y′ =
σx −σy
2.1. 应力的符号规定
在法线方向沿坐标轴 正向的微元面上,与坐标 正向相同的应力分量为正; 反之为负。 在法线方向沿坐标轴负向 的微元面上,与坐标正向 相反的应力分量为正。反 之为负。 拉应力为正,压应力为负。
y
x
2.2. 数学准备
α n x cos 单位矢量 n:n = = n y sinα 矢量 a 在 n 方向上的投影
新疆大学机械工程学院力学教研室
材料力学
王 春 耀、闵 磊
授课教案—7 —应力状态分析
第8章 应力状态分析
1、应力状态概念,应力张量 应力状态概念, 2、坐标变换,平面应力分析 坐标变换, 3、主应力计算、最大切应力 主应力计算、 4、广义虎克定律 5、应变比能
应力状态概念
正应力和切应力
若干概念和定义
sin2α ′ = 2τ xy
σ x −σ y
2
tg2α ′ =
2τ xy
σ x −σ y
σ α ′ = (σ x + σ y ) ±
1 2
σ x −σ y 2
2 + τ xy
正负号规则
正负号规则
τ x'y'
τ xy
τ yx
切
应 力
使微元或其 局部顺时针方 向转动为正; 向转动为正; 反之为负。 反之为负。
平面应力状态分析
正负号规则
正负号规则
θ 角
由 x 轴正向 反时针转到 x ‘轴 正向者为正; 正向者为正;反 之为负。 之为负。
y' y
θ
x'
x
平面应力状态分析
平衡原理的应用
y n α x
an = ax cosα + ay sinα
= (ax nx ay ) ny
a
n
=a n
T
− n y n x
t
an
y
与 n 垂直方向上的单位矢量 t
t x t= = t y
− sin α cos α =
π/2 α
Problem 3
Problem: The element is shown in the figure blow and AC is a free surface (no stress in it).
Determine : x and τxy. :σ
The First Kind of Exercise: The Analysis of the Stress-State
x
2.4 主应力与主方向
1. 正应力的极值
σ α = (σ x + σ y ) + (σ x − σ y )cos2α + τ xysin2α
dσα =0 dα
cos2α ′
1 2
1 2
使法向应力取极值的角度应满足
1 (σ x − σ y ) ⋅ ( −2sin2α ′) + τ xy ( 2cos2α ′) = 0 2
特例
平 面 应 力 状 态
特例
单向应力状态
纯剪应力状态
应力状态的概念及其描述 铸 铁 低碳钢
韧性材料拉伸时为什么会出现 滑移线? 滑移线?
应力状态的概念及其描述 低碳钢 铸 铁
为什么脆性材料扭转时沿45 为什么脆性材料扭转时沿45º螺 45º 旋面断开? 旋面断开?
y'
σx
根据微元的局部平衡
x'
θ sin2 +τ xy cos2 θ
或写成
1 1 σ θ = (σ x + σ y ) + (σ x − σ y ) ⋅ cos2θ −τ xysin2θ 2 2 1 τ θ = (σ x − σ y ) ⋅ sin2θ + τ xy cos2θ 2
The First Kind of Exercise: The Analysis of the Stress-State
