1-例题和习题
第一章 行列式• 要点和公式 •1 全排列及其逆序数、对换排列的逆序数=各元素的逆序数之和.(一个元素的逆序数是指排在其前面并且大于它的元素个数) n 个元素所有排列的种数P n =n !，其中奇、偶排列各占一半。
一次对换改变排列的奇偶性。
2 行列式n 阶行列式的定义： 或 或 行列式的性质： ⑴ D=DT⑵ ⎪⎪⎪⎩⎪⎪⎪⎨⎧⇒++⨯⇒⨯⨯⇒↔↔不变符号外面的公因子可提到行列式列行列式某行或反号D kc c kr r k D k c k r D c c r r j i j i i i j i j i )( ])(,[ )( )(⑶ 以下都是行列式等于零的充分条件：①两行(列)完全相同； ②某一行(列)的元素全为零； ③两(列)的元素对应成比例.⑷ 若行列式的某一行(列)元素都是两数之和，则行列式可分解为两个行列式之和. 行列式按行(列)展开法则ij nk jkik D A a δ=∑=1或ij nk kj ki D A a δ=∑=1(i =1,2,…,n )(其中⎩⎨⎧≠==ji ji ij ,0 ,1δ，D 是原行列式的值)重要的特殊行列式⑴ 对角行列式 / 上三角行列式 / 下三角行列式n nλλλλλλΛO2121= (1-1)nn nnn n nn n na a a a a a a a a a a a a a a ΛΛO M M M OΛΛ22112122121122212111== (1-2) ⑵n n n nλλλλλλΛN212)1(21)1(--=(1-3)11,212)1(1,121,2111,22111,111)1(n n n n n nnn n n nn nn n n n a aa a a a a a a a a a a a a ΛΛM M N N M ΛΛ-------==(1-4)⑶ 分块对角行列式 / 分块上三角行列式 / 分块下三角行列式B A B OA B O A B O O A ⋅===** (1-5) ⑷B A B AOO B A O B A O km ⋅-===)1(** (1-6) 以上两式中，B A 、分别是k 阶、m 阶行列式.⑸ 范德蒙德行列式∏≤<≤-----=nni j j i n nn n n n n x x x x x x x x x x x x x x 111312112232221321)(1111ΛΛΛΛΛΛΛΛΛ (1-7)3 克拉默法则和有关定理克拉默法则: 对于n 个变量n 个方程的线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++.22112222212111212111n n nn n n n n n n b x a x a x a b x a x a x a b x a x a x a ΛΛΛΛΛΛΛΛΛΛΛΛΛΛ 简记为i n j j ij b x a =∑=1 (i =1,2,…,n )若系数行列式D ≠0，则方程组有唯一解：DD x j j =(i =1,2,…,n )其中D j 是用方程组的常数项b 1, b 2, …, b n 替换系数行列式D 的第j 列得到的行列式。
定理：对于非齐次．．．线性方程组 i nj j ij b x a =∑=1(i =1,2,…,n )⑴ 方程组有唯一解 ⇔ 系数行列式D ≠0； ⑵ (等价命题) 方程组无解或有多组解 ⇔ D =0. 定理：对于齐次．．线性方程组 01=∑=nj j ij x a (i =1,2,…,n )⑴ 方程组只有零解⇔系数行列式D ≠0；⑵ (等价命题) 方程组(除零解外)有非零解 ⇔ D =0.∑-np p p t na a a Λ2121)1(∑+-nn qp q p q p t t a a a Λ221121)1(∑-n np p p ta a a Λ2121)1(• 典型题型 •1 全排列的逆序数、奇偶性计算n 元排列的逆序数的常用方法是：算出排列中每个元素前面比它大的元素的个数(即每个元素的逆序数)，这些元素的逆序数之和就是所求排列的逆序数.判断排列的奇偶性的常用方法有两种：方法一：算出排列的逆序数，若逆序数为奇数，则为奇排列；若逆序数为偶数，则为偶排列；方法二：将所给排列进行对换，使其变成标准排列(偶排列)，若所需对换次数为奇数，则为奇排列；若所需对换次数为偶数，则为偶排列. (因为每次对换都会改变排列的奇偶性)[练习1] 求排列13…(2n -1)24…(2n ) 的逆序数, 并讨论奇偶性. [答案] t =n (n -1)/2当n =4k ,4k +1时，为偶排列；n =4k +2, 4k +3时，为奇排列.2 求行列式中的项[练习2] 写出四阶行列式中所有带负号且包含a 23的项. [答案] -a 11a 23a 32a 44 -a 12a 23a 34a 41 -a 14a 23a 32a 41[练习3] 对例6中的行列式f (x )，求33)(dx x f d[提示] f (x )是x 的4次多项式，设f (x )=c 0+c 1x +c 2x 2+c 3x 3+c 4x 4，则d 3f (x )/dx 3= 6a 3+24a 4x ，故本题需先求行列式中x 4和x 3的系数. [答案]12144)(33+=x x f x d[练习4] 求44434241343332312423222114131211)(a x a a a a a x a a a a a x a a a a a x x f ++++=中x 4、x 3的系数以及常数项。
[提示] 行列式中涉及x 4和x 3的项只有1项，即主对角线上四个元素的乘积(-1)t (1234)))()()((44332211a x a x a x a x ++++，其余的项至多含x 2；而f (x )的常数项就是f (0).[答案] 1, a 11+a 22+a 33+a 44, 44434241343332312423222114131211)0(a a a a a a a a a a a a a a a a f =3 行列式的性质[练习5] 设1212222111211==nn n n nn a a a a aa a a a D ΛΛΛΛΛΛΛ, 则==------111,111,11,1,111,~a a a a a a a a a D n nn n n n n n n n nnΛΛΛΛΛΛΛ … … … ( ) (A) 1 (B) -1 (C) (-1)n (D)2[提示] 将D 左右翻转、再上下翻转(或者, 将D 依副对角线翻转) 可得到D ~，而左右或上下翻转可通过n (n -1)/2次相邻的列(行)对换实现. [答案] (A)4 行列式的计算和证明计算行列式的方法比较灵活，同一行列式可以有多种计算方法；有的行列式计算需要几种方法综合应用. 除了本章介绍的方法，以后还会陆续学习到一些新的方法，平时应注意归纳、整理. 在计算行列式时，首先要仔细考察行列式在构造上的特点，利用行列式的性质对它进行变换后，再考察是否能用常用的几种方法. ⑴ 对角线法则，只适用于二、三阶行列式 ⑵ 利用n 阶行列式的定义利用定义计算行列式是最基本的方法。
“要点和公式”中的公式(1-1)~ (1-4)就是用定义法证明的.[练习6] 用行列式的定义计算nn n 000000001000200020001000ΛΛΛΛΛΛΛΛΛΛΛ-- (n ≥2) [答案] 行列式的n ！项中只有1项不等于0，即!)1()1(2)2)(1(,1,12,21,1]21)2)(1[(n a a a a D n n n n n n n n n n t --------=-=ΛΛ⑶ 利用行列式性质，化为三角形行列式利用性质将行列式化为三角形行列式是最常用的方法之一. “要点和公式”中的公式(1-5)和(1-6)就是用此法证明的.其基本步骤是，利用r i +kr j (c i +kc j )、提取公因子、r i ↔r j (c i ↔c j )等运算，将对角线以下或以上的元素化为零，然后利用公式(1-1)~(1-4)计算出结果.注 对于以上关于 型行列式的例题，它们的翻转、旋转等形式，可循类似的思路进行计算.[练习7] 计算n 阶行列式xxx xx x a a a a D n n n --+=-NNN Λ121[答案]112)1()1(-=-⎪⎪⎭⎫ ⎝⎛+-∑n n i i n n x a x[练习8]. 计算4阶行列式xx x x +-----+---1111111111111111.[提示]利用各行元素之和相等的特点进行计算，或者化为爪型. [答案] 4x .[练习9] 计算(n ≥2)阶行列式)det(ij n a D =, 其中)1,max(+-=j n i a ij , ),,2,1,(n j i Λ= [提示] 依题意，有1111333122311231nnnnnn n n n n n n n n n n D n ΛΛΛΛΛΛΛΛΛΛΛ-------=在副对角线及其上方，各行的对应元素相同. 从第一行开始，前行减后行，即r i -r i +1 (i =1, 2, …, n -1)，可将副对角线以上元素全化为0，即得公式(1-4)的形式. 或者，也可利用副对角线下方相邻列元素相同的特点计算. [答案]n n n ⋅-+-2)2)(1()1(⑷ 分块法若行列式是公式(1-5)和(1-6)所示的分块三角形，或者容易变换成这种形式，则可用分块法计算. 注意公式中的A 和B 必须是“行数=列数”的数表.[练习10] 用分块法计算“练习6”中的行列式.[练习11] 用分块法计算行列式443322110000000x y x y y x y x [提示] 对换第2,3行，再对换第2,3列，然后分块计算 [答案] ))((42423131y y x x y y x x -- ⑸ 拆分法若行列式的某些行(列)为几个数之和，则可以考虑将行列式按这些行(列)拆分为几个行列式之和，前面的例8采用的就是拆分法. 特别是，当每个元素都是两数之和时，行列式可拆分为2n 个行列式之和，在某些情况下，这个2n 个行列式中有很多等于零，那些不等于零的行列式也很容易计算.[练习12] 用拆分法计算nn n n nn n b a b a b a b a ba b a b a b a b a D ---------=ΛΛΛΛΛΛΛ212221212111(n ≥2) [答案] 当n =2时，))((21212b b a a D --=当n ≥3时，D n =0[练习13] 用拆分法计算“练习8”中的行列式.[练习14] 用拆分法解“练习4”.⑹ 降阶展开法 - 行列式按行(列)展开法则利用行列式的性质，将行列式的某行(列)元素尽可能多地化为零，然后将行列式按该行(列)展开，从而变成n -1阶行列式的计算，这称为降阶展开法，也是最常用的计算方法之一.[练习15] 用降阶展开法计算“练习6”中的行列式. [提示] 按最后一行(列)展开.[练习16] 用降阶展开法计算4433221100000000a b a b b a b a[提示] 按第一行(列)展开后分块计算. [答案] (a 2a 3-b 2a 3)(a 1a 4-b 1b 4) ⑺ 递推法当n 阶行列式的结构具有重复性时，可通过按某行(列)展开，得出它的线性递推公式，然后递推出结果.[练习17] 用递推法证明以下n 阶行列式的结论： ① nn aa a a a a a -------111111133221O OOn na a a a a a ΛΛ21211)1(1-+++-=② x a x a x a a x n 111321---+M OO n n n n n a x a x a x a x +++++=---12211Λ ③ 111323211nnb b b a a a b a OM Λ+∑=-++=ni i i b a b a b a 11111)([提示] 这三个行列式按最后一行展开，可得递推公式如下：①21)1(--+-=n n n n n D a D a D ⇒ n n n n a a a D D Λ211)1(-+=- ②n n n a xD D +=-1 ③n n n n b a D D -=-1[练习18] 试用递推法计算“例12-14”中的n 阶行列式.[练习19] 计算n 阶行列式 xyx y x y x y x xy x y x yx yx x y x y x y x y x x ΛΛΛΛΛΛΛΛΛ---+--++-+++(n ≥2) [提示] 方法⑴：采用例25的方法，可得D n =-yD n -1+(x+y )y n-1和D n =yD n -1+(x-y )(-y )n -1；方法⑵：先“r 1-r 2”，“c 1-c 2”，然后按第一行展开，再按第一列展开，可得22-=n n D y D .[答案] n 为偶数时, D n =y n ; n 为奇数时, D n =xy n -1.⑻ 归纳法如果得出的递推公式难以计算，可考虑通过n =1,2,3…的低阶行列式去猜想一般结果，然后结合递推公式用归纳法证明猜想成立. 如果行列式已告诉结果，而要证明与自然数n 有关的结论时，也可考虑用数学归纳法证明.[练习20] 设a ≠b , 用数学归纳法证明：ab b x a a x b xbbba xb baa xb a a a x D nn n ----==)()(ΛΛΛΛΛΛΛΛΛ [提示] 采用例25的方法，得递推公式11)()(---+-=n n n b x a D a x D⑼ 加边法加边法是一种升阶计算的方法：对行列式添加一行一列，构成与D n 相等的n +1阶行列式. 通常，所加的行(列)为 1, 0, …, 0，而所加的列(行)则根据具体情况而定.[练习21] 用加边法计算“例20”和“例21”中的行列式.⑽ 利用范德蒙德行列式法范德蒙德行列式是重要的特殊行列式，要善于识别其变式，得出展开结果.[练习22] 已知0121≠+n n a a a a Λ，计算如下的n +1阶行列式：nn n n n n n n n n n n n n n n n n n n n n nn b b a b a b a a b b a b a b a a b b a b a b a a D 111212111112122222221221111212111111+-++-++-++------+=ΛΛΛΛΛΛΛΛΛ[提示] 对各第1, 2, …, n +1行分别提取n n nn a a a 121,,,+Λ[答案]()∏∏∏+≤≤≤+≤≤≤+=-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛111111 n i j j i i j n i j j j i i n i n i b a b a a b a b a⑾ 析因子法如果行列式中某些元素是x 的多项式，则行列式可作为一个多项式f (x ).若通过某些变换，求出了多项式f (x )的全部互素线性因式(一次因式)，则这些因式的乘积g (x )与行列式多项式f (x )只相差常数乘因子k ，于是，根据多项式恒等的定义，通过比较g (x )和f (x )的某一项系数，可进一步求出k .[练习23] 用析因子法计算xa a a a a x a a a a a x a a a a a x a a a a a x D n n nn n n n n n 13213211211211211----+=ΛΛΛΛΛΛΛΛΛΛΛ [提示] D n +1是x 的n +1次多项式，其n +1个根分别是, , , , ,121∑=-ni i n a a a a Λ[答案] ∏∑==-⋅⎪⎪⎭⎫ ⎝⎛+ni i n i i a x a x 11)( [注] 本题也可以利用行列式各行元素之和相等的特点进行计算.5 和代数余子式有关的计算[练习24] 对“例34”中的行列式，求: 423222126324M M M M +++- [提示] 将余子式变换成代数余子式，可看出所求的和式就是第三列元素与第二列对应元素的代数余子式乘积之和，或者，通过替换行列式的第二列元素进行计算.[答案] 0632463244232221242322212=+-+=+++-A A A A M M M M[练习25] 设nnD n 13121321O M Λ=, 求所有元素的代数余子式之和. [提示] 第一列元素的代数余子式之和就是D n ，而其它各列元素的代数余子式之和皆为0. [答案] n -2[练习26] 设行列式3165424532223335412311444=D , 求: ①232221A A A ++; ②2524A A +.[答案] ① 0; ② 06 克拉默法则⑴ 利用克拉默法则求线性方程组的解克拉默法则的适用条件是：①线性方程组的方程个数与未知数个数相等；②系数行列式不等于零.为了避免在计算中出现分数，可对某些方程乘以适当整数，把原方程组变成系数及常数项都是整数的线性方程组后再求解.例36 用克拉默法则求解:⎪⎪⎩⎪⎪⎨⎧=-+=-+-=+--=+-5534125 23432 543 321421431432x x x x x x x x x x x x解 系数行列式0240534502332014310≠=----=D ，方程组有唯一解.用常数项分别替换系数行列式的各列，得24053550212320443151=------=D ； 48055450123324143502=------=D ；24053451223340145103=---=D ； 24553412023420153104-=-----=D于是，方程组的解为 111==D D x , 222==D D x , 133==D D x , 144-==DDx[练习27] 解线性方程组⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++---111132211232222111321211n n n n n n n n n x a x a x a x x a x a x a x x a x a x a x ΛΛΛΛΛΛΛΛΛΛΛΛ,其中),,2,1, ,( n j i j i a a j i Λ=≠≠[提示] 系数行列式是范德蒙德行列式的转置行列式. [答案] x 1 =1, x 2=x 3=…=x n =0⑵ 已知线性方程组以及解的情况，求方程组的系数的条件练习28 当λ取何值时, 齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=+=+=-=+02002043214131x x x x x x x x λλ有非零解？[提示] 齐次线性方程组有非零解 ⇔ 系数行列式D =0 [答案] 4/1=λ⑶ 克拉默法则的应用[练习 29] 求过点(1,1,2), (3,-2,0), (0,5,-5)三点的平面方程. [提示] 设平面方程为0=+++d cz by ax ，其中a ,b ,c 不全为零[答案]055516291550102312111=-++=--z y x z y x[练习30] 证明: 对平面上的n 个横坐标互不相同的点(x i , y i ) (1≤i ≤n )， 必存在唯一的一个次数不超过n -1的多项式f (x )通过此n 个点.[提示] 设112210)(--++++=n n x a x a x a a x f Λ，然后证明以a 0 , a 1 , a 2 , …, a n -1为未知量的齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++------n n n n n nn n n n yx a x a x a a y x a x a x a a y x a x a x a a 11221021212222101111212110 ΛΛΛΛΛΛΛΛΛΛΛΛΛ 有唯一解.。
自动控制原理例题与习题[1]
![自动控制原理例题与习题[1]](https://360docs-1393072327.cos.ap-beijing.myqcloud.com/11fb309951e79b8968022688.webp)
自动控制原理例题与习题第一章自动控制的一般概念【例1】试述开环控制系统的主要优缺点。
【答】开环控制系统的优点有：1. 1.构造简单，维护容易。
2. 2.成本比相应的死循环系统低。
3. 3.不存在稳定性问题。
4. 4.当输出量难以测量，或者要测量输出量在经济上不允许时，采用开环系统比较合适（例如在洗衣机系统中，要提供一个测量洗衣机输出品质，即衣服的清洁程度的装置，必须花费很大）。
开环控制系统的缺点有：1. 1.扰动和标定尺度的变化将引起误差，从而使系统的输出量偏离希望的数值。
2. 2.为了保持必要的输出品质，需要对标定尺度随时修正。
【例2】图1.1为液位自动控制系统示意图。
在任何情况下，希望液面高度c维持不变，试说明系统工作原理，并画出系统原理方框图。
图1.1 液位自动控制系统示意图【解】系统的控制任务是保持液面高度不变。
水箱是被控对象，水箱液位是被控量，电位器设定电压u r(表征液位的希望值c r)是给定量。
当电位器电刷位于中点位置(对应u r)时，电动机不动，控制阀门有一定的开度、使水箱中流入水量与流出水量相等。
从而液面保持在希望高度c r上。
一旦流入水量或流出水量发生变化，例如当液面升高时，浮子位置也相应升高，通过杠杆作用使电位器电刷从中点位置下移，从而给电动机提供一定的控制电压，驱动电动初通过减速器减小阀门开度，使进入水箱的液体流量减少。
这时，水箱液面下降，浮子位置相应下降，直到电位器电刷回到中点位置，系统重新处于平衡状态，液面恢复给定高度。
反之，若水箱液位下降，则系统会自动增大阀门开度，加大流入水量，使液位升到给定高度c r。
系统原理方框图如图1.2所示。
图1.2 系统原理方框图习题1．题图1-1是一晶体管稳压电源。
试将其画成方块图并说明在该电源里哪些起着测量、放大、执行的作用以及系统里的干扰量和给定量是什么？题图1-12．如题图1-2（a）、（b）所示两水位控制系统，要求(1)画出方块图（包括给定输入量和扰动输入量）；(2)分析工作原理，讨论误差和扰动的关系。
宾语从句总复习经典例题、习题(word)(1)
宾语从句总复习经典例题、习题（word）(1)一、初中英语宾语从句1．— Could you tell me ?一"Rome was not built in a day." You should try to give it enough chances to become strong. A．what I could do to have a good memory B．what I can do to have a good memory C．what could I do to have a good memory D．what can I do to have a good memory【答案】B【解析】句意：——你能告诉我怎样才能有好的记忆力吗？——“罗马不是一天建成的”，你应该试着给它足够的机会变得强大。
考查宾语从句。
宾语从句需用陈述句语序，CD两项都是疑问语序，可排除。
主句的could表示请求，从句用一般现在时，可排除A；根据句意语境，可知选B。
2．—I'd like to know ________ for the party.—I have no idea.A．why did she buy so little foodB．what she has preparedC．whether will she danceD．when is she leaving【答案】B【解析】句意：--我想知道她为晚会做了什么。
—我不知道。
答案A,C,D的语序是疑问语序，不正确。
宾语从句的语序应该是陈述语序。
故选B。
3．"I want to know ." said the boy opening the box.A．what's inside the box B．where the box isC．that there's some candy D．how big is the box【答案】A【解析】句意：“我想知道盒子里边是什么”这个男孩打开盒子说。
基础工程例题及习题集
e 0.1W A 的条件，作用于基底的力矩最大值不能超过下列何值？（注：W 为基础底面的
抵抗矩，A 为基础底面积）。（06 年试题） 3、边长为 3m 的正方形基础，荷载作用点有基础形心沿 x 轴向右偏心 0.6m，则基础底面的
基底压力分布面积最接近于多少？（06 年试题）
例 5------持力层以及软弱下卧层承载力验算(确定基础底面积)
按 3m 计算； 2、土的重度取值问题（加权重度以及地下水的处理）； 3、能够利用理论公式进行计算承载力的条件；
例 3 ------地基承载力的深宽修正
某混合结构基础埋深 1.5m，基础宽度 4m，场地为均质粘土，重度 17.5 kN m3 ，孔隙
比 e 0.8 ，液性指数 IL 0.78 ,地基承载力特征值 fak 190kPa ，则修正后的地基承载力
某轴心受压基础，相应于荷载效应的标准组合上部结构传来的轴向力 Fk 780kN .地质剖
面如下，试确定基础底面积并验算软弱下卧层。
d 1.2m
Fk
15.7kN/m3
Es 2.6MPa
z 2m 第一步：地基承载力修正
18.6kN/m3 Es 10MPa fak 196kN/m2
ห้องสมุดไป่ตู้
2500 ηd=1.6
1、解：持力层承载力验算：
F F1 F2 G 2000 200 486.7 2686.7kN
M 0 M V h F2 a 1000 200 1.3 200 0.62 1383kN.m
e M 0 1383 0.515m 5.2 0.87m
为多少？ 基础宽度大于 3m，埋深大于 0.5m，所以需要对承载力进行修正。
力学题库1(例题与作业)
第一章质点运动学例1、质点沿x轴正向运动，加速度a=-kv，k为常数。
设从原点出发时速度为v0，求运动方程x=x(t)与速度—位移关系v=v(x)。
例2、已知斜抛运动的抛射角为θ，初速度为v0。
求其轨迹方程。
例3、如图，小船在绳子的匀速v0牵引下运动，已知h。
求θ位置时船的速度与加速度大小。
（两种方法）例4、有一轮以匀角速ω旋转，一质点自轮心沿水平轮轴以匀速v0向轮边移动。
求质点的轨迹方程，以及t时刻质点的速度和加速度大小。
*例5、一只狼沿着半径为R的圆形岛边缘按逆时针方向匀速跑动，当狼经过某点时，一只猎犬以相同的速率从岛中心出发追逐狼。
设追逐过程中犬、狼、岛中心始终在一直线上，求猎犬的轨迹和追上狼时的位置。
*例6、（上海高考题改编）下图为平静海面上拖船A、B拖着驳船C运动的示意图。
已知A、B的速度分别沿缆绳CA、CB方向，且A、B、C不共线。
以下说法正确的是（）（多选）（A）C的速度大小可能介于A、B的速度大小之间（B）C的速度一定不小于A、B的速度（C）C的速度方向可能在CA、CB的夹角之外（D）C的速度方向一定在CA、CB的夹角之内**例7、已知点P0(l,0)处有一小船，以长为l的线，拉着小船从原点向上走，小船沿着绳运动，PQ为P点切线，Q点恒在y轴上。
（1）以图中θ为参数，求P点的轨迹方程。
（曳物线）（2）若Q 点以匀速u 向上运动，求θ位置处P 点的加速度。
练习题1、一质点沿x 轴运动，其速度—时间关系为⎪⎭⎫ ⎝⎛+=t t v 6sin 23ππ，式中各量均取国际单位。
已知当t =0时质点在x =-2m 处。
求：（1）2s 时质点的位置；（2）0s 至2s 质点的位移；（3）0s 和2s 两时刻质点的加速度。
2、一质点以初速度v 0=5i 开始离开原点，其运动加速度为a =-i -j 。
求：（1）质点到达x 坐标最大值时的速度；（2）上述时刻质点的位置。
3、如图所示，长为l 的棒的一端A 靠在墙上，另一端B 搁在地面上，A 端以恒定速率u 向下运动。
中级微观例题与练习题第一章 供求行为与市场均衡
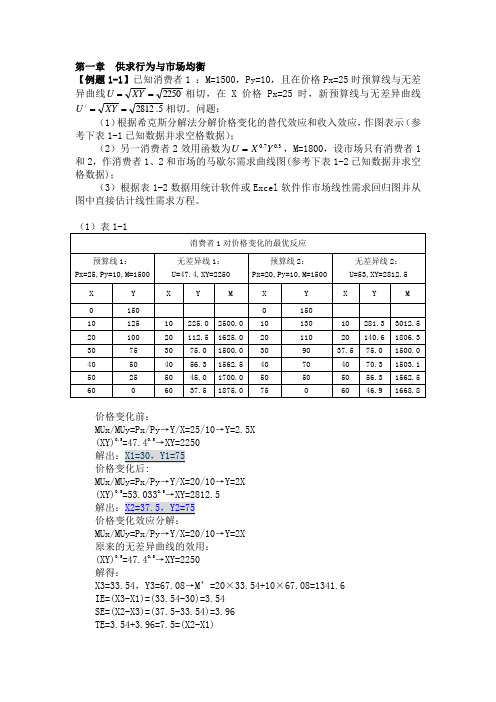
第一章 供求行为与市场均衡【例题1-1】已知消费者1 ：M=1500，Py=10，且在价格Px=25时预算线与无差异曲线2250==XY U 相切，在X 价格Px=25时，新预算线与无差异曲线5.2812/==XY U相切。
问题：（1）根据希克斯分解法分解价格变化的替代效应和收入效应，作图表示（参考下表1-1已知数据并求空格数据）；（2）另一消费者2效用函数为3.07.0Y X U =，M=1800，设市场只有消费者1和2，作消费者1、2和市场的马歇尔需求曲线图(参考下表1-2已知数据并求空格数据)；（3）根据表1-2数据用统计软件或Excel 软件作市场线性需求回归图并从图中直接估计线性需求方程。
（1）表1-1消费者1对价格变化的最优反应预算线1：Px=25,Py=10,M=1500无差异线1：U=47.4,XY=2250 预算线2：Px=20,Py=10,M=1500 无差异线2：U=53,XY=2812.5 X Y X Y M X Y X Y M 0 1500 15010 125 10 225.0 2500.0 10 130 10 281.3 3012.5 20 100 20 112.5 1625.0 20 110 20 140.6 1806.3 30 75 30 75.0 1500.0 30 90 37.5 75.0 1500.0 40 50 40 56.3 1562.5 40 70 40 70.3 1503.1 50 25 50 45.0 1700.0 50 50 50 56.3 1562.5 606037.5 1875.0756046.9 1668.8价格变化前：MUx/MUy=Px/Py →Y/X=25/10→Y=2.5X (XY)0.5=47.40.5→XY=2250 解出：X1=30，Y1=75 价格变化后:MUx/MUy=Px/Py →Y/X=20/10→Y=2X (XY)0.5=53.0330.5→XY=2812.5 解出：X2=37.5，Y2=75 价格变化效应分解：MUx/MUy=Px/Py →Y/X=20/10→Y=2X 原来的无差异曲线的效用： (XY)0.5=47.40.5→XY=2250 解得：X3=33.54，Y3=67.08→M ’=20×33.54+10×67.08=1341.6 IE=(X3-X1)=(33.54-30)=3.54 SE=(X2-X3)=(37.5-33.54)=3.96 TE=3.54+3.96=7.5=(X2-X1)（2）根据MU(X)/MU(Y)=Px/Py →Y/X=Px/Py →PyY=PxX ，代入预算线方程整理得：X=(1/2)M/Px=(1/2)*1500/Px,Y=(1500-PxX)/Py当Px 发生如下表变化，可得下表1-2消费者1均衡及价格效应E 0(30,75)(37.5,75)E 105010015020025030001020304050607080XY表1-2消费者1消费者2市场需求Px X1=0.5*1500/Px Y1=(1500-XPx)/Py X2=0.7*1800/Px Y2=(1800-XPx)/Py Q=X1+X2 25 30 75 50.4 54 80.4 20 37.5 75 63 54 100.5 15 50.0 75 84.00 54 134.0 10757512654201（3）用Excel 软件回归得：市场线性需求方程Qx= -7.906Px+ 267.33R 2 = 0.9320501001502002500102030PxQx【例题1-2】已知线性需求方程为Qxd=25-2Px+0.01M+2.5Py-1.25Pz ，其中，Px=10，Py=8，Pz=12，M=3000，求：（1）需求价格弹性、收入弹性和交叉弹性； （2）消费者总剩余（CS ）； （3）其他因素不变，分别求Py ’=10，Pz ’=16，M ’=4000的线性需求方程。
【英语】名词性从句总复习经典例题、习题经典1
【英语】名词性从句总复习经典例题、习题经典1一、名词性从句1． ---- Let's send him home. Do you know _________?---- I have no idea.A. where does he liveB. where he livesC. he where livesD. he lives where【答案】 B【解析】【分析】句意:----让我们把他送回家。
你知道他住在哪里吗?----我不知道。
宾语从句就是一个句子作动词或介词的宾语。
宾语从句由特殊疑问句变来就用原来的疑问词作引导。
在宾语从句中只能使用陈述句语序，不能用疑问句语序。
所以选B。
2．While some behaviors may seem strange to you, remember you consider normal probably seems just as unusual to others.A. it; thatB. what; thatC. that; whatD. which; that【答案】 C【解析】【分析】句意：虽然有些行为对你来说可能很奇怪，但请记住，你认为正常的行为对别人来说可能也不寻常。
第一空为宾语从句，从句结构完整用that起连接作用，第二空为主语从句，从句中consider缺少宾语，应该用what，故选C。
【点评】考查名词性从句，本题涉及that引导的宾语从句和what引导的主语从句。
3． is even more important is the earth cooled down, water began to appear on its surface.A. When; that; whenB. What; whether; asC. What; that; asD. lt; whether; as 【答案】 C【解析】【分析】这题考查从句的用法，第一空填what引导主语从句，在主语从句中what做主语，第二空填that引导表语从句，在表语从句中，as是引导时间状语从句，句意是：甚至更重要的是：随着地球的冷却，水开始出现在表面。
弹性力学-例题、习题和总复习
∂ 4φ ∂ 4φ + 2 4 ∂x ∂x 2∂y
2
∂ 4φ + = 0 4 ∂y
d 4 f1 ( x ) =0 4 dx
⑶
⑵式积分，得： f ( x ) = Ax 3 + Bx 2 + Cx + D 式积分， 故应力函数为： 故应力函数为：
f1 ( x ) = Ex 3 + Fx 2 + Gx + H ⑵式积分，得： 式积分，
σ
x
∂ 2φ = = 0 2 ∂y
积分得： 积分得： φ = yf ( x ) + f1 ( x )
⑴
⑴式必须要满足相容条件，代入相容方程中得到： 式必须要满足相容条件，代入相容方程中得到：
弹性力学 主讲
邹祖军
弹性力学例题、习题和总复习 弹性力学例题、
φ = yf ( x ) + f1 (x )
yd 4 f ( x ) d 4 f1 ( x ) + =0 4 4 dx dx d 4 f (x ) 必须有： 必须有： =0 ⑵ 4 dx
邹祖军
弹性力学例题、习题和总复习 弹性力学例题、
习题1 习题
σy = 0 σz = −300 105 N / m2 τ yz = −750 105 N / m2 τxz = 800 105 N / m2 × × × 5 2 试求法线方向余弦为 l = 1 , m = 1 , n = 1 τxy = 500 10 N / m × 2 2 2
50 80 1 106.6 2 1 ⋅ 0 − 75 2 = − 28.0MPa − 75 − 30 12 −18.7
X v2 + Yv2 + Z v2
2016初级会计实务(03)第1章4节习题
第四节存货习题阜阳校区王卫例题1-单选•1.（2013无纸化考题）某企业对材料采用计划成本核算。
2013年12月1日，结存材料的计划成本为800万元，材料成本差异贷方余额为12万元；本月入库材料的计划成本为3 200万元，材料成本差异借方发生额为60万元；本月发出材料的计划成本为3 000万元。
该企业2013年12月31日结存材料的实际成本为（）万元。
• A.1 000 B.3 000 C.1 012 D.3 036•『正确答案』C•『答案解析』材料成本差异率=（-12+60）/（800+3200）=0.012，800+3 200-3 000=1 000万元，1 000+1 000×0.012=1 012万元。
例题2-单选•2.（2013无纸化考题）存货发出计价采用先进先出法，11月1日结存200件，单位成本4元，2日发出150件，5日购入300件，单位成本4.4元，7日发出100件，11月7日发出存货实际成本（）万元。
• A.424 B.400 C.420 D.440•『正确答案』C•『答案解析』先进先出法，是指根据先入库先发出的原则，对于发出的存货以先入库存货的单价计算发出存货成本的方法。
采用这种方法的具体做法是：先按存货的期初余额的单价计算发出的存货的成本，领发完毕后，再按第一批入库的存货的单价计算，依此从前向后类推，计算发出存货和结存存货的成本。
11月7日发出存货实际成本=50×4+50×4.4=420万元。
例题3-单选•（2013无纸化考题）某商场采用毛利率法计算期末存货成本，甲商品4月1日期初成本3 600万元，本月购入6 000万元，当月销售收入6 800万元，该商品第一季度毛利率为25%，4月30日，期末结存成本为（）万元• A.4 500 B.1 100 C.5 100 D.7 900•『正确答案』A•『答案解析』期末结存成本=（3 600+6 000）-6 800×（1-25%）=4 500万元。
进制转换练习题
进制转换练习题【例题1-1】十进制数1000对应二进制数为______，对应十六进制数为______。
供选择的答案A：①1111101010 ②1111101000 ③1111101100④1111101110B：①3C8 ②3D8 ③3E8 ④3F8 【例题1-2】十进制小数为0.96875对应的二进制数为______，对应的十六进制数为______。
供选择的答案A：①0.11111 ②0.111101 ③0.111111④0.1111111B：①0.FC ②0.F8 ③0.F2 ④0.F1【例题1-3】二进制的1000001相当十进制的______，二进制的100.001可以表示为______。
供选择的答案A：①62 ②63 ③64 ④65B：①23+2–3②22+2–2③23+2–2④22+2–3【例题1-4】十进制的100相当于二进制______，二进制的0.110011相当十进制的______。
供选择的答案A：①1000000 ②1100000 ③1100100 ④1101000B：①2–1+2–2+2–4+2–5②1–(2–3+2–4)③1+(–2–3–2–4) ④1–2–3–2–4–2–6资料【例题1-5】八进制的100化为十进制为______，十六进制的100化为十进制为______。
供选择的答案A：①80 ②72 ③64 ④56B：①160 ②180 ③230 ④256【例题1-6】在答案群所给出的关系式中正确的为______，在给出的等式中不正确的为______。
供选择的答案A：①0.1112<0.7510②0.78>0.C16③0.610>0.AB16④0.1012<0.A16B：①0.87510=0.E16②0.748=0.937510③0.1012=0.A16④0.3116=0.1418【例题1-7】十六进制数FFF.C H相当十进制数______。
函数的连续性的例题和习题[一]
函数的连续性的例题与习题函数连续性这个内容所涉及到的练习与考试题目，大致有3大类。
第一类是计算或证明连续性；第二类是对间断点（或区间）的判断，包括间断点的类型；第三类是利用闭区间上的连续函数的几个性质（最值性质，零点存在性质），进行理论分析。
下面就这三大类问题，提供若干例题和习题。
还是那句老话：看到题目不要看解答，而是先思考先试着做！这是与看文学小说的最大区别。
要提醒的是，例题里有不少是《函数连续性（一）（二）》中没有给出解答的例题，你事先独立做了吗？如果没有做，是不会做好是根本不想做，还是没有时间？一．函数的连续例1.1（例1.20（一），这个序号值的是《函数连续性（一）中的例题号，请对照）设()f x 满足()()()f x y f x f y +=+，且()f x 在0x =连续。
证明：()f x 在任意点x 处连续。
分析：证明题是我们很多同学的软肋，不知道从何下手。
其实，如果你的基本概念比较清晰，证明题要比计算题号做，因为它有明确的方向，不像计算题，不知道正确的答案是什么在本题里，要证的是“()f x 在任意点x 处连续”，那么我们就先固定一个点x ，用函数连续的定义来证明在x 处连续。
你可能要问：函数连续的定义有好几个，用哪一个? 这要看已知条件，哪个容易用，就用那一个。
在本题中，提供了条件()()()f x y f x f y +=+，也就是()()()f x y f x f y +-=，你的脑海里就要想到，如果设y x =∆，那么就有 ()()()y f x x f x f x ∆=+∆-=∆；这个时候，你应该立即“闪过”，要用题目给的第二个条件了：()f x 在0x =连续！它意味着：0lim (0)(0)x f x f ∆→+∆=。
证明的思路就此产生！证明：因为 ()()()f x y f x f y +=+，取0y =，则有 ()()(0)f x f x f =+，所以(0)0f =。