西交大苏州附中2013-2014学年度第一学期期中复习卷(5)
2013-2014年陕西省西安交大附中八年级上学期期中数学试卷和答案

2013-2014学年陕西省西安交大附中八年级(上)期中数学试卷一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.(3分)在下列实数中,无理数是()A.B.C.﹣D.02.(3分)3的平方根是()A.±B.9 C.D.±93.(3分)﹣64的立方根是()A.﹣8 B.8 C.﹣4 D.44.(3分)在下列各组数据中,不能作为直角三角形的三边边长的是()A.5,12,13 B.6,8,10 C.7,24,25 D.8,15,165.(3分)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是()A.48 B.60 C.76 D.806.(3分)如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(﹣40,﹣30)表示,那么(﹣10,20)表示的位置是()A.点A B.点B C.点C D.点D7.(3分)如果m是任意实数,则点P(m﹣4,m+1)一定不在()A.第一象限B.第二象限C.第三象限D.第四象限8.(3分)如果一个正比例函数的图象经过不同象限的两点A(3,m),B(n,2),那么一定有()A.m>0,n>0 B.m<0,n<0 C.m>0,n<0 D.m<0,n>09.(3分)如图,直线AB对应的函数表达式是()A.y=﹣x+3 B.y=x+3 C.y=﹣x+3 D.y=x+310.(3分)某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:设鸭的质量为x千克,烤制时间为t,估计当x=3.2千克时,t的值为()A.140 B.138 C.148 D.160二、填空题(共4小题,每小题3分,计12分)11.(3分)写出一个大于2且小于4的无理数:.12.(3分)如图,是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离为mm.13.(3分)已知点A的坐标为(﹣2,3),点B与点A关于x轴对称,点C与点B关于y轴对称,则点C的坐标为.14.(3分)某函数的图象经过(1,﹣1),且函数y的值随自变量x的值增大而增大.请你写出一个符合上述条件的函数关系式:.三、解答题(共8小题,计58分.解答应写出过程)15.(6分)作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).(1)作△ABC关于直线l:x=﹣1对称的△A1B1C1,其中,点A、B、C的对应点分别为A1、B1、C1;(2)写出点A 1、B1、C1的坐标.16.(6分)计算:(1)(2+)(﹣5)(2)(﹣)÷.17.(6分)计算:(1)﹣×(2)﹣﹣.18.(7分)座钟的摆针摆动一个来回所需的时间称为一个周期,其计算公式为T=2π,其中T表示周期(单位:秒),L表示摆长(单位:米),g=9.8米/秒2,假若一台座钟摆长为0.5米,它每摆动一个来回发生一次滴答声,那么在1分钟内,该座钟大约发出了多少次滴答声(π≈3.14)19.(7分)如图,长方体的底面是边长为1cm 的正方形,高为3cm.(1)如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,请利用侧面展开图计算所用细线最短需要多少cm?(2)如果从点A开始经过4个侧面缠绕2圈到达点B,那么所用细线最短需要cm.(直接填空)20.(7分)如图,在平面直角坐标系中,等边三角形ABC的边长为2.(1)写出顶点A,B,C的坐标.(2)求出直线AC,BC的函数表达式.21.(9分)某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:(1)填空:甲种收费的函数关系式是.乙种收费的函数关系式是.(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算?22.(10分)如图,四边形ABCD是一正方形,已知A(1,2),B(5,2)(1)求点C,D的坐标;(2)若一次函数y=kx﹣2(k≠0)的图象过C点,求k的值.(3)若y=kx﹣2的直线与x轴、y轴分别交于M,N两点,且△OMN的面积等于2,求k的值.2013-2014学年陕西省西安交大附中八年级(上)期中数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.(3分)在下列实数中,无理数是()A.B.C.﹣D.0【解答】解:=2,则无理数为﹣.故选:C.2.(3分)3的平方根是()A.±B.9 C.D.±9【解答】解:∵()2=3,∴3的平方根是为.故选:A.3.(3分)﹣64的立方根是()A.﹣8 B.8 C.﹣4 D.4【解答】解:∵﹣4的立方等于﹣64,∴﹣64的立方根等于﹣4.故选:C.4.(3分)在下列各组数据中,不能作为直角三角形的三边边长的是()A.5,12,13 B.6,8,10 C.7,24,25 D.8,15,16【解答】解:A、52+122=25+144=169=132,所以5,12,13可以作为直角三角形的三边;B、62+82=36+64=100=102,所以6,8,10可以作为直角三角形的三边;C、72+242=49+576=625=252,所以7,24,25可以作为直角三角形的三边;D、82+152=64+225=289=172≠162,所以8,15,16不能作为直角三角形的三边长;故选:D.5.(3分)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是()A.48 B.60 C.76 D.80【解答】解:∵∠AEB=90°,AE=6,BE=8,∴在Rt△ABE中,AB2=AE2+BE2=100,∴S阴影部分=S正方形ABCD﹣S△ABE,=AB2﹣×AE×BE=100﹣×6×8=76.故选:C.6.(3分)如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(﹣40,﹣30)表示,那么(﹣10,20)表示的位置是()A.点A B.点B C.点C D.点D【解答】解:∵点M的位置用(﹣40,﹣30)表示,∴(﹣10,20)表示的位置是点A.故选:A.7.(3分)如果m是任意实数,则点P(m﹣4,m+1)一定不在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵(m+1)﹣(m﹣4)=m+1﹣m+4=5,∴点P的纵坐标一定大于横坐标,∵第四象限的点的横坐标是正数,纵坐标是负数,∴第四象限的点的横坐标一定大于纵坐标,∴点P一定不在第四象限.故选:D.8.(3分)如果一个正比例函数的图象经过不同象限的两点A(3,m),B(n,2),那么一定有()A.m>0,n>0 B.m<0,n<0 C.m>0,n<0 D.m<0,n>0【解答】解:∵点A(3,m)的横坐标为3>0,∴此点在一、四象限;∵点B(n,2)的纵坐标为2>0,∴此点在一、二象限,∴此函数的图象一定经过二四象限,∴点A(3,m)在第四象限,点B(n,2)在第二象限,∴m<0,n<0.故选:B.9.(3分)如图,直线AB对应的函数表达式是()A.y=﹣x+3 B.y=x+3 C.y=﹣x+3 D.y=x+3【解答】解:设直线AB对应的函数表达式是y=kx+b,把A(0,3),B(2,0)代入,得,解得,故直线AB对应的函数表达式是y=﹣x+3.故选:A.10.(3分)某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:设鸭的质量为x千克,烤制时间为t,估计当x=3.2千克时,t的值为()A.140 B.138 C.148 D.160【解答】解:从表中可以看出,烤鸭的质量每增加0.5千克,烤制的时间增加20分钟,由此可知烤制时间是烤鸭质量的一次函数.设烤制时间为t分钟,烤鸭的质量为x千克,t与x的一次函数关系式为:t=kx+b,,解得所以t=40x+20.当x=3.2千克时,t=40×3.2+20=148.故选:C.二、填空题(共4小题,每小题3分,计12分)11.(3分)写出一个大于2且小于4的无理数:(答案不唯一).【解答】解:∵大于2且小于4的无理数为:<x<,∴x可以为:x=(答案不唯一).故答案为:(答案不唯一).12.(3分)如图,是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离为5mm.【解答】解:∵AC=5﹣2=3mm,BC=6﹣2=4mm,∴AB===5mm.故答案为:5.13.(3分)已知点A的坐标为(﹣2,3),点B与点A关于x轴对称,点C与点B关于y轴对称,则点C的坐标为(2,﹣3).【解答】解:∵点A的坐标为(﹣2,3),∴点B坐标为(﹣2,﹣3),∴点C的坐标为(2,﹣3),故答案为:(2,﹣3).14.(3分)某函数的图象经过(1,﹣1),且函数y的值随自变量x的值增大而增大.请你写出一个符合上述条件的函数关系式:y=x﹣2.【解答】解:设此函数关系式是y=kx+b,把(1,﹣1)代入,得:k+b=﹣1,即b=﹣k﹣1.又函数y的值随自变量x的值增大而增大,则k>0.不妨取k=1,则b=﹣2,即y=x﹣2.(答案不唯一)三、解答题(共8小题,计58分.解答应写出过程)15.(6分)作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).(1)作△ABC关于直线l:x=﹣1对称的△A1B1C1,其中,点A、B、C的对应点分别为A1、B1、C1;(2)写出点A1、B1、C1的坐标.【解答】解:(1)△A1B1C1如图所示;(2)A1(0,1),B1(2,5),C1(3,2).16.(6分)计算:(1)(2+)(﹣5)(2)(﹣)÷.【解答】解:(1)原式=2﹣10+10﹣5 =﹣3;(2)原式=﹣=﹣2=﹣.17.(6分)计算:(1)﹣×(2)﹣﹣.【解答】解:(1)原式=﹣=﹣=﹣;(2)原式=﹣﹣=4﹣﹣2=.18.(7分)座钟的摆针摆动一个来回所需的时间称为一个周期,其计算公式为T=2π,其中T表示周期(单位:秒),L表示摆长(单位:米),g=9.8米/秒2,假若一台座钟摆长为0.5米,它每摆动一个来回发生一次滴答声,那么在1分钟内,该座钟大约发出了多少次滴答声(π≈3.14)【解答】解:T=2π≈1.42≈42次∴在1分钟内,该座钟大约发出了42次滴答声.19.(7分)如图,长方体的底面是边长为1cm 的正方形,高为3cm.(1)如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,请利用侧面展开图计算所用细线最短需要多少cm?(2)如果从点A开始经过4个侧面缠绕2圈到达点B,那么所用细线最短需要cm.(直接填空)【解答】解:(1)将长方体展开,连接A、B,根据两点之间线段最短,AB==5cm;(2)如果从点A开始经过4个侧面缠绕2圈到达点B,相当于直角三角形的两条直角边分别是8和3,根据勾股定理可知所用细线最短需要=cm.故答案为:.20.(7分)如图,在平面直角坐标系中,等边三角形ABC的边长为2.(1)写出顶点A,B,C的坐标.(2)求出直线AC,BC的函数表达式.【解答】解:(1)由题意得:OA=OB=1,OC==,∴A(﹣1,0),B(1,0),C(0,);(2)设直线AC解析式为y=kx+,把x=﹣1,y=0代入得:k=,∴直线AC解析式为y=x+;设直线BC解析式为y=mx+,把x=1,y=0代入得:m=﹣,则直线BC解析式为y=﹣x+.21.(9分)某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:(1)填空:甲种收费的函数关系式是y1=0.1x+6(x≥0).乙种收费的函数关系式是y2=0.12x(x≥0).(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算?【解答】解:(1)设甲种收费的函数关系式y1=kx+b,乙种收费的函数关系式是y2=k1x,由题意,得,12=100k1,解得:,k1=0.12,∴y1=0.1x+6(x≥0),y2=0.12x(x≥0);(2)由题意,得当y1>y2时,0.1x+6>0.12x,得x<300;当y1=y2时,0.1x+6=0.12x,得x=300;当y1<y2时,0.1x+6<0.12x,得x>300;∴当100≤x<300时,选择乙种方式合算;当x=300时,甲、乙两种方式一样合算;当300<x≤450时,选择甲种方式合算.答:印制100~300(含100)份学案,选择乙种印刷方式较合算,印制300份学案,甲、乙两种印刷方式都一样合算,印制300~450(含450)份学案,选择甲种印刷方式较合算.22.(10分)如图,四边形ABCD是一正方形,已知A(1,2),B(5,2)(1)求点C,D的坐标;(2)若一次函数y=kx﹣2(k≠0)的图象过C点,求k的值.(3)若y=kx﹣2的直线与x轴、y轴分别交于M,N两点,且△OMN的面积等于2,求k的值.【解答】解:(1)∵ABCD为正方形,又A(1,2),B(5,2)则AB=4,∴C(5,6),D(1,6)(2分)(2)∵y=kx﹣2经过C点,∴6=5k﹣2,∴k==1.6 (4分)(3)y=kx﹣2与x轴的交点为My=0时,kx﹣2=0,x=,M(,0),N(0,﹣2)又S=|OM|•|ON|=×|﹣2|•||=2△OMA∴|K|=1,k=±1故k=±1时,△OMN的面积为2个单位(少一个k值扣1分)(6分).赠送初中数学几何模型【模型一】“一线三等角”模型: 图形特征:60°60°60°45°45°45°运用举例:1.如图,若点B 在x 轴正半轴上,点A (4,4)、C (1,-1),且AB =BC ,AB ⊥BC ,求点B 的坐标;2.如图,在直线l 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是1S 、2S 、3S 、4S ,则14S S += .ls 4s 3s 2s 13213. 如图,Rt △ABC 中,∠BAC =90°,AB =AC =2,点D 在BC 上运动(不与点B ,C 重合),过D 作∠ADE =45°,DE 交AC 于E . (1)求证:△ABD ∽△DCE ;(2)设BD =x ,AE =y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (3)当△ADE 是等腰三角形时,求AE 的长.EB4.如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
西交大苏州附中2013-2014学年度第一学期期中复习总结卷(5)

西交大苏州附中2013-2014学年度第一学期期中复习数学试卷卷(5)一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上. 1.两个平面最多可以将空间分成 部分. 2.直线053=+-y x 的倾斜角是 .3.若一个球的表面积为12π,则该球的半径为 .4.两平行直线0962043=-+=-+y x y x 与的距离是 . 5.已/知圆044222=+-++y x y x 关于直线b x y +=2成轴对称,则b = .. 6.关于直线,m n 与平面,αβ,有以下四个命题:①若//,//m n αβ且//αβ,则//m n ;②若,m n αβ⊥⊥且αβ⊥,则m n ⊥; ③若,//m n αβ⊥且//αβ,则m n ⊥;④若//,m n αβ⊥且αβ⊥,则//m n ; 其中正确命题的序号是 .7.正三棱锥的底面边长为3,则其体积为 .8.过点P(2,3)且在两轴上的截距相等的直线方程是_________________. 9.圆柱形容器的内壁底半径是10cm ,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了53cm ,则这个铁球的表面积为 2cm . 10.圆心在y 轴上,且与直线y x =相切于点(1,1)的圆的方程为________ ___________.11.点P 在平面ABC 上的射影为O ,且PA 、PB 、PC 两两垂直,那么O 是△ABC 的 .(填:外心,内心,重心,垂心)12.若直线y x b =+与曲线x =b 的取值范围是 .13.已知04,k <<直线1:2280l kx y k --+=和直线222:2440l x k y k +--=与两坐标轴围成一个四边形,则使得这个四边形面积最小的k 值为 .14.若圆2244100x y x y +---=上至少有三个不同的点到直线0ax by +=的距离为_______________________.ABCD D1C1B1A1二、解答题:本大题共6小题,共计14+14+15+15+16+16=90分.解答应写出文字说明、证明过程或演算步骤.请把答案写在答卷纸...相应位置上. 15(本小题满分14分)如图,矩形ABCD 的两条对角线相交于点M (2,0),AB 边所在直线的方程为x -3y -6=0,点T (-1,1)在AD 边所在的直线上.(1)分别求AD 边,CD 边所在直线的方程; (2)求矩形ABCD 外接圆的方程.16.(本小题满分15分)如图,在六面体1111ABCD A B C D -中,11//AA CC ,11A B A D =,AB AD =.求证:(1)1AA BD ⊥;(2)11//BB DD .在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABDC 是菱形.(1)求证:平面ADC1⊥平面BCC1B1;(2)求该多面体的体积.18.(本小题满分15分)过圆x2+y2=2外一点P(4,2)向圆引切线.(1)求过点P的圆的切线方程;(2)若切点为P1、P2,,求直线P1P2的方程;(3)求P1、P2两点间的距离.C1B1A1 DCBA设圆221:106320C x y x y +--+=,动圆222:22(8)4120 C x y ax a y a +---++=. (1)求证:圆1C 、圆2C 相交于两个定点;(2)设点P 是圆221x y +=上的点,过点P 作圆1C 的一条切线,切点为1T ,过点P 作圆2C 的一条切线,切点为2T ,问:是否存在点P ,使无穷多个圆2C ,满足12PT PT =?如果存在,求出所有这样的点P ;如果不存在,说明理由.20.(本小题满分16分)如图,在平面直角坐标系xOy 中,已知圆1C :22(1)1x y ++=,圆2C :22(3)(4)1x y -+-=.(1)若过点1(1 0)C -,的直线l 被圆2C 截得的弦长为65,求直线l 的方程;(2)设动圆C 同时平分圆1C 的周长、圆2C 的周长. ①证明:动圆圆心C 在一条定直线上运动;②动圆C 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.参考答案一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上. 1.两个平面最多可以将空间分成 部分. 4 2.直线053=+-y x 的倾斜角是 .6003.若一个球的表面积为12π4.两平行直线0962043=-+=-+y x y x 与的距离是 。
交大附中2014届高三上学期期中考试物理试题

上海交通大学附属中学2013-2014学年度第一学期高三物理期中试卷(满分150分,120分钟完成答案一律写在答题纸上)命题:苏俊杰审核:王晓敏考生注意:1.全卷共9页,共33题.2. g取10m/s2.3.第30、31、32、33题要求写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案,而未写出主要演算过程的,不能得分,有数字计算的问题,答案中必须明确写出数值和单位.一.(56分)选择题. 本大题分单项选择题和多项选择题,共20小题.I.单项选择题. 每小题给出的四个答案中只有一个是正确的,选对得2分,共16分. 1.物体以初速度v o竖直上抛,经3s到达最高点,空气阻力不计,则( A )。
A.物体的初速度v o为30m/sB.物体在5s内的位移为45mC.物体在第1s内、第2s内、第3s内的平均速度之比为9∶4∶1D.物体在1s内、2s内、3s内的平均速度之比为9∶4∶12.液体与固体具有的相同特点是( B )。
(A)都具有确定的形状(B)体积都不易被压缩(C)物质分子的位置都确定(D)物质分子都在固定位置附近振动3.只要知道下列哪一组物理量,就可以估算出气体中分子间的平均距离( B ) (A)阿伏加德罗常量,该气体的质量和摩尔质量(B)阿伏加德罗常量,该气体的摩尔质量和密度(C)阿伏加德罗常量,该气体的质量和体积(D)该气体的密度、体积和摩尔质量4.秋千的吊绳有些磨损。
在摆动过程中,吊绳最容易断裂的时候是秋千( D )。
(A)在下摆过程中(B)在上摆过程中(C)摆到最高点时(D)摆到最低点时5、在冬季,剩有半瓶热水的暖水瓶经过一个夜晚后,第二天拔瓶口的软木塞时感觉很紧,不易拔出来,这主要是因为:(D)。
A.软木塞受潮膨胀 B .瓶口因温度降低而收缩变小C.白天气温升高,大气压强变大D.瓶内气体因温度降低而压强减小6. 如图所示的一段圆弧为某运动物体的速度随时间变化图像,由图可知,物体是做下列哪种运动( D )A. 圆周运动B. 匀变速直线运动C. 曲线运动D.减速直线运动7. 伽利略曾设计如图所示的一个实验,将摆球拉至M 点放开,摆球会达到同一水平高度上的N 点。
2013-2014学年七年级上册数学期中试卷及答案【苏州市高新区】(精编文档).doc

【最新整理,下载后即可编辑】苏州市高新区2013-2014学年度第一学期期中测试七年级数学试卷2013年11月(满分:100分考试时间:100分钟)一、选择题(每小题2分,共20分,请将正确答案填写在下面表格里)1.-3的相反数是A.3 B.-3 C.13D.-132.下列比较大小的式子中,正确的是A.2<-(+5) B.-1>-0.01 C.33-<+D.-(-5)>+(-7)3.下列运算正确的是A、3a+2b=5abB、3a2b-3ba2=0C、3x2+2x3=5x5D、3m4-2m4=14.在-227,-π,0,3.14,0.1010010001,-313中,无理数的个数有A、1个B、2个C、3个D、4个5.下列说法不正确的是A.任何一个有理数的绝对值都是正数B.0既不是正数也不是负数C.有理数可以分为正有理数,负有理数和零D.0的绝对值等于它的相反数6.如图,数轴的单位长度为1.如果点B、C表示的数的绝对值相等,那么点A表示的数是A.-2 B.-5 C.-4 D.-6 7.数a、b、c在数轴上对应的位置如下图,化简a b c b+--的结果是A .a +cB .c -aC .-c -aD .a +2b -c8.若m -n =-1,则(m -n)2-2m +2n 的值是A .3B .2C .1D .-19.若a =2,b =a ,则a +b 为A .±4B .0C .0、±4D .以上都不对10.今年苹果的价格比去年便宜了20%,已知今年苹果的价格是每千克a 元,则去年的价格是每千克( )元A .(1+20%) aB .(1-20%)aC .120%a - D .120%a + 二、填空题(每小题2分,共20分)11.如果“+200元”表示收入200元,那么“-100元”的实际意义是_______.12.我国南海面积约为350万平方千米,“350万”这个数用科学记数法表示为_______13.写出在-212和1之间的负整数:_______. 14.已知(b +3)2+2a -=0,则b a 的值是_______.15.在数轴上,点A 表示数-1,距A 点2.5个单位长度的点表示的数是_______.16.如图,是一个简单的数值运算程序,当输入x 的值为-4时,则输出的数值为_______.17.若a ,b 互为相反数,c ,d 互为倒数,m 的绝对值为2,则2a b m cd m ++-的值是_______.18.当k =_______时,多项式x 2+(k -1)xy -3y 2-2xy -5中不含xy 项.19.下列图形是由一些小正方形和实心圆按一定规律排列而成的,如图所示,按此规律排列下去,第n 个图形中有_______个实心圆.20.设[x)表示大于x 的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是_______.(填写所有正确结论的序号)①[0)=0;②[x)-x 的最小值是0;③[x)-x 的最大值是0;④存在实数x ,使[x)-x =0.5成立。
2013-2014期中试卷+交大附中

交大附中初二年级(数学)第一学期期中考试考试时间:90分钟 满分:100分班级 姓名一、选择题:(每小题3分,共30分) 1.下列运算不正确的是( ) A .5552a a a += B .()32622aa -=-C .2122a a a -⋅=D .()322221a a a a -÷=-2.下列图形中,轴对称图形.....的是( )3.代数式21,,,13x x ax x x π+中,分式的个数是( ) A .1 B .2 C .3 D .4 4.(—2,6)关于x 轴对称点的坐标为( )A.(—2,6)B.(2,6)C.(2,—6)D.(—2,—6) 5.如图所示,把一个长方形纸片沿EF 折叠后,点D ,C 分别落在D ′,C ′的位置.若∠EFB =65°,则∠AED ′等于 ( ) A .70° B.65° C . 50°D . 25°6. 在2222222)())(3(,)()2(),5)(5()5()1(b a b a y x y x x x x +=--+=+-+=-+(4)ab ab ab a b b a =-=--23)2)(3(中错误的有( ) A.1个 B.2个 C.3个 D.4个 7.如图,已知△ABC ,求作一点P ,使P 到∠A 两边的距离相等, 且PA =PB .下列确定P 点的方法正确的是( )A.P 为∠A 、∠B 两角平分线的交点B.P 为∠A 的角平分线与AB 的垂直平分线的交点 C.P 为AC 、AB 两边上的高的交点 D.P 为AC 、AB 两边的垂直平分线的交点8.如图,在△ABC 中,AB =AC =20cm ,DE 垂直平分AB ,垂足为E , 交AC 于D ,若△DBC 的周长为35cm ,则BC 的长为( )A B C DEDBC′FCD ′A8题图AB7题图A .5cmB .10cmC .15cmD .17.5cm9.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式.....,如a b c ++就是完全对称式.下列三个代数式:①2)(b a -;②ab bc ca ++;③222a b b c c a ++.其中是完全对称式的是( )A .①②B .①③C . ②③D .①②③10.如图(1)所示的Rt△ABC 中,∠A =90°,三边a b c >>.现以△ABC 某一边的垂直平分线为对称轴,将△ABC 翻折一次,记作一次操作.例如,若图(1)中△ABC 以a 边的垂直平分线为对称轴翻折后,变成图(2)中的△ABC ,记作“a 操作”一次;图(2)中△ABC 继续以b 边的垂直平分线为对称轴翻折后,变成图(3)中的△ABC ,记作“b 操作”一次.现对图(1)中的△ABC 分别按以下顺序连续进行若干次操作,则最后得到的△ABC 与图(1)中△ABC 重合的是( )A . a 操作-b 操作-c 操作B . b 操作-c 操作-b 操作-c 操作C . a 操作-c 操作-b 操作-a 操作D . b 操作-a 操作-b 操作-a 操作(1)ABC (2) a 操作 (3) b 操作BC二、填空题:(每小题2分,共16分) 11.2,3==n mx x, m n x += .12.计算⎪⎪⎭⎫⎝⎛-÷⎪⎪⎭⎫ ⎝⎛-⋅24382342y x y x y x 的结果为 .13.如果,6ab ,13b a 22-==+那么=+2)b a ( . 14.当x =__________时,分式33--x x 的值为0.15.已知511=-b a ,则bab a b ab a ---+2232的值是___________. 16.x 2-mx+16是一个完全平方式,则m=________.17.在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式44y x -,因式分解的结果是))()((22y x y x y x ++-,若取9,9==y x 时,则各个因式的值是:162)(,18)(,0)(22=+=+=-y x y x y x ,于是就可以把“018162”作为一个六位数的密码.对于多项式2249y x x -,取11,8==y x 时,用上述方法产生的密码是: __________. (写出一个即可)18. 如图,已知△ABC 中,∠BAC =120°,分别作AC ,AB 边的 垂直平分线PM ,PN 交于点P ,分别交BC 于点E 和点F .则以下各说法中:①∠P =60°,②∠EAF =60°,③点P 到点B 和点C 的距离相等,④PE =PF ,正确的说法是______________.(填序号) 三、解答题:(共54分)19.计算:(每小题3分,共12分)20(1)(4)(1)m m m +-+ (2)()()---x y y x()()()()+--223a b a b a b 2312(4)224xx x x -++-- 20.因式分解(每小题4分,共8分) (1)3222x x y xy -+ (2)()()2211x a y a -+-21. (本题5分)如图, ∠MAN 中,点C 、E 在射线AM 上,点B 、D 、F 在射线AN 上,其中AB=BC=CD=DE=EF ,∠DEF = 36°,求∠A 的度数.A22. (本题5分)先化简:22121111x x x x x -⎛⎫+÷ ⎪+--⎝⎭,然后选取一个使原式有意义的x 的值代入求值.23.(本题5分)如图,在等边三角形ABC 中,D 、E 分别为AB 、BC 上的点,且BD =CE ,AE 、CD 相交于点F ,AG ⊥CD ,垂足为G . 求证:AF =2FG .B24.(本题5分)如图,△ABC 中,点D 为BC 边的中点,∠1=∠2.求证:AB=AC.25.(本题4分)探索题:11)(1(2-=+-x x x ) 1)1)(1(32-=++-x x x x 1)1)(1(423-=+++-x x x x x 1)1)(1(5234-=++++-x x x x x x......①试求122222223456++++++的值; ②判断1222222200620072008++++++ 的值的个位数是几?26.(本题4分)已知三个数x ,y ,z 满足xy x y +=-2,yz y z+=43,zx z x +=-43.求xyzxy yz zx++的值.27.(本题6分)如图,△ABC 中,∠C =90°,∠B <45°.请依次按以下要求作图并回答问题:(1)在AB 上找一点D ,使得点D 到点C 的距离与点D 到线段BC 的距离之和最小,请在图(a)中画出图形(不要求尺规作图)并写出点...D .的作法...; (2)在(1)中作图的基础上,连接CD ,求证:CD =CA ;(3)在(1)和(2)中作图的基础上,继续在线段BC 上找一点E ,使得∠DEC =2∠B ,直线DE 交直线AC 于点F ;再在直线BC 上找点P ,使得PA =CF ,探究所得线段AP 与线段CD 的关系如何.关于这个问题,小马经过探究后说:“AP 与CD 相交,交点恰好是AP 的中点”,你同意他的结论吗?为什么?(可以利用备用图进行探究,也可自己重新作图.)图(a)备用图1备用图2。
西交大苏州附中高一5月考

高一年级英语2014年5月第一部分:听力理解(共两节,满分20分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转到答题卡上。
第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What time is it now?A. 5:50B. 5:10C. 5:302.What does the woman plan to do this Sunday?A. Go fishingB. Go shoppingC. Go swimming3.What‘s the woman‘s problem?A.She failed to pass the exam?B.She missed the bus.C.She lost her cellphone.4.Where are they probably now?A. In a bookstoreB. In the classroomC. In a library5.What is the woman going to do tomorrow morning?A. To wait for a callB. To meet her managerC. To see Mary off第二节(共10小题;每小题1分,满分15分)请听下面5段对话或独自。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独自读两遍。
听第6段材料,回答第6至7题。
6.Where is the woman now?A. At a storeB. On a busC. In front of a cinema7.How do the two speakers probably feel now?A. DisappointedB. InterestedC. Worried听第7段材料,回答第8至9题。
西安交大初三期末考试2013--2014上学期

交大附中分校2013--2014学年第一学期期末考试初三年级数学试题一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)1、在下列实数中,无理数是( )A.2B.3.14C.-21 D.3 2、下列图形中,既是轴对称图形,又是中心对称图形的是( )A.平行四边形B.矩形C. 正三角形D.等腰梯形3、在△ABC 中,∠C=90°,AB=5,BC=3,则sinA 的值是( ) A.43 B.34 C.53 D.54 4、某人抛硬币抛10次,其中正面朝上6次,反面朝上4次,下列说法正确的是( )A.出现正面的频率是6B.出现正面的频率是4C.出现正面的频率是40%D.出现反面的频率是40%5、方程21 x -x3=0的解为( ) A.x=2 B.x=-2 C.x=3 D.x=-36、如图,△ABC 内接于圆O ,∠A=50°,则∠OBC 的度数为( )A.40°B.50°C.80°D.100°7、如果函数y=ax+b(a <0,b <0)和y=kx(k >0)的图象交于点P ,那么点P 应该位于( )A .第一象限B .第二象限C .第三象限D .第四象限8、如图,在平行四边形ABCD 中,点E 在AD 上,连接CE 并延长与BA 的延长线交于点F ,若AE=2ED,CD=3cm ,则AF 的长为( )A.5cmB.6cmC.7cmD.8cm9、如图,点P (2a,a )是反比例函数y=x8在第一象限内的图像上的一个点,以点P 为顶点作等边ΔPAB ,使A 、B 落在x 轴上,则ΔPOA 的面积是( )A 、3B 、4C 、3324-D 、3348- 10、如图,二次函数c bx ax y ++=2的图像经过点(0,-2),与x 轴交点的横坐标分别为1x 、2x ,且-1<1x <0,1<2x <2,下列结论正确的是( )A.a <0B.a-b+c <0C.a b ac 842--<D.12>ab -二、填空题(本大题有6个小题,没小题3分,共18分)11、计算:2cos30°=_______ 12、如图,AB ∥CD ,点E 在BC 上,且CD=CE ,∠B=32°,则∠D 的度数为________13、 不等式组⎩⎨⎧->>+32012x x x 的正整数解__________ 14、圆锥的母线长为8cm,底面周长为5πcm,则圆锥的侧面积为________15、为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有______名16、在矩形ABCD 中,AB=4,AD=6,如图折叠使点A 落在矩形ABCD 内或边上,落点为A 1,折痕与矩形的一边交点为E ,连接AA 1,则当三角形EAA 1的面积最大时,DE 的长为________三、解答题(共7小题,计52分,解答题应写出过程)17、(本题满分5分) 化简a a a a 4)2121(2-∙-++18、如图所示,某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边DE 选取两点A 、B ,观察对岸的点C ,测得∠CAD=45°,∠CBD=30°,且AB=50m .求该河段的宽度。
2013-2014学年江苏省苏州市七年级(上)期中数学试卷(解析版)

)
【解答】解:在数轴上,4 和﹣4 到原点的距离为 4. ∴点 A 所表示的数是 4 和﹣4. 故选:C.
3. (2 分)下列各数中:+3ห้องสมุดไป่ตู้﹣2.1、 理数有( )
15. (2 分)靖江 2008 年人口普查结果显示,靖江人口已达 66.5 万,请你将 66.5 万用科学记数法表示应是 . .
16. (2 分)4﹣(+1)+(﹣6)﹣(﹣5)写成省略加号的和的形式为
17. (2 分)冬天某日上午的温度是 3℃,中午上升了 5℃达到最高温度,到夜间 最冷时下降了 10℃,则这天的日温差是 ℃.
2013-2014 学年江苏省苏州市七年级(上)期中数学试卷
一、选择题(每小题 2 分,计 20 分) 1. (2 分)有理数 的相反数是( A.﹣ B. C.﹣2 D.2 ) )
2. (2 分)数轴上的点 A 到原点的距离是 4,则点 A 表示的数为( A.4 B.﹣4 C.4 或﹣4 D.2 或﹣2
A.+2 B.±2 C.+10 D.﹣2 或+10
二、填充(每小题 2 分,计 20 分) 11. (2 分)最大的负整数是 . . .
12. (2 分)绝对值大于 3 小于 6 的所有整数是 13. (2 分)“x 的 4 倍与﹣2 的和除以 5”列式为
14 . ( 2 分)如图是一数值转换机,若输出的结果为﹣ 32 ,则输入的 x 的值 为 .
C.﹣|﹣2|与﹣(﹣2)
6. (2 分)在代数式 A.3 个 B.4 个 C.5 个 D.6 个
7. (2 分)某种细菌在培养过程中,每半个小时分裂一次(由 1 个分裂成 2 个, 两个裂成 4 个…) , 若这种细菌由 1 个分裂成 128 个, 那么这个过程需要经过 ( 小时. A.2 B.3 C.3.5 D.4 是关于 x 的四次三项式,则 m 的值是( ) )
苏州市2013-2014学年第一学期初二历史期中模拟试卷
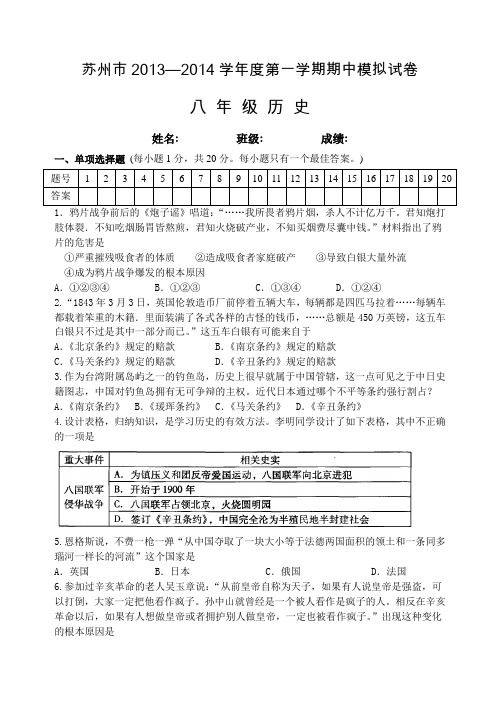
苏州市2013—2014学年度第一学期期中模拟试卷八年级历史姓名: 班级: 成绩:一、单项选择题(每小题1分,共20分。
每小题只有一个最佳答案。
)肢体裂.不知吃烟肠胃皆熬煎,君知火烧破产业,不知买烟费尽囊中钱。
”材料指出了鸦片的危害是①严重摧残吸食者的体质②造成吸食者家庭破产③导致白银大量外流④成为鸦片战争爆发的根本原因A.①②③④B.①②③C.①③④D.①②④2.“1843年3月3日,英国伦敦造币厂前停着五辆大车,每辆都是四匹马拉着……每辆车都载着笨重的木籍.里面装满了各式各样的古怪的钱币,……总额是450万英镑,这五车白银只不过是其中一部分而已。
”这五车白银有可能来自于A.《北京条约》规定的赔款B.《南京条约》规定的赔款C.《马关条约》规定的赔款D.《辛丑条约》规定的赔款3.作为台湾附属岛屿之一的钓鱼岛,历史上很早就属于中国管辖,这一点可见之于中日史籍图志,中国对钓鱼岛拥有无可争辩的主权。
近代日本通过哪个不平等条约强行割占?A.《南京条约》 B.《瑗珲条约》 C.《马关条约》 D.《辛丑条约》4.设计表格,归纳知识,是学习历史的有效方法。
李明同学设计了如下表格,其中不正确的一项是5.恩格斯说,不费一枪一弹“从中国夺取了一块大小等于法德两国面积的领土和一条同多瑙河一样长的河流”这个国家是A.英国 B.日本 C.俄国 D.法国6.参加过辛亥革命的老人吴玉章说:“从前皇帝自称为天子,如果有人说皇帝是强盗,可以打倒,大家一定把他看作疯子。
孙中山就曾经是一个被人看作是疯子的人。
相反在辛亥革命以后,如果有人想做皇帝或者拥护别人做皇帝,一定也被看作疯子。
”出现这种变化的根本原因是A.民主共和观念深入人心B.帝国主义扶植袁世凯C.民族资本主义进一步发展D.民主与科学在中国实现7.斯塔夫里阿诺斯在《全球通史》中指出:当1911年革命到来时,……革命者利用了这种不满,并在学生和士兵中做了有效的工作。
在广东,小规模的革命党人起义虽遭镇压,可是在汉口,1911年10月10日,革命者的一家炸弹制造厂的意外爆炸,导致了附近帝国军队的兵变,……革命运动仍迅速传遍全国。
苏州市2013—2014学年第一学期期中模拟试卷 初二英语(含答案)

苏州市2013—2014学年第一学期期中模拟试卷初二英语(时间:90分钟总分:100分)一.单项选择(15分)( )1. Max is _______honest boy. He has _______ useful book.A. an; anB. a; aC. a; anD. an; a( )2. Of all the streets in Beijing, Wangfujing is _______.A. the busierB. the busyestC. busiestD. the busiest( )3. Today is Wednesday. He _______be at home. He _______be at school.A. can't; canB. can't; mustC. mustn't; mustD. mustn't; can( )4. Kate is my good friend. She often _______a smile _______her face.A. wears; onB. with; inC. with; onD. has; in( )5. The text is _______easier and _______interesting than that one.A. more; muchB. much; moreC. more; moreD. much; much( )6. -Our team won the basketball final today!- _______.A. I hope not.B. I'm not sure.C. I know.D. That's great!( )7. Shanghai is bigger than _______in Jiangsu and bigger than _______in China.A. any city; any cityB. any city; any other cityC. any other city; the other citiesD. any other city; any city( )8. -What _______your Chinese teacher _______?-She is tall and beautiful.A. does; likeB. is; likeC. is; look likeD. does; look( )9. We were all _______at the _______ news.A. exciting; excitingB. excited; excitedC. exciting; excitedD. excited; exciting( )10. After a long walk in the sun, they wanted to drink _______.A. cold somethingB. something coldC. nothing coldD. cold anything( )11.一Your tea smells great!一It’s from India.Would you like ________?A.it B.this C.some D.1ittle( )12.Fishing with Dad was so for little Sam that he almost fell asleep.A. excitedB. excitingC. boredD. boring( )13.一Hi, guys. How was your party yesterday?一Wonderful! We had a big meal and enjoyed __________.A. themselvesB. myselfC. yourselvesD. ourselves( )14.一Shall I take my swimming suit?一No, you ______. We will just go hiking on the mountain.A.mustn’t B.couldn’t C.needn’t D.can’t( )15.—I believe this is the best movie of the year.—Well, . Anyway, the ending is OK.A. that’s a good ideaB. that may not be a good ideaC. I’m not sure if you’re rightD. I think you’re right二、完形填空(10分)One day a rich man wanted to sell some goods in another town and buy some things there. He 1 to take ten servants(仆人) with him. They would carry the goods and also some 2 to eat on their way. The rich man said to 3 of his servants, "Ali, you are the 4 and the weakest one. You may 5 the lightest load(担子) to carry." Ali thanked him and chose the 6 load. It was their food-bread. The rich man said, "How foolish you are! That's the heaviest one. " But Ali was 7 to lift it up. And so they set off. Four hours 8 , they stopped for a rest. They all 9 some of the bread. Then there was 10 bread for Ali to carry. Each time they ate some, the load became smaller and lighter. At last the clever servant had nothing to carry.( )1. A. agreed B. liked C. decided D. refused( )2. A. food B. goods C. water D. meat( )3. A. all B. both C. none D. one( )4. A. tallest B. smallest C. busiest D. fastest( )5. A. find B. give C. choose D. carry( )6. A. lightest B. smallest C. best D. biggest( )7. A. glad B. worry C. sorry D. tired( )8. A. early B.later C.past D.last( )9. A. loved B.put C.called D.ate( )10. A. more B.little C.less D.no三、阅读理解。
江苏省西安交通大学苏州附属中学2013—2014学年第一学期高一暑期自主学习检测数学试题

江苏省西安交通大学苏州附属中学2013—2014学年第一学期高一暑期自主学习检测数学试题西安交通大学苏州附属中学2013—2014学年第一学期高一暑期自主学习检测班级姓名成绩一、填空题(每小题5分,共60分)1.若式子在实数范围内有意义,则x 的取值范围是▲ .2.若点(m ,n )在函数y=2x+1的图象上,则2m ﹣n 的值是▲ .3.若3×9m ×27m =311,则m 的值为▲ .4.若双曲线y = k x 与直线y =2x +1的一个交点的横坐标为-1,则k 的值是▲ 5.若a=2,a+b=3,则a 2+ab= ▲6.分解因式(x -1)2-2(x -1)+1的结果是▲7.方程 4 x - 3 x -2 =0的解为▲ 8.如图,直线y =k 1x +b 与双曲线y =k 2 x 交于A 、B 两点,它们的横坐标分别为1和5,则不等式k 1x < k 2 x-b 的解集是▲ 9.设m 、n 是一元二次方程x 2+3x -7=0的两个根,则m 2+4m +n =▲ .10.若代数式232++x x 可以表示为b x a x +-+-)1()1(2的形式,则a +b 的值是▲ .11.已知x=y+4,则代数式22x 2xy+y 25--的值为▲ .12.大于1的正整数m 的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m 3分裂后,其中有一个奇数是2013,则m 的值是▲ .答题栏1. 2. 3. 4.5. 6. 7. 8.9. 10. 11. 12.二、解答题(共40分)13.已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当△P AC的周长最小时,求点P的坐标;(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.14.如图,已知一次函数b kx y +=1的图象与x 轴相交于点A ,与反比例函数x c y =2的图象相交于B (-1,5)、C (25,d )两点.点P (m 、n )是一次函数b kx y +=1的图象上的动点.(1)求k 、b 的值;(2)设231<<-m ,过点P 作x 轴的平行线与函数xc y =2的图象相交于点D .试问△P AD 的面积是否存在最大值?若存在,请求出面积的最大值及此时点P 的坐标;若不存在,请说明理由;(3)设a m -=1,如果在两个实数m 与n 之间(不包括m 和n )有且只有一个整数,求实数a 的取值范围.15.如图1,点C、B分别为抛物线C1:y1=x2+1,抛物线C2:y2=a2x2+b2x+c2的顶点.分别过点B、C作x轴的平行线,交抛物线C1、C2于点A、D,且AB=BD.(1)求点A的坐标:(2)如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=2x2+b1x+c1”.其他条件不变,求CD的长和a2的值;(3)如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=4x2+b1x+c1”,其他条件不变,求b1+b2的值(直接写结果).1.x ≥2 2.﹣1 3. 2 4. 1 5.66.(x -2)2 7.X=8 8.-5<x <-1或x >0 9.410.11 11.-9 12.4513.解:(1)将A (-1,0)、B (3,0)、C (0,3)代入抛物线y =ax 2+bx +c 中,得:∴抛物线的解析式:y =-x 2+2x +3. (2)连接BC ,直线BC 与直线l 的交点为P ;设直线BC 的解析式为y =kx +b ,将B (3,0),C (0,3)代入上式,得:,解得:∴直线BC 的函数关系式y =-x +3;当x -1时,y =2,即P 的坐标(1,2).(3)抛物线的解析式为:x =-=1,设M (1,m ),已知A (-1,0)、C (0,3),则:MA 2=m 2+4,MC 2=m 2-6m +10,AC 2=10;①若MA =MC ,则MA 2=MC 2,得:m 2+4=m 2-6m +10,得:m =1;②若MA =AC ,则MA 2=AC 2,得:m 2+4=10,得:m =±;③若MC =AC ,则MC 2=AC 2,得:m 2-6m +10=10,得:m =0,m =6;当m =6时,M 、A 、C 三点共线,构不成三角形,不合题意,故综上可知,符合条件的M 点,且坐标为 M (1,)(1,-)(1,1)(1,0).14.(1)12y2c=-5d=-233y =0,(,0);223-n 5n x y y =n -n 2n113-n 51349=y =+5=-n-+222n 4216-2m+3=n 0P B B C A P AB P D PD ∴∴∴ ? ? D P 将点坐标代入,;将点C 横坐标代入,得;将点、代入、直线解析式,求得k=-2,b=3;(2)令,x=由题意,点在线段上运动(不含A 、B )。
西安交通大学附属中学分校初三化学上册期中试题及答案知识讲解

西安交通大学附属中学分校初三化学上册期中试题及答案知识讲解一、选择题(培优题较难)1.科学理论在传承中不断发展,科学家们传承前人的正确观点,纠正错误观点,形成科学理论,关于原子结构的学说有:①在球体内充斥正电荷,电子镶嵌其中②原子是可分的③原子呈球形④原子中有带负电的电子⑤原子中有带正电的原子核⑥原子核很小,但集中了原子的大部分质量其中经过卢瑟福传承和发展后形成的观点是()A.②③④⑤⑥B.①②③④C.④⑤⑥D.⑤⑥2.某反应的微观示意图如下,其中“”和“”表示不同元素的原子,下列说法不正确的是( )A.反应物有4种分子B.反应前后原子个数不变C.反应前后元素种类不变D.化学变化中的最小粒子是原子3.下列实验操作正确的是A.塞紧橡皮塞B.加热液体C.取用液体D.读出液体的体积4.石墨烯是一种革命性材料,具有优异的光学、电学和力学特性。
图为金刚石、石墨和石墨烯的结构模型图,图中小球代表碳原子。
下列说法正确的是( )①石墨烯是一种新型化合物②三种物质分别在足量的氧气中完全燃烧的产物相同③金刚石和石墨烯是组成相同但结构不同的两种物质④石墨烯有超强的导电性和导热性,说明石墨烯的化学性质和金属相似A.①④B.②③C.①③D.②③④5.下列图示中的“错误实验操作”与图下面对应的“可能产生的后果”不一致的是()A.液体喷出B.污染试剂C.酒精溅出D.读数偏大6.质量相等的两份氯酸钾,只向其中一份加入少量二氧化锰,同时放在两只试管内加热。
下列有关放出氧气质量(g)与反应时间(t)关系图象(图中是a纯氯酸钾曲线,b是混有二氧化锰的曲线)其中正确是A.A B.B C.C D.D7.化学实验操作应严谨规范,下列操作符合要求的是A.看B.听C.闻D.吹8.下列关于过滤操作的叙述不正确的是A.滤纸的边缘要低于漏斗口B.液面不要低于滤纸的边缘C.玻璃棒要靠在三层滤纸的一边D.漏斗下端的管口要紧靠烧杯内壁9.科学家用单个分子制戚的“纳米车”能在人工操纵下运输药物分子到病源处释放,杀死癌细胞。
人教新课标版数学高二-西安交通大学苏州附属中学2013-2014高二上学期期初测试数学试卷

西安交通大学苏州附属中学2013-2014学年高二数学期初测试一、填空题:本大题共14小题,每小题5分,共70分.把答案填在答卷相应位置上. 1.函数()sin cos f x x x =的最小正周期是 ▲ .2.根据表格中的数据,可以判定方程e x ﹣x﹣2=0的一个根所在的区间为 ▲ .x ﹣1 0 1 2 3 e x 0.37 1 2.72 7.39 20.08 x+2123453.若关于x 的不等式2112x ax -+>-的解集为{}12x x -<<,则实数a = ▲ . 4.如图,已知集合A={2,3,4,5,6,8},B={1,3,4,5,7},C={2,4,5,7,8,9},用列举法写出图中阴影部分表示的集合为 ▲ .5.执行如图所示的程序框图,若输入A 的值为2,则输出P 的值为 ▲ . 6.已知π(,π)2α∈,3sin 5α=,则πsin()4α+= ▲ . 7.将一个骰子连续抛掷三次,它落地时向上的点数能组成等差数列的概率为 ▲ . 8.已知向量(34)a =-, ,(11)a =-, ,则向量a 在b 方向上的投影为 ▲ . 9.在△ABC 中,已知2a =,b x =,30B =.如果△ABC 有两解,那么x 的取值范围 ▲ .10.在数列{}n a 中,1=0a , 1313n n na a a ++=-,则2013a = ▲ .11.已知函数()(2)2af x x x x =+>-的图象过点A (3,7),则此函的最小值是 ▲ . 12.在△ABC 中, 若2222sin sin 2cos cos b C c B bc B C +=,则△ABC 的形状是 ▲ .13.如图,已知正三角形ABC 的边长为2,点D 为边AC 的中点, 点E 为边AB 上离点A 较近的三等分点,则BD CE ⋅= ▲ .(第13题图)EDBA C14.已知数列}{n a 满足:114a =,2122n n n a a a +=+,用][x 表示 不超过x 的最大整数,n S 表示数列⎭⎬⎫⎩⎨⎧+21n a 的前n 项和.现给出下列命题:①数列}{n a 单调递增; ② 数列}{1n n a a -+单调递减;③ 21111+-=+n n n a a a ; ④[].32013=S以上命题中正确的是 ▲ (填写你认为正确的所有命题的序号).二、解答题(本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤) 15.(本小题满分14分)已知a ,b ,c 是同一平面内的三个向量,其中=(1,2)a . (Ⅰ)若35b =,且//b a ,求b 的坐标;(Ⅱ)若c 与a 的夹角θ的余弦值为()(9)a c a c +⊥-,求c .16.(本小题满分14分)已知函数22π()cos ()sin 6f x x x =--. (Ⅰ)求π()12f 的值; (Ⅱ)求函数()f x 在π[0,]2上的最大值.17.(本小题满分16分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .(Ⅰ)若3cos sin 3a B b A c +=,求角A ; (Ⅱ)若3b a =,2c =,且△ABC 的面积为3,求a 的值.18.(本小题满分16分)已知函数()241x x f x a a =---(a >0且a ≠1). (1)求函数()f x 的定义域、值域;(2)是否存在实数a ,使得函数()f x 满足:对于任意x ∈﹣1,+∞),都有f (x )≤0?若存在,求出a 的取值范围;若不存在,请说明理由.解:(1)由4﹣a x ≥0,得a x ≤4.当a >1时,x ≤log a 4;当0<a <1时,x ≥log a 4. 即当a >1时,f (x )的定义域为(﹣∞,log a 4log a 4,+∞). 令t=,则0≤t <2,且a x =4﹣t 2,∴f (x )=g (t )=4﹣t 2﹣2t ﹣1=﹣(t+1)2+4,当t≥0时,g (x )是t 的单调减函数,∴g (2)<g (t )≤g (0),即﹣5<f (x )≤3,∴函数f (x )的值域是(﹣5,3﹣1,+∞),都有f (x )≤0,则区间﹣1,+∞),有a x ≤3恒成立,因为0<a <1,所以对任意x ∈﹣1,+∞),都有f (x )≤0. 19.(本小题满分16分)要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD 是一个矩形,EFCD 是一个等腰梯形,梯形高h=AB ,tan ∠FED=,设AB=x 米,BC=y 米. (Ⅰ)求y 关于x 的表达式;(Ⅱ)如何设计x ,y 的长度,才能使所用材料最少?解:(1)如图,等腰梯形EFCD 中,DH 是高,依题意:DH=AB=x ,EH===, ∴=xy+(x+x+)=xy+,∴y=, ∵x >0,y >0,∴,解得0<x <, ∴所求的表达式为:y=,(0<x <)(2)在RT △DEH 中,∵tan ∠FED=,∴sin ∠FED=, ∴DE===,∴l=(2x+2y )+2×+(2×)=2y+6x==+≥2=26,当且仅当=,即x=3时取等号,此时y==4,∴AB=3米,BC=4米时,用材料最少 20.(本小题满分16分)已知公差不为0的等差数列{}n a 满足23a =,1a ,3a ,7a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)数列{}n b 满足11n n n n na ab a a ++=+,求数列{}n b 的前n 项和n S ; (Ⅲ)设12()n n n a c nλ+=-,若数列{}n c 是单调递减数列,求实数λ的取值范围. 解:(Ⅰ)由题知2317a a a =,设{}n a 的公差为d ,则()()211126a d a a d +=+,212a d d =,0d ≠ ∴12a d =.又23a =,∴13a d += 12,1a d == 1n a n ∴=+.(Ⅱ)11121122112n n n n n a a n n b a a n n n n ++++=+=+=+-++++. 12111111222233412n n S b b b n n =++=+-++-+++-++ 1122222(2)nn n n n =+-=+++. (III )1(2)2()=2()n n n n a n c n n λλ++=--,使数列{}n c 是单调递减数列, 则12(3)22()01n n n n n c c n nλ+++-=--<+对*∈N n 都成立即max 2(3)22(3)20()11n n n n n n n nλλ++++--<⇒>-++设2(3)2()1n n f n n n++=-+ 2(4)32(3)2(1)()211n n n n f n f n n n n n +++++-=--++++2(4)23(3)21n n n n n n +++=+-++ 42621321n n n =+++--++()()()2212n n n n -=++(1)(2)(3)(4)(5)f f f f f ∴<=>>>当2n =或3n =时,max 4()3f n = 所以max 2(3)24()13n n n n ++-=+ 所以43λ>.。
江苏省西安交通大学苏州附属中学高二数学上学期期初测试试题苏教版

西安交通大学苏州附属中学2013-2014学年高二数学期初测试一、填空题:本大题共14小题,每小题5分,共70分.把答案填在答卷相应位置上. 1.函数()sin cos f x x x =的最小正周期是 ▲ .2.根据表格中的数据,可以判定方程e x﹣x ﹣2=0的一个根所在的区间为 ▲ .3.若关于x 的不等式212x ax -+>-的解集为{}12x x -<<,则实数a = ▲ . 4.如图,已知集合A={2,3,4,5,6,8},B={1,3,4,5,7},C={2,4,5,7,8,9},用列举法写出图中阴影部分表示的集合为 ▲ .5.执行如图所示的程序框图,若输入A 的值为2,则输出P 的值为 ▲ . 6.已知π(,π)2α∈,3sin 5α=,则πsin()4α+=▲ . 7.将一个骰子连续抛掷三次,它落地时向上的点数能组成等差数列的概率为 ▲ . 8.已知向量(34)a =-, ,(11)a =-, ,则向量a 在b 方向上的投影为 ▲ . 9.在△ABC 中,已知2a =,b x =,30B =.如果△ABC 有两解,那么x 的取值范围 ▲ .10.在数列{}n a 中,1=0a , 1n a +=2013a = ▲ .11.已知函数()(2)2af x x x x =+>-的图象过点A (3,7),则此函的最小值是 ▲. 12.在△ABC 中, 若2222sin sin 2cos cos b C c B bc B C +=,则△ABC 的形状是 ▲ .13.如图,已知正三角形ABC 的边长为2,点D 为边AC 的中点, 点E 为边AB 上离点A 较近的三等分点,则BD CE ⋅= ▲ .(第13题图)EDBA C14.已知数列}{n a 满足:114a =,2122n n n a a a +=+,用][x 表示 不超过x 的最大整数,n S 表示数列⎭⎬⎫⎩⎨⎧+21n a 的前n 项和.现给出下列命题:① 数列}{n a 单调递增; ② 数列}{1n n a a -+单调递减;③ 21111+-=+n n n a a a ; ④[].32013=S以上命题中正确的是 ▲ (填写你认为正确的所有命题的序号).二、解答题(本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分14分)已知a ,b ,c 是同一平面内的三个向量,其中=(1,2)a . (Ⅰ)若35b =,且//b a ,求b 的坐标;(Ⅱ)若c 与a 的夹角θ的余弦值为()(9)a c a c +⊥-,求c .16.(本小题满分14分)已知函数22π()cos ()sin 6f x x x =--. (Ⅰ)求π()12f 的值;(Ⅱ)求函数()f x 在π[0,]2上的最大值.17.(本小题满分16分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .cos sin B b A +=,求角A ;(Ⅱ)若b =,2c =,且△ABC ,求a 的值.18.(本小题满分16分)已知函数()1x f x a =-(a >0且a≠1). (1)求函数()f x 的定义域、值域;(2)是否存在实数a ,使得函数()f x 满足:对于任意x∈[﹣1,+∞),都有()f x ≤0?若存在,求出a 的取值范围;若不存在,请说明理由.19.(本小题满分16分)要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD 是一个矩形,EFCD 是一个等腰梯形,梯形高h=AB ,tan ∠FED=,设AB=x 米,BC=y 米.(Ⅰ)求y 关于x 的表达式;(Ⅱ)如何设计x ,y 的长度,才能使所用材料最少?20.(本小题满分16分)已知公差不为0的等差数列{}n a 满足23a =,1a ,3a ,7a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)数列{}n b 满足11n n n n na ab a a ++=+,求数列{}n b 的前n 项和n S ;(Ⅲ)设12()n n n a c nλ+=-,若数列{}n c 是单调递减数列,求实数λ的取值范围.西安交通大学苏州附属中学高二数学期初测试1.函数()sin cos f x x x =的最小正周期是 ▲ .π2.根据表格中的数据,可以判定方程e x﹣x ﹣2=0的一个根所在的区间为 ▲ .(1,2)3.若关于x 的不等式212x ax -+>-的解集为{}12x x -<<,则实数a = ▲ .124.如图,已知集合A={2,3,4,5,6,8},B={1,3,4,5,7},C={2,4,5,7,8,9},用列举法写出图中阴影部分表示的集合为 ▲ .{2,8}5.已知π(,π)2α∈,3sin 5α=,则πsin()4α+= ▲ .6.执行如图所示的程序框图,若输入A 的值为2,则输出P 的值为 ▲ .47.将一个骰子连续抛掷三次,它落地时向上的点数能组成等差数列的概率为 ▲ .8.已知向量(34)a =-, ,(11)a =-, ,则向量a 在b 方向上的投影为 ▲. 9.在△ABC 中,已知2a =,b x =,30B =.如果△ABC 有两解,那么x 的取值范围 ▲ .12x <<10.在数列{}n a 中,1=0a ,1n a +=2013a = ▲ .11.已知函数的图象过点A (3,7),则此函的最小值是▲ . 6 .12.在△ABC 中, 若2222sin sin 2cos cos b C c B bc B C +=,则△ABC 的形状是直角三角形13.如图,已知正三角形ABC 的边长为2,点D 为边AC 的中点, 点E 为边AB 上离点A 较近的三等分点,则BD CE ⋅= ▲ .1-14.已知数列}{n a 满足:114a =,2122n n n a a a +=+,用][x 表示 不超过x 的最大整数,n S 表示数列⎭⎬⎫⎩⎨⎧+21n a 的前n 项和.现给出下列命题: ⑤数列}{n a 单调递增;(第13题图)EDBA C⑥ 数列}{1n n a a -+单调递减;⑦ 21111+-=+n n n a a a ; ⑧[].32013=S以上命题中正确的是 ▲ (填写你认为正确的所有命题的序号). 答案:①③④15.(本小题满分14分)已知a ,b ,c 是同一平面内的三个向量,其中=(1,2)a . (Ⅰ)若35b =,且//b a ,求b 的坐标;(Ⅱ)若c 与a 的夹角θ的余弦值为()(9)a c a c +⊥-,求c . 解:(Ⅰ)//b a , 设(,2)b a λλλ==,则222445b λλ=+=, ∴29λ=∴3λ=±∴(3,6)b =或(3,6)b =--.(Ⅱ)cos θ=5a =, ∴1cos 2a c a c c θ⋅==-. 又()(9)a c a c +⊥-,∴()(9)0a c a c +⋅-=∴22890a c a c -⋅-= ∴25490c c +-= 解得1c =或59c =-(舍) ∴1c =16.(本小题满分14分)已知函数22π()cos ()sin 6f x x x =--.(Ⅰ)求π()12f 的值; (Ⅱ)求函数()f x 在π[0,]2上的最大值.解:(Ⅰ)22()cos ()sin 121212f πππ=-- cos6π= =. (Ⅱ)11()[1cos(2)](1cos 2)232f x x x π=+---1[cos(2)cos 2]23x x π=-+132cos 2))223x x x π=+=+因为[0,]2x π∈,所以42[,]333x πππ+∈,所以当232x ππ+=,即12x π=时,()f x .17.(本小题满分16分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .cos sin B b A +=,求角A ;(Ⅱ)若b =,2c =,且△ABC ,求a 的值.解:(Ⅰ)3cos sin a B b A +=,由正弦定理可得cos sin sin A B B A C +=)A B =+.cos sin sin cos sin A B B A A B A B +=+.即sin sin sin B A A B =,sin A A ∴=tan A ∴=,60A ∴=︒.注:利用A b B a c cos cos +=直接得A A cos 3sin =同样给分(Ⅱ)b =,ABC ∆,∴1sin 2ABC S ab C ∆==. 2sin 2a C ∴=,22sin C a∴=①由余弦定理2222cos c a b ab C =+- ∴224cos 4a C -=,cos C ∴= ②由①,②得:22221a ⎛⎫+= ⎪⎝⎭, 化简得428160a a -+=,()2240a ∴-=, ∴2a =(Ⅱ)或解:由1sin 2ABC S ab C ∆==得 2sin 2a C = ①由224cos 4a C -=得 2(2cos )2a C = ②由①,②得:sin 2C C =,即πsin()13C +=, π6C ∴=,224sin a C==.∴2a =. 18.(本小题满分16分) 已知函数f (x )=(a >0且a≠1).(1)求函数f (x )的定义域、值域;(2)是否存在实数a ,使得函数f (x )满足:对于任意x ∈[﹣1,+∞),都有f (x )≤0?若存在,求出a 的取值范围;若不存在,请说明理由.解:(1)由4﹣a x≥0,得a x≤4.当a >1时,x≤log a 4;当0<a <1时,x≥log a 4. 即当a >1时,f (x )的定义域为(﹣∞,log a 4];当0<a <1时,f (x )的定义域为[log a 4,+∞). 令t=,则0≤t<2,且a x=4﹣t 2,∴f (x )=g (t )=4﹣t 2﹣2t ﹣1=﹣(t+1)2+4,当t≥0时,g (x )是t 的单调减函数,∴g (2)<g (t )≤g(0),即﹣5<f (x )≤3,∴函数f (x )的值域是(﹣5,3].(2)若存在实数a ,使得对于任意x ∈[﹣1,+∞),都有f (x )≤0,则区间[﹣1,+∞)是定义域的子集.由(1)知,a >1不满足条件;所以0<a <1,且log a 4≤﹣1,即.令t=,由(1)知,f (x )=4﹣t 2﹣2t ﹣1=﹣(t+1)2+4,由f (x )≤0,解得t≤﹣3(舍)或t≥1,即有≥1解得a x≤3,由题意知对任意x ∈[﹣1,+∞),有a x≤3恒成立,因为0<a <1,所以对任意x ∈[﹣1,+∞),都有a x≤a ﹣1.所以有a ﹣1≤3,解得,即.∴存在,对任意x ∈[﹣1,+∞),都有f (x )≤0. 19.(本小题满分16分)要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD 是一个矩形,EFCD 是一个等腰梯形,梯形高h=AB ,tan ∠FED=,设AB=x 米,BC=y 米. (Ⅰ)求y 关于x 的表达式;(Ⅱ)如何设计x ,y 的长度,才能使所用材料最少?解:(1)如图,等腰梯形EFCD 中,DH 是高,依题意:DH=AB=x ,EH===, ∴=xy+(x+x+)=xy+,∴y=, ∵x >0,y >0,∴,解得0<x <, ∴所求的表达式为:y=,(0<x <)(2)在RT △DEH 中,∵tan ∠FED=,∴sin ∠FED=, ∴DE===,∴l=(2x+2y )+2×+(2×)=2y+6x==+≥2=26,当且仅当=,即x=3时取等号,此时y==4,∴AB=3米,BC=4米时,用材料最少 20.(本小题满分16分)已知公差不为0的等差数列{}n a 满足23a =,1a ,3a ,7a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)数列{}n b 满足11n n n n na ab a a ++=+,求数列{}n b 的前n 项和n S ;(Ⅲ)设12()n n n a c nλ+=-,若数列{}n c 是单调递减数列,求实数λ的取值范围. 解:(Ⅰ)由题知2317a a a =,设{}n a 的公差为d ,则()()211126a d a a d +=+,212a d d =,0d ≠ ∴12a d =. 又23a =,∴13a d += 12,1a d == 1n a n ∴=+. (Ⅱ)11121122112n n n n n a a n n b a a n n n n ++++=+=+=+-++++. 12111111222233412n n S b b b n n =++=+-++-+++-++ 1122222(2)n n n n n =+-=+++. (III )1(2)2()=2()n n n n a n c n nλλ++=--,使数列{}n c 是单调递减数列, 则12(3)22()01n n n n n c c n n λ+++-=--<+对*∈N n 都成立 即max 2(3)22(3)20()11n n n n n n n n λλ++++--<⇒>-++ 设2(3)2()1n n f n n n ++=-+ 2(4)32(3)2(1)()211n n n n f n f n n n n n +++++-=--++++2(4)23(3)21n n n n n n +++=+-++ 42621321n n n =+++--++()()()2212n n n n -=++ (1)(2)(3)(4)(5)f f f f f ∴<=>>>当2n =或3n =时,max 4()3f n =所以max 2(3)24()13n n n n ++-=+ 所以43λ>.。
西交大苏州附中高二文科数学期中试卷

2013-2014学年第二学期七校期中考试联考高 二 数 学 (文 科)一、填空题:本大题共14小题,每小题5分,共70分。
请将答案填写在答题卷的相应位置。
1.已知集合(]2 1A =-,,[)1 2B =-,,则A B =U ▲ . 2.设复数z 满足(34i)50z ++=(i 是虚数单位),则复数z 的模为 ▲ . 3. 已知命题:,sin 1p x R x ∃∈≥,则p ⌝为 ▲ . 4.“M N >”是“22log log M N >”成立的 ▲ 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写)5. 函数()f x =的定义域为 ▲ .6. 设函数2()23f x ax x =+-在区间(-∞,4)上是单调递增函数,则实数a 的取值范围 是 ▲ .7.若关于x 的方程ln 2100x x +-=的唯一解在区间(,1)()k k k Z +∈内,则k = ▲ . 8. 下列说法正确的有 ▲ .(填序号)(1)若函数f (x )为奇函数,则f (0)=0; (2)函数1()1f x x =-在(,1)(1,)-∞+∞上是减函数; (3)若函数(2)y f x =+为偶函数,则函数()y f x =的图像关于直线x =2对称; (4)若函数2()(2)f x ax a x b =+-+是定义在(b ,a -1)上的偶函数,则b = -1. 9.设,a b R ∈,且2a ≠,若定义在区间(,)b b -内的函数1()lg 12axf x x+=+是奇函数,则a b +的取值范围是 ▲ .10. 已知l ,m 是两条不同的直线,α,β,γ是三个不同的平面,给出下列命题: (1) ,l m l m αα⊥⊂⇒⊥;(2)//,//l m l m αα⊂⇒; (3),//αβαγβγ⊥⊥⇒;(4),//l l αββα⊥⊥⇒. 上述命题中,所有真命题的序号为 ▲ .11.已知()f x 是R 上的偶函数,且在区间(0,)+∞上是增函数,若有(23)(21)f a f a -+>-成立,实数a 的取值范围是 ▲ .12. 已知函数()f x 对任意实数x 均有()2(2)f x f x =-+,且()f x 在区间[]0,2上有表达式()(2)f x x x =-,则()f x 在区间[]2,4上的表达式为 ▲ .13.已知函数22 (0)()12 (0)xx f x x x x x ⎧>⎪=+⎨⎪+≤⎩,若函数()()g x f x m =-有3个零点,则实数m 的取值范围是 ▲ .14.已知定义在(0,)+∞上的函数()f x 为单调函数,且2()(())2f x f f x x⋅+=,则(1)f =▲ .二、解答题(请在指定区域....内作答,解答要给出必要的文字说明和验算步骤,本大题共6小题,共计90分)15. (本小题满分14分)设集合}341|{},4|{2+<=<=x x B x x A . (1)求集合B A ⋂;(2)若不等式022<++b ax x 的解集为B ,求b a ,的值.16. (本小题满分14分) 已知命题p :11[1,3],()102x x m -∀∈+-<,命题q :2(0,),40x mx x ∃∈+∞+-=.若“p 且q ”为真命题,求实数m 的取值范围.17. (本小题满分15分) 如图,在三棱锥P -ABC 中,PC ⊥平面ABC ,△ABC 为正三角形,D ,E ,F 分别是BC ,PB ,CA 的中点. (1) 证明:ED //平面P AC ;(2) 证明:平面PBF ⊥平面P AC ;(3) 判断AE 是否平行于平面PFD ,并说明理由.18. (本小题满分15分)经市场调查,某旅游城市在过去的一个月内(以30天计),日旅游人数()f t (万人..)与时间t (天)的函数关系近似满足1()4f t t=+,人均消费()g t (元.)与时间t (天)的函数关系近似满足()115|15|g t t =--.(1)求该城市的旅游日收益()w t (万元..)与时间(130,)t t t N ≤≤∈的函数关系式; (2)求该城市旅游日收益的最小值(万元..).ACB19. (本小题满分16分)已知函数[]11()()2()3,1,193x xf x a x =-+∈-.(1)当a =1时,求函数f (x )的值域; (2)求f (x )的最小值h (a );(3)否存在实数m ,同时满足以下条件:① 3m n >>;② 当()h a 的定义域为[,]n m 时值域为22[,]n m ;若存在,求出,m n 的值;若不存在,说明理由.20. (本小题满分16分) 已知函数21()ln ,()2f x xg x x bx ==-(b 为常数). (1)函数f (x )的图像在点(1,f (1))处的切线与g (x )的图像相切,求实数b 的值;(2)设()()()h x f x g x =+,若函数h (x )在定义域上存在单调减区间,求实数b 的取值范围; (3) 若b >1,对于区间[1,2]上的任意两个不相等的实数12,x x ,都有1212()()()()f x f x g x g x ->-成立,求b 的取值范围.2013-2014学年第二学期七校期中考试联考高二数学文科一、填空题1. 2. 3. 4.5. 6. 7. 8.9. 10. 11. 12.13. 14.18.ACBP.参考答案1、(2 2)-,2、13、,sin 1x R x ∀∈<4、必要不充分5、(,0]-∞6、1[,0]4-7、4 8、(3)(4) 9、3(2,]2-- 10、(1) 11、a <1 12、1(2)(4)2x x --- 13、1(0,)214、1±15、解:(1)}212|{}4|{2<<=<=x x x x A}13|{}341|{<<-=-<=x x x x B }12|{<<-=⋂∴x x B A ……………………………………………………………7分(2)由题意及(1)有-3,1是方程02=++b ax x 的两根根据韦达定理有:⎪⎪⎩⎪⎪⎨⎧-=⨯-=-=+-=-31322132b a6,4-==⇒b a …………………………14分16、解:p 真:m >0………………………………………………………………………………5分q 真:116m ≥………………………………………………………………………………10分 p 且q 为真,则1[,0)16m ∈-………………………………………………………………14分17、(1)5分 (2)10分(3)不平行 15分18、解:(1)由题意得,1()()()(4)(115|15|)w t f t g t t t=⋅=+--…………………………5分(2)因为**1(4)(100),(115,)()1(4)(130),(1530,)t t t N t w t t t t N t ⎧++≤<∈⎪⎪=⎨⎪+-≤≤∈⎪⎩………………………………………7分 ①当115t ≤<时,125()(4)(100)4()401w t t t t t=++=++4401441≥⨯= 当且仅当25t t=,即5t =时取等号…………………………………………………………10分 ②当1530t ≤≤时,1130()(4)(130)519(4)w t t t t t=+-=+-,可证()w t 在[15,30]t ∈上单调递减,所以当30t =时,()w t 取最小值14033…………………………………………13分由于14034413<,所以该城市旅游日收益的最小值为14033万元……………………15分19、解:(1)()[2,6]f x ∈…………………………………………………………………3分 (2) 1()3x t =,∵[1,1]x ∈-, ∴ 11()[,3]33x t =∈则原函数可化为2221()23()333t t at t a a t ϕ⎡⎤=-+=-+-∈⎢⎥⎣⎦,,讨论 ① 当13a <时,min 1282()()()393ah a t ϕϕ===-② 当133a ≤≤时,2min ()()()3h a t a a ϕϕ===-③ 当3a >时,min ()()(3)126h a t a ϕϕ===-22821()9331()3(3)3126(3)a a h a a a a a ⎧-<⎪⎪⎪∴=-≤≤⎨⎪->⎪⎪⎩………………………………………………………………10分 (3)因为()126h a a =-在(3,)+∞上为减函数,而3m n >> ()h a ∴在[,]n m 上的值域为[(),()]h m h n又()h a 在[,]n m 上的值域为22[,]n m ,22()()h m n h n m ⎧=∴⎨=⎩即: 22126126m n n m ⎧-=⎨-=⎩ …12分 两式相减得: 6()()()m n m n m n -=-+ 又3m n >>6m n ∴+=, 而3m n >>时有6m n +>,矛盾.西交大苏州附中高二文科数学期中试卷11 / 11 故满足条件的实数,m n 不存在. ………………………………………………………16分20、(1)y =x -1 …………………………………………………………………………………2分 2112y x y x bx =+⎧⎪⎨=-⎪⎩,得22(1)20x b x -++=,由24(1)80,1b b ∆=+-==-±4分 (2) 21()ln (0)2h x x x bx x =+-> 2,1()0x bx h x x-+=<在(0,)+∞上有解 只要1b x x>+在(0,)+∞上有解,解得b>2, 即(2,)b ∈+∞……………………………………………………8分(3)y =f (x )在[1,2]上是增函数,当12x x <时,12()()f x f x <由1212()()()()f x f x g x g x ->-可得121221()()()()()()f x f x g x g x f x f x -<-<-;即1122()()()()f x g x f x g x -<-与1122()()()()f x g x f x g x +<+在[1,2]上恒成立;()()()h x f x g x =-在[1,2]上单调递增;'1()0h x x b x =-+≥在在[1,2]上恒成立,32b ≥ ()()()r x f x g x =+在[1,2]上单调递增;'1()0r x x b x =+-≥在[1,2]上恒成立,2b ≤ 综上3,22b ⎡⎤∈⎢⎥⎣⎦.………………………………………………………………………………16分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西交大苏州附中2013-2014学年度第一学期期中复习数学试卷卷(5)一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上. 1.两个平面最多可以将空间分成 部分. 2.直线053=+-y x 的倾斜角是 .3.若一个球的表面积为12π,则该球的半径为 .4.两平行直线0962043=-+=-+y x y x 与的距离是 . 5.已/知圆044222=+-++y x y x 关于直线b x y +=2成轴对称,则b = .. 6.关于直线,m n 与平面,αβ,有以下四个命题:①若//,//m n αβ且//αβ,则//m n ;②若,m n αβ⊥⊥且αβ⊥,则m n ⊥; ③若,//m n αβ⊥且//αβ,则m n ⊥;④若//,m n αβ⊥且αβ⊥,则//m n ; 其中正确命题的序号是 .7.正三棱锥的底面边长为3,则其体积为 .8.过点P(2,3)且在两轴上的截距相等的直线方程是_________________. 9.圆柱形容器的内壁底半径是10cm ,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了53cm ,则这个铁球的表面积为 2cm . 10.圆心在y 轴上,且与直线y x =相切于点(1,1)的圆的方程为________ ___________.11.点P 在平面ABC 上的射影为O ,且PA 、PB 、PC 两两垂直,那么O 是△ABC 的 .(填:外心,内心,重心,垂心)12.若直线y x b =+与曲线x =b 的取值范围是 .13.已知04,k <<直线1:2280l kx y k --+=和直线222:2440l x k y k +--=与两坐标轴围成一个四边形,则使得这个四边形面积最小的k 值为 .14.若圆2244100x y x y +---=上至少有三个不同的点到直线0ax by +=的距离为_______________________.ABCD D1C1B1A1二、解答题:本大题共6小题,共计14+14+15+15+16+16=90分.解答应写出文字说明、证明过程或演算步骤.请把答案写在答卷纸...相应位置上. 15(本小题满分14分)如图,矩形ABCD 的两条对角线相交于点M (2,0),AB 边所在直线的方程为x -3y -6=0,点T (-1,1)在AD 边所在的直线上.(1)分别求AD 边,CD 边所在直线的方程; (2)求矩形ABCD 外接圆的方程.16.(本小题满分15分)如图,在六面体1111ABCD A B C D -中,11//AA CC ,11A B A D =,AB AD =.求证:(1)1AA BD ⊥;(2)11//BB DD .在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABDC 是菱形.(1)求证:平面ADC1⊥平面BCC1B1;(2)求该多面体的体积.18.(本小题满分15分)过圆x2+y2=2外一点P(4,2)向圆引切线.(1)求过点P的圆的切线方程;(2)若切点为P1、P2,,求直线P1P2的方程;(3)求P1、P2两点间的距离.C1B1A1 DCBA设圆221:106320C x y x y +--+=,动圆222:22(8)4120 C x y ax a y a +---++=. (1)求证:圆1C 、圆2C 相交于两个定点;(2)设点P 是圆221x y +=上的点,过点P 作圆1C 的一条切线,切点为1T ,过点P 作圆2C 的一条切线,切点为2T ,问:是否存在点P ,使无穷多个圆2C ,满足12PT PT =?如果存在,求出所有这样的点P ;如果不存在,说明理由.20.(本小题满分16分)如图,在平面直角坐标系xOy 中,已知圆1C :22(1)1x y ++=,圆2C :22(3)(4)1x y -+-=.(1)若过点1(1 0)C -,的直线l 被圆2C 截得的弦长为6,求直线l 的方程;(2)设动圆C 同时平分圆1C 的周长、圆2C 的周长. ①证明:动圆圆心C 在一条定直线上运动;②动圆C 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.参考答案一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上. 1.两个平面最多可以将空间分成 部分. 4 2.直线053=+-y x 的倾斜角是 .6003.若一个球的表面积为12π4.两平行直线0962043=-+=-+y x y x 与的距离是 。
205.已/知圆044222=+-++y x y x 关于直线b x y +=2成轴对称,则b = . 4 6.关于直线,m n 与平面,αβ,有以下四个命题:①若//,//m n αβ且//αβ,则//m n ;②若,m n αβ⊥⊥且αβ⊥,则m n ⊥; ③若,//m n αβ⊥且//αβ,则m n ⊥;④若//,m n αβ⊥且αβ⊥,则//m n ; 其中正确命题的序号是 ②③7.正三棱锥的底面边长为3,则其体积为 . 答案: 9/48.过点P(2,3)且在两轴上的截距相等的直线方程是__________________.32050x y x y -=+-=与9.圆柱形容器的内壁底半径是10cm ,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了53cm ,则这个铁球的表面积为 2cm .100π. 10.圆心在y 轴上,且与直线y x =相切于点(1,1)的圆的方程为________ ___________.22(2)2x y +-=11.点P 在平面ABC 上的射影为O ,且PA 、PB 、PC 两两垂直,那么O 是△ABC 的 心垂心;12.若直线y x b =+与曲线x =b 的取值范围是 .(-2,2]⋃{-13.已知04,k <<直线1:2280l kx y k --+=和直线222:2440l x k y k +--=与两坐标轴围成一个四边形,则使得这个四边形面积最小的k 值为 .1/8ABCD D1C1 B1A114.若圆2244100x y x y +---=上至少有三个不同的点到直线0axby +=的距离为_______________________.答案: [22-+二、解答题:(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.) 15(本小题满分14分)如图,矩形ABCD 的两条对角线相交于点M (2,0),AB 边所在直线的方程为x -3y -6=0,点T (-1,1)在AD 边所在的直线上.(1)求AD 边,CD 边所在直线的方程; (2)求矩形ABCD 外接圆的方程.解:(1) 因为AB 边所在直线的方程为x -3y -6=0,且AD 与AB 垂直, 所以直线AD 的斜率为-3.……………………………………2分又因为点T (-1,1)在直线AD 上,所以AD 边所在直线的方程为y -1=-3(x +1), 即3x +y +2=0.…………………………………………………………4分由360320{x y x y --=++=解得点A 的坐标为(0,-2). …………6分因为矩形ABCD 的两条对角线的交点为M (2,0),所以C(4,2) …………8分 所以CD 边所在直线的方程为x-3y+2=0, …………10分 (2) M 为矩形ABCD 外接圆的圆心.又|AM =………………………………12分 从而矩形ABCD 外接圆的方程为(x -2)2+y 2=8.…………………… 14分 16.(本小题满分14分)如图,在六面体1111ABCD A B C D -中,11//AA CC ,11A B A D =,AB AD =.求证:(1)1AA BD ⊥;(2)11//BB DD . 证明:(1)取线段BD 的中点M ,连结AM 、1A M , 因为11A D A B =,AD AB =,所以BD AM ⊥,1BD A M ⊥.…………3分又1AM A M M = ,1AM A M ⊂、平面1A AM , 所以BD ⊥平面1A AM .而1AA ⊂平面1A AM ,所以1AA BD ⊥.……………………………7分 (2)因为11//AA CC ,1AA ⊄平面11D DCC ,1CC ⊂平面11D DCC ,所以1//AA 平面11D DCC .…………………………………………………10分 又1AA ⊂平面11A ADD ,平面11A ADD 平面111D DCC DD =,……11分 所以11//AA DD .同理得11//AA BB ,所以11//BB DD .…………………………………………………14分 17.(本小题满分15分)在如图所示的多面体中,已知正三棱柱ABC-A 1B 1C 1的所有棱长均为2,四边形ABDC 是菱形.(1)求证:平面ADC 1⊥平面BCC 1B 1 (2)求该多面体的体积.(1)证:由正三棱柱111ABC A B C -,得1BB AD ⊥,而四边形ABDC 是菱形,所以AD BC ⊥,又1,BB BC ⊂平面11,BB C C 且1BC BB B = ,所以AD ⊥平面11BCC B …5分 则由AD ⊂平面1ADC ,得平面1ADC ⊥平面11BCC B …………………… 7分 (2)因为正三棱柱111ABC A B C -的体积为11ABC V S AA ∆=⨯=………10分 四棱锥11D B C CB -的体积为11211()32BCC B V S AD =⨯=3分所以该多面体的体积为V =5分 18.(本小题满分15分)过⊙:x 2+y 2=2外一点P(4,2)向圆引切线. (1)求过点P 的圆的切线方程.(2)若切点为P 1、P 2求过切点P 1、P 2的直线方程. (3)求P 1、P 2两点间的距离.解:(1)设过点P(4,2)的切线方程为y -2=k(x -4) 即kx -y+2-4k =0 ① 则d =2142kk +-C 1B 1A 1DCBA∴2142k k +-=2 解得k =1或k =71…………3分∴切线方程为:x -y -2=0或x -7y +10=0………………………………………5分(2) 设切点P1(x 1,y 1)、P 2(x 2,y 2),则两切线的方程可写成l 1: x 1x +y 1y =2,l 2:x 2x +y 2y =2因为点(4,2)在l 1和l 2上.则有4 x 1+2y 1=2 4x 2+2y 2=2这表明两点都在直线4x +2y =2上,由于两点只能确定一条直线,故直线2 x +y -1=0即为所求……………………………………10分 (3)12P P 5=……………………15分 19.(本小题满分16分)设圆221:106320C x y x y +--+=,动圆222:22(8)4120 C x y ax a y a +---++=, (1)求证:圆1C 、圆2C 相交于两个定点;(2)设点P 是圆221x y +=上的点,过点P 作圆1C 的一条切线,切点为1T ,过点P 作圆2C 的一条切线,切点为2T ,问:是否存在点P ,使无穷多个圆2C ,满足12PT PT =?如果存在,求出所有这样的点P ;如果不存在,说明理由.19.解(1)将方程2222(8)4120 x y ax a y a +---++=化为221612(224)0x y y x y a +-++-++=,令22161202240x y y x y ⎧+-+=⎨-++=⎩得42x y =⎧⎨=⎩或64x y =⎧⎨=⎩,所以圆2C 过定点(4,2)和(6,4),……………4分 将42x y =⎧⎨=⎩代入22106320x y x y +--+=,左边=1644012320+--+==右边,故点(4,2)在圆1C 上,同理可得点(6,4)也在圆1C 上,所以圆1C 、圆2C 相交于两个定点(4,2)和(6,4);……………6分(2)设00(,)P x y,则1PT =8分2PT =, …………………………………10分 12PT PT =即00001063222(8)412x y ax a y a --+=---++,整理得00(2)(5)0x y a ---=(*)………………………………………………12分 存在无穷多个圆2C ,满足12PT PT =的条件为00220201x y x y --=⎧⎪⎨+=⎪⎩(1)有解, …………………14分而(1)无解,故不存在点P ,使无穷多个圆2C ,满足12PT PT =.………………16分20(本小题满分16分)如图,在平面直角坐标系xOy 中,已知圆1C :22(1)1x y ++=,圆2C :22(3)(4)1x y -+-=.(1)若过点1(1 0)C -,的直线l 被圆2C 截得的弦长为65,求直线l 的方程;(2)设动圆C 同时平分圆1C 的周长、圆2C 的周长. ①证明:动圆圆心C 在一条定直线上运动;②动圆C 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.解:(1)设直线l 的方程为(1)y k x =+,即0kx y k -+= 因为直线l 被圆2C 截得的弦长为65,而圆2C 的半径为1,所以圆心2(3 4)C ,到l :0kx y k -+=的45=.…………………………3分化简,得21225120k k -+=,解得43k =或34k =.所以直线l 的方程为4340x y -+=或3430x y -+=.…………………6分 (2)①证明:设圆心( )C x y ,,由题意,得12CCCC =,.化简得30x y +-=,即动圆圆心C 在定直线30x y +-=上运动.…………………………10分②圆C过定点,设(3)Cm m -,,则动圆C .于是动圆C 的方程为2222()(3)1(1)(3)x m y m m m -+-+=+++-. 整理,得22622(1)0x y y m x y +----+=.…………………………14分由2210 620x y x y y-+=⎧⎨+--=⎩,,得1 2x y⎧=+⎪⎨⎪=+⎩或1 2x y ⎧=⎪⎨⎪=⎩所以定点的坐标为(1,(1+.………16分。
