湖南省长郡中学2011届高三暑期分班考试(数学理)(pdf版)答案
2011年普通高等学校招生全国统一考试数学卷(湖南.理)含详解

2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分150分。
参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高。
(3)球的体积公式343V R π=,其中R 为求的半径。
一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B .1,1a b =-=C .1,1a b =-=-D .1,1a b ==- 答案:D解析:因()1a i i ai b i +=-+=+,根据复数相等的条件可知1,1a b ==-。
2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( )A .充分不必要条件B .必要不充分条件C .充分必要条件 D .既不充分又不必要条件 答案:A解析:因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”。
3.设图一是某几何体的三视图,则该几何体的体积为( )A .9122π+B .9182π+C .942π+D .3618π+答案:B解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+()。
4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表: 男 女 总计 爱好 40 20 60 不爱好 20 30 50 总计 60 50 110由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:正视图侧视图俯视图图12()P K k ≥ 0.0500.010 0.001 k3.8416.63510.828参照附表,得到的正确结论是( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关” 答案:C解析:由27.8 6.635K ≈>,而2( 6.635)0.010P K ≥=,故由独立性检验的意义可知选C.5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为( ) A .4 B .3 C .2 D .1答案:C解析:由双曲线方程可知渐近线方程为3y x a=±,故可知2a =。
湖南省长郡中学2011届高三分班考试

湖南省长郡中学2011届高三分班考试湖南省长郡中学2011届高三分班考试语文试题时量:150分钟总分:100分一、语言知识及表达(共15分,每小题3分)1.下列各组词语中加点字读音完全相同的一组是()A.熨帖与会卖官鬻爵毁家纾难B.饯行践诺图穷匕见从谏如流C.瑰丽皈依大家闺秀岿然不动D.秩序对峙鳞次栉比博闻强识2.下列各句中,没有错别字的一项是()A.他暝思苦想人死后是否有知,想那从来不曾有一个旅人回来过的神密之国。
他的著名的独白生存还是毁灭或者正是他内心深处灵魂的自言自语?B.历史上曾经有过无数发明,今天更是如此——每天都有很多发明被完成,很多专利被注册,但是大多数都如同白驹过隙,瞬即逝,并未在物质文明的发展史上留下影响。
C.浓郁的情韵和深刻的哲理在文章中水乳交溶,增强了文章的艺术魅力,强烈地振撼着读者的心灵。
D.商务部副部长高虎城指出,有个别媒体的报道以偏盖全,蓄意炒作,其中不乏对中国产品提出质疑,甚至有损中国产品声誉的报道,对此,中国政府持保留态度,并坚决反对。
3.下列各句中加点的词语,使用最恰当的一句是()A.由于留在家的都是老弱病残人员,该村发展十分迟钝土地撂荒很多,曾经令人骄傲的林果经济逐步萎缩,烤烟产业更是由以前的上千亩下降到几十亩。
B.程海波案警示着我们的党员干部,当官特别是手中有一定权力的官员,更应树立自己正确的人生观、价值观和世界观,淡薄名利、甘于寂寞、守住清贫。
C.药品中的儿童酌减字样,的确让人难以操作,这样的文字看似一种善意的消费提示,实则似是而非减到多少才合适大多没有明确说明。
D.我们对曹操墓开展现代意义上的考古调查已经有四十多年了,这次震惊中外的考古大发现只是冰山一角大量珍宝还流失民间。
4.下列各句中,没有语病的一句是()A.2009年CCTV中国经济年度人物评选日前在北京揭晓,当选人覆盖了证券、新能源等行业和领域。
解读名单,我们可以清晰地辨认出2009年中国经济的热点和脉搏。
2011年普通高等学校招生全国统一考试数学理试题(湖南卷,含答案)

2011年普通高等学校招生全国统一考试数学理试题(湖南卷,含答案)本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分150分。
参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高。
(3)球的体积公式343V R π=,其中R 为求的半径。
一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B .1,1a b =-=C .1,1a b =-=-D .1,1a b ==- 答案:D2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 答案:A3.设图一是某几何体的三视图,则该几何体的体积为( )A .9122π+B .9182π+C .942π+D .3618π+答案:B4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:参照附表,得到的正确结论是( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关”答案:C5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为( ) A .4 B .3 C .2 D .1答案:C 6. 由直线,,033x x y ππ=-==与曲线cos y x =所围成的封闭图形的面积为( )A .12 B .1 CD答案:D7. 设1m >,在约束条件1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值小于2,则m 的取值范围为( )A.(1,1 B.(1)+∞ C .(1,3) D .(3,)+∞ 答案:A8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为( )A .1B .12 C答案:D二填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上。
2011年湖南省长沙市长郡中学理科实验班招生考试数学试卷
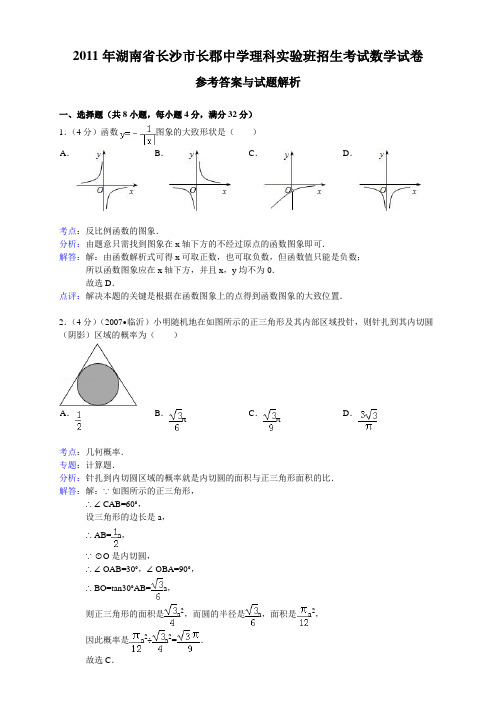
2011年湖南省长沙市长郡中学理科实验班招生考试数学试卷参考答案与试题解析一、选择题(共8小题,每小题4分,满分32分)1.(4分)函数图象的大致形状是( ) C D2.(4分)(2007•临沂)小明随机地在如图所示的正三角形及其内部区域投针,则针扎到其内切圆(阴影)区域的概率为( )π C π D a 则正三角形的面积是,而圆的半径是a ,面积是因此概率是a ÷.的正三角形的面积为:a2003004.(4分)甲、乙两车分别从A,B两车站同时开出相向而行,相遇后甲行驶1小时到达B站,乙.又相遇后甲行驶车站的时间不变可列出方程=+1车站的时间不变可列出方程=+4的值,从而得出正确选项.由题意,有.5.(4分)图中的矩形被分成四部分,其中三部分面积分别为2,3,4,那么,阴影三角形的面积为()6.(4分)如图,AB是圆的直径,CD是平行于AB的弦,且AC和BD相交于E,∠AED=α,那么△CDE与△ABE的面积之比是()=AED=,=cos=7.(4分)两杯等量的液体,一杯是咖啡,一杯是奶油.舀一勺奶油到咖啡杯里,搅匀后舀一勺混合液注入到奶油杯里.这时,设咖啡杯里的奶油量为a,奶油杯里的咖啡量为b,那么a和b的大小奶油杯里的咖啡量为第二次:咖啡杯里的奶油量为奶油杯里的咖啡量为二、填空题(共6小题,每小题5分,满分30分)9.(5分)用数字1,2,3,4,5,6,7,8不重复地填写在下面连等式的方框中,使这个连等式成立:1+□+□=9+□+□=8+□+□=6+□+□1+8+6=9+5+1=8+3+4=6+7+2.10.(5分)如图,正三角形与正六边形的边长分别为2和1,正六边形的顶点O是正三角形的中心,则四边形OABC的面积等于.即正三角形面积的正三角形的面积为×=故答案为11.(5分)计算:=.=.12.(5分)五支篮球队举行单循坏赛(就是每两队必须比赛1场,并且只比赛一场),当赛程进行到某一天时,A队已赛了4场,B队已赛了3场,C队已赛了2场,D队已赛了1场,那么到这一天为止一共已经赛了6场,E队比赛了2场.13.(5分)(2006•无锡)已知∠AOB=30°,C是射线OB上的一点,且OC=4.若以C为圆心,r 为半径的圆与射线OA有两个不同的交点,则r的取值范围是2<r≤4.OC=×14.(5分)如图,△ABC为等腰直角三角形,若AD=AC,CE=BC,则∠1=∠2(填“>”、“<”或“=”)EF=BF=,AC=1CE=﹣,=,三、解答题(共3小题,满分38分)15.(12分)(2009•深圳)迎接大运,美化深圳,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?解这个不等式组得16.(12分)如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中上一点,延长DA至点E,使CE=CD.(1)求证:AE=BD;(2)若AC⊥BC,求证:AD+BD=CD.DE=CD17.(14分)(2007•河北)如图,在等腰梯形ABCD中,AD∥BC,AB=DC=50,AD=75,BC=135.点P从点B出发沿折线段BA﹣AD﹣DC以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD﹣DA﹣AB于点E.点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当点P到达终点C时,求t的值,并指出此时BQ的长;(2)当点P运动到AD上时,t为何值能使PQ∥DC;(3)设射线QK扫过梯形ABCD的面积为S,分别求出点E运动到CD、DA上时,S与t的函数关系式;(不必写出t的取值范围)(4)△PQE能否成为直角三角形?若能,写出t的取值范围;若不能,请说明理由.,在.t=.t==4tQE(或或≠或。
湖南长郡中学2011届高三第四次月考(数学理)
湖南长郡中学 2011届高三第四次月考数 学 试 题(理)(考试范围:集合与逻辑、算法与框图、函数、三角函数、平面向量、数列、推理与证明、不等式、计数原理、概率与统计、空间几何及空间向量、4—1、4—4、4—5)本试题卷包括选择题、填空题和解答题三部分。
时间120分钟。
满分150分。
一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{|},{|12},A x x a B x x R =<=<<表示实数集,且()U A C B R =,则实数a 的取值范围是( )A .2a ≤B .1a <C .2a ≥D .2a >2.已知函数()22()xxf x P x R -=+∈为奇函数,则下列结论正确的是 ( )A .1,()P f x =为R 上的减函数B .1,()P f x =-为R 上的减函数C .P=1,f (x )为R 上的增函数D .P=-1,f (x )为R 上的增函数3.函数2sin()cos()((0,))36y x x x πππ=--+∈,则y( )A .有最小值-1,无最大值B .有最大值1,无最小值C .有最小值 1D .有最小值-14.某企业三月中旬生产A 、B 、C 三种产品共3000件,根据分层抽样的结果,企业统计员制作了如下的统计表格。
由于不小心,表格中A 、C 产品的有关数据己被污染看不清楚,统计员记得A 产品的样本容量比C 产品的样本容量多10件,根据以上信息,可得C 产品的数量是 ( )A .900件B .800件C .90件D .80件5.如图,AC 为⊙O 的直径,BD AC ⊥于P 点,PC=2,AP=8,则BC 的长为 ( )A B .3C .4D .6.已知,,l m n 是三条不重合的直线,,,αγβ是三具不重合的平面,给出下列四个命题:①若,//,m m αβαβ⊥⊥则;②若直线m ,n 与平面α所成的角相等,则m//n ;③存在异面直线m ,n ,使得m//α,m//β,n//β,则α//β; ④若,,,//,l m n l αββγγαγ===则m//n ;A .1B .2C .3D .47.已知向量(,),(1,2),(,),//,a m n b c k t a b b ===且⊥c ,|a+c 则mt 的取值范围是( )A .(,1]-∞B .(0,1]C .[—1,1]D .(—1,1)8.将正整数排成下表:1 2 3 4 4 56 7 8 9 10 11 12 13 14 15 16 …… 则数表中的数2010出现在 ( ) A .第44行第75列 B .第45行第75列 C .第44行第74列 D .第45行第74列二、填空题:本大题共7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上。
湖南省长郡中学2011届高三分班考试物理试题

绝密★启用前湖南省长郡中学2011届高三分班考试物理试题试卷副标题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.一物体做匀减速直线运动,初速度大小为10m/s ,加速度大小为1m/s2,则物体在停止运动前1s 内的平均速度大小为 ( ) A .0.5m/s B .5m/s C .1m/s D .5.5m/s 2.关于近代物理学的结论中,哪些是正确的: ( ) A .宏观物体的物质波波长非常小,极易观察到它的波动性 B .氢原子的能级是不连续的,辐射光子的能量也是不连续的 C .光电效应现象中,光电子的最大初动能与照射光的频率成正比 D .光的干涉现象中,干涉亮条纹部分是光子到达几率大的地方 3.类比是一种有效的学习方法,通过归类和比较,有助于掌握新知识,提高学习效率.在类比过程中,既要找出共同之处,又要抓住不同之处.某同学对机械波和电磁波进行类比,总结出下列内容,其中不正确的是 ( ) A .机械波的频率、波长和波速三者满足的关系,对电磁波也适用 B .机械波和电磁波都能产生干涉和衍射现象 C .机械波的传播依赖于介质,而电磁波可以在真空中传播 D .机械波既有横波又有纵波,而电磁波只有纵波4.点电荷A 和B ,分别带正电和负电,电量分别为4Q 和Q ,在AB 连线上,如图所示,电场强度为零的地方在 ( )A .A 和B 之间 B .A 右侧C .B 左侧D .A 的右侧及B 的左侧5.物体在两个相互垂直的力作用下运动,力F1对物体做功6J ,物体克服力F2做功8J ,则F1、F2的合力对物体做功为 ( ) A .14J B .10J C .2J D .-2J重力),恰能沿直线从左向右飞越此区域,则若电子以相同的速率从右向左水平飞入该区域,则电子将 ( )A .沿直线飞越此区域B .电子将向上偏转C .电子将向下偏转D .电子将向纸外偏转7.地球和木星绕太阳运行的轨道都可以看作是圆形的.已知木星的轨道半径约为地球轨道半径的5.2倍,则木星与地球绕太阳运行的线速度之比约为 ( ) A .0.19 B .0.44 C .2.3 D .5.28.在光滑水平面上有三个完全相同的小球排成一条直线.2、3小球静止,并靠在一起,1球以速度v 0射向它们,如图所示.设碰撞中不损失机械能,则碰后三个小球的速度可能值是 ( )A .032131v v v v ===B .032121,0v v v v ===C .032121,0v v v v ===D .0321,0v v v v ===9.如图所示,正方形容器处在匀强磁场中,一束电子从a 孔垂直进入磁场射入容器中,其中一部分从c 孔射出,一部分从d 孔射出,则下列说法正确的是 ( )A .从两孔射出的电子速率之比为1:2==d c v vB .从两孔射出的电子在容器中运动所用时间之比为1:2:=d c t tC .从两孔射出的电子在容器中运动时的加速度大小之比1:2:=d c a aD .从两孔射出的电子在容器中运动时的加速度大小之比1:2:=d c a a电压表并联在A、C两点间时,电压表读数为U;当并联在A、B两点间时,电压表读数也为U;当并联在B、C两点间时,电压表读数为零,则出现此种情况的原因可能是(R1、R2阻值相差不大)()A.AB段断路B.BC段断路 C.AB段短路D.BC段短路第II 卷(非选择题)请点击修改第II 卷的文字说明 二、实验题11.(4分)如图所示,螺旋测微器的读数是 .12.(4分)在欧姆表测电阻的实验中,用“×10”挡测量一个电阻的阻值,发现表针偏转角度较小,正确的判断和做法是下列选项中的 和 . A .这个电阻阻值较小 B .这个电阻阻值较大 C .为了把电阻测得更准确一些,应换用“×1”挡,重新测量 D .为了把电阻测得更准确一些,应换用“×100”挡,重新测量 13.(4分)如图是用打点计时器打出一系列点的纸带,纸带固定在一个做匀加速直线运动的小车后面,A 、B 、C 、D 、E 为选好的计数点.相邻计数点间的时间间隔为0.04s .由图上数据可从纸带上求出小车在运动中的加速度a= m/s 2以及打点计时器打下C点时小车的瞬时速度= m/s .14.(8分)热敏电阻是传感电路中常用的电子元件.现用伏安法研究热敏电阻在不同温度下的伏安特性曲线(伏安特性曲线是指用电器的电流I 与所加电压U 的关系在U-I 坐标中所作出的图线),要求特性曲线尽可能完整,实验用的原理图如图所示.已知常温下待测热敏电阻的阻值约4~5毟.热敏电阻和温度计插入带塞的保温杯中,杯内有一定量的冷水,其它备用的仪表和器具有: 盛有热水的热水杯电源(3V 、内阻可忽略) 直流电流表(内阻约1Ω) 直流电压表(内阻约5kΩ) 滑动变阻器(0~20Ω) 开关、导线若干.请在空格内填上适当的内容:a .往保温杯中加入一些热水,待温度稳定时读出 的值;b .调节滑动变阻器,快速读出 的值;d .绘出各测量温度下热敏电阻的 . 三、简答题15.(8分)一物体做匀变速直线运动,从某时刻开始计时,即t=0,在此后连续两个2s 内物体通过的位移分别为8m 和16m ,求: (1)物体的加速度大小; (2)t=0时物体的速度大小 四、计算题16.(10分)如图所示,A 和B 之间的距离为0.1m ,电子在A 点的速度70100.1⨯=v m/s .已知电子的电量19106.1-⨯=e C ,电子质量301091.0-⨯=m kg .(1)要使电子沿半圆周由A 运动到B ,求所加匀强磁场的大小和方向; (2)电子从A 运动到B 需要多少时间?17.(10分)如图所示,在光滑水平的地面上,有一辆上表面光滑的正在以速度0v 向右运动的小车,车上的木块一样与车一起以0v 向右运动,车左端有一固定挡板P ,挡板和车的质量为M=16kg ,在挡板P 和质量为M=9kg 的木块之间有少量炸药,炸药爆炸提供给小车和木块的总机械能为E 0=1800J .若要使炸药爆炸后木块的动能等于E 0,在爆炸前小车的速度0v 为多少?18.(12分)如图所示,一带电粒子以速度0v 沿上板边缘垂直于电场线射入匀强电场,它刚好贴着下板边缘飞出.已知匀强电场两极板长为l ,间距为d ,求:(1)如果带电粒子的速度变为20v ,则离开电场时,沿场强方向偏转的距离y 为多少?(2)如果带电粒子的速度变为20v ,板长l 不变,当它的竖直位移仍为d 时,它的水平位移x 为多少?(粒子的重力忽略不计)参考答案1.A【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】2.BD【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】3.D【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】4.C【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】5.D【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】6.C【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】7.B【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】8.D【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】9.AD【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】10.AD【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】11.5.824mm~5.826mm【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】12.B D【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】13.2.5m/s20.75m/s【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】14.a.温度计b.电流表和电压表c.温度d.伏安特性曲线【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】15.(1)2m/s2(2)2m/s【来源】湖南省长郡中学2011届高三分班考试物理试题 【解析】 16.(1)垂直纸面向里 0.0011T (2)1.57×10-8s 【来源】湖南省长郡中学2011届高三分班考试物理试题 【解析】 17.0v =4m/s【来源】湖南省长郡中学2011届高三分班考试物理试题 【解析】 18.(1)14y d =(2)2.5l【来源】湖南省长郡中学2011届高三分班考试物理试题【解析】因为带电粒子在电场中运动,受到的电场力与速度无关,所以a 是一定的⎪⎩⎪⎨⎧==2021at d t v l 2202l dv a =(1)t v l '=02d v l l dv t a y 41422121222202=⋅⋅='=(2)如图示:将速度反向延长交上板的中点,由相似△l x d d l x 5.1,414321='='l x l x 5.2='+=∴水平位移。
2011年长郡中学实验班招生数学试卷卷20110317(复赛卷)

2011年长郡中学实验班招生数学试题欢迎你参加考试!做题时要认真审题,积极思考,细心答题,充分发挥你的水平(时量: 60分钟;满分:100分 注意合理分配时间 )一、选择题:(每个题目只有一个正确答案,每题6分,共36分)1、计算20102011(1(1+-的结果是( )A.1-B.1C .1D .1-2、如图,在Rt A B C 中,90,60,,A B B C C A B C B D A B C C DC D∠=∠=∠- 平分则的值为( )A.3B.3- C.6- D3、初三(1)班在今年的植树节领有平均每人植树6棵的任务,如果只由女同学完成,每人应植树15棵,如果只由男同学完成,每人应植树( )棵A .9B .10C .12D .144、如图是一个正方体盒的平面展开图,如果在其中的在三个正方形A 、B 、C 中分别填入适当的数,使得它们折成正方体后,相对的面上的两个数互为相反数,那么填入A 、B 、C 的三个数依次是 ( )A . 1,-2,0 B. -1,2,0 C. -2,0,1 D. -2,1,0 5、根据下列表格的对应值,判断方程02=++c x b x a (a ≠0, a ,b ,c 为常数)一个解x 的范围是( )A. 3<x <3.23;B. 3.23<x <3.24;C. 3.24<x <3.25;D. 3.25<x <3.266.、已知实数b a ≠,且满足)1(33)1(2+-=+a a ,2)1(3)1(3+-=+b b .则ba aab b+的值为( ).A.23B. 23-C. 2-D. 13-二.填空题:(每题5分,共30分)7、一个西瓜,横切两刀,再竖切两刀(刀刃足够长,都不靠边切),吃完瓜瓤,剩下 块西瓜皮. 8、如图,点A ,B ,C ,D ,E 均在⊙O 上,∠A=30°,∠O=48°,则∠E= °9、如图2,正比例函数x y -=与反比例函数xy 1-=的图象相交于A 、C 两点,AB ⊥x 轴于B ,CD ⊥x 轴于D ,则四边形ABCD 的面积为10、如图3是由棱长为a 的小正方体堆积成的图形.若按照这样的规律继续摆放,第n 层需要块小正方体(用含n 的代数式表示)=学校 姓名 性别 联系电话1-20AB C BO A D E第1层 第2层第3层第4层 图3第n 层 … 第8题图学校 姓名 性别 联系电话11、如图,在△A BC 中,AB =AC ,A D ⊥BC ,CG ∥A B ,BG 分别交AD ,A C 于E ,F .若ba BEEF =,那么BEGE 等于____________.12、如图,在两个直角三角形中,∠ACB =∠ADC =90º,AC =6,AD =2,那么当AB 的长等于____ _时,使得两个三角形相似.三、解答题(本大题共3题,13、14题11分,15每题12分,共34分)13、已知:如图,BC 为半圆的半径,O 为圆心,D 是⌒AC 的中点,四边形ABCD 的对角线AC 、BD 交于点E . (1)试判断:△ABE ∽△DBC 成立吗?说明理由; (2)已知BC =25,CD =25,求sin ∠AEB 的值;(3)在(2)的条件下,求弦AB 的长.ABCDABCDE123O ABCDGEF H14、推理能力都很强的甲、乙、丙站成一列,丙可以看见甲、乙,乙可以看见甲但看不见丙,甲看不见乙、丙.现有5顶帽子,3顶白色,2顶黑色.老师分别给每人戴上一顶帽子(在各自不知道的情况下).老师先问丙是否知道头上的帽子颜色,丙回答说不知道;老师再问乙是否知道头上的帽子颜色,乙也回答说不知道;老师最后问甲是否知道头上的帽子颜色,甲回答说知道.请你说出甲戴了什么颜色的帽子,并写出推理过程. 解:15、如图9,在平面直角坐标系中,二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点,与y 轴交于C 点,与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),OB =OC ,tan∠ACO=31.(1)求这个二次函数的表达式.(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.(4)如图10,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.参考答案及评分标准:一.选择题:(每题6分,共36分)1-6:ADB, ACB二.填空题:(每题5分,共30分)7. 10 8. 54 9. 210. )1(21+n n 11. ab12. 3或23(只填一个得2分)三、解答题:(13、14每题11分,15题12分,共34分)13 (1)△ABE ∽△DBC 成立.∵⌒AC =⌒CD ,∴∠1=∠2.又BC 是⊙O 的直径, ∴∠BAC =∠BDC =︒90.∴△ABE ∽△DBC .……………………………………3分(2)∵△ABE ∽△DBC ,∴∠AEB =∠DCB .在R t △BCD 中,BC =25,CD =25,∴BD =22CDBC-=5.∴AEB ∠sin =DCB ∠sin =552255==BCBD .………………7分(3)∵∠1=∠2,∠2=∠3,∴∠1=∠3.又∠ADE 是公共角,∴△AED ∽△BAD . ∴AD DE BD AD =,即BD DE AD ⋅=2. 又CD =AD =25,∴5)5()25(2⋅-=BE ,BE =453.……9分在R t △ABE 中,AB =BE ·AEB ∠sin =453·552=23.……11分14、甲戴的是白帽子。
湖南省高考数学试卷理科答案与解析

2011年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)(2011?湖南)若a,b∈R,i为虚数单位,且(a+i)i=b+i则()A.a=1,b=1 B.a=﹣1,b=1 C.a=﹣1,b=﹣1 D.a=1,b=﹣1 【考点】复数相等的充要条件.【专题】计算题.【分析】利用复数的乘法运算将等式化简;利用复数相等实部、虚部分别相等;列出方程求出a,b的值.【解答】解:(a+i)i=b+i即﹣1+ai=b+i∴a=1,b=﹣1故选D【点评】本题考查两个复数相等的充要条件:实部、虚部分别相等.2.(5分)(2011?湖南)设集合M={1,2},N={a2},则“a=1”是“N?M”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件【考点】集合关系中的参数取值问题.【专题】集合.【分析】先由a=1判断是否能推出“N?M”;再由“N?M”判断是否能推出“a=1”,利用充要条件的定义得到结论.【解答】解:当a=1时,M={1,2},N={1}有N?M当N?M时,a2=1或a2=2有所以“a=1”是“N?M”的充分不必要条件.故选A.【点评】本题考查利用充要条件的定义判断一个命题是另一个命题的条件问题.3.(5分)(2011?湖南)设如图是某几何体的三视图,则该几何体的体积为()A.9π+42B.36π+18 C.D.【考点】由三视图求面积、体积.【专题】计算题.【分析】由三视图可知,下面是一个底面边长是3的正方形且高是2的一个四棱柱,上面是一个球,球的直径是3,该几何体的体积是两个体积之和,分别做出两个几何体的体积相加.【解答】解:由三视图可知,几何体是一个简单的组合体,下面是一个底面边长是3的正方形且高是2的一个四棱柱,上面是一个球,球的直径是3,该几何体的体积是两个体积之和,四棱柱的体积3×3×2=18,球的体积是,∴几何体的体积是18+,故选D.【点评】本题考查由三视图求面积和体积,考查球体的体积公式,考查四棱柱的体积公式,本题解题的关键是由三视图看出几何图形,是一个基础题.4.(5分)(2011?湖南)通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女总计爱好40 20 60不爱好20 30 50总计60 50 110由算得,.P(K2≥k)0.050 0.010 0.001k 3.841 6.635 10.828参照附表,得到的正确结论是()A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”【考点】独立性检验的应用.【专题】常规题型.【分析】题目的条件中已经给出这组数据的观测值,我们只要把所给的观测值同节选的观测值表进行比较,发现它大于6.635,得到有99%以上的把握认为“爱好这项运动与性别有关”.【解答】解:由题意算得,.∵7.8>6.635,∴有0.01=1%的机会错误,即有99%以上的把握认为“爱好这项运动与性别有关”故选:C.【点评】本题考查独立性检验的应用,这种问题一般运算量比较大,通常是为考查运算能力设计的,本题有创新的地方就是给出了观测值,只要进行比较就可以,本题是一个基础题.5.(5分)(2011?湖南)设双曲线的渐近线方程为3x±2y=0,则a的值为()A.4 B.3 C.2 D.1【考点】双曲线的简单性质.【专题】计算题.【分析】先求出双曲线的渐近线方程,再求a的值.【解答】解:的渐近线为y=,∵y=与3x±2y=0重合,∴a=2.故选C.【点评】本题考查双曲线的性质和应用,解题时要注意公式的灵活运用.6.(5分)(2011?湖南)由直线与曲线y=cosx 所围成的封闭图形的面积为()A.B.1 C.D.【考点】定积分在求面积中的应用.【专题】计算题.【分析】为了求得与x轴所围成的不规则的封闭图形的面积,可利用定积分求解,积分的上下限分别为与,cosx即为被积函数.【解答】解:由定积分可求得阴影部分的面积S=cosxdx==﹣(﹣)=,所以围成的封闭图形的面积是.故选D.【点评】本小题主要考查定积分的简单应用、定积分、导数的应用等基础知识,考查运算求解能力,化归与转化思想、考查数形结合思想,属于基础题.7.(5分)(2011?湖南)设m>1,在约束条件下,目标函数z=x+my的最大值小于2,则m的取值范围为()A.(1,)B.(,+∞) C.(1,3)D.(3,+∞)【考点】简单线性规划的应用.【专题】压轴题;数形结合.【分析】根据m>1,我们可以判断直线y=mx的倾斜角位于区间(,)上,由此我们不难判断出满足约束条件的平面区域的形状,再根据目标函数Z=X+my对应的直线与直线y=mx垂直,且在直线y=mx与直线x+y=1交点处取得最大值,由此构造出关于m的不等式组,解不等式组即可求出m的取值范围.【解答】解:∵m>1故直线y=mx与直线x+y=1交于点,目标函数Z=X+my对应的直线与直线y=mx垂直,且在点,取得最大值其关系如下图所示:即,解得1﹣<m<又∵m>1解得m∈(1,)故选:A.【点评】本题考查的知识点是简单线性规划的应用,其中根据平面直线方程判断出目标函数Z=X+my对应的直线与直线y=mx垂直,且在点取得最大值,并由此构造出关于m的不等式组是解答本题的关键.8.(5分)(2011?湖南)设直线x=t与函数f(x)=x2,g(x)=lnx的图象分别交于点M,N,则当|MN|达到最小时t的值为()A.1 B.C.D.【考点】导数在最大值、最小值问题中的应用.【专题】计算题;压轴题;转化思想.【分析】将两个函数作差,得到函数y=f(x)﹣g(x),再求此函数的最小值对应的自变量x的值.【解答】解:设函数y=f(x)﹣g(x)=x2﹣lnx,求导数得=当时,y′<0,函数在上为单调减函数,当时,y′>0,函数在上为单调增函数所以当时,所设函数的最小值为所求t的值为故选D【点评】可以结合两个函数的草图,发现在(0,+∞)上x2>lnx 恒成立,问题转化为求两个函数差的最小值对应的自变量x的值.二、填空题(共8小题,每小题5分,满分35分)9.(5分)(2011?湖南)在直角坐标系xOy中,曲线C1的参数方程为(α为参数)在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为p(cosθ﹣sinθ)+1=0,则C1与C2的交点个数为 2 .【考点】简单曲线的极坐标方程;双曲线的参数方程.【专题】计算题.【分析】先根据sin2α+cos2α=1,求出曲线C1的直角坐标方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,求出曲线C2的直角坐标方程,然后判定交点个数即可.【解答】解:∵曲线C1的参数方程为(α为参数),sin2α+cos2α=1∴曲线C1的直角坐标方程为x2+(y﹣1)2=1∵ρcosθ=x,ρsinθ=y,p(cosθ﹣sinθ)+1=0∴曲线C2的方程为x﹣y+1=0而圆心到直线的距离d=0<r,故C1与C2的交点个数为2故答案为:2【点评】本题考查点的极坐标和直角坐标的互化,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互,属于基础题.10.(5分)(2011?湖南)设x,y∈R,且xy≠0,则的最小值为9 .【考点】基本不等式.【专题】计算题.【分析】对展开,利用基本不等式即可求得其最小值.【解答】解:∵x,y∈R,且xy≠0,∴=1+4+≥5+2=9 当且仅当时等号成立,∴的最小值为9.故答案为9.【点评】此题是个基础题.考查利用基本不等式求最值,注意正、定、等,考查学生利用知识分析解决问题的能力和计算能力.11.(2011?湖南)如图,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为.【考点】与圆有关的比例线段.【专题】选作题.【分析】根据半圆的三等分点,得到三个弧对应的角度是60°,根据直径所对的圆周角是直角得到直角三角形的有关长度,做出要求的线段的长度.【解答】解:∵A,E是半圆周上的两个三等分点∴弧EC是一个60°的弧,∴∠EBC=30°,则CE=2,连接BA,则BA=2,∴在含有30°角的直角三角形中,BD=1,DF=,AD=∴AF=,故答案为:【点评】本题考查与圆有关的比例线段,考查圆周角定理,考查含有30°角的直角三角形的有关运算,本题是一个基础题.12.(5分)(2011?湖南)设S n是等差数列{a n}(n∈N*)的前n 项和,且a1=1,a4=7,则S9= 81 .【考点】等差数列的前n项和.【专题】计算题.【分析】先根据数列{a n}为等差数列,求出公差d,然后根据等差数列的前n项和公式求得S9.【解答】解:∵数列{a n}为等差数列,∴a n=a1+(n﹣1)d,S n=na1+∵a1=1,a4=7∴a4=1+(4﹣1)d=7∴d=2∴S9=9×1+×2=81故答案为:81【点评】本题主要考查了等差数列的通项公式和前n项和公式.13.(5分)(2011?湖南)若执行如图所示的框图,输入x1=1,x 2=2,x3=3,=2,则输出的数等于.【考点】循环结构.【专题】图表型.【分析】先弄清该算法功能,S=0+(1﹣2)2=1,i=1,满足条件i<3,执行循环体,依此类推,当i=3,不满足条件i<3,退出循环体,输出所求即可.【解答】解:S=0+(1﹣2)2=1,i=1,满足条件i<3,执行循环体,i=2S=1+(2﹣2)2=1,i=2,满足条件i<3,执行循环体,i=3S=1+(3﹣2)2=2,i=3,不满足条件i<3,退出循环体,则S=×2=故答案为:【点评】本题主要考查了方差的计算,算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.14.(5分)(2011?湖南)在边长为1的正三角形ABC中,设,,则= ﹣.【考点】向量在几何中的应用.【专题】计算题;数形结合;转化思想.【分析】根据,,确定点D,E在正三角形ABC中的位置,根据向量加法满足三角形法则,把用表示出来,利用向量的数量积的运算法则和定义式即可求得的值.【解答】解:∵,∴D为BC的中点,∴,∵,∴,∴=)==﹣,故答案为:﹣.【点评】此题是个中档题,考查向量的加法和数量积的运算法则和定义,体现了数形结合的思想.15.(5分)(2011?湖南)如图,EFGH是以O为圆心,半径为1的圆的内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则(1)P(A)= ;(2)P(B|A)= .【考点】条件概率与独立事件.【专题】计算题;压轴题.【分析】此题是个几何概型.用面积法求出事件A“豆子落在正方形EFGH内”的概率p(A),同理求出P(AB),根据条件概率公式P(B|A)=即可求得结果.【解答】解:用A表示事件“豆子落在正方形EFGH内”,∴P (A)==,B表示事件“豆子落在扇形OHE(阴影部分)内”,P(AB)==,∴P(B|A)=.故答案为:.【点评】此题是个基础题.考查条件概率的计算公式,同时考查学生对基础知识的记忆、理解和熟练程度.16.(5分)(2011?湖南)对于n∈N+,将n表示n=a0×2k+a1×2k﹣1+a2×2k﹣2+…+a k﹣1×21+a k×20,当i=0时,a i=1,当1≤i≤k时,a1为0或1.记I(n)为上述表示中a i为0的个数(例如:1=1×20,4=1×22+0×21+0×20,故I(1)=0,I(4)=2),则(1)I(12)= 2 ;(2)= 1093 .【考点】带余除法.【专题】计算题;压轴题;分类讨论;转化思想.【分析】(1)根据题意,分析可得,将n表示n=a0×2k+a1×2k﹣1+a2×2k﹣2+…+a k﹣1×21+a k×20,实际是将十进制的数转化为二进制的数,易得12=1×23+1×22+0×21+0×20,由I(n)的意义,可得答案;(2)将n分为n=127,64≤n≤126,32≤n≤63,…n=1等7种情况,有组合数的性质,分析其中I(n)的取值情况,与二项式定理结合,可转化为等比数列的前7项和,计算可得答案.【解答】解:(1)根据题意,12=1×23+1×22+0×21+0×20,则I (12)=2;(2)127=1×26+1×25+1×24+1×23+1×22+1×21+1×20,设64≤n≤126,且n为整数;则n=1×26+a1×25+a2×24+a3×23+a4×22+a5×21+a6×20,a1,a2,a3,a4,a5,a6中6个数都为0或1,其中没有一个为1时,有C60种情况,即有C60个I(n)=6;其中有一个为1时,有C61种情况,即有C61个I(n)=5;其中有2个为1时,有C62种情况,即有C62个I(n)=4;…2I(n)=C6026+C61×25+C62×24+C63×23+C64×22+C65×2+1=(2+1)n=36,同理可得:=35,…=31,2I(1)=1;则=1+3+32+…+36==1093;故答案为:(1)2;(2)1093.【点评】解本题关键在于分析题意,透彻理解I(n)的含义的运算,注意转化思想,结合二项式定理与等比数列的前n项和公式进行计算.三、解答题(共6小题,满分75分)17.(12分)(2011?湖南)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC.(1)求角C的大小;(2)求sinA﹣cos(B+)的最大值,并求取得最大值时角A、B的大小.【考点】三角函数的恒等变换及化简求值.【专题】三角函数的图像与性质.【分析】(1)利用正弦定理化简csinA=acosC.求出tanC=1,得到C=.(2)B=﹣A ,化简sinA﹣cos(B+)=2sin(A+).因为0<A <,推出求出2sin(A+)取得最大值2.得到A=,B=【解答】解:(1)由正弦定理得sinCsinA=sinAcosC,因为0<A<π,所以sinA>0.从而sinC=cosC,又cosC≠0,所以tanC=1,C=.(2)有(1)知,B=﹣A,于是=sinA+cosA=2sin(A+).因为0<A <,所以从而当A+,即A=时2sin(A+)取得最大值2.综上所述,cos(B+)的最大值为2,此时A=,B=【点评】本题是中档题,考查三角形的有关知识,正弦定理的应用,三角函数的最值,常考题型.18.(12分)(2011?湖南)某商店试销某种商品20天,获得如下数据:日销售量0 1 2 3(件)频数 1 5 9 5试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率.(Ⅰ)求当天商品不进货的概率;(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望.【考点】离散型随机变量的期望与方差;古典概型及其概率计算公式;离散型随机变量及其分布列.【专题】应用题.【分析】(I)“当天商品不进货”包含两个事件的和事件,利用古典概型概率公式求出两个事件的概率;再利用互斥事件的和事件概率公式求出当天商品不进货的概率.(II)求出x可取的值,利用古典概型概率公式及互斥事件和事件的概率公式求出x取每一个值的概率值;列出分布列;利用随机变量的期望公式求出x的期望.【解答】解:(I)P(“当天商店不进货”)=P(“当天商品销售量为0件”)+(“当天的商品销售量为1件”)=(II)由题意知,X的可能取值为2,3P(X=2)=P(“当天商品销售量为1件”)=P(X=3)=(“当天的销售量为0”)+P(“当天的销售量为2件”)+P(“当天的销售量为3件”)=故x的分布列x 23pX的数学期望为EX=【点评】本题考查古典概型的概率公式、互斥随机的概率公式、随机变量的数学期望公式、求随机变量的分布列的步骤.19.(12分)(2011?湖南)如图,在圆锥PO中,已知PO=,⊙O的直径AB=2,C是的中点,D为AC的中点.(Ⅰ)证明:平面POD⊥平面PAC;(Ⅱ)求二面角B﹣PA﹣C的余弦值.【考点】平面与平面垂直的判定;二面角的平面角及求法.【专题】计算题;证明题.【分析】(Ⅰ)连接OC,先根据△AOC是等腰直角三角形证出中线OD⊥AC,再结合PO⊥AC证出AC⊥POD,利用平面与平面垂直的判定定理,可证出平面POD⊥平面PAC;(Ⅱ)过O分别作OH⊥PD于H,OG⊥PA于G,再连接GH,根据三垂线定理证明∠OGH为二面角B﹣PA﹣C的平面角,最后分别在Rt△ODA、Rt△ODP、Rt△OGH中计算出OH、OG和sin∠OGH,最后求出所求二面角的余弦值.【解答】解:(Ⅰ)连接OC,∵OA=OC,D是AC的中点∴AC⊥OD又∵PO⊥底面⊙O,AC?底面⊙O∴AC⊥PO∵OD、PO是平面POD内的两条相交直线∴AC⊥平面POD,而AC?平面PAC∴平面POD⊥平面PAC(Ⅱ)在平面POD中,过O作OH⊥PD于H,由(Ⅰ)知,平面POD⊥平面PAC所以OH⊥平面PAC,又∵PA?平面PAC∴PA⊥HO在平面PAO中,过O作OG⊥PA于G,连接GH,则有PA⊥平面OGH,从而PA⊥HG.故∠OGH为二面角B﹣PA﹣C的平面角在Rt△ODA中,OD=OA?sin45°=在Rt△ODP中,OH=在Rt△OPA中,OG=在Rt△OGH中,sin∠OGH=所以cos∠OGH=故二面角B﹣PA﹣C的余弦值为【点评】直线与平面垂直是证明空间垂直的关键,立体几何常常利用三垂线定理作辅助线,来求与二面角的平面角有关的问题.20.(13分)(2011?湖南)如图,长方形物体E在雨中沿面P (面积为S)的垂直方向作匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R).E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与|v﹣c|×S成正比,比例系数为;(2)其它面的淋雨量之和,其值为,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S=时.(Ⅰ)写出y的表达式(Ⅱ)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度v,使总淋雨量y最少.【考点】函数模型的选择与应用.【分析】(Ⅰ)E移动时的总淋雨量应该等于单位时间内的淋雨量乘以所用的时间,可先求出单位时间内的淋雨量的式子,再乘以时间即可;(Ⅱ)根据绝对值的性质,将(Ⅰ)中的函数分解为分段函数的形式,再由c的不同取值范围讨论函数的单调性,在不同的情况下,单调区间不同,总淋雨量最小值对应的v值也不同.【解答】解:(Ⅰ)由题意知,E移动时单位时间内的淋雨量为,故(Ⅱ)由(Ⅰ)知,当0<v≤c时,当c≤v≤10时,故(1)当0<c<时,y是关于v的减函数,故当v=10时,;(2)当时,在(0,c]上y是关于v的减函数,在(c,10]上,y是关于v的增函数,故当v=c时,答:(Ⅰ)函数y的表达式为(Ⅱ)(1)在0<c的情况下,当v=10时,总淋雨量y最少;(2)在的情况下,当v=c时,总淋雨量y最少.【点评】本题着重考查函数应用能力,所建立的函数式为含有绝对值的式子.解决问题的关键一是要能根据v的范围将式子化简为分段函数,二是要将常数c进行讨论得出函数的单调性,从而得出不同情形下的最小值点.21.(13分)(2011?湖南)如图,椭圆C1:=1(a>b>0)的离心率为,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.(Ⅰ)求C1,C2的方程;(Ⅱ)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于D,E.(i)证明:MD⊥ME;(ii)记△MAB,△MDE的面积分别是S1,S2.问:是否存在直线l,使得=?请说明理由.【考点】圆锥曲线的综合.【专题】计算题;综合题;压轴题;转化思想.【分析】(Ⅰ)先利用离心率得到一个关于参数的方程,再利用x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长得另一个方程,两个方程联立即可求出参数进而求出C1,C2的方程;(Ⅱ)(i)把直线l的方程与抛物线方程联立可得关于点A、B 坐标的等量关系,再代入求出k MA?k MB=﹣1,即可证明:MD⊥ME;(ii)先把直线MA的方程与抛物线方程联立可得点A的坐标,再利用弦长公式求出|MA|,同样的方法求出|MB|进而求出S1,同理可求S2.再代入已知就可知道是否存在直线l满足题中条件了.【解答】解:(Ⅰ)由题得e=,从而a=2b,又2=a,解得a=2,b=1,故C1,C2的方程分别为,y=x2﹣1.(Ⅱ)(i)由题得,直线l的斜率存在,设为k,则直线l的方程为y=kx,由得x2﹣kx﹣1=0.设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根,于是x1+x2=k,x1x2=﹣1,又点M的坐标为(0,﹣1),所以k MA?k MB=====﹣1.故MA⊥MB,即MD⊥ME.(ii)设直线MA的斜率为k1,则直线MA的方程为y=k1x﹣1.由,解得或.则点A的坐标为(k1,k12﹣1).又直线MB的斜率为﹣,同理可得点B的坐标为(﹣,﹣1).于是s 1=|MA|?|MB|=?|k1|??|﹣|=.由得(1+4k12)x2﹣8k1x=0.解得或,,则点D的坐标为(,).又直线ME的斜率为﹣.同理可得点E的坐标为(,).于是s22=|MD|?|ME|=.故=,解得k12=4或k12=.又由点A,B的坐标得,k==k1﹣.所以k=±.故满足条件的直线存在,且有两条,其方程为y=x和y=﹣x.【点评】本题是对椭圆与抛物线以及直线与抛物线和直线与椭圆的综合问题的考查.是一道整理过程很麻烦的题,需要要认真,细致的态度才能把题目作好.22.(13分)(2011?湖南)已知函数f(x)=x 3,g(x)=x+.(Ⅰ)求函数h(x)=f(x)﹣g(x)的零点个数.并说明理由;(Ⅱ)设数列{a n}(n∈N*)满足a1=a(a>0),f(a n+1)=g(a n),证明:存在常数M,使得对于任意的n∈N*,都有a n≤M.【考点】数列与不等式的综合;根的存在性及根的个数判断.【专题】综合题;压轴题.【分析】(Ⅰ)由h(x)=知,x∈[0,+∞),而h(0)=0,且h(1)=﹣1<0,h(2)=6﹣,再研究函数在(0,+∞)上的单调性,以确定零点个数即可(Ⅱ)记h(x)的正零点为x0,即,当a<x0时,由a1=a,即a1<x0,而,a2<x0.由此猜测a n<x0.当a≥x0时,由(Ⅰ)知,当x∈(x1,+∞)时,h(x)单调递增,h(a)>h (x0)=0,从而a2<a,由此猜测a n<a.然后用数学归纳法证明.【解答】解:(Ⅰ)由h(x)=知,x∈[0,+∞),而h (0)=0,且h(1)=﹣1<0,h(2)=6﹣,则x=0为h(x)的一个零点,且h(x)在(1,2)内有零点,∴h(x)至少有两个零点.由h(x)=,记,则,当x∈(0,+∞)时,g(x)单调递增,故可判断出h(x)在(0,+∞)仅有一个零点,综上所述,h(x)有且只有两个零点.(Ⅱ)记h(x)的正零点为x 0,即,(1)当a<x0时,由a1=a,即a1<x0,而,∴a2<x0.由此猜测a n<x0.下面用数学归纳法证明:①当n=1时,a1<x0,成立.②假设当n=k时a k<x0成立,则当n=k+1时,由,知a k+1<x0.因此当n=k+1时,a k+1<x0成立.故对任意的n∈N*,a n≤x0成立.(2)当a≥x0时,由(Ⅰ)知,当x∈(x0,+∞)时,h(x)单调递增,∴h(a)>h(x0)=0,从而a2≤a,由此猜测a n≤a.下面用数学归纳法证明:①当n=1时,a1≤a,成立.②假设当n=k时a k<a成立,则当n=k+1时,由,知a k+1<a.因此当n=k+1时,a k+1<a成立.故对任意的n∈N*,a n≤a成立.综上所述,存在常数M,使得对于任意的n∈N*,都有a n≤M.【点评】本题考查数列的性质和运用,解题时要注意不等式性质的合理运用和数学归纳法的证明过程.。
2011年湖南省高中数学夏令营试题及答案

2011年湖南省高中数学夏令营试题及答案营号: 姓名: 学校:一、填空题:(本题满分90分,每小题9分) 1、函数()f x 的反函数是1xy x =+,1()()f x f x =,且对于1()n n N +>∈有11()[()]n fn x f f x -=,则1()n f x = . 答:1n x -2、设正实数,,a b c 满足2223a b c ++=,则222M abc a bc a b c =++的最大值为 .答:33、设A 是一个六位数(十进制表示).将A 的首位数字移至末尾得数B ,再将B 的首位数字移至末尾得数C ,若C 是A 的倍35,则A= .答:714285. 4、若集合{}1,A ax x ==+∈R 为空集,则实数a 的取值范围是 . 答:11(,)(,)36-∞-+∞5、在数列{}n a 中,已知()*11122,2N n a a a n n n ∈=-=++,则使10>n a 成立的最小正整数n 的值为 . 答:3 6、已知函数()()32134,,a x a f x x x ⎧-+-=⎨-⎩x tx t ≤>,无论t 取何值时,函数()f x 在R 上总是不单调.则实数a 的取值范围为 . 答:1(,]2-∞.7、设,G H 分别是ABC ∆的重心、垂心,其外接圆半径为1. 若F 为线段GH 的中点,则222AF BF CF ++ 的值为 . 答:3.8、椭圆长轴为6,左顶点在圆4)2()3(22=-+-y x 上,左准线为y 轴,则椭圆离心率e 的取值范围为 .答:33[,]84.9、函数y =的值域为 .答:10、正方体1111ABCD A BC D -棱长为1,E 是DC 中点,F 是1BB 中点,则四面体1AD EF 的体积是 .答: 524二、解答题(本题满分60分,每小题20分)11、设数列{}n a 满足11n n a a +-≤,*n N ∈,数列{}n b 定义为12nn a a a b n+++=.求证: 112n n b b +-≤. 证明: 依题设,结合绝对值不等式,对*,,m n N m n ∀∈>,有1121m n m m m m n n a a a a a a a a ---+-=-+-++- 11m m n n a a a a m n -+≤-++-≤- .从而 1121211211(1)n n n nn n na a a a a a a a a a b b n n n n +++----++++++-=-=++ 1112111121(1)(1)n n n nn n n na a a a a a a a a a a a n n n n ++++++-+-++--+-++-=≤++(1)11(1)2n n n n +-++≤=+ .12、设△ABC 的内切圆⊙I 切BC 、CA 边分别于点D 、E ,AB 、AC 边上的中点分别为M 、N ,求证:.(1)设BI 与DE 的交点为G ,则AG ⊥BG ; (2)直线MN ,BI ,DE 交于一点. 证明:(1)联结,AI IE ,则1902oAIB C ∠=+∠, 从而1180902ooAIG AIB C ∠=-∠=-∠ 又1902oAEG DEC C ∠=∠=-∠故,,,A I E G 四点共圆,即90oAGI AEI ∠=∠=,从而AG ⊥BG .(2)设直线MG 交AC 于'N ,在Rt AGB 中,M 为AB 中点.则BM MG =. 即GBD ABG MGB ∠=∠=∠.即有//MG BC ,从而'N 为AC 中点,即'N 与N 重合. 故直线MN ,BI ,DE 交于一点.G13、设A 为平面上的一个有限点集,现将A 中的点染三色使得任何两个同色点所连成的线段上恰有另外颜色的一个点,求证:A 中最多有6个点满足要求.解:首先证明 6n ≤.若7n ≥,由抽屉原理,必有一种色染上三个点;且同色三点不共线(否则不妨设123,,A A A同色且依次排在一条直线上,则有12A A 间有异色点B ,23A A 间有异色点C ,于是13A A 间有两个异色点,与任何两个同色点所连成的线段上恰有另外颜色的一个点,矛盾),从而必出现同色三角形.考察同色三角形中面积最小的一个,如图所示(用○, □, * 代表三色1, 2, 3 )三边中各有一个不为1色的点.若这三个点均为 * 或 □,则其面积必小于上述三角形. 所以,这三点不同色,设有两个2色,1个3色(如图所示). 若A 1A 2连线之间的点为1色,设为T ,则 S △PQT < S △PQR ,矛盾! 所以,A 1A 2之间的点必为3色.考虑T 与A 3之间的点S .若S 为2色,则S △A 1A 2S < S △PQR ; 若S 为3色,则S △PQS < S △PQR . 矛盾!因此,6n ≤.当6n =时,如右图满足条件,得证.2A**□□T RPQA A 132A**□RP QA A 13*□□*。
2011年高考理科数学试卷解析(湖南卷)

2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分1 50分。
一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.若,为虚数单位,且,则()A.B.C.D.答案:D解析:因,根据复数相等的条件可知。
2.设,,则“”是“”则()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件答案:A解析:因“”,即,满足“”,反之”,则,或,不一定有“”。
3.设图一是某几何体的三视图,则该几何体的体积为()A.B.C.D.答案:B解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积。
4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:由算得附表:参照附表,得到的正确结论是()A.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别无关”C.有以上的把握认为“爱好该项运动与性别有关”D.有以上的把握认为“爱好该项运动与性别有关”答案:C解析:由,而,故由独立性检验的意义可知选C.5.设双曲线的渐近线方程为,则的值为()A.4 B.3 C.2 D.1答案:C解析:由双曲线方程可知渐近线方程为,故可知。
6. 由直线与曲线所围成的封闭图形的面积为()A.B.1 C.D.答案:D解析:由定积分知识可得,故选D。
7. 设,在约束条件下,目标函数的最大值小于2,则的取值范围为()A.B.C.D.答案:A解析:画出可行域,可知在点取最大值,由解得。
8.设直线与函数的图像分别交于点,则当达到最小时的值为()A.1B.C.D.答案:D解析:由题,不妨令,则,令解得,因时,,当时,,所以当时,达到最小。
即。
二填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上。
2011届长郡中学高三月考试卷5理数(答案)

炎德·英才大联考理科数学参考答案(长郡版)-1炎德·英才大联考长郡中学2011届高三月考试卷(五)数学(理科)参考答案一㊁选择题题 号12345678答 案D C D A C C B D 二㊁填空题9.102 10.14 11.12 12.45 13.3 14.(2b ,2a ) 14a b s i n α15.S n -S n -1=22n -2(n ≥2) S n =4n 3+23三㊁解答题16.解:(1)由条件,→O P =(12,c o s 2θ),→O Q =(s i n 2θ,-1),∴→O P ㊃→O Q =12s i n 2θ-c o s 2θ=-12,∴12(1-c o s 2θ)-c o s 2θ=-12,∴c o s 2θ=23,∴c o s 2θ=2c o s 2θ-1=13.(6分)…………………………………………………………………………………(2)由(1)知c o s 2θ=23,s i n 2θ=13,∴P (12,23),Q (13,-1).又点P 在角α的终边上,点Q 在角β的终边上,∴由三角函数的定义,s i n α=2314+49=45,c o s α=35,s i n β=-119+1=-31010,c o s β=1010,∴s i n (α+β)=s i n αc o s β+c o s αs i n β=45×1010+35×(-31010)=-1010.(12分)…………………………17.解:(1)由该几何体的三视图知A C ⊥面B C E D ,且E C =B C =A C =4,B D =1,∴S 梯形B C E D =12×(4+1)×4=10,∴V =13㊃S 梯形B C E D ㊃A C =13×10×4=403,即该几何体的体积V 为403.(5分)………………………………………………………………………………(2)解法1:D E 上存在点Q ,使得A Q ⊥B Q ,取B C 中点O ,过点O 作O Q ⊥D E 于点Q ,则点Q 满足题设.连结E O ㊁O D ,在R t △E C O 和R t △O B D 中,∵E C C O =O B B D =2,∴R t △E C O ∽R t △O B D ,∴∠C E O =∠D O B .∵∠E O C +∠C E O =90°,∴∠E O C +∠D O B =90°,∴∠E O D =90°.∵O E =C E 2+C O 2=25,O D =O B 2+B D 2=5,∴O Q =O E ㊃O D E D =25㊃55=2,∴以O 为圆心㊁以B C 为直径的圆与D E 相切,切点为Q ,∴B Q ⊥C Q .∵A C ⊥面B C E D ,B Q ⊂面C E D B ,∴B Q ⊥A C ,∴B Q ⊥面A C Q .又∵A Q ⊂面A C Q ,∴B Q ⊥A Q .(12分)…………………………………………………………………………解法2:以C 为原点,以C A ,C B ,C E 所在直线为x ,y ,z 轴建立空间直角坐标系.设满足题设的点Q 存在,其坐标为(0,m ,n ),则→A Q =(-4,m ,n ),→B Q =(0,m -4,n ),→E Q =(0,m ,n -4),→Q D =(0,4-m ,1-n ).∵A Q ⊥B Q ,∴m (m -4)+n 2=0. ①炎德·英才大联考理科数学参考答案(长郡版)-2∵点Q 在E D 上,∴存在λ∈R (λ>0)使得→E Q =λ→Q D ,∴(0,m ,n -4)=λ(0,4-m ,1-n )⇒m =4λ1+λ,n =4+λ1+λ. ②②代入①得(λ+41+λ)2=16λ(1+λ)2⇒λ2-8λ+16=0,解得λ=4.∴满足题设的点Q 存在,其坐标为(0,165,85).(12分)………………………………………………………18.解:记 小球落入A 袋中”为事件A , 小球落入B 袋中”为事件B ,则小球落入A 袋中当且仅当小球一直向左落下或一直向右落下,故P (A )=(12)3+(12)3=14,P (B )=1-P (A )=34.(3分)……………………(1)获得两次一等奖的概率为P =P (A )㊃P (A )=116.(5分)…………………………………………………(2)X 可以取20,30,40,P (X =20)=(34)2=916;P (X =30)=C 1214㊃34=38;P (X =40)=(14)2=116.(9分)…………………………………………………………………………………分布列为:X203040P 91638116所以E X =20×916+30×38+40×116=25.(11分)……………………………………………………………(3)参加摇奖,可节省25元;打折优惠,可节省24元.故参加摇奖.(13分)…………………………………19.解:(1)P x =1000+5x +110x 2x (3分)……………………………………………………………………………=1000x +x 10+5≥25(当且仅当x =100时,取等号),∴生产100套时,每套成本费用最低.(6分)……………………………………………………………………(2)由题设,利润f (x )=(a x +b )x -(1000+5x +110x 2)=-110x 2+(b -5)x +a -1000,x ∈(0,200].(8分)…………………………………当5(b -5)≤200,即b ≤45时,f m a x (x )=f [5(b -5)]=52(b -5)2+a -1000,∴当产量为5b -25套时,利润最大.(11分)……………………………………………………………………当5(b -5)>200,即b >45时,函数f (x )在(0,200]上是增函数,∴当产量为200套时,f m ax (x )=200b +a -6000.综上所述,当b ≤45时,产量为5b -25套时,最大利润为52(b -5)2+a -1000元;当b >45时,产量为200套时,最大利润为200b +a -6000元.(13分)………………………………………20.解:(1)由2b =2,得b =1.又由点M 在直线x =a 2c 上,得a 2c =2.故1+c 2c =2,∴c =1,从而a =2.所以椭圆方程为x 22+y 2=1.(3分)………………………………………………………………………………(2)以O M 为直径的圆的方程为x (x -2)+y (y -t )=0,即(x -1)2+(y -t 2)2=t 24+1,炎德·英才大联考理科数学参考答案(长郡版)-3 其圆心为(1,t 2),半径r =t 24+1.(5分)……………………………………………………………………因为以O M 为直径的圆被直线3x -4y -5=0截得的弦长为2,所以圆心到直线3x -4y -5=0的距离d =r 2-1=t 2,所以|3-2t -5|5=t 2,解得t =4.所求圆的方程为(x -1)2+(y -2)2=5.(8分)…………………………………………………………………(3)方法一:由平几知:|O N |2=|O K ||O M |,其中K 为F N 与O M 的交点.直线O M :y =t 2x ,直线F N :y =-2t (x -1).由y =t 2x y =-2t(x -1ìîíïïïï)得x K =4t 2+4,∴|O N |2=1+t 24x K ㊃1+t 24x M =(1+t 24)㊃4t 2+4㊃2=2.所以线段O N 的长为定值2.(13分)……………………………………………………………………………方法二:设N (x 0,y 0),则→F N =(x 0-1,y 0),→O M =(2,t ),→MN =(x 0-2,y 0-t ),→O N =(x 0,y 0).∵→F N ⊥→O M ,∴2(x 0-1)+t y 0=0,∴2x 0+t y 0=2. ①又→MN ⊥→O N ,∴x 0(x 0-2)+y 0(y 0-t )=0,∴x 20+y 20=2x 0+t y 0. ②∴由①②可得x 20+y 20=2.所以,|→O N |=x 20+y 20=2为定值.(13分)……………………………………………………………………21.解:(1)∵f '(x )=2x -a x ,∴f '(1)=2-a =0,∴a =2.(2分)………………………………………………………………………………∴g (x )=x -2x .由g '(x )=1-1x >0⇒x >1,g '(x )=1-1x <0⇒0<x <1,∴g (x )的单调减区间是(0,1),单调增区间是[1,+∞).(4分)…………………………………………………………………………………(2)证明:∵1<x <e 2,∴0<l n x <2,∴2-l n x >0.欲证x <2+l n x 2-l n x ,只需证明2x -x l n x <2+l n x ,即只需证l n x >2(x -1)x +1.记h (x )=l n x -2(x -1)x +1,则h '(x )=(x -1)2x (x +1)2.当1<x <e 2时,h '(x )>0,∴h (x )在(1,e 2)上是增函数.又h (x )在[1,e 2)上是连续的,∴h (x )>h (1)=0,∴h (x )>0,即l n x -2(x -1)x +1>0,∴l n x >2(x -1)x +1,故结论成立.(8分)……………………………………………………………………………(3)由题意知C 1:H (x )=x -2x +6.问题转化为G (x )=x 2-2l n x -(x -2x +6)=0在x ∈(0,+∞)上解的个数.(10分)……………………∵G '(x )=2x -21x -1+1x =2x 2-2-x +x x =(x -1)(2x x +2x +x +2)x ,∴G '(x )>0⇒x >1,G '(x )<0⇒0<x <1,∴G (1)是G (x )在x >0上的最小值.又G (1)=-4<0,G (1e 4)>0,G (e 2)>0,且G (x )在x >0上是连续的,所以G (x )=x 2-2l n x -(x -2x +6)=0在x ∈(0,+∞)上有2个解,即C 1与f (x )对应曲线C 2的交点个数是2个.(13分)………………………………………………………。
2011年高考湖南省数学试卷-理科(含详细答案)

2011年高考湖南省数学试卷-理科(含详细答案)D男 女 总计 爱好 40 20 60 不爱好 20 30 50 总计 60 50 110由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯附表:2()P K k ≥ 0.050 0.010 0.001k3.841 6.635 10.828 参照附表,得到的正确结论是( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关”5.设双曲线2221(0)9x y a a-=>的渐近线方程为320x y ±=,则a 的值为( )A .4B .3C .2D .16. 由直线,,033x x y ππ=-==与曲线cos y x =所围成的封闭图形的面积为( )A .12B .1C .32D 37. 设1m >,在约束条件1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my=+的最大值小于2,则m 的取值范围为( )A .(1,12)B .(12,)++∞C .(1,3)D .(3,)+∞8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为( )A .1B .12C 5D 2二填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上。
一、选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题记分)9.在直角坐标系xoy 中,曲线C 1的参数方程为cos ,1sin x y αα=⎧⎨=+⎩(α为参数)在极坐标系(与直角坐标系xoy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为()cos sin 10ρθθ-+=,则1C 与2C 的交点个数为 。
湖南省长郡中学2011届高三分班考试(数学文)

绝密★启用前湖南省长郡中学2011届高三分班考试(数学文)试卷副标题考试范围:xxx ;考试时间:90分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、设函数的取值范围是 ( )A .B .C .D .2、若等差数列=" " ( )A .2B .C .D .3、已知双曲线,则双曲线的离心率为 ( )A .B .C .D .4、如图,是一个几何体的三视图,侧视图和正视图均为矩 形,俯视图为正三角形,尺寸如图,则该几何体的 侧面积 ( )A .6B .C .24D .35、若=" " ( )A .1B .—1C .2D .—26、命题:“”的否定是 ( ) A . B .C .D .7、已知全集=" " ( )A .{4}B .{3,4}C .{2,3,4}D .{1,2,3,4}8、按如下程序框图,若输出结果为170,则判断框内应补充的条件为 ( )A .B .C .D .9、设a ,b 是两个单位向量,命题:“”是命题:“”成立的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件10、函数的图象如图所示,为了得到的图象,则只要将的图象 ( )A .向右平移个单位长度B .向右平移个单位长度C .向左平移个单位长度D .向左平移个单位长度第II卷(非选择题)二、填空题(题型注释)11、将所有3的幂,或者是若干个不相等的3的幂之和,由小到大依次排列成数列1,3,4,9,10,12,13,…,则此数列的第100项为 . 12、已知圆C的极坐标方程为的极坐标方程为则圆心C到直线l的距离是。
13、如图,在正方体ABCD—A1B1C1D1中,直线A1B与平面A1B1CD 所成的角的大小等于 .14、在区间[1,9]上随机取一实数,则该实数在区间[4,7]上的概率为 .15、已知一种材料的最佳加入量在100g到200g之间,若按照0.618法优选,则第2次试点的加入量为 g.三、解答题(题型注释)16、(本题满分13分)已知函数处取得极小值,其图象过点A(0,1),且在点A处切线的斜率为—1。
长郡中学高二进高三分班考试理科数学试题

长郡中学高二进高三分班考试理科数学试题时量120分钟 总分150分一 选择题:本大题个8小题,每小题5分,共40分,在每小题给出的选项中,只有一项符合题目要求1、与两条不共面的直线都垂直的直线 A 、恰有一条 B 、恰有两条 C 、有无数条 D 、可能一条也没有2、已知,114|⎭⎬⎫⎩⎨⎧>+=x x A {},|||a x x B <=若,A B ⊆则实数a 的取值范围是 A 、1<a B 、1≤a C 、31≤<-a D 、10≤<a3、要从已编号1到60的60枚最新研制的某种导弹中随机抽取6枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是 A 5,10,15,20,25,30 B 3,13,23,33,43,53 C 1,2,3,4,5,6 D 2,4,8,16,32,48 4,如果执行下面的程序框图,那么输出的S = A.2550B.-2550C. 2548D.-25525、不等式组⎩⎨⎧≤≤≥++-300))(5(x y x y x 表示的平面区域是A .矩形B .三角形C .直角梯形D .等腰梯形6、与参数方程)x t y ⎧=⎪⎨=⎪⎩为参数等价的普通方程为 A .214y +=2x B .21(01)4y x +=≤≤2xC .21(02)4y y +=≤≤2x D .21(01,02)4y x y +=≤≤≤≤2x7、已知实数z y x ,,满足:132=++z y x ,则222z y x ++的最小值是A .91 B.121 C.141 D.33618、已知P 是以F1、F2为焦点的椭圆)0(12222>>=+b a b y a x 上一点,若21PF PF⋅=0, 21t a nF PF ∠=2,则椭圆的离心率为A .21B .32C .31D .35二 填空题:本大题共7个小题,每小题5分,共35分,把答案填在答题中卡对应题号的横线上 9、 在△ABC 中,若sin A ∶sin B ∶sin C =7∶8∶13,则C =_____________ 10、设lg2x -lgx2-2=0的两个零点是、,则log +log的值=____________11、3|2|x dx -⎰=_____________12.设nxx )13(3+的展开式中的各项系数之和与它的二项式系数和之差为240,那么n=____________13、从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,其中甲、乙两名志愿者不能从事翻译工作,则不同的选排方法共有____________种(用数字作答) 14、对于命题①化极坐标方程2cos 0ρθρ-=为直角坐标方程为1y = ②“a b Z +∈”是“20x ax b ++=有且仅有整数解”的必要非充分条件③i 1的虚部为-1④ 如果函数y=f(x) 有最大值M ,则使得不等式f(x)≤k 有解时,k 的范围是k ≥M , 其中正确的有____________②③(填写你认为正确的序号)15、已知命题:“若数列}{n a 为等差数列,且),,(,,*∈<==N n m n m b a a a n m,则m n ma nb a n m --=+··”,现已知数列}{n b ),0(*∈>N n b n 为等比数列,且,,b b a b n m ==),,(*∈<N n m n m ,若类比上述结论,则可得=+n m b三 :解答题:本大题共6个小题,共75分,解答应写出文字说明 证明过程或演算步骤16、((本小题满分12分)已知等差数列{}n a 的前n 项和为n S ,且416S =,47a =.(1)求数列{}n a 的通项公式;(2)求100993221111a a a a a a +⋅⋅⋅++的值.17、(本小题满分12分)若锐角35)sin(,713tan tan ,=-=⋅βαβαβα且满足,求值:(1))cos(βα-; (2))cos(βα+.18、(本小题满分12分)从装有3个红球,2个白球袋中随机取出2个球,求至少摸到一个红球的概率设摸到红球的个数为ξ,求ξ的概率分布列及期望19、(本小题满分13分)如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.⑴求证:A1C⊥平面BED;⑵求A1B与平面BDE所成的角的正弦值.20、(本小题满分13分)已知函数).(ln21)(2Raxaxxf∈-=(1)求函数f (x)的单调区间;(2)当x > 1时,试比较xx ln212+与.323x的大小,并证明D CA1 B1D1 C1EF21.(本小题满分13分)已知动点M 在y 轴右侧,M 到点(0,41)的距离比它到直线y=-21的距离小41.(1)求动点M 轨迹C 的方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长郡中学2011届高三分班考试试卷
理科数学参考答案
一㊁选择题:本大题共8小题,每小题3分,满分24分.
题 号12345678
答 案A B C C D A B C
二㊁填空题:本大题共7小题,每小题3分,共21分.
9.823 10.(-∞,-54] 11.4 12.②④ 13.ρ=2c o sθ 14.10 15.13
三㊁解答题:本大题共6小题,满分55分.
16.解:(1)∵m∥n,∴c(c-a)=(b-a)(a+b),
∴c2-a c=b2-a2,∴a2+c2-b2
a c=1.
由余弦定理得c o s B=12,B=π3.(4分)
………………………………(2)∵A+B+C=π,∴A+C=2π3,
∴s i n A+s i n C=s i n A+s i n(2π3-A)=s i n A+s i n2π3c o s A-c o s2π3s i n A=
3
2s i n A+3
2c o s A=3s i n(A+
π
6).
∵0<A<2π3,∴π6<A+π6<5π6,
∴12<s i n(A+π6)≤1,∴32<s i n A+s i n C≤3.(8分)
……………
17.解:(1)设 世博会会徽”卡有n张,由C2n C2
10=215,得n=4.(1分)
………
故 海宝”卡有6张,抽奖者获奖的概率为C26C210=13.(3分)
……………(2)ξ可能取的值为0,1,2,3,4,则(4分)
………………………………
P(ξ=0)=(23)4=1681;
P(ξ=1)=C1413(23)3=3281;
P(ξ=2)=C24(13)2(23)2=2481;
P(ξ=3)=C34(13)323=881;
P(ξ=4)=(13)4=181.
所以ξ的分布列为ξ01234 P168132812481881181
Eξ=0×1681+1×3281+2×2481+3×881+4×181=43.(8分)
…………18.解:方法一(1)取E C的中点F,连结B F,
则B F//D E,∴∠F B A或其补角即为异面直线D E与A B所成的角.在△B A F中,A B=42,B F=A F=25,∴c o s∠A B F=105,
∴异面直线D E与A B所成的角的余弦值为105.(3分)
……………(2)A C⊥平面B C E,过C作C G⊥D E交D E于G,连结A G,可得D E⊥平面A C G,从而A G⊥D E,
∴∠A G C为二面角A E D B的平面角.
在△A C G中,∠A C G=90°,A C=4,C G=855,
∴t a n∠A G C=52,∴s i n∠A G C=53,
∴二面角A E D B的正弦值为53.(6分)
…………………………(3)V=13㊃S B C E D㊃A C=16,∴几何体的体积V为16.(9分)
………
方法二:(坐标法)(1)以C为原点,以C A,C B,C E所在直线为x,y,z 轴建立空间直角坐标系,
则A(4,0,0),B(0,4,0),D(0,4,2),E(0,0,4),
→D E=(0,-4,2),→A B=(-4,4,0),∴c o s<→D E,→A B>=-10
5,
∴异面直线D E与A B所成的角的余弦值为105.(3分)
……………(2)平面B D E的一个法向量为→C A=(4,0,0),
设平面A D E的一个法向量为n=(x,y,z),
n⊥→A D,n⊥→D E,→A D=(-4,4,2),→D E=(0,-4,2),
∴n㊃→A D=0,n㊃→D E=0,
从而-4x+4y+2z=0,-4y+2z=0,令y=1,
则n=(2,1,2),c o s<→C A,n>=23,
∴二面角A E D B的正弦值为53.(6分)
…………………………(3)V=13㊃S B C E D㊃A C=16,∴几何体的体积V为16.(9分)
………
19.解:(1)∵f(t)=3
4+a㊃2-t×100%(t为学习时间),且f(2)=60%,则3
4+a㊃2-2×100%=60%,可解得a=4,
∴f(t)=3㊃-t㊃100%=3(-t)(t≥0),
∴f (0)=34(1+1
)=38=37.5%.f (
0)表示某项学习任务在开始学习时已掌握的程度为37.5%.(4分)………………………………………………………………………(2
)令学习效率指数y =f (t )t
,即y =f (t )t =34t (1+2-t )=34(t +t 2
t
)
(t >0),现研究g (t )=t +t 2
t 的单调性,g '(t )=1+2t -t ㊃2t l n 2(2t )2=2t
-t l n 2+12t (t >0).(6分)…………………又已知x >0时,2x
>x l n 2恒成立,∴2t
-t l n 2>0,即g (t )>0恒成立,
∴g (t )在(0,+∞)上为增函数且g (t
)为正数,∴y =f (t )t =34(t +t 2t )
(t >0)在(0,+∞)上为减函数.(8分)………而y |t =1=f (1)1=12,y |t =2=f (2)2=310,∴y =f (t
)t ∈(310,12
).
故所求学习效率指数的取值范围是(310,12
).(10
分)………………20.解:(1)∵f '(x )=1x
,直线l 是函数f (x )=
l n x 的图象在点(1,0)处的切线,
∴其斜率为k =f '(1)=1,
∴直线l 的方程为y =x -1.(1分)……………………………………又因为直线l 与g (x )的图象相切,∴
y =x -1
y =12x 2+m x +{
72
⇒12x 2+(m -1)x +92=0,得Δ=(m -1)2
-9=0⇒m =-2(m =4不合题意,舍去).(3分)
……(2)由(1)知g (x )=12x 2-2x +72
,
∴h (x )=f (x +1)-g '(x )=l n (x +1)-x +2(x >-1),∴h '(x )=1x +1-1=-x x +1(x >-1).(4分)…………………………当-1<x <0时,h '(x )>0;当x >0时,h '(x )<0.
于是,h (x )在(-1,0)上单调递增,在(0,+∞)上单调递减.(5分)…所以,当x =0时,h (x )取得最大值h (0)=2.(6分)
…………………(3)由(2)知:当-1<x <0时,h (x )<2,即l n (1+x )<x ;(8分)……当0<a <1时,-1<a -12
<0
,∴f (1+a )-f (2)=l n 1+a 2=l n (1+a -12)<a -12.(10分)…………
21.解:(1
)由题意知e =c a =12,所以e 2
=c 2a 2=a 2-b 2
a
2
=14,即a 2=43b 2.又因为b =
61+1
=3,所以a 2=4,b 2
=3.
故椭圆C 的方程为x 24+y 2
3
=1.(2分)
…………………………………(2)由题意知直线P B 的斜率存在,设直线P B 的方程为y =k (x -4).由y =
k (x -4),x 24+y
23
=1{
.得(4k 2+3)x 2-32k 2x +64k 2-12=0.①…………设点B (x 1,y 1),E (x 2,y
2),则A (x 1,-y 1).直线A E 的方程为y -y 2=y 2+y 1
x 2-x 1(x -x 2)
.令y =0,得x =x 2-y 2(x 2-x 1)y 2+y
1.将y 1=k (x 1-4),y
2=k (x 2-4)代入整理,得x =2x 1x 2-4(x 1+x 2)x 1+x 2-8.②
……………………………………………………………………由①得x 1+x 2=32k 24k 2+3,x 1x 2=64k 2
-124k 2+3
代入②整理,得x =1.所以直线A E 与x 轴相交于定点Q (1,0).(6分)……………………(3
)当过点Q 的直线MN 的斜率存在时,设直线MN 的方程为y =m (x -1),且M (x M ,y M ),N (x N ,y N )在椭圆C 上.
由y =m (
x -1)x 24+y
23
{
=1得(4m 2+3)x 2-8m 2x +4m 2-12=0,易知Δ>0,所以x M +x N =8m 24m 2+3,x M x N =4m 2-124m 2+3,y M y N =-9m 24m 2+3,则→O M ㊃→O N =x M x N +y M y N =-5m 2+124m 2+3=-54-334(4m 2+3
).因为m 2≥0,所以-114≤-334(4m 2+3)<0,所以→O M ㊃→O N ∈[-4,-54
).
当过点Q 的直线MN 的斜率不存在时,其方程为x =1.解得M (1,32),N (1,-32),此时→O M ㊃→O N =-54
,
所以→O M ㊃→O N 的取值范围是[-4,-54
].(10分)
……………………。
