角的特殊关系 一、教学目标
角的分类教学设计(优秀5篇)

角的分类教学设计(优秀5篇)角的分类教学设计篇一一、教学内容:人教版小学数学第七册第二单元。
二、教学目标:1、使学生认识、理解直角、锐角、钝角、平角和周角的概念,知道它们之间的关系,并能按一定标准分类。
2、培养学生动手操作、合作学习与探究学习能力。
发展学生的空间观念。
三、教学重点、难点:重点:依据角的度数区分各种角。
难点:平角、周角的认识及三种特殊角之间的关系。
四、教学方法:教法:直观演示法、自主探究法、小组合作法。
学法:实践操作法。
五、教学具准备:教具:多媒体课件一套。
学具:活动角、量角器、长方形纸和圆形纸各一张等。
教学资源:七巧板、量角器、课件。
教学过程:一、教学导入:出示各种不同的角,谁愿意说说什么叫做角?角有大有小,可以用什么来度量?角的大小与什么无关?与什么有关呢?“生活中存在着许许多多的角。
正是因为角有大有小,所以需要把角进行分类,下面这节课我们就来学习角的分类。
板书课题:角分分类。
二、教学新授:师:“请大家拿出四张卡片,用水彩笔和尺出画四个不同大小的角。
每张卡片画一个。
比一比谁画的又好又快!”学生在卡片上画角。
师:“请组长将大家画的角收集起来,平铺在桌面上。
比一比哪一组动作最快!”组长工作。
师:“下面我们要给这些角分分类。
在分类之前,老师要说几点要求:1、每人先要认真的观察这些角。
2、为了提高我们小组合作学习的效度,分类前组长一定要带领大家展开充分的讨论,确定分法后再分。
3、分好后,每组选一名发言人,准备向大家汇报分类的情况。
”小组合作学习,给角分类。
教师巡视,做好记录。
师:“哪一组愿意汇报?”小组汇报,汇报时请其用三角尺验证。
贴出直角。
师:“你们认为他们分的怎么样?”1.认识直角。
通过测量是90度的角数学上称作直角。
从而得出:直角是90度。
板书:直角90度举例生活中的直角。
2、认识锐角观察特征,小结锐角的定义,并板书。
举锐角的例子。
从而让学生发现锐角有无数个。
活动角转锐角。
3、认识钝角观察特征,小结钝角的定义,并板书。
四年级数学上册《认识平角周角和各种角的关系》教案、教学设计

1.教师将学生分成若干小组,每组4-6人,确保每个学生都能参与讨论。
2.各小组针对以下问题展开讨论:
-平角和周角在实际生活中的应用;
-如何区分平角、周角与其他角度;
-角度测量过程中遇到的问题及解决方法。
3.教师巡回指导,解答学生疑问,引导学生深入思考。
(四)课堂练习
1.设计不同难度的练习题,涵盖平角、周角的识别、测量及应用等,让学生独立完成。
四、教学内容与过程
(一)导入新课
1.教师通过展示生活中的实例,如时钟上时针和分针形成的角度、三角板上的角度等,引导学生回顾已学的角度知识。
2.提问:“同学们,我们已经学过哪些角度?它们有什么特点?”让学生回答,巩固已有知识。
3.逐步引出平角、周角的概念,并提出问题:“今天我们要学习的平角和周角有什么特别之处呢?”激发学生的好奇心和求知欲。
4.设计丰富多样的练习题,让学生在练习中巩固所学知识,提高解决问题的能力。
(三)情感态度与价值观
1.培养学生对数学学习的兴趣,激发学生主动探究数学问题的热情。
2.培养学生的空间观念,使学生能够运用角度知识观察、分析生活中的实际问题。
3.培养学生的耐心和细心,使学生养成严谨的学习态度,对待数学问题认真负责。
四年级数学上册《认识平角周角和各种角的关系》教案、教学设计
一、教学目标
(一)知识与技能
1.了解平角、周角的定义,能够识别并正确画出这两种特殊角度。
2.理解锐角、直角、钝角和平角、周角之间的关系,能够准确判断各种角度的大小。
3.学会使用量角器测量角度,提高角度测量的准确性。
4.能够运用角度知识解决实际问题,如判断物体间的角度关系、计算角度和等。
-采用启发式教学法,引导学生主动思考、探索,培养学生的数学思维。
小学二年级数学上(第三单元角的认识:1 角的认识)教学设计

小学二年级数学上(第三单元角的认识:1 角的认识)教学设计一、教学目标1.知识与技能:–了解角的概念;–能够用小于直角大于零的表示法表示角;–能够用角度尺测量和画角。
2.过程与方法:–采用示例教学法,引导学生观察角的形状和特点;–培养学生观察问题、提出问题、解决问题的能力;–注重手脑结合,让学生通过实际操作来理解角的概念。
3.情感态度价值观:–培养学生对数学学习的兴趣和信心;–培养学生合作学习和探究精神;–培养学生对准确性和细致性的追求。
二、教学重点与难点重点1.角的基本概念;2.用度量制表示角。
难点1.如何正确理解角的概念;2.如何准确度量和画出角。
三、教学准备1.教学工具:角尺、图形练习册;2.教学资源:角度尺、角度模型;3.教学环境:教室黑板、投影仪。
四、教学过程第一节角的概念1.引入:通过投影仪展示各种角的形状,引起学生对角的好奇和兴趣;2.讲解角的定义和符号表示:介绍角的定义,让学生了解角的起点、顶点和终点的概念;3.实例讲解:给出几个实际的角度,让学生观察并用度量尺测量;4.练习环节:让学生观察周围环境中的角,并用角尺测量,找出各种不同大小的角。
第二节角的度量和画角1.讲解角的度量:介绍度量角的方法和度量制的概念;2.示范画角:讲解如何用角度尺画出各种角,并让学生跟着练习;3.练习环节:让学生用角度尺画出特定的角度,并互相检查。
五、课堂小结与思考1.回顾本节课的重点内容:角的概念和度量;2.思考:在日常生活中还有哪些实际应用可以用到对角的认识;3.布置作业:要求学生完成练习册的相关题目,巩固所学知识。
六、拓展延伸1.鼓励学生自行寻找周围环境中的角,并用角度尺进行测量;2.让学生带来一些有趣的角度题目,进行小组讨论和解答。
以上是本节课的教学设计,希望能够帮助学生更好地理解和掌握角的概念。
二年级上册角的初步认识教案

二年级上册角的初步认识教案第一章:认识角教学目标:1. 让学生通过观察和操作,初步认识角。
2. 让学生能够找出生活中的各种角。
教学重点:1. 让学生掌握角的定义。
2. 让学生能够找出生活中的各种角。
教学难点:1. 让学生理解角的概念。
教学准备:1. 教师准备一些图片,展示各种角。
2. 学生准备一些三角形纸片。
教学过程:1. 导入:让学生观察教室里的各种角,引导学生关注角的存在。
2. 讲解:讲解角的定义,让学生通过观察和操作,理解角的概念。
3. 练习:让学生找出生活中的各种角,并画出来。
教学反思:1. 学生在找角的过程中,可能对一些特殊的角理解不透彻,需要在课后进行针对性的辅导。
2. 学生在画角的过程中,可能对角的大小把握不准,需要加强练习。
第二章:比较角的大小教学目标:1. 让学生通过观察和操作,学会比较角的大小。
2. 让学生能够判断两个角的大小关系。
教学重点:1. 让学生掌握比较角大小的方法。
2. 让学生能够判断两个角的大小关系。
教学难点:1. 让学生理解角的大小与边的长短无关。
教学准备:1. 教师准备一些大小不同的角。
2. 学生准备一些三角形纸片。
教学过程:1. 导入:让学生观察教师准备的大小不同的角,引导学生关注角的大小。
2. 讲解:讲解比较角大小的方法,让学生通过观察和操作,理解角的大小与边的长短无关。
3. 练习:让学生通过观察和操作,判断两个角的大小关系。
教学反思:1. 学生在判断角的大小关系时,可能对一些特殊的角理解不透彻,需要在课后进行针对性的辅导。
2. 学生在比较角的过程中,可能对角的大小把握不准,需要加强练习。
第三章:画角教学目标:1. 让学生通过观察和操作,学会画角。
2. 让学生能够准确地画出各种角。
教学重点:1. 让学生掌握画角的方法。
2. 让学生能够准确地画出各种角。
教学难点:1. 让学生理解画角的方法。
教学准备:1. 教师准备一些画角的工具。
2. 学生准备一些三角形纸片。
数学四年级上册《角的概念》教案设计

数学四年级上册《角的概念》教案设计。
为了能够更好地帮助学生掌握数学这门学科,数学教育在每个年级都有着相应的课程设计和教材。
在四年级上册中,学生们将会学习到《角的概念》这一知识点。
为此,本文将会以此为背景,为大家介绍一下有关这部分教学内容的设计方。
一、教学目标本节课的教学目标主要是引导学生了解角的概念、特征,并运用角的知识解决一些相关问题。
二、教学重点和难点1.角的概念和特征2.角的角度的表示方法3.角的分类和判别三、教学方式1.讲授型2.图像呈现与分析3.讨论与教师引导四、教学过程1.导入环节在本课的导入环节中,可以通过以下问题引导学生对于角的了解:a.你知道什么是角吗?b.角的特征有哪些?c.角与图形有什么关系?通过提出这些问题,可以引导学生通过图像的观察来建立对于角的概念和特征的认知,并且能够引导学生关注到角在图形中的重要性。
2. 角的概念和特征讲解接下来,通过教师的讲解来详细地介绍角的概念和特征,例如角的定义、角度的表示方法和角度的分类等。
教师需要注意在讲解中让学生理解到角是由两个射线共同构成的,并且强调角的度数表示的方法。
3. 角度的作用与计算在本节课的第三部分内容中,教师可以通过具体例子来展示角在实际问题中的应用。
例如,通过计算多个角度的大小来帮助学生理解角度计算的复杂性,这样学生将会更加深入地理解角的作用和重要性。
4. 练习环节为了巩固学生对于角的认知,教师可以安排一些实际习题,例如让学生在画好角度图形的前提下,计算角度的大小等等。
这些习题可以帮助学生快速记忆角的各项特征和知识点,并且让学生更加熟练地运用所学知识解决实际问题。
5. 总结环节在本课的最后部分,教师可以通过总结环节来确保学生完全掌握了本课的核心知识点。
教师可以借助回答问题的方式来检测学生的掌握程度,也可以通过简单的考试来检验。
本节课最终的目标就是让学生充分理解角的实际应用和特征,同时让他们能够应用所学知识来解决实际问题。
九年级数学《特殊角的三角函数值》教案

教案:特殊角的三角函数值一、教学目标:1.理解特殊角的概念和特征。
2.掌握特殊角的三角函数值。
3.运用特殊角的三角函数值解决实际问题。
4.培养学生的逻辑思维能力和解决问题的能力。
二、教学内容:1.特殊角的概念。
2.特殊角的特征。
3.特殊角的三角函数值。
4.运用特殊角的三角函数值解决实际问题。
三、教学过程:Step 1 导入新课1.让学生回忆和复习正弦、余弦、正切的定义和性质。
2.引入特殊角的概念。
解释特殊角是指在单位圆上的角度是特殊的角度。
Step 2 学习特殊角的特征1.讲解特殊角的三种特殊情况:a)0度。
b)90度。
c)180度。
2.引导学生思考其他特殊角的特征和三种特殊角的函数值。
3.提示学生特殊角的函数值与直角三角形的边长有关。
Step 3 推导特殊角的三角函数值1.推导0度特殊角的三角函数值。
a)角度为0度时,对应的三角函数值:- sin0° = 0- cos0° = 1- tan0° = 0b)解释特殊角的三角函数值与单位圆上的点位置的关系。
2.推导90度特殊角的三角函数值。
a)角度为90度时,对应的三角函数值:- sin90° = 1- cos90° = 0- tan90° = 无定义(不存在)b)解释特殊角的三角函数值与单位圆上的点位置的关系。
3.推导180度特殊角的三角函数值。
a)角度为180度时,对应的三角函数值:- sin180° = 0- cos180° = -1- tan180° = 0b)解释特殊角的三角函数值与单位圆上的点位置的关系。
Step 4 运用特殊角的三角函数值解决实际问题1.将上述推导结果应用于实际问题。
a) 比如:已知角度为45度,求解sin45°、cos45°和tan45°的值。
b)引导学生根据特殊角的三角函数值和单位圆上的三角关系进行计算。
角的特殊关系

°
3.任意一个直角三角形的两个锐角之和是多少度 任意一个直角三角形的两个锐角之和是多少度? 任意一个直角三角形的两个锐角之和是多少度
两个角的和等于90° 直角 两个角的和等于90°(直角 ,就说这两个角互为 90 直角), 余角,简称互余.即如果∠ 余角,简称互余.即如果∠1+∠2=90 ° ,那 互余,也可以说∠ 的余角, 么∠1与∠2互余,也可以说∠1是∠2的余角, 的余角. 或∠2是∠1的余角.
结论: 同角(等角 等角)的补角相等 结论 同角 等角 的补角相等
例2: 填空
你发现 了什么? 了什么?
某个角 它的余角 它的补角
34° 34° 56° 56° 146° 146°
49° 50° 105° 49° 50°30′ 105° 41° 39° 41° 39°30′
x° (90-x)° (90-x)°
角的特殊关系
执教者 李涛
本课要求: 本课要求 1.能够对余角和补角及对顶角进行识别和 能够对余角和补角及对顶角进行识别和 角度的计算; 角度的计算 2.能够运用本节课的知识解决实际问 能够运用本节课的知识解决实际问 题.
建筑工人的难题
要测量两堵墙所成的角AOB的度数,但人不 的度数, 要测量两堵墙所成的角 的度数 能进入围墙,如何测量? 能进入围墙,如何测量
×
(4)相等的角是对顶角.( 相等的角是对顶角.( (5)对顶角一定相等.( 对顶角一定相等.(
√
×
)
)
(6)如果两个角相等,且有公共顶点,那么这两个角是对顶 如果两个角相等,且有公共顶点, 角.( × ) 的角的余角是62° .( (7)28°30′的角的余角是 °30′.( ° 的角的余角是 (8)任何一个角都有余角.( 任何一个角都有余角.( ) ×
直角三角形 的边角关系(一) 优秀教案

《直角三角形的边角关系复习课》(一)教学设计一. 教学任务与目标1、能从整个学段梳理并掌握直角三角形中边、角关系,掌握解直角三角形及一般三角形的方法,理解锐角三角函数本质.2、能用这些关系来解决复杂几何图形中的相关计算,渗透转化与方程思想方法,为综合数学应用问题的解决提供基础.3、能利用解直角三角形解决生活中的实际问题,培养学生建模、识图、计算能力.二.教学重点:利用锐角三角函数解三角形及有关的实际问题.教学难点:把一般三角形问题转化成直角三角形问题.把实际问题转化成解三角形问题.三. 教学设计第一环节:前置学习任务一:知识点整理与回顾如图Rt△ABC中,∠C=90°。
1、直角三角形三边的关系: .2、直角三角形两锐角的关系: .3、直角三角形边与角之间的关系:锐角三角函数的定义:4、互余两角之间的三角函数关系: sin(900-A)= cos(900-A)=5、同角之间的三角函数关系: sin2A+cos2A=AAcossin=6、特殊角300,450,600角的三角函数值.7、锐角三角函数的变化规律:锐角的正弦值或正切值随角度的增大而,锐角的余弦值或余切值随角度的增大而。
8、会识别仰角、俯角、方向角,掌握坡度(坡比)和坡角的定义:==BA cossin==BA sincos==BA cottan54sin =B 00)60(tan2-21-⎪⎭⎫ ⎝⎛图一中的角叫: 图二中的角叫: 。
图三中A 在B 的 方向上, C 在B 的 方向上。
图四中迎水坡坡面是AD,则坡角为 ,坡面AD 的坡度(也叫 )i= =任务二:基础热身练习1、(类型一:考察定义)在Rt △ABC 中,∠C =900,AC =8 , ,则BC= cosB= .2、(类型二:考察特殊三角函数值的准确记忆)计算 + +3、(类型三:由特殊函数值求角度)若 ,则∠a = .4、(类型四:锐角三角函数的增减性)若锐角a 满足cosa<22,tana<3,则a 的取值范围是5、(类型四:转化求等角的函数值或利用cosa=sin(900-a ))如图Rt △ABC 中,∠ACB=90°,CD ⊥AB ,AC=5,BC=2,则=∠DCB cos 。
数学四年级上册《角的分类》教案设计

数学四年级上册《角的分类》教案设计“角的分类”教学设计篇一一、教学目标:1、认识平角、周角,会根据角的度数区分锐角、直角、钝角、平角和周角,并知道直角、平角和周角的关系。
2、通过观察、操作,经历平角和周角的形成过程,建立平角、周角的表象。
3、体会数学知识与实际生活的紧密联系,激发学习数学的兴趣。
二、教学重点:认识平角、周角,会根据角的度数区分直角、锐角、钝角、平角和周角。
三、教学难点:形成平角和周角的表象。
四、教具准备:量角器、活动角、三角板、课件。
五、教学过程:一)导入师:同学们,我们已经认识了角,这节课老师将与大家一起来学习《角的分类》。
如果我们要将角分类,你想按照什么进行划分?生:我们可以按照角的度数来划分。
生:我们可以按照角的大小来划分。
师:好,就按你们说的办,我们按照角度数的大小来划分。
师:其实有一类角,我们在上二年级时就已经认识了,还记得是什么角吗?生:直角。
师:你能说出在我们的生活中那些物体和平面中存在直角吗?生1:我们黑板的四个角是直角。
生2:电视,电脑屏幕面上的四个角也是直角。
生3:我们用的书桌的四个角是直角。
生4:我们数学书的和这张白纸的角也是直角。
生5:我三角板的这个角是直角。
(用手指出)师:同学们找的可真多,可见直角在我们的生活中应用的是多么广泛!那么谁知道直角是多少度的角?生1:90度。
师:他们都说是90度,让我们一起来验证一下好不好,你们可以量书桌的一角,也可以量书的一角,还可以量三角板的直角,可以量一个直角也可以量几个直角,看看直角是不是90度的角。
(教师巡视看学生量角的方法是否准确)师:结果怎么样?用你自己的话来说说。
生:90度的角是直角,直角都是90度。
二)认识平角师:老师这里还有一个图形想让你来帮老师判断一下,它是不是角,(演示折扇抽象为平角的过程)在演示之前我想问同学们一个问题,怎样的图形才称为角。
生1:有一个顶点,两条射线。
生2:从一个顶点引出两条射线所组成的图形叫做角。
4.6.3角的特殊关系
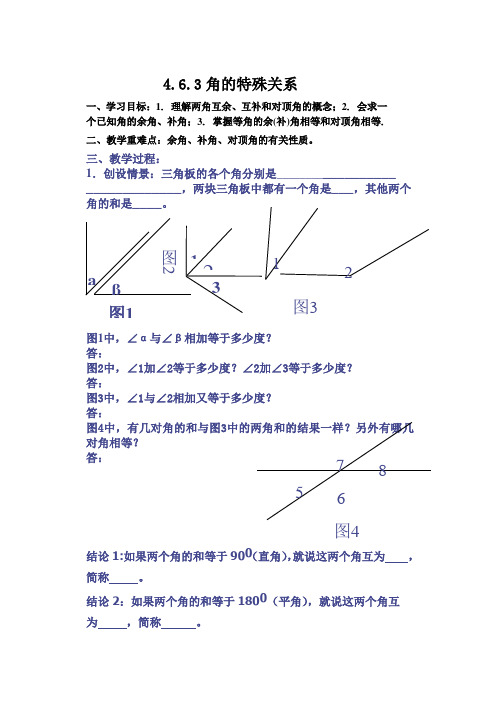
4.6.3角的特殊关系一、学习目标:1. 理解两角互余、互补和对顶角的概念;2. 会求一个已知角的余角、补角;3. 掌握等角的余(补)角相等和对顶角相等.二、教学重难点:余角、补角、对顶角的有关性质。
三、教学过程:1.创设情景:三角板的各个角分别是__________________ _____________,两块三角板中都有一个角是___,其他两个角的和是____。
图1中,∠α与∠β相加等于多少度?答:图2中,∠1加∠2等于多少度?∠2加∠3等于多少度? 答:图3中,∠1与∠2相加又等于多少度?答:图4中,有几对角的和与图3中的两角和的结果一样?另外有哪几对角相等?答:结论1:如果两个角的和等于900(直角),就说这两个角互为 ,简称 。
结论2:如果两个角的和等于1800(平角),就说这两个角互为 ,简称 。
a ß 图1 图3 1 2 1 23 图2图4 7 8 6 52.动动脑筋:(图1)若∠α和∠β互余,按照右图所示把∠α与∠β拼在一起,∠AOB等于多少度?(图3)若∠1和∠2互补,按照右图所示把∠1与∠2拼在一起,∠AOB等于多少度?选择:1、两个角互余,那么它们一定是( )。
A、锐角B、钝角C、直角D、不能确定2、一个锐角的补角一定是()。
A、锐角B、钝角C、直角D、不能确定练一练:P158 练习1问题3:图四∠6和∠7分别是∠5的什么角?∠6和∠7有什么关系?为什么?答:结论:同角的补角。
∠5是∠6的什么角?∠8是∠7的什么角?∠5和∠8有什么关系?为什么?答:结论:等角的补角。
问题4:图2中,∠1与∠2具有什么关系?∠2与∠3具有什么关系?∠1与∠3又有何关系?答:结论:同角的余角。
若∠1+∠2=900,∠3+∠4=900,∠2=∠4,那么∠1与∠3具有什么关系?答:结论:等角的余角。
动动手:已知∠α=50017′,求∠α的余角和补角。
3.思考:∠α的补角是__________,∠α的余角是__________,如果∠α的补角是∠α的余角的3倍,则∠α等于____。
数学四年级上册《角的特点》教案设计

数学四年级上册《角的特点》教案设计。
【教学目标】1.知道角的基本概念,能够识别角。
2.掌握角的特点,能够根据角的特点进行分类。
3.了解角和直线、线段的关系。
【重难点】1.学生初步认识角这一概念,需要在图形中简单理解角的概念,逐渐深化角的特点。
2.学生需要掌握角的度量单位。
3.角的垂直、相对等特点要求学生有较好的空间认知和图形思维能力。
【教学流程】第一步:导入通过展示多个图形,引导学生对“角”的概念进行预习,感受角的存在,即从图形认识角。
第二步:讲授1.讲解角的概念(一定程度上是引导、提问,让学生发现规律,引导学习)。
2.角的度量:讲解角和圆的关系,弧度的概念,度分秒表示法,加深学生对角度的认知。
3.角的特点:以图形多个角为例,引导学生分析角的特点,归纳总结,建立对角的分类的认知。
第三步:巩固1.图形应用(单选题、多选题、填空题):即通过图形、文字提问培养学生对角度量、角分类的感性认知。
2.角分类游戏:通过分组比赛的形式,让学生对角的分类有更深入的理解。
第四步:拓展引导学生探讨直线、线段和角之间的关系,通过实际的生活经验,让学生深刻认识到身边的角度,加深学生对角和其它几何图形的认知。
【板书设计】<ul><li>角的概念</li><li>角的度量</li><li>角的特点</li></ul>【教学总结】数学四年级上册《角的特点》教案设计通过引导学生逐渐理解角的概念和度量,并让学生认识到角和直线、线段的关系,深化学生对角的特点的认知,同时强化对角的分类的理解。
通过板书设计,加深学生对角的印象,确保学生对各个概念建立稳定的认知。
这里提醒老师,不同教学内容之前要注意较好的衔接,确保学生掌握的知识点能够相互理解。
1.3.4 角的特殊关系

1.3.4 角的特殊关系【知识精华点击】课标要求⑴认识一个角的余角和补角,掌握余角和补角的性质;⑵了解方位角,能确定具体物体的方位。
本节课的重点是认识角的互余、互补关系及其性质,确定方位. 通过简单的推理,归纳出余角、补角的性质,并能用规范的语言描述性质是难点。
教材详析1.互为余角、互为补角正确理解概念(1)互为余角的定义:如果两个角的和等于直角,称这两个角互为余角.符号表示:若∠1+∠2=900,那么∠1与∠2叫做互为余角,其中∠1是∠2的余角,∠2也是∠1的余角.理解这个定义要注意下列三个条件:①两个角之间的关系;②两个角相加等于900;③只与角的度数有关,与角的位置无关.(2)互为补角的定义:如果两个角的和等于平角,称这两个角互为补角符号表示:若∠1+∠2=1800,那么∠1与∠2叫做互为补角,其中∠1是∠2的补角,∠2也是∠1的补角.理解这个定义要注意下列三个条件:①两个角之间的关系;②两个角相加等于1800;③只与角的度数有关,与角的位置无关.(3)互为余角与余角、互为补角与补角区别它们都是不同的概念,互为余角或互为补角是指两角之间的特定的数量关系,余角与补角是一个角相对于另一个角而言的.(4)同一个角的余角与补角的关系∠α的余角是90°-∠α;∠α的补角是180°-∠α.一个角的补角比它的余角大90°.2. 余角、补角的性质(1)同角或等角的余角相等.推理格式如:∵∠A+∠1=90°, ∠A+∠2=90°,∴∠1=∠2;∵∠A+∠1=90°, ∠B+∠2=90°, ∠A=∠B,∴∠1=∠2.(2)同角或等角的补角相等.推理格式如:∵∠A+∠1=180°, ∠A+∠2=180°,∴∠1=∠2;∵∠A+∠1=180°, ∠B+∠2=180°, ∠A=∠B,∴∠1=∠2. 说明:同角或等角的余角相等,包含两方面内容:一是:同一个角的余角相等;二是相等的角的余角相等.同角或等角的补角相等也是这样理解的. 3.方位角如图1-3.4-1,画两条互相垂直的直线AB 和CD 相交于点O ,其中一条为水平线,图中四条射线所指方向分别是东西南北四大方向:向上的射线OA表示正北方向,向下的射线OB表示正南A北 图1-3.4-1 O 东 D 西 C B南方向,向右的射线OD表示正东方向,向左的射线OC表示正西方向.这四大方向简称为上北下南左西右东.建立这四方向线后,对于点P,如果点P在射线OA 上,则称点P在正北方向;如果点P在射线OB 上,则称点P在正南方向;如果点P在射线 OC 上,则称点P在正西方向;如果点P在射线OD 上,则称点P在正东方向.如果点P在正北方向线OA 与正东(或正西)方向线OD (或OC )的夹角内,且射线 OP 与正北方向线OA 的夹角是m°,则称点P在北偏东(或西)m°方向;如果点P在正南方向线OB 与正东(或正西)方向线OD (或OC )的夹角内,且射线OOP 与正南方向线OB 的夹角为m°,则称点P在南偏东(或西)m°方向. 如图1-3.4-2中的射线OA 、OB 、OC 、OD 分别称为:北偏东40°、北偏西65°、南偏西45°、南偏东20°. 这里要注意OD 不要说成是东偏南70°,同样,OC 也不要说成是西偏南45°. 对于偏向45°的方位角,有时也可以说成东南(北)方向或西南(北)方向.如图1-3.4-2中的OC ,除了说成南偏西45°外,还可以说是西南方向,但不要说成南西方向.【名师优质讲堂】例题精析例1 已知∠α,用两种不同的方法,画出∠α的余角∠β和∠α的补角∠γ.图1-3.4-3分析(1)作∠α的余角:①在顶点处作一边的垂线,这条垂线与另一边组成的锐角为∠α的余角;②在顶点处作另一边的垂线,与一边组成的锐角即为∠α的余角.(2)作∠α的补角:①过∠α的一边作其反向延长线,延长线与另一边所组成的角为∠α的补角;②过另一条边作其反向延长线,延长线与一边所组成的钝角即为∠α的补角.解 ∠α的余角如图1-3.4-4(1)、(2),∠α的补角如图1-3.4-4(3)、(4):图1-3.4-4说明 一个角的余角与这个角刚好拼成一个直角;一个角的补角与这个角刚好拼成一个平角.【变式1】下列四个角中,最有可能与70°角互补的是( )A .B .C .D . 65° 北 图1-3.4-2 O 东 西 南 C B A 70° 45° 40° D分析 先求出70°角的补角,然后结合各选项即可选择.解 70°角的补角=180°-70°=110°,是钝角,只有D 选项是钝角,所以,最有可能与70°角互补的是D 选项的角.故选D .例2 一个角的补角是它的余角的3倍,那么这个角的度数是( )A .60° B.45° C.30° D.15°分析 由于一个角和它的补角的和是平角,与它的余角的和是直角,如果设这个角为∠A ,则它的补角是180°-∠A ,余角是90°-∠A ,由题目中的所给的数量关系列出等式,便可以解决问题.解 设这个角的∠A ,则根据题意,得180°-∠A=3(90°-∠A),所以180°-∠A=270°-3∠A ,所以∠A=45°,选B.【变式1】互余两个角的差是20°,求这两个角中较小的那个角的补角.分析 “互余两个角的和是90°”,它们的差又是20°,所以设其中一个角为x°,则它的余角是90°- x°,根据已知条件可列方程求这两个角,进而求到较小角的余角.解 设其中一个角是x°,则另一个角是90°- x°,根据题意,得90°- x°- x°=20°,所以x =35,90°- x°=55°,所以较小的角的补角是180°-35°=145°.【变式2】∠α和∠β互余,且∠α:∠β=1:5,求∠α和∠β的补角各是多少度? 分析 先根据∠α和∠β互余,且∠α:∠β=1:5,设∠α=x ,则∠β=5x ,利用余角的性质求出∠α和∠β的度数,再根据补角的性质即可解答.解 ∵∠α和∠β互余,且∠α:∠β=1:5,∴设∠α=x ,则∠β=5x ,∴x+5x=90,解得x=15°,∴∠α=15°,∠β=5×15°=75°,∴∠α的补角是180°-15°=165°,∠β的补角是180°-75°=105°.例3 如图1-3.4-6,直线AB 与CD 相交于O ,OE 平分∠AOB ,OF 平分∠COD .(1)图中与∠COA 互补的角是 ;(把符合条件的所有角都写出来)(2)如果∠AOC=35°,求∠EOF 的度数.分析(1)找与∠COA刚好拼成一个平角的角即是∠COA的补角.(2)根据OE平分∠AOB,OF平分∠COD求得∠AOE=90°,∠COF=90°然后即可求得∠EOF的度数.图1-3.4-6解(1)图中与∠COA互补的角是∠AOD或∠COB.(2)∵OE平分∠AOB,OF平分∠COD.∴∠AOE=90°,∠COF=90°,∵∠AOC=35°,∴∠EOF=∠AOE+∠COF-∠AOC=90°+90°-35°=145°.说明从图形中寻找互余的角和互补的角,是我们必须练就的本领.的余角.∠AOC-∠AOB 表示出∠MON 并求出其度数是解题的关键,也是本题的难点【变式】如图1-3.4-10所示,∠AOB 是平角,∠AOC=30°,∠BOD=60°,OM ,ON 分别是∠AOC ,∠BOD 的平分线,∠MON 等于 度.图1-3.4-10分析 根据平角和角平分线的定义求得.解 ∵∠AOB 是平角,∠AOC=30°,∠BOD=60°,∴∠COD=90°(互为补角)∵OM ,ON 分别是∠AOC ,∠BOD 的平分线,∴∠MOC+∠NOD=21(30°+60°)=45°(角平分线定义) ∴∠MON=90°+45°=135°.例5 将一张长方形纸ABCD 的两个角按如图1-3.4-11所示方式折叠,且BE 与EC 的一部分重合,请问,∠α与∠β是有什么关系的两个角,并说明理由.图1-3.4-11 图1-3.4-12分析 由折叠的性质知,∠B′EF=∠BEF ,∠GEC′=∠CEG ,则这四个角的和为180°进而求解得∠α+∠β的值.解 互余(即∠α+∠β=90°),理由:由折叠可知∠B′EF=∠α,∠GEC′=∠β,而∠BEC=180°,所以∠α+∠FEB′+∠GEC+∠GEC′=180°,即2∠α+2∠β=180°,所以∠α+∠β=90°. 说明 本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②一个平角是180度.【变式】如图1-3.4-12所示,将书面折过去,该角顶点A 落在A ′处,BC 为折痕,BD 为∠A ′BE 的平分线,则∠CBD 等于多少度?试着说明其中的道理.分析 根据角平分线的定义得到∠A ′BC=21∠A ′BA ,∠A ′BD=21∠A ′BE ,∴∠CBD=∠A ′BC+∠A′BD=21(∠A ′BA+∠A ′BE ),(∠A ′BA+∠A ′BE )是平角180°,这样就可求出∠CBD 的度数.解 ∠CBD=90°,理由如下:由折线的过程可知,∵∠A′BC=21∠A′BA ,∠A′BD=21∠A′BE , ∴∠CBD=∠A′BC+∠A′BD=21(∠A′BA+∠A′BE )=21×180°=90度. 故∠CBD 为90°.例6 如图1-3.4-13所示,OA 是表示北偏东30°方向的一条射线,依照这条射线,画出表示下列方向的射线.(1)南偏东25°;(2)北偏西60°.分析 由图(1)可知,点O 的左边是西,右边是东,上边表示北,下边表示南. 南偏东25°即是从正南方向的射线绕点O 向东旋转25°后的位置,北偏西60°则是从正北方向的射线绕点O 向西旋转60°后的位置.解 如图(20所示.(1)射线OB 表示南偏东25°方向;(2)射线OC 表示北偏西60°方向.说明 (1)方向是针对某一具体点来说的,东、南、西、北也是针对这一点而言的,这一点也是射线的端点;(2)画表示某一方向(相对于这一点)的射线时,首先要找准端点、基准线,然后再根据射线的偏向(偏东或偏西)和方位角的度数画图.【变式】如图1-3.4-14,下列说法中错误的是( )A.OA 方向是北偏东40°B.OB 方向是北偏西15°C.OC 方向是南偏西30°D.OD 方向是东南方向分析 图中OA 偏离正东方向40°,故射线OA 绕点A 从正北向东旋转90°-40°=50°,即射线OA 表示北偏东50°的方向而不是北偏东40°方向. A 的说法是错误的,选A.说明 (1)方位角是表示方向的射线与正北(或正南)方向的夹角,如B 中射线OB 与正北方向的夹角为90°-75°=15°,故它表示北偏西15°的方向;射线OD 与正南方向的夹角为90°-45°=45°,故它表示南偏东45°即东南方向.(2)东南方向表示南偏东45°方向,东北方向表示北偏东45°方向,西南方向表示南偏西45°方向,西北方向表示北偏西45°方向. 为什么错 1.理解错误例7 如果∠AOC=∠COD=∠BOD=60°,则图1-3.4-15中互补的角有 对. 错解 ∵∠AOC=∠COD=∠BOD=60°,∴图中互补的角有7对,∠AOC 与∠COB ,∠AOC 与∠AOD ,∠AOD 与∠COD ,∠BOC 与∠COD ,∠BOD 与∠AOD ,∠BOD 与∠COB ,∠AOC 、∠COD 与∠BOD .北 O 南 东 西 30° A (1) 北O东 西 25°60° C 南 B (2) 图1-3.4-13图1-3.4-14例8 如图1-3.4-16,已知∠AOC=∠BOC=∠DOE=90°,问图中是否有与∠COE 互补的角? 错解 观察图形可知,图中没有与∠COE 互补的角.分析 图中真的没有与∠COE 互补的角吗?由∠AOC=90°可知,∠AOD 与∠COD 互为余角;由∠DOE =90°可知,∠COE 与∠COD 互为余角,根据“同角的余角相等”得∠COE =∠AOD.可见,要找与∠COE 互补的角,可转化为找与∠AOD 互补的角,观察图形知,∠BOD 与∠AOD 互为补角,因此与∠COE 互补的角是∠BOD.由上可知,在识图时,我们不单单要认真观察图形,而且还要仔细分析题设条件,这样才能作出正确的判断.正解 图中有与∠COE 互补的角,它是∠BOD.探究平台例9 如图1-3.4-17是一个由16个小正方形拼成的大正方形,则∠1+∠2+∠3+…∠16的度数是( )A .840°B .720°C .675°D .630°图1-3.4-17分析 把正方形沿对角线对折,就会发现这些角分8对,每对中的两个角拼成一个直角,如:∠1+∠16=90°;而对角线上的每个角都是45°。
小学二年级数学上(第三单元角的认识:1 角的认识)说课稿

小学二年级数学上(第三单元角的认识:1 角的认识)说课稿一、说教材本节课是二年级数学上册第三单元的第一课,主要内容为角的认识。
通过引入角的概念,让学生初步认识几何形状,培养学生的观察能力和逻辑思维能力。
二、说教学目标1.基本技能–能正确说出角的定义。
–能辨认图中的角形。
2.基本知识–了解角是由两条射线共同起点组成的图形。
–了解角的三要素:顶点、边、角度。
3.学习态度–培养学生对几何图形的兴趣,激发学生学习数学的热情。
三、说教学重点和难点1.重点–角的定义和特点。
–角的分类及命名。
2.难点–角的概念对小学生来说较为抽象,需要形象化的教学方法来引导学生理解。
四、说教学内容和方法1.教学内容–角的概念及命名方法。
–角形的分类。
2.教学方法–利用实物教具或图片引入角的概念,让学生观察、比较。
–结合生活实例解释角的命名方法,如门角、桌角等。
–设计互动游戏巩固学生对角的理解。
五、说教学过程1.导入–通过展示一张图片,让学生观察其中的角形,引起学生的兴趣。
2.讲授–向学生介绍角的定义和特点,帮助学生建立概念。
–根据角的不同特点,分类讨论,让学生明确各种角形的名称。
3.训练–布置一些练习题,巩固学生对角形的认识。
–组织小组活动,让学生相互交流,共同解答问题。
4.总结–总结本节课的重点内容,强调角的特点和命名方法。
六、说教学反思通过本节课的教学,我发现学生对角的抽象概念理解较为困难,需要将概念形象化,多通过实物、图片等教具的引入来帮助学生理解。
同时,在教学过程中,要注重培养学生的观察能力和逻辑思维能力,让学生在互动中更好地消化所学知识。
数学教师手册_直角三角形的边角关系

三角壹﹑教学目标与节数贰﹑教材地位分析参﹑教学摘要本章由锐角的正弦﹑余弦﹑正切函数开始介绍﹐进而了解正弦﹑余弦﹑正切函数之间的基本关系﹐并逐步引入广义角三角函数的概念。
其次﹐再由三角形的边角关系导出正弦定理与余弦定理及海龙公式。
接着介绍差角公式与和角公式﹐并引进倍角及半角公式。
最后介绍基本的三角测量。
本章共分五节﹐内容重点如下:1-1直角三角形的边角关系1. 直角三角形边的比例:固定θ之直角三角形﹐不论大小﹐其任两边长的比值恒为定值﹐依此定义正弦﹑余弦及正切;介绍30°﹐45°﹐60°之正弦﹑余弦﹑正切值及一些简单求值问题。
2. sin θ﹐cos θ﹐tan θ的性质:根据正弦﹑余弦及正切函数之定义﹐引出商数关系﹑平方关系﹑余角关系﹐利用这些关系式﹐能处理求值问题及证明简单三角恒等式。
3. 锐角的三角函数:透过特殊角函数值及四分之一单位圆的图形﹐能了解θ为锐角时﹐当θ增加﹐正弦值变大﹐余弦值变小﹐正切值变大之事实;并建立当θ确定时﹐正弦﹑余弦及正切唯一确定之函数关系。
1-2广义角与极坐标1. 广义角:介绍广义角之定义﹐再介绍标准位置角及同界角之定义。
2. 广义角的三角函数:在标准位置角之终边上取一点﹐利用该点坐标及其至原点的距离来定义广义角的三角函数;并能判断正弦﹑余弦及正切函数在不同象限之正负情形并求值。
3. 广义角三角函数的性质:根据正弦﹑余弦及正切函数之广义角定义﹐可得商数关系及平方关系;接着再利用负角关系﹑补角关系﹑余角关系及同界角关系﹐得将任意角度以参考角来表示的公式。
4. 极坐标:介绍极坐目标表示法﹐并能将极坐标所表示的点与直角坐目标点互相转换。
5. 弧度:藉由观察弧長半徑的大小与圆心角的大小成正比,且这个比值与单位无关,也与圆形的大小无关,因此我们可以利用此值来衡量角度的大小,此即弧度的概念;其次让学生了解角度有弧度量与度度量两种表示方式,并能熟练单位换算。
4.6角第三课时角的特殊关系

第四章图形的初步认识§4.6 角课时三角的特殊关系【学习目标】1.理解补角、余角的定义和性质,并会进行有关计算.2.理解对顶角的定义,能准确找出对顶角.【课前导习】1._________________________________,就说这两个角互为余角,简称_________.2.己知∠α与∠β互余,且∠α=150 ,则∠β=__________.3.如图,请问∠1与∠2的关系为_________.4.________________________________,就说这两个角互为补角,简称_________.5.己知∠α与∠β互余,且∠α=1050,则∠β=__________.6.如图,∠3与∠4的关系为__________.7.找出图中相等的对顶角.______=_______; ________=________;______=_______; ________=________;【主动探究】1.仿照书上例3完成:已知∠α=40°27',求∠α的余角和补角.2. 若∠1+∠2=90°,∠2+∠3 = 90°,则∠2与∠3的关系是.【当堂训练】1.已知∠AOB,用直尺和量角器画出∠AOB的余角,∠AOB的补角及∠AOB的角平分线.2. 72°20'的角的余角等于;25°31'的角的补角等于.3. 如右图,CO⊥AB,垂足为O,DO⊥OE,则图中互余的角有()A 3对B 4对C 5对D 6对4.一个角的补角比它的余角大_____度。
5. 互为补角的两个角可以都是_______角,或者一个是______角,一个是____角.(填“钝角”、“锐角”、DC ABNM(2)F E “直角”)6. 若一个角的余角是这个角的4•倍,•则这个角是_______,•这个角的补角是______.7.如图2,三条直线AB 、CD 、EF 相交于一点O ,则共有对顶角( )A 3对B 4对C 5对D 6对【回学反馈】1.已知∠1=43°27′,则∠1的余角是_______,补角是________. 2、互补的两个角的差为︒60,求较小的角的余角。
角的相互关系教案

角的相互关系教案一、教学目的1. 知识目标(1) 掌握角的概念和符号表示;(2) 理解两角相等、补角、邻补角、余角、同位角等角度关系;(3) 能够应用所学知识解决实际问题。
2. 能力目标(1) 发现问题并加以解决的能力;(2) 运用数学语言和符号表示角度关系的能力;(3) 分析、归纳角度关系的能力。
3. 情感目标(1) 培养学生的观察能力和创新思维能力;(2) 培养学生的合作精神和自学能力。
二、教学重点与难点1. 教重点(1) 掌握角的概念和符号表示;(2) 理解两角相等、补角、邻补角、余角、同位角等角度关系。
2. 教学难点(1) 运用数学语言和符号表示角度关系;(2) 分析、归纳角度关系。
三、教学过程设计1. 预习导入(5分钟)请同学们在课前预习课本内容,回答下列问题:(1) 什么是角?(2) 如何表示角?(3) 两角什么情况下相等?2. 概念讲解(15分钟)(1) 角的定义讲师出示一个角的图像,引导同学们探究角的定义,并给出角的定义:角是由两条半直线(称为角的边)和一个公共端点(称为角的顶点)组成的图形。
(2) 角的符号表示讲师给出角的符号表示,即用一个大写的字母表示角的顶点,如∠A,用“角度符号”度(°)表示角的大小,如∠A= 60°。
(3) 角的基本性质结合实例引导同学们发现角度的大小在0度到360度之间,任何一个角都可以表示成这个范围中的一个真实数。
3. 师生互动(15分钟)(1) 两角相等讲师出示两角相等的示意图,引导同学们探究两角相等的概念,给出两角相等的定义:若两角的度数相等,则这两个角相等。
(2) 补角讲师出示补角的示意图,引导同学们探究补角的概念,给出补角的定义:两角的度数之和为180度的两个角互为补角。
(3) 邻补角讲师出示邻补角的示意图,引导同学们探究邻补角的概念,给出邻补角的定义:互为补角且有公共边的两个角互为邻补角。
4. 小组讨论(20分钟)同学们分小组讨论,结合实际问题,设计符合实际的问题,讨论解决问题的方案。
高中数学的角的概念教案

高中数学的角的概念教案
教学目标:
1. 了解角的定义及相关术语
2. 掌握角的度量和角的种类
3. 能够运用角的性质解题
教学重点:
1. 角的定义及相关术语的理解
2. 角的度量和角的种类
3. 角的性质应用
教学难点:
1. 角度量的理解和运用
2. 角的种类的辨别和分类
3. 角的性质的应用
教学过程:
一、导入
1. 角的概念引入:让学生看图,提问引导学生思考角的概念。
2. 角的定义:通过示意图和解释,让学生理解什么是角。
二、角的度量和种类
1. 角的度量法:介绍度量角的方法和单位。
2. 角的种类:讲解锐角、直角、钝角和平角的分类及特点。
三、角的性质
1. 角的性质:介绍相邻角、对顶角、余角等角的性质。
2. 角的性质应用:通过解决角的性质相关问题,让学生掌握角的性质的运用方法。
四、练习与巩固
1. 小组讨论练习:让学生分组进行练习,巩固所学知识。
2. 课堂练习:布置适量练习题,让学生在课堂上解答,加深理解。
五、作业布置
1. 布置课后作业:让学生自主练习,巩固所学知识。
2. 鼓励学生多做题目,加深对角的理解和应用。
教学反思:
本节课通过引入角的概念,让学生初步了解了角的定义和相关术语,通过讲解角的度量和种类,让学生对角的分类有了更深入的了解。
通过讲解角的性质和应用,能够让学生掌握角的基本性质和应用方法。
在练习和作业中,让学生巩固所学知识,提高解题能力。
希望学生通过本节课的学习,能够对角有更深刻的理解,提高数学学习的兴趣和能力。
小学四年级数学《角的分类》教案

小学四年级数学《角的分类》教案小学四班级数学《角的分类》教案模板1教学目标:认知目标1. 知道角的计量单位是“度”,符号是“°”。
2. 掌握3个特殊角“直角、平角、周角”。
3. 掌握“锐角、直角、钝角、平角、周角”之间的关系。
能力目标让学生经历观察、操作的主动探索过程。
情感目标让学生享受学习的快乐,分享成功的喜悦。
教学重点:理解“周角、平角、直角”的含义。
教学难点:理解“旋转成角”。
教学准备:多媒体课件及量角器。
教学过程:一、出示课题1. 情景导入角的计量单位。
(课件演示)2. “度”是角的计量单位,读作“度”,用符号“°”标示。
3. 1度可以简写成“1°”4. 出示37°,“37”表示数值,是“量数”,“°”是“计量单位”。
5. 作为计量单位“度”,生活中的应用范围很广:水沸腾时为100度,结冰时为0度;正常体温是摄氏37度,高于它就是发烧了;一盏100瓦的灯,连续开10小时,用电1千瓦小时,我们常称作1度电;近视眼患者佩戴300度的眼镜;某种白酒38度;上海位于北纬32度、东经122度,等等。
说明:通过课件的演示和生活中实例的介绍,生动的引导角的度量单位“度”,体会数学与生活的联系,激发学生的学习爱好。
二、学习直角、平角、周角的定义。
1. 请你仔细地读读上面3句话,你觉得有什么问题。
2. 出示P68、P69出现的定义i. 一点(O)和从这一点(O)出发的两条射线(OA和OB)所组成的图形叫做角;ii. 直角:一条射线绕它的端点旋转四分之一周,所成的角叫做直角;iii. 一条射线绕它的端点旋转半周(二分之一周),所成的角叫做平角;iv. 一条射线绕它的端点旋转一周,所成的角叫做周角;3. 理解“旋转、端点、射线”。
v. 端点——一点(O)、曾经叫做“一个点、顶点”vi. 旋转——利用圆规画圆,体会旋转,绕圆心旋转;vii. 射线——没有尽头,也就无法表示长度,所以角度与射线的长度无关;viii. 重新定义锐角和钝角ix. 锐角:小于直角的角叫做锐角。
课时12 角的特殊关系

角的特殊关系教学目的:1、认识互为余角和补角的概念,理解互为余角和补角主要反映了角数量关系.2、认识对顶角的概念,理解对顶角主要反映角的一种位置关系。
教学过程: 一、复习:填空⑴若∠1=34°20′,∠2=55°40′,则∠1+∠2= . ⑵若∠3=54°12′,∠4=125°48′,则∠3+∠4= . ⑶在△ABC 中,若∠C =90°,则∠A +∠B = . ⑷如图,△ABC 中,延长线段BC ,得射线CD ,则∠ACB +∠ACD = .二、新授定义(1)如果两个角的和等于90°(直角),那么这两个角叫做互为补角,简称互余。
其中一个角是另一个角的余角.符号语言:若∠1+∠2=90°,则∠1与∠2互为余角(反之亦成立) 余角的性质:同角或等角的余角相等.定义(2)如果两个角的和等于180°(平角),那么这两个角叫做互为补角,简称互补。
其中一个角是另一个角的补角.用符号语言表示:若∠1+∠2=180°,则∠1、∠2互为补角. 补角的性质:同角或等角的补角相等。
说明:余角、补角是指两个角之间的相互数量关系,一个角不能叫做余角或补角. 例1:已知∠1=50°17′,求∠1的余角和补角。
说明:一个锐角的补角一定比这个锐角的余角大90°。
例2:给出下列判断:⑴如果∠1+∠2+∠3=180°,那么∠1、∠2、∠3互为补角;⑵90°的角叫做余角;⑶如果∠1是∠2的补角,那么∠1一定是钝角;⑷如果∠1是∠2的余角,那么∠1一定是锐角。
其中正确的判断的序号是 (请把所有正确的序号都填上) 定义(3)两边互为反向延长线的两个角是对顶角. 说明:(1)两相交直线是形成对顶角的前提条件. (2)性质:对顶角相等。
应用:∵AB 、CD 相交于O 点(已知)∴∠AOC =∠BOD (对顶角相等)(3)判别方法:两边互为反向延长线. 三、应用例3、(1)一个角的补角是它的3倍,求这个角.(2)一个角的补角是它余角的3倍,求这个角.(3)一个角的补角是它余角的10倍,求这个角(学生练习). (4)一个角的余角的补角比这个角的余角大45°,求这个角. 变化题:(1)一个角与它的余角相等,这个角等于 度.(2)一个角与它的补角相等,这个角等于 度.(3)若∠α=55°,则∠α的余角是 度,∠α的补角是 度.例4、如图(1)∵∠AOC =90°(已知)∴∠ 与∠ 互余,∠ 与∠ 互余( ) (2)∵∠BOD =90°(已知)∴∠ 与∠ 互余,∠ 与∠ 互余( ) (3)∴∠2=∠ ,∠1= ( )∠AOD 的补角是 .(4)若∠2=50°,说出图中其余角的度数?B C DAE O AB CD4 321例5、⑴判断下列各图中的∠1、∠2是否对顶角?为什么?⑵判断题:(1)有公共顶点的两个角是对顶角. ( ) (2)顶点公共,且有一边互为反向延长线的两个角是对顶角. ( ) (3)同一个角的两个邻补角是对顶角. ( ) ⑶(1)过同一点的三条直线两两相交,能构成 组对顶角. (2)不过同一点的三条直线两两相交,能构成 组对顶角. 例6、已知如图直线AB 与CD 相交于O 点,求证:∠1=∠3证明:∵AB 与CD 相交于O 点 ( ) ∴∠1与∠2互补,∠2与∠3互补( ) ∴∠1=∠3 ( )注意:(1)这个性质反之不成立;如图(3)若∠1=∠2,但∠1与∠2不是对顶角. (2)如图中,若∠1=40º,则∠2= ,∠3= ,∠4= . 思考题1、如图直线AB 、CD 相交于O 点,∠AOC =20º,OE 平分∠AOD .求∠EOB 的度数.2、已知AB 、CD 交于O 点,且OD 是∠BOE 的平分线,∠BOE =80º.求∠AOC 变化题:上题中,若∠AOF =Rt ∠,则∠COF 的余角是 ,∠AOD练习: 当堂课内练习1、2、3、4、5 本课课外作业:课课练1(1) 212(2) 1 2(3) 12(4)A C O 4B D 21 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角的特殊关系
一、教学目标
⑴理解余角、补角和对顶角的概念及其性质。
⑵学会运用所学数学知识去分析问题、解决问题
二、教学重点.难点
余角、补角和对顶角的概念及其性质。
余角、补角和对顶角的性质及其探索过程。
一、、走进生活,引入新课
1.为了引入余角的概念,我首先让学生回顾、思考如下问题:
(1)你平时所用的直角三角板的三个内角分别是多少度?其中两个锐角的和是多少度?
(3)如图是一只破损的直角三角形板,你能用α表示断掉的那个角吗?
二、动手实践,展示新知
我认为学生通过分析思考,能够顺利完成以上问题的解答,并对几何图形中存在大量的两个锐角之和等于90°有了深刻的印象。
这时我向学生指出:两个角的和等于90°(直角),就说这两个角互为余角,简称互余。
即,如果∠1+∠2=90°,那么∠1与∠2互为余角
为了揭示余角的本质特征,我给出如图的角AOB=90°,然后通过
电脑动画演示,将∠1∠2分离,由于∠1、∠2的大小没有变化,所以∠1+∠2 = 90°这样可以让学生感受到:
互为余角的两个角有如下特征:①成对出现;②只考虑数量关系,与位置无关。
为了巩固了余角的概念,又能达到训练学生的文字语言、符号语言的表述能力,动手操作能力,在这里我作了这样的安排:
三、⑴如图,∠1+∠2=90°,那么①∠1与∠2互为;
②∠1的余角是;
③∠1是的余角。
⑵(如图)画出∠COB的余角
基于对学生思维训练的考虑和数学方法运用的引导,在画图题的基础上我又设计了如下问题,让学生通过猜想找到规律,再实际量一量,动手折一折,最终用代数方法解决问题。
猜一猜、量一量、折一折:
如图∠AOB=90°,∠COD=90°,(电脑演示∠COD绕点O旋转)。
(2)任意一个直角三角形的两个锐角之和是多少度?
四、总结
这节课我们都学习了哪些内容和主要的思维方法?
五、板书。
