小学奥数5-8-2 进制的应用.专项练习
五年级奥数学练习试卷思维培训资料 数的进制

第四讲 数的进制卷Ⅰ教学目标数的进制问题一直是我们教学大纲的一个漏洞,只在三年级春季班讲了一次简单的二进制与十进制的互化之外,再也没有讲过,到了六年级也只是简单提一下.这几年随着二进制与计算机的联系、一年12个月、一周7天等生活中的其它进制问题的凸显,数的进制问题将来一定会是命题的热点.我们常用十进制,可是这并不代表其它进制没有学习的必要,就像我们56个民族,汉族是多数,但其它民族也有可以学习和借鉴之处,更何况在生活中我们用的很多就是二进制、三进制、七进制等等.所以调整了大纲,放了这么一讲,大部分题目都是原创题,不妥之处请批评指教.本讲主要从两个方面来系统地介绍数的进制:一是从进制的基本计数关系、运算法则出发,使学生从十进制的计数思维中解脱出来;二是从进制的转化及应用来说,进一步巩固进制的使用(还有各种进制的整除特征及法则,怕学生难以接受就没放).建议教师专题回顾讲起,先介绍几种进制的计数单位及运算法则,再引出想挑战吗.中间穿插了两个信息点,教师可以简单介绍.下表是十进制与二进制、三进制 、八进制、十六进制的位值(计数单位)对比图:十进制 … 105 104 103 102 101 100 二进制 … 25 24 23 22 21 20 三进制 … 35 34 33 32 31 30 八进制 … 85 84 83 82 81 80 十六进制…16516416316216116n 进制的运算法则是“逢n 进一”、“借一当n”.n 进制的四则混合运算和十进制一样:先乘除,后加减;同级运算,先左后右;有括号,先算括号里面的.7进制乘法表 8进制乘法表12345611234562461113153121521244222633534426511234567112345672461012141631114172225420243034531364364452761我们都学过十进制乘法口诀表,那么聪明的你能写出七进制的乘法口诀表吗?八进制的呢?想挑战吗?专题回顾计算:(1) ;(2) ;(3) ;(4)22(101)(111)+22(1101)(110)-22(1101)(101)⨯22(101101)(111)÷分析:和十进制一样列数式计算,“逢二进一”、“借一当二”.(1)(2)1011111100+1101110111-(3)(4)1101101110111011000001⨯110111101101111100011111专题精讲(一)进制的概念及性质【例1】 (奥数网原创题)在八进制中,1234-456-322=________. 分析:十进制中,两个数的和是整十整百整千的话,我们称为“互补数”,凑出“互补数”的这种方法叫“凑整法”,在n 进制中也有“凑整法”,要凑的就是整n. 原式=1234-(456+322)=1234-1000=234.[前铺] (奥数网原创题)在十进制中,1234-456-544=________.分析:观察两个减数,会发现它们的和是1000.所以,原式=1234-(456+544)=1234-1000=234.[拓展1] (奥数网原创题)在八进制中,63121-1247-16034-26531-1744=________.分析:原式=63121-(1247+26531)-(16034+1744)=63121-30000-20000=13121.[拓展2] (奥数网原创题)在九进制中,14438+3123-7120-11770+5766=________.分析:原式=14438+(3123+5766)-(7120+11770)=14438+10000-20000=4438.[信息提示] 关于八进制的奥秘来自外星世界的太空飞船突然出现在我们上空时将会发生什么样的情况?科学家曾经仔细研究过来自外形世界的信号并发现信息是采用的八进制编码.地球上流行十进制,换句话说,我们有0到9共10个数码.在十进制计数法中,每个数码表示10的某个乘幂,但是,没有任何理由假定外星生物也会使用十进制,来自外星的信息不大可能用十进制编码.在地球上,我们的数学计算用的是十进制,因为我们恰好有10个手指.事实上,我们的语言已经提示了手指同数制的联系——“digit”这个单词兼有两种意思:数或手指.由于十进制来自我们的10只手指,那么八进制会不会透漏一点外星生物的解剖学结构呢?也许八进制会意味着:外星人的每只手上有一个大拇指,3个手指;或者是有着8根触须的怪物;或者是:这种动物长着4只手,而每只手上有一个大拇指,一个小指.甚至还有更荒唐的设想:外星人长着3个头颅,点头和摇头的全部组合刚好是8种!(当然也有可能他们的计数制同其身体结构毫无关系.毕竟,古巴比伦的60进制不能为我们提供关于人体结构的任何信息).【例2】 (奥数网原创题)在六进制中,15+255+3555+45555+555555=________.分析:利用凑整法,十进制中,接近整十整百整千的数,后面会有若干个9,那么类似地,在n 进制中,接近一个比较整的数,后面会有若干位是n-1.原式=(20-1)+(300-1)+(4000-1)+(50000-1)+(1000000-1)=1054320-5=1054311.[前铺] (奥数网原创题)在十进制中,19+299+3999+49999+599999=________.分析:观察各个数,发现每一个都比一个整十整百整千之类的数少1.所以,也可以利用凑整法,原式=(20-1)+(300-1)+(4000-1)+(50000-1)+(600000-1)=654320-5=654315.[拓展] (奥数网原创题)在七进制中,666661-66662-6663-664-65-6=________.分析:原式=(1000000-6)-(100000-5)-(10000-4)-(1000-3)-(100-2)-(10-1)=(1000000-111110)-6+21=555560+12=555602.【例3】 (仁华考题)若是的4倍,那么化为十进制是多少? (62)n (14)n (41)n分析:因为,所以(62)4(14)n n =, 1010(62)4(4)624167n n n n n +=⨯+⎧⎪+=+⎨⎪=⎩710.(41)471(29)=⨯+=[前铺] 表示n 进制数,若,求n. (54)n 10(54)(64)n =【例4】 (仁华考题)在几进制中有4×13=100.分析:我们利用尾数分析来求解这个问题:不管在几进制均有(4)×(3)=(12).但是,式中为100,101010尾数为0.也就是说已经将12全部进到上一位. 所以说进位制为12的约数,也就是12,6,4,3,2.但n 是出现了4,所以不可能是4,3,2进制.我们知道(4)×(13)=(52),因52 < 100,也就是说不到10101010就已经进位,才能是100,于是我们知道<10.所以,只能是6. n n[前铺] 计算:(234)7+(656)7分析:7进制的运算是逢7进1,所以原式=(1223)7.【例5】 (仁华考题)证明10101在任何进制的记数法中,都是一个合数.分析:设在a 进制,则, 4222222(10101)111(1)(1)(1)a a a a a a a a a =⨯+⨯+=+-=+-++可以将其表达为两个均不为1的整数乘积,显然为合数.[前铺] 证明10201在大于2的任何进制的记数法中,都是一个合数.分析:设在b 进制,则,所以不管在任何进制,均是一个非1的4222(10201)121(1)b b b b =⨯+⨯+=+完全平方数,当然是一个合数.卷Ⅱ(二)进制的转化及应用【例6】 (奥数网原创题)把二进制自然数10100001101转化为八进制自然数.分析:二进制数转化为八进制是从个位开始往前每三位转化为八进制.对应关系如下: 二进制 000 001 010 011 100 101 110 111 八进制 0 1 2 3 4 5 6 7 对其进行分组,情况如下:(一定要从后往前)有: 10 100 001 101 2进制 2 4 1 5 8进制 (10100001101)=(2415). 28[拓展1] (奥数网原创题)把二进制小数11.0010010001转化为八进制小数.分析:小数和整数转化的方法类似,只不过是从小数点处,向前和向后都要三位三位数.但是本题的小数点后位数不是3的倍数,所以必须补0. 11. 001 001 000 100 3. 1 1 0 4所以,二进制11.0010010001转化为八进制是3.1104.[拓展2] (奥数网原创题)把二进制循环小数转化为八进制循环小数. 0.10011分析:循环小数转化的方法也类似,但是循环节长度不是3的倍数,所以需要把循环节连写三遍,如下: 0. 100 111 001 110 011 0. 4 7 1 6 3所以,二进制转化为八进制是. 0.100110.47163[拓展3] (奥数网原创题)在几进制中,是一个整数的倒数? 0.1463分析:看到这类问题不知道如何入手的话,可以这样想: 大家都熟悉的十进制循环小数中,循环节的前一半和后一半“互补”,也就是对应位相加10.1428577= 等于9,也就是进制数减1.而的循环节前一半和后一半对应位相加等于7,所以应该是八进制.经0.1463 检验,. 10.14635= [信息提示] 莫尔斯-瑟厄数列在管乐声中有两个调子,用 表示长调,用 表示短调,所有乐曲都可以用类似或表示,就是这种看似既非完全规则、又非全然不规则节奏的神奇模式就是著名的、奇异的二进制数字模式——莫尔斯-瑟厄数列,它可以用0和1的数字串来表示.莫尔斯-瑟厄数列是为了纪念挪威数学家阿克塞尔-瑟厄和普林斯顿大学的马斯登-莫尔斯而命名的.瑟厄引入这个数列,作为一种非周期性的、但又可以通过递推办法而算出来的实例.有好几种办法可以生成莫尔斯-瑟厄数列.第一种:从数0开始,反复进行下列置换:0→01,1→10.换句话说,你一旦见到0,就用01取代它,见到1就用10来取代,从一个单独的0开始,我们就可以得出以下各“代”:你可以用一支笔、一张纸来形成这个数列.从0开始,代之以01,现在你已有了一个两个数码的数列,用01代替0,10代替.从而有了数列0110,下一个二进数模式是01101001,请注意0110是对称的,它是一个回文数,然而01101001则不是.但是,你要顶住!再下面一个模式0110100110010110又是回文了.这种现象是否交替出现?显然,数列的神奇性质只是刚刚开始,奥妙还在后面呢.注意数列的第四行可以译成管乐声中的8个手指记号,如果 表示0, 表示1的话,真是令人惊讶! (未完,见数学知识)【例7】 (奥数网原创题)在三进制中的数12120120110110121121,则将其改写为九进制,其从左向右数第l 位数字是几?分析:我们如果通过十进制来将三进制转化为九进制,那运算量很大.注意到,三进制进动两位则我们注意到进动了3个3,于是为9.所以变为遇9进1.也就是九进制.于是,两个数一组,两个数一组,每两个数改写为九进制,如下表:3进制 12 12 0l 20 11 01 10 12 11 21 9进制 5 5 l 6 4 1 3 5 4 7 所以,首位为5.[总结] 若原为进制的数,转化为进制,则从右往左数每个数一组化为进制.n n kk n k【例8】 (仁华考题)N 是整数,它的b 进制表示是777,求最小的正整数b ,使得N 是十进制整数的四次方.分析:先化为十进制数,,则有,因为N 是7的倍数,2(777)777b b b =⨯+⨯+24777b b x ⨯+⨯+=所以也是7的倍数,又7为质数,所以是7的倍数.于是令,则,4x x 7x t =247772401b b t ⨯+⨯+=则,,则.因为最小,所以也是最小的.即有最小在18进制有21343b b ++=(1)342b b +=18b =t b41810.(777)(7)=[前铺] 在7进制中有三位数,化为9进制是,求这个三位数在十进制中是多少? abc cba分析:都化为十进制数,,27()77497abc a b c a b c =⨯+⨯+=++,于是,,即29()99819cba c b a c b a =⨯+⨯+=++497819a b c c b a ++=++48802a c b =+,因为是8的倍数,也是8的倍数,所以也是8的倍数.于是或,2440a c b =+24a 40c b 0b =8b =但在7进制不可能有8.所以,即,则,所以为5 的倍数,为3的倍数,有0b =2440a c =35a c =a c 或,首位不可以是0,所以,那么,所以0a =5a =5a =3c =77()(503)5493248.abc ==⨯+=[拓展] 设1987可以在进制中写成三位数,且=1+9+8+7,试确定出所有可能的、、b xyz x y z ++x y z 及. b分析:我们注意2()19871987b xyz b x by z x y z ⎧=++=⎨++=+++⎩①②①-②得:(-1)+(-1)=1987-25,则(-1)(+1)+(-1)=1962,即(-1)[(+1)2b x b y b b x b y b b x +]=1962.所以,1962是(-1)的倍数.1962=2×9×109, y b 当-1=9时,=10,显然不满足;b b 当-1=18时,=19,则(-1)[(+1)+]=18×(20+)=1962;则20+=109,b b b b x y x y x y 所以, 545,(929911b x x x y y y z ⎧⎪===⎧⎧⎪⎨⎨⎨===⎩⎩⎪⎪=⎩=19不满足),......则显然,当=109不满足,=2×109不满足,当=9×109也不满足.于是为(59B)=(1987),B 代表11. b b b 1910【例9】 (仁华考题)若能被15整除,自然数n 可以取哪些值? n21-分析:因为,而,如果能被15整除,即 nn 1n 02221=10001111⎛⎫⎛⎫--= ⎪ ⎪ ⎪⎝⎭⎝⎭ 个个2151111=()n21- n 12111⎛⎫ ⎪⎝⎭ 个能被整除,所以n 是4的倍数,n=4,8,12,… 21111()[前铺] 求证:能被7整除.1821-分析:直接用十进制比较困难,我们考虑化为二进制的整除问题.因为.而,于是18181180222110001111⎛⎫⎛⎫-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭ 个个27111=(),所以能被7整除.182218122171111111001001001001001⎛⎫÷÷= ⎪⎝⎭ 个(-)=()()1821-[拓展] 计算:÷26的余数.2003333 3...31⎛⎫⨯⨯⨯- ⎪ ⎪⎝⎭个分析:==,26=(222), 2003333 3...31⎛⎫⨯⨯⨯- ⎪ ⎪⎝⎭ 个2003331000...01⎛⎫⨯- ⎪ ⎪⎝⎭个20033222...2⎛⎫⎪ ⎪⎝⎭ 个23所以÷26=÷(222),(222)整除(222),2003÷3=667……2,所以余数2003333 3...31⎛⎫⨯⨯⨯- ⎪ ⎪⎝⎭个20033222 (2)⎛⎫ ⎪ ⎪⎝⎭ 个2333是(22)=8.3【例10】 (仁华考题)三个两位数恰构成公差为6的等差数列,而在五进制的表示中,这三个数的数字和是依次减少的,那么符合这样要求的等差数列有多少个?分析:设等差数列中最小的那个数表示为5进制为,最大可为5(abc ),最小可为.那么有、、的数字5(322)996287=-⨯=5(20)10=5()abc 55()(11)abc +55()(22)abc +和依次减少,所以、在运算时均必须有进位,不难发现有、55()(11)abc +55()(22)abc +5(24)a 5(43)a 满足,而a 可以取0,1,2,于是共有6组符合要求的数列.[前铺] 用、、、、分别表示五进制中互不相同的数字,如果、、是由小a b c d e 5()ade 5()adc 5()aab 到大排列的连续正整数,那么所表示的整数写成十进制的表示是多少?5()cde 分析:由题意知,,根据进位原则知,.又,55()1()ade adc +=55()1()adc aab +=4,0c b ==1c e -=所以.,且、只能在1,2中取值,所以.即,转化为十进3e =1a d -=a d 2,1a d ==55()(413)cde =制的表示为.22510(413)45153(108)=⨯+⨯+=【例11】 (奥数网原创题)一串数:1,3,4,9,10,12,13,…,由一些正整数组成,它们或者是3的幂,或者是若干个不同的3的幂的和,求这串数中的第100项是多少?分析:将已知数改写成三进制数,得:1 3 4 9 10 12 13110 11 100 101 110 111十进制:三进制:观察发现,在三进制数中,各位上的数字均不是2,若将它们看成二进制数,可以看出,它们与十进制数1,2,3,4,5,6,7,…对应,第100项与十进制数100对应.因为10010=26+25+22=11001002,所【例12】 (仁华考题)称n 个相同的数a 相乘叫做a 的n 次方,记做,并规定.如果某个自然n a 01a =数可以写成2的两个不同次方(包括零次方)的和,我们就称这样的数为“双子数”,如,.它们都是双子数,那么小于1040的双子数有多少个?30922=+523622=+分析:双子数与二进制的联系,,310102(9)(22)(1001)=+=,写成2的两个不同次方(包括零次方)的和,这样的数改写成二进制5210102(36)(22)(100100)=+=后只含有2个1,有,这样的二进制数为11位数,但104101022(1040)(22)(1000000000010000)(10000010000)=+=+=是11位数有限制:先看10位数,于是,这样10位数,选择2个数位填1,其它为0,()**********所以为,再考虑11位数,于是,只有4个“”和紧邻的“1”,于是有5种选择,210C (1000001)*****所以共有种选择方法,所以这样的“双子数”为50个.210550C +=[拓展] 一个非零自然数,如果它的二进制表示中数码l 的个数是偶数,则称之为“坏数”.例如:是“坏数”.试求小于1024的所有坏数的个数. 218=10010()分析:我们现把1024转化为二进制:(1024)=2=(10000000000)2.于是,在二进制中为11位数,但1010是我们只用看10位数中情况.并且,我们把不足10位数的在前面补上0,如=502111...10000...0⎛⎫⎪ ⎪⎝⎭ 5个1个或以上912111...1⎛⎫⎪ ⎪⎝⎭ 个则,可以含2个l ,4个1,6个1,8个l ,10个1.于是为9120111...1⎛⎫ ⎪ ⎪⎝⎭ 个10* * * * * * * * * *⎛⎫ ⎪ ⎪⎝⎭个位置 2268101010101010C C C C C ++++=10910987109876510987654312123412345612345678⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯+++=45+210+210+45+1=511,于是,小于1024的“坏数”有511个.【例13】 (奥数网原创题)在地球上有一个矮人国,这个国家不用通常的十进制,而是用大于十的另一种进制.但是该国家的钟表与中国的本质上相同(当然可能钟面标的数字有区别,这不是本质区别).一名司机开车在笔直的公路上匀速行驶,每小时的速度是整数.当钟表的时针与分针垂直的时候,司机发现他刚好经过路边的一个里程碑,上面的数字是一个两位数.当钟表的时针与分针再次垂直的时候,司机再次发现他刚好经过路边的里程碑,上面的数字是刚才那个两位数的数字颠倒过来.当钟表的时针与分针第三次垂直的时候,司机第三次发现他刚好经过路边的里程碑,上面的数字是一个三位数,是在第一次的那个两位数中间插了一个数字.在该国家的进制数尽量小的情况下,司机的时速是多少?(请把答案转化成十进制)分析:每个小时,时针走过周,分针走过1周,也就是分针比时针多走过周.两次垂直之间,分1121112针比时针多走过半周,所以时间为小时. 111621211÷=显然,第三次所经过的里程碑的首位是1.设矮人国用N 进制,设第一次的里程数是,则第二次的1X 里程数是,再设第三次的里程数是.则有.从个位上看,X+X 个位是2,所1X 1YX 1112X YX X +=⨯以2X=N+2,N 必须是偶数,. 12NX =+.也就是说,车的时速等于(1)111(1)1(1)222N N N N X X NX N X N N --=+--=++--+=,所以N 最小是12,时速是121. (1)611(1)21112N N N N --÷=专题展望六年级还会继续学习数的进制哦!练习四1. (例4)在几进制中有125×125=16324.分析:因为,且,所以.再来看尾数,101010(125)(125)(15626)⨯=1562516324 10n ,16324的末位是4,所以25-4=21进到上一位.即n 为21的约数,也就是1,3,101010(5)(5)(25)⨯=7,21,因为原式中出现了6,所以n 只能是7.2. (例8)在6进制中有三位数,化为9进制为,求这个三位数在十进制中为多少? abc cba分析:()=×62+×6+=36+6+;()=×92+×9+=81+9+.所以36+6abc 6a b c a b c cba 9c b a c b a a b +=81+9+;于是35=3b+80;因为35是5的倍数,80也是5的倍数.所以3也必须是5c c b a a c a c b 的倍数,又(3,5)=1.所以,=0或5.b ①当=0,则35=80;则7=16;(7,16)=1,并且、≠0,所以=16,=7:但是在6,9进b ac a c a c a c 制,不可以有一个数字为16.②当=5,则35=3×5+80;则7=3+16;mod 7后,3+2≡0,所以=2或者2+7(为整数).因b a c a c c c k k 为有6进制,所以不可能有9或者9以上的数,于是=2.于是,35=15+80×2;=5.于是() c a a abc 6=(552)=5×62+5×6+2=212.所以.这个三位数在十进制中为212.63. (例9)试求除以992的余数是多少?200621(-)分析:因为被除数与2的次幂有关,所以我们可以用二进制来解决.,,在二进制中一定能整除1029921111100000=()() 2006220061221111⎛⎫= ⎪⎝⎭ 个(-) 515502111000⎛⎫ ⎪ ⎪⎝⎭ 个个或个以上的,因为能整除,所以余数为21111100000() 20001602111000⎛⎫ ⎪ ⎪⎝⎭ 个个21111100000(),所以原式的余数为63.543210211111122222263=+++++=()4. (例9)求证能被5整除. 151413121110982222222221-+-+-+-++-分析:15141312111098151311914121081010222222222222122222222211010101010101010101010101010101101010101010101-+-+-+-++-=+++++-+++++=-= ()()()()()又,显然能被整除,所以得证.25101=()2101010101010101()2101()5. (例10)一个10进制的三位数,把它分别化为9进制和8进制数后,就又得到了2个三位数.老师发现这3个三位数的最高位数字恰好是3、4、5,那这样的三位数一共有多少个?分析:我们设(3)=(4)=(5);我们知道(4) 在(400)~(488)之间,也就是4×92~ab 10cd 9ef 8cd 9995×92-1,也就是324~406;还知道(5) 在(500)~(577)之间,也就是5×82~6×82-1,也就是ef 888320~383;又知道(3) 在(300)~(399)之间.所以,这样的三位数应该在324~383之间,于是ab 101010有383-324+1=60个三位数满足条件.6. 一个g 进制数,,要计算它的十进制数时,有一54321543210N a g a g a g a g a g a =⋅+⋅+⋅+⋅+⋅+个简便算法:,这样进行5次乘法和5次加法,543210(((())))N a g a g a g a g a g a =⋅+⋅+⋅+⋅++现在请你用简便算法求出六进制数的N.=(6)312150N =(10)_____分析:如按,则需进行15(=5+4+3+2+1)次乘法和5次加54321543210a g a g a g a g a g a ⋅+⋅+⋅+⋅+⋅+法,显然浪费时间.根据题目中给出的简便算法 =(6)312150N =543210361626165606⨯+⨯+⨯+⨯+⨯+⨯=((((3×6+1)×6+2)×6+1)×6+5)×6+0=(10)25211数学知识莫尔斯-瑟厄数列也可以用别的办法来生成乐音数列:每一代都可以由其前代挂上它的“补数列”而得出,这意味着如果你看到了0110,就在它的后面加挂1001.此外,还有第三种办法来生成它.一开始先写0,1,2,3,…,然后把它们改写成二进制数:0,1,10,11,100,101,110,111,….(本书第21节的“第一步探索”中将详细阐述二进制数,如果你渴望了解背景信息,不妨直接跳到那里去阅读.)现在,对每个二进制数字求和,并取其模2同余.也就是说,把每个和数用2去除,并取其余数.例如,二进数11求数字和后奖成为2,在最后的数列中就应当用0表达,通过这种办法可以得出数列0,1,1,0,1,0,0,1……同欺其他办法是一致的!让果戈尔博士来告诉你,何以这一数列如此迷人.首先,它是自相似的,这意味着你可以取数列的一段而生成全部无穷数列!例如,逐项相间地截取,可以复制全部数列.也就是说,你可以取最前面的二个数,再跳过二个,如此等等.其次,数列没有任何周期性.例如,不会出现,诸如00,11,00,11这类情况.然而,数列虽然没有周期可言,它去决非随机,它具有极强的短程与长程结构.例如,不可能有两个以上相邻的项是完全一样的.发现数列中所存在的模式的方法是傅里叶频谱,用它来分析本数列时显示出了明显的波峰.采用这种数学方法,你可以绘出一个图像,表明数列中项的位置与数据频度,在第三维上有着更稠密的频率分量,而在二维图像上不过是极其简单的一个黑点.数列的生长极其迅速,下面是第8代:有时候,按此种方式把数列堆积在它自身之上时会冒出一些模式,在这里,你能看出什么名堂来吗?表示莫尔斯——瑟厄数列的另外一种办法是使用超市里常用的商品分类的“条形码”,看到1的时候是一根垂直线段,而在出现0时则跳过一段空白.为了使肉眼更易辨识,当两个1连续出现时,可以用短横加以联接.我们可以用喜欢的植物图形来描述莫尔斯——瑟厄数列,用花朵表示1,空档表示0:倘若采用较高的树木,图形甚至更加好看.你能否对行、列作出巧妙安排以便更好地显示出数列的模式?在这种神奇的森林里漫步会有什么感受?不妨去想一想,你握着心上人的玉手,走入这个一望无际的莫尔斯——瑟厄森林中去的美妙情景哦!。
小学奥数-数的进制问题B提高版

数的进制问题B知识梳理一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:例题精选例题1 ① 222(101)(1011)(11011)⨯-=________;② 2222(11000111(10101(11(-÷=))) );③88888(63121)(1247)(16034)(26531)(1744)----=________;【解析】 ① 对于这种进位制计算,一般先将其转化成我们熟悉的十进制,再将结果转化成相应的进制: 2221010101010(101)(1011)(11011)(5)(11)(27)(28)(11100)⨯-=⨯-==; ② 可转化成十进制来计算:222101010102(11000111(10101(11(199)(21)(3)(192)(11000000-÷=-÷==)))); 如果对进制的知识较熟悉,可直接在二进制下对22(10101(11÷))进行除法计算,只是每次借位都是2,可得222222(11000111(10101(11(11000111(111(11000000-÷=-=))))));③十进制中,两个数的和是整十整百整千的话,我们称为“互补数”,凑出“互补数”的这种方法叫“凑整法”,在n 进制中也有“凑整法”,要凑的就是整n . 原式88888(63121)[(1247)(26531)][(16034)(1744)]=-+-+ 8888(63121)(30000)(20000)(13121)=--=;【答案】(1)、10(11100),(2)、2(11000000),(3)、8(13121)例题2 在几进制中有413100⨯=? 【解析】 利用尾数分析来解决这个问题:由于101010(4)(3)(12)⨯=,由于式中为100,尾数为0,也就是说已经将12全部进到上一位.所以说进位制n 为12的约数,也就是12,6,4,3,2中的一个. 但是式子中出现了4,所以n 要比4大,不可能是4,3,2进制.十进制 二进制十六进制八进制另外,由于101010(4)(13)(52)⨯=,因为52100<,也就是说不到10就已经进位,才能是100,于是知道10n <,那么n 不能是12. 所以,n 只能是6.【答案】6例题3 在几进制中有12512516324⨯=?【解析】 注意101010(125)(125)(15625)⨯=,因为1562516324<,所以一定是不到10就已经进位,才能得到16324,所以10n <.再注意尾数分析,101010(5)(5)(25)⨯=,而16324的末位为4,于是25421-=进到上一位.所以说进位制n 为21的约数,又小于10,也就是可能为7或3. 因为出现了6,所以n 只能是7.【答案】7例题4 10个砝码,每个砝码重量都是整数克,无论怎样放都不能使天平平衡,这堆砝码总重量最少为_________克。
奥数:小学奥数.进制的性质及应用(ABC级).学生版 (2)

一、 数的进制(1) 十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
(2) 二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
(3) k 进制:一般地,对于k 进位制,每个数是由0,1,2, ,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k , .如二进位制的计数单位是02,12,22, ,八进位制的计数单位是08,18,28, .(4) k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+ () 十进制表示形式:1010101010n n n n N a a a --=+++ ; 二进制表示形式:1010222n n n n N a a a --=+++ ;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.(5) k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、 进制间的转换:知识结构进制的性质与应用一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果. 如右图所示:1. 几进制就是逢几进一,借一当几。
小学奥数之进制的应用(完整版)

小学奥数之进制的应用1. 了解进制;2. 会对进制进行相应的转换;3. 能够运用进制进行解题一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++;二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果. 如右图所示:5-8-2.进制的应用教学目标知识点拨模块一、进制在生活中的运用【例 1】 有个吝啬的老财主,总是不想付钱给长工。
五年级奥数专题 数的进制(学生版)
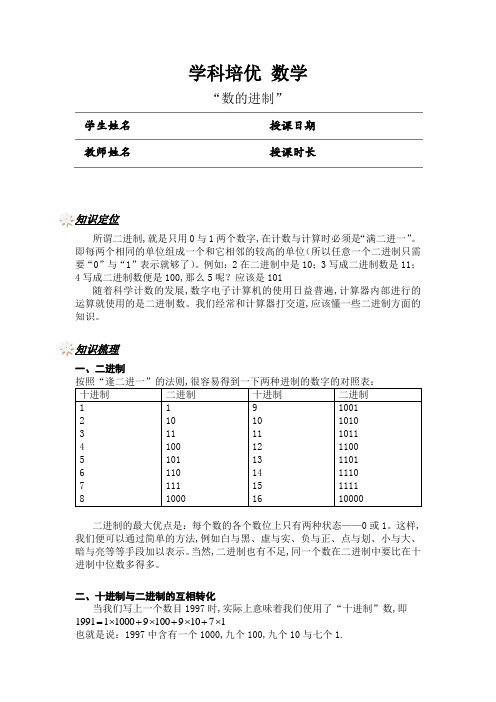
学科培优 数学 “数的进制” 学生姓名授课日期 教师姓名授课时长 知识定位 所谓二进制,就是只用0与1两个数字,在计数与计算时必须是“满二进一”。
即每两个相同的单位组成一个和它相邻的较高的单位(所以任意一个二进制只需要“0”与“1”表示就够了)。
例如:2在二进制中是10;3写成二进制数是11;4写成二进制数便是100,那么5呢?应该是101随着科学计数的发展,数字电子计算机的使用日益普遍,计算器内部进行的运算就使用的是二进制数。
我们经常和计算器打交道,应该懂一些二进制方面的知识。
知识梳理一、二进制按照“逢二进一”的法则,很容易得到一下两种进制的数字的对照表: 十进制 二进制 十进制 二进制 1 2 3 4 5 6 7 8 1 10 11 100 101 110 111 1000 9 10 11 12 13 14 15 16 100110101011110011011110111110000二进制的最大优点是:每个数的各个数位上只有两种状态——0或1。
这样,我们便可以通过简单的方法,例如白与黑、虚与实、负与正、点与划、小与大、暗与亮等等手段加以表示。
当然,二进制也有不足,同一个数在二进制中要比在十进制中位数多得多。
二、十进制与二进制的互相转化当我们写上一个数目1997时,实际上意味着我们使用了“十进制”数,即也就是说:1997中含有一个1000,九个100,九个10与七个1.199111000910091071=⨯+⨯+⨯+⨯在上表中可以看到,二进制数10表示十进制2;二进制数100表示十进制数4;二进制数1000表示十进制数8;二进制数10000表示十进制数16;……可以看出规律:二进制数100000应该表示十进制数32,……。
那么我们写下一个二进制数10110,则应表示它含有一个16,一个4与一个2,也就是明白了上面所说的两点,则二进制与十进制之间的转化的道理就容易懂了。
为了叙述的方便,我们约定:用表示括号内写的是二进制数,如;用表示括号中写的数是十进制数,如。
进制计算练习题

进制计算练习题在计算机科学和数学领域中,进制计算是一项基础而重要的技能。
掌握进制计算有助于我们更好地理解数字系统的运作原理,并且在编程、数据处理以及逻辑推理等方面有着广泛的应用。
本文将提供一系列进制计算练习题,以帮助读者巩固和提高自己的进制计算能力。
1. 二进制转换成十进制:a) 1010b) 110101c) 1111d) 100112. 十进制转换成二进制:a) 10b) 23c) 7d) 453. 二进制转换成十六进制:a) 101101b) 1101110c) 111d) 10011014. 十六进制转换成二进制:a) Ab) F3c) 2Ed) D15. 八进制转换成十六进制:a) 73b) 127c) 56d) 246. 十六进制转换成八进制:a) 3Ab) 9Ec) D7d) 177. 八进制转换成二进制:a) 56b) 127c) 22d) 138. 二进制转换成八进制:a) 1101b) 1010c) 100111d) 1111119. 十六进制转换成十进制:a) A5b) Fc) 2Ed) D110. 十进制转换成十六进制:a) 255b) 1024c) 100d) 30解答:1. 二进制转换成十进制:a) 1010 = 10b) 110101 = 53c) 1111 = 15d) 10011 = 192. 十进制转换成二进制:a) 10 = 1010b) 23 = 10111c) 7 = 111d) 45 = 1011013. 二进制转换成十六进制:a) 101101 = 2Db) 1101110 = 76c) 111 = 7d) 1001101 = 4D4. 十六进制转换成二进制:a) A = 1010b) F3 = 11110011c) 2E = 101110d) D1 = 110100015. 八进制转换成十六进制:a) 73 = 3Bb) 127 = 57c) 56 = 2Ed) 24 = 146. 十六进制转换成八进制:a) 3A = 72b) 9E = 236c) D7 = 327d) 17 = 277. 八进制转换成二进制:a) 56 = 101110b) 127 = 1011111c) 22 = 10010d) 13 = 10118. 二进制转换成八进制:a) 1101 = 15b) 1010 = 12c) 100111 = 47d) 111111 = 779. 十六进制转换成十进制:a) A5 = 165b) F = 15c) 2E = 46d) D1 = 20910. 十进制转换成十六进制:a) 255 = FFb) 1024 = 400c) 100 = 64d) 30 = 1E通过完成以上练习题,相信你已经对进制计算有了更深入的理解和熟练运用。
小学奥数数论专题--数位与进制(六年级)竞赛测试.doc

小学奥数数论专题--数位与进制(六年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx 分)【题文】某三位数和它的反序数的差被99除,商等于______与______的差;【答案】a-c【解析】本题属于基础型题型。
我们不妨设a>b>c。
(-)÷99=[(100a+10b+c)-(100c+10b+a)]÷99=(99a-99c)÷99=a-c;【题文】与的差被9除,商等于______与______的差;【答案】a-b【解析】(-)÷9=[(10a+b)-(10b+a)]÷9=(9a-9b)÷9=a-b;【题文】与的和被11除,商等于______与______的和。
【答案】a+b【解析】 (+)÷11=[(10a+b)+(10b+a)]÷11=(11a+11b)÷11=a+b。
【题文】(美国小学数学奥林匹克)把一个两位数的十位与个位上的数字加以交换,得到一个新的两位数.如果原来的两位数和交换后的新的两位数的差是45,试求这样的两位数中最大的是多少?【答案】94【解析】设原来的两位数为,交换后的新的两位数为,根据题意,,,原两位数最大时,十位数字至多为9,即,,原来的两位数中最大的是94.【题文】将一个四位数的数字顺序颠倒过来,得到一个新的四位数(这个数也叫原数的反序数),新数比原数大8802.求原来的四位数.【答案】1099【解析】设原数为,则新数为,.根据题意,有,.推知,,得到,,,,原数为1099.【题文】如果一个自然数的各个数码之积加上各个数码之和,正好等于这个自然数,我们就称这个自然数为“巧数”。
例如,99就是一个巧数,因为9×9+(9+9)=99。
六年级奥数进制的应用学生版

1. 六年级奥数进制的应用学生版2. 会对进制进行相应的转换;3. 能够运用进制进行解题一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+() 十进制表示形式:1010101010n n n n N a a a --=+++;二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:知识点拨 教学目标5-8-2.进制的应用一般地,十进制整数化为k进制数的方法是:除以k取余数,一直除到被除数小于k为止,余数由下到上按从左到右顺序排列即为k进制数.反过来,k进制数化为十进制数的一般方法是:首先将k进制数按k的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:八进制十进制二进制十六进制例题精讲模块一、进制在生活中的运用【例1】有个吝啬的老财主,总是不想付钱给长工。
进制的练习题

进制的练习题进制的练习题在我们日常生活中,进制是一个非常重要的概念。
无论是计算机科学、数学、物理学还是经济学,我们都会涉及到进制的概念和运算。
进制是一种表示数字的方式,常见的进制有十进制、二进制、八进制和十六进制。
今天,我们来一起做一些有关进制的练习题,加深对进制的理解。
1. 将十进制数34转换为二进制数。
解答:我们知道,二进制是由0和1组成的,所以我们需要找到34的二进制表示。
我们可以使用除2取余法来进行转换。
首先,我们将34除以2,得到商17和余数0。
然后,我们将商17再次除以2,得到商8和余数1。
接着,我们将商8再次除以2,得到商4和余数0。
再次除以2,得到商2和余数0。
最后,我们将商2再次除以2,得到商1和余数1。
将这些余数从下往上排列,我们得到34的二进制表示为100010。
2. 将二进制数101011转换为八进制数。
解答:我们知道,八进制是由0到7这八个数字组成的。
我们可以将二进制数101011每三位一组进行分组,然后将每组转换为对应的八进制数。
将101011分组为10和101,然后将10转换为八进制数2,将101转换为八进制数5。
所以,101011的八进制表示为25。
3. 将八进制数73转换为十进制数。
解答:我们知道,八进制数是由0到7这八个数字组成的。
将八进制数73分解为7和3,然后将7乘以8的1次方,再加上3乘以8的0次方,即可得到十进制数的结果。
计算得到7乘以8的1次方等于56,3乘以8的0次方等于3,所以73的十进制表示为59。
4. 将十六进制数A3转换为二进制数。
解答:我们知道,十六进制数是由0到9和A到F这十六个数字组成的。
将十六进制数A3分解为A和3,然后将A转换为二进制数1010,将3转换为二进制数0011。
所以,A3的二进制表示为10100011。
5. 将二进制数11011011转换为十六进制数。
解答:我们可以将二进制数11011011每四位一组进行分组,然后将每组转换为对应的十六进制数。
奥数:小学奥数.进制的性质及应用(ABC级).学生版

一、 数的进制(1) 十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
(2) 二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
(3) k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.(4) k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+() 十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.(5) k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、 进制间的转换:知识结构进制的性质与应用一般地,十进制整数化为k进制数的方法是:除以k取余数,一直除到被除数小于k为止,余数由下到上按从左到右顺序排列即为k进制数.反过来,k进制数化为十进制数的一般方法是:首先将k进制数按k的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:八进制十进制二进制十六进制重难点1.几进制就是逢几进一,借一当几。
小学奥数知识名师点拨 例题精讲 进制的计算.教师版

5-8-1.进制的计算.题库
教师版
page 4 of 4
在计算机中,所采用的计数法是二进制,即“逢二进一”。因此,二进制中只用两个数字 0 和 1。二进制的 计数单位分别是 1、21、22、23、……,二进制数也可以写做展开式的形式,例如 100110 在二进制中表示为: (100110)2=1×25+0×24+0×23+1×22+1×21+0×20。 二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。 注意:对于任意自然数 n,我们有 n0=1。 3. k 进制:
代表 13……。根据取四合一法,二进制 11101001.1011 转换为十六进制为 E9.B。 【答案】E9.B
【例 6】 某数在三进制中为 12120120110110121121,则将其改写为九进制,其从左向右数第1 位数字是几? 【考点】多进制转化成多进制 【难度】4 星 【题型】解答 【解析】由于 32=9,所以由三进制化为 9 进制需要取二合一。从后两个两个的取,取至最前边为 12,用位值
(9865)10 (303430)5
(9865)10 (23211)8
【答案】 (9865)10 (10011010001001)2 , (9865)10 (303430)5 , (9865)10 (23211)8
【巩固】 567 (
)8 (
)5 (
)2 ;
【考点】十进制化成多进制 【难度】3 星 【题型】解答
( 3021)4 (605)7 (3 43 2 4 1)10 (6 72 5)10 (500)10 【答案】 (500)10
模块五、多进制的判断
【例 9】 若 (1030)n 140 ,则 n ________. 【考点】多进制的判断 【难度】5 星 【题型】填空 【解析】若 (1030)n 140 ,则 n3 3n 140 ,经试验可得 n 5 . 【答案】 5
小学奥数之进制的计算(含详细解析)

1. 了解进制;2. 会将十进制数转换成多进制;3. 会将多进制转换成十进制;4. 会多进制的混合计算;5. 能够判断进制.一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
小学奥数5-8-1 进制的计算.专项练习及答案解析

1. 了解进制;2. 会将十进制数转换成多进制;3. 会将多进制转换成十进制;4. 会多进制的混合计算;5. 能够判断进制.一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.知识点拨教学目标5-8-1.进制的计算4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+() 十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
小学奥数5-8-2 进制的应用.专项练习及答案解析

1. 了解进制;2. 会对进制进行相应的转换;3. 能够运用进制进行解题一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:5-8-2.进制的应用教学目标知识点拨一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果. 如右图所示:模块一、进制在生活中的运用【例 1】 有个吝啬的老财主,总是不想付钱给长工。
小学五年级奥数 进制问题

2
2
2
②
Hale Waihona Puke 11010 101 2
2
2
【例3】 (★★★)
① (101)2(1011)2 (11011)2 ( )2
② ③
((131002010)4111)(6205)(17 01(0 1)2 )(1101)2
(
)2
④ (63121)8 (1247)8 (16034)8 (26531)8 (1744)8 ( )8
知识大总结 1. 进制转换:
⑴ 10转n:短除、取余、倒写 ⑵ n转10:写指、相乘、求和 2. n进制计算: ⑴ 同进制下,可以直接计算. ⑵ 不同进制,借助十进制转换计算. 3. 位值原理: ⑴ 借助数位,按数位进行计算. ⑵ 根据具体位置特征进行估算.
【今日讲题】 例1,例2,例3,例4
【讲题心得】 ______________________________________________________________
10
3
4. 关于进位制 ⑴ 本质:n进制就是逢n进一 ⑵ n进制下的数字最大为(n-1) 特别的:超过9的一般用大写英文字母表示. 例如,十六进制中,10、11、12、13、14、15、分别用A、B、C、D、E、 F表示.
5. n进制转十进制: 写指、相乘、求和. 例如:
101001 2
1
25
0
24
1
23
0
22
0
21
1
20
41 10
【例1】 (★★) ⑴将(2009)10写成二进制数 ⑵把十进制数 2008转化为十六进制数;
小学奥数模块之二进制及其应用

小学奥数模块之二进制及其应用
小学奥数模块之二进制及其应用
十进制:用0~9十个数字表示,逢10进1;不同数位上的数字表示不同的含义,十位上的`2表示20,百位上的2表示200。
所以234=200+30+4=2×102+3×10+4。
=An×10n-1+An-1×10n-2+An-2×10n-3+An-3×10n-4+An-4×10n-5+An-6×10n-7+……+A3×102+A2×101+A1×100注意:N0=1;N1=N(其中N是任意自然数)
二进制:用0~1两个数字表示,逢2进1;不同数位上的数字表示不同的含义。
(2)= An×2n-1+An-1×2n-2+An-2×2n-3+An-3×2n-4+An-4×2n-5+An-6×2n-7+……+A3×22+A2×21+A1×20
注意:An不是0就是1。
十进制化成二进制:
①根据二进制满2进1的特点,用2连续去除这个数,直到商为0,然后把每次所得的余数按自下而上依次写出即可。
②先找出不大于该数的2的n次方,再求它们的差,再找不大于这个差的2的n次方,依此方法一直找到差为0,按照二进制展开式特点即可写出。
小学奥数之进制的计算(含详细解析)

⼩学奥数之进制的计算(含详细解析)1. 了解进制;2. 会将⼗进制数转换成多进制;3. 会将多进制转换成⼗进制;4. 会多进制的混合计算;5. 能够判断进制.⼀、数的进制1.⼗进制:我们常⽤的进制为⼗进制,特点是“逢⼗进⼀”。
在实际⽣活中,除了⼗进制计数法外,还有其他的⼤于1的⾃然数进位制。
⽐如⼆进制,⼋进制,⼗六进制等。
2.⼆进制:在计算机中,所采⽤的计数法是⼆进制,即“逢⼆进⼀”。
因此,⼆进制中只⽤两个数字0和1。
⼆进制的计数单位分别是1、21、22、23、……,⼆进制数也可以写做展开式的形式,例如100110在⼆进制中表⽰为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
⼆进制的运算法则:“满⼆进⼀”、“借⼀当⼆”,乘法⼝诀是:零零得零,⼀零得零,零⼀得零,⼀⼀得⼀。
注意:对于任意⾃然数n ,我们有n 0=1。
3.k 进制:⼀般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进⼀”.1k k >()进位制计数单位是0k ,1k ,2k ,.如⼆进位制的计数单位是02,12,22,,⼋进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=?+?++?+()⼗进制表⽰形式:1010101010n n n n N a a a --=+++;⼆进制表⽰形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下⽅写上k ,表⽰是k 进位制的数如:8352(),21010(),123145(),分别表⽰⼋进位制,⼆进位制,⼗⼆进位制中的数.5.k 进制的四则混合运算和⼗进制⼀样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
小学奥数专题-进制的应用

1. 了解进制;2. 会对进制进行相应的转换;3. 能够运用进制进行解题一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:知识点拨教学目标5-8-2.进制的应用八进制十进制二进制十六进制例题精讲模块一、进制在生活中的运用【例1】有个吝啬的老财主,总是不想付钱给长工。
小学奥数全国推荐三年级奥数通用学案附带练习题解析答案29进制问题(一)

年 级三年级 学 科 奥数 版 本 通用版 课程标题进制问题(一)同学们在进行整数四则运算时,用的都是十进制,即“满10进1”,对于其他进制则感到陌生。
实际上,在我们的日常生活中,不仅使用十进制,还使用许多其他类型的进制。
比如,两只手为一双,两只手套为一副,这里使用的是二进制;60秒是1分钟,60分钟是1小时,这里使用的是六十进制;二十四小时为一天,这里使用的是二十四进制;1000米等于1千米,1000克等于1千克,这里使用的是一千进制等等。
计算器内部进行的计算使用的就是二进制数。
今天我们一起来研究一下二进制。
一、二进制:就是只用0与1两个数字,在计数与计算时必须是“满二进一”。
二、二进制的特点:每个数的各个数位上只有两种状态——0或1。
这样,我们便可以通过简单的方法加以表示。
当然,二进制也有不足,正如大家看到的那样,同一个数在二进制中要比在十进制中位数多得多。
三、表示方法:为了叙述的方便,我们约定:用( )2表示括号内写的数是二进制数,如(1011)2;用( )10表示括号中写的数是十进制数,如(37)10 ;十进制的标志可省略,37就代表十进制下的数。
例1 下列数不是八进制数的是( )A. 125B. 126C. 127D. 128分析与解:八进制采用0,1,2,3,4,5,6,7八个数码,逢八进位,所以八进制数中不可能出现7以上的阿拉伯数字,故选D 。
例2 计算简单的二进制加法()()221001011+等于多少?分析与解:二进制数据的算术运算的基本规律和十进制数的运算十分相似,本题中没有进位,所以()()22211111001011)=(+。
即例3 计算简单的二进制加法()()221011011+等于多少?分析与解:我们平时计算用的十进制都是逢十进一,二进制算法的关键之处是“逢二进一”,所以()()222100*********)=(+。
即二进制加法运算有四种情况:0+0=0;0+1=1;1+0=1 ;1+1=10,满二就要向高位进1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.
了解进制;
2. 会对进制进行相应的转换;
3.
能够运用进制进行解题
一、数的进制
1.十进制:
我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:
在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23
、……,二进制数也可以写做展开式的形式,例如100110在二
进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0
=1。
3.k 进制:
一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢
k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,
,八进位制的计数单位是08,18,28,.
4.k 进位制数可以写成不同计数单位的数之和的形式
1
1
10110n n n n k n n a a a a a k a k
a k a ---=⨯+⨯++⨯+()
十进制表示形式:1010101010n n n n N a a a --=+++;
二进制表示形式:1010222n n n n N a a a --=++
+;
为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数
如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.
5.k 进制的四则混合运算和十进制一样
先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
5-8-2.进制的应用
教学目标
知识点拨
二、进制间的转换:
一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k
进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.
如右图所示:
模块一、进制在生活中的运用
【例 1】 有个吝啬的老财主,总是不想付钱给长工。
这一次,拖了一个月的工钱,还是不想付。
可是
不付又说不过去,便故作大方地拿出一条金链,共有7环。
对长工说:“我不是要拖欠工资,只是想连这一个月加上再做半年的工资,都以这根金链来付。
”他望向吃惊的长工,心中很是得意,“本人说话,从不食言,可以请大老爷作证。
”大老爷可是说一不二的人,谁请他作证,他当作一种荣耀,总是分文不取,并会以命相拼也要兑现的。
这越发让长工不敢相信,要知道,这在以往,这样的金链中的一环三个月的工钱也不止。
老财主越发得意,终于拿出杀手锏:“不过,我请大老爷作证的时候,提到一项附加条件,就是这样的金链实在不能都把它断开,请你只能打开一环,以后按月来取才行!”当长工明白了老财主的要求后,不仅不为难,反倒爽快地答应了,而且,从第一个月到第七个月,顺利地拿到了这条金链,你知道怎么断开这条金链吗?
【巩固】 现有1克,2克,4克,8克,16克的砝码各1枚,在天平上能称多少种不同重量的物体?
【例 2】 茶叶店老板要求员工提高服务质量,开展“零等待”活动,当顾客要买茶叶的时候,看谁最
快
十进制 二进制
十六进制
八进制
例题精讲
满足顾客的需要则为优秀。
结果有一个员工总是第一名,而且顾客到他那儿不需要等待。
原来他把茶叶先称出若干包来,放在柜台上,顾客告诉他重量,他就拿出相应重量的茶叶。
别的伙计看在眼里,立即学习,可是柜台上却放不下许多包。
奇怪的是,最佳员工的柜台上的茶叶包裹却不是很多。
于是有员工去取经,发现最佳员工准备的茶叶数量是:1,2,4,8,16,32,64,128,256。
你能解释一下其中的道理么?这些重量可以应付的顾客需要的最高重量是多少?
【巩固】如果只考虑100克以内的重量,至少需要多少包?
【巩固】如果只许在天平的一边放砝码,要称量100g以内的各种整数克数,至少需要多少个砝码?
【巩固】古代英国的一位商人有一个15磅的砝码,由于跌落在地碎成4块,后来,称得每块碎片的重量都是整磅数,而且可以用这4块来称从1至15磅之间的任意整数磅的重物(砝码只能放在天平的一边)。
那么这4块砝码碎片各重,,,
【例3】有10箱钢珠,每个钢珠重10克,每箱600个.如果这10箱钢珠中有1箱次品,次品钢珠每个重9克,那么,要找出这箱次品最少要称几次?
【例4】小马虎将一些零件装箱,每个零件10g,装了10箱,结果发现,混进了几箱次品进去,每个次
品零件9克,但从外观上看不出来,聪明的你能只称量一次就能把所有的次品零件都找出来么?
【例5】计算机存储容量的基本单位是字节,用B表示,一般用KB、MB、GB作为存储容量的单位,它们之间的关系是1KB=10
2B,1MB=102KB,1GB=102MB。
小明新买了一个MP3播放器,存储容量为256MB,它相当于_____B。
【例6】向电脑输入汉字,每个页面最多可输入1677个五号字。
现在页面中有1个五号字,将它复制后粘贴到该页面,就得到2个字;再将这2个字复制后粘贴到该页面,就得到4个字。
每次复制和粘贴为1次操作,要使整个页面都排满五号字,至少需要操作次。
【例7】成语“愚公移山”比喻做事有毅力,不怕困难。
假设愚公家门口的大山有80万吨重,愚公有两个儿子,他的两个儿子又分别有两个儿子,依此类推。
愚公和它的子孙每人一生能搬运100吨石头。
如果愚公是第1代,那么到了第代,这座大山可以搬完。
(已知10个2连乘之积等于1024)
【例8】123456789012345678901234567890……1234567890,共10000个数字。
第一轮去掉在奇数位置(从左数起)上的数字,剩下5000个数字;第二轮再去掉这5000个数字中奇数位置上的数字,剩下2500个;第三轮,……;直到只剩下一个数字。
最后剩下的数字是__ ,这时已经操作了轮。
【例9】10个砝码,每个砝码重量都是整数克,无论怎样放都不能使天平平衡,这堆砝码总重量最少为_________克。
【例10】将6个灯泡排成一行,用○和●表示灯亮和灯不亮,下图是这一行灯的五种情况,分别表示五个数字:1,2,3,4,5。
那么●○○●○●表示的数是。
5
4321●○○○
●○○●○○●●●●●●●●●●●●●●●●●●●●
模块二、巧求余数问题
【例 11】 已知正整数N 的八进制表示为8(12345654321)N =,那么在十进制下,
N 除以7的余数与N 除以9的余数之和是多少?
【巩固】 在8进制中,一个多位数的数字和为十进制中的68,求除以7的余数为多少?
【例 12】
试求()
200610
21
-除以992的余数是多少?
【例 13】
计算2003(21)-除以7的余数. 【例 14】
计算2003(31)-除以26的余数.
模块三、进制与位值的综合运用
【例15】在美洲的一个小镇中,对于200以下的数字读法都是采取20进制的。
如果十进制中的147在20进制中的读音是“seyth ha seyth ugens”,而十进制中的49在20进制中的读音是“naw ha dew
ugens”,那么20进制中读音是“dew ha naw ugens”的数指的是十进制中的数
【例16】一个自然数,在3进制中的数字和是2007,它在9进制中的数字和最小是,最大是。
【例17】在6进制中有三位数abc,化为9进制为cba,求这个三位数在十进制中为多少?
【例18】在7进制中有三位数abc,化为9进制为cba,求这个三位数在十进制中为多少?
【例19】一个人的年龄用十进制数和三进制数表示,若在十进制数末尾添个“0”就是三进制数,求此人的年龄.
【例20】N是整数,它的b进制表示是777,求最小的正整数b,使得N是十进制整数的四次方.。
