控制理论基础 课件 第四章 频率特性新的
合集下载
自动控制理论第四章

若用一个复数G(jω)来表示,则有 指数表示法: G(jω)=∣G(jω)∣· j∠G(jω)=A(ω)· j e e 幅角表示法: G(jω)=A(ω)∠ (ω) G(jω)就是频率特性通用的表示形式,是ω的函数。 当ω是一个特定的值时,可以在复平面上用一个 向量去表示 G ( jω)。向量的长度为 A(ω),向量与 正实轴之间的夹角为 (ω),并规定逆时针方向为正, 即相角超前;规定顺时针方向为负,即相角滞后。 可由图4.3表示。
对输出求拉氏反变换可得
c(t ) ( K1e
p1t
K 2e
p2t
Kne
pn t
) (K c e
jt
K c e )
jt
系统的输出分为两部分,第一部分为指数瞬态分量, 对应特征根为单根时的响应;第二部分为稳态分量, 它取决于输入信号的形式。对于一个稳定系统,系统 所有的特征根的实部均为负,瞬态分量必将随时间趋 于无穷大而衰减到零。因此,系统响应正弦信号的稳 态分量为:
r(t)
sint 线 性 定 Asin(ωt+)
Css(t) t
常系统
图4-2,线性系统及频率响应示意图
4.1.2频率特性
一、基本概念 对系统的频率响应作进一步的分析,由于输入输出 的幅值比A与相位差 只与系统的结构、参数及输入正 弦信号的频率ω有关。在系统结构、参数给定的前提下, 幅值比 A与相位差 仅是ω的函数,可以分别表示为A (ω)与(ω)。 若输入信号的频率ω在0→∞的范围内连续变化,则 系统输出与输入信号的幅值比与相位差将随输入频率的 变化而变化,反映出系统在不同频率输入信号下的不同 性能,这种变化规律可以在频域内全面描述系统的性能。
第四章 控制系统的频率特性PPT课件

一·乃氏图的一般作图法
1·写出 G ( j w ) 和G( jw)表达式; 2·分别求出 w 0 和 w时的 G ( j w ) ;
3·求乃氏图与实轴的交点,交点可利用 ImG(jw)0或 G(jw)n180o
的关系式求出;
4·求乃氏图与虚轴的交点,交点可利用 ReG(jw)0或 G(jw)n90o
K;
(T 1s1 )(T 2s1 )
K ,T 1,T 20
试概略绘制系统开环幅相曲线。
解:由于惯性环节的角度变化为 ~-900,故该系统开环幅
相曲线中
起点为:
终点为:
系统开环频率特性
A (0)K,
(0)00
A ( ) 0 , ( )2 ( 90) 0 10 80
G (j)K [1 (1 T 1 T T 12 2 2 2) 1 (j (T T 1 22 T 22 ))]
即多环节传递函数的幅频特性是各环节模的乘积,相频特性是各环节 相位角之和。
7
自动控制原理
§4-2频率响应的极 频率响应G(jw)是输入频率w的复变函数,是一种变换,当w从0逐渐增长至
时,G(jw)作为一个矢量,其端点在复平面相对应的轨迹就是频率响
应的极坐标图,亦叫坐做乃标氏图图((Nyq乃uist氏曲线图) )
传递函数G(s)
S=jw
频率特性G(jw)
注:系统频率特性分析法是一种用“稳态”的方法(即输出稳态时 的正弦信号,不考虑过度过程)来分析系统的动态特性(稳,准, 快)
5
自动控制原理
二·频率特性的一些概念
G (jw ) U (w )jV (w )
幅频特性 A (w ) G (jw )[U (w )]2 [V (w )]2
(jw K)(j(wjw1T11)1()j(wjw2T21).1..)...
1·写出 G ( j w ) 和G( jw)表达式; 2·分别求出 w 0 和 w时的 G ( j w ) ;
3·求乃氏图与实轴的交点,交点可利用 ImG(jw)0或 G(jw)n180o
的关系式求出;
4·求乃氏图与虚轴的交点,交点可利用 ReG(jw)0或 G(jw)n90o
K;
(T 1s1 )(T 2s1 )
K ,T 1,T 20
试概略绘制系统开环幅相曲线。
解:由于惯性环节的角度变化为 ~-900,故该系统开环幅
相曲线中
起点为:
终点为:
系统开环频率特性
A (0)K,
(0)00
A ( ) 0 , ( )2 ( 90) 0 10 80
G (j)K [1 (1 T 1 T T 12 2 2 2) 1 (j (T T 1 22 T 22 ))]
即多环节传递函数的幅频特性是各环节模的乘积,相频特性是各环节 相位角之和。
7
自动控制原理
§4-2频率响应的极 频率响应G(jw)是输入频率w的复变函数,是一种变换,当w从0逐渐增长至
时,G(jw)作为一个矢量,其端点在复平面相对应的轨迹就是频率响
应的极坐标图,亦叫坐做乃标氏图图((Nyq乃uist氏曲线图) )
传递函数G(s)
S=jw
频率特性G(jw)
注:系统频率特性分析法是一种用“稳态”的方法(即输出稳态时 的正弦信号,不考虑过度过程)来分析系统的动态特性(稳,准, 快)
5
自动控制原理
二·频率特性的一些概念
G (jw ) U (w )jV (w )
幅频特性 A (w ) G (jw )[U (w )]2 [V (w )]2
(jw K)(j(wjw1T11)1()j(wjw2T21).1..)...
第4章 控制系统的频率特性

Bode图
对数幅频特性: 对数幅频特性:
ω L( ) dB
20lgK 0 0.1 1
L(ω) = 20lg A(ω) = 20lg K
φ ( ) ω
0 0.1
对数相频特性: 对数相频特性: ϕ(ω) = ∠G( jω) = 00
ω ω
1
典型环节的频率特性曲线图
Nyquist 图
1 G(S) = 传递函数: S
∠( AωG ( jω ) ) = ∠ ( jeω + f ) ⇒ t g−1 eω = ∠G ( jω ) f
(
)
2
+∑
j =1
q
dj S + pj
+
eS + f s2 + ω 2
几点认识: 频率特性概述 (1)频率特性有明确的物理意义,可以用实验的手段准确地 得到系统的频率响应,当系统传递函数未知时,可以通过 r(t) = Asin( t) ω 测量频率响应来推导系统的传递函数; R(S) C(S) css (t ) = A G( jω) sin[ωt + ∠G( jω)] G(S) 系统 (2)系统频率特性能间接地揭示系统的动态特性和稳态特性, 可简单迅速地判断某些环节或参数对系统性能的影响,指 系统在正弦信号作用下的稳态输出是与输入同频率 出系统改进方向。 的正弦信号,输出与输入的幅值之比为|G(jω)|,稳态 (3)频率特性是在系统稳定的条件下分析稳态响应得到的, 它与传递函数一样,也表征了系统的运动规律,是系统频 输出与输入间的相位差为∠G(jω)。 域分析的理论依据,但只适应于线性定常系统。 频率特性: 频率特性: G( jω) = G( jω) ⋅ e∠G( jω) = A(ω) ⋅ e jϕ(ω) (4)频率特性正好是线性系统的傅里叶变换。 幅频特性: 幅频特性:A(ω) = G( jω) G( jω) = G( s) s= jω 相频特性: 相频特性:ϕ(ω) = ∠G( jω)
控制工程基础第4章 控制系统的频率特性

( ) G ( j ) arctanT
As 0, 1) ( gain G ( j ) 1 L( ) 20lg G ( j ) 0
( ) 0
As 1 gain G ( j ) T L( ) 20lg G ( j ) 20 lg(T )
第四章 控制系统的频率特性
4.1 机电系统频率特性的概念及其实验基本方 法 4.2 极坐标图 4.3 对数坐标图 4.4 由频率特性曲线求系统的频率特性 4.5 控制系统的闭环频响
4.1 机电系统频率特性的概念及其实验基本方法
频率响应: 系统对正弦函数输入的问题响应。当输入正弦信号时, 系统的稳态输出也是正弦信号,且其频率与输入信号的 频率相同,其幅值及相角随着输入信号频率的变化而变 化。 当输入为非正弦的周期信号时,可将输入信号利用傅立 叶级数展开成正弦函数叠加的形式,系统的响应也是其 相应正弦函数响应的叠加 输入为非周期信号时也可以将它看作是周期为无穷大的 周期信号
V ( )
相频特性
A( )
( )
U ( )
4.2 极坐标图
Im( )
G ( j n )
Re( )
G ( j 2 )
G ( j1 )
4.2.1 典型环节的乃氏图
k
0
积分环节 比例环节
0
G (s) k G ( j ) k A( ) G ( j ) k
系统开环传递函数为: 100(0.05s+1) G(s)= s(0.1s+1)(0.2s+1) 试绘制其开环对数频率特性图
40 20 1 20lgk 5 10 20
1 -90 -180 -270
5
10
第4章 控制系统的频率特性

= A(ω )[cos ϕ (ω ) + j sin ϕ (ω )]
欧拉公式
15
G ( jω ) =
k Tjω + 1
(频域法)的幅频特性与相频特性、
实频特性与虚频特性的详细求法。
1/ k 1/ k 1 − Tjω 1 / k (1 − Tjω ) G ( jω ) = = × = 2 Tjω + 1 Tjω + 1 1 − Tjω 1 + (Tω ) A(ω ) = G ( jω ) = 1 / k (1 − Tjω ) 1 + (Tω )
19
K 试求: 试求: G ( jω ) = jω (T1 jω + 1)(T2 jω + 1)
的幅频特性与相频特性、实频特性与虚频特性。 的幅频特性与相频特性、实频特性与虚频特性。 K 解: ( jω) = G jω(T1 jω +1)(T2 jω +1)
=K e 1
π j − 2
系统对正弦输入的稳态响应称为频率响应。 系统对正弦输入的稳态响应称为频率响应。 频率响应 线性定常系统对于正弦信号的响应也和其他典型信 号的响应一样,包含瞬态响应和稳态响应,其瞬态响应 号的响应一样,包含瞬态响应和稳态响应, 瞬态响应和稳态响应 部分不是正弦波形, 部分不是正弦波形, t→∞,瞬态响应为零 ;稳态响应 , 部分和输入的正弦信号的频率相同的正弦波形, 部分和输入的正弦信号的频率相同的正弦波形,但振幅 和相位均与输入量不同, 和相位均与输入量不同 随着输入正弦信号频率的变化 而有规律的变化。输入为非正弦信号的周期信号时, 而有规律的变化。输入为非正弦信号的周期信号时,其 输入可以利用傅立叶级数展开成正弦波的叠加,其输出 输入可以利用傅立叶级数展开成正弦波的叠加, 为相应的正弦波的叠加。如果输入为非周期信号时, 为相应的正弦波的叠加。如果输入为非周期信号时,可 以将非周期信号看作T→∞。 以将非周期信号看作 。
第四章控制系统的频率特性分析课件

4-0 引言
频率响应法是二十世纪三十年代发展起来的一种经典工 程实用方法,是一种利用频率特性进行控制系统分析的图解方 法,可方便地用于控制工程中的系统分析与设计。频率法用于 分析和设计系统有如下优点:
(1)不必求解系统的特征根,采用较为简单的图解方法 就可研究系统的稳定性。由于频率响应法主要通过开环频率特 性的图形对系统进行分析,因而具有形象直观和计算量少的特 点。
❖数学本质
输入 xi(t) Xi sin(t)
输出
xo(t ) ae jt ae jt G( jw) e j ( )e jt Xi G( jw) e e j ( ) jt Xi
2j
2j
G( jw) Xi sin(t ( ))
Xo() sin(t ())
式中:Xo(ω) 为输出正弦信号的幅值,Φ(ω)为输出正弦
当在0~变化时,向量G( j)H(j)的幅值和相角随而变化,与此对应 的向量G( j)H(j)的端点在复平面G( j)H(j)上的运动轨迹就称为幅相 频率特性或 Nyqusit曲线。画有Nyqusit曲线的坐标图称为极坐标图或 Nyqusit图。
4-1 频率特性的基本概念
2.伯德图(Bode图) 如将系统频率特性G( j)的幅值和相角分别绘在半对数坐标
4-0 引言
(2)系统的频率特性可用实验方法测出。频率特性具 有明确的物理意义,它可以用实验的方法来确定,这对于难 以列写微分方程式的元部件或系统来说,具有重要的实际意 义。
(3)可推广应用于某些非线性系统。频率响应法不仅适 用于线性定常系统,而且还适用于传递函数中含有延迟环节 的系统和部分非线性系统的分析。
所以,
G(
j
)
Xo( )
A( )
Hale Waihona Puke XiG( j) ()
频率响应法是二十世纪三十年代发展起来的一种经典工 程实用方法,是一种利用频率特性进行控制系统分析的图解方 法,可方便地用于控制工程中的系统分析与设计。频率法用于 分析和设计系统有如下优点:
(1)不必求解系统的特征根,采用较为简单的图解方法 就可研究系统的稳定性。由于频率响应法主要通过开环频率特 性的图形对系统进行分析,因而具有形象直观和计算量少的特 点。
❖数学本质
输入 xi(t) Xi sin(t)
输出
xo(t ) ae jt ae jt G( jw) e j ( )e jt Xi G( jw) e e j ( ) jt Xi
2j
2j
G( jw) Xi sin(t ( ))
Xo() sin(t ())
式中:Xo(ω) 为输出正弦信号的幅值,Φ(ω)为输出正弦
当在0~变化时,向量G( j)H(j)的幅值和相角随而变化,与此对应 的向量G( j)H(j)的端点在复平面G( j)H(j)上的运动轨迹就称为幅相 频率特性或 Nyqusit曲线。画有Nyqusit曲线的坐标图称为极坐标图或 Nyqusit图。
4-1 频率特性的基本概念
2.伯德图(Bode图) 如将系统频率特性G( j)的幅值和相角分别绘在半对数坐标
4-0 引言
(2)系统的频率特性可用实验方法测出。频率特性具 有明确的物理意义,它可以用实验的方法来确定,这对于难 以列写微分方程式的元部件或系统来说,具有重要的实际意 义。
(3)可推广应用于某些非线性系统。频率响应法不仅适 用于线性定常系统,而且还适用于传递函数中含有延迟环节 的系统和部分非线性系统的分析。
所以,
G(
j
)
Xo( )
A( )
Hale Waihona Puke XiG( j) ()
【控制工程基础-清华课件】第四章频率特性

定义系统输出信号的稳态响应相对 其正弦输入信号的相移 φ(ω) = ∠G( jω) 为系统的相频特性。
相频特性描述系统在稳态下响应不 同频率的正弦输入时在相位上产生的滞 后(φ < 0)或超前(φ > 0)特性。
频率特性的定义(续)
上述定义的幅频特性 A(ω) = G( jω) 和相频特性 φ(ω) = ∠G( jω) 统称为系统 的频率特性,它描述了系统对正弦输入 的稳态响应。
傅里叶反变换式
∫ F −1[ X (ω)] = x(t ) = 1 +∞ X (ω )e jωtdω
2π −∞
傅氏变换与拉氏变换
傅氏正变换式
∫ X (ω) = +∞x(t)e−jωt dt −∞
拉氏正变换式
∫ X (s) = +∞ x(t)e−stdt 0
傅氏变换与拉氏变换是类似的。
除了积分下限不同外,只要将 s 换
频率特性是系统对不同频率正弦输入信号 的响应特性。
频率特性分析法(频域法) 是利用系统的频 率特性来分析系统性能的方法,研究的问题仍 然是系统的稳定性、快速性和准确性等,是工 程上广为采用的控制系统分析和综合的方法。
第四章 控制系统的频率特性
频率特性分析法是一种图解的分析方法。 不必直接求解系统输出的时域表达式,可 以间接地运用系统的开环频率特性去分析闭环 系统的响应性能,不需要求解系统的闭环特征 根。 系统的频域指标和时域指标之间存在着对 应关系。频率特性分析中大量使用简洁的曲 线、图表及经验公式,使得控制系统的分析十 分方便、直观。
频率特性的物理背景
图4-1 电路网络正弦输入的稳态响应
RC电路网络正弦输入的稳态响应
R
ui (t )
C
相频特性描述系统在稳态下响应不 同频率的正弦输入时在相位上产生的滞 后(φ < 0)或超前(φ > 0)特性。
频率特性的定义(续)
上述定义的幅频特性 A(ω) = G( jω) 和相频特性 φ(ω) = ∠G( jω) 统称为系统 的频率特性,它描述了系统对正弦输入 的稳态响应。
傅里叶反变换式
∫ F −1[ X (ω)] = x(t ) = 1 +∞ X (ω )e jωtdω
2π −∞
傅氏变换与拉氏变换
傅氏正变换式
∫ X (ω) = +∞x(t)e−jωt dt −∞
拉氏正变换式
∫ X (s) = +∞ x(t)e−stdt 0
傅氏变换与拉氏变换是类似的。
除了积分下限不同外,只要将 s 换
频率特性是系统对不同频率正弦输入信号 的响应特性。
频率特性分析法(频域法) 是利用系统的频 率特性来分析系统性能的方法,研究的问题仍 然是系统的稳定性、快速性和准确性等,是工 程上广为采用的控制系统分析和综合的方法。
第四章 控制系统的频率特性
频率特性分析法是一种图解的分析方法。 不必直接求解系统输出的时域表达式,可 以间接地运用系统的开环频率特性去分析闭环 系统的响应性能,不需要求解系统的闭环特征 根。 系统的频域指标和时域指标之间存在着对 应关系。频率特性分析中大量使用简洁的曲 线、图表及经验公式,使得控制系统的分析十 分方便、直观。
频率特性的物理背景
图4-1 电路网络正弦输入的稳态响应
RC电路网络正弦输入的稳态响应
R
ui (t )
C
机械工程控制基础第四章频率特性分析 PPT课件

2020/3/30
31
可编辑
Logo
4.2极坐标图(Polar plots) , 或乃氏图
极坐标图是反映频率特性的几何表示。
▪ 当ω从0逐渐增长至+∞时,频率特性G(jω)作为一个 矢量,其端点在复平面相对应的轨迹就是频率特性的 极坐标图。
极坐标图也称为乃氏图或乃奎斯特曲线。
2020/3/30
函数适合进行拉氏变换的条件比傅氏变换的 条件弱一些, 因此适合函数的范围也宽一些。
大多数机电系统可简单地将拉氏变换G(s)中 s换成jω而直接得到相应的傅氏变换式
2020/3/30
24
可编辑
Logo
4.1 频率特性概述
系统频率特性的表示形式
▪ 系统的频率特性函数是一种复变函数,可以表示成如 下形式:
Logo
2020/3/30
RC网络对正弦输入的稳态响应
16
可编辑
4.1 频率特性概述
频率特性的物理背景实例 --RC电路网络正弦输入的稳态响应
Logo
2020/3/30
17
可编辑
4.1 频率特性概述
频率特性的物理背景实例 --RC电路网络正弦输入的稳态响应
Logo
2020/3/30
18
可编辑
▪ 重点讨论过程的响应形式; ▪ 分析控制系统的直接方法; ▪ 优点:直观、精确; ▪ 缺点:比较繁琐。
• 高阶系统难以求解; • 难以研究系统结构参数变化对系统性能的影响; • 当系统某些元件的传递函数难以列写时,整个系统难以分析。
2020/3/30
6
可编辑
Logo
复习—基本环节典型输入响应小结
→幅频特性描述系统在稳态下,响应不同频率的正弦输入 时,在幅值上的增益特性(衰减或放大)。
控制工程基础 第4章 控制系统的频域特性

1
0.5
0
-0.5
-1
-1.5 y(t) u(t)
-20
1
2
3
4
5
6
数学本质 例:如图所示的RC电路
i (t) R ui(t)
C u0(t)
G(s) Uo (s) 1 1 1 / T Ui (s) RCs 1 Ts 1 S 1 / T
如:Ui (t) =
ASin t
, 即:Ui (s) =
第四章 控制系统的频率特性
频率特性及其表示法 极坐标图
对数坐标图 由频率特性曲线求传递函数 由单位脉冲响应求传递函数
对数幅相图 控制系统的闭环频率响应
系统常用的数学模型
常微分方程
线性定常系统 传递函数 频率特性
频率特性的特点
时域(分析方法) 复频域(分析方法) 频域(分析方法)
(1)频率特性具有明确的物理意义,它可以用实验的方 法来确定,这对于难以列写微分方程式的元部件或系统来 说,具有重要的实际意义。
1 T 2 2
一般线性定常系统,设输入信号为正弦函数,即:
x(t)=Xsint
式中: X—输入信号的振幅; X(s) —输入信号的角频率。
(4.1)
G(s) Y(s)
其拉氏变换为:
X
X
X ( s ) s2 2 ( s j )( s j )
(4.2)
一般情况下,传递函数可以写成如下形式:
出Ysin(t+),仍是一个正弦信号。其特点是:
①.频率与输入信号相同;
振幅Y和相移都
是输入信号频率的函
②.振幅Y为输入振幅X的 G( j) 倍;数,对于确定的值来
③.相移为 (ω)=∠G(j)。
控制工程第四版第4讲_频率特性_02.pptx

第四章 控制系统的频率特性
Y 则 X X Y 0 N 配方整理,可得
2 2
1 1 1 1 X Y 2 2 N 4 2 N
2
2
2
由上式可看出,等相角轨迹是一个圆心
1 1 为 , j ,半径为 2 2N
闭环截止频率 b: 对数幅频特性的幅值下 降到-3dB时对应的频率。
第四章 控制系统的频率特性 4.8 机械系统动刚度概念 一个典型的由质量-弹簧-阻尼构成的机械系 统的质量块在输入力f(t) 作用下产生的输出位移 为y(t),其传递函数为
Y s 1 1k G s 2 2 2 F s ms Ds k s n 2 s n 1
2 2
Im G j arc tan Re
第四章 控制系统的频率特性 4.5节小结 频率特性函数的求取方法:
1.根据系统的传递函数求取
2.根据系统的微分方程求取 3.实验方法:
输入不同频率的正弦信号
输入脉冲信号
第四章 控制系统的频率特性 4.6 对数幅相特性图(Nichols 图)
第四章 控制系统的频率特性
在由开环频率特性确定闭环频率特性时,应 用相同的比例尺,将尼柯尔斯图线绘制在透明 片上,然后再把它覆盖在以相同比例尺绘制的 系统开环传递函数对数幅相图上,则开环频率 特性曲线G( j ) 与M轨线和N 轨线的交点,就给出 了每一频率上闭环频率特性的幅值M 和相角φ。
若 G( j ) 轨迹与M轨线相切,切点 处频率就是谐振频率,谐振峰值由M轨 线对应的幅值确定。
系统单位脉冲响应的傅氏变换即为 系统的频率特性。
第四章 控制系统的频率特性
为了识别系统的传递函数,我们可以产生一 个近似的单位脉冲信号 (t ) 作为系统的输入,记 录系统响应的曲线 g (t ) ,则系统的频率特性为
《自动控制原理》教学课件 第四章 频率特性法 4.1
G(cjωs(t))==√jω1+T1(A+ω1T=)2 1S+i(nω1(Tω)t2-tg-j1ω1+Tω()ωTT)2
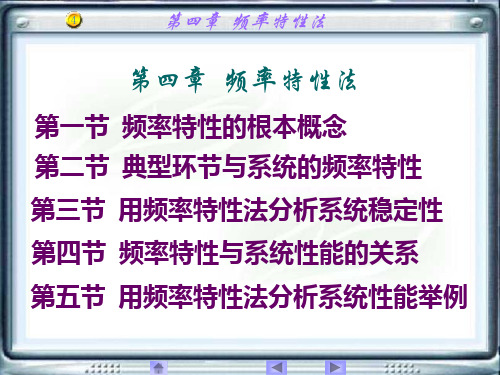
第一节 频率特性的根本概念
频率特性可表示为:
G(jω)= A(ω)e jφ (ω=)P(ω)+jQ(ω)
A(ω) =√ P2(ω)+Q2(ω)
φ (ω ) = tg-1QP((ωω))
1.幅相频率特性曲线
幅相频率特性曲线 又称奈魁斯特曲线.
也称极坐标图。
幅相频率特性曲线
Im
ω∞
0 Re
ω ω= 0
第一节 频率特性的根本概念
2.对数频率特性曲线
L性也纵为特 坐 分性德特数线频称记(单曲是坐Φω纵性标度曲图性相组率为作由)对位(对线标l=坐gω曲采。对线曲频成变.对十d2数为ω数的那e)0标线用数又线。化数特倍cl频。分g相横么d为的.幅A称和十幅性频l率B度g频坐表(横频ω伯 对 倍频曲程ω特,特标 示),,-1---29842400000000
第一节 频率特性的根本概念
系统输入输出曲线
第一节 频率特性的根本概念
定义 :
系统的频率特性 :
j
G(jω)=G(s)
S
=|G(jω)|e
=-jω
e G(jω)
= A(ω)
jφ (ω )
系统的幅频特性: A(ω) =|G(jω)|
系统的相频特性: φ (ω ) = G(jω)
频率特性与表征系统性能的传递函数 之间有着直接的内在联系,故可由频率特 性来分析系统性能。
第一节 频率特性的根本概念
RC电路的频率特性曲线
A(ω)
1A 0.8A
Φ(ω)
自动控制原理与系统__课件第四章控制系统的频率特性

图4-3
4.2 典型环节的Bode图
一 、 比例环节 传递函数 :
G( s) C ( s) K R( s)
频率特性 :
G ( j )
C ( j ) K R ( j )
对数频率特性 : L 20 lg K dB 0 图4-4 Bode图 : 对数幅频特性L(ω)为水平直线,其高度为20lgK。 对数相频特性φ(ω)为与横轴重合的水平直线。 如图4-4所示。 比例环节放大倍数K变化,系统的L(ω)上下平移,但φ(ω)不变。
12
四、惯性环节
C (s) 1 R( s) Ts 1 C ( j ) 1 G( j ) 频率特性 : R( j ) jT 1
传递函数 : G ( s)
对数频率特性 : L( ) 20lg Bode图 :
1 (T ) 2 1
20lg (T ) 2 1
11
三、 理想微分环节
传递函数 : C ( s)
G(s) R( s ) s
频率特性 : C ( j ) G( j ) j R( j ) 对数频率特性 :
L 20 lg dB 90
图4-6 Bode图 : 对数幅频特性L(ω)为过点(1/τ,0)、斜率为20dB/dec的 一条直线。 对数相频特性φ(ω) φ(ω)为一条90o 的水平直线。 如图4-6所示。
图4-8
16
六、振荡环节
1. 传递函数 2. 频率特性
2 n 1 G( s) 2 2 2 2 s 2 s 1 s 2n s n
jarctan 1 1 1 2 2 G ( j ) 2 e ( j ) 2 2 ( j ) 1 (1 2 2 ) 2 (2 ) 2
《机械控制工程基础》第四章 控制系统的频率特性

解:列写力平衡方程
f(t)
Kx(t) Cx(t) f (t)
其传递函数为:G(s) X (s)
1
1 K
1 K
F(s) Cs K C K s 1 Ts 1
K
X(t)
c
f (t) F sin wt 拉氏变换:
F(s) F w s2 w2
输出位移 X (s) G(s)F(s)
x(t)
F K
( T )w 1 Tw2
(1,j0)
w
U
τ<T
当w=0 A(w)=1 w→∞
(w) 0 A(w)
T
() 0
要画准确的奈氏曲线需计算不同频率下的幅值和相位,或实部 和虚部,得到相应的各点,将各点顺次连接得到奈氏曲线。
若系统传递函数是由多个环节组成,幅频特性曲线其幅值 是各环节幅值的乘积,相角是各环节相位相加。
U (w)
比例环节的特点:不改变曲线的形状,只改变L(w)的大小 。
2.积分环节
G( jw) 1 j 1 jw w
L(w)/dB
20
L(w) 20lg A(w) 20lg 1 20lg w 0.1 w
-20dB/dec
1
(w) arctg V (w) 90
U (w)
φ(w)°
-90°
8.延时环节 传递函数 G(s) eτs
频率特性 G( jw) ejw cosTw j sin Tw
U (w) cosTw
jV
V (w) sinTw
A(w) U 2 (w) V 2 (w) 1
(w) arctg V (w) Tw
U (w)
(1,j0) U
w
例3. 已知系统传递函数为 G(s) s 1 ,试画其奈氏曲线图
控制工程,第四章ppt课件

Ai
2、输出信号与输入信号的相位差也是 的非线
性函,称为系统的相频特性,记为 () 。
3、幅频特性和相频特性总称为系统的频率特性,
记作:A() () 或 A()ej() 。
故,频率特性定义为 的复变函数,其幅值
为 A() ,相位为 () 。
控制工程基础
二、频率特性的求法
1、利用频率特性的定义来求取:
G(j) T2 2 T
G(j)arctg T
2l0 g G (j )2l0 g T 2 2 2l0 g T
讨论:
第四章 频域分析法
控制工程基础
第四章 频域分析法
当 T 时
2 lG g ( 0 j) 2 lg T 0 2 lg T 0 0 d , B G ( j) 0 0
控制工程基础
G(j) r 0
r n 122
进而求得谐振峰值:
G(jr)
2
1
12
G(jr)arctg122
第四章 频域分析法
Im
1 Re
n
0
n
n
r
控制工程基础
第四章 频域分析法
7、延时环节:
Im
G(s)es
Re 0
G (j)ej co sjsin
幅值特性 : G( j) 1
相频特性 : G(j)
控制工程基础
2、对数相频特性图: G(j)
第四章 频域分析法
0 0.010.1 1 10 100 (ra/ds)
三、典型环节的对数坐标图
1、比例环节:G(s)=K
G(j)K
控制工程基础
第四章 频域分析法
2lG 0 g (j) w 2lK 0 g , G (j) w 0 o
2、输出信号与输入信号的相位差也是 的非线
性函,称为系统的相频特性,记为 () 。
3、幅频特性和相频特性总称为系统的频率特性,
记作:A() () 或 A()ej() 。
故,频率特性定义为 的复变函数,其幅值
为 A() ,相位为 () 。
控制工程基础
二、频率特性的求法
1、利用频率特性的定义来求取:
G(j) T2 2 T
G(j)arctg T
2l0 g G (j )2l0 g T 2 2 2l0 g T
讨论:
第四章 频域分析法
控制工程基础
第四章 频域分析法
当 T 时
2 lG g ( 0 j) 2 lg T 0 2 lg T 0 0 d , B G ( j) 0 0
控制工程基础
G(j) r 0
r n 122
进而求得谐振峰值:
G(jr)
2
1
12
G(jr)arctg122
第四章 频域分析法
Im
1 Re
n
0
n
n
r
控制工程基础
第四章 频域分析法
7、延时环节:
Im
G(s)es
Re 0
G (j)ej co sjsin
幅值特性 : G( j) 1
相频特性 : G(j)
控制工程基础
2、对数相频特性图: G(j)
第四章 频域分析法
0 0.010.1 1 10 100 (ra/ds)
三、典型环节的对数坐标图
1、比例环节:G(s)=K
G(j)K
控制工程基础
第四章 频域分析法
2lG 0 g (j) w 2lK 0 g , G (j) w 0 o
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
幅频特性 相频特性 实频特性 虚频特性
A() | G ( j) | U 2 () V 2 () 1 V ( ) ( ) G( j ) tan U ( ) U() A() cos()
V() A() sin ()
湖南工程学院机械工程学院
机械控制工程基础
时域分析法是分析控制系统的直接方法,比 较直观、精确。频域分析法,是一种工程上广为 采用的分析和综合系统的间接方法。 频域分析法是一种图解分析法。它依据系统 的又一种数学模型——频率特性,对系统的性能 (如稳定性、快速性和准确性)进行分析。频率 特性是研究控制系统的一种工程方法,应用频率 特性可间接地分析系统的动态性能和稳态性能。 频域分析法的突出优点是可以通过实验直接求得 频率特性来分析系统的品质,应用频率特性分析 系统可以得出定性和定量的结论,并具有明显的物 理含义,频域法分析系统可利用曲线、图表及经 验公式。
第四章 频率特性
T RC
G( j)
U 2 ( j) 1 A()e j( ) U1 ( j) 1 jT
A()
1 1 (T) 2
() arctan( T )
幅值A()随着频率升高而衰减 对于低频信号 (T 1) 对于高频信号 (T 1)
V() A() sin ()
湖南工程学院机械工程学院
机械特性? 联系系统的参数和结构
X r (t ) A sin wt X r (s)= As /( s w )
2 2
增加2个极点
s jw, s jw
X c (s)= G(s) X r (s)
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
•信号的频率特性是信号的内在本质,信号的时域波形是信号的外在形式, 从本质上处理问题将会更深入,全面,方便,更具优越性。
•频率法是应用频率特性研究线性控制系统的一种经典方法,它具有以下特点:
1 .利用奈氏判据,可以根据系统的开环频率特性研究闭环系统的稳定性,而不用 求出特征根。
第四章 频率特性
4.1.3 频率特性的物理意义 频率特性与传递函数的关系: G(jω)=G(s)|s=jω 频率特性表征了系统或元件对不同频率正弦 输入的响应特性。
(ω)大于零时称为 相角超前,小于零 时称为相角滞后。
湖南工程学院机械工程学院
机械控制工程基础
G(s) U 2 (s) 1 U1 (s) 1 T s
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
R
C
r (t ) A sin t c(t ) A | G( j ) | sin(t G( j ))
频率特性与传递函数的关系: G(jω)=G(s)|s=jω
b0 ( j) m b1 ( j) m1 ... b m1 ( j) b m G( j) a 0 ( j) n a1 ( j) n 1 ... a n 1 ( j) a n
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
Part 4.2 频率特性图 4.2.1 频率特性图的定义
4.2.2 典型环节的频率特性图 Nyquist/Bode
积分环节 惯性环节
放大环节 纯微分环节
一阶微分环节
二阶微分环节
振荡环节
延滞环节
湖南工程学院机械工程学院
6 .频率分析法不仅适用于线性定常系统,还可以推广应用于 某些非线性系统。
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
频域分析法的特点是可以根据开环频 率特性去分析闭环系统的性能,并能较方 便地分析系统参数对系统性能的影响,从 而进一步提出改善系统性能的途径。此外 ,除了一些超低频的热工系统,频率特性 都可以方便地由实验确定。频率特性主要 适用于线性定常系统。在线性定常系统中 ,频率特性与输入正弦信号的幅值和相位 无关。但是,这种方法也可以有条件地推 广应用到非线性系统中。
G( j) A()e j( ) U() jV()
幅频特性 相频特性 实频特性 虚频特性
A() | G ( j) | U 2 () V 2 () V ( ) ( ) G( j ) arctan U ( ) U() A() cos()
2、根据系统的频率性能间接地揭示系统的动态特性和稳态特性,可以简单迅速 地判断某些环节或参数对系统性能的影响,指出系统改进的方向。 3 .频率特性物理意义明确,很多元部件的这一特性可用实验方法确定,这对于难 于从分析物理规律着手来列写动态方程的系统有很大意义。
正弦信号发生器
系统或元件
双踪示波器
一路测输入/输出的幅值比,一路测输入/输出的相位之差 不断改变正弦输入的角频率,可得系统的频率特性
a G(s)
a G (s)
A AG( j) (s j) |s j s 2 2 2j
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
a
AG( j) 2j
AG( j) a 2j
G( j) | G( j) | e jG( j) | G( j) | e jG( j)
通过实验直接求取数学模型 扫频试验,无需理论建模。 适用于非线性系统的分析 无需对非线性系统拉氏变换(非常微分方 程,无法进行拉氏变换)。
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
4.1.2 频率特性的求取
1 已知系统的系统方程,输入正弦函数求其稳态 解,取输出稳态分量和输入正弦的复数比;
机械控制工程基础
第四章 频率特性
幅频特性和 相频特性随ω 变化的曲线 如图所示。
A(ω)和φ(ω)曲线
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
G(j)=稳态输出量与输入量的变化
C ( j ) G( j ) C ( j ) R( j ) R( j ) C ( j ) | G ( j ) || | R( j )
设
x c (t) ae jt ae jt b1es1t b2es2t ... b1esn t
A AG( j) (s j) |s j s 2 2 2j
( t 0)
对于稳定的系统, -s1,s2,…,sn 其有负实部
x c (t) ae jt ae jt
G( j) | G( j) | e jG( j)
x c ( t ) ae jt ae jt e j( t G ( j)) e j( t G ( j)) A | G ( j) | 2j A | G ( j) | sin(t G ( j))
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
4.2.1.1 幅相频率特性图-Nyquist图
系统频率特性可表示为
G( j ) A( )e j ( )
用一向量表示某一频率 i 下的 G( j i ) 向 量的长度A( i ),向量极坐标角为 ( i ) , ( ) 的 正方向取为逆时针方向,选极坐标与直角坐标 重合,极坐标的顶点在坐标原点。 如下图所示。
x r (t ) xrm sin(t )
x c (t ) A() xrm sin(t ())
稳态输出量与输入量的频率相同,仅振幅和相位不同。
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
湖南工程学院机械工程学院
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
G( j) G( j) X c ( j) X r ( j) | G( j) ||
X c ( j) X r ( j)
X c ( j) | X r ( j)
G( j) A()e j( ) U() jV()
机械控制工程基础
第四章 频率特性
机械控制工程基础
任课教师:伍新
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
第四章 频率特性
本章主要内容: 4.I 频率特性的基本概念
4.2 频率特性图
4.3 系统开环频率特性
4.4
最小相位和非最小相位系统
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
机械控制工程基础
第四章 频率特性
4.2.1 频率特性图的定义 幅相频率特性 极坐标图 (Nyquist) 对数频率特性 (Bode)
频率对数分度 幅值/相角线性分度
对数幅相频率特性 (Nichols)
以频率为参变量表示对数幅值和相角关系:L(ω) —(ω)图
虚频图/实频图
频率线性分度 幅值/相角线性分度
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
知识要点
频率特性是系统的一种数学模型;频率特性 的三种图形:幅相频率特性曲线(又称极坐标或 Nyquist曲线),对数频率特性曲线(又称Bode 图),对数幅相频率特性曲线(又称Nichols曲 线)。最小相位系统的幅频和相频特性之间存在 唯一的对应关系,利用Nyquist稳定判据可由开 环频率特性判别闭环系统的稳定性,用幅值裕量 和相角裕量来反映系统的相对稳定性。利用等M 圆和等N圆可由开环频率特性求闭环频率特性, 进而定性或定量分析系统的时域响应。
A() 1
A () 1 0 T
() 0
() 90
!频率特性反映了系统(电路)的内在性质,与外界因素无关。
湖南工程学院机械工程学院
机械控制工程基础
第四章 频率特性
频率特性与传递函数的关系: G (jω)=G(s)|s=jω
