高中数学人教a版高一必修一_第一章_集合与函数概念_学业分层测评5 有答案
2019-2020学年高一数学人教A版必修1练习:第一章 集合与函数概念 测评 Word版含解析

{������,������ ≤ ������,
解析根据运算 ab= ������,������ > ������, 得 f(x)=x2|x|
{������2,������ < - 1或������ > 1,
= |������|, - 1 ≤ ������ ≤ 1, 由此可得图象如图所示. 答案 B 12.定义在 R 上的偶函数 f(x)满足:对任意的 x1,x2∈(-∞,0](x1≠x2),有(x2-x1)[f(x2)-f(x1)]>0.则当 n∈N*时,有( ) A.f(-n)<f(n-1)<f(n+1) B.f(n-1)<f(-n)<f(n+1) C.f(n+1)<f(-n)<f(n-1) D.f(n+1)<f(n-1)<f(-n) 解析由(x2-x1)[f(x2)-f(x1)]>0 得 f(x)在(-∞,0]上为增函数. 又 f(x)为偶函数,所以 f(x)在[0,+∞)上为减函数.又 f(-n)=f(n)且 0≤n-1<n<n+1, 故 f(n+1)<f(n)<f(n-1), 即 f(n+1)<f(-n)<f(n-1).故选 C. 答案 C
{������ - 5 < - 3, 3
所以当 A⊆C 时,有 2������ + 3 > 6,解得2<m<2,
3
所以实数 m 的取值范围是2<m<2.
2������ + 1
18.(本小题满分 12 分)已知函数 f(x+1)= ������ + 2 .
(1)求 f(2),f(x); (2)证明:函数 f(x)在[1,17]上为增函数; (3)求函数 f(x)在[1,17]的最大值和最小值. 解(1)f(2)=f(1+1)=1,
高中数学 第一章 集合与函数概念综合测评(含解析)新人教A版必修1-新人教A版高一必修1数学试题

综合测评(一) 集合与函数概念(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.(2014·某某高考)已知全集U={1,2,3,4,5,6,7},集合A={1,3,5,6},则∁U A=( )A.{1,3,5,6} B.{2,3,7}C.{2,4,7} D.{2,5,7}【解析】∵全集U={1,2,3,4,5,6,7},集合A={1,3,5,6},∴∁U A={2,4,7}.【答案】C2.已知集合A={x∈N|-3≤x≤3},则必有( )A.-1∈A B.0∈AC.3∈A D.2∈A【解析】∵A={x∈N|-3≤x≤3}={0,1},∴0∈A.【答案】B3.设集合A={-1,3,5},若f:x→2x-1是集合A到集合B的映射,则集合B可以是( )A.{0,2,3} B.{1,2,3}C.{-3,5} D.{-3,5,9}【解析】将A中的元素-1代入得-3,A中的元素3代入得5,A中的元素5代入得9,故选D.1 / 112 / 11【答案】D4.(2014·某某高一检测)下列各组函数表示相等函数的是( )A .f (x )=x -2,g (x )=x 2-4x +2B .f (x )=|x |x,g (x )=1 C .f (x )=x 2-2x -1,g (t )=t 2-2t -1D .f (x )=12,g (x )=(x -1)02【解析】D 中f (x )、g (x )的定义域不同,因此不是相等函数;而C 只是表示变量的字母不一样,表示的函数是相等的.【答案】A5.已知y =f (x )是偶函数,且f (4)=5,那么f (4)+f (-4)的值为( )A .5B .10C .8D .不确定 【解析】 ∵y =f (x )是偶函数,∴f (-4)=f (4)=5,∴f (4)+f (-4)=10.【答案】B6.(2014·高考)已知集合A ={x |x 2-2x =0},B ={0,1,2},则A ∩B =( )A .{0}B .{0,1}C .{0,2}D .{0,1,2}3 / 11【解析】 ∵A ={x |x 2-2x =0}={0,2},B ={0,1,2},∴A ∩B ={0,2}.【答案】C7.函数f (x )=x|x |的图象是( )A B C D【解析】 由于f (x )=x |x |=⎩⎪⎨⎪⎧1,x >0,-1,x <0,所以其图象为C. 【答案】C8.若函数f (x )满足f (3x +2)=9x +8,则f (x )的解析式是( )A .f (x )=9x +8B .f (x )=3x +2C .f (x )=-3x -4D .f (x )=3x +2或f (x )=-3x -4【解析】f (3x +2)=9x +8=3(3x +2)+2,∴f (x )=3x +2.【答案】B4 / 11 9.(2013·某某高考)(3-a )(a +6)(-6≤a ≤3)的最大值为( )A .9B.92 C .3D.322【解析】(3-a )(a +6)=-a 2-3a +18 =-⎝ ⎛⎭⎪⎫a 2+3a +94+814 = -⎝ ⎛⎭⎪⎫a +322+814,由于-6≤a ≤3, ∴当a =-32时,(3-a )(a +6)有最大值92.【答案】B10.若函数f (3-2x )的定义域为[-1,2],则函数f (x )的定义域为() A.⎣⎢⎡⎦⎥⎤-52,-1 B .[-1,2] C.[]-1,5 D.⎣⎢⎡⎦⎥⎤12,2【解析】 由-1≤x ≤2,得-1≤3-2x ≤5,故选C.【答案】C5 / 1111.若函数f (x )=⎩⎪⎨⎪⎧2,x >0,x 2,x ≤0,则满足f (a )=1的实数a 的值为( ) A .-1 B .1 C .-2 D .2【解析】 依题意,知满足f (a )=1的实数a 必不超过零,于是有⎩⎪⎨⎪⎧a ≤0,a 2=1,由此解得a =-1, 选A.【答案】A12.函数f (x )是定义在[0,+∞)上的增函数,则满足f (2x -1)<f ⎝ ⎛⎭⎪⎫13的x 的取值X 围是( ) A.⎝ ⎛⎭⎪⎫13,23 B.⎣⎢⎡⎭⎪⎫13,23 C.⎝ ⎛⎭⎪⎫12,23 D.⎣⎢⎡⎭⎪⎫12,23 【解析】 根据题意,得⎩⎪⎨⎪⎧2x -1≥0,2x -1<13,解得12≤x <23,选D. 【答案】D二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.设集合M ={x |x 是小于5的质数},则M 的真子集的个数为________.【解析】 由题意可知M ={2,3},∴M 的真子集有∅,{2},{3}共3个.【答案】 36 / 1114.用列举法表示集合:M =⎩⎨⎧⎭⎬⎫m ⎪⎪⎪10m +1∈Z,m ∈Z =________. 【解析】 由10m +1∈Z ,且m ∈Z,知m +1是10的约数,故|m +1|=1,2,5,10,从而m 的值为-11,-6,-3,-2,0,1,4,9. 【答案】 {-11,-6,-3,-2,0,1,4,9}15.已知集合A ={x |x ≥2},B ={x |x ≥m },且A ∪B =A ,则实数m 的取值X 围是________.【解析】 ∵A ∪B =A ,即B ⊆A ,∴实数m 的取值X 围为[2,+∞).【答案】 [2,+∞)16.设函数f (x )=x 2+(a +1)x +a x为奇函数,则实数a =________. 【解析】f (x )=x 2+(a +1)x +a x =x +a x +a +1,因此有f (-x )=-x +a -x+a +1,又f (x )为奇函数,所以f (-x )+f (x )=0,即2a +2=0,所以a =-1.【答案】 -1三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)已知全集U =R ,集合A ={x |1≤x <4},B ={x |3x -1<x +5},求:(1)A ∩B ;(2)∁U A ∪B .7 / 11【解】 (1)由已知得:B =(-∞,3),A =[1,4),∴A ∩B =[1,3).(2)由已知得:∁U A =(-∞,1)∪[4,+∞),∁U A ∪B =(-∞,3)∪[4,+∞).18.(本小题满分12分)(2014·某某高一检测)已知函数f (x )=⎩⎪⎨⎪⎧-x +3,x ≤0,4x ,x >0. (1)求f (f (-1)).(2)若f (x 0)>2,求x 0的取值X 围.【解】 (1)因为f (-1)=-(-1)+3=4,所以f (f (-1))=f (4)=4×4=16.(2)当x 0≤0时,令2<-x 0+3,得x 0<1,此时x 0≤0;当x 0>0时,令2<4x 0,得x 0>12. 所以x 0≤0或x 0>12. 19.(本小题满分12分)设全集U ={2,4,-(a -3)2},集合A ={2,a 2-a +2},若∁U A ={-1},某某数a 的值.8 / 11【解】 由∁U A ={-1},可得⎩⎪⎨⎪⎧-1∈U ,-1∉A , 所以⎩⎪⎨⎪⎧-(a -3)2=-1,a 2-a +2≠-1, 解得a =4或a =2.当a =2时,A ={2,4},满足A ⊆U ,符合题意;当a =4时,A ={2,14},不满足A ⊆U ,故舍去.综上,a 的值为2.20.(本小题满分12分)某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一天能来回16次,如果每次拖7节车厢,则每天能来回10次.(1)若每天来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式;(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数.【解】 (1)设每天来回y 次,每次挂x 节车厢,由题意设y =kx +b .当x =4时,y =16,当x =7时,y =10,得到16=4k +b ,10=7k +b .得到16=4k +b ,10=7k +b .解得k =-2,b =24,∴y =-2x +24.(2)设每天来回y 次,每次挂x 节车厢,由题意知,每天挂车厢最多时,运营人数最多,设每天运营S 节车厢,则S =xy =x (-2x +24)=-2x 2+24x =-2(x -6)2+72,所以当x =6时,S max =72,此时y =12,则每日最多运营人数为110×72=7 920(人).9 / 11即这列火车每天来回12次,才能使运营人数最多,每天最多运营人数为7 920人.21.(本小题满分12分)已知函数f (x )=2x +1x +1. (1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论;(2)求该函数在区间[]1,4上的最大值与最小值.【解】 (1)f (x )在[1,+∞)上是增函数.证明如下:任取x 1,x 2∈[1,+∞),且x 1<x 2,f (x 1)-f (x 2)=2x 1+1x 1+1-2x 2+1x 2+1=x 1-x 2(x 1+1)(x 2+1). ∵x 1-x 2<0,(x 1+1)(x 2+1)>0,∴f (x 1)<f (x 2),∴函数f (x )在[1,+∞)上是增函数.(2)由(1)知函数f (x )在[1,4]上是增函数,∴最大值为f (4)=2×4+14+1=95,最小值为f (1)=2×1+11+1=32. 22.(本小题满分12分)已知函数f (x )=ax +b x 2+1是定义在(-1,1)上的奇函数,且f ⎝ ⎛⎭⎪⎫12=25. (1)确定函数f (x )的解析式;(2)当x ∈(-1,1)时判断函数f (x )的单调性,并证明;(3)解不等式f (2x -1)+f (x )<0.【解】 (1)由题意可知f (-x )=-f (x ),10 / 11 ∴-ax +b 1+x 2=-ax +b1+x 2,∴b =0.∴f (x )=ax1+x 2.∵f ⎝ ⎛⎭⎪⎫12=25,∴a =1.∴f (x )=x1+x 2.(2)f (x )在(-1,1)上为增函数.证明:设-1<x 1<x 2<1,则f (x 1)-f (x 2)=x 11+x 21-x 21+x 22=(x 1-x 2)(1-x 1x 2)(1+x 21)(1+x 22)∵-1<x 1<x 2<1,∴x 1-x 2<0,∴1-x 1x 2>0, 1+x 21>0,1+x 22>0,∴(x 1-x 2)(1-x 1x 2)(1+x 21)(1+x 22)<0.∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2). ∴f (x )在(-1,1)上为增函数.(3)∵f (2x -1)+f (x )<0,∴f (2x -1)<-f (x ),word11 / 11 又f (x )是定义在(-1,1)上的奇函数, ∴f (2x -1)<f (-x ),∴⎩⎪⎨⎪⎧-1<2x -1<1,-1<-x <1,2x -1<-x ,∴0<x <13.∴不等式f (2x -1)+f (x )<0的解集为⎝ ⎛⎭⎪⎫0,13.。
人教版 高中数学必修一课后习题配套参考答案(解析版)

人教版高中数学必修1课后习题答案(第一章集合与函数概念)人教A版习题1.2(第24页)练习(第32页)1.答:在一定的范围内,生产效率随着工人数量的增加而提高,当工人数量达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率随着工人数量的增加而降低.由此可见,并非是工人越多,生产效率就越高.2.解:图象如下[8,12]是递增区间,[12,13]是递减区间,[13,18]是递增区间,[18,20]是递减区间.3.解:该函数在[1,0]-上是减函数,在[0,2]上是增函数,在[2,4]上是减函数,在[4,5]上是增函数. 4.证明:设12,x x R∈,且12x x <, 因为121221()()2()2()0f x f x x x x x -=--=->,即12()()f x f x >, 所以函数()21f x x =-+在R 上是减函数.5.最小值.练习(第36页)1.解:(1)对于函数42()23f x x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有4242()2()3()23()f x x x x x f x -=-+-=+=,所以函数42()23f x x x =+为偶函数;(2)对于函数3()2f x x x =-,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有33()()2()(2)()f x x x x x f x -=---=--=-,所以函数3()2f x x x =-为奇函数;(3)对于函数21()x f x x+=,其定义域为(,0)(0,)-∞+∞U ,因为对定义域内每一个x 都有22()11()()x x f x f x x x-++-==-=--,所以函数21()x f x x+=为奇函数;(4)对于函数2()1f x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有22()()11()f x x x f x -=-+=+=,所以函数2()1f x x =+为偶函数.2.解:()f x 是偶函数,其图象是关于y 轴对称的;()g x 是奇函数,其图象是关于原点对称的.习题1.3(第39页)1.解:(1)函数在5(,)2-∞上递减;函数在5[,)2+∞上递增; (2)函数在(,0)-∞上递增;函数在[0,)+∞上递减.2.证明:(1)设120x x <<,而2212121212()()()()f x f x x x x x x x -=-=+-, 由12120,0x x x x +<-<,得12()()0f x f x ->,即12()()f x f x >,所以函数2()1f x x =+在(,0)-∞上是减函数;(2)设120x x <<,而1212211211()()x x f x f x x x x x --=-=,由12120,0x x x x >-<,得12()()0f x f x -<,即12()()f x f x <,所以函数1()1f x x=-在(,0)-∞上是增函数. 3.解:当0m >时,一次函数y mx b =+在(,)-∞+∞上是增函数;当0m <时,一次函数y mx b =+在(,)-∞+∞上是减函数,令()f x mx b =+,设12x x <, 而1212()()()f x f x m x x -=-,当0m >时,12()0m x x -<,即12()()f x f x <, 得一次函数y mx b =+在(,)-∞+∞上是增函数;当0m <时,12()0m x x ->,即12()()f x f x >, 得一次函数y mx b =+在(,)-∞+∞上是减函数.4.解:自服药那一刻起,心率关于时间的一个可能的图象为5.解:对于函数21622100050x y x =-+-, 当162405012()50x=-=⨯-时,max 307050y =(元), 即每辆车的月租金为4050元时,租赁公司最大月收益为307050元. 6.解:当0x <时,0x ->,而当0x ≥时,()(1)f x x x =+,即()(1)f x x x -=--,而由已知函数是奇函数,得()()f x f x -=-,得()(1)f x x x -=--,即()(1)f x x x =-,所以函数的解析式为(1),0()(1),0x x x f x x x x +≥⎧=⎨-<⎩. B 组1.解:(1)二次函数2()2f x x x =-的对称轴为1x =,则函数()f x 的单调区间为(,1),[1,)-∞+∞,且函数()f x 在(,1)-∞上为减函数,在[1,)+∞上为增函数,函数()g x 的单调区间为[2,4], 且函数()g x 在[2,4]上为增函数; (2)当1x =时,min ()1f x =-,因为函数()g x 在[2,4]上为增函数,所以2min ()(2)2220g x g ==-⨯=.2.解:由矩形的宽为xm ,得矩形的长为3032xm -,设矩形的面积为S , 则23033(10)22x x x S x --==-, 当5x =时,2max 37.5S m =,即宽5x =m 才能使建造的每间熊猫居室面积最大,且每间熊猫居室的最大面积是237.5m .3.判断()f x 在(,0)-∞上是增函数,证明如下: 设120x x <<,则120x x ->->,因为函数()f x 在(0,)+∞上是减函数,得12()()f x f x -<-, 又因为函数()f x 是偶函数,得12()()f x f x <,所以()f x 在(,0)-∞上是增函数.复习参考题(第44页)A 组1.解:(1)方程29x =的解为123,3x x =-=,即集合{3,3}A =-;(2)12x ≤≤,且x N ∈,则1,2x =,即集合{1,2}B =;(3)方程2320xx -+=的解为121,2x x ==,即集合{1,2}C =.2.解:(1)由PA PB =,得点P 到线段AB 的两个端点的距离相等,即{|}P PA PB =表示的点组成线段AB 的垂直平分线;(2){|3}P POcm =表示的点组成以定点O 为圆心,半径为3cm 的圆. 3.解:集合{|}P PA PB =表示的点组成线段AB 的垂直平分线, 集合{|}P PA PC =表示的点组成线段AC 的垂直平分线,得{|}{|}P PA PB P PA PC ==I 的点是线段AB 的垂直平分线与线段AC 的垂直平分线的交点,即ABC ∆的外心.4.解:显然集合{1,1}A =-,对于集合{|1}B x ax ==,当0a=时,集合B =∅,满足B A ⊆,即0a =;当0a ≠时,集合1{}B a=,而B A ⊆,则11a =-,或11a =,得1a =-,或1a =,综上得:实数a 的值为1,0-,或1.5.解:集合20(,)|{(0,0)}30x y A B x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭I ,即{(0,0)}A B =I ;集合20(,)|23x y A C x y x y ⎧-=⎫⎧==∅⎨⎨⎬-=⎩⎩⎭I,即A C =∅I ;集合3039(,)|{(,)}2355x y B C x y x y ⎧+=⎫⎧==-⎨⎨⎬-=⎩⎩⎭I; 则39()(){(0,0),(,)}55A B B C =-IU I .6.解:(1)要使原式有意义,则2050x x -≥⎧⎨+≥⎩,即2x ≥,得函数的定义域为[2,)+∞;(2)要使原式有意义,则40||50x x -≥⎧⎨-≠⎩,即4x ≥,且5x ≠,得函数的定义域为[4,5)(5,)+∞U .7.解:(1)因为1()1x f x x -=+, 所以1()1a f a a -=+,得12()1111a f a a a -+=+=++, 即2()11f a a +=+;(2)因为1()1xf x x-=+,所以1(1)(1)112a af a a a -++==-+++, 即(1)2af a a +=-+.8.证明:(1)因为221()1x f x x +=-,所以22221()1()()1()1x x f x f x x x +-+-===---,即()()f x f x -=;(2)因为221()1x f x x+=-, 所以222211()11()()111()x x f f x x x x++===---, 即1()()f f x x=-.9.解:该二次函数的对称轴为8k x=, 函数2()48f x x kx =--在[5,20]上具有单调性, 则208k ≥,或58k ≤,得160k ≥,或40k ≤, 即实数k 的取值范围为160k ≥,或40k ≤.10.解:(1)令2()f x x -=,而22()()()f x x x f x ---=-==,即函数2y x -=是偶函数; (2)函数2y x -=的图象关于y 轴对称; (3)函数2y x -=在(0,)+∞上是减函数; (4)函数2y x -=在(,0)-∞上是增函数.B 组1.解:设同时参加田径和球类比赛的有x 人, 则158143328x ++---=,得3x =,只参加游泳一项比赛的有15339--=(人),即同时参加田径和球类比赛的有3人,只参加游泳一项比赛的有9人.2.解:因为集合A ≠∅,且20x ≥,所以0a ≥.3.解:由(){1,3}U A B =U ð,得{2,4,5,6,7,8,9}A B =U ,集合A B U 里除去()U A B I ð,得集合B , 所以集合{5,6,7,8,9}B =.4.解:当0x ≥时,()(4)f x x x =+,得(1)1(14)5f =⨯+=; 当0x <时,()(4)f x x x =-,得(3)3(34)21f -=-⨯--=;(1)(5),1(1)(1)(3),1a a a f a a a a ++≥-⎧+=⎨+-<-⎩. .5.证明:(1)因为()f x ax b =+,得121212()()222x x x x a f a b x x b ++=+=++, 121212()()()222f x f x ax b ax b a x x b ++++==++, 所以1212()()()22x x f x f x f ++=; (2)因为2()g x x ax b =++,得22121212121()(2)()242x x x x g x x x x a b ++=++++, 22121122()()1[()()]22g x g x x ax b x ax b +=+++++ 2212121()()22x x x x a b +=+++, 因为2222212121212111(2)()()0424x x x x x x x x ++-+=--≤, 即222212121211(2)()42x x x x x x ++≤+, 所以1212()()()22x x g x g x g ++≤. 6.解:(1)函数()f x 在[,]b a --上也是减函数,证明如下:设12b x x a -<<<-,则21a x x b <-<-<, 因为函数()f x 在[,]a b 上是减函数,则21()()f x f x ->-,又因为函数()f x 是奇函数,则21()()f x f x ->-,即12()()f x f x >, 所以函数()f x 在[,]b a --上也是减函数;(2)函数()g x 在[,]b a --上是减函数,证明如下: 设12b x x a -<<<-,则21a x x b <-<-<,因为函数()g x 在[,]a b 上是增函数,则21()()g x g x -<-, 又因为函数()g x 是偶函数,则21()()g x g x <,即12()()g x g x >, 所以函数()g x 在[,]b a --上是减函数.7.解:设某人的全月工资、薪金所得为x 元,应纳此项税款为y 元,则 0,02000(2000)5%,2000250025(2500)10%,25004000175(4000)15%,40005000x x x y x x x x ≤≤⎧⎪-⨯<≤⎪=⎨+-⨯<≤⎪⎪+-⨯<≤⎩ 由该人一月份应交纳此项税款为26.78元,得25004000x <≤, 25(2500)10%26.78x +-⨯=,得2517.8x =, 所以该人当月的工资、薪金所得是2517.8元.。
高中数学 人教A版必修一 第一章集合与函数的概念课后作业答案

高一数学必修一第一章课时作业 1.1.1 集合的含义与表示第1课时 集合的含义 一、基础过关1. 下列各项中,不可以组成集合的是( )A .所有的正数B .等于2的数C .接近于0的数D .不等于0的偶数2. 集合A 中只含有元素a ,则下列各式正确的是( )A .0∈AB .a ∉AC .a ∈AD .a =A 3. 由实数x ,-x ,|x |,x 2,-3x 3所组成的集合,最多含( )A .2个元素B .3个元素C .4个元素D .5个元素4. 由下列对象组成的集体属于集合的是________.(填序号)①不超过π的正整数;②本班中成绩好的同学;③高一数学课本中所有的简单题;④平方后等于自身的数.5. 如果有一集合含有三个元素1,x ,x 2-x ,则实数x 的取值范围是________. 6. 判断下列说法是否正确?并说明理由.(1)参加2012年伦敦奥运会的所有国家构成一个集合; (2)未来世界的高科技产品构成一个集合; (3)1,0.5,32,12组成的集合含有四个元素;(4)某校的年轻教师.7.已知集合A 是由a -2,2a 2+5a,12三个元素组成的,且-3∈A ,求a .二、能力提升8. 已知集合S 中三个元素a ,b ,c 是△ABC 的三边长,那么△ABC 一定不是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形9. 已知集合A 是由0,m ,m 2-3m +2三个元素组成的集合,且2∈A ,则实数m 为( )A .2B .3C .0或3D .0,2,3均可10.方程x 2-2x -3=0的解集与集合A 相等,若集合A 中的元素是a ,b ,则a +b =________.11.设P 、Q 为两个非空实数集合,P 中含有0,2,5三个元素,Q 中含有1,2,6三个元素,定义集合P +Q 中的元素是a +b ,其中a ∈P ,b ∈Q ,则P +Q 中元素的个数是多少?三、探究与拓展12.设A 为实数集,且满足条件:若a ∈A ,则11-a∈A (a ≠1).求证:(1)若2∈A ,则A 中必还有另外两个元素; (2)集合A 不可能是单元素集.需要高中数学的朋友请加QQ :182337727,有你想要的精心整理的导学案、专题训练、综合训练、单元试题第2课时 集合的表示一、基础过关1. 集合{x ∈N +|x -3<2}用列举法可表示为( )A .{0,1,2,3,4}B .{1,2,3,4}C .{0,1,2,3,4,5}D .{1,2,3,4,5} 2. 集合{(x ,y )|y =2x -1}表示( )A .方程y =2x -1B .点(x ,y )C .平面直角坐标系中的所有点组成的集合D .函数y =2x -1图象上的所有点组成的集合3. 将集合⎩⎪⎨⎪⎧(x ,y )|⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x +y =52x -y =1表示成列举法,正确的是 ( )A .{2,3}B .{(2,3)}C .{(3,2)}D .(2,3)4. 若集合A ={-1,1},B ={0,2},则集合{z |z =x +y ,x ∈A ,y ∈B }中的元素的个数为( )A .5B .4C .3D .25. 用列举法表示下列集合:(1)A ={x ∈N ||x |≤2}=________;(2)B ={x ∈Z ||x |≤2}=________; (3)C ={(x ,y )|x 2+y 2=4,x ∈Z ,y ∈Z }=______. 6. 下列各组集合中,满足P =Q 的有________.(填序号)①P ={(1,2)},Q ={(2,1)};②P ={1,2,3},Q ={3,1,2}; ③P ={(x ,y )|y =x -1,x ∈R },Q ={y |y =x -1,x ∈R }. 7. 用适当的方法表示下列集合.(1)方程x (x 2+2x +1)=0的解集;(2)在自然数集内,小于1 000的奇数构成的集合; (3)不等式x -2>6的解的集合;(4)大于0.5且不大于6的自然数的全体构成的集合.8. 已知集合A ={x |y =x 2+3},B ={y |y =x 2+3},C ={(x ,y )|y =x 2+3},它们三个集合相等吗?试说明理由.二、能力提升9. 下列集合中,不同于另外三个集合的是( )A .{x |x =1}B .{y |(y -1)2=0}C .{x =1}D .{1} 10.集合M ={(x ,y )|xy <0,x ∈R ,y ∈R }是( )A .第一象限内的点集B .第三象限内的点集C .第四象限内的点集D .第二、四象限内的点集11.下列各组中的两个集合M 和N ,表示同一集合的是______.(填序号)①M ={π},N ={3.141 59}; ②M ={2,3},N ={(2,3)};③M ={x |-1<x ≤1,x ∈N },N ={1}; ④M ={1,3,π},N ={π,1,|-3|}.12.集合A ={x |kx 2-8x +16=0},若集合A 只有一个元素,试求实数k 的值,并用列举法表示集合A .三、探究与拓展13.定义集合运算A *B ={z |z =xy ,x ∈A ,y ∈B }.设A ={1,2},B ={0,2},则集合A *B 的所有元素之和是多少?1.1.2 集合间的基本关系一、基础过关1. 下列集合中,结果是空集的是( )A .{x ∈R |x 2-1=0}B .{x |x >6或x <1}C .{(x ,y )|x 2+y 2=0}D .{x |x >6且x <1}2. 集合P ={x |y =x +1},集合Q ={y |y =x -1},则P 与Q 的关系是( )A .P =QB .P QC .QPD .P ∩Q =∅3. 下列命题:①空集没有子集;②任何集合至少有两个子集;③空集是任何集合的真子集;④若∅A ,则A ≠∅. 其中正确的个数是( )A .0B .1C .2D .34. 下列正确表示集合M ={-1,0,1}和N ={x |x 2+x =0}关系的Venn 图是()5. 已知M ={x |x ≥22,x ∈R },给定下列关系:①π∈M ;②{π}M ;③πM ;④{π}∈M .其中正确的有________.(填序号)6. 已知集合A ={x |1<x <2},B ={x |x <a },若A B ,则实数a 的取值范围是________. 7. 已知集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},若B ⊆A ,求实数m 的取值范围.8. 若集合A ={x |x 2+x -6=0},B ={x |x 2+x +a =0},且B ⊆A ,求实数a 的取值范围.二、能力提升9. 适合条件{1}⊆A {1,2,3,4,5}的集合A 的个数是( )A .15个B .16个C .31个D .32个10.集合M ={x |x =3k -2,k ∈Z },P ={y |y =3n +1,n ∈Z },S ={z |z =6m +1,m Z ∈}之间的关系是 ( )A .S P MB .S =P MC .S P =MD .P =M S11.已知集合A {2,3,7},且A 中至多有1个奇数,则这样的集合共有________个. 12.已知集合A ={x |1<ax <2},B ={x |-1<x <1},求满足A ⊆B 的实数a 的取值范围.三、探究与拓展13.已知集合A ={x ||x -a |=4},B ={1,2,b }.问是否存在实数a ,使得对于任意实数b (b ≠1,b ≠2)都有A ⊆B .若存在,求出对应的a 值;若不存在,说明理由.1.1.3 集合的基本运算第1课时 并集与交集一、基础过关1. 若集合A ={0,1,2,3},B ={1,2,4},则集合A ∪B 等于( )A .{0,1,2,3,4}B .{1,2,3,4}C .{1,2}D .{0}2. 集合A ={x |-1≤x ≤2},B ={x |x <1},则A ∩B 等于( )A .{x |x <1}B .{x |-1≤x ≤2}C .{x |-1≤x ≤1}D .{x |-1≤x <1}3. 若集合A ={参加伦敦奥运会比赛的运动员},集合B ={参加伦敦奥运会比赛的男运动员},集合C ={参加伦敦奥运会比赛的女运动员},则下列关系正确的是( )A .A ⊆B B .B ⊆C C .A ∩B =CD .B ∪C =A4. 已知集合M ={(x ,y )|x +y =2},N ={(x ,y )|x -y =4},那么集合M ∩N 为( )A .x =3,y =-1B .(3,-1)C .{3,-1}D .{(3,-1)} 5. 设集合M ={-1,0,1},N ={x |x 2≤x },则M ∩N 等于( )A .{0}B .{0,1}C .{-1,1}D .{-1,0,1}6. 设集合A ={-1,1,3},B ={a +2,a 2+4},A ∩B ={3},则实数a =________. 7. 设A ={-4,2a -1,a 2},B ={a -5,1-a,9},已知A ∩B ={9},求A ∪B .8. 设集合A ={-2},B ={x |ax +1=0,a R ∈},若A ∩B =B ,求a 的值.二、能力提升9. 已知集合A ={1,3,m },B ={1,m },A ∪B =A ,则m 等于( )A .0或 3B .0或3C .1或 3D .1或310.设集合A={-3,0,1},B={t 2-t+1}.若A∪B=A,则t=________.11.设集合A={x|-1≤x≤2},B={x|-1<x≤4},C={x|-3<x<2}且集合A∩(B∪C)={x|a≤x≤b},则a=________,b=________.12.已知方程x2+px+q=0的两个不相等实根分别为α,β,集合A={α,β},B={2,4,5,6},C={1,2,3,4},A∩C=A,A∩B=∅.求p,q的值.三、探究与拓展13.已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.(1)A∩B=∅;(2)A⊆(A∩B).第2课时补集及综合应用一、基础过关1.已知集合U={1,3,5,7,9},A={1,5,7},则∁U A等于() A.{1,3} B.{3,7,9} C.{3,5,9} D.{3,9}2.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁U A)∪B为() A.{1,2,4} B.{2,3,4} C.{0,2,4} D.{0,2,3,4}3.设集合A={x|1<x<4},集合B={x|-1≤x≤3},则A∩(∁R B)等于() A.(1,4) B.(3,4) C.(1,3) D.(1,2)∪(3,4)4.设全集U和集合A、B、P满足A=∁U B,B=∁U P,则A与P的关系是() A.A=∁U P B.A=P C.A P D.P A5.设U={0,1,2,3},A={x∈U|x2+mx=0},若∁U A={1,2},则实数m=________.6.设全集U={x|x<9且x∈N},A={2,4,6},B={0,1,2,3,4,5,6},则∁U A=____________,∁U B=________,∁B A=________.7.设全集是数集U={2,3,a2+2a-3},已知A={b,2},∁U A={5},求实数a,b的值.8.(1)设全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},求N∩(∁U M);(2)设集合M={m∈Z|-3<m<2},N={n∈Z|-1≤n≤3},求M∪N.二、能力提升9.如图,I是全集,M、P、S是I的3个子集,则阴影部分所表示的集合是()A.(M∩P)∩S B.(M∩P)∪S C.(M∩P)∩(∁I S) D.(M∩P)∪(∁I S)10.已知全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8},则(∁U A)∩(∁U B)等于()A.{5,8} B.{7,9} C.{0,1,3} D.{2,4,6}11.已知全集U,A B,则∁U A与∁U B的关系是____________________.12.已知集合A={1,3,x},B={1,x2},设全集为U,若B∪(∁U B)=A,求∁U B.三、探究与拓展13.学校开运动会,某班有30名学生,其中20人报名参加赛跑项目,11人报名参加跳跃项目,两项都没有报名的有4人,问两项都参加的有几人?习题课一、基础过关1.设P={x|x<4},Q={x|x2<4},则()A.P⊆Q B.Q⊆P C.P⊆∁R Q D.Q⊆∁R P2.符合条件{a} P⊆{a,b,c}的集合P的个数是()A.2 B.3 C.4 D.53.已知集合A,B均为集合U={1,3,5,7,9}的子集,若A∩B={1,3},(∁U A)∩B={5},则集合B等于() A.{1,3} B.{3,5} C.{1,5} D.{1,3,5}4.设M={x|x=a2+1,a∈N*},P={y|y=b2-4b+5,b∈N*},则下列关系正确的是()A.M=P B.M P C.P M D.M与P没有公共元素5.全集U={1,2,3,4,5,6},集合M={2,3,5},N={4,5},则∁U(M∪N)等于()A.{1,3,5} B.{2,4,6} C.{1,5} D.{1,6}6.已知集合A={x|x≤2},B={x|x>a},如果A∪B=R,那么a的取值范围是________.7.已知集合A={x|-1≤x<3},B={x|2x-4≥x-2}.(1)求A∩B;(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.8.设A={x|x2+ax+b=0},B={x|x2+cx+15=0},又A∪B={3,5},A∩B={3},求实数a,b,c的值.二、能力提升9.已知集合A={x|x<3或x≥7},B={x|x<a}.若(∁U A)∩B≠∅,则a的取值范围为()A.a>3 B.a≥3 C.a≥7 D.a>710.集合A={1,2,3,5},当x∈A时,若x-1∉A,x+1∉A,则称x为A的一个“孤立元素”,则A中孤立元素的个数为____.11.设U =R ,M ={x |x ≥1},N ={x |0≤x <5},则(∁U M )∪(∁U N )=________.12.某班50名同学参加一次智力竞猜活动,对其中A ,B ,C 三道知识题作答情况如下:答错A 者17人,答错B 者15人,答错C 者11人,答错A ,B 者5人,答错A ,C 者3人,答错B ,C 者4人,A ,B ,C 都答错的有1人,问A ,B ,C 都答对的有多少人?三、探究与拓展13.已知集合A ={x |1<x <3},B ={x |2≤x ≤4}.(1)试定义一种新的集合运算Δ,使A ΔB ={x |1<x <2}; (2)按(1)的运算,求B ΔA .需要高中数学的朋友请加QQ :182337727,有你想要的精心整理的导学案、专题训练、综合训练、单元试题1.2.1 函数的概念一、基础过关 1. 下列对应:①M =R ,N =N +,对应关系f :“对集合M 中的元素,取绝对值与N 中的元素对应”; ②M ={1,-1,2,-2},N ={1,4},对应关系f :x →y =x 2,x ∈M ,y ∈N ;③M ={三角形},N ={x |x >0},对应关系f :“对M 中的三角形求面积与N 中元素对应”. 是集合M 到集合N 上的函数的有( )A .1个B .2个C .3个D .0个 2. 下列各组函数中,表示同一个函数的是( )A .y =x -1和y =x 2-1x +1B .y =x 0和y =1C .f (x )=x 2和g (x )=(x +1)2D .f (x )=(x )2x 和g (x )=x(x )23. 函数y =1-x +x 的定义域为( )A .{x |x ≤1}B .{x |x ≥0}C .{x |x ≥1或x ≤0}D .{x |0≤x ≤1}4. 函数y =x +1的值域为( )A .[-1,+∞)B .[0,+∞)C .(-∞,0]D .(-∞,-1]5. 已知函数f (x )=2x -3,x ∈{x ∈N |1≤x ≤5},则函数f (x )的值域为________. 6. 若A ={x |y =x +1},B ={y |y =x 2+1},则A ∩B =________ 7. 判断下列对应是否为集合A 到集合B 的函数.(1)A =R ,B ={x |x >0},f :x →y =|x |; (2)A =Z ,B =Z ,f :x →y =x 2;(3)A =Z ,B =Z ,f :x →y =x ; (4)A ={x |-1≤x ≤1},B ={0},f :x →y =0. 8. 已知函数f (1-x1+x )=x ,求f (2)的值.二、能力提升9. 设集合M ={x |0≤x ≤2},N ={y |0≤y ≤2},那么下面的4个图形中,能表示集合M 到集合N 的函数关系的有( )A .①②③④B .①②③C .②③D .② 10.下列函数中,不满足...f (2x )=2f (x )的是( )A .f (x )=|x |B .f (x )=x -|x |C .f (x )=x +1D .f (x )=-x11.若函数f (x )的定义域是[0,1],则函数f (2x )+f (x +23)的定义域为________.12.如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.根据这个曲线图,请你回答下列问题:(1)最初到达离家最远的地方是什么时间?离家多远? (2)何时开始第一次休息?休息多长时间? (3)第一次休息时,离家多远? (4)11∶00到12∶00他骑了多少千米?(5)他在9∶00~10∶00和10∶00~10∶30的平均速度分别是多少? (6)他在哪段时间里停止前进并休息用午餐?三、探究与拓展13.如图,某灌溉渠的横断面是等腰梯形,底宽为2 m ,渠深为1.8 m ,斜坡的倾斜角是45°.(临界状态不考虑)(1)试将横断面中水的面积A (m 2)表示成水深h (m)的函数;(2)确定函数的定义域和值域; (3)画出函数的图象.1.2.2 函数的表示法第1课时 函数的表示法一、基础过关1. 一个面积为100 cm 2的等腰梯形,上底长为x cm ,下底长为上底长的3倍,则把它的高y 表示成x 的函数为( )A .y =50x (x >0)B .y =100x (x >0)C .y =50x(x >0)D .y =100x(x >0)2. 一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则正确论断的个数是( ) A .0B .1C .2D .33. 已知x ≠0时,函数f (x )满足f (x -1x )=x 2+1x2,则f (x )的表达式为( )A .f (x )=x +1x (x ≠0)B .f (x )=x 2+2(x ≠0)C .f (x )=x 2(x ≠0)D .f (x )=(x -1x )2(x ≠0)4. 已知在x 克a %的盐水中,加入y 克b %(a ≠b )的盐水,浓度变为c %,将y 表示成x 的函数关系式为( )A .y =c -ac -bxB .y =c -a b -c xC .y =c -bc -axD .y =b -cc -ax5. 如图,函数f (x )的图象是折线段ABC ,其中点A ,B ,C 的坐标分别为(0,4),(2,0),(6,4),则f {f [f (2)]}=________.6. 已知f (x )是一次函数,若f (f (x ))=4x +8,则f (x )的解析式为________. 7. 已知f (x )为二次函数且f (0)=3,f (x +2)-f (x )=4x +2.求f (x )的解析式.8. 已知二次函数f (x )满足f (0)=f (4),且f (x )=0的两根的平方和为10,图象过(0,3)点,求f (x )的解析式.二、能力提升9. 如果f (1x )=x1-x,则当x ≠0,1时,f (x )等于( )A .1xB .1x -1C .11-xD .1x-110.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于..6·时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为( )A .y =[x10]B .y =[x +310]C .y =[x +410]D .y =[x +510]11.已知函数y =f (x )满足f (x )=2f (1x )+x ,则f (x )的解析式为____________.12.画出函数f (x )=-x 2+2x +3的图象,并根据图象回答下列问题:(1)比较f (0)、f (1)、f (3)的大小; (2)若x 1<x 2<1,比较f (x 1)与f (x 2)的大小; (3)求函数f (x )的值域.三、探究与拓展13.已知函数y =1ax +1(a <0且a 为常数)在区间(-∞,1]上有意义,求实数a 的值.第2课时 分段函数及映射一、基础过关1. 已知函数f (x )=⎩⎪⎨⎪⎧2x , x >0,x +1, x ≤0,若f (a )+f (1)=0,则实数a 的值等于( )A .-3或-1B .-1C .1D .-3 2. 已知f (x )=⎩⎪⎨⎪⎧x -5 (x ≥6),f (x +2) (x <6),则f (3)为( )A .2B .3C .4D .53. 某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m 元收费.某职工某月缴水费16m 元,则该职工这个月实际用水为( )A .13立方米B .14立方米C .18立方米D .26立方米4. 已知集合P ={x |0≤x ≤4},Q ={y |0≤y ≤2},下列不能表示从P 到Q 的映射的是( )A .f :x →y =12xB .f :x →y =13xC .f :x →y =23xD .f :x →y =x5. 下列对应关系f 中,构成从集合P 到S 的映射的是( )A .P =R ,S =(-∞,0),x ∈P ,y ∈S ,f ∶x →y =|x |B .P =N ,S =N +,x ∈P ,y ∈S ,f ∶y =x 2C .P ={有理数},S ={数轴上的点},x ∈P ,f ∶x →数轴上表示x 的点D .P =R ,S ={y |y >0},x ∈P ,y ∈S ,f ∶x →y =1x26. 设A =Z ,B ={x |x =2n +1,n ∈Z },C =R ,且从A 到B 的映射是x →2x -1,从B 到C 的映射是y →12y +1,则经过两次映射,A 中元素1在C 中的象为________. 7. 化简f (x )=x +|x |x ,并作图求值域.8. 已知f (x )=⎩⎪⎨⎪⎧x 2 (-1≤x ≤1)1 (x >1或x <-1),(1)画出f (x )的图象; (2)求f (x )的定义域和值域. 二、能力提升9. 已知函数y =⎩⎪⎨⎪⎧x 2+1(x ≤0),-2x (x >0),使函数值为5的x 的值是( )A .-2B .2或-52 C .2或-2D .2或-2或-5210.已知函数f (x )的图象如下图所示,则f (x )的解析式是________.11.设f (x )=⎩⎪⎨⎪⎧2x +2, -1≤x <0,-12x , 0<x <2,3, x ≥2,则f {f [f (-34)]}的值为______,f (x )的定义域是_ __.12. 如图,动点P 从边长为4的正方形ABCD 的顶点B 开始,顺次经C 、D 、A 绕边界运动,用x 表示点P 的行程,y 表示△APB 的面积,求函数y =f (x ) 的解析式.三、探究与拓展13.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v (单位:千米/小时)是车流密度x (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当20≤x ≤200时,车流速度v 是车流密度x 的一次函数.当0≤x ≤200时,求函数v (x )的表达式.1.3.1 单调性与最大(小)值第1课时 函数的单调性一、基础过关1. 下列函数中,在(-∞,0]内为增函数的是( )A .y =x 2-2B .y =3xC .y =1+2xD .y =-(x +2)22. 已知f (x )为R 上的减函数,则满足f ⎝⎛⎭⎫⎪⎪⎪⎪1x <f (1)的实数x 的取值范围是( )A .(-1,1)B .(0,1)C .(-1,0)∪(0,1)D .(-∞,-1)∪(1,+∞)3. 如果函数f (x )=ax 2+2x -3在区间(-∞,4)上是单调递增的,则实数a 的取值范围是( )A .a >-14B .a ≥-14C .-14≤a <0D .-14≤a ≤04. 如果函数f (x )在[a ,b ]上是增函数,对于任意的x 1,x 2∈ [a ,b ](x 1≠x 2),则下列结论中不正确的是( )A .f (x 1)-f (x 2)x 1-x 2>0B .(x 1-x 2)[f (x 1)-f (x 2)]>0C .f (a )<f (x 1)<f (x 2)<f (b )D .x 1-x 2f (x 1)-f (x 2)>05. 设函数f (x )是R 上的减函数,若f (m -1)>f (2m -1),则实数m 的取值范围是________.6. 函数f (x )=2x 2-mx +3,当x ∈ [2,+∞)时是增函数,当x ∈ (-∞,2]时是减函数,则f (1)=______________. 7. 画出函数y =-x 2+2|x |+3的图象,并指出函数的单调区间.8. 已知f (x )=x 2-1,试判断f (x )在[1,+∞)上的单调性,并证明.二、能力提升9. 已知函数f (x )的图象是不间断的曲线,f (x )在区间[a ,b ]上单调,且f (a )·f (b )<0,则方程f (x )=0在区间[a ,b ]上( )A .至少有一个根B .至多有一个根C .无实根D .必有唯一的实根10.若定义在R 上的二次函数f (x )=ax 2-4ax +b 在区间[0,2]上是增函数,且f (m )≥f (0),则实数m 的取值范围是( )A .0≤m ≤4B .0≤m ≤2C .m ≤0D .m ≤0或m ≥411.函数f (x )=ax +1x +2(a 为常数)在(-2,2)内为增函数,则实数a 的取值范围是________.12.求证:函数f (x )=-x 3+1在(-∞,+∞)上是减函数.三、探究与拓展13.已知函数f (x )=x 2+ax (a >0)在(2,+∞)上递增,求实数a 的取值范围.第2课时 函数的最大(小)值一、基础过关1. 函数f (x )=1x在[1,+∞)上( )A .有最大值无最小值B .有最小值无最大值C .有最大值也有最小值D .无最大值也无最小值 2. 函数y =x +2x -1( )A .有最小值12,无最大值B .有最大值12,无最小值C .有最小值12,有最大值2 D .无最大值,也无最小值3. 函数f (x )=⎩⎪⎨⎪⎧2x +6, x ∈[1,2]x +7, x ∈[-1,1],则f (x )的最大值、最小值为( )A .10,6B .10,8C .8,6D .以上都不对 4. 函数y =|x -3|-|x +1|的( )A .最小值是0,最大值是4B .最小值是-4,最大值是0C .最小值是-4,最大值是4D .没有最大值也没有最小值 5. 函数f (x )=11-x (1-x )的最大值是( )A .45B .54C .34D .436. 函数y =-x 2+6x +9在区间[a ,b ](a <b <3)上有最大值9,最小值-7,则a =______,b =________. 7. 已知函数f (x )=x 2-x +1,求f (x )在区间[-1,1]上的最大值和最小值.8. 已知函数f (x )=x 2-2x +2.(1)求f (x )在区间[12,3]上的最大值和最小值;(2)若g (x )=f (x )-mx 在[2,4]上是单调函数,求m 的取值范围.二、能力提升9. 函数f (x )=x 2-4x +5在区间[0,m ]上的最大值为5,最小值为1,则m 的取值范围是( )A .[2,+∞)B .[2,4]C .(-∞,2]D .[0,2]10.某公司在甲乙两地同时销售一种品牌车,利润(单位:万元)分别为L 1=-x 2+21x 和L 2=2x ,其中x 为销售量(单位:辆).若该公司在两地共销售15辆,则能获得的最大利润为 ( ) A .90万元B .60万元C .120万元D .120.25万元11.当x ∈ (1,2)时,不等式x 2+mx +4<0恒成立,则m 的取值范围是________. 12.已知函数f (x )=1a -1x(a >0,x >0),(1)求证:f (x )在(0,+∞)上是单调递增函数; (2)若f (x )在[12,2]上的值域是[12,2],求a 的值.三、探究与拓展13.若二次函数满足f (x +1)-f (x )=2x 且f (0)=1. (1)求f (x )的解析式;(2)若在区间[-1,1]上不等式f (x )>2x +m 恒成立,求实数m 的取值范围.1.3.2 奇偶性第1课时 奇偶性的概念一、基础过关1. 下列说法正确的是( )A .如果一个函数的定义域关于坐标原点对称,则这个函数为奇函数B .如果一个函数为偶函数,则它的定义域关于坐标原点对称C .如果一个函数的定义域关于坐标原点对称,则这个函数为偶函数D .如果一个函数的图象关于y 轴对称,则这个函数为奇函数 2. f (x )是定义在R 上的奇函数,下列结论中,不正确的是( )A .f (-x )+f (x )=0B .f (-x )-f (x )=-2f (x )C .f (x )·f (-x )≤0D .f (x )f (-x )=-13. 下列函数中,在其定义域内既是奇函数又是增函数的是( )A .y =-x 2+5(x ∈R )B .y =-xC .y =x 3(x ∈R )D .y =-1x (x ∈R ,x ≠0)4. 已知y =f (x ),x ∈(-a ,a ),F (x )=f (x )+f (-x ),则F (x )是( )A .奇函数B .偶函数C .既是奇函数又是偶函数D .非奇非偶函数 5. 设奇函数f (x )的定义域为[-5,5],若当x ∈[0,5]时,f (x )的图象如图所示,则不等式f (x )<0的解集是______.6. 若函数f (x )=⎩⎪⎨⎪⎧x 2+2x (x ≥0)g (x )(x <0)为奇函数,则f (g (-1))=________.7. 判断下列函数的奇偶性:(1)f (x )=3,x ∈R ; (2)f (x )=5x 4-4x 2+7,x ∈[-3,3]; (3)f (x )=|2x -1|-|2x +1|; (4)f (x )=⎩⎪⎨⎪⎧1-x 2, x >0,0, x =0,x 2-1, x <0.8. 已知函数f (x )=ax 2+1bx +c (a ,b ,c ∈Z )是奇函数,又f (1)=2,f (2)<3,求a ,b ,c 的值.二、能力提升9. 给出函数f (x )=|x 3+1|+|x 3-1|,则下列坐标表示的点一定在函数y =f (x )的图象上的是 ( )A .(a ,-f (a ))B .(a ,f (-a ))C .(-a ,-f (a ))D .(-a ,-f (-a ))10.已知定义在R 上的奇函数f (x )满足f (x )=x 2+2x (x ≥0),若f (3-a 2)>f (2a -a 2),则实数a 的取值范围是________. 11.已知函数f (x )=1-2x.(1)若g (x )=f (x )-a 为奇函数,求a 的值;(2)试判断f (x )在(0,+∞)内的单调性,并用定义证明.12.已知奇函数f (x )=⎩⎪⎨⎪⎧-x 2+2x (x >0)0 (x =0)x 2+mx (x <0).(1)求实数m 的值,并画出y =f (x )的图象;(2)若函数f (x )在区间[-1,a -2]上单调递增,试确定a 的取值范围.三、探究与拓展13.已知函数f (x )=x 2+ax(x ≠0).(1)判断f (x )的奇偶性,并说明理由;(2)若f (1)=2,试判断f (x )在[2,+∞)上的单调性.第2课时 奇偶性的应用一、基础过关1. 下面四个结论:①偶函数的图象一定与y 轴相交;②奇函数的图象一定过原点;③偶函数的图象关于y轴对称;④没有一个函数既是奇函数,又是偶函数. 其中正确命题的个数是( )A .1B .2C .3D .42. 已知函数f (x )=(m -1)x 2-2mx +3是偶函数,则在(-∞,0)上此函数( )A .是增函数B .不是单调函数C .是减函数D .不能确定3. 定义在R 上的函数f (x )在(-∞,2)上是增函数,且f (x +2)的图象关于y 轴对称,则( )A .f (-1)<f (3)B .f (0)>f (3)C .f (-1)=f (3)D .f (0)=f (3)4. 设奇函数f (x )在(0,+∞)上为减函数,且f (1)=0,则不等式f (x )-f (-x )x<0的解集为( )A .(-1,0)∪(1,+∞)B .(-∞,-1)∪(0,1)C .(-∞,-1)∪(1,+∞)D .(-1,0)∪(0,1) 5. 已知定义在R 上的奇函数f (x ),当x >0时,f (x )=x 2+|x |-1,那么x <0时,f (x )=________.6. 设f (x )是(-∞,+∞)上的奇函数,且f (x +2)=-f (x ),当0≤x ≤1时,f (x )=x ,则f (7.5)=________. 7. 设函数f (x )在R 上是偶函数,在区间(-∞,0)上递增,且f (2a 2+a +1)<f (2a 2-2a +3),求a 的取值范围.8. 已知函数f (x )是定义在R 上的单调函数,满足f (-3)=2,且对任意的实数a ∈R 有f (-a )+f (a )=0恒成立.(1)试判断f (x )在R 上的单调性,并说明理由. (2)解关于x 的不等式f (2-xx )<2.二、能力提升9. 已知偶函数f (x )在区间[0,+∞)上单调递增,则满足f (x )<f (1)的x 的取值范围是( )A .(-1,1)B .(-1,0)C .(0,1)D .[-1,1)10.设偶函数f (x )的定义域为R ,当x ∈[0,+∞)时,f (x )是增函数,则f (-2),f (π),f (-3)的大小关系是 ( )A .f (π)>f (-3)>f (-2)B .f (π)>f (-2)>f (-3)C .f (π)<f (-3)<f (-2)D .f (π)<f (-2)<f (-3) 11.y =f (x )在(0,2)上是增函数,y =f (x +2)是偶函数,则f (1),f (52),f (72)的大小关系是________________.12.已知函数f (x )=ax +1x2(x ≠0,常数a ∈R ).(1)讨论函数f (x )的奇偶性,并说明理由;(2)若函数f (x )在x ∈[3,+∞)上为增函数,求a 的取值范围.三、探究与拓展13.已知函数f (x )=ax 2+bx +1(a ,b 为常数),x ∈R.F (x )=⎩⎪⎨⎪⎧f (x ) (x >0)-f (x ) (x <0).(1)若f (-1)=0,且函数f (x )的值域为[0,+∞),求F (x )的表达式;(2)在(1)的条件下,当x ∈[-2,2]时,g (x )=f (x )-kx 是单调函数,求实数k 的取值范围; (3)设m ·n <0,m +n >0,a >0,且f (x )为偶函数,判断F (m )+F (n )能否大于零?【章末检测】一、选择题1. 若集合A ={x ||x |≤1,x ∈R },B ={y |y =x 2,x ∈R },则A ∩B 等于( ) A .{x |-1≤x ≤1}B .{x |x ≥0}C .{x |0≤x ≤1}D .∅ 2. 已知函数f (x )=ax 2+(a 3-a )x +1在(-∞,-1]上递增,则a 的取值范围是( )A .a ≤ 3B .-3≤a ≤ 3C .0<a ≤ 3D .-3≤a <0 3. 若f (x )=ax 2-2(a >0),且f (2)=2,则a 等于( )A .1+22B .1-22C .0D .24. 若函数f (x )满足f (3x +2)=9x +8,则f (x )的解析式是( )A .f (x )=9x +8B .f (x )=3x +2C .f (x )=-3x -4D .f (x )=3x +2或f (x )=-3x -45. 已知M ,N 为集合I 的非空真子集,且M ,N 不相等,若N ∩(∁I M )=∅,则M ∪N 等于( )A .MB .NC .ID .∅6. 已知函数f :A →B (A 、B 为非空数集),定义域为M ,值域为N ,则A 、B 、M 、N 的关系是 ( )A .M =A ,N =BB .M ⊆A ,N =BC .M =A ,N ⊆BD .M ⊆A ,N ⊆B 7. 下列函数中,既是奇函数又是增函数的为( )A .y =x +1B .y =-x 3C .y =1xD .y =x |x |8. 已知函数f (x )=1x在区间[1,2]上的最大值为A ,最小值为B ,则A -B 等于 ( )A.12B .-12C .1D .-1 9. 设f (x )=⎩⎪⎨⎪⎧x +3 (x >10)f (f (x +5)) (x ≤10),则f (5)的值是( )A .24B .21C .18D .16 10.f (x )=(m -1)x 2+2mx +3为偶函数,则f (x )在区间(2,5)上是( )A .增函数B .减函数C .有增有减D .增减性不确定11.若f (x )和g (x )都是奇函数,且F (x )=f (x )+g (x )+2在(0,+∞)上有最大值8,则在(-∞,0)上F (x )有 ( )A .最小值-8B .最大值-8C .最小值-6D .最小值-412. 在函数y =|x |(x ∈[-1,1])的图象上有一点P (t ,|t |),此函数与x 轴、直线x =-1及x =t 围成图形(如图阴影部分)的面积为S ,则S 与t 的函数关系的图象可表示为()二、填空题13.已知f (x )在R 上是奇函数,且满足f (x +4)=f (x ),当x ∈(0,2)时,f (x )=2x 2,则f (7)=______.14.已知函数f (x )=4x 2-mx +5在区间[-2,+∞)上是增函数,则f (1)的取值范围是________.15.若定义运算a ⊙b =⎩⎪⎨⎪⎧b ,a ≥ba ,a <b ,则函数f (x )=x ⊙(2-x )的值域为________.16.用描述法表示如图中阴影部分的点(含边界)的坐标的集合(不含虚线)为________.三、解答题17.设集合A ={x |2x 2+3px +2=0},B ={x |2x 2+x +q =0},其中p 、q 为常数,x ∈R ,当A ∩B ={12}时,求p 、q 的值和A ∪B .18.已知f (x ),g (x )在(a ,b )上是增函数,且a <g (x )<b ,求证:f (g (x ))在(a ,b )上也是增函数.19.函数f (x )=4x 2-4ax +a 2-2a +2在区间[0,2]上有最小值3,求a 的值.20.已知f (x )=xx -a(x ≠a ).(1)若a =-2,试证f (x )在(-∞,-2)内单调递增;(2)若a >0且f (x )在(1,+∞)内单调递减,求a 的取值范围.21.某公司计划投资A 、B 两种金融产品,根据市场调查与预测,A 产品的利润与投资量成正比例,其关系如图1,B 产品的利润与投资量的算术平方根成正比例,其关系如图2(注:利润与投资量的单位:万元). (1)分别将A 、B 两产品的利润表示为投资量的函数关系式;(2)该公司已有10万元资金,并全部投入A 、B 两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?22.已知函数y =x +tx有如下性质:如果常数t >0,那么该函数在(0,t ]上是减函数,在[t ,+∞)上是增函数.(1)已知f (x )=4x 2-12x -32x +1,x ∈ [0,1],利用上述性质,求函数f (x )的单调区间和值域;(2)对于(1)中的函数f (x )和函数g (x )=-x -2a ,若对任意x 1∈[0,1],总存在x 2∈[0,1],使得g (x 2)=f (x 1)成立,求实数a 的值.第一章参考答案第一节 集合的含义与表示参考答案1. C 2.C 3.A 4.①④ 5.x ≠0,1,2,1±52.6. 解 (1)正确.因为参加2012年伦敦奥运会的国家是确定的,明确的.(2)不正确.因为高科技产品的标准不确定.(3)不正确.对一个集合,它的元素必须是互异的,由于0.5=12,在这个集合中只能作为一个元素,故这个集合含有三个元素.(4)不正确.因为年轻没有明确的标准.7. 解 由-3∈A ,可得-3=a -2或-3=2a 2+5a ,∴a =-1或a =-32.则当a =-1时,a -2=-3,2a 2+5a =-3,不符合集合中元素的互异性,故a =-1应舍去. 当a =-32时,a -2=-72,2a 2+5a =-3,∴a =-32.8. D 9.B 10.211.解 ∵当a =0时,b 依次取1,2,6,得a +b 的值分别为1,2,6;当a =2时,b 依次取1,2,6,得a +b 的值分别为3,4,8; 当a =5时,b 依次取1,2,6,得a +b 的值分别为6,7,11.由集合元素的互异性知P +Q 中元素为1,2,3,4,6,7,8,11,共8个. 12.证明 (1)若a ∈A ,则11-a∈A .又∵2∈A ,∴11-2=-1∈A . ∵-1∈A ,∴11-(-1)=12∈A .∵12∈A ,∴11-12=2∈A . ∴A 中另外两个元素为-1,12.(2)若A 为单元素集,则a =11-a, 即a 2-a +1=0,方程无解. ∴a ≠11-a,∴集合A 不可能是单元素集.第一节 集合的含义与表示(2)答案1. B 2.D 3.B 4.C 5.(1){0,1,2} (2){-2,-1,0,1,2} (3){(2,0),(-2,0),(0,2),(0,-2)} 6.②7. 解 (1)∵方程x (x 2+2x +1)=0的解为0和-1,∴解集为{0,-1};(2){x |x =2n +1,且x <1 000,n ∈N }; (3){x |x >8}; (4){1,2,3,4,5,6}.8. 解 因为三个集合中代表的元素性质互不相同,所以它们是互不相同的集合.理由如下:集合A 中代表的元素是x ,满足条件y =x 2+3中的x ∈R ,所以A =R ;集合B 中代表的元素是y ,满足条件y =x 2+3中y 的取值范围是y ≥3,所以B ={y |y ≥3}.集合C 中代表的元素是(x ,y ),这是个点集,这些点在抛物线y =x 2+3上,所以C ={P |P 是抛物线y =x 2+3上的点}. 9. C 10.D 11.④12.解 (1)当k =0时,原方程变为-8x +16=0,x =2.此时集合A ={2}.(2)当k ≠0时,要使一元二次方程kx 2-8x +16=0有一个实根. 只需Δ=64-64k =0,即k =1.此时方程的解为x 1=x 2=4,集合A ={4},满足题意. 综上所述,实数k 的值为0或1.当k =0时,A ={2}; 当k =1时,A ={4}.13.解 当x =1或2,y =0时,z =0;当x =1,y =2时,z =2;当x =2,y =2时,z =4.所以A *B ={0,2,4},所以元素之和为0+2+4=6.第二节 集合间的基本关系答案1. D 2.B 3.B 4.B 5.①② 6.a ≥27. 解 A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},且B ⊆A .①若B =∅,则m +1>2m -1,解得m <2, 此时有B ⊆A ;②若B ≠∅,则m +1≤2m -1,即m ≥2, 由B ⊆A ,得⎩⎪⎨⎪⎧m ≥2m +1≥-22m -1≤5,解得2≤m ≤3. 由①②得m ≤3.∴实数m 的取值范围是{m |m ≤3}. 8. 解 A ={-3,2}.对于x 2+x +a =0,①当Δ=1-4a <0,即a >14时,B =∅,B ⊆A 成立;②当Δ=1-4a =0,即a =14时,B ={-12},B ⊆A 不成立;③当Δ=1-4a >0,即a <14时,若B ⊆A 成立,则B ={-3,2},∴a =-3×2=-6. 综上:a 的取值范围为a >14或a =-6.9. A 10.C 11.612.解 ①当a =0时,A =∅,满足A ⊆B .②当a >0时,A ={x |1a <x <2a }.又∵B ={x |-1<x <1},A ⊆B ,∴⎩⎨⎧1a≥-1,2a ≤1,∴a ≥2.③当a <0时,A ={x |2a <x <1a}.∵A ⊆B ,∴⎩⎨⎧2a≥-1,1a ≤1,∴a ≤-2.综上所述,a =0或a ≥2或a ≤-2.13.解 不存在.理由如下:要使对任意的实数b 都有A ⊆B ,则1,2是A 中的元素,又因A ={a -4,a +4},所以⎩⎪⎨⎪⎧ a -4=1,a +4=2,或⎩⎪⎨⎪⎧a +4=1,a -4=2.这两个方程组均无解,故这样的实数不存在.第三节 集合间的运算(1)答案1. A 2.D 3.D 4.D 5.B 6.17. 解 ∵A ∩B ={9},∴9∈A ,所以a 2=9或2a -1=9,解得a =±3或a =5.当a =3时,A ={9,5,-4},B ={-2,-2,9},B 中元素违背了互异性,舍去.当a =-3时,A ={9,-7,-4},B ={-8,4,9},A ∩B ={9}满足题意,故A ∪B ={-7,-4,-8,4,9}. 当a =5时,A ={25,9,-4},B ={0,-4,9},此时A ∩B ={-4,9},与A ∩B ={9}矛盾,故舍去. 综上所述,A ∪B ={-7,-4,-8,4,9}. 8. 解 ∵A ∩B =B ,∴B ⊆A .∵A ={-2}≠∅,∴B =∅或B ≠∅.当B =∅时,方程ax +1=0无解,此时a =0. 当B ≠∅时,此时a ≠0,则B ={-1a },∴-1a ∈A ,即有-1a =-2,得a =12.综上,a =0或a =12.9. B 10.0或1 11.-1 212.解 由A ∩C =A ,A ∩B =∅,可得:A ={1,3},即方程x 2+px +q =0的两个实根为1,3.∴⎩⎪⎨⎪⎧ 1+3=-p 1×3=q ,∴⎩⎪⎨⎪⎧p =-4q =3. 13.解 (1)若A =∅,则A ∩B =∅成立.此时2a +1>3a -5, 即a <6.若A ≠∅,如图所示,则⎩⎪⎨⎪⎧2a +1≤3a -5,2a +1≥-1,3a -5≤16,解得6≤a ≤7.综上,满足条件A ∩B =∅的实数a 的取值范围是{a |a ≤7}. (2)因为A ⊆(A ∩B ),且(A ∩B )⊆A , 所以A ∩B =A ,即A ⊆B . 显然A =∅满足条件,此时a <6.若A ≠∅,如图所示,则⎩⎪⎨⎪⎧ 2a +1≤3a -5,3a -5<-1或⎩⎪⎨⎪⎧2a +1≤3a -5,2a +1>16.由⎩⎪⎨⎪⎧ 2a +1≤3a -5,3a -5<-1解得a ∈∅; 由⎩⎪⎨⎪⎧2a +1≤3a -5,2a +1>16解得a >152.综上,满足条件A ⊆(A ∩B )的实数a 的取值范围是{a |a <6或a >152}. 第三节 集合间的运算(2)1. D 2.C 3.B 4.B 5.-3 6.{0,1,3,5,7,8} {7,8} {0,1,3,5} 7. 解 ∵∁U A ={5},∴5∈U 且5∉A .又b ∈A ,∴b ∈U ,由此得⎩⎪⎨⎪⎧a 2+2a -3=5,b =3.解得⎩⎪⎨⎪⎧ a =2,b =3或⎩⎪⎨⎪⎧a =-4,b =3经检验都符合题意.8. 解 (1)∵U ={1,2,3,4,5},M ={1,4},∴∁U M ={2,3,5}.又∵N ={1,3,5}, ∴N ∩(∁U M )={3,5}. (2)∵M ={m ∈Z |-3<m <2}, ∴M ={-2,-1,0,1};∵N ={n ∈Z |-1≤n ≤3},∴N ={-1,0,1,2,3},∴M ∪N ={-2,-1,0,1,2,3}.9. C 10.B 11.(∁U B ) (∁U A ) 12.解 因为B ∪(∁U B )=A ,所以B ⊆A ,U =A ,因而x 2=3或x 2=x . ①若x 2=3,则x =±3.当x =3时,A ={1,3,3},B ={1,3}, U =A ={1,3,3},此时∁U B ={3};当x =-3时,A ={1,3,-3},B ={1,3},U =A ={1,3,-3},此时∁U B ={-3}.②若x 2=x ,则x =0或x =1.当x =1时,A 中元素x 与1相同,B 中元素x 2与1也相同,不符合元素的互异性,故x ≠1;当x =0时,A ={1,3,0},B ={1,0},U =A ={1,3,0},从而∁U B ={3}. 综上所述,∁U B ={3}或{-3}或{3}.13.解 如图所示,设只参加赛跑、只参加跳跃、两项都参加的人数分别为a ,b ,x.根据题意有⎩⎪⎨⎪⎧a +x =20,b +x =11,a +b +x =30-4.解得x =5,即两项都参加的有5人.结合习题课答案1. B 2.B 3.D 4.B 5.D 6.a ≤2 7. 解 (1)∵B ={x |x ≥2},∴A ∩B ={x |2≤x <3}. (2)∵C ={x |x >-a2},B ∪C =C ⇔B ⊆C , ∴-a2<2,∴a >-4.8. 解 ∵A ∩B ={3},∴3∈B ,∴32+3c +15=0,∴c =-8.由方程x 2-8x +15=0解得x =3或x =5, ∴B ={3,5}.由A ⊆(A ∪B )={3,5}知,3∈A,5A (否则5∈A ∩B ,与A ∩B ={3}矛盾)故必有A ={3},∴方程x 2+ax +b =0有两相同的根3,由根与系数的关系得3+3=-a,3×3=b ,即a=-6,b =9,c =-8.9. A 10.1 11.{x |x <1或x ≥5}12. 解 由题意,设全班同学为全集U ,画出Venn 图,A 表示答错A的集合,B 表示答错B 的集合,C 表示答错C 的集合,将其集合中 元素数目填入图中,自中心区域向四周的各区域数目分别为 1,2,3,4,10,7,5,因此A ∪B ∪C 中元素数目为32,从而至少错一题的 共32人,因此A ,B ,C 全对的有50-32=18(人). 13.解 A ={x |1<x <3},B ={x |2≤x ≤4}.(1)∵A ΔB ={x |1<x <2},由上图可知A ΔB 中的元素都在A 中但不在B 中, ∴定义A ΔB ={x |x ∈A ,且xB }.(2)由(1)可知B ΔA ={x |x ∈B ,且x A }={x |3≤x ≤4}.函数部分第一节 函数及其表示(1)1. A 2.D 3.D 4.B 5.{-1,1,3,5,7} 6.[1,+∞) 7. 解 (1)A 中的元素0在B 中没有对应元素,故不是集合A 到集合B 的函数.(2)对于集合A 中的任意一个整数x ,按照对应关系f :x →y =x 2在集合B 中都有唯一一个确定的整数x 2与其对应,故是集合A 到集合B 的函数.(3)集合A 中的负整数没有平方根,故在集合B 中没有对应的元素,故不是集合A 到集合B 的函数. (4)对于集合A 中任意一个实数x ,按照对应关系f :x →y =0在集合B 中都有唯一一个确定的数0和它对应,故是集合A 到集合B 的函数. 8. 解 由1-x 1+x=2,解得x =-13,所以f (2)=-13.9. C 10.C 11.[0,13]12.解 (1)最初到达离家最远的地方的时间是12时,离家30千米.(2)10∶30开始第一次休息,休息了半小时. (3)第一次休息时,离家17千米. (4)11∶00至12∶00他骑了13千米.(5)9∶00~10∶00的平均速度是10千米/时;10∶00~10∶30的平均速度是14千米/时. (6)从12时到13时停止前进,并休息用午餐较为符合实际情形.13.解 (1)由已知,横断面为等腰梯形,下底为2 m ,上底为(2+2h )m ,高为h m ,∴水的面积A =[2+(2+2h )]h 2=h 2+2h (m 2).(2)定义域为{h |0<h <1.8}.值域由二次函数A =h 2+2h (0<h <1.8)求得.由函数A =h 2+2h =(h +1)2-1的图象可知,在区间(0,1.8)上函数值随自变量的增大而增大,∴0<A <6.84.故值域为{A |0<A <6.84}.(3)由于A =(h +1)2-1,对称轴为直线h =-1,顶点坐标为(-1,-1),且图象过(0,0)和(-2,0)两点,又考虑到0<h <1.8,∴A =h 2+2h 的图象仅是抛物线的一部分,如图所示.第一节 函数及其表示(2)答案1. C 2.B 3.B 4.B 5.2 6.f (x )=2x +83或f (x )=-2x -87. 解 设f (x )=ax 2+bx +c (a ≠0),∴f (x +2)=a (x +2)2+b (x +2)+c , 则f (x +2)-f (x )=4ax +4a +2b =4x +2.∴⎩⎪⎨⎪⎧4a =4,4a +2b =2. ∴⎩⎪⎨⎪⎧a =1,b =-1. 又f (0)=3,∴c =3,∴f (x )=x 2-x +3. 8. 解 设f (x )=ax 2+bx +c (a ≠0).由f (0)=f (4)知⎩⎪⎨⎪⎧f (0)=c ,f (4)=16a +4b +c ,f (0)=f (4),得4a +b =0.①又图象过(0,3)点,所以c =3.② 设f (x )=0的两实根为x 1,x 2, 则x 1+x 2=-b a ,x 1x 2=ca.所以x 21+x 22=(x 1+x 2)2-2x 1x 2=(-b a )2-2·ca =10.即b 2-2ac =10a 2.③由①②③得a =1,b =-4,c =3. 所以f (x )=x 2-4x +3.9. B 10.B 11.f (x )=-x 2+23x(x ≠0)12.解 因为函数f (x )=-x 2+2x +3的定义域为R ,列表:(1)根据图象,容易发现f (0)=3,f (1)=4,f (3)=0, 所以f (3)<f (0)<f (1).(2)根据图象,容易发现当x 1<x 2<1时,有f (x 1)<f (x 2).(3)根据图象,可以看出函数的图象是以(1,4)为顶点,开口向下的抛物线,因此,函数的值域为(-∞,4]. 13.解 要使函数y =1a x +1(a <0且a 为常数)在区间(-∞,1]上有意义,必须有1ax +1≥0,a <0,∴x ≤-a,即函数的定义域为(-∞,-a ], ∵函数在区间(-∞,1]上有意义,∴(-∞,1]⊆(-∞,-a ],∴-a ≥1,即a ≤-1,∴a 的取值范围是(-∞,-1].第一节 函数及其表示(3)答案 1. D 2.A 3.A 4.C 5.C 6.137. 解 f (x )=x +|x |x =⎩⎪⎨⎪⎧x +1,x >0,x -1,x <0.其图象如图所示.由图象可知,f (x )的值域为(-∞,-1)∪(1,+∞). 8. 解 (1)利用描点法,作出f (x )的图象,如图所示.(2)由条件知,函数f (x )的定义域为R .由图象知,当-1≤x ≤1时,f (x )=x 2的值域为[0,1], 当x >1或x <-1时,f (x )=1, 所以f (x )的值域为[0,1].9. A 10.f (x )=⎩⎪⎨⎪⎧x +1, -1≤x <0,-x , 0≤x ≤111.32 {x |x ≥-1且x ≠0}12.解 当点P 在BC 上运动,即0≤x ≤4时,y =12×4x =2x ;当点P 在CD 上运动,即4<x ≤8时,y =12×4×4=8;当点P 在DA 上运动,即8<x ≤12时, y =12×4×(12-x )=24-2x . 综上可知,f (x )=⎩⎪⎨⎪⎧2x , 0≤x ≤4,8, 4<x ≤8,24-2x , 8<x ≤12.13.解 由题意,当0≤x ≤20时,v (x )=60;当20≤x ≤200时,设v (x )=ax +b .。
人教新课标A版必修一第一章集合与函数的概念单元测试(带答案)

新课标人教A 版第一章集合与函数的概念单元测试一、单选题(每小题5分)1. 已知集合和集合2{}B y y x ==,则A B 等于( )A.(0,1)B.[0,1]C.(0,+∞)D.{(0,1),(1,0)}2.函数()f x =的定义域为( ) A.[3,+∞) B.[3,4)∪(4,+∞) C.(3,+∞) D.[3,4)3. (2018•卷Ⅰ)已知集合2{20}A x x x =-->,则∁R A=( ) A.{12}x x -<< B.{12}x x -≤≤ C.{1}{2}x x x x <-> D.{1}{2}x x x x ≤-≥4. 函数f (x )=|x 2﹣6x+8|的单调递增区间为( )A.[3,+∞) B.(﹣∞,2)(4,+∞) C.(2,3)(4,+∞) D.(﹣∞,2][3,4]5. (2018•卷Ⅰ)已知集合A={0,2},B={-2,-1,0,1,2},则A ∩B=( )A.{0,2}B.{1,2}C.{0}D.{-2,-1,0,1,2}6. 已知全集U={1,2,3,4,5,6},A={1,2,6},B={2,4,5},则(∁UA )∩B=( )A.{4,5}B.{1,2,3,4,5,6}C.{2,4,5}D.{3,4,5}7. 若函数f (x )对于任意实数x 恒有f (x )﹣2f (﹣x )=3x ﹣1,则f (x )等于( ) A.x+1 B.x ﹣1 C.2x+1 D.3x+38. 已知函数21,2()22,2x x f x x x x ⎧+>⎪=-⎨⎪+≤⎩,则f[f (1)]=( ) A.12- B.2 C.4 D.11 9. 已知集合A={x ∈N *|x ﹣3<0},则满足条件B ⊆A 的集合B 的个数为( )A.2B.3C.4D.810. 函数2()23f x x mx =-+,当[2,)x ∈-+∞时是增函数,当(,2]x ∈-∞-时是减函数,则(1)f 等于( )A.-3B.13C.7D.511. 已知函数22,1()2,1a x f x x x x x ⎧+>⎪=⎨⎪-+≤⎩在R 上单调递增,则实数a 的取值范围是( )A.[﹣1,+∞)B.(﹣1,+∞) .[﹣1,0) D.(﹣1,0)12. 下列有关集合的写法正确的是( )A.{0}{0,1,2}∈B.{0}∅=C.0∈∅D.{}∅∈∅二、填空题(每题5分)13. 非空数集A 与B 之间定义长度(,)d x y ,使得()1212d y y y y -=-,其中1y A ∈,2y B ∈,若所有的(,)d x y 中存在最小值()12','d y y ,则称()12','d y y 为集合A 与B 之间的距离,现已知集合11{21}A y a y a =≤≤-,222111{1,}B y y y y y A ==++∈,且()12','d y y =4,则a 的值为_______.14. 已知f(x)为奇函数,()()9,(2)3g x f x g =+-=,则f(2)=__________.15. 设集合A ={x|-1<x<2},集合B ={x|1<x<3},则A ∪B 等于________16. 若集合{12}M x x =-<<,2{1,}N y y x x R ==+∈,则集合M N =___三、解答题(17-22题,12分+12分+12分+12分+12分+12分+10分)17. 设集合2{40,}A x x x x R =+=∈,22{2(1)10,}B x x a x a x R =+++-=∈.(1)若A B B =,求实数a 的值;(2)若A B B =,求实数a 的范围.18. 已知函数239,2()1,211,1x x f x x x x x +≤-⎧⎪=--<<⎨⎪-+>⎩.(1)做出函数图象;(2)说明函数()f x 的单调区间(不需要证明);(3)若函数()y f x =的图象与函数y m =的图象有四个交点,求实数m 的取值范围.19. 已知函数21 ()1xf xx+=+.(1)判断函数()f x在区间[1,+)∞上的单调性,并用定义证明你的结论;(2)求该函数在区间[1,4]上的最大值与最小值.20. 已知函数f(x)对任意的实数m,n都有:f(m+n)=f(m)+f(n)-1,且当x >0时,有f(x)>1.(1)求f(0).(2)求证:f(x)在R上为增函数.(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.21. 已知二次函数f(x)的图象过点(0,4),对任意x满足f(3﹣x)=f(x),且f(1)=2.(1)若f(x)在(a,2a﹣1)上单调递减,求实数a的取值范围.(2)设函数h(x)=f(x)﹣(2t﹣3)x,其中t∈R,求h(x)在区间[0,1]上的最小值g (t).22. 若集合A={x|x2+5x﹣6=0},B={x|x2+2(m+1)x+m2﹣3=0}.(1)若m=0,写出A∪B的子集;(2)若A∩B=B,求实数m的取值范围.答案:1-5.BBBCA 6-10.AACCB 11-12.CD13. a=214. 615. {x|-1<x <3}16. [1,3)17. (1)a=1 (2)a=1或a ≤-118. (2)单调增区间(-∞,-2)和(0,1)单调减区间(-2,0)和(1,+∞) (3)(1,0)m ∈-19. (1)函数f(x)在[1,+∞)上是增函数 (2)最小值f(1)=32 最大值9(4)5f =20. (1)f(0)=1(2)略 (3)(1)-∞21. (1)5(1,]4a ∈ (2) 0(5)4t g ≤=时, 201()4t g t t<<=-时, 1()52t g t t ≥=-时, 22. (1){6,3,1}A B =--{-6}{-3}{1}{-6-3}{-6,1}{-3,A B ∅的子集:,,,,,,,,, (2)∞(-,-2]。
高中人教A版数学必修1单元测试:第一章 集合与函数概念Word版含解析

高中人教A版数学必修1单元测试第一章集合与函数概念(一)(集合)第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列四个集合中,是空集的是()A.{x|x+3=3} B.{(x,y)|y=-x2,x,y∈R}C.{x|x2≤0} D.{x|x2-x+1=0,x∈R}2.已知集合A={x∈N|x<6},则下列关系式错误的是()A.0∈A B.1.5∉A C.-1∉A D.6∈A3.已知集合U={1,3,5,7,9},A={1,5,7},则∁U A=()A.{1,3} B.{3,7,9} C.{3,5,9} D.{3,9}4.设集合A={1,2},B={1,2,3},C={2,3,4},则(A∩B)∪C=()A.{1,2,3} B.{1,2,4} C.{2,3,4} D.{1,2,3,4}5.满足条件{1,2}∪A={1,2}的所有非空集合A的个数是()A.1个B.2个C.3个D.4个6.若集合A={1,4,x},B={1,x2},A∪B={1,4,x},则满足条件的实数x有()A.1个B.2个C.3个D.4个7.已知集合M={y|x+y=2},N={(x,y)|x-y=4},那么集合M∩N为() A.{x=3,y=-1} B.{(x,y)|x=3或y=-1}C.∅D.{(3,-1)}8.已知集合A={0,1,2,3},B={1,3,4},则A∩B的子集个数为()A.2 B.3 C.4 D.169.设全集U 是实数集R ,M ={x |x >2或x <-2},N ={x |x ≥3或x <1}都是U 的子集,则图中阴影部分所表示的集合是( )A .{x |-2≤x <1}B .{x |-2≤x ≤2}C .{x |1<x ≤2}D .{x |x <2}10.如果集合A ={x |ax 2+2x +1=0}中只有一个元素,则a 的值是( ) A .0 B .0或1 C .1 D .不能确定11.集合⎩⎨⎧⎭⎬⎫x ∈N *⎪⎪⎪12x ∈Z 中含有的元素个数为( )A .4B .6C .8D .1212.设a ,b 都是非零实数,则y =a |a |+b |b |+ab|ab |可能取的值组成的集合为( ) A .{3} B .{3,2,1} C .{3,-2,1}D .{3,-1}第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)13.若集合A ={x |-1≤x <2},B ={x |x ≤a },若A ∩B ≠∅,则实数a 的取值范围是________.14.已知集合A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =a +16,a ∈Z ,B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x =b 2-13,b ∈Z ,C =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x =c 2+16,c ∈Z ,则A ,B ,C 之间的关系是________.15.若集合A ={x |x 2+x -6=0},B ={x |mx +1=0},且B ⊆A ,则m 的取值集合为________.16.若三个非零且互不相等的实数a ,b ,c ,满足1a +1b =2c ,则称a ,b ,c 是调和的;若满足a +c =2b ,则称a ,b ,c 是等差的.若集合P 中元素a ,b ,c 既是调和的,又是等差的,则称集合P 为“好集”.若集合M ={x ||x |≤2014,x ∈Z },集合P ={a ,b ,c }⊆M ,则“好集”P 的个数为________.三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)设全集为R ,A ={x |3≤x <7},B ={x |2<x <10}. 求:A ∪B ,∁R (A ∩B ),(∁R A )∩B .18.(本小题满分12分)(1)已知全集U =R ,集合M ={x |x +3≤0},N ={x |x 2=x +12},求(∁U M )∩N ; (2)已知全集U =R ,集合A ={x |x <-1或x >1},B ={x |-1≤x <0},求A ∪(∁U B ).19.(本小题满分12分)已知集合A={x|-2<x<-1或x>1},B={x|a≤x<b},A∪B={x|x>-2},A∩B={x|1<x<3},求实数a,b的值.20.(本小题满分12分)已知集合A={x|x≤a+3},B={x|x<-1或x>5}.(1)若a=-2,求A∩∁R B;(2)若A⊆B,求a的取值范围.21.(本小题满分12分)设集合A ={x |x 2-8x +15=0},B ={x |ax -1=0}. (1)若a =15,判断集合A 与B 的关系; (2)若A ∩B =B ,求实数a 组成的集合C .22.(本小题满分12分)已知集合A ={x |(a -1)x 2+3x -2=0},B ={x |x 2-3x +2=0}. (1)若A ≠∅,求实数a 的取值范围; (2)若A ∩B =A ,求实数a 的取值范围.详解答案第一章 集合与函数概念(一)(集 合)1.D 解析:选项D 中Δ=(-1)2-4×1×1=-3<0,所以方程x 2-x +1=0无实数根.2.D 解析:∵集合A ={x ∈N |x <6}={0,1,2,3,4,5},∴6∉A .故选D. 3.D 解析:∵U ={1,3,5,7,9},A ={1,5,7},∴∁U A ={3,9}.故选D. 4.D 解析:∵A ∩B ={1,2},C ={2,3,4},∴(A ∩B )∪C ={1,2,3,4}. 5.C 解析:∵{1,2}∪A ={1,2}∴集合A 可取集合{1,2}的非空子集.∴集合A 有3个.故选C.6.C 解析:∵A ∪B ={1,4,x },∴x 2=4或x 2=x .解得x =±2或x =1或x=0.检验当x =1时,A ={1,4,1}不符合集合的性质,∴x =2或x =-2或x =0.故选C.7.C 解析:∵集合M 的代表元素是实数,集合N 的代表元素是点,∴M ∩N =∅.故选C.8.C 解析:∵A ∩B ={1,3},∴A ∩B 的子集分别是∅,{1},{3},{1,3}.故选C.解题技巧:本题主要考查了列举法表示两个集合的交集,考查了子集的求法,解决本题的关键是确定出A ∩B 所含元素的个数n ,因此所有子集的个数为2n 个.9.A 解析:∵图中阴影部分表示:x ∈N 且x ∉M ,∴x ∈N ∩∁U M .∴∁U M ={x |-2≤x ≤2},∴N ∩∁U M ={x |-2≤x <1}.故选A.10.B 解析:∵集合A ={x |ax 2+2x +1=0}中只有一个元素,∴①当a =0时,集合A ={x |2x +1=0}只有一个元素,符合题意;②当a ≠0时,一元二次方程ax 2+2x +1=0只有一解,∴Δ=0,即4-4a =0,∴a =1.故选B.11.B 解析:∵x ∈N *,12x ∈Z ,∴x =1时,12x =12∈Z ;x =2时,12x =6∈Z ;x =3时,12x =4∈Z ;x =4时,12x =3∈Z ;x =6时,12x =2∈Z ;x =12时,12x =1∈Z .12.D 解析:①当a >0,b >0时,y =3;②当a >0,b <0时,y =-1;③当a <0,b >0时,y =-1;④当a <0,b <0时,y =-1.13.a ≥-1 解析:如图:∵A ∩B ≠∅,且A ={x |-1≤x <2},B ={x |x ≤a },∴a ≥-1. 14.AB =C 解析:A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x =a +16,a ∈Z=⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =16(6a +1),a ∈Z ,B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =b 2-13,b ∈Z =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =16(3b -2),b ∈Z =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =16[3(b +1)-2],b ∈Z ,C =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =c 2+16,c ∈Z =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =16(3c +1),c ∈Z .∴A B =C .15.m =⎩⎨⎧⎭⎬⎫0,-12,13 解析:集合A ={2,-3},又∵B ⊆A ,∴B =∅,{-3},{2}.∴m =0或m =-12或m =13.16.1 006 解析:因为若集合P 中元素a ,b ,c 既是调和的,又是等差的,则1a +1b =2c 且a +c =2b ,则a =-2b ,c =4b ,因此满足条件的“好集”为形如{-2b ,b,4b }(b ≠0)的形式,则-2 014≤4b ≤2 014,解得-503≤b ≤503,且b ≠0,符合条件的b 的值可取1 006个,故“好集”P 的个数为1 006个.解题技巧:本题主要考查了以集合为背景的新概念题,解决本题的关键是弄清楚新概念、新运算、新方法的含义,转化为集合问题求解.17.解:∵全集为R ,A ={x |3≤x <7},B ={x |2<x <10}, ∴A ∪B ={x |2<x <10},A ∩B ={x |3≤x <7}, ∴∁R (A ∩B )={x |x ≥7或x <3}. ∵∁R A ={x |x ≥7或x <3},∴(∁R A )∩B ={x |2<x <3或7≤x <10}.18.解:(1)M ={x |x +3=0}={-3},N ={x |x 2=x +12}={-3,4}, ∴(∁U M )∩N ={4}.(2)∵A ={x |x <-1或x >1},B ={x |-1≤x <0}, ∴∁U B ={x |x <-1或x ≥0}. ∴A ∪(∁U B )={x |x <-1或x ≥0}.19.解:∵A ∩B ={x |1<x <3},∴b =3, 又A ∪B ={x |x >-2}, ∴-2<a ≤-1, 又A ∩B ={x |1<x <3}, ∴-1≤a <1, ∴a =-1.20.解:(1)当a =-2时,集合A ={x |x ≤1},∁R B ={x |-1≤x ≤5}, ∴A ∩∁R B ={x |-1≤x ≤1}.(2)∵A ={x |x ≤a +3},B ={x |x <-1或x >5},A ⊆B , ∴a +3<-1,∴ a <-4.解题技巧:本题主要考查了描述法表示的集合的运算,集合间的关系,解决本题的关键是借助于数轴求出符合题意的值.在解决(2)时,特别注意参数a 是否取到不等式的端点值.21.解:A ={x |x 2-8x +15=0}={3,5}. (1)若a =15,则B ={5},所以B A . (2)若A ∩B =B ,则B ⊆A . 当a =0时,B =∅,满足B ⊆A ;当a ≠0时,B =⎩⎨⎧⎭⎬⎫1a ,因为B ⊆A ,所以1a =3或1a =5,即a =13或a =15;综上所述,实数a 组成的集合C 为⎩⎨⎧⎭⎬⎫0,13,15.22.解:(1)①当a =1时,A =⎩⎨⎧⎭⎬⎫23≠∅;②当a ≠1时,Δ≥0,即a ≥-18且a ≠1,综上,a ≥-18;(2)∵B ={1,2},A ∩B =A ,∴A =∅或{1}或{2}或{1,2}. ①A =∅,Δ<0,即a <-18;②当A ={1}或{2}时,Δ=0,即a =0且a =-18,不存在这样的实数; ③当A ={1,2},Δ>0,即a >-18且a ≠1,解得a =0. 综上,a <-18或a =0.第一章集合与函数概念(二)(函数的概念与基本性质)第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列四组函数中,表示同一函数的是()A.y=x-1与y=(x-1)2B.y=x-1与y=x-1 x-1C.y=4lg x与y=2lg x2D.y=lg x-2与y=lgx 1002.已知f:x→x2是集合A到集合B={0,1,4}的一个映射,则集合A中的元素个数最多有()A.3个B.4个C.5个D.6个3.函数f(x)=x+1x-1的定义域是()A.-1,1) B.-1,1)∪(1,+∞) C.-1,+∞) D.(1,+∞)4.函数y=2--x2+4x的值域是()A.-2,2] B.1,2]C.0,2] D.-2, 2 ] 5.已知f(x)的图象如图,则f(x)的解析式为()A .f (x )=⎩⎪⎨⎪⎧1,0≤x ≤1-x -2,1<x ≤2B .f (x )=⎩⎪⎨⎪⎧-1,0≤x ≤1x +2,1<x ≤2C .f (x )=⎩⎪⎨⎪⎧-1,0≤x ≤1x -2,1<x ≤2D .f (x )=⎩⎪⎨⎪⎧-1,0≤x ≤1-x +2,1<x ≤26.定义两种运算:a ⊕b =a 2-b 2,a b =(a -b )2,则函数f (x )=2⊕x (x2)-2的解析式为( )A .f (x )=4-x 2x ,x ∈-2,0)∪(0,2]B .f (x )=x 2-4x ,x ∈(-∞,-2]∪2,+∞) C .f (x )=-x 2-4x ,x ∈(-∞,-2]∪2,+∞) D .f (x )=-4-x 2x ,x ∈-2,0)∪(0,2]7.函数f (x )=1x -x 的图象关于( ) A .坐标原点对称 B .x 轴对称 C .y 轴对称D .直线y =x 对称8.设f (x )是定义在-6,6]上的偶函数,且f (4)>f (1),则下列各式一定成立的是( )A .f (0)<f (6)B .f (4)>f (3)C .f (2)>f (0)D .f (-1)<f (4)9.若奇函数f (x )在1,3]上为增函数,且有最小值0,则它在-3,-1]上( ) A .是减函数,有最小值0 B .是增函数,有最小值0 C .是减函数,有最大值0D .是增函数,有最大值010.已知函数f (x )=⎩⎪⎨⎪⎧a x (x <0),(a -3)x +4a (x ≥0),满足对任意x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2<0成立,则a 的取值范围是( )A.⎝ ⎛⎦⎥⎤0,14 B .(0,1) C.⎣⎢⎡⎭⎪⎫14,1 D .(0,3)11.若f (x )是R 上的减函数,且f (x )的图象经过点A (0,4)和点B (3,-2),则当不等式|f (x +t )-1|<3的解集为(-1,2)时,t 的值为( )A .0B .-1C .1D .212.已知函数y =f (x )满足:①y =f (x +1)是偶函数;②在1,+∞)上为增函数.若x 1<0,x 2>0,且x 1+x 2<-2,则f (-x 1)与f (-x 2)的大小关系是( )A .f (-x 1)>f (-x 2)B .f (-x 1)<f (-x 2)C .f (-x 1)=f (-x 2)D .无法确定第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)13.若函数f (x )=ax 7+bx -2,且f (2 014)=10,则f (-2 014)的值为________. 14.若函数f (x )=ax +1x +2在x ∈(-2,+∞)上单调递减,则实数a 的取值范围是________.15.已知函数f (x )=x +3x +1,记f (1)+f (2)+f (4)+f (8)+f (16)=m ,f ⎝ ⎛⎭⎪⎫12+f ⎝ ⎛⎭⎪⎫14+f ⎝ ⎛⎭⎪⎫18+f ⎝ ⎛⎭⎪⎫116=n ,则m +n =________. 16.设a 为常数且a <0,y =f (x )是定义在R 上的奇函数,当x <0时,f (x )=x +a 2x -2.若f (x )≥a 2-1对一切x ≥0都成立,则a 的取值范围为________.三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)(1)已知f (x -2)=3x -5,求f (x );(2)若f (f (f (x )))=27x +26,求一次函数f (x )的解析式.18.(本小题满分12分) 已知f (x )=1x -1,x ∈2,6].(1)证明:f (x )是定义域上的减函数; (2)求f (x )的最大值和最小值.19.(本小题满分12分)某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R (x )=⎩⎨⎧400x -12x 2,0≤x ≤400,80 000,x >400,其中x 是仪器的月产量.(1)将利润f (x )表示为月产量x 的函数;(2)当月产量x 为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)20.(本小题满分12分)已知函数f(x)=x2+2ax+2,x∈-5,5].(1)当a=-1时,求函数的最大值和最小值;(2)若y=f(x)在区间-5,5]上是单调函数,求实数a的取值范围.21.(本小题满分12分)已知二次函数f(x)=ax2+bx(a,b∈R),若f(1)=-1且函数f(x)的图象关于直线x=1对称.(1)求a,b的值;(2)若函数f(x)在k,k+1](k≥1)上的最大值为8,求实数k的值.22.(本小题满分12分)已知二次函数f(x)的图象过点(0,4),对任意x满足f(3-x)=f(x),且有最小值74.(1)求f(x)的解析式;(2)求函数h(x)=f(x)-(2t-3)x在区间0,1]上的最小值,其中t∈R;(3)在区间-1,3]上,y=f(x)的图象恒在函数y=2x+m的图象上方,试确定实数m的范围.详解答案第一章集合与函数概念(二)(函数的概念与基本性质)1.D解析:∵y=x-1与y=(x-1)2=|x-1|的对应关系不同,∴它们不是同一函数;y=x-1(x≥1)与y=x-1x-1(x>1)的定义域不同,∴它们不是同一函数;又y=4lg x(x>0)与y=2lg x2(x≠0)的定义域不同,因此它们也不是同一函数,而y=lg x-2(x>0)与y=lg x100=lg x-2(x>0)有相同的定义域、值域与对应关系,因此它们是同一函数.2.C解析:令x2=0,1,4,解得x=0,±1,±2.故选C.3.B 解析:由⎩⎪⎨⎪⎧x +1≥0,x -1≠0,解得x ≥-1,且x ≠1.4.C 解析:令t =-x 2+4x ,x ∈0,4],∴t ∈0,4].又∵y 1=x ,x ∈0,+∞)是增函数∴ t ∈0,2],-t ∈-2,0],∴y ∈0,2].故选C.5.C 解析:当0≤x ≤1时,f (x )=-1;当1<x ≤2时,设f (x )=kx +b (k ≠0),把点(1,-1),(2,0)代入f (x )=kx +b (k ≠0),则f (x )=x -2.所以f (x )=⎩⎪⎨⎪⎧-1,0≤x ≤1,x -2,1<x ≤2.故选C. 6.D 解析:f (x )=2⊕x (x2)-2=22-x 2(x -2)2-2=4-x 2|x -2|-2.由⎩⎪⎨⎪⎧4-x 2≥0,|x -2|-2≠0,得-2≤x ≤2且x ≠0.∴f (x )=-4-x 2x .7.A 解析:函数f (x )的定义域关于原点对称,又∵f (-x )=1-x+x =-⎝ ⎛⎭⎪⎫1x -x =-f (x ),∴f (x )为奇函数,其图象关于坐标原点对称.8.D 解析:∵f (x )是定义在-6,6]上的偶函数,∴f (-1)=f (1).又f (4)>f (1),f (4)>f (-1).9.D 解析:因为奇函数f (x )在1,3]上为增函数,且有最小值0,所以f (x )在-3,-1]上是增函数,且有最大值0.10.A 解析:由于函数f (x )=⎩⎪⎨⎪⎧a x (x <0),(a -3)x +4a (x ≥0)满足对任意x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2<0成立,所以该函数为R 上的减函数,所以⎩⎪⎨⎪⎧0<a <1,a -3<0,4a ≤a 0,解得0<a ≤14.解题技巧:本题主要考查了分段函数的单调性,解决本题的关键是利用好该函数为R 上的减函数这一条件.应特别注意隐含条件“a 0≥4a ”.11.C 解析:由不等式|f (x +t )-1|<3,得-3<f (x +t )-1<3,即-2<f (x +t )<4.又因为f (x )的图象经过点A (0,4)和点B (3,-2),所以f (0)=4,f (3)=-2,所以f (3)<f (x +t )<f (0).又f (x )在R 上为减函数,则3>x +t >0,即-t <x <3-t ,解集为(-t,3-t ).∵不等式的解集为(-1,2),∴-t =-1,3-t =2,解得t =1.故选C.12.A 解析:由y =f (x +1)是偶函数且把y =f (x +1)的图象向右平移1个单位可得函数y =f (x )的图象,所以函数y =f (x )的图象关于x =1对称,即f (2+x )=f (-x ).因为x 1<0,x 2>0,且x 1+x 2<-2,所以2<2+x 2<-x 1.因为函数在1,+∞)上为增函数,所以f (2+x 2)<f (-x 1),即f (-x 1)>f (-x 2),故选A.13.-14 解析:设g (x )=ax 7+bx ,则g (x )是奇函数,g (-2 014)=-g (2 014).∵f (2 014)=10且f (2 014)=g (2 014)-2,∴g (2 014)=12,∴g (-2 014)=-12,∴f (-2 014)=g (-2 014)-2,∴f (-2 014)=-14.14.a <12 解析:f (x )=ax +1x +2=a +1-2a x +2.∵y =1x +2在x ∈(-2,+∞)上是减函数,∴1-2a >0,∴a <12.15.18 解析:因为函数f (x )=x +3x +1,所以f ⎝ ⎛⎭⎪⎫1x =1+3xx +1.又因为f (x )+f ⎝ ⎛⎭⎪⎫1x =4(x +1)x +1=4,f (1)+f (2)+f (4)+f (8)+f (16)+f ⎝ ⎛⎭⎪⎫12+f ⎝ ⎛⎭⎪⎫14+f ⎝ ⎛⎭⎪⎫18+f ⎝ ⎛⎭⎪⎫116 =f (1)+f (2)+f ⎝ ⎛⎭⎪⎫12+f (4)+f ⎝ ⎛⎭⎪⎫14+f (8)+f ⎝ ⎛⎭⎪⎫18+f (16)+f ⎝ ⎛⎭⎪⎫116=f (1)+4×4=18, 所以m +n =18.解题技巧:本题主要考查了学生的观察、归纳、推理的能力,解决本题的关键是挖掘出题目中隐含的规律f (x )+f ⎝ ⎛⎭⎪⎫1x =4.16.-1≤a <0 解析:当x =0时,f (x )=0,则0≥a 2-1,解得-1≤a ≤1,所以-1≤a <0.当x >0时,-x <0,f (-x )=-x +a 2-x -2,则f (x )=-f (-x )=x +a 2x +2.由对数函数的图象可知,当x =a 2=|a |=-a 时,有f (x )min =-2a +2, 所以-2a +2≥a 2-1,即a 2+2a -3≤0,解得-3≤a ≤1.又a <0, 所以-3≤a <0. 综上所述,-1≤a <0.17.解:(1)令t =x -2,则x =t +2,t ∈R ,由已知有f (t )=3(t +2)-5=3t +1,故f (x )=3x +1.(2)设f (x )=ax +b (a ≠0),f (f (x ))=a 2x +ab +b , f (f (f (x )))=a (a 2x +ab +b )+b =a 3x +a 2b +ab +b ,∴⎩⎪⎨⎪⎧a 3=27,a 2b +ab +b =26,解得a =3,b =2.则f (x )=3x +2.18.(1)证明:设2≤x 1<x 2≤6,则f (x 1)-f (x 2)=1x 1-1-1x 2-1=x 2-x 1(x 1-1)(x 2-1),因为x 1-1>0,x 2-1>0,x 2-x 1>0,所以f (x 1)-f (x 2)>0, 即f (x 1)>f (x 2).所以f (x )是定义域上的减函数.(2)由(1)的结论可得,f (x )min =f (6)=15,f (x )max =f (2)=1. 19.解:(1)当0≤x ≤400时,f (x )=400x -12x 2-100x -20 000=-12x 2+300x -20 000. 当x >400时,f (x )=80 000-100x -20 000=60 000-100x ,所以f (x )=⎩⎨⎧-12x 2+300x -20 000,0≤x ≤400,60 000-100x ,x >400.(2)当0≤x ≤400时,f (x )=-12x 2+300x -20 000=-12(x -300)2+25 000; 当x =300时,f (x )max =25 000; 当x >400时,f (x )=60 000-100x <f (400)=20 000<25 000; 所以当x =300时,f (x )max =25 000.故当月产量x 为300台时,公司获利润最大,最大利润为25 000元. 20.解:(1)当a =-1时,f (x )=x 2-2x +2=(x -1)2+1. 又因为x ∈-5,5].所以函数的最大值为37,最小值为1. (2)若y =f (x )在区间-5,5]上是单调函数, 则有-a ≤-5或-a ≥5解得a ≤-5或a ≥5.解题技巧:本题主要考查了二次函数在给定区间上的最值与单调性.解决本题的关键是确定对称轴和区间端点的关系.注意分类讨论.21.解:(1)由题意可得f (1)=a +b =-1且-b2a =1, 解得a =1,b =-2. (2)f (x )=x 2-2x =(x -1)2-1.因为k ≥1,所以f (x )在k ,k +1]上单调递增, 所以f (x )max =f (k +1)=(k +1)2-2(k +1)=8, 解得k =±3. 又k ≥1,所以k =3.22.解:(1)由题知二次函数图象的对称轴为x =32,又最小值是74,则可设f (x )=a ⎝ ⎛⎭⎪⎫x -322+74(a ≠0), 又图象过点(0,4),则a ⎝ ⎛⎭⎪⎫0-322+74=4,解得a =1. ∴f (x )=⎝ ⎛⎭⎪⎫x -322+74=x 2-3x +4. (2)h (x )=f (x )-(2t -3)x =x 2-2tx +4=(x -t )2+4-t 2,其对称轴x =t . ①t ≤0时,函数h (x )在0,1]上单调递增,最小值为h (0)=4;②当0<t <1时,函数h (x )的最小值为h (t )=4-t 2;③当t ≥1时,函数h (x )在0,1]上单调递减,最小值为h (1)=5-2t ,所以h (x )min =⎩⎪⎨⎪⎧ 4,t ≤0,4-t 2,0<t <1,5-2t ,t ≥1.(3)由已知:f (x )>2x +m 对x ∈-1,3]恒成立,∴m <x 2-5x +4对x ∈-1,3]恒成立.∴m <(x 2-5x +4)min (x ∈-1,3]).∵g (x )=x 2-5x +4在x ∈-1,3]上的最小值为-94, ∴m <-94.。
人教A版数学必修一第一章集合和函数的概念答案.docx

高中数学学习材料鼎尚图文*整理制作高一数学单元卷(一)必修1答案(第一章集合和函数的概念)一.选择题(本大题12小题,每小题5分,共60分)1.答案:A (1)错的原因是元素不确定,(2)前者是数集,而后者是点集,种类不同,(3)361,0.5242=-=,有重复的元素,应该是3个元素,(4)本集合还包括坐标轴 2.答案:B,{}32x x ∈-<+N ={}5+N x x ∈<={}1,2,3,4,故选B.3. A 阴影部分完全覆盖了C 部分,这样就要求交集运算的两边都含有C 部分; 4答案:B ,T S = 1,3,5,6 ,)(T S C U ={}2,4,7,85.答案:B, =M Z k k x x ∈+=,412| , N = Z k k x x ∈++=,41)1(| ,1k +属于全体整数,2k 属于偶数, M N ⊆6.答案:C,判断两个函数是否同一函数,看其定义域和对应关系是否相同.7. C 有可能是没有交点的,如果有交点,那么对于1x =仅有一个函数值;8.答案:D, 该分段函数的三段各自的值域为(][)[),1,0,4,4,-∞+∞,而[)30,4∈∴2()3,3,12,f x x x x ===±-<<而∴ 3x =;9.答案:A,1,2x y =-=,所以3,1x y x y -=-+=10. C 22224(2)44,042,240x x x x x x x -+=--+≤≤-+≤-≤--+≤ 20242,02x x y ≤--+≤≤≤;11.答案:A,奇函数关于原点对称,左右两边有相同的单调性12.答案:B, 对称轴2,24,2x a a a =--≤≥-二.填空题: (本大题4小题,每小题4分,共16分)13. []4,9 021,3,49x x ≤-≤≤≤≤≤得2x 即14.答案:1|12k k ⎧⎫-≤≤⎨⎬⎩⎭ ; 213212k k -≥-⎧⎨+≤⎩得112k -≤≤ 15.(](2,0)2,5- 奇函数关于原点对称,补足左边的图象16.答案:3(1)x x -, 设0x <,则0x ->,33()(1)(1)f x x x x x -=-+-=-- ∵()()f x f x -=-∴3()()(1)f x f x x x =--=-三.解答题:(本大题共六小题,共74分)17.解:∵{}3A B =-,∴3B -∈,而213a +≠-, 4分∴当{}{}33,0,0,1,3,3,1,1a a A B -=-==-=--,这样{}3,1A B =-与{}3A B =-矛盾; 8分当213,1,a a -=-=-符合{}3AB =- ∴1a =- 12分18.解:由A ∩C =A ,A ∩B =φ 得{}1,3A =, 5分 0px q ++=2即方程x 的两个根是1,3,由韦达定理,得 7分 则1+3=-p p=-41×3=q q=3 12分19.解:令12,(0)x t t -=≥, 2分则2221111,2222t t x y t t t --==+=-++ 5分 21(1)12y t =--+, 9分 当1t =时,(]max 1,,1y y =∈-∞所以 12分20.解: 设OE=x,则当0≤x ≤2时,△OEF 的高EF=241212121x x x s x =⋅=∴ 3分 当2<x ≤3时,△BEF 的高EF=3-x ,∴)3)(3(211321x x s ---⨯⨯= 6分 当3x >时,32s = 9分 P x x -=+21 q x x =⋅21⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤<-+-≤≤==323323321204)(22x x x x x x x f S 10分12分21.解:()f x 是奇函数,∴()()f x f x \-=-,∴22(1)(1)f a f a \--=-∴22(1)(1)(1)f a f a f a -<--=-,6分 ()f x 的定义域为()1,1-且在定义域上单调递减,则2211111111a a a a -<-<⎧⎪-<-<⎨⎪->-⎩, 10分∴01a << 12分22.解:(1)依题意得(0)012()25f f ì=ïïïíï=ïïî 即2010221514b a b ìïï=ïï+ïïïí+ïï=ïïï+ïïïî得10a b ì=ïïíï=ïî ∴2()1x f x x\=+ 4分 (2)证明:任取1211x x -<<<,则12122212()()11x x f x f x x x -=-++12122212()(1)(1)(1)x x x x x x --=++ 121211,0x x x x -<<<\-<,221210,10x x +>+> 又121211,10x x x x -<<\->12()()0f x f x \-< 3 2 x 1 0 y∴ ()f x 在(1,1)-上是增函数。
高中数学人教A版必修一 学业分层测评(一) Word版含答案

学业分层测评(一) 集合的含义(建议用时:45分钟)[学业达标]一、选择题1.下列对象能构成集合的是()①NBA联盟中所有优秀的篮球运动员,②所有的钝角三角形,③2015年诺贝尔经济学奖得主,④大于等于0的整数,⑤莘县第一中学所有聪明的学生.A.①②④B.②⑤C.③④⑤D.②③④【解析】由集合中元素的确定性知,①中“优秀的篮球运动员”和⑤中“聪明的学生”不确定,所以不能构成集合.【答案】 D2.已知集合M中的元素a,b,c是△ABC的三边,则△ABC一定不是() A.锐角三角形B.钝角三角形C.直角三角形D.等腰三角形【解析】因为集合中元素具有互异性,所以a,b,c互不相等,因此选D.【答案】 D3.下面有三个命题:①集合N中最小的数是1;②若-a∉N,则a∈N;③若a∈N,b∈N,则a+b的最小值是2.其中正确命题的个数是()A.0个B.1个C.2个D.3个【解析】因为自然数集中最小的数是0,而不是1,所以①错;对于②,取a=2,则-2∉N,2∉N,所以②错;对于③,a=0,b=0时,a+b取得最小值是0,而不是2,所以③错.【答案】 A4.下列正确的命题的个数有( )①1∈N ;②2∈N *;③12∈Q ;④2+2∉R ;⑤42∉Z .A .1个B .2个C .3个D .4个【解析】 ∵1是自然数,∴1∈N ,故①正确;∵2不是正整数,∴2∉N *,故②不正确;∵12是有理数,∴12∈Q ,故③正确;∵2+2是实数,∴2+2∈R ,所以④不正确; ∵42=2是整数,∴42∈Z ,故⑤不正确.【答案】 B5.给出下列说法,其中正确的个数为( )(1)由1,32,64,⎪⎪⎪⎪⎪⎪-12,12这些数组成的集合有5个元素; (2)方程(x -3)(x -2)2=0的解组成的集合有3个元素;(3)由一条边为2,一个内角为30°的等腰三角形组成的集合中含有4个元素.A .0B .1C .2D .3【解析】 (1)不正确.对于一个给定的集合,它的元素必须是互异的,即集合中的任意两个元素都是不同的,而32与64相同,⎪⎪⎪⎪⎪⎪-12与12相同,故这些数组成的集合只有3个元素.(2)不正确.方程(x -3)(x -2)2=0的解是x 1=3,x 2=x 3=2,因此写入集合时只有3和2两个元素.(3)正确.若2为底边长,则30°角可以是顶角或底角;若2为腰长,则30°角也可以是顶角或底角,故集合中有4个元素.【答案】 B二、填空题6.由m -1,3m ,m 2-1组成的三元素集合中含有-1,则m 的值是________. 【导学号:97030003】【解析】 当m =0时,三个数分别为-1,0,-1,组成的集合中只有两个元素,不合题意;当m =-13时,三个数分别为-43,-1,-89,符合题意,即m 只能取-13.【答案】 -137.设集合A 是由1,k 2为元素组成的集合,则实数k 的取值范围是________.【解析】 ∵1∈A ,k 2∈A ,结合集合中元素的性质可知k 2≠1,解得k ≠±1.【答案】 k ≠±18.由实数t ,|t |,t 2,-t ,t 3所构成的集合M 中最多含有________个元素.【解析】 由于|t |至少与t 和-t 中的一个相等,故集合M 中至多有4个元素. 当t =-2时,t ,-t ,t 2,t 3互不相同,此时集合M 中元素最多,为4个.【答案】 4三、解答题9.设非空数集A 满足以下条件:若a ∈A ,则11-a∈A ,且1∉A . (1)若2∈A ,你还能求出A 中哪些元素?(2)“3∈A ”和“4∈A ”能否同时成立?【解】 (1)若2∈A ,则11-2=-1∈A ,于是11-(-1)=12∈A ,而11-12=2. 所以集合A 中还有-1,12这两个元素.(2)若“3∈A ”和“4∈A ”能同时成立,则11-a =3且11-a =4,由11-a =3解得a =23,由11-a=4解得a =34,矛盾,所以“3∈A ”和“4∈A ”不能同时成立. 10.设P 、Q 为两个非空实数集合,P 中含有0,2,5三个元素,Q 中含有1,2,6三个元素,定义集合P +Q 中的元素是a +b ,其中a ∈P ,b ∈Q ,则P +Q 中元素的个数是多少? 【导学号:97030004】【解】 ∵当a =0时,b 依次取1,2,6,得a +b 的值分别为1,2,6;当a =2时,b 依次取1,2,6,得a +b 的值分别为3,4,8;当a =5时,b 依次取1,2,6,得a +b 的值分别为6,7,11.由集合元素的互异性知P +Q 中元素为1,2,3,4,6,7,8,11,共8个.[能力提升]1.集合A 含有两个元素a -3和2a -1,则实数a 的取值范围是________.【解析】 由集合中元素的互异性,可得a -3≠2a -1,所以a ≠-2.即实数a 的取值范围为a ≠-2.【答案】 a ≠-22.设P 、Q 是两个数集,P 中含有0,2两个元素,Q 中含有1,2两个元素,定义集合P +Q 中的元素是a +b ,其中a ∈P ,b ∈Q ,则P +Q 中元素的个数是________.【解析】 由于a ∈P ,a =0或2,b ∈Q ,b =1或2,因此a +b 的值为1,2,3,4,共4个.【答案】 43.集合A 中的元素y ∈N 且y =-x 2+1,若t ∈A ,则t 的值为________.【解析】 依题意A ={y ∈N |y =-x 2+1}={y ∈N |y ≤1}={0,1}.又t ∈A ,∴t =0或1.【答案】 0或14.若所有形如3a +2b (a ∈Z ,b ∈Z )的数组成集合A ,判断32-9是否是集合A 中的元素.【解】∵32-9=-9+32=3×(-3)+2×3. 令a=-3,b=3,则-3∈Z,3∈Z.∴32-9是集合A中的元素.。
人教A版高中数学必修1课后习题及答案(全部三章)

高中数学必修1课后习题答案 第一章 集合与函数概念1.1集合1.1.1集合的含义与表示练习(第5页)1.用符号“∈”或“∉”填空:(1)设A 为所有亚洲国家组成的集合,则:中国_______A ,美国_______A ,印度_______A ,英国_______A ; (2)若2{|}A x x x ==,则1-_______A ; (3)若2{|60}B x x x =+-=,则3_______B ;(4)若{|110}C x N x =∈≤≤,则8_______C ,9.1_______C . 1.(1)中国∈A ,美国∉A ,印度∈A ,英国∉A ;中国和印度是属于亚洲的国家,美国在北美洲,英国在欧洲.(2)1-∉A 2{|}{0,1}A x x x ===.(3)3∉B 2{|60}{3,2}B x x x =+-==-. (4)8∈C ,9.1∉C 9.1N ∉.2.试选择适当的方法表示下列集合:(1)由方程290x -=的所有实数根组成的集合; (2)由小于8的所有素数组成的集合;(3)一次函数3y x =+与26y x =-+的图象的交点组成的集合; (4)不等式453x -<的解集.2.解:(1)因为方程290x -=的实数根为123,3x x =-=,所以由方程290x -=的所有实数根组成的集合为{3,3}-; (2)因为小于8的素数为2,3,5,7,所以由小于8的所有素数组成的集合为{2,3,5,7};(3)由326y x y x =+⎧⎨=-+⎩,得14x y =⎧⎨=⎩,即一次函数3y x =+与26y x =-+的图象的交点为(1,4),所以一次函数3y x =+与26y x =-+的图象的交点组成的集合为{(1,4)};(4)由453x -<,得2x <,所以不等式453x -<的解集为{|2}x x <.1.1.2集合间的基本关系练习(第7页)1.写出集合{,,}a b c 的所有子集.1.解:按子集元素个数来分类,不取任何元素,得∅;取一个元素,得{},{},{}a b c ; 取两个元素,得{,},{,},{,}a b a c b c ; 取三个元素,得{,,}a b c ,即集合{,,}a b c 的所有子集为,{},{},{},{,},{,},{,},{,,}a b c a b a c b c a b c ∅.2.用适当的符号填空:(1)a ______{,,}a b c ; (2)0______2{|0}x x =; (3)∅______2{|10}x R x ∈+=; (4){0,1}______N ;(5){0}______2{|}x x x =; (6){2,1}______2{|320}x x x -+=. 2.(1){,,}a a b c ∈ a 是集合{,,}a b c 中的一个元素;(2)20{|0}x x ∈= 2{|0}{0}x x ==;(3)2{|10}x R x ∅=∈+= 方程210x +=无实数根,2{|10}x R x ∈+==∅; (4){0,1}N (或{0,1}N ⊆) {0,1}是自然数集合N 的子集,也是真子集; (5){0}2{|}x x x = (或2{0}{|}x x x ⊆=) 2{|}{0,1}x x x ==;(6)2{2,1}{|320}x x x =-+= 方程2320x x -+=两根为121,2x x ==.3.判断下列两个集合之间的关系:(1){1,2,4}A =,{|8}B x x =是的约数;(2){|3,}A x x k k N ==∈,{|6,}B x x z z N ==∈;(3){|410}A x x x N +=∈是与的公倍数,,{|20,}B x x m m N +==∈. 3.解:(1)因为{|8}{1,2,4,8}B x x ==是的约数,所以AB ;(2)当2k z =时,36k z =;当21k z =+时,363k z =+,即B 是A 的真子集,B A ;(3)因为4与10的最小公倍数是20,所以A B =.1.1.3集合的基本运算练习(第11页)1.设{3,5,6,8},{4,5,7,8}A B ==,求,A B A B .1.解:{3,5,6,8}{4,5,7,8}{5,8}A B ==,{3,5,6,8}{4,5,7,8}{3,4,5,6,7,8}AB ==.2.设22{|450},{|1}A x x x B x x =--===,求,A B A B .2.解:方程2450x x --=的两根为121,5x x =-=, 方程210x -=的两根为121,1x x =-=, 得{1,5},{1,1}A B =-=-, 即{1},{1,1,5}AB A B =-=-.3.已知{|}A x x =是等腰三角形,{|}B x x =是直角三角形,求,A B A B .3.解:{|}A B x x =是等腰直角三角形,{|}AB x x =是等腰三角形或直角三角形.4.已知全集{1,2,3,4,5,6,7}U =,{2,4,5},{1,3,5,7}A B ==, 求(),()()U U U AB A B 痧?. 4.解:显然{2,4,6}U B =ð,{1,3,6,7}U A =ð, 则(){2,4}U AB =ð,()(){6}U U A B =痧. 1.1集合习题1.1 (第11页) A 组1.用符号“∈”或“∉”填空:(1)237_______Q ; (2)23______N ; (3)π_______Q ;(4_______R ; (5Z ; (6)2_______N .1.(1)237Q ∈ 237是有理数; (2)23N ∈ 239=是个自然数;(3)Q π∉ π是个无理数,不是有理数; (4R 是实数;(5Z3=是个整数; (6)2N ∈ 2)5=是个自然数.2.已知{|31,}A x x k k Z ==-∈,用 “∈”或“∉” 符号填空: (1)5_______A ; (2)7_______A ; (3)10-_______A .2.(1)5A ∈; (2)7A ∉; (3)10A -∈.当2k =时,315k -=;当3k =-时,3110k -=-; 3.用列举法表示下列给定的集合: (1)大于1且小于6的整数; (2){|(1)(2)0}A x x x =-+=; (3){|3213}B x Z x =∈-<-≤.3.解:(1)大于1且小于6的整数为2,3,4,5,即{2,3,4,5}为所求;(2)方程(1)(2)0x x -+=的两个实根为122,1x x =-=,即{2,1}-为所求; (3)由不等式3213x -<-≤,得12x -<≤,且x Z ∈,即{0,1,2}为所求. 4.试选择适当的方法表示下列集合:(1)二次函数24y x =-的函数值组成的集合;(2)反比例函数2y x=的自变量的值组成的集合; (3)不等式342x x ≥-的解集.4.解:(1)显然有20x ≥,得244x -≥-,即4y ≥-,得二次函数24y x =-的函数值组成的集合为{|4}y y ≥-;(2)显然有0x ≠,得反比例函数2y x =的自变量的值组成的集合为{|0}x x ≠; (3)由不等式342x x ≥-,得45x ≥,即不等式342x x ≥-的解集为4{|}5x x ≥.5.选用适当的符号填空:(1)已知集合{|233},{|2}A x x x B x x =-<=≥,则有:4-_______B ; 3-_______A ; {2}_______B ; B _______A ; (2)已知集合2{|10}A x x =-=,则有:1_______A ; {1}-_______A ; ∅_______A ; {1,1}-_______A ; (3){|}x x 是菱形_______{|}x x 是平行四边形;{|}x x 是等腰三角形_______{|}x x 是等边三角形. 5.(1)4B -∉; 3A -∉; {2}B ; BA ;2333x x x -<⇒>-,即{|3},{|2}A x x B x x =>-=≥; (2)1A ∈; {1}-A ; ∅A ; {1,1}-=A ; 2{|10}{1,1}A x x =-==-; (3){|}x x 是菱形{|}x x 是平行四边形;菱形一定是平行四边形,是特殊的平行四边形,但是平行四边形不一定是菱形;{|}x x 是等边三角形{|}x x 是等腰三角形.等边三角形一定是等腰三角形,但是等腰三角形不一定是等边三角形.6.设集合{|24},{|3782}A x x B x x x =≤<=-≥-,求,AB A B .6.解:3782x x -≥-,即3x ≥,得{|24},{|3}A x x B x x =≤<=≥, 则{|2}AB x x =≥,{|34}A B x x =≤<.7.设集合{|9}A x x =是小于的正整数,{1,2,3},{3,4,5,6}B C ==,求A B ,AC ,()A B C ,()A B C .7.解:{|9}{1,2,3,4,5,6,7,8}A x x ==是小于的正整数, 则{1,2,3}AB =,{3,4,5,6}AC =, 而{1,2,3,4,5,6}B C =,{3}B C =, 则(){1,2,3,4,5,6}AB C =,(){1,2,3,4,5,6,7,8}A B C =.8.学校里开运动会,设{|}A x x =是参加一百米跑的同学,{|}B x x =是参加二百米跑的同学,{|}C x x =是参加四百米跑的同学,学校规定,每个参加上述的同学最多只能参加两项,请你用集合的语言说明这项规定, 并解释以下集合运算的含义:(1)A B ;(2)A C . 8.解:用集合的语言说明这项规定:每个参加上述的同学最多只能参加两项, 即为()A B C =∅.(1){|}AB x x =是参加一百米跑或参加二百米跑的同学;(2){|}A C x x =是既参加一百米跑又参加四百米跑的同学.9.设{|}S x x =是平行四边形或梯形,{|}A x x =是平行四边形,{|}B x x =是菱形,{|}C x x =是矩形,求BC ,A B ð,S A ð.9.解:同时满足菱形和矩形特征的是正方形,即{|}B C x x =是正方形,平行四边形按照邻边是否相等可以分为两类,而邻边相等的平行四边形就是菱形, 即{|}A B x x =是邻边不相等的平行四边形ð, {|}S A x x =是梯形ð.10.已知集合{|37},{|210}A x x B x x =≤<=<<,求()R AB ð,()R A B ð,()R A B ð,()R A B ð.10.解:{|210}AB x x =<<,{|37}A B x x =≤<,{|3,7}R A x x x =<≥或ð,{|2,10}R B x x x =≤≥或ð, 得(){|2,10}R A B x x x =≤≥或ð, (){|3,7}R A B x x x =<≥或ð, (){|23,710}R A B x x x =<<≤<或ð,(){|2,3710}R AB x x x x =≤≤<≥或或ð.B 组1.已知集合{1,2}A =,集合B 满足{1,2}A B =,则集合B 有 个.1.4 集合B 满足AB A =,则B A ⊆,即集合B 是集合A 的子集,得4个子集.2.在平面直角坐标系中,集合{(,)|}C x y y x ==表示直线y x =,从这个角度看, 集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示什么?集合,C D 之间有什么关系?2.解:集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示两条直线21,45x y x y -=+=的交点的集合,即21(,)|{(1,1)}45x y D x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭,点(1,1)D 显然在直线y x =上,得D C .3.设集合{|(3)()0,}A x x x a a R =--=∈,{|(4)(1)0}B x x x =--=,求,A B A B .3.解:显然有集合{|(4)(1)0}{1,4}B x x x =--==, 当3a =时,集合{3}A =,则{1,3,4},A B A B ==∅; 当1a =时,集合{1,3}A =,则{1,3,4},{1}A B A B ==; 当4a =时,集合{3,4}A =,则{1,3,4},{4}AB A B ==;当1a ≠,且3a ≠,且4a ≠时,集合{3,}A a =,则{1,3,4,},AB a A B ==∅.4.已知全集{|010}U AB x N x ==∈≤≤,(){1,3,5,7}U A B =ð,试求集合B . 4.解:显然{0,1,2,3,4,5,6,7,8,9,10}U =,由U AB =,得U B A ⊆ð,即()U UAB B =痧,而(){1,3,5,7}U A B =ð, 得{1,3,5,7}U B =ð,而()U UB B =痧,即{0,2,4,6,8.9,10}B =.第一章 集合与函数概念1.2函数及其表示1.2.1函数的概念练习(第19页)1.求下列函数的定义域:(1)1()47f x x =+; (2)()1f x =.1.解:(1)要使原式有意义,则470x +≠,即74x ≠-,得该函数的定义域为7{|}4x x ≠-;(2)要使原式有意义,则1030x x -≥⎧⎨+≥⎩,即31x -≤≤,得该函数的定义域为{|31}x x -≤≤. 2.已知函数2()32f x x x =+,(1)求(2),(2),(2)(2)f f f f -+-的值;(2)求(),(),()()f a f a f a f a -+-的值.2.解:(1)由2()32f x x x =+,得2(2)322218f =⨯+⨯=, 同理得2(2)3(2)2(2)8f -=⨯-+⨯-=,则(2)(2)18826f f +-=+=,即(2)18,(2)8,(2)(2)26f f f f =-=+-=;(2)由2()32f x x x =+,得22()3232f a a a a a =⨯+⨯=+, 同理得22()3()2()32f a a a a a -=⨯-+⨯-=-, 则222()()(32)(32)6f a f a a a a a a +-=++-=,即222()32,()32,()()6f a a a f a a a f a f a a =+-=-+-=.3.判断下列各组中的函数是否相等,并说明理由:(1)表示炮弹飞行高度h 与时间t 关系的函数21305h t t =-和二次函数21305y x x =-; (2)()1f x =和0()g x x =.3.解:(1)不相等,因为定义域不同,时间0t >; (2)不相等,因为定义域不同,0()(0)g x x x =≠. 1.2.2函数的表示法练习(第23页)1.如图,把截面半径为25cm 的圆形木头锯成矩形木料,如果矩形的一边长为xcm , 面积为2ycm ,把y 表示为x 的函数.1,y ==050x <<,即(050)y x =<<.2.下图中哪几个图象与下述三件事分别吻合得最好?请你为剩下的那个图象写出一件事. (1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;(2)我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间; (3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.2.解:图象(A )对应事件(2),在途中遇到一次交通堵塞表示离开家的距离不发生变化; 图象(B )对应事件(3),刚刚开始缓缓行进,后来为了赶时间开始加速; 图象(D )对应事件(1),返回家里的时刻,离开家的距离又为零;图象(C )我出发后,以为要迟到,赶时间开始加速,后来心情轻松,缓缓行进. 3.画出函数|2|y x =-的图象.3.解:2,2|2|2,2x x y x x x -≥⎧=-=⎨-+<⎩,图象如下所示.4.设{|},{0,1}A x x B ==是锐角,从A 到B 的映射是“求正弦”,与A 中元素60相对应的B 中的元素是什么?与B中的元素2相对应的A 中元素是什么? 4.解:因为3sin 60=,所以与A 中元素60相对应的B因为2sin 45=,所以与B相对应的A 中元素是45. 1.2函数及其表示 习题1.2(第23页)1.求下列函数的定义域: (1)3()4xf x x =-; (2)()f x = (3)26()32f x x x =-+; (4)()1f x x =-. 1.解:(1)要使原式有意义,则40x -≠,即4x ≠, 得该函数的定义域为{|4}x x ≠; (2)x R∈,()f x =即该函数的定义域为R ;(3)要使原式有意义,则2320x x -+≠,即1x ≠且2x ≠,得该函数的定义域为{|12}x x x ≠≠且;(A )(B )(C )(D )(4)要使原式有意义,则4010x x -≥⎧⎨-≠⎩,即4x ≤且1x ≠,得该函数的定义域为{|41}x x x ≤≠且. 2.下列哪一组中的函数()f x 与()g x 相等?(1)2()1,()1x f x x g x x=-=-; (2)24(),()f x x g x ==;(3)2(),()f x x g x =.2.解:(1)()1f x x =-的定义域为R ,而2()1x g x x=-的定义域为{|0}x x ≠, 即两函数的定义域不同,得函数()f x 与()g x 不相等;(2)2()f x x =的定义域为R ,而4()g x =的定义域为{|0}x x ≥,即两函数的定义域不同,得函数()f x 与()g x 不相等;(32x =,即这两函数的定义域相同,切对应法则相同,得函数()f x 与()g x 相等.3.画出下列函数的图象,并说出函数的定义域和值域. (1)3y x =; (2)8y x=; (3)45y x =-+; (4)267y x x =-+. 3.解:(1)义域是(,)-∞+∞,值域是(,)-∞+∞;定 (2)义域是(,0)(0,)-∞+∞,值域是(,0)(0,)-∞+∞;定(3)义域是(,)-∞+∞,值域是(,)-∞+∞; 定(4)义域是(,)-∞+∞,值域是[2,)-+∞.定2()352f x x x =-+,求(f ,()f a -,(3)f a +,4.已知函数()(3)f a f +.2()352f x x x =-+,所以4.解:因为2(3(5(28f =⨯-⨯+=+即(8f =+同理,22()3()5()2352f a a a a a -=⨯--⨯-+=++,即2()352f a a a -=++;22(3)3(3)5(3)231314f a a a a a +=⨯+-⨯++=++,即2(3)31314f a a a +=++;22()(3)352(3)3516f a f a a f a a +=-++=-+,即2()(3)3516f a f a a +=-+.5.已知函数2()6x f x x +=-, (1)点(3,14)在()f x 的图象上吗?(2)当4x =时,求()f x 的值;(3)当()2f x =时,求x 的值.5.解:(1)当3x =时,325(3)14363f +==-≠-, 即点(3,14)不在()f x 的图象上;(2)当4x =时,42(4)346f +==--, 即当4x =时,求()f x 的值为3-;(3)2()26x f x x +==-,得22(6)x x +=-, 即14x =. 6.若2()f x x bx c =++,且(1)0,(3)0f f ==,求(1)f -的值.6.解:由(1)0,(3)0f f ==,得1,3是方程20x bx c ++=的两个实数根, 即13,13b c +=-⨯=,得4,3b c =-=,即2()43f x x x =-+,得2(1)(1)4(1)38f -=--⨯-+=,即(1)f -的值为8.7.画出下列函数的图象:(1)0,0()1,0x F x x ≤⎧=⎨>⎩; (2)()31,{1,2,3}G n n n =+∈. 7.图象如下:8.如图,矩形的面积为10,如果矩形的长为x ,宽为y ,对角线为d ,周长为l ,那么你能获得关于这些量的哪些函数? 8.解:由矩形的面积为10,即10xy =,得10(0)y x x=>,10(0)x y y =>, 由对角线为d,即d =(0)d x =>, 由周长为l ,即22l x y =+,得202(0)l x x x =+>, 另外2()l x y =+,而22210,xy d x y ==+,得(0)l d ===>,即(0)l d =>.9.一个圆柱形容器的底部直径是dcm ,高是hcm ,现在以3/vcm s 的速度向容器内注入某种溶液.求溶液内溶液的高度xcm 关于注入溶液的时间ts 的函数解析式,并写出函数的定义域和值域.9.解:依题意,有2()2dx vt π=,即24v x t dπ=, 显然0x h ≤≤,即240v t h dπ≤≤,得204h d t v π≤≤, 得函数的定义域为2[0,]4h d vπ和值域为[0,]h . 10.设集合{,,},{0,1}A a b c B ==,试问:从A 到B 的映射共有几个?并将它们分别表示出来.10.解:从A 到B 的映射共有8个.分别是()0()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()0()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩.B组1.函数()r f p =的图象如图所示.(1)函数()r f p =的定义域是什么?(2)函数()r f p =的值域是什么?(3)r 取何值时,只有唯一的p 值与之对应?1.解:(1)函数()r f p =的定义域是[5,0][2,6)-;(2)函数()r f p =的值域是[0,)+∞;(3)当5r >,或02r ≤<时,只有唯一的p 值与之对应.2.画出定义域为{|38,5}x x x -≤≤≠且,值域为{|12,0}y y y -≤≤≠的一个函数的图象.(1)如果平面直角坐标系中点(,)P x y 的坐标满足38x -≤≤,12y -≤≤,那么其中哪些点不能在图象上?(2)将你的图象和其他同学的相比较,有什么差别吗?2.解:图象如下,(1)点(,0)x 和点(5,)y 不能在图象上;(2)省略.3.函数()[]f x x =的函数值表示不超过x 的最大整数,例如,[ 3.5]4-=-,[2.1]2=.当( 2.5,3]x ∈-时,写出函数()f x 的解析式,并作出函数的图象.3.解:3, 2.522,211,10()[]0,011,122,233,3x x x f x x x x x x --<<-⎧⎪--≤<-⎪⎪--≤<⎪==≤<⎨⎪≤<⎪≤<⎪⎪=⎩图象如下4.如图所示,一座小岛距离海岸线上最近的点P 的距离是2km ,从点P 沿海岸正东12km 处有一个城镇.(1)假设一个人驾驶的小船的平均速度为3/km h ,步行的速度是5/km h ,t (单位:h)表示他从小岛到城镇的时间,x (单位:km )表示此人将船停在海岸处距P 点的距离.请将t 表示为x 的函数.(2)如果将船停在距点P 4km 处,那么从小岛到城镇要多长时间(精确到1h )?4.解:(112x -,得1235x t -=+,(012)x ≤≤,即125x t -=+,(012)x ≤≤.(2)当4x =时,12483()55t h -==+≈. 第一章 集合与函数概念1.3函数的基本性质1.3.1单调性与最大(小)值练习(第32页)1.请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.1.答:在一定的范围内,生产效率随着工人数量的增加而提高,当工人数量达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率随着工人数量的增加而降低.由此可见,并非是工人越多,生产效率就越高.2.整个上午(8:0012:00)天气越来越暖,中午时分(12:0013:00)一场暴风雨使天气骤然凉爽了许多.暴风雨过后,天气转暖,直到太阳落山(18:00)才又开始转凉.画出这一天8:0020:00期间气温作为时间函数的一个可能的图象,并说出所画函数的单调区间.2.解:图象如下 [8,12]是递增区间,[12,13]是递减区间,[13,18]是递增区间,[18,20]是递减区间.3.根据下图说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数.3.解:该函数在[1,0]-上是减函数,在[0,2]上是增函数,在[2,4]上是减函数,在[4,5]上是增函数.4.证明函数()21f x x =-+在R 上是减函数.4.证明:设12,x x R ∈,且12x x <,因为121221()()2()2()0f x f x x x x x -=--=->,即12()()f x f x >,所以函数()21f x x =-+在R 上是减函数.5.设()f x 是定义在区间[6,11]-上的函数.如果()f x 在区间[6,2]--上递减,在区间[2,11]-上递增,画出()f x 的一个大致的图象,从图象上可以发现(2)f -是函数()f x 的一个 .5.最小值.1.3.2单调性与最大(小)值练习(第36页)1.判断下列函数的奇偶性:(1)42()23f x x x =+; (2)3()2f x x x =- (3)21()x f x x+=; (4)2()1f x x =+. 1.解:(1)对于函数42()23f x x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有4242()2()3()23()f x x x x x f x -=-+-=+=,所以函数42()23f x x x =+为偶函数;(2)对于函数3()2f x x x =-,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有33()()2()(2)()f x x x x x f x -=---=--=-,所以函数3()2f x x x =-为奇函数; (3)对于函数21()x f x x+=,其定义域为(,0)(0,)-∞+∞,因为对定义域内 每一个x 都有22()11()()x x f x f x x x-++-==-=--, 所以函数21()x f x x+=为奇函数; (4)对于函数2()1f x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有22()()11()f x x x f x -=-+=+=,所以函数2()1f x x =+为偶函数.2.已知()f x 是偶函数,()g x 是奇函数,试将下图补充完整.2.解:()f x 是偶函数,其图象是关于y 轴对称的;()g x 是奇函数,其图象是关于原点对称的.习题1.3A 组1.画出下列函数的图象,并根据图象说出函数()y f x =的单调区间,以及在各单调区间上函数()y f x =是增函数还是减函数.(1)256y x x =--; (2)29y x =-.1.解:(1)5(,)2-∞上递减;函数在5[,)2+∞上递 函数在增;(2)(,0)-∞上递增;函数在[0,)+∞上递 函数在减.2.证明:(1)函数2()1f x x =+在(,0)-∞上是减函数; (2)函数1()1f x x =-在(,0)-∞上是增函数.2.证明:(1)设120x x <<,而2212121212()()()()f x f x x x x x x x -=-=+-,由12120,0x x x x +<-<,得12()()0f x f x ->,即12()()f x f x >,所以函数2()1f x x =+在(,0)-∞上是减函数;(2)设120x x <<,而1212211211()()x x f x f x x x x x --=-=, 由12120,0x x x x >-<,得12()()0f x f x -<,即12()()f x f x <,所以函数1()1f x x=-在(,0)-∞上是增函数. 3.探究一次函数()y mx b x R =+∈的单调性,并证明你的结论.3.解:当0m >时,一次函数y mx b =+在(,)-∞+∞上是增函数;当0m <时,一次函数y mx b =+在(,)-∞+∞上是减函数,令()f x mx b =+,设12x x <,而1212()()()f x f x m x x -=-,当0m >时,12()0m x x -<,即12()()f x f x <,得一次函数y mx b =+在(,)-∞+∞上是增函数;当0m <时,12()0m x x ->,即12()()f x f x >,得一次函数y mx b =+在(,)-∞+∞上是减函数.4.一名心率过速患者服用某种药物后心率立刻明显减慢,之后随着药力的减退,心率再次慢慢升高.画出自服药那一刻起,心率关于时间的一个可能的图象(示意图).4.解:自服药那一刻起,心率关于时间的一个可能的图象为5.某汽车租赁公司的月收益y 元与每辆车的月租金x 元间的关系为21622100050x y x =-+-,那么,每辆车的月租金多少元时,租赁公司的月收益最大?最大月收益是多少?5.解:对于函数21622100050x y x =-+-, 当162405012()50x =-=⨯-时,max 307050y =(元), 即每辆车的月租金为4050元时,租赁公司最大月收益为307050元.6.已知函数()f x 是定义在R 上的奇函数,当0x ≥时,()(1)f x x x =+.画出函数()f x的图象,并求出函数的解析式.6.解:当0x <时,0x ->,而当0x ≥时,()(1)f x x x =+,即()(1)f x x x -=--,而由已知函数是奇函数,得()()f x f x -=-,得()(1)f x x x -=--,即()(1)f x x x =-,所以函数的解析式为(1),0()(1),0x x x f x x x x +≥⎧=⎨-<⎩.B 组1.已知函数2()2f x x x =-,2()2([2,4])g x x x x =-∈.(1)求()f x ,()g x 的单调区间; (2)求()f x ,()g x 的最小值.1.解:(1)二次函数2()2f x x x =-的对称轴为1x =,则函数()f x 的单调区间为(,1),[1,)-∞+∞,且函数()f x 在(,1)-∞上为减函数,在[1,)+∞上为增函数,函数()g x 的单调区间为[2,4],且函数()g x 在[2,4]上为增函数;(2)当1x =时,min ()1f x =-,因为函数()g x 在[2,4]上为增函数,所以2min ()(2)2220g x g ==-⨯=.2.如图所示,动物园要建造一面靠墙的2间面积相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m ,那么宽x (单位:m )为多少才能使建造的每间熊猫居室面积最大?每间熊猫居室的最大面积是多少?2.解:由矩形的宽为x m ,得矩形的长为3032x m -,设矩形的面积为S , 则23033(10)22x x x S x --==-, 当5x =时,2max 37.5S m =,即宽5x =m 才能使建造的每间熊猫居室面积最大,且每间熊猫居室的最大面积是237.5m .3.已知函数()f x 是偶函数,而且在(0,)+∞上是减函数,判断()f x 在(,0)-∞上是增函数还是减函数,并证明你的判断.3.判断()f x 在(,0)-∞上是增函数,证明如下:设120x x <<,则120x x ->->,因为函数()f x 在(0,)+∞上是减函数,得12()()f x f x -<-,又因为函数()f x 是偶函数,得12()()f x f x <,所以()f x 在(,0)-∞上是增函数. 复习参考题A 组1.用列举法表示下列集合:(1)2{|9}A x x ==;(2){|12}B x N x =∈≤≤;(3)2{|320}C x x x =-+=.1.解:(1)方程29x =的解为123,3x x =-=,即集合{3,3}A =-;(2)12x ≤≤,且x N ∈,则1,2x =,即集合{1,2}B =;(3)方程2320x x -+=的解为121,2x x ==,即集合{1,2}C =.2.设P 表示平面内的动点,属于下列集合的点组成什么图形?(1){|}P PA PB =(,)A B 是两个定点;(2){|3}P PO cm =()O 是定点.2.解:(1)由PA PB =,得点P 到线段AB 的两个端点的距离相等,即{|}P PA PB =表示的点组成线段AB 的垂直平分线;(2){|3}P PO cm =表示的点组成以定点O 为圆心,半径为3cm 的圆.3.设平面内有ABC ∆,且P 表示这个平面内的动点,指出属于集合 {|}{|}P PA PB P PA PC ==的点是什么.3.解:集合{|}P PA PB =表示的点组成线段AB 的垂直平分线,集合{|}P PA PC =表示的点组成线段AC 的垂直平分线,得{|}{|}P PA PB P PA PC ==的点是线段AB 的垂直平分线与线段AC 的垂直平分线的交点,即ABC ∆的外心.4.已知集合2{|1}A x x ==,{|1}B x ax ==.若B A ⊆,求实数a 的值.4.解:显然集合{1,1}A =-,对于集合{|1}B x ax ==,当0a =时,集合B =∅,满足B A ⊆,即0a =;当0a ≠时,集合1{}B a =,而B A ⊆,则11a =-,或11a =, 得1a =-,或1a =,综上得:实数a 的值为1,0-,或1.5.已知集合{(,)|20}A x y x y =-=,{(,)|30}B x y x y =+=,{(,)|23}C x y x y =-=,求A B ,A C ,()()A B B C .5.解:集合20(,)|{(0,0)}30x y A B x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭,即{(0,0)}A B =; 集合20(,)|23x y A C x y x y ⎧-=⎫⎧==∅⎨⎨⎬-=⎩⎩⎭,即A C =∅;集合3039(,)|{(,)}2355x y B C x y x y ⎧+=⎫⎧==-⎨⎨⎬-=⎩⎩⎭; 则39()(){(0,0),(,)}55A B B C =-. 6.求下列函数的定义域:(1)y =(2)||5y x =-. 6.解:(1)要使原式有意义,则2050x x -≥⎧⎨+≥⎩,即2x ≥,得函数的定义域为[2,)+∞;(2)要使原式有意义,则40||50x x -≥⎧⎨-≠⎩,即4x ≥,且5x ≠,得函数的定义域为[4,5)(5,)+∞. 7.已知函数1()1x f x x-=+,求: (1)()1(1)f a a +≠-; (2)(1)(2)f a a +≠-.7.解:(1)因为1()1x f x x-=+, 所以1()1a f a a -=+,得12()1111a f a a a-+=+=++, 即2()11f a a+=+; (2)因为1()1x f x x-=+, 所以1(1)(1)112a a f a a a -++==-+++, 即(1)2a f a a +=-+. 8.设221()1x f x x +=-,求证:(1)()()f x f x -=; (2)1()()f f x x=-.8.证明:(1)因为221()1x f x x +=-,所以22221()1()()1()1x x f x f x x x+-+-===---, 即()()f x f x -=;(2)因为221()1x f x x +=-,所以222211()11()()111()x x f f x x x x++===---, 即1()()f f x x=-.9.已知函数2()48f x x kx =--在[5,20]上具有单调性,求实数k 的取值范围. 9.解:该二次函数的对称轴为8k x =, 函数2()48f x x kx =--在[5,20]上具有单调性,则208k ≥,或58k≤,得160k ≥,或40k ≤, 即实数k 的取值范围为160k ≥,或40k ≤.10.已知函数2y x -=,(1)它是奇函数还是偶函数? (2)它的图象具有怎样的对称性? (3)它在(0,)+∞上是增函数还是减函数? (4)它在(,0)-∞上是增函数还是减函数? 10.解:(1)令2()f x x -=,而22()()()f x x x f x ---=-==,即函数2y x -=是偶函数;(2)函数2y x -=的图象关于y 轴对称; (3)函数2y x -=在(0,)+∞上是减函数; (4)函数2y x -=在(,0)-∞上是增函数.B 组1.学校举办运动会时,高一(1)班共有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳比赛和田径比赛的有3人,同时参加游泳比赛和球类比赛的有3人,没有人同时参加三项比赛.问同时参加田径和球类比赛的有多少人?只参加游泳一项比赛的有多少人? 1.解:设同时参加田径和球类比赛的有x 人, 则158143328x ++---=,得3x =, 只参加游泳一项比赛的有15339--=(人),即同时参加田径和球类比赛的有3人,只参加游泳一项比赛的有9人. 2.已知非空集合2{|}A x R x a =∈=,试求实数a 的取值范围. 2.解:因为集合A ≠∅,且20x ≥,所以0a ≥. 3.设全集{1,2,3,4,5,6,7,8,9}U =,(){1,3}U A B =ð,(){2,4}U A B =ð,求集合B .3.解:由(){1,3}U A B =ð,得{2,4,5,6,7,8,9}A B =,集合AB 里除去()U A B ð,得集合B ,所以集合{5,6,7,8,9}B =.4.已知函数(4),0()(4),0x x x f x x x x +≥⎧=⎨-<⎩.求(1)f ,(3)f -,(1)f a +的值.4.解:当0x ≥时,()(4)f x x x =+,得(1)1(14)5f =⨯+=; 当0x <时,()(4)f x x x =-,得(3)3(34)21f -=-⨯--=; (1)(5),1(1)(1)(3),1a a a f a a a a ++≥-⎧+=⎨+-<-⎩.5.证明:(1)若()f x ax b =+,则1212()()()22x x f x f x f ++=; (2)若2()g x x ax b =++,则1212()()()22x x g x g x g ++≤. 5.证明:(1)因为()f x ax b =+,得121212()()222x x x x af a b x x b ++=+=++,121212()()()222f x f x ax b ax b ax x b ++++==++,所以1212()()()22x x f x f x f ++=; (2)因为2()g x x ax b =++,得22121212121()(2)()242x x x x g x x x x a b ++=++++,2212121()()22x x x x a b +=+++, 因为2222212121212111(2)()()0424x x x x x x x x ++-+=--≤,即222212121211(2)()42x x x x x x ++≤+, 所以1212()()()22x x g x g x g ++≤. 6.(1)已知奇函数()f x 在[,]a b 上是减函数,试问:它在[,]b a --上是增函数还是减函数?(2)已知偶函数()g x 在[,]a b 上是增函数,试问:[,]b a --上是增函数还是减函数?它在(1)函数()f x 在[,]b a --上也是减函数,证明如6.下:设12b x x a -<<<-,则21a x x b <-<-<,因为函数()f x 在[,]a b 上是减函数,则21()()f x f x ->-,又因为函数()f x 是奇函数,则21()()f x f x ->-,即12()()f x f x >, 所以函数()f x 在[,]b a --上也是减函数; (2)函数()g x 在[,]b a --上是减函数,证明如下: 设12b x x a -<<<-,则21a x x b <-<-<,因为函数()g x 在[,]a b 上是增函数,则21()()g x g x -<-, 又因为函数()g x 是偶函数,则21()()g x g x <,即12()()g x g x >, 所以函数()g x 在[,]b a --上是减函数.7.《中华人民共和国个人所得税》规定,公民全月工资、薪金所得不超过2000元的部分不必纳税,超过2000元的部分为全月应纳税所得额.此项税款按下表分段累计计算: 某人一月份应交纳此项税款为26.78元,那么他当月的工资、薪金所得是多少? 7.解:设某人的全月工资、薪金所得为x 元,应纳此项税款为y 元,则 由该人一月份应交纳此项税款为26.78元,得25004000x <≤, 25(2500)10%26.78x +-⨯=,得2517.8x =, 所以该人当月的工资、薪金所得是2517.8元.新课程标准数学必修1第二章课后习题解答第二章 基本初等函数(I )2.1指数函数 练习(P54)1. a 21=a ,a 43=43a ,a53-=531a,a32-=321a.2. (1)32x =x 32, (2)43)(b a +=(a +b )43, (3)32n)-(m =(m -n )32,(4)4n)-(m =(m -n )2,(5)56q p =p 3q 25,(6)mm 3=m213-=m 25.3. (1)(4936)23=[(76)2]23=(76)3=343216;(2)23×35.1×612=2×321×(23)31×(3×22)61=231311--×3613121++=2×3=6;(3)a 21a 41a 81-=a814121-+=a 85; (4)2x31-(21x 31-2x 32-)=x 3131+--4x 3221--=1-4x -1=1x4-. 练习(P58)1.如图图2-1-2-142.(1)要使函数有意义,需x -2≥0,即x ≥2,所以函数y =32-x 的定义域为{x |x ≥2};(2)要使函数有意义,需x ≠0,即函数y =(21)x 1的定义域是{x ∣x ≠0}.3.y =2x (x ∈N *)习题2.1 A 组(P59)1.(1)100;(2)-0.1;(3)4-π;(4)x -y .2解:(1)623ba ab=212162122123)(⨯⨯⨯b a a b =23232121--⨯b a =a 0b 0=1. (2)a aa2121=212121a a a⨯=2121a a ⨯=a 21.(3)415643)(mm m m m ∙∙∙=4165413121mm m m m ∙∙=4165413121+++mm=m 0=1.点评:遇到多重根号的式子,可以由里向外依次去掉根号,也可根据幂的运算性质来进行. 3.解:对于(1),可先按底数5,再按键,再按12,最后按,即可求得它的值.答案:1.710 0; 对于(2),先按底数8.31,再按键,再按12,最后按即可. 答案:2.881 0; 对于(3)这种无理指数幂,先按底数3,再按键,再按键,再按2,最后按即可.答案:4.728 8;对于(4)这种无理指数幂,可先按底数2,其次按键,再按π键,最后按即可.答案:8.825 0.4.解:(1)a 31a 43a127=a 1274331++=a 35; (2)a 32a 43÷a 65=a654332-+=a 127;(3)(x 31y43-)12=12431231⨯-⨯yx =x 4y -9;(4)4a 32b 31-÷(32-a 31-b 31-)=(32-×4)31313132+-+b a =-6ab 0=-6a ;(5))2516(462rts -23-=)23(4)23(2)23(6)23(2)23(452-⨯-⨯-⨯--⨯-⨯rts=6393652----rt s =36964125s r r ; (6)(-2x 41y31-)(3x21-y 32)(-4x 41y 32)=[-2×3×(-4)]x 323231412141++-+-yx=24y ;(7)(2x 21+3y41-)(2x 21-3y41-)=(2x 21)2-(3y 41-)2=4x -9y21-;(8)4x 41 (-3x 41y31-)÷(-6x21-y32-)=3231214141643+-++-⨯-y x =2xy 31. 点评:进行有理数指数幂的运算时,要严格按法则和运算顺序,同时注意运算结果的形式,但结果不能既有分数指数又有根式,也不能既有分母又有负指数.5.(1)要使函数有意义,需3-x ∈R ,即x ∈R ,所以函数y =23-x 的定义域为R . (2)要使函数有意义,需2x +1∈R ,即x ∈R ,所以函数y =32x +1的定义域为R . (3)要使函数有意义,需5x ∈R,即x ∈R,所以函数y =(21)5x的定义域为R . (4)要使函数有意义,需x ≠0,所以函数y =0.7x1的定义域为{x |x ≠0}.点评:求函数的定义域一是分式的分母不为零,二是偶次根号的被开方数大于零,0的0次幂没有意义.6.解:设经过x 年的产量为y ,一年内的产量是a (1+100p ),两年内产量是a (1+100p )2,…,x 年内的产量是a (1+100p )x ,则y =a (1+100p )x(x ∈N *,x ≤m ). 点评:根据实际问题,归纳是关键,注意x 的取值范围.7.(1)30.8与30.7的底数都是3,它们可以看成函数y =3x ,当x =0.8和0.7时的函数值;因为3>1,所以函数y =3x 在R 上是增函数.而0.7<0.8,所以30.7<30.8.(2)0.75-0.1与0.750.1的底数都是0.75,它们可以看成函数y =0.75x ,当x =-0.1和0.1时的函数值; 因为1>0.75,所以函数y =0.75x 在R 上是减函数.而-0.1<0.1,所以0.750.1<0.75-0.1.(3)1.012.7与1.013.5的底数都是1.01,它们可以看成函数y =1.01x ,当x =2.7和3.5时的函数值; 因为1.01>1,所以函数y =1.01x 在R 上是增函数.而2.7<3.5,所以1.012.7<1.013.5. (4)0.993.3与0.994.5的底数都是0.99,它们可以看成函数y =0.99x ,当x =3.3和4.5时的函数值; 因为0.99<1,所以函数y =0.99x 在R 上是减函数.而3.3<4.5,所以0.994.5<0.993.3.8.(1)2m ,2n 可以看成函数y =2x ,当x =m 和n 时的函数值;因为2>1,所以函数y =2x 在R 上是增函数.因为2m <2n ,所以m <n . (2)0.2m ,0.2n 可以看成函数y =0.2x ,当x =m 和n 时的函数值;因为0.2<1, 所以函数y =0.2x 在R 上是减函数.因为0.2m <0.2n ,所以m >n . (3)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为0<a <1, 所以函数y =a x 在R 上是减函数.因为a m <a n ,所以m >n . (4)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为a >1, 所以函数y =a x 在R 上是增函数.因为a m >a n ,所以m >n . 点评:利用指数函数的单调性是解题的关键.9.(1)死亡生物组织内碳14的剩余量P 与时间t 的函数解析式为P=(21)57301.当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量为P=(21)573057309⨯=(21)9≈0.002. 答:当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前含量的2‰, 因此,还能用一般的放射性探测器测到碳14的存在.(2)设大约经过t 万年后,用一般的放射性探测器测不到碳14,那么(21)537010000t <0.001,解得t >5.7.答:大约经过6万年后,用一般的放射性探测器是测不到碳14的. B 组1. 当0<a <1时,a 2x -7>a 4x -12⇒x -7<4x -1⇒x >-3;当a >1时,a 2x -7>a 4x -1⇒2x -7>4x -1⇒x <-3. 综上,当0<a <1时,不等式的解集是{x |x >-3};当a >1时,不等式的解集是{x |x <-3}.2.分析:像这种条件求值,一般考虑整体的思想,同时观察指数的特点,要注重完全平方公式的运用. 解:(1)设y =x 21+x21-,那么y 2=(x 21+x21-)2=x +x -1+2.由于x +x -1=3,所以y =5.(2)设y =x 2+x -2,那么y =(x +x -1)2-2.由于x +x -1=3,所以y =7.(3)设y =x 2-x -2,那么y =(x +x -1)(x -x -1),而(x -x -1)2=x 2-2+x -2=5,所以y =±35.点评:整体代入和平方差,完全平方公式的灵活运用是解题的突破口. 3.解:已知本金为a 元.1期后的本利和为y 1=a +a ×r =a (1+r ), 2期后的本利和为y 2=a (1+r )+a (1+r )×r =a (1+r )2, 3期后的本利和为y 3=a (1+r )3, …x 期后的本利和为y =a (1+r )x .将a =1 000,r =0.022 5,x =5代入上式得y =a (1+r )x =1 000×(1+0.022 5)5=1 000×1.02255≈1118.答:本利和y 随存期x 变化的函数关系式为y =a (1+r )x ,5期后的本利和约为1 118元. 4.解:(1)因为y 1=y 2,所以a 3x +1=a -2x .所以3x +1=-2x .所以x =51-. (2)因为y 1>y 2,所以a 3x +1>a -2x . 所以当a >1时,3x +1>-2x .所以x >51-. 当0<a <1时,3x +1<-2x .所以x <51-.2.2对数函数 练习(P64)1.(1)2log 83=; (2)2log 325=; (3)21log 12=-; (4)2711log 33=-2.(1)239=; (2)35125=; (3)2124-=; (4)41381-=3.(1)设5log 25x =,则25255x ==,所以2x =; (2)设21log 16x =,则412216x -==,所以4x =-; (3)设lg1000x =,则310100010x ==,所以3x =; (4)设lg 0.001x =,则3100.00110x -==,所以3x =-;4.(1)1; (2)0; (3)2; (4)2; (5)3; (6)5.练习(P68)1.(1)lg()lg lg lg xyz x y z =++;(2)222lg lg()lg lg lg lg lg 2lg lg xy xy z x y z x y z z=-=++=++;(3)33311lg()lg lg lg lg 3lg lg22xy x y z x y z =-=+-=+-;(4)2211lg()lg (lg lg )lg 2lg lg 22y z x y z x y z ==-+=--. 2.(1)223433333log (279)log 27log 9log 3log 3347⨯=+=+=+=;(2)22lg1002lg1002lg104lg104====;(3)5lg 0.00001lg105lg105-==-=-; (4)11ln 22e ==3. (1)22226log 6log 3log log 213-===; (2)lg5lg 2lg101+==; (3)555511log 3log log (3)log 1033+=⨯==;(4)13333351log 5log 15log log log 31153--====-. 4.(1)1; (2)1; (3)54练习(P73)1.函数3log y x =及13log y x =的图象如右图所示.相同点:图象都在y 轴的右侧,都过点(1,0) 不同点:3log y x =的图象是上升的,13log y x =的图象是下降的关系:3log y x =和13log y x =的图象是关于x 轴对称的.2. (1)(,1)-∞; (2)(0,1)(1,)+∞; (3)1(,)3-∞; (4)[1,)+∞3. (1)1010log 6log 8< (2)0.50.5log 6log 4< (3)2233log 0.5log 0.6> (4) 1.5 1.5log 1.6log 1.4>习题2.2 A 组(P74) 1. (1)3log 1x =; (2)41log 6x =; (3)4log 2x =; (4)2log 0.5x = (5) lg 25x = (6)5log 6x =2. (1)527x = (2) 87x = (3) 43x = (4)173x =(5) 100.3x = (6) xe =3. (1)0; (2) 2; (3) 2-; (4)2; (5) 14-; (6) 2. 4. (1)lg6lg 2lg3a b =+=+; (2) 3lg 42lg 22log 4lg3lg3ab===; (3) 2lg122lg 2lg3lg3log 1222lg 2lg 2lg 2b a +===+=+; (4)3lg lg3lg 22b a =-=-5. (1)x ab =; (2) mx n=; (3) 3n x m =; (4)x =.6. 设x 年后我国的GDP 在1999年的GDP 的基础上翻两番,则(10.073)4x+=解得 1.073log 420x =≈. 答:设20年后我国的GDP 在1999年的GDP 的基础上翻两番.7. (1)(0,)+∞; (2) 3(,1]4.8. (1)m n <; (2) m n <; (3) m n >; (4)m n >. 9. 若火箭的最大速度12000v =,那么62000ln 112000ln(1)61402M M M M e mm m m ⎛⎫+=⇒+=⇒+=⇒≈ ⎪⎝⎭答:当燃料质量约为火箭质量的402倍时,火箭的最大速度可达12km/s.10. (1)当底数全大于1时,在1x =的右侧,底数越大的图象越在下方.所以,①对应函数lg y x =,②对应函数5log y x =,③对应函数2log y x =. (2)略. (3)与原函数关于x 轴对称. 11. (1)235lg 25lg 4lg92lg52lg 22lg3log 25log 4log 98lg 2lg3lg5lg 2lg3lg5⋅⋅=⨯⨯=⨯⨯= (2)lg lg lg log log log 1lg lg lg a b c b c a b c a a b c⋅⋅=⨯⨯= 12. (1)令2700O =,则312700log 2100v =,解得 1.5v =. 答:鲑鱼的游速为1.5米/秒. (2)令0v =,则31log 02100O=,解得100O =. 答:一条鱼静止时的耗氧量为100个单位.B 组1. 由3log 41x =得:143,43x x -==,于是11044333x x -+=+= 2. ①当1a >时,3log 14a<恒成立; ②当01a <<时,由3log 1log 4a a a <=,得34a <,所以304a <<.综上所述:实数a 的取值范围是3{04a a <<或1}a >3. (1)当1I = W/m 2时,112110lg 12010L -==;(2)当1210I -= W/m 2时,121121010lg 010L --==答:常人听觉的声强级范围为0120dB .4. (1)由10x +>,10x ->得11x -<<,∴函数()()f x g x +的定义域为(1,1)- (2)根据(1)知:函数()()f x g x +的定义域为(1,1)-∴ 函数()()f x g x +的定义域关于原点对称又∵ ()()l o g (1)l o g (1)()a a f x g x x x f x g x -+-=-++=+ ∴()()f x g x +是(1,1)-上的偶函数.5. (1)2log y x =,0.3log y x =; (2)3xy =,0.1x y =.习题2.3 A 组(P79)。
高一数学人教A版必修1单元测评第一章集合与函数的概念

B 卷本试卷满分:100分;考试时间:90分钟一、选择题(本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合要求的)1.下列函数中与函数y =x -1相同的是( ) A .y =(1-x )2 B .y =2)1(-xC .y =1123++-x x xD .y =112+-x x2.下列函数表示偶函数的是( ) A .y =2x B .y =x 3 C .y =x +1D .y =x 2(-1<x ≤1)3.函数y =242x x ---的定义域是( ) A .{2} B .{1,2} C .{x |x ≤-2} D .∅4.已知符号函数:sgn (x )=⎪⎩⎪⎨⎧<-=>).0(1),0(0),0(1x x x 不等式sgn (x -2)<1的解集是( )A .x ≤2B .x <2C .x ≥2D .x <3 5.已知f (x )是奇函数,且当x >0时,f (x )=x (1-x ),则x <0时,f (x )为( ) A .-x (1-x ) B .x (1-x ) C .x (1+x ) D .-x (1+x )6.已知集合A ={(x ,y )|2x -y =0},集合B ={(x ,y )|x -y =3},则集合A ∩B 是( ) A .{-6,-3} B .{(-3,-6)} C .{3,6} D .(-3,-6)7.函数f (x )=xx x -+-||1212的定义域是( ) A .{x |x ≤0}B .{x |x ≤-1)C .{x |x ≥1)D .{x |x ≤-1或x ≥1)8.已知狄利克雷函数的定义为:则D (x )的图象是( )A .两条平行直线B .两条平行直线上稠密的点C .两条相交直线D .两条相交直线上稠密的点 9.函数y =2x +x1(x ≥1)的值域是( ) A .{y |y ≥3} B .{y |y ≥22} C .{y |y ≥4} D .{y |22≤y ≤3} 10.函数y =x1-x 的大致图象是( )答案:1.C 2.A 3.A 4.A 5.C 6.B 7.B 8.B 9.A 10.B二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上) 11.在给定A →B 的映射f :(x ,y )→(x +y ,x -y )下,集合A 中的元素(2,1)对应着B 中的元素__________. 答案:(3,1)12.函数y -||x -3|的递减区间是__________. 答案:(-∞,3] 13.函数f (x )对于任意的x 1,x 2∈R +恒有f (x 1+x 2)=f (x 1)+f (x 2)成立,且f (1)=41,则f (2 008)=__________. 答案:50214.要修一个面积为800 m 2的长方形的网球场,并且四周修前后l m ,左右2 m 的小路(如图),则占地面积的最小值是__________m 2.答案:968三、解答题(本大题共5小题,每小题8分,共40分,解答应写出文字说明、证明过程或 演算步骤)15.甲、乙两地相距s km ,汽车从甲地匀速行驶到乙地:速率不超过c km /h .已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成.可变部分与速率钞km /h 的平方成正比,比例系数为b ,固定部分为a 元.(1)把全部运输成本y 元表示成速率v km /h 的函数,指出函数的定义域; (2)为了使全程运输成本最小,汽车应以多大的速率行驶? 答案:(1)y =v s (bv 2+a )=bsv +vsa(0<a ≤c ) (2)(i )若c b a ≤,即a ≤c 2b ,当v =b a 时,y m in =2s ab ;(ii )若c ba >,即a > c 2b ,当v =c 时,y m in =csa+bsc 16.函数y =f (x )的图象如图所示.(1)函数y =f (x )的定义域可能是什么? (2)函数y =f (x )的值域可能是什么? (3)y 的哪些值只与x 的一个值对应?答案:(1)定义域{x |-7≤x ≤0或2<x <6} (2)值域{y |0<y <+∞}(3){y |0<y <2或5<y <+∞) 17.先用定义判断函数f (x )=1+12-x 在区间[2,6]上的单调性,再求函数f (x )在区间[2,6]上的最大值和最小值.答案:易证f (x )在[2,6]上是减函数,∴f (x )max =3,f (x )max =57 18.(1)求下列函数的定义域: ①1231)(2-++-=x x x x f ;②03)1(1312)(-+++-=x x x x f .(2)已知函数f (x )= 213+++x x . ①求f (-3)、f (32)的值; ②当m >0时,求f (m -1)的值. 答案:(1)①{x |x >1且x ≠2};②{x |x ≥21且x ≠1) (2)①f (-3)=-1,f (32)=333+83;②f (m -1)=112+++m m19.设某公民的月所得(工资、薪金所得)x 元,每月纳所得税f (x )元是x 的函数.当前国家制定的《个人所得税率表》如下:(1)在表中填写函数f (x )表达式;(2)某人在某月缴纳个人所得税是240元,他那个月的工资、薪金收入是多少元?(结果保留整数)答案:(1)⎪⎪⎩⎪⎪⎨⎧≤<-≤<-≤<-≤<-216006600,6952.0,66003600,36515.0,36002100,1851.0,21001600,8005.0)(x x x x x x x x x f(2)0.15x -365=240,解之得x ≈4033页。
高一数学人教A版必修1单元测试第一章 集合与函数概念 Word版含解析

第一章过关检测(时间分钟,满分分) 一、选择题(每小题分,共分).设集合={}={}={},则(∩)等于( ).{}.{}.{}.{}.若函数()(()≠)为奇函数,则必有( )()·(-)>()·(-)<()<(-)()>(-).下列集合不同于其他三个集合的是( ).{=}.{(-)=}.{=}.{}.下列集合不能用区间形式表示的是( )①={}②{是三角形}③{>,且∈}④⑤{≤或≥}⑥{<≤∈}.①②③.③④⑤.⑤⑥.①②③④⑥.下列各图中,可表示函数=()的图象的只可能是图中的( ).设()=+(+)=(),则()等于( )+--+.下列函数中,在区间()上为增函数的是( )=-=+=-.已知函数,则[(-)]的值是( ).-.-.全集=={<-或≥}={-<<},则集合{-<<}是( ).()∪().(∪).()∩∩.给出下列函数表达式:①;②;③=+(∈且≠);④,其中奇函数的个数为( )二、填空题(每小题分,共分).若函数(+)的定义域为[-,-],则()=(+)+(-)的定义域为..用列举法表示集合={∈∈}=..已知集合{+}={},则整数==..若函数()=+(-)+是偶函数,则()的递减区间是.三、解答题(、小题各分、小题各分,共分).已知集合={≤≤}={<<}={>}=.()求∪,()∩;()若∩≠,求的取值范围..判断并证明在(-∞)上的增减性..设()是上的奇函数,且当∈(,+∞)时()=(+),求()在上的解析式..若()是定义在(,+∞)上的增函数,且对一切>,满足()=()-().()求()的值;()若()=,解不等式(+)-()<.参考答案解析:∵={}={},∴∩={}.又={},∴(∩)={}.答案解析:∵()是奇函数,∴(-)=-().∴()·(-)=-[()]<(()≠).答案解析、、都表示元素是的集合表示元素为“=”的集合.。
人教新课标版数学高一人教A版必修1测评 第一章 集合与函数概念

单元测评(一)集合与函数概念(时间:90分钟满分:120分)第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,共50分.1.已知集合A={0,1,2,3,4,5},B={1,3,6,9},C={3,7,8},则(A∩B)∪C等于()A.{0,1,2,6,8}B.{3,7,8}C.{1,3,7,8} D.{1,3,6,7,8}解析:A∩B={1,3},(A∩B)∪C={1,3,7,8},故选C.答案:C2.已知f(x),g(x)对应值如表则f(A.-1 B.0C.1 D.不存在解析:∵g(1)=0,f(0)=1,∴f(g(1))=1,故选C.答案:C3.已知函数f(x+1)=3x+2,则f(x)的解析式是()A.3x+2 B.3x+1C.3x-1 D.3x+4解析:设x +1=t ,则x =t -1,∴f (t )=3(t -1)+2=3t -1,∴f (x )=3x -1,故选C.答案:C4.已知f (x )=⎩⎪⎨⎪⎧2x -1 (x ≥2),-x 2+3x (x <2),则f (-1)+f (4)的值为( )A .-7B .3C .-8D .4解析:f (4)=2×4-1=7,f (-1)=-(-1)2+3×(-1)=-4,∴f (4)+f (-1)=3,故选B.答案:B5.若f (x )=-x 2+mx 在(-∞,1]上是增函数,则m 的取值范围是( )A .{2}B .(-∞,2]C .[2,+∞)D .(-∞,1]解析:f (x )=-⎝ ⎛⎭⎪⎫x -m 22+m 24的增区间为⎝ ⎛⎦⎥⎤-∞,m 2,由条件知m2≥1,∴m ≥2,故选C.答案:C6.已知集合A ={1,2,3,4,5},B ={(x ,y )|x ∈A ,y ∈A ,x -y ∈A },则B 中所含元素的个数为( )A .3B .6C .8D .10解析:x =5时,y =1,2,3,4;x =4时,y =1,2,3;x =3时,y =1, 2;x =2时,y =1,共10个,故选D.7.若f (x )是偶函数且在(0,+∞)上减函数,又f (-3)=1,则不等式f (x )<1的解集为( )A .{x |x >3或-3<x <0}B .{x |x <-3或0<x <3}C .{x |x <-3或x >3}D .{x |-3<x <0或0<x <3}解析:由于f (x )是偶函数,∴f (3)=f (-3)=1,f (x )在(-∞,0)上是增函数,∴当x >0时,f (x )<1即为f (x )<f (3),∴x >3,当x <0时,f (x )<1即f (x )<f (-3),∴x <-3,故选C.答案:C8.定义在R 上的偶函数f (x )满足:对任意的x 1,x 2∈[0,+∞)(x 1≠x 2),有f (x 2)-f (x 1)x 2-x 1<0,则( )A .f (3)<f (-2)<f (1)B .f (1)<f (-2)<f (3)C .f (-2)<f (1)<f (3)D .f (3)<f (1)<f (-2)解析:若x 2-x 1>0,则f (x 2)-f (x 1)<0,即f (x 2)<f (x 1),∴f (x )在[0,+∞)上是减函数,∵3>2>1,∴f (3)<f (2)<f (1). 又f (x )是偶函数,∴f (-2)=f (2), ∴f (3)<f (-2)<f (1),故选A.9.设函数f (x )(x ∈R )为奇函数,f (1)=12,f (x +2)=f (x )+f (2),则f (5)=( )A .0B .1 C.52D .5解析:f (1)=f (-1+2)=f (-1)+f (2)=12,又f (-1)=-f (1)=-12,∴f (2)=1,∴f (5)=f (3)+f (2)=f (1)+2f (2)=52,故选C. 答案:C10.已知f (x )=3-2|x |,g (x )=x 2-2x ,F (x )=⎩⎪⎨⎪⎧g (x ),若f (x )≥g (x ),f (x ),若f (x )<g (x ).则F (x )的最值是( )A .最大值为3,最小值-1B .最大值为7-27,无最小值C .最大值为3,无最小值D .既无最大值,又无最小值解析:作出F (x )的图像,如图实线部分,知有最大值而无最小值,且最大值不是3,故选B.答案:B第Ⅱ卷(非选择题,共70分)二、填空题:本大题共4小题,每小题5分,共20分. 11.设集合A ={-1,1,3},B ={a +2,a 2+4},A ∩B ={3},则实数a =__________.解析:∵A ∩B ={3},∴3∈B .∵a 2+4≥4,∴a +2=3,∴a =1. 答案:112.已知函数f (x )=3x 2+mx +2在区间[1,+∞)上是增函数,则f (2)的取值范围是__________.解析:∵-m6≤1,∴m ≥-6,f (2)=14+2m ≥14+2×(-6)=2. 答案:[2,+∞)13.如图所示,函数f (x )的图像是曲线OAB ,其中点O ,A ,B的坐标分别为(0,0),(1,2),(3,1),则f ⎝ ⎛⎭⎪⎫1f (3)=__________.解析:由已知,得f (3)=1,f (1)=2,则f ⎝ ⎛⎭⎪⎫1f (3)=f (1)=2. 答案:214.国家规定个人稿费的纳税办法是:不超过800元的不纳税;超过800元而不超过4 000元的按超过800元的14%纳税;超过4 000元的按全部稿酬的11%纳税.某人出版了一本书,共纳税420元,则这个人的稿费为__________.解析:由于4 000×11%=440>420,设稿费x 元,x <4 000,则(x -800)×14%=420,∴x =3 800(元).答案:3 800元三、解答题:本大题共4小题,满分50分.15.(12分)设集合A ={x |a ≤x ≤a +3},集合B ={x |x <-1或x >5}. (1)若A ∩B ≠∅,求实数a 的取值范围; (2)若A ∩B =A ,求实数a 的取值范围.解:(1)因为A ∩B ≠∅,所以a <-1或a +3>5,即a <-1或a >2.(6分)(2)因为A ∩B =A ,所以A ⊆B ,所以a >5或a +3<-1,即a >5或a<-4.(12分)16.(12分)图中给出了奇函数f(x)的局部图像,已知f(x)的定义域为[-5, 5],试补全其图像,并比较f(1)与f(3)的大小.解:奇函数的图像关于原点对称,可画出其图像如图.(8分)显然f(3)>f(1).(12分)17.(12分)已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.(1)求f(x)的解析式;(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围.解:(1)∵f(x)为二次函数且f(0)=f(2),∴对称轴为x =1.(4分) 又∵f (x )最小值为1,∴可设f (x )=a (x -1)2+1 (a >0).(6分) ∵f (0)=3,∴a =2,∴f (x )=2(x -1)2+1, 即f (x )=2x 2-4x +3.(10分) (2)由条件知2a <1<a +1,∴0<a <12. (12分)18.(14分)已知函数f (x )=|x -a |,g (x )=ax . (1)当a =2时,解关于x 的不等式f (x )<g (x );(2)记F (x )=f (x )-g (x ),求函数F (x )在(0,a ]上的最小值(a >0). 解:(1)由题意,得|x -2|<2x ,则⎩⎨⎧x ≥2,x -2<2x .或⎩⎨⎧x <2,2-x <2x .(4分)∴x ≥2或23<x <2,即x >23.(5分) ∴不等式的解集为{x |x >23}.(6分) (2)F (x )=|x -a |-ax . ∵0<x ≤a ,∴F (x )=-(a +1)x +a .(8分) ∵-(a +1)<0,∴函数F(x)在(0,a]上是单调减函数,(12分) ∴当x=a时,函数F(x)取得最小值为-a2. (14分)。
人教版高中数学必修一第一章《集合与函数》精选习题(含答案解析)

人教版高中数学必修一第一章《集合与函数》单元检测精选(含答案解析)(时间:120分钟 满分:150分) 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A ={0,2,a },B ={1,a 2},若A ∪B ={0,1,2,4,16},则a 的值为( ) A .0 B .1 C .2D .42.设函数f (x )=,则f (f(31)的值为( )A.128127B .-128127C.81D.1613.若函数y =f (x )的定义域是[0,2],则函数g (x )=x -1f(2x的定义域是( ) A .[0,1]B .[0,1)C .[0,1)∪(1,4]D .(0,1)4.已知f (x )=(m -1)x 2+3mx +3为偶函数,则f (x )在区间(-4,2)上为( ) A .增函数B .减函数C .先递增再递减D .先递减再递增5.三个数a =0.32,b =log 20.3,c =20.3之间的大小关系是( ) A .a <c <b B .a <b <c C .b <a <cD .b <c <a6.若函数f (x )唯一的一个零点同时在区间(0,16)、(0,8)、(0,4)、(0,2)内,那么下列命题中正确的是( )A .函数f (x )在区间(0,1)内有零点B .函数f (x )在区间(0,1)或(1,2)内有零点C .函数f (x )在区间[2,16)内无零点D .函数f (x )在区间(1,16)内无零点7.已知0<a <1,则方程a |x |=|log a x |的实根个数是( ) A .2 B .3C .4D .与a 值有关8.函数y =1+ln(x -1)(x >1)的反函数是( ) A .y =e x +1-1(x >0)B .y =e x -1+1(x >0)C .y =e x +1-1(x ∈R )D .y =e x -1+1(x ∈R )9.函数f (x )=x 2-2ax +1有两个零点,且分别在(0,1)与(1,2)内,则实数a 的取值范围是( )A .-1<a <1B .a <-1或a >1C .1<a <45D .-45<a <-110.若一系列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数y =x 2,x ∈[1,2]与函数y =x 2,x ∈[-2,-1]即为“同族函数”.请你找出下面函数解析式中能够被用来构造“同族函数”的是( )A .y =xB .y =|x -3|C .y =2xD .y =11.下列4个函数中: ①y =2008x -1;②y =log a 2 009+x 2 009-x(a >0且a ≠1); ③y =x +1x2 009+x2 008;④y =x (a -x -11+21)(a >0且a ≠1). 其中既不是奇函数,又不是偶函数的是( ) A .①B .②③C .①③D .①④12.设函数的集合P ={f (x )=log 2(x +a )+b |a =-21,0,21,1;b =-1,0,1},平面上点的集合Q ={(x ,y )|x =-21,0,21,1;y =-1,0,1},则在同一直角坐标系中,P 中函数f (x )的图象恰好经过Q 中两个点的函数的个数是( )A .4B .6C .8D .10第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)13.已知函数f (x ),g (x )分别由下表给出:x 1 2 3 f (x )131x 1 2 3 g (x )321则不等式f [g (x )]>g [f (x )]的解为________. 14.已知log a 21>0,若≤a 1,则实数x 的取值范围为______________.15.直线y =1与曲线y =x 2-+a 有四个交点,则a 的取值范围为________________.16.已知下表中的对数值有且只有一个是错误的.三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)设全集为R,A={x|3≤x<7},B={x|2<x<10}.求:A∪B,∁R(A∩B),(∁R A)∩B.18.(本小题满分12分)(1)已知全集U=R,集合M={x|≤0},N={x|x2=x+12},求(∁U M)∩N;(2)已知全集U=R,集合A={x|x<-1或x>1},B={x|-1≤x<0},求A∪(∁U B).19.(本小题满分12分)已知集合A={x|-2<x<-1或x>1},B={x|a≤x<b},A∪B={x|x>-2},A ∩B={x|1<x<3},求实数a,b的值.20.(本小题满分12分)已知集合A={x|x≤a+3},B={x|x<-1或x>5}.(1)若a=-2,求A∩∁R B;(2)若A⊆B,求a的取值范围.21.(本小题满分12分)设集合A={x|x2-8x+15=0},B={x|ax-1=0}.(1)若a=51,判断集合A与B的关系;(2)若A∩B=B,求实数a组成的集合C.22.(本小题满分12分)已知集合A={x|(a-1)x2+3x-2=0},B={x|x2-3x+2=0}.(1)若A≠∅,求实数a的取值范围;(2)若A∩B=A,求实数a的取值范围.参考答案与解析1.D [∵A ∪B ={0,1,2,a ,a 2}, 又∵A ∪B ={0,1,2,4,16}, ∴a2=16,a =4,即a =4. 否则有a2=4a =16矛盾.]2.A [∵f (3)=32+3×3-2=16, ∴f(31=161,∴f (f(31)=f (161)=1-2×(161)2=1-2562=128127.] 3.B [由题意得:x ≠10≤2x ≤2,∴0≤x <1.] 4.C [∵f (x )=(m -1)x 2+3mx +3是偶函数,∴m =0,f (x )=-x 2+3,函数图象是开口向下的抛物线,顶点坐标为(0,3),f (x )在(-4,2)上先增后减.]5.C [20.3>20=1=0.30>0.32>0=log 21>log 20.3.]6.C [函数f (x )唯一的一个零点在区间(0,2)内,故函数f (x )在区间[2,16)内无零点.] 7.A [分别画出函数y =a |x |与y =|log a x |的图象,通过数形结合法,可知交点个数为2.]8.D [∵函数y =1+ln(x -1)(x >1),∴ln(x -1)=y -1,x -1=e y -1,y =e x -1+1(x ∈R ).] 9.C [∵f (x )=x 2-2ax +1, ∴f (x )的图象是开口向上的抛物线.由题意得:f(2>0.f(1<0,即4-4a +1>0,1-2a +1<0,解得1<a <45.] 10.B11.C [其中①不过原点,则不可能为奇函数,而且也不可能为偶函数;③中定义域不关于原点对称,则既不是奇函数,又不是偶函数.] 12.B [当a =-21,f (x )=log 2(x -21)+b , ∵x >21,∴此时至多经过Q 中的一个点;当a =0时,f (x )=log 2x 经过(21,-1),(1,0), f (x )=log 2x +1经过(21,0),(1,1);当a =1时,f (x )=log 2(x +1)+1经过(-21,0),(0,1), f (x )=log 2(x +1)-1经过(0,-1),(1,0); 当a =21时,f (x )=log 2(x +21)经过(0,-1),(21,0) f (x )=log 2(x +21)+1经过(0,0),(21,1).]13.x =2解析 ∵f (x )、g (x )的定义域都是{1,2,3},∴当x =1时,f [g (1)]=f (3)=1,g [f (1)]=g (1)=3,不等式不成立; 当x =2时,f [g (2)]=f (2)=3,g [f (2)]=g (3)=1,此时不等式成立; 当x =3时,f [g (3)]=f (1)=1,g [f (3)]=g (1)=3, 此时,不等式不成立. 因此不等式的解为x =2. 14.(-∞,-3]∪[1,+∞) 解析 由log a 21>0得0<a <1. 由≤a 1得≤a -1,∴x 2+2x -4≥-1,解得x ≤-3或x ≥1. 15.1<a <45解析 y =x2+x +a ,x <0,x2-x +a ,x ≥0,作出图象,如图所示.此曲线与y 轴交于(0,a )点,最小值为a -41,要使y =1与其有四个交点,只需a -41<1<a ,∴1<a <45. 16.lg1.5解析 ∵lg9=2lg3,适合,故二者不可能错误,同理:lg8=3lg2=3(1-lg5),∴lg8,lg5正确.lg6=lg2+lg3=(1-lg5)+lg3=1-(a +c )+(2a -b )=1+a -b -c ,故lg6也正确.17.解:∵全集为R ,A ={x |3≤x <7},B ={x |2<x <10}, ∴A ∪B ={x |2<x <10},A ∩B ={x |3≤x <7}, ∴∁R (A ∩B )={x |x ≥7或x <3}. ∵∁R A ={x |x ≥7或x <3},∴(∁R A )∩B ={x |2<x <3或7≤x <10}.18.解:(1)M ={x |x +3=0}={-3},N ={x |x 2=x +12}={-3,4}, ∴(∁U M )∩N ={4}.(2)∵A ={x |x <-1或x >1},B ={x |-1≤x <0}, ∴∁U B ={x |x <-1或x ≥0}. ∴A ∪(∁U B )={x |x <-1或x ≥0}. 19.解:∵A ∩B ={x |1<x <3},∴b =3,又A∪B={x|x>-2},∴-2<a≤-1,又A∩B={x|1<x<3},∴-1≤a<1,∴a=-1.20.解:(1)当a=-2时,集合A={x|x≤1},∁R B={x|-1≤x≤5},∴A∩∁R B={x|-1≤x≤1}.(2)∵A={x|x≤a+3},B={x|x<-1或x>5},A⊆B,∴a+3<-1,∴a<-4.解题技巧:本题主要考查了描述法表示的集合的运算,集合间的关系,解决本题的关键是借助于数轴求出符合题意的值.在解决(2)时,特别注意参数a是否取到不等式的端点值.21.解:A={x|x2-8x+15=0}={3,5}.(1)若a=51,则B={5},所以B A.(2)若A∩B=B,则B⊆A.当a=0时,B=∅,满足B⊆A;当a≠0时,B=a1,因为B⊆A,所以a1=3或a1=5,即a=31或a=51;综上所述,实数a组成的集合C为51.22.解:(1)①当a=1时,A=32≠∅;②当a≠1时,Δ≥0,即a≥-81且a≠1,综上,a≥-81;(2)∵B={1,2},A∩B=A,∴A=∅或{1}或{2}或{1,2}.①A=∅,Δ<0,即a<-81;②当A={1}或{2}时,Δ=0,即a=0且a=-81,不存在这样的实数;③当A={1,2},Δ>0,即a>-81且a≠1,解得a=0.综上,a<-81或a=0.11。
人教A版高一数学上册第一章集合与函数概念测试题及答案解析

第一章 集合与函数概念一、选择题1.已知全集U ={0,1,2}且U A ={2},则集合A 的真子集共有( ). A .3个B .4个C .5个D .6个2.设集合A ={x |1<x ≤2},B ={ x |x <a },若A ⊆B ,则a 的取值范围是( ). A .{a |a ≥1}B .{a |a ≤1}C .{a |a ≥2}D .{a |a >2}3.A ={x |x 2+x -6=0},B ={x |mx +1=0},且A B A =,则m 的取值集合是( ).A .⎭⎬⎫⎩⎨⎧21- ,31B .⎭⎬⎫⎩⎨⎧21- ,31- ,0C .⎭⎬⎫⎩⎨⎧21- ,31 ,0 D .⎭⎬⎫⎩⎨⎧21 ,31 4.设I 为全集,集合M ,N ,P 都是其子集,则图中的阴影部分表示的集合为( ). A .M ∩(N ∪P )B .M ∩(P ∩I N )C .P ∩(I N ∩I M )D .(M ∩N )∪(M ∩P )5.设全集U ={(x ,y )| x ∈R ,y ∈R },集合M =⎭⎬⎫⎩⎨⎧1=2-3-,x y y x |)(, P ={(x ,y )|y ≠x +1},那么U (M ∪P )等于( ).A .∅B .{(2,3)}C .(2,3)D .{(x ,y )| y =x +1}6.下列四组中的f (x ),g (x ),表示同一个函数的是( ). A .f (x )=1,g (x )=x 0B .f (x )=x -1,g (x )=xx 2-1C .f (x )=x 2,g (x )=(x )4D .f (x )=x 3,g (x )=39x7.函数f (x )=x 1-x 的图象关于( ). A .y 轴对称B .直线y =-x 对称C .坐标原点对称D .直线y =x 对称8.函数f (x )=11+x 2(x ∈R )的值域是( ).A .(0,1)B .(0,1]C .[0,1)D .[0,1]二、填空题(第4题)9.函数x=1的定义域是.-y+x10.若f(x)=ax+b(a>0),且f(f(x))=4x+1,则f(3)=.11.已知函数f(x)=ax+2a-1在区间[0,1]上的值恒正,则实数a的取值范围是.12.已知I={不大于15的正奇数},集合M∩N={5,15},(I M)∩(I N)={3,13},M ∩(I N)={1,7},则M=,N=.13.已知集合A={x|-2≤x≤7},B={x|m+1<x<2m-1}且B≠∅,若A∪B=A,则m的取值范围是_________.14.设f(x)是R上的奇函数,且当x∈[0,+∞)时,f(x)=x(1+x3),那么当x∈(-∞,0]时,f(x)=.三、解答题15.已知A={x|x2-ax+a2-19=0},B={ x|x2-5x+6=0},C={x|x2+2x-8=0},且∅(A∩B),A∩C=∅,求a的值.16.求函数f(x)=2x2-2ax+3在区间[-1,1]上的最小值.参考答案一、选择题1.A解析:条件U A={2}决定了集合A={0,1},所以A的真子集有∅,{0},{1},故正确选项为A.2.D∈解析:在数轴上画出集合A,B的示意图,极易否定A,B.当a=2时,2 B,故不满足条件A⊆B,所以,正确选项为D.3.C解析:据条件A ∪B =A ,得B ⊆A ,而A ={-3,2},所以B 只可能是集合∅,{-3},{2},所以,m 的取值集合是C .4.B解析:阴影部分在集合N 外,可否A ,D ,阴影部分在集合M 内,可否C ,所以,正确选项为B .5.B解析:集合M 是由直线y =x +1上除去点(2,3)之后,其余点组成的集合.集合P 是坐标平面上不在直线y =x +1上的点组成的集合,那么M P 就是坐标平面上除去点(2,3)外的所有点组成的集合.由此U (M P )就是点(2,3)的集合,即U (M P )={(2,3)}.故正确选项为B .6.D解析:判断同一函数的标准是两函数的定义域与对应关系相同,选项A ,B ,C 中,两函数的定义域不同,正确选项为D .7.C解析:函数f (x )显然是奇函数,所以不难确定正确选项为C .取特殊值不难否定其它选项.如取x =1,-1,函数值不等,故否A ;点(1,0)在函数图象上,而点(0,1)不在图象上,否选项D ,点(0,-1)也不在图象上,否选项B .8.B解析:当x =0时,分母最小,函数值最大为1,所以否定选项A ,C ;当x 的绝对值取值越大时,函数值越小,但永远大于0,所以否定选项D .故正确选项为B .二、填空题9.参考答案:{x | x ≥1}.解析:由x -1≥0且x ≥0,得函数定义域是{x |x ≥1}. 10.参考答案:319. 解析:由f (f (x ))=af (x )+b =a 2x +ab +b =4x +1,所以a 2=4,ab +b =1(a >0),解得a =2,b =31,所以f (x )=2x +31,于是f (3)=319.11.参考答案:⎪⎭⎫ ⎝⎛ 21,. 解析:a =0时不满足条件,所以a ≠0.+∞(1)当a >0时,只需f (0)=2a -1>0; (2)当a <0时,只需f (1)=3a -1>0. 综上得实数a 的取值范围是⎪⎭⎫ ⎝⎛ 21,. 12.参考答案:{1,5,7,15},{5,9,11,15}.解析:根据条件I ={1,3,5,7,9,11,13,15},M ∩N ={5,15},M ∩(I N )={1,7},得集合M ={1,5,7,15},再根据条件(I M )∩(I N )={3,13},得N ={5,9,11,15}.13.参考答案:(2,4].解析:据题意得-2≤m +1<2m -1≤7,转化为不等式组⎪⎩⎪⎨⎧7 ≤1-21-2<1+2- ≥1+m m m m ,解得m 的取值范围是(2,4].14.参考答案:x (1-x 3).解析:∵任取x ∈(-∞,0],有-x ∈[0,+∞), ∴ f (-x )=-x [1+(-x )3]=-x (1-x 3), ∵ f (x )是奇函数,∴ f (-x )=-f (x ). ∴ f (x )=-f (-x )=x (1-x 3),即当x ∈(-∞,0]时,f (x )的表达式为f (x )=x (1-x 3). 三、解答题15.参考答案:∵B ={x |x 2-5x +6=0}={2,3}, C ={x |x 2+2x -8=0}={-4,2}, ∴由A ∩C =∅知,-4 ,2 A ; 由∅(A ∩B )知,3∈A .∴32-3a +a 2-19=0,解得a =5或a =-2.当a =5时,A ={x |x 2-5x +6=0}=B ,与A ∩C =∅矛盾. 当a =-2时,经检验,符合题意.16.参考答案: f (x )=222⎪⎭⎫ ⎝⎛a x -+3-22a .(1)当2a<-1,即a <-2时,f (x )的最小值为f (-1)=5+2a ; ∈A ∈ +∞(2)当-1≤2a ≤1,即-2≤a ≤2时,f (x )的最小值为⎪⎭⎫⎝⎛2a f =3-22a ;(3)当2a>1,即a >2时,f (x )的最小值为f (1)=5-2a . 综上可知,f (x )的最小值为⎪⎪⎪⎩⎪⎪⎪⎨⎧.> ,-,≤≤ ,-,<- ,+22522232252a a a a a a -。
人教A版必修1高一上学期第一章集合与函数概念单元测试卷解析版

人教A 版必修1高一上学期第一章集合与函数概念单元测试卷 解 析 版考生注意: 1.本试卷分第Ⅰ卷(选择题)和第二卷(非选择题)两部分,共150分,考试时间120分钟.2.请将各题答案填写在答题卡上.第Ⅰ卷(选择题 共60分)一、选择题(每小题5分,共60分)1. 设集合{}10,8,6,4,2,0=A ,{}8,4=B ,则C A B =【 】 (A ){}8,4 (B ){}6,2,0 (C ){}10,6,2,0 (D ){}10,8,6,4,2,0 答案 【 C 】解析 本题考查补集的定义:对于一个集合A ,由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集,简称为集合A 的补集,记作C U A ,即C U A {}A x U x x ∉∈=且,.根据补集的定义,本题中, C A B ={}10,6,2,0.2. 已知集合{}{}3,1,13,2,12-=--=N m m M ,若{}3=N M ,则m 的值为【 】 (A )1,4- (B )1- (C )1 , 4- (D )4 答案 【 A 】解析 ∵{}3=N M ,∴M ∈3.∴3132=--m m ,即0432=--m m ,解之得:4,121=-=m m .3. 全集=U R ,{}03<<-=x x N ,{}1-<=x x M ,则图中阴影部分表示的集合是【 】U4321B A (A ){}13-<<-x x (B ){}03<<-x x (C ){}01<≤-x x (D ){}3<x x 答案 【 C 】 解析 重要结论如图所示,集合A , B 将全集U 分成了四部分,这四部分用集合表示如下: (1)①表示B A ; (2)②表示 A (C U B ); (3)③表示 B (C U A ); (4)④表示(C U A ) (C U B ).根据上述结论,本题中阴影部分表示的集合是 N (C U M ). ∵=U R ,{}1-<=x x M ,∴C U M {}1-≥=x x . ∵{}03<<-=x x N ,∴ N (C U M ){}01<≤-=x x .4. 设函数()⎪⎩⎪⎨⎧<-≥=0,0,x x x x x f ,若()()21=-+f a f ,则=a 【 】(A )3- (B )3± (C )1- (D )1± 答案 【 D 】解析 ∵()⎪⎩⎪⎨⎧<-≥=0,0,x x x x x f ,∴()()111=--=-f .∵()()21=-+f a f ,∴()21=+a f ,∴()1=a f . ∴=a 1±.5. 下列各组函数是同一函数的是【 】①()32x x f -=与()x x x g 2-=; ②()x x f =与()2x x g =; ③()0x x f =与()01xx g =; ④()122--=x x x f 与()122--=t t t g . (A )①② (B )③④ (C )①③ (D )①④ 答案 【 B 】 解析 函数的相等只有当两个函数的定义域和对应关系分别相同时,这两个函数才相等,即为同一个函数. 对于①,函数()x f 与()x g 的定义域均为(]0,∞-,但是()322x x x x g --=-=,所以函数()x f 与()x g 表示的不是同一个函数;对于②,函数()x f 与()x g 的定义域均为R ,但是()⎩⎨⎧<-≥===0,0,2x x x x x x x g ,所以函数()x f 与()x g 表示的不是同一个函数;对于③,函数()x f 与()x g 的定义域均为()()+∞∞-,00, ,且()()1,1==x g x f ,所以函数()x f 与()x g 表示的是同一个函数;对于④,函数的相等与用什么字母表示自变量和因变量没有关系,函数()x f 和函数()t g 表示的是同一个函数. ∴是同一函数的是③④.6. 已知函数()x f 的定义域为()1,23+-a a ,且()1+x f 为奇函数,则a 的值可以是【 】 (A )2 (B )32(C )4 (D )6 答案 【 A 】解析 若一个函数为奇函数或偶函数,即具有奇偶性,则函数的定义域关于原点对称.用区间表示奇函数或偶函数的定义域时,区间左右端点的和等于0. ∵函数()x f 的定义域为()1,23+-a a ∴1123+<+<-a x a ,解之得:a x a <<-22. ∴函数()1+x f 的定义域为()a a ,22- ∵()1+x f 为奇函数∴022=+-a a ,解之得:2=a .7. 已知定义在R 上的增函数()x f ,满足()()0=-+x f x f ,∈321,,x x x R ,且021>+x x ,032>+x x ,013>+x x ,则()()()321x f x f x f ++的值【 】(A )一定大于0 (B )一定小于0 (C )等于0 (D )正负都有可能答案 【 A 】解析 由题意可知,函数()x f 为定义在R 上的奇函数. ∵021>+x x ,032>+x x ,013>+x x ∴133221,,x x x x x x ->->->∴()()()()()()()()()113332221,,x f x f x f x f x f x f x f x f x f -=->-=->-=-> ∴()()()()()()[]321321x f x f x f x f x f x f ++->++ ∴()()()[]02321>++x f x f x f ,∴()()()0321>++x f x f x f . 即()()()321x f x f x f ++的值一定大于0.8. 设0>a ,则函数()a x x y -=的图象的大致形状是【 】(A ) (B ) (C ) (D ) 答案 【 B 】解析 对于含有绝对值的函数,要把函数化为分段函数,将问题进行分段处理.()()()⎩⎨⎧<--≥-=-=0,0,x a x x x a x x a x x y易知函数的图象与x 轴有两个交点,分别为()0,0和()0,a .当x ≥0时,()a x x y -=的图象开口向上,对称轴为直线2ax =;当0<x 时,()a x x y --=的图象开口向下.故符合题意的图象是【 B 】.9. 已知函数()x f y =在()2,0上是增函数,函数()2+=x f y 是偶函数,则下列结论中正确的是【 】(A )()⎪⎭⎫⎝⎛<⎪⎭⎫⎝⎛<27251f f f (B )()⎪⎭⎫ ⎝⎛<<⎪⎭⎫⎝⎛27125f f f(C )()12527f f f <⎪⎭⎫⎝⎛<⎪⎭⎫⎝⎛ (D )()⎪⎭⎫ ⎝⎛<<⎪⎭⎫⎝⎛25127f f f 答案 【 D 】解析 函数()2+=x f y 的图象是由函数()x f y =的图象向左平移2个单位长度得到的,因为函数()2+=x f y 是偶函数,所以其图象的对称轴为y 轴,从而函数()x f y =的图象的对称轴为直线2=x .另外,因为函数()2+=x f y 是偶函数,所以()()22+-=+x f x f ,即()()x f x f -=+22,所以函数()x f y =的图象关于直线2=x 对称,有()()31f f =∵函数()x f y =在()2,0上是增函数,∴函数()x f y =在()4,2上为减函数 ∵27325<<,∴()⎪⎭⎫ ⎝⎛<<⎪⎭⎫⎝⎛25327f f f ,即()⎪⎭⎫ ⎝⎛<<⎪⎭⎫⎝⎛25127f f f . 10. 已知函数()⎪⎩⎪⎨⎧>≤---=1,1,52x xa x ax x x f 是R 上的增函数,则实数a 的取值范围是【 】(A )3-≤0<a (B )3-≤a ≤2- (C )a ≤2- (D )0<a 答案 【 B 】解析 本题考查分段函数的单调性.解决分段函数的单调性问题时,一般要从两个方面考虑: (1)分段函数在每一段上都具有相同的单调性,即各段同为增函数或各段同为减函数; (2)要注意各段端点处的衔接情况.要使分段函数()x f 是R 上的增函数,需要满足在每一段上都是增函数,且从左到右每一段的最大值都小于或等于后一段的最小值,即每一段都单调但转折点不反超.由以上描述,根据题意可得:⎪⎪⎩⎪⎪⎨⎧≤---<≥-a a a a 51012,解之得:3-≤a ≤2-.∴实数a 的取值范围是[]2,3--.11. 定义一种运算⎩⎨⎧>≤=⊗b a b ba ab a ,,,令()()t x x x x f -⊗-+=223(t 为常数),且[]3,3-∈x ,则使函数()x f 的最大值为3的t 的集合是【 】(A ){}3,3- (B ){}5,1- (C ){}1,3- (D ){}5,3- 答案 【 C 】解析 本题为定义新运算问题,由题意可知运算b a ⊗的本质其实就是我们常遇到的取小问题:{}⎩⎨⎧>≤=b a b b a a b a ,,,min ,所以=⊗b a {}⎩⎨⎧>≤=b a b ba ab a ,,,min ,这样新运算问题就转化为了我们熟悉的问题了.如果是两个函数构成的取小函数问题,反映在两个函数的图象上,那么哪一个函数的图象部分在下方,就取哪一个函数的图象部分,作为取小函数图象的一部分.本题中,()()t x x x x f -⊗-+=223(t 为常数),设()223x x x g -+=,()t x x h -=,且当()3=x g 时,3332=-+x x ,解之得:2,021==x x ,所以函数()x g 的图象经过()()3,2,3,0两点.函数()x g 和()x h 的图象如下图所示.根据函数()x g 和()x h 的图象可知,函数()()()x h x g x f ⊗=的的值图象如下图所示.分析可知,当[]3,3-∈x 时,要使函数()x f 的最大值为3,则函数()x h 的图象必须经过点()3,0或()3,2,分别如下页图所示.当函数()x h 的图象必须经过点()3,0时,30=-t ,解之得:3±=t . ∵当3-=t 时,函数()x f 的最大值大于3,不符合题意,舍去,∴3=t ; 当函数()x h 的图象必须经过点()3,2时,32=-t ,解之得:5=t 或1-=t . ∵当5=t 时,函数()x f 的最大值大于3,不符合题意,舍去,∴1-=t . 综上所述,t 的值构成的集合是{}1,3-.12. 已知函数()35335+---=x x x x f ,若()()62>-+a f a f ,则a 的取值范围是【 】 (A )()1,∞- (B )()3,∞- (C )()+∞,1 (D )()+∞,3 答案 【 A 】解析 ∵()35335+---=x x x x f ,∴()x x x x f 53335---=-.设()()3-=x f x F ,显然,函数()x F 为定义在R 上的奇函数,且为减函数,∴()()x F x F -=-. ∵()()62>-+a f a f ,∴()()0323>--+-a f a f ∴()()02>-+a F a F ,()()()a F a F a F -=-->22 ∵函数()x F 为R 上的减函数 ∴a a -<2,解之得:1<a . ∴a 的取值范围是()1,∞-.f x () = x 2 2∙x 3第Ⅱ卷 非选择题(共90分)二、填空题(每小题5分,共20分) 13. 函数()211-++=x x x f 的定义域是__________. 答案 [)()+∞-,22,1解析 由题意可知:⎩⎨⎧≠-≥+0201x x ,解之得:x ≥1-且2≠x .∴函数()x f 的定义域为[)()+∞-,22,1 .14. 已知集合(){}(){}4,,2,=-==+=y x y x N y x y x M ,那么=N M __________. 答案 (){}1,3-解析 根据集合代表元素的特征,集合M 是由直线2=+y x 上的所有点构成的集合,集合N 是由直线4=-y x 上的所有点构成的集合,两个集合表示的都是点集,因此,集合N M 表示的是由直线2=+y x 与直线4=-y x 的交点构成的集合,即方程组⎩⎨⎧=-=+42y x y x 的有序实数解.注意点集的表示.解方程组⎩⎨⎧=-=+42y x y x 得:⎩⎨⎧-==13y x ,所以(){}1,3-=N M .15. 已知定义在R 上的函数()322--=x x x f ,设()()()⎩⎨⎧>≤=0,0,x x f x x f x g ,若函数()t x g y -=与x 轴有且只有三个交点,则实数t 的取值范围是____________.答案 (]{}43,0解析 解决分段函数的问题,常用数形结合的方法. 函数()322--=x x x f 的图象如右图所示,根据函数()x f 的图象,可以确定函数()()()⎩⎨⎧>≤=0,0,x x f x x f x g的图象如下页图所示.函数()t x g y -=与x 轴有且只有三个交点,即方程()()t x g t x g ==-,0有三个不相等的实数根,设t y =,也即函数()x g 的图象与直线t y =有三个不同的交点. 如上右图所示,实数t 的取值范围是(]{}43,0 . 16. 设关于x 的不等式012<--ax ax 的解集为S ,且S S ∉∈3,2,则a 的取值范围是__________. 答案 (]9,421,31 ⎪⎭⎫⎢⎣⎡解析 ∵S S ∉∈3,2∴2满足不等式012<--ax ax ,即0412<--a a ; 3不满足不等式012<--a x ax ,即aa --913≥0,或者当3=x 时,分母09=-a ,9=a 不等式无意义. ∴⎪⎪⎩⎪⎪⎨⎧≥--<--09130412aa aa ,解之得:31≤21<a 或94<<a .∵9=a 也符合题意∴31≤21<a 或a <4≤9. ∴a 的取值范围是(]9,421,31 ⎪⎭⎫⎢⎣⎡.三、解答题(共70分,解答应写出文字说明,证明过程或演算步骤) 17.(本题满分10分)已知{}{}121,42-≤≤+-=≤≤=m x m x B x x A .(1)若2=m ,求 A B A ,C R B ; (2)若∅=B A ,求m 的取值范围. 解:(1)当2=m 时,{}31≤≤-=x x B . ∴{}32≤≤=x x B A , C R B {}31>-<=x x x 或 ∴ A C R B {}43≤<=x x ;(2)当∅=B 时,则有121->+-m m ,解之得:32<m ; 当∅≠B 时,则有:⎩⎨⎧<--≤+-212121m m m 或⎩⎨⎧>+--≤+-41121m m m ,解之得:32≤23<m .综上所述,m 的取值范围为⎪⎭⎫ ⎝⎛∞-23,.18.(本题满分12分) 已知函数()xmx x f +=,且()21=f . (1)判断函数()x f 的奇偶性;(2)判断函数()x f 在()+∞,1上的单调性,并用定义证明你的结论. 解:(1)∵()21=f ,∴21=+m ,解之得:1=m .∴()x x x f 1+=,函数()x f 的定义域为()()+∞∞-,00, ,关于原点对称. ∵()()x f x x x x x f -=⎪⎭⎫ ⎝⎛+-=--=-11∴函数()x f 为奇函数;(2)函数()x f 在()+∞,1上为增函数,理由如下: 任取()+∞∈,1,21x x ,且21x x <,则有:()()()()()212121212122112111111x x x x x x x x x x x x x x x f x f --=⎪⎪⎭⎫ ⎝⎛-+-=⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛+=-. ∵()+∞∈,1,21x x ,且21x x <,∴0,01,0212121>>-<-x x x x x x ∴()()021<-x f x f ,∴()()21x f x f <. ∴函数()x f 在()+∞,1上为增函数.19.(本题满分12分)已知函数()ax x x f +-=22(∈x R )有最小值.(1)求实数a 的取值范围;(2)设()x g 为定义在R 上的奇函数,且当0<x 时,()()x f x g =,求()x g 的解析式.解:(1)()ax x x f +-=22()()⎩⎨⎧<+-≥-+=2,422,42x x a x x a . ∵函数()x f 有最小值∴⎩⎨⎧≤-≥+0202a a ,解之得:2-≤a ≤2. ∴实数a 的取值范围为[]2,2-;(2)∵()x g 为定义在R 上的奇函数,∴()00=g .∵当0<x 时,()()x f x g =∴当0<x 时,()()42+-=x a x g .当0>x 时,0<-x ,则()()()x g x a x g -=+-=-42∴()()42--=x a x g .∴()()()⎪⎩⎪⎨⎧>--=<+-=0,420,00,42x x a x x x a x g .20.(本题满分12分)已知二次函数()12++=bx ax x f (0≠a )和()b x a bx x g 212+-=. (1)若()x f 为偶函数,试判断()x g 的奇偶性;(2)若方程()x x g =有两个不相等的实数根,当0>a 时,判断()x f 在()1,1-上的单调性;(3)当a b 2=时,问是否存在x 的值,使满足1-≤a ≤1且0≠a 的任意实数a ,不等式()4<x f 恒成立?并说明理由.解:(1)∵()x f 为偶函数,∴()()x f x f =-∴1122++=+-bx ax bx ax ,解之得:0=b .∴()xa x g 21-=,其定义域为()()+∞∞-,00, ,关于原点对称. ∵()()x g x a x g -==-21 ∴()x g 为奇函数;(2)由()x x g =得:0122=++bx x a .∵方程()x x g =有两个不相等的实数根∴0422>-=∆a b ,∴12>a b 或12-<ab . ∵0>a ,函数()12++=bx ax x f 的对称轴为直线a b x 2-= ∴当12>ab ,12-<-=a b x 时,()x f 在()1,1-上为增函数, 当12-<ab ,12>-=a b x 时,()x f 在()1,1-上为减函数; (3)存在,理由如下:∵()4<x f ,∴4122<++ax ax ,即0322<-+ax ax∵满足1-≤a ≤1且0≠a 的任意实数a ,不等式恒成立∴⎩⎨⎧<---<-+03203222x x x x ,解之得:13<<-x . ∴存在()1,3-∈x ,使满足1-≤a ≤1且0≠a 的任意实数a ,不等式()4<x f 恒成立.21.(本题满分12分)某工厂某种航空产品的年固定成本为250万元,每生产x 件,需另投入成本为()x C ,当年产量不足80件时,()x x x C 10312+=(万元);当年产量不小于80件时,()14501000051-+=x x x C (万元).每件商品售价为50万元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润()x L (万元)关于年产量x (件)的函数解析式;(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?解:(1)当800<<x 时,()()25040311031250502505022-+-=---=--=x x x x x x C x x L ; 当x ≥80时,()()⎪⎭⎫ ⎝⎛+-=+---=--=x x x x x x C x x L 100001200145010000512505025050 ∴()⎪⎪⎩⎪⎪⎨⎧≥⎪⎭⎫ ⎝⎛+-<<-+-=80,100001200800,25040312x x x x x x x L ; (2)当800<<x 时,()()9506031250403122+--=-+-=x x x x L ∴()()95060max ==L x L (万元);当x ≥80时,()⎪⎭⎫ ⎝⎛+-=x x x L 100001200在[]100,80上单调递增,在[)+∞,100上单调递减,所以当100=x 时,()x L 取得最大值,最大值为()1000100100001001200=⎪⎭⎫ ⎝⎛+-=x L (万元). ∵1000>950∴当年产量为100件时,该厂在这一商品的生产中所获利润最大,最大利润为1000万元.22.(本题满分12分)已知函数()c x b ax x f ++=2(∈a N *,∈b R ,c <0≤1)是定义在[]1,1-上的奇函数,()x f 的最大值为21. (1)求函数()x f 的解析式;(2)若关于x 方程()0log 2=-m x f 在⎥⎦⎤⎢⎣⎡1,21上有解,求实数m 的取值范围. 解:(1)∵函数()x f 是定义在[]1,1-上的奇函数∴()00=f ,得0=b .∴当0≠x 时,()x c x acx ax x f +=+=2. ∵c <0≤1,∴()212max ==c a x f ,∴c a =. ∵∈a N *,∴1,1==c a .∴函数()x f 的解析式为()12+=x x x f ; (2)∵关于x 方程()0log 2=-m x f 在⎥⎦⎤⎢⎣⎡1,21上有解∴方程()x f m 2log =在⎥⎦⎤⎢⎣⎡1,21上有解 设()()⎪⎪⎪⎪⎭⎫ ⎝⎛+=+==x x x x x f x g 11log 1log log 2222,则()x g 在⎥⎦⎤⎢⎣⎡1,21上单调递增 ∴()x g 在⎥⎦⎤⎢⎣⎡1,21上的值域为[]1,5log 12--. ∴实数m 的取值范围为[]1,5log 12--.。
高一数学人教A版必修1单元测评五:第一章集合与函数概念Word版含解析
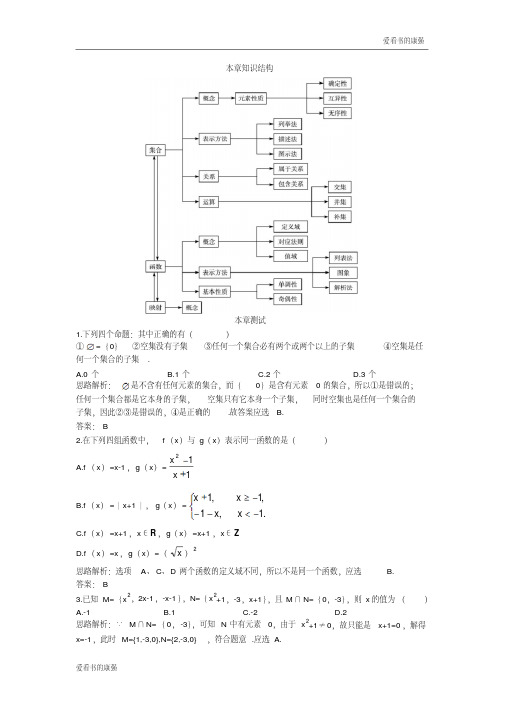
思路解析:选项 A、 C、 D 两个函数的定义域不同,所以不是同一个函数,应选
B.
答案: B
3.已知 M={x 2,2x-1 ,-x-1 },N={ x 2+1,-3,x+1},且 M ∩ N={ 0,-3},则 x 的值为 (
)
A.-1
B.1
C.-2
a
而 x 满足 a-2x>0 且 x> 0,所以 0< x< .
2
答案: V=x ( a-2x) 2
a {x|0 < x< }
2
14.给定映射 f :( x, y)→( x ,x+y ),在映射 f 下象( 2,12)的原象是( a, b),则函数
f ( x) =ax2+bx 的顶点坐标是 ____________________. 思路解析:根据题意有 a=2, a+b=12,解得 a=4, b=8, 所以函数 f(x)=4x 2+8x=4(x+1) 2-4,其顶点坐标为 (-1,-4). 答案: (-1,-4) 15.函数 f ( x) =x 2-2| x |的单调减区间是 ____________________. 思路解析:因为 f( -x )=x 2-2| x| =f ( x),所以 f(x) 是偶函数,我们可先考虑 x > 0 的情况, 当 x> 0 时, f(x)=x 2-2x ,函数在 (0,1) 上为减函数,在[ 1,+∞ )上为增函数;由于偶函数的图 象关于 y 轴对称,故函数在 (-1,0) 上为增函数,在 (-∞ ,-1)上为减函数 .
B.( -1, +∞)
C.(- ∞, 1)
D(- ∞, 1]
高一数学人教A版必修1本章测评一:第一章集合与函数概念_Word版含解析

高一数学人教A 版必修1本章测评一:第一章集合与函数概念本章测试一、选择题1.如图1-1,U 是全集,M 、P 、S 是U 的3个子集,则阴影部分所表示的集合是( )图1-1A.(M ∩P)∩SB.(M ∩N)∪SC.(M ∩P)∩SD.(M ∩N)∪S思路解析:符号语言、图形语言、文字语言三者的转译能力是高考命题的一个侧重点,应力求熟练准确. 图中阴影部分的元素x 的属性是:x ∈M 且x ∈P,但x ∉S.故选C.答案:C2.设f(x)、g(x)都是单调函数,有下列命题:①若f(x)是增函数,g(x)是增函数,则f(x)-g(x)是增函数;②若f(x)是增函数,g(x)是减函数,则f(x)-g(x)是增函数;③若f(x)是减函数,g(x)是增函数,则f(x)-g(x)是减函数;④若f(x)是减函数,g(x)是减函数,则f(x)-g(x)是减函数.其中正确的命题是( )A.①③B.①④C.②③D.②④思路解析:g(x)是单调函数,-g(x)也是单调函数,它与g(x)有相反的增减性.两个增函数的和仍是增函数,两个减函数的和仍是减函数,∴②③对.答案:C3.满足条件{1,2}⊆A {1,2,3,4}的集合A 的个数是( )A.1B.2C.3D.4思路解析:∵{1,2}⊆A {1,2,3,4},∴A 中至少有1、2两个元素,至多有1、2、3(4)三个元素.∴集合A 可能有三种情况:{1,2},{1,2,3},{1,2,4}.∴集合A 的个数是3.故选C.答案:C4.同时满足(1)M ⊆{1,2,3,4,5},(2)若a ∈M,则6-a ∈M 的非空集合M 有( )A.32个B.15个C.7个D.6个思路解析:∵M ⊆{1,2,3,4,5},a ∈M,则6-a ∈M,∴1、5应同属于M,2、4也应同属于M,3可单独出现.∴集合M 的情况有七种:{3},{1,5},{2,4},{1,3,5},{2,3,4},{1,2,4,5},{1,2,3,4,5}.故选C.答案:C5.f(x)=x 5+ax 3+bx-8,f(-2)=10,则f(2)等于( )A.-26B.-18C.-10D.10思路解析:∵f(x)=x 5+ax 3+bx-8,f(-2)=(x 5+ax 3+bx)-8=10,则(x 5+ax 3+bx)=18,f(2)=-(x 5+ax 3+bx)-8=-26.答案:A6.在一定范围内,某种产品的购买量y 吨与单价x 元之间满足一次函数关系,如果购买1 000吨,每吨为800元;购买2 000吨,每吨为700元.一客户购买400吨单价应该是( )A.820元B.840元C.860元D.880元 思路解析:设y=kx+b,由⎩⎨⎧+=+=,7002000,8001000b k b k ∴⎩⎨⎧=-=.9000,10b k ∴y=-10x+9 000.∴x=109000y -. 当y=400时,x=860元.故选C.答案:C7.设数集M={x|m ≤x ≤m+43},N={x|n-31≤x ≤n},且M 、N 都是集合{x|0≤x ≤1}的子集,如果把b-a 叫做集合{x|a ≤x ≤b}的“长度”,那么集合M ∩N 的“长度”的最小值是( ) A.31 B. 32 C.121 D.125 思路解析:根据定义,可知集合M 、N 的长度一定,分别为43、31,要使集合M ∩N 的“长度”最小,应取m=0,n=1,得M ∩N={x|32≤x ≤43},其区间长度为43-32=121.故选C. 答案:C8.若f(x)=122+x x ,则f(1)+f(2)+f(21)+f(3)+f(31)+f(4)+f(41)等于( ) A.3 B.27 C.4 D.29 思路解析:f(x)+f(x 1)=122+x x +112+x =1,∴f(2)+f(21)=f(3)+f(31)=f(4)+f(41)=1. 又f(1)= 21,∴原式=27. 答案:B9.设M 、P 是两个非空集合,定义M 与P 的差集为M-P={x|x ∈M 且x ∉P},则M-(M-P)等于( )A.PB.MC.M ∩PD.M ∪P思路解析:这是一道新定义的集合运算,关键是将M-P 用我们熟悉的交、并、补运算来表示.根据定义,“x ∈M 且x ∉P ”等价于“x ∈M ∩(P)”,为此,可设全集为U,则M-P=M ∩(P).于是有M-(M-P)=M-[M ∩(P)]=M ∩(M ∪P)=(M ∩M)∪(M ∩P)= ∅∪(M ∩P)=M ∩P.答案:C10.定义在R 上的偶函数在[0,7]上是增函数,在[7,+∞]上是减函数,又f(7)=6,则f(x)( )A.在[-7,0]上是增函数,且最大值是6B.在[-7,0]上是减函数,且最大值是6C.在[-7,0]上是增函数,且最小值是6D.在[-7,0]上是减函数,且最小值是6思路解析:f(x)是偶函数,得f(x)关于y 轴对称,如图1-2-,则f(x)在[-7,0]上是减函数,且最大值为6.图1-2 答案:B二、填空题11.已知集合A={x|x 2-2x-3=0},集合B={x|ax-1=0}.若B 是A 的真子集,则a 的值为_______.思路解析:因集合A 是确定的,所以先求出集合A={-1,3}.B 是A 的真子集,需考虑两种情况:(1)B 是空集时,a=0;(2)B 不是空集时,a=-1或a=31. 答案:0或-1或31 12.已知集合A={x|x 2+(m+2)x+1=0},若A ∩R +=∅〔R +=(0,+∞)〕,则实数m 的取值范围为_______________. 思路解析:本题综合考查方程的根与系数的关系以及集合的运算,同时此题还需特别注意空集的特殊性. A ∩R +=∅,且方程x 2+(m+2)x+1=0无零根,所以该方程只有两个负根或无实数根,即⎩⎨⎧<+-≥-+=∆0)2(,04)2(2m m 或Δ=(m+2)2-4<0.综上可得m>-4.答案:m>-413.f(x)的定义域为(0,1),则g(x)=f(x+31)+f(x-31)的定义域是__________. 思路解析:由已知得⎪⎪⎩⎪⎪⎨⎧≤-<≤+<.1310,1310x x 解得31<x ≤32. 答案: 31<x ≤32 14.设函数f(x)=x 2+x+21,则在其定义域[n,n+1],n ∈N 上,函数值域中共有个整数. 思路解析:不难判断函数f(x)=x 2+x+21在[n,n+1],n ∈N 上是增函数, 即n 2+n+21≤y ≤(n+1)2+(n+1)+ 21=n 2+3n+25成立. 又因为n 2+n+21和n 2+3n+25均非整数,而且[n 2+n+21,n 2+3n+25]上有(n 2+3n+25)-(n 2+n+21)=2n+2个整数,所以函数f(x)=x 2+x+21的值域中共有2n+2个整数. 答案:2n+2三、简答题15.设A={x|x 2+4x=0},B={x|x 2+2(a+1)x+a 2-1=0},其中a ∈R ,如果A ∩B=B,求实数a 的取值范围.思路分析:由题意易知B 有四种情况,再对四种情况讨论转化为一元二次方程根的讨论.解:化简A={0,-4},∵A ∩B=B,∴B ⊆A.(1)当B=∅时,Δ=4(a+1)2-4(a 2-1)<0,解得a<-1.(2)当B={0}或{4},即B A 时,Δ=4(a+1)2-4(a 2-1)=0,解得a=-1,此时B={0},满足B ⊆A.(3)当B={0,-4}时,⎪⎩⎪⎨⎧=--=+->--+=∆,01,4)1(2,0)1(4)1(4222a a a a 解得a=1.综上所述,实数a 的取值范围是a=1或a ≤-1.评述:由A ∩B=B 得到B ⊆A,再进行运算时,容易疏漏B=∅的情况.若改为A ∪B=A 同样有B ⊆A.16.已知函数f(x)是定义在(-1,1)上的偶函数,且在[0,1)上是增函数,若f(a-2)-f(4-a 2)<0,求a 的取值范围. 解:由函数的定义域知⎩⎨⎧<-<-<-<-,141,1212a a ∴3<a<5.又∵f(x)是定义在(-1,1)上的偶函数,∴f(4-a 2)=f(a 2-4).则f(a-2)-f(4-a 2)<0⇒f(a-2)<f(a 2-4). 结合3<a<5,可知(a-2)与(a 2-4)同号.又∵在[0,1]上f(x)是增函数,∴⎪⎩⎪⎨⎧-<-<<.|4||2|,532a a a 解得a ∈(3,2)∪(2, 5).17.上因特网的费用由两部分组成:电话费和上网费.以前,上海地区通过“上海热线”上因特网的费用为电话费0.12元/3分钟,上网费0.12元/分钟.根据信息产业部调整因特网资费的要求,自1999年3月1日起,上海地区上因特网的费用调整为电话费0.16元/3分钟,上网费每月不超过60小时,以4.00元/小时计算,超过60小时部分,以8.00元/小时计算.(1)根据调整后的规定,将每月上因特网的费用表示为上网时间(小时)的函数.(2)某网民在其家庭经济预算中一直有一笔每月上网60小时的费用支出,因特网费调整后,若要不超过其家庭经济预算中上网费的支出,该网民现在每月可上网约多少小时?(精确到0.01小时)(3)从涨价和降价的角度分析该地区调整前、后上因特网的费用情况.思路分析:理解题意,把实际问题转化为数学问题去处理.解:(1)由题意知,y=.60,600,2402.11,2.7>≤≤⎩⎨⎧-x x x x (2)调整前上网的费用与上网时间的函数关系为y 1=0.12×20x+0.12×60x=9.6x,当x=60时,y 1=576(元).由7.2×60=432<576,∴调整后该用户上网时间超过60小时.由11.2x-240=576,∴x ≈72.86(小时).答:该用户可上网约72.86小时.(3)调整前每小时平均费用9.6元.调整后,若x ∈[0,60]时每小时平均费用为7.2元;若x>60时,每小时平均费用为(11.2-x 240)元. 由11.2-x240≥9.6,则x ≥150.所以当用户上网时间小于150小时时上网费用是降低了, 而当上网时间大于150小时,上网费用是涨价了,但不会高于每小时11.2元.18.设集合A={x|2x 2+3px+2=0},B={x|2x 2+x+q=0},其中p 、q 、x ∈R ,当A ∩B={21}时,求p 的值和A ∪B. 思路分析:∵A ∩B={21},∴21∈A,且21∈B. ∴21既是方程2x 2+3px+2=0的根,又是方程2x 2+x+q=0的根. 代入易求得p 、q 的值,从而得集合A 、B,求得A ∪B.解:∵A ∩B={21},∴21∈A.∴2(21)2+3p(21)+2=0.∴p=-35.∴A={21,2}. 又∵A ∩B={21},∴21∈B.∴2(21)2+21+q=0.∴q=-1. ∴B={21,-1}.∴A ∪B={-1, 21,2}. 评述:本题考查了元素与集合的关系,应让学生深刻理解.会进行交集和并集的运算.19.设S 为满足下列两个条件的实数所构成的集合,①S 内不含1;②若a ∈S,则a-11∈S. 解答下列问题:(1)若2∈S,则S 中必有其他两个数,求出这两个数;(2)求证:若a ∈S,则1-a1∈S; (3)在集合S 中元素的个数能否只有一个?请说明理由.思路分析:理解集合中元素的属性是解决问题的突破口,由(1)、(2)知S 中不能只有一个元素,对问题(3),若从正面考虑有困难,可逆向思考,即正难则反.(1)解:∵2∈S,∴211-∈S,即-1∈S ∴)1(11--∈S,即21∈S. (2)证明:∵a ∈S,∴a -11∈S.∴a--1111=1-a 1∈S. (3)解:(用反证法)假设S 中只有一个元素,则有a=1-a 1,即a 2-a+1=0,方程无实数解, ∴集合S 中不能只有一个元素.评述:元素是否属于某个集合,关键是看它是否适合集合的公共属性.反证法是证明问题的一种重要方法,应让学生逐步掌握.20.已知函数f(x)对任意x 、y ∈R 都有f(x+y)=f(x)+f(y),且x>0时,f(x)<0,f(1)=-2.(1)判断函数f(x)的奇偶性.(2)当x ∈[-3,3]时,函数f(x)是否有最值?如果有,求出最值;如果没有,请说明理由.解:(1)∵f(x+y)=f(x)+f(y),∴f(0)=f(0)+f(0) ⇒f(0)=0.而0=x-x,因此0=f(0)=f(x-x)=f(x)+f(-x),即f(x)+f(-x)=0⇒f(-x)=-f(x).∴函数f(x)为奇函数.(2)设x 1<x 2,由f(x+y)=f(x)+f(y)知f(x 2-x 1)=f(x 2)+f(-x 1)=f(x 2)-f(x 1)〔f(x)为奇函数〕,∵(x 2-x 1)>0,且x>0时f(x)<0,∴f(x 2-x 1)=f(x 2)-f(x 1)<0,即f(x 2)<f(x 1).函数f(x)是定义域上的减函数,当x ∈[-3,3]时,函数f(x)有最值.当x=-3时,函数有最大值f(-3);当x=3时,函数有最小值f(3).f(3)=f(1+2)=f(1)+f(2)=f(1)+f(1+1)=f(1)+f(1)+f(1)=3f(1)=-6,f(-3)=-f(3)=6.∴当x=-3时,函数有最大值6;当x=3时,函数有最小值-6.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学人教a版高一必修一_第一章_集合与函数概念_学业分层测评5
有答案
学业分层测评(五)补集及综合应用
(建议用时:45分钟)
[学业达标]
一、选择题
1.若全集U={0,1,2,3}且∁U A={2},则集合A的真子集共有()
A.3个B.5个
C.7个D.8个
【解析】A={0,1,3},真子集有23-1=7.
【答案】 C
2.已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B)=()
A.{x|x≥0} B.{x|x≤1}
C.{x|0≤x≤1} D.{x|0<x<1}
【解析】由题意可知,A∪B={x|x≤0或x≥1},所以∁U(A∪B)={x|0<x<1}.【答案】 D
3.已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩∁U B=()
A.{2,5} B.{3,6}
C.{2,5,6} D.{2,3,5,6,8}
【解析】由题意得∁U B={2,5,8},∴A∩∁U B={2,3,5,6}∩{2,5,8}={2,5}.
【答案】 A
4.设全集U={1,2,3,4,5,6,7,8},集合A={1,2,3,5},B={2,4,6},则图1-1-2中的阴影部分表示的集合为()
图1-1-2
A.{2} B.{4,6}
C.{1,3,5} D.{4,6,7,8}
【解析】全集U={1,2,3,4,5,6,7,8},集合A={1,2,3,5},B={2,4,6},
由韦恩图可知阴影部分表示的集合为(∁U A)∩B,
∵∁U A={4,6,7,8},
∴(∁U A)∩B={4,6}.
故选B.
【答案】 B
5.已知集合A={x|x<a},B={x|1<x<2},且A∪(∁R B)=R,则实数a的取值范围是() 【导学号:97030023】
A.a≤2 B.a<1
C.a≥2 D.a>2
【解析】∵集合A={x|x<a},B={x|1<x<2},
∴∁R B={x|x≤1或x≥2},
因为A∪∁R B=R,所以a≥2,
故选C.
【答案】 C
二、填空题
6.州模拟)设集合S={x|x>-2},T={x|x2+3x-4≤0},则(∁R S)∪T=________.
【解析】∵集合S={x|x>-2},
∴∁R S={x|x≤-2},
由x2+3x-4≤0,得T={x|-4≤x≤1},
故(∁R S)∪T={x|x≤1}.
【答案】(-∞,1]
7.已知集合A、B均为全集U={1,2,3,4}的子集,且∁U(A∪B)={4},B={1,2},则A∩∁U B=________.
【解析】∵U={1,2,3,4},∁U(A∪B)={4},
∴A∪B={1,2,3},
又∵B={1,2},∴{3}⊆A⊆{1,2,3}.
又∁U B={3,4},∴A∩∁U B={3}.
【答案】{3}
8.设全集U=R,集合A={x|x≥0},B={y|y≥1},则∁U A与∁U B的包含关系是________.
【解析】∁U A={x|x<0},∁U B={y|y<1}={x|x<1}.∴∁U A⊆∁U B.
【答案】∁U A⊆∁U B
三、解答题
9.设A={x∈Z||x|<6},B={1,2,3},C={3,4,5},
求:(1)A∪(B∩C);
(2)A∩∁A(B∪C).
【解】A={-5,-4,-3,-2,-1,0,1,2,3,4,5},
(1)由B∩C={3},∴A∪(B∩C)=A={-5,-4,-3,-2,-1,0,1,2,3,4,5}.
(2)由B∪C={1,2,3,4,5},∁A(B∪C)={-5,-4,
-3,-2,-1,0},
∴A∩∁A(B∪C)={-5,-4,-3,-2,-1,0}.
10.设全集为R,A={x|3≤x<7},B={x|2<x<10},求:
(1)A∩B;
(2)∁R A;
(3)∁R(A∪B).
【解】(1)∵A={x|3≤x<7},B={x|2<x<10},
∴A∩B={x|3≤x<7}.
(2)又全集为R,A={x|3≤x<7},∴∁R A={x|x<3或x≥7}.
(3)∵A∪B={x|2<x<10},∴∁R(A∪B)={x|x≤2或x≥10}.
[能力提升]
1.(若全集U={1,2,3,4,5,6},M={2,3},N={1,4},则集合{5,6}等于()
A.M∪N B.M∩N
C.(∁U M)∪(∁U N) D.(∁U M)∩(∁U N)
【解析】∵全集U={1,2,3,4,5,6},M={2,3},N={1,4},∴M∪N={1,2,3,4},则(∁U M)∩(∁U N)=∁U(M∪N)={5,6}.故选D.
【答案】 D
2.已知全集U ={1,2,3,4,5},集合A ={x |x 2-3x +2=0},B ={x |x =2a ,a ∈A },则集合∁U (A ∪B )中元素个数为( )
A .1
B .2
C .3
D .4
【解析】 ∵A ={1,2},∴B ={2,4},∴A ∪B ={1,2,4},∴∁U (A ∪B )={3,5}.
【答案】 B
3.已知全集U ={2,3,a 2-a -1},A ={2,3},若∁U A ={1},则实数a 的值是________.
【解析】 ∵U ={2,3,a 2-a -1},A ={2,3},∁U A ={1},∴a 2-a -1=1,即a 2-a -2=0,解得a =-1或a =2.
【答案】 -1或2
4.集U =R ,集合A ={x |x ≤-2或x ≥5},B ={x |x ≤2}.求
(1)∁U (A ∪B );
(2)记∁U (A ∪B )=D ,C ={x |2a -3≤x ≤-a },且C ∩D =C ,求a 的取值范围. 【导学号:97030024】
【解】 (1)由题意知,A ={x |x ≤-2或x ≥5},B ={x |x ≤2},则A ∪B ={x |x ≤2或x ≥5},
又全集U =R ,∁U (A ∪B )={x |2<x <5}.
(2)由(1)得D ={x |2<x <5},由C ∩D =C 得C ⊆D ,
①当C =∅时,有-a <2a -3,解得a >1;
②当C ≠∅时,有⎩⎪⎨⎪⎧ 2a -3≤-a 2a -3>2
-a <5,
解得a ∈∅.
综上,a 的取值范围为(1,+∞).。
