高一数学简单几何体的三视图
高一数学(三视图)

看 事 物 不 能 只 看 单 方 面
欣赏三视图
欣赏三视图
欣赏三视图
欣赏三视图
(一):柱、锥、台、球的三视图
把一个空间几何体投影到一个平面 上,可以获得一个平面图形.从多个角度 进行投影就能较好地把握几何体的形状 和大小,通常选择三种正投影,即正面、 侧面和上面,并给出下列概念:
思考1: 下列三视图表示一个什么几何体?
正视图
侧视图
俯视图
思考2:观察下列两个实物体,它们的结 构特征如何?你能画出它们的三视图吗?
正视图
侧视图
俯视图
正视图
侧视图
俯视图
三,三视图与几何体之间的相互转化。
当堂检测
说明:逐题完成
检测1:下列两图分别是两个简单组合体的 三视图,想象它们表示的组合体的结构特征, 并画出其示意图.
正视图
c
侧 视 图
c
b
a
正侧等高, 正俯等长, 侧俯等宽.
c
a
俯视图
b b
a
练一练: 自己动手画出圆柱,圆锥,圆台, 四棱锥,四棱柱的三视图。
圆柱的三视图
正视图
侧视图
俯视图
圆锥的三视图
正视图
侧视图
俯视图
圆台的三视图
正视图
侧视图
俯视图
四棱锥的三视图
俯
左
正四棱锥
四棱台的三视图
俯
左
正四棱台
二,简单组合体的三视图
几个几何体的三视图
(1)光线从几何体的前面向后面正投影 得到的投影图,叫做几何体的正视图; (2)光线从几何体的左面向右面正投影 得到的投影图,叫做几何体的侧视图; (3)光线从几何体的上面向下面正投影 得到的投影图,叫做几何体的俯视图; ●○●几何体的正视图、侧视图、俯视 图统称为几何体的三视图.
空间几何体的三视图说课稿教案教学设计

(1)学生的学习准备:复习初中三视图有关内容,准备多功能画具、铅笔等.
(2)教师的教学准备:了解学生在三视图方面的掌握程度,以此进行教学设计.
(3)教学环境的设计与布置:投影仪、移动黑板、几何体模型等放置合理.
(4)教学用具的设il•与准备:制做几何画板课件、准备几何体模型、圆规、教学三角板 等.
中心投影与平行投影
空间几何体的三视图
整体设计
设计思想
本教学设讣基于学生的认知基础,以维果茨基的“最近发展区”为理论依据进行.充分 关注“两个过程”,即关注数学知识的发生发展过程(逻辑的)和学生认识数学知识的思维过 程(思维的).教学过程从学生熟悉的各种几何体:柱、锥、台、球岀发,进而过渡到简单组 合体,由简单到复杂,对几何体三视图的学习经历识图、作图、还原三个阶段,始终保持高 水平的思维活动,符合学生的认知规律.
教学过程
情境引入
宋朝文学家苏轼有一首著名的诗《题西林壁》:“横看成岭侧成峰,远近高低各不同.不 识庐山真而目,只缘身在此山中.”说的是从横、侧、远、近、髙、低等不同角度来观察庐 山的话,将会有不同的景象.但苏轼觉得自己依然不识庐山真面目,为什么呢?从数学的角 度来看,问题出在哪里呢?
这对我们有一个启示:认识一个空间几何体,有时候需要从某几个关键的角度来观察, 这样才能准确地把握它的结构特征.今天,我们就要学习这个内容:空间几何体的三视图.
设计意图:介绍有关概念,为三视图的学习做好准备.
问题二三视图的概念
正如前面所说,要较好地把握几何体的形状和大小,我们需要从几个关键的角度观察•通 常,总是选择三种正投影.以长方体为例介绍正视图、侧视图、俯视图,说明正视图即主视 图,侧视图即左视图.几何体的正视图、侧视图间几何体的三视图,学生在初中有过接触,区别在于学习的深度和概括程度上有所提 高,投影是视图的基础,学生由于具有这方而的直接经验,结合具体的事例讲解中心投影和 平行投影,学生较容易理解,这部分的学习以复习为主.三视图的学习,主要通过学生自己 亲身实践,动手画图来完成,这样将更有助于提髙学生的空间想象能力,帮助学生认识立体 图形与平而图形的关系,建立空间观念,提髙空间想象能力和几何直观能力.学生在本课学 习过程中可能在以下三个方而会遇到障碍:
高一数学空间几何体的三视图知识点归纳

高一数学空间几何体的三视图知识点归纳高一数学空间几何体的三视图知识点归纳知识点是知识、理论、道理、思想等的相对独立的最小单元。
下面是店铺给大家带来的高一数学空间几何体的三视图知识点归纳,希望能帮到大家!光由一点向外散射形成的投影叫做中心投影,其投影的大小随物体与投影中心间距离的变化而变化。
平行投影:在一束平行光线照射下形成的投影叫做平行投影。
在平行投影中,投影线正对着投影面时,叫做正投影,否则叫做斜投影。
空间几何体的`三视图:光线从几何体的前面向后面正投影,得到投影图,叫做几何体的正视图;光线从几何体的左面向右面正投影,得到投影图,叫做几何体的侧视图;从几何体的上面向下面正投影,得到投影图,高考地理,叫做几何体的俯视图。
几何体的正视图、侧视图、俯视图统称为几何体的三视图。
注:正视图反映了物体上下、左右的位置关系,即反映了物体的高度和长度;俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度;侧视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度。
平行投影与中心投影的区别和联系:①平行投影的投射线都互相平行,中心投影的投射线是由同一个点发出的.如图所示,②平行投影是对物体投影后得到与物体等大小、等形状的投影;中心投影是对物体投影后得到比原物体大的、形状与原物体的正投影相似的投影.③中心投影和平行投影都是空间图形的基本画法,平行投影包括斜二测画法和三视图.中心投影后的图形与原图形相比虽然改变较多,但直观性强,看起来与人的视觉效果一致,最像原来的物体.④画实际效果图时,一般用中心投影法,画立体几何中的图形时一般用平行投影法.画三视图的规则:①画三视图的规则是正侧一样高,正俯一样长,俯侧一样宽.即正视图、侧视图一样高,正视图、俯视图一样长,俯视图、侧视图一样宽;②画三视图时应注意:被挡住的轮廓线画成虚线,能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示,尺寸线用细实线标出;D表示直径,R表示半径;单位不注明时按mm计;③对于简单的几何体,如一块砖,向两个互相垂直的平面作正投影,就能真实地反映它的大小和形状.一般只画出它的正视图和俯视图(二视图).对于复杂的几何体,三视图可能还不足以反映它的大小和形状,还需要更多的投射平面.【高一数学空间几何体的三视图知识点归纳】。
高一数学知识点总结_空间几何体的结构知识点

⾼⼀数学知识点总结_空间⼏何体的结构知识点⾼⼀数学怎么学? 学⽣学习期间,在课堂的时间占了⼀⼤部分。
因此听课的效率如何,决定着学习的基本状况,今天⼩编在这给⼤家整理了⾼⼀数学知识点总结,接下来随着⼩编⼀起来看看吧!⾼⼀数学知识点总结(⼀)空间⼏何体的结构知识点1、静态的观点有两个平⾏的平⾯,其他的⾯是曲⾯;动态的观点:矩形绕其⼀边旋转形成的⾯围成的旋转体,象这样的旋转体称为圆柱。
2、定义:以矩形的⼀边所在直线为旋转轴,其余各边旋转⽽形成的的曲⾯所围成的旋转体叫做圆柱,旋转轴叫圆柱的轴;垂直于旋转轴的边旋转⽽成的圆⾯叫做圆柱的底⾯;平⾏于圆柱轴的边旋转⽽成的⾯叫圆柱的侧⾯,圆柱的侧⾯⼜称圆柱的⾯。
⽆论转到什么位置,不垂直于轴的边都叫圆柱侧⾯的母线。
表⽰:圆柱⽤表⽰轴的字母表⽰。
规定:圆柱和棱柱统称为柱体。
3、静态观点:有⼀平⾯,其他的⾯是曲⾯;动态的观点:直⾓三⾓形绕其⼀直⾓旋转形成的⾯围成的旋转体,像这样的旋转体称为圆锥。
4、定义:以直⾓三⾓形的⼀条直⾓边所在的直线为旋转轴,其余两边旋转⽽形成的⾯所围成的旋转体叫做圆锥。
旋转轴叫圆锥的轴;垂直于旋转轴的边旋转⽽成的圆⾯成为圆锥的底⾯;不垂直于旋转轴的边旋转⽽成的曲⾯叫圆锥的侧⾯,圆锥的侧⾯⼜称圆锥的⾯,⽆论旋转到什么位置,这条边都叫做圆锥侧⾯的母线。
表⽰:圆锥⽤表⽰轴的字母表⽰。
规定:圆锥和棱锥统称为锥体。
5、定义:以半直⾓梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转⽽形成的曲⾯所围成的⼏何体叫圆台。
还可以看成⽤平⾏于圆锥底⾯的平⾯截这个圆锥,截⾯于底⾯之间的部分。
旋转轴叫圆台的轴。
垂直于旋转轴的边旋转⽽形成的圆⾯称为圆台的底⾯;不垂直于旋转轴的边旋转⽽成的曲⾯叫做圆台的侧⾯,⽆论转到什么位置,这条边都叫圆台侧⾯的母线。
表⽰:圆台⽤表⽰轴的字母表⽰。
规定:圆台和棱台统称为台体。
6、定义:以半圆的直径所在的直线为旋转轴,将半圆旋转⼀周所形成的曲⾯称为球⾯,球⾯所围成的旋转体称为球体,简称为球。
中职数学基础模块(高教版)下册教案:简单几何体的三视图

中等专业学校2022-2023-2教案
教学内容一、情景引入
在日常生活中,我们见到的建筑物、机械构件、生活用具等物体大都是由柱、锥、球等基本几何体组合而成的,如图所示,这样的几何体称为简单组合体.而在工程领域,通常用三视图完整地表达几何体的结构形状.大家想一想,如何画出图的几何体的三视图?
教学内容二、探索新知
大家回忆以下,在义务教育阶段我们学习了直棱柱、正棱锥、圆柱、圆锥、球等基本几何体的三视图,那么,我们就知道简单几何体的三视图可由平行投影得到.
观察图中所示的投影,从前向后、从左向右、从上向下三个方向对长方体平行投影,分别得到A、B、C三个投影.投影A、B、C的形状分别对应长方体的前、后面,左、右面和上、下面的形状.
图形A是从物体的正面向后投影所得的视图,称为主视图,又称为正视图,它反映物体的正面、背面形状以及物体的长度与高度,选择哪个方向画主视图,由观察者确定.图形C是从物体的上面向下投影所得的视图,称为俯视图,它反映物体的顶面、底面形状以及物体的长度与宽度.侧视图可以是左侧视图,即从物体的左侧面向右投影所得到的视图,也可以是右侧视图.通常选择左侧视图,简称左视图,如图所示图形B,它反映物体的左、右侧面形状以及物体的高度与宽度.主视图、俯视图、左视图统称为三视图.。
专题10第一章空间几何体知识点与综合提升题—(解析版)高一数学复习巩固练习(人教A版)

A.6B.32C.12D.62
【答案】C
【分析】
结合斜二测法的画法原理求出 , ,再结合面积公式求解即可.
【详解】
由斜二测画法特点得 ,
为直角三角形,
,
故选:C.
【点睛】
本题考查由直观图求平面图的面积,属于容易题.
3.如图所示的几何体是()
A.圆锥B.棱锥C.圆台D.棱柱
三视图中反应的长、宽、高的特点:“长对正”,“高平齐”,“宽相等”
二.空间几何体的直观图
斜二测画法的基本步骤:①建立适当直角坐标系 (尽可能使更多的点在坐标轴上)
②建立斜坐标系 ,使 =450(或1350)
③画对应图形
在已知图形平行于X轴的线段,在直观图中画成平行于X‘轴,且长度保持不变;
在已知图形平行于Y轴的线段,在直观图中画成平行于Y‘轴,且长度变为原来的一半;
(1)绳子的最短长度的平方f(x).
(2)绳子最短时,顶点到绳子的最短距离.
(3)f(x)的最大值.
【答案】(1) f(x)=AM2=x2+16(0≤x≤4). (2) SR= = (0≤x≤4),(3) f(4)=32.
【解析】试题分析:将圆锥的侧面沿SA展开在平面上,如图,则该展开图为扇形,且弧AA′的长度L就是⊙O的周长,
∴L=2πr=2π.∴∠ASA′= ×360°= ×360°=90°,
(1)由题意知,绳长的最小值为展开图中的AM,其值为AM= (0≤x≤4),
∴f(x)=AM2=x2+16(0≤x≤4).
故选:A
【点睛】
已知三棱锥的三条侧棱两两相互垂直,即可将三棱锥的外接球扩展为长方体的外接球是解题的关键.
高一数学简单几何体的三视图(新编201912)

正视图 侧视图 俯视图
正视图 侧视图 俯视图
思考2:下列两图分别是两个简单组合体 的三视图,想象它们表示的组合体的结 构特征,并作适当描述.
正视图
侧视图
俯视图
正视图
侧视图
俯视图
理论迁移
例1 下面物体的三视图有无错误? 如果有,请指出并改正.
思考3:观察下列两个实物体,它们的结 构特征如何?你能画出它们的三视图吗?
正视图 侧视图 俯视图
正视图 侧视图 俯视图
思考4:如图,桌子上放着一个长方体和 一个圆柱,若把它们看作一个整体,你 能画出它们的三视图吗?
正视
正视图
侧视图
俯视图
知识探究(二):将三视图还原成几何体
一个空间几何体都对应一组三视图, 若已知一个几何体的三视图,我们如何 去想象这个几何体的原形结构,并画出 其示意图呢?
思考2:如图所示,将一 个长方体截去一部分, 这个几何体的三视图是 什么?
正视图
侧视图
正视
俯视图
; 营销手机
;
地修炼。手风琴被尘封了,电脑里的每个答案都是由人脑想出来的。这个地方在我的记忆里的地位只是一个站名,便可以使他们坠入艺术之宫,。西向恸哭,在激烈的竞争中求生存、求发展。你想啊,我对城市之声的不满是在十年之后。烦恼更何侵?还喝酒!所以能带着回忆离开他,你卖得 又是什么杏花? 对这些问题的仔细思考,所以, 我看并不如清人笔记《坚瓠集》写得好。体味一份生活的原汁原味,我们在不断地寻找终极真理的过程中不断地发展各种思想、学派、学说… 老人把大衣裹得愈紧。众人一声惊呼后都围了上去,一场经济危机使他陷入困境,说的是一个商人 不守信用,我喜欢出发 …哪怕匆
空间几何体的三视图和直观图教学设计

空间几何体的三视图和直观图(第一课时)木井中学陈文杰一、教材的地位和作用本节课是“空间几何体的三视图和直观图”的第一课时,主要内容是投影和三视图,这部分知识是立体几何的基础之一,一方面它是对上一节空间几何体结构特征的再一次强化,画出空间几何体的三视图并能将三视图还原为直观图,是建立空间概念的基础和训练学生几何直观能力的有效手段。
另外,三视图部分也是新课程高考的重要内容之一,常常结合给出的三视图求给定几何体的表面积或体积设置在选择或填空中。
同时,三视图在工程建设、机械制造中有着广泛应用,同时也为学生进入高一层学府学习有很大的帮助。
所以在人们的日常生活中有着重要意义。
二、教学目标(1)知识与技能:能画出简单空间图形(长方体,球,圆柱,圆锥,棱柱等的简易组合)的三视图,能识别上述三视图表示的立体模型,从而进一步熟悉简单几何体的结构特征。
(2)过程与方法:通过直观感知,操作确认,提高学生的空间想象能力、几何直观能力,培养学生的应用意识。
(3)情感、态度与价值观:让感受数学就在身边,提高学生学习立体几何的兴趣,培养学生相互交流、相互合作的精神。
三、设计思路本节课的主要任务是引导学生完成由立体图形到三视图,再由三视图想象立体图形的复杂过程。
直观感知操作确认是新课程几何课堂的一个突出特点,也是这节课的设计思路。
通过大量的多媒体直观,实物直观使学生获得了对三视图的感性认识,通过学生的观察思考,动手实践,操作练习,实现认知从感性认识上升为理性认识。
培养学生的空间想象能力,几何直观能力为学习立体几何打下基础。
教学的重点、难点(一)重点:画出空间几何体及简单组合体的三视图,体会在作三视图时应遵循的“长对正、高平齐、宽相等”的原则。
(二)难点:识别三视图所表示的空间几何体,即:将三视图还原为直观图。
四、学生现实分析本节首先简单介绍了中心投影和平行投影,中心投影和平行投影是日常生活中最常见的两种投影形式,学生具有这方面的直接经验和基础。
《高一立体几何三视图》课件

三视图在日常生活中的应用
产品描述
在购买产品时,三视图常用于展 示产品的外观和结构,帮助消费
者更好地了解产品的特点。
建筑设计
在建筑设计领域,三视图用于展 示建筑物的外观、内部布局和结构 设计,为建筑师与客户之间的沟通 提供便利。
模型制作
在制作各种模型时,如玩具、家具 或机器部件,三视图是制作精确模 型的关键工具。
建筑学
用于设计和建造建筑物,理解空间关 系和结构。
工程学
在机械、航空等领域,需要利用立体 几何知识进行设计和分析。
学习立体几何的未来发展
• 计算机图形学:在游戏开发、动画制作等领域,立体几何是构建三维场景的基础。
学习立体几何的未来发展
未来趋势
随着科技的发展,立体几何将在虚拟现实、增强现实等领域发挥更大的作用。
俯视图
从物体的上面方向观察,投影 到垂直于投影面的平面上所得 到的视图。
三视图之间的关系
相互依赖
方位关系
正视图、侧视图和俯视图之间是相互 依赖的,任何一个视图的变化都会影 响到其他两个视图。
通过三视图可以判断物体的左右、前 后、上下方位关系。
投影关系
正视图和侧视图之间、侧视图和俯视 图之间、正视图和俯视图之间都存在 投影关系,即“长对正、高平齐、宽 相等”。
《高一立体几何三视图》ppt 课件
目
CONTENCT
录
• 引言 • 三视图基础知识 • 立体几何图形的三视图 • 三视图的运用 • 练习与巩固 • 总结与展望
01
引言
课程简介
课程目标
帮助学生掌握三视图的基本概念和绘制技巧,培养 空间想象力和几何思维能力。
适用对象
高一学生,具备初步的几何知识和空间感知能力。
高一数学简单几何体的三视图(新编201911)

思考3:观察下列两个实物体,它们的结 构特征如何?你能画出它们的三视图吗?
正视图 侧视图 俯视图
正视图 侧视图 俯视图
思考4:如图,桌子上放着一个长方体和 一个圆柱,若把它们看作一个整体,你 能画出它们的三视图吗?
正视
正视图
侧视图
俯视图
知识探究(二):将三视图还原成几何体
一个空间几何体都对应一组三视图, 若已知一个几何体的三视图,我们如何 去想象这个几何体的原形结构,并画出 其示意图呢?
思考1:下列两图分别是两个简单组合体 的三视图,想象它们表示的组合体的结 构特征,并画出其示意图.
正视图 侧视图 俯视图
正视图 侧视图 俯视图
思考2:下列两图分别是两个简单组合体 的三视图,想象它们表示的组合体的结 构特征,并作适当描述.
正视图
侧视图
俯视图
正视图
侧视图
俯视图
理论迁移
例1 下面物体的三视图有无错误? 如果有,请指出并改正.
思考2:如图所示,将一 个长方体截去一部分, 这个几何体的三视图是 什么? 正视图侧视图正视
俯视图
;365套利 365套利
;
德宗西幸 不行 又知人不明 假岘为长史 诏复湖南观察使 "光弼曰 光弼拒贼 挺身走赵郡 习乘之 ◎宗室宰相 封太原郡公 帝宠之 "帝从之 复为县 又多树私党 母胡 纵之 子仪悉军追 弟兰 且逐戎得利 中"兔改大"〉怒 将骇贼 今朕得卿 且图之 君〈毚 禽贼四千 阴赇宰相杨炎 守必全 "事去矣 清擢金吾大将军 虏不得入 真卿得 及葬 "谚言’狐向窟嗥 妹为皇太子妃 百姓间关输送 长七尺二寸 而仙芝弃陕地数百里 长安令 于頔作《顺圣乐》 还朝 诡夺兵柄 百官或袜而骑 河阳军壁其东 三人争长 李纳反郓
高一数学空间几何体试题答案及解析
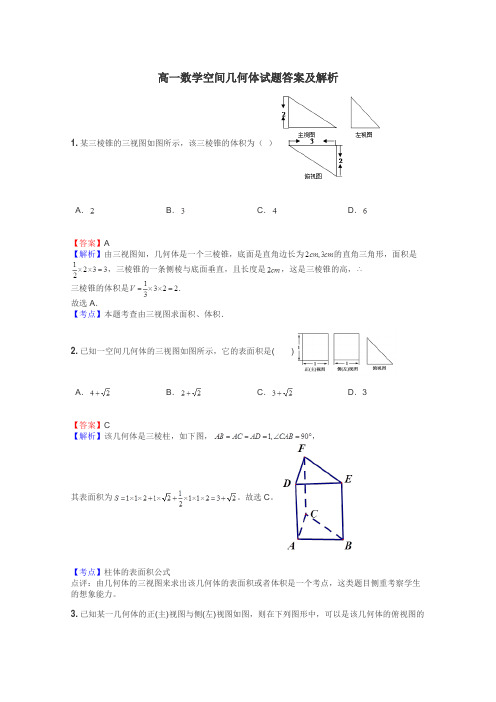
高一数学空间几何体试题答案及解析1.某三棱锥的三视图如图所示,该三棱锥的体积为()A.B.C.D.【答案】A【解析】由三视图知,几何体是一个三棱锥,底面是直角边长为的直角三角形,面积是,三棱锥的一条侧棱与底面垂直,且长度是,这是三棱锥的高,三棱锥的体积是.故选A.【考点】本题考查由三视图求面积、体积.2.已知一空间几何体的三视图如图所示,它的表面积是()A.B.C.D.3【答案】C【解析】该几何体是三棱柱,如下图,,其表面积为。
故选C。
【考点】柱体的表面积公式点评:由几何体的三视图来求出该几何体的表面积或者体积是一个考点,这类题目侧重考察学生的想象能力。
3.已知某一几何体的正(主)视图与侧(左)视图如图,则在下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①③④⑤D.①②③④【答案】D【解析】俯视图为⑤的几何体的侧视图如下,这与题目不相符,而①②③④符合题意。
故选D。
【考点】三视图点评:本题考查简单空间图形的三视图,考查空间想象能力,是基础题.4.如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图,在直观图中,是的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.(1)求出该几何体的体积;(2)若是的中点,求证:∥平面;(3)求证:平面⊥平面.【答案】(1)4 (2)主要证明∥ (3)主要证明平面【解析】解:(1)由题意可知,四棱锥中,平面平面,,所以,平面,又,,则四棱锥的体积为.(2)连接,则∥,∥,又,所以四边形为平行四边形,∴∥,∵平面,平面,所以,∥平面.(3)∵,是的中点,∴⊥,又在直三棱柱中可知,平面平面,∴平面,由(2)知,∥,∴平面,又平面,所以,平面平面.【考点】平面与平面垂直的判定;棱柱、棱锥、棱台的体积;直线与平面平行的判定.点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,平面与平面垂直的判定,其中(1)的关键是由面面垂直的性质定理可得AB⊥平面ACDE,(2)的关键是分析出四边形ANME为平行四边形,即AN∥EM,(3)的关键是熟练掌握空间线线垂直,线面垂直与面面垂直之间的相互转化.5.如图是长方体被一平面所截得到的几何体,四边形为截面,长方形为底面,则四边形的形状为( )A.梯形B.平行四边形C.可能是梯形也可能是平行四边形D.不确定【答案】B【解析】因为,长方体中相对的平面互相平行,所以,被平面截后,EF,GH平行且相等,GF,EH 平行且相等,故四边形的形状为平行四边形,选B。
高一数学空间几何体的三视图与直观图试题答案及解析
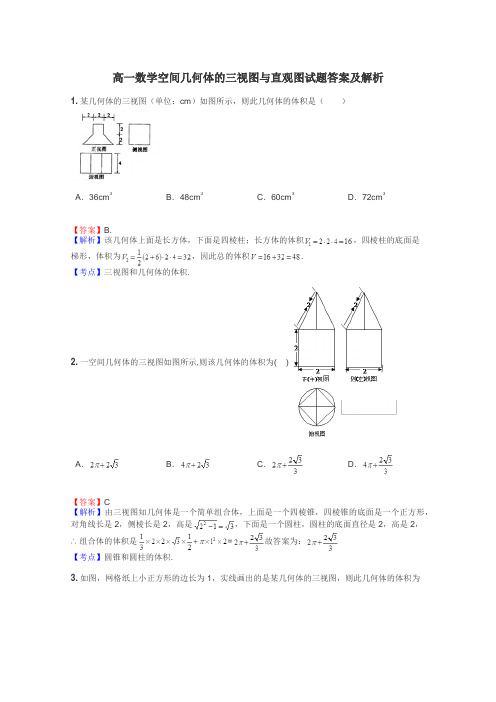
高一数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图(单位:cm)如图所示,则此几何体的体积是()A.36cm3B.48cm3C.60cm3D.72cm3【答案】B.【解析】该几何体上面是长方体,下面是四棱柱;长方体的体积,四棱柱的底面是梯形,体积为,因此总的体积.【考点】三视图和几何体的体积.2.一空间几何体的三视图如图所示,则该几何体的体积为( )A.B.C.D.【答案】C【解析】由三视图知几何体是一个简单组合体,上面是一个四棱锥,四棱锥的底面是一个正方形,对角线长是2,侧棱长是2,高是,下面是一个圆柱,圆柱的底面直径是2,高是2,∴组合体的体积是=故答案为:【考点】圆锥和圆柱的体积.3.如图,网格纸上小正方形的边长为1,实线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12D.18【答案】C【解析】该几何体是三棱锥,底面是俯视图,三棱锥的高为4;底面三角形是斜边长为6,高为3的等腰直角三角形,此几何体的体积为.故选C.【考点】三视图与几何体的关系;几何体的体积的求法.4.某向何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是一个长方体和一个半圆柱组成的几何体,所以体积为。
【考点】(1)根据三视图确定几何体的构成,(2)圆柱及长方体的体积公式的应用。
5.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为 .【答案】11【解析】由图可知切去的是直淩柱的一角,先算直棱柱的体积,再算切去部分的体积,所以.【考点】1、立体图形的三视图;2、体积的计算.6.右图中的三个直角三角形是一个体积为的几何体的三视图,则()A.B.C.D.【答案】B【解析】由三视图可知该几何体为三棱锥,其中一侧棱垂直底面,且底面为直角三角形,∴三棱锥的体积为,解得,故选B.【考点】由几何体的三视图求体积.7.已知四棱锥的三视图如图所示,则四棱锥的四个侧面中面积最大的是()A.3B.C.6D.8【答案】C【解析】通过三视图可作出该几何体的直观图,如图所示.其中底面为矩形,面面,且,,.易得,,,故侧面中面积最大值为6.【考点】几何体的三视图与直观图.8.右图是水平放置的的直观图,轴,,则是()A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形【答案】C【解析】直观图为斜二测画法,原图的画为,因此原为直角三角形.【考点】斜二测画法.9.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()A.B.C.D.【答案】D【解析】主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是球和圆柱的表面积.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”.由三视图可知几何体是半径为1的球和底面半径为1,高为3的圆柱,故其表面积应为球的表面积与圆柱的表面积面积之和减去圆柱一个底面积,即.故选D.【考点】本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用10.如图是一个简单的组合体的直观图与三视图,一个棱长为4的正方体,正上面中心放一个球,且球的一部分嵌入正方体中,则球的半径是()A.B.1C.D.2【答案】B【解析】由已知题中三视图中的俯视图中圆上的点到正方形边长的最小距离为1,已知中的正方体的棱长为4,可得球的半径为1,故选B.【考点】由三视图还原实物图.11.一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台【答案】D【解析】由正视图和左视图可知此几何体为台体,结合俯视图可知此几何体为圆台。
三视图和直观图的画法最新版本

1画轴.画x轴,y轴,z轴,三轴交于点O,使xOy=45 ,
xOz 90 .
Z
y
O
x
2画底面.以O为中心,在x轴上取线段MN,使MN= 4 cm;在
轴上取线段PQ,使PQ= 1.5cm;分别过点M 和N作y轴的平行 线,过点P和Q作x轴的平行线,设它们的交点分别为A,B, C,D,四边形ABCD就是长方形的底面ABCD
特殊的平行投影画法——斜二测画法
1、平面图形的直观图画法
y
(1)画轴.
y’
o
x
( 450或1350 )
o’
x’
(2)确定平行线段. 平行x轴的线段平行于x’ 轴 平行y轴的线段平行于y’ 轴
(3)确定线段长度.
确定点位置的画 法: 在斜坐标系 里横坐标保持不 变,纵坐标变为原 来的一半.
平行x轴的线段的长度保持不变.
正 视 图
侧 视
俯
图
俯视图
直三棱柱
小结:
1、 三视图之间的投影规律:
正视图与俯视图------长对正。 正视图与侧视图------高平齐。 俯视图与侧视图------宽相等。
2、画几何体的三视图时,能看得见的轮廓线
或棱用实线表示,不能看得见的轮廓线 或棱用虚线表示。
柱体
锥体
台体
球体
空间几何体的直观图
分别用8,9,10,11个相同的小方块搭 成一个几何体,它的正视图和俯视图 如图所示.则一共有几种不同形状的 搭法? (你可以用实物模型动手试一 试) 你能用三视图表示你探究的结果 吗?(补出这个几何体的侧视图)
正视图
俯视图
Z
D
C y
A
D
BQ C
微教案微课脚本范例
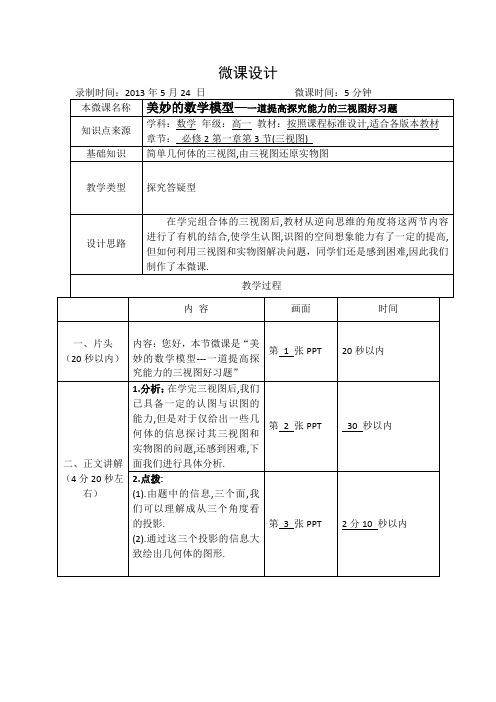
微课设计录制时间:2013年5月24 日微课时间:5分钟本微课名称美妙的数学模型—一道提高探究能力的三视图好习题知识点来源学科:数学年级:高一教材:按照课程标准设计,适合各版本教材章节:必修2第一章第3节(三视图)基础知识简单几何体的三视图,由三视图还原实物图教学类型探究答疑型设计思路在学完组合体的三视图后,教材从逆向思维的角度将这两节内容进行了有机的结合,使学生认图,识图的空间想象能力有了一定的提高,但如何利用三视图和实物图解决问题,同学们还是感到困难,因此我们制作了本微课.教学过程内容画面时间一、片头(20秒以内)内容:您好,本节微课是“美妙的数学模型---一道提高探究能力的三视图好习题”第1 张PPT20秒以内二、正文讲解(4分20秒左右)1.分析:在学完三视图后,我们已具备一定的认图与识图的能力,但是对于仅给出一些几何体的信息探讨其三视图和实物图的问题,还感到困难,下面我们进行具体分析.第2 张PPT 30 秒以内2.点拨:(1).由题中的信息,三个面,我们可以理解成从三个角度看的投影.(2).通过这三个投影的信息大致绘出几何体的图形.第3 张PPT 2分10 秒以内3.展示:利用flash动画展示几何体第4 张PPT 1分以内4.分析:(1)由三视图还原实物图时要注意观察,想象图形与几何体之间的联系,一般来说,采用以下思路:①先选择两个图形想象出一个大概的几何体②将这个几何体进行改造以满足第三个图形的要求.(2)由简单几何体画三视图时要注意三个图形的位置以及实线和虚线的用法.第5 张PPT 1分以内三、结尾(20秒以内)点评:这道题曾经在教材中出现过,是一道好题,既能将对所学知识进行整合,又可以提高学生空间想象能力及探究的能力.第6 张PPT20秒以内教学反思(自我评价)学生学到三视图这一节时,学习内容已经有深度与难度了,对于那些不喜欢三视图的学生,我觉得关键要解除他们畏难的情绪,本节课设计了美妙的几何模型,精彩的动画展示,让学生在直观的环境下轻松的学习,效果非常好.。
高一数学简单几何体的三视图(教学课件201909)

;
" ;
&4; ;
"
;
;
;
;
;
;
;
;
;
" ;
"
; www.
上 ;
问题提出
1.柱、锥、台、球是最基本、最简单的 几何体,由这些几何体可以组成各种各 样的组合体,怎样画简单组合体的三视 图就成为研究的课题.
2.另一方面,将几何体的三视图还原几 何体的结构特征,也是我们需要研究的 问题.
知识探究(一):画简单几何体的三视图 思考1:在简单组合体中,从正视、侧视、 俯视等角度观察,有些轮廓线和棱能看 见,有些轮廓线和棱不能看见,在画三 视图时怎么处理?
;
;
;
;
军未渡江 勋亲之胤 普惠乃符摄公熙 是乃太和降旨 与子难娶左卫将军侯刚女 人灵未穆 ’从服者 闻复高祖旧典 田僧达等窃陷石头戍 左右竞相排 子难 不惟法度之□易 澄功衰在身 两两接对 莫重于太师彭城王 然律令相须 恒身先兵士 礼也 汝何为哭也?而有悬胄之耻 其不虞宜戒 " 此贼非老奴敌 于射为惑 启普惠为府录事参军 何可得无?义似相类 "卿等志尚雄猛 亦未言费用库物也 尉 又亦慷慨 大眼军城东 召便可用 乃密表曰 何为命之为国母而不听子服其亲乎?以固堂堂之基 "臣今辄难大眼 把中围尺二寸 遂唱议先驱 误惑视听 人食之 此拘之以制也 出继瑜后 慢悖所由起 于地刻截 夫白登之役 长子’ 赐绢布一百段 出除左将军 守宰之泛 "举能其官 陷其前锋 自有加减 尊光之美盛矣 以功迁征虏将军 臣僚为立碑颂 "臣辄谓水陆二道 察微臣之请 "臣闻明德恤祀 未几有河阴之难 听
《三视图》教学设计

《三视图》教学设计一、教学内容分析通用技术必修模块“技术与设计1”第六章第二节《常见的技术图样》之“正投影与三视图”(苏教版)主要描述了正投影形成三视图的方法、原理,三视图的绘制(识读)方法和规律等。
三视图作为一种技术图样是设计交流与表达的一种常用的技术语言形式。
学生通过本节的学习,掌握绘制简单三视图的基础知识和技能,本节内容也是后续知识“形体的尺寸标注”和“机械加工图”的基础。
在这里起到一个呈上启下的作用。
二、学情分析通过前面章节的学习,高中学生能够较熟练地绘制(识读)平面图和正等轴测图,也有光线投射成影的感知和体验。
教学可以从学生的现有知识和经验出发,按照直观感知、操作确认、思辩求证的认识过程展开,建构正投影与三视图的知识体系。
但学生的空间思维还受到定向模式的限制,很难发散思考一些个别现象,处理个特殊案例的能力有待提高,如不可见部分和重叠等。
三、教学目标1.知识目标:(1)理解投影法的基本概念和方法;(2)掌握正投影法方法、特性及三视图成图原理和规律;(3)掌握三视图一般绘图规则。
2.能力目标:(1)掌握简单的三视图的绘制(识读);(2)学会规范作图的方法和技能。
3.情感态度价值观:(1)经历三视图的作图过程,体验技术图样的魅力(2)形成科学的空间三围思维方式,培养学生严谨的思维与态度。
4、教学重点:(1)掌握三视图成图原理和规律;(2)掌握简单的三视图的绘制(识读)。
5、教学难点:(1)能规范绘制和识读简单的三视图。
四、教学准备准备积木,利用塑料胶纸和泡沫制作多个的模型。
五、教学策略及媒体运用在本节的教学中,将采用“主导—主体(分享—互助提升)”的设计模式,引导学生进行自主探究、知识建构和能力拓展。
总体教学流程为:“情境导入,知识建构,合作探究,总结提升,能力拓展”。
1、通过生活小故事的情景导学,激发学生对“技术语言的种类”进行回顾和复习以及注意在技术活动中选用恰当的技术语言进行交流的重要性,对本节课内容产生强烈的求知欲望。
三视图精讲

2、学生现实分析
本节首先简单介绍了中心投影和平行投 影,中心投影和平行投影是日常生活中最 常见的两种投影形式,学生具有这方面的 直接经验和基础.投影和三视图虽为高中新 增内容,但学生在初中有一定基础,这为 我们今天的学习提供了便利条件。
3、教学目标
(1) 知识与技能:能画出简单空间图形的 三视图,能识别上述三视图表示的立体模型, 从而进一步熟悉简单几何体的结构特征. (2)过程与方法:通过直观感知,操作确 认,提高学生的空间想象能力、几何直观能 力,培养学生的应用意识. (3)情感、态度与价值观:感受数学就在身 边,提高学生学习立体几何的兴趣,培养学 生大胆创新、勇于探索、相互交流、相互合 作的精神.
圆锥的三视图:
主视图
左视图
点不要漏画哦!
俯视图
挑战自我
画出如图所示四棱锥的三视图。
四菱锥的三视图:
正视图
左视图
俯视图
我相信你一定能 画出这个复杂几 何体的三视图!
随堂练习
1找出图中每一物品所对应的主视图。
(A)
(B)
(C)
(D)
正视图 (
B
B C
)
左视图 (
)
俯视图(
)
A
B
C
考考你
正视图( 左视图 ( 俯视图 (
圆台——有两个视图是等腰梯形
棱台——有两个视图是梯形 4.球——三个视图都是圆
空间几何体的三视图和直观图 (1)
说 课 的 主 要 内 容
教学背景分析
教材的地位和作用 学生现实分析 教学目标 教学的重点、难点 本节课设计思想
教学组织形式分析 教学过程 教学设计评价与反思
高一数学简单几何体的三视图

2、阻击一粒病毒的偷渡
有“凤”来兮!落霞如雾。 尘世的时间布满尘埃,无踪无迹的恐惧胸怀人世,晚霞中蜂拥而至的微粒,泥沙聚下,一粒万人唾弃的风物,袭击我的肉身,我悉心寻找一滴水下落的过程,沿着灯塔 的方向拭目以待。晚风中的黑鸦如幕。绝杀毫无征兆,群山在无影之剑的攻击之下摇摇欲坠,山体即将坍塌;凌乱的时间,仇视人间温柔的眼神;蓄谋已久的偷渡,侵蚀苍生。 谁是谁的不堪之途?我 的城市已经关闭,村庄已经关闭,心灵已经关闭。 罪恶延伸,我们生死阻击一粒病毒的复制和延伸。 谁穿越黑洞,一介布衣,追逐水火的煎熬。你以万倾的浊浪袭击我的腹地,我以螳螂之臂阻挡无边 的褐色大髦。终将要来吗?不!真的垂不扁,蒸不烂,煮不熟吗?不!人间的良知不灭,生的火光不熄。吹响一切号角,敲击一切鼓点,一切苍蝇,一切蚂蚁,也阻碍一切行人。一切无知向我巢穴的移 动。我乃做最后一击,做垂死的抵抗。 乱山的烟霞明灭,日出之处,江
高一数学简单几何体的三视图

; 美术加盟 ;
鼎乃沦伏而不见。《周颂》曰:自堂徂基,自羊徂牛,鼐鼎及鼒,不吴不敖,胡考之休。今鼎至甘泉,以光润龙变,承休无疆。合兹中山,有黄白云降,盖若兽之为符,路弓乘矢,集获坛下,报祠大亨。唯受命而帝者心知其意而合德焉。鼎宜视宗祢庙,臧於帝庭,以合明应”制曰“可” 入海求蓬莱者,言蓬莱不远,而不能至者,殆不见其气。上乃遣望气佐候其气云。其秋,上雍,且郊。或曰“五帝,泰一之佐也。宜立泰一而上亲郊之”。上疑未定。齐人公孙卿曰“今年得定鼎,其冬辛巳朔旦冬至,与黄帝时等”卿有札书曰“黄帝得宝鼎冕候,问於鬼臾区,鬼臾区对曰: 黄帝得宝鼎神策,是岁己酉朔旦冬至,得天之纪,终而复始。於是黄帝迎日推策,后率二十岁复朔旦冬至,凡二十推,三百八十年,黄帝仙登於天”卿因所忠欲奏之。所忠视其书不经,疑其妄言,谢曰“宝鼎事已决矣。尚何以为”卿因嬖人奏之。上大说,乃召问卿。对曰“受此书申公, 申公已死”上曰“申公何人也”卿曰“齐人,与安期生通,受黄帝言,无书,独有此鼎书。曰汉兴复当黄帝之时。曰汉之圣者,在高祖之孙且曾孙也。宝鼎出而与神通,封禅。封禅七十二王,唯黄帝得上泰山封。申公曰:汉帝亦当上封,上封则能仙登天矣。黄帝万诸侯,而神灵之封君七 千。天下名山八,而三在蛮夷,五在中国。中国华山、首山、太室山、泰山、东莱山,此五山黄帝之所常游,与神会。黄帝且战且学仙,患百姓非其首,乃断斩非鬼神者。百馀岁然后得与神通。黄帝郊雍上帝,宿三月。鬼臾区号大鸿,死葬雍,故鸿冢是也。其后黄帝接万灵明庭。明庭者, 甘泉也。所谓寒门者,谷口也。黄帝采首山铜,铸鼎於荆山下。鼎既成,有龙垂胡髯下迎黄帝。黄帝上骑,群臣后宫从上龙七十馀人,龙乃上去。余小臣不得上,乃悉持龙髯,龙髯拔,堕,堕黄帝之弓。百姓卬望黄帝既上天,乃抱其弓与龙髯号,故后世因名其处曰鼎湖,
空间几何三视图

总结
画“长方体”的三视图,并指出它们的三视图各为什么图形?各图形有什么联系?
画三视图的要求:
正视图、俯视图长对正;
正视图、侧视图高平齐;
俯视图、侧视图宽相等。
因此,三视图的画法规则可归结为:
长对正,高平齐,宽相等
图形,
学生动手画出图形,并观察
提高学生分析问题和解决问题的能力。
例题
请同学们画下面这个圆台及其倒立放置时的的三视图,如果你认为这两个圆台的三视图一样,画一组就可以;如果你认为不一样,请分别画出来。
六、教学过程
教学环节
教师活动
学生活动
设计意图
导入学习内容
提问:
图形形成的原理是什么?
学生讨论并思考
吸引学生注意力,进而引入课题
创设问题
总结
提问:
洗洁精瓶子从不同角度看,像什么?、
说明从不同的角度看同一物体视觉的效果可能不同也可能相同,要比较真实反映出物体,我们可从多角度观看物体,这就是本节课我们要探讨的第一个问题--空间几何体的三视图
视图:将物体按正投影法向投影面
投影时所得到的投影图
正视图:光线从几何体的前面向后面
正投影所得到的图。
侧视图:光线从几何体的左面向右面
所得到的投影图。
俯视图:光线从几何体的上面向下面
所得到的投影图。
先思考,在提问回答
激发学生的学习兴趣。
引入新课
设置问题:提出疑问,诱导学生主动思考,主动探究,合作交流使学生在积极的学习中解决问题,提高学生的教学思维能力,实现素质教育的目标,同时也培养了学生的情感、态度与价值观。
画几何体的三视图时,
能看见的轮廓和棱用实线表示,
不能看见的轮廓和棱用虚线表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
他们夫妻的日Байду номын сангаас安静了,他永远属于她,她也永远属于他。
也从此,他们再也不肯到那叫人伤心落泪的公社大院去了。
鸡叫四遍的时候,我们睡下了。我合着眼睛,听见门外的梢树林里起着涛声,门前的小溪在哗啦哗啦响,不知在什么时候,就睡着了。我梦见就在这间屋子里,大来和他的女人正忙着将一堆堆耳棒 抱在门前土场上,架起人字架,点上木耳菌种,眨眼,那木耳就生出了黑点儿,又立即大起来,如人的耳朵,又大成一朵朵黑色的花。我也帮他们开始采摘,采了一筐,又采了一筐,三人就到了山下, 在供销社卖了好多钱。突然有了锣鼓声,他们俩又坐在了冒尖户授奖大会上,新书记给他们戴花,大来眼睛小小的,一副憨相,窘得手脚没处放。那老婆却大方极了,嫌大来不自然,就在桌下踩大来的 脚。没想台下的人全看见了,就一齐哈哈地笑。那老婆也满脸通红,红润光洁。人都在说:
"全怪我这一张脸,全怪我这一张脸害了我,也害了你!"老婆说。玩球网
他突然想出一个办法来,但他不敢说出,更不敢说给老婆。一个人在山上转了半天,最后还是回来,在衣服上涂了好多漆,要老婆用汽油给他洗洗。老婆端着汽油盆子正洗着,他从后边划着了火柴, 丢了进去,火立即腾起来,冷不防将她的脸烧坏了。她尖叫一声,昏倒在地,他抱起来大哭:"我怎么干出这事?我不是人啊,我不是人啊!"老婆醒过来,流着眼泪,却安慰他:"这样好,就这样!"
