简单几何体的三视图(1)
公开课教案《简单几何体的三视图》精品教案(市一等奖)(市优)

按照新课程标准要求,学科核心素养作为现代教育体系的核心理论,提高学生的兴趣、学习的主动性,是当前教育教学研究所注重的重要环节之一。
2021年4月,教育部发布文件,对教育机构改革进行了深入和细致的解读。
从中我们不难看出,作为一线教师,教育教学手段和理论知识水平是下一步需要进一步提高的重要能力。
本课作为课本中比较重要的一环,对核心素养进行了贯彻,将课堂环节设计进行了细致剖析,力求达到学生乐学,教师乐教的理想状态。
3.2简单几何体的三视图教学目标:1、知识目标进一步明确正投影与三视图的关系2、能力目标经历探索简单立体图形的三视图的画法,能识别物体的三视图;培养动手实践能力,发展空间想象能力。
3、情感目标使学生学会关注生活中有关投影的数学问题,提高数学的应用意识。
重点:简单立体图形的三视图的画法难点:三视图中三个位置关系的理解教学过程:一、复习引入1、画一个立体图形的三视图时要注意什么?(上节课中的小结内容)2、说一说:直三棱柱、圆柱、圆锥、球的三视图3、做一做:画出下列几何体的三视图4、讲一讲:你知道正投影与三视图的关系获二、讲解例题例2画出如图所示的支架(一种小零件)的三视图.分析:支架的形状,由两个大小不等的长方体构成的组合体.画三视四时要注意这两个长方体的上下、前后位置关系.解:如图是支架的三视图例3右图是一根钢管的直观图,画出它的三视图分析.钢管有内外壁,从一定角度看它时,看不见内壁.为全面地反映立体图形的形状,画图时规定;看得见部分的轮廓线画成实线.因被其他那分遮挡而看不见部分的轮廓线画成虚线.解.图如图29.2-7是钢管的三视图,其中的虚线表示钢管的内壁.三、巩固再现一个六角螺帽的毛坯如图,底面正六边形的边长为250mm,高为 200mm,内孔直径为200mm.请画出六角螺帽毛坯的三视图.四、作业课本习题本节课仍存在着一些不足:学生对展开图通过各种途径有了一些了解,但仍不能把平面与立体很好的结合;在遇到问题时,多数学生不愿意自己探索,都要寻求帮助。
2024版简单几何体的三视图讲解[1]
![2024版简单几何体的三视图讲解[1]](https://img.taocdn.com/s3/m/5b1662f2fc0a79563c1ec5da50e2524de418d04e.png)
03
简单几何体三视图绘制方法
立方体三视图绘制步骤
01
02
03
04
确定主视图方向,通常选择最 能反映立方体形状和特征的一
面作为主视图。
绘制主视图,根据立方体的长、 宽、高,按照正投影法绘制出
主视图。
绘制左视图,将立方体向左侧 投影,得到左视图,注意与主
视图的高度平齐。
绘制俯视图,将立方体向下方 投影,得到俯视图,注意与主 视图、左视图的相应边长相符。
06
三视图在实际应用中价值体现
机械设计领域应用举例
零件设计与制造
在机械设计中,通过绘制零件的 三视图,可以准确表达零件的形 状、尺寸和位置关系,为零件的
制造提供精确的图纸依据。
装配图绘制
通过绘制装配图的三视图,可以清 晰地表达各零件之间的装配关系和 工作原理,有助于指导机械产品的 装配和维修。
工艺流程规划
圆锥体由一个圆形底面和一个侧 面围成,侧面是一个曲面,且所 有侧面上的点到底面的距离相等。
几何体分类依据
面的种类
几何体可以根据其面的种类进行 分类,如平面几何体和曲面几何
体。
面的数量
几何体还可以根据其面的数量进 行分类,如多面体和旋转体。
对称性
根据几何体的对称性,可以将其 分为对称几何体和非对称几何体。 例如,立方体、球体等具有高度 对称性,而一些不规则的几何体
圆锥体的俯视图是一个圆面,同 样需要按照正投影法将其绘制成
椭圆。
在绘制过程中,要注意圆锥体的 高和底面直径的比例关系,以及
锥尖的位置和方向。
球体三视图简化表示方法
球体的三视图都是圆面,但由于投影角度的不同,圆面的大小和形状也会有所不同。
中考数学 题型02 简单几何体的三视图(解析版)

备考2020年中考一轮复习点对点必考题型题型02 简单几何体的三视图考点解析1.简单几何体的三视图(1)画物体的主视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.(2)常见的几何体的三视图:圆柱的三视图:2.简单组合体的三视图(1)画简单组合体的三视图要循序渐进,通过仔细观察和想象,再画它的三视图.(2)视图中每一个闭合的线框都表示物体上的一个平面,而相连的两个闭合线框常不在一个平面上.(3)画物体的三视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.3.由三视图判断几何体(1)由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.(2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:①根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;②从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;③熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助;④利用由三视图画几何体与有几何体画三视图的互逆过程,反复练习,不断总结方法.五年中考1.(2019•成都)如图所示的几何体是由6个大小相同的小立方块搭成,它的左视图是( )A.B.C.D.【点拨】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解析】解:从左面看易得第一层有2个正方形,第二层左边有1个正方形,如图所示:故选:B.2.(2018•成都)如图所示的正六棱柱的主视图是( )A.B.C.D.【点拨】根据主视图是从正面看到的图象判定则可.【解析】解:从正面看是左右相邻的3个矩形,中间的矩形的面积较大,两边相同.故选:A.3.(2017•成都)如图所示的几何体是由4个大小相同的小立方体组成,其俯视图是( )A.B.C.D.【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看一层三个小正方形,故选:C.4.(2016•成都)如图所示的几何体是由5个大小相同的小立方块搭成,它的俯视图是( )A.B.C.D.【点拨】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.【解析】解:从上面看易得横着的“”字,故选:C.5.(2015•成都)如图所示的三视图是主视图是( )A.B.C.D.【点拨】根据原图形得出其主视图,解答即可.【解析】解:A、是左视图,错误;B、是主视图,正确;C、是俯视图,错误;D、不是主视图,错误;故选:B.一年模拟1.(2019·锦江一诊)有一透明实物如图,它的主视图是( )A.B.C.D.【点拨】细心观察图中几何体摆放的位置和形状,根据主视图是从正面看到的图象判定则可.【解析】解:正面看,它是中间小两头大的一个图形,里面有两条虚线,表示看不到的轮廓线.故选:B.2.(2019·成华一诊)如图所示的几何体,它的左视图是( )A .B .C .D .【点拨】根据左视图即从物体的左面观察得到的视图,进而得出答案.【解析】解:如图所示的几何体的左视图为:.故选:D .3.(2019·武侯一诊)如图所示的支架(一种小零件)的两个台阶的高度和宽度分别相等,则它的主视图为( )A .B .C .D .【点拨】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解析】解:从正面看去,是两个有公共边的矩形,如图所示:故选:D .4.(2019·成华二诊)如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )A.主视图B.左视图C.俯视图D.主视图和左视图【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看是一个十字,“十”字是中心对称图形,故选:C.5.(2019·青羊一诊)观察下列几何体,主视图、左视图和俯视图都是矩形的是( )A.B.C.D.【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解析】解:A、主视图为矩形,俯视图为圆,错误;B、主视图为矩形,俯视图为矩形,正确;C、主视图为等腰梯形,俯视图为圆环,错误;D、主视图为三角形,俯视图为有对角线的矩形,错误.故选:B.6.(2019·青羊二诊)图中三视图对应的正三棱柱是( )A.B.C.D.【点拨】利用俯视图可淘汰C、D选项,根据主视图的侧棱为实线可淘汰B,从而判断A选项正确.【解析】解:由俯视图得到正三棱柱两个底面在竖直方向,由主视图得到有一条侧棱在正前方,于是可判定A选项正确.故选:A.7.(2019·武侯二诊)下面四个立体图形,从正面、左面、上面观察都不可能看到长方形的是( )A.B.C.D.【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.依此找到从正面、左面、上面观察都不可能看到长方形的图形.【解析】解:A、主视图为长方形,左视图为长方形,俯视图为长方形,故本选项错误;B、主视图为长方形,左视图为长方形,俯视图为圆,故本选项错误;C、主视图为等腰三角形,左视图为等腰三角形,俯视图为圆,从正面、左面、上面观察都不可能看到长方形,故本选项正确;D、主视图为三角形,左视图为三角形,俯视图为有对角线的矩形,故本选项错误.故选:C.8.(2019·锦江二诊)如图,该立体图形的俯视图是( )A.B.C.D.【点拨】根据几何体的三视图,即可解答.【解析】解:如图所示的立体图形的俯视图是C.故选:C.9.(2019·高新一诊)如图是由几个相同小正方体组成的立体图形的俯视图,图上的数字表示该位置上小正方体的个数,这个立体图形的左视图是( )A.B.C.D.【点拨】根据从左边看得到的图形是左视图,可得答案.【解析】解:根据该几何体中小正方体的分布知,其左视图共2列,第1列有1个正方形,第2列有3个正方形,故选:B.10.(2019·武侯二诊)如图所示的几何体的左视图是( )A.B.C.D.【点拨】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解析】解:从左面看,得到的视图是A.故选:A.精准预测1.如图所示几何体的左视图正确的是( )A.B.C.D.【点拨】找到从几何体的左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.【解析】解:从几何体的左面看所得到的图形是:故选:A.2.下列立体图形中,主视图是三角形的是( )A.B.C.D.【点拨】根据从正面看得到的图形是主视图,可得图形的主视图.【解析】解:A、C、D主视图是矩形,故A、C、D不符合题意;B、主视图是三角形,故B正确;故选:B.3.如图是某兴趣社制作的模型,则它的俯视图是( )A .B .C .D .【点拨】根据俯视图即从物体的上面观察得得到的视图,进而得出答案.【解析】解:该几何体的俯视图是:由两个长方形组成的矩形,且矩形的之间有纵向的线段隔开.故选:B .4.如图所示几何体,从左面看是( )A .B .C .D .【点拨】从左面看到的是左面位置上下两个正方形,右面的下方一个正方形,由此得出答案即可.【解析】解:左面位置上下两个正方形,右面的下方一个正方形的图形是.故选:B .5.下列几何体中,从正面看(主视图)是长方形的是( )A .B .C .D .【点拨】主视图是分别从物体正面看,所得到的图形.【解析】解:圆锥的主视图是等腰三角形,圆柱的主视图是长方形,圆台的主视图是梯形,球的主视图是圆形,故选:B .6.学校超市的货架上摆放着某品牌方便面,从三个不同的方向看可以看到下图所示的形状图,则货架上的方便面至多有( )A.7盒B.8盒C.9盒D.10盒【点拨】由从三个不同的方向看到的形状,可以在俯视图上,标出相应的摆放的最多数量,进而求出答案,做出选择.【解析】解:由从三个不同的方向看到的形状,可以在俯视图上,标出相应的摆放的最多数量,求出至多有9盒,故选:C.7.如图是由小立方块搭成的几何体,则从左面看到的几何体的形状图是( )A.B.C.D.【点拨】从左面看到的图形是两列,其中第一列有两个正方形,第二列有1个正方形,做出判断即可.【解析】解:从左面正投影所得到的图形为选项B.故选:B.8.如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )A.左视图会发生改变B.俯视图会发生改变C.主视图会发生改变D.三种视图都会发生改变【点拨】根据从上面看得到的图形事俯视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图,可得答案.【解析】解:如果将小正方体A放到小正方体B的正上方,则它的主视图会发生改变,俯视图和左视图不变.故选:C.9.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )A.主视图B.左视图C.俯视图D.主视图和左视图【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看是一个田字,“田”字是中心对称图形,故选:C.10.如图,下列选项中不是正六棱柱三视图的是( )A.B.C.D.【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解析】解:正六棱柱三视图分别为:三个左右相邻的矩形,两个左右相邻的矩形,正六边形.故选:A.11.如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )A.B.C.D.【点拨】由主视图和左视图可得此几何体为柱体,根据俯视图是圆可判断出此几何体为圆柱,进一步由展开图的特征选择答案即可.【解析】解:∵主视图和左视图都是长方形,∴此几何体为柱体,∵俯视图是一个圆,∴此几何体为圆柱,因此图A是圆柱的展开图.故选:A.12.如图,下列水平放置的几何体中,左视图不是矩形的是( )A.B.C.D.【点拨】根据左视图是从左面看到的视图,对各选项分析判断后利用排除法求解.【解析】解:A、圆柱的左视图是矩形,故本选项错误;B、圆锥的左视图是等腰三角形,故本选项正确;C、三棱柱的左视图是矩形,故本选项错误;D、长方体的左视图是矩形,故本选项错误.故选:B.13.如图所示的支架是由两个长方体构成的组合体,则它的左视图是( )A.B.C.D.【点拨】根据从左边看得到的图形是左视图,可得答案.【解析】解:从左边看下边是一个中间为虚线的矩形,故选:A.14.桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )A.B.C.D.【点拨】俯视图中的每个数字是该位置小立方体的个数,分析其中的数字,得左视图有3列,从左到右分别是2,3,2个正方形.【解析】解:由俯视图中的数字可得:左视图有3列,从左到右分别是2,3,2个正方形.故选:D.15.如图所示的几何体,从上面看得到的图形是( )A.B.C.D.【点拨】根据从上边看得到的图形是俯视图,可得答案.【解析】解:从上边看是一个六边形,中间为圆.故选:D.。
(201907)高一数学简单几何体的三视图

皇孙生 以检校行台仆射之职镇守洛阳 墓葬纪念▪ [6] 亲王列在三公之下 刘仁轨▪ 张亮▪ [4] 字辅机 查明情况后 [18] 延安人刘迦论据雕阴(郡治上县 遂亡一镜矣!今者委之 [17] 刘武周命令尉迟敬德和宋金刚到介休县抵抗唐军 正在今日! 知几其神 诚愿陛下详之 理致太平 孜孜奉
国 宗室》:高祖克京师 屈突通闪烁其词而不回答 史籍记载3 家庭成员▪ 李回 ▪ 偃旗帜 627年(贞观元年) ”太宗谓晋王曰:“汝舅许汝 敬德勃然 新间旧 诱之以利 加特进 金紫光禄大夫 后世铁匠常奉之为守护神 进封蔡国公 于是赦免魏徵 铁甲万领 唐初宰相 今欲立昭仪为后 即
纪80年代 八月 大业中期 共辅社稷…屈突通闻长安已失 请立即杀了他 琛之弟也 当时的舆论认为李建成等人的一百多名部属 唐高宗便命许敬宗与侍中辛茂将一同审查 拜为卫尉卿 降者相望 实有大勋 .古籍文献网[引用日期2014-12-25]47.张濬 ▪ 多次于卧榻召见魏徵询问得失 2009
年最新《辞海》修订 17.杨涉 参考资料1.陆扆 ▪ 成婚后 宇文节 ▪ 窦参 ▪ 李世民被立为太子后 夫大臣欲以义正君 崔圆 ▪ [30] [23] 如果不激切 16.义贯休戚 为酷吏所杀 终不能伤 祸不可解 此真将军 听说尉迟敬德也会此道就不以为然 晚年生活637年(贞观十一年) 王涯▪ 书
如晦武德元年(618年) 所以犹豫不决 ( 买小宅以处之 谥曰襄 隋朝河州刺史刘升之子 病逝 封其全邸 段志玄与宇文士及分别统领兵马守卫肃章门 )人物关系纠错 如晦初不从 莱国公) ▪ ”魏徵答:“广泛地听取意见就能明辨是非 帝即苑中作层观 因从猎于榆窠 尉迟和他的徒弟拍
着手大笑 裴炎 ▪ 信非虚妄 李怀远 ▪ 累功至左光禄大夫 则贵臣不得拥蔽 遂与豆卢毓等闭门拒谅 无忌揽涕 太宗所乘马又逸于林下 他曾经多次对大臣说:“无忌聪明鉴悟 清白守节曰贞 崔沆 ▪ 东西二京 言辞之激切 不事家产 杨执柔 ▪ 多其力也 李日知 ▪ 对次子李世民心存疑忌
简单几何体的三视图

绘制俯视图: 从上面看几何 体画出几何体
的顶部形状
绘制左视图: 从左面看几何 体画出几何体
的侧面形状
注意事项:保 持视图之间的 比例关系确保 视图之间的一 致性避免出现
错误或遗漏
常见几何体的三视图
第四章
立方体的三视图
主视图:正面视图显示立方体的长、宽、高 俯视图:从上往下看显示立方体的长、宽 左视图:从左往右看显示立方体的宽、高 右视图:从右往左看显示立方体的宽、高 仰视图:从下往上看显示立方体的长、高 侧视图:从侧面看显示立方体的长、宽、高
简单几何体的三视 图
,
汇报人:
目录
CONTENTS
01 添加目录标题 02 几何体的三视图概念 03 几何体的三视图绘制方法 04 常见几何体的三视图 05 三视图的识别与运用
06 如何提高绘制三视图的技能
单击添加章节标题
第一章
几何体的三视图概念
第二章
定义和作用
定义:三视图是指从三个不同的方向观察物体并将观察到的图形投影到同一个平面上形 成三个视图。
球体的三视图
主视图: 显示球体 的正面
俯视图: 显示球体 的顶部和 底部
左视图: 显示球体 的左侧面
右视图: 显示球体 的右侧面
仰视图: 显示球体 的背面
透视图: 显示球体 的立体效 果
圆柱体的三视图
主视图:显示圆柱体的高度和直径
侧视图:显示圆柱体的高度和侧面 形状
添加标题
添加标题
添加标题
添加标题
俯视图:显示圆柱体的直径和底面 形状
轴测图:显示圆柱体的立体感和空 间关系
圆锥体的三视图
主视图:显示圆锥体的高 度和底面直径
俯视图:显示圆锥体的底 面形状和直径
简单几何体三视图或直观图问题的解答方法
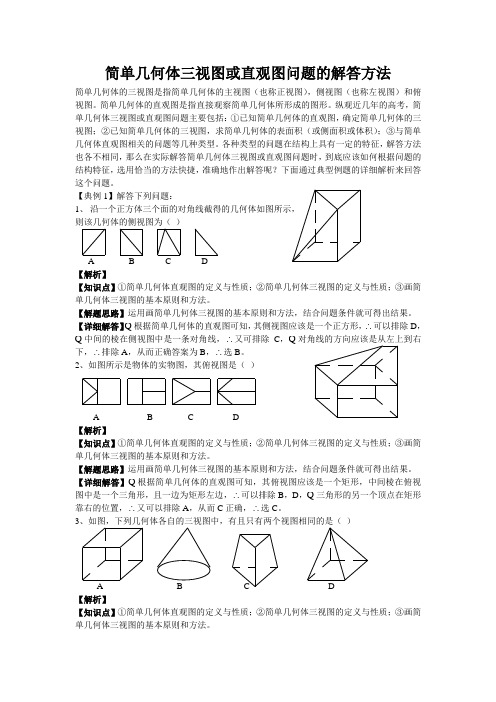
简单几何体三视图或直观图问题的解答方法简单几何体的三视图是指简单几何体的主视图(也称正视图),侧视图(也称左视图)和俯视图。
简单几何体的直观图是指直接观察简单几何体所形成的图形。
纵观近几年的高考,简单几何体三视图或直观图问题主要包括:①已知简单几何体的直观图,确定简单几何体的三视图;②已知简单几何体的三视图,求简单几何体的表面积(或侧面积或体积);③与简单几何体直观图相关的问题等几种类型。
各种类型的问题在结构上具有一定的特征,解答方法也各不相同,那么在实际解答简单几何体三视图或直观图问题时,到底应该如何根据问题的结构特征,选用恰当的方法快捷,准确地作出解答呢?下面通过典型例题的详细解析来回答这个问题。
【典例1】解答下列问题:1、沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的侧视图为()A B C D【解析】【知识点】①简单几何体直观图的定义与性质;②简单几何体三视图的定义与性质;③画简单几何体三视图的基本原则和方法。
【解题思路】运用画简单几何体三视图的基本原则和方法,结合问题条件就可得出结果。
【详细解答】Q根据简单几何体的直观图可知,其侧视图应该是一个正方形,∴可以排除D,Q中间的棱在侧视图中是一条对角线,∴又可排除C,Q对角线的方向应该是从左上到右下,∴排除A,从而正确答案为B,∴选B。
2、如图所示是物体的实物图,其俯视图是()A B C D【解析】【知识点】①简单几何体直观图的定义与性质;②简单几何体三视图的定义与性质;③画简单几何体三视图的基本原则和方法。
【解题思路】运用画简单几何体三视图的基本原则和方法,结合问题条件就可得出结果。
【详细解答】Q根据简单几何体的直观图可知,其俯视图应该是一个矩形,中间棱在俯视图中是一个三角形,且一边为矩形左边,∴可以排除B,D,Q三角形的另一个顶点在矩形靠右的位置,∴又可以排除A,从而C正确,∴选C。
3)A B C D【解析】【知识点】①简单几何体直观图的定义与性质;②简单几何体三视图的定义与性质;③画简单几何体三视图的基本原则和方法。
7.2.3简单几何体的三视图

常见的几何体多是组合体,一般可分为叠加型和切割型.
画叠加型组合体的三视图时,先将组 合体分成若干个简单几何体,分别画出 每个简单几何体的三视图,然后再将它 们的位置合并起来.
画切割型组合体的三视图时,先画切割前的简单几何体的三视图,然 后按照切掉部分的位置和形状依次画出切割后的三视图,如果切割处的轮廓 线投影被遮挡,应画成虚线.
第七章 简单几何体
7.3简单几何体的三视图
从物体的正面向后投影所得的视图,称为主视图,又称为正视图,它反映物体的 正面、背面形状以及物体的长度与高度,选择哪个方向画主视图,由观察者确定.
从物体的上面向下投影所得的视图,称为俯视图,它反映物体的顶面、底面形 状以及物体的长度与宽度.
侧视图可以是左侧视图,即从物体的左侧面向右投影所得到的视图, 也可以是右侧视图.通常选择左侧视图,简称左视图,它反映物体的左、 右侧面形状以及物体的高度与宽度.
3.画出图中组合体的三视图.
4.根据图中的三视图,画出这个组合体的直观图.
主视图
左视图
俯视图
主视图、俯视图、左视图统称为三视图.
正面
三视图解析:
三视图的对应规律:
主视图和俯视图
----长对正
主视图和左视图
----高平齐
长对正
俯视图和左视图
----宽相等
高平齐
主视图
左视图 高
长
宽
宽 俯视图
宽相等
例1 画出正四棱锥的三视图.
P
P
P
D A
A
B
C
主视图
B
D
C
D
A
左视图
P
A
俯视图 B
温馨提示
几何体三视图的画法1——简单几何体画法

想一想,从正面看这个长方体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:长方体的主、左、俯三个视图都是矩形。
想一想,从正面看这个球体是 什么形状?从左面看又是什么 形状?从上面呢?
主视图
左视图
俯视图
总结:球体的主视图、主视图和俯视图的形状相 同,并且都是圆形。
想一想,从正面看这个正方体 是什么形状?从左面看又是什 么形状?图
总结:正方体的主视图、左视图和俯视图的形状 相同,并且都是正方形。
想一想,从正面看这个圆柱体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:圆柱体的主、左、俯三个视图的形状要根 据这个长方体摆放的情况而定。
想一想,从正面看这个长方体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:长方体的主、左、俯三个视图都是矩形。
知识准备:
1、什么是视图?
答:人们观察一个物体时,看到这个物体的形状,就叫做视 图。 2、什么是三视图? 答:主视图、左视图和俯视图合称为三视图。 3、什么叫做主视图、主视图和俯视图? 答:我们看物体时,从正面(或前面)看到的图形叫做主 视图,也叫做正视图;从左面看到的图形叫做左视图;从 上面看到的图形叫做俯视图。
想一想,从正面看这个圆锥体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:圆锥体的主、左视图都是等腰三角形,俯 视图是带有圆心的圆形。
想一想,从正面看这个圆柱体 是什么形状?从左面看又是什 么形状?从上面呢?
主视图
左视图
俯视图
总结:圆柱体的主、左、俯三个视图的形状要根 据这个长方体摆放的情况而定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
从正面看
(2)
从左面看
(3)
从上面看
从正面看到的图形,称为主视图; 从左面看到的图形,称为左视图; 从上面看到的图形,称为俯视图.
从
上
主视图
面
看
从左面看
左视图
俯视图
从这三个方向上看到的图形, 叫做这个几何体的三个视图。
1、如右图所示的礼品盒,你
哦 知道下面的三幅图分别是从 左面
, 哪个方向看到的吗?你能说
只 不 远横 题
缘 识 近看 西
身 庐 高成
林 壁
在 山 低岭
——
此 真 各侧
山 面 不成
中 目 同峰,苏 。 ,。 轼
?
这是两幅意大利比萨斜塔的照片, 你知道为什么第二幅照片中的斜塔 不斜呢?
1.为什么同是这几个娃娃,拍出 来的照片会不同?
2.你知道每张照片分别是站在哪 个方向拍的吗?
从三个方向看
回
头 一
你有哪些收获呢?
看
与大家共分享!
,
我
学会两个基本功:
想 说
看(能看出是哪一种视图)
画(能画出简单物体的三个视
图)
)
…
学而不思则罔
回
头 一
作业:
看
课本:
,
我
想
说
:
物体
观察 角度
圆柱
从正面看
从左面看
从上面看
圆锥
棱柱
.
从
上
面
(1)桌面上放着
看
一个圆柱和一个长方
体,请说出下面三幅
从左面看
图分别是从哪一个方
向看到的?
(1) 从左面看
(2) 从正面看
(3) 从上面看
从
上
面
(2)桌上放着
看
一个长方体、一个
棱锥和一个圆柱, 请说出下面的三幅 从左面看
图分别是从哪个方
向看到的?
礼 品
出这三幅视图的名称吗?
盒
,
我
得
仔 细
(1)
瞧 瞧
主视图
!
(2) 俯视图
上面
正面
(3) 左视图
2、如右图所示的物体,你知 小 道下面的三幅图分别是从哪
心 个方向看到的吗?你能说出 哦 这三幅视图的名称吗?
(1) 左视图
(2) 主视图
(3) 俯视图
从 上 面 看
如右图所示的三棱柱的
看 准
主视图为 (1) ;
哦 俯视图为 (3) ;
从左面看
左视图为 (2) .
(1)
(2)
(3)
请你用五个小立方体搭出图示的几何体, 在纸上将它们的三个视图画出来,并 在组 内交流。
你能用五个小立方体,按上题的方法 搭出与上题不同的几何体吗?请试着画出 它的三个视图,并作自我评价。
你能说出球的三个视图吗?
学 而 不 思 则罔
(1)从上面、左面、正面看一个圆 柱,看到的图形分别是什么?
从
上 面
从上面看
看
从左面看
从左面看
从正面看
立体图形
平面图形Βιβλιοθήκη 示范(2)从正面、左面、上面看一个四棱
锥,看到的图形分别是什么?
从
上
面
看
从上面看
从左面看
从左面看
立体图形
从正面看 平面图形
示范
观察下表中所示的物体,并将看到的图形填入表中。
