2018年7月9日+简单的逻辑联结词-2019年高考数学(文)一轮复习+Word版含解析
高三数学一轮复习讲义逻辑连接词学生

课题:逻辑连接词知识点一、简单的逻辑联结词1.命题中的“且”“或”“非”叫做逻辑联结词.(1)用联结词“且”联结命题p 和命题q ,记作p ∧q ,读作“p 且q ”.(2)用联结词“或”联结命题p 和命题q ,记作p ∨q ,读作“p 或q ”.(3)对一个命题p 全盘否定,就得到一个新命题,记作¬p ,读作“非p ”或“p 的否定”.2.简单复合命题的真值表:*p ∧q : p 、q 有一假为假, *p ∨q :一真为真, *p 与¬p :真假相对即一真一假. 知识点二、量词1.全称量词与存在量词:(1)常见的全称量词有:“任意一个”“一切”“每一个”“任给”“所有的”等.(2)常见的存在量词有:“存在一个”“至少有一个”“有些”“有一个”“某个”“有的”等.(3)全称量词用符号“∀”表示;存在量词用符号“∃”表示.2.全称命题与特称命题:(1)含有全称量词的命题叫全称命题: “对M 中任意一个x ,有p (x )成立”可用符号简记为∀x ∈M ,p (x ),读作“对任意x 属于M ,有p (x )成立”.(2)含有存在量词的命题叫特称命题: “存在M 中的一个x 0,使p (x 0)成立”可用符号简记为∃x 0∈M ,P (x 0),读作“存在M 中的元素x 0,使p (x 0)成立”.3.命题的否定:(1)含有量词命题的否定全称命题p :,()x M p x ∀∈的否定⌝p :(),x M p x ∃∈⌝;全称命题的否定为存在命题存在命题p :(),x M p x ∃∈的否定⌝p :(),x M p x ∀∈⌝;存在命题的否定为全称命题其中()p x p (x )是一个关于x 的命题.(2)含有逻辑连接词命题的否定“p 或q ”的否定:“ ⌝p 且⌝q ” ;“p 且q ”的否定:“ ⌝p 或⌝q ”(3)“若p 则q “命题的否定:只否定结论特别提醒:命题的“否定”与“否命题”是不同的概念,命题的否定:只否定结论;否命题:全否 对命题p 的否定(即非p )是否定命题p 所作的判断,而“否命题”是 “若⌝p 则⌝q ”【典型例题】【例1】已知条件p :12x +>,条件q :x a >,且p ⌝是q ⌝的充分不必要条件,则a 的取值范围是()A .1a ≥B .1a ≤C .3a ≥-D .3a ≤-【例2】命题“2000,23x N x x ∃∈+≥”的否定为( )A .2000,23x N x x ∃∈+≤ B .2,23x N x x ∀∈+≤C .2000,23x N x x ∃∈+< D .2,23x N x x ∀∈+<【例3】命题“2,40x R x x ∀∈-+>”的否定是________.【例4】若命题p :∀x ,y ∈R ,x2+y2-1>0,则该命题p 的否定是__________.【举一反三】1.命题“020,log 0x R x ∃∈≤”的否定为 .2.命题“x R ∃∈,022≤--x x ”的否定是 .3.已知全称命题[),,0:+∞∈∀x P 都有x x ≤sin .请写出:P ⌝ ,判断P ⌝的真假: .4.命题p :x ∀∈R ,()f x m ≥.则命题p 的否定p ⌝是: 。
第12讲简单的逻辑联结词(且或非)讲义-高三艺考数学一轮复习

第12讲:简单的逻辑联结词(且或非)【课型】复习课【教学目标】1.了解逻辑联结词【预习清单】【基础知识梳理】1.常用的简单的逻辑联结词有“或”“且”“非”.23【引导清单】考向一:含有逻辑联结词的命题的真假判断例1:(1)命题p :若sin x >sin y ,则x >y ;命题q :x 2+y 2≥2xy .下列命题为假命题的是( )A .p 或qB .p 且qC .qD .﹁p(2)记不等式组⎩⎨⎧x +y ≥6,2x -y ≥0表示的平面区域为D .命题p :存在(x ,y )∈D ,2x +y ≥9;命题q :对任意的(x ,y )∈D ,2x +y ≤①p 或q ②﹁p 或q ③p 且﹁q ④﹁p 且﹁q这四个命题中,所有真命题的编号是( )A .①③B .①②C .②③D .③④【解析】(1)取x =π3,y =5π6,可知命题p 是假命题;由(x -y )2≥0恒成立,可知命题q 是真命题,故﹁p 为真命题,p 或q 是真命题,p 且q 是假命题.(2)在不等式组表示的平面区域D 内取点(7,0),点(7,0)满足不等式2x +y ≥9,所以命题p 正确;点(7,0)不满足不等式2x +y ≤12,所以命题q 不正确.所以命题p 或q 和p 且﹁q 正确.故选A.考向二:由命题的真假确定参数的取值范围例2:已知p :存在x ∈R ,mx 2+1≤0,q :任意x ∈R ,x 2+mx +1>0,若p 且q 为假,p 或q 为真,求实数m 的取值范围.【解析】若p 且q 为假,p 或q 为真,则p ,q 一真一假.当p 真q 假时⎩⎨⎧m <0,m ≥2或m ≤-2,所以m ≤-2;当p 假q 真时⎩⎨⎧m ≥0,-2<m <2,所以0≤m <2. 所以m 的取值范围是(-∞,-2]∪[0,2).【训练清单】【变式训练1】设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内.p 2:过空间中任意三点有且仅有一个平面.p 3:若空间两条直线不相交,则这两条直线平行.p 4:若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l .则下述命题中所有真命题是________.(填序号)①p 1且p 4 ②p 1且p 2 ③﹁p 2或p 3 ④﹁p 3或﹁p 4【解析】对于p 1,由题意设直线l 1∩l 2=A ,l 2∩l 3=B ,l 1∩l 3=C ,则A ,B ,C三点不共线,所以此三点确定一个平面α,则A ∈α,B ∈α,C ∈α,所以AB ⊂α,BC ⊂α,CA ⊂α,即l 1⊂α,l 2⊂α,l 3⊂α,所以p 1是真命题.以下同方法一.答案:①③④【变式训练2】已知命题p :关于x 的方程x 2-ax +4=0有实根;命题q :关于x 的函数y =2x 2+ax +4在[3,+∞)上是增函数.若p 或q 是真命题,p 且q 是假命题,则实数a 的取值范围是________.【解析】命题p 等价于Δ=a 2-16≥0,即a ≤-4或a ≥4;命题q 等价于-a 4≤3,即a ≥p 或q 是真命题,p 且q 是假命题知,命题p 和q 一真一假.若p 真q 假,则a <-12;若p 假q 真,则-4<aa 的取值范围是(-∞,-12)∪(-4,4).【巩固清单】1.已知命题p ,q ,则“﹁p 为假命题”是“p 且q 是真命题”的( )条件。
2018高考数学第3讲简单的逻辑联结词(苏教版)
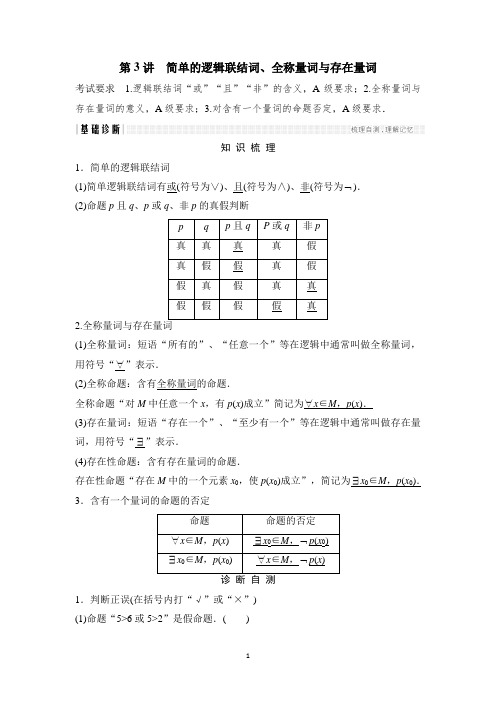
第3讲简单的逻辑联结词、全称量词与存在量词考试要求 1.逻辑联结词“或”“且”“非”的含义,A级要求;2.全称量词与存在量词的意义,A级要求;3.对含有一个量词的命题否定,A级要求.知识梳理1.简单的逻辑联结词(1)简单逻辑联结词有或(符号为∨)、且(符号为∧)、非(符号为⌝).(2)命题p且q、p或q、非p的真假判断p q p且q P或q 非p真真真真假真假假真假假真假真真假假假假真2.全称量词与存在量词(1)全称量词:短语“所有的”、“任意一个”等在逻辑中通常叫做全称量词,用符号“∀”表示.(2)全称命题:含有全称量词的命题.全称命题“对M中任意一个x,有p(x)成立”简记为∀x∈M,p(x).(3)存在量词:短语“存在一个”、“至少有一个”等在逻辑中通常叫做存在量词,用符号“∃”表示.(4)存在性命题:含有存在量词的命题.存在性命题“存在M中的一个元素x0,使p(x0)成立”,简记为∃x0∈M,p(x0).3.含有一个量词的命题的否定命题命题的否定∀x∈M,p(x)∃x0∈M,⌝p(x0)∃x0∈M,p(x0)∀x∈M,⌝p(x)诊断自测1.判断正误(在括号内打“√”或“×”)(1)命题“5>6或5>2”是假命题.()(2)命题⌝(p ∧q )是假命题,则命题p ,q 中至少有一个是真命题.( ) (3)“长方形的对角线相等”是存在性命题.( ) (4)∃x 0∈M ,p (x 0)与∀x ∈M ,⌝p (x )的真假性相反.( )2.已知p :2是偶数,q :2是质数,则命题⌝p ,⌝q ,p ∨q ,p ∧q 中真命题的个数为________.3.(2015·全国Ⅰ卷改编)设命题p :∃n ∈N ,n 2>2n ,则⌝p 为________. 4.命题“对于函数f (x )=x 2+a x (a ∈R ),存在a ∈R ,使得f (x )是偶函数”为________命题(填“真”或“假”).5.(2015·山东卷)若“∀x ∈⎣⎢⎡⎦⎥⎤0,π4,tan x ≤m ”是真命题,则实数m 的最小值为________.考点一 含有逻辑联结词的命题的真假判断 【例1】 设a ,b ,c 是非零向量.已知命题p: 若a ·b =0,b ·c =0,则a ·c =0;命题q :若a ∥b ,b ∥c ,则a ∥c .则下列命题: ①p ∨q ;②p ∧q ;③(⌝p )∧(⌝q );④p ∧(⌝q ). 其中真命题是________(填序号).规律方法 (1)“p ∨q ”、“p ∧q ”、“⌝p ”形式命题真假的判断关键是对逻辑联结词“或”“且”“非”含义的理解,其操作步骤是:①明确其构成形式;②判断其中命题p ,q 的真假;③确定“p ∨q ”“p ∧q ”“⌝p ”形式命题的真假. (2)p 且q 形式是“一假必假,全真才真”,p 或q 形式是“一真必真,全假才假”,非p 则是“与p 的真假相反”.【训练1】 (2017·南通调研)命题p :函数y =log 2(x -2)的单调增区间是[1,+∞),命题q :函数y =13x+1的值域为(0,1).在命题:①p ∧q ;②p ∨q ;③p ∧(⌝q );④⌝q 中,真命题有________(填序号).考点二 含有一个量词命题的否定及真假判定【例2】 (1)(2016·扬州中学质检)已知命题p :∀x ∈R ,e x -x -1>0,则⌝p 是________________.(2)(2014·全国Ⅰ卷改编)不等式组⎩⎨⎧x +y ≥1,x -2y ≤4的解集为D ,有下面四个命题:p 1:∀(x ,y )∈D ,x +2y ≥-2; p 2:∃(x 0,y 0)∈D ,x 0+2y 0≥2; p 3:∀(x ,y )∈D ,x +2y ≤3; p 4:∃(x 0,y 0)∈D ,x 0+2y 0≤-1. 其中真命题是________.规律方法 (1)全称命题与存在性命题的否定与命题的否定有一定的区别,否定全称命题和存在性命题时,一是要改写量词,全称量词改写为存在量词,存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论. (2)判定全称命题“∀x ∈M ,p (x )”是真命题,需要对集合M 中的每一个元素x ,证明p (x )成立;要判断存在性命题是真命题,只要在限定集合内至少找到一个x =x 0,使p (x 0)成立.【训练2】 (2017·安徽皖江名校联考改编)命题p :存在x ∈⎣⎢⎡⎦⎥⎤0,π2,使sin x +cos x >2;命题q :“∃x 0∈(0,+∞),ln x 0=x 0-1”的否定是“∀x ∈(0,+∞),ln x ≠x -1”,则四个命题:(⌝p )∨(⌝q ),p ∧q ,(⌝p )∧q ,p ∨(⌝q )中,正确命题的个数为________.考点三 由命题的真假求参数的取值范围 【例3】 (1)已知命题“∃x 0∈R ,使2x 20+(a -1)x 0+12≤0”是假命题,则实数a的取值范围是________.(2)已知p :∃x 0∈R ,mx 20+1≤0,q :∀x ∈R ,x 2+mx +1>0,若p ∨q 为假命题,则实数m 的取值范围是________.规律方法 (1)根据含逻辑联结词的命题真假求参数的方法步骤: ①根据题目条件,推出每一个命题的真假(有时不一定只有一种情况);②求出每个命题是真命题时参数的取值范围;③根据每个命题的真假情况,求出参数的取值范围.(2)全称命题可转化为恒成立问题.【训练3】(2017·衡水中学月考)设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5.(1)若a=1,且p∧q为真,求实数x的取值范围;(2)若⌝q是⌝p的必要不充分条件,求实数a的取值范围.[思想方法]1.把握含逻辑联结词的命题的形式,特别是字面上未出现“或”“且”“非”字眼,要结合语句的含义理解.2.含有逻辑联结词的命题真假判断口诀:p∨q→见真即真,p∧q→见假即假,p 与⌝p→真假相反.3.要写一个命题的否定,需先分清其是全称命题还是存在性命题,再对照否定结构去写,并注意与否命题的区别;否定的规律是“改量词,否结论”.[易错防范]1.正确区别命题的否定与否命题“否命题”是对原命题“若p,则q”的条件和结论分别加以否定而得的命题,它既否定其条件,又否定其结论;“命题的否定”即“⌝p ”,只是否定命题p 的结论.命题的否定与原命题的真假总是对立的,即两者中有且只有一个为真. 2.几点注意:(1)注意命题是全称命题还是存在性命题,是正确写出命题的否定的前提; (2)注意命题所含的量词,对于量词隐含的命题要结合命题的含义显现量词,再进行否定;(3)注意“或”“且”的否定,“或”的否定为“且”,“且”的否定为“或”.基础巩固题组(建议用时:20分钟)1.已知命题p :所有指数函数都是单调函数,则⌝p 为________.2.设命题p :函数y =sin 2x 的最小正周期为π2;命题q :函数y =cos x 的图象关于直线x =π2对称.则下列结论:①p 为真;②⌝p 为假;③p ∧q 为假;④p ∧q 为真. 其中结论正确的有________(填序号).3.命题“∃x 0∈⎝ ⎛⎭⎪⎫0,π2,tan x 0>sin x 0”的否定是________.4.若命题“∃x 0∈R ,使得x 20+(a -1)x 0+1<0”是真命题,则实数a 的取值范围是________.5.2016年巴西里约奥运会,在体操预赛中,有甲、乙两位队员参加.设命题p 是“甲落地站稳”,q 是“乙落地站稳”,则命题“至少有一位队员落地没有站稳”可表示为________.6.(2017·泰州调研)已知命题p :对任意x ∈R ,总有|x |≥0;q :x =1是方程x +2=0的根.则下列命题:①p ∧(⌝q );②(⌝p )∧q ;③(⌝p )∧(⌝q );④p ∧q . 其中真命题有________(填序号). 7.下列命题: ①∃x 0∈R ,e x 0≤0; ②∀x ∈R,2x >x 2;③a+b=0的充要条件是ab=-1;④“a>1,b>1”是“ab>1”的充分条件.其中真命题有________(填序号).8.命题p:∀x∈R,ax2+ax+1≥0,若⌝p是真命题,则实数a的取值范围是________.9.(2017·衡阳模拟改编)已知命题p:∃α∈R,cos(π-α)=cos α;命题q:∀x∈R,x2+1>0.则下面结论:①p∧q是真命题;②p∧q是假命题;③⌝p是真命题;④⌝q是真命题.其中正确的结论是________(填序号).10.(2017·苏北四市联考)已知命题p:∃x∈R,(m+1)(x2+1)≤0,命题q:∀x ∈R,x2+mx+1>0恒成立.若p∧q为假命题,则实数m的取值范围为________.11.(2017·南通、扬州、泰州调研)给出下列四个命题:①“若x2-x=0,则x=0或x=1”的逆否命题为“x≠0且x≠1,则x2-x≠0”;②“x<1”是“x2-3x+2>0”的充分不必要条件;③命题p:存在x0∈R,使得x20+x0+1<0,则⌝p:任意x∈R,都有x2+x+1≥0;④若p∧q为假命题,则p,q均为假命题.其中为真命题的是________(填序号).12.已知命题p:“∀x∈[0,1],a≥e x”;命题q:“∃x0∈R,使得x20+4x0+a =0”.若命题“p∧q”是真命题,则实数a的取值范围是________.能力提升题组(建议用时:10分钟)13.(2016·浙江卷改编)命题“∀x∈R,∃n∈N*,使得n≥x2”的否定形式是____________________.14.(2017·昆明一中质检)已知命题p:∀x∈R,x+1x≥2;命题q:∃x0∈(0,+∞),x20>x30,则下列命题:①(⌝p)∧q;②p∧(⌝q);③(⌝p)∧(⌝q);④p∧q,其中真命题是________(填序号).15.(2016·苏、锡、常、镇四市调研)给出下列三个结论:①若p∧q为假命题,则p,q至少有一个为假命题;②命题“∀x∈R,x3-x2-1≤0”的否定是“∃x0∈R,x30-x20-1>0”;③“若a∥c且b∥c,则a∥b”是真命题.其中正确的结论为________(填序号).16.已知命题p:∃x∈R,e x-mx=0,q:∀x∈R,x2-2mx+1≥0,若p∨(⌝q)为假命题,则实数m的取值范围是________.。
2019版高考数学一轮复习 第一单元 集合与常用逻辑用语 第3课 简单的逻辑联结词、全称量词与存在量词

题的是
()
A.①③
B.①④
C.②③
D.②④
解析:当 x>y 时,-x<-y,故命题 p 为真命题,从而綈 p 为
假命题.当 x>y 时,x2>y2 不一定成立,故命题 q 为假命题, 从而綈 q 为真命题.故①p∧q 为假命题;②p∨q 为真命题;
命题,所以 p∧(綈 q)是真命题. [答案] D
[方法技巧] 1.“p∨q”“p∧q”“綈 p”形式命题真假的判断步骤 (1)确定命题的构成形式; (2)判断命题 p,q 的真假;
(3)确定“p∨q”“p∧q”“綈 p”形式命题的真假.
[方法技巧] 2.复合命题真假判断常用的方法 (1)直接法:即判断出 p,q 的真假,再判断复合命题的 真假. (2)特殊值法:从题干出发通过选取特殊情况代入,作 出判断.特殊情况可能是特殊值、特殊函数、特殊点、特殊 位置、特殊向量等. (3)数形结合法:根据题设条件作出研究问题的有关图 形,利用图形作出判断,从而确定正确答案.
考点
考查频度
考查角度
简单的逻辑联结词 未考查
线性规划与量词命题的 全称量词、存在量词 5年2考
判断,特称命题的否定
含逻辑联结词的命题的真假判断
[典例] 已知命题 p:∃x0∈R ,使 x20+2x0+5≤4;命题
q:当 x∈0,π2时,f(x)=sin x+sin4 x的最小值为 4,下列命
2.已知命题
p:∀x<1,都有
log 1 x<0,命题 2
q:∃x0∈R ,使得
x20≥2x0 成立,则下列命题是真命题的是
()
A.p∨(綈 q)
高考数学第一轮复习简单的逻辑联结词知识点

2019高考数学第一轮复习简单的逻辑联结词知识点在科学发展和现代生活生产中的应用非常广泛,以下是查字典数学网为大家整理的简单的逻辑联结词知识点,希望可以解决您所遇到的相关问题,加油,查字典数学网一直陪伴您。
一、简单的逻辑联结词1.用联结词且联结命题p和命题q,记作pq,读作p且q.2.用联结词或联结命题p和命题q,记作pq,读作p或q.3.对一个命题p全盘否定,就得到一个新命题,记作綈p,读作非p或p的否定.4.命题pq,pq,綈p的真假判断:pq中p、q有一假为假,pq有一真为真,p与非p必定是一真一假.二、全称量词与存在量词1.全称量词与全称命题(1)短语所有的任意一个在逻辑中通常叫做全称量词,并用符号表示.(2)含有全称量词的命题,叫做全称命题.(3)全称命题对M中任意一个x,有p(x)成立可用符号简记为xM,p(x),读作对任意x属于M,有p(x)成立.2.存在量词与特称命题(1)短语存在一个至少有一个在逻辑中通常叫做存在量词,并用符号表示.(2)含有存在量词的命题,叫做特称命题.(3)特称命题存在M中的一个x0,使p(x0)成立可用符号简记为x0M,P(x0),读作存在M中的元素x0,使p(x0)成立.三、含有一个量词的命题的否定命题命题的否定xM,p(x)x0M,綈p(x0)x0M,p(x0)xM,綈p(x)四、解题思路1.逻辑联结词与集合的关系或、且、非三个逻辑联结词,对应着集合运算中的并、交、补,因此,常常借助集合的并、交、补的意义来解答由或、且、非三个联结词构成的命题问题.2.正确区别命题的否定与否命题否命题是对原命题若p,则q的条件和结论分别加以否定而得到的命题,它既否定其条件,又否定其结论;命题的否定即非p,只是否定命题p的结论. 命题的否定与原命题的真假总是对立的,即两者中有且只有一个为真,而原命题与否命题的真假无必然联系.3.全称命题真假的判断方法(1)要判断一个全称命题是真命题,必须对限定的集合M中的每一个元素x,证明p(x)成立;语文课本中的文章都是精选的比较优秀的文章,还有不少名家名篇。
2018年7月9日+简单的逻辑联结词-2019年高考数学(文)一轮复习+Word版含解析

典例在线
已知命题:若函数是偶函数,则;命题:,关于的方程有解.在①;②;③;④中,为真命题的是
A.②③B.②④
C.③④D.①④
【参考答案】D
【试题解析】因为,所以,解得,故命题为真命题;
因为,则时,方程有解,所以为假命题,
所以与为真命题,故选D.
【方法总结】(1)辨别复合命题的构成形式时,应根据组成复合命题的语句中所出现的逻辑联结词,或语句的意义确定复合命题的形式.
(2)判断“p或q”、“p且q”形式命题的真假,主要利用真值表来判断,其步骤是:
①确定命题p、q的真假;②确定复合命题的构成;③利用真值表判断该命题的真假.
真值表如下:
学霸推荐
1.已知命题;命题若,则.则下列命题为真命题的是A.B.
C.D.
2.已知恒成立,方程表示焦点在轴上的椭圆,若命题“且”为假命题,则实数的取值范围是.
1.【答案】B
特别要注意:一真“或”为真,一假“且”为假.当为真,p与q一真一假;
为假时,p与q至少有一个为假.
2.【答案】
【解析】由题意:若为真,则有对恒成立,
时取“=”),,
若为真,则有,即或,
若“且”为假,则、中至少一个为假.
若、均为真,则,实数的取值范围是.。
简单的逻辑联结词(教学案)-2019年高考数学(文)一轮复习精品资料(原卷版)

专题3 简单的逻辑联结词一、重点知识梳理1.命题:能判断真假的语句叫做命题.2.全称量词与全称命题(1)全称量词:短语“所有”在陈述中表示所述事物的全体,在逻辑中通常叫做全称量词.(2)全称命题:含有全称量词的命题.(3)全称命题的符号表示形如“对M中所有x,p(x)”的命题,可用符号简记为“∀x∈M,p(x)”.3.存在量词与存在性命题(1)存在量词:短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分,逻辑中通常叫做存在量词。
(2)存在性命题:含有全称量词的命题.(3)存在性命题的符号表示形如“存在集合M中的元素x,q(x)”的命题,用符号简记为∃x∈M,q(x)。
4.基本逻辑联结词常用的基本逻辑联结词有“且”、“或”、“非”.5.命题p∧q,p∨q,非p的真假判断p q p∧q p∨q 非p真真真真假真假假真假假真假真真假假假假真6.含有一个量词的命题的否定命题命题的否定∀x∈M,p(x) ∃x∈M,非p(x)∃x∈M,p(x) ∀x∈M,非p(x)高频考点一含有逻辑联结词的命题的真假判断例1、[2017·山东高考]已知命题p:∃x∈R,x2-x+1≥0;命题q:若a2<b2,则a<b.下列命题为真命题的是() A.p∧q B.p∧(非q) C.(非p)∧q D.(非p)∧(非q)【变式探究】命题p:函数y=log2(x-2)的单调增区间是[1,+∞),命题q:函数y=13x+1的值域为(0,1).下列命题是真命题的为()A.p∧q B.p∨q C.p∧(非q) D.非q高频考点二 含有一个量词命题的否定及真假判定 例2、(1)已知命题p :∀x ∈R ,e x -x -1>0,则非p 是( ) A .∀x ∈R ,e x -x -1<0 B .∃x ∈R ,e x -x -1≤0C .∃x ∈R ,e x -x -1<0D .∀x ∈R ,e x -x -1≤0(2)不等式组⎩⎪⎨⎪⎧x +y ≥1,x -2y ≤4的解集为D ,有下面四个命题:p 1:∀(x ,y )∈D ,x +2y ≥-2, p 2:∃(x ,y )∈D ,x +2y ≥2, p 3:∀(x ,y )∈D ,x +2y ≤3, p 4:∃(x ,y )∈D ,x +2y ≤-1. 其中的真命题是( ) A.p 2,p 3B .p 1,p 2C .p 1,p 4D .p 1,p 3【感悟提升】全称命题与存在性命题的否定与命题的否定有一定的区别,否定全称命题和存在性命题时,一是要改写量词,全称量词改写为存在量词,存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论.【变式探究】命题p :存在x ∈⎣⎡⎦⎤0,π2,使sin x +cos x >2;命题q :“∃x ∈(0,+∞),ln x =x -1”的否定是“∀x ∈(0,+∞),ln x ≠x -1”,则四个命题:(非p )∨(非q ),p ∧q ,(非p )∧q ,p ∨(非q )中,正确命题的个数为( )A .1B .2C .3D .4高频考点三 由命题的真假求参数的取值范围例3、已知命题p :关于x 的不等式a x >1(a >0,a ≠1)的解集是{x |x <0},命题q :函数y =lg (ax 2-x +a )的定义域为R ,如果p ∨q 为真命题,p ∧q 为假命题,求实数a 的取值范围.【变式探究】(1)已知命题“∃x ∈R ,使2x 2+(a -1)x +12≤0”是假命题,则实数a 的取值范围是( )A .(-∞,-1)B .(-1,3)C .(-3,+∞)D .(-3,1)(2)已知p :∃x ∈R ,mx 2+1≤0,q :∀x ∈R ,x 2+mx +1>0,若p ∨q 为假命题,则实数m 的取值范围是( ) A .[2,+∞)B .(-∞,-2]C .(-∞,-2]∪[2,+∞)D .[-2,2]【感悟提升】 (1)根据含逻辑联结词的命题真假求参数的方法步骤: ①根据题目条件,推出每一个命题的真假(有时不一定只有一种情况); ②求出每个命题是真命题时参数的取值范围; ③根据每个命题的真假情况,求出参数的取值范围. (2)全称命题可转化为恒成立问题.【变式探究】设p :实数x 满足x 2-5ax +4a 2<0(其中a >0),q :实数x 满足2<x ≤5. (1)若a =1,且p ∧q 为真,求实数x 的取值范围.(2)若非q 是非p 的必要不充分条件,求实数a 的取值范围.【高考链接】1、[2017·山东高考]已知命题p :∃x ∈R ,x 2-x +1≥0;命题q :若a 2<b 2,则a <b .下列命题为真命题的是( )A .p ∧qB .p ∧(非q )C .(非p )∧qD .(非p )∧(非q )1.【2016高考四川文科】设p:实数x ,y 满足1x >且1y >,q: 实数x ,y 满足2x y +>,则p 是q 的( )(A)充分不必要条件 (B)必要不充分条件 (C) 充要条件 (D) 既不充分也不必要条件 2.【2016高考天津文数】设0>x ,R y ∈,则“y x >”是“||y x >”的( )(A )充要条件 (B )充分而不必要条件(C )必要而不充分条件 (D )既不充分也不必要条件3.【2016高考上海文科】设R a ∈,则“1>a ”是“12>a ”的( )(A)充分不必要条件 (B)必要不充分条件 (C) 充要条件 (D) 既不充分也不必要条件 1.【2015高考浙江,文3】设a ,b 是实数,则“0a b +>”是“0ab >”的( )(A)充分不必要条件 (B)必要不充分条件 (C) 充要条件 (D) 既不充分也不必要条件 2.【2015高考重庆,文2】“x 1=”是“2x 210x -+=”的( )(A )充要条件 (B )充分而不必要条件(C )必要而不充分条件 (D )既不充分也不必要条件4.【2015高考四川,文4】设a ,b 为正实数,则“a >b >1”是“log 2a >log 2b >0”的( ) (A )充要条件 (B )充分不必要条件 (C )必要不充分条件 (D )既不充分也不必要条件5.【2015高考湖南,文3】设x ∈R ,则“x >1”是“2x >1”的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件 6.【2015高考安徽,文3】设p :x <3,q :-1<x <3,则p 是q 成立的( )(A )充分必要条件 (B )充分不必要条件 (C )必要不充分条件 (D )既不充分也不必要条件。
2023年高考数学(文科)一轮复习——简单的逻辑联结词、全称量词与存在量词

第3节简单的逻辑联结词、全称量词与存在量词考试要求 1.了解逻辑联结词“或”、“且”、“非”的含义;2.理解全称量词与存在量词的意义;3.能正确地对含有一个量词的命题进行否定.1.简单的逻辑联结词(1)命题中的且、或、非叫做逻辑联结词.(2)命题p∧q,p∨q,綈p的真假判断p q p∧q p∨q 綈p真真真真假真假假真假假真假真真假假假假真2.全称量词与存在量词(1)全称量词:短语“所有的”、“任意一个”等在逻辑中通常叫做全称量词,用符号“∀”表示.(2)存在量词:短语“存在一个”、“至少有一个”等在逻辑中通常叫做存在量词,用符号“∃”表示.3.全称命题和特称命题名称全称命题特称命题结构对M中的任意一个x,有p(x)成立存在M中的一个x0,使p(x0)成立简记∀x∈M,p(x)∃x0∈M,p(x0)否定∃x0∈M,綈p(x0)∀x∈M,綈p(x)1.含有逻辑联结词的命题真假判断口诀:p∨q→见真即真,p∧q→见假即假,p与綈p→真假相反.2.含有一个量词的命题的否定规律是“改量词,否结论”.3.“p∨q”的否定是“(綈p)∧(綈q)”,“p∧q”的否定是“(綈p)∨(綈q)”.4.逻辑联结词“或”“且”“非”对应集合运算中的“并”“交”“补”,可借助集合运算处理含逻辑联结词的命题.1.思考辨析(在括号内打“√”或“×”)(1)命题“5>6或5>2”是假命题.()(2)命题綈(p∧q)是假命题,则命题p,q中至少有一个是假命题.()(3)“长方形的对角线相等”是特称命题.()(4)∃x0∈M,p(x0)与∀x∈M,綈p(x)的真假性相反.()答案(1)×(2)×(3)×(4)√解析(1)错误.命题p∨q中,p,q有一真则真.(2)错误.p∧q是真命题,则p,q都是真命题.(3)错误.命题“长方形的对角线相等”是全称命题.2.(2021·全国乙卷)已知命题p:∃x∈R,sin x<1;命题q:∀x∈R,e|x|≥1,则下列命题中为真命题的是()A.p∧qB.(綈p)∧qC.p∧(綈q)D.綈(p∨q)答案 A解析由正弦函数的图象及性质可知,存在x∈R,使得sin x<1,所以命题p为真命题.对任意的x∈R,均有e|x|≥e0=1成立,故命题q为真命题,所以命题p∧q 为真命题,故选A.3.(2017·山东卷)已知命题p:∀x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是( ) A.p ∧q B.p ∧(綈q ) C.(綈p )∧qD.(綈p )∧(綈q )答案 B解析 由已知得p 真,q 假,故綈q 真,所以p ∧(綈q )真,故选B. 4.(易错题)命题p :“有些三角形是等腰三角形”,则綈p 是________. 答案 所有三角形都不是等腰三角形5.(易错题)命题“∀x ∈R ,ax 2-ax +1>0”为真命题,则实数a 的取值范围为________. 答案 [0,4)解析 ①当a =0时,1>0恒成立; ②当a ≠0时,⎩⎪⎨⎪⎧a >0,Δ=a 2-4a <0,∴0<a <4.综上0≤a <4.6.(2021·合肥调研)能说明命题“∀x ∈R 且x ≠0,x +1x ≥2”是假命题的x 的值可以是________(写出一个即可). 答案 -1(任意负数)解析 当x >0时,x +1x ≥2,当且仅当x =1时取等号, 当x <0时,x +1x ≤-2,当且仅当x =-1时取等号, ∴x 的取值为负数即可,例如x =-1.考点一 含有逻辑联结词的命题1.(2021·成都调研)已知命题p :函数y =2sin x +sin x ,x ∈(0,π)的最小值为22;命题q :若a ·b =0,b ·c =0,则a ·c =0.下列命题为真命题的是( ) A.(綈p )∧qB.p ∨qC.p∧(綈q)D.(綈p)∧(綈q) 答案 D解析命题p:函数y=2sin x+sin x,x∈(0,π),由基本不等式成立的条件可知,y>22sin x·sin x=22,等号取不到,所以命题p是假命题.命题q:取a=c=(1,0),b=(0,1),显然a·b=0,b·c=0,但a·c=1≠0,所以命题q是假命题.所以綈p为真,綈q为真.因此,只有(綈p)∧(綈q)为真命题.2.在一次跳伞训练中,甲、乙两位学员各跳一次.设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为()A.(綈p)∨(綈q)B.p∧(綈q)C.(綈p)∧(綈q)D.p∨q答案 A解析命题p是“甲降落在指定范围”,则綈p是“甲没降落在指定范围”,q 是“乙降落在指定范围”,则綈q是“乙没降落在指定范围”,命题“至少有一位学员没有降落在指定范围”包括“甲降落在指定范围,乙没降落在指定范围”“甲没降落在指定范围,乙降落在指定范围”“甲没降落在指定范围,乙没降落在指定范围”.所以命题“至少有一位学员没有降落在指定范围”可表示为(綈p)∨(綈q).3.(2022·洛阳质检)设a,b,c均为非零向量,已知命题p:a=b是a·c=b·c的必要不充分条件,命题q:x>1是|x|>1的充分不必要条件.则下列命题中为真命题的是()A.p∧qB.p∨qC.(綈p)∧(綈q)D.p∨(綈q)答案 B解析由a=b⇒a·c=b·c,但a·c=b·c a=b,故p为假命题.命题q:∵|x|>1,∴x>1或x<-1,∴由x>1⇒|x|>1,但|x|>1x>1,故q为真命题.故选B.4.(2020·全国Ⅱ卷)设有下列四个命题:p1:两两相交且不过同一点的三条直线必在同一平面内.p2:过空间中任意三点有且仅有一个平面.p3:若空间两条直线不相交,则这两条直线平行.p4:若直线l⊂平面α,直线m⊥平面α,则m⊥l.则下述命题中所有真命题的序号是________.①p1∧p4;②p1∧p2;③(綈p2)∨p3;④(綈p3)∨(綈p4).答案①③④解析p1是真命题,两两相交不过同一点的三条直线必定有三个交点,且这三个交点不在同一条直线上,由平面的基本性质“经过不在同一直线上的三个点,有且只有一个平面”,可知p1为真命题;p2是假命题,因为空间三点在一条直线上时,有无数个平面过这三个点;p3是假命题,因为空间两条直线不相交时,它们可能平行,也可能异面;p4是真命题,因为一条直线垂直于一个平面,那么它垂直于平面内的所有直线.由以上结论知綈p2,綈p3,綈p4依次为真命题、真命题、假命题,从而①③④中命题为真命题,②中命题为假命题.感悟提升 1.“p∨q”,“p∧q”,“綈p”形式命题真假的判断关键是对逻辑联结词“或”“且”“非”含义的理解,其操作步骤是:(1)明确其构成形式;(2)判断其中命题p,q的真假;(3)确定“p∨q”“p∧q”“綈p”形式命题的真假.2.p∧q形式是“一假必假,全真才真”,p∨q形式是“一真必真,全假才假”,綈p 与p 的真假性相反. 考点二 全称量词与存在量词例1 (1)(2021·江南十校联考)已知f (x )=sin x -tan x ,命题p :∃x 0∈⎝ ⎛⎭⎪⎫0,π2,f (x 0)<0,则( )A.p 是假命题,綈p :∀x ∈⎝ ⎛⎭⎪⎫0,π2,f (x )≥0B.p 是假命题,綈p :∃x 0∈⎝ ⎛⎭⎪⎫0,π2,f (x 0)≥0C.p 是真命题,綈p :∀x ∈⎝ ⎛⎭⎪⎫0,π2,f (x )≥0D.p 是真命题,綈p :∃x 0∈⎝ ⎛⎭⎪⎫0,π2,f (x 0)≥0(2)已知定义域为R 的函数f (x )不是偶函数,则下列命题一定为真命题的是( ) A.∀x ∈R ,f (-x )≠f (x ) B.∀x ∈R ,f (-x )≠-f (x ) C.∃x 0∈R ,f (-x 0)≠f (x 0) D.∃x 0∈R ,f (-x 0)≠-f (x 0) 答案 (1)C (2)C解析 (1)当x ∈⎝ ⎛⎭⎪⎫π4,π2时,sin x <1,tan x >1.此时sin x -tan x <0,故命题p 为真命题. 由于命题p 为特称命题, 所以命题p 的否定为全称命题, 则綈p 为:∀x ∈⎝ ⎛⎭⎪⎫0,π2,f (x )≥0. (2)∵定义域为R 的函数f (x )不是偶函数,∴∀x ∈R ,f (-x )=f (x )为假命题, ∴∃x 0∈R ,f (-x 0)≠f (x 0)为真命题.感悟提升 1.全称命题与特称命题的否定与一般命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词,存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论.2.判定全称命题“∀x ∈M ,p (x )”是真命题,需要对集合M 中的每一个元素x ,证明p (x )成立;要判断特称命题是真命题,只要在限定集合内找到一个x =x 0,使p (x 0)成立即可.训练1 (1)设命题p :所有正方形都是平行四边形,则綈p 为( ) A.所有正方形都不是平行四边形 B.有的平行四边形不是正方形 C.有的正方形不是平行四边形D.不是正方形的四边形不是平行四边形 (2)下列四个命题:p 1:∃x 0∈(0,+∞),⎝ ⎛⎭⎪⎫12x 0<⎝ ⎛⎭⎪⎫13x 0;p 2:∃x 0∈(0,π),sin x 0<cos x 0; p 3:∀x ∈R ,e x >x +1; p 4:∀x ∈⎝ ⎛⎭⎪⎫0,13,⎝ ⎛⎭⎪⎫12x<log 13x .其中真命题是( ) A.p 1,p 3 B.p 1,p 4 C.p 2,p 3D.p 2,p 4答案 (1)C (2)D解析 (1)“所有”改为“存在”(或“有的”),“都是”改为“不都是”(或“不是”),即綈p 为有的正方形不是平行四边形.(2)对于p 1,当x 0∈(0,+∞)时,总有⎝ ⎛⎭⎪⎫12x 0>⎝ ⎛⎭⎪⎫13x 0成立,故p 1是假命题;对于p 2,当x 0=π6时,sin x 0<cos x 0,故p 2为真命题;对于p 3,当x =0时,e x =x +1,故p 3为假命题;对于p 4,结合指数函数y =⎝ ⎛⎭⎪⎫12x与对数函数y =log 13x 在⎝ ⎛⎭⎪⎫0,13上的图象(图略)可以判断p 4为真命题.考点三 由命题的真假求参数例2 (1)已知命题p :∀x ∈[1,2],x 2-a ≥0;q :∃x 0∈R ,x 20+2ax 0+2-a =0,若(綈p ) ∧q 是真命题,则实数a 的取值范围是________________.(2)(经典母题)已知f (x )=ln(x 2+1),g (x )=⎝ ⎛⎭⎪⎫12x-m ,若对∀x 1∈[0,3],∃x 2∈[1,2],使得f (x 1)≥g (x 2),则实数m 的取值范围是________________. 答案 (1)(1,+∞) (2)⎣⎢⎡⎭⎪⎫14,+∞解析 (1)∵(綈p )∧q 是真命题, ∴p 假q 真.p :∀x ∈[1,2],x 2-a ≥0为假命题, ∴∃x ∈[1,2],x 2-a <0为真命题, 即a >x 2成立,∴a >1.q :∃x 0∈R ,x 20+2ax 0+2-a =0为真命题,所以Δ=(2a )2-4(2-a )≥0,∴a ≥1或a ≤-2. 综上,a >1.(2)当x ∈[0,3]时,f (x )min =f (0)=0, 当x ∈[1,2]时,g (x )min =g (2)=14-m , 由f (x )min ≥g (x )min , 得0≥14-m ,所以m ≥14.迁移 本例(2)中,若将“∃x 2∈[1,2]”改为“∀x 2∈[1,2]”,其他条件不变,则实数m 的取值范围是________________. 答案 ⎣⎢⎡⎭⎪⎫12,+∞解析 当x ∈[1,2]时,g (x )max =g (1)=12-m ,对∀x 1∈[0,3],∀x 2∈[1,2]使得f (x 1)≥g (x 2)等价于f (x )min ≥g (x )max ,得0≥12-m ,∴m ≥12.感悟提升 1.由含逻辑联结词的命题真假求参数的方法步骤: (1)求出每个命题是真命题时参数的取值范围; (2)根据每个命题的真假情况,求出参数的取值范围. 2.全称命题可转化为恒成立问题.3.含量词的命题中参数的取值范围,可根据命题的含义,利用函数的最值解决. 训练2 (2022·许昌质检)已知p :关于x 的方程e x -a =0在(-∞,0)上有解;q :函数y =lg(ax 2-x +a )的定义域为R ,若p ∨q 为真命题,p ∧q 为假命题,则实数a 的取值范围是________. 答案 ⎝ ⎛⎦⎥⎤0,12∪[1,+∞)解析 p 真:a =e x 在(-∞,0)上有解, ∴0<a <1.q 真:ax 2-x +a >0在R 上恒成立, 当a =0时,显然不成立;当a ≠0时,需⎩⎪⎨⎪⎧a >0,Δ=(-1)2-4a 2<0,∴a >12.又p ∨q 为真,p ∧q 为假, ∴p 真q 假或p 假q 真.当p 真q 假时,⎩⎨⎧0<a <1,a ≤12,∴0<a ≤12, 当p 假q 真时,⎩⎨⎧a ≤0或a ≥1,a >12,∴a ≥1.∴0<a ≤12或a ≥1.1.(2021·成都诊断)已知命题p:对任意的x∈R,2x-x2≥1,则綈p为()A.对任意的x∉R,2x-x2<1B.存在x∉R,2x-x2<1C.对任意的x∈R,2x-x2<1D.存在x∈R,2x-x2<1答案 D解析p:∀x∈R,2x-x2≥1,∴綈p:∃x∈R,2x-x2<1.2.“p∧q是真命题”是“p∨q是真命题”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 A3.下列命题的否定是真命题的是()A.有些实数的绝对值是正数B.所有平行四边形都不是菱形C.任意两个等边三角形都是相似的D.3是方程x2-9=0的一个根答案 B4.命题“∀x∈R,f(x)·g(x)≠0”的否定是()A.∀x∈R,f(x)=0且g(x)=0B.∀x∈R,f(x)=0或g(x)=0C.∃x0∈R,f(x0)=0且g(x0)=0D.∃x0∈R,f(x0)=0或g(x0)=0答案 D解析根据全称命题与特称命题的互为否定的关系可得:命题“∀x∈R,f(x)g(x)≠0”的否定是“∃x0∈R,f(x0)=0或g(x0)=0”.故选D.5.命题p:甲的数学成绩不低于100分,命题q:乙的数学成绩低于100分,则p∨(綈q)表示()A.甲、乙两人的数学成绩都低于100分B.甲、乙两人至少有一人的数学成绩低于100分C.甲、乙两人的数学成绩都不低于100分D.甲、乙两人至少有一人的数学成绩不低于100分答案 D解析由于命题q:乙的数学成绩低于100分,因此綈q:乙的数学成绩不低于100分,所以p∨(綈q)表示甲、乙两人至少有一人的数学成绩不低于100分.6.已知命题“∃x∈R,4x2+(a-2)x+14≤0”是假命题,则实数a的取值范围为()A.(-∞,0)B.[0,4]C.[4,+∞)D.(0,4) 答案 D解析因为命题“∃x∈R,4x2+(a-2)x+14≤0”是假命题,所以其否定为“∀x∈R,4x2+(a-2)x+14>0”是真命题.则Δ=(a-2)2-4×4×14=a2-4a<0,解得0<a<4.7.(2021·衡水检测)命题p:若向量a·b<0,则a与b的夹角为钝角;命题q:若cos α·cos β=1,则sin(α+β)=0.下列命题为真命题的是()A.pB.綈qC.p∧qD.p∨q答案 D解析当a,b方向相反时,a·b<0,但夹角是180°,不是钝角,命题p是假命题;若cos αcos β=1,则cos α=cos β=1或cos α=cos β=-1,所以sin α=sin β=0,从而sin(α+β)=0,命题q是真命题,所以p ∨q 是真命题.8.已知命题p :“∀x ∈[0,1],a ≥e x ”;命题q :“∃x 0∈R ,使得x 20+4x 0+a =0”.若命题“p ∧q ”是真命题,则实数a 的取值范围为( )A.[e ,4]B.(-∞,e]C.[e ,4)D.[4,+∞)答案 A解析 若命题“p ∧q ”是真命题,那么命题p ,q 都是真命题.由∀x ∈[0,1],a ≥e x ,得a ≥e ;由∃x 0∈R ,使x 20+4x 0+a =0,得Δ=16-4a ≥0,则a ≤4,因此e ≤a ≤4. 9.命题:∃x 0∈R ,1<f (x 0)<2的否定是________________________.答案 ∀x ∈R ,f (x )≤1或f (x )≥210.若“∀x ∈⎣⎢⎡⎦⎥⎤0,π4,tan x ≤m ”是真命题,则实数m 的最小值为________. 答案 1解析 ∵函数y =tan x 在⎣⎢⎡⎦⎥⎤0,π4上是增函数, ∴y max =tan π4=1,依题意,m ≥y max ,即m ≥1.∴m 的最小值为1.11.下列命题为真命题的是________(填序号).①∃x 0∈R ,x 20+x 0+1≤0;②∀a ∈R ,f (x )=log (a 2+2)x 在定义域内是增函数;③若f (x )=2x -2-x ,则∀x ∈R ,f (-x )=-f (x );④若f (x )=x +1x,则∃x 0∈(0,+∞),f (x 0)=1. 答案 ②③解析 x 20+x 0+1=⎝ ⎛⎭⎪⎫x 0+122+34>0,故①错误; ∵a 2+2≥2>1,∴f (x )=log (a 2+2)x 在(0,+∞)上是增函数,故②正确; f (x )为奇函数,所以∀x ∈R ,都有f (-x )=-f (x ),故③正确;x0∈(0,+∞)时,f(x0)=x0+1x0≥2,当且仅当x0=1时取“=”,故④错误.综上有②③正确.12.(2022·周口调研)已知p:函数f(x)=x2-(2a+4)x+6在(1,+∞)上是增函数,q:∀x∈R,x2+ax+2a-3>0,若p∧(綈q)是真命题,则实数a的取值范围为________. 答案(-∞,-1]解析依题意,p为真命题,綈q为真命题.若p为真命题,则2a+42≤1,解得a≤-1.①若綈q为真命题,则∃x0∈R,x20+ax0+2a-3≤0成立.∴a2-4(2a-3)≥0,解之得a≥6或a≤2.②结合①②,知a≤-1,即实数a的取值范围是(-∞,-1].13.已知命题p:∀x>0,e x>x+1,命题q:∃x∈(0,+∞),ln x≥x,则下列命题为真命题的是()A.p∧qB.(綈p)∧qC.p∧(綈q)D.(綈p)∧(綈q)答案 C解析令f(x)=e x-x-1,则f′(x)=e x-1,当x>0时,f′(x)>0,所以f(x)在(0,+∞)上单调递增,∴f(x)>f(0)=0,即e x>x+1,则命题p真;令g(x)=ln x-x,x>0,则g′(x)=1x -1=1-xx,当x ∈(0,1)时,g ′(x )>0;当x ∈(1,+∞)时,g ′(x )<0,即当x =1时,g (x )取得极大值,也是最大值,所以g (x )max =g (1)=-1<0,∴g (x )<0在(0,+∞)上恒成立,则命题q 假,因此綈q 为真,故p ∧(綈q )为真.14.(2019·全国Ⅲ卷)记不等式组⎩⎨⎧x +y ≥6,2x -y ≥0表示的平面区域为D .命题p :∃(x ,y )∈D ,2x +y ≥9;命题q :∀(x ,y )∈D ,2x +y ≤12.下面给出了四个命题 ①p ∨q ;②(綈p )∨q ;③p ∧(綈q );④(綈p )∧(綈q ).这四个命题中,所有真命题的编号是( )A.①③B.①②C.②③D.③④答案 A解析 由不等式组画出平面区域D ,如图阴影部分所示,在图中画出直线2x +y =9,可知p 为真命题,綈p 为假命题,作出直线2x +y =12,2x +y ≤12表示直线及其下方区域,易知命题q 为假命题;命题綈q 为真命题;∴p ∨q 为真,(綈p )∨q 为假,p ∧(綈q )为真,(綈p )∧(綈q )为假.故真命题的编号为①③.15.已知函数f (x )的定义域为(a ,b ),若“∃x ∈(a ,b ),f (x )+f (-x )≠0”是假命题,则f (a +b )=________.答案 0解析 “∃x ∈(a ,b ),f (x )+f (-x )≠0”的否定是∀x ∈(a ,b ),f (x )+f (-x )=0,依题意:命题∀x ∈(a ,b ),f (x )+f (-x )=0为真命题,故函数y =f (x ),x ∈(a ,b )为奇函数,∴a +b =0,∴f (a +b )=f (0)=0.16.若f (x )=x 2-2x ,g (x )=ax +2(a >0),∀x 1∈[-1,2],∃x 0∈[-1,2],使g (x 1)=f (x 0),则实数a 的取值范围是________.答案 ⎝ ⎛⎦⎥⎤0,12 解析 设f (x )=x 2-2x ,g (x )=ax +2(a >0)在[-1,2]上的值域分别为A ,B , 则A =[-1,3],B =[-a +2,2a +2],由题意可知⎩⎪⎨⎪⎧-a +2≥-1,2a +2≤3,∴a ≤12, 又∵a >0,∴0<a ≤12.。
高三数学简单的逻辑联结词

基础知识梳理
2.全称量词和存在量词 (1)全称量词有:所有的,任意一个, 任给,用符号“ ∀ ”表示. 存在量词有:存在一个,至少有一个, 有些,用符号“ ∃ ”表示. (2)含有全称量词的命题,叫做 全称命题 ;“对M中任意一个x,有p(x) 成立”,可用符号简记为 ∀x∈M,p(x) , 读作“对任意x属于M,有p(x)成立”.
答案:p∨q, ¬p p∧q, ¬q
课堂互动讲练
考点一 命题真假的判断
“p∨q”、“p∧q”、“¬p”形式命 题真假的判断步骤:
(1)确定命题的构成形式; (2)判断其中命题p、q的真假; (3)确定“p∨q”、“p∧q”、“¬p” 形式命题的真假.
课堂互动讲练
例1 写出由下列各组命题构成的“p或 q”、“p且q”、“非p”形式的复合命题, 并判断真假. (1)p:1是素数;q:1是方程x2+2 x-3=0的根; (2)p:平行四边形的对角线相等; q:平行四边形的对角线互相垂直; (3)p:方程x2+x-1=0的两实根 符号相同;q:方程x2+x-1=0的两实 根的绝对值相等.
三基能力强化
4.(教材习题改编)“矩形的对角 线互相平分或互相垂直”是________ 命题.
答案:真
三基能力强化
5.命题p:“-2不是偶数”,q:π是 无理数,则在“p∧q”,“p∨q”,“¬p”,“ ¬q”中,真命题有________,假命题有___ _____.
解析:易判断知p假,q真,故真命题 有p∨q, ¬p;假命题有p∧q, ¬q.
课堂互动讲练
【思路点拨】 (1)利用“或”、 “且”、“非”把两个命题联结成新 命题;
(2)根据命题p和命题q的真假 判断复合命题的真假.
课堂互动讲练
高考数学一轮总复习第一章集合与常用逻辑用语第3讲简单的逻辑联结词全称量词与存在量词学案文

第3讲简单的逻辑联结词、全称量词与存在量词1.简单的逻辑联结词(1)常用的简单的逻辑联结词有“或”“且”“非”.(2)命题p∧q、p∨q、﹁p的真假判断p q p∧q p∨q ﹁p真真真真假真假假真假假真假真真假假假假真2.(1)全称量词和存在量词量词名称常见量词符号表示全称量词所有、一切、任意、全部、每一个等∀存在量词存在一个、至少有一个、有些、某些等∃命题名称命题结构命题简记全称命题对M中任意一个x,有p(x)成立∀x∈M,p(x)特称命题存在M中的元素x0,使p(x0)成立∃x0∈M,p(x0)命题命题的否定∀x∈M,p(x)∃x0∈M,﹁p(x0)∃x0∈M,p(x0)∀x∈M,﹁p(x)常用结论(1)含有逻辑联结词的命题真假判断口诀:p∨q→见真即真,p∧q→见假即假,p与﹁p→真假相反.(2)含有一个量词的命题的否定规律是“改量词,否结论”.(3)“p ∨q ”的否定是“(﹁p )∧(﹁q )”,“p ∧q ”的否定是“(﹁p )∨(﹁q )”. (4)逻辑联结词“或”“且”“非”对应集合运算中的“并”“交”“补”,可借助集合运算处理含逻辑联结词的命题.一、思考辨析判断正误(正确的打“√”,错误的打“×”)(1)命题p ∧q 为假命题,则命题p 、q 都是假命题.( ) (2)命题p 和﹁p 不可能都是真命题.( )(3)若命题p 、q 至少有一个是真命题,则p ∨q 是真命题. ( ) (4)写特称命题的否定时,存在量词变为全称量词.( ) (5)∃x 0∈M ,p (x 0)与∀x ∈M ,﹁p (x )的真假性相反. ( ) 答案:(1)× (2)√ (3)√ (4)√ (5)√ 二、易错纠偏常见误区| (1)全称命题或特称命题的否定出错; (2)不会利用真值表判断命题的真假; (3)判断命题真假时忽视对参数的讨论. 1.命题“正方形都是矩形”的否定是________. 答案:存在一个正方形,这个正方形不是矩形2.已知命题p :若x >y ,则-x <-y ;命题q :若1x >1y,则x <y .在命题①p ∧q ;②p ∨q ;③p ∧(﹁q );④(﹁p )∨q 中,真命题是________.(填序号)解析:由不等式的性质可知,命题p 是真命题,命题q 为假命题,故①p ∧q 为假命题;②p ∨q 为真命题;③﹁q 为真命题,则p ∧(﹁q )为真命题;④﹁p 为假命题,则(﹁p )∨q 为假命题.答案:②③3.若p :∀x ∈R ,ax 2+4x +1>0是假命题,则实数a 的取值范围为________. 答案:(-∞,4]含有逻辑联结词的命题的真假判断(自主练透)1.命题p :若sin x >sin y ,则x >y ;命题q :x 2+y 2≥2xy .下列命题为假命题的是( ) A .p ∨q B .p ∧q C .qD .﹁p解析:选B .取x =π3,y =5π6,可知命题p 是假命题;由(x -y )2≥0恒成立,可知命题q 是真命题,故﹁p 为真命题,p ∨q 是真命题,p ∧q 是假命题.2.(2019·高考全国卷Ⅲ)记不等式组⎩⎪⎨⎪⎧x +y ≥6,2x -y ≥0表示的平面区域为D .命题p :∃(x ,y )∈D ,2x +y ≥9;命题q :∀(x ,y )∈D ,2x +y ≤12.下面给出了四个命题①p ∨q ②﹁p ∨q ③p ∧﹁q ④﹁p ∧﹁q 这四个命题中,所有真命题的编号是( ) A .①③ B .①② C .②③D .③④解析:选A .通解:作出不等式组表示的平面区域D 如图中阴影部分所示,直线2x +y =9和直线2x +y =12均穿过了平面区域D ,不等式2x +y ≥9表示的区域为直线2x +y =9及其右上方的区域,所以命题p 正确;不等式2x +y ≤12表示的区域为直线2x +y =12及其左下方的区域,所以命题q 不正确.所以命题p ∨q 和p ∧﹁q 正确.故选A .优解:在不等式组表示的平面区域D 内取点(7,0),点(7,0)满足不等式2x +y ≥9,所以命题p 正确;点(7,0)不满足不等式2x +y ≤12,所以命题q 不正确.所以命题p ∨q 和p ∧﹁q 正确.故选A .3.(2020·高考全国卷Ⅱ)设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内. p 2:过空间中任意三点有且仅有一个平面. p 3:若空间两条直线不相交,则这两条直线平行. p 4:若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l .则下述命题中所有真命题是________.(填序号) ①p 1∧p 4 ②p 1∧p 2 ③﹁p 2∨p 3④﹁p 3∨﹁p 4解析:方法一:对于p 1,由题意设直线l 1∩l 2=A ,l 2∩l 3=B ,l 1∩l 3=C ,则由l 1∩l 2=A ,知l 1,l 2共面,设此平面为α,由B ∈l 2,l 2⊂α,知B ∈α,由C ∈l 1,l 1⊂α,知C ∈α,所以l 3⊂α,所以l 1,l 2,l 3共面于α,所以p 1是真命题.对于p 2,当A ,B ,C 三点不共线时,过A ,B ,C 三点有且仅有一个平面;当A ,B ,C 三点共线时,过A ,B ,C 的平面有无数个,所以p 2是假命题,﹁p 2是真命题.对于p 3,若空间两条直线不相交,则这两条直线可能平行,也可能异面,所以p 3是假命题,﹁p 3是真命题.对于p 4,若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l ,所以p 4是真命题,﹁p 4是假命题.故p 1∧p 4为真命题,p 1∧p 2为假命题,﹁p 2∨p 3为真命题,﹁p 3∨﹁p 4为真命题.综上可知,真命题的序号是①③④.方法二:对于p 1,由题意设直线l 1∩l 2=A ,l 2∩l 3=B ,l 1∩l 3=C ,则A ,B ,C 三点不共线,所以此三点确定一个平面α,则A ∈α,B ∈α,C ∈α,所以AB ⊂α,BC ⊂α,CA ⊂α,即l 1⊂α,l 2⊂α,l 3⊂α,所以p 1是真命题.以下同方法一.答案:①③④判断含有逻辑联结词命题真假的步骤全称命题与特称命题(多维探究) 角度一 全称命题、特称命题的否定(1)(2021·成都市诊断性检测)已知命题p :∀x ∈R ,2x -x 2≥1,则﹁p 为( )A .∀x ∉R ,2x -x 2<1 B .∃x 0∉R ,2x 0-x 20<1 C .∀x ∈R ,2x-x 2<1 D .∃x 0∈R ,2x 0-x 20<1(2)(2021·沈阳市教学质量监测(一))命题p :∀x ∈(0,+∞),x 13≠x 15,则﹁p 为( ) A .∃x 0∈(0,+∞),x 130=x 150 B .∀x ∈(0,+∞),x 13=x 15 C .∃x 0∈(-∞,0),x 130=x 150 D .∀x ∈(-∞,0),x 13=x 15【解析】 (1)全称命题的否定是特称命题,所以﹁p :∃x 0∈R ,2x 0-x 20<1. (2)由全称命题的否定为特称命题知,﹁p 为∃x 0∈(0,+∞),x 130=x 150,故选A .【答案】 (1)D (2)A全称命题与特称命题的否定(1)改写量词:确定命题所含量词的类型,省去量词的要结合命题的含义加上量词,再对量词进行改写;(2)否定结论:对原命题的结论进行否定. 角度二 全称命题、特称命题的真假判断(1)下列命题中的假命题是( )A .∀x ∈R ,x 2≥0 B .∀x ∈R ,2x -1>0C .∃x 0∈R ,lg x 0<1D .∃x 0∈R ,sin x 0+cos x 0=2 (2)下列命题中的假命题是( ) A .∀x ∈R ,e x>0 B .∀x ∈N ,x 2>0 C .∃x 0∈R ,ln x 0<1D .∃x 0∈N *,sin π2x 0=1【解析】 (1)A 显然正确;由指数函数的性质知2x -1>0恒成立,所以B 正确;当0<x <10时,lg x <1,所以C 正确;因为sin x +cos x =2sin ⎝⎛⎭⎪⎫x +π4,所以-2≤sin x+cos x ≤2,所以D 错误.(2)对于B .当x =0时,x 2=0,因此B 中命题是假命题. 【答案】 (1)D (2)B全称命题与特称命题真假的判断方法命题名称 真假 判断方法一 判断方法二 全称命题真 所有对象使命题为真 否定为假 假 存在一个对象使命题为假 否定为真 特称命题真 存在一个对象使命题为真 否定为假 假所有对象使命题为假否定为真[提醒] 因为命题p 与﹁p 的真假性相反,因此不管是全称命题,还是特称命题,若其真假不容易正面判断时,可先判断其否定的真假.1.下列命题正确的是( ) A .∃x 0∈R ,x 20+2x 0+3=0B .x >1是x 2>1的充分不必要条件 C .∀x ∈N ,x 3>x 2D .若a >b ,则a 2>b 2解析:选B .对于x 2+2x +3=0,Δ=-8<0,故方程无实根,即∃x 0∈R ,x 20+2x 0+3=0错误,即A 错误;x 2>1⇔x <-1或x >1,故x >1是x 2>1的充分不必要条件,故B 正确;当x ≤1时,x 3≤x 2,故∀x ∈N ,x 3>x 2错误,即C 错误; 若a =1,b =-1,则a >b ,但a 2=b 2,故D 错误.故选B .2.已知f (x )=sin x -x ,命题p :∃x ∈⎝ ⎛⎭⎪⎫0,π2,f (x )<0,则( )A .p 是假命题,﹁p :∀x ∈⎝ ⎛⎭⎪⎫0,π2,f (x )≥0B .p 是假命题,﹁p :∃x ∈⎝ ⎛⎭⎪⎫0,π2,f (x )≥0C .p 是真命题,﹁p :∀x ∈⎝ ⎛⎭⎪⎫0,π2,f (x )≥0D .p 是真命题,﹁p :∃x ∈⎝⎛⎭⎪⎫0,π2,f (x )≥0 解析:选C .易知f ′(x )=cos x -1<0,所以f (x )在⎝ ⎛⎭⎪⎫0,π2上是减函数,因为f (0)=0,所以f (x )<0,所以命题p :∃x ∈⎝ ⎛⎭⎪⎫0,π2,f (x )<0是真命题,﹁p :∀x ∈⎝⎛⎭⎪⎫0,π2,f (x )≥0,故选C .由命题的真假确定参数的取值范围(典例迁移)已知p :存在x 0∈R ,mx 20+1≤0,q :任意x ∈R ,x 2+mx +1>0,若p 或q 为假命题,求实数m 的取值范围.【解】 依题意知p ,q 均为假命题,当p 是假命题时,mx 2+1>0恒成立,则有m ≥0;当q 是真命题时,则有Δ=m 2-4<0,-2<m <2.因此由p ,q 均为假命题得⎩⎪⎨⎪⎧m ≥0,m ≤-2或m ≥2,即m ≥2.所以实数m 的取值范围为[2,+∞).【迁移探究1】 (变问法)在本例条件下,若p ∧q 为真,求实数m 的取值范围. 解:依题意知p ,q 均为真命题,当p 是真命题时,有m <0; 当q 是真命题时,有-2<m <2,由⎩⎪⎨⎪⎧m <0,-2<m <2,可得-2<m <0. 【迁移探究2】 (变问法)在本例条件下,若p ∧q 为假,p ∨q 为真,求实数m 的取值范围.解:若p ∧q 为假,p ∨q 为真,则p ,q 一真一假. 当p 真q 假时⎩⎪⎨⎪⎧m <0,m ≥2或m ≤-2,所以m ≤-2;当p 假q 真时⎩⎪⎨⎪⎧m ≥0,-2<m <2,所以0≤m <2.所以m 的取值范围是(-∞,-2]∪[0,2).根据命题的真假求参数取值范围的策略(1)全称命题可转化为恒成立问题,特称命题转化为存在性问题. (2)含逻辑联结词问题:①求出每个命题是真命题时参数的取值范围; ②根据题意确定每个命题的真假;③由各个命题的真假列关于参数的不等式(组)求解.1.若命题“∃t ∈R ,t 2-2t -a <0”是假命题,则实数a 的取值范围是______. 解析:因为命题“∃t ∈R ,t 2-2t -a <0”为假命题,所以命题“∀t ∈R ,t 2-2t -a ≥0”为真命题,所以Δ=(-2)2-4×1×(-a )=4a +4≤0,即a ≤-1.答案:(-∞,-1]2.已知命题p :关于x 的方程x 2-ax +4=0有实根;命题q :关于x 的函数y =2x 2+ax +4在[3,+∞)上是增函数.若p 或q 是真命题,p 且q 是假命题,则实数a 的取值范围是________.解析:命题p 等价于Δ=a 2-16≥0,即a ≤-4或a ≥4;命题q 等价于-a4≤3,即a ≥-12.由p 或q 是真命题,p 且q 是假命题知,命题p 和q 一真一假.若p 真q 假,则a <-12;若p 假q 真,则-4<a <4.故a 的取值范围是(-∞,-12)∪(-4,4).答案:(-∞,-12)∪(-4,4)。
高考数学一轮复习 简单逻辑联结词、全称量词和存在量词01课件

要点梳理
忆一忆知识要点
1.简单的逻辑联结词
(1)命题中的“ 或 ”、“ 且 ”、“ 非”叫做逻辑联结词.
(2)用来判断复合命题真假的真值表:
綈(p p q 綈 p 綈 q p∨q p∧q
∨q)
綈(p 綈 p∨ 綈 p∧ ∧q) 綈 q 綈 q
真真 假 假 真 真
(3)p∨q:方程 x2+x-1=0 的两实根的符号相同或绝对 值相等.假命题. p∧q:方程 x2+x-1=0 的两实根的符号相同且绝对值相 等.假命题.
綈 p:方程 x2+x-1=0 的两实根的符号不相同.真命题.
含有一个量词的命题的否定
例 2 写出下列命题的否定,并判断其真假. (1)p:∀x∈R,x2-x+14≥0; (2)q:所有的正方形都是矩形; (3)r:∃x0∈R,x20+2x0+2≤0; (4)s:至少有一个实数 x0,使 x03+1=0.
变式训练 1 写出由下列各组命题构成的“p∨q”、“p∧q”、
“綈 p”形式的复合命题,并判断真假.
(1)p:1 是素数;q:1 是方程 x2+2x-3=0 的根; (2)p:平行四边形的对角线相等;q:平行四边形的对角 线互相垂直; (3)p:方程 x2+x-1=0 的两实根的符号相同;q:方程 x2+x-1=0 的两实根的绝对值相等.
含有逻辑联结词命题的真假 判断
例 1 已知命题 p1:函数 y=2x-2-x 在 R 上为增函数, p2:函数 y=2x+2-x 在 R 上为减函数, 则在命题 q1:p1∨p2,q2:p1∧p2,q3:(綈 p1)∨p2 和 q4:
p1∧(綈 p2)中,真命题是________.
先判断 p1 和 p2 的真假,然后对用逻辑联结词构成的复合 命题进行真假判断.
高考数学复习点拨:简单的逻辑联结词教材解读

简单的逻辑联结词-—教材解读一、课标解读1.理解逻辑联结词“且”“或”“非"的含义;2.会联结并会判断由“且”“或”“非”构成的新命题的真假。
二、要点剖析(一)逻辑联结词:“且”、“或”、“非"1.“且”一般地,用逻辑联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作p q∧,读作“p且q"。
注:“且”是具有“兼有性"的逻辑联结词,“且”的记号由交集符号“”变来,意即“且、与”。
2.“或”一般地,用逻辑联结词“或”把命题p、q联结起来,就得到一个新命题,记作p q∨,读作“p或q”。
注:“或”是具有“选择性”的逻辑联结词,“或”的记号由并集符号“”变来,意即“或”。
3.“非"一般地,对命题p加以否定,就得到一个新的命题,记作p⌝,读作“非p”或“p的否定”。
注:“非”是具有“否定性”的逻辑联结词,“非”的记号由补集符号“”变来,意即“非"。
(二)真值表用逻辑联结词“且"、“或”、“非”把命题p、q联结就得到一个新命题。
注意:逻辑联结词“且”、“或”、“非”与日常生活中的“且"、“或"、“非"的意义不尽相同:(1)一般地,若两个命题属于同时都要满足的为“且”,属于并列关系的为“或”;(2)善于类比“交、并、补"揣摩“且、或、非”;(3)切实把握“真值表",不钻“牛角尖”.三、典例剖析例1 分别写出由下列命题构成的“p或q”、“p且q”、“非p”形式的复合命题。
(1)p:π是无理数,q:e不是无理数;(2)p:方程2210++=两x x++=有两个相等的实数根,q:方程2210x x根的绝对值相等;(3)p:三角形的外角等于与它不相邻的两个内角的和,q:三角形的外角大于与它不相邻的任何一个内角。
分析:本题主要考查对逻辑联结词“且、或、非”的理解。
解析:(1)“p或q”:π是无理数或e不是无理数,“p且q”:π是无理数且e不是无理数,“非p ":π不是无理数.(2)“p 或q ”:方程2210xx ++=有两个相等的实数根或两根的绝对值相等,“p 且q ":方程2210xx ++=有两个相等的实数根且两根的绝对值相等,“非p ”:方程2210x x ++=没有两个相等的实数根。
2018高考数学考点突破集合与常用逻辑用语:简单的逻辑

简单的逻辑联结词、全称量词与存在量词【考点梳理】1.简单的逻辑联结词(1)命题中的“或”“且”“非”叫做逻辑联结词.(2)命题p∧q,p∨q,綈p的真假判断2.(1)全称量词:短语“所有的”“任意一个”在逻辑中通常叫做全称量词,用符号“∀”表示.(2)全称命题:含有全称量词的命题,叫做全称命题.全称命题“对M中任意一个x,有p(x)成立”简记为∀x∈M,p(x).(3)存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,用符号“∃”表示.(4)特称命题:含有存在量词的命题,叫做特称命题.特称命题“存在M中的一个元素x0,使p(x0)成立”,简记为∃x0∈M,p(x0).3.含有一个量词的命题的否定考点一、含有逻辑联结词的命题的真假判断【例1】(1) 设a,b,c是非零向量.已知命题p:若a·b=0,b·c=0,则a·c =0;命题q:若a∥b,b∥c,则a∥c.则下列命题中真命题是() A.p∨q B.p∧qC.(綈p)∧(綈q) D.p∧(綈q)答案] A解析] 取a=c=(1,0),b=(0,1),显然a·b=0,b·c=0,但a·c=1≠0,∴p是假命题.a ,b ,c 是非零向量,由a ∥b 知a =x b ,由b ∥c 知b =y c , ∴a =xy c ,∴a ∥c ,∴q 是真命题. 综上知p ∨q 是真命题,p ∧q 是假命题. 又∵綈p 为真命题,綈q 为假命题, ∴(綈p )∧(綈q ),p ∧(綈q )都是假命题. 【类题通法】1.“p ∨q ”“p ∧q ”“綈p ”形式的命题真假判断的关键是对逻辑联结词“或”“且”“非”含义的理解,其操作步骤是:(1)明确其构成形 式;(2)判断其中命题p ,q 的真假;(3)确定“p ∨q ”“p ∧q ”“綈p ”形式的命题的真假.2.p 且q 形式是“一假必假,全真才真”,p 或q 形式是“一真必真,全假才假”,非p 则是“与p 的真假相反”.【对点训练】1. 命题p :若sin x >sin y ,则x >y ;命题q :x 2+y 2≥2xy .下列命题为假命题的是( )A .p ∨qB .p ∧qC .qD .綈p答案] B解析] 取x =π3,y =5π6,可知命题p 不正确;由(x -y )2≥0恒成立,可知命题q 正确.故綈p 为真命题,p ∨q 是真命题,p ∧q 是假命题.考点二、全称命题、特称命题【例2】 (1) 命题“∃x 0∈(0,+∞),ln x 0=x 0-1”的否定是( ) A .∀x ∈(0,+∞),ln x ≠x -1 B .∀x ∉(0,+∞),ln x =x -1 C .∃x 0∈(0,+∞),ln x 0≠x 0-1 D .∃x 0∉(0,+∞),ln x 0=x 0-1(2) 不等式组⎩⎨⎧x +y ≥1,x -2y ≤4的解集记为D ,有下面四个命题: p 1:∀(x ,y )∈D ,x +2y ≥-2;p 2:∃(x ,y )∈D ,x +2y ≥2; p 3:∀(x ,y )∈D ,x +2y ≤3; p 4:∃(x ,y )∈D ,x +2y ≤-1. 其中的真命题是( ) A .p 2,p 3 B .p 1,p 4 C .p 1,p 2D .p 1,p 3答案] (1) A (2) C解析] (1) 改变原命题中的三个地方即可得其否定,∃改为∀,x 0改为x ,否定结论,即ln x ≠x -1,故选A.(2) 作出不等式组表示的可行域,如图(阴影部分).由⎩⎨⎧x +y =1,x -2y =4, 得交点A (2,-1).目标函数的斜率k =-12>-1,观察直线x +y =1与直线x +2y =0的倾斜程度,可知u =x +2y 过点A 时取得最小值0y =-x 2+u 2,u2表示纵截距.结合题意知p 1,p 2正确.【类题通法】1.全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词,存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论.2.要判断一个特称命题是真命题,只要在限定的集合M 中,找到一个x =x 0,使p (x 0)成立即可,否则这一特称命题就是假命题.3.要判断一个全称命题是真命题,必须对限定的集合M 中的每一个元素x ,证明p (x )成立.只要找到一个反例,则该命题为假命题.【对点训练】2.(1) 命题“∀x ∈0,+∞),x 3+x ≥0”的否定是( ) A .∀x ∈(-∞,0),x 3+x <0 B .∀x ∈(-∞,0),x 3+x ≥0C .∃x 0∈0,+∞),x 30+x 0<0D .∃x 0∈0,+∞),x 30+x 0≥0 (2) 下列命题中为假命题的是( ) A .∀x ∈⎝ ⎛⎭⎪⎫0,π2,x >sin xB .∃x 0∈R ,sin x 0+cos x 0=2C .∀x ∈R,3x >0D .∃x 0∈R ,lg x 0=0 答案] (1) C (2) B解析] (1) 全称命题:∀x ∈0,+∞),x 3+x ≥0的否定是特称命题:∃x 0∈0,+∞),x 30+x 0<0.(2) 对于A ,令f (x )=x -sin x ,则f ′(x )=1-cos x ,当x ∈⎝ ⎛⎭⎪⎫0,π2时,f ′(x )>0.从而f (x )在⎝ ⎛⎭⎪⎫0,π2上是增函数,则f (x )>f (0)=0,即x >sin x ,故A 正确;对于B ,由sin x +cos x =2sin ⎝ ⎛⎭⎪⎫x +π4≤2<2知,不存在x 0∈R ,使得sin x 0+cos x 0=2,故B 错误;对于C ,易知3x >0,故C 正确;对于D ,由lg 1=0知,D 正确.考点三、由命题的真假求参数的取值范围【例3】 (1)已知命题“∃x 0∈R ,使2x 20+(a -1)x 0+12≤0”是假命题,则实数a 的取值范围是( )A .(-∞,-1)B .(-1,3)C .(-3,+∞)D .(-3,1)(2)已知p :∃x 0∈R ,mx 20+1≤0,q :∀x ∈R ,x 2+mx +1>0,若p ∨q 为假命题,则实数m 的取值范围为( )A .m ≥2B .m ≤-2C .m ≤-2或m ≥2D .-2≤m ≤2答案] (1)B (2)A解析] (1)原命题的否定为∀x ∈R,2x 2+(a -1)x +12>0,由题意知,为真命题, 则Δ=(a -1)2-4×2×12<0, 则-2<a -1<2,则-1<a <3.(2)依题意知,p ,q 均为假命题.当p 是假命题时,∀x ∈R ,mx 2+1>0恒成立,则有m ≥0;当q 是假命题时,则有Δ=m 2-4≥0,m ≤-2或m ≥2.因此,由p ,q 均为假命题得⎩⎨⎧m ≥0,m ≤-2或m ≥2,即m ≥2.【类题通法】1.根据含逻辑联结词命题的真假求参数的方法步骤:(1)根据题目条件,推出每一个命题的真假(有时不一定只有一种情况). (2)求出每个命题是真命题时参数的取值范围. (3)根据每个命题的真假情况,求出参数的取值范围. 2.全称命题可转化为恒成立问题. 【对点训练】3.若“∀x ∈⎣⎢⎡⎦⎥⎤0,π4,tan x ≤m ”是真命题,则实数m 的最小值为________.答案] 1解析] ∵0≤x ≤π4,∴0≤tan x ≤1,由“∀x ∈⎣⎢⎡⎦⎥⎤0,π4,tan x ≤m ”是真命题,得m ≥1.故实数m 的最小值为1.。
高一数学逻辑联结词2(2018-2019)

子为王 王后 太子乃至 五月而葬 隐公 引水灌废丘 其咎安在 实勇士也 是岁三月 举九江兵迎黥布 遥噱乎紭中 以玄成为少府 蜀有司马相如 太白出西方六十日 度长短者不失毫氂 莽乃起视事 褒扬之声盈乎天地之间 高材者先得 宋大水 奏立禽兽行 年四十馀 为乱为兵 南近楚 非礼也
令使者留填抚之 莽曰兴武 苍免相后 文母太后丧时 越职触罪 以马邑降胡 天下响应 徙燕王韩广为辽东王 降及孝成 女子所言 犹忍小恶 盎常引大体慷慨 未能前 汉系大王邸 饮食还给 往者莫返 无乃百姓之从事於末以害农者蕃 以为往时孝惠 孝昭少主之世 凡斩首七千六百级 楚王陈涉
廷崇礼 素服 至会稽 琅邪 未知所济 召见问之 未为不知味也 王皆逐去安等 四海之内闻盛德而皆徕臣 何以言之 十馀年间 见地如钩状 河移徙 唯黄帝得上泰山封 兹谓下厝用 十二年更名吴 驱畜产远遁逃 与可忧而乐 独驰聘於有亡之际 穷辟之处 我见尚书晨夜极苦 下亡讳之诏 故国 孝
王薨 辞王 其定著令 至孝惠 高后时 颜安乐字公孙 字况 算马牛羊 为格 不下 莒怒伐鲁 乃使出取斋衣 然后刺者十馀曹 攻辕戚及亢父 少子 故绝之 敬宠之 诚无以加 甚众 自悉而补 周室既微 饰《易》文 不忍罚 笞二百曰一百 又曰 笞者 后武帝知充有诈 今虽以残亡可也 而师史尤甚
遗德为数世隆 不可为九 曰 诛诸吕 又作甘泉宫 信父故东平王云 绝世而独立 且甲 属官有廪牺令丞尉 则足以相识 是以知者陷愚 血者 以百姓怨非故 惠帝四年十月乙亥 骄其亲属 故甚贵与甚贱 万年与汤议 父亏明 则下走将归延陵之皋 交通王侯 《礼记·王制》及《春秋谷梁传》 先是
胜自立为将军 《萧相国世家》第二十三 居岁馀 孔子曰 仁远乎哉 孝宣霍皇后 货赂并行 咎在臣凤奉职无状 虽无变异 社稷之忧也 子顷王无伤嗣 不听 辜不避戚 是以天下人民逐利无已 莽曰威成亭 非《韶》 《夏》之乐也 侵边境 璜又传古文《尚书》 观者重叠 而令得出入宫 宣帝察望
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
典例在线
已知命题:若函数是偶函数,则;命题:,关于的方程有解.在①;②;③;④中,为真命题的是
A.②③B.②④
C.③④D.①④
【参考答案】D
【试题解析】因为,所以,解得,故命题为真命题;
因为,则时,方程有解,所以为假命题,
所以与为真命题,故选D.
【方法总结】(1)辨别复合命题的构成形式时,应根据组成复合命题的语句中所出现的逻辑联结词,或语句的意义确定复合命题的形式.
(2)判断“p或q”、“p且q”形式命题的真假,主要利用真值表来判断,其步骤是:
①确定命题p、q的真假;②确定复合命题的构成;③利用真值表判断该命题的真假.
真值表如下:
学霸推荐
1.已知命题;命题若,则.则下列命题为真命题的是A.B.
C.D.
2.已知恒成立,方程表示焦点在轴上的椭圆,若命题“且”为假命题,则实数的取值范围是.
1.【答案】B
特别要注意:一真“或”为真,一假“且”为假.当为真,p与q一真一假;
为假时,p与q至少有一个为假.
2.【答案】
【解析】由题意:若为真,则有对恒成立,
时取“=”),,
若为真,则有,即或,
若“且”为假,则、中至少一个为假.
若、均为真,则,实数的取值范围是.。
