巧用圆的平面几何性质处理解几题

合集下载

妙用圆的几何性质速解题

＂Ｙ
－
初中已经研究过．高中学习解析几何离不开平面
几何知识，尤其是圆的很多几何性质．若在解决相关问题时善于灵活运用圆的几何性质，仅可为不顺利得出解题思路扫除障碍、平道路。而且可铺
Ｂ
大大简化计算过程，高解题速度，增强求简意提
所＿ｎＯ一以ＰｔＡ。ａＰＺ
故所求直线方程为一．
一，譬
４，Ｐ是圆的弦．直线ＡＰ与ＡＱ倾斜角互补，）Ｑ若
求证：直线Ｐ的斜率为定值．Ｑ解：如图４作ＡＡ，上ｚ轴交Ｏｏ于Ａ，则
解设（ ’ （，：一Ｉ，碚一蒜）
（，，Ｌｌ２≠ ｏ，ｌ≠ ２Ｙ）｜，Ｙ．
一
横坐标的取值范围．解：如图３以０为圆心，Ｏ，Ｆ，的长为半径作
圆Ｙ一，椭等十ｚ一。５与圆等一ｌ立解两卜联，得曲
又该
所以一
鼬
（一
＋２３（一）３一ｏ解得一１一，．
所以，７＝３一３．
ｆＣｉｚ一￣， — Ｏ／即点Ｃ为（／６０．￣，） “
１３圆内角大于圆周角．．
一
例２如图ｌ设Ａ、，Ｂ为抛物线Ｙ。一４上如
由・一・卷
得Ｙ，？一一ｌ６
：
—，ｏ
①
线交点的横坐标分别为一，．

巧用平面几何解高中数学题

x2 + xz + z2 > y2 + yz + z2 .
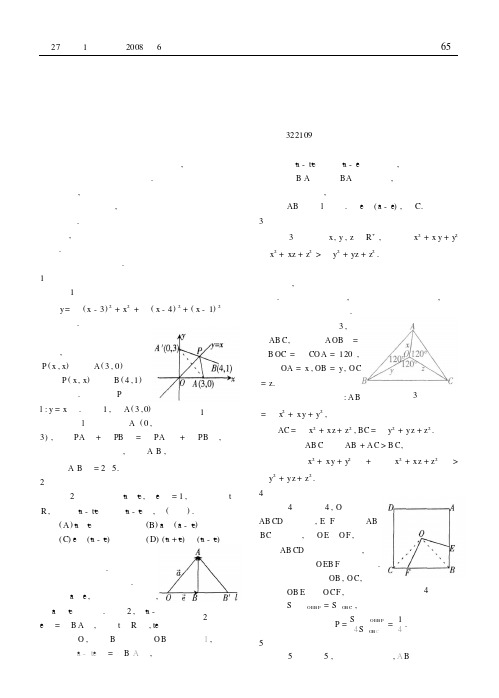
x2 + x y + y2
解析从整体上联想到 “三角形两边之和大于第三边” , 而三个被开方数的结构又可以联想到余弦定理. 结合这两个方面 , 设法构造一个三角形 , 利用平面几何知识解决问题 . 证明如图 3 , 作 △AB C, 使 ∠ A OB
方形 AB CD 内部任取一点 , 求该点落在四边形 O EB F 内的概率. 解析连接 OB , O C, 容易证明 △OB E ≌ △ O CF , ∴S四边形O EB F = S △OB C , 图2 故所求的概率 P =
S四边形O EB F 1 = . 4 S △OB C 4
图4
=
例 1 求函数
y= ( x - 3 ) 2 + x2 + ( x - 4 ) 2 + ( x - 1) 2
的最小值 . 解析由两点距离公式可知 , 该函数的几何意义是点
P ( x , x) 到点 A ( 3 , 0 ) 的距离
∠ B OC = ∠CO A = 120° , 且令 OA = x , OB = y , O C
∴
x2 + x y + y2
2
+
x2 + x z + z 2
>
y + yz + z . 4 在概率中的应用
例 2 已知向量 � a≠ � e , │� e │ = 1 , 对于任意 t ∈
). R , 恒有 │ � a - t� e │≥│ � a- � e │, 则 ( ( A) � a⊥ � e (B ) � a ⊥( � a- � e) ( C) � e ⊥( � a- � e) ( D) ( � a +� e) ⊥( � a- � e)

专题1 巧构圆，妙解题（含答案）

第一章圆专题1巧构圆，妙解题知识解读在处理平面几何中的许多问题时，常常需要借助圆的性质，问题才能解决.而有时候我们需要的圆并不存在，这就需要我们能利用已知的条件，借助图形的特点把实际存在的圆找出来，从而运用圆中的性质来解决问题，往往有事半功倍的效果，使问题获得巧解或简解，这是我们解题必须要掌握的技巧. 作辅助圆的常用依据有以下几种：①圆的定义：若几个点到某个固定点的距离相等，则这几个点在同一个圆上； ②有公共斜边的两个直角三角形的顶点在同一个圆上；③对角互补的四边形四个顶点在同一个圆上，简记为：对角互补，四点共圆；④若两个三角形有一条公共边，这条边所对的角相等，并且在公共边的同侧，则这两个三角形有公共的外接圆，简记为：同旁张等角，四点共圆.培优学案典例示范例1将线段AB 绕点A 逆时针旋转60°得到线段AC ，继续旋转(0120)αα<<得到线段AD ，连接CD . (1)连接BD .①如图1-1-1①，若α=80°，则∠BDC 的度数为；②在第二次旋转过程中，请探究∠BDC 的大小是否改变？若不变，求出∠BDC 的度数；若改变，请说明理由；(2)如图1-1-1②，以AB 为斜边作Rt △ABE ，使得∠B =∠ACD ，连接CE ，DE .若∠CED =90°，求α的值.图1-1-1②①EDCBADCBA【提示】(1)①∠BDC =∠ADC -∠ADB ，利用“等边对等角及三角形内角和为180°”可求出∠BDC 为30°； ②由题意知，AB =AC =AD ，则点B ，C ，D 在以A 为圆心，AB 为半径的圆上，利用“一条弧所对的圆周角等于它所对的圆心角的一半”可快速求出∠BDC 仍然为30°；(2)过点A 作AM ⊥CD 于点M ，连接EM ，证明“点A ，C ，D 在以M 为圆心，MC 为半径的圆上”. 【解答】跟踪训练如图1-1-2，菱形ABCD 中，∠B =60°，点E 在边BC 上，点F 在边CD 上.若∠EAF =60°，求证：△AEF是等边三角形.【提示】不难发现∠EAF +∠ECF =60°+120°=180°，所以点A ，E ，C ，F 共圆，再利用“同弧所对的圆周角相等”获证.图1-1-2BFEDC A【解答】例2 (1)如图1-1-3①，正方形ABCD 中，点E 是BC 边上的任意一点，∠AEF =90°，且EF 交正方形外角平分线CF 于点F .求证：AE =EF ；(2)若把(1)中的条件“点E 是BC 边上的任意一点”，改为“点E 是BC 边延长线上的一点”，其余条件不变，如图1-1-3②，那么结论AE =EF 是否还成立？若成立，请证明；若不成立，请说明理由.①②图1-1-3A B E CFDFDCEBA【提示】连接AC ，AF ，显然∠ACF =∠AEF =90°，所以A ，E ，C ，F 四点在以AF 为直径的圆上. (1)如图1-1-4①，当点E 在BC 边上，则∠AFE =∠ACE =45°，于是△AEF 是等腰直角三角形，AE =EF 获证；(2)如图1-1-4②，当点E 在BC 边的延长线上，则∠F AE =∠FCE =45°，于是△AEF 是等腰直角三角形，AE=EF 获证.OOABECDFDFEB图1-1-4②①【拓展】本题将“正方形”改为“正三角形”，“∠AEF =90°”相应改为“∠AEF =60°”，仍然可以运用构造“辅助圆”的思路.还可进一步拓展为“正n 边形”，360180AEF n=-∠，仍然可延续这种思路，读者可自己完成. 【解答】跟踪训练已知，将一副三角板(Rt △ABC 和Rt △DEF )如图1-1-5①摆放，点E ，A ，D ，B 在一条直线上，且D 是AB的中点.将Rt △DEF 绕点D 顺时针方向旋转角(090)αα<<，在旋转过程中，直线DE ，AC 相交于点M ，直线DF ，BC 相交于点N ，分别过点M ，N 作直线AB 的垂线，垂足为G ，H . (1)如图1-1-5②，当α=30°时，求证：AG =DH ； (2)如图1-1-5③，当α=60°时，(1)中的结论是否成立？请写出你的结论，并说明理由； (3)当090α<<时，(1)中的结论是否成立？请写出你的结论，并根据图1-1-5④说明理由.③④图1-1-5②①BCD AEH G G H HGEAFD CB EAF D C (N )BFE DCBA【提示】本题除了常规解法外，还可考虑构造“辅助圆”. 【解答】例3 已知，在△ABC 中，AB =AC ，过A 点的直线a 从与边AC 重合的位置开始绕点A 按顺时针方向旋转角θ，直线a 交BC 边于点P (点P 不与点B ，点C 重合)，△BMN 的边MN 始终在直线a 上(点M 在点N 的上方)，且BM =BN ，连接CN . (1)当∠BAC =∠MBN =90°时.①如图1-1-6①，当θ=45时，∠ANC 的度数为；②如图1-1-6②，当45θ≠时，①中的结论是否发生变化？说明理由；(2)如图1-1-6③，当∠BAC =∠MBN ≠90°时，请直接写出∠ANC 与∠BAC 之间的数量关系，不必证明.③①②图1-1-6MaA BPN CM BA CP Naa NPCA (M )Bθθθ【提示】由于在旋转过程中不变的关系是：∠BAC =∠MBN ，AB =AC ，BM =BN ，易知∠ABC =∠ACB =∠BMN =∠BNM .由∠ACB =∠BNM 可知A ，B ，N ，C 四个点在同一个圆上(如图1-1-7)，则∠ANC =∠ABC =1902BAC -∠，这样思考，所有问题都会迎刃而解.①a N PCABM CNPBAaM 图1-1-7②【解答】跟踪训练在△ABC 中，BA =BC ，∠BAC =α，M 是AC 的中点，P 是线段BM 上的动点，将线段P A 绕点P 顺时针旋转2α得到线段PQ . (1)若α=60°且点P 与点M 重合(如图1-1-8①)，线段CQ 的延长线交射线BM 于点D ，请补全图形，并写出∠CDB 的度数；(2)在图1-1-8②中，点P 不与点B ，M 重合，线段CQ 的延长线与射线BM 交于点D ，猜想∠CDB 的大小(用含α的代数式表示)，并加以证明；(3)对于适当大小的α，当点P 在线段BM 上运动到某一位置(不与点B ，M 重合)时，能使得线段CQ 的延长线与射线BM 交于点D ，且PQ =QD ，请直接写出α的范围.①图1-1-8②DP BACMQQM (P )CB A【解答】例4如图1-1-9，点A 与点B 的坐标分别是（1，0），（5，0），点P 是该直角坐标系内的一个动点．（1）使∠APB ＝30°的点P 有个；（2）若点P 在y 轴上，且∠APB ＝30°，求满足条件的点P 的坐标；（3）当点P 在y 轴上移动时，∠APB 是否有最大值？若有，求点P 的坐标，并说明此时∠APB 最大的理由；若没有，也请说明理由．图1-1-9【提示】（1）已知点A 、点B 是定点，要使∠APB ＝30°，只需点P 在过点A 、点B 的圆上，且弧AB所对的圆心角为60°即可，显然符合条件的点P有无数个．（2）结合（1）中的分析可知：当点P在y轴的正半轴上时，点P是（1）中的圆与y轴的交点，借助于垂径定理、等边三角形的性质、勾股定理等知识即可求出符合条件的点P的坐标；当点P在y轴的负半轴上时，同理可求出符合条件的点P的坐标．（3）由三角形外角的性质可证得：在同圆或等圆中，同弧所对的圆周角大于同弧所对的圆外角．要∠APB最大，只需构造过点A、点B且与y轴相切的圆，切点就是使得∠APB最大的点P，然后结合切线的性质、三角形外角的性质、矩形的判定与性质、勾股定理等知识即可解决问题．【解答】跟踪训练已知，如图1-1-10①，，∠MON＝60°，点A，B为射线OM，ON上的动点（点A，B不与点O重合），且AB＝43，在∠MON的内部，△AOB的外部有一点P，且AP＝BP，∠APB＝120°．（1）求AP的长；（2）求证：点P在∠MON的平分线上．（3）如图1-1-10②，点C，D，E，F分别是四边形AOBP的边AO，OB，BP，P A的中点，连接CD，DE，EF，FC，OP．若四边形CDEF的周长用t表示，请直接写出t的取值范围．图1-1-10 【解答】例5已知，在矩形ABCD中，AB＝a，BC＝b，动点M从点A出发沿边AD向点D运动．（1）如图1，当b＝2a，点M运动到边AD的中点时，请证明∠BMC＝90°；（2）如图2，当b＞2a时，点M在运动的过程中，是否存在∠BMC＝90°，若存在，请给与证明；若不存在，请说明理由；（3）如图3，当b＜2a时，（2）中的结论是否仍然成立？请说明理由．、① ②③图1-1-11【提示】本题除了建立方程模型，将问题转化为方程是否有解的判断外，还可以通过构造辅助圆，将问题转化为直线与圆的位置关系来讨论．【解答】跟踪训练1.如图1-1-12，直线y＝﹣x+3与x，y轴分别交于点A，B，与反比例函数的图象交于点P（2，1）．（1）求该反比例函数的关系式；（2）设PC⊥y轴于点C，点A关于y轴的对称点为A′；①求△A′BC的周长和sin∠BA′C的值；②对大于1的常数m，求x轴上的点M的坐标，使得sin∠BMC1m．图1-1-12【提示】（1）①由直线y=-x+3写出OA=3，OB=3；由等腰直角三角形的边长关系，可得AB2；由PC⊥y轴，可得QC=1，BC=2；由对称知A'B=AB2，OA'=0A=3，然后用勾股定理求出A'C的长，也就可以求出△A'BC的周长；（2）②如果选用上一题的思路求∠BMC的正弦值，会陷入计算的麻烦，这里采用转化的思想，找到△BCM的外接圆，把∠BCM转化为圆心角的一半，即图中的∠BMC=∠CND，从而把m转化为△BCM的外接圆的半径，另外还应分类讨论。

巧解初中几何问题——以构造辅助圆为例

２０２３年１２月下半月㊀解法探究㊀㊀㊀㊀巧解初中几何问题以构造辅助圆为例◉江苏省靖江市外国语龙馨园学校㊀徐㊀乐㊀㊀圆是初中数学平面几何中非常重要的一个知识点,与初中数学中其他几何问题有着紧密的联系．所以在解决几何问题时,一些无法利用常规思路求解的综合问题可以尝试通过构造辅助圆的方式来解决．因此,在初中数学几何问题解题教学中,教会学生如何正确使用辅助圆来巧解几何问题是教师需要重点研究的问题．下面将通过例题对辅助圆的应用进行说明．１角的问题例１㊀在әA B C 中,A B ＝A C ,øA B C 的平分线交A C 于点D ,已知B C ＝B D ＋A D ,求øA 的度数．分析:根据题中所给已知条件,可以判定әA B C为等腰三角形,但是想要根据已知条件通过常规方式求øA 的度数存在一定困难．结合题中所给的角平分线,可以联想圆中共顶点的角的问题,作әA B D 的外图１接圆,与әA B C 的B C 边交于点E ,连接D E ,如图１．根据B D 是øA B C 的角平分线,可以知道A D ＝D E ,同时还能得到这个辅助圆为四边形A B E D 的外接圆．根据圆内接四边形的对角互补的性质可得øA B C ＝øE D C ,根据әA B C 为等腰三角形可知øA B C ＝øE D C ＝øC ,于是可得øB E D ＝２øC ,且әE D C 为等腰三角形．所以D E ＝C E ,则A D ＝D E ＝C E ,然后结合B C ＝B E ＋A D 得到B D ＝B E ,所以øB D E ＝øB E D ＝２øC ．这样就可以在әB D E 中计算øC 的度数,即１２øC ＋２øC ＋２øC ＝１８０ʎ,所以øC ＝４０ʎ,最后计算得出øA ＝１００ʎ．在初中数学几何问题中构造辅助线需要充分结合试题的情况来进行．本题中辅助圆的构造就是结合了本题所给定的角平分线的关系,根据相等的圆周角所对应的弧和弦长相等的性质来实现;然后通过辅助圆及相关线段关系来与相关角取得联系;最后利用三角形的性质求解．教师要对学生进行相应的引导,让学生掌握通过角的关系来构造辅助圆,进而借助辅助圆解决问题．２线段长度的问题图２例２㊀如图２所示,在R t әA B C中,A B ʅB C ,A B ＝６,B C ＝４,P 是R t әA B C 内部的一个动点,且满足øP A B ＝øP B C ,则线段C P 的最小值为(㊀㊀)．A．３２㊀㊀㊀㊀㊀㊀B ．２C ．８１３１３D．１２１３１３图３分析:根据A B ʅB C 可以知道øA B C ＝９０ʎ,结合øP A B ＝øP B C 可得到øA P B ＝９０ʎ,所以әA B P 是直角三角形．根据直角三角形中斜边的中线等于斜边的一半以及圆的直径所对的圆周角是９０ʎ,可知点P 在以A B 为直径的圆上．以A B 的中点O 为圆心,A B 为直径作圆,如图３所示．这样就可得到当P C 的值最小时,点P 正好在线段O C 上．因为A B ＝６,所以O B ＝３．在R t әO B C 中,B C ＝４,根据勾股定理得到O C ＝５,于是可求出P C 的最小值为２．所以正确答案是选项B ．例２的解题关键是需要判断点P 的轨迹,首先根据试题中所给定的关系得到øA P B ＝９０ʎ,结合直角三角形的性质和圆的性质很容易判断出点P 在以直线A B 为直径的圆上,然后就能够求解最小值．因此,在解题的过程中,只有认真分析题目条件,才能顺利找到解题思路．教师在进行解题教学时需要教会学生如何根据题目中所给定的已知条件来进行分析,从而找到解题思路．很多几何问题都是需要在解题的过程中才能够找到相应的解题思路,并不是通过对试题的观察就能得到解题思路的．因此结合已知条件来对试９７解法探究２０２３年１２月下半月㊀㊀㊀题中存在的关系进行分析,在解题的过程中发现解题思路,是解决问题最好的方式．教师需要引导学生先根据已知条件尝试找到解题的思路,进而解决问题．３三角形相似的问题例３㊀әA B C 中,A D 是øB A C 的外角平分线,交B C 的延长线于点D ,求证:B D D C ＝A BA C．分析:A B ,A C 是әA B C 的两条边,而B D ,D C则是线段B D 上的两条线段,根据所学的知识,要证明B D D C ＝A BA C ,线段成比例关系可以通过证明三角形相似来解决．因此需要将线段B A 延长至点F ,连接D F ,构建出әB A C ʐәB D F ,得到A B A C ＝B DD F,然后证明C D ＝D F 就可以了,从而将证明的关键转化为证明C D ＝D F ．结合题意,øB A C 的外角平分线交B C的图４延长线于点D ,如图４,根据例题１中的方式构造әA C D 的外接圆,B A 的延长线与圆交于点F ,连接D F ．根据圆的性质可以得到C D ＝D F ,通过相似三角形的证明就可以解决问题．几何问题中需要求证的结论存在线段比例关系或者线段等积关系时,都会涉及三角形相似或者全等的证明,通过构造圆为三角形相似或者全等提供条件,实现对问题的求解．在这个过程中,需要充分结合例题１和例题２中辅助圆构造的方式来找到相应的关系．４动点的问题图５例４㊀如图５所示,边长为３的等边三角形A B C ,D ,E 分别是B C ,A C 边上的两个动点,且B D ＝C E ,A D ,B E 交于点P ,求点P 的运动路径长和C P 的最小值．分析:首先需要对点P 的运动路径进行判定．根据等边三角形的相关性质和B D ＝C E 可以得到әA B D ɸәB C E ,这样就得到øC B E ＝øB A D ,然后通过øC B E ＋øA B P ＝６０ʎ得到øB A P ＋øA B P ＝øA P E ＝６０ʎ,于是øA P B ＝１２０ʎ．可以发现在点D 和点E 移动的过程中,øA P B ＝１２０ʎ是恒成立的,所以可以认为点P 在A B 为弦的圆上．假设弦A B 所在圆的圆心为O ,连接O P ,O A ,O B ,根据圆的性质㊁әA B C 的边长为３可计算出圆O 的半径O A ＝３,然后计算出点P 的运动路径长度为２３３π,C P 的最小值为３．解:由A B ＝B C ,øA B D ＝øB C E ,B D ＝C E 得әA B D ɸәB C E ．由øC B E ＋øA B P ＝６０ʎ,得øB A P ＋øA B P ＝øA P E ＝６０ʎ．所以øA P B ＝１２０ʎ．故点P 的运动轨迹是以A B 为弦的圆上的一段弧．图６如图６所示,作әA B P 的外接圆,圆心为O ,连接O A ,O B ,O P ,O C ．由O A ＝O B ,A C ＝B C ,得әA O C ɸәB O C ．所以øO A C ＝øO B C ,øA C O ＝øB C O ＝１２øA C B ＝３０ʎ,øA O C ＝øB O C ＝１２øA P B ＝６０ʎ．故øO A C ＝９０ʎ．根据勾股定理,可得O A ＝３,O C ＝２３．所以,弦A B 所对的弧长为３ˑ２３π＝２３３π;当O ,P ,C 三点共线时,C P 最小,且最小值为３．在三角形的动点问题中,如果动点与一条线段所构成的角度固定,则说明这个动点的轨迹是以这个线段为弦的圆上的一段弧,通过这个关系可以构造辅助圆,然后利用圆的性质来求解问题．本题给定的是正三角形,当然不同的三角形中所呈现的关系可能会存在差别,但是本质没有变化．例如,在例题２中通过计算所得到的角度为９０ʎ的特殊角,这个辅助圆的圆心就在直角三角形的斜边上．例４中这个角度为１２０ʎ,圆心在三角形的外部,通过辅助圆来充分利用圆的相关性质,能够更好地对问题进行求解,实现问题的解决．本文中对辅助圆在初中数学平面几何中的应用进行了总结,并通过相关例题对其用法进行了说明．在初中数学平面几何问题中巧用辅助圆能够优化试题解法,实现快速求解．因此,教师在解题教学的过程中需要对学生进行有效地引导,让学生掌握辅助圆的应用,从而提升解题能力;提升数学素养．Z０８。

圆综合题技巧大全

圆综合题技巧大全
1.理解圆的基本概念和性质：了解圆的中心、半径、直径、弧、弦等基本概念，并熟悉圆的切线、切点、切角等性质。

2.运用正弦、余弦、正切等三角函数：在求解圆的综合问题时，将圆分解成三角形或者扇形，运用三角函数求解问题。

3.运用勾股定理：求解圆心距离或圆心到某一点的距离时，可以将圆分解成直角三角形，运用勾股定理求解。

4.运用相似性质：当两个圆相似时，它们的半径比相等，可以利用这一性质求解问题。

5.运用平面几何知识：如利用圆的割线定理、相交弧定理、角平分线定理等解决问题。

6.运用向量知识：利用向量的始末点等代数性质求解圆的位置关系。

7.利用方程求解：通过列方程、解方程的方式求解圆的位置关系或者面积等问题。

8.综合思考：圆的综合问题往往不止一个解法，需要综合考虑题目所给信息，灵活运用不同的方法求解。

同时，需要进行多次验算，确保答案正确。

2019中考数学高频考点剖析专题23平面几何之圆的性质问题—解析卷

备考2019中考数学高频考点剖析专题二十三平面几何之圆的性质问题考点扫描☆聚焦中考圆的性质，是每年中考的必考内容之一，考查的知识点包括垂径定理、圆心角和圆周角等关系，总体来看，难度系数低，以选择填空为主。

也有少量的解析题。

解析题主要以关于圆的综合性问题为主。

结合2018年全国各地中考的实例，我们从三方面进行圆的基本性质问题的探讨：（1）垂径典例相关问题；（2）圆心角相关问题；（3）圆周角相关问题．考点剖析☆典型例题2018·湖北荆州·3分）如图，平面直角坐标系中，⊙P经过三点A（8，0），O（0，0），B （0，6），点D是⊙P上的一动点．当点D到弦OB的距离最大时，tan∠BOD的值是（）A．2 B．3 C．4 D．5【解答】解：连接AB，过点P作PE⊥BO，并延长EP交⊙P于点D，此时点D到弦OB的距离最大，∵A（8，0），B（0，6），∴AO=8，BO=6，∵∠BOA=90°，∴AB==10，则⊙P的半径为5，∵PE⊥BO，∴BE=EO=3，∴PE==4，∴ED=9，∴tan∠BOD==3．故选：B．3分）《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸）”，问这块圆形木材的直径是多少？”如图所示，请根据所学知识计算：圆形木材的直径AC是（）A．13寸B．20寸C．26寸D．28寸解：设⊙O的半径为r．在Rt△ADO中，AD=5，OD=r﹣1，OA=r，则有r2=52+（r﹣1）2，解得r=13，∴⊙O的直径为26寸．故选C．2018·四川自贡·4分）如图，若△ABC内接于半径为R的⊙O，且∠A=60°，连接OB、OC，则边BC的长为（）A． B． C． D．【分析】延长BO交圆于D，连接CD，则∠BCD=90°，∠D=∠A=60°；又BD=2R，根据锐角三角函数的定义得BC=R．【解答】解：延长BO交⊙O于D，连接CD，则∠BCD=90°，∠D=∠A=60°，∴∠CBD=30°，∵BD=2R，∴DC=R，∴BC=R，故选：D．【点评】此题综合运用了圆周角定理、直角三角形30°角的性质、勾股定理，注意：作直径构造直角三角形是解决本题的关键．2018•江苏扬州•3分）如图，已知⊙O的半径为2，△ABC内接于⊙O，∠ACB=135°，则AB= 2．【分析】根据圆内接四边形对边互补和同弧所对的圆心角是圆周角的二倍，可以求得∠AOB的度数，然后根据勾股定理即可求得AB的长．【解答】解：连接AD、AE、OA、OB，∵⊙O的半径为2，△ABC内接于⊙O，∠ACB=135°，∴∠ADB=45°，∴∠AOB=90°，∵OA=OB=2，∴AB=2，故答案为：2．【点评】本题考查三角形的外接圆和外心，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．2018·天津·10分）已知是的直径，弦与相交，.（Ⅰ）如图①，若为的中点，求和的大小；（Ⅱ）如图②，过点作的切线，与的延长线交于点，若，求的大小.【答案】（1）52°，45°；（2）26°【解析】分析：（Ⅰ）运用直径所对的圆周角是直角以及圆周角的度数等于它所对弧的度数求解即可；（Ⅱ）运用圆周角定理求解即可.详解：（Ⅰ）∵是的直径，∴.∴.又∴，∴.由为的中点，得.∴.∴.（Ⅱ）如图，连接.∵切于点，∴，即.由，又，∴是的外角，∴.∴.又，得.∴.点睛：本题考查了圆周角定理，切线的性质以及等腰三角形的性质，正确的作出辅助线是解题的关键．考点过关☆专项突破类型一垂径定理相关问题1. （2018•张家界）如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=（）A．8cm B．5cm C．3cm D．2cm【分析】根据垂径定理可得出CE的长度，在Rt△OCE中，利用勾股定理可得出OE的长度，再利用AE=AO+OE即可得出AE的长度．【解答】解：∵弦CD⊥AB于点E，CD=8cm，∴CE=CD=4cm．在Rt△OCE中，OC=5cm，CE=4cm，∴OE==3cm，∴AE=AO+OE=5+3=8cm．故选：A．2. （2018•通辽）已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是（）A．30° B．60°C．30°或150°D．60°或120°【分析】由图可知，OA=10，OD=5．根据特殊角的三角函数值求角度即可．【解答】解：由图可知，OA=10，OD=5，在Rt△OAD中，∵OA=10，OD=5，AD=，∴tan∠1=，∠1=60°，同理可得∠2=60°，∴∠AOB=∠1+∠2=60°+60°=120°，∴圆周角的度数是60°或120°．故选：D．3. （2018•安顺）已知⊙O的直径CD=10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB=8cm，则AC的长为（）A．2cm B．4cm C．2cm或4cm D．2cm或4cm【分析】先根据题意画出图形，由于点C的位置不能确定，故应分两种情况进行讨论．【解答】解：连接AC，AO，∵⊙O的直径CD=10cm，AB⊥CD，AB=8cm，∴AM=AB=×8=4cm，OD=OC=5cm，当C点位置如图1所示时，∵OA=5cm，AM=4cm，CD⊥AB，∴OM===3cm，∴CM=OC+OM=5+3=8cm，∴AC===4cm；当C点位置如图2所示时，同理可得OM=3cm，∵OC=5cm，∴MC=5﹣3=2cm，在Rt△AMC中，AC===2cm．故选：C．4. （2016海南4分）如图，AB是⊙O的直径，AC、BC是⊙O的弦，直径DE⊥AC于点P．若点D在优弧上，AB=8，BC=3，则DP= 5.5 ．【考点】圆周角定理；垂径定理．【分析】解：由AB和DE是⊙O的直径，可推出OA=OB=OD=4，∠C=90°，又有DE⊥AC，得到OP∥BC，于是有△AOP∽△ABC，根据相似三角形的性质即可得到结论．【解答】解：∵AB和DE是⊙O的直径，∴OA=OB=OD=4，∠C=90°，又∵DE⊥AC，∴OP∥BC，∴△AOP∽△ABC，∴，即，∴OP=1.5．∴DP=OP+OP=5.5，故答案为：5.5．【点评】本题主要考查了圆周角定理，平行线的判定，相似三角形的判定和性质，熟练掌握圆周角定理是解决问题的关键．5. （2018•孝感）已知⊙O的半径为10cm，AB，CD是⊙O的两条弦，AB∥CD，AB=16cm，CD=12cm，则弦AB和CD之间的距离是2或14 cm．【分析】分两种情况进行讨论：①弦AB和CD在圆心同侧；②弦AB和CD在圆心异侧；作出半径和弦心距，利用勾股定理和垂径定理求解即可，小心别漏解．【解答】解：①当弦AB和CD在圆心同侧时，如图，∵AB=16cm，CD=12cm，∴AE=8cm，CF=6cm，∵OA=OC=10cm，∴EO=6cm，OF=8cm，∴EF=OF﹣OE=2cm；②当弦AB和CD在圆心异侧时，如图，∵AB=16cm，CD=12cm，∴AF=8cm，CE=6cm，∵OA=OC=10cm，∴OF=6cm，OE=8cm，∴EF=OF+OE=14cm．∴AB与CD之间的距离为14cm或2cm．故答案为：2或14．6. （2018•杭州）如图，AB是⊙O的直轻，点C是半径OA的中点，过点C作DE⊥AB，交⊙O于D，E 两点，过点D作直径DF，连结AF，则∠DFA= 30°．【分析】利用垂径定理和三角函数得出∠CDO=30°，进而得出∠DOA=60°，利用圆周角定理得出∠DFA=30°即可．【解答】解：∵点C是半径OA的中点，∴OC=OD，∵DE⊥AB，∴∠CDO=30°，∴∠DOA=60°，∴∠DFA=30°，故答案为：30°7. （2018•宜昌）如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE 至点F，使EF=AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD=7，BE=2，求半圆和菱形ABFC的面积．【分析】（1）根据对角线相互平分的四边形是平行四边形，证明是平行四边形，再根据邻边相等的平行四边形是菱形即可证明；（2）设CD=x，连接BD．利用勾股定理构建方程即可解决问题；【解答】（1）证明：∵AB是直径，∴∠AEB=90°，∴AE⊥BC，∵AB=AC，∴BE=CE，∵AE=EF，∴四边形ABFC是平行四边形，∵AC=AB，∴四边形ABFC是菱形．（2）设CD=x．连接BD．∵AB是直径，∴∠ADB=∠BDC=90°，∴AB2﹣AD2=CB2﹣CD2，∴（7+x）2﹣72=42﹣x2，解得x=1或﹣8（舍弃）∴AC=8，BD==，∴S菱形ABFC=8．∴S半圆=•π•42=8π．类型二圆心角相关问题1. （2018•四川凉州•3分）如图，⊙O是△ABC的外接圆，已知∠ABO=50°，则∠ACB的大小为（）A．40° B．30°C．45°D．50°【分析】首先根据等腰三角形的性质及三角形内角和定理求出∠AOB的度数，再利用圆周角与圆心角的关系求出∠ACB的度数．【解答】解：△AOB中，OA=OB，∠ABO=50°，∴∠AOB=180°﹣2∠ABO=80°，∴∠ACB=∠AOB=40°，故选：A．【点评】本题主要考查了圆周角定理的应用，涉及到的知识点还有：等腰三角形的性质以及三角形内角和定理．2．（2018·山东青岛·3分）如图，点A、B、C、D在⊙O上，∠AOC=140°，点B是的中点，则∠D的度数是（）A．70° B．55° C．35.5° D．35°【分析】根据圆心角、弧、弦的关系定理得到∠AOB=∠AOC，再根据圆周角定理解答．【解答】解：连接OB，∵点B是的中点，∴∠AOB=∠AOC=70°，由圆周角定理得，∠D=∠AOB=35°，故选：D．【点评】本题考查的是圆心角、弧、弦的关系定理、圆周角定理，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．3．（2018·浙江衢州·3分）如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（）A．75°B．70°C．65°D．35°【考点】圆周角定理【分析】直接根据圆周角定理求解．【解答】解：∵∠ACB=35°，∴∠AOB=2∠ACB=70°．故选B．【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．4. （2018·广东·3分）同圆中，已知弧AB所对的圆心角是100°，则弧AB所对的圆周角是50°．【分析】直接利用圆周角定理求解．【解答】解：弧AB所对的圆心角是100°，则弧AB所对的圆周角为50°．故答案为50°．【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．类型三圆周角相关问题1．（2018•铜仁市）如图，已知圆心角∠AOB=110°，则圆周角∠ACB=（）A．55° B．110°C．120°D．125°【分析】根据圆周角定理进行求解．一条弧所对的圆周角等于它所对的圆心角的一半．【解答】解：根据圆周角定理，得∠ACB=（360°﹣∠AOB）=×250°=125°．故选：D．2．（2018•南充）如图，BC是⊙O的直径，A是⊙O上的一点，∠OAC=32°，则∠B的度数是（）A．58° B．60° C．64° D．68°【分析】根据半径相等，得出OC=OA，进而得出∠C=32°，利用直径和圆周角定理解答即可．【解答】解：∵OA=OC，∴∠C=∠OAC=32°，∵BC是直径，∴∠B=90°﹣32°=58°，故选：A．3．（2017广西河池）如图，⊙O的直径AB垂直于弦CD，∠CAB=36°，则∠BCD的大小是（）A．18°B．36° C．54° D．72°【考点】M5：圆周角定理；M2：垂径定理．【分析】根据垂径定理推出=，推出∠CAB=∠BAD=36°，再由∠BCD=∠BAD即可解决问题．【解答】解：∵AB是直径，AB⊥CD，∴=，∴∠CAB=∠BAD=36°，∵∠BCD=∠BAD，∴∠BCD=36°，故选B．4. （2017山东泰安）如图，△ABC内接于⊙O，若∠A=α，则∠OBC等于（）A．180°﹣2αB．2αC．90°+αD．90°﹣α【考点】M5：圆周角定理．【分析】首先连接OC，由圆周角定理，可求得∠BOC的度数，又由等腰三角形的性质，即可求得∠OBC 的度数．【解答】解：∵连接OC，∵△ABC内接于⊙O，∠A=α，∴∠BOC=2∠A=2α，∵OB=OC，∴∠OBC=∠OCB==90°﹣α．故选D．5. （2017•新疆）如图，⊙O的半径OD垂直于弦AB，垂足为点C，连接AO并延长交⊙O于点E，连接BE，CE．若AB=8，CD=2，则△BCE的面积为（）A．12 B．15 C．16 D．18【考点】M5：圆周角定理；M2：垂径定理．【分析】先根据垂径定理求出AC的长，再设OA=r，则OC=r﹣2，在Rt△AOC中利用勾股定理求出r 的值，再求出BE的长，利用三角形的面积公式即可得出结论．【解答】解：∵⊙O的半径OD垂直于弦AB，垂足为点C，AB=8，∴AC=BC=AB=4．设OA=r，则OC=r﹣2，在Rt△AOC中，∵AC2+OC2=OA2，即42+（r﹣2）2=r2，解得r=5，∴AE=10，∴BE===6，∴△BCE的面积=BC•BE=×4×6=12．故选A．【点评】本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．6. （2018·湖北咸宁·3分）如图，已知⊙O的半径为5，弦AB，CD所对的圆心角分别是∠AOB，COD，若∠AOB与∠COD互补，弦CD=6，则弦AB的长为（）A. 6B. 8C. 5D. 5【答案】B【解析】【分析】延长AO交⊙O于点E，连接BE，由∠AOB+∠BOE=∠AOB+∠COD知∠BOE=∠COD，据此可得BE=CD=6，在Rt△ABE中利用勾股定理求解可得．【详解】如图，延长AO交⊙O于点E，连接BE，则∠AOB+∠BOE=180°，又∵∠AOB+∠COD=180°，∴∠BOE=∠COD，∴BE=CD=6，∵AE为⊙O的直径，∴∠ABE=90°，∴AB==8，故选B．【点睛】本题考查了弧、弦、圆心角的关系，圆周角定理等，正确添加辅助线以及熟练应用相关的性质与定理是解题的关键.7. （2018·新疆生产建设兵团·5分）如图，△ABC是⊙O的内接正三角形，⊙O的半径为2，则图中阴影部的面积是．【分析】根据等边三角形性质及圆周角定理可得扇形对应的圆心角度数，再根据扇形面积公式计算即可．【解答】解：∵△ABC是等边三角形，∴∠C=60°，根据圆周角定理可得∠AOB=2∠C=120°，∴阴影部分的面积是=π，故答案为：【点评】本题主要考查扇形面积的计算和圆周角定理，根据等边三角形性质和圆周角定理求得圆心角度数是解题的关键．8. （2018·广西梧州·3分）如图，已知在⊙O中，半径OA=，弦AB=2，∠BAD=18°，OD与AB 交于点C，则∠ACO=81 度．【分析】根据勾股定理的逆定理可以判断△AOB的形状，由圆周角定理可以求得∠BOD的度数，再根据三角形的外角和不相邻的内角的关系，即可求得∠AOC的度数．【解答】解：∵OA=，OB=，AB=2，∴OA2+OB2=AB2，OA=OB，∴△AOB是等腰直角三角形，∠AOB=90°，∴∠OBA=45°，∵∠BAD=18°，∴∠BOD=36°，∴∠ACO=∠OBA+∠BOD=45°+36°=81°，故答案为：81．【点评】本题考查圆周角定理、勾股定理的逆定理、等腰三角形的性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．。

高中数学数形结合_巧解“与圆有关的最值问题” 知识点+例题

数形结合，巧解“与圆有关的最值问题”例1 平面上有两点A （1-，0），B （1，0），P 为圆x y x y 2268210+--+=上的一点，试求S AP BP =+||||22最小值．解析：把已知圆的一般方程化为标准方程得()()x y -+-=34422，设点P 的坐标为(,)x y 00,则2222220000||||(1)(1)S AP BP x y x y =+=+++-+222002(1)2(1)x y OP =++=+ 要使22||||BP AP S +=最小,需||OP 最小,即使圆上的点到原点的距离最小.结合图形,容易知道325||min =-=-=r OC OP ,所以20)13(22min =+=S ．点评：设 P （x ，y ），使要求的式子转化为求圆上的点到原点的距离问题，利用数形结合法求最值，实质上是利用初中学过的“连结两点的线段中，直线段最短”这一性质．例２点A 在圆()()x y -+-=53922上，则点A 到直线3420x y +-=的最短距离为（）A. 9B. 8C. 5D. 2解析：过C 作CD ⊥直线3420x y +-=于D ，交圆C 于A ，则AD CD r =-为所求．∴AD例３ )0,3(P 在圆0122822=+--+y x y x 内一点．求（1）过P 的圆的最短弦所在直线方程（2）过P 的圆的最长弦所在直线方程解析：圆方程可以化成5)1()4(22=-+-y x ，圆心)1,4(O 1=OP k∴ 短l ：)3(--=x y 即 03=-+y x ；长l ：)3(-=x y 即03=--y x ．点评：最长弦当然是直径了，而最短弦是与直径垂直的弦．例４已知实数x ，y 满足方程22(2)3x y -+=．（1）求y x的最大值与最小值；（2）求y x -的最大值与最小值；（3）求22x y +的最大值和最小值．分析：22(2)3x y -+=为圆的方程，(,)P x y 是圆心为（2，0）点．y x的几何意义是圆上一点与原点连线的斜率，y x -的几何意义是直线y x b =+在轴上的截距，22x y +的几何意义是圆上一点到原点距离的平方．解：（1）设y k x=，即y kx =．当直线y kx =与圆相切时，斜率k 取最大值与最小值，=k =．所以y xk = （2）设y x b -=，当直线y x b -=与圆相切时，纵截距b 取得最大值与最小值，=解得2b =-所以y x -的最大值为2-，最小值2-．（3表示圆上一点到原点距离，由平面几何知识知，其最大值为圆心到原点的距离加上圆的半径，其最小值为圆心到原点的距离减去圆的半径，分别是2与222x y +的最大值和最小值分别为7+7-．例5 过直线1y =上一点P （x ，y ）作圆22(1)(1)1x y +++=的切线，求切线长的最小值．解析：如图所示，切线长2221PM PC CM PC =-=-，所以要求PM 的最小值，只需求PC 的最小值．PC 是直线上一点到圆心的距离，由于经直线外一点所引直线的垂线段的长度是该点到直线的距离的最小值，所以当PC 垂直于直线时，min 2PC =，此时，切线长最小，为3．小结与提升：圆的知识在初中与高中都要学习，是一典型的知识交汇点．现在的数学高考非常重视初高中知识的衔接问题，所以同学们在处理与圆有关的小题时，一定要数形结合，多联想一下与之有关的平面几何知识，以免“小题大作”．。

巧用三则平面几何知识简解解析几何问题

引玉．
例２设ａ，＞Ｏ定点Ｆ（，）直线ｌｚ一ｎ交ａｏ，：一轴于点Ｈ，Ｂ是ｚ上的动点，点Ｂ垂直于ｚ的直点过线与线段Ｂ的垂直平分线交于点Ｍ，１求点Ｍ的Ｆ（）轨迹Ｃ的方程；２设直线Ｂ与曲线Ｃ交于Ｐ、（）ＦＱ２
‘
图１
Ａ椭圆左准线与轴的交点；Ｂ坐标原点；Ｃ椭圆右准线与ｘ轴的交点；Ｄ右焦点
‘
，
三角形的有关性质，得知可
△ Ｐ ∽ ＡＱＦ，以ＡＦＣ所
ＰＡ
—
Ｄ
分析
这是一类涉及到角平分线的解析几何问
，
堕ＡＧＨＡＦ一一Ｂ，
，
②
◇
浙江
洪建松
由式 ① ② 可得 △ ＢＨＭ ∽ △ＡＧ，此Ｂ一』因Ｍ
ＨＭ
，
在解析几何中，一类涉及到平面几何初步知识有
的问题，如相似三角形性质、行四边形的边长关系、平重心的性质，类题往往与平面向量、这圆锥曲线等有机结合，通过稍加改变而成创新题．类问题若仅通这过联立方程等手段破解，往往事倍功半，至无功则甚
ＰＦ
／
ｃ
】
题，破解的思路往往是通过联立方程等手段，一时但难以得解，能结合平面几何相似三角形的性质，若则

平面几何知识在解析几何问题中的巧用

标分别为一、、、，／／
）］
・
．
．
Ｃ点纵坐标范围为（一
）
，
３
）．
点评：上点对直径所张角为９。，内点对直径圆周０圆
所张角大于９。，０圆外点对直径所张角小于９。，０这一再
能注意巧用、活用，将会取得事半功倍的效果。但有许多学
生在解题中不知、会应用，文旨在通过几个例题的分不本析，达到抛砖弓玉的目的。ｌ
ＩＡ＋Ｆ＝ＰＩＰＩ只需求ＰＩＩＩＩＱ＋Ａ，ＰＩ
ＩＱ＋Ａ取最小值时Ｐ点坐标ＰＩＩＩＰ
ｒ＝
（当点Ｃ在直线Ｌ上圆周２）
￣Ｐ＝－！Ｉ测２Ｍ．
Ｍ到定点Ｐ一，）（４０距离与它到定直线ＬＸ一距离之：－１
ｆ
上（Ｌ与圆两交点）时，即
ＡＣＢ－９０：－。
比为定值２由双曲线第二定义知Ｍ点轨迹为以Ｐ一，），（４０为左焦点，：一１左准线的双曲线的左支，Ｌ为可求得其方
，
方程是ｘ１＋４由平面几何 —）ｙ，＝知识知：
。。
ＩＰＩＭＢＩＩＡＩｒＭ＝Ｉ－Ｍ＝．
“
、
（当点Ｃ在直线Ｌ上圆内１）部分时ＡＢ９。；Ｃ＞０
在ＡＡＭ中，ＭＮｊＡＢ作＿Ｂ于Ｎ，ｌＩｌｌ则ＭＮ一ＭＢ＝

巧用圆的平面几何性质处理解几问题

与方向相反，・一ＩｉＯｌ３则郦Ｏ・Ｑ＝．ＰＩ一
４巧用圆心角、周角等的性质．圆
例５设直线Ｌ：ｘ４＋０圆Ｃ：ｙ＋一ｙ０交于Ｐ：３＋ｙｍ＝与．＋ｘ２＝￣ｘ、
分析：Ｃ为圆上的动点，设出Ｂ、的坐标，进角参Ｂ、都若Ｃ引
数，导致繁复的运算．果注意到由“ 径定理 ” 知Ｏ上将如垂可Ｍ
１
Ｂ（为原点）再结合ＣＢ９。ＩＩＢ＝Ｍ＝ＢＩＣ０，Ａ＝０，Ｍ＝ＭＩＣＩ÷Ｉ，ＡＩＩＣ即
Ｚ
Ｏ点，当Ｉ为何值时，Ｐ上Ｏ两则ｎＯＱ？
可迅速解题．解：Ｍ（，）连接ＯＯＭＡ，设ｘＹ，Ｃ，Ｍ，则由“ 径定理 ” 垂，Ｍ为Ｂ的中点Ｃ
‘ 。
解：如图２因圆ｃ：ｙｘ２＝过原点０，ＬＰＱ，－一ｙ０＋＋则Ｏ是圆ｃ
的圆周角，为直角．据 “ 中９。圆周角所对的弦是直且根圆０的
径 ” 知Ｐ可Ｑ￣ＩＣ的直径，直线３＋ｙｍ＝过圆，。一１￥。Ｉ即ｘ４＋０ＬＣ（
…
９
４
‘
Ｐ２Ｆ为钝角时，横坐标的取值范围是— 点Ｐ
图１
—
．
，一
２巧用 “ 割线长定理 ” ．切
例２已知直线ｙｍ（：＝ｘｍ∈Ｒ）圆Ｃ：‘ｖ一ｘ５０交于两与ｘ＋‘６＋＝相

圆的方程的求法例析

例#! 已知 2(') 的三个顶点所对应的坐标为
()"&!"*!')"!!*!))!!"!*!则 2(') 的外接圆的
方程为
!
! "&
Copyright©博看网. All Rights Reserved.
复习
!"!!年!月上半月!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!解法探究
!
根据题目条件中圆心在已知直线上可设
出所求的圆的标准方程将已知圆上两点的坐标代入
圆的标准方程圆心代入已知的直线方程联立方程
组进而确定对应的参数值得以求解圆的方程!
解析设所求圆的方程为)&"7*!*)%"H*!$N!! /)+"7*! * )""H*! $N!!
说条件更为广泛运算更为简单处理起来更加方便
快捷!圆的系数方程法可选择的两种方程都可以达到破解问题的目的!
$ 平面几何法
应用平面几何法求解圆的方程时!常用到圆的几
个性质%)#*直径所对的圆周角为直角&)!*圆心在任
意一弦的垂直平分线上&),*圆心在过切点且垂直于
")=! *>! "&4 &"*!通过待定系数法求出常数 =! >!4 的值!从而得以求解圆的方程!
例"!)!"#-年高考数学天津卷文科第#!题*在
平面直角坐标系中!经过三点 )"!"*!)#!#*!)!!"*的

用圆的几何性质解决椭圆问题

用圆研究椭圆
椭圆是高中数学中的重点和难点，原因在于它不像圆。圆上每一点到原点的距离都相等，并由此产生许多特别的性质，如垂径定理、切线长定理、圆周角定理等。而圆的这些定理就很难应用到椭圆上。如垂径定理、切线长定理，只能适用于椭圆的两个对称轴，而圆周角定理更是完全不适用。于是很多求线段长度、斜率大小、角度大小的题目，都只能通过复杂的数学运算来解决。如果能把椭圆变成圆，用圆的几何特性来解决椭圆的问题，将能使计算量大幅减少，不仅能节约大量宝贵的时间，还能提高解题的正确率。
��
= =
acos⁡�� sin⁡��
而圆的参数方程为：
��
= =
rcos rsin
��
可见，当椭圆长短轴相等时，就是一个圆了。
��
��′�
=
0
如果在变换后的坐标中，通过圆的性质求得某线段长度��’，根据：
��’
=
��1′
−
��2′�2
+
��1′
−
��2′�2
椭圆的方程
接着，我们来看椭圆的方程（假设长轴在 x 轴上）。
椭圆的标准方程为：
而圆的标准方程为：两边同时除以��2得：
我们再看椭圆的参数方程：
��2 ��2 ��2 + ��2 = 1 ��2 + ��2 = ��2 ��2 ��2 ��2 + ��2 = 1

活用“平面几何”,巧解“解析几何”问题

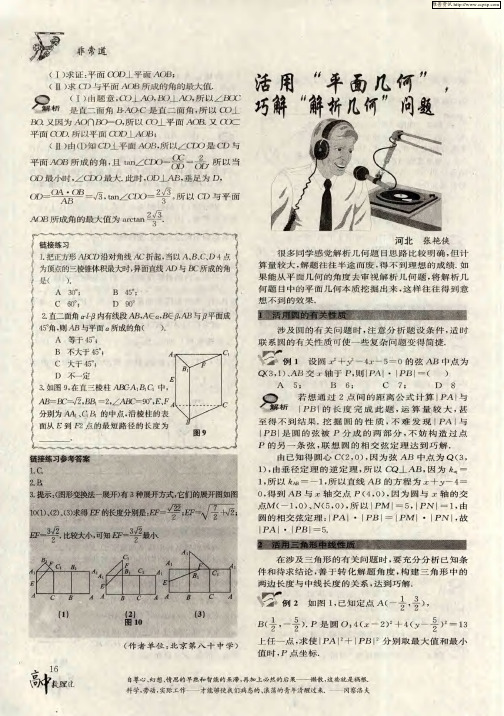
中点为
)
8
Q(3
， 1 )
A B
5
；
轴于
B 2
P 6
，
则
lP A
l
C
．I P B
7
；
(
D
A
；
，解析，
◇
B
若想通过
l
P B
点间的距离公式计算 l
，
P A
I与
，
l 的长度完成此题
．
运算量较大
甚
至得不到结果
挖掘圆的性质
P
，
不难发现 1P A J 与
，
，
件和待求结论 l善于转化解题角度构建
，
，
三
角形中的
两边长度与中线长度的关系达到巧解
，
．
崞例萝 ?磊
。
》
2
如图
P
l
，
已知定点 A (
4 (
z
一
1
一
3
，
百
百
)
，
B (
专
一
一
，
号)
，
．
是圆 O
：
2 )
。
。
+ 4 (
y
一
号)
。
= = =
13
(作
是直二面角所以 ∞ 上平面
A OB
．
B O 又因为 A O
0
，
所以 (] 吐
；
，
又 ( D [ =二
平面

利用外接圆的性质巧解几何题

利用外接圆的性质巧解几何题[摘要]通过巧作外接圆的辅助线，利用外接圆的性质转化原有的题设条件，开阔解题思路，给出有关三角形、四边形等的几何问题解题的新思路，以与托勒密定理在有关几何题的解题的应用，最后进一步推测正多边形外接圆上点的一些其他性质并给出证明。

[关键词]三角形外接圆四边形外接圆托勒密定理正多边形外接圆上点的性质Using the nature of circumscribed circle to slove geometryskillfully[Abstract]Through making the auxiliary line of circumscribed circleskillfully, use the nature of circumscribed circle to transform the original problem set conditions, widen our trains of thought in solving problems, then give some new thoughts to slove related triangle, quadrilateral and other geometric problems. Finally, giving a further speculation about some nature of dots on circumscribed circle of regular polygon and proving it.[Keywords] Triangle circumscribed circle Quadrilateral circumscribedcircle Ptolemy theorem Nature of dots on circumscribed circle of regular polygon目录摘要I关键词：I第一章引言1第二章多边形外接圆的性质与作图依据1（一）多边形外接圆的定义1（二）多边形外接圆的性质1（三）作外接圆辅助线的依据1第三章巧作外接圆在有关三角形几何问题上的应用1（一）证明角相等1（二）求线段长3（三）证明线段间的关系3（四）最值问题4第四章巧作外接圆在有关四边形几何问题上的应用5（一）证明角相等5（二）证明线段间的关系61、证明两条线段相等62、证明线段成比例6（三）证明两线间的位置关系71、证明两线平行72、证明两线垂直8（四）证明三点共线8（五）证明多点共圆9第五章利用托勒密定理与其逆定理证明有关几何题10（一）托勒密定理10（二）托勒密逆定理10（三）定理的应用111、证明“勾股定理”112、证明等腰梯形一性质123、借助定理巧变原式妙构图形12第六章进一步推测并证明正多边形外接圆上点的一些其他性质14 （一）正三角形外接圆上点的性质14性质114（二）正多边形外接圆上点的性质与其推广151、性质2与其推广152、性质3与其推广17结论22致语23References23第一章引言众所周知，圆是一种基本图形,也是一种重要的辅助线。

巧用图形变化,妙解几何试题

质，找出解决问题的途径．例２（２０１３年广东佛山市）我们知道，矩形是特殊的平行四边形，所以矩形除了具备平行四边形的一切性质，
展开、平移变换、对称变换、旋转变换、相似变换、等积变
换” 等手段转化为解决问题需要的基本图形或特殊位置．
Ｚ
对于一类几何题，通过对图形的折叠来增加试题的活力和新颖性，在折叠过程中所蕴含的几何性质主要有：线段相等、角相等、面积相等以及图形的对称性．几何图形的折叠问题较好地继承和发展了传统几何的优点，结
合现代数学的知识和方法，使数学问题更具有创新性、开
系，再利用几何图形的性质列出等式，使问题得以解决．
２．巧用图形分割．妙解几何试题
对于一类几何题，题目所给出的图形是图形的特征和题设的要求，把已知原
图形分割成几个平面图形，再根据分割后的新图形的性
１，有一张一个角为３０。，最小边长为２
．
的直角三角形纸片，沿图中所示的中
Ｌ／
７
图４
曰
位线剪开后，将两部分拼成一个四边
形，所得四边形的周长是（）．Ａ贼２Ｂ．１０或４＋２图
图５
Ｃ．１０或２、／一
２０１３年１１月
解法探究
巧用图形变化，妙解几何试题
◎江苏省启东市鹤城中学潘立新
图形的操作与图形的变换是新课程实施以来对传统

充分利用平面几何性质巧解解析几何题

一． ’ ‘ （、１（）ｖＴ（Ｍ３（２Ａ）／０Ｂ２ｆＣ）Ｄ）ＶＴ
．
且麻．￣则Ｉ＋ｌＰ赢：Ｆ－－Ｏ（）
一
解法（ ‘ 分别是双曲线Ｉ）。．、
＝１的左、焦点．右
通竺要题训让生方解竺。械套翟过量的练学列程方机用大的主习程弦
（）剪出的所有的正方形。成原来的正方形，画况，集数据，析数据，就 “ 何理财 ” 向父母提出自己５将拼并收分并如，出平面图形，过观察这个图形你发现了什么规律？通
，
．（／，￣／－）．一ｉ’）（ｉ，＾、ｘ … ｏ＇ｏ－ｄ “ ’
‘ 。Ｆ－．上．Ｐ．０ ’ 踢￣明则点Ｐ是为以即 △ 为直角三角形为直径的圆与双曲线的交点（四有
长公式，一元二次方程根的判别式等进行大量繁杂的计算，完全当成了纯代数ｉＳ来解决。至连必要的图形都没有，￣ｌｉ甚
范后。生动手操作。把结果填于表中：学
性、放性问题的设计，习形式要有趣味性。法要多样开练方
剪的次数（】ｎ
正方形的个数（）ｓ
１
２
３
４
５
６
性，有足够的探索与交流的时间。现数学课程标准中：要实 “ 同的人在数学上得到不同的发展 ” 要求。尊重学生的不的个体差异。学生不断感到成功和愉悦。使

巧用圆性质,妙定磁偏转轨迹七法

怨
Ａ
（）以Ｏ为圆心，０Ａ为半径作３
圆，弧ＡＢ即为带电粒子在磁场中的运动轨迹。此法的依据是同圆的半径相等，两条半径和一条弦构成一个等腰三角形的顶点即为圆心，故取名等腰三角形法。３．直角三角形法如图４示，此法作图步骤为：所
（）Ｏ为圆心，Ａ为半径作圆，４以Ｏ弧ＡＢ即为粒子在磁场中的运动轨迹。此法的依据是半圆上的圆周角为直角，此直角的两边与圆的两个交点和直角顶点构成的三角形为直角三角形，而直角三角形的斜边即为直径，故此法的关键是作出一个符合条件的直角三角形，因此该法命名为直角三角形法。４．切线半径法如图５示，此法的作图步骤为：所
Ｂ
图５ＩＩ墨３
（）过Ａ点作直线ＡＣ垂直于入１射速度ｖ矢量ｌ（）过Ｂ点作ＡＢＣ２Ｏ＝ＡＢ，
且Ｂ交ＡＣ于Ｏ点，０点即为圆心。Ｏ
（）过Ａ点作直线ＡＣ垂直于入１
射速度ｖ矢量；（２）在ＡＣ上截ＡＯ＝ｍｖｑ＝ｒ／Ｂ，Ｏ点即为圆心；取
（）过Ｂ点作Ｂ２Ｄ上ＡＢ，交ＡＣ
于Ｄ，ＡＤ必为圆的直径；
图６
新地２１．９天０１０４１１
课改案例
（）过Ａ点作直线ＡＣ垂直于入１射速度ｖ矢量；（）过Ｂ点作出射速度ｖ矢量与２ＡＢ的延长线成０角；由圆的几何性质（可知出射速度ｖ矢量与ＡＢ延长线必定夹ｅ角）的距离；并给出去除和射线的方

巧借平面三点共线求解立体几何最值

㊃题根研究㊃Җ㊀江苏㊀陆海琴㊀㊀空间几何体是由点㊁线㊁面构成的,在处理立体几何问题时,巧用平面几何性质,可使问题简洁求解.本文利用三点共线原理,探究一类立体几何最值问题.题根㊀平面四边形A B C D 中,在对角线A C 上寻找一点P ,使其到点B ㊁D 距离之和最小.利用三点共线原理易知B D 与A C 的交点,即为所求的点P .下面就此性质的应用,进行变式探究.1㊀直接应用求最值㊀㊀图1例1㊀(2015年福建卷)如图1所示,A B 是圆O 的直径,点C 是圆O 上异于A ㊁B 的点,P O 垂直于圆O 所在平面,且P O =O B =1.(1)若D 为线段A C的中点,求证A C ʅ平面P D O ;(2)求三棱锥P -A B C 体积的最大值;(3)若B C =2,点E 在线段P B 上,求C E +O E 的最小值.(1)㊁(2)略.(3)在әP O B 中,P O =O B =1,øP O B =90ʎ,所以P B =12+12=2.同理P C =2,所以P B =P C =B C .㊀㊀图2在三棱锥P -A B C 中,将侧面B C P 绕P B 旋转至平面B C ᶄP ,使之与平面A B P 共面,如图2所示.当O ㊁E ㊁C ᶄ共线时,C E +O E 取得最小值.又因为P O =O B ,C ᶄP =C ᶄB ,所以O C ᶄ垂直平分P B ,故O C ᶄ=O E+E C ᶄ=22+62=2+62,即C E +O E 的最小值为2+62.将面P B C 旋转至与面P A B 共面的位置时,即可直接应用题根的形式求此最值.2㊀多角度展开求最值例2㊀如图3所示,在直三棱柱A B C -㊀㊀图3A 1B 1C 1中,A B =B C =2,B B 1=2,øA BC =90ʎ,M ㊁N 分别为A A 1㊁C 1B 1的中点,求沿棱柱的表面从点M 到N 的最短路径.最短路径可按如下3种展开方式求解.1)沿棱B B 1展开,如图4.所以MN =1+(322)2=222.2)沿棱A 1B 1展开,如图5.过点M 作MP ʅB B 1于点P ,故MN =(2)2+(1+22)2=72+2.3)沿棱A 1C 1展开,如图6所示.图4㊀㊀㊀㊀㊀㊀㊀图5㊀㊀㊀㊀㊀㊀㊀图6过点M 作A A 1的垂线,过点N 作A 1C 1的垂线,2线交于点Q ,所以MN =(32)2+(32)2=322.综上可知MN 的最小值为322.本题通过运用平面化策略将几何体展开后利用题根求最值,但展开的方式并不唯一,因此应就其可能情况分别求最值,再将所得结果进行比较得出最小值.3㊀借助共线原理确定点的位置例3㊀(2012年福建卷)在长方体A B C D -A 1B 1C 1D 1中,A B =A D =1,A A 1=2,M 为棱D D 1上的一点.(1)求三棱锥A -M C C 1的体积;(2)当A 1M +M C 取得最小值时,求证:B 1M ʅ平面MA C .(1)略.(2)证明:将侧面C D D 1C 1绕DD 1逆时针转90ʎ展开,与侧面A D D 1A 1共面(如图7).当A 1㊁M ㊁C ᶄ共线时,A 1M +M C 取得最小值.由A D =C D =1,A A 1=2,得M 为D D 1中点.连接C 1M ,在әC 1M C 中,M C 1=2,M C =2,C C 1=2,故C C 21=3㊃通法研究㊃㊀图7M C 21+M C 2,得øC M C 1=90ʎ,即C M ʅM C 1.又由长方体A B C D -A 1B 1C 1D 1可知B 1C 1ʅ平面C D D 1C 1,所以B 1C 1ʅC M .又B 1C 1ɘC 1M =C 1,所以C M ʅ平面B 1C 1M ,得C M ʅB 1M .同理可证B 1M ʅAM .又AM ɘM C =M ,所以B 1Mʅ平面MA C .本题将最值问题作为条件来确定点的位置,从而利用题根将侧面展开后,由3点共线原理得到了点M 的位置,为后续解题创造了条件.4㊀变化应用到点面距例4㊀在长方体A B C D -A 1B 1C 1D 1中,A B =2,B C =A A 1=1,点P 为对角线A C 1上的动点,点Q 为底面A B C D 上的动点(点P ㊁Q 可以重合),则B 1P +P Q 的最小值为(㊀㊀).A㊀2;㊀㊀B ㊀3;㊀㊀C ㊀32;㊀㊀D㊀2如图8所示,求B 1P +P Q 的最小值,易知当点Q 位于A C 上时,P Q 可取到最小值.连接A B 1,将面A B 1C 旋转至与面A C C 1在同一平面(如图9),过点B 1作A C 的垂线,交A C 于点Q ,则B 1即为所求最小距离.㊀图8㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀图9由题目条件知A C ʅC C 1,A B 1ʅB 1C 1,A B 1=3,øC A C 1=øB 1A C 1=30ʎ,所以øA B 1Q =30ʎ,所以A Q =32,由勾股定理得B 1Q =32,即为所求.故正确选项为C .本题将点到点的距离变化为点到面的距离,同样利用平面化策略,将问题转化为点到线的最小值问题.综上,空间问题平面化是处理立体几何问题常用策略,平面化后再利用平面图形的性质原理解题.当然问题的考查形式不仅局限于本文所述,请同学们不断进行归纳总结,进而提高解题能力.(作者单位:江苏省海安县实验中学)Җ㊀河北㊀王崇艳㊀㊀空间向量的引入,利用点的坐标将几何问题代数化处理,降低了立体几何问题求解的难度,特别是空间角问题的求解.空间角主要包括2条异面直线所成的角㊁直线与平面所成的角㊁2个平面所成的角.本文引例说明向量法在求解空间问题中的理论基础及注意事项,以期对同学们复习此部分内容有所帮助㊀图1引例㊀(2015年天津卷)如图1所示,在四棱柱A B C D -A 1B 1C 1D 1中,侧棱A 1A ʅ面A B C D ,A B ʅA C ,A B =1,A C =A A 1=2,A D =C D =5,且点M ㊁N 分别为B 1C ㊁D 1D 的中点.(1)求直线MN 与C D 1夹角的余弦值(改编);(2)求二面角D 1-A C -B 1的正弦值;(3)设E 为棱A 1B 1上的点,若直线N E 和平面A B C D 所成角的正弦值为1/3,求线段A 1E 的长.1㊀恰当建系㊀准确找坐标建立坐标系是利用向量法求解立体几何问题的出发点.建系以充分利用题目条件中直接或间接给出的垂直关系为依据,尽可能使更多的点落在坐标轴上.间接的垂直关系常存在于特殊的平面几何图形中,如菱形㊁等腰三角形等.本题直接给出侧棱A 1A ʅ面A B C D ,A B ʅA C 为坐标系的建立奠定了基础.图如图2,以A 为原点建立空间直角坐标系,依题意可得A (0,0,0)㊁B (0,1,0)㊁C (2,0,0)㊁D (1,-2,0)㊁A 1(0,0,2)㊁B 1(0,1,2)㊁C 1(2,0,2)㊁D 1(1,-2,2).因为M ㊁N 分别为B 1C ㊁D 1D 的中点,得M (1,1/2,1)㊁N (1,-2,1).2㊀把握空间角求解的理论基础1)异面直线所成的角用传统方法求异面直线所成的角,首先需找到所成的角或其补角再求解,难度大,易出错.利用直线上4。

初中数学圆中常见的两解及多解问题_徐静

线 MN 的交点以每秒 1 cm 的速度（左边的交点）向左、（右边的
交点）向右运动，两圆相切有四种情形，①当 2t + t = 9 时，即 t =
3
秒时，两圆第一次相切；
②当
2t
+
t
=
11
时，即
t
=
11 3
秒时，两圆
第二次相切； ③当 2t － t = 11 时，即 t = 11 时，两圆第三次相切；
例 5 圆 O1 的半径为 17，圆 O2 的半径为 10，两圆相交于 A、B 两
点，AB = 16，求 O1 O2 ．分析：两种情况（ 1）两圆圆心在公共弦两侧，如图 5 （ 1 ），
（ 2）两圆圆心在公共弦同侧，如图 5（ 2）．
图5
解析：（ 1）连接 O1 A，O2 A，O1 O2 交 AB 于点 C，如图 5（ 1）．由
现在的问题是点 P 是假设出来的，点 A 已知，点 B 可以任意确定，但点 C 的位置是不确定的．因此在作图时，可以先任意确定点 C 的位置，也就是在直线 l 上，任意截取线段 BC（如图 6），然后过这三点作平行四边形．
图5
图6
图7
此图中，AB、BC 都是确定的线段，我们可以分别以 A、B 为
动，与此同时，⊙B 的半径也不断增大，其半径 r（ cm）与时间 t
（秒）之间的关系式为 r = 1 + t（ t≥0），当点 A 出发后
秒两圆相切．
分析： ⊙A 以每秒 2cm 的速度自左向右运动，则⊙A 与直线
MN 的交点也以每秒 2cm 的速度自左向右运动，⊙B 的半径 r
（ cm）与时间 t（秒）之间的关系式为 r = 1 + t（ t≥0），则⊙B 与直

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

巧用圆的平面几何性质处理解几问题
“圆”是一个特殊的图形，它有许多重要的性质。

在解析几何中，涉及到直线和圆的有关问题时，若能抓住题设中图形特征和数量关系，充分利用平面几何中圆的有关性质，常常可以得到简捷而巧妙的解法。

今举以下几例来说明。

1。

巧用“垂径定理”
例1 已知A（3，0）是圆x2+y2=25内的一个定点，以A为直角顶点作直角三角形ABC，且点B、C在圆上，试求BC中点M的轨迹方程。

分析：B、C都为圆上的动点，若设出B、C的坐标，引进角参数，将导致繁复的运算。

如果注意到由“垂径定理”知OM⊥BC（O为原点），那么再结合∠CAB=900，|AM|=|BM|=
1|BC|，即可迅速解题。

|CM|=
解：设M(x,y),连结OC，OM，MA，
则由“垂径定理”知，∵M为BC的中点∴OM⊥BC
∴|OM|2+|MC|2=|OC|2
1|BC|
∵在直角三角形ABC中，|AM|=|BM|=|CM|=
2
∴|OM|2+|AM|2=|OC|2
即x2+y2+(x-3)2+y2=25 （图1）
∴M点的轨迹方程为x2+y2-3x-8=0 。

2。

巧用“切割线长定理”
例 2 已知直线y=mx (m∈R)与圆C：x2+y2-6x+5=0相交于两点P、Q，则OP∙=_______________________。

OQ
分析：将直线方程代入到圆方程(x-3)2+y2=4中，进行消元，利用韦达定理解题，运算较繁。

注意到向量与方向相同，用“切割线长定理”来解题，可得以下两种简解。

解法一：过原点O作圆的切线，设切点为M、N，
则由“切割线长定理”知，|OP|•|OQ|=|OM|2=|OC|2-4=5
OP∙=|OP|•|OQ|=5 。

∵向量OP与OQ方向相同, ∴OQ
解法二：圆C与x轴有两个交点A（1，0）、B（5，0）
∵向量OP与方向相同,
OP∙=|OP|•|OQ|=|OA|•|OB|=5 。

∴由“切割线长定理”知，OQ
3。

巧用“相交弦定理”
例3 已知f(x)=(x+2002)(x-2003)图象与x轴交于两点A、B，与y轴交于一点C，过A、B、C三点作一圆，则该圆与y轴的另一个交点D的坐标为_____________。

分析：若写出圆的方程再求点D的坐标，将会导致繁复的运算。

注意到A、B两点的指标分别为（-2002，0）、（2003，0），而点C的坐标为（0，-2002•2003），根据“相交弦定理”可得，|OA|•|OB|=|OC|•|OD|，所以|OD|=1，从而D（0，1）。

例4过原点O且方向向量为（m，1）的直线L与圆C：(x-1)2+y2=4相交于两点P、Q，则∙=________________________。

分析：圆C 与x 轴交于两点A （-1，0）、B （3，0）。

利用“相交弦定理”得|OA|•|OB|=|OP|•|OQ|，因而|OP|•|OQ|=3。

注意到向量与方向相反，则∙= -|OP|•|OQ|= -3 。

4。

巧用圆心角、圆周角等的性质
例5 设直线L ：3x+4y+m=0与圆C 1：x 2+y 2+x-2y=0相交于P 、Q 两点，则当m 为何值
时，OP ⊥OQ ？
解：如图2，因圆C 1：x 2+y 2+x-2y=0过原点O ，则
∠POQ 是圆C 1的圆周角，且为直角。

根据“圆中900的
圆周角所对的弦是直径”可知PQ 为圆C 1的直径，即直
线3x+4y+m=0过圆心C 1（2
1-，1），代入直线L 方程得， 014)(31=+⨯+-⨯m ，∴2
5-=m 。

（图2）例6椭圆14
92
2=+y x 的焦点为F 1、F 2，点P 在椭圆上，当 ∠F 1PF 2为钝角时，点P 横坐标的取值范围是____________。

解：以F 1F 2为直径作圆x 2+y 2=5，与椭圆
14
92
2=+y x 联立，解得两曲线交点的横坐标分别为53
-和53。

根据“圆中同一条弦所对的圆周角小于
它所对的圆内角”这一性质知，点P 在椭圆的AB 或
CD 弧线（如图3，在辅助圆内）上时，∠F 1PF 2为钝
角，故点P 横坐标的取值范围是53
53
<<-x 即为结果。

（图3）
例7如图2，平面直角坐标系中，给定y 轴正半轴上两点A （0，a ）,B(0,b)(a>b>0)，试在x 轴正半轴上求一点C ，使∠ACB 取得最大值。

解：设C 是x 轴正半轴上一点，在⊿ABC 中，由正弦定理，有
sin ∠ACB=b a
-,其中R 是⊿ABC 的外接圆的半径。

可见，当R 取最小值时，∠ACB 取得最大值。

在过A 、B 两定点且与x 轴正向有交点C 的诸圆中，当且仅当点C
是与x 轴的切点时，半径最小。

故切点C 即为所求。

由切割线定理，得OC 2=OA •OB=ab
∴OC=x=ab ,即点C 的坐标为（ab ，0）时，∠ACB 取得最大值。

（图4）由以上几例可以看出，在解决与圆有关的问题时，只要充分挖掘圆的几何性质，再将几何条件代数化，既可以迅速获得解题途径，又可以减少解析几何的运算量。