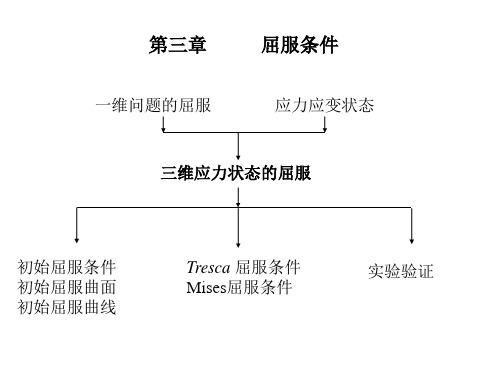
第3章 屈服条件
合集下载
3屈服准则
过P点作一条与ON平行的直线，
在上面取一点P1
NP N1P 1
材料屈服只和偏应力有关系 与平均应力无关
因此， P1点也可使材料屈服 因此， AP线上任意一点都可 使材料屈服
因此，
屈服表面必然是由平行于等倾斜轴OE的母线所构成的 与三个主应力轴等倾斜的柱面。
当主应力空间内任意一点P
位于该柱面以内时，该点处于弹性状态； 位于该柱面上时，该点处于塑性状态； 对于理想塑性材料，P点不可能在柱面之外
12 23 31
在上式中，只要有一式成立，该点就进入塑性 状态，因此，也可以用一个公式来表示，即
1 2 4k 2
2
2
3 4k
2
2
3
1 4k 2 0
2
3 2 2 2 4 6 4I 2 27 I 3 36k I 2 96k I 2 64k 0
8 塑性成形时的屈服准则与应力应变关系
8.1 屈服准则的一般概念 8.2 两个常用的屈服准则 8.3 塑性应力应变关系
8.1 屈服准则的一般概念
屈服准则是描述不同应力状态下，变形体内 某点由弹性状态进入塑性状态，并使塑性变 形状态持续进行所必须遵守的条件。
屈服准则又称为塑性条件或屈服条件
单向应力状态
但是，对于任意应力状态下的屈服准则 不可能用一般的实验方法来确定材料是否进入 塑性状态 目前描述其由弹性变形状态进入塑性变形状态 的判据，仅是一种假说
在任意应力状态下，不同应力分量之间的组合对材料 屈服的影响，可以用如下的屈服函数来描述，即
f ( ij , ij , T , t ,......) C
第3章屈服条件解析
2 2 2
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2
'
3J 2
s
物理意义：
1 当材料质点内单位体积的弹性形变能（即形状变化的能 量）达到某临界时，材料形状就屈服。
2 当八面体剪应力为某一临界值时，材料形状就屈服了。
对于绝大多数金属材料，密席斯准则更接近于试验数据。 对于各向同性理想塑性材料共同特点： 1).等式左边都是不变量的函数。 2).拉应力和压应力的作用是一样的。
三个主剪力
当 1 2 3
( 1 2 ) / 2 ( 2 3 ) / 2 ( ) / 2 3 1
1 3 C
可用最简单的应力状态，如单向拉伸或纯剪（薄壁管扭转）试 验求C。
单向拉伸时，有
1 s , 2 3 0
3 2
` 8 3J 2
1 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 )]2 C 2
单向拉伸时，有
1 s , 2 3 0
1 2 1 2 ( x y ) 2 ( y z ) 2 ( z x ) 2 6( xy yz zx )
π平面上的屈服轨迹
3.4 中间主应力的影响 设σ 1 ≥σ 2 ≥σ 3 则：屈雷斯加准则可写成：
1 3 s
这时，中间主应力 准则中是有影响的。 罗氏应力参数 当 2 在
2 不影响材料的屈服，但在密席斯
2 1 3
2 2
1 3
1 至 3 之间变化时，
则： C=
s
屈雷斯加屈服准则：
1 3 s
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2
'
3J 2
s
物理意义：
1 当材料质点内单位体积的弹性形变能（即形状变化的能 量）达到某临界时，材料形状就屈服。
2 当八面体剪应力为某一临界值时，材料形状就屈服了。
对于绝大多数金属材料，密席斯准则更接近于试验数据。 对于各向同性理想塑性材料共同特点： 1).等式左边都是不变量的函数。 2).拉应力和压应力的作用是一样的。
三个主剪力
当 1 2 3
( 1 2 ) / 2 ( 2 3 ) / 2 ( ) / 2 3 1
1 3 C
可用最简单的应力状态，如单向拉伸或纯剪（薄壁管扭转）试 验求C。
单向拉伸时，有
1 s , 2 3 0
3 2
` 8 3J 2
1 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 )]2 C 2
单向拉伸时，有
1 s , 2 3 0
1 2 1 2 ( x y ) 2 ( y z ) 2 ( z x ) 2 6( xy yz zx )
π平面上的屈服轨迹
3.4 中间主应力的影响 设σ 1 ≥σ 2 ≥σ 3 则：屈雷斯加准则可写成：
1 3 s
这时，中间主应力 准则中是有影响的。 罗氏应力参数 当 2 在
2 不影响材料的屈服，但在密席斯
2 1 3
2 2
1 3
1 至 3 之间变化时，
则： C=
s
屈雷斯加屈服准则：
1 3 s
屈服与破坏准则
S
A
C
D
E B
o
图中A点之后的曲线均称屈服曲线。 称 S 为初始屈服应力，A点之后曲线上任一点均称为相 继屈服点。
§3.1 概述
一、基本概念 1. 屈服、相继屈服与破坏 物体屈服后曲线如AB线的材料 称为理想塑性材料；如ACD线的材 料称为应变硬化（强化）材料；如 ACE线的材料称为应变软化材料。
内切圆
内接圆时： 外接圆时：
2sin 9 3sin 2 2sin 9 3sin 2
, k
6c cos 9 3sin 2 6c cos 9 3sin 2
' 2
1'
, k
见左图。 实际应用时选择要慎重，因为 极限荷载相差很大。
' 3
莫尔－库仑屈服准则的优点：它能反映岩土类材料的抗 压抗拉强度的不对称性；材料对静水压力的敏感性；而且模 型简单实用，材料参数少，c、 可以通过各种不同的常规 试验测定。因此，它在岩土力学和塑性理论中得到广泛应用， 并且积累了丰富的试验资料与应用经验。 但是，莫尔－库仑屈服准则不能反映中间主应力对屈服 和破坏的影响，不能反映单纯的静水压力可以引起岩土屈服 的特性，而且，屈服面有棱角，不便于数值计算。
§3.2 C-M准则
一、C-M准则
即 Coulomb-Mohe 准则，我们已经很熟悉了。当知道主 应力的大小，即 1 2 3 时，表示为：
f tan c 0
f (1 3 ) (1 3 )sin 2c cos 0
屈服与破坏准则
任务：如何来理解屈服与破坏准则？
何为屈服？何为破坏？何为准则？如何得 到屈服和破坏的准则？ 屈服：由弹性进入塑性！ 破坏：变形过大丧失对外力的抵抗！ 准则：寻找一种数学上的联系！ 那么，如何得到这种联系呢？
A
C
D
E B
o
图中A点之后的曲线均称屈服曲线。 称 S 为初始屈服应力，A点之后曲线上任一点均称为相 继屈服点。
§3.1 概述
一、基本概念 1. 屈服、相继屈服与破坏 物体屈服后曲线如AB线的材料 称为理想塑性材料；如ACD线的材 料称为应变硬化（强化）材料；如 ACE线的材料称为应变软化材料。
内切圆
内接圆时： 外接圆时：
2sin 9 3sin 2 2sin 9 3sin 2
, k
6c cos 9 3sin 2 6c cos 9 3sin 2
' 2
1'
, k
见左图。 实际应用时选择要慎重，因为 极限荷载相差很大。
' 3
莫尔－库仑屈服准则的优点：它能反映岩土类材料的抗 压抗拉强度的不对称性；材料对静水压力的敏感性；而且模 型简单实用，材料参数少，c、 可以通过各种不同的常规 试验测定。因此，它在岩土力学和塑性理论中得到广泛应用， 并且积累了丰富的试验资料与应用经验。 但是，莫尔－库仑屈服准则不能反映中间主应力对屈服 和破坏的影响，不能反映单纯的静水压力可以引起岩土屈服 的特性，而且，屈服面有棱角，不便于数值计算。
§3.2 C-M准则
一、C-M准则
即 Coulomb-Mohe 准则，我们已经很熟悉了。当知道主 应力的大小，即 1 2 3 时，表示为：
f tan c 0
f (1 3 ) (1 3 )sin 2c cos 0
屈服与破坏准则
任务：如何来理解屈服与破坏准则？
何为屈服？何为破坏？何为准则？如何得 到屈服和破坏的准则？ 屈服：由弹性进入塑性！ 破坏：变形过大丧失对外力的抵抗！ 准则：寻找一种数学上的联系！ 那么，如何得到这种联系呢？
第3章金属塑性变形的力学基础之屈服准则
1924年汉基（H.Hencky） NWPU
变形体单位体积内的总弹性变形能
1 1 m
m
3
1 An = ij ij 2
体积变化引起的单位体积弹性变形能
2
3 AV = m m 2
2 m m
m
3
m
18
3.6 形状变化引起的单位体积弹性变形能
3.6 Deformation energy per unit volume induced by shape change
max min s 2 K
10
2.3 任意应力状态下的Tresca屈服准则
2.3 Tresca yield criterion of any stress state
x xy xz yx y yz zx zy z
形状变化引起的单位体积弹性变形能
NWPU 广义胡克定律
A An AV
1 3 = ij ij m m 2 2
1 A [( x y )2 ( y z )2 ( z x )2 6( xy 2 yz 2 zx 2 )] 12G 1 2 1 2 1 E J2 G 19 2G 2 1 6G 3E
第四节 屈服准则
Part 4. Yield Criterion
P105-P116
1
本节主要内容 Contents
NWPU
1. 2.
基本概念★ ★Concepts 屈雷斯加屈服准则★ ★ ★ Tresca yield criterion
掌握标准 ★ ★ ★要求熟练掌 握并能应用 ★ ★要求熟练掌握 ★ 要求了解
等倾线定义 任意应力矢量
变形体单位体积内的总弹性变形能
1 1 m
m
3
1 An = ij ij 2
体积变化引起的单位体积弹性变形能
2
3 AV = m m 2
2 m m
m
3
m
18
3.6 形状变化引起的单位体积弹性变形能
3.6 Deformation energy per unit volume induced by shape change
max min s 2 K
10
2.3 任意应力状态下的Tresca屈服准则
2.3 Tresca yield criterion of any stress state
x xy xz yx y yz zx zy z
形状变化引起的单位体积弹性变形能
NWPU 广义胡克定律
A An AV
1 3 = ij ij m m 2 2
1 A [( x y )2 ( y z )2 ( z x )2 6( xy 2 yz 2 zx 2 )] 12G 1 2 1 2 1 E J2 G 19 2G 2 1 6G 3E
第四节 屈服准则
Part 4. Yield Criterion
P105-P116
1
本节主要内容 Contents
NWPU
1. 2.
基本概念★ ★Concepts 屈雷斯加屈服准则★ ★ ★ Tresca yield criterion
掌握标准 ★ ★ ★要求熟练掌 握并能应用 ★ ★要求熟练掌握 ★ 要求了解
等倾线定义 任意应力矢量
第三章应力分析应变分析屈服准则复习讲诉
a 0 0
1 ij
0
b
0
0 0 0
ab
2
ab 2
0
2 ij
a
b 2
ab 2
0
0
0 0
一、应力张量不变量及其应用
例题解答
对于
1 ij
J1 a b0 a b
J2
a 0
0b
b0
00
00
0
a
ab
a00 J3 0 b 0 0
000
同理，对于
2 ij
J1
a
2
b
a
2
b
0
a
b
ab
J2
试问上述应变场在什么情况下成立？
例题解答
2 xy xy
1 2
2 x y 2
2 y x2
(1)
2 xy 2 (2bxy) 2b xy xy
1
2
2 x y 2
2 y x2
1
2
2
a x2 y2 y 2
2
axy
x2
a
a 2b 即当a 2b时，上述应变场存在。
应变分析问题小 结
max min
2
C
2.2 单向拉伸时的Tresca屈服准则
2.2 Tresca yield criterion in uniaxial stretch test
三、应变连续方程问题
知识要点回顾
小应变几何方程
2 x y2
2 y2
u x
2 xy
u
y
(1)
2 y x2
2 x2
v y
2 v xy x
(2)
第三章 屈服准则
• 这一章研究材料的屈服. 我们已经知道,对于单向拉伸情况比 较简单,只有一个应力,实验可以得到应力应变的曲线, 应力应 变关系是一目了然. 但对于复杂应力状态, 材料在什么情况下 屈服这就不太好说了.这章的Tresca屈服条件和Mises屈服条件 就是解决这个问题的.
• 下一章来解决材料屈服后的应力应变的本构关系.
弹塑性力学基础－－－主讲：韩志仁
1. 屈服
物体受到荷载作用后，
随着荷载增大，由弹性状
态到塑性状态的这种过渡，
叫做屈服。
加载路径
2. 屈服条件
屈服点
物体内某一点开始产 生塑性应变时，应力或应 变所必需满足的条件，叫 做屈服条件。
only twist
Twist and extension
著名的Taylor和Quinney铜管拉扭 屈服试验(1931)
弹塑性力学基础－－－主讲：韩志仁
3. 屈服函数
一般情况下，屈服条件 与应力、应变、时间、温度 等有关，而且是它们的函数， 这个函数F称为屈服函数。
在不考虑时间效应(如应 变率)和温度的条件下：
在不考虑应力主轴旋转 情况下，可以用三个主应力 分量或应力不变量表示：
F( ij ,ij ,t,T ) 0
弹塑性力学基础－－－主讲：韩志仁
第三章 屈服准则
(yield criteria)
弹塑性力学基础－－－主讲：韩志仁
塑性模型三要素
屈服条件 流动法则
硬化规律
判断何时 达到屈服
屈服后塑性应变 增量的方向，也 即各分量的比值
决定给定的应力 增量引起的塑性 应变增量大小
弹塑性计算分 析的首要条件
弹塑性力学基础－－－主讲：韩志仁
这条曲线如图所示的红色曲线. 如果一个应力状态在这条曲线
• 下一章来解决材料屈服后的应力应变的本构关系.
弹塑性力学基础－－－主讲：韩志仁
1. 屈服
物体受到荷载作用后，
随着荷载增大，由弹性状
态到塑性状态的这种过渡，
叫做屈服。
加载路径
2. 屈服条件
屈服点
物体内某一点开始产 生塑性应变时，应力或应 变所必需满足的条件，叫 做屈服条件。
only twist
Twist and extension
著名的Taylor和Quinney铜管拉扭 屈服试验(1931)
弹塑性力学基础－－－主讲：韩志仁
3. 屈服函数
一般情况下，屈服条件 与应力、应变、时间、温度 等有关，而且是它们的函数， 这个函数F称为屈服函数。
在不考虑时间效应(如应 变率)和温度的条件下：
在不考虑应力主轴旋转 情况下，可以用三个主应力 分量或应力不变量表示：
F( ij ,ij ,t,T ) 0
弹塑性力学基础－－－主讲：韩志仁
第三章 屈服准则
(yield criteria)
弹塑性力学基础－－－主讲：韩志仁
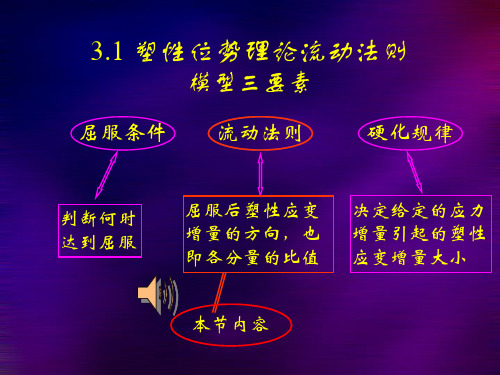
塑性模型三要素
屈服条件 流动法则
硬化规律
判断何时 达到屈服
屈服后塑性应变 增量的方向，也 即各分量的比值
决定给定的应力 增量引起的塑性 应变增量大小
弹塑性计算分 析的首要条件
弹塑性力学基础－－－主讲：韩志仁
这条曲线如图所示的红色曲线. 如果一个应力状态在这条曲线
五种常见的屈服准则及其适用范围
五种常见的屈服准则及其适用范围 屈服准则表示在复杂应力状态下材料开始进入屈服的条件，它的作用是控制塑性变形的开始阶段。
屈服条件在主应力空间中为屈服方程。
1.几种常用的屈服准则五种常用的屈服准则，它们分别是Tresca 准则，Von-Mises 准则 ，Mnhr- Coulomb 准则，Drucker Prager 准则，Zienkiewicz-Pande 准则。
其中后三种适用于混凝土和岩土材料的准则1.1 Tresca 屈服准则当最大剪应力达到一定数值时，材料开始屈服。
这就是Tresca 屈服条件，也称为最大剪应力条件。
k =max τ规定时321σσσ≥≥，上式可表示为：k 2-31=σσ 如果不知道321、、σσσ的大小顺序，则屈服条件可写为:0]4)][(4)][(4)[(221322322221=------k k k σσσσσσ换言之当变形体或质点中的最大切应力达到某一定值时，材料就发生屈服。
或者说，材料处于塑性状态时，其最大切应力是一个不变的定值，该定值只取决于材料在变形条件下的性质，而与应力状态无关。
所以Tresca 屈服准则又称为最大切应力不变条件。
这种模型与静水压力无关，也不考虑中间应力的影响。
在平面上屈服条件为一个正六边形，在主应力空间内，屈服曲面为一个正六面柱体。
Tresca 屈服准则不足之处就是不包含中间主应力，没有反映中间主应力对材料屈服的影响。
1.2 Mises 屈服准则当与物体中的一点应力状态对应的畸变能达到某一极限值时，该点便产生屈服，其表达式为22k J =或22132322216)()()(k =-+-+-σσσσσσ其中， k 为常数，可根据简单拉伸试验求得3/222s k J σ==，或根据纯剪切试验来确定， 222s k J τ==它所代表的屈服面是一个以空间对角线为轴的圆柱体，在平面上屈服条件是一个圆。
这时有:const k J r ===222σ 换言之当等效应力达到定值时，材料质点发生屈服，该定值与应力状态无关。
几种常见的屈服准则及其适用条件
几种常见的屈服准则及其适用条件屈服准则表示在复杂应力状态下材料开始进入屈服的条件，它的作用是控制塑性变形的开始阶段。
屈服条件在主应力空间中为屈服方程。
1.几种常用的屈服准则五种常用的屈服准则，它们分别是Tresca 准则，Von-Mises 准则 ，Mnhr- Coulomb 准则，Drucker Prager 准则，Zienkiewicz-Pande 准则。
其中后三种适用于混凝土和岩土材料的准则1.1 Tresca 屈服准则当最大剪应力达到一定数值时，材料开始屈服。
这就是Tresca 屈服条件，也称为最大剪应力条件。
k =max τ规定时321σσσ≥≥，上式可表示为：k 2-31=σσ如果不知道321、、σσσ的大小顺序，则屈服条件可写为:0]4)][(4)][(4)[(221322322221=------k k k σσσσσσ换言之当变形体或质点中的最大切应力达到某一定值时，材料就发生屈服。
或者说，材料处于塑性状态时，其最大切应力是一个不变的定值，该定值只取决于材料在变形条件下的性质，而与应力状态无关。
所以Tresca 屈服准则又称为最大切应力不变条件。
这种模型与静水压力无关，也不考虑中间应力的影响。
在平面上屈服条件为一个正六边形，在主应力空间内，屈服曲面为一个正六面柱体。
Tresca 屈服准则不足之处就是不包含中间主应力，没有反映中间主应力对材料屈服的影响。
1.2 Mises 屈服准则当与物体中的一点应力状态对应的畸变能达到某一极限值时，该点便产生屈服，其表达式为22k J =或22132322216)()()(k =-+-+-σσσσσσ其中， k 为常数，可根据简单拉伸试验求得3/222s k J σ==，或根据纯剪切试验来确定，222s k J τ==它所代表的屈服面是一个以空间对角线为轴的圆柱体，在平面上屈服条件是一个圆。
这时有:const k J r ===222σ 换言之当等效应力达到定值时，材料质点发生屈服，该定值与应力状态无关。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ij 3. 若变形体屈服时的应力状态为：
试分别按Mises和Tresca塑性条件计算该材料的屈服应力 s 及β 值，并分析差异大小。
30 23 3 ×10MPa ＝ 3 15
4、某理想塑性材料，其屈服应力为100N/mm2 ，某
点的应力状态为
f d ij 0 时，为卸载，表示应力由初始屈服表 ij
面向内移动，产生了弹性卸载。
df 0 时，塑性流动继续，仍为加载，不 对于理想塑性材料， f df d ij 0 ij 会出现 df ＞0 的情况。当 df ＜0 时，表示弹性应力状态。
思考
什么是屈服准则、屈服表面、屈服轨迹？ 常用的屈服准则有哪两种？它们有何差别？在什么情况下
第3章 屈服条件
第3章 屈服条件
3.1 基本假设 3.2 屈服准则
回顾并思考
均匀塑性变形 塑性失稳
屈服 断 裂
弹性变形
应力增加到什么程度材料屈服？
3.1 基本假设
材料为均匀连续，且各向同性；
体积变化为弹性的,塑性变形时体积不变；
静水压力不影响塑性变形，只引起体积弹性 变化； 不考虑时间因素，认为变形为准静态；
2 2
2
x s x s
xy 4 1 s xy 3 1 s
2 2
2
2
T resca Von Mises
3.6 应变硬化材料的屈服准则 材料经塑性变形后，要产生应变硬化，因此屈服应力并非 常数，在变形过程的每一瞬间，都有一后继的瞬时屈服表 面和屈服轨迹。而米赛斯和屈雷斯加两个屈服准则只适用
2 2 2
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2
'
3J 2
s
物理意义：
1 当材料质点内单位体积的弹性形变能（即形状变化的能 量）达到某临界时，材料形状就屈服。
2 当八面体剪应力为某一临界值时，材料形状就屈服了。
对于绝大多数金属材料，密席斯准则更接近于试验数据。 对于各向同性理想塑性材料共同特点： 1).等式左边都是不变量的函数。 2).拉应力和压应力的作用是一样的。
屈服表面几何意义： 主
应力空间中一点应力状态矢
1 2 s 2 3 s 3 1 s
量的端点 P 点位于屈服表面 上，该点处于塑性状态，若 P 点位于屈服表面内，则该 点处于弹性性状态。
π平面：在主应力空间中，通过坐标原点并垂 直于等倾角直线ON的平面。
屈雷斯加屈服准则：
1 3 s
2
密席斯屈服准则：
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 2 S
3.5 平面问题和轴对称问题中屈服准则的简化 对于密席斯屈服准则：
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 2 S
不考虑包辛格(Banschinger)效应。
基本概念： 屈服应力：质点处于单向应力状态，只要单 向应力达到材料的屈服点，则该点由弹性变 形状态进入塑性变形状态临界的应力。 塑性条件 或屈服条件：多向应力状态下变形 体某点进入塑性状态并使塑性变形继续进行 所必须满足的力学条件。
f ( ij ) C
3).各表达式都和应力球张量无关。
3.3 屈服准则的几何表达-------屈服轨迹和屈服表面
一、两向应力状态的屈服轨迹
3 0
即可得到两向应力状态的密席斯屈服准则：
2 12 1 2 2 s2
1 2 坐标平面上是一个椭圆，它的中心在原点，对称轴与坐标轴
成45°，长半轴为 2 s ，短半轴为 这个椭圆就叫
2
2
4 2 S 4K 2 3
轴对称问题：
z 0
3.6 屈服准则的实验验证
以上两种屈服条件最主要的差别在于中间主应力是否有影 响。以下介绍的一个实验结果表明Von Mises条件比Tresca条
件更接近于实际。
平面应力状态 ： 承受均匀的拉应力及剪应力。
求主应力（应力特征方程）
1 2
1 3 s 320MPa, 3 320 10 -330MPa
例2 已知一点的应力状态为：
1.2 s ij 0 0 0 0.1 s 0 0 0 0
试用屈雷斯加屈服准则该判断应力是否存在？如果 存在，材料处于弹性还是塑性变形状态（材料为理 想塑性材料，屈服强度为σs） 解：由屈雷斯加屈服准则 max 1 2 , 2 3 , 3 1 2k σ1=1.2σs，σ2=0.1σs，σ3=0 σ1-σ3=1.2σs-0＞σs， 因是理想塑性材料，屈服强度为σs，故此应力不 存在。
将在-1～1之间变化
我们利用
将密席斯准则改写成接近于屈雷斯加准则
的形式：
2
1 3
2
2
1 3
2
2
1 3
3
2
s
若设
3
2
1 3 s
值的变化范围为1～1.155
两个屈服准则的数学表达式相同
1
1.155 两个屈服准则差别最大
平面应变（纯剪叠加球张量），两个准则相差最大，为15.5%。
1 K ( 1 3 ) S 2 2
（K表示屈服时的最大剪应力）
K 0.5 S 屈雷斯加屈服准则 1 3 2 K S K （0.5 ~ 0.577 ） S 按密席斯准则
的形式，则屈服轨迹的 所确定的，而常数
决定了轨迹的大小。根据上述假设，各向同性硬化材料的屈服准则 来表示，但此时等式右边的常数C改变成 随变形程度而改变的变量。设这一变量用Y(材料为理想刚塑性材料 时，Y=C)表示。则各向同性硬化材料和理想刚塑性材料的屈服准则 都可表示为:
f ( ijij)
f ( )
π平面上的屈服轨迹
3.4 中间主应力的影响 设σ 1 ≥σ 2 ≥σ 3 则：屈雷斯加准则可写成：
1 3 s
这时，中间主应力 准则中是有影响的。 罗氏应力参数 当 2 在
2 不影响材料的屈服，但在密席斯
2 1 3
2 2
1 3
1 至 3 之间变化时，
它们相同?在什么应力状态下它们差别最大？分别写出其
数学表达式。
对各向同性的硬化材料的屈服准则是如何考虑的？ 米塞斯屈服准则的物理意义？
例题讲解
例1 一直径为50mm的圆柱体试样，在无摩擦的光滑 平板间墩粗，当总压力到达628KN时，试样屈服，现 设在圆柱体周围方向上加10MPa的压力，试求试样屈 服时所需的总压力。 4 628 103 320MPa 解：材料屈服应力： s 2 50 圆柱体加压后： 10MPa, 10MPa 由Mise屈服准则得：
则： C=
s
屈雷斯加屈服准则：
1 3 s
2、密席斯准则
因为材料的塑性变形是由应力偏张量引起的，且只 与应力偏张量的第二不变量有关。 将应力偏张量和第二不变量作为屈服准则的判据。 表述1 当应力偏张量的第二不变量达到某一定值时， 该点进入塑性变形状态。
表述2 当点应力状态的等效应力达到某一与应力状态无关的 定值，材料就屈服。
1 2 2 ( 4 x xy ) 1 2 x 2 0 1 2 2 3 ( x x 4 xy ) 2
代入屈雷斯加准则：
1 3 x 2 4 xy 2 s
代入密席斯准则：
x 3 xy S
3 2
` 8 3J 2
1 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 )]2 C 2
单向拉伸时，有
1 s , 2 3 0
1 2 1 2 ( x y ) 2 ( y z ) 2 ( z x ) 2 6( xy yz zx )
在这六点上，两个准则的差别都是15.5%。
如果P点在屈服轨迹的里面，则材料的质点处于弹性状态；如P点在轨迹上， 则质点处于塑性状态；对于理想塑性材料，P点不可能在屈服轨迹的外面。
密席斯屈 服准则
屈雷斯加 屈服准则
屈服准则都是空间曲面，叫做屈服表面。
主应力空间中，屈雷斯 加屈服表面是一个内接 于米塞斯圆柱面的正六 棱柱面
平面应力时，
2
z 3 yz zx 0
12 1 2 22 S 2
平面变形时：
zX zy 0, z 3 (1 2 ) / 2
1 2
2 3
S 2 K或( x y ) 4 xy
解：由由密席斯屈服准则：
s
1 2 2 2 x y 2 y z 2 z x 2 6 xy yz xz 2
1 75 15 2 15 02 0 75 2 615 2 0 0 73.5MPa s 2
应力分量的函数
与材料性质有关的常数
有关材料性质的一些基本概念
无明显物理屈服点 有物理屈服点
实际金属材料
b)理想弹塑性
c)理想刚塑性材料
d)弹塑性硬化
e)刚塑性硬化
3.2 屈服准则
1、屈雷斯加准则 法国工程师屈雷斯加（H.Tresca）提出 材料的屈服与最大切应力有关，即当受力材 料中的最大切应力达到某一极限值（定值） 时，材料发生屈服。