自然坐标系
直角坐标系和自然坐标系的转化

直角坐标系和自然坐标系的转化直角坐标系和自然坐标系是我们在数学和物理学中经常接触到的两种坐标系。
它们在表达平面或空间中的点的位置和运动方向时具有重要作用。
两种坐标系结合使用,可以更加准确地描述物理现象和解答数学问题。
直角坐标系直角坐标系是我们最为熟悉的坐标系,通常在平面直角坐标系中,我们将平面分成了四个象限,以原点为中心,横轴为X轴,竖轴为Y轴。
其中X轴和Y轴互相垂直,它们所形成的角度是90度。
在直角坐标系中,我们用一个有序数对(x, y)来表示平面上一个点的坐标位置,其中x是该点在X轴上的投影长度,y 是该点在Y轴上的投影长度。
按照惯例,在平面直角坐标系中选取X轴向右为正方向,Y 轴向上为正方向。
自然坐标系自然坐标系是一种身体坐标系,也称为物体坐标系,通常是将一个物体或者人体作为基准,以该物体或人体的中心点作为坐标系的原点。
人类自然坐标系起源于解剖学,我们通常用xyz三轴表示人体(或动物)在三维空间中的位置。
x轴代表从前往后方向,y轴代表从左到右方向,z轴代表从上到下方向。
同样的,自然坐标系也可以用有序数对(x,y,z)来表示三维空间中一个点的坐标位置。
不同于平面直角坐标系,自然坐标系是三维的,它可以很方便地描述三维物理现象。
此外,自然坐标系还有其他一些特点,例如坐标值可以为负数,和三个坐标轴可以任意排列。
由于自然坐标系和直角坐标系都有各自的优点和适用范围,因此在实际应用中,我们常常需要将自然坐标系转换为直角坐标系,或者将直角坐标系转换为自然坐标系,以便更加准确地描述和解决问题。
当我们需要将自然坐标系转换为直角坐标系时,需要判断当前自然坐标系的x、y、z 轴分别对应直角坐标系中的哪个轴。
为此,我们需要测量该物体或人体的朝向和方向,通常使用惯性导航仪或者静电陀螺仪等设备进行测量。
拿人体为例,可以根据人体的面朝方向,将自然坐标系中的x、y、z轴重组成一个新的坐标系。
假设x轴对应人体的前后方向,y轴对应人体左右方向,z轴对应人体的上下方向,则人体的中心点就是该新坐标系的原点。
1-3 坐标系的运用

r r
r
ω
r
r
υ
r
ω
r
r r υ = ω×r
d ω d 2θ 角加速度: 角加速度: β = = 2 dt dt
r
P
3、 角加速度 (Angular Acceleration ) 、
14
1.3 坐标系的运用
圆周运动的角量与线量的关系: 圆周运动的角量与线量的关系: 的关系
第1章 质点运动学
ds r dθ υ= = = rω dt dt dυ dω aτ = =r = rβ dt dt
8
1.3 坐标系的运用
曲线运动的 加速度小结: 加速度小结:
第1章 质点运动学
2
r dυ υ ˆ ˆ ˆ a = aττ + ann = n τˆ + dt ρ
r υ2 法向加速度: 法向加速度: a = ˆ n n
大小: 大小:
切向加速度: r 切向加速度:a = dυ τ ˆ τ dt dυ 大小: 大小: aτ = dt
1.3 坐标系的运用
第1章 质点运动学
1.3 坐标系的运用
1
1.3 坐标系的运用
一、自然坐标系
第1章 质点运动学 S为弧坐标。 为弧坐标。
在已知运动轨道上任取一参照点 O,由质点 已知运动轨道上任取一参照点 , 来表示质点的位置 质点的位置。 与参考点之间轨迹的长度 s 来表示质点的位置。 速度方向为切向坐标方向;指向曲率中心的 速度方向为切向坐标方向; 切向坐标方向 方向为法向坐标方向 与速度的方向垂直) 法向坐标方向( 方向为法向坐标方向(与速度的方向垂直)。
ds = v0 − bt 解:1) v = ) dt dv = −b 2) at = ) dt 2 2 v (v0 − bt ) an = = R R
自然坐标系

r
t
t 0
AB .
t R
ern
v2 R
en
法向加速度
a
an
v2 R
vB
B vA
R
O
A
大小,方向,作用
2. 一般圆周运动的
切向加速度和法向加速度 分析方法
vB r
v vB vA vrn vr v
vrn 表示速度方向改变量 vr 表示速度大小改变量
lim lim vr
t 0
rr t
t 0
s t
er
ds dt
er
ds dt
三、 自然坐标系下的加速度
1. 匀速圆周运动, 法向加速度
v vB
vA
v vB
vA
Δv vB vA ,
AB R
lim lim ar
t 0
则:a an2 a 2 (1.88)2 (1.2)2 2.23(m / s2 )
tg an
a
12233'
总结解题策略:
(1)分析问题特点,建立恰当的坐标系 (2)由运动方程求解速度随时间变化的表达式 (3)分别计算出切向加速度与法向加速度,再 求解合加速度的大小和方向
解:根据加速度的定义:
ar
anern
a er
v2 R
ern
dv dt
er
a an2 a 2
v
ds dt
2
R
a
d
dt
1.2t
7自然坐标系

University ຫໍສະໝຸດ hysics三. 角加速度(描述质点转动角速度变化快
慢的物理量)
o
t : t t :
r
P
lim
(t t ) (t )
dt
角加速度的方向与 dω 的方向相同
t 0
d d 2 k k 2 k dt dt
aτ
aτ
思考 求抛体运动过程中的曲率半径? 对B 点
a
y
2 2 2
aτ 0, an g , v B v 0cos
vo
B
vB (v 0cos ) xm ρ B an g 8 ym
o
C x
Xu Zhongfeng, Xi’an Jiaotong University, 2010
法向加速度
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
2 2 v d v d s ds 2 1 a an n aτ τ n τ 2 τ ( ) n dt dt dt 2 v 对匀速率圆周运动 a 0 an an n n r 加速度的正交分解 a an n aτ τ Pv • a an a aτ 2 an 2 , tg n
两类问题(圆周运动的角量描述) 1. 第一类问题 已知运动学方程, (t ) 求 ,
P
aτ v
d ω k dt
d d d 2 k 2 k dt dt dt
Xu Zhongfeng, Xi’an Jiaotong University, 2010
自然坐标圆周运动相对运动

伽利略所取得的巨大成就,开创了近代物理学 的新纪元。
自然坐标、圆周运动、角量描述、相对运动
3、绝对运动、牵连运动、相对运动
(1)位矢的关系
r
r'
质点P在相对作匀速直线运动
的两个坐标系中的移动 y y' u
自然坐标、圆周运动、角量描述、相对运动
2、相对运动
物体运动的轨迹依赖于观察者所处的参考系
自然坐标、圆周运动、角量描述、相对运动
伽利略(Galileo Galilei,1564—1642)
伽利略杰出的意大利物理学家和 天文学家,实验物理学的先驱者。
他提出著名的相对性原理、惯性 原理、抛体的运动定律、摆振动的等 时性等。
2
1 x2g
y 2
v02
y
an
a
g
自然坐标、圆周运动、角量描述、相对运动
(2)
o v0
x
vx v0, vy gt
an
a
y
v
vx2 vy2
v02 g 2t 2
tan 1
gt v0
a
dv dt
g2t v02 g2t2
an g2 a 2
g
v0 g v02 g2t 2
与速度同向
与切向加速度垂直
总结:自然坐标
v v
a a an a ann
a
a
an
切向加速度
法向加速度
反映速度大小变 化的快慢
反映速度方向变 化的快慢程度
dv a dt
an
v2
aa
a 2 an 2
自然坐标系

1 2 βt 2
****************************************************** 匀速圆周运动 匀速直线运动 θ = θ 0 + ωt x = x0 + Vt 匀变速圆周运动 匀加速直线运动 ω = ω 0 + βt V = V0 + at 1 1 θ − θ 0 = ω 0t + βt 2 x − x0 = V0 t + at 2 2 2 2 2 2 2 ω − ω 0 = 2 β (θ − θ 0 ) V − V0 = 2 a ( x − x 0 ) ******************************************************
4
V2
V2 ⇒ρ= :计算曲率半径 (4) a n = ρ an 例: R =800m 的圆形轨道,汽车,静止开始,
速率均匀增加, t =3(分) , V =20m/s r , a , at , a n 求: t =2(分) 解:设 V = kt ,t=3(分)=180s, V =20m/s
k =20/180=1/9, V = t /9 dV at = = 1 / 9 = 0.111(m / s 2 ) dt t =2(分)=120s, V =120/9(m/s) V2 = 0.222m / s 2 an = R
at
α
an R
O
r a
2 a = at2 + a n = 0.248m / s 2 , tgα = a n / at =2, α = 63.4 o
第5节
P
相对运动
S ′ 相对于 S 作平动运动 r r r r = r ′ + r0 r r r ∆r = ∆r ′ + ∆r0 r r r dr dr ′ dr0 = + dt dt dt
自然坐标系
v 2 (t ) an R
ˆ v v(t )
3 一般平面曲线运动
dv v 2 a n dt
曲线变化缓慢大 曲线变化急大
详细推导
ˆ v v
ˆ dv dv d ˆ a v dt dt dt
ˆ d的大小为 d 1
• 随质点一起运动,自然变换位置和方向。
举例:圆周运动 1 匀速圆周运动 速度 大小:v=衡量
ˆ n
ˆ
方向:切向
ˆ v v
v ˆ ˆ a an n n R
2
a 加速度 大小: n v / R
2
方向:指向圆心
2 变速率圆周运动 速度 加速度
ˆ ˆ a a an a an n
dv a dt 2 v an
a
a a
a 2 an 2
2 2 2
dv v dt
a tg an
加速度总是指向曲线的凹侧,因为正是加速 度的法向分量改变了质点的运动方向。
1.3 角量描述
v2 B v1
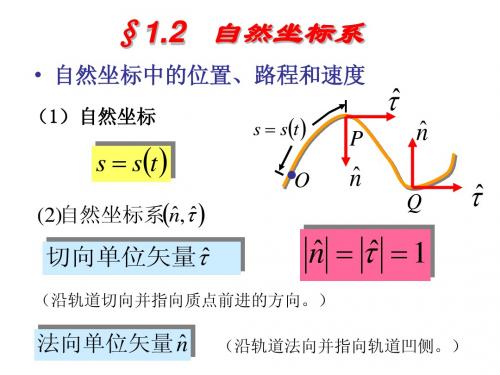
§1.2 自然坐标系
• 自然坐标中的位置、路程和速度
(1)自然坐标
s st
ˆ
s st
ˆ ˆ (2) 自然坐标系n,
P
ˆ n
Q
O
ˆ n
ˆ
ˆ 切向单位矢量
ˆ ˆ n 1
(沿轨道法向并指向轨道凹侧。)
(沿轨道切向并指向质点前进的方向。)
ˆ 法向单位矢量 n
自然坐标的特点
ˆ 方向为n
dˆ d d dr v ˆ ˆ ˆ ˆ n n n n dt dt dt dt
自然坐标系

自然坐标系
自然坐标系是指一个基于自然规律和观测事件的坐标系。
在物理学、地理学、
生物学等领域中,自然坐标系被广泛应用于描述和研究自然现象。
自然坐标系的建立通常以某个客观参照物或事件为基准点,以此构建具有一定方向和单位的坐标轴。
在物理学中,自然坐标系常用于描述空间位置、运动和力等物理量。
其中,笛
卡尔坐标系是最常见的一种自然坐标系,由三个垂直的坐标轴构成,分别代表空间中的长度、宽度和高度。
物体在笛卡尔坐标系中的位置可以通过三个坐标值来确定,这种描述方法简单直观。
在地理学中,地球表面的经纬度坐标就是一种自然坐标系。
经线和纬线交叉形
成网格状结构,用于描述地球表面上的位置。
经纬度坐标在导航、地图绘制等方面有着重要的应用,能够准确描述地球上任意点的位置。
生态学中也常常使用自然坐标系来描述生物群落的分布和生态系统的结构。
例如,树种分布图就是利用自然坐标系进行绘制的,通过对树木种类和数量在空间中的分布进行记录和统计,可以帮助研究者了解生态环境的特点和动态变化。
总的来说,自然坐标系是描述和研究自然现象不可或缺的工具之一。
通过建立
合适的坐标系,可以更好地理解和解释自然规律,促进科学研究和技术发展的进步。
对于不同领域的研究者来说,熟练掌握各种自然坐标系的原理和应用方法非常重要,能够帮助他们更准确地进行科学分析和实验推断。
自然坐标极坐标

dt
dt 2
注意:角加速度不是矢量 (参看《教与学参考》P71)
5.角量与线量的关系 s = Rθ ∆s = R∆θ
P′( t + ∆t )
∆s
R ∆θ
Oθ
P( t )
s
O' 参考
方向
v = ds = R dθ = Rω
dt
dt
aτ
=
dv dt
=
R dω
dt
=
Rβ
an
=
v2
ρ
=
( Rω
R
)2
=
Rω 2
A
B
第一项
r
∆ vτ
lim
∆t→ 0
∆t
=
lim
∆t→ 0
∆v ∆t
τr
=
d v τv
dt
v
v
∆v
v
A
v ∆s
v A
B
A
v
r
v B
rD r
vA ∆vn
∆v
∆v r C
∆ vτ
∆θ
r vB
E
B
第二项
r
lim
∆t→ 0
∆vn ∆t
=
v∆θ
lim
∆t→ 0
∆t
r n
=
vdθ
dt
r n
y
∆s ∆θ
A
x
o
=
练习
教材第44页例6
某发动机工作时,主轴边缘一点作圆周运动方程为
θ = t 3 + 4 t + 3 ( SI )
(1)t =2s 时,该点的角速度和角加速度为多大?
自然坐标系中的描述及相对运动

(2) vx v0 , v y gt
o v0
x
v
vx2
v
2 y
v02 g 2t 2
tan1( gt )
v0
y
an
a
g
切向加速度
at
dv dt
g2t v02 g2t 2
与速度同向
总加速度总是竖直向下的重力加速度 g
法向
an
g2 at2
v0 g 与切向加速度垂直 v02 g2t 2
A v1
n B
C
v2
法向加速度大小等于速率平方除以曲率半径, 方向沿轨道的法线指向。
第二讲 自然坐标系:切向加速度和法向加速度、相对运动
a
a
an
dv dt
v2
n
a
an
a
a a a 2 an 2
dv dt
2
v2
2
tg a
an
加速度总是指向曲线的凹侧,因为正 是加速度的法向分量改变了质点的运动方向。
2-2 圆周运动 角量
1、圆周运动中的切向加速度和法向加速度
曲率半径是恒量 a dv v2 n
dt R
匀速圆周运动v c a v2 n 向心加速度
R
2、圆周运动的角量描述
t A
角位置
t t B 角位移
v2 B v1
R s A
沿逆时针转动,角位移取正值
O
X
沿顺时针转动,角位移取负值
第二讲 自然坐标系:切向加速度和法向加速度、相对运动
第二讲 自然坐标系:切向加速度和法向加速度、相对运动
例2:手球运动员以初速度v0与水平方向成α0 角抛出一球,如图所示。当球到达M点处,与水 平线夹角为θ,求(1)球在M点速度的大小;(2)球 在M点处的切向加速度和法向加速度大小;(3)M 点处的曲率半径。
2 6_自然坐标·切向和法向加速度

2 6_自然坐标·切向和法向加速度
自然坐标:
在机械系统中,物体运动的轨迹往往是复杂的曲线,假设物体在曲线上运动。
我们可以根据物体在曲线上的位置,将坐标系重新定义,使之简化成两个自由度。
这样,物体的位置就可以用曲线上的一个参量来描述,这个参数称为自然参数;在这个参数的变化下,这个物体距离运动曲线的距离是不会改变的。
自然坐标系便是以这个自然参数为一坐标,另一个坐标是位置垂线于切线的方向,一般叫切线坐标,或称为法线坐标。
对于物体在曲线上的运动,根据牛顿第二定律,物体的加速度可以拆解成沿着曲线切向和法向的两个方向的加速度。
切向加速度:
物体在曲线上运动时,有一个切向的加速度,即切线方向上的加速度。
在自然坐标系中,我们可以通过物体在曲线上的两个连续位置的坐标求出物体在曲线上运动时的切向单位向量,然后对物体的速度向量进行投影,就可以求出物体在切向方向上的分量,进而求出物体在切向方向上的加速度。
$$a_t = \frac{d}{dt}\left(\frac{ds}{dt}\right) = \frac{d^2s}{dt^2}$$
其中,$a_t$代表切向加速度,$s$表示曲线的自然参数,$t$表示时间。
$$a_n = \frac{v^2}{\rho}$$
其中,$a$表示物体在曲线上的总加速度。
大学物理精品课件1.2 自然坐标系

vA
B
vB v A at 23.3m s 2 t 2 vB 2 an 106m s r
在点 B 的加速度
AB 3.5km
r a n
at
o
a
vB
a 与法向之间夹角
a
2 at
2 an
109m s
为
2
at arctan 12.4 an
1.3
自然坐标系
1
第一章 运动的描述
已知: vA 1940km h
所转过的角度 为 (2)在时间 t 内矢径 r
A
t 3s
AB 3.5km
vB 2192km h 1
vA
B
1 2 At t 2
飞机经过的路程为
r a n
at
o
a
vB
o
R
第一章 运动的描述 1.3 自然坐标系 2.判断下列说法的正、误: a. 加速度恒定不变时,物体的运动方向必定不变。 b. 平均速率等于平均速度的大小。
v s / t 依据 平均速率 平均速度的大小 v r / t
c. 不论加速度如何,平均速率的表达式总可以写成
v (v1 v2 ) / 2 ,其中 v1是初速度, v2 是末速度。
d. 运动物体的速率不变时,速度可以变化。 例如:物体做抛体运动,加速度恒定,而速度方 向改变。
1.3
自然坐标系
第一章 运动的描述
例 如图一超音速歼击机在高空 A 时的水平速率为 1940 km/h , 沿近似于圆弧的曲线俯冲到点 B ,其速率为 2192 km/h , 所经历的时间为 3s , 设圆弧 AB 的半径约为 3.5km , 且飞机从A 到B 的俯冲过程可视为匀变速率圆 周运动 , 若不计重力加速度的影响, 求: (1) 飞机在点B 的加速度; (2)飞机由点A 到点B 所经历的路程 . 解(1)因飞机作匀变速率 vA A 运动所以 a t 和 为常量 . B dv
自然坐标系圆周运动的角量描述

角加速度与向心加速度关系
在圆周运动中,向心加速度是描 述物体向圆心方向加速或减速的
物理量,其单位为米/秒²。
向心加速度的大小等于角加速度 与半径的乘积,即 a_n = α × r。
当角加速度的方向与半径垂直时, 向心加速度的大小达到最大值。
04
转动动能与势能
转动动能公式
定义
意义
转动动能为物体因转动而具有的动能, 与转动惯量和角速度的平方成正比。
意义
转动势能反映了物体转 动的静态特性,是描述 物体转动状态的重要物 理量。
动能与势能关系
动能与势能之和为常数
01
在保守力场中,物体转动的动能与势能之和保持不变,即 $E_{k}
+ U = E_{k0}$。
动能与势能相互转化
02
在非保守力场中,物体转动的动能与势能可以相互转化,但总
和保持不变。
动能与势能的物理意义
圆周运动的周期与频率
周期
圆周运动的周期是指完成一个完整的圆周运动所需的时间,用符号$T$表示。对于匀速 圆周运动,周期的大小为$T = frac{2pi}{omega}$。
频率
圆周运动的频率是指单位时间内完成的圆周运动圈数,用符号$f$表示。频率与周期的 关系为$f = frac{1}{T}$。
06
线速度和线加速度
在自然坐标系中,线速度和线加速度 可以通过角速度和角加速度与半径的 乘积得到。线速度的大小等于质点在 单位时间内沿圆周运动的弧长,单位 为米/秒。线加速度的大小等于质点 在单位时间内沿圆周运动的弧长的变 化量,单位为米/秒²。
展望
更深入的理论研究
随着物理学的发展,对圆周运动的研究可以更加深入,例如研究更高阶的角量和线量描述,以及它们在不同坐标 系下的变换关系等。
自然坐标系

B
(1)角位置
质点所在位置的矢径与x轴 的夹角θ。
A
R
O
X
(2)角位移
t时刻:
A点,角位置为 t
t t时刻:B点,角位置为 t t
在t时间内,矢径转过角度 ,称为质点
对O点的角位移。
t t t
大小:dθ 方向规定: 逆时针方向 dθ>0;
顺时针方向 dθ<0。
单位:弧度rad
(3)角速度
a
dv dt
an
dv n dt
a 由于速度大小变化产生的加速度;
an 由于速度方向变化产生的加速度。
切向加速度、法向加速度/二、2 r
r 为运动轨迹的曲率半径。
大小
a
a 2
a
2 n
dv
2
v 2
2
dt r
对于平面曲线运动 a dv dv dt dt
vn 为速度增量在法线方向的分量; 0 切线方向的单位矢量;
n0 法线方向的单位矢量。
切向加速度、法向加速度/二、a、an
将(1)式两边同除 t 后取极限,
lim v
Δt 0 t
lim
Δ t 0
v t
0
Δlitm0
vn t
n0
有
dv dt
dv dt
0
dv n dt
n0
即 a a0 ann0
其中:
切向加速度、法向加速度/二、a、an
例:一质点作半径为R的圆周运动,其速
率满足 v kRt, k为常数,求:切向加 速度、法向加速度和加速度的大小。
解: 切向加速度
a
dv dt
kR
法向加速度
an
1.3 自然坐标系及运用
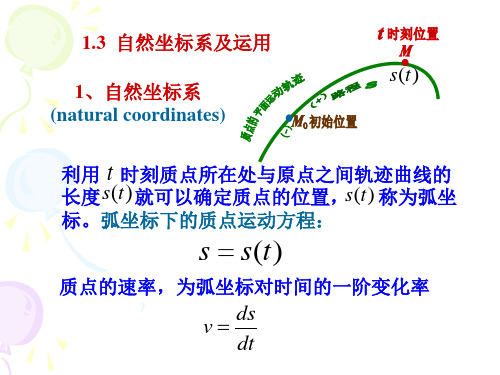
1、自然坐标系 (natural coordinates)
利用 t 时刻质点所在处与原点之间轨迹曲线的
长度s(t) 就可以确定质点的位置,s(t) 称为弧坐
标。弧坐标下的质点运动方程:
s s(t)
质点的速率,为弧坐标对时间的一阶变化率
v ds dt
将两个相互垂直的切向和法向所组成的平面
24tR
a an
an R 2 144t 4R
a
a an
24t 144t 4
3 3
2 4t3 2
2
t3 1/2 3 3.15rad
3
0 t t 0 5s
例2:质点沿半径R=0.1m作圆周运动,其角坐标与
时间的关系为 2 4t 3 (SI),当切向加速度的
大小恰为总加速度的一半时,则
。
解:切向加速度大小为总加速度的一半,则
30 a / an tan 30
v R R d 12t 2R
dt
a
R
d 2
R dt 2
an
v
dˆ
dtv2nˆFra bibliotek aa
an
dv ˆ
dt
v2
nˆ
大小:a
a2 an2
( dv )2 (v2 )2
dt
当质点做直线运动时 ,因此法向加速度为零;
当质点做圆周运动时, 为圆周运动的半径 R ;
如果 v 为常数,则切向加速度为零,合加速度方
向指向圆心,称为向心加速度;
3 圆周运动的角量描述
0t
0
0t
1 2
t2
2
2 0
2
(
直角坐标系和自然坐标系的转化

直角坐标系和自然坐标系的转化
直角坐标系和自然坐标系都是用来描述点在平面上的位置的工具。
直角坐标系是通过将平面分成水平和垂直的两个轴(x轴和y 轴),来表示点的位置。
而自然坐标系则是通过将平面上的点与它周围的物体(如墙角、街道等)的位置联系起来,来表示点的位置。
转换直角坐标系和自然坐标系之间的关系可以很有用,特别是在导航、地图制作和建筑设计方面。
转换的方法通常是通过观察平面上的物体,确定它们在直角坐标系中的坐标,然后将这些坐标用于转换其他点的位置。
在实际应用中,转换直角坐标系和自然坐标系的准确性非常重要,因为它涉及到测量、位置精度和方向。
因此,需要使用专门的工具和软件来进行这种转换,并根据具体情况进行调整和校正,以确保准确性和可靠性。
- 1 -。
有限元,自然坐标系的物理意义

有限元,自然坐标系的物理意义
有限元自然坐标系就是沿质点的运动轨道建立的坐标系。
在质点运动轨道上任取一点作为坐标原点O,质点在任意时刻的位置,都可用它到坐标原点O的轨迹的长度来表示。
在有限元自然坐标系中,两个单位矢量是这样定义的:切向单位矢量,沿质点所在点的轨道切线方向,法向单位矢量,垂直于在同一点的切向单位矢量而指向曲线的凹侧。
可见这两个单位矢量的方向,也是随质点位置的不同而不同的。
在有限元自然坐标系中表示质点速度,是非常简单的,因为无论质点处在什么位置上速度都只有切向分量,而没有法向分量。
有限元自然坐标系不仅适用于平面运动,也可以用于三维空间的运动。
不过在三维情况下,应该引入两个法向单位矢量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t)
-
et
(t)
当: t 0 , 0
et
t
t
O Δ P2
s
et t
有 det et d d
P1
方向
det
et
d et d
d t dt
即en方向
en
et
t
t
et
et
t
4
d ds
at
dv dt
c
an
v2 R
(b ct)2 R
(2) at an
解得 t b R cc
12
§1-3 相对运动
一 时间与空间
在两个作相对运动的参考系中,时间 的测量是绝对的,空间的测量也是绝对的, 与参考系无关.
时间和长度的的绝对性是经典力学或 牛顿力学的基础.
13
二 相对运动
o
at
0.4
M at
a
x
11
例5 一质点沿半径为R的圆周运动,其路程s随时
间t 的变化规律为 s bt 1 ct 2,式中b,c为大于
零的常数,且 b2 Rc 。求(2 1)质点的切向加速
度和法向加速度。(2)经过多长时间,切向加速
度等于法向加速度。
解: (1)
v ds b ct dt
解: 按题意作矢量图
y
v v0 v
v v0 tan 60 10 tan 60m s1
17.3 m s1
y´ x´
v0
v
速度:
v
vet
ds dt
et
2
质点的加速度:
a
dv dt
d(vet dt
)
dv dt
et
v
det dt
dv dt
et
:
速度大小的变化率,其方向指向曲线的切线方向
切向加速度:
at
dv dt
et
d2s dt 2
et
3
讨论
det
dt
et
et (t
1-2-5 自然坐标系:
把坐标建立在运动轨迹上的坐标系统。
P
s
et
en
s
• 切向规坐定标:轴O沿质点e前n 进方向Q的切向为正,et单位矢量为et
• 法向 坐标轴沿轨迹的法向凹侧为正,单位矢量为en
1
s
P
et
O
en s
Q
et
v
质点位置: s st
路程: s sQ sP
15
位移关系
r r'D 或 r r'ut
速度变换
r r' u t t v v'u
yy'
P P'
*
oo'
xx'
t0
y
o
y' u Q
P
D
r r'
P'
xx'
ut o' t t
16
v v u
伽利略速度变换
at R an R 2
ds R d
dt dt
dv R d
dt
dt
an
v2 R
R
2
8
可以把角速度看成是矢量 !
方向弯曲,拇指
的指向即为角速度矢量的方向。
线速度与角速度的关系:
v r
ω y v
R
d v d ω r ω d r
d et dt
ds ρdt
en
v ρ
en
et
t
t
O Δ P2
s
P1
et
t
v det
dt
v2 ρ
en
法向加速度:
沿法线方向
an
v det
dt
v2 ρ
en
5
综上所述:
a
at
an
dv dt
et
v2
en
加速度的大小:
物体运动的轨迹依赖于观察者所处的参考系
14
质点在相对作匀速 直线运动的两个坐标系 中的位移
S系 (Oxyz)
基本参考系
S'系(O' x' y' z')
运动参考系
u 是S’系相对S系
运动的速度
yy'
P P'
*
oo'
xx'
t0
y
o
y' u Q
P
D
r r'
P'
xx'
ut o' t t
绝对速度 v
dr
dt
绝对速度 v v
u 牵连速度
相对速度
相对速度
牵连速度 u
注意: 当物体运动速度 接近光速时,速度变换不 成立.
加速度关系
dv dv' du
dt
若
dudt 0
dt a a'
dt
17
例6 一观察者A坐在平板车上,车以10 m/s的速率沿 水平轨道前进。他以与车前进的反方向呈 60°角向上 斜抛出一石块,此时站在地面上的观察者B看到石块 沿铅垂线向上运动。求石块上升的高度。
dt dt
dt
r
O
x
z
9
a r ω v
r R 方向沿着运动的切线方向。
r为切向加速度
即 at r v v v 2R ω v 方向指向圆心
ω y v
R
r
O
x
为法向加速度
a an2 at2
加速度的方向(以与切线方向的夹角表示):
arctan an
at
例:抛体运动
an
at
g
6
1-2-6 圆周运动及其角量描述
角位置 : 质点所在的矢径与x 轴的夹角。
角位移: 质点从A到B矢径转过的角度 。
规定: 逆时针转向为正 顺时针转向为负
即
an
ω
v
z
10
例4 半径为r = 0.2 m的飞轮,可绕 O 轴转动。已知
轮缘上一点M的运动方程为 = -t2+4t ,求在1秒时
刻M点的速度和加速度。
解:
d
dt
2t 4
d
dt
2
v r r(2t 4) 0.2 (21 4) m s1 0.4 m s1
角速度:
lim t 0
t
d
dt
角加速度:
lim
t 0
t
d
dt
y
B
s
A
RO
x
7
角量表示匀加速圆周运动的基本公式:
0 t
0 0t
1 2
t2
2 02 2 0
角量和线量的关系:
s R
v R
at r (2) 0.2m s2 0.4 m s2 v
an r 2 0.2(21 4)2 m s2 0.8 m s2
a at2 an2 0.89 m s2
an
arctan an arctan 0.8 63.4
