振动力学第五章
大学物理第五章机械振动习题解答和分析要点
5-1 有一弹簧振子，振幅A=2.0⨯10-2m，周期T=1.0s，初相ϕ=3π/4.试写出它的振动位移、速度和加速度方程。
分析根据振动的标准形式得出振动方程，通过求导即可求解速度和加速度方程。
解：振动方程为：x=Acos[ωt+ϕ]=Acos[3π42πTt+ϕ] 代入有关数据得：x=0.02cos[2πt+振子的速度和加速度分别是：v=dx/dt=-0.04πsin[2πt+3π43π4](SI) ](SI) a=dx/dt=-0.08πcos[2πt+222](SI)5-2若简谐振动方程为x=0.1cos[20πt+π/4]m，求：（1）振幅、频率、角频率、周期和初相；（2）t=2s时的位移、速度和加速度.分析通过与简谐振动标准方程对比，得出特征参量。
解：(1)可用比较法求解.根据x=Acos[ωt+ϕ]=0.1cos[20πt+π/4] 得：振幅A=0.1m，角频率ω=20πrad/s，频率ν=ω/2π=10s 周期T=1/ν=0.1s，ϕ=π/4rad（2）t=2s时，振动相位为：ϕ=20πt+π/4=(40π+π/4)rad22 由x=Acosϕ，ν=-Aωsi nϕ，a=-Aωcosϕ=-ωx得 -1，x=0.0707m,ν=-4.44m/s,a=-279m/s5-3质量为2kg的质点，按方程x=0.2sin[5t-(π/6)](SI)沿着x轴振动.求：（1）t=0时，作用于质点的力的大小；（2）作用于质点的力的最大值和此时质点的位置.分析根据振动的动力学特征和已知的简谐振动方程求解，位移最大时受力最大。
2解：（1）跟据f=ma=-mωx，x=0.2sin[5t-(π/6)] 2将t=0代入上式中，得：f=5.0N2 （2）由f=-mωx可知，当x=-A=-0.2m时，质点受力最大，为f=10.0N5-4为了测得一物体的质量m，将其挂到一弹簧上并让其自由振动，测得振动频率ν1=1.0Hz；而当将另一已知质量为m'的物体单独挂到该弹簧上时，测得频率为ν2=2.0Hz.设振动均在弹簧的弹性限度内进行，求被测物体的质量.分析根据简谐振动频率公式比较即可。
振动力学 第5章
第五章 多自由度系统的振动5.1解：用Newton 第二定律或Dalembert 原理分别建立五个质点的动平衡方程1121314413213144131()()()()m xc x c x x c x x k x k x x k x x F ++-+-++-+-= 2272823728232()()m xc x c x x k x k x x F ++-++-= 33431534693832103543153469383210353()()()()()()()()()()m x c x x c x x c c x c x x c x x k x x k x x k k x k x x k x x F +-+-+++-+-+-+-+++-+-=4414341543143415434()()()()m xc x c x x c x x k x k x x k x x F ++-+-++-+-= 55105310535()()m xc x x k x x F +-+-= 整理得1123414334234143341()()m xc c c x c x c x k k k x k x k x F +++--+++--= 2278283782832()()m x c c x c x k k x k x F ++-++-= 3341824568910354105418245689103541053()()m x c x c x c c c c c c x c x c x k x k x k k k k k k x k x k x F --++++++----++++++--=44315335431533544()()m xc x c x c c x k x k x k k x F --++--++= 551031051031055m xc x c x k x k x F -+-+= 写成矩阵形式为MX+CX+KX =F 其中{}T12345F F F F F F = {}T12345X x x x x x =[]12345M diag m m m m m =234437884845689105103535101000000C 0000c c c c c c c c c c c c c c c c c c c c c c c c ++--⎡⎤⎢⎥+-⎢⎥⎢⎥=--+++++--⎢⎥--+⎢⎥⎢⎥-⎣⎦2344378848456891051035351010000000000k k k k k k k k k k k k k k k k k k k k k k k k ++--⎡⎤⎢⎥+-⎢⎥⎢⎥=--+++++--⎢⎥--+⎢⎥⎢⎥-⎣⎦K5.2解：（一）板和地基有四个立柱连接（1）取广义坐标B x 、C x 和D y 质心处的位移为:,,222B c B C B C O O D D x x x x x x lx y y y lθθ+--==+=+= 系统的势能为()222222222222211112222222222222222B C B C D D BCDBCDB C B D C D B C D B C B D C Dx x U kx kx ky k y l l kx kx ky k x x y x x x y x y kx kx ky kx x kx y kx y ⎡⎤-⎛⎫⎛⎫⎛⎫=++++⎢⎥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦=+++++-+-=++-+-其中, 312EI k l =系统的动能为2222222221112221112222211122222O O B C B C B C D B C B C B C D T mx my J xx x x x x m m y J l xx x x x x m m y J l θ=+++--⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭+--⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 其中, 22211()126J a b ml =+= 拉格朗日函数22222211122222222222B C B C B C D B C D B C B D C Dxx x x x x L T U m m y J l kx kx ky kx x kx y kx y +--⎛⎫⎛⎫⎛⎫=-=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭---+-+当系统发生位移B x 、C x 和D y 时，外力()F t 所做的功为111()()()()()222B C o D D B C x x W F t y F t y l F t y F t x F t x l -⎡⎤=⋅=+=⋅+⋅-⋅⎢⎥⎣⎦因此，等效结点力向量为T11Q ()()()22F t F t F t ⎧⎫=-⎨⎬⎩⎭代入Lagrange 方程d d i i i L LQ t qq ⎛⎫∂∂-= ⎪∂∂⎝⎭ (1,2,,)i n = 得 3332114824241()3622B C D B C D EI EI EI mx mx my x x y F t l l l -++-+= 3331212448241()6322B C D B C D EI EI EI mx mx my x x y F t l l l -+--+-=- 33311242448()22B C D B C D EI EI EI mx mx my x x y F t l l l-++-+= （2）取质心坐标o x 、o y 和θ为广义坐标 系统的势能为2222222211112222222222222222O O O O O O O O l l l l U k x k x k y k y l l l l k x k x k y k y θθθθθθθθ⎡⎤⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=++-+++-⎢⎥⎢⎥⎢⎥⎢⎥⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎛⎫⎛⎫⎛⎫⎛⎫=++-+++- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭其中, 312EI k l =系统的动能为222111222O O T mx my J θ=++ ， 其中, 22211()126J a b ml =+= 拉格朗日函数22222221112222222O O O O O O L T U mx my J l l l l k x k x k y k y θθθθθ=-=++⎛⎫⎛⎫⎛⎫⎛⎫-+---+-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭当系统发生位移o x 、o y 和θ时，外力()F t 所做的功为: ()o W F t y =⋅ 因此，等效结点力向量为:{}TQ 0()0F t =代入Lagrange d d i i i L LQ t qq ⎛⎫∂∂-= ⎪∂∂⎝⎭ (1,2,,)i n = 方程得 3480O O EImxx l += 348()O O EImyy F t l+= 212406EI ml l θθ+=（3）取质心坐标BD x 、AC y 和θ为广义坐标 系统的势能为2222222211112222221111222222AC AC AC AC BD BD BD BD U kx kx k x k x ky ky k y k y θθθθ⎛⎫⎛⎫=++++- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫+++++- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭其中, 312EI k l =系统的动能为222111222AC BD T mx my J θ=++ ， 其中, 22211()126J a b ml =+= 拉格朗日函数22222222211122211112222AC BD AC BD AC AC BD BD L T U mx my J kx ky k x k x k y k y θ=-=++--⎛⎫⎛⎫⎛⎫⎛⎫-+---- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭当系统发生位移BD x 、AC y 和θ时，外力()F t 所做的功为()()()AC BD AC BD W F t x y F t x t y ⎤=⋅+=⋅+⋅⎥⎣⎦因此，等效结点力向量为:TQ ()()022F t F t ⎫⎪=⎨⎬⎪⎪⎩⎭代入Lagrange d d i i i L LQ t qq ⎛⎫∂∂-= ⎪∂∂⎝⎭ (1,2,,)i n = 方程得348()AC AC EI mxx F t l +=348()BD BD EI myy F t l += 212406EI ml lθθ+= （二）板和地基有三个立柱连接 （1）取广义坐标B x 、C x 和D y质心处的位移为,,222B c B C B C O O D D x x x x x x lx y y y lθθ+--==+=+= 系统的势能为()22222222222221111222222112222233222222B CB C D D B C D B C D B C B D C D B C D B C B D C Dx x U kx kx ky k y l l kx kx ky k x x y x x x y x y kx kx ky kx x kx y kx y ⎡⎤-⎛⎫⎛⎫⎛⎫=++++⎢⎥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦=+++++-+-=++-+-其中，312EIk l=。
振动力学—连续系统
弦的横向振动
y(x,t)为弦上坐标为x处的横截面 在t时刻的横向位移l。
取微元，分析受力，如图
杆的纵向振动
假定：细长等截面杆, 振动时横截面仍保持为平面，横截 面上的质点只作沿杆件纵向的振动，横向变形忽略不计。 则同一横截面上各点在x方向作相等的位移。 参数：杆长l，截面积S，材料密度，弹性模量E
EI d 4Y d 2T a 2 , 4 Y IV , 2 T ，则上式为： 令 m dx dt IV T 2 Y a Y T
Y IV T a 2 Y T
2
梁的弯曲振动
方程
T 2T 0
Y
( 4)
2
a
2
Y 0
T Aei (t )
各态遍历过程
相关函数
自相关函数性质
1 偶函数
Rx ( ) Rx ( )
2 周期随机过程的自相关函数仍是周期函数 X (t ) X (t ) Rx ( ) Rx ( T ) 3 4
2 Rx (0) x
2 2 x x Rx ( ) Rx (0)
T(t ) 2T (t ) 0
X ( x)
2
a
2 0
X ( x) 0
杆的纵向振动
解为 时间域，初值问题 空间域，边值问题 固支边条件
T (t ) Aei (t )
X ( x) C1 sin
a0
x C2 cos
a0
x
x=0时，u(0,t)=X(0)· T(x)=0，即X(0)=0 x=l时，u(l,t)=X(0)· T(l)=0，即X(l)=0
x=H(0) f
机械振动的检测
5.2 机械振动的类型
1.简谐振动 简谐振动的振动量随时间的变化规律如图5-3所示，其位移
表达式为:
上一页 下一页 返回
5.2 机械振动的类型
将式(9-1)求导可得振动速度和振动加速度的表达式:
上一页 下一页 返回
5.2 机械振动的类型
由此可知，简谐振动的位移、速度和加速度的波形和频率都 为一定，其速度和加速度的幅值与频率有关，在相位上，速 度超前位移π/2，加速度又超前速度π/2。对于简谐振动， 只要测定出位移、速度、加速度和频率这四个参数中的任意 两个，便可推算出其余两个参数。
而且其振动量与时间也无一定的联系。诸如路面的不平对车 辆的激励;加工工件表面层几何物理状况的不均匀对机床刀具 的激励;波浪对船舶的激励;大气湍流对飞行器的激励等，都 将会产生随机振动。 随机振动的统计参数通常有均值、方均值、方差、相关函数 和功率谱密度函数等，与一般随机信号的处理一样。
上一页 下一页 返回
上一页 下一页 返回
5.2 机械振动的类型
3.准周期振动 准周期振动是由频率比不全为有理数的简谐振动迭加而成，
如
这种振动如果忽略其相位角，也可用离散频谱来表征，如 图5-5所示。因而称之为准周期振动。
实际工作中遇到的两个或几个不相关联的周期振动混合作 用时，便会产生这种振动状态。
上一页 下一页 返回
第五章 机械振动的检测
5.1 概述 5.2 机械振动的类型 5.3 振动的激励和激振器 5.4 测振传感器 5.5 振动的测量
5.1 概述
机械振动是自然界、工程技术和日常生活中普遍存在的物理 现象。各种机器、仪器和设备在其运行时，由于诸如回转件 的不平衡、负载的不均匀、结构刚度的各向异性、润滑状况 的不良及间隙等原因而引起力的变化、零部件之间的碰撞和 冲击，以及由于使用、运输和外界环境条件下能量的传递、 存储和释放等都会诱发或激励机械振动。所以说，任何一台 运行着的机器、仪器和设备都会存在着振动现象。
物理学教程(第二版)上册第五章课后习题答案详解
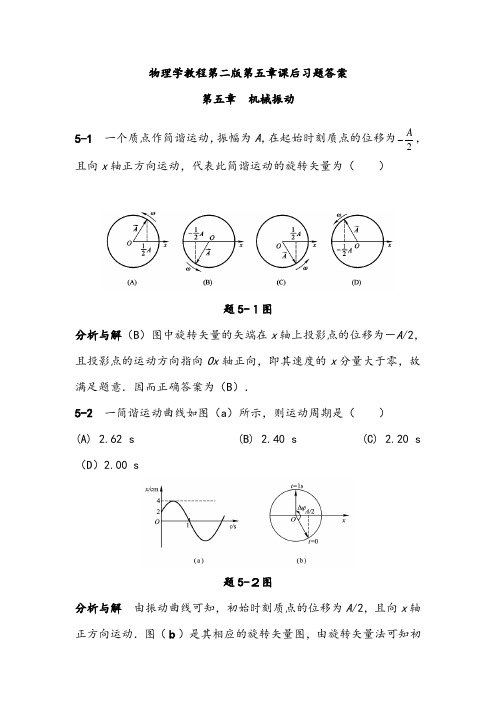
物理学教程第二版第五章课后习题答案第五章 机械振动5-1 一个质点作简谐运动，振幅为A ，在起始时刻质点的位移为2A，且向x 轴正方向运动，代表此简谐运动的旋转矢量为（ ）题5-１图分析与解（B ）图中旋转矢量的矢端在x 轴上投影点的位移为－A /2，且投影点的运动方向指向Ox 轴正向，即其速度的x 分量大于零，故满足题意．因而正确答案为（B ）．5-2 一简谐运动曲线如图（a ）所示，则运动周期是（ ）(A) 2.62 s (B) 2.40 s (C) 2.20 s（D ）2.00 s题5-２图分析与解 由振动曲线可知，初始时刻质点的位移为A /2，且向x 轴正方向运动．图（ｂ）是其相应的旋转矢量图，由旋转矢量法可知初相位为-3/π2．振动曲线上给出质点从A /2 处运动到x =0处所需时间为1 s ，由对应旋转矢量图可知相应的相位差65232πππϕ=+=∆，则角频率1s rad 65Δ/Δ-⋅==πϕωt ，周期s 40.22==ωπT .故选（B ）． 5-3 两个同周期简谐运动曲线如图（a ）所示， x 1的相位比x 2的相位（ ）（A ）落后2π（B ）超前2π（C ）落后π（D ）超前π分析与解 由振动曲线图作出相应的旋转矢量图（b ）即可得到答案为（B ）．题5 -３图5-4 两个同振动方向、同频率、振幅均为A 的简谐运动合成后，振幅仍为A ，则这两个简谐运动的相位差为（ ）（A ）60 （B ）90 （C ）120 （D ）180分析与解 由旋转矢量图可知两个简谐运动1和2的相位差为120 时，合成后的简谐运动3的振幅仍为A .正确答案为（C ）．题5-4图5-5 若简谐运动方程为⎪⎭⎫ ⎝⎛+=4ππ20cos 10.0t x ，式中x 的单位为m ，t 的单位为s.求：（1）振幅、频率、角频率、周期和初相；（2）s 2=t 时的位移、速度和加速度．分析 可采用比较法求解．将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较，即可求得各特征量．运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果．解 （1）将()()m π25.0π20cos 10.0+=t x 与()ϕω+=t A x cos 比较后可得：振幅A ＝0.10m ，角频率1s rad π20-⋅=ω，初相ϕ＝0.25π，则周期s 1.0/π2==ωT ，频率Hz /1T =v ．（２）s 2=t 时的位移、速度、加速度分别为()m 1007.7π25.0π40cos 10.02-⨯=+=t x()-1s m 44.4π25.0π40sin π2d /d ⋅-=+-==t x v()-22222s m 1079.2π25.0π40cos π40d /d ⋅⨯-=+-==t x a5-6 一远洋货轮，质量为m ，浮在水面时其水平截面积为S ．设在水面附近货轮的水平截面积近似相等，水的密度为ρ，且不计水的粘滞阻力，证明货轮在水中作振幅较小的竖直自由运动是简谐运动，并求振动周期．分析 要证明货轮作简谐运动，需要分析货轮在平衡位置附近上下运动时，它所受的合外力F 与位移x 间的关系，如果满足kx F -=，则货轮作简谐运动．通过kx F -=即可求得振动周期k m ωT /π2/π2==． 证 货轮处于平衡状态时［图（a ）］，浮力大小为F ＝mg ．当船上下作微小振动时，取货轮处于力平衡时的质心位置为坐标原点O ，竖直向下为x 轴正向，如图（b ）所示．则当货轮向下偏移x 位移时，受合外力为∑'+=F P F其中F '为此时货轮所受浮力，其方向向上，大小为gSx mg gSx F F ρρ+=+='题5-6图则货轮所受合外力为kx gSx F P F -=-='-=∑ρ式中gS k ρ=是一常数．这表明货轮在其平衡位置上下所作的微小振动是简谐运动．由∑=t x m F 22d d /可得货轮运动的微分方程为0d d 22=+m gSx t x //ρ令m gS /ρω=2，可得其振动周期为gS ρm πωT /2/π2==5-7 如图（a ）所示，两个轻弹簧的劲度系数分别为1k 、2k ．当物体在光滑斜面上振动时．（1）证明其运动仍是简谐运动；（2）求系统的振动频率．题5-7图分析 从上两题的求解知道，要证明一个系统作简谐运动，首先要分析受力情况，然后看是否满足简谐运动的受力特征（或简谐运动微分方程）．为此，建立如图（b ）所示的坐标．设系统平衡时物体所在位置为坐标原点O ，Ox 轴正向沿斜面向下，由受力分析可知，沿Ox 轴，物体受弹性力及重力分力的作用，其中弹性力是变力．利用串联时各弹簧受力相等，分析物体在任一位置时受力与位移的关系，即可证得物体作简谐运动，并可求出频率υ．证 设物体平衡时两弹簧伸长分别为1x 、2x ，则由物体受力平衡，有2211sin x k x k mg ==θ（1）按图（b ）所取坐标，物体沿x 轴移动位移x 时，两弹簧又分别被拉伸1x '和2x '，即21x x x '+'=．则物体受力为 ()()111222sin sin x x k mg x x k mg F '+-='+-=θθ（２） 将式（1）代入式（2）得1122x k x k F '-='-=（３） 由式（3）得11k F x /-='、22k F x /-='，而21x x x '+'=，则得到()[]kx x k k k k F -=+-=2121/式中()2121k k k k k +=/为常数，则物体作简谐运动，振动频率 ()m k k k k πm k ωv 2121/21/π21π2/+=== 讨论 （1）由本题的求证可知，斜面倾角θ对弹簧是否作简谐运动以及振动的频率均不产生影响．事实上，无论弹簧水平放置、斜置还是竖直悬挂，物体均作简谐运动．而且可以证明它们的频率相同，均由弹簧振子的固有性质决定，这就是称为固有频率的原因．（2）如果振动系统如图（c ）（弹簧并联）或如图（d ）所示，也可通过物体在某一位置的受力分析得出其作简谐运动，且振动频率均为()m k k v /π2121+=，读者可以一试．通过这些例子可以知道，证明物体是否作简谐运动的思路是相同的．5-8 一放置在水平桌面上的弹簧振子，振幅A ＝2.0 ×10-2 m ，周期T ＝0.50ｓ．当t ＝0 时，（1）物体在正方向端点；（2）物体在平衡位置、向负方向运动；（3）物体在x ＝-1.0×10-2m 处，向负方向运动；（4）物体在x ＝-1.0×10-2 m 处，向正方向运动．求以上各种情况的运动方程．分析 在振幅A 和周期T 已知的条件下，确定初相φ是求解简谐运动方程的关键．初相的确定通常有两种方法．（1）解析法：由振动方程出发，根据初始条件，即t ＝0 时，x ＝x 0和v ＝v 0来确定φ值．（2）旋转矢量法：如图（a ）所示，将质点P 在Ox 轴上振动的初始位置x 0和速度v 0的方向与旋转矢量图相对应来确定φ．旋转矢量法比较直观、方便，在分析中常采用．题5-8图解 由题给条件知A ＝2.0 ×10-2 m ，1s π4/2-==T ω，而初相φ可采用分析中的两种不同方法来求．解析法：根据简谐运动方程()ϕω+=t A x cos ，当0t =时有()ϕω+=t A x cos 0，sin 0ϕωA -=v ．当（1）A x =0时，1cos 1=ϕ，则01=ϕ；（2）00=x 时，0cos 2=ϕ，2π2±=ϕ，因00<v ，取2π2=ϕ；（3）m 100120-⨯=.x 时，50cos 3.=ϕ，3π3±=ϕ，由00<v ，取3π3=ϕ；（4）m 100120-⨯-=.x 时，50cos 4.-=ϕ，3ππ4±=ϕ，由00>v ，取3π44=ϕ． 旋转矢量法：分别画出四个不同初始状态的旋转矢量图，如图（b ）所示，它们所对应的初相分别为01=ϕ，2π2=ϕ，3π3=ϕ，3π44=ϕ． 振幅A 、角频率ω、初相φ均确定后，则各相应状态下的运动方程为（1）()m t πcos4100.22-⨯=x（2）()()m /2πt π4cos 100.22+⨯=-x（3）()()m /3πt π4cos 100.22+⨯=-x（4）()()m0.22+10=-xcos⨯/3π44tπ5-9有一弹簧，当其下端挂一质量为m的物体时，伸长量为9.8 ×10-2 m．若使物体上、下振动，且规定向下为正方向．（1）当t＝0 时，物体在平衡位置上方8.0 ×10-2ｍ处，由静止开始向下运动，求运动方程．（2）当t＝０时，物体在平衡位置并以0.6ｍ·s-1的速度向上运动，求运动方程．分析求运动方程，也就是要确定振动的三个特征物理量A、ω和φ．其中振动的角频率是由弹簧振子系统的固有性质（振子质量m及弹簧劲度系数k）决定的，即k mω=/，k可根据物体受力平衡时弹簧的伸长来计算；振幅A和初相φ需要根据初始条件确定．题5-9图解物体受力平衡时，弹性力F与重力P的大小相等，即F＝mg．而此时弹簧的伸长量Δl＝9.8 ×10-2m．则弹簧的劲度系数k＝F／Δl ＝mg／Δl．系统作简谐运动的角频率为1ωmk//g=s=l10-∆=（1）设系统平衡时，物体所在处为坐标原点，向下为x轴正向．由初始条件t ＝0 时，x10＝8.0 ×10-2m、v10＝0 可得振幅()m 10082210210-⨯=+=./ωv x A ；应用旋转矢量法可确定初相π1=ϕ［图（a ）］．则运动方程为()()m π10t cos 100.821+⨯=-x（2）t ＝０时，x 20＝0、v 20＝0.6 ｍ·s -1，同理可得()m 100622202202-⨯=+=./ωv x A ；2/π2=ϕ［图（b ）］．则运动方程为 ()()m π5.010t cos 100.622+⨯=-x5-10 某振动质点的x -t 曲线如图（a ）所示，试求：（1）运动方程；（2）点P 对应的相位；（3）到达点P 相应位置所需的时间．分析 由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题．本题就是要通过x －t 图线确定振动的三个特征量A 、ω和0ϕ，从而写出运动方程．曲线最大幅值即为振幅A ；而ω、0ϕ通常可通过旋转矢量法或解析法解出，一般采用旋转矢量法比较方便．解 （1）质点振动振幅A ＝0.10 ｍ．而由振动曲线可画出t 0＝0 和t 1＝4 ｓ时旋转矢量，如图（b ）所示．由图可见初相3/π0-=ϕ（或3/π50=ϕ），而由()3201//ππω+=-t t 得1s 24/π5-=ω，则运动方程为()m 3/π24π5cos 10.0⎪⎭⎫ ⎝⎛-=t x题5-10图（2）图（a ）中点P 的位置是质点从A ／2 处运动到正向的端点处．对应的旋转矢量图如图（c ）所示．当初相取3/π0-=ϕ时，点P 的相位为()000=-+=p p t ωϕϕ（如果初相取成3/π50=ϕ，则点P 相应的相位应表示为()π200=-+=p p t ωϕϕ．（3）由旋转矢量图可得()3/π0=-p t ω，则s 61.=p t ．5-11 质量为10 g 的物体沿x 的轴作简谐运动，振幅A =10 cm ，周期T =4.0 s ，t =0 时物体的位移为，cm 0.50-=x 且物体朝x 轴负方向运动，求（1）t =1.0 s 时物体的位移；（2）t =1.0 s 时物体受的力；（3）t =0之后何时物体第一次到达x =5.0 cm 处；（4）第二次和第一次经过x =5.0 cm 处的时间间隔.分析根据题给条件可以先写出物体简谐运动方程)cos(ϕω+=t A x .其中振幅A ，角频率Tπ2=ω均已知，而初相ϕ可由题给初始条件利用旋转矢量法方便求出. 有了运动方程，t 时刻位移x 和t 时刻物体受力x m ma F 2ω-==也就可以求出. 对于（3）、（4）两问均可通过作旋转矢量图并根据公式t ∆=∆ωϕ很方便求解.解由题给条件画出t =0时该简谐运动的旋转矢量图如图（a ）所示，可知初相3π2=ϕ.而A =0.10 m ，1s 2ππ2-==T ω.则简谐运动方程为m )3π22πcos(10.0+=t x (1)t =1.0 s 时物体的位移m 1066.8m )3π22π0.1cos(10.02-⨯-=+⨯=x（2）t =1.0 s 时物体受力N1014.2N)1066.8()2π(101032232---⨯=⨯-⨯⨯⨯-=-=x m F ω （3）设t =0时刻后，物体第一次到达x =5.0 cm 处的时刻为t 1，画出t =0和t =t 1时刻的旋转矢量图，如图（b ）所示，由图可知，A 1与A 的相位差为π，由t ∆=∆ωϕ得s 2s 2/ππ1==∆=ωϕt （4）设t =0时刻后，物体第二次到达x =5.0 cm 处的时刻为t 2,画出t =t 1和t = t 2时刻的旋转矢量图，如图（c ）所示，由图可知，A 2与A 1的相位差为3π2，故有 s 34s 2/π3/π212==∆=-=∆ωϕt t t题 5-11 图5-12 图（a ）为一简谐运动质点的速度与时间的关系曲线，且振幅为2cm ，求（1）振动周期；（2）加速度的最大值；（3）运动方程． 分析 根据v -t 图可知速度的最大值v max ，由v max ＝Aω可求出角频率ω，进而可求出周期T 和加速度的最大值a max ＝Aω2．在要求的简谐运动方程x ＝A cos （ωt ＋φ）中，因为A 和ω已得出，故只要求初相位φ即可．由v －t 曲线图可以知道，当t ＝0 时，质点运动速度v 0＝v max /2 ＝Aω/2，之后速度越来越大，因此可以判断出质点沿x 轴正向向着平衡点运动．利用v 0＝－Aωsinφ就可求出φ． 解 （1）由ωA v =max 得1s 51-=.ω，则s 2.4/π2==ωT（2）222max s m 1054--⋅⨯==.ωA a（3）从分析中已知2/sin 0ωA ωA =-=v ，即21sin /-=ϕ6/π5,6/π--=ϕ因为质点沿x 轴正向向平衡位置运动，则取6/π5-=，其旋转矢量图如图（b ）所示．则运动方程为()cm 6π55.1cos 2⎪⎭⎫⎝⎛-=t x题5-12图5-13 有一单摆，长为1.0m ，最大摆角为5°，如图所示．（1）求摆的角频率和周期；（2）设开始时摆角最大，试写出此单摆的运动方程；（3）摆角为3°时的角速度和摆球的线速度各为多少？题5-13图分析 单摆在摆角较小时（θ＜5°）的摆动，其角量θ与时间的关系可表示为简谐运动方程()ϕωθθ+=t cos max ，其中角频率ω仍由该系统的性质（重力加速度g 和绳长l ）决定，即l g /=ω．初相φ与摆角θ，质点的角速度与旋转矢量的角速度（角频率）均是不同的物理概念，必须注意区分． 解 （1）单摆角频率及周期分别为s 01.2/π2;s 13.3/1====-ωT l g ω（2）由0=t 时o max 5==θθ可得振动初相0=ϕ，则以角量表示的简谐运动方程为t θ13.3cos 36π=（３）摆角为3°时，有()60cos max ./==+θθϕωt ，则这时质点的角速度为()()1max 2max max s2180800cos 1sin /d d --=-=+--=+-=..ωθϕωωθϕωωθθt t t线速度的大小为1s m 218.0/d d -⋅-==t l v θ讨论 质点的线速度和角速度也可通过机械能守恒定律求解，但结果会有极微小的差别．这是因为在导出简谐运动方程时曾取θθ≈sin ，所以，单摆的简谐运动方程仅在θ较小时成立．*5-14 一飞轮质量为12kg ，内缘半径r ＝0.6ｍ，如图所示．为了测定其对质心轴的转动惯量，现让其绕内缘刃口摆动，在摆角较小时，测得周期为2.0s ，试求其绕质心轴的转动惯量．题5-14图分析 飞轮的运动相当于一个以刃口为转轴的复摆运动，复摆振动周期为c /π2mgl J T =，因此，只要知道复摆振动的周期和转轴到质心的距离c l ，其以刃口为转轴的转动惯量即可求得．再根据平行轴定理，可求出其绕质心轴的转动惯量．解 由复摆振动周期c /π2mgl J T =，可得22π4/m g r T J =（这里r l C ≈）．则由平行轴定理得222220m kg 83.2π4⋅=-=-=mr mgrT mr J J 5-15 如图（a ）所示，质量为 1.0 ×10-2kg 的子弹，以500m·s -1的速度射入木块，并嵌在木块中，同时使弹簧压缩从而作简谐运动，设木块的质量为4.99 kg ，弹簧的劲度系数为8.0 ×103 N·m -1，若以弹簧原长时物体所在处为坐标原点，向左为x 轴正向，求简谐运动方程．题5-15图分析 可分为两个过程讨论．首先是子弹射入木块的过程，在此过程中，子弹和木块组成的系统满足动量守恒，因而可以确定它们共同运动的初速度v 0，即振动的初速度．随后的过程是以子弹和木块为弹簧振子作简谐运动．它的角频率由振子质量m 1＋m 2和弹簧的劲度系数k 确定，振幅和初相可根据初始条件（初速度v 0和初位移x 0）求得．初相位仍可用旋转矢量法求． 解 振动系统的角频率为()121s 40-=+=m m k /ω由动量守恒定律得振动的初始速度即子弹和木块的共同运动初速度v 0为12110s m 0.1-⋅=+=m m vm v又因初始位移x 0＝0，则振动系统的振幅为()m 105.2//202020-⨯==+=ωωx A v v图（b ）给出了弹簧振子的旋转矢量图，从图中可知初相位2/π0=ϕ，则简谐运动方程为()()m π0.540cos 105.22+⨯=-t x5-16 如图（a ）所示，一劲度系数为k 的轻弹簧，其下挂有一质量为m 1的空盘．现有一质量为m 2的物体从盘上方高为h 处自由落入盘中，并和盘粘在一起振动．问：（1）此时的振动周期与空盘作振动的周期有何不同？（2）此时的振幅为多大？题5-16图分析 原有空盘振动系统由于下落物体的加入，振子质量由m 1变为m 1 + m 2，因此新系统的角频率（或周期）要改变．由于()2020/ωx A v +=，因此，确定初始速度v 0和初始位移x 0是求解振幅A 的关键．物体落到盘中，与盘作完全非弹性碰撞，由动量守恒定律可确定盘与物体的共同初速度v 0，这也是该振动系统的初始速度．在确定初始时刻的位移x 0时，应注意新振动系统的平衡位置应是盘和物体悬挂在弹簧上的平衡位置．因此，本题中初始位移x 0，也就是空盘时的平衡位置相对新系统的平衡位置的位移．解 （1）空盘时和物体落入盘中后的振动周期分别为k m ωT /π2/π21== ()k m m ωT /π2/π221+='='可见T ′＞T ，即振动周期变大了．（2）如图（b ）所示，取新系统的平衡位置为坐标原点O ．则根据分析中所述，初始位移为空盘时的平衡位置相对粘上物体后新系统平衡位置的位移，即g kmg k m m k g m l l x 2211210-=+-=-= 式中k g m l 11=为空盘静止时弹簧的伸长量，l 2＝g km m 21+为物体粘在盘上后，静止时弹簧的伸长量．由动量守恒定律可得振动系统的初始速度，即盘与物体相碰后的速度gh m m m m m m 22122120+=+=v v 式中gh 2=v 是物体由h 高下落至盘时的速度．故系统振动的振幅为()gm m khk g m x A )(21/2122020++='+=ωv 本题也可用机械能守恒定律求振幅A ．5-17 质量为0.10kg 的物体，以振幅1.0×10-2 m 作简谐运动，其最大加速度为4.0 ｍ·s -1求：（1）振动的周期；（2）物体通过平衡位置时的总能量与动能；（3）物体在何处其动能和势能相等？（4）当物体的位移大小为振幅的一半时，动能、势能各占总能量的多少？分析 在简谐运动过程中，物体的最大加速度2max ωA a =，由此可确定振动的周期T ．另外，在简谐运动过程中机械能是守恒的，其中动能和势能互相交替转化，其总能量E ＝kA 2/2．当动能与势能相等时，E k ＝E P ＝kA 2/4．因而可求解本题． 解 （1）由分析可得振动周期s 314.0/π2/π2max ===a A ωT（2）当物体处于平衡位置时，系统的势能为零，由机械能守恒可得系统的动能等于总能量，即J 100221213max22k -⨯====.m Aa m A E E ω （3）设振子在位移x 0处动能与势能相等，则有42220//kA kx =得m 100772230-⨯±=±=./A x（４）物体位移的大小为振幅的一半（即2x A =/）时的势能为4221212P /E A k kx E =⎪⎭⎫⎝⎛==则动能为43P K /E E E E =-=5-18 一劲度系数k =312 1m N -⋅的轻弹簧，一端固定，另一端连接一质量kg 3.00=m 的物体，放在光滑的水平面上，上面放一质量为kg 2.0=m 的物体，两物体间的最大静摩擦系数5.0=μ.求两物体间无相对滑动时，系统振动的最大能量.分析简谐运动系统的振动能量为2p k 21kA E E E =+=.因此只要求出两物体间无相对滑动条件下，该系统的最大振幅max A 即可求出系统振动的最大能量.因为两物体间无相对滑动，故可将它们视为一个整体，则根据简谐运动频率公式可得其振动角频率为mm k+=0ω.然后以物体m 为研究对象，它和m 0一起作简谐运动所需的回复力是由两物体间静摩擦力来提供的.而其运动中所需最大静摩擦力应对应其运动中具有最大加速度时，即max 2max A m ma mg ωμ==，由此可求出max A . 解根据分析，振动的角频率mm k+=0ω 由max 2max A m ma mg ωμ==得kgm m g A μωμ)(02max +=则最大能量J1062.92)(])([212132220202max max -⨯=+=+==kg m m kg m m k kA E μμ5-19 已知两同方向、同频率的简谐运动的运动方程分别为()()m π75.010cos 05.01+=t x ；()()m π25.010cos 06.02+=t x ．求：（1）合振动的振幅及初相；（2）若有另一同方向、同频率的简谐运动()()m 10cos 07033ϕ+=t x .，则3ϕ为多少时，x 1＋x 3的振幅最大？又3ϕ为多少时，x 2＋x 3的振幅最小？题5-19图分析 可采用解析法或旋转矢量法求解.由旋转矢量合成可知，两个同方向、同频率简谐运动的合成仍为一简谐运动，其角频率不变；合振动的振幅()12212221cos 2ϕϕ-++=A A A A A ，其大小与两个分振动的初相差12ϕϕ-相关．而合振动的初相位()()[]22112211cos cos sin sin arctanϕϕϕϕϕA A A A ++=/ 解 （1）作两个简谐运动合成的旋转矢量图（如图）．因为2/πΔ12-=-=ϕϕϕ，故合振动振幅为()m 1087cos 2212212221-⨯=-++=.ϕϕA A A A A合振动初相位()()[]rad1.48arctan11cos cos sin sin arctan22112211==++=ϕϕϕϕϕA A A A /（2）要使x 1＋x 3振幅最大，即两振动同相，则由π2Δk =ϕ得,...2,1,0,π75.0π2π213±±=+=+=k k k ϕϕ要使x 1＋x 3的振幅最小，即两振动反相，则由()π12Δ+=k ϕ得(),...2,1,0,π25.1π2π1223±±=+=++=k k k ϕϕ5-20 两个同频率的简谐运动1 和2 的振动曲线如图（a ）所示，求（1）两简谐运动的运动方程x 1和x 2；（2）在同一图中画出两简谐运动的旋转矢量，并比较两振动的相位关系；（3）若两简谐运动叠加，求合振动的运动方程．分析 振动图已给出了两个简谐运动的振幅和周期，因此只要利用图中所给初始条件，由旋转矢量法或解析法求出初相位，便可得两个简谐运动的方程．解 （1）由振动曲线可知，A ＝0.1 ｍ，T ＝2ｓ，则ω＝2π／T ＝πｓ-1．曲线1表示质点初始时刻在x ＝0 处且向x 轴正向运动，因此φ1＝－π／2；曲线2 表示质点初始时刻在x ＝A /2 处且向x 轴负向运动，因此φ2＝π／3．它们的旋转矢量图如图（b ）所示．则两振动的运动方程分别为()()m 2/ππcos 1.01-=t x 和()()m 3/ππcos 1.02+=t x（2）由图（b ）可知振动2超前振动1 的相位为5π／6． （3）()ϕω+'=+=t A x x x cos 21其中()m 0520cos 212212221.=-++='ϕϕA A A A A()12π0.268arctan cos cos sin sin arctan22112211-=-=++=ϕϕϕϕϕA A A A则合振动的运动方程为 ()()m π/12πcos 052.0-=t x题5-20 图5-21 将频率为348 Hz 的标准音叉振动和一待测频率的音叉振动合成，测得拍频为3.0Hz ．若在待测频率音叉的一端加上一小块物体，则拍频数将减少，求待测音叉的固有频率．分析 这是利用拍现象来测定振动频率的一种方法．在频率υ1和拍频数Δυ＝|υ2－υ1|已知的情况下，待测频率υ2可取两个值，即υ2＝υ1 ±Δυ．式中Δυ前正、负号的选取应根据待测音叉系统质量改变时，拍频数变化的情况来决定．解 根据分析可知，待测频率的可能值为υ2＝υ1 ±Δυ＝（348 ±3） Hz因振动系统的固有频率mkπ21=v ，即质量m 增加时，频率υ减小．从题意知，当待测音叉质量增加时拍频减少，即｜υ2－υ1｜变小．因此，在满足υ2与Δυ均变小的情况下，式中只能取正号，故待测频率为υ2＝υ1＋Δυ＝351 Hz*5-22 图示为测量液体阻尼系数的装置简图，将一质量为m 的物体挂在轻弹簧上，在空气中测得振动的频率为υ1，置于液体中测得的频率为υ2，求此系统的阻尼系数．题5-22图分析 在阻尼不太大的情况下，阻尼振动的角频率ω与无阻尼时系统的固有角频率ω0及阻尼系数δ有关系式220δωω-=．因此根据题中测得的υ1和υ2（即已知ω0、ω），就可求出δ．解 物体在空气和液体中的角频率为10π2v =ω和2π2v =ω，得阻尼系数为2221220π2v v -=-=ωωδ。
振动力学(倪振华)
6
而大多数情况下, 振动会产生不良、甚至严 重、灾难性的后果。 由于振动, 降低了机器的动态精度和其它使 用性能; 由于振动, 机器在使用过程中产生巨大的反 复变动的荷载, 导致使用寿命的降低; 有时候振动甚至酿成灾难性事故, 如大桥因 共振而倒塌, 烟囱因风振而倾倒, 飞机因颤振而 坠落等等。
通常系统设计要依赖于响应分析， 所以在实际工作中，响应分析和系统设 计这两个问题是交替进行的。
第1 章 导 论
13
（3）系统识别 已知振动系统的激励(输入)和响应(输出)求系
统参数,以便了解系统的特性。 系统识别包括物理参数识别(确定系统的物理
参数:质量、刚度、阻尼等)和模态参数识别(确定 或估计系统的固有特性:固有频率、振型等)。 （4）环境预测
确定性激励下的响应不一定是确定的 ，但随机激励下的响应一定是随机的。
第1 章 导 论
10
2. 工程振动分析的类别 振动分析：研究振动系统、激励(输入)和
响应(输出)三者之间的关系。
理论上讲，只要知道两者就可以确定第 三 者 。 这样，工程振动分析所要解决的问题 可以归纳为下面几类。
第1 章 导 论
周期的倒数称为频率，是系统每秒钟振动 的次数,单位为1/秒(1/s)或赫兹(Hz)。记作 f
f 1 n T 2
第2章 单自由度系统自由振动
2.2 自由振动系统
35
固有频率n和频率 f 只相差常数2，因
此经常通称为固有频率。是振动分析中极
其重要的参数。
显然
n
2
T
2
f
因此n的物理意义是在2时间内振动的
第2章 单自由度系统自由振动
2.2 自由振动系统
24
m-k系统的自由振动 (P6) m-k 系 统 虽 然 非 常 简 单 ，
理论力学 第5章 小振动
2. 单自由度系统的小振动
三、复摆系统的自由振动 绕不通过质心的光滑水平轴摆动的刚体
d M mgl sin I 2 d t ( 5 )
d mgl I 2 dt
2
2
M l F
转动正向 O 向外
l
*C
d 2 0 2 dt
2. 单自由度系统的小振动
例2：已知 m, OA=AB=L, 求系统微振动固有频率 解：系统的动能和势能 1 1 1 1 2 2 2 2 T J o mv c J c mv B 2 2 2 2 xc 1.5L cos , yc 0.5L sin , xB 2L cos 1 2 2 2 ~ T ( mL 6mL2 sin 2 ) k 6g 2 3 ~ V 4mgL(1 cos ) m L 2 2 1 1~ 2 ~ 2 m mL mq T m (0) q 3 2 2 1 1~ 2 ~ 2 V (q) V " (0)q k q k 4mgL 2 2
3.1 多自由度系统小振动问题（推导）
ˆ 0 ˆ A ˆ 2M K
本征值问题（求本征值 2 和本征矢量 A ）
f ( 2 ) det k m 2 0
即
k11 m11 2 k21 m21 2 ks1 ms1 2
k12 m12 2
T ——周期，每振动一次所经历的时间。 T
2
0
f —— 频率，每秒钟振动的次数， f = 1 / T 。
0 —— 固有频率，振体在2秒内振动的次数。
反映振动系统的动力学特性，只与系统本身的固有参数有关。
2. 单自由度系统的小振动
浙大《大学物理》第五章
五、简谐振动的能量 势能
线性回复力是保守力
1 2 E p x kxdx kx 2
0
1 2 1 2 1 2 E p kx kA cos (t ) m 2 A 2 cos 2 (t ) 2 2 2
动能
与弹性势能有相同的形式，但是两个不同的量
1 1 1 2 2 2 2 2 E k m v m A sin (t ) kA sin 2 (t ) 2 2 2
总机械能
1 1 2 1 2 1 2 E E k E p m v kx kA m 2 A 2 2 2 2 2
例
x
o
5-2 简谐振动的动力学方程
21 2011-4-14
解
（1） 角频率
k m
0.72N m 1 6.0s 1 0.02kg
x0=0.05， v0=0
由初始条件确定常数A和
2 A x0
2 v0 2
x0 0.05m
v0 tan 0 x0
0 或 π
T 2π
取 0
A
A
)
o
o
A
x
xt图
T
t
t
v
vt
图
v A sin( t ) A cos( t
2
2
T
A
a A cos(t ) A cos(t )
2
A 2
a
a t图
o
T
t
8 2011-4-14
d 2θ mglθ J 2 dt
A c o s ( t )
《汽车振动基础》课程教学大纲
《汽车振动基础》课程教学大纲一、课程基本信息课程类别：专业选修课适用专业：汽车车辆工程专业先修课程：汽车构造、汽车诊断与维修总学时：56学分：3二、课程教学目的与基本要求本课程主要任务是，学习汽车机械振动力学的基本理论和方法及分析振动问题的数学方法。
主要内容包括：单自由度系统的振动、两个自由度系统的振动、多自由度系统的振动，连续系统的振动，并介绍了求解特征值问题和系统响应的近似方法及数值计算方法，简要叙述了非线性振动和随机振动的基本概念和理论。
三、教学时数分配四、教学内容与要求第一章绪论（一）教学目的：理解机械振动的概念，了解振动系统研究方法，掌握振动的分类，会分析振动问题并提出解决方法。
（二）教学内容：1 基本要素 2 研究方法 3 分类和表示方法（三）重点：振动系统基本要素（四）难点：振动系统分类和表示方法第二章单自由度系统的振动（一）本章教学目的：理解单自由度系统的自由振动的概念，掌握单自由度系统的强迫振动，掌握汽车车身单自由度系统的振动。
（二）教学内容：1 自由振动 2 强迫振动 3 非简谐激励下的强迫振动4 汽车车身单自由度系统的振动（三）重点：单自由度系统的自由振动（四）难点：汽车车身单自由度系统的振动第三章二自由度系统的振动（一）教学目的：了解二自由度系统的运动微分方程，掌握无阻尼二自由度系统的振动，有阻尼二自由度振动系统和汽车的二自由度系统的振动。
（二）教学内容：1 二自由度系统的运动微分方程2 无阻尼二自由度系统的振动3 有阻尼二自由度振动系统4 汽车的二自由度系统的振动（三）重点：无阻尼二自由度系统的振动（四）难点：汽车的二自由度系统的振动第四章多自由度系统的振动（一）本章教学目的：理解多自由度振动系统的运动微分方程，掌握固有振型的正交性、模态坐标和正则坐标和汽车多自由度振动模型。
（二）教学内容：1 多自由度振动系统的运动微分方程2 固有振型的正交性、模态坐标和正则坐标3 多自由度系统的响应4 拉格朗日方程在振动分析中的应用5 汽车多自由度振动模型（三）重点：固有振型的正交性、模态坐标和正则坐标（四）难点：汽车多自由度振动模型第五章随机振动理论（一）教学目的：了解随机振动概述及随机振动的统计特性，线性振动系统的随机响应计算。
第五章小结 振动力学课件
一、随机振动的概念
确定性振动 随机振动 随机振动的两大特征 平稳随机过程 平稳遍历过程
定义及性质：
时间域 均值、自相关函数、互相关函数
频率域 自谱、互谱
时间域和频率域 均方值
窄带、宽带过程及理想白噪声特征
谱相干函数
Hale Waihona Puke FxSFx 2 SF Sx
完全线性系统，当测试系统出现 Fx 原因1：
线性系统对多个随机激励的响应
R x x h 1 R F F 1 2h T2d 1 d 2
S x x H * S F F H T
RFxRFFhTd
了解
S F xS F FH T
随机响应的模态分析法
• 随机响应主要方法： 直接应用脉冲响应函数和复频响应函数； 模态分析法 熟悉模态分析法的思路
振动力学第五章.
当cos(t ) 1时，动能达最大值
1 2 l 1 2 n 2 Tmax m( x) ( x)dx mi (i ) 2 0 2 2 i 1
由Tmax M max 得到
2
m( x) g ( x)dx F
l 2
2
从而得
EI 4 2 ym EI 4 3 2 4l 4 m 2 m l ym l 4
自振频率
2
l
2
EI m
精确解
（2）取振型为梁在自重荷载上的挠曲线。图（c）所示为匀布 自重荷载作用下简支梁的静力挠曲线，即 16 4 ( x) ym 4 ( x 2lx 3 l 3 x) 5l 最大动能
x ( x ) y sin m 解：（1）振型为 l
m 2 l x m 2 Tmax ym sin dx 2 ym l 0 2 l 4
V max EI 2 x EI 4 2 y sin dx ym m 2 3 0 2 l l 4l
因为 Tmax Wmax ,可以解得
9.8 EI l2 m
此值与精确解相比较，偏大约2％
例：计算重力坝沿水流方向 的自振频率时，可以取沿坝 轴线方向单位长度的坝体近 似地简化为图（a）所示的变 截面悬臂梁。试用瑞利法计 算其自振频率。
解：选变截面悬臂梁在其自重作用下所引起的挠曲线作为 近似振型，如图（b）所示，即 h 2 2 ( x) y ( x) 2 x
时刻，即
若只考虑弯曲变形的影响，系统的应变能为
2 1 l V EI ( x) y( x, t ) dx 2 0 (式中，y( x, t )表示y ( x, t )对坐标x求二阶偏导数）
大物第五章课后习题答案
简答题5.1 什么是简谐运动？说明下列运动是否是简谐运动?(１）活塞的往复运动；(2）皮球在硬地上的跳动;（3)一小球在半径很大的光滑凹球面底部的来回滑动,且经过的弧线很短；（4)锥摆的运动。
答:质点的简谐振动一定要有平衡位置，以平衡位置作为坐标原点,如果以x 表示质点偏离平衡位置的位移，质点所受合外力一定具有F kx =-的形式。
（１）活塞的往复运动不是简谐运动，因为活塞受力的方向和它的位移是同一方向,任一时刻所受的合外力不具有F kx =-的形式，所以活塞的往复运动是简谐运动。
（2）皮球在硬地上的跳动不是简谐运动，因为忽略空气阻力，皮球在上升和下落阶段，始终受到竖直向下的重力的作用，任一时刻所受的合外力不具有F kx =-的形式，所以皮球的运动不是简谐运动。
(3）一小球在半径很大的光滑凹球面底部的来回滑动，且经过的弧线很短是简谐运动。
符合简谐运动的定义。
(4)锥摆的运动不是简谐运动，此时锥摆受到重力和绳的拉力的作用,这两个力的合力的大小为恒量,而方向在不断的改变,任一时刻所受的合外力不具有F kx =-的形式，所以锥摆的运动不是简谐运动。
5.2(1)试述相位和初相的意义，如何确定初相?（2）在简谐振动表达式)cos(ϕω+=t A x 中，ｔ＝0是质点开始运动的时刻,还是开始观察的时刻?初相20/,πϕ=各表示从什么位置开始运动?答：１)相位是决定谐振动运动状态的物理量，初相是确定振动物体初始时刻运动状态的物理量。
由初始条件可以确定初相。
2）在简谐振动表达式)cos(ϕω+=t A x 中,t =０是质点开始计时时刻的运动状态,是开始观察的时刻。
初相0ϕ=是物体处于正最大位移处开始运动，初相/2ϕπ=是物体处于平衡位置且向初相x 轴负向开始运动。
5.3 一质点沿ｘ轴按)cos(ϕω+=t A x 作简谐振动，其振幅为A ,角频率为ω，今在下述情况下开始计时，试分别求振动的初相:(1)质点在ｘ＝+A 处；(2）质点在平衡位置处、且向正方向运动;（3)质点在平衡位置处、且向负方向运动；（4)质点在ｘ=A /２处、且向正方向运动;（5)质点的速度为零而加速度为正值。
《振动力学——研究性教程》评介
如固有振型节点数目和反共振机理；也有若干独创 性的新见解，如杆和梁的对偶分析、杆和梁与刚体壁 的碰撞冲击、对称结构的重频模态特征等。这给学生 的研究型学习做出了示范。学习需要独立思考，教材 和文献上的内容未必完全正确；创新要在掌握已有 知识基础上进行，并非是罔顾他人工作的异想天开。
该书也体现了工程和科学的统一。开篇作者基 于自己长期从事研究工作的经验和体会，从绳系卫 星初步论证、汽车液压与弹性隔振、结构动力消振、 太阳能帆板瞬态响应等实际工程问题中，提炼出连 续系统离散化条件、自由度退化振动系统的缩并与 分析、固有振型节点数目、波动和冲击响应的模态分 析等科学问题。后面5章分析这些科学问题，发展 相应的理论和方法，并指导工程问题的解决。这种工 程与科学的密切关系，体现了力学既是基础科学又 是技术科学的独特魅力。
70-72 6胡海岩.力学教育的几个问题及其对策.力学与实践，2020,
42(5): 598-602 Hu Haiyan. Some problems and their solutions in mechanics education. Mechanics in Engineering, 2020, 42(5): 598-602 (in Chinese) 7胡海岩.论工程科学的美学教育.南京航空航天大学学报(社会 科学版),1999(2): 71-74 8胡海岩.对振动学及其发展的美学思考.振动工程学报，2000, 13(2)： 161-169
该书共分7章，另加一个附录。前两章为准备 性工作。第一章从6个研究案例中提炼出12个科 学问题。第二章从科学美的角度归纳总结振动力学
振动力学经典教程
1）欧拉-----于1728年建立并解了有阻尼介质中运动的微分方程。
1739年他研究了无阻尼简谐受迫振动，从理论上解释了共振现 象 1747年他对n个等质量质点由等刚度弹簧连接的系统列出了微分 方程组并求出了精确解，从而发现了系统的振动是各阶简谐振动的 叠加。
5
0.2 振动的分类
1按系统分：连续系统和离散系统
1）连续系统（分布参数系统）-----是由杆、梁、 轴、板、壳等弹性元件组成的系统，有无穷多 自由度，数学描述为偏微分方程。
2）离散系统------是由彼此分离的有限个质量元 件、弹簧和阻尼器组成的系统，有有限个自由度， 数学描述为常微分方程。最简单的也是最基本的 离散系统就是单自由度系统。
结构物的水平振动
20
起重机突然起吊载荷时的振动
21
机器的隔振
22
柴油发电机扭转振动
23
第一章简谐振动与频谱分析
• 振动 1、 周期 1）简谐振动：表示以及合成 • 2）一般周期振动：利用傅立叶级数表
示成一系列简谐振动的叠加-----------谐波分析
•
2、非周期：利用傅立叶积分作谐波分析
0.1 振动和振动力学
一、 机械振动
1 振荡 ： 物体的往复运动或状态的循环变化 2 振动： 是一种特殊的振荡。 一种运动的物
理量时而增大，时而减少的反复变化。
3 机械振动： 工程技术所涉及的机械或结
构的振动称作机械振动。（运动的物理量为位移、 速度、加速度、应力和应变等）
二、
振动力学
1 振动力学是研究机械振动的运动学 和动力学的一门课程。 2 是一门力学分支学科。在统一的力 学模型的基础上，振动力学应用数学 分析、实验量测和数值计算等方法， 探讨各种振动现象的机理，阐明振动 的基本规律，从而为解决实践中可能 发生的振动问题提供理依据。
振动力学第五章
y(x,t)为静荷载（自 重、F等）引起的位 移，如自重等
n l 1 1 W sin(t ) m( x) g ( x)dx sin(t ) Fii 0 2 2 i 1
式中，g : 重力加速度 Fi : 集中质量mi 得重力荷载（ Fi＝mi g）
i : 集中质量作用点振幅
第五章 自振频率和振型的实用计算
第一节 能量法求自振频率
一，瑞利能量法 根据能量守恒，在任何瞬时（忽略能量散失）
T (t ) V (t ) 常数
设图示系统中任一质点的运动方程为 y( x, t ) ( x) sin(t )
振动速度
( x, t ) ( x) cos(t ) v y
i 1 j 1 ij i
n n
n
n
i 1 j 1 n n
ij
i
j
0
j
(i 1,2,, n)
即
n
2 Cij j
n
Dij i j
i 1 j 1
i 1 n
2( Cij i j )( Dij j )
i 1 j 1 n i 1
n
( Dij i j ) 2
Tmax m 2 16 4 ym 4 ( x 2lx 3 l 3 x) dx 0 2 5l
l 2
2 0.252 m l 2 y m 外力做功的最大值
1 l 16 4 Wmax m gym 4 ( x 2lx 3 l 3 x)dx 2 0 5l 5m gl 4 EI 2 式中， ym 0.320 m glym 24.6 3 ym 384EI l
2 3
Eb3 2 b 5 Eb3 2 2 b 6 ( h h )1 ( h h ) 2 0 6 15g 10 21g Eb3 2 2 b 6 Eb3 3 2 b 7 ( h h )1 ( h h ) 2 0 10 21g 10 28g
振动力学的专题精选
振动力学的专题精选Iliya I. Blekhman，Russian Academy of Science，Russia (Ed.)Selected Topics in Vibrational MechanicsSeries on Stability， Vibration and Control of Systems Vol.112022，409pp.Hardcover $ 92.00ISBN 981-238-055-8World Scientific本书是《系统的稳定性、振动和控制》系列丛书A系列的第11卷。
振动力学是非线性动力学和非线性振荡理论中新发展起来的一个分支，此书反映近几年来在振动力学的数学工具和在一起应用问题解这两方面所得到的主要成果。
全书分为六部分，共有20章。
第1部分振动力学的基本原理(有5章)；第1章关于若干非线性振荡效应和振动力学的主要概念；第2章振动力学和运动的直接分离方法的主要数学工具；第3章得到振动力的表达式和振动力学主要方程的其他方法；第4章最简单的例子：用非线性振荡理论的不同方法来解有振动悬挂轴的摆的问题；第5章结论：与非线性力学的其他方法相比，振动力学的方法和运动的直接分离方法的特点和优点。
第二部分在高频激励下的摆和摆系统——非平常效应(有5章)：第6章有周期振动轴的摆的拟平衡位置和稳态旋转；第7章高频激振对摆系统的非平常效应；第8章关于印度魔绳的理论；第9章摆在双调和激振下的共轭共振和分叉；第10章电机械系统的研究和高频磁场中摆型导体的性能。
第三部分自同步理论的一般定义(有4章)：第11章自同步的一般定义；第12章解一些自同步问题的指南；第13章有内自由度的动态物体自同步问题的建立及其解法；第14章有近拟均匀旋转的动态物体自同步问题中稳定性的积分符号应用域的扩展；第四部分产生动力物质的问题(有2章)：第15章关于动力物质；第16章用参数刚度调节来主动控制复合材料梁的振动。
大学物理学教程第二(马文蔚)练习册答案5第五章 机械振动
的速度射入并嵌在木块中，同时使弹簧压缩从而作简
谐运动。设木块的质量为 4.99kg ，弹簧的劲度系数为
8.00103 N/m。若以弹簧原长时物体所在处为坐标原
点，向左为 x 轴正向，求简谐运动方程。
解： 40(s1)
A 2.5102 (m)
v m1
m2 k
2
5-15 振动方程：
x 2.5102 cos(40t )(SI )
50 cos 3.13t
或
cos 3.13t
36
x/m
5-13
（3） j
d
dt
3.13sin 3.13t
36
30时 30 50 cos 3.13t
cos 3.13t 0.6
sin 3.13t 0.8 j 0.218s1
v = l 0.218m / s
10
第五章 习题分析
为 x1 0.05cos(10t 0.75 )(SI ), x2 0.06 cos(10t 0.25 )(SI ) 求：（1）合振动的振幅
及初相；（2）若有另一同方向同频率的简谐运动
x3 0.05cos(10t 3)(SI ), 则 3 为多少时，x1 x3 的 振幅最大？又 3 为多少时，x2 x3 的振幅最小。
曲线2 t 0时,x0
2
3
x2
2
cm
A 2
,
v0
0
10cos t
3
-0.10 -0.05
cm
0.10
0.05 x/m
17
第五章 习题分析
5-20 两个同频率简谐振动1和2的振动曲线如图所示，
求（1）两简谐运动的运动学方程；（2）在同一图中
画出两简谐运动的旋转矢量，并比较两简谐振动的相
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n
0
(i 1,2,, n)
简化上式并将 代入得 n 2 ( C ij Dij ) j 0
2
(i 1,2,, n)
j 1
或
(C 2 D) 0
上式为n个齐次线性方程，为了使方程组有非零解，必 须得到 C 2D 0 上式展开后得到一个 2 的n次方程，该方程有n个根。对 2 于其中的每一个根 j 都可求得一组常数ij (i 1,2,, n) ，因 此得到n个振型函数i ( x)
( x, t )表示y( x, t )对时间t求偏导数) (式中，y
系统的动能
1 l T m( x )v 2 dx 2 0
将振动速度代入得
l 1 2 2 T cos (t ) m( x) 2 ( x)dx 0 2
动能的最大值发生在 cos(t ) 1
Tmax 1 2 l m( x) 2 ( x)dx 0 2
2 3
Eb3 2 b 5 Eb3 2 2 b 6 ( h h )1 ( h h ) 2 0 6 15g 10 21g Eb3 2 2 b 6 Eb3 3 2 b 7 ( h h )1 ( h h ) 2 0 10 21g 10 28g
展开系数行列式，并令其等于零,得频率方程：
x ( x ) y sin m 解：（1）振型为 l
m 2 l x m 2 Tmax ym sin dx 2 ym l 0 2 l 4
V max EI 2 x EI 4 2 y sin dx ym m 2 3 0 2 l l 4l
4 3 2 2
因集中质量大于梁的分布质量，选用后一种试函数好
Vmax
1 l EI 2 ( x )dx T * 2 0
1 l 2 2 S ( x ) dx m ( x ) a 0 2
R ( )
Vmax T*
例.用能量法计算图示体系的基频. 解: m 2
y(x,t)为静荷载（自 重、F等）引起的位 移，如自重等
n l 1 1 W sin(t ) m( x) g ( x)dx sin(t ) Fii 0 2 2 i 1
式中，g : 重力加速度 Fi : 集中质量mi 得重力荷载（ Fi＝mi g）
i : 集中质量作用点振幅
因为 Tmax Wmax ,可以解得
9.8 EI l2 m
此值与精确解相比较，偏大约2％
例：计算重力坝沿水流方向 的自振频率时，可以取沿坝 轴线方向单位长度的坝体近 似地简化为图（a）所示的变 截面悬臂梁。试用瑞利法计 算其自振频率。
解：选变截面悬臂梁在其自重作用下所引起的挠曲线作为 近似振型，如图（b）所示，即 h 2 2 ( x) y ( x) 2 x
当 sin(t ) 1 时，应变能最大，即
V max
2 1 l EI ( x) ( x, t ) dx 2 0
使 Tmax V max ，即可得到
2
l
0
EI ( x) ( x) dx
2 l 0
m( x) 2 ( x)dx
瑞利商
用外力做功的数值代替系统应变能的数值 图（b）系统上外力所做的总功为 1 l 1 n W m( x) g y( x, t )dx Fi y( xi , t ) 2 0 2 i 1 将运动方程代入上式得
l 2
2
从而得
EI 4 2 ym EI 4 3 2 4l 4 m 2 m l ym l 4
自振频率
2
l
2
EI m
精确解
（2）取振型为梁在自重荷载上的挠曲线。图（c）所示为匀布 自重荷载作用下简支梁的静力挠曲线，即 16 4 ( x) ym 4 ( x 2lx 3 l 3 x) 5l 最大动能
3
2
1
二，李兹能量法
李兹给出了级数形式的近似振型
( x ) 1 f1 ( x ) 2 f 2 ( x ) n f n ( x )
i f i ( x)
i 1 n
其中，f1 ( x)，f 2 ( x)， ，f n ( x)为满足位移边界条件的 函数
1， 2，， n为待定参数。
j ( x) ij f i ( x)
i 1
n
(j 1,2,, n)
求得的 j , j ( x) 就是所研究的系统前n个自振频率和振型 函数的近似解。
例：试用李兹法求图所示重力坝 的第一和第二阶自振频率。
解：为了使级数各项都满足位移边界条件，近似振型函数选为
( x) 1x2 2 x3 n xn1
将上式代入瑞利商的表达式得
EI ( x ) f ( x ) i i dx 0 i 1 2 2 n l m ( x ) f ( x ) i i dx 0 i 1
l n 2
引进下列记号为
x) f j( x)dx Cij EI ( x) f i(
式中vi为各集中质体的振动速 度。
当cos(t ) 1时，动能达最大值
1 2 l 1 2 n 2 Tmax m( x) ( x)dx mi (i ) 2 0 2 2 i 1
由Tmax M max 得到
2
m( x) g ( x)dx F
当 sin(t ) 1 时，应变能达到最大值，此时外 力所作的功亦为最大值，
1 l 1 n W m( x) g ( x)dx Fii 2 0 2 i 1
这时系统的动能除了分布质量m(x)的动能外，还应 包括各集中质量mi (i 1,2,, n) 的动能，即 n 1 l 1 2 T m( x)v dx mi vi2 2 0 2 i 1 将振动速度代入得 l 1 2 2 T cos (t ) m( x) 2 ( x)dx 0 2 n 1 2 2 cos (t ) mi (i ) 2 2 i 1
0 l
Dij m( x) f i ( x) f j ( x)dx
0
l
所以
2
C D
i 1 j 1 ij i i 1 j 1 n n ij i
n
n
j
j
根据频率为极值的条件 ( 2 ) 0 i
(i 1,2,, n)
得到
i
C D
i 1 j 1 ij i
n n
n
n
i 1 j 1 n n
ij
i
j
0
j
(i 1,2,n
Dij i j
i 1 j 1
i 1 n
2( Cij i j )( Dij j )
i 1 j 1 n i 1
n
( Dij i j ) 2
假设经一次近似计算只取第一项，即
( x) 1x2
代入瑞利商的表达式得
1.581
b h2 Eg （与前面的结果完全一 样）
若取级数前两项，即
( x) 1x 2 2 x3
将 f1 ( x) x , f 2 ( x) x 代入相关式子计算出 Cij , Dij ，这时 (C 2 D) 0 成为
l 0 i 1
n
i i
l
0
m( x) ( x)dx mi (i ) 2
2 i 1
n
例：如图（a） 所示均质等截面简支 梁。单位梁长的质量为 m ，其抗弯 刚度EI为常数。若振型分别为图（b） x y ( x ) y sin 所示 （ m为梁中点的最大 m l 挠度）和图（c）所示梁在自重作用下 的挠曲线。分别计算自振频率，并将 所得结果进行比较。
m m m mg
k
3 2 1
y3
y2
m
m m
1 0 k k 1 2 1 0 1 1
k
k
1.取自重引起的位移
y1 3m g / k y2 y1 2m g / k 5m g / k
第五章 自振频率和振型的实用计算
第一节 能量法求自振频率
一，瑞利能量法 根据能量守恒，在任何瞬时（忽略能量散失）
T (t ) V (t ) 常数
设图示系统中任一质点的运动方程为 y( x, t ) ( x) sin(t )
振动速度
( x, t ) ( x) cos(t ) v y
根据Tmax Wmax 得到
b 1.581 2 h Eg （比精确解大 3.06 ％）
y
例：等截面悬臂梁
端部有一集中质量 m 2 Sl 用瑞利法估计基频
0
l
m
x
解：
选择等截面悬臂梁在均布载荷下的静挠度曲线作为试函数：
EI ( x) A1 ( x 4lx 6l x ) 1 1.1908 Sl 4 选择端部集中质量作用下的静挠度曲线作为试函数： EI ( x) A2 (3lx 2 x 3 ) 1 1.1584 Sl 4
从图（b）可以看出其分布质量为 b m( x ) (h x) hg 最大动能和外力功的最大值为 1 2 h Tmax m( x) 2 ( x)dx 0 2 1 2 3 h9 2 3 2 E b g 30
Eb 式中，为坝身材料单位体积的 重量。
1 h Wmax m( x) g ( x) dx 2 0 1 2 h2 2 Eb 12
y3 y1 mg / k 6mg / k