2018金衢十二校联考数学试题卷

合集下载

浙江省金丽衢十二校2018-2019学年高三数学第二次联考试卷

第1页，总18页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………姓名：____________班级：____________学号：___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………浙江省金丽衢十二校2018-2019学年高三数学第二次联考试卷考试时间：**分钟满分：**分姓名：____________班级：____________学号：___________题号一二三总分核分人得分注意事项：1、填写答题卡的内容用2B铅笔填写2、提前 15 分钟收取答题卡第Ⅰ卷客观题第Ⅰ卷的注释评卷人得分一、单选题（共10题)1. 集合，，则（）A .B .C .D .2. 点和是双曲线的两个焦点，则（）A .B . 2C .D . 43. 复数，，则（）A . 5B . 6C . 7D .4. 某几何体的三视图如图所示（图中单位：），则该几何体的表面积为（）答案第2页，总18页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………A .B .C .D .5. 已知直线平面，直线平面，则“”是“”的（）A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件6. 甲和乙两人独立的从五门选修课课程中任选三门进行学习，记两人所选课程相同的门数为，则为（）A . 1.2B . 1.5C . 1.8D . 2 7. 函数的图像大致为（）A .B .C .D .8. 已知，，和为空间中的4个单位向量，且，则不可能等于（） A . 3 B .C . 4D .9. 正三棱锥的底面边长为，高为，它在六条棱处的六个二面角（侧面与侧面或者侧面与底面）之和记为，则在从小到大的变化过程中，的变化情况是（） A . 一直增大 B . 一直减小 C . 先增大后减小 D . 先减小后增大 10. 数列满足：，，则的值所在区间为（） A .B .C .D .。

2018金衢十二校联考数学答题卷(2018.4)

请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
18．（本题6分）
解：(1)
(2)
19．（本题6分）
解：
20．（本题8分）
解：(1)
(2)
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
21．（本题8分）
解：(1)
(2)
22．（本题10分）
解：（1）表中的a=；并把频数分布直方图补充完整；
（2）这个样本数据的中位数落在从左到右数第组；
（3）
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
23．（本题10分）
4．（本题12分）
解：（1）点B的坐标为；用含t的式子表示点P的坐标为；
（2）
（3）
（3）请在各题目的答题来自域内作答，超出黑色矩形边框限定区域的答案无效
2018金衢十二校联考数学
数学答题纸
注意事项
1．答题前，考生先将自己的姓名、准考证号填写清楚。
2．卷必须使用2B铅笔填涂：卷的答案必须使用黑色字迹的钢笔或签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．作图时，可先使用2B铅笔，确定后必须使用黑色字迹的钢笔或签字笔描黑。
解：(1)
（2）
（3）
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效

浙江省金衢十二校2018届中考数学联合模拟试题

金衢十二校2018年中考联合模拟数学试卷考生须知：1.全卷共三大题，24 小题，全卷满分 120 分，考试时间 120 分钟．2.全卷分试卷Ⅰ（选择题）和试卷 II（非选择题）两部分，全部在答题卷上作答，卷Ⅰ的答案必须用2B 铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔答在答题卷的相应位置上．卷Ⅰ一、选择题（本大题有 10 小题，每小题 3 分，共 30 分.请选出各题中一个符合题意的正确选项.不选、多选、错选均不给分）1、0、1、－2 这四个数中，最小的数是( ▲ )．1.在2B．0 C．1 D．－2 A．122.据媒体报道，我国因环境污染造成的巨大经济损失，每年高达 680 000 000 元，这个数用科学记数法表示正确的是( ▲ )．A. 6.8×109 元B. 6.8×108 元C. 6.8×107 元D. 68×107 元3.下列事件中，必然事件是( ▲ )．A.今年夏季的雨量一定多B. 下雨天每个人都打着伞C. 二月份有30 天D. 我国冬季的平均气温比夏季的平均气温低4.如图，点A、B、C、D、O 都在方格纸的格点上，若△COD 是由A．30°B．45°C．90°D．135°5.一次函数y=2－2 的图象不．经．过．的象限是( ▲ )．A．第一象限B．第二象限C．第三象限D．第四象限（第4 题图）6.下列四个图形：其中是轴对称图形，且对称轴的条数为 2 的图形的个数是( ▲ )．A. 1 个B．2 个C．3 个D．4 个7.对于反比例函数y=2，下列说法不．正．确．的是( ▲ )．A．点(－2，－1)在它的图象上B．它的图象在第一、三象限C．当>0 时，y 随的增大而增大D．当<0 时，y 随的增大而减小8.如图，在菱形ABCD 中，对角线AC、BD 相交于点O，E 为B C 的中点，则下列式子中一定成立的是( ▲ )． A．AC=2OE B．BC=2OEC．AD=OE D．OB=OE9.如图，将长为 2，宽为 1 的矩形纸片分割成n 个三角形后，拼成面积为 2 的正方形，则n≠( ▲ )．A．2 B．3 C．4 D．5C(第 8 题图)(第 9 题图)10.小阳在如图①所示的扇形舞台上沿O﹣M﹣N 匀速行走，他从点O 出发，沿箭头所示的方向经过点M 再走到点N，共用时 70 秒．有一台摄像机选择了一个固定的位置记录了小阳的走路过程，设小阳走路的时间为t（单位：秒），他与摄像机的距离为y（单位：米），表示y 与t 的函数关系的图象大致如图②，则这个固定位置可能是图①中的( ▲ )．A．点Q B．点PC．点M D．点N(第 10 题图)卷Ⅱ二、填空题（本大题有 6 小题，每小题 4 分，共 24 分）11.使代数式+1有意义的的取值范围是▲．12.东山茶厂有甲、乙、丙三台包装机，同时分装质量为 200 克的茶叶. 从它们各自分装的茶叶中分别随机抽取了 15 盒，测得它们的实际质量的方差如下表所示：y l1 Array A1根据表中数据，三台包装机中，▲包装机包装的茶叶质量最稳定．213.如图，l1 是反比例函数y=在第一象限内的图象，且过点A(2，1) ，l2l2 与l1 关于轴对称，那么图象l2 的函数解析式为▲（＞(第 13 题图) 0）．14.将一个三角形经过放大后得到另一个三角形，如果所得三角形在原三角形的外部，这两个三角形各对应边平行且距离都相等，那么我们把这样的两个三角形叫做“等距三角形”，它们对应边之间的距离叫做“等距”．如果两个等边三角形是“等距三角形”，它们的“等距”是1，那么它们周长的差是▲．15.已知在直角坐标平面内，以点P（1，2）为圆心，r 为半径画圆，⊙P 与坐标轴恰好有三个交点，那么r的取值是▲．16.在平面直角坐标系Oy 中，抛物线y =-2+ 2m -m2-m +1交y 轴于点为A，顶点为D，对称轴与轴交于点H.（1）顶点D的坐标为▲（用含m的代数式表示）；（2）当抛物线顶点D在第二象限时，如果∠ADH=∠AHO，m 的值为▲．三、解答题（本大题共有8小题，共66 分）17．（本题 6 分）计算：3－2－2cos60°+(12－2006)0－|－1|．318．（本题 6 分）已知多项式 A=( +2)2+(1－)( 2+)－3．（1）化简多项式 A；（2）若(+1)2=6，求 A 的值．19．（本题 6 分）如图所示，巨型广告牌AB 背后有一看台CD，台阶每层高 0.3 米，且AC=17 米，现有一只小狗睡在台阶的FG 这层上晒太阳，设太阳光线与水平地面的夹角为α，当α=60°时，测得广告牌AB 在地面上的影长AE=10 米，过了一会，当α=45°，问小狗在FG 这层是否还能晒到太阳？请说明理由．20.（本题 8 分）杂技团进行杂技表演，演员从跷跷板右端A 处弹跳到人梯顶端椅子B 处，其身体（看成一个点）的路线是抛物线，已知起跳点A 距地面的高度为 1 米，弹跳的最大高度距地面 4.75 米，距起跳点A 的水平距离为 2.5 米，建立如图所示的平面直角坐标系，（1）求演员身体运行路线的抛物线的解析式？（2）已知人梯高BC=3.4 米，在一次表演中，人梯到起跳点A 的水平距离是 4 米，问这次表演是否成功？说明理由．(第 20 题图) 21.(本题 8 分）如图，已知⊙O 为△ABC 的外接圆，BC 为⊙O 的直径，作射线BF，使得BA 平分∠CBF，过点A 作AD⊥BF 于点D (1)求证DA 为⊙O 的切线；FADB O(2)若BD=1，tan∠ABD=2，求⊙O 的半径．22．（本题 8 分）C (第 21 题图)为了解八年级学生的身体素质情况，老师以八年级（1）班50 位学生为样本进行了一分钟跳绳次数测试．根据测试结果，绘制出部分频数分布表和部分频数分布直方图．请结合图表完成下列问题：八年级（1）班一分钟跳绳次数的频数分布直方图96380 100 120 140 160 180 跳绳次数（1）表中的a= ▲；并把频数分布直方图补充完整；（2）这个样本数据的中位数落在从左到右数第▲组；（3）已知该校八年级共有学生 800，请你估计一分钟跳绳次数不低于 120 次的八年级学生大约多少名？23. (本题 10 分)已知：矩形ABCD 中，AB=4，BC=3，点M、N 分别在边AB、CD 上，直线MN 交矩形对角线AC 于点E，将△AME 沿直线MN 翻折，点A 落在点P 处，且点P 在射线CB 上.（1）如图 1，当EP⊥BC 时，求CN 的长；（2）如图 2，当EP⊥AC 时，求AM 的长；（3）请写出线段CP 的长的取值范围，及当CP 的长最大时MN 的长.A DN MB P C（图 1）P BC（图 2）B C（备用图）24．（本题 12 分）已知A(3，2)，点B 是轴上的动点，设B(t，0), 过A 作AB 的垂线交y 轴与C，点D是BC 的中点．(1)当点D 在轴上时，求B 点坐标及直线AC 的解析式；(2)如图 1，当点D 在第一象限时，若直线OD 与过点D 的双曲线的另一支交于点F，将点B 关于y 轴作轴对称变换得点B′，连结DB′，FB′，FB．○ 1 求证：四边形DB′FB 为平行四边形；○ 2 当t 为何值时，四边形DB′FB 为矩形．(3)如图 2，设过点D 画y 轴的垂线与直线AC 交于点E，是否存在点B，使△CDE 成为等腰三角形？若存在，请求出点B 的坐标；若不存在，请说明理由．。

2018金衢十二校联考数学试题卷

金衢十二校联考数学试题卷考生须知：1.全卷共三大题，小题，全卷满分分，考试时间分钟．2.全卷分试卷Ⅰ（选择题）和试卷（非选择题）两部分，全部在答题卷上作答，卷Ⅰ的答案必须用铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔答在答题卷的相应位置上．卷Ⅰ一、选择题（本大题有小题，每小题分，共分.请选出各题中一个符合题意的正确选项.不选、多选、错选均不给分）1.在、、、－这四个数中，最小的数是( ▲ )．．．．．－2.据媒体报道，我国因环境污染造成的巨大经济损失，每年高达元，这个数用科学记数法表示正确的是( ▲ )．×元×元×元. ×元3.下列事件中，必然事件是( ▲ )．A.今年夏季的雨量一定多.下雨天每个人都打着伞.二月份有天.我国冬季的平均气温比夏季的平均气温低4.如图，点、、、、都在方格纸的格点上，若△是由△绕点按逆时针方向旋转而得，则旋转的角度为(▲ )．．°．°．°．°5.一次函数－的图象不．经．过．的象限是( ▲ )．．第一象限．第二象限．第三象限．第四象限（第题图）6.下列四个图形：其中是轴对称图形，且对称轴的条数为的图形的个数是( ▲ )．A.个．个．个．个7.对于反比例函数，下列说法不．正．确．的是( ▲ )．．点(－，－)在它的图象上．它的图象在第一、三象限．当> 时，随的增大而增大．当<时，随的增大而减小8.如图，在菱形中，对角线、相交于点，为的中点，则下列式子中一定成立的是(▲)．．．．．9.如图，将长为，宽为的矩形纸片分割成个三角形后，拼成面积为的正方形，则≠( ▲ )．．．．．(第题图)(第题图)10. 小阳在如图①所示的扇形舞台上沿 ﹣﹣匀速行走，他从点出发，沿箭头所示的方向经过点再走到点，共用时秒．有一台摄像机选择了一个固定的位置记录了小阳的走路过程，设小阳走路的时间为（单位：秒），他与摄像机的距离为（单位：米），表示与的函数关系的图象大致如图②，则这个固定位置可能是图①中的( ▲ )．．点．点．点．点(第题图)卷 Ⅱ二、填空题（本大题有小题，每小题分，共分） 11. 使代数式有意义的的取值范围是▲ ．12. 东山茶厂有甲、乙、丙三台包装机，同时分装质量为克的茶叶. 从它们各自分装的茶叶中分别随机抽取了盒，测得它们的实际质量的方差如下表所示：根据表中数据，三台包装机中，▲ 包装机包装的茶叶质量最稳定．13. 如图，是反比例函数在第一象限内的图象，且过点(，)，与关于轴对称，那么图象的函数解析式为▲（＞）．(第题图)14. 将一个三角形经过放大后得到另一个三角形，如果所得三角形在原三角形的外部，这两个三角形各对应边平行且距离都相等，那么我们把这样的两个三角形叫做“等距三角形”，它们对应边之间的距离叫做“等距”．如果两个等边三角形是“等距三角形”，它们的“等距”是，那么它们周长的差是 ▲ ．15. 已知在直角坐标平面内，以点（，）为圆心，为半径画圆，⊙与坐标轴恰好有三个交点，那么的取值是▲ ．16. 在平面直角坐标系中，抛物线交轴于点为，顶点为，对称轴与轴交于点 . （1）顶点的坐标为▲ （用含的代数式表示）；（2）当抛物线顶点在第二象限时，如果∠∠，的值为▲．三、解答题（本大题共有小题，共分）．（本题分）计算：－－°(－)－－．．（本题分）已知多项式 ( )(－)( )－．（1）化简多项式；（）若()，求的值．甲包装机乙包装机丙包装机方差（克）．（本题分）如图所示，巨型广告牌背后有一看台，台阶每层高米，且米，现有一只小狗睡在台阶的这层上晒太阳，设太阳光线与水平地面的夹角为α，当α°时，测得广告牌在地面上的影长米，过了一会，当α°，问小狗在这层是否还能晒到太阳？请说明理由．.（本题分）杂技团进行杂技表演，演员从跷跷板右端处弹跳到人梯顶端椅子处，其身体（看成一个点）的路线是抛物线，已知起跳点距地面的高度为米，弹跳的最大高度距地面米，距起跳点的水平距离为米，建立如图所示的平面直角坐标系，（1）求演员身体运行路线的抛物线的解析式？（2）已知人梯高米，在一次表演中，人梯到起跳点的水平距离是米，问这次表演是否成功？说明理由．(第题图)21. (本题分）如图，已知⊙为△的外接圆，为⊙的直径，作射线，使得平分∠，过点作 ⊥ 于点 (1) 求证为⊙ 的切线； (2) 若，∠，求⊙的半径．．（本题分）(第题图)为了解八年级学生的身体素质情况，老师以八年级（）班位学生为样本进行了一分钟跳绳次数测试．根据测试结果，绘制出部分频数分布表和部分频数分布直方图．（如下所示）：请结合图表完成下列问题：八年级（）班一分钟跳绳次数的频数分布直方图跳绳次数组别次数频数（人数）第组 ≤< 第组 ≤< 第组 ≤<第组 ≤< 第组 ≤<（1）表中的▲；并把频数分布直方图补充完整；（2）这个样本数据的中位数落在从左到右数第▲组；（3）已知该校八年级共有学生，请你估计一分钟跳绳次数不低于次的八年级学生大约多少名？. (本题分)已知：矩形中，，，点、分别在边、上，直线交矩形对角线于点，将△沿直线翻折，点落在点处，且点在射线上.（1）如图，当⊥时，求的长；（2）如图，当⊥时，求的长；（3）请写出线段的长的取值范围，及当的长最大时的长.AB（图）（图）（备用图）．（本题分）已知(，)，点是轴上的动点，设(，), 过作的垂线交轴与，点是的中点．(1)当点在轴上时，求点坐标及直线的解析式；(2)如图，当点在第一象限时，若直线与过点的双曲线的另一支交于点，将点关于轴作轴对称变换得点′，连结′，′，．○求证：四边形′为平行四边形；○当为何值时，四边形′为矩形．(3)如图，设过点画轴的垂线与直线交于点，是否存在点，使△成为等腰三角形？若存在，请求出点的坐标；若不存在，请说明理由．。

【数学】浙江省金丽衢十二校2018届高三第二次联考数学试题含答案

2017-2018学年浙江省金丽衢十二校高三（上）第二次联考数学试卷一、选择题（共10小题，每小题4分，满分40分）1．设集合M={x|}，N={x|0＜x＜2}，则M∪N=（）A．[0，1）B．（0，1）C．[0，2）D．（0，2）2．若双曲线的两条渐近线相互垂直，则它的离心率是（）A．B．C．2 D．3．某四面体的三视图如图所示，正视图、左视图都是腰长为2的等腰直角三角形，俯视图是边长为2的正方形，则此四面体的最大面的面积是（）A．2 B． C． D．44．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的图象如图，则φ=（）A．B．C．D．5．已知（﹣1+3i）（2﹣i）=4+3i（其中i是虚数单位，是z的共轭复数），则z的虚部为（）A．1 B．﹣1 C．i D．﹣i6．已知正项数列{a n}中，a1=1，a2=2，（n≥2），则a6=（）A．B．4 C．16 D．457．用0，1，2，3，4可以组成的无重复数字的能被3整除的三位数的个数是（）A．20 B．24 C．36 D．488．如果存在正实数a，使得f（x+a）为奇函数，f（x﹣a）为偶函数，我们称函数f（x）为“Θ函数”．给出下列四个函数：①f（x）=sinx ②f（x）=cosx ③f（x）=sinx﹣cosx ④f（x）=sin2（x+）．其中“Θ函数”的个数为（）A．1 B．2 C．3 D．49．设a＞b＞0，当+取得最小值c时，函数f（x）=|x﹣a|+|x﹣b|+|x﹣c|的最小值为（）A．3 B．2 C．5 D．410．如图，正方体ABCD﹣A1B1C1D1的棱长为1，线段线段B1D1上有两个动点E，F，且EF=0.6，则当E、F移动时，下列结论中错误的是（）A．AE∥平面C1BDB．四面体ACEF的体积为定值C．三棱锥A﹣BEF的体积为定值D．异面直线AF、BE所成的角为定值二、填空题（共7小题，每小题6分，满分36分）11．若f（x）为偶函数，当x≥0时，f（x）=x（1﹣x），则当x＜0时，f（x）= ；方程[5f（x）﹣1][f（x）+5]=0的实根个数为．12．在的展开式中，常数项为；系数最大的项是．13．已知向量，满足，，与的夹角为，则= ；与的夹角为．14．函数f（x）=x2+acosx+bx，非空数集A={x|f（x）=0}，B={x|f（f（x））=0}，已知A=B，则参数a的所有取值构成的集合为；参数b的所有取值构成的集合为．15．已知直线m，l，平面α，β，且m⊥α，l⊂β，给出下列命题：①若α∥β，则m⊥l；②若α⊥β，则m∥l；③若m⊥l，则α∥β④若m∥l，则α⊥β其中正确的命题的序号是．（注：把你认为正确的命题的序号都填上）．16．从放有标号为1、2、4、8、16、32的6个球的口袋里随机取出3个球（例如2、4、32），然后将3个球中标号最大和最小的球放回口袋（例子中放回2和32，留下4），则留在手中的球的标号的数学期望是．17．设直线2x+y﹣3=0与抛物线Γ：y2=8x交于A，B两点，过A，B的圆与抛物线Γ交于另外两点C，D，则直线CD的斜率k= ．三、解答题（共5小题，满分74分）18．（14分）已知函数f（x）=sin（x+）+sin（x﹣）+cosx．（Ⅰ）求f（x）的最小正周期；（Ⅱ）在△ABC中，f（A）=，△ABC的面积为，AB=，求BC的长．19．（15分）四棱锥S﹣ABCD的底面是边长为1的正方形，则棱SB垂直于底面．（Ⅰ）求证：平面SBD⊥平面SAC；（Ⅱ）若SA与平面SCD所成角为30°，求SB的长．20．（15分）已知函数f（x）=a x﹣xlna（a＞0且a≠1）．（Ⅰ）求函数f（x）在点（0，f（0））处的切线方程；（Ⅱ）求函数f（x）单调区间；（Ⅲ）若对任意x1，x2∈R，有|f（sinx1）﹣f（sinx2）|≤e﹣2（e是自然对数的底数），求实数a的取值范围．21．（15分）已知椭圆T的焦点在x轴上，一个顶点为A（﹣5，0），其右焦点到直线3x﹣4y+3=0的距离为3．（Ⅰ）求椭圆T的方程；（Ⅱ）设椭圆T的长轴为AA'，P为椭圆上除A和A'外任意一点，引AQ⊥AP，A'Q⊥A'P，AQ 和A'Q的交点为Q，求点Q的轨迹方程．22．（15分）已知数列{a n}的首项a1=1，前n项和为S n，且a n+1=S n+n+1（n∈N+）（Ⅰ）求证数列{a n+1}为等比数列；（Ⅱ）设数列{}的前n项和为T n，求证：．（Ⅲ）设函数，令，求数列{b n}的通项公式，并判断其单调性．2017-2018学年金丽衢十二校高三（上）第二次联考数学试卷参考答案三、解答题（共5小题，满分74分）18．解：函数f（x）=sin（x+）+sin（x﹣）+cosx．化简可得：f（x）=2sinxcos+cosx=sinx+cosx=2sin（x+）（Ⅰ）f（x）的最小正周期T=；（Ⅱ）由f（A）=，即2sin（A+）=，∴sin（A+）=，∵0＜A＜π，∴＜（A+）．可得：（A+）=或则A=或A=．当则A=时，△ABC的面积为=bcsinA，AB=c=，∴b=AC=2余弦定理：BC2=22+（2）2﹣2××cos，解得：BC=2当A=时，△ABC的面积为=bc，AB=c=，∴b=AC=1直角三角形性质可得：BC2=22+（2）2，解得：BC=．19．证明：（Ⅰ）连结AC，BD，∵四边形ABCD是正方形，∴AC⊥BD，∵SB⊥底面ABCD，∴AC⊥SB，∴AC⊥面SBD，又由AC⊂面SAC，∴面SAC⊥面SBD．解：（Ⅱ）将四棱锥补成正四棱柱ABCD﹣A′SC′D′，连结A′D，作AE⊥A′D于E，连结SE，由SA′∥CD，知平面SCD即为平面SCDA′，∵CD⊥侧面ADD′A′，∴CD⊥AE，又AE⊥A′D，∴AE⊥面SCD，∴∠ASE即为SA与平面SCD所成角的平面角，设SB=x，在直角△ABS中，SA=，在直角△DAA′中，∴=，解得x=1，∴SB的长为1．20．解：（Ⅰ）∵f′（x）=a x lna﹣lna=（a x﹣1）lna，∴f′（0）=0，又∵f（0）=1，∴所求切线方程是：y=1；（Ⅱ）当a＞1时，令f′（x）＞0，解得：x＞0，令f′（x）＜0，解得：x＜0，当0＜a＜1时，令f′（x）＞0，解得：x＞0，令f′（x）＜0，解得：x＜0，故对∀a＞0，且a≠1，f（x）在[0，+∞）递增，在（﹣∞，0]递减；（Ⅲ）记f（x）在x∈[﹣1，1]上的最大值是M，最小值是m，要使对任意x1，x2∈R，有|f（sinx1）﹣f（sinx2）|≤e﹣2，只需M﹣m≤e﹣2即可，根据f（x）的单调性可知，m=f（0）=1，M为f（﹣1），f（1）的最大值，f（﹣1）=+lna，f（1）=a﹣lna，f（﹣1）﹣f（1）=﹣a+2lna，令g（x）=﹣x+2lnx，g′（x）=﹣≤0，故g（x）在（0，+∞）递减，又∵g（1）=0，∴a＞1时，g（a）＜g（1）=0，即f（﹣1）＜f（1），此时M=a﹣lna，要使M﹣m≤e﹣2，即有a﹣lna﹣1≤e﹣2，再令h（x）=x﹣lnx，由h′（x）=可知h（x）在（1，+∞）递增，不等式a﹣lna≤e﹣1可化为h（a）≤h（e），解得：1＜a≤e，当0＜a＜1时，g（a）＞g（1）=0，即f（﹣1）＞f（1），此时M=+lna，要使M﹣m≤e﹣2，即有+lna﹣1≤e﹣2，再令l（x）=+lnx，由l′（x）=，可知l（x）在（0，1）递减，不等式+lna≤e﹣1可化为l（a）≤l（），解得：≤a＜1，综上，a的范围是[，1）∪（1，e]．21．解：（Ⅰ）设椭圆的方程为：（a＞b＞0），设椭圆的右焦点为（c，0），则=3，解得：c=4，由题意的焦点在x轴上，则a=5，b2=a2﹣c2=3，∴椭圆的标准方程：；（Ⅱ）设P（5cosθ，3sinθ），A'（5，0），θ≠kπ，k∈Z，设Q（x，y），x≠5且x≠﹣5，于是，×=﹣1，×=﹣1，两式相乘：×=1，化简，所求轨迹方程为：，x≠5且x≠﹣5，∴点Q的轨迹方程，x≠5且x≠﹣5．22．解：（Ⅰ）证明：a n+1=S n+n+1，可得当n≥2时，a n=S n﹣1+n，两式相减可得，a n+1﹣a n=a n+1，可得a n+1+1=2（a n+1），n≥2，由a1+1=2，a2+1=4，可得数列{a n+1}为公比为2的等比数列；（Ⅱ）a n+1=2•2n﹣1=2n，即有a n=2n﹣1，当n=1时，T1=1，当n=2时，T2=1+，当n=3时，T3=1++=显然有；n＞3时，T n=1++++…+＜1+++（++…+）=1+++＜1+++=1++＜1++=；（Ⅲ）设函数，令，f′n（x）=a n+2a n﹣1x+…+na1x n﹣1，则b n=f′n（1）=a n+2a n﹣1+…+na1=（2n﹣1）+2（2n﹣1﹣1）+3（2n﹣2﹣1）+…+n（21﹣1）=2n+2•2n﹣1+3•2n﹣2+…+n•21﹣．令A=2n+2•2n﹣1+3•2n﹣2+…+n•21，A=2n﹣1+2•2n﹣2+3•2n﹣3+…+n•20，两式相减可得，A=2n+2n﹣1+2n﹣2+…+2﹣n=2n+1﹣n﹣2，即A=2n+2﹣2n﹣4，b n=2n+2﹣2n﹣4﹣=2n+2﹣n2﹣n﹣4，{b n}递增，只需证明当n为自然数时，b n+1﹣b n=2n+2﹣n﹣3＞0．当n=1时，2n+2﹣n﹣3=4＞0，假设n=k时，2k+2﹣k﹣3＞0，则当n=k+1时，2k+3﹣k﹣4=（2k+2﹣k﹣3）+（2k+2﹣1）＞0恒成立，综上可得，当n为一切自然数时，b n+1＞b n．即数列{b n}为递增数列．。

2018金衢十二校联考数学参考答案及评分细则

2018 金衢十二校联考数学参考答案及评分细则二、填空题(本大题有 6 小题，每小题 4 分，共 24 分)11．x ≥－1； 12．丙； 13．y =－2；14． 6 3；x15．2 或；16. (1)（m , 1－m ）； (2) m = -1 或m = -2三、解答题17. （1） 1 1= －1+1－……………………各 1 分9 3 =－2 9 18. 3x +3，…………………2 分……………………各 3 分19. 解：当α=45°时，小狗仍可以晒到太阳．理由如下：假设没有台阶，当α=45°时，从点 B 射下的光线与地面 AD 的交点为点 F ，与 MC 的交点为点 H ．当α=60°时，在 Rt △ABE 中， ∴AB =10•tan60°=10 3． ∵∠BFA =45°，此时的影长 AF =AB =10 3米， ............. 3 分 ∴CF=AF-AC =10 3-17>0.3 米， ............. 2 分 ∴小狗能晒到太阳． ............. 1 分20. 解：(1) 故 y =－3（x －2.5）2+4.75， ............. 4 分5（2）当 x =4 时，y =－3.4=BC ，............. 3 分故这次表演成功． ............. 1 分 21. 解（1）连结 OA ， .............................. 1 分C∴∠DAO =∠DAB +∠BAO =∠DAB +∠ABO=∠DAB +∠ABD= 90°， ............... 1 分∵A 为圆上一点， ∴DA 为圆 O 切线． ............................ 1 分（2）由题意可知：AD =BD ·tan ∠ABD =2， ................. 1 分∴AB = 5，∴cos ∠ABD = 1， ............... 1 分5(第 21 题图)5 ±3 6．AB O∵AD ⊥BF ，∴∠ABD +∠BAD =90°，又∵BA 平分∠CBF ， ……………………1 分 F D∴∠ABD =∠ABO ， ……………………1 分又∵OA =OB ，∴∠ABO =∠OAB ， ……………………1 分∴BC =ABcos ∠ABD=5， ................ 1 分∴OB = 1BC =2.5．...................... 1 分 222. （1）12 ........................................................................................................................... 2 分频数分布直方图（略）（12 人，18 人）， ............................. 2 分（2）三 .............................................................. 2 分（3）800×36=576(人) .................................................................................................. 2 分5023. 解：（1）∵△AME 沿直线 MN 翻折，点 A 落在点 P 处，∴△AME ≌△PME . ∴∠AEM =∠PEM ，AE=PE . ∵ABCD 是矩形，∴AB ⊥BC . ∵EP ⊥BC ，∴AB // EP .∴∠AME =∠PEM . ∴∠AEM =∠AME . ∴AM =AE .∵ABCD 是矩形，∴AB // DC . ∴ AM = AE . ∴CN =CE .CNCE设 CN = CE =x .∵ABCD 是矩形，AB =4，BC =3，∴AC =5. ∴PE= AE=5- x .∵EP ⊥BC ，∴ EP = sin ∠ACB = 4.CE 5 ∴ 5 - x = 4 . ∴ x = 25 ，即CN = 25 ....................................... 3 分 x 5 99 （2）∵△AME 沿直线 MN 翻折，点 A 落在点 P 处，∴△AME ≌△PME . ∴AE=PE ，AM=PM .∵EP ⊥AC ，∴ EP = tan ∠ACB = 4. ∴AE = 4 . CE 3CE 3 ∵AC =5，∴AE = 20 ，15 .∴ PE = 20 .CE =77∵EP ⊥AC ，∴ PC =∴ PB = PC - BC = 25 - 3 = 4 .7 7=25 . 7在 Rt △PMB 中，∵ PM 2 = PB 2 + MB 2 ，AM=PM .∴ A M 2 = 4 2 2 . ∴AM =100 ........................................... 4 分( ) + (4 - AM ) 749（3）0 ≤ CP ≤ 5 , ............................... 2 分当 CP 最大时 MN = 35 ............................... 1 分224．(1)当点 D 在 x 轴上时,点 C 与 O 重合,可求得 B 点坐标为（133,0） ................. 2 分7直线 AC 的解析式为 y = 23x ； ............... 2 分(2) ○1 由双曲线和正比例函数图象的中心对称性可知，点 D ，F 关于点 O 成中心对称，则OD =OF ；由轴对称可知 OB =OB ′，则四边形 DB ′FB 为平行四边形；………2 分○ 2 由○1 得，四边形 DB ′FB 为平行四边形，若四边形 DB ′FB 为矩形，则 OB =OD =t ，又∵点 D 是 Rt △BOC 的斜边 BC 的中点， ∴OD =BD ，∴△OBD 为等边三角形， y ∴OC = 3BO ，C过点 A 分别作 AG ⊥y 轴，AH ⊥x 轴，垂足为 G ，H ．则，易得△AGC ∽△AHB G D∴HB GC ∴ ＝AH AG 9－3t O B H x CG = ；2 ∴ 13－3t OC =2∴13－3t = 3t213 26 3－39t = =……………………………………………………………………2 分 2 3+3 3 (3)Ⅰ 0<t <3当点 E 与点 A 重合时，△CDE 为等腰三角形即直线 DE 经过点 A 13－3t ∴ ＝24 ∴t ＝53 ∴B ( 5 3,0)； ................................... 1 分 Ⅱ 3<t <13 3设 CD ＝CE过 A 作 AM ⊥y 轴，易证△AMC ∽△DHC ∴HD HC t＝AM MC ∴2 3 ＝ 13－3t 13－3t 2－4 2 ∴t =± 13∴B ( 13 ,0)；……………………1 分yA ∴A13Ⅲt>3∠CED 为钝角，设CE＝DE ∴CG＝BG∴△OCG≌△ABG∴AB＝OC∴(13－3t2)2＝(t－3)2+22解得t1=3 (舍去)，t2=7.8∴B (7.8,0) .......................................................................... 1 分Ⅳt<0可求得OKyC 3t－13＝t－3当CD＝CE 时D E∴CB＝CK∴OB＝OK3t－13 A∴t－3＝－t解得t＝± 13 B O K x∴B (－13 ,0) .......................................................................................................................... 1 分综上所述,存在点 B 使△DCE 为等腰三角形,此时B 点坐标为B1(53,0)；B2( 13 ,0)；B3 (7.8,0)；B 4(－13 ,0)．AGOxBEDC。

浙江省金衢十二校2018届中考数学联合模拟试题

金衢十二校2018年中考联合模拟数学试卷考生须知：1.全卷共三大题，24 小题，全卷满分 120 分，考试时间 120 分钟．2.全卷分试卷Ⅰ（选择题）和试卷II（非选择题）两部分，全部在答题卷上作答，卷Ⅰ的答案必须用 2B 铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔答在答题卷的相应位置上．卷Ⅰ一、选择题（本大题有 10 小题，每小题 3 分，共 30 分.请选出各题中一个符合题意的正确选项.不选、多选、错选均不给分）1、0、1、－2 这四个数中，最小的数是( ▲ )．1.在2B．0 C．1 D．－2 A．122.据媒体报道，我国因环境污染造成的巨大经济损失，每年高达 680 000 000 元，这个数用科学记数法表示正确的是( ▲ )．A. 6.8×109 元B. 6.8×108 元C. 6.8×107 元D. 68×107 元3.下列事件中，必然事件是( ▲ )．A.今年夏季的雨量一定多B. 下雨天每个人都打着伞C. 二月份有30 天D. 我国冬季的平均气温比夏季的平均气温低4.如图，点A、B、C、D、O 都在方格纸的格点上，若△COD 是由A．30°B．45°C．90°D．135°5.一次函数y=2－2 的图象不．经．过．的象限是( ▲ )．A．第一象限B．第二象限C．第三象限D．第四象限（第4 题图）6.下列四个图形：其中是轴对称图形，且对称轴的条数为 2 的图形的个数是( ▲ )．A. 1 个B．2 个C．3 个D．4 个7.对于反比例函数y=2，下列说法不．正．确．的是( ▲ )．A．点(－2，－1)在它的图象上B．它的图象在第一、三象限C．当>0 时，y 随的增大而增大D．当<0 时，y 随的增大而减小8.如图，在菱形ABCD 中，对角线AC、BD 相交于点O，E 为B C 的中点，则下列式子中一定成立的是( ▲ )． A．AC=2OE B．BC=2OEC．AD=OE D．OB=OE9.如图，将长为 2，宽为 1 的矩形纸片分割成n 个三角形后，拼成面积为 2 的正方形，则n≠( ▲ )．A．2 B．3 C．4 D．5C(第 8 题图)(第 9 题图)10.小阳在如图①所示的扇形舞台上沿O﹣M﹣N 匀速行走，他从点O 出发，沿箭头所示的方向经过点M 再走到点N，共用时 70 秒．有一台摄像机选择了一个固定的位置记录了小阳的走路过程，设小阳走路的时间为t（单位：秒），他与摄像机的距离为y（单位：米），表示y 与t 的函数关系的图象大致如图②，则这个固定位置可能是图①中的( ▲ )．A．点Q B．点PC．点M D．点N(第 10 题图)卷Ⅱ二、填空题（本大题有 6 小题，每小题 4 分，共 24 分）11.使代数式+1有意义的的取值范围是▲．12.东山茶厂有甲、乙、丙三台包装机，同时分装质量为 200 克的茶叶. 从它们各自分装的茶叶中分别随机抽取了 15 盒，测得它们的实际质量的方差如下表所示：y l1 Array A1根据表中数据，三台包装机中，▲包装机包装的茶叶质量最稳定．213.如图，l1 是反比例函数y=在第一象限内的图象，且过点A(2，1) ，l2l2 与l1 关于轴对称，那么图象l2 的函数解析式为▲（＞(第 13 题图) 0）．14.将一个三角形经过放大后得到另一个三角形，如果所得三角形在原三角形的外部，这两个三角形各对应边平行且距离都相等，那么我们把这样的两个三角形叫做“等距三角形”，它们对应边之间的距离叫做“等距”．如果两个等边三角形是“等距三角形”，它们的“等距”是1，那么它们周长的差是▲．15.已知在直角坐标平面内，以点P（1，2）为圆心，r 为半径画圆，⊙P 与坐标轴恰好有三个交点，那么r的取值是▲．16.在平面直角坐标系Oy 中，抛物线y =-2+ 2m -m2-m +1交y 轴于点为A，顶点为D，对称轴与轴交于点H.（1）顶点D的坐标为▲（用含m的代数式表示）；（2）当抛物线顶点D在第二象限时，如果∠ADH=∠AHO，m 的值为▲．三、解答题（本大题共有8小题，共66 分）17．（本题 6 分）计算：3－2－2cos60°+(12－2006)0－|－1|．318．（本题 6 分）已知多项式 A=( +2)2+(1－)( 2+)－3．（1）化简多项式 A；（2）若(+1)2=6，求 A 的值．19．（本题 6 分）如图所示，巨型广告牌AB 背后有一看台CD，台阶每层高 0.3 米，且AC=17 米，现有一只小狗睡在台阶的FG 这层上晒太阳，设太阳光线与水平地面的夹角为α，当α=60°时，测得广告牌AB 在地面上的影长AE=10 米，过了一会，当α=45°，问小狗在FG 这层是否还能晒到太阳？请说明理由．20.（本题 8 分）杂技团进行杂技表演，演员从跷跷板右端A 处弹跳到人梯顶端椅子B 处，其身体（看成一个点）的路线是抛物线，已知起跳点A 距地面的高度为 1 米，弹跳的最大高度距地面 4.75 米，距起跳点A 的水平距离为 2.5 米，建立如图所示的平面直角坐标系，（1）求演员身体运行路线的抛物线的解析式？（2）已知人梯高BC=3.4 米，在一次表演中，人梯到起跳点A 的水平距离是 4 米，问这次表演是否成功？说明理由．(第 20 题图) 21.(本题 8 分）如图，已知⊙O 为△ABC 的外接圆，BC 为⊙O 的直径，作射线BF，使得BA 平分∠CBF，过点A 作AD⊥BF 于点D (1)求证DA 为⊙O 的切线；FADB O(2)若BD=1，tan∠ABD=2，求⊙O 的半径．22．（本题 8 分）C (第 21 题图)为了解八年级学生的身体素质情况，老师以八年级（1）班50 位学生为样本进行了一分钟跳绳次数测试．根据测试结果，绘制出部分频数分布表和部分频数分布直方图．请结合图表完成下列问题：1）班一分钟跳绳次数的频数分布直方96380 100 120 140 160 180 跳绳次数（1）表中的a= ▲；并把频数分布直方图补充完整；（2）这个样本数据的中位数落在从左到右数第▲组；（3）已知该校八年级共有学生 800，请你估计一分钟跳绳次数不低于 120 次的八年级学生大约多少名？23. (本题 10 分)已知：矩形ABCD 中，AB=4，BC=3，点M、N 分别在边AB、CD 上，直线MN 交矩形对角线AC 于点E，将△AME 沿直线MN 翻折，点A 落在点P 处，且点P 在射线CB 上.（1）如图 1，当EP⊥BC 时，求CN 的长；（2）如图 2，当EP⊥AC 时，求AM 的长；（3）请写出线段CP 的长的取值范围，及当CP 的长最大时MN 的长.A DN MB PC（图 1）P BC（图 2）B C（备用图）24．（本题 12 分）已知A(3，2)，点B 是轴上的动点，设B(t，0), 过A 作AB 的垂线交y 轴与C，点D是BC 的中点．(1)当点D 在轴上时，求B 点坐标及直线AC 的解析式；(2)如图 1，当点D 在第一象限时，若直线OD 与过点D 的双曲线的另一支交于点F，将点B 关于y 轴作轴对称变换得点B′，连结DB′，FB′，FB．○ 1 求证：四边形DB′FB 为平行四边形；○ 2 当t 为何值时，四边形DB′FB 为矩形．(3)如图 2，设过点D 画y 轴的垂线与直线AC 交于点E，是否存在点B，使△CDE 成为等腰三角形？若存在，请求出点B 的坐标；若不存在，请说明理由．。

金丽衢十二校2018学年高三第一次联考数学试题(含答案)

2018学年金丽衢十二校高三第一次联考数学参考答案一选择题（每小题4分，共40分）二填空题（多空题每题6分，单空题每题4分，共36分） 11．5212．23(0, 14] 13．2 1414．45 17 15．2- 16．23π 17．3三解答题18．解：（1）在△ABC 中，cos A =45，A ∈(0, π)，所以sin A 35==.同理可得，sin ∠ACB=1213.所以cos B =cos[π-(A +∠ACB )]= -cos(A +∠ACB )=sin A sin ∠ACB-cos A cos ∠ACB=312451651351364⨯-⨯=.…………………………7分（2）在△ABC 中，由正弦定理得，AB =sin BC Bsin ∠ACB =13123135⨯=20.又AD =3DB ，所以BD =14AB =5.在△BCD 中，由余弦定理得，CD ……………………………………14分19．（1）证明：连接ME ，因为点M ，E 分别是P A ，PD 的中点，所以ME =12AD ，ME ∥AD ，所以BC ∥ME ，BC =ME ，所以四边形BCEM 为平行四边形，所以CE ∥BM . 又因为BM ⊂平面BMD ，CE ⊄平面BMD ，所以CE //平面BMD ．……………………6分（2）如图，以A 为坐标原点建立空间坐标系O -xyz ，则又1,1,12CQ ⎛⎫=-- ⎪⎝⎭，()1,0,1CE =-设平面CEQ 的法向量为(),,x y z =n ，列方程组求得其中一个法向量为()2,1,2=n ，设直线P A 与平面CEQ 所成角大小为θ，于是2sin 3θ==，进而求得cos θ=…………………………15分 20．（1）a n +1+a n -1=2a n +2，则(a n +1-a n ) - (a n -a n -1)=2.所以{a n +1-a n }是公差为2的等差数列. ……………………… 5分（2）n ≥2，a n =(a n -a n -1)+…+(a 2-a 1)+a 1=2n +…+4+2=2·(1)2n n +=n (n +1).当n =1，a 1=2满足.则a n =n (n +1). ……………………………… 8分 b n =10(1)(!11012)2nn n n ++-=-∴S n =10(1+12+ (1))-2n ，∴S 2n =10(1+12+ (1)+11n ++12n ++…+12n )-22n ，设M n =S 2n -S n =10(11n ++12n ++ (12))-2n ，………………………………11分∴M n +1=10(12n ++13n ++…+12n+121n ++122n +)-12n +， ∴M n +1-M n =10(121n ++122n +-11n +)-12=10(121n +-122n +)-12=10(21)(22)n n ++-12，∴当n =1时，M n +1-M n =1034⨯-12＞0，即M 1＜M 2，当n ≥2时，M n +1-M n ＜0，即M 2＞M 3＞M 4＞…，∴(M n )max =M 2=10×(13+14)-1=296，则{S 2n -S n }的最大值为S 4-S 2=296……………………………………15分21．（1）11121122OMN S MN ∆=⨯⨯⨯⨯=≥………………………………6分（2）设),sin Eθθ，则AE方程为y x =+，则M为sin t t θ+⎛⎫⎝，同理N 为sin t t θ-⎛⎫ ⎝，因为OM ON ⊥，所以(2202t t -=，得2t =.………………15分【也可设E 为()00,x y 求出】22．（1）因为()2'31826f x x x =-+-，所以126x x +=，求得()12()6f x f x +=………6分（2）()()''61863f x x x =-+=--，所以函数()f x 在()0,3的图象为下凸，在()3,+∞的图象为上凸，记()()3,3P f ，求得P 处()f x 的切线为y x =，再记()0,Q a ，有求得()f x的极大值点为3339M ⎛⎝⎭，①当39a +≥时，直线y =kx +a 与曲线y =f (x )显然只有唯一公共点②当[3,39a ∈+时，直线QM 斜率为正，且与曲线y =f (x )有三个公共点，舍去.③当()0,3a ∈时，直线QP 斜率为正，且与曲线y =f (x )有三个公共点，舍去.④当(,0]a ∈-∞时，当()0,PQ k k ∈，P 在直线上方，直线y =kx +a 与曲线y =f (x )的上凸部分有唯一公共点，与下凸部分不相交；当PQ k k =时，直线y =kx +a 与曲线y =f (x )交于P 点，与上凸部分和下凸部分均不相交；当(),PQ k k ∈+∞，P 在直线下方，直线y =kx +a 与曲线y =f (x )的下凸部分有唯一公共点，与上凸部分不相交. 所以此种情况成立综上，a 的取值范围为23(,0][3,)9-∞++∞…………………………………15分。

浙江省金丽衢十二校2018-2019学年高三数学第二次联考试卷

浙江省金丽衢十二校2018-2019学年高三数学第二次联考试卷一、单选题 (共10题；共10分)1．（1分）集合A={x|x2−2x>0}，B={x}−3<x<3}，则（）A．B．C．D．2．（1分）点F1和F2是双曲线y2−x23=1的两个焦点，则|F1F2|=（）A．B．2C．D．43．（1分）复数z1=2−i，z2=3+i，则|z1⋅z2|=（）A．5B．6C．7D．4．（1分）某几何体的三视图如图所示（图中单位：cm），则该几何体的表面积为（）A．B．C．D．5．（1分）已知直线l⊥平面α，直线m∥平面β，则“ α∥β”是“ l⊥m”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件6．（1分）甲和乙两人独立的从五门选修课课程中任选三门进行学习，记两人所选课程相同的门数为ξ，则E(ξ)为（）A．1.2B．1.5C．1.8D．27．（1分）函数f(x)=lnx8−x的图像大致为（）A．B．C．D．8．（1分）已知a⇀，b⇀，c⇀和d⇀为空间中的4个单位向量，且a⇀+b⇀+c⇀=0，则|a⇀−d⇀|+|b⇀−d⇀|+|c⇀−d⇀|不可能等于（）A．3B．C．4D．9．（1分）正三棱锥P−ABC的底面边长为1cm，高为ℎcm，它在六条棱处的六个二面角（侧面与侧面或者侧面与底面）之和记为θ，则在ℎ从小到大的变化过程中，θ的变化情况是（）A．一直增大B．一直减小C．先增大后减小D．先减小后增大10．（1分）数列{a n}满足：a1=1，a n+1=a n+1an，则a2018的值所在区间为（）A．B．C．D．二、填空题 (共7题；共11分)11．（2分）《九章算术》第七章“盈不足”中第一题：“今有共买物，人出八，盈三钱；人出七，不足四，问人数物价各几何？”借用我们现在的说法可以表述为：有几个人合买一件物品，每人出8元，则付完钱后还多3元；若每人出7元，则还差4元才够付款.问他们的人数和物品价格？答：一共有人；所合买的物品价格为元．12．（2分）(1−2x)5展开式中x3的系数为；所有项的系数和为．13．（2分）若实数x，y满足约束条件{x+y≥1,x+2y≤2,x≤1,则目标函数Z=2x+3y的最小值为；最大值为．14．（2分）在ΔABC中，角A，B和C所对的边长为a，b和c，面积为13(a2+c2−b2)，且∠C为钝角，则tanB=；ca的取值范围是．15．（1分）安排3名支教老师去6所学校任教，每校至多2人，则不同的分配方案共有种.（用数字作答）16．（1分）定义在R上的偶函数f(x)满足：当x>0时有f(x+4)=13f(x)，且当0≤x≤4时，f(x)=3|x−3|，若方程f(x)−mx=0恰有三个实根，则m的取值范围是．17．（1分）过点P(1,1)的直线l与椭圆x24+y23=1交于点A和B，且AP⇀=λPB⇀.点Q满足AQ⇀=−λQB⇀，若O为坐标原点，则|OQ|的最小值为．三、解答题 (共5题；共10分)18．（2分）已知函数f(x)=sin2x+√3sinxsin(x+π2 ).（1）（1分）求f(x)的最小正周期；（2）（1分）求函数f(x)在区间[0,23π]上的取值范围.19．（1分）在三棱拄ABC−A1B1C1中，AB⊥侧面BB1C1C，已知BC=1，∠BCC1=π3，AB=C1C=2.（Ⅰ）求证：C1B⊥平面ABC；（Ⅱ）试在棱C1C(不包含端点C,C1)上确定一点E的位置，使得EA⊥EB1；（Ⅲ）在（Ⅱ）的条件下,求AE和平面ABC所成角正弦值的大小.20．（2分）数列{a n}的前n项和为S n，a1=1，对任意n∈N∗，有a n+1=2S n+1.（1）（1分）求数列{a n}的通项公式；（2）（1分）若b n=a n+1a n，求数列{log3b n}的前n项和T n.21．（2分）已知抛物线E：y=ax2(a>0)内有一点P(1,3)，过P的两条直线l1，l2分别与抛物线E交于A，C和B，D两点，且满足AP⇀=λPC⇀，BP⇀=λPD⇀(λ>0,λ≠1)，已知线段AB的中点为M，直线AB的斜率为k.（1）（1分）求证：点M的横坐标为定值；（2）（1分）如果k=2，点M的纵坐标小于3，求ΔPAB的面积的最大值.n(n−lnx)，其中n∈N∗，x∈(0,+∞).22．（3分）函数f(x)=√x（1）（1分）若n为定值，求f(x)的最大值；（2）（1分）求证：对任意m∈N∗，有ln1+ln2+ln3+⋯ln(m+1)>2(√m+1−1)2；（3）（1分）若n=2，lna≥1，求证：对任意k>0，直线y=−kx+a与曲线y= f(x)有唯一公共点.答案解析部分1．【答案】B【解析】【解答】解：A={x|x＜0，或x＞2}，B={x|﹣3＜x＜3}；∴A∩B={x|﹣3＜x＜0，或2＜x＜3}，A∪B=R；∵A∩B≠A，且A∩B≠B，∴B⊈A，A⊈B；即B符合题意．故答案为：B．【分析】通过解不等式求出集合A，根据集合的关系逐一判断即可. 2．【答案】D【解析】【解答】由y2−x 23=1可知a2=1,b2=3所以c2=a2+b2=4，则c=2,2c=4，所以|F1F2|=2c=4.故答案为：D【分析】根据双曲线的标准方程，得到两个焦点坐标，即可求出线段的长度.3．【答案】D【解析】【解答】因为|z1|=|2−i|=√5，|z2|=|3+i|=√10，所以|z1⋅z2|=|z1|⋅|z2|=√5×√10=5√2故答案为：D.【分析】根据复数的乘法运算，得到z1·z2，结合复数的模运算即可求出相应的值.4．【答案】B【解析】【解答】由三视图可知，该几何体的直观图为一个竖立的圆锥和一个倒立的圆锥组成，其表面积为S=2πrl=2×π×1×√2=2√2π，故答案为：B.【分析】根据三视图确定几何体的结构特征，即可求出几何体的表面积.5．【答案】A【解析】【解答】根据已知题意，由于直线l⊥平面α，直线m∥平面β，如果两个平面平行α//β，则必然能满足l⊥m，但是反之，如果l⊥m，则对于平面可能是相交的，故条件能推出结论，但是结论不能推出条件，故答案为：A【分析】根据直线与平面的位置关系，即可确定充分、必要性.6．【答案】C【解析】【解答】由已知得ξ=1,2,3，P(ξ=1)=C53C31C53C53=310, P(ξ=2)=C53C32C21C53C53=35, P(ξ=3)=C53C53C53=110,所以E(ξ)=1×310+2×610+3×110=1.8,故答案为：C【分析】求出随机变量的可能取值及相应的概率，即可求出数学期望. 7．【答案】A【解析】【解答】函数定义域为(0,8)，当x→0时，x8−x→0，lnx8−x→−∞，故排除B,D，当x→8时，x8−x→+∞，lnx8−x→+∞，故排除C,故答案为：A.【分析】根据函数的定义域及函数值的变化情况，逐一排除，即可确定函数的大致图象.8．【答案】A【解析】【解答】因为|a⇀−d⇀|+|b⇀−d⇀|+|c⇀−d⇀|≥|a⇀−d⇀+b⇀−d⇀+c⇀−d⇀|=|a⇀+b⇀+c⇀−3d⇀|而a⇀+b⇀+c⇀=0，所以|a⇀−d⇀|+|b⇀−d⇀|+|c⇀−d⇀|≥|−3d⇀|=3因为a⇀，b⇀，c⇀，d⇀是单位向量，且a⇀+b⇀+c⇀=0，所以a⇀−d⇀，b⇀−d⇀，c⇀−d⇀不共线，所以|a⇀−d⇀|+|b⇀−d⇀|+|c⇀−d⇀|>3，故答案为：A.【分析】根据向量的关系，求出|a⇀−d⇀|+|b⇀−d⇀|+|c⇀−d⇀|的最小值，即可确定|a⇀−d⇀|+|b⇀−d⇀|+ |c⇀−d⇀|不可能的取值.9．【答案】D【解析】【解答】当ℎ→0+（比0多一点点），有θ→θ1=3π；当ℎ→+∞，有θ→θ3=5π2；当ℎ刚好使得正三棱锥变为正四面体时，二面角之和记为θ2，则cosθ26=3+3−42×3=13，于是cos θ23=2×(13)2−1=−79>−√32，所以θ23<5π6，即θ2<5π2，所以与θ的变化情况相符合的只有选项D.故答案为：D【分析】根据几何体的结构特征，求出角的余弦值，即可得到角的变化情况. 10．【答案】A【解析】【解答】因为a1=1，所以a n+12=a n2+2+1a n2≤a n2+3an+12≤an2+3≤an−12+3+3…可得：a n+12<a12+3n所以a2018<√a12+3×2017<√10000=100.故答案为：A【分析】根据递推关系式得到数列项之间的关系，解不等式即可确定a2018的值所在区间.11．【答案】7；53【解析】【解答】设共有x人，由题意知8x−3=7x+4，解得x=7，可知商品价格为53元.即共有7人，商品价格为53元.【分析】设共有x人，通过解方程即可求出共有人数和商品价格.12．【答案】-80；-1【解析】【解答】因为T r+1=C5r(−2)r x r，令r=3，T4=−80x3，所以x3的系数为-80，设(1−2x)5=a0+a1x+⋯+a5x5，令x=1，则a0+a1…+a5=−1，所以所有项的系数和为-1.【分析】写出二项展开式的通项，即可求出特定项的系数及所有项的系数之和. 13．【答案】2；【解析】【解答】作出可行域如下：由Z=2x+3y可得y=−23x+z，作出直线y=−23x,平移直线过B(1,0)时，z有最小值z=2+0=2，平移直线过A(1，12）时，z有最大值z=2×1+3×12=72.【分析】作出可行域及目标函数相应的直线，平移该直线即可求出目标函数的最大值和最小值.14．【答案】；【解析】【解答】因为S=12acsinB=13(a2+c2−b2)，所以34sinB=a2+c2−b22ac=cosB即tanB=43，因为∠C为钝角，所以sinB=45,cosB=35，由正弦定理知ca=sinCsinA=sin(B+A)sinA=cosB+sinBcosAsinA=35+45cotA因为∠C为钝角，所以A+B<π2,即A<π2−B所以cotA>cot(π2−B)=tanB=43所以ca>35+45×43=53，即ca的取值范围是(53,+∞).【分析】通过面积公式及正弦定理，确定三角形边和角的关系，即可求出相应的值和取值范围. 15．【答案】210【解析】【解答】分两类，（1）每校1人：A63=120；（2）1校1人，1校2人：C32A62=90，不同的分配方案共有120+90=210．故答案为：210【分析】根据加法原理和乘法原理，即可确定不同的分配方案种数.16．【答案】【解析】【解答】因为当0≤x≤4时，f(x)=3|x−3|，设4≤x≤8，则0≤x−4≤4，所以f(x−4)=3|x−4−3|=3|x−7|，又f(x+4)=13f(x)，所以f(x)=13f(x−4)=|x−7|，可作出函数y=f(x)在x∈[0,8]上的图象，又函数为偶函数，可得函数在[−8,8]的图象，同时作出直线y=mx，如图：方程f(x)−mx=0恰有三个实根即y=f(x)与y=mx图象有三个交点，当m>0时，由图象可知，当直线y=mx过（8,1），即m=18时有4个交点，当直线y=mx过（4,3），即m=34时有2个交点，当18<m<34时有3个交点，同理可得当m<0时，满足−34<m<−18时，直线y=mx与y=f(x)有3个交点.故填(−34,−18)∪(18,34).【分析】通过函数的性质，作出函数的图象，数形结合即可求出实数m的取值范围. 17．【答案】【解析】【解答】设A(x1,y1)，B(x2,y2)，Q(m,n)则{x1+λx2=1+λ,x1−λx2=m(1−λ),于是x12−(λx2)2=m(1−λ2)，同理y12−(λy2)2=n(1−λ2)，于是我们可以得到(x124+y123)+λ2(x224+y223)=(1+λ2)(m4+n3).即m4+n3=1，所以Q点的轨迹是直线，|OQ|min即为原点到直线的距离，所以|OQ|min=1√116+19=125【分析】设出点A 和B 的坐标，根据向量的关系，确定Q 的轨迹是直线，即可求出线段长度的最小值.18．【答案】（1）解： f(x)=sin 2x +√3sinxsin(2x +π2)=1−cos2x 2+√32sin2x =sin(2x −π6)+12所以 T =π（2）解：由 −π2+2kπ≤2x −π6≤π2+2kπ 得 −π6+kπ≤x ≤π3+kπ,k ∈z 所以函数 f(x) 的单调递增区间是 [−π6+kπ,π3+kπ],k ∈z ．由 x ∈[0，2π3] 得 2x −π6∈[−π6,76π] ，所以 sin(2x −π6)∈[−12,1]所以 f(x)∈[0,32] ．【解析】【分析】（1）根据正弦和余弦的二倍角公式，结合辅助角公式，得到函数的表达式，即可求出函数的最小正周期；（2）根据正弦函数的单调性，确定函数f （x ）的单调区间，即可求出函数f （x ）的取值范围.19．【答案】解：（Ⅰ）因为 BC =1 ， ∠BCC 1=π3 ， C 1C =2 ，所以 BC 1=√3 ，BC 2+BC 12=CC 12 ，所以 BC 1⊥BC 因为 AB ⊥ 侧面 BB 1C 1C ， BC 1⊂ 平面 BB 1C 1C ，所以 BC 1⊥AB ，又 BC ∩AB =B ，所以， C 1B ⊥ 平面 ABC（Ⅱ）取 C 1C 的中点 E ，连接 BE ， BC =CE =1 ， ∠BCC 1=π3 ，等边 ΔBEB 1 中， ∠BEC =π3同理， B 1C 1=C 1E 1=1 ， ∠B 1C E 1=2π3，所以 ∠B 1EC 1=π6 ，可得 ∠BEB 1=π2 ，所以EB 1⊥EB因为 AB ⊥ 侧面 BB 1C 1C ， EB 1⊂ 平面 BB 1C 1C ，所以 EB 1⊥AB ，且 EB ∩AB =B ，所以 B 1E ⊥ 平面 ABE ，所以；（Ⅲ） AB ⊥ 侧面 BB 1C 1C ， AB ⊂ 平面，得平面 BCC 1B 1⊥ 平面 ABC 1 ，过 E 做 BC 1 的垂线交 BC 1 于 F ， EF ⊥ 平面 ABC 1连接AF，则∠EAF为所求，因为BC⊥BC1，EF⊥BC1，所以BC∥EF，E为CC1的中点得F为C1B的中点，EF=12，由（2）知AE=√5，所以sin∠EAF=12√5=√510【解析】【分析】根据线面垂直的判定定理，证明直线与平面内两条相交直线垂直即可；（2）根据线面垂直的定义，证明直线与平面垂直，即可说明直线与平面内任何一条直线垂直；（3）通过作垂线得到直线与平面所成的角，通过解三角形求出线面所成角的正弦即可. 20．【答案】（1）解：由a n+1=2S n+1知a n=2S n−1+1(n≥2)两式相减得：a n+1=3a n(n≥2)又a2=2s1+1=2a1+1=3，所以a2a1=3也成立，故a n+1=3a n,n∈N∗即数列{a n}是以1为首项，3为公比的等比数列，所以a n=3n−1(n∈N∗).（2）解：因为log3b n=log3a n+1an=3n−1log33n=n⋅3n−1，所以T n=1×30+2×31+3×32+⋯+n⋅3n−13T n=1×31+2×32+3×33+⋯+(n−1)⋅3n−1+n⋅3n两式相减得：−2Tn =(12−n)⋅3n−12，所以T n=(n2−14)3n+14.【解析】【分析】（1）根据等比数列的定义确定数列{a n}是以1为首项，3为公比的等比数列，即可求出的通项公式；（2）根据对数恒等式，结合错位相消求和法，即可求出前n项和T n.21．【答案】（1）证明：设CD中点为N，则由AP⇀=λPC⇀，BP⇀=λPD⇀可推得AB⇀=λDC⇀，MP⇀=λPN⇀，这说明AB⇀∥CD⇀，且M，P和N三点共线.对A，B使用点差法，可得y A−y B=a(x A−x B)(x A+x B)，即k AB=2a⋅x M.同理k CD=2a⋅x N.于是x M=x N，即MN⊥x轴，所以x M=x P=1为定值.（2）解：由k=2得到a=1，设y M=t∈(1,3)，|PM|=3−t，联立{y=x2,y−t=2(x−1),得x2−2x+2−t=0，所以|x A−x B|=2√t−1, |AB|=√1+k2|x A−x B|=√5⋅2√t−1,根据点到直线的距离公式知P到AB的距离为d=|t−3|√5，于是SΔPAB=(3−t)√t−1，令x= √t−1，x∈(0,2),则S=−x3+2x，S′=−3x2+2，令S′=0得x=√63，当x∈(0,√63)时，S′>0,函数为增函数，当x∈(√63，2)时，S′<0，函数为减函数，故当x=√63，即t=53时，SΔPAB有最大值4√69.【解析】【分析】（1）根据向量之间的关系，采用点差法，即可确定点M的坐标为定值；（2）根据点斜式写出直线方程，将直线方程与抛物线方程联立，通过弦长公式和点到直线的距离，表示出三角形的面积，求导数，利用导数研究函数的单调性，即可求出三角形面积的最大值.22．【答案】（1）解：n为定值，故f′(x)=1n x 1n−1(n−lnx)+√xn(−1x)=−√xn lnxx（x>0)，令f′(x)=0，得x=1，当0<x<1时，f′(x)>0，当x>1时，f′(x)<0，所以函数在(0,1)上单调递增，在(1,+∞)上单调递减，所以当x=1时，函数有极大值f(1)，也是最大值，所以f(x)max=f(1)=n.（2）解：由前一问可知lnx≥n−n√xn，取n=2得lnx≥2−2√x，于是∑m+1 i=1lni≥∑(2−2i)m+1i=2>2m−4∑m+1i=21√i+√i−1=2m−4∑(√i−√i−1)m+1i=2=2m−4√m+1+4=2(√m+1−1)2.（3）解：要证明当a≥e，k>0时，关于x的方程√x(2−lnx)=−kx+a有唯一解，令t=√x，即证明g(t)=kt2+2t−2tlnt−a有唯一零点，先证明g(t)存在零点，再利用导数得函数单调性，极值确定函数只有唯一零点.我们先证三个引理【引理1】x(1−lnx)≤1（由第1问取n=1即可）【引理2】lnx≥1−1x（由【引理1】变形得到）【引理3】lnx≤x−1（可直接证明也可由【引理2推出】证明：lnx=−ln 1x≤−(1−11x)=x−1.下面我们先证明函数g(t)存在零点，先由【引理2】得到：g(t)≤kt2+2t−2t(1−1t)−a=kt2+2−a.令t=√a−2k，可知g(t)≤0.再由【引理3】得到lnx<x，于是g(t)=t(kt−4ln√t)+(2t−a)>t√t(k√t−4)(2t−a).令t>16k2，且t>a2，可知g(t)>0.由连续性可知该函数一定存在零点.下面我们开始证明函数g(t)最多只能有一个零点.我们有g′(t)=2kt−2lnt=2t(k−lnt t).令ℎ(t)=lntt ，则ℎ′(t)=1−lntt2，则ℎ(t)在(0,e)递增，在(e,+∞)递减，即ℎ(t)max=1e.当k≥1e时，有g′(t)≥0恒成立，g(t)在(0,+∞)上递增，所以最多一个零点.当0<k<1e时，令g′(t1)=g′(t2)=0，t1<e<t2，即lnt1=kt1，于是g(t1)=t1lnt1+2t1−2t1lnt1−a=t1(2−lnt1)−a.再令t1=eT(0<T<1)，由【引理1】可以得到g(t1)=eT(1−lnT)−a<e×1−a≤0.因此函数g(t)在(0,t1)递增，(t1,t2)递减，(t2,+∞)递增，t=t1时，g(t)有极大值但其极大值g(t1)<0，所以最多只有一个零点.综上，当k>0，a≥e时，函数y=f(x)与y=−kx+a的图像有唯一交点.【解析】【分析】（1）求导数，利用导数确定函数的单调性，结合单调性求出函数的最大值即可；（2）由（1）可得不等式lnx≥n−n√xn，结合放缩法，即可证明相应的不等式；（3）构造函数，求导数，利用导数确定函数的单调性，求出函数的极值，根据函数零点与函数图象交点横坐标的关系，数形结合，即可证明相应的结论.。

浙江省金丽衢十二校2018-2019学年高三数学第二次联考试卷

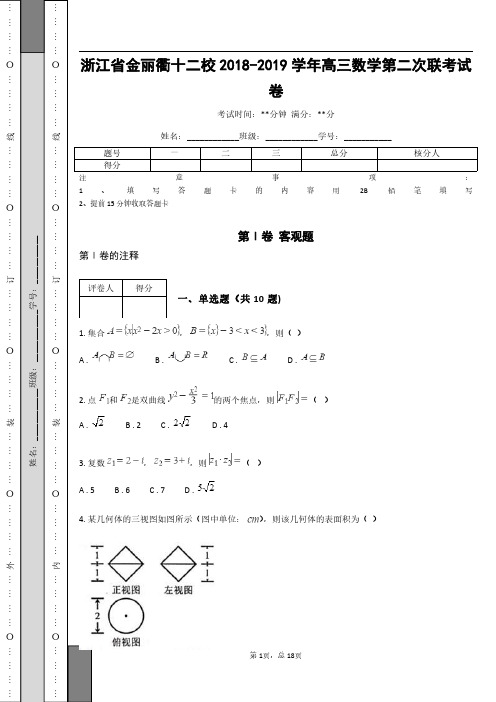
，对任意
，有
； .
（1）求数列的通项公式；
（2）若
，求数列
11. 已知抛物线：
和，两点，且满足斜率为 .
的前项和 .
内有一点
，过的两条直线，分别与抛物线交于，
，
，已知线段的中点为，直线的
答案第 4页，总 18页
…………○…………外…………○…………装…………○…………订…………○…………线…………○………… 姓名：____________班级：____________学号：___________
………○…………外…………○…………装…………○…………订…………○…………线…………○…………
A.
B.
C.
D.
5. 已知直线平面，直线平面，则“ ”是“ A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件
”的（）
6. 甲和乙两人独立的从五门选修课课程中任选三门进行学习，记两人所选课程相同的门数为，则为（） A . 1.2 B . 1.5 C . 1.8 D . 2
参数答案
第 5页，总 18页
与曲线
；
有唯一公共点.
…………○…………内…………○…………装…………○…………订…………○…………线…………○………… ※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
………○…………外…………○…………装…………○…………订…………○…………线…………○…………
种.（用数字作答）
6. 定义在上的偶函数满足：当
时有
，且当
时，
，
若方程
恰有三个实根，则的取值范围是

金丽衢十二校2018学年高三第一次联考数学试题(Word版)

金丽衢十二校2018学年高三第一次联考数学试题一、选择题1、若集合(,5)A =-∞,[3,)B =+∞，则(∁R A )∪(∁R B )=( )A 、RB 、∅C 、［3,5）D 、(,5)[5+-∞∞，）2、已知向量(4,3),(1,53)a b ==，则向量,a b 的夹角为（）A 、30°B 、45°C 、60°D 、90°3、等比数列{}n a 的前n 项和为n S ，己知23S =，415S =，则3S ＝（） A. 7 B 、－9 C 、7或－9 D 、6384、双曲线22941y x -=的渐近线方程为（） A 、49y x =±B 、94y x =±C 、23y x =±D 、32y x =± 5.己知一个几何体的三视图如图所示，则该几何体的体积为( ) A 、43 B 、83 C 、163 D 、3236.己知复数z 满足52(3)zi i π=+，则z 在复平面内对应的点位于（） A 、第一象限 B.第二象限 C.第三象限 D 、第四象限7.设函数()f x 的定义域为D ，如果对任惫的x ∈D ，存在y ∈D ，使得()()f x f y =-成立，则称函数()f x 为“H 函数”，下列为“H 函数”的是（）A 、2sin cos cos y x x x =+ B 、ln xy x e =+ C 、 2xy =D 、22y x x =- 8.如图，二面角BC αβ--的大小为6π，AB α⊂，CD β⊂，且AB ，BD ＝CD ＝2， ∠ABC ＝4π，∠BCD ＝3π，则AD 与β所成角的大小为（） A 、4π B 、3π C 、6πD 、12π9.五人进行过关游戏，每人随机出现左路和右路两种选择．若选择同一条路的人数超过2 人，则他们每人得1分：若选择同一条路的人数小于3人，则他们每人得0分。

2018金衢十二校联考数学试题卷

浙江省金丽衢十二校2018-2019学年高三数学第二次联考试卷

2018金衢十二校联考数学答题卷(2018.4)

浙江省金衢十二校2018届中考数学联合模拟试题

2018金衢十二校联考数学试题卷

【数学】浙江省金丽衢十二校2018届高三第二次联考数学试题 含答案

2018金衢十二校联考数学参考答案及评分细则

浙江省金衢十二校2018届中考数学联合模拟试题

金丽衢十二校2018学年高三第一次联考数学试题(含答案)

浙江省金丽衢十二校2018-2019学年高三数学第二次联考试卷

浙江省金丽衢十二校2018-2019学年高三数学第二次联考试卷

金丽衢十二校2018学年高三第一次联考数学试题(Word版)

【数学】浙江省金丽衢十二校2018届高三第二次联考数学试题含答案