人教版五年级数学奥数专题第10讲 数阵(基础卷+提高卷)
小学五年级奥数第10讲 数阵(含答案分析)

第10讲数阵一、知识要点填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,和同学们讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二、精讲精练【例题1】把5、6、7、8、9五个数分别填入下图的五个方格里,如图a 使横行三个数的和与竖行三个数的和都是21。
练习1:1.把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2.把1—9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3.将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
【例题2】将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
练习2:1.把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2.把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
3.将1——8八个数填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。
第1题第二题第三题【例题3】将1——6这六个数分别填入下图的圆中,使每条直线上三个圆内数的和相等、且最大。
练习3:1.将1——6六个数分别填入下图的○内,使每边上的三个○内数的和相等。
2.将1——9九个数分别填入下图○内,使每边上四个○内数的和都是17。
3.将1——8八个数分别填入下图的○内,使每条安上三个数的和相等。
第1题第二题第三题【例题4】将1——7分别填入下图的7个○内,使每条线段上三个○内数的和相等。
练习4:1.将1——9填入下图的○中,使横、竖行五个数相加的和都等于25。
奥数拓展第十讲排列组合问题-数学五年级上册人教版

奥数拓展第十讲:排列组合问题-数学五年级上册人教版一、选择题1.用7、8、9、0四张数字卡片,可以组成()个不同的四位数。
A.24B.18C.122.学校组织春游活动因故提前了,张老师要尽快通知到每一位学生,如果用打电话的方式,每分钟通知1人,每人接到电话后立即通知其他不知道这一信息的同学,全班40位同学,最快()分钟才能通知到全班同学。
A.4B.5C.6D.73.如图,小蚂蚁从点A爬到点B,走最短的路线,共有()种不同的路线。
A.6B.8C.10D.124.有1元、2元、5元和10元人民币各1张,任意取2张,可以有()种不同的取法。
A.4B.6C.10D.145.将7个点连成线段,任意三点不在同一条直线上,最多可以连成()。
A.7条B.12条C.21条D.28条6.四对情侣排成一队买演唱会门票,已知每对情侣必须排在一起,问共有多少种不同的排队顺序()。
A.24种B.96种C.384种D.40320种二、填空题7.小巧与同学们聚会,参加聚会的每两个人都合影一张。
聚会结束时,统计出一共拍照45张,参加这次聚会的同学共有( )人。
8.从下面三枚硬币中取硬币,一共可以取出( )种不同的钱数。
9.明明、红红、强强在平时的50m短跑训练比赛中,成绩相当。
他们要进行一场50m短跑比赛,你能算出比赛可能一共有( )种结果。
(不并列)。
10.从沈阳站始发的火车,途经辽中、锦州南站、唐山北站后到达终点北京站。
这趟列车单程需要准备( )种不同的车票。
11.要在人民公园大门的上方挂6只大灯笼(如图),如果把形状相同的灯笼挨在一起,可以有( )种不同的挂法。
12.小明从一楼到二楼,共要上9级台阶,他每次最多跨两级,那么他从一楼到二楼,一共有( )种走法。
13.5名象棋爱好者进行比赛,规定每两人比赛一局,经过一段时间后统计,甲已赛了4局,乙已赛了3局,丙已赛了2局,丁已赛了1局,则此时戊已赛了( )局。
14.2018年世界杯足球赛在俄罗斯举行。
五年级奥数举一反三第10周数阵

五年级奥数举一反三第10周数阵专题简析;填“幻方”是同学们比较熟悉的一种数学游戏’由幻方演变出来的数阵问题’也是一类比较常见的填数问题。
这里’和同学们讨论一些数阵的填法。
解答数阵问题通常用两种方法;一是待定数法’二是试验法。
待定数法就是先用字母[或符号]表示满足条件的数’通过分析、计算来确定这些字母[或符号]应具备的条件’为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口’确定填数的可能范围。
把分析推理和试验法结合起来’再由填数的可能情况’确定应填的数。
例题1 把5、6、7、8、9五个数分别填入下图的五个方格里’如图a使横行三个数的和与竖行三个数的和都是21。
先把五格方格中的数用字母A、B、C、D、E来表示’根据题意可知;A+B+C+D+E=35’A+E+B+C+E+D=21×2=42。
把两式相比较可知’E=42-35=7’即中间填7。
然后再根据5+9=6+8便可把五个数填进方格’如图b。
练习一1’把1——10各数填入“六一”的10个空格里’使在同一直线上的各数的和都是12。
2’把1——9各数填入“七一”的9个空格里’使在同一直线上的各数的和都是13。
3’将1——7七个自然数分别填入图中的圆圈里’使每条线上三个数的和相等。
例题2 将1——10这十个数填入下图小圆中’使每个大圆上六个数的和是30。
分析设中间两个圆中的数为a、b’则两个大圆的总和是1+2+3+……+10+a+b=30×2’即55+a+b=60’a+b=5。
在1——10这十个数中1+4=5’2+3=5。
当a和b是1和4时’每个大圆上另外四个数分别是[2’6’8’9]和[3’5’7’10];当a和b是2和3时’每个大圆上另外四个数分别为[1’5’9’10]和[4’6’7’8]。
练习二1’把1——8八个数分别填入下图的○内’使每个大圆上五个○内数的和相等。
2’把1——10这十个数分别填入下图的○内’使每个四边形顶点的○内四个数的和都相等’且和最大。
小学五年级奥数第10讲 数阵(含答案分析)

第10讲数阵一、知识要点填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,和同学们讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二、精讲精练【例题1】把5、6、7、8、9五个数分别填入下图的五个方格里,如图a 使横行三个数的和与竖行三个数的和都是21。
练习1:1.把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2.把1—9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3.将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
【例题2】将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
练习2:1.把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2.把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
3.将1——8八个数填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。
第1题第二题第三题【例题3】将1——6这六个数分别填入下图的圆中,使每条直线上三个圆内数的和相等、且最大。
练习3:1.将1——6六个数分别填入下图的○内,使每边上的三个○内数的和相等。
2.将1——9九个数分别填入下图○内,使每边上四个○内数的和都是17。
3.将1——8八个数分别填入下图的○内,使每条安上三个数的和相等。
第1题第二题第三题【例题4】将1——7分别填入下图的7个○内,使每条线段上三个○内数的和相等。
练习4:1.将1——9填入下图的○中,使横、竖行五个数相加的和都等于25。
人教版五年级奥数练习:数阵 (3)
人教版五年级奥数练习:数阵
例题
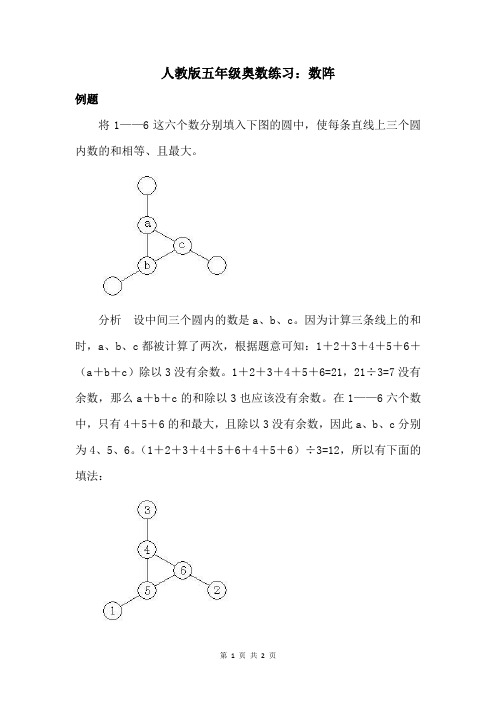
将1——6这六个数分别填入下图的圆中,使每条直线上三个圆内数的和相等、且最大。
分析设中间三个圆内的数是a、b、c。
因为计算三条线上的和时,a、b、c都被计算了两次,根据题意可知:1+2+3+4+5+6+(a+b+c)除以3没有余数。
1+2+3+4+5+6=21,21÷3=7没有余数,那么a+b+c的和除以3也应该没有余数。
在1——6六个数中,只有4+5+6的和最大,且除以3没有余数,因此a、b、c分别为4、5、6。
(1+2+3+4+5+6+4+5+6)÷3=12,所以有下面的填法:
练习
1,将1——6六个数分别填入下图的○内,使每边上的三个○内数的和相等。
2,将1——9九个数分别填入下图○内,使每边上四个○内数的和都是17。
3,将1——8八个数分别填入下图的○内,使每条安上三个数的和相等。
五年级奥数-数阵图(AB卷)
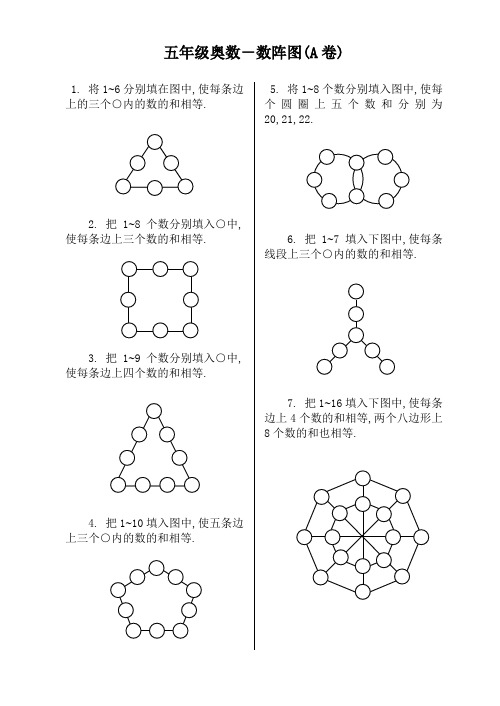
1. 将1~6分别填在图中,使每条边上的三个○内的数的和相等.
2. 把1~8个数分别填入○中,使每条边上三个数的和相等.
3. 把1~9个数分别填入○中,使每条边上四个数的和相等.
4. 把1~10填入图中,使五条边上三个○内的数的和相等.
5. 将1~8个数分别填入图中,使每个圆圈上五个数和分别为20,21,22.
6. 把1~7填入下图中,使每条线段上三个○内的数的和相等.
7. 把1~16填入下图中,使每条边上4个数的和相等,两个八边形上8个数的和也相等.
8. 把4~9填入下图中,使每条线上三个数的和相等,都是18.
9. 把1~8这8个数填入下图,使每边上的加、减、乘、除成立.
10. 把0~9填入10个小三角形中,使每4个小三角形组成的大三角形的和相等.
11. 把1~11填入图中,使每条线上三个数的和相等.
12. 把1~8,填入图中,使每条线及正方形四个顶点上的数的和相等.
13. 把1~9,填入下图中,使每条线段三个数和及四个顶点的和也相等.
14. 把17,23,25,31,46,53,58,66,72,88,94,100十二个数填入下图,使任意三个相邻的数相加的和除以7的余数相等.。
小学五年级奥数举一反三第10周数阵ppt课件

此,有这样的填法。
.
【练习4】
1,将1——9填入下图的○中,使横、竖行五个数相加的和都等于25。 2,将1——11这十一个数分别填进下图的○里,使每条线上3个○内 的数的和相等。 3,将1——8这八个数分别填入下图○内,使外圆四个数的和,内圆 四个数的和以及横行、竖行上四个数的和都等于18。
.
【例题5】如下图(a)四个小三角形的顶点处有六个圆圈。如果在这些 圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个 顶点上的数的和相等。问这六个质数的积是多少?
个数分别为(7,8,12,13)和(5,10,11,14);当a和b是
7和8时,每个大圆上另外四个数分别为(5,10,12,13)和(6,
9,11,14)。
.
【练习2】
1,把1——8八个数分别填入下图的○内,使每个大圆上五个○内数 的和相等。 2,把1——10这十个数分别填入下图的○内,使每个四边形顶点的 ○内四个数的和都相等,且和最大。 3,将1——8八个数填入下图方格里,使上面四格、下面四格、左 四格、右四格、中间四格以及对角线四格内四个数的和都是18。
【思路导航】设中间两个圆中的数为a、b,则两个大圆的总和是5 +6+7+……+14+a+b=55×2,即95+a+b=110,a+b=15。 在5—14这十个数中5+10=15,6+9=15, 7+8=15 。
当a和b是5和10时,每个大圆上另外四个数分别是(8,9,11,
12)和(6,7,13,14);当a和b是6和9时,每个大圆上另外四
.
【例题3】将1——6这六个数分别填入下图的圆中,使每条直线上三 个圆内数的和相等、且最大。
【思路导航】设中间三个圆内的数是a、b、c。因为计算三条线上的 和时,a、b、c都被计算了两次,根据题意可知:1+2+3+4+5+6 +(a+b+c)除以3没有余数。1+2+3+4+5+6=21,21÷3=7没 有余数,那么a+b+c的和除以3也应该没有余数。在1——6六个数中, 只有4+5+6的和最大,且除以3没有余数,因此a、b、c分别为4、5、 6。(1+2+3+4+5+6+4+5+6)÷3=12,所以有上面的填法:
小学五年级奥数举一反三第10周数阵教程文件

【练习4】
1,将1——9填入下图的○中,使横、竖行五个数相加的和都等于25。 2,将1——11这十一个数分别填进下图的○里,使每条线上3个○内 的数的和相等。 3,将1——8这八个数分别填入下图○内,使外圆四个数的和,内圆 四个数的和以及横行、竖行上四个数的和都等于18。
【例题5】如下图(a)四个小三角形的顶点处有六个圆圈。如果在这些 圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个 顶点上的数的和相等。问这六个质数的积是多少?
【思路导航】设中间两个圆中的数为a、b,则两个大圆的总和是5 +6+7+……+14+a+b=55×2,即95+a+b=110,a+b=15。 在5—14这十个数中5+10=15,6+9=15, 7+8=15 。 当a和b是5和10时,每个大圆上另外四个数分别是(8,9,11, 12)和(6,7,13,14);当a和b是6和9时,每个大圆上另外四 个数分别为(7,8,12,13)和(5,10,11,14);当a和b是 7和8时,每个大圆上另外四个数分别为(5,10,12,13)和(6, 9,11,14)。
【例题3】将1——6这六个数分别填入下图的圆中,使每条直线上三 个圆内数的和相等、且最大。
【思路导航】设中间三个圆内的数是a、b、c。因为计算三条线上的 和时,a、b、c都被计算了两次,根据题意可知:1+2+3+4+5+6 +(a+b+c)除以3没有余数。1+2+3+4+5+6=21,21÷3=7没 有余数,那么a+b+c的和除以3也应该没有余数。在1——6六个数中, 只有4+5+6的和最大,且除以3没有余数,因此a、b、c分别为4、5、 6。(1+2+3+4+5+6+4+5+6)÷3=12,所以有上面的填法:
小学五年级奥数举一反三第10周数阵
二、精讲精练
五年级奥数专题讲义-第10讲数阵通用版(含答案)

第 10 讲数阵基础卷1.把 3~10 分别填在下图中正方体的八个顶点上的圆圈里,使每个面四个顶点上圆圈中的数的和相等。
答案不唯一,只要每个面的和为262.把 1~14 分别填入下图中的方格内,使“十一” 三笔中每五个方格内的数的和相等。
答案不唯一,只要交叉部分是3的倍数都能填好3.把 1~9 分别填入下图的圆圈中,使七个三角形(四个小三角形、三个大三角形)中每个三角形的三个顶点圆圈内的数的和相等。
4.把 2~11 分别填入下图的方格中,每格填一个数,要求图中三个2×2 的正方形中四数之和相等。
上面第一行填的数分别为11,10,9中间行填入的数为2,3,4,5底下行填入8,7,6所有的和均为245.把 1~8 分别填入下图的空格中,使图中四边正好组成加、减、乘、除四种运算算式。
答案不唯一,被除数和被减数的位置是最大的数字8,能把8整除的数字只能是2和4,考虑下面的商还要做因数,完成乘法运算,所以只能是8除以4等于2,然后,依次凑数,填入2乘3等于6,8-7=1,1+5=6,即可得解.6.把 1~9 分别填入下图的圆圈中,使两条线段上的五个数的和相等,两个四边形顶点上数的和也相等。
答案不唯一提高卷1.如图,三个正方形组成八个三角形,现把每个正方形四个顶点上都分别填上 2, 3, 4, 5 这四个数,使得八个三角形三个顶点上数的和为连续的八个自然数,这连续的八个自然数各是多少?填数方法是(把大正方形摆正)大正方形和小正方形的左上角填2,中正方形的顶点填2,三个正方形都依次逆时针填入3 4 52.把 1~16 分别填入下图的十六个圆圈中,使每条线段上四个圆圈内的数的和相等,两个八边形顶点上的数的和也相等。
答案不唯一3.如图,内部四个交点上已经填好数,请你在四周的方格里填上适当的数,使交点上的数恰好等于四周四个方格内数的和,可以怎么填?5 5 55 5 55 4 54.在下图的七个圆圈内各填一个数,要求在每条线上的三个数中,当中的数是两边两个数的平均数,现已填好两个数,求 A。
小学五年级奥数举一反三第10周数阵ppt课件

线段上的和相等,所以(28+2a)除以3应该没有余数。由于
28÷3=9……1,那么2a除以3应该余2,因此,a可以为1、4或7。当
a=1时,(28+2×1)÷3-1=9,即每条线段上其他两数的和是9,
因此,有这样的填法。
可编辑课件PPT
9
【练习4】
1,将1——9填入下图的○中,使横、竖行五个数相加的和都等于 25。 2,将1——11这十一个数分别填进下图的○里,使每条线上3个○ 内的数的和相等。 3,将1——8这八个数分别填入下图○内,使外圆四个数的和,内圆 四个数的和以及横行、竖行上四个数的和都等于18。
定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。把
分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
可编辑课件PPT
2
二、精讲精练
【例题1】 把5、6、7、8、9五个数分别填入下图的五个方格里, 如图a使横行三个数的和与竖行三个数的和都是21。
五年级奥数 举一反三
第十讲 数阵
可编辑课件PPT
1
Байду номын сангаас 一、知识要点
填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来
的数阵问题,也是一类比较常见的填数问题。这里,和同学们讨论一
些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。待定数
法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确
可编辑课件PPT
4
【例题2】将5—14这十个数填入下图小圆中,使每个大圆上六个 数的和是55。
【思路导航】设中间两个圆中的数为a、b,则两个大圆的总和是5 +6+7+……+14+a+b=55×2,即95+a+b=110,a+b=15。 在5—14这十个数中5+10=15,6+9=15, 7+8=15 。
小学五年级奥数精品专项训练-数阵_周期问题

一、数阵一、知识要点填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,和同学们讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二、精讲精练【例题1】把5、6、7、8、9五个数分别填入下图的五个方格里,如图a 使横行三个数的和与竖行三个数的和都是21。
【思路导航】先把五格方格中的数用字母A、B、C、D、E来表示,根据题意可知:A+B+C+D+E=35,A+E+B+C+E+D=21×2=42。
把两式相比较可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8便可把五个数填进方格,如图b。
练习1:1.把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2.把1——9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3.将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
【答案】1.7、1、5、6、2、10、3、9、4、8(答案不唯一)2.1、2、3、8、5、4、9、6、7(答案不唯一)3.2、6、4、1、5、3、7(答案不唯一)【例题2】将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
【思路导航】设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3+……+10+a+b=30×2.即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a和b是1和4时,每个大圆上另外四个数分别是(2.6,8,9)和(3.5,7,10);当a和b是2和3时,每个大圆上另外四个数分别为(1.5,9,10)和(4,6,7,8)。
小三奥数 第10讲:数阵图

学员编号:年级:课时数:学员姓名:辅导科目:学科教师:授课T (同步知识主题) C (专题方法主题)T (学法与能力主题)类型授课日期时段教学内容第十讲:数阵图.把1~6这六个数字分别填入图10 - l的六个圈内.使得每个正方形顶点上的数的和都为13.从l到6这六个数的和是21.而两个正方形8个顶点上的数之和是26(=13×2),比六个数的总和大5.这是因为中间两个圈内的数,都被算了两次,所以,多出来的5就是中间两个圈内的数的和.每个正方形,去掉这中间的两个数,剩下的两个数,和都是8(=13 -5).解在1到6六个数中,两个数的和为8,只可能足2+6、3+5.所以中间两个圈内填1与4.得到如幽10 - 2的填法.将3、4、6这二个数填入图10-3的三个圆圈内,使得每条边上的三个数的和等于11..将2到7这六个数,填入图10- 4的圈中,使得每条线上的三个数的和相等.由2+7= 4+5=3+6=9.得到如图10-5的解将l到7这七个数填入图10-6,使得每条线上的三个数的和相等..将1到9这九个数填入图10-7,使得从中心出发的每条线段上的三个数的和相等..将1到9这九个数填入图10-7,使得从中心出发的每条线段上的三个数的和相等.l+2+…+9=45去掉中心的数后,每条线上两个数的和相等.4条线上8个数的和是每条线上的和乘以4.所以中心的数只能是1、5、9,去掉中心后的8个数的和分别是44、40、36,每条线上两个数的和分别是11、10、9.即有三种情况:(1)中心填1时,2与9、4与7、8与3、5与6两两搭配填入同一条线的两个圈内即可.(2)中心填5时,1与9、2与8、3与7、4与6搭配.(3)中心填9时,1与8、2与7、3与6、4与5搭配这样得到如图10-8所示的三个解将1~8填入图10-9,使两个正方形顶点上的数的和相等,并且用斜线连接的4对数的和也都相等..将1到5这五个数填入图10 - 10,使得圆周上四个数的和与每条直线上的三个数的和都相等.设中心的数是a.因为竖线上的三个数的和等于圆周上的四个数的和,所以a等于它左、右两个数的和.同理,a等于它上、下两个数的和.从而a是最大的数5.其余四个数,2与3搭配.1与4搭配,写在同一条线上,得到的解如图10-11所示.在图10 – 12中填上7、8、10、1 2,使得每个圆内的四个数的和相等..将l~6这六个数填入图10-13的六个圆圈内,使得每条边上的三个数的和相等.如果1与6都不在顶点处,那么在图10 -14中,a+l+c=b+6+c.所以a+1=6+b但6比a大,b比1大,所以a+l与6+b不可能相等.1与6至少有一个在顶点处.设1在顶点.2、3、4、5、6中取4个数,分成和相等的2组,只有3种可能:2+6=3+5.3+6=4+5.2+5=3+4前两种可得图10-15的(1),(2).第3种不可能,因为另一行3个数的和至少是2+3+6.超过1+2+5.同样,6在顶点时,可以得到图10 - 15的(3),(4)因此,本题的答案是图10-15的(1)~(4).用7减去1在顶点的图10 - 15(1)、(2)的每一个数,便得到(3)、(4).反过来也是这样.将l到16填入图10 -16,使得每条线段上四个数的和相等,两个八边形八个顶点上的数的和也相等.将1~16填入图10 - 17的正方形,使每行、每列、每条对角线的和都相等.本题也就是造一个四阶幻方四阶幻方的造法很多,解也不唯一.下面介绍一种最简的做法,可以称为调整法.先将1~16依照次序先左后右,先上后下逐一填入图10 - 18(1)中得四阶幻方中每行和、每列和、每条对角线的和都是(1+2+…+16)÷4= (1+16)×16÷2÷4=34现在图10 - 18(1)的两条对角线的和都已经是34,合乎要求所以对角线上的数不要再动.先来调整行,将第一行的2、3分别与第四行的14,1 5对调,第二行的5、8分别与第三行的9、12对调,得图10 - 18(2),这个图中,不但每条对角线的和是34,每一行的和也都是34.再调整列.将图10 - 18(2)第一列的9、5分别与第四列的12、8对调,第二列的14、2分别与15、3对调,得图10 -18(3),这个图就是一个合乎要求的幻方.比较例6所得的幻方与巩固练习5的答案.有何联系?可能与必然上节末,说到一个游戏“数独”数独怎么填呢?比如先看第一行,在上节末的图中,有6个空格,应填1、2、4、7、8、9这6个数字,每个空格填的数有6种可能,难以确定.如果看第二列,只有2个空格,心填2、7,每个空格有2种可能,但还不能惟一确定.可能性太多,需要逐个枚举讨论,比较麻烦.所以应先考虑可能较小的方格,最好能发现一些方格,只有一种填法,也就是说这些方格填什么数是必然的.将这些方格先填好,对填其他方格会有帮助.同时考虑几个方面的要求,可以得到必然的填法,比如中间的3×3的正方形,只有3个空格,应填2、6、8.再结合第四行已经有8,第六行也已经有8,所以8必须填在中央.接下去,因为第四行已经有6,所以6必须填在第六行,2填在第四行.现在再看第四行,只剩2个空格,应填9与3.第九列有9,所以第四行的9只能(必然)在第三列,3在第九列.同样,右中3×3的正方形中,9必然在第六行,第六行第一列必填2.左中3×3的正方形中,5必在第一列,7在笫三列.第八列3必填在第九行,9必填在第二行.右上3×3的正方形中,7必填在第七列.右下3×3的正方形中,5必在第八行第七列,2必在第八行,1在第九列第七行,6在第七行第七列.右中3×3的正方形中,6在第九列,2在第七列,左下3×3的正方形中,2、3、8、6的填法郡是必然的.左上3×3的正方形中.按行依次填2、1、4、7、6.右上3×3的正方形中,填4、8.中上3×3的正方形中填8、9、6、2、7、4.中下3×3的正方形中填9、3、6、4、1、7.填法都是必然的,最后结果如图.当然,上面填数的顺序可以变更但应尽量先填只有一种可能的方格,而不要先填邮些难以确定的方格.1.如果图中每行、每列、每条对角线的和都相等,那么填入的数a、b、c、d有什么关系?2.将1到8这八个数填入下图,使得每条线上的三个数的和相等.3.将1到9这九个数填入下图,使得每条边上的四个数的和相等.4.将6到10这五个数填入下图,使得每条边上的三个数的和相等.5.将5到12填入下图,使得每条边上的四个数的和相等.6.将2到11填入下图,使得每条线段上的三个数之和相等.7.将1到10填入下图,使得每条线上的四个数的和相等.8.将l到10填入下图,使每条线段上的四个数的和相等,每个三角形三个顶点上的数的和也相等.(三角形顶点上的数的和不必与线段上的数的和相等)9.将1到8填入圈内,使得每个圆上的五个数的和相等.10.将l到8填入圈内,使每一圆周上的四个数、每条线上的四个数的和相等.11.在下面由圆分割出的9个区域中,填入1到9这九个数,使得每个圆内的数的和都等于11.12.将1到12填入下图,使每条边上的五个数的和相等.你做对了吗?答案:巩固练习6 图中的4条对角线是四阶幻方的4行,另有4组共线的点,如l、12、8、13等是幻方的4列,外面八边形的4个相邻顶点上的数16、1、6、11是幻方的一条对角线,另4个相邻顶点上的数10,7,4,13是幻方的另一条对角线。
数阵问题 小学数学 随堂练习
一、填空题
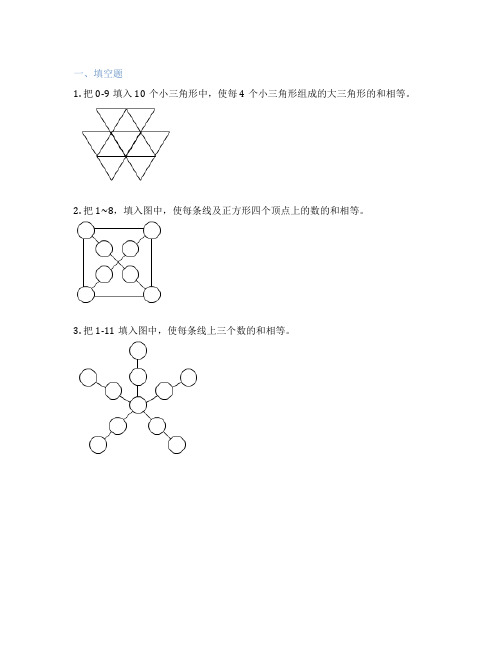
1. 把0-9填入10个小三角形中,使每4个小三角形组成的大三角形的和相等。
2. 把1~8,填入图中,使每条线及正方形四个顶点上的数的和相等。
3. 把1-11填入图中,使每条线上三个数的和相等。
4. 把 1~9 分别填入下图的圆圈中,使七个三角形(四个小三角形、三个大三角形)中每个三角形的三个顶点圆圈内的数的和相等。
5. 把 1~14 分别填入下图中的方格内,使“十一” 三笔中每五个方格内的数的和相等。
二、解答题
6. 把1,2,…,9填入图20﹣1中9个空白圆圈内,使得三个圆周及三条线段上
3个数之和都相等.
7. 请将1、2、3、4、5、6、7、8八个数字填入右图中的八块区域内,使得每一个圆圈与它相邻的区域内的数之和都相等。
8. 请将1~8填入图中的8个方格内,使得a、b、c、d四个方格内的数,恰好等于它上方与之有公共边的两个方格内所填数的差。
其中b填7。
9. 请将0、1、2、3、4、5六个数字填入图中的六块区域内,使得每一个圆圈与它相邻区域内的数之和都相等。
五年级奥数数阵问题

课时3 数阵问题(一)之南宫帮珍创作一.数阵填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较罕见的填数问题。
这里,主要讨论一些数阵的填法。
解答数阵问题通经常使用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)暗示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二.例题精析例1把5、6、7、8、9五个数分别填入下图的五个方格里,如图a使横行三个数的和与竖行三个数的和都是21。
先把五格方格中的数用字母A、B、C、D、E来暗示,根据题意可知:A+B+C+D+E=35,A+E+B+C+E+D=21×2=42。
把两式相比较可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8即可把五个数填进方格,如图b。
小试牛刀把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2、把1——9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3、将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
例2 将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
分析设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3+……+10+a+b=30×2、即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a和b是1和4时,每个大圆上另外四个数分别是(2、6,8,9)和(3、5,7,10);当a和b是2和3时,每个大圆上另外四个数分别为(1、5,9,10)和(4,6,7,8)。
小试牛刀1、把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2、把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
五年级下册奥数知识点:数阵图练习题
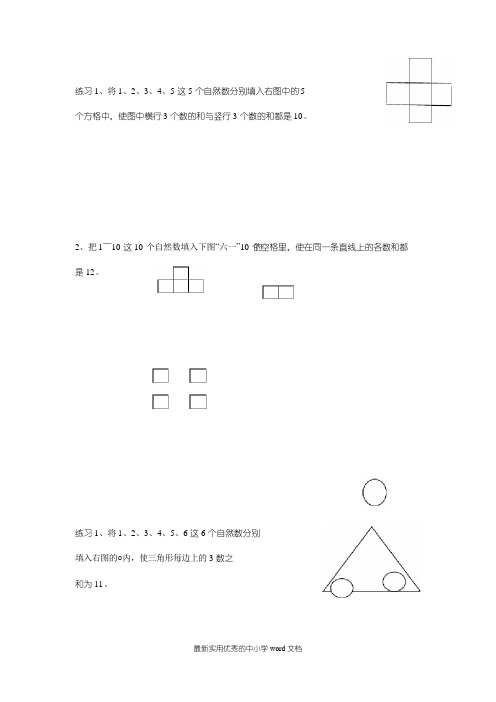
的练习1、将1、2、3、4、5这5个自然数分别填入右图中的5个方格中,使图中横行3个数的和与竖行3个数的和都是10。
2、把1~10这10个自然数填入下图“六一”10个空格里,使在同一条直线上的各数和都是12。
练习1、将1、2、3、4、5、6这6个自然数分别填入右图的○内,使三角形每边上的3数之和为11。
2、把1~9个数分别填入中○使每条边上四个数的和都是20.练习1、将1~6这6个自然数分别填入下图中两圆的○内,使每个圆上4个数的和相等,两圆交点上的两个○内的数有几种填法?例4、将1~10这10个自然数填入右图中的○内,使图中每条线段上的数之和都相等。
请写出各种填法。
3、下面一列数是按一定规律排列的,那么括号中的数是()。
1,4,7,28,5,20,(),12…4、王明参加一次数学竞赛,全卷共20道竞赛题,做对一道得5分,做错一道倒扣3分,王明20道题都做了,共得76分,他做对了()题。
5、同学们站成3层空心方阵,最外层每边站20人,一共有学生()人。
6、小明的邮票比小红多15张,小明的邮票张数是小红的4倍,小红有()张邮票7、一条小青虫,它的身长每天延长1倍,长到第10天的时候身长是20厘米,请问,在身长是10厘米的时候,它已经生长了()天。
8、士兵排成一个实心方阵,最外一层一周的人数为80人,问方阵外层每边有()人。
这个方阵共有()个士兵。
9、长方形的长是20厘米,截去一个最大的正方形后,余下一个长方形,这个长方形的周长是()厘米。
10、植树节到了,同学们在一条90米长的小路的一旁植树,每隔3米种一棵。
(1)如果两端都各栽一棵,需要()棵树。
(2)如果只有一端栽树,需要()棵树。
(3)如果两端都不栽树,需要()棵树。
11、甲班和乙班共有图书480本,甲班的图书本数是乙班的3倍,甲班有图书()本,乙班有图书()本。
13、小明买科技书和文艺书共34本,科技书比文艺书多6本。
小明买科技书()本,文艺书()本。
五年级下册奥数有趣的数阵图人教版

例1:把1~5这五个自然数,分别填入下图中的五个圆圈内, 使相交成十字的两条直线上三个数之和等于9。
假设重叠数是a 1+2+3+4+5+a=9×2
15+a=18 a=3
1 2 34
5
小结
解答数阵图的关键是重叠数,所以 填数阵时,一般优先考虑重叠数。可 以把这个数用括号或字母表示,列出 等式,再根据条件解答出来。
45+a+a+a是4的倍数 1+2+3+…+9+10+a+a
1
三个角上的数都加了两次,
1+2+…+6+7=28 解答数阵图的关键是重叠数,所以填数阵时,一般优先考虑重叠数。
先列出一个等式,再考虑三个未知的数吧。 三个角上的数都加了两次,
7
把1~7这七个数分别填入图中七个圆圈内,使每条直线上三个圆圈内各数之和都是12。
1+3+5+……+15=64
3
5
1
39×2-64=14
7
9
中间的两个圆圈数重叠一次, 15 13 11
两数之和为14
今天你学到了什么?
解答数阵图的关键是重叠数,所以 填数阵时,一般优先考虑重叠数。可 以把这个数用括号或字母表示,列出 等式,再根据条件解答出来。
先列出一个等式,再考虑三个未知的数吧。
1+5=6或2+4=6
哪个位置的数是重叠数?
1+2+…+7+8+a+b=21×2
45+a+a+a是4的倍数
中间的三个数只加一次, 1+2+3+…+9+a+a+a
五年级数阵10周练习题

五年级数阵10周练习题五年级数阵练习题是帮助学生巩固数学基础知识和提高解题技巧的有效方法。
以下是为期10周的练习题,每周的练习题都包含了不同的数学概念和技能,旨在全面提升学生的数学能力。
第1周:基础加法和减法- 完成以下加法:23 + 47 = ?- 完成以下减法:89 - 26 = ?- 解决实际问题:小明有55个苹果,他给了小华17个,还剩多少个?第2周:乘法和除法- 完成以下乘法:7 × 8 = ?- 完成以下除法:56 ÷ 8 = ?- 解决实际问题:一个班级有40名学生,每8人一组,可以分成几组?第3周:四则混合运算- 计算以下表达式:(36 + 24) ÷ 6- 计算以下表达式:90 - (15 × 3)- 解决实际问题:一个长方形的长是20米,宽是15米,它的面积是多少?第4周:分数的初步认识- 将一个整体分成4份,每份是多少?- 一个苹果分成2份,每份占整个苹果的几分之几?- 解决实际问题:一个蛋糕被平均分成了8份,小华吃了3份,吃了整个蛋糕的几分之几?第5周:小数的认识和运算- 将0.5写成分数形式。
- 完成以下小数加法:0.3 + 0.7 = ?- 完成以下小数减法:1.8 - 0.9 = ?第6周:几何图形的初步认识- 计算一个正方形的周长,如果它的边长是5厘米。
- 计算一个长方形的面积,如果它的长是8厘米,宽是4厘米。
- 解决实际问题:一个圆形花园的直径是10米,它的周长是多少?第7周:时间的计算- 如果现在是下午3点,3小时后是几点?- 一个活动从上午9点开始,持续2小时,结束时间是几点?- 解决实际问题:小明每天学习3小时,一周他总共学习了多少小时?第8周:简单的统计图表- 制作一个简单的条形图,表示班上同学喜欢不同水果的数量。
- 制作一个简单的饼图,表示一周内小明每天花费在不同活动上的时间比例。
第9周:逻辑推理- 根据给定的条件,找出符合条件的数字序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版五年级奥数专题第10讲数阵(基础卷+提高卷)
姓名:________ 班级:________ 成绩:________
小朋友,带上你一段时间的学习成果,一起来做个自我检测吧,相信你一定是最棒的!
一、填空题
1 . 把1~9这9个数分别填入○中,使每条边上四个数的和相等.
2 . 把4~9填入下图中,使每条线上三个数的和相等,都是18.
3 . 把1~10这10个数填入图中,使五条边上三个○内的数的和相等.
4 . 把1~14 分别填入下图中的方格内,使“十一” 三笔中每五个方格内的数的和相等。
5 . (2014•广州)在如图中的“○”里填上适当的数,使每个正方形的四个角的数之和为
1.
6 . 将1~8这8个数分别填入图中,使每个圆圈上五个数和分别为20,21,22.
7 . 把1~7填入下图中,使每条线段上三个○内的数的和相等.
8 . 把 1~12 分别填入下图的空格中,使四个椭圆、四个圆形、四个正方形及四条直线上的四个数之和都为 26。
二、解答题
9 . 将1~6填入右图的六个○中,使三角形每条边上的三个数之和都等于k,请指出k的取值范围。
10 . 海豚是很聪明的动物,它能将1~9填入下图的九个○内,并且使得每个圆周和每条直线上的三数之和都相等,并且7,8,9依次位于小、中、大圆周上,你能做到吗?
参考答案一、填空题
1、
2、
3、
4、
5、
6、
7、
8、
二、解答题1、
2、。
