五年级奥数“数阵问题” 第六讲
数阵图-奥数优秀课件

【经典例题】
例题1 把2~6这五个数分别填入下图的“○”中,使得横行三数之和与竖列三 数之和都等于13。
【经典例题】
例题1 把2~6这五个数分别填入下图的“○”中,使得横行三数之和与竖列三数之和都 等于13。
解析: 横行三数之和与竖列三数的和是 : 13×2=26 各个数的和是:
解析: 横行三数之和与竖列三数的和是 : 13×2=26 各个数的和是:
2+3+4+5+6=20 中间的数是 : 26-20=6 2+5=4+3=7
【经典例题】
例题1 把2~6这五个数分别填入下图的“○”中,使得横行三数之和与竖列三数之和都 等于13。
解析: 横行三数之和与竖列三数的和是 : 13×2=26 各个数的和是:
7个数字总和:(1+7)×7÷2=28
中间数字为:30-28=2
2÷2=1
边上的数字和:10-1=9,
2+7=4+5=3+6
(答案不唯一)
【课堂练习】
练习3: 把3~9这七个数字分别填入下图的各“○”中,使每条线上三个“○”内数的和等
于16.
【课堂练习】
练习3: 把3~9这七个数字分别填入下图的各“○”中,使每条线上三个“○”内数的和等
【思路导航】 设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3 +……+10+a+b=30×2,即55+a+b=60,a+b=5。在 1——10这十个数中1+4=5,2+3=5。 当a和b是1和4时,每个大圆上另外四个数分别是(2,6,8, 9)和(3,5,7,10);当a和b是2和3时,每个大圆上另 外四个数分别为(1,5,9,10)和(4,6,7,8)。
1.目录 五年级奥数教材智能思维训练教材

五年级奥数智能思维训练教材目录◆第一讲消去问题(一) (2)◆第二讲消去问题(二) (7)◆第三讲一般应用题 (12)◆第四讲盈亏问题(一) (16)◆第五讲盈亏问题(二) (17)◆第六讲流水问题 (19)◆第七讲等差数列 (23)◆第八讲找规律 (26)◆能力测试(一) (26)◆第九讲加法原理 (28)◆第十讲乘法法原理 (31)◆第十一讲周期问题(一) (35)◆第十二讲周期问题(二) (37)◆第十三讲巧算(一) (39)◆第十四讲巧算(二) (40)◆第十五讲数阵问题(一) (45)◆第十五讲数阵问题(二) (45)◆能力测试(二) (63)◆第16讲平面图形的计算(一)……………◆第17讲平面图形的计算(二)……………◆第18讲列方程解应用题(一)………………◆第19讲列方程解应用题(二)………………◆第20讲行程问题(一)…………………………◆第21讲行程问题(二)…………………………◆第22讲行程问题(三)…………………◆第23讲行程问题(四)……………………◆阶段测试(一)……………………◆第24讲平均数问题(一)………………………◆第25讲平均数问题(二)………………◆第26讲长方体和正方体(一)………………◆第27讲长方体和正方体(二)……………………◆第28讲数的整除特征……………………………◆第29讲奇偶性问题……………………◆第30讲最大公约数和最小公倍数…………………◆第30讲分解质因数(一)……………………◆第31讲分解质因数(二)……………………◆第32讲牛顿问题……………………◆综合测试………………………………………。
五年级奥数数阵问题

课时3 数阵问题(一)一.数阵填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,主要讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二.例题精析例1 把5、6、7、8、9五个数分别填入下图的五个方格里,如图a使横行三个数的和与竖行三个数的和都是21。
先把五格方格中的数用字母A、B、C、D、E来表示,根据题意可知:A+B+C+D +E=35,A+E+B+C+E+D=21×2=42。
把两式相比较可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8便可把五个数填进方格,如图b。
小试牛刀把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2、把1——9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3、将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
例2 将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
分析设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3+……+10+a+b=30×2、即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a和b是1和4时,每个大圆上另外四个数分别是(2、6,8,9)和(3、5,7,10);当a和b是2和3时,每个大圆上另外四个数分别为(1、5,9,10)和(4,6,7,8)。
小试牛刀1、把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2、把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
2019秋五年级精英班讲义 第6讲 数列与数阵解答

JY(5)第六讲数列与数阵解答姓名一、例题选讲1、将数列1,4,7,10,13…依次如下图排列,如果把最左边的一列叫做第一列,从左到右依次编号,那么数列中的数349 应排在第几行第几列?14710 1328 25 22 19 1631 34 37 40 4358 55 52 (49)…46答案:24;4。
解析:这个数列是一个公差为3的等差数列,(349-1)÷3+1=117,所以349 是这列数中的第 117 个数。
从排列可以看出,每两排为一个周期,每一周期有10 个数。
因为117÷10=11(组)……7,所以数“349”是第12 个周期的第7个数,也就是在第12×2=24(行)第4列。
2、将1~2011 的奇数排成一列,然后按每组1,2,3,2,l,2,3,2,1,…个数的规律分组如下(每个括号为一组):(1)(3,5) (7,9,11) (13,15) (17) (19,21) (23,25,27) (29,31)(33)…则最后一个括号内的各数之和是多少?答案:6027。
解析:4 个括号为一个周期,每个周期有1+2+3+2=8 个数。
1~2011 里面有(2011+1)÷2=1006(个)奇数,1006÷8=125……6。
1~2011 中最后6 个奇数为:(2001),(2003,2005),(2007,2009,2011)。
则最后一个括号内的各数之和为:2007+2009+2011=6027。
3、如图所示:数字排列形式,每一排由1 开始,由2 结束。
其他数则是上一排直接对着的两个数的和。
例如第四排的9 即是第三排两个对着的数 4 和5之和。
若按此排列形式继续下去,第十排数的总和是多少?答案:1536。
解析:我们可通过观察得到每一排和的规律:第一排:(1+ 2)⨯1 = (1+ 2)⨯ 20 ,第二排:(1+ 2)⨯ 2= (1+ 2)⨯ 21 ,第三排:(1+ 2)⨯ 4= (1+ 2)⨯ 22 ,+ ………第十排: (1+ 2)⨯ 29 =1536 。
五年级奥数数阵问题

课时3 数阵问题(一)一.数阵填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,主要讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二.例题精析例1 把5、6、7、8、9五个数分别填入下图的五个方格里,如图a使横行三个数的和与竖行三个数的和都是21。
先把五格方格中的数用字母A、B、C、D、E来表示,根据题意可知:A+B+C+D+E=35,A+E+B+C+E+D=21×2=42。
把两式相比较可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8便可把五个数填进方格,如图b。
小试牛刀把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2、把1——9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3、将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
例2 将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
分析设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3+……+10+a+b=30×2、即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a和b是1和4时,每个大圆上另外四个数分别是(2、6,8,9)和(3、5,7,10);当a和b是2和3时,每个大圆上另外四个数分别为(1、5,9,10)和(4,6,7,8)。
小试牛刀1、把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2、把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
五年级数学 奥数精品讲义1-34讲

五年级数学奥数精品讲义1-34讲第一讲消去问题(一)第二讲消去问题(二)第三讲一般应用题第四讲盈亏问题(一)第五讲盈亏问题(二)第六讲流水问题第七讲等差数列第八讲找规律能力测试(一)第九讲加法原理第十讲乘法法原理第十一讲周期问题(一)第十二讲周期问题(二)第十三讲巧算(一)第十四讲巧算(二)第十五讲数阵问题(一)第十六讲数阵问题(二)能力测试(二)第十七讲平面图形的计算(一)第十八讲平面图形的计算(二)第十九讲列方程解应用题(一)第二十讲列方程解应用题(二)第二十一讲行程问题(一)第二十二讲行程问题(二)第二十三讲行程问题(三)第二十四讲行程问题(四)能力测试(三)第二十五讲平均数问题(一)第二十六讲平均数问题(二)第二十七讲长方体和正方体(一)第二十八讲长方体和正方体(二)第二十九讲数的整除特征第三十讲奇偶性问题第三十一讲最大公约数和最小公倍数第三十二讲分解质因数(一)第三十三讲分解质因数(二)第三十四讲牛顿问题能力测试(四)第一讲消去问题(一)在有些应用题里;给出了两个或者两个以上的未知数量间的关系;要求出这些未知数的数量.我们在解题时;可以通过比较条件;分析对应的未知数量变化的情况;想办法消去其中的一个未知量;从而把一道数量关系较复杂的题目变成比较简单的题目解答出来.这样的解题方法;我们通常把它叫做“消去法”.例题与方法在学习例题前;我们先进行一些基本数量关系的练习;为用消去法解题作好准备.(1)买1个皮球和1个足球共用去40元;买同样的5个皮球和5个足球一共用去多少元?(2)3袋子、大米和3袋面粉共重225、千克;1袋大米和1袋面粉共重多少千克?(3)6行桃树和6行梨树一共120棵;照这样子计算8行桃树和8行梨树一共有多少棵?(4)学校买了4个水瓶和25个茶杯;一共用去172元;每个水瓶18元;每个茶杯多少元?例1 学校第一次买了3个水瓶和20个茶杯;共用去134元;第二次又买了同样的3个水瓶和16个差杯;共用去118元.水瓶和茶杯的单价各是多少元?例2 买3个篮球和5个足球共、用去480元;买同样的6个篮球和3个足球共用去519元.篮球和足球的单价各是多少元?练习与思考1、 1袋黄豆和1袋绿豆共重50千克;同样的7袋黄豆和7袋绿豆共重()千克.2、买5条毛巾和5条枕巾共用去90元;买1条毛巾和1条枕巾要()元.3、买4本字典和4本笔记本共、用去了68元;买同样的9本字典和9本笔记本一共要()元.4、9筐苹果和9筐梨共重495千克;找这样计算;2筐苹果和2筐梨共重()千克.5、妈妈买了5米画布和3米白布;一共用去102元.花布每米15元;白布每米多少元?6、果园里有14行桃树和20行梨树;桃树和梨树一共有440棵.每行梨树15棵;每行桃树多少棵?8、食堂第一次运来6袋大米和4袋面粉;一共重400千克;第二次又运来9袋大米和4袋面粉;一共重550千克.每袋大米和每袋面粉各重多少千克?9、3豹味精和7包糖共重3800克;同样的3包味精和14包糖共重7300克.每包味精和每包糖各重多少克?10、育新小学买了8个足球和12个篮球;一共用去了984元;青山小学买了同样的16个足球和10个篮球;一共用去1240元.每个足球和每个篮球各多少元?11、买15张桌子和25把椅子共用去3050元;买同样的 5张桌子和20张椅子;需要1600元.买一张桌子和一把椅子需要多少元?12、3头牛和6只羊一天共吃草93千克;6头牛和5只羊一天共吃草130千克.每头牛每天比每只羊多吃多少千克?第二讲消去问题(二)例1、7袋大米和3袋面粉共重425千克同样的3袋大米和7袋面粉共重325千克.求每袋大米和每袋面粉的重量.3..三头牛和8只羊每天共吃青草93千克;5头牛和15只羊每天吃青草165千克.一头牛和一只羊每天各吃青草多少千克?练习与思考1.3个皮球和5个足球共245元;同样的6个皮和10个足球共()元.2.5盒铅笔和9盒钢笔共190支;同样的2盒铅笔和6盒钢笔共100支.3盒铅笔和3盒钢笔共()支;1盒铅笔和1支钢笔共()支.3.育才小学体育组第一次买了4个篮球和3个排球;共用去了141元;第二次买了5个篮球和4个排球;共用去180元.每个篮球和每个排球各多少元?4.3筐苹果和5筐梨共重138千克;5筐同样的苹果和3筐同样的共重134千克.;每筐苹果和每筐梨各重多少千克?5.某食堂第一次运进大米5袋;面粉7袋;共重1350千克;第二次运进大米3袋;面粉5袋;共重850千克.一袋大米和一袋面粉各重多少千克?6.3件上衣和7条裤子共430元;同样的7件上衣和3条裤子共470元.每件上衣和每条棵子各多少元?7.2千克水果糖和5千克饼干共64元;同样的3千克水果糖和4千克饼干共68元.每千克水果糖和每千克饼干各多少元?8.5包科技书和7包故事书共620本;6包科技书和3包故事书共420本.每包科技书比每包故事书少多少本?9.3个水瓶和8个茶杯共92元;5个水瓶和6个茶杯共102元.每个水瓶和每个茶杯各多少元?10.甲有5盒糖;乙有4盒糕共值44元.如果甲、乙两人对换一盒;则每人所有物品的价值相等.一盒糖、一盒糕各值多少元?第三讲一般应用题在小学里;通常把应用题分为“一般应用题”和“典型应用题|”两大类.“典型应用题”有基本的数量关系、解题模式;较复杂的问题可以通过“转化”;向基本的问题靠拢.我们已经学过的“和差问题”、和“倍差问题”等等;都是“典型应用题”.“一般应用题|”没有各顶的数量关系;也没有可以以来的解题模式.解题时要具体问题具体分析;在认真审题;理解题意的基础上;理清一知条件与所求问题之间的数量关系;从而确定解题的方法.对于比较复杂的问题;可以借助线段图、示意图、直观演示等手段帮助分析.例题与方法例 1、把一条大鱼分成鱼头、鱼身、鱼尾三部分;鱼尾重4千克;鱼头的重量等于鱼尾的重量加身一般的重量;而鱼身体、的重量等于鱼头的重量加上鱼尾的重量.这条鱼重多少千克?例2、一所小学的五年级有四个班;其中五(1)班和五(2)班共有81人;五(2)班和五(3)班共有83人五(3)班和五(4)班共有86人;五(1)班比五(4)班多2人.这所学校五年级四个班各有多少人?例 3、甲、乙两位渔夫在和边掉鱼;甲钓了5条;乙钓了3条;吃鱼时;来了一位客人和甲、乙平均分吃这条鱼.吃完后来客付了8角钱作为餐费.问:甲、乙两为渔夫各应得这8角钱中的几角?例 4、一个工地用两台挖土机挖土;小挖土机工作6小时;大挖土机工作8小时;一共挖土312方.已知小挖土机5小时的挖土量等于大挖土机2小时的完土量;两种挖土机每小时各挖土多少方?例 5、甲、乙、丙三人用同样多的钱合买西瓜.分西瓜时;甲和丙都比乙多拿西瓜7.5千克.结果甲和丙各给乙1.5元钱.每千克西瓜多少元|?例 6、小红有一个储蓄筒;存放的都是硬币;其中2分币比5分币多22个.而按钱数算;5分币比2分币多4角.已知这些硬币中有36个1分币.问:小红的储蓄筒里共存了多少钱?练习与思考(第1~4题13分;其余每题12分;共100分.)1.有一段木头;不知它的长度.用一根绳子俩量它;绳子多15米;如果将绳子对折以后再来量;又不够04米.问:这段绳子长多少米?2.甲、乙两人拿出同样多的钱合买一段花布;原约定各拿花布同样多.结果甲拿了6米;乙拿了14米.这样;乙就要给甲12元钱.每米花布的单价是多少元?3.甲、乙丙合三人各出同样多的钱合买苹果若干千克.分苹果时;甲和丙都比乙多拿7.8千克苹果;这样甲和丙各应给乙6元钱.每千克苹果多少钱?4.学校买了2张桌子和5把椅子;共付了330元 .每张桌子的价钱是每把椅子的3倍.每张桌子多少元?5.某校六年级有甲、乙、丙丁四个班;不算甲班;期于三个班的总人数是131人;不算丁班;期于三个班的总人数是134人.已知乙、丙两个班的总人数比甲、丁两个班的总人数少1人;甲、乙丙、丁四个班共有多少人?6.李大伯买了15千克特制面粉和35千克大米;共用去31.2元.已知1千克特特制面粉的价格是1千克大米的 2倍.李大伯买特制面粉和大米各用去多少元?7.14千克大豆的价钱与8千克花生的价钱相等;已知1千克花生比1千克大豆贵12元;大豆和花生的单价各是多少元?8.某车间按计划每天应加工50个零件;实际每天加工56个零件.这样;不仅提前3天完成原计划加工凌驾的任务;而求多加工了120个零件.这个车间实际加工了多少个零件?9.用8千克丝可以织6分米宽的绸4米;现在有10千克的丝;要织75分米宽的绸;可以织几米?|第四讲盈亏问题(一)盈亏问题又叫盈不足问题;是指把一定数量的物品平均分给固定的对象;如果按某种标准分;则分配后会有剩余(盈);按另一种标准分;又会不足(亏);求物品的数量和分配对象的数量.例如:小朋友分苹果;如果每人分2个;就多余16个;如果每人分5个;就缺少14个.小朋友有多少个?苹果有多少个?比较两次分的结果;第一次余16个;第二次少14个;两次相差1+14=30(个).这是因为第二次比第一次每人多分了5-2=3(个)苹果.相差30个;就说明有30÷3=10(个)小朋友.请小读者自己算出苹果的个数.例题与方法例1、将一些糖果分给幼儿园小班的小朋友;如果每人分3 粒;就会余下糖果17粒;如果每人分5粒;就会缺少糖果13粒.问:幼儿园下班有多少个小朋友|这些糖果共有多少粒?例 2、学生搬一批砖;每人搬4块;其中5人要搬两次;如果么人搬5块;就有两人没有砖可搬.搬砖的学生有多少人?这批砖共有多少块?例3某校在植树活动中;把一批树苗分给各班;如果每班分18棵;就会有余下24棵;如果每班分20棵;正好分完.这个学校有多少个班?这批树苗共有多少棵?练习与思考1.小朋友分糖果若每人分4粒则多9粒;若每人呢分5粒则少6粒.问:有多少小朋友?有多少粒糖果?2.小朋友分糖果;每人分10粒正好分完;若每人呢分16粒;则有3个小朋友分不到糖果.问:有多少粒糖果?3.在桥上测量桥高.把绳长对折后垂到水面;还余4米;把绳长3折后垂到水面;还余1米.桥高多少米?绳长多少米?4.某校安排新生宿舍;如果每间住12人;就会有34人没有宿舍住;如果每间住14人就会有空出4间宿舍.这个学校有多少间?要安排多少个新生?5.在依次大扫除中;有一些同学被分配擦玻璃;他们当中如果有2人擦4块;其余的人各擦5块;就会多下12块玻璃没有人擦;如果么人擦6块;刚好擦完.擦玻璃的同学有多少人?玻璃共有多少块?6.有一个数;减去3所的差的4倍;等于它的2倍加上36.这个数是多少?7.体育老师和一个朋友一起上街买足球.他发现自己身边的钱;如果买10个“冠军”牌足球;还差42元;后来他向朋友借了1000元;买了31个“冠军”牌足球;结果多了13元.体育老师原来身边带了多少元?8.某小学生乘汽车去春游;如果每辆车坐65人;就会有15人不能乘车;如果每辆车多坐5人恰好多余了一辆车.一共有多少辆汽车?有多少个学生?第五讲盈亏问题(二)上一讲;我们讲了盈亏问题的一般情形;也就是在量词分配中恰好洋盈(多余);一次亏(不足).事实上;在许多问题里;也会出现两次都是盈(多余);或者两次都是亏(不足)的情况.例 1、学校将一批铅笔奖给三好学生;每人9支缺15支;每人7支就缺7支.问:三好学生有多少人;铅笔有多少支?例2、某小学的部分同学外出参观;如果每辆车坐55人就会余下30个座位;如果每辆车坐50人;就还可以坐10人.有多少辆车?去参观的学生多少人?例3、学校规定上午8时到校.王强上学去;如果每分钟走60米;可以提早10分钟到校;如果每分钟作呕50米可以提早8分钟到校.问:王强什么时候离开家?他家离学校多远?练习与思考(第1~4题13分;其余每题12分;共100分.)1.同学们打羽毛球;每两人一组.每组分6个羽毛球;少10个球;每组分4个羽毛球;少2个球.问:共、有多少个同学打球?有多少个羽毛球?2.学校将一批钢笔奖给三好学生;每人8支缺11支;每人7支缺7支.问:三好学生有多少人?钢笔有多少支?3.某小学的部分学生去春游;如果每辆车坐50人;就会余下30个座位;如果每辆车坐40个人;还可以坐10人.问有多少辆车?去春游的学生多少人?4.一筐苹果分给一个小组;每人5个剩16个;每人7个缺12个.这个小组有多少人?共有多少苹果?5.一些学生分练习本.其中两人每人分6本;其余每人分4本;就会多4本;如果有一人分10本;其余每人分6本;就会少18本.学生有多少人?练习本多少本?6.一个学生从家到学校;先用每分50米的速度走了2分;如果这样走下去;他会迟到8分;后来他改用每分60米的速度前进;结果早到学校5分.这个学生家到学校的路程是多少米?7.筑路对计划每天筑路720米;实际每天比原计划多筑802米;这样;在规定完成任务时间的前3天;就只剩下1160米未筑.这条路多长?8.老师给幼儿园小朋友分苹果.每2人3个苹果;多2个苹果;每3人5个苹果;少4个苹果.问:有多少小朋友?多少苹果?第六讲流水问题想一想:从南京长江逆流而上去长江三峡;与从长江三峡顺水而下回南京;哪个花的时间少?哪个花的时间多?为什么?原因很简单.在长江行船与在一个平静的湖这行船是不一样的;因为长江的水是一直从西向东(也就是从上游向下游)流着的;船的速度会受到江水的影响.而在平静的湖水中行船时;船的速度不会受到水流的影响.考虑船在水流速度的情况下行驶的问题;就是我们这一讲要讲的流水问题.船在顺水航行时(比方说;从长江三峡顺流而下到南京);船一方面按照自己本身的速度即船速(船在静水中行驶的速度)行驶;同时整个水面又按照水的流动速度在前进;水推动着船向前;所以;船顺水时的航行速度应该等于船本身的速度与水流速度的和.也就是顺水速度=船速+水速比方说;船在静水中行驶10千米;水流速度是每小时5千米;那么;船顺水航行的速度就是每小时10+5=15(千米).同学们可以想一想;上面的问题中;如果是问“船逆水航行的速度是多少?”答案又该怎么样呢?船逆水行驶;情况恰好相反.本来船每小时行驶10千米;但由于水每小时又把它往回推了5千米;结果船每小时只向上游行驶了10—5=5(千米).也就是船在逆水中的速度等于船速度与水速之差.即逆水速度=船速—水速例1、一艘每小时行驶30千米的客轮;在一河水中顺水航行165千米;水速每小时3千米.问:这艘客轮需要航行多少小时?例2、一艘船顺水行320千米需要8小时;水流速度是每小时15千米;这艘船逆水每小时行多少千米?这艘船逆水行这段路程;需要多少小时?例3、甲船逆水航行360千米需要18小时;返回原地需要10小时;乙船逆水航行同样的异端水路需要15小时;返回原地需要多少小时?练习与思考1.一只小船以每小时30千米的速度在176千米长的河中逆水而行;用了211小时.这只小船返回原处需要用多少小时?2.船在静水中的速度是每小时25千米;河水流速位每小时5千米;一只船往返甲、乙两港共花了9小时;两港相距多少千米?3.两地距280千米;一艘轮船在期间航行;顺流用去14小时;逆流用去20小时.求这艘轮船在静水中的速度和水流的速度.4.一架飞机所带的燃料;最多可以用6小时;飞机去是顺风;每小时可以飞1500千米;飞回时逆风;每小时可以飞1200千米.这架飞机最多飞出多少千米;就需要往回飞?5.乙船顺水航行2小时;行了120千米;返回原地用了4小时.甲船顺水航行同一段水路;用了3小时.甲船返回原地比去时多用多少小时?第七讲等差数列(1)1;2;3;4;5;6;7;8;…(2)2;4;6;8;10;12;14;16;…(3)1;4;9;16;25;36;49;…上面三组数都是数列.数列中称为项;第一个数叫第一项;又叫首项;第二个数叫第二项……以此类推;最后一个数叫做这个数列的末项.项的个数叫做项数.一个数列中;如果从第二项起;每一项与它前面一项的差都相等;这样的数列叫等差数列.后项与前项的差叫做这个等差数列的公差.如等差数列:4;7;10;13;16;19;22;25;28.首项是4;末项是28;共差是3.这一讲我们学习有关等差数列的知识.例题与方法例1、在等差数列1;5;9;13;17;…;401中401是第几项?例2、100个小朋友排成一排报数;每后一个同学报的数都比前一个同学报的数多3;小明站在第一个位置;小宏站在最后一个位置.已知小宏报的数是300;小明报的数是几?例3、有一堆粗细均匀的圆木;堆成梯形;最上面的一层有5根圆木;每向下一层增加一根;一共堆了28层.最下面一层有多少根?例4、1+2+3+4+5+6+…+97+98+99+100=?例5、求100以内所有被5除余10的自然数的和.例6、小王和小胡两个人赛跑;限定时间为10秒;谁跑的距离长谁就获胜.小王第一秒跑1米;以后每秒都比以前一秒多跑0.1米;小胡自始至终每秒跑1.5米;谁能取胜?练习与思考(每题10分;共100分.)1.数列4;7;10;……295;298中298是第几项?2.蜗牛每小时都比前一小时多爬0.1米;第10小时蜗牛爬了1.9米;第一小时蜗牛爬多少米?3.在树立俄;10;13;16;…中;907是第几个数?第907个数是多少?4.求自然数中所有三位数的和.5.求所有除以4余1的两位数的和.6.0.1+0.3+0.58.+0.7+0.9+0 11+0 13+0 15+…0 99的和是多少?7.梯子最高一级宽32厘米;最底一级宽110厘米;中间还有6级;各级的宽度成等差数列;中间一级宽多少厘米?8.有12个数组成等差数列;第六项与第七项的和是12;求这12个数的和.9.一个物体从高空落下;已知第一秒下落距离是4.9米;以后每秒落下的距离是都比前一秒多9.8米50秒后物体落地.求物体最初距地面的高度.10.求下面数字方阵中所有数的和.1;2;3;…;98;99;1002;3;4;…99;100;1013;4;5;…;100;101;102……100,101,102, …197,198,199第八讲找规律你能找出下面各数列暴烈的规律吗?请在括号内填上合适的数》(1)8;15;22;();36;…;(2)17;1;15;1;13;1;();();9;1;…;(3)45;1;43;3;41;5;();();37;9;…;(4)1;2;4;8;16;();64;…;(5)10;20;21;42;43;();();174;175;…;(6)1;2;3;5;8;13;21;();55.例1. 1;2;3;2;3;4;3;4;5;4;5;6;6;7;…从第一个数算起;前100个数的和是多少?.练习与思考(第1题30分;其余每题10分;共100分.)(1)找规律;在括号内填上合适的数.(1)1,3,9,27,( ),243;(2)2,7,12,17,22,( ),( ),37;(3)1,3,2,4,3,( ),4;(4)0,3,8,15,24,( ) ,.48;(5)6,3,8,5,10,7,12,9,( ),11;(6)2,3,5,( ),( ),17,23;(7)81,64,();36;();16;9;4;1;(8)21;26;19;24;();();15;20;(9)1;8;9;17;26;();69;(10)4;11;18;25;();39;46;2.一串数按下面规律排列:1;3;5;2;4;6;3;5;7;4;6;8;5;7;9;…从第一个数算起;前100个数的和是多少?3.有一串黑白相间的珠子(如下图);第100个黑珠前面一共有多少个白珠?4.在平面中任意作100条直线;这些直线最多能形成多少个交点?5.在平面中任意作20条直线;这些直线最多可把这个平面分成多少个部分?6.序号 1 2 3 4 5算式1+1 2+3 3+5 1+7 2+9序号 6 7 8 9 …算式3+11 1+13 2+15 3+17 …根据上面的规律;第40个序号的算式是什么?算式‘1+103“的序号上多少?7.小正方形的边长是1厘米;依次作出下面这些图形.已知第一幅图的周长是10厘米.(1)36个正方形组成的图形的周长是多少厘米?(2)周长是70厘米的图形;由多少个正方形组成?已知第一幅图的周长是10厘米.(1)36个正方形组成的图形的周厂是多少厘米?(2)周长是70厘米的图形;由多少个正方形组成?8在方格纸上画折线(如本讲例4图);小方格的边长是1;图中的1;2;3;4;…分别表示折线扩大第1;2;3;4;…段.求折线中第100段的长度.长度是30的是第几段?能力测试(一)一、填空题(每空3分;工39分).1.在下面的括号里按照规律填上适当的数字.(1)1;2;3;4;8;16;();64;128.(2)5;10;15;20;25;();35;40.(3)4;7;10;13;16;();22;25.(4)1;1;2;3;5;8;13;21;()(5)1024;512;256;();64;32;16;8;4.(6)2;5;11;20;32;();65;86.(7)1;3;2;4;3;5;();6;5.(8)1;4;9;16;25;();49;64.1.9个人9天共读书1620页;平均1个人1天共读书()页;照这样计算;5个同学5天读书()页.2.如果平均1个同学1天植树()棵;那么;3个同学4天共植树120棵.3.买3只足球和9只篮球共用了570元;买9只足球和27只篮球要用()元.二、计算题(每小题5分;共10分).1.2+4+6+8+10+ … +22+24+262.1+2+3+4+5+6+ … +1996+1997+1998三、应用题(第1~4题10其余每题10分;第5题11分;共51分).1.李老师将一叠练习本分给第一组的同学;如果每人分7本;还多7本.如果每人分9;那么有一个同学译本也分不到.第一组有多少同学?这叠练习本一共有多少本?2.一只小船在河中逆流航行176千米;用了11小时.一知水流速度是每小时4千米;这只小船返回原处要用多少小时?3.4只篮球和8只足球共买560元;6只篮球和3只足球共买390元.问:一只篮球和一只足球各买多少元?4.有10元钞票与5元钞票共128张;其中10元比5元多260元.两种面额的钞票各是多少张?5.下面是一种特殊数列的求和方法.要求数列2;4;8;16;32;64;…;1024;2048的和;方法如下:S= 2+4+8+16+32+64+ … +1024+204822S = 4+8+16+32+64+ … +1024+2048+4096用下面的式子减去上面的式子;就得到S =4096 – 2 = 4094即数列2;4;8;16;32;64;…;1024;2048的和是4094.仔细阅读上面的求和方法;然后利用这种方法求下面数列的和.1;3;9;27;81;243;…;177147;531441.第九讲加法原理在日常生活与实践中;我们经常会遇到分组、计数的问题.解答这一类问题;我们通常运用加法与那里与乘法原理这两个基本的计数原理.熟练掌握这两个原理;不仅可以顺利解答这类问题;而求可以为今后升入中学后学习排列组合等数学知识打下好的基础.什么叫做加法原理呢?我们先来看这样一个问题:从南京到上海;可以乘火车;也可以乘汽车、轮船或者飞机.假如一天中南京到上海有4班火车、6班汽车;3班轮船、2班飞机.那么一天中乘做这些交通工具从南京到上海共有多少种不同的走法?我们把乘坐不同班次的火车、汽车、轮船、飞机称为不同的走法;那么从南京到上海;乘火车有4种走法;乘汽车有6种走法;乘轮船有3种走法;乘坐飞机有2种走法.因为每一种走法都可以从南京到上海;因此;一天中从南京到上海共有4+6+3+2 = 15 (种)不同的走法.我们说;如果完成某一种工作可以有分类方法;一类方法中又有若干种不同的方法;那么完成这件任务工作的方法的总数就等于各类完成这件工作的总和.即N = m1 + m2 + … + m n (N代表完成一件工作的方法的总和;m1,m2, … m n 表示每一类完成工作的方法的种数).这个规律就乘做加法原理.例1 书架上有10本故事书;3本历史书;12本科普读物.志远任意从书架上取一本书;有多少种不同的取法?例2一列火车从上上海到南京;中途要经过6个站;这列火车要准备多少中不同的车票?例3在4 x 4的方格图中(如下图);共有多少个正方形?例4 妈妈;爸爸;和小明三人去公园照相:共有多少种不同的照法?练习与思考1.从甲城到乙城;可乘汽车;火车或飞机.已知一天中汽车有2班;火车有4班;甲城到乙城共有()种不同的走法.2.一列火车从上海开往杭州;中途要经过4个站;沿途应为这列火车准备____种不同的车票.3.下面图形中共有____个正方形.4.图中共有_____个角.5.书架上共有7种不同的的故事书;中层6本不同的科技书;下层有4钟不同的历史书.如果从书架上任取一本书;有____种不同的取法.6.平面上有8个点(其中没有任何三个点在一条直线上);经过每两个点画一条直线;共可以画_____条直线.7.图中共有_____个三角形.8.图中共有____个正方形.9.从2;3;5;7;11;13;这六个数中;每次取出两个数分别作为一个分数的分子和分母;一共可以组成_____个真分数.10.某铁路局从A站到F站共有6个火车站(包括A站和F站)铁路局要为在A站到F站之间运行的。
五年级奥数专题第六章 组合与推理

五年级奥数专题第六章组合与推理第一讲包含与排除【一】同学们站成一排报数,从左往右报数时,小明报8,从右往左报数时,小明报7,这排同学有多少人?练习1、一些同学站成一排报数,从左往右报数时,小明报11,从右往左报数时,小明报5,这排同学有多少人?2、中心小学某班进行队列练习,向前走时,小勇数了数,他前面有6人,老师喊:“向后转”的口令后,小勇数了数,他前面有7人,这行同学有多少人?【二】学校买来三种花,月季花和菊花一共有25盆,菊花和茶花一共有30盆,三种花一共有40盆,三种花各买来多少盆?练习1、苹果树、梨树和桃树共80棵,其中苹果树和梨树一共60棵,梨树和桃树一共有50棵,三种树各有多少棵?2、小丽从家到学校,走了60米后有一个商店,放学后小丽从学校回家,走了60米后超过了商店10米,小丽家离学校有多少米?【三】实验小学五年级196名学生都订了刊物,有165人订了少年报,有146人订了小学生报,问两种刊物都订的有多少人?练习1、五(1)班50人都在做语文和数学作业,有34人做完了语文作业,有30人做完了数学作业,这个班语文、数学作业都做完的有多少人?2、五年级有120人参加语文、数学考试,每人至少有一门功课得优,其中,语文得优的有76人,数学得优的有85人,问语文、数学都得优的有多少人?【四】中山市的外语教师中,每人至少懂得英语和日语中的一中语言。
已知有55人懂英语,32人懂日语,两种语言都懂的有20人,中山市有多少个外语教师?练习1、五年级的每个学生至少爱好体育和文娱中的一种活动,已知有780人爱好体育活动,有860人爱好文娱活动,其中320人两种活动都爱好。
五年级共有学生多少人?2、某班在一次测验中有26人语文获优,有30人数学获优,其中语、数双优的有12人,另外还有8人语、数均未获优,这个班共有多少个学生?【五】在100个外语教师中,懂英语的75人,懂日语的45人,其中必然有既懂英语又懂日语的老师,问:只懂英语的老师有多少人?练习1、40人都在做加法的两道题,并且至少做对了其中的一题,已知做对第一题的有35人,做对第二题的有20人,问:只做对第一题的有多少人?2、实验小学五年级120名同学参加语文、数学考试,每人至少有一门得优,已知语文64人得优,数学76人得优,求只有语文一门得优的人数。
一起学奥数有趣的数阵图资料讲解

因为1-12是一个等差数列,确定1-4为四个顶角,且按逆时针方向排列后,可以把剩下 的分成5-8,9-12两组,分别填在直线上对应的位置。
最后一步的规律必须让学生领会。可以把和都为22的条件去掉做讲解
例4、把1~7这七个数分别填入下图中的各个圆圈内,使每条线段上三个 ○内的数的和相等。
7
2
1
4 5
上两题相比较,图形特征与数字特征存在雷同性,但每条线上 三个数字和受限制。因此需要确定公共圆圈的值。
五条线段上的数字和相加为: 22×5=110 11个圆圈内的数字和为: 11×12÷2=66 则公共圆圈的数字为: (110-66)÷(5-1)=11
剩余圆圈上的填法,与之前题目相同。对剩下的10个数首尾取 数即可。
而 A+B+C+D+E+F+G+H+I=45
F
C
对上面等式进行简化,则: (D+E+F)-(G+H+I)=18
对1~9这9个数进行分析,最大三个数的和为: 7+8+9=24;最小为: 1+2+3=6 两者差为18。所以D+E+F=18
试试枚举法解这个题目(对枚举法也可以做初步分析)
例:将1~10这十个数填入下图的圆圈内,使每个正方形的四个数字之 和都等于23,应怎样填?
接着从这八个数中找出4个和为34的数的组合,放在正方形中。(1、4、13、16)、 (2、4、12、16)
没有条件四个数之和为34,是否可以解答本题?
例:把数字1~9分别填入下图的9个圈内,要求三角形ABC和三角形 DEF的每条边上三个圈内数字之和都等于18.下图中D、E、F的三个圈 中所填数之和为什么?
五年级奥数数阵问题

课时3 数阵问题〔一〕一.数阵填“幻方〞是同学们比拟熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比拟常见的填数问题。
这里,主要讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母〔或符号〕表示满足条件的数,通过分析、计算来确定这些字母〔或符号〕应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能X围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二.例题精析例1把5、6、7、8、9五个数分别填入下列图的五个方格里,如图a使横行三个数的和与竖行三个数的和都是21。
先把五格方格中的数用字母A、B、C、D、E来表示,根据题意可知:A+B+C+D +E=35,A+E+B+C+E+D=21×2=42。
把两式相比拟可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8便可把五个数填进方格,如图b。
小试牛刀把1——10各数填入“六一〞的10个空格里,使在同一直线上的各数的和都是12。
2、把1——9各数填入“七一〞的9个空格里,使在同一直线上的各数的和都是13。
3、将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
例2 将1——10这十个数填入下列图小圆中,使每个大圆上六个数的和是30。
分析设中间两个圆中的数为a、b,那么两个大圆的总和是1+2+3+……+10+a +b=30×2、即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a和b是1和4时,每个大圆上另外四个数分别是〔2、6,8,9〕和〔3、5,7,10〕;当a和b是2和3时,每个大圆上另外四个数分别为〔1、5,9,10〕和〔4,6,7,8〕。
小试牛刀1、把1——8八个数分别填入下列图的○,使每个大圆上五个○内数的和相等。
2、把1——10这十个数分别填入下列图的○,使每个四边形顶点的○内四个数的和都相等,且和最大。
五年级奥数教材

第1讲数阵一、精讲精练【例题1】把5、6、7、8、9五个数分别填入下图的五个方格里,如图a使横行三个数的和与竖行三个数的和都是21。
练习1:1.把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2.把1——9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
!3.将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
【例题2】将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
《练习2:1.把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2.把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
3.将1——8八个数填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。
|【例题3】将1——6这六个数分别填入下图的圆中,使每条直线上三个圆内数的和相等、且最大。
练习3:1.将1——6六个数分别填入下图的圆圈内,使每边上的三个数的和相等。
2.将1——9九个数分别填入下图圆圈内,使每边上四个数的和都是17。
3.将1——8八个数分别填入下图的圆圈内,使每条安上三个数的和相等。
》【例题4】将1——7分别填入下图的7个圆圈内,使每条线段上三个数的和相等。
练习4:¥1.将1——9填入下图的○中,使横、竖行五个数相加的和都等于25。
2.将1——11这十一个数分别填进下图的○里,使每条线上3个○内的数的和相等。
3.将1——8这八个数分别填入下图○内,使外圆四个数的和,内圆四个数的和以及横行、竖行上四个数的和都等于18。
>【例题5】如下图(a)四个小三角形的顶点处有六个圆圈。
如果在这些圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个顶点上的数的和相等。
问这六个质数的积是多少练习5:1.将九个不同的自然数填入下面方格中,使每行、每列、每条对角线上三个数的积都相等。
五年级奥数数阵问题

课时3 数阵问题(一)一.数阵填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,主要讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二.例题精析例1 把5、6、7、8、9五个数分别填入下图的五个方格里,如图a使横行三个数的和与竖行三个数的和都是21。
先把五格方格中的数用字母A、B、C、D、E来表示,根据题意可知:A+B+C+D +E=35,A+E+B+C+E+D=21×2=42。
把两式相比较可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8便可把五个数填进方格,如图b。
小试牛刀把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2、把1——9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3、将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
例2 将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
分析设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3+……+10+a+b=30×2、即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a和b是1和4时,每个大圆上另外四个数分别是(2、6,8,9)和(3、5,7,10);当a和b是2和3时,每个大圆上另外四个数分别为(1、5,9,10)和(4,6,7,8)。
小试牛刀1、把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2、把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
五年级奥数知识点:数阵与平均数

五年级奥数知识点:数阵与平均数小升初是孩子最重要的起步方向,我们需要关注怎样的信息才能对孩子的未来有帮助呢?店铺网小编告诉大家!五年级奥数知识点:平均数专题简析:把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数。
如何灵活运用平均数的数量关系解答一些稍复杂的问题呢?下面的数量关系必须牢记:平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1 有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?分析与解答:(1)1箱苹果+1箱梨+1箱橘子=42×3=136(个);(2)1箱桃+1箱梨+1箱橘子=36×3=108(个)(3)1箱苹果+1箱桃=37×2=72(个)由(1)(2)两个等式可知:1箱苹果比1箱桃多126-108=18(个),再根据等式(3)就可以算出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个)。
1箱苹果和1箱桃共有多少个:37×2=74(个)1箱苹果比1箱桃多多少个:42×3-36=18(个)1箱苹果有多少个:28+18=46(个)练习1,一次考试,甲、乙、丙三人平均分91分,乙、丙、丁三人平均分89分,甲、丁二人平均分95分。
问:甲、丁各得多少分?2,甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克。
求四人的平均体重是多少千克?3,甲、乙、丙三个小组的同学去植树,甲、乙两组平均每组植树18棵,甲、丙两组平均每组植树17棵,乙、丙两组平均每组植树19棵。
三个小组各植树多少棵?例2 一次数学测验,全班平均分是91.2分,已知女生有21人,平均每人92分;男生平均每人90.5分。
求这个班男生有多少人?分析:女生每人比全班平均分高92-91.2=0.8(分),而男生每人比全班平均分低91.2-90.5=0.7(分)。
五年级奥数6——迷人的数阵
1.把1~9这九个数填入“七一”的9个空格里,使在同一直线上各数的和都是13.
2.把1~7这七个自然数分别填入里,使每条线上的三个数和相等。
3.把1~8这八个数分别填入下图的里,使每个大圆上五个里数的和相等。
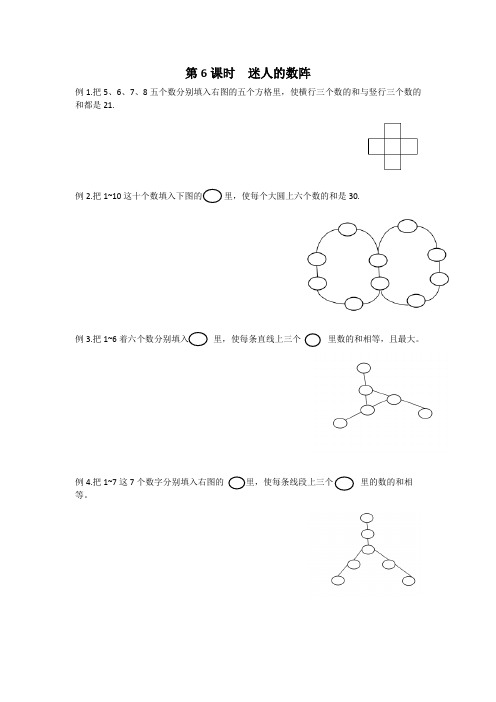
4.把1~10这十个数分别填入下图的里,使每个四边形顶点上的里四个数的和都相等,且和最大。第Fra bibliotek课时迷人的数阵
例1.把5、6、7、8五个数分别填入右图的五个方格里,使横行三个数的和与竖行三个数的和都是21.
例2.把1~10这十个数填入下图的里,使每个大圆上六个数的和是30.
例3.把1~6着六个数分别填入里,使每条直线上三个里数的和相等,且最大。
例4.把1~7这7个数字分别填入右图的里,使每条线段上三个里的数的和相等。
五年级奥数数阵问题

课时3 数阵问题(一)一.数阵填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,主要讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二.例题精析例1 把5、6、7、8、9五个数分别填入下图的五个方格里,如图a使横行三个数的和与竖行三个数的和都是21。
先把五格方格中的数用字母A、B、C、D、E来表示,根据题意可知:A+B+C+D +E=35,A+E+B+C+E+D=21×2=42。
把两式相比较可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8便可把五个数填进方格,如图b。
小试牛刀把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2、把1——9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3、将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
例2 将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
分析设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3+……+10+a+b=30×2、即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a和b是1和4时,每个大圆上另外四个数分别是(2、6,8,9)和(3、5,7,10);当a和b是2和3时,每个大圆上另外四个数分别为(1、5,9,10)和(4,6,7,8)。
小试牛刀1、把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2、把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上一页
练习5:将九个不同的自然数填入下面方格中,使每行、每列、每条对
习 题
角线上三个数的积都相等。
上一页
首页 结束
下一页
讲
个顶点上的数的和相等。问这六个质数的积是多少?
解:
设每个小三角形三个顶点处○内数的和为X。因为中间的小三 角形顶点处的数在求和时都用了三次,所以,四个小三角形 顶点处数的总和是4X=20+2X,解方程得X=10。由此可知, 每个小三角形顶点处的三个质数的和是10,这三个质数只能 是2、3、5。因此这6个质数的积是2×2×3×3×5×5=900。 如图(b)。
当a和b是1和4时,每个大圆上另外四个数分别是(2,6,8,9) 和(3,5,7,10);当a和b是2和3时,每个大圆上另外四个 数分别为(1,5,9,10)和(4,6,7,8)。
上一页
首页 结束
下一页
第4讲 数阵问题
练 习
练习2:把1——8八个数分别填入下图的○内,使每个大圆上五个○内 数的和相等。
上一页
首页 结束
下一页
第4讲 数阵问题
练 习
练习1:把1——10各数填入“六一”的10个空格里,使在同一直线上 的各数的和都是12。
题
上一页
首页 结束
下一页
第4讲 数阵问题
例 例2:将1——10这十个数填入下图小圆中,使每个大圆上六个数的
题 精
和是30。
讲
解: 设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3 +……+10+a+b=30×2,即55+a+b=60,a+b=5。在1— —10这十个数中1+4=5,2+3=5。
试验法就是根据题中所给条件选准突破口,确定填 数的可能范围。把分析推理和试验法结合起来,再 由填数的可能情况,确定应填的数。
上一页
首页 结束
下一页
第4讲 数阵问题
例 题
例1: 把5、6、7、8、9五个数分别填入下图的五个方格里,如图a使 横行三个数的和与竖行三个数的和都是21。
精
讲
解:
先把五格方格中的数用字母A、B、C、D、E来表示,根据题 意可知:A+B+C+D+E=35,A+E+B+C+E+ D=21×2=42。 把两式相比较可知,E=42-35=7,即中间填7。然后再根据5 +9=6+8便可把五个数填进方格,如图b。
5年级趣味数学
第4讲 数阵
第4讲 数阵问题
知 填“幻方”是同学们比较熟悉的一种数学游戏,
识 精 讲
由幻方演变出来的数阵问题,也是一类比较常见的 填数问题。这里,和同学们讨论一些数阵的填法。
解答数阵问题通常用两种方法: 一是待定数法,二是试验法。待定数法就是先用 字母(或符号)表示满足条件的数,通过分析、计 算来确定这些字母(或符号)应具备的条件,为解 答数阵问题提供方向。
题
上一页
首页 结束
下一页
第4讲 数阵问题
例 例3:将1——6这六个数分别填入下图的圆中,使每条直线上三个圆
题 精
内数的和相等、且最大。
讲
解:
设中间三个圆内的数是a、b、c。因为计算三条线上的和时, a、b、c都被计算了两次,根据题意可知:1+2+3+4+5+ 6+(a+b+c)除以3没有余数。1+2+3+4+5+6=21, 21÷3=7没有余数,那么a+b+c的和除以3也应该没有余数。 在1——6六个数中,只有4+5+6的和最大,且除以3没有余 数,因此a、b、c分别为4、5、6。(1+2+3+4+5+6+4 +5+6)÷3=12,所以有上面的填法:
上一页
首页 结束
下一页
第4讲 数阵问题
练 练习4:将1——11这十一个数分别填进下图的○里,使每条线上3个○
习 题
内的数的和相等。
上一页
首页 结束
下一页
第4讲 数阵问题
例 例5:如下图(a)四个小三角形的顶点处有六个圆圈。如果在这些圆
题 精
圈中分别填上六个质数,它们的和是20,而且每个小三角形三
上一页
首页 结束
下一页
第4讲 数阵问题
练 练习3:将1——9九个数分别填入下图○内,使每边上四个○内数的和
习 题
都是17.
上一页
首页 结束
下一页
第4讲 数阵问题
例 例4:将1——6这六个数分别填入下图的圆中,使每条直线上三个圆
题 精
内数的和相等、且最大。
讲
解:
首先要确定中心圆内的数,设中心○内的数是a,那么,三条 线段上的总和是1+2+3+4+5+6+7+2a=28+2a,由于 三条线段上的和相等,所以(28+2a)除以3应该没有余数。 由于28÷3=9……1,那么2a除以3应该余2,因此,a可以为 1、4或7。当a=1时,(28+2×1)÷3-1=9,即每条线段 上其他两数的和是9,因此,有这样的填法。
