24.3_正多边形和圆_同步测控优化训练(含答案) 3
2020-2021学年数学新人教九年级上册同步测控优化训练:(24.3-正多边形和圆)

2020-2021学年数学新人教九年级上册同步测控优化训练24.3 正多边形和圆5分钟训练(预习类训练,可用于课前)1.圆的半径扩大一倍,则它的相应的圆内接正n 边形的边长与半径之比( )A.扩大了一倍B.扩大了两倍C.扩大了四倍D.没有变化 思路解析:由题意知圆的半径扩大一倍,则相应的圆内接正n 边形的边长也扩大一倍,所以相应的圆内接正n 边形的边长与半径之比没有变化.答案:D2.正三角形的高、外接圆半径、边心距之比为( )A.3∶2∶1B.4∶3∶2C.4∶2∶1D.6∶4∶3 思路解析:如图,设正三角形的边长为a ,则高AD=23a ,外接圆半径OA=33a ,边心距OD=63a , 所以AD ∶OA ∶OD=3∶2∶1.答案:A3.正五边形共有__________条对称轴,正六边形共有__________条对称轴.思路解析:正n 边形的对称轴与它的边数相同.答案:5 64.中心角是45°的正多边形的边数是__________.思路解析:因为正n 边形的中心角为n ︒360,所以45°=n︒360,所以n=8. 答案:85.(2020上海静安检测)已知△ABC 的周长为20,△ABC 的内切圆与边AB 相切于点D,AD=4,那么BC=__________.思路解析:由切线长定理及三角形周长可得.答案:610分钟训练(强化类训练,可用于课中)1.若正n 边形的一个外角是一个内角的32时,此时该正n 边形有_________条对称轴. 思路解析:因为正n 边形的外角为n︒360,一个内角为n n ︒•-180)2(, 所以由题意得n ︒360=32·n n ︒•-180)2(,解这个方程得n=5. 答案:52.同圆的内接正三角形与内接正方形的边长的比是( )A.26B.43C.36D.34思路解析:画图分析,分别求出正三角形、正方形的边长,知应选A.答案:A3.周长相等的正三角形、正四边形、正六边形的面积S 3、S 4、S 6之间的大小关系是( )A.S 3>S 4>S 6B.S 6>S 4>S 3C.S 6>S 3>S 4D.S 4>S 6>S 3 思路解析:周长相等的正多边形的面积是边数越多面积越大.答案:B4.已知⊙O 和⊙O 上的一点A(如图24-3-1).(1)作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ;(2)在(1)题的作图中,如果点E 在弧AD 上,求证:DE 是⊙O 内接正十二边形的一边.图24-3-1思路分析:求作⊙O 的内接正六边形和正方形,依据定理应将⊙O 的圆周六等分、四等分,而正六边形的边长等于半径;互相垂直的两条直径由垂径定理知把圆四等分.要证明DE 是⊙O 内接正十二边形的一边,由定理知,只需证明DE 所对圆心角等于360°÷12=30°.(1)作法:①作直径AC;②作直径BD ⊥AC;③依次连结A 、B 、C 、D 四点,四边形ABCD 即为⊙O 的内接正方形;④分别以A 、C 为圆心,OA 长为半径作弧,交⊙O 于E 、H 、F 、G;⑤顺次连结A 、E 、F 、C 、G 、H 各点.六边形AEFCGH 即为⊙O 的内接正六边形.(2)证明:连结OE 、DE.∵∠AOD =4360︒=90°,∠AOE =6360︒=60°, ∴∠DOE =∠AOD -∠AOE =30°.∴DE 为⊙O 的内接正十二边形的一边.快乐时光有一位爱鸟人士,他特别喜欢鹦鹉,有一天,他经过一间鸟店发现里面正在拍卖一只鹦鹉,他见那只鹦鹉毛色很好决定要买,于是他喊道:“我愿意出10美金买下这只鹦鹉!”接着有人喊价:“我愿意出20美金!”那位爱鸟人士不愿把那只鹦鹉拱手让人,于是他又喊了30美金.可是另一个声音像在跟他作对,一直到那位爱鸟人士叫了200美金时才停.那人买到鹦鹉很高兴,可是他突然想到:我花了那么多钱才买到这鹦鹉,如果它不会说话那我不就亏大了吗?于是他就去问老板:“老板,你这只鹦鹉会不会说话啊?”接着他听到鹦鹉大叫:“不会说话?!你以为刚刚是谁在跟你喊价啊?!”30分钟训练(巩固类训练,可用于课后) 1.正六边形的两条平行边之间的距离为1,则它的边长为( ) A.63 B.43 C.332 D.33 思路解析:正六边形的两条平行边之间的距离为1,所以边心距为0.5,则边长为33. 答案:D2.已知正多边形的边心距与边长的比为21,则此正多边形为( ) A.正三角形 B.正方形C.正六边形D.正十二边形思路解析:将问题转化为直角三角形,由直角边的比知应选B.答案:B3.已知正六边形的半径为3 cm ,则这个正六边形的周长为__________ cm.思路解析:转化为直角三角形求出正六边形的边长,然后用P 6=6a n 求出周长.答案:184.(2020上海浦东新区模拟)正多边形的一个中心角为36度,那么这个正多边形的一个内角等于___________度.答案:144.5.如图24-3-2,两相交圆的公共弦AB 为23,在⊙O 1中为内接正三角形的一边,在⊙O 2中为内接正六边形的一边,求这两圆的面积之比.图24-3-2思路分析:欲求两圆的面积之比,根据圆的面积计算公式,只需求出两圆的半径R 3与R 6的平方比即可.解:设正三角形外接圆⊙O 1的半径为R 3,正六边形外接圆⊙O 2的半径为R 6,由题意得R 3=33AB ,R 6=AB ,∴R 3∶R 6=3∶3.∴⊙O 1的面积∶⊙O 2的面积=1∶3. 6.某正多边形的每个内角比其外角大100°,求这个正多边形的边数.思路分析:由正多边形的内角与外角公式可求.解:设此正多边形的边数为n ,则各内角为n n ︒•-180)2(,外角为n︒360,依题意得n n ︒•-180)2(-n︒360=100°.解得n =9. 7.如图24-3-3,在桌面上有半径为2 cm 的三个圆形纸片两两外切,现用一个大圆片把这三。
24.3 正多边形和圆同步练习(含答案)

则∠APB的度数是( ). A.36° B.60° C.72° D.108° 7.(2013•自贡)如图,点O是正六边形的对称中心,如果
用一副三角板的角,借助点O(使该角的顶点落在点O处), 第7题
把这个正六边形的面积n等分,那么n的所有可能取值的 个数是( )
22.已知⊙O和⊙O上的一点A. (1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH; (2)在(1)题的作图中,如果点E在弧AD上,求证:DE是⊙O内接 正十二边形的一边.
第22题
23.如图1、图2、图3、…、图n,M、N分别是⊙O的内接正三角形ABC、正 方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的 点,且BM=CN,连结OM、ON.
(2)每个内角的度数为:_______________________.
(3)每个外角的度数为:____________.
(4)周长为:_________,面积为:_________.
5.正n边形都是轴对称图形,当边数为偶数时,它的对称轴有_______
条,并且还是中心对称图形;当边数为奇数时,它只是
(2)都是轴对称图形(或都有外接圆和内切圆). 不同点:(1)正五边形的每个内角是108°,正六边形的每个内角是
120°; (2)正五边形的对称轴是5条,正六边形的对称轴是6条.
20. 21.
解:连结OB ∵在Rt△AOC中,AC==1 ∴AC=OC ∴∠AOC=∠OAC=45° ∵OA=OB OC⊥AB ∴AB=2AC=2 ∠AOB=2∠OAC=2×45°=90° ∴这个内接正多边形是正方形. ∴面积为22=4 ∴中心角为90°,边长为2,面积为4.
九年级数学上册同步测控优化训练(24.3正多边形和圆)

数学九年级上册同步测控优化训练24.3 正多边形和圆5分钟训练(预习类训练,可用于课前)1.圆的半径扩大一倍,则它的相应的圆内接正n 边形的边长与半径之比( )A.扩大了一倍B.扩大了两倍C.扩大了四倍D.没有变化思路解析:由题意知圆的半径扩大一倍,则相应的圆内接正n 边形的边长也扩大一倍,所以相应的圆内接正n 边形的边长与半径之比没有变化.答案:D2.正三角形的高、外接圆半径、边心距之比为( )A.3∶2∶1B.4∶3∶2C.4∶2∶1D.6∶4∶3思路解析:如图,设正三角形的边长为a ,则高AD=23a ,外接圆半径OA=33a ,边心距OD=63a ,所以AD ∶OA ∶OD=3∶2∶1.答案:A3.正五边形共有__________条对称轴,正六边形共有__________条对称轴.思路解析:正n 边形的对称轴与它的边数相同.答案:5 64.中心角是45°的正多边形的边数是__________.思路解析:因为正n 边形的中心角为n 360,所以45°=n360,所以n=8.答案:85.(2020上海静安检测)已知△ABC 的周长为20,△ABC 的内切圆与边AB 相切于点D,AD=4,那么BC=__________.思路解析:由切线长定理及三角形周长可得.答案:610分钟训练(强化类训练,可用于课中)1.若正n 边形的一个外角是一个内角的32时,此时该正n 边形有_________条对称轴.思路解析:因为正n 边形的外角为n 360,一个内角为n n180)2(,所以由题意得n 360=32·n n180)2(,解这个方程得n=5.答案:52.同圆的内接正三角形与内接正方形的边长的比是( )A.26 B.43 C.36 D.34思路解析:画图分析,分别求出正三角形、正方形的边长,知应选A.答案:A3.周长相等的正三角形、正四边形、正六边形的面积S 3、S 4、S 6之间的大小关系是( )A.S 3>S 4>S 6B.S 6>S 4>S 3C.S 6>S 3>S 4D.S 4>S 6>S 3思路解析:周长相等的正多边形的面积是边数越多面积越大.答案:B4.已知⊙O 和⊙O 上的一点A(如图24-3-1).(1)作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ;(2)在(1)题的作图中,如果点E 在弧AD 上,求证:DE 是⊙O 内接正十二边形的一边.图24-3-1思路分析:求作⊙O 的内接正六边形和正方形,依据定理应将⊙O 的圆周六等分、四等分,而正六边形的边长等于半径;互相垂直的两条直径由垂径定理知把圆四等分.要证明DE 是⊙O 内接正十二边形的一边,由定理知,只需证明DE 所对圆心角等于360°÷12=30°.(1)作法:①作直径AC;②作直径BD ⊥AC;③依次连结A 、B 、C 、D 四点,四边形ABCD 即为⊙O 的内接正方形;④分别以A 、C 为圆心,OA 长为半径作弧,交⊙O 于E 、H 、F 、G;⑤顺次连结A 、E 、F 、C 、G 、H 各点.六边形AEFCGH 即为⊙O 的内接正六边形.(2)证明:连结OE 、DE.∵∠AOD =4360 =90°,∠AOE =6360=60°,∴∠DOE =∠AOD -∠AOE =30°.∴DE 为⊙O 的内接正十二边形的一边.快乐时光有一位爱鸟人士,他特别喜欢鹦鹉,有一天,他经过一间鸟店发现里面正在拍卖一只鹦鹉,他见那只鹦鹉毛色很好决定要买,于是他喊道:“我愿意出10美金买下这只鹦鹉!”接着有人喊价:“我愿意出20美金!”那位爱鸟人士不愿把那只鹦鹉拱手让人,于是他又喊了30美金.可是另一个声音像在跟他作对,一直到那位爱鸟人士叫了200美金时才停.那人买到鹦鹉很高兴,可是他突然想到:我花了那么多钱才买到这鹦鹉,如果它不会说话那我不就亏大了吗?于是他就去问老板:“老板,你这只鹦鹉会不会说话啊?”接着他听到鹦鹉大叫:“不会说话?!你以为刚刚是谁在跟你喊价啊?!”30分钟训练(巩固类训练,可用于课后)1.正六边形的两条平行边之间的距离为1,则它的边长为( )A.63 B.43 C.332 D.33思路解析:正六边形的两条平行边之间的距离为1,所以边心距为0.5,则边长为33.答案:D2.已知正多边形的边心距与边长的比为21,则此正多边形为( )A.正三角形B.正方形C.正六边形D.正十二边形思路解析:将问题转化为直角三角形,由直角边的比知应选B.答案:B3.已知正六边形的半径为3 cm ,则这个正六边形的周长为__________ cm.思路解析:转化为直角三角形求出正六边形的边长,然后用P 6=6a n 求出周长.答案:184.(2020上海浦东新区模拟)正多边形的一个中心角为36度,那么这个正多边形的一个内角等于___________度.答案:144.5.如图24-3-2,两相交圆的公共弦AB 为23,在⊙O 1中为内接正三角形的一边,在⊙O 2中为内接正六边形的一边,求这两圆的面积之比.图24-3-2思路分析:欲求两圆的面积之比,根据圆的面积计算公式,只需求出两圆的半径R 3与R 6的平方比即可.解:设正三角形外接圆⊙O 1的半径为R 3,正六边形外接圆⊙O 2的半径为R 6,由题意得R 3=33AB ,R 6=AB ,∴R 3∶R 6=3∶3.∴⊙O 1的面积∶⊙O 2的面积=1∶3.6.某正多边形的每个内角比其外角大100°,求这个正多边形的边数.思路分析:由正多边形的内角与外角公式可求.。
【新】人教版九年级数学上册24.3 正多边形和圆同步练习 含答案

第24章 24.3《正多边形和圆》同步练习及答案 (2)1.下列边长为a 的正多边形与边长为a 的正方形组合起来,不能镶嵌成平面的是( )(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形A .(1)(2)B .(2)(3)C .(1)(3)D .(1)(4)2.以下说法正确的是A .每个内角都是120°的六边形一定是正六边形.B .正n 边形的对称轴不一定有n 条.C .正n 边形的每一个外角度数等于它的中心角度数.D .正多边形一定既是轴对称图形,又是中心对称图形.(3)(2006年天津市)若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r 3,r 4,r 6,则r 3:r 4:r 6等于( )A .BC .1:2:3D . 3:2:14. 已知正六边形ABCDEF 内接于⊙O ,图中阴影部分的面积为312,则⊙O 的半径为______________________.5.如图,正方形ABCD 内接于⊙O ,点E 在»AD 上,则∠BEC= . 6.将一块正六边形硬纸片(图1),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,见图2),需在每一个顶点处剪去一个四边形,例如图中的四边形AGA /H ,那么∠GA /H 的大小是 度.7.(2006年威海市)如图,若正方形A 1B 1C 1D 1内接于正方形ABCD 的内接圆,则ABB A 11的值为( ) A .21 B .22 C .41 D .42 8.从一个半径为10㎝的圆形纸片上裁出一个最大的正方形,则此正方形的边长为 .9.如图五边形ABCDE 内接于⊙O,∠A=∠B=∠C=∠D=∠E .求证:五边形ABCDE 是正五边形10.如图,10-1、10-2、10-3、…、10-n 分别是⊙O 的内接正三角形ABC ,正四边形ABCD 、正五边形ABCDE 、…、正n 边形ABCD …,点M 、N 分别从点B 、C 开始以相同的速度在⊙O 上逆时针运动。
人教版九年级数学上册 第24章 24.3正多边形和圆 教材同步培优、能力提升练习卷(含答案)

人教版九年级数学上册第24章24.3正多边形和圆教材同步培优、能力提升练习卷24.3正多边形和圆教材同步学习目标:1.能通过把一个圆n(n≥3)等分,得到圆的内接正n边形及外切正n边形.2.理解正多边形的中心、半径、中心角、边心距的概念,并能进行简单的计算.课堂学习检测一、基础知识填空1.各条边______,并且各个______也都相等的多边形叫做正多边形.2.把一个圆分成n(n≥3)等份,依次连结各等分点所得的多边形是这个圆的______.3.一个正多边形的______________叫做这个正多边形的中心;______________叫做正多边形的半径;正多边形每一边所对的______叫做正多边形的中心角;中心到正多边形的一边的__________叫做正多边形的边心距.4.正n边形的每一个内角等于__________,它的中心角等于__________,它的每一个外角等于______________.5.设正n边形的半径为R,边长为a n,边心距为r n,则它们之间的数量关系是______.这个正n边形的面积S n=________.6.正八边形的一个内角等于_______,它的中心角等于_______.7.正六边形的边长a,半径R,边心距r的比a∶R∶r=_______.8.同一圆的内接正方形和正六边形的周长比为_______.二、解答题9.在下图中,试分别按要求画出圆O的内接正多边形.(1)正三角形 (2)正方形 (3)正五边形(4)正六边形 (5)正八边形 (6)正十二边形综合、运用、诊断一、选择题10.等边三角形的外接圆面积是内切圆面积的( ).A .3倍B .5倍 C.4倍 D .2倍11.已知正方形的周长为x ,它的外接圆半径为y ,则y 与x 的函数关系式是( ).A .x y 42=B .x y 82=C .x y 21=D .x y 22= 12.有一个长为12cm 的正六边形,若要剪一张圆形纸片完全盖住这个圆形,则这个圆形纸片的半径最小是( ).A .10cmB .12cmC .14cmD .16cm 二、解答题13.已知:如图,正八边形A 1A 2A 3A 4A 5A 6A 7A 8内接于半径为R 的⊙O .(1)求A 1A 3的长;(2)求四边形A 1A 2A 3O 的面积;(3)求此正八边形的面积S .14.已知:如图,⊙O的半径为R,正方形ABCD,A′B′C′D分别是⊙O的内接正方形和外切正方形.求二者的边长比AB∶A′B′和面积比S内∶S外.拓广、探究、思考15.已知:如图,⊙O的半径为R,求⊙O的内接正六边形、⊙O的外切正六边形的边长比AB∶A′B′和面积比S内∶S外.参考答案:1.相等,角. 2.内接正n 边形.3.外接圆的圆心,外接圆的半径,圆心角,距离.4.⋅︒︒︒⋅-n n nn 360,360,180)2( 5.⋅+=n n n n a nr a r R 21,41222 6.135°,45°. 7.23:1:1(或3:2:2).8..3:22 9.略. 10.C . 11.B . 12.B .13.(1);231R A A = (2)222R (3).222R 14.AB ∶A ′B ′=1∶2,S 内∶S 外=1∶2.15.AB ∶A ′B ′=3∶2,S 内∶S 外=3∶4.。
人教版九年级数学上册《24.3 正多边形和圆》同步练习题-附答案

人教版九年级数学上册《24.3 正多边形和圆》同步练习题-附答案学校:___________班级:___________姓名:___________考号:___________考点 正多边形与圆1.定义:正多边形的 圆的圆心叫做这个正多边形的中心 圆的半径叫做正多边形的半径 正多边形每一边所对的 角叫做正多边形的中心角 到正多边形的一边的距离 叫做正多边形的边心距。
2.公式:正多边形的有关概念:边长(a ) 中心(O ) 中心角(∠AOB ) 半径(R )) 边心距(r ) 如图所示①.边心距222a r R ⎛⎫=- ⎪⎝⎭中心角360n ︒=关键点:三角形的内切圆与外接圆 关系定义圆心 实质半径图示外接圆经过三角形各顶点的圆外心三角形各边垂直平分线的交点交点到三角形三个顶点的距离相等内切圆与三角形各边都相切的圆内心三角形各内角平分线的交点交点到三角形各边的距离相等名校提高练习:一选择题:本题共10小题每小题3分共30分。
在每小题给出的选项中只有一项是符合题目要求的。
1.(2024·四川省泸州市·月考试卷)已知圆内接正三角形的面积为√ 3则该圆的内接正六边形的边心距是( )A. 2B. 1C. √ 3D. √ 322.同一个圆的内接正三角形正方形正六边形的边心距分别为r3r4r6则r3:r4:r6等于( )A. 1:√2:√3B. √3:√2:1C. 1:2:3D. 3:2:13.如图若干个全等的正五边形排成环状图中所示的是前3个正五边形要完成这一圆环还需正五边形的个数为( )A. 10B. 9C. 8D. 74.(2024·贵州省黔东南苗族侗族自治州·月考试卷)正六边形ABCDEF内接于⊙O正六边形的周长是12则⊙O的半径是( )A. √ 3B. 2C. 2√ 2D. 2√ 35.(2024·山东省·单元测试)《几何原本》中记载了用尺规作某种六边形的方法其步骤是:①在⊙O上任取一点A连接AO并延长交⊙O于点B②以点B为圆心BO为半径作圆弧分别交⊙O于C D两点③连接CO DO并延长分别交⊙O于点E F④顺次连接BC CF FA AE ED DB得到六边形AFCBDE.再连接AD EF AD EF交于点G.则下列结论不正确的是( )A. GF=GDB. ∠FGA=60°C. EFAE=√ 2 D. AF⊥AD6.(2024·江苏省·同步练习)以半径为2的圆的内接正三角形正方形正六边形的边心距为三边作三角形则该三角形的面积是( )A. √ 22B. √ 32C. √ 2D. √ 37.(2024·江苏省·同步练习)如图正十二边形A1A2…A12连接A3A7A7A10则∠A3A7A10的度数为( )A. 60°B. 65°C. 70°D. 75°8.(2024·江苏省·同步练习)如图若干个全等的正五边形排成环状.图中所示的是前3个正五边形要完成这一圆环还需正五边形的个数为( )A. 6B. 7C. 8D. 99.(2024·北京市市辖区·期末考试)如图正方形ABCD的边长为6且顶点A B C D都在⊙O上则⊙O 的半径为().A. 3B. 6C. 3√ 2D. 6√ 210.(2024·广东省广州市·月考试卷)如图已知⊙O的周长等于4πcm则圆内接正六边形的边长为()cm.A. √ 3B. 2C. 2√ 3D. 4二填空题:本题共6小题每小题3分共18分。
243正多边形和圆达标训练(含答案).docx

一、基础•巩固•达标i ・正五边形共有 ________ 条对称轴,正六边形共有 _________ 条对称轴.2•中心角是45。
的正多边形的边数是 _________ .3•若正〃边形的一个外角是一个内角的23吋,此吋该正n 边形有 __________ 条对称轴. 4 •圆的半径扩大一倍,则它的相应的圆内接正n 边形的边长与半径之比()・A.扩大了一倍B.扩大了两倍C.扩大了四倍D.没有变化5•正三角形的高"外接圆半径、边心距之比为() A. 3 : 2 : 1 B.4 : 3 : 2 C. 4 : 2 : 1 D. 6 : 4 : 36 •同圆的内接正三角形与内接正方形的边长的比是()A.62B.34C. 63D.43「7.周长相等的正三角形、正四边形、正六边形的而积S3、S4、S&Z 间的大小关系是()8•正六边形的两条平行边之间的距离为1,则它的边长为()A.9•己知OO 和(DO 上的一点A (如图24-3-2). (1)作<30的内接正方形ABCD 和内接正六边形AEFCGH ;(2)在(1)题的作图中,如果点E 在AD ±,求证:DE 是内接正十二边形的边.24.3 正多边形和圆 达标训练A ・S3>S<4>S6B.& A S4A S3 D.S4 > S6> S33图24-3-2二、综合•应用•创新 10・某正多边形的每个内角比其外角大100°,求这个正多边形的边数. H.如图24-3-3,在桌面上有半径为2纫7的三个圆形纸片两两外切,现用一个大圆片把这三个圆完全覆盖,这个大圆片的半径最小应为多少?12•如图24-3-4,两相交圆的公共弦在<30中为内接正三角形的一边,在©0 中为内接正六边形的一边,求这两圆的面积.之比.三、回顾•热身•展望13.如图24-3-5, /XABC 是等边三角形,OO 过点B 、C,且与34、CA 的延长线分别交于点D 、E.弦DF//AC, EF 的延长线交BC 的延长线于点G.图24-3-5(1)求证:是等边三角形; (2)若 BA 二4, CG=2,求 BF 的长.DE14.如图24 -3-6®、②、③、“、…、M 、N 分别是G )O 的内接正三角形4BC 、正方形ABCD 、正五边形ABCDE 、…、正〃边形ABCDE...的边AB. BC 上的点,且二CN,连接OM.ON.MF 的关系,并加以证明.15•将正方形CGEF 绕点C 旋转任意角度后(如图24-3-7), 其他条件不变•探究: 线段MD 、A图 24-3-6E图 24-3-7参考答案一、基础•巩固•达标1.正五边形共有_________ 条对称轴,正六边形共有________ 条对称轴.提示:正n边形的对称轴与它的边数相同.答案:5 62•中心角是45。
人教版九年级上册数学 24.3 正多边形和圆 同步练习(含答案)

24.3 正多边形和圆同步练习一、选择题1.一个正多边形的一个内角为120°,则这个正多边形的边数为( ) A.9 B.8 C.7 D.62.如图所示,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )A.23 cm B.3 cm C.233cm D.1 cm第2题图第5题图3.已知圆的半径是2,则该圆的内接正六边形的面积是()A.3B.9C.18D.364.正三角形、正方形、圆三者的周长都等于l,它们的面积分别为S1,S2、S3,则( ). A.S1=S2=S3 B.S3<S1<S2 C.S1<S2<S3 D.S2<S1<S35.中华人民共和国国旗上的五角星的画法通常是先把圆五等分,然后连接五个等分点而得到的(如图所示).五角星的每一个角的度数是( ).A.30° B.35° C.36° D.37°第6题图第7题图第9题图6.如图所示,是由5把相同的折扇组成的“蝶恋花”(如图①)和梅花图案(如图②)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为()A.36° B.42° C.45° D.48°二、填空题7.如图所示,平面上两个正方形与正五边形都有一条公共边,则∠ 等于________.8.要用圆形铁片裁出边长为4的正方形铁片,则选用的圆形铁片的直径最小是________. 9.如图所示,等边△ABC 内接于⊙O ,AB =10cm ,则⊙O 的半径是________. 10.如图,点O 是正五边形ABCDE 的中心,则∠BAO 的度数为 .11.正六边形的半径是5cm ,则边长6a =________,周长6P =________ ,边心距6r =________,面积6S =________.12. 正六边形的外接圆的半径与内切圆的半径之比为 .三、解答题13.如图所示,正△ABC 的外接圆的圆心为O ,半径为2,求△ABC 的边长a ,周长P ,边心距r ,面积S .14. 如图所示,半径为R 的圆绕周长为10πR 的正六边形外边作无滑动滚转,绕完正六边形后,圆一共转了多少圈?一位同学的解答过程:圆的周长为2πR ,所以它绕完正六边形后一共转了102RRππ圈,结果一共转了5圈.你认为这位同学的解答有无错误?如有错误,请更正.15.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.答案与解析一、选择题1.【答案】D;【解析】可求每个外角为60°,∴ 360÷60=6或(2)180120nn-⨯=°°∴ n=6.2.【答案】A;【解析】较长对角线与较短对角线及一边长构成一直角三角形,用勾股定理求解.3.【答案】C;【解析】连接正六边形的中心与各个顶点,得到六个等边三角形,等边三角形的边长是2,高为3,因而等边三角形的面积是3,∴正六边形的面积=18,故选C.4.【答案】C;【解析】当周长一定时,边数越多的正多边形其面积越大,当它成为圆时面积最大.5.【答案】C;【解析】五角星的每一个角所对的弧为圆的15,∴弧的度数为72°,因而每个角的度数为36°,故选C.6.【答案】D.【解析】如图③所示,正五边形ABCDE的中心角为72°,各内角为108°,故五角星五个锐角均为48°.二、填空题 7.【答案】72°;【解析】α=360°-90°-90°-108°=72°. 8.【答案】42;【解析】如图所示,△ABC 为等腰Rt△,242AC AB ==.9.【答案】1033cm ; 【解析】过O 作OD ⊥BC 于D ,连接OB ,在Rt △BOD 中,BD =12BC =1102⨯=5(cm). ∠BOD =180603=°°, ∴3BD OB =. ∴ BO =10333=(cm).10.【答案】54°; 【解析】连接OB ,则OB=OA ,∴∠BAO=∠ABO,∵点O 是正五边形ABCDE 的中心,∴∠AOB==72°,∴∠BAO=(180°﹣72°)=54°; 故答案为:54°.11.【答案】6a =5cm ,666P a ==30cm ,6532r =cm ,26753cm 2s =; 12.【答案】2:.【解析】设正六边形的半径是r ,则外接圆的半径r ,内切圆的半径是正六边形的边心距,因而是,因而正六边形的外接圆的半径与内切圆的半径之比为2:.三、解答题13.【答案与解析】作AD ⊥BC 于D .∵ △ABC 是正三角形,∴ 点O 在AD 上,a =BC =2CD ,∠OCD =30°,在Rt △COD 中,112r OD OC ===, 2222213CD OC OD =-=-=,∴ 223a BC CD ===,363P a ==. 又∵ AD =OA+OD =2+1=3, ∴ 112333322S BC AD ==⨯⨯=, ∴ 23a =,63P =,1r =,33S =.14.【答案与解析】有错误,由正六边形的每个顶点外圆要转60°角,应转了10162RRππ+=(圈). 15.【答案与解析】解:连接OB ,OC ,OD ,∵等边△ABC 内接于⊙O,BD 为内接正十二边形的一边,∴∠BOC=×360°=120°,∠BOD=×360°=30°,∴∠COD=∠BOC﹣∠BOD=90°,∵OC=OD,∴∠OCD=45°,∴OC=5×=5(cm).即⊙O的半径R=5cm.。
人教版九年级数学上册24.3 正多边形和圆同步练习含答案

第24章 24.3《正多边形和圆》同步练习及答案 (1) 1.边长为a的正六边形的边心距是__________,周长是____________,面积是___________。
2.如图1,正方形的边长为a,以顶点B、D为圆心,以边长a为半径分别画弧,在正方形内两弧所围成图形的面积是___________。
(1) (2) (3)3.圆内接正方形ABCD的边长为2,弦AE平分BC边,与BC交于F,则弦AE的长为__________。
4.正六边形的面积是183,则它的外接圆与内切圆所围成的圆环面积为_________。
5.圆内接正方形的一边截成的小弓形面积是2π-4,则正方形的边长等于__________。
6.正三角形的内切圆半径、外接圆半径和高的比为___________。
7.在半径为R的圆中,内接正方形与内接正六边形的边长之比为___________。
8.同圆的内接正n边形与外切正n边形边长之比是______________。
9.正三角形与它的内切圆及外接圆的三者面积之比为_____________。
10.正三角形的外接圆半径为4cm,以正三角形的一边为边作正方形,则此正方形的外接圆半径长为___________。
B卷1.正方形的内切圆半径为r,这个正方形将它的外接圆分割出四个弓形,其中一个弓形的面积为_________。
2.如果正三角形的边长为a,那么它的外接圆的周长是内切圆周长的_______倍。
3.如图2,正方形边长为2a,那么图中阴影部分的面积是__________。
4.正多边形的一个内角等于它的一个外角的8倍,那么这个正多边形的边数是________。
5.半径为R的圆的内接正n边形的面积等于__________。
6.如果圆的半径为a,它的内接正方形边长为b,该正方形的内切圆的内接正方形的边长为c,则a,b,c间满足的关系式为___________。
7.如图3,正△ABC内接于半径为1cm的圆,则阴影部分的面积为___________。
人教版 九年级数学上册 24.3 正多边形和圆 课后训练(含答案)

人教版九年级数学24.3 正多边形和圆课后训练一、选择题1. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是()A.正三角形B.正方形C.正五边形D.正六边形2. 2019·安徽月考如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是()A.AE∥BF B.AF∥CDC.DF=3AF D.AB=BF3. 一元硬币的直径约为24 mm,则用它能完全覆盖住的正六边形的边长最大为()A.12 mm B.12 3 mm C.6 mm D.6 3 mm4. 如图,边长为3的正五边形ABCDE的顶点A,B在半径为3的圆O上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆O 上时,点C转过的度数为()A.12°B.16°C.20°D.24°5. 如图,将两张完全相同的正六边形纸片(边长为2a)重合在一起,下面一张纸片保持不动,将上面一张纸片沿水平方向向左平移a个单位长度,则空白部分与阴影部分的面积之比是()A.5∶2 B.3∶2 C.3∶1 D.2∶16. 如图是由7个全等的正六边形组成的网格,正六边形的顶点称为格点,△ABC 的顶点都在格点上,设定AB边如图所示,则使△ABC是直角三角形的格点有()A.10个B.8个C.6个D.4个7. 正方形ABCD与正八边形EFGHKLMN的边长相等,初始位置如图所示,将正方形绕点F顺时针旋转使得BC与FG重合,再将正方形绕点G顺时针旋转使得CD与GH重合……按这样的方式将正方形ABCD旋转2020次后,正方形ABCD 中与正八边形EFGHKLMN的边重合的边是()A.AB B.BC C.CD D.DA8. 下列用尺规等分圆周的作法正确的有()①在圆上依次截取等于半径的弦,就可以六等分圆;②作相互垂直的两条直径,就可以四等分圆;③按①的方法将圆六等分,六个等分点中三个不相邻的点三等分圆;④按②的方法将圆四等分,再平分四条弧,就可以八等分圆.A.4个B.3个C.2个D.1个二、填空题9. 如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10 cm,则该脸盆的半径为________cm.10. (2019•海南)如图,O与正五边形ABCDE的边AB、DE分别相切于点B、D,的大小为__________度.则劣弧BD所对的圆心角BOD11. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是________.12. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形,则原来的纸带宽为________.13. 如图,AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,而BC恰好是⊙O内接正n边形的一边,则n等于________.14. 如图为一个半径为4 m 的圆形场地,其中放有六个宽为1 m 的长方形临时摊位,这些摊位均有两个顶点在场地边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为__________m.15. 佳佳对科技馆富有创意的科学方舟形象设计很有兴趣,他回家后将一正五边形纸片沿其对称轴对折(如图①所示),旋转放置,做成科学方舟模型(如图②所示).图①中正五边形的边心距OB 为2,图②中AC 为科学方舟船头A 到船底的距离,请你计算AC +12AB =________.三、解答题16. 如图,在正六边形ABCDEF 中,点O 是中心,AB =10,求这个正六边形的半径、边心距、周长、面积.17. 如图,P是⊙O 上的一点.(1)在⊙O 上求作一点B ,使PB 是⊙O 的内接正三角形的一边;(2)在BP ︵上求作一点A ,使P A 是⊙O 的内接正方形的一边; (3)连接OB ,求∠AOB 的度数; (4)求作⊙O 的内接正十二边形.18. 如图,A ,B ,C ,D ,E是⊙O 上的五等分点,连接AC ,CE ,EB ,BD ,DA ,得到一个五角星图形和五边形MNFGH. (1)计算∠CAD 的度数; (2)连接AE ,求证:AE =ME.人教版 九年级数学 24.3 正多边形和圆 课后训练-答案一、选择题1. 【答案】A[解析] ∵正三角形一条边所对的圆心角是360°÷3=120°,正方形一条边所对的圆心角是360°÷4=90°, 正五边形一条边所对的圆心角是360°÷5=72°, 正六边形一条边所对的圆心角是360°÷6=60°, ∴一条边所对的圆心角最大的图形是正三角形. 故选A.2. 【答案】C3. 【答案】A[解析] 正六边形外接圆的直径等于正六边形边长的2倍.4. 【答案】A[解析] 设点E第一次落在圆上时的对应点为E′,连接OA,OB,OE′,如图.∵五边形ABCDE为正五边形,∴∠EAB=108°.∵正五边形ABCDE绕点A逆时针旋转,点E第一次落在圆O上的点E′处,∴AE′=AE=3.∵OA=AB=OB=OE′=3,∴△OAE′,△OAB都为等边三角形,∴∠OAB=∠OAE′=60°,∴∠E′AB=120°,∴∠EAE′=12°,∴当点E第一次落在圆O上时,点C转过的度数为12°.5. 【答案】C[解析] 正六边形的面积=6×34×(2a)2=6 3a2,阴影部分的面积=a·2 3a=2 3a2,∴空白部分与阴影部分的面积之比是=6 3a2∶2 3a2=3∶1.6. 【答案】A[解析] 如图,当AB是直角边时,点C共有6个位置,即有6个直角三角形;当AB是斜边时,点C共有4个位置,即有4个直角三角形.综上所述,使△ABC是直角三角形的格点有6+4=10(个).故选A.7. 【答案】A[解析] 由题意可得正方形每旋转8次则回到原来的位置.∵2020÷8=252……4,∴正方形ABCD 旋转2020次后,AB 与正八边形EFGHKLMN 的边重合.8. 【答案】A二、填空题9.【答案】25 【解析】如解图,取圆心为O ,连接OA 、OC ,OC 交AB 于点D ,则OC ⊥AB.设⊙O的半径为r ,则OA =OC =r ,又∵CD =10,∴OD =r -10,∵AB =40,OC ⊥A B ,∴AD =20.在Rt △ADO 中,由勾股定理得:r 2=202+(r -10)2,解得r =25,即脸盆的半径为25 cm .10. 【答案】144【解析】五边形ABCDE 是正五边形,∴(52)1801085E A -⨯︒∠=∠==︒.∵AB 、DE 与O 相切,∴90OBA ODE ∠=∠=︒,∴(52)1809010810890144BOD ∠=-⨯----=︒︒︒︒︒︒,故答案为:144.11. 【答案】8+82 [解析] 易证四边形ABCD 是正方形.由题意可得AD =2+222×2=2+2 2, ∴四边形ABCD 的周长是4×(2+2 2)=8+8 2. 故答案为8+8 2.12. 【答案】3 [解析] 边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,所以原来的纸带宽度为 3.13. 【答案】12[解析] 连接OA ,OB ,OC ,如图.∵AB ,AC 分别为⊙O 的内接正四边形与内接正三角形的一边, ∴∠AOB =90°,∠AOC =120°, ∴∠BOC =∠AOC -∠AOB =30°,∴n =360°30°=12,即BC 恰好是⊙O 内接正十二边形的一边.14. 【答案】-3+3 72[解析] 设圆心是O ,连接OA ,OB ,过点O 作OC ⊥BC 于点C ,交AD 于点D .设长方形摊位的长是2x m .在Rt △OAD 中,∠AOD =30°,AD =x m ,则OD =3x m.在Rt △OBC 中,由勾股定理,得OC =16-x 2 m.∵OC -OD =CD =1 m , ∴16-x 2=3x +1, 解得x =-3+3 74(负值已舍去), 则2x =-3+3 72,∴长方形摊位的长为-3+3 72 m.15. 【答案】52 2 [解析] 如图①,连接OF ,OE .由题意,知AB ⊥EF ,则S 正五边形AGFED =5×S △OEF =5×(12EF ·OB )=2.5×2EF =5 2BE .如图②,连接AE .S 正五边形AGFED =2×S 四边形ABED =2×(S △ABE +S △ADE )=2×(12AB ·BE +12DE ·AC )=AB ·BE +DE ·AC =AB ·BE +2BE ·AC =BE ·(AB +2AC ),∴5 2BE =BE ·(AB +2AC ). ∴AB +2AC =5 2,∴AC +12AB =522.三、解答题16. 【答案】解:连接OB ,OC ,过点O 作OH ⊥BC 于点H.∵正六边形的中心角为360°6=60°,OB =OC ,∴△OBC 是等边三角形,∴半径R =OB =BC =AB =10.∵OH ⊥BC ,∴∠BOH =30°,∴BH =12OB =5. 在Rt △OBH 中,边心距r =OH =102-52=5 3,周长l =6AB =6×10=60. ∵S △OBC =12BC·OH =12×10×5 3=25 3,∴正六边形的面积S =6S △OBC =6×25 3=150 3.17. 【答案】解:(1)如图①,以点P 为圆心,OP 长为半径画圆弧交⊙O 于点M ,再以点M 为圆心,OM 长为半径画圆弧交⊙O 于点B ,连接PB ,则PB 即为所求. (2)如图①,作直径PH ,再过圆心作直径PH 的垂线交BP ︵于点A ,连接P A ,则P A 即为所求.(3)∵P A 是⊙O 的内接正方形的一边, ∴∠AOP =90°.∵PB 是⊙O 的内接正三角形的一边, ∴∠BOP =120°,∴∠AOB =30°.(4)如图②,以点P 为圆心,OP 长为半径在⊙O 上依次截取5个点,这5个点连同点P 是⊙O 的六等分点,再作各弧的中点,顺次连接12个点,得到⊙O 的内接正十二边形.18. 【答案】解:(1)∵A ,B ,C ,D ,E 是⊙O 上的五等分点, ∴∠COD =360°5=72°,∴∠CAD =12∠COD =36°.(2)证明:∵A ,B ,C ,D ,E 是⊙O 上的五等分点,∴CD ︵=DE ︵=AE ︵=AB ︵=BC ︵, ∴∠DAE =∠AEB =∠CAD =36°, ∴∠MAE =72°,∴∠AME =180°-∠MAE -∠AEB =72°=∠MAE ,∴AE =ME.。
人教版九年级数学上册24.3正多边形和圆同步测试及答案【精】

正多边形和圆1.正六边形的边心距与边长之比为( B ) A.3∶3 B.3∶2 C .1∶2 D.2∶2【解析】 如图:设正六边形的边长是a ,则半径长也是a ;经过正六边形的中心O 作边AB 的垂线OC ,则AC =12AB =12a , ∴OC =OA 2-AC 2=32a , ∴正六边形的边心距与边长之比为:32a ∶a =3∶2. 3-1,在⊙O 中,OA =AB ,OC ⊥AB ,则下列结论错误的是( D ) 图24-3-1A .弦AB 的长等于圆内接正六边形的边长B .弦AC 的长等于圆内接正十二边形的边长C.AC ︵=BC ︵D .∠BAC =30°【解析】 因为OA =AB =OB ,所以△OAB 是等边三角形,又OC ⊥AB ,所以∠AOC =∠BOC =30°,所以∠BAC =15°,D 不正确.3.如图24-3-2,点O 是正六边形的对称中心,如果用一副三角板的角,借助点O (使该角的顶点落在点O 处),把这个正六边形的面积n 等分,那么n 的所有可能取值的个数是( B )图24-3-2A .4B .5C .6D .7【解析】 360÷30=12;360÷60=6;360÷90=4;360÷120=3;360÷180=2.因此n 的所有可能的值共五种情况.4.如图24-3-3,要拧开一个边长为a =6 mm 的正六边形螺帽,扳手张开的开口b 至少为( C )图24-3-3 A .6 2 mm B .12 mmC .6 3 mmD .4 3 mm5.已知正六边形的边心距为3,则它的周长是( B )A .6B .12C .6 3D .12 3【解析】 正六边形的边长等于半径,设半径为R ,则⎝⎛⎭⎫12R 2+(3)2=R 2,∴R =2,它的周长是6R=6×2=12,故选B.6.若正六边形的边长为4 cm ,那么正六边形的中心角是__60__度,半径是__4__cm ,边心距是__23__cm ,它的每一个内角是__120°__.7.[2012·巴中]已知一个圆的半径为5 cm ,则它的内接正六边形的边长为__5__cm.8.已知一个正n 边形的中心角是它的一个内角的三分之一,则n =__8__.【解析】 由360n =180(n -2)n ×13,得n =8. 9.已知⊙O 和⊙O 上的一点A ,如图24-3-4所示.图24-3-4(1)作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ;(2)在(1)题所作的图中,如果点E 在AB ︵上,试证明EB 是⊙O 的内接正十二边形的一边.【解析】 (1)根据正四边形和正六边形的作图方法分别作出⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ;(2)计算EB 所对的圆心角的度数.解:(1)如图所示,在⊙O 中,用直尺和圆规作两条互相垂直的直径AC 和BD ,连接AB ,BC ,CD ,DA ,得⊙O 的内接正方形ABCD ;按正六边形的作法用直尺和圆规在⊙O 中作出正六边形AEFCGH . (2)如图,连接OE .∵AE 是正六边形的一边,∴∠AOE =360°6=60°.∵AB 是正方形的一边,∴∠AOB =360°4=90°,∴∠BOE =∠AOB -∠AOE =90°-60°=30°.设EB 是⊙O 的内接正n 边形的一边,则360°n=30°,∴n =12, ∴EB 是⊙O 的内接正十二边形的一边.10.小敏在作⊙O 的内接正五边形时,先做了如下几个步骤:(1)作⊙O 的两条互相垂直的直径,再作OA 的垂直平分线交OA 于点M ,如图1;(2)以M 为圆心,BM 长为半径作圆弧,交CA 于点D ,连接BD ,如图2.若⊙O 的半径为1,则由以上作图得到的关于正五边形边长BD 的等式是( C )图24-3-5 A .BD 2=5-12OD B .BD 2=5+12OD C .BD 2=5ODD .BD 2=52OD 11.[2013·徐州]如图24-3-6,在正八边形ABCDEFGH 中,四边形BCFG 的面积为20 cm 2,则正八边形的面积为____________cm 2.图24-3-6【解析】连接HE ,AD ,在正八边形ABCDEFGH 中,可得:HE ⊥BG 于点M ,AD ⊥BG 于点N ,∵正八边形每个内角为:(8-2)×180°8=135°, ∴∠HGM =45°,∴MN =MG ,设MH =MG =x ,则HG =AH =AB =GF =2x ,∴BG ×GF =2(2+1)x 2=20,四边形ABGH 面积=12(AH +BG )×HM =(2+1)x 2=10, ∴正八边形的面积为:10×2+20=40(cm 2).12.将固定宽度的纸条打个简单的结,然后系紧,使它成为平面的结(如图24-3-7),求证:五边形ABCDE 是正五边形.图24-3-7第13题答图证明:如图所示,连接BE ,AD ,设纸条的宽度为h ,则S △ABE =12AB ·h =12AE ·h , ∴AB =AE ,同理得AB =BC ,BC =CD ,∴AE =AB =BC =CD .∵纸条的宽度固定,∴AE ∥BD ,CD ∥BE ,∴∠1=∠2=∠3=∠4=∠5.由折叠性质得∠ABD +∠ABC =180°,从而得∠1=∠2=∠3=∠4=∠5=36°,由此易得∠ABC =∠BCD =∠CDE =∠DEA =∠EAB ,AE =AB =BC =CD =DE ,∴五边形ABCDE 是正五边形.13.如图24-3-8所示,已知△ABC 是⊙O 的内接等腰三角形,顶角∠BAC =36°,弦BD ,CE 分别平分∠ABC ,∠ACB ,求证:五边形AEBCD 是正五边形.图24-3-8 【解析】 要证明五边形AEBCD 是正五边形,只需证AE ︵=EB ︵=BC ︵=CD ︵=DA ︵即可.证明:∵△ABC 是等腰三角形,且∠BAC =36°,∴∠ABC =∠ACB =72°.又∵BD 平分∠ABC ,CE 平分∠ACB ,∴∠ABD =∠CBD =∠BCE =∠ACE =36°,即∠BAC =∠ABD =∠CBD =∠BCE =∠ACE ,∴BC ︵=AD ︵=CD ︵=BE ︵=AE ︵,∴A ,E ,B ,C ,D 是⊙O 的五等分点,∴五边形AEBCD 是正五边形.14.如图24-3-9,正五边形ABCDE ,连接对角线AC ,BD ,设AC 与BD 相交于O .(1)写出图中所有的等腰三角形;(2)判断四边形AODE 的形状,并说明理由.:学科图24-3-9解:(1)△ABO ,△ABC ,△BOC ,△DOC ,△BCD .(2)四边形AODE 是菱形,理由如下:∵AB =BC ,∠ABC =(5-2)×180°5=108°, ∴∠BAC =∠BCA =12×(180°-108°)=36°,同理得∠CBD =∠CDB =36°,∴∠ABO =∠ABC -∠CBD =72°,∠AOB =180°-∠ABO -∠BAC =72°,∴AB =AO ,同理得DO =DC ,∴OA =AE =ED =DO ,∴四边形AODE 是菱形.15.小刚现有一边长为a m 的正方形花布,准备做一个形状为正八边形的风筝,参加全校组织的风筝比赛,问:在这样的花布上怎样裁剪,才能得到一个面积最大的风筝?解:如图所示,在正方形ABCD 中,△DEF ,△CGH ,△BOP ,△AMN 为全等的等腰直角三角形,八边形EMNOPHGF 为正八边形.设直角边DE =DF =CG =CH =x .在Rt △DEF 中,EF =2x . ∵EF =FG ,且DC =DF +FG +CG ,∴x +x +2x =a ,解得x =2-22a ≈0.3a , 因此,从四个角上各剪去一个直角边长约为0.3a m 的等腰直角三角形,即可得到一个面积最大的正八边形风筝.16.小赵对芜湖科技馆富有创意的科学方舟形象设计很有兴趣,他回家后将一正五边形纸片沿其对称轴对折,旋转放置,做成科学方舟模型,如图24-3-10所示,该正五边形的边心距OB 长为2,AC 为科学方舟船头A 到船底的距离,请你计算AC +12AB =__522__. 图24-3-10【解析】 设正五边形的边长为a ,根据正五边形的面积等于科学方舟面积的2倍列方程求解,依题意,有12×2×a ×5=⎝⎛⎭⎫12×AB ×a 2+12×a ×AC ×2, 即522a =⎝⎛⎭⎫12AB +AC ×a ,∴12AB +AC =522.。
新人教版九年级上册24.3正多边形和圆同步练习(有答案)
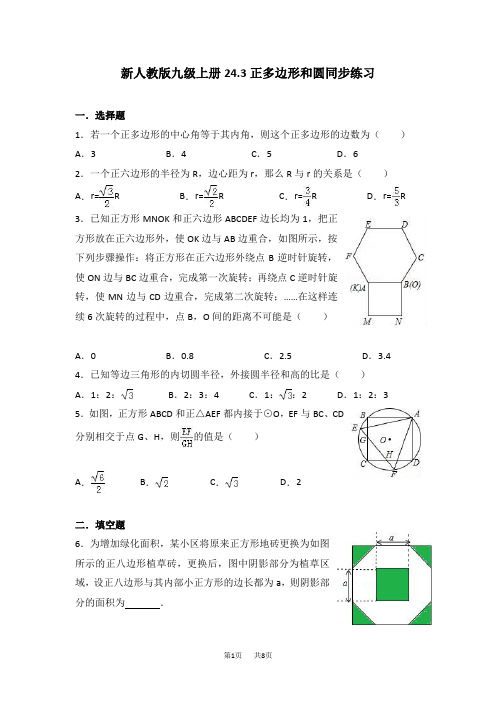
新人教版九级上册24.3正多边形和圆同步练习一.选择题1.若一个正多边形的中心角等于其内角,则这个正多边形的边数为()A.3 B.4 C.5 D.62.一个正六边形的半径为R,边心距为r,那么R与r的关系是()A.r=R B.r=R C.r=R D.r=R 3.已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形外,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B逆时针旋转,使ON边与BC边重合,完成第一次旋转;再绕点C逆时针旋转,使MN边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B,O间的距离不可能是()A.0 B.0.8 C.2.5 D.3.4 4.已知等边三角形的内切圆半径,外接圆半径和高的比是()A.1:2:B.2:3:4 C.1::2 D.1:2:3 5.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则的值是()A.B.C.D.2二.填空题6.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为.7.如图,AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,而BC恰好是同圆内接一个正n边形的一边,则n等于.8.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=.9.两个正三角形内接于一个半径为R的⊙O,设它的公共面积为S,则2S与的大小关系是.10.对于平面图形A,若存在一个或一个以上的圆,使图形A上任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖,图1中的三角形被一个圆所覆盖,图2中的四边形被两个圆所覆盖,若长宽分别为2cm与1cm的矩形被两个半径均为r的圆覆盖,则r的最小值为cm.三.解答题(共5小题)11.已知边长为1的正七边形ABCDEFG中,对角线AD,BG的长分别为a,b(a≠b),求证:(a+b)2(a﹣b)=ab2.12.如图,某圆形场地内有一个内接于⊙O的正方形中心场地,若⊙O的半径为10米,求图中所画的一块草地的面积.(计算结果保留π)13.在学习圆与正多边形时,马露、高静两位同学设计了一个画圆内接正三角形的方法:(1)如图,作直径AD;(2)作半径OD的垂直平分线,交⊙O于B,C两点;(3)联结AB、AC、BC,那么△ABC为所求的三角形.请你判断两位同学的作法是否正确,如果正确,请你按照两位同学设计的画法,画出△ABC,然后给出△ABC是等边三角形的证明过程;如果不正确,请说明理由.14.在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示:(1)通过计算(结果保留根号与π).(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为cm;(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为cm;(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为cm;(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.15.(1)已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=C N,证明△ABM≌△BCN,并求出∠BQM的度数.(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、正六边形ABCDEF、正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:正多边形正方形正五边形正六边形…正n边形∠BQM的度数…参考答案一.选择题1.B.2.A.3.D.4.D.5.C.二.填空题6.2a2.7.十二.8.48°.9.2S≥r2.10.cm.三.解答题11.证明:连结BD、EG、BE、DG,则BD=EG=GB=b,DG=BE=DA=a,DE=AB=AG=1,在四边形ABDG中,由托勒密协定理,得AD•BG=AB•DG+BD•AG,即ab=a+b ①,同理在四边形BDEG中,得BE•DG=DE•BG+BD•GE,即a2=b+b2,∴b=a2﹣b2=(a+b)(a﹣b)②,①×②,得ab2=(a+b)2(a﹣b).12.解:连AC,则AC为直径,即AC=20,∵正方形ABCD中,AB=BC,∠B=90°,∴在Rt△ABC中,AB2+BC2=AC2,2AB2=202,∴AB2=200,==(25π﹣50)米2.13.解:两位同学的方法正确.连BO、CO,∵BC垂直平分OD,∴直角△OEB中.cos∠BOE==,∠BOE=60°,由垂径定理得∠COE=∠BOE=60°,由于AD为直径,∴∠AOB=∠AOC=120°,∴AB=BC=CA,即△ABC为等边三角形.14.解:(1)(Ⅰ)连接BD,∵AD=3×5=15cm,AB=5cm,∴BD==cm;(Ⅱ)如图所示,∵三个正方形的边长均为5,∴A、B、C三点在以O为圆心,以OA为半径的圆上,∴OA==5cm,∴能盖住三个正方形所需的圆形硬纸板最小直径为10cm;(Ⅲ)如图所示,∵CE⊥AB,AC=BC,∴AD是过A、B、C三点的圆的直径,∵OA=OB=OD,∴O为圆心,∴⊙O的半径为OA,OA==5cm,∴能盖住三个正方形所需的圆形硬纸板最小直径为5×2=10 cm;(2)如图④为盖住三个正方形时直径最小的放置方法,连接OB,ON,延长OH交AB于点P,则OP⊥AB,P为AB中点,设OG=x,则OP=10﹣x,则有:,解得:,(8分)则ON=,∴直径为.15.(1)证明:∵△ABC为等边三角形,∴∠ABC=∠C=60°,在△ABM和△BCN中,,∴△ABM≌△BCN,∴∠BAM=∠CBN,∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=60°;(2)正方形ABCD中,由(1)得,△ABM≌△BCN,∴∠BAM=∠CBN,∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=90°,同理正五边形ABCDE中,∠BQM=108°,正六边形ABCDEF中,∠BQM=120°,正n边形ABCD…中,∠BQM=,故答案为:90°;108°;120°;.。
(完整)正多边形和圆同步练习(含答案),推荐文档

24.3 正多边形和圆知识点1. ______________ 相等,______________ 也相等的多边形叫做正多边形.2 •把一个圆分成几等份,连接各点所得到的多边形是_____________________ ,它的中心角等于3•—个正多边形的外接圆的_____________ 叫做这个正多边形的中心,外接圆的 _________ 叫做正多边形的半径,正多边形每一边所对的____________ 叫做正多边形的中心角,中心到正多边形的一边的_____________ 叫做正多边形的边心距.4•正n边形的半径为R,边心距为r,边长为a,(1)中心角的度数为:______________ .(2)每个内角的度数为:________________________ .(3)每个外角的度数为:____________ .(4)周长为:________ ,面积为:___________ .5. ___________________________________________________________ 正n边形都是轴对称图形,当边数为偶数时,它的对称轴有__________________________________ 条,并且还是中心对称图形;当边数为奇数时,它只是___________________ .(填轴对称图形”或中心对称图形”)1.下列说法正确的是()A. 各边相等的多边形是正多边形B. 各角相等的多边形是正多边形C.各边相等的圆内接多边形是正多边形D .各角相等的圆内接多边形是正多边形一、选择题2. (2013?天津)正六边形的边心距与边长之比为A . :;: 3 B. :;: 23.(2013山东滨州)若正方形的边长为C. 1:2 D.::.打:26,则其外接圆半径与内切圆半径的大小分别为C. 6, 3 D. 6.2 , 3.24. 如图所示,正六边形ABCDEF内接于O O,则/ ADB的度数是().A. 60 °B. 45 °C. 30 °D. 22. 55. 半径相等的圆的内接正三角形,正方形,正六边形的边长的比为A. 1: 2: 3B. .3: 2:1C.3:2:1D.1:2:317. 一个正三角形和一个正六边形的周长相等,则它们的面积比为 18. (2013?徐州)如图,在正八边形 ABCDEFGH 中,四边形BCFG 的面积为20cm 2,则正八边形的面积为 _______ cm 2.6. 圆内接正五边形 ABCD E 中,对角线 AC 和用一副三角板的角,借助点 O (使该角的顶点落在点 O 处), 把这个正六边形的面积 n 等分,那么n 的所有可能取值的 个数是( ) A.4B.5C.6D. 78•如图,△ PQR 是O O 的内接正三角形,四边形 ABCD 是O O的内接正方形,BC // QR ,则/ AOQ 的度数是 ()A.60 °B.65 °C.72 °D.75 °二、填空题9•一个正n 边形的边长为a ,面积为S ,则它的边心距为 ________________ 10•正多边形的一个中心角为 36度,那么这个正多边形的一个内角等于 11. 若正六边形的面积是24,3 cm 2,则这个正六边形的边长是 __________ . 12. 已知正六边形的边心距为3,则它的周长是 ________ .13. 点M 、N 分别是正八边形相邻的边 AB 、BC 上的点,且 AM= BN ,点O 是正八边形的中心,则/ MON= ________________ . 第13题14. 边长为a 的正三角形的边心距、半径(外接圆的半径)和高之比为 15.要用圆形铁片截出边长为4cm 的正方形铁片,则选用的圆形铁片的直径最小要_________ cm.16.若正多边形的边心距与边长的比为1:2,则这个正多边形的边数是第7题第18题三、解答题19. 比较正五边形与正六边形,可以发现它们的相同点与不同点例如 它们的一个相同点:正五边形的各边相等,正六边形的各边也相等 它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形 •请你再写出它们的两个相同点和不同点 相同点:(1)(2)不同点:(1)(2)20•已知,如图,正六边形 ABCDEF 的边长为6cm ,求这个正六边形的外接圆半径R 、边心距「6、面积S5.21.如图,O O 的半径为一 2,° O 的内接一个正多边形,边心距为 1,求它的中心角、边长、面积.正六边形第21题22•已知O O 和O O 上的一点A.(1 )作0 O 的内接正方形 ABCD 和内接正六边形 AEFCGH ; E 在弧AD 上,求证:DE 是O O 内接正十二边形的一边23.如图1、图2、图3、…、图n , M 、N 分别是O O 的内接正三角形 ABC 、正方形 ABCD 、正五边形 ABCDE 、…、正n 边形ABCDE …的边AB 、BC 上的点,且 BM=CN ,连结 OM 、ON.(1) 求图1中/ MON 的度数;(2) 图2中/ MON 的度数是 _________ ,图3中/ MON 的度数是 ___________ ⑶试探究/ MON 的度数与正n 边形边数n 的关系(直接写出答案).(2)在(1)题的作图中,如果点副 郅圏3 $圏n参考答案知识点1•各边各角2•正多边形正多边形每一边所对的圆心角3•圆心半径圆心角距离4 360 (n 2)gl80 360 nar4Q)—(2)____ (3)—(4 )na (5)--n n n 25.n轴对称图形一、选择题1.C2.B3.B4.C5.B6.C7. B解:根据圆内接正多边形的性质可知,只要把此正六边形再化为正多边形即可,即让周角除以30的倍数就可以解决问题.360 £0=12;360七0=6;360 为0=4;360勻20=3;360 勻80=2.因此n的所有可能的值共五种情况,故选B.8. D二、填空题9. 2S 10.144 11.4cm 12.12 13.45 ° 14.1:2:3 15. 4.2 16.四17.2:3na18.40三、解答题19.相同点:(1)每个内角都相等(或每个外角都相等或对角线都相等) ;(2)都是轴对称图形(或都有外接圆和内切圆)不同点:(1)正五边形的每个内角是108°正六边形的每个内角是120°20.(2)正五边形的对称轴是5条,正六边形的对称轴是6条.解:连接OA,OB. 过点0作OG AB于G. Q AOB =60 , OA 0B AOB是等边三角形OA OB 6 即R=6Q OA OB ,OGA11AG—A-6322在Rt AOG 中,心OG . OA2 AG1S666 3 354 36 2R 6 cm , r6 3 . 3 cm , S6 54、3cm 221.解:连结OB•••在Rt A AOC 中,AC= .OA2—OC2F7=1••• AC=OC •••/ AOC= / OAC =45°•/ OA=OB OC 丄AB• AB =2AC =2 / AOB=2 / OAC=2X45°=90°•这个内接正多边形是正方形.•面积为22=4•••中心角为90°边长为2,面积为4.22. (1)作法:①作直径AC;②作直径BD丄AC;③依次连结A、B、C、D四点,四边形ABCD即为O O的内接正方形;④分别以A、C为圆心,以OA长为半径作弧,交O⑤顺次连结A、E、F、C、G、H各点.六边形AEFCGH即为O O的内接正六边形⑵证明:连结OE DE/ 360 。
2022年人教版数学九上《正多边形和圆》同步练习(附答案)

24.3 正多边形和圆1.以下边长为a 的正多边形与边长为a 的正方形组合起来,不能镶嵌成平面的是( )(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形A .(1)(2)B .(2)(3)C .(1)(3)D .(1)(4) 2.以下说法正确的选项是A .每个内角都是120°的六边形一定是正六边形.B .正n 边形的对称轴不一定有n 条.C .正n 边形的每一个外角度数等于它的中心角度数.D .正多边形一定既是轴对称图形,又是中心对称图形.(3)(2006年天津市)假设同一个圆的内角正三角形、正方形、正六边形的边心距分别为r 3,r 4,r 6,那么r 3:r 4:r 6等于( )A .1:2:3B .3:2:1C .1:2:3D . 3:2:1 4. 正六边形ABCDEF 内接于⊙O ,图中阴影局部的面积为312,那么⊙O 的半径为______________________.5.如图,正方形ABCD 内接于⊙O ,点E 在AD 上,那么∠BEC= .6.将一块正六边形硬纸片〔图1〕,做成一个底面仍为正六边形且高相等的无盖纸盒〔侧面均垂直于底面,见图2〕,需在每一个顶点处剪去一个四边形,例如图中的四边形AGA /H ,那么∠GA /H 的大小是 度.7.〔2006年威海市〕如图,假设正方形A 1B 1C 1D 1内接于正方形ABCD 的内接圆,那么ABBA 11的值为〔 〕A .21B .22C .41D .42OBCD AEF EDCBAO8.从一个半径为10㎝的圆形纸片上裁出一个最大的正方形,那么此正方形的边长为 .9.如图五边形ABCDE 内接于⊙O,∠A =∠B=∠C=∠D=∠E . 求证:五边形ABCDE 是正五边形10.如图,10-1、10-2、10-3、…、10-n 分别是⊙O 的内接正三角形ABC ,正四边形ABCD 、正五边形ABCDE 、…、正n 边形ABCD …,点M 、N 分别从点B 、C 开始以相同的速度在⊙O 上逆时针运动。
2021年人教版九年级数学上册24.3正多边形和圆同步测试及答案【精修】

正多边形和圆1.正六边形的边心距与边长之比为( B ) A.3∶3 B.3∶2 C .1∶2 D.2∶2【解析】 如图:设正六边形的边长是a ,则半径长也是a ;经过正六边形的中心O 作边AB 的垂线OC ,则AC =12AB =12a , ∴OC =OA 2-AC 2=32a , ∴正六边形的边心距与边长之比为:32a ∶a =3∶2. 3-1,在⊙O 中,OA =AB ,OC ⊥AB ,则下列结论错误的是( D ) 图24-3-1A .弦AB 的长等于圆内接正六边形的边长B .弦AC 的长等于圆内接正十二边形的边长C.AC ︵=BC ︵D .∠BAC =30°【解析】 因为OA =AB =OB ,所以△OAB 是等边三角形,又OC ⊥AB ,所以∠AOC =∠BOC =30°,所以∠BAC =15°,D 不正确.3.如图24-3-2,点O 是正六边形的对称中心,如果用一副三角板的角,借助点O (使该角的顶点落在点O 处),把这个正六边形的面积n 等分,那么n 的所有可能取值的个数是( B )图24-3-2A .4B .5C .6D .7【解析】 360÷30=12;360÷60=6;360÷90=4;360÷120=3;360÷180=2.因此n 的所有可能的值共五种情况.4.如图24-3-3,要拧开一个边长为a =6 mm 的正六边形螺帽,扳手张开的开口b 至少为( C )图24-3-3 A .6 2 mm B .12 mmC .6 3 mmD .4 3 mm5.已知正六边形的边心距为3,则它的周长是( B )A .6B .12C .6 3D .12 3【解析】 正六边形的边长等于半径,设半径为R ,则⎝⎛⎭⎫12R 2+(3)2=R 2,∴R =2,它的周长是6R=6×2=12,故选B.6.若正六边形的边长为4 cm ,那么正六边形的中心角是__60__度,半径是__4__cm ,边心距是__23__cm ,它的每一个内角是__120°__.7.[2012·巴中]已知一个圆的半径为5 cm ,则它的内接正六边形的边长为__5__cm.8.已知一个正n 边形的中心角是它的一个内角的三分之一,则n =__8__.【解析】 由360n =180(n -2)n ×13,得n =8. 9.已知⊙O 和⊙O 上的一点A ,如图24-3-4所示.图24-3-4(1)作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ;(2)在(1)题所作的图中,如果点E 在AB ︵上,试证明EB 是⊙O 的内接正十二边形的一边.【解析】 (1)根据正四边形和正六边形的作图方法分别作出⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ;(2)计算EB 所对的圆心角的度数.解:(1)如图所示,在⊙O 中,用直尺和圆规作两条互相垂直的直径AC 和BD ,连接AB ,BC ,CD ,DA ,得⊙O 的内接正方形ABCD ;按正六边形的作法用直尺和圆规在⊙O 中作出正六边形AEFCGH . (2)如图,连接OE .∵AE 是正六边形的一边,∴∠AOE =360°6=60°.∵AB 是正方形的一边,∴∠AOB =360°4=90°,∴∠BOE =∠AOB -∠AOE =90°-60°=30°.设EB 是⊙O 的内接正n 边形的一边,则360°n=30°,∴n =12, ∴EB 是⊙O 的内接正十二边形的一边.10.小敏在作⊙O 的内接正五边形时,先做了如下几个步骤:(1)作⊙O 的两条互相垂直的直径,再作OA 的垂直平分线交OA 于点M ,如图1;(2)以M 为圆心,BM 长为半径作圆弧,交CA 于点D ,连接BD ,如图2.若⊙O 的半径为1,则由以上作图得到的关于正五边形边长BD 的等式是( C )图24-3-5 A .BD 2=5-12OD B .BD 2=5+12OD C .BD 2=5ODD .BD 2=52OD 11.[2013·徐州]如图24-3-6,在正八边形ABCDEFGH 中,四边形BCFG 的面积为20 cm 2,则正八边形的面积为____________cm 2.图24-3-6【解析】连接HE ,AD ,在正八边形ABCDEFGH 中,可得:HE ⊥BG 于点M ,AD ⊥BG 于点N ,∵正八边形每个内角为:(8-2)×180°8=135°, ∴∠HGM =45°,∴MN =MG ,设MH =MG =x ,则HG =AH =AB =GF =2x ,∴BG ×GF =2(2+1)x 2=20,四边形ABGH 面积=12(AH +BG )×HM =(2+1)x 2=10, ∴正八边形的面积为:10×2+20=40(cm 2).12.将固定宽度的纸条打个简单的结,然后系紧,使它成为平面的结(如图24-3-7),求证:五边形ABCDE 是正五边形.图24-3-7第13题答图证明:如图所示,连接BE ,AD ,设纸条的宽度为h ,则S △ABE =12AB ·h =12AE ·h , ∴AB =AE ,同理得AB =BC ,BC =CD ,∴AE =AB =BC =CD .∵纸条的宽度固定,∴AE ∥BD ,CD ∥BE ,∴∠1=∠2=∠3=∠4=∠5.由折叠性质得∠ABD +∠ABC =180°,从而得∠1=∠2=∠3=∠4=∠5=36°,由此易得∠ABC =∠BCD =∠CDE =∠DEA =∠EAB ,AE =AB =BC =CD =DE ,∴五边形ABCDE 是正五边形.13.如图24-3-8所示,已知△ABC 是⊙O 的内接等腰三角形,顶角∠BAC =36°,弦BD ,CE 分别平分∠ABC ,∠ACB ,求证:五边形AEBCD 是正五边形.图24-3-8 【解析】 要证明五边形AEBCD 是正五边形,只需证AE ︵=EB ︵=BC ︵=CD ︵=DA ︵即可.证明:∵△ABC 是等腰三角形,且∠BAC =36°,∴∠ABC =∠ACB =72°.又∵BD 平分∠ABC ,CE 平分∠ACB ,∴∠ABD =∠CBD =∠BCE =∠ACE =36°,即∠BAC =∠ABD =∠CBD =∠BCE =∠ACE ,∴BC ︵=AD ︵=CD ︵=BE ︵=AE ︵,∴A ,E ,B ,C ,D 是⊙O 的五等分点,∴五边形AEBCD 是正五边形.14.如图24-3-9,正五边形ABCDE ,连接对角线AC ,BD ,设AC 与BD 相交于O .(1)写出图中所有的等腰三角形;(2)判断四边形AODE 的形状,并说明理由.:学科图24-3-9解:(1)△ABO ,△ABC ,△BOC ,△DOC ,△BCD .(2)四边形AODE 是菱形,理由如下:∵AB =BC ,∠ABC =(5-2)×180°5=108°, ∴∠BAC =∠BCA =12×(180°-108°)=36°,同理得∠CBD =∠CDB =36°,∴∠ABO =∠ABC -∠CBD =72°,∠AOB =180°-∠ABO -∠BAC =72°,∴AB =AO ,同理得DO =DC ,∴OA =AE =ED =DO ,∴四边形AODE 是菱形.15.小刚现有一边长为a m 的正方形花布,准备做一个形状为正八边形的风筝,参加全校组织的风筝比赛,问:在这样的花布上怎样裁剪,才能得到一个面积最大的风筝?解:如图所示,在正方形ABCD 中,△DEF ,△CGH ,△BOP ,△AMN 为全等的等腰直角三角形,八边形EMNOPHGF 为正八边形.设直角边DE =DF =CG =CH =x .在Rt △DEF 中,EF =2x . ∵EF =FG ,且DC =DF +FG +CG ,∴x +x +2x =a ,解得x =2-22a ≈0.3a , 因此,从四个角上各剪去一个直角边长约为0.3a m 的等腰直角三角形,即可得到一个面积最大的正八边形风筝.16.小赵对芜湖科技馆富有创意的科学方舟形象设计很有兴趣,他回家后将一正五边形纸片沿其对称轴对折,旋转放置,做成科学方舟模型,如图24-3-10所示,该正五边形的边心距OB 长为2,AC 为科学方舟船头A 到船底的距离,请你计算AC +12AB =__522__. 图24-3-10【解析】 设正五边形的边长为a ,根据正五边形的面积等于科学方舟面积的2倍列方程求解,依题意,有12×2×a ×5=⎝⎛⎭⎫12×AB ×a 2+12×a ×AC ×2, 即522a =⎝⎛⎭⎫12AB +AC ×a ,∴12AB +AC =522.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24.3 正多边形和圆一、课前预习 (5分钟训练)1.圆的半径扩大一倍,则它的相应的圆内接正n 边形的边长与半径之比( )A.扩大了一倍B.扩大了两倍C.扩大了四倍D.没有变化 2.正三角形的高、外接圆半径、边心距之比为( )A.3∶2∶1B.4∶3∶2C.4∶2∶1D.6∶4∶3 3.正五边形共有__________条对称轴,正六边形共有__________条对称轴. 4.中心角是45°的正多边形的边数是__________.5.已知△ABC 的周长为20,△ABC 的内切圆与边AB 相切于点D,AD=4,那么BC=__________. 二、课中强化(10分钟训练)1.若正n 边形的一个外角是一个内角的32时,此时该正n 边形有_________条对称轴. 2.同圆的内接正三角形与内接正方形的边长的比是( )A.26 B.43 C.36D.343.周长相等的正三角形、正四边形、正六边形的面积S 3、S 4、S 6之间的大小关系是( )A.S 3>S 4>S 6B.S 6>S 4>S 3C.S 6>S 3>S 4D.S 4>S 6>S 3 4.已知⊙O 和⊙O 上的一点A(如图24-3-1).(1)作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ;(2)在(1)题的作图中,如果点E 在弧AD 上,求证:DE 是⊙O 内接正十二边形的一边.图24-3-1三、课后巩固(30分钟训练)1.正六边形的两条平行边之间的距离为1,则它的边长为( )A.63 B.43 C.332 D.332.已知正多边形的边心距与边长的比为21,则此正多边形为( ) A.正三角形 B.正方形 C.正六边形 D.正十二边形 3.已知正六边形的半径为3 cm ,则这个正六边形的周长为__________ cm.4.正多边形的一个中心角为36度,那么这个正多边形的一个内角等于___________度.5.如图24-3-2,两相交圆的公共弦AB 为23,在⊙O 1中为内接正三角形的一边,在⊙O 2中为内接正六边形的一边,求这两圆的面积之比.图24-3-26.某正多边形的每个内角比其外角大100°,求这个正多边形的边数.7.如图24-3-3,在桌面上有半径为2 cm的三个圆形纸片两两外切,现用一个大圆片把这三个圆完全覆盖,求这个大圆片的半径最小应为多少?图24-3-38.如图24-3-4,请同学们观察这两个图形是怎么画出来的?并请同学们画出这个图形(小组之间参与交流、评价).图24-3-49.用等分圆周的方法画出下列图案:图24-3-510.如图24-3-6(1)、24-3-6(2)、24-3-6(3)、…、24-3-6(n),M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连结OM、ON.图24-3-6(1)求图24-3-6(1)中∠MON的度数;(2)图24-3-6(2)中∠MON的度数是_________,图24-3-6(3)中∠MON的度数是_________;(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).参考答案一、课前预习 (5分钟训练)1.圆的半径扩大一倍,则它的相应的圆内接正n 边形的边长与半径之比( )A.扩大了一倍B.扩大了两倍C.扩大了四倍D.没有变化思路解析:由题意知圆的半径扩大一倍,则相应的圆内接正n 边形的边长也扩大一倍,所以相应的圆内接正n 边形的边长与半径之比没有变化. 答案:D2.正三角形的高、外接圆半径、边心距之比为( )A.3∶2∶1B.4∶3∶2C.4∶2∶1D.6∶4∶3思路解析:如图,设正三角形的边长为a ,则高AD=23a ,外接圆半径OA=33a ,边心距OD=63a , 所以AD ∶OA ∶OD=3∶2∶1.答案:A3.正五边形共有__________条对称轴,正六边形共有__________条对称轴.思路解析:正n 边形的对称轴与它的边数相同. 答案:5 6 4.中心角是45°的正多边形的边数是__________.思路解析:因为正n 边形的中心角为n ︒360,所以45°=n︒360,所以n=8. 答案:85.已知△ABC 的周长为20,△ABC 的内切圆与边AB 相切于点D,AD=4,那么BC=__________.思路解析:由切线长定理及三角形周长可得. 答案:6二、课中强化(10分钟训练)1.若正n 边形的一个外角是一个内角的32时,此时该正n 边形有_________条对称轴. 思路解析:因为正n 边形的外角为n ︒360,一个内角为nn ︒∙-180)2(,所以由题意得n ︒360=32·nn ︒∙-180)2(,解这个方程得n=5.答案:52.同圆的内接正三角形与内接正方形的边长的比是( )A.26 B.43 C.36D.34思路解析:画图分析,分别求出正三角形、正方形的边长,知应选A.答案:A3.周长相等的正三角形、正四边形、正六边形的面积S 3、S 4、S 6之间的大小关系是( )A.S 3>S 4>S 6B.S 6>S 4>S 3C.S 6>S 3>S 4D.S 4>S 6>S 3 思路解析:周长相等的正多边形的面积是边数越多面积越大. 答案:B4.已知⊙O 和⊙O 上的一点A(如图24-3-1).(1)作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ;(2)在(1)题的作图中,如果点E 在弧AD 上,求证:DE 是⊙O 内接正十二边形的一边.图24-3-1思路分析:求作⊙O 的内接正六边形和正方形,依据定理应将⊙O 的圆周六等分、四等分,而正六边形的边长等于半径;互相垂直的两条直径由垂径定理知把圆四等分.要证明DE 是⊙O 内接正十二边形的一边,由定理知,只需证明DE 所对圆心角等于360°÷12=30°.(1)作法: ①作直径AC;②作直径BD ⊥AC;③依次连结A 、B 、C 、D 四点,四边形ABCD 即为⊙O 的内接正方形;④分别以A 、C 为圆心,OA 长为半径作弧,交⊙O 于E 、H 、F 、G; ⑤顺次连结A 、E 、F 、C 、G 、H 各点. 六边形AEFCGH 即为⊙O 的内接正六边形. (2)证明:连结OE 、DE. ∵∠AOD =4360︒=90°,∠AOE =6360︒=60°, ∴∠DOE =∠AOD -∠AOE =30°.∴DE 为⊙O 的内接正十二边形的一边. 三、课后巩固(30分钟训练)1.正六边形的两条平行边之间的距离为1,则它的边长为( )A.63 B.43 C.332 D.33思路解析:正六边形的两条平行边之间的距离为1,所以边心距为0.5,则边长为33. 答案:D2.已知正多边形的边心距与边长的比为21,则此正多边形为( ) A.正三角形 B.正方形 C.正六边形 D.正十二边形 思路解析:将问题转化为直角三角形,由直角边的比知应选B. 答案:B3.已知正六边形的半径为3 cm ,则这个正六边形的周长为__________ cm.思路解析:转化为直角三角形求出正六边形的边长,然后用P 6=6a n 求出周长. 答案:184.正多边形的一个中心角为36度,那么这个正多边形的一个内角等于___________度.答案:144.5.如图24-3-2,两相交圆的公共弦AB 为23,在⊙O 1中为内接正三角形的一边,在⊙O 2中为内接正六边形的一边,求这两圆的面积之比.图24-3-2思路分析:欲求两圆的面积之比,根据圆的面积计算公式,只需求出两圆的半径R 3与R 6的平方比即可. 解:设正三角形外接圆⊙O 1的半径为R 3,正六边形外接圆⊙O 2的半径为R 6,由题意得R 3=33AB ,R 6=AB ,∴R 3∶R 6=3∶3.∴⊙O 1的面积∶⊙O 2的面积=1∶3. 6.某正多边形的每个内角比其外角大100°,求这个正多边形的边数. 思路分析:由正多边形的内角与外角公式可求.解:设此正多边形的边数为n ,则各内角为n n ︒∙-180)2(,外角为n ︒360,依题意得n n ︒∙-180)2(-n︒360=100°.解得n =9.7.如图24-3-3,在桌面上有半径为2 cm 的三个圆形纸片两两外切,现用一个大圆片把这三个圆完全覆盖,求这个大圆片的半径最小应为多少?图24-3-3思路分析:设三个圆的圆心为O 1、O 2、O 3,连结O 1O 2、O 2O 3、O 3O 1,可得边长为4 cm 的正△O 1O 2O 3,设大圆的圆心为O ,则点O 是正△O 1O 2O 3的中心,求出这个正△O 1O 2O 3外接圆的半径,再加上⊙O 1的半径即为所求. 解:设三个圆的圆心为O 1、O 2、O 3,连结O 1O 2、O 2O 3、O 3O 1,可得边长为4 cm 的正△O 1O 2O 3,则正△O 1O 2O 3外接圆的半径为334 cm ,所以大圆的半径为334+2=3634+ (cm).8.如图24-3-4,请同学们观察这两个图形是怎么画出来的?并请同学们画出这个图形(小组之间参与交流、评价).图24-3-4答案:略.9.用等分圆周的方法画出下列图案:图24-3-5作法:(1)分别以圆的4等分点为圆心,以圆的半径为半径,画4个圆;(2)分别以圆的6等分点为圆心,以圆的半径画弧.10.如图24-3-6(1)、24-3-6(2)、24-3-6(3)、…、24-3-6(n),M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连结OM、ON.图24-3-6(1)求图24-3-6(1)中∠MON的度数;(2)图24-3-6(2)中∠MON的度数是_________,图24-3-6(3)中∠MON的度数是_________;(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).答案:(1)方法一:连结OB、OC.∵正△ABC内接于⊙O,∴∠OBM=∠OCN=30°,∠BOC=120°.又∵BM=CN,OB=OC,∴△OBM≌△OCN.∴∠BOM=∠CON.∴∠MON=∠BOC=120°.方法二:连结OA、OB.∵正△ABC内接于⊙O,∴AB=AC,∠OAM=∠OBN=30°,∠AOB=120°.又∵BM=CN,∴AM=BN.又∵OA=OB,∴△AOM≌△BON.∴∠AOM=∠BON.∴∠MON=∠AOB=120°.(2)90°72°(3)∠MON=n360.。
