求a模b的约简 和 乘法逆
快速模乘法

快速模乘法快速模乘法是一种高效的计算模乘运算的方法,它主要应用于算法竞赛和密码学等领域。
以下是一些常见的快速模乘算法:蒙哥马利模乘法:这是一种广泛使用的快速模乘算法,它可以在不直接计算乘积的情况下计算出模乘结果,从而避免了大数乘法带来的溢出问题。
蒙哥马利方法通过一系列的变换,将模乘运算转化为更容易计算的形式。
巴雷特模乘法:这是另一种经典的快速模乘算法,它通过预计算一些值来加快模乘的计算速度。
巴雷特模乘法的核心在于找到一个近似倒数,从而将模乘运算转化为一系列更简单的操作。
快速幂算法:虽然严格来说快速幂算法是用来计算幂模的,但它也可以用于优化模乘运算。
当需要计算形如 a^b mod m 的表达式时,快速幂算法可以显著减少计算量,其时间复杂度为 O(log b)。
卡拉次乘法:这是一种用于计算大整数乘积在模下的快速算法,特别适用于大数的情况。
它通过将乘数分解为多个部分,然后分别计算这些部分的乘积和模,最后合并结果。
二进制方法:对于模数是2的幂的情况,可以使用二进制方法来优化模乘运算。
这种方法通过将乘数表示为二进制形式,然后只计算那些对应于二进制位为1的项,从而减少了计算量。
窗口方法:这是一种适用于多个模乘连续计算的情况,通过预计算和存储一些中间结果,可以减少重复计算的次数。
中国剩余定理(CRT):在处理多个模数的情况时,中国剩余定理可以用于优化模乘运算。
通过将问题分解为多个较小的子问题,然后在每个子问题上分别计算,最后合并结果,可以显著提高计算效率。
模重复平方法:这种方法适用于计算形如 (a * b) mod m 的表达式,其中 b 是一个非常大的整数。
通过将 b 分解为多个较小的部分,然后分别计算这些部分的模乘,最后合并结果,可以提高计算效率。
模加法链:这种方法适用于计算形如 (a + b) mod m 的表达式,其中 a和 b 都是非常大的整数。
通过将 a 和 b 分解为多个较小的部分,然后分别计算这些部分的模加,最后合并结果,可以提高计算效率。
数学中的模运算

数学中的模运算一、模运算的概念与性质模运算是一种特殊的整数运算方式,它是数论中的重要分支。
在模运算中,我们可以通过取余数来表示运算结果,例如a mod b表示a 除以b的余数。
模运算具有以下性质:1. 同余性质:若a与b对模m同余(记作a≡b(mod m)),则a 与b在模m下的余数相等。
同余关系满足以下性质:- 自反性:a≡a(mod m)- 反对称性:若a≡b(mod m),则b≡a(mod m)- 传递性:若a≡b(mod m)且b≡c(mod m),则a≡c(mod m)2. 模运算的加法性质:若a≡b(mod m)且c≡d(mod m),则a+c≡b+d(mod m)3. 模运算的乘法性质:若a≡b(mod m)且c≡d(mod m),则a×c≡b×d(mod m)4. 模运算的幂运算性质:对于任意整数a和非负整数n,有以下等式成立:- a^n≡(a mod m)^n(mod m)二、模运算的应用1. 同余方程:同余方程是模运算的重要应用之一。
同余方程的一般形式为ax≡b(mod m),其中a、b和m为已知整数,x为未知整数。
解同余方程的关键是求解x的值,满足方程使得等式成立。
2. 模逆元:模逆元是指在模m下,与整数a相乘恰好等于1的整数。
简单来说,若存在一个整数x,满足ax≡1(mod m),则称x为a 在模m下的模逆元。
模逆元在密码学、线性代数等领域有广泛应用。
3. 同余定理:同余定理是模运算中的重要定理之一,包括费马小定理和中国剩余定理。
- 费马小定理:若p为素数,且不整除整数a,则a^(p-1)≡1(mod p)- 中国剩余定理:若m1、m2、...、mn为两两互质的正整数,且a1、a2、...、an为任意整数,则以下同余方程存在解:- x≡a1(mod m1)- x≡a2(mod m2)- x≡an(mod mn)三、模运算的例题分析例题1:求解同余方程3x≡2(mod 5)解:根据同余方程的性质,我们可以通过试探法求解。
模运算

模运算“模”是“Mod”的音译,模运算多应用于程序编写中。
Mod的含义为求余。
模运算在数论和程序设计中都有着广泛的应用,从奇偶数的判别到素数的判别,从模幂运算到最大公约数的求法,从孙子问题到凯撒密码问题,无不充斥着模运算的身影。
虽然很多数论教材上对模运算都有一定的介绍,但多数都是以纯理论为主,对于模运算在程序设计中的应用涉及不多。
∙中文名模运算∙外文名Mod∙概述计算机编写程序∙领域数论和程序设计∙类型以纯理论为主举例11 Mod 2,值为1上述模运算多用于程序编写,举一例来说明模运算的原理:Turbo Pascal对mod的解释是这样的:A Mod B=A-(A div B) *B (div含义为整除)[1]概念及性质本文以c++语言为载体,对基本的模运算应用进行了分析和程序设计,以理论和实际相结合的方法向大家介绍模运算的基本应用。
基本概念给定一个正整数,任意一个整数,一定存在等式;其中、是整数,且,称为除以的商,为除以的余数。
对于正整数和整数 , ,定义如下运算:取模运算:a % p(或a mod p),表示a除以p的余数。
模p加法:(a + b) % p ,其结果是a+b算术和除以p的余数,也就是说,(a+b) = kp +r,则(a + b) % p = r。
模p减法:(a-b) % p ,其结果是a-b算术差除以p的余数。
模p乘法:(a * b) % p,其结果是 a * b算术乘法除以p的余数。
说明:1.同余式:正整数a,b对p取模,它们的余数相同,记做a ≡ b % p或者a ≡ b (mod p)。
2. n % p得到结果的正负由被除数n决定,与p无关。
例如:7%4 = 3, -7%4 = -3, 7%-4 = 3, -7%-4 = -3(在java、C/C++中%是取余,在python是模运算,此处%按取余处理)。
基本性质(1)若p|(a-b),则a≡b (% p)。
例如11 ≡ 4 (% 7),18 ≡ 4(% 7)(2)(a % p)=(b % p)意味a≡b (% p)(3)对称性:a≡b (% p)等价于b≡a (% p)(4)传递性:若a≡b (% p)且b≡c (% p) ,则a≡c (% p)运算规则模运算与基本四则运算有些相似,但是除法例外。
第一章第02讲 幂的乘方与积的乘方(5类热点题型讲练)(解析版)
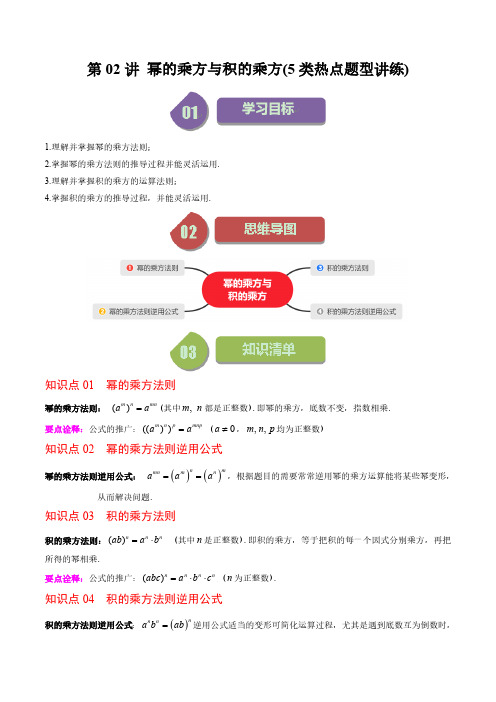
第02讲 幂的乘方与积的乘方(5类热点题型讲练)1.理解并掌握幂的乘方法则;2.掌握幂的乘方法则的推导过程并能灵活运用.3.理解并掌握积的乘方的运算法则;4.掌握积的乘方的推导过程,并能灵活运用.知识点01 幂的乘方法则幂的乘方法则: (其中都是正整数).即幂的乘方,底数不变,指数相乘.要点诠释:公式的推广: (,均为正整数)知识点02 幂的乘方法则逆用公式幂的乘方法则逆用公式: ,根据题目的需要常常逆用幂的乘方运算能将某些幂变形,从而解决问题.知识点03 积的乘方法则积的乘方法则: (其中是正整数).即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.要点诠释:公式的推广: (为正整数).知识点04 积的乘方法则逆用公式积的乘方法则逆用公式:逆用公式适当的变形可简化运算过程,尤其是遇到底数互为倒数时,()=m nmna a,m n (())=m n pmnpa a0¹a ,,m n p ()()n mmnm n aa a ==()=×nnnab a b n ()=××nnnnabc a b c n ()nn na b ab =计算更简便.如:题型01 幂的乘方运算【例题】(2023下·广东茂名·七年级统考期末)计算:()43a -=______.【答案】12a 【分析】直接运用幂的乘方法则进行运算即可.【详解】解:()()44333412a a a a ´-===,故答案为:12a .【点睛】本题主要考查的是幂的乘方法则知识内容,幂的乘方法则:幂的乘方,底数不变,指数相乘.【变式训练】1010101122 1.22æöæö´=´=ç÷ç÷èøèø题型02 幂的乘方的逆用【例题】(2023下·安徽蚌埠·七年级校考阶段练习)已知:105106a b ==,,求2310a b +的值.【答案】5400【分析】根据幂的乘方和同底数幂的乘法的运算法则,原式可化为()()231010a b ´,代入已知量,即可求解.【详解】解:2310a b+231010a b=´()()231010ab=´2356=´5400=.【点睛】本题考查幂的运算,掌握同底数幂的乘方的逆运算法则是解题关键.【变式训练】1.(2023下·江苏泰州·七年级校考阶段练习)已知3,2m n a a ==,求:(1)3()n a ;(2)23m n a +.【答案】(1)8(2)72【分析】(1)利用积的乘方的法则运算即可;(2)利用同底数幂的乘法与幂的乘方对式子进行运算即可.【详解】(1)解:∵3,2m n a a ==,∴3()n a 3()n a =328==(2)解:∵3,2m n a a ==,∴23m na +23m na a =´23()()m n a a =´2332=´98=´72=【点睛】本题主要考查幂的乘方,同底数幂的乘法,解答的关键是对相应的运算法则的掌握.2.(2023下·江苏苏州·七年级校考阶段练习)已知3x a =-,3y a =.求:(1)x y a +的值;(2)3x a 的值;(3)32x y a +的值.【答案】(1)9-(2)27-(3)243-【分析】(1)逆用同底数幂乘法运算法则进行计算即可;(2)逆用幂的乘方运算法则进行计算即可;(3)逆用同底数幂乘法和幂的乘方运算法则进行计算即可.【详解】(1)解:∵3x a =-,3y a =,∴339x y x y a a a +=×=-´=-;(2)解:∵3x a =-,∴()()333327xx a a ==-=-;(3)解:∵3x a =-,3y a =,∴3322x y x ya a a +=×()()32xya a =×()3233=-´243=-.【点睛】本题主要考查了幂的乘方,同底数幂乘法,解题的关键是熟练掌握幂的乘方,同底数幂乘法运算法则,准确计算.题型03 利用幂的乘方比较大小【例题】(2023上·八年级课时练习)已知34a =,118b =,试比较a ,b 的大小.【答案】a b>【分析】根据幂的乘方运算法则把它们化为指数相同的幂,再比较大小即可.【详解】解:∵()()1111311222422a ===,()()3311339822b ===,22922>,∴()()113311a b >.∴3333a b >,∴a b >.【点睛】本题主要考查了幂的乘方以及有理数大小比较,熟记幂的运算法则是解答本题的关键.【变式训练】1.(2023下·陕西西安·七年级校考阶段练习)比较1002,753,505这三个数的大小,并用“>”将它们连接起来.【答案】5010075532>>【分析】把它们化为指数相同的幂,再比较大小即可.【详解】解:()2525442100522216´===,()252533275533327´===()252522250555525´===,∵252525272516>>,∴5010075532>>【点睛】本题主要考查了幂的乘方的逆用:()=nmn m a a ,熟记幂的运算法则是解答本题的关键.2.(2023上·八年级课时练习)【阅读理解】特殊数大小的比较问题:比较553,444,335的大小.解:()115551133243==Q ,()114441144256==,()111133355125==,335544534\<<.【问题解决】学习以上解题思路和方法,然后完成下题:比较40403,30304,20205的大小.【答案】404030302020345>>【分析】根据幂的乘方逆运算法则解答.【详解】()10104040410103381==Q ,()10103030310104464==,()10102020210105525==,且816425>>,404030302020345\>>.【点睛】本题考查了幂的乘方,正确理解题意、熟练掌握幂的乘方法则是解题关键.题型04 积的乘方运算题型05积的乘方的逆用1.(2023下·江苏·七年级专题练习)(1)若34m x =,35n y =,求()()332242m n m n m n x y x y x y -××+×的值;(2)已知2530x y +-=,求432x y ×的值;(3)已知2n x =,3n y =,求()22nx y 的值.【答案】(1)59-;(2)8;(3)144【分析】(1)将待求式转化为含有x 3m ,y 3n 的式子后整体代入计算;(2)(3)利用积的乘方与幂的乘方的逆运算对所求式子化简,然后代入计算即可.【详解】解:(1)∵34m x =,35n y =,∴()()332242m n m n m n x y x y x y -××+×()()223333mn mnx y x y =+-×224545=+-´59=-;(2)∵2530x y +-=,∴2+5=3x y ,∴432x y×2522x y=×252x y+=32=8=;(3)∵2n x =,3n y =,∴()22nx y一、单选题1.(2024下·全国·七年级假期作业)计算()32a -的结果是( )A .6a -B .6aC .5a -D .5a 【答案】A 【解析】略2.(2023上·辽宁大连·八年级校联考阶段练习)下列各式计算正确的是( )A .()23639x x -=B .22(2)4a a -=-C .326a a a ×=D .()323ab ab =【答案】A【分析】本题考查了的乘方与积的乘方以及同底数幂的乘法,熟练掌握运算法则是解题的关键.【详解】解:A 、()23639x x -=,所以A 选项符合题意,B 、22(2)4a a -=,所以B 选项不符合题意,C 、325a a a ×=,所以C 选项不符合题意,D 、()3236ab a b =,所以D 选项不符合题意.故选:A .3.(2022上·广东肇庆·八年级统考期末)己知5,3m n a a ==,则2m n a +的值为( )A .75B .45C .30D .15【答案】B【分析】本题考查了幂的乘方与积的乘方,同底数幂的乘法等知识点,能正确根据幂的乘方和同底数幂的乘法法则进行计算是解此题的关键,先根据同底数幂的乘法法则进行变形,再根据幂的乘方进行变形,最后代入求出答案即可.【详解】解:5m a =Q ,3n a =,2m n a +\2m na a =×()2m n a a =×253=´59=´45=.故选:B .4.(2023上·河北廊坊·八年级校考阶段练习)若11393m ´=,则m 的值为( )A .2B .3C .4D .5【答案】D【分析】本题考查了同底数幂乘法运算,幂的乘方的逆运算,由11393m ´=得到121133m +=,即可求解,掌握同底数幂乘法运算和幂的乘方的逆运算的运算法则是解题的关键.【详解】解:∵21211393333m m m +´=´==,∴1211m +=,解得5m =,故选:D .5.(2023上·河北沧州·八年级校联考阶段练习)已知221192,3,12a b c ===,下列结论①a b >;②ab c >;③b c <中正确的有( )A .0个B .1个C .2个D .3个【答案】D【分析】本题考查了幂的运算,熟练掌握同底数幂的乘法公式,幂的乘方及其逆应用,积的乘方及其逆应用是解题的关键.【详解】∵221192,3,12a b c ===,∴()222111111224,3a b ====,∴a b >,故①正确;∵()11221111111123433412ab =´=´=´=,912c =,∴ab c >,故②正确;∵()9991192993,4339343123b c =´=´===´=´,994<,∴b c <,故③正确;故选:D .11.(2023上·八年级课时练习)计算:(1)()()6322423xy x y -+-;(2)()()32224323x x x x -+×--.【答案】(1)61237x y ;(2)616x -.【分析】(1)先利用积的乘方运算法则求解,再加减求解即可;(2)先利用同底数幂的乘法和积的乘方运算法则求解,再加减求解即可.【详解】(1)解:()()6322423xy x y -+-6126126427x y x y =-61237x y =;(2)解:()()32224323x x x x -+×--66689x x x =-+-616x =-.【点睛】本题考查同底数幂的乘法、积的乘方、合并同类项,熟练掌握运算法则并正确求解是解答的关键.12.(2024下·全国·七年级假期作业)计算:(1)()32352()x x x x ×+-+;(2)()()()322232223a a a a +-+×.【答案】(1)6x(2)618a 【详解】解:(1)原式5566x x x x =-+=.(2)原式()()()3223223222(3)a a a a =×+-×+×66689a a a =++6(891)a =++618a =.13.(2022上·上海闵行·七年级校考周测)计算:(1)224x x x x x ××+×;(2)()()()()22425223a a a a ×-×;(3)()()32233x x -+-;(4)()()()()4342343a a a a ×--×;【答案】(1)52x (2)0(3)68x (4)174a 【分析】(1)先计算同底数幂乘法然后再合并同类项;(2)先用幂的乘方和同底数幂乘法进行运算,然后再合并同类项;(3)先用幂的乘方进行运算,然后再合并同类项;(4)先用幂的乘方进行运算,然后再合并同类项.【详解】(1)解:224x x x x x××+×55x x =+52x =;(2)解:()()()()22425223a a a a ×-×10486a a a a =×-×1414a a =-0=;(3)解:()()32233x x -+-669x x =-+68x =;(4)解:()()()()4342343a a a a ×--×()89163a a a a =×--×(1)计算:①()2023202380.125´-;。
乘法公式ppt课件

乘法交换律
总结词
乘法交换律是数学中的基本定理之一,它描述了两个数相乘时,交换它们的顺序不会改变乘积的结果 。
详细描述
乘法交换律是指对于任何实数a和b,有a × b = b × a。这个定理说明了乘法的可交换性质,即两个 数的乘积与它们的顺序无关。
04
乘法公式的实例解析
实例一:整数乘法
总结词
整数乘法是乘法公式中最基础的形式,通过实例解析可以帮助学生更好地理解乘法的本 质。
详细描述
乘法分配律是指对于任何实数a、b和c,有a × (b + c) = a × b + a × c。这个定理在数学和物理中有广泛的应用,是学习 代数和微积分的基础。
乘法结合律
总结词
乘法结合律是数学中的基本定理之一 ,它描述了三个数相乘时,不论括号 如何组合,其结果都相同。
详细描述
乘法结合律是指对于任何实数a、b和 c,有(a × b) × c = a × (b × c)。这 个定理说明了乘法的结合性质,即乘 法的顺序不影响结果。
掌握同余式的性质和 运算规则
乘法公式的历史背景
古代数学中的乘法
在古代,人们通过重复加法来计算乘 法,随着数学的发展,逐渐形成了乘 法公式。
现代数学中的乘法
在现代数学中,乘法公式已经成为了 基础数学知识之一,被广泛应用于各 个领域。
乘法公式的应用场景
日常生活
在日常生活中,我们经常需要用到乘 法公式,比如购物时计算折扣、计算 利息等。
详细描述
分数乘法是指两个分数之间的相乘。在进行 分数乘法时,需要将分子和分母分别相乘, 然后化简得到最简分数形式。例如,1/2乘 以1/3等于1/6,表示为数学公式为 1/2x1/3=1/6。在进行分数乘法时,需要注 意分子和分母的约简问题,以确保结果的简 洁性和准确性。
a模b的乘法逆元

a模b的乘法逆元
在数学中,特别是在模运算中,一个整数a关于模m的乘法逆元是一个整数b,使得a乘以b模m等于1.换句话说,乘法逆元是满足以下等式的整数b:
(axb)modm=1
这里,mod表示取模运算。
不是所有的整数a都有关于模m的乘法逆元。
事实上,a有关于模m的乘法逆元当且仅当a和m互质,即它们的最大公约数为1.
如果m是质数,那么除了0以外的所有整数都有关于模m的乘法逆元,因为任何整数与质数都是互质的(除了该质数的倍数,但0不是任何数的倍数)。
乘法逆元在密码学和计算机科学中有重要应用,特别是在需要执行模运算的算法中。
要找到a关于模m的乘法逆元,可以使用扩展欧几里得算法。
这个算法可以找到整数x和y,使得ax+my=gcd(a,m),其中gcd(a,m)是a和m的最大公约数。
如果gcd(a,m)=1,那么x就是a关于模m的乘法逆元(可能需要调整为正数或加上m的倍数来得到一个正的结果)。
扩展欧几里得算法求模逆

扩展欧几里得算法求模逆
扩展欧几里得算法是求解两个整数a和b的最大公约数的同时,可以求出一个关于a和b的线性不定方程ax+by=d(其中d是a和b的最大公约数)的一组整数解x和y。
因为在求解过程中,得到的中间结果可以表示成形如sk=t*aj+rj的形式,其中s、t为整数,aj是第j 次迭代计算中的商,rj是该次迭代计算中的余数。
因此,在得到最大公约数d后,可以从最后一个迭代结果开始,逆向推导每一个迭代步骤中的商和余数,然后用反向的迭代公式更新s和t的值,最终求得关于a和b的线性不定方程的一组整数解x和y。
在求模逆的问题中,设正整数a和m满足gcd(a,m)=1,则存在整数x使得ax≡1(mod m)。
这个方程称为模逆的定义式。
利用扩展欧几里得算法可以求解该方程的解x,具体步骤如下:
1. 求解gcd(a,m)的值,如果gcd(a,m)≠1,则不存在模逆,否则继续求解。
2. 用扩展欧几里得算法求解形如ax+my=d(其中d=gcd(a,m))的一组整数解x和y。
3. 因为gcd(a,m)=d,所以有ax+my=d,将该式两侧同除以d,得到(a/d)x+(m/d)y=1,即意味着a/d的系数x就是所求解的模逆。
4. 由于我们只需要一个最小正整数解,因此将x对m取模,即可得到最终的模逆。
综上所述,扩展欧几里得算法可以用来求解模逆,具体步骤包括求最大公约数、求一组线性不定方程的解、将解化简为最小正整数解并取模。
数学中模的运算公式

数学中模的运算公式数学中的模运算公式,这可是个相当有趣的话题!咱先来说说啥是模运算。
比如说,你有一堆糖果,一共 15 个,要平均分给 4 个小朋友,每人能拿到几个呢?用 15 除以 4 ,商是 3 ,余数是 3 。
这个余数 3 就是 15 除以 4 的模。
在数学里,模运算常用的公式有不少呢。
比如说同余定理,若两个整数 a 和 b 除以正整数 m 的余数相同,我们就说 a 和 b 对模 m 同余,记作a ≡ b (mod m) 。
举个例子吧,假设今天是星期一,再过 7 天还是星期一,再过 14 天、21 天依然是星期一。
这是因为 7 、14 、21 除以 7 的余数都是 0 ,它们对模 7 同余。
再比如,在计算机编程里,模运算也经常被用到。
像计算一个数是不是偶数,就可以用这个数对 2 取模,如果余数是 0 ,那就是偶数,否则就是奇数。
我记得有一次给学生们讲模运算,有个小家伙特别迷糊,怎么都理解不了。
我就拿出一堆小积木,分成不同的组,给他比划。
我把 20 个积木分成每组 5 个,然后告诉他 20 除以 5 ,商是 4 ,没有余数,也就是 20 对模 5 同余于 0 。
这小家伙盯着积木看了半天,突然一拍脑袋,说:“老师,我懂啦!”那一刻,我心里那个乐呀,觉得所有的努力都值了。
模运算还有很多应用,比如在密码学中,通过模运算可以对信息进行加密和解密,保护我们的信息安全。
在数论中,模运算也是研究整数性质的重要工具。
总之,模运算公式虽然看起来有点复杂,但只要我们多琢磨,多练习,就会发现它其实挺好玩的,而且用处还特别大。
就像我们生活中的小窍门,掌握了就能解决很多问题。
所以呀,大家可别被它一开始的样子吓到,勇敢地去探索,你会发现数学的世界真是奇妙无穷!。
模逆运算 费马定理

模逆运算费马定理全文共四篇示例,供读者参考第一篇示例:模逆运算和费马定理是数论中两个非常重要的概念和定理。
模逆运算是指在模运算中找到某个数的乘法逆元,而费马定理则是指一种关于素数的性质。
这两个概念和定理在数论和密码学等领域有着广泛的应用和重要性。
首先我们来谈谈模逆运算。
在数学中,模逆运算是指在一个模数的情况下,找到一个数的乘法逆元。
当两个整数a和n互素时,a在模n下存在乘法逆元。
具体来说,如果存在一个整数b,使得ab ≡ 1 (mod n),则称b是a在模n下的乘法逆元。
对于任意一个整数a,在模n下的乘法逆元可能存在也可能不存在。
当存在时,我们可以通过一些数论算法来找到这个乘法逆元。
一种常见的方法是使用扩展欧几里得算法,通过该算法可以找到a在模n下的乘法逆元。
具体的算法过程不在此详述,有兴趣的读者可以自行查阅资料学习。
模逆运算在密码学中有着广泛的应用。
在RSA加密算法中,找到两个大素数p和q的乘法逆元是关键的一步。
只有找到p和q的乘法逆元才能生成RSA的公钥和私钥,从而实现加密和解密的过程。
模逆运算在密码学中扮演着非常重要的角色。
接下来我们来谈谈费马定理。
费马定理是数论中的一条重要定理,它由法国数学家费尔马在17世纪提出并证明。
费马定理的内容是:对于任意一个素数p和整数a,当a不是p的倍数时,有a^(p-1) ≡ 1 (mod p)。
简单来说,费马定理表明,对于素数p和不是p的倍数的整数a,a^(p-1)除以p的余数一定是1。
费马定理在数论中有着广泛的应用。
其中一个重要的应用是在素数检测中。
通过费马定理,我们可以获取一种新的检测素数的方法。
如果对于某个整数a,a^(p-1) ≡ 1 (mod p)不成立,那么p一定不是素数。
这种检测方法在密码学和计算机科学中有着很多重要的应用。
模逆运算和费马定理都是数论中非常重要的概念和定理。
它们在密码学、素数检测等领域有着重要的应用和价值。
深入理解和掌握这两个概念和定理,可以帮助我们更好地理解和应用数学在实际问题中的作用。
乘法原理推导过程

乘法原理推导过程乘法原理是概率论中的一项重要原则,用于计算复合事件的可能性。
它的推导过程如下:假设有两个事件A和B,A的概率为P(A),B的概率为P(B)。
我们希望计算同时发生A和B的概率。
首先,我们可以假设事件A发生的情况下,事件B发生的概率是多少。
这个条件概率可以表示为P(B|A),读作“在A发生的条件下,B 发生的概率”。
根据概率的定义,我们知道事件A和B同时发生的概率可以表示为P(A∩B),读作“A交B的概率”。
根据条件概率的定义,我们可以将P(A∩B)表示为P(A)乘以P(B|A)。
即:P(A∩B) = P(A) × P(B|A)这就是乘法原理的数学表达式。
如果我们希望计算多个事件同时发生的概率,可以通过多次应用乘法原理来推导。
例如,如果有三个事件A、B和C,我们希望计算这三个事件同时发生的概率。
根据乘法原理,我们可以将这个概率表示为:P(A∩B∩C) = P(A) × P(B|A) × P(C|A∩B)这样,我们可以根据需要依次应用乘法原理,计算复合事件的概率。
总而言之,乘法原理是基于条件概率的推导过程,用于计算复合事件的概率。
下面是乘法原理的推导过程:1. 假设有两个事件A和B,A的概率为P(A),B的概率为P(B)。
2. 假设A发生的条件下,B发生的概率为P(B|A)。
3. 根据概率的定义,事件A和B同时发生的概率可以表示为P(A∩B)。
4. 根据条件概率的定义,将P(A∩B)表示为P(A)乘以P(B|A)。
即:P(A∩B) = P(A) × P(B|A)。
5. 进一步应用乘法原理,可以推导出多个事件同时发生的概率。
例如,对于三个事件A、B和C,可以表示为:P(A∩B∩C) = P(A) × P(B|A) × P(C|A∩B)。
这个推导过程帮助我们理解乘法原理的数学表达及其在概率计算中的应用。
初中数学 如何使用乘法公式计算两个多项式的乘积

初中数学如何使用乘法公式计算两个多项式的乘积计算两个多项式的乘积可以使用乘法公式或直接进行乘法运算。
下面我将介绍如何使用乘法公式计算两个多项式的乘积,并给出示例来说明。
假设我们有两个多项式A(x) 和B(x),其中A(x) 和B(x) 的次数分别为m 和n,其表达式为:A(x) = a_m x^m + a_{m-1} x^{m-1} + ... + a_1 x + a_0B(x) = b_n x^n + b_{n-1} x^{n-1} + ... + b_1 x + b_0使用乘法公式计算两个多项式的乘积的具体步骤如下:步骤1:将每个多项式展开为单项式的和。
例如,我们可以将多项式A(x) 展开为:A(x) = a_m x^m + a_{m-1} x^{m-1} + ... + a_1 x + a_0= a_m x^m + (a_{m-1} x^{m-1} + ... + a_1 x + a_0)x^0步骤2:使用乘法公式计算每一对单项式的乘积。
对于每一对单项式的乘积,我们可以使用乘法公式计算。
具体的表达式如下:(a_k x^k) × (b_j x^j) = a_k b_j x^{k+j}步骤3:将所有乘积相加得到结果。
将所有乘积相加得到的结果就是两个多项式的乘积。
示例:计算多项式A(x) = 2x^2 + 3x + 1 和多项式B(x) = x + 1 的乘积。
首先,将每个多项式展开为单项式的和:A(x) = 2x^2 + 3x + 1B(x) = x + 1然后,使用乘法公式计算每一对单项式的乘积:(2x^2) × x = 2x^3(2x^2) × 1 = 2x^2(3x) × x = 3x^2(3x) × 1 = 3x(1) × x = x(1) × 1 = 1将所有乘积相加得到结果:(2x^3 + 3x^2 + 4x + 1)所以,多项式A(x) 和多项式B(x) 的乘积为2x^3 + 3x^2 + 4x + 1。
乘法逆元模的运算规则

乘法逆元模的运算规则模的运算规则运算规则模运算与基本四则运算有些相似,但是除法例外。
其规则如下:(a + b) % p = (a % p + b % p) % p (1)(a - b) % p = (a % p - b % p) % p (2)(a * b) % p = (a % p * b % p) % p (3)(a^b) % p = ((a % p)^b) % p (4)%运算法则1. (a*b) %p= ( a%p) *(b%p) 乘法的2. (a/b) %p= ( a *b^(-1)%p) 除法的结合律:((a+b) % p + c) % p = (a + (b+c) % p) % p (5)((a*b) % p * c)% p = (a * b*c) % p (6)// (a%p*b)%p=(a*b)%p交换律:(a + b) % p = (b+a) % p (7)(a * b) % p = (b * a) % p (8)分配律:((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p (9)重要定理:若a≡b (% p),则对于任意的c,都有(a + c) ≡ (b + c) (%p);(10)若a≡b (% p),则对于任意的c,都有(a * c) ≡ (b * c) (%p);(11)若a≡b (% p),c≡d (% p),则 (a + c) ≡ (b + d) (%p),(a - c) ≡ (b - d) (%p),(a * c) ≡ (b * d) (%p),(a / c) ≡ (b / d) (%p);(12)乘法逆元:定义:满足a*k≡1 (mod p)的k值就是a关于p的乘法逆元。
为什么要有乘法逆元呢?当我们要求(a/b) mod p的值,且a很大,无法直接求得a/b的值时,我们就要用到乘法逆元。
我们可以通过求b关于p的乘法逆元k,将a乘上k再模p,即(a*k) mod p。
人教课标版高中数学选修1-2《复数代数形式的乘除运算》疑难点拨

《复数代数形式的乘除运算》疑难点拨一、复数的乘法运算(1)两个复数相乘,类似于两个多项式相乘,只要在所得的结果中把2i 换成-1,并且把实部与虚部分别合并即可.(2)两个复数的积仍然是一个确定的复数.(3)复数的乘法运算满足交换律、结合律及乘法对加法的分配律,即对于任意123,,z z z C ∈,均有()()()12211231231231213,,z z z z z z z z z z z z z z z z z ⋅=⋅⋅⋅=⋅⋅⋅+=⋅+⋅.(4)实数集R 中正整数指数幂的运算律,在复数集C 中仍然成立,即对任意12,,z z z C ∈及,m n N *∈有()()1212,,n nm n m n m mn n n z z z z z z z z z +⋅==⋅=⋅. 实数集内乘法、乘方的一些重要结论和一些运算法则在复数集内不一定成立.如:①z R ∈时,22,z z z C =∈时,2z R ∈,而222,z C z z ∈∴≠. ②22221212121200,000,z R z z z z z C z z z z ∈+=⇔=∈+=⇒==时,=0且时,且2212120,00.z z z z ==⇒+=但. 例1(★★☆)(1)已知复数122,1z i z i =+=-,则12z z z =⋅在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限(2)以下四个命题:①()414i +=;②()()5743117i i i -+=-;③若复数()()21m i mi ++是实数,则实数1m =-;④若211,,,2222u i v v u =-+=--=则 其中错误的命题的序号为_____.解题导引(1)直接结合复数的乘法运算法则计算.(2)结合复数的乘法运算法则解答,注意2z z z =⋅.例2(★★☆)计算:(l) ()()()2111;i i i +--+(2)()()()1234564i i i i +++-.解题导引 根据复数的乘法法则进行求解.二、共轭复数的理解一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共扼复数.虚部不等于0的两个共轭复数也叫做共轭虚数.设(),z a bi a b R =+∈,则z 的共轭复数记为.z 容易得到22z z z z ⋅==. 特别地,实数a 的共轭复数仍是它本身.互为共扼复数的两个复数在复平面内所对应的点关于实轴对称.特别地,实数和它的共轭复数在复平面内所对应的点重合,且在实轴上.例3(★☆☆)已知21z i i=++,则复数z =( ) A.13i -+B .13i -C .13i --D .13i +解题导引 先求出z ,然后再求z .例4(★☆☆)复数z 满足()11z i i -=+,则复数z 的共轭复数在复平面内的对应点位于( )A.第一象限B.第二象限C.第三象限D.第四象限解题导引 先求1i +的值,然后再求z ,最后得到z ,从而结合复数的几何意义得结果. 三、复数的除法运算()()()22220ac bd bc ad a bi c di i c di c d c d+-+÷+=++≠++. 复数的除法是乘法的逆运算,两个复数相除(除数不为0),所得的商是一个确定的复数.在进行复数的除法运算时,通常先把()()a bi c di +÷+写成 a bi c di++的形式,再把分子与分母都乘分母的共轭复数c di -,化简后可得结果.这与做根式除法类似,在做根式除法时,分子与分母都乘分母的“有理化因式”,从而使分母“有理化”.在做复数除法时,分子与分母都乘分母的“实数化因式”(共轭复数),从而使分母“实数化”.例5(★☆☆)计算:(l)()()22i i +-;(2)()212i +.(3)6 11ii +⎛⎫ ⎪-⎝⎭解题导引直接利用复数的乘除法运算法则求解.参考答案例1答案:见解析解析:(l)()()12213,z z z i i i =⋅=+-=-∴它所对应的点位于第四象限.故选D.(2)①不正确,()()()242214124i i ⎡⎤+=+==-⎣⎦.②正确,因为57,i i i i ==-,故原式()()2431234117i i i i i i =--=--+=-.③正确,原式()()23=1m m m i =-+,由此复数为实数可得310m +=,即1m =-.④正确,2211312244222u i v ⎛⎫=-+=--=--= ⎪ ⎪⎝⎭.故答案为②③④. 导师点睛 (1)复数的乘法运算可将i 看作字母,按多项式乘法的运算法则进行,最后将21i =-代入合并“同类项”即可.(2)复数的乘法运算可以推广,因此,复数可进行乘方运算,常见的有:()()()()22222,,12a bi a b abi a b R i i ±=-±∈±=±等,即实数的乘方公式对复数也成立.例2答案:见解析解析:(1)()()()2111i i i +--+21222i i i =--=-.(2)()()()()()212345643468564i i i i i i i i i +++-=+++⋅+-= ()()25105642530506048516i i i i i i i i -++-=--++-=-+.导师点睛 三个或三个以上的复数相乘可按从左到右的顺序运算或利用结合律运算,复数的混合运算与实数的混合运算一样,对于能够使用乘法公式计算的,用乘法公式更简捷.例3答案:B 解析:()()2113z i i i =++=+,所以13z i =-,故选B.例4答案:D解析:()11122z i i z i -=+⇒==+-,所以22z i =-,对应的点位于第四象限,选D.导师点睛 计算复数(),a bi a b R +∈的共轭复数时,要明确实部为a 、虚部为b ,则其共轭复数为a bi -.例5答案:见解析解析:(1)原式=4-2i =4-(-1)=5.(2)原式=l+4i +(2i )2=l+4i +42i =-3+4i .(3)解法一:原式=())()()62622123125i i i i i ⎡⎤++-+=+=-+⎢⎥⎢⎥+⎣⎦.解法二:原式=()62611.2i i i i i ⎡⎤+=+=-+⎢⎥⎢⎥⎣⎦导师点睛 复数乘法可类比多项式乘法进行,注意21i =-;复数除法,若为÷“”连接的式子,应先写成分式的形式,然后分子、分母同时乘分母的共轭复数,完成分母“实数化”.。
除法求模中求逆元的两种方法

除法求模中求逆元的两种⽅法 ⾸先对于模运算来说,是没有对于除法的取模的(即没有(a/b)%mod==a%mod/b%mod),但是在很多题⽬中都涉及到除法取模,所以就必须要了解或者掌握,对于除法取模以(a/b)%mod来说,我们⾸先需要得到b的逆元,根据逆元的定理对于正整数a和m,如果有,那么把这个同余⽅程中x的最⼩正整数解叫做a模m的逆元。
然后就是求逆元的两种⽅法。
第⼀种⽅法就是⽐较普遍的,也是挺基础的,就是通过费马⼩定理来求,但是要求mod必须是素数(⼀般题⽬中都会是1e9+7)。
费马⼩定理:假如a是,p是,则a,p显然(即两者只有⼀个1),那么我们可以得到费马⼩定理的⼀个特例,即当p为质数时候, a^(p-1)≡1(mod p)。
即可以得到a*a^(p-1)=1(%M); 也是我们就可以将除法取模转化为乘法取模 (a/b)%mod==a*b^(mod-2)%mod,但是对于b^(mod-2)来说,也挺难算的,这⾥就需要⽤到快速幂。
最后贴上代码⽚段const long long mod=1e9+7;long long power_mod(long long a, long long b, long long mod){long long ans = 1;while (b){if (b & 1) ans = ans * a % mod;a = a * a % mod;b >>= 1;}return ans;}a*power_mod(b,mod-2,mod)%mod 第⼆种⽅法就是通过拓展欧⼏⾥得算法求逆元 扩展欧⼏⾥得定理:对于不完全为 0 的⾮负整数 a,b,gcd(a,b)表⽰ a,b 的最⼤公约数,必然存在整数对 x,y ,使得gcd(a,b)=ax+by。
对于乘法逆元来说 a*x≡1(mod m)也就等价于 a*x + m*y ==1 即当gcd(a,m)==1时就有拓展欧⼏⾥得定理,即求解这个⽅程解出的x就是a的逆元。
模逆运算快速算法

模逆运算快速算法模逆运算快速算法——扩展的Euclid 算法与扩展的Stein 算法(1)扩展的Euclid 算法求模逆的传统算法是扩展的Euclid 算法,该算法是在用Euclid 算法求取二个数的最大公因子时,若最大公因子为1,说明二个数互素,则可同时得出二者的乘法逆元。
算法描述如下:输入:二个整数a 、b ,设b a >输出:a 与b 的最大公因子;若二者互素,同时得出乘法逆元Step 1: ),0,1(),,(321a X X X ←,),1,0(),,(321N Y Y Y ← Step 2: if 03=Y then return ),gcd(3b a X =,no inverseStep 3: if 13=Y then return ),gcd(3b a Y =,a Y b mod 21=-,b b Y a mod )(11+=- Step 4: ??33X Q =Step 5: ),,(),,(332211321QY X QY X QY X T T T ---← Step 6: ),,(),,(321321Y Y Y X X X ← Step 7: ),,(),,(321321T T T Y Y Y ←Step 8: goto Step 2 (2)扩展的Stein 算法较之扩展的Euclid 算法,扩展的Stein 算法可以得到更高的执行效率。
Stein 算法基于以下求取二个数公因子的基本性质: 1)若a 与b 都是偶数,则)2,2gcd(2),gcd(b a b a = 2)若a 为偶数、b 为奇数,则),2gcd(),gcd(b a b a = 3)若a 与b 都是奇数,则),2)(gcd(),gcd(b b a b a -=由于除2在二进制运算中仅做一次移位操作,因此可以说Stein 算法主要只用到了减法,通过计算复杂性分析可知,在最坏情况下,Stein 算法所需减法次数为)13()(-+lb a lb 。
代数式的乘除运算

代数式的乘除运算代数式中的乘除运算是代数学中非常重要的一部分。
它涉及多个数的相乘或相除操作,是解决代数问题的基础。
在本文中,我将详细介绍代数式的乘法和除法运算,并提供一些实例帮助读者更好地理解这些概念。
一、代数式的乘法运算代数式的乘法运算是指将两个或多个代数项相乘,其中每个代数项可以包括变量和常数的乘积。
在乘法运算中,我们需要遵循以下几个原则:1. 乘法的交换律:a × b = b × a。
即乘法运算下,两个乘积的顺序可以交换。
2. 乘法的结合律:(a × b) × c = a × (b × c)。
即乘法运算下,多个乘积的组合方式不影响最终的结果。
3. 乘法的分配律:a × (b + c) = a × b + a × c。
即乘法运算可以通过分配律进行展开。
例如,考虑以下代数式:2x × (3y + 4)。
根据分配律,我们可以将该式子展开为:2x × 3y + 2x × 4。
然后,我们可以继续将这两个乘积进行计算,并化简得到最终结果。
二、代数式的除法运算代数式的除法运算是指将一个代数式除以另一个代数式,同样涉及到变量和常数间的相除操作。
在除法运算中,我们需要注意以下几个原则:1. 除法的除数不能为零。
若除数为零,则运算无意义。
2. 除法的整除关系:如果a能被b整除,即a ÷ b的结果为整数,则称a是b的倍数。
3. 除法的分配律:(a + b) ÷ c = a ÷ c + b ÷ c。
即除法运算可以通过分配律进行展开。
例如,考虑以下代数式:(6x^2 + 9x) ÷ 3。
根据分配律,我们可以将该式子展开为:6x^2 ÷ 3 + 9x ÷ 3。
然后,我们可以分别对这两个式子进行除法运算,并得到最终结果。
三、乘除运算的应用实例为了更好地理解代数式的乘除运算,以下是一些应用实例:实例一:计算表达式 (5x + 3) × (2x - 4) 的结果首先,根据乘法的分配律,我们可以展开该式子为:5x × 2x - 5x ×4 + 3 × 2x - 3 × 4。
模ab乘模ac

模ab乘模ac【原创实用版】目录一、引言二、模的概念与性质1.模的定义2.模的性质三、模 ab 乘模 ac 的运算方法1.模 ab 乘模 ac 的公式表示2.模 ab 乘模 ac 的具体计算过程四、模 ab 乘模 ac 的应用案例五、结论正文一、引言在数学领域,模运算是一种常见的运算方式,特别是在代数和数论等领域有广泛的应用。
在模运算中,我们经常会遇到模 ab 乘模 ac 的情况,那么我们应该如何进行计算呢?本文将从模的概念与性质入手,详细介绍模 ab 乘模 ac 的运算方法及其应用案例。
二、模的概念与性质1.模的定义模,又称模运算,是指在整数环中,对于给定的整数 a 和 b,将整数 m 按照 a 和 b 的最大公约数进行约分,得到的商即为模 ab。
通常表示为:m ≡ n (mod ab),其中 n 为整数,ab 为整数环中的整数。
2.模的性质模运算具有以下性质:(1)封闭性:对于任意整数 m、n,m ≡ n (mod ab) 时,m 与 n 的模 ab 运算结果相等。
(2)结合律:对于任意整数 m、n、p,(m ≡ n (mod ab)) ≡ (n ≡p (mod ab)) ≡ (m ≡ p (mod ab)) (mod ab)。
(3)分配律:对于任意整数 m、n、p,m ≡ n (mod ab) 且 n ≡ p (mod ac),则 m ≡ p (mod ac)。
(4)齐次性:对于任意整数 m、n,m ≡ n (mod ab) 当且仅当 m 与n 对模 ab 取模后相等。
三、模 ab 乘模 ac 的运算方法1.模 ab 乘模 ac 的公式表示模 ab 乘模 ac 的运算公式可以表示为:(m1 * m2) ≡ (m1 ≡ n1 (mod ab)) * (m2 ≡ n2 (mod ac)) ≡ n1 * n2 (mod ab * ac)。
2.模 ab 乘模 ac 的具体计算过程假设 m1 ≡ n1 (mod ab),m2 ≡ n2 (mod ac),我们需要计算 (m1 * m2) ≡ n1 * n2 (mod ab * ac)。
a-b的模公式

a-b的模公式模运算是计算机科学中非常重要的概念,它在密码学、计算机图形学、计算机网络和算法设计等诸多领域中被广泛应用。
在模运算中,一个数被取模后,所得的余数将在一个有限的范围内循环。
本文将介绍模运算的一种常见应用:求解a-b的模公式,并详细解释其计算原理和实际应用场景。
模运算的数学定义如下:对于整数a和正整数m,若存在整数q和r,使得a = qm + r 且0 ≤ r < m,则我们称r为a模m的余数,记作r ≡ a(mod m)。
a-b的模公式可以表示为:a-b ≡ (a mod N - b mod N + N) mod N,其中N是一个正整数。
在很多应用场景中,我们需要求解两个数之间的差值,并将其对一个给定的正整数取模。
在密码学中,我们需要使用模运算来加密和解密信息。
在图像处理和计算机视觉中,模运算被用来处理十六进制颜色码和像素点的坐标。
在计算机网络中,模运算被用来处理IP地址和端口号。
那么,如何求解a-b的模公式呢?考虑以下两种情况:1. 当a≥b时我们分别将a和b对N取模,并得到a mod N和b mod N。
然后,我们求出它们的差值,即(a mod N - b mod N),并加上N得到一个正数。
我们将其对N取模,即可得到a-b对N 取模的余数。
数学公式如下:a-b ≡ (a mod N - b mod N + N) mod N2. 当a<b时如果a<b,则可以将(a-b)改写为(a-b+N),使其成为一个正数,并进行与第一种情况相同的计算步骤。
我们可以得出a-b的模公式:a-b ≡ (a mod N - b mod N + N) mod N。
需要注意的是,N必须为正整数,否则无法进行模运算。
以上就是求解a-b的模公式的方法和原理,下面介绍一些实际应用场景。
1.密码学在密码学中,模运算被用来实现加密和解密算法。
私钥加密算法和公钥加密算法都需要使用模运算。
RSA算法就是一种基于模运算的公钥加密算法。
