大学物理练习册解答2

合集下载

大学物理（二）练习册答案

1 大学物理（二）练习册参考解答第12章真空中的静电场一、选择题1(D)，2(C)，3(C)，4(A)，5(C)，6(B)，7(C)，8(D)，9(D)，10(B)，二、填空题(1). 电场强度和电势，0/q F E=，l E q W U aaò×==00d /(U 0=0). (2). ()042e /q q+，q 1、q 2、q 3、q 4 ；(3). 0，l / (2e 0)；(4). s R / (2e 0) ；(5). 0 ；(6). ÷÷øöççèæ-p 00114r r qe ；(7). －2³103 V ；(8). ÷÷øöççèæ-p a br r q q 11400e (9). 0，pE sin a ；(10). ()i a x A2+-.三、计算题1. 如图所示，真空中一长为L 的均匀带电细直杆，总电荷为q ，试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度．解：设杆的左端为坐标原点O ，x 轴沿直杆方向．带电直杆的电荷线密度为l =q / L ，在x 处取一电荷元d q = l d x = q d x / L ，它在P 点的场强：()204d d x d L qE -+p =e ()204d x d L L xq -+p =e 总场强为ò+p =Lx d L x Lq E 020)(d 4－e ()d L d q +p =04e 方向沿x 轴，即杆的延长线方向．2．一个细玻璃棒被弯成半径为R 的半圆形，沿其上半部分均匀分布有电荷+Q ，沿其下半部分均匀分布有电荷－Q ，如图所示．试求圆心O 处的电场强度．解：把所有电荷都当作正电荷处理. 在q 处取微小电荷d q = l d l = 2Q d q / p 它在O 处产生场强Ldq P +Q－QROxyＰLdd qx (L+d －x ) d ExOq e e d 24d d 20220RQRq E p =p =按q 角变化，将d E 分解成二个分量：分解成二个分量：q q e q d sin 2sin d d 202RQE E x p ==q q e q d cos 2cos d d 202RQE E y p -=-=对各分量分别积分，积分时考虑到一半是负电荷对各分量分别积分，积分时考虑到一半是负电荷úûùêëé-p =òòpp p q q q q e 2/2/0202d sin d sin 2R QE x ＝0 2022/2/0202d cos d cos 2R Q R QE y e q q q q e pp p p -=úûùêëé-p -=òò所以所以j R Q j E i E E y x202e p -=+=3. “无限长”均匀带电的半圆柱面，半径为R ，设半圆柱面沿轴线OO'单位长度上的电荷为l ，试求轴线上一点的电场强度．，试求轴线上一点的电场强度．解:设坐标系如图所示．将半圆柱面划分成许多窄条．d l 宽的窄条的电荷线密度为荷线密度为q l l l d d d p=p =l R取q 位置处的一条，它在轴线上一点产生的场强为位置处的一条，它在轴线上一点产生的场强为q e l e l d 22d d 020RR E p =p =如图所示. 它在x 、y 轴上的二个分量为：轴上的二个分量为：d E x =d E sin q , d E y =－d E cos q 对各分量分别积分对各分量分别积分 R R E x 02002d sin 2e lq q e l pp =p =ò 0d c o s 202=p -=òp q q e lRE y场强场强 i Rj E i E E y x02e lp =+=4. 实验表明，在靠近地面处有相当强的电场，电场强度E垂直于地面向下，大小约为100 N/C ；在离地面1.5 km 高的地方，E也是垂直于地面向下的，大小约为25 N/C ． (1) 假设地面上各处E都是垂直于地面向下，试计算从地面到此高度大气中电荷的平均体密度；体密度；(2) 假设地表面内电场强度为零，假设地表面内电场强度为零，且地球表面处的电场强度完全是由均匀分布在地表面且地球表面处的电场强度完全是由均匀分布在地表面的电荷产生，求地面上的电荷面密度．(已知：真空介电常量0e ＝8.85³10-12 C 2²N -1²m -2) d qR Oxyqd qqq d E y y d l d q R q O d E xx d EOR’O'解：(1) 设电荷的平均体密度为r ，取圆柱形高斯面如图(1)(侧面垂直底面，底面D S 平行地面)上下底面处的上下底面处的场强分别为E 1和E 2，则通过高斯面的电场强度通量为：，则通过高斯面的电场强度通量为：òòE²S d ＝E 2D S -E 1D S ＝(E 2-E 1) D S 高斯面S 包围的电荷∑q i ＝h D S r由高斯定理(E 2－E 1) D S ＝h D S r /e∴ () E Eh121-=er ＝4.43³10-13 C/m 3(2) 设地面面电荷密度为s ．由于电荷只分布在地表面，所以电力线终止于地面，取高斯面如图(2) 由高斯定理由高斯定理òòE ²S d =åi 01q e-E D S =SD se1∴ s=－e 0 E ＝－8.9³10-10 C/m 35. 一半径为R 的带电球体，其电荷体密度分布为的带电球体，其电荷体密度分布为r =Ar (r ≤R ) ， r =0 (r ＞R )， A 为一常量．试求球体内外的场强分布．为一常量．试求球体内外的场强分布．解：在球内取半径为r 、厚为d r 的薄球壳，该壳内所包含的电荷为的薄球壳，该壳内所包含的电荷为 r r Ar V q d 4d d 2p ×==r在半径为r 的球面内包含的总电荷为的球面内包含的总电荷为 403d 4Ar r Ar dV q rV p =p ==òòr (r ≤R) 以该球面为高斯面，按高斯定理有以该球面为高斯面，按高斯定理有 0421/4e Ar r E p =p ×得到得到 ()0214/e ArE =， (r ≤R ) 方向沿径向，A >0时向外, A <0时向里．时向里．在球体外作一半径为r 的同心高斯球面，按高斯定理有的同心高斯球面，按高斯定理有0422/4e AR r E p =p ×得到得到 ()20424/rAR E e =， (r >R ) 方向沿径向，A >0时向外，A <0时向里．时向里．6. 如图所示，一厚为b 的“无限大”带电平板的“无限大”带电平板，其电荷体密度分布为r ＝kx (0≤x ≤b )，式中，式中k 为一正的常量．求：为一正的常量．求： (1) 平板外两侧任一点P 1和P 2处的电场强度大小；处的电场强度大小；(2) 平板内任一点P 处的电场强度；处的电场强度； (3) 场强为零的点在何处？场强为零的点在何处？解：解： (1) 由对称分析知，平板外两侧场强大小处处相等、方向垂直于平面且背离平面．设场强大小为E ．作一柱形高斯面垂直于平面．其底面大小为S ，如图所示．，如图所示．E(2)xbP 1 P 2Px OSE 2D SE 1(1) h按高斯定理åò=×0e /d q S E S ，即，即 020002d d 12e e r e kSbx x kSxS SEb b ===òò得到得到 E = k b kb 2 / (4e 0) (板外两侧) (2) 过P 点垂直平板作一柱形高斯面，底面为S ．设该处场强为E ¢，如图所示．按高斯定理有定理有()022ee k S bx d x kSSE Ex==+¢ò得到得到 ÷÷øöççèæ-=¢22220b x k E e (0≤x ≤b ) (3) E ¢=0，必须是0222=-bx ，可得2/b x =7. 一“无限大”平面，中部有一半径为R 的圆孔，设平面上均匀带电，电荷面密度为s ．如图所示，试求通过小孔中心O 并与平面垂直的直线上各点的场强和电势(选O 点的电势为零)．解：将题中的电荷分布看作为面密度为s 的大平面和面密度为－s 的圆盘叠加的的圆盘叠加的结果．选x 轴垂直于平面，坐标原点Ｏ在圆盘中心，大平面在x 处产生的场强为处产生的场强为 i xx E012e σ=圆盘在该处的场强为圆盘在该处的场强为i x R x x E÷÷øöççèæ+--=2202112e σ ∴ i xR xE E E 220212+=+=e σ 该点电势为该点电势为()22222d 2xRR xR xx U x+-=+=òe se s8. 一半径为R 的“无限长”圆柱形带电体，其电荷体密度为r =Ar (r ≤R )，式中A 为常量．试求：求：(1) 圆柱体内、外各点场强大小分布；圆柱体内、外各点场强大小分布； (2) 选与圆柱轴线的距离为l (l ＞R ) 处为电势零点，计算圆柱体内、外各点的电势分布．解：(1) 取半径为r 、高为h 的高斯圆柱面(如图所示)．面上各点场强大小为E 并垂直于柱面．则穿过该柱面的电场强度通量为：面．则穿过该柱面的电场强度通量为：xS P SE ESSEd xb E ¢sOROxPòp =×SrhE S E2d 为求高斯面内的电荷，r ＜R 时，取一半径为r ¢，厚d r ¢、高h 的圆筒，其电荷为的圆筒，其电荷为r r Ah V ¢¢p =d 2d 2r则包围在高斯面内的总电荷为则包围在高斯面内的总电荷为3/2d 2d 32Ahrr r Ah V rVp =¢¢p =òòr由高斯定理得由高斯定理得 ()033/22e Ahr rhE p =p 解出解出 ()023/e Ar E = (r ≤R ) r ＞R 时，包围在高斯面内总电荷为：时，包围在高斯面内总电荷为：3/2d 2d 32AhRrrAh VRVp=¢¢p=òòr由高斯定理由高斯定理 ()033/22e A h R r h E p =p 解出解出 ()r AR E 033/e = (r >R ) (2) 计算电势分布计算电势分布r ≤R 时 òòò×+==lRRrlrrr AR r r A r E U d 3d 3d 0320e e()Rl AR rR A ln 3903330e e +-=r ＞R 时 rl AR rr AR rE Ulrl rln3d 3d 033e e =×==òò9．一真空二极管，其主要构件是一个半径R 1＝5³10-4 m 的圆柱形阴极A 和一个套在阴极外的半径R 2＝4.5³10-3 m 的同轴圆筒形阳极B ，如图所示．阳极电势比阴极高300 300 VV ，忽略边缘效应. 求电子刚从阴极射出时所受的电场力．(基本电荷e ＝1.6³10-19 C) 解：与阴极同轴作半径为r (R 1＜r ＜R 2 )的单位长度的圆柱形高斯面，设阴极上电荷线密度为l ．按高斯定理有．按高斯定理有 2p rE = l / e 0 得到得到 E = l / (2p e 0r ) (R 1＜r ＜R 2) 方向沿半径指向轴线．两极之间电势差方向沿半径指向轴线．两极之间电势差òòp -=×=-21d 2d 0R R BAB A rr r E U U el120ln 2R R elp -=得到得到()120/ln 2R R UUAB-=p e l，所以所以 ()rR R UUE AB1/ln 12×-=在阴极表面处电子受电场力的大小为在阴极表面处电子受电场力的大小为 ()()11211/c R RR UUeReE F AB×-==＝4.37³10-14 N 方向沿半径指向阳极．方向沿半径指向阳极．RrhABR 2 R 1四研讨题1. 真空中点电荷q 的静电场场强大小为的静电场场强大小为 241rq E pe=式中r 为场点离点电荷的距离．当r →0时，E →∞，这一推论显然是没有物理意义的，应如何解释？何解释？参考解答：参考解答：点电荷的场强公式仅适用于点电荷，当r →0时，任何带电体都不能视为点电荷，所以点电荷场强公式已不适用．点电荷场强公式已不适用．若仍用此式求场强E ，其结论必然是错误的．当r →0时，需要具体考虑带电体的大小和电荷分布，这样求得的E 就有确定值．就有确定值．2. 用静电场的环路定理证明电场线如图分布的电场不可能是静电场．参考解答：参考解答：证：在电场中作如图所示的扇形环路abcda ．在ab 和cd 段场强方向与路径方向垂直．在bc 和da 段场强大小不相等（电力线疏密程度不同）而路径相等．因而同）而路径相等．因而d d d ¹×¢-×=×òòòc ba d l E l E l E 按静电场环路定理应有0d =×òl E ，此场不满足静电场环路定理，所以不可能是静电场．此场不满足静电场环路定理，所以不可能是静电场．3. 如果只知道电场中某点的场强，能否求出该点的电势？如果只知道电场中某点的电势，能否求出该点的场强？为什么？能否求出该点的场强？为什么？参考解答：参考解答：由电势的定义：由电势的定义： ò×=零势点场点l E U d式中E为所选场点到零势点的积分路径上各点的场强，所以，如果只知道电场中某点的场强，而不知道路径上各点的场强表达式，不能求出该点的电势。

大学物理练习册答案(下册)-

（1） x Acos( 2π t )
T
（2）
x Acos( 2π t 1 )
T2
（3）x Acos( 2π t 1 ) （4） x Acos( 2π t 3 )
T3
T4
2.两位外星人A和B生活在一个没有自转，没有大气，表面光滑的匀质球形小星球上。有一次他们决定进行一场比赛，从他们所在的位置出发，各自采用航天技术看谁能先达到星球的对径位置。A计划穿过星体直径凿一条通道，采用自由下落方式到达目标位置；B计划沿着紧贴着星球表面的空间轨道，象人造卫星一样航行到目标位置。试问A和B谁会赢得比赛？
C. 1 , 1 ,0.05 22
D. 2,2,0.05
9. 一列机械横波在t时刻的波形曲线如图所示，则该时刻能量为最大值的媒y质质元的位置是:
A. o, b, d, f B. a, c, e, g O'
C. o, d
D. b, f O
d
a
eg
c
b
fx
(二) 填空题 1.一横波的波动方程为: y 0.01cos(250πt 10πx)(m)
解: 以星球中心为原点在直径通道上设置x轴，A在x处受引力:
Fx
G
Mm R3
x
（注: 只有半径为x的星球部分对A有引力）
式中M为星球质量, R为星球半径, m为A的质量
A做简谐振动, 周期为 T 2 m / k k GMm / R3
A到达目标所需的时间为 tA T / 2 R R / GM B以第一宇宙速度做圆周运动 vB GM / R B到达目标所需的时间为 tB R / vB R R / GM
4. 一质点在x轴上作谐振动振幅A=4cm, 周期T=2s, 其平衡位置取作坐标原点, 若t=0时刻近质点第一次通过x=-2cm处, 且向x轴正方向运动, 则质点第二次通过 x=-2cm,处时刻为:[]

(完整版)《大学物理》习题册题目及答案第2单元动量守恒定律

第2单元动量守恒定律序号学号姓名专业、班级一选择题[ B ]1. 力i F t 12=(SI)作用在质量m ＝2 kg 的物体上，使物体由原点从静止开始运动，则它在3秒末的动量应为：(A) －54i kg ⋅m ⋅s -1(B) 54i kg ⋅m ⋅s -1(C) －27i kg ⋅m ⋅s -1 (D) 27i kg ⋅m ⋅s-1[ C ]2. 如图所示，圆锥摆的摆球质量为m ，速率为v ，圆半径为R ，当摆球在轨道上运动半周时，摆球所受重力冲量的大小为：(A) mv 2 (B)()()22/2v R mg mv π+(C)vRmgπ (D) 0[ A ]3 .粒子B 的质量是粒子A 的质量的4倍。

开始时粒子A 的速度为()j i ϖϖ43+，粒子B 的速度为(j i ϖϖ72-)。

由于两者的相互作用，粒子A 的速度为()j i ϖϖ47-，此时粒子B 的速度等于：(A) j i 5- (B) j i ϖϖ72- (C) 0 (D) j i ϖϖ35-[ C ]4. 水平冰面上以一定速度向东行驶的炮车，向东南（斜向上）方向发射一炮弹，对于炮车和炮弹这一系统，在此过程中（忽略冰面摩擦及空气阻力）（A ）总动量守恒（B ）总动量在炮身前进的方向上的分量守恒，其它方向动量不守恒 (C) 总动量在水平面上任意方向的分量守恒，竖直方向分量不守恒（D ）动量在任何方向的分量均不守恒二填空题1. 一颗子弹在枪筒里前进时所受的合力大小为t F 31044005⨯-=(SI)，子弹从枪口射出的速率为3001s m -⋅。

假设子弹离开枪口时合力刚好为零，则(1) 子弹走完枪筒全长所用的时间 t ＝ 0.003 s ,(2) 子弹在枪筒中所受的冲量 I ＝ s N 6.0⋅ ， (3) 子弹的质量 m ＝ 2 ×10-3 kg 。

2. 质量m 为10kg 的木箱放在地面上，在水平拉力F 的作用下由静止开始沿直线运动，其拉力随时间的变化关系如图所示。

大学物理习题册及解答第二版刚体的定轴转动

Z
R
由平行轴定理，关于刀口的转动惯量为 J zo J zc MR 2 2MR 2
（2）由垂直轴定理有： J J 1 J MR2
由平行轴定理有：
J
xC
J
yC
2
MR2
zC
3
2 MR 2
PP
xC
（3）复摆的摆动周期为 T 2π J
2
mgl
T 2 2R T 2 3R
T1 4 1.1547
2.力矩的定义式为_M_____r__F_．
在力矩作用下，一个绕轴转动的物体作_变__角__动_量_运动．若系统所受的合外力矩为零，则系统的____角__动_量_____守恒．
3 质量为20 kg、边长为1.0 m的均匀立方物体，放在水平地面上．有一拉力F作用在该物体一顶边的中点，且与包含该顶边的物体侧面垂直，如图所示．地面极粗糙，物体不可能滑动．若要使该立方体翻转90°，则拉力F不能小于___
(A) 动量守恒．
(B) 机械能守恒．
(C) 对转轴的角动量守恒．
(D) 动量、机械能和角动量都守恒．
(E) 动量、机械能和角动量都不守恒．
7．花样滑冰运动员绕通过自身的竖直轴转动，开始时两臂伸开，
转动惯量为J0，角速度为0，然后她将两臂收回，使转动惯量减少
为J0
/3,这时她转动的角速度变为
(A) 1 (B) 1
分析：
2as
2 0
2 02
a r
0 r0
s
r
N
2
13.3圈
02 0.024rad / s2 2
4．一轻绳跨过一具有水平光滑轴、质量为M的定滑轮，绳的两端分别悬有质量为m1和m2的物体(m1 >m2）．绳与轮之间无相对滑动．若某时刻滑轮沿逆时针方向转动，则绳中的张力

大学物理练习册习题解答(1-22上)

练习一运动的描述（一）1．（D ）2.（D ） 3．217,5s m sm 4．mmπ5,105．（1）s m t x V 5.0-=∆∆= （2）()s m v t t dt dx v 62,692-=-==（3）()()()()质点反向运动时，,05.125.25.1215.1===⨯-⨯+⨯-⨯=v s t m S6．答：矢径是从坐标原点至质点所在位置的有向线段。

位移是由前一时刻质点所在位置引向后一时刻质点所在位置的有向线段，它们的一般关系为0r r r -=∆ 若把坐标原点选在质点的初始位置，则00=r，任意时刻质点对此位置的位移为r r =∆，即此时r既是矢径也是位移。

练习二运动的描述（一）1．()()s m t t s radtt 612,34223-- 2．（c ） 3．三，三至六 4．s m s m s m 20,3103.17=5．1032,224,432102+===∴===⎰⎰⎰⎰t x dt t dx tv tdt dv t dt dv a txvt6．根据已知条件确定常量K 222224,4,4RtR v t s d ra Rtv tk ======ωωω22222228.3532168841sm a a a sm R v a s m Rt dt v d a sm Rtv s t n n =+=========ττ时，练习三运动定律与力学中的守恒定律（一）1．（D ） 2. （C ）3．4．5．因绳子质量不计，所以环受到的摩擦力在数值上等于张力T ，设2m 对地加速度为/2a ，取向上为正；1m 对地加速度为1a （亦即绳子的加速度）向下为正，⎪⎩⎪⎨⎧-==-=-21/2/222111aa a a m g m T a m T g m()()()212121/22121221222112m m a m g m m a m m m m a g T m m a m g m m a +--=+-=++-=解得：6．(1)子弹进入沙土后受力为－kv,由牛顿定律有mt k vv tev v v dv dt mk vdv dt mk dtdv mkv -=∴=-=-∴=-⎰⎰00,,（2）求最大深度()()kv mv x ev k m x dtev dx dt dx v mkt mkt 00max 00,1,=-=∴=∴=--练习四运动定律与力学中的守恒定律（二）1．（C ）2.（B ） 3．s m S N 24,140⋅()()sm m mv I v mv mv I sN dtt dt F I t t 24,14040301212221=+=∴-=⋅=+==⎰⎰4．2221221,m t F m m t F m m t F ∆++∆+∆5．（1）系统在水平方向动量守恒。

四川大学物理习题册第五章解答2

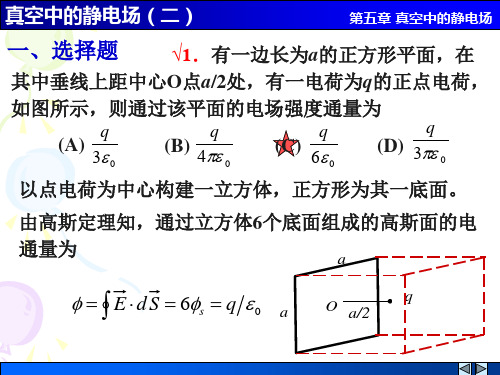
x2
r02

真空中的静电场（二）
第五章真空中的静电场
s E1 2 0
取x轴正方向为正
E2

s 2 0
1
x
x2

r02

x 0,
E

E1

E2

s 2 0

s 2 0
1
x x2
r02

2 0
sx
x2 r02
x 0,
面上均匀带电，电荷面密度为s．试求通过小孔中心O并
与平面垂直的直线上各点的场强和电势．（提示：选O 点的电势为零）．
解: 用割补法，该带电体=无限大平面(+s) +圆屏(-s)
由高斯定理可得，无限大平面场强
s E1 2 0 x 由场强叠加原理可得，圆屏场强
E2

s 2 0
1
x
为常数，则场强分布为 Ex=
，Ey=
.
U Ex x 2Ax
Ey
U y
2By
真空中的静Hale Waihona Puke 场（二）第五章真空中的静电场
三、计算题 1. 如图,带电细线弯成半径为R的半圆形，
电荷线密度为=0sinq，式中0为一常数，q为半径R与
x轴所成的夹角．试求环心O处的电场强度．
解: 在细线取一线段元,由点电荷的场强公式有
d
E

dq
4 0R2
er

0
sinq Rdq 4 0R2
cosq i sinq j
y E
dE
0

sinq cosq i sin2 q j dq

大学物理上练习册第2章《刚体定轴转动》答案-2013

第2章刚体定轴转动一、选择题1(B)，2(B)，3(C)，4(C)，5(C) 二、填空题(1). 62.5 1.67ｓ (2). 4.0 rad/ (3). 0.25 kg ·m 2(4). mgl μ21参考解：M ＝⎰M d ＝()mgl r r l gm l μμ21d /0=⎰(5). 2E 0三、计算题1. 如图所示，半径为r 1＝0.3 m 的A 轮通过皮带被半径为r 2＝0.75 m 的B 轮带动，B 轮以匀角加速度π rad /s 2由静止起动，轮与皮带间无滑动发生．试求A 轮达到转速3000 rev/min 所需要的时间．解：设A 、B 轮的角加速度分别为βA 和βB ，由于两轮边缘的切向加速度相同， a t = βA r 1 = βB r 2则 βA = βB r 2 / r 1 A 轮角速度达到ω所需时间为()75.03.060/2300021⨯π⨯π⨯===r r t B Aβωβωs ＝40 s2.一砂轮直径为1 m 质量为50 kg ，以 900 rev / min 的转速转动．撤去动力后，一工件以 200 N 的正压力作用在轮边缘上，使砂轮在11.8 s 内停止．求砂轮和工件间的摩擦系数．(砂轮轴的摩擦可忽略不计，砂轮绕轴的转动惯量为21mR 2，其中m 和R 分别为砂轮的质量和半径).解：R = 0.5 m ，ω0 = 900 rev/min = 30π rad/s ，根据转动定律 M = -J β ① 这里 M = -μNR ②μ为摩擦系数，N 为正压力，221mR J =． ③ 设在时刻t 砂轮开始停转，则有： 00=+=t t βωω从而得 β＝-ω0 / t ④将②、③、④式代入①式，得 )/(2102t mR NR ωμ-=- ∴ m =μR ω0 / (2Nt )≈0.5r1. 有一半径为R 的圆形平板平放在水平桌面上，平板与水平桌面的摩擦系数为μ，若平板绕通过其中心且垂直板面的固定轴以角速度ω0开始旋转，它将在旋转几圈后停止？（已知圆形平板的转动惯量221mR J =，其中m 为圆形平板的质量）解：在r 处的宽度为d r 的环带面积上摩擦力矩为r r r R mgM d 2d 2⋅π⋅π=μ总摩擦力矩 mgR M M R μ32d 0==⎰故平板角加速度 β =M /J设停止前转数为n ，则转角 θ = 2πn由 J /Mn π==4220θβω可得 g R MJ n μωωπ16/342020=π=2. 一转动惯量为J 的圆盘绕一固定轴转动，起初角速度为ω0．设它所受阻力矩与转动角速度成正比，即M ＝－k ω (k 为正的常数)，求圆盘的角速度从ω0变为021ω时所需的时间．解：根据转动定律： J d ω / d t = -k ω ∴ t J kd d -=ωω两边积分：⎰⎰-=t t J k02/d d 100ωωωω得 ln2 = kt / J∴ t ＝(J ln2) / k5.一质量为m 的物体悬于一条轻绳的一端，绳另一端绕在一轮轴的轴上，如图所示．轴水平且垂直于轮轴面，其半径为r ，整个装置架在光滑的固定轴承之上．当物体从静止释放后，在时间t 内下降了一段距离S ．试求整个轮轴的转动惯量(用m 、r 、t 和S 表示)．解：设绳子对物体(或绳子对轮轴)的拉力为T ，则根据牛顿运动定律和转动定律得：mg T ＝ma ① T r ＝J β ② 由运动学关系有： a = r β ③ 由①、②、③式解得： J ＝m ( g －a ) r 2 / a ④ 又根据已知条件 v 0＝0 ∴ S ＝221at ， a ＝2S / t 2 ⑤将⑤式代入④式得：J ＝mr 2(Sgt22－1)3.如图所示，设两重物的质量分别为m 1和m 2，且m 1＞m 2，定滑轮的半径为r ，对转轴的转动惯量为J ，轻绳与滑轮间无滑动，滑轮轴上摩擦不计．设开始时系统静止，试求t 时刻滑轮的角速度．解：作示力图．两重物加速度大小a 相同，方向如图.m 1g －T 1＝m 1a T 2－m 2g ＝m 2a 设滑轮的角加速度为β，则 (T 1－T 2)r ＝J β 且有 a ＝r β 由以上四式消去T 1，T 2得： ()()J r m m gr m m ++-=22121β 开始时系统静止，故t 时刻滑轮的角速度．()()Jrm m grt m m t ++-==22121 βω7.一根放在水平光滑桌面上的匀质棒，可绕通过其一端的竖直固定光滑轴O 转动．棒的质量为m = 1.5 kg ，长度为l = 1.0 m ，对轴的转动惯量为J = 231ml ．初始时棒静止．今有一水平运动的子弹垂直地射入棒的另一端，并留在棒中，如图所示．子弹的质量为m '= 0.020 kg ，速率为v = 400 m ·s -1．试问：(1) 棒开始和子弹一起转动时角速度ω有多大？(2) 若棒转动时受到大小为M r = 4.0 N ·m 的恒定阻力矩作用，棒能转过多大的角度θ？解：(1) 角动量守恒：ω⎪⎭⎫ ⎝⎛'+='2231l m ml l m v ∴ l m m m ⎪⎭⎫ ⎝⎛'+'=31vω＝15.4 rad ·s -1(2) 由转动定律，得：－M r ＝(231ml ＋2l m ')β0－ω 2＝2βθ∴ rM l m m 23122ωθ⎪⎭⎫ ⎝⎛'+=＝15.4 rad8.如图所示，A 和B 两飞轮的轴杆在同一中心线上，设两轮的转动惯量分别为 J ＝10 kg ·m 2 和 J ＝20 kg ·m 2．开始时，A 轮转速为600 rev/min ，B 轮静止．C 为摩擦啮合器，其转动惯量可忽略不计．A 、B 分别与C 的左、右两个组件相连，当C 的左右组件啮合时，B 轮得到加速而A 轮减速，直到两轮的转速相等为止．设轴光滑，求： mm , lOm '(1) 两轮啮合后的转速n ； (2) 两轮各自所受的冲量矩．解：(1) 选择A 、B 两轮为系统，啮合过程中只有内力矩作用，故系统角动量守恒J A ωA ＋J B ωB = (J A ＋J B )ω，又ωB ＝0得： ω ≈ J A ωA / (J A ＋J B ) = 20.9 rad / s 转速 ≈n 200 rev/min (2) A 轮受的冲量矩⎰t MAd = J A (J A ＋J B ) = -4.19×10 2 N ·m ·s负号表示与A ωϖ方向相反． B 轮受的冲量矩⎰t MBd = J B (ω - 0) = 4.19×102 N ·m ·s方向与A ωϖ相同．4.一匀质细棒长为2L ，质量为m ，以与棒长方向相垂直的速度v 0在光滑水平面内平动时，与前方一固定的光滑支点O 发生完全非弹性碰撞．碰撞点位于棒中心的一侧L 21处，如图所示．求棒在碰撞后的瞬时绕O 点转动的角速度ω．(细棒绕通过其端点且与其垂直的轴转动时的转动惯量为231ml ，式中的m 和l 分别为棒的质量和长度．)解：碰撞前瞬时，杆对O 点的角动量为L m L x x x x L L 0202/002/30021d d v v v v ==-⎰⎰ρρρ式中ρ为杆的线密度．碰撞后瞬时，杆对O 点的角动量为ωωω2221272141234331mL L m L m J =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=因碰撞前后角动量守恒，所以 L m mL 022112/7v =ω ∴ ω = 6v 0 / (7L)10. 空心圆环可绕光滑的竖直固定轴AC 自由转动，转动惯量为J 0，环的半径为R ，初始时环的角速度为ω0．质量为m 的小球静止在环内最高处A 点，由于某种微小干扰，小球沿环向下滑动，问小球滑到与环心O 在同一高度的B 点和环的最低处的C 点时，环的角速度及小球相对于环的速度各为多大?(设环的内壁和小球都是光滑的，小球可视为质点，环截面半径r <<R .)解：选小球和环为系统．运动过程中所受合外力矩为零，角动量守恒．对地球、小球和环系统机械能守恒．取过环心的水平面为势能零点．小球到B 点时： J 0ω0＝(J 0＋mR 2)ω ①2121()22220200212121BR m J mgR J v ++=+ωωω ② 式中v B 表示小球在B 点时相对于地面的竖直分速度，也等于它相对于环的速度．由式①得：ω＝J 0ω 0 / (J 0 + mR 2) 1分代入式②得222002J mR RJ gR B ++=ωv 当小球滑到C 点时，由角动量守恒定律，系统的角速度又回复至ω0，又由机械能守恒定律知，小球在C 的动能完全由重力势能转换而来．即： ()R mg m C 2212=v , gR C 4=v 四研讨题1. 计算一个刚体对某转轴的转动惯量时，一般能不能认为它的质量集中于其质心，成为一质点，然后计算这个质点对该轴的转动惯量？为什么？举例说明你的结论。

大学物理课后习题答案(上下册全)武汉大学出版社习题2详解

2-1 如题2-1图所示，弹簧秤挂一滑轮，滑轮两边各挂一质量为m 和2m 的物体，绳子与滑轮的质量忽略不计，轴承处摩擦忽略不计，在m 及2m 的运动过程中，弹簧秤的读数为[ ]A. 3mg .B. 2mg .C. 1mg .D. 8mg / 3.答案： D题 2-1图 2-2 一质点作匀速率圆周运动时，[ ] A.它的动量不变，对圆心的角动量也不变。

B.它的动量不变，对圆心的角动量不断改变。

C.它的动量不断改变，对圆心的角动量不变。

D.它的动量不断改变，对圆心的角动量也不断改变。

答案： C2-3 质点系的内力可以改变[ ] A.系统的总质量。

B.系统的总动量。

C.系统的总动能。

D.系统的总角动量。

答案： C2-4 一船浮于静水中，船长L ，质量为m ，一个质量也为m 的人从船尾走到船头。

不计水和空气阻力，则在此过程中船将：[ ] A.不动 B.后退LC.后退L 21 D.后退L 31答案： C2-5 对功的概念有以下几种说法：[ ]①保守力作正功时，系统内相应的势能增加。

②质点运动经一闭合路径，保守力对质点作的功为零。

③作用力与反作用力大小相等、方向相反，所以两者所作功的代数和必为零。

在上述说法中：A.①、②是正确的。

B.②、③是正确的。

C.只有②是正确的。

D.只有③是正确的。

答案： C2-6 某质点在力(45)F x i =+（SI ）的作用下沿x 轴作直线运动。

在从x=0移动到x=10m的过程中，力F所做功为。

答案： 290J2-7 如果一个箱子与货车底板之间的静摩擦系数为μ，当这货车爬一与水平方向成θ角的平缓山坡时，要不使箱子在车底板上滑动，车的最小加速度。

＜＜＜＜＜m 2m答案： ()cos sin g μθθ-2-8 一质量为1Kg 的球A ，以5m /s 的速率与原来静止的另一球B 作弹性碰撞，碰后A 球以4m /s 的速率垂直于它原来的运动方向，则B 球的动量大小为。

答案二

( 6)
εr =
C 5 .31 ×10 −10 = =3 C 0 1. 77 × 10 −10
13
大学物理练习册解答
9、平行板电容器极板面积为 S，两板间距离为 d，当极板上充以等量异号电荷 Q 后断 σ1 σ2 开电源，然后在电容器的左半面插入相对介电常数为 εr =3 的陶瓷介质板(忽略边缘效应)，求： (1) 极板上的自由电荷 b a 面密度分布σ1 、σ2 ； (2) 两极板之间 a、b 两点电场强度 E、电位移矢量 D 和极化强度 P； (3) 陶瓷板插入前、后两极板 ε r 电势差变化多少? σ1 σ σ=3 σ 解：（1）左右两边电势差相等 E 1 d = E 2 d d= 2 d→ 1 = 2 (1)
0
d−a λ a − ln a 2 πε 0 d − a
=
λ d−a ln πε 0 a πε 0 d −a ln a
q C=
l = UA − U B
12
大学物理练习册解答
7、如图，连接三个电容器， C1 = 50 µF , C2 = 30µF , C3 = 20 µF , （1）求该连接的总电容；（2）当在 AB 两端加 100V 的电压后，各电容器上的电压和电量各是多少？ A 1 1 1 解：（1）设总电容为 C, 则 = +
� � ∫ D ⋅ dS = ∑ q r<R R < r <a a < r <b r >b D= D1 = 0 D2 = q 4πr E1 = 0 E= D D = ε ε 0ε r
Q Q , E2 = 2 4πr 4 πε 0 r 2 Q Q D3 = , E3 = 2 4πr 4 πε 0 ε r r 2 Q Q D4 = ,E4 = 4πr 2 4 πε 0 r 2 P = ε 0 (ε r − 1) E 3 = ε 0 (ε r − 1)

大学物理习题册及解答(第二版)第二章质点的运动定律

µgR
(D) 还应由汽车的质量M决定
解：汽车不发生侧向打滑的条件是，它所受的摩擦力不得小于向心力，即有：
υ f = µN = µmg ≥ m R υ ≤ µgR
2
5．质量为m的质点，以不变速率v沿图中正三角形ABC 的水平光滑轨道运动．质点越过A角时，轨道作用于质点的冲量的大小为 A
(A) mυ (C) 3mυ
M g =G R
E 2
F −m g a= m +m
2 1 2
v F
v T
m1 m2
m T= (F + m g) m +m
2 1 1 2
6．质量为m的小球自高为y0处沿水平方向以速率v0抛出, 与地面碰撞后跳起的最大高度为y0/2，水平速率为v0/2. 则碰撞过程中 (1)地面对小球的竖直冲量的大小为___________； (2) 地面对小球的水平冲量的大小为_________．解：碰前小球沿x和y方向的速度分别为：
第二章质点的运动定律（二）质点的运动定律（一选择题
1．一小珠可在半径为R竖直的圆环上无摩擦地滑动，且圆环能以其竖直直径为轴转动．当圆环以一适当的恒定角速度ω转动，小珠偏离圆环转轴而且相对圆环静止时，小珠所在处圆环半径偏离竖直方向的角度为 g
Rω (C) θ = arctg( ) g
dυ k dυ = d υ ⋅ dx F =υ ∴a = = − 2 = dx dt mx dt m dx
k vdv = − dx 2 mx
k dx ∫ vdv = ∫ − 2 mx 0 x
v x
0
v2 k 1 1 = − 2 m x x0
v=
k 1 − 1 2 m x x 0

大学物理练习册解答2

M
x O l0
解：(1) 容器中每滴入一油滴的前后，水平方向动量值不变，而且在容器回到O点滴入下一油滴前，水平方向动量的大小与刚滴入上一油滴后的瞬间后的相同。依此，设容器第一次过O点油滴滴入前的速度为 v，刚滴入第个油滴后的速度 Mv (M nm)v ① 为v′,则有
1 1 系统机械能守恒 kl02 Mv 2 2 2
A/2
A
•
5．一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为
x(m)
A＝
10m
．．
10 5
＝

6 rad/s
＝

O
1
4
7
10
3
．
三、计算题 • 1. 一物体作简谐运动 , 其速度最大值 vm=3×10-2 m· -1, 其振幅 A＝ 2×10s 2m．若t＝0时，物体位于平衡位置且向x轴的负方向运动．求： (1) 振动周期T． (2) 加速度的最大值． (3) 振动方程的数值式．

•
3．如图，劲度系数为k的弹簧一端固定在墙上，另一端连接一质量为M的容器，容器可在光滑水平面上运动．当弹簧未变形时容器位于 O处，今使容器自O点左侧l0处从静止开始运动，每经过O点一次时，从上方滴管中滴入一质量为m的油滴，求： (1) 容器中滴入n滴以后，容器运动到距O点的最远距离； (2) 容器滴入第(n+1)滴与第n滴的时间间隔．
2 2
(C) x2 A cos(t 3 π)
2
(D) x2 A cos( t )
[ B ]
•
2．一质点沿x轴作简谐运动，振动方程为（SI），从t＝0时刻起，到质点位置在x＝－2cm处，且向x轴正方向运动的最短时间间隔为 (A)1/8s． (B)1/4s．(C)1/2s．(D)1/3s．(E)1/6s． [ C ]

大学物理二练习册答案

3. 如图所示，一电容器由两个同轴圆筒组成，内筒半径为 a，外筒半径为 b，筒长都是 L，中间充满相对介电常量为r 的各向同性均匀电介质．内、外筒分别带有等量异号电荷+Q 和-Q．设 (b- a) << a，L >> b，可以忽略边缘效应，求： (1) 圆柱形电容器的电容； (2) 电容器贮存的能量．
思考题 3：有一上下极板成 θ 角的非平行板电容器（长为 a ,宽为 b），其电容如何计算？
参考解答：设一平行板电容器是由长为 a , 宽为 b 的两导体板构成 , 板间距为 d , 则电容为
ab , 若该电容器沿两极板的长度同一方向有 d x的长度增 d a (b d x ) a d x 量,则电容为 C C0 , 在此基础上推广到 d d
L b a
解：由题给条件 ( b a) a 和 L b ，忽略边缘效应, 应用高斯定理可求出两筒之间的场强为：两筒间的电势差电容器的电容电容器贮存的能量
E Q /(2 0 r Lr )
b
U
Q dr Q b ln 2 0 r L r 2 0 r L a a
3
参考解答：由极性分子组成的电介质（极性电介质）放在外电场中时，极性分子的固有电矩将沿外电场的方向取向而使电介质极化。由于极性分子还有无规则热运动存在，这种取向不可能完全整齐。当电介质的温度升高时，极性分子的无规则热运动更加剧烈，取向更加不整齐，极化的 pi 效果更差。此情形下，电极化强度 P 将会比温度升高前减小。 V 在电介质中的电场 E 不太强时，各向同性电介质的 P 和 E 间的关系为 P 0 ( r 1) E . 很明显，在同样的电场下，当温度升高后，相对介电常量 εr 要减小。

大学物理学练习册答案

大物练习册参考答案二、判断题01. × 02. × 03. × 04. √ 05. √ 06. × 07. × 08. √ 09. √ 10. √ 11. √ 12. √ 13. √ 14. × 15. √三、计算题1. 解：根据连续性原理可知，出口处流速为：112221120.16)010.0()020.0(0.4--•=•⨯==s m s m S S v v 选流入处为参考平面，即令01=h ，根据伯努利方程可求的高处的压强为：22222112121gh v p v p ρρρ++=+ Pa gh v v p p 52222112103.22121⨯=--+=ρρρ2. 解：以油滴为研究对象, 设油滴的半径为r ，不存在竖直向下的匀强电场时，其受力情况为：竖直向下的重力：g r mg G ρπ334== 竖直向上的浮力：g r F 0334ρπ=竖直向上的黏滞阻力：rv f πη6= 三力达到平衡时,即:G=F+f,油滴以最大速度0v 下降。

由受力平衡：003363434rv g r g r πηρπρπ+=(1) 当存在竖直向下的匀强电场时，仍然以油滴为研究对象, 其受力情况为：竖直向下的重力：g r mg G ρπ334== 竖直向上的浮力：g r F 0334ρπ=竖直向上的黏滞阻力：rv f πη6= 竖直向上的电场力：qE F =1四力达到平衡时,即:f F F G ++=1时，油滴以最大速度v 下降。

由受力平衡：rv qE g r g r πηρπρπ63434033++=(2) 由方程（1）和（2）可以求出q 为：E v v v g q 210021023)((1)29(34-⎥⎦⎤⎢⎣⎡-=ρρηπ 3. 解：设总的水滴数目为N 个，根据融合前后水的体积不变，可得： 6333420105010(1.010)3N π--⨯⨯⨯=⨯g（1）则融合前后水的表面积改变量为：3264(1.010)2010S N π-∆=⨯-⨯g (2) 释放出的能量为E S α∆=∆ (3) 根据（1），（2），（3）方程可得 82.1810E J ∆=⨯4. 解：将虹吸管取为一流管。

湖南大学大学物理练习册答案(一二上下两册全)

大学物理（一）练习册参考解答第1章质点运动学一、选择题1(D)，2(D)，3(B)，4(D)，5(D)，6(D)，7(D)，8(D )，9(B)，10(B)，二、填空题(1). s i n2t A ωω，()ωπ+1221n (n = 0,1,… ), (2). 8 m ，10 m. (3). 23 m/s.(4). 16Rt 2 ，4 rad /s 2(5). 4t 3-3t 2 (rad/s)，12t 2-6t (m/s 2). (6).331ct ，2ct ，c 2t 4/R . (7). 2.24 m/s 2，104o(8). )5cos 5sin (50j t i t+-m/s ，0，圆.(9). h 1v /(h 1-h 2) (10). 0321=++v v v三、计算题1. 有一质点沿x 轴作直线运动，t 时刻的坐标为x = 4.5 t 2 – 2 t 3 (SI) ．试求：(1) 第2秒内的平均速度； (2) 第2秒末的瞬时速度； (3) 第2秒内的路程．解：(1) 5.0/-==∆∆t x v m/s(2) v = d x /d t = 9t - 6t 2, v (2) =-6 m/s. (3) S = |x (1.5)-x (1)| + |x (2)-x (1.5)| = 2.25 m.2. 一质点沿x 轴运动，其加速度为a = 4t (SI)，已知t = 0时，质点位于x 0=10 m 处，初速度v 0 = 0．试求其位置和时间的关系式．解： =a d v /d t 4=t ， d v 4=t d t⎰⎰=vv 0d 4d tt t v = 2t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰=x 2= t 3 /3+x 0 (SI)3. 质点沿x 轴运动，其加速度a 与位置坐标x 的关系为 a ＝2＋6 x 2 (SI)，如果质点在原点处的速度为零，试求其在任意位置处的速度．解：设质点在x 处的速度为v ，62d d d d d d 2x txx t a +=⋅==v v ()x x xd 62d 02⎰⎰+=v v v()2213x x +=v4. 一物体悬挂在弹簧上作竖直振动，其加速度为-=a ky ，式中k 为常量，y 是以平衡位置为原点所测得的坐标. 假定振动的物体在坐标y 0处的速度为v 0，试求速度v 与坐标y 的函数关系式．解： yt y y t a d d d d d d d d vvv v ===又 -=a ky ∴ -k =y v d v / d y⎰⎰+=-=-C ky y ky 222121 , d d v v v已知 =y y 0 ，=v v 0 则 20202121ky C --=v)(220202y y k -+=v v5. 一质点沿半径为R 的圆周运动．质点所经过的弧长与时间的关系为221ct bt S += 其中b 、c 是大于零的常量，求从0=t 开始到切向加速度与法向加速度大小相等时所经历的时间．解： ct b t S +==d /d v c t a t ==d /d v ()R ct b a n /2+=根据题意： a t = a n 即 ()R ct b c /2+=解得 cb c R t -=6. 如图所示，质点P 在水平面内沿一半径为R =2 m 的圆轨道转动．转动的角速度ω与时间t 的函数关系为2kt =ω (k 为常量)．已知s t 2=时，质点P 的速度值为32 m/s ．试求1=t s 时，质点P 的速度与加速度的大小．解：根据已知条件确定常量k()222/rad 4//s Rt t k ===v ω24t =ω, 24Rt R ==ωvs t 1=时， v = 4Rt 2 = 8 m/s2s /168/m Rt dt d a t ===v 22s /32/m R a n ==v()8.352/122=+=nt a a a m/s 27. (1)对于在xy 平面内，以原点O 为圆心作匀速圆周运动的质点，试用半径r 、角速度ω和单位矢量i 、j表示其t 时刻的位置矢量．已知在t = 0时，y = 0, x = r , 角速度ω如图所示；(2)由(1)导出速度 v 与加速度 a的矢量表示式； (3)试证加速度指向圆心．解：(1) j t r i t r j y i x rsin cos ωω+=+=(2) j t r i t r t rcos sin d d ωωωω+-==v j t r i t r ta sin cos d d 22ωωωω--==v(3) ()r j t r i t r a sin cos 22ωωωω-=+-=这说明 a 与 r方向相反，即a 指向圆心8. 一飞机驾驶员想往正北方向航行，而风以60 km/h 的速度由东向西刮来，如果飞机的航速（在静止空气中的速率）为 180 km/h ，试问驾驶员应取什么航向？飞机相对于地面的速率为多少？试用矢量图说明．解：设下标A 指飞机，F 指空气，E 指地面，由题可知：v FE =60 km/h 正西方向 v AF =180 km/h 方向未知v AE 大小未知，正北方向由相对速度关系有： FE AF AE v v v +=AE v 、 AF v 、EE v 构成直角三角形，可得 ()()k m /h 17022 v v v =-=FE AF AE () 4.19/tg 1==-AE FE v v θ（飞机应取向北偏东19.4︒的航向）．西北θFE v vAFv vAE v v四研讨题1. 在下列各图中质点M 作曲线运动，指出哪些运动是不可能的？参考解答： (1)、(3)、(4)是不可能的．(1) 曲线运动有法向加速度，加速度不可能为零；(3) 曲线运动法向加速度要指向曲率圆心；(4) 曲线运动法向加速度不可能为零.2. 设质点的运动方程为)(t x x =，)(t y y =在计算质点的速度和加速度时：第一种方法是，先求出22y x r +=，然后根据 td d r=v 及 22d d t r a =而求得结果；第二种方法是，先计算速度和加速度的分量，再合成求得结果，即22)d d ()d d (t y t x +=v 和 222222)d d ()d d (ty t x a +=.你认为两种方法中哪种方法正确？参考解答：第二种方法是正确的。

大学物理II练习册答案

大学物理练习十五一．选择题：1．如图所示，平行单色光垂直照射到薄膜上，经上下两表面反射的两束光发生干涉，若薄膜的厚度为e ，并且n 1<n 2 ，n 2>n 3，1λ为入射光在折射率为n 1的媒质中的波长，则两束反射光在相遇点的位相差为 [ C ](A) )/(2112λπn e n (B) πλπ+)/(4121n e n (C) πλπ+)/(4112n e n (D) )/(4112λπn e n解: n 1<n 2 ，n 2>n 3 有半波损失.2.在双缝干涉实验中，屏幕E 上的P 点处是明条纹。

若将缝S 2盖住，并在S 1S 2连线的垂直平分面处放一反射镜M ，如图所示，则此时 (A) P 点处仍为明条纹。

(B) P 点处为暗条纹。

(D) 无干涉条纹。

[B ]解: 反射镜M 有半波损失. （屏幕E 上的P 点处原是明条纹。

）3．如图所示，用波长为λ的单色光照射双缝干涉实验装置，若将一折射率为n 、劈角为α的透明劈尖b 插入光线2中，则当劈尖b 缓慢地向上移动时（只遮住S 2），屏C 上的干涉条纹 (A) 间隔变大，向下移动。

(B) 间隔变小，向上移动。

(D) 间隔不变，向上移动.。

[C ]解:当劈尖b 缓慢地向上移动时，改n 13λ1S屏λ4．如图，用单色光垂直照射在观察牛顿环的装置上。

当平凸透镜垂直向上缓慢平移而远离平面玻璃时，可以观察到这些环状干涉条纹 [B ](A) 向右平移. (B) 向中心收缩. (C) 向外扩张. (D) 静止不动. (E) 向左平移.解: 当平凸透镜垂直向上缓慢平移，薄膜厚增加. 环状干涉条纹向中心收缩.5. 在迈克尔逊干涉仪的一支光路中，放入一片折射率为n 的透明介质薄膜后，测出两束光的光程差的改变量为一个波长λ，则薄膜的厚度是 [ D ] (A) 2λ (B) ()n 2λ (C) n λ (D) )1(2-n λ解: λ=-=-=∆d n d nd )1(2226．如图所示，两个直径有微小差别的彼此平行的滚柱之间的距离为L ，夹在两块平晶的中间，形成空气劈尖，当单色光垂直入射时，产生等厚干涉条纹。

南华大学大物练习册二参考答案教材

第二章运动的守恒量和守恒定律练习一一. 选择题1. 关于质心，有以下几种说法，你认为正确的应该是（ C ）(A ) 质心与重心总是重合的； (B ) 任何物体的质心都在该物体内部； (C ) 物体一定有质心，但不一定有重心； (D ) 质心是质量集中之处，质心处一定有质量分布。

2. 任何一个质点系，其质心的运动只决定于（ D ）(A )该质点系所受到的内力和外力； (B) 该质点系所受到的外力；(C) 该质点系所受到的内力及初始条件； (D) 该质点系所受到的外力及初始条件。

3.从一个质量均匀分布的半径为R 的圆盘中挖出一个半径为2R 的小圆盘，两圆盘中心的距离恰好也为2R 。

如以两圆盘中心的连线为x 轴，以大圆盘中心为坐标原点，则该圆盘质心位置的x 坐标应为（ B ） (A )R 4； (B) R 6; (C) R 8； (D R12。

4. 质量为10 kg 的物体，开始的速度为2m/s ，由于受到外力作用，经一段时间后速度变为6 m/s ，而且方向转过90度，则该物体在此段时间内受到的冲量大小为（ B ） (A )s N ⋅820； (B) s N ⋅1020； (C) s N ⋅620； (D) s N ⋅520。

二、填空题1. 有一人造地球卫星，质量为m ，在地球表面上空2倍于地球半径R 的高度沿圆轨道运行，用m 、R 、引力常数G 和地球的质量M 表示，则卫星的动量大小为RGMm3。

2．三艘质量相等的小船在水平湖面上鱼贯而行，速度均等于0v ，如果从中间小船上同时以相对于地球的速度v 将两个质量均为m 的物体分别抛到前后两船上，设速度v 和0v 的方向在同一直线上，问中间小船在抛出物体前后的速度大小有什么变化:大小不变。

3. 如图1所示，两块并排的木块A 和B ，质量分别为m 1和m 2，静止地放在光滑的水平面上，一子弹水平地穿过两木块。

设子弹穿过两木块所用的时间分别为∆t 1和∆t 2，木块对子弹的阻力为恒力F ，则子弹穿出后，木块A 的速度大小为 1A BF t m m ⋅∆+，木块B 的速度大小为12F t A BBF t m m m ⋅∆⋅∆++。

大学物理练习册解答2

大学物理（二）练习册答案

大学物理练习册答案(下册)-

(完整版)《大学物理》习题册题目及答案第2单元 动量守恒定律

大学物理习题册及解答 第二版 刚体的定轴转动

大学物理练习册习题解答(1-22上)

四川大学物理习题册第五章解答2

大学物理上练习册 第2章《刚体定轴转动》答案-2013

大学物理课后习题答案(上下册全)武汉大学出版社 习题2详解

答案二

大学物理习题册及解答(第二版)第二章 质点的运动定律

大学物理练习册解答2

大学物理二练习册答案

大学物理学练习册答案

湖南大学大学物理练习册答案(一二上下两册全)

大学物理II练习册答案

南华大学大物练习册二参考答案教材

(完整版)《大学物理》习题册题目及答案第2单元动量守恒定律

大学物理习题册及解答第二版刚体的定轴转动

大学物理上练习册第2章《刚体定轴转动》答案-2013

大学物理课后习题答案(上下册全)武汉大学出版社习题2详解

大学物理习题册及解答(第二版)第二章质点的运动定律