鲁教版五四制初一第一学期期中测试题

合集下载

鲁教版五四制英语七年级上册期中考试试题

初中英语学习材料madeofjingetieji2015-2016学年七年级英语第一学期期中综合检测(100分钟120分)第Ⅰ卷(共60分)Ⅰ. 听力(20分)(Ⅰ)录音中有五个句子, 听一遍后, 选择与之相符的图片(5分)(Ⅱ)录音中有五组对话及五个问题, 听一遍后, 选择最佳答案(5分)6．What's in the fridge?A. Beef.B. Oranges.C. Fruit.7. What colour is Lisa's computer?A. Blue.B. Red.C. Black.8．Where are the shoes?A. They're behind the chair.B. They're beside the bed.C. They're under the bed.9. How many people are there in Mary's family?A. Three.B. Four.C. Five10. What animal does Betty like?A. Pandas.B. Elephants.C. Giraffe(Ⅲ)录音中有一段对话, 听两遍后, 选择最佳答案(5分)11. Why does Maria call Sam?A. She says happy birthday to Sam.B. She asks Sam some questions.C. She only wants to talk with Sam.12. What are Sam's family doing?A. Eating a cake.B. Visiting Sam's grandfather.C. Having a party for Sam.13. What are Sam and Maria doing?A. They're staying at home.B. They’re having lunch.C. They're making a telephone call.（打电话）14. What's the weather like in Moscow?A. Cold.B. Hot.C. Warm15. Who lives in London?A. Maria's grandfather.B. Sam's family.C. Maria's family（Ⅳ）录音中有一篇短文，听两遍后，选择最佳答案。

鲁教版五四制英语七年级上册期中综合检测

关闭Word文档返回原板块。

期中综合检测Units 1～4(120分钟120分)第Ⅰ卷(共65分)一、听力(20分)(一)录音中有五个句子,每个句子听一遍,然后选出与其相符的图片。

(5分)1. 2. 3. 4. 5.(二)录音中有五组对话,每组对话听一遍,然后从每小题A、B、C中选出能回答每个问题的正确答案。

(5分)6.The criminal is.A.a short and heavy studentB.a short and old womanC.a short and heavy old man7.Eggs are a symbol of.A.love and good luckB.love and good lifeC.life and good luck8.The woman.A.ate some chickenB.watched some chickenC.fed some chickens9.The girl went.A.campingB.shoppingC.swimming10.The woman would like.A.beef noodlesB.tomato noodlesC.beef noodles with tomato(三)录音中有两段对话,每段对话听两遍,然后从每小题A、B、C中选出能回答每个问题的正确答案。

(5分)听第一段对话,回答第11、12小题。

11.How was Mike’s school trip?A.Great.B.Terrible.C.Boring.12.What did Mike do on the farm?ked cows.B.Fed cows.C.Picked strawberries.听第二段对话,回答第13~15小题。

综合能力训练五四制(配鲁教版) 七年级上册期中综合测试

!'!

"#$ "%, "# '
, '
! #", '
垂直平分 $#"-
,.
直线的交点在上则 &# #.$,
"-

!%./#"%')./ #"$'
!

是等边三角形 (#%,.

如图所示在中 !.!
"#$ #')./,-"#
第!.题图

到直线"# 的距离是
!
"#*
$#0

&#'
(#)

!!!是我伞缩国柄的拢"/制始伞"终工,%平艺分与十同分"一巧-平妙%面始如内终图两保条伞持伞不全骨论等所张因成开的此还
角#"$从而保证伞圈% 能沿着伞柄滑动!请
第!*题图
问的理由是 ",%"-%
!
%
%%!如图所示是一个四边形的边角料木工师傅

通过测量获得了如下数据"#''12#$' 木工师傅由 !%12$%'!'12"% ')12 此认为这个四边形中" 恰好是直角你认

如图所示在中分别为 !4!
第!3题图
"#$ %,
#$"%
是!
长为!

第'题图

第0题图
"#!

鲁教版五四制七年级(上)数学期中试题(含答案) - 副本

第一学期期中质量调研七年级数学试题（时间：90分钟，满分120分）一、选择题（每题3分，共30分）1．运用等式性质进行的变形，不正确的是（）A．如果a=b，那么a﹣c=b﹣c B．如果a=b，那么a+c=b+cC．如果a=b，那么ac=bc D．如果ac=bc，那么a=b2.在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（）A B C D3．下图中，由AB∥CD，能得到∠1＝∠2的是( )4．某人在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来相同，这两次拐弯的角度可能是()A.第一次左拐30°，第二次右拐30°B. 第一次右拐50°，第二次左拐130°C.第一次右拐50°，第二次右拐130°D.第一次向左拐50°，第二次向左拐120°已知5．在解方程13132x xx-++=时，方程两边同时乘以6，去分母后，正确的是（）A．2x﹣1+6x=3（3x+1）B．2（x﹣1）+6x=3（3x+1）C．2（x﹣1）+x=3（3x+1）D．（x﹣1）+x=3（x+1）6．若A、B、C是直线l上的三点，P是直线l外一点，且P A=6cm，PB=5cm，PC=4cm，则点P到直线l 的距离（）A．等于4cm B．大于4cm而小于5cmC．不大于4cm D．小于4cm7．∠α的补角为125°12′，则它的余角为（）A．35°12′ B．35°48′ C．55°12′ D．55°48′8．如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1=35°，则∠2等于（）A．55°B．45°C．35°D．65°9．小李在解方程5a－x＝13(x为未知数)时，错将－x看作＋x，得方程的解为x=－2，则原方程的解为( ) A．x=－3 B．x=0 C．x=2 D．x=110. 足球比赛的记分规则是：胜一场得3分，平一场得1分，负一场得0分，若一个队打了14场比赛得17分，其中负了5场，那么这个队胜了（）场。

鲁教版(五四制)数学七年级上册期中达标测试卷(含答案)

期中达标测试卷一、选择题（本大题共10小题，每小题3分，共30分）1．对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上．在下列苏州园林的窗户简图中，不是轴对称图形的是（）A B C D 2．如果将一副三角尺按图1方式叠放，那么∠1的度数是（）A．90°B．100°C．105°D．135°图1 图2 图33．图2是作△ABC的作图痕迹，则此作图的已知条件是（）A．已知两边及夹角B．已知三边C．已知两角及夹边D．已知两边及一边对角4．如图3，在四边形ABCD中，AB＝AD，CB＝CD，AC，BD相交于点O，则图中全等三角形共有()A．1对B．2对C．3对D．4对5．图4为由四个全等的直角三角形拼成的图形，设CE=a，HG=b，则斜边BD2等于（）A．a2+b2B．a2－b2C．222a b-D．222a b+图4 图56．某木材市场上木棒规格与对应价格如下表：小明的爷爷要做一个三角形木架养鱼用，现有两根长度分别为3 m和5 m的木棒，还需要到该木材市场购买一根木棒，则小明的爷爷至少带的钱数为（）A．10 B．15 C．20 D．257．如图5，已知△ABC中，CD⊥AB，垂足为D，CE平分∠ACD交AD于点E，若CD＝12，BC＝13，且△BCE的面积为48，则点E到AC的距离为（）A．5 B．3 C．4 D．18．图6－①是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC＝12，BC＝7，将四个直角三角形中边长为12的直角边分别向外延长一倍，得到如图6－②所示的“数学风车”，则这个风车的外围周长是（）A．148 B．100 C．196 D．144图6 图7 图89．如图7，在△ABC中，∠A＝20°，沿BE将此三角形对折，又沿BA′再一次对折，点C落在BE上的C′处，此时∠C′DB＝74°，则原三角形的∠C的度数为（）A．27°B．59°C．69°D．79°10．如图8，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，连接AC，BD交于点M，连接OM．下列结论：①AC＝BD；②∠AMB＝40°；③OM平分∠BOC；④MO平分∠BMC．其中正确的有（）A．①B．①②C．①②③D．①②④二、填空题（本大题共6小题，每小题4分，共24分）11．如图9，△ACF≌△DBE，若AD＝11，BC＝3，则线段AB的长为．图9 图10 图1112．如图10，一条船从海岛A处出发，向正北方向航行8海里到达海岛B处，从C处望海岛A，A在C的南偏东42°方向上；从B处望灯塔C，C在B的北偏西84°方向上，则海岛B 到灯塔C的距离是海里．13．如图11，有一座小山，现要在小山A，B的两端开一条隧道，施工队要知道A，B两端的距离，于是先在平地上取一个可以直接到达点A和点B的点C，且使AC⊥BC，连接AC并延长到点D，使CD＝CA，连接BC并延长到点E，使CE＝CB，连接DE．经测量EC，DC的长度分别为300 m，400 m，则A，B之间的距离为m．14．如图12，在△ABC中，AD为中线，DE⊥AB于点E，DF⊥AC于点F，AB＝3，AC＝4，DF＝1.5，则DE＝．图12 图13 图1415．图13是放在地面上的一个长方体盒子，其中AB＝18 cm，BC＝12 cm，BF＝10 cm，点M在棱AB上，且AM＝6 cm，点N是FG的中点，一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，它需要爬行的最短路程为cm．16．如图14，在△ABC中，AI平分∠BAC，BI平分∠ABC，点O是AC，BC的垂直平分线的交点，连接AO，BO，若∠AIB＝α，则∠AOB的大小为．三、解答题（本大题共7小题，共66分）17．（6分）如图15，已知△ABC是等边三角形，D是BC边的中点，点E在AC的延长线上，且∠CDE＝30°．若AD＝5，求DE的长．图15 图1618．（8分）如图16，MN为我国领海线，MN以西为我国领海，以东为公海．上午9时50分我国缉私艇A发现在其正东方向有一走私艇C正以每小时16海里的速度偷偷向我国领海驶来，便立即通知距其6海里，正在MN上巡逻的缉私艇B密切注意，且已知A和C两艇的距离是10海里，缉私艇B与走私艇C的距离为8海里，若走私艇C 的速度不变，最早在什么时间进入我国领海？19．（8分）如图17，在△ABC中，AB＝AC，AD⊥BC于点D．（1）若∠B＝39°，求∠CAD的度数；（2）若点E在边AC上，EF∥AB交AD的延长线于点F．试说明：AE＝FE．图17 图1820．（8分）如图18，三角形纸片ABC中，∠C＝90°，AC＝BC＝2，D为BC的中点，折叠三角形纸片使点A与点D重合，EF为折痕，求AF的长．21．（10分）如图19，△ABC的顶点A，B，C都在小正方形的顶点上，利用网格线按下列要求画图．（1）画△A1B1C1，使它与△ABC关于直线l成轴对称；（2）在直线l上找一点P，使点P到点A，B的距离之和最短；（3）在直线l上找一点Q，使点Q到边AC，BC的距离相等．图1922．（12分）如图20，在△ABC中，AB＝4，AC＝3，BC＝5，DE是BC的垂直平分线，交BC于点D，交AB于点E．（1）试说明：△ABC为直角三角形；（2）求DE的长．图2023．（14分）如图21，在△ABC中，AM是△ABC的中线，MP平分∠AMB，MQ平分∠AMC，且BP⊥MP于点P，CQ⊥MQ于点Q，连接PQ．试说明：（1）MP⊥MQ；（2）△BMP≌△MCQ．图21期中达标测试卷参考答案：一、1．B 2．C 3．C 4．C 5．D 6．C 7．B 8．A 9．D 10．D二、11．4 12．8 13．500 14．2 15．20 16．4α－360°三、17．解：因为△ABC是等边三角形，D是BC边的中点，所以AD⊥BC，∠DAC＝12∠BAC＝30°．因为∠ACB＝60°，∠CDE＝30°，所以∠E＝30°，所以∠DAC＝∠E，所以DE＝AD ＝5．18．解：设MN与AC相交于点E，则∠BEC=90°．因为AB2+BC2=62+82=102=AC2，所以△ABC为直角三角形，且∠ABC=90°．由于MN⊥CE，所以走私艇C进入我领海的最近距离是CE．由S△ABC=12AB×BC=12AC×BE，得BE=4.8．由勾股定理，得CE2+BE2=BC2，所以CE=6.4，所以6.4÷16=0.4（h）=24（min）．9时50分+24分=10时14分．所以走私艇C最早在10时14分进入我领海．19．解：（1）因为AB＝AC，AD⊥BC于点D，所以∠BAD＝∠CAD，∠ADC＝90°．因为∠B＝39°，所以∠BAD＝∠CAD＝90°－39°＝51°．（2）因为AB＝AC，AD⊥BC于点D，所以∠BAD＝∠CAD．因为EF∥AC，所以∠F＝∠BAD．所以∠BAD＝∠F，所以AE＝FE．20．解：因为BC＝2，D为BC的中点，所以CD＝1．由折叠的性质，得AF＝DF．所以CF＝AC－AF＝2－DF．在Rt△CDF中，由勾股定理，得DF2＝CF2+CD2，即DF2＝（2－DF）2+12，解得DF＝54．所以AF＝54．21．解：（1）如图所示，△A1B1C1即为所求作的三角形；（2）如图所示，连接A1B交直线l于点P，点P即为所求作的点；（3）如图所示，由网格的特征易知射线CC1为∠ACB的平分线，其与直线l交于点Q，点Q即为所求作的点．22．解：（1）在△ABC中，AB＝4，AC＝3，BC＝5，因为42+32＝52，即AB2+AC2＝BC2，所以△ABC是直角三角形．（2）连接CE．因为DE是BC的垂直平分线，所以EC＝EB．设AE＝x，则EC＝4－x，所以x2+32＝（4－x）2，解得x＝78，即AE=78．所以BE＝4－78＝258．因为BD＝12BC＝5 2，所以DE2＝BE2－BD2＝（258）2－（52）2＝22564，所以DE＝158．23．解：（1）因为MP平分∠AMB，MQ平分∠AMC，所以∠AMP＝12∠AMB，∠AMQ＝1 2∠AMC，所以∠PMQ＝∠AMP+∠AMQ＝12∠AMB+12∠AMC＝12（∠AMB+∠AMC）＝12×180°＝90°，所以MP⊥MQ．（2）由（1）知，MP⊥MQ．因为BP⊥MP，所以BP∥QM，∠BPM＝90°，∠CQM＝90°，所以∠PBM＝∠QMC．因为AM是△ABC的中线，所以BM＝MC．在△BMP和△MCQ中，∠BPM＝∠MQC，∠MBP＝∠CMQ，BM＝MC，所以△BMP≌△MCQ．。

鲁教版(五四制)七年级英语上册期中达标测试卷含答案

鲁教版（五四制）七年级英语上册期中达标测试卷(限时：60分钟满分：100分)听力部分(20 分)一、听句子, 选择适当的应答语，每个句子读一遍(每小题1 分, 共5 分) ()1. A. Beef noodles.B. Yes, I like them.C. No, I don’t.()2. A. He is popular.B. He’s short.C. He likes reading.()3. A. I played basketball.B. I went fishing.C. It was excellent.()4. A. Yes, I did.B. Yes, they are.C. It was great.()5. A. She went to a farm.B. Gina did.C. I did my homework.二、听五段对话, 选择正确答案, 每段对话读两遍(每小题1 分, 共5 分) ()6. Where did Mike go last Saturday?A. To the park.B. To the zoo.C. To the bookstore.()7. What does Tom’s mother want?A. Tomato and egg rice.B. Mutton noodles.C. Beef dumplings.()8. Where was Li Mei over the weekend?A. She was at home.B. She was at school.C. She studied math.()9. What does the girl’s best friend look like?A. She has small eyes.B. She is short.C. She has big eyes.()10. Who did the girl go shopping with?A. Her friend.B. Her classmate.C. Her mother.三、听两段长对话, 选择正确答案，每段对话读两遍(每小题1 分, 共5 分) 听第一段对话, 回答第11、12 小题。

鲁教版(五四制)七年级英语上册期中综合测试卷含答案

鲁教版（五四制）七年级英语上册期中综合测试卷限时：120分钟满分：100分听力部分(20分)一、听句子, 选择正确的应答语, 每个句子读一遍(每小题1分, 共5分)1. A. Beef noodles. B. Yes, I like them. C. No, I don't.2. A. He is popular. B. He's short. C. He likes reading.3. A. I played basketball. B. I went fishing. C. It was excellent.4. A. Yes, I did. B. Yes, they are. C. It was great.5. A. She went to a farm. B. Gina did.C. I did my homework.二、听五段对话, 选择正确答案, 每段对话读两遍(每小题1分, 共5分)6. Does Lily agree to watch a football game?A. Yes, she does.B. No, she doesn't.C. She's very busy.7. What is the woman's sister?A. She is a nurse.B. He is a doctor.C. She is a doctor.8. How does Han Mei usually come to school?A. By bus.B. On foot.C. By car.9. What are they going to do this Sunday?A. Go hiking.B. Go boating.C. Go swimming.10. What's near here?A. A post office.B. A hotel.C. A hospital.三、听两段长对话, 选择正确答案, 每段对话读两遍(每小题1分, 共5分)听第一段对话, 回答第11、12小题。

初中数学鲁教版(五四制)七年级上册期中-章节测试习题(3)

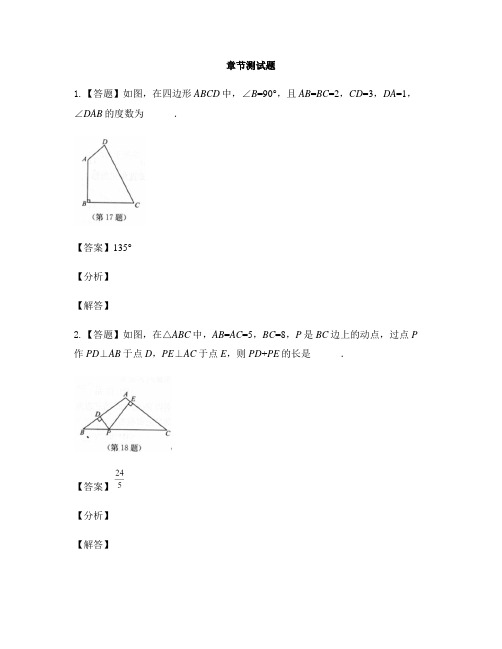
章节测试题1.【答题】如图，在四边形ABCD中，∠B=90°，且AB=BC=2，CD=3，DA=1，∠DAB的度数为______．【答案】135°【分析】【解答】2.【答题】如图，在△ABC中，AB=AC=5，BC=8，P是BC边上的动点，过点P 作PD⊥AB于点D，PE⊥AC于点E，则PD+PE的长是______．【答案】【分析】【解答】3.【题文】（7分）如图，已知直线AE∥BC，AD平分∠BAE，交BC于点C，∠BCD=140°，求∠B的度数．【答案】【分析】【解答】∵∠BCD=140°，∴∠ACB=180°-140°=40°．∵AE∥BC．∴∠CAE=∠ACB=40°．∵AD平分∠BAE，∴∠CAE=∠CAB=40°．∴∠B=180°-40°-40°=100°．4.【题文】（7分）一架梯子AB长25m，如图所示，斜靠在一面墙上，此时梯子底端B离墙7m如果梯子的顶端A下滑4m至点A'，那么梯子的底端水平滑动的距离BB'是多少米?【答案】【分析】【解答】∵AB=25m，BO=7m，由勾股定理得，AO=24m，∴A'O=AO-AA'=24-4=20（m）．由题意得，AB'=25m，A'O=20m，由勾股定理得，OB'=15m，∴BB'=OB'-OB=15-7=8（m）．答：梯子的底端水平滑动的距离BB'为8m．5.【题文】（10分）如图，在正方形网格中，有一个格点三角形ABC（即三角形的顶点都在格点上）和一条直线l．请在网格中按要求画图．（1）画出与△ABC关于直线l对称的△A1B1C1（要求A与A1，B与B1，C与C1相对应）；（2）在直线l上找一点P，使得△PBC的周长最小，并标出点P．【答案】略【分析】【解答】6.【题文】（10分）已知由若干个大小相同且边长为1的小正方形组成的网格．（1）如图①，A，B，C是三个格点（即小正方形的顶点），判断AB与BC的位置关系，并说明理由；（2）在图②中画出一个面积为10的正方形．【答案】【分析】【解答】（1）如图①，连接AC，由勾股定理，得AB2=32+22=13，BC2=42+62=52，AC2=1+82=65，∴AB2+BC2=AC2．∴△ABC是直角三角形，且∠ABC=90°．∴AB⊥BC．（2）如图②，四边形ABCD即为所求．7.【题文】（10分）如图，已知点B，E，C，F在同一条直线上，AB=DE，∠A=∠D，AC∥DF．请你判断，BE与CF相等吗?请说明理由．【答案】【分析】【解答】BE与CF相等．理由如下：∵AC∥DF，∴∠ACB=∠F．在△ABC和△DEF中，∴△ABC≌△DEF（AAS）．∴BC=EF．∴BC-CE=EF-CE，即BE=CF．8.【题文】（10分）如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O．（1）求证：△AEC≌△BED；（2）若∠1=42°，求∠BDE的度数．【答案】【分析】【解答】（1）证明：∵AE和BD相交于点O，∴∠AOD=∠BOE．在△AOD和△BOE中，∵∠A=∠B，∴∠BEO=∠2．又∵∠1=∠2，∴∠BEO=∠1．∴∠AEC=∠BED．在△AEC和△BED中，∴△AEC≌△BED（ASA）．（2）∵△AEC≌△BED，∴EC=ED，∴∠C=∠BDE．在△EDC中，∵∠1=42°，∴．∴∠BDE=∠C=69°．9.【题文】（12分）如图，△ABC和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．（1）猜想线段AD，BE之间的数量关系，并说明理由；（2）求∠AEB的度数．【答案】【分析】【解答】（1）猜想线段AD=BE，理由如下：∵△ACB和△DCE均为等边三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=60°，∴∠ACD=60°-∠DCB=∠BCE．在△ACD和△BCE中，AC=BC，∠BCE=∠DCA，DC=CE，∴△ACD≌△BCE（SAS）．∴AD=BE.（2）∵△ACD≌△BCE，∴∠ADC=∠BEC．∵△DCE为等边三角形，∴∠CDE=∠CED=60°．∵点A，D，E在同一直线上，∴∠ADC=120°，∴∠BEC=120°．∴∠AEB=∠BEC-∠CED=60°．10.【题文】（12分）如图，已知∠ACB=∠DCE=90°，AC=BC=6，CD=CE，AE=3，∠CAE=45°．（1）从图中找出一对全等三角形，并说明理由；（2）求AD的长．【答案】【分析】【解答】（1）△ACD≌△BCE．理由如下：∵∠ACB=∠DCE=90°，∴∠ACB+∠ACE=∠DCE+∠ACE，即∠BCE=∠ACD．在△ACD和△BCE中，∵AC=BC，∠BCE=∠ACD，DC=EC，∴△ACD≌△BCE（SAS）．（2）∵∠BAC=∠CAE=45°，∴∠BAE=90°．在Rt△BAC中，∵AC=BC=6，∴AB2=62+62=72．在Rt△BAE中，∵AE=3，∴BE2=AB2+AE2=72+32=81．∴BE=9．∵△ACD≌△BCE，∴AD=BE=9．11.【答题】下列图形中，是轴对称图形的为（）A. B. C. D.【答案】D【分析】【解答】12.【答题】等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边长为（）A. 3cmB. 7cmC. 3cm或7cmD. 5cm【答案】A【分析】【解答】13.【答题】下列长度的线段中不能组成直角三角形的是（）A. a=6，b=8，c=10B. a=0.3，b=0.4，c=0.5C. ，b=1，D. a=9，b=16，c=25【答案】D【分析】【解答】14.【答题】如图，为估计池塘两岸A，B间的距离，小杨在池塘一侧选取了一点P，测得PA=26m，PB=14m，那么AB之间的距离可能是（）A. 40mB. 15mC. 12mD. 10m【答案】B【分析】【解答】15.【答题】如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②AB=DE，∠B=∠E，BC=EF；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，AC=DF，∠B=∠E.其中，能判定△ABC≌△DEF的共有（）A. 1组B. 2组C. 3组D. 4组【答案】C【分析】【解答】16.【答题】如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是（）A. 10B. 20C. 30D. 15【答案】D【分析】【解答】17.【答题】如图，在△ABC中，按以下步骤作图：①分别以A，B为圆心，大于的长为半径画弧，交于两点M，N；②作直线MN交AC于点D，连接BD.若CD=BC，∠A=35°，则∠C的度数为（）A. 40°B. 50°C. 60°D. 70°【答案】A【分析】【解答】18.【答题】如图，在一个规格为6×12（即有6×12个小正方形）的球台上，有两个小球A，B. 若击打小球A，经过球台边的反弹后，恰好击中小球B，那么击打小球A时，应瞄准球台边上的点（）A. P1B. P2C. P3D. P4【答案】B【分析】【解答】19.【答题】如图是一株美丽的“勾股树”，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的边长分别为3，5，2，3，则最大的正方形E的面积是（）A. 13B. 26C. 47D. 94【答案】C【分析】【解答】20.【答题】如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB，垂足为E. 若AB=10，AC=6，则DE的长度为（）A. 2B. 3C. 4D. 5【答案】B【分析】【解答】。

鲁教版七年级英语上册期中期末试题及答案(五四制)

鲁教版七年级英语上册期中期末试题及答案（五四制）期中测试(限时：100分钟满分：120分)听力部分(20分)一、听句子, 选择适当的应答语。

每个句子读一遍(每小题1分, 共5分)1. A. Beef noodles. B. Yes, I like them. C. No, I don't.2. A. He is popular. B. He's short. C. He likes reading.3. A. I played basketball. B. I went fishing. C. It was excellent.4. A. Yes, I did. B. Yes, they are. C. It was great.5. A. She went to a farm. B. Gina did. C. I did my homework.二、听五段对话, 选择正确答案。

每段对话读两遍(每小题1分, 共5分)6. Does Lily agree to watch a football game?A. Yes, she does.B. No, she doesn't.C. She's very busy.7. What is the woman's sister?A. She is a nurse.B. He is a doctor.C. She is a doctor.8. How does Han Mei come to school?A. By bus.B. On foot.C. By car.9. What are they going to do this Sunday?A. Go hiking.B. Go boating.C. Go swimming.10. What's near here?A. A post office.B. A hotel.C. A hospital.三、请听录音中两段较长的对话。

鲁教版五四制英语七年级上册期中试卷

A. has; has B. is; has C. has; is D. is; is of
( )31.–What ______ his daughter _________? --She has long curly hair.
A. is; look like B. does; look like C. is; look D. is; looking like
16. ________ 17.________ 18.________ 19.________ 20._________
笔试部分（共80分）
二、单选（15分）
A.B C D四个选项中选出一个最佳答案，将其标号填入题前括号内。
( )21. --Do you know Jackie Chan?
--Yes.He is _______ actor.
( )25. My friend has many books.He often _______them on weekends.
A. reads B. looks C. sees D watches
( )26. --Would you like some juice, Jane?--___________.
A. an B. a C. the D. /
( )22.–Does Peter like beef?
--Yes.But hedoesn'tlike fish _____ mutton.
A. and B. or C. but D. so
( )23. ---Does your sister like music?
( )32.–Who cleaned up the room?It’s so tidy.–Tom ___________.

2022-2023学年鲁教版五四制七年级上期中复习数学试卷含答案解析

2022-2023学年鲁教版（五四制）七年级上册数学期中复习试卷一．选择题（共12小题，满分48分，每小题4分）1．如图对称图形中，是轴对称图形有（）个．A．1B．2C．3D．42．如果三角形的两条边长分别是8厘米、6厘米，那么第三边的长不可能是（）A．9厘米B．4厘米C．3厘米D．2厘米3．下列四组线段中，不能作为直角三角形三条边的是（）A．3，4，5B．2，2，2C．2，5，6D．5，12，134．若AD是△ABC的中线，则下列结论正确的是（）A．AD⊥BC B．BD＝CD C．∠BAD＝∠CAD D．AD＝BC5．△ABC≌△DEF，且△ABC的周长为80cm，A、B分别与D、E对应，且AB＝25cm，DF＝35cm，则EF 的长为（）A．20cm B．30cm C．45cm D．55cm6．如图，已知CD⊥AB，BE⊥AC，且AO平分∠BAC，那么图中全等三角形共有（）A．2对B．3对C．4对D．5对7．一个等腰三角形的两边长分别是2、4，那么它的周长是（）A．10B．8C．10或8D．不能确定8．如图，在△ABC中，AB＝10，AC＝6，BC的垂直平分线交AB于D，交BC于E，则△ADC的周长等于（）A．4B．6C．10D．169．如图，有三块菜地△ACD，△ABD，△BDE分别种植三种蔬菜，点D为AE与BC的交点，AD平分∠BAC，AD＝DE，AB＝3AC，菜地△BDE的面积为96，则菜地△ACD的面积是（）A．24B．27C．32D．3610．如图，△ABC中，点D是BC边上一点，DE⊥AB于点E，DF⊥BC，且BD＝FC，BE＝DC，∠AFD ＝155°．则∠EDF的度数是（）A．50°B．55°C．60°D．65°11．具备下列条件的三角形中，不是直角三角形的是（）A．∠A+∠B＝∠C B．C．∠A＝90°﹣∠B D．∠A﹣∠B＝90°12．如图，已知：∠MON＝30°，点A1，A2，A3……在射线ON上，点B1，B2，B3……在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4……均为等边三角形，若OA1＝1，则△A7B7A8的边长为（）A．64B．32C．16D．128二．填空题（共6小题，满分24分，每小题4分）13．若正六边形ABCDEF与正方形ABGH按图中所示摆放，连接FH，则∠AFH+∠AHF＝．14．如图是一棵勾股树，它是由正方形和直角三角形拼成的，若正方形A，B，C，D的边长分别是3、5、2、3，则最大正方形E的面积是．15．如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE＝DG，△ADG和△EFD的面积分别为50和4.5，则△AED的面积为．16．如图，△ABC中，AB＝AC，∠A＝40°，DE垂直平分AC交AB于E，则∠BCE＝17．在一个长11cm，宽5cm的长方形纸片上，如图放置一根正三棱柱的木块，它的侧棱平行且大于纸片的宽AD，它的底面边长为1cm的等边三角形，一只蚂蚁从点A处到点C处的最短路程是cm．18．如图，把一张长为4，宽为2的矩形纸片，沿对角线折叠，则重叠部分的面积为．三．解答题（共9小题，满分78分）19．（6分）△ABC中，∠B＝∠C+10°，∠A＝∠B+10°，求△ABC的各内角的度数．20．（6分）点B、E在线段CF上，AC∥DF，CE＝BF，AB∥DE，求证：△ABC≌△DEF．21．（6分）如图，AB＝AC，AB的垂直平分线DE交BC延长线于E，交AC于F，∠A＝40°，AB+BC＝6．（1）△BCF的周长为多少？（2）∠E的度数为多少？22．（8分）有一块土地形状如图所示，∠B＝∠D＝90°，AB＝20米，BC＝15米，CD＝7米，请计算这块地的面积．23．（8分）如图，在5×5的方格纸中，每一个小正方形的边长为1．（1）∠BCD是不是直角？请说明理由（可以适当添加字母）（2）求出四边形ABCD的面积；（3）连接BD，求△ABD边AD上的高．24．（10分）如图，点D在AB上，点E在AC上，AB＝AC，∠B＝∠C．CD与BE交于点O．求证：△DOB≌△EOC．25．（10分）【感知】如图①，点B、A、C在同﹣条直线上，DB⊥BC，EC⊥BC，且∠DAE＝90°，AD ＝AE，易证△DBA≌△ACE【探究】如图②，在△DBA和△ACE中，AD＝AE，若∠DAE＝α（0°＜α＜90°），∠BAC＝2α，∠B ＝∠C＝180°﹣α，求证：△DBA≌△ACE【应用】如图②，在△DBA和△ACE中，AD＝AE，若∠DAE＝70°，∠BAC＝140°，∠B＝∠C＝110°，则当∠D＝°时，∠DAC的度数是∠E的3倍．26．（12分）如图，在△ABC中，AD⊥BC于点D，BE⊥AE，连接DE，M是AB的中点，N是DE的中点．求证：MN是DE的中垂线．27．（12分）如图在△ABC中，AB＝BC＝6，∠ABC＝90°，直线l∥BC，点E是直线l上的一个动点，连接BE，将BE绕E逆时针旋转90°得到EF，连接BF交直线AC于点G．（1）如图1，当点E与点A重合时，线段BG和线段GF的数量关系是；（2）如图2，当点E在点A的右侧时，（1）问中的关系是否成立，请证明，若不成立，请写出你的结论并说明理由；（3）连接CF，若AE＝2，请直接写出△CFG面积大小．参考答案解析一．选择题（共12小题，满分48分，每小题4分）1．解：第一、第二、第四个图形都能找到这样的一条直线，使这些图形沿着一条直线对折后两部分完全重合，所以是轴对称图形，第三个图形找到这样的一条直线，使这个图形沿着一条直线对折后两部分完全重合，所以不是轴对称图形，所以是轴对称图形有3个．故选：C．2．解：设第三边为a，根据三角形的三边关系可得：8﹣6＜a＜8+6，解得：2＜a＜14．故第三边不可能是2，故选：D．3．解：A，32+42＝25＝52，符合勾股定理的逆定理，是直角三角形；B，22+22＝8＝（2）2，符合勾股定理的逆定理，是直角三角形；C，22+52≠62，不符合勾股定理的逆定理，不是直角三角形；D、52+122＝132，符合勾股定理的逆定理，是直角三角形．故选：C．4．解：∵AD是△ABC的中线，∴BD＝DC，故选：B．5．解：∵△ABC≌△DEF，△ABC的周长为80cm，∴△DEF的周长为80cm，DE＝AB＝25cm，又∵DF＝35cm，∴EF＝80﹣25﹣35＝20cm．故选：A．6．解：∵CD⊥AB，BE⊥AC，AO平分∠BAC，∴∠ADO＝∠AEO＝90°，∠DAO＝∠EAO，∵AO＝AO∴△ADO ≌△AEO （AAS ）；∴OD ＝OE ，AD ＝AE∵∠DOB ＝∠EOC ，∠ODB ＝∠OEC ＝90°∴△BOD ≌△COE （ASA ）；∴BD ＝CE ，OB ＝OC ，∠B ＝∠C∵AE ＝AD ，∠DAC ＝∠CAB ，∠ADC ＝∠AEB ＝90°，∴△ADC ≌△AEB （ASA ）；∵AD ＝AE ，BD ＝CE∴AB ＝AC∵OB ＝OC ，AO ＝AO∴△ABO ≌△ACO （SSS ）．所以共有四对全等三角形．故选：C ．7．解：2是腰长时，三角形的三边分别为2、2、4，∵2+2＝4，∴不能组成三角形，2是底边时，三角形的三边分别为2、4、4，能组成三角形，周长＝2+4+4＝10．故选：A ．8．解：∵DE 是BC 的垂直平分线，∴DC ＝DB ，∴△ADC 的周长＝AC +AD +DC ＝AC +AD +DB ＝AC +AB ＝16，故选：D ．9．解：在AB 上截取AF ＝AC ，∵AD 平分∠BAC ，∴∠CAD ＝∠FAD ，在△ACD 与△AFD 中，，∴△ACD ≌△AFD （SAS ），∴S △ACD ＝S △AFD ，∵AD ＝DE ，地△BDE 的面积为96，∴S △ABD ＝S △BDE ＝96，∵AB ＝3AC ，∴AB ＝3AF ，∴S △ADF ＝×96＝32，∴菜地△ACD 的面积是32，故选：C ．10．解：∵∠AFD ＝155°，∴∠DFC ＝25°，∵DF ⊥BC ，DE ⊥AB ，∴∠FDC ＝∠AED ＝90°，在Rt △FDC 和Rt △DEB 中，，∴Rt △FDC ≌Rt △DEB （HL ），∴∠DFC ＝∠EDB ＝25°，∴∠EDF ＝180°﹣∠BDE ﹣∠FDC ＝180°﹣25°﹣90°＝65°．故选：D ．11．解：A 、∵∠A +∠B ＝∠C ，∠A +∠B +∠C ＝180°，∴2∠C ＝180°，解得∠C ＝90°，∴此三角形是直角三角形，故本选项不合题意；B 、∵∠B ＝∠C ＝∠A ，∴设∠B ＝∠C ＝x ，则∠A ＝2x ．∵∠A +∠B +∠C ＝180°，∴x +x +2x ＝180°，解得x ＝45°，∴∠A ＝2x ＝90°，∴此三角形是直角三角形，故本选项不合题意；C 、∵∠A ＝90°﹣∠B ，∴∠A +∠B ＝90°，∴∠C ＝90°，∴此三角形是直角三角形，故本选项不符合题意；D、∵∠A﹣∠B＝90°，∴∠A＝90°+∠B＞90°，∴此三角形是钝角三角形，故本选项符合题意；故选：D．12．解：∵△A1B1A2是等边三角形，∴∠B1A1A2＝60°，∵∠MON＝30°，∴∠OB1A1＝30°∴A1B1＝OA1＝1，∴A2B1＝1，∵△A2B2A3、△A3B3A4是等边三角形，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴A2B2＝2B1A2，B3A3＝2B2A3，∴A3B3＝4B1A2＝4，A4B4＝8B1A2＝8，A5B5＝16B1A2＝16，以此类推：△A7B7A8的边长为26＝64，故选：A．二．填空题（共6小题，满分24分，每小题4分）13．解：∵正六边形ABCDEF的每一个内角是4×180°÷6＝120°，正方形ABGH的每个内角是90°，∴∠FAH＝360°﹣120°﹣90°＝150°，∴∠AFH+∠AHF＝180°﹣150°＝30°；故答案为：30°．14．解：如图所示：∵正方形A、B、C、D的边长分别是3、5、2、3，∴正方形A、B、C、D的面积分别是32＝9，52＝25，22＝4，32＝9，∵∠GFH＝90°，∴GH2＝GF2+FH2＝9+25＝34，∴正方形GHMN的面积＝34，同理：正方形MKLS的面积＝4+9＝13，同理：正方形E的面积＝34+13＝47；故答案是：47．15．解：作DM ⊥AC ，垂足为M ，如图，∵AD 是△ABC 的角平分线，DF ⊥AB ，DM ⊥AC ， ∴DF ＝DM ，∵AD ＝AD ，DF ＝DM ，∴△ADF ≌△ADM （HL ），∵DE ＝DG ，DF ＝DM ，∴△DFE ≌△DMG （HL ），∴S △ADM ＝S △ADF ＝S △ADG ﹣S △EFD ＝50﹣4.5＝45.5， ∴S △AED ＝S △ADF ﹣S △EFD ＝45.5﹣4.5＝41．故答案为：41．16．解：∵DE 垂直平分AC ，∠A ＝40°， ∴AE ＝CE ，∴∠ACE ＝∠A ＝40°，∵∠A ＝40°，AB ＝AC ，∴∠ACB ＝70°，∴∠BCE ＝∠ACB ﹣∠ACE ＝70°﹣40°＝30°．故∠BCE 的度数是30°．故答案为：30°．17．解：由题意可知，将木块展开，相当于是AB +1个等边三角形的边长，∴长为11+1＝12（m ）；宽为5cm ．于是最短路径为：＝13（cm ），故答案为：13．18．解：设BF长为x，则FD＝4﹣x，∵∠ACB＝∠BCE＝∠CBD，∴△BCF为等腰三角形，BF＝CF＝x，在Rt△CDF中，（4﹣x）2+22＝x2，解得：x＝2.5，∴BF＝2.5，＝BF×CD＝×2.5×2＝2.5．∴S△BFC即重叠部分面积为2.5．故答案为：2.5．三．解答题（共9小题，满分78分）19．解：由题意：，解得即∠A＝70°，∠B＝60°，∠C＝50°．20．解：∵AC∥DF，∴∠C＝∠F．∵AB∥DE，∴∠ABC＝∠DEF．∵CE＝BF，∴CE+EB＝BF+BE．∴CB＝EF．在△ABC和△DEF中，，∴△ABC≌△DEF（ASA）．21．解：（1）∵DF是AB的垂直平分线，∴AF＝BF，∵AB+BC＝6，AB＝AC，∴△BCF的周长为＝BC+CF+BF＝BC+CF+AF＝BC+AC＝AB+BC＝6；（2）∵AB＝AC，∠A＝40°，∴∠ACB＝∠ABC＝（180°﹣40°）＝70°，∵AB的垂直平分线DE交BC延长线于E，∴∠BDE＝90°，∴∠E＝90°﹣∠ABC＝20°．22．解：连接AC，将四边形分割成两个三角形，其面积为两个三角形的面积之和，在直角△ABC中，AC为斜边，则AC＝＝25米，在直角△ACD中，AC为斜边则AD＝＝24米，四边形ABCD面积S＝AB×BC+AD×CD＝234平方米．答：此块地的面积为234平方米．23．解：（1）∵BC2＝CE2+BE2＝22+42＝20，CD2＝CF2+DF2＝12+22＝5，BD2＝GD2+BG2＝32+42＝25，（勾股定理）∴BD2＝BC2+CD2根据勾股定理的逆定理可得∠BCD是直角．（2）根据图示知，S 四边形ABCD ＝S 正方形AHEJ ﹣S △BCE ﹣S △ABH ﹣S △ADI ﹣S △DCF ﹣S 正方形DFJI ，则S 四边形ABCD ＝5×5﹣×2×4﹣×1×5﹣×1×4﹣×2×1﹣1×1＝，即四边形ABCD 的面积是；（3）设△ABD 边AD 上的高为h ．由（2）知，S 四边形ABCD ＝．根据图示知，S △ABD ＝S 四边形ABCD ﹣S △BCD ，由（1）知，BD ＝5，BC ＝2，CD ＝，则×•h ＝﹣××2，解得，h ＝．所以，△ABD 边AD 上的高是．24．证明：在△ACD 和△ABE 中，，∴△ACD ≌△ABE （ASA ）．∴AD ＝AE ．∵AB ＝AC ，∴BD ＝CE ．在△DOB 和△EOC 中，，∴△DOB ≌△EOC （AAS ）．25．解：探究：∵∠BAC ＝2α，∠DAE ＝α，∴∠DAB+∠EAC＝α，∵∠B＝180°﹣α，∴∠DAB+∠D＝α，∴∠EAC＝∠D，在△DBA和△ACE中，，∴△DBA≌△ACE．应用：∵∠DAE＝70°，∠BAC＝140°，∠B＝∠C＝110°，∴∠DAC＝∠DAE+∠EAC＝70°+∠EAC，∠EAC＝180°﹣∠C﹣∠E＝180°﹣110°﹣∠E＝70°﹣∠E，∴∠DAC＝70°+70°﹣∠E，当∠DAC＝3∠E，∴3∠E＝70°+70°﹣∠E，解得：∠E＝35°，同理可证△DBA≌△ACE．∴∠D＝∠ACE＝35°．故答案为：35．26．证明：如图，连接MD、ME，∵AD⊥BC于点D，BE⊥AE，M为AB的中点，∴MD＝ME＝AB，∵N为DE的中点，∴MN⊥DE，∴MN是DE的中垂线．27．解：（1）∵AB＝BC＝6，∠ABC＝90°，∴∠BAC＝∠ACB＝45°，∵将BE绕E逆时针旋转90°得到EF，∴BE＝EF，∠BEF＝90°，∴∠BEC＝∠FEC＝45°，又∵EB＝EF，∴BG＝GF，故答案为：BG＝GF．（2）成立理由：过点E作EH⊥AE交AC于点H，连接FH，∴∠AEH＝90°∵AB＝BC＝6，∠ABC＝90°，∴∠BAC＝∠C＝45°，∵AE∥BC∴∠C＝∠CAE＝45°，∠BAE＝∠ABC＝90°，∵∠AEH＝90°，∴∠AHE＝∠CAE＝45°，∴AE＝EH，∵BE绕E逆时针旋转90°得到EF，∴BE＝EF，∠BEF＝90°，∵∠BEF＝∠AEH＝90°，∴∠AEB＝∠HEF，∴△ABE≌△HEF（SAS），∴AB＝HF，∠BAE＝∠EHF＝90°，∴∠CHF＝∠C＝45°，∵AB＝BC，∴HF＝BC，又∵∠HGF＝∠BGC，∴△HGF≌△BGC（AAS），∴BG＝GF；（3）如图2﹣1，当点E 在点A 右侧，过点B 作BN ⊥AC 于N ，∵AE ＝2＝EH ，∠AEH ＝90°，∴AH ＝2，∵AB ＝BC ＝6，BN ⊥AC ，∠ABC ＝90°，∴AC ＝6，BN ＝AC ＝3，∴CH ＝4， ∵△HGF ≌△BGC ，∴CG ＝GH ＝2，∴S △BGC ＝CG ×BN ＝×2×3＝6， ∵BG ＝GF ，∴S △CFG ＝S △BGC ＝6；如图2﹣2，过点E 作EH ⊥AE 交CA 的延长线于H ，连接HF ，过点B 作BN ⊥AC 于N ，同理可证△HGF ≌△BGC ，∴BG ＝GF ，GH ＝CG ，∵AE ＝2＝EH ，∠AEH ＝90°，∴AH ＝2，∵AB ＝BC ＝6，BN ⊥AC ，∠ABC ＝90°，∴AC ＝6，BN ＝AC ＝3，∴CH ＝8， ∴CG ＝4，∴S △BGC ＝CG ×BN ＝×4×3＝12， ∵BG ＝GF ，∴S △CFG ＝S △BGC ＝12，综上所述：S △CFG ＝6或12．。

鲁教版七年级(上)期中数学试卷(含答案)(五四制)

七年级数学上学期期中试题（时间120分钟，满分120分）得分表题号一二三总分19 20 21 22 23 24 25 26 得分阅卷人一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一个是正确的．每小题选对得３分，选错、不选或多选，均不得分．把正确选项的字母代号填在下面的答案表中）题号１２３４５６７８９１0 1１１2 得分答案1．下列各数是无理数的是( )A. 3.14B.16-C.3πD.362．如图，在Rt △ABC 中，∠C ＝90°，D 为AC 上一点，且DA ＝DB ＝5，又△DAB 的面积为10，那么DC 的长是 ( )A. 3B. 4C.5D. 63.如图，在ABC 中,DE 是AC 的垂直平分线，AE =3cm , ABD 的周长为12cm ，ABC 的周长为 ( ) cm .A. 15B. 16C.17D.18 4．在下列长度的四组线段中，不能组成直角三角形的是（）． A ．a =9 b =41 c =40 B ．a =b =5 C =52 C ．a :b :c =3:4:5 D ．a =11 b =12 c =15得分阅卷人第2题AED CB第3题图5．等腰三角形的腰长为10，底边长为12，则这个等腰三角形的面积是( )A．24 B．48 C．96 D．366．三角形的三个内角比为1∶2∶3，最小的边长为1，则最大的边长为( )A．2 B．4 C．6 D．87．下列图形不是轴对称图形的是()8．如图，四边形ABCD中，AB=4cm，BC=3cm，CD=12cm，DA=13cm，且∠ABC=90°，则四边形ABCD的面积为（）A、6cm2B、30cm2C、24cm2D、72cm29．如图所示，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超，使超市到三个小区的距离相等，则超市应建在（）（A）在AC、BC两边高线的交点处（B）在AC、BC两边中线的交点处（C）在AC、BC两边垂直平分线的交点处;（D）在A、B两内角平分线的交点处10.BE⊥AC于点D，且AD＝CD，BD＝ED，若∠ABC＝54°，则∠E＝（）（A）25°（B）27°（C）30°（D）45°11. 如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分为三个三角形，则S△ABO︰S△BCO︰S△CAO等于（）（A）1︰1︰1 （B）1︰2︰3 （C）2︰3︰4 （D）3︰4︰5第12题图12．如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A与点B重合，折痕为DE，则S△BCE：S△ADE等于（）A．2：5 B．16：25 C．14：25 D．14：21 CBAD AC EB10题ABO第11题图二、填空题（本大题共6小题，每小题3分，共18分，只要求填出最后结果）13．36的平方根是．14．等腰三角形的一个外角是100°，它的底角__________. 15．如图是“俄罗斯方块”游戏中的一个图案，由四个完全相同的小正方形拼成，则∠ABC 的度数为__________.16．如图，OP 平分∠MON ，PA ⊥ON 于点A ，点Q 是射线OM 上的一个动点，若PA =2，则PQ范围是．17．如图，一架梯子斜靠在一面墙上，梯子顶端离地面8米，底端距墙面6米，当梯子滑动到与地面成30︒角时，梯子的顶端向下水平滑动了米18．如图，△ABC 中，AB =AC ，∠BAC 和∠ACD 的平分线相交于点D ，∠ADC =130°，则∠BAC 的度数__________.三、解答题（本大题共8小题，共66分）19．（本题满分6分）若622=----y x x 求y x 的算术平方根．得分阅卷人得分阅卷人第18题第16题第17题AC用直尺和圆规作图（不写做法，只保留作图痕迹）：（1）在线段AB 上找一点P ，使点P 到BC ，AC 所在直线的距离相等；（2）在线段AC 上找一点Q ，使点Q 到点B ，C 的距离相等．21．（本题满分9分）如图，已知OA=O B.（1）说出数轴上点A 所表示的数；（2）比较点A 所表示的数与-3.5的大小；（3）在数轴上找出表示数17的点.（保留作图痕迹）22．（本题满分9分）如图，△ABC 中，D 是BC 上的一点，若AB =10，BD =6，AD =8，AC =17，求△ABC 的面积。

鲁教版五四制七年级(上)数学期中试题(含答案)

鲁教版五四制英语七年级上册-第一学期期中质量检测

2014-2015学年第一学期期中质量检测
初一英语
注意事项：
1.本试卷分第I卷和第II卷两部分，共120分。

考试时间90分钟。

2.用2B铅笔将第I卷答案涂在答题卡上，将第II卷答案直接写在试卷上。

考试结
束，考生只交第II卷。

第I卷
一．听力测试（共25小题，计25分）
友情提示：静下心，听仔细。

先将答案勾在题上，录音听完后，再涂写答题卡。

（一）听句子，选择与画面一致的选项。

每组句子听一遍。

1.（ＡＢＣ）２．（ＡＢＣ）３．（ＡＢＣ）
鲁K A 9083
４．（ＡＢＣ）5．（ＡＢＣ）
（二）听句子，选择适当的答语。

每个句子听两遍。

6. A. I’m OK. B. How are you? C. I’m good.
7. A. Hello! And you?. B.Thank you. C. Nice to meet you,too.
8. A. My telephone number is 6629238.
B. His telephone number is 6623529.
C. Her telephone number is 6635282.
9. A. Please spell it. B.B-I-K-E. C. It’s a bike.
10. A.She is my friend. B. They’re my brothers C.This is my cousin.。

鲁教版数学七年级上册期中考试试题含答案(五四制)

鲁教版数学七年级上册期中考试试卷注意事项：1、答题前请考生务必在答题卡及试卷的规定位置将自己的姓名、考试号、考试科目等内容填、写（涂）准确。

2、本试题分第I卷和第II卷两个部分，第I卷为选择题共42分，第II卷为非选择题共78分，共120分，考试时间为120分钟。

3、第I卷每小题选出答案后，必须用2B铅笔把答题卡上，对应题目的答案标号（AB-CD）涂黑，如需改动，须先用橡皮擦干净再改涂其它答案，第II卷须用蓝黑钢笔或圆珠笔直接答在试卷上，考试时，不允许使用计算器。

4、考试结束后，由监考教师把第I卷和第II卷及答题卡一并收回。

第I卷（选择题共42分）一、选择题：本题共14小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项涂在答题卡的相应位置上，每小题3分，错选、不选或选出的答案超过一个，均记0分1．0.49的算术平方根是（）A．±0.7 B．-0.7 C．0.7 D．0.72．下列各数中，是无理数的有（）2，31000，π， 3.1416-，13，9，0.571 43，31-．A．2个B．3个C．4个D．5个3．下列四幅图案，其中是轴对称图形的个数（）A．1个 B．2个 C．3个 D．4个4．两根木棒长分别为5cm和7cm，要选择第三根木棒，将其钉成三角形，则第三根木棒的长可以是（）．A．2cm B．4cm C．12cm D．17cm5．按下列各组数据能组成直角三角形的是（）A．11，15，13 B．1，4，5 C．8，15，17 D．4，5，6（6题图）（7 题图）（8题图）6．如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A．SSS B．SAS C．AAS D．ASA7．如图所示，一棵大树高8米，一场大风过后，大树在离地面3米处折断倒下，树的顶端落在地上，则此时树的顶端离树的底部有（）米．A．4 B．3.5 C．5 D．13.68．如图，直线l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它的三条公路的距离相等，则可供选择的地址有（）A．一处 B．二处 C．三处 D．四处9．若等腰三角形的腰长为10，底边长为12，则底边上的高为（）A．6 B．7 C．8 D．910．如图，PM=PN，MQ为△PMN的角平分线．若∠MQN=72°，则∠P的度数是（）A．18°B．36°C．48°D．60°（10题图）（11题图）（12题图）（13题图）11．如图，已知CF垂直平分AB于点E，∠ACD=70°，则∠A的度数是（）A．25° B．35° C．40° D．45°12．如图是一张直角三角形的纸片，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（）A．4 cm B．5 cm C．6 cm D．10 cm13.如图，一圆柱高8cm ，底面半径为2cm ，一只蚂蚁从点A 爬到点B 处吃食，要爬行的最短路程（π取3）是（）A ．20 cmB ．10 cmC ．14cmD ．无法确定 14．一块木板如图所示，已知AB ＝4，BC ＝3，DC ＝12，AD ＝13，∠B ＝90°，木板的面积为（） A ．60 B ．30 C ．24 D ．12二、填空题：本题共8小题，满分24分，只要求填写最后结果，每小题对得3分。

鲁教版五四制七年级上册期中学业水平测试

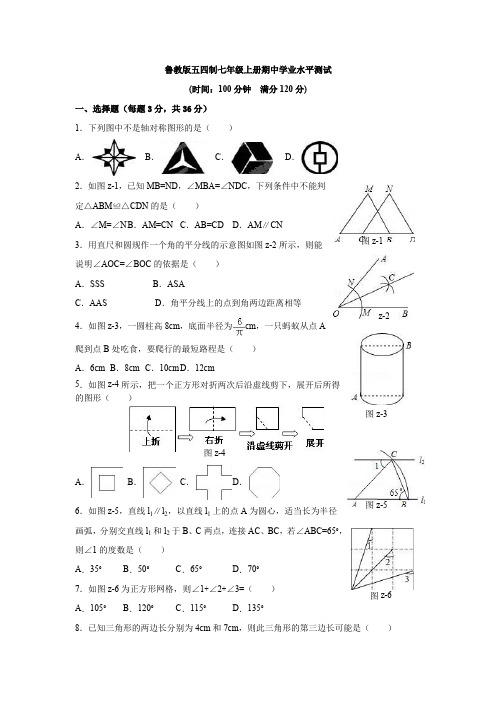
图z-4鲁教版五四制七年级上册期中学业水平测试(时间：100分钟满分120分)一、选择题（每题3分，共36分）1．下列图中不是轴对称图形的是（）A． B． C． D．2．如图z-1，已知MB=ND ，∠MBA=∠NDC ，下列条件中不能判定△ABM ≌△CDN 的是（）A ．∠M=∠NB ．AM=CNC ．AB=CD D ．AM ∥CN3．用直尺和圆规作一个角的平分线的示意图如图z-2所示，则能说明∠AOC=∠BOC 的依据是（）A ．SSSB ．ASAC ．AASD ．角平分线上的点到角两边距离相等4．如图z-3，一圆柱高8cm，底面半径为cm ，一只蚂蚁从点A 爬到点B 处吃食，要爬行的最短路程是（）A ．6cmB ．8cmC ．10cmD ．12cm5．如图z-4所示，把一个正方形对折两次后沿虚线剪下，展开后所得的图形（）A． B． C． D．6．如图z-5，直线l 1∥l 2，以直线l 1上的点A 为圆心，适当长为半径画弧，分别交直线l 1和l 2于B 、C 两点，连接AC 、BC ，若∠ABC=65°，则∠1的度数是（）A ．35°B ．50°C ．65°D ．70°7．如图z-6为正方形网格，则∠1+∠2+∠3=（）A ．105°B ．120°C ．115°D ．135° 8．已知三角形的两边长分别为4cm 和7cm ，则此三角形的第三边长可能是（）图z-1z-2图z-3 图z-5 图z-6图z-10 图z-11 图z-12 A ．3cm B ．11cm C ．7cm D ．15cm9．如图z-7，将△ABC 沿直线DE 折叠后，使得点B 与点A 重合．已知AC=5cm ，△ADC 的周长为17cm ，则BC 的长为（）A ．7cmB ．10cmC ．12cmD ．22cm10．等腰三角形一腰上的高与另一腰的夹角为40°，则这个等腰三角形的一个底角的度数为（）A ．50°B ．80°C ．50°或80°D ．25°或65° 11．如图z-8，在△ABC 中，∠C=90°，∠B=30°，以A 为圆心，任意长为半径画弧分别交AB 、AC 于点M 和N ，再分别以M 、N 为圆心，大于MN 的长为半径画弧，两弧交于点P ，连结AP 并延长交BC 于点D ，则下列说法中正确的个数是（）①AD 是∠BAC 的平分线；②∠ADC=60°；③点D 在AB 的中垂线上；④BD=2CD ．A ．4B ．3C ．2D ．1 12．如图z-9是4×4正方形网格，其中已有3个小正方形涂成了黑色，现在要从其余13个白色小方格中选出一个也涂成黑色的图形称为轴对称图形，这样的白色小方格有（）A ．2个B ．3个C ．4个D ．5个二、填空题（每题4分，共24分）13．如图z-10放置在一凹槽内，顶点A 、B 、C 分别落在凹槽内壁上，∠ADE=∠BED=90°，测得AD=5cm ，BE=7cm ，则该零件的面积为．14．如图z-11，AB ∥EF ，∠C=∠D=85°，CF=BD ，若∠A=40°，则∠EFD= ．15．如图z-12，将长方形纸片ABCD 折叠，使边DC 落在对角线AC 上，折痕为CE ，且D 点落在D ′处，若AB=3，AD=4，则S △CED ′：S△CEA = ．16．如图z-13，长方体的底面边长分别为1cm 和3cm ，高为6cm ．图z-7图z-8图z-9 图z-13如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B ，那么所用细线最短需要17．如图z-14，已知在△ABC 中，∠B 与∠C 的平分线交于点P ．当∠BPC=118°时，则∠A 的度数为．18．如图z-15所示，在△ABC 中，∠ACB=90°，AC=12，BC=5，AM=AC ，BN=BC ，则MN 的长为．三、解答题（共7个小题，60分）19．某地拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉P 到广场的两个入口A 、B 的距离相等，且到广场管理处C 的距离等于A 和B 之间距离的一半，A 、B 、C 的位置如图所示．请利用尺规作图作出音乐喷泉P 的位置．（要求：不写作法，但要保留作图痕迹，必须用铅笔作图）．20．如图z-16，已知AB ⊥CD ，△ABD 和△BCE 都是等腰直角三角形，CD=17，BE=5，则AC 的长为多少？21．如图z-17，△ABC 是等边三角形，D 是AC 上一点，BD=CE ，∠1=∠2，试判断BC 与AE 的位置关系，并证明你的结论．22．在8×8的方格纸中，设小方格的边长为1．（1）请判断△ABC 的形状并说明理由．（2）画出△ABC 以CO 所在直线为对称轴的对称图形△A ′B ′C ′，并在所画图中标明字母．23．在△ABC 中，AB=AC ，点D 是BC 的中点，点E 是图z-14图z-15图z-16 A E C B D 图z-17AD 上任意一点．（1）如图1，连接BE 、CE ，问：BE=CE成立吗？并说明理由；（2）如图2，若∠BAC=45°，BE 的延长线与AC 垂直相交于点F 时，问：EF=CF成立吗？并说明理由．24．在甲村至乙村的公路旁有一块山地正在开发，现有一C 处需要爆破，已知点C 与公路上的停靠站A 的距离为300米，与公路上另一停靠站B 的距离为400米，且CA ⊥CB ，如图z-18，为了安全起见，爆破点C 周围半径250米范围内不得进入，问在进行爆破时，公路AB 段是否有危险，是否而需要暂时封锁？请通过计算进行说明．25．如图z-19，已知△ABC 中∠BAC=135°，点E ，点F 在BC 上，EM 垂直平分AB 交AB 于点M ，FN 垂直平分AC 交AC 于点N ，BE=12，CF=9．（1）判断△EAF 的形状，并说明理由；（2）求△EAF 的周长．图z-18图z-19答案一、选择题1.【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．据此对图中的图形进行判断．【解答】解：A、有四条对称轴，是轴对称图形，故本选项错误；B、有三条对称轴，是轴对称图形，故本选项错误；C、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，故本选项正确；D、有二条对称轴，是轴对称图形，故本选项错误．故选C．【点评】本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2．【分析】根据普通三角形全等的判定定理，有AAS、SSS、ASA、SAS四种．逐条验证．【解答】解：A、∠M=∠N，符合ASA，能判定△ABM≌△CDN，故A选项不符合题意；B、根据条件AM=CN，MB=ND，∠MBA=∠NDC，不能判定△ABM≌△CDN，故B选项符合题意；C、AB=CD，符合SAS，能判定△ABM≌△CDN，故C选项不符合题意；D、AM∥CN，得出∠MAB=∠NCD，符合AAS，能判定△ABM≌△CDN，故D选项不符合题意．故选：B．3．【分析】连接NC，MC，根据SSS证△ONC≌△OMC，即可推出答案．【解答】解：连接NC，MC，在△ONC和△OMC中，∴△ONC≌△OMC（SSS），∴∠AOC=∠BOC，故选A．4．【分析】此题最直接的解法，就是将圆柱展开，然后利用两点之间线段最短解答．【解答】解：底面圆周长为2πr，底面半圆弧长为πr，即半圆弧长为：×2π×=6（cm），展开得：∵BC=8cm，AC=6cm，根据勾股定理得：AB==10（cm）．故选C．5．【分析】此类问题只有动手操作一下，按照题意的顺序折叠，剪开，观察所得的图形，可得正确的选项．【解答】解：按照题意，动手操作一下，可知展开后所得的图形是选项B．故选B．6．【分析】首先由题意可得：AB=AC，根据等边对等角的性质，即可求得∠ACB的度数，又由直线l1∥l2，根据两直线平行，内错角相等，即可求得∠2的度数，然后根据平角的定义，即可求得∠1的度数．【解答】解：根据题意得：AB=AC，∴∠ACB=∠ABC=67°，∵直线l1∥l2，∴∠2=∠ABC=65°，∵∠1+∠ACB+∠2=180°，∴∠1=180°﹣∠2﹣∠ACB=180°﹣65°﹣65°=50°．故选B．7．【分析】首先证明△ABC≌△AEF，然后证明∠1+∠3=90°，再根据等腰直角三角形的性质可得∠2=45°，进而可得答案．【解答】解：∵在△ABC和△AEF中，，∴△ABC≌△AEF（SAS），∴∠4=∠3，∵∠1+∠4=90°，∴∠1+∠3=90°，∵AD=MD，∠ADM=90°，∴∠2=45°，∴∠1+∠2+∠3=135°，故选：D．8．【分析】已知三角形的两边长分别为4cm和7cm，根据在三角形中任意两边之和＞第三边，任意两边之差＜第三边；即可求第三边长的范围．【解答】解：设第三边长为x，则由三角形三边关系定理得7﹣4＜x＜7+4，即3＜x＜11．因此，本题的第三边应满足3＜x＜11，把各项代入不等式符合的即为答案．3，11，15都不符合不等式3＜x＜11，只有7符合不等式，故答案为7cm．故选C．9．【分析】首先根据折叠可得AD=BD，再由△ADC的周长为17cm可以得到AD+DC的长，利用等量代换可得BC的长．【解答】解：根据折叠可得：AD=BD，∵△ADC的周长为17cm，AC=5cm，∴AD+DC=17﹣5=12（cm），∵AD=BD，∴BD+CD=12cm．故选：C．10．【分析】本题已知没有明确三角形的类型，所以应分这个等腰三角形是锐角三角形和钝角三角形两种情况讨论．【解答】解：当这个三角形是锐角三角形时：高与另一腰的夹角为40，则顶角是50°，因而底角是65°；如图所示：当这个三角形是钝角三角形时：∠ABD=50°，BD⊥CD，故∠BAD=50°，所以∠B=∠C=25°因此这个等腰三角形的一个底角的度数为25°或65°．故选：D．11．【分析】①根据作图的过程可以判定AD是∠BAC的角平分线；②利用角平分线的定义可以推知∠CAD=30°，则由直角三角形的性质来求∠ADC的度数；③利用等角对等边可以证得△ADB的等腰三角形，由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上；④根据直角三角形的性质得出AD=2CD，再由线段垂直平分线的性质得出AD=BD，进而可得出结论．【解答】解：①根据作图的过程可知，AD是∠BAC的平分线．故①正确；②如图，∵在△ABC中，∠C=90°，∠B=30°，∴∠CAB=60°．又∵AD是∠BAC的平分线，∴∠1=∠2=∠CAB=30°，∴∠3=90°﹣∠2=60°，即∠ADC=60°．故②正确；③∵∠1=∠B=30°，∴AD=BD，∴点D在AB的中垂线上．故③正确；∵∠2=30°，∴AD=2CD．∵点D在AB的中垂线上，∴AD=BD，∴BD=2CD．故④正确．故选A．12．【分析】根据轴对称图形的概念求解．【解答】解：如图所示，有4个位置使之成为轴对称图形．故选C．二、填空题13．【分析】首先证明△ADC≌△CEB，根据全等三角形的性质可得DC=BE=7cm，再利用勾股定理计算出AC长，然后利用三角形的面积公式计算出该零件的面积即可．【解答】解：∵△ABC是等腰直角三角形，∴AC=BC，∠ACB=90°，∴∠ACD+∠BCE=90°，∵∠ADC=90°，∴∠ACD+∠DAC=90°，∴∠DAC=∠BCE，在△ADC和△CEB中，，∴△ADC≌△CEB（AAS），∴DC=BE=7cm，∴AC===（cm），∴BC=cm，∴该零件的面积为：××=37（cm2）．故答案为：37cm2．14．【分析】利用已知条件证明△ABC≌△DFE（ASA），得到∠A=∠E=40°，再利用三角形的内角和为180°，即可解答．【解答】解：∵AB∥EF，∴∠ABC=∠EFD，∵CF=BD，∴CF+BF=BD+BF，∴BC=DF，在△ABC和△DFE中，∴△ABC≌△DFE（ASA），∴∠A=∠E=40°，∴∠EFD=180°﹣∠D﹣∠E=180°﹣85°﹣40°=55°．15．【分析】由矩形的性质可知DC=AB=3，由勾股定理可求得AC=5，由翻折的性质可知D′C=DC=3，最后根据S△CED′：S△CEA=D′C：AC求解即可．【解答】解：∵四边形ABCD为长方形，∴DC=AB=3．在Rt△ADC中，AC==5．∵由翻折的性质可知：D′C=DC=3，∴S△ECD′：S△CEA=D′C：AC=3：5．故答案为：3：5．16．【分析】要求所用细线的最短距离，需将长方体的侧面展开，进而根据“两点之间线段最短”得出结果．【解答】解：将长方体展开，如图，连接A、B′，∵AA′=1+3+1+3=8（cm），A′B′=6cm，∴根据两点之间线段最短，AB′==10cm．17．【分析】据三角形的内角和等于180°，求出∠PBC+∠PCB的度数，再根据角平分线的定义，求得∠ABC+∠ACB．在△ABC中，根据三角形内角和定理，即可求出∠BAC的度数．【解答】解：在△PBC中，∵∠BPC=118°，∴∠PBC+∠PCB=180°﹣118°=62°．∵PB、PC 分别是∠ABC和∠ACB的角平分线，∴∠ABC+∠ACB=2（∠PBC+∠PCB）=2×62°=124°，在△ABC中，∠A=180°﹣（∠ABC+∠ACB）=180°﹣124°=56°．故答案为：56°．18．【分析】由图示知：MN=AM+BN﹣AB，所以结合已知条件，根据勾股定理求出AC 的长即可解答．【解答】解：在Rt△ABC中，根据勾股定理，AB==13，又∵AC=12，BC=5，AM=AC，BN=BC，∴AM=12，BN=5，∴MN=AM+BN﹣AB=12+5﹣13=4．故答案是：4．三、解答题19．【分析】由题意可知，M在AB的垂直平分线上，且到C的距离等于AB的一半．【解答】解：如图，20．【分析】由等腰直角三角形的性质可知BE=BC=5，所以DB=CD﹣BC=12，在Rt△ABC中求出AC的长即可．【解答】解：∵△BEC是等腰直角三角形，∴BC=BE=5，∴DB=CD﹣BC=12，由等腰△ABD 得出AB=BD=12，Rt△ABC中，由勾股定理可得AC=13．21．【分析】由△ABC是等边三角形，得出∠BAD=∠BCA=60°，AB=AC，由SAS证得△ABD≌△ACE，得出∠BAD=∠CAE=∠BCA，即可得出结论．【解答】解：BC与AE的位置关系是：BC∥AE；理由如下：∵△ABC是等边三角形，∴∠BAD=∠BCA=60°，AB=AC，在△ABD和△ACE中，，∴△ABD≌△ACE （SAS），∴∠BAD=∠CAE=60°，∴∠CAE=∠BCA，∴BC∥AE．22．【分析】（1）根据勾股定理求出各边的平方，进而可得出结论；（2）画出各点关于直线CO的对称点，再顺次连接即可．【解答】解：（1）∵AB2=12+22=5，AC2=22+42=20，BC2=32+42=25，∴AB2+AC2=BC2，∴△ABC是直角三角形；（2）如图所示．23．【分析】（1）成立，根据等腰三角形的性质就可以求出∠BAE=∠CAE，再证明△ABE ≌△ACE就可以得出结论；（2）成立，由BF⊥AC，∠BAC=45°就可以求出AF=BF，在由条件证明△AEF≌△BCF就可以得出结论．【解答】解：（1）成立．理由：∵AB=AC，D是BC的中点，∴∠BAE=∠CAE．在△ABE和△ACE中，∴△ABE≌△ACE（SAS）∴BE=CE．（2）成立．理由：∵∠BAC=45°，BF⊥AF．∴△ABF为等腰直角三角形∴AF=BF，由（1）知AD⊥BC，∴∠EAF=∠CBF在△AEF和△BCF中，．∴△AEF≌△BCF （AAS），∴EF=CF．24．【分析】如图，本题需要判断点C到AB的距离是否小于250米，如果小于则有危险，大于则没有危险．因此过C作CD⊥AB于D，然后根据勾股定理在直角三角形ABC中即可求出AB的长度，然后利用三角形的公式即可求出CD，然后和250米比较大小即可判断需要暂时封锁．【解答】解：如图，过C作CD⊥AB于D，∵BC=400米，AC=300米，∠ACB=90°，∴根据勾股定理得AB=500米，∵ABCD=BCAC，∴CD=240米．∵240米＜250米，故有危险，因此AB段公路需要暂时封锁．25．【分析】（1）根据线段垂直平分线的性质得出BE=AE，AF=CF，再由∠BAC=135°得出∠B+∠C=180°﹣∠BAC=180°﹣135°=45°，故∠BAE+∠CAF=45°，∠EAF=135°﹣45°=90°由此可得出结论；（2）由（1）知△EAF是直角三角形，再根据勾股定理求出EF的长，进而可得出结论．【解答】解：（1）△EAF为直角三角形．∵EM是AB的垂直平分线，∴BE=AE，∴∠BAE=∠B．∵FN是AC的垂直平分线，∴AF=CF，∴∠CAF=∠C．∵∠BAC=135°，∴∠B+∠C=180°﹣∠BAC=180°﹣135°=45°，∴∠BAE+∠CAF=45°，∴∠EAF=135°﹣45°=90°，∴△EAF为直角三角形；（2）在△EAF中，∵∠EAF=90°，∴EF2=AE2+AF2，∵BE=4，CF=3，∴EF2=42+32=25，∴EF=5，∴△EAF的周长=12．。

2022年鲁教版五四制七年级数学上册期中测试题及答案

一、选择题(每小题4分，共48分)1.如图所示，下列图形中，是轴对称图形的是( D )2.(2021淄博桓台期中)已知三角形的两边长分别为7 cm和9 cm，则该三角形第三边的长不可能是( A )A.2 cmB.3 cmC.5 cmD.6 cm3.如图所示，D是线段AC，AB的垂直平分线的交点，若∠CAD=32°，∠ABD=28°，则∠BCD的大小是( C )A.32°B.28°C.30°D.60°第3题图4.小强家有两块三角形的菜地，他想判断这两块三角形菜地的形状大小是否完全一样，他设想了如下四种方法，下列方法中，不一定能判定两个三角形全等的是( C )A.测量三边对应相等B.测量两角及其夹边对应相等C.测量两边及除夹角外的另一角对应相等D.测量两边及其夹角对应相等5.如图所示，在△ABC中，∠C=90°，∠B=30°，分别以A，B为圆AB的长为半径画弧交于点E和F，连接FE并延长交BC于心，大于12点D，则下列说法中不正确的是( B )A.AD是∠BAC的平分线B.S△ABD=3S△DACC.点D在AB的垂直平分线上D.∠ADC=60°第5题图6.(2021泰安东平实验中学期中)如图所示，在△ABC中，ED∥BC，∠ABC和∠ACB的平分线分别交ED于点G，F，若FG=2，ED=6，则EB+DC 的值为( C )A.6B.7C.8D.9第6题图7.如图所示，在△ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC，交AC于点M，若CM=5，则CE2+CF2等于( B )A.75B.100C.120D.125第7题图8.如图所示，在△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于点D，交AB于点E，下列结论错误的是( D )A.BD平分∠ABCB.△BCD的周长等于AB+BCC.AD=BD=BCD.点D是线段AC的中点第8题图9.如图所示，BD是△ABC的角平分线，AE⊥BD，垂足为F，若∠ABC=40°，∠C=45°，则∠CDE的度数为( D )A.35°B.40°C.45°D.50°第9题图10.如图所示，△ABC的面积为8 cm2，AP垂直∠ABC的平分线BP于点P，则△PBC的面积为( B )A.3 cm2B.4 cm2C.5 cm2D.6 cm2第10题图11.如图所示，将矩形ABCD沿对角线BD折叠，点C落在了点E处，BE与AD交于点F，再将△DEF沿DF折叠，点E落到了点G处，此时DG为∠ADB的平分线，则∠BDE的度数为( A )A.54°B.60°C.72°D.48°第11题图12.如图所示，在△ABC与△AEF中，AB=AE，BC=EF，∠ABC=∠AEF，∠EAB=40°，AB交EF于点D，连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EBC=110°;④AD=AC;⑤∠EFB=40°，其中正确的有( C )A.1个B.2个C.3个D.4个第12题图二、填空题(每小题4分，共24分)13.(2021泰安东平期中)在Rt△ABC中，斜边AB=2，则AB2+BC2+ CA2= 8 .14.(2021聊城)如图所示，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为点D和点E，AD与CE交于点O，连接BO并延长交AC于点F，若AB=5， BC=4，AC=6，则CE∶AD∶BF值为12∶15∶10 .第14题图15.如图所示，在三角形ABC中，∠ACB=86°，点D为AB边上一个动点，连接CD，把三角形ACD沿着CD折叠，当∠A′CB=20°时，∠DCB= 33°.第15题图16.如图所示的是由5个正方形和5个等腰直角三角形组成的图形，已知③号正方形的面积是1，那么①号正方形的面积是16 .第16题图17.如图所示，有一个棱柱，底面是边长为2.5 cm的正方形，侧面都是长为12 cm的长方形.在棱柱一底面的顶点A处有一只蚂蚁，它想吃B点的食物，那它需要爬行的最短路程是13 cm.第17题图18.如图所示，在四边形ABCD中，AB=AD=6，∠A=60°，∠ADC=150°，BC-CD=4，则四边形ABCD的周长是21 .第18题图三、解答题(共78分)19.(8分)如图所示，在3×3的正方形网格图中，△ABC和△DEF是关于某条直线成轴对称的两个格点三角形，现给出了△ABC，在下面的图中画出4个符合条件的△DEF，并画出对称轴.解:(答案不唯一)如图所示.20.(8分)如图所示，在四边形ABCD中，AD∥BC，∠A=90°，AD=4 cm，BD=BC=7 cm，CE⊥BD于点E，求DE的长.解:因为AD∥BC，所以∠ADB=∠DBC.因为CE⊥BD，所以∠BEC=90°.因为∠A=90°，所以∠A=∠BEC.在△ABD 和△ECB 中，因为∠A=∠BEC ，∠ADB=∠DBC ，BD=BC ，所以△ABD ≌△ECB(AAS).所以BE=AD=4 cm.所以DE=BD-BE=3 cm.21.(12分)如图所示，在△ABC 中，点D 是BC 边的中点，DE ⊥BC 交AB 于点E ，且BE 2-EA 2=AC 2.(1)试说明:∠A=90°;(2)若AC=6，BD=5，求AE 的长度.解:(1)连接CE(图略)，因为D 是BC 的中点，DE ⊥BC ，所以CE=BE. 因为BE 2-EA 2=AC 2，所以CE 2-EA 2=AC 2，所以EA 2+AC 2=CE 2，所以△ACE 是直角三角形，即∠A=90°.(2)因为D 是BC 的中点，BD=5，所以BC=2BD=10.因为∠A=90°，AC=6，所以根据勾股定理求得AB=8.在Rt △AEC 中，EA 2+AC 2=CE 2.因为CE=BE ，所以62+AE 2=(8-AE)2，解得AE=74，所以AE 的长为74. 22.(12分)如图所示，将长方形ABCD 沿着对角线BD 折叠，使点C 落在C ′处，BC ′交AD 于点E.(1)试判断△BDE 的形状，并说明理由;(2)若AB=4，AD=8，求△BDE 的面积.解:(1)△BDE 是等腰三角形.理由如下:由折叠的性质，知∠CBD=∠EBD.在长方形ABCD 中，AD ∥BC ，所以∠CBD=∠EDB.所以∠EBD=∠EDB.所以BE=DE.所以△BDE 是等腰三角形.(2)设DE=x ，则BE=x ，AE=8-x.在Rt △ABE 中，根据勾股定理，有AB 2+AE 2=BE 2，即42+(8-x)2=x 2，解得x=5.所以S △BDE =12DE ·AB=12×5×4=10. 23.(12分)某校一班学生到野外活动，为测量一池塘两端A ，B 之间的距离，设计出如下几种方案:方案a:如图①所示，先在平地上取一个可直接到达A ，B 的点C ，再连接AC ，BC ，并分别延长AC 至D ，BC 至E ，使DC=AC ，EC=BC ，最后测出DE 的长即为A ，B 之间的距离;方案b:如图②所示，过点B作AB的垂线BF，再在BF上取C，D两点，使BC=CD，接着过点D作BD的垂线DE，交AC的延长线于点E，则测出DE的长即为A，B之间的距离.阅读后回答下列问题:(1)方案a是否可行?请说明理由.(2)方案b是否可行?请说明理由.(3)方案b中作BF⊥AB，ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE，方案b的结论是否成立?①②解:(1)可行.理由:在△ABC和△DEC中，AC=DC，∠ACB=∠DCE(对顶角相等)，BC=EC，所以△ACB≌△DCE(SAS)，所以DE=AB.(2)可行，理由:因为AB⊥BF，ED⊥BF，所以∠B=∠CDE=90°.因为BC=DC，∠ACB=∠ECD(对顶角相等)，所以△ABC≌△EDC(ASA)，所以DE=AB.(3)作BF⊥AB，ED⊥BF的目的是使对应角∠ABD=∠BDE=90°，只要∠ABC=∠BDE，方案b的结论仍成立.24.(12分)(2021威海乳山期中)如图所示，两根旗杆间相距11 m，某人从B点沿BA走向A点，一定时间后到达点M，此时他仰望旗杆的顶点C和D，两次视线的夹角为90°，且CM=DM.已知旗杆AC的高度为5 m，该人运动速度为1.5 m/s.(1)求这个人还需运动多长时间到达点A;(2)求旗杆DB有多高.解:(1)因为∠CMD=90°，所以∠CMA+∠DMB=90°.因为∠CAM=90°，所以∠CMA+∠ACM=90°.所以∠ACM=∠DMB.在△ACM和△BMD中，因为∠A=∠B，∠ACM=∠BMD，CM=DM，根据AAS，所以△ACM≌△BMD.所以BM=AC=5 m.所以AM=11-5=6(m).所以他到达点A时，运动时间为6÷1.5=4(s).答:这个人还需运动4 s到达点A.(2)因为Rt△ACM≌Rt△BMD，所以DB=AM=6 m.答:旗杆DB高6 m.25. (14分)如图所示，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE，BE，延长AE交BC的延长线于点F.(1)判断FC与AD的数量关系，并说明理由;(2)若AB=BC+AD，判断BE与AF的位置关系，并说明理由.解:(1)FC=AD.理由如下:在△ADE和△FCE中，因为AD∥BC，所以∠ADC=∠ECF.因为E是CD的中点，所以DE=EC.因为∠AED=∠FEC，根据ASA，所以△ADE≌△FCE.所以FC=AD.(2)BE⊥AF.理由如下:因为AB=BC+AD，AD=CF，所以AB=BC+CF，即AB=BF.所以△ABF是等腰三角形.因为△ADE≌△FCE，所以AE=EF.所以BE⊥AF.。