《勾股定理》典型练习题
《勾股定理》专项训练练习

60 120140 60BACC A BDE 1015《勾股定理》专项训练练习基础篇1、下列各组线段中,能构成直角三角形的是( )A .2,3,4B .3,4,6C .5,12,13D .4,6,7 2、在△ABC 中,∠C=90°,周长为60,斜边与一直角边比是13:5,•则这个三角形三边长分别是( )A .5,4,3 B .13,12,5 C .10,8,6 D .26,24,10 3、若等边△ABC 的边长为2cm ,那么△ABC 的面积为( ). A. 3cm2B. 32cm2C. 33cm 2D. 4cm 24. 三角形的三边为a 、b 、c ,由下列条件不能判断它是直角三角形的是( )A .a :b :c=8∶16∶17B . a 2-b 2=c 2C .a 2=(b+c)(b-c)D . a :b :c =13∶5∶12 5. 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A . 等边三角形B . 钝角三角形C . 直角三角形D . 锐角三角形.6.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( ) A .121 B .120 C .90 D .不能确定7、放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( ) A .600米 B . 800米 C . 1000米 D. 不能确定8、ΔABC 中∠B=90°,两直角边AB=7,BC=24,在三角形内有一点P 到各边的距离相等,则这个距离是( )A.1B.3C.6D.非以上答案9、在△ABC 中,AB=12cm , BC=16cm , AC=20cm , 则△ABC 的面积是( )A. 96cm 2B. 120cm 2C. 160cm 2D. 200cm 210、已知如图,水厂A 和工厂B 、C 正好构成等边△ABC ,现由水厂A 和B 、C 两厂供水,要在A 、B 、C 间铺设输水管道,有如下四种设计方案,(图中实线为铺设管道路线),•其中最合理的方案是( )11、在△ABC 中,∠C=90°, AB =5,则2AB +2AC +2BC =_______.12、如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有______米.13、如图所示,是一个外轮廓为矩形的机器零件平面示意图,根据图中标出尺寸(单位:mm )计算两圆孔中心A 和B 的距离为 .14、已知Rt △ABC 中,∠C=90°,若a+b=14,c=10,则Rt △ABC 的面积是_____15、如图,梯子AB 靠在墙上,梯子的底端A 到墙根O 的距离为2米,梯子的顶端B 到地面的距离为7米.现将梯子的底端A 向外移动到A ’,使梯子的底端A ’到墙根O 的距离等于3米,同时梯子的顶端 B 下降至 B ’,那么 BB ’的值: ①等于1米;②大于1米5;③小于1米.其中正确结论的序号是 .16、如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和103㎝的长方体无盖盒子中,求细木棒露在盒外面的最短长度是多少?17、小东拿着一根长竹竿进一个宽为3米的城门,他先横着拿不进去,又竖起来拿,结果竿比城门高1米,当他把竿斜着时,两端刚好顶着城门的对角,问竿长多少米?18、如图,铁路上A 、B 两点相距25km , C 、D 为两村庄,若DA =10km ,CB =15km ,DA ⊥AB 于A ,CB ⊥AB 于B ,现要在AB 上建一个中转站E ,使得C 、D 两村到E 站的距离相等.(1)求E 应建在距A 多远处? (2)DE 和EC 垂直吗?试说明理由19、如图,在△ABC 中,∠BAC =120°,∠B =30°,AD ⊥AB ,垂足为A,CD=2cm,求AB 的长.第12题图 第13题图 第15题图A B D专题篇一、勾股定理与梯子问题1、如图1,一个梯子AB长2.5米,顶端A靠在墙上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,如图2,测得BD长为0.5米,求梯子顶端A下落了多少米.2、比较梯子沿墙壁滑行时其在墙壁和地面上滑行距离的大小关系例2如图3,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2米,梯子的顶端B到地面的距离为7米.现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3米,同时梯子的顶端B下降至B′,那么BB①等于1米;②大于1米;③小于1米.其中正确结论的序号是________.(要求写出过程)二、勾股定理中的数学思想1、面积法.已知△ABC中,∠ACB=90°,AB=5㎝.BC=3㎝,CD⊥AB于点D,求CD的长.2、构造法.如图,已知△ABC中,∠B=30°,∠C=45°,AB=4,AC=22.求△ABC的面积.3、转化思想.如图3,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13.求四边形ABCD的面积.4、分类讨论思想.已知Rt△ABC中,其中两边的长分别是3,5,求第三边的长.5、方程思想.如图4,AB为一棵大树,在树上距地面10米的D处有两只猴子,它们同时发现C处有一筐苹果,一只猴子从D往上爬到树顶A又沿滑绳AC滑到C处,另一只猴子从D滑到B,再由B跑到C.已知两只猴子所经路程都是15米.试求大树AB的高度.如图,在△ABC中,AB=15,BC=14,CA=13,求BC边上的高AD.6、逆向思维的方法如图1,在△ABC中,D为BC边上一点,已知AB=13,AD=12,AC=15,BD=5,那么DC=_____.图3DABC图4DCBAABC三、勾股定理在影响范围问题中的运用1、如图1,公路MN 和公路PQ 在点P 处交汇,且30QPN ∠=︒,点A 处有一所中学,AP =160m 。
勾股定理练习题及答案(共6套)

勾股定理课时练(1)1.在直角三角形ABC中,斜边AB=1,则AB222ACBC++的值是()A.2B.4C.6D.82.如图18-2-4所示,有一个形状为直角梯形的零件ABCD,AD∥BC,斜腰DC的长为10 cm,∠D=120°,则该零件另一腰AB的长是______ cm(结果不取近似值).3.直角三角形两直角边长分别为5和12,则它斜边上的高为_______.4.一根旗杆于离地面12m处断裂,犹如装有铰链那样倒向地面,旗杆顶落于离旗杆地步16m,旗杆在断裂之前高多少m?5.如图,如下图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是米.6.飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行多少千米?7.如图所示,无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的容器的上口外侧距开口1cm的F处有一苍蝇,试求急于扑货苍蝇充饥的蜘蛛,所走的最短路线的长度. 8.一个零件的形状如图所示,已知AC=3cm,AB=4cm,BD=12cm。
求CD的长.9.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长.10.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?11如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?12.甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?第一课时答案:1.A ,提示:根据勾股定理得122=+AC BC,所以AB 222AC BC ++=1+1=2;2.4,提示:由勾股定理可得斜边的长为5m ,而3+4-5=2m ,所以他们少走了4步.3.1360 ,提示:设斜边的高为x ,根据勾股定理求斜边为1316951222==+ ,再利用面积法得,1360,132112521=⨯⨯=⨯⨯x x ;4. 解:依题意,AB=16m ,AC=12m ,在直角三角形ABC 中,由勾股定理,222222201216=+=+=AC AB BC ,所以BC=20m ,20+12=32(m ), 故旗杆在断裂之前有32m 高. 5.86. 解:如图,由题意得,AC=4000米,∠C=90°,AB=5000米,由勾股定理得BC=30004000500022=-(米),所以飞机飞行的速度为5403600203=(千米/小时) 7. 解:将曲线沿AB 展开,如图所示,过点C 作CE ⊥AB 于E. 在R 90,=∠∆CEF CEF t ,EF=18-1-1=16(cm ),CE=)(3060.21cm =⨯,由勾股定理,得CF=)(3416302222cm EF CE =+=+8.解:在直角三角形ABC 中,根据勾股定理,得254322222=+=+=AB AC BC在直角三角形CBD 中,根据勾股定理,得CD 2=BC 2+BD 2=25+122=169,所以CD=13.9. 解:延长BC 、AD 交于点E.(如图所示)∵∠B=90°,∠A=60°,∴∠E=30°又∵CD=3,∴CE=6,∴BE=8, 设AB=x ,则AE=2x ,由勾股定理。
勾股定理练习题及答案(共6套)

- 1 -勾股定理课时练(1)1. 在直角三角形ABC 中,斜边AB=1,则AB 222AC BC ++的值是( )A.2B.4C.6D.82.如图18-2-4所示,有一个形状为直角梯形的零件ABCD ,AD∥BC,斜腰DC 的长为10 cm ,∠D=120°,则该零件另一腰AB 的长是______ cm (结果不取近似值).3. 直角三角形两直角边长分别为5和12,则它斜边上的高为_______.4.一根旗杆于离地面12m 处断裂,犹如装有铰链那样倒向地面,旗杆顶落于离旗杆地步16m ,旗杆在断裂之前高多少m ?5.如图,如下图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是 米.6.飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行多少千米?7. 如图所示,无盖玻璃容器,高18cm ,底面周长为60cm ,在外侧距下底1cm 的点C 处有一蜘蛛,与蜘蛛相对的容器的上口外侧距开口1cm 的F 处有一苍蝇,试求急于扑货苍蝇充饥的蜘蛛,所走的最短路线的长度.8. 一个零件的形状如图所示,已知AC=3cm ,AB=4cm ,BD=12cm 。
求CD 的长.9. 如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长.10. 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?11如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?12. 甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?- 2 -。
《勾股定理》练习题及答案

《勾股定理》练习题测试1勾股定理(一)课堂学习检测一、填空题1.若一个直角三角形的两边长分别为12和5,则此三角形的第三边长为______.2.甲、乙两人同时从同一地点出发,已知甲往东走了4km ,乙往南走了3km ,此时甲、乙两人相距______km .3.如图,有一块长方形花圃,有少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了______m 路,却踩伤了花草.4.如图,有两棵树,一棵高8m ,另一棵高2m ,两树相距8m ,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少要飞______m .二、选择题5.如图,一棵大树被台风刮断,若树在离地面3m处折断, 树顶端落在离树底部4m 处,则树折断之前高().(A)5m (B)7m (C)8m (D)10m 6.如图,从台阶的下端点B 到上端点A 的直线距离为(). (A)212 (B)310(C)56 (D)58三、解答题7.在一棵树的10米高B 处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A 处;另一只爬到树顶D 后直接跃到A 处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高多少米8.在平静的湖面上,有一支红莲,高出水面1米,一阵风吹来,红莲移到一边,花朵齐及水面,已知红莲移动的水平距离为2米,求这里的水深是多少米综合、运用、诊断一、填空题9.如图,一电线杆AB的高为10米,当太阳光线与地面的夹角为60°时,其影长AC为______米.10.如图,有一个圆柱体,它的高为20,底面半径为5.如果一只蚂蚁要从圆柱体下底面的A点,沿圆柱表面爬到与A相对的上底面B点,则蚂蚁爬的最短路线长约为______(?取3)二、解答题:11.长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了______m.12.如图,在高为3米,斜坡长为5米的楼梯表面铺地毯,则地毯的长度至少需要多少米若楼梯宽2米,地毯每平方米30元,那么这块地毯需花多少元9101112拓展、探究、思考13.如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W .测试2勾股定理(三)学习要求熟练应用勾股定理解决直角三角形中的问题,进一步运用方程思想解决问题.课堂学习检测一、填空题1.在△ABC 中,若∠A +∠B =90°,AC =5,BC =3,则AB =______,AB 边上的高CE =______.2.在△ABC 中,若AB =AC =20,BC =24,则BC 边上的高AD =______,AC 边上的高BE =______.3.在△ABC 中,若AC =BC ,∠ACB =90°,AB =10,则AC =______,AB 边上的高CD =______.4.在△ABC 中,若AB =BC =CA =a ,则△ABC 的面积为______.5.在△ABC 中,若∠ACB =120°,AC =BC ,AB 边上的高CD =3,则AC =______,AB =______,BC 边上的高AE =______.二、选择题6.已知直角三角形的周长为62 ,斜边为2,则该三角形的面积是(). (A)41(B)43(C)21(D)17.若等腰三角形两边长分别为4和6,则底边上的高等于(). (A)7 (B)7或41 (C)24 (D)24或7三、解答题8.如图,在Rt△ABC中,∠C=90°,D、E分别为BC和AC的中点,AD=5,BE =102求AB的长.9.在数轴上画出表示10及13的点.综合、运用、诊断10.如图,△ABC中,∠A=90°,AC=20,AB=10,延长AB到D,使CD+DB=AC+AB,求BD的长.11.如图,将矩形ABCD沿EF折叠,使点D与点B重合,已知AB=3,AD=9,求BE的长.12.如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.13.已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC 上,且DE⊥DF.求证:AE2+BF2=EF2.拓展、探究、思考14.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,求AC的长是多少15.如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,……已知正方形ABCD的面积S 1为1,按上述方法所作的正方形的面积依次为S2,S3,…,S n(n为正整数),那么第8个正方形的面积S8=______,第n个正方形的面积S n=______.测试3勾股定理的逆定理学习要求掌握勾股定理的逆定理及其应用.理解原命题与其逆命题,原定理与其逆定理的概念及它们之间的关系.课堂学习检测一、填空题1.如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是______三角形,我们把这个定理叫做勾股定理的______.2.在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做____________;如果把其中一个命题叫做原命题,那么另一个命题叫做它的____________.3.分别以下列四组数为一个三角形的边长:(1)6、8、10,(2)5、12、13,(3)8、15、17,(4)4、5、6,其中能构成直角三角形的有____________.(填序号) 4.在△ABC中,a、b、c分别是∠A、∠B、∠C的对边,①若a2+b2>c2,则∠c为____________;②若a2+b2=c2,则∠c为____________;③若a2+b2<c2,则∠c为____________.5.若△ABC中,(b-a)(b+a)=c2,则∠B=____________;6.如图,正方形网格中,每个小正方形的边长为1,则网格上的△ABC是______三角形.7.若一个三角形的三边长分别为1、a、8(其中a为正整数),则以a-2、a、a +2为边的三角形的面积为______.8.△ABC 的两边a ,b 分别为5,12,另一边c 为奇数,且a +b +c 是3的倍数,则c 应为______,此三角形为______.二、选择题9.下列线段不能组成直角三角形的是().(A)a =6,b =8,c =10(B)3,2,1===c b a (C)43,1,45===c b a (D)6,3,2===c b a 10.下面各选项给出的是三角形中各边的长度的平方比,其中不是直角三角形的是().(A)1∶1∶2 (B)1∶3∶4(C)9∶25∶26 (D)25∶144∶16911.已知三角形的三边长为n 、n +1、m (其中m 2=2n +1),则此三角形().(A)一定是等边三角形(B)一定是等腰三角形(C)一定是直角三角形(D)形状无法确定综合、运用、诊断一、解答题12.如图,在△ABC 中,D 为BC 边上的一点,已知AB =13,AD =12,AC =15,BD =5,求CD 的长.13.已知:如图,四边形ABCD 中,AB ⊥BC ,AB =1,BC =2,CD =2,AD =3,求四边形ABCD 的面积.14.已知:如图,在正方形ABCD 中,F 为DC 的中点,E 为CB 的四等分点且CE =CB 41,求证:AF ⊥FE .15.在B 港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里的速度前进,乙船沿南偏东某个角度以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗拓展、探究、思考16.已知△ABC中,a2+b2+c2=10a+24b+26c-338,试判定△ABC的形状,并说明你的理由.17.已知a、b、c是△ABC的三边,且a2c2-b2c2=a4-b4,试判断三角形的形状.18.观察下列各式:32+42=52,82+62=102,152+82=172,242+102=262,…,你有没有发现其中的规律请用含n的代数式表示此规律并证明,再根据规律写出接下来的式子.参考答案3测试1勾股定理(二)1.13或.1192.5.3.2.4.10.5.C .6.A .7.15米.8.23米.9.⋅331010.25.11..2232-12.7米,420元.13.10万元.提示:作A 点关于CD 的对称点A ′,连结A ′B ,与CD 交点为O .测试2勾股定理(三)1.;343415,342.16,19.2.3.52,5.4..432a 5.6,36,33.6.C .7.D8..132提示:设BD =DC =m ,CE =EA =k ,则k 2+4m 2=40,4k 2+m 2=25.AB =.1324422=+k m9.,3213,31102222+=+=图略.10.BD =5.提示:设BD =x ,则CD =30-x .在Rt △ACD 中根据勾股定理列出(30-x )2=(x +10)2+202,解得x =5.11.BE =5.提示:设BE =x ,则DE =BE =x ,AE =AD -DE =9-x .在Rt △ABE中,AB 2+AE 2=BE 2,∴32+(9-x )2=x 2.解得x =5.12.EC =3cm .提示:设EC =x ,则DE =EF =8-x ,AF =AD =10,BF =622=-AB AF ,CF =4.在Rt △CEF 中(8-x )2=x 2+42,解得x =3.13.提示:延长FD 到M 使DM =DF ,连结AM ,EM .14.提示:过A ,C 分别作l 3的垂线,垂足分别为M ,N ,则易得△AMB ≌△BNC ,则.=ACAB34=∴,17215.128,2n-1.测试3勾股定理的逆定理1.直角,逆定理.2.互逆命题,逆命题.3.(1)(2)(3).4.①锐角;②直角;③钝角.5.90°.6.直角.7.24.提示:7<a<9,∴a=8.8.13,直角三角形.提示:7<c<17.9.D.10.C.11.C.12.CD=9.13..51+14.提示:连结AE,设正方形的边长为4a,计算得出AF,EF,AE的长,由AF2+EF2=AE2得结论.15.南偏东30°.16.直角三角形.提示:原式变为(a-5)2+(b-12)2+(c-13)2=0.17.等腰三角形或直角三角形.提示:原式可变形为(a2-b2)(a2+b2-c2)=0.18.352+122=372,[(n+1)2-1]2+[2(n+1)]2=[(n+1)2+1]2.(n≥1且n为整数)。
勾股定理常见练习题

勾股定理应用题题型一:已知两边求第三边1、直角三角形中;以直角边为边长的两个正方形的面积为72cm ;82cm ;则以斜边为边长的正方形的面积为_________2cm .2、已知直角三角形的两边长为5、12;则另一条边长是________________.3、作出长度为10的线段..4、一种盛饮料的圆柱形杯;测得内部底面半径为2.5㎝;高为12㎝;吸管放进杯里;杯口外面至少要露出4.6㎝;问吸管要做多长针对练习1、以下列各组数为边长;能组成直角三角形的是 A .2;3;4 B .10;8;4 C .7;25;24 D .7;15;122、已知一个Rt △的两边长分别为3和4;则第三边长的平方是A .25B .14C .7D .7或25 3、以面积为9 cm 2 的正方形对角线为边作正方形;其面积为A .9 cm 2B .13 cm 2C .18 cm 2D .24 cm 2题型二:利用勾股定理测量长度例1: 如果梯子的底端离建筑物9米;那么15米长的梯子可以到达建筑物的高度是多少米A B例2:如图8;水池中离岸边D点1.5米的C处;直立长着一根芦苇;出水部分BC的长是0.5米;把芦苇拉到岸边;它的顶端B恰好落到D点;并求水池的深度AC.例3:如图所示;一棵大树在一次强烈台风中于离地面10m处折断倒下;树顶落在离树根24m处. 大树在折断之前高多少题型三:转化思想例:如图;有一圆柱;其高为12cm;它的底面半径为3cm;在圆柱下底面A处有一只蚂蚁;它想得到上面B处的食物;则蚂蚁经过的最短距离为________ cm..π取3题型四:利用勾股定理解决实际问题例:如图;在一个高为3米;长为5米的楼梯表面铺地毯; 则地毯长度为多少米巩固练习1、如图1;直角△ABC的周长为24;且AB:AC=5:3;则BC=A.6 B.8 C.10 D.12图1 图22、如图2;一架云梯长25米;斜靠在一面墙上;梯子底端离墙7米;如果梯子的顶端下滑4米;那么梯子的底部在水平方向上滑动了A.4米 B.6米 C.8米 D.10米3、将一根长24 cm的筷子;置于底面直径为5cm、高为12cm的圆柱形水杯中;设筷子露在杯子外面的长为hcm;则h的取值范围是A.5≤h≤12 B.5≤h≤24 C.11≤h≤12 D.12≤h≤244、已知;如图;长方形ABCD中;AB=3cm;AD=9cm;将此长方形折叠;使点B与点D重合;折痕为EF;则△ABE的面积为A.6cm2 B.8cm2 C.10cm2 D.12cm24题 5题6题5、已知;如图;四边形ABCD中;AB=3cm;AD=4cm;BC=13cm;CD=12cm;且∠A=90°;则四边形ABCD的面积为A、36;B、22C、18D、126、如图中阴影部分是一个正方形;如果正方形的面积为64厘米2;则X的长为厘米..7、如图;从电线杆离地面6米处向地面拉一条长10米的缆绳;这条缆绳在地面的固定点距离电线杆底部为米..7题8题8、如图;在等腰直角△ABC中;AD是斜边BC上的高;AB=8;则AD2= ..9、小华和小红都从同一点O出发;小华向北走了9米到A点;小红向东走了12米到了B点;则________AB米..10、如图;所有的四边形都是正方形;所有的三角形都是直角三角形;其中最大的正方形的边长为6cm;则正方形A;B;C;D的面积之和为_____cm2..11、如图;某人欲横渡一条河;由于水流的影响;实际上岸地点C偏离欲到达点B200m;结果他在水中实际游了520m;求该河流的宽度为多少课后思考题如图;一个三级台阶;它的每一级的长、宽和高分别为20、3、2;A 和B是这个台阶两个相对的端点;A点有一只蚂蚁;想到B点去吃可口的食物;则蚂蚁沿着台阶面爬到B点最短路程是..。
勾股定理经典例题(含答案)
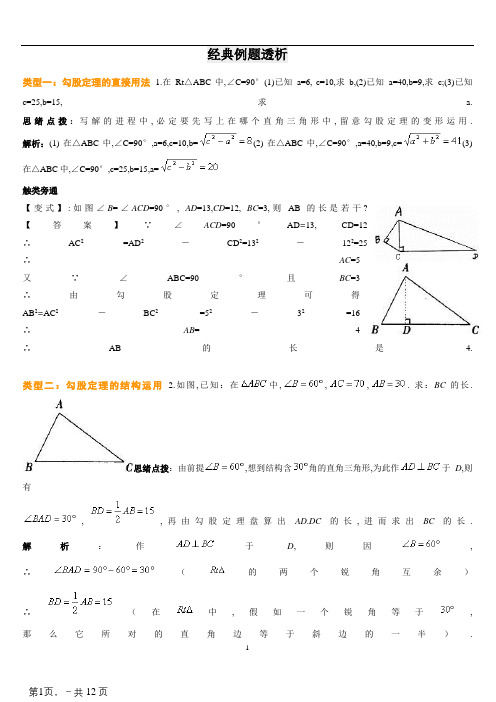
经典例题透析类型一:勾股定理的直接用法 1.在Rt△ABC中,∠C=90°(1)已知a=6, c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求 a. 思绪点拨:写解的进程中,必定要先写上在哪个直角三角形中,留意勾股定理的变形运用. 解析:(1) 在△ABC中,∠C=90°,a=6,c=10,b=(2) 在△ABC中,∠C=90°,a=40,b=9,c=(3) 在△ABC中,∠C=90°,c=25,b=15,a=触类旁通【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是若干?【答案】∵∠ACD=90°AD=13, CD=12∴AC2 =AD2-CD2=132-122=25∴AC=5又∵∠ABC=90°且BC=3∴由勾股定理可得AB2=AC2-BC2=52-32=16∴AB= 4∴AB的长是 4. 类型二:勾股定理的结构运用 2.如图,已知:在中,,,. 求:BC的长.思绪点拨:由前提,想到结构含角的直角三角形,为此作于D,则有,,再由勾股定理盘算出AD.DC的长,进而求出BC的长. 解析:作于D,则因, ∴(的两个锐角互余)∴(在中,假如一个锐角等于, 那么它所对的直角边等于斜边的一半).依据勾股定理,在中,. 依据勾股定理,在中,. ∴.触类旁通【变式1】如图,已知:,,于P. 求证:.解析:贯穿连接BM,依据勾股定理,在中,. 而在中,则依据勾股定理有. ∴又∵(已知), ∴. 在中,依据勾股定理有, ∴. 【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求:四边形ABCD的面积.剖析:若何结构直角三角形是解本题的症结,可以贯穿连接AC,或延伸AB.DC交于F,或延伸AD.BC交于点E,依据本题给定的角应选后两种,进一步依据本题给定的边选第三种较为简略. 解析:延伸AD.BC交于 E.∵∠A=∠60°,∠B=90°,∴∠E=30°.∴AE=2AB=8,CE=2CD=4,∴BE2=AE2-AB2=82-42=48,BE==.∵DE2= CE2-CD2=42-22=12,∴DE==. ∴S四边形ABCD=S△ABE-S△CDE=AB·BE-CD·DE=类型三:勾股定理的现实运用(一)用勾股定理求两点之间的距离问题 3.如图所示,在一次夏令营运动中,小明从营地A点动身,沿北偏东60°偏向走了到达B点,然后再沿北偏西30°偏向走了500m到达目标地C点. (1)求A.C两点之间的距离.(2)肯定目标地C在营地A的什么偏向.解析:(1)过B点作BE//AD∴∠DAB=∠ABE=60°∵30°+∠CBA+∠ABE=180°∴∠CBA=90°即△ABC为直角三角形由已知可得:BC=500m,AB=由勾股定理可得:所以(2)在Rt△ABC中, ∵BC=500m,AC=1000m ∴∠CAB=30°∵∠DAB=60°∴∠DAC=30°即点C在点A的北偏东30°的偏向触类旁通【变式】一辆装满货色的卡车,其外形高2.5米,宽1.6米,要开进厂门外形如图的某工场,问这辆卡车可否经由过程该工场的厂门?【答案】因为厂门宽度是否足够卡车经由过程,只要看当卡车位于厂门正中央时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.解:OC=1米(大门宽度一半), OD=0.8米(卡车宽度一半)在Rt△OCD中,由勾股定理得:CD===0.6米, CH=0.6+2.3=2.9(米)>2.5(米).是以高度上有0.4米的余量,所以卡车能经由过程厂门.(二)用勾股定理求最短问题4.国度电力总公司为了改良农村用电电费过高的近况,今朝正在全国各地农村进行电网改革,某地有四个村庄A.B.C.D,且正好位于一个正方形的四个极点,现筹划在四个村庄结合架设一条线路,他们设计了四种架设筹划,如图实线部分.请你关心盘算一下,哪种架设筹划最省电线.思绪点拨:解答本题的思绪是:最省电线就是线路长最短,经由过程运用勾股定理盘算线路长,然落后行比较,得出结论.解析:设正方形的边长为1,则图(1).图(2)中的总线路长分离为AB+BC+CD=3,AB+BC+CD= 3 图(3)中,在Rt△ABC中同理∴图(3)中的路线长为图(4)中,延伸EF交BC于H,则FH ⊥BC,BH=CH由∠FBH=及勾股定理得:EA=ED=FB=FC=∴EF=1-2FH=1-∴此图中总线路的长为4EA+EF=3> 2.828>2.732 ∴图(4)的衔接线路最短,即图(4)的架设筹划最省电线.触类旁通【变式】如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A动身,沿着圆柱的侧面爬行到点C,试求出爬行的最短旅程.解:如图,在Rt△ABC中,BC=底面周长的一半=10cm,依据勾股定理得(提问:勾股定理)∴ AC===≈10.77(cm)(勾股定理).答:最短旅程约为10.77cm.类型四:运用勾股定理作长为的线段5.作长为..的线段.思绪点拨:由勾股定理得,直角边为1的等腰直角三角形,斜边长就等于,直角边为和1的直角三角形斜边长就是,相似地可作.作法:如图所示(1)作直角边为1(单位长)的等腰直角△ACB,使AB为斜边;(2)以AB为一条直角边,作另一向角边为1的直角.斜边为;(3)按序如许做下去,最后做到直角三角形,如许斜边...的长度就是....触类旁通【变式】在数轴上表示的点.解析:可以把看作是直角三角形的斜边,,为了有利于绘图让其他双方的长为整数,而10又是9和1这两个完整平方数的和,得别的双方分离是3和1.作法:如图所示在数轴上找到A点,使OA=3,作AC⊥OA且截取AC=1,以OC为半径,以O为圆心做弧,弧与数轴的交点B即为.类型五:逆命题与勾股定理逆定理6.写出下列原命题的逆命题并断定是否准确1.原命题:猫有四只脚.(准确)2.原命题:对顶角相等(准确)3.原命题:线段垂直等分线上的点,到这条线段两头距离相等.(准确)4.原命题:角等分线上的点,到这个角的双方距离相等.(准确)思绪点拨:控制原命题与逆命题的关系.解析:1. 逆命题:有四只脚的是猫(不准确)2. 逆命题:相等的角是对顶角(不准确)3. 逆命题:到线段两头距离相等的点,在这条线段的垂直等分线上.•(准确)4. 逆命题:到角双方距离相等的点,在这个角的等分线上.(准确)总结升华:本题是为了进修勾股定理的逆命题做预备.7.假如ΔABC的三边分离为a.b.c,且知足a2+b2+c2+50=6a+8b+10c,断定ΔABC的外形.思绪点拨:要断定ΔABC的外形,须要找到a.b.c的关系,而标题中只有前提a2+b2+c2+50=6a+8b+10c,故只有从该前提入手,解决问题.解析:由a2+b2+c2+50=6a+8b+10c,得:a2-6a+9+b2-8b+16+c2-10c+25=0,∴ (a-3)2+(b-4)2+(c-5)2=0.∵ (a-3)2≥0, (b-4)2≥0, (c-5)2≥0.∴ a=3,b=4,c=5.∵ 32+42=52,∴ a2+b2=c2.由勾股定理的逆定理,得ΔABC是直角三角形.总结升华:勾股定理的逆定理是经由过程数目关系来研讨图形的地位关系的,在证实中也常要用到.触类旁通【变式1】四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.【答案】:贯穿连接AC∵∠B=90°,AB=3,BC=4∴AC2=AB2+BC2=25(勾股定理)∴AC=5∵AC2+CD2=169,AD2=169∴AC2+CD2=AD2∴∠ACD=90°(勾股定理逆定理)【变式2】已知:△ABC的三边分离为m2-n2,2mn,m2+n2(m,n为正整数,且m>n),断定△ABC是否为直角三角形.剖析:本题是运用勾股定理的的逆定理, 只要证实:a2+b2=c2即可证实:所以△ABC是直角三角形.【变式3】如图正方形ABCD,E为BC中点,F为AB上一点,且BF=AB.请问FE与DE是否垂直?请解释.【答案】答:DE⊥EF.证实:设BF=a,则BE=EC=2a, AF=3a,AB=4a,∴ EF2=BF2+BE2=a2+4a2=5a2;DE2=CE2+CD2=4a2+16a2=20a2.衔接DF(如图)DF2=AF2+AD2=9a2+16a2=25a2.∴ DF2=EF2+DE2,∴ FE⊥DE.经典例题精析类型一:勾股定理及其逆定理的根本用法 1.若直角三角形两直角边的比是3:4,斜边长是20,求此直角三角形的面积.思绪点拨:在直角三角形中知道双方的比值和第三边的长度,求面积,可以先经由过程比值设未知数,再依据勾股定理列出方程,求出未知数的值进而求面积.解析:设此直角三角形两直角边分离是3x,4x,依据题意得:(3x)2+(4x)2=202化简得x2=16; ∴直角三角形的面积=×3x×4x=6x2=96 总结升华:直角三角形边的有关盘算中,常常要设未知数,然后用勾股定理列方程(组)求解. 触类旁通【变式1】等边三角形的边长为2,求它的面积.【答案】如图,等边△ABC,作AD⊥BC于 D 则:BD=BC(等腰三角形底边上的高与底边上的中线互相重合)∵AB=AC=BC=2(等边三角形各边都相等)∴BD= 1 在直角三角形ABD中,AB2=AD2+BD2,即:AD2=AB2-BD2=4-1= 3 ∴AD=S△ABC=BC·AD=注:等边三角形面积公式:若等边三角形边长为a,则其面积为 a.【变式2】直角三角形周长为12cm,斜边长为5cm,求直角三角形的面积. 【答案】设此直角三角形两直角边长分离是x,y,依据题意得:由(1)得:x+y=7, (x+y)2=49,x2+2xy+y2=49 (3) (3)-(2),得:xy=12∴直角三角形的面积是xy=×12=6(cm2)【变式3】若直角三角形的三边长分离是n+1,n+2,n+3,求n. 思绪点拨:起首要肯定斜边(最长的边)长n+3,然后运用勾股定理列方程求解. 解:此直角三角形的斜边长为n+3,由勾股定理可得:(n+1)2+(n+2)2=(n+3)2化简得:n2= 4 ∴n=±2,但当n=-2时,n+1=-1<0,∴n= 2 总结升华:留意直角三角形中两“直角边”的平方和等于“斜边”的平方,在标题没有给出哪条是直角边哪条是斜边的情形下,起首要先肯定斜边,直角边. 【变式4】以下列各组数为边长,能构成直角三角形的是()A.8,15,17 B.4,5,6 C.5,8,10 D.8,39,40 解析:此题可直接用勾股定理的逆定理来进行断定, 对数据较大的可以用c2=a2+b2的变形:b2=c2-a2=(c-a)(c+a)来断定. 例如:对于选择D, ∵82≠(40+39)×(40-39), ∴以8,39,40为边长不能构成直角三角形. 同理可以断定其它选项.【答案】:A【变式5】四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.解:贯穿连接AC∵∠B=90°,AB=3,BC=4∴AC2=AB2+BC2=25(勾股定理)∴AC=5∵AC2+CD2=169,AD2=169 ∴AC2+CD2=AD2∴∠ACD=90°(勾股定理逆定理)∴S四边形ABCD=S△ABC+S△ACD=AB·BC+AC·CD=36类型二:勾股定理的运用2.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.假设拖沓机行驶时,四周100m以内会受到噪音的影响,那么拖沓机在公路MN上沿PN偏向行驶时,黉舍是否会受到噪声影响?请解释来由,假如受影响,已知拖沓机的速度为18km/h,那么黉舍受影响的时光为若干秒?思绪点拨:(1)要断定拖沓机的噪音是否影响黉舍A,本质上是看A到公路的距离是否小于100m, 小于100m则受影响,大于100m则不受影响,故作垂线段AB并盘算其长度.(2)请求出黉舍受影响的时光,本质是请求拖沓机对黉舍A的影响所行驶的旅程.是以必须找到拖沓机行至哪一点开端影响黉舍,行至哪一点后停止影响黉舍. 解析:作AB⊥MN,垂足为 B. 在RtΔABP中,∵∠ABP=90°,∠APB=30°, AP=160,∴AB=AP=80. (在直角三角形中,30°所对的直角边等于斜边的一半)∵点A到直线MN的距离小于100m, ∴这所中学会受到噪声的影响. 如图,假设拖沓机在公路MN上沿PN偏向行驶到点C处黉舍开端受到影响,那么AC=100(m), 由勾股定理得:BC2=1002-802=3600,∴BC=60.同理,拖沓机行驶到点D处黉舍开端离开影响,那么,AD=100(m),BD=60(m), ∴CD=120(m). 拖沓机行驶的速度为: 18km/h=5m/s t=120m÷5m/s=24s.答:拖沓机在公路MN上沿PN偏向行驶时,黉舍会受到噪声影响,黉舍受影响的时光为24秒. 总结升华:勾股定理是求线段的长度的很主要的办法,若图形缺乏直角前提,则可以经由过程作关心垂线的办法,结构直角三角形以便运用勾股定理.触类旁通【变式1】如图黉舍有一块长方形花圃,有少少数工资了避开拐角而走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了__________步路(假设2步为1m),却踩伤了花卉.解析:他们本来走的路为3+4=7(m) 设走“捷径”的路长为xm,则故少走的路长为7-5=2(m) 又因为2步为1m,所以他们仅仅少走了4步路.【答案】4【变式2】如图中的虚线网格我们称之为正三角形网格,它的每一个小三角形都是边长为1的正三角形,如许的三角形称为单位正三角形. (1)直接写出单位正三角形的高与面积. (2)图中的平行四边形ABCD含有若干个单位正三角形?平行四边形ABCD的面积是若干?(3)求出图中线段AC的长(可作关心线).【答案】(1)单位正三角形的高为,面积是. (2)如图可直接得出平行四边形ABCD含有24个单位正三角形,是以其面积. (3)过A作AK⊥BC于点K(如图所示),则在Rt△ACK中,,,故类型三:数学思惟办法(一)转化的思惟办法我们在求三角形的边或角,或进行推理论证时,常常作垂线,结构直角三角形,将问题转化为直角三角形问题来解决.3.如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E.F分离是AB.AC边上的点,且DE⊥DF,若BE=12,CF=5.求线段EF的长.思绪点拨:现已知BE.CF,请求EF,但这三条线段不在统一三角形中,所以症结是线段的转化,依据直角三角形的特点,三角形的中线有特别的性质,不妨先衔接AD.解:衔接AD.因为∠BAC=90°,AB=AC.又因为AD为△ABC的中线, 所以AD=DC=DB.AD⊥BC.且∠BAD=∠C=45°.因为∠EDA+∠ADF=90°.又因为∠CDF+∠ADF=90°.所以∠EDA=∠CDF.所以△AED≌△CFD(ASA).所以AE=FC=5.同理:AF=BE=12.在Rt△AEF中,依据勾股定理得:,所以EF=13.总结升华:此题考核了等腰直角三角形的性质及勾股定理等常识.经由过程此题,我们可以懂得:当已知的线段和所求的线段不在统一三角形中时,应经由过程恰当的转化把它们放在统一向角三角形中求解.(二)方程的思惟办法4.如图所示,已知△ABC中,∠C=90°,∠A=60°,,求..的值.思绪点拨:由,再找出.的关系即可求出和的值. 解:在Rt△ABC中,∠A=60°,∠B=90°-∠A=30°, 则,由勾股定理,得. 因为,所以,,,. 总结升华:在直角三角形中,30°的锐角的所对的直角边是斜边的一半. 触类旁通:【变式】如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EF的长. 解:因为△ADE与△AFE关于AE对称,所以AD=AF,DE=EF. 因为四边形ABCD是矩形,所以∠B=∠C=90°, 在Rt△ABF中,AF=AD=BC=10cm,AB=8cm,所以.所以. 设,则. 在Rt△ECF中,,即,解得.即EF的长为5cm.。
勾股定理练习题(含答案)

勾股定理练习题(含答案)一、基础达标:1. 下列说法正确的是( )A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2;B.若 a 、b 、c 是Rt △ABC 的三边,则a 2+b 2=c 2;C.若 a 、b 、c 是Rt △ABC 的三边, 90=∠A ,则a 2+b 2=c 2;D.若 a 、b 、c 是Rt △ABC 的三边, 90=∠C ,则a 2+b 2=c 2. 2. △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( )A .c b a =+ B. c b a >+ C. c b a <+ D. 222c b a =+ 3.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )A .121B .120C .90D .不能确定 4.△ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( ) A .42 B .32 C .42 或 32 D .37 或 33 5.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 .6.假如有一个三角形是直角三角形,那么三边a 、b 、c 之间应满足 ,其中 边是直角所对的边;如果一个三角形的三边a 、b 、c 满足222b c a =+,那么这个三角形是 三角形,其中b 边是 边,b 边所对的角是 . 7.一个三角形三边之比是6:8:10,则按角分类它是 三角形.8. 若三角形的三个内角的比是3:2:1,最短边长为cm 1,最长边长为cm 2,则这个三角形三个角度数分别是 ,另外一边的平方是 .9.如图,已知ABC ∆中,︒=∠90C ,15=BA ,12=AC ,以直角边BC 为直径作半圆,则这个半圆的面积是 .10. 一长方形的一边长为cm 3,面积为212cm ,那么它的一条对角线长是 .二、综合发展:11.如图,一个高4m 、宽3m 的大门,需要在对角线的顶点间加固一个木条,求木条的长.AB12.一个三角形三条边的长分别为cm 15,cm 20,cm 25,这个三角形最长边上的高是多少?13.如图,小李准备建一个蔬菜大棚,棚宽4m ,高3m ,长20m ,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.14.如图,有一只小鸟在一棵高13m 12m ,高8m 的一棵小树树梢上发出友好的叫声,它立刻以2m/s 的速度飞向小树树梢,那么这只小鸟至少几秒才可能到达小树和伙伴在一起?15.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m 处,过了2s 后,测得小汽车与车速检测仪间距离为50m ,这辆小汽车超速了吗?观测点答案: 一、基础达标1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.答案: D.2. 解析:本题考察三角形的三边关系和勾股定理.答案:B.3. 解析:设另一条直角边为x ,则斜边为(x+1)利用勾股定理可得方程,可以求出x .然后再求它的周长. 答案:C . 4.解析:解决本题关键是要画出图形来,作图时应注意高AD 是在三角形的内部还是在三角形的外部,有两种情况,分别求解. 答案:C.5. 解析: 勾股定理得到:22215817=-,另一条直角边是15,所求直角三角形面积为21158602cm ⨯⨯=. 答案: 260cm .6. 解析:本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立.答案:222c b a =+,c ,直角,斜,直角.7. 解析:本题由边长之比是6:8:10 可知满足勾股定理,即是直角三角形.答案:直角.8. 解析:由三角形的内角和定理知三个角的度数,断定是直角三角形.答案:︒30、︒60、︒90,3.9. 解析:由勾股定理知道:22222291215=-=-=AC AB BC所以以直角边9=BC 为直径的半圆面积为10.125π. 答案:10.125π.10. 解析:长方形面积长×宽,即12长×3,长4=,所以一条对角线长为5.答案:cm 5. 二、综合发展11. 解析:木条长的平方=门高长的平方+门宽长的平方.答案:5m .12解析:因为222252015=+,所以这三角形是直角三角形,设最长边(斜边)上的高为xcm ,由直角三角形面积关系,可得1115202522x ⨯⨯=⨯⋅,∴ 12=x (cm ).答案:12=x (cm ).13.解析:透阳光最大面积是塑料薄膜的面积,需要求出它的另一边的长是多少,可以借助勾股定理求出.答案:在直角三角形中,由勾股定理可得:直角三角形的斜边长为5m,所以矩形塑料薄膜的面积是:5×20=100(m2) .14.解析:本题的关键是构造直角三角形,利用勾股定理求斜边的值是13m,也就是两树树梢之间的距离是13m,两再利用时间关系式求解.答案:6.5s.15.解析:本题和14题相似,可以求出BC的值,再利用速度等于路程除以时间后比较.BC=40米,时间是2s,可得速度是20m/s=72km/h>70km/h.答案:这辆小汽车超速了.。
勾股定理经典例题(含答案)

勾股定理经典例题(含答案)勾股定理经典例题类型⼀:勾股定理的直接⽤法1、在Rt△ABC中,∠C=90°(1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.思路点拨: 写解的过程中,⼀定要先写上在哪个直⾓三⾓形中,注意勾股定理的变形使⽤。
举⼀反三【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?类型⼆:勾股定理的构造应⽤2、如图,已知:在中,,,. 求:BC的长.1、某市在旧城改造中,计划在市内⼀块如图所⽰的三⾓形空地上种植草⽪以美化环境,已知这种草⽪每平⽅⽶售价a元,则购买这种草⽪⾄少需要()A、450a元B、225a 元C、150a元D、300a元举⼀反三【变式1】如图,已知:,,于P. 求证:.150°20m 30m【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD的⾯积。
类型三:勾股定理的实际应⽤(⼀)⽤勾股定理求两点之间的距离问题3、如图所⽰,在⼀次夏令营活动中,⼩明从营地A点出发,沿北偏东60°⽅向⾛了到达B 点,然后再沿北偏西30°⽅向⾛了500m到达⽬的地C点。
(1)求A、C两点之间的距离。
(2)确定⽬的地C在营地A的什么⽅向。
举⼀反三【变式】⼀辆装满货物的卡车,其外形⾼2.5⽶,宽1.6⽶,要开进⼚门形状如图的某⼯⼚,问这辆卡车能否通过该⼯⼚的⼚门?(⼆)⽤勾股定理求最短问题4、如图,⼀圆柱体的底⾯周长为20cm,⾼AB为4cm,BC是上底⾯的直径.⼀只蚂蚁从点A出发,沿着圆柱的侧⾯爬⾏到点C,试求出爬⾏的最短路程.类型四:利⽤勾股定理作长为的线段5、作长为、、的线段。
作法:如图所⽰举⼀反三【变式】在数轴上表⽰的点。
解析:可以把看作是直⾓三⾓形的斜边,,为了有利于画图让其他两边的长为整数,⽽10⼜是9和1这两个完全平⽅数的和,得另外两边分别是3和1。
勾股定理典型例题
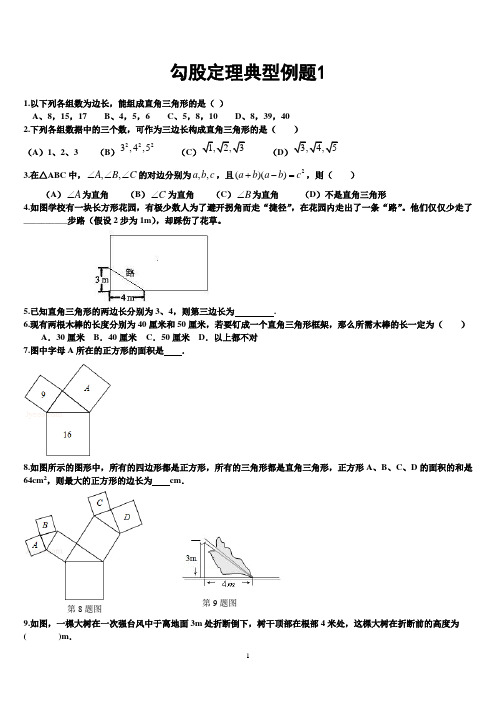
勾股定理典型例题11.以下列各组数为边长,能组成直角三角形的是( )A 、8,15,17B 、4,5,6C 、5,8,10D 、8,39,40 2.下列各组数据中的三个数,可作为三边长构成直角三角形的是( )(A )1、2、3 (B )2223,4,5 (C )1,2,3 (D )3,4,53.在△ABC 中,,,A B C ∠∠∠的对边分别为,,a b c ,且2()()a b a b c +-=,则( )(A )A ∠为直角 (B )C ∠为直角 (C )B ∠为直角 (D )不是直角三角形4.如图学校有一块长方形花园,有极少数人为了避开拐角而走“捷径”,在花园内走出了一条“路”。
他们仅仅少走了__________步路(假设2步为1m ),却踩伤了花草。
5.已知直角三角形的两边长分别为3、4,则第三边长为 .6.现有两根木棒的长度分别为40厘米和50厘米,若要钉成一个直角三角形框架,那么所需木棒的长一定为( ) A .30厘米 B .40厘米 C .50厘米 D .以上都不对7.图中字母A 所在的正方形的面积是 .8.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,正方形A 、B 、C 、D 的面积的和是64cm 2,则最大的正方形的边长为 cm .9.如图,一棵大树在一次强台风中于离地面3m 处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为 ( )m .第8题图第9题图10.如图,分别以直角三角形三边向外作三个半圆,若S1=30,S2=40,则S3=.11,如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是()A.6cm B.12cm C.13cm D.16cm12.长方体的长、宽、高分别为8cm,4cm,5cm.一只蚂蚁沿着长方体的表面从点A爬到点B.则蚂蚁爬行的最短路径的长是cm.13.如图,已知:在中,,,. 求:BC的长.14.已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
勾股定理练习题及答案(共6套)

勾股定理课时练(1)1.在直角三角形ABC 中,斜边AB=1,则AB 222AC BC ++的值是()A.2B.4C.6D.82.如图18-2-4所示,有一个形状为直角梯形的零件ABCD ,AD ∥BC ,斜腰DC 的长为10cm ,∠D=120°,则该零件另一腰AB 的长是______cm (结果不取近似值).3.直角三角形两直角边长分别为5和12,则它斜边上的高为_______.4.一根旗杆于离地面12m 处断裂,犹如装有铰链那样倒向地6.飞机在空中水平飞行上方4000米处,过了209.如图,在四边形CD=3,求AB 的长10.如图,一个牧童在小河的南的小屋B 的西8km 2m 的楼道上铺地毯,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?12.甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗? 第一课时答案:1.A ,提示:根据勾股定理得122=+AC BC ,所以AB222AC BC ++=1+1=2;2.4,提示:由勾股定理可得斜边的长为5m ,而3+4-5=2m ,所以他们少走了4步.3.1360,提示:设斜边的高为x ,根据勾股定理求斜边为1316951222==+,再利用面积法得,136011米,由勾所以飞机飞行的速度为CE=60.2⨯,由勾股定理,得CF=)(3416302222cm EF CE =+=+8.解:在直角三角形ABC 中,根据勾股定理,得在直角三角形CBD 中,根据勾股定理,得CD 2=BC 2+BD 2=25+122=169,所以CD=13. 9.解:延长BC 、AD 交于点E.(如图所示)第5题图第8题∵∠B=90°,∠A=60°,∴∠E=30°又∵CD=3,∴CE=6,∴BE=8, 设AB=x ,则AE=2x ,由勾股定理。
勾股定理10题

勾股定理10题
以下是10道关于勾股定理的题目:
1.已知直角三角形的两条直角边分别为3和4,求斜边的长度。
2.在一个直角三角形中,斜边长为5,一条直角边长为3,求另一条直角边的长度。
3.一个直角三角形的斜边长为13,其中一条直角边长为5,求另一条直角边的长度。
4.一个直角三角形的两条直角边分别为6和8,求斜边上的高。
5.已知直角三角形的斜边长为10,一条直角边与斜边的夹角为30°,求另一条直角边
的长度。
6.一个直角三角形的斜边长为17,其中一条直角边长为8,求这个直角三角形的面
积。
7.一个直角三角形的两条直角边分别为a和b,斜边长为c,且a ️c = 3:4:5,求这个
直角三角形的面积。
8.已知直角三角形的斜边长为13,且两条直角边的比为3:4,求这个直角三角形的面
积。
9.一个直角三角形的斜边长为25,其中一条直角边长为15,求这个直角三角形的一
个锐角的正切值。
10.一个直角三角形的两条直角边分别为6和8,求这个直角三角形的外接圆半径。
这些题目涵盖了勾股定理的基本应用,包括求斜边长度、求直角边长度、求高、求面积、求角度正切值以及求外接圆半径等。
通过练习这些题目,可以加深对勾股定理的理解和掌握。
勾股定理练习题(含答案)

勾股定理练习题一、基础达标:1。
下列说法正确的是( )A 。
若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2; B.若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;C 。
若 a 、b 、c 是Rt△ABC 的三边, 90=∠A ,则a 2+b 2=c 2;D 。
若 a 、b 、c 是Rt△ABC 的三边, 90=∠C ,则a 2+b 2=c 2.2。
Rt △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( )A .c b a =+B 。
c b a >+C 。
c b a <+D 。
222c b a =+ 3. 如果Rt △的两直角边长分别为k 2-1,2k(k >1),那么它的斜边长是( )A 、2kB 、k+1C 、k 2-1D 、k 2+14。
已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )A 。
直角三角形B.等腰三角形C.等腰直角三角形D 。
等腰三角形或直角三角形5. 直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )A .121B .120C .90D .不能确定6. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( ) A .42 B .32 C .42 或 32 D .37 或 337.※直角三角形的面积为S ,斜边上的中线长为d ,则这个三角形周长为( )(A 2d d(C )2d (D )d8、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( )A :3 B :4C:5 D :79.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( )A .17B 。
3 C.17或3 D 。
以上都不对10.已知a 、b 、c 是三角形的三边长,如果满足2(6)100a c --=则三角形的形状是( )A :底与边不相等的等腰三角形B :等边三角形 C:钝角三角形 D :直角三角形11.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 . 12. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__。
勾股定理练习题(含答案)

勾股定理练习题一、基础达标:1. 下列说法正确的是( )A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2;B 。
若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;C.若 a 、b 、c 是Rt△ABC 的三边, 90=∠A ,则a 2+b 2=c 2;D.若 a 、b 、c 是Rt△ABC 的三边, 90=∠C ,则a 2+b 2=c 2. 2。
Rt △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( )A .c b a =+B 。
c b a >+C 。
c b a <+ D. 222c b a =+3. 如果Rt △的两直角边长分别为k 2-1,2k (k 〉1),那么它的斜边长是( )A 、2kB 、k+1C 、k 2-1D 、k 2+1 4。
已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形 5. 直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )A .121B .120C .90D .不能确定6. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( )A .42B .32C .42 或 32D .37 或 337。
※直角三角形的面积为S ,斜边上的中线长为d ,则这个三角形周长为( )(A 2d (B d(C )2d (D )d8、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( )A :3 B :4 C :5 D :79.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( )A .17B 。
3C 。
17或3D 。
以上都不对10.已知a 、b 、c 是三角形的三边长,如果满足2(6)100a c --=则三角形的形状是( )A :底与边不相等的等腰三角形 B:等边三角形C:钝角三角形 D :直角三角形11.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 .12. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__。
勾股定理练习题(含答案)

勾股定理练习题一、基础达标:1. 下列说法正确的是( )A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2;B.若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;C.若 a 、b 、c 是Rt△ABC 的三边, 90=∠A ,则a 2+b 2=c 2;D.若 a 、b 、c 是Rt△ABC 的三边, 90=∠C ,则a 2+b 2=c 2.2. Rt △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( )A .c b a =+ B. c b a >+ C. c b a <+ D. 222c b a =+3. 如果Rt △的两直角边长分别为k 2-1,2k (k >1),那么它的斜边长是( )A 、2kB 、k+1C 、k 2-1D 、k 2+1 4. 已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形 5. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( ) A .42 B .32 C .42 或 32 D .37 或 33 6、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( )A :3B :4C :5D :77.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( )A .17 B.3 C.17或3 D.以上都不对 8.已知a 、b 、c 是三角形的三边长,如果满足2(6)100a c --=则三角形的形状是( )A :底与边不相等的等腰三角形B :等边三角形C :钝角三角形D :直角三角形 9.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 .10. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__. 11. 一个直角三角形的三边长的平方和为200,则斜边长为12.一个三角形三边之比是6:8:10,则按角分类它是 三角形. 13. 一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是___.14. 在Rt △ABC 中,斜边AB=4,则AB 2+BC 2+AC 2=_____. 15.如图,已知ABC ∆中,︒=∠90C ,15=BA ,12=AC ,以直角边BC 为直径作半圆,则这个半圆的面积是 .二:应用提升1.如图,一个高4m 、宽3m 的大门,需要在对角线的顶点间加固一个木条,求木条的长.2、有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗?3.一个三角形三条边的长分别为cm 15,cm 20,cm 25,这个三角形最长边上的高是多少?ABAEB4.如图,要修建一个育苗棚,棚高h=3m ,棚宽a=4m ,棚的长为12m ,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?5.如图,有一只小鸟在一棵高13m 的大树树梢上捉虫子,它的伙伴在离该树12m ,高8m 的一棵小树树梢上发出友好的叫声,它立刻以2m/s 的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?15.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m 处,过了2s 后,测得小汽车与车速检测仪间距离为50m ,这辆小汽车超速了吗?小汽车小汽车观测点答案:一、基础达标1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.答案: D.2. 解析:本题考察三角形的三边关系和勾股定理.答案:B.3. 解析:设另一条直角边为x ,则斜边为(x+1)利用勾股定理可得方程,可以求出x .然后再求它的周长. 答案:C .4.解析:解决本题关键是要画出图形来,作图时应注意高AD 是在三角形的内部还是在三角形的外部,有两种情况,分别求解. 答案:C.5. 解析: 勾股定理得到:22215817=-,另一条直角边是15,所求直角三角形面积为21158602cm ⨯⨯=.答案: 260cm .6. 解析:本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立.答案:222c b a =+,c ,直角,斜,直角.7. 解析:本题由边长之比是6:8:10 可知满足勾股定理,即是直角三角形.答案:直角. 8. 解析:由三角形的内角和定理知三个角的度数,断定是直角三角形.答案:︒30、︒60、︒90,3.9. 解析:由勾股定理知道:22222291215=-=-=AC AB BC ,所以以直角边9=BC 为直径的半圆面积为10.125π.答案:10.125π.10. 解析:长方形面积长×宽,即12长×3,长4=,所以一条对角线长为5. 答案:cm 5. 二、综合发展11. 解析:木条长的平方=门高长的平方+门宽长的平方.答案:5m .12解析:因为222252015=+,所以这三角形是直角三角形,设最长边(斜边)上的高为xcm ,由直角三角形面积关系,可得1115202522x ⨯⨯=⨯⋅,∴12=x .答案:12cm13.解析:透阳光最大面积是塑料薄膜的面积,需要求出它的另一边的长是多少,可以借助勾股定理求出.答案:在直角三角形中,由勾股定理可得:直角三角形的斜边长为5m,所以矩形塑料薄膜的面积是:5×20=100(m 2) .14.解析:本题的关键是构造直角三角形,利用勾股定理求斜边的值是13m ,也就是两树树梢之间的距离是13m ,两再利用时间关系式求解. 答案:6.5s . 15.解析:本题和14题相似,可以求出BC 的值,再利用速度等于路程除以时间后比较.BC=40米,时间是2s ,可得速度是20m/s=72km/h >70km/h . 答案:这辆小汽车超速了.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《勾股定理》总结与提升一、知识要点:1、勾股定理勾股定理:直角三角形两直角边的平方和等于斜边的平方。
也就是说:如果直角三角形的两直角边为a、b,斜边为c ,那么 a2 + b2= c2。
公式的变形:a2 = c2- b2, b2= c2-a2 。
2、勾股定理的逆定理如果三角形ABC的三边长分别是a,b,c,且满足a2 + b2= c2,那么三角形ABC 是直角三角形。
这个定理叫做勾股定理的逆定理.该定理在应用时,要注意处理好如下几个要点:①已知的条件:某三角形的三条边的长度.②满足的条件:最大边的平方=最小边的平方+中间边的平方.③得到的结论:这个三角形是直角三角形,并且最大边的对角是直角.④如果不满足条件,就说明这个三角形不是直角三角形。
3、勾股数满足a2 + b2= c2的三个正整数,称为勾股数。
注意:①勾股数必须是正整数,不能是分数或小数。
②一组勾股数扩大相同的正整数倍后,仍是勾股数。
常见勾股数有:(3,4,5)(5,12,13) (6,8,10)(7,24,25)(8,15,17)(9,12,15)4、最短距离问题:主要运用的依据是两点之间线段最短。
二、考点剖析考点一:利用勾股定理求面积1、求阴影部分面积:(1)阴影部分是形;(2)阴影部分是长方形;(3)阴影部分是半圆.2. 如图,以Rt△ABC的三边为直径分别向外作三个半圆,试探索三个半圆的面积之间的关系.3、如图所示,分别以直角三角形的三边向外作三个正三角形,其面积分别是S 1、S 2、S 3,则它们之间的关系是( )A. S 1- S 2= S 3B. S 1+ S 2= S 3C. S 2+S 3< S 1D. S 2- S 3=S 14、四边形ABCD 中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD 的面积。
5、在直线l 上依次摆放着七个形(如图4所示)。
已知斜放置的三个形的面积分别是1、2、3,正放置的四个形的面积依次是S S 12、、S S S S S S 341234、,则+++=_____________。
考点二:在直角三角形中,已知两边求第三边1.在直角三角形中,若两直角边的长分别为1cm ,2cm ,则斜边长为. 2.(易错题、注意分类的思想)已知直角三角形的两边长为3、2,则另一条边长的平方是3、已知直角三角形两直角边长分别为5和12, 求斜边上的高.4、把直角三角形的两条直角边同时扩大到原来的2倍,则斜边扩大到原来的( ) A . 2倍 B . 4倍 C . 6倍 D . 8倍5、在Rt △ABC 中,∠C=90°①若a=5,b=12,则c=___________; ②若a=15,c=25,则b=___________;S 3S 2S 1③若c=61,b=60,则a=__________;④若a∶b=3∶4,c=10则Rt△ABC的面积是=________。
6、如果直角三角形的两直角边长分别为1n2-,2n(n>1),那么它的斜边长是()A、2nB、n+1C、n2-1D、1n2+7、在Rt△ABC中,a,b,c为三边长,则下列关系中正确的是()A. 222c b a+= C. 222+= D.以上都有可能a b c+= B. 222a c b8、已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是()A、242c m D、602c mc m C、482c m B、36 29、已知x、y为正数,且│x2-4│+(y2-3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的形的面积为()A、5B、25C、7D、15考点三:应用勾股定理在等腰三角形中求底边上的高及面积例、如图1所示,等腰中,,是底边上的高,若,求①AD的长;②ΔABC的面积.考点四:勾股数的应用、利用勾股定理逆定理判断三角形的形状、最大、最小角的问题1、下列各组数据中的三个数,可作为三边长构成直角三角形的是()A. 4,5,6B. 2,3,4C. 11,12,13D. 8,15,172、若线段a,b,c组成直角三角形,则它们的比为()A、2∶3∶4B、3∶4∶6C、5∶12∶13D、4∶6∶73、下面的三角形中:①△ABC中,∠C=∠A-∠B;②△ABC中,∠A:∠B:∠C=1:2:3;③△ABC中,a:b:c=3:4:5;④△ABC中,三边长分别为8,15,17.其中是直角三角形的个数有().A.1个 B.2个 C.3个 D.4个4、若三角形的三边之比为2::12,则这个三角形一定是()A.等腰三角形B.直角三角形C.等腰直角三角形D.不等边三角形5、已知a ,b,c为△ABC三边,且满足(a2-b2)(a2+b2-c2)=0,则它的形状为()A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形6、将直角三角形的三条边长同时扩一倍数, 得到的三角形是( )A.钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等腰三角形7、若△ABC的三边长a,b,c满足222a b c20012a16b20c+++=++,试判断△ABC的形状。
8、△ABC的两边分别为5,12,另一边为奇数,且a+b+c是3的倍数,则c应为,此三角形为。
例3:求(1)若三角形三条边的长分别是7,24,25,则这个三角形的最大角是度。
(2)已知三角形三边的比为1:3:2,则其最小角为。
考点五:应用勾股定理解决楼梯上铺地毯问题某楼梯的侧面视图如图3所示,其中米,,,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的长度应为米。
考点六、利用列方程求线段的长(方程思想)1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?BC2、一架长2.5m的梯子,斜立在一竖起的墙上,梯子底端距离墙底0.7m(如图),如果梯子的顶端沿墙下滑0.4m,那么梯子底端将向左滑动米3、如图,一个长为10米的梯子,斜靠在墙面上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端下滑1米,那么,梯子底端的滑动距离 1米,(填“大于”,“等于”,或“小于”)4、在一棵树10 m高的B处,有两只猴子,一只爬下树走到离树20m处的池塘A处;•另外一只爬到树顶D处后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,试问这棵树有多高?5、如图,是一个外轮廓为矩形的机器零件平面示意图,根据图中标出尺寸(单位:mm)计算两圆孔中心A和B的距离为 .6、如图:有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了米.6012140B6AC8米CADB7、如图18-15所示,某人到一个荒岛上去探宝,在A 处登陆后,往东走8km ,又往北走2km ,遇到障碍后又往西走3km ,再折向北方走到5km 处往东一拐,仅1km •就找到了宝藏,问:登陆点(A 处)到宝藏埋藏点(B 处)的直线距离是多少?考点七:折叠问题1、如图,有一直角三角形纸片,两直角边AC=6,BC=8,将△ABC 折叠,使点B 与点A 重合,折痕为DE ,则CD 等于( )A. 425B. 322C. 47D. 352、如图所示,已知△ABC 中,∠C=90°,AB 的垂直平分线交BC •于M ,交AB 于N ,若AC=4,MB=2MC ,求AB 的长.3、折叠矩形ABCD 的一边AD,点D 落在BC 边上的点F 处,已知AB=8CM,BC=10CM ,求CF 和EC 。
4、如图,在长方形ABCD 中,DC=5,在DC 边上存在一点E ,沿直线AE 把△ABC 折叠,使点D 恰好在BC 边上,设此点为F ,若△ABF 的面积为30,求折叠的△AED 的面积DCBAF E图18-1515328B A A BCE DB CED5、如图,矩形纸片ABCD的长AD=9㎝,宽AB=3㎝,将其折叠,使点D与点B重合,那么折叠后DE的长是多少?6、如图,在长方形ABCD中,将∆ABC沿AC对折至∆AEC位置,CE与AD交于点F。
(1)试说明:AF=FC;(2)如果AB=3,BC=4,求AF的长7、如图2所示,将长方形ABCD沿直线AE折叠,顶点D正好落在BC边上F点处,已知CE=3cm,AB=8cm,则图中阴影部分面积为_______.8、如图2-3,把矩形ABCD沿直线BD向上折叠,使点C落在C′的位置上,已知AB=•3,BC=7,重合部分△EBD的面积为________.9、如图5,将形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G。
如果M为CD边的中点,求证:DE:DM:EM=3:4:5。
10、如图2-5,长方形ABCD中,AB=3,BC=4,若将该矩形折叠,使C点与A点重合,•则折叠后痕迹EF的长为()A.3.74 B.3.75 C.3.76 D.3.772-511、如图1-3-11,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P:①能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时 AP 的长;若不能,请说明理由.②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH 始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请你说明理由.12、如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5.求线段EF的长。
13、如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m。
假设拖拉机行驶时,周围100m以会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?请说明理由,如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?考点八:应用勾股定理解决勾股树问题1、如图所示,所有的四边形都是形,所有的三角形都是直角三角形,其中 最大的形的边长为5,则形A ,B ,C ,D 的面积的和为2、已知△ABC 是边长为1的等腰直角三角形,以Rt △ABC 的斜边AC 为直角边,画第二个等腰Rt △ACD ,再以Rt △ACD 的斜边AD 为直角边,画第三个等腰Rt △ADE ,…,依此类推,第n 个等腰直角三角形的斜边长是 .考点九、图形问题1、如图1,求该四边形的面积2、如图2,已知,在△ABC 中,∠A = 45°,AC = 2,AB = 3+1,则边BC 的长为 .3、某公司的大门如图所示,其中四边形ABCD是长方形,上部是以AD为直径的半圆,其中AB=2.3m,BC=2m,现有一辆装满货物的卡车,高为2.5m,宽为1.6m,问这辆卡车能否通过公司的大门?并说明你的理由 .AB CD E FG431213BC D4、将一根长24㎝的筷子置于地面直径为5㎝,高为12㎝的圆柱形水杯中,设筷子露在杯子外面的长为h㎝,则h的取值围。
