新北师版初中数学八年级上册2.3立方根1公开课优质课教学设计
北师大版八年级数学上册:2.3《立方根》教学设计2

北师大版八年级数学上册:2.3《立方根》教学设计2一. 教材分析《立方根》是北师大版八年级数学上册第二章第三节的内容。
本节内容是在学生已经掌握了有理数的乘方、平方根和算术平方根的基础上进行学习的,是进一步深化学生对数的概念的理解,也是进一步培养学生的抽象思维能力。
二. 学情分析学生在学习本节课之前,已经掌握了有理数的乘方、平方根和算术平方根的概念和性质,能够进行相关的运算。
但是,对于立方根的概念和性质的理解可能还存在一定的困难。
因此,在教学过程中,需要引导学生通过实际操作和思考,来理解和掌握立方根的概念和性质。
三. 教学目标1.知识与技能:使学生理解立方根的概念,掌握立方根的性质,能够进行立方根的运算。
2.过程与方法:通过实际操作和思考,培养学生的抽象思维能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的探索精神。
四. 教学重难点1.重点:立方根的概念和性质。
2.难点:立方根的运算。
五. 教学方法采用问题驱动法,通过引导学生思考和探索,让学生在实际操作中理解和掌握立方根的概念和性质。
六. 教学准备1.准备一些立方体的教具,用于引导学生直观地理解立方根的概念。
2.准备一些有关立方根的练习题,用于巩固学生的学习成果。
七. 教学过程1.导入(5分钟)通过向学生展示一些立方体的教具,引导学生直观地感受立方体的形状,从而引出立方根的概念。
2.呈现(10分钟)向学生介绍立方根的概念,并引导学生通过实际操作,理解立方根的性质。
3.操练(10分钟)让学生通过实际的计算,来理解和掌握立方根的运算方法。
4.巩固(10分钟)让学生通过做一些有关立方根的练习题,来巩固所学的知识。
5.拓展(10分钟)引导学生思考:除了立方根,还有哪些其他的根呢?它们的性质又是怎样的呢?6.小结(5分钟)让学生总结一下,今天学到了什么,有哪些收获。
7.家庭作业(5分钟)布置一些有关立方根的家庭作业,让学生在家里进行练习。
8.板书(5分钟)在黑板上写出立方根的概念和性质,以及立方根的运算方法。
北师大版八年级数学上册:2.3《立方根》教学设计1

北师大版八年级数学上册:2.3《立方根》教学设计1一. 教材分析《立方根》是北师大版八年级数学上册第二章第三节的内容。
本节主要让学生掌握立方根的概念,学会求一个数的立方根,以及理解立方根的性质。
教材通过引入立方根的概念,让学生通过观察、操作、思考、交流等活动,体会数学知识之间的联系,提高学生分析问题、解决问题的能力。
二. 学情分析学生在学习本节内容前,已经掌握了有理数的乘方、实数等知识,具备了一定的观察、操作、思考能力。
但部分学生对抽象的数学概念理解仍有困难,因此,在教学过程中,要关注学生的个体差异,引导他们积极参与课堂活动,提高他们的数学素养。
三. 教学目标1.理解立方根的概念,掌握求一个数的立方根的方法。
2.会运用立方根解决实际问题,提高解决问题的能力。
3.培养学生的观察、操作、思考能力,提高学生的数学素养。
四. 教学重难点1.重点:立方根的概念,求一个数的立方根的方法。
2.难点:理解立方根的性质,运用立方根解决实际问题。
五. 教学方法1.引导法:教师引导学生观察、操作、思考,让学生在活动中体验数学知识。
2.交流法:教师学生进行小组讨论,分享学习心得,提高学生的沟通能力。
3.实践法:教师设计具有实践性的数学问题,让学生在实践中掌握数学知识。
六. 教学准备1.教学课件:制作与本节内容相关的课件,辅助教学。
2.教学素材:准备一些实际问题,供学生练习。
3.学生活动材料:为学生提供观察、操作、思考的材料。
七. 教学过程1.导入(5分钟)教师通过一个实际问题引入本节内容,引导学生思考:如何求一个数的立方根?2.呈现(10分钟)教师展示立方根的定义,让学生观察、思考,引导学生发现立方根的性质。
3.操练(10分钟)教师设计一些练习题,让学生求一个数的立方根,巩固所学知识。
4.巩固(5分钟)教师学生进行小组讨论,分享解题心得,提高学生的沟通能力。
5.拓展(5分钟)教师提出一些具有挑战性的问题,引导学生进行思考,提高学生的分析问题、解决问题的能力。
八年级数学上册(北大师版)配套教学教案:2.3立方根

一、情境导入 填空并回答问题:
(1)(
)
3
=
0.001
;
(2)(
3
) = 0;
(3) 若正方体的棱长为 a,体积为 8,根 据正方体的体积公式得 a3= 8,那么 a 叫做 8
的什么呢? 二、合作探究 探究点一:立方根的概念及性质 【类型一】 立方根的概念及性质 立方根等于本身的数有 ________
个.
3 解析: 在正数中, 1 = 1,在负数中,
3
3
- 1=- 1,又 0= 0,∴立方根等于本身
的数有 1,- 1, 0. 故填 3. 方法总结: 不论正数、负数还是零,都
有立方根.
【类型二】 立方根与平方根的综合问
2
2
+ 7= 27,把 x= 6 代入解得 y= 8,∴x + y
2
2
2
2
= 6 + 8 =100. ∴x+y 的算术平方根为 10.
2
2
+ 7 的立方根是 3,求 x + y 的算术平方根.
解析: 根据平方根、 立方根的定义和已 知条件可知 x- 2= 4, 2x + y+7= 27,从而 解出 x,y ,最后代入 x2+ y2 求其算术平方根
即可.
解: ∵x- 2 的平方根是 ±2,∴x- 2=
4. ∴x=6. ∵2x +y+ 7 的立方根是 3,∴2x+ y
方法总结: 本题先根据平方根和立方根
的定义,运用方程思想列方程求出 值, 再根据算术平方根的定义求出
x, y 的 x 2+ y 2 的
算术平方根.
【类型三】 立方根的实际应用
已知球的体积公式是
V=
4 3πr
3(r
为
八年级数学上册2.3立方根教学设计 (新版北师大版)

八年级数学上册2.3立方根教学设计(新版北师大版)一. 教材分析《八年级数学上册2.3立方根教学设计》是人教版初中数学八年级上册的一部分。
这部分内容主要介绍了立方根的概念、性质和运算方法。
教材通过丰富的实例和练习,使学生掌握立方根的知识,并能够运用到实际问题中。
本节课的内容对于学生来说是比较抽象的,需要通过实例和练习来理解和掌握。
二. 学情分析学生在学习本节课之前,已经学习了平方根的知识,对根的概念有一定的了解。
但是,立方根的概念和平方根有所不同,需要学生通过实例和练习来理解和掌握。
此外,学生对于实数的运算也有一定的了解,但还需要进一步的学习和巩固。
三. 教学目标1.知识与技能目标:使学生理解立方根的概念,掌握立方根的性质和运算方法,能够运用立方根解决实际问题。
2.过程与方法目标:通过实例和练习,培养学生的观察能力、思考能力和运算能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的耐心和细心,使学生感受到数学在生活中的应用。
四. 教学重难点1.教学重点:立方根的概念、性质和运算方法。
2.教学难点:立方根的概念和运算方法的理解和应用。
五. 教学方法1.实例教学法:通过丰富的实例,使学生理解和掌握立方根的概念和运算方法。
2.练习法:通过大量的练习,巩固学生的知识,提高学生的运算能力。
3.小组合作学习法:学生分组讨论和解决问题,培养学生的合作意识和沟通能力。
六. 教学准备1.教材和教辅:准备教材和相关的教辅资料,以便于学生学习和练习。
2.多媒体教学设备:准备多媒体教学设备,以便于展示实例和练习。
七. 教学过程1.导入(5分钟)通过一个实例,引出立方根的概念。
例如,展示一个正方体,让学生计算其体积,进而引出立方根的概念。
2.呈现(10分钟)介绍立方根的性质和运算方法,通过多媒体展示,使学生理解和掌握。
同时,引导学生与平方根进行对比,加深对立方根的理解。
3.操练(10分钟)让学生进行大量的练习,巩固立方根的知识。
八年级数学北师大版上册 第2章《2.3立方根》教学设计 教案(1)

《2.3立方根》一、教材分析《立方根》是义务教育课程标准实验教科书北师大版八年级(上)第二章《实数》第三节.本节内容安排了1个学时完成.主要是通过对立方根与平方根的比较与归类,探索立方根的概念、计算和简单性质.因此,除了具体的知识技能(如知道一个数的立方根的意义,会用根号表示一个数的立方根,掌握立方根运算,掌握求一个数的立方根的方法和技巧)外,还需要让学生感受类比的思想方法,为今后的学习打下基础.二、学情分析在学习了平方根概念的基础上学习立方根的概念,学生比较容易接受,因此教学重点放在立方根具有唯一性(实数范围内)的讨论上.在学生对数的立方根概念及个数的唯一性有了一定理解的基础上,再提出数的立方根与数的平方根有什么区别,学生就容易解决问题.三、目标分析教学目标●知识与技能目标1.了解立方根的概念,会用根号表示一个数的立方根.2.会用立方运算求一个数的立方根,了解开立方与立方互为逆运算.3.了解立方根的性质.4.区分立方根与平方根的不同.●过程与方法目标1.经历对立方根的探究过程,在探究中学会解决立方根的一些基本方法和策略.2.在学习了平方根的基础上,学生经历用类比的方法学习立方根的有关知识,领会类比思想.3.通过对立方根性质的探究,在探究中培养学生的逆向思维能力和分类讨论的意识.●情感与态度目标:1.在立方根概念、符号、运算及性质的探究过程中,培养学生联系实际、善于观察、勇于探索和勤于思考的精神.2.学生通过对实际问题的解决,体会数学的实用价值.●教学重点:立方根的概念及计算.●教学难点:立方根的求法,立方根与平方根的联系及区别.四、教法学法:类比法.五、教学过程第一环节:创设问题情境:复习:1、平方根的定义( 填空:(1)16的平方根是______2、2)6(2)的平方根是;(3)若a的平方根只有一个,那么a = ;(4)若数b的一个平方根是 1.2,那么b的另一个平方根是;3.要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?你是怎么知道的?思考:如果问题中正方体的体积为5cm3,正方体的棱长又该是多少?意图:通过实际情境引入,让学生感受新知学习的必要性,激发学生的求知欲望.效果:在思考问题的同时,学生既感受了数学的应用价值,激发了学生的学习热情,有很快将问题归结为如何确定一个数,从而顺利引入新课。
【教案】2.3立方根北师大版八年级数学上册

3 立方根教学目标【知识与技能】掌握立方根的定义以及正数、负数、0 的立方根的特点.【过程与方法】正确理解立方根的定义.【情感、态度与价值观】体验数学在实际生活中的作用.教学重难点【重点】掌握立方根的定义.【难点】运用所学知识解决问题.教学过程一、创设情境,引入新课师:请同学们观看大屏幕: 多媒体展示问题:要制作一种容积为27 m3的正方体形状的包装箱,这种包装箱的边长应该是多少?师:设这种包装箱的边长为x m,则X3=27,这就是要求一个数,使它的立方等于27. •••33=27,「.X=3.即这种包装箱的边长为3 m.师:一般地,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根•即:如果x3=a,即么X叫做a的立方根.比如:•,33=27,A3是27的立方根. 师:什么是开立方?生:求一个数的立方根的运算,叫做开立方.师:正如开平方与平方互为逆运算一样,开立方与立方也互为逆运算,据此我们可以求一个数的立方根.师: 请看大屏幕.根据立方根的意义填空,看看正数、0 和负数的立方根各有什么特点?因为23=8,所以8 的立方根是( );因为( )3=0.125,所以0. 125 的立方根是( );因为()3=0所以0的立方根是();因为()3=-8所以-8的立方根是();因为()3=-所以-的立方根是().•.23=8, -^8的立方根是2;•••(0. 5)3=0. 125,「O 125 的立方根是0. 5;•.•(0)3=0,「0的立方根是0;•.•(_2)3=_8, .•- 8 的立方根是-2;•.•(_)3=-,.•.-的立方根是-.师生共同归纳:正数的立方根是正数.负数的立方根是负数.0的立方根是0.师:你能说说数的平方根与数的立方根有什么不同吗?生:每一个数均有一个立方根,而负数没有平方根.师:一个数a的立方根的表示方法:3,读作“三次根号a” .其中a是被开方数,3是根指数.如3表示8的立方根,即3=2.3表示-8的立方根,即3=-2.3中的根指数3不能省略.注:算术平方根的符号,实际上省略了2中的根指数2,因此也可读作“二次根号a”师:请同学们填空:-3= -3=• _______ ,_________ ■・3_ 3-• 33・3_ 3-・3 3一般地,3 _______ -3.师:请同学们做题:求下列各式的值:(1)3;(2)3;(3)(3)3.学生尝试独立完成,一学生上黑板板演•教师巡视、指导•师生共同完成:解:(1)3=4; (2)3=-5;(3)(3)3=()3=.通过计算可知(3)3=a,3=a.注:其实,很多有理数的立方根是无限不循环小数.如3、3等都是无限不循环小数,可以用有理数、近似数表示它们、例题讲解【例1】求下列各数的立方根:(1) 27;(2)-27;(3); (4)-0. 064;(5)0.【答案】(1) -.33=27. /-27的立方根是3,即3=3;(2) 3)3=- 27,/-27 的立方根是-3,即3=- 3;⑶T()3=. /•的立方根是,即3=;(4) v(-0. 4)3=-0. 064. ./-0. 064 的立方根是-0. 4,即3=-0. 4;(5) v03=0. /.0的立方根是0,即3=0.【例2】求下列各式的值:(1)3;(2)3;(3)-3;(4)(3)3.【答案】( 1)3=3;(2)3=3=0. 4;(3)- 3=- 3=(4)(3)3=9.三、课堂小结师:通过本节课的学习,你有哪些收获?请与同桌交流学生发言,教师点评.。
北师大版八年级数学上册:2.3 立方根 教案1

立方根【教学目标】1.在一定的情境只,理解立方根的概念,使学生不断获得解决问题的经验,提高思维水平,学习中要注意感悟“类比”在知识产生和发展过程中的作用。2.了解立方根的概念,会用根号表示一个数的立方根,了解开立方与立方互为逆运算,能用立方运算求一些数的立方根3.能用立方根解决一些简单的实际问题。【教学重难点】正确地理解立方根的概念及符号表示能熟练应用【教学方法】观察、比较、合作、交流、探索。【教学过程】一、创设情境,感悟新知情境一体积为1的正方体,棱长为多少?体积增加1,棱长为多少? 情境二做一个正方体纸盒,使它的容积为64cm 3,正方体纸盒的棱长是多少?如果要使正方体纸盒容积为25cm 3,它的棱长是多少?二、引入课题 立方根从实际问题的计算,感受学习立方根的必要性,教学中引导学生借助平方根的定义,平方根的符号表示,开平方运算,自己给立方根下定义,给出立方根的符号表示和什么叫开立方运算三、探索活动问题一根据立方根的定义,你能举出某个数的立方根吗?你能用符号表示吗?例题求下列各数的立方根 (1)-64 (2)-1258 (3)9 (4)0 问题一 根据计算结果,与平方根作比较有什么不同?与同学交流巩固练习:1.下列说法正确的是( )A.任意数a 的平方根有2个,它们互为相反数B.任意数a 的立方根有1个C.-3是27的负的立方根D. (-1)2的立方根是-12.下列判断正确的是( )A.64的立方根是±4B.(-1)1-的立方根是1C.64的立方根是2D.如果3a =a,则a=03.求下列各式中的Xx 3+729=0 (x-3)3=64思维拓展,运用新知1.讨论(38-)3等于多少?(32)3等于多少? 33)8(-等于多少?332等于多少?四、课堂小结,内化新知立方根和平方根有何异同? 利用立方根概念进行有关计算作业布置一、填空题1.(-1)2005的立方根是 ,—0.0027的立方根是2.已知x 2=64,则3x =3.38515-= , 312)1(--n = 4.a 为何值时,则a , a 2,3a ,a 中,必是非负数的有 二、选择题1.-6的立方根用符号表示,正确的是( ) A 36- B -36 C -36- D ±36-三、求下列各式中的x1.27x ³-512=0 2.(2-x)3+1=64四、如果一个正方体的体积增大为原来的27倍,那么它的棱长增大为原来的多少倍?。
北师大版八年级上册2.3立方根优秀教学案例

3.引导学生运用立方根解决实际问题,培养学生的数学应用能力和创新思维。
(三)情感态度与价值观
1.培养学生对数学学科的兴趣和自信心,让学生感受到数学的实用性和魅力。
2.培养学生的团队合作意识,让学生在探究活动中互相学习、互相帮助。
(四)总结归纳
1.引导学生对所学内容进行总结和归纳,让学生明确立方根的概念、性质和应用,建立完整的知识体系。
2.通过总结归纳,帮助学生梳理学习思路,提高学生的概括和表达能力。
3.引导学生发现学习中存在的问题和不足,激发学生的自我改进和自我提高的意识。
(五)作业小结
1.布置相关的作业,让学生在课后巩固所学知识,提高学生的应用能力。
3.创设具有挑战性和探究性的问题情境,如立方根的谜题、立方根的魔术等,激发学生的探究欲望。
(二)讲授新知
1.通过讲解和示例,引导学生理解立方根的概念,明确立方根的性质和求法。
2.利用数学实验、探究活动等方法,让学生亲身体验和发现立方根的性质,加深学生对立方根的理解。
3.引导学生通过观察、实验、归纳等方法,探索立方根的性质和规律,培养学生的探究能力。
2.问题导向:设计了一系列由浅入深的问题,引导学生主动思考和探究立方根的概念和性质,使学生在解决问题的过程中自然地掌握立方根的知识,提高了学生的思维能力和问题解决能力。
3.小组合作:组织学生进行小组讨论和合作探究,让学生在互动中交流思想、分享成果,培养了学生的团队合作能力和协作精神,提高了学生的学习效果。
二、教学掌握立方根的性质,能够正确求一个数的立方根。
2.能够区分立方根与平方根、四次方根等其它根的概念,明确它们之间的联系与区别。
北师大版八年级数学上册:2.3《立方根》教案2

北师大版八年级数学上册:2.3《立方根》教案2一. 教材分析《立方根》是北师大版八年级数学上册第二章第三节的内容。
本节内容是在学生已经掌握了有理数的乘方、实数的概念等知识的基础上进行学习的。
通过本节课的学习,使学生理解立方根的概念,会正确地计算立方根,培养学生的逻辑思维能力。
二. 学情分析学生在七年级时已经学习过平方根的概念,对于算术平方根、平方根等概念有一定的了解。
但是,对于立方根的概念和计算方法还不够熟悉。
因此,在教学过程中,教师需要通过实例和练习,帮助学生理解和掌握立方根的概念和计算方法。
三. 教学目标1.知识与技能:使学生理解立方根的概念,会正确地计算立方根。
2.过程与方法:通过实例和练习,培养学生的逻辑思维能力。
3.情感态度价值观:激发学生学习数学的兴趣,培养学生的团队合作精神。
四. 教学重难点1.重点:立方根的概念和计算方法。
2.难点:立方根的计算方法。
五. 教学方法采用问题驱动法、实例教学法、合作学习法等教学方法,引导学生通过自主学习、合作交流,掌握立方根的概念和计算方法。
六. 教学准备1.教学课件:制作教学课件,包括立方根的定义、计算方法、实例等。
2.练习题:准备一些关于立方根的练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)利用PPT展示一个正方体,引导学生思考正方体的体积是多少。
通过这个实例,激发学生的学习兴趣,引出立方根的概念。
2.呈现(15分钟)介绍立方根的定义,展示立方根的计算方法。
通过PPT和实物模型的展示,使学生直观地理解立方根的概念和计算方法。
3.操练(10分钟)让学生独立完成一些关于立方根的计算题。
教师在旁边辅导,解答学生的疑问。
4.巩固(10分钟)让学生分组讨论,总结立方根的计算方法。
教师选取一些学生的总结,进行点评和讲解。
5.拓展(10分钟)引导学生思考:立方根有哪些性质?如何判断一个数是否有立方根?通过这些问题,拓展学生的知识面。
6.小结(5分钟)对本节课的内容进行总结,强调立方根的概念和计算方法。
八年级数学上册 2.3 立方根教案 (新版)北师大版

立方根教学目标知识与技能1.使学生了解一个数的立方根概念,并会用根号表示一个数的立方根;2.理解开立方的概念;3.明确立方根个数的性质,分清一个数的立方根与平方根的区别.过程与方法1、创设情境,激发学生的求知欲。
2、鼓励学生积极思维,体会类比的数学方法。
情感与价值观培养学生团结协作的团队精神。
教学重点和难点重点:立方根的概念及求法.难点:立方根与平方根的区别.教学过程设计一、复习:请同学回答下列问题:(1)什么叫一个数a 的平方根?如何用符号表示数a(≥0)的平方根?(2)正数有几个平方根?它们之间的关系是什么?负数有没有平方根?0平方根是什么?(3)当a≥0时,式子a ,-a ,±a,的意义各是什么?答:(1)如果一个数x 的平方等于a ,即x2=a ,那么x 叫做a 的平方根,表示为x=±a.(2)正数有两个平方根,它们互为相反数,负数没有平方根,0的平方根是0.(3)a≥0,a 表示a 的算术平方根,-a 表示a 的负平方根,±a 表示a 的平方根.二、引入新课1.计算下列各题:(1) 31.0; (2) 33)2(-; (3) 30.答:(1) 31.0=0.001; (2) 33)2(-=-827; (3) 30=0.指出:上面各题是已知底数和乘方指数求三次幂的运算,也叫乘方运算.怎样求下列括号内的数?各题中已知什么?求什么?(1)( )3=18; (2)( )3=-27 125; (3)( )3=0. 答:已知乘方指数和3次幂,求底数,也就是“已知某数的立方,求某数”.设某数为x ,则(1)式为3x =18,求x ; (2)式为3x =-27125,求x ;(3)式为x3=0求x 。
2.立方根的概念.一般地,如果一个数的立方等于a ,这个数就叫做a 的立方根(也叫做三次方根).用式子表示,就是,如果3x =a ,那么x 叫做a 的立方根.数a 的立方根用符号“3a ”表示,读作“三次根号a ,其中a 是被开方数,3是根指数.(注意:根指数3不能省略).3.开立方.求一个数的立方根的运算,叫做开立方.开立方与立方也是互为逆运算,因此求一个数的立方根可以通过立方运算来求.做一做(1)2的立方是多少?是否还有其它的数它的立方也是8?(2)-3的立方等于多少?是否还有其它的数它的立方也是-27?正数的立方根是正数;0的立方根是0;负数的立方是负数。
八年级数学上册2.3立方根说课稿 (新版北师大版)

八年级数学上册2.3立方根说课稿(新版北师大版)一. 教材分析《八年级数学上册2.3立方根说课稿(新版北师大版)》的教材分析,首先要从整体上了解本节课的内容。
《北师大版》的教材在设计上,注重引导学生自主探究,培养学生的动手操作能力和思维能力。
在2.3立方根这一节,教材通过引入生活中的实例,让学生感受立方根的概念,从而引出立方根的定义,并通过例题和练习,让学生掌握求立方根的方法。
二. 学情分析在设计说课稿时,我们需要充分考虑学生的实际情况。
八年级的学生已经学习了有理数、无理数等基础知识,对数学概念和运算方法有一定的了解。
但他们在学习过程中,可能对立方根的概念和求法理解不深,容易混淆。
因此,在教学过程中,我们需要注重引导学生通过实例感受立方根的概念,并通过练习巩固所学知识。
三. 说教学目标本节课的教学目标主要包括三个方面:知识与技能目标、过程与方法目标、情感态度与价值观目标。
1.知识与技能目标:让学生掌握立方根的概念,学会求一个数的立方根。
2.过程与方法目标:通过实例引入立方根的概念,引导学生自主探究,培养学生的动手操作能力和思维能力。
3.情感态度与价值观目标:培养学生对数学的兴趣,增强学生的自信心,使学生体验到成功的喜悦。
四. 说教学重难点本节课的重难点是立方根的概念和求法。
学生可能对立方根的理解不够深入,容易与平方根混淆。
因此,在教学过程中,我们需要注重引导学生通过实例感受立方根的概念,并通过练习巩固所学知识。
五. 说教学方法与手段为了实现本节课的教学目标,我采用了以下教学方法和手段:1.情境教学法:通过引入生活中的实例,让学生感受立方根的概念。
2.引导发现法:引导学生通过自主探究,发现立方根的求法。
3.练习法:通过布置不同难度的练习题,让学生巩固所学知识。
4.多媒体辅助教学:利用多媒体课件,生动形象地展示立方根的概念和求法。
六. 说教学过程1.导入新课:通过展示生活中的实例,如冰雪融化、盐水浓度等,引导学生思考这些现象与立方根的关系,从而引出立方根的概念。
北师大版八年级数学上册:2.3立方根(教案)

-难点解释:学生可能会在将立方根应用于实际问题时感到困惑,需要通过案例分析、小组讨论等方式,帮助学生理解立方根在生活中的应用。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《立方根》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要求解一个数的立方根的情况?”(如:求解一个正方体的棱长。)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索立方根的奥秘。
6.数学应用:培养学生将数学知识应用于实际生活中的意识,增强数学在实际生活中的价值认识。
三、教学难点与重点
1.教学重点
-立方根的定义:理解立方根的概念,明确一个数的立方根是什么,这是本节课的核心内容。
-举例:解释2的立方根是8,因为8×8×8=512,而512是2的三次方。
-立方根的计算:掌握计算立方根的方法,包括计算器使用和手算技巧。
在学生小组讨论环节,我注意到有的小组在分享成果时表达不够清晰,可能是因为他们对立方根的理解还不够深入。为了提高学生的表达能力和加深他们对立方根的理解,我打算在接下来的课程中增加一些课堂展示和口头报告的环节。
另外,我还发现有些学生对立方根在实际生活中的应用了解不足。在今后的教学中,我会尽量多举一些生活中的例子,让学生们更好地认识到数学知识在实际生活中的重要性。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“立方根在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
北师大版初中数学八年级上册《第二章实数3立方根》公开课教学设计_1

立方根一、教材分析《立方根》是义务教育课程标准实验教科书北师大版八年级(上)第二章《实数》第三节.本节内容安排了1 个学时完成.主要是通过对立方根与平方根的比较与归类,探索立方根的概念、计算和简单性质.因此,除了具体的知识技能(如知道一个数的立方根的意义,会用根号表示一个数的立方根,掌握立方根运算,掌握求一个数的立方根的方法和技巧)外,还需要昂学生感受类比的思想方法,为今后的学习打下基础.二、学情分析在学习了平方根概念的基础上学习立方根的概念,学生比较容易接受,因此教学重点放在立方根具有唯一性(实数范围内)的讨论上.在学生对数的立方根概念及个数的唯一性有了一定理解的基础上,再提出数的立方根与数的平方根有什么区别,学生就容易解决问题.三、目标分析教学目标(1) 知识与技能目标1.了解立方根的概念,会用根号表示一个数的立方根.2.会用立方运算求一个数的立方根,了解开立方与立方互为逆运算.3.了解立方根的性质.4.区分立方根与平方根的不同.(2) 过程与方法目标1.经历对立方根的探究过程,在探究中学会解决立方根的一些基本方法和策略.2.在学习平方根的基础上,学生经历用类比的方法学习立方根的有关知识,领会类比思想.3.通过对立方根性质的探究,在探究中培养学生的逆向思维能力和分类讨论的意识.(3) 情感与态度目标:1.在立方根概念、符号、运算及性质的探究过程中,培养学生联系实际、善于观察、勇于探索和勤于思考的精神.2.学生通过对实际问题的解决,体会数学的实用价值.(4) 教学重点立方根的概念及计算.(5) 教学难点立方根的求法,立方根与平方根的联系及区别.四、教法学法1.教学方法:类比法.2 •课前准备:教具:教材,软件Microsoft PowerPoint 2007,电脑.学具:教材,练习本.五、教学过程本节课设计了七个教学环节:第一环节:创设问题情境;第二环节:复习引入、类比学习; 第三环节:初步探究;第四环节:尝试反馈,巩固练习;第五环节:深入探究;第六环节:课时小结;探究与思考;第七环节:作业布置及课外探究.第一环节:复习引入、类比学习(1)什么叫一个数a的平方根?如何用符号表示数a ( a> 0)的平方根?(2)正数的平方根有几个?它们之间的关系是什么?负数有没有平方根?0的平方根是什么?(3)平方和开平方运算有何关系?(4)算术平方根和平方根有何区别和联系?强调:一个正数的平方根有两个,且互为相反数;一个负数没有平方根;0的平方根是0.意图:学生通过回顾上节课的学习内容,为进一步研究立方根的概念及性质做好铺垫,同时突出平方根与立方根的对比,以利于弄清两者的区别和联系.效果:复习引入既复习了平方根的知识,又利于学生类比学习法学习立方根知识第二环节:创设问题情境:问题1:某化工厂使用一种球形储气罐储藏气体,现在要造一个新的球形储气罐,如果它的体积是原来的8倍,那么它的半径是原储气罐的多少倍?如果储气罐的体积是原来的4倍呢?4 3(球的体积公式为v= R3, R为球的半径)3提问:怎样求出半径R ?学完本节知识后,相信你会有一个满意的答案.有关体积的运算和面积的运算有类似之处,让我们用上节课解决问题的方法来学习新知识.问题2:要制作一种容积为27m3的正方体的包装箱,这种包装箱的边长应该是多少?解:设这种包装箱的边长为x m,则这就是要求一个数,使它的的立方等于27.27因为33=所以x= 3,即这种包装箱的边长应为 3 m.意图:通过实际情境引入,让学生感受新知学习的必要性,激发学生的求知欲望.效果:在思考问题的同时,学生既感受了数学的应用价值,激发了学生的学习热情,有很快将问题归结为如何确定一个数,它的立方等于4,从而顺利引入新课.在现实的一些场景的问题中,需要引出一个新的运算,你将如何定义这个新运算?般地,如果一个数x 的立方等于a ,即x 3=a,那么这个数x 就叫做a 的立方根(cube root,也叫做三次方根)第三环节:初步探究1 做一做:怎样求下列括号内的数?各题中已知什么数?求什么数?27 (1) ()3 = 0.001 ; (2) ()3=- 27 ;(3) ( )3=0.64意图:通过计算练习,使学生进一步了解求一个数的立方,与求一个数的立方根是互为逆运算,感受一个数的立方根的唯一性,计算中对 a 的取值分别选为正数、负数、 0,这样设计,在此过程中渗透分类讨论的思想方法.2、议一议:(1) 正数有几个立方根? (2) 0有几个立方根 (3) 负数呢?意图:提问,是为了指出平方根与立方根的对比,以利于弄清两者的区别和联系.3在上面的基础上明晰下列内容,对知识进行梳理(1) 每个数a 都只有一个立方根,记为“ Va ”读作“三次根号a ”例如x 3=7时,x 是7的立方根,即3 7 =x ;与数的平方根的表示比较,数的立方根中根号前 没有“土”符号,但根指数3不能省略.(2 )正数的立方根是正数;0的立方根是0 ;负数的立方根是负数.(3)求一个数a 的立方根的运算叫做 开立方(extrction of cubic root),其中a 叫做被开方数.开 立方与立方互为逆运算.效果:通过亲自运算、探究学习立方运算的逆运算,培养了学生的探究能力,初步掌握立 方根的概念.第四环节:尝试反馈,巩固练习 例1、求下列各数的立方根:83(1) -27 ;(2);(3) 3125 8解:(1)因为(一3)3=- 27,所以一27的立方根是一3,即3 — 27=- 3;(4) 0.216 ; (5) -5.(2)因为8,所以1258 1252的立方根是2,即53 27 3 3(3)因为(-)3=——=3-,所以33的立方根是2 8 8 8(4)因为(0.6)3=0.216,所以0.216 的立方根是0.6,即3 0.216=0.6 ;(5) -5的立方根是3- 5.例2、求下列各式的值:所以 3 二 _ -38.(2) ________________ 因为-~2^= ________ , -3 27 =.所以 3 -27' ____ -3 27. 例4 .求下列各数的立方根:____ _______ _______ ______ _____ 3 30.125 3 -64; —164 ; 3 53; 3 16 .2 •通过上面的计算结果,你发现了什么规律?意图:例1着眼于弄清立方根的概念,因此这里不仅用立方的方法求立方根,而且书写上 采用了语言叙述和符号表示互相补充的做法,学生在熟练以后可以简化写法•例 2则巩固立方根的计算,弓I 导学生思考立方根的性质.效果:学生通过练习掌握立方根的概念和计算,通过对计算结果的分析得出立方根的性质,若学生不能发现规律,教师可以再给出几个例子,如:3.33二3 27 = 3; (3 8)3 = (2)3=8. 3二二3 — 23 = — 2;引导学生观察被开方数、根指数及运算结果之间的关系,从而得出立方根的性质;也可以安排学生分小组讨论,通过交流,展示学生发现的规律; 若学生的讨论不够深入,可由教师补充得出结论.第五环节:深入探究想一想:(1) V a 表示a 的立方根,那么(V a 3等于什么? 睛 呢?(2) 3 — a 与一3 a 有何关系?意图:明晰 3a 3 =a , 3 a 3 =a 。
北师大版数学八年级上册2.3立方根教案

2.3立方根【学习目标】1.了解立方根的概念,会用根号表示一个数的立方根.2.能用立方运算求某些数的立方根,了解开立方与立方互为逆运算.3.了解立方根的性质.【学习重点】立方根的概念.【学习难点】1.正确理解立方根的概念.2.会求一个数的立方根.3.区分立方根与平方根的不同之处.【学法指导】合作交流自主学习【学习过程】(一)自学指导平方根与立方根的联系与区别.联系:(1)0的平方根、立方根都有一个是0.(2)平方根、立方根都是开方的结果.区别:(1)定义不同:“如果一个数的平方等于a ,这个数就叫做a 的平方根”;“如果一个数的立方等于a ,这个数就叫做a 的立方根.”(2)个数不同:一个正数有两个平方根,一个正数有一个立方根;一个负数没有平方根,一个负数有一个立方根.(3)表示法不同正数a 的平方根表示为±a ,a 的立方根表示为3a .(4)被开方数的取值范围不同 ±a 中的被开方数a 是非负数;3a 中的被开方数可以是任何数.(二)课堂反馈[例1]求下列各数的立方根:(1)-27;(2)1258;(3)0.216;(4)-5. [例2]求下列各式的值: (1)38 ;(2)3064.0;(3)-31258;(4)(39)3 (三)合作探究 3a 表示a 的立方根,则(3a )3等于什么?33a 等于什么? 【应用拓展】1.某化工厂使用一种球形储气罐储藏气体.现在要造一个新的球形储气罐,如果它的体积是原来的8倍,那么它的半径是原储气罐半径的多少倍?2.一个正方体的体积变为原来的n 倍,它的棱长变为原来的多少倍?解:设原正方体的棱长为a ,后来的正方体的棱长为b ,得na 3=b 3∴3333n a b =∴b =a n n a 333=.即后来的棱长变为原来的3n 倍. 【达标测评】1.(1)如果一个数的立方根等于它本身,那么这个数是________. (2)3271-=________, (38)3=________ (3)364的平方根是________.2.求下列各数的立方根:0,1,-8127,6,-1000125,0.001 3.求下列各式的值:3233333333)278(;)2(;)2(;16463;1251;1;027.0------ 4.求下列各式中的x .(1)8x 3+27=0;(2)(x -1)3-0.343=0;(3)81(x +1)4=16;(4)32x 5-1=0. 【总结评价】本节的内容最好在熟练掌握平方根的内容的前提下进行学习,这样就能用类推的方法得出立方根的相关结论。
八年级数学上册2.3立方根教案1北师大版(new)

2.3 立方根1.了解立方根的概念及性质,会用根号表示一个数的立方根;(重点)2.了解开立方与立方是互逆运算,会用开立方运算求一个数的立方根.(难点)一、情境导入填空并回答问题:(1)()3=0.001;(2)()3=0;(3)若正方体的棱长为a,体积为8,根据正方体的体积公式得a3=8,那么a叫做8的什么呢?二、合作探究探究点一:立方根的概念及性质【类型一】立方根的概念及性质立方根等于本身的数有________个.解析:在正数中,错误!=1,在负数中,3,-1=-1,又错误!=0,∴立方根等于本身的数有1,-1,0.故填3。
方法总结:不论正数、负数还是零,都有立方根.【类型二】立方根与平方根的综合问题已知x-2的平方根是±2,2x+y+7的立方根是3,求x2+y2的算术平方根.解析:根据平方根、立方根的定义和已知条件可知x-2=4,2x+y+7=27,从而解出x,y,最后代入x2+y2求其算术平方根即可.解:∵x-2的平方根是±2,∴x -2=4。
∴x=6。
∵2x+y+7的立方根是3,∴2x+y+7=27,把x=6代入解得y=8,∴x2+y2=62+82=100。
∴x2+y2的算术平方根为10。
方法总结:本题先根据平方根和立方根的定义,运用方程思想列方程求出x,y的值,再根据算术平方根的定义求出x2+y2的算术平方根.【类型三】立方根的实际应用已知球的体积公式是V=错误!πr3(r为球的半径,π取3.14),现已知一个小皮球的体积是113。
04cm3,求这个小皮球的半径r.解析:将公式变形为r3=错误!,从而求r.解:由V=错误!πr3,得r3=错误!,∴r=错误!.∵V=113。
04cm3,π取3。
14,∴r≈错误!=错误!=3(cm).故这个小皮球的半径r约为3cm。
方法总结:解此题的关键是灵活应用球的体积公式,并将公式适当变形.探究点二:开立方运算求下列各式的值.(1)-错误!;(2)错误!;(3)-3,-8÷错误!+错误!。
北师大版数学八年级上册2.3立方根教案

《2.3立方根》教学设计一、教材分析《立方根》是义务教育课程标准实验教科书北师大版八年级(上)第二章《实数》第三节.本节内容安排了1个学时完成.主要是通过对立方根与平方根的比较与归类,探索立方根的概念、计算和简单性质.因此,除了具体的知识技能(如知道一个数的立方根的意义,会用根号表示一个数的立方根,掌握立方根运算,掌握求一个数的立方根的方法和技巧)外,还需要让学生感受类比的思想方法,为今后的学习打下基础.二、学情分析在学习了平方根概念的基础上学习立方根的概念,学生比较容易接受,因此教学重点放在立方根具有唯一性(实数范围内)的讨论上.在学生对数的立方根概念及个数的唯一性有了一定理解的基础上,再提出数的立方根与数的平方根有什么区别,学生就容易解决问题.三、目标分析教学目标●知识与技能目标1.了解立方根的概念,会用根号表示一个数的立方根.2.会用立方运算求一个数的立方根,了解开立方与立方互为逆运算.3.了解立方根的性质.4.区分立方根与平方根的不同.●过程与方法目标1.经历对立方根的探究过程,在探究中学会解决立方根的一些基本方法和策略.2.在学习了平方根的基础上,学生经历用类比的方法学习立方根的有关知识,领会类比思想.3.通过对立方根性质的探究,在探究中培养学生的逆向思维能力和分类讨论的意识.●情感与态度目标:1.在立方根概念、符号、运算及性质的探究过程中,培养学生联系实际、善于观察、勇于探索和勤于思考的精神.2.学生通过对实际问题的解决,体会数学的实用价值.●教学重点:立方根的概念及计算.●教学难点:立方根的求法,立方根与平方根的联系及区别.四、教法学法:类比法.五、教学过程第一环节:创设问题情境:复习:1、平方根的定义2、填空: (1)16的平方根是______ (2) 的平方根是 ; (3)若a 的平方根只有一个,那么a = ;(4)若数 b 的一个平方根是 1.2,那么 b 的另一个平方根是 ; 3.要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?你是怎么知道的? 思考:如果问题中正方体的体积为5cm3,正方体的棱长又该是多少?意图:通过实际情境引入,让学生感受新知学习的必要性,激发学生的求知欲望.效果:在思考问题的同时,学生既感受了数学的应用价值,激发了学生的学习热情,有很快将问题归结为如何确定一个数,从而顺利引入新课。
初中数学北师大版八年级上册《2.3立方根》教学设计
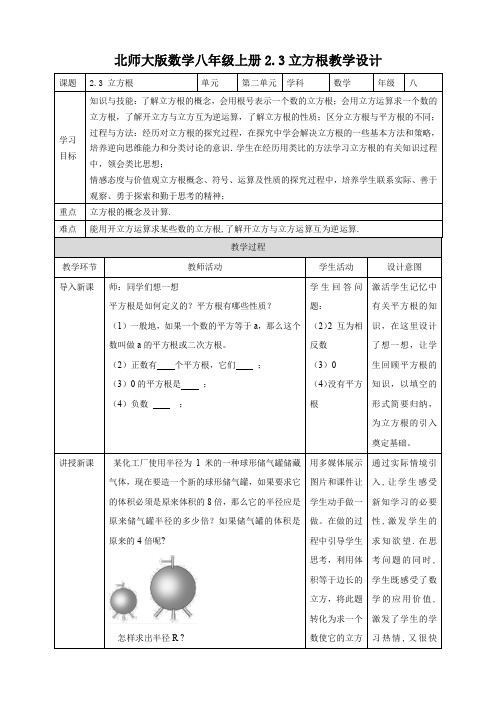
北师大版数学八年级上册2.3立方根教学设计某化工厂使用半径为1米的一种球形储气罐储藏气体,现在要造一个新的球形储气罐,如果要求它的体积必须是原来体积的8倍,那么它的半径应是原来储气罐半径的多少倍?如果储气罐的体积是原来的4倍呢?怎样求出半径R ?【议一议】(1)正数有几个立方根? (2)负数有几个立方根? (3)0有几个立方根?师:如何表示一个数的立方根?一个数a 的立方根可表示为:3a ,读作:三次根号a其中a 是被开方数,3是根指数,3不能省略. 【思考】正数、0和负数的的平方根和立方根各有什么特点?【想一想】类比开平方的概念,你能总结出开立方的概念吗? 求一个数a 的立方根的运算叫做开立方,a 叫做被开方数.例1求下列各数的立方根:(1)27-; (2)1258; (3)833 ; (4)216.0 ; (5)5-.解:(1)因为2733=-)(-,所以27-的立方根是3-,即3273=--;(2)因为1258523=⎪⎭⎫⎝⎛,所以1258的立方根是52,即5212583=; (3)因为833827233==)(,所以833的立方根是23,即238333=;(1)一个正方体的体积变为原来的8倍,它的棱长变为原来的___2____倍;(2)体积变为原来的n 倍,它的棱长变为原来的 _______倍;(3)当x__为任意数_____时, 有意义;(4)若x 是64的立方根,则x 的平方根是±2 ; (5)若x 是64的平方根,则x 的立方根是±2 . 2.求下列各数的立方根.(1)0.001; (2)-512 ; (3)827()31 0.001=0.1;3.(1)填表.(2)由上表你发现了什么规律?从表中发现被开方数小数点向右移动三位,立方根向右移动一位。
4.已知x -2的平方根是±2,2x +y +7的立方根是3,求x2+y2的算术平方根.解:∵x -2的平方根是±2,∴x -2=4.∴x =6.∵2x +y +7的立方根是3,∴2x +y +7=27,把x =6代入解得y =8,x2+y2=62+82=100. ∴x2+y2的算术平方根为10.5. (2019•大庆)有理数-8的立方根为( A )a0.0000010.001110001000000(2)由上表你发现了什么规律?3a 0.010.1110100从表中发现被开方数小数点向右移动三位,立方根向右移动一位。
最新北师版八年级数学上册精品教案2.3《立方根》

2.3立方根教学目标知识与技能1.使学生了解一个数的立方根概念,并会用根号表示一个数的立方根;2.理解开立方的概念;3.明确立方根的性质,分清一个数的立方根与平方根的区别.过程与方法创设情境,鼓励学生积极思考,体会类比的数学方法。
情感与价值观培养学生团结协作的团队精神。
重点难点重点:立方根的概念及计算.难点:立方根与平方根的区别,了解开立方与立方运算互为逆运算.教学过程【新课导入】(1)面积为2的正方形的边长为多少?(2)体积为2 的正方体的棱长是多少?请同学们回忆求解a 2=2时的情境,那么a 3=2呢?【新知构建】一、共同探究某化工厂使用半径为1 m 的一种球形储气罐储藏气体.现在要造一个新的球形储气罐,如果它的体积是原来的8倍,那么它的半径是原储气罐半径的多少倍?如果储气罐的体积是原来的4倍呢?(球的体积公式为V =πR 3,R 为球的半径)提问:怎样求出半径R ?计算下列各题:(1) 31.0; (2) 33)2(-; (3) 30. (1) 31.0=0.001; (2) 33)2(-=-827; (3) 30=0.指出:上面各题是已知底数和乘方指数求三次幂的运算,也叫乘方运算.怎样求下列括号内的数?各题中已知什么?求什么?(1)( )3=18; (2)( )3=-27 125; (3)( )3=0.已知乘方指数和3次幂,求底数,也就是“已知某数的立方,求某数”.设某数为x ,则(1)式为3x =18,求x ;(2)式为3x =-27 125,求x ;(3)式为x 3=0求x 。
立方根的概念:一般地,如果一个数x 的立方等于a ,即3x =a ,那么这个数x 就叫做a 的立方根(也叫做三次方根).如2是8的立方根,32-是278-的立方根,0是0的立方根. 做一做(1)2的立方是多少?是否还有其它的数它的立方也是8?(2)-3的立方等于多少?是否还有其它的数它的立方也是-27?立方根的性质:每个数a 都有一个立方根,记作“3a ”,读作“三次根号a ”.例如3x =7时,x 是7的立方根,即x=37.结论:正数的立方根是正数,0的立方根是0,负数的立方根是负数.开立方:求一个数a 的立方根的运算叫做开立方.开立方与立方也是互为逆运算,因此求一个数的立方根可以通过立方运算来求.其中a 是被开方数,3是根指数.(注意:根指数3不能省略).二、例题讲解例1 求下列各数的立方根:(1)-27; (2)1258; (3)0.216; (4)-5; 分析:求一个数的立方根,我们可以通过立方运算来求. 解:(1)因为3)3(-=-27,所以-27的立方根是-3,即327-=-3.问:除-3以外,还有什么数的立方等于-27?也就是说,-27还有别的立方根吗?答:除-3以外,没有其它的数的立方等于-27,也就是说,-27的立方根只有一个.(2)因为3)52(=1258,所以1258的立方根是52即31258=52.(3)因为36.0=0.216,所以0.216的立方根是0.6,即3216.0=0.6.(4)-5的立方根是35-.问:一个正数有几个立方根?一个负数有几个立方根?零的立方根是什么?答:正数有一个正的立方根;负数有一个负的立方根;零的立方根仍旧是零.指出:立方根的性质可以概括为立方根的唯一性,即一个数的立方根是唯一的. 例2 求下列各式的值:(1) 38-; (2) 3064.0-; (3) 31258-.(4)33)9( 解: (1) 38- =-2;(2) 3064.0-=-0.4; (3) 31258-=52-; (4)33)9(=9. 知识拓展:平方根与立方根的区别与联系区别:(1)在用根号表示平方根时,根指数2可以省略,而用根号表示立方根时,根指数3不能省略;(2)平方根只有非负数才有,而立方根任何数都有,并且每个数都只有一个立方根;(3)正数的平方根有两个,而正数的立方根只有一个.联系:(1)开平方与开立方运算都与相应的乘方运算互为逆运算;(2)都可归结为非负数的非负方根来研究,平方根主要通过算术平方根来研究,而负数的立方根也可转化为正数的立方根来研究;(3)0的平方根和立方根都是0.【课堂小结】1.了解立方根的概念,会用三次根号表示一个数的立方根,能用开立方运算求一个数的立方根.2.在学习中应注意以下5点:(1)符号中的根指数“3”不能省略;(2)对于立方根,被开方数没有限制,正数、零、负数都有一个立方根;(3)平方根和立方根的区别:正数有两个平方根,但只有一个立方根;负数没有平方根,但却有一个立方根;(4)灵活运用公式:(3a )3=a ;(5)立方与开立方也互为逆运算.我们可以用立方运算求一个数的立方根,或检验一个数是不是另一个数的立方根.【课后作业】教材第31页随堂练习第1,2题.教材第32页习题2.5第2,3题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3 立方根
1.了解立方根的概念及性质,会用根号表示一个数的立方根;(重点)
2.了解开立方与立方是互逆运算,会用开立方运算求一个数的立方根.(难点)
一、情境导入
填空并回答问题:
(1)( )3=0.001;(2)( )3=0;
(3)若正方体的棱长为a,体积为8,根据正方体的体积公式得a3=8,那么a叫做8的什么呢?
二、合作探究
探究点一:立方根的概念及性质
【类型一】立方根的概念及性质
立方根等于本身的数有________个.
解析:在正数中,3
1=1,在负数中,
3
-1=-1,又
3
0=0,∴立方根等于本身的数有1,
-1,0.故填3.
方法总结:不论正数、负数还是零,都有立方根.
【类型二】立方根与平方根的综合问题
已知x-2的平方根是±2,2x+y+7的立方根是3,求x2+y2的算术平方根.解析:根据平方根、立方根的定义和已知条件可知x-2=4,2x+y+7=27,从而解出x,y,最后代入x2+y2求其算术平方根即可.
解:∵x-2的平方根是±2,∴x-2=4.∴x=6.∵2x+y+7的立方根是3,∴2x+y+7=27,
把x =6代入解得y =8,∴x 2+y 2=62+82=100.∴x 2+y 2
的算术平方根为10.
方法总结:本题先根据平方根和立方根的定义,运用方程思想列方程求出x ,y 的值,再根据算术平方根的定义求出x 2+y 2的算术平方根.
【类型三】 立方根的实际应用
已知球的体积公式是V =4
3
πr 3(r 为球的半径,π取3.14),现已知一个小皮球的体积是113.04cm 3,求这个小皮球的半径r.
解析:将公式变形为r 3=3V 4π
,从而求r. 解:由V =43πr 3,得r 3=3V 4π,∴r =33V 4π.∵V =113.04cm 3,π取3.14,∴r ≈33×113.044×3.14
=327=3(cm).故这个小皮球的半径r 约为3cm.
方法总结:解此题的关键是灵活应用球的体积公式,并将公式适当变形.
探究点二:开立方运算
求下列各式的值.
(1)-3343;(2)31027-5;(3)-3-8÷214+(-1)100. 解:(1)-3343=-7;
(2)31027-5=3-12527=-53
; (3)-3-8÷214+(-1)100=2÷94+1=2÷32+1=2×23+1=73. 方法总结:做开平方或开立方运算时,一般都是利用它们的定义去掉根号;当被开方数不是单独一个数时,则需先将它们进行化简,再进行开方运算.
三、板书设计
1.每个数a都只有一个立方根,记为“3
a”,读作“三次根号a”.
2.正数的立方根是正数;0的立方根是0;负数的立方根是负数.
3.求一个数a的立方根的运算叫做开立方,其中a叫做被开方数.开立方与立方互为逆运算.
本节课让学生应用类比法学习立方根的概念、性质和运算.学生在以后的数学学习中,要注意渗透类比的思维方式,让学生在学习新知识的同时巩固已学的知识,并通过新旧对比更好地掌握知识.。
