概率论与数理统计(第9章)习题详解

合集下载

概率论与数理统计课后习题答案浙江大学第四版完整版.pdf

完全版概率论与数理统计课后习题答案第四版盛骤(浙江大学)浙大第四版（高等教育出版社）第一章概率论的基本概念1.[一]写出下列随机试验的样本空间（1）记录一个小班一次数学考试的平均分数（充以百分制记分）（[一]1）nn n n o S1001, ，n 表小班人数（3）生产产品直到得到10件正品，记录生产产品的总件数。

（[一]2）S={10，11，12，………，n ，………}（4）对某工厂出厂的产品进行检查，合格的盖上“正品”，不合格的盖上“次品”，如连续查出二个次品就停止检查，或检查4个产品就停止检查，记录检查的结果。

查出合格品记为“1”，查出次品记为“0”，连续出现两个“0”就停止检查，或查满4次才停止检查。

（[一](3)）S={00，100，0100，0101，1010，0110，1100，0111，1011，1101，1110，1111，}2.[二]设A ，B ，C 为三事件，用A ，B ，C 的运算关系表示下列事件。

（1）A 发生，B 与C 不发生。

表示为：C B A 或A －(AB+AC )或A －(B ∪C )（2）A ，B 都发生，而C 不发生。

表示为：C AB 或AB －ABC 或AB －C（3）A ，B ，C 中至少有一个发生表示为：A+B+C（4）A ，B ，C 都发生，表示为：ABC（5）A ，B ，C 都不发生，表示为：C B A 或S －(A+B+C)或CB A（6）A ，B ，C 中不多于一个发生，即A ，B ，C 中至少有两个同时不发生相当于C A C B B A ,,中至少有一个发生。

故表示为：C A C B B A 。

（7）A ，B ，C 中不多于二个发生。

相当于：C B A ,,中至少有一个发生。

故表示为：ABCC B A 或（8）A ，B ，C 中至少有二个发生。

相当于：AB ，BC ，AC 中至少有一个发生。

故表示为：AB +BC +AC6.[三]设A ，B 是两事件且P (A )=0.6，P (B )=0.7.问(1)在什么条件下P (AB )取到最大值，最大值是多少？（2）在什么条件下P (AB )取到最小值，最小值是多少？解：由P (A )=0.6，P (B )=0.7即知AB ≠φ，（否则AB =φ依互斥事件加法定理，P (A ∪B )=P (A )+P (B )=0.6+0.7=1.3>1与P (A ∪B )≤1矛盾）.从而由加法定理得P (AB )=P (A )+P (B )－P (A ∪B )(*)（1）从0≤P (AB )≤P (A )知，当AB =A ，即A ∩B 时P (AB )取到最大值，最大值为P (AB )=P (A )=0.6，（2）从(*)式知，当A ∪B=S 时，P (AB )取最小值，最小值为P (AB )=0.6+0.7－1=0.3。

浙大版概率论与数理统计答案---第九章

第九章方差分析与回归分析注意：这是第一稿（存在一些错误）1．解：()()()211,,n niii i i i L f y y f y x αβσεαβ======--∏∏()()()221222211122ni i i i i y x y x nni e eαβαβσσπσπσ=------=∑==∏()()()()22212,,ln ,,ln22ni i i y x l L n αβαβσαβσπσσ=--==--∑()()()()()()212212221242,,0,,0,,1022ni i i n i i i i n i i i y x l y x x l y x l n αβαβσασαβαβσβσαβαβσσσσ===⎧--⎪∂⎪==∂⎪⎪--⎪∂⎪==⎨∂⎪⎪--⎪∂⎪=-=⎪∂⎪⎩∑∑∑ 解得2ˆˆ,ˆ,ˆ.xyxxy x s s SSE n αββσ⎧⎪=-⎪⎪=⎨⎪⎪=⎪⎩则α、β的极大似然估计与最小二乘估计一致。

2σ的极大似然估计为SSE n ，最小二乘估计为2SSE n -，为2σ的无偏估计。

2．解：（1）由题意，知0123:H μμμ==，1123:,,H μμμ不全相等计算有112312.54ni i i x n x n n n ⋅===++∑ 321()0.738i A i i S n x x ⋅==-=∑，321() 5.534in T ij i i jS x x ===-=∑∑4.796E T A S S S =-=，/(31)0.369A A MS S =-=123/(3)0.178E E MS S n n n =++-=，/ 2.077A E F MS MS == 所以单因素方差分析表为：方差来源自由度平方和均方 F 比因素A 2 0.738 0.369 2.077 误差 27 4.796 0.178 总和295.534由于 2.077F =<(2,27) 3.3541F α=，接受0H（2）2σ的无偏估计量为：123/(3)0.178E E MS S n n n =++-=3．解：(1)61n =，4r =,(2)0.05(3,57) 2.76 3.564F ≈<,则拒绝原假设，即认为不同年级学生的月生活费水平有显著差异。

概率论与数理统计第四版习题答案全

概率论与数理统计习（第四版）题解答第一章随机事件及其概率·样本空间·事件的关系及运算一、任意抛掷一颗骰子，观察出现的点数。

设事件A 表示“出现偶数点”，事件B 表示“出现的点数能被3整除”．（1）写出试验的样本点及样本空间；（2）把事件A 及B 分别表示为样本点的集合；（3）事件B A AB B A B A ,,,,分别表示什么事件？并把它们表示为样本点的集合．解：设i ω表示“出现i 点”)6,,2,1( =i ，则（1）样本点为654321,,,,,ωωωωωω；样本空间为}.,,,,,{654321ωωωωωω=Ω （2）},,{642ωωωA =； }.,{63ωωB = （3）},,{531ωωωA =，表示“出现奇数点”；},,,{5421ωωωωB =，表示“出现的点数不能被3整除”；},,,{6432ωωωωB A =⋃，表示“出现的点数能被2或3整除”；}{6ωAB =，表示“出现的点数能被2整除且能被3整除”；},{B A 51ωω= ，表示“出现的点数既不能被2整除也不能被3整除”二、写出下列随机试验的样本空间及各个事件中的样本点：（1）同时掷三枚骰子，记录三枚骰子的点数之和．A —“点数之和大于10”，B —“点数之和小于15”．（2）一盒中有5只外形相同的电子元件，分别标有1，2，3，4，5．从中任取3只，A —“最小为1”．解：(1) 设i ω表示“点数之和等于i ”)18,,4,3( =i ，则},,,{1843ωωω =Ω；},,,{181211ωωωA =；}.,,,{1443ωωωB =(2) 设ijk ω表示“出现为k j i ,,”);5,,2,1,,(k j i k j i ≠≠= ，则},,,,,,,,,{345245235234145135134125124123ωωωωωωωωωω=Ω }.,,,,,{145135134125124123ωωωωωωA =三、设C B A ,,为三个事件，用事件之间的运算表示下列事件： (1) A 发生, B 与C 都不发生； (2) C B A ,,都发生；(3) C B A ,,中至少有两个发生； (4) C B A ,,中至多有两个发生．解：(1) C B A ；(2) ABC ；(3) ABC C AB C B A BC A ⋃⋃⋃或CA BC AB ⋃⋃(4) BC A C B A C AB C B A C B A C B A C B A ⋃⋃⋃⋃⋃⋃或C B A ⋃⋃或.ABC四、一个工人生产了n 个零件，以i A 表示他生产的第 i 个零件是合格品（n i ≤≤1）．用i A 表示下列事件：（1）没有一个零件是不合格品；（2）至少有一个零件是不合格品；（3）仅有一个零件是不合格品；（4）至少有一个零件不是不合格品．解：(1) n A A A 21；(2) n A A A 21或n A A A ⋃⋃⋃ 21； (3) n n n A A A A A A A A A 212121⋃⋃⋃ (4) n A A A ⋃⋃⋃ 21或.21n A A A第二章概率的古典定义·概率加法定理一、由七个数字组成，每个数字可以是0，1，2，…，9中的任一个数（但第一个数字不能为0），由完全不同的数字组成的概率．解：基本事件总数为611011011011011011019109⨯=C C C C C C C 有利事件总数为456789214151617181919⨯⨯⨯⨯⨯=C C C C C C C 设A 表示“是由完全不同的数字组成”，则0605.0109456789)(62≈⨯⨯⨯⨯⨯⨯=A P 二、把十本书任意地放在书架上，求其中指定的三本书放在一起的概率．解：基本事件总数为!101010=A 指定的三本书按某确定顺序排在书架上的所有可能为!777=A 种；这三本书按确定的顺序放在书架上的所以可能的位置共818=C 种；这三本书的排列顺序数为!333=A ；故有利事件总数为!3!8!38!7⨯=⨯⨯(亦可理解为)3388P P设A 表示“指定的三本书放在一起”，则067.0151!10!3!8)(≈=⨯=A P三、为了减少比赛场次，把二十个队任意分成两组（每组十队）进行比赛，求最强的两个队被分在不同组的概率．解：20个队任意分成两组（每组10队）的所以排法，构成基本事件总数1020C ；两个最强的队不被分在一组的所有排法，构成有利事件总数91812C C 设A 表示“最强的两队被分在不同组”，则526.01910)(102091812≈==C C C A P四、某工厂生产的产品共有100个，其中有5个次品．从这批产品中任取一半来检查，求发现次品不多于1个的概率．解：设i A 表示“出现的次品为i 件”)5,4,3,2,1,0(=i ，A 表示“取出的产品中次品不多于 1个”，则 .10A A A ⋃=因为V A A =10，所以).()()(10A P A P A P +=而0281.0979942347)(5010050950≈⨯⨯⨯==C C A P 1529.09799447255)(501004995151≈⨯⨯⨯⨯==C C C A P 故 181.01529.00281.0)(=+≈A P五、一批产品共有200件, 其中有6件废品．求 (1) 任取3件产品恰有1件是废品的概率; (2) 任取3件产品没有废品的概率; (3) 任取3件产品中废品不少于2件的概率．解：设A 表示“取出的3件产品中恰有1件废品”；B 表示“取出的3件产品中没有废品”；C 表示“取出的3件产品中废品不少于2件”，则 (1) 0855.019819920019319418)(3200219416≈⨯⨯⨯⨯==C C C A P (2) 912.0198199200192193194)(32003194≈⨯⨯⨯⨯==C C B P(3) 00223.019819920012019490)(3200019436119426≈⨯⨯⨯⨯=+=C C C C C C P六、设41)( ,0 ,31)()()(======BC P P(AC)P(AB)C P B P A P ．求A , B , C 至少有一事件发生的概率．解：因为0==P(AC)P(AB)，所以V AC V AB ==,，从而V C AB =)(可推出0)(=ABC P设D 表示“A , B , C 至少有一事件发生”，则C B A D ⋃⋃=，于是有)()()()()()()()()(ABC P CA P BC P AB P C P B P A P C B A P D P +---++=⋃⋃= 75.04341313131==-++=第三章条件概率与概率乘法定理·全概率公式与贝叶斯公式一、设,6.0)|(,4.0)(,5.0)(===B A P B P A P 求)|(,)(B A A P AB P ．解：因为B A AB B B A A +=+=)(，所以)()()(B A P AB P A P +=，即14.06.0)4.01(5.0)()()()()()(=⨯--=-=-=B A P B P A P B A P A P AB P68.074.05.036.0)4.01(5.05.0)()()()()()]([)|(≈=--+=-+==B A P B P A P A P B A P B A A P B A A P二、某人忘记了的最后一个数字，因而他随意地拨号，求他拨号不超过两次而接通所需的概率．若已知最后一个数字是奇数，那么此概率是多少？解：设A 表示“第一次拨通”，B 表示“第二次拨通”，C 表示“拨号不超过两次而拨通”（1）2.0101101)()()(19111101911011=+=⋅+=+=C C C C C C A B P A P C P（2）4.05151)()()(2511141511=+=+=+=A A A A A A B P A P C P三、两台车床加工同样的零件，第一台出现废品的概率是0.03，第二台出现废品的概率是0.02．加工出来的零件放在一起，并且已知第一台加工的零件比第二台加工的零件多一倍．（1）求任意取出的零件是合格品的概率；（2）如果任意取出的零件是废品，求它是第二台车床加工的概率．解：设i A 表示“第i 台机床加工的零件”)2,1(=i ；B 表示“出现废品”；C 表示“出现合格品”（1）)()()()()()()()(22112121A C P A P A C P A P C A P C A P C A C A P C P +=+=+= 973.0)02.01(31)03.01(32≈-⨯+-⨯=（2）25.002.03103.03202.031)()()()()()()()()(22112222=⨯+⨯⨯=+==A B P A P A B P A P A B P A P B P B A P B A P四、猎人在距离100米处射击一动物，击中的概率为0.6；如果第一次未击中，则进行第二次射击，但由于动物逃跑而使距离变为150米；如果第二次又未击中，则进行第三次射击，这时距离变为200米．假定击中的概率与距离成反比，求猎人三次之击中动物的概率．解：设i A 表示“第i 次击中”)3,2,1(=i ，则由题设，有1006.0)(1kA P ==，得60=k ，从而有4.015060150)(2===k A P ，.3.020060200)(3===k A P设A 表示“三次之击中”，则321211A A A A A A A ++=，故有)()()()()()()(321211A P A P A P A P A P A P A P ++=832.03.0)4.01()6.01(4.0)6.01(6.0=⨯-⨯-+⨯-+= （另解）设B 表示“猎人三次均未击中”，则168.0)3.01)(4.01)(6.01()(=---=B P故所求为 832.0)(1)(=-=B P B P五、盒中放有12个乒乓球，其中有9个是新的．第一次比赛时从其中任取3个来用，比赛后仍放回盒中．第二次比赛时再从盒中任取3个，求第二次取出的都是新球的概率．解：设i A 表示“第一次取得i 个新球”)3,2,1,0(=i ，则2201)(312330==C C A P 22027)(31219231==C C C A P 220108)(31229132==C C C A P 22084)(31239033==C C C A P 设B 表示“第二次取出的都是新球”，则312363123731238312393022084220108220272201)()()(C C C C C C C C A B P A P B P i i i ⋅+⋅+⋅+⋅==∑=146.0532400776161112208444722010855142202755212201≈=⋅+⋅+⋅+⋅=第四章随机事件的独立性·独立试验序列一、一个工人看管三台车床，在一小时车床不需要工人照管的概率：第一台等于0.9，第二台等于0.8，第三台等于0.7．求在一小时三台车床中最多有一台需要工人照管的概率．解：设i A 表示“第i 台机床不需要照管”)3,2,1(=i ，则9.0)(1=A P 8.0)(2=A P 7.0)(3=A P再设B 表示“在一小时三台车床中最多有一台需要工人照管”，则321321321321A A A A A A A A A A A A B +++=于是有)()()()()()()()()()()()()(321321321321A P A P A P A P A P A P A P A P A P A P A P A P B P +++= )7.01(8.09.07.0)8.01(9.07.08.0)9.01(7.08.09.0-⨯⨯+⨯-⨯+⨯⨯-+⨯⨯=902.0=．（另解）设i B 表示“有i 台机床需要照管”)1,0(=i ，B 表示“在一小时三台车床中最多有一台需要工人照管”，则10B B B +=且0B 、1B 互斥，另外有 504.07.08.09.0)(0=⨯⨯=B P398.0)7.01(8.09.07.0)8.01(9.07.08.0)9.01()(1=-⨯⨯+⨯-⨯+⨯⨯-=B P 故902.0398.0504.0)()()()(1010=+=+=+=B P B P B B P B P ．二、电路由电池a 与两个并联的电池b 及c 串联而成．设电池c b a ,,损坏的概率分别是0.3、0.2、0.2，求电路发生间断的概率．解：设1A 表示“a 损坏”；2A 表示“b 损坏”；3A 表示“c 损坏”；则3.0)(1=A P 2.0)()(32==A P A P又设B 表示“电路发生间断”，则321A A A B +=于是有)()()()()(321321321A A A P A A P A P A A A P B P -+=+=)()()()()()(321321A P A P A P A P A P A P -+= 328.02.02.03.02.02.03.0=⨯⨯-⨯+=．三、三个人独立地去破译一个密码，他们能译出的概率分别为51、31、41，求能将此密码译出的概率．解：设A 表示“甲能译出”；B 表示“乙能译出”；C 表示“丙能译出”，则51)(=A P 31)(=B P 41)(=C P设D 表示“此密码能被译出”，则C B A D ⋃⋃=，从而有)()()()()()()()()(ABC P CA P BC P AB P C P B P A P C B A P D P +---++=⋃⋃=)()()()()()()()()()()()(C P B P A P A P C P C P B P B P A P C P B P A P +---++=6.0413151415141513151413151=⨯⨯+⨯-⨯-⨯-++=．（另解）52)411)(311)(511()()()()()(=---===C P B P A P C B A P D P ，从而有6.053521)(1)(==-=-=D P D P四、甲、乙、丙三人同时对飞机进行射击，三人的命中概率分别为7.0,5.0,4.0．飞机被一人击中而被击落的概率为2.0，被两人击中而被击落的概率为6.0，若三人都击中，则飞机必被击落．求飞机被击落的概率．解：设1A 表示“甲命中”；2A 表示“乙命中”；3A 表示“丙命中”；则4.0)(1=A P5.0)(2=A P 7.0)(3=A P设i B 表示“i 人击中飞机” )3,2,1,0(=i ，则09.0)7.01)(5.01)(4.01()())(()()(3213210=---===A P A P A P A A A P B P)()(3213213211A A A A A A A A A P B P ++=)()()(321321321A A A P A A A P A A A P ++=)()()()()()()()()(321321321A P A P A P A P A P A P A P A P A P ++=36.07.0)5.01)(4.01()7.01(5.0)4.01()7.01)(5.01(4.0=⨯--+-⨯⨯-+--⨯=)()(3213213212A A A A A A A A A P B P ++= )()()(321321321A A A P A A A P A A A P ++=)()()()()()()()()(321321321A P A P A P A P A P A P A P A P A P ++=41.07.0)5.01)(4.01()7.01(5.0)4.01()7.01)(5.01(4.0=⨯--+-⨯⨯-+--⨯=14.07.05.04.0)()()()()(3213213=⨯⨯===A P A P A P A A A P B P 设A 表示“飞机被击落”，则由题设有0)(0=B A P 2.0)(1=B A P 6.0)(2=B A P 1)(3=B A P故有458.0114.06.041.02.036.0009.0)()()(30=⨯+⨯+⨯+⨯==∑=i i i B A P B P A P ．五、某机构有一个9人组成的顾问小组，若每个顾问贡献正确意见的概率都是0.7，现在该机构就某事可行与否个别征求每个顾问的意见，并按多数人意见作出决策，求作出正确决策的概率．解：设i A 表示“第i 人贡献正确意见”，则7.0)(=i A P )9,,2,1( =i ．又设m 为作出正确意见的人数，A 表示“作出正确决策”，则 )9()8()7()6()5()5()(99999P P P P P m P A P ++++=≥=+⋅⋅+⋅⋅+⋅⋅=277936694559)3.0()7.0()3.0()7.0()3.0()7.0(C C C 9991889)7.0()3.0()7.0(⋅+⋅⋅+C C+⋅⋅+⋅⋅+⋅⋅=273645)3.0()7.0(36)3.0()7.0(84)3.0()7.0(126918)7.0()3.0()7.0(9+⋅⋅+0403.01556.02668.02668.01715.0++++= 901.0=．六、每次试验中事件A 发生的概率为p ，为了使事件A 在独立试验序列中至少发生一次的概率不小于p ，问至少需要进行多少次试验？解：设做n 次试验，则n p A P A P )1(1}{1}{--=-=一次都不发生至少发生一次要p p n ≥--)1(1，即要p p n -≤-1)1(，从而有.1)1(log )1(=-≥-p n p 答：至少需要进行一次试验．第五章离散随机变量的概率分布·超几何分布·二项分布·泊松分布一、一批零件中有9个合格品与3个废品．安装机器时从这批零件中任取1个．如果每次取出的废品不再放回去，求在取得合格品以前已取出的废品数的概率分布．解：设X 表示“在取得合格品以前已取出的废品数”，则X 的概率分布为即亦即二、自动生产线在调整以后出现废品的概率为p ．生产过程中出现废品时立即进行调整．求在两次调整之间生产的合格品数的概率分布．解：设X 表示“在两次调整之间生产的合格品数”，且设p q -=1，则ξ的概率分布为三、已知一批产品共20个，其中有４个次品．（１）不放回抽样．抽取６个产品，求样品中次品数的概率分布；（２）放回抽样．抽取６个产品，求样品中次品数的概率分布．解：（1）设X 表示“取出的样本中的次品数”，则X 服从超几何分布，即X 的概率函数为)4,3,2,0()(6206164===-x C C C x X P xx从而X 的概率分布为即（2）设X 表示“取出的样本中的次品数”，则X 服从超几何分布，即X 的概率函数为)6,5,4,3,2,0()2.01()2.0()(66=-==-x C x X P xx x从而X即四、总机为300个用户服务．在一小时每一用户使用的概率等于0.01，求在一小时有4个用户使用的概率（先用二项分布计算，再用泊松分布近似计算，并求相对误差）．解：（1）用二项分布计算)01.0(=p168877.0)01.01()01.0()1()4(2964430029644300≈-=-==C p p C ξP（2）用泊松分布计算)301.0300(=⨯==np λ168031355.0!43)4(34≈==-e ξP相对误差为.5168877.0168031355.0168877.0000≈-=δ五、设事件A 在每一次试验中发生的概率为0.3，当A 发生次数不少于3次时，指示灯发出信号．现进行了5次独立试验，求指示灯发出信号的概率．解：设X 表示“事件A 发生的次数”，则3.0)(==p A P ，5=n ，).3.0,5(~B X 于是有)5()4()3()3(=+=+==≥X P X P X P X P5554452335)1()1(p C p p C p p C +-+-=16308.000243.002835.01323.0≈++≈（另解） )2()1()0(1)3(1)3(=-=-=-=<-=≥X P X P X P X P X P322541155005)1()1()1(11p p C p p C p p C ------= 16308.0≈六、设随机变量X 的概率分布为2, 1, ,0 , !)(===k k ak X P kλ；其中λ>0为常数，试确定常数a ．解：因为∑∞===01)(k k X P ，即∑∞==01!k kk λa ，亦即1=λae ，所以.λe a -=第六章随机变量的分布函数·连续随机变量的概率密度一、函数211x +可否是连续随机变量X 的分布函数？为什么？如果X 的可能值充满区间：（1）（∞+∞- ,）；（2）（0,∞-）．解：（1）设211)(xx F +=，则1)(0<<x F 因为0)(lim =-∞→x F x ，0)(lim =+∞→x F x ，所以)(x F 不能是X 的分布函数．（2）设211)(x x F +=，则1)(0<<x F 且0)(lim =-∞→x F x ，1)(lim 0=-→x F x因为)0( 0)1(2)('22<>+-=x x xx F ，所以)(x F 在（0,∞-）上单增．综上述，故)(x F 可作为X 的分布函数．二、函数x x f sin )(=可否是连续随机变量X 的概率密度？为什么？如果X 的可能值充满区间：（1）⎥⎦⎤⎢⎣⎡2,0π；（2）[]π,0；（3）⎥⎦⎤⎢⎣⎡23,0π．解：（1）因为⎥⎦⎤⎢⎣⎡∈2,0πx ，所以0sin )(≥=x x f ；又因为1cos )(2020=-=⎰ππx dx x f ，所以当⎥⎦⎤⎢⎣⎡∈2,0πx 时，函数x x f sin )(=可作为某随机变量X 的概率密度．（2）因为[]πx ,0∈，所以0sin )(≥=x x f ；但12cos )(00≠=-=⎰ππx dx x f ，所以当[]πx ,0∈时，函数x x f sin )(=不可能是某随机变量X 的概率密度．（3）因为⎥⎦⎤⎢⎣⎡∈23,0πx ，所以x x f sin )(=不是非负函数，从而它不可能是随机变量X 的概率密度．二、一批零件中有9个合格品与3个废品．安装机器时从这批零件中任取1个．如果每次取出的废品不再放回去，求在取得合格品以前已取出的废品数的分布函数，并作出分布函数的图形．解：设X 表示“取出的废品数”，则X 的分布律为于是，⎪⎩>3,1x四、（柯西分布）设连续随机变量X 的分布函数为+∞<<∞-+=x x B A x F ,arctan )(．求：（1）系数A 及B ；（2）随机变量X 落在区间)1 ,1(-的概率；(3) X 的概率密度．解：(1) 由0)2()(lim =-⋅+=-∞→πB A x F x ，12)(lim =⋅+=-∞→πB A x F x ，解得.1,21πB A ==即)( ,arctan 121)(+∞<<-∞+=x x πx F ．(2) .21)]1arctan(121[]1arctan 121[)1()1()11(=-+-+=--=<<-ππF F X P (3) X 的概率密度为)1(1)()(2x x F x f +='=π．五、（拉普拉斯分布）设随机变量X 的概率密度为+∞<<∞-=-x Ae x f x,)(．求：（1）系数A ；（2）随机变量X 落在区间)1,0(的概率；（3）随机变量X 的分布函数．解：(1) 由1)(⎰+∞∞-=dx x f ，得1220⎰⎰+∞∞-+∞--===A dx e A dx Ae xx ，解得21=A ，即有).( ,21)(+∞<<-∞=-x e x f x(2) ).11(21)(2121)()10(101010ee dx e dx xf X P x x -=-===<<--⎰⎰(3) 随机变量X 的分布函数为⎪⎩⎪⎨⎧>-≤===-∞--∞-⎰⎰021102121)()(x e x e dx e dx x f x F x xx xx ．第七章均匀分布·指数分布·随机变量函数的概率分布一、公共汽车站每隔5分钟有一辆汽车通过．乘客到达汽车站的任一时刻是等可能的．求乘客候车时间不超过3分钟的概率．解：设随机变量X 表示“乘客的候车时间”，则X 服从]5,0[上的均匀分布，其密度函数为⎩⎨⎧∉∈=]5,0[,0]5,0[,51)(x x x f 于是有.6.053)()30(3===≤≤⎰dx x f X P二、已知某种电子元件的使用寿命X (单位:h)服从指数分布，概率密度为⎪⎩⎪⎨⎧≤>=-.0,0;0,8001)(800x x e x f x任取３个这种电子元件，求至少有１个能使用1000h 以上的概率．解：设A 表示“至少有１个电子元件能使用1000h 以上”；321A 、A 、A 分别表示“元件甲、乙、丙能使用1000h 以上”．则287.08001)1000()()()(4510008001000800321≈=-==>===-∞+-∞+-⎰e e dx e X P A P A P A P xx)()()()()()()()()(321313221321321A A A P A A P A A P A A P A P A P A P A A A P A P +---++=⋃⋃=638.0287.0287.03287.0332≈+⨯-⨯=（另解）设A 表示“至少有１个电子元件能使用1000h 以上”．则287.08001)1000(4510008001000800≈=-==>-∞+-∞+-⎰ee dx e X P xx从而有713.01)1000(1)1000(45≈-=>-=≤-eX P X P ，进一步有638.0713.01)]1000([1)(33≈-≈≤-=X P A P三、(1) 设随机变量X 服从指数分布)(λe ．证明：对于任意非负实数s 及t ，有).()(t X P s X t s X P ≥=≥+≥这个性质叫做指数分布的无记忆性．(2) 设电视机的使用年数X 服从指数分布)10(．e ．某人买了一台旧电视机，求还能使用５年以上的概率．解：（１）因为)(~λe X ，所以R x ∈∀，有xex F λ--=1)(，其中)(x F 为X 的分布函数．设t s X A +≥=，t X B ≥=．因为s 及t 都是非负实数，所以B A ⊂，从而A AB =．根据条件概率公式，我们有)(1)(1)()()()()()()()(s X P t s X P s X P t s X P B P A P B P AB P B A P s X t s X P <-+<-=≥+≥====≥+≥tst s e e e λλλ--+-=----=]1[1]1[1)(．另一方面，我们有t t e e t F t X P t X P t X P λλ--=--=-=≤-=<-=≥)1(1)(1)(1)(1)(．综上所述，故有)()(t X P s X t s X P ≥=≥+≥．（２）由题设，知X 的概率密度为⎩⎨⎧≤>=-．，；，0001.0)(1.0x x e x f x 设某人购买的这台旧电视机已经使用了s 年，则根据上述证明的（１）的结论，该电视机还能使用5年以上的概率为6065.01.0)()5()5(5.051.051.05≈=-===≥=≥+≥-∞+-∞+-∞+⎰⎰e e dx e dx xf X P s X s X P xx ．答：该电视机还能使用5年以上的概率约为6065.0．四、设随机变量X 服从二项分布)4.0 ,3(B ，求下列随机变量函数的概率分布：（1）X Y 211-=；（2）2)3(2X X Y -=．解：X 的分布律为（1）X Y 211-=的分布律为（2）2)3(2X X Y -=的分布律为即五、设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤>+=.0,0;0,)1(2)(2x x x x f π求随机变量函数X Y ln =的概率密度．解：因为)()()(ln )()(yX yY e F e X P y X P y Y P y F =<=<=<= 所以随机变量函数X Y ln =的概率密度为)( )1(2)()()()(2''+∞<<-∞+====y e e e e f e e F y F y f yyyyyyXYY π，即 )( )1(2)(2+∞<<-∞+=y e e y f y yY π．第八章二维随机变量的联合分布与边缘分布一、把一颗均匀的骰子随机地掷两次．设随机变量X 表示第一次出现的点数，随机变量Y 表示两次出现点数的最大值，求二维随机变量),(Y X 的联合概率分布及Y 的边缘概率分布．解：二维随机变量),(Y X 的联合概率分布为Y 的边缘概率分布为二、设二维随机变量（X ，Y ）的联合分布函数)3arctan )(2arctan (),(yC x B A y x F ++=．求：（1）系数A 、B 及C ；（2）（X ，Y ）的联合概率密度：（3）边缘分布函数及边缘概率密度．解：（1）由0)0,(,0),0(,1),(=-∞=∞-=∞+-∞F F F ，得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=--=++0)2(0)2)(0(1)2)(2(πB AC πC B A πC πB A 解得2πC B ==，.12πA = （2）因为)3arctan 2)(2arctan 2(1),(2yx y x F ++=πππ，所以（X ，Y ）的联合概率密度为.)9)(4(6),(),(222"y x y x F y x f xy ++==π（3）X 及Y 的边缘分布函数分别为xx x X x dx x dy y x f dx x F ∞-∞-∞-+∞∞-=+==⎰⎰⎰2arctan 1)4(2),()(2ππ 2arctan 121xπ+=yx y Y y dy y dx y x f dy x F ∞-∞-∞-+∞∞-=+==⎰⎰⎰3arctan 1)9(3),()(2ππ 3arctan 121yπ+=X 及Y 的边缘概率密度分别为⎰⎰⎰+∞+∞∞-+∞∞-++⋅=++==0222222)9(1)4(112)9)(4(6),()(dy y x dy y x dy y x f x f X ππ )4(2)3arctan 31()4(1122022x y x +=+⋅=∞+ππ ⎰⎰⎰+∞+∞∞-+∞∞-++=++==022222241)9(12)9)(4(6),()(dx x y dx y x dx y x f y f Y ππ)9(3)2arctan 21()9(122022y x y +=+=∞+ππ三、设),(Y X 的联合概率密度为⎩⎨⎧>>=+-., 00;0,,Ae ),(3y)(2x 其它y x y x f求：（1）系数A ；（2）),(Y X 的联合分布函数；（3）X 及Y 的边缘概率密度；（4）),(Y X落在区域R ：632 ,0 ,0<+>>y x y x 的概率．解：（1）由1),(=⎰⎰+∞∞-+∞∞-dy dx y x f ，有16132==⎰⎰∞+∞+--A dy e dx e A y x ，解得.6=A （2）),(Y X 的联合分布函数为⎪⎩⎪⎨⎧>>==⎰⎰⎰⎰--∞-∞-其它0,06),(),(0032y x dy e dx e dy y x f dx y x F x y y x xy⎩⎨⎧>>--=--其它0,0)1)(1(32y x e e y x （3）X 及Y 的边缘概率密度分别为⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>==-+∞--∞+∞-⎰⎰00020006),()(2032x x ex x dy e e dy y x f x f x y x X⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>==-+∞--∞+∞-⎰⎰00030006),()(3032y y ex x dx e e dx y x f y f y y x Y（4）⎰⎰⎰⎰---==∈x y xR dy e dx edxdy y x f R Y X P 32203326),(}),{(6306271)(2---⎰-=-=e dx e e x四、设二维随机变量),(Y X 在抛物线2x y =与直线2+=x y 所围成的区域R 上服从均匀分布．求：(1) ),(Y X 的联合概率密度；(2) 概率)2(≥+Y X P ．解：(1) 设),(Y X 的联合概率密度为⎩⎨⎧∉∈=.),(, 0;),(,),(R y x R y x C y x f 则由129)322()2(21322122212==-+=-+==--+-⎰⎰⎰⎰⎰C x x x C dx x x C dy dx C Cdxdy x x R解得92=C ．故有⎪⎩⎪⎨⎧∉∈=.),(, 0;),(,92),(R y x R y x y x f(2) ⎰⎰⎰⎰⎰⎰++-≥++==≥+x x x x y x dy dx dy dx dxdy y x f Y X P 2212210229292),()2(⎰⎰-++=21210)2(92292dx x x xdx481.02713)322(92922132102≈=-++=x x x x ．第九章随机变量的独立性·二维随机变量函数的分布一、设X 与Y 是两个相互独立的随机变量，X 在]1,0[上服从均匀分布，Y 的概率密度为⎪⎩⎪⎨⎧≤>=-.0,0;0,21)(2y y e y f yY求 (1) ),(Y X 的联合概率密度; (2) 概率)(X Y P ≥．解: (1)X 的概率密度为⎩⎨⎧∉∈=)1,0(,0)1,0(,1)(x x x f X ，),(Y X 的联合概率密度为（注意Y X ,相互独立）⎪⎩⎪⎨⎧><<==-其它,00,10,21)()(),(2y x e y f x f y x f yY X（2）dx edx edy e dx dxdy y x f X Y P x xyxyxy ⎰⎰⎰⎰⎰⎰-∞+-∞+-≥=-===≥1021022102)(21),()(7869.0)1(2221122≈-=-=--e e x二、设随机变量X 与Y 独立，并且都服从二项分布：.,,2 ,1 ,0 ,)(; ,,2 ,1 ,0 ,)(212211n j qp C j p n i q p C i p jn jj n Y i n i in X ====--证明它们的和Y X Z +=也服从二项分布．证明: 设j i k +=, 则ik n i k i k n ki i n i i n k i Y X Z q p C q p C i k P i P k Z P k P +---=-=∑∑=-===22110)()()()( ∑=-+=ki k n n k i n in q p C C2121)( 由knm ki ik nk m C C C +=-=∑, 有k n n ki in i n C C C21210+==∑. 于是有 ),,2,1,0( )(212121n n k q p C k P kn n k i n n Z +==-++ 由此知Y X Z +=也服从二项分布.三、设随机变量X 与Y 独立，并且X 在区间[0，1]服从均匀分布，Y 在区间[0，2]服从辛普森分布：⎪⎩⎪⎨⎧><≤<-≤≤=.20 0,; 2 1 ,2;10 ,)(y y y y y y y f Y 或求随机变量Y X Z +=的概率密度．解: X 的概率密度为 ⎩⎨⎧∉∈=]1,0[,0]1,0[,1)(x x y f ξ . 于是),(Y X 的联合概率密度为⎪⎩⎪⎨⎧≤<≤≤-≤≤≤≤=. 0, 2 1,10 ,210,10,),(其它当当y x y y x y y x fY X Z +=的联合分布函数为}),{(}{}{)(D y x P z Y X P z Z P z F Z ∈=≤+=≤=，其中D 是zy x ≤+与),(y x f 的定义域的公共部分.故有 ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<+-≤<-+-≤≤><=3229321212331023,00)(222z z z z z z z zz z z F Z 从而随机变量Y X Z +=的概率密度为⎪⎪⎩⎪⎪⎨⎧≤<-≤<+-≤≤><=3232132103,00)(z z z z z z z z z f Z三、电子仪器由六个相互独立的部件ij L （3,2,1;2,1==j i ）组成，联接方式如右图所示．设各个部件的使用寿命ij X 服从相同的指数分布)(λe ，求仪器使用寿命的概率密度．解: 由题设，知ij X 的分布函数为⎩⎨⎧≤>-=-0,00,1x x e F x X ij λ 先求各个并联组的使用寿命)3,2,1( =i Y i 的分布函数.因为当并联的两个部件都损坏时,第i 个并联组才停止工作,所以有)3,2,1(),m ax (21==i Y i i i ξξ从而有)3,2,1( =i Y i 的分布函数为⎩⎨⎧≤>-==-0,00,)1()(221y y e F F y F y X X Y i i i λ 设Z "仪器使用寿命".因为当三个并联组中任一个损坏时,仪器停止工作.所以有),,min(321Y Y Y Z =.从而有Z 的分布函数为⎩⎨⎧≤>---=⎩⎨⎧≤>----=-0,00,])1(1[10,00)],(1)][(1)][(1[1)(32321z z e z z z F z F z F z F z Y Y Y Z λ 故Z 的概率密度为⎩⎨⎧≤>--=---0,00,)2)(1(6)(23z z e e e z f z z z Z λλλλ第十章随机变量的数学期望与方差一、一批零件中有9个合格品与3个废品．安装机器时从这批零件中任取一个．如果取出的废品不再放回去，求在取得合格品以前已取出的废品数的数学期望、方差与标准差．解：设X 表示“在取得合格品以前已取出的废品数”，则X 的概率分布为即1103322013220924491430=⨯+⨯+⨯+⨯=EX 即3.0004.03041.02205.0175.00≈⨯+⨯+⨯+⨯=EX2X 的分布为2X0 1 4 9即于是有229220192209444914302=⨯+⨯+⨯+⨯=EX 即4091.0004.09041.04205.0175.002≈⨯+⨯+⨯+⨯=EX从而有3191.013310042471)11033(229)(222≈=-=-=EX EX DX 565.03191.0≈==DX Xσ二、对某一目标进行射击，直至击中为止．如果每次射击命中率为p ，求射击次数的数学期望及方差．解：设X 表示“第i 次击中”),2,1( =i ，则X 的分布为p q p q q p q p iqp ipqEX i i i i i i 1)1()1()(211111=-='-='===∑∑∑∞=∞=-∞=- 2X p pp p q q p q p q q p pqi EX i i i ii i 122)1()1()(])([223111122-=-=-+='=''==∑∑∑∞=∞=∞=- 进一步有p pp p p EX EX DX 11)1(12)(22222-=--=-=三、设离散型随机变量X 的概率函数为,,2,1,21]2)1([ ==-=k k X P k k k问X 的数学期望是否存在？若存在，请计算)(X E ；若不存在，请解释为什么．解：因为∑∑∑∑∞=∞=∞=∞=-=⋅-=-=-==1111)1(212)1(]2)1([2)1()(k k k k k k k k k k ki i i k k k X P k x X P x 不绝对收敛，所以ξ没有数学期望．四、设随机变量X 的概率密度为⎪⎩⎪⎨⎧≥<-=.1, 0;1,11)(2x x xx f π 求数学期望)(X E 及方差)(X D ．解：011)()(112=-⋅==⎰⎰-+∞∞-dx xx dx x xf X E πdx x x dx x x dx x f x X D ⎰⎰⎰-=-⋅==-∞+∞-1022112221211)()(πππ21]arcsin 2112[2102=+--=x x x π五、（拉普拉斯分布）设随机变量X 的概率密度为 )( ,21)(+∞<<-∞=-x e x f x．求数学期望)(X E 及方差)(X D ．解：021)(===⎰⎰+∞∞--+∞∞-dx xe dx x xf EX x2!2)3(21)(0222==Γ====⎰⎰⎰+∞-+∞∞--+∞∞-dx e x dx e x dx x f x DX x x（分部积分亦可）第十一章随机变量函数的数学期望·关于数学期望与方差的定理一、设随机变量X 服从二项分布)4.0,3(B ，求2)3(X X Y -=的数学期望及方差．解：X 的概率分布为Y 的概率分布为2Y 的分布为72.072.0128.00=⨯+⨯=EY 72.072.0128.002=⨯+⨯=EY2016.0)72.0(72.0)(222=-=-=EY EY DY二、过半径为R 的圆周上一点任意作这圆的弦，求所有这些弦的平均长度．解：在圆周上任取一点O ，并通过该点作圆得直径OA ．建立平面直角坐标系，以O 为原点，且让OA 在x 轴的正半轴上．通过O 任作圆的一条弦OB ，使OB 与x 轴的夹角为θ，则θ服从]2,2[ππ-上的均匀分布，其概率密度为⎪⎩⎪⎨⎧-∉-∈=]2,2[,0]2,2[,1)(ππθππθπθf ．弦OB 的长为 ]2,2[cos 2)(ππθθθ-∈=R L ，故所有弦的平均长度为⎰⎰-∞+∞-⋅==22cos 21)()()]([ππθθπθθθθd R d L f L EπθπθθπππRR d R4sin 4cos 42020===⎰．三、一工厂生产的某种设备的寿命X （以年计）服从指数分布，概率密度为⎪⎩⎪⎨⎧≤>=-. 0,0 ;0 ,41)(4x x e x f x工厂规定，出售的设备若在售出一年之损坏可予以调换．若工厂售出一台设备赢利100元，调换一台设备厂方需花费300元．试求厂方出售一台设备的平均净赢利．解：由题设，有⎰⎰---∞--=-===<104110441141)()1(e e dx e dx x f X P x x进而有 41)1(1)1(-=<-=≥eX P X P设Y 表示“厂方出售一台设备获得的净赢利”，则Y 的概率分布为从而有64.33200300100)1(200414141≈-⨯=⨯+-⨯-=---ee e EY答：厂方出售一台设备获得的平均净赢利约为64.33元．四、设随机变量n X X X ,,21相互独立，并且服从同一分布，数学期望为μ，方差为2σ．求这些随机变量的算术平均值∑==ni i X n X 11的数学期望与方差．解：因为μ=)(i X E ，2)(σ=i X D ，且随机变量n X X X ,,21相互独立．所以有μμ=====∑∑∑∑====ni n i i ni i n i i n X E n X E n X n E X E 11111)(1)(1)1()(，nn X D n X D n X n D X D ni ni in i i n i i 2122121211)(1)(1)1()(σσ=====∑∑∑∑====．五、一民航送客车载有20位旅客自机场开出，沿途有10个车站可以下车，到达一个车站时如没有旅客下车就不停车．假设每位旅客在各车站下车是等可能的，且各旅客是否下车相互独立．求该车停车次数的数学期望．解: 设i X 表示"第i 站的停车次数" (10,,2,1 =i ). 则i X 服从"10-"分布. 其中⎩⎨⎧=站有人下车若在第站无人下车若在第i i X i ,1,0 于是i X 的概率分布为设∑==ni iXX 1, 则X 表示沿途停车次数, 故有]})10110(1[1)10110(0{10)(2020101101--⨯+-⨯===∑∑==i i i i EX X E EX748.8)9.01(1020≈-= 即停车次数的数学期望为748.8.第十二章二维随机变量的数字特征·切比雪夫不等式与大数定律一、设二维随机变量),(Y X 的联合概率密度为()(). 1,222++=y xAy x f求：（1）系数A ；（2）数学期望)(X E 及)(Y E ，方差)(X D 及)(Y D ，协方差),cov(Y X ．解: (1) 由⎰⎰+∞∞-+∞∞-=1),(dxdy y x f . 有()()⎰⎰⎰⎰∞+∞-∞+∞-∞+==+=++1112022222A dr rrd A dxdy y xAπθπ解得, π1=A .(2) ()011),()(222⎰⎰⎰⎰∞+∞-∞+∞-∞+∞-∞+∞-=++==dx y xxdy dxdy y x xf X E π.由对称性, 知 0)(=Y E .⎰⎰+∞∞-+∞∞-==-=dxdy y x f x EX EX X E X D ),(])[()(222()⎰⎰∞+∞-∞+∞-++=dx y xx dy 222211π()()+∞=+++=+-+=+=∞+∞+∞+⎰⎰⎰022022220223]11)1ln([1)1(211r r dr r rr r dr rr d πθπ同理, 有 +∞=)(Y D .)()])([(),cov(XY E EY Y Ex X E Y X =--=⎰⎰+∞∞-+∞∞-=dxdy y x xyf ),(()011),(222⎰⎰⎰⎰∞+∞-∞+∞-∞+∞-∞+∞-=++==dx y xxydy dxdy y x xyf π.二、设二维随机变量),(Y X 的联合概率密度为⎩⎨⎧<<<=其它．,0;10,,1),(x x y y x f求(1) ),cov(Y X ；(2) X 与Y 是否独立，是否相关，为什么？解: (1) 因为 ⎰⎰⎰⎰⎰====-∞+∞-∞+∞-1210322),(dx x dy xdx dxdy y x xf EX x x0),(1===⎰⎰⎰⎰-+∞∞-+∞∞-xx ydy dx dxdy y x yf EY0),()(1===⎰⎰⎰⎰-+∞∞-+∞∞-xx ydy xdx dxdy y x xyf XY E所以有])32[()])([(),cov(Y X E EY Y EX X E Y X -=--=⎰⎰+∞∞-+∞∞-=dxdy y x xyf ),(010==⎰⎰-xxydy xdx ．(2) 当)1,0(∈x 时,有 ⎰⎰+∞∞--===x dy dy y x f x f xxX 2),()(; 当)1,0(∉x 时, 有0)(=x f X .即⎩⎨⎧∉∈=)1,0(0)1,0(2)(X x x x x f 同理有 ⎩⎨⎧∉+∈-=⎪⎩⎪⎨⎧∉∈=⎰⎰-)1,0(1)1,0(1)1,0()1,0()(11Y x y x y x dx x dx y f y y因为 ),()()(y x f y f x f Y X ≠, 所以X 与Y 不是独立的．又因为0),cov(=Y X , 所以X 与Y 是不相关的．三、利用切比雪夫不等式估计随机变量X 与其数学期望)(X E 的差的绝对值大于三倍标准差)(X σ的概率．解：91)3()3(2=≤>-ξξξξξD D D E P ．四、为了确定事件A 的概率，进行10000次重复独立试验．利用切比雪夫不等式估计：用事件A在10000次试验中发生的频率作为事件A 的概率的近似值时，误差小于0.01的概率．解：设ξ表示“在10000次试验中事件A 的次数”，则)5.0,10000(~B ξ且有50005.010000=⨯==np E ξ 2500)5.01(5.010000=-⨯⨯==npq D ξ于是有npqp npq p np m P p n m P 22)01.0(1)01.0(1)01.0()01.0(-=-≥<-=<- 75.025.011=-=-=pq五、样检查产品质量时，如果发现次品多于10个，则认为这批产品不能接受．应该检查多少个产品，可使次品率为10%的一批产品不被接受的概率达到0.9？解：设ξ表示“发现的次品件数”，则)1.0,(~n B ξ，现要求.nn ξE 1.0= n ξD 09.0=要使得9.0)10(=>ξP ，即9.0)10(=≤<n ξP ，因为9.0)10(=≤<n ξP ，所以)3.01.03.01.03.01.010()10(nn n n n ξn n P ξD ξE n ξD ξE ξξD ξE P -≤-<-=-≤-<-)3.01.010()3()33.01.03.01.010(1,01,0nn n n n n ξn n P --≈≤-<-=ΦΦ1)3.0101.0()3(1,01,0--+nn n ΦΦ （德莫威尔—Laplace 定理）因为10>n ，所以53>n ，从而有1)3(1,0≈n Φ，故9.0)3.0101.0(1,0≈-nn Φ．查表有8997.0)28.1(1,0=Φ，故有28.13.0101.0≈-nn ，解得.146≈n答：应该检查约146个产品，方可使次品率为10%的一批产品不被接受的概率达到0.9．第十三章正态分布的概率密度、分布函数、数学期望与方差一、设随机变量X 服从正态分布)2,1(2N ，求（1）)8.56.1(<≤-X P ；（2）)56.4(≥X P ．解：(1) )4.2213.1()8.416.2()8.56.1(<-≤-=<-≤-=<≤-X P X P X P 8950.09032.019918.0)]3.1(1[)4.2()3.1()4.2(1,01,01,01,0=+-=--=--=ΦΦΦΦ(2) )78.12178.2(1)56.4(1)56.4(<-<--=<-=≥X P X P X P )]78.2(1)78.1(1)]78.2()78.1([11,01,01,01,0ΦΦΦΦ-+-=---=.0402.09973.09625.02=--二、已知某种机械零件的直径X （mm ）服从正态分布)6.0,100(2N ．规定直径在2.1100±（mm ）之间为合格品，求这种机械零件的不合格品率．解：设p 表示这种机械零件的不合格品率，则)2.1100(1)2.1100(≤--=>-=X P X P p ．而)26.01002()6.02.16.01006.02.1()2.1100(≤-≤-=≤-≤-=≤-X P X P X P 1)2(2)]2(1[)2()2()2(-Φ=Φ--Φ=-Φ-Φ= 9544.019772.02=-⨯= 故0456.09544.01=-=p ．三、测量到某一目标的距离时发生的误差X (m)具有概率密度3200)20(22401)(--=x ex f π求在三次测量中至少有一次误差的绝对值不超过30m 的概率．解：三次测量中每次误差绝对值都超过30米可表为}30{}30{}30{>⋃>⋃>=ξξξD 第三次第二次第一次因为)40,20(~2N ξ，所以由事件的相互独立性，有31,01,033)]25.0(1)25.1([})3030{(})30{()(ΦΦ-+-=>+-<=>=ξξP ξP D P13025.05069.0)8944.05987.02(33≈=--= 于是有86975.013025.01)(1}30{=-=-=<D P P 米至少有一次绝对值三次测量中ξ．四、设随机变量),(~2σμN X ，求随机变量函数Xe Y =的概率密度（所得的概率分布称为对数正态分布）．解：由题设，知X 的概率密度为)(21)(222)(+∞<<-∞=--x ex f x X σμσπ从而可得随机变量Y 的分布函数为)()()(y e P y Y P y F X Y ≤=≤=．当0≤y 时，有0)(=y F Y ；此时亦有0)(='y F Y ．当0>y 时，有dx ey X P y F yx Y ⎰∞---=≤=ln 2)(2221)ln ()(σμσπ．此时亦有222)(ln 21)(σμσπ--='y Y eyy F ．从而可得随机变量Y 的概率密度为⎪⎩⎪⎨⎧>≤=--.0,21;0,0)(222)(ln y e yy y f y Y σμσπ五、设随机变量X 与Y 独立，),(~211σμN X ，),(~222σμN Y ，求：(1) 随机变量函数bY aX Z +=1的数学期望与方差，其中a 及b 为常数； (2) 随机变量函数XY Z=2的数学期望与方差．解：由题设，有211)(,)(σμ==X D X E ；222)(,)(σμ==Y D Y E ．从而有(1)211)()()()()()(μμb a Y bE X aE bY E aX E bY aX E Z E +=+=+=+=； 222212221)()()()()()(σσb a Y D b X D a bY D aX D bY aX D Z D +=+=+=+=． (2)212)()()()(μμ===Y E X E XY E Z E ；)()()()()()()()(22222222Y E X E Y E X E XY E Y X E XY D Z D -=-== )()()]()()][()([2222Y E X E Y E Y D X E X D -++= )()()()()()(22X E Y D Y E X D Y D X D ++= 212222212221μσμσσσ++=．第十四章二维正态分布·正态随机变量线性函数的分布中心极限定理一、设二维随机变量),(Y X 服从二维正态分布，已知0)()(==Y E X E ，16)(=X D ，25)(=Y D ，并且12),cov(=Y X ，求),(Y X 的联合概率密度．解：已知0==y x μμ，416==x σ，525==y σ，53),cov(),(===y x Y X Y X r σσ．从而 2516)53(1122=-=-r ，5412=-r ．进一步按公式])())((2)([)1(21222222121),(yy y x y x x x y y x r x r y x ery x f σμσσμμσμσπσ-+-------=，可得),(Y X 的联合概率密度为)2550316((322522321),(y xy x e y x f +--=π．。

概率论与数理统计课后习题答案1-8章-习题解答

第一章思考题1．事件的和或者差的运算的等式两端能“移项”吗？为什么？2．医生在检查完病人的时候摇摇头“你的病很重，在十个得这种病的人中只有一个能救活. ”当病人被这个消息吓得够呛时，医生继续说“但你是幸运的.因为你找到了我，我已经看过九个病人了，他们都死于此病，所以你不会死” ，医生的说法对吗？为什么？３．圆周率 1415926.3=π是一个无限不循环小数, 我国数学家祖冲之第一次把它计算到小数点后七位, 这个记录保持了1000多年! 以后有人不断把它算得更精确. 1873年, 英国学者沈克士公布了一个π的数值, 它的数目在小数点后一共有707位之多! 但几十年后, 曼彻斯特的费林生对它产生了怀疑. 他统计了π的608位小数, 得到了下表:675844625664686762609876543210出现次数数字你能说出他产生怀疑的理由吗?答：因为π是一个无限不循环小数，所以，理论上每个数字出现的次数应近似相等，或它们出现的频率应都接近于0.1，但7出现的频率过小.这就是费林产生怀疑的理由.4．你能用概率证明“三个臭皮匠胜过一个诸葛亮”吗？５．两事件A 、B 相互独立与A 、B 互不相容这两个概念有何关系？对立事件与互不相容事件又有何区别和联系？６．条件概率是否是概率？为什么？习题1．写出下列试验下的样本空间：（1）将一枚硬币抛掷两次答：样本空间由如下4个样本点组成{(,)(,)(,)(,)}Ω=正正，正反，反正，反反（2）将两枚骰子抛掷一次答：样本空间由如下36个样本点组成{(,),1,2,3,4,5,6}i j i j Ω==（3）调查城市居民（以户为单位）烟、酒的年支出答：结果可以用（x ，y ）表示，x ，y 分别是烟、酒年支出的元数.这时，样本空间由坐标平面第一象限内一切点构成 .{(,)0,0}x y x y Ω=≥≥2．甲，乙，丙三人各射一次靶，记-A “甲中靶” -B “乙中靶” -C “丙中靶” 则可用上述三个事件的运算来分别表示下列各事件： (1) “甲未中靶”： ;A (2) “甲中靶而乙未中靶”： ;B A (3) “三人中只有丙未中靶”： ;C AB(4) “三人中恰好有一人中靶”： ;C B A C B A C B A (5)“ 三人中至少有一人中靶”： ;C B A(6)“三人中至少有一人未中靶”： ;C B A 或;ABC (7)“三人中恰有两人中靶”： ;BC A C B A C AB(8)“三人中至少两人中靶”： ;BC AC AB (9)“三人均未中靶”： ;C B A (10)“三人中至多一人中靶”： ;C B A C B A C B A C B A(11)“三人中至多两人中靶”： ;ABC 或;C B A 3 .设,A B 是两随机事件，化简事件 (1)()()AB A B (2) ()()A B A B解:(1)()()AB A B AB AB B B ==,(2) ()()AB AB ()A BA B B A A B B ==Ω=.4．某城市的电话号码由5个数字组成，每个数字可能是从0-9这十个数字中的任一个，求电话号码由五个不同数字组成的概率.解：51050.302410P P ==.5．n 张奖券中含有m 张有奖的，k 个人购买，每人一张，求其中至少有一人中奖的概率。

(完整版)概率论与数理统计习题答案详解版(廖茂新复旦版)

概率论与数理统计习题答案详解版（廖茂新复旦版）习题一1. 设A，B，C 为三个事件，用A，B，C 的运算式表示下列事件：（1）A 发生而B与 C 都不发生；（2）A，B，C 至少有一个事件发生；（3）A，B，C 至少有两个事件发生；（4）A，B，C 恰好有两个事件发生；（5）A，B至少有一个发生而 C 不发生；（6）A，B，C 都不发生.解：（1）A BC或 A B C或 A （B∪C）.（2）A∪B∪C.（3）（AB）∪（AC）∪（BC）.（4）（AB C ）∪（AC B ）∪（BC A）.（5）（A∪B）C.（6） A B C 或ABC.2. 对于任意事件A，B，C，证明下列关系式：（1）（A+B）（A+B ）（ A + B）（ A + B ）= ；（2）AB+A B +A B+A B AB= AB；(3)A-(B+C)= (A-B)-C. 证明：略.3.设A，B为两事件，P（A）=0.5,P（B）=0.3,P（AB）=0.1，求：（1）A发生但B不发生的概率；（2）A，B 都不发生的概率；（3）至少有一个事件不发生的概率.解（1）P（A B ）=P（A-B）=P（A-AB）=P（A）-P（AB）=0.4；（2） P（AB）=P（ A B）=1-P（A∪B）=1-0.7=0.3；（3） P（A∪B）=P（AB ）=1-P（AB）=1-0.1=0.9.4.调查某单位得知。

购买空调的占15％，购买电脑占12％，购买DVD 的占20%；其中购买空调与电脑占6%，购买空调与DVD占10%，购买电脑和DVD占5％，三种电器都购买占2％。

求下列事件的概率。

（1）至少购买一种电器的；（2）至多购买一种电器的；（3）三种电器都没购买的.解：（1）0.28, （2）0.83, （3）0.725.10 把钥匙中有 3 把能打开门，今任意取两把，求能打开门的概率。

解：8/156. 任意将10 本书放在书架上。

其中有两套书，一套 3 本，另一套4 本。

概率论与数理统计_浙大四版_习题解_第9章_回归分析

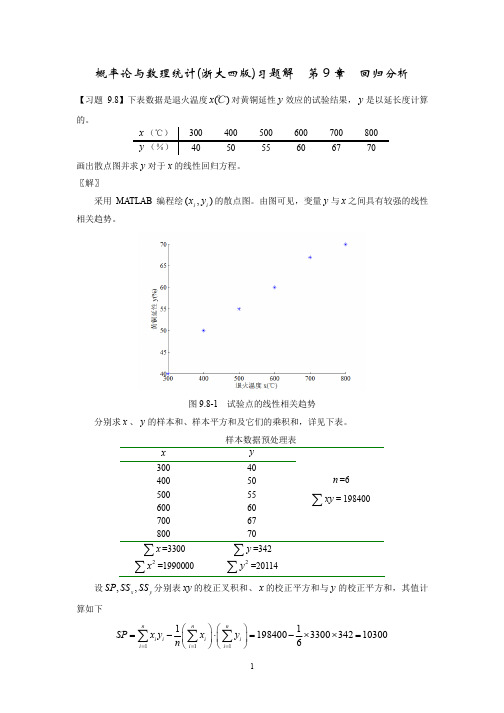
图 9.10-1 试验点的线性相关趋势〖解（2）〗分别计算 x 、 y 的样本和、样本平方和及它们的乘积和如下表。样本数据预处理表
x
17.1 10.5 13.8 15.7 11.9 10.4 15.0 16.0 17.8 15.8 15.1 12.1
1 n 1 SS x x xi 2.595 3.82 0.532142857 n i 1 7 i 1
2 i
n
2
1 n 1 SS y y yi 3104.2 145.4 2 84.0342858 n i 1 7 i 1
图 9.8-1 试验点的线性相关趋势分别求 x 、 y 的样本和、样本平方和及它们的乘积和，详见下表。样本数据预处理表
x
300 400 500 600 700 800
y
40 50 55 60 67 70
n =6
xy = 198400
x =3300 x =1990000
2
y =342 y =20114
2
采用 MATLAB 编程绘 ( xi , y i ) 的散点图。由图可见，变量 y 与 x 之间具有很强的线性相关趋势。
图 9.9-1 试验点的线性相关趋势〖解（2）〗分别求 x 、 y 的样本和、样本平方和及它们的乘积和，详见下表。样本数据预处理表
x
0.10 0.30 0.40 0.55 0.70 0.80 0.95
旅分布
2 ˆ N b, b SS x
ˆb b t df E MSE SS x
故 b 的置信水平为 0.95 的置信区间为：
ˆ MSE 0.043194636 b t 2 (df E ) 12.55033558 t0.025 (5) SS x 0.532142857 0.043194636 12.55033558 2.5706 0.532142857 12.55033558 0.732378006

概率论与数理统计课后习题答案高等教育出版社

概率论与数理统计课后习题答案高等教育出版社习题1.1解答1. 将一枚均匀的硬币抛两次，事件C B A ,,分别表示“第一次出现正面”，“两次出现同一面”，“至少有一次出现正面”。

试写出样本空间及事件C B A ,,中的样本点。

解：{=Ω(正，正)，（正，反），（反，正），（反，反）}{=A (正，正)，（正，反）}；{=B （正，正），（反，反）} {=C (正，正)，（正，反），（反，正）}2. 在掷两颗骰子的试验中，事件D C B A ,,,分别表示“点数之和为偶数”，“点数之和小于5”，“点数相等”，“至少有一颗骰子的点数为3”。

试写出样本空间及事件D C B A BC C A B A AB ---+,,,,中的样本点。

解：{})6,6(,),2,6(),1,6(,),6,2(,),2,2(),1,2(),6,1(,),2,1(),1,1( =Ω； {})1,3(),2,2(),3,1(),1,1(=AB ；{})1,2(),2,1(),6,6(),4,6(),2,6(,),5,1(),3,1(),1,1( =+B A ； Φ=C A ；{})2,2(),1,1(=BC ；{})4,6(),2,6(),1,5(),6,4(),2,4(),6,2(),4,2(),5,1(=---D C B A3. 以C B A ,,分别表示某城市居民订阅日报、晚报和体育报。

试用C B A ,,表示以下事件：（1）只订阅日报；（2）只订日报和晚报；（3）只订一种报；（4）正好订两种报；（5）至少订阅一种报；（6）不订阅任何报；（7）至多订阅一种报；（8）三种报纸都订阅；（9）三种报纸不全订阅。

解：（1）C B A ；（2）C AB ；（3）C B A C B A C B A ++；（4）BC A C B A C AB ++; （5）C B A ++；（6）C B A ；（7）C B A C B A C B A C B A +++或C B C A B A ++ （8）ABC ；（9）C B A ++4. 甲、乙、丙三人各射击一次，事件321,,A A A 分别表示甲、乙、丙射中。

概率论与数理统计第9章

n
x i 127 . 5
n
i1

n
y i 113 . 1
n
i1

n
x i 829 . 61
2
i1

yi

2
650 . 93
i1

x i y i 731 . 6
15
i1
x
n
n
1
n
xi
127 . 5 24
2
5 . 31
n
y 1 n
n
i1
n
2
1
5
若考虑两个变量
x和 y
且假定 x 和 y 之间具有线性相关关系 y 一元线性回归方程为 ~ f ( x ) 0 1 x
一元线性回归模型为 Y f ( x ) 0 1 x
0 , 1 称为回归系数
若根据样本得到
0 , 1的估计量（值）
其中 X i 是可以控制或精确观测
Y 是依赖 X i 变化的量 , 但 X i 取一固定值时
不过 Y 是一个随机变量
, 并可以确定 Y 的概率分布
y 的数学期望 EY 与 X i 有关 , 并且是 X i的函数 , 记为
EY f ( x 1 , x 2 , , x m )
因此可用函数
~ y f ( x1 , x 2 , , x m )
27
ˆ ˆ ˆ y 0 1x
ˆ ˆ 0,1
则称方程
为 y 对 x 的样本线性回归方程
6
三、样本线性回归方程的建立 1.散点图例1.考察某种纤维的强度与其拉伸倍数的关系,下表是
实际测定的24个纤维样品的强度与相应的拉伸倍数的

概率论与数理统计第九章方差分析

第九章方差分析在生产过程和科学实验中，我们经常遇到这样的问题：影响产品产量、质量的因素很多.例如，在化工生产中，影响结果的因素有：配方、设备、温度、压力、催化剂、操作人员等.我们需要通过观察或试验来判断哪些因素对产品的产量、质量有显著的影响.方差分析(Analysis of variance)就是用来解决这类问题的一种有效方法.它是在20世纪20年代由英国统计学家费舍尔首先使用到农业试验上去的.后来发现这种方法的应用范围十分广阔，可以成功地应用在试验工作的很多方面.第一节单因素试验的方差分析在试验中，我们将要考察的指标称为试验指标，影响试验指标的条件称为因素.因素可分为两类，一类是人们可以控制的；一类是人们不能控制的.例如，原料成分、反应温度、溶液浓度等是可以控制的，而测量误差、气象条件等一般是难以控制的.以下我们所说的因素都是可控因素，因素所处的状态称为该因素的水平.如果在一项试验中只有一个因素在改变，这样的试验称为单因素试验，如果多于一个因素在改变，就称为多因素试验.本节通过实例来讨论单因素试验.1.数学模型例9.1某试验室对钢锭模进行选材试验.其方法是将试件加热到700℃后，投入到20℃的水中急冷，这样反复进行到试件断裂为止，试验次数越多，试件质量越好.试验结果如表9-1.表9-1试验的目的是确定4种生铁试件的抗热疲劳性能是否有显著差异.这里，试验的指标是钢锭模的热疲劳值，钢锭模的材质是因素，4种不同的材质表示钢锭模的4个水平，这项试验叫做4水平单因素试验.例9.2考察一种人造纤维在不同温度的水中浸泡后的缩水率，在40℃，50℃, (90)的水中分别进行4次试验.得到该种纤维在每次试验中的缩水率如表92.试问浸泡水的温度对缩水率有无显著的影响？表9-2 （%）单因素试验的一般数学模型为：因素A 有s 个水平A 1，A 2，…，A s ,在水平A j (j =1,2,…,s )下进行n j (n j ≥2)次独立试验，得到如表9-3的结果：表9-3x 11 x 12 … x 1s x 21 x 22 … x 2s … … … … 11n x 22n x … s n s xT ·1 T ·2 … T ·s1x • 2x • … s x •μ1 μ2 … μs假定：各水平A j (j =1,2,…,s )下的样本x ij ~N (j ,),i =1,2,…,n j ,j =1,2,…,s ,且相互独立. 故x ij -μj 可看成随机误差，它们是试验中无法控制的各种因素所引起的，记x ij -μj =εij ,则⎪⎩⎪⎨⎧==+=.,),0(~,,,2,1;,,2,1,2相互独立各ij ij j ij j ij N s j n i x εσεεμ (9.1) 其中μj 与σ2均为未知参数.（9.1）式称为单因素试验方差分析的数学模型.方差分析的任务是对于模型（9.1），检验s 个总体N (μ１，σ2),…,N (μs ,σ2)的均值是否相等，即检验假设012112:;:,,,s s H H μμμσσσ===⎧⎨⎩不全相等. (9.2) 为将问题（9.2）写成便于讨论的形式，采用记号μ=11sj j j n n μ=∑，其中n =1sjj n=∑，μ表示μ１，μ2,…,μs 的加权平均，μ称为总平均.δj =μj -μ, j =1,2,…,s ，δj 表示水平Aj 下的总体平均值与总平均的差异.习惯上将δj 称为水平A j 的效应.利用这些记号，模型（9.1）可改写成：x ij =μ+δj +εij ,x ij 可分解成总平均、水平A j 的效应及随机误差三部分之和120,~(0,),.1,2,,;1,2,,.sj j j ijij j n N i n j s δεσε=⎧=⎪⎨⎪==⎩∑各相互独立 (9.1)′假设（9.2）等价于假设012112:0;:,,,s s H H δδδδδδ====⎧⎨⎩不全零.（9.2）′ 2.平方和分解我们寻找适当的统计量，对参数作假设检验.下面从平方和的分解着手，导出假设检验（9.2）′的检验统计量.记S T =211()jn sijj i xx ==-∑∑， (9.3)这里111jns ij j i x x n ===∑∑，S T 能反应全部试验数据之间的差异.又称为总变差.A j 下的样本均值 11jn j iji jx xn •==∑. (9.4)注意到2222()()()()2()()ij ij j j ij j j ij j j x x x x x x x x x x x x x x ••••••-=-+-=-+-+--，而 1111()()()()jj n n ssij j j j ij j j i j i x x x x x x x x ••••====⎡⎤--=--⎢⎥⎣⎦∑∑∑∑=11()0.j n sj ij j j j i x x x n x ••==⎛⎫--= ⎪ ⎪⎝⎭∑∑记 S E =211()jn sijj j i xx •==-∑∑，（9.5）S E 称为误差平方和;记 S A =22111()()jn ssjj j j i j xx n x x ••===-=-∑∑∑，（9.6）S A 称为因素A 的效应平方和.于是S T =S E +S A . （9.7）利用εij 可更清楚地看到S E ,S A 的含义，记111jns ij j i n εε===∑∑为随机误差的总平均,11jn j iji jn εε•==∑, j =1,2,…,s .于是S E =221111()()jjn n ssijj ij j j i j i xx εε••====-=-∑∑∑∑; (9.8)S A =2211()()ssj jj j j j j n xx n δεε••==-=+-∑∑. (9.9)平方和的分解公式（9.7）说明.总平方和分解成误差平方和与因素A 的效应平方和.（9.8）式说明S E 完全是由随机波动引起的.而（9.9）式说明S A 除随机误差外还含有各水平的效应δj ，当δj 不全为零时，S A 主要反映了这些效应的差异.若H 0成立，各水平的效应为零，S A 中也只含随机误差，因而S A 与S E 相比较相对于某一显著性水平来说不应太大.方差分析的目的是研究S A 相对于S E 有多大，若S A 比S E 显著地大，这表明各水平对指标的影响有显著差异.故需研究与S A /S E 有关的统计量.3.假设检验问题当H 0成立时，设x ij ~N (μ,σ2)(i =1,2,…,n j ；j =1,2,…,s )且相互独立，利用抽样分布的有关定理，我们有22~(1)AS s χσ-, (9.10) 22~()ES n s χσ-, (9.11)F =()(1)AEn s S s S -- ~F (s -1,n -s ). (9.12)于是，对于给定的显著性水平α(0<α<1),由于P {F ≥F α(s -1,n -s )}=α, (9.13)由此得检验问题（9.2）′的拒绝域为F ≥F α(s -1,n -s ).（9.14）由样本值计算F 的值，若F ≥F α,则拒绝H 0，即认为水平的改变对指标有显著性的影响；若F <F α,则接受原假设H 0，即认为水平的改变对指标无显著影响. 上面的分析结果可排成表9-4的形式，称为方差分析表.当F ≥F 0.05(s -1,n -s )时，称为显著，当F ≥F 0.01(s -1,n -s )时，称为高度显著.在实际中，我们可以按以下较简便的公式来计算S T ，S A 和S E .记T ·j =1jn iji x=∑, j =1,2,…,s ,T ··=11jn sijj i x==∑∑，即有22221111222211,,.j jn n s s T ij ij j i j i s s j A j j j j j E T AT S x nx x n T T S n x nx n n S S S ••====••••==⎧=-=-⎪⎪⎪⎪=-=-⎨⎪⎪=-⎪⎪⎩∑∑∑∑∑∑ (9.15) 例9.3 如上所述，在例9.1中需检验假设H 0:μ1=μ2=μ3=μ4；H 1:μ1,μ2,μ3,μ4不全相等.给定α=0.05,完成这一假设检验.解 s =4,n 1=7,n 2=5,n 3=8,n 4=6,n =26.S T =22211(4257)69895926jn sij j i T x n ••==-=-∑∑=1957.12， S A =2221(4257)697445.4926sj j j T T n n •••=-=-∑=443.61， S E =S T -S A =1513.51.得方差分析表9-5.表9-5因 F (3,22)=2.15<F 0.05(3,22)=3.05. 则接受H 0，即认为4种生铁试样的热疲劳性无显著差异.例9.4 如上所述，在例9.2中需检验假设H 0:μ1=μ2=…=μ6； H 1:μ1,μ2,…,μ6不全相等.试取α=0.05,α=0.01，完成这一假设检验.解 s =6, n 1=n 2=…=n 6=4,n =24.S T =2211jn sij j i T x n ••==-∑∑=112.27,S A =221sj j j T T n n•••=-∑=56,S E=S T-S A=56.27.得方差分析表9-6.0.050.01由于 4.25=F0.01(5,18)>F A=3.583>F0.05(5,18)=2.77,故浸泡水的温度对缩水率有显著影响，但不能说有高度显著的影响.本节的方差分析是在这两项假设下，检验各个正态总体均值是否相等.一是正态性假设，假定数据服从正态分布；二是等方差性假设，假定各正态总体方差相等.由大数定律及中心极限定理，以及多年来的方差分析应用，知正态性和等方差性这两项假设是合理的.第二节双因素试验的方差分析进行某一项试验，当影响指标的因素不是一个而是多个时，要分析各因素的作用是否显著，就要用到多因素的方差分析.本节就两个因素的方差分析作一简介.当有两个因素时，除每个因素的影响之外，还有这两个因素的搭配问题.如表9-7中的两组试验结果，都有两个因素A和B，每个因素取两个水平.表9-7(b)表9-7（a）中，无论B在什么水平（B1还是B2），水平A2下的结果总比A1下的高20；同样地，无论A是什么水平，B2下的结果总比B1下的高40.这说明A和B单独地各自影响结果，互相之间没有作用.表9-7(b)中，当B为B1时，A2下的结果比A1的高，而且当B为B2时，A1下的结果比A2的高；类似地，当A为A1时，B2下的结果比B1的高70，而A为A2时，B2下的结果比B1的高30.这表明A的作用与B所取的水平有关，而B的作用也与A所取的水平有关.即A 和B不仅各自对结果有影响，而且它们的搭配方式也有影响.我们把这种影响称作因素A和B的交互作用，记作A×B.在双因素试验的方差分析中，我们不仅要检验水平A和B的作用，还要检验它们的交互作用.1.双因素等重复试验的方差分析设有两个因素A，B作用于试验的指标，因素A有r个水平A1,A2,…,Ar,因素B有s个水平B1,B2,…,B s,现对因素A，B的水平的每对组合(A i,B j),i=1,2,…,r；j=1,2,…,s都作t(t≥2)次试验（称为等重复试验），得到如表9-8的结果：表9-8设x ijk ~N (ij ,), i =1,2,…,r ； j =1,2,…,s ； k =1,2,…,t ,各x ijk 独立.这里ij ,均为未知参数.或写为⎪⎩⎪⎨⎧===+=.,,,2,1),,0(~,,,2,1;,,2,1,2相互独立各ijkijk ijk ij ijk t k N s j r j x εσεεμ (9.16) 记μ=111,r s ij i j rs μ==∑∑, 11si ij j s μμ•==∑, i =1,2,…,r ,11rj ij i r μμ•==∑, j =1,2,…,s ,,i i αμμ•=-, i =1,2,…,r , j j βμμ•=-, j =1,2,…,s ,ij ij i j γμμμμ••=--+.于是 μij =μ+αi +βj +γij . (9.17)称μ为总平均，αi 为水平A i 的效应，βj 为水平B j 的效应，γij 为水平A i 和水平B j 的交互效应，这是由A i ,B j 搭配起来联合作用而引起的.易知1rii α=∑=0,1sjj β=∑=0，1riji γ=∑=0, j =1,2,…,s ,1sijj γ=∑=0, i =1,2,…,r ，这样（9.16）式可写成⎪⎪⎪⎩⎪⎪⎪⎨⎧=======++++=∑∑∑∑====.,,,2,1;,,2,1;,,2,1),,0(~,0,0,0,0,21111相互独立各ijkijk s j ij r i ij s j j r i i ijk ij j i ijk t k s j r i N x εσεγγβαεγβαμ (9.18) 其中μ,αi ,βj ,γij 及σ2都为未知参数.（9.18）式就是我们所要研究的双因素试验方差分析的数学模型.我们要检验因素A ，B 及交互作用A ×B 是否显著.要检验以下3个假设：⎩⎨⎧=====.,,:,0:21112101不全为零r r H H αααααα ⎩⎨⎧=====.,,:,0:21122102不全为零s s H H ββββββ ⎩⎨⎧=====.,,:,0:121113121103不全为零rs rs H H γγγγγγ 类似于单因素情况，对这些问题的检验方法也是建立在平方和分解上的.记1111r s tijk i j k x x rst ====∑∑∑, 11tij ijk k x x t •==∑, i =1,2,…,r ； j =1,2,…,s ，111s ti ijk j k x x st ••===∑∑, i =1,2,…,r ， 111r tj ijk i k x x rt ••===∑∑, j =1,2,…,s ， S T =2111()rstijk i j k x x ===-∑∑∑. 不难验证,,,i j ij x x x x •••••分别是μ,μi ·,μ·j ,μij 的无偏估计.由 ()()()()ijk ijk ij i j ij i j x x x x x x x x x x x x ••••••••••-=-+-+-+--+，1≤i ≤r ,1≤j ≤s ,1≤k ≤t得平方和的分解式：S T =S E ＋S A ＋S B ＋S A ×B ， (9.19)其中S E =2111()rstijkij i j k xx •===-∑∑∑，S A =1()2ri i stxx ••=-∑，S B =21()sj j rtxx ••=-∑，S A ×B =211()rsij i j i j txx x x •••••==--+∑∑.S E 称为误差平方和，S A ，S B 分别称为因素A ，B 的效应平方和，SA ×B 称为A ，B 交互效应平方和.当H 01:α1=α2=…=αr =0为真时，F A =[](1)(1)A ES S r rs t -- ~F (r -1,rs (t -1))；当假设H 02为真时，F B =[](1)(1)BES S s rs t --~F (s -1,rs (t -1))；当假设H 03为真时，F A ×B =[](1)(1)(1)A BES S r s rs t ⨯--- ~F ((r -1)(s -1),rs (t -1)).当给定显著性水平α后，假设H 01，H 02，H 03的拒绝域分别为：(1,(1));(1,(1));(1)(1),(1)).A B A BF F r rs t F F s rs t F F r s rs t ααα⨯≥--⎧⎪≥--⎨⎪≥---⎩ (9.20) 经过上面的分析和计算，可得出双因素试验的方差分析表9-9.在实际中，与单因素方差分析类似可按以下较简便的公式来计算S T ，S A ，S B ，S A ×B ,S E . 记 T ···=111r s tijki j k x===∑∑∑，T ij ·=1tijkk x=∑, i =1,2,…,r ; j =1,2,…,s ，T i ··=11stijkj k x==∑∑, i =1,2,…,r ,T ·j ·=11r tijki k x==∑∑, j =1,2,…,s ,即有221112212212211,1,1,1,.r s tT ijk i j k r A i i s B j j r s A B ij A B i j E T A B A B T S x rst T S T st rst T S T rt rst T S T S S t rst S S S S S •••===•••••=•••••=•••⨯•==⨯⎧=-⎪⎪⎪=-⎪⎪⎪⎨=-⎪⎪⎪=---⎪⎪⎪=---⎩∑∑∑∑∑∑∑ (9.21) 例9.5 用不同的生产方法（不同的硫化时间和不同的加速剂）制造的硬橡胶的抗牵拉强度（以kg ·cm -2为单位）的观察数据如表9-10所示.试在显著水平0.10下分析不同的硫化时间（A ），加速剂（B ）以及它们的交互作用（A ×B ）对抗牵拉强度有无显著影响.表9-10010203r =s =3, t =2， T ···,T ij ·,T i ··,T ·j ·的计算如表9-11.表9-11S T =22111,r s tijki j k T xrst•••===-∑∑∑=178.44， S A =2211r i i T T st rst•••••=-∑=15.44，S B =2211s j j T T rt rst •••••=-∑=30.11，S A ×B =22111r s ij A B i j T T S S t rst••••==---∑∑ =2.89，S E =S T -S A -S B -S A ×B =130，得方差分析表9-12.由于F 0.10(2,9)=3.01>F A ,F 0.10(2,9)>F B ,F 0.10(4,9)=2.69>F A ×B ,因而接受假设H 01,H 02,H 03,即硫化时间、加速剂以及它们的交互作用对硬橡胶的抗牵拉强度的影响不显著.2.双因素无重复试验的方差分析在双因素试验中，如果对每一对水平的组合（A i ,B j ）只做一次试验，即不重复试验，所得结果如表9-13.这时ij x •=x ijk ,S E =0,S E 的自由度为0，故不能利用双因素等重复试验中的公式进行方差分析.但是，如果我们认为A ，B 两因素无交互作用，或已知交互作用对试验指标影响很小，则可将S A ×B 取作S E ，仍可利用等重复的双因素试验对因素A ，B 进行方差分析.对这种情况下的数学模型及统计分析表示如下：由（9.18）式,112,0,0,~(0,),1,2,,;1,2,,,.ij i j ij r si j i j ij ijk x N i r j s μαβεαβεσε===+++⎧⎪⎪==⎪⎨⎪==⎪⎪⎩∑∑各相互独立 (9.22)要检验的假设有以下两个：⎩⎨⎧=====.,,:,0:21112101不全为零r r H H αααααα ⎩⎨⎧=====.,,:,0:21122102不全为零s s H H ββββββ 记 1111111,,,r s s rij i ij j ij i j j i x x x x x x rs s r ••=======∑∑∑∑平方和分解公式为：S T =S A +S B +S E ， (9.23)其中 22111(),(),rssT ijA i i j j S xx S s x x •====-=-∑∑∑22111(),(),srsB j E ij i j j i j S r x x S x x x x •••====-=--+∑∑∑分别为总平方和、因素A ，B 的效应平方和和误差平方和.取显著性水平为α,当H 01成立时，F A =(1)AEs S S - ~F ((r -1),(r -1)(s -1))， H 01拒绝域为F A ≥F α((r -1),(r -1)(s -1)). (9.24)当H 02成立时，F B =(1)BEr S S - ~F ((s -1),(r -1)(s -1))， H 02拒绝域为F B ≥F α((s -1),(r -1)(s -1)). (9.25)得方差分析表9-14.例9.6 测试某种钢不同含铜量在各种温度下的冲击值（单位：kg ·m ·cm ），表9-15列出了试验的数据（冲击值），问试验温度、含铜量对钢的冲击值的影响是否显著？（α=0.01）解由已知，r =4,s =3,需检验假设H 01,H 02，经计算得方差分析表9-16.0.01A 01F 0.01（2,6）=10.92<F B ,拒绝H 02.检验结果表明，试验温度、含铜量对钢冲击值的影响是显著的.第三节正交试验设计及其方差分析在工农业生产和科学实验中，为改革旧工艺，寻求最优生产条件等，经常要做许多试验，而影响这些试验结果的因素很多，我们把含有两个以上因素的试验称为多因素试验.前两节讨论的单因素试验和双因素试验均属于全面试验（即每一个因素的各种水平的相互搭配都要进行试验），多因素试验由于要考虑的因素较多，当每个因素的水平数较大时，若进行全面试验，则试验次数将会更大.因此，对于多因素试验，存在一个如何安排好试验的问题.正交试验设计是研究和处理多因素试验的一种科学方法，它利用一套现存规格化的表——正交表，来安排试验，通过少量的试验，获得满意的试验结果.1.正交试验设计的基本方法正交试验设计包含两个内容：（1）怎样安排试验方案；（2）如何分析试验结果.先介绍正交表.正交表是预先编制好的一种表格.比如表9-17即为正交表L4(23),其中字母L表示正交，它的3个数字有3种不同的含义：(1) L4（23）表的结构：有4行、3列，表中出现2个反映水平的数码1，2.列数↓L4 （23）↑↑行数水平数（2）L4（23）表的用法：做4次试验，最多可安排2水平的因素3个.最多能安排的因素数↓L4(23)↑↑试验次数水平数(3) L4（23）表的效率：3个2水平的因素.它的全面试验数为23=8次，使用正交表只需从8次试验中选出4次来做试验，效率是高的.L4(23)↑↑实际试验数理论上的试验数正交表的特点：（1）表中任一列，不同数字出现的次数相同.如正交表L4(23)中，数字1，2在每列中均出现2次.（2）表中任两列，其横向形成的有序数对出现的次数相同.如表L4（23）中任意两列，数字1，2间的搭配是均衡的.凡满足上述两性质的表都称为正交表(Orthogonal table).常用的正交表有L9（34），L8（27），L16（45）等，见附表.用正交表来安排试验的方法，就叫正交试验设计.一般正交表L p（n m）中，p=m(n-1)+1.下面通过实例来说明如何用正交表来安排试验.例9.7 提高某化工产品转化率的试验.某种化工产品的转化率可能与反应温度A，反应时间B，某两种原料之配比C和真空度D有关.为了寻找最优的生产条件，因此考虑对A，B，C，D这4个因素进行试验.根据以往的经验，确定各个因素的3个不同水平，如表9-18所示.表9-18分析各因素对产品的转化率是否产生显著影响，并指出最好生产条件.解本题是4因素3水平，选用正交表L9（34）.将各因素的诸水平所表示的实际状态或条件代入正交表中，得到9个试验方案，如表9-20所示.表9-20从表9-20看出，第一行是1号试验，其试验条件是：反应温度为60℃，反应时间为2.5小时，原料配比为1.1∶1，真空度为500毫米汞柱，记作A1B1C1D1.依此类推，第9号试验条件是A3B3C2D1.由此可见，因素和水平可以任意排，但一经排定，试验条件也就完全确定.按正交试验表9-20安排试验，试验的结果依次记于试验方案右侧，见表9-21.2.试验结果的直观分析正交试验设计的直观分析就是要通过计算，将各因素、水平对试验结果指标的影响大小，通过极差分析，综合比较，以确定最优化试验方案的方法.有时也称为极差分析法.例9.7中试验结果转化率列在表9-21中，在9次试验中，以第9次试验的指标86为最高，其生产条件是A 3B 3C 2D 1.由于全面搭配试验有81种，现只做了9次.9次试验中最好的结果是否一定是全面搭配试验中最好的结果呢？还需进一步分析. （1）极差计算在代表因素A 的表9-21的第1列中，将与水平“1”相对应的第1，2，3号3个试验结果相加，记作T 11，求得T 11=151.同样，将第1列中与水平“2”对应的第4，5，6号试验结果相加，记作T 21，求得T 21=183.一般地，定义T ij 为表9-21的第j 列中，与水平i 对应的各次试验结果之和(i =1,2,3; j =1,2,3,4).记T 为9次试验结果的总和，R j 为第j 列的3个T ij 中最大值与最小值之差，称为极差.显然T =31iji T=∑，j =1,2,3,4.此处T 11大致反映了A 1对试验结果的影响，T 21大致反映了A 2对试验结果的影响， T 31大致反映了A 3对试验结果的影响，T 12，T 22和T 32分别反映了B 1，B 2，B 3对试验结果的影响， T 13，T 23和T 33分别反映了C 1，C 2，C 3对试验结果的影响， T 14，T 24和T 34分别反映了D 1，D 2，D 3对试验结果的影响.R j 反映了第j 列因素的水平改变对试验结果的影响大小，R j 越大反映第j 列因素影响越大.上述结果列表9-22.(2) 极差分析(Analysis of range)由极差大小顺序排出因素的主次顺序：主→次 B ；A 、D ；C这里，R j 值相近的两因素间用“、”号隔开，而R j 值相差较大的两因素间用“；”号隔开.由此看出，特别要求在生产过程中控制好因素B ，即反应时间.其次是要考虑因素A 和D ，即要控制好反应温度和真空度.至于原料配比就不那么重要了.选择较好的因素水平搭配与所要求的指标有关.若要求指标越大越好，则应选取指标大的水平.反之，若希望指标越小越好，应选取指标小的水平.例9.7中，希望转化率越高越好，所以应在第1列选最大的T 31=185；即取水平A 3，同理可选B 3C 1D 3.故例9.7中较好的因素水平搭配是A 3B 3C 1D 3.例9.8 某试验被考察的因素有5个：A ，B ，C ，D ，E .每个因素有两个水平.选用正交表L 8(27)，现分别把A ，B ，C ，D ，E 安排在表L 8(27)的第1，2，4，5，7列上，空出第3，6列仿例9.7做法，按方案试验.记下试验结果，进行极差计算，得表9-23.试验目的要找出试验结果最小的工艺条件及因素影响的主次顺序.从表9-23的极差R j的大小顺序排出因素的主次顺序为主 → 次 A 、B ；D ；C 、E最优工艺条件为A 2B 1C 1D 2E 1.表9-23中因没有安排因素而空出了第3，6列.从理论上说，这两列的极差R j 应为0，但因存有随机误差，这两个空列的极差值实际上是相当小的.3.方差分析正交试验设计的极差分析简便易行，计算量小，也较直观，但极差分析精度较差，判断因素的作用时缺乏一个定量的标准.这些问题要用方差分析解决.设有一试验，使用正交表L p (n m ),试验的p 个结果为y 1,y 2,…,y p ,记T =1pi i y =∑, y =11p i i Ty p p ==∑，S T =21()pii yy =-∑为试验的p 个结果的总变差；S j =222111nn ij ij i i T T T r T r p r p ==⎛⎫-=- ⎪⎝⎭∑∑ 为第j 列上安排因素的变差平方和，其中r =p/n .可证明S T =1mij S=∑即总变差为各列变差平方和之和，且S T 的自由度为p -1，S j 的自由度为n -1.当正交表的所有列没被排满因素时，即有空列时，所有空列的S j 之和就是误差的变差平方和S e ，这时S e 的自由度f e 也为这些空列自由度之和.当正交表的所有列都排有因素时，即无空列时，取S j 中的最小值作为误差的变差平方和S e .从以上分析知，在使用正交表L p (n m )的正交试验方差分析中，对正交表所安排的因素选用的统计量为：F =1jeeS S n f -.当因素作用不显著时，F ~F (n -1,f e ),其中第j 列安排的是被检因素.在实际应用时，先求出各列的S j /(n -1)及S e /f e ,若某个S j /(n -1)比S e /f e 还小时，则这第j 列就可当作误差列并入S e 中去，这样使误差S e 的自由度增大，在作F 检验时会更灵敏，将所有可当作误差列的S j 全并入S e 后得新的误差变差平方和，记为S e Δ,其相应的自由度为f e Δ,这时选用统计量F =1je eS S n f - ~F (n -1,f e Δ).例9.9 对例9.8的表9-23作方差分析.解由表9-23的最后一行的极差值R j ，利用公式S j =2211n ij i T T r p=-∑,得表9-24.表9-24表9-24中第3，6列为空列，因此S e =S 3+S 6=1.250,其中f e =1+1=2,所以S e /f e =0.625,而第7列的S 7=0.125，S 7/f 7=0.1251=0.125比S e /f e 小，故将它并入误差. S e Δ=S e +S 7=1.375,f e Δ=3.整理成方差分析表9-25.eeS fC 3.125 1 3.125 6.818D 6.125 1 6.125 13.364E Δ 0.125 1 0.125 e 1.1250 2 0.625 e Δ 1.37530.458由于F 0.05(1,3)=10.13, F 0.01(1,3)=34.12,故因素A ，B 作用高度显著，因素C 作用不显著，因素D 作用显著，这与前面极差分析的结果是一致的.F 检验法要求选取S e ，且希望f e 要大，故在安排试验时，适当留出些空列会有好处的.前面的方差分析中，讨论因素A 和B 的交互作用A ×B .这类交互作用在正交试验设计中同样有表现，即一个因素A 的水平对试验结果指标的影响同另一个因素B 的水平选取有关.当试验考虑交互作用时，也可用前面讲的基本方法来处理.本章就不再介绍了.小结本章介绍了数理统计的基本方法之一：方差分析.在生产实践中，试验结果往往要受到一种或多种因素的影响.方差分析就是通过对试验数据进行分析，检验方差相同的多个正态总体的均值是否相等，用以判断各因素对试验结果的影响是否显著.方差分析按影响试验结果的因素的个数分为单因素方差分析、双因素方差分析和多因素方差分析.1. 单因素方差分析的情况.试验数据总是参差不齐，我们用总偏差平方和S T =211()jn sijj i xx ==-∑∑来度量数据间的离散程度.将S T 分解为试验随机误差的平方和(S E )与因素A 的偏差平方和（S A ）之和.若S A 比S E 大得较多，则有理由认为因素的各个水平对应的试验结果有显著差异，从而拒绝因素各水平对应的正态总体的均值相等这一原假设.这就是单因素方差分析法的基本思想.2. 双因素方差分析的基本思想类似于单因素方差分析.但双因素试验的方差分析中，我们不仅要检验因素A 和B 各自的作用，还要检验它们之间的交互作用.3. 正交试验设计及其方差分析.根据因素的个数及各个因素的水平个数，选取适当的正交表并按表进行试验.我们通过对这少数的试验数据进行分析，推断出各因素对试验结果影响的大小.对正交试验结果的分析，通常采用两种方法，一种是直观分析法（极差分析法）,它通过对各因素极差R j 的排序来确定各因素对试验结果影响的大小.一种是方差分析法，它的基本思想类似于双因素的方差分析. 重要术语及主题单因素试验方差分析的数学模型 S T =S E +S A单因素方差分析表双因素方差分析表正交试验表极差分析表习题九1.灯泡厂用4种不同的材料制成灯丝，检验灯线材料这一因素对灯泡寿命的影响.若灯泡寿命服从正态分布，不同材料的灯丝制成的灯泡寿命的方差相同，试根据表中试验结果记录，在显著性水平0.05下检验灯泡寿命是否因灯丝材料不同而有显著差异？2.一个年级有三个小班，他们进行了一次数学考试，现从各个班级随机地抽取了一些学生，试在显著性水平0.05下检验各班级的平均分数有无显著差异.设各个总体服从正态分布，且方差相等.4.为了解3种不同配比的饲料对仔猪生长影响的差异，对3种不同品种的猪各选3头进行试验，分别测得其3个月间体重增加量如下表所示，取显著性水平α=0.05，试分析不同饲料与不同品种对猪的生长有无显著影响？假定其体重增长量服从正态分布，且各种配比的方5.研究氯乙醇胶在各种硫化系统下的性能（油体膨胀绝对值越小越好）需要考察补强剂（A）、防老剂（B）、硫化系统（C）3个因素（各取3个水平），根据专业理论经验，交互4(2) 给定α=0.05,作方差分析与(1)比较.6.某农科站进行早稻品种试验（产量越高越好），需考察品种（A），施氮肥量（B），氮、磷、钾肥比例（C），插植规格（D）4个因素，根据专业理论和经验，交互作用全忽略，早(1) 试作出最优生产条件的直观分析，并对4因素排出主次关系.(2) 给定α=0.05,作方差分析，与(1)比较.。

概率论与数理统计(第二版)课后答案

各章大体题详解习题一一、选择题1. （A ）A B A B B ⊂−−→=;（B ）B A A B A B B ⊂−−→⊂−−→=; （C ）AB A B A B B φ=−−→⊂−−→=;（D ）AB B A φ=−−→⊂ 不必然能推出A B B =（除非A B =）所以选（D ）2. ()()()()()()()P A B P AB P AB P A P B P A P B -==--++ ()()()P A P B P AB =+-所以选（C ）3. )()()()()()()()|(A P B P A P B P A P B P AB P B A P B A ≥−→−==−→−⊂所以选（B ）4. 1)(0)()()()()(==−→−==B P A P B P A P AB P A P 或所以选（B ）5. （A ）若B A =，则φ=AB ，且φ==A A B A ，即B A ,不相容（B ）若φ≠⊃B A ，且Ω≠A ，则φ≠AB ，且φ≠=A B A ，即B A ,相容（C ）若φφ≠=B A ,，则φ=AB ，且φ≠=B B A ，即B A ,相容（D ）若φ≠AB ，不必然能推出φ=B A 所以选（D ）6. （A ）若φ≠AB ，不必然能推出)()()(B P A P AB P =（B ）若1)(=A P ，且φ≠⊃B A ，则)()()()(B P A P B P AB P ==，即A,B 独立（C ）若φ=AB ，1)(0<<A P ,1)(0<<B P ，则)()()(B P A P AB P ≠ （D ）若1)(=A P ，则A 与任何事件都彼此独立所以选（B ）7. 射击n 次才命中k 次，即前1-n 次射击恰好命中1-k 次，且第n 次射击时命中目标，所以选（C ）二、填空题8. C A C A C A A C A C A C A C A )())((= C C C C A A C C A C A C ==== ))(()()( 所以 C B =9. 共有44⨯种大体事件，向后两个邮筒投信有22⨯种大体事件，故所求概率为414422=⨯⨯ 10. 设事件A 表示两数之和大于21，则样本空间}10,10|),{(<<<<=Ωy x y x ，}10,10,21|),{(<<<<>+=y x y x y x A 872121211=⋅⋅-==ΩS S P A 11. 由1.0)(,8.0)(=-=B A P A P ，得7.0)(=AB P ，故3.0)(=AB P 12. 由4.0)(,3.0)(,2.0)(===B A P B P A P ，得1.0)(=AB P ，故2.0)()()(=-=AB P B P A B P 13. 2.0)|()()(==A B P A P AB P ，故8.0)|()()(==B A P AB P B P14. )()()()()()()()(ABC P CA P BC P AB P C P B P A P C B A P +---++=)()()()()()()()()()()()(C P B P A P A P C P C P B P B P A P C P B P A P +---++=2719=15. 由于A,B 彼此独立，可得91)()()(==B P A P B A P ，)()(B A P B A P =，于是31)()(==B P A P ，故32)(=B P 三、计算题16.（1）)},,(),,,(),,,(),,,(),,,(),,,(),,,(),,,{(T T T H T T T H T H H T T T H H T H T H H H H H =Ω；（2）}3,2,1,0{=Ω；（3）}1|),{(22≤+=Ωy x y x ；（4）}5:0,5:1,5:2,5:3,5:4,4:5,3:5,2:5,1:5,0:5{=Ω 17.（1）C B A ；（2）)(C B A ；（3）C B A C B A C B A ；（4）AC BC AB ；（5）C B A ；（6）C B A ；（7）ABC18. 法一，由古典概率可知，所求概率为：2016420109⋅C ；法二，由伯努利定理可知，所求概率为：1644209.01.0⋅⋅C19. 只有唯一的一个六位数号码开能打开锁。

概率论与数理统计第六章至第九章

═══════════════════════════════════════════════════════════════本套试题共分15页，当前页是第1页-概率论与数理统计(经管类)第六章至第九章试题课程代码：04183一、单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．设总体X ~ N(2,σμ)，其中μ未知，x 1，x 2，x 3，x 4为来自总体X 的一个样本，则以下关于μ的四个估计：)(41ˆ43211x x x x +++=μ，3212515151ˆx x x ++=μ，2136261ˆx x +=μ，1471ˆx =μ中，哪一个是无偏估计？( )A ．1ˆμB ．2ˆμC ．3ˆμD ．4ˆμ2．设x 1, x 2, …, x 100为来自总体X ~ N(0，42)的一个样本，以x 表示样本均值，则x ~( ) A ．N(0，16) B ．N(0，0.16) C ．N(0，0.04)D ．N(0，1.6)3．要检验变量y 和x 之间的线性关系是否显著，即考察由一组观测数据(x i ，y i )，i =1，2，…，n ，得到的回归方程x y 10ˆˆˆββ+=是否有实际意义，需要检验假设( ) A ．0∶,00100≠=ββH H ∶B ．0∶,0∶1110≠=ββH HC ．0ˆ∶,0ˆ∶0100≠=ββH HD ．0ˆ∶,0ˆ∶1110≠=ββH H4．设x 1,x 2,…，x 100为来自总体X ~N （μ,42）的一个样本，而y 1,y 2,…，y 100为来自总体Y~N （μ,32）的一个样本，且两个样本独立，以y x ,分别表示这两个样本的样本均值，则y x -~（）A ．N ⎪⎭⎫⎝⎛1007,0 B ．N ⎪⎭⎫ ⎝⎛41,0C ．N （0，7）D ．N （0，25）5．设总体X ~N （μ2σ）其中μ未知，x 1,x 2,x 3,x 4为来自总体X 的一个样本，则以下关于μ的四个无偏估计：1ˆμ=),(414321x x x x +++4321252515151ˆx x x x +++=μ 4321361626261ˆx x x x +++=μ，4321471737271ˆx x x x +++=μ中，哪一个方差最小？（）═══════════════════════════════════════════════════════════════本套试题共分15页，当前页是第2页-A ．1ˆμB ．2ˆμC ．3ˆμD ．4ˆμ6.设n 1X ,,X 为正态总体N(2,σμ)的样本,记∑=--=ni i x x n S 122)(11,则下列选项中正确的是（） A.)1(~)1(222--n S n χσB.)(~)1(222n S n χσ-C.)1(~)1(22--n S n χD.)1(~222-n S χσ7．设有一组观测数据(x i ,y i )，i =1，2，…，n ,其散点图呈线性趋势，若要拟合一元线性回归方程x y 10ˆˆˆββ+=，且n i x y i i ,,2,1,ˆˆˆ10 =+=ββ，则估计参数β0，β1时应使（） A ．∑=-ni i i yy 1)ˆ(最小 B ．∑=-ni i i yy 1)ˆ(最大 C ．∑=-ni i i yy 1)ˆ(2最小 D ．∑=-ni i i yy 1)ˆ(2最大 8．设x 1,x 2，…，1n x 与y 1,y 2，…，2n y 分别是来自总体),(21σμN 与),(22σμN 的两个样本，它们相互独立，且x ，y 分别为两个样本的样本均值，则y x -所服从的分布为（）A ．))11(,(22121σμμn n N +- B ．))11(,(22121σμμn n N -- C ．))11(,(2222121σμμn n N +-D ．))11(,(2222121σμμn n N --9．设总体n X X X N X ,,,),,(~212 σμ为来自总体X 的样本，2,σμ均未知，则2σ的无偏估计是（）A ．∑=--ni iX Xn 12)(11B ．∑=--ni iXn 12)(11μC ．∑=-ni iX Xn12)(1D ．∑=-+ni iXn 12)(11μ10.设总体X 服从正态分布N （μ，1），x 1，x 2，…，x n 为来自该总体的样本，x 为样本均值，s 为样本标准差，欲检验假设H 0∶μ=μ0，H 1∶μ≠μ0，则检验用的统计量是（）═══════════════════════════════════════════════════════════════本套试题共分15页，当前页是第3页-A.n/s x 0μ-B.)(0μ-x nC.10-μ-n /s xD.)(10μ--x n11．设总体X~N （μ，σ2），X 1，X 2，…，X n 为来自该总体的一个样本，X 为样本均值，S 2为样本方差.对假设检验问题：H 0：μ=μ0↔H 1：μ≠μ0，在σ2未知的情况下，应该选用的检验统计量为（） A ．n X σμ0- B ．10--n X σμ C ．n SX 0μ-D ．10--n SX μ12．在假设检验问题中，犯第一类错误的概率α的意义是（） A ．在H 0不成立的条件下，经检验H 0被拒绝的概率 B ．在H 0不成立的条件下，经检验H 0被接受的概率 C ．在H 0成立的条件下，经检验H 0被拒绝的概率 D ．在H 0成立的条件下，经检验H 0被接受的概率13．设总体X 服从[0，2θ]上的均匀分布（θ>0），x 1, x 2, …, x n 是来自该总体的样本，x 为样本均值，则θ的矩估计θˆ=（） A ．x 2 B ．x C ．2xD ．x2114．设总体X~N （μ,σ2），σ2未知，X 为样本均值，S n 2=n1∑=-n1i i X X ()2，S 2=1n 1-∑=-n1i iX X()2，检验假设H o :μ=μ0时采用的统计量是（） A ．Z=n /X 0σμ- B ．T=n /S X n 0μ-C ．T=n/X 0σμ- D ．T=n/S X 0μ-15．F 0.05（7，9）=（） A ．F 0. 95（9，7）B ．)7,9(195.0F═══════════════════════════════════════════════════════════════本套试题共分15页，当前页是第4页-C ．)9,7(105.0FD ．)7,9(105.0F16．设（X 1，X 2）是来自总体X 的一个容量为2的样本，则在下列E （X ）的无偏估计量中，最有效的估计量是（） A ．)(2121X X +B ．213132X X +C ．214143X X +D ．215253X X +17．设总体X~N(0,0.25)，从总体中取一个容量为6的样本X 1,…,X 6，设Y=26543221)X X X (X )X (X ++++，若CY 服从F(1,1)分布，则C 为( ) A.2 B.21 C.2D.2118．设α、β分别是假设检验中第一、二类错误的概率，且H 0、H 1分别为原假设和备择假设，则下列结论中正确的是( )A.在H 0成立的条件下，经检验H 1被接受的概率为βB.在H 1成立的条件下，经检验H 0被接受的概率为αC.α=βD.若要同时减少α、β，需要增加样本容量二、填空题请在每小题的空格中填上正确答案。

概率论与数理统计_浙大四版_习题解_第9章_方差分析

概率论与数理统计(浙大四版)习题解第9章方差分析约定：以下各个习题所涉及的方差分析问题均满足方差分析模型所要求的条件。

【习题9.1】今有某种型号的电池三批，它们分别是C B A ,,三个工厂所生产的。

为评比其质量，各随机抽取5只电池为样品，经试验得其寿命（小时）如下表。

三批电池样品的寿命检测结果 A B C 40 42 26 28 39 50 48 45 34 32 40 50 383043（1）试在显著性水平0.05下检验电池的平均寿命有无显著的差异。

（2）若差异显著，试求B A μμ-、C A μμ-及C B μμ-的置信水平为0.95的置信区间。

〖解（1）〗设,,A B C μμμ分别表C B A ,,三厂所产电池的寿命均值，则问题（1）归结为检验下面的假设（单因素方差分析）01::,,不全相等A B CA B C H H μμμμμμ==设A 表因素（工厂），设,,,T R A CR 分别表样本和、样本平方和、因素A 计算数、矫正数，其值的计算过程和结果如下表。

样本数据预处理表A B C 预处理结果40 42 26 28 39 50 n=15 48 45 34 32 40 50 a=338 30 43 CR=22815 j T 213 150 222 T=585 2j j T n9073.8 4500 9856.8 A=23430.6 2ijx∑913745409970R=23647112221121158558522815152364723430.6jjj n aij j i n aijj i n a ij j j i T x T CR n R x A x n =============⎛⎫== ⎪ ⎪⎝⎭∑∑∑∑∑∑计算平方和及自由度如下23647228158321151142364723430.6216.41531223430.622815615.61312T E A SST R CR df n SSE R A df n a SSA A CR df a =-=-==-=-==-=-==-=-==-=-==-=-= 方差分析表方差来源平方和自由度均方 F 值()0.052,12F因素A 615.6 2 307.8 17.07 3.89 误差 216.4 12 18.0333总和83214因17.07 3.89值F =>在拒绝域内，故在0.05水平上拒绝0H ，即认定各厂生产的电池寿命有显著的差异。

(完整版)概率论与数理统计课后习题答案

·1·习题一1．写出下列随机试验的样本空间及下列事件中的样本点：（1）掷一颗骰子，记录出现的点数. A =‘出现奇数点’；（2）将一颗骰子掷两次，记录出现点数. A =‘两次点数之和为10’，B =‘第一次的点数，比第二次的点数大2’；（3）一个口袋中有5只外形完全相同的球，编号分别为1,2,3,4,5；从中同时取出3只球，观察其结果，A =‘球的最小号码为1’；（4）将,a b 两个球，随机地放入到甲、乙、丙三个盒子中去，观察放球情况，A =‘甲盒中至少有一球’；（5）记录在一段时间内，通过某桥的汽车流量，A =‘通过汽车不足5台’，B =‘通过的汽车不少于3台’。

解（1）123456{,,,,,}S e e e e e e =其中i e =‘出现i 点’1,2,,6i =，135{,,}A e e e =。

（2）{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)S = (2,1),(2,2),(2,3),(2,4),(2,5),(2,6) (3,1),(3,2),(3,3),(3,4),(3,5),(3,6) (4,1),(4,2),(4,3),(4,4),(4,5),(4,6)(5,1),(5,2),(5,3),(5,4),(5,5),(5,6) (6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}； {(4,6),(5,5),(6,4)}A =； {(3,1),(4,2),(5,3),(6,4)}B =。

（3）{(1,2,3),(2,3,4),(3,4,5),(1,3,4),(1,4,5),(1,2,4),(1,2,5)S =(2,3,5),(2,4,5),(1,3,5)}{(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5)}A =（4）{(,,),(,,),(,,),(,,),(,,),(,,),S ab ab ab a b a b b a =---------(,,),(,,,),(,,)}b a a b b a ---，其中‘-’表示空盒；{(,,),(,,),(,,),(,,),(,,)}A ab a b a b b a b a =------。

《概率论与数理统计》第三版课后习题答案第9章

n
xi yi
i 1 n
xi 2
i 1
n
i 1
xi
n
xi 2
i 1
yi
n
ci yi ,
i 1
你仅购买了个人使用权
这里 ci
xi
n
是常数。所以 ˆ 也服从正态分布。
xi2
i 1
注意到，误差服从高斯-马尔科夫假设，即 1, 2 ,, n 不相关（正态分布不相关等价于独立），从而 y1, y2 ,, yn 也相互独立，所以
你仅购买了个人使用权
《概率论与数理统计》习题解答王松桂、张忠占、程维虎等，第三版，科学出版社
第九章
9.1 对一元线性回归模型
yi xi i ， i 1,2,3,, n
它不包含常数项，假设误差服从高斯-马尔科夫假设。
（1）求斜率的最小二乘估计 ˆ ；
（2）若进一步假设误差 i ~ N (0, 2 ) ，试求 ˆ 的分布；（3）导出假设 H0 : 0 的检验统计量。解：（1）本题也采用 9.1.1 小节的方法，求斜率的最小二乘估计 ˆ 。
0.24 0.24 0.24 0.25 0.26 0.29 0.32
56 53 53 54.5 61.5 59.5 64
（1）求 0 和 1 的最小二乘估计，并写出经验回归方程；（2）作回归方程的显著性检验，并列出方差分析表（取 0.05 ）；（3）求 0 和 1 各自的置信系数为 0.95 的置信区间。
假设这些数据服从一元线性回归模型
yi 0 1xi i ， i ~ N (0, 2 ) ， i 1,2,3,,92
序 X(%) 号
1 0.03 2 0.04 3 0.04 4 0.05 5 0.05 6 0.05 7 0.05 8 0.06 9 0.06 10 0.07 11 0.07 12 0.07 13 0.08 14 0.08 15 0.08 16 0.08 17 0.08 18 0.08 19 0.08 20 0.09 21 0.09 22 0.09 23 0.09 24 0.09 25 0.09

（完整版）概率论与数理统计习题答案详解版（廖茂新复旦版）

（完整版）概率论与数理统计习题答案详解版（廖茂新复旦版）概率论与数理统计习题答案详解版(廖茂新复旦版)习题⼀1.设A，B，C为三个事件，⽤A，B，C的运算式表⽰下列事件：（1）A发⽣⽽B与C都不发⽣；（2）A，B，C⾄少有⼀个事件发⽣；（3）A，B，C⾄少有两个事件发⽣；（4）A，B，C恰好有两个事件发⽣；（5）A，B⾄少有⼀个发⽣⽽C不发⽣；（6）A，B，C都不发⽣.解：（1）A CB或A-B-C或A-（B∪C）.（2）A∪B∪C.（3）（AB）∪（AC）∪（BC）.（4）（AB C）∪（AC B）∪（BC A）.（5）（A∪B）C.（6）CY或CBA IA.B2.对于任意事件A，B，C，证明下列关系式：（1）(A+B) (A+B)(A+ B)(A+B)= ?；（2）AB+A B +A B+A B AB-= AB；（3）A-(B+C)=(A-B)-C.证明：略.3.设A，B为两事件，P（A）=0.5,P(B)=0.3,P(AB)=0.1，求：（1）A发⽣但B不发⽣的概率；（2）A，B都不发⽣的概率；（3）⾄少有⼀个事件不发⽣的概率.解（1）P（A B）=P（A-B）=P（A-AB）=P（A）-P（AB）=0.4；(2) P(B A)=P(BA )=1-P(A∪B)=1-0.7=0.3；(3) P(A∪B）=P(AB）=1-P(AB)=1-0.1=0.9.4.调查某单位得知。

购买空调的占15％，购买电脑占12％，购买DVD 的占20%；其中购买空调与电脑占6%，购买空调与DVD 占10%，购买电脑和DVD占5％，三种电器都购买占2％。