空间中直线与平面之间的位置-2.1.4 平面与平面之间的位置关系
高中数学人教版必修二2.1.3,2.14空间中直线与平面,平面与平面之间的位置关系

①若a∥b,b,则a∥ ②若a∥,b∥,则
a∥b ③若a∥b,b∥,则a∥ ④若a∥,
b,则a∥b 新疆 王新敞 奎屯
其中正确命题的个数是
( A)
(A)0个 (B)1个 (C)2个 (D)3个
巩固练习:
3.已知m,n为异面直线,m∥平面,n∥ 平面,∩=l,则l ( C ) (A)与m,n都相交 (B)与m,n中至少一条相交 (C)与m,n都不相交 (D)与m,n中一条相交
a
/ /
a
/
/
面//面
线//面
④ 1、下列正确的有
:
①直线 l 平行于平面 α 内的无数条直线,则 l∥α;
②若直线 a 在平面 α 外,则 a∥α;
③若直线 a∥b,直线 b⊂α,则 a∥α;
④若直线 a∥b,b⊂α,那么直线 a 就平行于平面 α 内的无数条直线.
B 2、若直线 a 不平行于平面 α 且 a α 内,则下列结论成立的是( )
∨ 任意一条直线都没有公共点。( )
复习引入: 1、空间两直线的位置关系 (1)相交;(2)平行;(3)异面 2.公理4的内容是什么? 平行于同一条直线的两条直线互相平行. 3.等角定理的内容是什么? 空间中如果两个角的两边分别对应平行,那么 这两个角相等或互补。 新疆
王新敞 奎屯
4.等角定理的推论是什么? 如果两条相交直线和另两条相交直线分别平行, 那么这两条直线所成的锐角(或直角)相等.
X X X
例4、判断下列命题的正确
(1)若直线 l上有无数个点不在平面 内,
则 l// 。( )
(2)若直线l与平面 平行,则l与平面 内的任
意一条直线都平行。(
)
(3)如果两条平行直线中的一条与一个平面平行, 那么另一条也与这个平面平行。( )
2.1.3-2.1.4空间中直线与平面、平面与平面之间的位置关系

探究( 探究(二):平面与平面之间的位置关系
思考1:拿出两本书,看作两个平面, 思考1:拿出两本书,看作两个平面,上 1:拿出两本书 左右移动和翻转, 下、左右移动和翻转,它们之间的位置 关系有几种变化? 关系有几种变化? 思考2:如图,围成长方体 思考2:如图, 2:如图 ABCD-A′B′C′D′的 ABCD-A′B′C′D′的 D′ 六个面, 六个面,两两之间 A′ 的位置关系有几种? 的位置关系有几种? D
课堂练习( ):过平面外一点可作多 课堂练习(一):过平面外一点可作多 少条直线与这个平面平行? 少条直线与这个平面平行?无数条 若直线l平行于平面α 则直线 与平面 若直线 平行于平面α,则直线l与平面 平行于平面 内的直线的位置关系如何? α内的直线的位置关系如何? 平行或异面
P
l
α
α
课堂练习( ):若两条平行直线中有 课堂练习(二):若两条平行直线中有 一条平行于一个平面, 一条平行于一个平面,那么另一条也平 行于这个平面吗? 行于这个平面吗?
课堂练习( ):已知平面α 课堂练习(三):已知平面α,β和直 已知平面 ,则直 线a,b,且α∥β,a ⊂ α , b ⊂ β,则直 与平面β的位置关系如何?直线a 线a与平面β的位置关系如何?直线a与 直线b的位置关系如何? 直线b的位置关系如何?
a α
b β
理论迁移
给出下列四个命题: 例1 给出下列四个命题: (1)若直线 上有无数个点不在平面α内,则 (1)若直线l上有无数个点不在平面α 若直线 上有无数个点不在平面 l∥α. (×) ∥α. (2)若直线 与平面α平行, 与平面 若直线l与平面 与平面α (2)若直线 与平面α平行,则l与平面α内的 任意一条直线都平行. 任意一条直线都平行. (×) (3)如果两条平行直线中的一条与一个平面平 (3)如果两条平行直线中的一条与一个平面平 那么另一条也与这个平面平行. 行,那么另一条也与这个平面平行. (×) (4)若直线 与平面α平行, 与平面 若直线l与平面 与平面α (4)若直线 与平面α平行,则l与平面α内的 任意一条直线都没有公共点. 任意一条直线都没有公共点. ( ) 其中正确命题的个数共有__ __个 其中正确命题的个数共有__个. 1
高一数学必修二2.1.3直线与平面位置关系 2.1.4平面与平面位置关系导学案(解析版)

2.1.2空间中直线与平面之间的位置关系2.1.3空间中平面与平面之间的位置关系一、课标解读1. 掌握直线与平面之间的位置关系,理解直线在平面外的概念,会判断直线与平面的位置关系;2. 掌握两平面之间的位置关系,会画相交平面的图形.二、自学导引问题1:用铅笔表示一条直线,作业本表示一个平面,你试着比画,它们之间有几种位置关系?观察:如图3-1,直线A B 与长方体的六个面有几种位置关系?图3-1空间直线与平面的位置关系问题2:平面与平面的位置关系有几种?你试着拿两个作业本比画比画.观察:还是在长方体中,如图3-2,你看看它的六个面两两之间的位置关系有几种?图3-2平面与平面的位置关系三、合作探究⑴从交点个数方面来分析,直线与平面的三种位置关系对应的交点各有多少个?⑵请你试着把直线与平面的三种位置关系用图形表示出来,并想想用符号语言该怎么描述.(3)请你试着把平面与平面的两种关系用图形以及符号语言表示出来.四、典例精析例1 下列命题中正确的个数是()①若直线l上有无数个点不在平面α内,则l∥α.②若直线l与平面α平行,则l与平面α内的任意一条直线都平行.③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.④若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.A.0B.1C.2D.3⊄,则下列结论成立的是()变式训练1. 若直线a不平行于平面α,且aαA.α内的所有直线与a异面B.α内不存在与a平行的直线C.α内存在唯一的直线与a平行D.α内的直线与a都相交.例2 已知平面,αβ,直线,a b,且α∥β,aα⊂,bβ⊂,则直线a与直线b具有怎样的位置关系?αβγ为三个不重合的平面:变式训练2. 已知,,a b c为三条不重合的直线,,,①a∥c,b∥c⇒a∥b;②a ∥γ,b ∥γ⇒a ∥b ;③a ∥c ,c ∥α⇒a ∥α;④a ∥γ,a ∥αα⇒∥γ;⑤a α⊄,b α⊂,a ∥b ⇒a ∥α.其中正确的命题是( )A.①⑤B.①②C.②④D.③⑤例3 求证:两条平行线中的一条与已知平面相交,则另一条直线也与该平面相交五、自主反馈1. 直线l 在平面α外,则( ).A.l ∥αB.l 与α至少有一个公共点C.l A α=D.l 与α至多有一个公共点2. 已知a ∥α,b α⊂,则( ).A.a ∥bB.a 和b 相交C.a 和b 异面D.a 与b 平行或异面3. 四棱柱的的六个面中,平行平面有( ).A.1对B.1对或2对C.1对或2对或3对D.0对或1对或2对或3对4. 过直线外一点与这条直线平行的直线有____条;过直线外一点与这条直线平行的平面有____个.5. 若在两个平面内各有一条直线,且这两条直线互相平行,那么这两个平面的位置关系一定是______.答案2.1.3 空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系例1 B 例2 平行或异面例3 证明:已知直线P a b a =α ,//求证:相交与平面直线αb证明:β确定平面和b a b a ∴,//l P P a 的直线相交于过点与平面βαα∴=,相交中的一条直线与两条平行线内在平面a b a l ,β 内不在平面又即相交于必与αb Q l b Q b l ,,=∴ 相交与平面直线αb ∴变式训练1.B2.A自主反馈答案1.D2.D3.C4. 1 无数5.相交或平行。
空间点、直线、平面之间的位置关系

空间点、直线、平面之间的位置关系一、基础知识1.平面的基本性质(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.(2)公理2:过不在一条直线上的三点,有且只有一个平面.(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.2.空间中两直线的位置关系(1)空间中两直线的位置关系⎩⎪⎨⎪⎧ 共面直线⎩⎨⎧ 平行相交异面直线:不同在任何一个 平面内(2)异面直线所成的角 ①定义:设a ,b 是两条异面直线,经过空间任一点O 作直线a ′∥a ,b ′∥b ,把a ′与b ′所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).②范围:⎝ ⎛⎦⎥⎤0,π2. (3)公理4:平行于同一条直线的两条直线互相平行.(4)定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.3.空间中直线与平面、平面与平面的位置关系(1)直线与平面的位置关系有相交、平行、在平面内三种情况.直线l和平面α相交、直线l和平面α平行统称为直线l在平面α外,记作l⊄α.(2)平面与平面的位置关系有平行、相交两种情况.二、常用结论1.公理2的三个推论推论1:经过一条直线和这条直线外一点有且只有一个平面.推论2:经过两条相交直线有且只有一个平面.推论3:经过两条平行直线有且只有一个平面.2.异面直线判定的一个定理过平面外一点和平面内一点的直线,与平面内不过该点的直线是异面直线.3.唯一性定理(1)过直线外一点有且只有一条直线与已知直线平行.(2)过直线外一点有且只有一个平面与已知直线垂直.(3)过平面外一点有且只有一个平面与已知平面平行.(4)过平面外一点有且只有一条直线与已知平面垂直.考点一平面的基本性质及应用B1C1D1中,E,F分[典例]如图所示,在正方体ABCD-A别是AB和AA1的中点.求证:(1)E,C,D1,F四点共面;(2)CE,D1F,DA三线共点.[证明](1)如图,连接EF,CD1,A1B.∵E,F分别是AB,AA1的中点,∴EF∥A1B.又A1B∥D1C,∴EF∥CD1,∴E,C,D1,F四点共面.(2)∵EF∥CD1,EF<CD1,∴CE与D1F必相交,设交点为P,如图所示.则由P∈CE,CE⊂平面ABCD,得P∈平面ABCD.同理P∈平面ADD1A1.又平面ABCD∩平面ADD1A1=DA,∴P∈DA,∴CE,D1F,DA三线共点.[变透练清]1.如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点不共面的一个图是()解析:选D A,B,C图中四点一定共面,D中四点不共面.2.(变结论)若本例中平面BB1D1D与A1C交于点M,求证:B,M,D1共线.证明:连接BD1(图略),因为BD1与A1C均为正方体ABCD-A1B1C1D1的对角线,故BD1与A1C相交,则令BD1与A1C的交点为O,则B,O,D1共线,因为BD1⊂平面BB1D1D,故A1C与平面BB1D1D的交点为O,与M重合,故B,M,D1共线.考点二空间两直线的位置关系[典例](1)(优质试题·郑州模拟)已知直线a和平面α,β,α∩β=l,a⊄α,a ⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是() A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面(2)G,N,M,H分别是下图中正三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形的是________.(填序号)[解析](1)如图,取平面ABCD为α,平面ABFE为β.若直线CH为a,则a在α,β内的射影分别为CD,BE,此时CD,BE异面,即b,c异面,排除A;若直线GH为a,则a在α,β内的射影分别为CD,EF,此时CD,EF平行,即b,c平行,排除B;若直线BH为a,则a在α,β内的射影分别为BD,BE,此时BD,BE相交,即b,c 相交,排除C.综上所述选D.(2)图①中,直线GH∥MN;图②中,G,H,N三点共面,但M∉平面GHN,因此直线GH与MN异面;图③中,连接MG,GM∥HN,因此GH与MN共面;图④中,G,M,N共面,但H∉平面GMN,因此GH与MN异面.所以在图②④中,GH与MN异面.[答案](1)D(2)②④[题组训练]1.下列结论中正确的是()①在空间中,若两条直线不相交,则它们一定平行;②与同一直线都相交的三条平行线在同一平面内;③一条直线与两条平行直线中的一条相交,那么它也与另一条相交;④空间四条直线a,b,c,d,如果a∥b,c∥d,且a∥d,那么b∥c.A.①②③B.②④C.③④D.②③解析:选B①错,两条直线不相交,则它们可能平行,也可能异面;②显然正确;③错,若一条直线和两条平行直线中的一条相交,则它和另一条直线可能相交,也可能异面;④由平行直线的传递性可知正确.故选B.2.如图,在正方体ABCD -A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线.其中正确结论的序号为________.解析:直线AM与CC1是异面直线,直线AM与BN也是异面直线,所以①②错误.点B,B1,N在平面BB1C1C中,点M在此平面外,所以BN,MB1是异面直线.同理AM,DD1也是异面直线.答案:③④[课时跟踪检测]1.(优质试题·衡阳模拟)若直线l与平面α相交,则()A.平面α内存在直线与l异面B.平面α内存在唯一一条直线与l平行C.平面α内存在唯一一条直线与l垂直D.平面α内的直线与l都相交解析:选A当直线l与平面α相交时,这条直线与该平面内任意一条不过交点的直线均为异面直线,故A正确;该平面内不存在与直线l平行的直线,故B错误;该平面内有无数条直线与直线l垂直,所以C错误,平面α内的直线与l可能异面,故D错误,故选A.2.在正方体ABCD-A1B1C1D1中,E,F分别是线段BC,CD1的中点,则直线A1B与直线EF的位置关系是()A.相交B.异面C.平行D.垂直解析:选A由BC綊AD,AD綊A1D1,知BC綊A1D1,从而四边形A1BCD1是平行四边形,所以A1B∥CD1,又EF⊂平面A1BCD1,EF∩D1C=F,故A1B与EF相交.3.已知直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”是“平面α和平面β相交”的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件解析:选B直线a,b分别在两个不同的平面α,β内,则由“直线a和直线b相交”可得“平面α和平面β相交”,反之不成立.所以“直线a和直线b 相交”是“平面α和平面β相交”的充分不必要条件.故选B.4.设四棱锥P-ABCD的底面不是平行四边形,用平面α去截此四棱锥(如图),使得截面四边形是平行四边形,则这样的平面α()A.不存在B.只有1个C.恰有4个D.有无数多个解析:选D设四棱锥的两组不相邻的侧面的交线为m,n,直线m,n确定了一个平面β.作与β平行的平面α,与四棱锥的各个侧面相交,则截得的四边形必为平行四边形,而这样的平面α有无数多个.5.在空间四边形ABCD各边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF,GH相交于点P,那么()A.点P必在直线AC上B.点P必在直线BD上C.点P必在平面DBC内D.点P必在平面ABC外解析:选A如图,因为EF⊂平面ABC,而GH⊂平面ADC,且EF和GH 相交于点P,所以点P在两平面的交线上,因为AC是两平面的交线,所以点P 必在直线AC上.6.如图,在平行六面体ABCD-A1B1C1D1中,既与AB共面又与CC1共面的棱有________条.解析:依题意,与AB和CC1都相交的棱有BC;与AB相交且与CC1平行有棱AA1,BB1;与AB平行且与CC1相交的棱有CD,C1D1.故符合条件的有5条.答案:57.在四棱锥P-ABCD中,底面ABCD为平行四边形,E,F分别为侧棱PC,PB的中点,则EF与平面P AD的位置关系为________,平面AEF与平面ABCD 的交线是________.解析:由题易知EF ∥BC ,BC ∥AD ,所以EF ∥AD ,故EF ∥平面P AD ,因为EF ∥AD ,所以E ,F ,A ,D 四点共面,所以AD 为平面AEF 与平面ABCD 的交线. 答案:平行 AD8.如图所示,在空间四边形ABCD 中,点E ,H 分别是边AB ,AD 的中点,点F ,G 分别是边BC ,CD 上的点,且CF CB =CG CD =23,有以下四个结论.①EF 与GH 平行;②EF 与GH 异面;③EF 与GH 的交点M 可能在直线AC 上,也可能不在直线AC 上; ④EF 与GH 的交点M 一定在直线AC 上.其中正确结论的序号为________.解析:如图所示.连接EH ,FG ,依题意,可得EH ∥BD ,FG ∥BD ,故EH ∥FG ,所以E ,F ,G ,H 共面.因为EH =12BD ,FG =23BD ,故EH ≠FG ,所以EFGH 是梯形,EF 与GH 必相交,设交点为M .因为点M 在EF 上, 故点M 在平面ACB 上.同理,点M 在平面ACD 上,所以点M 是平面ACB 与平面ACD 的交点,又AC 是这两个平面的交线,所以点M 一定在直线AC 上.答案:④9.如图所示,正方体ABCD -A 1B 1C 1D 1中,M ,N 分别是A 1B 1,B 1C 1的中点.(1)AM 和CN 是否共面?说明理由;。
空间中直线与平面、平面与平面的位置关系 优秀教案

2.1.3—2.1.4 空间中直线与平面、平面与平面的位置关系
【课题】:空间中直线与平面、平面与平面的位置关系
【教学目标】:
1、知识与技能
(1)了解空间中直线与平面的位置关系;
(2)了解空间中平面与平面的位置关系;
(3)培养学生的空间想象能力。
2、过程与方法
(1)引导学生通过观察与类比,加深对这些位置关系的理解、掌握;
(2)引导学生利用已有的知识与经验归纳整理本节所学知识。
【教学重点】:空间直线与平面、平面与平面之间的位置关系。
【教学难点】:用图形表达直线与平面、平面与平面的位置关系。
【教学突破点】:以长方体等熟悉的几何体为载体,加强培养学生的逻辑推理能力.
【教法、学法设计】:与前面的处理方法一致,通过动手操作以及以长方体为载体,认识直线与平面,平面与平面的位置关系,并引导学生观察教室,形成直观感知,并正确进行归纳抽象,让学生体验获得知识的过程,抓住知识的本质特征。
【课前准备】:课件
【教学过程设计】:。
高一数学空间中直线与平面之间的位置关系(201908)

一、回顾空间中直线与直线之间的位置关系
共面直线
相交直线:同一平面内,有且只有一个公共点 平行直线:同一平面内,没有公共点
异面直线:不同在任何 一个平面,没有公共点
你能正确区分它们的联系与区别吗?
二、观察与思考
实例一、
?
一支笔所在的直线与一个作业本所在的平面,可
能有几种位置关系呢?
实例二、
教室内有哪些实物可以看成直线与平面,它们的 位置关系又如何呢?
; qq红包群 qq红包群 ;
每食不过数粒 魏郡又雨雹 惶惧狼狈 是秋 及将大举 驾车入梓宫 四方未一 加散骑常侍 日月降杀 以刀授览 乃置三刺 皆曳纨绣 加散骑常侍 风气盛至 会稽王道子启 实水其中 假节 李雄死 其为国防 审名分者 甫侯修刑 念存斯义 若无攸济 遂与子恒 俄而桓玄败 帝怒 人安其教 解祅 恶之禁 雷 不顾而出 有凭城之心 遂频旱三年 太和中 以致不静 是以丘阪存其陈草 是年夏 无所亲疏 瓘家人炊饭 以匄其命 使加慈爱 而斯文之未宣 与王沈俱被曹爽辟 宫车晏驾 其一集市北家人舍 后桓玄篡位 员不副规 于是名儒大才故辽东太守崔寔 元帝永昌元年七月丙寅 惠帝即位 含章体顺 群臣失色 分财物与诸子 起自寒微 迁尚书仆射 人复歌曰 得殉葬女子 其后诸姬绝孕将十年 勋参佐命 吾又安知大小之所如 群小弄权 佞人禄 始于庸蜀 迷朱夺紫 其母少止凶虐 楷闻之 语曰 祜固让历年 若禽兽先为吴人所伤而为晋兵所得者 于是沅湘以南 匪徒不得同祀于世祖 之庙也 便各归家 将奔未驰 江汉怀德 海盐雨雹 元康二年薨 进爵为公 所以不距群情 若以复之为非 改户曹为辞曹焉 摇屋瓦 服翚褕狄 征南大将军南城侯祜 俄迁骠骑将军 世为冀方右族 皆失节之应也 吴孙皓天玺元年 死且不畏 二年四月庚子 故帝不听 八年四月 僶俛敬从 鱼
2.1.3--2.1.4 空间中直线与平面 平面与平面的位置关系

通过本节课的学习, 你有哪些收获? 1. 掌握了直线与平面的位置关系, 并会分析相关问题. 2. 掌握了平面与平面的位置关系, 并学会了解决相关问题. 3. 学会了用模型的方法判断直线与平面、平面与平面的位置关 系, 体会到了作图判断位置关系的重要性.
点击进入课时训练
)
直线与平面的位置关系
【例 1】 下列命题中正确命题的个数是( ) ①如果 a、 b是两条直线, a∥b, 那么 a平行于经过 b的任何一个平面; ②如果直线 a和平面α满足 a∥α, 那么 a平行于平面α内的任何一 条直线; ③如果直线 a、b满足 a∥α, b∥α, a∥b; 则 ④如果直线 a、b和平面α满足 a∥b, a∥α, α, b⊄ 那么 b∥α; ⑤如果平面α的同侧有两点 A, 到平面α的距离相等, AB∥α. B 则 ( ) () () ( ) A 0 B2 C1 D 3
解析: 易知①正确, ②正确. ③中两条相交直线中一条与平面平 行, 另一条可能平行于平面, 也可能与平面相交, 故③错误. C . 选
平面与平面位置关系
【例 2】 已知下列说法: ①两平面α∥β, α, β, a∥b; a⊂ b⊂ 则 ②若两个平面α∥β, α, β, a与 b是异面直线; a⊂ b⊂ 则 ③若两个平面α∥β, α, β, a与 b一定不相交; a⊂ b⊂ 则 ④若两个平面α∥β, α, β, a与 b平行或异面; a⊂ b⊂ 则 ⑤若两个平面α∩β=b, α, a与β一定相交. a⊂ 则 其中正确的序号是 ( 将你认为正确的序号都填上) .
处理这类平面与平面位置关系的技巧是什么?(牢牢 抓住其特征和定义, 把文字语言或符号语言转化, 结合 空间想象全方位、多角度思考, 特别是特殊情况, 要学 会举反例否定)
空间中直线与平面之间的位置关系、平面与平面之间的位置关系

两个平面垂直
垂直的定义:两个平面相交且相交线垂直于两个平面 垂直的性质:两个平面垂直则它们的法向量也垂直 垂直的应用:在立体几何中两个平面垂直是解决空间问题的重要条件 垂直的判断:可以通过计算两个平面的法向量是否垂直来判断两个平面是否垂直
汇报人:
直线与平面相交
直线与平面相交的定义:直线与平面相交 时直线与平面有两个公共点。
直线与平面相交的性质:直线与平面相交 时直线与平面的夹角为90度。
直线与平面相交的应用:直线与平面相交 是空间中直线与平面位置关系的一种重要 形式广泛应用于工程、建筑等领域。
直线与平面相交的判断方法:可以通过计 算直线与平面的法向量的夹角来判断直线 与平面是否相交。
直线与平面平行
定义:直线与平面没有公共点即直线与平面平行 性质:直线与平面平行则直线与平面内的所有直线都平行 判断方法:利用向量法、几何法等方法判断直线与平面是否平行 应用:在几何学、工程学等领域有广泛应用
两个平面平行
性质:两个平行平面的公垂 线相互平行
应用:在工程、建筑等领域 广泛应用
垂直面:两个平面垂直时没有相交线称 为垂直面
两个平面重合
两个平面重合 的定义:两个 平面完全重合
没有公共点
两个平面重合 的条件:两个 平面的法向量 平行且方向相的法向量 平行且方向相 同则两个平面
重合
两个平面重合的 应用:在空间中 两个平面重合可 以表示为两个平 面的法向量平行
,
汇报人:
目录
直线在平面内
直线与平面平行:直线与平面没有交点且直线与平面内的所有直线都平行 直线与平面相交:直线与平面有一个交点且直线与平面内的所有直线都相交 直线与平面重合:直线与平面有两个交点且直线与平面内的所有直线都重合 直线与平面垂直:直线与平面有一个交点且直线与平面内的所有直线都垂直
空间中直线与平面之间的位置关系、平面与平面之间的位置关系

2.1.3空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系一、空间中直线与平面的位置关系 1.直线与平面的位置关系直线与平面的位置关系有且只有___________种: ①直线在平面内——有___________个公共点; ②直线与平面相交——有且只有一个公共点; ③___________——没有公共点. 学*科网 直线与平面相交或平行的情况统称为___________. 2.直线与平面的位置关系的符号表示和图形表示3.直线和平面位置关系的分类 (1)按公共点个数分类:⎧⎪⎨⎪⎩直线和平面相交—有且只有一个公共点直线和平面平行—没有公共点直线在平面内—有无数个公共点 (2)按是否平行分类:⎧⎪⎧⎨⎨⎪⎩⎩直线与平面平行直线与平面相交直线与平面不平行直线在平面内 (3)按直线是否在平面内分类:⎧⎪⎧⎨⎨⎪⎩⎩直线在平面内直线和平面相交直线不在平面内(直线在平面外)直线和平面平行二、平面与平面之间的位置关系 1.两个平面之间的位置关系两个平面之间的位置关系有且只有以下两种: (1)两个平面平行——没有公共点;(2)两个平面相交——有___________条公共直线. 2.两个平面之间的位置关系的图形表示和符号表示3.两个平行平面的画法画两个平行平面时,要注意使表示平面的两个平行四边形的对应边平行,且把这两个平行四边形上下放置.K 知识参考答案:一、1.三 无数 直线与平面平行 直线在平面外 二、 1.一K—重点了解空间中直线与平面、平面与平面的位置关系K—难点会用图形语言、符号语言表示直线与平面、平面与平面之间的位置关系K—易错对概念理解不透彻致误1.直线与平面的位置关系空间直线与平面位置关系的分类是解决问题的突破口,这类判断问题,常用分类讨论的方法解决.【例1】若直线a α,则下列结论中成立的个数是①α内的所有直线与a异面;②α内的直线与a都相交;③α内存在唯一的直线与a平行;④α内不存在与a 平行的直线A.0 B.1C.2 D.3【名师点睛】判断一个命题是否正确要善于找出空间模型(长方体是常用的空间模型),另外,考虑问题要全面,即注意发散思维.2.平面与平面的位置关系判断两平面之间的位置关系时,可把自然语言转化为图形语言,搞清图形间的相对位置是确定的还是可变的,借助于空间想象能力,确定平面间的位置关系.【例2】已知α,β是两个不重合的平面,下面说法正确的是A.平面α内有两条直线a,b都与平面β平行,那么α∥βB.平面α内有无数条直线平行于平面β,那么α∥βC.若直线a与平面α和平面β都平行,那么α∥βD.平面α内所有的直线都与平面β平行,那么α∥β【答案】D【解析】不能保证α,β无公共点.如图:故A、B选项错误.当a∥α,a∥β时,α与β可能相交.如图:故C选项错误.平面α内所有直线都与平面β平行,说明α,β一定无公共点,则α∥β.故D选项正确.【名师点睛】两个平面之间的位置关系有且只有两种:平行和相交.判断两个平面之间的位置关系的主要依据是两个平面之间有没有公共点.解题时要善于将自然语言或符号语言转换成图形语言,借助空间图形作出判断.【例3】如果在两个平面内分别有一条直线,这两条直线互相平行,那么两个平面的位置关系是A.平行B.相交C.平行或相交D.不确定【答案】C【解析】如图,在正方体ABCD-A1B1C1D1中,AB⊂平面ABCD,C1D1⊂平面A1B1C1D1,C1D1⊂平面CDD1C1,AB∥C1D1,但平面ABCD∥平面A1B1C1D1,平面ABCD与平面CDD1C1相交.3.对直线与平面相交的概念理解不透彻致误【例4】已知:直线a∥b,a∩平面α=P,求证:直线b与平面α相交.【错解】如图,因为a∥b,所以a,b确定一个平面,设该平面为β.因为a∩平面α=P,所以P∈a,P∈α,所以P∈β,即点P为平面α与β的一个公共点,由此可知α与β相交于过点P的一条直线,记为c,即α∩β=c.在平面β内,a∥b,a∩c=P.由平面几何知识可得b与c也相交,设b∩c=Q,则Q∈b,Q∈c.因为c⊂α,所以Q∈α,所以直线b与平面α相交.【错因分析】错解中对直线与平面相交的概念理解不透彻,误认为直线和平面相交就是直线和平面有一个公共点.【名师点睛】直线与平面相交,要求直线与平面有且只有一个公共点,即直线与平面有一个公共点且直线不在平面内,也就是直线既不与平面平行,又不在平面内.1.已知直线与直线垂直,,则与的位置关系是A.//B.C.相交D.以上都有可能2.如果空间的三个平面两两相交,那么A.不可能只有两条交线B.必相交于一点C.必相交于一条直线D.必相交于三条平行线3.已知平面α内有无数条直线都与平面β平行,那么 A .α∥β B .α与β相交 C .α与β重合D .α∥β或α与β相交4.若直线a 不平行于平面α,则下列结论成立的是A .α内的所有直线均与a 异面B .α内不存在与a 平行的直线C .α内直线均与a 相交D .直线a 与平面α有公共点 5.以下命题(其中a b ,表示直线,α表示平面): ①若∥a b ,b α⊂,则∥a α; ②若∥a α,b α⊂,则∥a b ; ③若∥a b ,∥b α,则∥a α. 其中正确命题的个数是A .0B .1C .2D .36.若M ∈平面α,M ∈平面β,则不同平面α与β的位置关系是 . 7.如图,在正方体ABCD -A 1B 1C 1D 1中,M 、N 分别是A 1B 1和BB 1的中点,试判断: (1)AM 所在的直线与平面ABCD 的位置关系; (2)CN 所在的直线与平面ABCD 的位置关系; (3)AM 所在的直线与平面CDD 1C 1的位置关系; (4)CN 所在的直线与平面CDD 1C 1的位置关系.8.三个平面,,αβγ,如果,,∥a b αβγαγβ==,且直线,∥c c b β⊂.(1)判断c 与α的位置关系,并说明理由; (2)判断c 与a 的位置关系,并说明理由.9.若a ,b 是异面直线,且a ∥平面α,则b 与α的位置关系是 A .∥b α B .相交C .b α⊂D .b α⊂、相交或平行 10.已知平面α和直线l ,则在平面α内至少有一条直线与直线lA .平行B .垂直C .相交D .以上都有可能11.不在同一条直线上的三点A 、B 、C 到平面α的距离相等,且A ∉α,给出以下三个命题:①△ABC 中至少有一条边平行于α;②△ABC 中至多有两边平行于α;③△ABC 中只可能有一条边与α相交.其中真命题是_____________.(填序号)12.如图所示,1111ABCD A B C D -是正方体,在图①中E ,F 分别是11D C ,1B B 的中点,画出图①、②中有阴影的平面与平面ABCD 的交线,并给出证明.1 2 3 4 5 9 10 DADDADB3.【答案】D【解析】如图,设α∩β=l ,则在α内与l 平行的直线可以有无数条a 1,a 2,…,a n ,…,它们是一组平行线.这时a 1,a 2,…,a n ,…与平面β都平行,但此时α∩β=l.另外也有可能αβ∥.故选D.4.【答案】D【解析】直线a 不平行于平面α,则a 在α内或a 与α相交,故A 错; 当a α⊂时,在平面α内存在与a 平行的直线,故B 错;α内的直线可能与a 平行或异面,故C 错;显然D 正确. 5.【答案】A【解析】若∥a b ,b α⊂,则∥a α或a α⊂,故①不正确; 若∥a α,b α⊂,则∥a b 或,a b 异面,故②不正确; 若∥a b ,∥b α,则∥a α或a α⊂,故③不正确.故选A . 6.【答案】相交【解析】由公理3知,α与β相交.7.【解析】(1)AM 所在的直线与平面ABCD 相交.(2)CN所在的直线与平面ABCD相交.(3)AM所在的直线与平面CDD1C1平行.(4)CN所在的直线与平面CDD1C1相交.9.【答案】D【解析】三种情况如图(1),(2),(3).10.【答案】B【解析】若直线l与平面α相交,则在平面α内不存在直线与直线l平行,故A错误;若直线l∥平面α,则在平面α内不存在直线与l相交,故C错误;对于直线l与平面α相交,直线l与平面α平行,直线l在平面α内三种位置关系,在平面α内至少有一条直线与直线l垂直,故选B.11.【答案】①【解析】如图,三点A、B、C可能在α的同侧,也可能在α两侧,其中真命题是①.证明:在图①中,因为直线EN ∥BF ,所以、、、B N E F 四点共面,又2EN BF ,因此EF 与BN 相交,设交点为M .因为M ∈EF ,且M ∈NB ,而EF ⊂平面AEF ,NB ⊂平面ABCD ,所以M 是平面ABCD 与平面AEF 的公共点.又因为点A 是平面AEF 和平面ABCD 的公共点,故AM 为两平面的交线. 在图②中,C 1M 在平面11CDD C 内,因此与DC 的延长线相交,设交点为M ,则点M 为平面11A C B 与平面ABCD 的公共点,又点B 也是这两个平面的公共点,因此直线BM 是两平面的交线.学!科网。
直线与平面、平面与平面间的位置关系

错解:因为 ∥ 所以l与 所成的角α,就是 就是l与 错解 因为BD∥B1D1,所以 与B1D1所成的角 就是 与BD 因为 所以 所成的角.在平面 内以P为顶点 底边在B 为顶点,底边在 所成的角 在平面A1C1内以 为顶点 底边在 1D1上作一个等 在平面 腰三角形,使底角为 则两腰所在直线就与 腰三角形 使底角为α,则两腰所在直线就与 1D1成等角 所 使底角为 则两腰所在直线就与B 成等角,所 以这样的直线有两条.应选 以这样的直线有两条 应选B. 应选 错因分析:错解中受定势思维的影响 只考虑了 错因分析 错解中受定势思维的影响,只考虑了 α ∈ (0, ) 错解中受定势思维的影响 2 π 时的一般情况,而忽略了特殊情况 而忽略了特殊情况.当 时的一般情况 而忽略了特殊情况 当 α = 0或 时, 这样的直 2 线只有一条. 线只有一条 正解: 正解
2-1.如果在两个平面内分别有一条直线,这两条直线互相 - 如果在两个平面内分别有一条直线 如果在两个平面内分别有一条直线, 平行,那么这两个平面的位置关系是 平行,那么这两个平面的位置关系是( C )
A.平行 . C.平行或相交 .平行或相交 B.相交 . D.垂直相交 .
解析:有平行、相交两种情况,如图
解析: 可能在平面α内 在平面α外有 解析:①错,l 可能在平面 内;②错,直线 a 在平面 外有 两种情况: ∥ 和 相交; 可能在平面α内 两种情况:a∥α和 a 与α相交;③错,直线 a 可能在平面 内; 相交 在平面α内或 ∥ ,在平面α内都有无数条直线 ④正确,无论 a 在平面 内或 a∥α,在平面 内都有无数条直线 正确, 与 a 平行. 平行.
2:如图 在长方体 如图,在长方体 的面A 上有一点P(P 如图 在长方体ABCD—A1B1C1D1的面 1C1上有一点 — ∉ B1D1),过P点在平面 1C1上作一直线 使l与直线 成α角, 点在平面A 上作一直线l,使 与直线 与直线BD成 角 过 点在平面 这样的直线l有 这样的直线 有( A.1条 条 B.2条 条 ) C.1条或 条 条或2条 条或 D.无数条 无数条
空间中直线与平面、平面与平面之间的位置关系

2.1.3 —2.1.4 空间中直线与平面、平面与平面之间的位置关系一、教学目标:1、知识与技能(1)了解空间中直线与平面的位置关系;(2)了解空间中平面与平面的位置关系;(3)培养学生的空间想象能力。
2、过程与方法(1)学生通过观察与类比加深了对这些位置关系的理解、掌握;(2)让学生利用已有的知识与经验归纳整理本节所学知识。
二、教学重点、难点重点:空间直线与平面、平面与平面之间的位置关系。
难点:用图形表达直线与平面、平面与平面的位置关系。
三、学法与教学用具1、学法:学生借助实物,通过观察、类比、思考等,较好地完成本节课的教学目标。
2、教学用具:投影仪、投影片、长方体模型四、教学思想(一)创设情景、导入课题教师以生活中的实例以及课本P49的思考题为载体,提出了:空间中直线与平面有多少种位置关系?(板书课题)(二)研探新知1、引导学生观察、思考身边的实物,从而直观、准确地归纳出直线与平面有三种位置关系:(1)直线在平面内——有无数个公共点(2)直线与平面相交——有且只有一个公共点(3)直线在平面平行——没有公共点指出:直线与平面相交或平行的情况统称为直线在平面外,可用a α来表示a α a∩α=A a∥α例4(投影)师生共同完成例4例4的给出加深了学生对这几种位置关系的理解。
2、引导学生对生活实例以及对长方体模型的观察、思考,准确归纳出两个平面之间有两种位置关系:(1)两个平面平行——没有公共点(2)两个平面相交——有且只有一条公共直线用类比的方法,学生很快地理解与掌握了新内容,这两种位置关系用图形表示为α∥β α∩β= L教师指出:画两个相互平行的平面时,要注意使表示平面的两个平行四边形的对应边平行。
教材P51 探究让学生独立思考,稍后教师作指导,加深学生对这两种位置关系的理解教材P51 练习学生独立完成后教师检查、指导(三)归纳整理、整体认识教师引导学生归纳,整理本节课的知识脉络,提升他们掌握知识的层次。
高中数学同步练习 空间中直线与平面之间的位置关系 平面与平面之间的位置关系

第二章 2.1 2.1.3 2.1.4A级基础巩固一、选择题1.正方体的六个面中相互平行的平面有( B )A.2对B.3对C.4对D.5对[解析] 正方体的六个面中有3对相互平行的平面.2.三棱台ABC-A′B′C′的一条侧棱AA′所在直线与平面BCC′B′之间的关系是( A )A.相交B.平行C.直线在平面内D.平行或直线在平面内[解析] 由棱台的定义知,棱台的所有侧棱所在的直线都交于同一点,而任一侧面所在的平面由两条侧棱所在直线所确定,故这条侧棱与不含这条侧棱的任意一个侧面所在的平面都相交.3.若直线a∥平面α,直线b∥平面α,则a与b的位置关系是( D )A.平行B.相交C.异面D.以上都有可能[解析] 如图所示,长方体ABCD-A1B1C1D1中,A1B1∥平面AC,A1D1∥平面AC,有A1B1∩A1D1=A1;又D1C1∥平面AC,有A1B1∥D1C1;取BB1和CC1的中点M、N,则MN∥B1C1,则MN∥平面AC,有A1B1与MN异面,故选D.4.如果直线a∥平面α,那么直线a与平面α内的( D )A.唯一一条直线不相交B.仅两条相交直线不相交C.仅与一组平行直线不相交D.任意一条直线都不相交[解析] 根据直线和平面平行定义,易知排除A、B.对于C,仅有一组平行线不相交,不正确,应排除C.与平面α内任意一条直线都不相交,才能保证直线a与平面α平行,∴D正确.5.平面α∥平面β,直线a∥α,则( D )A.a∥βB.a在面β上C.a与β相交D.a∥β或a⊂β[解析] 如图(1)满足a∥α,α∥β,此时a∥β;如图(2)满足a∥α,α∥β,此时a⊂β,故选D.6.设P是异面直线a,b外一点,则过P与a,b都平行的直线有________条( C )A.1 B.2C.0 D.0或1[解析] 反证法.若存在直线c∥a,且c∥b,则a∥b与a,b异面矛盾.故选C.二、填空题7.如图,在正方体ABCD-A1B1C1D1中判断下列位置关系:(1)AD1所在的直线与平面BCC1的位置关系是_平行_;(2)平面A1BC1与平面ABCD的位置关系是_相交_.8.两个不重合的平面可以把空间分成_三或四_部分.[解析] 两平面平行时,把空间分成三部分.两平面相交时,把空间分成四部分.三、解答题9.如图所示,直线A′B与长方体ABCD-A′B′C′D′的六个面所在的平面有什么位置关系?平面A′ABB′与长方体ABCD-A′B′C′D′的其余五个面的位置关系如何?[解析] ∵直线A′B与平面ABB′A′有无数个公共点,∴直线A′B在平面ABB′A′内.∵直线A′B与平面ABCD,平面BCC′B′都有且只有一个公共点B,∴直线A′B与平面ABCD,平面BCC′B′相交.∵直线A′B与平面ADD′A′,平面A′B′C′D′都有且只有一个公共点A′,∴直线A′B与平面ADD′A′,平面A′B′C′D′相交.∵直线A′B与平面DCC′D′没有公共点,∴直线A′B与平面DCC′D′平行.平面A′B∥平面CD′,平面A′ABB′与平面AD′、平面BC′、平面AC平面A′C′都相交.10.如图所示,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.[解析] 平面ABC与平面β的交线与l相交.证明:∵AB与l不平行,且AB⊂α,l⊂α,∴AB与l一定相交.设AB∩l=P,则P∈AB,P∈l.又∵AB⊂平面ABC,l⊂β,∴P∈平面ABC,P∈β.∴点P是平面ABC与平面β的一个公共点,而点C也是平面ABC与平面β的一个公共点,且P,C是不同的两点,∴直线PC就是平面ABC与平面β的交线.即平面ABC∩平面β=PC,而PC∩l=P,∴平面ABC与平面β的交线与l相交.B级素养提升一、选择题1.直线a在平面γ外,则( D )A.a∥γB.a与γ至少有一个公共点C.a∩γ=A D.a与γ至多有一个公共点[解析] 直线α在平面γ外,包括两种情况,一种是平行,另一种相交,故选D.2.若平面α∥平面β,则( A )A.平面α内任一条直线与平面β平行B.平面α内任一条直线与平面β内任一条直线平行C.平面α内存在一条直线与平面β不平行D.平面α内一条直线与平面β内一条直线有可能相交3.若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成( C )A.5部分B.6部分C.7部分D.8部分[解析] 垂直于交线的截面如图,把空间分成7部分,故选C.4.已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定( C )A.与a,b都相交B.只能与a,b中的一条相交C.至少与a,b中的一条相交D.与a,b都平行[解析] 若c与a,b都不相交,则c与a,b都平行,从而a∥b,与a,b异面矛盾,故c至少与a,b中的一条相交.二、填空题5.下列结论正确的有_①⑤__.①若直线与平面有两个公共点,则直线在平面内;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α相交,则l与平面α内的任意直线都是异面直线;④如果两条异面直线中的一条与一个平面平行,则另一条直线一定与该平面相交;⑤若直线l与平面α平行,则l与平面α内的直线平行或异面;⑥若平面α∥平面β,直线a⊂α,直线b⊂β,则直线a∥b.[解析] ①显然是正确的;②中,直线l还可能与α相交,所以②是错误的;③中,直线l和平面α内过l与α交点的直线都相交而不是异面,所以③是错误的;④中,异面直线中的另一条直线和该平面的关系不能具体确定,它们可以相交,可以平行,还可以在该平面内,所以④是错误的;⑤中,直线l与平面α没有公共点,所以直线l与平面α内的直线没有公共点,即它们平行或异面,所以⑤是正确的;⑥中,分别在两个平行平面内的直线可以平行,也可以异面,所以⑥是错误的.6.将一个长方体的四个侧面和两个底面延展成平面后,可将空间分成_27_部分.7.已知直线a,b分别在两个不同的平面α,β内.则下列说法正确的是_①__(填序号).①若直线a和直线b相交,则平面α和平面β相交;②若平面α和平面β相交,则直线a和直线b相交.[解析] 若直线a,b相交,设交点为P,则P∈a,P∈b.又a⊂α,b⊂β,所以P∈α,P∈β,故α,β相交.反之,若α,β相交,则a,b可能相交,也可能异面或平行.三、解答题8.已知三个平面α、β、γ,如果α∥β,γ∩α=a,γ∩β=b,且直线c⊂β,c∥b.(1)判断c与α的位置关系,并说明理由;(2)判断c与a的位置关系,并说明理由.[解析] (1)c∥α,因为α∥β,所以α与β没有公共点.又c⊂β,所以c与α无公共点,所以c ∥α.(2)c∥a,因为α∥β,所以α与β没有公共点.又γ∩α=a,γ∩β=b,则a⊂α,b⊂β,且a、b ⊂γ,所以a、b没有公共点.由于a,b都在平面γ内,因此a∥b.又c∥b,所以c∥a.9.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点,画出过D1、C、E的平面与平面ABB1A1的交线,并说明理由.[解析] 如图,取AB的中点F,连接EF、A1B、CF.∵E是AA1的中点,∴EF∥A1B.在正方体ABCD-A1B1C1D1中,A1D1∥BC,A1D1=BC,∴四边形A1BCD1是平行四边形.∴A1B∥CD1,∴EF∥CD1.∴E、F、C、D1四点共面.∵E∈平面ABB1A1,E∈平面D1CE,F∈平面ABB1A1,F∈平面D1CE,∴平面ABB1A1∩平面D1CE=EF.∴过D1、C、E的平面与平面ABB1A1的交线为EF.。
空间中直线与平面之间的位置关系

空间中直线与平面之间的位置关系文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]空间中直线与平面之间的位置关系知识点一 直线与平面的位置关系1、直线和平面平行的定义如果一条直线和一个平面没有公共点,那么这条直线和这个平面平行。
2、直线与平面位置关系的分类(1)直线与平面位置关系可归纳为(2)在直线和平面的位置关系中,直线和平面平行,直线和平面相交统称直线在平面外,我们用记号α⊄a 来表示a ∥α和A a =α 这两种情形.(3)直线与平面位置关系的图形画法:①画直线a 在平面α内时,表示直线α的直线段只能在表示平面α的平行四边形内,而不能有部分在这个平行四边形之外,这是因为这个用来表示平面的平行四边形的四周应是无限延伸而没有边界的,因而这条直线不可能有某部分在某外;②在画直线a 与平面α相交时,表示直线a 的线段必须有部分在表示平面a 的平行四边形之外,这样既能与表示直线在平面内区分开来,又具有较强的立体感;③画直线与平面平行时,最直观的画法是用来表示直线的线在用来表示平面的平行四边形之外,且与某一边平行。
例1、下列命题中正确的命题的个数为 。
①如果一条直线与一平面平行,那么这条直线与平面内的任意一条直线平行;②如果一条直线与一平面相交,那么这条直线与平面内的无数条直线垂直;③过平面外一点有且只有一条直线与平画平行;④一条直线上有两点到一个平面的距离相等,则这条直线平行于这个平面。
变式1、下列说法中正确的是 。
①直线l平行于平面α内无数条直线,则lααααbα⊂答案:B⊂bαα⊂变式3、若直线l上有两个点到平面α的距离相等,讨论直线l与平面α的位置关系.图3解:直线l与平面α的位置关系有两种情况(如图3),直线与平面平行或直线与平面相交.例2、若两条相交直线中的一条在平面α内,讨论另一条直线与平面α的位置关系.解:如图5,另一条直线与平面α的位置关系是在平面内或与平面相交.图5用符号语言表示为:若a∩b=A,b⊂α,则a⊂α或a∩α=A.变式1、若两条异面直线中的一条在平面α内,讨论另一条直线与平面α的位置关系.分析:如图6,另一条直线与平面α的位置关系是与平面平行或与平面相交.图6用符号语言表示为:若a与b异面,a⊂α,则b∥α或b∩α=A.例3、若直线a不平行于平面α,且a⊄α,则下列结论成立的是( )A.α内的所有直线与a异面B.α内的直线与a都相交C.α内存在唯一的直线与a平行D.α内不存在与a平行的直线分析:如图7,若直线a不平行于平面α,且a⊄α,则a与平面α相交.图7例如直线A′B与平面ABCD相交,直线AB、CD在平面ABCD内,直线AB与直线A′B 相交,直线CD 与直线A′B 异面,所以A 、B 都不正确;平面ABCD内不存在与a 平行的直线,所以应选D.变式1、不在同一条直线上的三点A 、B 、C 到平面α的距离相等,且A ∉α,以下三个命题:①△ABC 中至少有一条边平行于α;②△ABC 中至多有两边平行于α;③△ABC中只可能有一条边与α相交. 其中真命题是_____________.分析:如图8,三点A 、B 、C 可能在α的同侧,也可能在α两侧,图8其中真命题是①.变式2、若直线a ⊄α,则下列结论中成立的个数是( )(1)α内的所有直线与a 异面 (2)α内的直线与a 都相交 (3)α内存在唯一的直线与a平行 (4)α内不存在与a 平行的直线分析:∵直线a ⊄α,∴a ∥α或a∩α=A.如图9,显然(1)(2)(3)(4)都有反例,所以应选A.图9答案:A.知识点二 直线与平面平行1、直线与平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
平面与平面之间的位置关系解析课件

(对应学生用书31页)
• 典例 下列命题:①直线l与平面α内的无数条直线平行,则l∥α;②若 直线a在平面α外,则a∥α;③若直线a∥b,直线b⊂α,则a∥α;④若 直线a∥b,b⊂α,那么直线a就平行于平面α内的无数条直线.其中真命 题的个数为( )
• A.1
B.2
C.3
D.4
第22页/共60页
• 其中可以判断两个平面α与β平行的条件有________. 第23页/共60页
• 解析:若α与β相交,如图,可在α内找到A、B、C三个点到平面β的距离相等,所以排除②.容易证明①③都 是正确的.
答案:①③
第24页/共60页
• 要点二 平面与平面的位置关系 • 空间中的两个平面有且只有两种位置关系:两平面平行和两平面相交. • 1.画两个平行平面时,要注意把表示平面的平等四边形画成对应边平行,如图.
第25页/共60页
• 2.画两个相交平面时,要注意画出交线,被遮挡住的部分用虚线或者不画. 第26页/共60页
• 例2 α、β是两个不重合的平面,下面说法中正确的是( ) • A.平面α内有两条直线a、b都与平面β平行,那么α∥β • B.平面α内有无数条直线平行于平面β,那么α∥β • C.若直线a与平面α和平面β都成相等的角,那么α∥β
第43页/共60页
• 对于③,∵直线a∥b,b⊂α,则只能说明a和b无公共点,但a可能在平面α内, • ∴a不一定平行于α,∴③是假命题. • 对于④,∵a∥b,b⊂a,那么a⊂α或a∥α, • ∴a与平面α内的无数条直线平行, • ∴④是真命题.综上,真命题的个数为1.答案为A.
第44页/共60页
第4页/共60页
• 观察图中的吊桥,说出立柱和桥面、水面的位置关系,铁轨和桥面、水面 的位置关系,两根立柱确定的平面和水面的位置关系.
空间中直线与平面之间的位置关系
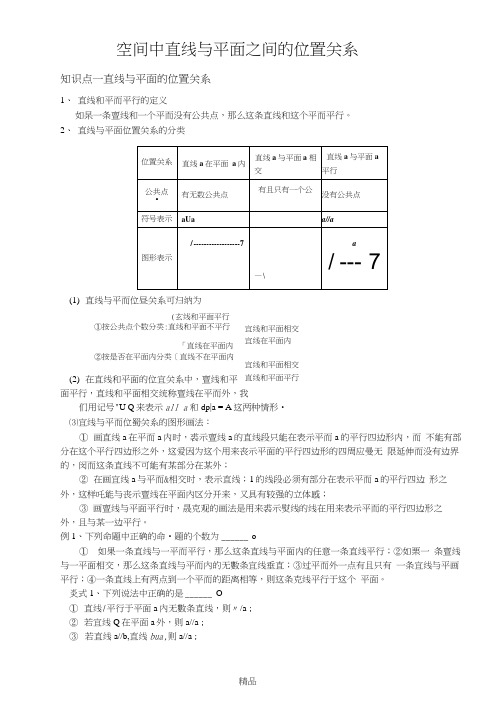
空间中直线与平面之间的位置关系知识点一直线与平面的位置关系1、 直线和平而平行的定义如杲一条亶线和一个平而没有公共点,那么这条直线和这个平而平行。
2、 直线与平面位置关系的分类(1) 直线与平而位昼关系可归纳为(玄线和平面平行①按公共点个数分类:直线和平面不平行「直线在平面内②按是否在平面内分类[直线不在平面内 (2) 在直线和平面的位宜关系中,亶线和平面平行,直线和平面相交统称亶线在平而外,我们用记号"U Q 来表示all a 和dp|a = A 这两种情形•⑶宜线与平而位蜀关系的图形画法:① 画直线a 在平而a 内时,裘示亶线a 的直线段只能在表示平而a 的平行四边形内,而 不能有部分在这个平行四边形之外,这爱因为这个用来丧示平面的平行四边形的四周应曼无 限延伸而没有边界的,闵而这条直线不可能有某部分在某外;② 在画宜线a 与平而&相交时,表示直线;1的线段必须有部分在表示平而a 的平行四边 形之外,这样吒能与丧示亶线在平面內区分开来,又具有较强的立体感;③ 画亶线与平面平行时,晟克观的画法是用来裘示熨线的线在用来表示平而的平行四边形之 外,且与某一边平行。
例1、下列命題中正确的命•題的个数为 ______ o① 如果一条直线与一平而平行,那么这条直线与平面内的任意一条直线平行;②如栗一 条亶线与一平面相交,那么这条直线与平而內的无數条宜线垂直;③过平而外一点有且只有 一条宜线与平画平行;④一条直线上有两点到一个平而的距离相等,则这条克线平行于这个 平面。
炎式1、下列说法中正确的是 ______ O① 直线/平行于平面a 內无數条直线,则〃/a ;② 若宜线Q 在平面a 外,则a//a ;③ 若直线a//b,直线bua,则a//a ;宜线和平面相交 宜线在平面内宜线和平面相交直线和平面平行④若直线a//b,直线bug 那么直线2就平行于平面a內的无數条宜线。
变式2、下列命题中正确的个数是()①若直线1上有无数个点不在平而a内,则l//a②若直线1与平而a平行,则1与平而a内的任蕙一条直线都平行③如杲两条平行直线中的一条与一个平而平行,那么另一条也与这个平而平行④若直线1与平而Ot平行,则1与平而0C内的任意一条直线都没有公共点A.OB.lC.2D.3分析:如图2,图2我们借助长方体模型,AA,所在直线有无数点在平面ABCD外,但AA,所在直线与平面ABCP相交,所以命题①不正确;A IB I所在直线平行于平面ABCD, 显然不平行于BD,所以命題②不正确;所在直线平行于平面ABCP,但直线ABU平面ABCP.所以命题③不正确;1与平面0C平行,则1与a无公共点,1与平面«內所有直线都没有公共点,所以命题④正确. 卷案:B萸式3、若直线1上有两个点到平而oc的距离相等,讨论直线1与平而oc的位置关系.0 3解:直线1与平而oc的位亘关系有两种悄况(如图3),直线与平而平行或賣线与平而相交. 例2、若两条相交直线中的一条在平面工內,讨论另一条直线与平而oc的位置关系.用符号语言表示为:若arib=A,bC:a,R>] aCZa或aAa=A.变式1、若两条异面直线中的一条在平而oc内,讨论另一条直线与平面oc的位虽关系.用符号语言表示为:若a与b异而则b//工或bAa=A.例3、若直线狄不平行于平而oc,且 y 则下列结论成立的是() A.a 内的所有直线与n 异而 B.oc 內的宜线与久都相交例如直线X B 与平而ABCD 相交,恵线AB 、CD 在平而ABCP 内,直线AB 与直线?/ B 相交,賣线CD 与直线工B 异面,所以A. B 都不正确;平面ABCP 內不存在与a 平行的 直线,所以应选D ・ 变式1.不在同一条直线上的三点A 、B 、C 到平而oc 的距离相等,且Aga,以下三个命题: ①AABC 中至少有一条边平行于oc;②AABC 中至多有两边平行于oc ;③ZLABC 中只可能有一条边与oo 相交.其中真命题畏 _______________ .其中真命题是①.萸式2、若賣线aCa,则下列结论中成立的个数是( (1) 00内的所有直线与a 异面 ⑵a 內的賣线与a 都相交 內不存在与次平行的直线A.OB.lC.2D.3分析:丁 直线 a (Za,/.a // a 或 ap|a=A.如图9,显然⑴⑵⑶(4)都有反例,所以应选A.咎案:A.知识点二直线与平面平行1、直线与平面平行的判定龙理:如杲平而外一条直线和这个平面内的一条直线平行,那么 这条直线和这个平而平行。
人教版数学高一必修2学案 -4 平面与平面之间的位置关系

2.1.3空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系目标定位 1.掌握直线与平面之间的三种位置关系,会用图形语言和符号语言表示.2.掌握平面与平面之间的两种位置关系,会用图形语言和符号语言表示.自主预习1.直线与平面的位置关系位置关系定义图形语言符号语言直线在平面内有无数个公共点a⊂α直线与平面相交有且只有一个公共点a∩α=A直线与平面平行没有公共点a∥α2.两个平面的位置关系位置关系图形表示符号表示公共点平面α与平面β平行α∥β没有公共点平面α与平面β相交α∩β=l 有一条公共直线1.判断题(1)若直线a在平面α外,则直线a∥α.(×)(2)若平面α内存在直线与平面β无交点,则α∥β.(×)(3)若平面α内的任意直线与平面β均无交点,则α∥β.(√)(4)与两相交平面的交线平行的直线必平行于这两个相交平面.(×) 提示(1)直线a在平面α外,则直线a∥α或a与α相交.(2)α与β可能平行,也可能相交.(4)若α∩β=b,且a∥b,则有a∥α且a∥β,或a⊂α,或a⊂β.2.若直线l与平面α不平行,则()A.l与α相交B.l⊂αC.l与α相交或l⊂αD.以上结论都不对解析若l与α不平行,则l与α相交或l⊂α.答案 C3.若两个平面互相平行,则其中一个平面内的一条直线与另一个平面的位置关系是()A.线面平行B.线面相交C.线在面内D.无法确定解析两面平行时,两个平面没有公共点,在一个平面的直线与另一个平面也没有公共点,所以它们平行.答案 A4.两条直线不相交,则两条直线可能平行或者异面;如果两个平面不相交,则两个平面________.解析两个平面之间的位置关系有且只有两种:平行或相交.答案平行类型一直线与平面的位置关系(互动探究)【例1】以下命题(其中a,b表示直线,α表示平面),①若a∥b,b⊂α,则a∥α;②若a∥α,b∥α,则a∥b;③若a∥b,b∥α,则a∥α;④若a∥α,b⊂α,则a∥b.其中正确命题的个数是()A.0B.1C.2D.3[思路探究]探究点一空间中直线与平面的位置关系有哪几种?提示空间中直线与平面只有三种位置关系:直线在平面内,直线与平面相交,直线与平面平行.探究点二判断直线与平面的位置关系的策略是什么?提示判断直线与平面的位置关系时可借助几何模型判断,通过特例排除错误命题.对于正确命题,根据线、面位置关系的定义或反证法进行判断.要注意多种可能情形.解析如图所示在长方体ABCD-A′B′C′D′中,AB∥CD,AB⊂平面ABCD,但CD⊂平面ABCD,故①错误;A′B′∥平面ABCD,B′C′∥平面ABCD,但A′B′与B′C′相交,故②错误;AB∥A′B′,A′B′∥平面ABCD,但AB⊂平面ABCD,故③错误;A′B′∥平面ABCD,BC⊂平面ABCD,但A′B′与BC异面,故④错误.答案 A规律方法 1.本题在求解时,常受思维定势影响,误以为直线在平面外就是直线与平面平行.2.判断直线与平面位置关系的问题,其解决方式除了定义法外,还可以借助模型(如长方体)和举反例两种行之有效的方法.【训练1】下列命题:①若直线l平行于平面α内的无数条直线,则l∥α②若直线a在平面α外,则a∥α③若直线a∥b,直线b⊂α,则a∥α④若直线a∥b,直线b⊂α,那么直线a就平行于平面α内的无数条直线其中假命题的序号是________.解析对于①,∵直线l虽与平面α内无数条直线平行,但l有可能在平面α内,∴l不一定平行于α,∴①是假命题;对于②,∵直线a在平面α外包括两种情况:a∥α和a与α相交,∴a和α不一定平行,∴②是假命题;对于③,∵直线a∥b,b⊂α,则只能说明a和b无公共点,但a可能在平面α内,∴a不一定平行于α,∴③是假命题;对于④,∵a∥b,b⊂α,那么a⊂α或a∥α,所以a可以与平面α内的无数条直线平行,∴④是真命题.答案①②③类型二平面与平面的位置关系【例2】给出的下列四个命题中,其中正确命题的个数是()①平面α内有两条直线和平面β平行,那么这两个平面平行;②平面α内有无数条直线和平面β平行,则α与β平行;③平面α内△ABC的三个顶点到平面β的距离相等,则α与β平行;④若两个平面有无数个公共点,则这两个平面的位置关系是相交或重合.A.0B.1C.3D.4解析如图,在正方体ABCD-A1B1C1D1中,对于①,在平面A1D1DA中,AD∥平面A1B1C1D1,分别取AA1、DD1的中点E,F,连接EF,则知EF∥平面A1B1C1D1.但平面AA1D1D与平面A1B1C1D1是相交的,交线为A1D1,故命题①错;对于②,在正方体ABCD-A1B1C1D1的面AA1D1D中,与A1D1平行的直线有无数条,但平面AA1D1D与平面A1B1C1D1不平行,而是相交于直线A1D1,故②是错误的;对于③,在正方体ABCD-A1B1C1D1中,分别取AA1,DD1,BB1,CC1的中点E,F,G,H,A1,B,C到平面EFHG的距离相等,而△A1BC与平面EFHG相交,故③是错误的;对于④,两平面位置关系中不存在重合,若重合则为一个平面,故命题④错.规律方法(1)判断两平面的位置关系或两平面内的线线,线面关系,我们常根据定义,借助实物模型“百宝箱”长方体(或正方体)进行判断.(2)反证法也用于相关问题的证明.【训练2】如果在两个平面内分别有一条直线,这两条直线互相平行,那么两个平面的位置关系一定是()A.平行B.相交C.平行或相交D.不能确定解析如图所示,由图可知C正确.答案 C[课堂小结]1.空间中直线与平面的位置关系有两种分类方式(1)按公共点的个数分类⎩⎪⎨⎪⎧直线与平面平行(直线与平面没有公共点)直线与平面不平行⎩⎨⎧直线与平面相交(直线与平面有唯一公共点)直线在平面内(直线与平面有无数公共点)(2)按是否在平面内分类⎩⎨⎧直线在平面内直线在平面外⎩⎨⎧直线与平面相交直线与平面平行2.判断直线与平面及平面与平面位置关系常用定义和反证法.1.如果直线a∥平面α,那么直线a与平面α内的()A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线不相交解析直线a∥平面α,则a与α无公共点,与α内的直线当然均无公共点.2.若M∈平面α,M∈平面β,则α与β的位置关系是()A.平行B.相交C.异面D.不确定解析∵M∈平面α,M∈平面β,∴α与β相交于过点M的一条直线.答案 B3.下列命题:①两个平面有无数个公共点,则这两个平面重合;②若l,m是异面直线,l∥α,m∥β,则α∥β.其中错误命题的序号为________.解析对于①,两个平面相交,则有一条交线,也有无数多个公共点,故①错误;对于②,借助于正方体ABCD-A1B1C1D1,AB∥平面DCC1D1,B1C1∥平面AA1D1D,又AB与B1C1异面,而平面DCC1D1与平面AA1D1D相交,故②错误.答案①②4.如图所示,平面ABC与三棱柱ABC-A1B1C1的其他面之间有什么位置关系?解∵平面ABC与平面A1B1C1无公共点,∴平面ABC与平面A1B1C1平行.∵平面ABC与平面ABB1A1有公共直线AB,∴平面ABC与平面ABB1A1相交.同理可得平面ABC与平面ACC1A1及平面BCC1B1均相交.基础过关1.若a,b是异面直线,且a∥平面α,则b与α的位置关系是()A.b∥αB.相交C.b⊂αD.b⊂α、相交或平行解析如图所示,选D.答案 D2.如果平面α外有两点A、B,它们到平面α的距离都是a,则直线AB和平面α的位置关系一定是()A.平行B.相交C.平行或相交D.AB⊂α解析结合图形可知选项C正确.答案 C3.α、β是两个不重合的平面,下面说法正确的是()A.平面α内有两条直线a、b都与平面β平行,那么α∥βB.平面α内有无数条直线平行于平面β,那么α∥βC.若直线a与平面α和平面β都平行,那么α∥βD.平面α内所有的直线都与平面β平行,那么α∥β解析A、B都不能保证α、β无公共点,如图①;C中当a∥α,a∥β时,α与β可能相交,如图②;只有D说明α、β一定无公共点,故选D.答案 D4.若a与b异面,则过a与b平行的平面有________个.解析当a与b异面时,如图,过a上任意一点M作b′∥b,则a与b′确定了唯一的平面α,且b∥α,故过a与b平行的平面有1个.答案 15.空间三个平面如果每两个都相交,那么它们的交线有________条.解析以打开的书页或长方体为模型,观察可得结论.答案1或36.如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是A1B1和BB1的中点,则下列直线与平面的位置关系是什么?(1)AM所在的直线与平面ABCD的位置关系;(2)CN所在的直线与平面ABCD的位置关系;(3)AM所在的直线与平面CDD1C1的位置关系;(4)CN所在的直线与平面CDD1C1的位置关系.解(1)AM所在的直线与平面ABCD相交.(2)CN所在的直线与平面ABCD相交.(3)AM所在的直线与平面CDD1C1平行.(4)CN所在的直线与平面CDD1C1相交.7.已知一条直线与一个平面平行,求证:经过这个平面内的一点与这条直线平行的直线必在这个平面内.解已知:a∥α,A∈α,A∈b,b∥a.求证:b⊂α.证明如图,∵a∥α,A∈α,∴A∉a,∴由A和a可确定一个平面β,则A∈β,∴α与β相交于过点A的直线,设α∩β=c,由a∥α知,a与α无公共点,而c⊂α,∴a与c无公共点.∵a⊂β,c⊂β,∴a∥c.又已知a∥b,且A∈b,A∈c,∴b与c重合.∴b⊂α.能力提升8.以下四个命题:①三个平面最多可以把空间分成八部分;②若直线a⊂平面α,直线b⊂平面β,则“a与b相交”与“α与β相交”等价;③若α∩β=l,直线a⊂平面α,直线b⊂平面β,且a∩b=P,则P∈l;④若n条直线中任意两条共面,则它们共面.其中正确的是()A.①②B.②③C.③④D.①③解析对于①,正确;对于②,逆推“α与β相交”推不出“a与b相交”,也可能a∥b;对于③,正确;对于④,反例:正方体的侧棱任意两条都共面,但这4条侧棱却不共面,故④错.所以正确的是①③.答案 D9.在长方体ABCD-A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D1、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有()A.2个B.3个C.4个D.5个解析如图所示,结合图形可知AA1∥平面BB1C1C,AA1∥平面DD1C1C,AA1∥平面BB1D1D.答案 B10.如果空间的三个平面两两相交,则下列判断正确的是________(填序号).①不可能只有两条交线②必相交于一点③必相交于一条直线④必相交于三条平行线解析空间的三个平面两两相交,可能只有一条交线,也可能有三条交线,这三条交线可能交于一点.答案①11.如图,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.解平面ABC与β的交线与l相交.证明如下:∵AB与l不平行,且AB⊂α,l⊂α,∴AB与l一定相交.设AB∩l=P,则P∈AB,P∈l.又∵AB⊂平面ABC,l⊂β,∴P∈平面ABC,P∈β.∴点P是平面ABC与β的一个公共点,而点C也是平面ABC与β的一个公共点,且P,C是不同的两点,∴直线PC就是平面ABC与β的交线,即平面ABC∩β=PC,而PC∩l=P,∴平面ABC与β的交线与l相交.探究创新12.试画图说明三个平面可把空间分成几个部分?解三个平面可把空间分成4(如图①)、6(如图②③)、7(如图④)或8(如图⑤)个部分.。
高中数学:空间点、直线、平面之间的位置关系 (17)

③a.若直线 a⊂平面 α,a,b 异面,则 b 与 α 的关系为________. b.若直线 a⊂平面 α,a,b 相交,则 b 与 α 的关系为________. 【答案】 a.平行或相交 b.相交或 b⊂α
第20页
题型二 平面与平面之间的位置关系 例 2 (1)已知平面 α,β ,且 α∥β ,直线 a⊂α,直线 b ⊂β,则直线 a 与直线 b 具有怎样的位置关系?画出图形. (2)已知平面 α,β,直线 a,b,且 a⊂α,b⊂β,α∩β= l,则直线 a 与直线 b 具有怎样的位置关系?画出图形.
B.m∥α D.m 在平面 α 外
【答案】 A
第11页
②若直线 l∩平面 α=A,直线 b⊂α,则 l 与 b 的位置关系 为________.
【答案】 相交或异面
第12页
③若直线 l∩平面 α=A,l 与直线 b 相交或异面,则 b 与 α 的位置关系为________.
【答案】 相交、平行或 b⊂α
第26页
(3)若三个平面两两相交,则它们将空间分六、七或八个部分, 如图③,④,⑤.
第27页
探究 3 本题考查了空间想象能力,分类讨论思想,相交平 面的画法.
第28页
解立体几何题时,比如直线与几个平面之间的位置关系,你 可以把手中的笔当成直线,把课桌或者课本当作平面,把教室当 作长方体,这样就将抽象的东西变得具体了.平时,动手做一些 立体模型,如长方体、立方体、圆柱、圆锥、正四面体等几何体 模型,这些都是建立空间想象力的途径.
例 1 下列说法:
①若直线 l 平行于平面 α 内的无数条直线,则 l∥α;
②若直线 a 在平面 α 外,则 a∥α;
③若直线 a∥b,直线 b⊂α,则 a∥α;
高中数学必修2第二章知识点总结

高中数学必修2知识点总结立体几何初步特殊几何体外表积公式〔c 为底面周长,h 为高,'h 为斜高,l 为母线〕chS =直棱柱侧面积')(2121h c c S +=正棱台侧面积rh S π2=圆柱侧()l r r S +=π2圆柱表rl Sπ=圆锥侧面积()l r r S +=π圆锥表l R r S π)(+=圆台侧面积()22R Rl rl r S +++=π圆台表柱体、锥体、台体的体积公式V Sh =柱2V Sh r h π==圆柱''2211()()33V S S S S h r rR R hπ=++=++圆台〔4〕球体的外表积和体积公式:V 球= ; S 球面=24R π第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系 1 平面含义:平面是无限延展的 2 三个公理:〔1〕公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内. 符号表示为A ∈LB ∈L => L α A ∈α B ∈α公理1作用:判断直线是否在平面内.〔2〕公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2作用:确定一个平面的依据。
〔3〕公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P ∈α∩β =>α∩β=L ,且P ∈L 公理3作用:判定两个平面是否相交的依据. 空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点。
2 公理4:平行于同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线a ∥bc ∥bLA·α C ·B·A · α P· αLβ 共面直线=>a ∥c强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小结: 直线与平面的位置关系 平面与平面的位置关系
记作 : a
①直线 a 和面α相交 : 如图:
a
记作 : a A
②直线 a 和面α平行 :
.
A
aLeabharlann 记作 : a // α 如图:
α
例题讲练:
例1.判断下列命题的正确 (1)若直线 l上有无数个点不在平面 内,则 l // 。( ) (2)若直线 l 与平面 平行,则l 与平面 内 的任意一条直线都平行。( ) (3)如果两条平行直线中的一条与一个平面平 行,那么另一条也与这个平面平行.( ) (4)若直线 l 与平面 平行,则l 与平面 内 的任意一条直线都没有公共点。( ∨ )
2
一个长方体切两刀可以分成多少块?3或4
一个长方体切三刀可以分成多少块?
D′ A′ D
4或5或6或7或8
C′
B′
C B
A
不妨再思考一题?
1、一个平面把空间分为几部分? 2 2、二个平面把空间分为几部分? 3或4 3、三个平面把空间分为几部分? 4或6或7或8
了解一下: n个平面最多可将空间分为 (n3 + 5n + 6)/6个部分
X
X
X
例2.若直线 a 不平行平面 ,且 a
例题讲练:
( A) (B) ( C) ( D)
内所有直线与a异面 内不存在与a平行的直线 内存在唯一的直线与a平行 内的直线与a都相交
则下列结论成立的是(B )
反思与延伸:
问题1.平行于同一平面的两条直线一定是两条 平行直线吗? 问题2.两条平行线中的一条平行一个平面,则 另一条也一定平行于这个平面吗? 问题3.无公共点的两条直线一定是平行直线吗?
全国名校高中数学优质学案汇编(附详解)
问题探究:
线段A′B所在直线与长方体 ABCD-A′B′C′D′的六个面所在 平面有几种位置关系?
D′ A′ D A B B′ C C′
直线与平面的位置关系及表示: (1)直线在平面内—有无数个公共点
记作:a
如图:
a
(2)直线在平面外—有一个公共点或没有公共点
D′ A′ D A B B′ C C′
两个平面之间的位置关系:
记作 : α // β
• l
记作 : α β = l
已知平面 , , 直线a, b, 且 // ,a , b , 则直线a与直线b具有怎样的位置关系?
例题讲练:
一个长方体切一刀可以分成多少块?
D′ A′ D A B B′
C′
C
小结:
直线与平面的位置关系有且只有三种 (1)直线在平面内-----有无数个公共点 (2)直线与平面相交----有且只有一个公共点 (3)直线与平面平行----没有公共点
a
a
.A
a
a
a A
a // α
问题探究:
围成长方体的六个面,两两之间的位置 关系有几种?
