10.2二重积分的计算(一)2011.4.11

合集下载

二重积分的定义和计算方法

二重积分的定义和计算方法引言：二重积分在数学中扮演着重要的角色，用于求解平面区域上的面积、质量分布、物理量等。

本文将介绍二重积分的定义以及常用的计算方法，帮助读者更好地理解和应用二重积分。

一、二重积分的定义二重积分用于计算平面上某个有界区域的面积或者其他类型的物理量。

其定义如下：设函数f(x,y)在闭区域D（边界为C）上连续，其中D的边界C由有限个简单光滑的曲线组成。

将D划分为m×n个小区域，区域在第i 行第j列的小区域记为ΔSij，并任选ΔSij上一点(xi,yi)。

当ΔSij趋近于零且区域D趋近于闭区间上的有限个点时，若二重极限$$\lim_{\substack{m,n \to\infty}}\sum_{i=1}^{m}\sum_{j=1}^{n}f(xi,yi)\Delta Sij$$存在，且与D的划分和点(xi,yi)的选择无关，则称该极限为函数f(x,y)在闭区域D上的二重积分，记为$$\iint_D f(x,y)dS$$其中，dS表示面积元素。

二、二重积分的计算方法1. 直角坐标系下的二重积分计算当函数f(x,y)在闭区域D上连续或者分段连续时，二重积分的计算可以通过以下两个步骤进行：步骤一：确定积分区域D的范围和边界方程。

根据题目的描述或者所给的图形，确定积分区域D的边界曲线的方程。

可以使用直线、圆等几何图形的方程来描述。

步骤二：建立二重积分的积分式，计算积分。

根据所给的积分区域D，在直角坐标系下建立对应的积分式，然后进行计算。

根据题目需求，可以选择使用直角坐标系的面积元素dS = dxdy或者极坐标系的面积元素dS = r dr dθ。

2. 极坐标系下的二重积分计算当函数f(r,θ)在极坐标系下连续或者分段连续时，二重积分的计算可以通过以下步骤进行：步骤一：确定积分区域D的范围和边界方程。

根据题目给出的信息或者图形，确定积分区域D在极坐标系下的范围和边界曲线的方程。

步骤二：建立二重积分的积分式，计算积分。

二重积分的计算

二重积分的计算二重积分的计算，是多元函数积分学的第一个难关，这一关过好了，对于其他类型（三重积分，曲线和曲面积分等）的积分，将开个好头，希望大家真正理解并掌握。

首先需要化点功夫弄明白二重积分的定义以及性质。

这里我就不写过多的内容，因为深入理解需要在具体的计算中才能加深理解，就事论事地背定义是很难有效果的。

二重积分的计算，最基本也是最根本的是要理解转化二重积分为累次积分的原理，即一个二重积分化为两个有先后次序的定积分，这2个定积分一般彼此存在着关系，先积分的那个定积分一般是后一个定积分的被积函数。

转化的前提是需要将被积区域D 表示为不等式形式。

二重积分的被积区域是个平面域，常用两种表示法：1）12()():x y x D a x b ϕϕ≤≤⎧⎨≤≤⎩，这时，累次积分的次序是“先y 后x ”，具体公式为2211()()()()(,)(,)(,)x x bb Da x a x f x y d f x y dy dx dx f x y dy ϕϕϕϕσ⎛⎫== ⎪ ⎪⎝⎭⎰⎰⎰⎰⎰⎰。

2）12()():y x y D c y d ψψ≤≤⎧⎨≤≤⎩，这时，累次积分的次序是“先x 后y ”，具体公式为2211()()()()(,)(,)(,)y y dd Dc y c y f x yd f x y dx dy dy f x y dx ψψψψσ⎛⎫== ⎪ ⎪⎝⎭⎰⎰⎰⎰⎰⎰。

上述公式表示的是在直角坐标系下的计算公式。

在直角坐标系下，对平面区域可以沿平行于坐标轴的直线来分划该区域，所以积分微元d dxdy σ=。

如果被积区域D 是一个矩形区域，则:c y dD a x b ≤≤⎧⎨≤≤⎩，而且被积函数可表为(,)()()f x y g x h y =，此时，二重积分实际变为两个独立定积分的乘积：(,)()()()()bd b dDa c a c f x y d g x h y dy dx g x dx h y dy σ⎛⎫== ⎪⎝⎭⎰⎰⎰⎰⎰⎰，这是二重积分计算中最简单的情况。

(完整版)第二节二重积分的计算

即等于两个定积分的乘积.
例2 求 x2e y2dxdy, 其中D 是以 (0,0),(1,1),(0,1)
D
为顶点的三角形.
解因 e y2dy 无法用初等函数表示,
所以, 积分时必须考虑次序.
x2e y2dxdy
1
dy
y x 2e y2 dx
0
0
D
e1 y2
y3 dy
1
1 y2e y2dy2 1 1 2
Oa
b x Oa
bx
f ( x, y)d
b
dx
2 ( x) f ( x, y)dy
a
1 ( x)
D
3. 若区域如图, 则必须分割. 在分割后的三个区域上分别使用积分公式. (利用积分区域的可加性)
y
D3
D1 D2
O
x
D
D1
D2
D3
例1 求 ( x2 y)dxdy,其中D是抛物线y x2和
0
3
60
6 e
例3 交换积分次序:
1
2 x x2
2
2 x
0 dx0
f ( x, y)dy 1 dx0 f ( x, y)dy
y
解积分区域:
y2 x
y 2x x2
O
1
2x
原式=
1
dy
2 y
f ( x, y)dx
0
1 1 y2
例4 计算积分 I
1
2 1
dy
1
y
y e x dx
(
x,
y)dx)dy
D
即
f y)dx.
D
c
1( y)

求二重积分的方法

求二重积分的方法在数学中，二重积分是一种重要的积分形式，它在物理、工程、经济学等领域都有广泛的应用。

求解二重积分的方法有很多种，本文将介绍几种常见的方法，希望能够帮助大家更好地理解和掌握二重积分的计算技巧。

一、直角坐标系下的二重积分。

在直角坐标系下，二重积分的计算通常采用先对x进行积分，再对y进行积分的方法。

对于给定的二元函数f(x,y)，其在有界区域D上的二重积分可以表示为：∬f(x,y)dxdy。

其中积分区域D可以用不等式形式表示为D={(x,y)|a≤x≤b,g1(x)≤y≤g2(x)}，此时二重积分可以表示为：∬f(x,y)dxdy=∫(∫f(x,y)dy)dx。

其中内层积分是对y进行积分，外层积分是对x进行积分。

在实际计算中，可以先对y进行积分，再对x进行积分，也可以反过来进行计算，选择合适的积分顺序可以简化计算过程。

二、极坐标系下的二重积分。

在某些情况下，使用极坐标系进行二重积分的计算会更加方便。

对于给定的二元函数f(x,y)，其在极坐标下的二重积分可以表示为：∬f(x,y)dxdy=∫(∫f(rcosθ,rsinθ)rdrdθ。

其中积分区域D可以用极坐标形式表示为D={(r,θ)|α≤θ≤β, h1(θ)≤r≤h2(θ)}。

在极坐标系下，二重积分的计算可以简化为对r和θ的积分，适用于一些具有极向对称性的函数。

三、变量代换法。

对于一些复杂的二重积分，可以通过变量代换的方法来简化计算。

常见的变量代换包括直角坐标系到极坐标系的转换、直角坐标系到柱坐标系的转换、直角坐标系到球坐标系的转换等。

通过适当的变量代换，可以将原积分区域D变换为一个更简单的区域，从而简化积分的计算。

四、二重积分的性质。

在计算二重积分时，还可以利用二重积分的性质来简化计算。

例如，二重积分具有线性性质，可以将一个复杂的二重积分拆分为若干个简单的二重积分相加；二重积分的积分区域可以进行分割，将原积分区域分割为若干个简单的子区域，分别计算再相加等。

二重积分运算

二重积分运算
二重积分运算是微积分中的一个重要概念，它是对二元函数在一个有限区域内的积分运算。

在实际应用中，二重积分运算被广泛应用于物理、工程、经济学等领域，是解决实际问题的重要工具。

二重积分运算的定义是：设f(x,y)在闭区域D上连续，则在D上的二重积分为：
∬Df(x,y)dxdy
其中，D表示二元函数f(x,y)的定义域，dxdy表示对x和y的积分运算。

二重积分运算的结果是一个数值，表示在D上f(x,y)的积分值。

二重积分运算的计算方法有两种：直接计算和变量代换法。

直接计算法是将二元函数f(x,y)在D上分割成若干个小区域，然后对每个小区域进行积分运算，最后将所有小区域的积分值相加得到二重积分的结果。

变量代换法是将二元函数f(x,y)在D上的积分转化为在另一个区域上的积分，然后再进行计算。

二重积分运算在实际应用中有着广泛的应用。

例如，在物理学中，二重积分运算可以用来计算物体的质心、重心、转动惯量等物理量；在工程学中，二重积分运算可以用来计算材料的强度、应力、变形等参数；在经济学中，二重积分运算可以用来计算市场需求、供给、价格等经济指标。

二重积分运算是微积分中的一个重要概念，它在实际应用中有着广泛的应用。

掌握二重积分运算的计算方法和应用技巧，对于解决实际问题具有重要的意义。

二重积分的数值计算和算法设计

二重积分的数值计算和算法设计二重积分是高等数学中重要的概念之一，它在实际应用中有着广泛的应用，比如物理学、金融学、统计学等一、什么是二重积分二重积分是在二维平面上求一个平面区域上的函数值的平均值，可以用于求面积、质心、惯性矩等.当被积函数 $f(x,y)$ 连续时，二重积分的计算公式为$$\iint_D f(x,y) \, \mathrm{d}A$$其中 $D$ 是平面上的一个有限闭区域，$\mathrm{d}A$ 是面积元。

二、二重积分的数值计算在很多情况下，二重积分很难通过解析的方式求解，这时我们需要使用数值计算的方式。

常用的数值计算算法有：矩形法、梯形法、辛普森法。

这些方法可以将二重积分变成多维积分，进一步转化为求解一维积分的问题，例如：矩形法的基本思想是将区域 $D$ 划分为若干个小矩形，然后把每个小矩形看作一面积元，对每个小矩形做一个面积公式，这样就相当于把二重积分转化为多个一重积分之和，然后再把它们相加即可得到原二重积分的近似值。

梯形法的基本思想是将区域 $D$ 划分为若干个小梯形，对每个小梯形做一个面积公式，这样就相当于把二重积分转化为多个一重积分之和，然后再把它们相加即可得到原二重积分的近似值.辛普森法的基本思想是将区域 $D$ 划分为若干个小梯形，不同于梯形法，辛普森法对每两个相邻的小梯形做一个简单二次函数的插值，然后将相邻两个小梯形和所在高度的三个位置计算一次牛顿-莱布尼茨公式，即可得到原二重积分的近似值。

当然，这些数值计算的方法都只是近似值，真实的二重积分值只有在精度趋于无穷时才能得到。

三、算法设计在实际应用中，需要根据具体问题的特点来选择合适的数值计算算法，并根据实际的输入数据的复杂度来选择合适的数据结构和算法。

例如，在求解面积的时候，我们可以先对平面区域进行参数化，然后使用梯形法或辛普森法进行计算；在求解质心时，我们需要用到面积元上的重心，可以通过参数方程和矩形法进行计算。

计算二重积分的几种简便方法

计算二重积分的几种简便方法计算二重积分是数学中的一个重要概念，在实际问题的建模和求解中有着广泛的应用。

但是对于初学者来说，计算二重积分可能是一个比较困难的任务。

有一些简便的方法可以帮助我们更轻松地计算二重积分。

本文将介绍几种简便方法来计算二重积分，希望能对大家的学习有所帮助。

一、直角坐标系下的计算我们首先回顾一下在直角坐标系下计算二重积分的过程。

设积分区域为D，函数为f(x, y)，则二重积分的计算公式为：∬ f(x, y) dA = ∫∫D f(x, y) dx dy其中D表示积分区域，dA表示面积元素，f(x, y)表示要被积的函数。

在直角坐标系下，我们通常通过将积分区域D分解为水平方向和垂直方向的两个部分，然后进行累次积分的方法来计算二重积分。

这种方法在处理一些复杂的积分区域时可能会比较繁琐，下面我们就介绍一些简便的方法来计算二重积分。

对于一些具有旋转对称性的积分区域，我们可以转换到极坐标系下来简化计算过程。

极坐标系的坐标变换公式为：x = rcosθy = rsinθr表示从原点到点(x, y)的距离，θ表示向量OP与x轴的夹角。

在极坐标系下，面积元素dA可以表示为:dA = rdrdθ利用这个变换，我们可以将二重积分转化为极坐标下的累次积分。

具体来说，我们首先确定极坐标系中r和θ的取值范围，然后进行r方向和θ方向的累次积分。

这样做可以帮助我们简化积分区域，并且在计算上也更加方便。

三、换元法除了极坐标系下的计算方法，换元法也是计算二重积分的一种简便方法。

换元法是一种常用的积分技巧，在解决一些复杂函数积分时特别有用。

换元法的基本思想是通过一些代数变换来简化被积函数或者积分区域。

对于二重积分来说，我们可以通过一些变换来将原积分转化为一个更容易计算的积分。

当积分区域为一个矩形时，我们可以通过线性变换来将其变为单位矩形，这样做可以大大简化计算过程。

换元法在实际应用中需要具体问题具体分析，需要我们灵活运用。

二重积分的计算方法

二重积分的计算方法在数学的广袤领域中，二重积分是一个重要的概念，它在许多实际问题和理论研究中都有着广泛的应用。

理解和掌握二重积分的计算方法，对于我们解决诸如计算平面区域的面积、物体的质量、重心等问题具有关键意义。

首先，让我们来明确一下二重积分的定义。

二重积分是用来计算在一个平面区域上的函数的累积量。

简单来说，就是把这个区域划分成无数个小的部分，对每个小部分上的函数值乘以小部分的面积，然后把这些乘积加起来。

接下来，我们探讨几种常见的二重积分计算方法。

直角坐标系下的计算方法是基础且重要的。

当积分区域是一个矩形时，计算相对简单。

假设积分区域为＄D ＝＼｛（x,y) ｜ a ＼leq x ＼leq b, c ＼leq y ＼leq d\｝＄，被积函数为＄f(x,y)＄，则二重积分可以表示为：＼＼iint_D f(x,y) ＼，dx\，dy ＝＼int_a^b ＼left(＼int_c^d f(x,y) ＼，dy ＼right)dx＼这意味着我们先对＄y$ 进行积分，把＄x$ 看作常数，得到一个关于＄x$ 的函数，然后再对＄x$ 进行积分。

如果积分区域不是矩形，而是由直线围成的一般区域，比如＄D ＝＼｛（x,y) ｜＼varphi_1(x) ＼leq y ＼leq ＼varphi_2(x)， a ＼leq x ＼leq b\｝＄，那么二重积分可以表示为：＼＼iint_D f(x,y) ＼，dx\，dy ＝＼int_a^b ＼left(＼int_{＼varphi_1(x)｝＾｛＼varphi_2(x)｝ f(x,y) ＼，dy ＼right)dx＼这种情况下，我们先对＄y$ 积分，然后对＄x$ 积分。

极坐标系下的计算方法在处理具有圆形或扇形特征的积分区域时非常有用。

在极坐标系中，点的坐标表示为＄（r,＼theta)＄，其中＄r$ 表示点到原点的距离，＄＼theta$ 表示极角。

如果积分区域可以用极坐标表示为＄D ＝＼｛（r,＼theta) ｜＼alpha ＼leq ＼theta ＼leq ＼beta, ＼varphi(＼theta) ＼leq r ＼leq ＼psi(＼theta)＼｝＄，被积函数为＄f(x,y) ＝ f(r\cos\theta, r\sin\theta)＄，那么二重积分可以表示为：＼＼iint_D f(x,y) ＼，dx\，dy ＝＼int_{＼alpha}＾｛＼beta} ＼left(＼int_{＼varphi(＼theta)｝＾｛＼psi(＼theta)｝ f(r\cos\theta, r\sin\theta) r ＼，dr ＼right)d\theta＼这里需要注意的是，多了一个＄r$ ，这是因为在极坐标下，面积元素＄dx\，dy$ 要换成＄r\，dr\，d\theta$ 。

二重积分的计算方法资料

二重积分的计算方法资料二重积分是微积分中的重要内容，在物理、工程、统计学等领域都有广泛应用。

本文将介绍二重积分的计算方法，包括定积分计算与几何应用两个方面。

一、定积分计算方法（一）极坐标下的二重积分计算：在极坐标下，平面上的一个点可以用极径和极角来表示。

设区域D由曲线r=f(θ)和两直线θ=a，θ=b（0≤a≤b≤2π）所围成。

要计算D上的二重积分，可以通过极坐标转换来简化计算。

1.若函数f为连续函数，则有二重积分I = ∬D f(x,y) dA = ∫ab ∫f(r，θ) r dθ dr2.计算时，先按θ积分，再按r积分。

3.需要注意的是，r的取值范围是由f(θ)和直线θ=a，θ=b所围成的区域。

（二）直角坐标下的二重积分计算：在直角坐标系下，可以利用定积分的性质计算二重积分。

设区域D的上下界分别为y=g1(x)和y=g2(x)（a≤x≤b），则有二重积分I = ∬D f(x,y) dA = ∫ab ∫g2(x) g1(x) f(x,y) dy dx1.计算时，先按y积分，再按x积分。

2.需要注意的是，y的取值范围是由g1(x)和g2(x)所围成的区域。

对于一些复杂的积分，可以通过换元法来简化计算。

一般来说，选择适当的变量替换可以使原积分转化为更简单的形式。

1.平面区域变换：设变换为x = φ(u,v)，y = ψ(u,v)，则有 dA = ，J， du dv，其中J为变换的雅可比行列式，可利用行列式的性质计算。

2.极坐标变换：设变换为x = r cos(θ)，y = r sin(θ)，则有dA = r dr dθ。

3.球坐标变换：设变换为x = ρ sinφ cosθ，y = ρ sinφ sinθ，z = ρcosφ，则有dV = ρ^2 sinφ dρ dφ dθ。

（四）离散型二重积分与曲边梯形面积：如果函数f(x,y)是有界函数，并且在区域D上有无穷多个不连续点，则可以通过计算曲边梯形面积来近似计算二重积分：I ≈ ∑f(xi,yi) ΔA = ∑f(xi,yi) Δx Δy其中(Δx,Δy)为曲边梯形的底边与两侧边长，(xi,yi)为底边上的任意点。

二重积分四则运算公式

二重积分四则运算公式二重积分有许多应用，如精密物理、化学和工程中物体的性质数学模型，是描述物体的物理性质或者内部结构的一种数学工具。

它的定义及应用非常清楚，但是它的四则运算的公式却一直都很模糊，很多人都不知道它的各种公式。

为了让大家明确了解二重积分四则运算的公式，本文将介绍二重积分的四则运算的公式，以及计算的实例和它们相关的理论。

首先，我们介绍二重积分四则运算的加法公式，它的计算方式为： $$ iint limits_U f(x,y) dx dy+iint limits_V g(x,y) dx dy=iint limits_{Ucup V} [f(x,y)+g(x,y)] dx dy $$ 其中，f(x,y)和g(x,y)分别为U和V区域上的函数，U和V构成的是两个二重积分的区域。

可以看出，在U和V区域上，可以计算出f和g函数的二重积分，将两个二重积分相加，就可以得到U和V构成的全新区域求出的函数f+g的二重积分。

计算它们的加法公式就是上述所示。

接下来，我们看看二重积分的减法公式，它的计算方式为：$$ iint limits_U f(x,y) dx dy-iint limits_V g(x,y) dx dy=iint limits_{Usetminus V} [f(x,y)-g(x,y)] dx dy $$ 它的计算方式与加法公式类似，也是将U和V区域构成的新区域求出的函数f-g的二重积分来计算，只不过是将f和g的函数进行减法运算，而加法是进行加法，其他的步骤都是一样的。

接下来，我们介绍二重积分的乘法公式，它的计算方式为：$$ iint limits_U f(x,y) dx dycdot iint limits_V g(x,y) dx dy=iint limits_Uiint limits_V [f(x,y) cdot g(x,y)] dx dy $$它的计算方式与上面两个公式不同，它不是求U和V构成的新区域求出的函数，而是在U和V区域分别求出函数f(x,y)和g(x,y)的乘积，然后求出U和V区域两两乘积的积分即可。

二重积分的计算(1)

1
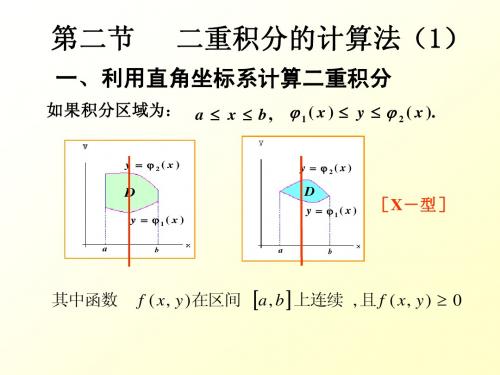
–1
例4 将二重积分换序 I =
∫
a
0
dx ∫
2 ax − x 2
x
f ( x , y )dy
0≤ x≤a D: x ≤ y ≤ 2ax − x 2
y 2 = 2ax − x 2
y
a
x = a − a2 − y2
即 y + ( x − a) = a
又Q x ≤ a,
2
2
2
∴x−a = − a − y
所围立体在 xoy 面上的投影是
Q 0 ≤ x + y ≤ 1, ∴ x + y ≥ xy ,
所求体积V =
1 1− x
∫∫ ( x + y − xy )dσ
D
= ∫0 dx ∫0 ( x + y − xy )dy
1 7 3 = ∫0 [ x (1 − x ) + (1 − x ) ]dx = . 24 2
a x
(练习)将二重积分化成二次积分将二重积分化成二次积分二先对 y 积分
y
I=
∫∫ f ( x , y )dxdy
D
b
o y D
I=
a x
∫
a
0
dx ∫
b x a 0
f ( x , y )dy
b
o y
.
D
I=
a x
x y + =1 a b .
∫
a
0
dx ∫b f ( x , y )dy
a x
0
∫
x
=
∫
1
0
xdx ∫ 2 ydy
x
x
1 1 1 3 5 = = ∫ ( x − x )dx 24 2 0

102二重积分的计算法一

分部积分法(略). (05/06学年第一学期考试题A卷)
解Ⅱ 化为二次积分,交换积分次序
原式=
1
(
xey2dy)dx
1
dx
xey2dy
1
dx
1ey2dy
01
01
0x
0x1 DX : xy1
DY
:
0y1 0xy
原式
1
dy
yey2dx
00
1ey2dy
y
dx
e 1 y2
ydy
0
公式1
上式称为 y后先 x对的对二次积分
几点小结
Df(x ,y )d x d ya b [ 1 2 (( x x ))f(x ,y )d y ]d x
9
①通过体积作 ,实为现过了渡二重积计分算的方一法种
通过计算两次(单定积积)来分分求. 解
②二重积分的计算关定键限是：投影穿线法
2(x0)
AA((xx0 )0 )
1(x0) oo aa xx00
xx
bbyy1(1x()x)
1(x0)
2(x0)
A A ((x x0)) 1 2 1 (2 ((x(x x)x 0 )0 ))ff(x (,xy 0,)y d)ydy
b
VaA(x)dx
即得
D D ff( (x ,y ) )d d a b a [ b d x 1 2 (( x x ) )1 2 (f( x x ) ()x f,y () x d ,y y ]) d d x y .
12
例1 计算 x d y ,其D ：中 y 由 1 ,x2 及 yx所围. 闭
D
解 Ⅰ
看作X－型域