有限自动机的一种化简方法
有限自动机理论06章图灵机-简化

使用=>+代表格局的多次变换 使用=>*代表格局的任意次变换
定义6-4
图灵机 M= ( Q , ∑,
q 0 , qα , δ ) 在字母表 ∑ 上接收的语言为 L(M) , 则 L(M)={w|存在w1,w2∈(∑′)* 有 q0w =>* w1qαw2 }
定义6-5 完全的图灵机
如果图灵机对于一切输入串都能够停 机----完全的图灵机。 完全的图灵机接收的语言 L 称为递归 语言(图灵可判定语言)
③在 seek_a 状态时,没有再发现 a ,需 检查是否所有的b都已经被扫描过。 <seek_a,$,check,$,R> <check,$,check,$,R> <check,B,accept,B,N>
某些不需要定义的规则 <start,b,? > //无a
<start,B,? > //无a 无b <del_b,B,? > //b少 <seek_a,B,? > //无b <seek_a,b,? > //不可能 <check,b,? > //b多
6.1 图灵机的基本模型
6.1.1 图灵机的定义
图灵机的物理模型
a1 a2 a3 … aj … an an+1 …
FSC
一个有限状态控制器(FSC) 一个外部的存储设备 可以向右扩展的无限长度带 带上具有左端点,使用“┣”表示 图灵机直接扫描输入带上左端点右边 的第一个符号。
带分解为单元,每个单元可以为 空或存放字母表上的字母符号 带的空白单元标记为B 有限状态控制器通过一个读/写头 与带进行耦合。
②处于状态 del_b ,扫描到 b ,用 # 代替 它,向左寻找a,(从①重复循环) <del_b,b,seek_a,#,L> <seek_a,#,seek_a,#,L> <seek_a,a,del_b,#,R> //最右的a
第3章-3-有限自动机.解析

种性质的FA称为非确定的FA(NFA:
Nondeterministic FA)
二、非确定有穷状态自动机
a A aa
S ab Z a
bB b a
例如:文法G3.1 Z → Za|Aa|Bb A → Ba|Za|a B → Ab|Ba|b
二、非确定有穷状态自动机
一个非确定的有穷自动机(NFA)M是一 个五元组:N=(K,Σ,f,S0,Z)其中
DFA f的定义
2.为定义DFA所接受(或识别)的符号串集合,我们
先将其转换函数f 的定义域拓广到 f^: K* : (1)f^ (s,)=s, sK; (2)f^ (s,aw)=f^ ( f(s,a),w), sK,a,w*;
对于x* ,f^(s,x)=t 的含义是,当自动机M从 状态s出发,依次扫描完x的各个符号后将进入状 态t.
第三章 词法分析
3.1 词法分析概述 3.2 正规文法和状态转换图 3.3 有限自动机 3.4 正规表达式和正规集 3.5 词法分析器的实现
3.3 有限自动机
一、确定有穷状态自动机(DFA) 二、非确定有穷状态自动机(NFA) 三、NFA和DFA的转换
四、具有ε-动作的NFA 五、ε-动作的NFA的确定化
实质:用自底向上方法识别句子 状态转换的下一状态不唯一,如何解决?
三、NFA和DFA的转换(NFA的确定化)
NFA状态转换的下一状态不唯一,如何解决? 确定化的概念 1.确定化:对任给的NFA,都能对应地构造一
DFA,它们有相同的接受集 2.确定化原理:令构造出的“新”DFA的状态 与“旧”NFA的某一状态子集对应,并使 “新”DFA对“旧”NFA的状态转移保持跟 踪。
1.K’=2k.即,由M的全部状态子集构成,特别地, 令 S0’=[S0].
DFA的化简分析

DFA(确定的有穷自动机)的化简1. 实验内容输入一个DFA M,输出一个与之等价的最小化的DFA M’,设计并实现将NFA确定化为DFA的子集构造算法,输入非确定有限(穷)状态自动机,输出确定化的有限(穷)状态自动机编写一个程序,将一个非确定有限自动机转换为确定有限自动机。
2. 实验设计分析2.1 实验设计思路首先输入边集找到状态与边的关系,然后输入终结点,这样一个没有简化的NFA图就表示出来了,然后利用求闭包的方式求move集合,画出状态转化图,重命名后进行集合划分,再次重新画出状态转换矩阵,输出简化后的DFA。
2.2 实验算法(1)构造具有两个组的状态集合的初始划分I:接受状态组 F 和非接受状态组Non-F。
(2)对I采用下面所述的过程来构造新的划分I-new.For I 中每个组G doBegin当且仅当对任意输入符号a,状态s和读入a后转换到I的同一组中;/*最坏情况下,一个状态就可能成为一个组*/用所有新形成的小组集代替I-new中的G;end(3)如果I-new=I,令I-final=I,再执行第(4)步,否则令I=I=new,重复步骤(2)。
(4)在划分I-final的每个状态组中选一个状态作为该组的代表。
这些代表构成了化简后的DFA M'状态。
令s是一个代表状态,而且假设:在DFA M 中,输入为a时有从s到t转换。
令t所在组的代表是r,那么在M’中有一个从s到r的转换,标记为a。
令包含s0的状态组的代表是M’的开始状态,并令M’的接受状态是那些属于F的状态所在组的代表。
注意,I-final的每个组或者仅含F中的状态,或者不含F中的状态。
(5)如果M’含有死状态(即一个对所有输入符号都有刀自身的转换的非接受状态d),则从M’中去掉它;删除从开始状态不可到达的状态;取消从任何其他状态到死状态的转换。
2.3 实验流程1. 输入NFA各边信息(起点条件[空为*] 终点),以#结束2. 输入终态3. 求e-clouse闭包,将结点移入相应的闭包集合,并重新排序4. 输出状态转换矩阵,转换成DFA并重命名5. 执行DFA最简化6. 重命名DFA,输出最简化DFA状态转换矩阵2.4 实验的基本技术设计方案实验中含有一些数据结构的知识,假设I是NFA M状态集K的一个子集(即I∈K),则定义ε-closure(I)为:若Q∈I,则Q∈ε-closure(I);若Q∈I,则从Q出发经过任意条ε弧而能到达的任何状态Q’,则Q’∈ε-closure(I)。
有限自动机理论-4章正则语言

可以简化为无ε的NFA
定理4-2
如果语言L被一个DFA所接收,则语言L可以用一个正则表达式来表示。
证明:
设语言L被DFA=(Q,∑,δ,q1,F)所接收;
状态集合Q中有n个状态,按任意顺序进行编号;即Q={q1,q2,q3,…,qn}。
使用记号Rijk代表字符串的集合,具体定义为:
Rijk={w|δ* (qi,w)= qj,且对于w的任何前缀x(x≠w,x≠ε),如果δ* (qi,x)= ql},则l≤k}
其中某些正则表达式已经被化简;
例如
r221= r210(r110)*r120+r220=0(ε)*0+ε,可以化简为00+ε;
01
03
02
又例如
r132=0(00)*(ε+0)1+1
r132= r121(r221)*r231+r131=0(ε+00)*(1+01)+1,由于(ε+00)*可以化简为(00)*,(1+01)可以化简为(ε+0)1,则
Rijk是所有那些将DFA从给定状态qi引导到状态qj,并且中间不经过(进入并离开)编号大于k的任何状态的所有字符串的集合,
要注意的是,i,j的大小与k的大小无关;
01
显然,Rijn是所有那些将DFA从给定状态qi引导到状态qj的字符串的集合。
02
01
根据定义,可以得出如下的递推公式:
02
{a|δ(qi,a)= qj} 若i≠j
从ε-NFA的开始状态出发,通过两个ε动作,可以直接进入NFA的惟一接收状态f0(以便能够接收空串ε);或者到达M1的开始状态q1,然后,从M1的开始状态q1出发,使用M1自己的δ函数,到达M1的惟一接收状态f1,
计算机编译原理课后习题及答案详细解析
在此深情而热烈的感谢沈仲秋同学的大力支持和帮助,同时希望本文档对各位有些帮助。
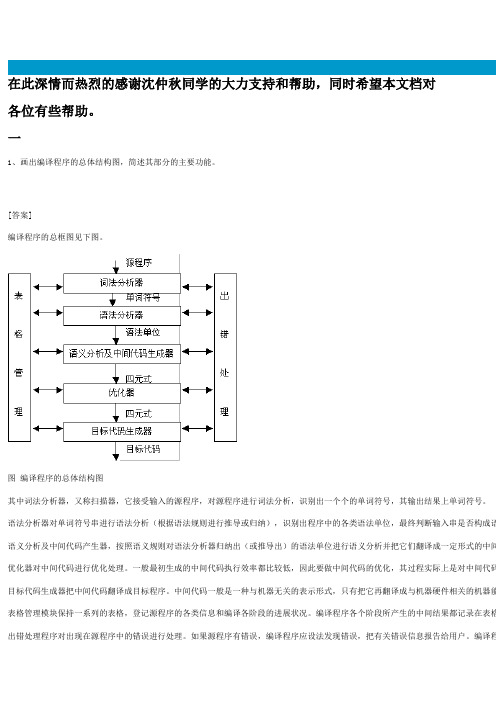
一1、画出编译程序的总体结构图,简述其部分的主要功能。
[答案]编译程序的总框图见下图。
图编译程序的总体结构图其中词法分析器,又称扫描器,它接受输入的源程序,对源程序进行词法分析,识别出一个个的单词符号,其输出结果上单词符号。
语法分析器对单词符号串进行语法分析(根据语法规则进行推导或归纳),识别出程序中的各类语法单位,最终判断输入串是否构成语语义分析及中间代码产生器,按照语义规则对语法分析器归纳出(或推导出)的语法单位进行语义分析并把它们翻译成一定形式的中间优化器对中间代码进行优化处理。
一般最初生成的中间代码执行效率都比较低,因此要做中间代码的优化,其过程实际上是对中间代码目标代码生成器把中间代码翻译成目标程序。
中间代码一般是一种与机器无关的表示形式,只有把它再翻译成与机器硬件相关的机器能表格管理模块保持一系列的表格,登记源程序的各类信息和编译各阶段的进展状况。
编译程序各个阶段所产生的中间结果都记录在表格出错处理程序对出现在源程序中的错误进行处理。
如果源程序有错误,编译程序应设法发现错误,把有关错误信息报告给用户。
编译程2、计算机执行用高级语言编写的程序有哪些途径?它们之间的主要区别是什么?[答案]计算机执行用高级语言编写的程序主要途径有两种,即解释与编译。
像Basic之类的语言,属于解释型的高级语言。
它们的特点是计算机并不事先对高级语言进行全盘翻译,将其变为机器代码,而是每读总而言之,是边翻译边执行。
像C,Pascal之类的语言,属于编译型的高级语言。
它们的特点是计算机事先对高级语言进行全盘翻译,将其全部变为机器代码,再统1.文法G[S]为:S->Ac|aBA->abB->bc写出L(G[S])的全部元素。
[答案]S=>Ac=>abc或S=>aB=>abc所以L(G[S])={abc}2. 文法G[N]为:N->D|NDD->0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?[答案]G[N]的语言是V+。
有限自动机最小化算法的实现

[ 摘 要]实现 D AM 一 ( 三, q , ) F Q, ,。 F 最小化算法 的关键 问题是如何编程求取商集 Q R ( / 即状态的 k阶区
分 ) 引入 等 价 关 系 S 与 商 集 Q/ 状 态 的 严 格 k阶 区 分 )证 明 了 R . s( , 一 R N S , 因此 Q 风 是 Q/  ̄。 / R- 中等
R 一 { q V ( ( )l ( E ,
^ l l 走 一 ≤ )
( P, ( )∈ F一 q )E F) } (, ).
显 然 , 与R R 是 Q上 的等价关 系. 关 于 R, 的等 q R
示 状态 之 间的 内在联 系[ , 于其 存储 实现 [ , 于 7便 ] 8便 ]
一
R = { P,)lV ∈ ( q (
一
论 与应 用仍是 一个 较 活跃 的研究 领域 . tmaa 简称 DF 的最 小 化 仍 是 有 限 自动 机 应 用 o t, A)
及 实现 方面 的重要 问题 之 一. A 的最小 化 可 以揭 DF
( , ( )∈ F一 q )E F) } (, ).
建立用 D A描述 的任务模 型 l , 些理论 问题 也与 F _ 一 g j 最 小化 思想 有关 _ jDF 的最 小 化是 指 构造 一 个 g . A 。 与之等 价且 状态 数 最 小 的 D A, F 即等 价最 小 D A. F
价类分 别记 为E 3与 E 3 q q .
作为新 的状态 , 而得 到 等价最 小 D A. 今 为止 , 从 F 迄
Q/ 一 [。 , = {q qE F) R, q] E3l ,
否 []n ( q , )一 [ ( , ) . a∈ . q n ] qE Q,
关于有限自动机的简介

特点:
程序短小,但占用存储空间多
DFA的实现2
状态转换图的形式: 每个状态对应一个带标号的case语句 转向边对应goto语句
a
i b
j
Li: case CurrentChar of
a
k b
:goto Lj
: goto Lk
特点: 程序长,但占用存储空间少
other : Error( )
NFA到DFA的转换
合并 (Close(S)) 1.对S状态寻找边,如果有令Ss={S} 2.对任意状态SiSs,如果有:f(Si,)= Sj则 消除边:Ss= SsSj 重复上述操作直至没有边 3.对a f(Ss,a)= f(Sk,a) Ss={S1,…,Sm},k=1,…,m. 4.如果Ss中包含初始状态则Ss也为初始状 态,如果有终止状态,则Ss为终止状态。
a
U
b a
a a,b
S
b
Q
b
V
状态转换图
字符 状态 S
a U
b V
U V
Q
Q U
Q
V Q
Q
状态转换表
DFA接受的字符串
对于*中的任何字符串t,若存在一条从初始 结点到某一终止结点的路径,且这条路上所 有弧的标记符连接成的字符串等于t,则称t 可为DFA M所接受(识别)。 DFA M 所能接受的字符串的全体记为L(M).
DFA的确定性
初始状态唯一。 转换函数f:SSSS是一个单值函数,也就 是说,对任何状态SSS,和输入符号a , f(S,a)唯一地确定了下一个状态。即转换函 数至多确定一个状态。 没有空边。即没有输入为()
编译原理第6讲 词法分析3--有限自动机等价性

{1,6,4,2,Y} {1,5,4,2,Y} {1,3,6,2,4,Y}
{1,5,4,2,Y} {1,3,5,2,4,Y} {1,6,4,2,Y}
DFA与NFA的等价性证明
把表看成状态转换矩阵,子 集视为状态
转换表唯一刻划了一个确定 的有限自动机M
初态是-closure({X})
M’ X
a
两个状态不等价,则称它们是可区别的
测试:状态的可区分性
两个状态s和t是可区分的,是指( )
A. 对于任意字,要么s读出停止于终态而t读出
停止于非终态,要么t读出停止于终态而s读
出停止于非终态
视频区域
B. 存在一个字,要么s读出停止于终态而t读出 停止于非终态,要么t读出停止于终态而s读 出停止于非终态
重复上述过程,直到所有第2, 3列子集全部出现在第一列为止
I
视I频a 区域 Ib
-Closure({X}) {...} {...}
{...}
{...} {...}
{...}
{...} {...}
DFA与NFA的等价性证明
M’
a
a5a
a
X 1 2
3 4 Y
b
b6 b
b
I -closure({X})={X,1,2}
DFA与NFA的等价性证明
确定化:不失一般性,设字母表只 包含两个 a 和b,我们构造一张计 算状态集的转换表:
首先,置第1行第1列为closure({X})求出这一列的Ia,Ib;
然后,检查这两个Ia,Ib,看它 们是否已在表中的第一列中出 现,把未曾出现的填入后面的 空行的第1列上,求出每行第2, 3列上的集合...
达的状态集合。
有限状态机设计与化简

有限状态机设计与化简
在设计和实现有限状态机时,我们经常遇到的一个问题是状态机可能会变得复杂和冗长,导致难以管理和维护。
因此,我们需要一个方法来对有限状态机进行化简,以简化设计和提高可读性。
1.确定状态集合:首先,我们需要明确系统中可能的所有状态。
这些状态应该能够完整地描述系统的行为和状态。
2.确定输入符号集合:然后,我们需要确定能够影响状态转移的所有输入符号。
3.确定输出符号集合:接下来,我们需要确定状态机可以产生的所有输出符号。
4.确定转移函数:转移函数定义了从一个状态到另一个状态的转移条件。
我们需要根据系统要求确定转移函数的具体形式和条件。
5.绘制状态转移图:借助状态转移图,我们可以直观地表示状态之间的转移关系。
图中的节点表示状态,边表示状态之间的转移,边上的标记表示触发该转移的输入符号。
6.确定等价状态:等价状态是指在任何输入序列下,状态机的行为是相同的。
我们可以使用不同的方法(如等价关系、状态等价识别算法等)来确定等价状态。
7.合并等价状态:一旦我们确定了等价状态,我们可以将它们合并成一个新的等价状态。
通过合并等价状态,我们可以显著减少状态机的复杂性和冗余。
8.重绘状态转移图:最后,我们需要使用新的等价状态更新状态转移图。
新的状态转移图应该更简洁和易读,同时保留了原始状态机的行为。
通过以上步骤,我们可以对有限状态机进行设计和化简,从而简化复杂的状态机,并提高其可读性和可维护性。
这对于开发和设计各种自动控制系统、软件系统和电路系统等具有重要意义。
确定有限自动机的化简

确定有限自动机的化简
一、准备知识
引论一:s1、s2是S中的两个等价状态,a 是符号表Σ中的一个符号,如果δ(s1,a)存在, 则δ(s2,a)亦存在,且δ(s1,a)与δ(s2,a)等价。 引论二:s1、s2是S中的两个状态,对Σ中 任意符号a,如果δ(s1,a)存在,则δ(s2,a)必存在 且二者等价,则s1与s2等价。 引论三:如果A、B是S中的两个子集,且 A与B中状态两两不等价,则对Σ中的一个符号a, δ-1(A,a)与δ-1(B,a)中状态两两不等价。
二、确定有限自动机的化简
1、令A1=F(终止状态集)、A·=S-A1。 则A1与A2之状态两两不等价。 2、设已构造出A1、A2、……、Ak,对任 意的i,j,Ai与Aj中状态两两不等价,对任意的符 号a,则δ-1(Ai,a)∩Aj,i,j=1,2,3,……,k中任两个 状态子集中状态是两两不等价。 3、重复2直到状态集数不增加止,则每一 个状态集中任两个状态等价。将等价状态合并 成一个状态,即为简化的DFA。
6}。 。
得如下分划π: 得如下分划 : 1பைடு நூலகம்{0}, , 4={3,4,5,6}。 , , , 。
2={1}, ,
3={2}, ,
简化后的确定有限自动机如下: 简化后的确定有限自动机如下:
a 0 b a 2
1 b
a
3 b
词法分析器自动生成
Lex语言定义: 辅助定义式 %% 识别规则 %% 用户子程序
三、举例
将下面不确定有限自动确定化并化简成最简型
有穷自动机的化简与确定化

1.2课题意义
编译程序的这些过程的执行先后就构成了编译程序的逻辑结构。有 穷自动机(也称有限自动机)作为一种识别装置,它能准确地识别正规 集,即识别正规文法所定义的语言和正规式所表示的集合,引入有穷自 动机这个理论,正是为词法分析程序的自动构造寻找特殊的方法和工 具。正规表达式与自动机理论在词法构造乃至整个编译器构造过程中起 着至关重要的作用,同时它们被广泛应用于计算机科学的各个领域,它 们与计算机其它学科之间也有着很大的联系。
目
1课题综述
1.1课题来源 1.2课题意义 1.3预期的目标 1.4面对的问题 1.5需解决的关键技术
录
2 系统分析
2.1涉及的知识基础 2.2总体方案 2.3解决问题的基本思路 2.4功能模块图
3 系统设计
3.1实现原理 3.2实现方法 3.3详细流程图
4代码编写
4.1 NFA到DFA的转化
5 程序调试
2.2总体方案
(1)如果读入正规式,则先将其转换为NFA,再将此NFA转换为DFA 并最小化,输入测试字符串,输出测试结果。 (2)如果读入NFA,则将其转化为DFA并最小化,输入测试字符串, 输出测试结果。 (3如果读入DFA,则直接将其最小化,输入测试字符串,输出测试结 果。
2.3解决问题的基本思路
11课题来12课题意13预期的目14面对的问15需解决的关键技21涉及的知识基22总体方23解决问题的基本思24功能模块31实现原32实现方33详细流程41nfa到dfa51调试步52发现的问53解决的方13参考文14编译原理课程设计报告课题综述11课题来源由于很多计算机系统都配有多个高级语言的编译程序对有些高级语言甚至配置了几个不同性能的编译程序
(1)按照设计的要求和内容先画出流程图,通过使用switch语句来完 成,对于头文件通过上网找了相应的资料正确地添加了程序中所需的头 文件: 用 .h 的头文件,就不用 using namespace std; 用 没有 .h 的头文件,就 必须 用 using namespace std。 conio.h是字符屏幕操作头文件。 (2)通过type(char re)函数实现:如果遇到操作符:|和*,则return OP;遇到操作数则return OP_D;其他则return -1。 (3)NFA构造算法
形式语言自动机有限自动机

2、子集构造,计算状态可达
0
1
p {q}
q { q { q, r
{p} {q
r } }
3、经筛选后的DFA
0, 1
{ q } }{ q
{r }
{ }p, q } { q
0
{ p, r }{ q
Start
1 {p} 0
{q} 1
{q,r}
1 }{ q, r { }p, q, r }
}{ q }{ q
转移图和转移表表示的NFA
0, 1
(1)
Start p 0 q 1 r
0
p {q q }{ q
r }
0, 1
(2)
0
Start p 1
q 0, 1 r
p {p q }{ r
注:转移表中的每一项都是一个集合。含空集Φ r }
1
{ q, r
}
1
{ p, q }{ r}
二、NFA的状态转移函数
与 DFA 唯一不同之处 : Q T 2Q
{ p, q } { p, q, r }
0, 1
q
r
0
{p,q}
1
1
1
Start {p}
0
1
{p,q,r}
0
0
{p,r}
证明:从 NFA 构造等价的 DFA
设 N = (QN, T, N , q0 , FN) 是一个 NFA , 通过子集构造法 得到相应的DFA D = (QD, T, D , [q0 ], FD ), 则 对任何ω T* , D ( {q0 } , ω ) = N (q0 , ω).
将过河问题模型化:
MG-WC (处于左岸的子集- 处于右岸的子集)
2.5 有限自动机的化简

极小有限自动机
• Myhill-Nerode定理 定理:米希尔-尼罗德定理,用字 定理 符串等价关系给出了正规语言的两个特征。是DFA 化简的理论依据。 • 极小有限自动机的唯一性 极小有限自动机的唯一性:正规语言的极小有限 自动机是同构的。 • 极小有限自动机的构造方法 极小有限自动机的构造方法:将给定的DFA转化为 等价的极小DFA。
q0 q1 q2 q4 q5 q6 q7
合并等价状态
q0 , q4
q1 , q7
q2
q5
q6
作业
• 习题2.20中的图2.32
填表算法
• 给定一个DFA M,找出相互等价的状态对。 • 用一个二维图表记录各个状态对是否等价,行标 与列标分别是M的各个状态。 • Step 1. 标记每个终结状态p与非终结状态q构成的 对(p,q)。 • Step 2. 对于尚未标记的状态对(p, q) ,若存在字母 a使得 (δ(p, a), δ(q, a)) 是已标记的对,则标记(p, q)。 • Step 3. 重复执行Step 2, 直到对任何尚未标记的(p, q)以及任何字母a, (δ(p, a), δ(q, a))都是未标记的状 态对时为止。 • Step 4. 此时未加标记的状态对就是所求的等价状 态对。
• 3)⇒ 1)根据右不变等价关系RL 构造识别L的DFA M如下。令M的状态集Q为RL的商集即等价类集合, 其中[ε]为起始状态,L中语句构成的等价类都是终 止状态。 • 再定义转移函数如下: • δ([x], a)=[xa] ∀[x]∈Q,∀a∈Σ ∀ • 则M是识别L的DFA。 □
有限自动机的最小化

有限自动机的最小化(齐齐哈尔大学)本文2000年5月14日收到.图2M ’的转移图摘要引进有限自动机中的不可区分状态概念,并给出一些已知结果新的、更简单的证明.关键词有限自动机状态不可区分状态等价类定义1设M =(Q ,Σ,δ,q 0,F )为有限自动机,且令q 1和q 2为不同的状态.如果存在x ∈Σ3,使q 1,x —3q 3,e ,q 2,x —3q 4,e ,且恰好q 3和q 4中只有一个在F 内,则称x 使得q 1和q 2可以区分.定义2设q 1和q 2为不同的状态且属于定义1中的Q .称q 1和q 2是K 阶不可区分,且写成q 1≡K q 2,当且仅当不存在x ≤K 的x ,使q 1和q 2可以区分.称两个状态q 1和q 2是不可区且写成q 1≡q 2,当且仅当对于所有的K ≥0存在q 1和q 2的K 阶不可区分.称状态q ∈Q 是不可到达的,假使不存在使得q 0,x —3q ,e 的输入字符串x .称M 是经过简化的,假使Q 没有一个状态是不可到达的和没有两个不同的状态是不可区分的.例1考虑转移图1所示的有限自动机M .|||第20卷第3期高师理科学刊Vol.20No.32000年8月Journal of Science of Teachers ’Colle g e and U niversit y A u g .2000图1M 的转移图为了简化M ,首先消去状态F 和G 不可到达的.在下面的算法中,将看出在等价关系“≡”之下的等价类是[A ]、[B ,C ]、[C ,E ],并依次以状态p 、q 、r 表示,从而得到图1经过简化有限自动机M ’.丁春欣定理设M =(Q ,Σ,δ,q 0,F )为具有n 个状态的有限自动机.若状态q 1和q 2是不可区分的,当且仅当它们是(n -2)阶不可区分.证由状态q 1和q 2不可区分的定义,定理中必要性结论显然.充分性如果F 中没有元素(空集)或F =Q ,则充分性也是显然的.以下假设F 含有大于0但小于n 个状态.按照K 阶不可区分性的定义,易知关系“≡K ”是Q 上的等价关系,Q 关于≡K 的商集记为Q /≡K,并以|Q /≡K |记为Q /≡K 中元素的个数,则下列情况成立:Q ≡0≤Q ≡1≤…≤Q ≡n -3≤Q ≡n -2=Q ≡n -1.为此,对于Q 中的q 1和q 2有(1)q 1≡0q 2当且仅当q 1和q 2都在F 中或都不在F 中,(2)q 1≡K q 2当且仅当q 1≡K -1q 2,同时对于Σ上的所有a ,δq 1,a ≡K -1δq 2,a .等价关系≡0对Q 是第一次等分类,它只是将状态集Q 划分成终态和非终态两类.如果存在≡K ≠≡K -1,则Q ≡K >Q ≡K -1.由于F 或Q -F 中至多有n -1个元素,故对于≡0至多只能进行n -2次相继分类.于是≡是使得≡K -1=≡K 的第一次的关系≡K,再由(2)必然得出k =n -2.证毕.下面的算法给出了如何使有限自动机的状态数极小化方法.算法构造规范的有限自动机输入:有限自动机M =(Q ,Σ,δ,q 0,F ).输出:简化的等价有限自动机M ’.方法:步骤1:使用参考文献[1]中算法0.3,按照M 的转移图找出由q 0出发的所有那些可以到达的状态,并且删去所有不可到达的状态.步骤2:依照前面定理的描述,构造等价关系≡0,≡1…,直到≡K =≡K -1,选取≡K作为等价关系.步骤3:构造有限自动机M ’=(Q ’,Σ,δ’,q 0’,F ’)其中(1)Q ’是≡之下的等价类的集合.令[p ]是≡之下状态p 的等价类.(2)若δ(p ,a )=q ,则δ’([p ],a )=[q ].(3)q 0’=[q 0].(4)F ’={[q ]|q ∈F }.易见L (M ’)=L (M ).以下证明不可能再有另外的等价自动机能接受L (M ),而它的状态却比M ’还要少.以下证明M ’的状态是最小的.假设M "比M ’的状态少且L (M ")=L (M ).由于在等价关系≡之下的每个等价类是非空的,所以M ’的每个状态都是可以到达的,于是有字符串序列x 1,x 2,…,x m (m =|Q ’|)使M ’每一个状态都可达.由于M "的状态少于M ’,那么在序列x 1,x 2,…,x m 中存在x ≠w ,使q 0",w —M "3q ,e 和q 0",x —M "3q ,e,其中q 0"是M "的初始状态,但w 和x 却推导M ’到不同的状态.因此,w 和x 同样推导M 到不同状态,记为p 和r ,且它们是可以区分的,即存在某个y ,使得只有w y 和x y 中之一属于L (M ).但w y 和x y 必定推导M "到相同状态,这与w y 和x y 之属于L (M ")相矛盾.||第3期丁春欣:有限自动机的最小化910高师理科学刊第20卷参考文献1[美]阿霍A V,厄尔曼J D.形式语言及其句法分析.科学出版社,19872[美]J E.霍普克罗夫特,J D厄尔曼.自动机理论、语言和计算导引.北京:科学出版社,19863谢邦杰.抽象代数学.上海科学技术出版社,1982Minimizatio n of Finite A uto matio nDin g Chunxin(Qi q ihar U niversit y)Abstract The indistin g uishable state in finite automation is int roduced in t his p a p er.The aut hor g ives new and ver y sim p le p roof s to some known result s.K e y Words Finite automation E q uivatence class State Indistin g uishable state重要声明为适应我国信息化建设的需要,扩大作者学术交流渠道,本刊已加入《中国学术期刊(光盘版)》和“中国期刊网”全文数据库。
有限自动机理论05章下推自动机(简化)

接收语言L={(ab)n|n≥0}
< q1,a,Z0,q2,AZ0> < q2,b,A,q1,ε> < q1,ε,Z0,q1,ε > 规则是不确定的。
n 接收语言L={(ab) |n>0}
< q0,a,Z0,q0,AZ0> < q0,b,A,q1,ε> < q1,a,Z0,q2,AZ0> < q2,b,A,q1,ε> < q1,ε,Z0,q1,ε> 规则是不确定的。
NFA:δ(q,x)= {q1,q2,… qn} 单态的PDA: <x,q, q1 > <x,q, q2 > … <x,q, qn >
NFA:
若 q ∈δ*(q0,w) 单态的PDA: 有 (*,w,q0)=>*(*,ε,q)
NFA:
若q∈F 则 单态的PDA: <ε,q,ε>
q0∈Q是开始状态 Z0∈Г是栈底符号 FQ是接收状态集合
δ:Q×(∑∪{ε})×Г→Q×Г* 对于确定的PDA,有 δ(q,x,D)=( q′,V) 对于不确定的PDA,有 ( q′,V) ∈δ(q,x,D)
一般
使用 <q,x,D,q′,V> 表示δ函数
定义5-2 PDA格局(或瞬间描述ID) 格局代表某个时刻PDA的情况 PDA的格局是一个三元式 (q,w,ζ)
不确定 PDA 对于某一格局可 能会有不同的下一格局。
+ 用=> 代表格局的多次变换
* 用=> 代表格局的任意次变换
5.1.3 PDA接收语言的两种方式
定义 5-3 PAD 以空栈方式接收的语 言为L(M),且 L(M)={w|(q0,w,Z0) =>*(q , ε , ε) q∈Q}
Mealy型模糊有限自动机的最小化算法

2007年7月系统工程理论与实践第7期 文章编号:1000 6788(2007)07 0122 05Mealy型模糊有限自动机的最小化算法洪晓蕾1,万美凯2,3,蒋 毅3,莫智文3(1 成都市树德中学,成都610031;2 西南交通大学峨嵋校区基础课部,峨嵋614202;3 四川师范大学数学与软件科学学院,成都610066)摘要: 提出了Mealy型模糊有限自动机的扩张概念并讨论了Mealy型模糊有限自动机的一些性质,进而得到了它与原Mealy型模糊有限自动机在模糊转移函数上的关系,在此基础上讨论了它的最小化算法.关键词: M ealy型模糊有限自动机;模糊字符串;最小化中图分类号: TP301 1 文献标志码: AMinimization Algorithm of Mealy Fuzzy Finite AutomataHONG Xiao lei1,WAN Mei kai2,3,JIANG Yi3,MO Zhi wen3(1 Shude High School,Chengdu610031,China;2 Sou th west Joatong University,Emei614202,China;3 College of Mathematics and Software Science,Sichuan Normal Uni versity,Chengdu610066,China)Abstract: Expansion of Mealy fuzzy finite au tomata is defined,and properties of Mealy fuzzy fini te automata arediscussed.It is worth noting that we obtain the relation between this automata and general Mealy fuzzy fini te automataon fuzzy transition function.We describe its minimization algorithm on the basis of foregoing analysis being shownabove.Key words: Mealy fuzzy finite automata;fuzzy words;minimization1 引言在有限自动机理论中,输入的仅仅是离散的字符或有限的字符串.而当Zadeh在1965年提出了模糊集理论[1],随之,模糊集理论率先由Wee[2]应用于自动机领域,D.S.Malik、J.N.Mordeson与M.Ksen在文[3]引入了一种模糊自动机.模糊有限自动机是有限自动机的一个推广,它的系统中的下一个状态是不确定的.模糊有限自动机在其应用过程中,常以设计工具的形式出现.作为一个设计工具,对于其价值的判别关键在于是否可以提供一种设计指引使设计者可以得到最佳的设计方案.而其中最重要的一个判断标准既是设计的最简化,即状态的最小化.前人在模糊有限自动机的工作中几乎都只考虑的是输入单个字符或字符串.从知识系统中来看,输入字母表中的字符可以看作是待处理的信息.因此,我们可以考虑这样一种模糊自动机,不仅它的下一个状态是不确定的,而且能识别不确定的字符或字符串.2002年,应明生率先把输入字符串扩张到了输入模糊字符串[4].按照程伟、莫智文提出的模糊有限自动机的分类思想[5],文[4]只扩张到了其中的一类,即有初始状态无输出字符的模糊有限自动机.本文在文[4]的基础上,讨论另一类模糊有限自动机,即无初始状态有输出字符的模糊有限自动机 Mealy型模糊有限自动机.最后还给出了当输入模糊字符串时的状态最小化方法.2 Mealy型模糊有限自动机收稿日期:2006 05 16资助项目:国家自然科学基金(60474022)作者简介:洪晓蕾(1981-),女,硕士研究生.定义1 一个经典的Mealy型有限自动机是一个由五元组M=(Q, , ,,!)所表示的系统,其中:Q 为有限状态集, 为有限输入字符集, 为有限输出字符集.:Q !Q为状态转移函数,!:Q ! 为输出函数.在Zadeh的模糊理论中,设在论域U上给定了一个映射A:U![0,1],u!A(u)则称A为U上的模糊集,A(u)称为A的隶属函数.我们用F(U)表示U的所有模糊子集的全体.定义2[3] 一个Mealy型模糊有限自动机是一个五元组M:M=(Q, , ,,!),其中:Q为有限状态集, 为有限输入字符集, 为有限输出字符集.:Q !F(Q)为模糊转移函数,!:Q !F( )为模糊输出函数,满足以下两个条件:1)q∀Q,x∀ ,!p∀Q,s.t.(q,x)(p)>0∀!y∀ ,s.t.!(q,x)(y)>0;2)q∀Q,x∀ ,!y∀ ,s.t.!(q,x)(y)>0∀!p∀Q,s.t.(q,x)(p)>0.我们用 *和 *分别表示 和 上所有有限长度的字符串的集合.∀表示空字符串,对任意x∀ *,y∀ *,|x|和|y|分别为x和y的长度.就输入字符串而言:#:Q *!F(Q)#(q#,∀)(q∃)=1 q#=q∃0 q#%q∃,#(q#,xa)(q∃)=&q∀Q[#(q#,x)(q)∋(q,a)(q∃)] !#:Q *!F( *)!#(q#,x)(y)=1 x=y=∀0 x=∀,y%∀;y=∀,x%∀,!#(q#,xa)(xb)=&q∀Q[!#(q#,x)(y)∋#(q#,x)(q)∋!(q,a)(b)]=!#(q#,x)(y)∋{&q∀Q[#(q#,x)(q)∋!(q,a)(b)]}其中q#,q∃∀Q,a∀ ,b∀ ,x∀ *,y∀ *.3 Mealy型模糊有限自动机的扩张模型在文[6]中,已经讨论过当输入字符串时,自动机最小化算法的问题,下面我们将利用Zadeh扩张原则定义当输入模糊有限字符串时的模糊转移函数*和模糊输出函数!*.定义3 M=(Q, , ,,!)是一Mealy型模糊有限自动机,F( )*表示输入字符集 上所有有限长度的模糊字符串的集合.任意W∀F( )*,|W|为模糊字符串W的长度.将 扩张到F( ),那么:Q F( )!F(Q),(q#,A)(q∃)=&a∀[A(a)∋(q#,a)(q∃)]!:Q F( )!F( ),!(q#,A)(b)=&a∀[A(a)∋!(q#,a)(b)]又将Q扩张到F(Q),那么:F(Q)F( )!F(Q),(P,A)(q∃)=&q#∀Q[P(q#)∋(q#,A)(q∃)]!:F(Q)F( )!F( ),!(P,A)(b)=&q#∀Q[P(q#)∋!(q#,A)(b)]当输入模糊字符串时,*:F(Q)F( )*!F(Q)*(P,∀)(q∃)=P(q∃),*(P,WA)(q∃)=&q∀Q[*(P,W)(q)∋(q,A)(q∃)] !*:F(Q)F( )*!F( *)!*(P,W)(y)=1 W=y=∀0 W=∀,y%∀;y=∀,W%∀,!*(P,WA)(y b)=&q∀Q[!*(P,W)(y)∋*(P,W)(q)∋!(q,A)(b)]123第7期Mealy型模糊有限自动机的最小化算法=!*(P,W)(y)∋{&q∀Q[*(P,W)(q)∋!(q,A)(b)]}其中q#,q∃∀Q,P∀F(Q),W∀F( )*,A∀F( ),y∀ *,b∀ .在进行如上扩张以后,我们可以得到如下定理1、2、3.定理1 M=(Q, , ,,!)是一Mealy型模糊有限自动机,任意q#,q∃∀Q,a∀ ,b∀ ,A∀F( ),则1)*(q#,a)(q∃)=(q#,a)(q∃),!*(q#,a)(b)=!(q#,a)(b)2)*(q#,A)(q∃)=(q#,A)(q∃),!*(q#,A)(b)=!(q#,A)(b)证明 1)*(q#,a)(q∃)=*(q#,∀a)(q∃)=&q∀Q[*(q#,∀)(q)∋(q,a)(q∃)]=1∋(q#,a)(q∃)= (q#,a)(q∃)2)的证明和(1)类似,故略.定理2 M=(Q, , ,,!)是一Mealy型模糊有限自动机,则任意q#∀Q,y∀ *,W∀F( )*,若| W|%|y|,那么!*(q#,W)(y)=0.证明 假定|W|>|y|,且设|y|=n,用数学归纳法对|y|作归纳证明.当n=0时,y=∀且W%∀,由定义2知!*(q#,W)(y)=0结论成立.当n(1时,假设任意V∀F( )*,z∀ *,|V|>|z|,且|z|=n-1命题成立,又设W=V A,y=zb,其中A∀F( ),b∀ ,|W|>|y|=n,由归纳假设!*(q#,V)(z)=0,而!*(q#,W)(y)=!*(q#,V A)(zb)=!*(q#,V)(z)∋{&q∀Q[*(q#,V)(q)∋!(q,A)(b)]}=0,所以,对于任意q#∀Q,y∀ *,W∀F ( )*,当|W|>|y|时,有!*(q#,W)(y)=0.同理可证当|W|<|y|时,有!*(q#,W)(y)=0,故定理得证.定理3 M=(Q, , ,,!)是一Mealy型模糊有限自动机,则1(a)和2(a)等价,1(b)和2(b)等价.1(a)q∀Q,a∀ ,!p∀Q,s.t.(q,a)(p)>0∀!b∀ ,s.t.!(q,a)(b)>01(b)q∀Q,a∀ ,!b∀ ,s.t.!(q,a)(b)>0∀!p∀Q,s.t.(q,a)(p)>02(a)q∀Q,W∀F( )*,!p∀Q,s.t.*(q,W)(p)>0∀!y∀ *,s.t.!*(q,W)(y)>02(b)q∀Q,W∀F( )*,!y∀ *,s.t.!*(q,W)(y)>0∀!p∀Q,s.t.*(q,W)(p)>0证明:1∀21(a)∀2(a):设|W|=n,对|W|作数学归纳.当n=0时,W=∀且p=q,取y=∀,则!*(q,∀)(∀)=1>0命题成立.当n(1时,假设对任意V∀F( )*,|V|=n-1,命题成立.设W=V A,A∀F( ),V∀F( )*且|V| =n-1,由定义2,*(q,W)(p)=*(q,V A)(p)=&q#∀Q[*(q,V)(q#)∋(q#,A)(p)]>0,则存在r∀Q,使*(q,V)(r)>0且(r,A)(p)>0,而(r,A)(p)=&a∀[A(a)∋(r,a)(p)],即是存在a#∀ ,使A(a#)>0,(r,a#)(p)>0,由1(a)知!b∀ ,s.t.!(r,a#)(b)>0,而!(r,A)(b)=&a∀[A(a)∋!(r,a) (b)](A(a#)∋!(r,a#)(b)>0,由归纳假设,存在z∀ *,使!*(q,V)(z)>0,设y=zb,那么:!*(q,W)(y)=!*(q,V A)(zb)=!*(q,V)(z)∋{&m∀Q[*(q,V)(m)∋!(m,A)(b)]}(!*(q,V)(z)∋*(q, V)(r)∋!(r,A)(b)>0.命题成立,故得证.1(b)∀2(b):由定理2知|W|=|y|=n当n=0时,W=y=∀,则*(q,∀)(q)=1>0,命题成立当n(1时,假设对任意V∀F( )*,z∀ *,|V|=|z|=n-1,命题成立.设W=V A,y=zb,A∀F( ),V∀F( )*且|V|=n-1,由定义2知:!*(q,W)(y)=!*(q,V A)(zb)=!*(q,V)(z)∋{&m∀Q[*(q,V)(m)∋!(m,A)(b)]}>0,则存在r∀Q,使!(r,A)(b)>0,*(q,V)(r)>0,而!(r,A)(b)=&a∀ [A(a)∋!(r,a)(b)]即存在a#∀ ,使A(a#)>0,!(r,a#)(b)>0.由1(b)知,!p∀Q,s.t.(r,a#)(p) >0,(r,A)(p)=&a∀[A(a)∋(r,a)(p)](A(a#)∋(r,a#)(p)>0,所以*(q,W)(p)=*(q,V A)(p)=&q#∀Q [*(q,V)(q#)∋(q#,A)(p)](*(q,V)(r)∋(r,A)(p)>0命题成立,故得证.124系统工程理论与实践2007年7月2∀1易证.定理4 M =(Q , , , ,!)是一Mealy 型模糊有限自动机,q #,q ∃∀Q ,A 1,A 2,),A n ∀F ( ),则有 *(q #,A 1,A 2,),A n )(q ∃)=&a 1,a 2,),a n∀∋[ #(q #,a 1,a 2,),a n )(q ∃),A 1(a 1),A 2(a 2),),A n (a n )]证明 由归纳证明,当k =0时, *(q #,∀)(q ∃)= #(q #,∀)(q ∃),结论成立.当n (1时,假设k =n 时,结论成立,那么k =n +1时,*(q #,A 1A 2)A n A n +1)(q ∃)=&q ∀Q[ *(q #,A 1A 2)A n )(q )∋ (q ,A n +1)(q ∃)],由归纳假设, *(q #,A 1A 2)A n A n +1)(q ∃)=&q ∀Q&a 1,a 2,),a n∀∋[ #(q #,a 1a 2)a n )(q ),A 1(a 1),A 2(a 2),),A n (a n )]∋&a n +1∀[A n +1(a n +1)∋ (q ,a n +1)(q ∃)]=&a 1,a 2,),a n,an +1∀ &q ∀Q∋[ #(q #,a 1a 2)a n )(q ), (q ,a n +1)(q ∃),A 1(a 1),A 2(a 2),),A n (a n ),A n +1(a n +1)]=&a 1,a 2,),a n,an +1∀∋&q ∀Q∋[ #(q #,a 1a 2)a n )(q ), (q ,a n +1)(q ∃)],A 1(a 1),A 2(a 2),),A n (a n ),A n +1(a n +1)=&a 1,a 2,),a n,an +1∀∋[ #(q #,a 1a 2)a n a n +1)(q ∃),A 1(a 1),A 2(a 2),),A n (a n ),A n +1(a n +1)],结论成立,故命题得证.至此,我们可以看出,在输入字符串和输入模糊字符串,这两种情形下的模糊转移函数通过定理4联系起来了.4 Mealy 型模糊有限自动机的最小化方法我们把等价∗和k 等价∗k 也作了相应的扩张.定义4 设M i =(Q i , , , i ,!i )是Mealy 型模糊有限自动机,i =1,2,q i ∀Q i ,则:1)q 1和q 2等价(q 1∗q 2)# W ∀F ( )*,y ∀ *,!*1(q 1,W )(y )=!*2(q 2,W )(y )2)对每一个正整数k ,q 1和q 2k 等价(q 1∗k q 2)# W ∀F ( )*,|W |+k ,y ∀ *,!*1(q 1,W )(y )=!*2(q 2,W )(y ).那么称M 是一个状态最小化自动机,当且仅当q ∗p ∀q =p , p ,q ∀Q .定义5 M =(Q , , , ,!)是一Mealy 型模糊有限自动机,M m =(Q ∗, , , m ,!m ), [q ],[p ]∀Q ∗,x ∀ ,y ∀ ,定义:m ([q ],x )([p ])=&{ (s ,x )(t )|s ,t ∀Q ,s ∗q ,t ∗p },!m ([q ],x )(y )=&{!(s ,x )(y )|s ∀Q ,s ∗q }.能够验证M m 是一状态最小化的Mealy 型模糊有限状态自动机,且与M 等价.定理5 M =(Q , , , ,!)是一Mealy 型模糊有限自动机,|Q |=n ,设|F ( )|=m ,则{ *(W )|W ∀F ( )*}中存在至多(mn 2)n2个不同的模糊矩阵.证明 因为模糊矩阵中出现的所有不同的元素至多有(mn 2)个,所以{ *(W )|W ∀F ( )*}中存在至多(mn 2)n2个不同的模糊矩阵.故能够证明:任意两个可分的状态能够被某个长度至多为(mn 2)n2+1的模糊字符串所区分.至此,我们可以获得一个与已知Mealy 型模糊有限自动机等价的状态最小化的M m =(Q ∗, , , m ,!m ),设模糊字符有A 1,A 2,),A m ,其中Q ∗可由如下算法得到:1)根据模糊字符计算 *(A 1),), *(A m )和!*(A 1),),!*(A m ),由!*(A 1),),!*(A m )可以获得∗1的等价类Q ∗1,令k =1.2)令k =k +1,由定义2计算!*(A i 1A i 2)A i k -1A i k ),i 1,i 2,),i k ∀{1,2,),m },i ∀{1,2,),m },由等价类Q ∗k -1求得Q ∗k .3)判断|Q ∗k |=n 或者k =(mn 2)n2+1,若满足,则转入4;不满足,则转入2.125第7期Mealy 型模糊有限自动机的最小化算法4)输出Q ∗k=Q ∗.例 设一个Mealy型模糊有限自动机M=(Q, , ,,!),其中 = ={0,1},Q={q1,q2,q3},其模糊转移函数和模糊输出函数!如下:(0)=q1q2q3q10 50 60q2100 4q3010 5,(1)=q1q2q3q110 20 9q200 60q30 410 6,!(0)=01q110 2q210 2q30 40 1,!(1)=01q10 70 1q20 70 1q310 4,令A1=0 40+11,A2=10+0 51.第1步:计算出!*(A1)=01q10 70 2q20 70 2q310 4,!*(A2)=01q110 2q210 2q30 50 4,可以得到Q ∗1={{q1,q2},{q3}},*(A1)=q1q2q3q110 40 9q20 40 60 4q30 410 6,*(A2)=q1q2q3q10 50 60 5q210 50 4q30 410 5第2步:计算!*(A1A1),!*(A1A2),!*(A2A1),!*(A2A2)!*(A1A1)=00011011q10 70 40 20 2q20 60 40 20 2q30 70 40 40 4,由!*(A1A1)就可以得到Q ∗2={{q1},{q2},{q3}}.第3步;|Q ∗2|=3=|Q|.第4步:输出Q ∗=Q ∗2.5 结论众所周知,经典的自动机理论在文字识别、语言识别以及人工智能等领域起着重要作用,它还是描述许多重要硬件和软件的有用模型.近些年来,随着模糊技术的飞速发展,由模糊理论和自动机结合构成的模糊有限状态自动机和模糊语言,在其应用及进一步发展中,不仅合理地拓展了分明有限自动机和语言理论,而且已经用来模拟一些动态或者不确定系统,如车辆公路系统.模糊自动机识别输入模糊字串时的一个有为的应用在于将描述和分析动态控制系统,其行为和控制规则来源于专家的经验或者自然语言.参考文献:[1] Zadeh L A.Fuzzy sets[J].Inform Control,1965,(8):338-353.[2] Wee W G.On generalizations of adaptive algori thm and application of the fuzzy sets concept to pattern classi fication[D].PurdueUniversi ty,1967.[3] Malik D S,Mordeson J N,Sen M K.Minimization of fuzzy finite automata[J].Information Science,1999,(113):323-330.[4] Ying M ingsheng.A formal model of computing with words[J].IEEE T ransactions on Fuzzy Systems,2002,(10):640-652.[5] Wei Cheng,Mo Zhi wen.A kind of classification of fuzzy fini te automata[J].B USEFAL,2000,(84):51-55.[6] Wei Cheng,Zhi wen Mo.Mini mization algorithm of fuzzy finite automata[J].Fuzzy Sets and Systems,2004,(4):439-448.126系统工程理论与实践2007年7月。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
技改援i 习
b
1 2 也 不宜合并 们这时 可 以看 到 , 和 , 非终态组 的
情 况 正 好 与 终 态 组 的 睛 对 应 且 相 反 ,因 此 可 以 让
表 3
状 态 1 2合并 , 态 6和 7合并 , 和 状 并重新 分别命 名 为状 态 1 6 由此得 出新 的转 换矩阵表 ( 5 . 和 , 表 ) 其
,
2 . 观察 表 2 出发状 志 3 4的到达状 态均 同样 )再 . 和
为 3 4 因 此 这 两 个 状 态 可 以 台 掉 . 重 命 名 为状 和 , 并 态 3 重 新 填写 转 换 矩 阵 表 ( 3 如 下 从 表 3n 表 ) r 知 . 到达状态均不 相 同 . 各 因 此 这 就 是 最 后 化简 的 结 果 根 据 表 3可 以 面 出 简
有 限 自动 机 在 构 造 时 往 往 运 用 转 换 矩 阵 来 消 除 标 记 为 e 夺 字 的 弧 ( 然 未 化 简 的 有 限 自动 机 也 能 的 当
例 如 : 简 化 的 有 限 自动 机 【 I 和 其 柑 斑 的 未 图 ) 转换矩 阵 ( 1i 表 } 在 转 换 矩 阵 表 中 s 为 出 发 状 态 ,a栏 为 经 a 栏 弧 后 到 达 的状 态 , 为 经 b弧 后 到达 的 状 态 b栏 化 简 过 程 如 F:首先 把 出 发 状 态 分 为 两 组 终 态组 { 4 5 6 , 终 态组 f, ,} 3 , , }非 0 I2 . 后 再 观 察 表 .然 1 出 发 状 态 3的两 个 到 达 状 态 为 3和 4 而 发 状 态 6的两 个 到 达 状 态 也 同 样 为 3和 4 因 此 状 忐 3 . 和 6可 以合 并 , 新 命 名 为 状 态 3 再看 出发 状 态 4和 重 一 5的 两 个 到 达 状 态 均 为 6和 5 因 此 状 态 4 5 可 , 和 也 以台 并 . 命名 为状 态 4 重新 填 重 q转 换 矩 阵 丧 { 表
相 应 的化 简 后 的 有 限 自动 机 转 换 图 图 4 。
÷
一
一
表 5
定条件下 也可以合并 。例如 , 有 限 自动 机 的 转
换 图 I 3 和 其 相 应 的转 换 矩 阵 4 如 下 : 图 ) ( ) 表
表 4
h 1 2 3 4 5 6
推出转换矩 阵 1 然后再将其进 行状态 分组 , . 重新逐
个 地 从 一 个状 态 经 某 道 路 到 达 另 一 个 状 态 进 行 检
查分析 , 消除 多余 状态 来得 到化简的 D A F 。而实际
E 种 ,法 显 然 是 一 种 重 复 .因此 利 用 转 换 矩 阵 直 这 j 接 进 行 化 简 成 勾 町能 一 这 里 介 绍 的 是 一 新 的 方 法 :在 简 化 时 .首 先 坪 用 未 简 化 的 有 限 自动 机 来 推 出 其 相 应 的 转 换 矩 阵 【 有 则 卣接 利 用 1 如 ,把 状 态 分 为 终 态 组 和 非 终 态
个出发状 态就可 合并 为一个状 态 , 成新的转换 形
矩 阵 根 据 新 的 转 换 矩 阵 来推 出 简 化后 的 有 限 少 , 并使得新 的有 限 自 动机 与未化 简 的有 限 自动机 等价 在计算 机教科 书 《 编译原坪 》 中也介绍 r 一些 化简方 法 , 未化简 的 其
7
;
l d l
—
6 7 I 4 7 4
4
3 3 5 6 3 1
2
从 以上 介绍 可以看 出, 该方法 简便 , 观 , 用 直 在 于 由转 换 矩阵 表 而推 出 的有 限 自动 机 的化 简 时 尤
为 快 捷 但 该 方 法 也 有 其 一 定 的局 限 性 . 下 面 情 在
襄 2
阿个绀 分别进 行简化 i 在转换 矩阵 的各分组 中 .
表 1
b
化 后 的 有 限 自动 机 的 转 换
图 ( 2 一 图 )
在 到 达 状 态 中 .如 只
图 1 来 简
有 部 分 栏 状 态 相 同 时 ,在
维普资讯
图 3 有 限 自动 机 的 转 换 图 化 简 过 程 如 下 :先 把 出 发 状 态 分 为 两 组 : 态 终 组 l . , } 非 终 态 组 { . . , l 从 表 4中我 们 可 56 7 , 123 4。 以 看 出 . 非 终 态 组 中 , 有 状 态 1 2 b 到 达 在 只 和 经 弧 状态 3 相 同的 , 经 a 却分 别到达状态 6 7 是 而 弧 和 , 不 宜 合 并 = 时 再 考 察 终 态组 , 有状 态 6和 7经 a 这 只
维普资讯
《 西 置信 斟 技)o: 山 2o 2年第 1 期
青 限 自 动 机 的 一 种 化 简 方 法
王 树 智
f 西 省 长 治 电缆 厂 ) 山
摘
要
利 用 转换 矩 阵 对有 限 自动 机 进 行 化 简。在 各 分 组 中 当两 十 不 同 的 出发 状 态 . 有 同样 的 到 达 具 状 态 时 , 两个 出发 状 态 就 可 以 合 并 为一 十 状 态 . 这
关键 词
有 限 自动机
转换 矩 阵
状态
化 简
在 计 算 机 程 序设 计语 自的 编 译 程 序 构 造 中 , 常 涉 及 到 有 限 自动 机 f F l 化 简 问题 有 限 自动 机 DA的 的 化 简 是 指 : 求 一 个新 的 有 限 自动 机 .其 状 态 的 寻
从 两 个不 同 的 出发 状 态 ,到 达 同 样 的 状 态 时 ,这 两
