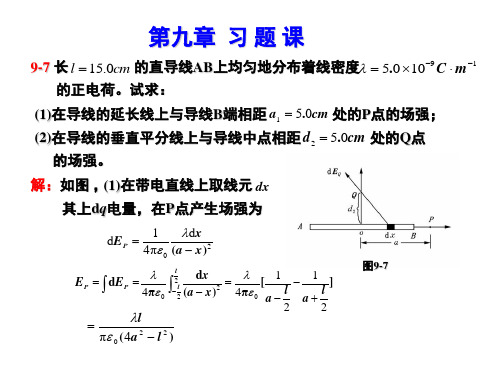
长L15cm的直导线AB上均匀地分布着线密度为
大物习题集
如果它包含q所在顶点则 e 0
9-12 半径为 R1 和 R2 ( R2 R1 )的两无限长同轴圆柱面,单位长度
上分别带有电量 和 ,试求: (1) r R1 ; (2) R1 r R2 ; (3) r R2 处各点的场强。
q 解: 高斯定理 E dS ,取同轴圆柱形高斯面,侧面积 S 2 πrl
11-6 如题11-5所示,在两平行载流的无限长直导线的平面内有一 矩形线圈。两导线中的电流方向相反、大小相等,且电流以
dI 的变化率增大,求: dt
(1)任一时刻线圈内所通过的磁通量; (2)线圈中的感应电动势。 解: 以向外磁通为正,则
(1)
m
ba
0 I
2 πr 2 πr Il ba d a 0 [l n ln ] 2π b d
s
0
E 则 dS E 2πrl
S
(1) 当 r R1 时
q 0 E 0
方向沿径向向外。 2π 0 r
(2)当 R1 r R2 时 q l E
(3) 当 r R2 时
q 0 E 0
9-17 如题9-17图所示,在A、B两点处放有电量分别为+q 和-q 的
图9-7
EQy
d λ dEQy 2 l 4πε0
l 2 l 2
dx (x d )
2 3 2 2 2
l
2 2π 0 l 2 4d 2
将 5.0 109 C m 1 , l 15cm, d 2 5cm 代入得
EQ EQy 14.96102 N C 1,方向沿y轴正向。
点电荷,AB间距离为2R,现将另一正试验点电荷我我 q0 从 O点经过半圆弧移到C点,求移动过程中电场力作的功。
第七章静止电荷的电场作业题目及解答

(3)金属球的电势
R Q Q Q 1 1 r U E d l dr dr ( ) 2 2 r R R 4 r 4 r 4 R R 0 r 0 0 r
e e e ee e
C F 7-64 电容 的电容器在800V的电 1 4 差下充电,然后切断电源,并将此电容器 的两个极板分别和原来不带电、电容为 的C 6 F 电容器两极板相连,求: 2 (1)每个电容器极板所带电荷量; (2)连接前后的静电场能
0
ε
q´
0
0
题号 结束
7-20 在半径为R,电荷体密度为ρ 的均 匀带电球内,挖去一个半径为 r 的小球,如 图所示。试求:O、O′、P、 P′各点的场 强。 O、O′、P、 P′在一条直线上。
P′.
P O . O . .′ r R
题号 结束
解:
E1 E2
带电荷-ρ 的小球的场强 带电荷ρ 的大球的场强
0 0
r1 . P
O O′ . . r R
0
ρ r2 E2 =
3 ε E1
0
EP = E2 =
r2 P.
3 ε
ρ
r2
0
r3 r12
O O′ . . r R
题号 结束
(4)P ´点的场强: 3 4 r 1 2 π r 1 r E1 4 π 1 = ρ ε 3 r 2 O O ′ P ′ 3 . . ρ . r E1 = r 2 r R 3 ε 1
UP =
4 π ε r> > re a = re cosq
0
1
q (r 1
Байду номын сангаас
2q + q ) r r2 r1 r a
大学物理课后习题答案第八单元

dE P =
1 λdx 4 πε 0 (a − x ) 2
λ E P = ∫ dE P = 4πε 0
=
∫
l 2 l − 2
dx (a − x ) 2
λ 1 1 [ − ] l l 4 πε 0 a− a+ 2 2
福建师范大学学生门户
整理
更多课件题库答案尽在
=
λl πε 0 (4a 2 − l 2 )
沿径向向外
∴
(3) ∴
r > R2
∑q = 0
E=0
题 8-12 图 8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为 σ 1 和 σ 2 , 试求空间各处场强. 解: 如题 8-12 图示,两带电平面均匀带电,电荷面密度分别为 σ 1 与 σ 2 , 两面间, E =
�
1 � (σ 1 − σ 2 )n 2ε 0
福建师范大学学生门户
整理
更多课件题库答案尽在
习题八 8-1 电量都是 q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1) 在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡 (即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形 的边长有无关系? 解: 如题 8-1 图示 (1) 以 A 处点电荷为研究对象,由力平衡知: q ′ 为负电荷
4λlr 4π ε 0 (r 2 +
l2 l2 ) r2 + 4 2
∵ ∴
λ= EP = qr
q 4l
方向沿 OP
l2 l2 4πε 0 (r 2 + ) r 2 + 4 2
8-9
(1)点电荷 q 位于一边长为a的立方体中பைடு நூலகம்,试求在该点电荷电场中穿
大学物理简明教程(第2版)(赵近芳)习题答案,习题7 静电场
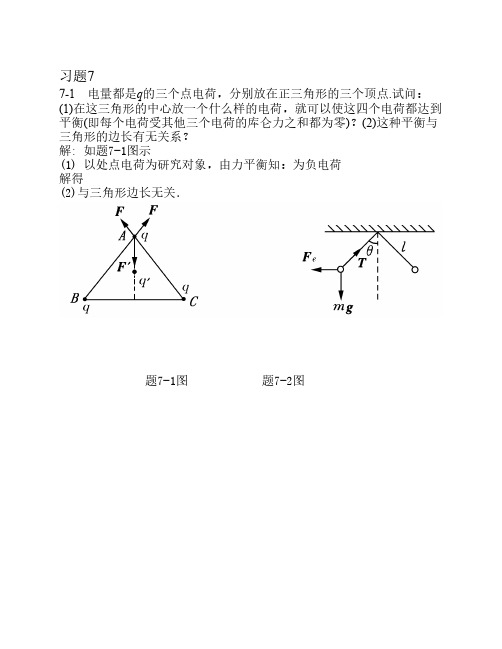
7-1 电量都是q的三个点电荷,分别放在正三角形的三个顶点.试问: (1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到 平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与 三角形的边长有无关系? 解: 如题7-1图示 (1) 以处点电荷为研究对象,由力平衡知:为负电荷 解得 (2)与三角形边长无关.
解: 电容上电量 电容与并联 其上电荷 ∴
题7-15图
题7-12图 (2)外壳接地时,外表面电荷入地,外表面不带电,内表面电荷仍为. 所以球壳电势由内球与内表面产生:
7-13 在半径为R1的金属球之外包有一层外半径为R2的均匀电介质球壳, 介质相对介电常数为r,金属球带电Q。试求: (1)电介质内、外的电场强度; (2)电介质层内、外的电势; (3)金属球的电势。 解: 利用有介质时的高斯定理 (1)介质内场强
; 介质外场强 (2)介质外电势 介质内电势 (3)金属球的电势
7-14 计算球形电容器的电容和能量。已知球形电容器的内外半径分别为 R1和R2,带电量分别为Q和-Q。为简单起见,设球内外介质介电常数均 为0。 解:,
R1 R2 r o 和, 体积元 能量 电容器的电容
7-15 如题7-15图所示,,,,上电压为50 V.求:.
题7-1图
题7-2图
题7-2图 7-2 两小球的质量都是m,都用长为l的细绳挂在同一点,它们带有相 同电量,静止时两线夹角为2θ,如题7--2图所示.设小球的半径和线的质 量都可以忽略不计,求每个小球所带的电量. 解: 如题7-2图示
解得
7-3 在真空中有A,B两平行板,相对距离为d,板面积为S,其带电量 分别为+q和-q.则这两板之间有相互作用力f,有人说,又有人说,因 为f=qE,,所以试问这两种说法对吗?为什么?f到底应等于多少? 解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不 对的,第二种说法把合场强看成是一个带电板在另一带电板处的场强也
大学物理(下)答案

⼤学物理(下)答案⼤学物理学答案【下】北京邮电⼤学出版社习题99.1选择题(1) 正⽅形的两对⾓线处各放置电荷Q,另两对⾓线各放置电荷q,若Q所受到合⼒为零,则Q与q的关系为:()(A)Q=-23/2q (B) Q=23/2q (C) Q=-2q (D) Q=2q[答案:A](2) 下⾯说法正确的是:()(A)若⾼斯⾯上的电场强度处处为零,则该⾯内必定没有电荷;(B)若⾼斯⾯内没有电荷,则该⾯上的电场强度必定处处为零;(C)若⾼斯⾯上的电场强度处处不为零,则该⾯内必定有电荷;(D)若⾼斯⾯内有电荷,则该⾯上的电场强度必定处处不为零。
[答案:D](3) ⼀半径为R的导体球表⾯的⾯点荷密度为σ,则在距球⾯R处的电场强度()(A)σ/ε0 (B)σ/2ε0 (C)σ/4ε0 (D)σ/8ε0[答案:C](4) 在电场中的导体内部的()(A)电场和电势均为零;(B)电场不为零,电势均为零;(C)电势和表⾯电势相等;(D)电势低于表⾯电势。
[答案:C]9.2填空题(1) 在静电场中,电势不变的区域,场强必定为[答案:相同](2) ⼀个点电荷q放在⽴⽅体中⼼,则穿过某⼀表⾯的电通量为若将点电荷由中⼼向外移动⾄⽆限远,则总通量将。
[答案:q/6ε0, 将为零](3) 电介质在电容器中作⽤(a)——(b)——。
[答案:(a)提⾼电容器的容量;(b) 延长电容器的使⽤寿命](4) 电量Q均匀分布在半径为R的球体内,则球内球外的静电能之⽐[答案:5:6]9.3 电量都是q的三个点电荷,分别放在正三⾓形的三个顶点.试问:(1)在这三⾓形的中⼼放⼀个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑⼒之和都为零)?(2)这种平衡与三⾓形的边长有⽆关系?解: 如题9.3图⽰(1) 以A处点电荷为研究对象,由⼒平衡知:q'为负电荷1q212cos30?=4πε0a24πε0qq'(2a)3解得q'=-q 3(2)与三⾓形边长⽆关.题9.3图题9.4图9.4 两⼩球的质量都是m,都⽤长为l的细绳挂在同⼀点,它们带有相同电量,静⽌时两线夹⾓为2θ ,如题9.4图所⽰.设⼩球的半径和线的质量都可以忽略不计,求每个⼩球所带的电量.解: 如题9.4图⽰Tcosθ=mg??q2 ?Tsinθ=F=1e?4πε0(2lsinθ)2?解得q=2lsinθ40mgtan9.5 根据点电荷场强公式E=q4πε0r2,当被考察的场点距源点电荷很近(r→0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解: E=q4πε0r2?r0仅对点电荷成⽴,当r→0时,带电体不能再视为点电荷,再⽤上式求场强是错误的,实际带电体有⼀定形状⼤⼩,考虑电荷在带电体上的分布求出的场强不会是⽆限⼤.9.6 在真空中有A,B两平⾏板,相对距离为d,板⾯积为S,其带电量分别为+q和-q.则这两板之间有相互作⽤⼒f,有⼈说f=q2 4πε0d2,⼜有⼈说,因为f=qE,E=q,所ε0Sq2以f=.试问这两种说法对吗?为什么? f到底应等于多少?ε0S解: 题中的两种说法均不对.第⼀种说法中把两带电板视为点电荷是不对的,第⼆种说法把合场强E=q看成是⼀个带电板在另⼀带电板处的场强也是不对的.正确解答应为⼀个ε0Sqqq2=板的电场为E=,另⼀板受它的作⽤⼒f=q,这是两板间相互作⽤2ε0S2ε0S2ε0S的电场⼒.-19.7 长l=15.0cm的直导线AB上均匀地分布着线密度λ=5.0x10-9C·m的正电荷.试求:(1)在导线的延长线上与导线B端相距a1=5.0cm处P点的场强;(2)在导线的垂直平分线上与导线中点相距d2=5.0cm 处Q点的场强.解:如题9.7图所⽰(1) 在带电直线上取线元dx,其上电量dq在P点产⽣场强为dEP=1λdx 24πε0(a-x)λEP=?dEP=4πε0?l2l-2dx 题9.7图2(a-x)=λ11[-] ll4πε0a-a+22=⽤l=15cm,λ=5.0?10-9λlπε0(4a2-l2) C?m-1, a=12.5cm代⼊得EP=6.74?102N?C-1 ⽅向⽔平向右(2)同理 dEQ=由于对称性dEQxl1λdx ⽅向如题9.7图所⽰4πε0x2+d22?=0,即EQ 只有y分量,1λdx=4πε0x2+d22d2x+d222?∵dEQyEQy=?dEQyldλ=24πε2l2l-2dx(x2+d22)32 =-9λl2πε0l+4d222以λ=5.0?10C?cm-1, l=15cm,d2=5cm代⼊得EQ=EQy=14.96?102N?C-1,⽅向沿y轴正向9.8 ⼀个半径为R的均匀带电半圆环,电荷线密度为λ,求环⼼处O 点的场强.解: 如9.8图在圆上取dl=Rd?题9.8图dq=λdl=Rλd?,它在O点产⽣场强⼤⼩为dE=λRd?⽅向沿半径向外4πε0R2则dEx=dEsin?=λsin?d?4πε0R-λcos?d?4πε0Rπ-?)= dEy=dEcos(积分Ex=?π0λλsin?d?=4πε0R2πε0REy=?π0-λcos?d?=0 4πε0R∴E=Ex=λ,⽅向沿x轴正向.2πε0R9.9 均匀带电的细线弯成正⽅形,边长为l,总电量为q.(1)求这正⽅形轴线上离中⼼为r处的场强E;(2)证明:在r>>l处,它相当于点电荷q产⽣的场强E.解: 如9.9图⽰,正⽅形⼀条边上电荷?q在P点产⽣物强dEP ⽅向如图,⼤⼩为4dEP=λ(cosθ1-cosθ2)4πε0r2+l42∵cosθ1=lr2+l22cosθ2=-cosθ1∴dEP=λ4πε0r2+l42lr2+l22dEP在垂直于平⾯上的分量dE⊥=dEPcosβ∴dE⊥=λl4πε0r2+l42rr2+l22r2+l42题9.9图由于对称性,P点场强沿OP⽅向,⼤⼩为EP=4?dE⊥=4λlr4πε0(r2+ll)r2+4222∵λ=∴EP=q 4l2qr4πε0(r2+ll)r2+422 ⽅向沿9.10 (1)点电荷q位于⼀边长为a的⽴⽅体中⼼,试求在该点电荷电场中穿过⽴⽅体的⼀个⾯的电通量;(2)如果该场源点电荷移动到该⽴⽅体的⼀个顶点上,这时穿过⽴⽅体各⾯的电通量是多少?q 解: (1)由⾼斯定理E?dS= sε0⽴⽅体六个⾯,当q在⽴⽅体中⼼时,每个⾯上电通量相等∴各⾯电通量Φe=q.6ε0(2)电荷在顶点时,将⽴⽅体延伸为边长2a的⽴⽅体,使q处于边长2a的⽴⽅体中⼼,则边长2a的正⽅形上电通量Φe=q 6ε0 对于边长a的正⽅形,如果它不包含q所在的顶点,则Φe=如果它包含q所在顶点则Φe=0.q,24ε0如题9.10图所⽰.题9.10 图9.11 均匀带电球壳内半径6cm,外半径10cm,电荷体密度为2×108cm ,12cm 各点的场强.解: ⾼斯定理E?dS=s-5C·m求距球⼼5cm,-3??∑q,E4πrε02=∑q ε0 ?当r=5cm时,∑q=0,E=0r=8cm时,∑q=p4π33) (r -r内3ρ∴E=4π32r-r内≈3.48?104N?C-1,⽅向沿半径向外.24πε0r()r=12cm时,∑q=ρ4π33)(r外-r内3ρ∴E=4π33r外-r内3≈4.10?104 N?C-1 沿半径向外. 24πε0r()9.12 半径为R1和R2(R2 >R1)的两⽆限长同轴圆柱⾯,单位长度上分别带有电量λ和-λ,试求:(1)r<R1;(2) R1<r<R2;(3) r >R2处各点的场强.解: ⾼斯定理E?dS=sq ε0取同轴圆柱形⾼斯⾯,侧⾯积S=2πrl则E?dS=E2πrl S对(1) r∑q=lλ (2) R1∴E=λ沿径向向外2πε0r(3) r>R2 ∑q=0∴E=0题9.13图9.13 两个⽆限⼤的平⾏平⾯都均匀带电,电荷的⾯密度分别为σ1和σ2,试求空间各处场强.解: 如题9.13图⽰,两带电平⾯均匀带电,电荷⾯密度分别为σ1与σ2,两⾯间,E=?1?(σ1-σ2)n 2ε01(σ1+σ2)n σ1⾯外,E=-2ε0σ2⾯外,E=?1?(σ1+σ2)n 2ε0n:垂直于两平⾯由σ1⾯指为σ2⾯.9.14 半径为R的均匀带电球体内的电荷体密度为ρ,若在球内挖去⼀块半径为r<R的⼩球体,如题9.14图所⽰.试求:两球⼼O 与O'点的场强,并证明⼩球空腔内的电场是均匀的.解: 将此带电体看作带正电ρ的均匀球与带电-ρ的均匀⼩球的组合,见题9.14图(a).(1) +ρ球在O点产⽣电场E10=0,-ρ球在O点产⽣电场E2043πrρ=OO' 4πε0d3r3ρ;∴O点电场E0=3ε0d343πdρ?(2) +ρ在O'产⽣电场E10'=34πε0d-ρ球在O'产⽣电场E20'=0ρOO∴O'点电场E0'=3ε0题9.14图(a) 题9.14图(b) ??(3)设空腔任⼀点P相对O'的位⽮为r',相对O点位⽮为r (如题8-13(b)图)ρr则EPO=,3ε0ρr'EPO'=-, 3ε0ρ??ρρd(r-r')=OO'=∴EP=EPO+EPO'= 3ε03ε03ε0∴腔内场强是均匀的.-69.15 ⼀电偶极⼦由q=1.0×10C的两个异号点电荷组成,两电荷距离d=0.2cm,把这电偶极⼦放在1.0×10N·C的外电场中,求外电场作⽤于电偶极⼦上的最⼤⼒矩. 5-1解: ∵电偶极⼦p在外场E中受⼒矩M=p?E∴Mmax=pE=qlE代⼊数字Mmax=1.0?10-6?2?10-3?1.0?105=2.0?10-4N?m9.16 两点电荷q1=1.5×10C,q2=3.0×10C,相距r1=42cm,要把它们之间的距离变为-8-8r2=25cm,需作多少功?解: A=?r2r1??r2qqdrqq11F?dr=?122=12(-) r24πεr4πε0r1r20=-6.55?10-6J外⼒需作的功A'=-A=-6.55?10 J-6题9.17图9.17 如题9.17图所⽰,在A,B两点处放有电量分别为+q,-q的点电荷,AB间距离为2R,现将另⼀正试验点电荷q0从O点经过半圆弧移到C点,求移动过程中电场⼒作的功.解: 如题9.17图⽰UO=1qq(-)=0 4πε0RRUO=1qqq (-)=-4πε03RR6πε0Rqoq 6πε0R∴A=q0(UO-UC)=9.18 如题9.18图所⽰的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R.试求环中⼼O点处的场强和电势.。
大学物理学第四版答案

大学物理学第四版答案【篇一:大学物理(第四版)课后习题及答案机械振动】13-1分析弹簧振子的振动是简谐运动。
振幅a、初相?、角频率?是简谐运动方程x?acos??t???的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除a、?已知外,?可通过关系式??2?确定。
振子运动的速度t和加速度的计算仍与质点运动学中的计算方法相同。
解因??2?,则运动方程 t?2?t?x?acos??t????acos?t??? ?t?根据题中给出的数据得x?(2.0?10?2m)cos[(2?s?1)t?0.75?]振子的速度和加速度分别为v?dx/dt??(4??10?2m?s?1)sin[(2?s?1)t?0.75?]a?d2x/dt2??(8?2?10?2m?s?1)cos[(2?s?1)t?0.75?x-t、v-t及a-t图如图13-l所示???13-2 若简谐运动方程为x?(0.01m)cos?(20?s?1)t??,求:(1)振幅、频率、角频率、周期和4??初相;(2)t=2s 时的位移、速度和加速度。
13-2分析可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式x?acos??t???作比较,即可求得各特征量。
运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t值后,即可求得结果。
解(l)将x?(0.10m)cos[(20?s?1)t?0.25?]与x?acos??t???比较后可得:振幅a= 0.10 m,角频率??20?s?1,初相??0.25?,则周期 t?2?/??0.1s,频率??1/t?10hz。
(2)t= 2s时的位移、速度、加速度分别为x?(0.10m)cos(40??0.25?)?7.07?10?2mv?dx/dt??(2?m?s?1)sin(40??0.25?)a?d2x/dt2??(40?2m?s?2)cos(40??0.25?)若有一质量为m的质点在此隧道内做无摩擦运动。
大学物理习题7详解

习题77.1 选择题(1) 下面说法正确的是: [ ](A )若高斯面上的电场强度处处为零,则该面内必无电荷; (B )若高斯面内无电荷,则高斯面上的电场强度处处为零;(C )若高斯面上的电场强度处处不为零,则高斯面内必定有电荷; (D )若高斯面内有净电荷,则通过高斯面的电通量必不为零; (E )高斯定理仅适用于具有高度对称性的电场。
[答案:D](2)点电荷Q 被曲面S 所包围 , 从无穷远处引入另一点电荷q 至曲面外一点,如题7.1(2)图所示,则引入前后, [ ] (A) 曲面S 的电场强度通量不变,曲面上各点场强不变.(B) 曲面S 的电场强度通量变化,曲面上各点场强不变. (C) 曲面S 的电场强度通量变化,曲面上各点场强变化.(D) 曲面S 的电场强度通量不变,曲面上各点场强变化. 题7.1(2)图[答案D ](3)在电场中的导体内部的 [ ](A )电场和电势均为零; (B )电场不为零,电势均为零;(C )电势和表面电势相等; (D )电势低于表面电势。
[答案:C](4)两个同心均匀带电球面,半径分别为R a 和R b (R a <R b ), 所带电荷分别为Q a 和Q b .设某点与球心相距r ,当R a <r <R b 时,该点的电场强度的大小为: [ ](A) 2014a b Q Q r ε+⋅π. (B) 2014a bQ Q r ε-⋅π. (C)22014a b b Q Q r R ε⎛⎫⋅+ ⎪⎝⎭π. (D) 2014a Q r ε⋅π.[答案 D](5)如果某带电体其电荷分布的体密度增大为原来的2倍,则其电场的能量变为原来的 [ ] (A) 2倍. (B) 1/2倍.(C) 4倍. (D) 1/4倍.[答案 C]7.2 填空题(1)在静电场中,电势不变的区域,场强必定为 。
[答案:相同](2)一个点电荷q 放在立方体中心,则穿过某一表面的电通量为 ,若将点电荷由中心向外移动至无限远,则总的电通量将 。
普通物理练习题及解析

第一章一、填空1、一飞轮边缘上一点的路程与时间的关系为2021btt v s -=,0v 、b 都是正的常量,已知飞轮的半径为R ,时刻t 的法向加速度为 ,切向加速度为 。
Rbt v 20)(-,-b2、一个作平面运动的质点,它的运动方程是)(),(t v v t r r==,如果0,0≠=dtr d dt dr质点作 运动;如果0,0≠=dtvd dt dv质点作 运动。
圆周;匀速率曲线二、选择题下列哪种情况不可能发生?( )(C ) A 一物体具有加速度而其速度为零B 一物体具有恒定速率但仍有变化的速度C 一物体具有恒定速度但仍有变化的速率D 一物体具有沿X 轴正方向的加速度而有沿X 轴负方向的速度 三、简述题1、位移和路程有何区别?答:位移表示位置的变化,是矢量;路程是位置变化的过程量,是标量。
2、速度和速率有何区别? 答:速度表示运动的快慢和方向的量,是矢量;速率只表示运动的快慢,是标量。
3、瞬时速度和平均速度的区别和联系是什么?答:瞬时速度表示瞬间运动的快慢和方向,它对时间的积分就得到位移;平均速度是位移对时间的平均。
四、计算题已知m =3kg 的质点,其运动方程的正交分解式为j t i t r )28(52++=(SI )。
试求: (1)质点在任意时刻t 的加速度矢量的正交分解式;(2)质点在时刻t=5s 时所受的合力。
解:(1)j t i dtr d v 165+==(m .s-1),a=16j(2)F=ma=48j (N )第二章1、凡是对一个惯性系作 运动的一切物体都是惯性系。
匀速直线2、凡是相对惯性系作 运动的物体都是非惯性系。
加速3、一物体 只具有机械能而无动量;一物体 只有动量而无机械能。
(填可以或不可以) 可以;可以 二、选择题让两小滑块1和2分别从等高的光滑斜面和光滑弧面的顶端由静止出发下滑至底部,则下述结论哪些是对的?( )A A .两滑块到达底部时速率相同; B .两滑块到达底部所作时间相同; C .下滑过程中重力所作的功必相同; D .正压力对物体的运动无影响 关于摩擦力,正确的说法是( )。
医用物理学静电场免费下载

6-4、如图,在直角三角形ABC的A点上有电荷q1=1.8×10-9C,B点上有点电荷q2=-4.8×10-9C,试求C点的电场强度(BC=0.04m,AC=0.03m)6-5、长为l=15cm的直导线AB,如图,均匀地分布着电荷线密度λ=5.0×10-9C·m-1的电荷.求(1)导线的延长线上与导线一端B相距R=0.05m处P点的场强,(2)在导线的垂直平分线上与导线中点相距R=0.05m处Q点的埸强.6-6、如图,将一根细玻璃棒弯曲成半径为R,圆心角2π/3的圆弧,其上均匀地分布着+q的电荷,求圆弧的圆心O点处的埸强和电势.6-7、如图,有2个均匀带电的1/4圆环与x轴对称放置,半径为R,x轴上端电荷线密度为λ1(λ1>0),x轴下端线电荷密度为λ2(λ2>0),求(1)曲率中心O处的电场强度,(2)曲率中心O处的电势.6-8、如图,2个均匀带电的金属同心球壳,内球壳半径R1=5.0cm,带电q1=0.60×10-8C,外球壳内半径R2=7.0cm,外半径R3=9.0cm,带电q2=-2.0×10-8cm,求距球心3.0cm,6.0cm,8.0cm,10.0cm各点处的埸强. 6-9、如图,有一半径为R的无限长薄壁圆筒,单位长度带电荷为λ,(1)用高斯定理求离圆筒轴线垂直距离为r处的电场强度E,并画出E-r曲线,若ra 和rb分别为a、b两点到圆筒轴线的垂直距离,且R<ra <rb,试求a、b两点间的电势差Uab.6-10,如图,两无限大带电平面相互平行,面电荷密度分别为+σ1和+σ2,分别求Ⅰ、Ⅱ、Ⅲ区的电场强度。
6-11,在电场力的作用下,一点电荷q从a点移动到b点时,电场力作功为A1,从b点移动到c点时,电场力作功为A2,则从c点移动a点时电场力作了多少功?6-13,电偶极子周围的电势分布与什么有关?当电偶极子绕其中心以匀角速度旋转时,用曲线描绘出某观察点的电势随时间变化的关系。
大学物理第05章 静电场习题解答

第5章 静电场习题解答5.1一带电体可作为点电荷处理的条件是( C ) (A )电荷必须呈球形分布。
(B )带电体的线度很小。
(C )带电体的线度与其它有关长度相比可忽略不计。
(D )电量很小。
5.2图中所示为一沿 x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+λ(x >0)和 -λ(x < 0),则 oxy 坐标平面上点(0,a )处的场强 E 为:( B ) ( A ) 0 ( B )02aλπεi ( C )04a λπεi ( D ) ()02aλπε+i j 5.3 两个均匀带电的同心球面,半径分别为R 1、R 2(R 1<R 2),小球带电Q ,大球带电-Q ,下列各图中哪一个正确表示了电场的分布 ( d )(C) (D)5.4 如图所示,任一闭合曲面S 内有一点电荷q ,O 为S 面上任一点,若将q 由闭合曲面内的P 点移到T 点,且OP =OT ,那么 ( d )(A) 穿过S 面的电通量改变,O 点的场强大小不变; (B) 穿过S 面的电通量改变,O 点的场强大小改变; (C) 穿过S 面的电通量不变,O 点的场强大小改变;(D) 穿过S 面的电通量不变,O 点的场强大小不变。
5.5如图所示,a 、b 、c 是电场中某条电场线上的三个点,由此可知 ( c ) (A) E a >E b >E c ; (B) E a <E b <E c ; (C) U a >U b >U c ; (D) U a <U b <U c 。
5.6关于高斯定理的理解有下面几种说法,其中正确的是 ( c )(A) 如果高斯面内无电荷,则高斯面上E处处为零;(B) 如果高斯面上E处处不为零,则该面内必无电荷; (C) 如果高斯面内有净电荷,则通过该面的电通量必不为零;(D) 如果高斯面上E处处为零,则该面内必无电荷。
5.7 下面说法正确的是 [ D ](A)等势面上各点场强的大小一定相等; (B)在电势高处,电势能也一定高; (C)场强大处,电势一定高;(D)场强的方向总是从电势高处指向低处.5.8 已知一高斯面所包围的体积内电量代数和0i q =∑ ,则可肯定:[ C ] (A )高斯面上各点场强均为零。
黄淮学院《大学物理》课后答案5

(
)
7 半径为 R1 和 R2 ( R2 > R1 )的两无限长同轴圆柱面,单位长度上分别带有电量 λ 和- λ , 解: 高斯定理 E ⋅ dS =
∫s
�
�
∑q
ε0
� � E ∫ ⋅ dS = E 2πrl
S
取同轴圆柱形高斯面,侧面积 S = 2 πrl 则 对(1) (2)
r < R1
∑ q = 0, E = 0 ∑ q = lλ
(3)设此时内球壳带电量为 q ′ ;则外壳内表面带电量为 − q ′ ,外壳外表面带电量为 − q + q ′ (电荷守恒),此时内球壳电势为零,且
UA =
q' q' − q + q' − + =0 4 πε 0 R1 4 πε 0 R2 4 πε 0 R2
得 外球壳上电势
q′ =
R1 q R2
UB =
Q1 = C1U 1
电容 C 2 与 C 3 并联 C 23 = C 2 + C 3 其上电荷 Q23 = Q1 ∴
U2 =
Q23 C1U 1 25 × 50 = = C 23 C 23 35
25 ) = 86 V 35
U AB = U 1 + U 2 = 50(1 +
5 (1)点电荷 q 位于一边长为a的立方体中心,试求在该点电荷电场中穿过立方体的一个面
解: (1)由高斯定理 E ⋅ dS =
∫s
�
�
q ε0
立方体六个面,当 q 在立方体中心时,每个面上电通量相等 ∴ 各面电通量 Φ e =
q . 6ε 0
(2)电荷在顶点时,将立方体延伸为边长 2a 的立方体,使 q 处于边长 2a 的立方体中心,则 边长 2a 的正方形上电通量 Φ e =
大学物理简明教程习题7详解

习题77.1 选择题(1) 下面说法正确的是: [ ](A )若高斯面上的电场强度处处为零,则该面内必无电荷; (B )若高斯面内无电荷,则高斯面上的电场强度处处为零;(C )若高斯面上的电场强度处处不为零,则高斯面内必定有电荷; (D )若高斯面内有净电荷,则通过高斯面的电通量必不为零; (E )高斯定理仅适用于具有高度对称性的电场。
[答案:D](2)点电荷Q 被曲面S 所包围 , 从无穷远处引入另一点电荷q 至曲面外一点,如题7.1(2)图所示,则引入前后, [ ](A) 曲面S 的电场强度通量不变,曲面上各点场强不变.(B) 曲面S 的电场强度通量变化,曲面上各点场强不变.(C) 曲面S 的电场强度通量变化,曲面上各点场强变化.(D) 曲面S 的电场强度通量不变,曲面上各点场强变化. 题7.1(2)图[答案D ](3)在电场中的导体内部的 [ ](A )电场和电势均为零; (B )电场不为零,电势均为零;(C )电势和表面电势相等; (D )电势低于表面电势。
[答案:C](4)两个同心均匀带电球面,半径分别为R a 和R b (R a <R b ), 所带电荷分别为Q a 和Q b .设某点与球心相距r ,当R a <r <R b 时,该点的电场强度的大小为: [ ] (A)2014a bQ Q r ε+⋅π. (B)2014a bQ Q r ε-⋅π.(C)22014a b b Q Q r R ε⎛⎫⋅+ ⎪⎝⎭π. (D)2014aQ rε⋅π.[答案 D](5)如果某带电体其电荷分布的体密度增大为原来的2倍,则其电场的能量变为原来的 [ ] (A) 2倍. (B) 1/2倍.(C) 4倍. (D) 1/4倍. [答案 C]7.2 填空题(1)在静电场中,电势不变的区域,场强必定为 。
[答案:相同](2)一个点电荷q 放在立方体中心,则穿过某一表面的电通量为 ,若将点电荷由中心向外移动至无限远,则总的电通量将 。
电学习题

= A / r ,在球心处有一点电荷Q,证明当A = Q /(2 π
a2)时,球壳区域内的场强的大小E 与 r 无关。 证:在球壳区域内任一高斯球面,半径为r 。 由高斯定理:
q内 E ds
s
E 4r
2
q内
0
0 q内 E 2 4r 0
Q
r a
b
证:在球壳区域内任一高斯球面,半径为r 。
2
1.以下说法中正确的是[
]
(A) 场强为零处,电势一定为零,电势为零处,场强
一定为零;
(B) 电势较高处,场强一定较大,电势较低处,场强
也一定较小;
(C) 在均匀电场中,各点的场强相等,各点的电势也
相等;
(D) 空间任意点的电势取值与电势零点的选取有关,
但空间任意两点间的电势差是固定的,与电势零点的
选取无关。
2. 在场强大小为E的均匀静电场中,取一半球面,其
半径为R,场强的方向和半球面的轴平行,则通过半
球面的电场强度通量为 [ (A) ] (B)
R E
2
2 R E
2
(C)
2 R 2 E
(D)
1 2 R E 2
3.在没有其它电荷存在的情况下,一个点电荷q1受另
一点电荷 q2 的作用力为f12,当放入第三个电荷Q后,
一、选择题
1、在静电场中,下列说法正确的是:
A)带正电荷的导体,其电势一定是正值。
B)等势面上各点的场强一定相等。
C)场强为零处,电势也一定为零。
√ D)场强相等处,电势梯度矢量一定相等。
2、若空间存在两根无限长直载流导线,空间的磁场 分布就不具有简单的对称性,则该磁场分布: A)不能用安培环路定理计算。
大学物理学第版修订版北京邮电大学出版社下册第九章习题答案

习题99.1选择题(1) 正方形的两对角线处各放置电荷Q ,另两对角线各放置电荷q ,若Q 所受到合力为零,则Q 与q的关系为:()(A )Q=-23/2q (B) Q=23/2q (C) Q=-2q (D) Q=2q[答案:A](2) 下面说法正确的是:()(A )若高斯面上的电场强度处处为零,则该面内必定没有电荷;(B )若高斯面内没有电荷,则该面上的电场强度必定处处为零; (C )若高斯面上的电场强度处处不为零,则该面内必定有电荷; (D )若高斯面内有电荷,则该面上的电场强度必定处处不为零。
[答案:D](3) 一半径为R 的导体球表面的面点荷密度为σ,则在距球面R 处的电场强度() (A )σ/ε0 (B )σ/2ε0 (C )σ/4ε0 (D )σ/8ε0[答案:C](4) 在电场中的导体内部的()(A )电场和电势均为零; (B )电场不为零,电势均为零;(C )电势和表面电势相等; (D )电势低于表面电势。
[答案:C]9.2填空题(1) 在静电场中,电势不变的区域,场强必定为 。
[答案:相同](2) 一个点电荷q 放在立方体中心,则穿过某一表面的电通量为 ,若将点电荷由中心向外移动至无限远,则总通量将 。
[答案:q/6ε0, 将为零](3) 电介质在电容器中作用(a )——(b )——。
[答案:(a)提高电容器的容量;(b) 延长电容器的使用寿命](4) 电量Q 均匀分布在半径为R 的球体内,则球内球外的静电能之比 。
[答案:5:6]9.3 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题9.3图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷 解得 q q 33-=' (2)与三角形边长无关.题9.3图 题9.4图9.4 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如题9.4解: 如题9.4图示解得θπεθtan 4sin 20mg l q =9.5 根据点电荷场强公式204rq E πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解: 020π4r r q Eε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.9.6 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024d q πε,又有人说,因为f =qE ,S q E 0ε=,所以f =S q 02ε.试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强SqE 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为Sq E 02ε=,另一板受它的作用力Sq S qq f 02022εε==,这是两板间相互作用的电场力. 9.7 长l =15.0cmAB 上均匀地分布着线密度λ=5.0x10-9C ·m-1(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q点的场强.解: 如题9.7图所示(1) 在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a xE P -=λε 222)(d π4d x a xE E l l P P -==⎰⎰-ελ题9.7图 用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅方向水平向右(2)2220d d π41d +=x xE Q λε 方向如题9.7图所示由于对称性⎰=l QxE 0d ,即Q E只有y 分量,∵ 22222220dd d d π41d ++=x x x E Qyλε以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅,方向沿y 轴正向9.8 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强.解: 如9.8图在圆上取ϕRd dl =题9.8图ϕλλd d d R l q ==,它在O 点产生场强大小为 20π4d d R R E εϕλ=方向沿半径向外 则 ϕϕελϕd sin π4sin d d 0RE E x ==积分R R E x 000π2d sin π4ελϕϕελπ==⎰ ∴ RE E x 0π2ελ==,方向沿x 轴正向.9.9 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E解: 如9.9图示,正方形一条边上电荷4q在P 点产生物强P E d 方向如图,大小为∵ 22cos 221l r l +=θ∴ 24π4d 22220l r l l r E P ++=ελP Ed 在垂直于平面上的分量βcos d d P E E =⊥∴ 424π4d 2222220l r rl r l r lE +++=⊥ελ题9.9图由于对称性,P 点场强沿OP 方向,大小为 ∵ lq4=λ ∴ 2)4(π422220l r l r qrE P ++=ε 方向沿9.10 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?解: (1)由高斯定理0d εqS E s ⎰=⋅立方体六个面,当q 在立方体中心时,每个面上电通量相等 ∴ 各面电通量06εqe =Φ. (2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εq e =Φ 对于边长a 的正方形,如果它不包含q 所在的顶点,则024εqe =Φ, 如果它包含q 所在顶点则0=Φe .如题9.10图所示. 题9.10 图9.11 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=q r E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm 时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=rr r E ερ内外 1C N -⋅ 沿半径向外. 9.12 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s取同轴圆柱形高斯面,侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰对(1) 1R r < 0,0==∑E q(2) 21R r R << λl q =∑ ∴ rE 0π2ελ=沿径向向外 (3) 2R r > 0=∑q ∴ 0=E题9.13图9.13 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ解: 如题9.13图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ, 两面间, n E)(21210σσε-=1σ面外, n E)(21210σσε+-= 2σ面外, n E)(21210σσε+=n:垂直于两平面由1σ面指为2σ面.9.14 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题9.14图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的.解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题9.14图(a).(1) ρ+球在O 点产生电场010=E ,ρ-球在O 点产生电场'dπ4π3430320OO r E ερ=∴ O 点电场'd33030OO r E ερ= ;(2) ρ+在O '产生电场'dπ4d 3430301OO E ερπ='ρ-球在O '产生电场002='E∴ O ' 点电场 003ερ='E 'OO 题9.14图(a) 题9.14图(b)(3)设空腔任一点P 相对O '的位矢为r',相对O 点位矢为r (如题8-13(b)图)则 03ερrE PO =,3ερr E O P '-=' ,∴ 00033)(3ερερερdr r E E E O P PO P=='-=+=' ∴腔内场强是均匀的.9.15 一电偶极子由q =1.0×10-6Cd=0.2cm ,把这电偶极子放在1.0×105N ·C-1解: ∵ 电偶极子p在外场E中受力矩 ∴ qlE pE M ==max 代入数字9.16 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解: ⎰⎰==⋅=22210212021π4π4d d r rr r q q r r q q r F A εε)11(21r r - 外力需作的功 61055.6-⨯-=-='A A J题9.17图9.17 如题9.17图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C解: 如题9.17图示∴ Rqq U U q A o C O 00π6)(ε=-= 9.18 如题9.18图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点Ed 如图,由于对称性,O 点场强沿y 轴负方向题9.18图R 0π4ελ=[)2sin(π-2sin π-] (2) AB 电荷在O 点产生电势,以0=∞U 同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U ∴ 0032142ln π2ελελ+=++=U U U U O 9.19 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强 电子受力大小 re eE F e 0π2ελ== ∴ rv m r e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅9.20 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm解: 平行板电容器内部近似为均匀电场9.21 证明:对于两个无限大的平行平面带电导体板(题9.21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)证: 如题9.21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题9.21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有 ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即 又∵ +2σ03=σ ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同.9.22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0 mm .B ,C 都接地,如题9.22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?解: 如题9.22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题9.22图(1)∵ AB AC U U =,即∴ AB AB AC AC E E d d = ∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A= 得 ,32S q A =σ Sq A 321=σ 而 7110232-⨯-=-=-=A C q S q σCC10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC AC AC A E U εσV 9.23两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳(2)*(3)解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势⎰⎰∞∞==⋅=22020π4π4d d RR Rqr r q r E U εε 题9.23图(2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q ' (电荷守恒),此时内球壳电势为零,且 得 q R R q 21=' 外球壳上电势9.24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题9.24图所示,设金属球感应电荷为q ',则球接地时电势0=O U题9.24图由电势叠加原理有:得 -='q 3q 9.25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F .试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力; (2)小球3依次交替接触小球1,2很多次后移去,小球1,2解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电2q q =', 小球3再与小球2接触后,小球2与小球3均带电 ∴ 此时小球1与小球2间相互作用力(2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为32q . ∴ 小球1、2间的作用力00294π432322F r q q F ==ε 9.26 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势.解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强303π4,π4r rQ E r r Q D r εε ==内; 介质外)(2R r <场强 (2)介质外)(2R r >电势介质内)(21R r R <<电势(3)金属球的电势9.27 如题9.27图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题9.27图所示,充满电介质部分场强为2E ,真空部分场强为1E,自由电荷面密度分别为2σ与1σ 由∑⎰=⋅0d q S D得11σ=D ,22σ=D而 101E D ε=,202E D r εε= ∴r r E E εεεεσσ==102012 题9.27图 题9.28图9.28 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求:(1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量;(2)电介质中的总电场能量; (3)圆柱形电容器的电容.解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰当)(21R r R <<时,Q q =∑∴ rlQD π2=(1)电场能量密度 22222π82l r Q D w εε==薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222===(2)电介质中总电场能量(3)电容:∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== 题9.29图9.29 如题9.29 图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量电容2C 与3C 并联3223C C C += 其上电荷123Q Q =∴ 355025231123232⨯===C U C C Q U 9.30 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少?如果两端加上1000 V?解: (1) 1C 与2C 串联后电容 (2)串联后电压比231221==C C U U ,而100021=+U U ∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿.9.31半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题9.31图(1)在1R r <和32R r R <<区域在21R r R <<时 301π4r rQ E ε=3R r >时 302π4rrQ E ε=∴在21R r R <<区域 在3R r >区域∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε(2)导体壳接地时,只有21R r R <<时30π4r rQ E ε=,02=W ∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容 )11/(π422102R R Q W C -==ε。
医用物理习题

第8章 振动与波
(含声和超声)
2-1、某波在空气中的波速为344m·s-1,波长为 0.671m,当它传入水中时,波长变为2.83m,求它在水 中的传播速度?
y
2-2、已知平面波的波动方程为
0.02
截面时,克服粘滞力所作的功是多少?
3-15、如图,牛顿粘性液体沿等粗水平管流动时压 力沿管路降低的情况,已知h=23cm,h1=15cm, h2=10cm,h3=5cm,a=10cm,求液体流动的平 均速度?
h
h1 h2 h3
a a aa 3-16、液体中有一空气泡,泡的直径为1mm,液体 的粘度为0.15Pa·s,密度为0.9×103kg·m-3,问(1) 空气泡在该液体中上升的收尾速度是多少?(2)若
6-14,正三角形的边长为0.6m,在三顶点分别放上点 电荷 q1 1.0 106 C, q2 2.0 106 C, q3 3.0 106 C, 今将一电子自A点沿圆弧移到B点需作多少功?A、B 分别为三角形两边的中点(如图所示)。
6-15,如图,AB=2L,OCD是以B为中心L为半径的 半圆。A点有正电荷+q,B点有电荷-q。(1)把单 位正电荷从O点沿OCD移到D点,电场力对它作了多 少功?(2)把单位负电荷从D点沿AB的延长线移到 无穷远处,电场力对它作了多少功?
7 8.如图,已知R1 R2 4.0, R3 R4 R5 8.0,
1 2.0V ,2 10.0V ,求I1, I2和Uab
7 9.如图,已知1 1.5V ,2 1.0V , R1 50.0, R2 80.0,
6-6、如图,将一根细玻璃棒弯曲成半径为R,圆心角 2π/3的圆弧,其上均匀地分布着+q的电荷,求圆弧的 圆心O点处的埸强和电势.
大学物理学课后答案第3版下册北京邮电大学出版社.pdf

大学物理习题及解答习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系? 解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷20220)33(π4130cos π412a q q a q '=︒εε解得q q 33−='(2)与三角形边长无关.题8-1图题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量. 解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得θπεθtan 4sin 20mg l q =8-3 根据点电荷场强公式204r qE πε=,当被考察的场点距源点电荷很近(r→0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解:20π4r r q E ε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024d q πε,又有人说,因为f =qE ,S qE 0ε=,所以f =S q 02ε.试问这两种说法对吗?为什么? f 到底应等于多少? 解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强S qE 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为S qE 02ε=,另一板受它的作用力S q S q q f 02022εε==,这是两板间相互作用的电场力.8-5 一电偶极子的电矩为l q p =,场点到偶极子中心O 点的距离为r ,矢量r 与l 的夹角为θ,(见题8-5图),且l r >>.试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin r p πεθ证: 如题8-5所示,将p 分解为与r 平行的分量θsin p 和垂直于r 的分量θsin p .∵ l r >> ∴ 场点P 在r 方向场强分量30π2cos r p E r εθ=垂直于r 方向,即θ方向场强分量300π4sin r p E εθ=题8-5图 题8-6图8-6 长l =15.0cm 的直导线AB 上均匀地分布着线密度λ=5.0x10-9C·m -1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强. 解: 如题8-6图所示(1)在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a x E P −=λε2220)(d π4d x a xE E llP P −==⎰⎰−ελ]2121[π40l a l a +−−=ελ)4(π220l a l−=ελ用15=l cm ,9100.5−⨯=λ1m C −⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N −⋅ 方向水平向右 (2)同理2220d d π41d +=x xE Q λε 方向如题8-6图所示 由于对称性⎰=l QxE 0d ,即Q E只有y 分量,∵22222220d d d d π41d ++=x x x E Qy λε22π4d d ελ⎰==lQyQy E E ⎰−+2223222)d (d l l x x2220d 4π2+=l lελ以9100.5−⨯=λ1cm C −⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N −⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强. 解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0R E E x ==ϕϕελϕπd cos π4)cos(d d 0R E E y −=−=积分R R E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=−=⎰ϕϕελπR E y∴R E E x 0π2ελ==,方向沿x 轴正向.8-8 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E .解: 如8-8图示,正方形一条边上电荷4q 在P 点产生物强P Ed 方向如图,大小为()4π4cos cos d 22021l r E P +−=εθθλ ∵22cos 221l r l +=θ 12cos cos θθ−= ∴24π4d 22220l r ll r E P ++=ελ P Ed 在垂直于平面上的分量βcos d d P E E =⊥∴424π4d 222222l r r l r l r lE +++=⊥ελ题8-8图由于对称性,P 点场强沿OP 方向,大小为2)4(π44d 422220l r l r lrE E P ++=⨯=⊥ελ ∵l q 4=λ∴2)4(π422220l r l r qrE P ++=ε 方向沿OP 8-9 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在点电荷q 的电场中取半径为R 的圆平面.q 在该平面轴线上的A 点处,求:通过圆平面的电通量.(x Rarctan=α)解: (1)由高斯定理0d εq S E s⎰=⋅ 立方体六个面,当q 在立方体中心时,每个面上电通量相等∴ 各面电通量06εqe =Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εq e =Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则024εqe =Φ,如果它包含q 所在顶点则=Φe .如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量,球冠面积*]1)[(π22222xR x x R S +−+=∴)(π42200x R Sq +=Φε02εq=[221x R x +−] *关于球冠面积的计算:见题8-9(c)图ααα⎰⋅=0d sin π2r r S ααα⎰⋅=02d sin π2r)cos 1(π22α−=r8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510−C·m -3求距球心5cm ,8cm ,12cm 各点的场强.解: 高斯定理,02π4ε∑=q r E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p =3(r )3内r −∴()2023π43π4r r r E ερ内−=41048.3⨯≈1C N −⋅, 方向沿半径向外. 12=r cm 时,3π4∑=ρq −3(外r )内3r∴ ()420331010.4π43π4⨯≈−=r r r E ερ内外 1C N −⋅ 沿半径向外.8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强. 解: 高斯定理0d ε∑⎰=⋅q S E s取同轴圆柱形高斯面,侧面积rl S π2=则rlE S E Sπ2d =⋅⎰对(1) 1R r < 0,0==∑E q(2) 21R r R <<λl q =∑∴r E 0π2ελ=沿径向向外(3) 2R r >=∑q∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强.解: 如题8-12图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,d ε ∑⎰= ⋅ q S E s两面间, nE )(21210σσε−=1σ面外, nE )(21210σσε+−= 2σ面外, nE )(21210σσε+=n:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题8-13图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的.解: 将此带电体看作带正电ρ的均匀球与带电ρ−的均匀小球的组合,见题8-13图(a).(1) ρ+球在O 点产生电场10=E,ρ− 球在O 点产生电场'd π4π3430320OO r E ερ=∴ O 点电场'd 33030OO r E ερ= ;(2) ρ+在O '产生电场'd π4d 3430301OO E ερπ=' ρ−球在O '产生电场002='E∴ O ' 点电场003ερ='E 'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r ',相对O 点位矢为r(如题8-13(b)图)则03ερrE PO =,03ερr E O P '−=' ,∴0003'3)(3ερερερd OO r r E E E O P PO P=='−=+='∴腔内场强是均匀的.8-14 一电偶极子由q =1.0×10-6C 的两个异号点电荷组成,两电荷距离d=0.2cm ,把这电偶极子放在1.0×105N·C -1的外电场中,求外电场作用于电偶极子上的最大力矩.解: ∵ 电偶极子p 在外场E中受力矩E p M ⨯= ∴qlEpE M ==m ax 代入数字4536max 100.2100.1102100.1−−−⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功? 解:⎰⎰==⋅=22210212021π4π4d d r r r r q q r rq q r F A εε )11(21r r −61055.6−⨯−=J外力需作的功 61055.6−⨯−=−='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点,求移动过程中电场力作的功.解: 如题8-16图示0π41ε=O U 0)(=−R qR q 0π41ε=O U )3(R q R q −R q 0π6ε−=∴R qq U U q A oC O 00π6)(ε=−=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点Ed 如图,由于对称性,O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰−==R R E E yR 0π4ελ=[)2sin(π−2sinπ−]R 0π2ελ−=(2) AB 电荷在O 点产生电势,以0=∞U⎰⎰===A B 200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U半圆环产生0034π4πελελ==R R U∴0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强r E 0π2ελ=电子受力大小r e eE F e 0π2ελ==∴r v m r e 20π2=ελ得1320105.12π2−⨯==e mv ελ1m C −⋅ 8-19 空气可以承受的场强的最大值为E =30kV·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm ,求此电容器可承受的最高电压.解: 平行板电容器内部近似为均匀电场∴ 4105.1d ⨯==E U V8-20 根据场强E与电势U 的关系U E −∇= ,求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q ,半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图).解: (1)点电荷r qU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ε=∂∂−= 0r 为r 方向单位矢量.(2)总电量q ,半径为R 的均匀带电圆环轴上一点电势220π4x R qU +=ε∴ ()ix R qx i x U E 2/3220π4+=∂∂−=ε(3)偶极子l q p=在l r >>处的一点电势200π4cos ])cos 21(1)cos 2(1[π4r ql l l r q U εθθθε=+−−=∴ 30π2cos r p r U E r εθ=∂∂−=30π4sin 1r p U r E εθθθ=∂∂−=8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同.证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有)(d 32=∆+=⋅⎰S S E sσσ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=−−−εσεσεσεσ又∵ +2σ03=σ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同.8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0 mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少? 解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ ABAC U U =,即∴ABAB AC AC E E d d =∴ 2d d 21===AC ABAB AC E E σσ且 1σ+2σS q A=得,32S q A =σ S q A321=σ 而7110232−⨯−=−=−=A C q S q σC C10172−⨯−=−=S q B σ(2)301103.2d d ⨯===AC AC AC A E U εσV8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势; *(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q +;球壳内表面带电则为q −,外表面带电为q +,且均匀分布,其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qr r q r E U εε (2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q −.所以球壳电势由内球q +与内表面q −产生:π4π42020=−=R qR qU εε(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '−,外壳外表面带电量为+−q q '(电荷守恒),此时内球壳电势为零,且π4'π4'π4'202010=+−+−=R q q R q R q U A εεε得 q R R q 21='外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε−=+−+−=8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+RqR q εε得 −='q 3q8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F.试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力; (2)小球3依次交替接触小球1,2很多次后移去,小球1,2之间的库仑力.解: 由题意知2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电2q q =',小球3再与小球2接触后,小球2与小球3均带电qq 43=''∴ 此时小球1与小球2间相互作用力0220183π483π4"'2F rqr q q F =−=εε (2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为32q.∴ 小球1、2间的作用力00294π432322F r q q F ==ε*8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+−==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得S q261==σσ S qd U 2032−=−=εσσ S qd U 2054+=−=εσσ所以CB 间电场S q d U E 00422εεσ+==)2d (212d 02S q U E U U CB C ε+===注意:因为C 片带电,所以2U U C ≠,若C 片不带电,显然2UU C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势. 解: 利用有介质时的高斯定理∑⎰=⋅qS D Sd(1)介质内)(21R r R <<场强303π4,π4r rQ E r r Q D r εε ==内;介质外)(2R r <场强303π4,π4r r Q E r Qr D ε ==外(2)介质外)(2R r >电势r Q E U 0rπ4r d ε=⋅=⎰∞ 外介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+−=)11(π420R r Q r r −+=εεε(3)金属球的电势rd r d 221⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=222020π44πdrR R R r r Qdrr Q εεε )11(π4210R R Q r r −+=εεε8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值. 解: 如题8-28图所示,充满电介质部分场强为2E ,真空部分场强为1E,自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D 得11σ=D ,22σ=D而101E D ε=,202E D r εε=d 21UE E ==∴ r D D εσσ==1212题8-28图 题8-29图rd r d ⋅+⋅=⎰⎰∞∞rrE E U 外内8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求:(1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量; (2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S 则 rlDS D S π2d )(=⋅⎰当)(21R r R <<时,Q q =∑∴rl QD π2=(1)电场能量密度22222π82l r Q D w εε== 薄壳中rl rQ rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R V R R l Q rl r Q W W εε(3)电容:∵C Q W 22=∴)/ln(π22122R R lW Q C ε==*8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1) 1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度. 解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即2210π41r q q F ε=但2q 处于金属球壳中心,它受合力为零,没有加速度. (2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41r q q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U . 解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C +=其上电荷123Q Q =∴355025231123232⨯===C U C C Q U86)35251(5021=+=+=U U U AB V8-32 1C 和2C 两电容器分别标明“200 pF、500 V”和“300 pF、900 V”,把它们串联起来后等值电容是多少?如果两端加上1000 V 的电压,是否会击穿? 解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF(2)串联后电压比231221==C C U U ,而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿.8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求: (1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==−=−=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+−=+−(2)电场能量损失WW W −=∆0)22()2121(2221212221C q C q U C U C +−+=221212UC C C C +=8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C 时,求:(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q −,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E在21R r R <<时 301π4r rQ E ε =3R r >时 302π4r rQ E ε =∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r r Q W εε ⎰−==21)11(π8π8d 2102202R R R R Q rr Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r r Q W εεε ∴ 总能量)111(π83210221R R R Q W W W +−=+=ε41082.1−⨯=J(2)导体壳接地时,只有21R r R <<时30π4r rQ E ε =,02=W∴ 4210211001.1)11(π8−⨯=−==R R Q W W ε J(3)电容器电容)11/(π422102R R Q W C −==ε121049.4−⨯=F习题九9-1 在同一磁感应线上,各点B 的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向?解: 在同一磁感应线上,各点B的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B 的方向.题9-2图9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B 的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)?(2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B = ∑⎰==−=⋅0d 021I bc B da B l B abcdμ∴ 21B B= (2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B 方向相反,即21B B≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.9-4 在载流长螺线管的情况下,我们导出其内部nIB 0μ=,外面B =0,所以在载流螺线管外面环绕一周(见题9-4图)的环路积分⎰外B L ·d l =0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为 ⎰外B L ·d l=I 0μ这是为什么? 解: 我们导出nl B 0μ=内,=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μ外,与⎰⎰=⋅=⋅Ll l B 0d 0d外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B 的轴向分量为零,而垂直于轴的圆周方向分量r IB πμ20=⊥,r 为管外一点到螺线管轴的距离.题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转. 9-6 已知磁感应强度0.2=B Wb·m-2的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是 24.04.03.00.211=⨯⨯=⋅=S BΦWb(2)通过befc 面积2S 的磁通量 022=⋅=S BΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb (或曰24.0−Wb ) 题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题9-7图所示,O 点磁场由AB 、C B、CD 三部分电流产生.其中AB 产生 01=BCD 产生R I B 1202μ=,方向垂直向里CD 段产生)231(2)60sin 90(sin 24003−πμ=−πμ=︒︒R I R I B ,方向⊥向里∴)6231(203210ππμ+−=++=R I B B B B ,方向⊥向里. 9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题9-8图解:如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2−⨯=⨯+−=πμπμI I B A T(2)设0=B 在2L 外侧距离2L 为r 处则 02)1.0(220=−+r I r Iπμπμ解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
2022年大学工程力学专业《大学物理(上册)》期末考试试卷 含答案

2022年大学工程力学专业《大学物理(上册)》期末考试试卷含答案姓名:______ 班级:______ 学号:______考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题(共10小题,每题2分,共20分)1、刚体绕定轴转动时,刚体的角加速度与它所受的合外力矩成______,与刚体本身的转动惯量成反比。
(填“正比”或“反比”)。
2、质量分别为m和2m的两物体(都可视为质点),用一长为l的轻质刚性细杆相连,系统绕通过杆且与杆垂直的竖直固定轴O转动,已知O轴离质量为2m的质点的距离为l,质量为m的质点的线速度为v且与杆垂直,则该系统对转轴的角动量(动量矩)大小为________。
3、两根相互平行的“无限长”均匀带正电直线1、2,相距为d,其电荷线密度分别为和如图所示,则场强等于零的点与直线1的距离a为_____________ 。
4、质量为M的物体A静止于水平面上,它与平面之间的滑动摩擦系数为μ,另一质量为的小球B以沿水平方向向右的速度与物体A发生完全非弹性碰撞.则碰后它们在水平方向滑过的距离L=__________。
5、简谐振动的振动曲线如图所示,相应的以余弦函数表示的振动方程为__________。
6、一条无限长直导线载有10A的电流.在离它 0.5m远的地方它产生的磁感强度B为____________。
一条长直载流导线,在离它1cm处产生的磁感强度是T,它所载的电流为____________。
7、一圆盘正绕垂直于盘面的水平光滑固定轴O转动,如图射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并留在盘内,则子弹射入后的瞬间,圆盘的角速度_____。
8、一个绕有500匝导线的平均周长50cm的细螺绕环,铁芯的相对磁导率为600,载有0.3A 电流时, 铁芯中的磁感应强度B的大小为___________;铁芯中的磁场强度H的大小为___________ 。
长L15cm的直导线AB上均匀地分布着线密度为

xa
2 0
dx
07-3
0x
kx
2 0
dx
xa
kx
2 0
dx
k (2x2 a2)
4 0
(3)场强最小值为零
k (2x2 a2) 0
4 0
x 2a
2
完
07-4
4.如图所示,在点电荷q的电场中,取半径为R的圆
形平面。设点电荷q在垂直于平面并通过圆心O的轴
线上A点处,A点与圆心的距离为d。试计算通过此平
07-1
1. 长L=15cm的直导线AB上均匀地分布着线密度为
=510-9C/m的电荷。求:在导线的延长线上与导线
一端B相距d=5cm处P点的场强。
解:建立如图所示的坐 标系,在导线上取电荷
元dq=dx ,电荷元在P
oA
x dx B P x
L
d dE
点所激发的场强大小
dE
1
4 0
(L
dx
d
x)2
P点的总场强大小
y
解:建立如图所示的坐标系,电
荷元dq=Rd 在o点所激发的场
强大小dEFra bibliotek14 0
Rd
R2
dE
d o
R
x
dl 0
dE y
1
4 0
Rd
R2
cos
d
07-2
E
dE y
0
0
4 0
cos
R
d
4 0
2 sin 0
R
4 0
d R2
9
109
3.12 109
2 0.5 0.02
0.02 0.52
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E 4 ( R h)
2
1.13 10 (C/m )
3
前页 后页 目录
12
完 16
2
4 0 ( L d x )
P点的总场强大小
前页 后页 目录
1
07-1
E 0
L
1
dx
2
4 0 ( L d x ) 1 1 ( ) 4 0 d d L
9 9
1 1 9 10 5 10 ( ) 0.05 0.20 675(V/m)
0.72(V/m)
前页 后页 目录
4
07-2 近似解法:
1 d E 2 4 0 R
y
0.72(V/m)
o
E
R
x
d
完
前页 后页 目录
5
07-3
3.一块厚度为a的无限大带电平板,电荷体密度为 =kx (0xa),k为正常数,求: (1)板外两侧任一点M1、M2的场强大小。 (2)板内任一点M的场强大小。 dx (3)场强最小的点在何处。
kx ka 2 a a dx E2 0 dx 0 2 0 2 0 4 0
x
2
M2处的场强
(2)M处的场强
a E 0 dx x dx 2 0 2 0
前页 后页 目录
7
07-3
kx kx a 0 dx x dx 2 0 2 0 k 2 2 (2 x a ) 4 0
6.(1)地球表面的场强近似为200V/m,方向指向地球 中心,地球的半径为6.37106m。试计算地球带的总 电荷量。 (2)在离地面1400 m处,场强降为20V/m,方向仍 指向地球中心,试计算这1400m厚的大气层里的平均 电荷密度。
解:设地球带的总电量为Q,大气层带电量为q。 (1)由高斯定理得
完
前页 后页 目录
2
07-2
2. 半径R为50cm的圆弧形细塑料棒,两端空隙d为 2cm,总电荷量为3.1210-9C的正电荷均匀地分布在 棒上。求圆心o处场强的大小和方向。
解:建立如图所示的坐标系,电 荷元dq=Rd 在o点所激发的场 强大小
y
1 Rd dE 2 4 0 R 1 Rd dE y cos 2 4 0 R
x
(3)场强最小值为零
k 2 2 (2 x a ) 0 4 0 2 x a 2
前页 后页 目录
完 8
07-4
4.如图所示,在点电荷q的电场中,取半径为R的圆 形平面。设点电荷q在垂直于平面并通过圆心O的轴 线上A点处,A点与圆心的距离为d。试计算通过此 平面的通量。 2 2 解:在圆形平面取半径 为r宽度为dr的同心圆环 作为面元,则
d
dl
o
R
dE
x
0
d
前页 后页 目录
3
07-2
E dE y 0
0
cos d 4 0 R
2 sin 0 d 2 4 0 R 4 0 R 9 3.12 10 0.02 9 9 10 2 2 0.5 0.02 0.5
解:在平板内任意x处取厚度为dx 的簿层作为电荷元,其电荷面密度 =dx,簿层两侧的场强
o x
x
dE dx 2 0 2 0
方向平行于x轴
M1
M
a
M2
前页 后页 目录
6
07-3 (1)M1处的场强
a
kx ka a E1 0 dx 0 dx 2 0 2 0 4 0
R dr r O
R d q d A
dS 2rdr r d tg d dr d 2 cos
前页 后页 目录
9
07-4 dS的电通量
d E E cos dS E cos 2rdr 1 q cos 2rdr 2 2 4 0 r d
q d cos 2 dtg d 2 4 0 ( d ) 2 cos cos 1 sin d 2 0
2
Q E 4R 0 1 6 2 200 (6.37 10 ) 9 105 (C) 9 9 10
前页 后页 目录
15
E 4R
2
Q
0
07-6 (2)由据高斯定理得
0 2 q E 4 0 ( R h) Q
1 6 2 5 20 (6.37 10 1400) 9 10 9 9 10 5 8.1 10 (C) 5 q 8.1 10 2 6 2 4R h 4 (6.37 10 ) 1400
前页 后页 目录
10
1
07-4 通过圆平面的电通量
q E d E 0 sin d 2 0 q (1 cos ) 2 0
q d (1 ) 2 2 2 0 R d
前页 后页 目录
11
07-4
另解:圆平面的电通量等于以 R 2 d 2 为半径, 以圆平面的边界为边界的球冠表面的电通量
4 3 4 3 R r 1 1 3 3 E P 2 2 4 0 rP O 4 0 (rP O rOO )
r R ( 2 ) 2 3 0 (rP O rOO ) rP O
3 3
场强沿水平方向,正值水平向右。
前页 后页 目录
完 14
07-6
E d E EdS E dS E 2rh
q 2 2 2 2 2 R d ( R d d ) 2 2 4 0 R d 1
q d (1 ) 2 2 2 0 R d
完
前页 后页 目录
12
07-5
5.在半径为R,电荷体密度为 的均匀带电球内,挖 去一个半径为r的小球,如图所示。试求:P和P点的 场强。(O、O、P、P在一条直线上。)
07-1
1. 长L=15cm的直导线AB上均匀地分布着线密度为 =510-9C/m的电荷。求:在导线的延长线上与导线 一端B相距d=5cm处P点的场强。
解:建立如图所示的坐 标系,在导线上取电荷 元dq=dx ,电荷元在 P点所激发的场强大小
A x o
dx B P x dE L d
dE
1
dx
解:用场强叠加原理求解
P
P
O O r R
4 3 4 3 rPO r 1 1 3 3 EP 2 2 4 0 rPO 4 0 (rPO rOO )
前页 后页 目录
13
07-5
r ( rPO ) 2 3 0 (rPO rOO )
场强沿水平方向,正值水平向右。
