长沙市2014年初中数学创新能力大赛
2013-2014学年第二学期八年级竞赛数学试卷(含答案)人教新课标

ADCB2013学年第二学期八年级竞赛数学试卷学号___________ 姓名____________ 得分___________一、 细心选一选(每题3分,共36分) 1.下列计算正确的是( ) A.B.C.D.2.要使二次根式有意义,则x 的取值范围是( )A .x B.x C. D.x3.一位卖运动鞋的经销商到一所学校对200名学生的鞋号进行了抽样调查,经销商最感兴趣的是这组鞋号的( )A .中位数 B.平均数 C.众数 D.方差 4.如果一个多边形的内角和为1800°则这是个( )边形A .9 B.10 C.11 D.125.下列各数中,可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是( ) A .5 B.4 C.2 D.86.若代数式x 2+5x +6与-x +1的值相等,则x 的值为( ) **=-1,x2=-5B.x1=-6,x2=1**=-2,x2=-3D.x=-17.在下列图形中,既是轴对称图形,又是中心对称图形的是( )8.如果等边三角形的边长为6,那么连接各边中点所成的三角形的周长为( ) ** B.9 C.12 D.18 9.用配方法解下列方程时,配方有错误的是( )**-2x -99=0化为(x -1)2=100 B.x2+8x+9=0化为(x+4)2=25 **-7t -4=0化为 D.3y2-4y -2=0化为10.平行四边形的对角线分别为a和b ,一边长为12,则a和b的值可能是下面各组的数据中的()A.8和4 B.10和14 C.18和20 D.10和3811. 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是()A.70 B. 110 C. 140 D. 15012.设min{,}x y表示x,y两个数中的最小值,例如min{0,2}=0 ,min{12,8}8=,则关于函数min{2,2}y x x=+可表示为()A.2(2)2(2)x xyx x<⎧=⎨+≥⎩B.2(2)2(2)x xyx x+<⎧=⎨≥⎩C.2y x= D.2y x=+二、填空题(每题3分,共24分)13.在直角坐标系中,点A(2,-3)关于原点对称的点的坐标是__________,关于x轴对称的点的坐标是_____________.14.已知x=-1是关于x的方程的一个根,则a=_____________15. 一组正整数2,3,4,x从小到大排列,已知这组数据的中位数和平均数相等,那么x的值是______________16.用反证法证明“在三角形中,至少有一个内角大于或等于60°”时,应假设__________________________________17.函数与y=x-2图象的交点的横坐标分别为a,b,则的值为______18. 如图,▱ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合,若△ACD的面积为3,则图中阴影部分两个三角形的面积和为______________第18题图19题图第20题图19. 学剪五角星:如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC剪下△ABC,展开即可得到一个五角星,若想得到一个正五角星(如图④,正五角星的5个角都是36°),则在图③中应沿什么角度剪即∠ABC的度数为_____________20.如图,在菱形ABCD 中,边长为10,∠A =60°.顺次连结菱形ABCD 各边中点,可得四边形A 1B 1C 1D 1;顺次连结四边形A 1B 1C 1D 1各边中点,可得四边形A 2B 2C 2D 2;顺次连结四边形A 2B 2C 2D 2各边中点,可得四边形A 3B 3C 3D 3;按此规律继续下去….则四边形A 2B 2C 2D 2的周长是________;四边形A 2012B 2012C 2012D 2012的周长是________ 三、 解答题(共60分) 21.(8分)化简计算:(1)1691214⨯⨯ (2)182)12)(12(12⨯+-++22.(8分)解方程(1)x 2+3x +1=0 (2)(x -2)(x -5)=-223.(8分)已知:如图,在正方形ABCD 中,AE ⊥BF ,垂足为P ,AE 与CD 交于点E ,•BF •与AD 交于点F ,求证:AE =BF .24.(8分)某校为了解学生“体育大课间”的锻炼效果,中考体育测试结束后,随机从学校720名考生中抽取部分学生的体育测试成绩绘制了条形统计图.试根据统计图提供的信息,回答下列问题:(1)共抽取了_____________名学生的体育测试成绩进行统计;(2)随机抽取的这部分学生中男生体育成绩的平均数是______,众数是______,女生体育成绩的中位数是___________(3)若将不低于27分的成绩评为优秀,估计这720名考生中,成绩为优秀的学生大约是多少?25.(8分)某百货大楼服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1050元,那么每件童装应降价多少元?26.(8分) 如图,病人按规定的剂量服用某药物,测得服药后2小时,每毫升血液中含药量达到最大值为4毫克.已知服药后,2小时前每毫升血液中含药量y (毫克)与时间x (小时)成正比例;2小时后y 与x 成反比例.(1)当0≤x ≤2时;x >2时,分别求y 与x 的函数关系式?(2)如果每毫升血液中含药量不低于2毫克时治疗有效,则那么服药一次,治疗疾病的有效时间是多长?27. (12分)将正方形ABCD 绕中心O 顺时针旋转角α得到正方形1111D C B A ,如图1所示. (1)当α=45o时(如图2),若线段OA 与边11D A 的交点为E ,线段1OA 与AB 的交点为F ,可得下列结论成立 ①EOP ∆≌FOP ∆②1PA PA =,试选择一个证明.(2)当o o 900<<α时,第(1)小题中的结论1PA PA =还成立吗?如果成立,请证明;如果不成立,请说明理由.(3)在旋转过程中,记正方形1111D C B A 与AB 边相交于P ,Q 两点,探究POQ ∠的度数是否发生变化?如果变化,请描述它与α之间的关系;如果不变,请直接写出POQ ∠的度数.答题卷一.选择题 (本大题共12小题, 每小题3分, 共36分)APBQ1B C1C D1DO图1DC1B BPFEOA1C1D图21A 1A二.填空题(本大题有8小题, 每小题3分, 共24分)13. 、 14. . 15. . 16. . 17. . 18. . 19. . 20. . 三、解答题(共8道小题,共50分) 21、(本题满分6分)化简计算:(1)1691214⨯⨯ (2)182)12)(12(12⨯+-++22、(本题满分6分)解方程(1)x 2+3x +1=0 (2)(x -2)(x -5)=-2 23.(8分)题号 1 2 3 4 5 6 7 8 9 10 11 12 答案24.(8分)(1)共抽取了_____________名学生的体育测试成绩进行统计;(2)随机抽取的这部分学生中男生体育成绩的平均数是______,众数是______;女生体育成绩的中位数是___________(3)若将不低于27分的成绩评为优秀,估计这720名考生中,成绩为优秀的学生大约是多少?25.(8分)26.(8分)27.(12分)APBQ1B C1C D1DO图1DC1B BP FEOA 1C1D图21A 1A参考答案一.选择题 (本大题共12小题, 每小题3分, 共36分) 二.填空题(本大题有8小题, 每小题3分, 共24分)13. (-2,3) 、 (2,3) 14. -2或1 . 15. 5 . 16. 三个内角都小于60° . 17. -2 . 18. 3 . 19. 126°. 20. 20 、21.(1)286 (2)7+22.(1) (2)x =3,或x =423.解:在(ASA ) AE =BF24.(1)80 (2) 26.4 27 27 (3)25.解:设每件童装应降价X 元,则26 (1) .(2)题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DACDCACBBCDA1A B1B C1CD1DOEFPQA 治疗疾病的有效时间是4小时。
2014年长沙市“学用杯”初中数学应用与创新能力大赛 八年级初赛试题

长沙市2014年初中数学创新能力大赛八 年 级 初 赛 试 题(时量:90分钟 满分:100分)一、选择题(本大题共10小题,每小题4分,共40分)1.计算)1011)(911)...(411)(311)(211(22222-----的值是 A .2110B .2113C .209D .20112.整数N =215×510的位数是A .10位B .11位C .12位D .13位 3.已知32233,796x y xyxyxy y x---==+-则4.已知△ABC 的三边的长分别为a 、b 、c ,且b c b c a+=+-,则△ABC 一定是A .等边三角形B .腰长为a 的等腰三角形C .底边长为a 的等腰三角形D .等腰三角形 5.如果代数式-2+38a b +的值为18,那么代数式962b a -+的值等于A .28B .-28C .-32D .326在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,则下列说法中错误的是 A .如果∠C -∠B =∠A ,那么△ABC 是直角三角形,∠C =90° B .如果5:4:3::=c b a ,则∠B =60°,∠A =30° C .如果3:2:5C :B :A =∠∠∠,那么△ABC 是直角三角形 D .如果2))((b a c a c =-+,那么△ABC 是直角三角形7.如图,在四边形ABCD 中,M 、N 分别是CD 、BC 的中点,且AM⊥CD,AN⊥BC,已知∠MAN=74°,∠DBC=41°,则∠ADC 度数为学校:姓名: 考场: 考号:☼……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼A .45°B .47°C .49°D .51°8.规定“Δ”为有序实数对的运算,且(a ,b )△(c ,d )=(ac +bd ,ad +bc ),如果对任意实数a ,b 都有(a ,b )△(x ,y )=(a ,b ),则(x ,y )为 A .(0,1) B .(1,0) C .(-1,0) D .(0,-1)9.甲、乙、丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲、乙各比赛了4局,丙当了3次裁判.问第2局的输者是A .甲B .乙C .丙D .不能确定10.某公交公司停车场内有15辆车,从上午6时开始发车(6时整第一辆车开出),以后每隔6分钟再开出一辆.第一辆车开出3分钟后有一辆车进场,以后每隔8分钟有一辆车进场,进场的车在原有的15辆车后依次再出车.则到第几辆车开出后,停车场内第一次出现无车辆? A 、55 B 、56 C 、57 D 、58 二、填空题(本大题共8小题,每小题4分,共32分) 11.已知a +b =1,ab =108,则a 2b +ab 2的值为__________. 12.关于x 的方程211x a x +=-的解是正数,则a 的取值范围是_________.13.已知31=+aa ,则221a a +的值是_______________. 14.如图,在ABC ∆中,90,50,30,ACB AB cm BC cm CD AB ∠=︒==⊥于D ,则CD=______ _____________cm .(第14题) (第17题) (第18题)15.已知4x -3y -6z =0,x +2y -7z =0,则=---+222222103225zy x z y x .16.已知:244x x -+与 |1y -| 互为相反数,则式子()x y x y y x⎛⎫-÷+ ⎪⎝⎭的值等于_________.17.如图,AD=8cm ,CD=6cm ,AD⊥CD,BC=24cm ,AB=26cm ,则S 四边形ABCD = . 18.如图,若AB=AC ,BD =BE ,AF=FD ,则∠BAC 的度数为 . 三、解答题(本大题共2小题,每小题14分,共28分) 19.(本题满分14分)已知:A =bca cb 2222-+,B =acb c a 2222-+,C =abc b a 2222-+,且a +b=c ,求A 2013+B 2014+C 2013的值.20.(本题满分14分)如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于点E . (1)若∠ADC +∠ABC =180°,求证:AD +AB =2AE ; (2)若AD +AB =2AE ,求证:CD =CB .八年级预赛参考答案及评分标准一、选择题(本大题共10小题,每小题4分,共40分)1、D2、C3、B4、B5、D6、B7、C8、B9、C10、B二、选择题(本大题共8小题,每小题4分,共32分)11、108 12、a <-1且a ≠-2 13、714、2.4cm15、-1316、1217、96 18、36︒三、选择题(本大题共2小题,每小题14分,共28分)19.、∵A =bc a c b 2222-+=bca c a cb 2))((2-++又由a +b =c 得c -a =b∴A =bca cb b 2)(2++=c a c b 2++=c c 22=1………………………………………………(4分)同理B =1,C =-1 ………………………………………………(12分) ∴A 2013+B 2014+C 2013=1。
2014年长沙市“学用杯”初中数学应用与创新能力大赛--九-年-级-初-赛-试-题及标准答案

CABD M 第15题2014年长沙市“学用杯”初中数学应用与创新能力大赛九 年 级 初 赛 试 题(时量:90分钟 满分:100分)一、选择题(本大题共10小题,每小题4分,共40分)题号 12345678910答案1.设P=121220132012++,Q=121220142013++,则P 与Q的大小关系是A.P >Q B .P=Q C .P<Q D .不能确定2.边长为整数,周长等于21的等腰三角形共有A.4个 B .5个 C .6个 D.7个3.在直角坐标系中,纵、横坐标都是整数的点,称为整点.设k 为整数,当直线2+=x y 与直线4-=kx y 的交点为整点时,k 的值可以取A.8个 ﻩﻩB .7个 ﻩﻩC.6个 D.5个 4.若二次函数2y ax bx c =++的图象如图所示,则点(b a +,ac )在A.第一象限 B .第二象限 C .第三象限 D.第四象限5.如图,矩形ABCD 被分割成六个正方形,其中最小正方形的面积等于1,则矩形ABCD 的面积等于A.152B.143C.132 D .1086.如图,⊙O 中,弦A D∥BC ,DA =DC ,∠AOC =160°,则∠BCO 等于ﻫA. 20° B. 30° C. 40° D . 50°7.已知锐角△A BC 中,∠A =60°,BD 和CE 都是△A BC 的高。
如果△A BC 的面积为12,那么四边形BCDE 的面积为 A.6 ﻩB.8 C.9 ﻩD .108.一个商人用m 元(m 是正整数)买来了n 台(n 为质数)电视机,其中有两台以成本的一半价钱卖给某个慈善机构,其余的电视机在商店出售,每台盈利500元,结果该商人获得利润为5500元,则n 的最小值是A.11 B .13 ﻩ C.17 ﻩ D.19 9.直线k x y +=21与x 轴的交点分别为A 、B,如果S △AOB ≤1,那么,k 的取值范围是 A.k ≤1 B. 0<k ≤1 C .-1≤k ≤1 D. k ≤-1或k ≥110.如图,在梯形ABCD 中,A B∥DC ,AB ⊥BC ,E 是AD 的中点,6AB BC CD ++=,5BE =,则梯形ABC D的面积等于A . 13B . 8C . 132D. 4二、填空题(本大题共8小题,每小题4分,共32分)11.实数a ,b 满足a b a b a =++-+-+-31)5(2)3(222,则=-b a . 12.若532=-+c b a , 8765=+-c b a ,则=-+c b a 529 .13.若m ,n 是一元二次方程0132=-+x x 的两个根,则=-+n m m 22.14.已知3=xy ,那么yxyx y x +的值是 . 15.如图,在△ABC 中,中线CM 与高线CD 三等分ACB ∠,则B ∠等于 度. 16.已知t bac a c b c b a =+=+=+,那么直线t tx y +=一定通过第 象限. 17.不论k 取什么实数,关于x 的方程1632=--+bkx a kx (a 、b 是常数)的根总是x =1,那么=+b a .18.如图, AB 是半径为R 的圆O 的直径, 四边形CDMN和DEFG 都是正方形. 其中,,C D E 在AB 上, ,F N学校: 姓名: 考场: 考号:☼……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼ABCD E 第10题Oxy第4题 A B C D 第6题O C B A D 第5题 第18题在半圆上,则两个正方形的面积之和为 .. ﻬ三、解答题(本大题共2小题,每小题14分,共28分) 19.(本题满分14分)如图,已知一次函数323+-=x y 的图象与x 轴、y 轴分别交于A 、B 两点,与正比例函数x y 3=的图象交于点C ,点D 是线段OB 上的一个动点(不包含O 、B 两点),以AD 为边在其一侧作等边三角形AD E,DE 交AB 于F,A D交OC 于G .(1)分别求出A 、B 、C 三点的坐标; (2)△ADF 和△ACG 是否相似,为什么? (3)证明CE总与AB 垂直.ﻮ20.(本题满分14分)如图1,在平面直角坐标系中,直角梯形ABCD 的直角顶点D 与原点重合,另一直角顶点A在y 轴的正半轴上,点B、C 的坐标分别为B (12,8)、C (14,0),AD 为⊙E 的直径.,点M 、N分别从A 、C两点同时出发做匀速运动,其中点M沿AB 向终点B运动,速度为每秒1个单位;点N 沿CD 向终点D 运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.(1)如图2,设点M 、N 的运动时间为t 秒,当t 为何值时,四边形MB CN 为平行四边形?(2)在(1)的条件下,连结DM 与⊙E 相交于点P ,求弦DP 的长;(3)已知二次函数的图象经过D 及(1)中的点M 、N ,求该二次函数的解析式;(4)在运动过程中,是否存在使直线MN 与⊙E 相切的情形?如果存在,请求出直线MN 的解析式;如果不存在,请说明理由.(图3供解答本小题用)2014年长沙市“学用杯”初中数学应用与创新能力大赛九 年 级 初 赛 试 题参考答案及评分标准一、选择题(本大题共10小题,每小题4分,共40分)题号12345678910x O B Ay C DGF E。
2014全国初中数学联合竞赛试题答案及评分标准

2014年全国初中数学联合竞赛试题参考答案及评分标准第一试一、选择题:(本题满分42分,每小题7分) 1.已知,x y 为整数,且满足22441111211()()()3x y x y x y++=--,错误!未找到引用源。
则x y +的可能的值有( )A. 1个B. 2个C. 3个D. 4个 【答】 C.由已知等式得2244224423x y x y x y xy x y x y++-? ,显然,x y 均不为0,所以x y +=0或32()xy x y =-. 若32()xy x y =-,则(32)(32)4x y +-=-.又,x y 为整数,可求得12,x y ì=-ïí=ïî,或21.x y =-⎧⎨=⎩,所以1x y +=或1x y +=-.因此,x y +的可能的值有3个.2.已知非负实数,,x y z 满足1x y z ++=,则22t xy yz zx =++的最大值为 ( ) A .47 B .59 C .916 D .1225【答】 A.21222()2()()4t xy yz zx x y z yz x y z y z =++=++≤+++212(1)(1)4x x x =-+-2731424x x =-++2734()477x =--+,易知:当37x =,27y z ==时,22t xy yz zx =++取得最大值47.3.在△ABC 中,AB AC =,D 为BC 的中点,BE AC ⊥于E ,交AD 于P ,已知3BP =,1PE =,则错误!未找到引用源。
=( )ABCD【答】 B .因为A D B C ⊥,BE AC ⊥,所以,,,P D C E 四点共圆,所以12BD BC BP BE ⋅=⋅=,又2B C B D =,所以BD =DP =.又易知△AEP ∽△BDP ,所以AE PEBD DP =,从而可得PE AE BD DP =⋅==. 4.6张不同的卡片上分别写有数字2,2,4,4,6,6,从中取出3张,则这3张卡片上所写的数字可以作为三角形的三边长的概率是 ( )A .12 B .25 C .23 D .34【答】 B.若取出的3张卡片上的数字互不相同,有2×2×2=8种取法;若取出的3张卡片上的数字有相同的,有3×4=12种取法.所以,从6张不同的卡片中取出3张,共有8+12=20种取法.要使得三个数字可以构成三角形的三边长,只可能是:(2,4,4),(4,4,6),(2,6,6),(4,6,6),由于不同的卡片上所写数字有重复,所以,取出的3张卡片上所写的数字可以作为三角形的三边长的情况共有4×2=8种.因此,所求概率为82205=. 5.设[]t 表示不超过实数t 的最大整数,令{}[]t t t =-.已知实数x 满足33118x x +=,则1{}{}x x+= ( )A .12 B.3 C.1(32D .1 【答】 D . 设1x a x +=,则32223211111()(1)()[()3](3)x x x x x a a x x x x x+=++-=++-=-,所以2(3)18a a -=,因式分解得2(3)(36)0a a a -++=,所以3a =.由13x x +=解得1(32x =,显然10{}1,0{}1x x <<<<,所以1{}{}x x +=1. 6.在△ABC 中,90C ∠=︒,60A ∠=︒错误!未找到引用源。
2014年长沙市首届中学数学教师解题能力大赛 初中组个人获奖光荣榜
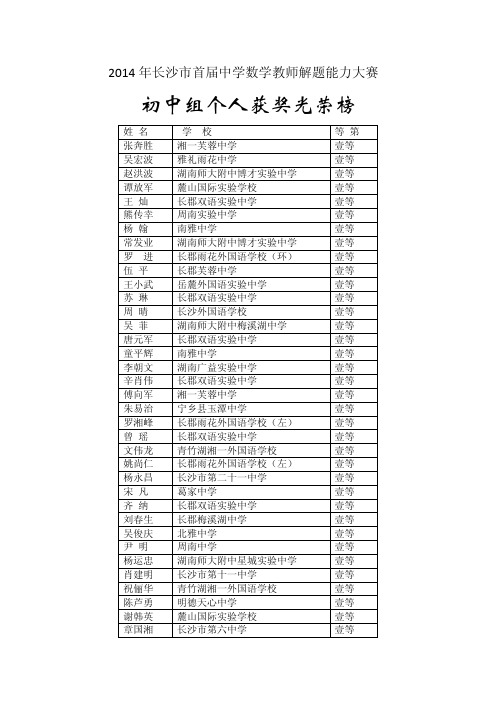
2014年长沙市首届中学数学教师解题能力大赛 初中组个人获奖光荣榜姓 名 学 校 等 第张奔胜 湘一芙蓉中学 壹等吴宏波 雅礼雨花中学 壹等赵洪波湖南师大附中博才实验中学 壹等谭放军 麓山国际实验学校 壹等王 灿 长郡双语实验中学 壹等熊传幸 周南实验中学 壹等杨 翰 南雅中学 壹等常发业 湖南师大附中博才实验中学 壹等罗 进 长郡雨花外国语学校(环) 壹等伍 平 长郡芙蓉中学 壹等王小武 岳麓外国语实验中学 壹等苏 琳 长郡双语实验中学 壹等周 晴长沙外国语学校 壹等吴 菲湖南师大附中梅溪湖中学 壹等唐元军 长郡双语实验中学 壹等童平辉 南雅中学 壹等李朝文湖南广益实验中学 壹等辛肖伟 长郡双语实验中学 壹等傅向军 湘一芙蓉中学 壹等朱易治 宁乡县玉潭中学 壹等罗湘峰 长郡雨花外国语学校(左) 壹等曾 瑶 长郡双语实验中学 壹等文伟龙青竹湖湘一外国语学校 壹等姚尚仁 长郡雨花外国语学校(左) 壹等杨永昌 长沙市第二十一中学 壹等宋 凡 葛家中学 壹等齐 纳 长郡双语实验中学 壹等刘春生 长郡梅溪湖中学 壹等吴俊庆 北雅中学 壹等尹 明 周南中学 壹等杨运忠 湖南师大附中星城实验中学 壹等肖建明 长沙市第十一中学 壹等祝俪华 青竹湖湘一外国语学校 壹等陈芦勇 明德天心中学 壹等谢韩英麓山国际实验学校 壹等章国湘 长沙市第六中学 壹等张文武 宁乡县实验中学 壹等 刘小妹 南雅中学 壹等 于佃刚 长郡雨花外国语学校(环) 壹等 冒敏娟 长郡双语实验中学 壹等 李志军雅礼实验中学 贰等 王乐龙 长沙市第一中学新华都学校 贰等 邓志强 青竹湖湘一外国语学校 贰等 王荣军 青竹湖湘一外国语学校 贰等 丁 丽 长郡雨花外国语学校(左) 贰等 廖永明 长郡双语实验中学 贰等 洪家佳 明德麓谷学校 贰等 李朝石 麓山国际实验学校 贰等 杨梦蕾 丰裕中学 贰等 王天乐 稻田中学 贰等 张玉杨 北雅中学 贰等 肖利民 望城金海学校 贰等 肖千民岳麓外国语实验中学 贰等 刘宗良 宁乡金海中学 贰等 宋贻才 南雅中学 贰等 李宇平 湖南师大附中高新实验中学 贰等 隆四化 雅礼天心中学 贰等 庄德全 雅礼实验中学 贰等 吴远觉 岳麓外国语实验中学 贰等 胡能兵 明德华兴中学 贰等 蒋宁波 湖南师大附中高新实验中学 贰等 戴冬梅 长沙市第六中学 贰等 黄海燕 长郡双语实验中学 贰等 伍友波 长沙大学附中 贰等 李 莉 湖南师大附中博才实验中学 贰等 李正荣 学士中学 贰等 王 静 长郡梅溪湖中学 贰等 敬海军 北雅中学 贰等 刘 旋 长沙市第十九中学 贰等 邓 超 青竹湖湘一外国语学校 贰等 石普余 宁乡金州中学 贰等 米 亮 明德华兴中学 贰等 鲁家兴 艺术学校 贰等 蒋 刚 雅礼雨花中学 贰等 邓 娟 雅礼雨花中学 贰等 刘 芸 雅礼实验中学 贰等 唐 镇 稻田中学 贰等宾定铸 长沙县星沙中学 贰等 白北胜 长沙县梨江中学 贰等 刘理坤 长郡双语实验中学 贰等 段华庭 长郡梅溪湖中学 贰等 杨帅红 艺术学校 贰等 杨智华 湖南师大附中星城实验中学 贰等 易 丹 湖南师大附中星城实验中学 贰等 陈香意 望城育红中学 贰等 唐正刚 望城高塘岭中学 贰等 王 伟 长沙市三十七中学 贰等 朱建才 青竹湖湘一外国语学校 贰等 刘林湘 集里中学 贰等 柳 红 湖南师大附中高新实验中学 贰等 辜 刚 长雅中学 贰等 张洁 长沙县松雅湖中学 贰等 潘海浩 长郡双语实验中学 贰等 殷 甜 湘一芙蓉第二中学 贰等 刘长安麓山滨江实验学校 贰等 唐崇耀 湖南广益实验中学 贰等 胡泽龙 湖南师大附中高新实验中学 贰等 王 宾 稻田中学 贰等 陈 旭 长沙县梨江中学 贰等 邹国斌 长沙县黄兴中学 贰等 何庆阳 长郡双语实验中学 贰等 杨君文 望城乔口中学 贰等 段晓莹 长沙市田家炳实验中学 贰等 阳文义 宁乡金海中学 贰等 张红春 明德洞井中学 贰等 欧超军 井湾子中学 贰等 邵国奎 丰裕中学 贰等 唐美旦 长雅中学 贰等 王应龙 长沙县黄兴中学 贰等 肖 毛 周南中学 贰等 何素贞 长沙市第十一中学 贰等 吴义东 长沙市三十七中学 贰等 伍梦珊 周南实验中学 贰等 徐树成 艺术学校 贰等 石 洁 湖南师大附中星城实验中学 贰等 唐星宇 长沙市第三十七中学 贰等 杨 玫 明德天心中学 贰等 陶宏伟 浏阳河中学 贰等肖雪晖 湖南师大附中高新实验中学 贰等 肖旭峰 宁乡城北中学 梅花校区 贰等 杨宗永 长沙县石门中学 贰等 田荣春 长郡雨花外国学校(左) 贰等 任彦斌 长郡双语实验中学 贰等 李光辉 湖南大学附中 贰等 王贵初 周南实验中学 贰等 刘冠佳 雅礼雨花中学 贰等 王艳文 雅礼天心中学 贰等 肖艳斌 湖南师大附中星城实验中学 贰等 陈伟根 新文学校 贰等 郑剑凯 湘仪学校 贰等 张泽湘 麓山滨江实验学校 贰等 李 勇 浏阳河中学 贰等 李青红 古港中学 贰等 张凌云 湖南师大附中高新实验中学 贰等 熊 坚 长沙市铁路第一中学 贰等 赵 欣 长郡双语实验中学 贰等 陈 遥 长郡梅溪湖中学 贰等 戴术军 艺术学校 贰等 唐玉分 湘一芙蓉第二中学 贰等 肖小华 明德洞井中学 贰等 何晓琼 明德洞井中学 贰等 蔡雄丽 湖南大学附中 贰等 熊昌辉 大瑶中学 贰等 谭建平 枨冲中学 贰等 马宏东 长沙县石常中学 贰等 黄 波 长郡雨花外国语学校(左) 贰等 沙永强 长郡梅溪湖中学 贰等 刘成文 沅丰坝中学 贰等 向 琼 沅丰坝中学 贰等 孟令申 雅礼雨花中学 贰等 余 娟 湘仪学校 贰等 陈丽娟 湘府中学 贰等 叶 滔 长郡双语实验中学 贰等 曹芳湘 望城金海学校 贰等 罗启明 长沙田家炳实验中学 贰等 王 畅 长沙外国语学校 贰等 杨 军 青竹湖湘一外国语学校 贰等 颜正伟 明德华兴中学 贰等 全建兴 麓山国际实验学校 贰等易祖辉 浏阳河中学 贰等 于爱文 北雅中学 贰等 杨万银湖南师大附中博才中学(南) 贰等 毛向荣 稻田中学 叁等 周奇峰 周南实验中学 叁等 曹德城 雅礼雨花中学 叁等 宋江伟 长沙市田家炳实验中学 叁等 龙 舟长沙市实验中学 叁等 何 强 青竹湖湘一外国语学校 叁等 吴 勇 宁乡县巷子口中学 叁等 苏东海 宁乡县实验中学 叁等 徐 玲 明德天心中学 叁等 刘安定 明德天心中学 叁等 付静文 井湾子中学 叁等 周春艳 关口中学 叁等 阳小强 湖南师大附中高新实验中学 叁等 文泽湘 长沙市第二十六中学 叁等 赵红柏 洞阳中学 叁等 汤达满 大瑶中学 叁等 宋喜盈 宁乡城北中学 振兴校区 叁等 苏 邦 长郡双语实验中学 叁等 龙安勇 长郡双语实验中学 叁等 卢帅华 沅丰坝中学 叁等 罗胜云 湘仪学校 叁等 李 垚 湘仪学校 叁等 曾婷婷 湘一芙蓉中学 叁等 罗欢欢 湘府中学 叁等 罗智勇 乌龙中学 叁等 廖 妮 长沙市田家炳实验中学 叁等 徐德群 双枫中学 叁等 段浩瀚 长沙市第十五中学 叁等 曾新美 宁乡金海中学 叁等 李万胜 明德洞井中学 叁等 侯 慧 湖南师大附中高新实验中学 叁等 胡冬情 长沙市第二十六中学 叁等 孙 瑞 长雅中学 叁等 刘萍萍 长沙县松雅湖中学 叁等 罗周清 长郡双语实验中学 叁等 袁 颖 长郡双语实验中学 叁等 李 祥 长沙市第一中学新华都学校 叁等 吴小燕 长沙外国语学校 叁等刘 畅 宁乡县白马桥中学 叁等 唐 华 明德天心中学 叁等 佘 科 明德华兴中学 叁等 凌 斌 麓山滨江实验学校 叁等 李 群 湖南广益实验中学 叁等 张巧如 宁乡城北中学 梅花校区 叁等 武才松 长沙县石常中学 叁等 肖 扬 长郡雨花外国语学校(环) 叁等 唐昌艺 长郡梅溪湖中学 叁等 刘林海 长郡梅溪湖中学 叁等 徐 敏 北雅中学 叁等 胡 勇 北雅中学 叁等 尹磊石 雅礼天心中学 叁等 于慧枚 湖南师大附中星城实验中学 叁等 秦姣平 长沙外国语学校 叁等 谢志坚 长沙市第七中学 叁等 谭林之 麓山滨江实验学校 叁等 黄永许 金刚中学 叁等 吴文明 金刚中学 叁等 吴孟然 金刚中学 叁等 郑兰香 湖南师大附中高新实验中学 叁等 谢慧霞 湖南师大附中高新实验中学 叁等 言 威 长沙铁路第一中学 叁等 唐 超 长郡双语实验中学 叁等 杨 诗 雅礼天心中学 叁等 屈松江 文家市中学 叁等 朱 光长沙市田家炳实验中学 叁等 邓月琴 双枫中学 叁等 阳承英 岳麓外国语实验中学 叁等 杨汉林长沙市第十五中学 叁等 谭建红 三口中学 叁等 刘建兵 宁乡县实验中学 叁等 欧扩军 宁乡县东湖塘中学 叁等 曹 珊 明德天心中学 叁等 张 云 井湾子中学 叁等 王健宇 湖南师大附中博才中学 叁等 匡懿龄 长雅中学 叁等 刘 琳 长郡双语实验中学 叁等 王建辉北雅中学 叁等 赵连华 周南实验中学 叁等 王孟乐 学士中学 叁等袁名焱 湖南师大附中星城实验中学 叁等 魏裕鸣 三口中学 叁等 黄国杰 湖南师大附中高新实验中学 叁等 金 峰 湖南师大附中博才中学(南) 叁等 何义华 湖南师大附中博才中学(南) 叁等 许 鹃 长沙县星沙中学 叁等 熊云丰 湖南师大附中星城实验中学 叁等 刘文芳 湘府中学 叁等 姚 娜 长沙市田家炳实验中学 叁等 刘 纯长沙市第十九中学 叁等 易 鹏 普迹中学 叁等 葛东伟 明德天心中学 叁等 杨 伟 湖南师大附中高新实验中学 叁等 龙四学 丰裕中学 叁等 何培柏 长沙县石门中学 叁等 粟 艳 长沙县石门中学 叁等 彭希望 长沙县梨江中学 叁等 杨海舟 长郡芙蓉中学 叁等 朱章桃 长沙大学附中 叁等 龚小芳 长沙大学附中 叁等 刘 惠 中和中学 叁等 朱小平 永和中学 叁等 肖芳芳 湖南师大附中星城实验中学 叁等 谭 咏 岳麓外国语实验中学 叁等 曹菲菲 湖南广益实验中学 叁等 郭满花 湖南师大附中高新实验中学 叁等 银日红 宁乡城北中学 梅花校区 叁等 李群玉长沙铁路第一中学 叁等 阳立松 湖南师大附中星城实验中学 叁等 卢长华 新文学校 叁等 崔 盛 长沙市第一中学新华都学校 叁等 蒋佐银 望城金海学校 叁等 朱灿维 望城高塘岭中学 叁等 柳健康 双狮坪中学 叁等 周文娟 长沙市第十五中学 叁等 黄明理 青草中学 叁等 李燕舞 普迹中学 叁等 欧智辉 宁乡县玉潭中学 叁等 谢荣昌 宁乡县巷子口中学 叁等 李岳文 明德麓谷学校 叁等 张建伟 麓山滨江实验学校 叁等朱运涛 湖南师大附中高新实验中学 叁等刘普缘湖南师大附中高新实验中学 叁等夏慧阳 湖南师大附中高新实验中学 叁等吴 婷 长沙县松雅湖中学 叁等王 芳 长郡双语实验中学 叁等邱赞荣 永和中学 叁等陶驷玖 雅礼雨花中学 叁等谭振荣 湘一芙蓉第二中学 叁等易谦柱 望城桥驿镇维新学校 叁等刘 洋 望城乔口中学 叁等佘亚力 望城高塘岭中学 叁等刘东安 长沙市第二十一中学 叁等陈继红 长沙市第十九中学 叁等陈 姣 普迹中学 叁等方有幸 宁乡县巷子口中学 叁等银 亮 宁乡县白马桥中学 叁等高建军 雷锋学校 叁等彭朝煌 集里中学 叁等李朝英 湖南师大附中博才中学(南) 叁等罗桂香 长沙市二十六中学 叁等曾令武 枨冲中学 叁等尧文涛 长沙县石常中学 叁等张琼方 长郡雨花外国语学校(左) 叁等佘月娥 长郡雨花外国语学校(左) 叁等雷雅慧 浏阳新文学校 叁等长沙市教育科学研究院长沙市数学学会长沙市教育学会中学数学专业委员会二零一四年 十二月。
2014初中数学联赛初二年级

.
17 n k 15
【答】144.
由条件得 7 k 8 ,由 k 的唯一性,得 k 1 7 且 k 1 8 ,所以 2 k 1 k 1 8 7 1 ,
8n9
n8 n9
n n n 9 8 72
所以 n 144 .
当 n 144 时,由 7 k 8 可得126 k 128 , k 可取唯一整数值 127. 8n9
()
A.21
B.20
C.31
D.30
【答】 C.
2014 年全国初中数学联合竞赛初二年级试题参考答案 第 1 页(共 4 页)
可以称出的重物的克数可以为 1、2、3、4、5、6、7、8、9、10、20、21、22、23、24、25、26、27、
28、29、30、31、32、33、34、35、36、37、38、39、40,共 31 种.
x 2, y 3, z 1, xyz 6 .
6.已知△ ABC 的三边长分别为 2,3,4, M 为三角形内一点,过点 M 作三边的平行线,交各边于
D 、 E 、 F 、 G 、 P 、 Q (如图),如果 DE FG PQ x ,则 x =
()
18
A.
13
20
B.
13
22
C.
13
24
PAE 1 (BAD CAE) 1 (66 30) 18 ,
2
2
所以 PAC PAE CAE 18 30 48 .
EP
C
D
A
4.已知 n 为正整数,且 n4 2n3 6n2 12n 25 为完全平方数,则 n =
.
【答】8.
易知 n 1 , n 2 均不符合题意,所以 n 3 ,此时一定有
雅礼实验中学2014年学科竞赛喜报

1205唐若凡108铜奖
1211张钰哲106铜奖
1213万易106铜奖
(四)2014年长沙市“学用杯”数学能力创新大赛(复赛)
班级姓名分数等级备注
1210曾新昊120一等奖长沙市第1名(唯一满分)
1206刘哲贤119一等奖长沙市第2名(全市共2人)
1205赵厚然116一等奖
1208曹博宇116一等奖
唐子及
金奖
杨吉胤陈三才黄嘉竟刘宗卓熊子恽陈子博欧阳乐陶
段昱王泽轩王志彪唐迦润李书展赵昶旭欧阳子绚
席铭基王佳骏
银奖
刘成之王钒唐家铮王奕桥谭婷方胡祖瑜刘子豪
许昶陈智鹏龚宇洁左常睿吴峒匡博文全若山
陈可铨吕新昱华宇阳陈一豪林湘宁刘洁松张子南
周昆煜陈凯旋张秋雨蔡语鸿欧阳慧杨运城金鹏
杨彦博李晟阳彭孝妍向晨宇何凌志彭洋漾
(二)2014长沙市初中八年级应用物理知识读书竞赛(复赛)
一等奖
王泽宇银浩然罗嘉铭彭毓聪张佳怡唐一忱
姜唯周谭吉张涵琦陈沫璇唐若凡黄思源
刘哲贤刘一苇李嘉懿黄千驰杨若漪周胤妤
李岚宇黄玺洋曾新昊童年伍树刘砚博
二等奖
方逸飞唐钰琪徐金健李尹汝刘雨潇伍欣仪
张千帆胡泷文张雅淇邹正阳刘臻睿杨思科
胥清雅
三等奖
李典和徐芊杨清云林毅欧阳悠悠
又,2014年中国青少年英语能力大赛湖南赛区竞赛(初赛)揭晓,我校初一、初二参赛学生发挥出色,成绩优异,共有448名同学获竞赛奖,其中一等奖112名,二等奖152名,三等奖174名。
特向全校师生报喜!
在各类比赛准备期间,我校参赛学生始终保持端正的学习态度和饱满的学习热情,他们凭着自己的兴趣和刻苦执著、力争上游的学习精神挑战强手如林的赛场。他们优异成绩的获得,离不开学校各级各部门的大力支持,离不开老师的精心指导,更离不开自己的扎实准备与奋勇拼搏。他们的优异成绩,充分体现了我雅实学子在语文、数学、物理及英语等方面的优良素养。
历年初联真题

2014年全国初中数学联合竞赛试题第一试一、选择题:(本题满分42分,每小题7分) 1.已知,x y 为整数,且满足22441111211()()()3x y x y x y++=--,则x y +的可能的值有( )A. 1个B. 2个C. 3个D. 4个2.已知非负实数,,x y z 满足1x y z ++=,则22t xy yz zx =++的最大值为 ( )A .47B .59C .916D .12253.在△ABC 中,AB AC =,D 为BC 的中点,BE AC ⊥于E ,交AD 于P ,已知3BP =,1PE =,则AE =( )A B C D 4.6张不同的卡片上分别写有数字2,2,4,4,6,6,从中取出3张,则这3张卡片上所写的数字可以作为三角形的三边长的概率是( )A .12 B .25 C .23 D .345.设[]t 表示不超过实数t 的最大整数,令{}[]t t t =-.已知实数x 满足33118x x+=,则1{}{}x x +=( )A .12B .3C .1(32- D .16.在△ABC 中,90C ∠=︒,60A ∠=︒,1AC =,D 在BC 上,E 在AB 上,使得△ADE 为等腰直角三角形, 90ADE ∠=︒ ,则BE 的长为( )A .4-B .2-C .11)2D 1二、填空题:(本题满分28分,每小题7分) 1.已知实数,,a b c 满足1a b c ++=,1111a b c b c a c a b++=+-+-+-,则abc =__ __. 2.使得不等式981715n n k <<+对唯一的整数k 成立的最大正整数n 为 . 3.已知P 为等腰△ABC 内一点,AB BC =,108BPC ∠=︒,D 为AC 的中点,BD 与PC 交于点E ,如果点P 为△ABE 的内心,则PAC ∠= .4.已知正整数,,a b c 满足:1a b c <<<,111a b c ++=,2b ac =,则b = .一、(本题满分20分)设实数,a b 满足22(1)(2)40a b b b a +++=,(1)8a b b ++=,求2211a b+的值.二.(本题满分25分)如图,在平行四边形ABCD 中,E 为对角线BD 上一点,且满足ECD ACB ∠=∠, AC 的延长线与△ABD 的外接圆交于点F . 证明:DFE AFB ∠=∠.三.(本题满分25分)设n 是整数,如果存在整数,,x y z 满足3333n x y z xyz =++-,则称n 具有性质P .在1,5,2013,2014这四个数中,哪些数具有性质P ,哪些数不具有性质P ?并说明理由.FB一.(本题满分20分)同(A )卷第一题.二.(本题满分25分)如图,已知O 为△ABC 的外心,AB AC =,D 为△OBC 的外接圆上一点,过点A 作直线OD 的垂线,垂足为H .若7BD =,3DC =,求AH .三.(本题满分25分)设n 是整数,如果存在整数,,x y z 满足3333n x y z xyz =++-,则称n 具有性质P . (1)试判断1,2,3是否具有性质P ;(2)在1,2,3,…,2013,2014这2014个连续整数中,不具有性质P 的数有多少个?2013年全国初中数学联合竞赛试题第一试一、选择题(本题满分42分,每小题7分)1.计算=( )(A 1 (B )1 (C (D )22.满足等式()2221m m m ---=的所有实数m 的和为( )(A )3 (B )4 (C )5 (D )63.已知AB 是圆O 的直径,C 为圆O 上一点,15CAB ∠=,ABC ∠的平分线交圆O 于点D ,若CD =AB=( )(A )2 (B(C )(D )34.不定方程23725170x xy x y +---=的全部正整数角(x,y )的组数为( ) (A )1 (B )2 (C )3 (D )45矩形ABCD 的边长AD=3,AB=2,E 为AB 的中点,F 在线段BC 上,且BF :FC=1:2, AF 分别与DE ,DB 交于点M ,N ,则MN=( )(A )7 (B )14 (C )28 (D )286.设n 为正整数,若不超过n 的正整数中质数的个数等于合个数,则称n 为“好数”,那么,所有“好数”之和为( ) (A )33 (B )34 (C )2013 (D )2014 二、填空题(本题满分28分,每小题7分)1.已知实数,,x y z 满足4,129,x y z xy y +=+=+-则23x y z ++=2.将一个正方体的表面都染成红色,再切割成3(2)n n >个相同的小正方体,若只有一面是红色的小正方体数目与任何面都不是红色的小正方体的数目相同,则n= 3.在ABC 中,60,75,10A C AB ∠=∠==,D ,E ,F 分别在AB ,BC ,CA 上,则DEF的周长最小值为4.如果实数,,x y z 满足()2228x y z xy yz zx ++-++=,用A 表示,,x y y z z x ---的最大值,则A 的最大值为第二试(A )一、(本题满分20分)已知实数,,,a b c d 满足()2222223236,a c b d ad bc +=+=-=求()()2222ab c d ++的值。
初中数学联赛(初联)历年真题

2014年全国初中数学联合竞赛试题第一试一、选择题:(本题满分42分,每小题7分) 1.已知,x y 为整数,且满足22441111211()()()3x y x y x y++=--,则x y +的可能的值有( )A. 1个B. 2个C. 3个D. 4个2.已知非负实数,,x y z 满足1x y z ++=,则22t xy yz zx =++的最大值为 ( )A .47B .59C .916D .1225 3.在△ABC 中,AB AC =,D 为BC 的中点,BE AC ⊥于E ,交AD 于P ,已知3BP =,1PE =,则AE =( )A .2B C D 4.6张不同的卡片上分别写有数字2,2,4,4,6,6,从中取出3张,则这3张卡片上所写的数字可以作为三角形的三边长的概率是( )A .12 B .25 C .23 D .345.设[]t 表示不超过实数t 的最大整数,令{}[]t t t =-.已知实数x 满足33118x x+=,则1{}{}x x +=( )A .12B .3-C .1(32- D .16.在△ABC 中,90C ∠=︒,60A ∠=︒,1AC =,D 在BC 上,E 在AB 上,使得△ADE 为等腰直角三角形, 90ADE ∠=︒ ,则BE 的长为( )A .4-B .2C .11)2D 1二、填空题:(本题满分28分,每小题7分) 1.已知实数,,a b c 满足1a b c ++=,1111a b c b c a c a b++=+-+-+-,则abc =__ __. 2.使得不等式981715n n k <<+对唯一的整数k 成立的最大正整数n 为 . 3.已知P 为等腰△ABC 内一点,AB BC =,108BPC ∠=︒,D 为AC 的中点,BD 与PC 交于点E ,如果点P 为△ABE 的内心,则PAC ∠= .4.已知正整数,,a b c 满足:1a b c <<<,111a b c ++=,2b ac =,则b = .一、(本题满分20分)设实数,a b 满足22(1)(2)40a b b b a +++=,(1)8a b b ++=,求2211a b+的值.二.(本题满分25分)如图,在平行四边形ABCD 中,E 为对角线BD 上一点,且满足ECD ACB ∠=∠,AC 的延长线与△ABD 的外接圆交于点F . 证明:DFE AFB ∠=∠.三.(本题满分25分)设n 是整数,如果存在整数,,x y z 满足3333n x y z xyz =++-,则称n 具有性质P .在1,5,2013,2014这四个数中,哪些数具有性质P ,哪些数不具有性质P ?并说明理由.FB一.(本题满分20分)同(A )卷第一题.二.(本题满分25分)如图,已知O 为△ABC 的外心,AB AC =,D 为△OBC 的外接圆上一点,过点A 作直线OD 的垂线,垂足为H .若7BD =,3DC =,求AH .三.(本题满分25分)设n 是整数,如果存在整数,,x y z 满足3333n x y z xyz =++-,则称n 具有性质P . (1)试判断1,2,3是否具有性质P ;(2)在1,2,3,…,2013,2014这2014个连续整数中,不具有性质P 的数有多少个?2013年全国初中数学联合竞赛试题第一试一、选择题(本题满分42分,每小题7分)1.计算=( )(A 1- (B )1 (C (D )22.满足等式()2221m m m ---=的所有实数m 的和为( )(A )3 (B )4 (C )5 (D )63.已知AB 是圆O 的直径,C 为圆O 上一点,15CAB ∠=o,ABC ∠的平分线交圆O 于点D ,若CD =AB=( )(A )2 (B(C )(D )34.不定方程23725170x xy x y +---=的全部正整数角(x,y )的组数为( ) (A )1 (B )2 (C )3 (D )45矩形ABCD 的边长AD=3,AB=2,E 为AB 的中点,F 在线段BC 上,且BF :FC=1:2, AF 分别与DE ,DB 交于点M ,N ,则MN=( )(A )7 (B )14 (C )28 (D )286.设n 为正整数,若不超过n 的正整数中质数的个数等于合个数,则称n 为“好数”,那么,所有“好数”之和为( ) (A )33 (B )34 (C )2013 (D )2014 二、填空题(本题满分28分,每小题7分)1.已知实数,,x y z 满足4,129,x y z xy y +=+=+-则23x y z ++=2.将一个正方体的表面都染成红色,再切割成3(2)n n >个相同的小正方体,若只有一面是红色的小正方体数目与任何面都不是红色的小正方体的数目相同,则n= 3.在ABC V 中,60,75,10A C AB ∠=∠==oo,D ,E ,F 分别在AB ,BC ,CA 上,则DEF V 的周长最小值为4.如果实数,,x y z 满足()2228x y z xy yz zx ++-++=,用A 表示,,x y y z z x ---的最大值,则A 的最大值为第二试(A )一、(本题满分20分)已知实数,,,a b c d 满足()2222223236,a c b d ad bc +=+=-=求()()2222ab c d ++的值。
2014年全国初中数学竞赛试题及答案

中国教育学会中学数学教学专业委员会2014年全国初中数学竞赛试题答题时注意:1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线; 3.草稿纸不上交.一、选择题(共5小题,每小题7分,共35分.每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的.请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设非零实数a ,b ,c 满足2302340a b c a b c ++=⎧⎨++=⎩,,则222ab bc caa b c ++++的值为( ). (A )12-(B )0 (C )12(D )12.已知关于x 的不等式组255332x x x t x +⎧->-⎪⎨+⎪-<⎩,恰有5个整数解,则t 的取值范围是( ).(A )6-<t <112-(B )6-≤t <112-(C )6-<t ≤112-(D )6-≤t ≤112-3.如图,在Rt △ABC 中,已知O 是斜边AB 的中点,CD ⊥AB ,垂足为D ,DE ⊥OC ,垂足为E .若AD ,DB ,CD 的长度都是有理数,则线段OD ,OE ,DE ,AC 的长度中,不.一定..是有理数的为( ). (A )OD (B )OE (C )DE(D )AC4.如图,已知△ABC 的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且4BC CF =,DCFE 是平行四边形,则图中阴影部分的面积为( ).(A )3 (B )4 (C )6(D )85.对于任意实数x ,y ,z ,定义运算“*”为:()()32233333451160x y x y xy x y x y +++*=+++-,且()x y z x y z **=**,则2013201232****的值为( ). (A )607967(B )1821967(C )5463967(D )16389967二、填空题(共5小题,每小题7分,共35分)6.设33a =,b 是a 的小数部分,c 是2a 的小数部分,则(4)b b c ++的值为 .7.一个质地均匀的正方体的六个面上分别标有数1,2,3,4,5,6.掷这个正方体三次,则其朝上的面的数和为3的倍数的概率是 .8.已知正整数a ,b ,c 满足2220+--=a b c ,2380-+=a b c ,则abc 的最大值为 .9.实数a ,b ,c ,d 满足:一元二次方程20x cx d ++=的两根为a ,b ,一元二次方程20x ax b ++=的两根为c ,d ,则所有满足条件的数组(),,,a b c d 为 .10.444444222222121231991001121231991001++++++++++-+-+-…的值为 .三、解答题(共4题,每题20分,共80分)11.如图,抛物线y=23ax bx+-,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线113y x=-+与y轴交于点D.求∠DBC ∠CBE.12.设△ABC的外心、垂心分别为O H、,若B C H O、、、共圆,对于所有的△ABC,求BAC∠所有可能的度数.13.如图,设点D 在△ABC 外接圆上,且为BC 的中点,点X 在BD 上,E 是AX 的中点,过△ABC 的内心I 作直线R T 平行于DE ,分别与BC ,AX 交于点R ,T ,设直线DR 与ET 交于点S .证明:点S 在△ABC 的外接圆上.14.如果将正整数M 放在正整数m 左侧,所得到的新数可被7整除,那么称M 为m 的“魔术数”(例如,把86放在415的左侧,得到的数86415能被7整除,所以称86为415的魔术数).求正整数n 的最小值,使得存在互不相同的正整数12n a a a ,,…,,满足对任意一个正整数m ,在12n a a a ,,…,中都至少有一个为m 的魔术数.中国教育学会中学数学教学专业委员会2013年全国初中数学竞赛试题参考答案一、选择题 1.A解:由已知得(234)(23)0a b c a b c a b c ++=++-++=,故2()0a b c ++=.于是2221()2ab bc ca a b c ++=-++,所以22212ab bc ca a b c ++=-++. 2.C解:根据题设知不等式组有解,解得,32t -<x <20.由于不等式组恰有5个整数解,这5个整数解只能为15,16,17,18,19,因此14≤32t -<15,解得6-<t ≤112-. 3.D解:因AD ,DB ,CD 的长度都是有理数,所以,OA =OB =OC =2AD BD+是有理数.于是,OD =OA -AD 是有理数.由Rt △DOE ∽Rt △COD ,知2OD OE OC =,·DC DODE OC =都是有理数,而AC=·AD AB 不一定是有理数. 4.C解:因为DCFE 是平行四边形,所以DE //CF ,且EF //DC .连接CE ,因为DE //CF ,即DE //BF ,所以S △DEB = S △DEC ,因此原来阴影部分的面积等于△ACE 的面积.连接AF ,因为EF //CD ,即EF //AC ,所以S △ACE = S △ACF .因为4BC CF =,所以S △ABC = 4S △ACF .故阴影部分的面积为6.5.C解:设201320124m ***=,则()20132012433m ****=*32323339274593316460m m m m m m ⨯+⨯+⨯+==++++-, 于是()201320123292****=*3223333923929245546310360967⨯⨯+⨯⨯+⨯+==+-.二、填空题 6.2解:由于2123a a <<<<,故1=-b a ,22=-c a .所以223(4)(1)(124)(1)(1)12b b c a a a a a a a ++=--+-+=-++=-=.7.13解:掷三次正方体,朝上的面的数和为3的倍数的是3,6,9,12,15,18,且3=1+1+1,6=1+1+4=1+2+3=2+2+2,9=1+2+6=1+3+5=1+4+4=2+2+5=2+3+4=3+3+3, 12=1+5+6=2+4+6=2+5+5=3+3+6=3+4+5=4+4+4, 15=3+6+6=4+5+6=5+5+5, 18=6+6+6.记掷三次正方体面朝上的数分别为x ,y ,z .则使x +y +z 为3的倍数的(x ,y ,z )中,3个数都不相等的有8组,恰有两个相等的有6组,3个数都相等的有6组.故所求概率为83263616663⨯⨯+⨯+=⨯⨯.8.2013解:由已知2220+--=a b c ,2380-+=a b c 消去c ,并整理得()228666b a a -++=.由a 为正整数及26a a +≤66,可得1≤a ≤3.若1a =,则()2859b -=,无正整数解; 若2a =,则()2840b -=,无正整数解;若3a =,则()289b -=,于是可解得11=b ,5b =. (i )若11b =,则61c =,从而可得311612013abc =⨯⨯=; (ii )若5b =,则13c =,从而可得3513195abc =⨯⨯=. 综上知abc 的最大值为2013.9.(1212),,,--,(00),,,-t t (t 为任意实数) 解:由韦达定理得,,,.+=-⎧⎪=⎪⎨+=-⎪=⎪⎩a b c ab d c d a cd b 由上式,可知b a c d =--=.若0b d =≠,则1==d a b ,1==bc d ,进而2b d a c ==--=-.若0b d ==,则c a =-,有()(00),,,,,,=-a b c d t t (t 为任意实数). 经检验,数组(1212)--,,,与(00),,,-t t (t 为任意实数)满足条件. 10解:设0k >,那么=11111(1)1k k k k ⎤⎫=+=+-⎪⎥++⎝⎭⎣⎦. 上式对1=k ,2,…,99求和,得原式11991100100100⎫⎫=+-=-=⎪⎪⎝⎭⎝⎭.三、解答题11.解:将0x =分别代入y =113x -+,23y ax bx =+-知,D (0,1),C (0,3-),所以B (3,0),A (1-,0).直线y =113x -+过点B .将点C (0,3-)的坐标代入y =(1)(3)a x x +-,得1a =.…………5分抛物线223y x x =--的顶点为E (1,4-).于是由勾股定理得BC =32,CE =2,BE =25. 因为BC 2+CE 2=BE 2,所以,△BCE 为直角三角形,90BCE ∠=︒.…………10分因此tan CBE ∠=CE CB =13.又tan ∠DBO =13OD OB =,则∠DBO =CBE ∠.所以,45DBC CBE DBC DBO OBC ∠-∠=∠-∠=∠=︒.…………20分12.解:分三种情况讨论. (i )若△ABC 为锐角三角形.因为1802BHC A BOC A ∠=︒-∠∠=∠,,所以由BHC BOC ∠=∠,可得1802A A ︒-∠=∠,于是60A ∠=︒.…………5分(ii )若△ABC 为钝角三角形.当90A ∠>︒时,因为()1802180BHC A BOC A ∠=︒-∠∠=︒-∠,,所以由180BHC BOC ∠+∠=︒,可得()3180180A ︒-∠=︒,于是120A ∠=︒;当90A ∠<︒时,不妨假设90B ∠>︒,因为2BHC A BOC A ∠=∠∠=∠,,所以由180BHC BOC ∠+∠=︒,可得3180A ∠=︒,于是60A ∠=︒.…………15分(iii )若△ABC 为直角三角形.当90A ∠=︒时,因为O 为边BC 的中点,B C H O ,,,不可能共圆,所以A ∠不可能等于90︒;当90A ∠<︒时,不妨假设90B ∠=︒,此时点B 与H 重合,于是总有B C H O ,,,共圆,因此A ∠可以是满足090A ︒<∠<︒的所有角.综上可得,A ∠所有可能取到的度数为所有锐角及120︒.…………20分13.证明:如图,设DR 与△ABC 的外接圆交于点S ',AX 与S E '交于点T ',连接S C CD S A AE AD '',,,,.由D 为BC 的中点知,A ,I ,D 三点共线,且∠CS D '=∠RCD ,△S CD '∽△CRD ,所以S D CDCD RD'=, ① 即2CD S D RD '=⋅. ②…………5分由E 为AX 的中点知,∠AS E '=∠T AE ',△AS E '∽△T AE ',所以S E AEAE T E'=', ③ 即2AE S E T E ''=⋅. ④由IR ∥DE ,知180IRD S'DE S'AE ∠=︒-∠=∠.又因为IDR S DA S EA ''∠=∠=∠,所以△IRD ∽△S AE ',则有ID S ERD AE'=. ⑤ …………10分由I 为△ABC 的内心,连接CI ,由CID CAI ACI DCB BCI ICD ∠=∠+∠=∠+∠=∠知ID CD =.由式①,⑤,得S D S ECD AE''=, 即S D CDS E AE'='. ⑥ 由式②,④,得22CD S D RDAE S E T E'⋅=''⋅. ⑦ 由式⑥,⑦得S D RDS E T E'='', …………15分于是RT '∥DE .又RT ∥DE ,故点T '与T 重合,即点S '在直线ET 上.从而,点S '与S 重合,即点S 在△ABC 的外接圆上.…………20分14.解:若n ≤6,取m =1,2,…,7,根据抽屉原理知,必有12na a a ,,…,中的一个正整数M 是(1i j ,≤i <j ≤7)的公共的魔术数,即7|(10M i +),7|(10M j +).则有7|(j i -),但0<j i -≤6,矛盾.故n ≥7.…………10分又当12n a a a ,,…,为1,2,…,7时,对任意一个正整数m ,设其为k 位数(k 为正整数).则10k i m +(12i =,,…,7)被7除的余数两两不同.若不然,存在正整数i ,(1j ≤i <j ≤7),满足7|[(10)(10)]k k j m i m +-+,即7|10()k j i -,从而7|()j i -,矛盾.故必存在一个正整数i (1≤i ≤7),使得7|(10)k i m +,即i 为m 的魔术数. 所以,n 的最小值为7.…………20分。
2014全国初中数学联赛参考答案及评分标准

H
O
N D E
F B M C
三. (本题满分 25 分) 设 n 是整数,如果存在整数 x, y, z 满足 n x3 y 3 z 3 3xyz ,则称 n 具有性质 P . (1)试判断 1,2,3 是否具有性质 P ; (2)在 1,2,3, …,2013,2014 这 2014 个连续整数中,不具有性质 P 的数有多少个? 解 取 x 1 , y z 0 ,可得1 13 03 0 3 3 1 0 0 ,所以 1 具有性质 P ; 取 x y 1 , z 0 ,可得 2 13 13 0 3 3 1 1 0 ,所以 2 具有性质 P ; 若 3 具有性质 P ,则存在整数 x, y, z 使得 3 ( x y z ) 3 3( x y z )( xy yz zx ) ,从而可得
1 2
B.
2 5
C.
2 3
D.
3 4
【答】 B. 若取出的 3 张卡片上的数字互不相同,有 2×2×2=8 种取法;若取出的 3 张卡片上的数字有相同的, 有 3×4=12 种取法.所以,从 6 张不同的卡片中取出 3 张,共有 8+12=20 种取法. 要使得三个数字可以构成三角形的三边长,只可能是: (2,4,4) , (4,4,6) , (2,6,6) , (4,6, 6) ,由于不同的卡片上所写数字有重复,所以,取出的 3 张卡片上所写的数字可以作为三角形的三边长的 情况共有 4×2=8 种. 因此,所求概率为
2014年长沙市首届中学数学教师解题能力大赛 高中组个人获奖光荣榜
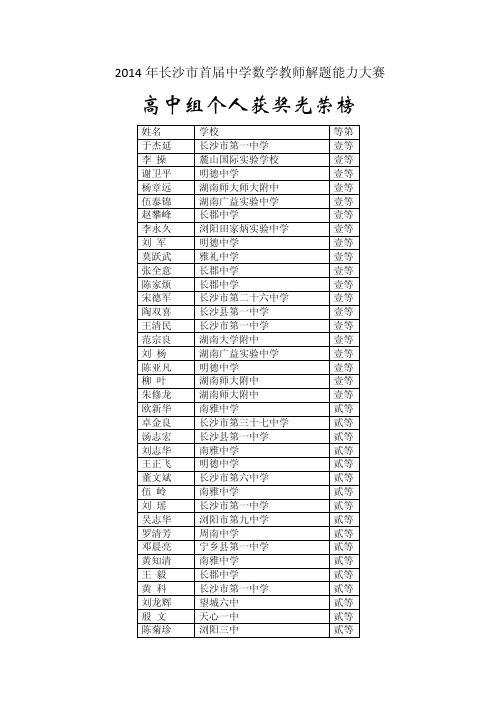
2014年长沙市首届中学数学教师解题能力大赛 高中组个人获奖光荣榜姓名 学校 等第于杰延 长沙市第一中学 壹等李 操 麓山国际实验学校 壹等谢卫平 明德中学 壹等杨章远 湖南师大师大附中 壹等伍泰锦 湖南广益实验中学 壹等赵攀峰 长郡中学 壹等李永久 浏阳田家炳实验中学 壹等刘 军 明德中学 壹等莫跃武 雅礼中学 壹等张全意 长郡中学 壹等陈家烦 长郡中学 壹等宋德军 长沙市第二十六中学 壹等陶双喜 长沙县第一中学 壹等王清民 长沙市第一中学 壹等范宗良 湖南大学附中 壹等刘 杨 湖南广益实验中学 壹等陈亚凡 明德中学 壹等柳 叶 湖南师大附中 壹等朱修龙 湖南师大附中 壹等欧新华 南雅中学 贰等卓金良 长沙市第三十七中学 贰等汤志宏 长沙县第一中学 贰等刘志华 南雅中学 贰等王正飞 明德中学 贰等董文斌 长沙市第六中学 贰等伍 岭 南雅中学 贰等刘 瑶 长沙市第一中学 贰等吴志华 浏阳市第九中学 贰等罗清芳 周南中学 贰等邓晨亮 宁乡县第一中学 贰等黄知清 南雅中学 贰等王 毅 长郡中学 贰等黄 科 长沙市第一中学 贰等刘龙辉 望城六中 贰等殷 文 天心一中 贰等陈菊珍 浏阳三中 贰等田志坚 浏阳五中 贰等 刘 伟 湖南师大附中梅溪湖中学 贰等 王辉沅 浏阳六中 贰等 叶运平 浏阳一中 贰等 谭泽阳 长郡中学 贰等 华接春 长郡中学 贰等 唐智明 湖南师大附中梅溪湖中学 贰等 汪光俊 浏阳市第十一中学 贰等 杨振新 周南中学 贰等 钟升阳 长沙县第六中学 贰等 刘文通 浏阳市第六中学 贰等 谢 娇 宁乡县第一中学 贰等 郭义生 长沙市第六中学 贰等 卢 琼 宁乡县第一中学 贰等 刘 超 长沙铁路第一中学 贰等 李碧涛 周南中学 贰等 蔡章平 长沙铁路第一中学 贰等 李 鑫 长沙市第一中学 贰等 王京臣 湘府中学 贰等 杨耀平 长沙外国语学校 贰等 吴 杰 望城一中 贰等 刘 琼 麓山滨江实验学校 贰等 陈湘栋 宁乡四中 贰等 刘 杰 浏阳六中 贰等 陈一星 湖南广益实验中学 贰等 易长保 周南中学 贰等 冷志强 长沙县三中 贰等 刘东红 湖南师大附中 贰等 汤礼达 湖南师大附中 贰等 黄爱钦 浏阳六中 贰等 李益保 浏阳三中 贰等 张家红 浏阳九中 贰等 袁立新 长沙县第一中学 贰等 朱学军 宁乡县第一中学 贰等 谢大寨 长沙县第六中学 贰等 陈淼君 湖南师大附中 贰等 邓有英 宁乡县实验中学 贰等 黄文辉 雅礼中学 贰等 罗跃东 长沙市第十一中学 贰等 罗 雄 浏阳田家炳实验中学 贰等 彭小平 浏阳八中 贰等沈望喜 浏阳八中 贰等 李双翔 长沙外国语学校 贰等 潘映山 浏阳五中 贰等 胡 玲 长沙县第七中学 贰等 蒋建平 湘府中学 贰等 张 勇 周南中学 贰等 李 论 长沙市第十九中学 贰等 罗定汩 浏阳三中 贰等 李 飞 长沙县第一中学 贰等 袁怀庆 浏阳一中 贰等 周江红 浏阳田家炳实验中学 贰等 周佳华 天心一中 叁等 胡 蓉 宁乡县第一中学 叁等 王忠富 湖南广益实验中学 叁等 杨庆芬 湖南师大附中梅溪湖中学 叁等 黄 刚 湖南师大附中 叁等 廖娟利 长沙市第十一中学 叁等 李毓安 浏阳一中 叁等 彭水珍 湖南师大附中梅溪湖中学 叁等 宋旭辉 长郡中学 叁等 胡安明 艺术学校 叁等 周春华 金桥学校 叁等 吴中华 宁乡十三中 叁等 戴志勇 宁乡四中 叁等 段 峰 长沙市第七中学 叁等 阳 松 麓山滨江实验学校 叁等 严文鸳 望城一中 叁等 阳才福 宁乡四中 叁等 张 蓉 长沙市第十一中学 叁等 林曙光 长沙县第九中学 叁等 罗春才 长沙大学附中 叁等 张台坡 地质中学 叁等 王华海 浏阳一中 叁等 钟建国 长沙市第一中学 叁等 黎尚青 浏阳二中 叁等 欧家祥 浏阳五中 叁等 许 敏 稻田中学 叁等 罗秋红 长沙县实验中学 叁等 付建军 长沙县实验中学 叁等 程广宇 望城六中 叁等 彭志中 麓山滨江实验学校 叁等陶玉玲 稻田中学 叁等 唐 强 麓山滨江实验学校 叁等 段建红 长沙市第十五中学 叁等 颜新国 长沙市实验中学 叁等 杨海艳 宁乡县第一中学 叁等 张先祥 浏阳一中 叁等 邓永生 周南中学 叁等 林海峰 周南中学 叁等 马远征 宁乡县第一中学 叁等 邹辉煌 浏阳六中 叁等 郭应兰 金桥学校 叁等 龙 航 长沙县九中 叁等 曾召勇 长沙市实验中学 叁等 张海江 长沙市第三十七中学 叁等 邱 勇 浏阳三中 叁等 曾 敏 浏阳三中 叁等 沈申文 浏阳田家炳实验中学 叁等 张在强 浏阳九中 叁等 张 强 浏阳十一中 叁等 唐 枫 长沙市第六中学 叁等 罗 敏 长沙市第十五中学 叁等 李撩原 宁乡一中 叁等 唐伯良 长沙市第十九中学 叁等 姚 蹈 湖南师大附中星城实验中学 叁等 罗志恒 长铁一中 叁等 曾 平 望城一中 叁等 陈红水 天心一中 叁等 吴向军 长沙县第六中学 叁等 李 义 长沙大学附中 叁等 甘林蛟 湖南师大附中梅溪湖中学 叁等 疗海伟 宁乡县第一中学 叁等 旷有元 周南梅溪湖中学 叁等 曹海军 长沙县第六中学 叁等 陈和珍 浏阳二中 叁等 袁满发 浏阳四中 叁等 谭建锋 湖南师大附中梅溪湖中学 叁等 向彩金 长沙市实验中学 叁等 吴 浩 湖南师大附中星城实验中学 叁等 肖海错 雅礼中学 叁等 袁跃良 长沙县第三中学 叁等 钟 波 长沙市第六中学 叁等罗瑞坤 长沙大学附中 叁等黎忐忑 浏阳二中 叁等长沙市教育科学研究院长沙市数学学会长沙市教育学会中学数学专业委员会二零一四年 十二月。
长沙市中学数学学用杯应用与创新能力大赛精编

长沙市中学数学学用杯应用与创新能力大赛精编Document number:WTT-LKK-GBB-08921-EIGG-229862011年长沙市中学数学“学用杯”应用与创新能力大赛八 年 级 决 赛 试 题(时量:120分钟 满分:100分)一、选择题(本题有10小题,每小题3分,共30分)(请将惟一正确的选项代号填在下面的答题卡内)1、多项式54222+--+b a b a 的值总为( )A 、非负数B 、零C 、负数D 、正数2、比较2的大小,正确的是( )A 、2<B 、2<C 2<D 、23、当230x ->时,|1|x -( )A 、2x -B 、34x -C 、2x -D 、43x -4、设c b a >>> 0,1=++c b a ,,,b c a c a b M N P abc+++===,则,,M N P 之间的大小关系是( )A 、M >P >NB 、N > P > MC 、P > M >ND 、P >N >M学校: 姓名: 考场: 考号:☼……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼5、下列五个命题:①若直角三角形的两条边长为3与4,则第三边长是5;②2();a a =③若点(,)P a b 在第三象限,则点)1,(+--b a Q 在第一象限;④连结对角线垂直且相等的四边形各边中点的四边形是正方形;⑤两边及其第三边上的中线对应相等的两个三角形全等. 其中正确的命题的个数是( )A 、2个B 、3个C 、4个D 、5个6、在⊿ABC 中,AC =5,中线AD =4,则AB 的取值范围是( )A 、3 <AB <13 B 、5 <AB <13C 、9 <AB <13D 、1 <AB <97、如图,直线l 和双曲线k y x=(0k >)交于A 、B 两点,P 是线段AB 上的点(不与A 、B 重合),过点A 、B 、P分别向x 轴作垂线,垂足分别为C 、D 、E ,连接OA 、OB 、OP ,设△AOC 的面积为1S 、△BOD 的面积为2S 、△POE的面积为3S ,则有( )第7题第10题A 、123S S S << B 、123S S S >> C 、123S S S =<D 、123SS S =>8、有铅笔,练习本,圆珠笔三种学习用品. 若购铅笔3支,练习本7本,圆珠笔1支共需元;若购铅笔4支,练习本10本,圆珠笔1支共需元. 现购铅笔、练习本、圆珠笔各1件,共需( )A 、元B 、元C 、元D 、元9、关于x 的方程211x a x +=-的解是正数,则a 的取值范围是( )A 、1a >-B 、10a a >-≠且C 、1a <-D 、12a a <-≠-且 10、如图所示,已知△ABC 和△DCE 均是等边三角形,点B 、C 、E在同一条直线上,AE 与BD 交于点O ,AE 与CD 交于点G ,AC 与BD交于点F ,连接OC 、FG ,则下列结论:①AE =BD ;②AG =BF ;③FG ∥BE ;④∠BOC =∠EOC ,其中正确结论的个数( )A 、1个B 、2个C 、3个D 、4个二、填空题(本题有8小题,每小题3分,共24分)11、若03=+ba ,则=-++÷+-222242)21(b a b ab a b a b . 12、已知01x ≤≤,若223x y +=,1xy =,则x y-= . 13、分解因式:2235294x xy y x y +-++-= . 14、如图,DC ∥AB ,∠BAE =∠BCD ,AE ⊥DE ,∠D = 130°,则∠B = .15、如图是根据某初中为地震灾区捐款的情况而制作的统计图,已知该校在校学生有2000人,请根据统计图计算该校共捐款 元.16、设多项式M d cx bx ax =+++35,已知当x =0时,5-=M ;当3-=x 时,7=M ,则当3=x 时, M = .17、如图,直线b kx y +=1过点A (0,2),且与直线mx y =2交于点P (1,m ),则关于x 的不等式组mx >kx +b >mx -2的解集是______________.18、如图,在平面直角坐标系中,边长为1的正方形 OA 1B 1C 的对角线A 1C 和OB 1交于点M 1;以M 1A 1为对角线作第二个正方形A 2A 1B 2M 1,对角线A 1 M 1和A 2B 2 交于点M 2;以M 2A 1为对角线作第三个正方形A 3A 1B 3 M 2,对角线A 1 M 2和A 3B 3 交第14题第15题第17题 A 1A 3 A 2B 1B 2B 3M 1M 2M 3COxy 第18题于点M3;……,依次类推,这样作的第n个正方形对角线交点的坐标为M n __________________.三、解答题(本题有4小题,共46分)19、(本题满分12分)“六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具x套,B种玩具y套,三种电动玩具的进价和售价如右表所示.⑴用含的代数x、y式表示购进C种玩具的套数;⑵求y与x之间的函数关系式;⑶假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元.①求出利润P(元)与x(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套.20、(本题满分12分)如图,在正方形ABCD 中,E 是AB 边上任意一点,BG ⊥CE ,垂足为点O ,交AC 于点F ,交AD 于点G.(1)证明:BE =AG ;(2)点E 位于什么位置时,∠AEF =∠CEB ,说明理由.21、(本题满分12分)在平面直角坐标系内有两点A (-2,0),B (4,0)和直线2521:+=x y l .在直线l 上是否存在点P ,使ABP∆为直角三角形,若存在,请求出P 点的坐标;若不存在,请说明理由.E BAO FG C D22、(本题满分10分)已知a ,b 是实数,若关于x ,y 的方程组⎩⎨⎧+=--=bax y bx ax x y ,23有整数解),(y x ,求a ,b 满足的关系式.2011年长沙市中学数学“学用杯”应用与创新能力大赛八年级试题参考答案与评分标准一、选择题(本题有10小题,每小题3分,共30分)二、填空题(本题有8小题,每小题3分,共24分) 11、25 12、-1 13、)12)(43(-++-y x y x 14、40° 15、2518016、-17 17、21<<x 18、(1-12n ,12n )或另一书写形式(2n-12n ,12n )三、解答题(本题有4小题,共46分)19、(本题满分12分)解:解:(1)购进C 种玩具套数为:50-x -y (或47-54x -1011y )………2分(2)由题意得405550()2350x y x y ++-=, 整理得230y x =- ……5分(3)①利润=销售收入-进价-其它费用(5040)(8055)(6550)(50)200p x y x y =-+-+----……………6分又∵230y x =- ∴整理得15250p x =+ …………………………………………………7分②购进C 种电动玩具的套数为:5050(230)803x y x x x --=---=-据题意列不等式组102301080310x x x ≥⎧⎪-≥⎨⎪-≥⎩,解得70203x ≤≤ …………………9分∴x 的范围为70203x ≤≤,且x 为整数 x 的最大值是23 ………10分∵在15250p x =+中,15k =>0 ∴P 随x 的增大而增大∴当x 取最大值23时,P 有最大值,最大值为595元.此时购进A 、B 、C 种玩具分别为23套、16套、11套. …………………………………12分 20、(本题满分12分)解(1)证明:∵四边形ABCD 是正方形,∴∠ABC =∠BAD =90°,∴∠1+∠3=90°,∵BG ⊥CE ,∴∠BOC =90°∴∠2+∠3=90°, ∴∠1=∠2. ………………………2分 在△GAB 和△EBC 中,∵∠GAB =∠EBC =90°,AB =BC ,∠1=∠2; ∴△GAB ≌△EBC (ASA) …………5分 ∴AG =BE . ………………………… 6分 (2)解:当点E 位于线段AB 中点时,∠AEF =∠CEB . ……………………7分1EB A OF G CD3 2理由如下:若当点E 位于线段AB 中点时,则AE =BE ,由(1)可知,AG =BE ∴AG =AE. ∵四边形ABCD 是正方形,∴∠GAF =∠EAF =45°.…………………………8分又∵AF =AF ,∴△GAF ≌△EAF (SAS),∴∠AGF =∠AEF. …………………10分由(1)知,△GAB ≌△EBC∴∠AGF =∠CEB ,∴∠AEF =∠CEB . ……12分 21、(本题满分12分)解:(1)如果点A 或点B 为直角顶点,则点P的横坐标为-2或4.易得)23,2(1-P ,)29,4(2P . …………………………………………………4分(2)如果点P 为直角顶点,则线段AB 为斜边,AB =6,AB 的中点为)0,1(C ,连结PC ,则PC =3. ……………………………6分设P 点的坐标为)2521,(+x x P ,作AB PD ⊥于点D ,则222PC PD CD =+,即2223)2521()1(=++-x x , …………………8分整理得07252=-+x x . 解得571-=x ,12=x .相应地 591=y ,32=y . )59,57(3-∴P ,)3,1(4P . (11)分综上,在直线l 上存在四个点P :)23,2(1-P ,)29,4(2P ,)59,57(3-P ,)3,1(4P ,使ABP ∆为直角三角形. …………………………………………………………12分22、(本题满分10分)解:将b ax y +=代入bx ax x y --=23,消去a 、b ,得xy x y -=3,即3)1(x y x =+. …………………………………………………………4分若x +1=0,即1-=x ,则上式左边为0,右边为1-不可能,所以x +1≠0.于是111123+-+-=+=x x x x x y .因为x 、y 都是整数,所以11±=+x ,即2-=x 或=x 0,进而y =8或=y 0. 故⎩⎨⎧=-=82y x 或⎩⎨⎧==00y x …………8分 当⎩⎨⎧=-=82y x 时,代入b ax y +=得,082=+-b a ;当⎩⎨⎧==00y x 时,代入b ax y +=得,0=b . 综上所述,a 、b 满足关系式是082=+-b a ,或者0=b ,a 是任意实数.…10分。
2014年湖南省长沙市中考数学试卷(含解析版)

2014年湖南省长沙市中考数学试卷一、选择题(共10小题,每小题3分,共30分)1.的倒数是()A、2B、-2C、D、-2.下列几何体中,主视图、左视图、俯视图完全相同的是()A.圆锥B.六棱柱C.球D.四棱锥3.(3分)(2014•长沙)一组数据3,3,4,2,8的中位数和平均数分别是()A.3和3 B.3和4 C.4和3 D.4和44.(3分)(2014•长沙)平行四边形的对角线一定具有的性质是()A.相等B.互相平分C.互相垂直D.互相垂直且相等5.(3分)(2014•长沙)下列计算正确的是()A.+= B.(ab2)2=ab4C.2a+3a=6a D.a•a3=a46.(3分)(2014•长沙)如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为()A.2cm B.3cm C.4cm D.6cm7.(3分)(2014•长沙)一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是()A.x>1 B.x≥1C.x>3 D.x≥38.(3分)(2014•长沙)如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是()A.1B.C.2 D.29.(3分)(2014•长沙)下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是()A.B.C.D.10.(3分)(2014•长沙)函数y=与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.二、填空题(共8小题,每小题3分,共24分)11.(3分)(2014•长沙)如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2=度.12.(3分)(2014•长沙)抛物线y=3(x﹣2)2+5的顶点坐标是.13.(3分)(2014•长沙)如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=度.14.(3分)(2014•长沙)已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1,则k= .15.(3分)(2014•长沙)100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是.16.(3分)(2014•长沙)如图,在△ABC中,DE∥BC,=,△ADE的面积是8,则△ABC的面积为.17.(3分)(2014•长沙)如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF= .18.(3分)(2014•长沙)如图,在平面直角坐标系中,已知点A(2,3),点B (﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是.三、解答题(共2小题,每小题6分,共12分)19.(6分)(2014•长沙)计算:(﹣1)2014+﹣()﹣1+sin45°.20.(6分)(2014•长沙)先简化,再求值:(1+)+,其中x=3.四、解答题(共2小题,每小题8分,共16分)21.(8分)(2014•长沙)某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:请根据所给信息解答以下问题:(1)请补全条形统计图;(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.22.(8分)(2014•长沙)如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.(1)求证:△AOE≌△COD;(2)若∠OCD=30°,AB=,求△AOC的面积.五、解答题(共2小题,每小题9分,共18分)23.(9分)(2014•长沙)为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼地进行,某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.(1)若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?(2)若购买甲种树苗的金额不少于购买一中树苗的金额,至少应购买甲种树苗多少棵?24.(9分)(2014•长沙)如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.(1)求证:DE⊥AC;(2)若AB=3DE,求tan∠ACB的值.六、解答题(共2小题,每小题10分,共20分)25.(10分)(2014•长沙)在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),(,),…都是“梦之点”,显然,这样的“梦之点”有无数个.(1)若点P(2,m)是反比例函数y=(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+,试求出t的取值范围.26.(10分)(2014•长沙)如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.2014年湖南省长沙市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.的倒数是()A、2B、-2C、D、-倒数.考点:分根据乘积为的1两个数倒数,可得一个数的倒数.析:解:的倒数是2,解答:故选:A.本题考查了倒数,分子分母交换位置是求一个数的倒数的关键.点评:2.下列几何体中,主视图、左视图、俯视图完全相同的是()A.圆锥B.六棱柱C.球D.四棱锥简单几何体的三视图.考点:分析:找到从物体正面、左面和上面看得到的图形全等的几何体即可.解答:解:A、圆锥的主视图、左视图、俯视图分别为等腰三角形,等腰三角形,圆及圆心,故A选项不符合题意;B、六棱柱的主视图、左视图、俯视图分别为四边形,四边形,六边形,故B选项不符合题意;C、球的主视图、左视图、俯视图分别为三个全等的圆,故C选项符合题意;D、四棱锥的主视图、左视图、俯视图分别为三角形,三角形,四边形,故D选项不符合题意;故选C.点评:考查三视图的有关知识,注意三视图都相同的常见的几何体有球和正方体.3.(3分)(2014•长沙)一组数据3,3,4,2,8的中位数和平均数分别是()A.3和3 B.3和4 C.4和3 D.4和4考点:中位数;算术平均数.分析:根据中位数及平均数的定义求解即可.解答:解:将数据从小到大排列为:2,3,3,4,8,则中位数是3,平均数==4.故选B.点评:本题考查了平均数及中位数的知识,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.4.(3分)(2014•长沙)平行四边形的对角线一定具有的性质是()A.相等B.互相平分C.互相垂直D.互相垂直且相等考点:平行四边形的性质.分析:根据平行四边形的对角线互相平分可得答案.解答:解:平行四边形的对角线互相平分,故选:B.。
2014年特长展示决赛数学试题答案

二○一四年初中特长展示决赛数学试题答案一、选择题A B B C B 二、填空题6.1981; 7.36;8. (1,1)b a +-+;9.10;10.110.三、解答题11.解:(1)矩形ABCD 的边AB =CD =200x,……………2分 由题意得400×(2x +200x +200x )+300×(200x +200x)+200×80=47200即800x +400700x⨯+200×80=47200.……………6分化简得x 2﹣39x +350=0. 解得x 1=14,x 2=25.……………9分经检验都是原方程的解,但x =25>16(不合题意舍去). 当x =14时,2001614<,符合题意. 因此当三级污水处理池的总造价为47200元时,池长14米.……………10分 (2)当以47200为总造价来修建三级污水处理池时,不是最合算;……………11分 当池长为16米时,池宽为12.5米<16米,故池长为16米符合题意,这时总造价为800×16+40070016⨯+200×80=46300<47200.……………13分因此当以47200为总造价来修污水处理池时,不是最合算.……………15分 12.证明:延长BH 交AC 于点M ,延长AH 交BC 于点N ,连接BE ,EH ,EC . ∵ 点H 是△ABC 的三条高的交点, ∴ BM ⊥AC ,AN ⊥BC .……………5分 ∵AD BD ⊥, ∴∠BDE =90°.∴ BE 为△BHC 外接圆的直径.………8分 ∴∠BHE =∠BCE =90°.即BH EH ⊥,CE BC ⊥.……………10分AEBDPM NHC又∵BH⊥AC, AH⊥BC,∴AH∥CE,AC∥HE.∴四边形ACEH为平行四边形.……………12分∵点P是对角线AE与HC的交点,∴点P为CH的中点.…………… 15分13.解:(1)如图,过点A作AH⊥x轴,垂足为H.∵AB=BO.∴∠∠OAB=AOB=30°.∴∠ABH=60°.……………… 1分在Rt△ABH中,AB=2,∴BH=1,AHA.……………∵抛物线与x轴交于O、B(2,0)两点,设y=ax(x-2),代入点A,可得a.∴抛物线的表达式为2(2)y x x=-=.…………… 4分(2)由221)3333y x x x=-=--得抛物线的顶点M的坐标为(1,.…………… 6分∴tan BOM∠=.∴∠BOM=30°.∴∠AOM=60°.…………… 8分(3)由A()3,3、B(2,0)、M(1,,AH⊥x轴,∠AOB=30°,∴322==AHAO.…………… 9分∵M(1,,∠BOM=30°,∴OM=∴3=OMOA.…………… 10分当点C在点B左侧时,∠ABC=120°,△AMO中不可能出现120°的角,不存在满足条件的点;…………… 11分当点C 在点B 右侧时,∵∠ABC =∠AOM =60°, ∴△ABC 与△AOM 相似,存在两种情况: ①如图2,当3==OM OA BC BA 时,3231==BA BC .此时C (83,0).…… 13分 ②如图3,当3==OMOABA BC 时,6233=⨯==BA BC .此时C (8,0).综上所述,C 点的坐标为(83,0)或(8,0).…………… 15分 14.解:(1)如图1,容易把一个正方形分成42=16个正方形,再把其中位于一角的9个拼成一个正方形,共得:16-9+1=8个正方形.…………… 5分(2)如图2,分成16个正方形后,把其中任意5个分成4个小正方形,共有16﹣5+5×4=31个正方形.…………… 10分(3)说明:把立方体分割成33=27个立方体,再把其中4个各分成23=8个立方体,共27-4+4×23=55个立方体.…………… 15分图1图2。
2014年长沙市“学用杯”初中数学应用与创新能力大赛--九-年-级-初-赛-试-题及答案

CABD M 第15题2014年市“学用杯”初中数学应用与创新能力大赛九 年 级 初 赛 试 题(时量:90分钟 满分:100分)一、选择题(本大题共10小题,每小题4分,共40分)题号 12345678910答案1.设P =121220132012++,Q =121220142013++,则P 与Q 的大小关系是A .P >QB .P =QC .P <QD .不能确定2.边长为整数,周长等于21的等腰三角形共有A .4个B .5个C .6个D .7个3.在直角坐标系中,纵、横坐标都是整数的点,称为整点.设k 为整数,当直线2+=x y 与直线4-=kx y 的交点为整点时,k 的值可以取 A .8个 B .7个 C .6个 D .5个 4.若二次函数2y ax bx c =++的图象如图所示,则点(b a +,ac )在A .第一象限B .第二象限C .第三象限D .第四象限5.如图,矩形ABCD 被分割成六个正方形,其中最小正方形的面积等于1,则矩形ABCD 的面积等于A .152B .143C .132D .108 6.如图,⊙O 中,弦AD ∥BC ,DA =DC ,∠AOC =160°,则∠BCO 等于 A . 20° B . 30° C . 40° D . 50°7.已知锐角△ABC 中,∠A =60°,BD 和CE 都是△ABC 的高。
如果△ABC 的面积为12, 那么四边形BCDE 的面积为 A .6 B .8 C .9 D .108.一个商人用m 元(m 是正整数)买来了n 台(n 为质数)电视机,其中有两台以成本的一半价钱卖给某个慈善机构,其余的电视机在商店出售,每台盈利500元,结果该商人获得利润为5500元,则n 的最小值是 A .11 B .13 C .17 D .19 9.直线k x y +=21与x 轴的交点分别为A 、B ,如果S △AOB ≤1,那么,k 的取值围是 A .k ≤1 B . 0<k ≤1 C .-1≤k ≤1 D . k ≤-1或k ≥110.如图,在梯形ABCD 中,AB ∥DC ,AB ⊥BC ,E 是AD 的中点,6AB BC CD ++=,5BE =,则梯形ABCD 的面积等于A . 13B . 8C . 132D . 4二、填空题(本大题共8小题,每小题4分,共32分)11.实数a ,b 满足a b a b a =++-+-+-31)5(2)3(222,则=-b a . 12.若532=-+c b a , 8765=+-c b a ,则=-+c b a 529 .13.若m ,n 是一元二次方程0132=-+x x 的两个根,则=-+n m m 22.14.已知3=xy ,那么yxyx y x +的值是 . 15.如图,在△ABC 中,中线CM 与高线CD 三等分ACB ∠,则B ∠等于 度. 16.已知t bac a c b c b a =+=+=+,那么直线t tx y +=一定通过第 象限. 17.不论k 取什么实数,关于x 的方程1632=--+bkx a kx (a 、b 是常数)的根总是x =1,那么=+b a .18.如图, AB 是半径为R 的圆O 的直径, 四边形CDMN学校: 姓名: 考场: 考号:…☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼ABCD E 第10题Oxy第4题A B C D 第6题O C B A D 第5题C D E在AB上, ,F N 和DEFG都是正方形. 其中,,在半圆上,则两个正方形的面积之和为..三、解答题(本大题共2小题,每小题14分,共28分)19.(本题满分14分)如图,已知一次函数323+-=x y 的图象与x 轴、y 轴分别交于A 、B 两点,与正比例函数x y 3=的图象交于点C ,点D 是线段OB 上的一个动点(不包含O 、B 两点),以AD 为边在其一侧作等边三角形ADE ,DE 交AB 于F ,AD 交OC 于G .(1)分别求出A 、B 、C 三点的坐标; (2)△ADF 和△ACG 是否相似,为什么? (3)证明CE 总与AB 垂直.如图1,在平面直角坐标系中,直角梯形ABCD 的直角顶点D 与原点重合,另一直角顶点A 在y 轴的正半轴上,点B 、C 的坐标分别为B (12,8)、C (14,0),AD 为⊙E 的直径.,点M 、N 分别从A 、C 两点同时出发做匀速运动,其中点M 沿AB 向终点B 运动,速度为每秒1个单位;点N 沿CD 向终点D 运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.(1)如图2,设点M 、N 的运动时间为t 秒,当t 为何值时,四边形MBCN 为平行四边形? (2)在(1)的条件下,连结DM 与⊙E 相交于点P ,求弦DP 的长;(3)已知二次函数的图象经过D 及(1)中的点M 、N ,求该二次函数的解析式;(4)在运动过程中,是否存在使直线MN 与⊙E 相切的情形?如果存在,请求出直线MN 的解析式;如果不存在,请说明理由.(图3供解答本小题用)x O B Ay C DGF E2014年市“学用杯”初中数学应用与创新能力大赛九 年 级 初 赛 试 题参考答案及评分标准一、选择题(本大题共10小题,每小题4分,共40分)题号 1 2 3 4 5 6 7 8 9 10答案ABDABBCCCD二、填空题(本大题共8小题,每小题4分,共32分)11、3; 12、28; 13、4; 14、32±; 15、30︒; 16、二、三; 17、21-; 18、2R三、解答题(本大题共2小题,每小题14分,共28分)19.(1)在y=-3x+23中,令x=0得y=23,令y=0得x=2, ∴A 的坐标为(2,0),B 的坐标为(0,23).由⎩⎨⎧=+-=x 3y 32x 3y 得⎩⎨⎧==3y 1x ,即C 的坐标为(1,3). ……………………………………(4分)(2) △ADF ∽△ACG. 由tan ∠OAB=3得∠OAB=60︒,由tan ∠AOC=3得∠AOC=60︒, ∴△OAC 为等边三角形。
xxxx年长沙市中学数学“学用杯”应用与创新能力大赛[]
![xxxx年长沙市中学数学“学用杯”应用与创新能力大赛[]](https://img.taocdn.com/s3/m/97a8ff24581b6bd97f19ea75.png)
2011年长沙市中学数学“学用杯”应用与创新能力大赛八 年 级 决 赛 试 题(时量:120分钟 满分:100分)一、选择题(本题有10小题,每小题3分,共30分)(请将惟一正确的选项代号填在下面的答题卡内) 题号 1 2 3 4 5 6 789 10 答案1、多项式54222+--+b a b a 的值总为( ) A 、非负数B 、零C 、负数D 、正数2、比较2,5,37的大小,正确的是( )A 、3257<< B 、3275<< C 、3725<< D 、3572<< 3、当230x ->时,2|1|9124x x x -+-+=( )A 、2x -B 、34x -C 、2x -D 、43x - 4、设c b a >>> 0,1=++c b a ,,,b c a c a bM N P a b c+++===,则,,M N P 之间的大小关系是( )A 、M >P >NB 、N > P > MC 、P > M >ND 、P >N >M5、下列五个命题:①若直角三角形的两条边长为3与4,则第三边长是5;②2();aa=③若点(,)P a b 在第三象限,则点)1,(+--b a Q 在第一象限;④连结对角线垂直且相等的四边形各边中点的四边形是正方形;⑤两边及其第三边上的中线对应相等的两个三角形全等. 其中正确的命题的个数是( )A 、2个B 、3个C 、4个D 、5个 6、在⊿ABC 中,AC =5,中线AD =4,则AB 的取值范围是( ) A 、3 <AB <13 B 、5 <AB <13 C 、9 <AB <13 D 、1 <AB <9 7、如图,直线l 和双曲线ky x=(0k >)交于A 、B 两点, P 是线段AB 上的点(不与A 、B 重合),过点A 、B 、P 分别向x 轴作垂线,垂足分别为C 、D 、E ,连接OA 、OB 、 OP ,设△AOC 的面积为1S 、△BOD 的面积为2S 、△POE 的面积为3S ,则有( )学校: 姓名: 考场: 考号:☼……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼第7题A D CB 第10题EG FO A 、123S S S << B 、123S S S >> C 、123S S S =< D 、123S S S =>8、有铅笔,练习本,圆珠笔三种学习用品. 若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本10本,圆珠笔1支共需4.2元. 现购铅笔、练习本、圆珠笔各1件,共需( )A 、1.2元B 、1.05元C 、0.95元D 、0.9元9、关于x 的方程211x ax +=-的解是正数,则a 的取值范围是( ) A 、1a >- B 、10a a >-≠且 C 、1a <- D 、12a a <-≠-且10、如图所示,已知△ABC 和△DCE 均是等边三角形,点B 、 C 、E 在同一条直线上,AE 与BD 交于点O ,AE 与CD 交于点G ,AC 与BD 交于点F ,连接OC 、FG ,则下列结论:①AE =BD ;②AG =BF ;③FG ∥BE ;④∠BOC =∠EOC ,其中正确结论的个数( ) A 、1个 B 、2个 C 、3个 D 、4个 二、填空题(本题有8小题,每小题3分,共24分)11、若03=+b a ,则=-++÷+-222242)21(b a b ab a b a b . 12、已知01x ≤≤,若223x y +=,1xy =,则x y -= .13、分解因式:2235294x xy y x y +-++-= . 14、如图,DC ∥AB ,∠BAE =∠BCD ,AE ⊥DE ,∠D = 130°,则∠B = .15、如图是根据某初中为地震灾区捐款的情况而制作的统计图,已知该校在校学生有2000人,请根据统计图计算该校共捐款 元. 16、设多项式M d cx bx ax =+++35,已知当x =0时,5-=M ;当3-=x 时,7=M ,则当3=x 时, M = .17、如图,直线b kx y +=1过点A (0,2),且与直线mx y =2交于点P (1,m ),则关于x 的不等式组 mx >kx +b >mx -2的解集是______________.18、如图,在平面直角坐标系中,边长为1的正方形OA 1B 1C 的对角线A 1C 和OB 1交于点M 1;以M 1A 1为对角线作第二个正方形A 2A 1B 2 M 1,对角线A 1 M 1和A 2B 2 交于点M 2;以M 2A 1为对角线作第三个正方形A 3A 1B 3 M 2,对角线A 1 M 2和A 3B 3 交于点M 3;……,依次类推,这样第14题 第15题 第17题A 1A 3 A 2B 1B 2B 3M 1M 2M 3 CO xy第18题作的第n个正方形对角线交点的坐标为M n __________________.三、解答题(本题有4小题,共46分) 19、(本题满分12分)“六一”前夕,某玩具经销商用去2350元购进A 、B 、C 三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A 种玩具x 套,B 种玩具y 套,三种电动玩具的进价和售价如右表所示.⑴ 用含x 、y 的代数式表示购进C 种玩具的套数; ⑵ 求y 与x 之间的函数关系式;⑶ 假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元.①求出利润P (元)与x (套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套. 20、(本题满分12分)如图,在正方形ABCD 中,E 是AB 边上任意一点,BG ⊥CE ,垂足为点O ,交AC 于点F ,交AD 于点G. (1)证明:BE =AG ;(2)点E 位于什么位置时,∠AEF =∠CEB ,说明理由.型 号 A BC 进价(元/套) 40 55 50 售价(元/套) 50 8065EBAOFGCD21、(本题满分12分)在平面直角坐标系内有两点A (-2,0),B (4,0)和直线2521:+=x y l .在直线l 上是否存在点P ,使ABP ∆为直角三角形,若存在,请求出P 点的坐标;若不存在,请说明理由.22、(本题满分10分)已知a ,b 是实数,若关于x ,y 的方程组⎩⎨⎧+=--=bax y bx ax x y ,23有整数解),(y x ,求a ,b 满足的关系式.2011年长沙市中学数学“学用杯”应用与创新能力大赛八年级试题参考答案与评分标准一、选择题(本题有10小题,每小题3分,共30分) 题号 1 2 3 4 5 6 7 8 9 10 答案 A C B D B A C BDD二、填空题(本题有8小题,每小题3分,共24分) 11、2512、-1 13、)12)(43(-++-y x y x 14、40° 15、25180 16、-17 17、21<<x 18、(1-12n ,12n )或另一书写形式(2n-12n ,12n )三、解答题(本题有4小题,共46分)19、(本题满分12分)解:解:(1)购进C 种玩具套数为:50-x -y (或47-54x -1011y )………2分 (2)由题意得405550()2350x y x y ++-=, 整理得230y x =- ……5分(3)①利润=销售收入-进价-其它费用(5040)(8055)(6550)(50)200p x y x y =-+-+----……………6分又∵230y x =-∴整理得15250p x =+ …………………………………………………7分 ②购进C 种电动玩具的套数为:5050(230)803x y x x x --=---=-据题意列不等式组102301080310x x x ≥⎧⎪-≥⎨⎪-≥⎩,解得70203x ≤≤ …………………9分∴x 的范围为70203x ≤≤,且x 为整数 x 的最大值是23 ………10分∵在15250p x =+中,15k =>0 ∴P 随x 的增大而增大∴当x 取最大值23时,P 有最大值,最大值为595元.此时购进A 、B 、C 种玩具分别为23套、16套、11套. …………………………………12分 20、(本题满分12分)解(1)证明:∵四边形ABCD 是正方形,∴∠ABC =∠BAD =90°,∴∠1+∠3=90°,∵BG ⊥CE ,∴∠BOC =90°∴∠2+∠3=90°,∴∠1=∠2. ………………………2分在△GAB 和△EBC 中, ∵∠GAB =∠EBC =90°,AB =BC ,∠1=∠2;∴△GAB ≌△EBC (ASA) …………5分∴AG =BE . ………………………… 6分1 E B AO FG C D32(2)解:当点E 位于线段AB 中点时,∠AEF =∠CEB . ……………………7分理由如下:若当点E 位于线段AB 中点时,则AE =BE , 由(1)可知,AG =BE ∴AG =AE.∵四边形ABCD 是正方形,∴∠GAF =∠EAF =45°.…………………………8分 又∵AF =AF ,∴△GAF ≌△EAF (SAS),∴∠AGF =∠AEF. …………………10分 由(1)知,△GAB ≌△EBC ∴∠AGF =∠CEB ,∴∠AEF =∠CEB . ……12分 21、(本题满分12分) 解:(1)如果点A 或点B 为直角顶点,则点P的横坐标为-2或4.易得)23,2(1-P ,)29,4(2P . …………………………………………………4分(2)如果点P 为直角顶点,则线段AB 为斜边,AB =6,AB 的中点为)0,1(C ,连结PC ,则PC =3. ……………………………6分设P 点的坐标为)2521,(+x x P ,作AB PD ⊥于点D , 则222PC PD CD =+,即2223)2521()1(=++-x x , …………………8分整理得07252=-+x x . 解得571-=x ,12=x .相应地 591=y ,32=y . )59,57(3-∴P ,)3,1(4P .…………………11分综上,在直线l 上存在四个点P :)23,2(1-P ,)29,4(2P ,)59,57(3-P ,)3,1(4P ,使ABP ∆为直角三角形. …………………………………………………………12分22、(本题满分10分)解:将b ax y +=代入bx ax x y --=23,消去a 、b ,得xy x y -=3,即3)1(x y x =+. …………………………………………………………4分 若x +1=0,即1-=x ,则上式左边为0,右边为1-不可能,所以x +1≠0.于是111123+-+-=+=x x x x x y .因为x 、y 都是整数,所以11±=+x ,即2-=x 或=x 0,进而y =8或=y 0. 故⎩⎨⎧=-=82y x 或⎩⎨⎧==0y x …………8分当⎩⎨⎧=-=82y x 时,代入b ax y +=得,082=+-b a ;当⎩⎨⎧==00y x 时,代入b ax y +=得,0=b . 综上所述,a 、b 满足关系式是082=+-b a ,或者0=b ,a 是任意实数.…10分。
2014年长沙市市直初中语文、数学、英语教师

2014年长沙市市直初中语文、数学、英语教师“课堂教学问题解析与应对”远程研修实施方案一、研修主题新课程背景下的学科课堂教学问题解析与应对二、研修目标通过实施本项目,达到以下目标:1.通过案例、对比、反思等途径,引领学员发现自己课堂里的教学问题,提升学员的问题意识。
2.通过探究解决问题的方法策略,引领学员关注自己教学行为的改善,提升学员的行为意识。
3.通过案例研究,反思研究和网上研讨,引领学员了解当前课堂教学中存在的普遍问题,并掌握解决这些问题的方法和策略。
4.通过组织学员参与案例研究、反思研究等过程,使学员了解行为研究的基本方法和过程,为开展校本研修和建设教师的研修社区打下基础。
三、研修对象市直初中语文、数学、英语三个学科的在职专任教师,1250人左右。
参加培训的教师应具备上网条件和网上交流的能力,保证培训期间平均每天不少于 1小时的网上学习与交流时间。
四、研修时间2014年9月11日—11月21日,共计72学时。
五、研修内容与研修方式(一)研修内容研修内容包含学科内容教学问题、学科思想教学问题、学科评价问题、学科教学基本技能问题等四个模块;每模块包含“案例研究”、“理论总结提升”、“思考作业”和“网上答疑”等环节。
1.案例研究。
案例研究是本课程的基本学习方式和基本内容单位,包含“案例展示”(揭示问题),“案例评析”(解析问题),“问题解决的方法策略建议”(引领教师研讨交流)。
每一个“案例研究”不超过20分钟,具有“微课”特点。
2.理论提升引领。
针对“案例研究”中涉及到的共性问题,聘请学科教学专家开设专题讲座,进行理论总结和提升。
理论提升讲座共5次,其中“学科内容教学问题”2次,其他模块每个1次。
每次1学时。
3.思考作业。
针对专家讲座,布置相应的思考作业。
4.网上答疑。
针对学员在研讨中提出的热点问题,每个模块网上答疑一次。
每次1学时。
(二)研修方式1.资源学习。
学员按照培训计划选定“多媒体课程资源包”自主学习,包括收看视频课程,阅读网络资源(含生成性资源)等。
长沙市八年级初中数学应用与创新能力大赛答案和试题

长沙市2014年初中数学应用与创新能力大赛八年级决赛参考答案及评分标准试题在最下面一、选择题(本大题共10小题,每小题4分,共40分)1、C2、A3、B4、D5、D6、C7、D8、B9、D10、A二、选择题(本大题共8小题,每小题4分,共32分)1112、113、8414、75 15、88 16、7017、426334,4,,8,8,1,a a a a a ---18、102三、选择题(本大题共2小题,每小题14分,共28分)19、由abc =1得:1111111111111111a b cab a bc b ac c b bc b ab a b ab a b aab a ab a ab a +++++++++=++++++=++++++=+=++++ 20、⑴设甲、乙两个工程队单独完成这项工程,分别需要x 、y 天,则⎪⎪⎩⎪⎪⎨⎧=+=+10912101616y x y x ,………………………………………… 4分解得⎩⎨⎧==3020y x ,经检验⎩⎨⎧==3020y x 是原方程组的解, ∴原方程组的解为⎩⎨⎧==3020y x . ………………………………………… 6分⑵设甲、乙两个工程队每天应得工程款a 元、b 元,则⎩⎨⎧=+=+1720001210196000616b a b a , ………………………………………… 8分解得⎩⎨⎧==600010000b a .………………………………………… 10分由于甲、乙两个工程队单独完成这项工程都超过了工期,故应合作完成。
为了节约工程款,应尽量安排乙工程队。
安排乙工作15天,完成工程的一半,同时安排甲工程队工作10天,完成另一半, 总工程款为190000元。
………………………………………… 12分 答:甲、乙两个工程队单独完成这项工程,分别需要20、30天;………………………………………… 4分………………………………………… 8分………………………………………… 12分安排甲工程队工作10天,同时安排乙工作15天,总工程款最少为190000元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长沙市2014年初中数学创新能力大赛
八 年 级 初 赛 试 题
(时量:90分钟 满分:100分)
1.计算)1011)(911)...(411)(311)(211(22222-----
的值是 A .2110 B .2113 C .20
9
D .
20
11
2.整数N =215
×510
的位数是
A .10位
B .11位
C .12位
D .13位
3.已知
32233,x y xy
---==则 4.已知△ABC 的三边的长分别为a 、b 、c ,且b c b c a
+=+-,则△ABC 一定是
A .等边三角形
B .腰长为a 的等腰三角形
C .底边长为a 的等腰三角形
D .等腰三角形
5.如果代数式-2+38a b +的值为18,那么代数式962b a -+的值等于
A .28
B .-28
C .-32
D .32
6.在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,则下列说法中错误的是 A .如果∠C -∠B =∠A ,那么△ABC 是直角三角形,∠C =90°
B .如果5:4:3::=c b a ,则∠B =60°,∠A =30°
C .如果3:2:5C :B :A =∠∠∠,那么△ABC 是直角三角形
D .如果2))((b a c a c =-+,那么△ABC 是直角三角形
7.如图,在四边形ABCD 中,M 、N 分别是CD 、BC 的中点,且AM ⊥CD ,AN ⊥BC ,已知∠MAN=74°,∠DBC=41°,则∠ADC 度数为 A .45° B .47° C .49° D .51°
8.规定“Δ”为有序实数对的运算,且(a ,b )△(c ,d )=(ac +bd ,ad +bc ),如果对任意实数a ,b 都有(a ,b )△(x ,y )=(a ,b ),则(x ,y )为 A .(0,1) B .(1,0) C .(-1,0) D .(0,-1)
9.甲、乙、丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲、乙各比赛了4局,丙当了3次裁判.问第2局的输者是 A .甲 B .乙 C .丙 D .不能确定
学校:
姓名: 考场: 考号:
☼……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼
10.某公交公司停车场内有15辆车,从上午6时开始发车(6时整第一辆车开出),以后每隔6分钟再开出一辆.第一辆车开出3分钟后有一辆车进场,以后每隔8分钟有一辆车进场,进场的车在原有的15辆车后依次再出车.则到第几辆车开出后,停车场内第一次出现无车辆?
A 、55
B 、56
C 、57
D 、58
二、填空题(本大题共8小题,每小题4分,共32分)
11.已知a +b =1,ab =108,则a 2b +ab 2的值为__________. 12.关于x 的方程211
x a x +=-的解是正数,则a 的取值范围是_________.
13.已知31=+
a a ,则221
a
a +的值是_______________. 14.如图,在ABC ∆中,90,50,30,ACB AB cm
BC cm CD AB ∠=︒==⊥于D ,则
CD=______ _____________cm .
(第14题)
(第17题)
(第18题)
15.已知4x -3y -6z =0,x +2y -7z =0,则
=---+2
22222103225z y x z y x .
16.已知:2
44x x -+与 |1y -| 互为相反数,则式子()x
y x y y x ⎛⎫
-÷+
⎪⎝⎭
的值等于_________. 17.如图,AD=8cm ,CD=6cm ,AD ⊥CD ,BC=24cm ,AB=26cm ,则S 四边形ABCD = . 18.如图,若AB=AC ,BD =BE ,AF=FD ,则∠BAC 的度数为 .
三、解答题(本大题共2小题,每小题14分,共28分)
19.(本题满分14分)已知:A=
bc a
c b
2
2 2
2-
+,B=
ac b
c a
2
2 2
2-
+,C=
ab c
b a
2
2 2
2-
+,且a+b=c,求A2013+B2014+C2013的值.
20.(本题满分14分)如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E.(1)若∠ADC+∠ABC=180°,求证:AD+AB =2AE;
(2)若AD+AB =2AE,求证:CD=CB.
长沙市2014年初中数学创新能力大赛
八年级预赛参考答案及评分标准
一、选择题(本大题共10小题,每小题4分,共40分)
1、D
2、C
3、B
4、B
5、D
6、B
7、C
8、B
9、C
10、B
二、选择题(本大题共8小题,每小题4分,共32分)
11、108 12、a <-1且a ≠-2 13、7
14、2.4cm
15、-13
16、
12
17、96 18、36︒
三、选择题(本大题共2小题,每小题14分,共28分)
19.、∵A =bc a c b 2222-+=bc
a c a c
b 2)
)((2-++
又由a +b =c 得c -a =b
∴A =bc
a c
b b 2)
(2++=c a c b 2++=c c 22=1
………………………………………………(4分) 同理B =1,C =-1
…………………………………………(12分) ∴A 2013+B 2014+C 2013=1。
…………………………………………(14分)
20、(1)如图.延长AB 到点M ,使AE =ME .………………………………………(2分)
又CE ⊥AB ,
故△ACM 为等腰三角形. 因此,AC =CM ,∠l =∠3.
……………(4分)
已知∠1 =∠2, 所以,∠3=∠2.
又∠ADC +∠ABC =180°, 于是,∠ADC =∠CBM .
…………………………………………(5分) 因此,△ADC ≌△MBC ,
…………………………………………(6分)
AD =BM ,故AM =2AE =AB + BM =AB +AD . …………………………………………(7分) (2)如图,延长AB 到点M ,使BM =AD .
…………………………………………(9分) 由2AE = AB +AD = AB + BM = AM , 故AE = ME .
…………………………………(10分)
∵CE ⊥AM ,同(1)得AC =MC ,∠2=∠3. …………………………………(12分)
∵BM=AD,
∴△ADC≌△MBC,从而,CD=CB. …………………………………………(14分)。
