青岛版【2014年新版】八年级数学下册期末复习检测题(五,无答案)
青岛版数学八年级下册期末测试卷(五)

期末测试卷(五)一、选择题)答案:D2.(贵州安顺)下列各数中,3.141 59,0.131 131 113…,-π,-17,无理数的个数有()A.1个B.2个C.3个D.4个答案:B3.下列命题中,真命题是()A.三个角相等的四边形是矩形B.对角线互相垂直且相等的四边形是正方形C.顺次连接矩形四边中点得到的四边形是菱形D.正五边形既是轴对称图形又是中心对称图形答案:C4.已知a,b均为有理数,且)2,则()A.a=9,b=12B.a=11,b=-6C.a=11,b=0D.a=9,b=6答案:B5.若一次函数y=kx+b的图象交y轴于正半轴,且y的值随x的值的增大而减小,则()A.k>0,b>0B.k>0,b<0C.k<0,b>0D.k<0,b<0答案:C6.一天早上小华步行上学,他离开家后不远便发现数学书忘在了家里,于是以相同的速度回家去拿,到家后发现弟弟把牛奶洒在了地上,就放下手中的东西,收拾好后才离开.为了不迟到,小华跑步到了学校,则小华离学校的距离y与时间t之间的函数关系的大致图象是( )答案:B7.如图,菱形ABCD 中,∠B=60°,AB=4,则以AC 为边长的正方形ACEF 的周长为( )A.14B.15C.16D.17答案:C8.如图,为测量池塘岸边AB 的距离,小亮在池塘的一侧选取一点O ,测得OA ,OB 的中点D ,E 之间的距离是14 m ,则A ,B 两点之间的距离是( )A.18 mB.24 mC.28 mD.30 m答案:C9.如图,ABCD 和矩形ACEF 的位置如图所示,点D 在EF 上,则ABCD 和矩形ACEF 的面积S 1,S 2的大小关系是( )A.S 1>S 2B.S 1=S 2C.S 1<S 2D.3S 1=2S 2答案:B10.如图,在Rt △ABC 中,CD ⊥AB ,垂足为D ,AD=8,DB=2,则CD 的长为( )答案:A11.在平面直角坐标系中,线段OP 的两个端点坐标分别为O (0,0),P (4,3),将线段OP 绕点O 逆时针90°旋转到OP ′位置,则点P ′的坐标为( )A.(3,4)B.(-4,3)C.(-3,4)D.(4,-3)答案:C12.已知关于x 的不等式组255,332x x x t x ⎧+-≥-+-<⎪⎪⎨⎪⎪⎩恰有6个整数解,则t 的取值范围是( ) A.-6<t<-112 B.-6≤t<-112C.-6<t ≤-112D.-6≤t ≤-112 答案:C二、填空题13.的结果是 . 答案:514.如图,Rt △ABC 中,∠ACB=90°,D 为斜边AB 的中点,AB=10 cm ,则CD 的长为cm .答案:515.如图,ABCD 是对角线互相垂直的四边形,且OB =OD ,请你添加一个适当的条件 ,使ABCD 成为菱形.(只需添加一个即可)答案:OA=OC ,答案不唯一16.(辽宁鞍山)如图,D 是△ABC 内一点,BD ⊥CD ,AD=6,BD=4,CD=3,E ,F ,G ,H 分别是AB ,AC ,CD ,BD 的中点,则四边形EFGH 的周长是 .答案:1117.已知长方形ABCD ,AB=3 cm ,AD=4 cm ,过对角线BD 的中点O 作BD 的垂直平分线EF ,分别交AD ,BC 于点E ,F ,则AE 的长为 . 答案:78cm 解析:如图,连接EB.∵EF 垂直平分BD ,∴ED=EB ,设AE=x cm ,则DE=EB=(4-x ) cm ,在Rt △AEB 中,AE 2+AB 2=BE 2,即x 2+32=2(4)x ,解得x=78. 18.如图,已知一次函数y=kx+b 和y=mx+n 的图象交于点P ,则根据图象可得不等式组0<mx+n <kx+b 的解集是 .答案:-3<x<-1三、解答题19.已知x 2-xy+y 2.答案:解:原式=2-+)2=()-(7-5)+()=22.20.先化简,再求值:2224x x x +-÷(x-2+82x x -),其中-1. 答案:解:原式=22(2)x x x +-÷24482x x x x -++- =22(2)x x x +-·()222x x -+=()122x x +. 当-1时,原式=12. 21.解不等式组()3151124,2x x x x -<+-≥-⎧⎪⎨⎪⎩,①②并指出它的所有的非负整数. 答案:解:解不等式①,得x>-2,解不等式②,得x ≤73, 该不等式的解集为-2<x ≤73. 它的非负整数解为x=0,1,2.22.(湖北黄冈)如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,DH ⊥AB 于点H ,连接OH ,求证:∠DHO=∠DCO.答案:证明:∵四边形ABCD 是菱形,∴OD=OB ,∠COD=90°.∵DH ⊥AB ,∴OH=12BD=OB , ∴∠OHB=∠OBH.又∵AB ∥CD ,∴∠OBH=∠ODC.在Rt △COD 中,∠ODC+∠DCO=90°.在Rt △DHB 中,∠DHO+∠OHB=90°,∴∠DHO=∠DCO.23.在某“三华李”种植基地有A,B两个品种的树苗出售,已知A种树苗比B 种树苗每株贵2元,买1株A种树苗和2株B种树苗共需20元.(1)问A,B两种树苗每株分别是多少元;(2)为扩大种植,某农户准备购买A,B两种树苗共360株,且A种树苗数量不少于B种数量的一半,请求出费用最省的购买方案.答案:解:(1)设A种树苗每株x元,B种树苗每株y元,根据题意得2220x yx y-==⎨+⎧⎩,,解得86.xy==⎧⎨⎩,答:A种树苗每株8元,B种树苗每株6元.(2)设购买A种树苗a株,则购买B种树苗(360-a)株,由题意得a≥12(360-a),解得a≥120.设总的购买费用为y,则y=8a+6(360-a)=2a+2 160,y随a的增大而增大.∵a≥120,∴当a=120,y取得最小值,最小值为y=2×120+2 160=2 400,故最省的购买方案为购买A种树苗120株,B种树苗240株.24.(江苏南京)小丽驾车从甲地到乙地,设她出发第x min时的速度为y km/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系.(1)小丽驾车的最高速度是 km/h;(2)当20≤x≤30时,求y与x之间的函数表达式,并求出小丽出发第22 min 时的速度;(3)如果汽车每行驶100 km耗油10 L,那么小丽驾车从甲地到乙地共耗油多少升?答案:解:(1)60(2)设y=kx+b ,由图可知,函数图象经过点(20,60),(30,24), ∴20603024k b k b ⎨+=+=⎧⎩,,解得 3.6132k b =-=⎧⎨⎩,, y 与x 之间的函数表达式为y=-3.6x+132,当x=22时,y=-3.6×22+132=52.8.故出发第22 min 时的速度为52.8 km/min.(3)OA 段的平均速度为0212+=6(km/h ), AB 段的平均速度为12260+=36(km/h ), CD 段的平均速度为60224+=42(km/h ), DE 段的平均速度为24248+=36(km/h ), FG 段的平均速度为0248+=24(km/h ), 行驶总路程为160(6×5+36×5+60×10+42×10+36×5+48×10+24×10)=33.5(km),小丽驾车从甲地到乙地共耗油33.5×10100=3.35(L).25.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.(1)求证:EB=GD;(2)判断EB与GD的位置关系,并说明理由;(3)若AB=2,,求EB的长.答案:解:(1)∵∠BAE=∠BAD+∠DAE,∠DAG=∠GAE+∠DAE,且∠BAD=∠GAE=90°,∴∠BAE=∠DAG.在△BAE和△DAG中,AB ADBAE DAGAE AG=∠=∠=⎧⎪⎨⎪⎩,,,∴△BAE≌△DAG,∴EB=GD.(2)EB⊥GD,如图,设GD与AE相交于点O,则∠EOH=∠AOG.∵△BAE≌△DAG,∴∠BEA=∠DGA,∴∠EHO=∠GAO=90°,∴EB⊥GD.(3)如图,连接AC,BD交于点P,∵AB=AD=2,由勾股定理得,∴,∴.由正方形的性质可知,∠DPG=90°,∴。
青岛版【2014年新版】八年级数学下册期末复习检测题(三,无答案)

青岛版八年级数学下册2013---2014学年期末检测三数 学 试 题注意事项:1.答卷请直接写在答题纸上,在试题上答题无效.务必将答题纸密封线内的项目填写清楚.2.本试题共4页,满分120分.考试时间120分钟.一、选择题(在下列各小题中只有一个正确答案,请将正确答案的字母代号填入答题纸的相应位置,每小题3分,共36分。
) 1、把不等式组2010x x -≥⎧⎨+<⎩的解在数轴上表示出来,正确的是( )2、下列关于矩形的说法中正确的是( )A .对角线相等的四边形是矩形B .对角线互相平分的四边形是矩形C .矩形的对角线互相垂直且平行D .矩形的对角线相等且互相平分3、下列各式一定是二次根式的是( )7-32m 21a +a b4、直角三角形的斜边比一直角边长2 cm ,另一直角边长为6 cm ,则它的斜边长(A )4 cm (B )8 cm (C )10 cm (D )12 cm 5、由图中左侧三角形仅经过一次平移、旋转或轴对称变换,不能得到的图形是( )-------------------------------------------------------------------------------------密-----------------------------封-------------------------线-----------------------------年级----------------- 班------------------ 姓名------------------- 考号-----------------6、如图1-1,菱形ABCD 中,∠B =60°,AB =2,E 、F 分别是BC 、CD 的中点,连接AE 、EF 、AF ,则△AEF 的周长为( ) A . 32 B . 33 C . 34 D . 37、若不等式组9514xx a-⎧>⎪⎨⎪<⎩的解集是x<1,则( )A .a<1B .a=1C .a>1D .a ≥1 8、能使等式22xxx x =--成立的x 的取值范围是( ) A. 2x ≠ B. 0x ≥ C. X>2 D. 2x ≥9、如图在矩形ABCD 中,1=AB ,3=AD ,AF 平分DAB ∠,过C 点作BD CE ⊥于E ,延长AF 、EC 交于点H ,下列结论中:①FH AF =;②BF BO =;③CH CA =;④ED BE 3=,正确的 ( )A .②③B .③④C .①②④D .②③④ 10、如图所示的计算程序中,y 与x 之间的函数关系所对应的图象应为( )11、已知函数y kx b =+的图象如图,则2y kx b =+的图象可能是【 】12、 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( )x Oy x -2 - 4 A D C B O 4 2 y O 2 - 4 y x O 4 - 2 y x 取相反数 ×2 +4输入x输出y(A ) 25 (B ) 12.5 (C ) 9 (D ) 8.5二、填空题:13、如图,三个边长均为2的正方形重叠在一起,O 1、O 2是其中两个正方形的中心,则阴影部分的面积是 .14、已知()222x x -=-,则x 的取值范围是 。
八年级下册数学期末检测试卷(青岛版)

八年级下册数学期末检测试卷(青岛版) 青岛版八年级下学期数学期末试题五一、选择题1、下列计算正确的是()A、(-)2=2B、=abC、1÷=D、=5-42、下列结论正确的是()(A)有两个锐角相等的两个直角三角形全等(B)一条斜边对应相等的两个直角三角形全等;(C)顶角和底边对应相等的两个等腰三角形全等;(D)两个等边三角形全等.3、下列说法错误的是()A、任意一个命题都有逆命题B、定理“全等三角形的对应角相等”有逆定理C、正方形都相似是真命题D、“画平行线”不是命题4、如图下列条件不能判定l1∥l2的是()A、∠2+∠1=1800B、∠3=∠2C、∠4=∠5D、∠3+∠4=18005、已知30°A.B.C.D.6、甲乙两同学在n次数学测试中平均分相等,但他们的方差不相等。
能正确评价他们的学习情况的是()A、因为他们的平均分相等,所以他们水平一样B、虽然平均分一样,单方差较大的学习潜力大,学习态度踏实C、虽然平均分一样,单方差小的学习成绩稳定D、平均分相等,方差不相等,说明学习水平不一样,方差小的同学,学习成绩不稳定,忽高忽低7、如图所示,将直角三角形ABC绕顶点A顺时针旋转600后,得到直角三角形AB′C′,且C′为BC的中点,则C′D:DB′=()A、1:2B、1:2C、1:D、1:38、如图,点O为小亮家的位置,他家门前有一条东西走向的公路,水塔A位于他家北偏东600的500米处,那么水塔所在的位置到公路的距离是()A.250米B、250C、150D、2509、如图△ABC中,AD垂直BC于点D,BE垂直AC于点E,AD与BE相交于点F,若BF=AC,那么∠ABC的大小是()A、400B、450C、500D、60010、如图,在△ABC中,D、E、F分别在AB、AC、BC上,DE∥BC,EF∥AB,且AD:AB=1:2,S四边形BFED:S△ABC=()A、1:2B、1:3C、4:9D、5:9二、填空题11、已知△ABC≌△ADE,∠B与∠D是对应角,那么AC与是对应边,∠BAC与是对应角.12、如图,已知AB=BE,BC=BD,∠1=∠2,那么图中13、已知:D、E分别是△ABC边AB、AC上的点,DE∥BC,AE=6,AD =3,AB=5,则AC=________。
青岛版八年级下册数学期末测试卷及含答案(全优)

青岛版八年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、关于x的一元一次不等式+2≤的解为()A.x≤B.x≥C.x≤D.x≥2、下列计算正确的是()A. B. C. D.3、下列y关于x的函数中,是正比例函数的为()A.y=x 2B.y=C.y=D.y=4、一次函数y=kx+b的图象经过(m,1)、(-1,m),其中m>1,则k、b ( )A.k>0且b<0B.k>0且b>0C.k<0且b<0D.k<0且b>05、下列二次根式中能与合并的二次根式的是()A. B. C. D.6、在同一直角坐标系中,函数y=ax2+b与y=ax+b(a,b都不为0)的图象的相对位置可以是( )A. B. C. D.7、下列各组数据中能作为直角三角形的三边长的是()A.1,1,B.6,8,11C.3,4,5D.1,3,8、下列图形中,是中心对称图形但不是轴对称图形的是()A. B. C. D.9、下列图案中是中心对称图形但不是轴对称图形的是()A. B. C.D.10、不等式组的解集在数轴上表示正确的是()A. B. C. D.11、如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PMN的面积;③△PAB的周长;④∠APB的大小;⑤直线MN,AB之间的距离.其中会随点P的移动而不改变的是()A.①②③B.①②⑤C.②③④D.②④⑤12、如图,点、、、、都在方格子的格点上,若是由绕点按顺时针方向旋转得到的,则旋转的角度为( )A.60°B.135°C.45°D.90°13、如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD 剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为()A.150°B.135°C.120°D.108°14、不等式组的解集是()A. x>4B.﹣2<x<0C.﹣2<x<4D.无解15、若二次根式有意义,则X的取值范围为()A.x≠1B.x≥1C.x<lD.全体实数二、填空题(共10题,共计30分)16、一个三角形的三边分别是、1、,这个三角形的面积是________.17、如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP 绕点A顺时针旋转后与△ACP1重合,如果AP=5,那么线段PP1的长等于________.18、已知:如图,四边形ABCD中,AB=BC=1,CD= ,AD=1,且∠B=90°.则四边形ABCD的面积为________.(结果保留根号)19、一次函数的图象不经过第________象限.20、如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值________.21、如图,在Rt△ABC中,∠ACB=90°,∠A=α,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的大小为________.22、点M是直线y=2x+3上的动点,过点M作MN⊥x轴于点N,当点M位于第二象限时,在y轴上有一点P,使△MNP为等腰直角三角形,则点P的坐标为________ .23、如图,一次函数y=ax+b的图象经过A(2,0)、B(0,﹣1)两点,则关于x的不等式ax+b<0的解集是________.24、如图,在直角坐标系中,的圆心A的坐标为,半径为1,点P 为直线上的动点,过点P作的切线,切点为Q,则切线长PQ 的最小值是________.25、如图,正方形ABCD的面积为2 cm2,对角线交于点O1,以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为________cm2.三、解答题(共5题,共计25分)26、计算①3 ﹣| |②.27、商店以7元/件的进价购入某种文具1 000件,按10元/件的售价销售了500件.现对剩下的这种文具降价销售,如果要保证总利润不低于2 000元,那么剩下的文具最低定价是多少元?28、嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1, R2,R3,其行经位置如图与表所示:路径编号图例行径位置第一条路径R1A→C→D→B第二条路径R2A→E→D→F→B第三条路径R3A→G→B已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.29、在△ABC中,若AC=15,BC=13,AB边上的高CD=12,求△ABC的周长.30、解不等式组,并将它的解集表示在如图所示的数轴上.参考答案一、单选题(共15题,共计45分)1、D2、D3、C4、D5、C7、C8、B9、C10、A11、B12、D13、B14、C15、B二、填空题(共10题,共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。
青岛版八年级下册数学期末测试卷及含答案(完整版)
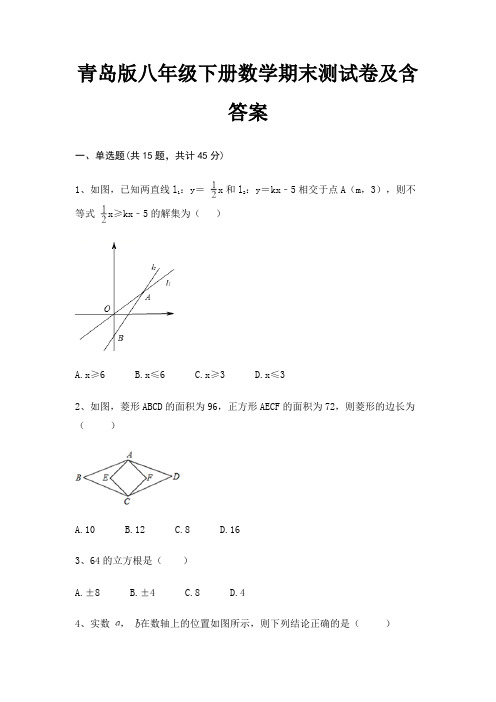
青岛版八年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图,已知两直线l1:y=x和l2:y=kx﹣5相交于点A(m,3),则不等式x≥kx﹣5的解集为()A.x≥6B.x≤6C.x≥3D.x≤32、如图,菱形ABCD的面积为96,正方形AECF的面积为72,则菱形的边长为()A.10B.12C.8D.163、64的立方根是()A.±8B.±4C.8D.44、实数,在数轴上的位置如图所示,则下列结论正确的是()A. B. C. D.5、如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么菱形ABCD周长是( )A.4B.8C.12D.166、某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往青岛,这列货车可挂两种不同规格的货厢50节.已知甲种货物35吨和乙种货物15吨可装满一节型货厢,甲种货物25吨和乙种货物35吨可装满一节型货厢,按此要求安排两种货厢的节数,有几种运输方案()A.1种B.2种C.3种D.4种7、如图,等腰直角三角形ABC的直角边AB的长为6cm,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点H,则图中△AHC′的面积等于()A.12﹣6B.14﹣6C.18﹣6D.18+68、下列说法中,错误的是()A.有一条对角线平分一个内角的平行四边形是菱形B.对角线互相垂直且平分的四边形是菱形C.一条对角线平分另一条对角线的四边形是平行四边形D.三角形的一条中位线与第三边上的中线互相平分9、若a>b,则不等式的解集为()A.x≤bB.x<aC.b≤x<aD.无解10、如图,在矩形ABCD中,F是BC中点,E是AD上一点,且∠ECD=30º,∠BEC=90º,EF=4cm,则矩形的面积为( )cm2.A.16B.C.D.3211、如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为()A. B.2 C.2 D.12、不等式组的解集在数轴上表示正确的是A. B.C.D.13、已知四边形ABCD是平行四边形,若要使它成为正方形,则应增加的条件是()A.AC⊥BDB.AC=BDC.AC=BD且AC⊥BDD.AC平分∠BAD14、如图所示,平移后得到,已知,,则()A. B. C. D.15、8的立方根是()A. 4B.2C.±2D.-2二、填空题(共10题,共计30分)16、若实数a、b满足,则=________.17、如图,矩形ABCD边AD沿折痕AE折叠,使点D落在BC上的点F处,已知AD=10,AB=6,则FC的长是________.18、将函数y=x2﹣x﹣2的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的图形是函数y=|x2﹣x﹣2|的图象,已知过点D(0,4)的直线y=kx+4恰好与y=|x2﹣x﹣2|的图象只有三个交点,则k的值为________.19、对于实数a,b,我们定义符号max{a,b},其意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如:max{4,﹣2}=4,max{3,3}=3,若y关于x的函数关系式为:y=max{x+3,﹣x+1},则该函数y的最小值是________.20、如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为________米(精确到0.1 ).21、如图,将矩形OABC置于一平面直角坐标系中,顶点A,C分别位于x轴,y 轴的正半轴上,点B的坐标为(5,6),双曲线y=(k≠0)在第一象限中的图象经过BC的中点D,与AB交于点E,P为y轴正半轴上一动点,把△OAP沿直线AP翻折,使点O落在点F处,连接FE,若FE∥x轴,则点P的坐标为________.22、如图,是一块钜形的场地,长=101米,宽=52米,从A、B两处入口的中路宽都为1米,两小路汇合处路口宽为2米,其余部分种植草坪面积为________米223、如图,在边长为8的菱形ABCD中,∠BAD=45°,BE⊥AD于点E,以B为圆心,BE为半径画弧,分别交AB、CB于点F、G,则图中阴影部分的面积为________(结果保留π)24、丁丁参加了一次智力竞赛,共回答了30道题,题目的评分标准是这样的:答对一题加5分,一题答错或不答倒扣1分.如果在这次竞赛中丁丁的得分要超过100分,那么他至少要答对________题.25、如图,∠A=15°,∠C=90°,DE垂直平分AB交AC于E,若BC=4cm,则AC=________cm.三、解答题(共5题,共计25分)26、计算:+ ﹣+3 ×.27、(1)计算:;(2)已知x=+1,y=﹣1,求代数式x2﹣y2的值.28、物理学中的自由落体公式:S= gt2, g是重力加速度,它的值约为10米/秒2,若物体降落的高度S=125米,那么降落的时间是多少秒?29、如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(≈1.414,精确到1米)30、如图,在△ABC中AC=BC,D,E,F分别是AB,AC,BC的中点,连接DE,DF.求证:四边形DFCE是菱形.参考答案一、单选题(共15题,共计45分)1、B2、A3、D4、D5、D6、C7、C8、C9、A10、C11、B12、A13、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、29、30、。
【完整版】青岛版八年级下册数学期末测试卷

青岛版八年级下册数学期末测试卷一、单选题(共15题,共计45分)1、若式子有意义,则x的取值范围为()A.x≤2B.x≤2且x≠1C.x≥2D.x≥12、不等式组的所有整数解是( )A.-1,0B.-2,-1C.0,1D.-2,-1,03、如图是一只鱼,将图案平移后得到的是()A. B. C. D.4、已知P1(x1, y1),P2(x2, y2)是一次函数y=﹣x+2图象上的两点,下列判断中,正确的是()A.y1>y2B.y1<y2C.当x1<x2时,y1<y2D.当x1<x2时,y1>y25、若一次函数的图象经过,两点,则的值为()A. B. C. D.6、在实数,π,,3.5,,0,3.02002,中,无理数共有()A.4个B.5个C.6个D.7个7、下列各式计算错误的是( )A. B. C.D.8、下列函数是y关于x的二次函数的是()A. B. C. D.9、八年级某班级部分同学去植树,若每人平均植树7课,还剩9棵,若每人平均植树9棵,则有1位同学植树的棵数不到8棵.若设同学人数为x人,植树的棵数为(7x+9)棵,下列各项能准确地求出同学人数与种植的树木的数量的是()A.7x+9≤8+9(x﹣1)B.7x+9≥9(x﹣1)C.D.10、下列图形中,既是轴对称图形又是中心对称图形的是()A. B. C. D.11、如果a=(-99)0,b=(-0.1)-1, c=(-)-2,那么a、b.c 三数的大小关系为()A.a>c>bB.c>a>bC.a>b>cD.c>b>a12、如图,将△ABC向右平移得到△DEF,已知A,D两点的距离为1,CE=2,则BF的长为()A.5B.4C.3D.213、如图所示,数轴上点A所表示的数为,则的值是( )A. B. C. D.14、在计算器上按键显示的结果是()A.3B.-3C.-1D.115、实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是()A.a﹣c>b﹣cB.a+c<b+cC.ac>bcD.二、填空题(共10题,共计30分)16、如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为________.17、已知+=y+4,则y x的值为________ .18、如果0<a<1,那么a,1和的大小关系(用“<”连接)是________.19、点(-2,3)关于原点对称的点的坐标是________20、已知一个矩形的对角线的长为4,它们的夹角是60°,则这个矩形的较短的边长为________,面积为 ________.21、如图,直线l是四边形ABCD的对称轴,请再添加一个条件:________,使四边形ABCD成为菱形(不再标注其它字母)。
八年级数学下学期期末考试试题 青岛版-青岛版初中八年级全册数学试题

某某省新泰市龙廷镇中心学校2014-2015学年八年级数学下学期期末考试试题注意事项:1.本试卷共7页,满分100分,考试时间120分钟。
2.答题前,请考生仔细阅读答题纸上的注意事项,并务必按照相关要求作答。
3.考试结束后,监考人员只收回答题纸。
一、选择题: 在下列各小题中,均给出四个答案,其中有且只有一个正确答案. 1.计算16结果是 A .4B .4-C .4±D .2±2.下列二次根式中,最简二次根式是A .31B .3.0C .3a 2+D .2ab3.如图,四边形ABCD 的对角线互相平分,要使它成为矩形, 那么需要添加的条件是 A .AB CD =B .AD BC =C .AB BC =D .AC BD = 4.下列各式中,计算不正确的是 A .5353⨯=⨯B .20812=+C .1065322=⨯D .255105=5.不等式组⎩⎨⎧->-≥-71212x x 的解集在数轴上表示正确的是6.如图,在平面直角坐标系中,将△ABC 绕点定P 旋转180º,得到△A 1B 1C 1,则A 1,B 1,C 1的坐标分别为 A.A 1(-4,-6),B 1(-3,-3),C 1(-5,-1) B.A 1(-6,-4),B 1(-3,-3),C 1(-5,-1) C.A 1(-4,-6),B 1(-3,-3),C 1(-1,-5) D.A 1(-6,-4),B 1(-3,-3),C 1(-1,-5) 7.能使等式33=--x xx x 成立的条件是 A .x ≥0 B.-3<x ≤0C .x >3 D .x >3或x <08.将一次函数12y x =的图像向上平移2个单位,平移后,若y >0,则x 的取值X 围是 A. x >4 B. x >-4 C. x >2 D. x >-29.如图,过A 点的一次函数图象与正比例函数2y x =的图象相交于点B ,则这个一次函数的解析式是 A .23y x =+ B .3y x =-C .23y x =- D .3y x =-+10.如图,在平行四边形ABCD 中,AB =4,∠BAD =平分线与BC 的延长线相交于点E ,与DC 交于点F ,且点F 为边DC 的中点,DG ⊥AE ,垂足为G ,若DG =1,则AE 的长为 A .23B .43C .4 D .811.直线1y x =+与2y x a =-+的交点在第一象限,则a 的取值可以是 A .-1B .0C . 1D .212.如图,函数2y x =和4y ax =+的图象相交于点A (m ,3),则不等式2x ≥4ax + 的解集为A .x ≥32B .x ≤3C.x ≤32D .x ≥313.如图,矩形ABCD 中,E 是AD 的中点,将△ABE 沿直线BE 折叠后得到△GBE ,延长BG 交CD 于点F ,若AB =6,BC =46,则FD 的长为A .2B .4C .6D .2314.实数a 在数轴上的位置如图所示,则22(4)(11)-+-a a 化简结果为A .7B .-7C .2a -15D .无法确定15.如图,正方形ABCD 中,AB =3,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连接AG ,CF .下列结论: ①点G 是BC 的中点;②FG =FC ;③S △FGC =910.其中正确的是 A .①②B .①③C .②③D .①②③二、填空题(本大题共5小题,只要求填写最后结果)954312612÷⨯的结果为_________.P (-2,a )是正比例函数y=-2x 图象上的一点,那么P 点关于y 轴对称点的坐标为_________.18.如图,在矩形ABCD 中,M ,N 分别是边AD ,BC 的中点,E 、F 分别是线段BM 、CMAB =8,AD =12,则四边形ENFM 的周长为_________.19.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y (米)与时间t (秒)之间的函数关系如图,则这次越野跑的全程为_________米.第9题图 第10题图 第12题图第13题图 第14题图 第15题图 a 1050第2题图0,122x a x x +≥⎧⎨->-⎩20.若不等式组有解,则a 的取值X围是_________.三、解答题(本大题共7小题,解答应写出必要的文字说明、证明过程或推演步骤)21.解不等式组12432362273(1)x x x x x ---⎧-≥⎪⎨⎪-≤-⎩,并把它的解集在数轴上表示出来.22.已知水银体温计的读数y (℃)与水银柱的长度x (cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.水银柱有长度x (cm) … 体温计的读数y (℃)…42.0(1)求y 关于x 的函数关系式(不需要写出函数的定义域);(2)用该体温计测体温时,水银柱的长度为6.2cm ,求此时体温计的读数.23.如图,四边形ABCD 的对角线AC 、BD 交于点O ,若O 是AC 的中点,AE=CF ,DF ∥BE .(1)求证:△BOE ≌△DOF ;(2)若OD =12AC ,则四边形ABCD 是什么特殊四边形?请证明你的结论.24. 如图所示,x 轴所在直线是一条东西走向的河,A (-2,3)、B (4,5)两个村庄位于河的北岸,现准备在河上修建一净水站P ,并利用管道为两个村庄供水(单位:千米).(1)欲使所修管道最短,应该把净水站P 修在什么位置,作出正确图形(用尺规作图),求出P 点坐标并及PB 所在直线解析式;(2)若管道每米费用需要200元,求修管道的最低费用.25. 如图,点E 、F 分别在正方形ABCD 的边CD 与BC 上,45EAF ∠=. (1)求证:EF =DE +BF ;(2)作AP ⊥EF 于点P ,若AD =10,求AP 的长.26.x 元,其中x >100.(1)根据题意,填写下表(单位:元):(2)当x 取何值时,小红在甲、乙两商场的实际花费相同?(3)当小红在同一商场累计购物超过100元时,在哪家商场的实际花费少?27.如图,△ABC 是直角三角形,且∠ABC=90°,四边形BCDE 是平行四边形,E 为AC的中点,BD 平分∠ABC ,点F 在AB 上,且BF =BC .求证:(1)DF=AE;(2)DF⊥AC.2014-2015学年度下学期期末教学质量监测 八年级数学试题参考答案一、选择题: 每小题3分,满分45分二、填空题:每小题3分,满分15分1617.(2,4) 18.20 19.2200 20.a >-1 三、解答题:本大题满分60分 21.(本题满分5分) 原式可化为2(12)(43)3(2)4---≥-⎧⎨≥-⎩x x x x ………………………………2分解得:﹣4≤x≤1.………………………………………………………………3分 数轴略……………………………………………………………………………5分 22.(本题满分8分)解:(1)设一次函数解析式为:y=kx+b , 由题意得:⎩⎨⎧+=+=b k bk 2.80.402.40.35,…………………………………………………3分解得:⎩⎨⎧==75.2925.1b k∴一次函数的解析式是:y=1.25x+29.75;………………………………………5分 (2)当x=6.2时,y=1.25×6.2+29.75=37.5. ℃. ………………………………………………8分 23.(本题满分9分) (1)证明:∵DF ∥BE , ∴∠FDO=∠EBO ,∠DFO=∠BEO ,∵O 为AC 的中点,即OA=OC ,AE=CF ,………………………………………………………………2分∴OA ﹣AE=OC ﹣CF ,即OE=OF , 在△BOE 和△DOF 中,FDO=EBO DFO=BEO OE=OF ⎧⎪⎨⎪⎩∠∠∠∠, ∴△BOE ≌△DOF……………………………………………………………………………………………………5分 (2)若OD=12AC ,则四边形ABCD 是矩形,……………………………………………………………7分 理由为:证明:∵△BOE ≌△DOF , ∴OB=OD ,∴OA=OB=OC=OD ,即BD=AC ,∴四边形ABCD 为矩形.……………………………………………………………9分 24.(本题满分9分)解:(1)作点A 关于x 轴的对称A ’,连接A ’B 交x 轴于点P ,则点P 就是所求…3分 设PB 所在直线解析式为=+y kx b , 因为PB 过点A ’(-2,-3),B(4,5),所以可得2345-+=-⎧⎨+=⎩k b k b ,解得4313⎧=⎪⎪⎨⎪=-⎪⎩k b所以PB 所在直线解析式为4133=-y x ……………………………………6分 (2)根据题意,A ’B 即为所修管道长,分别过A ’和B 作平行于x 轴和y 轴的直线交于点B ’,在直角三角形A ’B ’B 中,A ’B ’=6,B ’B=8,所以A ’B=10,所以最少费用为200×10×1000=2000000元…………………………………9分 25.(本题满分9分)(1)证明:将△ABC 绕以点A 为旋转中心顺时针旋转90,此时点D 位于CB 的延长线上D ’处………………………………………1分 根据旋转的性质,DE=BD ’,∠=∠'B DAE D A 又因为45EAF ∠=,90DAE BAC EAF ∠+∠+∠=所以45DAE BAF ∠+∠=……………………………………………………………………………2分 所以∠+∠=’45oD AB BAF …………………………………………………………3分即∠=’45D AF所以’45D AF EAF ∠=∠=在△EAF 与△D ’AF 中,另有AF=AF ,AE=AD ’所以△EAF ≌△D ’AF ………………………………………………………………5分 所以EF=D ’F=B D ’ +BF=DE+BF ……………………………………………………6分 (2)因为AP ⊥EF ,由(1)知,AP 与AB 同为全等三角形对应边上的高, 所以AP=AB=10…………………………………………………………………9分 26.(本题满分10分)解:(1)在甲商场:271, 0.9x+10: ……………………………………………2分 在乙商场:278, 0.95x+2.5. ……………………………………………4分 (2)根据题意,有0.9x+10=0.95x+2.5,解得x=150,∴当x=150时,小红在甲、乙两商场的实际花费相同;…………………7分 (3)由0.9x+10<0.95x+2.5,解得x>150, 由0.9x+10>0.95x+2.5,解得x<150.∴当小红累计购物超过150元时,在甲商场的实际花费少.当小红累计购物超过100元而不到150元时,在乙商场的实际花费少.…10分 27.(本题满分10分)证明:(1)延长DE 交AB 于点G ,连接AD. ∵ED ∥BC ,E 是AC 中点,∠ABC=90°∴AG=BG,DG⊥AB∴AD=BD………………………………………………………………………2分∵BD平分∠ABC∴∠ABC=45°,∠BAD=45°,∠BDG=∠ADG=45°…………………4分∵四边形BCDE是平行四边形.∴ED=BC,又∵BF=BC,∴BF=DE. ……………………………………………………………6分∴△AED≌△DFB∴AE=BE……………………………………………………………7分(2)∵△AED≌△DFB∴∠AED=∠DFB,∴∠DFG=∠DEC,∵∠DFG与∠FDG互余,…………………………………………………9分∴∠DEC与∠FDG互余,∴DF⊥AC. ………………………………………………………………10分。
青岛版数学八年级下册期末复习综合检测试题

期末复习综合检测试题(满分120分;时间:90分钟)一、选择题(本题共计9 小题,每题3 分,共计27分,)1. 下列说法中,错误的是()A.一组对边平行且相等的四边形是平行四边形B.两条对角线互相垂直且平分的四边形是菱形C.四个角都相等的四边形是矩形D.邻边相等的菱形是正方形2. 如图,在▱ABCD中,已知AC=5cm,若△ACD的周长为13cm,则▱ABCD的周长为()A.14cmB.16cmC.18cmD.20cm3. 下列说法错误的是()A.1是(−1)2的算术平方根B.0的平方根是0C.−27的立方根是−3D.√169=±134. 平行四边形、矩形、菱形、正方形共有的性质是()A.对角线相等B.对角线互相垂直C.对角线互相平分D.对角形互相垂直平分5. 三个数,−π,−3.14,−√3的大小关系正确的是()A.−π<−3.14<−√3B.−3.14<−π<−√3C.−3.14<−√3<−πD.−√3<−π<−3.146. 如图,点O是矩形ABCD的对角线AC的中点,M是CD边的中点.若AB=8,OM= 3,则线段OB的长为()A.5B.6C.8D.107. 下列运算错误的是( )A.√−0.1253=−0.5B.√−183+√183=0C.√4=±2D.√(−1)2+√(−1)33=0 8. 不等式6x +1≤2x −3的解集在数轴上表示正确的是( )A. B.C. D.9. 如图,F 是菱形ABCD 边CD 上的点,过点A 作AE ⊥CD ,若DE =EF ,∠CBF =9∘,则∠EAF 的度数为( )A.21∘B.24∘C.27∘D.30∘二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )10. 不等式−3x +6>0的解集为________.11. 对角线互相________的平行四边形是菱形.12. 已知对角线长为2的正方形的面积为________.13. 为了举行班级晚会,孔明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍作奖品,已知乒乓球每个1.5元,球拍每个22元,如果购买金额不超过200元,且买的球拍尽可能多,那么孔明应该买________个球拍.14. 不等式3x+2x−1>2的解是________.15. 如图,四边形ABCD 是矩形,对角线AC 、BD 相交于点O ,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是________.16. 已知不等式组{9x −a ≥08x −b ≤0,x 的整数解是1、2、3,则最大整数解b 和最小整数a 的差为________.17. 如图,BD 是△ABC 的角平分线,DE // BC ,交AB 于点E ,DF // AB ,交BC 于点F ,当△ABC 满足条件________时,四边形BEDF 是正方形.18. 如图,点D 、E 分别为△ABC 的边AB 、AC 的中点,同时,点F 在DE 上,且∠AFB =90∘,已知AB =5,BC =8,那么EF 的长为________.三、 解答题 (本题共计 7 小题 ,共计66分 , )19. √123÷√213×√125.20. 把下列数填入相应的集合中.√9,√43,5π3,0.6˙,−34,3. (1)整数集合( );(2)分数集合( );(3)有理数集合( );(4)无理数集合( );(5)实数集合( ).21. 小亮家里装修房子,爸爸想考一考他,爸爸拿出一块四条边都是80cm 的瓷砖(瓷砖的平面图如图所示),要求他检验一下四个角是否为直角,能用的工具只有10cm 的一段直尺,如果你是小亮,你认为能完成吗?22. 阅读下列内容:设a ,b ,c 是一个三角形的三条边的长,且a 是最长边,我们可以利用a ,b ,c 三条边长度之间的关系来判断这个三角形的形状:①若a 2=b 2+c 2,则该三角形是直角三角形;②若a 2>b 2+c 2,则该三角形是钝角三角形;③若a 2<b 2+c 2,则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,62=36<42+52,故由③可知该三角形是锐角三角形,请解答以下问题:(1)若一个三角形的三边长分别是7,8,9,则该三角形是________三角形.(2)若一个三角形的三边长分别是5,12,x ,且这个三角形是直角三角形,求x 的值.23. 勾股定理是一条古老的数学定理,它有很多种证明方法.(1)请你根据图1填空;勾股定理成立的条件是________三角形,结论是________(三边关系)(2)以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;24. 小明家有一块紧靠河边的四边形菜地,如图所示,他想知道该地的大小.于是他和同学小亮进行了测量,得到下列数据:∠B=90∘,AB=4米,BC=3米,CD=13米,AD=12米.你能帮助小明求出该菜地的面积吗?相信你自己,祝你成功!25. 如图,图象L1反映了某公司产品的销售收入与销售量之间的关系,图象L2反映了某公司产品的销售成本与销售量之间的关系,则:(1)当销售量为2吨时,销售收入为多少元?销售成本呢?此时公司是赢利还是亏损?(2)当销售量等于多少时该公司收入等于销售成本?(3)当销售量在什么范围内时,该公司亏损?(4)要使公司赢利,你对公司有何建议?。
2014青岛版初二数学下册期末综合练习题

2014 青岛版初二数学下册期末综合练习题1 、( 2013四川凉山州)如图,菱形中,,,则以为边长的正方形的周长为 A.14 B.15 C.16 D.17 2 、( 2013湖北宜昌)如图,在矩形 ABCD中, AB< BC, AC, BD 订交于点O,则图中等腰三角形的个数是() A.8B .6C.4D.23、( 2013 ? 聊城, 5 , 3 分)以下命题中的真命题是() A .三个角相等的四边形是矩形B.对角线相互垂直且相等的四边形是正方形C.按序连接矩形四边中点获得的四边形是菱形D .正五边形既是轴对称图形又是中心对称图形 4 、( 2013贵州省六盘水)在平面中,下列命题为真命题的是() A .四个角相等的四边形是矩形 B .对角线垂直的四边形是菱形 C .对角线相等的四边形是矩形 D.四边相等的四边形是正方形 5. 已知一次函数跟着的增大而减小,且,则在直角坐标系内它的大体图象是()6、若一次函数的象交于正半,且的随的的增大而减小,() A.B.C.D. 7、在如所示的平面直角坐系内,画在透明胶片上的? ABCD,点A的坐是(0 ,2).将胶片平移,使点A落在点A′( 5,?1),此平移可以是()A.先向右平移5个位,再向下平移1个位B.先向右平移5个位,再向下平移 3个位C.先向右平移4个位,再向下平移1个位D.先向右平移4个位,再向下平移3个位8、( 2013广广州,8,4分)若代数式有意,数 x的取范是() A.B.C.D.且 9 、(2013州安)以下各数中, 3.14159 ,,⋯⋯,-π,,,无理数的个数有()A.1个B. 2个 C . 3个D.4个 10 、( 2013?坊)如,ABCD 是角相互垂直的四形,且OB=OD,你增添一个适当的条件 ____________ ,使ABCD 成菱形.(只需添加一个即可)11、如,直一次函数州)如图所于E, AF⊥CD 的图象,则示,菱形ABCD于F,∠B=60°,. 12、(2013 贵的边长为4,且 AE⊥BC,则菱形的面积为.13、如图,将ABC沿直线AB向右平移后到达BDE 的位置,若CAB= 50°,ABC=100°,则CBE=.14.已知菱形的周长为 40 cm,一条对角线长为 16 cm,则这个菱形的面积是 .15、如图6,在中,,,将绕点沿逆时针方向旋转得到,则线段的长是;的度数是. 16(2013鞍山)如图,D是△ABC 内一点, BD⊥CD ,AD=6,BD=4 ,CD=3,E、 F、G 、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是.17 ( 2013?宁夏)若不等式组有解,则 a的取值范围是.18 (2013 白银,26,10分)如图,在△ABC 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点 F ,且AF=BD ,连接BF.(1)BD与CD有什么数目关系,并说明理由;(2)当△ABC 满足什么条件时,四边形AFBD 是矩形?并说明理由. 19 ( 2013?鞍山)如图,在正方形ABCD 中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?20 (2013?湘西州)如图, Rt△ABC中,∠C=90°, AD 平分∠CAB ,DE⊥AB 于E,若AC=6,BC=8,CD=3.( 1 )求DE 的长;(2)求△ADB 的面积.21(2013?南京中考)小丽驾车从甲地到乙地,设她出发第 x min时的速度为 y km/h,图中的折线表示她在整个驾车过程中 y与 x 之间的函数关系 .( 1 )小丽驾车的最高速度是 km/h. ( 2 )当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22 min时的速度.(3)如果汽车每行驶100 km 耗油10 L,那么小丽驾车从甲地到乙地共耗油多少升?22、如图,点是正方形对角线的延长线上任意一点,以线段为边作一个正方形,线段和订交于点.(1)求证:;(2)判断与的地点关系,并说明原由;(3)若,求的长.23、已知:如图①,在△ABC 中,AB=AC,∠BAC=90°,D 、 E分别是AB、AC边的中点.将△ABC 绕点 A顺时针旋转α角( 0°<α<180°),得到△AB’C’(如图②). (1)研究DB’与 EC’的数量关系,并给与证明;(2)DB’∥EA时,试求旋转角α 的度数 .24、解不等式组,并指出它的所有的非负整数解.25 、( 2013?茂名)在信宜市某“三华李”种植基地有A、B两个品种的树苗销售,已知A种比 B种每株多2元,买1株A种树苗和2株B 种树苗共需20元.(1)问A、B两种树苗每株分别是多少元?( 2)为扩大种植,某农户准备购买A、 B两种树苗共360株,且A种树苗数量不少于B种数量的一半,请求出费用最省的购买方案.。
八年级数学下学期期末质量检测 青岛版

年级下学期期末质量检测数 学 试 题一、选择题(在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号填入答题纸的相应位置)1.两个边数相同的多边形相似应具备的条件是 ( ) A .对应角相等B .对应边相等C .对应角相等,对应边相等D .对应角相等,对应边成比例2.下列运算错误的是 ( ) A .2×3=6 B .21=22C .22+23=25D .221()—=1-23.如图,在钝角△ABC 中,∠A =30°,则tan A 的值是( ) A .3 B .23C .33D . 无法确定4.下列统计量中不能反应数据波动情况的是 ( ) A .极差B .偏差C .方差D .标准差5.如图在△ABC ,P 为AB 上一点,连结CP ,以下各条件中不能判定△ACP ∽△ABC 的是 A .∠ACP =∠BB .∠APC =∠ACBC . AC AP =ABACD . AC AB =CP BC6.如图,在△ABC 和△AˊBˊC ˊ中, AB=AˊB ˊ, ∠B =∠B ˊ, 补充条件后仍不一定能保证△ABC ≌△AˊBˊCˊ, 则补充的这个条件是 ( ) A .BC=BˊCˊ B .∠A =∠A ˊC .AC =AˊCˊD .∠C =∠C ˊ(第3题图)ACBABC (第6题图)A’B’C’(第5题图)7.下列各组二次根式是同类二次根式的一组是( ) A .93和B .313和C .318和D .2412和8.在等腰△ABC 和等腰△DEF 中,∠A 与∠D 是顶角,下列判断①∠A=∠D 时,两三角形相似;②∠A =∠E 时,两三角形相似;③EFDE BCAB =时,两三角形相似; ④∠B =∠E 时,两三角形相似 其中正确的个数是 ( ) A .1个B .2个C .3个D .4个9.如图,等边ABC △的边长为3,P 为BC 上一点,且1BP =,D 为AC 上一点,若60APD ∠=°,则CD 的长为 ( )A .32B .23C .12 D .3410.下列代数式中,x 能取一切实数的是( ) A .42+xB . x1C .x 3D .1—x11.在△ABC 中,已知∠C =90°,sinB=53,则tan A 的值是 ( ) A .43B .34C .53D .5412. 如图,在△ABC 中,DE 垂直平分AB ,FG 垂直平分AC ,BC =13cm ,则△AEG 的周长为 ( )A .6.5cmB .13cmC .26cmD .15二、填空题(请将答案直接填写在答题纸的相应位置)13.命题“等腰三角形的两底角相等”的逆命题是 . 14.如图,ABC △与AEF △中,AB AE BC EF B E AB ==∠=∠,,,交EF 于 点D .给出下列结论:①AFC C ∠=∠;②DF CF =;③ADE FDB △∽△; ④BFD CAF ∠=∠.其中正确的结论是 (填写所有正确结论的序号).ADC PB (第9题图)60°15.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m .如果在坡度为0.75的山坡上种树,也要求株距为4m ,那么相邻两树间的坡面距离为 . 16.在二次根式x 31-中字母x 的取值范围为 . 17.已知x=23+,y=23-,则x 2+2xy+y 2的值是 . 18.一组数据5,8,x ,10,4的平均数是2x ,则x 的值为 .19.一个五边形各边的长分别是1,2,3,4,5,和它相似的另一个五边形的周长为21,则后一个五边形的最长边的长为 .三、解答题(本大题共7个小题,满分63分.请按要求将必要的解答过程呈现在答题纸的相应位置.) 20.化简下列各题(1) 3845cos 260sin 3+-οο(2) 213412÷⋅(3)20)21()23(3632918-+-++--AED B F C(第14题)(第15题)21.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连结DC.请你找出图2中的全等三角形,并给予证明.(说明:结论中不得含有未标识的字母)22.为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):编号一二三四五六七八九十类型甲种电子钟 1 -3 -4 4 2 -2 2 -1 -1 2乙种电子钟 4 -3 -1 2 -2 1 -2 2 -2 1(1)计算甲、乙两种电子钟走时误差的平均数;(2)计算甲、乙两种电子钟走时误差的方差;(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?23.如图,M 为线段AB 的中点,AE 与BD 交于点C ,∠DME =∠A =∠B ,且DM 交AC于F ,ME 交BC 于G .写出图中的所有相似三角形,并选择一对加以证明.24.如图在△ABC 中,∠ACB =90o,BC =3,AC =4,AB 的垂直平分线DE (垂足为D )交 BC 的延长线于点E ,求线段CE 的长.A BM FGDEC 第23题图25.阅读下题及证明过程:已知:如图, D 是△ABC 中BC 边上一点, E 是AD 上一点,EB=EC ,∠ABE =∠ACE ,求证:∠BAE =∠CAE . 证明:在△AEB 和△AEC 中, ∵EB =EC ,∠ABE =∠ACE ,AE =AE , ∴△AEB ≌△AEC …………………第一步 ∴∠BAE=∠CAE …………………第二步问上面证明过程是否正确?若正确,请写出每一步推理的依据; 若不正确,请指出错在哪一步,并写出你认为正确的证明过程.26.如图,在航线l 的两侧分别有观测点A 和B ,点A 到航线l 的距离为2km ,点B 位于点A 北偏东60°方向且与A 相距10km 处.现有一艘轮船从位于点B 南偏西76°方向的C 处,正沿该航线自西向东航行,5分钟后该轮船行至点A 的正北方向的D 处. (1)求观测点B 到航线l 的距离;(2)求该轮船航行的速度(结果精确到0.1千米/小时).(参考数据:73.13≈,97.076sin ≈ο,24.076cos ≈ο,01.476tan ≈ο)ACABD E 第25题图八年级数学(A)参考答案及评分标准一、 选择题(每小题3分,满分36分) DDCBD CBCBA BB 二、 填空题(每小题3分,满分21分)13.如果一个三角形有两个角相等,那么这个三角形是等腰三角形 14.①③④ 15.5m 16.x ≤1317.12 18.3 19.7 三、解答题(本题满分63分) 20.(本题三个小题,满分15分)(1)52……………………………………………………………………………………5分(2)4 2 ………………………………………………………………………………10分(3)解:原式(11|1=++.………………………………12分111=.………………………………………………13分1…………………………………………………………………………15分 21.(本题满分7分)解:图2中ABE ACD △≌△ ………………………………1分 证明:∵△A BC 与AED △均为等腰直角三角形AB AC ∴=,AE AD =,90BAC EAD ∠=∠=o ………………………………3分BAC CAE EAD CAE ∴∠+∠=∠+∠即BAE CAD ∠=∠………………………………………………………………5分 ABE ACD ∴△≌△………………………………………………………………7分22.(本题满分8分).解:(1)甲种电子钟走时误差的平均数是:1(1344222112)010--++-+--+= 乙种电子钟走时误差的平均数是:1(4312212221)010--+-+-+-+=∴两种电子钟走时误差的平均数都是0秒………………………………4分 (2)1012=甲S [])(660101)02()03()01(2222s =⨯=-++--+-K 1012=乙S [])(8.448101)01()03()04(2222s =⨯=-++--+-K∴甲乙两种电子钟走时误差的方差分别是6s 2和4.8s 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
青岛版八年级数学下册2013---2014学年期末检测五
数 学 试 题
注意事项:
1.答卷请直接写在答题纸上,在试题上答题无效.务必将答题纸密封线内的项目填写清楚.
2.本试题共4页,满分120分.考试时间120分钟.
填空题
:
11___________, 12___________, 13___________,
14____________,
15___________, 16___________,17___________,
18____________.
一. 选择题(每小题3分,共30分)
1.函数
x 取值范围是( )
A .x ≥3
B .x>3
C .x ≤3
D .x<3
4.若一次函数y=(3-k)x-k 的图象经过第二、三、四象限,则k 的取值范围是( )
A .k>3
B .0<k ≤3
C .0≤k<3
D .0<k<3 5.一元一次方程0=-b ax 的解3=x ,函数b ax y -=的图象与x 轴的交点坐标为( )
A.(3 ,0)
B.(-3 ,0)
C.(a ,0)
D.(-b ,0) 6.如图,矩形ABCD 中,AB =3,AD =1,AB 在数轴上,若以点A 为圆心,对角线AC 的长为半径作弧交数轴的正半轴于M ,则点M 的坐标为( ♣ )
A.(2,0) B.(,0) C.(,0) D .(,0)
7.如图,平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且AE=
BE,则∠BCD的度数是()
A.30° B.60°或120° C.60° D.120°
8.在一个标准大气压下,能反映水在均匀加热过程中,水的温度(T)随
加热时间(t)变化的函数图象大致是()
9.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、
AD的中点,
AB=6cm,BC=8cm,则ΔAEF的周长是()
A.14cm
B. 8cm
C. 9cm
D.
10cm
10.如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两
车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),
图中的折线表示y与x之间的函数关系.下列说法中正确的是()
A.B点表示此时快车到达乙地 B.B-C-D段表示慢车先加
速后减速最后到达甲地
C.快车的速度为h
km/
3
2
166 D.慢车的速度为125km/h
二、填空题(每小题4分,共32分)
11.直线y=x+3与y轴的交点坐标是()
12.已知直线y=(n-2)x-3与直线y=-3x+5平行,则n=()
13. 最简二次根式1
2+
b与17
--
a b是同类二次根式,则b-a=()
14. 已知y-2与x成正比例,且x=2时,y=4,则y与x的函数关系式是
()
10题
6题
17题
16题
7题9题
A. B. C. D.
15. 若,0836122=-++-b a a 则22b a + 的平方根是 ( )
16. 如图,四边形ABCD 是正方形,AE 垂直于BE ,且AE=3,BE=4,阴影部分的面积是 ( )
17. 如图,菱形ABCD 的对角线AC 、BD 相交于点O ,且AC =8,BD =6,过点O 作OH 丄AB , 垂足为H ,则点O 到边AB 的距离OH= ( ) 18. 金都超市利用“六、一”开展促销活动,店前公告如下:凡是一次性购买3件某种服装,每件仅售价80元,如超过3件,则其超过部分打8折,顾客所付款y (元)与所购买的件数x (x≥3)之间的函数关系式为y=( ) (x≥3).
三. 解答题(共88分)
19.计算:(10分)(1)224831
2123÷⎪⎪⎭
⎫
⎝⎛
+-(2)()
()
2013
2013
2
323-•+
20. (8分)先化简再求值,已知0
2--32)(=x ,求2
12312
+-÷
⎪⎭⎫ ⎝
⎛+-
x x x 的值.
21. (8分)如图,平行四边形ABCD 中,AC 丄BC ,E 为AB 的中点.若CE =2,求CD 的长?
22. (10分)如图,把长方形纸片ABCD 沿EF 折叠后.点D 与点B 重合,点C 落在点C ′的位置上.若∠1=60°,AE=1.(1)求∠2、∠3的度数; (2)求长方形纸片ABCD 的面积S .
23.(10分)如图所示的是函数y 1=kx+b 与y 2=mx+n 的图象,
(1)方程 ⎩⎨
⎧+=+=n
mx y b
kx y 的解是:__________。
(2)y 1中变量y 1随x 的增大而_________。
(3)在平面直角坐标系中,将点P (3,4)向下平移1个单位,恰好在正比例函数的图象上,求这个正比例函数的关系式.
24.(10分)甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y (m )与挖掘时间x (h )之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)乙队开挖到30m 时,用了_____ h .开挖到6h 时甲队比乙队多挖了_______m ;
(2)请你求出:
① 甲队在0≤x ≤6的时段内,y 与x 之间的函数关系式;
② 乙队在2≤x ≤6的时段内,y 与x 之间的函数关系式.
(3)当x为何值时,甲、乙两队在施工过程中所挖河渠的长度相等?
25.(10分)如图,L1直线y=2x与L2直线y=kx+3在同一平面直角坐标
系内交于点P.
(1)写出不等式2x>kx+3的解集:__________
(2)设直线L2与x轴交于点A,求△OAP的面积.
26. (10分)同学们喜爱手机上网,某网络公司看中了这种商机,推出
了两种手机上网的计费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月租费20元外,再以每分钟0.06元的价格按上网时间计费.假设某客户月上网时间为X分钟,上网费用为y元.
(1)分别写出该客户按A,B两种方式的上网费y(元)与每月上网时间X(分钟)函数关系式。
(2)在图的坐标系中画出这两个函数的图象;
(3)如何选择计费方式能使该客户上网费用更合算?
27.(12分)我校九年级学生共400人,学校决定组织该年级学生到三中
训练,并安排10位教师同行.经学校与汽车出租公司协商,有两种型号的客车可供选择,其座位(不含司机座位)与租金如下表,学校规定每
大巴中巴
座位数(个/辆)45 30
租金(元/辆)800 500
(1)为保证每人都有座位,显然座位总数不能少于410.设租大巴x 辆,根据要求,请你设计出可行的租车方案.
(2)设大巴、中巴的租金共y元,写出y与x之间的函数关系式.在上述租车方案中,哪种租车方案的租金最少?最少租金为多少元?。
