2019年安徽省江淮十校高三上学期第一次联考数学(理)试题
江淮十校理数试卷

江淮十校2019届高三第二次联考数学(理科)2018. 11命题单位:宿城一中命审人:黄力江廖晓三王占魁考生注意:1. 本试卷分笫1卷(选择题)和笫11卷(非选择题)两部分.满分150分,考试时间120分钟.2. 考生作答时,请将答案答在答题卡上.必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效第1卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一个选项是符合题目要求的.1. 设命题p:3xE R ,x 2 >2', 则•p是A .3xER ,x 飞2兀C.VxER,x 2 >2'()B.:l x E R ,x 2 =2'D.Vx E R,x 飞2名2.已知集合A ={x臣至2} , B = { x I l og 辽<0},则A nB =A .(0,1) B .(1,4]C.[4,+oo)D.03. 我国古代名著《九章算术》卷六中有这样一段话:“今有金箭,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”大致意思是:”有一根金锤,长5尺,头部l尺,重4斤,尾部l尺,重2斤,问每一尺各重几斤?"根据巳知条件,若金锤从头到尾,每一尺的重械构成等差数列,则中间一尺重拭为( )A.2.5斤B.3斤C.3.5斤D.4斤4.已知函数J(x )= {2父-i -2,x�l ,且f(a)=-2, 则f(4-a) =-lo g 2 (x + l) , x > I () 41-- .. A C B .-2D.O--+ --+ --+ 5.已知向量a,b满足lal=2,bl=l, 且向最a,b的夹角为卫,若入a+b与b垂直,则实数入的值为()3A.-1 互3cB .-—D.1数学(理科)试题第1页(共4页)。
安徽省江淮十校2019届高三上学期第一次联考数学(文)试题+Word版含解析

安徽省江淮十校2019届高三上学期第一次联考数学(文)试题:选择题。
1. 已知集合、:,集合- < .0,1,3,,则土Lh-: 'A. 1,、B.C. 0,1,'D. 1,【答案】A【解析】【分析】由题意,求得集合V- <-.:-,:■<;.,利用集合交集的运算,即可得到答案.【详解】由题意,集合:e ■- ■:■::' I 2 - <集合:m \:<,Sj,所以f门「二.故选:A.【点睛】本题主要考查了集合交集的运算,其中解答中熟记集合的交集的运算方法是解答的关键,着重考查了推理与运算能力,属于基础题2. 若复数i-;.i为虚数单位是纯虚数,则实数a的值为A. 0B.C.D. 1【答案】C【解析】【分析】a卜i直接由复数代数形式的除法运算化简,然后由实部等于0且虚部不等于0列式求解实数aI十1的值.a 卜i (a + i)(1 -1) a + 1 I (1 - a)i a i I 1 - a【详解】由题意,复数为纯虚数,1 十1 〔1 十-1)2 2 2-0,解得:卞- I,故选:C.【点睛】本题主要考查了复数的四则运算和复数的基本概念,其中解答中熟练应用复数的四则运算是解答的关键,着重考查了推理与运算能力,属于基础题3. 为了解户籍、性另恻生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为200的调查样本,其中城镇户籍与农村户籍各100人;男性120人,女性80人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图如图所示,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是100%80%60%40%20%0%城诡户籍农村户籍刃性女性A. 是否倾向选择生育二胎与户籍有关B. 是否倾向选择生育二胎与性别有关C. 倾向选择生育二胎的人群中,男性人数与女性人数相同D. 倾向选择不生育二胎的人群中,农村户籍人数少于城镇户籍人数【答案】C【解析】【分析】由题意,通过阅读理解、识图,将数据进行比对,通过计算可得出C选项错误.【详解】由比例图可知,是否倾向选择生育二胎与户籍、性别有关,倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数,倾向选择生育二胎的人员中,男性人数为人,女性人数为、人,男性人数与女性人数不相同,故C错误,故选:C.【点睛】本题主要考查了条形图的实际应用,其中解答中认真审题,正确理解条形图所表达的含义是解答的关键,着重考查了阅读理解能力、识图能力,属于基础题.4. 若公比为2的等比数列的前n项和为,且,9, 成等差数列,则A. B. C. D. “ - |【答案】B【解析】【分析】运用等比数列的通项公式和等差数列的中项性质,解方程可得首项,再由等比数列的求和公式,计算可得所求和.【详解】由题意,公比q为2的等比数列的前n项和为,且,9, 成等差数列,可得、宀' ■, I ■ | ,解得:-,川」订「I 、I ■则10I -q 1 -2故选:B.【点睛】本题主要考查了等比数列的通项公式和求和公式的运用,等差数列中项性质,其中解答中熟记等比数列的通项公式和前n项和公式,准确运算是解答的关键,着重考查了推理与运算能力,属于基础题•5. 已知函数是定义在R上的偶函数,且在V.上单调递增,则A. ■ - ■ i - :- i 2""B. i j" .- :■■:_.-C. :/ '■ :■ - I :-D. :< ■ I' - ■■【答案】C【解析】【分析】根据题意,由函数的奇偶性可得•-,祇'*;:一代,又由2 " - I-_: > . ■- J- ',结合函数的单调性分析可得答案.【详解】根据题意,函数是定义在R上的偶函数,则^ “ "丁丨;有J I- _: / -又由在上单调递增,则有'辽'■- \ --:故选:C.【点睛】本题主要考查了函数的奇偶性与单调性的综合应用,其中解答中合理利用函数的基本性质是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题(y > - 36. 已知实数x, y满足 J 」叮…的最大值是[3x-4y- 12>0A. 2B. 3C. 4D. 5【答案】D【解析】【分析】【点睛】本题主要考查的是古典概型及其概率计算公式 •,属于基础题•解题时要准确理解题画出约束条件的可行域,利用目标函数的几何意义,确定目标函数的最优解,即可求解最值, 得到答案. 【详解】由题意,画出约束条件的可行域,如图所示: 由,解得..•:、八■经过可行域的卜-二I 时,纵截距•丄十;.最小,此时z 最大, 所以-J -■1: -"-解是解答的关键,着重考查了数形结合思想,及推理与计算能力,属于基础题.7.用24个棱长为1的小正方体组成 S 的长方体,将共顶点的某三个面涂成红色, 然后将长方体拆散开,搅拌均匀后从中任取一个小正方体,则它的涂成红色的面数为1的概率为13 11 7 1 A.B.C. D.2424244【答案】B【解析】【分析】合理分类讨论思想、得出涂成红色的面数为 1的基本事件的总数,再由古典概型概率计算公式直接求解,即可得到答案.【详解】由题意得:有三个面涂成红色的小正方体仅有一个, 有两个面涂成红色的小正方体仅有;-I 「个, 仅有一个面涂成红色的小正方体有 I 「•十.「: + :\ - ■: - I 个,还剩下';-1 1' ■■-: 1 :;:个小正方体它的六个面都没有涂色,1 1'它的涂成红色的面数为 1的概率为:=.24故选:B .意,先要判断该概率模型是不是古典概型,正确找出随机事件 A 包含的基本事件的个数和试验中基本事件的总数,令古典概型及其概率的计算公式求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.【答案】D【解析】【分析】模拟执模拟执行程序,依次写出每次循环得到的s,i的值,当•时不满足条件,退出循环,输出的值为300,得到答案.【详解】行程序,可得..- :;,:- T;, - ..,满足条件;,满足条件,「- . 1 ,. -】,满足条件,,,不满足条件,退出循环,输出的值为300.故选:D.【点睛】本题主要考查了程序框图和算法问题,其中解答中依次写出每次循环得到的s , i的值是解题的关键,属于基础题,着重考查了推理与运算能力9•将函数:H 込"十d图象上所有点向左平移个单位,再将横坐标伸长为原来的2倍纵坐6标不变,得到的图象,则下列叙述正确的是2兀5兀A. :是厂化亍的对称轴B.〔二邛是:;-•::;-的对称中心」L 一【【解析】 【分析】可采用逆向法,直接利用三角函数关系式的恒等变变换和平移变换及诱导公式的应用求出结 果. 【详解】由题意,可采用逆向法,为得到:函数 -V ■. -忙图象,只需将:-ir.'.,的横坐标缩短为原来的 二,即:2兀7U兀兀再将图象向右平移 个单位,即: .. ,所以:im I ,.66 3 3丄匚2兀7?r故: , 故选:C.【点睛】本题主要考查了三角函数关系式的恒等变变换和平移变换的应用,三角函数诱导公 式的应用,其中解答中熟记三角函数的图象变换和合理应用诱导公式化简是解答的关键,着 重考查了运算能力和转化能力,属于基础题型.10. 一个几何体的三视图如图所示,则这个几何体的体积为A. I SO TLB. 144TTC. 2OO TED. 1667E【答案】A 【解析】 【分析】画出几何体的直观图,结合三视图的数据,禾U 用几何体的体积公式,即可求解,得到答案【答案】CI TL 2兀【详解】由题意可知几何体是一个底面半径和高都是 6的圆柱,挖去一个半圆锥的几何体如俯视图图:几何体的体积为:21 1 22 3故选:A.\ ■【点睛】本题考查了几何体的三视图及组合体的表面积的计算,在由三视图还原为空间几何体的实际形状时,要根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线•求解以三视图为载体的空间几何体的表面积与体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解•x y ,C: 的左、右焦点,点a2 b2M是的中点,且「二,讣“」,则双曲线的离心率为【解析】【分析】运用双曲线的定义和为直角三角形,则|:_二「,由离心率公式,即可求解双曲线的离心率,得到答案。
安徽省江淮名校2019届高三12月联考数学(理科)试题(精品Word版,含答案解析)

数学(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U R =,集合(){}30A x x x =-?,{}2B x y x =-,则()U A B Çð等于( ) A. ()0,2 B. ()0,3 C. Æ D. (]0,2【答案】D 【解析】 【分析】解不等式得集合A ,进而可得U A ð,求解函数定义域可得集合B ,利用交集求解即可. 【详解】因为集合(){}()300,3U A x x x =-<=ð,(],2B =-?,所以()(]0,2U A B ?ð,故选D.【点睛】本题主要考查了集合的补集及交集的运算,属于基础题.2.复数z 满足(32)43i z i -=+(i 为虚数单位),则复数z 在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】A 【解析】 由题意得,43(43)(32)11732(32)(32)1313i i i iz i i i +++===+--+,则复数z 在复平面内对应的点位于第一象限,故选A. 3.已知向量()1,3a =,(),1b m =,若//a b ,则m = ( ) A. 13-B. 13C. 3-D. 3 【答案】B 【解析】 【分析】利用两个向量平行的坐标表示列出方程求解即可.【详解】向量()()1,3,,1a b m ==,若//a b ,则113m ?,解得1m =.【点睛】本题主要考查了向量平行的坐标表示,属于基础题. 4.已知函数()1112xf x e =-+,则()f x 是( ) A. 奇函数,且在R 上是增函数 B. 偶函数,且在()0,+?上是增函数 C. 奇函数,且在R 上是减函数 D. 偶函数,且在()0,+?上是减函数【答案】C 【解析】 【分析】先判断定义域是否关于原点对称,进而利用()()0f x f x -+=可得函数为奇函数,再由指数函数的单调性可判断函数的单调性.【详解】定义域为R ,关于原点对称,()1112x f x e --=-+ 112x x e e =-+,有()()0f x f x -+=,所以()f x 是奇函数, 函数()1112xf x e =-+,显然是减函数. 故选C.【点睛】本题主要考查了函数的奇偶性和单调性的判断,属于基础题.5.已知一个四棱锥的三视图如图所示,则该四棱锥侧面的4个三角形面积的最大值为( )A. 2B. 3C. 5D. 23【答案】A 【解析】 【分析】还原几何体得四棱锥P ABCD -,其中PA ^面ABCD ,分别计算各侧面的面积即可得解.【详解】还原三视图可得几何体如图所示,四棱锥P ABCD -,其中PA ^面ABCD ,11151,?2,2222PADPABPCDSPA AD S PA AB S PD CD ======. PCB 中有6,2,22PC BC PB =222BC PC PB +=,所以90PCB ??.所以132PCBSPC BC ==. 所以面积最大值是PAB D 的面积,等于2.【点睛】本题主要考查了由三视图还原几何体,并计算几何体的侧面积,需要一定的空间想象力,属于中档题. 6.已知等比数列{}n a 的前n 项和为n S ,1352a a +=且2454a a +=,则55Sa ( ) A. 256 B. 255 C. 16 D. 31 【答案】D 【解析】 【分析】由等比数列的通项公式,利用基本量运算可得通项公式,进而可得前n 项和,从而可得nnS a ,令5n =求解即可.【详解】由1352a a +=,可得21152a a q +=; 由31154a q a q +=. 两式作比可得:可得12q =,12a =, 所以212n n a -骣琪=琪桫,2142n n S -骣琪=-琪桫,21n n n S a =-,所以5552131Sa =-=.【点睛】本题主要考查了等比数列的通项公式及前n 项公式,属于公式运用的题目,属于基础题. 7.把函数()sin cos f x x x =-的图象上每个点的横坐标扩大到原来的2倍,再向左平移3p,得到函数()g x 的图象,则函数()g x 的一个单调递增区间为( ) A. 175,66p p轾--犏犏臌 B. 57,66p p轾-犏犏臌 C. 24,33p p轾-犏犏臌 D. 719,66p p轾犏犏臌【答案】B 【解析】 【分析】利用三角函数的图象变换可得函数()2sin 212x g x x p骣琪=-琪桫,再由22212x k p p p -?22k pp ?,k Z Î,可解得单调增区间,即可得解. 【详解】函数()sin cos f x x x =-=2sin 4x x p骣琪-琪桫的图象上每个点的横坐标扩大到原来的2倍,可得24x y x p骣琪=-琪桫的图象,再向左平移3p ,得到函数()12sin 234g x x p p 轾骣犏琪+-琪犏桫臌2sin 212x x p 骣琪=-琪桫的图象. 由22212x k p pp -?22k p p ?,k Z Î,得574466k xk p pp p -#+,k Z Î. 当0k =时,函数()g x 的一个单调递增区间57,66p p轾-犏犏臌, 故选B.【点睛】本题主要考查了三角函数的图象变换及三角函数的单调性,注意三角函数的平移变换,平移是针对自变量“x”而言的,所以需要将x 的系数提出,属于中档题.8.若实数x ,y 满足约束条件2027030x y x y y ì--?ïï+-?íï-?ïî,则1x z y +=的最小值为( )A.23 B. 1 C. 2 D. 145【解析】 【分析】作出不等式的可行域,1x z y+=的几何意义是可行域内的点与点()1,0-连线的斜率的倒数,由斜率的最大值即可得解.【详解】作出不等式组构成的区域,1x z y+=的几何意义是可行域内的点与点()1,0D -连线的斜率的倒数,由图象知AD 的斜率最大,由2703x y y ì+-=ïí=ïî得13x y ì=ïí=ïî,所以()1,3A ,此时11233z +==. 故选A.【点睛】常见的非线性目标函数问题,利用其几何意义求解:z Ax By C =++的几何意义为可行域内的点到直线A 0x By C ++=22A B +()()22b z x a y =-+-的几何意义为可行域内的点到点()a,b 的距离的平方。
江淮十校2019届高三第一次联考

江淮十校2019 届高三第一次联考化学第I卷(选择题共48 分)一、选择题(本大题共16 小题,每题 3 分,共48 分。
在每题列出的四个选项中,只有一项为哪一项最切合题目要求的。
)1.“故近朱者赤,近墨者黑”出自晋朝傅玄的《傅鹑觚集·太子少傅箴》,这里的“朱”指的是朱砂,古代常用的一种红色颜料,也是先人“炼丹”的原料,有毒,它的主要成分是()A. HgSB.Cu 2OC.Fe2O3D.Cu2.化学与人类生产、生活、科研亲密有关,以下有关说法错误的选项是()A.“血液透析”利用的是渗析的原理B.“ 84”消毒液(主要成分NaClO )不可以够与“洁厕灵”(主要成分HCl) 混用C.高纯度的二氧化硅宽泛用于制作光导纤维D.熬制中药后的“箅渣取液”操作实质上相当于实验室里的萃取3.设 N A为阿伏加德罗常数的值,以下说法正确的选项是()A. 6.0 g 二氧化硅含有的 Si-O 键数为 0.4N AB. 1 mol Na 2O2与足量的水反响转移电子数量为2N AC.将 1 mol Cl 2通入水中, HClO 、 Cl -、 ClO -粒子数之和为 2N AD. 0.1 mol/L 的 HNO 3溶液中含有的H+ 数量为 0. 1N A4.《本草蒙筌》有关明矾[KAl(SO4).l2H O] 的记录以下:“禁便泻,塞齿疼,洗脱肛涩肠,敷脓疮收22水。
”以下有关明矾的说法正确的选项是()A.明矾的水溶液呈中性,所以不可以够用于冲洗铁锈B. Na +、 NH 4+、 CO32-、MnO 4-可与明矾溶液大批共存C.“敷脓疮收水”是由于明矾可让疮水聚沉结痂D.向明矾水溶液中滴加过度的Ba(OH) 2溶液发生的反响:Al 3+ +4OH -= AlO 2- +2H 2O 5.以下实验操作、现象和结论均正确且存在因果关系的是()6.以下有关说法正确的选项是()A.工业上能够用钢制容器运输浓硫酸,由于钢制容器遇浓硫酸能够钝化B.实验室用排饱和食盐水法采集氯气,此种做法与勒夏特列原理没关C.工业上合成氨时需要加入催化剂,由于催化剂能够提升氨的产率D.实验室用氨气做喷泉实验,而C02 气体不论怎么改良也没法做喷泉实验7.味精的主要成分中含有W、X、Y、Z、T五种元素,它们的原子序数挨次递加,此中W 和T分别是短周期半径最小和最大的主族原子,X、Y、Z同周期相邻,且它们的最外层电子数量之和为15,则()以下说法错误的选项是A. W 、X 可形成工业上用途极为宽泛的化合物X2W4 , X2W4 分子中既含极性共价键又含非极性共价键B.Y 、Z 原子半径和单原子离子半径均为前者大于后者C.简单氢化物的熔沸点从低到高X<Y<ZD.W 、 Y 、 T 的单原子离子均能够损坏水的电离均衡8.以下实验中,所使用的装置(部分夹持装置略)、试剂和操作方法都正确的选项是()A.用装置①配制250 mL0.1 mol . L -1的 NaOH 溶液B.用装置②制备少许Fe( OH) 2固体C.用装置③考证乙烯的生成 D .用装置④制取少许乙酸乙酯9.金属的腐化与防备和生活亲密有关,以下有关说法正确的选项是()A.银金饰表面变黑属于电化学腐化B.图中氧气传感器测得氧气体积分数变小,说明三颈瓶中发生的必定只有吸氧腐化C.图中压强传感器测得压强变小,说明三颈瓶中发生的必定以吸氧腐化为主D.海里在轮船外面连结一块废铜块保护轮船的方法叫牺牲阳极的阴极保护法10.类比推理是学习化学的重要的思想方法,以下陈说I 及类比推理陈说Ⅱ均正确的选项是11.不一样温度下,反响2CH3 OH( g) = CH 3OCH 3(g)+H 2O(g) 的均衡常数以下:以下说法正确的选项是()A .其正反响的AH >0B.207℃时,密闭容器中进行的该反响总压不变不可以够作为该反响达到均衡的标记C.387℃时, 1L密闭容器中投入0.2 mol 的 CH3OH(g) ,均衡时转变率为 80%D.387℃时, 1L密闭容器中充入CH OH 0.1 mol、 CH OCH30.2 mol 和 H O 0.10 mol ,则反响将向正反332应方向进行12.吡喃酮的构造宽泛存在于天然产物之中,吡喃酮有两种构造,α一吡喃酮和γ一吡喃酮,如图:下列有关吡喃酮的说法正确的选项是()A.α一吡喃酮和γ一吡喃酮均不可以与NaOH 溶液反响B.γ一吡喃酮的全部碳原子不行能共面C.γ一吡喃酮与甲基吡喃酮互为同系物D.α -吡喃酮和γ一吡喃酮互为同分异构体;甲基吡喃酮属于酚类的同分异构体有 3 种13. 25℃时,用0.1 mol/L 的 HC1 溶液滴定10. 00 mL0.1 mol/L的NH3.H20溶液,其滴定曲线以下图。
安徽省江淮十校2020届高三上学期第一次联考理数考试试题(无答案)

江淮十校2020届高三第一次联考数学(理科) 2019.8命题单位:阜阳一中 命题人:孙晓林 杨敏 王小云审题人:肖璐洋注意事项:1. 答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合1,0A y y x x x ⎧⎫==+≠⎨⎬⎩⎭,集合{}240B x x =-≤,若A B P =I ,则集合P 的子集个数为A.2B.4C.8D.162.复数z 满足342z i ++=,则z z ⋅的最大值是A.7B.49C.9D.813.设a ,b ,c 为正数,则“a b c +>”是“222a b c +>”的A.充分不必要条件B.必要不充分条件C.充要条件 D 既不充分也不必要条件.4.已知向量a r ,b r 均为非零向量,()2a b a -⊥r r r ,a b =r r,则a r ,b r 的夹角为A.6πB.3π C.23π D.56π 5.已知ln x π=,13y e-=,13log z π=,则A.x y z <<B.z x y <<C.z y x <<D.y z x <<6.勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.现在勒洛三角形中随机取一点,则此点取自正三角形外的概率为A.()23323ππ-- B.()323π- C.()323π+ D.()23323ππ-+7.如图,在正方体1111ABCD A B C D -中,F 是棱11A D 上的动点,下列说法正确的是A.对任意动点F ,在平面11ADD A 内不存在...与平面CBF 平行的直线B.对任意动点F ,在平面ABCD 内存在..与平面CBF 垂直的直线C.当点F 从1A 运动到1D 的过程中,FC 与平面ABCD 所成角变大..D.当点F 从1A 运动到1D 的过程中,点D 到平面CBF 的距离逐渐变小..8.某创业公司共有36名职工,为了了解该公司职工年龄构成情况,随机采访了9位代表,将数据制成茎叶图如图.若用样本估计总体,年龄在(),x s x s -+内的人数占公司总人数的百分比是(其中x 为平均数,s 为标准差,结果精确到1%)A.56%B.14%C.25%D.67%9.将余弦函数的图像向右平移2π个单位后,再保持图像上点的纵坐标不变,横坐标变为原来的一半,得到函数()f x 的图像,下列关于()f x 的叙述正确的是A.最大值为1,且关于3,04π⎛⎫⎪⎝⎭对称B.周期为π,关于直线2x π=对称C.在,68ππ⎛⎫-⎪⎝⎭上单调递增,且为奇函数 D.在0,4π⎛⎫⎪⎝⎭上单调递减,且为偶函数 10.对任意实数x ,恒有10xe ax --≥成立,关于x 的方程()ln 10x a x x ---=有两根为1x ,2x (12x x <),则下列结论正确的为A.122x x +=B.121x x ⋅=C.122x x =D.12xx e =11.已知双曲线2222:1x y C a b-=的两条渐近线分别为1l 与2l ,A 与B 为1l 上关于坐标原点对称的两点,M 为2l 上一点且AM BM k k e ⋅=,则双曲线离心率e 的值为A.B.12C.212.在四面体ABCD 中,若1AD DB AC CB ====,则当四面体ABCD 的体积最大时其外接球表面积为A.53πB.43πC.πD.2π二、填空题:本题共4小题,每小题5分,共20分13.已知实数x ,y 满足210020x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩,则目标函数2z x y =+的最小值为14.已知()()512x x a ++的展开式中各项系数和为2,则其展开式中含2x 项的系数是15.关于x 的方程sin 2cos 0x x a ++=在0,2π⎛⎫⎪⎝⎭内有解,则实数a 的取值范围是16.已知抛物线2:4C x y =的焦点为F ,过F 作直线l 交抛物线于A ,B 两点,且2AF FB λ=u u u r u u u r (λ为非零常数).以A 为切点作抛物线C 的切线交直线1y =-于M 点,则MF 的长度为 (结果用含λ式子表示).三、解答题:共70分。
2019届安徽省江淮六校高三上学期开学联考数学(理)试题(解析版)

2019届安徽省江淮六校高三上学期开学联考数学(理)试题一、单选题1.复数等于()A.B.C.D.【答案】C【解析】【分析】化简分式,分子、分母分别平方,再按照复数的除法运算法则化简可得结果.【详解】,故选:C【点睛】本题主要考查了复数代数形式的运算,是基础题.2.已知集合,则()A.B.C.D.【答案】C【解析】分析:先求出集合A,由此利用交集的定义能求出的值.详解:集合,,.故选:C.点睛:本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用. 3.函数的图象是()A.B.C.D.【答案】B【解析】【分析】由题意结合函数的性质排除错误选项即可确定函数的图象.【详解】由函数的解析式可知函数为偶函数,则函数图象关于y轴对称,选项AC错误;当时,,选项D错误;本题选择B选项.【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.4.已知两个单位向量和夹角为,则向量在向量方向上的投影为()A.B.C.D.【答案】D【解析】【分析】由题意首先求得的值,然后求解向量在向量方向上的投影即可.【详解】由题意可知:,则,,据此可得向量在向量方向上的投影为.本题选择D选项.【点睛】本题主要考查平面向量数量积的几何意义,数量积的运算法则及其应用等知识,意在考查学生的转化能力和计算求解能力.5.已知双曲线的虚轴长是实轴长的2倍,则双曲线的标准方程为()A.B.C.D.【答案】D【解析】【分析】由题意得到关于m的方程,解方程求得m的值即可确定双曲线方程.【详解】由题意可得:,则实轴长为:,虚轴长为,由题意有:,解得:,代入可得双曲线方程为.本题选择D选项.【点睛】本题主要考查双曲线方程的求解,意在考查学生的转化能力和计算求解能力.6.在中,,,,则角等于()A.或B.C.D.【答案】A【解析】【分析】由题意结合正弦定理求解角B的值即可.【详解】由正弦定理可得:,则角等于或.本题选择A选项.【点睛】本题主要考查正弦定理及其应用,特殊角的三角函数值等知识,意在考查学生的转化能力和计算求解能力.7.学校就如程序中的循环体,送走一届,又会招来一级。
2019届安徽省高三上学期第一次联考数学试卷(理科)Word版含解析
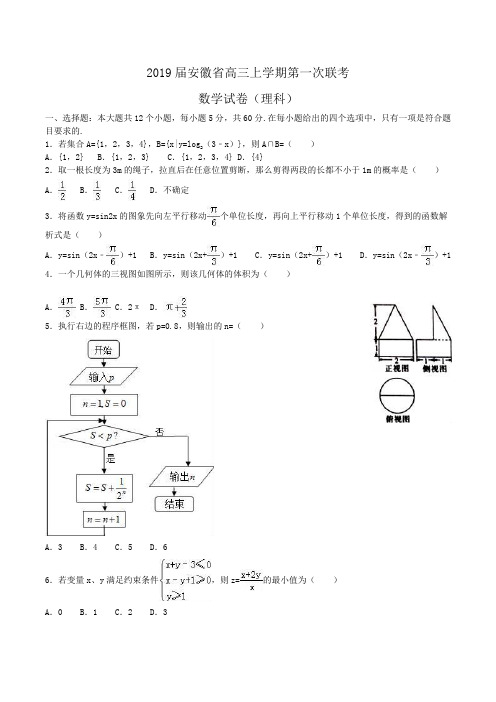
2019届安徽省高三上学期第一次联考数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={1,2,3,4},B={x|y=log(3﹣x)},则A∩B=()2A.{1,2} B.{1,2,3} C.{1,2,3,4} D.{4}2.取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1m的概率是()A.B.C.D.不确定3.将函数y=sin2x的图象先向左平行移动个单位长度,再向上平行移动1个单位长度,得到的函数解析式是()A.y=sin(2x﹣)+1 B.y=sin(2x+)+1 C.y=sin(2x+)+1 D.y=sin(2x﹣)+14.一个几何体的三视图如图所示,则该几何体的体积为()A. B. C.2πD.5.执行右边的程序框图,若p=0.8,则输出的n=()A.3 B.4 C.5 D.66.若变量x、y满足约束条件,则z=的最小值为()A.0 B.1 C.2 D.37.已知{an }为等差数列,a1+a2+a3=156,a2+a3+a4=147,{an}的前n项和为Sn,则使得Sn达到最大值的n是()A.19 B.20 C.21 D.228.设m、n是两条不同的直线α、β是两个不同的平面,有下列四个命题:①如果α∥β,m⊂α,那么m∥β;②如果m⊥α,β⊥α,那么m∥β;③如果m⊥n,m⊥α,n∥β,那么α⊥β;④如果m∥β,m⊂α,α∩β=n,那么m∥n其中正确的命题是()A.①② B.①③ C.①④ D.③④9.已知函数f(x)=是R上的增函数,则实数a的取值范围是()A.﹣1<a<1 B.﹣1<a≤1 C.D.10.设a>b>0,a+b=1,且x=()b,y=log ab,z=log a,则x、y、z的大小关系是()A.y<z<x B.z<y<x C.x<y<z D.y<x<z11.已知A、B是球O的球面上两点,且∠AOB=120°,C为球面上的动点,若三棱锥O﹣ABC体积的最大值为,则球O的表面积为()A.4πB.C.16π D.32π12.设函数f(x)、g(x)分别是定义在R上的奇函数和偶函数,且f(x)+g(x)=2x,若对x∈[1,2],不等式af(x)+g(2x)≥0恒成立,则实数a的取值范围是()A.[﹣1,+∞)B.C.D.二、填空题:本大题共4小题,每小题5分,共20分.13.经过圆x2+2x+y2=0的圆心C,且与直线x+y=0垂直的直线方程是.14.已知,则sin2x= .15.设函数f(x)=sin(wx+φ),其中|φ|<.若f(﹣)≤f(x)≤f()对任意x∈R恒成立,则正数w的最小值为,此时,φ= .16.已知,满足||=||=•=2,且(﹣)•(﹣)=0,则|2﹣|的最小值为.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.我国是世界上严重缺水的国家.某市政府为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3.5吨的人数,并说明理由;(3)若在该选取的100人的样本中,从月均用水量不低于3.5吨的居民中随机选取3人,求至少选到1名月均用水量不低于4吨的居民的概率.18.如图,在△ABC中,∠B=,AB=8,点D在边BC上,且CD=2,cos∠ADC=.(1)求sin∠BAD;(2)求BD,AC的长.19.如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,BC=,F为BE的中点.(1)若CE=2,求证:①DF∥平面ABC;②平面BDE⊥平面BCE;(2)若二面角E﹣AB﹣C为45°,求直线AE与平面BCE所成角.20.设数列{a n }的前n 项和为S n ,已知a 1=1,2S n =(n+1)a n ,n ∈N *.(1)求数列{a n }的通项公式;(2)令b n =,数列{b n }的前n 项和为T n ,试比较T n 与的大小.21.如图,已知直线l :y=x+4,圆O :x 2+y 2=3,直线m ∥l .(1)若直线m 与圆O 相交,求直线m 纵截距b 的取值范围;(2)设直线m 与圆O 相交于C 、D 两点,且A 、B 为直线l 上两点,如图所示,若四边形ABCD 是一个内角为60°的菱形,求直线m 纵截距b 的值.22.已知a >0,b ∈R ,函数f (x )=4ax 2﹣2bx ﹣a+b 的定义域为[0,1].(Ⅰ)当a=1时,函数f (x )在定义域内有两个不同的零点,求b 的取值范围;(Ⅱ)记f (x )的最大值为M ,证明:f (x )+M >0.2017-2018学年安徽省“江淮十校”高三(上)第一次联考数学试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(3﹣x)},则A∩B=()1.若集合A={1,2,3,4},B={x|y=log2A.{1,2} B.{1,2,3} C.{1,2,3,4} D.{4}【考点】交集及其运算.【分析】根据对数函数的定义求出集合B中元素的范围,再由交集的定义求出A∩B即可.【解答】解:∵A={1,2,3,4},B={x|y=log(3﹣x)}={x|x<3},2则A∩B={1,2},故选:A.2.取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1m的概率是()A.B.C.D.不确定【考点】几何概型;任意角的三角函数的定义.【分析】根据题意确定为几何概型中的长度类型,将长度为3m的绳子分成相等的三段,在中间一段任意位置剪断符合要求,从而找出中间1m处的两个界点,再求出其比值.【解答】解:记“两段的长都不小于1m”为事件A,则只能在中间1m的绳子上剪断,剪得两段的长都不小于1m,所以事件A发生的概率.故选B3.将函数y=sin2x的图象先向左平行移动个单位长度,再向上平行移动1个单位长度,得到的函数解析式是()A.y=sin(2x﹣)+1 B.y=sin(2x+)+1 C.y=sin(2x+)+1 D.y=sin(2x﹣)+1【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】第一次变换可得可得函数y=sin2(x+)的图象,第二次变换可得函数y=sin2(x+)+1的图象,从而得出结论.【解答】解:将函数y=sin2x的图象先向左平行移动个单位长度,可得函数y=sin2(x+)的图象,再向上平行移动1个单位长度,可得函数y=sin2(x+)+1=sin(2x+)+1 的图象,故选B.4.一个几何体的三视图如图所示,则该几何体的体积为()A. B. C.2πD.【考点】由三视图求面积、体积.【分析】由三视图可以看出,此几何体是一个上部为半圆锥、下部为圆柱的几何体,故可以分部分求出半圆锥与圆柱的体积再相加求出此简单组合体的体积.【解答】解:所求几何体为一个圆柱体和半圆锥体构成.其中半圆锥的高为2.其体积为=,圆柱的体积为π•12•1=π故此简单组合体的体积V=π+=.故选:A.5.执行右边的程序框图,若p=0.8,则输出的n=()A.3 B.4 C.5 D.6【考点】循环结构.【分析】根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用可知:该程序的作用是判断S=>0.8时,n+1的值.【解答】解:根据流程图所示的顺序,该程序的作用是判断S=>0.8时,n+1的值.当n=2时,当n=3时,,此时n+1=4.则输出的n=4故选B.6.若变量x、y满足约束条件,则z=的最小值为()A.0 B.1 C.2 D.3【考点】简单线性规划.【分析】先根据约束条件画出可行域,再利用目标函数的几何意义:平面区域内的一点与原点连线的斜率求最小值【解答】解:作出的可行域如图所示的阴影部分,由于z==1+2的几何意义是平面区域内的一点与原点连线的斜率的2倍加1,结合图形可知,直线OA的斜率最小,由可得A(2,1),此时z===2.故选:C.7.已知{an }为等差数列,a1+a2+a3=156,a2+a3+a4=147,{an}的前n项和为Sn,则使得Sn达到最大值的n是()A.19 B.20 C.21 D.22【考点】等差数列的前n项和.【分析】写出前n项和的函数解析式,再求此式的最值是最直观的思路,但注意n取正整数这一条件.【解答】解:设{an}的公差为d,由题意得:a 1+a2+a3=a1+a1+d+a1+2d=156,即a1+d=52,①a 2+a3+a4=a1+d+a1+2d+a1+3d=147,即a1+2d=49,②由①②联立得a1=55,d=﹣3,∴Sn=55n+×(﹣3)=﹣n2+n=﹣(n﹣)2+.∴观察选项,当n=19时,使得Sn达到最大值.故选:A.8.设m、n是两条不同的直线α、β是两个不同的平面,有下列四个命题:①如果α∥β,m⊂α,那么m∥β;②如果m⊥α,β⊥α,那么m∥β;③如果m⊥n,m⊥α,n∥β,那么α⊥β;④如果m∥β,m⊂α,α∩β=n,那么m∥n其中正确的命题是()A.①② B.①③ C.①④ D.③④【考点】命题的真假判断与应用.【分析】根据空间直线与直线,直线与平面的位置关系及几何特征,逐一分析四个命题的真假,可得答案.【解答】解:①如果α∥β,m⊂α,那么m∥β,故正确;②如果m⊥α,β⊥α,那么m∥β,或m⊂β,故错误;③如果m⊥n,m⊥α,n∥β,那么α,β关系不能确定,故错误;④如果m∥β,m⊂α,α∩β=n,那么m∥n,故正确故选:C9.已知函数f(x)=是R上的增函数,则实数a的取值范围是()A.﹣1<a<1 B.﹣1<a≤1 C.D.【考点】分段函数的应用.【分析】根据f(x)在R上单调递增便可知,二次函数x2﹣2ax+2在[1,+∞)上单调递增,一次函数(a+1)x+1在(﹣∞,1)上单调递增,列出不等式,即可得出实数a的取值范围.【解答】解:函数f(x)=是R上的增函数,;∴当x≥1时,f(x)=x2﹣2ax+2为增函数;∴a≤1;当x<1时,f(x)=(a+1)x+1为增函数;∴a+1>0;∴a >﹣1;且a+2≤3﹣2a ;解得;∴实数a 的取值范围为:(﹣1,].故选:D .10.设a >b >0,a+b=1,且x=()b ,y=log ab ,z=log a ,则x 、y 、z 的大小关系是( )A .y <z <xB .z <y <xC .x <y <zD .y <x <z【考点】对数值大小的比较.【分析】由已知得到a ,b 的具体范围,进一步得到ab ,,的范围,结合指数函数与对数函数的性质得答案.【解答】解:由a >b >0,a+b=1,得0,,且0<ab <1,则,,a <,∴x=()b >0,y=logab=﹣1,0=>z=log a >=﹣1,∴y <z <x .故选:A .11.已知A 、B 是球O 的球面上两点,且∠AOB=120°,C 为球面上的动点,若三棱锥O ﹣ABC 体积的最大值为,则球O 的表面积为( )A .4πB .C .16πD .32π 【考点】球的体积和表面积.【分析】当点C 位于垂直于面AOB 的直径端点时,三棱锥O ﹣ABC 的体积最大,利用三棱锥O ﹣ABC 体积的最大值为,求出半径,即可求出球O 的表面积.【解答】解:如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ﹣ABC 的体积最大,设球O 的半径为R ,此时V O ﹣ABC =V C ﹣AOB ==,故R=2,则球O 的表面积为4πR 2=16π,故选:C .12.设函数f(x)、g(x)分别是定义在R上的奇函数和偶函数,且f(x)+g(x)=2x,若对x∈[1,2],不等式af(x)+g(2x)≥0恒成立,则实数a的取值范围是()A.[﹣1,+∞)B.C.D.【考点】函数奇偶性的性质.【分析】先根据函数奇偶性定义,解出奇函数f(x)和偶函数g(x)的表达式,将这个表达式不等式af(x)+g(2x)≥0,令t=2x﹣2﹣x,则t>0,通过变形可得a≥﹣(t+),讨论出右边在x∈[1,2]的最大值,可以得出实数a的取值范围.【解答】解:∵f(x)为定义在R上的奇函数,g(x)为定义在R上的偶函数∴f(﹣x)=﹣f(x),g(﹣x)=g(x)又∵由f(x)+g(x)=2x,结合f(﹣x)+g(﹣x)=﹣f(x)+g(x)=2﹣x,∴f(x)=(2x﹣2﹣x),g(x)=(2x+2﹣x)不等式af(x)+g(2x)≥0,化简为(2x﹣2﹣x)+(22x+2﹣2x)≥0∵1≤x≤2∴≤2x﹣2﹣x≤令t=2x﹣2﹣x,则t>0,因此将上面不等式整理,得:a≥﹣(t+).∵≤t≤∴≤t+≤∴a≥﹣.故选:C.二、填空题:本大题共4小题,每小题5分,共20分.13.经过圆x2+2x+y2=0的圆心C,且与直线x+y=0垂直的直线方程是x﹣y+1=0 .【考点】直线的点斜式方程;两条直线垂直与倾斜角、斜率的关系.【分析】先求圆心,再求斜率,可求直线方程.【解答】解:易知点C为(﹣1,0),而直线与x+y=0垂直,我们设待求的直线的方程为y=x+b,将点C的坐标代入马上就能求出参数b的值为b=1,故待求的直线的方程为x﹣y+1=0.故答案为:x﹣y+1=0.14.已知,则sin2x= .【考点】二倍角的正弦.【分析】由诱导公式,二倍角的余弦函数公式化简所求,结合已知即可计算求值.【解答】解:∵,∴.故答案为:.15.设函数f(x)=sin(wx+φ),其中|φ|<.若f(﹣)≤f(x)≤f()对任意x∈R恒成立,则正数w的最小值为 2 ,此时,φ= ﹣.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】直接利用函数的周期的最大值,即可求解ω的最小值.通过函数的最大值求出φ【解答】解:因为函数f(x)=sin(ωx+φ),其中|φ|<.若f(﹣)≤f(x)≤f()对任意x∈R恒成立,所以的最大值为:,所以正数ω的最小值为:,ω=2,因为函数的最大值为f(),所以2×=,所以φ=,故答案为:2,.16.已知,满足||=||=•=2,且(﹣)•(﹣)=0,则|2﹣|的最小值为﹣1 .【考点】平面向量数量积的运算.【分析】求出的夹角,建立平面直角坐标系,设=(2,0),则=(1,),根据数量积的几何意义得出C的轨迹,利用点到圆的最短距离求出|2﹣|的最小值.【解答】解:∵||=||=•=2,∴cos<>==,∴<>=60°.设=(2,0),==(1,),,∵(﹣)•(﹣)=0,∴,∴C的轨迹为以AB为直径的圆M.其中M(,),半径r=1.延长OB到D,则D(2,2).连结DM,交圆M于C点,则CD为|2﹣|的最小值.DM==.∴CD=.故答案为:﹣1.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.我国是世界上严重缺水的国家.某市政府为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3.5吨的人数,并说明理由;(3)若在该选取的100人的样本中,从月均用水量不低于3.5吨的居民中随机选取3人,求至少选到1名月均用水量不低于4吨的居民的概率.【考点】古典概型及其概率计算公式;频率分布直方图.【分析】(1)由频率统计相关知识,各组频率之和的值为1,由此能求出a.(2)由图求出不低于3.5吨人数所占百分比,由此能估计全市月均用水量不低于3.5吨的人数.(3)由不低于3.5吨人数所占百分比为6%,得该选取的100人的样本中,月均用水量不低于3.5吨的居民有6人,其中[3.5,4)之间有4人,[4,4.5)之间有2人,由此能求出从6人中取出3人,至少选到1名月均用水量不低于4吨的居民的概率.【解答】解:(1)由频率统计相关知识,各组频率之和的值为1,∵频率=,∴0.5×(a+0.16+0.3+0.4+0.52+0.3+0.12+a+0.04)=1得a=0.08.(2)由图,不低于3.5吨人数所占百分比为0.5×(0.08+0.04)=6%,∴估计全市月均用水量不低于3.5吨的人数为:30×6%=1.8(万),(3)由(2)不低于3.5吨人数所占百分比为0.5×(0.08+0.04)=6%,因此该选取的100人的样本中,月均用水量不低于3.5吨的居民有100×6%=6人,其中[3.5,4)之间有4人,[4,4.5)之间有2人,从6人中取出3人,共有=20种取法,利用互斥事件分类讨论,3人中在[4,4.5)之间有1人,[3.5,4)之间有2人,共有12种取法,3人中在[4,4.5)之间有2人,[3.5,4)之间有1人,共有4种取法,所以至少选到1名月均用水量不低于4吨的居民的概率为:p==.18.如图,在△ABC中,∠B=,AB=8,点D在边BC上,且CD=2,cos∠ADC=.(1)求sin∠BAD;(2)求BD,AC的长.【考点】余弦定理的应用.【分析】根据三角形边角之间的关系,结合正弦定理和余弦定理即可得到结论.【解答】解:(1)在△ABC中,∵cos∠ADC=,∴sin∠ADC====,则sin∠BAD=sin(∠ADC﹣∠B)=sin∠ADC•cosB﹣cos∠ADC•sinB=×﹣=.(2)在△ABD中,由正弦定理得BD==,在△ABC中,由余弦定理得AC2=AB2+CB2﹣2AB•BCcosB=82+52﹣2×8×=49,即AC=7.19.如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,BC=,F为BE的中点.(1)若CE=2,求证:①DF∥平面ABC;②平面BDE⊥平面BCE;(2)若二面角E﹣AB﹣C为45°,求直线AE与平面BCE所成角.【考点】直线与平面所成的角;平面与平面垂直的判定.【分析】(1)①取BC作的中点G,连接GF,GA,证明四边形AGFD为平行四边形得出DF∥AG,故而DF∥平面ABC;②证明AG⊥平面BCE,得出DF⊥平面BCE,于是平面BDE⊥平面BCE;(2)连接AE,则∠EAC=45°,由AG⊥平面BCE得出∠AEG为所求角,利用勾股定理计算AG,AE,即可得出sin∠AEG.【解答】证明:(1)①取BC作的中点G,连接GF,GA,∴GF为三角形BCE的中位线,∴GF∥CE,GF=CE,∵DA⊥平面ABC,EC⊥平面ABC,∴DA∥CE,又DA=CE,∴GF∥AD,GF=AD.∴四边形GFDA为平行四边形,∴AG∥FD,又GA⊂平面ABC,DF⊄平面ABC,∴DF∥平面ABC.②∵AB=AC,G为BC的中点,∴AG⊥BC,∵CE⊥平面ABC,CE⊂平面BCE,∴平面BCE⊥平面ABC,又平面BCE∩平面ABC=BC,AG⊂平面ABC,∴AG⊥平面BCE,∵AG∥FD,∴FD⊥平面BCE,又FD⊂平面BDE,∴平面BDE⊥平面BCE.(2)连接AE.∵AD⊥平面ABC,AB⊂平面ABC,∴AD⊥AB,∵AB=AC=1,BC=,∴AC ⊥AB ,又AC ⊂平面ACE ,AD ⊂平面ACE ,AC∩AD=A,∴AB ⊥平面ACE ,又AE ⊂平面ACE ,∴AB ⊥AE ,∴E ﹣AB ﹣C 的平面角为∠EAC=45°,∴CE=AC=1;由(1)可知AG ⊥平面BCE ,∴直线AE 与平面BCE 所成角为∠AEG .∵AB=AC=1,AB ⊥AC ,∴AG=BC=,AE==,∴,∴∠AEG=30°.20.设数列{a n }的前n 项和为S n ,已知a 1=1,2S n =(n+1)a n ,n ∈N *.(1)求数列{a n }的通项公式;(2)令b n =,数列{b n }的前n 项和为T n ,试比较T n 与的大小.【考点】数列的求和;数列递推式.【分析】(1)由2S n =(n+1)a n ,当n ≥2,2S n ﹣1=na n ﹣1,两式相减可知:,即,a n =n ;(2)由(1)可知:,采用“裂项法”即可求得数列{b n }的前n 项和为T n ,即可比较T n 与的大小.【解答】解:(1)∵,∴,两式相减得:,…∴(n ≥2,且n ∈N *),又,∴,=n…∴an(2)由(1)可得…∴,=…21.如图,已知直线l:y=x+4,圆O:x2+y2=3,直线m∥l.(1)若直线m与圆O相交,求直线m纵截距b的取值范围;(2)设直线m与圆O相交于C、D两点,且A、B为直线l上两点,如图所示,若四边形ABCD是一个内角为60°的菱形,求直线m纵截距b的值.【考点】圆方程的综合应用;直线与圆的位置关系.【分析】(1)利用m∥l,求出直线l;设直线m的方程,利用设圆心O到直线m的距离为d,通过直线m与圆O相交,求解即可.(2)求出CD,利用AB与CD之间的距离,结合求解即可.【解答】解:(1)∵m∥l,直线,∴可设直线,即,设圆心O到直线m的距离为d,又因为直线m与圆O相交,∴,…即,∴…(2)由,①…AB与CD之间的距离,②…又③…联立①②③得到:b2﹣2b﹣5=0,又,解得:或…22.已知a>0,b∈R,函数f(x)=4ax2﹣2bx﹣a+b的定义域为[0,1].(Ⅰ)当a=1时,函数f(x)在定义域内有两个不同的零点,求b的取值范围;(Ⅱ)记f(x)的最大值为M,证明:f(x)+M>0.【考点】二次函数的性质.【分析】(1)由题意可得f(0)≥0,f(1)≥0,△>0,0<<1,解不等式即可得到所求范围;(2)求出对称轴,讨论对称轴和区间[0,1]的关系,可得最值,即可证明f(x)+M>0.【解答】解:(1)由题意可得f(x)=4x2﹣2bx﹣1+b在[0,1]内有两个不同的零点,即有,解得1≤b<2或2<b≤3;(2)记f(x)的最大值为M,证明:f(x)+M>0.只需证明f(x)最小值+M>0即可,设f(x)的最小值是m,问题转化为证明M+m>0,证明如下:f(x)的对称轴为x=,当>1时,区间[0,1]为减区间,可得M=f(0)=b﹣a,m=f(1)=3a﹣b,则M+m=2a>0;当<0时,区间[0,1]为增区间,可得m=f(0)=b﹣a,M=f(1)=3a﹣b,则M+m=2a>0;当0≤≤1时,区间[0,]为减区间,[,1]为增区间,可得m=f()=,若f(0)≤f(1),即b≤2a,可得M=f(1)=3a﹣b,M+m=≥=a>0;若f(0)>f(1),即2a<b≤4a,可得M=f(0)=b﹣a,M+m==,由于2a<b≤4a,可得M+m∈(a,2a],即为M+m>0.综上可得:f(x)max +f(x)min>0恒成立,即f(x)+M>0.。
安徽省江淮十校2024届高三第一次联考数学试题

安徽省江淮十校2024届高三第一次联考数学试题学校:___________姓名:___________班级:___________考号:___________
A .DF ⊥平面AEC
B .多面体ABCDEF
C .BG
D △的周长的最小值为D .EG 与平面AFC 三、填空题
13.某高校开设了乒乓球,羽毛球,篮球,小提琴,书法五门选修课程可供学习,要求每位同学每学年至多选的不同选修方式有
14.若601(21)x a a -=+(用数字作答)
15.将4个半径为6的球堆放在一起,且两两相切,记与这径为R ,记与这4个球都外切的小球的半径为16.已知函数()3sin f x =则满足条件的ω的个数为
四、解答题
17.在ABC 中,内角A (1)求B ;
(2)若3b =,且ABC 的面积为
(1)若平面PAB ⋂平面PCD l =,证明:(2)求二面角A BP C --的余弦值21.在平面直角坐标系xOy 中,已知双曲线C的中心为坐标原点,对称轴是坐标轴,右支与x 轴的交点为()1,0,其中一条渐近线的倾斜角为(1)求C 的标准方程;
(2)过点()2,0T 作直线l 与双曲线点E 满足AE TB EB AT ⋅=⋅,证明:点22.已知函数()2
k
f x x x
=+
,k (1)讨论()f x 的单调性;
(2)设函数()3
ln g x x x =-,313≤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年安徽省江淮十校高三上学期第一次联考(理)数学试题注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I 卷(选择题)一、单选题1.已知集合1|,0A y y x x x ⎧⎫==+≠⎨⎬⎩⎭,集合{}2|40B x x =-≤,若A B P ⋂=,则集合P 的子集个数为( )A .2B .4C .8D .162.复数z 满足342z i ++=,则z z ⋅的最大值是( )A .7B .49C .9D .813.设,,a b c 为正数,则“a b c +>”是“222a b c +>”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知向量a 、b 均为非零向量,(a -2b )⊥a ,|a |=|b |,则a 、b 的夹角为( ) A .6π B .3π C .23π D .56π 5.已知ln x π=,13y e -=,13log z π=,则( )A .x y z <<B .z x y <<C .z y x <<D .y z x <<6.勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形,现在勒洛三角形中随机取一点,则此点取自正三角形外的概率为( )ABC D7.如图,在正方体111ABCD A B C D -中,F 是棱11A D 上动点,下列说法正确的是( )A .对任意动点F ,在平面11ADD A 内不存在...与平面CBF 平行的直线B .对任意动点F ,在平面ABCD 内存在..与平面CBF 垂直的直线C .当点F 从1A 运动到1D 的过程中,FC 与平面ABCD 所成的角变大..D .当点F 从1A 运动到1D 的过程中,点D 到平面CBF 的距离逐渐变小..8.某创业公司共有36名职工,为了了解该公司职工的年龄构成情况,随机采访了9位代表,将数据制成茎叶图如图,若用样本估计总体,年龄在(,)x s x s -+内的人数占公司总人数的百分比是(精确到1%)( )A .56%B .14%C .25%D .67%9.将余弦函数的图象向右平移2π个单位后,再保持图象上点的纵坐标不变,横坐标变为原来的一半,得到函数()f x 的图象,下列关于()f x 的叙述正确的是( )A .最大值为1,且关于3,04π⎛⎫ ⎪⎝⎭对称 B .周期为π,关于直线2x π=对称 C .在,68ππ⎛⎫- ⎪⎝⎭上单调递增,且为奇函数 D .在0,4π⎛⎫ ⎪⎝⎭上单调递减,且为偶函数 10.对任意实数x ,恒有10x e ax --≥成立,关于x 的方程()ln 10x a x x ---=有两根为1x ,2x ()12x x <,则下列结论正确的为( )A .122x x +=B .121=x xC .122x x =D .12x x e =11.已知双曲线2222:1x y C a b-=的两条渐近线分别为1l 与2l ,A 与B 为1l 上关于原点对称的两点,M 为2l 上一点且AM BM k k e ⋅=,则双曲线离心率e 的值为( )A B .12 C .2 D12.在四面体ABCD 中,若1AD DB AC CB ====,则当四面体ABCD 的体积最大时其外接球表面积为( )A .53π B .43π C .π D .2π第II 卷(非选择题)二、填空题13.已知实数x 、y 满足210020x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩,则目标函数2z x y =+的最小值为_____________。
14.已知()()512x x a ++的展开式中各项系数和为2,则其展开式中含2x 项的系数是____________。
15.关于x 的方程sin 2cos 0x x a ++=在0,2π⎛⎫ ⎪⎝⎭内有解,则实数a 的取值范围是_____________。
16.已知抛物线2:4C x y =的焦点为F ,过F 作直线l 交抛物线于A 、B 两点,且2AF FB λ=(λ为非零常数).以A 为切点作抛物线C 的切线交直线1y =-于M 点,则MF 的长度为__________(结果用含λ式子表示)。
三、解答题17.数列{}n a 的前n 项和为n S ,且()()6121n S n n n =++.(1)求{}n a 的通项公式;(2)设141n n b a =-,数列{}n b 的前n 项和为n T ,证明12n T <。
18.ABC ∆中,角A 、B 、C 所对的边分别是a 、b 、c ,若sin 2A -sin 2B =3sin 2C ,sin A =,且0BA AC ⋅>。
(1)求sin sin B C; (2)若2a =,求ABC ∆的面积.19.如图,四面体ABCD 中,ABC ∆是正三角形,ACD ∆是直角三角形,∠ABD =∠CBD ,AB =BD .(1)证明:平面ACD ⊥平面ABC ;(2)若点E 为DB 中点,求二面角D AE C --的正弦值。
20.如图,已知A (-1,0)、B (1,0), Q 、G 分别为ABC △的外心,重心,QG //AB 。
(1)求点C 的轨迹E 的方程;(2)是否存在过()0,1P 的直线L 交曲线E 于M ,N 两点且满足2MP PN =,若存在求出L 的方程,若不存在请说明理由。
21.已知函数()21cos 14f x x x =+-. (1)证明:()0f x ≤,,22x ππ⎡⎤∈-⎢⎥⎣⎦; (2)判断()y f x =的零点个数,并给出证明过程。
22.棋盘上标有第0、1、2、、100站,棋子开始位于第0站,棋手抛掷均匀硬币走跳棋游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到调到第99站或第100站时,游戏结束.设棋子位于第n 站的概率为n P 。
(1)当游戏开始时,若抛掷均匀硬币3次后,求棋手所走步数之和X 的分布列与数学期望;(2)证明:()()1111982n n n n P P P P n +--=--≤≤; (3)求99P 、100P 的值。
2019年安徽省江淮十校高三上学期第一次联考(理)数学试题参考答案1.B【分析】求出集合A 、B ,得出集合P ,确定集合P 的元素个数,利用子集个数公式可得出集合P 的子集个数.【详解】当0x >时,12y x x =+≥=;当0x <时,()()112y x x x x ⎡⎤=+=--+≤-=-⎢⎥-⎣⎦. 所以,集合{}22A y y y =≤-≥或. 集合{}{}24022B x x x x =-≤=-≤≤,{}2,2P A B ∴==-I , 集合P 有两个元素,因此,集合P 的子集个数为224=,故选:B.【点睛】本题考查集合子集个数的计算,考查集合的交集、函数的值域以及一元二次不等式的解法,解题时要注意集合子集个数结论的应用,属于中等题.2.B 【分析】设z x yi =+,由342z i ++=可得出()()22344x y +++=,22z z x y ⋅=+,利用数形结合思想求出z z ⋅的最大值. 【详解】设z x yi =+,则()()34342z i x y i ++=+++==, ()()22344x y ∴+++=,则复数z 在复平面内所对应的点的轨迹是以()3,4--为圆心,以2为半径的圆,22z z x y ⋅=+,其几何意义是原点到圆()()22344x y +++=上一点距离5=, 因此,z z ⋅的最大值为()22549+=,故选:B.【点睛】本题考查复数的几何意义,考查复数对应点的轨迹,同时也涉及了点到圆上一点最值的求解,考查分析问题和解决问题的能力,属于中等题.3.B【分析】根据不等式的关系,结合充分条件和必要条件的定义进行判断即可.【详解】∵,,a b c 为正数,∴当2,2,3a b c ===时,满足a b c +>,但222a b c +>不成立,即充分性不成立, 若222a b c +>,则()222+->a b ab c ,即()2222+>+>a b c ab c ,>a b c +>,成立,即必要性成立,则“a b c +>”是“222a b c +>”的必要不充分条件,故选:B .【点睛】本题主要考查充分条件和必要条件的判断,结合不等式的关系是解决本题的关键,属于中档题.4.B【分析】,|a |=|b |设a 、b 的夹角为θ,由(a -2b )⊥a ,得出(a -2b )·a =0,利用平面向量数量积的运算律与定义可计算出cos θ的值,结合θ的取值范围得出θ的值.【详解】设a 、b 的夹角为θ,(a -2b )⊥a ,且|a |=|b |,(a -2b )⊥a =a 2-2a b =|a |2-2|a |2cos θ=0,解得1cos 2θ=, ,3πθ∴=.因此,a 、b 的夹角为3π,故选:B. 【点睛】本题考查利用平面向量的数量积求向量的夹角,在处理平面向量垂直时,要将其转化为两向量的数量积为零,利用平面向量数量积的定义和运算律来计算,考查运算求解能力,属于中等题. 5.C 【分析】利用中间值法,将这三个数与0、1比较大小,从而得出这三个数的大小关系. 【详解】由于对数函数ln y x =在其定义域上是增函数,则ln ln 1x e π=>=,指数函数xy e =在R 上为增函数,则10301e e -<<=,即01y <<,对数函数13log y x =在其定义域上是减函数,则1133log log 10π<=,即0z <.因此,z y x <<,故选:C. 【点睛】本题考查利用中间值法比较指数式、对数式的大小,常用的中间值为0和1,在实际问题中,中间值取多少要由具体问题来选择,同时在比较大小时,要充分利用指数函数与对数函数的单调性来求解,考查分析问题和解决问题的能力,属于中等题. 6.A 【分析】设2BC =,将圆心角为3π的扇形面积减去等边三角形的面积可得出弓形的面积,由此计算出图中“勒洛三角形”的面积,然后利用几何概型的概率公式可计算出所求事件的概率. 【详解】如下图所示,设2BC =,则以点B 为圆心的扇形面积为2122=233ππ⨯⨯,等边ABC ∆的面积为212sin 23π⨯⨯=23π- 所以,勒洛三角形的面积可视为一个扇形面积加上两个弓形的面积,即222233πππ⎛+⨯=- ⎝ ∴在勒洛三角形中随机取一点,此点取自正三角形外部的概率1=A.【点睛】本题考查几何概型概率的计算,解题的关键就是要求出图形相应区域的面积,解题时要熟悉一些常见平面图形的面积计算方法,考查计算能力,属于中等题. 7.C 【分析】利用直线与平面平行的判定定理可判断出A 选项中命题的正误;利用反证法判断出B 选项中命题的正误;利用线面角的定义判断出C 选项中命题的正误;利用三棱锥体积来判断出D 选项命题的正误. 【详解】 对于A 选项,//AD BC ,AD ⊄平面CBF ,BC ⊂平面CBF ,//AD ∴平面CBF ,又AD ⊂平面11ADD A ,所以,A 选项中的命题错误;对于B 选项,反设平面ABCD 内存在直线a 满足a ⊥平面CBF ,a ⊂Q 平面ABCD ,由平面与平面垂直的判定定理可得平面CBF ⊥平面ABCD ,事实上,平面CBF 与平面ABCD 不垂直,假设不存在,所以,B 选项中的命题错误;对于C 选项,由于F 到平面ABCD 的距离d 不变且FC 变小,设直线FC 与平面ABCD 所成的角为θ,则sin dFCθ=,可知θ在逐渐变大,C 选项中的命题正确; 对于D 选项,由于点F 到平面ABCD 的距离不变,BCD ∆的面积不变,则三棱锥F BCD -的体积不变,即三棱锥D BCF -的体积不变,在点F 的运动过程中,BCF ∆的面积不变,由等体积法可知,点D 到平面BCF 的距离不变,D 选项中的命题正确.故选:C. 【点睛】本题考查直线与平面平行、直线与平面垂直、直线与平面所成的角以及点到平面距离等命题的判断,判断时要从这些知识点的定义出发来理解,考查逻辑推理能力,属于中等题. 8.A 【分析】求出样本平均值与方差,可得年龄在(,)x s x s -+内的人数有5人,利用古典概型概率公式可得结果. 【详解】363637374440434443409x ++++++++==,2161699160916910099s ++++++++==103s =,年龄在(,)x s x s -+内,即110130,33⎛⎫⎪⎝⎭内的人数有5人, 所以年龄在(,)x s x s -+内的人数占公司总人数的百分比是等于505609≈,故选A.【点睛】样本数据的算术平均数公式 12n 1(++...+)x x x x n=. 样本方差公式2222121[()()...()]n s x x x x x x n=-+-++-,标准差s =9.C 【分析】根据图象变换求出函数()y f x =的解析式,然后结合正弦型函数的基本性质对各选项的正误进行判断. 【详解】将余弦函数的图象向右平移2π个单位后,得到函数cos sin 2y x x π⎛⎫=-= ⎪⎝⎭的图象,再保持图象上点的纵坐标不变,横坐标变为原来的一半,得到函数()sin 2f x x =的图象.对于A 选项,函数()sin 2f x x =的最大值为1,由于33sin 142f ππ⎛⎫==- ⎪⎝⎭,该函数的图象不关于点3,04π⎛⎫⎪⎝⎭对称,A 选项错误; 对于B 选项,函数()sin 2f x x =的最小正周期为22T ππ==,且sin 02f ππ⎛⎫== ⎪⎝⎭,则该函数的图象不关于直线2x π=对称,B 选项错误; 对于C 选项,当68x ππ-<<时,234x ππ-<<,则函数()sin 2f x x =在,68ππ⎛⎫-⎪⎝⎭上单调递增,且该函数为奇函数,C 选项正确; 对于D 选项,当04x π<<时,022x π<<,则函数()sin 2f x x =在0,4π⎛⎫⎪⎝⎭上单调递增,且为奇函数,D 选项错误.故选:C. 【点睛】本题考查三角函数的图象变换,同时也考查了正弦型函数基本性质的判断,解题时要根据图象的变换写出变换后的函数解析式,并结合正弦函数的基本性质进行判断,考查推理能力,属于中等题. 10.B 【分析】先由10x e ax --≥可得出1a =,再由()1ln 10x x x ---=,得出1ln 1x x x +=-,由题意得出1111ln 1x x x +=-和111111ln 11x x x +=-,由此得出211x x =,由此可得出正确选项.【详解】构造函数()1xf x e ax =--,则()00f =,由题意得出()()0f x f ≥,则()()min 0f x f=.且()xf x e a '=-.①当0a -≥时,即当0a ≤时,对任意的x ∈R ,()0f x '>,函数()y f x =在R 上单调递增,此时,函数()y f x =没有最小值;②当0a -<时,即当0a >时,令()0f x '=,得ln x a =. 当ln x a <时,()0f x '<;当ln x a >时,()0f x '>.此时,函数()y f x =在ln x a =处取得极小值,亦即最小值,即()()min ln f x f a =,ln 0a ∴=,得1a =.由题意可知,关于x 的方程()1ln 10x x x ---=有两个实根,即1ln 1x x x +=-有两个实数根. 方程1ln 1x x x +=-的其中一个实根为1x ,则1111ln 1x x x +=-,1111111ln 11x x x x x ++∴-=-=--, 即111111ln 11x x x +=-,又方程1ln 1x x x +=-的另一个实根为2x ,211x x ∴=,因此,121=x x , 故选:B. 【点睛】本题考查利用导数研究不等式恒成立问题,同时也考查了方程两根之间的关系,解题时要充分利用对数的运算性质来求解,考查分析问题和解决问题的能力,属于中等题. 11.B 【分析】设直线1l 的方程为b y x a =,则直线2l 的方程为b y x a =-,设点11,b A x x a ⎛⎫⎪⎝⎭、22,b M x x a ⎛⎫- ⎪⎝⎭,则点11,b B x x a ⎛⎫-- ⎪⎝⎭,利用AM BM k k e ⋅=,可得出21e e -=,解出即可.【详解】设直线1l 的方程为by x a=,则直线2l 的方程为b y x a =-,设点11,b A x x a ⎛⎫ ⎪⎝⎭、22,b M x x a ⎛⎫- ⎪⎝⎭,则点11,b B x x a ⎛⎫-- ⎪⎝⎭, ()1212AMb x x a k x x +=-,()12121212MB b b bx x x x a a a k x x x x -+-==--+,22AM BM b k k e a ∴⋅==,即21e e -=,即210e e --=,1e >Q ,解得e = B. 【点睛】本题考查双曲线离心率的求解,同时也涉及到渐近线方程,在求解离心率时,充分利用公式222221c b e a a==+可简化计算,考查运算求解能力,属于中等题.12.A 【分析】设()201AB x x =<<,可知当四面体ABCD 的体积最大时,平面ACB ⊥平面ADB ,计算出CE DE =求出四面体ABCD 的体积31133V x x =-,利用导数求出V 的最大值以及对应的x 的值,再利用四面体的结构得出计算出外接球的半径,最后利用球体表面积公式可得出结果. 【详解】如下图,取AB 的中点E ,连接CE 、DE ,设()201AB x x =<<,则CE DE ==ABCD 的体积最大时,平面ACB ⊥平面ADB ,四面体ABCD 的体积为3111123233V x x x =⨯⨯=-,213V x '=-.令0V '=,得3x =,当0x <<时,0V '>;当13x <<时,0V '<.所以,函数31133V x x =-在x =.此时,3CE ==,sin 3CE BAC AC ∠==,设ABC ∆和ABD ∆的外接圆半径为r,由正弦定理得2sin BC r BAC ==∠r ∴=设ABC ∆、ABD ∆的外接圆圆心分别为M 、N ,外接球的球心为点O ,如下图所示:在Rt BCE ∆中,BM r ==, 四边形OMEN是正方形,且边长为ME BE BM =-=, 所以,四面体ABCD的外接球半径R ==, 因此,该四面体的外接球表面积为25544123OB πππ⋅=⨯=,故选:A. 【点睛】本题考查四面体体积的最值,同时也考查了四面体外接球表面积的计算,要充分分析几何体的结构特征,考查分析问题和解决问题的能力,属于难题. 13.32【分析】作出不等式组所表示的可行域,平移直线2z x y =+经过可行域时在x 轴上取最小值时对应的最优解,再将最优解代入目标函数可得出答案. 【详解】作出不等式组210020x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩所表示的可行域如下图所示:联立2100x x y -=⎧⎨-=⎩,得12x y ==,可得点11,22A ⎛⎫⎪⎝⎭,平移直线2z x y =+,当直线2z x y =+经过可行域的顶点11,22A ⎛⎫⎪⎝⎭时,该直线在x 轴上的截距最小,此时z 取最小值,即min 1132222z =⨯+=,故答案为:32. 【点睛】本题考查简单的线性规划问题,考查线性目标函数的最值问题,通常利用平移直线在坐标轴上截距的最值来寻找最优解来求解,考查数形结合思想的应用,属于中等题. 14.30- 【分析】先将1x =代入二项式得出二项式的值为展开式各项系数和,可求出1a =-,然后将二项式变形为()()()()5551212121x x x x x +-=-+-,写出二项展开式的通项,令x 的指数为2,求出参数的值,再将参数的值代入通项可得出2x 项的系数. 【详解】由题意可知,()()512x x a ++的展开式中各项系数和为()()()551121222a a +⨯+=+=, 解得1a =-,()()()()()()5555121212121x x a x x x x x ++=+-=-+-, 二项展开式的通项为()()()()()5556555212121kkrrkkrkk k xC x C x C x ----⋅⋅-+⋅⋅-=⋅⋅-⋅+()55521rr r r C x --⋅⋅-⋅,令6252k r -=⎧⎨-=⎩,得43k r =⎧⎨=⎩,因此,展开式中含2x 项的系数为()()434132552121104030C C ⋅⋅-+⋅⋅-=-=-,故答案为:30-. 【点睛】本题考查二项式展开式各项系数和的概念,同时也考查了二项式中指定项的系数,解题时要充分利用展开式通项求解,考查运算求解能力,属于中等题.15.)1⎡-⎣【分析】将问题转化为方程sin 2cos a x x -=+在区间0,2π⎛⎫⎪⎝⎭上有解,可得出实数a -的取值范围即为函数()sin 2cos f x x x =+在区间0,2π⎛⎫⎪⎝⎭上的值域,利用辅助角公式求出函数()y f x =在区间0,2π⎛⎫⎪⎝⎭上的值域,即可得出实数a 的取值范围. 【详解】由题意可得sin 2cos a x x -=+,则关于x 的方程sin 2cos a x x -=+在区间0,2π⎛⎫⎪⎝⎭上有解.构造函数()sin 2cos f x x x =+,其中0,2x π⎛⎫∈ ⎪⎝⎭,由辅助角公式可得()()f x x ϕ+,ϕ为锐角,且cos 5ϕ=,sin 5ϕ=. 由于02x π<<,则2x πϕϕϕ<+<+,所以,函数()sin 2cos f x x x =+在区间0,2πϕ⎛⎫- ⎪⎝⎭上单调递增,在区间,22ππϕ⎛⎫- ⎪⎝⎭上单调递减,则()max f x =()02f =,12f π⎛⎫=⎪⎝⎭,所以,函数()sin 2cos f x x x =+在区间0,2π⎛⎫⎪⎝⎭上的值域为(,1a ∴<-≤解得1a <-,因此,实数a 的取值范围是)1⎡-⎣,故答案为:)1⎡-⎣.【点睛】本题考查三角函数的零点问题,解题时可以利用参变量分离法转化为函数的值域问题,充分利用辅助角公式和正弦函数的基本性质求解,考查运算求解能力,属于中中等题. 16.1λλ+【分析】设直线AB 的方程为1y kx =+,联立直线AB 的方程与抛物线C 的方程,列出韦达定理,结合2AF FB λ=得出点A 的横坐标,然后利用导数求出抛物线C 在点A 处的切线方程,并求出点M 的坐标,最后利用两点间的距离公式求出MF 的长度. 【详解】设点()11,A x y 、()22,B x y ,抛物线C 的焦点为()0,1F ,设直线AB 的方程为1y kx =+, 联立直线AB 的方程与抛物线C 的方程214y kx x y=+⎧⎨=⎩,消去y 得2440x kx --=, 由韦达定理得124x x k +=,124x x =-.()11,1AF x y =--uu u r ,()22,1FB x y =-uu r ,2AF FB λ=uu u r uu r Q ,212x x λ∴-=,2121x x λ∴=-,2121214x x x λ∴=-=-,得2214x λ=.抛物线C 的函数解析式为24x y =,求导得2x y '=,则抛物线C 在点A 处的切线方程为()1112x y y x x -=-,即21124x x y x =-,联立211124y x x y x =-⎧⎪⎨=-⎪⎩,解得11221x x x y ⎧=-⎪⎨⎪=-⎩,所点112,12x M x ⎛⎫-- ⎪⎝⎭, 因此,1MF λλ====+, 故答案为:1λλ+.【点睛】本题考查直线与抛物线的综合问题,涉及到切线方程以及两点间的距离公式的应用,对于直线与抛物线的综合问题,一般将直线方程与抛物线方程联立,利用韦达定理设而不求法进行求解,考查计算能力,属于中等题.17.(1)2n a n =;(2)证明见解析.【分析】(1)令1n =,由11a S =求出11a =,再令2n ≥,由1n n n a S S -=-求出n a 的表达式,再对11a =是否满足n a 的表达式进行验证,由此得出数列{}n a 的通项公式; (2)将数列{}n b 的通项公式裂项为11122121n b n n ⎛⎫=- ⎪-+⎝⎭,并利用裂项法求出n T ,即可证明出12n T <成立. 【详解】(1)当1n =时,11661236a S ==⨯⨯=,可得11a =;当2n ≥时,由()()6121n S n n n =++可得()()16121n S n n n -=--,上述两式相减得()()()()261211216n a n n n n n n =++---=⎡⎤⎣⎦,2n a n =. 11a =适合2n a n =,因此,对任意的n *∈N ,2n a n =;(2)()()21111114141212122121n n b a n n n n n ⎛⎫====- ⎪---+-+⎝⎭Q ,111111111111123235221212212n T n n n ⎛⎫⎛⎫⎛⎫⎛⎫∴=-+-++-=-< ⎪ ⎪ ⎪ ⎪-++⎝⎭⎝⎭⎝⎭⎝⎭L 成立.【点睛】本题考查由前n 项和公式求数列通项,同时也考查了利用裂项法求和,在由前n 项和公式求数列通项时,利用公式11,1,2n n n S n a S S n -=⎧=⎨-≥⎩来进行计算,考查计算能力,属于中等题.18.(1)3;(2)3. 【分析】(1)由0BA AC ⋅>可得出cos 0A <,利用同角三角函数的平方关系可求出cos A 的值,利用正弦定理边角互化思想得出2223a b c -=,再利用余弦定理可得出b c的值,从而可得出sin sin BC的值; (2)由(1)得出3b c =,利用余弦定理可求出b 、c 的值,再利用三角形的面积公式可求出ABC ∆的面积. 【详解】 (1),cos 0A ∴<.由同角三角函数的平方关系得1cos 3A ===-.,由正弦定理可得2223a b c -=.由余弦定理得2222231cos 223b c a c c c A bc bc b +--===-=-,3b c ∴=,由正弦定理边角互化思想得sin 3sin B bC c==; (2)由(1)可知3b c =,由余弦定理得2222222cos 10212a b c bc A c c c =+-=+=,2211123c a ∴==,则c =b =由三角形面积公式可知,ABC ∆的面积为11sin 22333ABC S bc A ∆===. 【点睛】本题考查正弦定理和余弦定理解三角形,同时也考查了三角形面积公式的应用,要根据三角形已知元素的类型合理选择正弦、余弦定理解三角形,同时也考查充分利用边角互化思想的应用,简化计算,考查运算求解能力,属于中等题.19.(1)证明见解析;(2. 【分析】(1)先证明出ABD CBD ∆≅∆,可得出AD CD =,可得出90ADC ∠=,然后取AC 的中点O ,连接OC 、OD ,并设OA OD a ==,利用勾股定理证明出OD OB ⊥,由等腰三角形三线合一得出OD AC ⊥,利用直线与平面垂直的判定定理可证明出OD ⊥平面ABC ,再利用平面与平面垂直的判定定理可得出平面ACD ⊥平面ABC ;(2)以点O 为坐标原点,OA 、OB 、OD 所在直线分别为x 、y 、z 轴建立空间直角坐标系,设2AB =,计算出平面ADE 和ACE 的法向量,利用空间向量法求出二面角D AE C --的余弦值,再利用同角三角函数的基本关系可得出答案.【详解】 (1)ABC ∆是等边三角形,AB BC ∴=,又ABD CBD ∠=∠,BD BD =,ABD CBD ∴∆≅∆,AD CD ∴=,ACD ∆为直角三角形,所以90ADC ∠=,取AC 的中点O ,连接OC 、OD ,则OD AC ⊥,OA OD =.设OA OD a ==,则tan 60OB OA =⋅=o ,又2BD AB AC a ===,222BD OB OD ∴=+,OB OD ∴⊥,又OB AC O =I ,OD ∴⊥平面ABC ,OD ⊂平面ACD ,因此,平面ACD ⊥平面ABC ;(2)由题设及(1)可知OA 、OB 、OD 两两垂直,以点O 为坐标原点,建立如下图所示的空间直角坐标系O xyz -,设2AB =,则()1,0,0A、()B、()1,0,0C -、()0,0,1D ,E 为BD的中点,则12E ⎛⎫ ⎪ ⎪⎝⎭,()1,0,1AD ∴=-uuu r ,()2,0,0AC =-uu u r,12AE ⎛⎫=- ⎪ ⎪⎝⎭uu u r . 设平面ADE 的一个法向量为(),,n x y z =,由00n AD n AE ⎧⋅=⎨⋅=⎩,得0102x z x y z -+=⎧⎪⎨-+=⎪⎩,得3z xy x =⎧⎪⎨=⎪⎩,令x =1y =,z =所以,平面ADE的一个法向量为(31,n =,.同理可得,平面ACE 的一个法向量为(0,m =-u r,cos ,7m n m n m n⋅∴===⋅u r ru r r u r r ,所以,二面角D AE C --=.【点睛】本题考查平面与平面垂直的判定,同时也考查了二面角的计算,在利用空间向量计算二面角时,关键就是要建立合适的空间直角坐标系,并计算出平面的法向量,考查逻辑推理能力与计算能力,属于中等题.20.(1)()22103y x xy +=≠;(2)不存在. 【分析】(1)设点()(),0C x y xy ≠,利用重心的坐标公式得出点G 的坐标为,33x y ⎛⎫⎪⎝⎭,可得出点0,3y Q ⎛⎫⎪⎝⎭,由QA QC =可得出点C 的轨迹E 的方程; (2)由题意得出直线L 的斜率存在,并设直线L 的方程为1y kx =+,设点()11,M x y 、()22,N x y ,将直线L 的方程与曲线E 的方程联立,并列出韦达定理,由2MP PN =,可得出122x x =-代入韦达定理求出k 的值,即可得出直线L 的方程,此时,直线L 过点()1,0-或()1,0,从而说明直线L 不存在. 【详解】(1)设点()(),0C x y xy ≠,则点,33x y G ⎛⎫⎪⎝⎭,由于//QG AB ,则点0,3y Q ⎛⎫⎪⎝⎭. 由QA QC =,可得出2224199y y x +=+,化简得2213y x +=.因此,轨迹E 的方程为()22103y x xy +=≠;(2)当L 与y 轴重合时不符合条件.假设存在直线:1L y kx =+,设点()11,M x y 、()22,N x y .将直线L 的方程与曲线E 的方程联立22113y kx y x =+⎧⎪⎨+=⎪⎩,消去y 得()223220k x kx ++-=,由韦达定理得12223k x x k +=-+,12223x x k =-+. ()11,1MP x y =--uuu r ,()22,1PN x y =-uu u r ,2MP PN =uuu r uuu rQ ,122x x ∴-=,得122x x =-,即122x x =-,()()22221222212432233x x k k k x x k k +⎛⎫+=⋅-=- ⎪+⎝⎭+Q , 另一方面()2212122122112223x x x x k x x x x k +=++=-=-+,得21k =,解得1k =±. 则直线L 过点()1,0-或()1,0,因此,直线L 不存在. 【点睛】本题考查动点的轨迹方程,同时也考查了椭圆中的向量问题,在求解时可充分利用韦达定理设而不求法进行求解,考查运算求解能力,属于中等题. 21.(1)证明见解析;(2)三个零点,证明见解析. 【分析】(1)由函数()y f x =是偶函数,只需利用导数证明函数()y f x =在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值()max 0f x ≤即可;(2)由(1)得出函数()y f x =在区间,22ππ⎡⎤-⎢⎥⎣⎦上只有一个零点,然后利用函数值符号得出该函数在区间[)3,+∞上无零点,利用导数分析函数的单调性,并分析极值的符号,结合零点存在定理得出该函数在区间,32π⎛⎫⎪⎝⎭上有且只有一个零点,由偶函数的性质得出该函数在区间,2π⎛⎫-∞- ⎪⎝⎭上也只有一个零点,从而得出函数()y f x =有三个零点.【详解】(1),,22x ππ⎡⎤∈-⎢⎥⎣⎦,则该函数为偶函数, 只需证()max 0f x ≤,其中0,2x π⎡⎤∈⎢⎥⎣⎦. ()1sin 2f x x x '=-+,()1cos 2f x x ''∴=-. 当0,2x π⎡⎤∈⎢⎥⎣⎦时,令()0f x ''=,得3x π=. 当0,3x π⎡⎤∈⎢⎥⎣⎦时,()0f x ''≤,此时,函数()y f x '=单调递减; 当,32x ππ⎡⎤∈⎢⎥⎣⎦时,()0f x ''≥,此时,函数()y f x '=单调递增.,1024f ππ⎛⎫'=-<⎪⎝⎭, 当0,2x π⎡⎤∈⎢⎥⎣⎦时,()0f x '≤,此时,函数()y f x =单调递减,则()()00f x f ≤=, 因此,对任意的,22x ππ⎡⎤∈-⎢⎥⎣⎦,()0f x ≤; (2)三个零点,证明如下: 由(1)可知,当,22x ππ⎡⎤∈-⎢⎥⎣⎦时,函数()y f x =有一个零点0x =. 当[)3,x ∈+∞时,()9cos 104f x x ≥-+>,此时,函数()y f x =无零点; 当,32x π⎛⎫∈⎪⎝⎭时,()1sin 2f x x x '=-,()1cos 02f x x ''=->.此时,函数()y f x '=单调递增,1024f ππ⎛⎫'=-<⎪⎝⎭,()33sin 302f '=->. 由零点存在定理可知,存在0,32x π⎛⎫∈⎪⎝⎭,使得()00f x '=. 当0,2x x π⎛⎫∈ ⎪⎝⎭时,()0f x '<,此时,函数()y f x =单调递减;当()0,3x x ∈时,()0f x '>,此时,函数()y f x =单调递增.,()002f x f π⎛⎫<<⎪⎝⎭,()53cos304f =+>. 由零点存在定理知,函数()y f x =在区间0,2x π⎛⎫⎪⎝⎭上无零点,在区间()0,3x 上有且只有一个零点,即函数()y f x =在区间,32π⎛⎫⎪⎝⎭上有且只有一个零点. 由于函数()y f x =为偶函数,所以,函数()y f x =在(],3-∞-上无零点,在3,2π⎛⎫-- ⎪⎝⎭上有且只有一个零点.综上所述,函数()y f x =有三个零点. 【点睛】本题考查利用导数证明不等式,以及利用导数研究函数的零点个数问题,解题时要充分利用导数研究函数的单调性,并结合零点存在定理进行分析,考查分析问题和解决问题的能力,属于难题.22.(1)分布列见解析,随机变量X 的数学期望为92;(2)证明见解析; (3)9910021132P ⎛⎫=- ⎪⎝⎭,1009911132P ⎛⎫=+⎪⎝⎭. 【分析】(1)根据题意得出随机变量X 的可能取值有3、4、5、6,利用独立重复试验的概率公式计算出随机变量X 在相应取值时的概率,可列出随机变量X 的分布列,由此计算出随机变量X 的数学期望;(2)根据题意,棋子要到第()1n +站,由两种情况,由第n 站跳1站得到,也可以由第()1n -站跳2站得到,由此得出111122n n n P P P +-=+,并在该等式两边同时减去n P ,可得出所证等式成立;(3)结合(1)、(2)可得1112n n n P P ++⎛⎫-=- ⎪⎝⎭,利用累加法求出数列{}n P 的通项公式,从而可求出99P 和100P 的值. 【详解】(1)由题意可知,随机变量X 的可能取值有3、4、5、6.()311328P X ⎛⎫=== ⎪⎝⎭,()31313428P X C ⎛⎫==⋅= ⎪⎝⎭,()32313528P X C ⎛⎫==⋅= ⎪⎝⎭,()311628P X ⎛⎫=== ⎪⎝⎭.所以,随机变量X 的分布列如下表所示:所以,随机变量X 的数学期望为13319345688882EX =⨯+⨯+⨯+⨯=; (2)根据题意,棋子要到第()1n +站,由两种情况,由第n 站跳1站得到,其概率为12n P ,也可以由第()1n -站跳2站得到,其概率为112n P -,所以,111122n n n P P P +-=+.等式两边同时减去n P 得()()111111198222n n n n n n P P P P P P n +---=-+=--≤≤; (3)由(2)可得01P =,112P =,210113224P P P =+=. 由(2)可知,数列{}1n n P P +-是首项为2114P P -=,公比为12-的等比数列, 111111422n n n n P P -++⎛⎫⎛⎫∴-=⋅-=- ⎪⎪⎝⎭⎝⎭,()()()23999912132999811112222P P P P P P P P ⎛⎫⎛⎫⎛⎫∴=+-+-++-=+-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L L98100111421211123212⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦=+=- ⎪⎛⎫⎝⎭-- ⎪⎝⎭, 又9999989911=22P P ⎛⎫--=- ⎪⎝⎭,则989921132P ⎛⎫=+ ⎪⎝⎭, 由于若跳到第99站时,自动停止游戏,故有10098991111232P P ⎛⎫==+ ⎪⎝⎭. 【点睛】本题考查相互独立事件的概率乘法公式以及等比数列的判定与应用,同时也考查了累加法求数列通项,综合性较强,属于难题.。
