课时作业(五十一)
高中英语课时作业(人教版选修第一册)课时作业 5

课时作业(五)Unit 2Section ⅡLearning AboutLanguage层级一课时跟踪检测维度1单句语法填空1.This time tomorrow, we ________ (sit) in the cinema and watching a film.2.I feel so excited! At that time tomorrow morning, I ________ (fly) to Shanghai.3.In the past three years, Liu Mei ________ (make) great progress in her study.4.Daniel's family ________ (enjoy) their holiday in Huangshan this time next week.5.I ________ (fly) from Miami to New York to meet the other members of the group at this time tomorrow.6.At 7 o'clock this evening we ________ (celebrate) Tom's birthday.7.The car ________ (go) at the present speed until it reaches the foot of the mountain at about nine o'clock tonight.8.Will you ________ (work)on your report this time tomorrow?9.I ________ (tell) him the news when he comes back.10.Look at the dark clouds over there. I think it ________ (rain) soon.11.She ________ (go) to the zoo to see the lovely bear next week.12.Next Friday I will go to another concert.They ________ (play) some music by Mozart at that time.维度2语法与写作1.下个星期的这时候,我们将在那个工厂劳动。
(2021版)课时作业(五)+第七章+一力(北师大版)

当我们在日常办公时,经常会遇到一些不太好编辑和制作的资料。
这些资料因为用的比较少,所以在全网范围内,都不易被找到。
您看到的资料,制作于2021年,是根据最新版课本编辑而成。
我们集合了衡中、洋思、毛毯厂等知名学校的多位名师,进行集体创作,将日常教学中的一些珍贵资料,融合以后进行再制作,形成了本套作品。
本套作品是集合了多位教学大咖的创作经验,经过创作、审核、优化、发布等环节,最终形成了本作品。
本作品为珍贵资源,如果您现在不用,请您收藏一下吧。
因为下次再搜索到我的机会不多哦!温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时作业(五)力(30分钟40分)一、选择题(本大题共5小题,每小题3分,共15分)1.关于力的认识,下列说法中错误的是( )A.力是物体对物体的作用B.力能使物体发生形变或改变物体运动状态C.物体间力的作用是相互的D.只有相互接触的物体才会产生力的作用2.下列哪个物体被托起时所用的力最接近10 N( )3.如图为伦敦奥运会运动项目图标,其中不是利用“力的作用是相互的”这一原理的是( )4.(2013·吉林中考)如图所示的几种现象,能体现出力改变物体运动状态的是( )5.如图所示的实验,表示力的作用效果与( )A.力的大小有关B.力的方向有关C.力的作用点有关D.力的大小、方向和作用点都有关二、填空题(本大题共3小题,每空2分,共10分)6.(2013·娄底中考)现在各中小学都坚持“每天锻炼一小时”。
如图所示是同学们课外活动在玩“造房子”的游戏。
小香同学单脚站立,依次将“物块”踢进事先在地上画好的框内,完成造房任务。
当“物块”被踢出时,主要表明力可以改变物体的。
7.人踢球时,对球施力的物体是,同时也受到球的作用力,这一事例说明。
8.用木棒撬石头时,手握在木棒的末端比握在木棒的中间更容易把石头撬起来,这说明力的不同,力的作用效果不同。
课时作业(五十一) 古典概型与条件概率(含答案)

课时作业(五十一) 古典概型与条件概率一、选择题1.在第1、3、4、5、8路公共汽车都要停靠的一个站(假定这个站只能停靠一辆汽车),有一位乘客等候第4路或第8路汽车.假定当时各路汽车首先到站的可能性相等,则首先到站的正好是这位乘客所需乘的汽车的概率等于( )12..2332..55A B C D 解析:根据题意,基本事件分别是第1、3、4、5、8路公共汽车到站,显然共有5个,而“该乘客所需乘的汽车”包括4路和8路两个,故所求概率P=2.5答案:D2.盒中有10个铁钉,其中8个是合格的,2个是不合格的,从中任取一个恰为合格铁钉的概率是( ) 11..5441..510A B C D 解析:从盒中任取一个铁钉包含基本事件总数为10,其中抽到合格铁钉(记为事件A)包含8个基本事件,所以,所求概率为P(A)84.105== 答案:C3.把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为m,第二次出现的点数为n,向量p =(m,n),q =(-2,1),则向量p ⊥q 的概率为( )1111 (181296)A B C D 解析:∵向量p ⊥q ,∴p ·q =-2m+n=0,∴n=2m,满足条件的(m,n)有3个:(1,2),(2,4),(3,6),∴P=31,3612=故选B. 答案:B4.抛掷甲、乙两枚骰子,若事件A:甲骰子的点数小于3,事件B:甲、乙两枚骰子的点数和等于6.则P(B|A)的值等于( )1111 (31869)A B C D 解析:事件A 包含的基本事件有(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),共12个,而A∩B 包含(1,5),(2,4)共2个.∴P(B|A)=2()136.12()636P AB P A == 答案:C5.设有两个独立事件A 和B 同时不发生的概率为p,A 发生B 不发生与B 发生A 不发生的概率相同,则事件A 发生的概率为( ).2.2.1.1p A pB C D 解析:设P(A)=a,P(B)=b,则P ()1,()1,A a P B b =-=-依题意得(1)(1),(1)(1)(1).(2)a b p a b b a --=⎧⎨-=-⎩ 由(2)得a=b,代入(1)解得a=1答案:C6.(2010·安徽卷)甲从正方形四个顶点中任意选择两个顶点连成直线,乙也从该正方形四个顶点中任意选择两个顶点连成直线,则所得的两条直线互相垂直的概率是( )3456 (18181818)A B C D 解析:由题意知,甲得直线6条,乙得直线6条,因此共得6×6=36对直线.其中互相垂直的有10对,故所求的概率为P 105.3618== 答案:C二、填空题7.将一个体积为27 cm 3的正方体木块表面涂上红色,然后锯成体积为1 cm 3的小正方体,从中任取一块,则这一块恰有两面涂有红色的概率为________.解析:依题意知,基本事件总数n=27,其中恰有两面涂有红色的小正方体个数m=12(每条棱上一个).故所求概率为124.279P == 答案:498.(2009·江苏高考)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为[CD#4].解析:在5个长度中一次抽取2个,则有(2.5,2.6),(2.5,2.7),(2.5,2.8),(2.5,2.9),(2.6,2.7),(2.6,2.8),(2.6,2.9),(2.7,2.8),(2.7,2.9),(2.8,2.9)共10种情况.满足长度恰好相差0.3m 的基本事件有(2.5,2.8),(2.6,2.9)共2种情况,所以它们的长度恰好相差0.3m 的概率为21.105P ==答案:1 59.袋中有3只白球和a只黑球,从中任取2只,全是白球的概率为1.7则a=________.解析:分别记白球为1,2,3号,黑球为4,5,…,a+3号,从中任取2只,有如下基本事件(1,2),(1,3),…,(1,a+3),(2,3),(2,4),…,(2,a+3),…,(a+2,a+3),共(a+2)+(a+1)+…+1=(3)(2)2a a++个,“全部是白球”记为事件A,事件A有(1,2),(1,3),(2,3)共3个,所以P(A)31(3)(2)72a a==++,解得a=4.答案:4三、解答题10.(2009·福建高考)袋中有大小、形状相同的红、黑球各一个,现依次有放回地随机摸取3次,每次摸取一个球.(1)试问:一共有多少种不同的结果?请列出所有可能的结果;(2)若摸到红球时得到2分,摸到黑球时得1分,求3次摸球所得总分为5的概率.解:(1)一共有8种不同的结果,列举如下:(红,红,红),(红,红,黑),(红,黑,红),(红,黑,黑),(黑,红,红),(黑,红,黑),(黑,黑,红),(黑,黑,黑).(2)记“摸球3次所得总分为5”的事件为A.事件A包含的基本事件为:(红,红,黑),(红,黑,红),(黑,红,红),事件A包含的基本事件数为3.由(1)知,基本事件总数为8,所以事件A的概率为P(A)=3 . 811.大世界购物中心拟在国庆节举行购物抽奖活动,规则是:从装有编号为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码之和等于5中一等奖,等于4中二等奖,等于3中三等奖.(1)求中三等奖的概率;(2)求中奖的概率.解:从编号为0,1,2,3的四个小球中,抽出两个,共有6种结果:0和1,0和2,0和3,1和2,1和3,2和3.(1)抽出的两个小球号码之和等于3的有0和3,1和2,共2个结果.故中三等奖的概率为21.63P== (2)记事件A为中奖,则事件A表示不中奖.A包含0和1,0和2两个结果,所以P21 (),63 A==故P(A)=1-2 ().3 P A=12.1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱中,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?解:记事件A:从2号箱中取出的是红球;事件B:从1号箱中取出的是红球.则42131431(),()1(),(|),(|),4233819813P B P B P B P A B P A B +===-=====+++∴P(A)=P(AB)+P ()AB =P(A|B)P(B)+ P(|)A B ·P 421111().933327B ⨯⨯=+=。
2022版高中数学一轮复习课时作业梯级练五十一两条直线的位置关系课时作业理含解析新人教A版

课时作业梯级练五十一两条直线的位置关系一、选择题(每小题5分,共35分)1.已知直线l的倾斜角为,直线l1经过点A(3,2)和B(a,-1),且直线l与l1平行,则实数a的值为( )A.0B.1C.6D.0或6【解析】选C.由直线l的倾斜角为得l的斜率为-1,因为直线l与l1平行,所以l1的斜率为-1.又直线l1经过点A(3,2)和B(a,-1),所以l1的斜率为,故=-1,解得a=6.2.过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是( )A.4x+3y-13=0B.4x-3y-19=0C.3x-4y-16=0D.3x+4y-8=0【解析】选A.因为两直线垂直,直线3x-4y+6=0的斜率为,所以所求直线的斜率k=-,则直线方程为y-(-1)=-(x-4),化简得4x+3y-13=0.3.已知点A,B,直线l的方程为kx-y-k+1=0,且与线段AB相交,则直线l的斜率k的取值X围为( )A.∪B.∪C.D.【解析】选A.直线l:kx-y-k+1=0整理为k-=0即可知道直线l过定点P,作出直线和点对应的图象如图:因为A(2,-3),B(-3,-2),P(1,1),所以k PA==-4,k PB==,要使直线l与线段AB相交,则直线l的斜率k满足k PB≤k或k≤k PA,所以k≤-4或k≥即直线l的斜率的取值X围是(-∞,-4]∪.4.将一X坐标纸折叠一次,使得点(0,2)与点(4,0)重合,点(7,3)与点(m,n)重合,则m+n等于( )A. B. C. D.【解析】选A.由题意可知,纸的折痕应是点(0,2)与点(4,0)连线的中垂线,即直线y=2x-3,它也是点(7,3)与点(m,n)连线的中垂线,于是解得故m+n=.5.已知直线p:3x-2y+1=0,直线q:ax+(b-1)y=0,且p∥q,若a,b均为正数,则+的最小值是( )A. B.C.8D.24【解析】选A.因为直线p:3x-2y+1=0,直线q:ax+(b-1)y=0,且p∥q,所以2a=3(1-b),即+b=1,因为a,b均为正数,所以+=·=+++3=+≥+2=+4=,当且仅当=,即a=b=时取等号,所以+的最小值为.6.已知P1与P2是直线y=kx+1(k为常数)上两个不同的点,则关于x和y的方程组的解的情况是( )A.无论k,P1,P2如何,总是无解B.无论k,P1,P2如何,总有唯一解C.存在k,P1,P2,使之恰有两解D.存在k,P1,P2,使之有无穷多解【解析】选B.由题意,点P1与P2是直线y=kx+1(k为常数)上两个不同的点,直线y=kx+1的斜率存在,所以k=,即a1≠a2,且b1=ka1+1,b2=ka2+1,所以a2b1-a1b2=ka1a2-ka1a2+a2-a1=a2-a1,由方程组(1)×b2-(2)×b1可得:(a1b2-a2b1)x=b2-b1,即(a1-a2)x=b2-b1,所以方程组有唯一的解.7.在平面直角坐标系内,过定点P的直线l:ax+y-1=0与过定点Q的直线m:x-ay+3=0相交于点M,则|MP|2+|MQ|2=( )A. B. C.5D.10【解析】选D.由题意知P(0,1),Q(-3,0),因为过定点P的直线ax+y-1=0与过定点Q的直线x-ay+3=0垂直,所以MP⊥MQ,所以|MP|2+|MQ|2=|PQ|2=9+1=10.二、填空题(每小题5分,共15分)8.已知A,B两点分别在两条互相垂直的直线2x-y=0和x+ay=5上,且线段AB的中点为P,则=.【解析】由于直线2x-y=0与直线x+ay=5垂直,则2-a=0,解得a=2,联立解得所以,直线2x-y=0与直线x+2y=5交于点C, 由直角三角形斜边上的中线的长度等于斜边的长度的一半,且AC⊥BC,所以=2=2=2.答案:29.已知直线l1:4x+y=4,l2:mx+y=0,l3:2x-3my=4.当m=时,这三条直线无法围成三角形. 【解析】当三条直线中的任两条平行,或三条直线交于一点时,三条直线无法围成三角形,当l1∥l2时,=⇔m=4,当l1∥l3时,=⇔m=-,当l2∥l3时,=,无解,当三条直线交于一点时,解得:x=,y=,将点代入直线l3:2x-3my=4,整理为3m2+m-2=0,解得m=-1或m=.综上可知:m=4,-,-1,.答案:4,-,-1,10.已知坐标原点关于直线l1:x-y+1=0的对称点为A,设直线l2经过点A,则当点B(2,-1)到直线l2的距离最大时,直线l2的方程为.【解析】设A(x0,y0),依题意可得解得即A(-1,1).设点B(2,-1)到直线l2的距离为d,当d=|AB|时取得最大值,此时直线l2垂直于直线AB,又-=,所以直线l2的方程为y-1=(x+1),即3x-2y+5=0 .答案:3x-2y+5=0【一题多解】作出直线y=x+1,原点关于直线y=x+1的对称点为A(-1,1),连接AB两点,过A 作AB的垂线,就是直线l2,所以直线l2的方程为3x-2y+5=0.答案:3x-2y+5=01.(5分)若a,b为正实数,直线2x+(2a-3)y+2=0与直线bx+2y-1=0互相垂直,则ab的最大值为( )A.B.C.D.【解析】选B.由直线2x+(2a-3)y+2=0与直线bx+2y-1=0互相垂直,所以2b+2(2a-3)=0,即2a+b=3,又a,b为正实数,所以2a+b≥2,即2ab≤=,当且仅当a=,b=时取“=”,所以ab的最大值为.2.(5分)“a=”是“直线(a+1)x+3ay+1=0与直线(a-1)x+(a+1)y-3=0相互垂直”的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解析】选A.由于直线(a+1)x+3ay+1=0与直线(a-1)x+(a+1)y-3=0,当a=0时,分别化为:x+1=0,-x+y-3=0,此时两条直线不垂直,舍去;当a=-1时,分别化为:-3y+1=0,-2x-3=0,此时两条直线相互垂直,因此a=-1满足条件;当a≠-1,0时,两条直线的斜率分别为:-,,由于两条直线垂直,可得-×=-1,解得a=或-1(舍去).综上可得:两条直线相互垂直的充要条件为:a=或-1.所以“a=”是“直线(a+1)x+3ay+1=0与直线(a-1)x+(a+1)y-3=0相互垂直”的充分而不必要条件.3.(5分)已知直线l1:y=x·sinα和直线l2:y=2x+c,则直线l1与l2( )A.通过平移可以重合B.不可能垂直C.可能与x轴围成等腰直角三角形D.通过绕l1上某点旋转可以重合【解析】选D.根据题意,由于直线l1:y=sin α·x和直线l2:y=2x+c,因为sin α∈[-1,1],所以不存在α,使得sin α=2,故A错误;当sin α×2=-1,即sin α=-时,l1⊥l2,故B错误;由于=2>0,x轴所在直线方程为y=0,要使l1,l2与x轴围成等腰直角三角形,则必有l1⊥l2,所以l1:y=-x,但此时围成的三角形不是等腰三角形,仅为直角三角形,故C错误.由于l1,l2斜率不相等,所以l1,l2相交,当l2绕l1,l2的交点旋转时可以与l1重合,故D正确.【加练备选·拔高】坐标原点O在动直线m(x-2)+n(y-2)=0上的投影为点P,若点Q(-1,-1),那么的取值X围为( )A. B.C. D.【解析】选A.因为动直线m+n(y-2)=0过定点M(2,2),点O在动直线m(x-2)+n=0上的投影为点P,所以∠OPM=90°,则P在以OM为直径的圆上,所以此圆的圆心A坐标为,即A(1,1),半径r=OM=,又Q,所以|AQ|=2>,则点Q在圆外,所以的取值X围为.4.(10分)已知直线l经过直线2x+y-5=0与x-2y=0的交点.(1)点A(5,0)到l的距离为3,求l的方程.(2)求点A(5,0)到l的距离的最大值.【解析】(1)经过两条已知直线交点的直线系方程为(2x+y-5)+λ(x-2y)=0,即(2+λ)x+(1-2λ)y-5=0.所以=3.即2λ2-5λ+2=0,所以λ=2或.所以l的方程为x=2或4x-3y-5=0.(2)由解得交点P(2,1),如图,过P作任一直线l,设d为点A到l的距离,则d≤|PA|(当l⊥PA时等号成立).(其余距离d与PA构成直角三角形,PA 为它们的斜边),所以d max=|PA|=.5.(10分)已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.试确定m,n的值,使(1)l1与l2相交于点P(m,-1);(2)l1∥l2;(3)l1⊥l2,且l1在y轴上的截距为-1.【解析】(1) 由题意得,解得m=1,n=7.(2)当m=0时,显然l1不平行于l2;当m≠0时,由=≠,得所以或即m=4,n≠-2或m=-4,n≠2时,l1∥l2.(3)当且仅当m·2+8·m=0,即m=0时,l1⊥l2.又-=-1,所以n=8.即m=0,n=8时,l1⊥l2,且l1在y轴上的截距为-1.【加练备选·拔高】1.已知直线l1:ax+2y+6=0,直线l2:x+y+a2-1=0.(1)求a为何值时,l1∥l2;(2)求a为何值时,l1⊥l2.【解析】(1)因为要使l1∥l2,所以解得a=-1或a=2(舍去),所以当a=-1时,l1∥l2.(2)因为要使l1⊥l2,所以a·1+2·=0,解得a=,所以当a=时,l1⊥l2.2.已知平面内两点M(4,-2),N(2,4).(1)求MN的垂直平分线方程;(2)直线l经过点A(3,0),且与直线MN平行,求直线l的方程.【解析】(1)因为M(4,-2),N(2,4),所以M,N的中点坐标为(3,1),又k MN==-3,所以MN的垂直平分线的斜率为,则MN的垂直平分线方程为y-1=(x-3),即x-3y=0;(2)因为直线l与直线MN平行,所以直线l的斜率为-3,又直线l经过点A(3,0),所以直线l的方程为y=-3(x-3),即3x+y-9=0.3.某县相邻两镇在一平面直角坐标系下的坐标为A(1,2)、B(4,0),一条河所在直线方程为l:x+2y-10=0,若在河边l上建一座供水站P使之到A,B两镇的管道最省,问供水站P应建在什么地方?此时|PA|+|PB|为多少?【解析】如图所示,过A作直线l的对称点A′,连接A′B交l于P,因为若P′(异于P)在直线l上,高考则|AP′|+|BP′|=|A′P′|+|BP′|>|A′B|.因此,供水站只能在点P处,才能取得最小值.设A′(a,b),则AA ′的中点在l 上,且AA′⊥l,即解得即A′(3,6).所以直线A′B的方程为6x+y-24=0.解方程组得所以P点的坐标为.故供水站应建在点P处,此时|PA|+|PB|=|A′B|==.- 11 - / 11。
新人教版高一语文必修一课时作业5

课时作业5作业时限:45分钟作业满分:60分积累运用1.下列词语中,加点字的读音全都正确的一项是()A.竹篙.(ɡāo)逮捕.(bǔ)潜.伏(qiān)卷帙.浩繁(zhì)B.慰藉.(jiè)淤.泥(wū)混.乱(hùn)垂头丧.气(sànɡ)C.漫溯.(sù)胡诌.(zōu)恍惚.(hú)呶.呶不休(náo)D.踩踏.(tà)狙.击(jū)笼.罩(lǒnɡ)繁文缛.节(rù)解析:A项,潜应读qián;B项,淤应读yū;C项,诌应读zhōu,惚应读hū。
答案:D2.下列句子中,加点的成语使用正确的一项是()A.国足再遭绝杀,无缘冲进2014巴西世界杯赛场的消息传来,中国球迷痛不欲生....。
B.今年我国许多地方的大旱警示我们,本来就水资源匮乏的北京离“水贵如油”的情形指日可待....,节水意识还需要进一步加强。
C.位于2011西安世园会主轴线上的自然馆,建筑体型独特,器宇轩昂....,是2011年西安世界园艺博览会的标志性建筑。
D.日前的李双江之子无照驾车打人事件,与河北大学李启铭交通肇事案如出一辙....,网民均认为事件发生的根本原因在于父母溺爱、管教无方,以及同阶层玩伴间相互影响。
解析:本题考查正确使用成语的能力。
抓语境、析词义是解答此类题的关键。
A项“痛不欲生”,悲痛得不想活下去,形容悲伤到极点。
程度过深,应改为“痛心疾首”。
B项“指日可待”,不久就可以实现。
重在“实现”,而不是“出现”,侧重希望发生的事。
不符合语境。
C项“器宇轩昂”,形容人气质、风度出众,不同一般。
对象误用。
D项“如出一辙”,好像出自同一个车辙。
比喻两件事情非常相似。
答案:D3.下列各句中,没有语病的一句是()A.温家宝总理9月7日主持召开国务院常务会议,听取关于蓬莱19-3油田溢油事故处理情况,研究部署加强环境保护工作。
高三数学第一轮复习课时作业(51)直线与圆锥曲线的位置关系

课时作业(五十一) 第51讲 直线与圆锥曲线的位置关系时间:45分钟 分值:100分基础热身1.2011²哈尔滨二模 已知椭圆C :x24+y2b=1,直线l :y =mx +1,若对任意的m ∈R ,直线l 与椭圆C 恒有公共点,则实数b 的取值范围是( )A .1,4)B .1,+∞)C .1,4)∪(4,+∞)D .(4,+∞)2.直线l 过点(2,0)且与双曲线x 2-y 2=2仅有一个公共点,这样的直线有( ) A .1条 B .2条 C .3条 D .4条3.直线x -y +3=0与曲线y 29-x |x |4=1的交点个数是( )A .4B .3C .2D .14.2011²西铁一中二模 若直线y =kx +2与双曲线x 2-y 2=6的右支交于不同的两点,则k 的取值范围是( )A.⎝ ⎛⎭⎪⎫-1531 B.⎝ ⎛⎭⎪⎫0,153 C.⎝⎛⎭⎪⎫-1530 D.⎝ ⎛⎭⎪⎫-153,153 能力提升5.设O 是坐标原点,F 是抛物线y 2=2px (p >0)的焦点,A 是抛物线上的一点,与x 轴正向的夹角为60°,则||为( )A.21p 4B.21p 2C.136p D.1336p 6.过抛物线y 2=4x 的焦点作一条直线与抛物线相交于A 、B 两点,它们的横坐标之和等于5,则这样的直线( )A .有且仅有一条B .有且仅有两条C .有无穷多条D .不存在7.2011²舟山七校联考 椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率e =23,A ,B 是椭圆上关于x 、y轴均不对称的两点,线段AB 的垂直平分线与x 轴交于点P (1,0).设AB 的中点为C (x 0,y 0),则x 0的值为( )A.95B.94C.49D.598.已知直线y =k (x +2)(k >0)与抛物线C :y 2=8x 相交于A 、B 两点,F 为C 的焦点,若|FA |=2|FB |,则k =( )A.13B.23C.23D.2239.2011²全国卷 已知抛物线C :y 2=4x 的焦点为F ,直线y =2x -4与C 交于A ,B 两点.则cos ∠AFB =( )A.45B.35C .-35D .-4510.若直线l :tx -y +6=0与曲线C :x 2-y 2=2有两个不同交点,则实数t 的取值范围是________.11.过点(0,2)的双曲线x 2-y 2=2的切线方程是________.12.设已知抛物线C 的顶点在坐标原点,焦点为F (1,0),直线l 与抛物线C 相交于A ,B 两点.若AB 的中点为(2,2),则直线l 的方程为________.13.已知双曲线x29-y216=1,过其右焦点F 的直线交双曲线于P ,Q 两点,PQ 的垂直平分线交x 轴于点M ,则|MF ||PQ |=________.14.(10分)已知抛物线y 2=2px (p >0)的对称轴上的定点M (m,0)(m >0),过点M 作直线AB 与抛物线相交于A ,B 两点.(1)试证明A ,B 两点的纵坐标之积为定值;(2)若点N 是定直线l :x =-m 上的任一点,证明:直线AN ,MN ,BN 的斜率成等差数列.15.(13分)2011²江西卷 P (x 0,y 0)(x 0≠±a )是双曲线E :x 2a 2-y2b 2=1(a >0,b >0)上一点,M ,N 分别是双曲线E 的左、右顶点,直线PM ,PN 的斜率之积为15.(1)求双曲线的离心率;(2)过双曲线E 的右焦点且斜率为1的直线交双曲线于A ,B 两点,O 为坐标原点,C 为双曲线上一点,满足=λ+,求λ的值.难点突破16.(12分)2011²银川一中月考 已知曲线C 上任意一点M 到点F (0,1)的距离比它到直线l :y =-2的距离小1.(1)求曲线C 的方程; (2)过点P (2,2)的直线m 与曲线C 交于A 、B 两点,设=λ,当△AOB 的面积为42时(O 为坐标原点),求λ的值.课时作业(五十一)【基础热身】1.C 解析 直线恒过定点(0,1),只要该点在椭圆内部或椭圆上即可,故只要b ≥1且b ≠4.2.C 解析 点(2,0)恰是双曲线的一个顶点,过该点仅有一条直线与双曲线相切,而过该点与双曲线的渐近线平行的两条直线也与双曲线仅有一个公共点,故这样的直线有3条.3.B 解析 当x ≥0时,方程是y29-x24=1,当x <0时,方程是y29+x24=1,作图即知.4.A 解析 联立方程⎩⎨⎧y =kx +2,x 2-y 2=6,消去y 后得 (1-k 2)x 2-4kx -10=0,设交点坐标为(x 1,y 1),(x 2,y 2),则1-k 2≠0,Δ=(-4k )2+40(1-k 2)>0,x 1+x 2=4k 1-k 2>0,x 1x 2=-101-k2>0,解不等式组得-153<k <-1. 【能力提升】5.B 解析 过A 作AD ⊥x 轴于D ,令|FD |=m ,则|FA |=2m ,p +m =2m ,m =p , ∴OA =⎝⎛⎭⎫p 2+p 2+(3p )2=212p .6.B 解析 方法1:该抛物线的通径长为4,而这样的弦AB 的长为x A +x B +p =7,故这样的直线有且仅有两条.方法二:①当该直线的斜率不存在时,它们的横坐标之和等于2,不合题意. ②当该直线的斜率存在时,设该直线方程为y =k (x -1),代入抛物线方程得 k 2x 2-(2k 2+4)x +k 2=0,由x 1+x 2=2k 2+4k 2=5⇒k 2=43⇒k =±233.故这样的直线有且仅有两条.7.B 解析 设A (x 1,y 1),B (x 2,y 2).由于点A ,B 在椭圆x 2a +y 2b =1(a >b >0)上,所以x 21a +y 21b1,x 22a 2+y 22b 2=1,两式相减得(x 1+x 2)(x 1-x 2)a 2+(y 1+y 2)(y 1-y 2)b 2=0.设直线AB 的斜率为k ,则得k =-b 2x 0a 2y 0,从而线段AB 的垂直平分线的斜率为a 2y 0b 2x 0,线段AB 的垂直平分线的方程为y -y 0=a 2y 0b 2x 0x-x 0).由于线段AB 的垂直平分线与x 轴交于点P (1,0),所以0-y 0=a 2y 0b 2x 0(1-x 0),解得x 0=a2a 2-b2.a 2a 2-b 2=a 2c 2=⎝⎛⎭⎫1e 2.所以x 0=94. 8.D 解析 设A (x 1,y 1),B (x 2,y 2),直线y =k (x +2)与抛物线y 2=8x 联立,消掉y 得k 2x 2+(4k 2-8)x +4k 2=0.根据韦达定理x 1x 2=4,(1).根据焦点半径公式,有|FA |=x 1+2,|FB |=x 2+2,由|FA |=2|FB |,得x 1=2x 2+2,(2),由(1)(2)解得x 2=1(负值舍去),故点B 的坐标为(1,22),将其代入y =k (x +2)(k >0)得k =223. 9.D 解析 法一:联立直线与抛物线的方程,消去y 得x 2-5x +4=0,∴x =1或4,得A (1,-2),B (4,4),则|AF |=2,|BF |=5,|AB |=35,由余弦定理得cos ∠AFB =-45.法二:联立方程⎩⎨⎧y =2x -4,y 2=4x ,解得x =1或x =4,所以交点坐标分别为A (1,-2),B (4,4),又F (1,0),∴=(3,4),=(0,-2),所以cos ∠AFB ==-85³2=-45.10.(-2,-1)∪(-1,1)∪(1,2) 解析 直线与曲线方程联立,消掉y 得(1-t 2)x 2-26tx -8=0,直线与双曲线交于不同两点的充要条件是1-t 2≠0且Δ=(26t )2-4(1-t 2)³(-8)>0,解得t 2<4且t 2≠1.11.y =±3x +2 解析 设切线方程为y =kx +2,代入双曲线方程得(1-k 2)x 2-4kx -6=0,由Δ=16k 2+24(1-k 2)=0,解得k =±3,故所求的切线方程为y =±3x +2.12.y =x 解析 由已知抛物线方程为y 2=4x .直线l 的斜率不存在时,根据抛物线的对称性,点(2,2)不可能是AB 的中点,故直线l 的斜率存在,设直线方程斜率为k ,则直线l 的方程是y-2=k (x -2)且k ≠0,与抛物线方程y 2=4x 联立消去x ,则y 2-4⎝⎛⎭⎫y -2k +2=0,即y 2-4k y +8k-8=0.设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=4k y 1+y 22=2,即2k=2,解得k =1,故所求的直线方程是y -2=x -2,即y =x .13.56 解析 右焦点F 的坐标是(5,0),设直线PQ 的方程是x =my +5,代入双曲线方程得(16m2-9)y 2+160my +162=0.设P (x 1,y 1),Q (x 2,y 2),则y 1+y 2=-160m 16m 2-9,y 1y 2=16216m 2-9, 则|PQ |=1+m2⎝⎛⎭⎫-160m 16m 2-92-4²16216m 2-9=96(1+m 2)|16m 2-9|. 设PQ 的中点N (x 0,y 0),则y 0=-80m 16m 2-9,x 0=-80m 216m 2-9+5=-4516m 2-9. 设M (t,0),则y 0x 0-t =-m ,即t =y 0m +x 0=-12516m 2-9故|MF |=|t -5|=⎪⎪⎪⎪-12516m 2-9-5=80(1+m 2)|16m 2-9|. 所以|MF ||PQ |=8096=56.14.解答 (1)证明:设A (x 1,y 1),B (x 2,y 2),则有y 1y 2=-2pm ,下证之:设直线AB 的方程为:x =ty +m ,与y 2=2px 联立得⎩⎨⎧y 2=2px ,x =ty +m ,消去x ,得y 2-2pty -2pm=0,由韦达定理得y 1y 2=-2pm .(2)证明:设点N (-m ,n ),则直线AN 的斜率为k AN =y 1-n x 1+m ,直线BN 的斜率为k BN =y 2-nx 2+m, ∴k AN +k BN =y 1-n y 212p +m +y 2-n y 222p +m =2p (y 1-n )y 21+2pm +2p (y 2-n )y 22+2pm =2p ⎝⎛⎫y 1-n y 1-y 1y 2+y 2-n y 2-y 1y 2=2p ²y 2(y 1-n )-y 1(y 2-n )y 1y 2(y 1-y 2)=2p ²n (y 1-y 2)y 1y 2(y 1-y 2)=2p ²n y 1y 2=2p ²n -2pm =-nm又∵直线MN 的斜率为k MN =n -0-m -m =-n2m,∴k AN +k BN =2k MN ,即直线AN ,MN ,BN 的斜率成等差数列.15.解答 (1)点P (x 0,y 0)(x 0≠±a )在双曲线a 2-b 2=1上,有x 20a 2-y 2b2=1,由题意又有y 0x 0-a ²y 0x 0+a =15,可得a 2=5b 2,c 2=a 2+b 2=6b 2,则e =c a =305.(2)联立⎩⎨⎧x 2-5y 2=5b 2,y =x -c得4x 2-10cx +35b 2=0,设A (x 1,y 1),B (x 2,y 2),则⎩⎨⎧x 1+x 2=5c 2,x 1x 2=35b24.①设=(x 3,y 3),=λ+,即⎩⎨⎧x 3=λx 1+x 2,y 3=λy 1+y 2,又C 为双曲线上一点,即x 23-5y 23=5b 2,有(λx 1+x 2)2-5(λy 1+y 2)2=5b 2,化简得:λ2(x 21-5y 21)+(x 22-5y 22)+2λ(x 1x 2-5y 1y 2)=5b 2. 又A (x 1,y 1),B (x 2,y 2)在双曲线上,所以x 21-5y 21=5b 2,x 22-5y 22=5b 2.②由①式又有x 1x 2-5y 1y 2=x 1x 2-5(x 1-c )(x 2-c )=-4x 1x 2+5c (x 1+x 2)-5c 2=10b 2,得:λ2+4λ=0,解得λ=0或λ=-4. 【难点突破】16.解答 (1)∵点M 到点F (0,1)的距离比它到直线l :y =-2的距离小1,∴点M 在直线l 的上方,点M 到F (0,1)的距离与它到直线l ′∶y =-1的距离相等, ∴点M 的轨迹C 是以F 为焦点,l ′为准线的抛物线,∴曲线C 的方程为x 2=4y .(2)当直线m 的斜率不存在时,它与曲线C 只有一个交点,不合题意, 设直线m 的方程为y -2=k (x -2),即y =kx +(2-2k ),代入x 2=4y 得x 2-4kx +8(k -1)=0(*),Δ=16(k 2-2k +2)>0对k ∈R 恒成立,所以直线m 与曲线C 恒有两个不同的交点. 设交点A ,B 的坐标分别为A (x 1,y 1),B (x 2,y 2), 则x 1+x 2=4k ,x 1x 2=8(k -1). ∴|AB |=(x 2-x 1)2+(y 2-y 1)2=(1+k 2)[(x 2+x 1)2-4x 1x 2]=4(1+k 2)(k 2-2k +2),点O 到直线m 的距离d =|2-2k |1+k2,∴S △ABO =12|AB |d =4|k -1|k 2-2k +2=4(k -1)4+(k -1)2,∵S △ABO =42,∴4(k -1)4+(k -1)2=42,∴(k -1)4+(k -1)2-2=0,∴(k -1)2=1或(k -1)2=-2(舍去), ∴k =0或k =2.当k=0时,方程(*)的解为x=±2 2. 若x1=22,x2=-22,2-22=3-22;则λ=-22-2若x1=-22,x2=22,2+22=3+2 2.则λ=22-2当k=2时,方程(*)的解为4±2 2. 若x1=4+22,x2=4-22,-2-22则λ==3+22;2-22若x1=4-22,x2=4+22,-2+22则λ==3-2 2.2+22所以λ=3+22或3-2 2.。
2019-2020学年新教材高中数学第五章三角函数5.5.1.4二倍角的正弦余弦正切公式
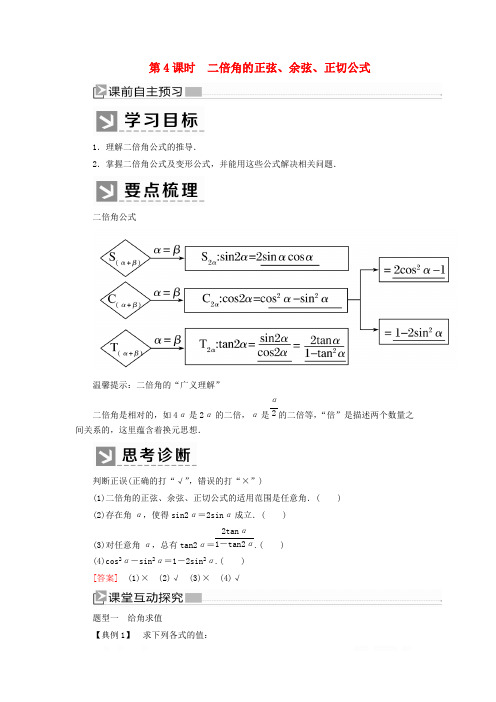
(4)原式=
2sin20°
2sin40°·cos40°·cos80° 2sin80°·cos80°
=
4sin20°
= 8sin20°
sin160° 1 =8sin20°=8.
(1)记住公式的推导过程及公式特征以便于应用. (2)与公式不符,但是适当变形后就可套用公式的,要先变形化简再求值.
[针对训练] 1.求下列各式的值.
( ) ( ) 12
5 120
-
-
因此,sin2α=2sinαcosα=2× 13 × 13 =169.
故选 D.
[答案] D
2.cos275°+cos215°+cos75°cos15°的值等于( )
635
3
A. 2 B.2 C.4 D.1+ 4
[解析] 原式=sin215°+cos215°+sin15°cos15°
[针对训练] 3.化简:(1) 1+sin20°+ 1-sin20°;
1+sin4α+cos4α (2)1+sin4α-cos4α. [解] (1)原式= sin210°+cos210°+2sin10°cos10°+
sin210°+cos210°-2sin10°cos10°
= sin10°+cos10°2+ sin10°-cos10°2 =|sin10°+cos10°|+|sin10°-cos10°|
[答案] B
π
π
2.sin412-cos4 12等于( )
1
31 3
A.-2 B.- 2 C.2 D. 2
( )( ) π
π
π
π
sin2 +cos2 sin2 -cos2
[解析] 原式= 12
12
12
【人教版】高一语文必修一全一册优质课时作业(含答案)

【人教版】高一语文必修一全一册优质课时作业(含答案)课时作业 1[基础演练]1.下列加点字的读音完全相同的一项是()A.百舸.孟轲.沉疴.枝柯.B.怅.惘蚊帐.苌.弘伥.鬼C.峥.嵘狰.狞挣.扎风筝.D.寥廓.城郭.敦.厚淳.厚解析:A项,“舸”读“ɡě”,其余都读“kē”;B项,读音依次为“chànɡ”“zhànɡ”“chánɡ”“chānɡ”;C项,都读“zhēn ɡ”;D项,读音依次为“kuò”“ɡuō”“dūn”“chún”。
答案:C2.下面加点词的解释都正确的一项是()A.挥斥..(力量)方遒怅.(失意)寥廓漫.(满)江B.浪遏.(阻止)飞舟主.(主宰)沉浮鹰击.(搏击)长空C.百侣.(同伴)激扬...(地位很高的人)..(激浊扬清)万户侯D.击水..(不平凡)岁月稠.(多)..(击打水)峥嵘解析:A项,“挥斥”的意思是“奔放”。
“怅”在这里表达由深思而引发的激昂慷慨的心绪。
C项,“万户侯”在本词中指大军阀、大官僚。
D项,“击水”的意思是“游泳”。
答案:B阅读下面的文字,完成3~5题。
《沁园春·长沙》这首词上阕主要是写景抒情,下阕主要是回忆往事,用诗中的“问苍茫大地,谁主沉浮?”把这首词的上阕和下阕联系起来,从“谁主沉浮”的设问到“粪土当年万户侯”的豪情,再到“到中流击水”的壮志,鲜明地彰显出诗人少年时期的________,含蓄地回答了“谁主沉浮”的问题,()。
诗人运用对比手法,把诗人心忧天下和人民的生活处于________之中的情景和祖国的大好河山形成了鲜明的对比,这种强烈的对比反差展现了人民无法做江山主人的悲哀,诗人在________,充分显露出诗人要改造旧天地,建立新世界的决心和胸怀。
从湖南农村走出的一个农民的儿子,到是一位“问苍茫大地谁主沉浮”的负重之人,再到“埋骨何须桑梓地”的有志之士,最后能够“指点江山,激扬文字”的血性青年。
河北省邯郸市重点中学高三数学规范性课时作业(五十一)(学生版)

课时作业(五十一)一、选择题1.中心在坐标原点的椭圆,焦点在x 轴上,焦距为4,离心率为22,则该椭圆的方程为( )A.x 216+y 212=1 B.x 212+y 28=1 C.x 212+y 24=1 D.x 28+y 24=1 2.已知椭圆C 的上、下顶点分别为B 1、B 2,左、右焦点分别为F 1、F 2,若四边形B 1F 1B 2F 2是正方形,则此椭圆的离心率e 等于( )A.13B.12C.22D.323.设F 1,F 2是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,P 为直线x =3a2上一点,△F 2PF 1是底角为30°的等腰三角形,则E 的离心率为( )A.12 B.23 C.34D.454.已知圆(x +2)2+y 2=36的圆心为M ,设A 为圆上任一点,N (2,0),线段AN 的垂直平分线交MA 于点P ,则动点P 的轨迹是( )A .圆B .椭圆C .双曲线D .抛物线5.若点O 和点F 分别为椭圆x 24+y 23=1的中心和左焦点,点P 为椭圆上的任意一点,则OP →·FP →的最大值为( )A .2B .3C .6D .86.过椭圆C :x 25+y 2=1的右焦点F 作直线l 交椭圆C 于A 、B 两点,交y 轴于点M ,若MA →=λ1AF →,MB →=λ2BF →,则λ1+λ2=( )A .10B .5C .-5D .-10二、填空题7.已知椭圆C :x 2a 2+y 2b 2=1(a >0,b >0)的右焦点为F (3,0),且点⎝ ⎛⎭⎪⎫-3,322在椭圆C上,则椭圆C 的标准方程为________.8.设F 1,F 2分别是椭圆x 216+y 212=1的左、右焦点,点P 在椭圆上,若△PF 1F 2为直角三角形,则△PF 1F 2的面积等于________.9.椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别是F 1,F 2,过F 2作倾斜角为120°的直线与椭圆的一个交点为M ,若MF 1垂直于x 轴,则椭圆的离心率为________.三、解答题10.根据下列条件求椭圆的标准方程:(1)已知P 点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为435和235,过P 作长轴的垂线恰好过椭圆的一个焦点;(2)经过两点A (0,2)和B ⎝⎛⎭⎫12,3.11.如图,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,上顶点为A ,在x 轴负半轴上有一点B ,满足BF 1→=F 1F 2→,AB ⊥AF 2.(1)求椭圆C 的离心率;(2)D 是过A ,B ,F 2三点的圆上的点,D 到直线l :x -3y -3=0的最大距离等于椭圆长轴的长,求椭圆C 的方程.12.已知动点M (x ,y )到直线l :x =4的距离是它到点N (1,0)的距离的2倍. (1)求动点M 的轨迹C 的方程;(2)过点P (0,3)的直线m 与轨迹C 交于A ,B 两点,若A 是PB 的中点,求直线m 的斜率.[热点预测]13.设F 1、F 2分别是椭圆x 24+y 2=1的左、右焦点.(1)若P 是第一象限内该椭圆上的一点,且PF 1→·PF 2→=-54,求点P 的坐标;(2)设过定点M (0,2)的直线l 与椭圆交于不同的两点A 、B ,且∠AOB 为锐角(其中O 为坐标原点),求直线l 的斜率k 的取值范围.。
2020高三数学一轮复习(人教版文):课时作业51圆 的 方 程

7.在圆x2+y2-2x-6y=0内,过点E(0,1)的最长弦和最短弦分别为AC
和BD,则四边形ABCD的面积为( )
A.5 2
B.10 2
C.15 2
D.20 2
解析 圆的标准方程为(x-1)2+(y-3)2=10,则圆心(1,3),半径r= 10,由题意知AC⊥BD,且|AC| =2 10,|BD|=2 10-5=2 5,所以四 边形ABCD的面积为S=12|AC|·|BD|=21×2 10×2 5=10 2。
解析 过点M的最短弦与CM垂直,圆C:x2+y2-4x-2y=0的圆心为
C(2,1),因为kCM=
1-0 2-1
=1,所以最短弦所在直线的方程为y-0=-(x-
1),即x+y-1=0。
答案 x+y-1=0
10.(2019·湖南湘东五校联考)圆心在抛物线y=
1 2
x2(x<0)上,且和该抛
物线的准线及y轴都相切的圆的标准方程为________。
答案 B
6.已知圆C:x2+y2+Dx+Ey+F=0,则“E=F=0且D<0”是“圆C 与y轴相切于原点”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
解析 圆C与y轴相切于原点⇔圆C的圆心在x轴上(设坐标为(a,0)),且 半径r=|a|,所以当E=F=0且D<0时,圆心为-D2 ,0,半径为D2,圆C 与y轴相切于原点;圆(x+1)2+y2=1与y轴相切于原点,但D=2>0,故选 A。
解析 直线x-y+1=0与x轴的交点(-1,0)。根据题意,圆C的圆心 坐标为(-1,0)。因为圆与直线x+y+3=0相切,所以半径为圆心到切线的 距离,即r=d=|-11+2+0+123|= 2,则圆的方程为(x+1)2+y2=2。
课时作业(五十一)

课时作业(五十一)数学建模案例(二):距离问题1.春节期间,佳怡去探望奶奶,她到商店买了一盒点心.为了美观起见.售货员对点
心盒做了一个捆扎(如图1),并在角上配了一个花结.售货员说:“这样的捆扎不仅漂亮,而且比一般的十字捆扎方式(如图2)包装更节省彩绳.你同意这种说法吗?请给出你的理由.(注:长方体点心盒的高小于长、宽)
2.如图,广场上有一盏路灯挂在高10 m的电线杆上,记电线杆的底部为A,顶部为S.把路灯看作一个点光源,身高1.5 m的女孩站在离点A5 m的点B处.回答下面的问题:
(1)若女孩以5 m为半径绕着电线杆走一个圆圈,人影扫过的是什么图形,求这个图形的面积;
(2)若女孩向点A前行4 m到达点D,然后从点D出发,沿着以BD为对角线的正方形走一圈,画出女孩走一圈时头顶影子的轨迹,说明轨迹的形状.。
课时作业5:Unit 1 Art

Unit 1 ArtⅠ.单词拼写1.The weather at the moment is not __________(典型的)for July.2.The artist combines different ________(技术) in the same painting.3.It was ________(荒谬的)that this should be so difficult to say.4.We may talk of beautiful things, but beauty itself is ______(抽象的).5.The museum has several lifesized__________(雕塑)of people and animals.6.We can't ________(预测)future events.7.I'm interested in ________(当代的)Chinese literature.8.They finally ________(采纳) our advice on how to finish the work.9.He ________(努力)to watch the wonderful film, but failed.10.Check your ________(财产)before you get off the bus.Ⅱ.用所给词的适当形式填空1.I missed the train and ________ (consequent) was late for work.2.When you get something wrong, it can shake your ________ (believe) in yourself.3.She was rewarded for her 30 years' ________ (faith) service with the community.4.I like her very much, and the ________ (behave) of the other students shows that they like her, too.5.Mahatma Gandhi was both a political and a ______________ (religion) figure in Indian history.6.The police arrested him and took ________ (possess) of certain substances found in his house.7.The outcome of the election was correspondent with my ________ (predict).8.I ________ (specific) told you not to go near the water.9.He worked very hard and gave a deep ________ (impress) on me.10.Two years ago he went to the USA and wanted to live ________ (permanent) there.Ⅲ.单句语法填空1.Over the last seventeenth century the painting styles ________ (change) a great deal.2.He was the first painter ________ (work) outdoors.3.It took ________ (little) money to build the house than before.4.This is the masterpiece ________ he is famous for.5.Mike is allergic ________ fresh flowers.6.It was up to me ________ do the cleaning.7.He visited a lot of places of interest, ________ (include) the West Lake and the Great Wall.8.The beautiful garden is well worth ________ (visit).9.The beauty of the charming girl appealed ________ the young man.10.He is considering ________ (buy) a flat in the town, which is considered ________ (be) convenient.Ⅳ.课文语法填空As is known __1__ all, art is influenced by the customs and faith of a people. Styles in Western art have changed many times.During the Middle Ages, the main aim of painters was __2__ (represent) religious themes.__3__ a result, some pictures at this time were full of religious symbols, __4__ created a feeling of respect and love for God.During the Renaissance, people began to concentrate less __5__ religious themes and adopt a more humanistic attitude __6__ life.In the late 19th century, some painters became the Impressionists. And they were the first painters __7__ (paint)outdoors.Paintings can reflect the __8__ (develop) of civilization, and it is interesting to predict__9__ styles of paintings there will be in the future. Why not try to visit some art galleries to appreciate different __10__ (style) of paintings?参考答案Ⅰ.单词拼写答案1.typical 2.technique 3.ridiculous 4.abstract5.sculptures 6.predict7.contemporary8.adopted9.attempted10.possessionsⅡ.用所给词的适当形式填空答案1.consequently 2.belief 3.faithful 4.behaviour5.religious 6.possession7.prediction8.specifically9.impression10.permanentlyⅢ.单句语法填空答案与解析1.have changed over the last seventeenth century与现在完成时连用。
课时作业51:第10课 劝学 师说

劝学师说一、语言应用1.下列句中加点词的解释,有误的一项是 ( )A.木直中.绳中:符合,合乎B.善假.于物也假:借助C.是故无.贵无贱无:无论,不分D.六艺经传皆通.习之通:精通2.下列各句中加点的虚词,意义与用法都相同的一组是 ( )A.师之.所存也欲人之.无惑也难矣B.冰,水为之,而.寒于水吾尝终日而.思矣C.善假于.物也于.其身也D.其.闻道也固先乎吾其.皆出于此乎3.下列句子中与其他三句句式不相同的一项是( )A.青,取之于蓝,而青于蓝B.师者,所以传道受业解惑也C.冰,水为之,而寒于水D.师不必贤于弟子4.从词类活用的角度看,下列各句中加点词的用法不同于其他三项的一项是 ( )A.惑.而不从师B.是故圣.益圣,愚益愚C.小.学而大遗D.位卑.则足羞5.(2019·石家庄高一检测)根据语境,下列三句话,依次填入横线处最恰当的一项是( )一位学生向老师请教做人、做事、做学问的方法。
老师说:“______ ,________,创业酌用兵家之权变,________,行文当如纵横家之灵活。
采百家之学问而集于一身,必成贤者。
”①治事应持法家之严明②待人应守儒家之诚信③读书当如墨家之兼爱A.①②③B.②①③C.③①②D.②③①6.翻译下面的句子。
(1)君子博学而日参省乎己,则知明而行无过矣。
(2)彼童子之师,授之书而习其句读者,非吾所谓传其道解其惑者也。
(3)闻道有先后,术业有专攻,如是而已。
7.补写出下列句子的空缺部分。
(1)孔子曰:“学而时习之。
”又说:“生而知之者,上也;学而知之者,次也。
”荀子在《劝学》中提出“____________”的观点,继承并发展了孔子对学习的认识。
(2)儒道两家都曾用行路来形象地论述积累的重要性。
《老子》中说“九层之台,起于累土。
千里之行,始于足下。
”荀子在《劝学》中说“____________,____________”。
(3)《劝学》中指出:“青,取之于蓝,而青于蓝。
课时作业51:立足文本,思考深广,探究丰富意蕴

对点专练六立足文本,思考深广,探究丰富意蕴一、阅读下面的文字,完成文后题目。
1956年元旦那场雪徐剑1956年新年,并非中国农历的元春之始,天气很冷。
2012年夏,李旭阁[注]在北戴河海滨回忆起来,记忆难免有误,但他非常确定地对我说,那年元旦,北京城里落了一场大雪。
雪是从1956年元旦凌晨下起来的,飞飞扬扬了一夜。
第二天清晨,人们推门一看,雪拥长街,行人稀落,北京城郭上下一抹白,若从空中俯瞰,犹如一张巨大宣纸铺陈其上,而匆匆而过的行人,就像泼墨于宣纸上的一滴墨、一个点、一行雁痕鸿爪。
天上一片雪,地下一世界。
李旭阁说,他记得昨天晚上离开中南海居仁堂时,天还晴得好。
早已过了下班时间,黄昏泛起,1955年最后一抹夕阳照在中南海居仁堂红墙黄瓦的林苑里。
时任军委作战部特种兵处技术组参谋的李旭阁少校,将最后一页台历撕下来,然后,走到窗前,将目光透过古老花格窗的玻璃,投向红墙内外。
一元复始春将至啊。
窗外,如火如荼的公私合营运动,遍及每个角隅,热火朝天的场面浮现于京畿的天空,新中国的青春之姿与萧索的北方冬季相峙。
明天就是元旦,终于可以放松一下,带着孩子妻子出去走走了。
李旭阁将目光从窗外收回来,收拾了东西,正准备穿上军大衣离去时,特种兵处处长杨坤上校突然走了进来。
“有要紧之事?”李旭阁问。
“是啊!”杨坤扬了扬手中一张入场券说,“明天下午三点新街口排练场有场很重要的讲座,让你参加。
”“什么讲座?”“我也不知道。
”杨坤处长颇有几分神秘地说,“作战部王尚荣部长点了你的名,据说,听讲座的都是驻京各大单位的上将、大将。
”“啊!”李旭阁一脸骇然,规格这么高呀。
“作战部就发了两张票,王部长和你一起参加,有困难吗?”“没有!”李旭阁摇了摇头。
“好!”暮霭落了下来,西天最后一抹紫阳被中南海冰湖的暮霭融尽。
李旭阁骑车从居仁堂出来,右拐,从六部口,绕着红墙北行,过毛家湾,从国管局门口向西,穿过红楼电影院,往武衣库总参作战部宿舍骑去。
这时,夜色如潮水泛起,街灯昏黄如豆,在薄暮中犹如一只只夏夜里的萤火虫,将北京的万家灯火引燃了,他的身前身后,便是一片灯河,一条人间天河。
课时作业(五十一) 机械波及其常见现象

课时作业(五十一) 机械波及其常见现象1.关于波的干涉和衍射,正确的说法是( )A .有的波能发生干涉现象,有的波不能发生干涉现象B .产生干涉现象的必要条件之一,就是两列波的频率相等C .只有在障碍物的尺寸与波长比较相差不多或小得多,才能发生衍射现象D .在干涉图样中,振动加强区域的质点,其位移始终保持最大;振动减弱区域的质点,其位移始终保持最小2.根据多普勒效应,下列说法中正确的有( ) A .多普勒效应只适用于声波B .当波源和观察者同向运动时,观察者接收到的频率一定比波源发出的频率低C .当波源和观察者相向运动时,观察者接收到的频率一定比波源发出的频率高D .当波源和观察者反向运动时,观察者接收到的频率一定比波源发出的频率高3.如图所示,S 是某介质中振源,MN 是带孔挡板,其中M 固定,N 可上下移动,为了使原来不振动的A 点振动起来,可采用( )第3题图A .增大S 的频率B .减小S 的频率C .N 上移D .N 下移4.一简谐横波以4m/s 的波速沿x 轴正方向传播.已知t =0时的波形如图所示,则( )第4题图A .波的周期为1sB .x =0处的质点在t =0时向y 轴负向运动C .x =0处的质点在t =14s 时速度为0D .x =0处的质点在t =14s 时速度值最大5.如图所示,S 1、 S 2是两个相干波源,它们振动同步且振幅相同.实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷.关于图中所标的a 、 b 、 c 、 d 四点,下列说法中正确的有( )第5题图A.该时刻a质点振动最弱,b、c质点振动最强,d质点振动既不是最强也不是最弱B.该时刻a质点振动最弱,b、c、d质点振动都最强C.a质点的振动始终是最弱的,b、c、d质点的振动始终是最强的D.再过T/4后的时刻a、b、c三个质点都将处于各自的平衡位置,因此振动最弱6.如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为4m/s,则()第6题图A.质点P此时刻的振动方向沿y轴正方向B.P点振幅比Q点振幅小C.经过Δt=3s,质点Q通过的路程是0.6mD.经过Δt=3s,质点P将向右移动12m7.沿x轴方向的一条细绳上有O、A、B、C四点,OA=AB,BC=5AB,质点O在垂直于x轴方向做简谐运动,沿x轴传播形成横波.t=0时刻,O点开始向上运动,经t=0.2s,O点第一次到达上方最大位移处,这时A点刚好开始运动.那么在t=2.5s时刻,关于质点B和C运动情况,以下描述中正确的是()第7题图A.B点位于x轴下方B.C点位于x轴下方C.B点正向上运动D.C点正向上运动8.(1)如图甲所示,水槽内有一振源,振动时产生的水波通过一个小缝隙发生衍射现象,为了使衍射现象更明显,可采用的方法是使小缝隙的宽度________;或者是使振源的振动频率________.(2)如图乙所示,实线表示两个相干波源S1、S2发出的波的波峰位置,图中的________点为振动加强的位置,图中的________点为振动减弱的位置.乙第8题图9.一根长绳左端位于平面直角坐标系的O点,t=0时某同学使绳子的左端开始做简谐运动,t =1s时形成如图所示波形.则该波的周期T=________s,传播速度v=________m/s.第9题图10.一列简谐横波在t=0时的波形图如图所示.介质中x=3m处的质点P沿y轴方向做简谐振运动的表达式为y=5sin(5πt)cm.则此波沿x轴________(选填“正”或“负”)方向传播,传播速度为________m/s.第10题图11.如图所示是一列沿x轴负方向传播的简谐横波在t=0时刻的波形图,已知波的传播速度v =2m/s,则x=1.5m处质点的振动函数表达式y=________ cm,x=2.0m处质点在0~1.5s通过的路程为________cm.第11题图12.如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,已知波的传播速度v =2m/s.试回答下列问题:①写出x=1.0m处质点的振动函数表达式;②求出x=2.5 m处质点在0~4.5 s内通过的路程及t=4.5 s时的位移.第12题图13.一列横波上有相距4 m的A、B两点,波的传播方向是由A向B,波长大于2 m.如图所示的是A、B两质点的振动图象,求这列波可能的波速.第13题图课时作业(五十一)机械波及其常见现象1.B【解析】两列波的频率相等时就能发生稳定干涉,A错,B对;波在障碍物尺寸与波长相差不多或小得多才能发生明显衍射现象,但并不是遇到尺寸较大障碍物不能发生衍射,只是不明显,C错;干涉图样中振动加强区并不是位移始终保持最大,而是振动加强,减弱区是振动减弱并不是位移始终最小,D错;选B.2.C【解析】当波源与观察者相互接近,f变大,音调变高,反之f变小,音调变低,故C 正确.3.BC【解析】要使A振动起来,必须发生衍射,原来A不振动,说明孔尺寸较大,故减小孔的尺寸或使波长增大即可.由于波速v一定,要使波长增大,由v=λf知减小频率即可.故B、C正确.4.AB【解析】由波形图可知,波长λ=4m,则波的周期T=λv =44s=1s,选项A正确;x=0处的质点在t=0时向y轴负方向运动,选项B正确;x=0处质点经Δt=T4时间后即不处于平衡位置也不处于波谷位置,选项C、D均错.5.BC【解析】该时刻a质点振动最弱,b、c质点振动最强,这不难理解.但是d既不是波峰和波峰叠加,又不是波谷和波谷叠加,如何判定其振动强弱?这就要用到充要条件:“到两波源的路程之差是波长的整数倍”时振动最强,从图中可以看出,d是s1、s2连线的中垂线上的一点,到s1、s2的距离相等,所以必然为振动最强点.描述振动强弱的物理量是振幅,而振幅不是位移.每个质点在振动过程中的位移是在不断改变的,但振幅是保持不变的,所以振动最强的点无论处于波峰还是波谷,振动始终是最强的.6.C【解析】在机械波的传播过程中,前一质点带动后一质点振动,而后一质点要“模仿”前一质点的振动,已知机械波沿x轴正方向传播,利用“带动”原理可知,质点P此时此刻的振动方向沿y轴负方向,选项A错误;沿波传播方向上各质点并不随波迁移,而是在平衡位置附近做简谐运动,并且各质点振动的幅度相同即振幅相同,据此可判断选项BD错误;根据波形图可知,波长λ=4m,振幅A=5cm,已知v=4m/s,所以T=λ/v=1s,Δt=3s=3T,所以质点Q通过的路程是12A =60cm =0.6m ,所以选项C 正确.本题答案为C.7.A 【解析】 根据题意,机械波的振动周期T =4t =0.8 s ,波长λ=4AB ,在t 1=0.4 s 时刻,B 点刚好开始向上运动,在t =2.5 s 时刻,即再经过2.1 s =258T. B 点位于x 轴下方,且正向下运动,所以选项A 正确,C 错误;在t 2=1.4 s 时刻,C 点刚好开始向上运动,在t =2.5 s 时刻,即再经过1.1 s =138T ,C 点位于x 轴上方,且正向下运动,所以选项BD 错误.本题答案为A.8.(1)变窄 变小 (2)b a 【解析】 当波遇到与波长相差不大的障碍物时才能发生明显的衍射现象;由波速公式v =λT =fλ可知,当波速一定时,频率降低波长增大;当两个相干波源的振动步调一致时,到两个波源的距离之差Δs =nλ处是加强区,Δs =(2n +1)λ2处是减弱区,故b 点为加强点位置,a 点是为减弱点位置.9.4 1 【解析】 由图可知,t =1s 时形成了14个波形,即1s =T 4, T =4s, v =λT =44 m/s =1m/s.10.负 10 m/s 【解析】 根据表达式可知,质点P 的位移按照正弦规律变化,所以在图示时刻质点P 正向上运动,据此可知,此波沿x 轴负方向传播;根据波形图可知,波长λ=4 m ,又周期T =2π/5π=0.4 s ,所以,波速v =λ/T =10 m/s.11.-5cos2πt 30 【解析】 在t =0时刻,x =1.5 m 处质点处于-5 cm ,x =1.5 m 处质点的振动函数表达式y =-5cos 2πt.波长为2.0 m ,波动周期T =1 s ,x =2.0 m 处质点在0~1.5 s 内通过的路程为6A =6×5 cm =30 cm.12.①y =5sin(2πt) cm ②90 cm -5 cm 【解析】 ①波长λ=2.0 m ,周期T =λv =1.0 s ,振幅A =5 cm ,则y =5sin (2πt) cm ②n =tT =4.5,则4.5 s 内路程s =4nA =90 cm ;x =2.5 m 处质点在t =0时位移为y =5 cm ,则经过4个周期后与初始时刻相同,经4.5个周期后该质点位移y =-5 cm.13.403m/s 或407m/s 【解析】 由振动图象得:质点振动周期T =0.4sB 点比A 点晚振动的时间Δt =nT +34T(n =0,1,2,3,…)所以A 、B 间的距离为Δs =kλ+34λ(k =0, 1, 2, 3, …)则波长为λ=4Δs 4k +3=164k +3 因为λ>2m ,所以k =0,1 当k =0时,λ1=163 m ,v 1=λ1T =163×0.4m/s =403m/s 当k =1时,λ2=167 m ,v 2=λ2T =167×0.4m/s =407m/s.。
2019新人教A版高中数学 必修第一册课时同步课时作业 5.5.1 第1课时 两角差的余弦公式 Word版含解析

第五章 5.5 5.5.1 第1课时A 组·素养自测一、选择题1.计算cos 5π12cos π6+cos π12sin π6=( C )A .0B .12C .22D .32[解析] cos 5π12cos π6+cos π12sin π6=cos 5π12cos π6+sin 5π12sin π6=cos(5π12-π6)=cos π4=22.2.cos(45°-α)cos(α+15°)-sin(45°-α)sin(α+15°)=( A ) A .12B .-12C .32D .-32[解析] 原式=cos(α-45°)cos(α+15°)+sin(α-45°)·sin(α+15°)=cos[(α-45°)-(α+15°)]=cos(-60°)=12.3.设α∈(0,π2),若sin α=35,则22cos(α-π4)=( B )A .110B .710C .-710D .-110[解析] α∈(0,π2),sin α=35,cos α=45,原式=22(cos α·22+sin α·22) =12(cos α+sin α)=710. 4.若sin(π+θ)=-35,θ是第二象限角,sin(π2+φ)=-255,φ是第三象限角,则cos(θ-φ)的值是( B )A .-55B .55C .11525D . 5[解析] ∵sin(π+θ)=-35,θ是第二象限角,可解得:sin θ=35,cos θ=-1-sin 2θ=-45,又∵sin(π2+φ)=-255,φ是第三象限角,cos φ=-255,sin φ=-1-cos 2φ=-55,∴cos(θ-φ)=cos θcos φ+sin θsin φ=(-45)×(-255)+35×(-55)=55.5.化简sin(x +y )sin(x -y )+cos(x +y )cos(x -y )的结果是( B ) A .sin2x B .cos2y C .-cos2xD .-cos2y[解析] 原式=cos(x +y )cos(x -y )+sin(x +y )·sin(x -y )=cos[(x +y )-(x -y )]=cos2y . 6.已知sin(30°+α)=35,60°<α<150°,则cos α=( A )A .3-4310B .3+4310C .4-3310D .4+3310[解析] ∵60°<α<150°,∴90°<30°+α<180°, ∴cos(30°+α)=-45,又cos α=cos[(30°+α)-30°]=cos(30°+α)cos30°+sin(30°+α)sin30°=-45×32+35×12=3-4310.二、填空题7.cos(61°+2α)cos(31°+2α)+sin(61°+2α)·sin(31°+2α)=2[解析] 原式=cos[(61°+2α)-(31°+2α)] =cos 30°=32.8.已知sin(π3+α)=1213,α∈(π6,2π3),则cos α的值为2631363∴π3+α∈(π2,π),cos(π3+α)=-513. ∴cos α=cos[(π3+α)-π3]=cos(π3+α)cos π3+sin(π3+α)sin π3=-513×12+1213×32=123-526.9.已知cos(α-π3)=cos α,则tanα=3[解析] ∵cos(α-π3)=cos αcos π3+sin α·sin π3=12cos α+32sin α=cos α, ∴32sin α=12cos α,∴sin αcos α=33, 即tan α=33. 三、解答题10.已知角α的终边过点P (-4,3). (1)求tan (3π+α)sin (5π-α)-cos (π2+α)的值; (2)若β为第三象限角,且tan β=43,求cos(α-β)的值.[解析] (1)因为角α的终边过点P (-4,3). 所以sin α=35,cos α=-45,所以tan (3π+α)sin (5π-α)-cos (π2+α)=sin αcos αsin α+sin α=12cos α=-58. (2)因为β为第三象限角,且tan β=43,所以sin β=-45,cos β=-35.由(1),知sin α=35,cos α=-45.所以cos(α-β)=cos αcos β+sin αsin β=-45×(-35)+35×(-45)=0.11.已知sin ⎝⎛⎭⎫α+π4=1213,且π4<α<3π4,求cos α的值.⎝⎭41344∴π2<α+π4<π. ∴cos ⎝⎛⎭⎫α+π4=-1-⎝⎛⎭⎫12132=-513. ∴cos α=cos ⎣⎡⎦⎤⎝⎛⎭⎫α+π4-π4=cos ⎝⎛⎭⎫α+π4cos π4+sin ⎝⎛⎭⎫α+π4sin π4 =-513×22+1213×22=7226.B 组·素养提升一、选择题1.cos(α+β)cos α+sin(α+β)sin α等于( D ) A .sin α B .cos α C .sin βD .cos β[解析] cos(α+β)cos α+sin(α+β)sin α=cos[(α+β)-α]=cos β,故选D .2.第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如图所示,会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形与大正方形面积之比为4∶9,且直角三角形的两锐角分别为α,β,则cos(α-β)的值为( A )A .59B .49C .23D .0[解析] 设大正方形的边长为1,由于小正方形与大正方形面积之比为4∶9,可得小正方形的边长为23,所以有sin α-cos α=23,①cos β-sin β=23,②由图可得cos α=sin β,sin α=cos β,①×②可得49=sin αcos β-cos αcos β-sin αsin β+cos αsin β=cos 2β-(cos αcos β+sin αsin β)+sin 2β=1-cos(α-β),解得cos(α-β)=59.3.(多选题)满足cos αcos β=32-sin αsin β的α,β的值可能是( BC ) A .α=1312π,β=3π4B .α=π2,β=π3C .α=π3,β=π6D .α=π3,β=π4[解析] 由条件cos αcos β=32-sin αsin β得cos αcos β+sin αsin β=32,即cos(α-β)=32,α=π2,β=π3,α=π3,β=π6都满足,故选BC . 4.(多选题)已知α,β,γ∈(0,π2),sin α+sin γ=sin β,cos β+cos γ=cos α,则下列说法正确的是( AC )A .cos(β-α)=12B .cos(β-α)=-12C .β-α=π3D .β-α=-π3[解析] 由已知,得sin γ=sin β-sin α,cos γ=cos α-cos β.两式分别平方相加,得(sin β-sin α)2+(cos α-cos β)2=1.∴-2cos(β-α)=-1,∴cos(β-α)=12,∴A 正确,B 错误.∵sinγ=sin β-sin α>0,∴β>α,∴β-α=π3,∴C 正确,D 错误,故选AC . 二、填空题5.已知cos(α-π6)+sin α=435,则cos(α-π3)的值是__45__.[解析] cos(α-π6)+sin α=32cos α+32sin α=435,12cos α+32sin α=45, ∴cos(α-π3)=12cos α+32sin α=45.6.已知α,β均为锐角,且sin α=55,cos β=1010,则α-β=__-π4__. [解析] ∵α为锐角,sin α=55,∴cos α=255. 又β为锐角,cos β=1010,∴sin β=31010.∴cos(α-β)=cos αcos β+sin αsin β =255×1010+55×31010=22.又α,β∈(0,π2),sin α<sin β,∴0<α<β<π2,∴-π2<α-β<0.故α-β=-π4.7.函数f (x )=sin2x sin π6-cos2x cos 5π6在[-π2,π2]上的单调递增区间为__[-5π12,π12]__.[解析] f (x )=sin2x sin π6-cos2x cos 5π6=sin2x sin π6+cos2x cos π6=cos(2x -π6).当2k π-π≤2x-π6≤2k π(k ∈Z ),即k π-5π12≤x ≤k π+π12(k ∈Z )时,函数f (x )单调递增.取k =0,得-5π12≤x ≤π12,故函数f (x )在[-π2,π2]上的单调递增区间为[-5π12,π12].三、解答题8.已知α、β∈(3π4,π),sin(α+β)=-35,sin(β-π4)=1213,求cos(α+π4)的值.[解析] ∵α、β∈(3π4,π),sin(α+β)=-35,sin(β-π4)=1213,∴α+β∈(3π2,2π),β-π4∈(π2,3π4),∴cos(α+β)=1-(-35)2=45,cos(β-π4)=-1-(1213)2=-513,∴cos(α+π4)=cos[(α+β)-(β-π4)]=cos(α+β)·cos(β-π4)+sin(α+β)sin(β-π4)=45×(-513)+(-35)×1213=-5665. 9.已知A (cos α,sin α),B (cos β,sin β),其中α,β为锐角,且|AB |=105. (1)求cos(α-β)的值; (2)若cos α=35,求cos β的值.[解析] (1)由|AB |=105,得(cos α-cos β)2+(sin α-sin β)2=105, ∴2-2(cos αcos β+sin αsin β)=25,∴cos(α-β)=45.(2)∵cos α=35,cos(α-β)=45,α,β为锐角,∴sin α=45,sin(α-β)=±35.当sin(α-β)=35时,cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=2425.当sin(α-β)=-35时,cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=0.∵β为锐角,∴cos β=2425.。
反冲运动-火箭教学设计
听讲,明确过反程及易错问题。
计 2. 原理
三.人船模型 意图:落实知思识目标(3)情感目标(1)
Hale Waihona Puke 生:杨凯玲引导学生运用动量守恒列式,并在最后给出 多次喷气问题的求解方法;
生:运用动量守恒列式,理解好解题方法 意图:落实能力目标(2)情感目标(1)
师:提出问题,请全体同学帮助王树桐解决问题 生:王树桐进行尝试,提出解决方案并。刘宇萌进行
(3)知道火箭飞行原理和主要用途。
学 目
过程与方法:
(1)通过对反冲运动实例的分析,能运用动 难
量守恒定律分析,解释反冲运动;
点
如何正确应用动量守恒定律分 析、解决反冲运动的问题
标
(2)提高运用动量守恒定律分析和解决实际 问题的能力。
情感态度与价值观: (1)通 过 对 生 活 中 反 冲 运 动 实 例 的 理 解 与
意图:落实情感目标(1)
新课教学
一.反冲运动
师:请孙显瑞等三名同学演示和讲解反冲运动
1。定义
生:2 名同学进行演示讲解,孙显锐负责讲解, 4
列式;其他同学认真理解
2。原理
意图:落实知识目标(1)(2)能力目标(1)
二.火箭 1.发射过程
2.工作原理
三.人船模型
师:请杨凯玲等七名同学演示火箭工作过程
生:6 名同学演示火箭工作原理,杨凯玲负责
中学课程设计 授课日期 2017 年 12 月 14 日
授课人
学校
年班
高三 八班
课题
反冲运动 火箭
课型
复习课
知识与技能:
(1)知道什么是反冲运动,能推举出反冲运
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业(五十一)一、选择题1.(2010·重庆卷)某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的青年职工为7人,则样本容量为( )A .7B .15C .25D .35答案 B解析 设样本容量为n ,则依题意有350750×n =7,n =15,选B. 2.某工厂生产A 、B 、C 三种不同型号的产品,产品的数量之比依次为3∶4∶7,现在用分层抽样的方法抽出容量为n 的样本,样本中A 型号产品有15件,那么样本容量n 为( )A .50B .60C .70D .80答案 C解析 由分层抽样方法得33+4+7×n =15,解之得n =70,故选C. 3.某高中在校学生2000人,高一级与高二级人数相同并都比高三级多1人,为了响应“阳光体育运动”号召,学校举行了“元旦”跑步和登山比赛活动.每个人都参加而且只参其中a ∶b ∶c =2∶3∶5,全校参与登山的人数占总人数的25,为了了解学生对本次活动的满意程度,从中抽取了一个200人的样本进行调查,则高二级参与跑步的学生中应抽取( )A .36人B .60人C .24人D .30人答案 A解析 ∵登山占总数的25,故跑步的占总数的35, 又跑步中高二级占32+3+5=310. ∴高二级跑步的占总人数的35×310=950. 由950=x 200得x =36,故选A. 4.问题:①某社区有500个家庭,其中高收入家庭125户,中等收入家庭280户,低收入家庭95户,为了了解社会购买力的某项指标,要从中抽出一个容量为100的样本;②从10名学生中抽出3个参加座谈会.方法一:Ⅰ简单随机抽样法;Ⅱ系统抽样法;Ⅲ分层抽样法.问题与方法配对正确的是( )A .①Ⅲ,②ⅠB .①Ⅰ,②ⅡC .①Ⅱ,②ⅢD .①Ⅲ,②Ⅱ答案 A解析 ①因为社会购买力与家庭收入有关,因此要采用分层抽样法;②从10名学生中抽取3名,样本和总体都比较少,适合采用简单随机抽样法.5.从2010名学生中选取50名学生参加全国数学联赛,若采用下面的方法选取:先用简单随机抽样从2010人中剔除10人,剩下的2000人再按系统抽样的方法抽取,则每人入选的概率( )A .不全相等B .均不相等C .都相等,且为502010D .都相等,且为502000答案 C6.(2010·湖北卷,理)将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( )A .26,16,8B .25,17,8C .25,16,9D .24,17,9答案 B解析 依题意及系统抽样的意义可知,将这600名学生按编号依次分成50组,每一组各有12名学生,第k (k ∈N*)组抽中的号码是3+12(k -1).令3+12(k -1)≤300得k ≤1034,因此第Ⅰ营区被抽中的人数是25;令300<3+12(k -1)≤495得1034<k ≤42,因此第Ⅱ营区被抽中的人数是42-25=17.结合各选项知,选B.7.(2011·陕西师大附中)某中学开学后从高一年级的学生中随机抽取90名学生进行家庭情况调查,经过一段时间后再次从这个年级随机抽取100名学生进行学情调查,发现有20名同学上次被抽到过,估计这个学校高一年级的学生人数为( )A .180B .400C .450D .2000答案 C解析 90x =20100,∴x =450.故选C. 8.某初级中学有学生270人,其中七年级108人,八、九年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按七、八、九年级依次统一编号为1、2、…、270;使用系统抽样时,将学生统一随机编号为1、2、…、270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:①7,34,61,88,115,142,169,196,223,250;②5,9,100,107,111,121,180,190,200,265;③11,38,65,92,119,146,173,200,227,254;④30,57,84,111,138,165,192,219,246,270;关于上述样本的下列结论中,正确的是( )A .②、③都不能为系统抽样B .②、④都不能为分层抽样C .①、④都可能为系统抽样D .①、③都可能为分层抽样答案 D解析 对于系统抽样,应在1~27、28~54、55~81、82~108、109~135、136~162、163~189、190~216、217~243、244~270中各抽取1个号;对于分层抽样,应在1~108中抽取4个号,109~189中抽取3个号,190~270中抽取3个号.点评 虽然三种抽样的方式、方法不同,但最终每个个体被抽取是等可能的,这正说明了三种抽样方法的科学性和可可行性.要根据不同的研究对象和不同的要求,采取不同的抽样方法.9.衡水中学为了提高学生的数学素养,开设了《数学史选讲》、《对称与群》、《球面上的几何》三门选修课程,供高二学生选修,已知高二年级共有学生600人,他们每人都参加且只参加一门课程的选修.为了了解学生对选修课的学习情况,现用分层抽样的方法从中抽取30名学生进行座谈.据统计,参加《数学史选讲》、《对称与群》、《球面上的几何》的人数依次组成一个公差为-40的等差数列,则应抽取参加《数学史选讲》的学生的人数为( )A .8B .10C .12D .16答案 C解析 根据题意可得,参加《数学史选讲》的学生人数为240人.抽取比例是30600=120,故应该抽取240×120=12人. 二、填空题10.(2010·上海,文)将一个总数为A 、B 、C 三层,其个体数之比为5 3 2。
若用分层抽样方法抽取容量为100的样本,则应从C 中抽取________个个体。
答案 2011.(2011·珠海质检)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2500,3000)月收入段应抽出________人.答案 25解析 由图可得月收入在[2500,3000)的频率为0.0005×500=0.25,所以[2500,3000)月收入段应抽出100×0.25=25(人).12.(09·辽宁)某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1∶2∶1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980 h,1020 h,1032 h ,则抽取的100件产品的使用寿命的平均值为________h.答案 1013解析 根据分层抽样知识可知,从3个分厂抽出的100件电子产品中,每个分厂抽取的个数比也为1∶2∶1,故分别有25个,50个,25个.再由3个分厂算出的使用寿命的平均值可得抽取的100件产品的使用寿命的平均值为980×25+1020×50+1032×25100=1013(h). 13.某校进行数学竞赛,将考生的成绩分成90分以下、90~120分、120~150分三种情况进行统计,发现三个成绩段的人数之比依次5∶3∶1,现用分层抽样的方法抽出一个容量为m 的样本,其中分数在90~120分的人数是45,则此样本的容量m =________答案 135解析 ∵个体容量样本容量=各层个体容量各层样本容量, ∴45m =35+3+1,即m =135. 三、解答题14.(09·广东)某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本.用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号、6~10号,…,196~200号).若第5组抽出的号码为22,则第8组抽出的号码应是________.若用分层抽样方法,则40岁以下年龄段应抽取________1人.答案 37 20解析 由系统抽样知识可知,将总体分成均等的若干部分指的是将总体分段,分段的间隔要求相等, 这时间隔为k =[N n].在第1段内采用简单随机抽样的方法确定一个起始编号,在此编号的基础上加上分段间隔的整数倍即为抽样编号.由题意,第5组抽出的号码为22,因为2+(5-1)×5=22,则第1组抽出的号码应该为2,第8组抽出的号码应该为2+(8-1)×5=37.由分层抽样知识可知,40岁以下年龄段的职工占50%,按比例应抽取40×50%=20(人).15.中央电视台在因特网上就观众对2011年春节晚会这一节目的喜爱程度进行调查,参加调查的总人数为人进行更为详细的调查,其中持“喜爱”态度的观众应抽取多少人?答案 23人解析 由于样本容量与总体容量的比为6012000=1200, ∴应抽取“喜爱”态度的观众人数为4600×1200=23(人). 16.2010年12月衡水市统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)).(1)求居民月收入在[3000,3500)的频率;(2)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中分层抽样方法抽出100人作进一步分析,则月收入在[2500,3000)的这段应抽多少人?解析 (1)月收入在[3000,3500)的频率为0.0003×(3500-3000)=0.15.(2)居民月收入在[2500,3000)的频率为0.0005×(3000-2500)=0.25,所以10000人中月收入在[2500,3000)的人数为0.25×10000=2500(人),再从10000人中分层抽样方法抽出100人,则月收入在[2500,3000)的这段应抽取100×250010000=25人.。
