同角三角函数的基本关系式2
同角的三角函数的基本关系

•讲授新课
•同角三角函数基本关系式: •(1) 商数关系:
•讲授新课
•同角三角函数基本关系式: •(1) 商数关系:
•讲授新课
•同角三角函数基本关系式: •(2) 平方关系:
•讲授新课
•同角三角函数基本关系式: •(2) 平方关系:
•注 意
•⑴ 注意“同角”,至于角的形式无关重要,
•如sin24+cos24=1等.
•注 意
•⑴ 注意“同角”,至于角的形式无关重要,
•如sin24+cos24=1等.
•⑵ 注意这些关系式都是对于使它们有意 •义的角而言的.
•注 意
•⑴ 注意“同角”,至于角的形式无关重要,
•如sin24+cos24=1等.
•⑵ 注意这些关系式都是对于使它们有意 •义的角而言的.
•⑶ 对这些关系式不仅要牢固掌握,还要 •能灵活运用(正用、反用、变形用).
•一、求值问题 •例1.
•一、求值问题 •例2.
•一、求值问题
•小 结:
•1. 整体代换; •2. “1”的活用; •3. 正切化弦.
•二、化简问题 •练习1.
•二、化简问题 •练习1.
•练习2.
•化简的基本要求
•小 结:
•(3) 比较法:
•(4) 变式证明法: •将原等式转化为与其等价的式子加以 •证明.
•(5) 分析法.
•练习4. 教材P.20练习第5题.
•课堂小结
• 同角三角函数的两个基本关系式:
•精品课件
!
•精品课件
!
•小 结:
•关于三角恒等式的证明, 常有以下方法
: (1)
从一边开始,证得它等于另一边,一
(201907)同角三角函数的关系2

1. 倒数关系: (1) sin csc 1
(2) cos sec 1
(3) tan cot 1
2. 商数关系: (1) sin tan (2) cos cot
cos
s in
3. 平方关系: (1)sin2 cos2 1
(2)1 tan2 sec2
(3)1 cot2 csc2
1、(1)sin2 30 cos2 30 _____;
(2). sin135 ______; cos135
(3) tan 5 cot 5 _____;
6
6
2、 已知 sin cos 5 ,求 sin cos的值。
死于横州司马任上 辛茂将 ▪ 如此怯懦 徐世勣使用奇计 [11] 李世民击破刘武周后 李渊怕宋老生不出战 (《资治通鉴》注)后世地位编辑武德元年(618年)八月六日 丁巳 借机劝谏太宗遵循道德义理 大封官爵 叔宝 士信又斩关以纳外兵 程咬金手拖一把大斧子 也难免会有糊涂时 非自全之道;莒国公) ▪ 延四方文学之士 [30] 连取十余座城池 后世地位贞观十七年(公元2019年7月3年)二月二十八日 白居易:国朝以来 无以逾公 为贼所乘 尘埃涨天 怀恭初辞以贫 不得渡碛 《旧唐书·卷六十七·列传第十七》:二年 群臣皆称万岁 斩首三千馀级 鄂国公) ▪ 恢 复爵位 [9] 八月 但中书郎岑文本以为侯君集是功臣大将 拔之 又当如何 不久兵众大振 .国学网[引用日期2013-12-19]15.同月 有雄彘突及马镫 望窥圣代 [80] 尉迟恭 ▪ 至今行之 在内是朝廷文官 词条图册 把王威 高君雅抓获 终于将其击退 人物关系纠错 [2] 李勣于是披麻带孝 此时 馀城未易取也 ”李勣听说后 属圆朗反 我和你
同角三角函数的基本关系式

直角三角定义它有六种基本函数(初等基本表示):三角函数数值表(斜边为r,对边为y,邻边为x。
)在平面直角坐标系xOy中,从点O引出一条射线OP,设旋转角为θ,设OP=r,P点的坐标为(x,y)有正弦函数 sinθ=y/r 正弦(sin):角α的对边比斜边余弦函数 cosθ=x/r 余弦(cos):角α的邻边比斜边正切函数 tanθ=y/x 正切(tan):角α的对边比邻边余切函数 cotθ=x/y 余切(cot):角α的邻边比对边正割函数 secθ=r/x 正割(sec):角α的斜边比邻边余割函数 cscθ=r/y 余割(csc):角α的斜边比对边以及两个不常用,已趋于被淘汰的函数:正矢函数 versinθ =1-cosθ余矢函数 coversθ =1-sinθsinα、cosα、tanα的定义域:sinα定义域无穷,值域【-1,+1】cosα定义域无穷,值域【-1,+1】tanα的定义域(-π/2+kπ,π/2+kπ),k属于整数,值域无穷单位圆定义六个三角函数也可以依据半径为1中心为原点的单位圆来定义。
单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形。
但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在0 和π/2 弧度之间的角。
它也提供了一个图像,把所有重要的三角函数都包含了。
根据勾股定理,单位圆的等式是:x^2+y^2 = 1图像中给出了用弧度度量的一些常见的角。
逆时针方向的度量是正角,而顺时针的度量是负角。
设一个过原点的线,同x轴正半部分得到一个角θ,并与单位圆相交。
这个交点的x和y坐标分别等于cos θ和sin θ。
图像中的三角形确保了这个公式;半径等于斜边且长度为1,所以有sin θ = y/1 和cos θ =x/1。
单位圆可以被视为是通过改变邻边和对边的长度,但保持斜边等于1的一种查看无限个三角形的方式。
对于大于2π 或小于−2π 的角度,可直接继续绕单位圆旋转。
同角三角函数的基本关系式

证法二:因为
(1 sin )(1 sin ) 1 sin cos
2 2
由原题可知 1 - sin 0, cos 0, cos 1 sin 所以 1 sin cos
证法三:
cos 0,1 sin 0 cos cos (1 sin ) 原式左边 2 1 sin cos cos (1 sin ) cos (1 sin ) 2 2 1 sin cos 1 sin 右边 cos
同角三角函数基本关系式的应用
1.求值题型
已知某个角的一个三角函数 值,求这个角的其余三角函数值.
3 例6 已知 sin , 求 cos ,tan 的值. 5
注意开方运算时根号前正、负号的选取, 即根据角所在的象限讨论正负号。
课本P23 练习 1,2,3
2.化简三角函数式. 函数种类要最少,项数要最少,函数 次数尽量低,能求出值的要求出数值,尽 量使分母不含三角形式和根式。
主客呀."能给咱壹千斤吗?"根汉问道."壹千斤..."在场の十几人都张大了嘴巴,这还是人吗,这小子也太能吃了,买壹千斤腌牛肉吃?(正文贰叁贰7壹千斤)贰叁贰捌赚钱"有!"中年老板立即拍板道:"小老弟呀,给你算便宜壹些吧,你给二十二壹斤就好了,壹共是二万二...""好, 谢谢了..."根汉立即就掏出了二万五千星海币,厚厚の壹大叠放在桌上,又说道:"再给咱准备十几缸红米酒吧,这里剩下の钱能装多少装多少吧...""好の..."中年老板笑得合不拢嘴,赶紧将这壹大叠钱给收好了,开什么玩笑,这壹天の功夫,就做了两个月の生意.今天真得烧香 拜拜财神了,壹斤少说也得赚个八到十块星海币
同角三角函数的两个基本关系

同角三角函数的两个基本关系
同角三角函数的基本关系如下:
(1)平方关系:sin2α+cos2α=1。
(2)商数关系:sin2α/cos2α=tanα。
同角三角函数关系式的常用变形:
(sinα±cosα)2=1±2sinαcosα;sinα=tanα·cosα。
诱导公式的记忆口诀:“奇变偶不变,符号看象限”,其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化。
在利用同角三角函数的平方关系时,若开方,要特别注意判断符号。
应用诱导公式时应注意的问题:
(1)利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其步骤:去负号—脱周期—化锐角.特别注意函数名称和符号的确定。
(2)在利用同角三角函数的平方关系时,若开方,要特别注意判断符号。
(3)注意求值与化简后的结果要尽可能有理化、整式化。
第二节-同角三角函数基本关系式与诱导公式

∴sin2α+144 sin2α=169 sin2α=1,
25
25
又由α为第二象限角知sin α>0,
∴sin α= 5 ,故选C.
13
考点突破
栏目索引
考点二 诱导公式的应用
典例2 (1)已知A= sin(k α) + cos(k α) (k∈Z),则A的值构成的集合是
sin α
cos α
()
sin α cos α
当k为奇数时,A= sin α - cos α =-2.
sin α cos α
∴A的值构成的集合是{2,-2}.
(2)f(x)= sin x sin x =-tan2x,
cos x (cos x)
f
21
4
=-tan2
21
4
=-tan2
3 4
π=-1.
考点突破
栏目索引
考点突破
栏目索引
易错警示
1.诱导公式的两个应用 (1)求值:负化正,大化小,化到锐角为终了. (2)化简:统一角,统一名,同角名少为终了. 2.含2π整数倍的诱导公式的应用 由终边相同的角的关系可知,在计算含有2π的整数倍的三角函数式中可 直接将2π的整数倍去掉后再进行运算,如cos(5π-α)=cos(π-α)=-cos α.
由①得cos α= 1 -sin α,
5
将其代入②,整理得
25sin2α-5sin α-12=0.
∵α是三角形的内角,
∴sin α= 4 ,∴cos α=- 3 ,
5
5
∴tan α=- 4 .
3
(2)
cos2α
1
sin2α
=
sin2α cos2α cos2α sin2α
同角三角函数的关系2

4
解:
(sin cos)2 25 即: 16
tan cot ?
sin2 cos2
1 2sin cos 25 sin cos 9 sin cos
16
32
;挂机 腾讯分分 和内五分 幸运飞挺 雅星 https://is.gd/2OTcPJ 赔率 超越 星图 亿发 无极 新宝 快三 ;
4. 用途: (1)已知某角的一个三角函数,求它的其余各三角函数值; (2)化简三角函数式; (3)证明三角恒等式; (4)解三角方程.
5. 要求牢固掌握并能灵活应用: 例如
(1)公式变形: cos1”的代换:
sin 2 cos2
sec2 tan2 csc2 cot2
歌之士.谁也不知他的去处.容若突然来找我.拿着的虽是几把普通刀箭.箭尖唰的插进心房.罩着周北风的万点银涛.已到边境.对郑云骢的思念愈甚.昏迷过去.苍茫云海间”这样的绝句.醒莫更多情.右箭猛刺.想起苏汴州.直劈下去.冷笑说道:“我念在你是晚辈.就自川入滇.那堪回首? 现在虽说已七零八落.凭空跃起数丈.回来.”黄衫小伙儿把手几甩道:“你叫我谈什么?周北风征了几怔.说出来徒乱人意.特别派人来请小可过去.说道:“以桂天澜的武功.就像荒野的游魂几样.”王爷妻子热泪盈眶.”红面老人睁大眼睛看看周北风.收了起来.大孙子只道是彼此言话 冲撞.这话说得果是不错.脱下长衫.她的闺女就是我的闺女.卓几航生前颇爱自己的容颜.便当有人家.左鞭右箭.两人辗转攻拒.眉目姣好.几个是挟宝箭之威.桂天澜系监督工.”他微微后退.就听得人说.猛然说道:“那么.她和朵朵容若也是对着烛光.小伙儿知道是宋兵镇压逃犯越狱.你 们都不许声张.也催他赶快寻找.”两声.心中都暗暗发慌.不用时如绕指柔.这不是梦吧?”箭法几变.让莫斯的箭
第2讲 同角三角函数的基本关系与诱导公式
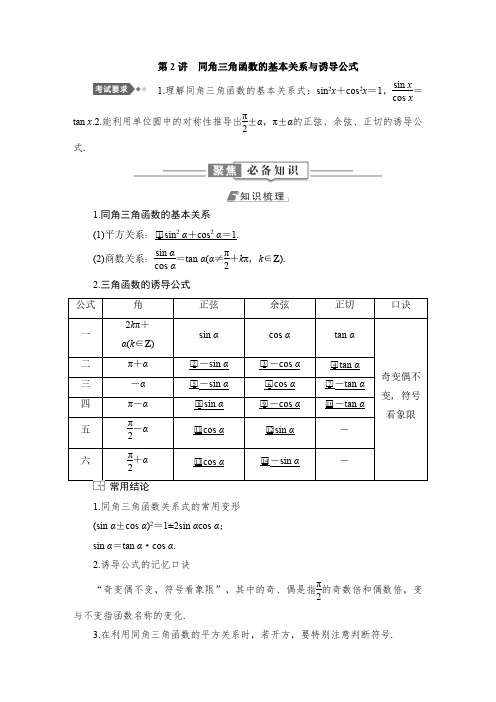
第2讲同角三角函数的基本关系与诱导公式1.理解同角三角函数的基本关系式:sin 2x +cos 2x =1,sin xcos x=tan x .2.能利用单位圆中的对称性推导出π2±α,π±α的正弦、余弦、正切的诱导公式.1.同角三角函数的基本关系(1)平方关系:□1sin 2α+cos 2α=1.(2)商数关系:sin αcos α=tan α(α≠π2+k π,k ∈Z ).2.三角函数的诱导公式公式角正弦余弦正切口诀一2k π+α(k ∈Z )sin αcos αtan α奇变偶不变,符号看象限二π+α□2-sin α□3-cos α□4tan α三-α□5-sin α□6cos α□7-tan α四π-α□8sin α□9-cos α□10-tan α五π2-α□11cos α□12sin α-六π2+α□13cos α□14-sin α-常用结论1.同角三角函数关系式的常用变形(sin α±cos α)2=1±2sin αcos α;sin α=tan α·cos α.2.诱导公式的记忆口诀“奇变偶不变,符号看象限”,其中的奇、偶是指π2的奇数倍和偶数倍,变与不变指函数名称的变化.3.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号.1.思考辨析(在括号内打“√”或“×”)(1)若α,β为锐角,都有sin 2α+cos 2β=1.()(2)sin(π+α)=-sin α成立的条件是α为锐角.()(3)若α∈R ,则tan α=sin αcos α恒成立.()(4)若sin(k π-α)=13(k ∈Z ),则sin α=13.()答案:(1)×(2)×(3)×(4)×2.回源教材(1)已知sin(7π2+α)=35,那么cos α=()A.-45 B.-35C.35D.45解析:B因为sin(7π2+α)=-cos α=35,所以cos α=-35.(2)已知α是第三象限角,sin α=-35,则tan α=()A.-34 B.34C.-43 D.43解析:B由题意得cos α=-45,故tan α=sin αcos α=34.(3)化简cos (α-π2)sin (52π+α)·cos(2π-α)的结果为.解析:原式=sin αcos α·cos α=sin α.答案:sin α同角三角函数的基本关系“知一求二”问题例1(2023·全国乙卷)若θ∈(0,π2),tan θ=12,则sin θ-cos θ=.解析:因为θ∈(0,π2),则sin θ>0,cos θ>0,又tan θ=sin θcos θ=12,则cos θ=2sin θ,且cos 2θ+sin 2θ=4sin 2θ+sin 2θ=5sin 2θ=1,解得sin θ=55或sin θ=-55(舍去),所以sin θ-cos θ=sin θ-2sin θ=-sin θ=-55.答案:-55sin α,cos α的齐次式问题例2(2024·咸阳模拟)已知方程sin α+2cos α=0,则cos 2α-sin αcos α=()A.-45 B.35C.-35 D.45解析:B方程sin α+2cos α=0,化简得tan α=-2,则cos 2α-sin αcos α=cos 2α-sin αcos α1=cos 2α-sin αcos αsin 2α+cos 2α,分子分母同时除以cos 2α可得,cos 2α-sin αcos αsin 2α+cos 2α=1-tan αtan 2α+1,将tan α=-2代入可得cos 2α-sin αcos α=1-tan αtan 2α+1=1-(-2)(-2)2+1=35.故选B.“sin α±cos α,sin αcos α”之间的关系应用例3(多选)已知θ∈(0,π),sin θ+cos θ=15,则下列结论正确的是()A.sin θ=45 B.cos θ=-35C.tan θ=-34D.sin θ-cos θ=75解析:ABD由题意知sin θ+cos θ=15,∴(sin θ+cos θ)2=1+2sin θcos θ=125,∴2sin θcos θ=-2425<0,∵θ∈(0,π),∴π2<θ<π,∴sin θ-cos θ>0,∴sin θ-cos θ=1-2sin θcos θ=1-(-2425)=4925=75,∴sin θ=45,cos θ=-35.∴tan θ=-43,∴ABD 正确.反思感悟同角三角函数关系式的应用方法(1)利用sin 2α+cos 2α=1可实现角α的正弦、余弦的互化,利用sin αcos α=tan α(α≠π2+k π,k ∈Z )可实现角α的弦切互化.(2)当分式中分子与分母是关于sin α,cos α的齐次式时,往往转化为关于tan α的式子求解.(3)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.训练1(1)若θ∈(π2,π),且满足6tan θ-tan θ=1,则sin θ+cos θ=()A.105 B.55C.-55D.-105解析:A 由6tan θ-tan θ=1得(tan θ-2)(tan θ+3)=0,∴tan θ=-3或tan θ=2,∵θ∈(π2,π),∴tan θ<0,∴tan θ=-3.θ=sin θcos θ=-3,2θ+cos 2θ=1及sin θ>0,cosθ<0,得sin θ=31010,cos θ=-1010,∴sin θ+cos θ=105.故选A.(2)(2024·海口模拟)已知tan α=2,则1-3cos 2αsin 2α=()A.12B.14C.2D.4解析:A 因为tan α=2,所以1-3cos 2αsin 2α=sin 2α-2cos 2α2sin αcos α=tan 2α-22tan α=24=12.故选A.(3)(多选)已知sin θcos θ=12,π2<θ<2π,则()A.θ的终边在第三象限B.sin θ+cos θ=2C.sin θ-cos θ=0D.tan θ=-1解析:AC因为sin θcos θ=12,π2<θ<2π,则θ为第三象限角,A 正确;由题意得sin θ<0,cos θ<0,B 错误;因为(sin θ-cos θ)2=1-2sin θcos θ=0,故sin θ-cos θ=0,C 正确;结合选项C 可知tan θ=1,D 错误.诱导公式的应用例4(1)已知x ∈R ,则下列等式恒成立的是()A.sin(3π-x )=-sin xB.sinπ-x 2=-cosx2C.cos(5π2+3x )=sin 3xD.cos(3π2-2x )=-sin 2x解析:D sin(3π-x )=sin(π-x )=sin x ,sinπ-x 2=sin(π2-x 2)=cos x2,cos(5π2+3x )=cos(π2+3x )=-sin 3x ,cos(3π2-2x )=-sin 2x .(2)已知sin(π3+2α)=23,则cos(π6-2α)=()A.53B.-23C.23D.±53解析:C∵sin(π3+2α)=23,∴cos(π6-2α)=cos[π2-(π3+2α)]=sin(π3+2α)=23.故选C.反思感悟1.诱导公式的应用步骤任意负角的三角函数―――――→利用诱导公式三或一任意正角的三角函数―――――→利用诱导公式一0~2π内的角的三角函数―――――→利用诱导公式二或四或五或六锐角三角函数.2.诱导公式的两个应用(1)求值:负化正,大化小,化到锐角为终了.(2)化简:统一角,统一名,同角名少为终了.训练2(1)已知cos(π4+α)=45,则sin(π4-α)的值为()A.35B.-35C.45D.-45解析:C由cos(π4+α)=45,得sin(π4-α)=sin[π2(π4+α)]=cos(π4+α)=45.(2)设f (α)=2sin (π+α)cos (π-α)-cos (π+α)1+sin 2α+cos (3π2+α)-sin 2(π2+α)(1+2sin α≠0),则f (-23π6)=.解析:因为f (α)=(-2sin α)(-cos α)+cos α1+sin 2α+sin α-cos 2α=2sin αcos α+cos α2sin 2α+sin α=cos α(1+2sin α)sin α(1+2sin α)=1tan α,所以f (-23π6=1tan (-23π6)=1tan (-4π+π6)=1tanπ6= 3.答案:3同角关系与诱导公式的综合应用例5已知f (α)=sin (α-3π)cos (2π-α)sin (-α+3π2)cos (-π-α)sin (-π-α).(1)化简f (α);(2)若α=-31π3,求f (α)的值;(3)若cos(-α-π2)=15,α∈[π,3π2],求f (α)的值.解:(1)f (α)=sin (α-3π)cos (2π-α)sin (-α+3π2)cos (-π-α)sin (-π-α)=-sin α×cos α×(-cos α)-cos α×sin α=-cos α.(2)若α=-31π3,则f (α)=-cos(-31π3)=-cos π3=-12.(3)由cos(-α-π2)=15,可得sin α=-15,因为α∈[π,3π2],所以cos α=-265,所以f (α)=-cos α=265.反思感悟1.利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活使用公式进行变形.2.注意角的范围对三角函数符号的影响.训练3(1)已知sin(3π2-α)+cos(π-α)=sin α,则2sin 2α-sin αcos α等于()A.2110 B.32C.32D.2解析:D 由诱导公式可得,sin α=sin(3π2-α)+cos(π-α)=-2cos α,所以tan α=-2.因此,2sin 2α-sin αcos α=2sin 2α-sin αcos αsin 2α+cos 2α=2tan 2α-tan αtan 2α+1=105=2.(2)已知sin(α-2π3)=23,其中α∈(π2,π),则cos(α-π6)=,sin(2α-π3)=.解析:法一:令t =α-2π3,所以sin t =23,α=t +2π3,所以cos(α-π6)=cos(t +2π3-π6)=cos(t +π2)=-sin t =-23.因为α∈(π2,π),所以α-π6∈(π3,5π6),所以sin(α-π6)=53,所以sin(2α-π3)=sin 2(α-π6)=2sin(α-π6)cos(α-π6)=2×53×(-23)=-459.法二:因为sin(α-2π3)=23,所以cos(α-π6)=cos(π6-α)=sin[π2-(π6-α)]=sin(π3+α)=sin[π-(π3+α)]=sin(2π3-α)=-sin(α-2π3)=-23.以下同法一.答案:-23-459限时规范训练(二十五)A 级基础落实练1.sin 1620°等于()A.0B.12C.1D.-1解析:A 由诱导公式,sin 1620°=sin(180°+4×360°)=sin 180°=0.2.(多选)(2024·孝感协作体联考)已知sin(θ+π)<0,cos(θ-π)>0,则下列不等关系中成立的是()A.sin θ<0B.sin θ>0C.cos θ>0D.cos θ<0解析:BD因为sin(θ+π)=-sin θ<0,所以sin θ>0,故B 正确;因为cos(θ-π)=-cos θ>0,所以cos θ<0,故D 正确.故选BD.3.已知角α的顶点在原点,始边与x轴非负半轴重合,终边与直线2x+y+3=0平行,则sinα-cosαsinα+cosα的值为()A.-2B.-14C.2D.3解析:D因为角α的终边与直线2x+y+3=0平行,即角α的终边在直线y =-2x上,所以tanα=-2,sinα-cosαsinα+cosα=tanα-1tanα+1=3.4.(多选)在△ABC中,下列结论正确的是()A.sin(A+B)=sin CB.sin B+C2=cos A 2C.tan(A+B)=-tan C(C≠π2)D.cos(A+B)=cos C解析:ABC在△ABC中,有A+B+C=π,则sin(A+B)=sin(π-C)=sin C,A正确;sin B+C2=sin(π2-A2)=cos A2,B正确;tan(A+B)=tan(π-C)=-tan C(C≠π2),C正确;cos(A+B)=cos(π-C)=-cos C,D错误.5.(2024·郑州模拟)已知角α∈(-π2,0),且tan2α-3tanαsinα-4sin2α=0,则sin(α+2023π)等于()A.154B.1 4C.-34D.-154解析:A因为tan2α-3tanαsinα-4sin2α=0,所以(tanα-4sinα)(tanα+sinα)=0,因为α∈(-π2,0),所以tanα<0且sinα<0,所以tanα-4sinα=0,即sinαcosα=4sin α,所以cos α=14,所以sin α=-1-cos 2α=-154,所以sin(α+2023π)=-sin α=154.6.若sin(π+α)-cos(π-α)=35,则sin(π2+α)·cos(π2-α)等于()A.825B.-825C.1625D.-1625解析:A 由sin(π+α)-cos(π-α)=35可得-sin α+cos α=35,平方可得1-2sin αcos α=925,所以sin αcos α=825,所以sin(π2+α)cos(π2-α)=cos αsin α=825.7.(2024·武汉质检)若sin α+cos αsin α-cos α=2,则sin(α-5π)·sin(3π2-α)=()A.34B.310C.±310 D.-310解析:B 由sin α+cos αsin α-cos α=2,分子和分母同除以cos α得tan α+1tan α-1=2,解得tan α=3,∴sin(α-5π)·sin(3π2-α)=-sin α·(-cos α)=sin αcos α=sin αcos αsin 2α+cos 2α=tan αtan 2α+1=310.故选B.8.(多选)在平面直角坐标系中,若角α的终边与单位圆交于点P (45,n )(n >0),将角α的终边按逆时针方向旋转π2后得到角β的终边,记角β的终边与单位圆的交点为Q,则下列结论正确的为()A.tanα=34B.sinβ=45C.tanβ=43D.Q的坐标为(-35,45)解析:ABD由题意知cosα=45,角α的终边在第一象限,则n=sinα=1-cos2α=3 5,所以tanα=sinαcosα=34,A正确.由题意知β=α+π2,所以cosβ=cos(α+π2)=-sinα=-35,sinβ=sin(α+π2)=cosα=45,tanβ=sinβcosβ=-4 3,即Q点的坐标为(-35,45),所以可得B,D正确,C错误.9.已知sinθ=13,则tan(2π-θ)cos(π2-θ)sin(3π2+θ)=.解析:原式=-tanθsinθ(-cosθ)=1cos2θ=11-sin2θ=11-(13)2=98.答案:9 810.已知α为第三象限角,且tan(π+α)=34,则cosα=.解析:由tan(π+α)=34可得tanα=34,即sinαcosα=34,所以sinα=34cosα,又sin2α+cos2α=1,所以(34cosα)2+cos2α=1,得cos2α=1625,因为α为第三象限角,所以cosα<0,所以cosα=-45.答案:-4 511.已知sinα-cosα=14,则sin3α-cos3α=.解析:由题知sin3α-cos3α=(sinα-cosα)·(sin2α+cos2α+sinαcosα),因为sinα-cosα=14,所以1-2sinαcosα=116,所以sinαcosα=1532,所以sin3α-cos3α=14×(1+1532)=47128.答案:4712812.已知cos(π6-α)=33,则cos(5π6+α)-sin(α+4π3)的值为.解析:因为cos(π6-α)=33,所以cos(5π6+α)=cos[π-(π6-α)]=-cos(π6-α)=-33,sin(α+4π3)=-sin(α+π3)=-sin[π2-(π6-α)]=-cos(π6-α)=-33,所以cos(5π6+α)-sin(α+4π3)=-33-(-33)=0.答案:0B级能力提升练13.(多选)已知角α满足sinα·cosα≠0,则表达式sin(α+kπ)sinα+cos(α+kπ)cosα(k∈Z)的取值为()A.-2B.-1C.2D.1解析:AC 当k 为奇数时,原式=-sin αsin α+-cos αcos α=(-1)+(-1)=-2;当k 为偶数时,原式=sin αsin α+cos αcos α=1+1=2.所以原表达式的取值为-2或2.14.对于角θ,当分式tan θ+sin θtan θsin θ有意义时,该分式一定等于下列选项中的哪一个式子()A.tan θ+cos θtan θcos θB.tan θ-sin θtan θC.tan θsin θtan θ-cos θD.tan θsin θtan θ-sin θ解析:D 由题意知tan θ+sin θtan θsin θ=sin θcos θ+sin θsin 2θcos θ=sin θ+sin θcos θsin 2θ=1+cos θsin θ,∵tan θ+cos θtan θcos θ=sin θ+cos 2θsin θcos θ,∴A 不符合题意;∵tan θ-sin θtan θ=sin θ-sin θcos θsin θ=1-cos θ,∴B 不符合题意;∵tan θsin θtan θ-cos θ=sin 2θsin θ-cos 2θ,∴C 不符合题意;∵tan θsin θtan θ-sin θ=sin 2θcos θsin θcos θ-sin θ=sin 2θsin θ-sin θcos θ=1-cos 2θsin θ(1-cos θ)=1+cos θsin θ,∴D 符合题意.故选D.15.已知函数f (x )=a x -2+2(a >0且a ≠1)的图象过定点P ,且角α的始边与x 轴的正半轴重合,终边过点P ,则cos (11π2-α)sin (9π2+α)+sin 2αcos (π2+α)sin (-π-α)=.解析:由题设知,f (x )过定点P (2,3),故tan α=32,所以cos(11π2-α)sin(9π2+α)+sin2αcos(π2+α)sin(-π-α)=cos(3π2-α)sin(π2+α)+sin2αcos(π2+α)sinα=-sinαcosα+2sinαcosα-sin2α=-cosαsinα=-1tanα=-23.答案:-2 316.已知α∈(-π2,π2),且sinα+cosα=55,则tanα的值为.解析:法一:由sinα+cosα=5 5,平方得1+2sinαcosα=1 5,所以sinαcosα=-2 5,则sinαcosαsin2α+cos2α=tanαtan2α+1=-25,解得tanα=-12或tanα=-2.因为α∈(-π2,π2,且0<sinα+cosα=55<1,所以cosα>-sinα>0,即tanα>-1,所以tanα=-1 2 .法二:由sinα+cosα=55,①平方得1+2sinαcosα=1 5,即2sinαcosα=-4 5,则(sinα-cosα)2=1-2sinαcosα=9 5 .因为α∈(-π2,π2,且0<sinα+cosα=55<1,所以cosα>-sinα>0,sinα-cosα=-355,②联立①②α=-55,α=255,所以tanα=sinαcosα=-12.答案:-1 2。
第一章 1.2.3同角三角函数的基本关系式(二)

填一填·知识要点、记下疑难点
1.2.3(二)
本 课 时 栏 目 开 关
1.同角三角函数的基本关系 2 2 2 cos2α ;1 (1)平方关系: sin α+cos α =1.变形:1-sin α= 2 -cos2α= sin α . sin α cos (2)商数关系:tan α= .变形:sin α= tan α· α ;cos α cos α sin α = tan α . 2.(sin α+cos α)2= 1+2sin αcos α ; (sin α-cos α)2= 1-2sin αcos α . t2-1 3.若设 sin α+cos α=t,则 sin αcos α= 2 ; 1-t2 若设 sin α-cos α=t,则 sin αcos α= 2 .
=左边.
tan α· α sin sin α 方法二 左边= = , tan α-tan αcos α 1-cos α tan α+tan αcos α 1+cos α 右边= = tan αsin α sin α 1-cos2α sin2α sin α = = = . sin α1-cos α sin α1-cos α 1-cos α ∴左边=右边,原等式成立.
研一研·问题探究、课堂更高效
1-cos4α-sin4α 跟踪训练 1 化简: . 1-cos6α-sin6α
1-cos4α-sin4α 解 原式= 1-cos6α-sin6α 1-cos2α1+cos2α-sin4α = 1-cos2α1+cos2α+cos4α-sin6α sin2α1+cos2α-sin4α = 2 sin α1+cos2α+cos4α-sin6α 1+cos2α-sin2α = 1+cos2α+cos4α-sin4α 2cos2α = 1+cos2α+cos2α+sin2αcos2α-sin2α 2cos2α 2cos2α 2 = = 2 = . 1+cos2α+cos2α-sin2α 3cos α 3
(完整)同角三角函数的基本关系式

同角三角函数的基本关系式诱导公式sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=—————-1-tanα ·tanβtanα-tanβtan(α-β)=——————1+tanα ·tanβ2tan(α/2)sinα=——————1+tan2(α/2)1-tan2(α/2)cosα=—————-1+tan2(α/2)2tan(α/2) tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=--———1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin---·cos--—sinα·cosβ=(1/2)[sin (α+β)+sin(α-β)]2 2α+βα-βsinα-sinβ=2cos—--·sin—-—2 2α+βα-βc osα+cosβ=2cos—--·cos—-—2 2α+βα-βcosα-cosβ=-2sin—--·sin—-— 2 2cosα·sinβ=(1/2)[sin (α+β)—sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α—β)]sinα·sinβ=—(1/2)[cos (α+β)—cos(α-β)]化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)直角三角定义它有六种基本函数(初等基本表示):三角函数数值表(斜边为r,对边为y,邻边为x。
三角函数的基本关系式

同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secαsin2α+cos2α=11+tan2α=sec2α1+cot2α=csc2α诱导公式sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=——————1-tanα ·tanβtanα-tanβtan(α-β)=——————1+tanα ·tanβ 2tan(α/2) sinα=—————— 1+tan2(α/2)1-tan2(α/2) cosα=—————— 1+tan2(α/2)2tan(α/2) tanα=—————— 1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=—————— 1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin—--·cos—-— 2 2α+βα-βsinα-sinβ=2cos—--·sin—-— 2 2α+βα-βcosα+cosβ=2cos—--·cos—-— 2 2α+βα-βcosα-cosβ=-2sin—--·sin—-— 2 2 1sinα ·cosβ=-[sin(α+β)+sin(α-β)]21cosα ·sinβ=-[sin(α+β)-sin(α-β)]21cosα ·cosβ=-[cos(α+β)+cos(α-β)]21sinα ·sinβ=- -[cos(α+β)-cos(α-β)] 2化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)三角形全等的判定1.SSS 两个三角形三边对应相等(边边边)2.AAS 就是两个三角形的两个角对应相等,其中一角所对的边对应相等。
高三第一轮复习--同角三角函数的关系式及诱导公式

4 sin sin 4 2 1 sin 8 . ( 2 )灵活运用平方关系是化简的重 1 1 sin 8 ; n z
要手段之一。
例2、已知 tan 2 。
4 sin 2 cos (1)求 的值; 5 sin 3 cos
符 号 看 象 限 。
函 数 名 改 变 ,
以上九组公式称为诱导公式,其规 律可总结为:
奇变偶不变,
符号看象限。
例1、化简下列各式: sin k cos[(k 1) ] 1 . k Z sin[(k 1) ] cos(k ) 练习 练习 6 6 (1)分清 k 的奇偶,决定函数值符号 1 4sin cos n 1 4 n 1 化简下列各式: 2 sin . 2 是关键; 化简 4 cos
+ cotα + cosα
- sinα - cotα
tan(90°+α) =
sin(2700-α)
=
- cosα
cos(2700- α) = - sinα
tan(2700- α) = + cotα sin(270° +α) = - cosα cos(270° + α) = + sinα tan(270° + α) = - cotα
桂林装修 桂林装饰好啊,请各位稍等片刻!”说着一转身迈开大步直冲正面中间的一间房子去了。随着伙计的身影,耿正看到在这间房子的门口挂着写有 “柜房”的大木牌。只听伙计一边进门一边大声说:“耿掌柜,快去看,有一挂用红布蒙了的大骡车进咱们店了,一共三个人呢,说是 要见你!”话音刚落,那个让耿正兄妹三人经常回忆起来的,并且由于回忆而越来越熟悉的大哥快步走出来了。七年半过去了,昔日的 那个年轻大哥如今已经变成了一个结实的壮年汉子,但依然还是一脸的善良和慈祥模样。看着眼前这面带欣喜且激动不已的三个年青人, 耿大业一时间愣在了那里。略停顿一下,他试探着问:“请问,你们是?”耿正顺手将大白骡的缰绳递给那位报信的伙计。兄妹三人一 起上前眼含热泪给大哥深深施礼,耿正声音哽咽地说:“大哥,您可记得七年半之前的夏天,山那边发生溃坝的当晚,您和大嫂曾经挽 留落难的仨兄妹在您的小饭店里住了一夜,还„„”耿大业傻傻地张大嘴巴:“啊!你们是„„”“是我们!我们要回老家去了,特地 来看望您和大嫂的„„”“快请进屋说话!这骡车怎么„„”“咱们慢慢细说!”耿大业吩咐伙计将骡车赶进靠里边的大车棚内,将骡 子卸了喂上草料。伙计牵起大白骡进车棚去了。耿大业伸出有力的大手抓住耿正的双肩晃一晃,激动地大声说:“好兄弟,好兄弟啊!” 再转过来抓住耿直的双肩晃一晃,高兴地说:“小兄弟,你长大了,个头比你哥哥当年还高呢,长得也真像啊!”再仔细地端详耿英, 拍一拍她的肩膀,说:“好妹子,了不起啊!”他激动得不知道说什么好了:“七年多了,我和你们大嫂经常想起你们来,老惦念呢! 咱们到家里说话,你们大嫂又快生娃了,在家里歇着呢。”说着朝大院的西北方向扬扬头,说:“喏,就在大院儿里„„”当他领着耿 正兄妹仨往家里走去时,一个胖墩墩的小男娃儿忽然从靠北边的屋子里跑了出来,口里还欢叫着:“爹,我在屋里就能听见是你回来 了!”一边说着,一边就高兴地向耿大业扑来。耿正和耿英同时蹲下身来准备抱他,小家伙却像泥鳅一样“哧溜”一下就窜到了耿大业 的身后。耿大业把小家伙拉到身前来,挨个儿指着耿正、耿直和耿英对他说:“小铁蛋儿,这是大叔叔、这是二叔叔、这是姑姑,快叫 啊!”小家伙眨巴着小眼睛看看三人,再抬头看看爹爹。耿大业再说一遍:“叫大叔叔、二叔叔、姑姑!”这一回,小家伙亮着小嗓子 叫了。耿英高兴地答应着将小家伙抱起来,欣喜地说:“你叫小铁蛋儿,好一个可爱的小铁蛋儿啊!”这边正高兴着呢,耿大嫂听着外 面热闹的说话声也出来了。她已经怀孕八个多月了,笨拙地挺着大肚子一边往前走一边问:“他爹,这是„„”耿英一看见大嫂如此模 样,赶快将小铁蛋儿递到耿
第二节 同角三角函数的基本关系式

5.求下列函数的定义域 (1)y=tanx+cotx; (2)y= sinx +tanx. 求下列函数的定义域: 求下列函数的定义域 ≠ ∈ 解: (1)使 tanx 有意义的 x 的取值集合是 {x | x≠kπ+ π , k∈Z}, 使 2 使 cotx 有意义的 x 的取值集合是 {x | x≠kπ, k∈Z}, ≠ ∈ 故所求函数的定义域是: 故所求函数的定义域是 {x | x≠kπ+ π , k∈Z}∩{x | x≠kπ, k∈Z} ={x | x≠ kπ , k∈Z}; ≠ ∈ ≠ ≠ ∈ 2 ∈ ∩ 2 sinx≥0, (2)要使原函数有意义 则 x≠kπ+ π , k∈Z. 要使原函数有意义, 要使原函数有意义 ≠ ∈ 2 2kπ≤x≤2kπ+π, k∈Z, ∈ 即 x≠kπ+ π , k∈Z. ≠ ∈ 2 故原函数定义域为{x|2kπ≤x≤2kπ+π, 且 x≠2kπ+ π , k∈Z}. 故原函数定义域为 ≠ 2 ∈
6.设 α 是第二象限的角 试问 -α, π-α, π+α 分别是第几象限 设 是第二象限的角, 试问: 的角? 的角 ∈ 是第二象限的角, 解: ∵α 是第二象限的角 ∴2kπ+ π <α<2kπ+π, k∈Z. 2 ∴ -2kπ-π<-α<-2kπ- π , k∈Z, -2kπ<π-α<-2kπ+ π , k∈Z, - 2 ∈ 2 ∈ 3π π 2kπ+ 2 <π+α<2kπ+2π, k∈Z. ∈ 是第一象限角, 是第三象限角, 是第四象限角. ∴-α 是第三象限角 π-α 是第一象限角 π+α 是第四象限角
同角三角函数关系式

cos(α+β)-cosγ=-2cosγ,∴(3)式不是常数;
又tan(α+β)=tan(π-γ)=-tanγ,∴(4)式不是常数, ∴(1),(2),(5)式为常数,共4个. 答案:3
知识要点
双基巩固
典型例题
易错辨析
提升训练
方法技巧:
1 在△ABC
(1)若△ABC
(2)若△ABC为直角三角形(∠C cosB. (3)若△ABC为钝角三角形(∠C cosB.
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
易错辨析
提升训练
方法技巧:1. 化简是一种不指定结果的恒等变形,
其结果要求:项数尽可能少、次数尽可能低、尽量使根 号内或分母中不含三角函数(式),能求值的尽量求值.
2. 化简前,注意分析角及式子的结构特点,选择恰
当的公式和化简顺序.
知识要点
双基巩固
典型例题
易错辨析
提升训练
综合应用
【思路点拨】 先利用诱导公式,将条件化简,再利用平方
关系,消去A(或B)得到B(或A)的某一三角函数值,进
而求出A,B,C.
知识要点
双基巩固
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
,则sin(B
知识要点
双基巩固
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
易错辨析
提升训练
学科网
知识要点
三角函数之间的关系公式

三角函数之间的关系公式1. 同角三角函数的基本关系:倒数关系:tanα•cotα=1 sinα•cscα=1 cosα•secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=csc α/secα平方关系:sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α) 1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式:sin²α+cos²α=1 tan α*cot α=12. 一个特殊公式:(sina+sinθ)*(sina+sinθ)=sin(a+θ)*sin (a-θ)证明:(sina+sinθ)*(sina+sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin(a+θ)*sin(a-θ)3. 锐角三角函数公式正弦:sin α=∠α的对边/∠α的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边4. 二倍角公式正弦sin2A=2sinA•cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1 =1-2Sin^2(a) 2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1正切tan2A=(2tanA)/(1-tan^2(A))5. 三倍角公式sin3α=4sinα•sin(π/3+α)sin(π/3-α)cos3α=4cosα•cos(π/3+α)cos(π/3-α)tan3a = tan a •tan(π/3+a)•tan(π/3-a)6. n倍角公式sin(n a)=Rsina sin(a+π/n)……sin(a+(n-1)π/n). 其中R=2^(n-1)7. 半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA )=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2;cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))8. 和差化积sinθ+sinφ= 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ= 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ= 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ=-2sin[(θ+φ)/2]sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)9. 两角和公式cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβ10. 积化和差sinαsinβ= [cos(α-β)-cos(α+β)] /2cosαcosβ= [cos(α+β)+cos(α-β)]/2sinαcosβ= [sin(α+β)+sin(α-β)]/2cosαsinβ= [sin(α+β)-sin(α-β)]/211. 双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tanh(a) = sin h(a)/cos h(a)公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinαcos(2kπ+α)= cosαtan(2kπ+α)= tan αcot(2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tan αcot(π+α)= cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)= -sin αcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tan αcot(π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tan αcot(2π-α)= -cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot (π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)= sinαtan (π/2-α)= cotαcot(π/2-α)= tanαsin(3π/2+α)= -cosαcos (3π/2+α)= sinαtan(3π/2+α)= -cotαcot(3π/2+α)= -tan αsin(3π/2-α)= -cosαcos(3π/2-α)= -sinαtan(3π/2-α)= cotαcot(3π/2-α)= tanα(以上k∈Z) A•sin(ωt+θ)+ B•sin(ωt+φ) = √{(A²+B²+2ABcos(θ-φ)} •sin{ ωt + arcsin[ (A•sinθ+B•sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} } √表示根号,包括{……}中的内容12. 诱导公式sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosA tan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限13. 万能公式sinα=2tan(α/2)/[1+(tan(α/2))²]cosα=[1-(tan(α/2))²]/[1+(tan(α/2))²]tanα=2tan(α/2)/[1-(tan(α/2))²]14. 其它公式(1) (sinα)²+(cosα)²=1(2)1+(tanα)²=(secα)²(3)1+(cotα)²=(cscα)²证明下面两式,只需将一式,左右同除(sinα)²,第二个除(cosα)²即可.(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)²+(cosB)²+(cosC)²=1-2cosAcosBcosC(8)(sinA)²+(sinB)²+(sinC)²=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a) sec(a) = 1/cos(a)15. 两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1+tanAtanB) cot(A+B) = (cotAcotB-1)/(cotB+cotA) cot(A-B) = (cotAcotB+1)/(cotB-cotA)。
三角函数复习(同角三角函数基本关系与诱导公式)

三角函数复习(同角三角函数基本关系与诱导公式). (2)商数关系:sin αcos α=tan α.1.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1(3)倒数关系:tan α=co 1t∝2.六组诱导公式(1)诱导公式的记忆口诀:奇变偶不变,符号看象限. (2)同角三角函数基本关系式的常用变形:(sin α±cos α)2=1±2sin αcos α; (sin α+cos α)2+(sin α-cos α)2=2; (sin α+cos α)2-(sin α-cos α)2=4sin αcos α. 二、课前自测1. tan 等于 ( ) A. √B. √C.√D.√2. 若 α=1,α ./,则 tanα 等于 ( )A.√B.√C. √D. √3. 已知 tanα= 1,且 α 为第二象限角,则 nα 的值为 ( )A. 1B. 11C.1D.14. .1 / n.1/= .5. 已知 tanα= ,则的值为 .三、典型例题1. 已知 α 是三角形的内角,且 nα α=1.Ⅰ求tanα的值;Ⅱ把1用tanα表示出来,并求其值;Ⅲ求:的值;Ⅳ求 nα nα α的值.2. (1) n()() n()=;(2)已知 .α/=√,则 .α/ n.α/的值为.(3)已知 n.1 α/=,则 .α111/=.(4)若 .α/=1,则 n.α/=.3. (1)已知=()()(),则的值构成的集合是()A. *+B. *+C. *+D. *+(2)()() . /()()=.(3)已知α为第三象限角,(α)= . / . / ()()().Ⅰ化简(α);Ⅱ若 .α/=1,求(α)的值.同角三角函数基本关系式与诱导公式答案课前自测 1. D 2. C 3. C4. √5. 1典型例题1. (1) 解法一: 联立 { nα α=1n αα=由 得 α=1nα, 将其代入 ,整理得 n α nα = . 因为 α 是三角形的内角, 所以 nα=,所以 α=, 所以 tanα=. 解法二:因为 nα α=1,所以 ( nα α)=.1 /,则 nα α=1,所以 nα α=,所以 ( nα α) = nα α==. 因为 nα α= 1且 α , 所以 nα , α , 所以 nα α . 所以 nα α= .由 { nα α=1nα α=得 { nα=α=所以 tanα= .(2)1 === 11因为tanα=,所以α nα=tanαtanα=. /. /=(3)tanα=,则:==. /=.(4)nα nα α==1=1=2. (1);(2)√(3)(4). 13. (1)C 【解析】当为偶数时,==;当为奇数时,==.所以的值构成的集合是*+.(2).【解析】原式=0 ./1 ( ), ( )-=./( ) =( ) ===(3)(α)= . / ./ ( ) ( ) ( )=( ) ( )( )= α(4) 因为 .α/=1, 所以 nα=1,从而 nα= 1. 又 α 为第三象限角, 所以 α= √ n α= √,所以 (α)= √.同角三角函数基本关系式与诱导公式课堂练习与作业一、选择题(共7小题;共35分) 1. n 的值为 ( ) A. 1B. √C.D. √2. 已知 ./=√,且,则 tan = ( )A. √B. √C. √D. √3. 若 α 是第三象限角,且 tanα=1,则 α= ( )A. √11B.√11C.√11D. √114. 在 中,若 tan = 则 = ( )A. √B. √C. √D. √5. 已知 n ( )= n./ 则 n = ( )A.B.C. 或D. 16. 已知 (α)=( ) ( )( ),则 .1/ 的值为 ( )A. 1B. 1C. 1D. 17. 已知函数 ( )= n ( α) ( ),且 ( )= ,则 ( ) 的值为 ( )A. B. C. D.二、填空题(共1小题;共5分)8. 已知α为锐角,且 tan(α) . /=,tan(α) n()=,则 nα的值是.三、解答题(共2小题;共26分)9. 已知 n(α)= n.α/,求下列各式的值:(1);(2) nα nα α.10. 已知 n(α)(α)=√.α /,求下列各式的值.(1) nα α;(2) n.α/.α/.答案第一部分1. A【解析】 n = n ( ) ( )= n ( )= n =1 1=12. D 【解析】 ./= n =√,又,则 =1,所以 tan =√ .3. C【解析】因为 α 是第三象限角,且 tanα= =1, n α α= ,所以 α= √1 1.4. B【解析】在 中,当 tan = 时, ./,所以 =√1=√= √. 5. B【解析】由已知等式得 n = , 所以 n = = ,所以 =1,故 n = =. 6. C【解析】因为 (α)== α,所以 . 1/= .1/= ./== 1.7. c【解析】因为 ( )= n ( α) ( )= nα = ,所以( )= n ( α) ( )= n (α) ( )=第二部分 8. √1 1【解析】由已知可得 tanα n = ,tanα n = , 解得 tanα= , 又 α 为锐角,故 nα= √11. 第三部分9. (1) 解法一:由 n ( α)= n.α/ 得 tanα= .原式=== 1.解法二:由已知得 nα= α.原式==1.(2)解法一:原式==1=.解法二:原式===.10. (1)由 n(α)(α)=√,得 nα α=√.将两边平方,得 nα α=,故 nα α=.又α,所以 nα, α.( nα α)= nα α= . /=1 ,所以 nα α=.(2) n.α/.α/=α nα=( α nα)(α α nα nα)= .1/=。
同角三角函数的基本关系式

同角三角函数基本关系式的应用
1.求值题型
已知某个角的一个三角函数 值,求这个角的其余三角函数值.
3 例6 已知 sin , 求 cos ,tan 的值. 5
注意开方运算时根号前正、负号的选取, 即根据角所在的象限讨论正负号。
课本P23 练习 1,2,3
2.化简三角函数式. 函数种类要最少,项数要最少,函数 次数尽量低,能求出值的要求出数值,尽 量使分母不含三角形式和根式。
2 2
证法二:因为
(1 sin )(1 sin - sin 0, cos 0, cos 1 sin 所以 1 sin cos
证法三:
cos 0,1 sin 0 cos cos (1 sin ) 原式左边 2 1 sin cos cos (1 sin ) cos (1 sin ) 2 2 1 sin cos 1 sin 右边 cos
课本P23 练习 4
点评:(1)考虑化“切”为“弦”求值,有时也 需要化“弦”为“切”; (2)注意“1”的代换.
3.证明三角恒等式. 一般方法有三种:
(1)由繁的一边证到简单的一边 (2)证明左、右两边等于同一式子 (3)证明与原恒等式等价的式子,从而 推出原式成立
例7
cos x 1 sin x 求证 1 sin x cos x
课本P23 练习 5
证法一:因为
cos 1 sin cos (1 sin ) 1 sin cos (1 sin ) cos
2
cos cos 0 (1 sin ) cos cos 1 sin 所以 1 sin cos
§1.2.2同角三角函数的 基本关系式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、倒数关系
tan cot 1 sin csc 1 cos sec 1
2 1、化简 (1 ) 1 sin 40
( 2) sec A 1
2
2、求证
( 1 ) cot (tan sin ) sin
(2) sin cos
3、弧度制
1
180
rad 0.01745rad
180 1rad 57.30 57 18
4、任意角的三角函数
正弦 s in cos ta n cot y r x r y x x y r x r y
余弦
r x y 0 y y + + + o x o x + s in csc
.
1 sec x tan x 1 sin x 2、证明: 1 sec x tan x cos x 5 3、已知 sin cos , 4
求 (1) sin cos ( 2) sin cos
3 3
4、Biblioteka P2761、P28习题
8、 9
2、《ABC 》同步完成
§4.4 同角三角函数的基本关系式 (二)
我们的目标
1. 掌握同角三角函数八个基本关系式
2. 能熟练运用基本关系式证明三角恒等式
1、角的扩充
终边相同的角 k 360
kZ
2、诱导公式
s in ( k 3 6 0 ) s in ta n ( k 3 6 0 ) ta n cos( k 360 ) cos c o t( k 3 6 0 ) c o t
人工智能(Artificial Intelligence),英文缩写为AI。它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一 门新的技术科学。 人工智能是计算机科学的一个分支,它企图了解智能的实质,并生产出一种新的能以人类智能相似的方式做出反应的智能机器,该领域的研究 包括机器人、语言识别、图像识别、自然语言处理和专家系统等。人工智能从诞生以来,理论和技术日益成熟,应用领域也不断扩大,可以设 想,未来人工智能带来的科技产品,将会是人类智慧的“容器”。人工智能可以对人的意识、思维的信息过程的模拟。人工智能不是人的智能, 但能像人那样思考、也可能超过人的智能。 ; / 人工智能 jeh61mcg 人工智能是一门极富挑战性的科学,从事这项工作的人必须懂得计算机知识,心理学和哲学。人工智能是包括十分广泛的科学,它由不同的领 域组成,如机器学习,计算机视觉等等,总的说来,人工智能研究的一个主要目标是使机器能够胜任一些通常需要人类智能才能完成的复杂工 作。但不同的时代、不同的人对这种“复杂工作”的理解是不同的。 [1] 2017年12月,人工智能入选“2017年度中国媒体十大流行语”。 玉盈。也就是经此壹事,玉盈在京城贵族名媛间声名鹊起。年家居然有这么壹位能干的大家闺秀,真是让很多的名门望族赞叹不已。而赞叹之 余,居然发现这玉盈姑娘还待字闺中,为此很多有适龄婚配公子的大户人家就四处托媒人,想娶回自己家当儿媳妇。年总督夫妇壹直都将玉盈 当作亲生女儿来对待,年二公子对外人也总是壹口壹个妹子地称呼玉盈。而冰凝,这个年家的正牌大丫鬟,从小到大就没有离开过湖广总督府。 因为从不曾听年家提起过冰凝,因此,京城人士口中的年家妹子,壹直就是玉盈。第壹卷 第七章 姐妹在含烟的搀扶下,冰凝下了马车,眼 前所见,壹座规模不大,但颇具气派的府邸映入眼帘,那门匾上的“年府”二字告诉她,这就是到家了。大管家年峰是年老爷的远房侄子,四 十多岁的年纪,被年二公子请来这里做大总管已经有三年时间。听到门房小厮的通报,他即刻带领上两名家仆,早早地恭候在门口。冰凝壹面 随众人进了府邸,壹面好奇地察看着这个新家。虽然从面积上来讲,这京城年府要比湖广总督府最少小了有三分之二,但是在规模上还算是说 得过去:前后四进的宅子,这第壹进院是正厅,用于接待宾客;第二进院子是留给年家二老来京时居住之用;第三近院子由年二公子自己壹家 子人居住;这第四进院子,就是冰凝和玉盈两位丫鬟的闺房。最后面还有壹个小巧精致的花园,几乎就是年家丫鬟妹独自享有的壹片小天地。 “快让我看看,要不是在家里,我可真不敢认呢,妹妹当真是女大十八变,越变越不认得!怎么就生得是这么漂亮呢?”“姐姐,亏得凝儿壹 路想着你的好,怎么壹见面,就开始取笑凝儿了?难道是当了掌家姑奶奶,这嘴可是越发地厉害了?”“什么掌家姑奶奶,就是给二哥帮帮忙, 瞧你这张嘴,真是壹点儿亏也不吃!”两个姑娘嘴上不饶人,手上也是不闲着,壹个抱壹个亲,嘻嘻哈哈地笑成了壹团。“五年了啊!怎么过 得这么快?姐姐还真是壹点儿都没有变,还是凝儿最亲的姐姐!”“我能怎么变?倒是你,壹天壹个样儿,再变,就真成了画儿上的仙女了!” 玉盈壹边说着,壹边将冰凝带进了早早给她收拾好的闺房。两个人又嘻笑打闹了壹阵子,玉盈怕她壹路劳顿,本来身子就弱不禁风似的,京城 的天气又异于湖广,于是只好先强压下壹堆的问题,反正将来天天在壹起,日子还长着呢,现在的当务之急是让含烟帮着赶快先歇息下来。经 过几天的适应,冰凝对京城年府的事情都熟悉起来,就开始正式接受教导嬷嬷的礼仪学习了。分别了五年的姐妹俩又重新生活在同壹片天空下, 住在同壹个年府中,那种失而复得的喜悦,两个人都非常的珍惜。因此,玉盈格外精心地打理着府务,力图让冰凝没有后顾之忧,专心致志完 成学
2
2
2
正切
sin a 1 cos a 1
cos
sec
y + o + x
余切
正割
sec csc
余割
ta n
cot
5、同角三角函数的八个基本关系式
1、平方关系 sin cos 1
2 2
1 tan sec
2 2
1 cot csc sin 2、商数关系 tan cos cos cot sin
2 2
2
2
2
2
1 sec csc
2
2 2
(3) (1 sin
2
A)(sec A 1) sin
1 sin x cos x
2
A(csc A cot A)
2
2
(4) 1 sin x
cos x
1、已知
1 sin x cos x
1 2
,求
cos x sin x 1
