八年级四边形难题综合
人教版八年级初二数学下学期平行四边形单元 易错题难题提高题学能测试试题
人教版八年级初二数学下学期平行四边形单元 易错题难题提高题学能测试试题一、选择题1.如图,菱形ABCD 中,AC 交BD 于点O ,DE BC ⊥于点E ,连接OE ,若50BCD ∠=︒,则OED ∠的度数是( )A .35°B .30°C .25°D .20°2.如图,四边形,ABCD AD 与BC 不平行,AB CD =.,AC BD 为四边形ABCD 的对角线,,,E F ,G H 分别是,,,BD BC AC AD 的中点下列结论:①EG FH ⊥;②四边形EFGH 是矩形;③HF 平分;EHG ∠④()1 2EG BC AD =-;⑤四边形EFGH 是菱形.其中正确的个数是 ( )A .1个B .2个C .3个D .4个3.如图,依次连结第一个菱形各边的中点得到一个矩形,再依次连结矩形各边的中点得到第二个菱形,按此方法继续下去.已知第一个菱形的面积为1,则第4个菱形的面积是( )A .14B .116C .132D .164 4.如图,正方形ABCD 中,点E 是AD 边的中点,BD 、CE 交于点H ,BE 、AH 交于点G ,则下列结论:①AG ⊥BE ;②5:2;③S △BHE =S △CHD ;④∠AHB=∠EHD .其中正确的个数是A .1B .2C .3D .45.矩形纸片ABCD 中,AB =5,AD =4,将纸片折叠,使点B 落在边CD 上的点B '处,折痕为AE .延长B E '交AB 的延长线于点M ,折痕AE 上有点P ,下列结论中:①M DAB '∠∠=;②PB PB '=;③AE =552;④MB CD '=;⑤若B P CD '⊥,则EB B P ''=.正确的有( )个A .2B .3C .4D .56.如图,在平行四边形ABCD 中,按以下步骤作图:①以A 为圆心,AB 长为半径画弧,交边AD 于点;②再分别以B ,F 为圆心画弧,两弧交于平行四边形ABCD 内部的点G 处;③连接AG 并延长交BC 于点E ,连接BF ,若BF =3,AB =2.5,则AE 的长为( )A .2B .4C .8D .57.如图,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC =185.其中正确结论的个数是( )A .1B .2C .3D .48.如图,在菱形ABCD 中,AB=AC=1,点E 、F 分别为边AB 、BC 上的点,且AE=BF ,连接CE 、AF 交于点H ,连接DH 交AC 于点O ,则下列结论:①△ABF ≌△CAE ;②∠FHC=∠B ;③△ADO ≌△ACH ;④=3ABCD S 菱形;其中正确的结论个数是( )A .1个B .2个C .3个D .4个9.如图,一个四边形花坛ABCD ,被两条线段MN , EF 分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S 1、S 2、S 3、S 4,若MN ∥AB ∥DC ,EF ∥DA ∥CB ,则有( )A .S 1= S 4B .S 1 + S 4 = S 2 + S 3C .S 1 + S 3 = S 2 + S 4D .S 1·S 4 = S 2·S 310.如图,正方形ABCD 中,延长CB 至E 使2CB EB =,以EB 为边作正方形EFGB ,延长FG 交DC 于M ,连接AM ,AF ,H 为AD 的中点,连接FH 分别与AB ,AM 交于点,N K .则下列说法:①ANH GNF △≌△;②DAM NFG ∠=∠;③2FN NK =;④:2:7AFN DMKH S S =△四边形.其中正确的有( )A .4个B .3个C .2个D .1个二、填空题11.如图,在矩形ABCD 中,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,点G 是EF 的中点,连接CG ,BG ,BD ,DG ,下列结论:①BC=DF ;②135DGF ︒∠=;③BG DG ⊥;④34AB AD =,则254BDG FDG S S =,正确的有__________________.12.如图,在正方形ABCD 中,点,E F 将对角线AC 三等分,且6AC =.点P 在正方形的边上,则满足5PE PF +=的点P 的个数是________个.13.如图,四边形ABCD 是菱形,∠DAB =48°,对角线AC ,BD 相交于点O ,DH ⊥AB 于H ,连接OH ,则∠DHO =_____度.14.已知在矩形ABCD 中,3,3,2AB BC ==点P 在直线BC 上,点Q 在直线CD 上,且,AP PQ ⊥当AP PQ =时,AP =________________.15.如图正方形 ABCD 中,E 是 BC 边的中点,将△ABE 沿 AE 对折至△AFE ,延长 EF 交 CD 于 G ,接 CF ,AG .下列结论:① AE ∥FC ; ②∠EAG = 45°,且BE + DG = EG ;③ABCD 19CEF S S ∆=正方形;④ AD = 3DG ,正确是_______ (填序号).16.如图,直线1l ,2l 分别经过点(1,0)和(4,0)且平行于y 轴.OABC 的顶点A ,C 分别在直线1l 和2l 上,O 是坐标原点,则对角线OB 长的最小值为_________.17.如图,在平面直角坐标系中,直线112y x =+与x 轴、y 轴分别交于A ,B 两点,以AB 为边在第二象限内作正方形ABCD ,则D 点坐标是_______;在y 轴上有一个动点M ,当MDC △的周长值最小时,则这个最小值是_______.18.如图,点E 、F 分别在平行四边形ABCD 边BC 和AD 上(E 、F 都不与两端点重合),连结AE 、DE 、BF 、CF ,其中AE 和BF 交于点G ,DE 和CF 交于点H .令AF n BC=,EC m BC=.若m n =,则图中有_______个平行四边形(不添加别的辅助线);若1m n +=,且四边形ABCD 的面积为28,则四边形FGEH 的面积为_______.19.如图,在四边形ABCD 中, //,5,18,AD BC AD BC E ==是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒3个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动,当运动时间为t 秒时,以点,,,P Q E D 为顶点的四边形是平行四边形,则t 的值等于_______.20.如图所示,在四边形ABCD 中,顺次连接四边中点E 、F 、G 、H ,构成一个新的四边形,请你对四边形ABCD 添加一个条件,使四边形EFGH 成一个菱形,这个条件是__________.三、解答题21.如图,在Rt ABC ∆中,090BAC ∠=,D 是BC 的中点,E 是AD 的中点,过点A 作//BC AF 交BE 的延长线于点F(1)求证:四边形ADCF 是菱形(2)若4,5AC AB ==,求菱形ADCF 的面积22.如图1,在正方形ABCD 和正方形BEFG 中,点,,A B E 在同一条直线上,P 是线段DF 的中点,连接,PG PC .(1)求证:,PG PC PG PC ⊥=.简析:由Р是线段DF 的中点,//DC CF ,不妨延长GP 交DC 于点M ,从而构造出一对全等的三角形,即_______≅________.由全等三角形的性质,易证CMG 是_______三角形,进而得出结论;(2)如图2,将原问题中的正方形ABCD 和正方形BEFG 换成菱形ABCD 和菱形BEFG ,且60ABC BEF ∠=∠=︒,探究PG 与PC 的位置关系及PG PC的值,写出你的猜想并加以证明;(3)当6,2AB BE ==时,菱形ABCD 和菱形BEFG 的顶点都按逆时针排列,且60ABC BEF ∠=∠=︒.若点A B E 、、在一条直线上,如图2,则CP =________;若点A B G 、、在一条直线上,如图3,则CP =________.23.如图1,在矩形纸片ABCD 中,AB =3cm ,AD =5cm ,折叠纸片使B 点落在边AD 上的E 处,折痕为PQ ,过点E 作EF ∥AB 交PQ 于F ,连接BF .(1)求证:四边形BFEP为菱形;(2)当E在AD边上移动时,折痕的端点P、Q也随着移动.①当点Q与点C重合时,(如图2),求菱形BFEP的边长;②如果限定P、Q分别在线段BA、BC上移动,直接写出菱形BFEP面积的变化范围.24.如图.正方形ABCD的边长为4,点E从点A出发,以每秒1个单位长度的速度沿射线AD运动,运动时间为t秒(t>0),以AE为一条边,在正方形ABCD左侧作正方形AEFG,连接BF.(1)当t=1时,求BF的长度;(2)在点E运动的过程中,求D、F两点之间距离的最小值;(3)连接AF、DF,当△ADF是等腰三角形时,求t的值.25.如图①,已知正方形ABCD的边长为3,点Q是AD边上的一个动点,点A关于直线BQ的对称点是点P,连接QP、DP、CP、BP,设AQ=x.(1)BP+DP的最小值是_______,此时x的值是_______;(2)如图②,若QP的延长线交CD边于点M,并且∠CPD=90°.①求证:点M是CD的中点;②求x的值.(3)若点Q是射线AD上的一个动点,请直接写出当△CDP为等腰三角形时x的值.26.如图1,在OAB 中,OAB 90∠=,30AOB ∠=,8OB =,以OB 为边,在OAB Λ外作等边OBC Λ,D 是OB 的中点,连接AD 并延长交OC 于E .(1)求证:四边形ABCE 是平行四边形;(2)连接AC ,BE 交于点P ,求AP 的长及AP 边上的高BH ;(3)在(2)的条件下,将四边形OABC 置于如图所示的平面直角坐标系中,以E 为坐标原点,其余条件不变,以AP 为边向右上方作正方形APMN :①M 点的坐标为 .②直接写出正方形APMN 与四边形OABC 重叠部分的面积(图中阴影部分).27.如图,在四边形ABCD 中,AD BC =,AD BC ∥,连接AC ,点P 、E 分别在AB 、CD 上,连接PE ,PE 与AC 交于点F ,连接PC ,D ∠=BAC ∠,DAE AEP ∠=∠. (1)判断四边形PBCE 的形状,并说明理由;(2)求证:CP AE =;(3)当P 为AB 的中点时,四边形APCE 是什么特殊四边形?请说明理由.28.定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径。
苏教版八年级下册 第9章:中心对称图形~平行四边形重难点题型训练 【含答案】

苏教版八年级下册第9章:中心对称图形——平行四边形重难点题型训练1.如图1,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接CE、OE,连接AE交OD于点F.(1)求证:OE=CD;(2)如图2,延长BC和DE相交于点G,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形ABCD和四边形OCED外)2.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且2DE=AC,连接AE交OD于点F,连接DE、OE.(1)求证:AF=EF;(2)已知AB=2,若AB=2DE,求AE的长.3.如图,四边形ABCD为平行四边形,延长BC到点E,使BE=CD,连接AE交CD 于点F.(1)求证:AE平分∠BAD;(2)连接BF,若BF⊥AE,∠E=60°,AB=4,求平行四边形ABCD的面积.4.如图,在△ABC中,点D是BC边的中点,点E,F分别在AC,AB上,且DE∥AB,EF∥BC.(1)求证:CD=EF;(2)已知∠ABC=60°,连接BE,若BE平分∠ABC,CD=6,求四边形BDEF 的周长.5.(1)如图①,点E、F分别在正方形ABCD的边AB、BC上,∠EDF=45°,连接EF,求证:EF=AE+FC.(2)如图②,点E,F在正方形ABCD的对角线AC上,∠EDF=45°,猜想EF、AE、FC的数量关系,并说明理由.6.如图,在▱ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.(1)求证:四边形ABEF是菱形;(2)若AE=6,BF=8,CE=,求▱ABCD的面积.7.如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.(1)当H(﹣2,6)时,求证:四边形EFGH是正方形;(2)若F(﹣5,0),求点G的坐标.8.如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.(1)当四边形ABCD分别是菱形、矩形、平行四边形时,相应的四边形EFGH一定是“平行四边形、菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:四边形ABCD菱形矩形平行四边形四边形EFGH (2)反之,当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时,相应的原四边形ABCD必须满足怎样的条件?当 时,四边形EFGH是矩形;当 时四边形EFGH是菱形.9.如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是点M、N(1)求证:AE=MN;(2)若AE=2,∠DAE=30°,求正方形的边长.10.如图,△ABC≌△DBC,AD平分∠BAC,AD交BC于点O.(1)如图1,求证:四边形ABDC是菱形;(2)如图2,点E为BD边的中点,连接AE交BC于点F,若∠AFO=∠ADC,在不添加任何辅助线和字母的条件下,请直接写出图2中所有长度是线段EF长度的偶数倍的线段.11.如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.(1)若PE⊥BC,求BQ的长;(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.12.已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.(1)若BF⊥AE,①求证:BF=AE;②连接OD,确定OD与AB的数量关系,并证明;(2)若正方形的边长为4,且BF=AE,求BO的长.13.如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.(1)求证:四边形ABCD为矩形;(2)若MD=6,BC=12,求BF的长度.(结果可保留根号)14.在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.(1)求证:四边形AFCE是平行四边形;(2)若AE⊥BD,AF=2,AB=4,求BF的长度.15.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)求证:△AEF≌△DEC;(2)当△ABC满足什么条件时,四边形AFBD是矩形?请说明理由.参考答案1.(1)证明:∵四边形ABCD是菱形,∴∠COD=90°,OC=AC,∵DE=AC,∴OC=DE,∵DE∥AC,∴四边形OCED是平行四边形,∴四边形OCED是矩形,∴OE=CD;(2)图中所有的平行四边形有:四边形AOED,四边形ACGD,四边形OBCE.由AO DE可得四边形AOED是平行四边形;由AC∥DG,AD∥CG可得四边形ACGD是平行四边形;由OE∥BC,OB∥CE可得四边形OBCE是平行四边形.2.(1)证明:∵四边形ABCD是菱形,∴OA=OC=AC,∵2DE=AC,∴DE=OA,又∵DE∥AC,∴四边形OADE是平行四边形,∴AF=EF;(2)解:连接CE,∵DE∥OC,DE=OC,∴四边形OCED是平行四边形,又∵菱形ABCD,∴AC⊥BD,∴四边形OCED是矩形,∴∠OCE=90°,又∵AB=2DE=AC,∴△ABC为等边三角形,∵在菱形ABCD中,∠ABC=60°,∴AC=AB=2,AO=AC=1,∴在矩形OCED中,CE=OD==,∴在Rt△ACE中,AE==.3.(1)证明:∵四边形ABCD为平行四边形,∴AB=CD,AD∥BE,∴∠DAE=∠E,∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠E,∴AB=BE,∴∠BAE=∠E,∴∠BAE=∠DAE,∴AE平分∠BAD;(2)解:由BE=AB,∠BEA=60°,∴△ABE为等边三角形,∴AB=AE=4,又∵BF⊥AE,∴AF=EF=2,∴BF==2,∵∠DAE=∠E,AF=EF,∠AFD=∠CFE,∴△ADF≌△ECF(ASA),∴平行四边形ABCD的面积=△ABE的面积=×4×2=4.4.(1)证明:∵DE∥AB,EF∥BC,∴四边形BDEF是平行四边形,∴EF=BD,∵点D是BC边的中点,∴BD=CD,∴CD=EF;(2)解:∵BE平分∠ABC,∴∠FBE=∠DBE,又∵四边形BDEF是平行四边形,∴BD=EF,BF=ED,EF∥BD,∴∠FEB=∠DBE,∴∠FBE=∠BEF,∴BF=EF,∴BD=EF=BF=ED,又∵BD=CD=6,∴BD=EF=BF=ED=6,∴四边形BDEF的周长=6×4=24.5.证明:(1)∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠C=∠ADC=∠DAB=90°,如图①:延长BA,使AM=CF,连接MD,在△AMD和△CFD中,,∴△AMD≌△CFD(SAS),∴∠MDA=∠CDF,MD=DF,∵∠EDF=45°,∴∠ADE+∠FDC=45°,∴∠ADM+∠ADE=45°=∠MDE,∴∠MDE=∠EDF,在△EDF和△EDM中,,∴△EDF≌△EDM(SAS),∴EF=EM,∵EM=AM+AE=AE+CF,∴EF=AE+CF;(2)EF2=AE2+CF2,理由如下:如图②,将△CDF绕点D顺时针旋转90°,可得△ADN,由旋转的性质可得DN=DF,AN=CF,∠DAN=∠DCF=45°,∠CDF=∠ADN,∴∠CAN=∠CAD+∠DAN=90°,∴EN2=AE2+AN2,∵∠EDF=45°,∴∠CDF+∠ADE=45°,∴∠ADE+∠ADN=45°=∠NDE=∠EDF,在△EDF和△EDN中,,∴△EDF≌△EDN(SAS),∴EF=EN,∴EF2=AE2+CF2.6.解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠AEB,∵∠BAD的平分线交BC于点E,∴∠DAE=∠BEA,∴∠BAE=∠BEA,∴AB=BE,同理可得AB=AF,∴AF=BE,∴四边形ABEF是平行四边形,∵AB=AF.∴四边形ABEF是菱形.(2)作FG⊥BC于G,∵四边形ABEF是菱形,AE=6,BF=8,∴AE⊥BF,OE=AE=3,OB=BF=4,∴BE==5,∵S菱形ABEF=•AE•BF=BE•FG,∴GF=,∴S平行四边形ABCD=BC•FG=(BE+EC)•GF=(5+)×=36.7.解:(1)∵四边形ABCD是正方形,∴∠BAO=∠AOC=90°,∵E(0,2),H(﹣2,6),∴AH=OE=2,∵四边形EFGH是菱形,∴EH=EF,在Rt△AHE和Rt△OEF中,,∴Rt△AHE≌Rt△OEF,∴∠AEH=∠EFO,∵∠EFO+∠FEO=90°,∴∠AEH+∠FEO=90°,∴∠HEF=90°,∵四边形EFGH是菱形,∴四边形EFGH是正方形.(2)连接EG交FH于K.∵HE=EF,∴AH2+AE2=EO2+OF2,∴AH2+16=4+25,∴AH=,∴H(﹣,6),∵KH=KF,∴K(﹣,3),∵GK=KE,∴G(﹣5﹣,4).8.解:(1)四边形ABCD是菱形时,平行四边形EFGH是矩形,四边形ABCD是矩形时,平行四边形EFGH是菱形,四边形ABCD是平行四边形时,四边形EFGH是平行四边形;故答案为:矩形;菱形;平行四边形;(2)当平行四边形是矩形时,原四边形ABCD必须满足的条件是对角线互相垂直,当平行四边形是菱形时,原四边形ABCD必须满足的条件是对角线相等.故答案为:对角线互相垂直(AC⊥BD);对角线相等(A C=BD).9.(1)证明:连接EC.∵四边形ABCD是正方形,EM⊥BC,EN⊥CD,∴∠NCM=∠CME=∠CNE=90°,∴四边形EMCN为矩形.∴MN=CE.又∵BD为正方形ABCD的对角线,∴∠ABE=∠CBE.在△ABE和△CBE中∵,∴△ABE≌△CBE(SAS).∴AE=EC.∴AE=MN.(2)解:过点E作EF⊥AD于点F,∵AE=2,∠DAE=30°,∴EF=AE=1,AF=AE•cos30°=2×=.∵BD是正方形ABCD的对角线,∴∠EDF=45°,∴DF=EF=1,∴AD=AF+DF=+1,即正方形的边长为+1.10.(1)证明:∵△ABC≌△DBC,∴AB=BD,AC=CD,∴∠BAD=∠BDA,∠CAD=∠CDA,∵AD平分∠BAC,∴∠DAB=∠DAC,∠ADC=∠ADC,在△ADB和△ADC中,,∴△ADB≌△ADC,∴AB=AC,∴AB=BD=CD=AC,∴四边形ABCD是菱形.(2)解:∵∠AFO=∠ADC=∠ADB,又∵∠AFO+∠EFO=180°,∴∠EFO+∠EDO=180°,∴∠FED+∠FOD=90°,∵四边形ABCD是菱形,∴AD⊥BC,∴∠FEO=∠FOD=90°,∵BE=ED,∴AB=AD,∴AB=AD=BD,∴△ABD是等边三角形,∴∠EBF=∠ABD=30°,在Rt△BEF中,BF=2EF,∵∠FBA=∠FAB=30°,∴FA=FB,在Rt△AFC中,CF=2AF=4EF,综上所述,长度是线段EF长度的偶数倍的线段有BF,AF,CF.11.解:(1)作AM⊥BC于M,设AC交PE于N.如图所示:∵∠BAC=90°,∠B=45°,∴∠C=45°=∠B,∴AB=AC,∴BM=CM,∴AM=BC=5,∵AD∥BC,∴∠PAN=∠C=45°,∵PE⊥BC,∴PE=AM=5,PE⊥AD,∴△APN和△CEN是等腰直角三角形,∴PN=AP=t,CE=NE=5﹣t,∵CE=CQ﹣QE=2t﹣2,∴5﹣t=2t﹣2,解得:t=,所以BQ=BC﹣CQ=10﹣2×=;(2)存在,t=4或12;理由如下:若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,∴t=10﹣2t+2或t=2t﹣2﹣10解得:t=4或12∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12.12.解:(1)①如图1①,∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠ABE=∠C=90°,∴∠BAE+∠AEB=90°,∵BF⊥AE,∴∠CBF+∠AEB=90°,∴∠BAE=∠CBF,在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴BF=AE;②OD=AB.证明:延长AD,交射线BM于点G,如图1②,∵△ABE≌△BCF,∴BE=CF.∵E为BC的中点,∴CF=BE=BC=DC,∴CF=DF.∵DG∥BC,∴∠DGF=∠CBF.在△DGF和△CBF中,,∴△DGF≌△CBF,∴DG=BC,∴DG=AD.∵BF⊥AE,∴OD=AG=AD=AB;(2)①若点F在CD上,如图2①,在Rt△ABE和Rt△BCF中,,∴Rt△ABE≌Rt△BCF(HL),∴∠BAE=∠CBF,∵∠BAE+∠AEB=90°,∴∠CBF+∠AEB=90°,∴∠AOB=90°.∵∠ABE=90°,AB=4,BE=2,∴AE==2.∵S△ABE=AB•BE=AE•BO,∴BO===.②若点F在AD上,如图2②,在Rt△ABE和Rt△BAF中,,∴Rt△ABE≌Rt△BAF(HL),∴∠BAE=∠ABF,∴OB=OA.∵∠BAE+∠AEB=90°,∠ABF+∠EBF=90°,∴∠AEB=∠EBF,∴OB=OE,∴OA=OB=OE.∵∠ABE=90°,AB=4,BE=2,∴AE==2,∴OB=AE=.综上所述:BO的长为或.13.(1)证明:∵在四边形ABCD中,AB∥CD,AB=CD,∴四边形ABCD是平行四边形,∴AB∥CD,∴∠A+∠ADC=180°,∵∠A=∠ADC,∴∠A=90°,∴四边形ABCD是矩形;(2)解:∵AB∥CD,∴∠ABE=∠M,∵E为AD的中点,∴AE=DE.在△ABE和△DME中,∴△ABE≌△DME(AAS),∴AB=DM=6,∵四边形ABCD是矩形,∴DC=AB=DM=6,∠C=90°,∵F为CD的中点,∴CF=CD=3,在Rt△BCF中,由勾股定理得:BF===3.14.(1)证明:连接AC,交BD于O,如图所示:∵四边形ABCD是矩形,∴∠BAD=90°,OA=OC,OB=OD,∵DE=FB,∴OE=OF,∴四边形AFCE是平行四边形;(2)解:∵DE=EF=BF,AE⊥BD,∴AD=AF=2,∴BD===2,∴BF=BD=.15.证明:(1)∵AF∥BC,∴∠AFE=∠DCE,∵点E为AD的中点,∴AE=DE,在△AEF和△DEC中,∴△AEF≌△DEC(AAS);(2)当△ABC满足:AB=AC时,四边形AFBD是矩形;∵△AEF≌△DEC,∴AF=CD,∵AF=BD,∴CD=BD;∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,∵AB=AC,BD=CD,∴∠ADB=90°,∴平行四边形AFBD是矩形.。
八年级下四边形知识点经典题型要点总结

八年级下四边形知识点经典题型要点总结在八年级下册的数学学习中,四边形是一个重要的几何图形,其中包括了矩形、正方形、菱形、平行四边形、梯形等等。
通过对于这些四边形的学习和掌握,不仅可以提高我们的空间想象力,还有助于解决实际问题。
在本文中,我们将总结四边形的知识点和经典题型要点,帮助大家更好地掌握这一部分内容。
1. 矩形矩形是一个具有四个直角的四边形,其特点是对角线相等,对边平行且相等。
矩形的相关要点包括:- 周长计算公式:周长 = 2 × (长 + 宽)- 面积计算公式:面积 = 长 ×宽- 对角线长度相等:对角线长度等于 $\sqrt{长^2 + 宽^2}$2. 正方形正方形是一种特殊的矩形,其特点是四个边和四个角都相等。
正方形的相关要点包括:- 周长计算公式:周长 = 4 ×边长- 面积计算公式:面积 = 边长 ×边长- 对角线长度:对角线长度等于边长 × $\sqrt{2}$3. 菱形菱形是一种具有对边平行且相等的四边形,其特点是所有角都是直角。
菱形的相关要点包括:- 周长计算公式:周长 = 4 ×边长- 面积计算公式:面积 = 对角线之积的一半- 对角线的长度关系:对角线互相垂直且相等4. 平行四边形平行四边形是一种具有对边平行且相等的四边形,其特点是对角线互相平分。
平行四边形的相关要点包括:- 周长计算公式:周长 = 2 × (边长1 + 边长2)- 面积计算公式:面积 = 底边 ×高- 对角线的长度和关系:对角线长度等于 $\sqrt{边长1^2 + 边长2^2 + 2×底边×高^2}$5. 梯形梯形是一种具有两条平行边的四边形,其特点是底边和顶边平行且相等。
梯形的相关要点包括:- 周长计算公式:周长 = 底边1 + 底边2 + 左斜边 + 右斜边- 面积计算公式:面积 = (底边1 + 底边2) ×高 / 2通过对于这些四边形的学习和掌握,我们可以更好地解决与其相关的问题。
初中八年级 平行四边形 拔高题 综合题 压轴题(含答案)

初中八年级平行四边形拔高题综合题压轴题(含答案)题目一已知平行四边形ABCD中,AB = 6cm,BC = 8cm,过点B作平行于AD的直线与AC交于点E,连接DE交BC的延长线于点F。
求EF的长度。
答案一连接DE并延长交BC于点G,根据平行四边形的性质,我们知道AG || DE。
所以AG || BF。
由此可得∆BFG与∆BCD为三角形对应边平行,则根据平行线截断比定理可知:$\frac{{BE}}{{BD}} = \frac{{FG}}{{GC}}$又已知$BE = BC + CE$,$CE = BD$,$BC = 8$,代入得:$\frac{{8+BD}}{{BD}} = \frac{{FG}}{{GC}}$整理可得:$\frac{{BD}}{{FG}} = \frac{{GC}}{{8+BD}}$ 由于$FG = GD$,所以:$\frac{{BD}}{{FG}} = \frac{{BD}}{{GD}} = 1$ 代入可得:$\frac{{1}}{{1}} = \frac{{GC}}{{8+BD}}$整理得:$BD = GC - 8$题目中已知BC=8,所以GC=16。
代入可得:$BD = 16 - 8 = 8$所以EF的长度等于BD,即EF=8cm。
题目二平行四边形PQRS中,已知PR = 5cm,PQ = 6cm,PS = 7cm。
点A在PS上,且PA的长度是PS的一半。
连接AQ并延长交QR 的延长线于点B,连接RP交QA的延长线于点C。
求BC的长度。
答案二设PS的长度为2x,则PA = x。
由平行四边形的性质可知AQ || RB,所以根据平行线截断比定理:$\frac{{RP}}{{PC}} = \frac{{AQ}}{{CQ}}$代入已知条件,得:$\frac{{2x + 6}}{{PC}} = \frac{{4}}{{2x - 6}}$ 整理可得:$(2x + 6)(2x - 6) = 4PC$解方程得:$x = 3$所以PA = 3cm。
苏科版八年级下册 第9章 中心对称图形~平行四边形 重难点题型训练【含答案】

苏科版八年级下册第9章中心对称图形~平行四边形重难点题型训练1.如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且AG=AB,垂足为G,则:(1)△ABF与△AGF全等吗?说明理由;(2)求∠EAF的度数;(3)若AG=7,△AEF的面积是21,求△CEF的面积.2.如图,在正方形ABCD中,AB=BC=CD=AD=10cm,∠A=∠B=∠C=∠D=90°,点E 在边AB上,且AE=4cm,如果点P在线段BC上以2cm/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.设运动时间为t秒.(1)若点Q与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由;(2)若点Q与点P的运动速度不相等,则当t为何值时,△BPE与△CQP全等?此时点Q的运动速度为多少?3.已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是线段OB、OC上的动点(1)如果动点E、F满足BE=OF(如图),且AE⊥BF时,问点E在什么位置?并证明你的结论;(2)如果动点E、F满足BE=CF(如图),写出所有以点E或F为顶点的全等三角形(不得添加辅助线).4.如图,正方形ABCD,点F在BC上,试在图中画出一条线段,构出另一个三角形,使得这个三角形全等于△DFC.(1)你能在图中画出几种不同位置的线段得到这个三角形?试写出能够画出的种数共有 种.(2)画出其中的1种位置的线段,并证明你构出的三角形全等于△DFC.5.已知正方形ABCD中,AB=BC=CD=DA=16,∠A=∠B=∠C=∠D=90°.动点P以每秒1个单位速度从点B出发沿射线BC方向运动,设点P的运动时间为t.连接PA.(1)如图1,动点Q同时以每秒4个单位速度从A点出发沿正方形的边AD运动,求t 为何值时,以点Q及正方形的某两个顶点组成的三角形和△PAB全等;(2)如图2,在(1)的基础上,当点Q到达点D以后,立即以原速沿线段DC向点C运动,当Q到达点C时,两点同时停止运动,求t为何值时,以点Q及正方形的某两个顶点组成的三角形和△PAB全等.6.已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.(1)求证:OE=OF;(2)若点O为CD的中点,求证:四边形DECF是矩形.7.在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.8.如图,在菱形ABCD中,AB=4,E为BC中点,AE⊥BC于点E,AF⊥CD于点F,CG∥AE,CG交AF于点H,交AD于点G.(1)求菱形ABCD的面积;(2)求∠CHA的度数.9.如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F,(1)证明:PC=PE;(2)求∠CPE的度数;(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.10.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE.(1)求证:OE=CD;(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.11.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.(1)求证:OE=OF;(2)如图(2)若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.12.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于D,交AB于E,且CF=BE.(1)求证:四边形BECF是菱形;(2)当∠A的大小满足什么条件时,菱形BECF是正方形?回答并证明你的结论.13.如图,四边形ABCD中,AD∥BC,AD=DC=BC,过AD的中点E作AC的垂线,交CB的延长线于F.求证:(1)四边形ABCD是菱形.(2)BF=DE.14.如图,在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AD=BC,AC,BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE,BF相交于点H.(1)图中有若干对三角形是全等的,请你任选一对进行证明;(不添加任何辅助线)(2)证明:四边形AHBG是菱形;(3)若使四边形AHBG是正方形,还需在Rt△ABC的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)15.如图:∠MON=90°,在∠MON的内部有一个正方形AOCD,点A、C分别在射线OM、ON 上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1.(1)连续D1D,求证:∠D1DA=90°;(2)连接CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论;(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1)、(2)的结论,请你再做出一个合理的判断.参考答案1.解:(1)结论:△ABF≌△AGF.理由:在Rt△ABF与Rt△AGF中,,∴△ABF≌△AGF(HL)(2)∵△ABF≌△AGF∴∠BAF=∠GAF,同理易得:△AGE≌△ADE,有∠GAE=∠DAE;即∠EAF=∠EAD+∠FAG=∠BAD=45°,故∠EAF=45°.(3)∵S△AEF=×EF×AG,AG=4∴21=×EF×AG,∴EF=6,∵BF=FG,EG=DE,AG=AB=BC=CD=7,设FC=x,EC=y,则BF=7﹣x,DE=7﹣y,∵BF+DE=FG+EG=EF=6,∴7﹣x+7﹣y=6,∴x+y=8 ①在Rt△EFC中,∵EF2=EC2+FC2,∴x2+y2=62②①2﹣②得到,2xy=28,∴S△CEF=xy=7.方法二:易知S△ABF=S△AGF,S△AED=S△AEG,∴S△ABF+S△ADE=S△AEF=21,∴S△EFC=S正方形ABCD﹣S五边形ABFED=49﹣42=7.2.解:(1)全等.理由:由题意:BP=CQ=2t当t=2时,BP=CQ=4∵AB=BC=10,AE=4∴BE=CP=10﹣4=6∵BP=CQ,∠B=∠C=90°,BE=CP∴△BPE≌△CQP(SAS)(2)∵P、Q运动速度不相等∴BP≠CQ∵∠B=∠C=90°∴当BP=CP,CQ=BE时,△BPE≌△CPQ,∴BP=CP=BC=5,CQ=BE=6∴当t=5÷2=(秒)时,△BPE≌△CPQ,此时点Q的运动速度为6÷=(cm/s)3.解:(1)当AE⊥BF时,点E在BO中点.证明如下:延长AE交BF于点M,如图所示:∵∠BME=∠AOE,∠BEM=∠AEO,∴△BEM∽△AEO,∴,∵∠MBE=∠OBF,∠BME=∠BOF,∴△BEM∽△BFO,∴,∵AO=BO,∴EO=OF,∵BE=OF,∴BE=EO,故当AE⊥BF时,点E在BO中点.(2)∵四边形ABCD是正方形,∴AO=CO=BO=DO,AC⊥BD,AB=BC=AD=CD,∠ACB=∠ABD=∠ADE=∠BAC=45°∵BE=CF,∴OE=OF,AF=DE,∵BE=CF,∠ABD=∠ACB,AB=BC∴△ABE≌△BCF(SAS)同理可得△AOE≌△BOF,△ADE≌△BAF;∴以点E或F为顶点的全等三角形有△ABE≌△BCF,△AOE≌△BOF,△ADE≌△BAF;4.解:(1)如图,共可以构造出8个满足条件的三角形;故答案为:8.(2)如图1,作AE=CF,则△DFC≌△DAE,证明如下:∵四边形ABCD是正方形,∴AD=CD,∠A=∠C=90°,在△DFC和△DAE中,,∴△DFC≌△DAE(SAS).5.解:(1)由题意,得BP=t,AQ=4t,QD=16﹣4t,∵△ABP≌△CDQ∴BP=QD∴t=16﹣4t解得:t=,∴当t=时,以点Q及正方形的某两个顶点组成的三角形和△PAB全等;(2)如图2,依题意有△ADQ≌△ABP或△BCQ≌△ABP∴DQ=BP或CQ=BP∵DQ=4t﹣16,CQ=32﹣4t∴4t﹣16=t或32﹣4t=t解得:t=或t=,∴当t=或t=时,以点Q及正方形的某两个顶点组成的三角形和△PAB全等.6.证明:(1)∵CE平分∠BCD、CF平分∠GCD,∴∠BCE=∠DCE,∠DCF=∠GCF,∵EF∥BC,∴∠BCE=∠FEC,∠EFC=∠GCF,∴∠DCE=∠FEC,∠EFC=∠DCF,∴OE=OC,OF=OC,∴OE=OF;(2)∵点O为CD的中点,∴OD=OC,又OE=OF,∴四边形DECF是平行四边形,∵CE平分∠BCD、CF平分∠GCD,∴∠DCE=∠BCD,∠DCF=∠DCG∴∠DCE+∠DCF=(∠BCD+∠DCG)=90°,即∠ECF=90°,∴四边形DECF是矩形.7.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD.∵BE∥DF,BE=DF,∴四边形BFDE是平行四边形.∵DE⊥AB,∴∠DEB=90°,∴四边形BFDE是矩形;(2)∵四边形ABCD是平行四边形,∴AB∥DC,∴∠DFA=∠FAB.在Rt△BCF中,由勾股定理,得BC==5,∴AD=BC=DF=5,∴∠DAF=∠DFA,∴∠DAF=∠FAB,即AF平分∠DAB.8.解:(1)如图,连接AC,∵E为BC的中点,AE⊥BC,∴AB=AC,又∵菱形的边AB=BC,∴△ABC是等边三角形,∴AE=AB=×4=2,∴菱形ABCD的面积=BC•AE=4×2=8;(2)在等边三角形ABC中,∵AE⊥BC,∴∠CAE=∠BAC=×60°=30°,同理∠CAF=30°,∴∠EAF=∠CAE+∠CAF=30°+30°=60°,∵AE∥CG,∴∠CHA=180°﹣∠EAF=180°﹣60°=120°.9.(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,在△ABP和△CBP中,,∴△ABP≌△CBP(SAS),∴PA=PC,∵PA=PE,∴PC=PE;(2)解:由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP,∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E,∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,即∠CPE=∠EDF=90°;(3)解:AP=CE;理由如下:在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,在△ABP和△CBP中,,∴△ABP≌△CBP(SAS),∴PA=PC,∠BAP=∠BCP,∵PA=PE,∴PC=PE,∴∠DAP=∠DCP,∵PA=PC,∴∠DAP=∠AEP,∴∠DCP=∠AEP∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,∴△EPC是等边三角形,∴PC=CE,∴AP=CE.10.(1)证明:在菱形ABCD中,OC=AC.∴DE=OC.∵DE∥AC,∴四边形OCED是平行四边形.∵AC⊥BD,∴平行四边形OCED是矩形.∴OE=CD.(2)解:在菱形ABCD中,∠ABC=60°,∴AC=AB=4,∴在矩形OCED中,CE=OD===2.在Rt△ACE中,AE==2.11.解:(1)∵四边形ABCD是正方形.∴∠BOE=∠AOF=90°,OB=OA.又∵AM⊥BE,∴∠MEA+∠MAE=90°=∠AFO+∠MAE,∴∠MEA=∠AFO.在△BOE和△AOF中,∵,∴△BOE≌△AOF.∴OE=OF.(2)OE=OF成立.∵四边形ABCD是正方形,∴∠BOE=∠AOF=90°,OB=OA.又∵AM⊥BE,∴∠F+∠MBF=90°,∠E+∠OBE=90°,又∵∠MBF=∠OBE,∴∠F=∠E.在△BOE和△AOF中,∵,∴△BOE≌△AOF.∴OE=OF.12.1)证法一:如图∵EF垂直平分BC,∴BE=EC,BF=CF,∵CF=BE,∴BE=EC=CF=BF,∴四边形BECF是菱形;证法二:如图∵EF垂直平分BC,∴BD=DC,EF⊥BC∵BE=CF,∴△BED≌△CFD,∴DE=DF∴四边形BECF是菱形;(2)解法一:当∠A=45°时,菱形BECF是正方形.∵∠A=45°,∠ACB=90°,∴∠EBC=45°∴∠EBF=2∠EBC=2×45°=90°∴菱形BECF是正方形.解法二:当∠A=45°时,菱形BECF是正方形.∵∠A=45°,∠ACB=90°,∴∠EBC=45°,∵BE=EC,∴∠ECB=∠EBC=45°∴∠BEC=90°,∴菱形BECF是正方形.13.证明:(1)∵AD∥BC,AD=BC(已知),∴四边形ABCD为平行四边形.又邻边AD=DC,∴四边形ABCD为菱形;(3分)(2)证法一:如图:记EF与AC交点为G,EF与AB的交点为M.由(1)证得四边形ABCD为菱形,所以对角线AC平分∠A,即∠BAC=∠DAC.又∵EF⊥AC,AG=AG,∴△AGM≌△AGE,∴AM=AE.(6分)又∵E为AD的中点,四边形ABCD为菱形,∴AM=BM.∠MAE=∠MBF.又∵∠BMF=∠AME,∴△BMF≌△AME.∴BF=AE.∴BF=DE.(8分)证法二:如图:连接BD∵四边形ABCD为菱形∴BD⊥AC∵EF⊥AC∴EF∥BD∵BF∥DE∴四边形BDEF是平行四边形∴BF=DE(8分)14.(1)解:△ABC≌△BAD.证明:∵AD=BC,∠ABC=∠BAD=90°,AB=BA,∴△ABC≌△BAD(SAS).(2)证明:∵AH∥GB,BH∥GA,∴四边形AHBG是平行四边形.∵△ABC≌△BAD,∴∠ABD=∠BAC.∴GA=GB.∴平行四边形AHBG是菱形.(3)解:需要添加的条件是AB=BC.15.(1)证明:∵∠D1AD+∠B1AD=90°,∠OAB1+∠B1AD=90°,∴∠B1AO=∠D1AD,∵AD1=AB1,AO=AD,∴△OAB1≌△DAD1,∴∠D1DA=∠O=90°;(D1,D,C在同一条直线上).(2)解:猜想∠C1CN=45°.证明:作C1H⊥ON于H.作C1G⊥CD1于G;则有C1G=CH.∵∠C1D1C+∠AD1D=90°,∠C1B1H+∠AB1O=90°∴∠C1D1C=∠C1B1H,∵C1D1=B1C1,∠D1C1E=∠C1HB1=90°,∴△C1GD1≌△C1B1H,∴C1G=C1H,又∵CH=C1G,∴直角三角形CHC1是个等腰直角三角形,∴∠C1CN=45°.(3)解:作图;得∠ADD2=90°(∠ADD2=90°、∠C2CN=45°均可).。
专题15 四边形的综合 题型全覆盖(16题)-2020-2021学年八年级数学下(人教版)(原卷版)

专题15 四边形的综合 题型全覆盖(16题)【思维导图】【考查题型】考查题型一 中点四边形1.(2020·天津河西区·八年级期中)如图,已知四边形ABCD 中,,,,E F G H 分别为,,,AB BC CD DA 上的点(不与端点重合).(1)若,,,E F G H 分别为,,,AB BC CD DA 的中点.求证:四边形EFGH 是平行四边形;(2)在(1)的条件下,根据题意填空:若四边形ABCD 的对角线AC 和BD 满足 时,四边形EFGH 是矩形;若四边形ABCD 的对角线AC 和BD 满足 时,四边形EFGH 是菱形;若四边形ABCD 的对角线AC 和BD 满足 时,四边形EFGH 是正方形.(3)判断对错:①若已知的四边形ABCD 是任意矩形,则存在无数个四边形EFGH 是菱形;( )②若已知的四边形ABCD 是任意矩形,则至少存在一个四边形EFGH 是正方形.( )2.(2020·山东济宁市·八年级期中)综合与实践问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD 中,点E ,F ,G ,H 分别为边AB ,BC ,CD ,DA 的中点.试说明中点四边形EFGH 是平行四边形.探究展示:勤奋小组的解题思路:反思交流:(1)①上述解题思路中的“依据1”、“依据2”分别是什么?依据1:;依据2:;②连接AC,若AC=BD时,则中点四边形EFGH的形状为;创新小组受到勤奋小组的启发,继续探究:(2)如图(2),点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并说明理由;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为.3.(2020·静宁县八年级期中)已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).(1)四边形EFGH的形状是,证明你的结论.(2)当四边形ABCD的对角线满足条件时,四边形EFGH是矩形;(3)你学过的哪种特殊四边形的中点四边形是矩形?.4.(2020·广东深圳市八年级期中)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)考查题型二 特殊四边形的动点问题5.(2020·菏泽市期末)如图,在长方形ABCD 中,6AB cm =,AD 2cm =,动点P 、Q 分别从点A 、C 同时出发,点P 以2厘米/秒的速度向终点B 移动,点Q 以1厘米/秒的速度向D 移动,当有一点到达终点时,另一点也停止运动.设运动的时间为t ,问:(1)当1t =秒时,四边形BCQP 面积是多少?(2)当t 为何值时,点P 和点Q 距离是3cm ?(3)当t =_________时,以点P 、Q 、D 为顶点的三角形是等腰三角形.(直接写出答案)6.(2020·四川成都市七年级期中)如图1,在长方形ABCD 中,12AB cm =,BC 10cm =,点P 从A 出发,沿A B C D →→→的路线运动,到D 停止;点Q 从D 点出发,沿D C B A →→→路线运动,到A 点停止.若P 、Q 两点同时出发,速度分别为每秒1cm 、2cm ,a 秒时P 、Q 两点同时改变速度,分别变为每秒2cm 、54cm (P 、Q 两点速度改变后一直保持此速度,直到停止),如图2是APD ∆的面积2()s cm 和运动时间x (秒)的图象.(1)求出a 值;(2)设点P 已行的路程为1()y cm ,点Q 还剩的路程为2()y cm ,请分别求出改变速度后,12,y y 和运动时间x (秒)的关系式;(3)求P 、Q 两点都在BC 边上,x 为何值时P ,Q 两点相距3cm ?7.(2020·耒阳市八年级期中)如图,在长方形ABCD中,AB=4cm,BE=5cm,点E是AD边上的一点,AE、DE分别长acm、bcm,满足(a﹣3)2+|2a+b﹣9|=0.动点P从B点出发,以2cm/s的速度沿B→C→D运动,最终到达点D.设运动时间为ts.(1)a=cm,b=cm;(2)t为何值时,EP把四边形BCDE的周长平分?(3)另有一点Q从点E出发,按照E→D→C的路径运动,且速度为1cm/s,若P、Q两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t为何值时,△BPQ的面积等于6cm2.8.(2020·石阡县期末)如图,在Rt ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s 的速度向点A匀速运动.同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)当t为何值时,DEF为直角三角形?请说明理由.考查题型三四边形中线段最值∆沿CD所在直线折叠,9.(2020·南宁市八年级期中)如图,矩形ABCD的对角线AC,BD相交于点O,将COD∆.得到CED(1)求证:四边形OCED 是菱形;(2)若2AB =,当四边形OCED 是正方形时,OC 等于多少?(3)若3BD =,30ACD ∠=︒,P 是CD 边上的动点,Q 是CE 边上的动点,那么PE PQ +的最小值是多少? 10.(2020·北京市八年级期中)如图,长方形ABCD 中,AB =8,BC =10,在边CD 上取一点E ,将△ADE 折叠后点D 恰好落在BC 边上的点F 处(1)求CE 的长;(2)在(1)的条件下,BC 边上是否存在一点P ,使得PA +PE 值最小?若存在,请求出最小值:若不存在,请说明理由.11.(2020·福建龙岩市·八年级期中)如图,在边长为2cm 的正方形ABCD 中,Q 为BC 边的中点,P 为对角线AC 上的一个动点,连接PB ,PQ ,求△PBQ 周长的最小值.12.(2020·河南周口市期末)如图,在Rt △ABC 中,∠ACB =90°,AC =4,BC =6,点E 是斜边AB 上的一个动点,连接CE ,过点B ,C 分别作BD ∥CE ,CD ∥BE ,BD 与CD 相交于点D .(1)当CE ⊥AB 时,求证:四边形BECD 是矩形;(2)填空:①当BE 的长为______时,四边形BECD 是菱形;②在①的结论下,若点P是BC上一动点,连接AP,EP,则AP+EP的最小值为______.考查题型四四边形其他综合问题13.(2020·黄石市八年级期中)如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.(1)当t为何值时,四边形ABQP是矩形;(2)当t为何值时,四边形AQCP是菱形;(3)分别求出(2)中菱形AQCP的周长和面积.14.(2020·四川广安市九年级期末)给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.①求证:△BCE是等边三角形;②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.15.(2020·山东临沂市·八年级期中)如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.16.(2020·山东德州市·八年级期末)以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是;(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.。
八年级下册数学平行四边形难题

八年级下册数学平行四边形难题平行四边形是几何学中一个非常重要的图形,它有许多重要的性质和应用。
在初二下学期的平行四边形单元中,学生们将学习如何证明平行四边形的性质和判定,以及解决一些相关的几何问题。
为了更好地帮助学生掌握这个单元的知识点,下面列举了一些常见的易错题和难题。
一、易错题1、已知平行四边形ABCD的对角线AC和BD相交于点O,AC=4,BD=2,则AB的取值范围是?这道题是一道易错题,很多学生会认为AB的取值范围是2<AB<4。
然而,这个答案是错误的。
因为在平行四边形ABCD中,对角线AC和BD互相平分,即AO=CO=2,BO=DO=1,根据三角形的三边关系,可以得到AB的取值范围是1<AB<5。
2、已知平行四边形ABCD的对角线AC和BD相交于点O,且AC垂直于AB,BD垂直于CD,AC=4,BD=3。
求平行四边形ABCD的面积。
3、这道题是一道易错题,很多学生会认为平行四边形ABCD的面积是12。
然而,这个答案是错误的。
因为在平行四边形ABCD中,对角线AC和BD互相平分,即AO=CO=2,BO=DO= 5,根据勾股定理可以得到AB= 5。
根据三角形的面积公式可以得到平行四边形ABCD的面积是25。
二、难题1、已知平行四边形ABCD的对角线AC和BD相交于点O,且AC垂直于AB,BD垂直于CD,AC=4,BD=3。
求平行四边形ABCD的周长。
这道题是一道难题,需要学生灵活运用平行四边形的性质和判定来解决。
在解决这道题时,需要先根据已知条件求出AB的长度,再利用平行四边形的对边相等的性质求出平行四边形ABCD的周长。
由于这道题涉及到的知识点较多,很多学生难以全面掌握并灵活运用。
2、已知平行四边形ABCD的对角线AC和BD相交于点O,且OA=OC,OB=OD。
求证:平行四边形ABCD是矩形。
这道题是一道难题,需要学生通过证明两条对角线互相平分来证明平行四边形是矩形。
人教版八年级初二数学下学期平行四边形单元 易错题难题同步练习试题

人教版八年级初二数学下学期平行四边形单元 易错题难题同步练习试题一、解答题1.如图,正方形ABCO 的边OA 、OC 在坐标轴上,点B 坐标为(6,6),将正方形ABCO 绕点C 逆时针旋转角度α(0°<α<90°),得到正方形CDEF ,ED 交线段AB 于点G ,ED 的延长线交线段OA 于点H ,连结CH 、CG .(1)求证:CG 平分∠DCB ;(2)在正方形ABCO 绕点C 逆时针旋转的过程中,求线段HG 、OH 、BG 之间的数量关系;(3)连结BD 、DA 、AE 、EB ,在旋转的过程中,四边形AEBD 是否能在点G 满足一定的条件下成为矩形?若能,试求出直线DE 的解析式;若不能,请说明理由.2.如图所示,四边形ABCD 是正方形, M 是AB 延长线上一点.直角三角尺的一条直角边经过点D ,且直角顶点E 在AB 边上滑动(点E 不与点A B 、重合),另一直角边与CBM ∠的平分线BF 相交于点F .(1)求证: ADE FEM ∠=∠;(2)如图(1),当点E 在AB 边的中点位置时,猜想DE 与EF 的数量关系,并证明你的猜想;(3)如图(2),当点E 在AB 边(除两端点)上的任意位置时,猜想此时DE 与EF 有怎样的数量关系,并证明你的猜想.3.在正方形ABCD 中,点E 是CD 边上任意一点,连接,AE 过点B 作BF AE ⊥于F ,交AD 于H .()1如图1,过点D 作DG AE ⊥于G .求证:BF DG FG -=;()2如图2,点E 为CD 的中点,连接DF ,试判断,,DF FH EF 存在什么数量关系并说明理由;()3如图3,1AB =,连接EH ,点Р为EH 的中点,在点E 从点D 运动到点C 的过程中,点Р随之运动,请直接写出点Р运动的路径长.4.(解决问题)如图1,在ABC ∆中,10AB AC ==,CG AB ⊥于点G .点P 是BC 边上任意一点,过点P 作PE AB ⊥,PF AC ⊥,垂足分别为点E ,点F .(1)若3PE =,5PF =,则ABP ∆的面积是______,CG =______.(2)猜想线段PE ,PF ,CG 的数量关系,并说明理由.(3)(变式探究)如图2,在ABC ∆中,若10AB AC BC ===,点P 是ABC ∆内任意一点,且PE BC ⊥,PF AC ⊥,PG AB ⊥,垂足分别为点E ,点F ,点G ,求PE PF PG ++的值.(4)(拓展延伸)如图3,将长方形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C '处,点P 为折痕EF 上的任意一点,过点P 作PG BE ⊥,PH BC ⊥,垂足分别为点G ,点H .若8AD =,3CF =,直接写出PG PH +的值.5.探究:如图①,△ABC是等边三角形,在边AB、BC的延长线上截取BM=CN,连结MC、AN,延长MC交AN于点P.(1)求证:△ACN≌△CBM;(2)∠CPN= °;(给出求解过程)(3)应用:将图①的△ABC分别改为正方形ABCD和正五边形ABCDE,如图②、③,在边AB、BC的延长线上截取BM=CN,连结MC、DN,延长MC交DN于点P,则图②中∠CPN= °;(直接写出答案)(4)图③中∠CPN= °;(直接写出答案)(5)拓展:若将图①的△ABC改为正n边形,其它条件不变,则∠CPN= °(用含n 的代数式表示,直接写出答案).6.已知:在矩形ABCD中,点F为AD中点,点E为AB边上一点,连接CE、EF、CF,EF平分∠AEC.(1)如图1,求证:CF⊥EF;(2)如图2,延长CE、DA交于点K, 过点F作FG∥AB交CE于点G若,点H为FG上一点,连接CH,若∠CHG=∠BCE, 求证:CH=FK;(3)如图3, 过点H作HN⊥CH交AB于点N,若EN=11,FH-GH=1,求GK长.7.如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).(1)求G 点坐标(2)求直线EF 解析式(3)点N 在坐标轴上,直线EF 上是否存在点M ,使以M 、N 、F 、G 为顶点的四边形是平行四边形?若存在,直接写出M 点坐标;若不存在,请说明理由8.如图,在矩形 ABCD 中, AB =16 , BC =18 ,点 E 在边 AB 上,点 F 是边 BC 上不与点 B 、C 重合的一个动点,把△EBF 沿 EF 折叠,点B 落在点 B' 处.(I)若 AE =0 时,且点 B' 恰好落在 AD 边上,请直接写出 DB' 的长;(II)若 AE =3 时, 且△CDB' 是以 DB' 为腰的等腰三角形,试求 DB' 的长;(III)若AE =8时,且点 B' 落在矩形内部(不含边长),试直接写出 DB' 的取值范围.9.如图①,在等腰Rt ABC 中,90BAC ∠=,点E 在AC 上(且不与点A 、C 重合),在ABC 的外部作等腰Rt CED ,使90CED ∠=,连接AD ,分别以AB ,AD 为邻边作平行四边形ABFD ,连接AF .()1请直接写出线段AF ,AE 的数量关系;()2①将CED 绕点C 逆时针旋转,当点E 在线段BC 上时,如图②,连接AE ,请判断线段AF ,AE 的数量关系,并证明你的结论;②若25AB =2CE =,在图②的基础上将CED 绕点C 继续逆时针旋转一周的过程中,当平行四边形ABFD 为菱形时,直接写出线段AE 的长度.10.如图,已知正方形ABCD与正方形CEFG如图放置,连接AG,AE.(1)求证:AG AE=(2)过点F作FP AE⊥于P,交AB、AD于M、N,交AE、AG于P、Q,交BC于H,.求证:NH=FM【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)见解析;(2)HG=OH+BG;(3)能成矩形,y33 42x=-.【分析】(1)根据旋转和正方形的性质可得出CD=CB,∠CDG=∠CBG=90,根据全等直角三角形的判定定理(HL)即可证出Rt△CDG≌Rt△CBG,即∠DCG=∠BCG,由此即可得出CG平分∠DCB;(2)由(1)的Rt△CDG≌Rt△CBG可得出BG=DG,根据全等直角三角形的判定定理(HL)即可证出Rt△CHO≌Rt△CHD,即OH=HD,再根据线段间的关系即可得出HG=HD+DG=OH+BG;(3)根据(2)的结论即可找出当G点为AB中点时,四边形AEBD为矩形,再根据正方形的性质以及点B的坐标可得出点G的坐标,设H点的坐标为(x,0),由此可得出HO=x,根据勾股定理即可求出x的值,即可得出点H的坐标,结合点H、G的坐标利用待定系数法即可求出直线DE的解析式.【详解】(1)∵正方形ABCO绕点C旋转得到正方形CDEF,∴CD=CB,∠CDG=∠CBG=90°.在Rt△CDG和Rt△CBG中,∵CG CGCD CB=⎧⎨=⎩,∴Rt△CDG≌Rt△CBG(HL),∴∠DCG=∠BCG,即CG平分∠DCB.(2)由(1)证得:Rt△CDG≌Rt△CBG,∴BG=DG.在Rt△CHO和Rt△CHD中,∵CH CHCO CD=⎧⎨=⎩,∴Rt△CHO≌Rt△CHD(HL),∴OH=HD,∴HG=HD+DG=OH+BG.(3)假设四边形AEBD可为矩形.当G点为AB中点时,四边形AEBD为矩形,如图所示.∵G点为AB中点,∴BG=GA12=AB,由(2)证得:BG=DG,则BG=GA=DG12=AB12=DE=GE,又AB=DE,∴四边形AEBD为矩形,∴AG=EG=BG=DG.∵AG12=AB=3,∴G点的坐标为(6,3).设H点的坐标为(x,0),则HO=x,∴HD=x,DG=3.在Rt△HGA中,HG=x+3,GA=3,HA=6﹣x,由勾股定理得:(x+3)2=32+(6﹣x)2,解得:x=2,∴H点的坐标为(2,0).设直线DE的解析式为:y=kx+b(k≠0),将点H(2,0)、G(6,3)代入y=kx+b中,得:2063k bk b+=⎧⎨+=⎩,解得:3432kb⎧=⎪⎪⎨⎪=-⎪⎩,∴直线DE的解析式为:y3342x=-.故四边形AEBD能为矩形,此时直线DE的解析式为:y33 42x=-.【点睛】本题考查了矩形的性质、旋转的性质、全等三角形的判定及性质、待定系数法求函数解析式以及勾股定理.解题的关键是:(1)证出Rt △CDG ≌Rt △CBG ;(2)找出BG =DG 、OH =HD ;(3)求出点H 、G 的坐标.本题属于中档题,难度不大,解决该题型题目时,根据全等三角形的性质找出相等的边和角是关键.2.(1)详见解析;(2)DE EF =,理由详见解析;(3)DE EF =,理由详见解析【分析】(1)根据90,90AED FEB ADE AED ∠+∠=︒∠+∠=︒,等量代换即可证明;(2)DE=EF ,连接NE ,在DA 边上截取DN=EB ,证出△DNE ≌△EBF 即可得出答案;(3)在DA 边上截取DN EB =,连接NE ,证出()DNE EBF ASA ≌即可得出答案.【详解】(1)证明:∵90DAB DEF ∠=∠=︒,∴90,90AED FEB ADE AED ∠+∠=︒∠+∠=︒,∴ADE FEM ∠=∠;(2) ;DE EF =理由如下:如图,取AD 的中点N ,连接NE ,∵四边形ABCD 为正方形,∴AD AB = ,∵,N E 分别为,AD AB 中点 ∴11,22AN DN AD AE EB AB ====, ∴,DN BE AN AE == 又∵90A ∠=︒∴45ANE ∠=︒∴180135DNE ANE ∠=︒-∠=︒,又∵90CBM ∠=︒,BF 平分CBM ∠∴45,135CBF EBF ∠=︒∠=︒.∴DNE EBF ∠=∠在DNE △和EBF △中ADE FEB DN EBDNE EBF ∠=∠⎧⎪=⎨⎪∠=∠⎩()DNE EBF ASA ≌,∴DE EF =(3) DE EF =.理由如下:如图,在DA 边上截取DN EB =,连接NE ,∵四边形ABCD 是正方形, DN EB =,∴AN AE =,∴AEN △为等腰直角三角形,∵45ANE ∠=︒∴18045135DNE ∠=︒-︒=︒,∵BF 平分CBM ∠, AN AE =,∴9045135EBF ∠=︒+︒=︒,∴DNE EBF ∠=∠,在DNE △和EBF △中ADE FEB DN EBDNE EBF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()DNE EBF ASA ≌,∴DE EF =.【点睛】此题主要考查了正方形的性质以及全等三角形的判定与性质等知识,解决本题的关键就是求证△DNE ≌△EBF .3.(1)见解析;(2)2DF ,理由见解析;(3)22【分析】(1)如图1中,证明△AFB≌△DGA(AAS)可得结论.(2)结论:FH+FE=2DF.如图2中,过点D作DK⊥AE于K,DJ⊥BF交BF的延长线于J,证明四边形DKFJ是正方形,可得结论.(3)如图3中,取AD的中点J,连接PJ,延长JP交CD于R,过点P作PT⊥CD于T,PK⊥AD于K.设PT=b.证明△KPJ是等腰直角三角形,推出点P在线段JR上运动,求出JR即可解决问题.【详解】解:(1)如图1中,∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∵DG⊥AE,AE⊥BH,∴∠AFB=∠DGH=90°,∴∠FAB+∠DAG=90°,∠DAG+∠ADG=90°,∴∠BAF=∠ADG,∴△AFB≌△DGA(AAS),∴AF=DG,BF=AG,∴BF-DG=AG-AF=FG.(2)结论:FH+FE=2DF.理由:如图2中,过点D作DK⊥AE于K,DJ⊥BF交BF的延长线于J,∵四边形ABCD是正方形,∴∠BAD=∠ADE=90°,AB=AD,∵AE⊥BH,∴∠AFB=90°,∴∠DAE+∠EAB=90°,∠EAB+∠ABH=90°,∴∠DAE=∠ABH,∴△ABH≌△DAE(ASA),∴AH=AE,∵DE=EC=12CD,CD=AD,∴AH=DH,∴DE=DH,∵DJ⊥BJ,DK⊥AE,∴∠J=∠DKE=∠KFJ=90°,∴四边形DKFJ是矩形,∴∠JDK=∠ADC=90°,∴∠JDH=∠KDE,∵∠J=∠DKE=90°,∴△DJH≌△DKE(AAS),∴DJ=DK,JH=EK,∴四边形DKFJ是正方形,∴FK=FJ=DK=DJ,∴DF=2FJ,∴FH+FE=FJ-HJ+FK+KE=2FJ=2DF;(3)如图3中,取AD的中点J,连接PJ,延长JP交CD于R,过点P作PT⊥CD于T,PK⊥AD于K.设PT=b.∵△ABH≌△DAE,∴AH=DE,∵∠EDH=90°,HP=PE,∴PD=PH=PE,∵PK⊥DH,PT⊥DE,∴∠PKD=∠KDT=∠PTD=90°,∴四边形PTDK是矩形,∴PT=DK=b,PK=DT,∵PH=PD=PE,PK⊥DH,PT⊥DE,∴DH=2DK=2b,DE=2DT,∴AH=DE=1-2b ,∴PK=12DE=12-b , JK=DJ-DK=12-b , ∴PK=KJ ,∵∠PKJ=90°,∴∠KJP=45°,∴点P 在线段JR 上运动,∵DJ=2,∴点P 的运动轨迹的长为2. 【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,轨迹等知识,解题的关键是正确寻找全等三角形解决问题,学会利用参数解决问题,属于中考压轴题.4.(1)15,8;(2)PE PF CG +=,见解析;(3)4)4【分析】解决问题(1)只需运用面积法:ABC ABP ACP S S S ∆∆∆=+,即可解决问题;(2)解法同(1);(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,由等边三角形的性质得出152BM BC ==,由勾股定理得出AM ==ABC ∆的面积12BC AM =⨯=ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积1111()2222BC PE AC PF AB PG AB PE PF PG =⨯+⨯+⨯=++=,即可得出答案; (4)过点E 作EQ BC ⊥,垂足为Q ,易证BE BF =,过点E 作EQ BF ⊥,垂足为Q ,由解决问题(1)可得PG PH EQ +=,易证EQ DC =,BF DF =,只需求出BF 即可.【详解】解:(1)∵PE AB ⊥,10AB =,3PE =,∴ABP ∆的面积111031522AB PE =⨯=⨯⨯=, ∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =,∴358CG PE PF =+=+=.故答案为:15,8.(2)∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =,∴CG PE PF =+.(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,如图2所示:∵10AB AC BC ===,∴ABC ∆是等边三角形,∵AM BC ⊥, ∴152BM BC ==, ∴222210553AM AB BM =-=-=,∴ABC ∆的面积11105325322BC AM =⨯=⨯⨯=, ∵PE BC ⊥,PF AC ⊥,PG AB ⊥,∴ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积111222BC PE AC PF AB PG =⨯+⨯+⨯1()2AB PE PF PG =++ 253=,∴225353PE PF PG ⨯++==. (4)过点E 作EQ BC ⊥,垂足为Q ,如图3所示:∵四边形ABCD 是矩形,∴AD BC =,90C ADC ∠=∠=︒,∵8AD =,3CF =,∴5BF BC CF AD CF =-=-=,由折叠可得:5DF BF ==,BEF DEF ∠=∠,∵90C ∠=︒,∴4DC ===,∵EQ BC ⊥,90C ADC ∠=∠=︒,∴90EQC C ADC ∠=︒=∠=∠,∴四边形EQCD 是矩形,∴4EQ DC ==,∵//AD BC ,∴DEF EFB ∠=∠,∵BEF DEF ∠=∠,∴BEF EFB ∠=∠,∴BE BF =,由解决问题(1)可得:PG PH EQ +=,∴4PG PH +=,即PG PH +的值为4.【点睛】本题是四边形综合题目,考查了矩形的性质与判定、等腰三角形的性质与判定、平行线的性质与判定、等边三角形的性质、勾股定理等知识,考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力,体现了自主探究与合作交流的新理念,是充分体现新课程理念难得的好题.5.(1)见解析;(2)120;(3)90;(4)72;(5)360n. 【分析】(1)利用等边三角形的性质得到BC=AC ,∠ACB=∠ABC ,从而得到△ACN ≌△CBM. (2)利用全等三角形的性质得到∠CAN=∠BCM ,再利用三角形的外角等于与它不相邻的两个内角的和,即可求解.(3)利用正方形(或正五边形)的性质得到BC=DC ,∠ABC=∠BCD ,从而判断出△DCN ≌△CBM ,再利用全等三角形的性质得到∠CDN=∠BCM ,再利用内角和定理即可得到答案.(4)由(3)的方法即可得到答案.(5)利用正三边形,正四边形,正五边形,分别求出∠CPN 的度数与边数的关系式,即可得到答案.【详解】(1)∵△ABC 是等边三角形,∴BC=AC ,∠ACB=∠BAC=∠ABC=60︒,∴∠ACN=∠CBM=120︒,在△CAN 和△CBM 中,CN BM ACN CBM AC BC =⎧⎪∠=∠⎨⎪=⎩,∴△ACN ≌△CBM.(2)∵△ACN ≌△CBM.∴∠CAN=∠BCM ,∵∠ABC=∠BMC+∠BCM ,∠BAN=∠BAC+∠CAN ,∴∠CPN=∠BMC+∠BAN=∠BMC+∠BAC+∠CAN=∠BMC+∠BAC+∠BCM=∠ABC+∠BAC=60︒+60︒,=120︒,故答案为:120.(3)将等边三角形换成正方形,∵四边形ABCD 是正方形,∴BC=DC ,∠ABC=∠BCD=90︒,∴∠MBC=∠DCN=90︒,在△DCN 和△CBM 中,DC BC DCN MBC CN BM =⎧⎪∠=∠⎨⎪=⎩,∴△DCN ≌△CBM ,∴∠CDN=∠BCM ,∵∠BCM=∠PCN ,∴∠CDN=∠PCN ,在Rt △DCN 中,∠CDN+∠CND=90︒,∴∠PCN+∠CND=90︒,∴∠CPN=90︒,故答案为:90.(4)将等边三角形换成正五边形,∴∠ABC=∠DCB=108︒,∴∠MBC=∠DCN=72︒,在△DCN 和△CBM 中,DC BC DCN MBC CN BM =⎧⎪∠=∠⎨⎪=⎩,∴△DCN ≌△CBM ,∴∠BMC=∠CND ,∠BCM=∠CDN ,∵∠BCM=∠PCN ,∴∠CND=∠PCN ,在△CDN 中,∠CDN+∠CND=∠BCD=108︒,∴∠CPN=180︒-(∠CND+∠PCN)=180︒-(∠CND+∠CDN)=180︒-108︒,=72︒,故答案为:72.(5)正三边形时,∠CPN=120︒=3603, 正四边形时,∠CPN=90︒=3604, 正五边形时,∠CPN=72︒=3605, 正n 边形时,∠CPN=360n , 故答案为:360n . 【点睛】此题考查正多边形的性质,三角形全等的判定及性质,图形在发生变化但是解题的思路是不变的,依据此特点进行解题是解此题的关键.6.(1)证明见解析;(2)证明见解析;(3)CN=25.【解析】【分析】(1)如图,延长EF 交CD 延长线于点Q ,先证明CQ=CE ,再证明△FQD ≌△FEA ,根据全等三角形的对应边相等可得EF=FQ ,再根据等腰三角形的性质即可得CF ⊥EF ;(2)分别过点F 、H 作FM ⊥CE ,HP ⊥CD ,垂足分别为M 、P ,证明四边形DFHP 是矩形,继而证明△HPC ≌△FMK ,根据全等三角形的性质即可得CH=FK ;(3)连接CN ,延长HG 交CN 于点T ,设∠DCF=α,则∠GCF=α, 先证明得到FG=CG=GE ,∠CGT=2α,再由FG 是BC 的中垂线,可得BG = CG , ∠CGT=∠FGK=∠BGT=2α,再证明HN ∥BG ,得到四边形HGBN 是平行四边形,继而证明△HNC ≌△KGF ,推导可得出HT=CT=TN ,由FH-HG=1,所以设GH=m ,则BN=m ,FH=m+1,CE=2FG=4m+2,继而根据22222BC CN BN CE BE =-=-,可得关于m 的方程,解方程求得m 的值即可求得答案.【详解】(1)如图,延长EF交CD延长线于点Q,∵矩形ABCD,AB∥CD,∴∠AEF=∠CQE,∠A=∠QDF,又∵EF 平分∠AEC ,∴∠AEF=∠CEF,∴∠CEF=∠CQE,∴CQ=CE,∵点F是AD中点,∴AF=DF,∴△FQD≌△FEA,∴EF=FQ,又∵CE=CQ,∴CF⊥EF;(2)分别过点F、H作FM⊥CE ,HP⊥CD,垂足分别为M、P,∵CQ=CE ,CF⊥EF,∴∠DCF=∠FCE,又∵FD⊥CD,∴FM=DF,∵FG//AB,∴∠DFH=∠DAC=90°,∴∠DFH=∠FDP=∠DPH=90°,∴四边形DFHP 是矩形,∴DF=HP ,∴FM= DF=HP ,∵∠CHG=∠BCE ,AD ∥BC ,FG ∥CD ,∴∠K=∠BCE=∠CHG=∠DCH ,又∵∠FMK=∠HPC=90°,∴△HPC ≌△FMK ,∴CH=FK ;(3)连接CN ,延长HG 交CN 于点T ,设∠DCF=α,则∠GCF=α,∵FG ∥CD ,∴∠DCF=∠CFG ,∴∠FCG=∠CFG ,∴FG=CG ,∵CF ⊥EF ,∴∠FEG+∠FCG=90°,∠CFG+∠GFE=90°,∴∠GFE=∠FEG ,∴GF=FE ,∴FG=CG=GE ,∠CGT=2α,∵FG 是BC 的中垂线,∴BG = CG , ∠CGT=∠FGK=∠BGT=2α,∵∠CHG=∠BCE=90°-2α,∠CHN=90°,∴∠GHN=∠FGK=∠BGT=2α,∴HN ∥BG ,∴四边形HGBN 是平行四边形,∴HG=BN ,HN=BG = CG =FG ,∴△HNC ≌△KGF ,∴GK=CN ,∠HNC=∠FGK=∠NHT=2α,∴HT=CT=TN ,∵FH-HG=1,∴设GH=m ,则BN=m ,FH=m+1,CE=2FG=4m+2,∵GT=1122EN =,∴CN=2HT=11+2m , ∵22222BC CN BN CE BE =-=-,∴2222(112)(42)(11)m m m m +-=+-+ ∴1176m =-(舍去),27m =, ∴CN=GK=2HT=25.【点睛】 本题考查的是四边形综合题,涉及了等腰三角形的判定与性质,全等三角形的判定与性质,平行四边形的判定与性质,矩形的性质与判定,三角形外角的性质等,综合性较强,难度较大,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.7.(1)G (0,2)4y =++3)234,,(1,4M M M -+⎝⎝⎝. 【解析】【分析】1(1)由F (1,4),B (3,4),得出AF=1,BF=2,根据折叠的性质得到GF=BF=2,在Rt △AGF 中,利用勾股定理求出AG =,那么OG=OA-AG=4-,于是G (0,);(2)先在Rt △AGF 中,由tan AG AFG AF ∠===,得出∠AFG=60°,再由折叠的性质得出∠GFE=∠BFE=60°,解Rt △BFE ,求出BE=BF tan60°,那么CE=4-2E (3,.设直线EF 的表达式为y=kx+b ,将E (3,F (1,4)代入,利用待定系数法即可求出直线EF 的解析.(3)因为M 、N 均为动点,只有F 、G 已经确定,所以可从此入手,结合图形,按照FG 为一边,N 点在x 轴上;FG 为一边,N 点在y 轴上;FG 为对角线的思路,顺序探究可能的平行四边形的形状.确定平行四边形的位置与形状之后,利用平行四边形及平移的性质求得M 点的坐标.【详解】解:(1)∵F (1,4),B (3,4),∴AF=1,BF=2,由折叠的性质得:GF=BF=2,在Rt △AGF 中,由勾股定理得,AG ==∵B (3,4),∴OA=4,∴∴G (0,(2)在Rt △AGF 中,∵tan 1AG AFG AF ∠===, ∴∠AFG=60°,由折叠的性质得知:∠GFE=∠BFE=60°,在Rt △BFE 中,∵BE=BF tan60°,.E (3,).设直线EF 的表达式为y=kx+b ,∵E (3,F (1,4),∴34234k b k b ⎧+=-⎪⎨+=⎪⎩解得343k b ⎧=-⎪⎨=+⎪⎩ ∴343y x =-++ ;(3)若以M 、N 、F 、G 为顶点的四边形是平行四边形,则分如下四种情况: ①FG 为平行四边形的一边,N 点在x 轴上,GFMN 为平行四边形,如图1所示. 过点G 作EF 的平行线,交x 轴于点N 1,再过点N :作GF 的平行线,交EF 于点M ,得平行四边形GFM 1N 1.∵GN 1∥EF ,直线EF 的解析式为343,(0,43)y x G =-++- ∴直线GN 1的解析式为34-3y x =-+,当y=0时,1433433,,033x N ⎛⎫--= ⎪ ⎪⎝⎭. ∵GFM 1N 1是平行四边形,且G (0,4-3),F (1,4),N 1(433- ,0), ∴M ,(433,3);②FG 为平行四边形的一边,N 点在x 轴上,GFNM 为平行四边形,如图2所示. ∵GFN 2M 2为平行四边形,∴GN ₂与FM 2互相平分.∴G (0,3N2点纵坐标为0∴GN:中点的纵坐标为322 -,设GN₂中点的坐标为(x,32-).∵GN2中点与FM2中点重合,∴3 34322 x-++=-∴x=439+∵.GN2的中点的坐标为(4393,2+-),.∴N2点的坐标为(4393+,0).∵GFN2M2为平行四边形,且G(0,4-3),F(1,4),N2(4393+,0),∴M2(436,3+-);③FG为平行四边形的一边,N点在y轴上,GFNM为平行四边形,如图3所示.∵GFN3M3为平行四边形,.∴GN3与FM3互相平分.∵G(0,3N2点横坐标为0,.∴GN3中点的横坐标为0,∴F与M3的横坐标互为相反数,∴M 3的横坐标为-1,当x=-1时,y=3(1)43423-⨯-++=+,∴M 3(-1,4+23);④FG 为平行四边形的对角线,GMFN 为平行四边形,如图4所示.过点G 作EF 的平行线,交x 轴于点N 4,连结N 4与GF 的中点并延长,交EF 于点M 。
八年级下册数学平行四边形难题

八年级下册数学平行四边形难题平行四边形是在数学中常见的几何形状之一,它具有特殊的性质和规律。
在本文中,我们将介绍一些关于平行四边形的难题,帮助大家更好地理解和运用这个概念。
1. 平行四边形的基本性质平行四边形指的是具有两对平行边的四边形。
首先,我们来看一道简单的题目:题目:在平行四边形ABCD中,若AB = 5cm,BC = 8cm,且∠BAD = 60°,求DC的长度。
解析:根据平行四边形的性质,我们知道对边是相等的,即AD = BC = 8cm。
同时,根据三角形的角度和为180°的性质,我们可以计算出∠ADB = 180° - 60° - 90° = 30°,再利用正弦定理可以求得DC的长度。
2. 平行四边形的面积计算平行四边形的面积计算方法与矩形相同,即面积等于底边乘以高。
下面是一个稍微复杂些的问题:题目:在平行四边形ABCD中,AB = 6cm,AD = 8cm,且∠ADC = 120°,求平行四边形ABCD的面积。
解析:我们可将平行四边形分成两个三角形和一个梯形。
首先,利用正弦定理可以计算出∠DAB = 180° - 120° = 60°。
然后,我们可以通过计算三角形的面积来求得梯形ABCD的面积。
这里使用的公式是:面积 = 底边乘以高除以2。
通过计算两个三角形的面积之和,再减去梯形内部的三角形的面积,即可得到平行四边形ABCD的面积。
3. 平行四边形的角度性质平行四边形的角度和为360°,其中对角线之间交叉的角是互补角。
我们来看一个与角度性质相关的问题:题目:在平行四边形ABCD中,已知∠A = 100°,求∠BCD 的度数。
解析:根据平行四边形的角度性质,我们可以得出∠ABC = 180° - ∠A = 80°。
由平行四边形的性质可知∠BCD = 180° - ∠ABC = 100°。
八年级四边形动点问题及难题

动点问题及四边形难题1如图1,在平面直角坐标系中,点0是坐标原点,四边形ABCO是菱形,点A的坐标为(一3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.(1)求直线AC的解析式;(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C 匀速运动,设△PMB的面积为S(SHO),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);2.已知:如图,在直角梯形COAB中,OC〃AB,A,B,C三点的坐标分别为A(8,0),B(8,10),C(0,4),点D为线段BC的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为t秒.(1)求直线BC的解析式;(2)若动点P在线段OA上移动,当t为何值时,四边形OPDC的面积是梯形COAB面积(3)动点P从点O出发,沿折线OABD的路线移动过程中,设A OPD的面积为S,请直接写出S与t的函数关系式,并指出自变量t的取值范围;简单作业练习题4.如图,已知AD 与BC 相交于E,Z1=Z2=Z3,BD=CD ,ZADB=90CH 丄AB 于H,CH 交AD 于F.(1) 求证:CD 〃AB ;(2) 求证:△BDE^AACE;1(3) 若0为AB 中点,求证:OF=BE. 2简单作业练习题5、如图1—4—21,在边长为a 的菱形ABCD 中,ZDAB=60°,E 是异于A 、D 两点的动点,F 是CD 上的动点,满足AE+CF=a ,说明:不论E 、F 怎样移动,三角形BEF 总是正三角形. 3.如图,已知A ABC 中,AB =AC =10厘米,BC =8厘米,点D 为AB 的中点.(1) 如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.① 若点Q 的运动速度与点P 的运动速度相等,经过1秒后,MPD 与A COP 是否全等, 请说明理由;② 若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使A BPD 与A COP 全等?(2) 若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点P 与点Q 第一次在厶ABC 的哪条边上相遇?PDF C6、如图1—4—38,等腰梯形ABCD中,AD〃BC,AB=CD,ZDBC=45O,翻折梯形使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8,求BE的长.7、在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:AB CF;(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.8、如图1—4—80,已知正方形ABCD的对角线AC、BD相交于点0,E是AC上一点,过点A 作AG丄EB,垂足为G,AG交BD于F.(1)请证明0E=0F(2)若点E在AC的延长线上,其他条件不变,0E=0F是否成立?若成立,请给出证明;若不成立,请说明理由.9已知:如图4-26所示,△ABC中,AB=AC,ZBAC=90°,D为BC的中点,P为BC的延长线上一点,PE丄直线AB于点E,PF丄直线AC于点F.求证:DE丄DF并且相等.中难度10已知:如图4-27,ABCD为矩形,CE丄BD于点E,ZBAD的平分线与直线CE相交于点F.求证:CA=CF.中难度11已知:如图4-56A.,直线l通过正方形ABCD的顶点D平行于对角线AC,E为l上U4—SB一点,EC=AC,并且EC与边AD相交于点F.求证:AE=AF.E本例中,点E与A位于BD同侧.如图4-56B.,点E与A位于BD异侧,直线EC与DA 的延长线交于点F,这时仍有AE=AF.请自己证明.AI12求证:矩形各内角平分线(对角的平分线不在一直线上)所围成的四边形EFGH是正方形.。
(完整版)八年级下平行四边形难题全面专题复习(最全面的平行四边形)
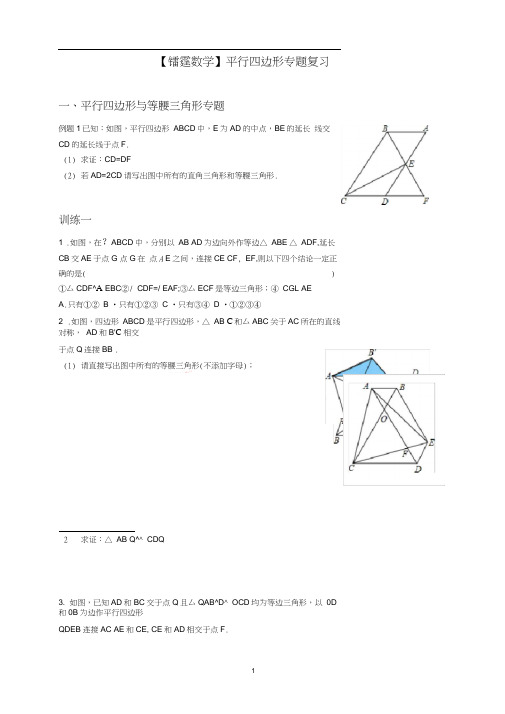
【镭霆数学】平行四边形专题复习一、平行四边形与等腰三角形专题例题1已知:如图,平行四边形ABCD中,E为AD的中点,BE的延长线交CD的延长线于点F.(1)求证:CD=DF(2)若AD=2CD请写出图中所有的直角三角形和等腰三角形.训练一1 .如图,在?ABCD中,分别以AB AD为边向外作等边△ ABE △ ADF,延长CB交AE于点G 点G在点A E之间,连接CE CF, EF,则以下四个结论一定正确的是( )①厶CDF^A EBC②/ CDF=/ EAF;③厶ECF是等边三角形;④ CGL AEA.只有①② B •只有①②③ C •只有③④ D •①②③④2 .如图,四边形ABCD是平行四边形,△ AB C和厶ABC关于AC所在的直线对称,AD和B'C相交于点Q连接BB .(1)请直接写出图中所有的等腰三角形(不添加字母);---------------- J—1 22 求证:△ AB Q^^ CDQ3. 如图,已知AD和BC交于点Q且厶QAB^D^ OCD均为等边三角形,以0D 和0B为边作平行四边形QDEB连接AC AE和CE, CE和AD相交于点F.求证:△ ACE为等边三角形.4. 如图,已知:平行四边形ABCD中, / BCD的平分线CE交边AD于E, / ABC的平分线BG交CE于F, 交AD于G.求证:AE=DG训练1.如图,过?ABCD 勺对角线BD 上一点M 分别作平行四边形两边的平行线 EF 与GH 那么图中的?AEMG的面积S i 与?HCFM 勺面积S 2的大小关系是( ) A. S i > S 2B . Sv S 2C. S i =SaD. 2S i =S 22.农业技术员在一块平行四边形的实验田里种植四种不同的农作物,现需将该实验田划成四个平行四边形地块(如图),已知其中三块田的面积分别是14m 2,10m 2,36m i ,则第四块田的面积为 _______3 .如图,AE// BD BE// DF, AB// CD 下面给出四个结论: (1) AB=CD (2) BE=DF ( 3) S ABD =S BDF ;(4) S A ABE =S ^DCF.其中正确的有( )BC 于点E ,作AF 垂直于直线CD 于 点 F ,若 AB=5, BC=6,则 CE+CF 的值为()A . 11 11 3B .2C .11 叩或 11 F A.1个 B.2 个 C.3 个 D.4 个4 .在面积为15的平行四边形 ABCD 中,过点A 作AE 垂直于直线5. 平行四边形ABCD的周长为20cm, AE± BC于点E, AF丄CD于点F,AE=2cm AF=3cm 求ABCD勺面积.CE6. 如图,四边形ABCD勺对角线AC BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF 且AP+AE=CP+CF(1)求证:PA=PC(2)若BD=12 AB=15, / DBA=45,求四边形ABCD勺面积.7 .如图,平行四边形ABCD中, AB: BC=3 2,/ DAB=60 , E在AB上,且AE EB=1: 2, F 是BC 的中点,过D分别作DPIAF于P, DQLCE于Q贝U DP DQ等于()A. 3: 4 B . .. 13 : . 5 C . 13 : 6 D . 13 : 5三、平行四边形与角度专题例题3 如图,在平行四边形ABCD中,/ BAD=32 .分别以BC C 为边向外作△ BCE^D^ DCF 使BE=BC DF=D(C Z EBC2 CDF 延长AB交边EC于点G,点G在E、C两点之间,连接AE AF.(1)求证:△ ABE^A FDA(2 )当AE± AF时,求/ EBG的度数.训练三1. 如图,将一平行四边形纸片ABCD沿AE,EF折叠,使点E, B ',C'在同一直线上,则/ AEF= 度.£2. 如图,已知平行四边形ABCD DE是/ ADQ的角平分线,交BC于点E.(1) 求证:CD=CE(2) 若BE=CE / B=80°,求/ DAE的度数.3. 如图,E、F是?ABCD对角线AC上的两点,且求证:(ABE^A CDF(2)Z 仁/ 2.四、平行四边形与线段专题DE交AC的延长线于F点,交BE于E点. 例题4如图,ABCD为平行四边形,AD=2, BE// AC,(1)求证:EF=DF(2 )若AC=2CF / ADC=60 , ACL DC 求DE 的长.E F D训练四1. 如图,口ABCD勺对角线相交于点0,过点0任引直线交AD于E,交BC于F,贝U OE _OF(填“〉”“ =”“v ”),并说明理由.2. 如图,在?ABCD中,对角线AC BD相交于点0,如果AC=14, BD=8, AB=x那么x的取值范围是.6. 已知:平行四边形 ABCD 中,对角线 AC 、BD 相交于点 O , BD=2AD , E , F , G 分别是0C , 0D , AB 的中点.求证:(1) BE 丄 AC ; (2) EG=EF .3.已知:如图,在 ?ABCD K/ ADC / DAB 的平分线DF 、AE 分别与线段 BC 相交于点F 、E , DF 与 AE 相交于点G.(1)求证:AE! DF ; (2 )若 AD=10 AB=6, AE=4,求 DF 的长. 4.如图,已知△ ABC 是等边三角形,点(1)求证:四边形 EFCD 是平行四边形; (2 )若 BF=EF 求证:AE=AD 5. 占 八、、 D F 分别在线段 BC AB 上,/ EFB=60 , DC=EF如图,E 、F 分别是?ABCD 的边AD BC 上的点,且 AE=CF AF 和BE 相交于点G, DF 和CE 相交于H,求证:EF 和GH 互相平分.7. _________________________________________________________ 如图,?ABCD中,点E在边AD 上,以BE为折痕,将厶ABE向上翻折,点A正好落在CD上的F点, 若厶FDE的周长为8 cm , △ FCB的周长为20 cm,贝U FC的长为 _____________________________________ cm.18.如图,已知:在△ ABC中,/ BAC=90,延长BA到点D,使AD—AB点G E、F分别为边AB2BC AC的中点.求证:DF=BE五、三角形中位线专题例题5如图,△ ABC的周长为26,点D, E都在边BC上, /ABC的平分线垂直于AE垂足为Q / ACB的平分线垂直于AD,垂足为P,若BC=1Q则PQ的长为()3 5A. — B . C . 3 D . 42 2训练五1.如图,AB// CD E , F分别为AC BD的中点,若AB=5 CD=3贝U EF的长是()A. 4 B . 3 C . 2 D . 12 .如图,在四边形ABCD中 ,点P是对角线BD的中点,点E、F分别是AB CD的中点,AD=BC /H分别是AB AG CD BD的PEF=30 ,则/ PFE的度数是()A. 15° B . 20°C . 25° D . 30°3 .如图,D是厶ABC内一点,BDL CD AD=6 BD=4, CD=3 E、F、G六、平行四边形综合探究专题例题6 如图所示,在□ABCD中, AB> BC, / A与/ D的平分线交于点E,/ B与/ C的平分线交于F 点,连接EF.(1)延长DE交AB于M点,则图中与线段EM—定相等的线段有哪几条?说明理由;(不再另外添加字母和辅助线)(2)EF、BC与AB之间有怎样的数量关系?为什么?(3)如果将条件“ AB> BC改为“ AB< BC , 图形并证明你的结论.其它条件不变,EF、BC与AB的关系又如何?请画出训练六1.如图,分别以Rt △ ABC的斜边AB直角边和厶ACE F为AB的中点,DE, AB相交于点AC为边向外作等边厶结论:①EF丄AC②四边形ADFE为平行四边形;③ AD=4AG④厶DB ◎ △ EFA其中正确结论的序号是2A浮F VB CG,若/ BAC=30,下列2 .如图所示,△ ABC为等边三角形,P是厶ABC内任一点,PD// AB,PE// BC PF/ AC 若厶ABC的周长为12,贝U PD+PE+PF ___________3.如图,?ABCD中,对角线AC与BD相交于点E,/ AEB=45 , BD=2将厶ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B',贝U DB的长为HEA4 .点A、B、C是平面内不在同一条直线上的三点,点恰能构成一个平行四边形,则在平面内符合这样条件的点D是平面内任意一点,若A、B、C、D四点D有( )5.在平行四边形ABCD中, E是AD上一点,AE=AB过点E作直线EF,在EF上取一点G,使得/ EGB/ EAB连接AG(1)如图①,当EF与AB相交时,若/ EAB=60,求证:EG=AG+B;(2)如图②,当EF与CD相交时,且/ EAB=90,请你写出线段EG AG BG之间的数量关系,并证明你的结论.6.在?ABCD中,对角线AG BD相交于点0,直线EF过点0,分别交AD BC于E、F,如图①(1)求证:AE=CF(2)将图①中?ABCD沿直线EF折叠,使得点A落在A处,点B落在B处,如图②设FB交CD于点G, AiBi分别交CD DE于点P、Q 求证:EQ=FG7. 如图1,在四边形ABCD中,AB=CD , E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD 的延长线交于点M、N,则/ BME= / CNE (不需证明).(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而/ 1= / 2,再利用平行线性质,可证得/ BME= / CNE .)问题一:如图2,在四边形ADBC中,AB与CD相交于点0, AB=CD , E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△ 0MN的形状,请直接写出结论;问题二:如图3,在△ ABC中,AC >AB , D点在AC 上, AB=CD , E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若/ EFC=60,连接GD,判断△ AGD的形状并证明.£ F C圍②11。
2019-2021北京初二(下)期中数学汇编:四边形章节综合3

2019-2021北京初二(下)期中数学汇编四边形章节综合3一、解答题1.(2021·北京市文汇中学八年级期中)如图,在□ABCD中,E,F分别在AD,BC上,且AE=CF,连结BE、DF.求证:BE=DF.2.(2019·北京五十五中八年级期中)如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.(1)若∠DBC=25°,求∠ADC′的度数;(2)若AB=4,AD=8,求△BDE的面积.3.(2019·北京市第三十一中学八年级期中)已知:如图,平行四边形ABCD中,E、F分别是边BC和AD上的点,且BE=DF,求证:AE=CF4.(2019·北京五十五中八年级期中)已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.5.(2020·北京铁路二中八年级期中)如图,在平行四边形ABCD中,E、F为对角线BD上的三等分点.求证:四边形AFCE是平行四边形.6.(2020·北京市第一六一中学八年级期中)已知,如图,E、F分别为□ABCD的边BC、AD上的点,且∠1=∠2,求证:AE=CF.7.(2021·北京广渠门中学教育集团八年级期中)如图,在矩形ABCD中,AB=5,BC=4,将矩形ABCD翻折,使得点B落在CD边上的点E处,折痕AF交BC于点F,求FC的长.8.(2021·北京·和平街第一中学八年级期中)如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF 与一组对边AB,CD分别相交于点E,F.(1)求证:AE=CF;(2)若AB=2,点E是AB中点,求EF的长.9.(2021·北京师大附中八年级期中)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB 于点H,连接OH,求证:∠DHO=∠DCO.10.(2021·北京一七一中八年级期中)如图,在平行四边形ABCD中,E为BC的中点,连接DE.延长DE交AB 的延长线于点F.求证:AB=BF.11.(2019·北京·海淀教师进修学校附属实验学校八年级期中)已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.求证:EA⊥AF.12.(2019·北京市第四十一中学八年级期中)如图,在▱ABCD中,点E在AD上,连接BE,DF//BE交BC于点F,AF与BE交于点M,CE与DF交于点N.(1)求证:DE=BF;(2)求证:四边形MFNE是平行四边形.13.(2019·北京市第三十一中学八年级期中)如图,在长方形ABCD中,AB=6,BC=8,将长方形ABCD沿CE 折叠后,使点D恰好落在对角线AC上的点F处.(1)求EF的长;(2)求四边形ABCE的面积.14.(2019·北京市第一六一中学八年级期中)如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.(1)在图1中画出一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;(2)在图2中画出线段AB的垂直平分线.15.(2019·北京市第四十一中学八年级期中)如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF,求证:AF⊥DE.16.(2020·北京市文汇中学八年级期中)阅读下列材料∶问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G.使得∠EGB=∠EAB,连接AG.求证∶EG=AG+BG.小明同学的思路是:作∠GAH=∠EAB交CE于点H,构造全等三角形,经过推理解决问题.参考小明同学的思路,探究并解决下列问题∶(1)完成上面问题中的证明;(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EC、AG、BG 之间的数量关系,并证明你的结论.解∶线段EG、AG、BG之间的数量关系为___________________________________________________.并证明.17.(2020·北京·北外附中八年级期中)如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.(1)求证:AE=EF;(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.18.(2020·北京市第一六一中学八年级期中)如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.实践与操作:根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).(1)作∠DAC的平分线AM;(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.猜想并证明:判断四边形AECF的形状并加以证明.19.(2020·北京·首都师范大学附属中学八年级期中)如图,点E是平行四边形ABCD边CD上的中点,AE、BC 的延长线交于点F,连接DF,求证:四边形ACFD为平行四边形20.(2020·北京市文汇中学八年级期中)如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.(1)求证:BF=CD;23(2)连接BE,若BE⊥AF,∠BFA=60°,BE=,求平行四边形ABCD的周长.21.(2020·北京市顺义区第五中学八年级期中)已知:如图,E,F为□ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.22.(2020·北京·北外附中八年级期中)如图,在△ABC中,AB=BC,BD平分∠ABC,四边形ABED是平行四边形,DE交BC于点F,连接CE求证:四边形BECD是矩形.23.(2021·北京·北大附中八年级期中)如图,在平行四边形ABCD中,DE,BF分别是∠ADC,∠ABC的角平分线.求证:四边形DEBF是平行四边形.24.(2021·北京师范大学昌平附属学校八年级期中)如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.(1)求证:四边形OCED是菱形;(2)若∠BAC=30°,AC=4,求菱形OCED的面积.25.(2021·北京广渠门中学教育集团八年级期中)如图所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两直角边长都为3,另一种纸片的两条直角边长分别为1和3.图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.⑴请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上(要求:所画图形各顶点必须与方格纸中的小正方形顶点重合;并要保留四块直角三角形纸片的拼接痕迹);⑵三种方法所拼得的平行四边形的面积和周长是否是定值?若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的面积和周长各是多少.26.(2021·北京一七一中八年级期中)如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.(1)求证:四边形DBEC是菱形;(2)若AD=3,DF=1,求四边形DBEC面积.27.(2019·北京十五中八年级期中)把一个含45°角的直角三角板BEF 和一个正方形ABCD 摆放在一起,使三角板的直角顶点和正方形的顶点B 重合,联结DF ,点M ,N 分别为DF ,EF 的中点,联结MA ,MN .(1)如图1,点E ,F 分别在正方形的边CB ,AB 上,请判断MA ,MN 的数量关系和位置关系,直接写出结论; (2)如图2,点E ,F 分别在正方形的边CB ,AB 的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.28.(2019·北京四中八年级期中)在▱ABCD 中,∠BAD 的平分线交直线BC 于点E ,交直线DC 于点F(1)在图1中证明CE =CF ;(2)若∠ABC =90°,G 是EF 的中点(如图2),直接写出∠BDG 的度数;(3)若∠ABC =120°,FG CE ,FG =CE ,分别连接DB 、DG (如图3),求∠BDG 的度数.∥29.(2020·北京铁路二中八年级期中)对于正数,用符号表示的整数部分,例如:,,x [x]x [0.1]=0[2.5]=2.点在第一象限内,以A 为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于轴[3]=3A(a,b)y 的边长为,垂直于轴的边长为,那么,把这个矩形覆盖的区域叫做点A 的矩形域.例如:点的矩形域a x [b]+1(3,32)是一个以为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6. (3,32)图1图2根据上面的定义,回答下列问题: (1)在图2所示的坐标系中画出点的矩形域,该矩形域的面积是 ;(2,72)(2)点的矩形域重叠部分面积为1,求的值;P(2,72),Q(a ,72)(a >0)a (3)已知点在直线上, 且点B 的矩形域的面积满足,那么的取值范围B(m, n)(m >0)y =x +1S 4<S <5m 是 .(直接写出结果)30.(2021·北京育才学校八年级期中)如图,在正方形ABCD 中,点M 在CD 边上,点N 在正方形ABCD 外部,且满足∠CMN =90°,CM =MN .连接AN ,CN ,取AN 的中点E ,连接BE ,AC ,交于F 点.(1)①依题意补全图形;②求证:BE ⊥AC .(2)请探究线段BE ,AD ,CN 所满足的等量关系,并证明你的结论.(3)设AB =1,若点M 沿着线段CD 从点C 运动到点D ,则在该运动过程中,线段EN 所扫过的面积为______________(直接写出答案).参考答案1.详见解析【分析】根据平行四边形性质得出AD∥BC,AD=BC,求出DE=BF,DE∥BF,得出四边形DEBF是平行四边形,根据平行四边形的性质推出即可.【详解】∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵AE=CF,∴DE=BF,DE∥BF,∴四边形DEBF是平行四边形,∴BE=DF.【点睛】本题考查了平行四边形的性质和判定;熟练掌握平行四边形的性质,证明四边形DEBF是平行四边形是解决问题的关键.2.(1) 40° (2)10【分析】(1)求出∠ADB,求出∠BDC,根据折叠求出∠C′DB,代入∠ADC′=∠BDC′-∠ADB即可;(2)先证BE=DE,然后设DE=x,则BE=x,AE=8-x,在Rt△ABE中,由勾股定理求出x的值,再由三角形的面积公式求出面积的值.【详解】解:(1)∵四边形ABCD是长方形,∴AD∥BC,∠ADC=∠C=90°,∵AD∥BC,∴∠BDA=∠DBC=25°,∴∠BDC=90°-25°=65°,∵沿BD折叠C和C′重合,∴∠C′DB=∠CDB=65°,∴∠ADC′=∠BDC′-∠BDA=65°-25°=40°;(2)由折叠可知,∠CBD=∠EBD,∵AD∥BC,∴∠CBD=∠EDB,∴∠EBD=∠EDB,∴BE=DE,设DE=x,则BE=x,AE=8-x,在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即42+(8-x)2=x2,解得:x =5,所以S △BDE =DE ×AB =×5×4=10.12123.详见解析【分析】根据平行四边形的性质和已知条件证明△ABE ≌△CDF ,再利用全等三角形的性质:即可得到AE=CF .【详解】证:∵四边形ABCD 是平行四边形,∴AB=CD ,∠B=∠D ,又∵BE=DF ,∴△ABE ≌△CDF ,∴AE=CF. (其他证法也可)4.证明见解析【分析】根据矩形的对边相等可得AB =CD ,四个角都是直角可得∠A =∠C =90°,然后利用“边角边”证明△ABE 和△CDF 全等,【详解】证明:∵四边形ABCD 为矩形,∴,.AB =CD ∠A =∠C =90°∵在和中, △ABE △CDF , {AE =CF ∠A =∠C AB =CD∴,△ABE≌△CDF ∴.BE =DF 【点睛】本题考查了矩形的性质及全等三角形的判定与性质,掌握矩形的对边相等的性质、四个角都是直角是解题的关键. 5.证明见解析.【分析】根据题意与平行四边形的性质得∠ADB =∠DBC ,DA =BC ,DE =BF ,则△ADE ≌△CBF ,所以AE =CF ,同理可证得AF =CE ,故可得四边形AFCE 是平行四边形.【详解】证明:∵四边形ABCD 为平行四边形,∴∠ADB =∠DBC ,DA =BC ,∵E ,F 为BD 的三等分点,∴DE =BF ,在△ADE 和△CBF 中,, {DA =BC ∠ADE =∠CBF DE =BF∴△ADE ≌△CBF (SAS ),∴AE =CF ,同理△CDE ≌△ABF ,∴AF =CE ,∴四边形AFCE 是平行四边形.【点睛】本题考查平行四边形的判定与性质和全等三角形的判定与性质,解此题的关键在于灵活运用平行四边形的性质来证明三角形全等,再利用全等三角形的性质证明已知四边形为平行四边形.6.详见解析【分析】通过证明三角形全等求得两线段相等即可.【详解】∵四边形ABCD 为平行四边形∴∠B =∠D ,AB =CD∵∠1=∠2,∠B =∠D ,AB =CD∴△ABE ≌△CDF∴AE =CF .【点睛】本题主要考查平行四边形性质与全等三角形,解题关键在于找到全等三角形.7.FC =32【分析】根据翻转前后,图形的对应边和对应角相等,可知EF =BF ,AB =AE ,故可求出DE 的长,然后设出FC 的长,则EF =4-FC ,再根据勾股定理的知识,即可求出答案.【详解】解:由题意,得AE =AB =5,AD =BC =4,EF =BF ,在Rt △ADE 中,由勾股定理,得DE =3.在矩形ABCD 中,DC =AB =5.∴CE =DC -DE =2.设FC =x ,则EF =4-x .在Rt △CEF 中,x 2+22=(4-x )2.解得x =.32即FC =.32【点睛】本题考查了翻转变换的知识,属于基础题,注意掌握图形翻转前后对应边和对应角相等.8.(1)见解析;(2)EF =2【分析】(1)由四边形ABCD 是菱形,可得AB ∥CD ,OA =OC ,继而证得△AOE ≌△COF ,则可证得结论.(2)利用平行四边形的判定和性质解答即可.(1)∵四边形ABCD 是菱形,∴AO =CO ,AB ∥CD ,∴∠EAO =∠FCO ,∠AEO =∠CFO .在△OAE 和△OCF 中,∠EAO =∠FCO ,AO =CO ,∠AEO =∠CFO ,∴△AOE ≌△COF ,∴AE =CF ;(2)∵E 是AB 中点,∴BE =AE =CF .∵BE ∥CF ,∴四边形BEFC 是平行四边形,∵AB =2,∴EF =BC =AB =2.【点睛】此题考查了菱形的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用. 9.证明见解析.【分析】根据菱形的对角线互相平分可得OD =OB ,再根据直角三角形斜边上的中线等于斜边的一半可得OH =OB ,然后根据等边对等角求出∠OHB =∠OBH ,根据两直线平行,内错角相等求出∠OBH =∠ODC ,然后根据等角的余角相等证明即可.【详解】∵四边形ABCD 是菱形,∴OD =OB ,∠COD =90°,∵DH ⊥AB ,∴OH =BD =OB ,12∴∠OHB =∠OBH ,又∵AB ∥CD ,∴∠OBH =∠ODC ,在Rt △COD 中,∠ODC +∠DCO =90°,在Rt △DHB 中,∠DHO +∠OHB =90°,∴∠DHO =∠DCO .10.见解析【分析】由平行四边形的性质知AB=CD ,再有中点定义得CE=BE ,从而可以由ASA 定理证明△CED △BEF ,则≌CD=BF ,故AB=BF .证明:∵E 是BC 的中点,∴CE=BE ,∵四边形ABCD 是平行四边形,∴AB ∥CD ,AB=CD ,∴∠DCB=∠FBE ,在△CED 和△BEF 中,, {∠DCB =∠FBE CE =BE ∠CED =∠BEF∴△CED △BEF (ASA ),≌∴CD=BF ,∴AB=BF .【点睛】本题考查了以下内容:1.平行四边形的性质 2.三角形全等的判定定理.11.见解析【分析】根据条件可以得出AD =AB ,∠ABF =∠ADE =90°,从而可以得出△ABF ≌△ADE ,就可以得出∠FAB =∠EAD ,就可以得出结论.【详解】证明:∵四边形ABCD 是正方形,∴AB =AD ,∠ABC =∠D =∠BAD =90°,∴∠ABF =90°.∵在△BAF 和△DAE 中, , {AB =AD ∠ABF =∠ADE BF =DE∴△BAF ≌△DAE (SAS ),∴∠FAB =∠EAD ,∵∠EAD +∠BAE =90°,∴∠FAB +∠BAE =90°,∴∠FAE =90°,∴EA ⊥AF .12.(1)证明见解析;(2)证明见解析.【分析】(1)根据两组对边分别平行的四边形是平行四边形可得四边形BFDE 是平行四边形,根据平行四边形的对边相等即可得;(2)根据一组对边平行且相等的四边形是平行四边形可得四边形AFCE 是平行四边形,从而得AF ∥CE ,再根据四边形BFDE 是平行四边形,从而可得DF ∥BE ,再根据两组对边分别平行的四边形是平行四边形即可得.【详解】解:(1)∵四边形ABCD 是平行四边形,∴AD //BC ,∵DF ∥BE ,∴四边形BFDE 是平行四边形,∴DE =BF ;(2)∵四边形ABCD 是平行四边形∴AD //BC 且AD =BC ,∵DE =BF ,∴AD -DE =BC -BF ,即AE =CF ,∴四边形AFCE 是平行四边形,∴AF ∥CE ,∵四边形BFDE 是平行四边形,∴DF //BE ,∴四边形MFNE 是平行四边形.【点睛】本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定方法与性质是解题的关键.13.(1)EF =3;(2)梯形ABCE 的面积为39.【详解】试题分析:(1)根据折叠的性质,折叠前后边相等,即 得: 在CF =CD ,DE =EF ,AE =AD−EF ,Rt △ACD 中,根据勾股定理,可将的长求出,知的长,可求出的长,在中,根据,可将AC CF AF Rt △AEF AE 2=EF 2+AF 2EF 的长求出;(2)根据S 梯形=,将各边的长代入进行求解即可. (AE +BC )×AB 2试题解析:(1)设EF =x 依题意知:△CDE ≌△CFE ,∴DE =EF =x ,CF =CD =6.∵在中,Rt △ACD AC =62+82=10,∴AF =AC −CF =4,AE =AD −DE =8−x .在中,有Rt △AEF AE 2=EF 2+AF 2即(8−x)2=42+x 2解得x =3,即:EF =3.(2)由(1)知:AE =8−3=5,梯形ABCE 的面积S =(AE +BC )×AB 2=(5+8)×62=39.14.(1)答案见解析;(2)答案见解析.【分析】(1)根据等腰直角三角形的性质即可解决问题.(2)根据正方形、长方形的性质对角线相等且互相平分,即可解决问题.【详解】解:(1)如图所示,∠ABC=45°.(AB、AC是小长方形的对角线).(2)线段AB的垂直平分线如图所示,点M是长方形AFBE是对角线交点,点N是正方形ABCD的对角线的交点,直线MN就是所求的线段AB的垂直平分线.【点睛】本题考查作图—应用与设计作图.15.见解析【分析】由题意先证明△ADE≌△BAF,得出∠EDA=∠FAB,再根据∠ADE+∠AED=90°,推得∠FAE+∠AED=90°,从而证出AF⊥DE.【详解】解:∵四边形ABCD为正方形,∴DA=AB,∠DAE=∠ABF=90°,又∵AE=BF,∴△DAE≌△ABF,∴∠ADE=∠BAF,∵∠ADE+∠AED=90°,∴∠FAE+∠AED=90°,∴∠AGE=90°,∴AF⊥DE.【点睛】本题考查正方形的性质,全等三角形的判定与性质,解题的关键是掌握三角形的判定定理.216.(1)详见解析;(2)EG+BG=AG,证明详见解析.【分析】(1)作∠GAH=∠EAB交GE于点H,证△ABG≌△AEH,再证ΔACH是等边三角形,得AG=HG,EG=AG+BG;(2)作∠GAH =∠EAB 交GE 的延长线于点H ,则∠GAB =∠HAE ,证ΔABG ≌ΔAEH ,得BG =EH ,AG =AH ,再证ΔAGH 是等腰直角三角形,可得AG =HG .故EG +BG =AG .22【详解】(1)证明:如图1,作∠GAH =∠EAB 交GE 于点H ,则∠GAB =∠HAE .∵∠EAB =∠EGB ,∠AOE =∠BOF ,∴∠ABG =∠AEH在ΔABG 和ΔAEH 中{∠GAB =∠HAE AB =AE ∠ABG =∠AEH所以△ABG ≌△AEH (ASA )∴BG =EH ,AG =AH∵∠GAH =∠EAB =60°∴ΔAGH 是等边三角形∴AG =HG . ∴EG =AG +BG(2)EG +BG =AG2证明:如图2,作∠GAH =∠EAB 交GE 的延长线于点H ,则∠GAB =∠HAE∵∠EGB =∠EAB =90°∴∠ABG +∠AEG =∠AEG +∠AEH =180°∴∠ABG =∠AEH .在ΔABG 和ΔAEH 中{∠HAE =∠GAB AB =AE ∠AEH =∠ABG∴ΔABG ≌ΔAEH (ASA )∴BG =EH ,AG =AH∵∠GAH =∠EAB =90°∴ΔAGH 是等腰直角三角形 ∴AG =HG2∴EG +BG =AG2【点睛】本题主要考查了等边三角形的性质与判定,等腰直角三角形的性质与判定,全等三角形的性质与判定,平行四边形的性质等等,正确作出辅助线构造全等三角形是解题的关键.17.(1)见解析;(2)α,β之间的数量关系式为2α+β=60°.【分析】(1)根据三角形的中位线的性质得到EF=CD ,根据直角三角形的性质得到AE=BD ,于是得到结论; 1212(2)根据题意得到△AEF 是等边三角形,求得∠AEF=60°,根据三角形中位线的性质和三角形外角的性质即可得到结论.【详解】(1)∵点E 、F 分别为DB 、BC 的中点,∴EF=CD ,12∵∠DAB=90°,∴AE=BD ,12∵DB=DC ,∴AE=EF ;(2)∵AF=AE ,AE=EF ,∴△AEF 是等边三角形,∴∠AEF=60°,∵∠DAB=90°,点E 、F 分别为DB 、BC 的中点,∴AE=DE ,EF ∥CD ,∴∠ADE=∠DAE=α,∠BEF=∠BDC=β,∴∠AEB=2∠ADE=2α,∴∠AEF=∠AEB+∠FEB=2α+β=60°,∴α,β之间的数量关系式为2α+β=60°.【点睛】本题考查了三角形中位线的性质,直角三角形的性质,平行线的性质,三角形外角的性质,正确的识别图形是解题的关键.18.(1)作图见解析;(2)菱形,证明见解析【详解】解:(1)如图所示,(2)四边形AECF 的形状为菱形.理由如下:∵AB=AC ,∴∠ABC=∠ACB ,∵AM 平分∠DAC ,∴∠DAM=∠CAM ,而∠DAC=∠ABC+∠ACB ,∴∠CAM=∠ACB ,∴EF 垂直平分AC ,∴OA=OC ,∠AOF=∠COE ,在△AOF 和△COE 中,, {∠FAO =∠ECO OA =OC ∠AOF =∠COE∴△AOF ≌△COE ,∴OF=OE ,即AC 和EF 互相垂直平分,∴四边形AECF 的形状为菱形.【点睛】本题考查①作图—复杂作图;②角平分线的性质;③线段垂直平分线的性质.19.证明见解析.【分析】根据平行四边形的性质证出∠ADC=∠FCD ,然后再证明△ADE ≌△FCE 可得AD=FC ,根据一组对边平行且相等的四边形是平行四边形可得结论【详解】证明:∵在▱ABCD 中,AD ∥BF .∴∠ADC=∠FCD .∵E 为CD 的中点,∴DE=CE .在△ADE 和△FCE 中,, {∠AED =∠FEC∠ADE =∠FCE DE =CE∴△ADE ≌△FCE (ASA )∴AD=FC .又∵AD ∥FC ,∴四边形ACFD 是平行四边形.【点睛】此题主要考查了平行四边形的判定和性质,关键是掌握平行四边形两组对边分别平行.20.(1)证明见解析;(2)12【分析】(1)由平行四边形的性质和角平分线得出∠BAF =∠BFA ,即可得出AB =BF ;(2)由题意可证△ABF 为等边三角形,点E 是AF 的中点. 可求EF 、BF 的值,即可得解.【详解】解:(1)证明:∵ 四边形ABCD 为平行四边形,∴ AB =CD ,∠FAD =∠AFB又∵ AF 平分∠BAD ,∴ ∠FAD =∠FAB∴ ∠AFB =∠FAB∴ AB =BF∴ BF =CD(2)解:由题意可证△ABF 为等边三角形,点E 是AF 的中点在Rt △BEF 中,∠BFA =60°,BE =,23可求EF =2,BF =4∴ 平行四边形ABCD 的周长为1221.证明见解析.【分析】利用SAS 证明△AEB ≌△CFD ,再根据全等三角形的对应边相等即可得.【详解】∵四边形ABCD 是平行四边形,∴AB //DC ,AB =DC ,∴∠BAE =∠DCF ,在△AEB 和△CFD 中,, {AB =CD ∠BAE =∠DCF AE =CF∴△AEB ≌△CFD (SAS ),∴BE =DF .【点睛】本题考查了平行四边形的性质以及全等三角形的判定与性质,熟练掌握相关的性质是解题的关键.22.见解析【分析】根据已知条件易推知四边形BECD 是平行四边形.结合等腰△ABC “三线合一”的性质证得BD ⊥AC ,即∠BDC =90°,所以由“有一内角为直角的平行四边形是矩形”得到▱BECD 是矩形.【详解】证明:∵AB =BC ,BD 平分∠ABC ,∴BD ⊥AC ,AD =CD .∵四边形ABED 是平行四边形,∴,BE =AD ,BE//AC ∴BE =CD ,∴四边形BECD 是平行四边形.∵BD ⊥AC ,∴∠BDC =90°,∴▱BECD 是矩形.【点睛】本题考查矩形的判定,等腰三角形三线合一的性质,平行四边形的判定和性质.解题的关键是掌握有一个角是直角的平行四边形是矩形.23.见解析.【分析】根据题意利用平行四边形的性质求出∠ABF =∠AED ,即DE ∥BF ,即可解答【详解】∵四边形ABCD 是平行四边形,∴∠ADC =∠ABC .又∵DE ,BF 分别是∠ADC ,∠ABC 的平分线,∴∠ABF =∠CDE .又∵∠CDE =∠AED ,∴∠ABF =∠AED ,∴DE ∥BF ,∵DE ∥BF ,DF ∥BE ,∴四边形DEBF 是平行四边形.【点睛】此题考查平行四边形的性质和判定,利用好角平分线的性质是解题关键24.(1)证明见解析;(2).23【分析】(1)由平行四边形的判定得出四边形OCED 是平行四边形,根据矩形的性质求出OC =OD ,根据菱形的判定得出即可.(2)解直角三角形求出BC =2,AB =DC =2,连接OE ,交CD 于点F ,根据菱形的性质得出F 为CD 中点,求出3OF =BC =1,求出OE =2OF =2,求出菱形的面积即可.12【详解】证明:,,(1)∵CE //OD DE //OC 四边形OCED 是平行四边形,∴矩形ABCD ,∵,,,∴AC =BD OC =12AC OD =12BD ,∴OC =OD 平行四边形OCED 是菱形;∴在矩形ABCD 中,,,,(2)∠ABC =90∘∠BAC =30∘AC =4,∴BC =2,∴AB =DC =23连接OE ,交CD 于点F ,四边形OCED 为菱形,∵为CD 中点,∴F 为BD 中点, ∵O ,∴OF =12BC =1,∴OE =2OF =2.∴S 菱形OCED =12×OE ×CD =12×2×23=23【点睛】 本题主要考查了矩形的性质和菱形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:菱形的面积等于对角线积的一半.25.(1)如图所示见解析;(2)面积均为12,周长分别为:8+6,8+2.210,210+62【分析】(1)用边长为1、3的直角三角形拼出矩形,再分别在边长为3的两侧拼上边长都为3的直角三角形;用边长都为3的直角三角形拼出矩形,再分别在边长为3的两侧拼上边长都为3、1的直角三角形;以四个直角三角形的直角边拼出对角线为4的平行四边形即可;(2)每个平行四边形的面积都等于四个直角三角形的面积之和,为定值,周长不是定值.【详解】(1)3种拼法;(2)三种方法所拼得的平行四边形的面积是定值,这个定值==12;三种方法所拼得的平2×(12×3×3+12×1×3)行四边形的周长不是定值,它们的周长分别是8+6,8+2.210,210+62【点睛】本题考查了四边形综合题,其中涉及到了平行四边形的判定与性质,平行四边形的面积,灵活掌握平行四边形与三角形之间关系是解题的难点.26.(1)见解析;(2)42【分析】(1)根据平行四边形的判定定理首先推知四边形DBEC 为平行四边形,然后由直角三角形斜边上的中线等于斜边的一半得到其邻边相等:CD =BD ,得证;(2)由三角形中位线定理和勾股定理求得AB 边的长度,然后根据菱形的性质和三角形的面积公式进行解答.【详解】(1)证明:∵CE ∥DB ,BE ∥DC ,∴四边形DBEC 为平行四边形.又∵Rt △ABC 中,∠ABC =90°,点D 是AC 的中点,∴CD =BD =AC ,12∴平行四边形DBEC 是菱形;(2)∵点D ,F 分别是AC ,AB 的中点,AD =3,DF =1,∴DF 是△ABC 的中位线,AC =2AD =6,S △BCD =S △ABC12∴BC =2DF =2.又∵∠ABC =90°,∴AB = = = 4.AC 2−BC 262−222∵平行四边形DBEC 是菱形,∴S 四边形DBEC =2S △BCD =S △ABC =AB •BC =×4×2=4. 121222【点睛】本题考查了菱形的判定与性质,直角三角形斜边上的中线等于斜边的一半,三角形中位线定理.由点D 是AC 的中点,得到CD =BD 是解答(1)的关键,由菱形的性质和三角形的面积公式得到S 四边形DBEC =S △ABC 是解(2)的关键.27.(1)MA=MN ,MA ⊥MN ;(2)成立,理由详见解析【详解】(1)解:连接DE ,∵四边形ABCD 是正方形,∴AD=CD=AB=BC ,∠DAB=∠DCE=90°,∵点M 是DF 的中点,∴AM=DF .12∵△BEF 是等腰直角三角形,∴AF=CE ,在△ADF 与△CDE 中,, {AB =CD∠DAF =∠DCE AF =CE∴△ADF ≌△CDE (SAS ),∴DE=DF .∵点M ,N 分别为DF ,EF 的中点,∴MN 是△EFD 的中位线,∴MN=DE ,12∴AM=MN ;∵MN 是△EFD 的中位线,∴MN ∥DE ,∴∠FMN=∠FDE .∵AM=MD ,∴∠MAD=∠ADM ,∵∠AMF 是△ADM 的外角,∴∠AMF=2∠ADM .∵△ADF ≌△CDE ,∴∠ADM=∠CDE ,∴∠ADM+∠CDE+∠FDE=∠FMN+∠AMF=90°,∴MA ⊥MN .∴MA=MN ,MA ⊥MN .(2)成立.理由:连接DE .∵四边形ABCD 是正方形,∴AB=BC=CD=DA ,∠ABC=∠BCD=∠CDA=∠DAB=90°.在Rt △ADF 中,∵点M 是DF 的中点,∴MA=DF=MD=MF ,12∴∠1=∠3.∵点N 是EF 的中点,∴MN 是△DEF 的中位线,∴MN=DE ,MN ∥DE .12∵△BEF 是等腰直角三角形,∴BF=BF ,∠EBF=90°.∵点E 、F 分别在正方形CB 、AB 的延长线上,∴AB+BF=CB+BE ,即AF=CE .在△ADF 与△CDE 中, {AD =CD∠DAF =∠DCE AF =DE∴△ADF ≌△CDE ,∴DF=DE ,∠1=∠2,∴MA=MN ,∠2=∠3.∵∠2+∠4=∠ABC=90°,∠4=∠5,∴∠3+∠5=90°,∴∠6=180°﹣(∠3+∠5)=90°,∴∠7=∠6=90°,MA ⊥MN .28.(1)见解析;(2)45°;(3)见解析【分析】(1)根据AF 平分∠BAD ,可得∠BAF =∠DAF ,利用四边形ABCD 是平行四边形,求证∠CEF =∠F 即可; (2)根据∠ABC =90°,G 是EF 的中点可直接求得;(3)分别连接GB 、GC ,求证四边形CEGF 是平行四边形,再求证△ECG 是等边三角形,由AD ∥BC 及AF 平分∠BAD 可得∠BAE =∠AEB ,求证△BEG ≌△DCG ,然后即可求得答案.【详解】(1)证明:如图1,∵AF 平分∠BAD ,∴∠BAF =∠DAF ,∵四边形ABCD 是平行四边形,∴AD BC ,AB CD ,∥∥∴∠DAF =∠CEF ,∠BAF =∠F ,∴∠CEF =∠F .∴CE =CF .(2)解:连接GC 、BG ,∵四边形ABCD 为平行四边形,∠ABC =90°,∴四边形ABCD 为矩形,∵AF 平分∠BAD ,∴∠DAF =∠BAF =45°,∵∠DCB =90°,DF ∥AB ,∴∠DFA =45°,∠ECF =90°∴△ECF 为等腰直角三角形,∵G 为EF 中点,∴EG =CG =FG ,CG ⊥EF ,∵△ABE 为等腰直角三角形,AB =DC ,∴BE =DC ,∵∠CEF =∠GCF =45°,∴∠BEG =∠DCG =135°在△BEG 与△DCG 中,∵,{EG =CG∠BEG =∠DCG BE =DC ∴△BEG ≌△DCG ,∴BG =DG ,∵CG ⊥EF ,∴∠DGC +∠DGA =90°,又∵∠DGC =∠BGA ,∴∠BGA +∠DGA =90°,∴△DGB 为等腰直角三角形,∴∠BDG =45°.(3)解:延长AB 、FG 交于H ,连接HD .∵AD GF ,AB DF ,∥∥∴四边形AHFD 为平行四边形∵∠ABC =120°,AF 平分∠BAD∴∠DAF =30°,∠ADC =120°,∠DFA =30°∴△DAF 为等腰三角形∴AD =DF ,∴CE =CF ,∴平行四边形AHFD 为菱形∴△ADH ,△DHF 为全等的等边三角形∴DH =DF ,∠BHD =∠GFD =60°∵FG =CE ,CE =CF ,CF =BH ,∴BH =GF在△BHD 与△GFD 中,∵ , {DH =DF ∠BHD =∠GFD BH =GF∴△BHD ≌△GFD ,∴∠BDH =∠GDF∴∠BDG =∠BDH +∠HDG =∠GDF +∠HDG =60°.【点睛】本题考查了平行四边形的判定方法,全等三角形的判定与性质,等边三角形的判定与性质,菱形的判定与性质等知识点,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.29.(1)8;(2)所以的值为或;(3)a 5611243< m <53【分析】(1)点(2,)的矩形域的定义,求出矩形边长分别为2,4,画出图形即可解决问题;72(2)分两种情形,重叠部分在(1)中矩形的左边或右边,分别构建方程即可解决问题;(3)利用特殊值法.推出平行于y 轴的矩形的边长为3,由此即可解决问题;【详解】解:(1)根据题意可得:点矩形域为,长为4,宽为2,(2,72)点的矩形域如图所示, (2,72)该该矩形域的面积是8;故答案为:8;(2)如图所示,因为点的矩形域重叠部分面积为1,且平行于轴的边长均为4, P (2,72),Q (a ,72)(a >0)y 所以点的矩形域重叠部分也是一个矩形,且平行于轴的边长为4,平行于轴的边长为. P (2,72),Q (a ,72)(a >0)y x 14①当时,,解得;0<a <2a +a 2=1+14a =56②当时,,解得. a >2a−a 2=3−14a =112所以的值为或.a 56112(3)当m =1时,S =3,当m =2时,S =8,∵4<S <5,∴1<m <2,∴平行于y 轴的矩形的边长为3,∴平行于x 轴的矩形的边长m 的范围为43< m <53。
人教版八年级数学下册-难点探究专题(选做):特殊四边形中的综合性问题

难点探究专题(选做):特殊四边形中的综合性问题◆类型一特殊平行四边形的动态探究问题一、动点问题1.(2016·枣庄中考)如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=63,∠BAD=60°,且AB>6 3.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值;(3)若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP的最大值和最小值.二、图形的变换问题2.如图①,点O是正方形ABCD两条对角线的交点.分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG,OE为邻边作正方形OEFG,连接AG,DE.(1)求证:DE⊥AG;(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图②.①在旋转过程中,当∠OAG′是直角时,求α的度数;②若正方形ABCD的边长为1,在旋转过程中,求AF′的最大值和此时α的度数,直接写出结果不必说明理由.◆类型二四边形间的综合性问题3.(2016·德州中考)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图②,点P是四边形ABCD内一点,且满足P A=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)参考答案与解析1.解:(1)如图①,过点P 作PG ⊥EF 于点G ,H 为PE 的中点,连接GH ,∴∠PGE=90°,GH =PH =HE =12PE =3.∵PF =PE ,∴∠FPG =∠EPG ,FG =GE =12EF =3 3.在Rt △PGE 中,由勾股定理得PG =PE 2-GE 2=62-(33)2=3.∴PG =GH =PH ,即△GPH 为等边三角形,∴∠GPH =60°,∴∠FPE =∠FPG +∠GPE =2∠GPE =2×60°=120°.(2)如图①,过点P 作PM ⊥AB 于点M ,作PN ⊥AD 于点N ,∴∠ANP =∠AMP =90°.∵AC为菱形ABCD 的对角线,∴∠DAC =∠BAC =12∠DAB =30°,PM =PN .在Rt △PME 和Rt △PNF 中,PM =PN ,PE =PF ,∴Rt △PME ≌Rt △PNF ,∴ME =NF .∵∠P AM =30°,AP=10,∴PM =12AP =5.由勾股定理得AM =P A 2-PM 2=5 3.在△ANP 和△AMP 中,⎩⎪⎨⎪⎧∠NAP =∠MAP ,∠ANP =∠AMP =90°,AP =AP ,∴△ANP ≌△AMP ,∴AN =AM =5 3.∴AE +AF =(AM +ME )+(AN -NF )=AM +AN +ME -NF =10 3.(3)如图②,△EFP 的三个顶点分别在AB ,AD ,AC 上运动,点P 在P 1,P 之间运动.P 1O =PO =12PE =3,AE =EF =63,AO =AE 2-EO 2=9.∴AP 的最大值为AO +OP =12,AP 的最小值为AO -OP 1=6.2.(1)证明:如图,延长ED 交AG 于点H .∵四边形ABCD 与OEFG 均为正方形,∴OA =OD ,OG =OE ,∠AOG =∠DOE =90°,∴Rt △AOG ≌Rt △DOE ,∴∠AGO =∠DEO .∵∠AGO +∠GAO =90°,∴∠DEO +∠GAO =90°,∴∠AHE =90°,即DE ⊥AG ;(2)解:①在旋转过程中,∠OAG ′成为直角有以下两种情况:a .α由0°增大到90°过程中,当∠OAG ′为直角时,∵OA =OD =12OG =12OG ′,∴∠AG ′O =30°,∠AOG ′=60°.∵OA ⊥OD ,∴∠DOG ′=90°-∠AOG ′=30°,即α=30°;b .α由90°增大到180°过程中,当∠OAG ′为直角时,同理可求的∠AOG ′=60°,∴α=90°+∠AOG ′=150°.综上,当∠OAG ′为直角时,α=30°或150°;②AF ′长的最大值是2+22,此时α=315°. 3.(1)证明:如图①中,连接BD .∵点E ,H 分别为边AB ,DA 的中点,∴EH ∥BD ,EH =12BD .∵点F ,G 分别为边BC ,CD 的中点,∴FG ∥BD ,FG =12BD ,∴EH ∥FG ,EH =GF ,∴中点四边形EFGH 是平行四边形.(2)解:四边形EFGH 是菱形.理由如下:如图②中,连接AC ,BD .∵∠APB =∠CPD ,∴∠APB +∠APD =∠CPD +∠APD ,即∠APC =∠BPD .在△APC 和△BPD 中,⎩⎪⎨⎪⎧AP =PB ,∠APC =∠BPD ,PC =PD ,∴△APC ≌△BPD ,∴AC =BD .∵点E ,F ,G 分别为边AB ,BC ,CD 的中点,∴EF =12AC ,FG =12BD ,∴EF =FG .∵四边形EFGH 是平行四边形,∴四边形EFGH 是菱形.(3)解:四边形EFGH 是正方形.理由如下:如图②中,设AC 与BD 交于点O .AC 与PD 交于点M ,AC 与EH 交于点N .∵△APC ≌△BPD ,∴∠ACP =∠BDP .∵∠DMO =∠CMP ,∴∠COD =∠CPD =90°.∵EH ∥BD ,AC ∥HG ,∴∠EHG =∠ENO =∠BOC =∠DOC =90°.∵四边形EFGH 是菱形,∴四边形EFGH 是正方形.19.2.3 一次函数与方程、不等式一.选择题(共8小题)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()A.x=2B.y=2C.x=﹣1D.y=﹣12.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为()A.x=﹣1B.x=2C.x=0D.x=33.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为()A.(3,0)B.(﹣3,0)C.(a,0)D.(﹣b,0)4.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A.B.C.D.5.若方程x﹣3=0的解也是直线y=(4k+1)x﹣15与x轴的交点的横坐标,则k的值为()A.﹣1B.0C.1D.±16.如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是()A.B.C.D.7.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m >nx+4n>0的整数解为()A.﹣1B.﹣5 C.﹣4D.﹣38.如图,一次函数y=kx+b的图象经过A、B两点,则不等式kx+b<0的解集是()A.x<0B.0<x<1C.x<1 D.x>1二.填空题(共10小题)9.若直线y=2x+b与x轴交于点(﹣3,0),则方程2x+b=0的解是_________.10.如图是一次函数y=kx+b的图象,则方程kx+b=0的解为_________.11.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为_________.12.如图,已知直线y=ax﹣b,则关于x的方程ax﹣1=b的解x=_________.13.如图,直线y=kx+b分别交x轴和y轴于点A、B,则关于x的方程kx+b=0的解为_________.14.如图,已知函数y=2x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),根据图象可得方程2x+b=ax﹣3的解是_________.15.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是_________.16.如图,直线y=kx+b过A(﹣1,2)、B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为_________.17.一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是_________.18.如图,函数y=kx和的图象相交于A (a,2),则不等式的解集为_________.三.解答题(共4小题)19.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=﹣3的解.20.如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:_________;(2)设直线l2与x轴交于点A,求△OAP的面积.21.在平面直角坐标系x0y中,直线y=kx+b(k≠0)过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点,求不等式kx+b≤0的解.22.在直角坐标系xOy中,直线y=kx+b(k≠0)经过(﹣2,1)和(2,3)两点,且与x 轴、y轴分别交于A、B两点,求不等式kx+b≥0的解集.19.2.3 一次函数与方程、不等式一.选择题(共8小题)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()A.x=2B.y=2C.x=﹣1D.y=﹣12.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为()A.x=﹣1B.x=2C.x=0D.x=33.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为()A.(3,0)B.(﹣3,0)C.(a,0)D.(﹣b,0)4.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A.B.C.D.5.若方程x﹣3=0的解也是直线y=(4k+1)x﹣15与x轴的交点的横坐标,则k的值为()A.﹣1B.0C.1D.±16.如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是()A.B.C.D.7.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m >nx+4n>0的整数解为()A.﹣1B.﹣5 C.﹣4D.﹣38.如图,一次函数y=kx+b的图象经过A、B两点,则不等式kx+b<0的解集是()A.x<0B.0<x<1C.x<1 D.x>1二.填空题(共10小题)9.若直线y=2x+b与x轴交于点(﹣3,0),则方程2x+b=0的解是_________.10.如图是一次函数y=kx+b的图象,则方程kx+b=0的解为_________.11.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为_________.12.如图,已知直线y=ax﹣b,则关于x的方程ax﹣1=b的解x=_________.13.如图,直线y=kx+b分别交x轴和y轴于点A、B,则关于x的方程kx+b=0的解为_________.14.如图,已知函数y=2x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),根据图象可得方程2x+b=ax﹣3的解是_________.15.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是_________.16.如图,直线y=kx+b过A(﹣1,2)、B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为_________.17.一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是_________.18.如图,函数y=kx和的图象相交于A (a,2),则不等式的解集为_________.三.解答题(共4小题)19.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=﹣3的解.20.如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:_________;(2)设直线l2与x轴交于点A,求△OAP的面积.21.在平面直角坐标系x0y中,直线y=kx+b(k≠0)过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点,求不等式kx+b≤0的解.22.在直角坐标系xOy中,直线y=kx+b(k≠0)经过(﹣2,1)和(2,3)两点,且与x 轴、y轴分别交于A、B两点,求不等式kx+b≥0的解集.。
八年级数学四边形专题复习(精编)

四边形专题复习【知识要点】 一 一般四边形1.四边形的内角和与外角和定理: (1)四边形的内角和等于360°;(2)四边形的外角和等于360°. 2.多边形的内角和与外角和定理: (1)n 边形的内角和等于(n -2)180°;(2)任意多边形的外角和等于360°.3.若n 是多边形的边数,则对角线条数公式是:2)3n (n -.二 平行四边形的判定与性质1. 平行四边形定义:两组对边分别平行的四边形叫做平行四边形。
2. 平行四边形是中心对称图形,对称中心是两条对角线的交点。
3.平行四边形的性质:因为ABCD 是平行四边形⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧.54321)邻角互补()对角线互相平分;()两组对角分别相等;()两组对边分别相等;()两组对边分别平行;( 4.平行四边形的判定:是平行四边形)对角线互相平分()一组对边平行且相等()两组对角分别相等()两组对边分别相等()两组对边分别平行(ABCD 54321⎪⎪⎪⎭⎪⎪⎪⎬⎫.三 矩形的判定与性质1. 矩形定义1:有一个角是直角的平行四边形叫做矩形2. 矩形定义2:有三个角是直角的四边形叫做矩形3. 矩形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点,对称轴是各边的垂直平分线。
4.矩形的性质:因为ABCD 是矩形⇒⎪⎩⎪⎨⎧.3;2;1)对角线相等()四个角都是直角(有通性)具有平行四边形的所( 5. 矩形的判定:⎪⎭⎪⎬⎫+边形)对角线相等的平行四()三个角都是直角(一个直角)平行四边形(321⇒四边形ABCD 是矩形.四 菱形的判定与性质1. 菱形定义1:有一组邻边相等的平行四边形叫做菱形.2. 菱形定义2:四条边都相等的四边形叫做菱形。
3. 菱形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点, 对称轴是对角线所在的直线。
A BCD 1234AB CDABDOCABDOCA D BCADBCOCDBAO4.菱形的性质: 因为ABCD 是菱形⇒⎪⎩⎪⎨⎧.321角)对角线垂直且平分对()四个边都相等;(有通性;)具有平行四边形的所( 5.菱形的判定:⎪⎭⎪⎬⎫+边形)对角线垂直的平行四()四个边都相等(一组邻边等)平行四边形(321⇒四边形四边形ABCD 是菱形. 五 正方形的判定与性质1. 正方形定义1:有一组邻边相等的矩形叫做正方形。
浙教版初中数学八年级下册第五单元《特殊平行四边形》(困难)(含答案解析)(含答案解析)

浙教版初中数学八年级下册第五单元《特殊平行四边形》(困难)(含答案解析)考试范围:第五单元; 考试时间:120分钟;总分:120分,第I卷(选择题)一、选择题(本大题共12小题,共36.0分。
在每小题列出的选项中,选出符合题目的一项)1. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )A. 5B. 4.8C. 4.6D. 4.42. 若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD一定是( )A. 矩形B. 菱形C. 对角线互相垂直的四边形D. 对角线相等的四边形3. 如图,在矩形ABCD中,点M在AB边上,把△BCM沿直线CM折叠,使点B落在AD边上的点E处,连接EC,过点B作BF⊥EC,垂足为F,若CD=1,CF=2,则线段AE的长为( )A. √5−2B. √3−1C. 13D. 124. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=6,∠DAC=60°,点F在线段AO 上从点A至点O运动,连接DF,以DF为边作等边三角形DFE,点E和点A分别位于DF两侧,下列结论:①∠BDE=∠EFC;②ED=EC;③∠ADF=∠ECF;④点E运动的路程是2√3,其中正确结论的序号为( )A. ①④B. ①②③C. ②③④D. ①②③④5. 如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③▵GDK和▵GKH的面积相等;④当点F与点C重合时,∠DEF= 75∘,其中正确的结论共有( )A. 1个B. 2个C. 3个D. 4个6. 如图,将三角形纸片△ABC沿DE折叠,使点A落在BC边上的点F处,且DE//BC,下列结论中,一定正确的个数是( )BC;①△BDF是等腰三角形;②DE =12③四边形ADFE是菱形;④∠BDF+∠FEC=2∠A.A. 1B. 2C. 3D. 47. 已知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设△BEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图象是( )A. B. C. D.8. 如图,菱形ABCD中,AB=4,∠ABC=120°,点E是边AB上一点,点F在BC上,在以下四个结论中不正确的是( )A. 若AE+CF=4,则△ADE≌△BDFB. 若DF⊥AD,DE⊥CD,则EF=2√3C. 若∠DEB=∠DFC,则△BEF周长的最小值(4+2√3)D. 若DE=DF,则∠ADE+∠FDC=60°9. 如图所示,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )A. 1个B. 2个C. 3个D. 4个10. 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=√5,下列结论:①△APD≌△AEB;②点B到直线AE的距离为√2;③EB⊥ED;④S△APD+S△APB=1+√6⑤S正方形ABCD=4+√6.其中正确的序号是( )A. ①③④B. ①②⑤C. ③④⑤D. ①③⑤11. 如图,正方形ABCD的面积为3,点E在边CD上,且CE=1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )A. √62B. √32C. 2−√3D. √6−√2212. 如图,在边长为a的正方形ABCD中,E是对角线BD上一点,且BE=BC,点P是CE上一动点,则点P到边BD,BC的距离之和PM+PN的值( )A. 有最大值aB. 有最小值√22a C. 是定值a D. 是定值√22a第II卷(非选择题)二、填空题(本大题共4小题,共12.0分)13. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E=______度.14. 如图,四边形OABC是矩形,点A的坐标为(8,0),点C的坐标为(0,4),把矩形OABC沿OB 折叠,点C落在点D处,则点D的坐标为______.15. 如图,在菱形ABCD中,∠A=60°,AB=3,点M为AB边上一点,AM=2,点N为AD边上的一动点,沿MN将△AMN翻折,点A落在点P处,当点P在菱形的对角线上时,AN的长度为_______.16. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B n的坐标是______.三、解答题(本大题共9小题,共72.0分。
2022年沪科版八年级数学下册第19章 四边形综合测评练习题(含详解)

沪科版八年级数学下册第19章四边形综合测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图是用若干个全等的等腰梯形拼成的图形,下列说法错误的是()A.梯形的下底是上底的两倍B.梯形最大角是120︒C.梯形的腰与上底相等D.梯形的底角是60︒2、如图所示,公路AC、BC互相垂直,点M为公路AB的中点,为测量湖泊两侧C、M两点间的距离,若测得AB的长为6km,则M、C两点间的距离为()A.2.5km B.4.5km C.5km D.3km∠+∠+∠+∠=()3、如图,在六边形ABCDEF中,若1290∠+∠=︒,则3456A.180°B.240°C.270°D.360°4、如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是()A.2.5 B.C D5、四边形四条边长分别是a,b,c,d,其中a,b为对边,且满足222222+,则这++=+a b c d ab cd个四边形是()A.任意四边形B.平行四边形C.对角线相等的四边形D.对角线垂直的四边形6、如图,四边形ABCD中,∠A=60°,AD=2,AB=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为()A B C D7、绿丝带是颜色丝带的一种,被用来象征许多事物,例如环境保护、大麻和解放农业等,同时绿丝带也代表健康,使人对健康的人生与生命的活力充满无限希望.某班同学在“做环保护航者”的主题班会课上制作象征“健康快乐”的绿丝带(丝带的对边平行且宽度相同),如图所示,丝带重叠部分形成的图形是()A.矩形B.菱形C.正方形D.等腰梯形8、在Rt△ABC中,∠C=90°,若D为斜边AB上的中点,AB的长为10,则DC的长为()A.5 B.4 C.3 D.29、下列测量方案中,能确定四边形门框为矩形的是()A.测量对角线是否互相平分B.测量两组对边是否分别相等C.测量对角线是否相等D.测量对角线交点到四个顶点的距离是否都相等10、如图,已知正方形ABCD的边长为6,点E,F分别在边AB,BC上,BE=CF=2,CE与DF交于点H,点G为DE的中点,连接GH,则GH的长为()A B C.4.5 D.4.3第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=50°.现将△ADE沿DE折叠点A落在三角形所在平面内的点为A1,则∠BDA1的度数为 _____.2、在平行四边形ABCD 中,BF 平分∠ABC ,交AD 于点F ,CE 平分∠BCD ,交AD 于点E ,AB =6,EF =2,则BC 的长为_____.3、如图,在四边形ABCD 中,90ABC DCB ∠+∠=︒,,E F 分别是,AD BC 的中点,分别以,AB CD 为直径作半圆,这两个半圆面积的和为8π,则EF 的长为_______.4、七边形内角和的度数是__________.5、在边长为4dm 的正方形纸片(厚度不计)上,按如图的实线裁剪,将阴影部分按虚线折叠成一个有盖的正方体盒子,则这个盒子的容积为______3dm .三、解答题(5小题,每小题10分,共计50分)1、已知矩形ABCD ,AB =6,BC =10,以BC 所在直线为x 轴,AB 所在直线为y 轴,建立如图所示的平面直角坐标系,在CD 边上取一点E ,将△ADE 沿AE 翻折,点D 恰好落在BC 边上的点F 处.(1)求线段EF 长;(2)在平面内找一点G ,①使得以A、B、F、G为顶点的四边形是平行四边形,请直接写出点G的坐标;②如图2,将图1翻折后的矩形沿y轴正半轴向上平移m(m>0)个单位,若以A、O、F、G为顶点的四边形为菱形,请求出m的值并写出点G的坐标.2、如图,在△ABC中,点D是BC边的中点,点E是AD的中点,过A点作AF∥BC,且交CE的延长线于点F,联结BF.(1)求证:四边形AFBD是平行四边形;(2)当AB=AC时,求证:四边形AFBD是矩形.3、如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.(1)求证:AE=CF;(2)若∠ABE=62°,求∠GFC+∠BCF的值.4、如图1,ABC 在平面直角坐标系中,且::2:3:4BO AO CO =;(1)试说明ABC 是等腰三角形;(2)已知2160cm ABC S =△.写出各点的坐标:A ( , ),B ( , ),C ( , ).(3)在(2)的条件下,若一动点M 从点B 出发沿线段BA 向点A 运动,同时动点N 从点A 出发以相同速度沿线段AC 向点C 运动,当其中一点到达终点时整个运动都停止.①若OMN 的一条边与BC 平行,求此时点M 的坐标;②若点E 是边AC 的中点,在点M 运动的过程中,MOE △能否成为等腰三角形?若能,求出此时点M的坐标;若不能,请说明理由.5、如图,矩形ABCD 中,8AB =,4BC =,过对角线BD 中点O 的直线分别交AB ,CD 边于点E ,F .(1)求证:四边形BEDF 是平行四边形.(2)当四边形BEDF 是菱形时,求EF 的长.-参考答案-一、单选题1、D【分析】如图(见解析),先根据平角的定义可得123180∠+∠+∠=︒,再根据123∠=∠=∠可求出12360∠=∠=∠=︒,由此可判断选项,B D ;先根据等边三角形的判定与性质可得,60DE CD CDE =∠=︒,再根据平行四边形的判定可得四边形ABCE 是平行四边形,根据平行四边形的性质可得AE BC =,然后根据菱形的判定可得四边形DEFG 是菱形,根据菱形的性质可得DE EF AD ==,最后根据线段的和差、等量代换可得,2CD AD BC AD ==,由此可判断选项,A C .【详解】解:如图,123180,123∠+∠+∠=︒∠=∠=∠,12360∴∠=∠=∠=︒,AD BC ,1801120ADC ∴∠=︒-∠=︒,梯形ABCD 是等腰梯形,160,120,ABC BAD ADC CD CE ∴∠=∠=︒∠=∠=︒=,则梯形最大角是120︒,选项B 正确;没有指明哪个角是底角,∴梯形的底角是60︒或120︒,选项D错误;如图,连接DE,=∠=︒,,260CD CE∴是等边三角形,CDE∴=∠=︒,DE CD CDE,60∴∠+∠=︒,180ADC CDEA D E共线,∴点,,∠=∠=︒,ABC360∴,AB CE=,AB CE∴四边形ABCE是平行四边形,∴=,AE BC∠=∠=︒,CGF CDE60∴,DE FGEF DG,EF FG=,∴四边形DEFG是菱形,∴==,DE EF AD==+=,选项A、C正确;BC AE AD DE AD∴=,2CD AD故选:D.【点睛】本题考查了等腰梯形、菱形的判定与性质、等边三角形的判定与性质等知识点,熟练掌握各判定与性质是解题关键.2、D【详解】AB,即可求出CM.根据直角三角形斜边上的中线性质得出CM=12【解答】解:∵公路AC,BC互相垂直,∴∠ACB=90°,∵M为AB的中点,AB,∴CM=12∵AB=6km,∴CM=3km,即M,C两点间的距离为3km,故选:D.【点睛】本题考查了直角三角形的性质,解题关键是掌握直角三角形斜边上的中线的性质:直角三角形斜边上的中线等于斜边的一半.3、C【分析】根据多边形外角和360 求解即可.【详解】解:123456360∠+∠+∠+∠+∠+∠=︒ ,1290∠+∠=︒()345636012270∴∠+∠+∠+∠=︒-∠+∠=︒,故选:C【点睛】本题考查了多边形的外角和定理,掌握多边形外角和360︒是解题的关键.4、D【分析】利用矩形的性质,求证明90OAB ∠=︒,进而在Rt AOB ∆中利用勾股定理求出OB 的长度,弧长就是OB 的长度,利用数轴上的点表示,求出弧与数轴交点表示的实数即可.【详解】 解:四边形OABC 是矩形,∴90OAB ∠=︒,在Rt AOB ∆中,由勾股定理可知:222OB OA AB =+,OB ∴==∴故选:D .【点睛】本题主要是考查了矩形的性质、勾股定理解三角形以及数轴上的点的表示,熟练利用矩形性质,得到直角三角形,然后通过勾股定理求边长,是解决该类问题的关键.5、B【分析】根据完全平方公式分解因式得到a=b ,c=d ,利用边的位置关系得到该四边形的形状.【详解】解:222222+,++=+a b c d ab cd22220a ab bc cd d-++-+=,2222-=a b+-(,c d()0)--=a b=,0,0c d∴a=b,c=d,∵四边形四条边长分别是a,b,c,d,其中a,b为对边,∴c、d是对边,∴该四边形是平行四边形,故选:B.【点睛】此题考查了完全平方公式分解因式,平行四边形的判定方法,熟练掌握完全平方公式分解因式是解题的关键.6、A【分析】DN,从而可知DN最大时,EF最大,因为N与B重合时DN最大,根据三角形的中位线定理得出EF=12此时根据勾股定理求得DN,从而求得EF的最大值.连接DB,过点D作DH⊥AB交AB于点H,再利用直角三角形的性质和勾股定理求解即可;【详解】解:∵ED=EM,MF=FN,DN,∴EF=12∴DN最大时,EF最大,∴N与B重合时DN=DB最大,在R t△ADH中,∵∠A=60°ADH∴∠=︒30∴AH=2×1=1,DH=2∴BH=AB﹣AH=3﹣1=2,∴DBDB,∴EF max=12∴EF故选A【点睛】本题考查了三角形的中位线定理,勾股定理,含30度角的直角三角形的性质,利用中位线求得EF=1DN是解题的关键.27、B【分析】首先可判断重叠部分为平行四边形,且两条丝带宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.【详解】解:过点A作AE⊥BC于E,AF⊥CD于F,因为两条彩带宽度相同,所以AB∥CD,AD∥BC,AE=AF.∴四边形ABCD是平行四边形.∵S▱ABCD=BC•AE=CD•AF.又AE=AF.∴BC=CD,∴四边形ABCD是菱形.故选:B【点睛】此题考查了菱形的判定,平行四边形的面积公式以及平行四边形的判定与性质,利用了数形结合的数学思想,其中菱形的判定方法有:一组邻边相等的平行四边形为菱形;对角线互相垂直的平行四边形为菱形;四条边相等的四边形为菱形,根据题意作出两条高AE和AF,熟练掌握菱形的判定方法是解本题的关键8、A【分析】利用直角三角形斜边的中线的性质可得答案.【详解】解:∵∠C=90°,若D为斜边AB上的中点,AB,∴CD=12∵AB的长为10,∴DC=5,故选:A.【点睛】此题主要考查了直角三角形斜边的中线,关键是掌握在直角三角形中,斜边上的中线等于斜边的一半.9、D【分析】由平行四边形的判定与性质、矩形的判定分别对各个选项进行判断即可.【详解】解:A、∵对角线互相平分的四边形是平行四边形,∴对角线互相平分且相等的四边形才是矩形,∴选项A不符合题意;B、∵两组对边分别相等是平行四边形,∴选项B不符合题意;C、∵对角线互相平分且相等的四边形才是矩形,∴对角线相等的四边形不是矩形,∴选项C不符合题意;D、∵对角线交点到四个顶点的距离都相等,∴对角线互相平分且相等,∵对角线互相平分且相等的四边形是矩形,∴选项D符合题意;故选:D.【点睛】本题考查了矩形的判定、平行四边形的判定与性质、解题的关键是熟记矩形的判定定理.【分析】根据正方形的四条边都相等可得BC =DC ,每一个角都是直角可得∠B =∠DCF =90°,然后利用“边角边”证明△CBE ≌△DCF ,得∠BCE =∠CDF ,进一步得∠DHC =∠DHE =90°,从而知GH =12DE ,利用勾股定理求出DE 的长即可得出答案.【详解】解:∵四边形ABCD 为正方形,∴∠B =∠DCF =90°,BC =DC ,在△CBE 和△DCF 中,BC CC B DCF BE CF =⎧⎪∠=∠⎨⎪=⎩, ∴△CBE ≌△DCF (SAS ),∴∠BCE =∠CDF ,∵∠BCE +∠DCH =90°,∴∠CDF +∠DCH =90°,∴∠DHC =∠DHE =90°,∵点G 为DE 的中点,∴GH =12DE ,∵AD =AB =6,AE =AB ﹣BE =6﹣2=4,∴DE == ∴GH【点睛】本题主要考查了正方形的性质,全等三角形的性质与判定,勾股定理,直角三角形斜边上的中线,解题的关键在于能够熟练掌握相关知识进行求解.二、填空题1、80°【分析】由翻折的性质得∠ADE=∠A1DE,由中位线的性质得DE//BC,由平行线的性质得∠ADE=∠B=50°,即可解决问题.【详解】解:由题意得:∠ADE=∠A1DE;∵D、E分别是边AB、AC的中点,∴DE//BC,∴∠ADE=∠B=∠A1DE=50°,∴∠A1DA=100°,∴∠BDA1=180°−100°=80°.故答案为:80°.【点睛】本题主要考查了翻折变换及其应用问题;同时还考查了三角形的中位线定理等几何知识点.熟练掌握各性质是解题的关键.2、10或14或10【分析】=,通过BF和CE 利用BF平分∠ABC, CE平分∠BCD,以及平行关系,分别求出AB AF=、DE DC是否相交,分两类情况讨论,最后通过边之间的关系,求出BC的长即可.解:四边形ABCD是平行四边形,∥,==,AD BCAB CDAD BC∴=,6∠=∠,AFE FBC∴∠=∠,DEC ECBBF平分∠ABC, CE平分∠BCD,∠=∠,ABF FBC∴∠=∠,DCE ECB∠=∠,AFE ABF∴∠=∠,DCE DEC∴由等角对等边可知:6==,DE DCAF AB==,6情况1:当BF与CE相交时,如下图所示:AD AF DE EF=+-,AD∴=,10∴=,BC10情况2:当BF与CE不相交时,如下图所示:=++AD AF DE EF∴=AD,14∴=,BC14故答案为:10或14.【点睛】本题主要是考查了平行四边形的性质,熟练运用平行关系+角平分线证边相等,是解决本题的关键,还要注意根据BF和CE是否相交,本题分两类情况,如果没考虑仔细,会漏掉一种情况.3、4【分析】根据题意连接BD,取BD的中点M,连接EM、FM,EM交BC于N,根据三角形的中位线定理推出EM=12 CD,EM∥AB,FM∥CD,推出∠ABC=∠ENC,∠MFN=∠C,求出∠EMF=90°,根据勾股定理求AB,FM=12出ME2+FM2=EF2,根据圆的面积公式求出阴影部分的面积即可.【详解】解:连接BD,取BD的中点M,连接EM、FM,延长EM交BC于N,∵∠ABC+∠DCB=90°,∵E、F、M分别是AD、BC、BD的中点,∴EM=12AB,FM=12CD,EM∥AB,FM∥CD,∴∠ABC=∠ENC,∠MFN=∠C,∴∠MNF+∠MFN=90°,∴∠NMF=180°-90°=90°,∴∠EMF=90°,由勾股定理得:ME2+FM2=EF2,∴阴影部分的面积是:12π(ME2+FM2)=12EF2π=8π,∴EF=4.故答案为:4.【点睛】本题主要考查对勾股定理,三角形的内角和定理,多边形的内角和定理,三角形的中位线定理,圆的面积,平行线的性质,面积与等积变形等知识点的理解和掌握,能正确作辅助线并求出ME2+FM2的值是解答此题的关键.4、900°900度【分析】根据多边形内角和公式计算即可.【详解】解:七边形内角和的度数是(72)180900-⨯︒=︒,故答案为:900°.【点睛】本题考查了多边形内角和公式,解题关键是熟记n 边形内角和公式:2180()n -⨯︒.5、【分析】根据题意可得,设正方体的棱长为a dm ,则减去的部分为2个边长为a dm 的正方形,将阴影部分按虚线折叠成一个有盖的正方体盒子,则四个角折叠后刚好凑成1个边长为a dm 的正方形,据此列一元二次方程求解,进而即可求得正方体的容积【详解】解:设正方体的棱长为a dm ()0a >,则222426a a -=解得a∴这个盒子的容积为3dm故答案为:【点睛】本题考查了一元二次方程的应用,立方体展开图,正方形的性质,根据题意列出一元二次方程是解题的关键.三、解答题1、(1)103;(2)①点G 的坐标为(﹣8,6)或(8,6)或(8,﹣6);②4,8,6m G 或6,8,6.m G 或732,8,33m G ⎛⎫= ⎪⎝⎭. 【分析】(1)由矩形的性质得AD =BC =OC =10,CD =AB =OA =6,∠AOC =∠ECF =90°,由折叠性质得EF =DE ,AF =AD =10,则CE =6﹣EF ,由勾股定理求出BF =OF =8,则FC =OC ﹣OF =2,在Rt △ECF 中,由勾股定理得出方程,解方程即可;(2)①分三种情况,当AB 为平行四边形的对角线时;当AF 为平行四边形的对角线时;当BF 为平行四边形的对角线时,分别求解点G 的坐标即可;②分三种情况讨论,当OF 为对角线时,由菱形的性质得OA =AF =10,则矩形ABCD 平移距离m =OA ﹣AB=4,即OB=4,设FG交x轴于H,证出四边形OBFH是矩形,得FH=OB=4,OH=BF=8,则HG=6,如图,当AO为菱形的对角线时,当AF为菱形的对角线时,结合矩形与菱形的性质同理可得出答案.【详解】解:(1)∵四边形ABCD是矩形,∴AD=BC=OC=10,CD=AB=OA=6,∠AOC=∠ECF=90°,由折叠性质得:EF=DE,AF=AD=10,∴CE=CD﹣DE=CD﹣EF=6﹣EF,由勾股定理得:BF=OF22221068AF OA,∴FC=OC﹣OF=10﹣8=2,在Rt△ECF中,由勾股定理得:EF2=CE2+FC2,即:EF2=(6﹣EF)2+22,解得:EF=103;(2)①如图所示:当AB为平行四边形的对角线时,AG=BF=8,AG BF∥,∴点G的坐标为:(﹣8,6);当AF为平行四边形的对角线时,AG'=BF=8,'AG BF,∴点G'的坐标为:(8,6);FG AB,当BF为平行四边形的对角线时,FG''=AB=6,''∴点G''的坐标为:(8,﹣6);综上所述,点G的坐标为(﹣8,6)或(8,6)或(8,﹣6);②如图,当OF为菱形的对角线时,∵四边形AOGF为菱形,∴OA=AF=10,∴矩形ABCD平移距离m=OA﹣AB=10﹣6=4,即OB=4,设FG交x轴于H,如图所示:∵OA FG∥轴,∥,BC x∴∠FBO=∠BOH=∠OHF=90°,∴四边形OBFH是矩形,∴FH=OB=4,OH=BF=8,∴HG=10﹣4=6,∴点G的坐标为:(8,﹣6).如图,当AO 为菱形的对角线时,则6,8,,AB OB GB BF AO GF6,8,6.m G 如图,当AF 为菱形的对角线时,同理可得:,6,OA OF OA m 且,,GF OA GF BC ∥0,6,8,,A m F m 22268,m m 解得:7,3m2570,,8,,33A F 所以7258,33G 即328,.3G 综上:平移距离m 与G 的坐标分别为:4,8,6m G 或()6,8,6m G =-或732,8,.33mG . 【点睛】本题是四边形综合题目,考查了矩形的判定与性质、菱形的判定与性质,坐标与图形性质、平行四边形的性质、勾股定理、折叠变换的性质、平移的性质等知识;熟练掌握矩形的性质和折叠的性质是解题的关键.2、(1)见解析(2)见解析【分析】(1)首先证明△AEF ≌△DEC (AAS ),得出AF =DC ,进而利用AF ∥B D 、AF =BD 得出答案;(2)利用等腰三角形的性质,结合矩形的判定方法得出答案.【小题1】解:证明:(1)∵AF ∥BC ,∴∠AFC =∠FC D .在△AFE 和△DCE 中,AEF DEC AFE DCE AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AEF ≌△DEC (AAS ).∴AF =DC ,∵BD =DC ,∴AF =BD ,∴四边形AFBD 是平行四边形;【小题2】∵AB =AC ,BD =DC ,∴AD ⊥B C .∴∠ADB =90°.∵四边形AFBD 是平行四边形,∴四边形AFBD 是矩形.【点睛】此题主要考查了平行四边形的判定以及矩形的判定方法、全等三角形的判定与性质,正确掌握平行四边形的判定方法是解题关键.3、(1)证明见解析;(2)73°.【分析】(1)根据正方形的性质及各角之间的关系可得:ABE CBF ∠=∠,由全等三角形的判定定理可得AEB CFB ≌,再根据其性质即可得证;(2)根据垂直及等腰三角形的性质可得45BEF EFB ∠=∠=︒,再由三角形的外角的性质可得EGC GFC BCF EBG BEF ∠=∠+∠=∠+∠,由此计算即可.【详解】(1)证明:∵四边形ABCD 是正方形,∴90ABC ∠=︒,AB BC =,∵BE BF ⊥,∴90FBE ∠=︒,∵90ABE EBC ∠+∠=°,90CBF EBC ∠+∠=︒,∴ABE CBF ∠=∠,在AEB 和CFB 中,AB BC ABE CBF BE BF =⎧⎪∠=∠⎨⎪=⎩, ∴AEB CFB ≌,∴AE CF =;(2)解:∵BE ⊥BF ,∴90FBE ∠=︒,又∵BE BF =,∴45BEF EFB ∠=∠=︒,∵四边形ABCD 是正方形,∴90ABC ∠=︒,∵62ABE ∠=︒,∴906228EBG ∠=︒-︒=︒,∴452873EGC GFC BCF EBG BEF ∠=∠+∠=∠+∠=︒+︒=︒.∴GFC BCF ∠+∠的值为73︒.【点睛】题目主要考查全等三角形的判定和性质,正方形的性质,三角形的外角性质,理解题意,熟练运用各个定理性质是解题关键.4、(1)见解析;(2)12,0;-8,0;0,16;(3)①当M 的坐标为(2,0)或(4,0)时,△OMN 的一条边与BC 平行;②当M 的坐标为(0,10)或(12,0)或(253,0)时,,△MOE 是等腰三角形.【分析】(1)设2BO m =,3AO m =,4CO m =,则5AB AO BO m =+=,由勾股定理求出AC ,即可得出结论;(2)由ABC 的面积求出m 的值,从而得到OB 、OA 、OC 的长,即可得到A 、B 、C 的坐标;(3)①分当//BC MN 时,AM AN =;当//ON BC 时,AO AN =;得出方程,解方程即可; ②由直角三角形的性质得出10cm OE =,根据题意得出MOE △为等腰三角形,有3种可能:如果OE OM =;如果EO EM =;如果MO ME =;分别得出方程,解方程即可.【详解】解:(1)证明:设2BO m =,3AO m =,4CO m =,则5AB AO BO m =+=,在Rt ACO 中,5AC m ==,AB AC ∴=,∴ABC 是等腰三角形;(2)∵115416022ABC S AB OC m m =⋅=⨯⋅=,0m >,∴4m =,∴8cm BO =,12cm AO =,16cm CO =,20cm AC =.∴A 点坐标为(12,0),B 点坐标为(-8,0),C 点坐标为(0,16),故答案为:12,0;-8,0;0,16;(3)①如图3-1所示,当MN ∥BC 时,∵AB =AC ,∴∠ABC =∠ACB ,∵MN ∥BC ,∴∠AMN =∠ABC ,∠ANM =∠ACB ,∴∠AMN=∠ANM,∴AM=AN,∴AM=BM,∴M为AB的中点,AB=,∵20cm∴10cmAM=,∴2cmOM=,∴点M的坐标为(2,0);如图3-2所示,当ON∥BC时,同理可得12cm===,OA AN BM∴4cm=-=,OM BM OB∴M点的坐标为(4,0);∴综上所述,当M的坐标为(2,0)或(4,0)时,△OMN的一条边与BC平行;②如图3-3所示,当OM=OE时,∵E是AC的中点,∠AOC=90°,20cmAC=,∴110cm2OM OE AE AC====,∴此时M的坐标为(0,10);如图3-4所示,当=10cmOE ME=时,∴此时M点与A点重合,∴M点的坐标为(12,0);如图3-5所示,当OM=ME时,过点E作EF⊥x轴于F,∵OE=AE,EF⊥OA,∴1=6cm2OF OA=,∴8cm EF,设cm OM ME n ==,则()6cm MF OM OF n =-=-,∵222ME EF FM =+,∴()22286n n =+-, 解得253n =, ∴M 点的坐标为(253,0); 综上所述,当M 的坐标为(0,10)或(12,0)或(253,0)时,,△MOE 是等腰三角形.【点睛】本题主要考查了坐标与图形,勾股定理,等腰三角形的性质与判定,直角三角形斜边上的直线,三角形面积等等,解题的关键在于能够利用数形结合和分类讨论的思想求解.5、(1)证明见解析;(2)EF=【分析】(1)由题意知BE DF ∥,OD OB =,通过BOE DOF ≌得到BE DF =,证明四边形BEDF 平行四边形.(2)四边形BEDF 为菱形,DB EF ⊥,DB =BE BF x ==,8CF AE x ==-;在Rt BCF 中用勾股定理,解出BF 的长,在Rt BOF 中用勾股定理,得到OF 的长,由2EF OF =得到EF 的值.【详解】(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点∴BE DF ∥,OD OB =OBE ODF ∴∠=∠在BOE △和DOF △中OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BOE DOF △△≌(ASA ) ∴BE DF =∴四边形BEDF 是平行四边形.(2)解:∵四边形BEDF 为菱形,∴BE BF =,DB EF ⊥又∵8AB =,4BC =∴BD ==BO =设BE BF x ==,则8CF AE x ==-在Rt BCF 中,()22248x x +-=∴5x =在Rt BOF中,OE =∴2EF OE ==【点睛】本题考察了平行四边形的判定,三角形全等,菱形的性质,勾股定理.解题的关键与难点在于对平行四边形的性质的灵活运用.。
2020年八年级数学下册四边形综合题重难点培优练习(含答案)

第 1 页 共 26 页 1.如图,在矩形ABCD 中,中,AB=4cm AB=4cm AB=4cm,,BC=8cm BC=8cm,点,点P 从点D 出发向点A 运动,运动到点A 即停止;同时点Q 从点B 出发向点C 运动,运动到点C 即停止.点P 、Q 的速度的速度都是1cm/s 1cm/s,连结,连结PQ PQ,,AQ AQ,,CP CP,设点,设点P 、Q 运动的时间为t (s ).).(1)当t 为何值时,四边形ABQP 是矩形?是矩形?(2)当t 为何值时,四边形AQCP 是菱形?是菱形? (3)分别求出()分别求出(22)中菱形AQCP 的周长和面积.的周长和面积.2.如图,在Rt Rt△△ABC 中,∠中,∠ACB=90ACB=90ACB=90°,过点°,过点C 的直线m ∥AB AB,,D 为AB 边上一点,过点D 作DE DE⊥⊥BC BC,交直线,交直线m 于点E ,垂足为点F ,连接CD CD,,BE BE..(1)求证:)求证:CE=AD CE=AD CE=AD;; (2)当点D 是AB 中点时,四边形BECD 是什么特殊四边形?说明你的理由;(3)当∠)当∠A A 的大小满足什么条件时,四边形BECD 是正方形?(不需要证明)3.如图1,在矩形,在矩形ABCD ABCD ABCD中,动点中,动点中,动点P P 从点从点A A 出发,沿出发,沿A A →D →C →B 的路径运动.设点的路径运动.设点P P 运动的路程为运动的路程为x x ,△PAB PAB的面积为的面积为的面积为y y .图2反映的是点反映的是点P P 在A →D →C 运动过程中,运动过程中,y y 与x 的函数关系.请根据图象回答以下问题:以下问题:(1)矩形)矩形ABCD ABCD ABCD的边的边的边AD= AD=,AB= ; (2)写出点)写出点P P 在C →B 运动过程中运动过程中y y 与x 的函数关系式,并在图2中补全函数图象.中补全函数图象.4.在图1,2,3中,已知▱ABCD ABCD,∠,∠,∠ABC=120ABC=120ABC=120°,点°,点E 为线段BC 上的动点,连接AE AE,以,以AE 为边向上作菱形AEFG AEFG,且∠,且∠,且∠EAG=120EAG=120EAG=120°.°.°.(1)(1)如图如图1,当点E 与点B 重合时,∠重合时,∠CEF= CEF= CEF= °;°;(2)(2)如图如图2,连接AF AF..①填空:∠①填空:∠FAD FAD FAD ∠EAB(EAB(填“>”,“<“,“填“>”,“<“,“填“>”,“<“,“==”);②求证:点F 在∠在∠ABC ABC 的平分线上;的平分线上;(3)(3)如图如图3,连接EG EG,,DG DG,并延长,并延长DG 交BA 的延长线于点H ,当四边形AEGH 是平行四边形时,是平行四边形时, 求的值.的值.5.如图,两个全等的△如图,两个全等的△ABC ABC 和△和△DEF DEF 重叠在一起,固定△重叠在一起,固定△ABC ABC ABC,将△,将△,将△DEF DEF 进行如下变换:进行如下变换:(1)如图1,△,△DEF DEF 沿直线CB 向右平移(即点F 在线段CB 上移动),连接AF AF、、AD AD、、BD BD,请直,请直接写出S △ABC 与S 四边形AFBD 的关系的关系(2)如图2,当点F 平移到线段BC 的中点时,若四边形AFBD 为正方形,那么△为正方形,那么△ABC ABC 应满足什么条件:请给出证明;么条件:请给出证明;(3)在()在(22)的条件下,将△)的条件下,将△DEF DEF 沿DF 折叠,点E 落在FA 的延长线上的点G 处,连接CG CG,请,请你画出图形,此时CG 与CF 有何数量关系有何数量关系. .6.菱形ABCD 中,点P 为CD 上一点,连接BP.(1)如图1,若BP BP⊥⊥CD CD,菱形,菱形ABCD 边长为1010,,PD=4PD=4,连接,连接AP AP,求,求AP 的长的长. .(2)如图2,连接对角线AC AC、、BD 相交于点O ,点N 为BP 的中点,过P 作PM PM⊥⊥AC 于M ,连接ON ON、、MN.MN.试判断△试判断△试判断△MON MON 的形状,并说明理由的形状,并说明理由. .7.如图,在Rt Rt△△ABC 中,∠ACB=90°,过点C 的直线MN∥AB,D 为AB 边上一点,过点D 作DE⊥BC,交直线MN 于E ,垂足为F ,连接CD CD、、BE.(1)求证:)求证:CE=AD CE=AD CE=AD;;(2)当D 在AB 中点时,四边形BECD 是什么特殊四边形?说明你的理由;是什么特殊四边形?说明你的理由;(3)若D 为AB 中点,则当∠A 的大小满足什么条件时,四边形BECD 是正方形?请说明你的理由.8.如图,在在四边形ABCD 中,中,AD AD AD∥∥BC BC,∠,∠,∠B=90B=90B=90°,且°,且AD=12cm AD=12cm,,AB=8cm AB=8cm,,DC=10cm DC=10cm,若动点,若动点P 从A 点出发,以每秒2cm 的速度沿线段AD 向点D 运动;动点Q 从C 点出发以每秒3cm 的速度沿CB 向B 点运动,当P 点到达D 点时,动点P 、Q 同时停止运动,设点P 、Q 同时出发,并运动了t 秒,回答下列问题:秒,回答下列问题:(1)BC= BC= cm cm;;(2)当t= t= 秒时,四边形PQBA 成为矩形.成为矩形.(3)当t 为多少时,为多少时,PQ=CD PQ=CD PQ=CD??(4)是否存在t ,使得△,使得△DQC DQC 是等腰三角形?若存在,请求出t 的值;若不存在,说明理由.的值;若不存在,说明理由.9.如图1,已知正方形已知正方形ABCD ABCD ABCD,,点E 、F 、G 、H 分别在边分别在边AB AB AB、、BC BC、、CD CD、、DA DA上,上,若EG EG⊥⊥FH FH,,则易证:EG=FH EG=FH..(1)如果把条件中的“正方形”改为“长方形”,并设,并设AB=2AB=2AB=2,,BC=3BC=3(如图(如图2),试探究,试探究EG EG EG、、FH FH之之间有怎样的数量关系,并证明你的结论;间有怎样的数量关系,并证明你的结论; (2)如果把条件中的“)如果把条件中的“EG EG EG⊥⊥FH FH”改为“”改为“”改为“EG EG EG与与FH FH的夹角为的夹角为4545°”°”,并假设正方形,并假设正方形ABCD ABCD ABCD的边长为的边长为1,FH FH的长为的长为(如图3),试求,试求EG EG EG的长度.的长度.的长度.10.如图,如图,P P 为正方形为正方形ABCD ABCD ABCD的边的边的边BC BC BC上一动点(上一动点(上一动点(P P 与B 、C 不重合),连接不重合),连接AP AP AP,过点,过点,过点B B 作BQ BQ⊥⊥AP AP交交CD CD于于点Q ,将△,将△BQC BQC BQC沿沿BQ BQ所在的直线对折得到△所在的直线对折得到△所在的直线对折得到△BQC BQC BQC′,延长′,延长′,延长QC QC QC′交′交′交BA BA BA的延长线于点的延长线于点的延长线于点M M . (1)试探究)试探究AP AP AP与与BQ BQ的数量关系,并证明你的结论;的数量关系,并证明你的结论;的数量关系,并证明你的结论;(2)当)当AB=3AB=3AB=3,,BP=2PC BP=2PC,求,求,求QM QM QM的长;的长;的长;(3)当)当BP=m BP=m BP=m,,PC=n PC=n时,求时,求时,求AM AM AM的长.的长.的长.11.11.如图,在矩形如图,在矩形如图,在矩形ABCD ABCD ABCD中,点中,点中,点E E 为CD CD上一点,将△上一点,将△上一点,将△BCE BCE BCE沿沿BE BE翻折后点翻折后点翻折后点C C 恰好落在恰好落在AD AD AD边上的点边上的点边上的点F F 处,将线段线段EF EF EF绕点绕点绕点F F 旋转,使点旋转,使点E E 落在落在BE BE BE上的点上的点上的点G G 处,连接处,连接CG. CG.(1)(1)证明:四边形证明:四边形证明:四边形CEFG CEFG CEFG是菱形;是菱形;是菱形;(2)(2)若若AB=8AB=8,,BC=10BC=10,求四边形,求四边形,求四边形CEFG CEFG CEFG的面积;的面积;的面积;(3)(3)试探究当线段试探究当线段试探究当线段AB AB AB与与BC BC满足什么数量关系时,满足什么数量关系时,满足什么数量关系时,BG=CG BG=CG BG=CG,请写出你的探究过程.,请写出你的探究过程.,请写出你的探究过程.12.四边形ABCD是正方形,点E在边BC上(不与端点B、C重合),点F在对角线AC上,且EFDF、、FG,点G是AE的中点,连接DF,连接AE⊥ACAC,连接AE,点(1)若AB=7,的长;BE=,求FG的长;FG;DF=FG;)求证:DF=(2)求证:中的△CEFCEF绕点C按顺时针旋转,使边CF的顶点F恰好在正方形ABCD的边BC上(如(3)将图1中的△之间的数量关系,并证明你的猜想. AE、点图2),连接AE、点G仍是AE的中点,猜想BF与FG之间的数量关系,并证明你的猜想.13.△ABC 和△和△DEF DEF 都是边长为6cm 的等边三角形,且A 、D 、B 、F 在同一直线上,连接CD CD、、BF BF..(1)求证:四边形BCDE 是平行四边形;是平行四边形;(2)若AD=2cm AD=2cm,△,△,△ABC ABC 沿着AF 的方向以每秒1cm 的速度运动,设△的速度运动,设△ABC ABC 运动的时间为t 秒.秒. (a )当t 为何值时,平行四边形BCDE 是菱形?说明理由;是菱形?说明理由;(b )平行四边形BCDE 有可能是矩形吗?若有可能,求出t 的值,并求出矩形的面积;若不可能,说明理由.能,说明理由.14.14.已知已知E,F 分别为正方形ABCD 的边BC,CD 上的点上的点,AF,DE ,AF,DE 相交于点G,G,当当E,F 分别为边BC,CD 的中点时中点时,,有AF=DE,AF AF=DE,AF⊥⊥DE 成立成立. . 试探究下列问题试探究下列问题: : (1)(1)如图①如图①如图①,,若点E 不是边BC 的中点的中点,F ,F 不是边CD 的中点的中点,,且CE=DF,CE=DF,上述结论是否仍然成立上述结论是否仍然成立上述结论是否仍然成立?(?(?(请请直接回答“成立”或“不成立”直接回答“成立”或“不成立”,,不需要证明不需要证明) ) (2)(2)如图②如图②如图②,,若点E,F 分别在CB 的延长线和DC 的延长线上的延长线上,,且CE=DF,CE=DF,此时此时此时,,上述结论是否仍然成立?若成立若成立,,请写出证明过程请写出证明过程,,若不成立若不成立,,请说明理由请说明理由; ; (3)(3)如图③如图③如图③,,在(2)(2)的基础上的基础上的基础上,,连接AE 和EF,EF,若点若点M,N,P,Q 分别为AE,EF,FD,AD 的中点的中点,,请判断四边形MNPQ 是“矩形、菱形、正方形”中的哪一种是“矩形、菱形、正方形”中的哪一种,,并证明你的结论并证明你的结论. .15.如图,在如图,在Rt Rt Rt△△ABC ABC中,∠中,∠中,∠B=90B=90B=90°,°,°,AC=60cm AC=60cm AC=60cm,∠,∠,∠A=60A=60A=60°,点°,点°,点D D 从点从点C C 出发沿出发沿CA CA CA方向以方向以4cm/s 4cm/s的速的速度向点度向点A A 匀速运动,同时点同时点E E 从点从点A A 出发沿出发沿AB AB AB方向以方向以2cm/s 2cm/s的速度向点的速度向点的速度向点B B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点达终点时,另一个点也随之停止运动.设点D D 、E 运动的时间是运动的时间是ts ts ts.过点.过点.过点D D 作DF DF⊥⊥BC BC于点于点于点F F ,连接DE DE、、EF EF.. (1)用)用t t 的代数式表示:的代数式表示:AE= AE= ;DF= ; (2)四边形)四边形AEFD AEFD AEFD能够成为菱形吗?如果能,求出相应的能够成为菱形吗?如果能,求出相应的能够成为菱形吗?如果能,求出相应的t t 值;如果不能,请说明理由;值;如果不能,请说明理由; (3)当)当t t 为何值时,△为何值时,△DEF DEF DEF为直角三角形?请说明理由.为直角三角形?请说明理由.为直角三角形?请说明理由.参考答案1.解:解:(1)当四边形ABQP 是矩形时,是矩形时,BQ=AP BQ=AP BQ=AP,即:,即:,即:t=8t=8t=8﹣﹣t ,解得t=4t=4.. 答:当t=4时,四边形ABQP 是矩形;是矩形; (2)设t 秒后,四边形AQCP 是菱形是菱形 当AQ=CQ AQ=CQ,即,即=8=8﹣﹣t 时,四边形AQCP 为菱形.解得:为菱形.解得:t=3t=3t=3..答:当t=3时,四边形AQCP 是菱形;是菱形;(3)当t=3时,时,CQ=5CQ=5CQ=5,则周长为:,则周长为:,则周长为:4CQ=20cm 4CQ=20cm 4CQ=20cm,面积为:,面积为:,面积为:44×8﹣2××3×4=204=20((cm 22).).2.(1)证明:∵直线m ∥AB AB,∴,∴,∴EC EC EC∥∥AD AD..又∵∠又∵∠ACB=90ACB=90ACB=90°,∴°,∴°,∴BC BC BC⊥⊥AC AC.又∵.又∵.又∵DE DE DE⊥⊥BC BC,∴,∴,∴DE DE DE∥∥AC AC.. ∵EC EC∥∥AD AD,,DE DE∥∥AC AC,∴四边形,∴四边形ADEC 是平行四边形.∴是平行四边形.∴CE=AD CE=AD CE=AD.. (2)当点D 是AB 中点时,四边形BECD 是菱形. 证明:∵证明:∵D D 是AB 中点,中点,DE DE DE∥∥AC AC(已证)(已证),∴,∴F F 为BC 中点,∴中点,∴BF=CF BF=CF BF=CF.. ∵直线m ∥AB AB,∴∠,∴∠,∴∠ECF=ECF=ECF=∠∠DBF DBF.∵∠.∵∠.∵∠BFD=BFD=BFD=∠∠CFE CFE,∴△,∴△,∴△BFD BFD BFD≌△≌△≌△CFE CFE CFE.∴.∴.∴DF=EF DF=EF DF=EF.. ∵DE DE⊥⊥BC BC,∴,∴,∴BC BC 和DE 垂直且互相平分.∴四边形BECD 是菱形. (3)当∠)当∠A A 的大小是4545°时,四边形°时,四边形BECD 是正方形. 理由是:∵∠理由是:∵∠ACB=90ACB=90ACB=90°,∠°,∠°,∠A=45A=45A=45°,∴∠°,∴∠°,∴∠ABC=ABC=ABC=∠∠A=45A=45°,∴°,∴°,∴AC=BC AC=BC AC=BC,, ∵D 为BA 中点,∴中点,∴CD CD CD⊥⊥AB AB,∴∠,∴∠,∴∠CDB=90CDB=90CDB=90°,°,∵四边形BECD 是菱形,∴四边形BECD 是正方形, 即当∠即当∠A=45A=45A=45°时,四边形°时,四边形BECD 是正方形.3.解:(解:(11)根据题意得:矩形)根据题意得:矩形ABCD ABCD ABCD的边的边的边AD=2AD=2AD=2,,AB=4AB=4;故答案为:;故答案为:;故答案为:22;4; (2)当点)当点P P 在C →B 运动过程中,运动过程中,PB=8PB=8PB=8﹣﹣x ,∴,∴y=S y=S △APB=×4×(×(88﹣x ),即),即y=y=y=﹣﹣2x+162x+16((6≤x ≤8),正确作出图象,如图所示:正确作出图象,如图所示:4.解:解:(1)(1)∵四边形∵四边形AEFG 是菱形,∴∠是菱形,∴∠AEF=180AEF=180AEF=180°﹣∠°﹣∠°﹣∠EAG=60EAG=60EAG=60°,°,°, ∴∠∴∠CEF=CEF=CEF=∠∠AEC AEC﹣∠﹣∠﹣∠AEF=60AEF=60AEF=60°,°,°, 故答案为:故答案为:606060°;°;°; (2)(2)①∵四边形①∵四边形ABCD 是平行四边形,∴∠是平行四边形,∴∠DAB=180DAB=180DAB=180°﹣∠°﹣∠°﹣∠ABC=60ABC=60ABC=60°,°,°, ∵四边形AEFG 是菱形,∠是菱形,∠EAG=120EAG=120EAG=120°,∴∠°,∴∠°,∴∠FAE=60FAE=60FAE=60°,°,°, ∴∠∴∠FAD=FAD=FAD=∠∠EAB EAB,, ②作FM FM⊥⊥BC 于M ,FN FN⊥⊥BA 交BA 的延长线于N ,则∠,则∠FNB=FNB=FNB=∠∠FMB=90FMB=90°,°,°, ∴∠∴∠NFM=60NFM=60NFM=60°,°,°, 又∠又∠AFE=60AFE=60AFE=60°,∴∠°,∴∠°,∴∠AFN=AFN=AFN=∠∠EFM EFM,, ∵EF=EA EF=EA,∠,∠,∠FAE=60FAE=60FAE=60°,∴△°,∴△°,∴△AEF AEF 为等边三角形,∴为等边三角形,∴FA=FE FA=FE FA=FE,, 在△在△AFN AFN 和△和△EFM EFM 中,,∴△,∴△AFN AFN AFN≌△≌△≌△EFM(AAS) EFM(AAS)∴FN=FM FN=FM,又,又FM FM⊥⊥BC BC,,FN FN⊥⊥BA BA,, ∴点F 在∠在∠ABC ABC 的平分线上;的平分线上; (3)(3)∵四边形∵四边形AEFG 是菱形,∠是菱形,∠EAG=120EAG=120EAG=120°,°,°, ∴∠∴∠AGF=60AGF=60AGF=60°,∴∠°,∴∠°,∴∠FGE=FGE=FGE=∠∠AGE=30AGE=30°,°,°,∵四边形AEGH 为平行四边形,∴为平行四边形,∴GE GE GE∥∥AH AH,, ∴∠∴∠GAH=GAH=GAH=∠∠AGE=30AGE=30°,∠°,∠°,∠H=H=H=∠∠FGE=30FGE=30°,°,°, ∴∠∴∠GAN=90GAN=90GAN=90°,又∠°,又∠°,又∠AGE=30AGE=30AGE=30°,∴°,∴°,∴GN=2AN GN=2AN GN=2AN,, ∵∠∵∠DAB=60DAB=60DAB=60°,∠°,∠°,∠H=30H=30H=30°,∴∠°,∴∠°,∴∠ADH=30ADH=30ADH=30°,∴°,∴°,∴AD=AH=GE AD=AH=GE AD=AH=GE,, ∵四边形ABCD 为平行四边形,∴为平行四边形,∴BC=AD BC=AD BC=AD,∴,∴,∴BC=GE BC=GE BC=GE,, ∵四边形ABEH 为平行四边形,∠为平行四边形,∠HAE=HAE=HAE=∠∠EAB=30EAB=30°,°,°, ∴平行四边形ABEN 为菱形,∴为菱形,∴AB=AN=NE AB=AN=NE AB=AN=NE,∴,∴,∴GE=3AB GE=3AB GE=3AB,, ∴=3=3..5.解:(解:(11)S △ABC =S 四边形AFBD ,理由:由题意可得:理由:由题意可得:AD AD AD∥∥EC EC,则,则S △ADF =S △ABD , 故S △ACF =S △ADF =S △ABD ,则S △ABC =S 四边形AFBD ; (2)△)△ABC ABC 为等腰直角三角形,即:为等腰直角三角形,即:AB=AC AB=AC AB=AC,∠,∠,∠BAC=90BAC=90BAC=90°,°,°, 理由如下:理由如下:∵F 为BC 的中点,∴的中点,∴CF=BF CF=BF CF=BF,∵,∵,∵CF=AD CF=AD CF=AD,∴,∴,∴AD=BF AD=BF AD=BF,, 又∵又∵AD AD AD∥∥BF BF,∴四边形,∴四边形AFBD 为平行四边形,为平行四边形, ∵AB=AC AB=AC,,F 为BC 的中点,∴的中点,∴AF AF AF⊥⊥BC BC,∴平行四边形,∴平行四边形AFBD 为矩形为矩形∵∠∵∠BAC=90BAC=90BAC=90°,°,°,F F 为BC 的中点,∴的中点,∴AF=AF=BC=BF BC=BF,,∴四边形AFBD 为正方形;为正方形; (3)如图3所示:所示: 由(由(22)知,△)知,△ABC ABC 为等腰直角三角形,为等腰直角三角形,AF AF AF⊥⊥BC BC,,设CF=k CF=k,,则GF=EF=CB=2k GF=EF=CB=2k,,由勾股定理得:CG=k ,∴CG=CF.6.6.解:解:(1)如图1中,∵四边形ABCD 是菱形,∴是菱形,∴AB=BC=CD=AD=10AB=BC=CD=AD=10AB=BC=CD=AD=10,,AB AB∥∥CD∵PD=4PD=4,∴,∴,∴PC=6PC=6PC=6,∵,∵,∵PB PB PB⊥⊥CD CD,∴,∴,∴PB PB PB⊥⊥AB AB,∴∠,∴∠,∴∠CPB=CPB=CPB=∠ABP=90°,∠ABP=90°,∠ABP=90°, 在RT RT△△PCB 中,∵∠CPB=90°P 中,∵∠CPB=90°PC=6C=6C=6,,BC=10BC=10,∴,∴,∴PB=PB===8=8,, 在RT RT△△ABP 中,∵∠ABP=90°,中,∵∠ABP=90°,AB=10AB=10AB=10,,PB=8PB=8,∴,∴,∴PA=PA===2.(2)△)△OMN OMN 是等腰三角形是等腰三角形..理由:如图2中,延长PM 交BC 于E. ∵四边形ABCD 是菱形,∴是菱形,∴AC AC AC⊥⊥BD BD,,CB=CD CB=CD,, ∵PE PE⊥⊥AC AC,∴,∴,∴PE PE PE∥∥BD BD,∴,∴=,∴,∴CP=CE CP=CE CP=CE,∴,∴,∴PD=BE PD=BE PD=BE,,∵CP=CE CP=CE,,CM CM⊥⊥PE PE,∴,∴,∴PM=ME PM=ME PM=ME,∵,∵,∵PN=NB PN=NB PN=NB,∴,∴,∴MN=MN=BE BE,,∵BO=OD BO=OD,,BN=NP BN=NP,∴,∴,∴ON=ON=PD PD,∴,∴,∴ON=MN ON=MN ON=MN,∴△,∴△,∴△OMN OMN 是等腰三角形是等腰三角形. .7.(1)证明:∵DE⊥BC,∴∠DFB=90°,)证明:∵DE⊥BC,∴∠DFB=90°,∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,∵MN∥AB,即CE∥AD,∴四边形ADEC 是平行四边形,∴是平行四边形,∴CE=AD CE=AD CE=AD;; (2)解:四边形BECD 是菱形,理由是:∵是菱形,理由是:∵D D 为AB 中点,∴中点,∴AD=BD AD=BD AD=BD,, ∵CE=AD CE=AD,∴,∴,∴BD=CE BD=CE BD=CE,∵BD∥CE,∴四边形,∵BD∥CE,∴四边形BECD 是平行四边形,是平行四边形, ∵∠ACB=90°,∵∠ACB=90°,D D 为AB 中点,∴中点,∴CD=BD CD=BD CD=BD,∴,∴▱四边形BECD 是菱形;是菱形; (3)当∠A=45°时,四边形BECD 是正方形,理由是:是正方形,理由是: 解:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°,∴解:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°,∴AC=BC AC=BC AC=BC,, ∵D 为BA 中点,∴CD⊥AB,∴∠CDB=90°,中点,∴CD⊥AB,∴∠CDB=90°, ∵四边形BECD 是菱形,∴菱形BECD 是正方形,是正方形, 即当∠A=45°时,四边形BECD 是正方形是正方形. . 8.解:解:9.(1)结论:)结论:EG EG EG::FH=3FH=3::2证明:过点证明:过点A A 作AM AM∥∥HF HF交交BC BC于点于点于点M M ,作,作AN AN AN∥∥EG EG交交CD CD的延长线于点的延长线于点的延长线于点N N ,如图1: ∴AM=HF AM=HF,,AN=EG AN=EG,∵长方形,∵长方形,∵长方形ABCD ABCD ABCD,∴∠,∴∠,∴∠BAD=BAD=BAD=∠∠ADN=90ADN=90°,°,°, ∵EG EG⊥⊥FH FH,∴∠,∴∠,∴∠NAM=90NAM=90NAM=90°,∴∠°,∴∠°,∴∠BAM=BAM=BAM=∠∠DAN DAN,∴△,∴△,∴△ABM ABM ABM∽△∽△∽△ADN ADN ADN,, ∴AM:AN=AB:AD AM:AN=AB:AD,∵,∵,∵AB=2BC=AD=3AB=2BC=AD=3AB=2BC=AD=3,∴,∴,∴EG:FH=1.5EG:FH=1.5EG:FH=1.5;; (2)解:过点)解:过点A A 作AM AM∥∥HF HF交交BC BC于点于点于点M M ,过点,过点A A 作AN AN∥∥EG EG交交CD CD于点于点于点N N ,如图2:∵AB=1AB=1,,AM=FH=,∴在,∴在Rt Rt Rt△△ABM ABM中,中,中,BM=0.5BM=0.5将△AND AND绕点绕点绕点A A 旋转到△旋转到△APB APB APB,, ∵EG EG与与FH FH的夹角为的夹角为4545°,∴∠°,∴∠°,∴∠MAN=45MAN=45MAN=45°,∴∠°,∴∠°,∴∠DAN+DAN+DAN+∠∠MAB=45 即∠即∠PAM=PAM=PAM=∠∠MAN=45MAN=45°,从而△°,从而△°,从而△APM APM APM≌△≌△≌△ANM ANM ANM,∴,∴,∴PM=NM PM=NM PM=NM,,设DN=x DN=x,则,则,则NC=1NC=1NC=1﹣﹣x ,NM=PM=0.5+x NM=PM=0.5+x在在Rt Rt△△CMN CMN中,中,中,(0.5 +x)(0.5 +x)2=0.25+(1=0.25+(1﹣﹣x)2,解得,解得x=1/3x=1/3x=1/3,,∴EG=AN=,答:,答:EG EG EG的长为的长为.10.11. (1)证明:证明:根据翻折的方法可得根据翻折的方法可得EF=EC EF=EC EF=EC,,∠FEG=FEG=∠∠CEG.CEG.又∵又∵又∵GE=GE GE=GE GE=GE,,∴△∴△EFG EFG EFG≌△≌△≌△ECG.ECG.ECG.∴∴FG=GC. ∵线段∵线段FG FG FG是由是由是由EF EF EF绕绕F 旋转得到的,∴旋转得到的,∴EF=FG.EF=FG.EF=FG.∴∴EF=EC=FG=GC.EF=EC=FG=GC.∴四边形∴四边形∴四边形FGCE FGCE FGCE是菱形.是菱形.是菱形. (2)连接)连接FC FC FC交交GE GE于于O 点.根据折叠可得点.根据折叠可得BF=BC=10.BF=BC=10.BF=BC=10.∵∵AB=8 ∴在∴在Rt Rt Rt△△ABF ABF中,根据勾股定理得中,根据勾股定理得中,根据勾股定理得AF=6.AF=6.AF=6.∴∴FD=AD FD=AD--AF=10AF=10--6=4.设EC=x EC=x,则,则,则DE=8DE=8DE=8--x ,EF=x EF=x,在,在,在Rt Rt Rt△△FDE FDE中,中,中,FD FD 2+DE 2=EF 2,即42+(8-x)2=x 2.解得解得x=5.x=5.x=5.即即CE=5.S 菱形菱形CEFG CEFG =CE =CE··FD=5FD=5××4=20.(3)当=时,时,BG=CG BG=CG BG=CG,理由:由折叠可得,理由:由折叠可得,理由:由折叠可得BF=BC BF=BC BF=BC,∠,∠,∠FBE=FBE=FBE=∠∠CBE CBE,,∵在∵在Rt Rt Rt△△ABF ABF中,中,=,∴,∴BF=2AF.BF=2AF.BF=2AF.∴∠∴∠∴∠ABF=30ABF=30ABF=30°°.又∵∠又∵∠ABC=90ABC=90ABC=90°,∴∠°,∴∠°,∴∠FBE=FBE=FBE=∠∠CBE=30CBE=30°,°,°,EC=0.5BE. EC=0.5BE.∵∠∵∠BCE=90BCE=90BCE=90°,∴∠°,∴∠°,∴∠BEC=60BEC=60BEC=60°°.又∵又∵GC=CE GC=CE GC=CE,∴△,∴△,∴△GCE GCE GCE为等边三角形.为等边三角形.为等边三角形. ∴GE=CG=CE=0.5BE.GE=CG=CE=0.5BE.∴∴G 为BE BE的中点.∴的中点.∴的中点.∴CG=BG=0.5BE. CG=BG=0.5BE. 12.13.(1)证明:∵△)证明:∵△ABC ABC 和△和△DEF DEF 是两个边长为6cm 的等边三角形,的等边三角形,∴BC=DE BC=DE,∠,∠,∠ABC=ABC=ABC=∠∠FDE=60FDE=60°,∴°,∴°,∴BC BC BC∥∥DE DE,∴四边形,∴四边形BCDE 是平行四边形;是平行四边形; (2)解:(a )当t=2秒时,▱BCDE 是菱形,此时A 与D 重合,∴重合,∴CD=DE CD=DE CD=DE,∴,∴▱ADEC 是菱形;是菱形; (b )若平行四边形BCDE 是矩形,则∠是矩形,则∠CDE=90CDE=90CDE=90°,如图所示:∴∠°,如图所示:∴∠°,如图所示:∴∠CDB=90CDB=90CDB=90°﹣°﹣°﹣606060°°=30=30°° 同理∠同理∠DCA=30DCA=30DCA=30°°=∠CDB CDB,∴,∴,∴AC=AD AC=AD AC=AD,同理,同理FB=EF FB=EF,∴,∴,∴F F 与B 重合,重合, ∴t=t=((6+26+2)÷)÷)÷1=81=8秒,∴当t=8秒时,平行四边形BCDE 是矩形.是矩形.14.14.解:解:解:(1)(1)(1)成立成立成立. .(2)(2)成立成立理由理由::∵四边形ABCD 为正方形为正方形,,∴AD=DC,AD=DC,∠∠BCD=BCD=∠∠ADC=90ADC=90°°. 在△在△ADF ADF 和△和△DCE DCE 中,DF=CE,,DF=CE,∠∠ADC=ADC=∠∠BCD,AD=CD BCD,AD=CD∴△∴△∴△ADF ADF ADF≌△≌△≌△DCE(SAS), DCE(SAS), ∴AF=DE,AF=DE,∠∠DAF=DAF=∠∠CDE. ∵∠∵∠ADG+ADG+ADG+∠∠EDC=90EDC=90°°,∴∠∴∠ADG+ADG+ADG+∠∠DAF=90DAF=90°°,∴∠∴∠AGD=90AGD=90AGD=90°°,即AF AF⊥⊥DE. (3)(3)四边形四边形MNPQ 是正方形是正方形. . 理由理由::如图如图,,设MQ 交AF 于点O,PQ 交DE 于点H, ∵点M,N,P,Q 分别为AE,EF,FD,AD 的中点的中点, ,∴MQ=PN=错误!未找到引用源。
中点四边形综合问题重难点培优八年级数学下册尖子生同步培优题典(解析版)【人教版】

八年级数学下册尖子生同步培优题典【人教版】专题18.13中点四边形综合问题(重难点培优)姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2019秋•龙岗区期末)如图,四边形ABCD 中,AC BD =,顺次连接四边形各边中点得到的图形是( )A .菱形B .矩形C .正方形D .以上都不对【分析】根据中位线定理证明中点四边形的四边相等,则顺次连接四边形各边中点得到的四边形是菱形. 【解析】E ,F 分别是DC ,AD 的中点, 12EF AC ∴=,//EF AC , 同理,12GH AC =,//GH AC ,12GF BD =, EF GH ∴=,//EF GH ,∴四边形EFGH 是平行四边形,AC BD =,EF GF ∴=,∴平行四边形EFGH 为菱形,故选:A .2.(2021春•宣城期末)下列说法:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相垂直的四边形是菱形;③四条边相等的四边形是正方形;④顺次连接菱形各边中点形成的四边形一定是矩形.其中正确的个数是( )A .4B .3C .2D .1【分析】根据平行四边形的判定和等腰梯形的判定即可判断①;画出图形,根据菱形的判定即可判断②;根据菱形和正方形的判定即可判断③;根据三角形的中位线性质得出//EF AC '',12EH B D ='',//EH B D '',12FG B D ='',//FG B D '',求出EH FG =,//EH FG ,根据平行四边形的判定得出四边形EFGH 是平行四边形,根据菱形的性质得出AC B D ''⊥'',求出90HEF ∠=︒,根据矩形的判定得出四边形EFGH 是矩形,即可判断④.【解析】①一组对边平行,另一组对边相等的四边形是等腰梯形,不一定是平行四边形,故①错误; ②如图,AC BD ⊥,但是四边形ABCD 不是菱形,即对角线互相垂直的四边形不一定是菱形,故②错误; ③四条边相等的四边形是菱形,不一定是正方形,故③错误;④如图,E 、F 、G 、H 分别是菱形A B C D ''''的边A B ''、B C ''、C D ''、A D ''的中点,//EF AC ∴'',12EH B D ='',//EH B D '',12FG B D ='',//FG B D '', EH FG ∴=,//EH FG ,∴四边形EFGH 是平行四边形,四边形A B C D''''是菱形,∴''⊥'',AC B DEH B D'',//EH AC∴⊥'',EF AC'',//∴⊥,EF EH即90∠=︒,HEF∴四边形EFGH是矩形,故④正确;所以正确的个数是1,故选:D.3.(2020秋•岐山县期中)如图,任意四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA 的中点,连接AC,BD,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是()A.若AC BD=,则四边形EFGH为菱形B.若AC BD⊥,则四边形EFGH为矩形C.若AC BD⊥,则四边形EFGH为正方形=,且AC BDD.若AC与BD互相平分,且AC BD=,则四边形EFGH是正方形【分析】连接四边形各边中点所得的四边形必为平行四边形,根据中点四边形的性质进行判断即可.【解析】A.当E,F,G,H是四边形ABCD各边中点,且AC BD===,=时,存在EF FG GH HE故四边形EFGH为菱形,故本选项不符合题意;B、当E,F,G,H是四边形ABCD各边中点,且AC BDEFG FGH GHE∠=∠=∠=︒,⊥时,存在90故四边形EFGH为矩形,故本选项不符合题意;===,⊥,存在EF FG GH HE C、当E,F,G,H是四边形ABCD各边中点,且AC BD=,且AC BD∠=∠=∠=︒,故四边形EFGH为正方形,故本选项不符合题意;90EFG FGH GHED、当E,F,G,H是四边形ABCD各边中点,且AC与BD互相平分,且AC BD=,故四边形EFGH 为菱形,故本选项符合题意;故选:D.4.(2021春•樊城区期末)如果一个四边形的对角线相等,顺次连接该四边形四条边的中点,可以得到( )A.平行四边形B.矩形C.菱形D.正方形【分析】根据三角形中位线定理得到//EF BD,//GH BD,12EF BD=,12GH BD=,12EH AC=,根据菱形的判定定理证明即可.【解析】E、F、G、H分别是边AD、AB、BC、CD的中点,//EF BD∴,//GH BD,12EF BD=,12GH BD=,12EH AC=,//EF GH∴,EF GH=,∴四边形EFGH是平行四边形.如图,连接AC、BD,AC BD=,12EF BD=,12EH AC=,EF EH∴=,∴平行四边形EFGH是菱形,故选:C.5.(2021春•武昌区校级期中)如图,顺次连接四边形ABCD各边中点得到中点四边形EFGH,下列说法中正确的是()A .当AC BD ⊥时,四边形EFGH 为菱形B .当AC BD =时,四边形EFGH 为矩形C .当AC BD ⊥,AC BD =时,四边形EFGH 为正方形D .以上说法都不对【分析】根据三角形中位线定理、平行四边形的判定定理得到四边形EFGH 为平行四边形,根据矩形、菱形、正方形的判定定理判断即可.【解析】点E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点,//EF AC ∴,12EF AC =,//GH AC ,12GH AC =,//EH BD ,12EH BD =, //EF GH ∴,EF GH =,∴四边形EFGH 为平行四边形,当AC BD ⊥时,EF EH ⊥,∴四边形EFGH 为矩形,A 选项说法错误;当AC BD =时,EH EF =,∴四边形EFGH 为菱形,B 选项说法错误;当AC BD ⊥,AC BD =时,EF EH ⊥,EF EH =,∴四边形EFGH 为正方形,C 选项说法正确;D 选项说法错误;故选:C .6.(2019•青神县一模)如图,正方形ABCD 四边的中点分别是E 、F 、G 、H ,若四边形EFGH 的面积是2,则正方形ABCD 的周长是( )A .4B .42C .8D .82【分析】根据正方形的性质得到AB BC CD AD ===,求得AE BE BF CF CG DG DH AH =======,根据全等三角形的性质得到EF FG HG EH ===,45AHE DHG ∠=∠=︒,求得90GHE ∠=︒,求得1AE AH ==,得到正方形ABCD 的边长为2,于是得到答案.【解析】正方形ABCD 四边的中点分别是E 、F 、G 、H ,AB BC CD AD∴===,∴=======,AE BE BF CF CG DG DH AH∠=∠=∠=∠=︒,A B C D90∴∆≅∆≅∆≅∆,AEH BFE CGF HDE SAS()∠=∠=︒,AHE DHGEF FG HG EH∴===,45GHE∴∠=︒,90∴四边形EFGH是正方形,四边形EFGH的面积是2,∴四边形EFGH2,∴==,AE AH1∴正方形ABCD的边长为2,∴正方形ABCD的周长是8,故选:C.7.(2019•江油市二模)我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形,下列说法正确的是()A.任意一个四边形的中点四边形是菱形B.任意一个平行四边形的中点四边形是平行四边形C.对角线相等的四边形的中点四边形是矩形D.对角线垂直的四边形的中点四边形是正方形【分析】利用三角形中位线定理可得新四边形的对边平行且等于原四边形一条对角线的一半,那么根据一组对边平行且相等的四边形是平行四边形可判定所得的四边形一定是平行四边形.【解析】A、任意一个四边形的中点四边形是平行四边形,故此选项错误;B、任意一个平行四边形的中点四边形是平行四边形,正确;C、对角线相等的四边形的中点四边形是菱形,故此选项错误;D、对角线垂直的四边形的中点四边形是矩形,故此选项错误.故选:B.8.(2019•临沂)如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点.则下列说法:①若AC BD=,则四边形EFGH为矩形;②若AC BD⊥,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是()A.1B.2C.3D.4【分析】因为一般四边形的中点四边形是平行四边形,当对角线BD AC=时,中点四边形是菱形,当对角线AC BD⊥时,中点四边形是正方形,=,且AC BD⊥时,中点四边形是矩形,当对角线AC BD【解析】因为一般四边形的中点四边形是平行四边形,当对角线BD AC⊥时,中点四边形是矩形,当对角线AC BD=,=时,中点四边形是菱形,当对角线AC BD且AC BD⊥时,中点四边形是正方形,故④选项正确,故选:A.9.(2021秋•金水区校级月考)如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点,则下列说法:①若AC BD=,则四边形EFGH为矩形;②若AC BD⊥,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;其中正确的个数是()A.0B.1C.2D.3【分析】根据“一般四边形的中点四边形是平行四边形,当对角线BD AC=时,中点四边形是菱形,当对角线AC BD⊥时,中点四边形是矩形”进行判断即可.【解析】因为一般四边形的中点四边形是平行四边形,故③错误;当对角线BD AC=时,中点四边形是菱形,当对角线AC BD⊥时,中点四边形是矩形,故①②错误,所以正确的有0个,故选:A.10.(2021春•德阳期末)如图,点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,则下列说法:①若AC BD=,则四边形EFGH为矩形;②若AC BD⊥,则四边形EFGH为菱形;③若四边形EFGH是菱形,则AC与BD互相垂直;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是()A.1B.2C.3D.4【分析】先证四边形EFGH是平行四边形,再由菱形、矩形以及正方形的判定分别对各个说法进行判断即可.【解析】E、F、G、H分别是AB、BC、CD、AD的中点,EH∴是ABD∆的中位线,FG是CBD∆的中位线,EF是ABC∆的中位线,//EH BD ∴,12EH BD=,//FG BD,12FG BD=,//EF AC,12EF AC=,//EH FG∴,EH FG=,∴四边形EFGH是平行四边形,①AC BD=,EH EF∴=,∴平行四边形EFGH是菱形,故①错误;②AC BD⊥,EF EH∴⊥,90FEH∴∠=︒,∴平行四边形EFGH 是矩形,故②错误;③若四边形EFGH 是菱形,则AC BD =,故③错误;④对角线AC BD =,且AC BD ⊥时,中点四边形EFGH 是正方形,故④正确,故选:A .二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上 11.(2021春•阿拉尔期末)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是 正方形 .【分析】由三角形中位线定理得//EH BD ,12EH BD =,//FG BD ,12FG BD =,//EF AC ,12EF AC =,则//EH FG ,EH FG =,得四边形EFGH 是平行四边形,再怎EH EF =,则平行四边形EFGH 是菱形,然后证90FEH ∠=︒,即可得出结论.【解析】如图,四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、AD 的中点,EH ∴是ABD ∆的中位线,FG 是CBD ∆的中位线,EF 是ABC ∆的中位线,//EH BD ∴,12EH BD =,//FG BD ,12FG BD =,//EF AC ,12EF AC =, //EH FG ∴,EH FG =,∴四边形EFGH 是平行四边形,AC BD =,EH EF ∴=,∴平行四边形EFGH 是菱形,又AC BD ⊥,EF EH ∴⊥,90FEH ∴∠=︒,∴四边形EFGH 是正方形,故答案为:正方形.12.(2021秋•寿光市期末)下列说法正确的是 A 、C .A .对角线相等的菱形是正方形B .顺次连接对角线互相垂直的四边形的四边中点,所得到的四边形是菱形C .成轴对称的两个图形全等D .有三个角相等的四边形是矩形【分析】利用正方形的判定方法、菱形的判定方法、矩形的判定方法及全等图形的定义分别判断后即可确定正确的答案.【解析】A 、对角线相等的菱形是正方形,正确,符合题意;B 、顺次连接对角线互相垂直的四边形的四边中点,所得到的四边形是矩形,故原命题错误,不符合题意;C 、成轴对称的两个图形全等,正确,符合题意;D 、有四个角相等的四边形是矩形,故原命题错误,不符合题意.故答案为:A 、C .13.(2020春•西华县期末)如图所示,AC 、BD 是四边形ABCD 的两条对角线,且AC BD ⊥,已知10AC =,8BD =,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,则EG 41 .【分析】易证四边形HEFG 是平行四边形,因为AC BD ⊥,所以HG EH ⊥,所以四边形HEFG 为矩形,进而由勾股定理得到22EG HE HG +.【解析】E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,152HG EF AC ∴===,142EH FG BD ===, E ,H ,是AB ,AD 中点,//HE BD ∴,12HE BD =, 同理//FG BD ,12FG BD =, ∴四边形HEFG 是平行四边形, AC BD ⊥,HG EH ∴⊥,∴四边形HEFG 为矩形,22224541EG HE HG ∴=+=+4114.(2020春•孝义市期末)如图,菱形ABCD 的对角线AC ,BD 相交于点O ,依次连接AO ,BO ,CO ,DO 的中点E ,F ,G ,H ,得到四边形EFGH ,点M 是EF 的中点,连接OM ,若10AB =,则OM 的长为 2.5 .【分析】根据菱形的性质得到AC BD ⊥,根据三角形中位线定理得到152EF AB ==,根据直角三角形的性质计算,得到答案.【解析】四边形ABCD 为菱形,AC BD ∴⊥, E 、F 分别为OA 、OB 的中点,152EF AB ∴==, 在Rt EOF ∆中,M 是EF 的中点,1 2.52OM EF ∴==, 故答案为:2.5.15.(2021秋•南海区月考)已知:在四边形ABCD 中,AD BC =,点E ,F ,G ,H 分别是AB ,CD ,AC ,BD 的中点,四边形EHFG 是 菱形 .【分析】由已知条件得出GF是ADC∆的中位线,GE是ABC∆的中位线,EH是ABD∆的中位线,由三角形中位线定理得出//GF EH,GF EH=,得出四边形EGFH是平行四边形,再证出GE EH=,即可得出四边形EHFG是菱形.【解析】证明:点E、F、G、H分别是AB、CD、AC、BD的中点,GF∴是ADC∆的中位线,GE是ABC∆的中位线,EH是ABD∆的中位线,//GF AD ∴,12GF AD=,12GE BC=,//EH AD,12EH AD=,//GF EH∴,GF EH=,∴四边形EGFH是平行四边形,又AD BC=,GE EH∴=,∴四边形EGFH是菱形.故答案是:菱形.16.(2021秋•榆阳区校级月考)点E、F、G、H分别是任意四边形ABCD中AD、AB、BC、CD各边的中点,对角线AC,BD交于点O,当四边形ABCD满足对角线垂直且相等条件时,四边形EFGH是正方形.【分析】根据三角形中位线定理得到//EF BD,12EF BD=,//GH BD,12GH BD=,12EH AC=,进而证明四边形EFGH为平行四边形,再根据正方形的判定定理解答即可.【解析】点E、F、G、H分别是任意四边形ABCD中AD、AB、BC、CD各边的中点,//EF BD ∴,12EF BD=,//GH BD,12GH BD=,12EH AC=,//EF GH∴,EF GH=,∴四边形EFGH为平行四边形,当AC BD=时,EF EH=,∴平行四边形EFGH为菱形,当AC BD⊥时,EF EH⊥,∴菱形EFGH为正方形,∴当四边形ABCD的对角线垂直且相等时,四边形EFGH是正方形,故答案为:对角线垂直且相等.17.(2021•西城区校级开学)如图,点A,B,C为平面内不在同一直线上的三点,点D为平面内一个动点,线段AB,BC,CD,DA的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④中点四边形MNPQ不可能是正方形;所有结论正确的序号是①②③.【分析】根据中点四边形的性质:一般中点四边形是平行四边形,对角线相等的四边形的中点四边形是菱形,对角线垂线的中点四边形是矩形,对角线相等且垂直的四边形的中点四边形是正方形解答.【解析】中点四边形都是平行四边形,对角线相等的四边形的中点四边形是菱形,对角线垂线的中点四边形是矩形,对角线相等且垂直的四边形的中点四边形是正方形,∴存在无数个中点四边形MNPQ是平行四边形,存在无数个中点四边形MNPQ是菱形,存在无数个中点四边形MNPQ是矩形.故答案为:①②③.18.(2020春•新乐市期末)对于任意矩形ABCD ,若M ,N ,P ,Q 分别为边AB ,BC ,CD ,DA 上的中点,下面四个结论中,①四边形MNPQ 是平行四边形;②四边形MNPQ 是矩形;③四边形MNPQ 是菱形; ④四边形MNPQ 是正方形.所有正确结论的序号是 ①③ .【分析】连接AC 、BD ,由三角形中位线定理得出//MN AC ,12MN AC =,//PQ AC ,12PQ AC =,//MQ BD ,12MQ BD =,则//MN PQ ,MN PQ =,MN MQ =,证出四边形MNPQ 是平行四边形,四边形MNPQ 是菱形;①③正确;当AC BD ⊥时,MN MQ ⊥,四边形MNPQ 是矩形,四边形MNPQ 是正方形,②④不正确,即可得出结论.【解析】连接AC 、BD ,如图:四边形ABCD 是矩形,AC BD ∴=,M ,N ,P ,Q 分别为边AB ,BC ,CD ,DA 上的中点,MN ∴是ABC ∆的中位线,PQ 是ACD ∆的中位线,MQ 是ABD ∆的中位线,//MN AC ∴,12MN AC =,//PQ AC ,12PQ AC =,//MQ BD ,12MQ BD =, //MN PQ ∴,MN PQ =,MN MQ =,∴四边形MNPQ 是平行四边形,∴四边形MNPQ 是菱形;故①③正确;当AC BD ⊥时,MN MQ ⊥,四边形MNPQ 是矩形,四边形MNPQ 是正方形.故②④不正确; 故答案为:①③.三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)19.(2020春•工业园区期末)已知:如图,在四边形ABCD 中,AB 与CD 不平行,E ,F ,G ,H 分别是AD ,BC ,BD ,AC 的中点.(1)求证:四边形EGFH 是平行四边形;(2)①当AB 与CD 满足条件 AB CD = 时,四边形EGFH 是菱形;②当AB 与CD 满足条件 时,四边形EGFH 是矩形.【分析】(1)根据三角形中位线定理得到12EG AB =,//EG AB ,12FH AB =,//FH AB ,根据平行四边形的判定定理证明结论;(2)①根据邻边相等的平行四边形是菱形解答;②根据矩形的判定定理解答.【解析】(1)证明:E ,G 分别是AD ,BD 的中点,EG ∴是DAB ∆的中位线,12EG AB ∴=,//EG AB , 同理,12FH AB =,//FH AB , EG FH ∴=,//EG FH ,∴四边形EGFH 是平行四边形;(2)①F ,G 分别是BC ,BD 的中点,FG ∴是DCB ∆的中位线,12FG CD ∴=,//FG CD , 当AB CD =时,EG FG =,∴四边形EGFH 是菱形;②//HF AB , HFC ABC ∴∠=∠,//FG CD ,GFB DCB ∴∠=∠,90ABC DCB∴∠+∠=︒,90HFC GFB∴∠+∠=︒,90GFH∴∠=︒,∴平行四边形EGFH是矩形,故答案为:①AB CD=;②AB CD⊥.20.(2020春•海陵区校级期中)如图,O为BAC∠内一点,E、F、G、H分别为AB,AC,OC,OB 的中点.(1)求证:四边形EFGH为平行四边形;(2)当AB AC=,AO平分BAC∠时,求证:四边形EFGH为矩形.【分析】(1)根据三角形中位线定理推知////EH AO FG,12EH FG AO==,则四边形EFGH是平行四边形.(2)根据平行线的性质和等腰AEF∆的性质推知:90HEF ADE∠=∠=︒,则四边形EFGH为矩形.【解析】证明:(1)EH是ABO∆的中位线,//EH AO ∴,12EH AO=.同理,FG是ACO∆的中位线,//FG OA ∴,12FG AO=.//EH FG∴,EH FG=,∴四边形EFGH是平行四边形.(2)设OA与EF的交点为D,AB AC=,E、F分别为AB,AC的中点,AE AF∴=.AO平分BAC∠,//EH AD,∴∠=∠=︒,HEF ADE90∴四边形EFGH为矩形.21.已知:如图,分别以BM、CM为边,向BMC∆形外作等边三角形ABM、CDM,E、F、G、H分别为AB、BC、CD、DA中点.(1)猜测四边形EFGH的形状;(2)证明你的猜想;(3)三角形BMC形状的改变是否对上述结论有影响?【分析】(1)由题意可猜测四边形EFGH是菱形;(2)首先连接AC,BD,易证得()∆≅∆,即可得AC BDAMC BMD SAS=,又由E、F、G、H分别为AB、===,即可得四边形EFGH是菱形;BC、CD、DA中点,则可证得EF FG GH EH(3)由(2)得:BMC∆形状的改变对上述结论没有影响.【解析】(1)解:四边形EFGH是菱形;(2)证明:连接AC,BD,∆和CDMABM∆是等边三角形,∴=,CM DMAM BM∠=∠=︒,=,60AMB CMD∴∠=∠,AMC BMD在AMC ∆和BMD ∆中,AM BM AMC BMD CM DM =⎧⎪∠=∠⎨⎪=⎩,()AMC BMD SAS ∴∆≅∆,AC BD ∴=,E 、F 、G 、H 分别为AB 、BC 、CD 、DA 中点,12EF GH AC ∴==,12EH FG BD ==, EF FG GH EH ∴===,∴四边形EFGH 是菱形;(3)解:BMC ∆形状的改变对上述结论没有影响.22.(2021春•东莞市期末)如图,在四边形ABCD 中,AC 、BD 是对角线,点E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点,依次连接E 、F 、G 、H .(1)证明:四边形EFGH 是平行四边形;(2)在四边形ABCD 中,若再补充一个条件: AC BD ⊥ ,则四边形EFGH 是矩形;(3)连接EG 、FH ,求证:222222EG FH EF FG GH HE +=+++.【分析】(1)由中位线定理证明://HG AC ,12HG AC =,//EF AC ,12EF AC =,从而//HG EF ,HG EF =,即可证明四边形EFGH 是平行四边形;(2)若AC BD ⊥,则90DOC ∠=︒,由//EF AC ,//FG BD ,即可得90GFE ∠=︒,故四边形EFGH 是矩形;(3)过H 作HP EG ⊥于P ,过F 作FQ EG ⊥于Q ,Rt HPE ∆中,22222EH HP OE OP OE OP =++-⋅,Rt HPG ∆中,22222HG HP OG OP OG OP =++-⋅,由四边形EFGH 是平行四边形,可得12OE OG EG ==,12OH OF HF ==,故2222222222112222EH HG HP OE OP OE OP HP OG OP OG OP HF EG +=++-⋅+++-⋅=+,同理可得:22221122EF FG HF EG +=+,从而可证明222222EG FH EF FG GH HE +=+++.【解析】(1)H 、G 是AD 、CD 的中点,HG ∴是ACD ∆的中位线,//HG AC ∴,12HG AC =,同理://EF AC ,12EF AC =,//HG EF ∴,HG EF =,∴四边形EFGH 是平行四边形;(2)解:补充的条件是:AC BD ⊥,证明如下:如图:若AC BD ⊥,则90DOC ∠=︒,//EF AC , 90OMF DOC ∴∠=∠=︒,FG 是BCD ∆的中位线,//FG BD ∴,18090GFE OMF ∴∠=︒-∠=︒,由(1)知:四边形EFGH 是平行四边形,∴四边形EFGH 是矩形;故答案为:AC BD ⊥;(3)过H 作HP EG ⊥于P ,过F 作FQ EG ⊥于Q ,如图:Rt HPE ∆中,22222222()2EH HP EP HP OE OP HP OE OP OE OP =+=+-=++-⋅, Rt HPG ∆中,22222222()2HG HP PG HP OG OP HP OG OP OG OP =+=++=++-⋅, 由(1)知:四边形EFGH 是平行四边形,12OE OG EG ∴==,12OH OF HF ==, 2222222222EH HG HP OE OP OE OP HP OG OP OG OP ∴+=++-⋅+++-⋅ 22222()HP OP OE OG =+++222112()()22OH EG EG =++ 22112()22HF EG =⨯+ 221122HF EG =+, 同理可得:22221122EF FG HF EG +=+, 222222EG FH EF FG GH HE ∴+=+++.23.(2021春•集贤县期末)在四边形ABCD 中,AB 、BC 、CD 、DA 的中点分别为P 、Q 、M 、N .(1)如图1,试判断四边形PQMN 怎样的四边形,并证明你的结论;(2)若在AB 上取一点E ,连结DE ,CE ,恰好ADE ∆和BCE ∆都是等边三角形(如图2),判断此时四边形PQMN 的形状,并证明你的结论.【分析】(1)连接AC 、BD .利用三角形中位线定理判定四边形PQMN 的对边平行且相等,易证该四边形是平行四边形;(2)①设ADE ∆的边长是x ,BCE ∆的边长是y ,由于2222213()()2DB x y x x xy y =++=++,2222213()()2AC x y y x xy y =++=++,可得平行四边形PQMN 的对角线相等,从而得出平行四边形PQMN 是菱形;【解析】四边形PQMN 为平行四边形;(1)连接AC 、BD .PQ 为ABC ∆的中位线,//PQ AC ∴,12PQ AC =, 同理//MN AC .12MN AC =. MN PQ ∴=,//MN PQ ,∴四边形PQMN 为平行四边形;(2)四边形PQMN 是菱形;理由如下:设ADE ∆的边长是x ,BCE ∆的边长是y ,2222213()()2DB x y x xy y ∴=++=++,2222213()()2AC x y y x xy y =++=++, 平行四边形PQMN 的对角线相等,∴平行四边形PQMN 是菱形;24.(2021春•泗阳县期末)已知:如图,在四边形ABCD 中,AB 与CD 不平行,E ,F ,G ,H 分别是AD ,BC ,BD ,AC 的中点.(1)求证:四边形EGFH 是平行四边形;(2)当AB CD =,四边形EGFH 是怎样的四边形?证明你的结论.【分析】(1)根据三角形中位线定理得到12EG AB =,//EG AB ,12FH AB =,//FH AB ,根据平行四边形的判定定理证明结论; (2)依据四边形ABCD 是平行四边形,再运用三角形中位线定理证明邻边相等,从而证明它是菱形.【解析】(1)证明:E ,G 分别是AD ,BD 的中点, EG ∴是DAB ∆的中位线,12EG AB ∴=,//EG AB , 同理,12FH AB =,//FH AB , EG FH ∴=,//EG FH ,∴四边形EGFH 是平行四边形;(2)菱形.理由:F ,G 分别是BC ,BD 的中点,FG ∴是DCB ∆的中位线,12FG CD ∴=,//FG CD ,又12EG AB =, ∴当AB CD =时,EG FG =,∴平行四边形EGFH 是z。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级四边形难题综合
【例题精选】:
例1:如图1,已知:□ABCD 中,
AE BD CF BD ⊥⊥,,垂足为E 、F ,G 、H
分别为AD 、BC 的中点,连结GE 、EH 、HF 、
FG 。
求证:EF 和GH 互相平分。
证明:
AE BD G AD ⊥,为中点
∴==GE GD AD 1
2
(直角三角形斜边上的中线等于斜边的一半)
∴∠=∠GED GDE (等边对等角)
同理可证:HF HB BC HFB HBF ==∠=∠1
2
,
□ABCD
∴∠=∠∴=∠=∠∴AD BC GDE HBF
GE HF GED HFB GE HF
////,,且 ∴四边形ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形) ∴EF 和GH 互相平分(平行四边形的对角线互相平分)
例2:如图3,已知:菱形ABCD ,E 、F 分别是BC 、
CD 上的点,∠=∠=︒∠=︒B EAF BAE 6018,
求:∠CEF 的度数
分析:由菱形ABCD ,∠=︒B ABC 60,可得∆是等
边三角形,所以∠=∠=︒BAC ACD 60,∠=︒EAF 60,得出∠BAE=∠CAF ,从而可证∆∆ABE ACF ≅,进而推出∆AEF 是等边三角形,求出∠CEF 的度数。
解:连结AC ∵菱形ABCD
∴BA=BC ,∠ACB=∠ACD ∵∠=︒B 60
∴∆ABC 是等边三角形
∴∠=∠=︒=∴∠=∠=︒
∠=∠=︒∴∠=∠∴≅BAC ACB AB AC
ACF B EAF BAC BAE CAF ABE ACF AAS 606060,()
∆∆
∴=∴∴∠=︒
AE AF
AEF AEF ∆是等边三角形60 ∠+∠=∠+∠∠=︒∴∠=︒
AEF CEF B BAE
BAE CEF 1818
例3:如图4,已知:正方形ABCD ,E 、F 为AB 、BC 上两点,且EF=AE+FC
求证:∠=︒EDF 45
证明:延长BC 至G ,使CG=AE ,连结DG
正方形,()又,公用()ABCD
AD CD A DCG DAE DCG SAS ADE CDG DE DG ADC EDG EF AE FC
EF CG FC FG DF EDF GDF SSS EDF GDF ∴=∠=∠=︒∴≅∴∠=∠=∠=︒∴∠=︒=+∴=+=∴≅∴∠=∠=︒
90909045∆∆∆∆,
例4:如图5,已知:正方形ABCD ,BE ∥AC ,且AE=AC 交BC 于F 求证CF=CE
分析:CF 、CE 在同一三角形中,故考虑用“等角对等边”易知
∠=
AEC 1802
︒-∠EAC
,∠CFE=∠EAC +∠ACF=∠EAC +︒45,从上述两
个式子无法直接判断∠AEC 是否与∠CFE 相等,若能分别求出∠AEC 和∠CFE 就可以判断了,故本题关键是如何求出∠EAC 的度数。
这就要充分
运用已知条件(包括题目中的隐含条件,如正方形具有的性质,对角线?)。
因此AE=AC 这个条件很重要。
因为AC 是正方形ABCD 的对角线。
证明:如图6,作EG AC ⊥于G ,连结BD 交AC 于O 。
∴⊥=
BO AC BO AC ,1
2
(正方形对角线相等,且互相垂直平分) ∴BO ∥EG (垂直于同一直线的两直线平行) 又∵BE ∥AC
∴BO=EG (夹在两条平行线间的平行线段相等)
∴=
=∴=EG AC AC AE EG AE Rt AEG 12
1
2
又,在中
∆
∴∠=︒EAC 30(在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30︒)
∆ACE 是等腰三角形
∴∠=
︒-∠=︒AEC EAC
1802
75 ∵AC 是正方形ABCD 的对角线。
∴∠=︒ACB AFC 45,在中,∆
∠=∠+∠=︒CFE EAC ACB 75(三角形的一个外角等于和它不相邻的两个内角的
和) 即(等角对等边)
∠=∠∴=AEC CFE
CF CE
例5:已知:如图7,∆ABC AB AC 中,=,延长AB 到D ,使BD=AB ,又CE 是AB 边上的中线。
求证:CE CD =1
2
证明:
如图8,过点B 作BF ∥AC 交CD 于F ∵AB=BD ,AB=AC
∴CF CD =
1
2
(过三角形一边中点与另一边平行的直线必平分第三边)
∴BF AC AB =
=121
2
(三角形中位线等于第三边的一半) ∵AE=EB ∴BF=BE
∵∠1=∠ACB ,∠2=∠ACB ∴∠1=∠2 又BC 公用
∴∆∆BEC BFC SAS ≅() ∴CE=CF 即:CE CD =
1
2
【专项训练】: 一、选择题: 1、下列图形中,是轴对称图形而不是中心对称图形的是: A .平行四边形 B .菱形 C .等腰梯形 D .直角梯形 2、下列四边形各边中点连线为菱形的是: A .平行四边形
B .菱形
C .矩形
D .直角梯形
3、下列命题中,不正确的是: A .平行四边形的对角线互相平分
B .对角线互相平分的四边形是平行四边形
C .菱形的对角线互相垂直
D .对角线互相垂直的四边形是菱形
4、直角梯形的一腰为10cm ,该腰与下底的夹角为45︒,且下底为上底长的2倍,则直角梯形的面积是:
A .75cm 2
B .100cm 2
C .1021()+cm 2
D .10221()+cm 2
二、证明:
1、已知:如图12,E 、F 为∆ABC 的边AB 、BC 的中点,在AC 上取G 、H 两点,使AG=GH=HC ,连结EG 、FH ,并延长交于D 点。
求证:四边形ABCD 是平行四边形。
2、已知:如图13,正方形ABCD ,P 是BD 上任意一点,
DQ AP ⊥,垂足是Q ,交AC 于R 。
求证:DP=CR
3、已知:如图14,矩形ABCD ,P 为矩形外一点,PA PC ⊥ 求证:PB CD ⊥
4、已知:如图15,正方形ABCD 中,F 为DC 中点,AE=EC +AD 求证:AF 平分∠EAD
5、已知:如图16,梯形ABCD ,AB ∥CD ,以AD 、AC 为邻边作□ACED ,DC 的延长线交BE 于
F 求证:F 是BE 的中点
【专项训练二】: 一、选择题:
1、下列命题中,错误的是: A .平行四边形的对角线互相平分
B .有两对邻角互补的四边形是平行四边形
C .对角线互相平分的四边形是平行四边形
D .两组对边分别相等的四边形是平行四边形 2、已知矩形的一条对角线与一边的夹角是40︒,则两条对角线所夹的锐角是: A .50︒ B .60︒ C .70︒ D .80︒
3、对角线互相垂直平分但不相等的四边形是:
A .正方形
B .矩形
C .菱形
D .非特殊平行四边形
4、已知四边形ABCD ,对角线AC=BD ,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,则四边形EFGH 是:
A .正方形
B .矩形
C .菱形
D .非特殊平行四边形
5、若等腰梯形上底长为a ,中位线长为b ,则连结两条对角线中点的线段的长是:
A .b a -2
B .b a -
C .
b a
-2
D .
b
a 2
- 二、填空题:
1、在平行四边形ABCD 中,若∠+∠=︒∠A C B 240,的大小是
2、等腰三角形的两条中位线的长分别是3和5,则它的周长是
3、菱形的周长是52cm ,一条对角线长是24cm ,那么另一条对角线长是 。
4、平行四边形ABCD 中(如图),AE 、AF 分别是BC 、CD 的高,若∠=︒BAE 48,则∠=EAF。
5、矩形的对角线长为8cm ,对角线与一边的夹角为30︒,则矩形的周长是。
三、已知:如图,等腰梯形ABCD 中,AD//BC ,中位线EF=9cm ,梯形的周长为34cm ,两条对角线的中点连线为3cm 。
求腰及两底的长度。
四、已知:如图,正方形ABCD 中,E 是CD 上一点,F 是BC 上一点,且∠=︒EAF 45。
求证:EF=BF+DE。
