六子棋中基于局部“路”扫描方式的博弈树生成算法
博弈大赛赛前培训_六棋子程序的实现

/
计算机博弈与人工智能
六子棋的棋型
活二:在同一直线上的2颗同色棋子,符合“再下两手 棋就能形成活四”的条件。
/
计算机博弈与人工智能
六子棋的棋型
眠二:在同一直线上的2颗同色棋子,符合“再下两手 棋只能形成眠四”的条件。
/
计算机博弈与人工智能
示例代码
//将着法转换成要发送的字符形式 y0 = (char)((int)('A') + y0); x0 = (char)((int)('S') - x0); y1 = (char)((int)('A') + y1); x1 = (char)((int)('S') - x1); //Move[] = "move AABB\n" //修改"AABB" 并发送 Move[5] = y0; Move[6] = x0; Move[7] = y1; Move[8] = x1; printf("%s",Move); fflush(stdout);
计算机博弈与人工智能
示例代码
结构定义: //棋子位置 typedef struct _stoneposition { BYTE x; BYTE y; }STONEPOS; //走法 typedef struct _stonemove { STONEPOS StonePos[2]; int Score; }STONEMOVE;
计算机博弈与人工智能
六子棋的棋型
活五:在同一直线上的5颗同色棋子,符合“对方必须 用两手棋才能挡住”的条件。“挡住”是指不让 另一方形成六连或长连。
/
计算机博弈与人工智能
六子棋博弈系统设计与实现

六子棋博弈系统设计与实现摘要:六子棋作为计算机博弈比赛项目越来越受到重视。
从棋局表示、估值函数设计、搜索算法、走法生成器以及开局库几个方面介绍了六子棋博弈系统的设计与实现。
该系统在“成理杯”2014届全国大学生计算机博弈大赛六子棋项目比赛中,获得了一等奖的好成绩。
大量模拟实验证明,该算法具有一定的有效性和实用性。
关键词:六子棋;估值函数设计;走法生成器;开局库中图分类号:TP319文献标识码:A 文章编号:1672-7800(2015)003-0092-030 引言人工智能是研究智能的理论、方法、技术及应用系统的科学,其最关心的是知识表示与搜索,也是计算机博弈要解决的问题。
计算机博弈也称为机器博弈,最早来源于博弈论思想。
目前计算机博弈研究主要针对人机对战的棋盘类游戏,因而人工智能相关技术在计算机博弈游戏中被广泛应用。
六子棋由五子棋演变而来,2003年由台湾新竹交通大学吴毅成教授提出,其规则简单、游戏公平、玩法复杂,受到玩家欢迎,逐渐得到推广。
六子棋标准棋盘为19×19,黑白双方轮流下棋,除了第一次由黑方先下一颗子外,其后各方每轮下两颗棋子,连成六子(或以上)者获胜,如图1所示。
六子棋没有禁手,长连(连成六子以上)即算赢棋,若全部棋盘填满仍未分出胜负则算和棋。
图1 六子棋棋盘本文主要从棋盘表示、走法生成器、估值函数设计、搜索算法实现以及开局库几个方面介绍六子棋博弈系统的设计与实现。
1 棋盘表示棋盘的表示一般有数组表示法和比特表示法,比特表示法又称为位棋盘。
六子棋棋盘一般为19×19,若用二维数组表示棋盘即为Board[19][19]。
采用位棋盘的作用就是记录棋盘上的某些布尔条件,根据布尔值放入对应的棋子。
位棋盘如今广泛应用在六子棋中,原因是效率高、占用空间小。
本文程序采用64位长度的变量,与数组表示法相比较,位棋盘每19个点需要38位。
用64位长度的变量表示,19行就需19×8B,即为152B,而数组表示法需要361B。
[转载]中国象棋软件-引擎实现(四)搜索算法
![[转载]中国象棋软件-引擎实现(四)搜索算法](https://img.taocdn.com/s3/m/d629d78bed3a87c24028915f804d2b160b4e8662.png)
// 执行着法,返回ptTo位置的棋子状况。即若吃掉子返回被吃掉的子,没有吃子则返回0 BYTE DoMove( CCHESSMOVE * move );
然而,下棋是一个你来我往的交替进行并且相互“较劲”的过程,由于每一方都会尽可能将局面导向对自己有利而对对方不利的形势。所以有些“暂时”看来很不错的局面由于可 能会产生很糟糕的局面因而根本没有考虑的价值。所以当你看到某个局面有可能产生很糟糕的局面时(确切地说这里的“很糟糕”是与之前所分析的情况相比较而言的),你 应当立刻停止对其剩余子结点的分析——不要对它再报任何幻想了,如果你选择了它,则你必将得到那个很糟糕的局面,甚至更糟……这样一来便可以很大程度上减少搜索 的工作量,提高搜索效率。这称为“树的剪裁”。为了便于大家理解,下面我援引ElephantBoard的主页上所翻译的《Alpha-Beta搜索》中的一个“口袋的例子”,原文作者是 Bruce Moreland (brucemo@)。 口袋的例子:
int iBestmove = -1;
for( i = 0; i < nCount; i ++ ) {
nCChessID = DoMove( & MoveList[nDepth][i] ); // 执行着法(生成新节点) nScore = - AlphaBeta_HH( nDepth - 1, -beta, -alpha );//递归调用AlphaBeta_HH UndoMove( & MoveList[nDepth][i], nCChessID ); // 撤销执行(删除节点)
六子棋机器博弈关键技术分析PPT课件

徐长明、徐心和、王翠 荣
2011. 06. 13
五子棋
入手
• 起源于中国 • 发展在日本(棋型棋) • Renju / Go-Moku • 棋盘 15×15
五子棋机器博弈研究现状
入手
• 两种常见的五子棋均已经被成功破解 • Go-moku(无禁手):于1994年解决 • Renju(禁手):于2001年解决,花费了9000小时=375 天。
复杂度: 计算复杂度为PSPACE-complete; 平均分枝因子约为300; 每盘棋平均30步。
入手
研究现状:涉及到k子棋(如五子棋和六子棋)复 杂度的文献均高估了它的复杂度。
零
万事开头难,从哪里入手?
参考文献
入手
1. 六子棋 发明人吴毅成教授网站: /web/index.php?option=com_content&t ask=view&id=15&Itemid=26.
标准的六子棋是connect(19, 19, 6, 2, 1),标准的五子 棋是connect(15, 15, 5, 1, 1) 。
复杂度
入手
二人博弈问题一般至少属于NP-hard类,而且,多 属于PSPACE-complete(如奥赛罗) 或EXPTIMEcomplete(如中国象棋、西洋跳棋、国际象棋和围 棋等)类问题。
• 破解五子棋的重要因素 • 借助了机器博弈 • 当时恰好发现新算法——TSS(Threat Space Search)+PNS(Proof Number Search)
• 新的五子棋其规则变得复杂,致使趣味性大减
六子棋简介
入手
• 棋盘 19×19 • 6子棋型为胜 • 复杂度显著提高
博弈树计算以及剪枝例题

博弈树计算以及剪枝例题博弈树是一种用于解决博弈问题的数学模型,它可以帮助我们分析博弈的各种可能走法以及对应的结果。
在计算博弈树时,我们需要考虑以下几个步骤:1. 确定博弈的参与者和规则,首先确定参与博弈的玩家以及博弈的规则,包括每个玩家的可行行动和胜利条件。
2. 构建博弈树的根节点,根节点表示博弈的初始状态,通常是一个空棋盘或者初始的游戏状态。
3. 生成博弈树的分支节点,从根节点开始,根据规则和玩家的行动选择生成各个可能的子节点,每个子节点代表一个可能的下一步行动。
4. 递归生成博弈树,对于每个子节点,重复步骤3,直到达到博弈的终止状态,例如达到胜利条件或者无法再进行下一步行动。
5. 评估叶子节点的结果,对于博弈树的叶子节点,根据游戏规则和胜利条件评估其结果,可以使用得分、胜利或失败等方式表示。
6. 向上回溯更新节点值,从叶子节点开始,通过向上回溯更新每个节点的值,例如选择最大值或最小值作为节点的值,以便在博弈过程中做出最优决策。
剪枝是一种优化博弈树计算的技术,它可以减少计算量,提高搜索效率。
常用的剪枝技术有Alpha-Beta剪枝和极小化极大剪枝。
以下是一个简单的例子来说明博弈树计算和剪枝的应用:假设我们玩一个简单的棋类游戏,如井字棋。
我们用X和O分别代表两个玩家。
我们的目标是找到最佳的下一步行动。
1. 首先,我们构建博弈树的根节点,表示当前的游戏状态,例如一个空棋盘。
2. 然后,我们生成所有可能的子节点,代表X玩家的所有可能行动。
3. 对于每个子节点,我们再生成对应O玩家的所有可能行动的子节点。
4. 重复步骤3,直到达到博弈的终止状态,例如棋盘上已经有了胜利的一方或者无法再进行下一步行动。
5. 对于博弈树的叶子节点,根据游戏规则评估其结果,例如胜利的一方得分为1,失败的一方得分为-1,平局得分为0。
6. 向上回溯更新每个节点的值,例如对于X玩家的节点,选择最大值作为节点的值;对于O玩家的节点,选择最小值作为节点的值。
博弈论算法棋设计

博弈论算法棋设计
博弈论算法在棋类游戏的设计和实现中起着关键作用。
以下是一些常见的博弈论算法和与棋类游戏设计相关的考虑:
极小极大算法(Minimax Algorithm):用于决策树搜索,通过最大化己方得分和最小化对手得分来进行决策。
在棋类游戏中,这种算法可以帮助计算出最优的移动。
Alpha-Beta剪枝算法:在极小极大算法的基础上进行优化,通过剪枝减少搜索树的节点数量,提高计算效率。
蒙特卡洛树搜索(Monte Carlo Tree Search,MCTS):通过模拟大量游戏局面来评估每个决策的优劣。
在棋类游戏中,MCTS常用于复杂且不确定性较大的情境。
启发式搜索算法:使用启发式评估函数来估算每个可能移动的价值,帮助算法更快地找到有望取得好结果的决策。
深度学习和神经网络:利用神经网络来学习和提高棋类游戏中的决策策略。
例如,AlphaGo就使用了深度学习技术。
状态空间表示:设计有效的状态表示方法,以便在算法中高效地搜索状态空间。
这可能涉及将棋盘状态编码为适当的数据结构。
优化算法:使用各种优化技术,例如并行计算、分布式计算,以提高搜索速度。
博弈规则和评估函数:明确定义博弈的规则和设计有效的评估函数,以便算法能够准确评估局势。
这些算法和考虑因素的选择取决于特定棋类游戏的规模和复杂性。
在设计中,需要根据游戏的性质选择合适的博弈论算法,并对其进行适当的调优和优化。
“理治棋壮”中国象棋计算机博弈引擎关键算法分析与设计

“理治棋壮”中国象棋计算机博弈引擎关键算法分析与设计“理治棋壮”中国象棋计算机博弈引擎开发小组在《程序架构设计与主要算法概述》一文中,我们阐述了中国象棋计算机博弈涉及的主要算法。
下面就其中的关键算法进行深入分析,并说明其设计实现方法。
一、核心搜索算法1、Principal Variable Search搜索算法是计算机博弈程序的核心算法。
如何选择适合的搜索算法,配以合理的剪枝条件,是决定搜索效率的关键所在。
博弈树不同于一般的搜索树,它是由对弈双方共同产生的一种“变性”搜索树。
应对这类问题,香农(Claude Shannon)教授早在1950年提出了极大-极小算法(Minimax Algorithm)。
这种算法常以一种形式上的改进——负极大值算法出现:记我方节点值为正,对方节点值为负,双方在每一节点分别选择其子节点中绝对值最大的一个。
递归深度优先遍历有限层次的树,找到使起始节点绝对值最大的一个叶子节点,然后回溯找到形成这一叶子节点的第一层子节点,作为最优解。
可以在博弈树深度优先搜索过程中记录2个附加值,α:我方搜索到的最好值,任何比它更小的值就没用了;β:对于对手来说最坏的值。
在搜索算法中,如果某个节点的结果小于或等于α,那么它就可以抛弃;如果某个着法的结果大于或等于β,那么整个结点就作废了,因为对手不希望走到这个局面。
如果某个节点值大于α但小于β,那么这个节点就是可以考虑走。
这便是所谓的α-β剪枝搜索。
由α和β可以形成一个节点预选窗口。
如何能够快速得到一个尽可能小而又尽可能准确的窗口?有不少窗口搜索算法被设计出来解决这个问题,如:Aspiration Search、Principal Variable Search、Tolerance Search等。
目前大多数国际象棋与中国象棋的算法核心青睐速度快而不会出现错误剪枝的Principal Variable Search,它的原理是第一个分枝以完整窗口搜索,产生一个解v,后继分枝则以一个极小窗口(v,v+1)搜索之,旨在建立高效的、极小的搜索树。
棋类计算机博弈系统的主要研究方法及在6子棋上的应用

20 年 9月 08
S p.2 0 e 08
Байду номын сангаас
V0 . 2 No. 12 9
棋 类计 算 机 博 弈 系统 的 主 要 研 究 方 法及 在 6子 棋 上 的 应 用
张 颖, 李祖 枢
4O 4) OO4
( 重庆大学 自动化 学院 , 庆 重
M an Te h lge fChes Co pu e — m e S se n i c noo iso s m tr Ga y tm a d
‘
计算机博 弈, 简单地说 , 就是让计算机像人一
样从事需要 高度智 能 的博 弈活 动 . 类 游戏是 对 而棋
现实生活 中各 种 矛 盾 、 战争 的模拟 , 棋 的 双方 无 下
1 棋 类计算机博弈发展 简史
计 算机 博弈 是人 工 智能 领 域 中一个 极 其 重要
时不在调动 自己的一 切智 能 , 充分 发 挥逻 辑思 维 、 形象思维 和 灵感 思 维 的 能力 . 同时 它规 则 简单 、 易 于实现 , 以, 所 在人 工 智 能领 域 始终 将 棋 类 的机 器 博弈作为常用 的研究 平 台之一 . 以棋类 游 戏为研 究
在计算机博 弈 中都可 以得 到广泛 的应用 .
收 稿 日期 :08 6 2 2 0 —0 —1
基金项 目 : 国家 自然科 学基 金资助项 目(0404 . 6430 ) 作者简介 : 张颖 (9 1 )男 , 18一 , 江苏人 , 硕士研究生 , 主要从 事计算机博弈 研究
维普资讯
张
颖, : 等 棋类计算机博弈 系统的主要研 究方法及在 6 子棋上的应用
9 9
开发 出“ 深 的 蓝 ” 以3 5z2 5 败 了卡 斯 帕 罗 更 , . I .击 t 夫 , 为人 工智 能发 展 的一个 里程 碑 . 成 在 国内 ,06年 , 人 工 智 能 概 念 提 出 5 20 在 0周
六子棋机器博弈关键技术分析

六子棋机器博弈关键技术分析六子棋是一种类似于五子棋的棋类游戏,双方轮流在棋盘上下子,先连成六子的一方获胜。
作为一项智力竞技游戏,六子棋的机器博弈涉及多个关键技术。
下面将对这些关键技术进行分析。
1.棋盘表示与状态表示棋盘表示是指如何将棋盘上的棋子和空位用数据结构表示。
在六子棋中,通常使用二维数组或位图来表示棋盘。
状态表示是指如何用数字或者其他方式表示一局棋局的状态,包括哪些位置有棋子,哪些位置是空的,以及当前轮到谁下子等等。
2.博弈树与算法博弈树是指将游戏的所有可能走法组织成树形结构的一种方法。
在六子棋中,博弈树的根节点表示初始局面,每个节点表示一种可能的下一步走法。
为了找到最好的下一步走法,需要对博弈树进行。
常用的算法包括极大极小值算法、Alpha-Beta剪枝算法等。
3.评估函数评估函数是指用来评估当前局面优劣的一种函数。
在六子棋中,评估函数可以考虑如下因素:棋子的连珠情况,即已经形成多少个连续的棋子;棋子的布局,即是否有可以形成连珠的可能;危险情况,即对手是否有可能在下一步形成连珠;以及其他一些附加条件。
4.深度与剪枝深度是指在博弈树中向下的层数。
深度越深,的时间和计算资源就会越多,但的精度也会更高。
然而,深度受限于计算资源和时间限制。
剪枝是一种在过程中提前终止一些分支的方法,以减少的时间和计算资源。
Alpha-Beta剪枝算法是一种常用的剪枝方法。
5.优化与加速技术为了提高六子棋机器博弈的效率和性能,还可以采用一些优化与加速技术。
例如,使用启发式算法,即根据一些启发式规则来指导;使用置换表,即保存之前的结果,避免重复;使用并行,即利用多个处理器或多线程同时;使用深度学习技术训练神经网络来评估局面等等。
总之,六子棋机器博弈涉及棋盘表示与状态表示、博弈树与算法、评估函数、深度与剪枝、以及优化与加速技术等多个关键技术。
这些技术的综合应用能够提高六子棋机器博弈的效率和性能,使得机器能够在游戏中更好地模拟和预测对手的走法,从而取得更好的胜率。
机器博弈中搜索策略和估值函数的设计
机器博弈中搜索策略和估值函数的设计作者:何轩洪迎伟王开译彭耶萍来源:《电脑知识与技术》2019年第34期摘要:机器博弈是人工智能的头部领域。
该文以六子棋为例,重点介绍了搜索策略和估值函数的设计,主要介绍了博弈树,极大极小值算法,α-β剪枝,MCTS以及基于“路”和“棋型”结合的估值函数。
关键词:六子棋;搜索算法;估值函数中图分类号:TP391 文献标识码:A文章编号:1009-3044(2019)34-0053-021 概述作为二十一世纪三大尖端技术之一的人工智能,其头部研究领域的机器博弈被认为是最富有挑战性的项目之一。
而由吴毅成教授所提出的六子棋,以其玩法简单,情况多变,丰富的乐趣性吸引了大量玩家,并且成为机器博弈的竞赛项目之一。
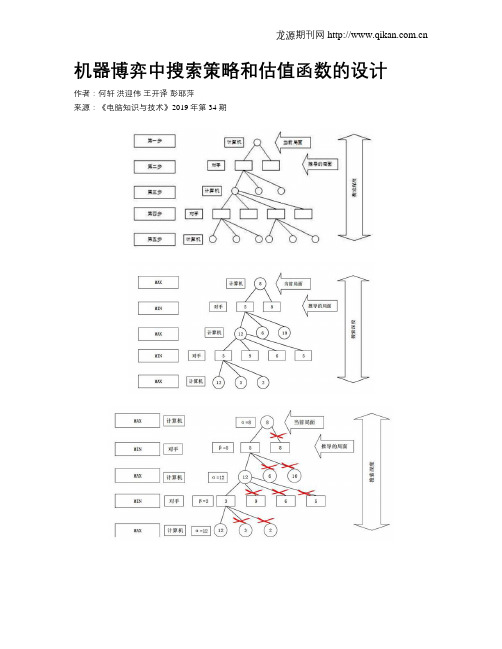
2 搜索算法2.1 博弈树搜索搜索的目的不仅是找出当前所有可以落子的地方,还要考虑到之后更多步数所产生的情况。
博弈树指的是以树的形式把对手和计算机所有落子的情况表示出来。
该博弈树以当前局面为根节点,每一个节点表示一个推导的局面,每一层表示一方所有可能的落子情况,树的层数表示搜索深度。
该树描述的是以当前局面为起始,走n步以后的所有情况。
单纯的博弈树效率很低,所以真正的棋手那样,过滤掉许多不需要考虑的情况,降低搜索的深度,通过改进算法实现在规定时间求出最佳路径。
2.2 极大极小值搜索假设双方都采用最佳的策略,每一种局面都通过估值函数来确定局面的好坏,那么对于己方来说每次都要选择最好的,每次都认为对方选择的是最佳策略,选择估值最低的局面展开博弈树。
2.3 α-β剪枝α—β剪枝是在极大极小值搜索的基础上,舍弃每一次局面没有必要继续搜索下去的情况。
对于MAX的情况来说,只保留最大的分支,对于MIN的情况,只保留最小的分支。
2.4 MCTS树搜索如果直接把α-β剪枝算法直接应用于实际的机器博弈,会有几个问题。
1)即使剪枝过后,推导的局面还是太多。
2)对于每一个局面,如果为了得出每一层准确的估值,而进行相同时间的搜索,会导致搜索的深度不够,无法建立更加深层次的博弈树。
六子棋计算机博弈系统的研究与实现

六子棋计算机博弈系统的研究与实现摘要:本文简述了目前计算机博弈技术的发展状况,通过将六子棋游戏作为计算机博弈技术的研究平台,提出了六子棋计算机博弈的概念。
通过对国外相关研究现状的综述,指出本课题研究的意义。
通过借鉴国际象棋和中国象棋计算机博弈中的成熟技术,提出了建立六子棋计算机博弈系统的关键技术。
关键词:人工智能;六子棋计算机博弈;状态表示;着法生成;棋局评估;博弈树搜索;开局库1 引言人工智能诞生50周年以来,在知识工程、模式识别、机器学习、进化计算、专家系统、自然语言处理、数据挖掘、机器人、图象识别、人工生命、分布式人工智能等各个领域得到了蓬勃的发展[1]。
计算机博弈作为人工智能领域的一个重要分支,也得到了极其快速的发展,并为人工智能带来了很多重要的方法和理论,同时也产生了广泛的社会影响和学术影响以及大量的研究成果。
博弈就是对策[2],是自然界中的普遍现象,它不仅存在于游戏、下棋之中,而且存在于政治、经济、军事和生物竞争中,博弈的参加者可以是个人、集体、某类生物或机器,他们都力图用自己的智力去击败对手。
体现计算机博弈技术的各种棋类游戏在其博弈技术研究中已取得相当丰硕的成果,且各种棋类游戏的计算机博弈系统也日趋完善,基本上能达到大师级水平。
六子棋作为最近两年才兴起的棋类游戏,其计算机博弈技术和算法的研究相对较少[3]。
2 六子棋计算机博弈的研究意义人们常常把计算机博弈描述为人工智能的果蝇,即人类在计算机博弈的研究中衍生了大量的研究成果,这些成果对更广泛的领域产生了重要影响。
通过博弈问题来研究人工智能典型问题,具有以下的优点[4]:(1)博弈问题局限在一个小的有典型意义的围,研究容易深入。
(2)博弈问题非常集中的体现了人类的智能,已经足以为现实世界提供新的方法和新的模型。
(3)专家经验容易获取。
(4)进展可以精确的展示和表现出来,不同方法和模型的优缺点也容易比较。
用一棵树来表示棋局发展的种种可能性,这种树叫做博弈树。
计算机博弈大赛-六子棋知识初步汇总

3:棋型之间的状态演变。
注:除红色标注知识需要必须掌握,其他知识均可后期学习。下附知识框架图,压缩包中具有相关资料。
计算机博弈大赛六子棋知识初步汇总知识比赛大赛计算机知识博弈大赛计算机博弈六子棋家有六子博弈论初步五子棋初步
计算机博弈大赛
一:计算机知识储备
1:C++会编程并会运用“类”,具有编程经验。
2:动态链接库(.dll)文件编程(可后期学习)。
二:数学知识储备
1:博弈论对博弈树,博弈树搜索进行学习(可后期学习)。
六子棋中基于局部“路”扫描方式的博弈树生成算法

六子棋中基于局部“路”扫描方式的博弈树生成算法李学俊;王小龙;吴蕾;刘慧婷【期刊名称】《智能系统学报》【年(卷),期】2015(000)002【摘要】针对六子棋博弈比赛中基于“路”的全局扫描方式的博弈树生成算法效率较低问题,首先分析了基于“路”的全局扫描方式的计算规则和估值分析,然后将博弈树生成算法中的全局扫描方式改进为局部扫描方式,并给出其计算规则和估值分析,接着设计了基于局部扫描方式的博弈树生成算法,并集成到Alpha⁃Beta 剪枝算法中。
最后从搜索效率和博弈水平2个角度对全局扫描和局部扫描进行实验,实验结果表明,局部扫描方式在比赛时间要求的情况下,能够大幅度提高搜索效率,并且博弈水平显著优于全局扫描方式。
%Aiming at the problem that the game⁃tree generation algorithm generated by global scanning method is low in efficiency in the connect 6, this paper analyzes the calculation rules and valuation analysis of the global scanning method based on"road". Secondly, it develops the global scanning method of the game⁃tree generation al⁃gorithm into local scanning method, and introduces the calculation rules and valuation analysis. The game⁃tree gen⁃eration algorithm is a local scanning method designed and integrated into the alpha⁃beta pruning search. Finally, the global and local scanning experiments are carried out from the two perspectives of search efficiency and playing skill. The experimental results showed that local scanningcould greatly improve search efficiency within the compe⁃tition time. The game ability is superior to that of the global scanning method.【总页数】6页(P267-272)【作者】李学俊;王小龙;吴蕾;刘慧婷【作者单位】安徽大学计算机科学与技术学院,安徽合肥230601; 安徽大学计算智能与信号处理重点实验室,安徽合肥230039;安徽大学计算机科学与技术学院,安徽合肥230601;安徽大学计算机科学与技术学院,安徽合肥230601;安徽大学计算机科学与技术学院,安徽合肥230601【正文语种】中文【中图分类】TP31【相关文献】1.六子棋博弈系统中机器学习算法设计与研究 [J], 于江明;袁斌杰;何灿辉;段琢华2.基于PVS算法的六子棋博弈系统的研究 [J], 王鸿菲;王静文;李媛3.基于PVS算法的六子棋博弈系统的研究 [J], 王鸿菲;王静文;李媛4.基于博弈树算法的五子棋游戏的设计与实现 [J], 曹晓燕;王辰5.基于遗传算法的六子棋博弈评估函数参数优化 [J], 李果因版权原因,仅展示原文概要,查看原文内容请购买。
六子棋局面评估以及算法研究

六子棋局面评估以及算法研究经相关专家证明五子棋黑子先手占有必胜的绝对优势,六子棋在k-in-a-row 家族中[1][2][3]由于他的复杂性以及公平性,受到越来越多的关注。
这里将向大家阐述六子棋的特点、攻防策略以及有关六子棋博弈理论以及局面评估如何以算法的形式实现。
Connect(m,n,k,p,q)公平性攻防理论博弈树局面评估搜索策略算法设计六子棋子起步较晚,但近两年已取得不小的进展。
一方面弥补了五子棋“先下者必胜”的窘境,一方面也因为其自身复杂程度引起了工程界广泛的兴趣。
六子棋的复杂性缘于他庞大的分支数。
另外棋局评估也是六子棋的研究重点。
我们可以把五子棋、六子棋归纳为 k-in-a-row的游戏。
游戏的胜利规则是在任意四个方向之一(水平,铅垂,倾角45?),达到k子一线。
台湾国立交通大学的吴毅成教授把他归纳为Connect(m,n,k,p,q)。
其中m,n 代表黑白双方要在m * n 的棋盘上对弈。
比较具有代表性的是19纵横361交叉点的围棋棋盘。
k代表胜利所需必要的连子数目。
q是黑子先手落子的数目,p是以后黑白双方每回合允许着子数目。
首先,有关公平性的定义[1](由吴毅成教授给出):定义1:如果能够证明某方可以赢得比赛,那么博弈是明确不公平(definite unfairness)的。
定义2:如果能证明其中一方不能赢得比赛,那么博弈是单调不公平(monotonicallyunfairness)的。
定义3:如果根据大多数专业棋手观点比赛是对某方有利的,那么博弈是经验主义上的不公平(empirically unfair)。
定义4:如果没有显示或证明以上三条结论一定成立的依据,那么比赛可能是公平的(potentially fair)。
下面,我们简单的阐述一下关五子棋的不公性:我们假设白子可以通过策略S赢得比赛。
黑子随机开局,然后可以更加容易的执行策略S,并赢得比赛。
如果理论S要求黑子在已经落过子的地方落子,那么黑子可以随机的重新选择其他的方格落子。
hex-六角棋ai初步设计(算法复杂度剖析)[最新]
![hex-六角棋ai初步设计(算法复杂度剖析)[最新]](https://img.taocdn.com/s3/m/12f3de1b53ea551810a6f524ccbff121dc36c552.png)
Hex游戏AI的初步设计摘要Hex游戏是一种在以六边形为单元格的棋盘上进行的对弈游戏。
与其他对弈一样,Hex游戏蕴含着丰富的数学知识和博弈技巧,吸引了许多博弈爱好者的关注。
Hex游戏存在先手必胜策略,然而寻找必胜策略被证明是NP难的问题。
本文介绍了Hex游戏的基本规则和特性,给出Hex游戏AI的初步设计,重点介绍极小极大搜索和alpha-beta剪枝策略。
最后将Hex棋抽象为网络流模型,提出基于最大流算法的估值函数,并对估值算法的时间复杂度进行分析。
关键字:Hex游戏,AI,极小极大,alpha-beta剪枝,网络流一、Hex游戏1.1 Hex游戏规则Hex游戏(或Hex棋、Hex博弈)是一种以正六边形为单元格的棋盘类游戏。
Hex棋由丹麦数学家Piet Hein于1942年发明;1948年,该游戏又被美国数学家John Nash重新独立发明,曾一度被称为“Nash Game”。
Hex棋的棋盘可以有不同大小,一般采用11阶,即共有11*11个六边形单元格,每个单元格最多与6个其他单元格相邻。
一个8*8 Hex棋盘如图1所示:图1棋子一般采用黑色和白色,对弈双方各执一种颜色的棋子。
棋盘的四个边界,每组对边由一种颜色标识,属于对弈的一方。
在上图中,黑白双方对弈,黑方执黑子,拥有黑色的一对边界;白方执白子,拥有白色的一对边界。
Hex游戏的对弈规则是:双方轮流下子,可以将自己的棋子下到棋盘中任意空闲的格子里,同种颜色的棋子相邻即认为它们相互连接。
任意一方将自己的两条边界用自己的棋子连接起来,该方则获胜,游戏结束。
我们把将一对边界连接起来的相同颜色棋子所组成的路径成为“获胜链”。
一般由黑方先下子。
1.2 先手必胜Hex棋的一个有趣的特点是,其对弈结果永远不会出现平局。
也就是说,在极端情况下,棋盘中的每个格子都被某种颜色的棋子所占据,那么一定能找到一条获胜链。
David Gale 于1979年通过Brouwer不动点理论加以证明[1]。
博弈树算法

博弈树算法博弈树算法是一种应用于博弈问题分析的算法。
它能够以一种树状结构的方式组织游戏的不同阶段,帮助研究者进行系统的游戏和决策的研究。
在这种研究中,博弈树算法被广泛用于对游戏和对策进行分析。
博弈树算法最初由John von Neumann发明,他是一位著名的数学家,曾发明过单晶格算法。
可以说,博弈树算法是他最突出的成果之一。
博弈树算法的概念是,在研究游戏时,要从游戏初始状态开始,假设玩家会依据某一策略移动,然后以游戏到达另一个状态,以此类推,将游戏的所有状态和可能的解组织成一棵树。
根据每个状态的特点和玩家的策略,游戏的决策者可以分析出每个状态的价值,并通过计算机模拟过程,得出最优的解决方案。
博弈树算法的最大特点就是能够得出一个最优的解决方案,它能够根据不同的游戏状态计算出最优的游戏策略,以获得最大的收益。
由于游戏状态间的相互关系,以及博弈树算法在研究分析中的特殊优势,博弈树算法已成为现代博弈问题研究的重要工具。
博弈树算法被广泛应用于许多不同领域,例如决策支持系统、经济学、金融、管理等领域。
例如,在决策支持系统中,它可以帮助管理者根据系统的决策模型,从而做出最佳的决策;在金融领域,博弈树算法可以帮助投资者分析投资时可能出现的各种情况,从而更好地管理投资风险;在管理领域,博弈树算法可以帮助管理者在处理复杂关系时,精确分析和评估各种可能出现的情况。
博弈树算法在不同领域的应用越来越广泛,被认为是博弈问题研究的重要工具,由此可见,它在系统模拟分析中发挥着重要的作用。
在游戏研究中,博弈树算法的优势进一步得到体现,它能够根据游戏的不同状态计算出最佳的游戏策略,从而帮助研究者从复杂的决策中挑选最佳方案,从而有效提高游戏决策的效率。
由此可见,博弈树算法不仅在游戏研究中发挥着重要作用,而且在多个领域也得到了广泛应用,使用起来非常方便,而且结果更加准确,可谓是一种重要的系统研究工具。
博弈树算法在未来的发展前景也非常可观,在游戏研究和多个领域中,都将发挥着重要的作用。
棋类游戏的算法有哪些

棋类游戏的算法有哪些棋类游戏的算法有哪些棋类游戏通常包含三大要素:棋盘、棋子和游戏规则,其中游戏规则又包括胜负判定规则、落子的规则以及游戏的基本策略。
下面店铺来给大家讲讲各类棋类游戏的算法。
除了棋盘和棋子的建模,棋类游戏最重要的部分就是AI算法的设计。
目前棋类游戏的AI基本上就是带启发的搜索算法,那么常用的搜索算法有哪些呢?1. 博弈与博弈树博弈可以理解为有限参与者进行有限策略选择的竞争性活动,比如下棋、打牌、竞技、战争等。
根据参与者种类和策略选择的方式可以将博弈分成很多种,比如“二人零和、全信息、非偶然”博弈,也就是我们常说的零和博弈(Zero-sum Game)。
所谓“零和”,就是有赢必有输,不存在双赢的结果。
所谓“全信息”,是指参与博弈的双方进行决策时能够了解的信息是公开和透明的,不存在信息不对称的情况。
比如棋类游戏的棋盘和棋子状态是公开的,下棋的双方都可以看到当前所有棋子的位置,但是很多牌类游戏则不满足全信息的条件,因为牌类游戏都不会公开自己手中的牌,也看不到对手手中的牌。
所谓的“非偶然”,是指参与博弈的双方的决策都是“理智”的行为,不存在失误和碰运气的情况。
在博弈过程中,任何一方都希望自己取得胜利,当某一方当前有多个行动方案可供选择时,他总是挑选对自己最为有利同时对对方最为不利的那个行动方案。
当然,博弈的另一方也会从多个行动方案中选择一个对自己最有利的方案进行对抗。
参与博弈的双方在对抗或博弈的过程中会遇到各种状态和移动(也可能是棋子落子)的选择,博弈双方交替选择,每一次选择都会产生一个新的棋局状态。
假设两个棋手(可能是两个人,也可能是两台计算机)MAX和MIN 正在一个棋盘上进行博弈。
当MAX做选择时,主动权在MAX手中,MAX可以从多个可选决策方案中任选一个行动,一旦MAX选定某个行动方案后,主动权就转移到了MIN手中。
MIN也会有若干个可选决策方案,MIN可能会选择任何一个方案行动,因此MAX必须对做好应对MIN的每一种选择。
基于遗传算法的六子棋博弈评估函数参数优化

第29卷第11期 西南大学学报(自然科学版) 2007年11月Vol129 No111Journal of Sout hwest University(Nat ural Science Edition)Nov1 2007文章编号:167329868(2007)1120138205基于遗传算法的六子棋博弈评估函数参数优化①李 果重庆大学自动化学院,重庆400044摘要:将博弈问题分解为搜索引擎、走法生成、评估函数和开局库4大模块,再将自适应遗传算法引入到评估函数中,并通过锦标赛算法对评估函数中的参数组合进行自动调整和优化,设计并开发出基于上述方法的离线自学习系统.关 键 词:六子棋计算机博弈;博弈树;评估函数;锦标赛算法;遗传算法中图分类号:TP11文献标识码:A计算机博弈[1]是人工智能领域一个极其重要且极具挑战性的研究方向,而棋类游戏则是计算机博弈的一个标准性问题.各种搜索算法、模式识别及智能方法在计算机博弈中都可以得到广泛的应用.目前,五子棋、中国象棋等棋类游戏的计算机博弈算法研究已相对成熟,六子棋作为一个刚刚兴起不久的棋类游戏,其计算机博弈算法的研究还相对较少.由于六子棋的特殊性,每次一方走下两颗棋子,其game2tree的复杂度可达10140(按30手计算),远大于五子棋,其state2space复杂度可达10172,与围棋相当.为此,有必要对六子棋的计算机博弈算法展开更加深入的研究,以促进六子棋运动以及计算机博弈的更进一步发展.六子棋计算机博弈可以分解为4个主要部分:搜索引擎、走法生成、评估函数和开局库.评估函数是模式识别和智能算法应用最为广泛的领域.不管多么复杂的评估函数,都可以表示为一个多项式.评估函数一般来说必须包括5个方面的要素,分别是固定子力值、棋子位置值、棋子灵活度值、威胁与保护值、动态调整值.每一方面的值又由许多参数值构成的.即使最简单的评估函数也有20多个参数,将这些值线性地组合在一起得到最终的评估值.由于六子棋无子与子的差别(对于某一方),其评估函数只跟当前棋子的位置以及其周边棋子的位置状态有关,是以上所述5要素的一个子集,因而可以得到简化.但评估函数的确定通常依赖于编程者的棋类知识,这就带来很大的局限性,通过手动调整其参数很难达到全局最优.为了解决这个参数优化的问题,在六子棋计算机博弈领域引入了遗传算法.通过离线自学习训练得到其评估函数的最佳参数组合.1 六子棋的常见棋型及其状态演变的计算机描述要把遗传算法引入到六子棋的评估函数,必须深入了解六子棋的一些常用基本棋型以便对六子棋的常①收稿日期:2007204219作者简介:李 果(19812),男,重庆人,硕士研究生,主要从事模式识别与智能系统的研究.用基本棋型之间的内部联系做更深一步的研究.下面分别给出六子棋的常用基本棋型以及基本棋型间的状态演变.111 六子棋的棋型六子棋常见棋型的定义、英文名称和符号表示如下:【六连】:在棋盘的纵向、横向或斜向的任意一条线上,形成的6颗同色棋子不间隔地相连.英文名称:Continuous six.符号表示:C6.【长连】:在棋盘的纵向、横向或斜向的任意一条线上,形成的7颗或7颗以上同色棋子不间隔地相连.英文名称:Co ntinuous long.符号表示:Cl.【活五】:在同一直线上的5颗同色棋子,符合“对方必须用两手棋才能挡住”的条件.“挡住”是指不让另一方形成六连或长连.英文名称:Active five.符号表示:A5.【眠五】:在同一直线上的5颗同色棋子,符合“对方用一手棋就能挡住”的条件.英文名称:Sleep five.符号表示:S5.【死五】:在同一直线上的5颗同色棋子,它们已无法形成【六连】或【长连】.英文名称:Dead five.符号表示:D5.其它【活四】【眠四】【死四】等定义类似,其符号表示分别为A4、S4、D4、A3、S3、D3、A2、S2、D2,除此之外,还有个比较特殊的棋型:【朦胧三】:在同一直线上的3颗同色棋子,符合“再下一手棋只能形成眠四,但如果再下两手棋的话就能形成活五”的条件.英文名称:Indistinct t hree.符号表示:I3.112 六子棋各棋型间的状态演变上文已对六子棋的常用基本棋型做出了简单的定义,每种棋型都包含不同的对应状态.下面给出六子棋中各棋型的状态演变情况:A5→(S5∪C6∪A4∪S4)S5→(C6∪A5∪A4∪A3∪S5∪D5∪D4∪S3∪I3∪D3∪S2∪D2)D5→(S3∪S4∪D3∪D2)A4→(A5∪S4)S4→(S5∪A5∪A3∪I3∪A2)D4→(D5∪D3∪S3∪S2∪I3)A3→(A4∪S4∪S3∪D3∪S2)I3→(S4∪S3∪D3∪S2∪D2)S3→(S4∪D4∪D3∪D2)D3→(D4)A2→(A3∪S2)S2→(S3∪D2)D2→(D3∪A2∪S2)其中,符号“∪”表示“或”的关系.上述的演变情况包括了本方走一步和对方走一步时的情况,而且每一种演变情况包括不止一种的对应状态,当然状态演变为自身的情况都存在,例如,A5→A5这种情况是肯定存在的,但没有给出.这里,A5→(S5∪C6∪A4∪S4)表示黑白双方的某一方在现有A5棋型的情况下,当己方或对方落下一子后,会转变成S5或C6或A4或S4的棋型.当然,每一种棋型包含不同的对应状态.以A5→S5为例,可能包含不同的棋型对应状态.把棋型之间演变情况的不同对应状态作为一个参数,那么所有可能的演变情况中的不同对应状态就组成了参数组.给每种状态赋予不同的值,组成不同的参数组,形成原始种群,这样就可以用遗传算法来做参数的调整和优化.2 基于遗传算法的六子棋评估函数已经有人尝试着把遗传算法引入评估函数[2],试图学习并发现棋子之间内部的动态联系,但其效果并不理想.本文应用遗传算法做六子棋评估函数的参数调整和优化,并且为了加强遗传算法的局部搜索能力,在进化过程中采用了改进的遗传算法———自适应遗传算法.211 六子棋评估函数的确定上文已经提到,六子棋的评估函数只是评估函数5要素的一个子集,只跟当前棋子的位置以及其周边931第11期 李 果:基于遗传算法的六子棋博弈评估函数参数优化041西南大学学报(自然科学版) 第29卷棋子的位置状态有关,因而可以得到简化.首先从当前落子和当前棋盘状态出发,以当前落子为中心,分别从横向、纵向、左斜向、右斜向4个方向定长地扫描步长为13的点,得到4个方向的状态数组horizonal2 CodeStat us,verticalCodeStat us,left SlopeCodeStat us,right SlopeCodeStat us,每个数组的长度为13.数组中的每一位有4个值:-1,0,1,2,分别表示棋盘外、黑棋、白棋、无子的情况.其中,当前的落子在状态数组的第7位.例如一个黑棋A3→A4的状态数组为{2,2,2,0,0,0,0,2,2,2,2,2,2}.然后通过下式将状态数组映射为一个数值value:value+=value×4+aStep Stat us[i]+1 i=0,1,…,12其中,aStep Stat us表示4个方向中其中一个方向的状态数组,每一个value将对应一个stepValue, stepValue的值首先靠编程者的经验人为的给出.程序预先把value作为“键”,把stepValue作为“值”存储在一个哈希表中.查找哈希表,通过value分别得到4个方向的stepValue:step HorizonalValue,stepVer2 ticalValue,stepLeft SlopeValue,step Right SlopeValue.如果value在哈希表中不存在,其对应的stepValue 默认为0,表示此时的value对于棋局影响不大或几乎没有影响.最终当前落子的评估函数: stepValue=step HorizonalValue+step VerticalValue+stepLeft SlopeValue+step Right SlopeValue212 适应度函数的计算———锦标赛算法遗传算法[3]在进化搜索中基本不需要外部信息,仅以适应度函数(fit ness f unction)为依据,利用种群中每个个体的适应度函数来进行搜索.一般而言,适应度函数是由目标函数变换而成的.但是六子棋的评估比较复杂,很难像一般优化问题那样找到真实准确的目标函数,因此本文设计了一个专门用于棋类优化问题的适应度函数计算方法———锦标赛算法.首先,对已开发的六子棋计算机博弈软件进行拓展,拓展后的程序包含两个评估函数,但是搜索引擎、走法生成都是共用的.两个评估函数通过读取不同的参数组来进行计算机与计算机的对弈,并决出胜负.这样,就可以通过竞赛的方式来确定下棋双方的适应度,也就是参数组的优劣.在相同适应度的初始状态下,赢的一方对适应度进行加运算(奖赏),输的一方对适应度进行减运算(惩罚),和棋则不操作.这样就解决了适应度函数不好确定的问题,实现了通过适应度函数来决定个体的优劣程度,体现了自然进化中的优胜劣汰原则.遗传算法处理的对象主要是个体[4-5].个体包括一组染色体串,其中每一个染色体对应于评估函数中的一个参数值,也就是上文提到的某一个状态数组的stepValue.将染色体串解码到评估函数中即可求得评估值.213 遗传操作过程21311 锦标赛选择锦标赛模式[6]的缺点在于速度过慢.为了加快速度对标准锦标赛做了改进.将包含m个个体的种群随机分成n组,分别记为Group[i](i=1,2,…,n),每组包含m/n个个体.分别在各组内进行锦标赛训练,得到每个组的冠军,分别记为Champion[i](i=1,2,3,…,n),其为筛选出的最佳.从而对n个冠军相互之间做交叉和变异操作产生m-n个新个体,分别记为NewBody[i](i=n+1,n+2,…,m),以Champion [i]和NewBody[i]为个体形成一个个体数为m的新种群,即下一代种群.经过优化后,以包含20个个体的种群为例,在保证优胜劣汰原则的基础上,可以节省约80%的时间.21312 均匀交叉交叉方法很多,有单点交叉、多点交叉、顺序交叉、循环交叉等等.为了使交叉在便于操作的同时更加广义化,选用均匀交叉,参数之间的间隔点作为潜在的交叉点.均匀交叉根据交叉率P c随机地产生与参数个数等长的0-1掩码,掩码中的片断表明了哪个父个体向子个体提供变量值.通过这个掩码和选择的父个体一起确定子个体.21313 变 异变异是指以等于变异率P m 的概率改变一个或几个基因,对于二进制串来说,就是根据变异率来实现基因的0-1翻转.变异是一种局部随机搜索,与选择/交叉算子结合在一起,保证了遗传算法的有效性,使遗传算法具有局部的随机搜索能力,同时使得遗传算法保持种群的多样性,以防止出现非成熟的收敛.214 改进的遗传算法在整个遗传算法实现的过程中,交叉率P c 和变异率P m 的选择是影响遗传算法行为和性能的关键所在,直接影响算法的效率以及收敛性.P c 越大,新个体产生的速度就越快,然而P c 过大时遗传模式或信息被破坏的可能性也越大,使得具有高适应度的个体结构很快就会被破坏;但是如果P c 过小,会使搜索过程缓慢,以至停滞不前,得不到适应度较高的个体.对于变异率P m ,如果P m 取值过小,就不容易产生新的个体结构;如果P m 取值过大,那么遗传算法就变成了纯粹的随机搜索算法,失去了其本来的意义.目前,还没有通用的一次性确定P c 和P m 的方法.针对不同的优化问题,需要反复通过实验和调试来确定P c 和P m ,这是一件非常繁琐的工作.为此,自适应遗传算法[7],P c 和P m 能够随着适应度自动改变.P c 和P m 的计算公式如下:p c =p c 1-(p c 1-p c 2)(f ′-f avg )f max -f avgf ′≥f avg p c 1f ′<f avg p m =p m 1-(p m 1-p m 2)(f max -f )f max -f avgf ′≥f max p m 1f ′<f max 其中:P c 1=019,P c 2=016,P m 1=011,P m 2=01001,f max 为群体中最大的适应度值,f avg 为每代群体的平均适应度值,f ′为要交叉的两个个体中较大的适应度值,f 为要变异个体的适应度值.经过改进的自适应遗传算法中的P c 和P m 能够提供相对某个解的最佳P c 和P m ,在保持群体多样性的同时,保证了遗传算法的效率和收敛性.图1 比赛结果3 实验设计及实验结果为了测试进化效果,找出较好的参数组,本文设计了一个测试实验,分别取出50代、100代、150代、200代、250代、300代的冠军以及两个随机选手组成一个小组,进行单循环比赛.每两个对手之间都要进行互换先后手的两场比赛,胜者积分加1,负者积分减1,平局双方积分不变,最后积分情况如图1.从图中可以看出,得分随着代数的增加而单调增加,而参加比赛的随机选手基本上没有获胜的机会.这里给出了进化到300代时的训练结果.用300代的参数组和完全用经验设定的参数组的程序进行了比赛,结果用进化到300代的参数组的胜率明显占优.5 结 论在六子棋的评估函数中,引入了自适应遗传算法优化参数组合,加强了传统的遗传算法的搜索能力,避免了传统的爬山法容易陷入局部最优的缺点,也不像模拟退火算法那样收敛过慢.它同时维护一组参数,既可以继承已有参数中的优良部分,又可以避免因局部震荡而失败,并且具有较高的效率和收敛速度,可以最大限度的发挥评估函数的作用,也为开发高质量的六子棋计算机博弈程序打下了坚实的基础.141第11期 李 果:基于遗传算法的六子棋博弈评估函数参数优化241西南大学学报(自然科学版) 第29卷参考文献:[1]王小春.PC游戏编程[M].重庆:重庆大学出版社,2002:1-27.[2] Lorenz D,Markovitch S.Derivative Evaluation Function Learning Using G enetic Operators[A].Proceedings oftheAAA I Fall Symposium on G ames:Planing and Learning[C].New Carolina,1993:106-114.[3] Holland J H.A Daptation in Nature and Artificial System[M].Ann Arbor:The University of Michigan Press,1975.[4] 米凯利维茨.演化程序遗传算法和数据编码的结合[M].北京:科学出版社,2000:20-23.[5] 李敏强,遗传算法的基本理论与应用[M].北京:科学出版社,2002:1-15.[6] 王小平,曹立明.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社,2002:195-210.[7] Angeline J,Pollack petitive Environments Evolve Better Solution for Complex Tasks[A].Proceedings of theFifth International Conference on Genetic Algorithms[C].SanMateo:Morgan Kauf man Publishers,1993:264-270.Adjustment and Optimization of the Connect6Evalu ationFunction P arameters B ased on G enetic AlgorithmL I GuoColle ge of Automation,Chongqing University,Chongqing400044,ChinaAbstract:Genetic Algorit hm(GA)is used in t he co mp uter game of Connect6.The p roblems of t he game are divided into four part s:search engine,move generator,evaluation f unction and starting step s database. Then t he modified GA is applied in t he evaluation f unction,so as to automatically adjust and optimize it s parameters t hrough t he Tournament Algorit hm.At last,a self2learning system is designed and developed based on t he met hod above.K ey w ords:comp uter game of connect6;game tree;evaluatio n f unction;tournament algorit hm;genetic al2 gorit hm责任编辑 张 栒 。
