2018北海市中考必备数学模拟试卷(19)附详细试题答案
2018年北海市重点初中入学模拟考试数学试题与答案

2018年北海市重点初中入学模拟考试数学试题与答案(满分100分,时间90分钟)一、填一填。
(1-3题每空1分,4-12题每空2分,共30分)1、0.572的小数单位是( ),它有( )个这样的单位。
2、5.07吨=()吨()千克 4升58毫升=()升5.03公顷=( )公顷( )平方米8千米21米=( )千米公元2018年第一季度()天。
3、4.385385385……,它的循环节是( ),用简便方法表示是( ),将它保留三位小数是( )。
4、六个自然数的平均数是7,其中前四个数的平均数是8,第4个数是11,那么后三个数的平均数是()。
5、大小两个圆的周长之比是4:1,那么这两个圆的面积之比是()。
6、在下面式子中的方框内填入同样的数字,使等式成立:7□×6432=□7×7296,那么,此□=()。
7、在两位自然数的十位与个位中间插入0~9中的一个数码,这个两位数就变成了三位数.某些两位数中间插入某个数码后变成的三位数,是原来两位数的9倍.这样的两位数共有()个。
8、10个连续偶数的和是从1开始的10个连续奇数和的3.5倍,其中最大的偶数是()。
9、一个正方体的棱长由5厘米变成8厘米,表面积增加了()平方厘米。
10、200个连续自然数的和是32300,取出其中所有的第偶数个数(第2个,第4个,……,第200个),将它们相加,则和是( )。
11、将一根长为1997厘米的铁丝截成199厘米和177厘米两种长度的铁丝,剩余部分最少是()厘米。
12、有55个棱长为1分米的正方体木块,在地面上摆成如图所示的形式,要在表面涂刷油漆,如果与地面接触的面不涂油漆,干后将小木块分开,则涂油漆的表面积与未涂油漆表面积的比是()。
二、判断。
(每小题1分,共6分)1、0是自然数。
( )2、梯形的面积等于上、下底的和与高的积的一半。
( )3、36和48的最大公约数是12,公约数是1、2、3、4、6、12。
〖2019数学中考首发〗广西北海市2018年中考数学试题含答案(Word版)

3 33 广西北海市2018年中考数学试题(考试时间:120 分钟 满分:120 分)注意事项:1. 本试卷分第 I 卷(选择题)和第 II 卷(非选择题)两部分,请在答题卡上作答,在试卷上作答无效。
2. 答题前,请认真阅读答题卡上的注意事项。
3. 不能使用计算器,考试结束前,将本试卷和答题卡一并交回。
一、选择题(本大题共 12 小题,每小题 3 分,共 36 分.在每小题给出的四个选项中只有一项是符合要求的,用 2B 铅笔把答题卡上对应题目的答案标号涂黑.)1. -3 的倒数是 A. -3B. 3C. -1D. 1【答案】C【考点】倒数定义,有理数乘法的运算律,【解析】根据倒数的定义,如果两个数的乘积等于 1,那么我们就说这两个数互为倒数.除 0 以外的数都存在倒数。
因此-3 的倒数为-1【点评】主要考察倒数的定义2. 下列美丽的壮锦图案是中心对称图形的是【答案】A【考点】中心对称图形【解析】在平面内,如果把一个图形绕某个点旋转180°后,能与自身重合,那么这个图形就叫做中心对称图形。
【点评】掌握中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180 度后两部分重合.3.2018 年俄罗斯世界杯开幕式于6 月14 日在莫斯科卢日尼基球场举行,该球场可容纳81000 名观众,其中数据81000 用科学计数法表示为()A. 81⨯103B. 8.1⨯104C. 8.1⨯105D. 0.81⨯105【答案】B【考点】科学计数法【解析】81000 = 8.1⨯104,故选B【点评】科学计数法的表示形式为a ⨯10n的形式,其中1 ≤a < 10,n为整数4.某球员参加一场篮球比赛,比赛分4 节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分为()A.7 分B.8 分C.9 分D.10 分【答案】B【考点】求平均分【解析】12 + 4 +10 + 6 = 84【点评】本题考查用折线图求数据的平均分问题5.下列运算正确的是A. a(a+1)=a2+1B. (a2)3=a5C. 3a2+a=4a3D. a5÷a2=a3【答案】D【考点】整式的乘法;幂的乘方;整式的加法;同底数幂的除法【解析】选项A 错误,直接运用整式的乘法法则,用单项式去乘多项式的每一项,再把结果相加,可得a(a+1)=a2+a;选项B 错误,直接运用幂的乘方法则,底数不变,指数相乘,可得(a2)3=a6;选项C 错误,直接运用整式的加法法则,3a2 和a 不是同类项,不可以合并;选项D 正确,直接运用同底数幂的除法,底数不变,指数相减,可得a5÷a2=a3.【点评】本题考查整式的四则运算,需要记住运算法则及其公式,属于基础题。
2018年广西北海市中考数学试卷

2018年广西北海市中考数学试卷一、选择题(本大题共12小题,每小题3分,共36分。
在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑。
)1.(3.00分)(2018•常州)﹣3的倒数是()A.﹣3 B.3 C.﹣ D.2.(3.00分)(2018•广西)下列美丽的壮锦图案是中心对称图形的是()A.B.C.D.3.(3.00分)(2018•广西)2018年俄罗斯世界杯开幕式于6月14日在莫斯科卢日尼基球场举行,该球场可容纳81000名观众,其中数据81000用科学记数法表示为()A.81×103 B.8.1×104C.8.1×105D.0.81×1054.(3.00分)(2018•广西)某球员参加一场篮球比赛,比赛分4节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分为()A.7分 B.8分 C.9分 D.10分5.(3.00分)(2018•广西)下列运算正确的是()A.a(a+1)=a2+1 B.(a2)3=a5C.3a2+a=4a3D.a5÷a2=a36.(3.00分)(2018•广西)如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于()A.40°B.45°C.50°D.55°7.(3.00分)(2018•广西)若m>n,则下列不等式正确的是()A.m﹣2<n﹣2 B.C.6m<6n D.﹣8m>﹣8n8.(3.00分)(2018•广西)从﹣2,﹣1,2这三个数中任取两个不同的数相乘,积为正数的概率是()A.B.C.D.9.(3.00分)(2018•广西)将抛物线y=x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为()A.y=(x﹣8)2+5 B.y=(x﹣4)2+5 C.y=(x﹣8)2+3 D.y=(x﹣4)2+3 10.(3.00分)(2018•广西)如图,分别以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为()A.B.C.2 D.211.(3.00分)(2018•广西)某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为()A.80(1+x)2=100 B.100(1﹣x)2=80 C.80(1+2x)=100 D.80(1+x2)=10012.(3.00分)(2018•广西)如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为()A.B.C.D.二、填空题(本大题共6小题,每小题3分,共18分)13.(3.00分)(2018•广西)要使二次根式在实数范围内有意义,则实数x 的取值范围是.14.(3.00分)(2018•广西)因式分解:2a2﹣2=.15.(3.00分)(2018•广西)已知一组数据6,x,3,3,5,1的众数是3和5,则这组数据的中位数是.16.(3.00分)(2018•广西)如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是m(结果保留根号)17.(3.00分)(2018•广西)观察下列等式:30=1,31=3,32=9,33=27,34=81,35=243,…,根据其中规律可得30+31+32+…+32018的结果的个位数字是.18.(3.00分)(2018•广西)如图,矩形ABCD的顶点A,B在x轴上,且关于y 轴对称,反比例函数y=(x>0)的图象经过点C,反比例函数y=(x<0)=7,k1+3k2=0,则k1等于.的图象分别与AD,CD交于点E,F,若S△BEF三、解答题(本大题共8小题,共66分,解答题因写出文字说明、证明过程或演算步骤)19.(6.00分)(2018•广西)计算:|﹣4|+3tan60°﹣﹣()﹣1 20.(6.00分)(2018•广西)解分式方程:﹣1=.21.(8.00分)(2018•广西)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)22.(8.00分)(2018•广西)某市将开展以“走进中国数学史”为主题的知识竞赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:(1)求m=,n=;(2)在扇形统计图中,求“C等级”所对应心角的度数;(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.23.(8.00分)(2018•广西)如图,在▱ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.(1)求证:▱ABCD是菱形;(2)若AB=5,AC=6,求▱ABCD的面积.24.(10.00分)(2018•广西)某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.(1)求甲、乙两仓库各存放原料多少吨?(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元/吨(10≤a ≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.25.(10.00分)(2018•广西)如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.(1)求证:PG与⊙O相切;(2)若=,求的值;(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.26.(10.00分)(2018•广西)如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD ⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.(1)求抛物线的解析式及点D的坐标;(2)当△CMN是直角三角形时,求点M的坐标;(3)试求出AM+AN的最小值.2018年广西北海市中考数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分。
2018年中考数学模拟试题及答案(共五套)

中考模拟试卷数学卷一、仔细选一选。
(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确答案. 1.下列四个运算中,结果最小的是( ). A 、2017的相反数 B 、2017的绝对值 C 、2017的0次幂 D 、2017的立方根 2.已知∠α=23°45′,则∠α的余角=( ).A .66°55′B .156°15′C .66°15′D .156°55′3.若代数式x 2+bx 可以分解因式,则常数b 不可以是( ). A .﹣1B .0C .1D .24.在代数式x ﹣y, 4a, y+,,yz, ,中有( ).A .5个整式B .3个单项式,4个多项式C .6个整式,4个单项式D .单项式与多项式的个数相同5.下图是小方送给她外婆的生日蛋糕,则下面关于三种视图判断正确的( ).A.主视图、俯视图、左视图都正确B.主视图、俯视图、左视图都错误C.主视图、左视图正确、俯视图错误D. 左视图、俯视图正确、主视图错误 6.已知⎩⎨⎧>≤-,,a xb x 则的值( ).A.大于0B.小于0C.大于或等于0D.小于或等于07.某超市举办促销活动,促销方式是将原价x 元的衣服以(45x -10) 元出售,则下列说法中,能正确表达该超市促销方式的是( ).A. 原价减去10元后再打8折B. 原价打8折后再减去10元C. 原价减去10元后再打2折D. 原价打2折后再减去10元8.如图为4×4的网格图,A ,B ,C ,D ,O 均在格点上,点O 是( ).(第8题图) A .△ACD 的外心 B .△ABC 的外心C .△ACD 的内心 D .△ABC 的内心9.在同一直角坐标系中,对于以下四个函数①y=-x-1;②y=x+1;③y=-x+1; ④y=-2(x+1)的图像。
2018年广西北海市中考数学试卷

2018年广西北海市中考数学试卷一、选择题(本大题共12小题,每小题3分,共36分。
在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑。
)1.(3.00分)﹣3的倒数是()A.﹣3 B.3 C.﹣D.2.(3.00分)下列美丽的壮锦图案是中心对称图形的是()A.B.C.D.3.(3.00分)2018年俄罗斯世界杯开幕式于6月14日在莫斯科卢日尼基球场举行,该球场可容纳81000名观众,其中数据81000用科学记数法表示为()A.81×103B.8.1×104C.8.1×105D.0.81×1054.(3.00分)某球员参加一场篮球比赛,比赛分4节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分为()A.7分B.8分C.9分D.10分5.(3.00分)下列运算正确的是()A.a(a+1)=a2+1 B.(a2)3=a5C.3a2+a=4a3D.a5÷a2=a36.(3.00分)如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于()A.40°B.45°C.50°D.55°7.(3.00分)若m>n,则下列不等式正确的是()A.m﹣2<n﹣2 B.C.6m<6n D.﹣8m>﹣8n8.(3.00分)从﹣2,﹣1,2这三个数中任取两个不同的数相乘,积为正数的概率是()A.B.C.D.9.(3.00分)将抛物线y=x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为()A.y=(x﹣8)2+5 B.y=(x﹣4)2+5C.y=(x﹣8)2+3 D.y=(x﹣4)2+310.(3.00分)如图,分别以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为()A.B.C.2 D.211.(3.00分)某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为()A.80(1+x)2=100 B.100(1﹣x)2=80C.80(1+2x)=100 D.80(1+x2)=10012.(3.00分)如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为()A.B.C.D.二、填空题(本大题共6小题,每小题3分,共18分)13.(3.00分)要使二次根式在实数范围内有意义,则实数x的取值范围是.14.(3.00分)因式分解:2a2﹣2=.15.(3.00分)已知一组数据6,x,3,3,5,1的众数是3和5,则这组数据的中位数是.16.(3.00分)如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是m(结果保留根号)17.(3.00分)观察下列等式:30=1,31=3,32=9,33=27,34=81,35=243,…,根据其中规律可得30+31+32+…+32018的结果的个位数字是.18.(3.00分)如图,矩形ABCD的顶点A,B在x轴上,且关于y轴对称,反比例函数y=(x>0)的图象经过点C,反比例函数y=(x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于.三、解答题(本大题共8小题,共66分,解答题因写出文字说明、证明过程或演算步骤)19.(6.00分)计算:|﹣4|+3tan60°﹣﹣()﹣120.(6.00分)解分式方程:﹣1=.21.(8.00分)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)22.(8.00分)某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:(1)求m=,n=;(2)在扇形统计图中,求“C等级”所对应心角的度数;(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.23.(8.00分)如图,在▱ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.(1)求证:▱ABCD是菱形;(2)若AB=5,AC=6,求▱ABCD的面积.24.(10.00分)某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.(1)求甲、乙两仓库各存放原料多少吨?(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a ≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.25.(10.00分)如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.(1)求证:PG与⊙O相切;(2)若=,求的值;(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.26.(10.00分)如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.(1)求抛物线的解析式及点D的坐标;(2)当△CMN是直角三角形时,求点M的坐标;(3)试求出AM+AN的最小值.参考答案1.C.2.A.3.B.4.B.5.D.6.C.7.B.8.C.9.D.10.D.11.A.12.C.13.x≥5.14.2(a+1)(a﹣1).15.4.16.40.17.3.18.919.解:原式=4+3﹣2﹣2=+2.20.解:两边都乘以3(x﹣1),得:3x﹣3(x﹣1)=2x,解得:x=1.5,检验:x=1.5时,3(x﹣1)=1.5≠0,所以分式方程的解为x=1.5.21.解:(1)如图所示,△A1B1C1即为所求:(2)如图所示,△A2B2C2即为所求:(3)三角形的形状为等腰直角三角形,OB=OA1=,A1B=,即,所以三角形的形状为等腰直角三角形.22.解:(1)参加本次比赛的学生有:4÷0.04=100(人);m=0.51×100=51(人),D组人数=100×15%=15(人),n=100﹣4﹣51﹣15=30(人)故答案为51,30;(2)B等级的学生共有:50﹣4﹣20﹣8﹣2=16(人).∴所占的百分比为:16÷50=32%∴C等级所对应扇形的圆心角度数为:360°×30%=108°.(3)列表如下:∵共有12种等可能的结果,选中1名男生和1名女生结果的有6种.∴P(选中1名男生和1名女生)==.23.(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D,∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°,∵BE=DF,∴△AEB≌△AFD∴AB=AD,∴四边形ABCD是平行四边形.(2)连接BD交AC于O.∵四边形ABCD是菱形,AC=6,∴AC⊥BD,AO=OC=AC=×6=3,∵AB=5,AO=3,∴BO===4,∴BD=2BO=8,=×AC×BD=24.∴S平行四边形ABCD24.解:(1)设甲仓库存放原料x吨,乙仓库存放原料y吨,由题意,得,解得,甲仓库存放原料240吨,乙仓库存放原料210吨;(2)由题意,从甲仓库运m吨原料到工厂,则从乙仓库云原料(300﹣m)吨到工厂,总运费W=(120﹣a)m+100(300﹣m)=(20﹣a)m+30000;(3)①当10≤a<20时,20﹣a>0,由一次函数的性质,得W随m的增大而增大,②当a=20是,20﹣a=0,W随m的增大没变化;③当20≤a≤30时,则20﹣a<0,W随m的增大而减小.25.解:(1)如图,连接OB,则OB=OD,∴∠BDC=∠DBO,∵∠BAC=∠BDC、∠BDC=∠GBC,∴∠GBC=∠BDC,∵CD是⊙O的切线,∴∠DBO+∠OBC=90°,∴∠GBC+∠OBC=90°,∴∠GBO=90°,∴PG与⊙O相切;(2)过点O作OM⊥AC于点M,连接OA,则∠AOM=∠COM=∠AOC,∵=,∴∠ABC=∠AOC,又∵∠EFB=∠OGA=90°,∴△BEF∽△OAM,∴=,∵AM=AC,OA=OC,∴=,又∵=,∴=2×=2×=;(3)∵PD=OD,∠PBO=90°,∴BD=OD=8,在Rt△DBC中,BC==8,又∵OD=OB,∴△DOB是等边三角形,∴∠DOB=60°,∵∠DOB=∠OBC+∠OCB,OB=OC,∴∠OCB=30°,∴=,=,∴可设EF=x,则EC=2x、FC=x,∴BF=8﹣x,在Rt△BEF中,BE2=EF2+BF2,∴100=x2+(8﹣x)2,解得:x=6±,∵6+>8,舍去,∴x=6﹣,∴EC=12﹣2,∴OE=8﹣(12﹣2)=2﹣4.26.解:(1)把A(﹣3,0),C(0,4)代入y=ax2﹣5ax+c得,解得,∴抛物线解析式为y=﹣x2+x+4;∵AC=BC,CO⊥AB,∴OB=OA=3,∴B(3,0),∵BD⊥x轴交抛物线于点D,∴D点的横坐标为3,当x=3时,y=﹣×9+×3+4=5,∴D点坐标为(3,5);(2)在Rt△OBC中,BC===5,设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,∵∠MCN=∠OCB,∴当=时,△CMN∽△COB,则∠CMN=∠COB=90°,即=,解得m=,此时M点坐标为(0,);当=时,△CMN∽△CBO,则∠CNM=∠COB=90°,即=,解得m=,此时M点坐标为(0,);综上所述,M点的坐标为(0,)或(0,);(3)连接DN,AD,如图,∵AC=BC,CO⊥AB,∴OC平分∠ACB,∴∠ACO=∠BCO,∵BD∥OC,∴∠BCO=∠DBC,∵DB=BC=AC=5,CM=BN,∴△ACM≌△DBN,∴AM=DN,∴AM+AN=DN+AN,而DN+AN≥AD(当且仅当点A、N、D共线时取等号),∴DN+AN的最小值==,∴AM+AN的最小值为.。
广西北海市2018届数学中考模拟试卷(6月份)

广西北海市2018届数学中考模拟试卷(6月份)一、单1.在0,﹣2,3,四个数中,最小的数是()A、0B、﹣2C、3D、+2.下列基本几何体中,三视图都是相同图形的是()A、B、C、D、+3.据报道,南宁创客城已于2015年10月开城,占地面积约为14400平方米,目前已引进创业团队30多家,将14400用科学记数法表示为()A、14.4×103B、144×102C、1.44×104D、1.44×10﹣4+4.下面调查中,适合采用全面调查的是()A、对南宁市市民进行“南宁地铁1号线线路”B、对你安宁市食品安全合格情况的调查C、对南宁市电视台《新闻在线》收视率的调查D、对你所在的班级同学的身高情况的调查+5.下列运算正确的是()A、=2B、4 ﹣=1C、=9D、=2+6.不等式组的解集在数轴上可表示为()C、A、B、D、+7.一个多边形的内角和是360°,则这个多边形的边数为()A、6B、5C、4D、3+8.一元二次方程x2﹣3x+1=0的根的情况()A、有两个相等的实数根B、有两个不相等的实数根C、没有实数根D、以上答案都不对+9.已知⊙O的半径为5.若OP=6,则点P与⊙O的位置关系是()A、点P在⊙O内B、点P在⊙O上C、点P在⊙O外D、无法判断+10.甲、乙两人分别以4m/s和5m/s的速度,同时从100m直线型跑道的起点向同一方向起跑,设乙的奔跑时间为t(s),甲乙两人的距离为S(m),则S关于t的函数图象为()A、B、C、D、+11.如图①是半径为2的半圆,点C是弧AB的中点,现将半圆如图②方式翻折,使得点C与圆心O重合,则图中阴影部分的面积是()A 、+ B 、 C 、 D 、12.如图,在△ABC 中,AB=AC ,AD 和CE 是高,∠ACE=45°,点F 是AC 的中点,AD 与FE ,CE 分别交于点G 、H ,∠BCE=∠CAD ,有下列结论:①图中存在两个等腰 直角三角形;②△AHE ≌△CBE ;③BC?AD= 其中正确的个数有()AE 2;④S △ABC =4S △ADF. A 、1 B 、2 C 、3 D 、4+二、填空题13.分解因式:2x 2﹣2= . +14.如图,平行线AB 、CD 被直线EF 所截,若∠2=130°,则∠1= .+15.某商品原售价为100元,经连续两次涨价后售价为121元,设平均每次涨价的百分率为x,则依题意所列的方程是.+16.如图,甲、乙两船同时从港口出发,甲船以60海里/时的速度沿北偏东60°方向航行,乙船沿北偏西30°方向航行,半小时后甲船到达C点,乙船正好到达甲船正西方向的B点,则乙船的路程(结果保留根号)+17.如图,在平面直角坐标系中,函数y=(k>0)的图象经过点A(1,2)、B两点,过点A作x轴的垂线,垂足为C,连接AB、BC.若三角形ABC的面积为3,则点B的坐标为.+18.如图所示,扇形OMN的圆心角为45°,正方形A1B1C1A2的边长为2,顶点A1,A2在线段OM上,顶点B1在弧MN上,顶点C1在线段ON上,在边A2C1上取点B 2,以A2B2为边长继续作正方形A2B2C2A3,使得点C2在线段ON上,点A3在线段OM上,……,依次规律,继续作正方形,则A2018 M= .+三、解答题19.计算:2﹣1+20160﹣|3tan30°+|﹣+20.解方程:+21.某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了以下两幅不完整的统计图:请根据以上统计图提供的信息,解答下列问题:(1)、共抽取名学生进行问卷调查;(2)、补全条形统计图,求出扇形统计图中“足球”所对应的圆心角的度数;(3)、该校共有3000名学生,请估计全校学生喜欢足球运动的人数.(4)、甲乙两名学生各选一项球类运动,请求出甲乙两人选同一项球类运动的概率.+22.已知BD平分∠ABF,且交AE于点D.(1)、求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);(2)、设AP交BD于点O,交BF于点C,连接CD,当AC⊥BD时,求证:四边形AB CD是菱形.+23.如图,直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣1),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CB O.(1)、请直接写出⊙M的直径,并求证BD平分∠ABO;(2)、在线段BD的延长线上寻找一点E,使得直线AE恰好与⊙M相切,求此时点E的坐标.+24.甲、乙两组工人同时加工某种零件,乙组在加工过程中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍,两组各组加工零件的数量y(件)与时间x(时)的函数图象如图所示.(1)、求甲组加工零件的数量y与时间x之间的函数关系式;(2)、求乙组加工零件总量a的值;(3)、甲、乙两组加工出的零件合在一起装箱,每次生产达到150件就装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第2箱?+25.矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.(1)、如图1,已知折痕与边BC交于点O,连接AP、OP、OA.①求证:△OCP∽△PDA;②若△OCP与△PDA的面积比为1:4,求边AB的长.(2)、如图2,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M、N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.+26.如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D,已知A(﹣1,0).(1)、求点B的坐标和抛物线的解析式;(2)、判断△CDB的形状并说明理由;(3)、将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.+。
广西北海市数学中考模拟试卷

广西北海市数学中考模拟试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2018·黄冈) 下列运算结果正确的是()A . 3a3·2a2=6a6B . (-2a)2= -4a2C . tan45°=D . cos30°=2. (2分)下列各组图形中,右边的图形与左边的图形成中心对称的是()A .B .C .D .3. (2分)“十二五”期间,我国将新建保障性住房36000000套,用于解决中低收入和新参加工作的大学生住房的需求,把36000000用科学记数法表示应是()A . 3.6×107B . 3.6×106C . 36×106D . 0.36×1084. (2分)(2018·哈尔滨) 已知反比例函数的图象经过点(1,1),则k的值为().A . -1B . 0C . 1D . 25. (2分)(2013·丽水) 用3个相同的立方块搭成的几何体如图所示,则它的主视图是()A .B .C .D .6. (2分)如图,△ABC内接于⊙O,∠A = 40°,则∠BOC的度数为()A . 20°B . 40°C . 60°D . 80°7. (2分)(2017·洛阳模拟) 下列各数中,最小的数是()A . 0B .C . ﹣D . ﹣38. (2分) (2017八下·邵阳期末) 如图,有一张一个角为30° ,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是()A . 8或B . 10或4+C . 10或D . 或4+9. (2分)(2020·武汉模拟) 如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为()A . 100°B . 120°C . 135°D . 150°10. (2分)已知反比例函数,有下列四个结论:① 图象必经过点(-1,2);② 图像经过(x1,y1),(x2,y2)两点,若x1<x2 ,则y1<y2;③ 图象分布在第二、四象限内;④ 若x>1,则y>-2.其中正确的有()A . 1个B . 2个C . 3个D . 4个11. (2分) (2016九上·嵊州期中) 当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m 的值为()A . ﹣B . 或﹣C . 2或﹣D . 2或或﹣12. (2分)如图,在Rt△ABC中,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得△A'B'O,那么点A'的坐标为()A . (, 1)B . (1,)C . (-1,)D . (, -1)二、填空题 (共6题;共6分)13. (1分)若x+y=2,x2﹣y2=6,则x﹣y=________.14. (1分)函数的图象如图所示,则结论:①两函数图象的交点的坐标为;②当时,;③当时,;④当逐渐增大时,随着的增大而增大,随着的增大而减小.其中正确结论的序号是________.15. (1分)从-2,-1,1,2,3这五个数中随机抽取一数,作为函数y=mx2+2mx+2中的m的值,若能使函数与x轴有两个不同的交点A、B,与y轴的交点为C,且△ABC的面积大于的概率为:________16. (1分)如图,在大小为的正方形网格中,是相似三角形的是________(请填上编号).17. (1分)(2017·海曙模拟) 已知,抛物线y=ax2+bx+3满足2a+b=0,写出该抛物线上可以确定的点的坐标________.18. (1分) (2019八下·海淀期中) 如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC= ,OC= ,则另一直角边BC的长为________.三、解答题 (共7题;共53分)19. (10分)用适当的方法解下列方程:(1)(2x+1)2=(x﹣1)2(2).20. (9分)(2018·恩施) 为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:(1) a=________,b=________,c=________;(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为________度;(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.21. (2分) (2017九上·湖州月考) 如图,的图像交x轴于O点和A点,将此抛物线绕原点旋转180°得图像y2 , y2与x轴交于O点和B点.(1)若y1=2x2-3x,则y2=________ .(2)设 y 1 的顶点为C,则当△ABC为直角三角形时,请你任写一个符合此条件的 y 1 的表达式________ .22. (5分)(2017·长乐模拟) 如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈ ,tan37°≈ ,sin67°≈ ,tan67°≈ )23. (15分) (2017九上·吴兴期中) 为鼓励大学生毕业后自主创业,市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给应届毕业生自主销售,成本价与出厂价之间的差价由政府承担.赵某按照相关政策投资销售本市生产的一种新型“儿童玩具枪”.已知这种“儿童玩具枪”的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.(1)赵某在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)设赵某获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?(3)物价部门规定,这种“儿童玩具枪”的销售单价不得高于28元.如果赵某想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?24. (5分)(2016·张家界) 已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.25. (7分) (2016九上·岑溪期中) 如图,在平面直角坐标系中,已知抛物线y=x2﹣bx+c经过A(0,3),B (1,0)两点,顶点为M.(1)则b=________,c=________;(2)将△OAB绕点B顺时针旋转90°后,点A落到点C的位置,该抛物线沿y轴上下平移后经过点C,求平移后所得抛物线的表达式.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共6题;共6分)13-1、14-1、15-1、16-1、17-1、18-1、三、解答题 (共7题;共53分)19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、23-1、23-2、23-3、24-1、25-1、25-2、。
(真题)广西北海市2018年中考数学试题有答案(Word版)AUPPPA

3 33广西北海市2018年中考数学试题(考试时间:120 分钟 满分:120 分)注意事项:1. 本试卷分第 I 卷(选择题)和第 II 卷(非选择题)两部分,请在答题卡上作答,在试卷上作答无效。
2. 答题前,请认真阅读答题卡上的注意事项。
3. 不能使用计算器,考试结束前,将本试卷和答题卡一并交回。
一、选择题(本大题共 12 小题,每小题 3 分,共 36 分.在每小题给出的四个选项中只有一项是符合要求的,用 2B 铅笔把答题卡上对应题目的答案标号涂黑.)1. -3 的倒数是A. -3B. 3C. -1D. 1 【答案】C【考点】倒数定义,有理数乘法的运算律,【解析】根据倒数的定义,如果两个数的乘积等于 1,那么我们就说这两个数互为倒数.除 0以外的数都存在倒数。
因此-3 的倒数为-1【点评】主要考察倒数的定义2. 下列美丽的壮锦图案是中心对称图形的是【答案】A【考点】中心对称图形【解析】在平面内,如果把一个图形绕某个点旋转180°后,能与自身重合,那么这个图形就叫做中心对称图形。
【点评】掌握中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180 度后两部分重合.3.2018 年俄罗斯世界杯开幕式于6 月14 日在莫斯科卢日尼基球场举行,该球场可容纳81000 名观众,其中数据81000 用科学计数法表示为()A. 81⨯103B. 8.1⨯104C. 8.1⨯105D. 0.81⨯105【答案】B【考点】科学计数法【解析】81000 = 8.1⨯104,故选B【点评】科学计数法的表示形式为a ⨯10n的形式,其中1 ≤a < 10,n为整数4.某球员参加一场篮球比赛,比赛分4 节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分为()A.7 分B.8 分C.9 分D.10 分【答案】B【考点】求平均分【解析】12 + 4 +10 + 6 = 84【点评】本题考查用折线图求数据的平均分问题5.下列运算正确的是A. a(a+1)=a2+1B. (a2)3=a5C. 3a2+a=4a3D. a5÷a2=a3【答案】D【考点】整式的乘法;幂的乘方;整式的加法;同底数幂的除法【解析】选项A 错误,直接运用整式的乘法法则,用单项式去乘多项式的每一项,再把结果相加,可得a(a+1)=a2+a;选项B 错误,直接运用幂的乘方法则,底数不变,指数相乘,可得(a2)3=a6;选项C 错误,直接运用整式的加法法则,3a2 和a 不是同类项,不可以合并;选项D 正确,直接运用同底数幂的除法,底数不变,指数相减,可得a5÷a2=a3.【点评】本题考查整式的四则运算,需要记住运算法则及其公式,属于基础题。
2018年北海市初中毕业升学考试数学试卷 精品
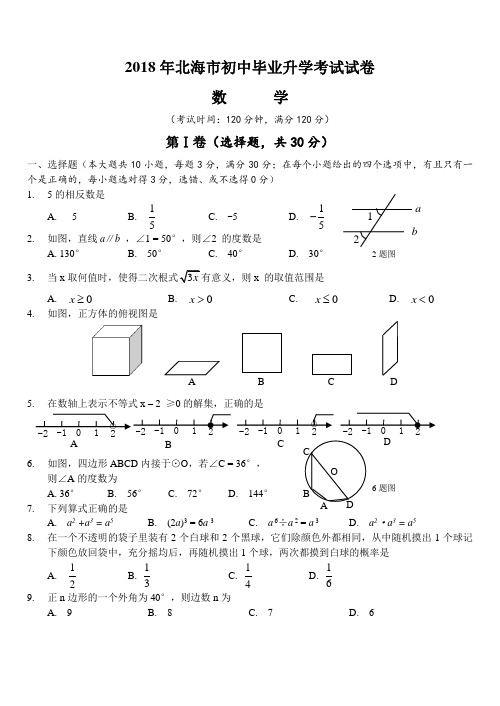
A B C D a b1 2A B C D2018年北海市初中毕业升学考试试卷数 学(考试时间:120分钟,满分120分)第Ⅰ卷(选择题,共30分)一、选择题(本大题共10小题,每题3分,满分30分;在每个小题给出的四个选项中,有且只有一个是正确的,每小题选对得3分,选错、或不选得0分) 1. 5的相反数是A.5B.15C. -5D. 15-2. 如图,直线a ∥b ,∠1 = 50°,则∠2 的度数是A. 130°B. 50°C. 40°D. 30°3. 当x x 的取值范围是A. 0x ≥B. 0x >C. 0x ≤D. 0x < 4. 如图,正方体的俯视图是5. 在数轴上表示不等式x – 2 ≥0的解集,正确的是6. 如图,四边形ABCD 内接于⊙O ,若∠C = 36°,则∠A 的度数为A. 36°B. 56°C. 72°D. 144°7. 下列算式正确的是A. a 2 +a 3 = a 5B. (2a )3 = 6a 3C. a 6÷a 2 = a 3D. a 2·a 3 = a 58. 在一个不透明的袋子里装有2个白球和2个黑球,它们除颜色外都相同,从中随机摸出1个球记下颜色放回袋中,充分摇均后,再随机摸出1个球,两次都摸到白球的概率是A.12B.13C.14D.169. 正n 边形的一个外角为40°,则边数n 为A. 9B. 8C. 7D. 62题图6题图15题图3●● 16题图10. 如图,A 、B 是双曲线ky x=上的点,分别过A 、B 两点作x 轴、y 轴的垂线段. S 1,S 2,S 3分别表示图中三个矩形的面积,若 S 3 = 1,且124S S +=,则k 值为 A. 1B. 2C. 3D. 4第Ⅱ卷(非选择题,共90分)6小题,每题3分,满分18分)11. 计算: 2 +(– 5)= ;12. 解方程(x + 2)(x – 3) = 0 ,则x = ;13. 随着“家电下乡” 活动的推进,我市今年一季度家电销售总额高达2950万元,用科学记数法表示为 万元; 14. 如图,在Rt △ABC 中,∠ C = 90°,作AB 的垂直平分线,交AB 于D ,交AC 于E ,连接BE. 已知∠CBE = 40°, 则∠A= 度;15. 如图,已知平行四边形ABCD ,E 是BD 上的点,BE :ED = 1:2,F 、G 分别是BC 、CD 上的点,EF ∥CD ,EG ∥BC ,若1ABCD S =,则EFCG S = .16. 如图,在直角坐标系xoy 中,∠OA 0A 1 = 90°, OA 0 = A 0A 1=1,以OA 1为直角边作等腰Rt △OA 1A 2,再以OA 2为直角边作 等腰Rt △OA 2A 3,……,以此类推, 则 A 21点的坐标为 ( , ) .三、(本题共2小题,每小题5分,满分10分)17. (本题满分5分)解方程组251x y x y +=⎧⎨-=⎩18. (本题满分5分)先化简再求值:211x x -⎛⎫- ⎪⎝⎭÷2321x x x -+,其中x = 2 .A B C D ●O四、(本题共2小题,每小题6分,满分12分)19. (本题满分6分)规定: 2!= 2×1;3!= 3×2×1;4!= 4×3×2×1,……,!(1)(2)21n n n n =⨯-⨯-⨯⋅⋅⋅⨯⨯,即称!n 为n 的阶乘. (1)计算:100!98!= ; (2)当x = 7是一元二次方程28!06!x kx +-=的一个根,求k 的值. 20. (本题满分6分)在矩形ABCD 中,对角线AC 、BD 交于点O ,AE ⊥BD ,且AE 平分∠BAO.求∠AOB 度数五、(本题共2小题,每小题6分,满分12分) 21. (本题满分6分)已知,如图在小正方形组成的网格中,矩形ABCD 的顶点和点O 都在格点上,将矩形ABCD 绕点O 顺时针方向旋转90 º,得到矩形''''A B C D .(1)在网格中,画出矩形''''A B C D ,并画出旋转过程点A 和B 分别划过的痕迹(不用写作法); (2)网格每个小正方形的边长为1,请求出线段AB 旋转时扫过的图形的面积. (结果保留π)扇形统计图)22. (本题满分6分)某商场计划为学校挑选一批运动鞋供学生选购,对全校学生所穿运动鞋鞋码进行调查,现随机抽取一部分学生,对他们所穿运动鞋鞋码作为数据样本进行分析,绘出部分条形图和部分扇形统计图,如下图所示:(1)结合统计图完成下列填空,并把条形图和扇形图补充完整. 这个样本的穿26码运动鞋的人数是 ,中位数是 ,众数是 ; (2)请你为该商场提出一条挑选这批运动鞋的合理建议. 六、(本题共2小题,每小题8分,共16分)23. (本题满分8分)某水库在60天中,一段时间蓄水量随时间的增加直线上升,由于灌溉的需要,一段时间蓄水量随时间的增加直线下降, 水库的蓄水量V (万立方米)与时间t (天)的关系如图所示.(1)分别求出水库蓄水量上升期及下降期V 与t 的函数关系式; (2)求水库的蓄水量为900万立方米以上(包含 900万立方米)的时间t 的取值范围.24. (本题满分8分)已知一台挖掘机的工作效率是一名工人工作效率的160倍. 挖掘800米道路,一台挖掘机比80名工人少用10天. 问一名工人和一台挖掘机每天各挖多少米?市道路建设工程指挥部,对城市1600米道路进行改建. 原计划只用一台挖掘机完成,在挖掘2天后,为了加快进度,加入80名工人一起工作,则完成这项工作比原计划能提前几天?图2图1七、(本题满分10分)三点,∠BAC = 30°,D是OB 延长线上的点,∠BDC = 30°,⊙O(1)求证:DC 是⊙O 的切线;(2)如果AC ∥BD ,证明四边形ACDB (3)在图1中,如果AO ⊥BO ,BO 与AC 交于E ,如图2,求ABC AEB S S ∆∆:的值.八、(本题满分12分),∠OAB = 90°,点B 坐标为(10,0). 过原点O 的抛物线,又过点A 和G ,点G 坐标为(7,0).(1)求抛物线的解析式;(2)边OB 上一动点T (t ,0),(T 不与点O 、B 过点T 作OA 、AB 的垂线,垂足分别为C 、D. 设△的面积为S ,求S 的表达式(用t 表示),并求S (3)已知M (2,0),过点M 作MK ⊥OA ,垂足为作MN ⊥OB ,交点OA 于N . 在线段OA 一点Q ,使得Rt △KMN 绕点Q 旋转180°后,点M 恰好落在(1)所求抛物线上,若存在请求出点Q 物线上与M 、K2018年北海市初中毕业升学考试数学试题参考答案及评分标准11. -3 ; 12. x = - 2 或3 ;13. 2. 95×103 ;14. 25° ;15.29;16. A 211010(2,2)-- 。
北海初级中学2018-2019学年七年级下学期数学期中考试模拟试卷含解析

∴原方程组的解是
.
故答案为:2,2,﹣4.
第 10 页,共 17 页
【分析】观察方程组中同一未知数的系数特点:三个方程中 c 的系数都是 1,因此①﹣②和①﹣③,就可求出 b 的值,再代入计算求出 a、c 的值。
18、( 1 分 ) 若方程组
的解也是方程 2x-ay=18 的解,则 a=________.
2、 ( 2 分 ) 16 的平方根与 27 的立方根的相反数的差是( )
A. 1
B. 7
【答案】C
【考点】平方根,立方根及开立方
C. 7 或-1
D. 7 或 1
第 1 页,共 17 页
【解析】【解答】解:∵16 的平方根为±4, 27 的立方根为 3, ∴3 的相反数为-3, ∴4-(-3)=7,或-4-(-3)=-1. 故答案为:C. 【分析】根据平方根和立方根的定义分别求出 16 的平方根和 27 的立方根的相反数 ,再列式、计算求出答案. 3、 ( 2 分 ) 已知方程 5m-2n=1,当 m 与 n 相等时,m 与 n 的值分别是( )
14、( 1 分 ) 写出一个比-1 小的无理数 ________.
【答案】
【考点】实数大小的比较
第 8 页,共 17 页
【解析】【解答】解:比-1 小的无理数为: 【分析】根据无理数的大小比较,写出一个比-1 小的无理数即可。此题答案不唯一。
15、( 1 分 ) 如图,已知直线 AB、CD、EF 相交于点 O,∠1=95°,∠2=32°,则∠BOE=________.
【解析】【解答】解:
由 ×3 得:6x-3y=3由Βιβλιοθήκη 得:(a+6)x=12
∵原方程组无解 ∴a+6=0 解之:a=-6
广西北海市中考数学模拟试卷

广西北海市中考数学模拟试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)(2018·赤峰) 2018的相反数是()A . ﹣2018B .C . 2018D .2. (2分)(2018·泰州) 下列运算正确的是()A .B .C .D .3. (2分) (2017八下·萧山期中) 下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是()A .B .C .D .4. (2分)若A(a1 , b1),B(a2 , b2)是反比例函数y=-图象上的两个点,且a1<a2 ,则b1与b2的大小关系是()A . b1<b2B . b1=b2C . b1>b2D . 大小不确定5. (2分)(2013·崇左) 如图所示的是三通管的立体图,则这个几何体的俯视图是()A .B .C .D .6. (2分)(2017·长安模拟) 不等式组的解集是()A . x<3B . 3<x<4C . x<4D . 无解7. (2分) (2017八下·吉安期末) 等腰三角形的底角是70°,则顶角为()A . 40°B . 70°C . 55°D . 45°8. (2分) 2016年9月28日﹣12月31日,山东临沂灯展中千万盏彩灯点亮300亩天然花海.某日,从晚上17时开始每小时进入灯展的人数约为900人(之前该灯展有游客 400人),同时每小时走出灯展的人数约为600人,已知该灯展的饱和人数约为1600人,则该灯展人数饱和时的时间约为()A . 21时B . 22时C . 23时D . 24时9. (2分)如图,已知∠1=∠2=∠3=55º,则∠4=()A . 135ºB . 125ºC . 110ºD . 无法确定10. (2分)某地修一条公路,若甲工程队单独承包要80天完成,乙工程队单独承包要120天完成.现在由甲、乙工程队合作承包,完成任务需要()A . 48天B . 60天C . 80天D . 100天二、填空题 (共10题;共10分)11. (1分)(2017·鹤岗模拟) 2016年7月11日是第二十二个世界人口日,本次世界人口日的主题是“面对74亿人的世界”,74亿人用科学记数法表示为________人.12. (1分) (2018九上·青浦期末) 函数的定义域是________.13. (1分)计算:5 ﹣2 =________.14. (1分)(2017·深圳模拟) 分解因式:ax2﹣9a=________.15. (1分) (2018九上·泰州月考) 如图,在半径为的中,劣弧的长为,则________度.16. (1分)(2018·柘城模拟) 如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为________.17. (1分) (2017八上·鄞州月考) 如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为________.18. (1分)(2017·安阳模拟) 一个不透明的袋子中装有3个红球和2个白球共5个球,这些球除颜色不同外,其余均相同,从中任意摸出一个球,这个球是白球的概率为________.19. (1分) (2017九上·拱墅期中) 如图,内接于⊙ ,于点,,,,则⊙ 的直径是________.20. (1分) (2017八下·海安期中) 如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE 于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②AB=HF,③BH=HF;④BC ﹣CF=2HE;⑤OE=OD;其中正确结论的序号是________三、解答题 (共7题;共70分)21. (5分) (2019九上·尚志期末) 先化简,再求代数式()÷ 的值,其中a=2sin45°+tan45°.22. (5分) (2020九上·郑州期末) 如图,已知∠ABC,求作:①∠ABC的平分线BD(写出作法,并保留作图痕迹);②在BD上任取一点P,作直线PQ,使PQ⊥AB(不写作法,保留作图痕迹).23. (12分)(2017·宜兴模拟) 学校为了解学生参加体育活动的情况,对学生“平均每天参加体育活动的时间”进行了随机抽样调查,下图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答以下问题:(1)“平均每天参加体育活动的时间”“为0.5~1小时”部分的扇形统计图的圆心角为________度;(2)本次一共调查了________名学生;(3)将条形统计图补充完整;(4)若该校有2000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.24. (8分) (2019九上·无锡月考) 如图l,在中,点,分别在边和上,点,在对角线上,且, .(1)求证:四边形是平行四边形:(2)若,, .①当四边形是菱形时,的长为________;②当四边形是正方形时,的长为________;③当四边形是矩形且时,的长为________.25. (10分)(2017·南充) 学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?26. (15分) (2019九上·许昌期末) 如图1,在平面直角坐标系中,已知抛物线y=ax2+bx-5与x轴交于A(-1,0),B(5,0)两点,与y轴交与点C.(1)求抛物线的函数表达式;(2)若点D是y轴上的点,且以B、C、D为顶点的三角形与△ABC相似,求点D的坐标;(3)如图2,CE//x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC、CE分别相交于点F,G,试探求当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积.27. (15分)(2017·淄博) 如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(,0),在第一象限内与直线y=x交于点B(2,t).(1)求这条抛物线的表达式;(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共10题;共10分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共7题;共70分)21-1、22-1、23-1、23-2、23-3、23-4、24-1、24-2、25-1、25-2、26-1、26-2、26-3、27-1、27-2、。
北海市初级中学2018-2019学年七年级下学期数学期中考试模拟试卷含解析

7、 ( 2 分 ) 判断下列现象中是平移的有几种?( ).
( 1 )篮球运动员投出篮球的运动;(2)升降机上上下下运送东西;(3)空中放飞的风筝的运动;(4)飞
机在跑道上滑行到停止的运动;(5)铝合金窗叶左右平移;(6)电脑的风叶的运动.
A. 2 种
B. 3 种
C. 4 种
D. 5 种
【答案】B
【考点】生活中的平移现象
6、 ( 2 分 ) 下列不等式中,是一元一次不等式的是( ) A.x+1>2 B.x2>9 C.2x+y≤5
D. >3 【答案】 A 【考点】一元一次不等式的定义
【解析】【解答】解:A.该不等式符合一元一次不等式的定义,符合题意;
第 3 页,共 16 页
B.未知数的次数是 2,不是一元一次不等式,不符合题意; C.该不等式中含有 2 个未知数,属于二元一次不等式,不符合题意; D.该不等式属于分式不等式,不符合题意; 故答案为:A. 【分析】根据一元一次不等式的定义判定.含有一个未知数,未知数的次数是 1 的不等式,叫做一元一次不等 式.
10、( 2 分 ) 5 名学生身高两两不同,把他们按从高到低排列,设前三名的平均身高为 a 米,后两名的平均 身高为 b 米.又前两名的平均身高为 c 米,后三名的平均身高为 d 米,则( )
A.
>
B.
>
C.
=
D.以上都不对
【答案】 B
【考点】不等式及其性质
【解析】【解答】解:根据把他们按从高到低排列,设前三名的平均身高为 a 米,后两名的平均身高为 b 米.又
【答案】A
【考点】点到直线的距离
C. 5
D. 以上都不对
【解析】【解答】解:∵∠C=90° ∴AC⊥BC ∴点 A 到直线 BC 的距离就是线段 AC 的长,即 AC=3 故答案为:A 【分析】根据点到直线的距离的定义求解即可。
北海市中考数学一模试卷

北海市中考数学一模试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2018七上·双台子月考) 下列几对数中,互为相反数的是()A . ﹣|﹣5|和﹣5B . π和﹣3.14C . 和﹣0.75D . 和﹣32. (2分)(2018·灌南模拟) 如图,观察这个立体图形,它的左视图是()A .B .C .D .3. (2分)(2011·宁波) 据宁波市统计局年报,去年我市人均生产总值为104485元,104485元用科学记数法表示为()A . 1.04485×106元B . 0.104485×106元C . 1.04485×105元D . 10.4485×104元4. (2分)一个正方形的面积是12,估计它的边长大小在()A . 2与3之间B . 3与4之间C . 4与5之间D . 5与6之间5. (2分)(2017·河北模拟) 下列等式成立的是()A . + =B . =C . =D . =﹣6. (2分)某商场销售某品牌童装,平均每天可以售出20件,每件盈利40元,为了扩大销售,增加利润,尽量减少库存,经调查发现,每件童装每降价1元,商场平均可多销售2件.若商场每天盈利1200元,设每件童装降价x元,则可列方程()A . (20+x)(20﹣2x)=1200B . (20﹣2x)(40+x)=1200C . (20﹣x)(40+2x)=1200D . (20+2x)(40﹣x)=12007. (2分) (2015八下·伊宁期中) 如图,菱形ABCD中,E,F分别是AB,AC的中点,若EF=3,则菱形ABCD 的周长是()A . 12B . 16C . 20D . 248. (2分)(2018·岳池模拟) 若一组数据2,4,,5,7的平均数为5,则这组数据中的和中位数分别为()A . 5,7B . 5,5C . 7,5D . 7,79. (2分) A、B两地相距480千米,一列慢车从A地出发,每小时行驶60千米,一列快车从B地出发,每小时行驶90千米,快车提前30分钟出发,两车相向而行,慢车行驶多少小时后两车相遇?设慢车行驶x小时后两车相遇,根据题意,下面所列方程正确的是()A . 60(x+30)+90x=480B . 60x+90(x+30)=480C . 60(x+ )+90x=480D . 60x+90(x+ )=48010. (2分) (2019八下·江城期中) 已知等腰三角形的一条腰长是15,底边长是18,则它底边上的高为()A . 9B . 12C . 15D . 18二、填空题 (共4题;共4分)11. (1分)因式分解:x3﹣4x=________ .12. (1分)(2018·龙湾模拟) 如图,点A是反比例函数y= (x>0)图象上的一点,点B是反比例函数y=﹣(x<0)图象上的点,连接OA、OB、AB,若∠AOB=90°,则sin∠A=________13. (1分)如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△ABE≌△DCF;②;③DP2=PH•PB;④.其中正确的是________ .(写出所有正确结论的序号)14. (1分) (2019九下·邓州模拟) 已知抛物线y=ax2+bx+c(a>0)的顶点为(2,4),若点(﹣2,m),(3,n)在抛物线上,则m________n(填“>”、“=”或“<”).三、解答题 (共9题;共73分)15. (5分)(2020·北京模拟) 计算:16. (5分) (2017七下·抚宁期末) 解不等式组解不等式组,并把它的解集表示在数轴上.18. (6分) (2017七上·启东期中) 观察下列三行数:①0,3,8,15,24,…②2,5,10,17,26,…③0,6,16,30,48,…(1)第①行数按什么规律排行?(2)第②行,第③行数与第①行数分别有什么关系?(3)分别从①②③行数中取出第a个数,并计算这三个数的和.(结果用含a的式子表示)19. (5分)如图是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面AC的倾斜角∠CAB=45°,在距A点10米处有一建筑物HQ.为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除?(计算最后结果保留一位小数).(参考数据: =1.414, =1.732)20. (6分)(2017·番禺模拟) 如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线.(1)用尺规作图:作∠AEC的平分线EN(保留作图痕迹,不写作法和证明);(2)设EN与AF交于点M,判断△AEM的形状,并说明理由.21. (11分)(2017·铁西模拟) 某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?22. (10分)(2017·云南) 已知二次函数y=﹣2x2+bx+c图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.(1)不等式b+2c+8≥0是否成立?请说明理由;(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.23. (10分) (2017八下·黄冈期中) 如图1,四边形ABCO为正方形.(1)若点A坐标为(0,)①求点B的坐标;②如图2,点D为y轴上一点,连接BD,若点A到BD的距离为l,求点C到BD的距离;(2)如图3,连接正方形ABCO的对角线AC,OB交于点Q,点F为线段BC上一点,以OF为直角边向上构造等腰Rt△EOF,∠EOF=90°,EF交AC于P.若PQ=1,求CF的长度.参考答案一、单选题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共4题;共4分)11-1、12-1、13-1、14-1、三、解答题 (共9题;共73分)15-1、16-1、18-1、18-2、18-3、19-1、20-1、20-2、21-1、21-2、22-1、22-2、23-1、。
