单纯形法例题讲解
运筹学单纯形法例题求解过程

运筹学单纯形法例题求解过程【实用版】目录一、运筹学单纯形法概述二、运筹学单纯形法的求解步骤1.确定基变量和初始基本可行解2.编制初始单纯形表3.判断基本可行解是否为最优解4.迭代求解下一个使目标函数更优的基本可行解5.重新计算机会费用和检验数三、运筹学单纯形法例题求解过程1.题目描述2.化为标准型3.建立初始单纯形表4.迭代计算四、总结正文一、运筹学单纯形法概述运筹学单纯形法是一种求解线性规划问题的方法,它是基于数学和经济学理论的基础上发展起来的。
线性规划问题是指在有限的资源约束下,寻求一个最优解的问题,例如最大化利润或最小化成本等。
单纯形法是求解线性规划问题的一种常用方法,它通过迭代计算来逐步优化解决方案,最终得到最优解。
二、运筹学单纯形法的求解步骤1.确定基变量和初始基本可行解在求解线性规划问题时,首先需要确定基变量,即在约束条件方程组中选择一部分变量作为基变量。
基变量的选取可以通过寻找或构造单位矩阵的方法来确定。
确定基变量后,可以求出初始基本可行解,即满足所有约束条件的变量值组合。
2.编制初始单纯形表根据初始基本可行解和线性规划模型提供的信息,可以编制初始单纯形表。
单纯形表是一个矩阵,其中包含基变量、非基变量、目标函数系数、约束条件系数和检验数等信息。
3.判断基本可行解是否为最优解在求解过程中,需要判断基本可行解是否为最优解。
这可以通过检验数来进行。
如果所有非基变量的检验数都小于 0,说明已经达到最优解;如果存在检验数大于 0 的非基变量,但所有这样的非基变量对应的列中至少有一个基变量系数大于 0,说明没有达到最优解;如果至少存在一个检验数大于 0 的非基变量,并且对应的列中至少有一个基变量系数小于0,说明没有达到最优解,需要继续迭代求解。
4.迭代求解下一个使目标函数更优的基本可行解在迭代过程中,需要通过更换基变量和非基变量的方法来求解下一个使目标函数更优的基本可行解。
更换的依据是检验数,原则上选择最大检验数对应的非基变量作为换入变量,选择最小检验数对应的非基变量作为换出变量。
单纯形法的计算题

单纯形法的计算题
单纯形法是一种求解线性规划问题的数学方法。
下面是一道使用单纯形法求解的线性规划问题的例子:
求最大化目标函数z = -2x1 + 3x2,
约束条件:
1. x1 + x2 <= 4
2. 3x1 + 4x2 <= 12
3. x1, x2 >= 0
用单纯形法求解此问题,需要进行以下步骤:
1. 建立初始单纯形表格:根据约束条件,我们可以确定初始单纯形表格的基变量和非基变量。
2. 计算目标函数的系数和:根据目标函数的系数,我们可以计算出目标函数的系数和。
3. 检查退出条件:如果目标函数的系数和大于零,则无法找到可行解;如果目标函数的系数和小于等于零,则已经找到最优解。
4. 迭代计算:如果未达到最优解,需要继续迭代计算,更新单纯形表格,直到找到最优解为止。
5. 输出结果:最终的单纯形表格中,最优解对应的基变量和非基变量的值即为所求的最优解。
具体到这个例子中,可以使用线性规划软件包或编程语言实现单纯形法来求解。
通过输入约束条件和目标函数,可以得到最优解。
单纯形法例题讲解

基可行解
单纯形法就是针对标准形式得线性规划问题进行演算得,任何线性规划问题都可以化为标准形式。
min (1)
s.t (2)
(3)
其中
假设,并设系数矩阵A得秩为m,即设约束方程(2)中没有多余得方程,用表示A得第列,于就是(2可写成
(4)
矩阵A得任意一个m阶非奇异子方阵为LP得一个基(或基阵),若
(5)
就是一个基,则对应变量,称关于B得基变量,其余变量成为关于B得非基变量,若令非基变量都取零值,则(4)变为
(6)
由于此方程组得系数矩阵B就是满秩方阵,故知(6)有唯一解,记为于就是按分量
所构成得向量就是约束方程组得一个解,称此为LP得对应于基B得基解(或基本解),也可称为方程组得一个基解,如果为一基解,且满足即它得所有分量都非负,则称此就是L P得一个基可行解,基可行解对应得基称为可行基。
设对应基阵,即为基变量,就是非基变量,记
从而A=(B,N),相应地分划,约束方程(2)可以写成
即由此解得
(7)
这就是用非基变量表达基变量得公式
在(7)中令而知
ﻬ求解线性规划问题
min
已知初始可行基
于就是可列出对应得单纯形表,如表所示
从表可以瞧出,检验数中仅有,故取为进基变量,由于最小比值
在第32行取得,故取第2行对应得基变量为离基变量,于就是元素就是上表得枢元
为求出新基对应得单纯形表,对作初等形变换,使对应得列变为单位列向量、在上表中枢元。
【精品】最优化单纯形法例题讲解

【精品】最优化单纯形法例题讲解最优化单纯形法是一种用于求解线性规划问题的常用方法。
它通过不断迭代调整基变量的取值来寻找使目标函数取得最大(或最小)值的最优解。
下面我们通过一个例题来详细讲解最优化单纯形法的求解过程。
例题:假设有如下线性规划问题:Max Z = 3x1 + 4x2 s.t. 2x1 + x2 ≤ 8 x1 + 2x2 ≤ 6 x1, x2 ≥ 0首先,我们将原问题转化为标准型,即将约束条件全部转化为等式,并引入松弛变量。
将原问题转化为如下形式:Max Z = 3x1 + 4x2 s.t. 2x1 + x2 + x3 = 8 x1 + 2x2 + x4 = 6 x1, x2, x3, x4 ≥ 0接下来,我们构造初始单纯形表。
单纯形表由目标函数系数矩阵、约束条件系数矩阵和右端常数向量组成。
目标函数系数矩阵: 3 4 0 0约束条件系数矩阵: 2 1 1 0 1 2 0 1右端常数向量: 8 6再构造一个松弛变量的列向量,也就是单位矩阵的第一列。
接下来,我们要选择一个入基变量和一个出基变量,通过迭代调整基变量的取值来逼近最优解。
选择入基变量:我们要选择一个非基变量进入基变量集合,使得目标函数系数矩阵中的相应列元素最大(如果是最小化问题,则选择最小的)。
选择出基变量:我们要选择一个基变量出基变量集合,使得约束条件系数矩阵中相应列元素最小的行对应的非基变量列元素大于等于0。
在初始单纯形表中,目标函数系数矩阵中3和4是最大的,所以我们选择x1和x2作为入基变量。
在约束条件系数矩阵中,对于x1,第一行的1最小,所以我们选择第一行的x4作为出基变量;对于x2,第二行的1最小,所以我们选择第二行的x3作为出基变量。
接下来,我们通过计算新的单纯形表来更新基变量的取值。
首先,我们计算新的基变量x1的系数矩阵。
将x1的列除以相应的出基变量的系数(即1),得到新的系数矩阵:1 0 1/2 0 0 1 -1/2 1然后,我们计算新的基变量x2的系数矩阵。
单纯形表例题详解易懂

单纯形法(Simplex Method)是线性规划问题的一种求解方法。
下面我将以一个简单的线性规划问题为例,详细解释如何使用单纯形法求解。
例题:假设我们有一个简单的线性规划问题,目标是最小化目标函数 z = 3x + 2y,约束条件是 x + y <= 10, x >= 0, y >= 0。
首先,我们需要构建问题的数学模型。
数学模型可以表示为以下形式:z = 3x + 2yx + y <= 10x >= 0y >= 0然后,我们可以将这个线性规划问题表示为一个单纯形表。
单纯形表的形式如下:| c | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | ||---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---||x | y | z | u | v | w | x1 | x2 | x3 | ... | xn | s.x | s.y | s.z | c.val | b.x | b.y | b.z | dual.val | dual.x1 | dual.x2 | ... | dual.xn ||在这个表中,c 是目标函数的系数,b 是约束条件的系数,s 是松弛变量的系数,dual 是对偶问题的系数,c.val 是当前解的目标函数值,b.x, b.y, b.z 是约束条件的边界值,s.x, s.y, s.z 是松弛变量的值。
现在,我们可以将例题中的数据填入单纯形表:c = [3, 2, 1]b = [1, 0, -10]s = [1, 1, 0]dual = []然后,我们可以开始迭代求解。
在每一次迭代中,我们首先找到进入变量和离开变量,然后更新单纯形表中的数据。
运筹学单纯形法例题求解过程

运筹学单纯形法例题求解过程(原创版)目录一、运筹学单纯形法的基本概念二、运筹学单纯形法的求解步骤1.确定基变量和初始基本可行解2.编制初始单纯形表3.判断基本可行解是否为最优解4.迭代求解下一个使目标函数更优的基本可行解5.重新计算机会费用和检验数三、运筹学单纯形法的应用实例正文一、运筹学单纯形法的基本概念运筹学单纯形法是一种求解线性规划问题的方法,它是基于数学和统计学的理论基础,通过逐步优化算法,寻找线性规划问题中最优解的一种方法。
线性规划问题是指在一定约束条件下,寻求目标函数的最小值或最大值的问题。
而单纯形法是线性规划问题中最常用的求解方法之一,它通过迭代计算,不断优化基变量,从而得到问题的最优解。
二、运筹学单纯形法的求解步骤1.确定基变量和初始基本可行解在求解线性规划问题时,首先需要确定问题的基变量,即在所有变量中选择若干个变量作为基变量。
基变量的选取可以通过寻找单位矩阵的方法来确定。
确定基变量后,可以求出初始基本可行解,即满足所有约束条件的变量值组合。
2.编制初始单纯形表根据初始基本可行解和线性规划模型提供的信息,可以编制初始单纯形表。
单纯形表是一个包含基变量、非基变量、目标函数系数、约束条件常数项和检验数等元素的矩阵表。
3.判断基本可行解是否为最优解在求解过程中,需要判断基本可行解是否为最优解。
这可以通过检验数来进行。
检验数是指非基变量与对应约束条件的乘积,如果所有非基变量的检验数都小于等于 0,说明已经达到最优解。
否则,需要继续迭代求解。
4.迭代求解下一个使目标函数更优的基本可行解如果基本可行解不是最优解,需要通过迭代求解来寻找下一个使目标函数更优的基本可行解。
迭代过程中,需要确定换入变量和换出变量,然后根据换入变量和换出变量生成新的单纯形表,并重新计算机会费用和检验数。
5.重新计算机会费用和检验数在迭代过程中,需要重新计算机会费用和检验数,以便判断新的基本可行解是否更优。
如果新的基本可行解的检验数满足条件,说明已经找到最优解,可以结束迭代求解过程。
单纯形法求解全过程详解共9页

(7)接下来,我们的任务就是找另一个基可行解。即转回到步骤(5)。
选择进基变量: max⎨⎧σ1 ⎩
=
5⎫
3
⎬ ⎭
=σk
= σ1 ,即
x1 进基成为基变量。
出基变量:
min
⎧
⎨ ⎩
b1 a11
,
b2 a21
⎫
⎬ ⎭
=
min⎨⎧30 × ⎩
3 5
= 18,10 × 3 = 30⎬⎫ ⎭
=
b1 a11
,即第
3
3
1
0
−
5
5
1
2
1
−
5
5
这时,我们可以得到基 B3 = [P1, P2 ] 对应的基可行解。
即令非基变量 x3 = 0, x4 = 0 ,根据表中的约束条件可得 x1 = 18, x2 = 4 (这两个值正好是表 中基变量对应的资源向量 b 对应的分量) 那么,第 3 个基可行解为 X 3 = [18,4,0,0]T 。 (8)找到了第 3 个基可行解,接下来的任务就是判断该基可行解是否为最优解,检验其是 否为最优解的标准前面已经详细讲述,这里就不啰唆了。即转回到步骤(4)。
1
0
1
10 × 3 = 30
3
σ
(2) j
=
cj
−
CB
⋅
Pj
5
0
0
−4
3
3
3
x1
1
0
4
x2
0
1
σ
(3) j
=cj
− CB
⋅ Pj
5
1
先来看主元 a11 所在的行。行的系数表示的是约束条件: 30 = 3 x1 + x3 − 3 x4 ①’。
min单纯形法简单例题详解

min单纯形法简单例题详解假设有一家工厂生产两种产品 A 和 B,目标是最大化利润。
已知每单位产品 A 的生产时间为 2 小时,产品 B 的生产时间为 3 小时。
每天工厂的总生产时间为 24 小时。
每单位产品 A的利润为 10 美元,产品 B 的利润为 8 美元。
现在要确定工厂每天应该生产多少单位的产品 A 和 B,以最大化总利润。
首先我们需要定义两个变量:x 和 y。
其中,x 表示每天生产的单位数目 A,y 表示每天生产的单位数目 B。
根据问题的要求,我们可以得到两个约束条件:1. 生产时间约束:2x + 3y <= 24(每天生产时间最大为 24 小时)2. 非负约束:x >= 0,y >= 0(生产单位数目不能为负)现在我们可以根据最大化利润的目标函数进行建模。
目标函数为:10x + 8y。
接下来,我们可以使用单纯形法来解决这个问题。
首先,我们将这个问题转化为标准形式。
通过引入两个松弛变量 s1 和 s2,我们可以将不等式约束转化为等式约束:2x + 3y + s1 = 24x + s2 = 0接下来,我们将目标函数进行转化。
由于目标是最大化,我们可以引入一个辅助变量 z,并将目标函数写为:z = -10x - 8y现在,我们可以构建一张初始单纯形表。
表格的第一行包含变量和约束条件的系数以及目标函数的系数。
第一列列出变量和约束条件的名字。
变量 |x |y |s1 |s2 |b |--------|----|----|----|----|----|z |-10 |-8 |0 |0 |0 |s1 |2 |3 |1 |0 |24 |s2 |1 |0 |0 |1 |0 |接下来,我们需要根据单纯形法的规则来迭代计算。
首先,选择一个入基变量和一个出基变量。
根据最大增益准则,我们找到目标函数中系数最小的变量,即 x。
然后,我们需要根据最小比率准则来选择出基变量。
计算每个约束条件右侧与对应入基变量系数的比率,并选择最小的非负比率对应的出基变量。
单纯形法基本原理及实例演示

③计算各非基变量xj的检验数j=Cj-CBPj ′,若所有j≤0,则问题已得
到最优解,停止计算,否则转入下步。
④在大于0的检验数中,若某个k所对应的系数列向量Pk≤0,则此问
题是无界解,停止计算,否则转入下步。
⑤根据max{j|j>0}=k原则,确定xk为换入变量(进基变量),再按 规则计算:=min{bi/aik| aik>0}=bl/ aik 确定xBl为换出变量。建 立新的单纯形表,此时基变量中xk取代了xBl的位置。
⑥以aik为主元素进行迭代,把xk所对应的列向量变为单位列向量,即 aik变为1,同列中其它元素为0,转第③ 步。
线性规划的例子
max z 4x1 3x2 2x1 2x2 1600 5x1 2.5x2 2500 x1 400 x1, x2 0
线性规划--标准化
● 引入变量:s1,s2,s3
检验系数区
Z=CBB-1b
初始单纯形表
迭代 基变 次数 量
CB
x1
x2
s1
s2
s3
50 100 0 0 0
比值
b bi ai 2
1 Zj=CBNj j cj zj
Z=CBB-1b
初始单纯形表
基
迭代 次数
变
CB
x1
X2
s1
s2 S3
量
50 100 0 0 0
比值
b bi ai 2
1 1 1 0 0 300
C向量
max z 50 100 0 0
CB
CN
x1
x2
0•
1 1 1
1 0 0
0 1 0
最优化单纯形法例题讲解

例1 用单纯形法解下列问题:解:将原问题化成标准形:x 4与添加的松弛变量x 5,x 6在约束方程组中其系数列正好构成一个3阶单位阵,它们可以作为初始基变量,初始基可行解为X =(0, 0, 0,10, 8, 4)T列出初始单纯形表,见表1。
22x 2的系数列的正分量对应去除常数列,最小比值所在行对应的基变量作为换出的基变量。
242)24,110(m in ===θ 因此确定2为主元素(表1中以防括号[]括起),意味着将以非基变量x 2去置换基变量x 6,采取的做法是对约束方程组的系数增广矩阵实施初等行变换,将x 2的系数列(1, -1, 2)T 变换成x 6的系数列(0, 0, 1)T ,变换之后重新计算检验数。
变换结果见表2。
1231234123123min 2..210,248,244,0,1,,4.j x x x s t x x x x x x x x x x x j -++-+=-+≤-+-≤≥=123123412351236max 2..210,248,244,0,1,,6.j x x x s t x x x x x x x x x x x x x j -+-+-+=-++=-+-+=≥=检验数σ3=3>0,当前基可行解仍然不是最优解。
继续“换基”,确定2为主元素,即以非基变量x 3置换基变量x 5。
变换结果见表3。
此时,3个非基变量的检验数都小于0,σ1= -9/4,σ5= -3/2,σ5= -7/4,表明已求得最优解:T)0,0,8,5,12,0(=*X 。
去除添加的松弛变量,原问题的最优解为:T )8,5,12,0(=*X ,最小值为-19例2 用大M 法求解下列问题:12312312313min 3..211,243,21,0,1,,3.j x x x s t x x x x x x x x x j +--+≤+-≥-=≥=解 引进松弛变量x 4、、剩余变量x 5和人工变量x 6、x 7,解下列问题:1234567123412356137min 300()..211243210,1,2,,7j x x x x x M x x s t x x x x x x x x x x x x x j +-++++-++=+--+=-+=≥=用单纯形法计算如下:由于σ1<σ2< 0,说明表中基可行解不是最优解,所以确定x 1为换入非基变量;以x 1的系数列的正分量对应去除常数列,最小比值所在行对应的基变量作为换出的基变量。
课件:单纯形法求解举例

1
1
0
-2 0
0
0
11
1-3M 1-M -3+6M 0 M
1
1
-3
0
0
b
x1
X2
x3
x4
x5
0
0
比较比值时,系数是
0或负数,不选
MM
x6
x7 bi/yi
11 0 -2
3
1
0
0 -1
1
0
1
0
0 -1
1 -2 1
1
1
0
-2
0
0
0
1
0 1-M -1 0 M
0 3M-1
Cj→
CB XB
b
1
1
-3 0
0
x1
上述模型有一组很明显的基变量x4,x6,x7,能够很容易地
求出一组初始基本可行解!
X4=11,x6=3,x7=1,其余非基变量=0,即X0=(0,0,0,11,0,3,1)’
由前面介绍的单纯形法,就能以此为基础,求出最优解!
Cj→
CB XB
0 X4 M X6 M X7
Cj-zj
Cj→ CB XB
0
但该解不是可行解!(因解的分量不全≥0) 这样就不能按照前面所介绍的单纯形表格法, 进行迭代变换以求出最优解!
为了便于找到初始基本可行解,再引入人工变量x6,x7,
使约束条件变成如下形式,但由于人工变量的特殊性,需要
在目标函数中作出相应的变化,实际上是对人工变量最终
取值的约束!
M为无限大的正数!作为惩 罚项,若人工变量不=0,则
X2
x3
x4
x5
MM
两阶段单纯形法例题详解

两阶段单纯形法引言在线性规划中,两阶段单纯形法是一种常用的求解方法。
它通过两个阶段的迭代,逐步优化目标函数值,从而找到最优解。
本文将详细介绍两阶段单纯形法的步骤和原理。
步骤两阶段单纯形法主要分为两个阶段:人工变量法和单纯形法。
人工变量法•将目标函数按照线性规划的标准形式化简。
•引入人工变量(artificial variables)来转换非标准化的约束条件为等式形式。
•新增的人工变量构成的目标函数为目标是最小化的。
•利用单纯形法求解这个新增的最小化目标函数,得到一个初始可行解。
•如果初始可行解的目标函数值为0,说明原问题有解;如果目标函数值不为0,则原问题无解。
单纯形法•判断初始基本可行解是否是最优解,如果不是,则进行下面的优化步骤。
•选择一个入基变量(entering variable),即将要进入基本解的变量。
•选择一个出基变量(leaving variable),即将要离开基本解的变量。
•使用基本变量和非基本变量之间的约束方程来计算新的基本解。
•迭代以上步骤,直到找到满足优化条件的最优解。
示例假设有一个线性规划问题如下:max Z = 5x1 + 3x2subject tox1 + 2x2 <= 62x1 + x2 >= 4x1, x2 >= 0首先,将目标函数和约束条件标准化,得到以下形式:max Z = 5x1 + 3x2subject to-x1 - 2x2 <= -62x1 + x2 >= 4x1, x2 >= 0然后,采用人工变量法引入人工变量(s1和s2),得到以下形式:max Z = 5x1 + 3x2subject to-x1 - 2x2 + s1 = -62x1 + x2 - s2 = 4x1, x2, s1, s2 >= 0接下来,我们利用单纯形法求解最小化目标函数s1 + s2的初始可行解。
根据单纯形表格的形式,我们可以得到初始表格如下:Cj | -1 | -1 | 0 | 0 |------- |----|----|----|----|Cb | 0 | 0 | 1 | 1 |------- |----|----|----|----|Var. |x1 |x2 |s1 |s2 |------- |----|----|----|----|-1 | -1 | -2 | 1 | 0 |------- |----|----|----|----|0 | 2 | 1 | 0 | -1 |按照单纯形法的步骤,我们选取入基变量s1和出基变量x2,进行迭代计算,得到新的表格:Cj | -1 | -4 | 1 | -3 |------- |----|----|----|----|Cb | 0 | 2 | -1 | 2 |------- |----|----|----|----|Var. |x1 |s2 |s1 |x2 |------- |----|----|----|----|-1 | -1 | 0 | 1 | 2 |------- |----|----|----|----|2 | 2 | 0 | 0 | -1 |继续迭代,直到得到满足优化条件的最优解。
求单纯形表中的未知数例题

求单纯形表中的未知数例题以下是一个求解线性规划问题的例题,涉及到单纯形法。
假设有如下线性规划问题:
最大化: 4x + 6y
约束条件:
x + 2y <= 12
x + y <= 8
x, y >= 0
目标函数系数:4 和6。
约束条件的系数分别是:1、2、1 和1。
首先,我们需要构建一个初始单纯形表。
在这个表中,我们有两个基变量和两个非基变量。
基变量的系数是约束条件的系数,而非基变量的系数是目标函数的系数。
初始单纯形表如下:
在这个表中:
B列是基变量的检验数,表示的是当前解是否可行或最优。
非基变量的检验数表示的是当非基变量进入基变量时,目标函数的增加值。
我们将其设置为负无穷,表示这是一个入基变量,其增加量可以被任意大。
最后一行的两个问号表示的是非基变量的值,我们将其设置为待求解的值。
然后,我们开始迭代。
在每一次迭代中,我们都会找到一个入基变量和出基变量,然后更新单纯形表。
这个过程会一直持续到所有的检验数都满足最优性条件(即所有的B列的值都大于等于0)。
单纯形法的几种特殊情况

达不到最优解。
下面一个是由E.Beale给出的循环的例子。
例5
目标函数
min f =-(3/4)x4+20x5-(1/2)x6+6x7.
约束条件:x1+(1/4)x4-8x5-x6+9x7=0,
x2+(1/2)x4-12x5-(1/2)x6+3x7=0,
x3+x6=1,
x1,x2,x3,x4,x5,x6,x7≥0.
50 150 250
12500
50/1 150/2 —
50 50 250
15000
— 50/1 250/1
8
§4 几种特殊情况
这样我们求得了最优解为x1=50,x2=250,s1=0,s2=50,s3=0,此线性规划的 最优值为15000。这个最优解是否是惟一的呢?由于在第2次迭代的检验数
中除了基变量的检验数 1,2,4 等于零外,非基变量s3的检验数也等
30 0 20 1 -M 0
1
1/10
-3/10
0
0
0
-7/10
-1
1
zj
20
30
3+M/10 11+7M/10
M
-M
cj-zj
0
0
-3-M/10 -11-7M/10
-M
0
管理运筹学
b
比值
150 30 40
-40M
150/10 — 40/1
15
15/(3/10)
30
30/1
25
25/(7/10)
例4.用单纯形表,求解下列线性规划问题。
解:加上松驰变量s1,s2,s3化为标准形式后,
单纯形法例题讲解

例1max z=2x1+3x2(标准形式即所有的变量均为负、所有约束条件为等式、所有的右端项系数非负)a=(2,3) b1=(80,160,120) A2=NULL b2=NULL A3=NULL b3=NULL n.iter=n+2*m maxi=TRUE ●simplex(a=a,A1=A1,b1=b1,maxi=TRUE): m1=3,m2=0,m3=0m=3,n=2 a.o=a=(2,3)if(maxi) a=-a(-2,-3) if(m2+m3==0) a=(-2,-3,0,0,0) b=(80,160,120) init=(0,0,0,80,160,120) basic=(3,4,5) eps=1e -10out1<-simplex1(a=a,A=A,b=b,init=init,basic=basic,eps=eps) ⏹ simplex1(a=a,A=A,b=b,init=init,basic=basic,eps=eps):N=5,M=3nonbasic=(1,2)if(stage==2) obfun=(-2,-3)it=1◆ while(!all(obfun > -eps) && (it <= n.iter))循环 pcol=3if(stage==2) neg=(1,3)x1+2x2<=804x1<=160 4x2<=120 x1,x2>=0A1= 1 2 4 0 0 4A= 1 2 1 0 0 4 0 0 1 0 0 4 0 0 1tableau= 80 -1 -2 160 -4 0 120 0 -4tableau= 80 -1 -2 160 -4 0120 0 -40 -2 -3转化为标准形式x1+2x2+x3=80 4x1+x4=160 4x2+x5=120x1,x2,x3,x4,x5>=0ratios=(40,30)prow=3pivot(tableau,prow ,pcol) 换基迭代 pv=tableau[3,3]=-4pcv=tableau[,3]=(-2,0,-4,-3)tableau[-3, ] = tableau[-3, ] - (tableau[-3, 3]/pv) %o% tableau[3,]tableau[3, ] = tableau[3, ]/(-pv)=(30,0,-1)tableau[3,3]=1/pv=-1/4tableau[-3, 3]=pcv[-3]/(-4)if(stage==1) else temp=basic[3]=5 basic[3]=nonbasic[2]=2 nonbasic[2]=5 obfun =tableau[4, -1L]=(-2,3/4) it=it+1=2至此进行了一次换基迭代(basic=(3,4,2) nonbasic=(1,5)) 再从while 循环头部开始,判断循环条件是否满足 pcol=2if(stage==2) neg=(1,2) ratios=(20,40)prow=1pivot(tableau,prow ,pcol) 换基迭代 pv=tableau[1,2]=-1pcv=tableau[,2]=(-1,-4,0,-2)tableau[-1, ] = tableau[-1, ] - (tableau[-1, 2]/pv) %o% tableau[1,]tableau[1, ] = tableau[1, ]/(-pv)=(20,-1,0)tableau= 20 -1 0 160 -4 0 120 0 -4 -90 -2 0tableau= 20 -1 0160 -4 030 0 -1/4-90 -2 0tableau= 20 -1 0 160 -4 0 30 0 -1 -90 -2 0tableau= 20 -1 1/2 160 -4 030 0 -1/4-90 -2 3/4tableau= 20 -1 1/2 80 0 -2 30 0 -1/4 -130 0 -1/4tableau= 20 -1 1/2 80 0 -2 30 0 -1/4 -130 0 -1/4tableau[1,2]=1/pv=-1/1tableau[-1,2]=pcv[-1]/(-1)if(stage==1) else temp=basic[1]=3 basic[1]=nonbasic[1]=1 nonbasic[21=3 obfun =tableau[4, -1L]=(2,-1/4) it=it+1=3至此进行了两次换基迭代(basic=(1,4,2) nonbasic=(3,5)) 再从while 循环头部开始,判断循环条件是否满足 pcol=3if(stage==2) neg=(2,3) ratios=(40,120) prow=2pivot(tableau,prow ,pcol) 换基迭代pv=tableau[2,3]=-2pcv=tableau[,3]=(1/2,-2,-1/4,-1/4)tableau[-2, ] = tableau[-2, ] - (tableau[-2, 3]/pv) %o% tableau[2,]tableau[2, ] = tableau[2, ]/(-pv)=(40,2,-1)tableau[2,3]=1/pv=-1/2tableau[-2,3]=pcv[-2]/(-2)if(stage==1) else temp=basic[2]=4 basic[2]=nonbasic[2]=5 nonbasic[21=4tableau= 20 -1 1/2 80 0 -2 30 0 -1/4 -130 0 -1/4 tableau=20 -1 1/2 80 4 -2 30 0 -1/4 -130 2 -1/4tableau= 40 0 080 4 -220 -1/2 0-140 3/2 0 tableau=40 0 040 2 -120 -1/2 0-140 3/2 0tableau=40 0 0 40 2 -1/2 20 -1/2 0 -140 3/2 0 tableau= 40 0 -1/4 40 2 -1/2 20 -1/2 1/8-140 3/2 1/8obfun =tableau[4, -1L]=(3/2,1/8)it=it+1=4至此进行了三次换基迭代(basic=(1,5,2) nonbasic=(3,4))再从while 循环头部开始,判断循环条件是否满足,发现!all(obfun > -eps)为false ,则跳出循环,循环结束。
单纯形法例题详解
x4
x5
0
x3 15/2 0
0Leabharlann 1 5/4 -15/22
x1
7/2
1
0
0 1/4 -1/2
1
x2
3/2
0
1
0 -1/4 3/2
cj zj
0
0
0 -1/4 -1/2
最后得到的表格中检验数这一行无正数则所得解为最优解。 本题最优解为 X=(7/2,3/2,15/2,0,0) 目标函数值 Z=8.5
单纯形法改进单纯形法matlab单纯形法下山单纯形法三角函数例题详解运筹学单纯形法单纯形法原理排列组合例题双代号网络图例题双倍余额递减法例题
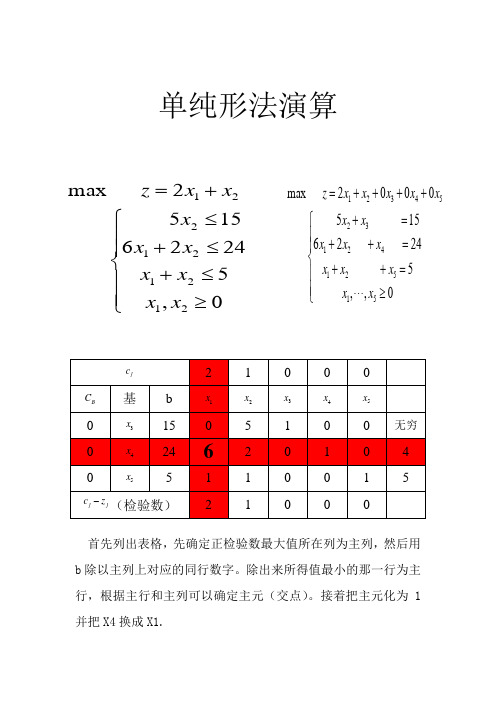
单纯形法演算
max z 2x1 x2
5x2 15
6
x1 2x2 x1 x2
24 5
x1, x2 0
max z 2x1 x2 0x3 0x4 0x5
cj
2
1
0
0
0
CB
基
b
x1
x2
x3
x4
x5
0
x3
15
0
5
1
0
0
2
x1
4
1 2/6 0 1/6 0
0
x5
5
1
1
0
0
1
cj zj
2
1
0
0
0
这时进行初等行列变换,把主列换单位向量,主元为 1。也就 是 X5 所在行减去 X1 所在行。并且重新计算检验数。
cj
2
1
0
0
0
CB
基
b
x1
x2
x3
x4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1
max z=2x1+3x2
(标准形式即所有的变量均为负、所有约束条件为等式、所有的右端项系数非负)
a=(2,3) b1=(80,160,120) A2=NULL b2=NULL b3=NULL n.iter=n+2*m maxi=TRUE
● simplex(a=a,A1=A1,b1=b1,maxi=TRUE): m1=3,m2=0,m3=0 m=3,n=2 a.o=a=(2,3)
if(maxi) a=-a(-2,-3) if(m2+m3==0) a=(-2,-3,0,0,0) b=(80,160,120) init=(0,0,0,80,160,120) eps=1e-10
out1<-simplex1(a=a,A=A,b=b,init=init,basic=basic,eps=eps)
⏹ simplex1(a=a,A=A,b=b,init=init,basic=basic,eps=eps):
N=5,M=3
nonbasic=(1,2)
if(stage==2) obfun=(-2,-3)
it=1
◆ while(!all(obfun > -eps) && (it <= n.iter))循环 pcol=3
if(stage==2) neg=(1,3)
ratios=(40,30) prow=3
➢ pivot(tableau,prow,pcol) 换基迭代 pv=tableau[3,3]=-4
pcv=tableau[,3]=(-2,0,-4,-3)
tableau[3, ] = tableau[3, ]/(-pv)=(30,0,-1)
tableau[3,3]=1/pv=-1/4
tableau[-3, 3]=pcv[-3]/(-4)
if(stage==1) else temp=basic[3]=5 basic[3]=nonbasic[2]=2 nonbasic[2]=5 obfun =tableau[4, -1L]=(-2,3/4) it=it+1=2
至此进行了一次换基迭代(basic=(3,4,2) nonbasic=(1,5)) 再从while 循环头部开始,判断循环条件是否满足 pcol=2
if(stage==2)
neg=(1,2) ratios=(20,40) prow=1
➢ pivot(tableau,prow,pcol) 换基迭代 pv=tableau[1,2]=-1
pcv=tableau[,2]=(-1,-4,0,-2)
tableau[-1, ] = tableau[-1, ] - (tableau[-1, 2]/pv) %o% tableau[1,] tableau[1, ] = tableau[1, ]/(-pv)=(20,-1,0)
tableau[1,2]=1/pv=-1/1
tableau[-1,2]=pcv[-1]/(-1)
if(stage==1) else temp=basic[1]=3 basic[1]=nonbasic[1]=1
nonbasic[21=3 obfun =tableau[4, -1L]=(2,-1/4) it=it+1=3
至此进行了两次换基迭代(basic=(1,4,2) nonbasic=(3,5)) 再从while 循环头部开始,判断循环条件是否满足 pcol=3
if(stage==2) neg=(2,3) ratios=(40,120) prow=2
➢ pivot(tableau,prow,pcol) 换基迭代 pv=tableau[2,3]=-2
pcv=tableau[,3]=(1/2,-2,-1/4,-1/4)
tableau[-2, ] = tableau[-2, ] - (tableau[-2, 3]/pv) %o% tableau[2,]
tableau[2, ] = tableau[2, ]/(-pv)=(40,2,-1)
tableau[2,3]=1/pv=-1/2
tableau[-2,3]=pcv[-2]/(-2)
if(stage==1) else
temp=basic[2]=4 basic[2]=nonbasic[2]=5 nonbasic[21=4
obfun =tableau[4, -1L]=(3/2,1/8) it=it+1=4
至此进行了三次换基迭代(basic=(1,5,2) nonbasic=(3,4))
再从while 循环头部开始,判断循环条件是否满足,发现!all(obfun > -eps)为false ,则跳出循环,循环结束。
输出:
if(stage==1) else soln=(0,0,0,0,0) soln[(1,5,2)]=(40,40,20) val=-140
a.out=(0,0,3/2,1/8,0)
if(maxi) out$value=-out$value=140
所以该线性问题的最优解为140
例2
a=(-3,1,1) A1=(1,-2,1) b1=11
A2=(-4,1,2) b2=3 A3=(2,0,-1) b3=-1 maxi=FALSE n.iter=n+2*m eps=1e-10
simplex(a=a,A1=A1,b1=b1,A2=A2,b2=b2,A3=A3,b3=b3,maxi=FALSE):
m1=1,m2=1,m3=1 m=3,n=3
a.o=a=(-3,1,1)
if(m2+m3==0) a=(-3,1,1,0,0,0,0) b=(11,3,1)
init=(0,0,0,11,0,3,1) basic=(4,6,7) stage=1 n.iter=n.iter eps=eps
out1<-simplex1(a=a,A=A,b=b,init=init,basic=basic,eps=eps,stage=1,n1=5,n.iter=n.iter) ⏹
N=7 M=3 nonbasic=(1,2,3,5)
if(stage==2) else obfun=(4,6,-1,-3,1)
obfun=(6,-1,-3,1)
it=1
◆while(!all(obfun > -eps) && (it <= n.iter))循环pcol=4
if(stage==2) selse neg=(2,3,4)
ratios=(11,3/2,1)
prow=4
➢pivot(tableau,prow,pcol) 换基迭代
pv=pv=tableau[4,4]=-1
pcv=tableau[,4]=(1,-1,-2,-3)
tableau[4, ] = tableau[4, ]/(-pv)=(1,2,0,-1,0)
tableau[4,4]=1/pv=-1
tableau[-4, 4]=pcv[-4]/(-1)
if(stage==1) temp=basic[3]=7 basic[3]=nonbasic[3]=3 nonbasic[2]=7 obfun =tableau[5, -1L]=(0,-1,3,1) it=it+1=2
至此进行了一次换基迭代(basic=(4,6,3) nonbasic=(1,2,7,5) 再从while 循环头部开始,判断循环条件是否满足 pcol=3
if(stage==2) selse neg=(2) ratios=(1) prow=3
➢ pivot(tableau,prow,pcol) 换基迭代 pv=pv=tableau[3,3]=-1 pcv=tableau[,3]=(1,2,0,-1)
tableau[-3, ] = tableau[-3, ] - (tableau[-3, 3]/pv) %o% tableau[3,]
tableau[3, ] = tableau[3, ]/(-pv)=(1,0,-1,2,1)
tableau[3,3]=1/pv=-1
tableau[-3, 3]=pcv[-3]/(-1)
if(stage==1) temp=basic[2]=6 basic[2]=nonbasic[2]=2
nonbasic[2]=6 obfun =tableau[5, -1L]=(0,-1,3,1) it=it+1=3
至此进行了两次换基迭代(basic=(4,2,3) nonbasic=(1,6,7,5)
再从while 循环头部开始,判断循环条件是否满足,发现!all(obfun > -eps)为false ,则跳出循环,循环结束,到此第一阶段结束。
接着判断第一阶段得到的人造优化函数的最优解,若该值为0则可扔掉人工变量进入第二阶段,在第二阶段仍然按照例1的步骤来求得最优解;否则说明原问题没有可行解。
