第04章 气体动理论
气体动理论

第十三章 气体动理论本章从理想气体的微观组成出发,假以统计性假设,推出理想气体的压强和温度公式,揭示了压强和温度的本质;提出了理想气体内能的概念,介绍了理想气体能量按自由度均分原理;阐述了理想气体的麦克斯韦速率分布率。
这称为气体动理论。
气体动理论的产生和发展凝聚了众多物理学家的智慧和心血。
早在1678年,胡克就提出了气体压强是由大量气体分子与器壁碰撞的结果的观点。
之后,在1738年,伯努利根据这一观点推导出压强公式,并且解释了玻意耳定律。
1744年,俄国的罗蒙诺索夫提出了热是分子运动表现的观点。
在19世纪中叶,气体动理论经克劳修斯、麦克斯韦和玻耳兹曼的努力而有了重大发展。
1858年,克劳修斯提出气体分子平均自由程的概念并导出相关公式。
1860年,麦克斯韦指出,气体分子的频繁碰撞并未使它们的速度趋于一致,而是达到稳定的分布,导出了平衡态气体分子的速率分布和速度分布。
之后,麦克斯韦又建立了输运过程的数学理论。
1868年,玻耳兹曼在麦克斯韦气体分子速率分布律中又引进重力场。
第一节理想气体状态方程一、状态参量1.状态参量概念如何描述系统的冷热变化规律,这就需要一些物理量。
假设气体的质量为 m ,其宏观状态一般可以用气体的压强p 、体积V 和温度T 三个物理量来描述。
如果在热力学过程中伴随着化学反应,还需要物质的量、摩尔质量 、物质各组分的质量等物理量来描述。
如果热力学系统处于磁场中,还需要电场强度E 、电极化矢量P 、磁场强度H 和磁化强度M 等物理量来描述。
选择几个描写系统状态的参量,称为状态参量。
2.状态参量分类按照不同的划分标准,状态参量可作如下划分:(1)按状态参量描写系统的性质划分可分为:V P E P H M几何参量:描述系统的空间广延性。
如体积 。
力学参量:描述系统的强度。
如压强 。
化学参量:描述系统的化学组分。
如各组分的质量,物质的量。
电磁参量:描述系统的电磁性质。
如电场强度 ,电极化强度 ,磁场强度 ,磁化强度 。
第四章气体动理论总结

第四章⽓体动理论总结第四章⽓体动理论单个分⼦的运动具有⽆序性布朗运动⼤量分⼦的运动具有规律性伽尔顿板热平衡定律(热⼒学第零定律)实验表明:若 A 与C 热平衡 B 与C 热平衡则 A 与B 热平衡意义:互为热平衡的物体必然存在⼀个相同的特征--- 它们的温度相同定义温度:处于同⼀热平衡态下的热⼒学系统所具有的共同的宏观性质,称为温度。
⼀切处于同⼀热平衡态的系统有相同的温度。
理想⽓体状态⽅程: 形式1:mol M PV =RT =νRTM形式2:222111T V p T V p =形式3: nkT P =n ----分⼦数密度(单位体积中的分⼦数) k = R/NA = 1.38*10 –23 J/K----玻⽿兹曼常数在通常的压强与温度下,各种实际⽓体都服从理想⽓体状态⽅程。
§4-2 ⽓体动理论的压强公式VNV N n ==d d 1)分⼦按位置的分布是均匀的2)分⼦各⽅向运动概率均等、速度各种平均值相等kj i iz iy ix iv v v v ++=分⼦运动速度单个分⼦碰撞器壁的作⽤⼒是不连续的、偶然的、不均匀的。
从总的效果上来看,⼀个持续的平均作⽤⼒。
2213212()323p nmvp n mv n ω===v----摩尔数R--普适⽓体恒量描述⽓体状态三个物理量: P,V T 压强公式122ω=mv理想⽓体的压强公式揭⽰了宏观量与微观量统计平均值之间的关系,说明压强具有统计意义;压强公式指出:有两个途径可以增加压强 1)增加分⼦数密度n 即增加碰壁的个数2)增加分⼦运动的平均平动能即增加每次碰壁的强度思考题:对于⼀定量的⽓体来说,当温度不变时,⽓体的压强随体积的减⼩⽽增⼤(玻意⽿定律);当体积不变时,压强随温度的升⾼⽽增⼤(查理定律)。
从宏观来看,这两种变化同样使压强增⼤,从微观(分⼦运动)来看,它们有什么区别?对⼀定量的⽓体,在温度不变时,体积减⼩使单位体积内的分⼦数增多,则单位时间内与器壁碰撞的分⼦数增多,器壁所受的平均冲⼒增⼤,因⽽压强增⼤。
大学物理04第四章

第四章 气体动理论一、基本要求1.理解平衡态的概念。
2.了解气体分子热运动图像和理想气体分子的微观模型,能从宏观和统计意义上理解压强、温度、内能等概念。
3.初步掌握气体动理论的研究方法,了解系统的宏观性质是微观运动的统计表现。
4.理解麦克斯韦速率分布律、速率分布函数和速率分布曲线的物理意义,理解气体分子运动的最概然速率、平均速率、方均根速率的意义,了解玻尔兹曼能量分布律。
5.理解能量按自由度均分定理及内能的概念,会用能量均分定理计算理想气体的内能。
6.了解气体分子平均碰撞频率及平均自由程的意义及其简单的计算。
二、基本内容1. 平衡态在不受外界影响的条件下,一个系统的宏观性质不随时间改变的状态。
2. 理想气体状态方程在平衡态下,理想气体各参量之间满足关系式pV vRT =或 nkT p =式中v 为气体摩尔数,R 为摩尔气体常量 118.31R J mol K --=⋅⋅,k 为玻尔兹曼常量 2311.3810k J K --=⨯⋅3. 理想气体压强的微观公式21233t p nm n ε==v4. 温度及其微观统计意义温度是决定一个系统能否与其它系统处于热平衡的宏观性质,在微观统计上32t kT ε=5. 能量均分定理在平衡态下,分子热运动的每个自由度的平均动能都相等,且等于2kT 。
以i 表示分子热运动的总自由度,则一个分子的总平均动能为2t i kT ε=6. 速率分布函数()dNf Nd =v v麦克斯韦速率分布函数232/22()4()2m kT m f e kTππ-=v v v7. 三种速率最概然速率p ==≈v 平均速率==≈v 方均根速率==≈8. 玻尔兹曼分布律平衡态下某状态区间(粒子能量为ε)的粒子数正比于kT e /ε-。
重力场中粒子数密度按高度的分布(温度均匀):kT mgh e n n /0-=9. 范德瓦尔斯方程采用相互作用的刚性球分子模型,对于1mol 气体RT b V V ap m m=-+))((2 10. 气体分子的平均自由程λ==11. 输运过程 内摩擦dS dz du df z 0)(η-=, 1133mn ηλρλ==v v 热传导dSdt dz dT dQ z 0)(κ-= 13v c κρλ=v 扩散dSdt dz d D dM z 0)(ρ-= 13D λ=v三、习题选解4-1 一根铜棒的两端分别与冰水混合物和沸水接触,经过足够长的时间后,系统也可以达到一个宏观性质不随时间变化的状态。
气体分子动理论

气体分子动理论气体分子动理论是描述气体分子运动行为的一种物理理论。
这个理论指出了分子在气体状态下的运动行为,包括分子的速率、轨道和碰撞等。
这个理论解释了许多与气体相关的现象,例如热力学原理、功率引擎行为、热导率等等。
本文将详细介绍气体分子动理论的概念、假设和实验验证,并探讨其在化学、工程和自然科学等领域中的应用。
概念气体分子动理论的概念可以从其名称中得知。
分子是气体的基本单位,而动力学则指出了这些气体分子在气体状态下的运动行为。
按照这个理论,气体分子是在三维空间中随机移动的,其运动速度和方向都是随机的,还会经常碰撞。
分子的速度和能量也很高,而且分子之间的压力和温度通常也非常高。
假设气体分子动理论是建立在一些基本假设的基础上,这些假设可以让我们从分子层面上研究气体状态。
以下是气体分子动理论的基本假设:1.分子运动规律是基于牛顿定律的:分子沿着匀速直线前进,如果有力作用于分子上,分子会产生加速度。
2.分子间的运动足够快、足够随机:分子的平均速度相比于分子间的相互作用力,可以看作是随机热运动。
3.分子之间的互相碰撞是弹性碰撞:分子之间的作用力很小,因此任何碰撞都是弹性碰撞。
4.分子间的空间相对大,可以看做是不存在相互作用的:引力、排斥力等作用力很小,因此新增分子不会对气体的性质产生影响。
这些假设允许我们通过原子和分子的运动来解释理论分析和实验结果,有效推导气体的性质和状态。
实验验证气体分子动理论建立在基础物理尺度上,如角动量守恒定律、速度分布和碰撞等。
因此,文章介绍了几种实验验证气体分子动理论的方法:1.光扩散实验:将悬浮于气体之中的微小颗粒照射红外线。
微小颗粒受到红外线的反射和散射,通过测量其在气体中的扩散行为,可以推断出气体分子的平均速度和碰撞频率。
2.均匀气体分子分布实验:将气体充入小孔振荡单元中,通过与空气的微小污染物有序混合,检测气体分子的运动行为和浓度。
3.气体热传导实验:通过传导热流并测定体系温度梯度,分析气体分子在高温区域的热传导和碰撞频率。
大学物理 气体动理论

三、 温 度
决定一个系统是否与其它系统达到热平衡的宏观性质。
处于热平衡的多个系统具有相同的温度
具有相同温度的几个系统放在一起必然处于热平衡。
温度测量
酒精或水银
A
B
A 和 B 热平衡,TA = TB
热胀冷缩特性,标准 状态下,冰水混合, B 上留一刻痕, 水沸 腾,又一刻痕,之间 百等份,就是摄氏温 标(Co)。
生碰撞的�数目为:Ni = nivix dt d A 速度为 vi 分子在 dt 时间对 dA 的冲量为:
�
x
vxi
dA
vidt
nivixdAdt ⋅ (2mvix )
∑ 所有分子在
dt
时间内对
dA 产生的总冲量为:dI = 1 2
i
2mni
v
2
ix
dAdt
∑ ∑ 气体对器壁的宏观压强为:
p=
mni
T0
273.15
= 8.31(Jmol⋅K)
若写成 ν = N NA
N A = 6.023 × 1023 / mol
N为气体分子总数 阿伏伽德罗常量
µN
R
pV = RT = N T
µNA
NA
令
k
≡
R NA
=
1.38 × 10−23
J
K
玻耳兹曼常数
pV = NkT
p = N kT = nkT V
n:气体分子数密度
2
三、气体分子的平均总动能
设分子有: 平动自由度 t 转动自由度 r
分子平均总动能:
1 εk = (t + r) 2 kT
单原子分子 刚性双原子分子
3
气体动理论知识点总结

气体动理论知识点总结注意:本章所有用到的温度指热力学温度,国际单位开尔文。
T=273.15+t 物态方程A NPV NkT P kT nkT V m PV NkT PV vN kT vRT RTM =→=='=→===(常用)一、 压强公式11()33P mn mn ==ρρ=22v v二、 自由度*单原子分子:平均能量=平均平动动能=(3/2)kT *刚性双原子分子:平均能量=平均平动动能+平均平动动能=325222kT kT kT += *刚性多原子分子:平均能量=平均平动动能+平均平动动能=33322kT kT kT +=能量均分定理:能量按自由度均等分布,每个自由度的能量为(1/2)kT 所以,每个气体分子的平均能量为2k i kT ε= 气体的内能为k E N =ε1 mol 气体的内能22k A ii E N N kT RT =ε== 四、三种速率p =v=≈v=≈三、 平均自由程和平均碰撞次数 平均碰撞次数:2Z d n =v 平均自由程:zλ==v根据物态方程:p p nkT n kT=⇒=平均自由程:zλ==v练习一1.关于温度的意义,有下列几种说法:(1)气体的温度是分子平均平动动能的量度。
(2)气体的温度是大量气体分子热运动的集体表现,具有统计意义。
(3)温度的高低反映物质内部分子热运动剧烈程度的不同。
(4)从微观上看,气体的温度表示每个气体分子的冷热程度。
(错) 解:温度是个统计量,对个别分子说它有多少温度是没有意义的。
3.若室内升起炉子后温度从15℃升高到27℃,而室内气压不变,则此时室内的分子数减少了: 解:PV NkT =2112273150.9627327N T N T +===+ 1210.04N N N N ∆=-=则此时室内的分子数减少了4%.4. 两容器内分别盛有氢气和氦气,若他们的温度和质量分别相等,则:(A )(A )两种气体分子的平均平动动能相等。
第四章 气体动理论

§4-1
分子动理论的基本观点
一、物质微观结构的物理图象 1、物质是由大量的微观粒子——原子或分子组 成的; 2、分子在作永不停息的无规则运动; 3、分子之间有相互作用力。 综上所述,一切宏观物体(不论它是气体、 液体、还是固体)都是由大量的原子或分子组 成的;所有分子都在不停的、无规则运动中; 分子之间有相互作用力。这就是关于物质微观 结构的三个基本观点。
(s t )
C2 引力: f1 t , C2、t均 0 r 斥力: f C 1 , C 、s均 0 2 1 s r t:4 ~ 7 s : 9 ~ 13
2、图线
(f—r图线)
三、分子间的势能曲线(Ep—r图线)
1、分子间的势能: dE p fdr
C1 C2 E p fdr ( s t )dr r r C1 C2 s 1 t 1 ( s 1)r (t 1)r
N pV RT NA
p nkT
温度 T 的物理意义
1 2 3 平 m v kT 2 2
1) 温度是分子平均平动动能的量度 平 T (反映热运动的剧烈程度).
2)温度是大量分子的集体表现,个别分子无意义.
3)在同一温度下,各种气体分子平均平动动能均 相等。 注意 热运动与宏观运动的区别:温度所反 映的是分子的无规则运动,它和物体的整 体运动无关,物体的整体运动是其中所有 分子的一种有规则运动的表现.
由于热力学方法的局限性,我们对平衡态下系统内 部的情况不了解,从而对温度和理想 气体的理解 也很肤浅,对气体的压强更是一无所知,因此,为 了全面了解平衡态下的基本热学信息,我们必须用 分子物理学的方法从微观本质上加以认识。
• 气体动理论是统计物理学的基础; • 气体动理论是从微观的观点来研究气体的热学 性质; • 解释气体的温度、压强、热容、内能等的微观 本质; • 建立统计的概念。
04章分子动理论

2 cos h gr
式 中 为 表 面 张 力 系 数 , 为 接 触 角 , 为 液 体 的 密 度,g为重力加速度,r为毛 细管的内半径.
1
S 4n r 2 ( n 1) 4 3 3m 由m n r n 3 4r 3
n 1 n 1 n
1 3 1 3 1 3
2 3
1 3
3m 则A 6.0 10 2 J r
§4-4 液体的表面现象 11
三、弯曲液面内外压强差(附加压强): 附加压强的概念:若液体表面为曲面,则表面张
§4-4 液体的表面现象 18
液体润湿固体:当附着力 大于内聚力时,情况正相反, 固 附着层内的分子受到的合力 体 f 指向固体,附着层里出现液 体相互推斥的力,分子在附 着层内比在液体内部有较小 的势能,附着层有扩展趋势, 宏观上表现为液体润湿固体.
液体
附 着 层
§4-4 液体的表面现象 19
表面活性物质降低了肺泡表面液体的表面张力系数,人类得以将空 气 吸入肺泡。
吸气时肺泡不会过分膨胀;呼气时肺泡不会过分萎缩。 小肺泡不会萎缩;大肺泡不会过分膨胀。
本 章 小 结
1. 表面张力系数 :沿液体表面垂直作用于单位长 度上的表面张力。 2. 表面张力:f = L 3. 表面能:E=A=S 4. 分子作用半径:分子引力的作用范围(约10-9m) 5. 附加压强:p=p=2 /R 6. 润湿:液体附着在固体表面的现象。 7. 不润湿:液体不附着在固体表面的现象。 8. 接触角:在液体与固体的分界处,液体表面的切 面和固体表面的切面在液体内部的夹角。
气体动理论

MpV 解: T不变,设每天用去m 质量的气体 m RT Mp1V1 使用前,气体质量为 m1 RT Mp2V1 m2 充气时,气体质量为 RT
使用天数:
m1 m2 ( p1 p2 )V1 N 9.6天 m pV
§7.4
理想气体压强公式与温度公式
一、理想气体的微观模型
热力学第零定律——测温原理 热平衡:两热力学系统互相热接触,经过一段时 间后它们的宏观性质不再变化,即达到了热平衡 状态。
热力学第零定律:在不受外界影响的条件下,如 果两个系统分别与第三个系统达到热平衡,则这 两个系统彼此也处于热平衡。
A A
B
C
B C
温度 T —— 表征物体的温暖程度
在宏观层次上:温度是表征热平衡状态下系统的 宏观性质的物理量。处于热平衡的两个系统,它 们的温度是相同的。 在微观层次上:温度是物 质分子无规则运动的量度。 这种微观运动在宏观上不 能直接观察,观察到的是 温度。随着温度的升高, 微观运动也加强。 温度 —— 某种温度计上的读数
1 2 kt v 分子平均平动动能 2
是大量分子运动的集体表现,决定于微观量 的统计平均值。 对少数分子压强无意义。
四、理想气体的温度公式 理想气体状态方程 压强公式
p nkT
说明: 温度是分子平均平动动能的量度,是分子热 运动剧烈程度的标志。 温度是大量分子热运动的集体表现,是统 计性概念,对个别分子无温度可言。
热运动:物质中大量微观粒子的无规则运动 热学:是研究与热现象(热运动的集体表现)有关 的规律的学科。 ①宏观理论:热力学(宏观理论) 从实验事实出发,以热力学基本规律为基础,用 逻辑推理的方法研究物质各宏观性质间的关系,以 及热运动过程进行的方向和限度。 ②微观理论:统计物理学(微观理论)
04章分子动理论

分子 t r i He, Ar 3 0 3 O2, N2 3 2 5 H2O 3 3 6 CH4 3 3 6
❖ 理想气体的内能
一定量理想气体的内能——组成气体的全部分
子的平均动能之和.
分子的平均动能
i kT
1mol理想气体的内能
2 E1mol
NA
i 2
kT
i 2
RT
一定质量m理想 气体的内能
接触角:在液体与固体接触处作液体表面和固体表面的 切线,此两切线在液体内部所夹的角。
❖ 毛细现象(capillarity):润湿液体在毛细管中上 升和不润湿液体在毛细管中下降,这种现象叫做 毛细现象.
上升或下降的高度 h 可用 下式计算:
h 2 cos gr
式 中 为表 面 张力 系 数 , 为 接 触 角 , 为 液 体 的 密
状态参量:
压强 p Pa
温度 T K
体积 V m3
❖ 理想气体的物态方程
压强不太高,温度不太低的实际气体都可视 为理想气体,遵守
pV m RT 或 p=nkT M
式中,m:气体质量, 单位为kg. M:气体摩尔质量,单位为kg·mol1. R = 8.31 Jmol1·K1.
二. 理想气体的微观模型
固体吸附:在固体表面吸附一层表面活性物质
❖ 弯曲液面的附加压强
在肥皂泡、小液滴等气体与液体接触的地方,液 面都是弯曲的.对于球面型的液面来说,可以证明 其附加压强为
Δp
p内
p外
2
R
对于中空的肥皂泡,由于液膜有内、外两个表面, 可以认为两个表面半径R相等,其附加压强为
p4
R
❖ 毛细现象 气体栓塞
附着层:在液体和固体接触处取一液体薄层,厚 度为分子引力的有效作用距离,这个液体薄层称 为附着层.
第4章气体动理论

00:30
kT B. v v v m0
2 x 2 y 2 z
3kT C. v v v m0
2 x 2 y 2 z
2 2 D. v x v2 v y z 0
投票人数:0
5. 关于温度的意义,有下列几种说法: 00:30 (1)气体的温度是分子平均平动动能的量度; (2)气体的温度是大量气体分子热运动的集体表现,具 有统计意义; (3)温度的高低反映物质内部分子运动剧烈程度的不同; (4)从微观上看,气体的温度表示每个气体分子的冷热 程度。 上述说法中正确的是( )。 A. B. C. D. (1)(2)(4) (1)(2)(3) (2)(3)(4) (1)(3)(4)
投票人数:0
23. 麦克斯韦速率分布曲线如图4-4所示,图中A,B
两部分面积相等,则由图可知( )。 00:30
A O B
f (v )
A. v0 为最概然速率
B. v0 为平均速率
C. v0 为方均根速率
D. 速率大于和小于 v0 的 分子数各占一半
v0 图4-4
v
投票人数:0
24. 一定量的理想气体,在容积不变的条件下,当温
H2 O2
)。
00:30
D. 无法判断
图4-1
投票人数:0
2. 一密闭容器中储有4 kg氢气和4 kg氦气,它们处于 平衡状态。那么,氢气和氦气的体积比和压强比分别 为( A. B. C. D. )。 2:1,1:1 2:1,2:1 1:1,1:1 1:1,2:1 00:30
投票人数:0
3. 在没有外力场作用下,分子质量为m0的大量气体分 子处于热动平衡态时,下列各式中成立的是( )。
气体动理论

率最大.
2020/9Leabharlann 2218气体动理论
五、平均自由程
1
kT
2 π d 2n
2 πd2p
平均碰撞频率
Z 2d 2n
六、气体内的迁移现象
粘滞现象 扩散现象 热传导现象
动量迁移 质量迁移 能量迁移
Z
2020/9/22
19
气体动理论
例1 (理想气体物态方程)容器中有密封的某种理
想气体,分别经历两次加热过程,获得两条过程 曲线,如图(a)(b)所示。试分析(1)图a中气体 的压强如何变化;(2)图b中气体的V体积如何变 化。
v
0
v
f
v
dv
v 8kT 8RT m M
平方平均速率
v2 v2 f v dv 0
方均根速率
vrms
v2
3kT m
3RT M
3.麦氏分布函数
f
v
4
m 2kT
3/2
mv2
e 2kT
v2
f (v)
fmax
o vp
v
4.三种统计速率
最概然速率 v p
2kT m
2RT M
2020/9/22
2
分子的平均平动动能
—— 3 kT
2
理想气体的内能——
i
RT
2
分子 单原子 双原子 多原子
自由度i
3
56
分子的平均 3
3
3
平动动能
kT kT
2
2
kT 2
分子的平均 转动动能
0
2 kT 3 kT
2
2
分子的 平均动能
3 kT 2
气体动理论

3
统计规律有以下几个特点: 2、统计规律有以下几个特点:
(1)只对大量偶然的事件才有意义。 只对大量偶然的事件才有意义。 (2)它是不同于个体规律的整体规律。 它是不同于个体规律的整体规律。 (3)总是伴随着涨落。 总是伴随着涨落。 但就前面其中的每一次实验来看, 但就前面其中的每一次实验来看,所得的分布曲线只能 近似重合,不能完全一致,由此说明,在统计规律中一 近似重合,不能完全一致,由此说明, 定出现起伏或涨落现象。 定出现起伏或涨落现象。
p,V ,T
2、气体压强 :作用于容器壁上单位 面积的正压力 压强-----帕斯卡 压强---帕斯卡 1 a =1 ⋅ m 2 P N −
1 atm= 760 m g = 1.013×105 P m H a
气体冷热程度的量度. 3、温度 : 气体冷热程度的量度. 温度---开尔文 温度---开尔文 --T ) = 273.15+ t(0C (K )
(N、V、M)
l3
l2 B
A
O
l1
X
设一个分子的质量为 m
Z
仅讨论大量分子与一面A的碰撞产生的压强 压 强
23
个分子与A面发生碰撞时 面发生碰撞时, 第i个分子与 面发生碰撞时,由于碰撞为完全弹性的 并且分子的质量远远小于器壁的质量。 ,并且分子的质量远远小于器壁的质量。 Y 面所受到的冲量为: 所以A面所受到的冲量为:
T1 = T2
p1 = p 2
M PV= R T M mol
(D) 那种的密度较大是无法判断的 那种的密度较大是无法判断的.
[A ]
M ρ= V
1
M mol 1 ρ1 = ρ 2 M mol 2
H2 O2
2
气体动理论

第四章气体动理论一、基本要求1. 理解理想气体微观模型。
理解理想气体压强、温度的概念及其微观本质。
掌握理想气体压强、温度的公式并会做相应计算。
通过推导气体压强公式,了解气体动理论的基本研究思想和方法。
2. 理解能量均分定理,掌握理想气体内能的概念、公式及有关计算。
3. 了解麦克斯韦速率分布律、速率分布函数和速率分布曲线的物理意义,了解气体分子热运动三种统计速率。
4. 了解玻耳兹曼能量分布律。
二、内容概要(一)统计概念1.理想气体压强(1)压强概念 垂直作用于器壁单位面积上的压力。
(2)压强公式 p=n 32ε=231_v nm 为分子平均平动动能。
(4-1) (3)适用条件 理想气体(大量分子组成),处于平衡态。
(4)微观本质①由大量气体分子对器壁的碰撞所产生,表示单位时间内气体分子作用于器壁单位面积上的平均冲量。
②一定温度的平衡态下,单位体积内的气体分子数(分子数密度n)越多,或分子平均平动动能(-ε)越大,压强就越高。
-n 、-ε为气体分子微观量的统计平均值。
2. 理想气体温度(1) 温度概念 表征系统处于热平衡态的物理量。
(2) 温度公式 -ε=kT 23 (3) 适用条件 理想气体(由大量分子组成)处于平衡态。
(4) 微观本质 反映了大量分子热运动的剧烈程度,是分子平均平动动能的量度。
(二)统计规律1. 能量均分定理(1) 内容要点物质分子每个自由度的平均动能kT 21 每个分子的平均动能 -k ε=kT i 2vmol 理想气体内能 E=v RT i 2 气体自由度 i=()()()⎪⎩⎪⎨⎧刚性多原子分子刚性双原子分子单原子分子653(2) 适用条件. 式 (4-2) (4-3)----任何物质分子,温度为 T 的平衡态。
式 (4-4)----理想气体,温度为 T (室温附近)的平衡态。
2. 麦克斯韦速率分布律(1) 气体速率分布函数f(v)=Ndv dN (4-6) 表示速率v 在附近单位速率区间内的分子分布概率(即分子数占总分子数的比率)。
第四章气体动理论

第四章气体动理论4.1 关于理想气体的基本假设是什么?【答】理想气体是气体分子运动论和热学所研究的,由大量做无规则热运动的分子组成的最简单的系统,它是客观实际存在的许多真实气体的理想化的物理模型。
关于理想气体的基本假设如下:(1)气体的密度很小,因而气体分子问的平均距离比,分子本身的几何线度大很多’(2)气体分子之间的相互作用力随分子间距离的增大,而急剧地减小,当分子问的距离超过分子本身的几何线度很。
多时,分子间的相互作用力变得非常小,以至于可以忽略不-计;(3)气体分子是完全弹性的刚性球,因此,气体分子之间的相互碰撞以及气体分子与容器壁的碰撞都是完全的弹-性碰撞;(4)气体分子之间的相互碰撞很少,即在绝大部分时间内,气体分子都是自由运动的。
也就是说,气体分子的运动轨道是由许多直线段组成的不规则的折线,各直线线段的长度比分子本身的几何线度大很多;(5)气体分子的运动速度很大,因此单位时间内气体分子之间的相互碰撞次数很多,在标准状态下,一般气体分子的运动速度为500米/秒左右,一个分子在1秒内所经历的碰撞次数为大约810次。
上述五条即是关于理想气体的基本假设,做了这样的基本假设后,气体的许多主要性质被突出了,例如,理想气体服从状态方程: PV=nRT这就为我们研究气体各状态参量——压强P、体积V和温度T之间的关系提供了方便。
做了上述基本假定之后,这样的理想气体虽然并不真实存在,它只是客观存在的真实气体的理想模型,但它与一般状态下的气体,例如,氢气、氨气和氧气等非常接近。
实际上,在压强不太高,温度不特别低的情况下,很多种真实气体都可以用理想气体来近似。
换句话说,由于对理想气体的基本假设是抓住了问题的本质,忽略了次要因素,因此,理想气体具有很好的普遍性和适用性,成为气体分子运动论和热学的典型的研究对象。
4.2 什么是动力学规律性?什么是统计规律性?【答】动力学规律性是从经典力学、经典电磁场理论以及其他物理学科的研究中总结出来的。
气体动理论 章节总结

气体动理论 章节总结第四章 气体动理论1.平衡态 在没有外界影响的条件下,系统的宏观物理性质不随时间变化的状态。
2.热力学第零定律系统A和系统B分别与系统C处于热平衡,那么当系统A和系统B接触时,它们也必定处于热平衡。
3.理想气体的状态方程RT M m pV =式中,普适气体常量8.31J /(mol K)R ∙=玻耳兹曼常量231.3810J /Kk -=⨯NkT pV =或4.理想气体的压强公式k n p ε32=压强是单位时间单位面积所受大量分子的平均冲量。
5.理想气体的温度公式kT k 23=ε 温度是分子的平均平动动能的统计平均值,反映了系统内大量分子无规则运动的剧烈程度。
6.自由度确定物体位置的独立坐标数目。
单原子分子 3 0 3双原子分子 3 2 5多原子分子 3 3 6t r i 分子自由度平动转动总刚性气体分子的自由度7.能量均分定理温度为T的平衡态下,气体分子每个自由度的平均能量都相等,而且等于kT 21根据能量均分定理,如果一个气体分子的自由度是 ,则它的平均能量就是i kT i 2=ε理想气体的内能为8.理想气体的内能mol μRT i E 2μ=9.麦克斯韦速率分布律速率分布函数NdvdN v f =)(物理意义:速率在v 附近的单位速率区间的分子数占分子总数的百分比麦克斯韦速率分布函数222/32)2(4)(v e kT m v f kT mv -=ππ三种统计速率最概然速率M RT M RT m kT v p 41.122≈==平均速率M RT M RT m kT v 60.188≈==ππ方均根速率M RTM RTm kT v v 73.1332rms ≈===。
第4章气体动理论
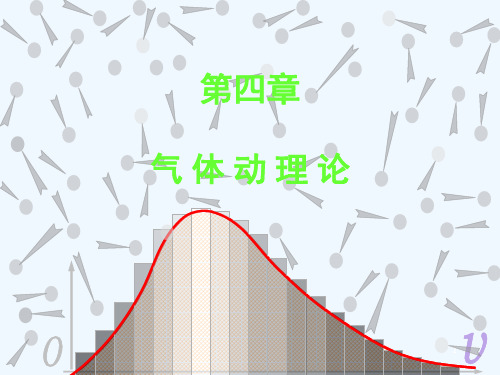
小球每次落入哪个狭槽是不
完全相同的,这表明在一次
实验中小球落入哪个狭槽中 是偶然的。 尽管一个小球落入哪个槽中 是偶然的,但大量小球的分 布规律则是确定的,即遵从
统计分布规律。
7
统计规律:当小球数N 足够大时小球的分布具有统计规律。
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
子,如果分子有 t 个平动自由度,r 个转动自由度,则气体分 子的平均动能为
1 i ( t r ) kT kT 2 2
单原子分子
双原子分子
多原子分子
3 kT 2
5 kT 2
6 kT 2
27
★ 理想气体的内能 实际气体的内能 气体分子热运动的各种形式的动能和势能的总和。 平动动能 分子动能 转动动能 振动动能 分子振动势能
i i
于1,称为概率的归一化条件。
6
小球在伽尔顿板中的分布规律
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
单位: 8.31J · mol-1 · K-1
4
★ 统计规律
一定条件下,大量偶然随机事件的整体具有确定的规律
性,这种规律称为统计规律。
对单个分子运用力学规律,对大量分子求统计平均值, 从而建立大量分子微观量的统计平均值与系统宏观量之 间的关系。这种关系就是所要寻求的统计规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.伽尔顿板实验
统计物理关心两件事:
1. 分布 2. 平均值
1.气体分子速率分布
离散:
f
vi : N i
N i
N
f (vi )
O f v 1 v 2 v 3 v4 v5 v
N i --分布函数 f (vi ) N
连续:
dN v v ~ v dv : dN v f (v )dv N
而系统以外的部分则称为外界。 热力学系统是一个由大量的 微观粒子(分子、原子)组 成的宏观系统。 热力学系统与外界之间通过 做功,热传递和粒子交换而 相互联系。
外界
热力学系统
2.平衡态
在不受外界影响的条件下,系统的宏观性质不 随时间改变的状态,称为平衡态。
2.1 力学平衡: 系统各部分受力平衡。在无外场条件下, 力学平衡的条件为系统内部压强处处相等,系统内外的压 强在分界处保持相等。
解: (1) pV RT
(0.10 / 32 10 3 ) 8.31 (47 273.15) V p 10 1.013 105 8.3110 3 (m 3 )
m' RT ' (2) p 'V RT ' M Mp'V 32 10 3 (5 / 8) 10 1.013 105 8.31 10 3 m' RT ' 8.31 (27 273.15)
§4-1 平衡态 状态方程 §4-2 分子热运动及其统计规律 §4-3 麦克斯韦速率分布 §4-4 玻尔兹曼分布 §4-5 理想气体的压强与温度 §4-6 能量均分定理 理想气体的内能 §4-7 真实气体 §4-8 平均碰撞频率与平均自由程 §4-9 输运现象
1.热力学系统
把研究的对象视为一个系统,称为热力学系统,
f(v)的性质: 1)存在最可几速率vp
2)T增大,速率大的分子数增多,vp增大
3)f(v)满足归一化条件: f (v )dv 1
0
f
T1
T1 T2
T2
O
vp1 vp2
v
3. 三个统计速率
1.最概然速率 vp:
df 2kT 2 RT 0 vp dv m M 2.平均速率 v :
1.热学的研究对象
研究一个与温度有关的各种宏观现象——热现象,
以及这些现象的微观机制。
热学研究的范围很广,任何与热(微观粒子热运动)相关 的现象都是热学的研究范围。 热学所研究的系统是一个由大量的微观粒子(分子、原子) 组成的宏观系统。
2.宏观与微观
2.1 宏观现象与宏观量: 宏观现象即一个系统所表现出来 的各种物理性质以及这些性质的变化规律。描述一个系统 宏观性质的物理量称为宏观量。例:P、V、T、E、C等。
p /T C
--查理定律
V /T C
pV C
--盖.吕萨克定律
--玻意耳定律
4.3 范德瓦耳斯方程
a ( p 2 )(Vm b) RT Vm
其中 V m
Vm
为摩尔体积,a、b 由实验确定。
例 4-1 一容器内贮有氧气 0.10kg, 压强为 10atm, 温度为 470C。因容器漏气,过一段时间后,压强 减到原来的 5/8,温度降到 270C。问: (1)容器体积为多大? (2)漏去了多少氧气?
23
10
2)每个分子都在作不停的运动──热运动。由于分 子之间频繁的碰撞,分子的运动是杂乱无章的。
2
v ~ 10 米 / 秒
Z ~ 10 次 / 秒
3 )气体分子之间的相互作用
力很小(一般可忽略)。
9
2.分子热运动的统计规律
个别分子的运动是杂1. 掷骰子
270C ,海平面上的气压 p0=1.0atm ,今测得某山顶
上的大气压p=0.8atm。 (1)分别求出海平面和山顶上空气的分子密度; ( 2 )山的高度约为多少?(设空气的平均分子量 为29)
m m pM RT 解: (1) pV M V RT
p0 M 0 0.94kg/m 3 RT
RT
6.67 10 2 (kg )
m m m' 0.10 6.67 10 2 3.33 10 2 ( kg )
1.气体分子热运动的微观模型
1)气体系统由大量的分子组成。
26 m ~ 10 千克 N A 6.02 10 个 / 摩尔 d ~ 10 米
pM 1.18kg/m 3 RT
(2) p ( z ) p0 e
mgz kT
p0 e
Mgz RT
p0 RT z ln 1.96 103 (m) Mg p
1.理想气体的微观模型及混沌性假设
1.1 理想气体的微观模型
① 分子本身的线度比起分子间的间距小得多而可 忽略不计。 ② 除了碰撞的瞬间外,分子之间以及分子与容器壁 之间的相互作用力可忽略不计。
x 2
2
0
x e
4
x 2
dx
3 8
2
……
麦克斯韦 Maxwell,James Clerk (1831~1879)
英国物理学家。经典电动力学的创始人,统计物理学 的奠基人之一。 1831 年 6 月 13 日生于爱丁堡, 1879 年 11 月 5 日 卒 于 剑 桥 。 1847 ~ 1850 年 在 爱 丁 堡 大 学 学 习 , 1850 ~1854年入剑桥三一学院攻读数学。1856~1860年担 任阿伯丁郡的马里查尔学院教授。 1860 ~ 1865 年在伦敦皇 家学院执教,并从事气体运动理论的研究 。 1860 年为英 国皇家学会会员。 1871 年任剑桥大学教授,创建并领导了 英国第一个专门的物理实验室 卡文迪什实验室 。麦克斯 韦的主要贡献是创立了经典电动力学。他发展了 M. 法拉第 关于电、磁相互作用必须通过中间媒质的思想,并把这种 中间媒质称为以太 ( 后来研究表明,不存在所谓的以太, 这种中间媒质实际上是电磁场 ),并在此基础上提出了位移 电流的概念 。
③ 气体分子分子的运动满足经典力学,分子之间以
n( z ) n 0 e
mgz kT
2.2 等温气压公式
mgz n( z ) n e kT 0 p nkT
p( z ) p 0 e
mgz kT
其中 p 0 n0 kT 为 z 0 处的压强。
例 4-3 设地球大气可近似看成是等温的,温度为
2.2 微观运动与微观量: 微观运动即系统内部的微观粒子 的热运动。描述微观粒子热运动的物理量称为微观量。例: m、v、 等。 2.3 宏观与微观的关系:微观粒子的热运动与系统的各种宏
观热现象之间存在着内在的联系。宏观量等于微观量的统计 平均值。
3.热学的两种研究方法
3.1 宏观方法:通过对热现象进行观察和实验测量,总结出 热力学基本定律;从基本的热力学定律出发,通过严密的逻 辑推理和演绎,研究物质的宏观性质以及宏观物理过程的运 行规律——热力学。 优点:可靠性,普遍性。 缺点:只研究宏观现象,未能揭示产生这些现象的原因(微 观机制)。 3.2 微观方法: 依据微观粒子热运动所满足的力学定律, 通过统计的方法求出各微观量的统计平均值,导出宏观量 与微观量的关系,从而揭示各种热现象的本质——统计物 理学。 优点:从更深层次(微观层次)揭示各种热现象的本质。 缺点: 数学上较复杂,为克服数学的困难而假设的各种微 观模型均有一定的局限性。
麦克斯韦研究了法拉第的电磁场设想,于 1864 年发表 了《电磁场动力学理论》,提出包括偏微分方程的麦克斯 韦方程组,概括了当时已知的关于电磁现象的一切实验结 果,从而创立了经典电动力学。他根据这一理论得出结论: 存在着电磁波;电磁波在真空中传播的速度等于光速;光 的本质是电磁波;电磁波会产生压力等 。 麦克斯韦在这 一 期 间 的 著 作 还 有 1855 ~ 1856 年 发 表 的 《 论 法 拉 第 力 线 》、 1861 ~ 1862 年发表的《论物理力线》、 1873 年发 表的《电学和磁学论》等。 1868 年继 W. 韦伯等之后,他以 更高的精确度测定了电荷的静电单位对电磁单位的比值, 并证实了它就等于光速。麦克斯韦在气体运动理论、光学、 热力学和弹性理论方面也作出了重要贡献 ,1860年得出了 理想气体分子按速度的统计分布律,计算了分子的自由程。 他在 1861 年提出,彩色是由红、绿、蓝三基色组成的,他 还是第一批彩色照片的制作者之一。 1873 ~ 1874 年他发现 了双折光现象。
k p
n 0 为势能为零处的分子数密度。
2.玻尔兹曼分布的应用
2.1 有力场时分子数密度的分布
dN r n0e
p
kT
m d r ( ) e 2 kT
p
mv 2 3/ 2 2 kT
d v n0e
p
kT
d r
kT n( r ) n 0 e
特别地,重力场中粒子数密度的分布:
解:(1)
0
6 f (v)dv 1 C 3 v0
v0 / 4
5 (2) N N f (v)dv N 0 32 v0 df (v) 0 vp (3) dv v v 2
p
(4) v
2
0
v0 vf (v)dv 2
2 1/ 2 0
v [ v f (v)dv]
v
0
8kT 8RT f (v)vdv v m M
1/ 2
3.方均根速率 v 2 :
2 v f (v)v dv 0 2
3kT 3RT v m M
