江西专版七年级数学下册.第课时平方根新版
合集下载
七级数学下册6.1平方根第1课时课件新版新人教版版

精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
◎第一阶
◎第二阶
8 ◎第三阶
)
精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
◎第一阶
◎第二阶
9 ◎第三阶
)
精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
◎第一阶
◎第二阶
10 ◎第三阶
)
精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
)
精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
◎第一阶
◎第二阶
15 ◎第三阶
)
谢谢观看!
最新精品中小学课件
◎第一阶
◎第二阶
11 ◎第三阶
)
精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
◎第一阶
◎第二阶
12 ◎第三阶
)
精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
◎第一阶
◎第二阶
13 ◎第三阶
)
精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
◎第一阶
◎第二阶
14 ◎第三阶
精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
◎第一阶
◎第二阶
1 ◎第三阶
)
选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
◎第一阶
◎第二阶
2 ◎第三阶
)
精选
◆知识导航
最新精品中小学课件 ◆典例导学 ◆反馈演练(
七年级下册:6.1《平方根》ppt课件市公开课一等奖省赛课获奖PPT课件

2 能正确地表示一个数平方根, 了解开平方运算和乘方运算之 间互逆关系.
第4页
三、研读课文
知识点一
认真阅读书本第44至46页内容 ,完 成下面练习并体验知识点形成过程.
平 方
1 、填空
x2 1
15 36 49
4 25
x
1 15 6 7
2 5
根 2、平方根:假如一个数平方等于a,那么
这个数就叫做a_____平__方或根_____二_次_方.根
方 (2)存在条件相同:平方根和算术平方根都是只
根
有_非__负___数才有. (3)0平方根、算术平方根都是___0.
和
算 术 2、区分:(1)定义不一样:“假如一个数_x___平方
等于,这个数就叫做a平方根” ; “非负数a非
平 负平方根叫a _______算__术__平_”方. 根
方
(2)个数不一样:一个正数有两___个平方根,而一 个正数算术平方根只有_一___个.
即 x2 =a时x叫做a平方根,记作x=____a.
温馨提醒:符号 a 只有当___a_≥0____时有意
义,___a_<0____时无意义.
3、求一个数平方根运算,叫做___;开平平方方 与开平方互为 ____运逆算.
第5页
知识点一
三、研读课文
例4 求以下各数平方根: (1)100; (2) 9 ; (3)0.25
根 (3)表示法不一样:正数a平方根表示为_±__a_,正
数算术平方根表示为___ a.
第10页
四、归纳小结
1、假如_一__个__数__平__方____等于a,那么这个数就叫做平方 根或二次方根; 2、非负数平方根表示为___±___a.
第4页
三、研读课文
知识点一
认真阅读书本第44至46页内容 ,完 成下面练习并体验知识点形成过程.
平 方
1 、填空
x2 1
15 36 49
4 25
x
1 15 6 7
2 5
根 2、平方根:假如一个数平方等于a,那么
这个数就叫做a_____平__方或根_____二_次_方.根
方 (2)存在条件相同:平方根和算术平方根都是只
根
有_非__负___数才有. (3)0平方根、算术平方根都是___0.
和
算 术 2、区分:(1)定义不一样:“假如一个数_x___平方
等于,这个数就叫做a平方根” ; “非负数a非
平 负平方根叫a _______算__术__平_”方. 根
方
(2)个数不一样:一个正数有两___个平方根,而一 个正数算术平方根只有_一___个.
即 x2 =a时x叫做a平方根,记作x=____a.
温馨提醒:符号 a 只有当___a_≥0____时有意
义,___a_<0____时无意义.
3、求一个数平方根运算,叫做___;开平平方方 与开平方互为 ____运逆算.
第5页
知识点一
三、研读课文
例4 求以下各数平方根: (1)100; (2) 9 ; (3)0.25
根 (3)表示法不一样:正数a平方根表示为_±__a_,正
数算术平方根表示为___ a.
第10页
四、归纳小结
1、假如_一__个__数__平__方____等于a,那么这个数就叫做平方 根或二次方根; 2、非负数平方根表示为___±___a.
(新人教版)七年级数学下册:6.1《平方根》PPT课件
a 与- a 互为相反数; (3) 在± a 中,a≥0.
(4)( a )2=a (a≥0),
a2
| a |
a,a≥0 a. a<0
(5)一个正数有两个平方根,它们互为 相反数.
零的平方根是零.
负数没有平方根.
平方根与算术平方根的 联系与区别:
联系:
1.算术平方根是平方根的一种; 2.只有非负数才有算术平方根和平方根; 3.0的算术平方根和平方根都是0.
所以7900 <v <11200
答: 要使宇宙飞船离开地球进入轨道正常 运行,必须使它的速度大于7900米/秒,小于 11200米/秒.
想一想
要做一张边长是4cm 的方桌面,它的面积是多 少?
这个问题实际上就是 求:42=?的问题.
根据乘方运算,可知 42=16cm2.
4cm
反过来,要做一张面积是16cm2的 桌面,它的边长是多少cm?
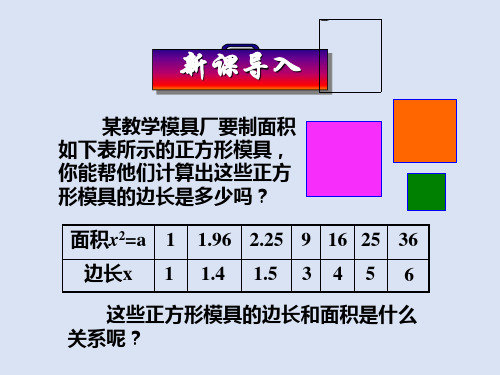
新课导入
某教学模具厂要制面积 如下表所示的正方形模具, 你能帮他们计算出这些正方 形模具的边长是多少吗?
面积x2=a 1 1.96 2.25 9 16 25 36 边长x 1 1.4 1.5 3 4 5 6
这些正方形模具的边长和面积是什么 关系呢?
教学目标
知识与能力
1.理解平方根和算术平方根的概念,了解平方 与开平方的关系;
毕达哥拉斯认为“宇宙间的一切现象都能 归结为整数或整数之比,即都可用有理数来描 述.
但后来,这学派的一位年轻成员希伯索斯 发现边长为1的正方形的对角线的长不能用有理 数来表示,这就动摇了毕达哥拉斯学派的信条, 引起了信徒们的恐慌,他们试图封锁这一发现, 然而希伯索斯偷偷将这一发现传播出去,这为 他招来了杀身之祸,在他逃回家的路上,遭到 毕氏成员的围捕,被投入大海.
(4)( a )2=a (a≥0),
a2
| a |
a,a≥0 a. a<0
(5)一个正数有两个平方根,它们互为 相反数.
零的平方根是零.
负数没有平方根.
平方根与算术平方根的 联系与区别:
联系:
1.算术平方根是平方根的一种; 2.只有非负数才有算术平方根和平方根; 3.0的算术平方根和平方根都是0.
所以7900 <v <11200
答: 要使宇宙飞船离开地球进入轨道正常 运行,必须使它的速度大于7900米/秒,小于 11200米/秒.
想一想
要做一张边长是4cm 的方桌面,它的面积是多 少?
这个问题实际上就是 求:42=?的问题.
根据乘方运算,可知 42=16cm2.
4cm
反过来,要做一张面积是16cm2的 桌面,它的边长是多少cm?
新课导入
某教学模具厂要制面积 如下表所示的正方形模具, 你能帮他们计算出这些正方 形模具的边长是多少吗?
面积x2=a 1 1.96 2.25 9 16 25 36 边长x 1 1.4 1.5 3 4 5 6
这些正方形模具的边长和面积是什么 关系呢?
教学目标
知识与能力
1.理解平方根和算术平方根的概念,了解平方 与开平方的关系;
毕达哥拉斯认为“宇宙间的一切现象都能 归结为整数或整数之比,即都可用有理数来描 述.
但后来,这学派的一位年轻成员希伯索斯 发现边长为1的正方形的对角线的长不能用有理 数来表示,这就动摇了毕达哥拉斯学派的信条, 引起了信徒们的恐慌,他们试图封锁这一发现, 然而希伯索斯偷偷将这一发现传播出去,这为 他招来了杀身之祸,在他逃回家的路上,遭到 毕氏成员的围捕,被投入大海.
平方根 第1课时 课件 2022—2023学年人教版数学七年级下

(3) 64 . 81
解:(1) 9 3 ;
(2) 0.49 0.7 ;
(3)因为
8 9
2
64 81
,所以
64 81
8 9
.
课堂小结
定义:如果一个数的平方等于a,即x2= a,那 么这个数叫做a 的平方根.
平方根
性质:(1)正数有两个平方根,两个平方根 互为相反数.(2)0的平方根还是0.(3)负数 没有平方根.
课程讲授
1 平方根
练一练:判断下列说法是否正确.
(1)49的平方根是7.( ×) (2)2是4的平方根;( √) (3)-5是25的平方根;( √) (4)64的平方根是±8;(√ ) (5)-16的平方根是-4.( ×个数a的平方根的运算,叫做开平方.
平方
+1 -1
(2)用计算器计算 3 (精确到0.001),并利用你在(1)中发现 的规律说出 0.03, 300, 30 000 的近似值,你能根据 3 的值
说出 30 是多少吗?
随堂练习
1.填一填 (1)9的算术平方根是____3____;
(2) 9 的算术平方根是____3____;
(3)0.01的算术平方根是 __0_.1_____; (4)10-6 的算术平方根是__1_0_-3____; (5)(-4)2的算术平方根是___4_____; (6)10的算术平方根是________.
D.x≠ 1 2
课程讲授
2 估算算术平方根
问题1: 2 有多大呢?
因为 12 = 1,22=4,所以1< 2 <2; 因为 1. 42 = 1. 96,1. 52=2. 25,所以 1.4< 2 <1.5; 因为 1.412 = 1.988 1,1.422 = 2.016 4, 所以 1.41< 2 <1.42; 因为 1. 4142 = 1. 999 396,1. 4152=2. 002 225, 所以 1.414< 2 <1.415; ……
平方根(第3课时)教学课件全

(3) ∵(±0.5)2=0.25,
∴100的平方根是±10; ∴0.25的平方根是±0.5.
(2)
∵(±
3 4
)2= 9
16
,
∴ 9 的平方根是±3 ;
16
4
巩固练习
列说法是否正确:
(1)0的平方根是0;
(√ )
(2)1的平方根是1;
(× )
(3)-1的平方根是-1;
(×)
(4)0.01是0.1的一个平方根.( × )
( )2 9
9平方分米
显然,括号里应是±3,但-3不符 题意. ∴方桌面的边长应是3分米.
你还能得到什么问题呢?
?分米
探究新知
问题: 如果一个数的平方等于9,这个数是多少?
由于 3 2 =9 ,
所以这个数是3或-3.
想一想:3和-3有什么特征? 3和-3互为相反 数,会不会是 巧合呢?
探究新知
做一做,想一想:
探究新知
1. 121的平方根是什么? 11
2. 0的平方根是什么? 0
16
3. 49
的平方根是什么?
4 7
4. -9有没有平方根?为什么?
没有,因为一个数的平方不可能是负数.
探究新知
通过这些题目的解答,你能发现什么?
问题:(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的 平方是负数?
(1) 4的平方等于16,那么16的算术平方根就是__4___.
(2)
2 5
的平方等于
4 25
,那么
4 25
的算术平方根就是__52__.
(3) 展厅地面为正方形,其面积是49 m2,则其边长为_7__m.
七下数学6.1平方根ppt课件

132 122 ==5 169-144= 25 =5
精选ppt课件2021
20
4.用大小完全相同的240块正方形地板砖,铺一间 面积为60 m2的会议室的地面,每块地板砖的边长 是多少?
解:设每块地板砖的边长为x m.由题意得
24x02 60,x2 1. 4
x 1 1 0.5 42
故每块地板砖的边长是0.5 m.
所以正数 t 42 (秒). 即铁球到达地面需要2秒.
精选ppt课件2021
17
当堂练习
1.填空:(看谁算得又对又快) (1) 一个数的算术平方根是3,则这个数是 9 . (2) 一个自然数的算术平方根为a,则这个自然数 是_a_2_;和这个自然数相邻的下一个自然数是 a2+1 .
(3) 81 的算术平方根为 3 . 81 9 (4) 2的算术平方根为___2 _.
2 1 .4 1 42 1 35 6 23 7 3 ......
小数位数无限,且 小数部分不循环
小数位数无限,且小数部分不循环的小数称为 无限不循环小数.
2 是一个无限不循环的小数
精选ppt课件2021
31
2
精选ppt课件2021
32
典例精析 例1:估算 19 -2的值 ( B ) A.在1和2之间 B.在2和3之间 C.在3和4之间 D.在4和5之间
出它们的算术平方根.
2 5
-36 , 0.09 , 1 2 1
, 0,
2,
3
2
.
-只36有没非有负算术数平才方有根算. 术平方根,算术平方根是非负的.
0.09 0.3
25 5 121 11
00
2
3 3
3.你知道 2 有多大吗? 2的算术平方根是 2 .
新人教版七年级下册初中数学 课时1 算数平方根 教学课件

第四页,共十九页。
新课讲解
问题3:学校要举行美术作品比赛,小鸥想裁出一块 面积为25 dm2的正方形画布,画上自己的得 意之作参加比赛,这块正方形画布的边长应
取多少?
你一定会算出边长应取5 dm. 说
一说,你是怎样算出来的? 因为52=25,所以这个正方形画
布的边长应取5 dm.
第五页,共十九页。
当堂小练
2.若 2x-1 +
)
C
A.x≥ 1
2
C.x= 1
2
1-2x +1有意义,则x满足的条件是(
B.x≤ 1
2
D.x≠ 1
2
第十八页,共十九页。
拓展与延伸
求 18 的算术平方根.
解:因为 18=9, 9 =3, 所以的算术平方根是3.
第十九页,共十九页。
新人教版七年级下册初中数学 课时1 算数平方根 教学课件
科 目:数学 适用版本:新人教版 适用范围:【教师教学】
第六章 实数
6.1 平方根
课时1 算数平方根
第一页,共十九页。
学习目标
算术平方根的定义
求算术平方根 算术平方根的非负性. (重点、难点)
第二页,共十九页。
新课导入
(1)根据图填空: x2=____2___, y2=____x_2_+_1, z2=____y2_+_1_, w2=___z_2+_1__,
术平方根是3,即
3=2 3.
第十二页,共十九页。
新课讲解
知识点3 算术平方根的非负性
问题1: (1)因为____8_2=64,所以64的算术平方根是 ____8__,即 6=4_____8_.
(2)因为___0_._52=0.25,所以0.25的算术平方根是______0,.5 即 0.25=___0_._5_.
新课讲解
问题3:学校要举行美术作品比赛,小鸥想裁出一块 面积为25 dm2的正方形画布,画上自己的得 意之作参加比赛,这块正方形画布的边长应
取多少?
你一定会算出边长应取5 dm. 说
一说,你是怎样算出来的? 因为52=25,所以这个正方形画
布的边长应取5 dm.
第五页,共十九页。
当堂小练
2.若 2x-1 +
)
C
A.x≥ 1
2
C.x= 1
2
1-2x +1有意义,则x满足的条件是(
B.x≤ 1
2
D.x≠ 1
2
第十八页,共十九页。
拓展与延伸
求 18 的算术平方根.
解:因为 18=9, 9 =3, 所以的算术平方根是3.
第十九页,共十九页。
新人教版七年级下册初中数学 课时1 算数平方根 教学课件
科 目:数学 适用版本:新人教版 适用范围:【教师教学】
第六章 实数
6.1 平方根
课时1 算数平方根
第一页,共十九页。
学习目标
算术平方根的定义
求算术平方根 算术平方根的非负性. (重点、难点)
第二页,共十九页。
新课导入
(1)根据图填空: x2=____2___, y2=____x_2_+_1, z2=____y2_+_1_, w2=___z_2+_1__,
术平方根是3,即
3=2 3.
第十二页,共十九页。
新课讲解
知识点3 算术平方根的非负性
问题1: (1)因为____8_2=64,所以64的算术平方根是 ____8__,即 6=4_____8_.
(2)因为___0_._52=0.25,所以0.25的算术平方根是______0,.5 即 0.25=___0_._5_.
2020-2021学年人教版数学七年级下册6.1平方根(教案)

3.重点难点解析:在讲授过程中,我会特别强调平方根的定义和求平方根的方法这两个重点。对于难点部分,如负数没有平方根,我会通过数轴和实际例子来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与平方根相关的实际问题,如估算平方根的大小。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作,如用纸张折叠和剪刀剪裁来演示平方根的基本原理。
其次,关于平方根的应用,我注意到部分学生在将理论知识运用到实际问题解决时,还存在一定的困难。这说明我在教学过程中需要进一步强化实际案例的分析,让学生更多地进行实际操作,从而提高他们解决问题的能力。
此外,课堂上的小组讨论环节,学生的参与度较高,但个别小组在讨论过程中仍然存在依赖心理,等待其他同学给出答案。针对这一问题,我计划在接下来的教学中,加强对学生的引导和鼓励,让他们更加积极主动地参与讨论,发挥自己的主观能动性。
2.教学难点
-理解负数没有平方根的概念:这是学生的常见疑惑点,需要通过数轴和数学定义来解释。
-估算平方根的大小:学生可能会在这一步骤上感到困难,需要通过实际例子和图形辅助来帮助学生建立直观感受。
-应用平方根解决实际问题:将平方根应用于实际问题,如求解土地面积、物体速度等,需要学生具备一定的抽象思维能力。
-平方根的运算规则应用:在实际运算中,学生可能会混淆平方根与乘法、除法的运算顺序和规则。
举例解释:
-对于负数没有平方根,可以通过数轴上的表示,说明负数的平方将导致结果为正数,从而无法在实数范围内找到对应的平方根。
-对于估算平方根的大小,可以让学生通过近似计算,如√16在4和5之间,因为4^2=16,5^2=25,从而估算出√16约等于4.5,然后逐步精确到整数4。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与平方根相关的实际问题,如估算平方根的大小。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作,如用纸张折叠和剪刀剪裁来演示平方根的基本原理。
其次,关于平方根的应用,我注意到部分学生在将理论知识运用到实际问题解决时,还存在一定的困难。这说明我在教学过程中需要进一步强化实际案例的分析,让学生更多地进行实际操作,从而提高他们解决问题的能力。
此外,课堂上的小组讨论环节,学生的参与度较高,但个别小组在讨论过程中仍然存在依赖心理,等待其他同学给出答案。针对这一问题,我计划在接下来的教学中,加强对学生的引导和鼓励,让他们更加积极主动地参与讨论,发挥自己的主观能动性。
2.教学难点
-理解负数没有平方根的概念:这是学生的常见疑惑点,需要通过数轴和数学定义来解释。
-估算平方根的大小:学生可能会在这一步骤上感到困难,需要通过实际例子和图形辅助来帮助学生建立直观感受。
-应用平方根解决实际问题:将平方根应用于实际问题,如求解土地面积、物体速度等,需要学生具备一定的抽象思维能力。
-平方根的运算规则应用:在实际运算中,学生可能会混淆平方根与乘法、除法的运算顺序和规则。
举例解释:
-对于负数没有平方根,可以通过数轴上的表示,说明负数的平方将导致结果为正数,从而无法在实数范围内找到对应的平方根。
-对于估算平方根的大小,可以让学生通过近似计算,如√16在4和5之间,因为4^2=16,5^2=25,从而估算出√16约等于4.5,然后逐步精确到整数4。
七年级下册数学《平方根》课件

应用场景
适用于需要快速得出平方根近似值的场合,如工程计算、物 理实验等。
精确计算步骤演示
01
确定被开方数的小数点 位置,将其表示为科学 记数法或普通数值形式 。
02
从最高位开始,依次计 算每一位数字的平方根 ,并保留余数。
03
将上一步得到的商与下 一位数字组合成新的被 开方数,继续进行计算 。
04
分组讨论:探讨疑难问题及解决方法
分组方式
根据学生的数学基础和学习能力 ,将班级学生分成若干小组,每 组4-6人,确保每组都有不同层
次的学生。
讨论内容
提前准备一些与平方根相关的疑 难问题或案例,引导学生围绕这 些问题展开讨论,探讨解决方法
。
教师指导
在讨论过程中,教师巡视各组, 倾听学生的发言,给予必要的指 导和帮助,确保讨论的有效进行
七年级下册数学《平方根》课件
目录
• 课程介绍与目标 • 平方根基础知识 • 平方根在实际问题中应用 • 平方根计算技巧与方法 • 平方根与其他数学概念联系 • 学生自主练习与互动环节
01
课程介绍与目标
平方根概念引入
平方根定义
平方根是指一个数自乘后得到的数,即若$a^2 = b$,则$a$是 $b$的平方根。
加减法运算
只有同类项(即同为正数 或负数的平方根)才能进 行加减运算。
乘方运算
平方根的乘方等于被开方 数的乘方。
典型例题解析
例题1
求下列各数的平方根:16、0、-9。
01
例题2
计算:(√5 + √3)(√5 - √3)。
03
例题3
化简:(√6 - √2)²。
05
02
解析
16的平方根为±4,0的平方根为0,-9没有 平方根。
适用于需要快速得出平方根近似值的场合,如工程计算、物 理实验等。
精确计算步骤演示
01
确定被开方数的小数点 位置,将其表示为科学 记数法或普通数值形式 。
02
从最高位开始,依次计 算每一位数字的平方根 ,并保留余数。
03
将上一步得到的商与下 一位数字组合成新的被 开方数,继续进行计算 。
04
分组讨论:探讨疑难问题及解决方法
分组方式
根据学生的数学基础和学习能力 ,将班级学生分成若干小组,每 组4-6人,确保每组都有不同层
次的学生。
讨论内容
提前准备一些与平方根相关的疑 难问题或案例,引导学生围绕这 些问题展开讨论,探讨解决方法
。
教师指导
在讨论过程中,教师巡视各组, 倾听学生的发言,给予必要的指 导和帮助,确保讨论的有效进行
七年级下册数学《平方根》课件
目录
• 课程介绍与目标 • 平方根基础知识 • 平方根在实际问题中应用 • 平方根计算技巧与方法 • 平方根与其他数学概念联系 • 学生自主练习与互动环节
01
课程介绍与目标
平方根概念引入
平方根定义
平方根是指一个数自乘后得到的数,即若$a^2 = b$,则$a$是 $b$的平方根。
加减法运算
只有同类项(即同为正数 或负数的平方根)才能进 行加减运算。
乘方运算
平方根的乘方等于被开方 数的乘方。
典型例题解析
例题1
求下列各数的平方根:16、0、-9。
01
例题2
计算:(√5 + √3)(√5 - √3)。
03
例题3
化简:(√6 - √2)²。
05
02
解析
16的平方根为±4,0的平方根为0,-9没有 平方根。
七年级下册数学6.1 第3课时 平方根

谢谢观看
Thank you for watching!
(3)49(x2+1)=50; 解:整理 49(x2+1)=50,得 x2= 1 ,
49 ∴开平方得 x=± 419=±17.
(4)(3x-1)2=(-5)2. 解:∵(3x-1)2=(-5)2, ∴开平方得 3x-1=±5. 当 3x-1=5 时,x=2; 当 3x-1=-5 时,x=-43. 综上所述,x=2 或-43.
丛书·舒心教辅 /
2021春季学期 数学·七年级下(RJ)
目 录页
要点归纳 典例导学 当堂检测
知识要点 平方根及开平方
定义
表示方法
性质
平
如果一个数 x 的
平方等于 a,即 x2=a ,那么这
a 的平方 根记作
(1)一个正数有两个 平方根,它们互为 相反数;
(4)(-4)2; (5) 81. 解:(4)∵(±4)2=(-4)2, ∴(-4)2 的平方根是±4. (5)∵(±3)2=9= 81, ∴ 81的平方根是±3.
5.求下列各式中 x 的值: (1)x2=361; (2)81x2-49=0; 解:(1)∵x2=361, ∴开平方得 x=± 361=±19. (2)整理 81x2-49=0,得 x2=4891, ∴开平方得 x=± 4891=±79.
算中,被开方数向左或向右移动两位,则平方
根的小数点向左或向右移动一位.
一个正数的两个平方根分别是 2a+1 和 a-4, 求这个数.
分析:因为一个正数的平方根有两个,且它们 互为相反数,所以 2a+1 和 a-4 互为相反数,根据 互为相反数的两个数的和为 0 列方程求解.
解:由于一个正数的两个平方根分别是 2a+1 和 a-4,
平方根课件2021—2022学年人教版数学七年级下册

(2)49的平方根是7 ;
( × ) 7
(3)(-2)2的平方根是±2 ( √ ) 22 4 (4)-1 是 1的平方根; ( √ )
(5)若X2 = 16 则X = 4 ( × )
(6)7的平方根是±49.
(× ) 7
四、总结评价
1.了解平方根的概念. 2.会求一些数的平方根,
并用平方根符号表示.
开 平 方 运 算
底数
幂
a的算术平方根 被开方数
一、导入展示
如果这里的x不是一个正数,而是一个数,那么 这个表格你还能填对吗?
x2 a 1
9 16 36 0.25
x 1 3 4 6 0.5
一、导入展示
1.了解平方根的概念. 2.会求一些数的平方根,
并用平方根符号表示.
4
二、自主学习
请阅读教科书第44~46页并思考: 1.什么是平方根?数a的平方根怎样表示? 2.平方根与算术平方根有什么不同? 3.平方根的性质是什么? 8分钟后全班交流展示!
0.81 ;(3)
49 9
。
36 6
0.81 0.9
49 7 93
三、合作释疑
平方根的性质
一个正数a有_两___个平方根,它们__互__为__相__反___数; 0只有_一__个___平方根,它是__0_本__身___; 负数__没__有___平方根.
开平方与平方的对比
运算 适用 运算结 符号 范围 果名称
三、合作释疑
一般地,如果一个__数__x___的平方等于 a,即 x2 =a,那么这个__数__x__叫做a的 平方根。
即:x2 a, x叫做a的平方根, 记作:x a
三、合作释疑
平方根的表示法:
七年级数学下册平方根 第1课时新人教版

七年级数学下册平方根第1课时新人教版七年级数学下册平方根第1课时新人教版
平方根
一、创设情景、谈话导入
问:小欧很高兴学校将举办艺术比赛。
他想剪出一幅面积为25平方米的正方形画布,画出他最喜欢的作品来参加比赛。
正方形画布的侧面应该有多长?
二、精讲点拨、质疑问难⒈填表:4正方形的面积1916253649边长上面的问题,实际上是已知一个正数的平方,求这个正数的问题⒉一般地,如果一个正数x的平方等于a,
即x2=a,那么这个正数x叫做a的算术平方根。
3.非负数a的算术平方根记录为a,读作“根符号a”,a称为要打开的平方。
4.规定
0的算术平方根为0。
⒌对于a来说,a≥0,即被开方数a是非负数,算术平方根a也是非负数,即a≥0
三、课堂活动和强化培训
例1.求下列各数的算术平方根:⑴100⑵
49(3)0.0001(4)16(5)172-152(6)-6)264例2。
计算:⑴ 10000 (2)
25⑶172?82⑷(?0.41)2121
四、扩展、扩展和巩固内部化
例3.x为何值时,下列各式有意义。
⑴2?3x⑵
12倍?51⑶⑷⑸x5?十、
(1?x)233x?61
例4。
如果是?3+2b?1=0,求a和B的值。
例5.小丽用一块面积为400cm2的正方形纸片,沿着边的方向裁出一块面积为
300厘米长方形。
如果长宽比为3:2,是否可以切割则通过试算来解释。
2。
