【小初高学习]2017年中考数学专题训练 特殊平行四边形(无答案)
初中数学特殊的平行四边形50题(含答案)

特殊的平行四边形练习题(50题)菱形、矩形、正方形一、单选题(共18题;共36分)1.下列条件中,能判定一个四边形为矩形的条件是( )A. 对角线互相平分的四边形B. 对角线相等且平分的四边形C. 对角线相等的四边形D. 对角线相等且互相垂直的四边形【答案】B【解析】【解答】解:A、对角线互相平分的四边形是平行四边形,故A不符合题意;B、对角线相等且平分的四边形是矩形,故B符合题意;C、对角线相等的四边形不是矩形,故C不符合题意;D、对角线相等且互相垂直的四边形不是矩形,故D不符合题意.故答案为:B.【分析】根据矩形的判定方法,逐项进行判断,即可求解2.如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a ,EF=b ,NH= c ,则下列各式中正确的是()A. a > b > cB. a =b =cC. c > a > bD. b > c > a【答案】B【解析】【解答】解:连接OA、OD、OM,如图所示:则OA=OD=OM,∵四边形ABOC、DEOF、HNMO均为矩形,∴OA=BC=a,OD=EF=b,OM=NH=c,∴a=b=c;故答案为:B.【分析】连接OA、OD、OM,则OA=OD=OM,由矩形的对角线相等得出OA=BC=a,OD=EF=b,OM=NH=c,再由同圆的半径相等即可得出a=b=c.3.如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( )A. 1B. 2C.D.【答案】 D【解析】【解答】解:连接DE交AC于P,连接BD,BP,由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB,∴PE+PB=PE+PD=DE,即DE就是PE+PB的最小值,∵∠BAD=60°,AD=AB,∴△ABD是等边三角形,∴AD=BD,∵AE=BE=AB=1,∴DE⊥AB,在Rt△ADE中,DE=,∴ PE+PB的最小值是.故答案为:D.【分析】连接DE交AC于P,连接BD,BP,根据菱形的性质得出B、D关于AC对称,得出DE就是PE+PB 的最小值,根据等边三角形的判定与性质得出DE⊥AB,再根据勾股定理求出DE的长,即可求解.4.若正方形的对角线长为2 cm,则这个正方形的面积为()A. 4B. 2C.D.【答案】B【解析】【解答】解:设正方形的边长为xcm,根据题意得:x2+x2=22,∴x2=2,∴正方形的面积=x2=2(cm2).故答案为:B.【分析】设正方形的边长为xcm,利用勾股定理列出方程,求出x2=2,即可求出正方形的面积为2.5.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为()A. 72B. 24C. 48D. 96【答案】C【解析】【解答】解:∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD,∵DH⊥AB,∴∠BHD=90°,∴BD=2OH,∵OH=4,∴BD=8,∵OA=6,∴AC=12,∴菱形ABCD的面积= AC•BD=×12×8=48.故答案为:C.【分析】根据菱形的性质得O为BD的中点,再由直角三角形斜边上的中线等于斜边的一半,得BD的长度,最后由菱形的面积公式求得面积.6.将一张长方形纸片折叠成如图所示的形状,则∠ABC等于( )A. 73°B. 56°C. 68°D. 146°【答案】A【解析】【解答】如图,∵∠CBD=34°,∴∠CBE=180°﹣∠CBD=146°,由折叠的性质可得∠ABC=∠ABE= ∠CBE=73°.故答案为:A【分析】根据补角的知识可求出∠CBE,从而根据折叠的性质∠ABC=∠ABE= ∠CBE,可得出∠ABC的度数.7.如图,已知矩形AOBC的顶点O(0,0),A(0,3),B(4,0),按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OC,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠BOC内交于点F;③作射线OF,交边BC于点G,则点G的坐标为()A. (4,1)B. (4,)C. (4,)D. (4,)【答案】B【解析】【解答】解:∵四边形AOBC是矩形,A(0,3),B(4,0),∴OB=4,OA=BC=3,∠OBC=90°,∴OC==5,作GH⊥OC于H,如图,由题意可知:OG平分∠BOC,∵GB⊥OB,GH⊥OC,∴GB=GH,设GB=GH=x,由S△OBC=×3×4=×5×x+ ×4×x,解得:x=,∴G(4,).故答案为:B.【分析】根据勾股定理可得OC的长,作GH⊥OC于H,根据角平分线的性质可得GB=GH,然后利用面积法求出GB即可.8.如图1,在矩形ABCD中,点E在CD上,∠AEB=90°,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q,设点P运动的路程为x,PQ长为y,若y与x之间的函数关系图象如图2所示,当x=6时,PQ的值是( )A. 2B.C.D. 1【答案】B【解析】【解答】解:由图象可知:AE=3,BE=4,在Rt ABE中,∠AEB=90°AB= =5当x=6时,点P在BE上,如图,此时PE=4-(7-x)=x-3=6-3=3∵∠AEB=90°, PQ⊥CD∴∠AEB=∠PQE=90°,在矩形ABCD中,AB//CD∴∠QEP=∠ABE∴PQE BAE, ∴=∴=∴PQ=故答案为:B.【分析】由图象可知:AE=3,BE=4,根据勾股定理可得AB=5,当x=6时,点P在BE上,先求出PE的长,再根据△ PQE ∽△ BAE,求出PQ的长.9.如图,在平面直角坐标系中,已知点,.若平移点到点,使以点,,,为顶点的四边形是菱形,则正确的平移方法是()A. 向左平移1个单位,再向下平移1个单位B. 向左平移个单位,再向上平移1个单位C. 向右平移个单位,再向上平移1个单位D. 向右平移1个单位,再向上平移1个单位【答案】 D【解析】【解答】解:因为B(1,1)由勾股定理可得OB=,所以OA=OB,而AB<OA.故以AB为对角线,OB//AC,由O(0,0)移到点B(1,1)需要向右平移1个单位,再向上平移1个单位,由平移的性质可得由A(,0)移到点C需要向右平移1个单位,再向上平移1个单位,故选D.【分析】根据平移的性质可得OB//AC,平移A到C,有两种平移的方法可使O,A,B,C四点构成的四边形是平行四边形;而OA=OB>AB,故当OA,OB为边时O,A,B,C四点构成的四边形是菱形,故点A平移到C的运动与点O平移到B的相同.10.如图,把长方形ABCD沿EF对折,若∠1=500,则∠AEF的度数等于()A. 25ºB. 50ºC. 100ºD. 115º【答案】 D【解析】解析:∵把矩形ABCD沿EF对折,∴AD∥BC,∠BFE=∠2,∵∠1=50°,∠1+∠2+∠BFE=180°,∴∠BFE==65°,∵∠AEF+∠BFE=180°,∴∠AEF=115°.故选D11.在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是()A. ②③B. ③④C. ①②④D. ②③④【答案】 D【解析】【解答】∵AB=1,AD=,∴BD=AC=2,OB=OA=OD=OC=1.∴△OAB,△OCD为正三角形.AF平分∠DAB,∴∠FAB=45°,即△ABF是一个等腰直角三角形.∴BF=AB=1,BF=BO=1.∵AF平分∠DAB,∴∠FAB=45°,∴∠CAH=45°﹣30°=15°.∵∠ACE=30°(正三角形上的高的性质)∴∠AHC=15°,∴CA=CH由正三角形上的高的性质可知:DE=OD÷2,OD=OB,∴BE=3ED.所以正确的是②③④.故选D.【分析】这是一个特殊的矩形:对角线相交成60°的角.利用等边三角形的性质结合图中的特殊角度解答.本题主要考查了矩形的性质及正三角形的性质.12.矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB 上,当△CDE的周长最小时,点E的坐标为()A. (3,1)B. (3,)C. (3,)D. (3,2)【答案】B【解析】【解答】解:如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.∵D(,0),A(3,0),∴H(,0),∴直线CH解析式为y=﹣x+4,∴x=3时,y= ,∴点E坐标(3,)故选:B.【分析】如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,先求出直线CH解析式,再求出直线CH与AB的交点即可解决问题.本题考查矩形的性质、坐标与图形的性质、轴对称﹣最短问题、一次函数等知识,解题的关键是利用轴对称找到点E位置,学会利用一次函数解决交点问题,属于中考常考题型.13.如图,正方形ABCD的边长为4,M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为().A. 3B. 4C. 5D.【答案】C【解析】【分析】由正方形的对称性可知点B与D关于直线AC对称,连接BM交AC于N′点,N′即为所求在Rt△BCM中利用勾股定理即可求出BM的长即可.【解答】∵四边形ABCD是正方形,∴点B与D关于直线AC对称,连接BD,BM交AC于N′,连接DN′,N′即为所求的点,则BM的长即为DN+MN的最小值,∴AC是线段BD的垂直平分线,又CM=CD-DM=4-1=3,在Rt△BCM中,BM==5,故DN+MN的最小值是5.故选C.【点评】本题考查的是轴对称-最短路线问题及正方形的性质,先作出M关于直线AC的对称点M′,由轴对称及正方形的性质判断出点M′在BC上是解答此题的关键.14.将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是,则点C的坐标是()A. (4,2)B. (2,4)C. (,3)D. (3,)【答案】 D【解析】【解答】解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,过点A作AN⊥BF于点N,过点C作CM⊥x轴于点M,∵∠EAO+∠AOE=90°,∠AOE+∠MOC=90°,∴∠EAO=∠COM,又∵∠AEO=∠CMO,∴∠AEO∽△COM,∴=,∵∠BAN+∠OAN=90°,∠EAO+∠OAN=90°,∴∠BAN=∠EAO=∠COM,在△ABN和△OCM中∴△ABN≌△OCM(AAS),∴BN=CM,∵点A(−1,2),点B的纵坐标是,∴BN= ,∴CM= ,∴MO==2CM=3,∴点C的坐标是:(3, ).故选:D.【分析】次题主要考查了矩形的性质以及相似三角形的判定与性质以及结合全等三角形的判定与性质等知识.构造直角三角形,正确得出CM的长是解题的关键.15.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是()A. 1B. 2C. 3D. 4【答案】 D【解析】【解答】解:∵四边形ADEF为正方形,∴∠FAD=90°,AD=AF=EF,∴∠CAD+∠FAG=90°,∵FG⊥CA,∴∠C=90°=∠ACB,∴∠CAD=∠AFG,在△FGA和△ACD中,,∴△FGA≌△ACD(AAS),∴AC=FG,①正确;∵BC=AC,∴FG=BC,∵∠ACB=90°,FG⊥CA,∴FG∥BC,∴四边形CBFG是矩形,∴∠CBF=90°,S△FAB= FB•FG= S四边形CBFG,②正确;∵CA=CB,∠C=∠CBF=90°,∴∠ABC=∠ABF=45°,③正确;∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,∴△ACD∽△FEQ,∴AC:AD=FE:FQ,∴AD•FE=AD2=FQ•AC,④正确;故选:D.【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;证明四边形CBFG是矩形,得出S△FAB= FB•FG= S四边形CEFG,②正确;由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;证出△ACD∽△FEQ,得出对应边成比例,得出D•FE=AD2=FQ•AC,④正确.16.如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M 为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为()A. 5B.C.D.【答案】B【解析】【解答】设BE=x,则CE=6-x,∵四边形ABCD矩形,AB=4,∴AB=CD=4,∠C=∠B=90°,∴∠DEC+∠CDE=90°,又∵F是AB的中点,∴BF=2,又∵EF⊥ED,∴∠FED=90°,∴∠FEB+∠DEC=90°,∴∠FEB=∠CDE,∴△BFE∽△CED,∴=,∴=,∴(x-2)(x-4)=0,∴x=2,或x=4,①当x=2时,∴EF=2,DE=4,DF=2,∴AM=ME=,∴AE===2,②当x=4时,∴EF=2,DE=2,DF=2,∴AM=ME=,∴AE==2,AE==4,∴x=4不合题意,舍去故答案为:B.【分析】设BE=x,则CE=6-x,由矩形性质得出AB=CD=4,∠C=∠B=90°,又由EF⊥ED,根据同角的余角相等可得出∠FEB=∠CDE;由相似三角形的判定得出△BFE∽△CED,再根据相似三角形的性质得出=,由此列出方程从而求出x=2或x=4,分情况讨论:①当x=2时,由勾股定理算出AE===2,②当x=4时,由勾股定理算出AE==2,AE==4,故x=4不合题意,舍去.17.如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有()A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【解答】∵四边形ABCD是正方形,∴∠B=∠DCB=90°,AB=BC,∵AG=CE,∴BG=BE,由勾股定理得:BE=GE,∴①错误;∵BG=BE,∠B=90°,∴∠BGE=∠BEG=45°,∴∠AGE=135°,∴∠GAE+∠AEG=45°,∵AE⊥EF,∴∠AEF=90°,∵∠BEG=45°,∴∠AEG+∠FEC=45°,∴∠GAE=∠FEC,在△GAE和△CEF中∴△GAE≌△CEF,∴②正确;∴∠AGE=∠ECF=135°,∴∠FCD=135°﹣90°=45°,∴③正确;∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,∴∠FEC<45°,∴△GBE和△ECH不相似,∴④错误;即正确的有2个.故选B.【分析】根据正方形的性质得出∠B=∠DCB=90°,AB=BC,求出BG=BE,根据勾股定理得出BE=GE,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△GAE≌△CEF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.18.如图,P是正方形ABCD内一点,∠APB=135,BP=1,AP=,求PC的值()A. B. 3 C. D. 2【答案】B【解析】【分析】解答此题的关键是利用旋转构建直角三角形,由勾股定理求解.如图,把△PBC绕点B逆时针旋转90°得到△ABP′,点C的对应点C′与点A重合.根据旋转的性质可得AP′=PC,BP′=BP,△PBP′是等腰直角三角形,利用勾股定理求出,然后由∠APB=135,可得出∠APP′=90°,再利用勾股定理列式计算求出.故选B.二、填空题(共15题;共16分)19.如图所示,△ABC为边长为4的等边三角形,AD为BC边上的高,以AD为边的正方形ADEF的面积为________。
中考数学复习《特殊的平行四边形》专题练习(含答案)

三、解答题
31. (2018·湘西州)如图,在矩形 中, 是 的中点,连接 .
(1)求证: ;
(2)若 ,求 的周长.
32. (2018连云港)如图,在矩形 中, 是 的中点,延长 交于点 ,连接 .
(1)求证:四边形 是平行四边形;
A. B. C. D.
二、填空题
13. (2018·株洲)如图,矩形 的对角线 与 相交点 , 分别为 的中点,则 的长度为.
14.(2018·成都)如图,在矩形 中,按以下步骤作图:①分别以点 和 为圆心,以大于 的长为半径作弧,两弧相交于点 和 ;②作直线 交 于点 .若 ,则矩形的对角线 的长为.
38. (2018·乌鲁木齐)如图,在四边形 中, , 是 的中点, , , 于点 .
(1)求证:四边形 是菱形;
(2)若 ,求 的长.
39. (2018·广安)如图,四边形 是正方形, 为 上一点,连接 ,延长 至点 ,使得 ,过点 作 ,垂足为 ,求证: .
40. (2018·盐城)如图,在正方形 中,对角线 所在的直线上有两点 满足 ,连接 .
(2)在(1)的条件下,连接 ,求 的度数.
36.(2018·娄底)如图,在四边形 中,对角线 相交于点 ,且
,过点 作 ,分别交 于点 .
(1)求证: ;
(2)判断四边形 的形状,并说明理由.
37. (2018·南京)如图,在四边形 中, , . 是四边形 内一点,且 .求证:
(1) ;
(2)四边形 是菱形.
9. (2018·宿迁)如图,菱形 的对角线 相交于点 , 为边 的中点.若菱
中考数学总复习《特殊的平行四边形》专项测试卷

中考数学总复习《特殊的平行四边形》专项测试卷学校:___________班级:___________姓名:___________考号:___________【例题】如图①,在正方形ABCD和正方形BEFG 中,点 A,B,E在同一条直线上,P 是线段DF 的中点,连接 PG,PC。
的值(写出结论,不需要证明);(1)探究 PG与PC 的位置关系及PGPC(2)如图②,将原问题中的正方形ABCD和正方形BEFG 换成菱形ABCD 和菱形BEFG,且∠的值,写出你的猜想并加以证明:ABC=∠BEF=60度。
探究 PG 与PC的位置关系及PGPC(3)如图③,将图②中的菱形 BEFG绕点 B 顺时针旋转,使菱形 BEFG 的边BG 恰好与菱形ABCD的边AB 在同一条直线上,问题(2)中的其他条件不变。
你在(2)中得到的两个结论是否发生变化?写出你的猜想并加以证明。
课后练习一、选择题(共6 小题)1.如图4.把含30°的直角三角板 PMN放置在正方形ABCD 中,∠PMN=30°,直角顶点 P 在正方形ABCD 的对角线BD 上.点M. N分别在AB 和CD边上. MN与BD 交于点O,且点O为MN 的中点.则∠AMP的度数为 ( )。
A.60°B.65°C.75°D.80°2.如图5.在菱形 ABCD中.∠A=60°.点E,F 分别在边AB,BC上,AE=BF=2.△DEF 的周长为3√6.则AD的长为 ( )。
A. √6B.2 √3C.√3+1D.2√3−13.如图6是一个由5张纸片拼成的平行四边形ABCD.相邻纸片之间互不重叠也无缝隙.其中两张等腰直角三角形纸片的面积都为S ₁,另两张直角三角形纸片的面积都为S ₂,中间一张矩形纸片 EFGH 的面积为S ₃,FH 与GE 相交于点O 。
当△AEO,△BFO,△CGO,△DHO 的面积相等时,下列结论一定成立的是 ( )。
特殊平行四边形练习题

特殊的平行四边形1. 平行四边形、矩形、菱形、正方形的性质:2. 识别方法小结:(1) 识别平行四边形的方法:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形。
(2) 识别矩形的方法:①有一个角是直角的平行四边形是矩形;②对角线相等的平行四边形是矩形;③有三个角是直角的四边形是矩形;④对角线相等且互相平分的四边形是矩形。
(3) 识别菱形的方法:①有一组邻边相等的平行四边形是菱形;②对角线互相垂直的平行四边形是菱形;③四边都相等的四边形是菱形;④对角线互相垂直平分的四边形是菱形。
(4) 识别正方形的方法:①有一组邻边相等且有一个角是直角的平行四边形是正方形;②对角线互相垂直且相等的平行四边形是正方形;③有一组邻边相等的矩形是正方形;④对角线互相垂直的矩形是正方形;⑤有一个角是直角的菱形是正方形;⑥对角线相等的菱形是正方形;⑦对角线互相垂直平分且相等的四边形是正方形。
小结:把以上识别方法的编号分别填入下图中的每一条带方向的线上:(如平行四边形的第一种识别方法的编号为(1) ①,其他方法类似)一、基础达标训练:(A组)1.填空:(1)两条对角线的四边形是平行四边形;(2)两条对角线的四边形是矩形;(3)两条对角线的四边形是菱形;(4)两条对角线的四边形是正方形;(5)两条对角线的平行四边形是矩形;(6)两条对角线的平行四边形是菱形;(7)两条对角线的平行四边形是正方形;(8)两条对角线的矩形是正方形;(9)两条对角线的菱形是正方形。
2.已知□ABCD的周长为42cm,AB:AD = 2∶5,则AB+AD=________3.已知矩形ABCD的一条对角线AC = 24,则另一条对角线BD = .4.矩形的两条对角线一夹角为60°,一条对角线与较短边的和为21cm,则对角线的长为.5.菱形的两条对角线长为7和16,则菱形的面积为.6.正方形的边长是5cm时,它的周长是,面积是.7.正方形的一条对角线长为8,则正方形的面积为.8.中点四边形:(1) 顺次连接四边形各边中点所得的四边形是.(2) 顺次连接平行四边形各边中点所得的四边形是.(3) 顺次连接矩形各边中点所得的四边形是.(4) 顺次连接菱形各边中点所得的四边形是.(5) 顺次连接正方形各边中点所得的四边形是.9.(2006年黑龙江省)如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF ,AE 、BF 相交于点D ,下列结论①AE=BF ; ②AE ⊥BF ;③ AO=OE ; ④S △AOB =S 四边形DEOF 中,错误的有( ) A .1个 B .2个 C .3个 D .4个10. (2006年黑龙江省) 如图,在矩形ABCD 中,EF ∥AB ,GH ∥BC , 11. EF 、GH 的交点P 在BD 上,图中面积相等的四边形有( )A .3对B .4对C .5对D .6对12. (2006年海南省)如图,在菱形ABCD 中,E 、F 、G 、H 分别是菱形四边的 中点,连结EG 与FH 交于点O ,则图中的菱形共有( ) A .4个 B .5个 C .6个 D .7个13. (2006年云南省昆明市)己知:如图,菱形ABCD 中,∠B=600,AB =4,则以AC 为边长的正方形ACEF 的周长为 .14. (2006年宁夏回族自治区)菱形的周长为20cm ,一条对角线长为8cm ,则菱形的面积为 2cm .15. 矩形ABCD 的对角线AC 、BD 相交于点O ,∠1=2∠2,若AC =1.8cm ,试求AB 的长。
中考数学专题复习:特殊平行四边形
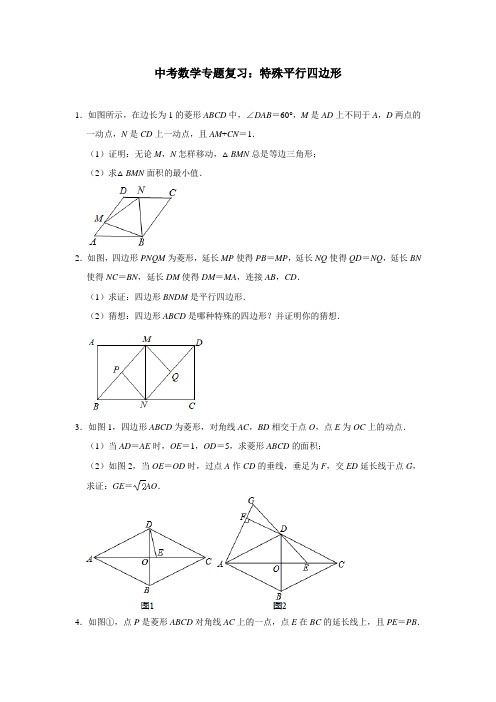
中考数学专题复习:特殊平行四边形1.如图所示,在边长为1的菱形ABCD中,∠DAB=60°,M是AD上不同于A,D两点的一动点,N是CD上一动点,且AM+CN=1.(1)证明:无论M,N怎样移动,△BMN总是等边三角形;(2)求△BMN面积的最小值.2.如图,四边形PNQM为菱形,延长MP使得PB=MP,延长NQ使得QD=NQ,延长BN 使得NC=BN,延长DM使得DM=MA,连接AB,CD.(1)求证:四边形BNDM是平行四边形.(2)猜想:四边形ABCD是哪种特殊的四边形?并证明你的猜想.3.如图1,四边形ABCD为菱形,对角线AC,BD相交于点O,点E为OC上的动点.(1)当AD=AE时,OE=1,OD=5,求菱形ABCD的面积;(2)如图2,当OE=OD时,过点A作CD的垂线,垂足为F,交ED延长线于点G,求证:GE=AO.4.如图①,点P是菱形ABCD对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)求证:PD=PE;(2)如图②,当∠ABC=90°时,连接DE,则是否为定值?如果是,请求其值;如果不是,请说明理由.5.如图1,菱形ABCD中,∠A=60°,F,E分别为AD,BD边上的点,且DE=AF,CF 交BD于点G,AD=2.(1)求证:CE=BF;(2)当E点和G点重合时,求DF的长;(3)如图2,延长CE交BF于点H,连接HG,当F为AD的中点时,求证:GH⊥BF.6.在菱形ABCD中,E、F分别是AD和AB的中点,连接BE、DF.(1)如图(1),求证:BE=DF;(2)如图(2),设BE,DF交于点G,连接AC,EF,在不添加任何辅助线的情况下,直接写出图中所有的等腰三角形.7.如图,在▱ABCD中,E、F分别为AD、BC的中点,点M、N在对角线AC上,且AM =CN.(1)求证:四边形EMFN是平行四边形;(2)若AB⊥AC,求证:四边形EMFN是菱形.8.点E、F分别在菱形ABCD的边BC、CD上,BE=DF,作FG∥AE,交AC的延长线于点G,连接AF、EG.(1)如图1,求证:四边形AEGF是菱形;(2)如图2,当AF平分∠CAD时,在不添加辅助线及字母的情况下,请直接写出图中所有的等腰三角形(不包括腰长等于AB的等腰三角形).9.如图1,已知平行四边形ABCD中,BD平分∠CBA.(1)求证:平行四边形ABCD是菱形;(2)如图2,E为边AB上一动点,连接CE,作CE的垂直平分线交CE于F,交DB于G,连接AG、EG,①求证:△AGE为等腰三角形;②若∠CBA=60°,求的值.10.四边形ABCD为矩形,E是AB延长线上的一点.(1)若AC=EC,如图1,求证:四边形BECD为平行四边形;(2)若AB=AD,点F是AB上的点,AF=BE,EG⊥AC于点G,如图2,求证:△DGF 是等腰直角三角形.11.在矩形ABCD中,AB=6,AD=8,E是边BC上一点,以点E为直角顶点,在AE的右侧作等腰直角△AEF.(1)如图1,当点F在CD边上时,求BE的长;(2)如图2,若EF⊥DF,求BE的长.12.小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,求矩形ABCD长与宽的比值.13.矩形ABCD,点E在直线CD上,CF⊥AE垂足为F,连接BF、DF.(1)如图1,点E在线段CD上,写出线段BF与DF的位置关系并证明;(2)如图2,点E不在线段CD上,请补全图形,写出线段BF与DF的位置关系并证明.14.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向C、A运动.(1)四边形DEBF是平行四边形吗?请说明理由;(2)若BD=12cm,AC=16cm,当四边形DEBF是矩形,求运动时间t为何值?15.如图,四边形ABCD是矩形,∠ACP=90°,∠APC=∠P AD+∠PCD.(1)求∠ACD的度数;(2)过点D作DE⊥AP,垂足为点E,延长DE交AC于点F.请补全图形,探究线段AF,CF,PC的数量关系,并证明.16.如图,在矩形ABCD中,AB=8,BC=6.动点P、Q分别从点D、A同时出发向右运动,点P的运动速度为2个单位/秒,点Q的运动速度为1个单位/秒,当一个点到达终点时两个点都停止运动.设运动的时间为t(s)(1)当t=2时,PQ的长为________;(2)若PQ=PB,求运动时间t的值;(3)若BQ=PQ,求运动时间t的值.17.在矩形ABCD中,AB=4,BC=3,E是AB边上一点,连接CE,过点E作EF⊥CE交AD于点F,作∠AEH=∠BEC,交射线FD于点H,交射线CD于点N.(1)如图1,当点H与点F重合时,求BE的长;(2)如图2,当点H在线段FD上时,用等式表示线段BE与DN之间的数量关系(其中2<BE≤3),并证明.18.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=60°.(1)如图1,求证:△AOB为等边三角形.(2)如图2,若AE平分∠BAD交BC于点E,连接OE,请直接写出图中除等边三角形外的所有等腰三角形.19.如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足AE=CG,AH=CF.(1)求证:四边形EFGH是平行四边形;(2)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.20.如图,点E为▱ABCD的边AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH,AF.(1)若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)求证:当∠F AD=90°时,四边形AFHD为矩形.21.如图,在▱ABCD中,延长AB到点E,使BE=AB,DE交BC于点O,连接EC.(1)求证:四边形BECD是平行四边形;(2)若∠A=40°,当∠BOD等于多少度时四边形BECD是矩形,并说明理由.22.如图,在▱ABCD中,E,F分别是AD,BC边上的点,DE=BF,连接EF,∠EFB,∠FED的平分线分别交AB,CD边于点M,N,连接ME,NF.(1)求证:四边形EMFN是平行四边形;(2)小明在完成(1)的证明后继续探索,他猜想:当M为AB的中点时,四边形EMFN 是矩形,请补全他的证明思路.小明的证明思路:连接MN.由(1)知四边形EMFN是平行四边形.要证▱EMFN是矩形,只要证MN=EF.故只要证∠FEN=∠MNE.由已知条件________,故只要证MN∥AD,即证四边形AMND为平行四边形,易证________,故只要证AM=DN,易证AM=BM,故只要证________,易证△BMF≌△DNE,即可得证.23.在▱ABCD中,点E、F均在AD边上,AE=FD.连接BE、CF并延长,它们交于点G,且GB=GC.(1)如图1,求证:四边形ABCD是矩形;(2)如图2,连接BF、CE,若EF=AE,在不添加任何字母和辅助线的前提下,请直接写出所有面积是△GEF面积8倍的四边形.24.如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.(1)求证:△ABM≌△BCN.(2)请判定△OMN的形状,并说明理由.(3)若点K在线段AD上运动(不包括端点),当AK=时,求△OMN的面积.25.如图1,M为正方形ABCD的对角线BD上一点,过M作BD的垂线交AD于E,连BE,取BE中点O.(1)如图1,连AO、MO,求证:∠AOM=90°;(2)如图2,若M在对角线DB的延长线上,连接AM,使得∠MAN=135°,AN与DB的反向延长线相交于点N,求证:2AM 2﹣MB 2=MN 2﹣BN 2.26.如图,已知正方形ABCD,AB=2,E是对角线BD上一点,且不与B、D两点重合,F 是射线CB上一点,且EF=EC.(1)求证:AE=EF;(2)若BE=AB,请在图2中补全图形,判断AF与EC的数量关系并加以证明.27.[问题呈现]如图①,点E是正方形ABCD的边CD上的一点,点F是CB的延长线上的一点,且EA⊥AF.求证:DE=BF.[拓展探究]如图②,在△ABC中,∠ACB=90°,AC=CB=2,CD⊥AB,垂足为点D,点E是边AC上的动点,点F是边CB上的一点,且ED⊥DF.(1)直接写出四边形EDFC的面积.(2)若∠CDE=15°,则四边形EDFC的周长为________.28.在矩形ABCD中,AB=3,BC=4,动点E从B出发,以每秒1个单位的速度,沿射线BC方向运动,连接AE,以AE为边向上作正方形AEFG.设点E的运动时间为t(t>0).(1)如图1,EF与CD边交于点M,当DM=EM时,求此时t的值;(2)如图2,当点F恰好落在矩形任意两个顶点的所在直线上时,请求出所有符合条件的t的值.29.在正方形ABCD中,对角线AC、BD相交于点O,点E在线段OC上,点F在线段AB 上,连接BE,连接EF交BD于点M,已知∠AEB=∠OME.(1)如图1,求证:EB=EF;(2)如图2,点N在线段EF上,AN=EN,AN延长线交DB于H,连接DF,求证:DF=AH.30.在正方形ABCD中,E是BC中点,F是CD上一点,且CF=CD.(1)如图1,求证:∠AEF=90°;(2)如图2,连接DE,延长FE交AB的延长线于点G,过点B作BH⊥AF交AD于点H,垂足为M,交AE于点N,在不添加任何辅助线的情况下,请直接写出图2中的所有等腰三角形.31.如图,在正方形ABCD中,点E在边BC上,AE交BD于点F,DG⊥AE于G,∠DGE 的平分线GH分别交BD,CD于点P,H,连接FH.(1)求证:∠DHG=∠DF A;(2)求证:FH∥BC;(3)求:的值.32.正方形ABCD,点E在射线CD上,连接AE,以AE为斜边,作Rt△AEF,FE=F A(点F,B在直线AE的两侧),连接DF.(1)如图,点E在线段CD上.①求∠ADF的度数.②求证:CE=DF.(2)若DE=2,以A,E,D,F为顶点的四边形的面积为6时,请直接写出DF的长.33.如图,正方形ABCD中,点G是CD边上的一点(点G不与点C,点D重合),以CG 为一边向正方形ABCD外做正方形GCEF,联结DE交BG的延长线于点H.(1)求证:BH⊥DE;(2)若正方形ABCD的边长为1,当点H为DE中点时,求CG的长.34.如图,点O为正方形ABCD的中心.DE=AG,连接EG,过点O作OF⊥EG交AD于点F.(1)连接EF,△EDF的周长与AD的长有怎样的数量关系,并证明;(2)连接OE,求∠EOF的度数;(3)若AF:CE=m,OF:OE=n,求证:m=n2.35.正方形ABCD,点E在AB上,过点E作AD的平行线交CD于点F点G在EF上,CG 平分∠BCD,点H在CG上,HE=HD.(1)如图(1),求证:HG=HC;(2)如图(2),连接DE,FH,在不添加任何辅助线的情况下,请直接写出图(2)中的所有的等腰直角三角形.36.如图,已知四边形ABCD是正方形,对角线AC、BD相交于O.(1)如图1,设E、F分别是AD、AB上的点,且∠EOF=90°,线段AF、BF和EF之间存在一定的数量关系.请你用等式直接写出这个数量关系;(2)如图2,设E、F分别是AB上不同的两个点,且∠EOF=45°,请你用等式表示线段AE、BF和EF之间的数量关系,并证明.37.点E在正方形AOCD的边AD上,点H在边AO上,AH=DE.(1)如图1,求证:DH⊥CE;(2)如图2,EF⊥CE,FH⊥AO,垂足为点H.求证:FH=AH.38.已知边长为2的正方形ABCD中,P是对角线AC上的一个动点(与点A,C不重合),过点P作PE⊥PB,PE交DC于点E,过点E作EF⊥AC,垂足为点F.(1)求证:PB=PE;(2)在点P的运动过程中,PF的长度是否发生变化?若不变,求出这个不变的值;若变化,试说明理由.39.如图1,在正方形ABCD中,对角线AC、BD相交于点O,点E为线段BO上一点,FC⊥EC 于点C,且EC=FC,连接EF交CD于点G.(1)若AB=4,BE=,求△CEF的面积.(2)如图2,线段FE的延长线交AB于点H,过点F作FM⊥CD于点M,求证:BH+MG =BE.40.如图,ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F,G,求证:BF=FG+DG.41.如图,正方形ABCD和正方形AEFG有公共点A,点B在线段DG上.(1)判断DG与BE的位置关系,并说明理由;(2)若正方形ABCD的边长为1,正方形AEFG的边长为,求BE的长.42.如图,在正方形ABCD中,E是边AB上的一动点(不与点A,B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE 交DG的延长线于点H,连接BH.(1)直接写出GF与GC的数量关系:________;(2)用等式表示线段BH与AE的数量关系,并证明.43.如图1,△ABC是以∠ACB为直角的直角三角形,分别以AB,BC为边向外作正方形ABFG,BCED,连接AD,CF,AD与CF交于点M,AB与CF交于点N.(1)求证:△ABD≌△FBC;(2)如图2,在图1基础上连接AF和FD,若AD=6,求四边形ACDF的面积.44.如图,已知正方形ABCD,点E在BC上,点F在CD延长线上,BE=DF(1)求证:AE=AF;(2)若BD与EF交于点M,连接AM,试判断AM与EF的数量与位置关系,并说明理由.45.如图,已知正方形ABCD的边长为,连接AC、BD交于点O,CE平分∠ACD交BD 于点E,(1)求DE的长;(2)过点E作EF⊥CE,交AB于点F,求BF的长;(3)过点E作EG⊥CE,交CD于点G,求DG的长.46.如图1,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.则有结论EF=BE+FD成立;(1)如图2,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请说明理由.(2)若将(1)中的条件改为:如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,延长BC到点E,延长CD到点F,使得∠EAF仍然是∠BAD的一半,则结论EF=BE+FD 是否仍然成立?若成立,请证明;不成立,请写出它们的数量关系并证明.47.如图,在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AD=BC,AC,BD相交于点G.过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE,BF相交于点H.(1)求证:△ABC≌△BAD;(2)若AB=BC,四边形AHBG是什么特殊四边形?请说明理由.48.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图,求证:矩形DEFG是正方形;(2)若AB=4,CE=2,求CG的长度;(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.参考答案1.(1)证明:如图所示,连接BD,在菱形ABCD中,∠DAB=60°,∴∠ADB=∠NDB=60°,故△ADB是等边三角形,∴AB=BD,又AM+CN=1,DN+CN=1,∴AM=DN,在△AMB和△DNB中,,∴△AMB≌△DNB(SAS),∴BM=BN,∠MBA=∠NBD,又∠MBA+∠DBM=60°,∴∠NBD+∠DBM=60°,即∠MBN=60°,∴△BMN是等边三角形;(2)解:过点B作BE⊥MN于点E.设BM=BN=MN=x,则,故,∴当BM⊥AD时,x最小,此时,,.∴△BMN面积的最小值为.2.(1)证明:∵四边形PNQM为菱形,∴MP=NQ,MP∥NQ,∵PB=MP,QD=NQ,∴MB=DN,∵MP∥NQ,∴四边形BNDM是平行四边形;(2)四边形ABCD是矩形.证明:∵四边形BNDM是平行四边形.∴DM=BN,∵NC=BN,∴DM=NC,∵DM∥NC,∴四边形DMNC是平行四边形.∴MN=DC,MN∥DC,∵DM=MA,∴MA=BN,∴四边形AMNB是平行四边形.∴AB∥MN,AB=MN,∴AB=DC,AB∥DC,∴四边形ABCD是平行四边形.∵四边形PNQM为菱形,∴MQ=NQ,∵QD=NQ,∴QD=NQ=MQ,∴∠NMD=90°,∴∠CDM=90°,∴四边形ABCD是矩形.3.解:(1)∵四边形ABCD是菱形,∴AC⊥BD,AC=2AO,BD=2DO=10,∵AD=AE,∴AD=AE=AO+OE=1+OA,∵AD2=OD2+AO2,∴(1+OA)2=25+AO2,∴AO=12,∴AC=24,∴菱形ABCD的面积==120;(2)如图,过点G作GH⊥AC于H,∵四边形ABCD是菱形,∴AC⊥BD,AO=CO,AD=CD,∠DAC=∠DCA,∵OE=OD,∴∠DEO=∠EDO=45°,∵GH⊥AC,∴∠HED=∠HGE=45°,∴GH=HE,GE=GH,设∠DAC=∠DCA=x,∴∠EDC=45°﹣x=∠GDF,∵AF⊥CF,∴∠FGD=90°﹣∠GDF=45°+x,∵∠DAF=90°﹣2x,∴∠ADC=180°﹣∠GAD﹣∠AGD=45°+x,∴∠ADC=∠AGD,∴AG=AD,在△AHG和△DOA中,,∴△AHG≌△DOA(AAS),∴GH=AO,∴GE=GH=AO.4.证明:(1)∵四边形ABCD是菱形,∴BC=DC,∠BCP=∠DCP,AB∥DC,在△BCP和△DCP中,,∴△BCP≌△DCP(SAS),∴PB=PD,∵PE=PB,∴PD=PE;(2),理由如下:∵∠ABC=90°,∴四边形ABCD是正方形,由(1)知,△BCP≌△DCP,∴∠CBP=∠CDP,∵PE=PB,∴∠CBP=∠E,∵∠CFE=∠DFP(对顶角相等),∴180°﹣∠DFP﹣∠CDP=180°﹣∠CFE﹣∠E,即∠DPE=∠DCE,∵AB∥CD,∴∠DCE=∠ABC,∴∠DPE=∠ABC=90°,又∵PD=PE,∴DE=PE,∴.5.(1)证明:∵四边形ABCD为菱形,∠A=60°,∴AB=BC=CD=DA=BD,在△ABF和△DCE中,∴△ABF≌△DCE(SAS),∴CE=BF.(2)DF的长是﹣1.(3)证明:∵F为AD的中点,∴BF⊥AD,AF=DF,∠DBF=30°,由(1)知:AF=DE,∴AF=DF=DE=BE,∴CE⊥BD,∴∠BFD=∠BEH=90°,∴∠EBH=∠FBD,∴BH=,HG=,由(2)知DF:BC=DG:BG=1:2,∴,∴BH2+HG2=BG2,∴△BHG为直角三角形,∴∠BHG=90°,∴GH⊥BF.6.证明:(1)∵四边形ABCD是菱形,∴AB=AD=BC=CD,∠BAC=∠DAC,∵E、F分别是AD和AB的中点,∴AF=AE=BF=DE,在△ABE和△ADF中,,∴△ABE≌△ADF(SAS),∴BE=DF;(2)∵AE=AF,∴△AEF是等腰三角形,∵AB=AD=BC=CD,∴△ABC,△ADC是等腰三角形,∵AE=AF,∠BAC=∠DAC,∴AG垂直平分EF,∴FG=EG,∴△GEF是等腰三角形.7.证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠EAM=∠FCN,∵E、F分别为AD、BC的中点,∴AE=DE=BF=CF,在△AEM和△CFN中,,∴△AEM≌△CFN(SAS),∴EM=FN,∠AME=∠CNF,∴∠EMN=∠FNM,∴EM∥FN,∴四边形EMFN是平行四边形;(2)连接EF交AC于O,如图所示:由(1)得:AE∥BF,AE=BF,∴四边形AEFB是平行四边形,∴AB∥EF,∵AB⊥AC,∴∠BAC=90°,∴∠COF=∠BAC=90°,∴EF⊥MN,∴四边形EMFN是菱形.8.(1)证明:∵菱形ABCD,∴AB=AD,∠B=∠D,∠BAC=∠DAC,∵BE=DF,∴△ABE≌△ADF(SAS),∴AE=AF,∠BAE=∠DAF,∴∠EAG=∠F AG,∵FG∥AE,∴∠EAG=∠FGA,∴∠F AG=∠FGA,∴FG=AF=AE,∵FG∥AE,∴四边形AECF是平行四边形,又∵AF=AE,∴四边形AECF是菱形;(2)解:△AEG、△AFG、△CEG、△CFG.理由如下:由(1)及菱形的性质可得△AEG、△AFG是等腰三角形,∴∠F AC=∠FGA,∵∠DAC=2∠F AC,∴∠DAC=2∠FGA,∵AD=DC,∴∠DAC=∠DCA,∵∠DCA=∠FGA+∠CFG,∴2∠FGA=∠FGA+∠CFG,∴∠FGA=∠CFG,∴△CFG是等腰三角形,同理可得△CEG是等腰三角形,∴符合要求的等腰三角形为△AEG、△AFG、△CEG、△CFG.9.证明:(1)∵四边形ABCD是平行四边形,∴DC∥AB,∴∠CDB=∠ABD,∵BD平分∠ABC,∴∠CBD=∠ABD,∴∠CDB=∠CBD,∴DC=BC,∵四边形ABCD是平行四边形,∴四边形ABCD是菱形;(2)①∵四边形ABCD是菱形,∴DC=DA,∠CDG=∠ADG,在△ADG和△CDG中,∴△ADG≌△CDG(SAS),∴AG=CG,∵GF是EC的垂直平分线,∴CG=EG,∴AG=EG,即△AGE是等腰三角形;②连接AC交BD于O,∵GC=GE,∴∠GCE=∠GEC,∵AG=CG=GE,∴∠GCA=∠GAC,∠GAE=∠GEA,∵∠CBA=60°,BC=AB,∴∠CAB=∠ACB=60°,∴∠GAC+∠GAE=60°,∴∠GAC+∠GCA+∠GAE+∠GEA=120°,∴∠AGC+∠AGE=240°,∴∠CGE=120°,∴∠GCE=30°,∴CG=2GF,∴AG=2GF,∴=.10.证明:(1)∵四边形ABCD为矩形,∴AB∥CD,AB=CD,CB⊥AE,又∵AC=EC,∴AB=BE,∴BE=CD,BE∥CD,∴四边形BECD为平行四边形;(2)∵AB=AD,∴矩形ABCD是正方形,∵EG⊥AC,∴∠E=∠GAE=45°,∴GE=GA,又∵AF=BE,∴AB=FE,∴FE=AD,在△EGF和△AGD中,,∴△EGF≌△AGD(SAS),∴GF=GD,∠DGA=∠FGE,∠DGF=∠DGA+∠AGF=∠EGF+∠AGF=∠AGE=90°,∴△DGF是等腰直角三角形.11.解:(1)如图1中,∵四边形ABCD是矩形,∴∠B=∠C=90°,AD=BC,∵EF⊥AE,∠AEF=90°,∴∠AEB=∠EFC,∵△AEF是等腰直角三角形,∴EF=AE,在△ABE和△ECF中,,∴△ABE≌△ECF(AAS),∴CE=AB,∵AB=6,∴CE=6,∵AD=8,∴BC=8,∴BE=BC﹣CE=2.(2)如图2中,延长DF,BC交于点N,过点F作FM⊥BN于点M,同理可证△ABE≌△EMF,∴AB=EM,BE=FM,设BE=x,则EM=AB=6,FM=BE=x,EC=8﹣x,∵EF⊥DF,∴∠NFE=∠DCB=90°,∴∠CDF+∠N=90°,∠FEC+∠N=90°,∴∠FEC=∠CDF,在矩形ABCD中,AB=DC,∴CD=AB=EM,在△EFM和△DNC中,,∴△EFM≌△DNC(AAS),∴NC=FM=x,EN=EC+NC=8,NM=EN﹣EM=2,即在Rt△FMN中,FN2=FM2+NM2=x2+22,在Rt△EFM中,EF2=FM2+EM2=x2+62,在Rt△EFN中,FN2+EF2=EN2,即x2+22+x2+62=82,解得x=2或﹣2舍弃),即BE=2.12.解:连接DE,如图:∵沿过A点的直线折叠,使得B点落在AD边上的点F处,∴四边形ABEF为正方形,∴∠EAD=45°,由第二次折叠知,M点正好在∠NDG的平分线上,∴DE平分∠GDC,∴∠GDE=∠CDE,∵DG为折痕,∴∠DGE=90°=∠C,而DE=DE,∴Rt△DGE≌Rt△DCE(AAS),∴DC=DG,∵∠EAD=45°,∠DGA=90°,∴△AGD为等腰直角三角形,∴AD=DG=CD,∴矩形ABCD长与宽的比值为,故答案为.13.解:(1)BF⊥DF,如图1,连接AC,BD交于点O,连接OF,∵四边形ABCD是矩形,∴AC与BD相等且互相平分,∴OA=OC=OB=OD,∵CF⊥AE垂足为F,∴∠AFC=90°,∵在Rt△ACF中,OA=OC,∴OF=AC=OA=OB=OD,∴OF=OB=OD,∴∠DBF=∠OFB,∠BDF=∠OFD,∵∠BFD+∠BDF+∠DBF=180°,∴∠OFB+∠OFD+∠OFB+∠OFD=180°,∴∠OFB+∠OFD=90°,∴∠BFD=∠OFB+∠OFD=90°,即BF⊥DF.(2)补全图形如图2或图3,BF⊥DF,连接AC,BD交于点O,连接OF,∵四边形ABCD是矩形,∴AC与BD相等且互相平分,∴OA=OC=OB=OD,∵CF⊥AE垂足为F,∴∠AFC=90°,∵在Rt△ACF,OA=OC,∴OF=AC=OA=OB=OD,∴OF=OB=OD,∴∠DBF=∠OFB,∠BDF=∠OFD,∵∠BFD+∠BDF+∠OFB+∠OFD=180°,∴∠OFB+∠OFD=90°,∴∠BFD=∠OFB+∠OFD=90°,即BF⊥DF.14.解:(1)是.理由:∵四边形ABCD是平行四边形,∴OD=OB,OA=OC,∵E、F两点移动的速度相同,即AE=CF,∴OE=OF,∵OD=OB,∴四边形DEBF是平行四边形.(2)因为矩形对角线相等,所以EF=12时,其为矩形,即AE=CF=(16﹣12)=2,或者AE=CF=(16+12)=14,所以当t=2或14时,四边形DEBF是矩形.15.解:(1)∵四边形ABCD是矩形,∴∠D=90°,∴∠DAC+∠DCA=90°,即∠DAP+∠P AC+∠DCA=90°,∵∠ACP=90°,∴∠APC+∠CAP=90°,∵∠APC=∠P AD+∠PCD.∴∠CAP+∠P AD+∠PCD=90°,∴∠PCD=∠ACD,∵∠ACP=90°,∴∠PCD+∠ACD=90°,∴∠ACD=45°;(2)AF=CF+PC.连接BD,交AC于点O,过点C作CN∥AP交BD于点N,如图.证明:由(1)知,∠ACD=45°,∴∠CAD=∠ACD=45°,∴AD=CD,∴矩形ABCD是正方形,∴∠DAO=∠CDO=45°,∠AOD=90°,∵∠ACP=∠AOD=90°,∴MN∥PC,∵AP∥CN,∴∠1=∠2,四边形PCNM为平行四边形,∴PC=MN,∵∠1+∠3=90°,∠2+∠4=90°,∴∠3=∠4,在△ADF和△DCN中,,∴△ADF≌△DCN(AAS),∴AF=DN,∵∠7+∠ADE=90°,∠8+∠ADE=90°,∴∠7=∠8,在△ADM和△DCF中,,∴△ADM≌△DCF(ASA),∴DM=CF,∵AF=DN,PC=MN,∴AF=DN=DM+MN=CF+PC.16.解:(1)如图所示:作PH⊥AB于H,由题意得,DP=4,AQ=2,则QH=2,又PH=AD=6,由勾股定理的,PQ===2,故答案为:2;(2)当PQ=PB时,如图,QH=BH,则t+2t=8,解得,t=;(3)当PQ=BQ时,(2t﹣t)2+62=(8﹣t)2,解得,t=.17.解:(1)如图,∵EF⊥EC,∴∠NEC=90°,∴∠AEF+∠BEC=90°,∵∠AEF=∠BEC,∴∠BEC=45°,∵四边形ABCD是矩形,∴∠B=90°,∴BE=BC,∵BC=3,∴BE=3;(2)线段BE与DN之间的数量关系为DN=2BE﹣4.证明:如图,过点E作EG⊥CN,垂足为点G,∵四边形ABCD是矩形,∴AB∥CN,∴∠B=∠BCG=90°=∠EGC,∴四边形BEGC是矩形,∴BE=CG,∵AB∥CN,∴∠AEH=∠N,∠BEC=∠ECN,∵∠AEH=∠BEC,∴∠N=∠ECN,∴EN=EC,∴CN=2CG=2BE,∵CD=AB=4,∴CN=2CG=2BE=DN+4,∴DN=2BE﹣4.18.(1)证明:∵矩形ABCD的对角线AC,BD相交于点O,∴OA=OB,又∵∠AOB=60°,∴△AOB为等边三角形.(2)解∵矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AE平分∠BAD交BC于点E,∴OA=OD=OB=AB=OC,∠BAE=45°,∴AB=BE,∴BE=OB,所以△ABE是等腰三角形,△OAD,△OBC,△BEO是等腰三角形.19.(1)证明:∵四边形ABCD是矩形,∴∠A=∠C.∴在△AEH与△CGF中,,∴△AEH≌△CGF(SAS),∴EH=GF,同理证得△EBF≌△GDH,则EF=GH,∴四边形EFGH是平行四边形;(2)解:四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.理由如下:作G关于BC的对称点G′,连接EG′,可得EG′的长度就是EF+FG的最小值.连接AC,∵CG′=CG=AE,AB∥CG′,∴四边形AEG′C为平行四边形,∴EG′=AC.在△EFG′中,∵EF+FG′>EG′=AC,∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.20.(1)解:∵四边形ABCD是平行四边形,∴∠BAE=∠BCD=70°,AD∥BC,∵∠DCE=20°,AB∥CD,∴∠CDE=180°﹣∠BAE=110°,∴∠DEC=180°﹣∠DCE﹣∠CDE=50°;(2)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠BAE=∠BCD,∵BF=BE,CG=CE,∴BC是△EFG的中位线,∴BC∥FG,BC=FG,∵H为FG的中点,∴FH=FG,∴BC∥FH,BC=FH,∴AD∥FH,AD=FH,∴四边形AFHD是平行四边形,∵∠F AD=90°,∴四边形AFHD为矩形.21.(1)证明:∵四边形ABCD为平行四边形,∴AB∥DC,AB=CD,∵BE=AB,∴BE=CD,BE∥CD,∴四边形BECD是平行四边形;(2)解:若∠A=40°,当∠BOD=80°时,四边形BECD是矩形,理由如下:∵四边形ABCD是平行四边形,∴∠BCD=∠A=40°,∵∠BOD=∠BCD+∠ODC,∴∠ODC=80°﹣40°=40°=∠BCD,∴OC=OD,∵BO=CO,OD=OE,∴DE=BC,∵四边形BECD是平行四边形,∴四边形BECD是矩形.22.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∠B=∠D,∴∠FED=∠EFB,∵EN,FM分别平分∠FED,∠EFB,∴∠FEN=∠DEN=FED,∠EFM=∠BFM=EFB,∴∠FEN=∠EFM,∠DEN=∠BFM,∴FM∥EN,在△BFM与△DEN中,,∴△BFM≌△DEN(ASA),∴FM=EN,∴四边形EMFN是平行四边形;(2)连接MN.由(1)知四边形EMFN是平行四边形.要证▱EMFN是矩形,只要证MN=EF.故只要证∠FEN=∠MNE.由已知条件EN平分∠FED,故只要证MN∥AD,即证四边形AMND为平行四边形,易证AM∥DN,故只要证AM=DN,易证AM=BM,故只要证BM=DN,易证△BMF≌△DNE,即可得证.故答案为:EN平分∠FED;AM∥DN;BM=DN.23.(1)证明:∵▱ABCD,∴AD∥BC,∠A+∠D=180°,∴∠GBC=∠GEF,∠GCB=∠GFE,∵GB=GC,∴∠GBC=∠GCB,∴∠GEF=∠GFE,∴GE=GF,∠AEB=∠DFC,∴GB﹣GE=GC﹣GF,即EB=FC,在△ABE和△DCF中,,∴△ABE≌△DCF(SAS),∴∠A=∠D,又∠A+∠D=180°,∴∠A=∠D=90°,∴四边形ABCD是矩形;(2)∵▱ABCD,∴AD∥BC,AD=BC,∴∠GBC=∠GEF,∠GCB=∠GFE,∴S四边形EBCF=8S△GEF,∵AE=FD=EF,∴S△AEB=S△EFB=S△EFC=S△FDC,∴S△AEB+S△BCE=S△EFC+S△BCE,S△EFB+S△BCF=S△FDC+S△BCF,即S四边形ABCE=S四边形EBCF,S四边形EBCF=S四边形DCBF,∴S四边形ABCE=S四边形EBCF=S四边形DCBF=8S△GEF.面积是△GEF面积8倍的四边形有:四边形ABCE,四边形EBCF,四边形DCBF.24.证明:(1)∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,∴∠ABM+∠CBM=90°,∵AM⊥BM,CN⊥BN,∴∠AMB=∠BNC=90°,∴∠MAB+∠MBA=90°,∴∠MAB=∠CBM,在△ABM和△BCN中,,∴△ABM≌△BCN(AAS);(2)△OMN是等腰直角三角形,理由如下:如图,连接OB,∵点O是正方形ABCD的中心,∴OA=OB,∠OBA=∠OAB=45°=∠OBC,AO⊥BO,∵∠MAB=∠CBM,∴∠MAB﹣∠OAB=∠CBM﹣∠OBC,∴∠MAO=∠NBO,又∵AM=BN,OA=OB,∴△AOM≌△BON(SAS),∴MO=NO,∠AOM=∠BON,∵∠AON+∠BON=90°,∴∠AON+∠AOM=90°,∴∠MON=90°,∴△MON是等腰直角三角形;解:(3)设AK=x(0<x<1),在Rt△ABK中,BK==, ∵S△ABK=×AK×AB=×BK×AM,∴AM==,∴BN=AM=,∴BM==,∴MN=BM﹣BN=,∵S△OMN=MN2==(0<x<1),将x=代入得:S△OMN===,∴当AK=时,S△OMN=.25.(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠BAD=90°,∠ABD=∠ADB=45°,∵ME⊥BD,∴∠BME=90°,∵O是BE的中点,∴AO=MO=BE=BO=EO,∴∠ABO=∠BAO,∠OBM=∠OMB,∴∠AOE=2∠ABO,∠MOE=2∠MBO,∴∠AOM=∠AOE+∠MOE=2∠ABO+2∠MBO=2∠ABD=90°;(2)∵四边形ABCD是正方形,∴∠ADB=45°,即∠N+∠DAN=45°,∵∠MAN=135°,∴∠MAB+∠DAN=135°﹣∠BAD=45°,∴∠MAB=∠N,又∠M=∠M,∴MA2=MN•MB∴2AM2=MN•2BM=MN•(BM+BM)=MN•(MN﹣BN+BM)=MN2﹣MN((BN﹣BM)=MN2﹣(BN+BM)•(BN﹣BM)=MN2﹣BN2+BM2,∴2AM2﹣MB2=MN2﹣BN2.26.证明:(1)∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠ADB=∠CDB=45°,在△ADE与△CDE中,,∴△ADE≌△CDE(SAS),∴AE=EC,∵EF=EC,∴AE=EF;(2)AF=CE,理由如下:∵AB=BE=BC,∠ABD=∠DBC=45°,∴∠BAE=∠AEB=∠BEC=∠BCE=67.5°,∵EF=EC,∴∠EFC=∠ECF=67.5°,∴∠FEC=45°,∠BFE=112.5°,∵∠BAE+∠AEF+∠BFE+∠ABF=360°,∴∠AEF=90°,且AE=EF,∴∠AFE=45°,∴∠AFE=∠FEC=45°,∴AF=EF,∴AF=CE.27.证明:[问题呈现]∵四边形ABCD是正方形,∴AD=AB,∠BAD=∠D=∠ABF=90°.∵EA⊥AF,∴∠F AE=90°.∴∠DAE+∠BAE=∠BAF+∠BAE=90°,∴∠BAF=∠DAE.在△ADE和△ABF中,,∴△ADE≌△ABF(ASA),∴DE=BF.[拓展探究](1)∵∠ACB=90°,ED⊥DF,∴∠CED+∠CFD=180°,∵∠BFD=∠CFD=180°,∴∠CED=∠BFD,又∵AC=CB=2,CD⊥AB,∴△ABC为等腰直角三角形,∴CD=BD=AD,∠B=∠DCE=45°,∴△DCE≌DBF(AAS).∴S四边形CEDF=S△CDB=S△ABC=AC•BC=3.(2)作DM⊥AC于点M,则CM=AM=DM=AC=,∵∠CDE=15°,∠ACD=45°,∴∠MED=∠CDE+∠ACD=60°,∴ED=2.∵△DCE≌DBF,∴ED=FD,EC=BF,∴四边形EDFC的周长=ED+FD+EC+BF=2ED+BC=4+2.故答案为:4+2.28.解:(1)连接AM,如图,∵正方形AEFG,矩形ABCD,∴∠AEM=∠ADM=∠ABE=90°,AD=BC=4,在Rt△AEM和Rt△ADM中,,∴Rt△AEM≌Rt△ADM(HL),∴AE=AD=4,在Rt△ABE中,BE==,∵动点E从B出发,以每秒1个单位的速度,∴;(2)分四种情况,1°当点F在CD上时,如图,∵矩形ABCD,∴∠ABE=∠ECF=90°,∴∠BAE+∠AEB=90°,∠FEC+∠EFC=90°,∵正方形AEFG,∴∠AEF=90°,AE=EF,∴∠FEC+∠AEB=90°,∴∠BAE=∠FEC,∠AEB=∠EFC,在△BAE和△CEF中,,∴△BAE≌△CEF(ASA),∴AB=EC=3,∴BE=BC﹣CE=4﹣3=1,∵动点E从B出发,以每秒1个单位的速度,∴t=1;2°当点F落在AD上时,如图,∵AF时正方形AEFG的对角线,∴∠EAF=45°,∵矩形ABCD,∴∠B=∠BAD=90°,∴∠BAE=45°=∠AEB,∴BE=AB=3,∵动点E从B出发,以每秒1个单位的速度,∴t=3;3°当点F落在AC上时,过点F作FM⊥BC交BC于点M,如图,∵正方形AEFG,∴AE=EF,∠AEF=90°,∴∠AEB+∠FEM=90°,∵矩形ABCD,∴∠ABE=90°,∴∠BAE+∠AEB=90°,∴∠BAE=∠FEM,在△BAE和△MEF中,,∴△BAE≌△MEF(AAS),∴FM=BE,EM=AB=3,设FM=BE=x,则MC=4﹣3﹣x=1﹣x,∵∠FCM=∠ACM,∠FMC=∠ABC,∴△FMC~△ABC,∴x=,即FM=BE=,∵动点E从B出发,以每秒1个单位的速度,∴;4°当点F落在BD上时,过点F作FM⊥BC交BC于点M,如图,∵正方形AEFG,∴AE=EF,∠AEF=90°,∴∠AEB+∠FEM=90°,∵矩形ABCD,∴∠ABE=90°,∴∠BAE+∠AEB=90°,∴∠BAE=∠FEM,在△BAE和△MEF中,,∴△BAE≌△MEF(AAS),∴FM=BE,EM=AB=3,设CE=a,,则FM=BE=4+a,BM=7+a,∵∠DBC=∠FBM,∠FMB=∠BCD=90°,∴a=5,∴BE=4+a=9,∵动点E从B出发,以每秒1个单位的速度,∴t=9;故所有符合条件的t的值t=1或t=3或t=9或.29.证明:(1)如图所示:∵四边形ABCD是正方形,∴AC⊥BD,∠1=∠2=45°,∴在Rt△OME和Rt△OEB中,∠3+∠OME=∠4+∠OEB=90°,∵∠OME=∠OEB,∴∠3=∠4,∴∠5=∠1+∠3=∠2+∠4=∠FBE,∴EF=EB;(2)连接DE,∵AN=EN,∴∠3=∠5,∵∠3=∠4,∴∠4=∠5,∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠7=∠8=90°,在△AOH和△BOE中,,∴△AOH≌△BOE(ASA),∵四边形ABCD是正方形,∴DC=BC,∠1=∠2=45°,在△DCE和△BCE中,,∴△DCE≌△BCE(SAS),∴DE=BE=AH=EF,∵AC⊥BD,∴∠6=∠AEB,∵∠3=∠4,∠4+∠AEB=90°,∴∠3+∠6=90°,即∠DEF=90°,∴△DEF是等腰直角三角形,∴.30.解:(1)证明:∵四边形ABCD为正方形,∴∠B=∠C=90°,AB=BC=CD.∵E是BC中点,∴,EC=BC=CD.∴∠BAE=∠CEF.∵∠BAE+∠BEA=90°,∴∠BEA+∠CEF=90°.∴∠AEF=90°.(2)∵四边形ABCD为正方形,∴∠GBE=∠C=90°,AB∥CD.∴∠G=∠CFE.在△BEG和△CEF中,.∴△BEG≌△CEF(AAS).∵∠AEF=90°,∴AE是GF的垂直平分线.∴AG=AF.∴△AGF为等腰三角形.∴∠GAE=∠F AE.∵BH⊥AF,∴∠MAH+∠AHM=90°.∵AD∥BC,∴∠AHM=∠HBC.∵∠ABC=90°,∴∠HBC+∠ABH=90°.∴∠ABH=∠MAH.∵∠ANH=∠ABH+∠GAE,∴∠ANH=∠MAH+∠EAF=∠NAH.∴HA=HN.∴△HAN为等腰三角形.∵AD∥BC,∴∠HAN=∠BEN.∵∠ANH=∠BNE,∴∠BEN=∠BNE.∴△BEN为等腰三角形.在△ABE和△DCE中,.∴△ABE≌△DCE(SAS).∴EA=ED.∴△AED为等腰三角形.综上,等腰三角形有:△AED,△BEN,△AHN,△AGF.31.证明:(1)∵四边形ABCD是正方形,∴∠BDC=45°,∵DG⊥AE,∴∠DGE=90°,∵GH平分∠DGE,∴∠DGH=∠EGH=45°,∴∠BDC=∠EGH=45°,∵∠DPH=∠GPF,∴∠DHG=∠DF A.(2)由(1)可知:∠BDC=∠EGH=45°,∠DPH=∠GPF,∴∠DGP=∠HFP=45°,又∠DBC=45°,∴∠DBC=∠HFP=45°,∴FH∥BC.(3)连接P A,过点P作PM⊥AE于M,PN⊥DG于N,QP⊥GP交GD于Q,如图所示.由(2)证法,易证∠P AG=∠PDG,∵PM⊥AE,PN⊥DG,GH平分∠DGE,∴PM=PN,∴Rt△PMA≌Rt△PND(AAS),∴P A=PD,∵四边形ABCD是正方形,∠ADB=45°,∴∠APD=90°=∠GPQ,∴∠APG=∠DPQ,∴△APG≌△DPQ(ASA),∴QD=AG,∵∠PGQ=45°,∴△PGQ是等腰直角三角形,∴GQ=PG,∴DG﹣AG=DG﹣DQ=GQ=PG,∴.32.解:(1)①连接AC,∵四边形ABCD是正方形,∴∠CAD=45°,Rt△AEF中,FE=F A,∴∠EAF=45°,即∠CAE=∠DAF,∴∠ADF=∠ACE=45°.∴CE=DF;(2)①当点E在线段CD上时,则S△ADE+S△ADF=6,过点F作FH⊥AD,∵∠ADF=45°,∴HF=DF,设方形ABCD的边长为a,则CE=a﹣2,DF=CE=(a﹣2),∴2a+a×(a﹣2)×=6,解得:a=4,∴CE=4﹣2=2,∴DF=CE=×2=,②当点E在CD的延长线上时,则S△ADE+S△AEF=6,过点F作FM⊥AE,FN⊥AD,连接AC,设正方形ABCD的边长为a,则AE==,MF=,∴×2a+×=6,解得a=2﹣2或a=﹣2﹣2(舍去),∴CE=2﹣2+2=2,∴DF=CE=×2=2,综上所述:DF=或2.33.(1)证明:∵正方形ABCD,∴∠BCD=90°,BC=CD,同理:CG=CE,∠GCE=90°,∴∠BCD=∠GCE=90°,,∴△BCG≌△DCE(SAS),∴∠GBC=∠CDE,在Rt△DCE中∠CDE+∠CED=90°,∴∠GBC+∠BEH=90°,∴∠BHE=180°﹣(∠GBC+∠BEH)=90°,。
中考数学 真题精选 专题试卷 特殊的平行四边形(含答案解析) (含答案解析)

特殊的平行四边形一.选择题(共19小题)1.(•河北)如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB 的大小.其中会随点P的移动而变化的是()A.②③ B.②⑤ C.①③④ D.④⑤考点:三角形中位线定理;平行线之间的距离.分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=AB,从而判断出①不变;再根据三角形的周长的定义判断出②是变化的;确定出点P到MN的距离不变,然后根据等底等高的三角形的面积相等确定出③不变;根据平行线间的距离相等判断出④不变;根据角的定义判断出⑤变化.解答:解:∵点A,B为定点,点M,N分别为PA,PB的中点,∴MN是△PAB的中位线,∴MN=AB,即线段MN的长度不变,故①错误;PA、PB的长度随点P的移动而变化,所以,△PAB的周长会随点P的移动而变化,故②正确;∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,∴△PMN的面积不变,故③错误;直线MN,AB之间的距离不随点P的移动而变化,故④错误;∠APB的大小点P的移动而变化,故⑤正确.综上所述,会随点P的移动而变化的是②⑤.故选B.点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等底等高的三角形的面积相等,平行线间的距离的定义,熟记定理是解题的关键.2.(•山西)如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC 的周长是()A.8 B.10 C.12 D.14考点:三角形中位线定理.分析:首先根据点D、E分别是边AB,BC的中点,可得DE是三角形BC的中位线,然后根据三角形中位线定理,可得DE=AC,最后根据三角形周长的含义,判断出△ABC的周长和△DBE的周长的关系,再结合△DBE的周长是6,即可求出△ABC的周长是多少.解答:解:∵点D、E分别是边AB,BC的中点,∴DE是三角形BC的中位线,AB=2BD,BC=2BE,∴DE∥BC且DE=AC,又∵AB=2BD,BC=2BE,∴AB+BC+AC=2(BD+BE+DE),即△ABC的周长是△DBE的周长的2倍,∵△DBE的周长是6,∴△ABC的周长是:6×2=12.故选:C.点评:(1)此题主要考查了三角形中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.(2)此题还考查了三角形的周长和含义的求法,要熟练掌握.3.(•铁岭)如图,点D、E、F分别为△ABC各边中点,下列说法正确的是()A.DE=DF B.EF=AB C.S△ABD=S△ACD D.AD平分∠BAC考点:三角形中位线定理.分析:根据三角形中位线定理逐项分析即可.解答:解:A、∵点D、E、F分别为△ABC各边中点,∴DE=AC,DF=AB,∵AC≠AB,∴DE≠DF,故该选项错误;B、由A选项的思路可知,B选项错误、C、∵S△ABD=BD•h,S△ACD=CD•h,BD=CD,∴S△ABD=S△ACD,故该选项正确;D、∵BD=CD,AB≠AC,∴AD不平分∠BAC,故选C.点评:本题考查了三角形中位线定理的运用,解题的根据是熟记其定理:三角形的中位线平行于第三边,并且等于第三边的一半.4.(•安顺)如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于()A.3:2 B.3:1 C.1:1 D.1:2考点:平行四边形的性质;相似三角形的判定与性质.专题:几何图形问题.分析:根据题意得出△DEF∽△BCF,进而得出=,利用点E是边AD的中点得出答案即可.解答:解:∵▱ABCD,故AD∥BC,∴△DEF∽△BCF,∴=,∵点E是边AD的中点,∴AE=DE=AD,∴=.故选:D.点评:此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识,得出△DEF∽△BCF是解题关键.5.(•衢州)如图,在▱ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于()A.8cm B.6cm C.4cm D.2cm考点:平行四边形的性质.分析:由平行四边形的性质得出BC=AD=12cm,AD∥BC,得出∠DAE=∠BEA,证出∠BEA=∠BAE,得出BE=AB,即可得出CE的长.解答:解:∵四边形ABCD是平行四边形,∴BC=AD=12cm,AD∥BC,∴∠DAE=∠BEA,∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BEA=∠BAE,∴BE=AB=8cm,∴CE=BC﹣BE=4cm;故答案为:C.点评:本题考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.6.(•玉林)如图,在▱ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,▱ABCD的周长是在14,则DM等于()A.1 B. 2 C. 3 D. 4考点:平行四边形的性质.分析:根据BM是∠ABC的平分线和AB∥CD,求出BC=MC=2,根据▱ABCD的周长是14,求出CD=5,得到DM的长.解答:解:∵BM是∠ABC的平分线,∴∠ABM=∠CBM,∵AB∥CD,∴∠ABM=∠BMC,∴∠BMC=∠CBM,∴BC=MC=2,∵▱ABCD的周长是14,∴BC+CD=7,∴CD=5,则DM=CD﹣MC=3,故选:C.点评:本题考查的是平行四边形的性质和角平分线的定义,根据平行四边形的对边相等求出BC+CD 是解题的关键,注意等腰三角形的性质的正确运用.7.(•绥化)如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=BC,成立的个数有()A.1个B.2个C.3个D.4个考点:平行四边形的性质;等腰三角形的判定与性质;等边三角形的判定与性质;含30度角的直角三角形.分析:由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S▱ABCD=AB•AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.解答:解:∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,∴AE=AB=BE,∵AB=BC,∴AE=BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;∵AC⊥AB,∴S▱ABCD=AB•AC,故②正确,∵AB=BC,OB=BD,∵BD>BC,∴AB≠OB,故③错误;∵CE=BE,CO=OA,∴OE=AB,∴OE=BC,故④正确.故选C.点评:本题考查了平行四边形的性质,等边三角形的判定和性质,直角三角形的性质,平行四边形的面积公式,熟练掌握性质定理和判定定理是解题的关键.8.(•河南)如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为()A.4 B. 6 C.8 D.10考点:平行四边形的性质;等腰三角形的判定与性质;勾股定理;作图—基本作图.专题:计算题.分析:由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.解答:解:连结EF,AE与BF交于点O,如图,∵AB=AF,AO平分∠BAD,∴AO⊥BF,BO=FO=BF=3,∵四边形ABCD为平行四边形,∴AF∥BE,∴∠1=∠3,∴∠2=∠3,∴AB=EB,而BO⊥AE,∴AO=OE,在Rt△AOB中,AO===4,∴AE=2AO=8.故选C.点评:本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.9.(•本溪)如图,▱ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是()A.10cm B.8cm C.6cm D.4cm考点:平行四边形的性质.分析:根据平行四边形的性质得出AB=CD,AD=BC,AD∥BC,推出∠DAE=∠BAE,求出∠BAE=∠AEB,推出AB=BE,设AB=CD=xcm,则AD=BC=(x+2)cm,得出方程x+x+2=10,求出方程的解即可.解答:解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,AD∥BC,∴∠DAE=∠BAE,∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠AEB,∴AB=BE,设AB=CD=xcm,则AD=BC=(x+2)cm,∵▱ABCD的周长为20cm,∴x+x+2=10,解得:x=4,即AB=4cm,故选D.点评:本题考查了平行四边形的在,平行线的性质,等腰三角形的判定的应用,解此题的关键是能推出AB=BE,题目比较好,难度适中.10.(•福建)如图,在▱ABCD中,O是对角线AC,BD的交点,下列结论错误的是()A.AB∥CD B.AB=CD C.AC=BD D.OA=OC考点:平行四边形的性质.分析:根据平行四边形的性质推出即可.解答:解:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,OA=OC,但是AC和BD不一定相等,故选C.点评:本题考查了平行四边形的性质的应用,能熟记平行四边形的性质是解此题的关键,注意:平行四边形的对边相等且平行,平行四边形的对角线互相平分.11.(•陕西)在▱ABCD中,AB=10,BC=14,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为()A.7 B.4或10 C.5或9 D.6或8考点:平行四边形的性质;勾股定理;正方形的性质.专题:分类讨论.分析:设AE的长为x,根据正方形的性质可得BE=14﹣x,根据勾股定理得到关于x的方程,解方程即可得到AE的长.解答:解:如图:设AE的长为x,根据正方形的性质可得BE=14﹣x,在△ABE中,根据勾股定理可得x2+(14﹣x)2=102,解得x1=6,x2=8.故AE的长为6或8.故选:D.点评:考查了平行四边形的性质,正方形的性质,勾股定理,关键是根据勾股定理得到关于AE的方程.12.(•营口)▱ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是()A.61° B.63° C.65° D.67°考点:平行四边形的性质.分析:由平行四边形的性质可知:AD∥BC,进而可得∠DAC=∠BCA,再根据三角形外角和定理即可求出∠COD的度数.解答:解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠BCA=42°,∴∠COD=∠CBD+∠BCA=65°,故选C.点评:本题考查了平行四边形的性质以及三角形的外角和定理,题目比较简单,解题的关键是灵活运用平行四边形的性质,将四边形的问题转化为三角形问题.13.(•巴彦淖尔)如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为()A.24 B.12 C.6 D.3考点:平行四边形的性质;三角形中位线定理.分析:过P作PQ平行于DC,由DC与AB平行,得到PQ平行于AB,可得出四边形PQCD与ABQP都为平行四边形,进而确定出△PDC与△PCQ面积相等,△PQB与△ABP面积相等,再由EF为△BPC的中位线,利用中位线定理得到EF为BC的一半,且EF平行于BC,得出△PEF与△PBC 相似,相似比为1:2,面积之比为1:4,求出△PBC的面积,而△PBC面积=△CPQ面积+△PBQ 面积,即为△PDC面积+△PAB面积,即为平行四边形面积的一半,即可求出所求的面积.解答:解:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,∴四边形PQCD与四边形APQB都为平行四边形,∴△PDC≌△CQP,△ABP≌△QPB,∴S△PDC=S△CQP,S△ABP=S△QPB,∵EF为△PCB的中位线,∴EF∥BC,EF=BC,∴△PEF∽△PBC,且相似比为1:2,∴S△PEF:S△PBC=1:4,S△PEF=3,∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=12.故选:B.点评:此题考查了平行四边形的性质,相似三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.14.(•常州)如图,▱ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是()A.AO=OD B.AO⊥OD C.AO=OC D.AO⊥AB考点:平行四边形的性质.分析:根据平行四边形的性质:对边平行且相等,对角线互相平分进行判断即可.解答:解:对角线不一定相等,A错误;对角线不一定互相垂直,B错误;对角线互相平分,C正确;对角线与边不一定垂直,D错误.故选:C.点评:本题考查度数平行四边形的性质,掌握平行四边形的对边平行且相等,对角线互相平分是解题的关键.15.(•淄博)如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有()A.4个B.3个C.2个D.1个考点:平行四边形的性质;等边三角形的判定;翻折变换(折叠问题).分析:根据折叠的性质可得∠E=∠B=60°,进而可证明△BEC是等边三角形,再根据平行四边形的性质可得:AD∥BC,所以可得∠EAF=60°,进而可证明△EFA是等边三角形,由等边三角形的性质可得∠EFA=∠DFC=60°,又因为∠D=∠B=60°,进而可证明△DFC是等边三角形,问题得解.解答:解:∵将△ABC沿对角线AC折叠,点B的对应点落在点E处,∴∠E=∠B=60°,∴△BEC是等边三角形,∵四边形ABCD是平行四边形,∴AD∥BC,∠D=∠B=60°,∴∠B=∠EAF=60°,∴△EFA是等边三角形,∵∠EFA=∠DFC=60°,∠D=∠B=60°,∴△DFC是等边三角形,∴图中等边三角形共有3个,故选B.点评:本题考查了平行四边形的性质、折叠的性质以及等边三角形的判定和性质,解题的关键是熟记等边三角形的各种判定方法特别是经常用到的判定方法:三个角都相等的三角形是等边三角形.16.(•连云港)已知四边形ABCD,下列说法正确的是()A.当AD=BC,AB∥DC时,四边形ABCD是平行四边形B.当AD=BC,AB=DC时,四边形ABCD是平行四边形C.当AC=BD,AC平分BD时,四边形ABCD是矩形D.当AC=BD,AC⊥BD时,四边形ABCD是正方形考点:平行四边形的判定;矩形的判定;正方形的判定.分析:由平行四边形的判定方法得出A不正确、B正确;由矩形和正方形的判定方法得出C、D不正确.解答:解:∵一组对边平行且相等的四边形是平行四边形,∴A不正确;∵两组对边分别相等的四边形是平行四边形,∴B正确;∵对角线互相平分且相等的四边形是矩形,∴C不正确;∵对角线互相垂直平分且相等的四边形是正方形,∴D不正确;故选:B.点评:本题考查了平行四边形的判定、矩形的判定、正方形的判定;熟练掌握平行四边形、矩形、正方形的判定方法是解决问题的关键.17.(•台湾)坐标平面上,二次函数y=﹣x2+6x﹣9的图形的顶点为A,且此函数图形与y轴交于B 点.若在此函数图形上取一点C,在x轴上取一点D,使得四边形ABCD为平行四边形,则D点坐标为何?()A.(6,0)B.(9,0)C.(﹣6,0)D.(﹣9,0)考点:平行四边形的判定;二次函数的性质.分析:首先将二次函数配方求得顶点A的坐标,然后求得抛物线与y轴的交点坐标,根据电C和点B的纵坐标相同求得点C的坐标,从而求得线段BC的长,根据平行四边形的性质求得AD的长即可求得点D的坐标.解答:解:∵y=﹣x2+6x﹣9=﹣(x﹣3)2,∴顶点A的坐标为(3,0),令x=0得到y=﹣9,∴点B的坐标为(0,﹣9),令y=﹣x2+6x﹣9=﹣9,解得:x=0或x=6,∴点C的坐标为(6,﹣9),∴BC=AD=6,∴OD=OA+AD=3+6=9,∴点D的坐标为(9,0),故选B.点评:本题考查了平行四边形的判定、二次函数的性质等知识,主要利用了抛物线与坐标轴交点的求法,平行四边形的对边平行且相等的性质,综合题,但难度不大.18.(•绵阳)如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为()A.6 B.12 C.20 D.24考点:平行四边形的判定与性质;全等三角形的判定与性质;勾股定理.分析:根据勾股定理,可得EC的长,根据平行四边形的判定,可得四边形ABCD的形状,根据平行四边形的面积公式,可得答案.解答:解:在Rt△BCE中,由勾股定理,得CE===5.∵BE=DE=3,AE=CE=5,∴四边形ABCD是平行四边形.四边形ABCD的面积为BC•BD=4×(3+3)=24,故选:D.点评:本题考查了平行四边形的判定与性质,利用了勾股定理得出CE的长,又利用对角线互相平分的四边形是平行四边形,最后利用了平行四边形的面积公式.19.(•泰安)如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为()A.6 B.7 C.8 D.10考点:三角形中位线定理;直角三角形斜边上的中线.分析:根据直角三角形斜边上的中线等于斜边的一半得到CD=AB=3,则结合已知条件CE=CD 可以求得ED=4.然后由三角形中位线定理可以求得BF=2ED=8.解答:解:如图,∵∠ACB=90°,D为AB的中点,AB=6,∴CD=AB=3.又CE=CD,∴CE=1,∴ED=CE+CD=4.又∵BF∥DE,点D是AB的中点,∴ED是△AFB的中位线,∴BF=2ED=8.故选:C.点评:本题考查了三角形中位线定理和直角三角形斜边上的中线.根据已知条件求得ED的长度是解题的关键与难点.二.填空题(共11小题)20.(•泰安)如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM 的中点.若AB=8,AD=12,则四边形ENFM的周长为20.考点:三角形中位线定理;勾股定理;矩形的性质.分析:根据M是边AD的中点,得AM=DM=6,根据勾股定理得出BM=CM=10,再根据E、F分别是线段BM、CM的中点,即可得出EM=FM=5,再根据N是边BC的中点,得出EM=FN,EN=FM,从而得出四边形EN,FM的周长.解答:解:∵M、N分别是边AD、BC的中点,AB=8,AD=12,∴AM=DM=6,∵四边形ABCD为矩形,∴∠A=∠D=90°,∴BM=CM=10,∵E、F分别是线段BM、CM的中点,∴EM=FM=5,∴EN,FN都是△BCM的中位线,∴EN=FN=5,∴四边形ENFM的周长为5+5+5+5=20,故答案为20.点评:本题考查了三角形的中位线,勾股定理以及矩形的性质,是年中考常见的题型,难度不大,比较容易理解.21.(•巴中)如图,在△ABC中,AB=5,AC=3,AD、AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连结DH,则线段DH的长为1.考点:三角形中位线定理;等腰三角形的判定与性质.分析:首先证明△ACF是等腰三角形,则AF=AC=3,HF=CH,则DH是△BCF的中位线,利用三角形的中位线定理即可求解.解答:解:∵AE为△ABC的角平分线,CH⊥AE,∴△ACF是等腰三角形,∴AF=AC,∵AC=3,∴AF=AC=3,HF=CH,∵AD为△ABC的中线,∴DH是△BCF的中位线,∴DH=BF,∵AB=5,∴BF=AB﹣AF=5﹣3=2.∴DH=1,故答案为:1.点评:本题考查了等腰三角形的判定以及三角形的中位线定理,正确证明HF=CH是关键.22.(•盐城)如图,点D、E、F分别是△ABC各边的中点,连接DE、EF、DF.若△ABC的周长为10,则△DEF的周长为5.考点:三角形中位线定理.分析:由于D、E分别是AB、BC的中点,则DE是△ABC的中位线,那么DE=AC,同理有EF=AB,DF=BC,于是易求△DEF的周长.解答:解:如上图所示,∵D、E分别是AB、BC的中点,∴DE是△ABC的中位线,∴DE=AC,同理有EF=AB,DF=BC,∴△DEF的周长=(AC+BC+AB)=×10=5.故答案为5.点评:本题考查了三角形中位线定理.解题的关键是根据中位线定理得出边之间的数量关系.23.(•无锡)已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长等于.考点:三角形中位线定理;勾股定理.专题:计算题.分析:延长AD至F,使DF=AD,过点F作平行BE与AC延长线交于点G,过点C作CH∥BE,交AF于点H,连接BF,如图所示,在直角三角形AGF中,利用勾股定理求出AG的长,利用SAS 证得△BDF≌△CDA,利用全等三角形对应角相等得到∠ACD=∠BFD,证得AG∥BF,从而证得四边形EBFG是平行四边形,得到FG=BE=6,利用AAS得到三角形BOD与三角形CHD全等,利用全等三角形对应边相等得到OD=DH=3,得出AH=9,然后根据△AHC∽△AFG,对应边成比例即可求得AC.解答:解:延长AD至F,使DF=AD,过点F作FG∥BE与AC延长线交于点G,过点C作CH∥BE,交AF于点H,连接BF,如图所示,在Rt△AFG中,AF=2AD=12,FG=BE=6,根据勾股定理得:AG==6,在△BDF和△CDA中,∴△BDF≌△CDA(SAS),∴∠ACD=∠BFD,∴AG∥BF,∴四边形EBFG是平行四边形,∴FG=BE=6,在△BOD和△CHD中,,∴△BOD≌△CHD(AAS),∴OD=DH=3,∵CH∥FG,∴△AHC∽△AFG,∴=,即=,解得:AC=,故答案为:点评:本题考查了三角形全等的判定和性质,三角形相似的判定和性质,平行四边形的判定和性质以及勾股定理的应用,作出辅助线构建直角三角形和平行四边形是解题的关键.24.(•宿迁)如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为5.考点:三角形中位线定理;直角三角形斜边上的中线.分析:已知CD是Rt△ABC斜边AB的中线,那么AB=2CD;EF是△ABC的中位线,则EF应等于AB的一半.解答:解:∵△ABC是直角三角形,CD是斜边的中线,∴CD=AB,又∵EF是△ABC的中位线,∴AB=2CD=2×5=10cm,∴EF=×10=5cm.故答案为:5.点评:此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识,用到的知识点为:(1)直角三角形斜边的中线等于斜边的一半;(2)三角形的中位线等于对应边的一半.25.(•广州)如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB 上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为3.考点:三角形中位线定理;勾股定理.专题:动点型.分析:根据三角形的中位线定理得出EF=DN,从而可知DN最大时,EF最大,因为N与B重合时DN最大,此时根据勾股定理求得DN=DB=6,从而求得EF的最大值为3.解答:解:∵ED=EM,MF=FN,∴EF=DN,∴DN最大时,EF最大,∵N与B重合时DN最大,此时DN=DB==6,∴EF的最大值为3.故答案为3.点评:本题考查了三角形中位线定理,勾股定理的应用,熟练掌握定理是解题的关键.26.(•云南)如图,在△ABC中,BC=1,点P1,M1分别是AB,AC边的中点,点P2,M2分别是AP1,AM1的中点,点P3,M3分别是AP2,AM2的中点,按这样的规律下去,P n M n的长为(n 为正整数).考点:三角形中位线定理.专题:规律型.分析:根据中位线的定理得出规律解答即可.解答:解:在△ABC中,BC=1,点P1,M1分别是AB,AC边的中点,点P2,M2分别是AP1,AM1的中点,点P3,M3分别是AP2,AM2的中点,可得:P1M1=,P2M2=,故P n M n=,故答案为:点评:此题考查三角形中位线定理,关键是根据中位线得出规律进行解答.27.(•珠海)如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点得△A3B3C3,…,则△A5B5C5的周长为1.考点:三角形中位线定理.专题:规律型.分析:由三角形的中位线定理得:A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半,所以△A2B2C2的周长等于△A1B1C1的周长的一半,以此类推可求出△A5B5C5的周长为△A1B1C1的周长的.解答:解:∵A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半,∴以此类推:△A5B5C5的周长为△A1B1C1的周长的,∴则△A5B5C5的周长为(7+4+5)÷16=1.故答案为:1点评:本题主要考查了三角形的中位线定理,关键是根据三角形的中位线定理得:A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半,所以△A2B2C2的周长等于△A1B1C1的周长的一半.28.(•衢州)如图,小聪与小慧玩跷跷板,跷跷板支架高EF为0.6米,E是AB的中点,那么小聪能将小慧翘起的最大高度BC等于 1.2米.考点:三角形中位线定理.专题:应用题.分析:先求出F为AC的中点,根据三角形的中位线求出BC=2EF,代入求出即可.解答:解:∵EF⊥AC,BC⊥AC,∴EF∥BC,∵E是AB的中点,∴F为AC的中点,∴BC=2EF,∵EF=0.6米,∴BC=1.2米,故答案为:1.2.点评:本题考查了三角形的中位线性质,平行线的性质和判定的应用,解此题的关键是求出BC=2EF,注意:垂直于同一直线的两直线平行.29.(•昆明)如图,在△ABC中,AB=8,点D、E分别是BC、CA的中点,连接DE,则DE=4.考点:三角形中位线定理.分析:根据三角形的中位线等于第三边的一半即可得出DE=AB=4.解答:解:∵在△ABC中,点D、E分别是BC、CA的中点,AB=8,∴DE是△ABC的中位线,∴DE=AB=×8=4.故答案为4.点评:本题考查了三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.30.(•陕西)如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是3.考点:三角形中位线定理;等腰直角三角形;圆周角定理.分析:根据中位线定理得到MN的最大时,AC最大,当AC最大时是直径,从而求得直径后就可以求得最大值.解答:解:∵点M,N分别是AB,BC的中点,∴MN=AC,∴当AC取得最大值时,MN就取得最大值,当AC时直径时,最大,如图,∵∠ACB=∠D=45°,AB=6,∴AD=6,∴MN=AD=3故答案为:3.点评:本题考查了三角形的中位线定理、等腰直角三角形的性质及圆周角定理,解题的关键是了解当什么时候MN的值最大,难度不大.1.(•苏州)如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F 作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为27.考点:三角形中位线定理;等腰三角形的性质;轴对称的性质.分析:先根据点A、D关于点F对称可知点F是AD的中点,再由CD⊥AB,FG∥CD可知FG是△ACD的中位线,故可得出CG的长,再根据点E是AB的中点可知GE是△ABC的中位线,故可得出GE的长,由此可得出结论.解答:解:∵点A、D关于点F对称,∴点F是AD的中点.∵CD⊥AB,FG∥CD,∴FG是△ACD的中位线,AC=18,BC=12,∴CG=AC=9.∵点E是AB的中点,∴GE是△ABC的中位线,∵CE=CB=12,∴GE=BC=6,∴△CEG的周长=CG+GE+CE=9+6+12=27.故答案为:27.点评:本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.2.(•铜仁市)如图,∠ACB=9O°,D为AB中点,连接DC并延长到点E,使CE=CD,过点B作BF∥DE交AE的延长线于点F.若BF=10,则AB的长为8.考点:三角形中位线定理;直角三角形斜边上的中线.分析:先根据点D是AB的中点,BF∥DE可知DE是△ABF的中位线,故可得出DE的长,根据CE=CD可得出CD的长,再根据直角三角形的性质即可得出结论.解答:解:∵点D是AB的中点,BF∥DE,∴DE是△ABF的中位线.∵BF=10,∴DE=BF=5.∵CE=CD,∴CD=5,解得CD=4.∵△ABC是直角三角形,∴AB=2CD=8.故答案为:8.点评:本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.3.(•淮安)如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是720米.考点:三角形中位线定理.专题:应用题.分析:首先根据D、E分别是CA,CB的中点,可得DE是△ABC的中位线,然后根据三角形的中位线定理,可得DE∥AB,且DE=,再根据DE的长度为360米,求出A、B两地之间的距离是多少米即可.解答:解:∵D、E分别是CA,CB的中点,∴DE是△ABC的中位线,∴DE∥AB,且DE=,∵DE=360(米),∴AB=360×2=720(米).即A、B两地之间的距离是720米.故答案为:720.点评:此题主要考查了三角形中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.4.(•梅州)如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于20.考点:平行四边形的性质.分析:根据四边形ABCD为平行四边形可得AE∥BC,根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB,继而可得AB=AE,然后根据已知可求得结果.解答:解:∵四边形ABCD为平行四边形,∴AE∥BC,AD=BC,AD=BC,∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE,∴AE+DE=AD=BC=6,∴AE+2=6,∴AE=4,∴AB=CD=4,∴▱ABCD的周长=4+4+6+6=20,故答案为:20.点评:本题考查了平行四边形的性质,解答本题的关键是根据平行线的性质和角平分线的性质得出∠ABE=∠AEB.5.(•大连)如图,在▱ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB=cm.考点:平行四边形的性质;勾股定理.分析:由平行四边形的性质得出BC=AD=8cm,OA=OC=AC,由勾股定理求出AC,得出OC,再由勾股定理求出OB即可.解答:解:∵四边形ABCD是平行四边形,∴BC=AD=8cm,OA=OC=AC,∵AC⊥BC,∴∠ACB=90°,∴AC===6,。
20170210中考特殊平行四边形证明及计算经典习题及答案

初中数学中考特殊四边形证明及计算组卷参考答案与试题解析一.解答题(共30小题)1.(2012•威海)(1)如图①,▱ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.(2)如图②,将▱ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.,∴△6.如图,以△ABC三边为边在BC同侧作三个等边△ABD、△BCE、△ACF.请回答下列问题:(1)求证:四边形ADEF是平行四边形;(2)当△ABC满足什么条件时,四边形ADEF是矩形.9.(2009•龙岩)在边长为6的菱形ABCD中,动点M从点A出发,沿A⇒B⇒C向终点C运动,连接DM交AC 于点N.(1)如图1,当点M在AB边上时,连接BN:①求证:△ABN≌△ADN;②若∠ABC=60°,AM=4,∠ABN=α,求点M到AD的距离及tanα的值.(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x(6≤x≤12).试问:x为何值时,△ADN为等腰三角形.MH=AM•sin60°=4×sin60°=2.2MDH=tanα=AC=66.610.(2007•常德)如图1,已知四边形ABCD是菱形,G是线段CD上的任意一点时,连接BG交AC于F,过F作FH∥CD交BC于H,可以证明结论成立.(考生不必证明)(1)探究:如图2,上述条件中,若G在CD的延长线上,其它条件不变时,其结论是否成立?若成立,请给出证明;若不成立,请说明理由;(2)计算:若菱形ABCD中AB=6,∠ADC=60°,G在直线CD上,且CG=16,连接BG交AC所在的直线于F,过F作FH∥CD交BC所在的直线于H,求BG与FG的长.(3)发现:通过上述过程,你发现G在直线CD上时,结论还成立吗?)借助中间比进行证明,根据平行线分线段成比例定理分别证明两个比都等于)结论成立,.,可得,,)知,,可得,.BF=14×÷16=..的延长线上时,,11.(2001•河北)如图,在菱形ABCD中,AB=10,∠BAD=60度.点M从点A以每秒1个单位长的速度沿着AD 边向点D移动;设点M移动的时间为t秒(0≤t≤10).(1)点N为BC边上任意一点,在点M移动过程中,线段MN是否一定可以将菱形分割成面积相等的两部分并说明理由;(2)点N从点B(与点M出发的时刻相同)以每秒2个单位长的速度沿着BC边向点C移动,在什么时刻,梯形ABNM的面积最大并求出面积的最大值;(3)点N从点B(与点M出发的时刻相同)以每秒a(a≥2)个单位长的速度沿着射线BC方向(可以超越C点)移动,过点M作MP∥AB,交BC于点P.当△MPN≌△ABC时,设△MPN与菱形ABCD重叠部分的面积为S,求出用t表示S的关系式,井求当S=0时的值.,5×=t.点外,所以不重合处面积为×S=25﹣,12.(2002•无锡)已知:如图,矩形ABCD中,AB=2,AD=3,E、F分别是AB、CD的中点.(1)在边AD上取一点M,使点A关于BM的对称点C恰好落在EF上.设BM与EF相交于点N,求证:四边形ANGM是菱形;(2)设P是AD上一点,∠PFB=3∠FBC,求线段AP的长.PA=..14.在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.(1)如图1,证明平行四边形ECFG为菱形;(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.,,15.如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE、AC和BE相交于点O.(1)判断四边形ABCE是怎样的四边形,说明理由;(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED 的面积.××17.(2010•大庆)已知:如图①,正方形ABCD与矩形DEFG的边AD、DE在同一直线l上,点G在CD上.正方形ABCD的边长为a,矩形DEFG的长DE为b,宽DG为3(其中a>b>3).若矩形DEFG沿直线l向左以每秒1个单位的长度的速度运动(点D、E始终在直线l上).若矩形DEFG在运动过程中与正方形ABCD的重叠部分的面积记作S,运动时间记为t秒(0≤t≤m),其中S与t的函数图象如图②所示.矩形DEFG的顶点经运动后的对应点分别记作D′、E′、F′、G′.(1)根据题目所提供的信息,可求得b=4,a=5,m=9;(2)连接AG′、CF′,设以AG′和CF′为边的两个正方形的面积之和为y,求当0≤t≤5时,y与时间t之间的函数关系式,并求出y的最小值以及y取最小值时t的值;(3)如图③,这是在矩形DEFG运动过程中,直线AG′第一次与直线CF′垂直的情形,求此时t的值.并探究:在矩形DEFG继续运动的过程中,直线AG′与直线CF′是否存在平行或再次垂直的情形?如果存在,请画出图形,并求出t的值;否则,请说明理由.),时,.,=,,=,,即18.(2005•淮安)已知:平行四边形ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD,A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).(1)求证:四边形ABCD是矩形;(2)在四边形ABCD中,求的值.,易求解则21.(2012•黑龙江)在△ABC中,∠BAC=90°,AB=AC,若点D在线段BC上,以AD为边长作正方形ADEF,如图1,易证:∠AFC=∠ACB+∠DAC;(1)若点D在BC延长线上,其他条件不变,写出∠AFC、∠ACB、∠DAC的关系,并结合图2给出证明;(2)若点D在CB延长线上,其他条件不变,直接写出∠AFC、∠ACB、∠DAC的关系式.,,22.(2012•常德)已知四边形ABCD是正方形,O为正方形对角线的交点,一动点P从B开始,沿射线BC运动,连接DP,作CN⊥DP于点M,且交直线AB于点N,连接OP,ON.(当P在线段BC上时,如图1:当P在BC 的延长线上时,如图2)(1)请从图1,图2中任选一图证明下面结论:①BN=CP;②OP=ON,且OP⊥ON;(2)设AB=4,BP=x,试确定以O、P、B、N为顶点的四边形的面积y与x的函数关系.,,=2+×=2+×=的函数关系是:23.(2011•来宾)已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点,(1)如果动点E、F满足BE=CF(如图1):①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);②证明:AE⊥BF;(2)如果动点E、F满足BE=OF(如图2),问当AE⊥BF时,点E在什么位置,并证明你的结论.,==,AO==,==,BO==,24.(2011•河北)如图,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.(1)求证:①DE=DG;②DE⊥DG(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想:(4)当时,请直接写出的值.)由已知表示出=.25.(2011•阜新)如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O 为AC中点.(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;(2)如图2,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由;(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形(尺规作图,保留作图痕迹,不写作法),并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.,26.(2006•内江)如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连接E、F、G、H,把四边形EFGH 称为中点四边形.连接AC、BD,容易证明:中点四边形EFGH一定是平行四边形.(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD 的对角线满足AC=BD时,四边形EFGH为菱形.当四边形ABCD的对角线满足AC⊥BD时,四边形EFGH为矩形;当四边形ABCD的对角线满足AC⊥BD且AC=BD时,四边形EFGH为正方形;(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明;(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少?EF=AC BD=EF=AC BDSBDSS(S(S(SS27.如图,四边形ABCD是正方形,点P是BC上任意一点,DE⊥AP于点E,BF⊥AP于点F,CH⊥DE于点H,BF的延长线交CH于点G.(1)求证:AF﹣BF=EF;(2)四边形EFGH是什么四边形?并证明;(3)若AB=2,BP=1,求四边形EFGH的面积.AP=×AP=×BF×2×,==,﹣.28.如图,在正方形ABCD中,点M在边AB上,点N在边AD的延长线上,且BM=DN.点E为MN的中点,DE的延长线与AC相交于点F.试猜想线段DF与线段AC的关系,并证你的猜想.ACACACAC29.在图1到图3中,点O是正方形ABCD对角线AC的中点,△MPN为直角三角形,∠MPN=90°.正方形ABCD 保持不动,△MPN沿射线AC向右平移,平移过程中P点始终在射线AC上,且保持PM垂直于直线AB于点E,PN垂直于直线BC于点F.(1)如图1,当点P与点O重合时,OE与OF的数量关系为OE=OF;(2)如图2,当P在线段OC上时,猜想OE与OF有怎样的数量关系与位置关系?并对你的猜想结果给予证明;(3)如图3,当点P在AC的延长线上时,OE与OF的数量关系为OE=OF;位置关系为OE⊥OF.30.以△ABC的各边,在边BC的同侧分别作三个正方形.他们分别是正方形ABDI,BCFE,ACHG,试探究:(1)如图中四边形ADEG是什么四边形?并说明理由.(2)当△ABC满足什么条件时,四边形ADEG是矩形?(3)当△ABC满足什么条件时,四边形ADEG是正方形?ABABABAC=。
中考数学总复习《(特殊)平行四边形的动点问题》专题训练(附答案)

中考数学总复习《(特殊)平行四边形的动点问题》专题训练(附答案)学校:___________班级:___________姓名:___________考号:___________1.已知,矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .(1)如图1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长;(2)如图2,动点P 、Q 分别从A 、C 两点同时出发,沿△AFB 和△CDE 各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P 、Q 的运动路程分别为a 、b (单位:cm ,ab ≠0),已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.2.(1)如图1,点P 为矩形ABCD 对角线BD 上一点,过点P 作//EF BC ,分别交AB 、CD 于点E 、F .若2BE =,PF=6,AEP △的面积为1S ,CFP 的面积为2S ,则12S S +=________;(2)如图2,点P 为ABCD 内一点(点P 不在BD 上),点E 、F 、G 、H 分别为各边的中点.设四边形AEPH 的面积为1S ,四边形PFCG 的面积为2S (其中21S S >),求PBD △的面积(用含1S 、S的代数式表示);2(3)如图3,点P为ABCD内一点(点P不在BD上)过点P作//EF AD,HG//AB与各边分别相交于点E、F、G、H设四边形AEPH的面积为1S,四边形PGCF的面积为2S(其中21),S S求PBD△的面积(用含1S、2S的代数式表示);(4)如图4 点A B C D把O四等分.请你在圆内选一点P(点P不在AC BD 上)设PB PC BC围成的封闭图形的面积为1S PA PD AD围成的封闭图形的面积为2S PBD△的面积为3S PAC△的面积为4S.根据你选的点P的位置直接写出一个含有1S2S3S4S的等式(写出一种情况即可).3.已知直线y=x+4与x轴y轴分别交于A B两点∠ABC=60°BC与x轴交于点C.(1)试确定直线BC的解析式.(2)若动点P从A点出发沿AC向点C运动(不与A C重合)同时动点Q从C点出发沿CBA向点A运动(不与C A重合) 动点P的运动速度是每秒1个单位长度动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S P点的运动时间为t秒求S与t的函数关系式并写出自变量的取值范围.(3)在(2)的条件下当△APQ的面积最大时y轴上有一点M 平面内是否存在一点N 使以A Q M N为顶点的四边形为菱形?若存在请直接写出N点的坐标;若不存在请说明理由.4.如图在等腰梯形ABCD中AB∥DC AB=8cm CD=2cm AD=6cm.点P 从点A出发以2cm/s的速度沿AB向终点B运动;点Q从点C出发以1cm/s的速度沿CD DA向终点A运动(P Q两点中有一个点运动到终点时所有运动即终止).设P Q同时出发并运动了t秒.(1)当PQ将梯形ABCD分成两个直角梯形时求t的值;(2)试问是否存在这样的t 使四边形PBCQ的面积是梯形ABCD面积的一半?若存在求出这样的t的值若不存在请说明理由.5.如图在平面直角坐标系中以坐标原点O为圆心2为半径画⊙O P是⊙O上一动点且P在第一象限内过点P作⊙O的切线与轴相交于点A与轴相交于点B.(1)点P在运动时线段AB的长度也在发生变化请写出线段AB长度的最小值并说明理由;(2)在⊙O上是否存在一点Q使得以Q O A P为顶点的四边形时平行四边形?若存在请求出Q点的坐标;若不存在请说明理由.6.如图已知长方形ABCD中AD=6cm AB=4cm 点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动同时点Q在线段BC上由点B向点C运动.(1)若点Q的运动速度与点P的运动速度相等经过1秒后△AEP与△BPQ是否全等请说明理由并判断此时线段PE和线段PQ的位置关系;(2)若点Q的运动速度与点P的运动速度相等运动时间为t秒设△PEQ的面积为Scm2请用t的代数式表示S;(3)若点Q的运动速度与点P的运动速度不相等当点Q的运动速度为多少时能够使△AEP与△BPQ全等?7.如图长方形ABCD中5cm,8cm==现有一动点P从A出发以2cm/s的速度沿AB BC----返回到点A停止设点P运动的时间为t秒.长方形的边A B C D At=时BP=___________cm;(1)当2(2)当t为何值时连接,,△是等腰三角形;CP DP CDP(3)Q为AD边上的点且6DQ=P与Q不重合当t为何值时以长方形的两个顶点及点P为顶点的三角形与DCQ全等.8.如图平行四边形ABCD中6cmB∠︒G是CD的中点E是BC==60AB=8cm边AD上的动点EG的延长线与BC的延长线交于点F连接CE DF.(1)求证:四边形CEDF是平行四边形;(2)①AE=______时四边形CEDF是矩形;②AE=______时四边形CEDF是菱形.9.在平面直角坐标系中点A在第一象限AB⊥x轴于点B AC⊥y轴于点C已知点B(b0)C(0 c)其中b c满足|b﹣8|6+-=0.c(1)直接写出点A坐标.(2)如图2 点D从点O出发以每秒1个单位的速度沿y轴正方向运动同时点E从点A出发以每秒2个单位的速度沿射线BA运动过点E作GE⊥y轴于点G设运动时间为t 秒当S四边形AEGC<S△DEG时求t的取值范围.(3)如图3 将线段BC平移使点B的对应点M恰好落在y轴负半轴上点C的对应点为N连接BN交y轴于点P当OM=4OP时求点M的坐标.10.如图在平面直角坐标系中点A B的坐标分别是(﹣4 0)(0 8)动点P从点O出发沿x轴正方向以每秒1个单位的速度运动同时动点C从点B出发沿12.在四边形ABCD中//,90,10cm,8cm∠=︒===点P从点A出发沿折线AB CD BCD AB AD BCABCD方向以3cm/s的速度匀速运动;点Q从点D出发沿线段DC方向以2cm/s的速度匀速运动.已知两点同时出发当一个点到达终点时另一点也停止运动设运动时间为()s t.(1)求CD的长;(2)当四边形PBQD为平行四边形时求四边形PBQD的周长;(3)在点P Q的运动过程中是否存在某一时刻使得BPQ的面积为220cm若存在请求出所有满足条件的t的值;若不存在请说明理由.13.在平面直角坐标系中矩形OABC的边OA任x轴上OC在y轴上B(4 3)点M从点A开始以每秒1个单位长度的速度沿AB→BC→CO运动设△AOM的面积为S 点M运动的时间为t.(1)当0<t<3时AM=当7<t<10时OM=;(用t的代数式表示)(2)当△AOM为等腰三角形时t=;(3)当7<t<10时求S关于t的函数关系式;(4)当S=4时求t的值.14.如图1 在平面直角坐标系中正方形OABC的边长为6 点A C分别在x y 正半轴上点B在第一象限.点P是x正半轴上的一动点且OP=t连结PC将线段PC绕点P顺时针旋转90度至PQ连结CQ取CQ中点M.(1)当t=2时求Q与M的坐标;(2)如图2 连结AM以AM AP为邻边构造平行四边形APNM.记平行四边形APNM 的面积为S.①用含t的代数式表示S(0<t<6).②当N落在△CPQ的直角边上时求∠CPA的度数;(3)在(2)的条件下连结AQ记△AMQ的面积为S'若S=S'则t=(直接写出答案).15.如图平面直角坐标系中矩形OABC的顶点B的坐标为(7 5)顶点A C 分别在x轴y轴上点D的坐标为(0 1)过点D的直线与矩形OABC的边BC交于点G 且点G不与点C重合以DG为一边作菱形DEFG 点E在矩形OABC的边OA 上设直线DG的函数表达式为y=kx+b(1)当CG=OD时求直线DG的函数表达式;(2)当点E的坐标为(5 0)时求直线DG的函数表达式;(3)连接BF 设△FBG的面积为S CG的长为a 请直接写出S与a的函数表达式及自变量a 的取值范围.16.如图 在四边形ABCD 中 //AD BC 3AD = 5DC = 42AB = 45B ∠=︒ 动点M 从点B 出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从点C 出发沿线段CD 以每秒1个单位长度的速度向终点D 运动 设运动的时间为s t .(1)求BC 的长.(2)当//MN AB 时 求t 的值(3)试探究:t 为何值时 MNC ∆为等腰三角形?参考答案:1.(1)证明:∵四边形ABCD 是矩形∴AD ∥BC∴∠CAD =∠ACB ∠AEF =∠CFE∵EF 垂直平分AC 垂足为O∴OA =OC∴△AOE ≌△COF∴OE =OF∴四边形AFCE 为平行四边形又∵EF ⊥AC∴四边形AFCE 为菱形设菱形的边长AF =CF =x cm 则BF =(8﹣x )cm在Rt △ABF 中 AB =4cm由勾股定理得42+(8﹣x )2=x 2解得x =5iii )如图3 当P 点在AB 上 Q 点在CD 上时 AP =CQ 即12﹣a =b 得a +b =12. 综上所述 a 与b 满足的数量关系式是a +b =12(ab ≠0).2.(1)过P 点作AB∥MN∵S 矩形AEPM +S 矩形DFPM =S 矩形CFPN +S 矩形DFPM =S 矩形ABCD -S 矩形BEPN又∵11,,22AEP CFP AEPM CFPN SS S S ==矩形矩形 ∴1==26=62AEP CFP S S ⨯⨯, ∴1212.S S +=(2)如图 连接PA PC在APB △中 因为点E 是AB 中点可设APE BPE S S a ==同理 ,,BPF CPF CPG DFG DPH APH S S b S S c S S d ======所以APE APH CPF AEPH PFCG CPG S S SS a b d S S c =+++=++++四边形四边形 BPE BPF DPH DPH EDFP HPGD S S S S S S a b c d +=+++=+++四边形四边形.所以12EBFP HPGD AEPH PFCG S S S S S S +++=+四边形四边形四边形四边形所以1212ABD ABCD SS S S ==+ 所以1DPH APH S S S a ==-. ()()()1121121PBD ABD BPE PDH S S S S S S S S a S a S S =-++=+-++-=-.(3)易证四边形EBGP 四边形HPFD 是平行四边形.EBP SHPD S .()()121211122222ABD ABCD EBF HPD EBP HPD SS S S S S S S S S ==+++=+++ ()()12112FBD ABD EBP HPD S S S S S S S =-++=-. (4)试题解析:(1)由已知得A 点坐标(﹣4﹐0) B 点坐标(0﹐43﹚ ∵OB=3OA ∴∠BAO=60° ∵∠ABC=60° ∴△ABC 是等边三角形 ∵O C=OA=4 ∴C 点坐标﹙4 0﹚ 设直线BC 解析式为y kx b =+∴ ∴直线BC 的解析式为343y x =-+; ﹙2﹚当P 点在AO 之间运动时 作QH⊥x 轴 ∵QH CQ OB CB= ∴2843QH t = ∴QH=3t ∴S △APQ =AP•QH=132t t ⋅=232t ﹙0<t≤4﹚ 同理可得S △APQ =t·﹙833t -﹚=23432t t -+﹙4≤t<8﹚∴223(04)2{343?(48)2t t S t t t <≤=-+≤<; (3)存在 如图当Q 与B 重合时 四边形AMNQ 为菱形 此时N 坐标为(4 0) 其它类似还有(﹣4 8)或(﹣4 ﹣8)或(﹣4 ).4.(1)53(2)存在 使四边形PBCQ 的面积是梯形ABCD 面积的一半.(1)过D 作DE⊥AB 于E 过C 作CF⊥AB 于F 通过Rt ADE Rt BCF ∆≅∆ 得AE BF = 若四边形APQD 是直角梯形 则四边形DEPQ 为矩形 通过AP AE EP =+ 代入t 值 即可求解(2)假设当时 通过点Q 在CD 上或在AD 上 两种情况进行讨论求解5.(1)线段AB 长度的最小值为4理由如下:连接OP如图② 设四边形APQO 为平行四边形因为OQ PA ∥ 90APO ︒∠=所以90POQ ︒∠= 又因为OP OQ =所以45PQO ︒∠= 因为PQ OA ∥所以PQ y ⊥轴.设PQ y ⊥轴于点H在Rt △OHQ 中 根据2,45OQ HQO ︒=∠= 得Q 点坐标为(2,2-)所以符合条件的点Q 的坐标为(2,2-)或(2,2-).6.(1)∵长方形ABCD∴∠A =∠B =90°∵点E 为AD 的中点 AD =6cm∴AE =3cm又∵P 和Q 的速度相等可得出AP =BQ =1cm BP =3 ∴AE =BP在△AEP 和△BQP 中∴y=xy 3=4-y⎧⎨⎩ 解得:x=1y=1⎧⎨⎩ (舍去). 综上所述,点Q 的运动速度为32cm /s 时能使两三角形全等.7.(1)1(2)54t =或4或232 (3) 3.5t = 5.5或10(1)解:动点P 的速度是2cm/s∴当2t =时 224AP =⨯=∵5cm AB =∴BP =1cm ;(2)解:①当点P 在AB 上时 CDP △是等腰三角形∴PD CP =在长方形ABCD 中 ,90AD BC A B =∠=∠=︒∴()HL DAP CBP ≌∴AP BP =∴1522AP AB ==∵动点P 的速度是2cm/s∵90D5DP CD == 2AB CB CD t ++=∴要使一个三角形与DCQ 全等①当点P运动到1P时16△≌△DCQ CDPCP DQ==此时1∴点P的路程为:1527AB BP+=+=∴72 3.5t=÷=;②当点P运动到2P时26△≌△CDQ ABPBP DQ==此时2∴点P的路程为:25611+=+=AB BP∴112 5.5t=÷=③当点P运动到3P时35△≌△CDQ BAP==此时3AP DQ∴点P的路程为:3585220AB BC CD DP+++=+++=∴20210t=÷=④当点P运动到4P时即P与Q重合时46△≌△CDQ CDPDP DQ==此时4∴点P的路程为:4585624+++=+++=AB BC CD DPt=÷=此结果舍去不符合题意∴24212综上所述t的值可以是: 3.5t= 5.5或10.8.(1)四边形ABCD是平行四边形∥∴BC AD∴∠=∠FCG EDGG是CD的中点∴=CG DG△中在CFG△和DEGCFG∴≅(ASA)DEGFG EG∴=又CG DG=∴四边形CEDF是平行四边形.2)①当5AE=如图过60B∠=12BM∴=5AE=DE AD∴=在MBA△BM DEB=⎧⎪∠=∠⎨⎪(SAS)MBA EDC∴≅CED AMB∴∠=∠四边形CEDF是平行四边形∴平行四边形CEDF②当2AE cm =时 四边形CEDF 是菱形 理由如下:四边形ABCD 是平行四边形8AD ∴= 6CD AB == 60CDE B ∠=∠=︒2AE =6DE AD AE ∴=-=DE CD ∴=CDE ∴∆是等边三角形CE DE ∴=四边形CEDF 是平行四边形∴平行四边形CEDF 是菱形故答案为:2;9.(1)解:∵|b ﹣8|6c +-=0∴b -8=0 c -6=0∴b =8 c =6∵B (b 0) C (0 c )∴B (8 0) C (0 6)又∵AB ⊥x 轴 AC ⊥y 轴∴A (8 6);(2)∵AB ⊥x 轴 AC ⊥y 轴 GE ⊥y 轴∴四边形AEGC 是矩形设运动时间为t 秒∴OD =t AE =2t DG =6+2t-t =6+t∴S 四边形AEGC =8×2t =16t S △DEG =12×(6+t )×8=4t +242∵OM=4OP∴-m=-4×62m解得m=-12综上所述m的值为-4或-12.10.(1)∵点A B的坐标分别是(﹣4 0)(0 8)∴OA=4 OB=8∵点C运动到线段OB的中点∴OC=BC=12OB=4∵动点C从点B出发沿射线BO方向以每秒2个单位的速度运动∴2t=4解之:t=2;∵PE=OA=4 动点P从点O出发沿x轴正方向以每秒1个单位的速度运动∴OE=OP+PE=t+4=2+4=6∴点E(6 0)(2)证明:∵四边形PCOD是平行四边形∴OC=PD OC∥PD当点C在y轴的负半轴上时③如果点M在DE上时24163(3)22t tt--=++解得423t=+④当N在CE上时28(3)8214tt tt-⋅++-=-+解得12t=综上分析可得满足条件的t的值为:t1=28﹣16 3t2=2 t3=4+2 3t4=12.11.(1) ()30D,,()1,3E;(2)933022933222572222t tS t tt t⎧⎛⎫-+≤≤⎪⎪⎝⎭⎪⎪⎛⎫=-<≤⎨ ⎪⎝⎭⎪⎪⎛⎫-≤⎪ ⎪⎝⎭⎩<(3)198s解:(1)3922y x=-+当y=0时39=022x-+则x=3 即点()30D,当y=3时39=322x-+则x=1 故点()1,3E故:()30D,,()1,3E;(2)如图1 ①当点P在OD段时此时0≤t<32119()2223233S PD OC t t=⨯⨯=⨯-⨯=-+;②当点P在点D时此时t=32此时三角形不存在0S=;''6ADP BEP S S -=-30232t t ⎛⎫≤≤ ⎪⎝⎭⎫<≤⎪;即当点P 在边AB 上运动 且PD PE +的值最小时 运动时间t 为198s . 12.(1)16cm ;(2)(8813)cm +;(3)53t =秒或395秒 解:(1)如图1过A 作AM DC ⊥于M在四边形ABCD 中 //AB CD 90BCD ∠=︒//AM BC ∴∴四边形AMCB 是矩形10AB AD cm == 8BC cm =8AM BC cm ∴== 10CM AB cm ==在Rt AMD ∆中 由勾股定理得:6DM cm =10616CD DM CM cm cm cm =+=+=;(2)如图2当四边形PBQD 是平行四边形时 PB DQ =即1032t t -=解得2t =此时4DQ = 12CQ = 22413BQ BC CQ =+=所以()28813PBQD C BQ DQ =+=+;1003t 14(102BPQ BP BC ==解得53t =;P 在BC 上时 63t1(32BP CQ t =此方程没有实数解;CD 上时:在点Q 的右侧54(34PQ BC =6< 不合题意若P 在Q 的左侧 如图6 即3485t <14(534)202BPQ S PQ BC t ∆==-= 解得395t =; 综上所述 当53t =秒或395秒时 BPQ ∆的面积为220cm . 13.(1)t 10-t ;(2)5;(3)S =20-2t ;(4)2或8. 解:(1)当0<t <3时 点M 在线段AB 上 即AM =t 当7<t <10时 点M 在线段OC 上 OM =10-t故填:t 10-t ;(2)∵四边形ABCO 是矩形 B (4 3)∴OA =BC =4 AB =OC =3∵△AOM 为等腰三角形∴只有当MA =MO 此时点M 在线段BC 上 CM =BM =2 ∴t =3+2=5故填:5;(3)∵当7<t <10时 点M 在线段OC 上∴114(10)20222S OA OM t t =⋅⋅=⨯⨯-=-;(4)①当点M 在线段AB 上时 4=12×4t 解得t =2;②当点M 在线段BC 上时 S =6 不符合题意;当点M 在线段OC 上时 4=20-2t 解得t =8.∴OD =OP +PD =8∴Q (8 2)∵M 是CQ 的中点 C (0 6)∴M (4 4);(2)①∵△COP ≌△PDQ∴OP =OQ =t OC =PD =6∴OD =t +6∴Q (t +6 t )∵C (0 6)∴M (62t + 62t +) 当0<t <6时 S =AP ×y M =(6﹣t )×62t +=2362t -; ②分两种情况:a 当N 在PC 上时 连接OB PM 如图2﹣1所示:∵点M 的横 纵坐标相等∴点M 在对角线BD 上∵四边形OABC 是正方形∴OC =OA ∠COM =∠AOM∴∠MPA =12(180°﹣45°)=67.5° ∴∠CPA =67.5﹣45=22.5°;综上所述 当点N 在△CPQ 的直角边上时 ∠CPA 的度数为112.5°或22.5°;(3)过点M 作MH ⊥x 轴于点H 过点Q 作QG ⊥x 轴于点G∵AMQ AHM AGQ MHGQ S S S S =--△△△梯形∴S '=12(62t ++t )•62t +﹣12(6﹣62t +)•62t +﹣12t •t =3t ①当0<t <6时 即点AP 在点A 左侧时 如图3所示:∵S =S '∴2362t -=3t 解得:t =﹣3+35 或t =﹣3﹣35(舍去);②当t >6时 即点P 在点A 右侧时 如图4所示:S =AP ×y M =(t ﹣6)×62t +=2362t - ∵S =S '将D (0 1)G (10 5)代入y=kx+b 得:1105b k b =⎧⎪⎨+=⎪⎩解得:21051k b ⎧=⎪⎨⎪=⎩∴当CG=OD 时 直线DG 的函数表达式为y=2105x+1.(3)设DG 交x 轴于点P 过点F 作FM⊥x 轴于点M 延长MF 交BC 于点N 如图所示.∵DG∥EF∴∠FEM=∠GPO.∵BC∥OA∴∠DGC=∠GPO=∠FEM.在△DCG 和△FME 中90DCG FME DGC FEMDG FE⎧∠=∠=⎪∠=∠⎨⎪=⎩ ∴△DCG≌△FME(AAS )∴FM=DC=4.∵MN⊥x 轴∴四边形OMNC 为矩形在Rt△CDH 中 由勾股定理可得: HC=22543-=∴BC=BK+KH+HC=4+3+3=10;(2)如图② 过D 作DG∥AB 交BC 于G 点 则四边形ADGB 为平行四边形 ∴BG=AD=3∴GC=BC−BC=10−3=7由题意得 当M N 运动t 秒后 CN=t CM=10−2t∵AB∥DG MN∥AB∴DG∥MN∴∠NMC=∠DGC又∵∠C=∠C∴△MNC ~△GDC∴CN CM CD CG=, ∴10257tt -=解得t=5017; (3)第一种情况:当NC=MC 时 如图③22∵∠C=∠C∠MFC=∠DHC=90°∴△MFC~△DHC∴FC MCHC DC=即:1 102253tt-=解得:t=6017;综上所述当t=103t=258或t=6017时△MNC为等腰三角形.。
中考数学专题训练:特殊平行四边形(附参考答案)

中考数学专题训练:特殊平行四边形(附参考答案)1.如图,在矩形ABCD和△BDE中,点A在BE上.若矩形ABCD的面积为20,△BDE的面积为24,则△ADE的面积为( )A.10 B.12C.14 D.162.如图,矩形ABCD的对角线AC,BD交于点O,AB=3,BC=4,过点O作OM⊥AC,交BC于点M,过点M作MN⊥BD,垂足为点N,则OM+MN的值为( )A.245B.165C.125D.653.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,E是AC 的中点,则BE的长为( )A.2 B.52C.√5D.34.关于菱形的性质,以下说法不正确的是( )A.四条边相等B.对角线相等C.对角线互相垂直D.是轴对称图形5.下列选项中能使□ABCD成为菱形的是( )A.AB=CD B.AB=BCC.∠BAD=90°D.AC=BD6.如图,在菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC-CD方向移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是( )A.直角三角形→等边三角形→等腰三角形→直角三角形B.直角三角形→等腰三角形→直角三角形→等边三角形C.直角三角形→等边三角形→直角三角形→等腰三角形D.等腰三角形→等边三角形→直角三角形→等腰三角形7.如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( )A.2 B.52C.3 D.48.如图,在菱形ABCD中,E,F分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( )A.2 B.3C.4 D.59.如图,将矩形ABCD对折,使边AB与DC,BC与AD分别重合,展开后得到四边形EFGH.若AB=2,BC=4,则四边形EFGH的面积为( )A.2 B.4C.5 D.610.一个四边形顺次添加下列条件中的三个条件便得到正方形:a.两组对边分别相等;b.一组对边平行且相等;c.一组邻边相等;d.一个角是直角.顺次添加的条件:①a→c→d ②b→d→c ③a→b→c,则正确的是( )A.仅①B.仅③C.①②D.②③11.如图,在正方形ABCD中,点E,F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则CG的长是( )A.2 B.√5C.3√22D.12512.如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( )A.BE=12AE B.PC=PDC.∠EAF+∠AFD=90°D.PE=EC13.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( )A.1 B.√2C.√3D.214.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则OE的长度为( )A.√6B.√62C.2√2D.2√315.如图,在△ABC中,D,E,F分别是边AB,BC和AC的中点,请添加一个条件________________________,使四边形BEFD为矩形.(填一个即可)16.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.若AC=12,BD=16,则OE的长为______.17.如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点,点FAC,连接EF.若AC=10,则EF=______.在对角线AC上,且AF=1418.如图,E是矩形ABCD边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为_____.19.如图,菱形ABCD的对角线AC,BD相交于点O,OE⊥AD,垂足为点E,AC=8,BD=6,则OE的长为______.20.如图,菱形ABCD的边长为6 cm,∠BAD=60°,将该菱形沿AC方向平移2√3 cm得到四边形A′B′C′D′,A′D′交CD于点E,则点E到AC的距离为_____cm.21.如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE 的中点,AF与DE相交于点G,则GF的长等于______.22.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°得到正方形AB1C1D1,则阴影部分的面积是_________.23.如图,在正方形ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于______.24.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是_______.参考答案1.C 2.C 3.C 4.B 5.B 6.C 7.B 8.B 9.B 10.C 11.D 12.C 13.C 14.B15.AB⊥BC(答案不唯一) 16.10 17.52 18.3 19.12520.221.√19422.2-2√3323.2α 24.8√5。
2017年中考数学专题 特殊平行四边形
互相平分
中心对称图形
互相平分且相等
中心对称图形 轴对称图形
互相垂直平分,且每一 中心对称图形 条对角线平分一组对角 轴对称图形
中心对称图形 互相垂直平分且相等,每 一条对角线平分一组对角 轴对称图形
等腰梯形
两底平行 两腰相等
同一底上 的角相等
相等
轴对称图形
三、几种特殊四边形的常用判定方法:
四边形
条件
(2)若M是AD上的一 A
M
D
个动点,ME+MF的长度 是否发生改变?
F
E
(3)当M点运动到何
O
处时,四边形MFOE的面
积最大?
B
C
综合练习:
1、如图,平行四边形ABCD中,ABACAB 1 BC 5
对角线AC、BD交于点O,将直线AC绕O点顺时针旋 转,分别交BC、AD于点E、F。
(1)证明:当旋转角为 9 0 时,四边形ABEF是平行
E
AC=BD且AC ⊥ BD
D G
B
F
C
那么,特殊平行四边形的“中点 四边形”会是怎样的图形呢?
1.矩形的“中点四边形”是菱 形;
2.菱形的“中点四边形”是矩 形;
3.正方形的“中点四边形”是正方 形。
已知正方形ABCD, ME⊥ BD,MF⊥ AC,垂足分别为E、F
(1) M是AD上的点,若对角线AC=12cm, 求ME+MF的长。
想一想
还有什么方法可以说明这
个铝合金窗框是合格的?
∠A= A∠CB==B∠D C=90 °
A
BA
B
D
C
D
C
若这个铝合金窗框ABCD两条对角线的夹 角∠ AOB为60 ° , △ AOB的周长为3 m。
特殊的平行四边形(中考试题)

1特殊的平行四边形(中考试题)一、选择题1.如图,正方形ABCD 的边长是4,DAC ∠的平分线交DC 于点E .若点P ,Q 分别是AD 和AE 上的动点,则DQ PQ +的最小值是( )A .2B .4 C..2.如图,在菱形ABCD 中,,AB BD =点E F ,分别在AB AD ,上,且.AE DF =连接BF 与DE 相交于点,G 连接CG 与BD 相交于点,H 下列结论:①AED DFB △≌△;②2DCBG S =四边形; ③若2AF DF =,则6.BG GF =其中正确的结论( )A . 只有①② B.只有①③ C.只有②③ D.①②③3. 如图,已知正方形ABCD的对角线长为ABCD 沿直线EF 折叠,则图中阴影部分的周长为( )(A)(B )(C )8 (D )64.如图,在菱形ABCD 中,60A ∠=°,E F ,分别是AB AD ,的中点,DE BF ,相交于点G ,连结BD 、CG .有下列结论:①120BGD ∠=°;②BG D G C G +=;③B D F C G B △≌△;④2ABD S AB =△. 其中正确的结论有( ).(A )1个 (B )2个 (C )3个 (D )4个25.如图,在ABC △中,90C =∠,4AC BC ==,D 是AB 的中点,点E 、F 分别在AC 、BC 边上运动(点E 不与点A 、C 重合),且保持AE CF =,连接DE 、DF 、EF .在此运动变化的过程中,有下列结论:①DFE △是等腰直角三角形; ②四边形CEDF 不可能为正方形;③四边形CEDF 的面积随点E 位置的改变而发生变化;④点C 到线段EF)(A )1个 (B )2个 (C )3个 (D )4个6.Rt ABC △中,AB AC =,点D 为BC 中点,90MDN ∠=°,MDN ∠绕点D 旋转,DM DN 、分别与边AB AC 、交于E F 、两点.下列结论①()2BE CF BC +=;②14A E F A B C S S △△≤;③A E D F S A D E F =∙四边形;④A D E F ≥;⑤AD 与EF 可能互相平分,其中正确结论的个数是( )(A )1个 (B )2个 (C )3个 (D )4个7.如图,将矩形ABCD 的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH ,若12EH =厘米,16EF =厘米,则边AD 的长是( ).(A )12厘米 (B )16厘米 (C )20厘米 (D )28厘米8.如图,矩形ABCD 中,E 是AD 的中点,将ABE △沿BE 折叠后得到GBE △,延长BG 交CD 于点F ,若12CF FD ==,,则BC 的长为( ).(A)(B)(C)(D)9. 如图,矩形ABCD 的对角线108AC BC ==,,则图中五个小矩形的周长之和为( )A .14B .16C .20D .2810.如图,正方形A BCD 和EFGC 中,正方形EFGC 的边长为a ,用a 的代数式表示阴影部分△AEG 的面积为( )(A )232a (B )223a (C )212a (D )2a3A F C D BE 11.如图,四边形ABCD 四边的中点分别为E ,F ,G ,H ,对角线AC 与BD 相交于点O ,若四边形EFGH 的面积是3,则四边形ABCD 的面积是( )A .3B .6C .9D .1212. 如图所示,矩形纸片ABCD 中,6cm AB =,8cm BC =,现将其沿EF 对折,使得点C 与点A 重合,则AF 长为( )(A )25cm 8 (B )25cm 4 (C )25cm 2(D )8cm 二、填空题13.如图,在ABC △中,点D 、E 、F 分别在边AB 、BC 、CA 上,且DE CA ∥,DF BA ∥.下列四种说法: ①四边形AEDF 是平行四边形;②如果90BAC ∠=,那么四边形AEDF 是矩形;③如果AD 平分BAC ∠,那么四边形AEDF 是菱形;④如果AD BC ⊥且AB AC =,那么四边形AEDF 是菱形.其中,正确的有 .(只填写序号)14.如图,三个边长均为2的正方形重叠在一起,O 1、O 2是其中两个正方形的中心,则阴影部分的面积是 .15.如图,DE 为△ABC 的中位线,点F 在DE 上,且∠AFB =90°,若AB =5,BC =8,则EF 的长为________.16.矩形ABCD 中,AB =10,BC =3,E 为AB 边的中点,P 为CD 边上的点,且△AEP 是腰长为5的等腰三角形,则DP = .17. (2012 湖北省十堰市) 如图,矩形ABCD 中,24AB AD ==,,AC 的垂直平分线EF 交AD 于点E 、交BC 于点F ,则=EF .18.如图,将两张长为4,宽为1的矩形纸条交叉并旋转,使重叠部分成为一个菱形. 旋转过程中,当两张纸条垂直时,菱形周长的最小值是4,那么菱形周长的最大值是 .19.如图,矩形ABCD 中,15AB =cm ,点E 在AD 上,且9AE =cm ,连接EC ,将矩形ABCD 沿直线BE 翻折,点A 恰好落在EC 上的点A '处,则A C '=_______cm.4三、证明题20.如图,在△ABC 中,∠ACB=90°,BC 的垂直平分线DE 交BC 于D ,交AB 于E ,F 在DE 上,且AF=CE=AE .(1)说明四边形ACEF 是平行四边形;(2)当∠B 满足什么条件时,四边形ACEF 是菱形,并说明理由.21.如图,在正方形ABCD 中,对角线AC 、BD 相交于点O ,E 、F 分别在OD 、OC 上,且DE CF =,连接DF 、AE ,AE 的延长线交DF 于点M .求证:AM DF ⊥.22.矩形ABCD 中,53AD AB ==,,将矩形ABCD 沿某直线折叠,使点A 的对应点A '落在线段BC 上,再打开得到折痕EF .(1)当A '与B 重合时(如图1),EF =_______;当折痕EF 过点D 时(如图2),求线段EF 的长;(2)观察图3和图4,设BA x '=,①当x 的取值范围是_______时,四边形AEA F '是菱形;②在①的条件下,利用图4证明四边形AEA F '是菱形.523. 已知:如图,D 是△ABC 的边AB 上一点,CN ∥AB ,DN 交AC 于点M ,MA=MC.(1)求证:CD=AN ;(2)若∠AMD=2∠MCD ,求证:四边形ADCN 是矩形.24.已知□ABCD ,对角线AC 与BD 相交于点O ,点P 在边AD 上,过点P 分别作PE ⊥AC 、PF ⊥BD ,垂足分别为E 、F ,PE =PF .(1)如图10,若PE =3,EO =1,求∠EPF 的度数;(2)若点P 是AD 的中点,点F 是DO 的中点, BF =BC +32-4,求BC 的长.25. 已知:如图,在菱形ABCD 中,F 为边BC 的中点,DF 与对角线AC 交于点M ,过M 作ME CD ⊥于点E ,∠1=∠2.(1)若1CE =,求BC 的长;(2)求证AM DF ME =+.26.如图,点O 在线段AB 上的一点,OA OC =,OD 平分AOC ∠交AC 于点D ,OF 平分COB ∠,CF OF ⊥于点F .(1)求证:四边形CDOF 是矩形;(2)当AOC ∠多少度时,四边形CDOF 是正方形?并说明理由.E F 图10A B C D OP6 27.如图1,在ABC △中,点P 为BC 边中点,直线a 绕顶点A 旋转,若点B P 、在直线a 的异侧,BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,连接.PM PN 、(1)延长MP 交CN 于点E (如图2),①求证:BPM CPE △≌△;②求证:PM PN =;(2)若直线a 绕点A 旋转到图3的位置时,点B P 、在直线a 的同侧,其它条件不变.此时PM PN =还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a 绕点A 旋转到与BC 边平行的位置时,其它条件不变,请直接判断四边形MBCN 的形状及此时PM PN =还成立吗?不必说明理由.28.如图所示,在菱形ABCD 中,4AB =,120BAD AEF =∠°,△为正三角形,点E F 、分别在菱形的边BC CD 、上滑动,且E F 、不与B C D 、、重合.(1)证明不论E F 、在BC CD 、上如何滑动,总有BE CF =;(2)当点E F 、在BC CD 、上滑动时,分别探讨四边形AECF 和CEF △的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.29.如图,∠C=90°,点A 、B 在∠C 的两边上,CA=30,CB=20,连结AB .点P 从点B 出发,以每秒4个单位长度的速度沿BC 方向运动,到点C 停止.当点P 与B 、C 两点不重合时,作PD ⊥BC 交AB 于D ,作DE ⊥AC 于E .F 为射线CB 上一点,且∠CEF=∠ABC .设点P 的运动时间为x (秒).(1)用含有x 的代数式表示CF 的长.(2)求点F 与点B 重合时x 的值.(3)当点F 在线段CB 上时,设四边形DECP 与四边形DEFB 重叠部分图形的面积为y (平方单位).求y 与x 之间的函数关系式.(4)当x 为某个值时,沿PD 将以D 、E 、F 、B 为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x 值.图1 图2 图3。
中考数学特殊的平行四边形复习训练试题含答案

适用精选文件资料分享中考数学特别的平行四边形复习训练试题(含答案 )第 2 课时特别的平行四边形一级训练 1 .(2012 年江苏宜昌 ) 如图 4-3-23,在菱形 ABCD中,AB =5,∠ BCD=120°,则△ ABC的周长等于 () A.20 B.15 C.10 D.5 图 4-3-23 2 .以下说法不正确的选项是 () A .一组邻边相等的矩形是正方形; B .对角线相等的菱形是正方形C.对角线相互垂直的矩形是正方形;D.有一个角是直角的平行四边形是正方形 3 .(2011 年江苏无锡 ) 菱形拥有而矩形不必定拥有的性质是() A .对角线相互垂直 B .对角线相等 C.对角线相互均分D.对角互补 4 .(2012 年湖南张家界 ) 按序连接矩形四边中点所得的四边形必定是 () A.正方形 B .矩形 C.菱形 D.等腰梯形 5 .如图 4-3-24,矩形 ABCD的两条对角线订交于点O,∠ AOD=120°,AB=2,则矩形的对角线AC的长是 () A .2 B.4 C.2 3 D .4 3图 4-3-24 图 4-3-25 图 4-3-26 6 .(2012 年天津 ) 如图 4-3-25,在边长为 2 的正方形 ABCD中, M为边 AD的中点,延长 MD至点 E,使 ME=MC,以 DE为边作正方形 DEFG,点 G在边 CD上,则DG的长为 () A. 3-1 B.3-5 C.5+1 D. 5-1 7.(2011年江苏南京) 如图4-3-26,菱形ABCD的边长是2 cm,E 是AB的中点,且DE⊥AB,则菱形 ABCD的面积为 ________cm2. 8.(2011 年江苏淮安 )在四边形 ABCD中, AB=DC,AD=BC.请再增添一个条件,使四边形ABCD是矩形.你增添的条件是 __________(写出一种即可 ) .9 .(2012年吉林长春 ) 如图 4-3-27,?ABCD的极点 B在矩形 AEFC的边 EF上,点 B 与点 E,F 不重合,若△ ACD的面积为 3,则图中暗影部分两个三角形的面积和为 ______.图 4-3-27 10 .(2011 年广东模拟 ) 已知菱形 ABCD的边长为 6,∠ A=60°,假如点 P 是菱形内的一点,且 PB=P D=2 3 ,那么 AP的长为 __________. 11 .(2011 年陕西 ) 如图 4-3-28,在正方形 ABCD中,点 G是 BC上任意一点,连接 AG,过B,D两点分别作 BE⊥AG,DF⊥AG,垂足分别为 E,F 两点,求证:△ADF≌△ BAE.12.如图 4-3-29,O为矩形 ABCD对角线的交点, DE∥AC,CE∥BD.(1) 试判断四边形 OCED的形状,并说明原由; (2) 若 AB=6,BC=8,求四边形 OCED的面积.二级训练 13 .如图 4-3-30,在矩形纸片 ABCD中,已知 AD=8,折叠纸片使 AB边与对角线 AC重合,点 B 落在点 F 处,折痕为 AE,且EF=3,则 AB的长为 () A.3B .4C.5D.6图 4-3-30 图 4-3-31 14.(2012 年四川宜宾 ) 如图 4-3-31,已知正方形 ABCD的边长为 1,连接 AC,BD,CE均分∠ ACD交 BD于点 E,则 DE=______. 15 .(2010 年山东青岛 ) 已知:如图 4-3-32,在正方形 ABCD中,点 E,F 分别在 BC和 CD上, AE=AF. (1) 求证: BE=DF; (2) 连接 AC交 EF于点 O,延长 OC至点 M,使 OM=OA,连接EM,FM.判断四边形 AEMF是什么特别四边形?并证明你的结论.三级训练 16 .(2011 年广东深圳 ) 如图 4-3-33(1) ,一张矩形纸片ABCD,此中 AD=8 cm,AB=6 cm,先沿对角线 BD对折,点 C落在点C′的地点, BC′交 AD于点 G. (1) 求证: AG=C′G; (2) 如图 4-3-33(2) ,再折叠一次,使点 D与点 A 重合,得折痕 EN,EN交 AD于点 M,求 EM的长. (1)(2) 图 4-3-33参照答案 1 .B 2.D 3.A 4.C 5.B 6.D 7 .2 3 8 .∠ A=90°或∠B=90°或∠ C=90°或∠ D=90°或 AC=BD(答案不独一,写出一种即可 ) 9 .3 10.2 3或4311.证明:∵四边形 ABCD是正方形,∴DA= AB,∠ 1+∠ 2=90°.又∵ BE⊥AG,DF⊥AG,∴∠ 1+∠ 3=90°,∠ 2+∠ 4=90°.∴∠ 2=∠ 3,∠ 1=∠ 4.又∵ AD=AB,∴△ ADF≌△ BAE. 12.解: (1) 四边形 OCED是菱形.原由以下:∵DE∥AC,CE∥BD,∴四边形 OCED是平行四边形.又∵在矩形 ABCD 中, OC=OD,∴四边形 OCED是菱形 . (2)连接OE.由菱形OCED,得CD⊥OE,∴OE∥BC. 又∵ CE∥BD,∴四边形BCEO是平行四边形.∴OE= BC=8. ∴S四边形 OCED=12OE?CD=12×8×6= 24. 13.D 14.2 -1 15 .(1) 证明:∵四边形 ABCD是正方形,∴AB=AD,∠B =∠ D=90°. ∵AE= AF,∴ Rt△ABE≌Rt△ADF. ∴BE= DF. (2) 解:四边形 AEMF是菱形.证明以下:∵四边形 ABCD是正方形,∴∠ BCA =∠DCA=45°, BC=DC. ∵BE= DF,∴ BC-BE=DC-DF,即 CE=CF.∴OE=OF. ∵OM=OA,∴四边形 AEMF是平行四边形.∵AE=AF,∴平行四边形 AEMF是菱形. 16 .(1) 证明:∵沿对角线 BD对折,点 C落在点 C′的地点,∴∠ A=∠ C′,AB=C′D,∴在△ GAB与△ GC′D中,∠A=∠ C′,∠AGB=∠ C′GD,AB=C′D,∴△ GAB≌△ GC′D. ∴AG=C′G. (2) 解:∵点 D与点 A 重合,得折痕 EN,∴DM=4 cm,NM=3 cm.由折叠及平行线的性质,得∠END=∠ NDC=∠ NDE,∴EN=E D.设 EM=x,则 ED=EN=x+3. 由勾股定理,得 ED2=EM2+DM2,即(x +3)2 =x2+42. 解得 x=76,即 EM=76.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊平行四边形
一、基础知识点复习:
(一)矩形:
1.矩形的定义:__________________________的平行四边形叫矩形.
2.矩形的性质:①.矩形的四个角都是______;矩形的对角线______________。
②.矩形既是对称图形,又是图形,它有条对称轴.
3.矩形的判定:①.有_____个是直角的四边形是矩形②.对角线___________平行四边形是矩形.
③.对角线_________________的四边形是矩形.
4.练习:①矩形ABCD的两条对角线相交于O,∠AOD=120°,AB=4cm,则矩形对角线AC长为______cm.
②.四边形ABCD的对角线AC,BD相交于点O,能判断它为矩形的题设是()
A.AO=CO,BO=DO B.AO=BO=CO=DO C.AB=BC,AO=CO D.AO=CO,BO=DO,AC⊥BD
③.四边形ABCD中,AD//BC,则四边形ABCD是 ___________,又对角线AC,BD交于点O,
若∠1=∠2,则四边形ABCD是_______________.
(二)菱形:
1.菱形的定义:有一组______________相等的平行四边形叫菱形.
2.菱形的性质:①.菱形的四条边______;菱形的对角线__________,且每条对角线________。
②.菱形既是对称图形,又是图形,它有条对称轴.
3.菱形的判定:①.___________边都相等的四边形菱形②.对角线___________的平行四边形
是菱形。
③.对角线____________的四边形是菱形.
4.菱形的面积与两对角线的关系是________________________
5.练习:①.如图,BD是菱形ABCD的一条对角线,若∠ABD=65°,则∠A=_____.
②.一个菱形的两条对角线分别是6cm,8cm,则这个菱形的周长等于 cm,
面积= cm2
③.若菱形的周长为8cm,高为1cm,则菱形两邻角的度数比为
(三)正方形:
1.正方形的定义:的平行四边形叫正方形。
2.正方形的性质:①.正方形的四个角是_____角,四条边_____,对角线_____________.
②.正方形是______对称图形,又是对称图形,它有______条对称轴.
3.正方形的判定:先判定这个四边形是矩形,•再判定这个矩形还是_____形;或者先判定四边形是菱形,再判定这个菱形也是_____形.
4.练习:①正方形的面积为4,则它的边长为____,对角线长为_____.
②已知正方形的对角线长是4,则它的边长是,面积是。
③如图所示,在△ABC中,AB=AC,点D,E,F分别是边AB,BC,AC的中点,
连接DE ,EF ,要使四边形ADEF 是正方形,还需增加条件:_______.
二.复习专题练习: (一)、选择题:
1.如图1,矩形ABCD 的长AD=15cm ,宽AB=10cm ,∠ABC 的平分线分AD 边为 AE 、ED 两部分,这AE 、ED 的长分别为( )
A .11cm 和4cm
B .10cm 和5cm
C .9cm 和6cm
D .8cm 和7cm
2.四边形ABCD 的对角线互相平分,要使它变为矩形,需要添加的条件是( ) A .AB=CD B .AD=BC C .AB=BC D .AC=BD
3.如图,在正方形ABCD 的外侧,作等边三角形ADE ,则∠AED ( )
A. 10° B .15° C .20° D .12.5°
4.如图,在菱形ABCD 中,E 、F 分别是AD 、BD 的中点,如果EF=2, 那么菱形ABCD 的周长是( )
A. 4 B .8 C .12 D .16
(二)、填空题
5.知正方形ABCD 对角线AC ,BD 相交于点O ,•且AC=•16cm ,•则DO=•_____cm , BO=____cm ,∠OCD=____度.
6.平面直角坐标系中,四边形ABCD 是菱形,∠ABC=60°,且点A 的坐标 为(0,2),则点B 坐标( ),点C 坐标为( ),点D
7.一平行四边形的一条边长是9
,两条对角线长分别是12和
它是 形,它的面积是 ,周长是 。
8.如图ABCD 是一块正方形场地,在AB 边上取定了一点E ,量得 EC=30 cm ,EB=10 cm ,则这块场地的面积是 cm 2
, 对角线的长是 cm 。
(三)解答题:
9.如图,四边形ABCD 是菱形 ,∠ACD=30°,BD=6,求:
(1)∠BAD,∠ABC 的度数; (2)边AB 及对角线AC 的长。
C
B
A
E E
10.如图,四边形ABCD 是菱形,对角线AC=8cm ,DB=6cm,DH ⊥AB 于点H ,求DH 的长.
11.如图,矩形ABCD 的对角线相交于点O ,DE ∥AC ,CE ∥BD ,求证:四边形OCED 是菱形。
12.如图:AE ∥BF ,AC 平分∠BAD ,且交BF 于点C ,BD 平分∠ABC ,且交AE 于点D ,连接CD , 求证:四边形ABCD 是菱形
13.如图,E 、F 、M 、N 分别是正方形ABCD 四条边上的点,且AE=BF=CM=DN , 求证,四边形EFMN 是正方形 。
14.如图,四边形ABCD 是正方形,点G 是BC 上的任意一点,DE ⊥AG 于点E ,BF ∥DE , 且交AG 于点F 。
求证:AF=BF+EF
H
A
B
C
D
O E
F
15.如图,已知四边形ABCD中,AD//BC,OB=OC,E、F、G、H分别是AB、BC、CD、DA边上的中点,求证:四边形EFGH是菱形.
16.若以直角三角形ABC的边AB为边,在三角形ABC的外部作正方形ABDE,AF是BC边的高,延长FA使AG=BC,求证:BG=CD.
17.在正方形ABCD的对角线BD上,取BE=AB,若过E作BD的垂线EF交CD于F,求证:CF=ED.
18.如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF
下列问题(不要求证明):
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
第13题图
C
_B
A
B
C
D
O
E F
G
H。
