一元二次方程经典例题及练习
一元二次方程100道计算题练习(含答案)

一元二次方程100道计算题练习(含答案)1、(x+4)=5(x+4)解:将等式两边展开,得到x+4=5x+20,移项化简得4x=-16,因此x=-4.2、(x+1)=4x解:将等式两边展开,得到x+1=4x,移项化简得3x=1,因此x=1/3.3、(x+3)=(1-2x)2解:将等式两边展开,得到x+3=1-4x+4x2,移项化简得4x2-4x-2=0,因此x=1+√3或x=1-√3.4、2x2-10x=3解:将等式两边移项化简,得到2x2-10x-3=0,利用求根公式得到x=(5+√37)/2或x=(5-√37)/2.5、(x+5)2=16解:将等式两边展开,得到x2+10x+25=16,移项化简得x2+10x+9=0,因此x=-1或x=-9.6、2(2x-1)-x(1-2x)=0解:将等式两边展开,得到4x-2-x+2x2=0,移项化简得2x2+3x-2=0,因此x=1/2或x=-2.7、x2+6x-5=0解:利用求根公式得到x=(-6±√56)/2,化简得到x=-3+√14或x=-3-√14.8、5x2-2/5=0解:将等式两边乘以5,得到25x2-2=0,移项化简得到x=±√(2/25)=±2/5.9、8(3-x)2-72=0解:将等式两边移项化简,得到8(3-x)2=72,化简得到(3-x)2=9,因此x=0或x=6.10、3x(x+2)=5(x+2)解:将等式两边移项化简,得到3x(x+2)-5(x+2)=0,因此(3x-5)(x+2)=0,因此x=5/3或x=-2.11、(1-3y)2+2(3y-1)=0解:将等式展开化简,得到9y2-18y+9+6y-2=0,移项化简得到9y2-12y+7=0,利用求根公式得到y=(6±√12)/9.12、x2+2x+3=0解:利用求根公式得到x=(-2±√(-8))/2,因为无实数解,所以方程无解。
一元二次方程经典练习题(6套)附带详细答案

丄-2=0,③2 x 2 +3x=(1+2x)(2+x),④3- J =0,⑤ x 元二次方程的个数是 个 B2个 个4.方程x 2=6x 的根是()5.方2X 2-3X +1=0经为(x+a )2=b 的形式,正确的是D. ± 157. 不解方程判断下列方程中无实数根的是8.某超市一月份的营业额为 200万元,已知第一季度的总营业额共1000万元,如果平均每月增长率为X ,则由题意列方程应为() (1+x )2=1000 +200 X 2x=1000+200 X 3x=1000[1+(1+x )+(1+x )2]=1000二、填空题:(每小题3分,共24分)(x 1} 59•方程——-3x -化为一元二次方程的一般形式是________ ,它的一次项系数是、选择题:(每小题3分,共24分) 1•下列方程中 ,常数项为零的是() +x=1=12; 练习一(x<1)=3(x-1) (X 2+1)=X +2 3.把方程(x- . 5) (x+ 5) +(2X -1)2=0化为一元二次方程的一般形式是 =0=0 +1=0 +6=02•下列方程:①X 2=0,② 竺-8x+仁0中,x=0,X 2=_6=0,X 2=6 =6 =02 3 A. x16; 223 1 B. 2 x416C.D.以上都不对6.若两个连续整数的积是56,则它们的和是( 16=2x-1+4x+ — =0; C. \ 2x 24D.(x+2)(x-3)==-52 210. 关于x的一元二次方程x2+bx+c=0有实数解的条件是____________ .11. 用_____ 法解方程3(X-2)2=2X-4比较简便.12. 如果2X2+1与4X2-2X-5互为相反数,则x的值为__________ .13. 如果关于x的一元二次方程2x(kx-4)-x2+6=0没有实数根,那么k的最小整数值是14. 如果关于x的方程4mx2-mx+1=0有两个相等实数根,那么它的根是________ .15. 若一元二次方程(心1)/-4乂-5=0有两个不相等实数根,则k的取值范围是________ .16. 某种型号的微机,原售价7200元/台,经连续两次降价后,现售价为3528元/台,则平均每次降价的百分率为_________________ .三、解答题(2分)17. 用适当的方法解下列一元二次方程.(每小题5分,共15分)(1)5x(x-3)=6-2x; (2)3y2+仁2、、3y; (3)(x-a)2=1-2a+a2(a 是常数)18. (7分)已知关于x的一元二次方程x2+mx+ n=0的一个解是2,另一个解是正数,而且也是方程(X+4)2-52=3X的解,你能求出m和n的值吗119. (10分)已知关于x的一元二次方程x2-2kx+ k2-2=0.(1)求证:不论k为何值,方程总有两不相等实数根⑵设X1,x2是方程的根,且x12-2kx1+2x1X2=5,求k的值.四、列方程解应用题(每题10 分,共20 分)20.某电视机厂计划用两年的时间把某种型号的电视机的成本降低36%, 若每年下降的百分数相同,求这个百分数21.某商场今年1月份销售额为100 万元,2 月份销售额下降了10%, 该商场马上采取措施,改进经营管理,使月销售额大幅上升,4 月份的销售额达到万元,求3, 4 月份平均每月销售额增长的百分率练习二一、选择题(共8 题,每题有四个选项,其中只有一项符合题意。
一元二次方程100道计算题练习(含答案)

一元二次方程100道计算题练习(含答案)1、(x+4)=5(x+4)^22、(x+1)=4x3、(x+3)=(1-2x)24、2x^2-10x=35、(x+5)^2=166、2(2x-1)-x(1-2x)=07、8x=648、5x^2-2=09、8(3-x)^2/5-72=010、3x(x+2)=5(x+2)11、(1-3y)^2+2(3y-1)=012、x^2+2x+3=013、x^2-4x+3=014、x^2-2x-1=015、3x^2+2x-1=016、5x^2-3x+2=017、-x^2+x+12=018、7x-4x-3=019、x-6x+9=020、(3x-2)=(2x-3)21、x-2x-4=022、(2x-3)-12=2(2x+2)23、x^2-9x+8=024、x=3/425、3x^2+8x-3=026、(3x+2)(x+3)=x+1427、无解28、2(x-3)^2=x^2-929、-3x^2+22x-24=030、(2x-1)+3(2x-1)+2=031、2x^2-9x+8=032、3x^2=x(5-x)33、(x+2)^2=8x34、x^2-4x+4=2x+335、7x+2x=3636、4t-4t+1=037、5x^2-2x-3=038、7x-31x+35=039、(2x-3)-12=2^240、2x^2-23x+65=0补充练:1、(x-2)^2=(2x-3)^22、x^2-4x+3=03、(x-5)-8(x-5)+16=24、(2y-1)^2=115、4(x-3)^2=256、(3x-2)^2=3(x-6)7、2x^2-5x+2=08、2x^2-7x+10=09、(x+1)^2-3(x+1)+2=(2x+1)^2-910、x^2-2x-3=01、某商场每天平均售出20件名牌衬衫,每件衬衫盈利40元。
为了增加销售和盈利,商场采取降价措施。
调查发现,每降价1元,每天可多售出2件衬衫。
一元二次方程50道计算题

一元二次方程50道计算题1. 解下列方程:$x^2-5x+6=0$2. 解下列方程:$2x^2+3x-2=0$3. 解下列方程:$3x^2-4x-4=0$4. 解下列方程:$4x^2-12x+9=0$5. 解下列方程:$x^2+7x+10=0$6. 解下列方程:$2x^2-11x+5=0$7. 解下列方程:$3x^2-8x-3=0$8. 解下列方程:$4x^2-16x+16=0$9. 解下列方程:$x^2-9=0$10. 解下列方程:$2x^2-5x+3=0$11. 解下列方程:$3x^2+5x-2=0$12. 解下列方程:$4x^2-7x-2=0$13. 解下列方程:$x^2-6x+9=0$14. 解下列方程:$2x^2-4x-2=0$15. 解下列方程:$3x^2-10x+7=0$16. 解下列方程:$4x^2-15x+14=0$17. 解下列方程:$x^2-3=0$18. 解下列方程:$2x^2-9x+6=0$19. 解下列方程:$3x^2+2x-1=0$20. 解下列方程:$4x^2-3x-1=0$21. 解下列方程:$x^2-4x+4=0$22. 解下列方程:$2x^2-3x-1=0$23. 解下列方程:$3x^2-7x-2=0$24. 解下列方程:$4x^2-13x+10=0$25. 解下列方程:$x^2-1=0$26. 解下列方程:$2x^2-7x+6=0$27. 解下列方程:$3x^2-6x-1=0$28. 解下列方程:$4x^2-9x+4=0$29. 解下列方程:$x^2-2x+1=0$30. 解下列方程:$2x^2-4x+2=0$31. 解下列方程:$3x^2-9x+6=0$32. 解下列方程:$4x^2-11x+6=0$33. 解下列方程:$x^2=0$34. 解下列方程:$2x^2-3x-2=0$35. 解下列方程:$3x^2-4x-1=0$36. 解下列方程:$4x^2-5x-1=0$37. 解下列方程:$x^2+5=0$38. 解下列方程:$2x^2-8x+8=0$39. 解下列方程:$3x^2+3x-6=0$40. 解下列方程:$4x^2-2x-2=0$41. 解下列方程:$x^2+6x+9=0$42. 解下列方程:$2x^2-5x-3=0$43. 解下列方程:$3x^2-10x+5=0$44. 解下列方程:$4x^2-17x+16=0$45. 解下列方程:$x^2=3$46. 解下列方程:$2x^2-6x+4=0$47. 解下列方程:$3x^2+4x-1=0$48. 解下列方程:$4x^2-4x-4=0$49. 解下列方程:$x^2+2x+1=0$50. 解下列方程:$2x^2-2x-4=0$本篇文章提供了50道一元二次方程的计算题,希望大家能够通过解答这些题目,熟练掌握一元二次方程的求解方法。
完整版)一元二次方程100道计算题练习(附答案)

完整版)一元二次方程100道计算题练习(附答案)1、(x+4)=5(x+4)^22、(x+1)=4x3、(x+3)=(1-2x)^24、2x^2-10x=35、x^2=646、(x+5)^2=167、2(2x-1)-x(1-2x)=08、5x^2-2/5=09、8(3-x)^2-72=010、3x(x+2)=5(x+2)11、(1-3y)^2+2(3y-1)=012、x^2+2x+3=013、x^2+6x-5=014、x^2-4x+3=015、x^2-2x-1=016、2x^2+3x+1=017、3x^2+2x-1=018、5x^2-3x+2=019、3x-3=020、-2x+12=021、x^2-6x+9=022、3x-2=2x+323、x-2x-4=024、x=3/425、3x^2+8x-3=026、3x^2+11x+14=027、x=-9 or x=-228、2(x-3)^2=x^2-929、-3x^2+22x-24=030、4t^2-4t+1=031、(2x-3)^2-121=032、x^2-4x=033、(x+2)^2=8x34、x=1/3 or x=-235、7x^2+2x-36=036、x=1 or x=-1 or x=3/237、4(x-3)^2+x(x-3)=038、6x^2-31x+35=039、x=1/2 or x=140、2x^2-23x+65=0这是一组一元二次方程的计算题练,需要用不同的方法来解决这些问题。
为了方便,我们可以将这些方程按照不同的方法分类。
一种方法是因式分解法,另一种方法是开平方法,还有一种方法是配方法,最后一种方法是公式法。
根据不同的题目,我们可以选择不同的方法来解决问题。
例如,对于方程(x-2)^2=(2x-3)^2,我们可以使用因式分解法来解决。
将方程化简后,得到x=5/3或x=-1/3.对于方程2x^2-5x+2=0,我们可以使用配方法来解决。
将方程化简后,得到x=1/2或x=2.对于方程-3x^2+22x-24=0,我们可以使用公式法来解决。
一元二次函数经典题目带答案附解析
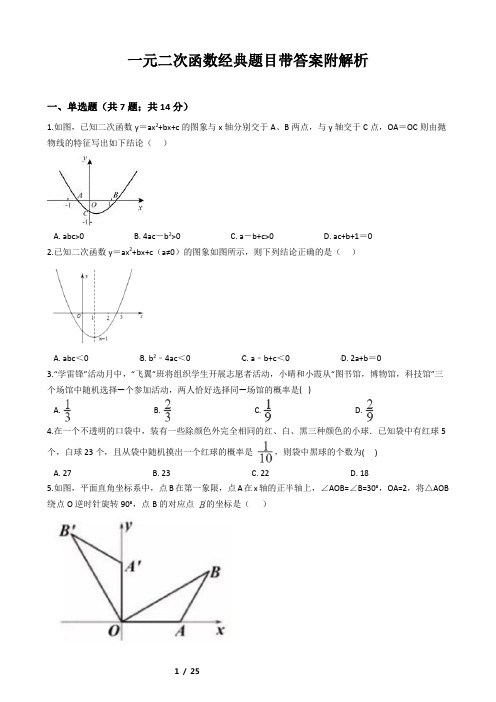
一元二次函数经典题目带答案附解析一、单选题(共7题;共14分)1.如图,已知二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于C点,OA=OC则由抛物线的特征写出如下结论()A. abc>0B. 4ac-b2>0C. a-b+c>0D. ac+b+1=02.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是()A. abc<0B. b2﹣4ac<0C. a﹣b+c<0D. 2a+b=03.“学雷锋”活动月中,“飞翼”班将组织学生开展志愿者活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择—个参加活动,两人恰好选择同—场馆的概率是( )A. B. C. D.4.在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为( )A. 27B. 23C. 22D. 185.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB 绕点O逆时针旋转90°,点B的对应点的坐标是()A. B. C. D.6.如图,一条公路的转弯处是一段圆弧(AB),点O是这段弧所在圆的圆心,AB=40m,点C是AB的中点,且CD=10m,则这段弯路所在圆的半径为()A. 25mB. 24mC. 30mD. 60m7.如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为()A. B. 2 C. 2 D. (1+2 )二、填空题(共2题;共2分)8.柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:种子数n 30 75 130 210 480 856 1250 2300发芽数m 28 72 125 200 457 814 1187 21850.9333 0.9600 0.9615 0.9524 0.9521 0.9509 0.9496 0.9500发芽频率依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是________(结果精确到0.01). 9.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是________.三、作图题(共1题;共5分)10.已知:在平面直角坐标系中,的三个顶点的坐标分别为,,.①画出关于原点成中心对称的,并写出点的坐标;②画出将绕点按顺时针旋转所得的.四、综合题(共13题;共178分)11.如图,已知抛物线y=ax2+bx+c的顶点为A(4,3),与y轴相交于点B(0,﹣5),对称轴为直线l,点M是线段AB的中点.(1)求抛物线的表达式;(2)写出点M的坐标并求直线AB的表达式;(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.12.已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4)(1)求b,c满足的关系式(2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式(3)若该函数的图象不经过第三象限,当-5sx≤1时,函数的最大值与最小值之差为16,求b的值13.已知抛物线y=2x2-4x+c与x轴有两个不同的交点.(1)求c的取值范围;(2)若抛物线y=2x2-4x+c经过点A(2,m)和点B(3,n),试比较m与n的大小,并说明理由.14.超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加元,每天售出件.(1)请写出与之间的函数表达式;(2)当为多少时,超市每天销售这种玩具可获利润2250元?(3)设超市每天销售这种玩具可获利元,当为多少时最大,最大值是多少?15.如图所示・二次函数的图像与一次函数的图像交于A、B两点,点B 在点A的右側,直线AB分别与x、y轴交于C、D两点,其中k<0.(1)求A、B两点的横坐标;(2)若△OAB是以OA为腰的等腰三角形,求k的值;(3)二次函数图像的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.16.如图,已知二次函数y=x2+ax+3的图象经过点P(-2,3).(1)求a的值和图象的顶点坐标。
一元二次方程40道题及过程

降
次
∴x+1= 或x+1=- ,
即x1=-1+ ,x2=-1- .
2
【例3】解方程(1)x -4x+4=5;
2
2
(1)分析:x -4x+4 =(x-2) ,
2
(2)(2x-1) =(x-2)2 .
(2)分析:如果把2x-1看成
同样可以用直接开平方法
是(x-2)2的平方根,同样可
求解.
以用直接开平方法求解.
(4)4x²-121=0;
(5)3x(2x+1)=4x+2;
(6)(x-4)²=(5-2x)².
则有 x = 0 或 x + 1 =0,
x1=0, x2=-1.
【例1】解下列方程
(1)x2-1.21=0
解:(1)移项,得x2=1.21,
(2)4x2-1=0
(2)移项,得4x2=1,
∵x是1.21的平方根,
2
解:(1) (x-2) =5,
(2)2x-1=± ( − )²,
即 x-2=± ,
即 2x-1=±(x-2),
即x-2= 或x-2=- ,
∴2x-1=x-2或2x-1=-x+2,
所以x1=2+ ,x2=2- .
即x1=-1,x2=1.
2.解下列方程:
(1)x2-0.81=0;
解:(1)x²=0.81,
【例1】 用公式法解下列方程:
(1)2x²-x-1=0;
(2) 4x²-3x+2=0;
(3) 2x²-2 x+1=0.
解:(2)a=4,b=-3,c=2,
b²-4ac=(-3)²-4×4×2=-7<0,
一元二次方程练习题含答案(解法20题题海111题)

经典解法20题(1) (3x+1F2=7(2) 9x A2-24x+16=11⑶(x+3)(x-6)=-8⑷ 2xA2+3x=0⑸ 6xA2+5x-50=0 选学)⑹ xA2-4x+4=0 (选学)(7) (x-2) A2=4 (2x+3)(8) yA2+2V2y-4=0(9)( x+1) A2-3 (x+1)+2=0(10) xA2+2ax-3aA2=0 (a 为常数)(11)2xA2 + 7x =4.(12) x A2 - 1 = 2 x(13) xA2 + 6x+5=0(14) x A2-4x+ 3=0(15网2 —4x- 3 =0(16) x A2 - 6x+9 =0(17) x2+8x+16=9(18) (x2-5)2=16(19) x(x+2)=x(3-x)+1(20) 6xA2+x-2=0海量111题1)xA2-9x+8=0⑵ xA2+6x-27=0⑶ x A2-2x-80=0(4) xH+10x-200=0(5) xA2-20x+96=0⑹ xA2+23x+76=0(7) xA2-25x+154=0(8) xA2-12x-108=0(9) xA2+4x-252=0(10) xA2-11x-102=0(11) xA2+15x-54=0(12) xA2+11x+18=0(13) xA2-9x+20=0(14) xA2+19x+90=0(15) xA2-25x+156=0(16) xA2-22x+57=0(17) xA2-5x-176=0(18) xA2-26x+133=0(19) xA2+10x-11=0(20) xA2-3x-304=0(21) xA2+13x-140=0(22) xA2+13x-48=0(23) xA2+5x-176=0(24) xA2+28x+171=0(25) xA2+14x+45=0(26) xA2-9x-136=0(28) xT+23x+126=0(29) xA2+9x-70=0(30) xA2-1x-56=0(31) xA2+7x-60=0(32) xA2+10x-39=0(33) xA2+19x+34=0(34) xA2-6x-160=0(35) xA2-6x-55=0(36) xA2-7x-144=0(37) xA2+20x+5 仁0(38) xA2-9x+14=0(39) xA2-29x+208=0(40) xA2+19x-20=0(41) xA2-13x-48=0(42) xA2+10x+24=0(43) xA2+28x+180=0(44) xA2-8x-209=0(45) xA2+23x+90=0(46) xA2+7x+6=0(47) xA2+16x+28=0(48) xA2+5x-50=0(49) xA2+13x-14=0(50) xA2-23x+102=0(52) x A2-8x-20=0(53) xA2-16x+39=0(54) xA2+32x+240=0(55) xA2+34x+288=0(56) xA2+22x+105=0(57) xA2+19x-20=0(58) xA2-7x+6=0(59) xA2+4x-221=0(60) xA2+6x-9 仁0(61) xA2+8x+12=0(62) xA2+7x-120=0(63) xA2-18x+17=0(64) xA2+7x-170=0(65) xA2+6x+8=0(66) xA2+13x+12=0(67) xA2+24x+119=0(68) xA2+11x-42=0(69) xA20x-289=0(70) xA2+13x+30=0(71) xA2-24x+140=0(72) xA2+4x-60=0(73) xA2+27x+170=0(74) xA2+27x+152=0(76) x A2+12x+11=0(77) xA2+17x+70=0(78) xA2+20x+19=0(79) xA2-2x-168=0(80) xA2-13x+30=0(81) xA2-10x-119=0(82) xA2+16x-17=0(83) xA2-1x-20=0(84) xA2-2x-288=0(85) xA2-20x+64=0(86) xA2+22x+105=0(87) xA2+13x+12=0(88) xA2-4x-285=0(89) xA2+26x+133=0(90) xA2-17x+16=0(91) xA2+3x-4=0(92) xA2-14x+48=0(93) xA2-12x-133=0(94) xA2+5x+4=0(95) xA2+6x-9 仁0(96) xA2+3x-4=0(97) xA2-13x+12=0(98) xA2+7x-44=0(99) x A2-6x-7=0 (100) x A2-9x-90=0 (101) xA2+17x+72=0 (102) xA2+13x-14=0 (103) xA2+9x-36=0 (104) xA2-9x-90=0 (105) xA2+14x+13=0 (106) xA2-16x+63=0 (107) xA2-15x+44=0 (108) xA2+2x-168=0 (109) xA2-6x-216=0 (110) xA2-6x-55=0 (111) xA2+18x+32=0答案(1) (3x+1F2=7解:(3x+1F2=7 /• (3x+1)A2=7 二3x+1=±V7(注意不要丢解)二x= (±V7-1)/3(2) 9xA2-24x+16=11解:9xA2-24x+16=11 二(3x-4F2=11 二3x-4=±V 11 二x= (±V 11+4)/3 •••原方程的解为x仁(211+4)/3 x2=(-V 11+4)/3(3) (x+3)(x-6)=-8解:(x+3)(x-6)=-8化简整理得xA2-3x-10=0方程左边为二次三项式,右边为零) (x-5)(x+2)=0方程左边分解因式)二x-5=0或x+2=0转化成两个一元一次方程)••• x1=5,x2=-2是原方程的解。
初三数学一元二次方程经典例题及答案解析

初三数学一元二次方程经典例题1.某网店专门销售某种品牌的工艺品,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,如图所示.(1)求y与x之间的函数关系式;(2)如果规定每天工艺品的销售量不低于240件,销售单价应定在什么范围?(3)如果在(2)的条件下,网店每天销售的利润为3750元,求该种工艺品销售单价是多少元?2.已知关于x的元二次方程(x+2)(x﹣3)=|k|(1)求证:对于任何实数k,方程总有两个不相等的实数根;(2)设(x+2)(x﹣3)=|k|的两个实数根分别为x1、x2,若x12+x22=21,求k的值.3.解下列方程:(1)x2+6x﹣1=0;(2)3x(1﹣x)=2﹣2x.4.直接写出下列方程的根.(1)x2=4x;(2)3(x﹣1)2﹣18=0;(3)2y2﹣y=6;(4)(2x﹣1)2+3(2x﹣1)﹣2=0.5.某商店出售A、B两种商品,一月份这两种商品的利润都是10万元,后因某种原因确定增加出售A种商品的数量,使A种商品每月利润的增长率都为a,同时减少B种商品的数量,使B种商品每月利润减少的百分率也都是a,(1)分别求出二月份出售A和B两种商品的利润是多少万元?(2)求出三月份出售A、B两种商品的总利润是多少万元?初三数学一元二次方程经典例题答案1.某网店专门销售某种品牌的工艺品,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,如图所示.(1)求y与x之间的函数关系式;(2)如果规定每天工艺品的销售量不低于240件,销售单价应定在什么范围?(3)如果在(2)的条件下,网店每天销售的利润为3750元,求该种工艺品销售单价是多少元?【分析】(1)根据点的坐标,利用待定系数法可求出y与x之间的函数关系式;(2)由销售量不低于240件,可得出关于x的一元一次不等式,解之即可得出x的取值范围,再结合该工艺品的成本价,即可得出结论;(3)根据总利润=单件利润×销售数量,即可得出关于x的一元二次方程,解之即可得出x的值,再结合(2)的结论即可确定该种工艺品销售单价.【解答】解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),将(40,300),(55,150)代入y=kx+b,得:,解得:,∴y与x之间的函数关系式为y=﹣10x+700.(2)当y≥240时,﹣10x+700≥240,解得:x≤46,∵成本为30元/件,∴30<x≤46.答:销售单价应大于30元/件,小于等于46元/件.(3)依题意,得:(x﹣30)(﹣10x+700)=3750,整理,得:x2﹣100x+2475=0,解得:x1=45,x2=55.∵30<x≤46,∴x=45.答:该种工艺品销售单价是45元/件.【点评】本题考查了一元二次方程的应用以及一次函数的应用,解题的关键是:(1)根据点的坐标,利用待定系数法求出一次函数解析式;(2)利用一次函数图象上点的坐标特征,找出关于x的一元一次不等式;(3)找准等量关系,正确列出一元二次方程.2.已知关于x的元二次方程(x+2)(x﹣3)=|k|(1)求证:对于任何实数k,方程总有两个不相等的实数根;(2)设(x+2)(x﹣3)=|k|的两个实数根分别为x1、x2,若x12+x22=21,求k的值.【分析】(1)将方程化为一般式后根据判别式即可求出答案;(2)利用根与系数的关系即可求出答案.【解答】解:(1)由题意可知:x2﹣x﹣6﹣|k|=0,△=1+4(6+|k|)=25+4|k|>0,∴对于任何实数k,方程总有两个不相等的实数根;(2)原方程可化为x2﹣x﹣6﹣|k|=0,∴x1+x2=1,x1x2=﹣6﹣|k|,∵x12+x22=21,∴(x1+x2)2﹣2x1x2=21,∴1﹣2(﹣6﹣|k|)=21,∴|k|=4,∴k=±4,【点评】本题考查一元二次方程,解题的关键是判别式以及根与系数的关系,本题属于基础题型.3.解下列方程:(1)x2+6x﹣1=0;(2)3x(1﹣x)=2﹣2x.【分析】(1)利用配方法求解可得;(2)利用因式分解法求解可得.【解答】解:(1)∵x2+6x=1,∴x2+6x+9=1+9,即(x+3)2=10,则x+3=±,∴x1=﹣3+,x2=﹣3﹣;(2)∵3x(1﹣x)=2(1﹣x),∴3x(1﹣x)﹣2(1﹣x)=0,则(1﹣x)(3x﹣2)=0,∴1﹣x=0或3x﹣2=0,解得x=1或x=.【点评】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.4.直接写出下列方程的根.(1)x2=4x;(2)3(x﹣1)2﹣18=0;(3)2y2﹣y=6;(4)(2x﹣1)2+3(2x﹣1)﹣2=0.【分析】(1)利用因式分解法求解;(2)利用直接开平方法求解;(3)利用因式分解法求解;(4)利用因式分解法求解.【解答】解:(1)x2=4x,x2﹣4x=0.x(x﹣4)=0,解得x1=0,x2=4;(2)3(x﹣1)2﹣18=0,(x﹣1)2=6,∴x﹣1=±,解得x1=1+,x2=1﹣;(3)2y2﹣y=6,2y2﹣y﹣6=0,(2y+3)(y﹣2)=0,解得y1=﹣,y2=2;(4)(2x﹣1)2+3(2x﹣1)﹣2=0,2x﹣1=,∴x1=,x2=.【点评】此题主要考查一元二次方程的一般解法:直接开平方法、因式分解法等,对不同的方程要选择合适的方法.5.某商店出售A、B两种商品,一月份这两种商品的利润都是10万元,后因某种原因确定增加出售A种商品的数量,使A种商品每月利润的增长率都为a,同时减少B种商品的数量,使B种商品每月利润减少的百分率也都是a,(1)分别求出二月份出售A和B两种商品的利润是多少万元?(2)求出三月份出售A、B两种商品的总利润是多少万元?【分析】(1)根据“A种商品每月利润的增长率都为a,使B种商品每月利润减少的百分率也都是a”列出代数式;(2)在(1)的基础上分别求得三月份出售A和B两种商品的利润,然后求和即可.【解答】解:(1)由题意,得二月份出售A商品的利润:10(1+a)万元.二月份出售A商品的利润:10(1﹣a)万元.(2)根据题意,得10(1+a)2+10(1﹣a)2=20a2+20(万元)答:三月份出售A、B两种商品的总利润是(20a2+20)万元.【点评】考查了一元二次方程的应用,解题的关键是读懂题意,找到等量关系.。
一元二次方程10道例题

一元二次方程10道例题一、直接开平方法例1:解方程(x - 3)^2=16解析:对于方程(x - 3)^2 = 16,根据直接开平方法,我们得到:x-3=±4当x - 3=4时,x=4 + 3=7;当x-3=-4时,x=- 4+3=-1。
所以方程的解为x_1 = 7,x_2=-1。
二、配方法例2:解方程x^2+6x - 7 = 0解析:在方程x^2+6x-7 = 0中,1. 移项得x^2+6x=7。
2. 配方:在等式两边加上一次项系数一半的平方,即x^2+6x + 9=7 + 9,得到(x + 3)^2=16。
3. 然后用直接开平方法,x+3=±4。
- 当x+3 = 4时,x=1。
- 当x + 3=-4时,x=-7。
所以方程的解为x_1=1,x_2 = - 7。
三、公式法例3:解方程2x^2-5x+3=0解析:对于一元二次方程ax^2+bx + c=0(a≠0),其求根公式为x=(-b±√(b^2 - 4ac))/(2a)。
在方程2x^2-5x + 3=0中,a = 2,b=-5,c = 3。
1. 先计算判别式Δ=b^2-4ac=(-5)^2-4×2×3=25 - 24 = 1。
2. 把a、b、Δ的值代入求根公式,得到x=(5±√(1))/(4)。
- 当取正号时,x=(5 + 1)/(4)=(3)/(2)。
- 当取负号时,x=(5-1)/(4)=1。
所以方程的解为x_1=(3)/(2),x_2 = 1。
四、因式分解法例4:解方程x^2-3x+2=0解析:1. 对x^2-3x + 2进行因式分解,得到(x - 1)(x - 2)=0。
2. 则有x-1=0或者x - 2=0。
- 当x-1=0时,x = 1。
- 当x-2=0时,x=2。
所以方程的解为x_1=1,x_2=2。
例5:解方程6x^2+x - 1=0解析:1. 对6x^2+x - 1进行因式分解,得到(2x + 1)(3x - 1)=0。
一元二次方程经典例题与练习

一元二次方程练习题1. 用直接开平方法解下列方程:(1)2225x =; (2)21440y -=.2. 解下列方程:(1)2(1)9x -=; (2)2(21)3x +=;(3)2(61)250x --=. (4)281(2)16x -=.3. 用直接开平方法解下列方程:(1)25(21)180y -=; (2)21(31)644x +=;(3)26(2)1x +=; (4)2()(00)ax c b b a -=≠,≥4. 填空(1)28x x ++( )=(x + )2. (2)223x x -+( )=(x - )2. (3)2b y y a -+( )=(y - )2. 5. 用适当的数(式)填空:23x x -+ (x =- 2);2x px -+ =(x -2) 23223(x x x +-=+2)+. 6. 用配方法解下列方程 1).210x x +-= 2).23610x x +-= 3).21(1)2(1)02x x ---+=7. 方程22103x x -+=左边配成一个完全平方式,所得的方程是 .8. 用配方法解方程.23610x x --= 22540x x --=9. 关于x 的方程22291240x a ab b ---=的根1x = ,2x = .10. 关于x 的方程22220x ax b a +-+=的解为11. 用配方法解方程(1)210x x --=; (2)23920x x -+=.12. 用适当的方法解方程(1)23(1)12x +=; (2)2410y y ++=;(3)2884x x -=; (4)2310y y ++=.13. 已知关于x 的一元二次方程22(21)10m x m x +-+=有两个不相等的实数根,则m 的取值围是 .一元二次方程综合测试(一):____________ 分数:___________一、填空题(每小题5分,计35分)1、()x x 6542=+-化成一般形式是___________________________________,其中一次项系数是___________2、()22________________3+=++x x x 3、若()()______________054==-+x x x ,则4、若代数式242-+x x 的值为3,则x 的值为_______________________________5、已知一元二次方程022=+-mx mx 有两个相等的实数根,则m 的值为____________________6、已知三角形的两边长分别为1和2,第三边的数值是方程03522=+-x x 的根,则这个三角形的周长为_______________________7、我国政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品经过两次降价,由每盒60元调至52元,若设每次平均降价的百分率为x ,则由题意可列方程为_______________________________________二、选择题(每小题5分,计20分)8、下列方程是一元二次方程的是( )A 、0523=-x xB 、()06122=--xC 、022312=-+x xD 、02122=-+x x 9、方程0562=--x x 左边配成一个完全平方式后,所得方程为( )A 、()4162=-xB 、()432=-xC 、()1432=-xD 、()3662=-x10、要使方程()()0132=+++-c x b x a 是关于x 的一元二次方程,则( ) A 、0≠a B 、3≠a C 、13-≠≠b a ,且 D 、013≠-≠≠c b a ,且,11、某种商品因换季准备打折出售,如果按原价的七五折出售,将赔25元,二按原价的九折出售,将赚20元,则这种商品的原价是( )A 、500元B 、400元C 、300元D 、200元三、解答题12、用适当的方法解下列方程(每小题6分,计24分)(1)()9322=-x ; (2)162=-x x ;(3)051632=++x x ; (4)()()2231623-=+x x13、(10分)无论m 为何值时,方程04222=---m mx x 总有两个不相等的实数根吗?给出答案并说明理由14、(11分)百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?一元二次方程综合测试(二):____________ 分数:___________一、填空题(每小题5分,计40分)1、已知方程2(m+1)x 2+4mx+3m -2=0是关于x 的一元二次方程,那么m 的取值围是 。
一元二次方程100道计算题练习(附答案)+一元二次方程经典练习题(6套)附带详细答案

一元二次方程100道计算题练习1、)4(5)4(2+=+x x 2、x x 4)1(2=+ 3、22)21()3(x x -=+4、31022=-x x 5、(x+5)2=16 6、2(2x -1)-x (1-2x )=07、x 2 =64 8、5x 2 - 52=0 9、8(3 -x )2 –72=010、3x(x+2)=5(x+2) 11、(1-3y )2+2(3y -1)=0 12、x 2+ 2x + 3=013、x 2+ 6x -5=0 14、x 2-4x+ 3=0 15、x 2-2x -1 =016、2x 2+3x+1=0 17、3x 2+2x -1 =0 18、5x 2-3x+2 =019、7x 2-4x -3 =0 20、 -x 2-x+12 =0 21、x 2-6x+9 =022、22(32)(23)x x -=- 23、x 2-2x-4=0 24、x 2-3=4x25、3x 2+8 x -3=0(配方法) 26、(3x +2)(x +3)=x +14 27、(x+1)(x+8)=-1228、2(x -3) 2=x 2-9 29、-3x 2+22x -24=0 30、(2x-1)2+3(2x-1)+2=031、2x 2-9x +8=0 32、3(x-5)2=x(5-x) 33、(x +2) 2=8x34、(x -2) 2=(2x +3)2 35、2720x x += 36、24410t t -+=37、()()24330x x x -+-= 38、2631350x x -+= 39、()2231210x --=40、2223650x x -+=补充练习:一、利用因式分解法解下列方程(x -2) 2=(2x-3)2 042=-x x 3(1)33x x x +=+x 2 ()()0165852=+---x x二、利用开平方法解下列方程51)12(212=-y 4(x-3)2=25 24)23(2=+x三、利用配方法解下列方程25220x x -+= 012632=--x x01072=+-x x四、利用公式法解下列方程-3x 2+22x -24=0 2x (x -3)=x -3. 3x 2+5(2x+1)=0五、选用适当的方法解下列方程(x +1) 2-3 (x +1)+2=0 22(21)9(3)x x +=- 2230x x --=21302x x ++= 4)2)(1(13)1(+-=-+x x x x--xx x(x+1)-5x=0. 3x(x-3) =2(x-1) (x+1).23(=)2)(11应用题:1、某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为扩大销售增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价一元,市场每天可多售2件,若商场平均每天盈利1250元,每件衬衫应降价多少元?2、两个正方形,小正方形的边长比大正方形的边长的一半多4 cm,大正方形的面积比小正方形的面积的2倍少32平方厘米,求大小两个正方形的边长.3、如图,有一块梯形铁板ABCD,AB∥CD,∠A=90°,AB=6 m,CD=4 m,AD=2 m,现在梯形中裁出一内接矩形铁板AEFG,使E在AB上,F在BC上,G在AD上,若矩形铁板的面积为5 m2,则矩形的一边EF长为多少?4、如右图,某小在长32米,区规划宽20米的矩形场地ABCD上修建三条同样宽的3条小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为566米2,问小路应为多宽?5、某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,商店想在月销售成本不超过1万元的情况下,使得月销售利润达到8000元,销售单价应定为多少?6.某工厂1998年初投资100万元生产某种新产品,1998年底将获得的利润与年初的投资的和作为1999年初的投资,到1999年底,两年共获利润56万元,已知1999年的年获利率比1998年的年获利率多10个百分点,求1998年和1999年的年获利率各是多少? 思考:1、关于x 的一元二次方程()04222=-++-a x x a 的一个根为0,则a 的值为 。
(完整版)一元二次方程100道计算题练习(附答案)

一元二次方程100道计算题练习1、)4(5)4(2+=+x x 2、x x 4)1(2=+ 3、22)21()3(x x -=+4、31022=-x x 5、(x+5)2=16 6、2(2x -1)-x (1-2x )=07、x 2 =64 8、5x 2 - 52=0 9、8(3 -x )2 –72=010、3x(x+2)=5(x+2) 11、(1-3y )2+2(3y -1)=0 12、x 2+ 2x + 3=013、x 2+ 6x -5=0 14、x 2-4x+ 3=0 15、x 2-2x -1 =016、2x 2+3x+1=0 17、3x 2+2x -1 =0 18、5x 2-3x+2 =019、7x 2-4x -3 =0 20、 -x 2-x+12 =0 21、x 2-6x+9 =022、22(32)(23)x x -=- 23、x 2-2x-4=0 24、x 2-3=4x25、3x 2+8 x -3=0(配方法) 26、(3x +2)(x +3)=x +14 27、(x+1)(x+8)=-1228、2(x -3) 2=x 2-9 29、-3x 2+22x -24=0 30、(2x-1)2+3(2x-1)+2=031、2x 2-9x +8=0 32、3(x-5)2=x(5-x) 33、(x +2) 2=8x34、(x -2) 2=(2x +3)2 35、2720x x += 36、24410t t -+=37、()()24330x x x -+-= 38、2631350x x -+= 39、()2231210x --=40、2223650x x -+=一、用因式分解法解下列方程(x -2) 2=(2x-3)2 042=-x x 3(1)33x x x +=+x 2-23x+3=0 ()()0165852=+---x x二、利用开平方法解下列方程51)12(212=-y 4(x-3)2=25 24)23(2=+x三、利用配方法解下列方程25220x x -+= 012632=--x x01072=+-x x四、利用公式法解下列方程-3x 2+22x -24=0 2x (x -3)=x -3. 3x 2+5(2x+1)=0五、选用适当的方法解下列方程(x +1) 2-3 (x +1)+2=0 22(21)9(3)x x +=- 2230x x --=21302x x ++= 4)2)(1(13)1(+-=-+x x x x--xx x(x+1)-5x=0. 3x(x-3) =2(x-1) (x+1). 3(=11)2)(2答案第二章 一元二次方程备注:每题2.5分,共计100分,配方法、公式法、分解因式法,方法自选,家长批阅,错题需在旁边纠错。
一元二次方程经典练习题(6套)附带详细答案

练习一一、选择题:(每小题3分,共24分)1.下列方程中,常数项为零的是( )A.x 2+x=1B.2x 2-x-12=12;C.2(x 2-1)=3(x-1)D.2(x 2+1)=x+22.下列方程:①x 2=0,② 21x -2=0,③22x +3x=(1+2x)(2+x),④32x-=0,⑤32x x-8x+ 1=0中,一元二次方程的个数是( )A.1个 B2个 C.3个D.4个3.把方程())+(2x-1)2=0化为一元二次方程的一般形式是( )A.5x 2-4x-4=0B.x 2-5=0C.5x 2-2x+1=0D.5x 2-4x+6=04.方程x 2=6x 的根是( ) A.x 1=0,x 2=-6 B.x 1=0,x 2=6C.x=6D.x=05.方2x 2-3x+1=0经为(x+a)2=b 的形式,正确的是( )A.23162x ⎛⎫-= ⎪⎝⎭; B.2312416x ⎛⎫-= ⎪⎝⎭; C. 231416x ⎛⎫-= ⎪⎝⎭; D.以上都不对6.若两个连续整数的积是56,则它们的和是( )A.11B.15C.-15D.±157.不解方程判断下列方程中无实数根的是( )A.-x2=2x-1B.4x2+4x+5=0;4C.20-= D.(x+2)(x-3)==-5x8.某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )A.200(1+x)2=1000B.200+200×2x=1000C.200+200×3x=1000D.200[1+(1+x)+(1+x)2]=1000二、填空题:(每小题3分,共24分)9.方程2(1)5322x x -+=化为一元二次方程的一般形式是________,它的一次项系数是______.10.关于x 的一元二次方程x 2+bx+c=0有实数解的条件是__________.11.用______法解方程3(x-2)2=2x-4比较简便.12.如果2x 2+1与4x 2-2x-5互为相反数,则x 的值为________.13.如果关于x的一元二次方程2x(kx-4)-x2+6=0没有实数根,那么k 的最小整数值是__________. 14.如果关于x的方程4mx2-mx+1=0有两个相等实数根,那么它的根是_______.15.若一元二次方程(k-1)x2-4x-5=0 有两个不相等实数根, 则k 的取值范围是_______.16.某种型号的微机,原售价7200元/台,经连续两次降价后,现售价为3528元/台,则平均每次降价的百分率为______________.三、解答题(2分)17.用适当的方法解下列一元二次方程.(每小题5分,共15分)(1)5x(x-3)=6-2x;(2)3y2+1=;(3)(x-a)2=1-2a+a2(a是常数)18.(7分)已知关于x的一元二次方程x2+mx+n=0的一个解是2,另一个解是正数, 而且也是方程(x+4)2-52=3x的解,你能求出m和n的值吗?19.(10分)已知关于x的一元二次方程x2-2kx+1k2-2=0.2(1)求证:不论k为何值,方程总有两不相等实数根.(2)设x1,x2是方程的根,且x12-2kx1+2x1x2=5,求k的值.四、列方程解应用题(每题10分,共20分)20.某电视机厂计划用两年的时间把某种型号的电视机的成本降低36%, 若每年下降的百分数相同,求这个百分数.21.某商场今年1月份销售额为100万元,2月份销售额下降了10%,该商场马上采取措施,改进经营管理,使月销售额大幅上升,4月份的销售额达到129.6万元,求3, 4月份平均每月销售额增长的百分率.练习二一、选择题(共8题,每题有四个选项,其中只有一项符合题意。
一元二次方程的应用专项练习60题(有答案)

一元二次方程的应用专项练习60题(有答案)1.某单位组织职工旅游,旅行社的收费标准如下:人数不超过25人,每人旅游费用为100元;超过25人,每增加1人,人均旅游费用降低2元,但不低于70元。
该单位按照旅行社的收费标准组团,结束后,共支付给旅行社2700元。
求该单位这次旅游共有多少人参加?2.国务院于4月7日公布了《医药卫生体制改革近期重点实施方案(2009~20XX年)》。
某市政府决定用于改善医疗卫生服务的经费为6000万元,并计划到20XX年提高到7260万元。
如果从现在到20XX年每年的资金投入按相同的增长率递增,求到20XX年的平均增长率。
3.某商场按照定价销售某种电器时,每台可获利48元。
如果按照定价的九折销售该电器6台,则将定价降低30元销售该电器9台所获得的利润相等。
1)该电器每台进价和定价各是多少元?2)按照(1)的定价,该商场一年可销售1000台。
经市场调查,每降低一元,一年可多卖该种电器10台。
如果商场想在一年中使该种电器获利元,那么商场应该按几折销售?4.5月1日,杭州湾跨海大桥通车。
通车后,苏南A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地。
如果有一批货物(不超过10车)从A地按照外运路线运到B地,运费为8320元。
其中,从A地经杭州湾跨海大桥到宁波港的每车运输费用为380元。
从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元。
如果这批货物有x车。
1)用含x的代数式表示每车从宁波港到B地的海上运费;2)求x的值。
5.有一块矩形铁皮,长100cm,宽50cm。
在它的四角各切去一个同样大的正方形,然后将四周突出部分折起,就能制作成一个无盖的方盒。
如果制成的无盖方盒的底面积为3600cm²,那么铁皮各角应切去多大的正方形?6.近年来,我市某乡的蔬菜产值不断增加,蔬菜的产值从640万元增加到1000万元。
一元二次方程练习题-含答案(解法20题-题海111题)

经典解法20题(1)(3x+1)^2=7(2)9x^2-24x+16=11(3) (x+3)(x-6)=-8(4) 2x^2+3x=0(5) 6x^2+5x-50=0 (选学)(6)x^2-4x+4=0 (选学)(7)(x-2)^2=4(2x+3)^2(8)y^2+2√2y-4=0(9)(x+1)^2-3(x+1)+2=0(10)x^2+2ax-3a^2=0(a为常数)(11)2x^2+7x=4.(12)x^2-1=2 x (13)x^2 + 6x+5=0(14) x ^2-4x+ 3=0(15)7x^2 -4x-3 =0(16)x ^2-6x+9 =0(17)x²+8x+16=9(18)(x²-5)²=16(19)x(x+2)=x(3-x)+1(20) 6x^2+x-2=0海量111题1)x^2-9x+8=0(2)x^2+6x-27=0(3)x^2-2x-80=0(4)x^2+10x-200=0(5)x^2-20x+96=0(6)x^2+23x+76=0(7)x^2-25x+154=0(8)x^2-12x-108=0(9)x^2+4x-252=0(10)x^2-11x-102=0(11)x^2+15x-54=0(12)x^2+11x+18=0(13)x^2-9x+20=0(14)x^2+19x+90=0(15)x^2-25x+156=0(16)x^2-22x+57=0(17)x^2-5x-176=0(18)x^2-26x+133=0(19)x^2+10x-11=0(20)x^2-3x-304=0(21)x^2+13x-140=0(23)x^2+5x-176=0(24)x^2+28x+171=0(25)x^2+14x+45=0(26)x^2-9x-136=0(27)x^2-15x-76=0(28)x^2+23x+126=0(29)x^2+9x-70=0(30)x^2-1x-56=0(31)x^2+7x-60=0(32)x^2+10x-39=0(33)x^2+19x+34=0(34)x^2-6x-160=0(35)x^2-6x-55=0(36)x^2-7x-144=0(37)x^2+20x+51=0(38)x^2-9x+14=0(39)x^2-29x+208=0(40)x^2+19x-20=0(41)x^2-13x-48=0(42)x^2+10x+24=0(43)x^2+28x+180=0(45)x^2+23x+90=0(46)x^2+7x+6=0(47)x^2+16x+28=0(48)x^2+5x-50=0(49)x^2+13x-14=0(50)x^2-23x+102=0(51)x^2+5x-176=0(52)x^2-8x-20=0(53)x^2-16x+39=0(54)x^2+32x+240=0(55)x^2+34x+288=0(56)x^2+22x+105=0(57)x^2+19x-20=0(58)x^2-7x+6=0(59)x^2+4x-221=0(60)x^2+6x-91=0(61)x^2+8x+12=0(62)x^2+7x-120=0(63)x^2-18x+17=0(64)x^2+7x-170=0(65)x^2+6x+8=0(67)x^2+24x+119=0(68)x^2+11x-42=0(69)x^20x-289=0(70)x^2+13x+30=0(71)x^2-24x+140=0(72)x^2+4x-60=0(73)x^2+27x+170=0(74)x^2+27x+152=0(75)x^2-2x-99=0(76)x^2+12x+11=0(77)x^2+17x+70=0(78)x^2+20x+19=0(79)x^2-2x-168=0(80)x^2-13x+30=0(81)x^2-10x-119=0(82)x^2+16x-17=0(83)x^2-1x-20=0(84)x^2-2x-288=0(85)x^2-20x+64=0(86)x^2+22x+105=0(87)x^2+13x+12=0(89)x^2+26x+133=0(90)x^2-17x+16=0(91)x^2+3x-4=0(92)x^2-14x+48=0(93)x^2-12x-133=0(94)x^2+5x+4=0(95)x^2+6x-91=0(96)x^2+3x-4=0(97)x^2-13x+12=0(98)x^2+7x-44=0(99)x^2-6x-7=0 (100)x^2-9x-90=0 (101)x^2+17x+72=0 (102)x^2+13x-14=0 (103)x^2+9x-36=0 (104)x^2-9x-90=0 (105)x^2+14x+13=0 (106)x^2-16x+63=0 (107)x^2-15x+44=0 (108)x^2+2x-168=0 (109)x^2-6x-216=0(111)x^2+18x+32=0答案(1)(3x+1)^2=7解:(3x+1)^2=7 ∴(3x+1)^2=7 ∴3x+1=±√7(注意不要丢解) ∴x= (±√7-1)/3(2)9x^2-24x+16=11解:9x^2-24x+16=11 ∴(3x-4)^2=11 ∴3x-4=±√11 ∴x= (±√11+4)/3 ∴原方程的解为x1=(√11+4)/3 x2=(-√11+4)/3(3) (x+3)(x-6)=-8解:(x+3)(x-6)=-8 化简整理得x^2-3x-10=0 (方程左边为二次三项式,右边为零) (x-5)(x+2)=0 (方程左边分解因式) ∴x-5=0或x+2=0 (转化成两个一元一次方程) ∴x1=5,x2=-2是原方程的解。
一元二次方程经典例题及练习

一元二次方程练习题1. 用直接开平方法解以下方程:〔1〕2225x =; 〔2〕21440y -=.2. 解以下方程:〔1〕2(1)9x -=; 〔2〕2(21)3x +=;〔3〕2(61)250x --=. 〔4〕281(2)16x -=.3. 用直接开平方法解以下方程:〔1〕25(21)180y -=; 〔2〕21(31)644x +=;〔3〕26(2)1x +=; 〔4〕2()(00)ax c b b a -=≠,≥4. 填空〔1〕28x x ++〔 〕=〔x + 〕2. 〔2〕223x x -+〔 〕=〔x - 〕2. 〔3〕2b y y a -+〔 〕=〔y - 〕2. 5. 用适当的数〔式〕填空:23x x -+ (x =- 2);2x px -+ =(x -2) 23223(x x x +-=+2)+. 6. 用配方法解以下方程 1〕.210x x +-= 2〕.23610x x +-= 3〕.21(1)2(1)02x x ---+=7. 方程22103x x -+=左边配成一个完全平方式,所得的方程是 .8. 用配方法解方程.23610x x --= 22540x x --=9. 关于x 的方程22291240x a ab b ---=的根1x = ,2x = .10. 关于x 的方程22220x ax b a +-+=的解为11. 用配方法解方程〔1〕210x x --=; 〔2〕23920x x -+=.12. 用适当的方法解方程〔1〕23(1)12x +=; 〔2〕2410y y ++=;〔3〕2884x x -=; 〔4〕2310y y ++=.13. 关于x 的一元二次方程22(21)10m x m x +-+=有两个不相等的实数根,那么m 的取值范围是 .一元二次方程综合测试〔一〕姓名:____________ 分数:___________一、填空题〔每题5分,计35分〕1、()x x 6542=+-化成一般形式是___________________________________,其中一次项系数是___________2、()22________________3+=++x x x 3、假设()()______________054==-+x x x ,则4、假设代数式242-+x x 的值为3,那么x 的值为_______________________________5、一元二次方程022=+-mx mx 有两个相等的实数根,那么m 的值为____________________6、三角形的两边长分别为1和2,第三边的数值是方程03522=+-x x 的根,那么这个三角形的周长为_______________________7、我国政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品经过两次降价,由每盒60元调至52元,假设设每次平均降价的百分率为x ,那么由题意可列方程为_______________________________________二、选择题〔每题5分,计20分〕8、以下方程是一元二次方程的是〔 〕A 、0523=-x xB 、()06122=--xC 、022312=-+x x D 、02122=-+xx 9、方程0562=--x x 左边配成一个完全平方式后,所得方程为〔 〕A 、()4162=-xB 、()432=-xC 、()1432=-xD 、()3662=-x10、要使方程()()0132=+++-c x b x a 是关于x 的一元二次方程,那么〔 〕A 、0≠aB 、3≠aC 、13-≠≠b a ,且D 、013≠-≠≠c b a ,且,11、某种商品因换季准备打折出售,假如按原价的七五折出售,将赔25元,二按原价的九折出售,将赚20元,那么这种商品的原价是〔 〕A 、500元B 、400元C 、300元D 、200元三、解答题12、用适当的方法解以下方程〔每题6分,计24分〕〔1〕()9322=-x ; 〔2〕162=-x x ;〔3〕051632=++x x ; 〔4〕()()2231623-=+x x13、〔10分〕无论m 为何值时,方程04222=---m mx x 总有两个不相等的实数根吗?给出答案并说明理由“六一〞国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:假如每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?一元二次方程综合测试〔二〕姓名:____________ 分数:___________一、填空题〔每题5分,计40分〕1、方程2(m+1)x 2+4mx+3m -2=0是关于x 的一元二次方程,那么m 的取值范围是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元二次方程练习题1. 用直接开平方法解下列方程:(1)2225x =; (2)21440y -=.2. 解下列方程:(1)2(1)9x -=; (2)2(21)3x +=;(3)2(61)250x --=. (4)281(2)16x -=.3. 用直接开平方法解下列方程:(1)25(21)180y -=; (2)21(31)644x +=;(3)26(2)1x +=; (4)2()(00)ax c b b a -=≠,≥ 4. 填空(1)28x x ++( )=(x + )2.(2)223x x -+( )=(x - )2. (3)2b y y a-+( )=(y - )2.5. 用适当的数(式)填空:23x x -+(x =-2); 2x px -+=(x -2)23223(x x x +-=+2)+.6. 用配方法解下列方程1).210x x +-= 2).23610x x +-= 3).21(1)2(1)02x x ---+=7. 方程22103x x -+=左边配成一个完全平方式,所得的方程是 .8. 用配方法解方程.23610x x --= 22540x x --=9. 关于x 的方程22291240x a ab b ---=的根1x = ,2x = . 10. 关于x 的方程22220x ax b a +-+=的解为 11. 用配方法解方程(1)210x x --=; (2)23920x x -+=.12. 用适当的方法解方程(1)23(1)12x +=; (2)2410y y ++=;(3)2884x x -=; (4)2310y y ++=.13. 已知关于x 的一元二次方程22(21)10m x m x +-+=有两个不相等的实数根,则m 的取值范围是 .一元二次方程综合测试(一)姓名:____________ 分数:___________一、填空题(每小题5分,计35分)1、()x x 6542=+-化成一般形式是___________________________________,其中一次项系数是___________2、()22________________3+=++x x x3、若()()______________054==-+x x x ,则4、若代数式242-+x x 的值为3,则x 的值为_______________________________5、已知一元二次方程022=+-mx mx 有两个相等的实数根,则m 的值为____________________ 6、已知三角形的两边长分别为1和2,第三边的数值是方程03522=+-x x 的根,则这个三角形的周长为_______________________7、我国政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品经过两次降价,由每盒60元调至52元,若设每次平均降价的百分率为x ,则由题意可列方程为_______________________________________ 二、选择题(每小题5分,计20分)8、下列方程是一元二次方程的是( )A 、0523=-x x B 、()06122=--x C 、022312=-+x x D 、02122=-+xx 9、方程0562=--x x 左边配成一个完全平方式后,所得方程为( )A 、()4162=-x B 、()432=-x C 、()1432=-x D 、()3662=-x10、要使方程()()0132=+++-c x b x a 是关于x 的一元二次方程,则( )A 、0≠aB 、3≠aC 、13-≠≠b a ,且D 、013≠-≠≠c b a ,且,11、某种商品因换季准备打折出售,如果按原价的七五折出售,将赔25元,二按原价的九折出售,将赚20元,则这种商品的原价是( )A 、500元B 、400元C 、300元D 、200元 三、解答题12、用适当的方法解下列方程(每小题6分,计24分)(1)()9322=-x ; (2)162=-x x ;(3)051632=++x x ; (4)()()2231623-=+x x13、(10分)无论m 为何值时,方程04222=---m mx x 总有两个不相等的实数根吗?给出答案并说明理由 14、(11分)百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?一元二次方程综合测试(二)姓名:____________ 分数:___________一、填空题(每小题5分,计40分)1、已知方程2(m+1)x 2+4mx+3m -2=0是关于x 的一元二次方程,那么m 的取值范围是 。
2、一元二次方程(1-3x)(x+3)=2x 2+1的一般形式是 它的二次项系数是 ;一次项系数是 ;常数项是 。
3、已知关于x 的一元二次方程(2m -1)x 2+3mx+5=0有一根是x=-1,则m= 。
4、 关于x 的方程2310x x -+= 实数根。
(注:填写“有”或“没有”) 5、若代数式x 2-2x 与代数式 -9+4x 的值相等,则x 的值为 。
6、在实数范围内定义一种运算 “*” , 其规则为 22a b a b *=-, 根据这个规则, 方程(x+3)*2=0的解为 。
7、在参加足球世界杯预选赛的球队中,每两支队都要进行两次比赛,共要比赛30场,则参赛队有 支。
8、如右图,是一个正方体的展开图,标注了字母A 的面是正方体的正面, 如果正方体的左面和右面所标注代数式的值相等,则x 的值是 。
二、选择题(每小题4分,计20分) 9、下列方程,是一元二次方程的是( ) ①3x 2+x=20,②2x 2-3xy+4=0,③x 2-1x =4,④x 2=0,⑤x 2-3x+3=0 A .①② B .①②④⑤ C .①③④ D .①④⑤ 102(7)x -=7-x ,则x 的取值范围是( )A .x ≥7B .x ≤7C .x>7D .x<711、方程(x-3)2=(x-3)的根为( )A .3B .4C .4或3D .-4或312、若c (c ≠0)为关于x 的一元二次方程x 2+bx+c=0的根,则c+b 的值为( ) A .1 B .-1 C .2 D .-213、从正方形铁片上截去2cm 宽的一个长方形,剩余矩形的面积为80cm 2,•则原来正方形的面积为( ) A .100cm 2 B .121cm 2 C .144cm 2 D .169cm 2 三、解答题14、用适当的方法解下列方程(每小题6分,计24分)(1)(3)(1)5x x +-=; (2)231060x x -+=(3)2(3)2(3)x x x -=-; (4)2(3)2(1)7x x x --+=-15、(10分)已知方程2(m+1)x 2+4mx+3m=2,根据下列条件之一求m 的值. (1)方程有两个相等的实数根;(2)方程有两个相反的实数根;(3)方程的一个根为0. 16、(11分)某农户在山上种了脐橙果树44株,现进入第三年收获。
收获时,先随意采摘5株果树上的脐橙,称得每株果树上的脐橙质量如下(单位:千克):35,35,34,39,37(1)根据样本平均数估计,这年脐橙的总产量约是多少?(2)若市场上的脐橙售价为每千克5元,则这年该农户卖脐橙的收入将达多少元?(3)已知该农户第一年卖脐橙的收入为5500元,根据以上估算,试求第二年、第三年卖脐橙收入的年平均增长率。
(四)一元一次方程的实际应用(1)与数字有关的问题例11:一个两位数,十位数字与个位数字之和是5,把这个数的个位数字与十位数字对调后,所得的新两位数与原来的两位数的乘积为736,求原来的两位数解:设原两位数的十位数字为x ,则个位数字为x -5. 根据题意,得()[]()[]736510510=+--+x x x x整理后,得0652=+-x x 解方程,得3221==x x ,当2=x 时,35=-x ,两位数为23;当3=x 时,25=-x ,两位数为32 答:原来的两位数为23或32 一元二次方程实际应用练习题11:1.一个两位数,个位数字比十位数字大3,个位数字的平方恰好等于这个两位数,则这个两位数是多少?2、某两位数的十位数字是082=-x x 的解,则其十位数字是多少;某两位数的个位数字是方程082=-x x 的解,则其个位数是多少?3、一个两位数,个位上数字比十位数字小4,且个位数字与十位数字的平方和比这两位数小4,设个位数字为x ,求这个两位数?4、一个两位数,个位上的数字是十位数字的平方还多1,若把个位上的数字与十位上的数字对调,所得的两位数比原数大27,求原两位数?5、一个三位数,百位上数字为2,十位上数字比个位上数字小3,这个三位数个位、十位、百位上的数字之积的6倍比这个三位数小20,求这个三位数?例12:三个连续奇数,它们的平方和为251,求这三个数?解:设中间的一个奇数为x ,则另两个奇数分别为22+-x x ,.由题意,得()()25122222=++-+x x x整理,得24332=x ∴9921-==x x ,当91=x 时,11272=+=-x x ,;当92-=x 时,72112-=+-=-x x ,答:三个连续奇数分别为7,9,11或7911---,,一元二次方程实际应用练习题12:1、 两个数的和为16,积为48,则这两个正整数各是多少?2、 若两个连续正整数的平方和为313,则这两个正整数的和是多少?3、 三个连续正整数中,前两个数的平方和等于第三个数的平方,则这三个数从小到大依次是多少?4、 三个连续偶数,使第三个数的平方等于前两个数的平方和,求这三个数?5、 有四个连续整数,已知它们的和等于其中最大的与最小的两个整数的积,求这四个数?(2)与几何图形面积有关的问题例13:一个直角三角形三边的长是三个连续整数,求这三条边的长和它的面积解:设三条边的长分别为()()11+-x x x ,, 由勾股定理,得()()22211+=+-x x x整理,得042=-x x . ∴4021==x x , ∵01=x ,不合题意,舍去∴4=x 从而5131=+=-x x , ∴S △=64321=⨯⨯一元二次方程实际应用练习题13:1.直角三角形两直角边的比是8:15,而斜边的长等于6.8cm ,那么这个直角三角形的面积等于多少?2、直角三角形的面积为6,两直角边的和为7,则斜边长为多少?3、用一条长12厘米的铁丝折成一个斜边长是5厘米的直角三角形,则两直角边的长是多少?4、一个三角形的两边长为2和4,第三边长是方程0121022=+-x x 的解,则三角形的周长为多少6、 若三角形的三边长均满足方程0862=+-x x ,则此三角形的周长为多少?例14:一块长80cm ,宽60cm 的薄钢片,在四个角截去四个相同的小正方形,然后将四边折起,做成如图所示的底面积是15002cm 且无盖的长方体盒子. 求截去的小正方形的边长.解:设截去的小正方形的边长为x cm ,则()()1500260280=--x x整理,得0825702=++x x 解得551521==x x ,因为0260>-x ,所以55=x 不合题意,舍去 所以 15=x答:截去的小正方形的边长为15cm一元二次方程实际应用练习题14:1.一块矩形的地,长是24米,宽是12米,要在它的中央划一块矩形的花坛,四周铺上草地,其宽都相同,花坛占大块矩形面积的95,求草地的宽?2、从一块正方形的木板上锯下2m 宽的长方形木条,剩下部分的面积是482m ,则这块木板的面积是多少?3、有一间长18m ,宽7m 的会议室,在它的中间铺一块地毯,地毯的面积是会议室面积的31,四周未铺地毯处的宽度相同,则求所留宽度是多少?4、一根铁丝长48cm ,围成一个面积为140cm 2的矩形,求这个矩形的长和宽分别是多少?5、建一个面积为480平方米的长方形存车处,存车处的一面靠墙,另三面用铁栅栏围起来,已知铁栅栏的长是92米,求存车处的长和宽各是多少?(3)有关增长率的问题例15:将进货单价为30元的商品按40元售出时,每天能卖出500个. 已知这种商品每涨价1元,其每天销售量就减少10个,为了每天能赚取8000元的利润,且尽量减少库存,售价应定为多少?解:设售价应定为x 元,则()()[]8000401050030=---x x整理,得035001202=+-x x解得705021==x x ,因为要尽量减少库存,所以70=x 不合题意,舍去所以50=x答:售价应定为50元一元二次方程实际应用练习题15:1、 某商店的童装按标价的九折出售,仍可获利20%,若进价为每件21元,求每件标价为多少元?2、 一个小组有若干个人,新年互送贺卡一张,已知全组共送贺卡72张,求这个小组有多少人?3、 生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共赠送了182件,求全组有多少名同学?4、 有一种植物的主干长出了若干数目的支干,每个支干又长出同样数目的小分支,主干、分支和小分支的总数是111,每个支干长出多少小分支?例16:某工厂1月份产值为50万元,采用先进技术后,第一季度产值共为182万元,2月份和3月份的平均增长率为多少?解:设2月份和3月份的平均增长率为x ,则()()182150150502=++++x x 整理,得01675252=-+x x解得2.32.021-==x x ,因为02.3<-=x ,所以2.3-=x 不合题意,舍去所以%202.0==x答:2月份和3月份的平均增长率为%20一元二次方程实际应用练习题16:1、 某农场的产量两年从50万公斤增加到60.5万公斤,平均每年增产百分之几??2、 某化肥厂今年一月份的化肥产量为4万吨,第一季度共生产化肥13.2万吨,问2、3月份平均每月的增长率是多少?3、 某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,求平均每月增长率为多少?4、 某种粮大户今年产粮20万千克,计划后年产粮达到28.8万千克,若每年粮食增产的百分率相同,求平均每年增产的百分数?5、某钢厂今年一月份产量为4万吨,第一季度共生产13.24万吨,问二、三月份平均每月的增长率是多少?。
