2015年长郡澄池杯复赛数学试卷及解析
2015年上学期长郡系七年级段考数学模拟试卷(A4修订稿答案与解析)

1 1 , ,AB 中点所表示的数为 m ,在 10.1 和它的相 4 6
2012
n m ( m) (2) 3 _____ 0 (3 分)
2
(2)若 x nx m 0 ,求 3 x [ 34 x 2( 4 x 3) 5 x ] 的值(3 分)
2
5
金钥匙爱未来培训学校
2015 年上学期长郡系七年级段考数学模拟试卷(一)答案
班级: 姓名: 得分: 一、选择题(在下列各题的四个选项中,只有一项是符合题意的。本题共 10 个小题,每小题 3 分,共 30 分)
题号 答案 1 2 3 4 5 6 7 8 9 10
1 、(有理数) 若 a 的负倒数的相反数是 8,b 的相反数的负倒数也是 8,则( A )。 A.a=b B.a<b C.a>b D.ab=1 2、(整式) 单项式-xy2z的 ( A.系数是0,次数是2 C.系数是0,次数是4 3、(有理数) 下面说法正确的有( A D ) B.系数是-1,次数是2 D.系数是-1,次数是4 )
3a x 0 有共同的解,则 a 的值等于( 3D、 0)Fra bibliotek1 3
B、 2
C、 1
7 、(一元一次方程) 如图,若两个天平都是平衡的,则与 2 个球体相等质量的正方体的个数为(
)
A.5
B.4
5
C.3
D.2 )
8、(一元一次方程) 已知 1 3m 5 有最大值,则方程 5m-4=3x+2 的解是( A.
( 2)
x4 x3 x2 ( x 5) 5 3 2
21、 (6分) 已知 a 2 a
1 1 求 a 2b {3ab 2 (a 2b 2 abc) 2[a 2b ( a 2b 2 2abc)]} c (c 3) 2 0 , 2 b
长郡澄池杯初赛2015年数试卷A

长郡澄池杯初赛2015年数试卷A满分:100分时量:70分钟一、选择题(每题5分,共30分)1、现在网购越来越多地成为人们的一种消费方式,在 2014 年的 "双 11 ' 网上促销活动中天猫和淘宝的支付交易额突破 57000 000 000 元,将数字57000 000 000 用科学记数法表示为()A. 5.7 ×109B. 5.7×1010C. 0.57×lO11D. 57×l092、菜农机厂囚月份生产零件 50 万个,第二季度共生产零件 182 万个,设该厂五、六月份平均每月的增长率为 x ,那么 x 满足的方程是()A、50(1+ x)2 = 182 B. 50 + 50(1+ x)十 50( l +x)2 = 182c、50(1+ 2x)=182 D.50 + 50(l + x) + 50(1+ 2x) = l 823、如图,点A, B是棱长为 l 的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A, B 两点间的距离为()A. 2 B . C. . D.o(第 3 题应)(第 4 题图)(第 5 题图)4、如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是()A. B. C. D.5、如图,直径为 10 的⊙A 经过点 C (O, 5) 和点B (0, 0) ,B 是 y 轴右侧⊙A 优弧上一点 ,则 cos ∠OBC 的值为( ) A .B.C .D.6、如图,在矩形ABCD 中,垂直于对角线 BD 的直线1,点B 开始沿着线段BD 匀速平移到D.设直线l 被矩形所截线段EF 的长度为y,运动时间为t ,则y 关于t 的函数的大致图像是( )二、填空题(每题5分,共30分〉 7、计算:( )。
8、函数中自变量 x 的取值范围是 。
9、化简 (的结果为 。
10、如图,AB 是⊙0 的直径,弦AC=2 ,∠ABC=30°,则图中阴影部分的面积是 。
2015年长郡双语八年级数学复习测试卷

2015年长郡双语八年级数学复习测试卷一、选择题:(每小题3分,共30分)1、下列方程中,关于x 的一元二次方程是( )A 、3(x+1)2=2(x+1)B 、21x +x 1-2=0C 、ax 2+bx+c=0D 、x 2+2x=x 2-1 2、( 2014•广西玉林市、防城港市,第9题3分)x 1,x 2是关于x 的一元二次方程x 2﹣mx +m ﹣2=0的两个实数根,是否存在实数m 使+=0成立?则正确的是结论是( A ) A . m =0时成立 B . m =2时成立 C . m =0或2时成立 D . 不存在3、⊙O 的半径为5cm ,点P 是⊙O 内一点,OP=2cm ,⊙P 与⊙O 内切,则⊙P 的半径是( D )A 、3cmB 、7cmC 、10cmD 、3cm 或7cm 4、(2014•丽水,第9题3分)如图,半径为5的⊙A 中,弦BC ,ED 所对的圆心角分别是∠BAC ,∠EAD .已知DE=6,∠BAC+∠EAD=180°,则弦BC 的弦心距等于( D )A .B .C . 4D . 35、(4分)(2014•绍兴)如图,圆锥的侧面展开图使半径为3,圆心角为90°的扇形,则该圆锥的底面周长为( B )A . πB . πC .D .解:设底面圆的半径为r ,则:2πr==π.∴r=,∴圆锥的底面周长为. 6、(2014年山东烟台)如图,将△ABC 绕点P 顺时针旋转90°得到△A ′B ′C ′,则点P 的坐标是( B )A .(1,1)B . (1,2)C . (1,3)D . (1,4)7、某市决定改善城市容貌,绿化环境,计划过两年时间,绿地面积增加44%,这两地平均每年绿地面积的增长率是( )A 、19%B 、20%C 、21%D 、22%8、(2013浙江丽水)若二次函数2y 的图象经过点P(-2,4),则该图象ax必经过点(A )A. (2,4)B. (-2,-4)C. (-4,2)D. (4,-2)9、(3分)(2014•金华)如图是二次函数y=﹣x2+2x+4的图象,使y≤1成立的x的取值范围是()A、﹣1≤x≤3B、x≤﹣1C、x≥1D、x≤﹣1或x≥310、(2013•内江)若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( C )A.抛物线开口向上B.抛物线的对称轴是x=1C.当x=1时,y的最大值为﹣4 D.抛物线与x轴的交点为(﹣1,0),(3,0)解:∵抛物线过点(0,﹣3),∴抛物线的解析式为:y=x2﹣2x﹣3.A、抛物线的二次项系数为1>0,抛物线的开口向上,正确.B、根据抛物线的对称轴x=﹣=﹣=1,正确.C、由A知抛物线的开口向上,二次函数有最小值,当x=1时,y的最小值为﹣4,而不是最大值.故本选项错误.D、当y=0时,有x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,抛物线与x轴的交点坐标为(﹣1,0),(3,0).正确.11、(2014•宁波)已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( D )A、(﹣3,7)B、(﹣1,7)C、(﹣4,10)D、(0,10)解:∵点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,∴(a﹣2b)2+4×(a﹣2b)+10=2﹣4ab,a2﹣4ab+4b2+4a﹣8ab+10=2﹣4ab,(a+2)2+4(b﹣1)2=0,∴a+2=0,b﹣1=0,解得a=﹣2,b=1,∴a﹣2b=﹣2﹣2×1=﹣4,2﹣4ab=2﹣4×(﹣2)×1=10,∴点A的坐标为(﹣4,10),∵对称轴为直线x=﹣=﹣2,∴点A关于对称轴的对称点的坐标为(0,10).12、(2014年四川资阳,第10题3分)二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是(B)A. 4个B.3个C.2个D.1个解:∵抛物线和x轴有两个交点,∴b2﹣4ac>0,∴4ac﹣b2<0,∴①正确;∵对称轴是直线x﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,∴4a+c>2b,∴②错误;∵把(1,0)代入抛物线得:y=a+b+c<0,∴2a+2b+2c<0,∵b=2a,∴3b+2c<0,∴③正确;∵抛物线的对称轴是直线x=﹣1,∴y=a﹣b+c的值最大,即把(m,0)(m≠0)代入得:y=am2+bm+c<a﹣b+c,∴am2+bm+b<a,即m(am+b)+b<a,∴④正确;二、填空题13、设a,b是方程x2+x-2009=0是两个实数根,则a2+2a+b的值为 .14、已知:如图,PA,PB,DC分别切⊙O于A、B、E点,若PA=10cm,则△PCD的周长为。
长郡澄池杯数学试题及解析

1 初三·数学 2018长郡集团“澄池”杯初赛数学试题满分:100分时量:90分钟一、选择题(每小题6分,共36分)1.如果a b -=,那么代数式222a b ab a a b ⎛⎫+-⋅⎪-⎝⎭的值为( ) AB. C. D.2.如图是一个沿3×3正方形格纸的对角线AB 剪下的图形,一质点P 由A 点出发,沿格点线每次向右或向上运动1个单位长度,则点P 由A 点运动到B 点的不同路径共有( )A .4条B .5条C .6条D .7条3.如图,点E 在DBC ∆的边DB 上,点A 在DBC ∆内部,90DAE BAC ∠=∠=︒,AD AE =,AB AC =.给出下列结论:①BD CE =;②45ABD ECB ∠+∠=︒;③BD CE ⊥;④()22222BE AD AB CD =+-.其中正确的是( )A .②④B .①②③C .①③④D .①②③④4.若关于x 的分式方程2213m x x x+-=-无解,则m 的值为( ) A . 1.5-B .1C .0.5-或 1.5-D . 1.5-或25.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y (米)与甲出发的时间t (分)之间的关系如图所示,下列结论: ①甲步行的速度为60米/分;2 初三·数学②乙走完全程用了32分钟; ③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米. 其中正确的结论有( )A .1个B .2个C .3个D .4个6.如图,菱形ABCD 的边长是4厘米,60B ∠=︒,动点P 以1厘米/秒的速度自A 点出发沿AB 方向运动至B 点停止,动点Q 以2厘米/秒的速度自B 点出发沿折线BCD 运动至D 点停止.若点P 、Q 同时出发运动了t 秒,记BPQ ∆的面积为S 厘米2,下面图象中能表示S 与t 之间的函数关系的是( )A .B .C .D .二、填空题(每小题6分,共24分)7.按一定顺序排列的一列数叫做数列,如数列:1111261220⋅⋅⋅,,,,则这个数列的前2018个数的和为________.8.如图,正方形ABCD 的边长为1,点A 与原点重合,点B 在y 轴的正半轴上,点D 在x 轴的负半轴上,将正方形ABCD 绕点A 逆时针旋转至正方形'''AB C D 的位置,''B C 与CD 相交于点M ,则点M 的坐标为________.3 初三·数学9.如图,抛物线2y ax bx c =++(a ,b ,c 是常数,0a ≠)与x 轴交于A ,B 两点,顶点(),P m n .给出下列结论:①20a c +<;②若13,2y ⎛⎫- ⎪⎝⎭,21,2y ⎛⎫- ⎪⎝⎭,31,2y ⎛⎫⎪⎝⎭在抛物线上,则123y y y >>;③关于x 的方程20ax bx k ++=有实数解,则k c n ->; ④当1n a=-时,ABP ∆为等腰直角三角形.其中正确结论是________(填写序号).10.如图,在平面直角坐标系中,点1A ,2A ,3A ,…和1B ,2B ,3B ,…分别在直线15y x b =+和x 轴上.11OA B ∆,122B A B ∆,233B A B ∆,…都是等腰直角三角形.如果点()11,1A ,那么点2018A 的纵坐标是________.三、解答题(共40分)11.(共12分)某销售商准备在长沙采购一批丝绸,经调查,用10000元采购A型丝绸的件数与用8000元采购B型丝绸的件数相等,一件A型丝绸进价比一件B型丝绸进价多100元.⑴求一件A型、B型丝绸的进价分别为多少元?⑵若销售商购进A型、B型丝绸共50件,其中A型的件数不大于B型的件数,且不少于16件,设购进A型丝绸m件.①求m的取值范围.②已知A型的售价是800元/件,销售成本为2n元/件;B型的售价为600元/件,销售成本为n 元/件.如果50150n≤≤,求销售这批丝绸的最大利润w(元)与n(元)的函数关系式(每件销售利润=售价﹣进价﹣销售成本).12.(共12分)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB AE=,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.⑴若3AH=,1HE=,求ABE∆的面积;⑵若45ACB∠=︒,求证:DF=.4 初三·数学5 初三·数学13.(共16分)如图,抛物线26y ax x c =++交x 轴于A ,B 两点,交y 轴于点C .直线5y x =-经过点B ,C . ⑴求抛物线的解析式;⑵过点A 的直线交直线BC 于点M .①当AM BC ⊥时,过抛物线上一动点P (不与点B ,C 重合),作直线AM 的平行线交直线BC 于点Q ,若以点A ,M ,P ,Q 为顶点的四边形是平行四边形,求点P 的横坐标; ②连接AC ,当直线AM 与直线BC 的夹角等于ACB ∠的2倍时,请直接写出点M 的坐标.1 初三·数学2018长郡集团“澄池”杯初赛数学试题解析一、选择题 1-6 ABDCAD二、填空题 7.20182019. 8.3(1,)3-. 9.②和④. 10.20173()2.三、解答题 11.(1)设B 型丝绸的进价为x 元,则B 型丝绸的进价为(100)x +元 则100008000100x x=+,解得400x = 经检验得:400x =是原方程的解 100500x ∴+=一件A 型丝绸进价为500元,一件B 型丝绸进价为400元 (2)①由题意得5016m mm ≤-⎧⎨≥⎩解得:1625m ≤≤②(8005002)(600400)(50)w n m n m =--+---化简得:(100)1000050w n m n =-+-已知50150n ≤≤i. 当50100n ≤<时,1000n ->,即y 随m 的增大而增大当25m =时,销售这批丝绸的利润最大最大利润25(100+10000-507512500w n n n =-=-+) ii. 当100n =时,1000n -=10000501005000y =-⨯=,即最大利润为5000w =。
2015年高中数学竞赛复赛试题及答案

2015年高中数学竞赛 复赛试题及答案一、选择题(本大题共6小题,每小题6分,共36分.每小题各有四个选择支,仅有一个选择支正确.请把正确选择支号填在答题卡的相应位置.)1.从集合{1,3,6,8}中任取两个数相乘,积是偶数的概率是A .56B .23C .12D .132.若α是第四象限角,且2cos2sin212cos2sinαααα-=-,则2α是A .第一象限角B .第二象限角C .第三象限角D .第四象限角3. 已知点O A B 、、不在同一条直线上,点P 为该平面上一点,且22+OP OA BA =,则A .点P 不在直线AB 上 B .点P 在线段AB 上C .点P 在线段AB 的延长线上D .点P 在线段AB 的反向延长线上4.设+∈R n m ,,若直线04)1()1(=-+++y n x m 与圆4)2()2(22=-+-y x 相切,则m n +的取值范围是A .]31,0(+B .),31[+∞+C . ),222[+∞+D .]222,0(+ 5. 已知正方体C 1的棱长为C 1的各个面的中心为顶点的凸多面体记为C 2,以C 2的各个面的中心为顶点的凸多面体记为C 3,则凸多面体C 3的棱长为A .18B .29C .9D .266. 已知定义在R 上的奇函数)(x f ,满足(3)()f x f x +=-,且在区间]23,0[上是增函数,若方程m x f =)()0(<m 在区间[]6,6-上有四个不同的根1234,,,x x x x ,则1234x x x x +++=A .6-B . 6C .8-D .8 二、填空题(本大题共6小题,每小题6分,共36分.请把答案填在答题卡相应题的横线上.)7.已知1ln ,0()1,0x xf x x x⎧>⎪⎪=⎨⎪<⎪⎩,则不等式()1f x >-的解集为 ▲ .8.随机抽查某中学高二年级100名学生的视力情况,发现学生的视力全部介于4.3至5.2.现将这些数据分成9组,得其频率分布直方图如下.又知前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.6到5.0之间的学生有 ▲ 人.9.在ABC ∆中,角,,A B C 所对应的边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为 ▲ . 10.给出下列四个命题:(1)如果平面α与平面β相交,那么平面α内所有的直线都与平面β相交; (2)如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β;(3)如果平面α⊥平面β,那么平面α内与它们的交线不垂直的直线与平面β也不垂直; (4)如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β.其中真命题...的序号是 ▲ .(写出所有真命题的序号) 11.若动点00(,)M x y 在直线20x y --=上运动,且满足2200(2)(2)x y -++≤8,则2200x y +的取值范围是▲ .12.设函数()1121++⎪⎭⎫⎝⎛=x x x f x,0A 为坐标原点,n A 为函数()x f y =图象上横坐标为n (n ∈N *)的点,向量∑=-=nk k k n A A a 11,向量)0,1(=i ,设n θ为向量n a 与向量i 的夹角,满足15tan 3n k k θ=<∑的最大整数n 是▲ .答 题 卡一、选择题(本大题共6小题,每小题6分,共36分.)二、填空题(本大题共6小题,每小题6分,共36分.)7. 8. 9. 10. 11. 12.4.3 4.4 4.5 4.6 4.7 4.8 4.95.0 5.1.5.2三、解答题(本大题共6小题,共78分.解答应写出必要的文字说明、证明过程或演算步骤.) 13.(本小题满分12分)已知函数2()2sincos 222x x xf x =-+. (1)求函数()f x 的单调减区间;(2)该函数的图象可由)(sin R x x y ∈=的图象经过怎样的变换得到?(3)已知2π,63πα⎛⎫∈ ⎪⎝⎭,且6()5f α=,求()6f πα-的值.菱形ABCD 中,)2,1(A ,)0,6(=AB ,点M 是线段AB 的中点,线段CM 与BD 交于点P . (1)若向量)7,3(=AD ,求点C 的坐标; (2)当点D 运动时,求点P 的轨迹.如图,四边形ABCD 是边长为2的正方形,△ABE 为等腰三角形,AE =BE ,平面ABCD ⊥平面ABE ,点F 在CE 上,且BF ⊥平面ACE. (1)判断平面ADE 与平面BCE 是否垂直,并说明理由; (2)求点D 到平面ACE 的距离. ABCDEF如图,某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.根据环保部门的要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两个工厂都必须各自处理一部分污水.(1)设甲、乙两个化工厂每天各自处理的污水分别为x、y万m3,试根据环保部门的要求写出x、y 所满足的所有条件;(2)已知甲厂处理污水的成本是1200元/万m3,乙厂处理污水的成本是1000元/万m3,在满足环保部门要求的条件下,甲、乙两个化工厂每天应分别各自处理污水多少万m3,才能使这两个工厂处理污水的总费用最小?最小总费用是多少元?已知),,(42)(2R c b a c bx ax x f ∈++=.(1)当0≠a 时,若函数)(x f 的图象与直线x y ±=均无公共点,求证:;4142>-b ac (2)43,4==c b 时,对于给定的负数8-≤a ,记使不等式5|)(|≤x f 成立的x 的最大值为)(a M .问a 为何值时,)(a M 最大,并求出这个最大的)(a M ,证明你的结论.2014年高中数学竞赛决赛参考答案11.24一、选择题(本大题共6小题,每小题6分,共36分.)二、填空题(本大题共6小题,每小题6分,共36分.)7.),0()1,(e --∞ 8. 78 9.1210. (3)(4) 11. [2,8] 12. 3三、解答题(本大题共6小题,共78分.解答应写出必要的文字说明、证明过程或演算步骤.) 13.(本小题满分12分)解:(1)2()sin 2sin)2x f x x =+- sin x x =π2sin 3x ⎛⎫=+ ⎪⎝⎭. …………………2分 令πππππk x k 223322+≤+≤+,Z k ∈. 得ππππk x k 26726+≤≤+,Z k ∈. ()f x ∴的单调减区间为]267,26[ππππk k ++,Z k ∈. …………………5分 (2)先把函数)(sin R x x y ∈=的图象向左平移3π个单位,就得到函数))(3sin(R x x y ∈+=π的图象;再把其纵坐标伸长为原来的2倍,横坐标不变,就得到π2sin 3y x ⎛⎫=+ ⎪⎝⎭)(R x ∈的图象.…………7分(3)由56)(=αf 得:π62sin(),35α+=即π3sin(),35α+= …………………8分 因为2π,63πα⎛⎫∈⎪⎝⎭,所以π()(,)32παπ+∈.从而π4cos()35α+==- …………………10分 于是()2sin[()]2[sin()cos cos()sin ]6363636f πππππππαααα-=+-=+-+ 5433]21542353[2+=⨯+⨯=. …………………12分14.(本小题满分12分)解:(1)菱形ABCD 中,)7,9()0,6()7,3(=+=+=AB AD AC ,且)2,1(A ,所以)9,10(C .…4分 (2)设),(y x P ,则)2,7()0,6()2,1(--=---=-=y x y x AB AP BP . …………………5分又因为点M 是线段AB 的中点,线段CM 与BD 交于点P ,即点P 是ABC ∆的重心,从而有MP MC 3=,所以11133()3222AC AM MC AB MP AB AP AB AP AB =+=+=+-=-3(1,2)(6,0)(39,36)x y x y =---=-- …………………7分菱形ABCD 的对角线互相垂直,所以AC BP ⊥, 即 0)63,93()2,7(=--⋅--y x y x , 亦即0)63)(2()93()7(=--+-⋅-y y x x ,整理得:4)2()5(22=-+-y x (2≠y ), …………………11分 故P 点的轨迹是以)2,5(为圆心,2为半径的圆,除去与2=y 的交点. …………………12分15.(本题满分13分)解:(1)平面ADE 与平面BCE 垂直. …………………1分证明如下:因为BF ⊥平面ACE ,所以BF ⊥AE. …………………3分 因为平面ABCD ⊥平面ABE ,且ABCD 是正方形,BC ⊥AB ,CD平面ABCD ∩平面ABE =AB ,所以BC ⊥平面ABE ,从而BC ⊥AE. …………………6分 于是AE ⊥平面BCE ,故平面ADE ⊥平面BCE. ………………7分 (2)连结BD 交AC 与点M ,则点M 是BD 的中点,所以点D 与点B 到平面ACE 的距离相等. …………………8分 因为BF ⊥平面ACE ,所以BF 为点B 到平面ACE 的距离. …9分 因为AE ⊥平面BCE ,所以AE ⊥BE.又AE =BE ,所以△AEB 是等腰直角三角形. …………………10分 因为AB =2,所以BE=2sin 45︒= …………………11分在Rt △CBE 中,CE = 3B C B E BF CE ⨯=== 故点D 到平面ACE 的距离是332. …………………13分16.(本题满分13分)解:(1)据题意,x 、y 所满足的所有条件是()20.25001000.8(2) 1.40.2700100020 1.4x x y x y -⎧≤⎪⎪-+-⎪≤⎨⎪≤≤⎪⎪≤≤⎩, …………………4分即⎪⎩⎪⎨⎧≤≤≤≤≥+4.1021854y x y x . …………………5分 (2)设甲、乙两厂处理污水的总费用为z 元,则目标函数z =1200x +1000y =200(6x +5y ).…………7分 作可行域,如图. ……………10分 平移直线l :6x +5y=0,当直线经过点A (1,0.8)时,z 取最大值,此时ABCDEFMGz =1200×1+1000×0.8=2000(元). ……………12分故甲、乙两厂每天应分别处理1万m3、0.8万m3污水,才能使两厂处理污水的总费用最小,且最小总费用是2000元. …………………13分17.(本题满分14分)解:(1)由),,(42)(2R c b a c bx ax x f ∈++=与直线x y ±=均无公共点(0≠a ),可知x c bx ax ±=++422无解, ………………1分 由04)12(2=+++c x b ax 无解,得:016)12(2<-+=∆ac b , 整理得:b b ac +>-4142(1) ………………3分 由04)12(2=+-+c x b ax 无解,得:016)12(2<--=∆ac b ,整理得:b b ac ->-4142(2) ………………5分 由(1),(2)得: 4142>-b ac . ………………6分(2) 由43,4==c b ,所以38)(2++=x ax x f ………………7分因为a a f 163)4(-=-, 由8-≤a 得,5163)4(≤-=-aa f ………………9分 所以()5f x ≤恒成立,故不等式5|)(|≤x f 成立的x 的最大值也就是不等式()5f x ≥-成立的x 的最大值,…………10分 因此)(a M 为方程5382-=++x ax 的较大根,即aaa M 2424)(---=(8-≤a ) ………………11分当8-≤a 时,()M a ==a 的增函数, ………………13分 所以,当8a =-时,)(a M 取得最大值,其最大值为251)(+=a M . ………………14分 18.(本题满分14分)解:(1)由条件可得3n n x =,45n y n =+,根据题意知,23n n c =. …………………1分由k c 为数列{}n y 中的第m 项,则有2345km =+, …………………2分因910m *+∈N ,所以1k c +是数列{}n y 中的第910m +项. …………………5分(2)设在区间[1,2]上存在实数b 使得数列{}n x 和{}n y 有公共项,即存在正整数s ,t 使(1)sa a tb =++,∴1+-=a b a t s , 因自然数2a ≥,s ,t 为正整数,∴sa b -能被1a +整除. …………………6分 ①当1s =时,1s a b t a -=<+1a a *∉+N . ②当2s n = (n *∈N )时,若1b =,2222111[1()()()]111()s n nn a b a a a a a a a a ----==-=-+-+-++-++-- 2422(1)[1]n a a a a -*=-+++∈N ,即s a b -能被1a +整除, …………………8分 此时数列{}n x 和{}n y 有公共项组成的数列{}n z ,通项公式为2n n z a =(n *∈N );若2b =, 显然,222111111s n n a b a a a a a a *---==-∉++++N ,即s a b -不能被1a +整除. ………………9分 ③当21s n =+(n *∈N )时, 2()11n sb a a a b a t a a --==++, …………………10分 若2a >,则2n b a a *-∉N ,又a 与1a +互质,故此时2()1n b a a a t a *-=∉+N . ………………11分 若2a =,要2n b a a *-∈N ,则要2b =,此时221n n b a a a-=-, …………………12分 由②知,21n a -能被1a +整除, 故2()1n b a a a t a *-=∈+N ,即s a b -能被1a +整除. 当且仅当2b a ==时,b a S -能被1a +整除. …………………13分此时数列{}n x 和{}n y 有公共项组成的数列{}n z ,通项公式为212n n z +=(n *∈N ).综上所述,存在{1,2}b ∈,使得数列{}n x 和{}n y 有公共项组成的数列{}n z ,且当1b =时,数列2n n z a=(n *∈N );当2b a ==时,数列212n n z +=(n *∈N ). ……………14分18.(本题满分14分)已知数列{}n x 和{}n y 的通项公式分别为n n x a =和()1,n y a n b n N +=++∈.(1)当3,5a b ==时,记2n n c x =,若k c 是{}n y 中的第m 项(,)k m N +∈,试问:1k c +是数列{}n y 中的第几项?请说明理由.(2)对给定自然数2a ≥,试问是否存在{}1,2b ∈,使得数列{}n x 和{}n y 有公共项?若存在,求出b 的值及相应的公共项组成的数列{}n z ,若不存在,请说明理由.。
湖南省长沙市2018年长郡集团“澄池杯”复赛九年级数学试卷(含解析)

2018年长郡集团“澄池杯”复赛初三数学试卷一.选择题(共6小题)1.规定:在平面直角坐标系中,如果点P的坐标为(m,n),向量可以用点P的坐标表示为:=(m,n).已知:=(x1,y1),=(x2,y2),如果x1•x2+y1•y2=0,那么与互相垂直.下列四组向量,互相垂直的是()A.=(3,2),=(﹣2,3)B.=(﹣1,1),=(+1,1)C.=(3,20180),=(﹣,﹣1)D.=(,﹣),=(()2,4)2.某篮球队10名队员的年龄结构如表,已知该队队员年龄的中位数为21.5,则众数与方差分别为()A.22,3 B.22,4 C.21,3 D.21,43.二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①4a+2b+c>0;②5a﹣b+c=0;③若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1;④若方程|ax2+bx+c|=1有四个根,则这四个根的和为﹣4.其中正确的结论有()A.1个B.2个C.3个D.4个4.已知关于x的一元二次方程mx2﹣(m+2)x+=0有两个不相等的实数根x1,x2.若+=4m,则m的值是()A.2 B.﹣1 C.2或﹣1 D.不存在5.若数a使关于x的不等式组,有且仅有三个整数解,且使关于y的分式方程+=1有整数解,则满足条件的所有a的值之和是()A.﹣10 B.﹣12 C.﹣16 D.﹣186.如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD 与△PMN重叠部分的面积为y,则y与x的大致图象是()A.B.C.D.二.填空题(共4小题)7.在平面直角坐标系内有两点A、B,其坐标为A(﹣1,﹣1),B(2,7),点M为x轴上的一个动点,若要使MB﹣MA的值最大,则点M的坐标为.8.折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在线段AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=.9.在﹣4、﹣2,1、2四个数中、随机取两个数分别作为函数y=ax2+bx+1中a,b的值,则该二次函数图象恰好经过第一、二、四象限的概率为.10.定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推……△A n﹣1B n﹣1C n﹣1经γ(n,180°)变换后得△A n B n∁n,则点A1的坐标是,点A2018的坐标是.三.解答题(共3小题)11.随着龙虾节的火热举办,某龙虾养殖大户为了发挥技术优势,一次性收购了10000kg 小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养10天的总成本为166000,放养30天的总成本为178000元.设这批小龙虾放养t天后的质量为akg,销售单价为y元/kg,根据往年的行情预测,a与t的函数关系为a=,y与t的函数关系如图所示.(1)设每天的养殖成本为m元,收购成本为n元,求m与n的值;(2)求y与t的函数关系式;(3)如果将这批小龙虾放养t天后一次性出售所得利润为W元.问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大?最大利润是多少?(总成本=放养总费用+收购成本;利润=销售总额﹣总成本)12.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.13.如图,在边长为1的正方形ABCD中,动点E、F分别在边AB、CD上,将正方形ABCD 沿直线EF折叠,使点B的对应点M始终落在边AD上(点M不与点A、D重合),点C落在点N处,MN与CD交于点P,设BE=x.(1)当AM=时,求x的值;(2)随着点M在边AD上位置的变化,△PDM的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;(3)设四边形BEFC的面积为S,求S与x之间的函数表达式,并求出S的最小值.参考答案与试题解析一.选择题(共6小题)1.规定:在平面直角坐标系中,如果点P的坐标为(m,n),向量可以用点P的坐标表示为:=(m,n).已知:=(x1,y1),=(x2,y2),如果x1•x2+y1•y2=0,那么与互相垂直.下列四组向量,互相垂直的是()A.=(3,2),=(﹣2,3)B.=(﹣1,1),=(+1,1)C.=(3,20180),=(﹣,﹣1)D.=(,﹣),=(()2,4)【分析】根据垂直的向量满足的条件判断即可;【解答】解:A、∵3×(﹣2)+2×3=0,∴与垂直,故本选项符合题意;B、∵(﹣1)(+1)+1×1=2≠0,∴与不垂直,故本选项不符合题意;C、∵3×(﹣)+1×(﹣1)=﹣2≠0,∴与不垂直,故本选项不符合题意;D、∵×()2+(﹣)×4=2≠0,∴与不垂直,故本选项不符合题意,故选:A.2.某篮球队10名队员的年龄结构如表,已知该队队员年龄的中位数为21.5,则众数与方差分别为()A.22,3 B.22,4 C.21,3 D.21,4【分析】先根据数据的总个数及中位数得出x=3、y=2,再利用众数和方差的定义求解可得.【解答】解:∵共有10个数据,∴x+y=5,又该队队员年龄的中位数为21.5,即,∴x=3、y=2,则这组数据的众数为21,平均数为=22,所以方差为×[(19﹣22)2+(20﹣22)2+3×(21﹣22)2+2×(22﹣22)2+2×(24﹣22)2+(26﹣22)2]=4,故选:D.3.二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①4a+2b+c>0;②5a﹣b+c=0;③若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1;④若方程|ax2+bx+c|=1有四个根,则这四个根的和为﹣4.其中正确的结论有()A.1个B.2个C.3个D.4个【分析】根据二次函数的性质一一判断即可.【解答】解:∵抛物线的顶点坐标(﹣2,﹣9a),∴﹣=﹣2,=﹣9a,∴b=4a,c=﹣5a,∴抛物线的解析式为y=ax2+4ax﹣5a,∴4a+2b+c=4a+8a﹣5a=7a>0,故①正确,5a﹣b+c=5a﹣4a﹣5a=﹣4a<0,故②错误,∵抛物线y=ax2+4ax﹣5a交x轴于(﹣5,0),(1,0),∴若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1,正确,故③正确,若方程|ax2+bx+c|=1有四个根,设方程ax2+bx+c=1的两根分别为x1,x2,则=﹣2,可得x1+x2=﹣4,设方程ax2+bx+c=﹣1的两根分别为x3,x4,则=﹣2,可得x3+x4=﹣4,所以这四个根的和为﹣8,故④错误,故选:B.4.已知关于x的一元二次方程mx2﹣(m+2)x+=0有两个不相等的实数根x1,x2.若+=4m,则m的值是()A.2 B.﹣1 C.2或﹣1 D.不存在【分析】先由二次项系数非零及根的判别式△>0,得出关于m的不等式组,解之得出m 的取值范围,再根据根与系数的关系可得出x1+x2=,x1x2=,结合+=4m,即可求出m的值.【解答】解:∵关于x的一元二次方程mx2﹣(m+2)x+=0有两个不相等的实数根x1、x2,∴,解得:m>﹣1且m≠0.∵x1、x2是方程mx2﹣(m+2)x+=0的两个实数根,∴x1+x2=,x1x2=,∵+=4m,∴=4m,∴m=2或﹣1,∵m>﹣1,∴m=2.故选:A.5.若数a使关于x的不等式组,有且仅有三个整数解,且使关于y的分式方程+=1有整数解,则满足条件的所有a的值之和是()A.﹣10 B.﹣12 C.﹣16 D.﹣18【分析】思想利用不等式组根据已知条件确定a的取值范围,求出分式方程的解,求出满足有整数解的a的值即可解决问题;【解答】解:,由①得到:x≥﹣3,由②得到:x≤,∵不等式组有且仅有三个整数解,∴﹣1≤<0,解得﹣8≤a<﹣3.由分式方程+=1,解得y=﹣,∵有整数解,∴a=﹣8或﹣4,﹣8﹣4=﹣12,故选:B.6.如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD 与△PMN重叠部分的面积为y,则y与x的大致图象是()A.B.C.D.【分析】在Rt△PMN中解题,要充分运用好垂直关系和45度角,因为此题也是点的移动问题,可知矩形ABCD以每秒1cm的速度由开始向右移动到停止,和Rt△PMN重叠部分的形状可分为下列三种情况,(1)0≤x≤2;(2)2<x≤4;(3)4<x≤6;根据重叠图形确定面积的求法,作出判断即可.【解答】解:∵∠P=90°,PM=PN,∴∠PMN=∠PNM=45°,由题意得:CM=x,分三种情况:①当0≤x≤2时,如图1,边CD与PM交于点E,∵∠PMN=45°,∴△MEC是等腰直角三角形,此时矩形ABCD与△PMN重叠部分是△EMC,∴y=S△EMC=CM•CE=;故选项B和D不正确;②如图2,当D在边PN上时,过P作PF⊥MN于F,交AD于G,∵∠N=45°,CD=2,∴CN=CD=2,∴CM=6﹣2=4,即此时x=4,当2<x≤4时,如图3,矩形ABCD与△PMN重叠部分是四边形EMCD,过E作EF⊥MN于F,∴EF=MF=2,∴ED=CF=x﹣2,∴y=S梯形EMCD=CD•(DE+CM)==2x﹣2;③当4<x≤6时,如图4,矩形ABCD与△PMN重叠部分是五边形EMCGF,过E作EH⊥MN于H,∴EH=MH=2,DE=CH=x﹣2,∵MN=6,CM=x,∴CG=CN=6﹣x,∴DF=DG=2﹣(6﹣x)=x﹣4,∴y=S梯形EMCD﹣S△FDG=﹣=×2×(x﹣2+x)﹣=﹣+6x﹣10,故选项A正确;故选:A.二.填空题(共4小题)7.在平面直角坐标系内有两点A、B,其坐标为A(﹣1,﹣1),B(2,7),点M为x轴上的一个动点,若要使MB﹣MA的值最大,则点M的坐标为.【分析】要使得MB﹣MA的值最大,只需取其中一点关于x轴的对称点,与另一点连成直线,然后求该直线x轴交点即为所求.【解答】解:取点B关于x轴的对称点B′,则直线AB′交x轴于点M.点M即为所求.设直线AB′解析式为:y=kx+b把点A(﹣1,﹣1)B′(2,﹣7)代入解得∴直线AB′为:y=﹣2x﹣3,当y=0时,x=﹣∴M坐标为(﹣,0)故答案为:(﹣,0)8.折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在线段AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=3+2.【分析】设AD=x,则AB=x+2,利用折叠的性质得DF=AD,EA=EF,∠DFE=∠A=90°,则可判断四边形AEFD为正方形,所以AE=AD=x,再根据折叠的性质得DH=DC=x+2,当AH=AE﹣HE=x﹣1,然后根据勾股定理得到x2+(x﹣1)2=(x+2)2,再解方程求出x 即可.【解答】解:设AD=x,则AB=x+2,∵把△ADE翻折,点A落在DC边上的点F处,∴DF=AD,EA=EF,∠DFE=∠A=90°,∴四边形AEFD为正方形,∴AE=AD=x,∵把△CDG翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,∴DH=DC=x+2,∵HE=1,当AH=AE﹣HE=x﹣1,在Rt△ADH中,∵AD2+AH2=DH2,∴x2+(x﹣1)2=(x+2)2,整理得x2﹣6x﹣3=0,解得x1=3+2,x2=3﹣2(舍去),即AD的长为3+2.故答案为3+2.9.在﹣4、﹣2,1、2四个数中、随机取两个数分别作为函数y=ax2+bx+1中a,b的值,则该二次函数图象恰好经过第一、二、四象限的概率为.【分析】画树状图展示所有12种等可能的结果数,根据二次函数的性质,找出满足a>0,b<0的结果数,然后根据概率公式求解.【解答】解:画树状图为:共有12种等可能的结果数,满足a>0,b<0的结果数为4,但a=1,b=﹣2和a=2,b=﹣2时,抛物线不过第四象限,所以满足该二次函数图象恰好经过第一、二、四象限的结果数为2,所以该二次函数图象恰好经过第一、二、四象限的概率==.故答案为.10.定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推……△A n﹣1B n﹣1C n﹣1经γ(n,180°)变换后得△A n B n∁n,则点A1的坐标是(﹣,﹣),点A2018的坐标是(﹣,).【分析】分析图形的γ(a,θ)变换的定义可知:对图形γ(n,180°)变换,就是先进行向右平移n个单位变换,再进行关于原点作中心对称变换.向右平移n个单位变换就是横坐标加n,纵坐标不变,关于原点作中心对称变换就是横纵坐标都变为相反数.写出几次变换后的坐标可以发现其中规律.【解答】解:根据图形的γ(a,θ)变换的定义可知:对图形γ(n,180°)变换,就是先进行向右平移n个单位变换,再进行关于原点作中心对称变换.△ABC经γ(1,180°)变换后得△A1B1C1,A1 坐标(﹣,﹣)△A1B1C1经γ(2,180°)变换后得△A2B2C2,A2坐标(﹣,)△A2B2C2经γ(3,180°)变换后得△A3B3C3,A3坐标(﹣,﹣)△A3B3C3经γ(4,180°)变换后得△A4B4C4,A4坐标(﹣,)△A4B4C4经γ(5,180°)变换后得△A5B5C5,A5坐标(﹣,﹣)依此类推……可以发现规律:A n纵坐标为:当n是奇数,A n横坐标为:﹣当n是偶数,A n横横坐标为:﹣当n=2018时,是偶数,A2018横坐标是﹣,纵坐标为故答案为:(﹣,﹣),(﹣,).三.解答题(共3小题)11.随着龙虾节的火热举办,某龙虾养殖大户为了发挥技术优势,一次性收购了10000kg 小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养10天的总成本为166000,放养30天的总成本为178000元.设这批小龙虾放养t天后的质量为akg,销售单价为y元/kg,根据往年的行情预测,a与t的函数关系为a=,y与t的函数关系如图所示.(1)设每天的养殖成本为m元,收购成本为n元,求m与n的值;(2)求y与t的函数关系式;(3)如果将这批小龙虾放养t天后一次性出售所得利润为W元.问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大?最大利润是多少?(总成本=放养总费用+收购成本;利润=销售总额﹣总成本)【分析】(1)根据题意列出方程组,求出方程组的解得到m与n的值即可;(2)根据图象,分类讨论利用待定系数法求出y与P的解析式即可;(3)根据W=ya﹣mt﹣n,表示出W与t的函数解析式,利用一次函数与二次函数的性质求出所求即可.【解答】解:(1)依题意得,解得:;(2)当0≤t≤20时,设y=k1t+b1,由图象得:,解得:∴y=t+16;当20<t≤50时,设y=k2t+b2,由图象得:,解得:,∴y=﹣t+32,综上,;(3)W=ya﹣mt﹣n,当0≤t≤20时,W=10000(t+16)﹣600t﹣160000=5400t,∵5400>0,∴当t=20时,W最大=5400×20=108000,当20<t≤50时,W=(﹣t+32)(100t+8000)﹣600t﹣160000=﹣20t2+1000t+96000=﹣20(t﹣25)2+108500,∵﹣20<0,抛物线开口向下,∴当t=25,W最大=108500,∵108500>108000,∴当t=25时,W取得最大值,该最大值为108500元.12.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.【分析】(1)设出抛物线顶点坐标,把C坐标代入求出即可;(2)由△BCQ与△BCP的面积相等,得到PQ与BC平行,①过P作PQ∥BC,交抛物线于点Q,如图1所示;②设G(1,2),可得PG=GH=2,过H作直线Q2Q3∥BC,交x轴于点H,分别求出Q的坐标即可;(3)存在点M,N使四边形MNED为正方形,如图2所示,过M作MF∥y轴,过N作NF ∥x轴,过N作NH∥y轴,则有△MNF与△NEH都为等腰直角三角形,设M(x1,y1),N (x2,y2),设直线MN解析式为y=﹣x+b,与二次函数解析式联立,消去y得到关于x 的一元二次方程,利用根与系数关系表示出NF2,由△MNF为等腰直角三角形,得到MN2=2NF2,若四边形MNED为正方形,得到NE2=MN2,求出b的值,进而确定出MN的长,即为正方形边长.【解答】解:(1)设y=a(x﹣1)2+4(a≠0),把C(0,3)代入抛物线解析式得:a+4=3,即a=﹣1,则抛物线解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3;(2)由B(3,0),C(0,3),得到直线BC解析式为y=﹣x+3,∵S△PBC=S△QBC,∴PQ∥BC,①过P作PQ∥BC,交抛物线于点Q,如图1所示,∵P(1,4),∴直线PQ解析式为y=﹣x+5,联立得:,解得:或,即(1,4)与P重合,Q1(2,3);②∵S△BCQ=S△BCP,∴PG=GH∵直线BC的解析式为y=﹣x+3,P(1,4)∴G(1,2),∴PG=GH=2,过H作直线Q2Q3∥BC,交x轴于点H,则直线Q2Q3解析式为y=﹣x+1,联立得:,解得:或,∴Q2(,),Q3(,);(3)存在点M,N使四边形MNED为正方形,如图2所示,过M作MF∥y轴,过N作NF∥x轴,过N作NH∥y轴,则有△MNF与△NEH 都为等腰直角三角形,设M(x1,y1),N(x2,y2),设直线MN解析式为y=﹣x+b,联立得:,消去y得:x2﹣3x+b﹣3=0,∴NF2=|x1﹣x2|2=(x1+x2)2﹣4x1x2=21﹣4b,∵△MNF为等腰直角三角形,∴MN2=2NF2=42﹣8b,∵H(x2,﹣x2+3),∴NH2=[y2﹣(﹣x2+3)]2=(﹣x2+b+x2﹣3)2=(b﹣3)2,∴NE2=(b﹣3)2,若四边形MNED为正方形,则有NE2=MN2,∴42﹣8b=(b2﹣6b+9),整理得:b2+10b﹣75=0,解得:b=﹣15或b=5,∵正方形边长为MN=,∴MN=9或.13.如图,在边长为1的正方形ABCD中,动点E、F分别在边AB、CD上,将正方形ABCD 沿直线EF折叠,使点B的对应点M始终落在边AD上(点M不与点A、D重合),点C落在点N处,MN与CD交于点P,设BE=x.(1)当AM=时,求x的值;(2)随着点M在边AD上位置的变化,△PDM的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;(3)设四边形BEFC的面积为S,求S与x之间的函数表达式,并求出S的最小值.【分析】(1)利用勾股定理构建方程,即可解决问题;(2)设AM=y,则BE=EM=x,MD=1﹣y,在Rt△AEM中,由勾股定理得出x、y的关系式,可证Rt△AEM∽Rt△DMP,根据相似三角形的周长比等于相似比求△DMP的周长;(3)作FH⊥AB于H.则四边形BCFH是矩形.连接BM交EF于O,交FH于K.根据梯形的面积公式构建二次函数,利用二次函数的性质解决最值问题即可;【解答】解:(1)如图,在Rt△AEM中,AE=1﹣x,EM=BE=x,AM=,∵AE2+AM2=EM2,∴(1﹣x)2+()2=x2,∴x=.(2)△PDM的周长不变,为2.理由:设AM=y,则BE=EM=x,MD=1﹣y,在Rt△AEM中,由勾股定理得AE2+AM2=EM2,(1﹣x)2+y2=x2,解得1+y2=2x,∴1﹣y2=2(1﹣x)∵∠EMP=90°,∠A=∠D,∴Rt△AEM∽Rt△DMP,∴=,即=,解得DM+MP+DP==2.∴△DMP的周长为2.(3)作FH⊥AB于H.则四边形BCFH是矩形.连接BM交EF于O,交FH于K.在Rt△AEM中,AM==,∵B、M关于EF对称,∴BM⊥EF,∴∠KOF=∠KHB,∵∠OKF=∠BKH,∴∠KFO=∠KBH,∵AB=BC=FH,∠A=∠FHE=90°,∴△ABM≌△HFE,∴EH=AM=,∴CF=BH=x﹣,∴S=(BE+CF)•BC=(x+x﹣)=[()2﹣+1]=(﹣)2+.当=时,S有最小值=.。
2018.9.16长郡集团澄池杯复赛-数学解析(高清版)

A.
B.
C.
D.
【解答】解:
∵∠P=90°,PM=PN, ∴∠PMN=∠PNM=45°,
4
由题意得:CM=x, 分三种情况: ①当 0≤x≤2 时,如图 1,边 CD 与 PM 交于点 E, ∵∠PMN=45°, ∴△MEC 是等腰直角三角形, 此时矩形 ABCD 与△PMN 重叠部分是△EMC, ∴y=S△EMC= CM•CE= ;
A.1 个
B.2 个
C.3 个
【解答】解:
ቤተ መጻሕፍቲ ባይዱ
∵抛物线的顶点坐标(﹣2,﹣9a),
D.4 个
∴﹣ =﹣2,
=﹣9a,
∴b=4a,c=﹣5a, ∴抛物线的解析式为 y=ax2+4ax﹣5a, ∴4a+2b+c=4a+8a﹣5a=7a>0,故①正确, 5a﹣b+c=5a﹣4a﹣5a=﹣4a<0,故②错误, ∵抛物线 y=ax2+4ax﹣5a 交 x 轴于(﹣5,0),(1,0), ∴若方程 a(x+5)(x﹣1)=﹣1 有两个根 x1 和 x2,且 x1<x2,则﹣5<x1<x2 <1,正确,故③正确, 若方程|ax2+bx+c|=1 有四个根,则这四个根的和为﹣8,故④错误, 故选:B.
1
则这组数据的众数为 21,平均数为
=22,
所以方差为 ×[(19﹣22)2+(20﹣22)2+3×(21﹣22)2+2×(22﹣
22)2+2×(24﹣22)2+(26﹣22)2]=4, 故选:D.
3.二次函数 y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2, ﹣9a),下列结论:①4a+2b+c>0;②5a﹣b+c=0;③若方程 a(x+5)(x﹣1) =﹣1 有两个根 x1 和 x2,且 x1<x2,则﹣5<x1<x2<1;④若方程|ax2+bx+c|=1 有四个根,则这四个根的和为﹣4.其中正确的结论有( )
2015年湖南长沙长郡中学初一数学竞赛试题

2015年湖南长沙长郡中学初一数学竞赛试题2015年5月24日考试时量:60分钟 满分:100分一、选择题:(每个题目只有一个正确答案,每题5分,共30分) 1、若不等式组⎩⎨⎧>-<+m x x x 148的解集是x >3,则m 的取值范围是 ( )A. m >3 B .m ≥3 C .m ≤3 D .m <3 2、用去分母方法解分式方程xx x x m x x 11122+=++-+,产生增根,则m 的值为( ) A .–1或–2 B. 1或–2 C.1或2 D. –1或23、 已知31)53(-=a ,21)35(=b ,21)34(-=c ,则a,b,c 三个数的大小关系是A .a b c << B. b a c << C. c b a << D. c a b << 4、点P 是直线04=-+y x 上一动点,O 为原点,则|OP|的最小值为( ) A. 2 B. 2 C. 22 D. 45、已知梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于O ,△AOD 的面积为4,△BOC 的面积为9,则梯形ABCD 的面积为( )(A )25 (B )24 (C )22 (D )266、矩形纸片ABCD 中,AB=3cm ,BC=4cm ,现将纸片折叠压平,使A 与C 重合,设折痕为EF ,则重叠部分△AEF 的面积等于( ).(A )73757375()()()881616B C D二.填空题:(每题6分,共36分) 7、已知=-=+xx x x 1,41则_________ 8、方程xx x x 34=-的解为 9、在△ABC 中,AB =10,AC =26,BC =10,设能完全覆盖△ABC 的圆的半径为R .则R 的最小值是 .10、若βα、是方程0532=--x x 的两个实数根,则ββα3222-+的值=11、分解因式:8)43)(3322-++-+x x x x (=12、已知x 为实数,则分式12156322++++x x x x 的最小值为学校 姓名 性别 联系电话三、解答题(本大题共3题,13题10分,14,15每题12分,共34分)13、如图:已知△ABC ,E 为AB 的中点,D 为AE 的中点,且AE=AC, 求证:BC=2CD14、“六一”前夕,某玩具经销商用去2350元购进A 、B 、C 三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A 种玩具x 套,B 种玩具y 套,三种电动玩具的进价和售价如表中所示: ⑴用含x 、y 的代数式表示购进C 种玩具的套数;⑵求y 与x 之间的函数关系式;⑶假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元。
2018年长郡集团澄池杯复赛数学试卷高清解析(含试题来源)
D.4 个
4. ( 2018• 潍坊)已知关于 x 的一元二次方程 mx2 ﹣( m+2 ) x+
m =0 有两个不相等的实数根 x1 , x2 .若 4
1 1 4m ,则 m 的值是( x1 x2
A.2 B.﹣1Leabharlann ) C.2 或﹣1 D.不存在
1 1 x 1 x 1 5. (2018•重庆)若数 a 使关于 x 的不等式组 3 ,有且仅有三个整数解,且使关于 y 的分 2 2 x a 31 x
m2 1 1 1 ,x1 x2 ,结合 4m ,即可求出 m 的值. m 4 x1 x2 m =0 有两个不相等的实数根 x1、x2, 4
【解答】解:∵关于 x 的一元二次方程 mx2﹣(m+2)x+
∴
m 0 m 2 m 2 4m 0 4
第 6 页 共 18 页
2018 年长郡集团“澄池”杯复赛数学试卷 试题解析
一.选择题(共 6 小题) 1. 【分析】根据垂直的向量满足的条件判断即可; 【解答】解:A.∵3×(﹣2)+2×3=0,∴ B.∵( 2 ﹣1) ( 2 +1)+1×1=2≠0,∴ C.∵3×(﹣ 与 与 垂直,故本选项符合题意; 不垂直,故本选项不符合题意;
第 2 页 共 18 页
式方程
3y a 12 1 有整数解,则满足条件的所有 a 的值之和是( y2 2 y
B.﹣12 C.﹣16
) D.﹣18
A.﹣10
6. (2018•黄石)如图,在 Rt△PMN 中,∠P=90°,PM=PN,MN=6cm,矩形 ABCD 中 AB=2cm,BC=10cm, 点 C 和点 M 重合,点 B、C(M) 、N 在同一直线上,令 Rt△PMN 不动,矩形 ABCD 沿 MN 所在直线以每秒 1cm 的速度向右移动,至点 C 与点 N 重合为止,设移动 x 秒后,矩形 ABCD 与△PMN 重叠部分的面积为 y, 则 y 与 x 的大致图象是( )
2015年下学期九年级数学竞赛试题及答案

2015年下学期九年级数学竞赛试题时量:120分钟 满分:120分一、选择题(共8道小题,每小题4分,满分32分)1.若y 与x 成反比例,x 与z 成反比例,则y 是z 的( )A .正比例函数B .反比例函数C .一次函数D .不能确定2.反比例函数k y x =和正比例函数y mx =的图象如图.由此可以得到方程k mx x=的实数根为( ) A .2x =- B .1x =C .12x =,22x =-D .11x =,22x =-第2题图 第3题图 第4题图 第5题图A .12AE AC =B .12DE BC = C .13ADE ABC =△的周长△的周长D .13ADE ABC =△的面积△的面积 4.如上图,在网格中,小正方形的边长均为1,点A ,B ,C 都在格点上,则ABC ∠的正切值是( )A .2B .5C .5D .125.如上图,四边形ABCD 为O ⊙的内接四边形,已知100BOD ∠=︒,则BCD ∠的度数为( )A .50°B .80°C .100°D .130°6.已知1sin cos 8αα⋅=,4590α︒<<︒,则cos sin αα-=( )A .2B .2-C .34D .2±7.要估计鱼塘中的鱼数,养鱼者首先从鱼塘中打捞了50条鱼,在每条鱼身上做好记号后把这些鱼放归鱼塘,再从鱼塘中打捞出100条鱼,发现只有两条鱼是刚才做了记号的鱼.假设鱼在鱼塘内均匀分布,那么估计这个鱼塘的鱼数约为( )A .5000条B .2500条C .1750条D .1250条8.已知二次函数223y x x =-++,当2x ≥时,y 的取值范围是( )A .3y ≥B .3y ≤C .3y >D .3y <二、填空题(共7道小题,每小题4分,满分28分)9.如下图,在平面直角坐标系中,反比例函数()0k y x x=>的图象交矩形OABC 的边AB 于点D ,交边BC 于点E ,且2BE EC =.若四边形ODBE 的面积为6,则k = .第9题图 第11题图 第14题图 第15题图10.若()()222223100x y x y +-+-=,则22x y += .11.如上图,AD DF FB ==,DE FG BC ∥∥,则 S S S =ⅠⅡⅢ∶∶ . 12.已知α是锐角且3tan 4α=,则sin cos αα+= . 13.抛物线在223y x x =--在x 轴上截得的线段长度是 .14.如上图,已知点A (0,1),B (0,﹣1),以点A 为圆心,AB 为半径作圆,交x 轴的正半轴于点C ,则BAC ∠等于 度.15.已知二次函数()20y ax bx c a =++≠的图象如图所示,给出以下结论:0a b c ++<①;0a b c -+<②;20b a +<③;0abc >④,其中所有正确结论的序号是 .三、解答题(共六道小题,每小题10分,满分60分)16.(10分)若m 、n 满足2320m m +-==0,2320n n +-=,求m n n m+的值.17.(10分)如图,建筑物AB后有一座假山,其坡度为 1 i =,山坡上E 点处有一凉亭,测得假山坡脚C 与建筑物水平距离25BC =米,与凉亭距离20CE =米,某人从建筑物顶端测得E 点的俯角为45︒,求建筑物AB 的高.18.(10分)随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业旅游年消费情况进行了问卷调查,随机抽取部分员工,记录每个人消费金额,并将调查数据(1)a = ,b = ,c = .并将条形统计图补充完整;(2)这次调查中,个人年消费金额的中位数出现在 组;(3)若这个企业有3000多名员工,请你估计个人旅游年消费金额在6000元以上的人数.19.(10分)如图,在ABC △中,AB AC =,以AC 为直径的O ⊙交AB 于点D ,交BC 于点E .(1)求证:BE CE =;(2)若2BD =,3BE =,求AC 的长.20.(10分)如图,在ABC △中,AB AC =,点P 、D 分别是BC 、AC 边上的点,且APD B ∠=∠.(1)求证:AC CD CP BP ⋅=⋅;(2)若10AB =,12BC =,PD AB ∥,求BP 的长.21.(10分)如图,在平面直角坐标系中,正方形OABC 的边长为4,顶点A 、C 分别在x 轴、y 轴的正半轴,抛物线212y x bx c =-++经过B 、C 两点,点D 为抛物线的顶点,连接AC 、BD 、CD . (1)求此抛物线的解析式.(2)求此抛物线顶点D 的坐标和四边形ABCD 的面积.参考答案16.解:∵m 2+3m ﹣2=0,n 2+3n ﹣2=0,∴当m=n 时,原式=1+1=2; ………………………………………………………3分当m ≠n 时,m 、n 可看作一元二次方程x 2+3x ﹣2=0的两不等根,∴m+n=﹣3,mn=﹣2,………………………………………………………………6分 ∴原式= ===﹣,…………………………………………9分∴的值为2或﹣.…………………………………………………………10分17.解:过点E 作EF ⊥BC 于点F ,过点E 作EN ⊥AB 于点N ,∵建筑物AB 后有一座假山,其坡度为i=1:,∴设EF=x ,则FC=x ,……………………………………………………………2分∵CE=20米,∴x 2+(x )2=400,…………………………………………………………………4分 解得:x=10,则FC=10m ,…………………………………………………………………………6分∵BC=25m ,∴BF=NE=(25+10)m ,)∴AB=AN+BN=NE+EF=10+25+10=(35+10)m ,……………………………9分答:建筑物AB 的高为(35+10)m .……………………………………………10分18.解:(1)a=36,b=0.30,c=120, ………………………………………………………3分 C 组的频数为120﹣18﹣36﹣24﹣12=30,补充图见右上图……………………………………5分(2)∵共120人,∴中位数为第60和第61人的平均数,∴中位数应该落在C 小组内;…7分(3)个人旅游年消费金额在6000元以上的人数3000×(0.10+0.20)=900人.………………10分3019.(1)证明:连结AE,如图,∵AC为⊙O的直径,∴∠AEC=90°,………………………………………………………………2分∴AE⊥BC,……………………………………………………………………………………………3分而AB=AC,∴BE=CE;………………………………………………………………………………5分(2)连结DE,如图,∵BE=CE=3,∴BC=6,………………………………………………………………………………6分∵∠BED=∠BAC,而∠DBE=∠CBA,∴△BED∽△BAC,……………………………………8分∴=,即=,∴BA=9,∴AC=BA=9.……………………………………………………10分20.解:(1)∵AB=AC,∴∠B=∠C.∵∠APD=∠B,∴∠APD=∠B=∠C.∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,∴∠BAP=∠DPC,∴△ABP∽△PCD,∴=,∴AB•CD=CP•BP.∵AB=AC,∴AC•CD=CP•BP;……………………………………………………………………5分(2)∵PD∥AB,∴∠APD=∠BAP.∵∠APD=∠C,∴∠BAP=∠C.∵∠B=∠B,∴△BAP∽△BCA,∴=.∵AB=10,BC=12,∴=,∴BP=.………………………………………………………10分21.解:(1)由已知得:C(0,4),B(4,4),把B与C坐标代入y=﹣x2+bx+c得:,……………………………………………2分解得:b=2,c=4,……………………………………………………………………………………4分则解析式为y=﹣x2+2x+4;…………………………………………………………………………5分(2)∵y=﹣x2+2x+4=﹣(x﹣2)2+6,∴抛物线顶点坐标为(2,6),……………………7分则S四边形ABDC=S△ABC+S△BCD=×4×4+×4×2=8+4=12.…………………………………………10分。
2016年长郡集团澄池杯初赛数学试卷及答案解析

(2)已知距观测点 D 处 100 海里范围内有暗礁。若巡逻船 A 沿直线 AC 去 营救船 C,在去营救的途中有无触暗礁危险?(参考数据:√2≈1.41,√3≈1.73)
14.(10 分) 某欢乐谷为回馈广大谷迷, 在暑假期间退出学生个人门票优惠价, 各票价如下:
8. 当x = √2 − 1 时,代数式
÷ ������ 2 +������ + ������ 的值是
9. 关于 x 的分式方程
������
������−1
+
3 1−�ห้องสมุดไป่ตู้����
= 1 的解是正数,则 m 的取值范围为
10. 如图,直线 y=x+4 与双曲线 y =
k ������
(k≠0)相交于 A(−1,a)、B
三、解答题(共 52 分) 13. 如图,在南北方向的海岸线 MN 上,有 A. B 两艘巡逻船,现均收到故障船 C 的求救信号。 已知 A. B 两船相距 100(√3+1)海里,船 C 在船 A 的北偏东 60∘方向上,船 C 在船 B 的东南 方向上,MN 上有一观测点 D,测得船 C 正好在观测点 D 的南偏东 75°方向上。 (1)分别求出 A 与 C,A 与 D 之间的距离 AC 和 AD(如果运算结果有根号,请保留根号).
四边形
OEBF : S
正方形
ABCD=1:4;
C、3 个
(3)BE+BF=√2OA; (4) OG⋅BD=AE2+CF2. D、4 个
二、填空题(每题 4 分,共 24 分) 7. 计算:(3 − ������)0 + 4 sin 45° − √8 + |1 − √3| =
2018年长郡集团澄池杯复赛数学试卷高清解析(含试题来源)
题号
来源
知识点
备注
1 2018•菏泽中考真题 材料理解
2 2018•潍坊中考真题 中位数、众数、方差
二次函数的性质、二次函数图象上的点的特征、抛物线 3 2018•荆门中考真题
与坐标轴的交点
4 2018•潍坊中考真题 根与系数的关系;一元二次方程的定义以及根的判别式
一.选择题(每小题 6 分,共 36 分)
1.(2018•菏泽)规定:在平面直角坐标系中,如果点 P 的坐标为(m,n),向量 OP 可以用点 P 的坐标表
示为: OP =(m,n).已知: OA =(x1,y1), OB =(x2,y2),如果 x1•x2+y1•y2=0,那么 OA 与 OB 互相垂
H 处,折痕为 DG,点 G 在 BC 边上,若 AB=AD+2,EH=1,则 AD=
.
9.(2018•黄冈)在﹣4、﹣2,1、2 四个数中、随机取两个数分别作为函数 y=ax2+bx+1 中 a,b 的值,则该
二次函数图象恰好经过第一、二、四象限的概率为
.
10.(2018•衢州)定义:在平面直角坐标系中,一个图形先向右平移 a 个单位,再绕原点按顺时针方向旋转
A.2
B.﹣1
C.2 或﹣1
D.不存在
1 x 1 1 x 1
5.(2018•重庆)若数 a 使关于 x 的不等式组 3
2
,有且仅有三个整数解,且使关于 y 的分
2x a 31 x
第 2 页 共 18 页
式方程 3y a 12 1 有整数解,则满足条件的所有 a 的值之和是( ) y2 2 y
小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养 10 天的总成本为 166000,放养
2015 年全国初中数学联合竞赛试题参考答案及评分标准

AB AC , EF BC ,则 C B ____________.
【答】 60 .
E
作 EM BC 于点 M , FN BC 于点 N , FP EM 于点 P .
∵ E 、 F 分别为△ ABD 、△ ACD 的外心,∴ M 、 N 分别为 BD 、CD 的中
点.又 EF BC ,∴ PF MN 1 BC 1 EF ,∴ PEF 30 .
6. 设 n 是小于 100 的正整数且使 5n2 3n 5 是 15 的倍数,则符合条件的所有正整数 n 的和是( )
A.285. 【答】D.
B.350.
C.540.
D.635.
∵ 5n2 3n 5 是 15 的倍数,∴ 5 | (5n2 3n 5) ,∴ 5 | 3n ,∴ 5 | n ,设 n 5m ( m 是正整数),
∴符合条件的所有正整数 n 的和是(2+8+14+…+86+92+98)+(4+10+16+…+82+88+94)
=1634. 二、填空题:(本题满分 28 分,每小题 7 分) 1.题目和解答与(A)卷第 1 题相同. 2. 三边长均为整数且周长为 24 的三角形的个数为________. 【答】12.
C E
B
G
∴ GF 11, GE 10 ,∴ EF GE2 GF 2 221 .
4. 已知 O 为坐标原点,位于第一象限的点 A 在反比例函数 y 1 (x 0) 的图象上,位于第二象限的 x
点 B 在反比例函数 y 4 (x 0) 的图象上,且 OA OB ,则 tan ABO 的值为 x
同理可知: C 不小于 9, D 不小于 12, E 不小于 15, F 不小于 18.
因此,第三列所填 6 个数字之和 A + B + C + D + E + F 3 6 9 12 15 18 63.
2018.9.16长郡集团澄池杯复赛-数学试卷(高清版)
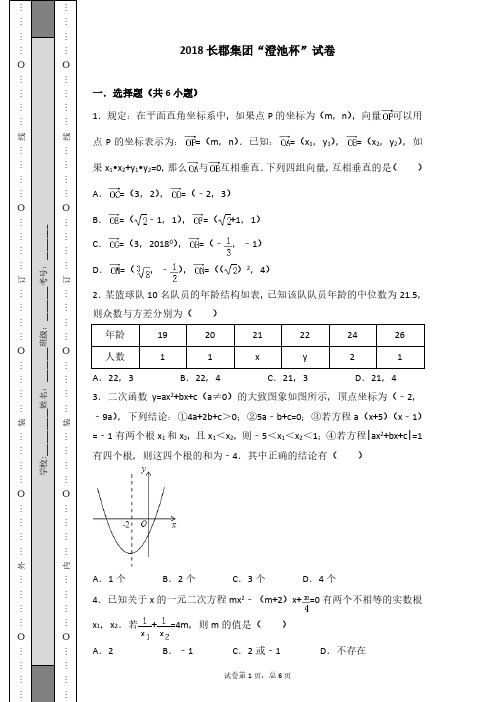
有四个根,则这四个根的和为﹣4.其中正确的结论有( )
A.1 个
B.2 个
C.3 个
D.4 个
4.已知关于 x 的一元二次方程 mx2﹣(m+2)x+ =0 有两个不相等的实数根
x1,x2.若 + =4m,则 m 的值是( )
A.2
B.﹣1
C.2 或﹣1
D.不存在
试卷第 1 页,总 6 页
…………○…………内…………○…………装…………○…………订…………○…………线…………○………… ※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
B. =( ﹣1,1), =( +1,1) C. =(3,20180), =(﹣ ,﹣1)
D. =( ,﹣ ), =(( )2,4)
2.某篮球队 10 名队员的年龄结构如表,已知该队队员年龄的中位数为 21.5, 则众数与方差分别为( )
年龄
19
20
21
22
24
26
人数
1
1
x
y
21Biblioteka A.22,3B.22,4
C.21,3
D.21,4
3.二次函数 y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,
﹣9a),下列结论:①4a+2b+c>0;②5a﹣b+c=0;③若方程 a(x+5)(x﹣1)
=﹣1 有两个根 x1 和 x2,且 x1<x2,则﹣5<x1<x2<1;④若方程|ax2+bx+c|=1
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
2015年湖南省长沙市长郡澄池杯英语竞赛复赛考试试卷 Word版

2015年湖南省长沙市长郡澄池杯英语竞赛复赛考试试卷 Word版2015 年长郡澄池杯英语决赛试卷(考试时间50 分钟,总分100 分)一、单项选择(每题 2 分,共60 分)( ) 1. —How do you like the song Let It Go ? — Sounds beautiful, it’s worth .A. call; listenB. called; listeningC. called; listenedD. calls; to listen( ) 2. Lisa her friend’s house to have a chat when coming back from work yesterday.A. drop byB. dropped byC. drop offD. dropped off ( ) 3.Xie Na her way to make faces to make others laugh.A. goes out ofB. goes outC. go ofD. go out of( ) 4. My parents are me because I didn’t finish my homework on time.A. madB. mad atC. mad withD. mad to( ) 5. After the earthquake, we heard tons of stories and we were deeply .A. moved; movedB. moving; movedC. moving; movingD. moved; moving( ) 6. It is that you didn’t watch the film Our Times is very interesting.A.a pain; thatB. a pity; whoC. a pity; whichD. pities; which ( ) 7. Zuckerberg his dream and finally sets up a social networking site called Facebook. A. stick to B. sticks to C. stick with D. sticks with ( ) 8. — Whose volleyball is this?— It Lily’s, she loves playing volleyball very much.A. must belong toB. must beC. can’t beD. might belong( ) 9. Thanksgiving Day_ a time for people to give thanks for what they have is on the fourth Thursday of November.A. whichB. thatC. which isD. that be( ) 10. Not only kind but also very smart.A. she isB. is sheC. do sheD. she does( ) 11. The cartoon the Pleasant Goat and the Gray is fun to watch.A. wolfB. wolfsC. wolvesD. wolfes( ) 12. Jack’s parents don’t allow him as much as he’d like to .A. to trainB. trainsC. trainingD. trained( ) 13. Teenagers should the net bar.A. keep themsevles away fromB. prevent them fromC. stop themselves fromD. keep away( ) 14. I am excited about the concert tomorrow, because I am crazy about EXO.A. is heldB. holdC. being heldD. be holded( ) 15. It China will become one of the strongest countries in the world.A. is believe thatB. is believed thatC. believesD. believed( ) 16. Great changes in Changsha,a more and more thriving city in central China.A. have took placeB. have taken placeC. has been taken placeD. has taken( )17. Switzerland is the clocks and watches,such as IWC, Rolex and so on.A. well-known forB. famous asC. well-know forD. well-known as( )18.Whenever I shopping, he says he’s too busy to be with me.A. mention goB. mention goingC. mention to goD. mention to going( )19. The paper is made wood while the book is made paper.A. of; fromB. of; ofC. from; fromD. from; of( )20. Not only the young but also the old are interested WeChat.A. forB. atC. aboutD. in( )21. He wants to take part in the Voice of China, so he makes to practice .A. an effort; singB. an effort; singingC. a effort; to singD. a effort; sing( )22.—Could you please tell me to Huanghua Airport?—Sorry, I don’t know.A. how can I getB. how I can getC. how do I getD. how I can arrive( )23. Grace spends more time than she used to English with foreigners.A. speakB. speakingC. spokenD. speaks( ) 24. China is stronger and stronger so she can properly all kinds if situations in the world .A. deal withB. do withC. deals withD. does with( )25. Parents are the best teacher for their children because their behaviors always them. A. have an influence to B. have an influence onC. has influences withD. has an influence at( )26. —Can you tell me something about Jeremy Lin?—Yes, he is a player can play basketball very well.A. whichB. whoseC. whoD. whom( )27. Hengdian has been one of tourist places for Chinese because it is the locations for many TV plays.A. the hotestB. the hottestC. hottestD. hot( )28. A number of teenagers know Li Y ifeng by Swords of Legends.A. watchedB. to watchC. watchingD. watches( )29. —Food safety is becoming more and more important .—So some rules help us.A.must makeB. must be made toC.must be madeD. be made( )30. —I am so crazy about playing volleyball that I don't have time to finish my homework.—Playing volleyball is a good idea but it can’t your study.A. in the wayB. get in the way ofC. be in the wayD. by the way二、完形填空(每题 2 分,共40 分)AThere is a new substance(物质)that is harder than 31 . It's called Q-carbon, and it was 32 by researchers at North Carolina State University. "The only 33 it may be found in the natural world would be possibly in the core of some planets(行星内核)," Jay Narayan said Before its discovery, there were two 34 of solid carbon: graphite(石墨)and diamond. Q-carbon is not only harder than diamond, but also glows(发光)even when exposed to 35 levels of energy. That could make it very 36 for creating strong, bright screens for electronic devices. " Researchers created the Q-carbon at room 37 and at ambient atmosphere( 大气环境) — we're basically using a 38 like the ones used for laser eye surgery," Narayan said. "So, not only does this allow us to 39 new applications, but the process itself is relatively 40 .( )31. A. diamond B. graphite C. stone D. sand( )32. A. find B. looked for C. created D. met( )33. A. time B. place C. mystery D. thing ( )34. A. kinds B. differences C. styles D. forms( )35. A. low B. high C. strong D. bright( )36. A. useless B. useful C. uses D. use( )37. A. condition B. environment C. temperature D. situation ( )38. A. laser B. tool C. way D. knife( )39. A. develop B. invents C. found D. created( )40. A. expensive B. inexpensive C. difficult D. EasilyBDear Basketball,As a six-year-old boy,deeply in love with you,I never saw the 41 of the tunnel(隧道). I only saw myself 42 out of one.And so I ran. I ran up and down every court( 球场) after every loose ball for you. You asked for my 43 . I gave you my heart because it came with so 44 . I played through the sweat( 汗水) and 45 , not because challenge called me but because YOU called me. I did everything for YOU. Because that's 46 you do when someone makes you feel as alive as you've made me feel. You gave a six-year-old boy his Laker(湖人)47 . And I'll always love you for it. But I 48 love you obsessively(过度的)for much longer. This season is all I have left to give. My heart can take the pounding. My mind can handle the grind. But my body knows it's time to 49 . I'm ready to let you go. I want you to know now. So we both can savor (品尝) every moment we have left together, the good and the bad. We have given each other all that we have.And we both know, no matter what I do next ,I'll always be that six-year-old 50 .Love you always,Kobe( )41. A. start B. end C. way D. look( )42. A. living B. jumping C. running D. calling( )43. A. money B. help C. efforts D. heart ( )44. A. much more B. less C. nothing D. something( )45. A. wound B. hurt C. painful D. blood( )46. A. what B. how C.that D. where( )47. A. confidence B. dream C. game D. experience( )48. A. can B. must C. mustn’t D. can’t( )49. A. say hello B. say yes C. say goodbye D. say no( )50. A. runner B. children C. kid D. basketball player2015年湖南省长沙市长郡澄池杯英语竞赛复赛考试试卷 Word版2015 年长郡澄池杯英语决赛试卷答案(考试时间50 分钟,总分100 分)一、单项选择(每题2 分,共60 分)二、完形填空(每题 2 分,共40 分)。
2015.11.15长郡系小升初数学答案

参考答案一、填空题1.12.5,242.9,2773.4254.4:3 5.5% 6.15:147.24 8.14.13 9.7510.311.405解析1.1平方米=100平方分米,110012.58⨯=,则18平方米=12.5平方米. 1小时=60分钟,260245⨯=,则25小时=24分钟.2.27197⎛⎫⨯+= ⎪⎝⎭(米);227777+=(米).注意区分“量”与“率”.3.锯成4段需要锯3次,每次需要用时121355÷=(分钟).锯成8段需要锯7次,需要用时214472555⨯==(分钟). 4.丽丽和丹丹走的路程之比为8:9,所花的时间之比我2:3,所以丽丽和丹丹的速度之比是89:4:323=. 5.2015%100%5%2040⨯⨯=+,所以现在盐水的含盐率是5%.6.甲:乙=5:6=15:18,乙:丙=9:7=18:14,所以甲:丙=15:14.7.因为三角形任意两边长度之和不大于第三边,则腰长:底长=5:2,该三角形的底长为21045⨯=(厘米),所以周长为102424⨯+=(厘米). 8.设这个半圆的半径为r 厘米,则13.142215.422r r ⨯⨯+=,解得3r =,所以这个半圆的面积为213.14314.132⨯⨯=(平方厘米).9.20点30分即晚上8点30分,830240⨯=(度),()24060.53075--⨯=(度),所以20点30分,时针和分针形成的夹角是75度.10.把这项工作的工作总量看作单位“1”,则甲组每人的工作效率为113824÷÷=,乙组每人的工作效率为114728÷÷=.甲组2人和乙组7人的工作效率之和为1112724283⨯+⨯=,1133÷=(天),所以甲组2人和乙组7人合作需要3天完成这项工作. 11.从10个数字任意选出两个不同的数字,共有2101094521C ⨯==⨯种不同的选法(此步也可经枚举得到).将所得两个数字中较大的数放在十位,较小的数放在个位,百位的数字可以为1~9共9个不同的数字,945405⨯=,所以所有十位比个位大的三位数共有405个.二、选择题解析1.在1~100中,有25个质数,1既不是质数也不是合数,10025174--=,所以共有74个合数.2.30.3758÷==甲乙,则83=甲乙,甲:乙=3:8.3.112015-的结果比1小,112015+的结果比1大,所以A 、C 的计算结果比2014小,B 、D 的计算结果比2014大.B 的计算结果比2014大12015,2014比D 的计算结果小12015,根据单位1的不同可得,D 的计算结果更大一些. 4.1111124612+++=,所以去掉的是18和110.5.三个星期日的日期都是偶数说明这个月共有5天是星期日,且最后一个星期日的日期为30日,所以20日是星期四.三、计算题1.630135161775572 1001162.原式=()3331718171815777⨯+⨯=⨯+=原式=3111311111551555515313115311515⎛⎫+⨯=⨯+⨯=+= ⎪⎝⎭原式=()555559867198671322088888⨯-⨯+⨯=⨯-+=⨯=原式()()111122012232021120201111112223202112101212021021⎛⎫=+++++++ ⎪⨯⨯⨯⎝⎭+⨯⎛⎫=+-+-++- ⎪⎝⎭=+-=L L L四、图形计算1.15.44cm 2【解析】()()22114104 3.1442812.5615.4424S S S cm =-=⨯+⨯-⨯⨯=-=阴影梯形扇形2.45平方厘米 【解析】如图,因为AE ∥CD ,::15:103:2EB BC AE DC ===,而15EB BC EC +==(cm),则215632BC =⨯=+(厘米),所以1615452ABC S =⨯⨯=V (平方厘米).五、解决问题1.10米【解析】设这根水管全长是x 米,则11 1.2 3.844x x x ⎛⎫--+= ⎪⎝⎭,解得10x =,所以这根水管全长10米.2.姐姐养了70只;妹妹养了50只【解析】设姐姐养了x 只兔,则妹妹养了120x -只兔,根据题意可列方程11120107x x ⎛⎫-=-+ ⎪⎝⎭,解得70x =,1207050-=(只),所以姐姐养了70只兔,妹妹养了50只兔. 3.44吨【解析】第二天用去余下的13少2吨,还剩下余下的23多2吨,则第一天用完后还余下了()2162213-÷=(吨).第一天用去了12多1吨,则余下12少1吨,()1211442+÷=(吨),所以原来这堆水泥有44吨.4.30千克【解析】设需添加x 千克含盐30%的盐水,则()2010%30%2022%x x ⨯+⨯=+⨯,解得30x =,所以需要添加30千克含盐30%的盐水. 5.154小时 【解析】把这件工作的工作总量看作单位“1”,则甲的工作效率为115525÷=,乙的工作效率为111165215⎛⎫-⨯÷= ⎪⎝⎭.甲、乙合做的工作效率之和为118251575+=,11815152754⎛⎫-⨯÷= ⎪⎝⎭(小时). 6.100级【解析】由题可得,女孩每秒钟向上走32 1.5÷=梯级.设扶梯每秒钟向上走x 梯级,则()()240 1.550x x +⨯=+⨯,解得0.5x =.则当扶梯静止时,扶梯可看到的梯级共有()20.540100+⨯=(级).E 1510AB CD。
【全国百强校】湖南省长沙市长郡中学2015年自主招生考试数学试题(含解析)

2015年湖南省长沙市长郡中学自主招生考试数学试卷(理实班)一、选择题:本题有6小题,每小题5分,共30分.1.方程(x2+x﹣1)x+3=1的所有整数解的个数是()A.5个B.4个C.3个D.2个2.如图,已知等边△ABC外有一点P,P落在∠BAC内,设P到BC、CA、AB的距离分别为h1,h2,h3,满足h2+h3﹣h1=6,那么等边△ABC的面积为()A.4 B.8 C.9 D.123.若﹣1<a<0,则一定是()A.最小,a3最大B.最小,a最大C.最小,a最大D.最小,最大4.如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连接EF交AB于H,则下列结论错误的是()A.AE⊥AF B.EF:AF=:1 C.AF2=FH•FE D.FB:FC=HB:EC5.在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为10,△BCF 的面积为20,△CEF的面积为16,则四边形区域ADFE的面积等于()A.22 B.24 C.36 D.446.某医院内科病房有护士15人,每2人一班,轮流值班,每8小时换班一次,某两人同值一班后,到下次两人再同班,最长需要的天数是()A.30 B.35 C.56 D.448二、填空题:本题有6小题,每小题5分,共30分.7.若4sin2A﹣4sinAcosA+cos2A=0,则tanA= .8.在某海防观测站的正东方向12海浬处有A、B两艘船相会之后,A船以每小时12海浬的速度往南航行,B船则以每小时3海浬的速度向北漂流.则经过小时后,观测站及A、B两船恰成一个直角三角形.9.如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是.10.桌面上有大小两颗球,相互靠在一起.已知大球的半径为20cm,小球半径5cm,则这两颗球分别与桌面相接触的两点之间的距离等于 cm.11.物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以1单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2015次相遇地点的坐标是.12.设C1,C2,C3,…为一群圆,其作法如下:C1是半径为a的圆,在C1的圆内作四个相等的圆C2(如图),每个圆C2和圆C1都内切,且相邻的两个圆C2均外切,再在每一个圆C2中,用同样的方法作四个相等的圆C3,依此类推作出C4,C5,C6,…,则(1)圆C2的半径长等于(用a表示);(2)圆C k的半径为(k为正整数,用a表示,不必证明)三、解答题:本题有4个小题,共60分.13.如图,四边形ABCD内接于圆O,且AD是圆O的直径,DC与AB的延长线相交于E点,OC∥AB.(1)求证:AD=AE;(2)若OC=AB=4,求△BCE的面积.14.已知抛物线y=x2+2px+2p﹣2的顶点为M,(1)求证抛物线与x轴必有两个不同交点;(2)设抛物线与x轴的交点分别为A,B,求实数p的值使△ABM面积达到最小.15.某次足球邀请赛的记分规则及奖励方案如下表:胜一场平一场负一场积分 3 1 0奖励(元/每人)1500 700 0当比赛进行到12轮结束已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y=x﹣1经过这两个顶点中的一个.(1)求出矩形的顶点A、B、C、D的坐标;(2)以AB为直径作⊙M,经过A、B两点的抛物线,y=ax2+bx+c的顶点是P点.①若点P位于⊙M外侧且在矩形ABCD内部,求a的取值范围;②过点C作⊙M的切线交AD于F点,当PF∥AB时,试判断抛物线与y轴的交点Q是位于直线y=x﹣1的上方?还是下方?还是正好落在此直线上?并说明理由.2015年湖南省长沙市长郡中学自主招生考试数学试卷(理实班)参考答案与试题解析一、选择题:本题有6小题,每小题5分,共30分.1.方程(x2+x﹣1)x+3=1的所有整数解的个数是()A.5个B.4个C.3个D.2个【考点】零指数幂.【专题】分类讨论.【分析】方程的右边是1,有三种可能,需要分类讨论.第1种可能:指数为0,底数不为0;第2种可能:底数为1;第3种可能:底数为﹣1,指数为偶数.【解答】解:(1)当x+3=0,x2+x﹣1≠0时,解得x=﹣3;(2)当x2+x﹣1=1时,解得x=﹣2或1.(3)当x2+x﹣1=﹣1,x+3为偶数时,解得x=﹣1因而原方程所有整数解是﹣3,﹣2,1,﹣1共4个.故选B.【点评】本题考查了:a0=1(a是不为0的任意数)以及1的任何次方都等于1.本题容易遗漏第3种可能情况而导致误选C,需特别注意.2.如图,已知等边△ABC外有一点P,P落在∠BAC内,设P到BC、CA、AB的距离分别为h1,h2,h3,满足h2+h3﹣h1=6,那么等边△ABC的面积为()A.4 B.8 C.9 D.12【考点】等边三角形的性质.【专题】面积法.【分析】先设等边三角形ABC的边长为a,连接PA、PB、PC,根据S△PAB+S△PAC﹣S△PCB=S△CAB,得出ah1+ ah2﹣ah3=,再根据h2+h3﹣h1=6,求得a=4即可得到等边△ABC的面积.【解答】解:设等边三角形ABC的边长为a,连接PA、PB、PC,则S△PAB+S△PAC﹣S△PCB=S△CAB,即ah1+ah2﹣ah3=,∴a(h2+h3﹣h1)=,∵h2+h3﹣h1=6,∴a=4,∴S△CAB==12,故选(D).【点评】本题主要考查了等边三角形面积的计算,等边三角形高线长与边长之间的关系.根据等边三角形的高计算等边三角形的面积是解决问题的关键.3.若﹣1<a<0,则一定是()A.最小,a3最大B.最小,a最大C.最小,a最大D.最小,最大【考点】实数大小比较.【分析】在所给范围内选择一个具体的数,代入后比较即可.【解答】解:∵若﹣1<a<0,∴a可取﹣0.001,那么a3=﹣0.000 000 001,=﹣0.1,=﹣1000,∴最小,a3最大,故选A.【点评】考查实数的大小比较;选择一个合适的具体的数,代入所给代数式比较,可以简化比较的步骤.4.如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连接EF交AB于H,则下列结论错误的是()A.AE⊥AF B.EF:AF=:1 C.AF2=FH•FE D.FB:FC=HB:EC【考点】旋转的性质;正方形的性质;相似三角形的判定与性质.【分析】由旋转得到△AFB≌△AED,根据相似三角对应边的比等于相似比,即可求得.【解答】解:由题意知,△AFB≌△AED∴AF=AE,∠FAB=∠EAD,∠FAB+∠BAE=∠EAD+∠BAE=∠BAD=90°.∴AE⊥AF,所以A正确;∴△AEF是等腰直角三角形,有EF:AF=:1,所以B正确;∵HB∥EC,∴△FBH∽△FCE,∴FB:FC=HB:EC,所以D正确.∵△AEF与△AHF不相似,∴AF2=FH•FE不正确.故选:C.【点评】本题利用了正方形的性质,等腰直角三角形的性质,全等三角形的判定和性质求解.5.在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为10,△BCF 的面积为20,△CEF的面积为16,则四边形区域ADFE的面积等于()A.22 B.24 C.36 D.44【考点】三角形的面积.【分析】可设S△ADF=m,根据题中条件可得出三角形的面积与边长之间的关系,进而用m表示出△AEF,求出m的值,进而可得四边形的面积.【解答】解:如图,连AF,设S△ADF=m,∵S△BDF:S△BCF=10:20=1:2=DF:CF,则有2m=S△AEF+S△EFC,S△AEF=2m﹣16,而S△BFC:S△EFC=20:16=5:4=BF:EF,又∵S△ABF:S△AEF=BF:EF=5:4,而S△ABF=m+S△BDF=m+10,∴S△ABF:S△AEF=BF:EF=5:4=(m+10):(2m﹣16),解得m=20.S△AEF=2×20﹣16=24,S ADEF=S△AEF+S△ADF=24+20=44.故选D.【点评】本题主要考查了三角形的面积计算问题,能够利用三角形的性质进行一些简单的计算.6.某医院内科病房有护士15人,每2人一班,轮流值班,每8小时换班一次,某两人同值一班后,到下次两人再同班,最长需要的天数是()A.30 B.35 C.56 D.448【考点】整数问题的综合运用.【专题】数字问题.【分析】此题可运用排列组合解答,15人,每2人一班,轮流值班,则有C152=105种组合,一天是24小时,8小时1班,24除以3=每天3个班再用105除以3=35天.【解答】解:由已知护士15人,每2人一班,轮流值班,得:有C152=105种组合,又已知每8小时换班一次,某两人同值一班后,到下次两人再同班,所以最长需要的天数是105÷(24÷8)=35(天).故选:B.【点评】此题考查的知识点是整数问题的综合运用,关键是先求出15人,每2人一班有多少种组合,再由每8小时换班一次,某两人同值一班后,到下次两人再同班求出最长需要的天数.二、填空题:本题有6小题,每小题5分,共30分.7.若4sin2A﹣4sinAcosA+cos2A=0,则tanA= .【考点】解一元二次方程﹣配方法;锐角三角函数的定义.【分析】先解一元二次方程,再根据锐角三角函数的定义得出即可.【解答】解:4sin2A﹣4sinAcosA+cos2A=0,(2sinA﹣cosA)2=0,2sinA﹣cosA=0,2sinA=cosA,tanA==,故答案为:【点评】本题考查了锐角三角函数的定义和解一元二次方程等知识点,比较简单,注意锐角三角函数定义的掌握.8.在某海防观测站的正东方向12海浬处有A、B两艘船相会之后,A船以每小时12海浬的速度往南航行,B船则以每小时3海浬的速度向北漂流.则经过 2 小时后,观测站及A、B两船恰成一个直角三角形.【考点】勾股定理的应用.【专题】计算题.【分析】根据题意画出图形,设经过x小时后,观测站及A、B两船恰成一个直角三角形,在Rt△OBC、Rt△OCA和Rt△ABO中分别应用勾股定理,即可求出x的值.【解答】解:如下图所示,设经过x小时后,观测站及A、B两船恰成一个直角三角形,则BC=3x,AC=12x,在Rt△OBC中,根据勾股定理得:122+(3x)2=OB2;在Rt△OCA中,根据勾股定理得:122+(12x)2=AO2;在Rt△ABO中,根据勾股定理得:OB2+AO2=AB2=(15x)2;∴122+(3x)2+122+(12x)2=(15x)2,解得:x=2或﹣2(舍去).即经过2小时后,观测站及A、B两船恰成一个直角三角形.故答案为:2.【点评】本题考查勾股定理的实际应用,难度适中,先根据题意画出图形是解题关键.9.如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是y=﹣x2﹣x+.【考点】二次函数综合题.【分析】根据矩形的性质,利用矩形边长得出A,B,C三点的坐标,再利用待定系数法求出二次函数解析式即可.【解答】解:∵沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,∴A点的坐标为:(﹣4,2),B点的坐标为:(﹣2,6),C点的坐标为:(2,4),将A,B,C代入y=ax2+bx+c,,解得:,∴二次函数解析式为:y=﹣x2﹣x+.故答案为:y=﹣x2﹣x+.【点评】此题主要考查了矩形的性质以及待定系数法求二次函数解析式,根据矩形边长得出A,B,C三点坐标是解决问题的关键.10.桌面上有大小两颗球,相互靠在一起.已知大球的半径为20cm,小球半径5cm,则这两颗球分别与桌面相接触的两点之间的距离等于20 cm.【考点】相切两圆的性质.【分析】首先根据题意作图,可得:⊙A与⊙B外切,⊙A,⊙B与CD分别相切于C,D,AC=20cm,BD=5cm,然后过点B作BE⊥AC,又由切线的性质,即可得四边形ECDB是矩形,则在Rt△AEB中,即可求得BE的长,即可求得这两颗球分别与桌面相接触的两点之间的距离CD的长.【解答】解:如图,根据题意得:⊙A与⊙B外切,⊙A,⊙B与CD分别相切于C,D,AC=20cm,BD=5cm,∴AB=25cm,AC⊥CD,BD⊥CD,∴∠ACD=∠BDC=90°,过点B作BE⊥AC,∴∠BEC=90°,∴四边形ECDB是矩形,∴BE=CD,EC=BD=5cm,∴AE=AC﹣EC=15cm,在Rt△AEB中,BE===20(cm),∴CD=20cm.故答案为:20.【点评】此题考查了外切两圆的性质,切线的性质,以及矩形的性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用与辅助线的作法.11.物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以1单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2015次相遇地点的坐标是(﹣,﹣2).【考点】规律型:点的坐标.【分析】此题利用行程问题中的相遇问题,由于正方形的边长为4,物质B是物质A的速度的2倍,求得每一次相遇的地点,找出规律即可解答.【解答】解:正方形的边长为4,因为物质B是物质A的速度的2倍,时间相同,物质A与物质B 的路程比为1:2,由题意知:①第一次相遇物质A与物质B行的路程和为16×1,物质A行的路程为16×=,物质B行的路程为16×=,在BC边相遇;②第二次相遇物质A与物质B行的路程和为16×2,物质A行的路程为16×2×=,物质B行的路程为16×2×=,在DE边相遇;③第三次相遇物质A与物质B行的路程和为16×3,物质A行的路程为16×3×=16,物质B行的路程为16×3×=32,在A点相遇;④第四次相遇物质A与物质B行的路程和为16×4,物质A行的路程为16×4×=,物质B行的路程为16×4×=,在BC边相遇;⑤第五次相遇物质A与物质B行的路程和为16×5,物质A行的路程为16×5×=,物质B行的路程为16×5×=,在DE边相遇;…综上可得相遇三次一个循环,因为2015=3×671+2,即第2015次相遇和第二次相遇的地点相同,所以它们第2015次相遇在边DE 上,点的坐标是(﹣,﹣2).故答案为:(﹣,﹣2).【点评】此题属于应用类问题,主要考查行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题,难度较大.12.设C1,C2,C3,…为一群圆,其作法如下:C1是半径为a的圆,在C1的圆内作四个相等的圆C2(如图),每个圆C2和圆C1都内切,且相邻的两个圆C2均外切,再在每一个圆C2中,用同样的方法作四个相等的圆C3,依此类推作出C4,C5,C6,…,则(1)圆C2的半径长等于(用a表示);(2)圆C k的半径为(﹣1 )k﹣1 a (k为正整数,用a表示,不必证明)【考点】相切两圆的性质;勾股定理;正方形的判定与性质.【专题】规律型.【分析】(1)连接AB、BC、CD、AD,AC,设小圆的半径是r,根据圆与圆相切,得到AC=2a﹣2r,根据正方形的性质和勾股定理得到AC=2r,推出方程2a﹣2r=2r,求出即可;(2)求出r=(﹣1)a,r3=(﹣1)r=a,r4=,得出圆C k的半径为r k=(﹣1 )k﹣1 a即可.【解答】(1)解:连接AB、BC、CD、AD,AC,设小圆的半径是r,根据圆与圆相切,∴AC=2a﹣2r,∴四边形ABCD是正方形,∴AB=BC,∠B=90°,由勾股定理得:AC=2r,∴2a﹣2r=2r,解得:r=(﹣1)a,故答案为:(﹣1)a.(2)解:由(1)得:r=(﹣1)a,同理圆C3的半径是r3=(﹣1)r=a,C4的半径是r4=,…圆C k的半径为r k=(﹣1 )k﹣1 a,故答案为:r k=(﹣1 )k﹣1 a.【点评】本题主要考查对正方形的性质和判定,勾股定理,相切两圆的性质等知识点的理解和掌握,能根据计算结果得出规律是解此题的关键.三、解答题:本题有4个小题,共60分.13.如图,四边形ABCD内接于圆O,且AD是圆O的直径,DC与AB的延长线相交于E点,OC∥AB.(1)求证:AD=AE;(2)若OC=AB=4,求△BCE的面积.【考点】圆周角定理;等边三角形的判定与性质;平行四边形的判定与性质.【分析】(1)根据O为AD中点,OC∥AE,得到2OC=AE,再根据AD是圆O的直径,得到2OC=AD,从而得到AD=AE;(2)根据平行四边形的性质得到BC∥AD,再根据C为中点,得到AB=BE=4,从而求得BC=BE=4,然后连接BD,得到∠DBE=90°,进而得到BE=BC=CE=4,然后求面积即可.【解答】(本小题满分12分)解:(1)∵O为AD中点,OC∥AE,∴2OC=AE,又∵AD是圆O的直径,∴2OC=AD,∴AD=AE.(2)由条件得ABCO是平行四边形,∴BC∥AD,又C为中点,∴AB=BE=4,∵AD=AE,∴BC=BE=4,连接BD,∵点B在圆O上,∴∠DBE=90°,∴CE=BC=4,即BE=BC=CE=4,∴所求面积为4.【点评】本题考查了圆周角定理及平行四边形的性质及判定,解题的关键正确的应用圆周角定理.14.已知抛物线y=x2+2px+2p﹣2的顶点为M,(1)求证抛物线与x轴必有两个不同交点;(2)设抛物线与x轴的交点分别为A,B,求实数p的值使△ABM面积达到最小.【考点】抛物线与x轴的交点.【专题】探究型.【分析】(1)先判断出△的符号即可得出结论;(2)设A(x1,0),B(x2,0),利用两点间的距离公式即可得出|AB|的表达式,设顶点M(a,b),再把原式化为顶点式的形式,即可得到b=﹣(p﹣1)2﹣1,根据二次函数的最值及三角形的面积公式即可解答.【解答】解:(1)∵△=4p2﹣8p+8=4(p﹣1)2+4>0,∴抛物线与x轴必有两个不同交点.(2)设A(x1,0),B(x2,0),则|AB|2=|x2﹣x1|2=(x1+x2)2﹣4x1x2=4p2﹣8p+8=4(p﹣1)2+4,∴|AB|=2.又设顶点M(a,b),由y=(x+p)2﹣(p﹣1)2﹣1.得b=﹣(p﹣1)2﹣1.当p=1时,|b|及|AB|均取最小,此时S△ABM=|AB||b|取最小值1.【点评】本题考查的是抛物线与x轴的交点问题,涉及到的知识点为:根的判别式、两点间的距离公式、二次函数的顶点式及三角形的面积,熟知以上知识是解答此题的关键.15.某次足球邀请赛的记分规则及奖励方案如下表:胜一场平一场负一场积分 3 1 0奖励(元/每人)1500 700 0当比赛进行到12轮结束(2015•天心区校级自主招生)已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y=x﹣1经过这两个顶点中的一个.(1)求出矩形的顶点A、B、C、D的坐标;(2)以AB为直径作⊙M,经过A、B两点的抛物线,y=ax2+bx+c的顶点是P点.①若点P位于⊙M外侧且在矩形ABCD内部,求a的取值范围;②过点C作⊙M的切线交AD于F点,当PF∥AB时,试判断抛物线与y轴的交点Q是位于直线y=x ﹣1的上方?还是下方?还是正好落在此直线上?并说明理由.【考点】二次函数综合题.【分析】(1)首先建立平面直角坐标系,由矩形ABCD中,AB=3,AD=2,设A(m,0)(m>0),则有B(m+3,0);C(m+3,2),D(m,2);然后若C点过y=x﹣1与C点不过y=x﹣1分析,即可求得矩形的顶点A、B、C、D的坐标;(2)⊙M以AB为直径,即可求得M点的坐标,又由y=ax2+bx+c过A(2,0)和B(5,0)两点,利用待定系数法即可求得二次函数的图象,然后顶点同时在⊙M外侧和在矩形ABCD内部,即可求得a 的取值范围;②首先设切线CF与⊙M相切于Q,交AD于F,设AF=n,n>0;由AD、BC、CF均为⊙M切线,求得CF与DF的长;在Rt△DCF中,由勾股定理求得n的值,可得F的坐标,然后由当PF∥AB时,求得抛物线的解析式与抛物线与y轴的交点Q的坐标,则可得Q在直线y=x﹣1下方.【解答】解:(1)如图,建立平面直角坐标系,∵矩形ABCD中,AB=3,AD=2,设A(m,0)(m>0),则有B(m+3,0);C(m+3,2),D(m,2);若C点过y=x﹣1;则2=(m+3)﹣1,m=﹣1与m>0不合;∴C点不过y=x﹣1;若点D过y=x﹣1,则2=m﹣1,m=2,∴A(2,0),B(5,0),C(5,2),D(2,2);(2)①∵⊙M以AB为直径,∴M(,0),由于y=ax2+bx+c过A(2,0)和B(5,0)两点,∴,∴,∴y=ax2﹣7ax+10a(也可得:y=a(x﹣2)(x﹣5)=a(x2﹣7x+10)=ax2﹣7ax+10a)∴y=a(x﹣)2﹣a;∴抛物线顶点P(,﹣ a)∵顶点同时在⊙M外侧和在矩形ABCD内部,∴<﹣a<2,∴﹣<a<﹣.②设切线CF与⊙M相切于Q,交AD于F,设AF=n,n>0;∵AD、BC、CF均为⊙M切线,∴AF=QF,CQ=BC=2,∴CF=n+2,DF=2﹣n;在Rt△DCF中,∵DF2+DC2=CF2;∴32+(2﹣n)2=(n+2)2,∴n=,∴F(2,)∴当PF∥AB时,P点纵坐标为;∴﹣a=,∴a=﹣;∴抛物线的解析式为:y=﹣x2+x﹣5,抛物线与y轴的交点为Q(0,﹣5),又直线y=x﹣1与y轴交点(0,﹣1);∴Q在直线y=x﹣1下方.【点评】此题考查了待定系数法求二次函数的解析式,矩形的性质,勾股定理的应用以及点与函数的关系等知识.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用.。
湖南省长郡中学2015届高三月考试卷(二)数学(理)试题Word版含答案

长郡中学2015届高三月考试卷(二)数学(理科)长郡中学高三数学命题组组稿得分:____________ 本试题卷包括选择题、填空题和解答题三部分,共8页。
时量120分钟。
满分150分。
一、选择题:本大题共10小题,没小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.“0x ”是“ln 10x ”的A.充分不必要条件B.必要不充分条件C. 充分必要条件D. 既不充分也不必要条件2.已知函数33y x x c 的图像与x 轴恰有两个公共点,则c A.-2或 2 B.-9或3C.-1或 1D.-3或1 3.已知函数()sin f x x 在0,4上单调递增且在这个区间上的最大值为32,则实数的一个值可以是A.23 B.83C.43D.1034.已知向量a 与b 的夹角为,定义a b 为a 与b 的“向量积”,且a b 是一个向量,它的长度sin a b a b ,若2,0,1,3,则A,43 B.3 C.6 D.235.一几何体的三视图如图,该几何体的顶点都在球O 的球面上,球O 的表面积是A.2 B.4 C.6 D.166.设l 为直线,,是两个不同的平面,下列命题中正确的是A.若//,//,//l l 则B.//l l 若,,则C.,//,//l l 若则D.,//,l l若则7.已知n S 是等差数列n a 的前n 项和,下列选项中不可能是关于,n n S 的图像的是8.在数列n a 中,11a ,对于任意自然数n ,都有12nn n a a n ,则15a A.151422 B. 141322 C. 151423 D. 1513239.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V ,求其直径d 的一个近似公式3169d V,人们还用过一些类似的近似公式.根据π=3.14159…判断,下列近似公式中最精确的一个是A.3169d VB. 32d V C. 3300157d V D. 32111d V10.已知数列n a 的通项公式为13n a n ,则满足119102k k k a a a 的整数kA.有3个B.有2个C.有1个D.不存在选择题答题卡题号 1 2 3 4 5 6 7 8 9 10 得分答案二、填空题:本大题共5小题,每小题5分,共25分。
长郡中学2015届高三第五次月考数学理试题含答案

7.湖南省长郡中学2015届高三第五次月考数学(理)试题本试题卷包括选择题、填空题和解答题三部分。
时量 120分钟。
满分150分。
一、选择题:本大题共 10小题,每小题5分,共50分•在每小题给出的四个选项中,只有 一项是符合题目要求的.1.复数 2i 所对应的点位于复平面内2 iA .第一象限B .第二象限 C.第三象限 D .第四象限2 .已知离散型随机变量 X 的分布列为A1Ja訂JJ F1 K Jv3 A .4C. 33 5A .B . 2c.— D . 3223 .已知f (x )是定义在 R 上的奇函数,当 , 2 小 x^0 时,f (x ) =x — 3x , 则函数 g (x ) =f (x )—x+3的零点的集合为A . {1 , 3}B . {-3, -1 , 1, 3} C. {27 , 1, 3}D . { — 27 1, 3}在(1+x ) (1, 2) 6 (1+y ) 4的展开式中,记 x m +f (0, 3)=A . 45 已知命题 A . x 不属于AB . 60 A B ,则非p 是BC. 120C. x 不属于 A 且x 不属于B 若执行如图所示的程序框图,输出B . x 不属于A 或x 不属于D . x A BS 的值为3,则判断框中应填人的条件是 B . C. kk k kD . 已知三棱锥的底面是边长为侧视图的面积为1的正三角形,其正视图与俯视图如图所示,B . D . 1则X 的数学期4.y n 项的系数为f (m , n ),贝U f ( 3,0) +f(2,1) +fD .4 7.1 x&已知函数f (x )=e x , g(x )=ln x 1的图象分别与直线y =m 交于A , B 两点,贝U |AB|2 2的最小值为213 A . 2B 2+1n 2C. e 2+—D . 2e — ln229 .设函数f (x )=3sin(2x )+cos (2 x) ||',且其图象关于直线 x=0210. 对于三次函数 f (x ) =ax 3+bx 2+cx+d (a 0),给出定义:设导数,f(x )是f (x )的导数,若方程f(x ) =0有实数解x o ,则称点(x o ,f ( x o)),且在(0,)上为增函数2-,且在(0,-) 上为增函数24,且在(0,-)上为减函数2-,且在(0,-) 上为减函数24对称,则A. y=f ( x )的最小正周期为B. y=f (x )的最小正周期为C. y=f (x )的最小正周期为D. y=f (x )的最小正周期为(x )是函数y=f (x )的为函数y=f (x )的拐点”某同学经过探究发现:任何一个三次函数都有1一个三次函数都有对称中心, 且 拐点”就是对称中心,设函数g( x) = 1x 33拐点”任何1 2 x 2+3x5 121 2015+g2015+…+g2014 2015A . 2 013B . 2 014C. 2 015 D . 2 01613.不等式|a 2 | sin y对一切非零实数x, y均成立,则实数a的取值范围、填空题:本大题共6小题,考生作答5小题,每小题5分,共25分.把答案填在答题卡中对应题号后的横线上.(一)选做题(请考生在第11,12 ,13三题中任选两题作答,如果全做,则按前两题记分)11. 如图,AB是半圆O的直径,点C在半圆上,CD丄AB,垂足为D,且AD=5DB,设/ COD=,贝U tan 的值为12 .已知在平面直角坐标系xOy中,圆C的参数方程为x 3 3cos y 1 3si n(为参数),Ox为极轴建立极坐标系,直线I的极坐标方程为cos 0,则6圆C截直线l所得的弦长为2216.等边△ ABC 的边长为2,取各边的三等分点并连线, 可以将△ ABC分成如图所示的9个全等的小正三角形,记这 9个小正三角形的 重心分别为 G 1,G 2,G 3,…,G 9,贝屮(AG 1 BG 1 )+( AG 2 BG 2 )三、解答题:本大题共 6小题,共75分•解答应写出文字说明、证明过程或演算步骤. 17. (本小题满分12分)某车间甲组有10名工人,其中有4名女工人;乙组有 5名工人,其中有3名女工人, 现采用分层抽样方法(层内采用不放回简单随机抽样) 从甲、乙两组中共抽取3名工人进行技术考核.(1)求从甲、乙两组各抽取的人数;(2)记 表示抽取的3名工人中男工人数,求的分布列及数学期望.(二)必做题(14〜16题) 14 .已知点A 是不等式组x 2y 1x y 3 0所表示的平面区域内的一个动点,点x 1B ( -1,1),O 为坐标原点,则 OA • OB 的取值范围是 ____________________15.如图,已知过椭圆2x2a2y2 1(a b 0)的左顶点 A (-a , 0)作直线lb 2交y 轴于点P,交椭圆于点0,若厶AOP 是等腰三角形,且PQ =2QA ,则椭圆的离心率为 ________________ +…+ ( AG 9 BG 9) |= ____________________(2 )若a=3,A ABC的面积为33,求CA • AB的值.在厶ABC中,角A,B,C的对边分别是a, b , c,若』3acos C=csin A.(1)求角C的大小;2如图,在四棱锥 P — ABCD 中,底面ABCD 为矩形,PA 丄平面ABCD,AB= PA=1,AD= 3 , F 是PB 中点,E 为BC 上一点. (1) 求证:AF 丄平面PBC ;(2) 当BE 为何值时,二面角 C — PE — D 为45°.20. (本小题满分13分)已知数列{a n }的前n 项和为S n , S=21 a n (n 》1(1)求证:数列n是等比数列;(2)设数列{ 2n a n }的前 n 项和为T n ,A n =T 11 1 1 2+ — +—+- + 丄.试比较 A n 与 的大小.T 2 T 3 T n na n21. (本小题满分13分)如图,O为坐标原点,点F为抛物线C1: /=2py ( p 0)的焦点,且抛物线C1上点P 处的切线与圆Q: x2+『=1相切于点Q.(1)当直线PQ的方程为x-y \ 2 =0时,求抛物线C的方程;51(2)当正数p变化时,记S1, S2分别为△ FPQ △ FOQ的面积,求—的最小值.5222. (本小题满分13分)2已知函数 f (X)=21 nx —x - ax.1(1 )当a》3寸,讨论函数f (x)在,上的单调性;2(2)如果X1, x2是函数f( x)的两个零点,且X1 x2 4x-! , f (x)是函数f( x)的导函数,用X1, x2表示a并证明:f 空一x203・ 1数学(理科)参考答案1 2 3 4 ■ G ■ i«< 10 & 条 B A 1) (・ c C (・BB一 •逸择题 【 ] 「 (";—(「一/、・•・• - / —\i )=*1二、填空题 :…;.h ("= U 八〃”=十尺・• L •…、-f > ・.“ (7> • ■( "=—/<■■■"““=万厂二 一二 T R / — /T —3co> 0 o • y=l +3>in 0 •r (.r /!)・ + ($ 1X=9 ......... ①. th (” ・专)—「〉• r :p(co9 •、— 即/T J y=0 ....... ②.亡=£•故沁诗.12. 4 /2【解析】曲「心(•(/?■】)餌鼻汽・・匚 — :/s= /(/T )2+( — 1)2 丹汉点汽/彼制(・所最得的徐识为Ali\=2 尺— =4 72. 4 /T.13. [h3]【解析】•••「+丄€(—8・2]U[2・+8)・ sin 十)「+亠€ [2. +乂)•其说小伉为2. 2 4-sin y 金成.方.时.有 … . 負为[】.3]・14. [- 1.11【解析】作出卜孑犬纽对M 的平面R 城知图: 3] .4(/■〉•)・<:—"A • OH — .「一>・• 曲z=・「+,■(¥,=・/•+<炭尔针年为1纵価厢为z 的・・纽・1•幵点线・ -:-i:- *L y~ 1 —二 耳 I • '.、・=" —二汽 ;I) Ef ・ v=./•— c P-;先 论 航 小•此时Z 边小. 当点買y= r A " = ' o &斜冯V L 「+y 3=0 I; ,f.r —3 y+ 1 =0 一…1 ilH ■ v ..., , i#+y —3=0i )=l 为[一1•叮. 2 yr15. ^-【胡析】•••_“川 ・\ ..・•・; i< Q( ./\. •〉、)・•••"&= 2 Q A• •*• (./Q • y Q “)= 2( a f*0. jv +x "、it 也 H E ;• JtlK v= / ― z i ;・:、•'「.:・* 1 r=L 即〃(1.2)■此时1+2-1.・y =2 •解僭即LK2.1)此时z2+】=• • 2m =亍恥=1■“4 2 1 W ~<r Zr 1代入鶴肉方锐奇 一+「— = 】•?!:为——==・: a IfcC J一[解析】•••_〒.・U+〃FdO.试)一・・・+(才小一片=| 54 K (^ \ =G /X 故咨蓬为G 民三•解答題】7 •解:(1)因为屮纽有10各工人•乙幼有5各工人.从甲■乙两怨中头抽M3 L 匸人進行技术等卞・笊诺》层抽却的邸理可JL 按矗列•在甲中抽取2名•乙中抽取1名......................................... (4少)(2)^的丐能施位为O.I.2.3.2S泌宀(G 1 28贰 r<=«—-* .—7o 751& 解:⑴•••屁心 C=< sin A ■d| 正我 < f-T t r : /^sin Aa >s ( — >in ("sin A ♦ VIA z* >in .A.. ':・二 、(’二、i ・:(’• • • i * — • . . I -.i— ..................(2 > *.\z=3 .匚.4〃(° :: ' :-^-. .*. S .<7»sin ( '-—- 专=•、; ....»=三.ilj .令£、L * ' ;:.• — ! -,■即tCOS A.2 +(疗) 护—g.2X2X7?14嚥I 「A • A/J=/jt cos (x 一 ・4) = 2 /7x ( 计)=—I. .................................................................................. 19•解:(1)证呱以A 为斥点.AD 为/轴2〃为y 轴・AP 为z 軸・迟立空问点用*祐系.V.4B=PA=hAD=/3< F 芯P 〃中点••••.•W 」」)・P(0・0・l )・〃(0・l ・0).(・(/T ・l ・0)・D(/T ・・・ "〃=(0丄 1).P(・=(/T.1・ l)・F (0吕•£).AF ・(0・+ •斗)■•••・*•• P"0.AF ・ P(J0・ 乙 乙 JJ:.XV . PlhAF I "( ••••AF L F 面 Pin \ .......................................................................................................(2)il HK=a.:.E(aA.0)J)E=(a /?• 1.0) • PU=(/T.0・ 1)> 汝平血mE 的注向》” =(/•)“)•n • l)P^ = (u yT)./-r n • P />= /T./z=0•••J" 〃卜二〒H ;./丿(w 」)31 —j /•: t_;s. _ ■ ■p7S(12・皐./= 1 • f'r n =( 1 ♦ /T “ • /T )••刃 ir 2 yr丁〃匸+Mf )A (A<r + /rz > ----------- (.4(匚一从”卫+律卫=卫— ■■ • • ■■ ■■ . •3点F (0•# )列切线PQ n ;厢离:i d =•piftRY :的法向黄为 AF=(O •斗・+)••••二亦;(・ PE I ) h 43v . n. \F 〒• J 圧_ 2斥<+7 小朋■悟时•二耐C-PE D7T狞•迓fr “20. W :(l )dja.=S,=2 也.再“・= —・ 询 3=2(打+ 1)“•滋 S. .=2 ( 于建心=筑S ・=(宀+1)心・ 角+ %.・-(鬥)“・・"‘仔一$沽(心2〉・一 閱 W 及公:旳为*"比魏列・••… ⑵由⑴待严二亠*(*)八=右.T . —■ — _ 1 I n I o I I _"(〃+】)1 _ 三 _打 1 ] \ A =?r (i 亠)_(丄 亠)+•••+(丄—-亠心、2 丿 I 2 3 1 、〃———— -—• — ;小・na n u* n" “― I ir “一 I " n咲 /(”)=;T ・&S )=Lf ・..〜、、〜、2叮讥〃 2)./(w-r I ) /(〃) - p '丄 2 •7 I 〃(”+l ) r5 ej 4/(w4- 1) /(w )>*0< :■ 5 心3时/(〃)单调递堵. A Ji f! I • I •—'・ '' :・.I 经盼验W-U2.3时•仍有/(〃)>£(”)•9 日此•对任惡正牛做心郭有/(〃):>*(〃)•叩4,<—・ ....................... 仪』■ 21 •解:(】)汉点卩(./ ・—)-k /* —-/<v ( p • :-.v —T ;・ —丄・ \ 匕p > 厶pp旁歴・0•解jf p ・2住,.1 : /Q , :】•所汉血■] H , P 丙以祀场汽(・.的方糧为.? =4 /2y ・ ............ •• i … .: 2P I?渕切线与闵切.歼d~ T. . /!~ Arg + 4/r2・心丿2py J Z =0曲方程殂{/+〉,= 1.fo 4./g 4^r —0才(./ .r o ) ♦即 2/o ./ 2py ・f£j . - —I , 巧以屮Q= /F H F I ./ P ・g 2 = 7/r 5 兴 2./O P ・帀歼汉 S.=*|PQ • d=+ xS -=T OF /■2 .r 0(13 ;?)而 d/ ./J — 4.7? +4“•加•=./i 4./S ■ <7 ./01 ?>2<当H 仪占匚二=— d 取“=”号•即 启= 4+2 /T •此时•〃=、/2+2 /T z .r$ —4 丙以卷的说小債为2血+3. ................................................................................22. ^:(1)法一:V/(.r)=2ln j-j z -ar.2, “■ ,(Q0)・ 令/(・/)= 0存< =“+严空(贡抿介戈)■ ;•“a 1 + 1G + 4“+4 ■ /•、/“■ + ]G £“_2 ■ .I “ + J 圧 + ] G£2« -------------------- - ---- --------- 4 • Z 亠・+乂>)上f (G 迄0怛戎工.・•・:.[*•・「• 一2 ./•) =— - 2.r a • &十•+>□)•匕是减函4JL “忑上3・ ^;x/(.r)=-^ 2.i “乞4 1 3=0 花[[■ + =)上•世成辺. 斗• + = )上吕疑/(.「)P 冏违•戏. ........ .•/ ‘ ・ .; .. .•*•/(./. )=2ln ./. ./: a.i\ =0./(.# >) = 2ln ./ V/(.r)=2ln .r-.r 2 In 亠— ,. "TT : l.r ・■*•) “・a ')In—— -/. . z . - G 2 心------------ (r 2 + r.)〒 ---------- —(2心—r. Zr.十小 3u.r> =0.In ———儿2+匚3/ 3 . . \ 9 F 帀+4 (/ 1)(/ ・1) / + 2 … '一7 一(/+2)2 — 心+2卩 J AA(z)/£(k4).L 单调递减1)・0・戈 — <0.丄(・「・-r> )>0- A/ ( 2/\; Z - )>0. ........................................................................ —才. .i \ 3 / <0. (13 亍)・ 「J;」*) 4(13 ;?)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与直线 BC 交于点 E,则 CE=
.
10.如图,点 G 是正方形 ABCD 对角线 CA 的延长线上任意一点,以线段 AG 为边
作一个正方形 AEFG,线段 EB 和 GD 相交于点 H.若 AB= 2 ,AG=1,则
EB=
.
11.如右上图:在四边形 ABCD 中,AD∥BC,∠ABC=90°,AB=BC,E 为 AB 边上
一点,∠BCE=15°,且 AE=AD.连接 DE 交对角线 AC 于 H,连接 BH.下列结论
正确的是
SBEH DH .
SBEC AC
BE 1 .(填序号)①AC⊥DE;② ;③CD=2DH;④
HE 2
12.设 a1,a2 ,..., a2014 是从 1, 0, 1 这三个数中取值的一列数,若 a1 a2 ... a2014 69 ,
2015 澄池杯复赛数学试卷(A)
满分:100 分 时量:70 分钟
一、选择题(每题 5 分,共 30 分)
1、点 A、B、C 在同一条数轴上,其中点 A、B 表示的数分别为﹣3、1,若 BC=2,
则 AC 等于【 】
A.3
B.2
C.3 或 5
D.2 或 6
2.、关于 x 的二次函数 y=-(x-1)2+2,下列说法正确的是【 】
结算)报销看病的医疗费用.表一:
居民个人当年看病的医疗费用
医疗费用报销办法
不超过 n 元的部分
全部由医保基金承担(即全额报销)
超过 n 元但不超过 6000 元的部分
个人承担 k%,其余由医保基金承担
超过 6000 元的部分
个人承担 20%,其余由医保基金承担
设一位居民当年看病的医疗费用为 x 元,他个人实际承担的医疗费用(包括医疗费
800
1500
(元)
个人实际承担的医疗费用 y 70
190
470
(元)
(3)该地居民周大爷 2013 年看病的医疗费用共 32000 元,那么他这一年个人实际
承担的医疗费用是多少元?
14. (14 分)如图(1),E 是正方形 ABCD 的边 BC 上的一个点(E 与 B、C 两点 不重合),过点 E 作射线 EP⊥AE,在射线 EP 上截取线段 EF,使得 EF=AE;过点 F 作 FG⊥BC 交 BC 的延长线于点 G. (1)求证:FG=BE; (2)连接 CF,如图(2),求证:CF 平分∠DCG;
…
依此规律,在第 10 个数、第 11 个数、第 12 个数、第 13 个数中,最大的数是【 】
A. 第 10 个数
B. 第 11 个数
C. 第 12 个数
D. 第 13 个数
4.如图,在四边形 ABCD 中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60º,点 M、 N 分别在 AB、AD 边上,若 AM:MB=AN:ND=1:2,则 tan MCN 【 】
BE 3 (3)当 时,求 sin∠CFE 的值.
BC 4
9
15. (14 分)如图,在平面直角坐标系 xOy 中,顶点为 M 的抛物线是由抛物线 y=x2 ﹣3 向右平移一个单位后得到的,它与 y 轴负半轴交于点 A,点 B 在该抛物线上, 且横坐标为 3. (1)求点 M、A、B 坐标; (2)连结 AB、AM、BM,求∠ABM 的正切值; (3)点 P 是顶点为 M 的抛物线上一点,且位于对称轴的右侧,设 PO 与 x 正半轴 的夹角为α,当α=∠ABM 时,求 P 点坐标.
A、图象的开口向上
B、当 x>1 时,y 随 x 的增大而减小
C、图象的顶点坐标是(-1,2) D、图象与 y 轴的交点坐标为(0,2)
3.下面是按照一定规律排列的一列数:
第
1
个数:
1 2
1
1 2
;
1 1 12 13
第
2
个数:
3
1
2
1
3
1
4
;
1 1 12 13 14 15
第 3 个数: 1 1 1 1 1 ; 4 2 3 4 5 6
6.如图,矩形 ABCD 中,AB=3,BC=5,点 P 是 BC 边上的一个动点(点 P 不与点 B,C 重合),现将△PCD 沿直线 PD 折叠,使点 C 落下点 C1 处;作∠BPC1 的平
7
分线交 AB 于点 E.设 BP=x,BE=y,那么 y 关于 x 的函数图象大致应为【 】
A.
ቤተ መጻሕፍቲ ባይዱ
B.
33 A.
13
25 B.
11
23 C.
9
D. 5 2
5.在直角坐标系中,已知点 A(1, 3 ),O 是坐标原点,若连结 OA,将线段 OA
绕点 O 逆时针旋转 90°得到线段 OB,则点 B 的坐标是【 】
A、( 3 ,1)
B、(- 3 ,-1)
C、( 3 ,-1)或(- 3 ,1)
D、(- 3 ,1)
用中个人承担的部分和年初缴纳的医保基金)记为 y 元.
(1)当 0≤x≤n 时,y=70;当 n<x≤6000 时,y=
(用含 n、k、x 的代数式
表示)
(2)表二是该地 A、B、C 三位居民 2013 年看病的医疗费和个人实际承担的医疗
费用,根据表中的数据,求出 n、k 的值.表二:
居民
A
B
C
个人看病所花费的医费用 x 400
(a1 1)2 (a 2 1)2 ... (a 2014 1)2 4001 ,则 a1,a2 ,...,a2014 中为 0 的个数是
.
三、解答题
13.(12 分)某地实行医保制度,并规定:
8
一、每位居民年初缴纳医保基金 70 元;
二、居民个人当年看病的医疗费(以定点医院的医疗发票为准,年底按表一的方式
10
2015 澄池杯复赛数学真题详解
C.
D.
二、填空题(每题 5 分,共 30 分)
x -1
7、函数 y=
自变量 x 的取值范围是_________
x-2
8. .已知实数 m,n 满足 m n2 1 ,则代数式 m2 2n2 4m 1的最小值等
于
.
9. 矩形 ABCD 中,AB=2,BC=1,点 P 是直线 BD 上一点,且 DP=DA,直线 AP
