八年级数学上册衔接训练课件(新版)新人教版
人教版八年级数学上册专题训练(二)PPT

7.(中考改编题)如图①,线段AB,CD相交于点O,连接AC,DB. (1)求证:∠A+∠C=∠D+∠B; (2)如图②,已知∠A=50°,∠D=40°,若BE平分∠ABD交CD于点F, CE平分∠ACD交AB于点G,求∠E的度数; (3)如图③,若直线BM平分∠ABD交CD于点F,CM平分∠DCH交直线 BF于点M,直接写出∠M与∠A,∠D之间相等的数量关系.
类型四 利用方程思想探究角与角之间的关系 8.【探究与发现】如图①,在△ABC中,∠B=∠C=45°,点D在BC 边上,点E在AC边上,且∠ADE=∠AED,连接DE. (1)当∠BAD=60°时,求∠CDE的度数; (2)当点D在BC(点B,C除外)边上运动时,试猜想∠BAD与∠CDE的数量 关系,并说明理由; (3)【深入探究】如图②,若∠B=∠C,但∠C≠45°,其他条件不变,试 探究∠BAD与∠CDE的数量关系.
解:(2)如图②,2∠A=∠1+∠2. 理 由 如 下 : ∵ ∠ 1 + ∠ A′DA + ∠ 2 + ∠ A′EA = 360° , ∠ A + ∠ A′ + ∠A′DA+∠A′EA=360°, ∴∠A′+∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2, ∴∠1=∠A+∠A′+∠2=2∠A+∠2, ∴2∠A=∠1-∠2=56°, 解得∠A=28°
解:(1)证明:在△BOD中,∠BOD=180°-∠D-∠B, 在△AOC中,∠AOC=180°-∠A-∠C,∵∠AOC=∠BOD, ∴180°-∠A-∠C=180°-∠D-∠B,∴∠A+∠C=∠D+∠B
(2)∠DBE+∠D=∠E+∠DCE,① ∠ECA+∠A=∠EBA+∠E,② ∵∠DBA和∠ACD的平分线BE和CE相交于点E,∴∠DBE=∠EBA, ∠ECA=∠DCE, 由 ① + ② , 得 ∠ DBE + ∠ D + ∠ ECA + ∠ A = ∠ E + ∠ DCE + ∠ EBA + ∠E,即2∠E=∠D+∠A, 又∠D=40°,∠A=50°,∴2∠E=40°+50°=90°,∴∠E=45° (3)2∠M=180°-∠A-∠D
新人教版八年级上册数学课件

新人教版八年级上册数学课件注:直接按Ctrl键点击你所要下载的课件即可.可以长期关注11.1 全等三角形PPT课件.ppt11.2 三角形全等的判定PPT课件1.ppt11.2 三角形全等的判定PPT课件2.ppt11.2 三角形全等的判定(ASA AAS) PPT课件.ppt11.2 三角形全等的判定(SAS) PPT课件.ppt11.2 三角形全等的判定(SSS) PPT课件.ppt11.2 三角形全等的判定2PPT课件.ppt11.2 三角形全等的条件PPT课件.ppt11.3 角的平分线的性质PPT课件1.ppt11.3 角的平分线的性质PPT课件2.ppt12.1 轴对称 PPT课件1a.ppt12.1 轴对称 PPT课件2a.ppt12.1 轴对称 PPT课件3a.ppt12.2 作轴对称图形PPT课件1.ppt12.2 作轴对称图形PPT课件2.ppt12.2 作轴对称图形PPT课件3.ppt12.2 作轴对称图形PPT课件4.ppt12.2.1 作轴对称图形PPT课件.ppt 12.2.2 用坐标表示轴对称PPT课件.ppt 12.3.1 等腰三角形PPT课件1.ppt12.3.1 等腰三角形PPT课件2.ppt12.3.1 等腰三角形的判定课件.ppt 12.3.1 等腰三角形的性质课件1.ppt 12.3.1 等腰三角形的性质课件2.ppt 12.3.1 等腰三角形的性质课件3.ppt 12.3.2 等边三角形PPT课件1.ppt12.3.2 等边三角形PPT课件2.ppt12.3.2 等边三角形PPT课件3.ppt13.1 平方根PPT课件1.ppt13.1 平方根PPT课件2.ppt13.1 平方根PPT课件3.ppt13.1 平方根PPT课件4.ppt13.1 平方根PPT课件5.ppt13.1 算术平方根PPT课件.ppt13.1 习题讲解PPT课件.ppt13.2 立方根PPT课件1.ppt13.2 立方根PPT课件2.ppt13.2 立方根PPT课件3.ppt13.2 平方根、立方根习题课课件.ppt13.2 习题讲解PPT课件.ppt13.3 实数PPT课件1.ppt13.3 实数PPT课件2.ppt13.3 实数PPT课件3.ppt13.3 实数(实数的概念)课件.ppt13.3 实数习题讲解课件.ppt14.1 变量与函数的初步认识课件.ppt14.1.1 变量PPT课件.ppt14.1.2 变量与函数PPT课件1.ppt 14.1.2 变量与函数PPT课件2.ppt 14.1.2 函数PPT课件.ppt14.1.3 函数的图象PPT课件1.ppt 14.1.3 函数的图象PPT课件2.ppt 14.2 一次函数_待定系数法PPT课件.ppt 14.2 一次函数_复习课PPT课件.ppt 14.2 一次函数_实际问题PPT课件.ppt 14.2 一次函数_正比例函数PPT课件.ppt 14.2 一次函数的图象和性质课件.ppt 14.2.1正比例函数(第1课时)课件.ppt 14.2.1正比例函数(第2课时)课件.ppt 14.3 一次函数与一元一次方程(1课时).ppt 14.3 一次函数与一元一次方程(2课时).ppt14.3 一次函数与一元一次方程(3课时).ppt 14.3.1一次函数与一元一次方程课件.ppt 14.3.2一次函数与与一元一次不等式.ppt 14.3.3一次函数与二元一次方程组.ppt14.3.4用函数观点看方程(组)与不等式1.ppt 14.3.4用函数观点看方程(组)与不等式2.ppt14.3.4用函数观点看方程(组)与不等式3.ppt15.1 整式的乘法PPT课件1.ppt15.1 整式的乘法PPT课件2.ppt15.1 整式的乘法(1)PPT课件.ppt15.1 整式的乘法(2)PPT课件.ppt15.1.1 单项式乘以单项式PPT课件.ppt 15.1.2 单项式与多项式相乘课件1.ppt 15.1.2 单项式与多项式相乘课件2.ppt 15.1.3 多项式与多项式相乘课件.ppt15.1.4 同底数幂的乘法PPT课件.ppt15.2 乘法公式(第1课时)PPT课件.ppt 15.2 乘法公式(第2课时)PPT课件.ppt 15.2 乘法公式(第3课时)PPT课件.ppt 15.2 乘法公式_平方差公式课件.ppt15.2.1 平方差公式PPT课件.ppt15.2.2 完全平方公式PPT课件.ppt15.3 整式的除法(第1课时)课件.ppt 15.3 整式的除法(第2课时)课件.ppt 15.3.2 单项式除单项式PPT课件.ppt 15.3.2 整式的除法PPT课件.ppt15.4 因式分解.ppt15.4 因式分解(1).ppt15.4 因式分解(2)(平方差公式).ppt 15.4 因式分解(3)(完全平方公式法).ppt 15.4《因式分解》复习ppt课件.ppt。
新人教版八年级上册数学全册课件

2020/10/21
注意:
A
知1-讲
c
b
1.三角形的三边用字母表示时,字
母没有顺序限制.
B
aC
2.三角形的三边,有时也用一个小写字母来表示.
如:△ABC的三边中,顶点A所对的边BC也可表示为a,
顶点B所对的边AC也可表示为b,顶点C所对的边AB也可
表示为c.
3.一般情况下,我们把边BC叫做 A的对边,AC,AB叫
2020/10/21
知2-讲
按 角 分
按 边 分
2020/10/21
三角形的分类
锐角三角形
直角三角形 钝角三角形
三边都不相等的三角形 底边和腰不相等
等腰三
三边都 角形
不相等
的三角 等边三
形
角形
等腰三角形 的等腰三角形
三角形
等边三角形
知2-练
1 下列说法:①等边三角形是等腰三角形;②等腰 三角形也可能是直角三角形;③三角形按边分类 可分为等腰三角形、等边三角形和三边都不相等 的三角形;④三角形按角分类应分为锐角三角形、 直角三角形和钝角三角形.其中正确的有( C ) A.1个 B.2个 C.3个 D.4个
同理有
AC+BC>AB,
②
AB+BC>AC.
③
一般地,我们有
三角形两边的和大于第三边. 由不等式②③移项可得BC>AB-AC,BC>AC-AB. 这就是说,三角形两边的差小于第三边.
2020/10/21
知3-导
例1 用一条长为18 cm的细绳围成一个等腰三角形. (1) 如果腰长是底边长的2倍,那么各边的长是多少? (2) 能围成有一边的长是4 cm的等腰三角形吗?为什么?
八年级数学上册 13.3-13.4课件 (新版)新人教版

3.等腰三角形底边长为5 cm,一腰上的中线把其周长分为 两部分的差为3 cm,则腰长为 8 cm .
等腰三角形与全等三角形的综合问题
例4 某校八(3)班在一次数学探究性学习活动中,探究“一般三角形具 备哪些条件,就能断定其是等腰三角形”的过程中,其中一个小组提出下列问题: 如图所示,△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O,给出下列四个条 件: ①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC. (1)上述四个条件中,哪两个条件组合可判定△ABC是等腰三角形?(用序号写出所 有情况) (解2):选(1)择①第和(③1)问,①中和的④一,②种和情③况,②,证和明④△四AB种C情是况等,腰三角形. 均可判定△ABC是等腰三角形. (2)证明满足①和③的情形,理由如下:
A
C
B C , ∴ △ADC≌△BDC(SSS),
D C D C ,
∴∠BCD=∠ACD=
1 2
ACB=30°,∴∠P=30°.
等腰三角形与含有30°角的直角三角形的综合问题
例5 如图所示,在等边三角形ABC中,BD平分∠ABC 交AC于点D,过点D作DE⊥BC于点E,且CE=1, 求BC的长. 解:∵△ABC是等边三角形, ∴∠ABC=∠C=60°,AB=BC=AC, ∵DE⊥BC,∴∠CDE=30°, ∵EC=1,∴CD=2EC=2, ∵BD平分∠ABC交AC于点D, ∴AD=CD=2, ∴BC=AC=AD+CD=4.
1 ∴∠BDC+ 2
∠ABC=
1 ∠ACE,∠BAC+∠ABC=∠ACE, 2
∴∠BDC+
1 2
【推荐】新人教版八年级数学上(全书)课件PPT(共556张)(2020年最新)

B
C
D
【练习】 用同样的方法,你能画出
△ABC的另两条边上的中线吗?
根据你的观察,
三角形的三条中线交于几个点呢?
A
三角形的三条中线交于一点. F
E
B
D
C
【巩固练习】 你能分别画出直角三角形和钝角三角
形的三条中线吗?
A
A
F
E
F
E
B
D
B
C
D
C
任意三角形的三条中线都在三角形的内部.
你能根据自己的观察,画 出三角形的一条角平分线吗?
图中∠1与∠2有什么关系?为什么?
A
E
F 12
B
D
C
盖房子时,在窗框未安装 好之前,木工师傅常常现在窗 框上斜钉一根木条.为什么要 这样做?
三角形 具有稳定性,
四边形 不具有稳定性.
思考: 如图(1),将三根木条用钉子钉成一个三角形 木架,然后扭动它,它的形状会改变吗? 如图(2),将四根木条用钉子钉成一个四边形 木架,然后扭动它,它的形状会改变吗? 如图(3),在四边形木架上再钉一根木条,将 它的一对顶点连接起来,然后再扭动它,这时 木架的形状还会改变吗?为什么?
C
∠A, ∠B, ∠C, 是相邻两边组成 的角,
叫做三角形的内角,简称三角形的 角.
1. 图中有几个三角形?用符号表示这些三 角形.
5个 △ABE, △DCE, △ABC, △BCD, △BCE
A E
B
D C
A
D
B
C
如图,按要求完成下列填空.
(1)用符号表示图中的三角△A形BD,△BCD,△ABC
角平分线,则∠1= ∠2 , ∠3 =1/2 ∠AB,C
暑假 人教版八年级上册数学衔接班讲义第5讲:全等三角形
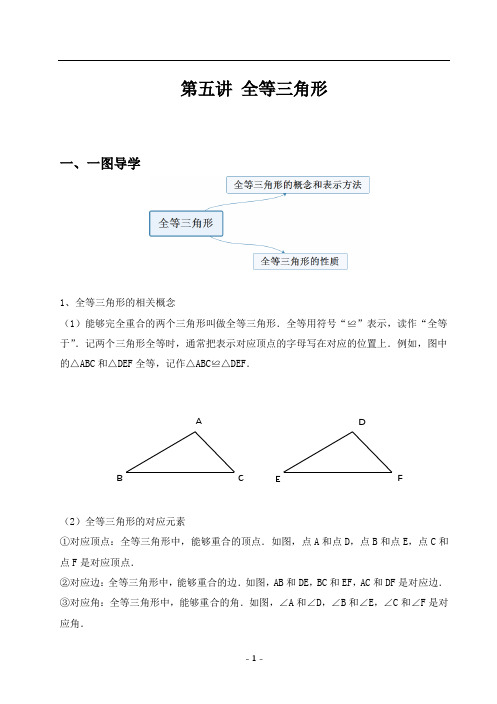
第五讲 全等三角形一、一图导学1、全等三角形的相关概念(1)能够完全重合的两个三角形叫做全等三角形.全等用符号“≌”表示,读作“全等于”.记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.例如,图中的△ABC 和△DEF 全等,记作△ABC ≌△DEF .(2)全等三角形的对应元素①对应顶点:全等三角形中,能够重合的顶点.如图,点A 和点D ,点B 和点E ,点C 和点F 是对应顶点.②对应边:全等三角形中,能够重合的边.如图,AB 和DE ,BC 和EF ,AC 和DF 是对应边. ③对应角:全等三角形中,能够重合的角.如图,∠A 和∠D ,∠B 和∠E ,∠C 和∠F 是对应角. A B C DE F探究交流:如图,将△ACB向右平移得到△DEF,先写出全等式,再指出它们的对应边和对应角.如图,△ABC与△ABD关于AB对称,先写出全等式,再指出它们的对应边和对应角.如图,将△AOC旋转得到△BOD,先写出全等式,再指出它们的对应边和对应角.2、对应元素的确定方法(1)图形特征法:①最长边对最长边,最短边对最短边.②最大角对最大角,最小角对最小角.(2)位置关系法:①公共角(对顶角)为对应角,公共边为对应边.②对应角的对边为对应边,两个对应角所夹的边是对应边.③对应边的对角为对应角,两条对应边所夹的角是对应角.3、全等三角形的性质(1)全等三角形的对应边相等,全等三角形的对应角相等.(2)全等三角形的周长相等,面积相等,对应边上的中线相等,对应角的角平分线相等,对应边上的高相等.例1、如图,将△ABC沿AC对折,点B与点E重合,则全等的三角形有( )A.1对 B.2对C.3对 D.4对例2、如图所示,△ACF≌△DBE,且点A,B,C,D在同一条直线上.AD=9cm,BC=5cm,求AB的长.折叠中的全等三角形问题例3、如图所示,将长方形ABCD沿DE折叠,使点C恰好落在BA边上,得到点C′,若∠C′EB=40°,求∠EDC′的度数.例4、如图,A、D、E三点在同一直线上,且△BAD≌△ACE.(1)试说明BD=DE+CE;(2)△ABD满足什么条件时,BD∥CE?请说明理由.1、如图,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是( ) A.AC=CE B.∠BAC=∠ECDC.∠ACB=∠ECD D.∠B=∠D2、如图,△ABC中,D,E分别是边BC,AC上的点,若△EAB≌△EDB≌△EDC,则∠C为( )A.15° B.20°C.25° D.30°3、已知△ABC与△DEF是全等的两个三角形,∠A=80°,∠E-∠F=50°.求∠D的度数.4、如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数为( )A.30° B.40°C.50° D.65°。
新人教版八年级数学上册全册课件

巩固并运用“三角形两边的和大于第三边”
追问 解决这类问题我们通常用哪两条线段的和与 第三条线段做比较就可以了?为什么?
用较小两条线段的和与第三条线段做比较; 若较小两条线段的和大于第三条线段,就能保证 任意两条线段的和大于第三条线段.
巩固并运用“三角形两边的和大于第三边”
例2 用一条长为18 cm的细绳围成一个等腰三角 形.(1)如果腰长是底边的2倍,那么各边的长是多 少?
△BDC.
B
C
课堂练习
练习2 下列说法正确的有_(__4_)___. (1)锐角三角形是三条边都不相等的三角形; (2)直角三角形不是等腰三角形; (3)等腰三角形是等边三角形; (4)等边三角形是等腰三角形.
探索与证明三角形三边的关系
问题3 如图,任意画一个△ABC,一只小虫从点 B 出发,沿三角形的边爬到点C,它有几条路线可以选 择?各条线路的长一样吗?你能运用所学知识解释你的 结果吗?你能由此推出三条边之间有怎样的关系?
三边都不相等的三角形
三角形
底边和腰不相等的等腰三角形
等腰三角形 等边三角形
理解三角形的分类
追问 按边分类后的特殊三角形之间有什么关系? 它们的边和角怎样命名?
课堂练习
练习1 图中有几个三角形?用符号表示这些三角 形.
图中有5个三角形. A
D
三角形的表示为:
△ABE, △ABC,
E
△BEC, △EDC,
八年级 上册
11.1 与三角形有关的线段 (第2课时)
课件说明
• 在已学过的过直线外一点作已知直线的垂线、线段的 中点、角的平分线等知识的基础上,本节课学习与三 角形有关的三种重要线段及三角形的稳定性.
课件说明
新人教版初二上册(八上)数学全册课件PPT

全册教学课件
11.1
与三角形有关的线段
11.1.1 三角形的边
导入新知
观察与思考
1. 你能从中找出4个不同的三角形吗?与同学交流
各自找出的三角形。
A
2. 这些三角形有什么共同
特点?
EE
F
B
D
G
C
探究新知
知识点 1
探究
三角形的有关概念
三角形是我们熟悉的图形,观察下列图片,你能
D.2,3,5
课堂检测
基 础 巩 固 题
3.下列说法:①等边三角形是等腰三角形;②三
角形按边分类可分为等腰三角形、等边三角形、不等边
三角形;③三角形的两边之差大于第三边;④三角形按
角分类应分为锐角三角形、直角三角形、钝角三角形.
其中正确的有( B )
A.1个
B.2个
C.3个
D.4个
课堂检测
能力提升题
1. (2018•长沙)下列长度的三条线段,能组成三角形的
是( B )
A.4cm,5cm,9cm
B.8cm,8cm,15c
C.5cm,5cm,10cm
D.6cm,7cm,14cm
2. (2018•常德)已知三角形两边的长分别是3和7,则此三角形
第三边的长可能是( C )
A.1 B.2 C.8 D.11
厘米.
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角
平分线
导入新知
定义
复
垂线
当两条直线相交所成的四个角中,有一个
角是直角时,就说这两条直线互相垂直,
其中一条直线叫做另一条直线的垂线
习
线段
2024八年级数学上册第二部分期末专题复习专题2图形与几何习题课件新版新人教版

(1)图中与 MF 相等的线段是
;
CE
(2)当 BF + CE 取最小值时,∠ AFB
= 95
1
2
3
4
°.
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
19. [2023北京海淀区期中] 如图,在△ ABC 中, AC = BC ,
∠ ACB =90°, AD 平分∠ CAB ,交 BC 于点 D . 点 A
与点 E 关于直线 BC 对称,连接 BE , CE ,延长 AD 交
BE 于点 F .
(2)求证:△ BDF 是等腰三角形;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
(2)证明:∵ AC = BC ,∠ ACB =90°,
∴∠ CAB =∠ CBA =45°.
∵ AD 是∠ CAB 的平分线,
∴△ BDF 是等腰三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
19. [2023北京海淀区期中] 如图,在△ ABC 中, AC = BC ,
∠ ACB =90°, AD 平分∠ CAB ,交 BC 于点 D . 点 A
初中数学人教版八年级上全册课件ppt(全等三角形等40个) 人教版20

练习:1、填空 (1)正比例函数 y=kx(k≠0) 的图象是 直线 它一定经过点 (0,0) 和 (1,k) 。 (2)如果函数 y= - kx 的图象在一,三象 限,那么y = kx 的图象经过 二,四象限。 m 2 1 m )x (3)如果 y( 是正比例函数, 且y随x的增大而减小,那么m= 3 。
§14.2.1正比例函数
2、已知y与x成正比例,且当x =-1时, y =-2,求y与x之间的函数关系式。
知识回顾
1、正比例的解析式是什么?
y=kx(k≠0)
y=2x
例1:画正比例函数 y=2x 的图象
画图步骤:
1、列表; 2、描点;
3、连线。
y=2x 的图象为: x … -3 -2 -1 0 1 2 3 … y … -6 -4 -2 0 2 4 6 …
y
5 4 3 2 1 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 1 2 3
y=2x
4
5
x
练习:画出正比例函数y=-2x的图象?
y 5 4 3 2 1
y=2x
结论 正比例 函数y= kx (k≠0) 的图 象是经过 原点(0,0)点 和(1,k)点 的一条直 线。
-5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5
③当 |k| 越大时,图象越靠近y轴
布置作业:
必做题:课本P35习题11.2 第1、2题
作业本 选做题:习题精选P18—19
再见
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
1、聪明的人有长的耳朵和短的舌头。 ——弗莱格 2、重复是学习之母。 ——狄慈根 3、当你还不能对自己说今天学到了什么东西时,你就不要去睡觉。 ——利希顿堡 4、人天天都学到一点东西,而往往所学到的是发现昨日学到的是错的。 ——B.V 5、学到很多东西的诀窍,就是一下子不要学很多。 ——洛 克 6、学问是异常珍贵的东西,从任何源泉吸收都不可耻。 ——阿卜· 日· 法拉兹 7、学习是劳动,是充满思想的劳动。 ——乌申斯基 8、聪明出于勤奋,天才在于积累 --华罗庚 9、好学而不勤问非真好学者。 10、书山有路勤为径,学海无涯苦作舟。 11、人的大脑和肢体一样,多用则灵,不用则废 -茅以升 12、你想成为幸福的人吗?但愿你首先学会吃得起苦 --屠格涅夫 13、成功=艰苦劳动+正确方法+少说空话 --爱因斯坦 14、不经历风雨,怎能见彩虹 -《真心英雄》 15、只有登上山顶,才能看到那边的风光。 16只会幻想而不行动的人,永远也体会不到收获果实时的喜悦。 17、勤奋是你生命的密码,能译出你一部壮丽的史诗。 1 8.成功,往往住在失败的隔壁! 1 9 生命不是要超越别人,而是要超越自己. 2 0.命运是那些懦弱和认命的人发明的! 21.人生最大的喜悦是每个人都说你做不到,你却完成它了! 22.世界上大部分的事情,都是觉得不太舒服的人做出来的. 23.昨天是失效的支票,明天是未兑现的支票,今天才是现金. 24.一直割舍不下一件事,永远成不了! 25.扫地,要连心地一起扫! 26.不为模糊不清的未来担忧,只为清清楚楚的现在努力. 27.当你停止尝试时,就是失败的时候. 28.心灵激情不在,就可能被打败. 29.凡事不要说"我不会"或"不可能",因为你根本还没有去做! 30.成功不是靠梦想和希望,而是靠努力和实践. 31.只有在天空最暗的时候,才可以看到天上的星星. 32.上帝说:你要什么便取什么,但是要付出相当的代价. 33.现在站在什么地方不重要,重要的是你往什么方向移动。 34.宁可辛苦一阵子,不要苦一辈子. 35.为成功找方法,不为失败找借口. 36.不断反思自己的弱点,是让自己获得更好成功的优良习惯。 37.垃圾桶哲学:别人不要做的事,我拣来做! 38.不一定要做最大的,但要做最好的. 39.死的方式由上帝决定,活的方式由自己决定! 40.成功是动词,不是名词! 20、不要只会吃奶,要学会吃干粮,尤其是粗茶淡饭。
八年级数学上册 第一章 勾股定理学期衔接训练课件

A.3个球都是黑球 B.3个球都是白球
C.3个球中有黑球
D.3个球中有白球
第三页,共十一页。
3.图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(xūxiàn)(对称轴)剪开,
Байду номын сангаас
把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则
中间空的部分的面积是( )
第五页,共十一页。
5.(2019·陕西)如图,OC是∠AOB的角平分线,l∥OB,若∠1=52°,则∠2的度数(dù shu)
为( )
C
A.52°
B.54°
C.64°
D.69°
第六页,共十一页。
二、填空题
6.(2019·毕节)如图,以△ABC的顶点B为圆心,BA长为半径(bànjìng)画弧,交BC边于点D, 连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为_____度.
第九页,共十一页。
9.如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格 点△ABC(即三角形的顶点都在格点上). (1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求(yāoqiú):A与A1,B与B1,C与C1相对 应) (2)在(1)问的结果下,连接BB1,CC1.求四边形BB1C1C的面积.
Image
12/13/2021
第十一页,共十一页。
C
A.2mn
B.(m+n)2
C.(m-n)2
D.m2-n2
第四页,共十一页。
4.(2019·安顺(ān shùn))如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加 下列一个条件后,仍无法判定△ABC≌△DEF的是(A) A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC
人教版数学八年级上册同步教学课件份ppt3

人教版数学八年级上册同步教学课件 份ppt3 (PPT优 秀课件 )
人教版数学八年级上册同步教学课件 份ppt3 (PPT优 秀课件 )
“HL”判定方法的运用
变式1 如图,AC⊥BC,BD⊥AD,要证△ABC ≌△BAD,需要添加一个什么条件?请说明理由. (1) AD = BC( H)L;
(2) AC = BD( H)L;
现象:两个直角三角形能重合. 说明:这两个直角三角形全等.
人教版数学八年级上册同步教学课件 份ppt3 (PPT优 秀课件 )
M B'
A
C N
A'
C'
人教版数学八年级上册同步教学课件 份ppt3 (PPT优 秀课件 )
归纳概括“HL”判定方法
斜边和一条直角边分别相等的两个直角三角形全 等(简写为“斜边、直角边”或“HL”).
∠ABC +∠DFE =90°
人教版数学八年级上册同步教学课件 份ppt3 (PPT优 秀课件 )
人教版数学八年级上册同步教学课件 份ppt3 (PPT优 秀课件 )
“HL”判定方法的运用
例2 如图,有两个长度相同的滑梯,左边滑梯的 高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯 的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?
• 学习重点: 理解并运用“HL”判定方法.
创设情境引出“HL”判定方法
问题1 如图,舞台背景的形状是两个直角三角形, 为了美观,工作人员想知道这两个直角三角形是否全 等,但每个三角形都有一条直角边被花盆遮住无法测 量.你能帮工作人员想个办法吗?
(1)如果用直尺和量角器两种工具,你能解决这个 问题吗?
(3) ∠DAB = ∠CB(A AA)S;
初中数学人教版八年级上全册课件 PPT课件 (全等三角形等40个) 人教版36

目的要求:
1、通过一元二次方程求根公式的推导,加强推理技 能训练,发展逻辑思维能力。 2、会运用求根公式解一元二次方程。
复习提 1.给下列各式配上适当的数,使其成为恒等式 问 5
5 ( ) 2 1) x 5 x (x 2 2 1 2 1 ( ) 2 2) x x (x 6
方程的求解问题转化为 代数式的值的计算问题 ,从而可简化
式了 .
例2
解方程
2x2 5x 2 0
a 2 , b 5 , c 2 解:
2 2 b 4 ac 5 4 2 2 9 0
5 9 5 3 x 4 4
1 x , x 2 1 2 2
2
b 2 b 4 ac 即 (x ) 2 2 a 4 a
2
ax2 bx c 0(a 0) 的求根公式
一般地,对于一元二次方程
2 当b 4 ac 0时,它的根是 :
ax bx c 0 ( a 0 )
2
2 b b 4 ac 2 x ( b 4 ac 0 ) 2 a
2 2
谢谢!
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
何。” 大意是:已知长方形门的高比宽多6尺8寸,门 的对角线长1丈,那么门的高和宽各是多少?
小 结 谈谈本节课你有哪些收获?
作业:
初中数学人教版八年级上全册课件ppt(全等三角形等40个) 人教版1

1、能够
的两个图形叫做
全等图形。两个三角形重合时,互
相
的顶点叫做对应顶点。
记两个全等三角形时,通常把表示
顶点的字母写在
的位置上。
2、如图△ABC≌ △ADE若
∠D= ∠B,
∠C= ∠AED,则
D
∠DAE=
;
∠DAB=
。
B
A
E
C
3、如图△ ABD ≌ △CDB, 若AB=4,AD=5,BD=6,则 BC= ,CD= 。
全等三角形的对应边相等; 全等三角形的对应角相等;
1、观察上图中的全等三角形应表示为: △ ABC ≌ △ DEF 。
2、根椐全等三角形的定义我们知道了对应边、对 应角的关系?请完成下面填空:
∵ △ ABC ≌ △ DEF(已知) ∴AB =DE,BC = EF,AC = DF ∠A = ∠D,∠B = ∠E,∠C = ∠F。
找一找
A
E
BD
C
如图,已知△ABC≌△ADE, ∠C=∠E,BC=DE,其它的对应边 有 :_____________ 对应角有:_____________
练习: P92——93
A
D
B
CEFFra bibliotek全等三角形的性质:对应边相等,对应角相等
全等三角形的符号表示: “≌”
读作:全等于
如图:∵ △ABC≌△DEF
•
8、有些人,因为陪你走的时间长了,你便淡然了,其实是他们给你撑起了生命的天空;有些人,分开了,就忘了吧,残缺是一种大美。
•
9、照自己的意思去理解自己,不要小看自己,被别人的意见引入歧途。
•
10、没人能让我输,除非我不想赢!
•
暑假 人教版八年级上册数学衔接班讲义第7讲:全等三角形的判定(ASA,AAS,HL)

第七讲全等三角形的判定一、一图导学继续探讨三角形全等的条件:两角一边思考:已知一个三角形的两个角和一条边,那么两个角与这条边的位置上有几种可能性呢?在图1中,边AB是∠A与∠B的夹边,我们称这种位置关系为两角及其夹边.在图2中,边BC是∠A的对边,我们称这种位置关系为两角及其中一角的对边.观察下图中的△ABC,画一个△A′B′C′,使A′B′=AB,∠A =∠A′,∠B =∠B′.角边角:两角和它们的夹边对应相等的两个三角形全等.简写为“角边角”或“ASA”.如图,在△ABC 和△DEF 中,若则△ABC ≌△DEF(ASA).如果两个三角形有两个角分别对应相等,且其中一组相等的角的对边相等,那么这两个三角形是否一定全等?因为三角形的内角和等于180°,因此有两个角分别对应相等,那么第三个角必定对应相等,于是由“角边角”,这两个三角形全等.角角边:两个角和其中一个角的对边对应相等的两个三角形全等.简写为“角角边”或“AAS ”.如图,在△ABC 和△DEF 中,若则△ABC ≌△DEF(AAS).直角三角形全等的条件除了可以用SSS ,SAS ,ASA ,AAS 来判定两个直角三角形全等外,还有一般三角形所没有的特殊判定方法:斜边和一条直角边对应相等的两个直角三角形全等.简写为“斜边、直角边”或“HL ”.,,,A D AB DE B E ∠=∠⎧⎪=⎨⎪∠=∠⎩,,,A D B E BC EF ∠=∠⎧⎪∠=∠⎨⎪=⎩ A B C DE F例1、如图,AB=DE,∠ABC=∠DEF.下列条件中不能证明△ABC≌△DEF的是()A.∠A=∠D B.AC=DFC.BE=FC D.∠ACB=∠DFE例2、如图,∠1=∠2,∠3=∠4,求证:AC=AD.例3、如图,已知在△AFD和△CEB中,点A,E,F,C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:AD=BC.例4、如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则下列结论正确的是( )①△APC≌△BPD;②△ADO≌△BCO;③△AOP≌△BOP;④△OCP≌△ODP.A.①②③④ B.①②③ C.②③④ D.①③④例5.如图,在△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD,CE交于点O,试判断BE,CD,BC的数量关系,并加以证明.1、如图,在下列条件中,不能证明△ABC≌△DCB的是( )A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCBC.BO=CO,∠A=∠D D.AB=DC,∠A=∠D2、如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是___________(填出一个即可).3.如图,BE⊥CD,BE=DE,BC=DA,求证:(1)△BEC≌△DEA;(2)DF⊥BC.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阶梯 电量 电价 0-180度 0.6元/度 一档 二档 181-400度 二档电价 三档 401度及以上 三档电价
解:设二档电价是x元/度,三档电价是y元/度,
180×0.6+220x+100y=352, x=0.7, 根据题意得 解得 y=0.9, 180×0.6+220x+60y=316,
衔接训练
1.(2015·日照) 4 的算术平方根是( C ) A.2 B.±2 C. 2 D.± 2 2.下列调查中,适宜采用普查方式的是( D A.了解一批圆珠笔的寿命 B.了解全国八年级学生身高的现状 C.考察人们保护海洋的意识 D.检查一枚用于发射卫星的运载火箭的各零部件 )
3.下列图形中,由∠1=∠2能得到AB∥CD的是( B)
则二档电价是0.7元/度,三档电价是0.9元/度
解答下列问题:
50 ,并补全频数分布直方图; (1)这次抽样调查的样本容量是____ 72 度; (2)在扇形统计图中D组的圆心角是____
(3)请你估计该校九年级体重超过60 kg的学生大约有多少名?
解:(1)补图略 (3)样本中体重超过60 kg的学生数为10+8=18(名),则该校九年级体 18 重超过60 kg的学生数为 ×1000=360(名) 50
那么第一架轰炸机C的平面坐标是 (2,-1) .
2a-b=2, 7.(2015·枣庄)已知a,b满足方程组 a+2b=5,
26 则2a+b的值为 5
.
8.有10名菜农,每人可种茄子3亩或辣椒2亩,已知茄子每亩可收入0.5 万元,辣椒每亩可收入0.8万元,要使总收入不低于15.6万元,则最多只能 4 人种茄子. 安排____
x+2≥1, 4.不等式组 的解集在数轴上表示正确的是( B ) 3-x≥0
二、填空题
5.如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=
110°,则∠AON的度数为____ 145度.
6.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标
分别为A(-2,1)和B(-2,-3),
三、解答题
9.(2015· 朝阳)为响应国家节能减排的号召,鼓励居民节约用电,各
省先后出台了居民用电“阶梯价格”制度,如表中是某省的电价标准( 每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档
电价+100×三档电价=352元;李先生家5月份用电460度,交费316元
,请问表中二档电价、三档电价各是多少?
