二次根式复习专题讲义(补课用)
初二数学经典讲义 二次根式(基础)知识讲解

《二次根式》全章复习与巩固--知识讲解(基础)【学习目标】1、理解并掌握二次根式、最简二次根式、同类二次根式的定义和性质.2、熟练掌握二次根式的加、减、乘、除运算,会用它们进行有关实数的四则运算.3、了解代数式的概念,进一步体会代数式在表示数量关系方面的作用. 【知识网络】【要点梳理】要点一、二次根式的相关概念和性质 1. 二次根式形如(0)a a ≥的式子叫做二次根式,如13,,0.02,02等式子,都叫做二次根式. 要点诠释:二次根式a 有意义的条件是0a ≥,即只有被开方数0a ≥时,式子a 才是二次根式,a 才有意义. 2.二次根式的性质 (1); (2);(3).要点诠释:(1) 一个非负数a 可以写成它的算术平方根的平方的形式,即a 2a =(0a ≥),如2221122););)33x x ===(0x ≥). (2)2a a 的取值范围可以是任意实数,即不论a 2a .(3a ,再根据绝对值的意义来进行化简.(42的异同a可以取任何实数,而2中的a 必须取非负数;a,2=a (0a ≥).相同点:被开方数都是非负数,当a2.3. 最简二次根式(1)被开方数是整数或整式;(2)被开方数中不含能开方的因数或因式.满足上述两个条件的二次根式,叫做最简二次根式.次根式.要点诠释:最简二次根式有两个要求:(1)被开方数不含分母;(2)被开方数中每个因式的指数都小于根指数2. 4.同类二次根式几个二次根式化成最简二次根式后,被开方数相同,这几个二次根式就叫同类二次根式. 要点诠释:判断是否是同类二次根式,一定要化简到最简二次根式后,看被开方数是否相同,再判断.显然是同类二次根式. 要点二、二次根式的运算 1. 乘除法(1)乘除法法则: 类型 法则逆用法则二次根式的乘法0,0)a b =≥≥积的算术平方根化简公式:0,0)a b =≥≥二次根式的除法0,0)a b ≥>商的算术平方根化简公式:0,0)a b =≥>要点诠释:(1)当二次根式的前面有系数时,可类比单项式与单项式相乘(或相除)的法则,如= (2)被开方数a 、b 一定是非负数(在分母上时只能为正数).≠. 2.加减法将二次根式化为最简二次根式后,将同类二次根式的系数相加减,被开方数和根指数不变,即合并同类二次根式. 要点诠释:二次根式相加减时,要先将各个二次根式化成最简二次根式,再找出同类二次根式,最后合并同类二次根式.如23252(135)22+-=+-=-. 【典型例题】类型一、二次根式的概念与性质1. 当________时,二次根式3x -在实数范围内有意义. 【答案】x ≥3.【解析】根据二次根式的性质,必须3x -≥0才有意义.【总结升华】本例考查了二次根式成立的条件,要牢记,只有0a ≥时a 才是二次根式. 举一反三【高清课堂:二次根式 高清ID 号:388065 关联的位置名称:填空题5】 【变式】①242x x =-成立的条件是 . ②2233x x x x--=--成立的条件是 . 【答案】① x ≤0;(2422x x x x ==-∴≤0.)② 2≤3x <.(20,30,x x -->∴≥2≤3x <)2.当0≤x <1时,化简21x x +-的结果是__________.【答案】 1.【解析】因为x ≥0,所以2x =x ;又因为x <1,即x -1<0,所以1(1)1x x x -=--=-,所以21x x +-=x +1-x =1.【总结升华】利用二次根式的性质化简二次根式,即2a =a ,同时联系绝对值的意义正确解答. 举一反三【变式】已知0a <,化简二次根式3a b -的正确结果是( ).A.a ab --B. a ab -C. a abD.a ab -【答案】A.3.下列二次根式中属于最简二次根式的是( ).1448ab44a +【答案】A.【解析】选项B :48=43;选项C :有分母;选项D :44a +=21a +,所以选A. 【总结升华】本题考查了最简二次根式的定义.最简二次根式要满足:(1)被开方数是整数或是整式;(2)被开方数中不含能开方的因式或因数. 类型二、二次根式的运算4.下列计算错误的是( ).A. 14772⨯=B. 60523÷=C. 9258a a a +=D. 3223-= 【答案】 D.【解析】选项A : 14714727772⨯=⨯=⨯⨯= 故正确;选项B :605605123423÷=÷==⨯=,故正确;选项C925358a a a a a +=+=故正确;选项D :32222-= 故错误.【总结升华】本题主要考查了二次根式的加减乘除运算,属于基础性考题. 举一反三 【变式】计算:48(54453)833-+⨯ 【答案】243610-.5.化简20102011(32)(32)⋅. 【答案与解析】201020102010=(32)32)(32)(32)32)32)132)3 2.⋅⋅⎡⎤=⋅⋅⎣⎦=⋅=原式【总结升华】本题的求解用到了积的乘方的性质,乘法运算律,平方差公式及根式的性质,是一道综合运算题型.6 已知2231,12x x x x=-+求.【答案与解析】2231,1=30,(1)1313331=3x x x xx x x =+∴->∴=--++==原式当时,原式【总结升华】 化简求值时要注意x 的取值范围,如果未确定要注意分类讨论. 举一反三【高清课堂:二次根式 高清ID 号:388065关联的位置名称:计算技巧6-7】 【变式】已知a b +=-3, ab =1,求ab b a +的值. 【答案】∵a b +=-3,ab =1,∴<0a ,<0b11+==-(+)=-=3--ab ab a bb a b a ab∴+原式.。
专题04二次根式的核心知识点精讲(讲义)(原卷版)中考数学一轮复习

专题04 二次根式的核心知识点精讲1.了解二次根式的概念及其有意义的条件.2.了解最简二次根式的概念,并会把二次根式化成最简二次根式.3.掌握二次根式(根号下仅限于数)加、减、乘、除、乘方运算法则,会用它们进行有管的简单四则运算.【题型1:二次根式有意义的条件】【典例1】(2023•济宁)若代数式有意义,则实数x的取值范围是()A.x≠2B.x≥0C.x≥2D.x≥0且x≠21.(2023•金华)要使有意义,则x的值可以是()A.0B.﹣1C.﹣2D.22.(2023•通辽)二次根式在实数范围内有意义,则实数x的取值范围在数轴上表示为()A.B.C.D.3.(2023•湘西州)若二次根式在实数范围内有意义,则x的取值范围是.【题型2:二次根式的性质】【典例2】(2023•泰州)计算等于()A.±2B.2C.4D.1.(2021•苏州)计算()2的结果是()A.B.3C.2D.92.(2023•青岛)下列计算正确的是()A.B.C.D.3.(2021•娄底)2、5、m是某三角形三边的长,则+等于()A.2m﹣10B.10﹣2m C.10D.44.(2022•遂宁)实数a、b在数轴上的位置如图所示,化简|a+1|﹣+=2.【题型3:二次根式的运算】【典例3】(2023•金昌)计算:÷×2﹣6.1.(2023•聊城)计算:(﹣3)÷=.2.(2023•山西)计算:的结果为.3.(2023•兰州)计算:.4.(2023•陕西)计算:.1.(2023秋•福鼎市期中)下列各数不能与合并的是()A.B.C.D.2.(2023秋•云岩区校级期中)下列式子中,属于最简二次根式的是()A.B.C.D.3.(2022秋•泉州期末)若二次根式有意义,则x的取值范围是()A.x<3B.x≠3C.x≤3D.x≥3 4.(2023秋•龙泉驿区期中)下列运算中,正确的是()A.B.C.D.5.(2023秋•锦江区校级期中)若a>b>0,则的结果是()A.a B.2b﹣a C.a﹣2b D.﹣a6.(2023春•河东区期中)把x根号外的因数移到根号内,结果是()A.B.C.﹣D.﹣7.(2023春•铁岭县期末)计算:的结果是()A.2B.0C.﹣2D.﹣8.(2023春•抚顺月考)二次根式的计算结果是()A.B.C.±D.9.(2023春•西丰县期中)已知a=+2,b=﹣2,则a﹣b的值是()A.2B.4C.2+4D.2﹣410.(2023春•工业园区期末)下列各组二次根式中,是同类二次根式的是()A.与B.与C.与D.与11.(2023春•武昌区校级期中)若是整数,则满足条件的最小正整数n的值为.12.(2023春•固镇县月考)计算=.13.(2023春•高安市期中)化简计算:=.14.(2023秋•高新区校级期中)计算:(1)×;(2).15.(2023秋•秦都区校级期中)计算:﹣×.1.(2022秋•鼓楼区校级期末)实数a在数轴上的位置如图所示,则化简结果为()A.7B.﹣7C.2a﹣15D.无法确定2.(2023春•新郑市校级期末)若=在实数范围内成立,则x的取值范围是()A.x≥1B.x≥4C.1≤x≤4D.x>43.(2023秋•西安校级月考)若x,y都是实数,且,则xy的值是()A.0B.4C.2D.不能确定4.(2023•商水县一模)我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记,则其面积,这个公式也被称为海伦一秦九韶公式.若p=5,c=2,则此三角形面积的最大值为()A.B.C.D.55.(2023秋•闵行区期中)计算:=.6.(2023春•科左中旗校级期末)观察下列等式:第1个等式:a1==﹣1,第2个等式:a2==,第3个等式:a3==2﹣,第4个等式:a4==﹣2,…按上述规律,计算a1+a2+a3+…+a n=.7.(2023春•中江县月考)已知的值是.8.(2023春•禹州市期中)如图,在数学课上,老师用5个完全相同的小长方形在无重叠的情况下拼成了一个大长方形,已知小长方形的长为,宽为,则这个大长方形的周长为.9.(2023春•宿豫区期末)计算的结果为.10.(2023秋•双流区校级期中)已知a=3+,b=3﹣,分别求下列代数式的值:(1)a2﹣b2;(2)a2﹣3ab+b2.11.(2023春•双柏县期中)阅读下面问题:==﹣1;==﹣;==﹣2.(1)求的值;(2)计算:+++…++.12.(2023秋•二七区校级月考)阅读材料:我们来看看完全平方公式在无理数化简中的作用.问题提出:该如何化简?建立模型:形如的化简,只要我们找到两个数a,b,使a+b=m,ab=n,这样()2+()2=m,•=.那么便有:(a>b),问题解决:化简:,解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12,即,.∴,模型应用1:利用上述解决问题的方法化简下列各式:(1);(2).模型应用2:(3)在Rt△ABC中,∠C=90°,AB=4﹣,AC=,那么BC边的长为多少?(直接写出结果,结果化成最简).1.(2022•桂林)化简的结果是()A.2B.3C.2D.22.(2022•内蒙古)实数a在数轴上的对应位置如图所示,则+1+|a﹣1|的化简结果是()A.1B.2C.2a D.1﹣2a3.(2022•河北)下列正确的是()A.=2+3B.=2×3C.=32D.=0.7 4.(2022•湖北)下列各式计算正确的是()A.B.C.D.5.(2022•青岛)计算(﹣)×的结果是()A.B.1C.D.36.(2022•安顺)估计(+)×的值应在()A.4和5之间B.5和6之间C.6和7之间D.7和8之间7.(2023•绵阳)若式子在实数范围内有意义,则x的最小值为.8.(2023•丹东)若代数式在实数范围内有意义,则实数x的取值范围是.9.(2022•武汉)计算的结果是.10.(2023•内蒙古)实数m在数轴上对应点的位置如图所示,化简:=.11.(2022•荆州)若3﹣的整数部分为a,小数部分为b,则代数式(2+a)•b的值是.12.(2022•泰安)计算:•﹣3=.13.(2022•济宁)已知a=2+,b=2﹣,求代数式a2b+ab2的值.。
二次根式辅导讲义

二次根式一、知识梳理1、二次根式的概念和性质二次根式的定义:形如a (0a ≥)的式子叫做二次根式.注意点:(1)被开方数是正数或0;(2)二次根式a (0a ≥)表示非负数a 的算术平方根.二次根式的性质:(1)二次根式的非负性:0a ≥;(2)2()(0)a a a =≥;(3)2(0)(0)(0)a a a a a a a a >⎧⎪===⎨⎪-<⎩;(4)当0a ≥时,22()a a =.2、最简二次根式最简二次根式最简二次根式的定义:①被开方数的因数是整数,因式是整式(分母中不含根号);②被开方数中不含能开 得尽方的因数或因式.这样的二次根式叫做最简二次根式.最简二次根式的满足条件:(1)被开放数的因数是整数,因式是整式(被开方数不能存在小数、分数形式);(2)被开方数中不含能开得尽方的因数或因式;(3)分母中不含二次根式.说明:二次根式的计算结果要写成最简根式的形式.3、二次根式的加减同类二次根式几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫同类二次根式.二次根式的加减同类二次根式:几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次 根式.合并同类二次根式:()a x b x a b x +=+,同类二次根式才可加减合并.分母有理化分母有理化:把分母中的根号化去叫做分母有理化.互为有理化因式:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,说这两个代数式互为有理化因式.a b+与a b-互为有理化因式;分式有理化时,一定要保证有理化因式不为0.4、二次根式综合运算二次根式的综合运算法则:先算乘除法,再算加减法,有括号的先算括号里面的,最终结果二次根式部分要化为最简二次根式.注意:在二次根式的计算题中,如果题目中没有明确说明字母的取值范围,按照字母使二次根式有意义计算.5、二次根式化简求值二次根式的化简求值:先把二次根式化为最简二次根式,然后进行二次根式的加减乘除运算,化为较为简单的一个式子(或直接得出结果),最后代入未知数的值求解,有时候也会存在整体代入的情况.注意:对于二次根式的化简求值如果字母没有明确说明取值范围,必须要进行分类讨论.6、根式的大小比较比较大小的方法1.作差法:比较a、b的大小,0,0,0,a b a b a ba b>>⎧⎪-==⎨⎪<<⎩2.作商法:比较a、b的大小,当0,0a b>>时,可以采用作商法,1,1,1,a b aa b ba b>>⎧⎪==⎨⎪<<⎩二次根式比较大小的方法(1)0a b a b>>⇔>(2)二次根式比较大小:能直接比较大小的直接比较;不能直接比较大小的,先平方再比较.(3)估算法(4)分子有理化(5)倒数法7、二次根式的乘除二次根式的乘除法二次根式的乘法法则:a b ab⋅=(0a≥,0b≥).二次根式的除法法则:a abb=(0a≥,0b>).说明:利用乘除法则时注意a、b的取值范围,对于ab a b=⋅,a、b都非负,否则不成立.二、典型例题题型一、二次根式的概念和性质例1: 函数1x y x =-中自变量x 的取值范围是( ) A .1x ≥B .1x <且0x ≠C .1x >D .1x ≥且0x ≠【答案】C【解析】该题考查的是函数的定义域.根式下的式子在非负条件下有意义,分数在分母不为0的条件下有意义,综上所述,10x -≥,且10x -≠,∴1x >,故本题答案为C .例2: 若320-+-=x y ,则xy 的值为____.A .8B .6C .5D .9【答案】A【解析】该题考查的是的非负性.根据题意得:3020x y -=⎧⎨-=⎩解得:32x y =⎧⎨=⎩∴32x y =,故选A .变式: 已知:()322512012x x y x -+-=+--,求x y 的值. 【答案】25【解析】该题考查的是二次根式的性质.∵()322512012x xy x -+-=+--有意义∴()32020120120x x x ⎧-≥⎪⎪-≥⎨⎪--≠⎪⎩所以2x =,055y =+=∴2525x y ==题型二、最简二次根式例1、下列二次根式中,最简二次根式是( )A .22xB .0.5C .22x y +D .1x 【答案】C【解析】该题考查最简二次根式.A 、x x 222=被开方数含能开得尽方的因数,不是最简二次根式;故本选项错误; B 、120.522==,被开方数含分母,不是最简二次根式;故本选项错误; C 、22x y +满足最简二次根式的定义,是最简二次根式;D 、1x x x=,被开方数含能开得尽方的因数,不是最简二次根式. 故选C .例2、若最简二次根式2342a +与22613a -是同类二次根式,则a =_________【答案】1±【解析】该题考查的是二次根式.满足下列两个条件的二次根式,叫做最简二次根式:(1)被开方数的因数是整数,因式是整式;(2)被开方数中不含能开得尽方的因数或因式.几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫做同类二次根式. 根据题意可列:22461a a +=-解得:1a =±变式、若2,m ,4为三角形三边,化简:()()2226m m -+-=____________.【答案】4【解析】该题考查的是根式的化简求值.∵2,m ,4为三角形三边,可知包括如下关系:①24m +>,即6m <②24m +>,即2m >∴原式264m m =-+-=题型三、二次根式的加减例1、计算124183-⨯=__________.【答案】6【解析】该题考查的是二次根式的计算.原式346923=⨯-⨯⨯326323=-⨯ 2666=-=例2、111115533131317+++=++++____.【答案】1714-【解析】该题考查根式的分母有理化.11115135133171317144444155********-----+++=+++=++++ 故答案为1714-. 变式、已知32x =+,32y =-,则33_________x y xy +=.【答案】10【解析】因为32x =+,32y =-,所以()()32321xy =+-=,()()323223x y +=++-=,所以()()()22332221232110x y xy xy x y xy x y xy ⎡⎤⎡⎤+=+=+-=⨯-⨯=⎢⎥⎣⎦⎣⎦题型四、二次根式综合运算例1、化简:2244112a a a a -+--+(112a ≤≤)【答案】32a -【解析】()()222244112211211a a a a a a a a -+--+---=---,因为112a ≤≤,所以原式21121132a a a a a =---=-+-=-例2、若352x y +=-,325x y -=-,求xy .【答案】52-【解析】2()352x y +=-;2()325x y -=-∴22()()352(325)5244x y x y xy +-----===-变式、化简22691025a a a a +++-+【答案】当3a <-时,原式=22a -+;当35a -≤<时,原式=8;当5a ≥时,原式=22a -;【解析】()()22226910253535a a a a a a a a +++-+=++-=++-,当3a <-时,原式353522a a a a a =++-=---+=-+;当35a -≤<时,原式35358a a a a =++-=+-+=;当5a ≥时,原式353522a a a a a =++-=++-=-题型五、二次根式化简求值例1、化简:()221269x x x -+-+=____【答案】43x -【解析】该题考查根式的化简.()()2221269123x x x x x -+-+=-+-∵由题得120x -≥,12x ≤∴()2333x x x -=-=-.∴原式12343x x x =-+-=-.故答案为43x -.例2、化简:108322++.【答案】42+【解析】22108322108(12)108(12)1882(42)42++=++=++=+=+=+变式、化简:(1)412-(2)415+【答案】(1)31-(2)1062+【解析】(1)()24124233131-=-=-=- (2)221064158215(53)222++=+=+=题型六、根式的大小比较例1、比较大小:512-_______12.(填“>”、“<”或“=”). 【答案】>【解析】该题考查的是二次根式比大小.5115115254022222------===>,即511022-->, 即51122->. 例2、设120082006,2007A B =-=,比较大小:A ____B .【答案】A B >【解析】222008200620082006A ==+-,22220072007B ==;2008200622007+< ∴22A B< ∴A B >变式、已知21a =-,226b =-,62c =-,那么a ,b ,c 的大小关系是( )A .a b c >>B .b a c >>C .c b a >>D .c b a <<【答案】B【解析】()()221,223,2322a b c ⎛⎫=-=-=- ⎪ ⎪⎝⎭2222(231)2(13)(2223)0222b a -=--+=-+=+->,b a > 2222(132)2(13)(2223)0222a c -=--+=-+=+->,a c >b ac >>题型七、二次根式的乘除例1、下列计算正确的是( )A .235⋅=B .236⋅=C .84=D .2(3)3-=-【答案】B【解析】根据二次根式的乘法运算法则,可得236⋅=,故答案为B 选项.例2、下列计算结果正确的是( )A .257+=B .2510⨯=C .3223-=D .25105=【答案】B【解析】该题考查的是二次根式计算.A 选项2与5不是同类项,不能合并,故本选项错误;B 选项252510⨯=⨯=,故本选项正确;C 选项32222-=,故本选项错误;D 选项21055=,故本选项错误. 故答案是B .变式、已知:4322232b a a =-+-+,求11a b +的平方根.【答案】2±【解析】该题考查的是二次根式.4322232b a a =-+-+,根据被开方数的非负性我们知道320230a a -≥⎧⎨-≥⎩,所以23a =, 代入得43222322b a a =-+-+=,所以1131222a b +=+=,平方根为2±三、课堂巩固1、函数11y x =-中自变量的取值范围是( B )A .1x ≠B .1x >C .1x ≥D .1x ≥-2、对于所有实数,a b ,下列等式总能成立的是( C )A .()2a b a b +=+B .22a b a b +=+C .()22222a b a b +=+ D .()2a b a b +=+ 3、函数12y x =+中,自变量x 的取值范围是2->x 4、实数P 在数轴上的位置如图所示,化简()()2223p p -+-=15、计算:=⨯121726,=--)84)(213(24, =⨯-03.027.02-0.18,=÷-327348-5.6、化简:()221269x x x -+-+=x 34-.7、设120082006,2007A B =-=,比较大小:A >B . 8、已知: 21x =-,求223x x +-的值.()()()()2222231322-=-+=+-=-+x x x x 9、已知:,x y 为实数,且113y x x <-+-+,化简:23816y y y ---+. 1=x 3<y 原式=()1-4343=---=---y y y y1 2 3 4 p课后作业1、函数2x y x-=中,自变量x 的取值范围是( A ) A .2x ≤且0x ≠B .2x ≤C .2x <且0x ≠D .0x ≠2、若()424A a =+,则A =( A ) A .24a +B .22a +C .()222a + D .()224a + 3、若2(2)10m n ++-= 则m n -= -3 .4、在下列二次根式22211025312232322a a a a b m x a b x a b +-++,,,,,,,,,,中,最简二次根式有6个.5、若最简二次根式35a -与3a +是同类二次根式,则a =___4___.6、若231604b a a +-+=-,则3223a b a b +=-___-18___.7、比较大小:512-___>___12.(填“>”、“<”或“=”). 8、计算:01186(121)221+---- 原式=01232212=--++9、化简:(1)412-原式=()13132-=- (2)415+221064158215(53)222++=+=+=。
二次根式全章复习讲义

知识点一 二次根式的概念和性质 【知识梳理】一、二次根式概念1.二次根式:一般地,我们把形如(a ≥0)•的式子叫做二次根式,“”称为二次根号.要点诠释:二次根式的两个要素:①根指数为2;②被开方数为非负数. 二、二次根式的性质1.a ≥0,(a ≥0);2. (a ≥0);3..【典例精讲】类型一、二次根式的概念1下列各式中,一定是二次根式的有( )个.A.2B.3C.4D.5举一反三:【变式】下列式子中二次根式的个数有( ). (1)13;(2)3-; (3)21x -+;(4)38; (5)21()3-;(6)1x -(1x >)A .2 B.3 C.4 D.52. x 取何值时,下列函数在实数范围内有意义?(1)1y x =-; (2)y=2+x -x 23-;举一反三:【变式】下列格式中,一定是二次根式的是( ). A. 23- B. ()20.3- C. 2- D. x类型二、二次根式的性质3. 计算下列各式:232()4-⨯-2(3.14)π-(1) (2)举一反三:【变式】(1)2)252(-=_____________. (2)2)2(2a a ---=_____________.4.已知实数a ,b ,c 在数轴上的位置如图所示,化简:22||()||a a c c b b -++---|.举一反三:【变式】若整数m 满足条件22(1)1,,5m m m +=+<且则m 的值是___________.【巩固练习】一.选择题1要使代数式有意义,则x 的( ).A. 最大值是23 B .最小值是23 C. 最大值是32 D. 最小值是322. 若1a <,化简2(1)-1=a - ( ).A.2a -B.2a -C.aD.a - 3.下列说法正确的是( )A .4是一个无理数B .函数11y x =-的自变量x 的取值范围是x ≥1C .8的立方根是2± D.若点(2,)-3)P a Q和点(b ,关于x 轴对称,则a b +的值为5. 4. 若a 不等于0,a 、b 互为相反数,则下列各对数中互为相反数的一对数是( ). A.与B.与C.与D.与5.下列根式是最简二次根式的是( ). A .8 B .24x y + C . D .6. 已知,化简二次根式的正确结果为( ).A.B. C.D.二. 填空题7.当x______时,式子x -在实数范围有意义;当x_______时,式子2x -在实数范围有意义.8.=____________. 若,则____________.9.(1)2)53(-=_____________. (2)9622++-a a a (a>0)=__________________________.10.求值(1)已知a 、b 满足,解关于x 的方程(a+2)x+b 2=a ﹣1.(2)已知x 、y 都是实数,且,求y x的平方根.知识点二二次根式的乘除法计算化简一、二次根式的乘法及积的算术平方根:(≥0,≥0),即两个二次根式相乘,根指数不变,只把被1.乘法法则a b开方数相乘.二、二次根式的除法及商的算术平方根:(≥0,>0),即两个二次根式相除,根指数不变,把被开方数相1.a b除.。
《二次根式复习课》课件

简化表达式
利用二次根式的性质和运 算法则,简化复杂的代数 表达式。
解方程
利用二次根式解一元二次 方程或二元一次方程组。
不等式求解
利用二次根式求解一元二 次不等式。
二次根式在实际问题中的应用
计算实际问题中的数值
解决概率和统计问题
利用二次根式解决一些实际问题,如 物体运动、速度、加速度等。
利用二次根式解决一些概率和统计问 题,如方差、标准差等。
二次根式的加减法
01
总结词
掌握二次根式的加减法规则
02 03
详细描述
二次根式的加减法需要先将根号内的数进行加减运算,再将根号外的系 数进行加减运算。如果根号内的数是相同的,可以直接相加或相减其系 数。
举例
$sqrt{5} + sqrt{5} = 2sqrt{5}$,$sqrt{5} - sqrt{5} = 0$,$sqrt{10} + 2sqrt{10} = 3sqrt{10}$。
二次根式的简化
总结词
描述二次根式的简化方法
1. 化简二次根式
通过因式分解、平方差公式等 方法,将复杂的二次根式化简 为简单的形式。
2. 合并同类项
将二次根式中的同类项进行合 并,简化表达式。
3. 分母有理化
对于分母含有二次根式的式子 ,通过有理化分母的方法,将
式子转化为更简单的形式。
02 二次根式的运算
二次根式的混合运算
总结词
掌握二次根式的混合运算规则
详细描述
二次根式的混合运算需要按照先乘除后加减的顺序进行,同时需要注意运算优先级,如括号、指数等。在运算过程中 ,需要注意化简和合并同类项。
举例
$(sqrt{5} + 2)^2 = (sqrt{5})^2 + 2 times 2sqrt{5} + 4 = 5 + 4sqrt{5} + 4 = 9 + 4sqrt{5}$, $3sqrt{10} times frac{sqrt{5}}{2} = frac{3sqrt{10} times sqrt{5}}{2} = frac{15}{2}$。
二次根式培优复习讲义

人教版八年级下学期二次根式(01)姓名:________ 得分:_____一、知识点梳理:1、二次根式的定义. 一般地,式子 a (a ≥0)叫做二次根式,a 叫做被开方数。
两个非负数:(1)a ≥0 ;(2) a ≥02、二次根式的性质:(1).()0≥a a 是一个________ 数 ; (2)()=2a __________(a ≥0) (3)()()()⎪⎩⎪⎨⎧〈=〉==0_______0_______0_______2a a a a a3、二次根式的乘除: 积的算术平方根的性质:)0,0(≥≥⋅=b a b a ab ,二次根式乘法法则:__________=⋅b a (a≥0,b ≥0)商的算术平方根的性质: b a b a =).0,0(>≥b a 二次根式除法法则:)0,0(>≥=b a b a b a 1.被开方数不含分母;4、最简二次根式 2.分母中不含根号;3. 被开方数中不含能开得尽方的因数或因式.分母有理化:是指把分母中的根号化去,达到化去分母中的根号的目的.二、典型例题:例1:当x 是怎样实数时,下列各式在实数范围内有意义?⑴2-x ⑵x x -+2)1(0 ⑶13-+-x x ⑷12+x (5)12-+x x小结:代数式有意义应考虑以下三个方面:(1)二次根式的被开方数为非负数。
(2)分式的分母不为0.(3)零指数幂、负整数指数幂的底数不能为0例2:化简:(1)|21|)22(2-+- (2)|3254|)3253(2-+-例3: (1)已知y=x -3+62-x +5,求x y的值. (2) 已知01442=-+++-y x y y ,求xy 的值.例4:化简:(1)32; (2)2b a 33; (3)48.0 (4)y x x 2 (5)2925x y例5:计算:(1)351223⨯ (2) 21335÷ (3) ()0,02123〉〉⎪⎪⎭⎫ ⎝⎛-÷b a b a b a例6:化去下列各式分母中的二次根式:(1)323+ (2)813 (3)251+ (4)()0,03〉〉y x xy三、强化训练:1x 的取值范围是( ) A 、x ≤1; B 、x ≤1且2x ≠-; C 、2x ≠-; D 、x <1且2x ≠-.2、已知0<x<1时,化简()21--x x 的结果是( )A 2X-1B 1-2XC -1D 13、 已知直角三角形的一条直角边为9,斜边长为10,则别一条直角边长为( )A 、1; BC 、19; D4n 的最小值是( )A 、4;B 、5;C 、6;D 、7.5、下列二次根式中,是最简二次根式的是( ) A 、a 16 B 、b 3 C 、ab D 、456、下列计算正确的是( ) A ()()69494-=-⨯-=-⨯- B 188142712=⨯=⨯ C 624416416=+=+=+ D 1212414414=⨯=⨯= 7、等式33-=-x x x x 成立的条件是( ) A x ≠3 B x ≥0 C x ≥0且x ≠3 D x>38、已知053232=--+--y x y x 则y x 8-的值为9、23231+-与的关系是 。
二次根式复习专题讲义(补课用)汇总

二次根式复习专题讲义(补课用)汇总二次根式复专题讲义一、二次根式的概念:1.二次根式:形如 $\sqrt{a}$ ($a\geq 0$)的式子叫做二次根式,也称为二次根号。
①.式子中,被开方数(式)必须大于等于零。
②.$a$($a\geq 0$)是一个非负数。
即$\sqrt{a^2}=a$($a\geq 0$);③。
$\sqrt{a^2}=|a|$($a$为任意实数)2.二次根式的乘:①.一般的,有$\frac{a}{b}\cdot\frac{\sqrt{b}}{\sqrt{b}}=\frac{a\sqrt{b}}{b}$($a\geq 0$,$b>0$)②.反过来,有$\frac{a\sqrt{b}}{b}=\sqrt{ab}$($a\geq 0$,$b>0$)3.二次根式的除:①.一般地,对二次根式的除法规定:$\frac{\sqrt{a}}{\sqrt{b}}=\frac{\sqrt{a}}{\sqrt{b}}\cdot\frac{\sqrt{b}}{\sqrt{b}}=\frac{\sqrt{ab}}{b}$($a\geq 0$,$b>0$),即 $\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$($a\geq 0$,$b>0$)②.反过来,$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$($a\geq 0$,$b>0$)4.二次根式的加减法则:二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并。
典型例题分析:例1.下列式子,哪些是二次根式,哪些不是二次根式:2、33、$\frac{1}{x}$、$\sqrt{x}$($x>0$)、$\sqrt{42}$、-2、$\frac{1}{\sqrt{x}+\sqrt{y}}$($x\geq 0$,$y\geq 0$).例2.当$x$是多少时,$\frac{2x+3}{x+1}$在实数范围内有意义?frac{3x-1}{x+2}$在实数范围内有意义?变式题2:①.当$x$是多少时,$\frac{\sqrt{x-2}}{x-1}$有意义?例3.①.已知$y=\frac{2x+3}{x^2}$在实数范围内有意义,求$x$的取值范围和$y$的值.②.若$a+1+\frac{1}{b-1}=0$,求$a^{2004}+b^{2004}$的值.③.已知$\frac{x-y+1}{x-3}=0$,求$xy$的值.例4.计算:1.$\left(\frac{3}{2}\right)^2$2.$\left(\frac{3\sqrt{5}}{2}\right)^2$3.$\left(\frac{3}{\sqrt{2}}\right)^2$4.$\left(\frac{5}{\sqrt{3}}\right)^2$5.$\left(\frac{\sqrt{5}}{2}\right)^2$6.$\left(\frac{7}{\sqrt{2}}\right)^2$7.$\left(\frac{2}{\sqrt{5}}\right)^2$例5.计算:1.$\frac{(x+1)^2}{x^2}$($x\geq 0$)2.$\frac{a^2}{a^2+2a+1}$3.$\frac{a^2}{a^2-2a+1}$4.$\frac{9}{25}+\frac{4}{9}$变式题:计算1.$\left(-\frac{3}{2}\right)^2$2.$(23^2-32^2)$例6.在实数范围内分解下列因式:1)$x^2-3$(2)$x^4-4$(3)$2x^2-3$例7.化简:1)$\frac{9}{\sqrt{25}}$2)$(-4)^2$3)$\frac{a^2}{25}$($a\neq 0$)4)$(-3)^2$例8.填空:当$a\geq 0$时,$\sqrt{a^2}=$ $a$;当$a<0$时,$\sqrt{a^2}=$ $-a$,并根据这一性质回答下列问题.1)若$a^2=a$,则$a$可以是什么数?2)若$a^2=-a$,则$a$可以是什么数?3)若$a^2>a$,则$a$可以是什么数?例9.当$x>2$,化简$(x-2)^2-(1-2x)^2$.例10.先化简再求值:当$a=9$时,求$a^2+1-2a$的值,甲乙两人的解答如下:甲的解答为:原式=a+(1-a)^2=a+1-2a+a^2=1+a-a^2乙的解答为:原式=a+(1-a)^2/(1-a)^2=a+1-a=1;a+(a-1)/(1-a)=2a-1=17.两种解答中,甲的解答是错误的,错误的原因是少写了一步展开式子的步骤.变式题1.根据题目条件,得到|1995-a|+a-2=a,即|1995-a|=a-2,因为a-200≥-199,所以当a≥197时,1995-a为正数,此时a-1995=|1995-a|=a-2-1995=-1993-a;当a<197时,1995-a为负数,此时a-1995=|1995-a|=1995-a-2=1993+a,综上所述,a-1995的值为-1993-a(a≥197)或1993+a(a<197)。
二次根式的讲义

专题一 二次根式【知识点1】二次根式的概念:一般地,我们把形如)0(0≥≥a a 的式子叫做二次根式。
二次根式的实质是一个非负数数a 的算数平方根。
【注】二次根式的概念有两个要点:一是从形式上看,应含有二次根号;二是被开方数的取值范围有限制:被开方数a 必须是非负数。
例1 以下各式1〕22211,2)5,3)2,4)4,5)(),6)1,7)2153x a a a --+---+, 其中是二次根式的是_________〔填序号〕. 例2 使x +1x-2有意义的x 的取值范围是〔 〕 A .x ≥0 B .x ≠2 C .x>2 D .x ≥0且x ≠2. 例3 假设y=5-x +x -5+2021,那么x+y=练习1使代数式43--x x 有意义的x 的取值范围是〔 〕 A 、x>3 B 、x ≥3 C 、 x>4D 、x ≥3且x ≠4练习2假设11x x ---2()x y =+,那么x -y 的值为〔 〕A .-1B .1C .2D .3例4 假设230a b -+-=,那么 2a b -= 。
例5 在实数的范围内分解因式:X 4 - 4X 2+ 4= ________ 例6 假设a 、b 为正实数,以下等式中一定成立的是〔 〕: A 、a 2 +b 2 =a 2+b 2 ; B 、〔a 2+b 2〕2 =a 2+b 2; C 、〔 a + b 〕2= a 2+b 2; D 、〔a —b 〕2 =a —b ;【知识点2】二次根式的性质:〔1〕二次根式的非负性,)0(0≥≥a a 的最小值是0;也就是说〔〕是一个非负数,即0〔〕。
注:因为二次根式〔〕表示a 的算术平方根,而正数的算术平方根是正数,0的算术平方根是0,所以非负数〔〕的算术平方根是非负数,即0〔〕,这个性质也就是非负数的算术平方根的性质,和绝对值、偶次方类似。
这个性质在解答题目时应用较多,如假设,那么a=0,b=0;假设,那么a=0,b=0;假设,那么a=0,b=0。
二次根式复习专题讲义(补课用)详解

二次根式复习专题讲义一、二次根式的概念:1.二次根式:a ≥0)的式子叫做二次根式,“”称为二次根号。
①.式子中,被开方数(式)必须大于等于零。
②.a ≥0)是一个非负数。
③.2=a (a ≥0)(a ≥0)2.二次根式的乘:①.②. 3.二次根式的除:①. 一般地,对二次根式的除法规定:②. 4. 二次根式的加减法则:二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并。
典型例题分析:例1. 下列式子,哪些是二次根式,哪些不是二次根式:、1xx>0)1x y+x ≥0,y•≥0).例2.当x+11x+在实数范围内有意义?变式题1:当x在实数范围内有意义?变式题2:①.当x2在实数范围内有意义?例3.①.已知,求xy的值.②.=0,求a2004+b2004的值.③.,求x y的值.例4.计算1.22.()23.24.(2)2例5. 计算1.2(x≥0)2.23.24.2变式题:计算1.(-)22.例6.在实数范围内分解下列因式:(1)x2-3 (2)x4-4 (3) 2x2-3例7.化简(2(3(4(1例8.填空:当a≥0时,=_____;当a<0时,=_______,•并根据这一性质回答下列问题.(1,则a可以是什么数?(2,则a可以是什么数?(3,则a可以是什么数?例9.当x>2.例10.先化简再求值:当a=9时,求的值,甲乙两人的解答如下:甲的解答为:原式=a+(1-a)=1;乙的解答为:原式=a+(a-1)=2a-1=17.两种解答中,_______的解答是错误的,错误的原因是__________.=a,求a-19952的值.变式题1.若│1995-a│变式题2.若-3≤x≤2时,试化简│x-2│。
(2(3(4)(1a≥0,b≥0)计算即可.分析:(2(3(4例12 .化简(2(3(1(5(4例13 .判断下列各式是否正确,不正确的请予以改正:(1=4(2变式题1:和,•那么此直角三角形斜边长是().变式题2:化简a)..√169×6变式题3变式题5:探究过程:观察下列各式及其验证过程.(1)验证:(2)验证:同理可得:,……通过上述探究你能猜测出:a=_______(a>0),并验证你的结论.例14.计算:(1(2÷(3÷(4)例15.化简:(1(2(3(4例16.,且x为偶数,求(1+x的值.变式题1.的结果是().变式题2.阅读下列运算过程:,化”).变式题3.已知x=3,y=4,z=5,是_______.变式题4.有一种房梁的截面积是一个矩形,且矩形的长:1,•现用直径为的一种圆木做原料加工这种房梁,那么加工后的房染的最大截面积是多少?变式题5.计算(1·(m>0,n>0)(2)(a>0)例17.把它们化成最简二次根式:(1)3; (2)总结:二次根式有如下两个特点:1.被开方数不含分母;2.被开方数中不含能开得尽方的因数或因式.我们把满足上述两个条件的二次根式,叫做最简二次根式.例18.如图,在Rt△ABC中,∠C=90°,AC=2.5cm,BC=6cm,求AB的长.B A C例19.观察下列各式,通过分母有理数,把不是最简二次根式的化成最简二次根式:-1,=,,……从计算结果中找出规律,并利用这一规律计算++(+1)的值.练习:一、选择题1(y>0)是二次根式,那么,化为最简二次根式是().y>0) B y>0) C y>0)AD.以上都不对2.把(a-1中根号外的(a-1)移入根号内得().C. D.ABA=a2DC4的结果是()B.C.D.A.二、填空题1.(x≥0)2.化简二次根式号后的结果是_________.三、综合提高题1.已知a 过程,请判断是否正确?若不正确,•请写出正确的解答过程:2.若x 、y 为实数,且y=y x y -的值.例20.计算 (1(2总结:二次根式加减时,可以先将二次根式化成最简二次根式,•再将被开方数相同的二次根式进行合并.例21.计算(1)(2))+例22.已知4x 2+y 2-4x-6y+10=0,求(23+y-(x -5x)的值.练习: 一、选择题1中,与是同类二次根式的是( ).A .①和②B .②和③C .①和④D .③和④ 2.下列各式:①3+3=6;②17=1;③=;④,其中错误的有( ).A .3个B .2个C .1个D .0个 二、填空题1、、与是同类二次根式的有________.2.计算二次根式5-3-7+9的最后结果是________.三、综合提高题1.已知≈2.236,求(-)-+)的值.(结果精确到0.01) 2.先化简,再求值.()-(,其中x=32,y=27.例23.如图所示的Rt △ABC 中,∠B=90°,点P 从点B 开始沿BA 边以1厘米/•秒的速度向点A 移动;同时,点Q 也从点B 开始沿BC 边以2厘米/秒的速度向点C 移动.问:几秒后△PBQ 的面积为35平方厘米?PQ 的距离是多少厘米?(结果用最简二次根式表示)BAC QP例23.要焊接如图所示的钢架,大约需要多少米钢材(精确到0.1m )?例24.若最简根式3是同类二次根式,求a 、b 的值.(•同类二次根式就是被开方数相同的最简二次根式)练习: 一、选择题1.已知直角三角形的两条直角边的长分别为5和5,那么斜边的长应为( ).(•结果用最简二次根式) A .BC .D .以上都不对2.小明想自己钉一个长与宽分别为30cm 和20cm 的长方形的木框,•为了增加其稳定性,他沿长方形的对角线又钉上了一根木条,木条的长应为()米.(结果同最简二次根式表示)A.. D.二、填空题1.某地有一长方形鱼塘,已知鱼塘的长是宽的2倍,它的面积是1600m2,•鱼塘的宽是_______m.(结果用最简二次根式)2.,•那么这简二次根式)三、综合提高题1.若最简二次根式与n是同类二次根式,求m、n的值.2.同学们,我们以前学过完全平方公式a2±2ab+b2=(a ±b)2,你一定熟练掌握了吧!现在,我们又学习了二次根式,那么所有的正数(包括0)都可以看作是一个数的平方,如3=)2,5=(2,你知道是谁的二次根式呢?下面我们观察:-1)2=)2-2·1+12+1=3-2反之,∴-1求:(1(2;(3吗?(√3-1)(4,则m 、n 与a 、b 的关系是什么?并说明理由.例25.计算: (1)+(2)(4)÷例26.计算 (1))(3-) (2)))例27.已知xba-=2-xa b-,其中a 、b 是实数,且a+b ≠0,练习: 一、选择题1.).AC2( ).A.2 B.3 C.4 D.1二、填空题+)2的计算结果(用最简根式表示)是 1.(-12________.)()-()2的计算结果(用最简2.(二次根式表示)是_______.-1,则x2+2x+1=________.3.若4.已知a=3+2,,则a2b-ab2=_________.三、综合提高题12.当+的值.(结果用最简二次根式表示)课外知识1.同类二次根式:几个二次根式化成最简二次根式后,它们的被开方数相同,•这些二次根式就称为同类二次根式,就是本书中所讲的被开方数相同的二次根式.练习:下列各组二次根式中,是同类二次根式的是().AC2.互为有理化因式:•互为有理化因式是指两个二次根式的乘积可以运用平方差公式(a+b)(a-b)=a2-b2,同时它们的积是有理数,不含有二次根式:如x+1-与x+1+与也是互为有理化因式.+的有理化因式是________;的有理化因式是_________._______.3.分母有理化是指把分母中的根号化去,通常在分子、•分母上同乘以一个二次根式,达到化去分母中的根号的目的.练习:把下列各式的分母有理化(1(2;(3(44.其它材料:如果n是任意正整数,=_____=_______.例28.-1的大小。
二次根式专题复习课件 (共21张PPT)

次 根
三个性质 2 ab a ba 0,b 0
式
3
a b
a
(a 0,b 0)
b
四种运算
加 、减、乘、除
二次根式的概念
1.二次根式的定义:形如 a(a 0)的式子
叫做二次根式
2.二次根式的识别:(1)被开方数 a 0
(2)根指数是2
例.下列各式中哪些是二次根式? 那些不是?为什么?
练习与反馈:
1.要使下列式子有意义,求字母X
的取值范围
1(1) 3 x(2) Nhomakorabea2x 5
(3) 1 x (4) x 2 2 x
x
(5) x2 2x 1
2.(1) ( 3)2 ____
(2)当 x 1 时, (1 x)2 ____ (3) (x 2)2 x 2
则X的取值范围是___
八年级下册
二次根式专题复习
杉川 备课组
考点复习目标:
1. 知道二次根式有关概念,能正确做出相关判断。 2.明确二次根式的性质,并灵活运用计算。 3.掌握二次根式的概念及性质解题。
知识重难点:
运用二次根式概念及性质解决相关问题。
知识结构
三个概念
二次根式 最简二次根式 同类二次根式
二
1 a 0 (a 0)
4.已知: x 4 + 2x y =0,求 x-y 的值.
解:由题意,得 x-4=0 且 2x+y=0 解得 x=4,y=-8
x-y=4-(-8)= 4+ 8 =12
5.(2016.湖北黄冈市)已知x,y为实数,且
x 1 +3(y-2)2 =0,则x-y的值为( D )
A.3
B.-3
考点02 二次根式(解析版)

考点二二次根式知识点整合1.二次根式的有关概念(1)二次根式的概念形如)0(≥a a 的式子叫做二次根式.其中符号“”叫做二次根号,二次根号下的数叫做被开方数.【注意】被开方数a 只能是非负数.即要使二次根式a 有意义,则a ≥0.(2)最简二次根式被开方数所含因数是整数,因式是整式,不含能开得尽方的因数或因式的二次根式,叫做最简二次根式.(3)同类二次根式化成最简二次根式后,被开方数相同的几个二次根式,叫做同类二次根式.2.二次根式的性质(1)a ≥0(a ≥0);(2))0()(2≥=a a a ;(32(0)0(0)(0)a a a a a a a >⎧⎪===⎨⎪-<⎩;(40,0)ab a b a b =≥≥;(50,0)a a a b b b=≥>.3.二次根式的运算(1)二次根式的加减合并同类二次根式:在二次根式的加减运算中,把几个二次根式化为最简二次根式后,若有同类二次根式,可把同类二次根式合并成一个二次根式.(2)二次根式的乘除0,0)a b ab a b =≥≥;除法法则:(0,0)a aa b bb=≥>.(3)二次根式的混合运算二次根式的混合运算顺序与实数的运算顺序一样,先乘方,后乘除,最后加减,有括号的先算括号内的.在运算过程中,乘法公式和有理数的运算律在二次根式的运算中仍然适用.考向一二次根式的概念及性质1.二次根式的有关概念(1)二次根式的概念形如)0(≥a a 的式子叫做二次根式.其中符号“”叫做二次根号,二次根号下的数叫做被开方数.2.二次根式的性质(1)a ≥0(a ≥0);(2))0()(2≥=a a a ;(32(0)0(0)(0)a a a a a a a >⎧⎪===⎨⎪-<⎩;(40,0)ab a b a b =≥≥;(50,0)a a a b b b=≥>.1.在函数12x y x -=-中,自变量x 的取值范围是()A .0x ≥且2x ≠B .2x >C .1x ≥且2x ≠D .1x >且2x ≠【答案】C【分析】本题考查了函数的自变量有意义的条件,分式有意义的条件、二次根式有意义的条件.根据分式的分母不能为0,被开方数不0即可得.【详解】解:在函数12x y x -=-中,.B..D.【答案】B【分析】根据二次根式有意义的条件列出不等式组求解即可.考向二二次根式的运算(1)二次根式的加减合并同类二次根式:在二次根式的加减运算中,把几个二次根式化为最简二次根式后,若有同类二次根式,可把同类二次根式合并成一个二次根式.(2)二次根式的乘除0,0)a b =≥≥;0,0)a b≥>.(3)二次根式的混合运算二次根式的混合运算顺序与实数的运算顺序一样,先乘方,后乘除,最后加减,有括号的先算括号内的.在运算过程中,乘法公式和有理数的运算律在二次根式的运算中仍然适用.-【答案】2a-【答案】(1)5;(2)2a(1)______的解法是错误的;(2)当2a =时,求26911a a a -++-的值.【答案】(1)小亮OA=__________(1)填空:210(2)请用含有n(n为正整数)的式子填空:(133+(1)求出这个魔方的棱长.(2)图甲中阴影部分是一个正方形ABCD,求出阴影部分正方形(3)把正方形ABCD放置在数轴上,如图乙所示,使得点的数为______.【答案】(1)4cm(1)则原来大正方形的边长为号)(2)求这个长方体盒子的底面边长和体积分别是多少2 1.414,3 1.732,≈≈【答案】(1)42;2A.20cm B.5【答案】A【分析】本题考查二次根式的应用,出关系式,去括号合并即可得到结果.。
专题01 二次根式的概念及性质(知识点串讲)(解析版)

专题01 二次根式的概念及性质知识框架重难突破一、二次根式及代数式的概念1.二次根式的概念:一般地,我们把形如(a ≥0)•的式子叫做二次根式,“”称为二次根号. 备注:二次根式的两个要素:①必须含有,②被开方数可以是数、字母和代数式,但必须大于等于0. 2.代数式的概念:形如5,a ,a+b ,ab ,,x 3,这些式子,用基本的运算符号(基本运算包括加、减、乘、除、乘方、开方)把数和表示数的字母连接起来的式子,我们称这样的式子为代数式. 例1.(2019·上海市建平中学西校初二月考)下列各式中,一定是二次根式的是( ) A 1a +B 1a -C 21a -D 222a a ++【答案】D【解析】A 、被开方数可能为负数,二次根式无意义,故选项错误;B 、被开方数可能为负数,二次根式无意义,故选项错误;C 、被开方数可能为负数,二次根式无意义,故选项错误;D 、正确.故选:D .练习1.(2019·郑州枫杨外国语学校初二月考)下列式子:7,2x ,1π-,22a b +,100,21a -,1a +( )A .3个B .4个C .5个D .6个【答案】B【解析】解:7,22a b +,100,1a +是二次根式,共4个,故选:B . 练习2.(2019·上海市闵行区上虹中学初二月考)下列各式中,一定是二次根式的有( ) ①2 ②a ③21a + ④4 ⑤x - A .2个B .3个C .4个D .5个 【答案】B【解析】解:①2是二次根式;②a 不是二次根式;③21a +,∵a 2≥0,∴a 2+1>0,故21a +是二次根式;④4是二次根式;⑤x -不是二次根式. 故选B.例2.(2019·上海初二期末)下列各式中,是代数式的是 ( )A .s vt =B .()2a 10+≥C .2x x -D .x 5≠【答案】C【解析】解:A. s vt =式子中包含等号,不是代数式,所以错误;B. ()2a 10+≥式子中包含不等号,不是代数式,所以错误;C. 2x x -式子是由数和字母的乘方、减法运算得到的式子,是代数式,所以正确;D. x 5≠式子中包含不等号,不是代数式,所以错误;故答案选C.练习1.(2019·全国初一课时练习)以下是代数式的是( )A .m ab =B .22()()a b a b a b +-=-C .1a +D .2S R π= 【答案】C【解析】因为代数式中不含“=”号,所以是代数式的是C .故选C .二、二次根式的性质及双重非负性1.二次根式双重非负性:a ≥0,(a ≥0);2. 二次根式的性质:(1)(a ≥0);(2).备注:(1)二次根式(a ≥0)的值是非负数。
二次根式及其运算知识讲义(解析版)
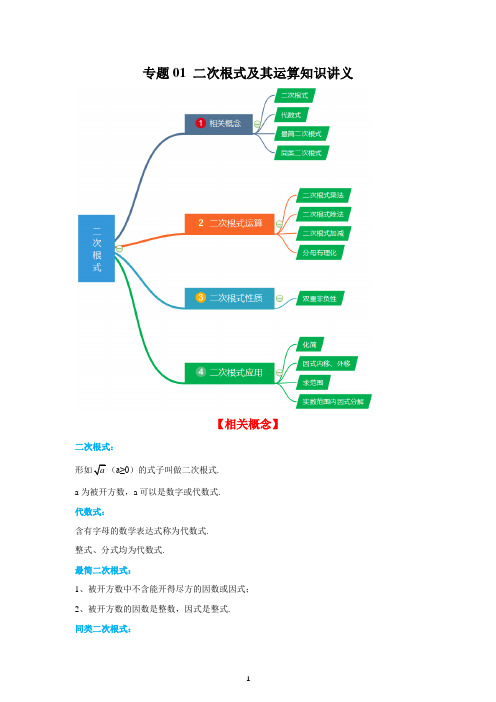
专题01 二次根式及其运算知识讲义【相关概念】二次根式:a≥0)的式子叫做二次根式.a为被开方数,a可以是数字或代数式.代数式:含有字母的数学表达式称为代数式.整式、分式均为代数式.最简二次根式:1、被开方数中不含能开得尽方的因数或因式;2、被开方数的因数是整数,因式是整式.同类二次根式:几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫做同类二次根式.【二次根式运算】乘法=a≥0,b≥0)除法=(a≥0,b >0)加(减)法先把各根式化成最简根式,再合并同类根式分母有理化====【二次根式性质】,a≥0非负数:|a|,a 2n()()00a a a a ≥⎧=⎨-≤⎩2a =【二次根式应用】因式的内移和外移:(1)负号不能移到根号下;(2)根号下的负号不能移到根号外.【题型一】二次根式有意义条件例1. (2020·m 能取的最小整数值是()A .m = 0B .m = 1C .m = 2D .m = 3【答案】B.3m -1≥0,解得:m≥13, 所以,m 能取的最小整数值是1.故答案为:B .例2. (2020·=-,那么x 的取值范围是_______. 【答案】-3≤x≤0.【解析】解:∵233x x +-∴x≤0,且x+3≥0,解得:-3≤x≤0,故答案为:-3≤x≤0.例3.(2019·=x 的取值范围是______. 【答案】x≥2.=∴x≥0,x−2≥0,∴x≥2.故答案为:x≥2.【题型二】同类二次根式例4. (2020·是同类二次根式,那么满足条件的m 中最小正整数是________.【答案】4.【解析】解:当5m+8=7时,m=-15,不合题意,,即5m+8=28时,m=4,是同类二次根式,那么m 的最小正整数是4,故答案为:4.例5. mn =_________.【答案】10.∴n=2,2m-5=5,∴m=5,n=2∴mn=10故答案为:10.例6. mn=________.【答案】21.∴1221343nm m-=⎧⎨-=-⎩,解得,73mn=⎧⎨=⎩,∴mn=21故答案为:21.【题型三】变式考查例7. (2020·浙江宁波市期中)我们把形如b(a,b为最简二次根式)32是()A型无理数B C型无理数D型无理数【答案】B.【解析】解:2故答案为:B.例8. (1n所有可能的值;(2是整数,求正整数n的最小值.【答案】(1)自然数n 的值为2、9、14、17、18;(2)正整数n 的最小值为6.【解析】解:(1是整数,∴18-n=0或1或4或9或16,解得:n=18或17或14或9或2,则自然数n 的值为2,9,14,17,18;(2=是整数,n 为正整数,∴正整数n 的最小值为6.例9.(2020·21x =-,则x=__________. 【答案】12或1.21x =-,∴2x-1=0或2x-1=1,解得:x=12或x=1. 故答案为12或1. 【题型四】二次根式运算例10.(2020·周长为( )A .B .C .D .无法确定【答案】A.若,,则周长为若,∴,此三角形不存在,∴个三角形的周长为故答案为:A .例11)2211-.)2211--1313=--+-=例12.(2020·福建省泉州月考)已知1x =,x 的整数部分为a ,小数部分为b ,求a b的值..【解析】解:∵3,∴+1<4,故a=3,-2,∴)3232274a b ====-. 例13.(2020·广东佛山市月考)先阅读,再解答:由222=-= 可以看出,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式,在进行二次根式计算时,利用有理化因式,有时可以化去分母中的根号,例如:==,请完成下列问题:1的有理化因式是;(2)= .(直接写结果)>或<)(4)利用你发现的规律计算下列式子的值:)1+【答案】(1+1;(2);(3)<;(4)2017.【解析】解:(1+1;(2333==+;(3=>(4)原式=)120181+=)11=2018-1=2017.例14. 若a,b都是正整数,且a<b是可以合并的二次根式,是否存在a,b,=a,b的值;若不存在,请说明理由.【答案】当a=3,b=48;当a=12,b=27.,m、n为正整数,m<n,∴m=1,n=4或m=2,n=3故a=3,b=48或a=12,b=27.例15.(2019·辽宁大连市期中)[观察]请你观察下列式子的特点,并直接写出结果:11112=+-=;11123=+-=;11134=+-=;……[发现]根据你的阅读回答下列问题:(1)请根据上面式子的规律填空:=(n为正整数);(2)请证明(1) 中你所发现的规律.[应用]请直接写出下面式子的结果:11n++=.【答案】[观察]32,76,1312;[发现](1)1111n n+-+或221n nn n+++;(2)证明见解析;[应用]221n nn++.【解析】[观察]32,76,1312,[发现](1)1111n n+-+或221n nn n+++(2)左边=====∵n 为正整数,∴()11111011n n n n +-=+>++ ∴左边=右边[应用11n +++111111111111223341n n =+-++-++-+++-+…… 1111n n =⨯+-+ 1n n n =++ 22=1n n n ++. 【题型五】化简求值例16. (2021·江苏南通市期末)化简2+的结果是( ) A .152x -B .1-C .27x -D .1 【答案】A.【解析】解:∵二次根式被开方数为非负数,∴7-x≥0,则x≤7∴x-8<0,原式=7-x+8-x=15-2x故答案为:A .例17.(2020·浙江杭州期中)实数a ,b 在数轴上的位置如图,||a b -的结果为( )A .2aB .2a -C .2bD .2b -【答案】B.【解析】解:由题意得:a >b ,|a |<|b |,a >0,b <0,∴a -b >0,a +b <0,∴原式=-a -b -a +b =-2a ,故答案为:B .例18.若数轴上表示数x 的点在原点的左边,则化简3x + ) A .4x - B .4x C .2x - D .2x【答案】C.【解析】解:∵数x 的点在原点的左边,∴x <0,∴原式=|3x +|x ||=|3x -x |=|2x |=-2x .故答案为:C .例19.(2020·温州月考)下列四个式子中,与(a -的值相等的是() AB .CD .【答案】D.【解析】解:由题意得:2021-a>0,得:a<2021,∴a-2021<0,∴原式=(2021a --== 故答案为:D . 例20.下列给出的四个命题:①若a b = ,则a a b b =;②若a 2﹣5a+5=01a =- ;③(1a -=其中是真命题是【答案】②.【解析】解:①当a=-1,b=1时,命题不成立,是假命题,②a 2=5a-5,∴5a-5≥0,即a≥1,,是真命题;③(a -==,是假命题, 故答案为:②.【题型六】阅读材料例21.(2021·北京延庆区期末)我们规定用(a ,b )表示一对数对.给出如下定义:记m=,n = a > 0,b > 0),将(m ,n )与(n ,m )称为数对(a ,b )的一对“对称数对”.例如:(4,1)的一对“对称数对”为(12,1)和(1,12); (1)数对(9,3)的一对“对称数对”是 ;(2)若数对(3,y )的一对“对称数对”相同,则y 的值为 ;(3)若数对(x ,2)的一个“对称数对”,1),则x 的值为 ;(4)若数对(a ,b )的一个“对称数对”,,求ab 的值.【答案】(1)1(3与1)3, ;(2)13;(3)1 ;(4)16或6.【解析】解:(1)由题意得13=,∴数对(9,3)的一对“对称数对”是1(3与1)3,;(2)由题意得,∴数对(3,y )的一对“对称数对”为⎝与⎭, ∵数对(3,y )的一对“对称数对”相同,= ∴y=13;(3)∵数对(x ,2)的一对“对称数对”是与而数对(x ,2)的一个“对称数对”,1), 1=, ∴x=1;(4)∵数对(a ,b)的一对“对称数对”是与,而数对(a ,b)的一个“对称数对”是,==1,183a b == ∴11863ab =⨯=;==1,318a b ==, ∴113186ab =⨯=,综上所述,16ab =或6ab =. 例22. 阅读理解:二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式..11==. 类比应用:(1= ; (29++=+ . 拓展延伸:的矩形叫黄金矩形.如图①,已知黄金矩形ABCD 的宽AB =1. (1)黄金矩形ABCD 的长BC = ;(2)如图②,将图①中的黄金矩形裁剪掉一个以AB 为边的正方形ABEF ,得到新的矩形DCEF ,猜想矩形DCEF 是否为黄金矩形,并证明你的结论;(3)在图②中,连结AE ,则点D 到线段AE 的距离为 .【答案】类比应用:(1);(2)2;拓展延伸:(1)12;(2)矩形DCEF为黄金矩形,理由见解析;(3【解析】解:类比应用:(1)根据题意可得:== (2)根据题意可得:9++(9+++19-+-1=2;拓展延伸:(1的矩形叫黄金矩形, 若黄金矩形ABCD 的宽AB =1,则黄金矩形ABCD 的长BC; (2)矩形DCEF 为黄金矩形,理由是:由裁剪可知:AB=AF=BE=EF=CD=1,根据黄金矩形的性质可得:AD=BC=1=∴FD=EC=AD-AF=112-=12,∴DF EF =11122÷=,故矩形DCEF 为黄金矩形;(3)连接AE ,DE ,过D 作DG ⊥AE 于点G ,∵AB=EF=1,,∴=在△AED 中,S △AED =1122AD EF AE DG ⨯⨯=⨯⨯,即AD EF AE DG ⨯=⨯1DG =,解得∴点D 到线段AE 的距离为4+. 例23. (2019·四川月考)阅读下列材料,然后回答问题.一样的式子,其实我们还可以将其进一步化简:====1以上这种化简的步骤叫做分母有理化.②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 a +b =2,ab = -3 ,求 a 2 + b 2 .我们可以把a +b 和ab 看成是一个整体,令 x =a +b , y = ab ,则 a 2 + b 2 = (a + b)2 - 2ab = x 2- 2y = 4+ 6=10.这样,我们不用求出a ,b ,就可以得到最后的结果.(1...+(2)已知 m 是正整数, ab且 2a 2+ 1823ab + 2b 2 = 2019 .求 m . (31=【答案】(1)12;(2)2;(3)9. 【解析】解:(1)原式12019+2222=+++2019++== (2)∵ab∴=2(2m+1),=1∵2a 2+ 1823ab + 2b 2 = 2019∴2(a 2+b 2)+1823=2019∴a 2+b 2=98∴4(2m+1)2=100∴m=2或m=-3∵m是正整数∴m=2.(31=,得:21=20=2281=-+=0≥≥.例24.(2020·湖南怀化市期末)同学们,我们以前学过完全平方公式222)2(a ab b a b ±+=±,你一定熟练掌握了吧!现在,我们又学习了二次根式,那么所有的非负数(以及0)都可以看作是一个数的平方,如23=,25=,下面我们观察:)2221211213=-⨯=-=-23211)-=-=,∴231)-=1= 求:(1;(2(3=,则m 、n 与a 、b 的关系是什么?并说明理由.【答案】(11;(21;(3)m+n=a ,mn=b ,理由见解析.【解析】解:(11;(21==;(3)m+n =a ,mn =b.=∴2a =+,∴,∴m+n =a ,mn =b.例25.(2020·安徽安庆市)阅读理解题,下面我们观察:2221)211213=-⨯=-=-反之23211)-=-=,所以231)-=1= 完成下列各题:(1)在实数范围内因式分解:(2(3.【答案】(1)2(1+;(21;(3【解析】解:(1)22231(1+=+=+(21==(3==。
二次根式讲义

二次根式复习讲义知识点一:二次根式的概念【知识要点】二次根式的定义:形如的式子叫二次根式,其中a 叫被开方数,只有当a 是一个非负数时,才有意义.【典型例题】【例1】 12)解题思路:式子a ≥0),50,50x x -≥⎧⎨-≥⎩ 5x =,y=2009,则x+y=2014举一反三:12()x y =+,则x -y 的值为( )A .-1B .1C .2D .32、若x 、y 都是实数,且y=4x 233x 2+-+-,求xy 的值【例4】已知a b 是 的小数部分,求12a b ++的值。
举一反三:1、若3的整数部分是a ,小数部分是b ,则=-b a 3 。
知识点二:二次根式的性质 【知识要点】1. 非负性:a a ()≥0是一个非负数.注意:此性质可作公式记住,后面根式运算中经常用到. (.举一反三:1、若0)1(32=++-n m ,则m n +的值为 。
二次根式的性质2 (公式)0()(2≥=a a a 的运用)【例6】 化简:21a -+的结果为( )A 、4—2aB 、0C 、2a —4D 、4举一反三:1、在实数范围内分解因式:429__________,2__________x x -=-+=二次根式的性质3 (公式⎩⎨⎧<-≥==)0a (a )0a (a a a 2的应用) 【例7】已知2x <,)A 、2x -B 、2x +C 、2x --D 、2x - 举一反三:【例 A. -a B. --a C. -aD. a知识点三:最简二次根式和同类二次根式【知识要点】1、最简二次根式: 最简二次根式的定义:①被开方数是整数,因式是整式;②被开方数中不含能开得尽方的数或因式.2、同类二次根式(可合并根式):几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式就叫做同类二次根式,即可以合并的两个根式。
【典型例题】 下列根式中,不是..最简二次根式的是( )A B C . 21 D【例11】 举一反三:1、下列根式不是最简二次根式的是( ) 是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次根式复习专题讲义一、二次根式的概念:1.二次根式:形如a (a ≥0)的式子叫做二次根式,“”称为二次根号。
①.式子中,被开方数(式)必须大于等于零。
②.a (a ≥0)是一个非负数。
③. (a )2=a (a ≥0);2a =a (a ≥0)2.二次根式的乘: ①.一般的,有a·b=a b.(a ≥0,b ≥0)②. 反过来,有ab =a ×b( a ≥ 0 ,b ≥ 0 )3.二次根式的除:①. 一般地,对二次根式的除法规定:ab=a b(a ≥0,b>0), ②. 反过来,a b=a b(a ≥0,b>0)4. 二次根式的加减法则:二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并。
典型例题分析:例1. 下列式子,哪些是二次根式,哪些不是二次根式:2、33、1x、x (x>0)、0、42、-2、1x y+、x y +(x ≥0,y •≥0).分析:二次根式应满足两个条件:第一,有二次根号“”;第二,被开方数是正数或0。
解:二次根式有:2、x (x>0)、0、-2、x y +(x≥0,y ≥0);不是二次根式的有:33、1x、42、1x y+。
例2.当x 是多少时,23x ++11x +在实数范围内有意义? 分析:要使23x ++11x +在实数范围内有意义,必须同时满足23x +中的≥0和11x +中的x+1≠0.解:依题意,得23010x x +≥⎧⎨+≠⎩由①得:x ≥-32由②得:x ≠-1当x ≥-32且x ≠-1时,23x ++11x +在实数范围内有意义。
变式题1:当x 是多少时,31x -在实数范围内有意义?分析:由二次根式的定义可知,被开方数一定要大于或等于0,所以3x-1≥0,•31x -才能有意义.解:由3x-1≥0,得:x ≥13当x ≥13时,31x -在实数范围内有意义.变式题2:①.当x 是多少时,23x x++x 2在实数范围内有意义?解:依题意得:2300x x +≥⎧⎨≠⎩,320x x ⎧≥-⎪⎨⎪≠⎩∴当x>-32且x≠0时,23xx++x2在实数范围内没有意义。
②.若3x-+3x-有意义,则2x-=_______。
③.使式子2(5)x--有意义的未知数x有()个。
例3. ①.已知y=2x-+2x-+5,求xy 的值.(答案:25)②.若1a++1b-=0,求a2004+b2004的值.(答案: 2) ③.已知1x y-++3x-=0,求x y的值.(答案:81)例4.计算1.(32)2 2.(35)23.(56)2 4.(72)2分析:我们可以直接利用(a)2=a(a≥0)的结论解题.解:(32)2 =32,(35)2 =32·(5)2=32·5=45,(56)2=56,(72)2=22(7)724=.例5. 计算1.(1x+)2(x≥0) 2.(2a)23.(221a a++)2 4.(24129x x-+)2分析:(1)因为x≥0,所以x+1>0;(2)a2≥0;(3)a2+2a+1=(a+1)2≥0;(4)4x2-12x+9=(2x)2-2·2x·3+32=(2x-3)2≥0.所以上面的4题都可以运用(a)2=a(a≥0)的重要结论解题.解:(1)因为x≥0,所以x+1>0(1x+)2=x+1(2)∵a2≥0,∴(2a)2=a2(3)∵a2+2a+1=(a+1)2又∵(a+1)2≥0,∴a2+2a+1≥0 ,∴221++=a2+2a+1a a(4)∵4x2-12x+9=(2x)2-2·2x·3+32=(2x-3)2又∵(2x-3)2≥0∴4x2-12x+9≥0,∴(2-+)2=4x2-12x+94129x x变式题:计算)21.(-3232.(2332)(2332)+-例6.在实数范围内分解下列因式:(1)x2-3 (2)x4-4 (3) 2x2-3例7.化简(1)9(2)2-(3)(4)-(3)25(4)2分析:因为(1)9=-32,(2)(-4)2=42,(3)25=52,(4)(-3)2=32,所以都可运用2a=a(a≥0)•去化简。
解:(1)9=23=3 (2)2-=24=4(4)(3)25=25=5 (4)2-=23=3(3)例8.填空:当a≥0时,2a=_____;当a<0时,2a=_______,•并根据这一性质回答下列问题.(1)若2a=a,则a可以是什么数?(2)若2a=-a,则a可以是什么数?(3)2a>a,则a可以是什么数?分析:∵2a=a(a≥0),∴要填第一个空格可以根据这个结论,第二空格就不行,应变形,使“()2”中的数是正数,因为,当a≤0时,2a=2()a-,那么-a≥0.(1)根据结论求条件;(2)根据第二个填空的分析,逆向思想;(3)根据(1)、(2)可知2a=│a│,而│a│要大于a,只有什么时候才能保证呢?a<0.解:(1)因为2a=a,所以a≥0;(2)因为2a=-a,所以a≤0;(3)因为当a≥0时2a=a,要使2a>a,即使a>a所以a 不存在;当a<0时,2a=-a,要使2a>a,即使-a>a,a<0综上,a<0例9.当x>2,化简2(12)x-.x--2(2)例10.先化简再求值:当a=9时,求a+2-+的值,12a a甲乙两人的解答如下:甲的解答为:原式=a+2-=a+(1-a)=1;(1)a乙的解答为:原式=a+2-=a+(a-1)=2a-1=17.(1)a两种解答中,_______的解答是错误的,错误的原因是__________.变式题1.若│1995-a │+2000a -=a ,求a-19952的值.(提示:先由a-2000≥0,判断1995-a •的值是正数还是负数,去掉绝对值)变式题2.若-3≤x ≤2时,试化简│x-2│+2(3)x ++21025x x -+。
(答案:10-x) 例11.计算 (1)5×7(2)13×9(3)9×27(4)12×6分析:直接利用a·b=a b(a ≥0,b ≥0)计算即可.解:(1)5×7=35(2)13×9=193⨯=3(3)9×27=292793⨯=⨯=93(4)12×6=162⨯=3例12 . 化简(1)916⨯ (2)1681⨯ (3)81100⨯(4)229x y (5)54分析:利用a b=a·b(a ≥0,b ≥0)直接化简即可. 解:(1)916⨯=9×16=3×4=12(2)1681⨯=16×81=4×9=36(3)81100⨯=81×100=9×10=90(4)229x y=23×22x y=23×2x×2y=3xy (5)54=96⨯=23×6=36例13 .判断下列各式是否正确,不正确的请予以改正:(1)(4)(9)49-⨯-=-⨯-(2)12425×25=4×1225×25=41225×25=412=83解:(1)不正确.改正:(4)(9)-⨯-=49⨯=4×9=2×3=6 (2)不正确.改正:12425×25=11225×25=1122525⨯=112=167⨯=47变式题1:若直角三角形两条直角边的边长分别为15cm 和12cm,•那么此直角三角形斜边长是().变式题2:化简a1a-的结果是().变式题3:1014=_______.√169×6变式题4:一个底面为30cm×30cm长方体玻璃容器中装满水,•现将一部分水例入一个底面为正方形、高为10cm 铁桶中,当铁桶装满水时,容器中的水面下降了20cm,铁桶的底面边长是多少厘米?设:底面正方形铁桶的底面边长为x,则x 2×10=30×30×20,x 2=30×30×2,x=3030⨯×2=302.变式题5:探究过程:观察下列各式及其验证过程. (1)223=223+验证:223=22×23=2223⨯=332(22)233-+==3222222222(21)221212121--+=+----=223+(2)338=338+验证:338=23×38=338=3233331-+-=222223(31)33(31)3313131-+-=+---=338+同理可得:44441515=+ 55552424=+,…… 通过上述探究你能猜测出: a 21a a -=_______(a>0),并验证你的结论.解: a 21a a -=21aa a +- 验证:a 21a a -=322211a a a a a ⨯=-- =33222111a aa a a a a a a -+-=+---=222(1)11aa aa a -+--=21a a a +-.例14.计算: (1)123(2)3128÷ (3)11416÷ (4)648分析:上面4小题利用a b=a b(a ≥0,b>0)便可直接得出答案.解:(1)123=123=4=2(2)3128÷=313834282÷=⨯=⨯=3×=23(3)11416÷=111164164÷=⨯=4=2(4)648=648=8=22例15.化简: (1)364(2)22649b a (3)2964x y (4)25169x y分析:直接利用a b=a b(a ≥0,b>0)就可以达到化简之目的.解:(1)364=33864=(2)22649b a =2264839b baa = (3)2964x y =293864x x y y=(4)25169x y =25513169x x yy =例16.已知9966x xx x --=--,且x 为偶数,求(1+x )22541x x x -+-的值. 分析:式子ab=a b,只有a ≥0,b>0时才能成立.因此得到9-x ≥0且x-6>0,即6<x ≤9,又因为x 为偶数,所以x=8.解:由题意得9060x x -≥⎧⎨->⎩,即96x x ≤⎧⎨>⎩∴6<x ≤9 ∵x 为偶数 ∴x=8∴原式=(1+x )(4)(1)(1)(1)x x x x --+-=(1+x )41x x -+ =(1+x )4(1)x x -+=(1)(4)x x +-∴当x=8时,原式的值=49⨯=6.变式题1.计算112121335÷÷的结果是( ). 变式题2.阅读下列运算过程:1333333==⨯,225255555==⨯ 数学上将这种把分母的根号去掉的过程称作“分母有理化”,那么,化简26的结果是( ).变式题3.已知x=3,y=4,z=5,那么y z x y ÷的最后结果是_______.变式题4.有一种房梁的截面积是一个矩形,且矩形的长与宽之比为3:1,•现用直径为315cm 的一种圆木做原料加工这种房梁,那么加工后的房染的最大截面积是多少? 解:设:矩形房梁的宽为x (cm ),则长为3xcm ,依题意,得:(3x )2+x 2=(315)2,4x 2=9×15,x=3215(cm ), 3x ·x=3x 2=13543(cm 2).变式题5.计算 (1)32nn m m ·(-331n mm )÷32n m(m>0,n>0)(2)-3222332m n a -÷(232m n a +)×2a m n- (a>0)解:(1)原式=-4252n n mm ÷32n m=-432522n n mm m n⨯=-3222n n n n n m m m m ⨯=-⨯=-23n nm(2)原式=-22223()()2m n m n a a a m nm n +-⨯⨯+-=-2232a =-6a例17.把它们化成最简二次根式:(1) 5312; (2)2442x y x y +; (3)238x y点评:二次根式有如下两个特点:1.被开方数不含分母;2.被开方数中不含能开得尽方的因数或因式. 我们把满足上述两个条件的二次根式,叫做最简二次根式.例18.如图,在Rt △ABC 中,∠C=90°,AC=2.5cm ,BC=6cm ,求AB 的长.BAC解:因为AB 2=AC 2+BC 2所以AB=222.56+=2516916913()362424+====6.5(cm )因此AB 的长为6.5cm .例19.观察下列各式,通过分母有理数,把不是最简二次根式的化成最简二次根式:121+=1(21)2121(21)(21)⨯--=-+-=2-1,132+=1(32)3232(32)(32)⨯--=-+-=3-2,同理可得:143+=4-3,……从计算结果中找出规律,并利用这一规律计算 (121++132++143++……120022001+)(2002+1)的值.分析:由题意可知,本题所给的是一组分母有理化的式子,因此,分母有理化后就可以达到化简的目的. 解:原式=(2-1+3-2+4-3+……+2002-2001)×(2002+1)=(2002-1)(2002+1) =2002-1=2001 练习: 一、选择题 1.如果xy(y>0)是二次根式,那么,化为最简二次根式是( ). A .xy(y>0) B .x y(y>0) C .x y y(y>0)D .以上都不对 2.把(a-1)11a --中根号外的(a-1)移入根号内得( ).A .1a - B .1a - C .-1a - D .-1a-3.在下列各式中,化简正确的是( )A .53=315B .12=±122C .4a b=a 2bD .32x x -=x 1x -4.化简3227-的结果是( )A .-23B .-23C .-63D .-2二、填空题 1.化简422x x y +=_________.(x ≥0) 2.a21a a +-化简二次根式号后的结果是_________.三、综合提高题 1.已知a 为实数,化简:3a --a1a-,阅读下面的解答过程,请判断是否正确?若不正确,•请写出正确的解答过程: 解:3a --a1a-=aa--a ·1aa-=(a-1)a-2.若x 、y 为实数,且y=224412x x x -+-++,求xy x y +-的值. 答案:一、1.C 2.D 3.C 4.C 二、1.x22x y + 2.-1a --三、1.不正确,正确解答:因为3010a a⎧->⎪⎨->⎪⎩,所以a<0,原式=2a a --a ·2a a -=a-·2a -a ·2a a-=-aa-+a-=(1-a)a-2.∵224040x x ⎧-≥⎪⎨-≥⎪⎩ ∴x-4=0,∴x=±2,但∵x+2≠0,∴x=2,y=14∴221634164x y x y x y +-=-=-=.例20.计算 (1)8+18(2)16x+64x分析:第一步,将不是最简二次根式的项化为最简二次根式;第二步,将相同的最简二次根式进行合并. 解:(1)8+18=22+32=(2+3)2=52 (2)16x+64x=4x+8x=(4+8)x=12x点评:二次根式加减时,可以先将二次根式化成最简二次根式,•再将被开方数相同的二次根式进行合并.例21.计算(1)348-913+312(2)(48+20)+(12-5)解:(1)348-913+312=123-33+63=(12-3+6)3=153(2)(48+20)+(12-5)=48+20+12-5=43+25+23-5=63+5例22.已知4x 2+y 2-4x-6y+10=0,求(293xx+y23x y)-(x21x-5x yx)的值.分析:本题首先将已知等式进行变形,把它配成完全平方式,得(2x-1)2+(y-3)2=0,即x=12,y=3.其次,根据二次根式的加减运算,先把各项化成最简二次根式,•再合并同类二次根式,最后代入求值. 解:∵4x 2+y 2-4x-6y+10=0 ∵4x 2-4x+1+y 2-6y+9=0 ∴(2x-1)2+(y-3)2=0 ∴x=12,y=3原式=293xx+y23x y-x21x+5xy x=2x x+x y -x x+5x y=xx+6x y当x=12,y=3时, 原式=12×12+632=24+36练习: 一、选择题 1.以下二次根式:①12;②22;③23;④27中,与3是同类二次根式的是( ).A .①和②B .②和③C .①和④D .③和④ 2.下列各式:①33+3=63;②177=1;③2+6=8=22;④243=22,其中错误的有( ).A .3个B .2个C .1个D .0个二、填空题1.在8、1753a、293a、125、323aa、30.2、-218中,与3a是同类二次根式的有________.2.计算二次根式5a-3b-7a+9b的最后结果是________.三、综合提高题1.已知5≈2.236,求(80-415)-(135+4455)的值.(结果精确到0.01) 2.先化简,再求值.(6x yx +33x yy)-(4x xy+36xy),其中x=32,y=27.答案:一、1.C 2.A二、1.1753a323aa2.6b-2a三、1.原式=45-355-455-1255=155≈15×2.236≈0.452.原式=6x y+3x y-(4x y+6x y)=√xy(3-4x/y)=12.5√2例23.如图所示的Rt△ABC中,∠B=90°,点P从点B开始沿BA边以1厘米/•秒的速度向点A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为35平方厘米?PQ的距离是多少厘米?(结果用最简二次根式表示)BAC QP分析:设x 秒后△PBQ 的面积为35平方厘米,那么PB=x ,BQ=2x ,•根据三角形面积公式就可以求出x 的值. 解:设x 后△PBQ 的面积为35平方厘米. 则有PB=x ,BQ=2x 依题意,得:12x ·2x=35x 2=35 x=35所以35秒后△PBQ 的面积为35平方厘米.PQ=2222245535P B B Q x x x +=+==⨯=57答:35秒后△PBQ 的面积为35平方厘米,PQ 的距离为57厘米.例23.要焊接如图所示的钢架,大约需要多少米钢材(精确到0.1m )?分析:此框架是由AB 、BC 、BD 、AC 组成,所以要求钢架的钢材,•只需知道这四段的长度.BAC2m1m4mD解:由勾股定理,得 AB=22224220A D B D +=+==25BC=222221B D C D +=+=5所需钢材长度为 AB+BC+AC+BD =25+5+5+2=35+7≈3×2.24+7≈13.7(m )答:要焊接一个如图所示的钢架,大约需要13.7m 的钢材.例24.若最简根式343a b a b -+与根式23226a b b b -+是同类二次根式,求a 、b 的值.(•同类二次根式就是被开方数相同的最简二次根式)分析:同类二次根式是指几个二次根式化成最简二次根式后,被开方数相同;•事实上,根式23226a b b b -+不是最简二次根式,因此把23226a b b b -+化简成|b|·26a b -+,才由同类二次根式的定义得3a-•b=•2,2a-b+6=4a+3b . 解:首先把根式23226a b b b -+化为最简二次根式:23226a b b b -+=2(216)ba -+=|b|·26ab -+ 由题意得432632a b a b a b +=-+⎧⎨-=⎩∴24632a b a b +=⎧⎨-=⎩∴a=1,b=1 练习: 一、选择题1.已知直角三角形的两条直角边的长分别为5和5,那么斜边的长应为( ).(•结果用最简二次根式) A .52B .50C .25D .以上都不对2.小明想自己钉一个长与宽分别为30cm 和20cm 的长方形的木框,•为了增加其稳定性,他沿长方形的对角线又钉上了一根木条,木条的长应为( )米.(结果同最简二次根式表示) A .13100B .1300C .1013D .513二、填空题1.某地有一长方形鱼塘,已知鱼塘的长是宽的2倍,它的面积是1600m 2,•鱼塘的宽是_______m .(结果用最简二次根式)2.已知等腰直角三角形的直角边的边长为2,•那么这个等腰直角三角形的周长是________.(结果用最简二次根式)三、综合提高题 1.若最简二次根式22323m -与212410n m --是同类二次根式,求m 、n 的值.2.同学们,我们以前学过完全平方公式a 2±2ab+b 2=(a ±b )2,你一定熟练掌握了吧!现在,我们又学习了二次根式,那么所有的正数(包括0)都可以看作是一个数的平方,如3=(3)2,5=(5)2,你知道是谁的二次根式呢?下面我们观察: (2-1)2=(2)2-2·1·2+12=2-22+1=3-22反之,3-22=2-22+1=(2-1)2∴3-22=(2-1)2∴322-=2-1求:(1)322+; (2)423+;(3)你会算412-吗?(√3-1)(4)若2a b ±=m n ±,则m 、n 与a 、b 的关系是什么?并说明理由. 答案: 一、1.A 2.C 二、1.2022.2+22三、1.依题意,得2223241012m m n ⎧-=-⎪⎨-=⎪⎩ ,2283m n ⎧=⎪⎨=⎪⎩ ,223m n ⎧=±⎪⎨=±⎪⎩所以223m n ⎧=⎪⎨=⎪⎩或223m n ⎧=-⎪⎨=⎪⎩ 或223m n ⎧=⎪⎨=-⎪⎩ 或223m n ⎧=-⎪⎨=-⎪⎩2.(1)322+=2(21)+=2+1(2)423+=2(31)+=3+1(3)412-=2423(31)-=-=3-1 (4)m n amn b+=⎧⎨=⎩ 理由:两边平方得a ±2b=m+n ±2m n所以a m n b mn =+⎧⎨=⎩例25.计算: (1)(6+8)×3(2)(46-32)÷22分析:刚才已经分析,二次根式仍然满足整式的运算规律,•所以直接可用整式的运算规律. 解:(1)(6+8)×3=6×3+8×3=18+24=32+26解:(46-32)÷22=46÷22-32÷22=23-32例26.计算 (1)(5+6)(3-5) (2)(10+7)(10-7)分析:刚才已经分析,二次根式的多项式乘以多项式运算在乘法公式运算中仍然成立. 解:(1)(5+6)(3-5)=35-(5)2+18-65=13-35(2)(10+7)(10-7)=(10)2-(7)2=10-7=3 例27.已知xba-=2-xa b-,其中a 、b 是实数,且a+b ≠0,化简11x x x x+-+++11x x x x+++-,并求值。
