一线三等角中点相似模型证明
一线三等角模型相似证明

一线三等角模型相似证明好嘞,今天咱们聊聊一线三等角模型相似证明的事儿。
听起来挺高大上的,但其实说白了就是个有趣的几何故事。
你想啊,几何这个东西,跟生活其实是有很多相似之处的。
就像我们在生活中总是喜欢找到一些规律、一些相似性,这些其实也能帮助我们理解这个世界。
一线三等角模型,其实就是一个很简单的图形构造。
你可以想象一下,就像把三根小棒子拼成一个三角形,哎呀,没事儿,别紧张,这三角形可不复杂。
它的角都是等的,等于是给你一个平等的机会,不管你是哪个角,都是那样的。
这个想法,感觉就像是朋友之间的公平交易,大家都有发言权。
每个角都在发光发热,绝对不是“独角戏”。
再说这相似证明,哈哈,感觉就像是在做一道拼图。
你只要找到那几个对应的边和角,就能搞定。
就像生活中,朋友之间的默契,彼此之间总有些共同点,这种相似感就像是在说:“嘿,我也懂你!”每当你发现这种相似性,心里那个乐啊,真是巴适得很。
想象一下,假如我们把这个模型带到生活中,大家都在一个大舞台上,三角形的三个角分别代表不同的人。
有的人热情似火,有的人冷静如水,还有的人嘛,幽默搞笑,三者相辅相成,缺一不可。
就像在团队中,每个人的特长都能让这个团队更加出彩。
这个时候,你就会发现,只要大家心往一处想,劲往一处使,那绝对能完成一场精彩的表演。
这时候就要提到相似的概念了。
模型里的每个部分都有相同的比例,就像我们生活中那些互相借鉴的经验。
你说我今天遇到的麻烦,你也可能经历过,咱俩一交流,嘿,问题就解决了。
这种相似就像是生活的魔法,能让我们从彼此的经验中获益。
别小看这种分享,生活中的每一份理解都是让人暖心的存在。
咱们再说说那些三等角的性质吧。
这可是个亮点,三角形的内角加起来就是180度,哦,真是太妙了。
这就像是在说,无论你的人生经历如何,最终都要回归到一个平衡的状态。
这种平衡在我们的生活中也很重要。
就像一盘菜,调料、主料、辅料,每样东西都得有适量,才能做出美味佳肴。
否则,光放盐可不行啊,得有个搭配,才能味道更佳。
一线三等角模型结论及证明

一线三等角模型结论及证明
摘要
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,它们的夹角均为120度。
本文将详细阐述一线三等角模型的结论及证明,以及如何使用它来解决实际问题。
一、定义
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,它们的夹角均为120度。
二、结论
一线三等角模型的结论如下:
1、如果在一条直线上有三个等角,则它们的夹角均为120度。
2、如果三条直线的夹角均为120度,则它们共线。
三、证明
1、证明一:假设在一条直线上有三个等角,设它们的夹角为α,β,γ,则有
α+β+γ=360°,由等角性质可知α=β=γ=120°,得证。
2、证明二:假设三条直线的夹角均为120°,设它们的夹角分别为α,β,γ,则有α+β+γ=360°,此时α=β=γ=120°,由此可知,三条直线共线,得证。
四、实际应用
一线三等角模型可以用来解决实际问题,比如,在建筑设计中,可以根据一线三等角模型设计出美观的建筑结构,如三角形的屋顶,具有特殊的视觉效果。
结论
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,
它们的夹角均为120度。
本文详细阐述了一线三等角模型的结论及证明,并且给出了如何使用它来解决实际问题的实例。
相似三角形的基本模型(一线三等角)

【根本模子】
1.如图 , ∽ (一线三等角)
如图 , ∽ (一线三直角)
如图 ,特殊地,当 是 中点时: ∽ ∽ 等分 , 等分 .
2.一线三等角帮助线添加:一般情形下,已知一条直线上有两个等角(直角)或一个直角时,可结构“一线三等角”型类似.
【巩固进步】
1.已知 中 , 是 的中点, 边上有一点 延伸线上有一点 ,使 已知 ,则
提醒:作过点 作 ∥ ,分离交 . 于 . .
∵ ,
∴
设 ,由翻折可得:
∵ ∽
∴ ,即
∴ ,∴
5.已知△ , , ,边长 ,点 在 上,且 ,点 是 上一动点,联络 ,将线段 绕点 逆时针扭转 得到线段 ,要使点 正好落在 上,则 的长是 .
提醒:结构“一线三等角”
∴△ ≌△
∴ , ,
∴
6.如图,已知 ∥ , , ,点 是射线 上的一个动点(点 与点 不重合),点 是线段 上的一个动点(点 与点 . 不重合),联络 ,过点 作 的垂线,交射线 于点 ,联络 .设 , .
提醒: , 是 的中点
∴
由 ∽
∴ ,
2.如图,等边 中, 是边 上的一点,且 ,把 折叠,使点 落在 边上的点 处.那么 的值为 .
提醒:由翻折可得:
设: 则
∵ ∽ ,
∴
3.在矩形 中, , ,把矩形 沿直线 翻折,点 落在边 上的 点处,若 ,那么 的长等于
提醒:作 于 ,则
∵ ∽ ,
∴
∵
∴
4.在矩形 中, ,点 在边 上,联络 ,△ 沿直线 翻折后点 落到点 ,过点 作 ,垂足为点 ,假如 ,那么 .
(1)当 时,求 关于 的函数关系式,并写出它的界说域;
一线三等角中点相似模型证明

一线三等角中点相似模型证明一线三等角中点相似模型是指在一个三角形中,如果从一个顶点引一条线段,使其与对边中点相连,那么这条线段将把三角形分成两个相似的三角形。
这个模型可以用来证明一些三角形的性质。
我们来证明一个三角形的中线相等。
假设三角形ABC的中线DE与BC相交于点F,我们需要证明EF=FD。
根据一线三等角中点相似模型,我们可以将三角形ABC分成两个相似的三角形ADE和BDE。
因为ADE和BDE相似,所以我们可以得到以下比例:AD/BD = AE/BE = DE/DE因为DE/DE=1,所以我们可以得到AD=BD。
因此,EF=FD,证明了三角形ABC的中线相等。
接下来,我们来证明一个三角形的中线平行于另一边。
假设三角形ABC的中线DE与AB相交于点F,我们需要证明DE平行于BC。
根据一线三等角中点相似模型,我们可以将三角形ABC分成两个相似的三角形ADE和CDE。
因为ADE和CDE相似,所以我们可以得到以下比例:AD/CD = AE/CE = DE/DE因为DE/DE=1,所以我们可以得到AD=CD。
因此,DE平行于BC,证明了一个三角形的中线平行于另一边。
我们来证明一个三角形的中线长度等于半周长。
假设三角形ABC 的中线DE与BC相交于点F,我们需要证明DE=1/2(AB+AC)。
根据一线三等角中点相似模型,我们可以将三角形ABC分成两个相似的三角形ADE和BDE。
因为ADE和BDE相似,所以我们可以得到以下比例:AD/BD = AE/BE = DE/DE因为DE/DE=1,所以我们可以得到AD=BD。
因此,DE=2AD=AB+AC,证明了一个三角形的中线长度等于半周长。
一线三等角中点相似模型是一个非常有用的工具,可以用来证明一些三角形的性质。
通过这个模型,我们可以更深入地理解三角形的性质,从而更好地解决相关问题。
相似的一线三等角模型
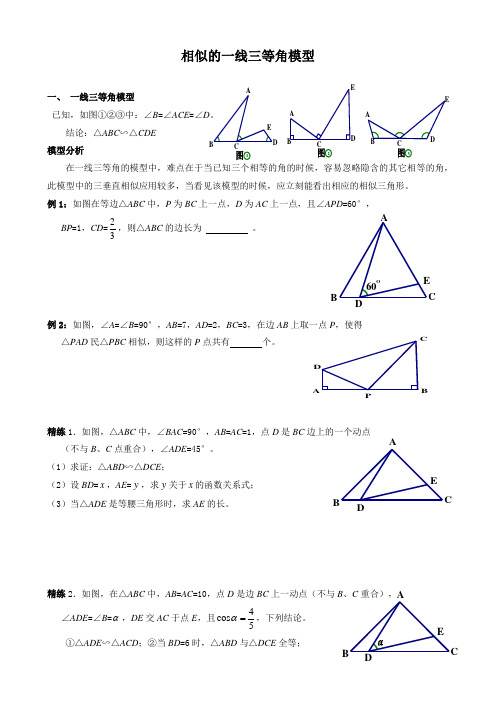
相似的一线三等角模型一、 一线三等角模型已知,如图①②③中:∠B =∠ACE =∠D 。
结论:△ABC ∽△CDE 模型分析在一线三等角的模型中,难点在于当已知三个相等的角的时候,容易忽略隐含的其它相等的角,此模型中的三垂直相似应用较多,当看见该模型的时候,应立刻能看出相应的相似三角形。
例1:如图在等边△ABC 中,P 为BC 上一点,D 为AC 上一点,且∠APD =60°,BP =1,CD =23,则△ABC 的边长为 。
例2:如图,∠A =∠B =90°,AB =7,AD =2,BC =3,在边AB 上取一点P ,使得△PAD 民△PBC 相似,则这样的P 点共有 个。
精练1.如图,△ABC 中,∠BAC =90°,AB =AC =1,点D 是BC 边上的一个动点 (不与B 、C 点重合),∠ADE =45°。
(1)求证:△ABD ∽△DCE ;(2)设BD =x ,AE =y ,求y 关于x 的函数关系式; (3)当△ADE 是等腰三角形时,求AE 的长。
精练2.如图,在△ABC 中,AB =AC =10,点D 是边BC 上一动点(不与B 、C 重合), ∠ADE =∠B =α,DE 交AC 于点E ,且4cos 5α=,下列结论。
①△ADE ∽△ACD ;②当BD =6时,△ABD 与△DCE 全等;图3BCAED图2BCAED1图ABDCE O60ABDCE BCAPDABDCEA BDCE③△DCE 为直角三角形时,BD 等于8或12.5;④0<CE ≤6.4.其中正确的结论是 。
(把你认为正确结论的序号都填上) 精练3.如图,已知矩形ABCD 的一条边AD =8,将矩形ABCD 折叠,使得顶点B 落在CD 边上 的P 点外,折痕与边BC 交于O ,连接AP 、OP 、OA 。
(1)求证:△OCP ∽△PDA ;(2)若△OCP 与△PDA 的面积比为1:4,求边AB 的长。
初中数学几何模型(五)一线三等角模型

初中数学几何模型(五)一线三等角模型一线三等角模型:指有三个相等角的顶点在同一直线上构成的相似或全等(相等角所对的边相等)图形,相等的角可以是锐角,也可以是直角或钝角。
(一)全等1、相等的三个角和全等三角形在直线同侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,且CD=CE,则△ACD≌△BEC。
证明:∵∠BCD=∠1+∠D,∠BCD=∠3+∠BCE,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,CD=CE,∴△ACD≌△BEC(AAS)。
2、相等的三个角和全等三角形在直线异侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,且CD=CE,则△ACD ≌△BEC。
证明:∵∠2=∠D+∠ACD,∠3=∠BCE+∠ACD,∠2=∠3,∴∠D=∠BCE,∵∠2=∠1,∴∠DAC=∠CBE,∵CD=CE,∴△ACD≌△BEC(AAS)。
一线三等角结论1:当等角所对边相等时,则两个三角形全等。
(二)相似1、相等的三个角和相似三角形在直线同侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,则△ACD∽△BEC。
证明:∵∠BCD+∠1+∠D,∠BCD=∠3+∠BCE,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,∴△ACD∽△BEC。
2、相等的三个角和相似三角形在直线异侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,则△ACD∽△BEC。
证明:∵∠1=∠D+∠ACD,∠3=∠BCE+∠ACD,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,∴∠DAC=∠CBE,∴△ACD∽△BEC。
一线三等角结论2:一线三等角两个三角形相似。
(三)一线三等角变式:中点型如图,点C在相等AB上,且AC=BC,∠1=∠2=∠3。
求证:△ACD∽△BEC∽△CED证明:∵∠1=∠2=∠3,∴△ACD ∽△BEC ,∴AD BC =CD CE , ∵AC=BC ,∴AD AC =CD CE ,∵∠1=∠3,∴△ACD ∽△CED ,∴△ACD ∽△BEC ∽△CED ,∴∠4=∠5=∠8,∠9=∠6=∠7。
一线三等角相似模型

在物理学中,可以利用一线三等角 相似模型来研究物理现象和规律, 如光的反射和折射、波的传播等。
04 一线三等角相似模型的证 明方法
直接证明法
定义
直接证明法是通过直接使用已知条件和定理来证明结论的 方法。
步骤
首先,根据已知条件,明确一线三等角的定义和性质;然后, 通过比较两个三角形中的角度和边长,利用相似三角形的性质
03
注意事项
反证法需要熟练掌握反证法的原理和 推理技巧,以及能够灵活运用已知条 件。
综合法与分析法
定义
综合法是从已知条件出发,逐步推导出结论的方法;分析法是从结论出发,逐步推导出已知条件的方法。
步骤
在综合法中,首先明确已知条件和目标结论;然后,根据已知条件逐步推导所需结论;最后,总结推导过程。在分析 法中,首先明确目标结论和已知条件;然后,根据结论逐步推导所需条件;最后,总结推导过程。
,逐步推导出所需的结论。
注意事项
直接证明法需要熟练掌握相似三角形的性质和定理,以及 灵活运用已知条件。
反证法
01
定义
反证法是通过假设结论不成立,然后 推导出矛盾,从而证明结论成立的方 法。
02
步骤
首先,假设结论不成立;然后,根据 已知条件和反证法的原理,推导出与 已知条件相矛盾的结论;最后,根据 矛盾的结论,得出结论成立。
相似变换的性质
相似变换具有一些重要的性质,如保持角度不变、线 段长度比例不变等。
相似变换的应用
相似变换在几何学、物理学、工程学等领域有着广泛 的应用,如建筑设计、机械制造、航天技术等。
相似多边形的性质与应用
1 2
相似多边形的定义
相似多边形是指各对应角相等、各对应边成比例 的多边形。
相似三角形中的 “一线三等角”模型-2023年新九年级数学核心知识点与常见题型(沪教版)(解析版)

重难点专项突破:相似三角形中的“一线三等角”模型【知识梳理】一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
或叫“K字模型”。
三直角相似可以看着是“一线三等角”中当角为直角时的特例,三直角型相似通常是以矩形或者正方形形为背景,或者在一条直线上有一个顶点在该直线上移动或者旋转的直角,几种常见的基本图形如下:当题目的条件中只有一个或者两个直角时,就要考虑通过添加辅助线构造完整的三直角型相似,这往往是很多压轴题的突破口,进而将三角型的条件进行转化。
一般类型:基本类型:同侧“一线三等角”异侧“一线三等角”【考点剖析】例1.如图,直角梯形ABCD 中,AB // CD ,90ABC ∠=︒,点E 在边BC 上,且34AB BE EC CD ==, AD = 10,求AED ∆的面积.【答案】24.【解析】90ABC ∠=,//AB CD , ∴90DCB ABC ∠=∠=.又34AB BE EC CD ==, ABE ECD ∴∆∆∽.∴AEB EDC ∠=∠. ∴34AE AB ED EC ==.90EDC DEC ∠+∠=,∴90AEB DEC ∠+∠=. ∴90AED ∠=.在Rt AED ∆中,10AD =,68AE ED ∴==,. 24AED S ∆∴=.【总结】本题考查一线三等角模型的相似问题,还有外角知识、平行的判定等.例2.已知:如图,△ABC 是等边三角形,点D 、E 分别在边BC 、AC 上,∠ADE =60°.(1)求证:△ABD ∽△DCE ;(2)如果AB =3,EC =,求DC 的长.【分析】(1)△ABC 是等边三角形,得到∠B =∠C =60°,AB =AC ,推出∠BAD =∠CDE ,得到△ABD∽△A B C DEDCE ;(2)由△ABD ∽△DCE ,得到=,然后代入数值求得结果.【解答】(1)证明:∵△ABC 是等边三角形,∴∠B =∠C =60°,AB =AC ,∵∠B+∠BAD =∠ADE+∠CDE ,∠B =∠ADE =60°,∴∠BAD =∠CDE∴△ABD ∽△DCE ;(2)解:由(1)证得△ABD ∽△DCE ,∴=,设CD =x ,则BD =3﹣x ,∴=,∴x =1或x =2,∴DC =1或DC =2.【点评】本题考查了等边三角形的性质,相似三角形的判定和性质,注意数形结合和方程思想的应用. 例3.已知,在等腰ABC ∆中,AB = AC = 10,以BC 的中点D 为顶点作EDF B ∠=∠, 分别交AB 、AC 于点E 、F ,AE = 6,AF = 4,求底边BC 的长.【答案】46.【解析】EDC B BED ∠=∠+∠,而EDC EDF FDC ∠=∠+∠,∴B BED EDF FDC ∠+∠=∠+∠. 又EDF B ∠=∠,∴BED FDC ∠=∠.AB C D EFAB AC=,∴B C∠=∠.EDB DCF∴∆∆∽.BE BDDC CF∴=.106104BDDC−∴=−,24DC BD∴=.又12CD DB BC==,BC∴=【总结】本题是对“一线三等角”模型的考查.例4.已知:如图,AB⊥BC,AD // BC, AB = 3,AD = 2.点P在线段AB上,联结PD,过点D作PD的垂线,与BC相交于点C.设线段AP的长为x.(1)当AP = AD时,求线段PC的长;(2)设△PDC的面积为y,求y关于x的函数解析式,并写出函数的定义域;(3)当△APD∽△DPC时,求线段BC的长.满分解答:(1)过点C作CE⊥AD,交AD的延长线于点E.∵AB⊥BC,CE⊥AD,PD⊥CD,AD // BC,∴∠ABC =∠AEC =∠PDC = 90°,CE = AB = 3.∵AD // BC,∴∠A +∠ABC = 180°.即得∠A = 90°.又∵∠ADC =∠DCE +∠DEC,∠ADC =∠ADP +∠PDC,∴∠ADP =∠DCE.又由∠A =∠DEC = 90°,得△APD∽△DCE.∴AD APCE DE=.于是,由AP = AD = 2,得DE = CE = 3.…………………………(2分)在Rt△APD和Rt△DCE中,得PD=,CD=1分)AB CDPAB CD(备用图)于是,在Rt △PDC 中,得 PC = (1分)(2)在Rt △APD 中,由 AD = 2,AP = x ,得 PD 1分)∵ △APD ∽△DCE ,∴AD PD CE CD =.∴ 32CD PD ==1分)在Rt △PCD 中,22113332224PCD S PD CD x ∆=⋅⋅=⨯=+.∴ 所求函数解析式为2334y x =+.…………………………………(2分) 函数的定义域为 0 < x ≤ 3.…………………………………………(1分)(3)当△APD ∽△DPC 时,即得 △APD ∽△DPC ∽△DCE .…………(1分)根据题意,当△APD ∽△DPC 时,有下列两种情况:(ⅰ)当点P 与点B 不重合时,可知 ∠APD =∠DPC .由 △APD ∽△DCE ,得 AP PD DE DC =.即得AP DE PD CD =. 由 △APD ∽△DPC ,得AP AD PD DC =. ∴AD DE CD CD =.即得 DE = AD = 2. ∴ AE = 4.易证得四边形ABCE 是矩形,∴ BC = AE = 4.…………………(2分)(ⅱ)当点P 与点B 重合时,可知 ∠ABD =∠DBC .在Rt △ABD 中,由 AD = 2,AB = 3,得 BD =.由 △ABD ∽△DBC ,得AD BD BD BC =.即得 =. 解得 132BC =.………………………………………………………(2分)∴ △APD ∽△DPC 时,线段BC 的长分别为4或132.方法总结本题重点在于:过点C 作CE ⊥AD ,交AD 的延长线于点E .(构造一线三角,出现相似三角形,进行求解) 例5.在梯形ABCD 中,AD ∥BC ,︒=∠===90,2,1A BC AB AD .(如图1)(1)试求C ∠的度数;(2)若E 、F 分别为边AD 、CD 上的两个动点(不与端点A 、D 、C 重合),且始终保持︒=∠45EBF ,BD 与EF交于点P .(如图2)①求证:BDE ∆∽BCF ∆;②试判断BEF ∆的形状(从边、角两个方面考虑),并加以说明;③设y DP x AE ==,,试求y 关于x 的函数解析式,并写出定义域.答案:(1)作BC DH ⊥,垂足为H ,在四边形ABHD 中,AD ∥BC ,︒=∠==90,1A AB AD ,则四边形ABHD 为正方形又在CDH ∆中,1,1,90=−====∠︒BH BC CH AB DH DHC , ∴︒︒=∠−=∠452180DHC C .(2)①∵四边形ABHD 为正方形,∴︒=∠45CBD ,︒=∠45ADB ,又∵︒=∠45EBF ,∴CBF DBE ∠=∠又∵︒=∠=∠45C BDE ,∴BDE ∆∽BCF ∆.②BEF ∆是等腰直角三角形,∵BDE ∆∽BCF ∆, ∴CB FB BD BE =,又∵︒=∠=∠45DBC EBF ,∴EBF ∆∽DBC ∆,又在DBC ∆中,︒=∠=∠45C DBC ,为等腰直角三角形,∴BEF ∆是等腰直角三角形. ③x x x x x x y +−=+−⨯=1221222,(0<x <1).方法总结 第三问方法提示:过点P 作AD 的垂线于点H ,构造一线三直角相似,进行求解,很简单。
专题 相似三角形中的一线三等角模型(学生版)
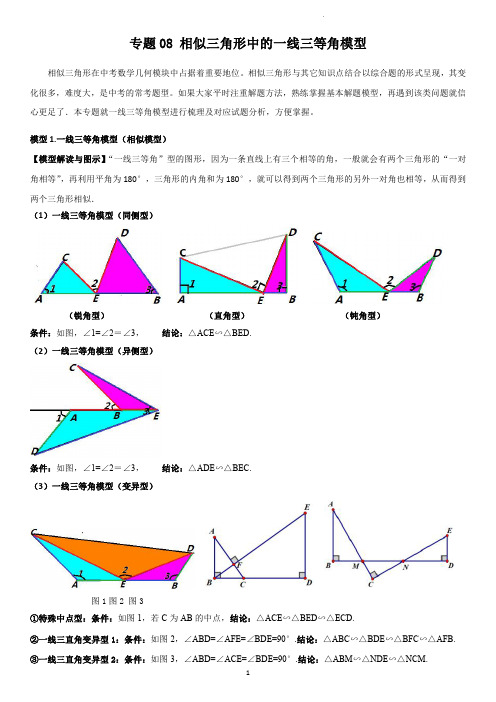
专题08相似三角形中的一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.(1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.(2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.(3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.A.1.8B.2.4例3.(2022·河南新乡·九年级期中)某学习小组在探究三角形相似时,发现了下面这种典型的基本图形.(1)如图1,在ABC中,∠BAC=90°,ABAC=k,直线l经过点A,BD⊥直线I,CE上直线l,垂足分别为D、E.求证:BDAE=k.(2)组员小刘想,如果三个角都不是直角,那么结论是否仍然成立呢?如图2,将(1)中的条件做以下修改:在ABC中,ABAC=k,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中的结论还成立吗?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,在ABC中,沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG,ABAE=ACAG=12,AH是BC边上的高,延长HA交EG于点I.①求证:I是EG的中点.②直接写出线段BC与AI之间的数量关系:.例4.(2022·四川·一模)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:(1)如图1,已知:在△ABC 中,AB AC =,D 、A 、E 三点都在直线m 上,并且有BDA AEC BAC α∠=∠=∠=.试猜想DE 、BD 、CE 有怎样的数量关系,请证明你的结论;(2)老师鼓励学习小组继续探索相似的情形.于是,学习小组又研究以下问题:如图2,△ABC 中,(060)B C αα∠=∠=<<︒.将一把三角尺中30°角顶点P 放在BC 边上,当P 在BC 边上移动时,三角尺中30°角的一条边始终过点A ,另一条边交AC 边于点Q ,P 、Q 不与三角形顶点重合.设CPQ β∠=.当β在许可范围内变化时,α取何值总有△ABP ∽△PCQ ?当α在许可范围内变化时,β取何值总有△ABP ∽△QCP ?(3)试探索有无可能使△ABP 、△QPC 、△ABC 两两相似?若可能,写出所有α、β的值(不写过程);若不可能,请说明理由.例5.(2022·山西晋中·一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在ABC 中,90ACB ∠=︒,AC BC =,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:ADC CEB △≌△.(1)探究问题:如果AC BC ≠,其他条件不变,如图②,可得到结论;ADC CEB △∽△.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线12y x =与直线CD 交于点()2,1M ,且两直线夹角为α,且3tan 2α=,请你求出直线CD 的解析式.(3)拓展应用:如图④,在矩形ABCD 中,3AB =,5BC =,点E 为BC 边上—个动点,连接AE ,将线段AE 绕点E 顺时针旋转90︒,点A 落在点P 处,当点P 在矩形ABCD 外部时,连接PC ,PD .若DPC △为直角三角形时,请你探究并直接写出BE 的长.的中点,校考三模)某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探【观察与猜想】(1)如图1,在正方形ABCD中,E,F分别是AB,AD上的两点,连接则DECF的值为___________;A.2个B.3个2.(2023·浙江·九年级专题练习)如图,四边形3.(2022·安徽·九年级专题练习)如图,矩形△CEF面积的最小值是.是12.(2022·山东济宁·二模)情境观察:将含45°角的三角板的直角顶点R 放在直线l 上,分别过两锐角的顶点M ,N 作l 的垂线,垂足分别为P ,Q ,(1)如图1.观察图1可知:与NQ 相等的线段是______________,与NRQ ∠相等的角是_____(2)问题探究直角ABC 中,90B ∠=︒,在AB 边上任取一点D ,连接CD ,分别以AC ,DC 为边作正方形ACEF 和正方形CDGH ,如图2,过E ,H 分别作BC 所在直线的垂线,垂足分别为K ,L .试探究EK 与HL 之间的数量关系,并证明你的结论.(3)拓展延伸:直角ABC 中,90B ∠=︒,在AB 边上任取一点D ,连接CD ,分别以AC ,DC 为边作矩形ACEF 和矩形CDGH ,连接EH 交BC 所在的直线于点T ,如图3.如果AC kCE =,CD kCH =,试探究TE 与TH 之间的数量关系,并证明你的结论.问题探究(2)如图2,在矩形ABCD 中,6cm,9cm AB BC ==,点P 是AD 边上一动点,点Q 是CD 的中点将.ABP 沿着BP 折叠,点A 的对应点是A ',将QDP △沿着PQ 折叠,点D 的对应点是D ¢.请问是否存在这样的点P ,使得中,,在平面直角坐标系中,点16.(2020·四川雅安·中考真题)如图,已知边长为10的正方形ABCD E ,是BC 边上一动点(与B C 、不重合),连结AE G ,是BC 延长线上的点,过点E 作AE 的垂线交DCG ∠的角平分线于点F ,若FG BG ⊥.(1)求证:ABE EGF ∽△△;(2)若2EC =,求CEF △的面积;(3)请直接写出EC 为何值时,CEF △的面积最大.17.(2023·湖南株洲·九年级统考期末)如图,正方形ABCD 的边长为1,点E 是AD 边上的动点,从点A 沿AD 向点D 运动,以BE 为边,在BE 的上方作正方形BEFG ,连接CG .(1)求证:AEB CGB △≌△;(2)若设AE=x ,DH=y ,当x 取何值时,y 有最大值?并求出这个最大值;(3)连接BH ,当点E 运动到AD 的何位置时有BEH BAE ∽?∆BCE。
相似专题:一线三等角相似模型

注意事项:需要熟练掌握代数公式和定理以及灵活运用代数方法进行证明
三角函数证明法
利用三角函数的性质通过角度相等来证明三角形相似 利用三角函数的诱导公式将角度相等转化为边长比例相等 利用三角函数的和差公式将角度相等转化为边长比例相等 利用三角函数的倍角公式将角度相等转化为边长比例相等
一线三等角相似的判定条件
两个三角形中如果一个角分别与另两个角相等则这两个三角形相似。
在两个三角形中如果一个角的对边与另一个角的对边成比例则这两个三角形相似。 在两个三角形中如果一个角的对边与另一个角的邻边成比例则这两个三角形相似。
在两个三角形中如果一个角的对边与另一个角相等则这两个三角形相似。
一线三等角相似模型的 应用
单击添加标题
题目:在三角形BC中D是B上一点E是C上一点DE平行于BC且E:EC=1:2 则S△DE:S△BC=?
代数表达式简化:利用一线三等角 相似模型可以将复杂的代数表达式 进行简化。
代数应用实例
代数不等式证明:利用一线三等角 相似模型可以证明一些代数不等式。
添加标题
添加标题
添加标题
添加标题
代数方程求解:通过一线三等角相 似模型可以求解一些代数方程。
一线三等角相似模型的 应用实例
几何证明实例
单击添加标题
题目:已知三角形BC中D是B上一点E是C上一点DE平行于BC且D:DB=2: 1则S△DE:S△BC=?
单击添加标题
题目:在三角形BC中D是B上一点E是C上一点DE平行于BC且E:EC=2:1 则S△DE:S△BC=?
单击添加标题
题目:在三角形BC中D是B上一点E是C上一点DE平行于BC且BD:B=1:3 则S△DE:S△BC=?
完整版相似三角形模型讲一线三等角问题讲义解答

」、相似三角形判定的基本模型认识(一) A 字型、反 A 字型(斜A 字型)(二) 8字型、反8字型(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(六)双垂型: A(平行)(不平行)△B(平行) (三)母子型(蝴蝶型)相似三角形判定的变化模型一线三直角的2AB=AC ADL BC 于 D, CG// AB BG 分别交 AD AC 于 E 、F .求证:BE=EF? EG2 .如图,在△ ABC 中,AB=AC=10 BC=16点D 是边BC 上(不与 B, C 重合)一动点,/ ADE=Z B=a, DE 交 AC 于点E .下列结论:①AD 2=AE? A B ② 3.6 W AE V 10;③当 AD=2 i 时,△ ABD^A DCE ④厶DCE 为直角三角形时, BD 为8或12.5 . 其中正确的结论是 _____________ .(把你认为正确结论的序号都填上)3.已知:如图,△ ABC 中,点 E 在中线 AD 上,/ DEB=/ ABC 求证:(1) DB=DE? D A(2 )Z DCE=/ DACAD// BC,对角线 AG BD 交于点O, BE// CD 交CA 延长线于 E.求证:OC=OA?OE6.已知:如图,在 Rt △ ABC 中,/ C=90°, BC=2 AC=4 P 是斜边 AB 上的一个动点, PD 丄AB 交边 AC 于点 D (点D 与点A C 都不重合),E 是射线DC 上一点,且/ EPD=/ A.设A P 两点的距离为 x ,A BEP 的面积为 (1)求证:AE=2PE(2)求y 关于x 的函数解析式,并写出它的定义域;8.如图,已知△ ABC 是等边三角形,点 D B C E 在同一条直线上,且/ DAE=120 (1) 图中有哪几对三角形相似?请证明其中的一对三角形相似;9.(已知:如图,在 Rt △ ABC 中,AB=AC / DAE=45 .求证:BC=2DE10.如图,在等边厶 ABC 中,边长为 6, D 是BC 边上的动点,/ EDF=60 (1) 求证:△ BD 0A CFD②若BP=x CQ=y 求y 与x 之间的函数关系式,并写出函数的定义域;(2) 正方形ABCD 勺边长为5 (如图),点P 、Q 分别在直线CB DC 上 (点P 不与点C 点B 重合),且保持 / APQ=90度.当CQ=1时,写出线段BP 的长(不需要计算过程,请直接写出结果)13 .已知梯形 ABCD 中, AD// BC,且 AD< BC, AD=5, AB=DC=2 (1) 如图,P 为AD 上的一点,满足/ BPC=ZA ,求AP 的长;(2) 如果点P 在AD 边上移动(点 P 与点A D 不重合),且满足/ BPE=Z A, PE 交直线BC 于点E ,同时交直 线DC 于点Q.①当点Q 在线段DC 的延长线上时,设 AP=x CQ=y 求y 关于x 的函数关系式,并写出自变量 x的取值范围;求BE 的长.11. (1)在厶ABC 中,AB=AC=5 BC=8点P 、Q 分别在射线 CB AC 上(点P 不与点 C 点B 重合),且保持 / APQ 2 ABC14.如图,在梯形ABCD中, AD// BC, AB=CD=BC=,6 AD=3.点M为边BC的中点,以M为顶点作/ EMF M B, 射线ME交腰AB于点E,射线MF交腰CD于点F,连接EF.(1)求证:△ ME®A BEM(2)若厶BEM是以BM为腰的等腰三角形,求EF的长;(3 )若EF丄CD求BE的长.15 .已知在梯形ABCD中, AD// BC AD< BC 且BC=6 AB=DC=4 点E 是AB 的中点.(1) 如图,P为BC上的一点,且BP=2.求证:△ BEP^A CPD(2) 如果点P在BC边上移动(点P与点B C不重合),且满足/ EPF=Z C, PF交直线CD于点F,同时交直线AD于点M,那么①当点F在线段CD的延长线上时,设BP=x, DF=y,求y关于x的函数解析式,并写出函数的定义域;16.如图所示,已知边长为3的等边△ ABC点F在边BC上, CF=1,点E是射线BA上一动点,以线段EF为边向右侧作等边厶EFG直线EG FG交直线AC于点M, N,(1)写出图中与△ BEF相似的三角形;(2)证明其中一对三角形相似;(3)设BE=x , MN=y求y与x之间的函数关系式,并写出自变量x的取值范围;(4)若AE=1,试求△ GMN勺面积.丄CP 交直线AB 于点E ,设PD=x AE=y,(1)写出y 与x 的函数解析式,并指出自变量的取值范围; (2)如果△ PCD 的面积是△ AEP 面积的4倍,求CE 的长;(3) 是否存在点 卩,使厶APE 沿PE 翻折后,点A 落在BC 上?证明你的结论.18. 如图,在 Rt △ ABC 中,/ C=90°, AB=5,工匸-=,点D 是BC 的中点,点 E 是AB 边上的动点, 交射线AC 于点F .(1 )求AC 和BC 的长;(2) 当 EF// BC 时,求 BE 的长;(3) 连接EF ,当厶DEF 和△ ABC 相似时,求 BE 的长.(备用图)19. 如图,在 Rt △ ABC 中,/ C=90°, AC=BC D 是AB 边上一点,E 是在AC 边上的一个动点(与点 重合),DF 丄DE DF 与射线BC 相交于点F .(1) 如图2,如果点 D 是边AB 的中点,求证:DE=DF (2) 如果 AD: DB=m 求DE DF 的值;17.如图所示,已知矩形 ABCD 中, CD=2 AD=3,点P 是AD 上的一个动点(与 A 、D 不重合),过点 P 作PEDF 丄DEA 、C 不(3)如果AC=BC=6 AD DB=1: 2,设AE=x BF=y,①求y关于x的函数关系式,并写出定义域;(2)如果以线段BC 为直径的圆与以线段 AE 为直径的圆相切,求线段 BE 的长;421. 如图,在梯形 ABCD 中, AB// CD AB=2 AD=4, tanC=^,/ ADC M DAB=90 , P 是腰 BC 上一个动点(不J含点B C ),作PQLAP 交CD 于点Q.(图1) (1 )求BC 的长与梯形 ABCD 勺面积;(2)当PQ=DQ 寸,求BP 的长;(图2)20. 如图,在厶ABC 中,/ C=90° EF 交射线BC 于点F .设BE=x , (1 )求y 关于x 的函数关系式, ,AC=6 •斗_彳,D 是BC 边的中点, △ BED 的面积为y .并写出自变量 x 的取值范围; E 为AB 边上的一个动点, 作/ DEF=90 ,②以CE 为直径的圆与直线 AB 是否可相切?若可能,求出此时 x 的值;若不可能,请说明理由.BED 相似,求△ BED 的面积.(2)••• AD 是中线,• CD=BD • C D=AD? DE,又/ ADC N CDE DEC^A DCA :丄 DCE N DAC证明:连接CE 如右图所示,•/ AB=AC AD L BC, • AD 是/ BAC 的角平分线,• BE=CE •••/ EBC=z ECB 又•••/ ABC=Z ACBABC- / EBC 2 ACB-Z ECB1. 解 答:2. 解 答: 证明:••• AD// BC4,又 BE// CD •••丄』,二二丄,即 OC=OA? OEOC OBOB OE OC OE解:①••• AB=ACB=Z C ,又•••/ ADE=Z B.••/ ADE N C ,「.A ADE^A ACD •••4 仝,.•• AE J =AE ? AB,AE AD故①正确,②易证得厶 CDE^A BAD T BC=16 设 BD=y, CE=x •••魁=—,•1° 工,整理得: CD CE 16-y x2即(y - 8) =64 - 10x , • O v x < 6.4 ,•/ AE=AC- CE=10- x , • 3.6 < AE< 10.故②正确. 2y - 16y+64=64 - 10x ,3.解 答: ③作AGL BC 于G •/ AB=AC=10 / ADE 玄 B=a ,COS a_4•/ BC=1Q • AG=6 •/ AD=2 I ,• DG=2 • CD=8 • AB=CD •△ ABD-与^ DCE 全等;故③正确; ④当/ AED=90 时,由①可知:△ ADE^A ACD •/ ADC=Z AED •••/ AED=90 , ADC=90 , 即 AD L BC, •/ AB=AC • BD=CD ADE 玄 B=a 且 COS a = , AB=10, BD=8/ B=a 且 COS a J. AB=10, ••• cosB=二 •• BD 」.故④正确5 BD 5 2当/ CDE=90 时,易厶 CDE^A BAD •••/ CDE=90 , BAD=90 ,故答案为:①②④.B U G C证明:(1)在厶BDE 和A DAB 中•••/ DEB=/ ABC / BDE=/ ADB BDE^A ADBD£__BD • BE J =AD ? DE4.解 答:.CD 二 AD'DE _CD实用文档即/ ABEK ACE又••• CGI AB,:/ ABEh CGF :丄 CGF 2 FCE 又/ FEC=/ CEGCEF^A GEC 二 CE EF=EG CE 即 C^=EF? EG 又 CE=BE ••• BU=EF? EG又 EF 为 AD 的垂直平分线,• AF=FD / DAF=/ ADF, DAC / CAF=/ B+/ BAD•••/ CAF=/ B ,•// AFC 玄 AFC •△ ACF^A BAF,即丄仝,• AF "=CF? BF ,即 F[J=CF? BF.AF B?ripr r>ri i •// EPD=/ A, /PED=/ AER EPD^A EAR •定义域是 0< x v 一-—5得 「二_二= 21寸PEAP 2 (2)由厶 EPD^A EAR6.解 答:PD BC 1AP AC 2• PE=2DE • AE=2PE=4DE 作EHL AB,垂足为点H,•/ AP=x •- PD 二x , •/ PD// HE2又AB=2 ■ , y =—•-上J 亠- 'PD AD 3.(2 _ ";- x)? —x ,即 y=-3^ • HE :x .3X 2+二' 3x .另解:由厶EPD^A EAR 得DE PD 1 PE• PE=2DE • AE=2PE=4DE • AE --S AAB =—X y x ——X X 2=1 x , • ABx .定义域是 0< x < —'.厂丄• PE 二x? • HE AC ,当厶BEP-与^ ABC 相似时,只有两种情形:/(3)由厶 PEH ^A BAC 得x .32BEP=/ C=90° 或/ EBP=/ C=90°.• △ ADP ^A ABC • A=/ A ,X2 x,2SAABE 2 1…y= - — x2 37.解 答:8.解 答:证明:••• BD CE 分别是AC 与AB 边上的高,•/ BEC 2 BDC• B 、C D E 四点共圆,•/ AED=/ ACB 而/ A=Z A, • △ AED^A ACB •- -丄; BC AR•/ BD 丄AC,且/ A=60°,A Z ABD=30 , AD=迅,• BC=2DE•/△ ABC 是等边三角形•/ ABC=/ ACB 玄 BAC=60 . •/ D+Z DAB=60 , •••/ DAE=120,•/ DAB+Z EAC=60 . •/ D=Z CAE / E=Z DAB •••/ D=Z D,Z E=Z E ,「.A DAE^A DBA^A ACE(2)•••△ DBA^A ACE •- DB: AC=AB CE•/ AB=AC=BC DB=2 CE=6i BC ?=DB? CE=12 •/ BO0, • BC=2,/ £.Z E+Z CAE=60 .9.解证明:(1)在Rt △ ABC 中, 答: •/ AB=AC •/ B=Z C=45.•••/ BAE=/ BAD+Z DAE Z DAE=45,•/ BAE=/ BAD+45 . 而/ ADC Z BAD+Z B=Z BAD+45 , • Z BAE=/ CDA • △ ABE^A DCA(2)由厶 ABE^^ DCA 得翌• BE? CD=AB AC.AB CD2 2 2 2 2 2而 AB=AC BC=AB+AC ,「. BC=2AB . • BC=2BE? CD10.解(1)证明:•••△ ABC 为等边三角形,•/ B=Z C=60°, 答: vZ EDF=60,•/ BED+Z EDB 玄 EDB+Z FDC=120 ,• Z BED Z FDC •△ BD 0A CFD(2)解:由(1 )知厶 BDE^A CFDBE =BD CD =CF(i )当/ BEP=90时,旦县,•••罗》=丄.解得x 型迈.PB 起药厂V5 4• y=-二x X_X 5+''X …亠.31&3 4 16(ii )当/ EBP=90时,同理可得 x=邑匹,y=J .24•/ BC=6 BD=1,「. CD=B G BD=5, •••翌=丄,解得 BE 壬.5 3 3解解:(1)①•••/ APQ+Z CPQ 2 B+Z BAP, / APQ 2 ABC BAP=Z CQP又••• AB=AC •••/ B=Z C.• △ CPQ^A BAP若点P 在线段CB 的延长线上,如图.•••/ APQ M APB 亡 CPQ/ ABC 玄 APB+Z PAB /APQ M ABC •••/ CPQ MPAB又 T Z ABP=180 -Z ABC Z PCQ=180 -Z ACB Z ABC Z ACB • Z ABP=/ PCQ11. 答:BP AB•/ AB=AC=5 BC=8 BP=6 CP=8- 6=2 , • CQ CP•/ BP=x, BC=8,「. CP=BC- BP=8- x , ,即丁 _ 7 y5②若点P 在线段CB 上,由(1 )知又••• CQ=y AB=5 •工E _ 1X 5故所求的函数关系式为CQ 2» 12 6 3CQ 飞CQ PC ■/ BP=x CP=BC+BP=8+, AB=5, CQ=y实用文档QCP^ PBA 里/:.实用文档圉①(2)①当点P 在线段BC 上,•••/ APQ=90,•/ APB+Z QPC=90 , •••/ PAB 亡 APB=90,•/ PAB=/ QPC•••/ B=/ C=90°.・.A ABP^A PCQ • AB: PC=BP CQ-J : 或. | -②当点P 在线段BC 的延长线上,则点 Q 在线段 同理可得:△ ABN A PCQ • AB: PC=BP CQ即 5: ( 5 - BP ) =BP 1,解得:2DC 的延长线上,••• 5: (BP- 5) =BP: 1,解得: BP=— ③当点P 在线段CB 的延长线上,则点 Q 在线段 同理可得:△ ABN A PCQ • AB: PC=BP CQ • 5: (BP+5) =BP 1,解得:E _ . DC 的延长线上, A=Z D 13.解 解:(1)v ABCD 是梯形,AD// BC AB=DC 「./ •••/ ABP+/ APB+/ A=180°,Z APB-/ DPC / BPC=180 , / BPC 玄 A 解得:AP=1 或 AP=4.答: •••/ ABPK DPC ABN A DPC. AP 民即. AP 2 CD FD 2 ~5-AP 14. 答: (2)①由(1) •;」即:DQ~PD②当CE=1时,富二22fy~ 5-i•/△ PDQ^A ECQ • CE_CQPD~DQ ,:,解得:AP=2或(舍去).G怙 ■ 4. 『-t * -i;\Fi/i解证明:(1)在梯形ABCD 中,•/ AD// BC, AB=CD 「・/ B=/ C ,•••/ BMF / EMB / EMF / C+/ MFC又•••/ EMF=/ B, •/ EMB / MFC •△ EMB^A MFC •- _L "一EM ~MF ' •/ MC=M , • 一 UL關—和,又丄即匕B’iEi B EM(2)解:若△ BEM 是以BM 为腰的等腰三角形,则有两种情况:① BM=ME 那么根据厶 ME &A BEM .•.二1="- ,•. £=也,即 EF=MFHE 01 ME EF根据第(1)问中已证厶BM 0A MFC ■ ■, 即 MF=FC •••/ FMC 2 C,HE FC又•••/ B=Z C,.Z FMC M B ,. MF// AB延长BA 和CD 相交于点 G 又点M 是BC 的中点, • MF >^ GBC 的中位线,• MF=GB2!又••• AD// BC,GAD^A GBC • 塑=型=丄4 ,•.塑=1, 即 AG=AB=6GB BC 6 2 AG• GB=12 • MF=EF=6② BM=BE=3 .•点E 是AB 的中点,又厶 MEF^A BEM.•.型=世=1,即MF=ME • EF 是梯形 ABCD 勺中位线,• EF 丄(AD+BC — ( 3+6)戈;Bg ME 2 2 2(3 )T EF ± CD• / BEP=/ FPC •△ BEP^A CPF , • ^^^-4 (2< x v 4)•②当点F 在线段CD 的延长线上时,•••/ FDM Z C=Z B, / BEP=/ FPCK FMD •△ BEP^A DMF DF 3 y.T , • x - 3x+8=0 , △< 0.•此方程无实数根..•尸gF - 3K +4 .2 ____________、,15. 答:• / EFC=90 , △ MEF^A BEM / MFE / MFC / BME=45 ,解一:过点E 作EH! BC,则可得△ EHM 等腰直角三角形, EH=MH 」 故 EH=MH 设 BE=x 贝U BH 丄•-, 4解二:过点M 作MN L DC MC=3由厶 MEF^A MFCt • T ,即 P 旳TCI 5 4NIC 』.M43弓&亏"解 (1)证明:•••在梯形 ABCD 中 , AD// BC, AB=DC=FN FC= i i : - - 2BE —— 丨.• / B=Z C.BE=2, BP=2, CP=4 CD=4 •••里=!!?.•••△ BEP^A CPDCP CD(2)解:①•••/ B=Z C=Z EPF• 180 —/ B=180-Z EPF=/ BEP+Z BPE=Z BPE+Z CPFHE 閏.•crP 2 si 6-iSZ1DJIF^43ABEP, … DF BP"3 y 八. △ BEP^A CPF , • EB BPl • 1 2 xCP '"cr£ - 工 4 _ y.、/9•当 £ADMF ^^ABEP,得 2故当点F 在线段CD 的延长线上时,不存在点 P 使SADMF =-|SABEP ; 当点F 在线段 CD 上时,同理△ BEP^A DMF• x - 9x+8=0 ,解得X1=1 , X2=8.由于X2=8 不合题意舍去.• x=1 ,即BP=1. 时,BP的长为1.实用文档16.解解:(BE&A AM 0A CFW A GMN 答:证明:(2)在厶BEF 与厶AME 中,•••/ B=Z A=60°,「./ AEM 社 AME=120 ,•/△ BEF^A AME •- BE: AM=BF AE ,同理可证厶 BEF ^A CFN • BE: CF=BF CN即:x : 1=2: CN •- CN 丄,即: x : AM=2 (3- x ) , • AM=•••/ GEF=60 ,•••/ AEM # BEF=120BEF=Z AME :, △ BEF ^A AME备用图一备甲图二解:(3) (i )当点E 在线段AB 上,点M N 在线段AC 上时,如图,实用文档(ii )当点E 在线段AB 上,点6在厶ABC 内时,如备用图一,同上可得:AM= 丁 i ;, C N L ,2x•/ AC=AM+CN MN ••• 3= _ /+%+上—yy=— J %*民 一 4 ( o v x < 1 );2 x2x(iii )当点E 在线段BA 的延长线上时,如备用图二,AM= -------- 二,CN=,2 £ •/ AC=MN+C Z AM • 3=y+Z - ' _ 刃,• y=J 一 彳&张—° ( x > 3);± 2 2x综上所述:y= -£-娄细竺( o v x < 1),或y=^-3,十6豪 -4( x > 1); 2x 2x(4) (i )当AE=1时,△ GMN 是边长为1等边三角形,S MM =_X 1 X 二=丄;(1 分)::(ii )当 AE=1 时,△ GMN1 有一个角为 30° 的 Rt △, ••• x=4,. y= 「一,一丄,NG=FG FN=4X ;- 1 X ・;=;, 2X4 2 222• s =1X22 2 g17. 答: 解(1)解:T PEI CP,.可得:△ y 3 _ Xx" 2(2)解:当△ PCD 的面积是厶AEP 面积的4倍, 则:相似比为2: 1 , •又••• CD=2 AD=3 设 PD=x, AE=y,.・.AF PAEAP^^ PDC ••亠-PD CD• y = — 1 2 卫 ,…y = - r ,0v x v 3;................... .AE AP_1'PD"CD"2,_•/ CD=2 • AP=1, PD=2 • PE= - , PC=2 :■: , • EC= 111. (3 )不存在.作AF 丄PE,交PE 于O, BC 于 F ,连接EFT AF 丄 PE, CP 丄 PE/. AF=CP= , •, PE=::,-.',(3-7~2 •/△ CDP^A POA=£2 23x —6x+4=0,OA=PA PC (3- x)x =l 2△ =6 — 4 X 4 X 3= — 12 x 无解因此,不存在.实用文档y—, •••设 AC=3k, BC=4k, /• AB=5k=5,「. k=1,「. AC=3 BC=4 BC 4| (2)过点E 作EH! BC,垂足为 H.易得△ EHB^A ACB 设 EH=CF=3k BH=4k, BE=5k ; •/ EF// BC ••/ EFD=/ FDC•••/ FDE 玄 C=90°A ^ EFD^^ FDC ・ —F D=EF? CD,即 9k 2+4=2 (4 -4k )化简,得 9k 2+8k - 4=0(负值舍去),•••二_■丨 ';19.解(1)证明:如图2,连接DC答: •••/ ACB=90 , AC=BC A=Z B=45° ,•••点 D 是 AB 中点,BCD 2 ACD=45 , CD=BD ACD=/ B=45°•/ ED ! DF , CD!AB,•••/ EDC 丄 CDF=90 , / CDF+Z FDB=90 , EDC M FDB•••△ CED^A BFD (ASA ) , • DE=DF(2) 解:如图1,作DP ! AC, DQL BC,垂足分别为点 Q, P.•••/ B=Z A , / APD=/ BQD=90 , ADP^A BDQ• DP DQ=AD DB=m•••/ CPD / CQD=90 , / C=90°, •/ QDP=90 , •/ DF 丄 DE, •/ EDF=90 , •/ QDF / PDE•••/ DQF / DPE=90 , DQF^A DPE• DE DF=DP DQ • DE DF=DP DQ=AD DB=m(3) 解:①如备用图1,作EGL AB, FH! AB,垂足分别为点 G H. 在 Rt △ ABC 中,/ C=90° , AC=BC=6 •- AB= ■:,18. 答: E 作EH! BC,垂足为H.易得△ BE=5k(3)过点 设 EH=3k, •••/ HED 丄 HDE=90 / FDC+ZHDE=90EHB^A ACB•••/ EHD 2 C=90°•••△ EHD^A DCF•••/ HED=/FDC • I 方五,当厶DEF 和△ ABC 相似时,有两种情况:1°CD~4,即.解得••-丄,24 K 厲 DE BC 4 综合1°、2 ° , 2° 2,•呼5匸卫 • 即亠CD -3 2 "3 当厶DEF 和△ ABCt 目似时,BE 的长为上或丄 2 g 解得w ,—丄.FD _CD解 解:(1)在 Rt △ ABC 中,/C=90°实用文档20. 答:•/ AD DB=1: 2,:. AD三•:, DB= 「由/ AGE M BHF=90,/ A=Z B=45°可得AG=EG= 一.,BH=FH2 K 2易证△ DG0A FHD :• DG GE匸」「,GD= —_ .,<2 V2----- 資 ----- V2 2rW2②如备用图2,取CE的中点0,作OM L AB于M.可得CE=6- x, A0=-十二,HD=:'7,0M=]:「_±,.AB相切,贝U —2 _ 2 2若以CE为直径的圆与直线解得.•:当八时,以,•: y=8 -2x,CE为直径的圆与直线AB相切.备冒图1 备用图』解解: (1)T在厶ABC中,/ C=90°, AC=6 t述斗,•:BC=8 AB=10,定义域是•: CD=DB=4过点E作EH! CB于H.则可求得EH丄x.54 x '■ x= x (0 V x <5 5-'或5V x w 10).(2)取AE OGL BC于G 连接OD则x10+y32 '(10+x), GD=C- CG=4-I (10-x)4 2-- T •251 2 2两圆外切,则可得*BC1;AE=OD:.( BC+AE =4OD,2 Q 2+——x ]25•: 0D=2:•( 8+10- x) =4[ (10+x)100若两圆内切,得|-;BC--;AEFOD,解得4实用文档•••( BC — AE ) 2=4OD ,.・.(8 - 10+x )2=4[— ( 10+x )100解得x=-二J (舍去),所以两圆内切不存在•所以,线段7(3)由题意知/ BEF M 90°,故可以分两种情况. ①当/ BEF 为锐角时,由已知以 B E 、F 为顶点的三角形与△ BED 相似,又知/ EBF=Z DBE / BEF <Z BED 所以/ BEF=Z BDE过点D 作DM L BA 于M 过E 作EH L BC 于H. 根据等角的余角相等,可证得/ MDE N HDE • EM=EH21.解解:(1)作BHLCD ,垂足为H,则四边形 ABHD 为矩形;答: • BH=DA=4 DH=AB=2在 Rt △ BCH 中,上皿二寻• 6冷讣■=$,(1 分)BC 討E H '+CH~5; 又 CD=CH+DH=5 • S 梯形 ABCI ^ (血+CD) AD =14;2(2)连接AQ由 DQ=PQ 可知△ APQ AP=AD=4 作PE! AB 交AB 的延长线于点 E , (1分)在 Rt △ BPE 中,二工_;二上--口一-二,令 BE=3k PE=4k. 则在Rt △ APE 中, AF ^A W+P E ,2224A /21 - &即 4=(2+3k ) + (4k ),解得:2+—x 2]25BE 的长为二丄3又 EM=M — EB — - x ,5由(1)知:EH 士 x ,「亍冗兀②当/ BEF 为钝角时,同理可求得 x - ,• x=2.•16 =3x=8.「. y=§X 8=坐 5 512或 48 55x ,•所以,△ BED 的面积是实用文档•『'i :■ - ' | :厂-「- -(3)作PF丄CD交CD于点F,由/ AEF=/ EFD=/ APQ=90 , 可得:△ AEP^A PFQaQF _屮芹H• OF EPPF~AE,化简得:QF二一16 卫二"SO+ISX5 50+15X3010•….定义域为(0v x v 5).。
1_例说一个“中点三相似”模型的应用

/_DOF=90。,从而构造“中点三相似”模型求解,心中 有模型在。2 J,解题方法也就自然生成了. 简解:如图7,易得/_DOF=900,从而构造“中点
数学教育,2017(11):47—50. [2] 姜黄飞.心中有模型解法自然来[J].数理化
学习:初中版,2016(7):39—42. [浙江省海盐滨海中学(314300)]
三相似”模型,由模型得筹=A历O=了2,得日F=÷,所 以CF=÷,所以tan/CDF=历CF=老,故选择B.
B
函”:囫。
E c 口E C
图8
图9
・稿・
万方数据
证明:如图5,过c作CF∥DE交BD的延长线于 点F,则[DCF=/CDE=/__ADB,又因为AD平分
/_BAC,所以/BAD=LDAC,又/__ADB=/_ACD,所 以AABD—AADC,AABD=AADC,所以AABD— ADFC,所以AABD—AADC—ADFC,由模型得D 为BG中点,所以E为BC中点.
AABP—AECB,所以AABP一△CBP—AECB,由 模型得B为AE中点,所以BE=AB=4,所以CD=AE
P 曰
+/ACP,又厶4=/CPD,所 以/_BPD=AACP,所以
AACP”ABPD,所以筹:彳
历CP,又P为AB中点,所以AP=
=8,从而CD的长是一个定值,长为8.
图1 例2
如图4,AABC中,AD平分A_BAC,点E在
分析:由/_BPC=£BPA,BC上曰P,又AB上MN,
所以可以构造“中点三相似”模型. 笔者称之为“中点三相似”模型.
二、证明 如图1,因为[BPC=[A
简解:如图3,过c作CE上AB交AB的延长线于点
中点一线三等角模型结论以及证明

中点一线三等角模型结论以及证明1.引言1.1 概述概述部分的内容可以写作:引言是文章中的开篇部分,用于引入我们要讨论的主题,并对整篇文章进行概括和介绍。
本文主要讲述的是中点一线三等角模型的结论以及其证明过程。
中点一线三等角模型是一个几何图形模型,它涉及到三角形的中点、角平分线和三等角关系。
通过研究这一模型,我们可以深入了解三角形内部的特殊性质与关系。
在本文中,我们将首先概述整篇文章的内容和结构。
然后,我们会详细探讨中点一线三等角模型的要点,并展示相关的证明过程。
最后,我们会对整个模型的结论进行总结和概述,以便读者能够更好地理解和应用该模型。
本文的目的是为读者提供清晰的论述和证明过程,使其能够深入理解中点一线三等角模型背后的原理和应用。
同时,通过学习这一模型,读者还可以培养逻辑思维和几何推理的能力,从而在解决实际问题时能够灵活运用相关知识。
接下来,我们将进入正文部分,通过介绍该模型的要点和证明过程,帮助读者逐步理解中点一线三等角模型的内涵和重要性。
1.2文章结构1.2 文章结构本文将按照以下结构进行论述和分析:1. 引言:在引言部分,将对中点一线三等角模型进行概述,并明确本文的目的和意义。
2. 正文:正文部分将包括两个要点的详细阐述:2.1 第一个要点:首先,将介绍中点一线三等角模型的概念和基本性质。
然后,将详细探讨该模型的应用场景和实际意义,并给出相关例证或案例分析。
最后,将进一步讨论与该模型相关的数学原理和运用方法。
2.2 第二个要点:接着,将详细分析中点一线三等角模型的证明过程。
首先,将介绍该模型的基本假设和前提条件。
然后,将给出证明过程的详细步骤和推导过程,通过逻辑推理和数学运算来证明该模型的正确性。
最后,将对证明结果进行验证,并探讨可能的应用和推广方向。
3. 结论:在结论部分,将对中点一线三等角模型的结论进行总结概述,强调该模型的重要性和实用性。
同时,将详细解释并证明该结论的正确性,通过对证明过程的回顾和总结,进一步巩固读者对该模型的理解和认知。
一线三等角相似模型

1、如图,等边△ABC的边长为3
,点D是BC上一点,且BD=1,在
AC上取点E,使∠ADE=60度,AE
长为( c )
A. 3 B. 2
2
3
C.
7 3
D. 3
4
2.在矩形ABCD中,AB=4,BC=5,AF平 分∠DAE,EF⊥AE,
1.5 则CF= ______
5
• ∴BE= 3
【2014德州中考试题】 24.(2)是否存在点P,使得△ACP是以AC为直角边的 直角三角形?若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由.
(2016呼市T9)如图,面积为24的正方形ABCD中,有一
个小正方形EFGH,其中E,F,G分别在AB,BC,FD
上.若BF= 6 ,则小正方形的周长为( ) 2
• (3)当M点运动到什么位置时,Rt△ABM∽Rt△AMN?求此时x的 值.
如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不 与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
(1)求证:△ABP∽△PCM; (2)设BP=x,CM=y.求 y与x的函数解析式,并写出函数的取值范
A型
基本 8型 图形
K型
一线三等角是一个常见的相似模型,指的是有三 个等角的顶点在同一条直线上构成的相似图形, 这个角可以是直角,也可以是锐角或钝角。
三角形基架
K型 矩形基架
梯形基架
毕达哥拉斯证法
赵爽弦图
K字型的一般形式
你能证明吗?
证明: 在ABC中 1 A ACB 180 又 2 DCE ACB 180
围. (3)当△APM为等腰三角形时, 求PB的长.
中考数学解题策略研究之等边相似模型
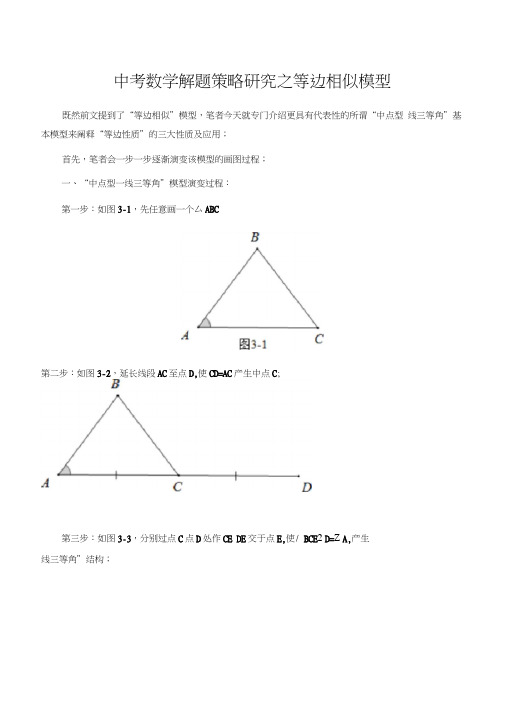
中考数学解题策略研究之等边相似模型既然前文提到了“等边相似”模型,笔者今天就专门介绍更具有代表性的所谓“中点型线三等角”基本模型来阐释“等边性质”的三大性质及应用;首先,笔者会一步一步逐渐演变该模型的画图过程;一、“中点型一线三等角”模型演变过程:第一步:如图3-1,先任意画一个厶ABC第二步:如图3-2,延长线段AC至点D,使CD=AC产生中点C;第三步:如图3-3,分别过点C点D处作CE DE交于点E,使/ BCE2 D=Z A,产生线三等角”结构;图3-3之所以把上面的画图过程展示出来,旨在培养学生的画图意识,很多老师都有感觉学生的画图能力越来越差,计算能力也有所下降,作为老师就更不能畏首畏尾,而应该迎难而上,有意识地去培养学生的画图能力及计算能力,平时训练有素,才能真正形成意识,从而应用娴熟,或许可能跟我们教师平时也忽略了这些能力的培养有直接关联吧!这样通过“三角形的外角模型”去导角,很容易推出/ ECD M B,Z ACB M E,则有△ ABCDCE(注意对应字母的顺序以及对应边与对应角),如图3-4所示;这就是所谓的“中点型一线三等角”相似模型;^3-4中点型一线三等角”模型性质探究:性质1 :“中点型一线三等角”结构中三个三角形两两相似由"相協三角形的对电边成比例烯空=俎•又由'仲点啣DOAC.则空=空富EC DC CE AC 若是此时#iSBB连接起来■狛图3T所示,结合N迥二上扎由“两组对应边成比例聂夹気相等的两个三角形相fcT ■简而言之就是"SAS"梟得△CffisAABG同理舄薄△CEE S A DCE,聞在如图3-5所示的'『中点型一线三著甫模型”中,三个三角形两两刿似,即△CBEsA ABC^A D CE I从上面的证明过程来看.这里中点C的作用,简而言之就星起“换边”之效,同学们可用心体悟辛03-5若此模型仅仅研究到这就停下来,那就太没意思了,这里还有值得我们继续探索的“秘密”,它竟然可以跟三角形的内心或者旁心产生关联,也会跟正方形中著名的“半角模型”产生瓜葛,不得不让人感叹数学的无穷魅力之所在,继续我们的探究之路.性质2: “中点型一线三等角”结构中两条公共边都是相应的角平分线•由性质1 中厶CB0A ABB A DCE可知,/ CBE M CBA1/ CEB M CED 即BC平分/ ABE且EC平分/ DEB即公共边BC及EC分别是相应的角平分线,如图3-6所示.图3-6性质3: “中点型一线三等角”结构中的中点是其所对的三条边所在直线构成的三角形的旁心(即旁切圆的圆心)或内心(即内切圆的圆心),且当“三等角”为锐角时,对应的中点是旁心;当“三等角”是钝角时,对应的中点是内心•情形一:如图3-7所示,当/ BCE2 D=Z A,且为锐角时,延长AB与DE交于点F,则易知厶ADF是以/ F为顶角的等腰三角形;因此“一线三等角”结构,包括“中点型一线三等角”结构,经常会在等腰三角形或等腰梯形等大背景里出现;如图3-8所示,锁定△ BEF由性质1知BC及EC都是其外角平分线;联想到“角平分线上的点到角的两边的距离相等”,采取“见角平分线,作双垂”策略, 如图3-9所示,过点C作三条垂线段,易知CG=CH=CK由CG=C K 结合“角的内部,到角的两边距离相等的点一定在角的平分线上”这个角平分 线判定定理可知:如图3-10所示,连接FC,则FC 也是/ AFD 的平分线;其实FC 是/AFD 的平分线,也可以由等腰厶ADF 及 CA=CD 结合“三线合一”定理得到, 上面的证法反而绕了些,但我们琢磨到这里,竟然发现“中点型一线三等角”模型与如此多重 要的基本图形有关联,还是蛮有趣的,这或许就是探索数学的情怀吧!如图3-11所示,由CG=CH=C 发现中点。
中考数学解题策略研究之等边相似模型
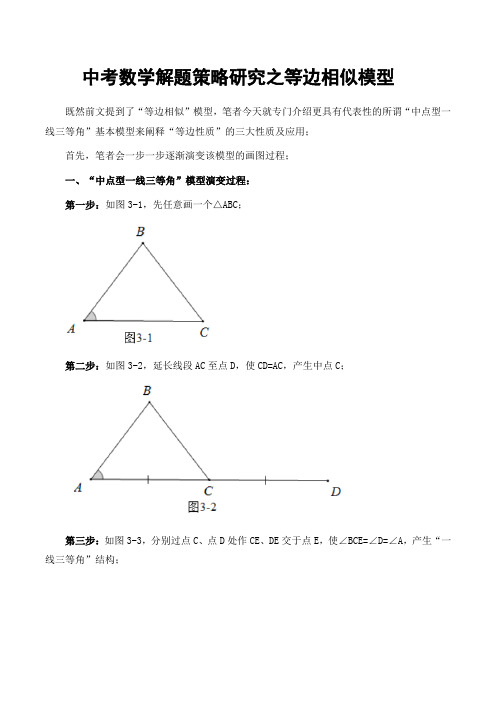
中考数学解题策略研究之等边相似模型既然前文提到了“等边相似”模型,笔者今天就专门介绍更具有代表性的所谓“中点型一线三等角”基本模型来阐释“等边性质”的三大性质及应用;首先,笔者会一步一步逐渐演变该模型的画图过程;一、“中点型一线三等角”模型演变过程:第一步:如图3-1,先任意画一个△ABC;第二步:如图3-2,延长线段AC至点D,使CD=AC,产生中点C;第三步:如图3-3,分别过点C、点D处作CE、DE交于点E,使∠BCE=∠D=∠A,产生“一线三等角”结构;之所以把上面的画图过程展示出来,旨在培养学生的画图意识,很多老师都有感觉学生的画图能力越来越差,计算能力也有所下降,作为老师就更不能畏首畏尾,而应该迎难而上,有意识地去培养学生的画图能力及计算能力,平时训练有素,才能真正形成意识,从而应用娴熟,或许可能跟我们教师平时也忽略了这些能力的培养有直接关联吧!这样通过“三角形的外角模型”去导角,很容易推出∠ECD=∠B,∠ACB=∠E,则有△ABC ∽△DCE(注意对应字母的顺序以及对应边与对应角),如图3-4所示;这就是所谓的“中点型一线三等角”相似模型;二、“中点型一线三等角”模型性质探究:性质1:“中点型一线三等角”结构中三个三角形两两相似.若此模型仅仅研究到这就停下来,那就太没意思了,这里还有值得我们继续探索的“秘密”,它竟然可以跟三角形的内心或者旁心产生关联,也会跟正方形中著名的“半角模型”产生瓜葛,不得不让人感叹数学的无穷魅力之所在,继续我们的探究之路.性质2:“中点型一线三等角”结构中两条公共边都是相应的角平分线.由性质1中△CBE∽△ABC∽△DCE可知,∠CBE=∠CBA且∠CEB=∠CED,即BC平分∠ABE且EC平分∠DEB,即公共边BC及EC分别是相应的角平分线,如图3-6所示.性质3:“中点型一线三等角”结构中的中点是其所对的三条边所在直线构成的三角形的旁心(即旁切圆的圆心)或内心(即内切圆的圆心),且当“三等角”为锐角时,对应的中点是旁心;当“三等角”是钝角时,对应的中点是内心.情形一:如图3-7所示,当∠BCE=∠D=∠A,且为锐角时,延长AB与DE交于点F,则易知△ADF是以∠F为顶角的等腰三角形;因此“一线三等角”结构,包括“中点型一线三等角”结构,经常会在等腰三角形或等腰梯形等大背景里出现;如图3-8所示,锁定△BEF,由性质1知BC及EC都是其外角平分线;联想到“角平分线上的点到角的两边的距离相等”,采取“见角平分线,作双垂”策略,如图3-9所示,过点C作三条垂线段,易知CG=CH=CK;由CG=CK,结合“角的内部,到角的两边距离相等的点一定在角的平分线上”这个角平分线判定定理可知:如图3-10所示,连接FC,则FC也是∠AFD的平分线;其实FC是∠AFD的平分线,也可以由等腰△ADF及CA=CD,结合“三线合一”定理得到,上面的证法反而绕了些,但我们琢磨到这里,竟然发现“中点型一线三等角”模型与如此多重要的基本图形有关联,还是蛮有趣的,这或许就是探索数学的情怀吧!如图3-11所示,由CG=CH=CK发现中点C到△BEF的三边所在的直线的距离相等,以C为圆心,CG为半径作⊙C,则⊙C与△BEF的三边所在的直线相切,可称为△BEF的旁切圆,圆心C称为△BEF的旁心,旁心C到△BEF的三边所在的直线的距离相等;有关三角形旁切圆的研究具体可参见本人作品《三角形内切圆、旁切圆半径的研究》;即对于“中点型一线三等角”结构,当这里的“三等角”为锐角时,这里的中点是其所对三条边所在直线构成的三角形的旁心(即旁切圆的圆心);情形二:如图3-12所示,当∠BCE=∠D=∠A且为直角时,这种特殊结构还可以称之为“一线三直角”,此时若延长AB与DE,根本就不会有交点了;图3-12中的三个直角三角形依然两两相似,公共边BC及EC依然分别是相应的角平分线;“见角平分线,作双垂”,如图3-13所示,过点C作CH⊥BE于点H,由角平分线则会产生两组全等的直角三角形,易知CH=CA=CD,BA=BH,ED=EH,BE=AB+DE等系列结论,甚至以BE 为直径的圆一定与AD相切(学生可自行琢磨,提示:利用d=r,遗憾地是可能用梯形的中位线说理最简单);下面是情形二的特例:如图3-14所示,点E是正方形ABCD边AD的中点,EF⊥BE交CD于点F,很明显这个正方形里出现了一个“中点型一线三直角”结构,不再赘述;图3-15中的相关结论,也是一目了然,不再详述;此时若是将延长EH交CD于点N,如图3-16所示,由BH=BA=BC,结合“HL”易证Rt△BNH≌Rt△BNC,故∠NBC=∠NBH,又由∠EBH=∠EBA易得∠EBN=45°;哇塞,这不就出现大名鼎鼎的正方形中“半角模型”了嘛,如图3-17所示!有关这个模型有数值不清的结论,笔者也在慢慢沉淀,接下来的题3中也会专门讲到这个模型,此处不再赘述;情形三:当∠BCE=∠D=∠A,且为钝角时,如图3-18所示;反向延长线段AB与DE交于点F,则易知△ADF是以∠F为顶角的等腰三角形,如图3-19所示;如图3-20所示,锁定△BEF,由性质1知BC及EC都是其内角平分线;联想到“角平分线上的点到角的两边的距离相等”,采取“见角平分线,作双垂”策略,如图3-21所示,过点C作三条垂线段,易知CG=CH=CK;由CG=CK,结合“角的内部,到角的两边距离相等的点一定在角的平分线上”这个角平分线判定定理可知:如图3-21所示,连接FC,则FC也是∠AFD的平分线,其实FC是∠AFD的平分线,也可以由等腰△ADF及CA=CD,结合“三线合一”定理得到;如图3-21所示,由CG=CH=CK发现中点C到△BEF的三边所在的直线的距离相等,以C为圆心,CG为半径作⊙C,则⊙C与△BEF的三边所在的直线相切,可称为△BEF的内切圆,圆心C称为△BEF的内心,内心C到△BEF的三边所在的直线的距离相等;即对于“中点型一线三等角”结构,当这里的“三等角”为钝角时,这里的中点是其所对三条边所在直线构成的三角形的内心(即内切圆的圆心);情形一的“中点型一线三锐角”与情形三的“中点型一线三钝角”,其实探究思路差不多,唯一的区别就是旁心变成了内心,这就是类比思想,这就是“图形变了,方法未变”的统一性;有关“中点型一线三等角”结构的性质探究,至此就差不多了,在探究的过程中,笔者惊喜地发现这个结构可以演变出蛮多学生熟知的基本图形,这种探究的乐趣传递,才是我主要想表达的东西;其实,笔者本来仅仅想随便构造一个“中点型一线三等角”结构,然后结合于特的“等边相似”模型三性质分析一下即可,但没想到一发不可收,搞了这么多,这就是写作的魅力,越写越有劲,越写越有灵感,建议广大教师们可以行动起来,执起手中的笔,开启你们的写作之路吧,大家一起加油!最后我们结合“中点型一线三锐角”结构,强化于特的“等边相似”三大性质,这也是笔者的初衷啊!为方便起见,将图3-6复制下来,接下来对照此图进行分析;这里的“中点型一线三等角”模型就是典型的“等边相似”模型,所谓“等边”就是中点C提供的两边CA与CD;下面再举一例,谈谈“等边相似”在中考实战中的应用:简析:下面提供一般情况下解反比例函数有关问题的两种常见的通解通法:一是代数设坐标法;二是几何特征面积法;方法一(设坐标暴力计算代数法):一般情况下,反比例函数的考题大多都可以回归定义,利用“设坐标法”进行求解,只不过有的可能计算量偏大而已,但只要“硬着头皮”坚持到底,基本都能搞定,可称之为“代数法”;设坐标时,一般情况下都是设出主动点的坐标,“牵一发而动全身”,紧接着产生“连锁反应”,表示出其他各从动点的坐标,再想办法列方程求解即可;题目中还有一个关键条件QE:DP=4:9没有用,如何利用这个比值呢?QE与DP这两条线段都是“斜线段”,它们之间的比值,我称之为“斜比值”,一般遇到“斜比值”的话,都是通过依托于这两条线段的四个端点构造系列“水平—竖直辅助线”,构造相似,将“斜比值”转化为“直比值”进行处理,是的,这里又采用了“改斜归正”大法,这种斜化直思想的重要性不言而喻,应用极其广泛;如图4-1所示,分别过点D、点E向x轴、y轴作垂线,垂足依次为点F、点G,则Rt△QEG∽Rt△DPF,从而有QE:DP=QG:DF,即QG:DF=4:9;题目中还有一个关键条件QE:DP=4:9没有用,如何利用这个比值呢?QE与DP这两条线段都是“斜线段”,它们之间的比值,我称之为“斜比值”,一般遇到“斜比值”的话,都是通过依托于这两条线段的四个端点构造系列“水平—竖直辅助线”,构造相似,将“斜比值”转化为“直比值”进行处理,是的,这里又采用了“改斜归正”大法,这种斜化直思想的重要性不言而喻,应用极其广泛;如图4-1所示,分别过点D、点E向x轴、y轴作垂线,垂足依次为点F、点G,则Rt△QEG∽Rt△DPF,从而有QE:DP=QG:DF,即QG:DF=4:9;解题后反思:上面的代数计算法,一般情况下都是行得通的,但因其几乎没什么思维量而言,导致其计算量一般会很大,甚至可能会超出学生的计算能力,凡事皆有利有弊,唯有坚持,方能胜利;代数解法是处理反比例函数的一种通解通法,当你无路可走时,就果断去算吧!除了上面“繁琐”的代数暴力计算法外,还有没有比较巧妙机智的“几何构造解法”呢?下面提供本人偶像于特的“等边相似”大法:解题后反思:解法二几乎就是纯几何解法,巧妙借助这里的“等边相似型”,即Rt△QEG ∽Rt△DPF,结合巧设,最后利用特征矩形的面积得到所求,妙不可言;本题中Rt△QEG∽Rt△EDA∽Rt△DPF,这三个三角形两两相似,两头的直角三角形都与中间的直角三角形组成了“等边相似型”;除了可以利用“等边相似型”Rt△QEG∽Rt△DPF求解外,还可以利用另一组“等边相似型”Rt△QEG∽Rt△EDA进行求解,笔者不再详述,有兴趣的同学可自行研究,加深印象;此外,此题还可将代数设坐标法与几何构造“等边相似”三角形法混合在一起使用,不妨称之为“混搭”,具体操作如下;注意:这里最后提及的混合解法,是夹杂代数设坐标法以及几何构造及特征面积法,是同学们最值得思考的地方,只有对每种解法的优缺点熟悉了,才能灵活运用;另外这里的“等边相似”基本图形为寻找解题思路及突破口,甚至口算结果都发挥了重大作用,应引起同学们足够的重视,建议自己再找些更一般意识上的“等边相似”结构,研究琢磨上面的三大性质,将之烂熟于心,了如指掌,才是正道!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一线三等角中点相似模型证明
在初中数学学习中,一线三等角中点相似模型是一个重要的知识点。
它不仅是数学学科中的基础概念,也是日常生活中的实用知识型模型。
一线三等角中点相似模型包含了三个关键要素,即一线、三等角和中
点相似。
其中,一线指在一个三角形中连接两个角的线段,三等角指
三角形中三个角的度数相等,中点相似则是指两个图形中对应线段的
长度相等。
理解这个模型需要我们首先了解一些基础概念。
在三角形中,连接一
个角的两边的线段称为这个角的平分线,平分线的中点称为这个角的
顶点角平分线中点。
而三角形中线则是一条连接两个角的中点的线段。
在一个三角形中,三个顶点连成一条线段即为三角形的一条边。
有了这些基础概念之后,我们可以开始理解一线三等角中点相似模型
的证明过程。
在证明这个模型时,我们需要使用到的基本公式是:在
一个三角形中,连接一个角的两边的长度的比等于另外一个角的两边
的长度的比,那么这个角的平分线上任意一点到两边的距离之比等于
这两边的长度之比。
首先,证明一线三等角中点相似模型的前提是三角形ABC和DEF中,∠A=∠D,∠B=∠E,∠C=∠F。
我们需要构造中线DG与CB、EH与AC的交点K,LK为EF的平行线,并证明LK=AB/BG=AC/CH。
我们先考虑LK=AB/BG的证明。
因为LK∥EF,我们可以通过小学奥数中的对应角相等的定理,得出∠LBL~∠ABC,∠LKF~∠ACB。
由于LK是EF的平行线,所以LK=EF×BL/AC=AB/BG,得证。
接下来,我们需要证明LK=AC/CH。
由于AC是三角形ABC的中线,所以AC=2CH。
而LK=EF×BL/AC,因为∠LBL~∠ABC,所以
BL=AC/AB。
代入LK中得LK=EF/AB×AC/CH=AC/CH,得证。
综上可知,LK=AB/BG=AC/CH,所以三角形ABC与DEF是相似的。
由于ABC与DEF相似,因此它们的相应线段比例相等。
因为CB与EF平行且有相同比例,在DG与EH交于K的情况下,由于ABC与DEF相似,所以三角形ABE与CDG也相似。
因此,AB/CD=BE/DG,而BE=BG。
又因为AC是三角形ABC的中线,DG是三角形DEF的中线,所以AC=2DG。
代入AB/CD=BE/DG中得到
AB/BG=CD/DG=2CA/DG。
即在三角形ABC和DEF中,一线三等角中点相似模型成立,证毕。
总之,一线三等角中点相似模型证明过程依照基础概念和公式推导,考虑到图形间的相似性以及平行线理论,需要使用一定的数学知识点和算式。
在数学学习中,我们需要加强对基础概念的理解,掌握一定的几何知识和推理能力,才能更好地理解和应用这些模型。
