货币时间价值、资产收益率的计算和比较、Excel函数、达成理财目标的计算方法、生涯仿真表
货币时间价值、资产收益率的计算和比较、Excel函数、达成理财目标的计算方法、生涯仿真表

货币时间价值、资产收益率的计算和比较、Excel函数、达成理财目标的计算方法、生涯仿真表一、货币时间价值货币时间价值的基本概念:PV 即现值,也即期间所发生的现金流在期初的价值FV 即终值,也即期间所发生的现金流在期末的价值t 表示终值和现值之间的这段时间r 表示市场利率二、资产收益率的计算和比较(一)、现金流量时间图通常,现金流入为正(如 C2),现金流出为负(如C0 )。
(二)、现值与终值的计算单期情况多期情况1、终值利率因子与现值利率因子(1)单期中的终值单期中终值计算公式为:FV = PV×(1 + r)其中,PV是第0期的现金流,r是利率。
(2)单期中的现值单期中现值的计算公式为:其中, FV是在1时期的现金流,r是利率。
(3)多期中的终值计算多期中的终值公式:FV = PV×(1 + r)tPV是第0期的价值r 是利率t 是投资时间(4)终值利率因子(复利终值系数)一般说来,经过t时期后,今天投入的1元的终值将是FVt =1 *(1 + r)t(1 + r)t 是终值利率因子(FVIF),也称为复利终值系数现值利率因子(复利现值系数)年利率为r时,要计算t时期价值1元的投资的现值,可以用以下公式:PV = 1/(1 + r )t1/(1 + r )t称为现值利率因子(PVIF),也称复利现值系数。
例题1:已知时间、利率和终值,求现值假如你现在21岁,每年收益率10%,要想在65岁时成为百万富翁,今天你要一次性拿出多少钱来投资?确定变量:FV = 1,000,000元 r = 10%t = 65 - 21 = 44 年 PV = ?代入终值算式中并求解现值:1,000,000= PV ´ (1+10%)44PV = 1,000,000/(1+10%) 44 = 15,091元当然我们忽略了税收和其他的复杂部分,但是现在你需要的是筹集15,000元!例题2:已知现值、时间和利率,求终值据研究,美国1802-1997年间普通股票的年均收益率是8.4%。
用EXCEL计算货币的时间价值

RATE利率函数 RATE(N,PMT,
PV,FV,0/1) N为期数 PMT为年金 PV为现值 FV为终值 0代表期末年金 1代表期初年金
练习EXCEL财务函数运用
题目
1
2
3
4
5
6
RATE 10% 10% 0.83% 2%
8%
?
NPER 5
5
60
10
?
10
PMT -5
0
?
2.5
-1
-6
PV
-20
?
0
?
-20
-20
FV
?
30
30
100
100
100
0E/1B 0
0
0
0
0
0
结果
使用EXCEL财务函数进行计算
1.1.1 Excel使用注意事项
按顺序输入Rate、Nper、Pmt、Pv、Fv、Type Rate输入:例如:10%,应输入0.1或10% ,与计算
器输入10 i 不同。 Type:1为期初,0为期末,如为0,可缺省。 输入数字时,如投资、存款、生活费用支出、房贷本
练习:NPER函数与RATE函数
问题1:现有资产20万元,年投资1万元,报酬率8%,几 年后可以累计100万元退休金Nper? 解:NPER(8%,-1,-20,100,0)=16.13年
问题2:现有资产20万元,每年可投资6万元,理财目标 为10年累积资产100万元,实现该理财目标应有的报酬率 Rate是少? 解:RATE(10,-6,-20,100,0)=3.73%
技能分享——巧用EXCEL函数,算清各种收益利率
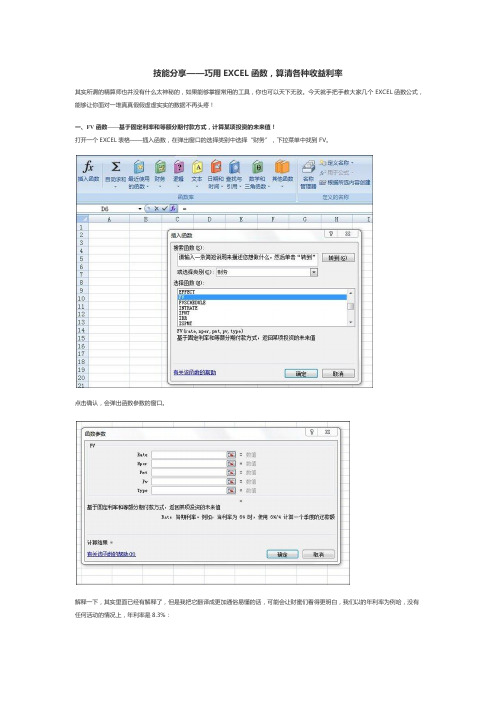
技能分享——巧用EXCEL函数,算清各种收益利率其实所谓的精算师也并没有什么太神秘的,如果能够掌握常用的工具,你也可以天下无敌。
今天就手把手教大家几个EXCEL函数公式,能够让你面对一堆真真假假虚虚实实的数据不再头疼!一、FV函数——基于固定利率和等额分期付款方式,计算某项投资的未来值!打开一个EXCEL表格——插入函数,在弹出窗口的选择类别中选择“财务”,下拉菜单中找到FV。
点击确认,会弹出函数参数的窗口。
解释一下,其实里面已经有解释了,但是我把它翻译成更加通俗易懂的话,可能会让财蜜们看得更明白,我们以的年利率为例哈,没有任何活动的情况上,年利率是8.3%:Rate——各期利率。
这里,年利率为8.3%,如果我们选择正常的12存单法,即每月月初存入一笔2000块,那么这里的Rate值就输入"8.3%/12",但是如果我们选择52周那种做法,为了保持本金和周期一致,我会选择48周,每周存入500元,那么这里的Rate值就输入"8.3%/48"。
Nper——总投资期。
12存单就输入12,代表12个月,每月1期。
48周就输入48,代表48周,每周为1期。
Ptm——各期支出金额。
注意,因为是投入,所以值为负值,12个月是各期支出金额是-2000,48周各期支出金额是-500。
Pv——从该项投资开始计算时已经入账的款项。
因为我们是从现在开始投入,那么之前就是没有,所以填0就好啦。
Type——指定付款时间是期初还是期末,如果是期初选择1,期末的话选择0,我们假定为每月或者是每周投入,那么就是期初,输入1。
如下图,第一种,12个月存入,到期本息为25106.第二种,48周存入,到期本息是25044.所以亲爱的财蜜们,如果不考虑资金灵活性的话,关于52周攒门槛提高的问题,其实也是有另外的解决途径的是不是?上面这个分析可以看出,全部选择月初存12单,最后到期的本息比48周还要多那么一点点呢。
学习情境二 Excel在货币时间价值计算中的应用

学习情境二 Excel 在货币时间价值计算中的应用复习思考题1. 一笔现金流如何计算单利终值?一笔现金流的单利终值是指现在的一笔资金按单利的方法只对最初的本金计算利息,而不对各期产生的利息计算利息,在一定时期之后所得到的本利和。
其计算公式如下:)(n i P n i P P F S S S ⋅+⋅=⋅⋅+=1 式中,S F 为单利终值;P 为现在的一笔资金;S i 为单利年利率;n 为计息期限。
2. 一笔现金流如何计算复利终值?一笔现金流的复利终值是指现在的一笔资金按复利的方法不仅对最初的本金计息,还对各期产生的利息计息,在一定时期以后所得到的本利和。
其计算公式如下:n i P F )1(+⋅= 或 n i F V I F P F ,⋅=式中,F 为复利终值;P 为现在的一笔资金;i 为复利年利率;n 为计息期限;n i FVIF ,=n i )1(+称为复利终值系数,表示现在的1元钱在n 年后的价值。
3. 一笔款项如何计算单利现值?单利现值的计算实质上是单利终值计算的逆运算过程,即在已知一定时期后单利终值的基础上,求其按给定贴现率计算的现在时刻的价值。
其计算公式为:P =F /(1+i ·n )式中,P 表示现值;F 表示未来值;i 为单利年利率;n 为计息期限。
4. 一笔款项如何计算复利现值?若已知现在收入或支出的一笔款项在n 年末的复利终值F 和贴现率i ,则可以计算求出这笔款项现在时刻的价值P 。
其计算公式为:n i F P )1/(+= 或 n i P V I F F P ,⋅=式中,n n i i PVIF )1/(1,+=称为复利现值系数。
5. 如何计算名义年利率与有效年利率?在给定了年利率i 且每年计息m 次的情况下,给定的年利率仅是名义年利率,而按一年的实际年利息与本金之比所计算的年利率称为有效年利率。
有效年利率r 与名义年利率之间的关系为:1-)1(m mi r += 式中,m 为每年计息次数。
用Excel计算货币时间价值

单利和复利的对比
单利是指按照固定的本金计算的利息,而本金所产生的利息不再计算利息。 复利是指在每经过一个计息期后,都要将所生利息加入本金,以计算下期的利息。 如果分别使用单利和复利两种方式来计算收益,随着期数增多,两者的差异越大。
实际利率转为名义利率
实际利率转为名义利率的公式为:
其中I为名义利率,r为实际利率,m为一年内计息的次数。 NOMINAL函数 NOMINAL函数能够基于给定的实际利率和年复利期数,返回名义年利率。该函数语法为: NOMINAL(effect_rate, npery) 第一参数effect_rate为实际利率。 第二参数npery为每年的复利期数。
04 单利现值计算
单利现值计算相当于单利终值计算的逆运算过程,是在已知一定时期后单利终值的基础上,按照指定的利率计算出 的当前的价值。 单利计算的规则为: 现值=未来值/(1+年利率*期限)
05 普通复利现值计算
PV函数 PV函数用于返回普通复利情况下的投资现值,该函数语法为: PV(rate,nper,pmt,[fv],[type]) 第1个参数rate表示利率,本例中为6.25%。 第2个参数nper表示期限,本例中为3年。 第3个参数pmt代表每期等额支付金额,本例为0。 第4个参数fv代表未来值,与FV函数一样,如果希望计算结果为正数,则该参数应该用负数表示。 第5个参数type是可选参数,值为数字 0 或 1,用以指定各期的付款时间是在期初还是期末。本例中省略该参数,表示 期末。
Excel Home
Excel在财务中的应用
06
第六章
用Excel计算货币时间价值
PART 06
01 终值计算
终值是指现在的一笔资金在一定时期之后的本利或未来值。 单利终值是指对一笔资金按单利的方法对最初的本金计算利息,而不对各期产生的利息再次计算利息,在一定 时期内得到的本金利息之和。
Excel公式提升个人理财规划能力

Excel公式提升个人理财规划能力在个人理财规划中,准确的数据分析和计算是至关重要的。
而Excel公式作为一种强大的数据处理工具,可以帮助我们提升个人理财规划能力。
本文将介绍关于如何使用Excel公式来辅助个人理财规划的几个方面内容。
一、收入管理与分析个人理财规划的第一步是对收入进行有效的管理与分析。
我们需要了解自己的收入来源和收入情况,以便更好地进行预算和支出计划。
在Excel中,可以通过SUM函数来计算一段时间内的总收入。
例如,假设我们要计算某年度的总收入,我们可以在一个单元格中输入“=SUM(A1:A12)”,其中A1到A12是分别表示每个月份收入的单元格。
通过使用SUM函数,我们可以方便地得出整个年度的总收入。
此外,我们还可以使用AVERAGE函数来计算平均收入。
比如我们想计算某一时期(比如三个月)的平均月收入,我们可以在一个单元格中输入“=AVERAGE(A1:A3)”,其中A1到A3是分别表示每个月份收入的单元格。
通过使用AVERAGE函数,我们可以得到某一时期的平均收入,帮助我们更加全面地了解自己的收入水平。
二、支出管理与分析除了收入管理外,个人理财规划还需要对支出进行有效的管理与分析。
我们需要清楚地掌握自己的支出情况,并合理分配资金。
在Excel中,我们可以使用SUM函数同样来计算一段时间内总支出。
例如,我们想计算某年度的总支出,我们可以在一个单元格中输入“=SUM(A1:A12)”,其中A1到A12是分别表示每个月份支出的单元格。
通过使用SUM函数,我们可以得知整个年度的总支出情况。
此外,我们还可以使用COUNT函数来计算支出次数。
比如我们想计算某一时期(比如三个月)的支出次数,我们可以在一个单元格中输入“=COUNT(A1:A3)”,其中A1到A3是分别表示每个月份支出的单元格。
通过使用COUNT函数,我们可以了解到某一时期内的支出次数,有助于我们更好地评估自己的消费情况。
三、投资回报率计算投资是个人理财规划中重要的一环。
第三讲EXCEL在资金时间价值计算的应用

第三讲EXCEL在资金时间价值计算的应用在资金管理和财务决策中,时间价值是一个非常重要的概念。
它指的是钱在不同时间点的价值不同,即在不同时间点上的一定金额的现金流具有不同的价值。
EXCEL是一个非常强大和广泛应用的电子表格软件,它可以帮助我们进行资金时间价值的计算和分析,下面将介绍EXCEL在资金时间价值计算中的应用。
首先,我们可以使用EXCEL的函数来计算一笔未来现金流的现值或未来值。
例如,我们可以使用PV函数来计算一笔未来现金流在当前时点的现值。
在计算时,需要输入一些参数,如未来现金流的金额、折现率(即贴现率)和未来现金流的时间点。
EXCEL可以轻松地计算出未来现金流的现值,并帮助我们做出明智的决策。
其次,我们可以使用EXCEL来计算资金的复利增长。
复利是指投资从一定的本金再投资收益后,下一期的投资收益又会继续以同样的利率投资,使得投资额逐渐增加的过程。
在EXCEL中,可以使用FV函数来计算出资金在未来时点的复利增长额。
同样,需要输入一些参数,如本金、利率和投资期限等。
EXCEL的计算结果可以帮助我们了解资金的增长情况,并作出相应的决策。
此外,EXCEL还可以帮助我们进行不同项目的财务比较和评估。
在资金管理和财务决策中,常常需要比较和评估不同项目或决策对资金时间价值的影响。
通过使用EXCEL的函数和工具,我们可以将不同项目的现金流进行系统地比较和评估。
例如,可以使用IRR函数计算不同项目的内部收益率,并对比选择最佳的项目。
此外,EXCEL还提供了一些工具和图表,帮助我们对资金时间价值进行可视化和分析。
例如,可以使用折线图来显示不同时间点上的现金流量或资金增长情况,从而更直观地比较和分析不同项目的现金流。
可以使用柱状图来显示不同项目的现金流差异,进一步帮助我们做出决策。
总之,EXCEL是一个非常强大和灵活的工具,可以帮助我们进行资金时间价值的计算和分析,从而更好地进行资金管理和财务决策。
通过使用EXCEL的函数、工具和图表,我们可以更直观地理解和比较不同项目的现金流和资金增长情况,以做出更明智的决策。
excel怎么计算收益率与年化收益率

excel怎么计算收益率与年化收益率通过比较年化收益率,我们可以比较直观地看出一项投资是否成功。
EXCEL通过简单的操作,就能帮助我们快速方便地自动计算出年化收益率。
excel计算收益率与年化收益率的方法excel计算收益率与年化收益率的步骤:【新建一个工作簿】打开EXCEL后,我们首先新建一个空白的工作簿。
excel计算收益率与年化收益率的步骤:【输入项目】如图,分别输入项目:购入成本,当下价值,累计收益,买入日期,卖出日期,持有时间,收益率年,化收益率。
excel计算收益率与年化收益率的步骤:【建立函数】(1)累计收益=当下价值-购入成本。
所以在D2栏输入【=C2-B2】输入完毕后点击回车。
excel计算收益率与年化收益率的步骤:【建立函数】(2)持有时间=卖出日期-买入日期。
所以在G2栏输入【=DATEDIF(E2,F2,"d")】输入完毕后点击回车。
excel计算收益率与年化收益率的步骤:【建立函数】(3)收益率=累计收益/购入成本。
所以在H2栏输入【=D2/B2】输入完毕后点击回车。
excel计算收益率与年化收益率的步骤:【建立函数】(4)年化收益率=(累计收益/购入成本)/持有时间*365天。
所以在最后一栏输入【=H2/G2*365】输入完毕后点击回车。
excel计算收益率与年化收益率的步骤:【改变单元格格式】分别右键H栏和I栏的最顶端,点击【设置单元格格式】,点击【百分比】,点击【确定】。
excel计算收益率与年化收益率的步骤:【在各栏中输入数值】我在这里随便输入了一些数值做测试,如图。
Excel公式提升个人理财规划效率

Excel公式提升个人理财规划效率在当今社会,个人理财规划已经成为人们生活中的重要一环。
人们希望能够通过科学的方法管理自己的财务,实现财务自由和稳定的收入。
而Excel作为一款强大的电子表格软件,可以帮助我们提升个人理财规划的效率。
本文将介绍如何使用Excel公式来优化个人理财规划。
一、基本的理财公式1.1 计算收入总和在个人理财中,我们需要计算所有的收入总和。
这可以通过Excel的SUM函数实现。
例如,假设你有多个来源的收入,请将这些收入金额输入到单独的单元格,然后使用SUM函数计算总和。
具体公式如下:=SUM(金额1, 金额2, 金额3, ...)1.2 计算支出总和同样地,我们还需要计算所有支出的总和。
同样可以使用SUM函数来实现。
将每个支出金额输入到单独的单元格,然后使用SUM函数计算总和。
具体公式如下:=SUM(金额1, 金额2, 金额3, ...)1.3 计算净收入个人理财规划中,我们需要计算净收入,即收入减去支出。
这可以通过如下公式实现:=总收入 - 总支出1.4 计算月均收入月均收入是指在一个月内的平均收入金额。
可以使用AVERAGE函数来实现。
假设收入数据存储在A1到A30单元格里,具体公式如下:=AVERAGE(A1:A30)二、高级的理财公式2.1 计算复利在投资中,复利是非常重要的概念。
我们可以使用Excel的POWER函数(幂函数)来计算复利。
假设初始投资金额存储在A1单元格,年利率为r,投资年限为n年,具体公式如下:=A1 * POWER(1 + r, n)2.2 计算投资回报率投资回报率可以帮助我们评估投资的效果和盈利能力。
在Excel中,可以使用RATE函数来计算投资回报率。
假设初始投资金额存储在A1单元格,投资期限为n年,结束时的价值存储在A2单元格,具体公式如下:=RATE(n, 0, -A1, A2)2.3 计算财务目标的达成时间有时候,我们会设定一个财务目标,希望在一定时间内达到。
用excle计算货币的时间价值

案例1:计算复利现值。某企业计划在5年后获得一笔资金1000000元,假设年投资报酬率为10%,问现在应该一次性地投入多少资金?
在Excel工作表的单元格中录入:=PV(10%,5,0,-1000000),回车确认,结果自动显示为620921.32元。
案例2:计算普通年金现值。购买一项基金,购买成本为80000元,该基金可以在以后20年内于每月月末回报600元。若要求的最低年回报率为8%,问投资该项基金是否合算?在Excel工作表的单元格中录入:=PV(8%/12,12*20,-600),回车确认,结果自动显示为71732.58元。71732.58元为应该投资金额,如果实际购买成本要80000元,那么投资该项基金是不合算的。
三、终值计算
在Excel中,计算终值的函数是FV,其语法格式为:FV(rate,nper,pmt,[pv],[type])。其中:参数rate为各期利率,参数nper为期数,参数pmt为各期支付的金额。省略pmt参数则不能省略pv参数;参数pv为现值,省略参数pv即假设其值为零,此时不能省略pmt参数。type参数值为1或0,用以指定付款时间是在期初还是在期末,如果省略type则假设值为0,即默认付款时间在期末。
案例15:计算还款期。按揭方式购房,首付后贷款600000元,假设贷款的年利率为7.95%,每月还款能力为5000元,问需多少年能够还清贷款?在Excel工作表的单元格中录入:=NPER(7.95%/12,5000,-600000)/12,回车确认,结果显示为20年。
EXCEL在财务管理中应用 项目二 货币时间价值计算(授课)

√
4年后:10750*(1+2*3.75%)=11556.25(元)
难点释疑:
3. 关于现值与终值
存入1万,年利率10%,问1年后,2年后,3年后的本利和:
0 1 2 3
P0
F1
F2
F3
1万
P0*(1+10%) FV(10 F1*(1+10%) FV(10%,2,,PO) FV(10%,1,,F1)
Excel年金函数介绍:
终值函数FV() 现值函数PV() 年金函数PMT()
年金的本金函数PPMT()
年金的利息函数IPMT() 利率函数RATE()
总期数函数NPER()
见操作演示 附实训任务
授课内容总结
1、资金时间价值的概念、计算 2、单利、复利终值和现值 3、年金终值和现值
难点释疑:
活动1 计算单利的终值和现值
由于货币在不同时点的价值不同,货币时间价值的表现形式则分为现值、
终值两种。
现值(P) 100元
1年期,年利率10% 2年期,年利率10% n年期,年利率10%
终值(F)
100×(1+1×10%)
100×(1+2×10%)
100×(1+n×10%)
单利终值:F=P×(1+i×n)
FV()、PV()
其中普通年金设置期末收付款项,预付年金设置期初收付款项。
工作实例
假设某项目在5年建设期内每年年末从银行借款100万元, 借款年利率为10%, 则该项目竣工时应付本息的总额为: 解析:属于普通年金终值。适用FV函数。
工作实例 假设张先生采用分期付款方式购入商品房一套,每年年 初支付15 000元,分10年付清,假设银行利率为6%,问该 项分期付款相当于一次性支付现金的购买价格是多少? 解析:属于预付年金现值。适用PV函数。
Excel中如何利用RATE函数计算年收益率

Excel中如何利用RATE函数计算年收益率
RATE函数,用来计算收益率,十分适合银行或者保险公司的文员学习。
以下是店铺为您带来的关于Excel中利用RATE函数计算年收益率,希望对您有所帮助。
Excel中利用RATE函数计算年收益率
①我们输入了保险金额、年底返还率、保险年限、银行利率,然后我们需要根据这些数据来计算收益率。
在单元格输入=RATE就能看到相关参数的说明。
②输入参数,可以参看下图的例子。
③按下回车键,计算出结果,收益率为8%,具体的计算过程我就不跟大家说了,不是银行专业人员,你是不懂的。
货币时间价值计算基础EXCEL

第一次课货币时间价值是理财规划过程中经常使用的重要工具,是金融理财的计算基础。
本章以案例的方式讲述货币时间价值的基本知识和计算方法,为以后的理财规划实务提供基础性知识准备。
第一节货币时间价值的本质案例2.1:西格资产理财公司的业务1987年,罗莎赢得了一项总价值超过130万美元的大奖,分20年等额付清。
在以后20年中,每年她都会收到65000美元的分期付款。
1993年,罗莎女士接到了位于佛罗里达州的西格资产理财公司的一位经纪人打来的电话,称该公司愿立即付给她160000美元以获得今后9年其博彩奖支票的一半款项(也就是,现在的160000美元交换未来9年共292500美元[32500美元×9]的分期付款)。
西格资产理财公司是一个奖金经纪公司,其主营业务就是通过跟踪类似罗莎女士这样的博彩大奖的获得者,公司可以获悉许多人会急于将他们获得奖项的部分马上变现成一笔大钱,进而收购这种获得未来现金流的权利再转售给一些机构投资者。
另一方面,西格公司已和汉考克共同生命保险公司谈好将它领取罗莎女士一半奖金的权利以206000美元的价格卖给了汉考克共同生命保险公司。
如果罗莎女士答应公司的报价,公司就能马上赚取46000美元。
最终罗莎女士接受报价,交易达成。
问题:为何西格公司能安排这笔交易并立即获得46000美元的利润呢?要理解本案例,必须了解货币的时间价值。
对于罗莎女士而言,未来九年每年的32500美元相当于当前的160000美元,而对于汉考克共同生命保险公司而言,它愿意以当前放弃206000美元的代价,获得未来9年里每年稳定的32500美元的现金流入。
可见,相同额度的货币,在不同的时间点,其价值量是不相等的。
一、什么是货币时间价值?货币时间价值是指货币经历一定时间的投资和再投资所增加的价值,也称资金的时间价值。
从经济学观点来说:同量货币在不同时间的价值是不相等的,货币持有者假如放弃现在使用此货币的机会,就可以在将来换取按其所放弃时间的长短来计算货币的时间价值,也就是我们常说的今天的一元钱比未来的一元钱更值钱。
EXCEL财务函数在资金时间价值计算中的应用

EXCEL财务函数在资金时间价值计算中的应用在当今信息时代,数据的收集和信息的处理显得尤为重要。
Excel作为一个应用广泛的电子表格软件被大众所熟知。
其强大的数据分析和处理能力,深受广大用户的喜爱。
Excel既能够帮助用户完成多种要求的数据运算汇总,提取及可视化图表的制作等工作,又帮助用户将复杂的数据转换为有用的信息。
目前大多数企业都引进了各种财务软件,这些软件用于处理基本的财务核算工作和常用财务报表的自动编制工作,而Excel可以在除了常规凭证、账表之外的范围内,可以根据企业自身的特点进行多种有针对性的经营分析与决策。
因此与其他财务软件相比,使用Excel既能高效、正确、灵活的处理会计数据,又能节约成本。
本文以PV函数为例,利用PV函数计算现值,对现有投资方案进行分析与判断。
一·PV函数Pv函数是用来计算一段时间内,连续收到、支出一系列固定金额的现值,或一次性收到、偿还额的现值。
Pv函数的格式为:PV(Rate,Nper,Pmt,Fv,Type)。
其中各参数的含义如下。
Rate:各期的利率、贴现率或投资者期望的最低报酬率。
Nper:付款的总期数或项目投资的使用年限。
Pmt:年金,各期支付的固定金额。
Fv:终值,一次性收到或偿还金额。
投资期终了时,本利和或若干期等额收付款后的本利和。
若不填则视为0。
Type:表示收款或付款日的类型——期初或期末收付款。
1表示每期期初收款或付款,不填或输入0则表示每期期末收款或付款。
二、复利情况下投资方案的选择(一)复利复利是指在整个投资期内,不仅本金要计算利息,本金产生的利息也要计算利息,就是俗称的“利滚利”。
(二)复利现值复利现值是指若干期后一定量资金折现到现在的金额。
其计算公式为:P=公式中P——现值,即本金;F——终值,即n年后的本利和;——复利现值系数,记为(P/F,i,n)。
(三)案例一次性投资300 000元,假设年回报率为4%,等待期限为30年,到期一次性返还800 000元,该投资方案是否可行?若到期一次性返还1 000 000元,该投资方案是否可行?依题意,求现在应存入多少钱实际为所求复利的现值,该现值与投资本金比较后判断投资方案是否可行。
excel收益率函数计算逻辑

excel收益率函数计算逻辑
Excel中的收益率函数是一种用来计算投资组合收益率的函数,通常用于计算股票、基金等金融资产的收益率。
这个函数的计算逻辑比较复杂,需要注意以下几个方面:
1. 收益率函数的语法
收益率函数的基本语法为:=XIRR(现金流,日期,[猜测值])其中,现金流是指投资组合每期的现金流,日期是指现金流对应的日期,而猜测值是指投资组合的年化收益率的猜测值。
如果不提供猜测值,则Excel会使用默认值0.1。
2. 收益率函数的输入数据
在使用收益率函数时,需要确保现金流和日期的输入顺序一致,且现金流的第一项必须为负数,表示初始投资的支出。
如果现金流中存在多个现金流值,则必须保证它们之间的间隔不超过180天。
3. 收益率函数的输出结果
收益率函数的输出结果为投资组合的年化收益率,通常用百分数表示。
如果猜测值参数被省略,则输出结果为内部收益率(IRR),即使得投资组合现值等于初始投资支出的年化收益率。
4. 收益率函数的应用场景
收益率函数通常用于计算投资组合的收益率和风险,以便投资者能够更好地评估投资风险和收益。
它也可以用于评估不同投资方案的优劣,以及预测未来收益。
- 1 -。
excel常用财务函数

4.3.2 年金中的本金函数PPMT() PPMT(rate,nper,pv, fv,type) rate——各期利率 nper——付款期总数 pv——现值, fv——终值,缺省为0 Type_0为期末,可缺省;1为期初。
4.3.3 年金中的利息函数IPMT() IPMT(rate,nper,pv, fv,type) rate——各期利率 nper——付款期总数 pv——现值, fv——终值,缺省为0 Type_0为期末,可缺省;1为期初。
A: 每年现金流
A(1+i)n-2
A(1+i)n-1
2020/3/8
5
①普通年金终值
FA=A+A(1+i)+A(1+i)2+…+A(1+i)n-1
=A
(1+i)n-1 i
年金终值系数 F/A,i,n
例:若每年年末存1万元,利率为8%,5年后的本利
和是多少?
FA = 10000
(1+8%)5-1 8%
NPV(rate,value1, value2……, valueN) 要求: value1……, valueN,所属各期间的长度必须相
等,而且支付及收入的时间都发生在期末。
4.3 年金、本金和利息函数
4.3.1年金函数PMT( ) PMT(rate,nper,pv, fv,type) rate——各期利率 nper——付款期总数 pv——现值, fv——终值,缺省为0 Type_0为期末,可缺省;1为期初。
[ ] 1-(1+i)-(n-1)
=A
+1
i
2020/3/8
预付年金现值系数和普通 年金现值系数的关系:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
货币时间价值、资产收益率的计算和比较、Excel函数、达成理财目标的计算方法、生涯仿真表
一、货币时间价值
货币时间价值的基本概念:
PV 即现值,也即期间所发生的现金流在期初的价值
FV 即终值,也即期间所发生的现金流在期末的价值
t 表示终值和现值之间的这段时间
r 表示市场利率
二、资产收益率的计算和比较
(一)、现金流量时间图
通常,现金流入为正(如 C2),现金流出为负(如C0 )。
(二)、现值与终值的计算
单期情况
多期情况
1、终值利率因子与现值利率因子
(1)单期中的终值
单期中终值计算公式为:FV = PV×(1 + r)
其中,PV是第0期的现金流,r是利率。
(2)单期中的现值
单期中现值的计算公式为:
其中, FV是在1时期的现金流,r是利率。
(3)多期中的终值
计算多期中的终值公式:
FV = PV×(1 + r)t
PV是第0期的价值
r 是利率
t 是投资时间
(4)终值利率因子(复利终值系数)
一般说来,经过t时期后,今天投入的1元的终值将是FVt =1 *(1 + r)t
(1 + r)t 是终值利率因子(FVIF),也称为复利终值系数
现值利率因子(复利现值系数)
年利率为r时,要计算t时期价值1元的投资的现值,可以用以下公式:
PV = 1/(1 + r )t
1/(1 + r )t称为现值利率因子(PVIF),也称复利现值系数。
例题1:已知时间、利率和终值,求现值
假如你现在21岁,每年收益率10%,要想在65岁时成为百万富翁,今天你要一次性拿出多少钱来投资?
确定变量:
FV = 1,000,000元 r = 10%
t = 65 - 21 = 44 年 PV = ?
代入终值算式中并求解现值:
1,000,000= PV ´ (1+10%)44
PV = 1,000,000/(1+10%) 44 = 15,091元
当然我们忽略了税收和其他的复杂部分,但是现在你需要的是筹集15,000元!
例题2:已知现值、时间和利率,求终值
据研究,美国1802-1997年间普通股票的年均收益率是8.4%。
假设Tom的祖先在1802年对一个充分分散风险的投资组合进行了1,000美元的投资。
1997年的时候,这个投资的价值是多少?
t = 195 r = 8.4%, FVIF(8.4,195) = 6,771,892.09695
所以该投资的价值应为:6,771,892,096.95美元。
案例3:已知现值、终值和时间,求利率
富兰克林死于1790年。
他在自己的遗嘱中写道,他将分别向波士顿和费城捐赠1,000元。
捐款将于他死后200年赠出。
1990年时,付给费城的捐款已经变成200万元,而给波士顿的已达到450万元。
请问两者的年投资回报率各为多少?
对于费城,有以下算式:
1,000 = 2,000,000/(1 + r )200
(1 + r )200 = 2,000.00
求解r,得到年投资回报率为3.87%。
同理我们可以得到波士顿的年投资回报率为4.3%。
2、72法则
如果年利率为r%, 你的投资将在大约72/r年后翻番。
例如,如果年收益率为6%,你的投资将于约12年后翻番。
为什么要说“大约”?因为如果利率过高,该法则不再适用。
假设r = 72% Þ FVIF(72,1) = 1.7200,即一年后仅为1.72倍,并未达到2倍。
类似,r = 36% Þ FVIF(36,2) = 1.8496,也未达到2倍。
可见,该法则只是一个近似估计。
(三)规则现金流的计算
永续年金
增长型年金
增长型永续年金
期末年金与期初年金
1、年金的分类
(1)年金(普通年金)
在一定期限内,时间间隔相同、不间断、金额相等、方向相同的一系列现金流。
(2)永续年金
在无限期内,时间间隔相同、不间断、金额相等、方向相同的一系列现金流。
(3)增长型年金(等比增长型年金)
在一定期限内,时间间隔相同、不间断、金额不相等但每期增长率相等、方向相同的一系列现金流。
(4)增长型永续年金
在无限期内,时间间隔相同、不间断、金额不相等但每期增长率相等、方向相同的一系列现金流。
(1)年金(Annuity)
(期末)年金现值的公式为:
(期末)年金终值的公式为:
(2)永续年金。
