2019中考数学一轮复习第六章圆第23讲圆的相关概念及性质实用课件
合集下载
中考数学 第一部分 教材知识梳理 第六单元 第23课时 圆的基本性质课件

_2_5__米.
【思路点拨】根据垂径定理和勾股定理,在Rt△AOD
中列方程即可求解.
【解析】在Rt△AOD 中,由垂径定理和勾股定理
可得,AD = 1 AB =20,OD =R -10,
∴R 2-(R
2 –10)
2=202,解得R
=
25(米).
拓展2 (’15广元)如图,
已知⊙O 的直AB⊥CD 于点E ,
(2)性质:三角形的外心到三角形各个15 _顶__点__ 的距离相等.
考点5 垂径定理及其推论
1. 垂径定理: 垂直于弦的直径 16 _平__分__这条弦,并且平分
弦所对的两条弧
【温馨提示】(1)平分弦(不是直径)的直径垂 直弦,并且平分弦所对的弧;(2)圆的两条平行 弦所夹的弧 17 _相__等___.
则下列结论错误的是 (B)
A. CE=DE
B. AE=OE
C. BC=BD
D. △OCE≌△ODE
【解析】∵AB 是⊙O的直径且AB⊥CD ,∴CE =DE ,BC =BD ,选项A、C 均正确.易知△OCE ≌△ODE ,选项D 正确.而由已知不能判定AE =OE ,选项B 不正确,故选B .
失分点16 圆中的计算谨防漏解
第一部分 教材知识梳理
第六单元 圆
第23课时 圆的基本性质
中考考点清单
考点1 圆及其相关概念 考点2 弦、弧与圆心角关系 考点3 圆周角定理及其推论(高频考点) 考点4 圆内接四边形、三角形的 外接圆 考点5 垂径定理及其推论
考点1 圆及其相关概念
1. 圆的基本概念(参考图(1)) (1)圆的定义:平面内到定点距 离等于定长的所有点组成的图形 叫做圆,这个定点叫做①_圆__心__,
【思路点拨】根据垂径定理和勾股定理,在Rt△AOD
中列方程即可求解.
【解析】在Rt△AOD 中,由垂径定理和勾股定理
可得,AD = 1 AB =20,OD =R -10,
∴R 2-(R
2 –10)
2=202,解得R
=
25(米).
拓展2 (’15广元)如图,
已知⊙O 的直AB⊥CD 于点E ,
(2)性质:三角形的外心到三角形各个15 _顶__点__ 的距离相等.
考点5 垂径定理及其推论
1. 垂径定理: 垂直于弦的直径 16 _平__分__这条弦,并且平分
弦所对的两条弧
【温馨提示】(1)平分弦(不是直径)的直径垂 直弦,并且平分弦所对的弧;(2)圆的两条平行 弦所夹的弧 17 _相__等___.
则下列结论错误的是 (B)
A. CE=DE
B. AE=OE
C. BC=BD
D. △OCE≌△ODE
【解析】∵AB 是⊙O的直径且AB⊥CD ,∴CE =DE ,BC =BD ,选项A、C 均正确.易知△OCE ≌△ODE ,选项D 正确.而由已知不能判定AE =OE ,选项B 不正确,故选B .
失分点16 圆中的计算谨防漏解
第一部分 教材知识梳理
第六单元 圆
第23课时 圆的基本性质
中考考点清单
考点1 圆及其相关概念 考点2 弦、弧与圆心角关系 考点3 圆周角定理及其推论(高频考点) 考点4 圆内接四边形、三角形的 外接圆 考点5 垂径定理及其推论
考点1 圆及其相关概念
1. 圆的基本概念(参考图(1)) (1)圆的定义:平面内到定点距 离等于定长的所有点组成的图形 叫做圆,这个定点叫做①_圆__心__,
圆的概念及性质 ppt课件

析
圆中”,而所谓“等圆”,是指圆心不同,但半径相等的
圆,如“面积相等”“周长相等”的两个圆都是等圆.正确
理解这两个概念是避免出现错误的关键.
28.1 圆的概念及性质
方 ■方法:利用圆的定义证明多点共圆问题(数形结合)
法
这类问题一般是给出一个圆和另一个几何图形,判断几
技
巧 何图形上某些点是否在同一个圆上.解决此类问题时,可运
[答案] 解:连接 OC,如图,∵CE=AO,OA=OC,
重
难
题 ∴OC=EC,∴ ∠E = ∠1,∴∠2 =∠E+∠1 =2∠E,
型 ∵OC=OD,∴∠D=∠2=2∠E,∵∠BOD=∠E+∠D,
突
破 ∴∠E+2∠E=75°,∴∠E=25°.
28.1 圆的概念及性质
变式衍生 如图,OA 是⊙O 的半径,B 为 OA 上一点
重
难
题 (且不与点 O,A 重合),过点 B 作 OA 的垂线交⊙O 于
型 点 C.以 OB,BC 为边作矩形 OBCD,连接 BD.若 BD=10
突
破 ,BC=8,则 AB 的长为 ______.
4
28.1 圆的概念及性质
易 ■判断“等弧”忽略在“在同圆或等圆中”
错
例 下列说法错误的是 (
)
易
混
读
续表
优弧
大于半圆的弧(用三个点表示,如图中的
ABC,读作“弧 ABC”)叫做优弧
弧
劣弧
图示
小于半圆的弧(如图中的AC,读作“弧
AC”)叫做劣弧
28.1 圆的概念及性质
考
点
清
单
解
读
续表
能够完全重合的两个圆叫做等圆
圆中”,而所谓“等圆”,是指圆心不同,但半径相等的
圆,如“面积相等”“周长相等”的两个圆都是等圆.正确
理解这两个概念是避免出现错误的关键.
28.1 圆的概念及性质
方 ■方法:利用圆的定义证明多点共圆问题(数形结合)
法
这类问题一般是给出一个圆和另一个几何图形,判断几
技
巧 何图形上某些点是否在同一个圆上.解决此类问题时,可运
[答案] 解:连接 OC,如图,∵CE=AO,OA=OC,
重
难
题 ∴OC=EC,∴ ∠E = ∠1,∴∠2 =∠E+∠1 =2∠E,
型 ∵OC=OD,∴∠D=∠2=2∠E,∵∠BOD=∠E+∠D,
突
破 ∴∠E+2∠E=75°,∴∠E=25°.
28.1 圆的概念及性质
变式衍生 如图,OA 是⊙O 的半径,B 为 OA 上一点
重
难
题 (且不与点 O,A 重合),过点 B 作 OA 的垂线交⊙O 于
型 点 C.以 OB,BC 为边作矩形 OBCD,连接 BD.若 BD=10
突
破 ,BC=8,则 AB 的长为 ______.
4
28.1 圆的概念及性质
易 ■判断“等弧”忽略在“在同圆或等圆中”
错
例 下列说法错误的是 (
)
易
混
读
续表
优弧
大于半圆的弧(用三个点表示,如图中的
ABC,读作“弧 ABC”)叫做优弧
弧
劣弧
图示
小于半圆的弧(如图中的AC,读作“弧
AC”)叫做劣弧
28.1 圆的概念及性质
考
点
清
单
解
读
续表
能够完全重合的两个圆叫做等圆
圆的基本概念和性质PPT课件

第14页/共19页
圆的相关概念
1、弧:圆上任意两点间的部分叫做圆弧,简称弧.
AB”. 以A,B两点为端点的弧.记作 A⌒B 读作“弧
2、弦:连接圆上任意两点间的线段叫做弦(如弦AB).
3、直径:经过圆心的弦叫做直径(如直径AC).
4、半圆:直径将圆分成两部分,每一部分都叫做半圆(如
弧 ABC).
B
定义二:圆是到定点的距离等于定长的点的集合。
2、点与圆的位置关系:
设⊙O的半径为r,则点P与⊙O的位置关系有: (1)点P在⊙O上 OP=r
(2)点P在⊙O内 (3)点P在⊙O外
OP<r OP>r
3、证明几个点在同一个圆上的方法。
要证明几个点在同一个圆上,只要证明这几个点 与一个定点的距离相等。
第17页/共19页
1:在以AB=5cm为直径的圆上到直线AB的距离为2.5cm 的点有 ( C ) A.无数个 B.1个 C.2个 D.4个
2:圆的半径是5cm,圆心的坐标是(0,0),点P 的坐标为(4,2),点P与⊙O的位置关系是(A )
A.点P在⊙O内 C.点P在⊙O外
B.点P在⊙O上 D.点P在⊙O上或⊙O外
(分别以点A、B为圆心,2厘米长为
半径的⊙A的内部与⊙ B的内部的公共
AA
BB
部分,即图中阴影部分,不包括阴影的
边界)
第12页/共19页
设AB=3cm,作图说明满足下列要求的图形:
(5)到点A的距离小于2cm,且到点B的距离大于2 cm的所有点组成的图形.
(分别以点A、B为圆心分,即图中阴影部分,不包括阴影的
边界)
A
B
第13页/共19页
如图菱形ABCD的对角线AC和BD相交于点O,E、 F、G、H分别是边AB、BC、CD、AD的中点,求证: E、F、G、H在同一个圆上。
圆的相关概念
1、弧:圆上任意两点间的部分叫做圆弧,简称弧.
AB”. 以A,B两点为端点的弧.记作 A⌒B 读作“弧
2、弦:连接圆上任意两点间的线段叫做弦(如弦AB).
3、直径:经过圆心的弦叫做直径(如直径AC).
4、半圆:直径将圆分成两部分,每一部分都叫做半圆(如
弧 ABC).
B
定义二:圆是到定点的距离等于定长的点的集合。
2、点与圆的位置关系:
设⊙O的半径为r,则点P与⊙O的位置关系有: (1)点P在⊙O上 OP=r
(2)点P在⊙O内 (3)点P在⊙O外
OP<r OP>r
3、证明几个点在同一个圆上的方法。
要证明几个点在同一个圆上,只要证明这几个点 与一个定点的距离相等。
第17页/共19页
1:在以AB=5cm为直径的圆上到直线AB的距离为2.5cm 的点有 ( C ) A.无数个 B.1个 C.2个 D.4个
2:圆的半径是5cm,圆心的坐标是(0,0),点P 的坐标为(4,2),点P与⊙O的位置关系是(A )
A.点P在⊙O内 C.点P在⊙O外
B.点P在⊙O上 D.点P在⊙O上或⊙O外
(分别以点A、B为圆心,2厘米长为
半径的⊙A的内部与⊙ B的内部的公共
AA
BB
部分,即图中阴影部分,不包括阴影的
边界)
第12页/共19页
设AB=3cm,作图说明满足下列要求的图形:
(5)到点A的距离小于2cm,且到点B的距离大于2 cm的所有点组成的图形.
(分别以点A、B为圆心分,即图中阴影部分,不包括阴影的
边界)
A
B
第13页/共19页
如图菱形ABCD的对角线AC和BD相交于点O,E、 F、G、H分别是边AB、BC、CD、AD的中点,求证: E、F、G、H在同一个圆上。
圆的有关概念及性质复习课件

可推出
①∠AOB=∠A′O′B′
⌒⌒
②AB=A′B′ ④ OD=O′D′
4、圆周角定理及推论
D
C
C
B
E
●O A
●O
BA
●O
B
A
C
定理:一条弧所对的圆周角等于这弧所对的
圆心角的一半.
推论: 在同圆或等圆中,同弧或等弧所对的圆 周角相等.
90°的圆周角所对的弦是 直径 .
直径所对的圆周角是 直角 .
三、【基本能力练习】
B. O.
.
C
B
.
O C
三角形的外心就是三角形各边垂直平分线的交点. 三角形的内心就是三角形各角平分线的交点.
二. 圆的基本性质
圆的对称性: (1)圆是轴对称图形,经过圆心的每一条直 线都是它的对称轴.圆有无数条对称轴. (2)圆是中心对称图形,并且绕圆心旋转 任何一个角度都能与自身重合,即圆具 有旋转不变性.
.
1、垂径定理
垂径定理 : 垂直于弦的直径平分弦,并且
平分这条弦所对的两条弧. C
A
B
M└
若 ① CD是直径
●O
② CD⊥AB
可推得
③AM=BM,
④A⌒C=B⌒C, ⑤A⌒D=B⌒D.
D
重视:模型“垂径定理直角三角形”
2、垂径定理的逆定理
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
∠BOD=100°, 则∠DAB的度数为( ) A.50°B.80° C.100°D.130°
五、【强化训练 】
5.如图,四边形ABCD为⊙O的内接四边形,点E在 CD的延长线上,
如果∠BOD=120°,那么∠BCE等于( )
2019届中考数学复习第六章圆6.1圆的性质课件

【提分必练】
1.如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC 的度数是( D )
A.30°
第1题图 B.45°
C.55°
D.60°
陕西考点解读
考点2 垂径定理及其推论
1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。 2.垂径定理的推论 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
【特别提示】
(1)一条直线如果具有:a.经过圆心,b.垂直于弦,c.平分弦(被平分的弦不是直径),d. 平分弦所对的优弧,e.平分弦所对的劣弧,以上这五条中的任意两条,则具备其余三条; (2)在同圆或等圆中,两条平行弦所夹的弧相等。
【提分必练】
2.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连 接CO,AD,∠BAD=20°,则下列说法正确的是( D )
A.AD=2OB C.∠OCE=40°
B.CE=EO D.∠BOC=2∠BAD
第2题图
陕西考点解读
考点3 弦、弧、弦心距、圆心角的关系定理及推论
(1)弦、弧、弦心距、圆心角的关系定理:在同圆或等圆中,相等的圆心角所对的 弧相等,所对的弦相等,所对的弦心距相等。 (2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两条弦心距中有 一组量相等,那么它们所对应的其余各组量都分别相等。
【特别提示】
结合图形理解定理中“所对的”一词的含义,如一条弦对应着两条弧(一条优弧,一 条劣弧),所对的弧相等是指优弧对应相等或劣弧对应相等。
【特别提示】
3.如图,在⊙O中,AB=AC,∠AOB=40°,则∠ADC的
1.如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC 的度数是( D )
A.30°
第1题图 B.45°
C.55°
D.60°
陕西考点解读
考点2 垂径定理及其推论
1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。 2.垂径定理的推论 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
【特别提示】
(1)一条直线如果具有:a.经过圆心,b.垂直于弦,c.平分弦(被平分的弦不是直径),d. 平分弦所对的优弧,e.平分弦所对的劣弧,以上这五条中的任意两条,则具备其余三条; (2)在同圆或等圆中,两条平行弦所夹的弧相等。
【提分必练】
2.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连 接CO,AD,∠BAD=20°,则下列说法正确的是( D )
A.AD=2OB C.∠OCE=40°
B.CE=EO D.∠BOC=2∠BAD
第2题图
陕西考点解读
考点3 弦、弧、弦心距、圆心角的关系定理及推论
(1)弦、弧、弦心距、圆心角的关系定理:在同圆或等圆中,相等的圆心角所对的 弧相等,所对的弦相等,所对的弦心距相等。 (2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两条弦心距中有 一组量相等,那么它们所对应的其余各组量都分别相等。
【特别提示】
结合图形理解定理中“所对的”一词的含义,如一条弦对应着两条弧(一条优弧,一 条劣弧),所对的弧相等是指优弧对应相等或劣弧对应相等。
【特别提示】
3.如图,在⊙O中,AB=AC,∠AOB=40°,则∠ADC的
初三数学一轮复习课件 圆的基本概念和性质

C O A P D B
H
训练慧
1 请完成随堂练习的必做题, 并填写座位表. 2 再完成选做题. (比比谁更棒!)
A
F
B C
A
F E O ·
B D
O ·
C
D
E
两平行弦在
两平行弦在
圆心两旁
圆心同旁
注意圆的对称性
深思促
我巩固了哪些知识 我还有哪些困惑 我还有哪些方面需要改进 同学中值得我学习的地方 自评得 ____分 (满分100分)
C O
A
B
A C
Eபைடு நூலகம்
B
O
D
垂径定理:
垂直于弦的直径平分这条弦以及 弦所对的两条弧. C
∵CD是直径, CD⊥AB
⌒ ⌒ ⌒ ⌒ ∴AP=BP, AD=BD, AC=BC
A D
O P
B
(课本43页第8题)如图,⊙O的直径 ⌒ AB=4,半径OC⊥AB,点D在BC上, DE⊥OC,DF⊥AB,垂足分别为E、 F .求EF的长.
中考一轮复习课
东台市三仓镇中学 郭敏
揭题明
一 学习目标:
1.梳理并理解圆的有关概念与性质, 能熟练运用解决问题. 2.通过互学、精讲、训练等数学活 动,感受小组互助互学的乐趣,培 养合作交流的意识.
展示互
1. 将学案上的课前练习在小组 内交流. 2. 组长将仍有疑问的题号或 想要展示的题号写到黑板上.
连接半径,是圆中常用的辅助线
例1 (课本42页 习题第4题) 如图,BD、
CE是△ABC的高,M是BC的中点.点B、 C、D、E是否在以点M为圆心的同一圆 上?为什么?
变式题1 ∠BDC在BC下方时,点B、C、
H
训练慧
1 请完成随堂练习的必做题, 并填写座位表. 2 再完成选做题. (比比谁更棒!)
A
F
B C
A
F E O ·
B D
O ·
C
D
E
两平行弦在
两平行弦在
圆心两旁
圆心同旁
注意圆的对称性
深思促
我巩固了哪些知识 我还有哪些困惑 我还有哪些方面需要改进 同学中值得我学习的地方 自评得 ____分 (满分100分)
C O
A
B
A C
Eபைடு நூலகம்
B
O
D
垂径定理:
垂直于弦的直径平分这条弦以及 弦所对的两条弧. C
∵CD是直径, CD⊥AB
⌒ ⌒ ⌒ ⌒ ∴AP=BP, AD=BD, AC=BC
A D
O P
B
(课本43页第8题)如图,⊙O的直径 ⌒ AB=4,半径OC⊥AB,点D在BC上, DE⊥OC,DF⊥AB,垂足分别为E、 F .求EF的长.
中考一轮复习课
东台市三仓镇中学 郭敏
揭题明
一 学习目标:
1.梳理并理解圆的有关概念与性质, 能熟练运用解决问题. 2.通过互学、精讲、训练等数学活 动,感受小组互助互学的乐趣,培 养合作交流的意识.
展示互
1. 将学案上的课前练习在小组 内交流. 2. 组长将仍有疑问的题号或 想要展示的题号写到黑板上.
连接半径,是圆中常用的辅助线
例1 (课本42页 习题第4题) 如图,BD、
CE是△ABC的高,M是BC的中点.点B、 C、D、E是否在以点M为圆心的同一圆 上?为什么?
变式题1 ∠BDC在BC下方时,点B、C、
2019中考数学一轮复习教材同步复习第六章圆第23讲圆的相关概念及性质实用课件
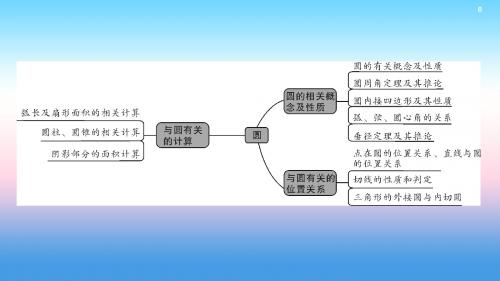
未给出两条平行弦的位置,而要求圆中两条平行弦间的距离时,就要分情况讨论,
再利用垂径定理进行计算,图形如下:
12
3.垂径定理与推论的延伸 根据圆的对称轴,如图所示,有以下五条结论:①AC =BC ;②AD =BD ; ③AE=BE;④AB⊥CD;⑤CD 是直径.只要满足其中两个,另外三个结论一定成 立,即知二推三.
9
知识点四 1.定理
弧、弦、圆心角的关系
在同圆或等圆中,相等的圆心角所对的弧①________ 相等 ,所对的弦也②________. 相等 2.推论
相等 (1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角③__________ , 所对的弦也④__________. 相等
(2) 在同圆 或等圆 中 , 如果 两 条弦 ⑤ __________ 相等 , 那么它 们 所对的 圆 心角 ⑥ __________ ,所对的弧也相等. 相等
内容
直径 __________
表示 形式
如图,(1)∵BD =BD ,∴∠1 如图,(1)∵AB 是⊙O 的直径,∴∠C=
∠2 =⑥__________ ; 90° ; ⑦__________
︵
︵
(2)∵DE =BD ,∴∠2=∠3
︵
︵
(2)∵∠C=90° ,∴AB 是⊙O 的直径
7
推论 1
推论 2
解题思路.另外,在圆中求线段长,三角形相似也是常用的方法.
17
1.(2018· 枣庄)如图,AB 是⊙O 的直径,弦 CD 交 AB 于点 P,AP=2,BP=6, ∠APC=30° ,则 CD 的长为( C ) A. 15 C.2 15 B. 2 5 D.8
18
重难点2 例2
圆的有关概念及性质 中考数学一轮复习 教学PPT课件

2.圆上任意两点间的部分叫做弧;小于半圆的 弧叫劣弧;大于半圆的弧叫优弧.
3.连接圆上任意两点的线段叫做弦;经过圆心 的弦叫做直径;直径是圆内最长的弦;直径等于半径 的2倍.
4.圆的对称性 (1)圆是轴对称图形,经过圆心的每一条直线都是 它的对称轴. (2)圆是以圆心为对称中心的中心对称图形. (3)圆绕圆心旋转任意角度,都能和原来的图形重 合,这就是圆的旋转不变性.
本题考查了圆心角弧弦的关系等边三角形的判定与性质以及菱形的判定解题的关键是根据圆的性质得出特殊三角形等边三角形和直角三角形再根据其性质进行求解
圆的有关概念及性质
考点一 圆的有关概念及性质 1.圆的概念有两种方式 (1)在一个平面内,线段OA绕它固定的一个端点O 旋转一周,另一个端点A所形成的图形叫做圆.固定 的端点O叫做圆心,线段OA叫做半径. (2)圆是到定点的距离等于定长的点的集合.
答案:3 3
5.在直径为52 cm的圆柱形油槽内装入一些油 后,截面如图所示,如果油的最大深度为16 cm,那 么油面宽度AB是 cm.
解析:如图,连接OB,过点O作OD⊥AB于点 D,并延长交⊙O于点C,
则
AD
=
BD
=
1 2
AB.
根
据
题
意
可
知
OB= OC=
26 cm,CD=16 cm,∴OD=10 cm.在 Rt△BOD 中,
BD= OB2-OD2= 262-102=24(cm),∴AB=2BD
=48 (cm).
答案:48
6.如图,⊙O是△ABC的外接圆,AB是⊙O的直 径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC; (2)当∠ODB=30°时,求证:BC=OD.
【数学课件】2019中考数学一轮复习第23讲圆的相关概念及性质课件
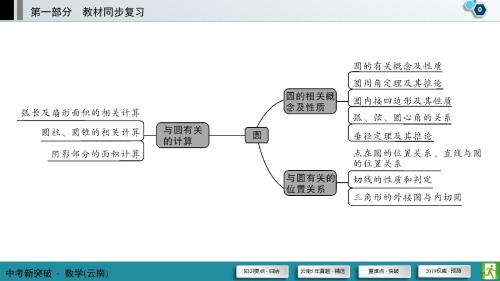
直径
长 圆心 经过②__________ 的弦叫做直径;直径是圆内最③__________
半径 的弦,直径等于④__________ 的2倍
中考新突破 · 数学(云南)
知识要点 · 归纳
云南5 年真题 · 精选
重难点 · 突破
2019权威 · 预测
第一部分 教材同步复习
2
弧定义 弧 劣弧 优弧 等弧
中考新突破 · 数学(云南)
知识要点 · 归纳
云南5 年真题 · 精选
重难点 · 突破
2019权威 · 预测
第一部分 教材同步复习
7
推论 1
推论 2
图形
辅助线作法
有直径时, 连接过直径端点的弦, 构造直角三角形, 构造同弧所对的圆周角
中考新突破 · 数学(云南)
知识要点 · 归纳
云南5 年真题 · 精选
圆上任意两点间的部分叫做弧.弧有优弧、半 圆、劣弧之分 小于半圆的弧叫劣弧,如AC ,BC 大于半圆的弧叫优弧,如ABC ,ACB 在同圆或等圆中,能够互相重合的弧叫做等弧
︵
︵
︵
︵
圆心角 顶点在圆心且两边都和圆相交的角叫做圆心角,如∠AOB 圆周角 顶点在圆上且两边都和圆相交的角叫做圆周角,如∠ACB 等圆 能够重合的两个圆叫做等圆 同心圆 圆心相同的圆叫做同心圆
1 (∠ACB= α) 2
1 (∠ACB=180° - α) 2
中考新突破 · 数学(云南)
知识要点 · 归纳
云南5 年真题 · 精选
重难点 · 突破
2019权威 · 预测
第一部分 教材同步复习
6
2.推论
推论 1 同弧或等弧所对的圆周角③
相等 __________
中考数学总复习 第一部分 考点全解 第六章 圆 第23讲 与圆有关的计算课件

12/10/2021
11.(2018·信阳一模)如图,在▱ABCD 中,AD=2,AB=4,∠A=30°,以点 A 为圆心,AD 的长为半径画弧交 AB 于点 E,连接 CE,则图中阴影部分的面积是 ___3_-__π3___ (结果保留 π).
12/10/2021
12.(2018·新乡一模)如图所示,半圆 O 的直径 AB=4,以点 B 为圆心,2 3为半 径作弧,交半圆 O 于点 C,交直径 AB 于点 D,则图中阴影部分的面积是___3_-__π3___.
12/10/2021
3.正多边形都是轴对称图形.一个正 n 边形共有____n___条对称轴,每条对称轴 都通过正 n 边形的___中__心____;边数为___偶__数__的正多边形还是中心对称图形,它的对 称中心是正多边形的____中__心___.
12/10/2021
)
3.(2018·河南 14 题)如图,在△ABC 中,∠ACB=90°,AC=BC=2,将△ABC
12/10/2021
类型三 阴影部分面积的计算 (2018·安顺)如图,C 为半圆内一点,点 O 为圆心,直径 AB 的长为 2 cm,
∠BOC=60°,∠BCO=90°,将△BOC 绕圆心 O 逆时针旋转至△B′OC′,点 C′在 OA 上,则边 BC 扫过的区域(图中阴影部分)的面积为________ cm2.(结果保留 π)
12/10/2021
3.弓形的面积 (1)由弦及其所对的弧组成的图形叫做弓形. (2)弓形面积可以在计算扇形面积和三角形面积的基础上求得.如果弓形的弧是劣 弧,则弓形面积等于扇形面积__减__去_____三角形面积;若弓形的弧是优弧,则弓形面 积等于扇形面积___加__上____三角形面积.
11.(2018·信阳一模)如图,在▱ABCD 中,AD=2,AB=4,∠A=30°,以点 A 为圆心,AD 的长为半径画弧交 AB 于点 E,连接 CE,则图中阴影部分的面积是 ___3_-__π3___ (结果保留 π).
12/10/2021
12.(2018·新乡一模)如图所示,半圆 O 的直径 AB=4,以点 B 为圆心,2 3为半 径作弧,交半圆 O 于点 C,交直径 AB 于点 D,则图中阴影部分的面积是___3_-__π3___.
12/10/2021
3.正多边形都是轴对称图形.一个正 n 边形共有____n___条对称轴,每条对称轴 都通过正 n 边形的___中__心____;边数为___偶__数__的正多边形还是中心对称图形,它的对 称中心是正多边形的____中__心___.
12/10/2021
)
3.(2018·河南 14 题)如图,在△ABC 中,∠ACB=90°,AC=BC=2,将△ABC
12/10/2021
类型三 阴影部分面积的计算 (2018·安顺)如图,C 为半圆内一点,点 O 为圆心,直径 AB 的长为 2 cm,
∠BOC=60°,∠BCO=90°,将△BOC 绕圆心 O 逆时针旋转至△B′OC′,点 C′在 OA 上,则边 BC 扫过的区域(图中阴影部分)的面积为________ cm2.(结果保留 π)
12/10/2021
3.弓形的面积 (1)由弦及其所对的弧组成的图形叫做弓形. (2)弓形面积可以在计算扇形面积和三角形面积的基础上求得.如果弓形的弧是劣 弧,则弓形面积等于扇形面积__减__去_____三角形面积;若弓形的弧是优弧,则弓形面 积等于扇形面积___加__上____三角形面积.
中考数学总复习第一部分基础知识复习圆圆的有关概念及性质PPT

★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★热点分类解析 ★热点分类解析 ★热点分类解析 ★知识要点导航 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★知识要点导航 ★热点分类解析
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识点5 ★知识点6
★知识点5 ★知识点6 ★知识点5 ★知识点6
★知识点5 ★知识点6 ★知识点5 ★知识点6
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
2019届百色市中考《第23课时:圆的有关概念及性质》复习课件

百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
ห้องสมุดไป่ตู้
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
百色中考命题规律与预测
百色中考考题感知与试做
核心考点解读
典题精讲精练
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 ∴CE= CD=4 cm. 2 在 Rt△OCE 中,∵OC=5 cm,CE=4 cm, ∴OE= OC2-CE2=3 cm, ∴AE=AO+OE=5+3=8 cm.
16
解题技巧
(1)利用垂径定理及其推论进行计算时,常涉及弦长 a,弦心距 d,半径 r 及弓形 a2 高 h(弦所对的弧的中点到弦中点的距离), 如图所示, 它们之间的关系是 r =d +( ) , 2
11
知识点五 1.定理
垂径定理及其推论
垂直于弦的直径①__________ 平分 弦,并且②__________ 平分 弦所对的两条弧. 2.推论
平分弦 ( 不是直径 ) 的直径③ __________ 于弦,并且④ __________ 垂直 平分 弦所对的两条
弧.
12
【易错警示】
由于圆内两条平行弦可以在圆心的同侧或异侧,故若题干中并
内容
直径 __________
表示 形式
如图,(1)∵BD =BD ,∴∠1 如图,(1)∵AB 是⊙O 的直径,∴∠C=
∠2 =⑥__________ ; 90° ; ⑦__________
︵
︵
(2)∵DE =BD ,∴∠2=∠3
︵
︵
(2)∵∠C=90° ,∴AB 是⊙O 的直径
8
推论 1
推论 2
未给出两条平行弦的位置,而要求圆中两条平行弦间的距离时,就要分情况讨论,
再利用垂径定理进行计算,图形如下:
13
3.垂径定理与推论的延伸 根据圆的对称轴,如图所示,有以下五条结论:①AC =BC ;②AD =BD ; ③AE=BE;④AB⊥CD;⑤CD 是直径.只要满足其中两个,另外三个结论一定成 立,即知二推三.
4
2.圆的有关性质 直径 所在的直线都是圆的对 (1)轴对称性:圆是轴对称图形,任何一条⑤__________
称轴.
圆心 (2)中心对称性:圆是中心对称图形,对称中心是⑥__________.
任意 (3)圆具有旋转不变性,即圆绕着它的圆心旋转⑦__________ 角度,都能与原来
的图形重合.
5
重点
(2018· 杭州 ) 如图, AB 是⊙ O 的直径,点 C 是半径 OA 的中点,过点 C 作
30° DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连接AF,则∠DFA=__________.
【解答】
∵点 C 是半径 OA 的中点,
10
知识点四 1.定理
弧、弦、圆心角的关系
在同圆或等圆中,相等的圆心角所对的弧①________ 相等 ,所对的弦也②________. 相等 2.推论
相等 (1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角③__________ , 所对的弦也④__________. 相等
(2) 在同圆 或等圆 中 , 如果 两 条弦 ⑤ __________ 相等 , 那么它 们 所对的 圆 一段弦对应的圆周角的度数时,就要分情况讨论,图形如下:
1 (∠ACB= α) 2
1 (∠ACB=180° - α) 2
7
2.推论
推论 1 同弧或等弧所对的圆周角③
相等 __________
推论 2 半圆(或直径)所对的圆周角是④
直角 __________,90° 的圆周角所对的弦是⑤
2 2
r=d+h;
17
(2)运用垂径定理解题时应注意: ①两条辅助线:过圆心作弦的垂线;连接圆心和弦的一端 ( 即半径 ) ,这样把半 径、弦心距、弦的一半构建在一个直角三角形中,运用勾股定理或锐角三角函数求
解;
②方程思想:在直接运用垂径定理求线段的长度时,常将未知的一条线段设为 x,利用勾股定理构造关于 x的方程解决问题,这是一种用代数方法解决几何问题的
︵
︵
︵
︵
14
重难点 ·突破
重难点1 例1 垂径定理及其推论的相关计算 重点
(2018· 张家界 ) 如图, AB 是⊙ O的直径,弦 CD⊥AB于点 E, OC= 5 cm , B.5 cm D.2 cm
CD=8 cm,则AE=( A ) A.8 cm C.3 cm
15
【解答】
∵弦 CD⊥AB 于点 E,CD=8 cm,
第一部分
教材同步复习
第六章 圆
1
2
第23讲
圆的相关概念及性质
知识要点 ·归纳
知识点一 圆的有关概念及性质
1.圆的有关概念 叫做弦 弦定义 连接圆上任意两点的①__________ 线段 弦 直径
经过②__________ 的弦叫做直径;直径是圆内最③__________ 长 圆心
的弦,直径等于④__________ 的2倍 半径
3
弧定义 弧 劣弧 优弧 等弧
圆上任意两点间的部分叫做弧.弧有优弧、半 圆、劣弧之分 小于半圆的弧叫劣弧,如AC ,BC 大于半圆的弧叫优弧,如ABC ,ACB 在同圆或等圆中,能够互相重合的弧叫做等弧
︵
︵
︵
︵
圆心角 顶点在圆心且两边都和圆相交的角叫做圆心角,如∠AOB 圆周角 顶点在圆上且两边都和圆相交的角叫做圆周角,如∠ACB 等圆 能够重合的两个圆叫做等圆 同心圆 圆心相同的圆叫做同心圆
图形
辅助线作法
有直径时, 连接过直径端点的弦, 构造直角三角形, 构造同弧所对的圆周角
9
知识点三
圆内接四边形及其性质
1.圆内接四边形的对角①__________. 如图,∠A+∠BCD=180°; 互补 2.圆内接四边形的任意一个外角等于它的② __________( 内对角 和它相邻的内角的对 ∠A 角).如图,∠DCE=③__________.
解题思路.另外,在圆中求线段长,三角形相似也是常用的方法.
18
1.(2018· 枣庄)如图,AB 是⊙O 的直径,弦 CD 交 AB 于点 P,AP=2,BP=6, ∠APC=30° ,则 CD 的长为( C ) A. 15 C.2 15 B. 2 5 D.8
19
重难点2 例2
圆周角定理及其推论的相关计算
知识点二 1.定理
圆周角定理及其推论
内容 一条弧所对的圆周角等于它所对的圆心角的①__________ 一半 情况 圆心在圆周角的一条边上 圆心在圆周角内部 圆心在圆周角外部
图形
结论
1 ∠AOB ∠APB=②__________ 2
6
【易错警示】
由于圆中一条弦对应两段弧,故若题干中并未明确弦对应哪段
