D5_4反常积分
反常积分的几种计算方法

反常积分的几种计算方法目录摘要 (1)关键词 (1)Abstract (1)Keywords (1)0 前言 (1)1反常积分的定义 (1)1.1无穷积分的定义 (1)1.2 瑕积分的定义 (2)2 反常积分的计算方法 (3)2.1利用Newton—Leibniz公式计算反常积分…………………………………………32.2利用变量替换法计算反常积分 (3)2.3利用分部积分法计算反常积分 (5)2.4利用分段积分自我消去法计算反常积分 (7)2.5利用方程法计算反常积分 (7)2.6利用级数法计算反常积分 (9)2.7利用待定系数法计算反常积分 (10)结束语 (11)参考文献…………………………………………………………………⎰=+∞→uau Jdx x f )(lim ,)1(则称此极限J 为函数f 在[)+∞,a 上的无穷限反常积分(简称无穷积分),记作⎰+∞=adxx f J )(,)1('并称⎰+∞adx x f )(收敛.如果极限)1(不存在,为方便起见,亦称⎰+∞adx x f )(发散.类似地,可定义f 在(]b ,∞-上的无穷积分:⎰⎰-∞→∞-=buu bdxx f dx x f )(lim )(.)2(对于f 在()+∞∞-,上的无穷积分,它用前面两种无穷积分来定义:dxx f dx x f dx x f aa ⎰⎰⎰+∞∞-+∞∞-+=)()()(.)3(1.2瑕积分的定义定义2设函数f 定义在区间(]b a ,上,在点a 的任一右领域上无界,但在任何内闭区间[](]b a b u ,,⊂上有界且可积.如果存在极限⎰=+→bua u Jdx x f )(lim ,)4(则称此极限为无界函数f 在(]b a ,上的反常积分,记作⎰=badxx f J )(,)4('并称反常积分⎰b adx x f )(收敛.如果极限)4(不存在,这时也说反常积分⎰badx x f )(发散.在定义中,被积函数f 在点a 近旁是无界的,这时点a 称为f 的瑕点,而无界函数反常积分⎰badx x f )(又称为瑕积分.类似地,可定义瑕点为b 时的瑕积分:⎰⎰-→=uabu badx x f dx x f )(lim )(.)5(其中f 在[)b a ,有定义,在点b 的任一左领域上无界,但在任何[][)b a u a ,,⊂上可积.若f 的瑕点()b a c ,⊂,则定义瑕积分dx x f dx x f dx x f bcc aba⎰⎰⎰+=)()()(=⎰⎰+-→→+bvcv u acu dx x f dx x f )(lim )(lim .)6(其中f 在[)(]b c c a ,,⋃上有定义,在点c 的任一领域上无界,但在任何[][)c a u a ,,⊂和[](]b c b v ,,⊂上都可积.当且仅当)6(式右边两个瑕积分都收敛时,左边的瑕积分才是收敛的.又若b a ,两点都是f 的瑕点,而f 在任何[]()b a v u ,,⊂上可积,这时定义瑕积分dx x f dx x f dx x f bcc aba⎰⎰⎰+=)()()(=⎰⎰-+→→+vcbv cuau dx x f dx x f )(lim )(lim , )7( 其中c 为()b a ,上任一实数.同样地,当且仅当)7(式右边两个瑕积分都收敛时,左边的瑕积分才是收敛的.2反常积分的计算方法在计算反常积分时有三大基本方法:Newton —Leibniz 公式、利用变量替换、利用分部积分法.设dx x f ba⎰)(是反常积分, b 为唯一的奇点(b 为有限数,或∞+),计算dx x f ba⎰)(:2.1利用Newton —Leibniz 公式计算反常积分若)(x f 在[)b a ,连续,且)(x F 为)(x f 的原函数,则)()0(|)()(0a Fb F x F dx x f b a ba--==-⎰.)8(例1 计算⎰-b apa x dx)(的值.解: pa x x f )(1)(-=在(]b a ,上连续,从而在任何[](]b a b u ,,⊂上可积,ax =为其瑕点,故⎰⎰-=-+→b u pa ub ap a x dx a x dx )(lim)(⎪⎩⎪⎨⎧=---≠-----=⎪⎪⎩⎪⎪⎨⎧=-≠--=----⎰.1),ln()ln(,1,1)(1)(.1,)ln(,1,1)()(111p a u a b p p a u p a b p a x p pa x a x dx pp bu bu p b u p⎪⎩⎪⎨⎧≥∞<--=-=--→⎰⎰+.1,,1,1)()(lim )(1p p p a b a x dx a x dx pb u p a u b a p2.2利用变量替换法计算反常积分若)(t ϕ在[)βα,上单调,有连续的导数)(t ϕ',b a a =-=)0(,)(βϕϕ(β为有限数或无穷大),则⎰⎰'=βαϕϕdtt t f dx x f ba)())(()(.(9) 例2 计算⎰--bax b a x dx))((2的值.解:令θθ22sin cos b a x +=则θθθθcos sin 2sin cos 2b a dx +-=,θθθθθθθ2222222sin )(sin sin sin )1(cos sin cos a b b a b a a b a a x -=+-=+-=-+=-θθθθθθθ2222222cos )(cos cos cos )sin 1(sin cos a b a b a b b a b x b -=-=--=--=-πθθθθθθππ24cos sin )(cos sin )(22))((22020==--=--⎰⎰⎰d a b d a b x b a x dx ba.例 3 证明等式dt ab t f a dx x b ax f ⎰⎰+∞+∞+=+020)4(1)(,其中0,>b a (假设二积分有意义).分析:比较该等式的两边,我们必须使得ab t xbax 42+=+, 因0,,>x b a ,此即要求ab t x b ax 422+=⎪⎭⎫ ⎝⎛+,亦即 22t x b ax =⎪⎭⎫ ⎝⎛-.因此我们选取的变换如下: 证明:令t xbax =-, 此时ab t xbax 42+=+成立,因此可得 )4(212ab t t ax ++=,dt abt a ab t t dx 42422+++=.于是dt abt ab t t ab t f a dx x b ax f 44)4(21)(222000++++⎪⎭⎫ ⎝⎛+=+⎰⎰⎰∞+∞-∞+, 在上式的右边的第一个积分里,令u t -=,⎥⎥⎦⎤⎢⎢⎣⎡++++++-++=+⎰⎰⎰∞+∞+∞+00222222044)4(44)4(21)(dt ab t ab u t ab t f du ab u u ab u ab u f a dx x b ax f 再将u 改写成t ,二积分合并,得dt ab t f a dx x b ax f ⎰⎰+∞+∞+=+020)4(1)(.因此该式得证.2.3利用分部积分法计算反常积分设)(),(x v v x u u ==在[)b a ,上有连续的导数,则⎰⎰⎰'-=='-bab a babadxx u x v x v x u udv dx x v x u )()()()()()(0.(10)例4 计算dx x x ⎰10ln 的值.解:⎰⎰=1021ln 21ln xdx dx x x )1ln (21102102dx xx x x ⎰⋅-⋅=41-=例5 计算积分dx x nx ⎰20cos ln 2cos π.解:(困难在于被积函数中有对数符号ln"",用分部积分法消去ln"")原式nx d x n2sin cos ln 2120⎰=πdx xx nx n x nx n ⎰--=2020cos )sin (2sin 21cos ln 2sin 21ππdx xxnx n ⎰=20cos sin 2sin 21π(我们看到,这里如果被积函数没有分母的x cos ,用积化和差公式,立即可以算出积分值.因此,我们希望设法应用公式∑=+=+nk kt t tn 12cos 21sin )12sin(将被积函数拆开).因为x n x nx x nx )12cos(cos 2cos sin 2sin +-=⋅,dx xx n dx nx n dx x x nx n ⎰⎰⎰+-=202020cos )12cos(2cos 21cos sin 2sin 21πππ, 第一个积分为0,第二个积分令t x -=2π,dx xxn n dx x x nx n ⎰⎰+-=2020cos )12cos(21cos sin 2sin 21ππdt ttn nn ⎰+-=-201sin )12sin(2)1(πdt kt nnk n ⎰∑⎪⎭⎫ ⎝⎛+-==-20112cos 212)1(πnn 4)1(1π--=.例6 计算⎰+∞∞-++nx x dx)22(2.解:()[]⎰⎰+∞∞-+∞∞-++=++n nx dxx x dx 11)22(22 ()⎰+∞∞-+=+=nx t tdt121()n nI tdt21202=+=⎰+∞,分部积分可建立n I 的递推公式: ()()()⎰⎰∞+++∞∞++--+=+=01220221211n n nn tdtnt tttdtI122+-=n n nI nI , 即n n I n n I 2121-=+. 21021π=+=⎰+∞t dt I ,2!)!22(!)!32(21425222321π⋅--=⋅⋅⋅--⋅--=n n I n n n n I n . 在计算n I 时我们也可以利用变量替换法进行求解,令θtan =t ,()()θθπd tdtI n nn ⎰⎰-∞+=+=202202cos 1,再直接引用Walls 公式2!)!22(!)!32(π⋅--=n n .利用分部积分法我们常常可以得到递推公式从而简化运算.除了上述的三种基本方法外,根据具体情况,经常用的还有下列几种方法: 2.4利用分段积分自我消去法计算反常积分在这种方法的计算中主要分为两步:第一步:将所需计算的积分区间进行分段;第二步:进行变量替换,通过变量替换可以将分段后的某些积分区间与其中的某些区间相抵消或者合并.例7 计算dx x x⎰+∞+021ln 2的值.解:dx x xdx x x dx x x ⎰⎰⎰+∞+∞+++=+12102021ln 21ln 21ln 2=)11ln 1ln (2122102dx x x x dx x x ⎰⎰∞++++=))1(111ln 1ln (212102xd xx dx x x ⎰⎰∞++++ ))(1ln 1ln (20121021t d t t dx x xxt ⎰⎰+++===))(1ln 1ln (2102102t d t tdx x x ⎰⎰+-+ =0通过上述计算我们可以发现这种方法可以省略很多计算,关键在于对积分区间的分段和变量替换要找到最合适的,否则适得其反. 2.5利用方程法计算反常积分使用方程法计算反常积分是分为两步:第一步:通过变量替换,将原积分进行变形;第二步:将原积分与变形后的积分相加,通过计算相加后的积分从而求出原积分.例8 计算积分⎰=20sin ln 2πxdx I .解:⎰⎰===402202sin ln 4sin ln 2ππtdt xdx I tx=⎰40cos sin 2ln 4πtdt t=)cos ln sin ln 2ln (4404040⎰⎰⎰++πππtdt tdt dt=))2sin(ln sin ln (42ln 4040⎰⎰-++⋅ππππdt t tdt)sin ln sin ln (42ln 42402⎰⎰-+=-=πππππudu tdt tu=⎰+20sin ln 42ln ππtdt=I 42ln +π通过解方程得:32ln π-=I .例9 计算积分dx x I ⎰+∞+=0412.解:dx x x x dx x I ⎰⎰∞+∞++=+=022241212 )1(12022x d x x ⎰+∞+-=dt tt xt ⎰∞+=+-=022112J dx x x =+=⎰∞+04212 则()dx xx J I I ⎰∞+++=+=0421222121 dx xx ⎰∞+++=04211 dx x x x ⎰∞+++=0222111 )1(11022x x d x x -+=⎰+∞ )1(2)1(102x x d xx -+-=⎰+∞ dt t xx t ⎰∞+∞---+=2121 dt t ⎰+∞+=02212+∞=02arctan2t22π=. 2.6利用级数法计算反常积分在运用级数法求反常积分时,关键在于积分区间进行分段,使所求的反常积分可以表示成级数的求和运算,从而简化运算.例10 证明[]⎪⎭⎫⎝⎛--+++=⎭⎬⎫⎩⎨⎧-∞→∞+⎰n n dx x x n ln 11211lim 111 .证明: (1) 当2>x 时,[]xx x x )1(111-≤-,由于dx x x ⎰+∞-1)1(1积分收敛,故[]dx x x ⎰∞+⎭⎬⎫⎩⎨⎧-111收敛. (2) [][]dx x x dx x x n n ⎰⎰⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-+∞→∞+1111lim 11[][][][]dx x x dx x x dx x x dx x x n n n⎰⎰⎰⎰-⎭⎬⎫⎩⎨⎧-+⎭⎬⎫⎩⎨⎧-+⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-13221111111111 dx x n dx x dx x n n ⎰⎰⎰-⎭⎬⎫⎩⎨⎧--+⎭⎬⎫⎩⎨⎧-+⎭⎬⎫⎩⎨⎧-=13221111121111 dx x n n ⎰--+++=1111211 n n ln 11211--+++= .因此:[]⎪⎭⎫⎝⎛--+++=⎭⎬⎫⎩⎨⎧-∞→∞+⎰n n dx x x n ln 11211lim 111 .2.7利用待定系数法计算反常积分在使用待定系数法时通常先将有理分式化为部分分式,再通过待定系数求解,在使用这种方法时通常结合多种方法求解. 例11 计算积分⎰+∞++=1)()1(n x x x dxI n .解:(拆为部分分式)设nx A k x A x A x A n x x x n k ++++++++=++ 1)()1(110(n A A A ,,,10 为待定系数).将)()1(n x x x ++ 同乘等式两边.然后k x -=,得)(21)1()1)((1n k k k A k +-⋅⋅⋅-+--=)!(!1)1(k n k k--=!)1(n C k nk-= ),,2,1,0(n k =,其中)!(!!k n k n C kn -=于是dx k x n C I nk k n kn ⎰∑∞+=+-=10)1!)1((dx kx n C nk knk∑⎰=∞++-=011!)1( ∑=∞++-=n k kn k k x C n 01)ln()1(!1.注意到∑∑==⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-=+-nk kn k n k knkx k x C k x C 001ln )1()ln()1(∑∑==⎪⎭⎫ ⎝⎛+-+-⋅=n k nk kn k knkx k C C x 001ln )1()1(ln∑=→⎪⎭⎫ ⎝⎛+-+-⋅=nk kn k nx k C x 001ln )1()11(ln (当+∞→x 时),因此 ∑=++-=n k kn k n k C n I 01)1ln()1(!1.结束语反常积分的计算方法灵活多变,对于任一问题都存在多种计算方法,我们在计算时要提取最简便的方法,除了上述的几种计算方法还有很多的计算方法需要我们去探究、归纳、总结,更重要的是我们要学会这些方法的灵活使用.参考文献:[1] 费定辉等,基米多继奇数学分析习题[M],山东:山东科技出版社,1990.[2] 同济大学应用数学系,高等数学[M],北京:高等教育出版社,2002.[3]刘玉莲,傅沛仁.数学分析讲义[M].第二版.北京:高等教育出版社,1996.43-47.[4]周建莹,李正元.高等数学解题指南[M].北京:北京大学出版社,2002.212-214.[5]数学分析第四版上册 .华东师范大学数学系编[M].高等教育出版社,2010.[6] Tom M.Apostol著. Mathematical Analysis[M]. 机械工业出版社,2004.[7] Zorich,. Mathematical. Analysis. [M]. Springer,2004.。
高等数学同济第三版D5_4反常积分

f ( x) dx F (x)
F () F (a) F (b) F () F () F ()
b
f ( x) dx F (x)
f ( x) dx F (x)
目录
上页
下页
返回
结束
例1. 计算反常积分
解:
[ arctan x ] π π ( ) π 2 2
收敛 ; 如果上述极限不存在, 发散 .
类似地 , 若 f ( x) C ( , b] , 则定义
目录
上页
下页
返回
结束
若 f ( x) C ( , ) , 则定义
lim a f ( x) dx b c f ( x) dx a lim
( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 .
第四节 反常积分
常义积分
推广
第五章
积分限有限 被积函数有界
反常积分 (广义积分)
一、无穷限的反常积分
目录
上页
下页
返回
结束
一、无穷限的反常积分
定义1. 设 f ( x) C [a , ) , 取 b a , 若
存在 , 则称此极限为 f (x) 的无穷限反常积分, 记作
这时称反常积分 就称反常积分
c b
无穷限的反常积分也称为第一类反常积分.
说明: 上述定义中若出现 , 并非不定型 ,
它表明该反常积分发散 .
目录
上页
下页
返回
结束
引入记号
F () lim F ( x) ; F () lim F ( x)
x
x
高等数学5-4反常积分

电磁学
在电磁学中,反常积分用于计算电磁波的传播 和散射特性。
热力学
在热力学中,反常积分用于计算热传导、热辐射和热对流等过程的热能分布。
在概率论中的应用
随机过程
在随机过程中,反常积分用于计算随机事件 的概率分布和概率密度函数。
统计推断
在统计推断中,反常积分用于计算样本数据 的统计特征和参数估计。
贝叶斯推断
05
反常积分的注意事项
计算过程中的常见错误
1 2 3
积分区间选择不当
在计算反常积分时,选择正确的积分区间至关重 要。如果积分区间选择不当,可能会导致计算结 果不准确或错误。
积分上限或下限错误
在计算反常积分时,需要注意积分上限或下限的 取值。如果取值错误,会导致计算结果偏离正确 值。
积分函数处理不当
感谢您的观看
THANKS
比较法
通过比较两个反常积分的敛散性来判断其敛散性。如果两个反 常积分具有相同的敛散性,则可以判断它们的敛散性。
如何处理无界函数和瑕点
无界函数的处理
在处理无界函数时,需要将其限制在 有界区间内进行积分。这样可以避免 无界函数对积分结果的影响。
瑕点的处理
在处理瑕点时,需要将其排除在积分 区间外。这样可以避免瑕点对积分结 果的影响。
Байду номын сангаас
反常积分的可加性
定义
如果两个反常积分 $int_{a}^{b}f(x)dx$ 和 $int_{c}^{d}f(x)dx$ 的极限都存在, 且 $lim_{x to a+}(F(x)-F(a))=lim_{x to c+}(F(x)-F(c))$,则称反常积分具 有可加性。
应用
在处理反常积分时,可加性可以帮助 我们简化计算,将复杂的积分拆分成 几个简单的积分进行处理。
7反常积分——反常积分的概念和计算

7反常积分——反常积分的概念和计算反常积分是微积分中的一个重要概念,是对一些函数在一些区间上的积分进行无穷求和的过程。
与定积分不同,反常积分是对未能被定积分求解的函数进行求解的方法,常见于一些函数在一些点上无界或不连续。
本文将详细介绍反常积分的概念和计算方法。
一、反常积分的概念反常积分是对一些在一些点不连续或无界的函数进行积分求解的方法。
在实际应用中,我们常遇到一些函数在一些点附近出现无穷大的情况,或者在其中一点上不连续的情况,这时就需要用到反常积分进行求解。
具体来说,反常积分可以分为以下两种情况:1.类型一:函数在积分区间其中一点附近无界的情况。
设函数f(x)在区间(a,b]上有定义,且x=b是f(x)的发散点,则反常积分的定义为:∫f(x)dx = lim┬(t→b)〖∫[a,t] f(x)dx〗即求解函数在区间[a,t]上的定积分,然后将t无限趋近于b来求解该反常积分。
2.类型二:函数在积分区间其中一点不连续的情况。
设函数f(x)在区间[a,b]上有定义,且x=c是f(x)的不连续点,则反常积分的定义为:∫f(x)dx = ∫[a,c) f(x)dx + ∫[c,b] f(x)dx即将不连续点c拆分成两个积分区间,在每个区间上分别求解定积分,然后求和。
需要注意的是,反常积分只在函数在一些点附近出现无界或不连续时才有意义。
如果函数在积分区间上连续且有界,那么反常积分与定积分是等价的。
二、反常积分的计算方法对于类型一的反常积分,我们可以通过以下几种方法进行计算:1.无界函数的积分计算当函数f(x)在x=b附近无界时,我们可以通过计算一个足够大的正数M,使得对于任意t>b有,f(x),<M。
然后计算定积分∫[a,t] f(x)dx,再令t无限趋近于b,即可求得反常积分的值。
2.函数在无穷远点(正无穷和负无穷)处的积分计算如果函数在正无穷远点处无界且不连续,可以将反常积分转化为辐角积分的形式。
第五章 积分 5-4 反常积分

b
1
t (x a) p d x
|
1 1
p
(x
a) 1
p
b
,
t
p1 ,
|
ln
(x
a)
b
,
t
p1
《高等数学》课件 (第五章第四节)
所以
b
1
lim
ta
t
(x a) p d x
1 (b a) 1 p , 1 p ,
p1 p1,
,
p1
所以, 反常积分 (1) 当 p < 1 时收敛, p 1时发散. 类似地, 反常积分 (1) 当 p < 1 时收敛, p 1时发散.
《高等数学》课件 (第五章第四节)
5.4.1 无限区间上的反常积分 y
考虑由直线 x = a, y = 0 和曲线
y = f (x) ( 0) 围成的平面无穷区域
f (x)
的面积 A.
x Oa
视面积 A 为有限区域 0 y f (x), y
a x b 面积 A b
b f ( x) d x 的极限,
xa _
a 为 f (x) 的奇点或暇点. 同样若函数 f (x) 在 a < 0 附近有定义,
且 lim f (x) , 则称 x a 为 f (x) 的奇点或暇点.
xa
定义 5-4 设函数 y = f (x) 在 [a, b) 连续, b 是 f 的奇点, 若
t
lim f ( x) d x
0
解
In
x ne x d x
0
x n d e x
0
| x n e x
n
x n1 e x d x
54反常积分new

d(x
1 x
)
0
(x
1 x
)2
2
12arctanx 21 x0 12[2(2)]2.
dx x2
0
1x40
1x4dx 22
16
例
1
0 (1xn)(1x2)dx
ta t
tb a
否则,称反常积分 b f (x)dx发散. a
9
如 何 判 别 上 述 定 义 3 、 4 、 5 中 的 点 a , b , c 为 f ( x ) 的 瑕 点 ?
方 法 :
证 明 lim f(x ) , lim f(x ) , lim f(x ) .
x a
x b
x c
例 a dx (a0).
0 a2x2
解 由于lim 1 ,则xa是 瑕 点 .
xa a2x2
原式lim t ta 0
dx a2 x2
lim
ta
arcsin
x a
t 0
limarcsint 0.
ta
a2
10
例 证 明 : 0 1 x 1 qd x 当 q 1 时 收 敛 , 当 q 1 时 发 散 .
54反常积分new
•
•
•
练 习 : 证 明 e p x d x 当 p 0 时 收 敛 , 当 p 0 时 发 散 . a
证
epxdxlimbepxdx
a
b a
lim b
e pa p
epb p
e ap p
,
p0
, p 0
因 此 , e p x d x 当 p 0 时 收 敛 , 当 p 0 时 发 散 . a 6
即 ,bf(x)dxlimbf(x)dx
高等数学第五章:定积分-4反常积分

左邻域内无界.取 0,如果极限 lim b f ( x)dx 存 0 a
在,则称此极限为函数 f ( x)在区间[a, b)上的反常积分,
记作
b
a
f
(
x)dx
lim
0
b a
f ( x)dx .
当极限存在时,称反常积分收敛;当极限不存在时,称 反常积分发散.
Tianjin Polytechnic University
作
b
a
f
(
x
)dx
.
b f ( x)dx lim b f ( x)dx
a
0 a
当极限存在时,称反常积分收敛;当极限不存在时,称 反常积分发散.
Tianjin Polytechnic University
Teaching Plan on Advanced Mathematics
类似地,设函数 f ( x)在区间[a, b)在上连续,而点b 的
Teaching Plan on Advanced Mathematics
第四节 反常积分
一、无穷限的反常积分 二、无穷函数的反常积分
返回 Tianjin Polytechnic University
Teaching Plan on Advanced Mathematics
一、无穷限的反常积分
定义 1 设函数 f ( x)在区间[a,)上连续,取b a ,
例
5
证明反常积分
1 0
1 xq
dx当q
1时收敛,当q
1
时发散.
证
(1) q 1,
1
0
1 xq
dx
1
0
1 x
Teaching Plan on Advanced Mathematics
反常积分计算技巧

反常积分计算技巧嘿,朋友们!今天咱们来唠唠反常积分这个有点小调皮的家伙。
你可以把反常积分想象成一个在数学世界里不走寻常路的小怪兽。
首先呢,对于无穷区间上的反常积分,就像是一场没有尽头的马拉松。
比如说从a到正无穷的积分,就好比你在一条永远跑不到头的跑道上计算面积。
这个时候,极限就成了我们的魔法棒。
我们把这个无穷区间分成一段一段的,就像把马拉松分成一个个小赛程。
当这个小段不断趋近于无穷的时候,我们就用极限来抓住这个小怪兽的尾巴。
那遇到瑕积分呢,就像是在一个到处是陷阱的迷宫里找宝藏。
瑕点就像迷宫里的那些危险陷阱。
比如说函数在某一点无界,这个点就是瑕点。
我们要小心翼翼地绕过这个陷阱来计算积分。
这时候呢,把积分拆分成两部分,一部分在瑕点左边,一部分在瑕点右边,就像从陷阱的两边偷偷绕过去一样。
再说说换元法在反常积分里的运用吧。
换元就像是给这个小怪兽换了一身衣服,让它看起来没那么吓人。
比如说,我们用一个合适的变量替换,就像给它穿上了一件伪装服,原本复杂的积分可能就变得简单多啦。
这就好比你把一个看起来很凶的怪兽,通过一个魔法道具,变成了一只温顺的小绵羊。
分部积分法在反常积分里也是个有趣的家伙。
它就像两个小伙伴在玩跷跷板。
一个函数是跷跷板的这头,另一个函数是那头。
通过不断地让它们在跷跷板上上下下,我们就能算出反常积分的值。
有时候这个跷跷板会晃得很厉害,那我们就得更小心地控制两边的力量,也就是函数的选择。
比较判别法呢,就像是在一群小怪兽里找出最厉害的那个。
我们找一个已知的积分来和要计算的反常积分比较。
如果已知的积分像一个大力士,我们要算的积分像个小瘦子,而且小瘦子比大力士还小,那小瘦子的积分就是收敛的。
这就好比在一群小动物里,你看到一只小兔子比一头大象还小很多,那你就知道这只小兔子肯定没大象那么“占地方”。
还有极限判别法,这就像是给反常积分做一个身体检查。
通过检查它在某个点或者趋近于无穷的时候的极限情况,来判断它是健康的(收敛)还是生病的(发散)。
5-4反常积分(广义积分)

例6 计算广义积分
解: lim
x a 0
a
0
dx a2 x2
(a 0).
1 , 2 2 a x
dx a2 x2
x a 为被积函数的无穷间断点. 即x=a是瑕点
0
a
a dx lim 0 2 2 0 a x
a
a x 0 . lim arcsin lim arcsin 0 a a 0 0 2
e dx lim b p a
px
b
e ap pa pb e e , p0 p lim b p p , p0
e
pb
1 pb e
即当 p 0 时收敛,当 p 0 时发散.
2
1 1 1 1 sin dx 2 2 sin x d x x x
lim
b
b
2
1 1 lim cos 1 sin d b x 2 x x
b
1 lim cos cos b b 2
1 dx dx 所以 2 发散,从而 2 发散. 1 x 1 x 0
部分分散,全部发散.
例 8.证明广义积分 0 当 q 1时发散.
1
1
1 dx 当 q 1时收敛, q x
X=0是瑕点
11 1 1 证: (1) q 1, q dx dx ln x 0 , 0 x 0 x , q 1 1 q 1 1 1 x ( 2) q 1, q dx 1 ,q1 0 x 1 q 0 1 q 1 q
5-4广义积分反常积分
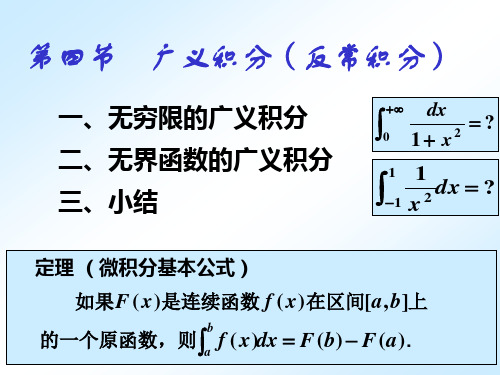
一、无穷限的广义积分 二、无界函数的广义积分 三、小结
dx ?
0 1 x2
1 1 dx ?
1 x 2
定理 (微积分基本公式)
如果F ( x)是连续函数 f ( x)在区间[a, b]上
的一个原函数,则
b
a
f
(
x)dx
F
(b)
F
(a).
返回
一、无穷限的广义积分
定义 1 设函数 f ( x)在区间[a,)上连续,取b a ,如果
dx
.
1 x 3x2 2x 1
(2) lim f ( x) lim
1
,
x1
x1 x 3 x2 2 x 1
x 1 为 f ( x) 的瑕点.
原式 lim 2
dx
x 0 1 3 x2 2 x 1
d(1 1 )
2
lim[
x]
0 1 22 (1 1 )2
1x
1
lim arcsin x
极限 lim b
b
a
f
(
x)dx
存在,则称此极限为函数
f
(
x)在无穷区
间[a,)
上的广义积分,记作
a
f
( x)dx.
b
a
f
( x)dx
lim
b a
f
( x)dx
当极限存在时,称广义
积分收敛;当极限不存
在时,称广义积分发散.
问: f(x)在 (-∞ b]上的反常 积分如何计算?
y f (x)
返回
积分
1
0
ln x x1
dx
的瑕点是哪几点?
常见反常积分

常见反常积分
反常积分是一种由定积分发展演变而来的特殊积分,比传统的定积分要复杂得多,因
此它的应用也就更加广泛,可以用于多种多样的物理和数学问题。
首先要说明的是,反常积分也是由定积分扩展而来的,它由原来的定积分公式扩展为
反常积分。
在定积分中,要求函数是连续和可积分,而反常积分不仅要求函数连续,而且
还要求函数在每个积分点处连续不变,这样的定义反常积分就比定积分更具有准确性。
反常积分的应用范围很广泛,可用于计算复杂的物理和数学问题。
例如,当分析复杂
装置中传输介质流速时,对物体供热或传导过程建模,计算机模拟中的正反向物理计算,
电力工程中的电磁学和振动过程,兰科法定律,传动学中的力学运算,天文学方面的流体
动力学模拟,生物物理过程,核物理应用等都需要反常积分的用到。
在实际的工程应用中,反常积分的优势在于能够以一定的精度准确地描述出未知参数,以此来预测系统的行为。
而在科学研究中,反常积分可以用来求解一些非线性的积分方程,建立复杂的计算模型,从而更好地理解自然界各种现象,从而为人类创造多种各种有用的
服务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
存在 , 则称此极限为 f (x) 的无穷限反常积分, 记作
这时称反常积分 就称反常积分
收敛 ; 如果上述极限不存在, 发散 .
类似地 , 若 f ( x) C ( , b] , 则定义
目录
上页
下页
返回
结束
若 f ( x) C ( , ) , 则定义
f ( x) dx lim f ( x) dx a a b c lim
目录 上页 下页 返回 结束
例3. 计算反常积分
t pt 解: 原式 e p
1 pt 2e p 1 2 p
1 p t e dt p 0
目录
上页
下页
返回
结束
二、无界函数的反常积分
引例:曲线 与 x 轴, y 轴和直线 所围成的
开口曲边梯形的面积可记作
y
1 y x
提示: P260 题2 d(ln x ) dx 2 x (ln x) k 2 (ln x) k dx 1 当 k 1 时, I (k ) 2 k x (ln x) (k 1)(ln 2) k 1
令 f (k ) (k 1)(ln 2)
k 1
, 求其最大值 .
0
1
目录
上页
下页
返回
结束
例6. 证明反常积分 时发散 .
当 q < 1 时收敛 ; q≥1
证 : 当 q = 1 时,
当 q≠1 时
ln x a
1 q
a
b
q 1 q 1
( x a) 1 q
(b a)1q , b 1 q a ,
x
则有类似牛 – 莱公式的计算表达式 :
a
f ( x ) dx F ( x)
F () F (a) F (b) F () F () F ()
f ( x) dx F ( x) f ( x) dx F ( x)
b
目录
上页
c 1 a
c
b
f ( x) dx lim
2 0
b
c 2
f ( x ) dx
无界函数的积分又称作第二类反常积分, 无界点常称 为瑕点(奇点) .
说明: 若被积函数在积分区间上仅存在有限个第一类 间断点, 则本质上是常义积分, 而不是反常积分. 例如,
目录 上页 下页 返回 结束
0 dx 下述解法是否正确 : 1 dx
的收敛性 .
1 1 解: 2 2 x x 1 x 0x 1 1 dx 0 1 1 2 1 1 2 , ∴积分收敛 1 x x 所以反常积分 1 发散 .
这时称反常积分 就称反常积分
收敛 ; 如果上述极限不存在, 发散 .
类似地 , 若 f ( x) C [a , b) , 而在 b 的左邻域内无界,
则定义
目录 上页 下页 返回 结束
而在点 c 的 邻域内无界 , 则定义
a f ( x) dx c f ( x) dx
lim
1 0
注意: 若瑕点 c (a , b) , 则
f ( x) dx F (b) F (c ) F (c ) F (a)
可相消吗?
目录 上页 下页 返回 结束
例4. 计算反常积分 解: 显然瑕点为 a , 所以 a x π arcsin 1 原式 arcsin a 0 2 例5. 讨论反常积分
a
c b lim f ( x ) dx f ( x ) dx c a 0
注意: 主值意义下反常积分存在不等于一般意义下反
常积分收敛 .
思考与练习
P260 题 1 (1) , (2) , (7) , (8)
目录 上页 下页 返回 结束
作业
P260 1 (4) , (5) , (6) , (9) , (10) ; 2; 3
3
f ( x) d f ( x) 1 f 2 ( x) d x 1 f 2 ( x) arctan f ( x) C
π ] 2
π 32 ] arctan 2 π 2 27
目录 上页 下页 返回 结束
内容小结
1. 反常积分 积分区间无限 被积函数无界 常义积分的极限
dx 2
b
1
b 1
b
1 dx lim 2 b x 1 x
O 1
b
x
1 lim 1 1 b b
目录 上页 下页 返回 结束
定义1. 设 f ( x) C [a , ) , 取 b a , 若
第五节 目录 上页 下页 返回 结束
备用题 试证
解:
0
dx x d x , 并求其值 . 4 4 0 1 x 1 x
2
令t1 x
1 1 1 14 t 2 d t
0 t
t2 dt 4 0 1 t 2 d x 1 dx x d x 4 4 4 0 1 x 0 1 x 2 0 1 x 1 1 x 2 d x 2 0 1 x4
则也有类似牛 – 莱公式的
计算表达式 :
若 b 为瑕点, 则
若 a 为瑕点, 则
a a
b
f ( x) dx F (b ) F (a) f ( x) dx F (b) F (a )
b
若 a , b 都为瑕点, 则
a a
b
b
f ( x) dx F (b ) F (a )
当 p >1 时收敛 ; p≤1
证:当 p =1 时有
ln x
当 p ≠ 1 时有
a
x 1 p a
1 p
,
a 1 p , p 1
p 1 p 1
a 1 p ; 因此, 当 p >1 时, 反常积分收敛 , 其值为 p 1 当 p≤1 时, 反常积分发散 .
( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 .
c b
无穷限的反常积分也称为第一类反常积分.
说明: 上述定义中若出现 , 并非不定型 ,
它表明该反常积分发散 .
目录
上页
下页
返回
结束
引入记号
F () lim F ( x) ;
x
F () lim F ( x)
第四节 反常积分
常义积分
推广
第五章
积分限有限 被积函数有界
反常积分 (广义积分)
一、无穷限的反常积分
二、无界函数的反常积分
目录 上页 下页 返回 结束
一、无穷限的反常积分
引例. 曲线 和直线 及 x 轴所围成的开口曲
边梯形的面积 可记作
y
1 y 2 x A
x 其含义可理解为 A lim
A
目录 上页 下页 返回 结束
1 2
1 1 x 2 1 x2 0 x2
dx
1 1 1 d (x ) 2 2 0 (x 1) 2 x
x
1 2 2
arctan
x1 x 2
0
目录
上页
下页
返回
结束
2. 两个重要的反常积分
, 1 , p 1 ( p 1) a
p 1 p 1
,
目录 上页
q 1
下页 返回 结束
说明: (1) 有时通过换元 , 反常积分和常义积分可以互
相转化 .
例如 ,
1 1 x2 0 x2 1 x2
1
dt
1
d( x 1 ) x 2
0 ( x 1)2 x
(b a)1q ; 所以当 q < 1 时, 该广义积分收敛 , 其值为 1 q 当 q ≥ 1 时, 该广义积分发散 .
目录 上页 下页 返回 结束
例7. 解: 积分.
求 的无穷间断点, 故 I 为反常
0
f ( x) I dx 2 11 f ( x )
f ( x) dx 2 2 1 f ( x)
dt 2 t 2 (2) 当一题同时含两类反常积分时, 应划分积分区间,
0
分别讨论每一区间上的反常积分.
目录 上页 下页 返回 结束
(3) 有时需考虑主值意义下的反常积分. 其定义为
v.p.
b
f ( x) dx lim
f ( x ) dx a a
a
v.p. f ( x) dx (c 为瑕点, a c b)
下页
返回
结束
例1. 计算反常积分
解:
[ arctan x ] π π ( ) π 2 2
y O
y
1 1 x 2
x
思考: 分析: 原积分发散 !
注意: 对反常积分, 只有在收敛的条件下才能使用 “偶倍奇零” 的性质, 否则会出现错误 .
目录 上页 下页 返回 结束
例2. 证明第一类 p 积分 时发散 .
其含义可理解为
A lim
0
1
dx 1 lim 2 x x 0
A
O
lim 2(1 ) 2
0
x
目录
上页
下页
返回
结束
定义2. 设 f ( x) C (a , b] , 而在点 a 的右邻域内无界,
